Table of Contents
एकक 5
द्रव्य की अवस्थाएँ
States of Matter
" गिरते हैं मखमली हिमकण धरती माँ की गोद में रह नहीं पाते वहाँ अधिक देर। सूर्य आकर उन्हें वाष्प और पहाड़ी ढलानों पर बहते झरनों को लौटा देता है। "
रोड ओ कोनोर
उद्देश्य
इस एकक के अध्ययन के बाद आप–
- द्रव्य की विभिन्न अवस्थाओं के अस्तित्त्व को कणों के मध्य अंतरा-अणुक बलों तथा ऊष्मीय ऊर्जा में परस्पर संतुलन के आधार पर समझ सकेंगे;
- आदर्श गैसों के व्यवहार को नियंत्रित करनेवाले नियमों की व्याख्या कर सकेंगे;
- वास्तविक जीवन की विभिन्न परिस्थितियों में गैस नियमों को अनुप्रयुक्त कर सकेंगे;
- गैसों के द्रवीकरण के लिए आवश्यक परिस्थितियों की व्याख्यां कर सकेंगे;
- गैसीय तथा द्रव अवस्था में निरंतरता को महसूस कर सकेंगे;
- गैसीय अवस्था तथा वाष्प में विभेद कर सकेंगे;
- अंतरा-अणुक आकर्षण के आधार पर द्रव के गुणों को स्पष्ट कर सकेंगे।
परिचय
इससे पूर्व के अध्यायों में हमने द्रव्य के एक कण से संबंधित गुणों जैसे– परमाण्विक आमाप, आयनन एन्थैल्पी, इलेक्ट्रॉनिक आवेश घनत्व, आण्विक आकार, ध्रुवता आदि का अध्ययन किया। रासायनिक तंत्रों के अधिकांश प्रेक्षित गुणधर्म, जिनसे हम परिचित हैं, द्रव्य के स्थूल गुणों को निरूपित करते हैं, अर्थात् वे गुणधर्म जो बड़ी संख्या में एकत्रित अणुओं, परमाणुओं या आयनों के समूह से संबंधित होते हैं। उदाहरणार्थ– द्रव का सिर्फ एक अणु नहीं, अपितु उनका समूह उबलता है। गीला करने का गुण जल के अणुओं के समूह का होता है एक अणु का नहीं। जल बर्फ के रूप में, जो एक ठोस है; द्रव अवस्था में तथा वाष्प अथवा भाप के रूप में गैसीय अवस्था में अस्तित्व में रहता है। बर्फ, जल तथा वाष्प में भौतिक गुण भिन्न-भिन्न होते हैं। तीनों ही अवस्थाओं में जल का रासायनिक संघटन H2O ही रहता है। जल की तीनों अवस्थाओं के गुणधर्म जल के अणुओं की ऊर्जा तथा उनके समूह में एकत्र होने के प्रकार पर निर्भर करते हैं। यह अन्य पदार्थों के लिए भी सत्य है।
किसी पदार्थ के रासायनिक गुणधर्म उसकी भौतिक अवस्था परिवर्तित होने से परिवर्तित नहीं होते हैं, परंतु रासायनिक अभिक्रिया की दर भौतिक अवस्था पर निर्भर करती है। कभी-कभी प्रयोगों के आँकड़ों की गणना करते समय द्रव्य की अवस्था के ज्ञान की आवश्यकता होती है। अतः पदार्थ की विभिन्न अवस्थाओं को नियंत्रित करनेवाले भौतिक नियमों को जानना एक रसायनज्ञ के लिए आवश्यक होता है। इस एकक में हम द्रव्य की इन तीन भौतिक अवस्थाओं, विशेषतः द्रव तथा गैसीय अवस्था के बारे में अधिक सीखेंगे। अंतरा आण्विक बलों की प्रकृति, आण्विक अन्योन्यक्रिया और कणों की गति पर ऊष्मीय ऊर्जा के प्रभाव को प्रारंभ में समझना आवश्यक है, क्योंकि इनके बीच संतुलन ही पदार्थ की अवस्था निर्धारित करता है।
5.1 अंतरा-आण्विक बल
अन्नोन्यक्रियाकारी कणों (परमाणुओं तथा अणुओं) के मध्य आकर्षण और प्रतिकर्षण बलों को ‘अंतरा-आण्विक बल’ कहते हैं। इस पद का तात्पर्य दो विपरीत आवेशित आयनों के मध्य वैद्युत बल से या उस बल से जो अणु में परमाणुओं को थामे रखता है, नहीं है।
अंतरा-आण्विक आकर्षण-बलों को जोहानन वांडरवाल्स (1837-1923) के सम्मान में ‘वांडरवाल्स बल’ कहते हैं। वांडरवाल्स ने आदर्श व्यवहार से वास्तविक गैसों के विचलन को उन बलों के द्वारा समझाया, जिनका अध्ययन हम इस अध्याय में आगे करेंगे। वांडरवाल्स बलों के परिमाण में विविधता होती है। इसके अंतर्गत लंडन बल, द्विध्रुव बल तथा प्रेरित द्विध्रुव बल आते हैैं। एक विशेष प्रबल प्रकार की द्विध्रुव-द्विध्रुव अन्योन्य क्रिया हाइड्रोजन बंधन है। केवल कुछ अणु ही हाइड्रोजन बंध निर्माण में भाग ले सकते हैं। अतः इसे पृथक् संवर्ग में रखा गया है। इस अन्योन्य क्रिया के बारे में हम पूर्व में एकक 4 में सीख चुके हैं।
यहाँ ध्यान देने योग्य तथ्य यह है कि एक आयन तथा एक द्विध्रुव के मध्य आकर्षण बल, जिन्हें ‘आयन-द्विध्रुव बल’ कहा जाता है, ‘वांडरवाल्स बल’ नहीं है। अब हम विभिन्न प्रकार के वांडरवाल्स बलों का अध्ययन करेंगे।
5.1.1 प्रकीर्णन बल अथवा लंडन बल
परमाणु तथा अध्रुवीय अणु वैद्युत सममित होते हैं। इनमें द्विध्रुव आघूर्ण नहीं होता है, क्याेंकि इनमें इलेक्ट्रॉनिक आवेश अभ्र सममित रूप से वितरित रहता है, परंतु उदासीन परमाणुओं या अणुओं में भी द्विध्रुव नियंत्रित रूप में उत्पन्न किया जा सकता है। इसे इस प्रकार समझा जा सकता है। माना कि दो परमाणु A तथा B एक-दूसरे के समीप हैं (चित्र 5.1 क)। एेसा हो सकता है कि कोई एक परमाणु माना A तात्क्षणिक रूप से असममित हो जाए, अर्थात् आवेश अभ्र एक ओर अधिक हो जाए (चित्र 5.1 ख तथा ग), तो इसका परिणाम यह होता है कि A परमाणु में कुछ समय के लिए तात्क्षणिक द्विध्रुव उत्पन्न हो जाता है। यह अल्पकालिक तात्क्षणिक द्विध्रुव अन्य परमाणु B, (जो इसके निकट हैं) के इलेक्ट्रॉन घनत्व को विरूपित कर देता है। परिणामस्वरूप परमाणु B में प्रेरित द्विध्रुव उत्पन्न हो जाता हैै।
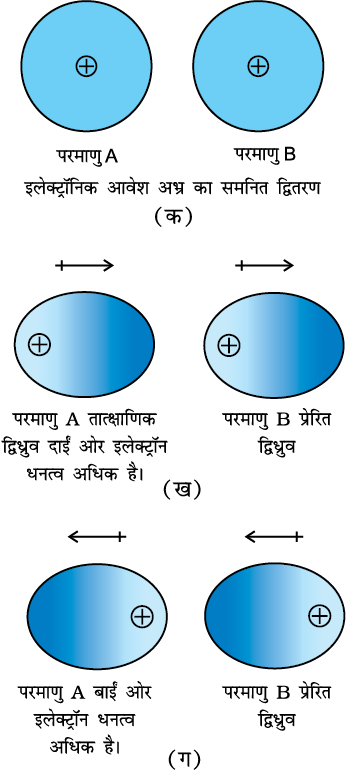
चित्र 5.1
परमाणु A तथा B के अस्थायी द्विध्रुव एक-दूसरे को आकर्षित करते हैं। इसी प्रकार का प्रेरित द्विध्रुव अणुओं में भी उत्पन्न किया जा सकता है। इस प्रकार के आकर्षण बल को पहली बार जर्मन भौतिक विज्ञानी फिट्ज लंडन ने प्रस्तावित किया। इसी कारण दो अस्थायी द्विध्रुव के बीच के आकर्षण को लंडन बल कहा जाता है। इस बल का एक अन्य नाम प्रकीर्णन बल है। इस प्रकार के बल हमेशा आकर्षण बल होते हैं तथा दो अन्योन्यक्रियाकारी कणों के मध्य की दूरी के छठे घात के व्युत्क्रमानुपाती (अर्थात् 1/r 6, जहाँ r दो कणों के मध्य दूरी) होते हैं। ये बल केवल लघु दूरी (~500 pm) तक ही महत्त्वपूर्ण होते हैं। इनका परिमाण कणों की ध्रुवता पर निर्भर करता है। सभी कणों में प्रकीर्णन बल उपस्थित रहते हैं।
5.1.2 द्विध्रुव-द्विध्रुव बल
स्थायी द्विध्रुव रखनेवाले अणुओं के मध्य द्विध्रुव-द्विध्रुव बल कार्य करते हैं। द्विध्रुव के सिरे ‘आंशिक आवेश’ रखते हैं। इन्हें ग्रीक अक्षर डेल्टा (δ) से प्रदर्शित किया जाता है। ‘आंशिक आवेश’ सदैव इकाई इलेक्ट्रॉनिक आवेश (1.6 × 10–19C) से कम होता है। ध्रुवीय अणु निकटवर्ती अणु से अन्योन्य किया करता है। चित्र 5.2 (क) हाइड्रोजन क्लोराइड के द्विध्रुव में इलेक्ट्रॉन अभ्र वितरण को तथा चित्र 5.2 (ख) दो HCl अणुओं के मध्य द्विध्रुव-द्विध्रुव अन्योन्य क्रिया को प्रदर्शित करता है। यह अन्योन्य क्रिया आयन-आयन की तुलना में दुर्बल होती है, क्योंकि इसमें केवल आंशिक आवेश ही भाग लेते हैं। द्विध्रुव के मध्य दूरी बढ़ने से ये आकर्षण बल घटते जाते हैं। यहाँ भी उपरोक्त स्थिति की ही तरह अन्योन्यक्रिया की ऊर्जा ध्रुवित अणुओं के मध्य दूरी के व्युत्क्रमानुपाती होती है। स्थिर ध्रुवित अणुओं (जैसे– ठोसों में) के मध्य अन्योन्यक्रिया की ऊर्जा 1/r3 के तथा घूर्णित ध्रुवित अणुओं के मध्य 1/r6 के समानुपाती होती है, जहाँ r ध्रुवीय अणुओं के मध्य की दूरी है। ध्रुवीय अणु लंडन बलों के द्वारा भी अन्योन्य क्रिया कर सकते हैं, जिसका सम्मिलित प्रभाव यह होता है कि ध्रुवीय अणुओं में कुल अंतरा-आण्विक बल बढ़ जाते हैं।
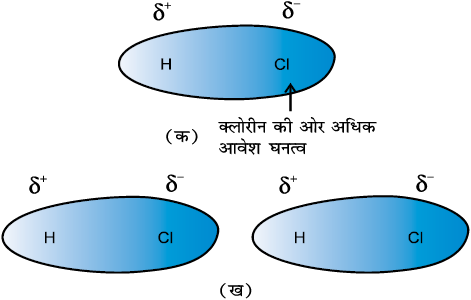
चित्र 5.2ः (क) एकध्रुवीय अणु HCl में इलेक्ट्रॉनिक आवेश का वितरण (ख) दो HCl अणुओं के मध्य द्विध्रुव-द्विध्रुव अन्योन्य किया
5.1.3 द्विध्रुव-प्रेरित द्विध्रुव बल
इस प्रकार के आकर्षण बल, स्थायी द्विध्रुव रखनेवाले ध्रुवीय अणुओं तथा स्थायी द्विध्रुव नहीं रखनेवाले अणुओं के मध्य कार्यरत होते हैं। स्थायी द्विध्रुव रखनेवाला अणु वैद्युत उदासीन अणु के इलेक्ट्रॉनिक अभ्र को विकृत करके द्विध्रुव प्रेरित कर देता है। इस प्रकार अन्य अणु में प्रेरित द्विध्रुव उत्पन्न हो जाता है। इस स्थिति में भी आकर्षण 1/r6 बल के समानुपाती होता है, जहाँ r दो अणुओं के मध्य की दूरी है। प्रेरित द्विध्रुव आघूर्ण, स्थायी द्विध्रुव के द्विध्रुव आघूर्ण तथा विद्युत् उदासीन अणु में ध्रुवता पर निर्भर करता है। एकक 4 में हम यह पढ़ चुके हैं कि बड़े आकार के अणुओं को आसानी से ध्रुवित किया जा सकता है। उच्च ध्रुवणीयता आकर्षण बलों की सामर्थ्य में वृद्धि करती है। इस स्थिति में भी प्रकीर्णन बलों तथा द्विध्रुव-प्रेरित द्विध्रुव अन्योन्य क्रिया (Interaction) के संयुक्त प्रभाव का अस्तित्व होता हैै।
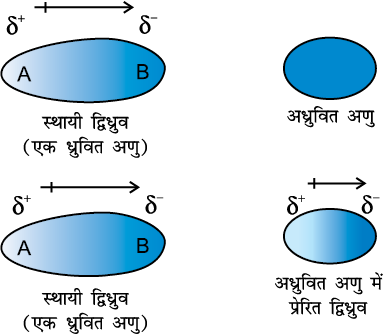
चित्र 5.3 स्थायी द्विध्रुव तथा प्रेरित द्विध्रुव अन्योन्य क्रिया
5.1.4 हाइड्रोजन आबंध
हम एकक 4 में ही यह सीख चुके हैं (जैसा खंड 5.1 दर्शाया गया है) कि यह द्विध्रुव-द्विध्रुव अन्योन्य क्रिया की एक विशेष स्थिति है। हाइड्रोजन आबंध उन अणुओं में मिलता है, जिनमें अति ध्रुवीय N—H, O—H अथवा H—F आबंध उपस्थित होते हैं। यद्यपि हाइड्रोजन आबंधन N, O तथा F तक ही सीमित होता है, परंतु Cl जैसे परमाणु भी हाइड्रोजन आबंधन में भाग लेते हैं। हाइड्रोजन आबंध की ऊर्जा 10 से 100kJ mol—1 के मध्य होती है। यह एक सार्थक मात्रा में ऊर्जा होती है। अतः अधिकतर यौगिकों (उदाहरणार्थ– प्रोटीन तथा न्यूक्लिक अम्ल) की संरचना तथा गुणों के निर्धारण में हाइड्रोजन आबंध एक महत्त्वपूर्ण बल है। एक अणु के विद्युत्ऋणी परमाणु तथा दूसरे अणु के धन-आवेशित हाइड्रोजन परमाणु के मध्य आकर्षण बल द्वारा हाइड्रोजन आबंध की सामर्थ्य निर्धारित होती है। नीचे दिया गया चित्र हाइड्रोजन आबंध के निर्माण को प्रदर्शित करता है–
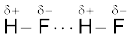
अंतरा-आण्विक बल, जिनकी व्याख्या अभी की गई है, आकर्षण बल होते हैं। अणुओं के मध्य एक-दूसरे के प्रति प्रतिकर्षण भी होता है। जब दो अणु एक-दूसरे के संपर्क में आते हैं, तब दोनों अणुओं के इलेक्ट्रॉन अभ्र (Cloud) के मध्य तथा दोनों अणुओं के नाभिकों के मध्य प्रतिकर्षण उत्पन्न होता है। दो पृथक्कारी अणुओं के मध्य की दूरी घटने से प्रतिकर्षण का परिमाण बढ़ जाता है। यही कारण है कि द्रव एवं ठोस को संपीडित करना कठिन है। इन स्थितियों में अणु पूर्व में ही एक-दूसरे के निकट संपर्क में होते हैं। अतः ये पुनः संपीडन का विरोध करते हैं। फलस्वरूप प्रतिकर्षण अन्योन्य क्रिया में वृद्धि होती है।
5.2 ऊष्मीय ऊर्जा
एक पदार्थ के अणु या परमाणुओं की गति के कारण ऊष्मीय ऊर्जा उत्पन्न होती है। यह पदार्थ के ताप के समानुपाती होती है। द्रव्य के कणों की औसत गतिज ऊर्जा का माप होने के कारण यह कणों के गमन के लिए उत्तरदायी होती है। कणों के इस गमन को ‘ऊष्मीय गमन’ कहते हैं।
5.3 अंतरा-आण्विक बल बनाम ऊष्मीय अन्योन्य क्रिया
हम जानते हैं कि अंतरा-आण्विक बल अणुओं को पास-पास रखता है, परंतु ऊष्मीय ऊर्जा अणुओं को एक-दूसरे से दूर करती है। द्रव्य की तीन अवस्थाएं अणुओं के अंतर आण्विक बलों तथा ऊष्मीय ऊर्जा के मध्य संतुलन का परिणाम हैं।
आण्विक अन्योन्य क्रिया बहुत दुर्बल होने की अवस्था में, जब तक ताप कम करके ऊर्जा कम न की जाए, तब तक अणु साथ-साथ अनुलग्न स्थिति में नहीं होते हैं तथा ठोस नहीं बनाते हैं। गैसों को केवल संपीडन द्वारा द्रवित नहीं किया जा सकता है, यद्यपि इसमें अणु एक-दूसरे के अत्यंत निकट आ जाते हैं तथा अंतर अणुक बल अधिकतम हो जाता है, तथापि यदि ताप कम करके अणुओं की ऊष्मीय ऊर्जा कम की जाती है, तब गैस को आसानी से द्रवित किया जा सकता है। एक पदार्थ की तीनों अवस्थाओं में ऊष्मीय ऊर्जा तथा आण्विक अन्योन्य क्रिया की पूर्वप्रभाविता को इस चित्र द्वारा दर्शाया जा सकता है–
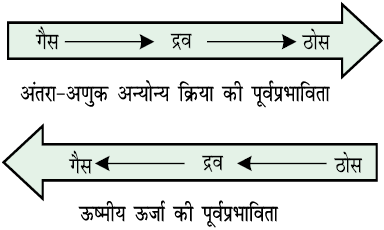
द्रव्य की तीनों अवस्थाओं के अस्तित्व के कारणों को हम पूर्व में ही समझ चुके हैं। अब हम गैसीय तथा द्रव अवस्था और द्रव्य की इन अवस्थाओं को नियंत्रित करनेवाले नियमों को विस्तार से पढ़ेंगे। ठोस अवस्था का अध्ययन हम कक्षा XII में करेंगे।
5.4 गैसीय अवस्था
यह द्रव्य की सरलतम अवस्था है। हम अपने पूर्ण जीवनकाल में वायु के महासागर में डूबे रहते हैं, जो गैसों का मिश्रण होता है। हम वायुमंडल की सबसे नीची परत ट्रोपोस्फीयर, जो गुरुत्वीय बल के द्वारा पृथ्वी से बंधी रहती है, में जीवन व्यतीत करते हैं। वायुमंडल की यह पतली परत हमारे जीवन के लिए महत्त्वपूर्ण है। यह परत हमारी हानिकारक विकिरणों से रक्षा करती है। इसमें डाइअॉक्सीजन, डाइनाइट्रोजन, कार्बन डाइअॉक्साइड, जलवाष्प आदि उपस्थित होती हैं।
अब हम अपना ध्यान पदार्थ के उस व्यवहार पर केंद्रित करेंगे, जो ताप एवं दाब की सामान्य परिस्थितियों में गैसीय अवस्था में होता है। सामान्य परिस्थितियों में आवर्त सारणी में केवल 11 तत्त्व गैसीय अवस्था में रहते हैं (चित्र 5.4)।
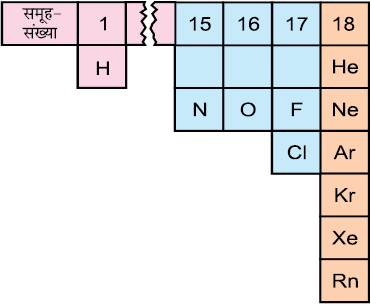
चित्र 5.4 गैसीय अवस्था में रहते ग्यारह तत्त्व
गैसीय अवस्था को निम्नलिखित भौतिक गुणों द्वारा चारित्रित किया जा सकता है–
• गैसें अत्यधिक संपीड्य होती हैं।
• गैसें सभी दिशाओं में समान दाब प्रेषित करती हैं।
• ठोसों तथा द्रवों की तुलना में गैसों का घनत्व अत्यंत कम होता है।
• गैसों का आयतन तथा आकृति अनिश्चित होती है। ये पात्र का आयतन तथा आकृति अपना लेती हैं।
• गैस किसी यांत्रिक सहायता के बिना प्रत्येक अनुपात में पूर्ण मिश्रित होती है।
गैसों की सरलता इस तथ्य से परिलक्षित होती है कि इनके अणुओं के मध्य आकर्षण बल नगण्य होते हैं। इनके व्यवहार कुछ सामान्य नियमों द्वारा संचालित होते हैं, जिन्हें प्रयोगों द्वारा खोजा गया है। ये नियम गैसों के मापनीय गुणों के मध्य संबंध को दर्शाते हैं। इनमें कुछ गुण (जैसे– दाब, आयतन, ताप तथा द्रव्यमान) बहुत महत्त्वपूर्ण हैं, क्योंकि इन चरों के मध्य संबंध ही गैस की अवस्था की व्याख्या करता है। इन चरों के मध्य अंतर्संबंध गैस नियमों का सूत्रपात्र करते हैं। अग्रिम खंड में हम गैस के नियमों के बारे में सीखेंगे।
5.5 गैस के नियम
गैस के नियम, जिनका अध्ययन अब हम करेंगे, गैस के भौतिक गुणों पर कई शताब्दियों तक किए गए शोध के परिणाम हैं। गैसों के इन गुणों पर प्रथम विश्वसनीय मापन एंग्लो-आयरिश वैज्ञानिक बॉयल ने सन् 1662 में किया था। वह नियम, जिसका सूत्रपात उन्होंने किया, ‘बॉयल का नियम’ कहलाता है। बाद में गरम वायु के गुब्बारे द्वारा वायु में उड़ने के प्रयासों ने अन्य नियमों को खोजने के लिए जैकर्स चार्ल्स तथा गै-लुसैक को प्रेरित किया। आवोगाद्रो तथा अन्य वैज्ञानिकों ने भी गैसीय अवस्था के बारे में अनेक सूचनाएँ दीं।
5.5.1 बॉयल का नियम (दाब-आयतन संबंध)
अपने प्रयोगों के आधार पर रॉबर्ट बॉयल इस निष्कर्ष पर पहुँचे कि ‘‘स्थिर ताप पर गैस की निश्चित मात्रा (अर्थात् मोलों की संख्या) का दाब उसके आयतन के व्युत्क्रमानुपाती होता है।’’ इसे ‘बॉयल का नियम’ कहते हैं। गणितीय रूप से इसे इस प्रकार लिखा जा सकता है–
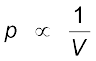 (स्थिर T तथा n पर) .................(5.1)
(स्थिर T तथा n पर) .................(5.1)
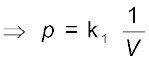 .................... (5.2)
.................... (5.2)
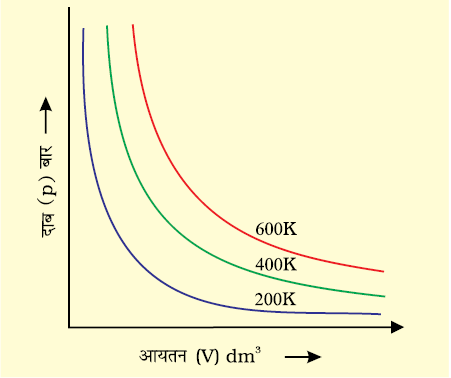
चित्र 5.5 (अ) विभिन्न तापों पर एक गैस के आयतन V तथा p के मध्य वक्र
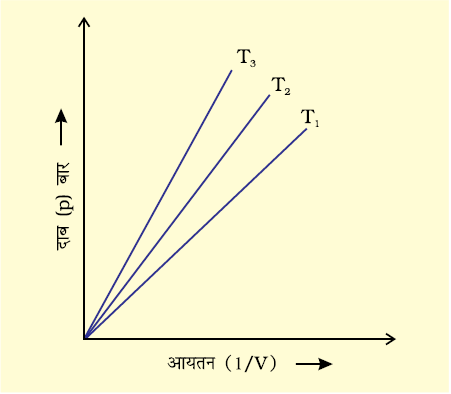
चित्र 5.5 (ब) गैस के दाब तथा 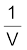 के मध्य वक्र
के मध्य वक्र
यहाँ k1 समानुपातिक स्थिरांक है। स्थिरांक k1 का मान गैस की मात्रा, गैस के ताप तथा उन इकाइयों, जिनके द्वारा p तथा V व्यक्त किए जाते हैं, पर निर्भर करता है। समीकरण 5.2 को पुनर्व्यवस्थित करने पर हम पाते हैं कि
pV = k1 .................(5.3)
अर्थात् ‘स्थिर ताप पर गैस की निश्चित मात्रा का आयतन तथा दाब का गुणनफल स्थिर होता है।’ यदि गैस की निश्चित मात्रा को स्थिर ताप T पर दाब p1 तथा आयतन V1 से प्रसारित किया जाता है (जिससे आयतन V2 तथा दाब P2 हो जाए), तो ‘बॉयल के नियम’ के अनुसार
p1V1 = p2V2 = स्थिरांक ..................(5.4)
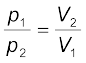 .................(5.5)
.................(5.5)
चित्र 5.5 में बॉयल के नियम को दो प्रकार के ग्राफीय निरूपण द्वारा प्रदर्शित किया गया है। चित्र 5.5 (अ) विभिन्न तापों पर समीकरण (5.3) का ग्राफ है। k1 का मान प्रत्येक वक्र के लिए पृथक्-पृथक् है, क्योंकि किसी गैस के दिए गए द्रव्यमान के लिए यह केवल ताप के साथ परिवर्तित होता है। प्रत्येक वक्र (Graph) भिन्न ताप से संबंधित है। इसे समतापी वक्र (स्थिर ताप वक्र) कहते हैं। उच्च वक्र उच्च ताप से संबंधित होते हैं। यह ध्यान देने योग्य बात है कि यदि गैस का दाब आधा किया जाता है, तो गैस का आयतन दोगुना हो जाता है। सारणी 5.1, 300 K पर 0.09 मोल CO2 के आयतन पर दाब के प्रभाव को दर्शाती है।
सारणी 5-1 300 K पर 0.09 मोल CO 2 के आयतन पर दाब का प्रभाव
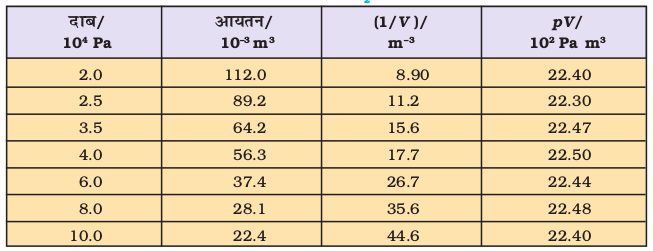
चित्र 5.5 (ब) p तथा 1/V के मध्य ग्राफ को व्यक्त करता है। यह मूल बिंदु से गुजरती हुई सरल रेखा है। उच्च दाब पर गैस बॉयल के नियम से विचलन दर्शाती है। एेसी परिस्थितियों में ग्राफ में सीधी रेखा प्राप्त नहीं होती है।
मात्रात्मक रूप से बॉयल के प्रयोग यह सिद्ध करते हैं कि गैस अत्यधिक संपीडिन होती है, क्योंकि जब एक गैस के दिए गए द्रव्यमान को संपीडित किया जाता है, तब उसके अणु कम स्थान घेरते हैं। इसका तात्पर्य यह है कि उच्च दाब पर गैस अधिक सघन हो जाती है। बॉयल के नियम का उपयोग करने पर गैस के दाब तथा घनतव के मध्य एक संबंध प्राप्त होता है। परिभाषा के अनुसार घनत्व d, आयतन V तथा द्रव्यमान m में संबंध 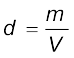 है। यदि हम बॉयल के नियम के समीकरण 5.3 में से आयतन का मान इस संबंध में रखें, तो हमें यह संबंध प्राप्त होता है–
है। यदि हम बॉयल के नियम के समीकरण 5.3 में से आयतन का मान इस संबंध में रखें, तो हमें यह संबंध प्राप्त होता है–
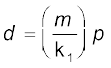
यह प्रदर्शित करता है कि स्थिर ताप पर गैस के निश्चित द्रव्यमान का दाब घनत्व के समानुपाती होता है।
उदाहरण 5.1
जितना भी हो, एक गुब्बारे में कमरे के ताप पर हाइड्रोजन गैस भरी जाती है। यदि दाब को 0.2 bar से अधिक कर दिया जाता है, तो यह गुब्बारा फूट जाता है। यदि 1 bar दाब पर गैस 2.27 L आयतन घेरती है, तो कितने आयतन तक गुब्बारे को फुलाया जा सकता है?
हल
बॉयल के नियमानुसार p1 V1 = p2 V2
यदि p1 = 1 bar तो, V1 = 2.27 L,
p2 = 0.2 bar तो,
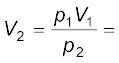
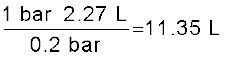
चूँकि गुब्बारा 0.2 bar दाब पर फूट जाता है, इसलिए उसे (गुब्बारे को) 11.35 L आयतन तक फुलाया जा सकता है।
5.5.2 चार्ल्स का नियम (ताप-आयतन संबंध)
गुब्बारा तकनीक को उन्नत बनाने के लिए चार्ल्स तथा गै-लुसैक ने गैसों पर विभिन्न प्रयोग किए। उनके अनुसंधान दर्शाते हैं कि स्थिर दाब पर निश्चित द्रव्यमान वाली गैस का आयतन ताप बढ़ाने पर बढ़ता तथा ताप कम करने पर घटता है। उन्होंने पाया कि ताप की प्रत्येक डिग्री में वृद्धि से गैस की निश्चित मात्रा के आयतन में उसके 0° C ताप के आयतन से  वें भाग की वृद्धि होती है। अतः यदि 0° तथा t° C पर किसी गैस का आयतन क्रमशः V0 तथा Vt हो, तो
वें भाग की वृद्धि होती है। अतः यदि 0° तथा t° C पर किसी गैस का आयतन क्रमशः V0 तथा Vt हो, तो
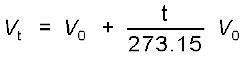
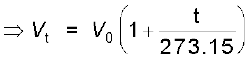
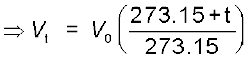 ................. (5.6)
................. (5.6)
इस स्थिति में हम ताप के एक नए मापक्रम को इस प्रकार निर्धारित करते हैं कि नए मापक्रम में t°C को Tt = 273.15 + t तथा 0°C को T0 = 273.15 द्वारा दिया जाता है। इस नए ताप मापक्रम को केल्विन ताप मा
* STP-प्रारंभ में STP की परिभाषा 0° से. तथा 1 Bar पर थी। इस परिभाषा के अनुसार STP पर आदर्श गैस का मोलर आयतन 22.4138 Litre mol–1 होता है।
मानक परिवेश ताप एवं दाब (SATP) की परिस्थितियाँ कुछ वैज्ञानिक कार्यों पर लागू होती हैं, जहाँ STP परिस्थितियों से तात्पर्य 298.15 K तथा 1 Bar (105 Pascal) है। अतः, STP (1 बार तथा 298.15 K) पर आदर्श गैस का मोलर आयतन 24.789 Litre mol–1 होता है।
पक्रम अथवा परम ताप (Absolute Temperature) मापक्रम कहते हैं।
अतः सेल्सियस मापक्रम पर 00C; परमताप मापक्रम पर 273.15 K के बराबर होता है। ध्यान देने योग्य तथ्य यह है कि परम ताप मापक्रम में ताप को लिखते समय डिग्री के चिह्न का प्रयोग नहीं लिया जाता है। केल्विन मापक्रम को ताप का ऊष्मागतिक मापक्रम भी कहते हैं। इसका उपयोग प्रत्येक वैज्ञानिक कार्य में किया जाता है।
अतः सेल्सियस मापक्रम से केल्विन मापक्रम प्राप्त करने के लिए हम 273 (अधिक परिशुद्ध रूप में 273.15) जोड़ देते हैं। यदि समीकरण 5.6 में हम Tt = 273.15 + t तथा T0 = 273.15 लिखें, तो निम्नलिखित संबंध प्राप्त होता है–
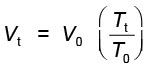
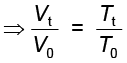 ..............(5.7)
..............(5.7)
अतः एक सामान्य समीकरण इस प्रकार लिखा जाता है–
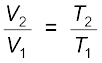 (5.8)
(5.8)
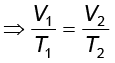
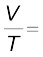 स्थिरांक = k2 ..............(5.9)
स्थिरांक = k2 ..............(5.9)
अतः V = k2 T ...........(5.10)
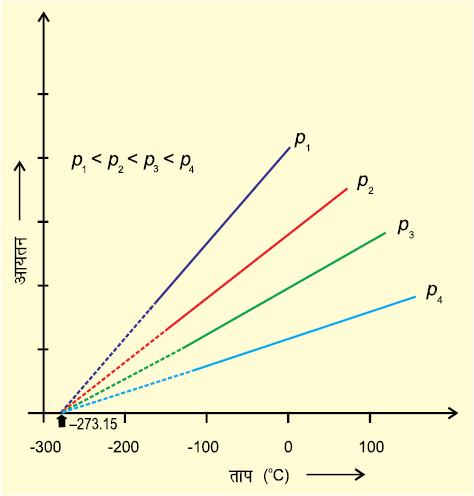
चित्र 5.6 आयतन एवं ताप (°C) के मध्य आरेख
स्थिरांक k2 का मान गैस की मात्रा, गैस के दाब तथा वह इकाई (जिसमें आयतन V व्यक्त किया गया है) से निर्धारित किया जाता है।
समीकरण (5.10) चार्ल्स के नियम का गणितीय रूप है, जो व्यक्त करता है कि स्थिर दाब पर एक गैस की निश्चित मात्रा का आयतन उसके परम ताप के समानुपाती होता है। चार्ल्स ने पाया कि दिए गए दाब पर ताप (सेल्सियस में) तथा आयतन के मध्य ग्राफ सरल रेखा में होता है। इन्हें शून्य आयतन तक बढ़ाने पर प्रत्येक रेखा ताप अक्ष के –273.15 °C
पर अंतः खंड बनाती है। विभिन्न दाब पर रेखाओं का ढाल भिन्न प्राप्त होता है, परंतु शून्य आयतन पर प्रत्येक रेखा ताप-अक्ष पर -273.15 °C पर मिलती है (चित्र 5.6)।
ताप तथा आयतन के मध्य ग्राफ की प्रत्येक रेखा को समदाब रेखा कहते हैं। यदि समीकरण 5.6 में t के मान को –273.15 °C द्वारा व्यक्त करें, तो चार्ल्स के प्रेक्षणों को व्यक्त किया जा सकता है। हम देखते हैं कि किसी गैस का आयतन -273.15 °C पर शून्य हो जाता है। इसका तात्पर्य यह है कि गैस का अस्तित्व नहीं रहता है। वास्तव में इस ताप पर पहुँचने से पूर्व ही प्रत्येक गैस द्रवित हो जाती है। वह न्यूनतम काल्पनिक ताप, जिसपर गैस शून्य आयतन घेरती है, को परम शून्य (Absolute Zero) कहते हैं। बहुत कम दाब तथा उच्च ताप पर प्रत्येक गैस ‘बॉयल के नियम’ का पालन करती है।
उदाहरण 5.2
प्रशांत महासागर में एक जहाज चलाते समय ताप
23.4°C पर एक गुब्बारे को 2L वायु से भरा गया। जब जहाज हिंद महासागर, जहाँ ताप 26.1°C पर पहुँचता है, में पहुँचेगा, तब गुब्बारे का आयतन क्या होगा ?
हल
V1 = 2 L T2 = 26.1 + 273
T1 = (23.4 + 273) K = 299.1 K
= 296.4 K
चार्ल्स के नियमानुसार
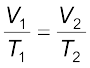
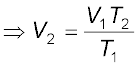
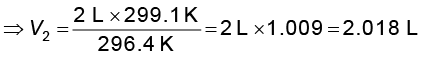
5.5.3 गै-लुसैक नियम (दाब-ताप संबंध)
स्वचालित वाहनों के टायरों में दाब प्रायः समान रहता है, परंतु गरमी के दिनों में यह अत्यधिक बढ़ जाता है। यदि दाब को अच्छी तरह समायोजित नहीं किया जाए, तो टायर फट जाएगा। सर्दी के दिनों में हम पाते हैं कि वाहन के टायर में दाब काफी कम हो जाता है। ताप एवं दाब के मध्य गणितीय संबंध को जोसेफ गै-लुसैक ने प्रतिपादित किया, जिसे गै-लुसैक नियम कहा जाता है। इसके अनुसार– "स्थिर आयतन पर किसी निश्चित मात्रा वाली गैस का दाब उसके आयतन के समानुपाती होता है।’’ गणितीय रूप में–

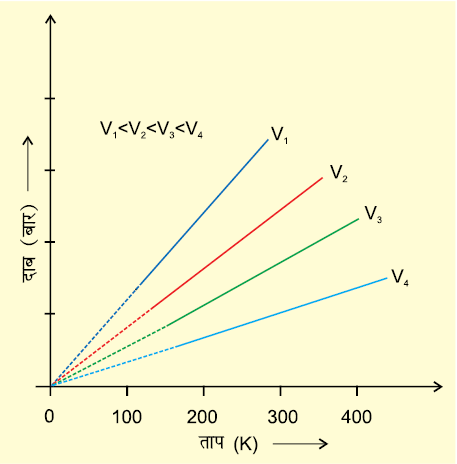
चित्र 5.7 ः एक गैस के दाब तथा ताप (K) के मध्य आरेख (सम-आयतनी आरेख)
इस संबंध को बॉयल के नियम या चार्ल्स के नियम द्वारा भी निरूपित किया जा सकता है। स्थिर मोलर आयतन पर दाब तथा ताप (केल्विन) के मध्य आरेख को चित्र 5.7 में दर्शाया गया है। इसकी प्रत्येक रेखा को ‘समायतनी’ कहते हैं।
5.5.4 आवोगाद्रो नियम (आयतन-मात्रा संबंध)
सन् 1811 में इटली के वैज्ञानिक आवोगाद्रो ने डाल्टन का परमाणु सिद्धांत तथा गै-लुसैक संयुक्त आयतन सिद्धांत के संयुक्त निष्कर्ष से एक परिकल्पना दी, जिसे ‘आवोगाद्रो नियम’ के रूप में जाना जाता है। इसके अनुसार– ताप तथा दाब की समान परिस्थितियों में समान आयतनवाली गैसों में समान संख्या में अणु होते हैं। इसका तात्पर्य यह है कि जब ताप एवं दाब स्थिर रहता है, तो गैस का आयतन उसके अणुओं की संख्या पर या अन्य शब्दों में गैस की मात्रा पर निर्भर करता है।
गणितीय रूप में हम लिख सकते हैं–
V ∝ n (जहाँ n गैस के मोलों की संख्या है)
V = K4n .............(5.11)
एक मोल गैस में अणुओं की संख्या 6.023×1023 निर्धारित की गई है, जिसे ‘आवोगाद्रो स्थिरांक’ कहते हैं। यह वही संख्या है, जिसकी व्याख्या एकक 1 में मोल की परिभाषा के संदर्भ में हमने की है।
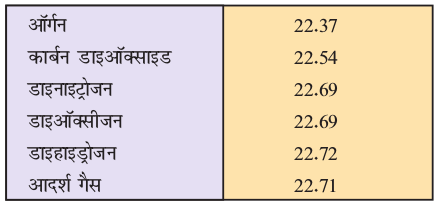
चूँकि गैस का आयतन मोलों की संख्या के समानुपाती होता है, अतः प्रत्येक गैस का एक मोल, मानक ताप एवं दाब (STP)*, जिसका तात्पर्य 273.15 K तथा 1 bar (105 Pascal) होता है, समान आयतन रखता है। STP पर आदर्श गैस का मोलर आयतन 22.7 L mol–1 होता है। कुछ गैसों का मोलर आयतन सारणी 5.2 में दिया गया है–
सारणी 5.2 ः 273.15 K तथा 1 bar (STP) पर कुछ गैसों का लिटर प्रति मोल में मोलर-आयतन
एक गैस के मोलों की संख्या की गणना इस प्रकार की जा सकती है–
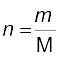 ..................(5.12)
..................(5.12)
जहाँ m = अन्वेषण के दौरान गैस का द्रव्यमान तथा मोलर द्रव्यमान है, अतः
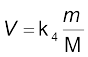 ..................(5.13)
..................(5.13)
समीकरण 5.13 को इस प्रकार पुनर्विन्यासित किया जा सकता है–
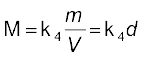 ................... (5.14)
................... (5.14)
यहाँ d गैस का घनत्व है। समीकरण 5.14 से हम निष्कर्ष निकालते हैं कि किसी गैस का घनत्व उसके मोलर द्रव्यमान का समानुपाती होता है।
एक गैस, जो बॉयल के नियम, चार्ल्स के नियम तथा आवोगाद्रो के नियम का पूर्णतः पालन करती है, आदर्श गैस कहलाती है। यह गैस काल्पनिक है। एेसा माना जाता है कि एक आदर्श गैस के अणुओं के मध्य बल अंतरा-अणुक बल उपस्थित नहीं होते हैं। वास्तविक गैस केवल कुछ विशेष परिस्थितियों में, जब अन्योन्य बल प्रायोगिक रूप से नगण्य होते हैं, इन नियमों का पालन करती है। अन्य सभी परिस्थितियों में वह आदर्श व्यवहार से विचलन दर्शाती है।
5.6 आदर्श गैस समीकरण
तीन नियमों, जिनका अध्ययन हम अब तक कर चुके हैं, को एक समीकरण के द्वारा जोड़ा जा सकता है। इसे आदर्श गैस समीकरण कहते हैं।
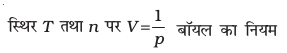
स्थिर p तथा n पर V ∝ T चार्ल्स का नियम
स्थिर p तथा T पर V ∝ n आवोगाद्रो का नियम
अतः 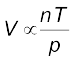 ...............(5.15)
...............(5.15)
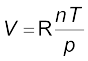 .................(5.16)
.................(5.16)
R एक समानुपातिक स्थिरांक है। समीकरण 5.16 को पुनर्विन्यासित करने पर हम पाते हैं कि
pV = n RT ...................(5.17)
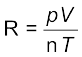 ..................(5.18)
..................(5.18)
R को ‘गैस नियतांक’ कहते हैं। यह सभी गैसों के लिए समान होता है। अतः इसे सार्वत्रिक गैस नियतांक भी कहते हैैं। समीकरण 5.17 को आदर्श गैस समीकरण कहते हैं। समीकरण 5.18 दर्शाती है कि R का मान उन इकाइयों पर निर्भर करता है, जिसमें p, V तथा T को मापा जाता है। यदि समीकरण में तीन चर ज्ञात हाें, तो चौथे की गणना की जा सकती है। इस समीकरण से हम देखते हैं कि स्थिर ताप एवं दाब पर किसी गैस के n मोल समान आयतन रखते हैं, क्योंकि 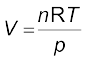 यहाँ n, R, T तथा p स्थिर है। जब किसी गैस का व्यवहार आदर्श व्यवहार के समान होता है, तो यह समीकरण किसी भी गैस पर लागू हो सकता है। STP परिस्थितियों में (273.15 K तथा 1 bar दाब) एक मोल आदर्श गैस का आयतन 22.7 Litre mol–1 होता है। इन परिस्थितियों में एक मोल आदर्श गैस के R के मान की गणना इस प्रकार की जा सकती है–
यहाँ n, R, T तथा p स्थिर है। जब किसी गैस का व्यवहार आदर्श व्यवहार के समान होता है, तो यह समीकरण किसी भी गैस पर लागू हो सकता है। STP परिस्थितियों में (273.15 K तथा 1 bar दाब) एक मोल आदर्श गैस का आयतन 22.7 Litre mol–1 होता है। इन परिस्थितियों में एक मोल आदर्श गैस के R के मान की गणना इस प्रकार की जा सकती है–
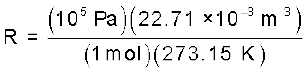
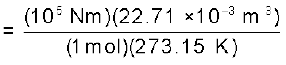
= 8.314 Pa m3 K–1 mol–1 (चूँकि 1Nm = 1J)
= 8.314 × 10–2 bar L K–1 mol–1
= 8.314 J K–1 mol–1
STP परिस्थितियों (0°C तथा 1 वायुमंडलीय दाब) पर R का मान = 8.20578 × 10—2 L atm K–1 mol–1 होता है।
आदर्श गैस समीकरण का संबंध इन चार चरों से है। किसी गैस की अवस्था की व्याख्या करता है। अतः इसे अवस्था समीकरण भी कहते हैं।
अब आदर्श गैस समीकरण पर पुनः विचार करें। यह चरों के समक्षणिक परिवर्तन के लिए है। यदि किसी निश्चित मात्रा वाली गैस का ताप T1, आयतन V1 तथा दाब p1 से T2, V2 तथा p2 तक परिवर्तित होता है, तो हम लिख सकते हैं कि
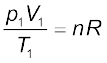 तथा
तथा 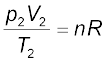

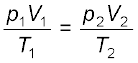 .....................(5.19)
.....................(5.19)
समीकरण 5.19 एक उपयोगी समीकरण है। यदि उपरोक्त छः चरों में से पाँच चरों के मान ज्ञात हों, तो अज्ञात चर की गणना समीकरण (5.19) द्वारा की जा सकती है । इस समीकरण को संयुक्त गैस नियम कहते हैं।
उदाहरण 5.3
25°C तथा 760 mm (Hg) दाब पर एक गैस 600 mL आयतन घेरती है। किसी अन्य स्थान पर, जहाँ ताप 10°C. आयतन 640 mL हो, गैस का दाब क्या होगा?
चित्र 5.9 300 K ताप पर क्लोरीन और नाइट्रोजन के अणुओं की गतियों का वितरण
हल
p1 = 760 mm (Hg), V1 = 600 ml;
T1 = 25 + 273 = 298 K
V2 = 640 mL, T2 = 10 + 273 = 283 K
संयुक्त गैस नियम के अनुसार 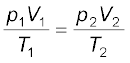
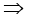
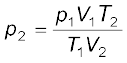
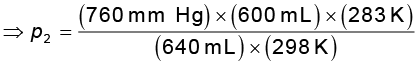
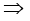 p2 = 676.6 mm (Hg)
p2 = 676.6 mm (Hg)
5.6.1 गैसीय पदार्थ का घनत्व एवं मोलर द्रव्यमान
आदर्श गैस समीकरण का पुनर्विन्यास करने पर हम पाते हैं कि
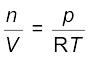
n को 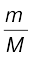 से प्रतिस्थापित करने पर हम पाते हैं कि
से प्रतिस्थापित करने पर हम पाते हैं कि
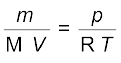 ...................(5.20)
...................(5.20)
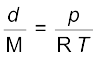 (जहाँ d घनत्व है) ....................(5.21)
(जहाँ d घनत्व है) ....................(5.21)
समीकरण (5.21) को पुनर्व्यवस्थित करने पर हम एक गैस के मोलर द्रव्यमान की गणना करने के लिए निम्नलिखित संबंध प्राप्त करते हैं —
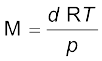 ..................(5.22)
..................(5.22)
5.6.2 डाल्टन का आंशिक दाब का नियम
इस नियम को जॉन डॉल्टन ने सन् 1801 में प्रतिपादित किया। इसके अनुसार अन्योन्य क्रिया से विहीन गैसों के मिश्रण का कुल दाब प्रत्येक गैस के आंशिक दाब के योग के बराबर होता है। अर्थात् वह दाब जब इन गैसों को ताप की समान परिस्थि्तियों में, समान आयतन वाले पात्र में पृथक्-पृथक् बंद किया जाता है, प्रत्येक गैस द्वारा उत्पन्न किए गए दाब को आंशिक दाब कहते हैं। गणितीय रूप में–
pकुल = p1+p2+p3+......(स्थिर T, V पर) ..............(5.23)
जहाँ pकुल गैसों के मिश्रण का कुल दाब है तथा p1, p2, p3 गैसों के आंशिक दाब हैं।
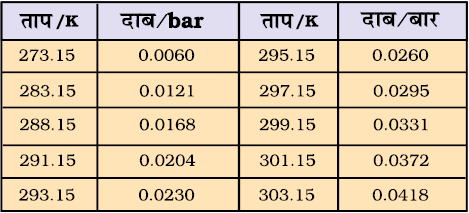
गैसों को सामान्यतः जल के ऊपर एकत्र किया जाता है। अतः ये नम होती हैं। नमीयुक्त गैस, जिसमें जलवाष्प भी होती है, के वाष्पदाब में से जलवाष्पदाब घटाने पर शुष्क गैस के दाब की गणना की जा सकती है। जलवाष्प द्वारा लगाए जानेवाले दाब को ‘जलीय तनाव’ कहते हैं। विभिन्न ताप पर जल के जलीय तनाव को सारणी 5.3 में दिया गया है।
pशुष्क गैस = pकुल – जलीय तनाव ....................(5.24)
सारणी 5.3 विभिन्न ताप पर जल का जलीय तनाव (वाष्प-दाब)
मोल अंश के रूप में आंशिक दाब—माना ताप T पर V आयतनवाले पात्र में तीन गैसें, जिनका आंशिक दाब क्रमशः p1, p2, तथा p3 है, रखी गई हैं, तो
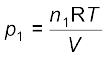 ................(5.25)
................(5.25)
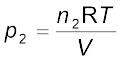 .................(5.26)
.................(5.26)
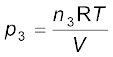 ..................(5.27)
..................(5.27)
जहाँ n1, n2, तथा n3 इन गैसों के मोलों की संख्या हैं
pकुल = p1 + p2 + p3
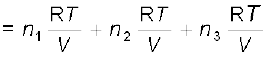
= (n1 + n2 + n3) 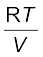 ...........(5.28)
...........(5.28)
p1 को pकुल से भाग देने पर हम पाते हैं कि–
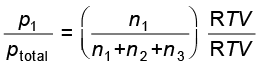
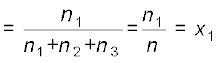
जहाँ n = n1 + n2 + n3
x1 को पहली गैस का मोल अंश कहते हैं।
अतः p1 = x1 pकुल
इसी प्रकार अन्य दो गैसों के लिए हम लिख सकते हैं–
p2 = x2 pकुल तथा p3 = x3 pकुल
अतः एक सामान्य समीकरण को इस प्रकार लिखा जा सकता है–
pi = xi pकुल ...........(5.29)
जहाँ pi तथा xi , i गैस के क्रमशः आंशिक दाब और मोल अंश हैं। यदि गैसों के मिश्रण का कुल दाब ज्ञात हो, तो समीकरण 5.29 के द्वारा प्रत्येक गैस से उत्पन्न आंशिक दाब को ज्ञात किया जा सकता है।
उदाहरण 5.4
एक नीअॉन-डाइअॉक्सीजन मिश्रण में 70.6 ग्राम डाइअॉक्सीजन तथा 167.5 ग्राम नीअॉन है, यदि गैसों के मिश्रण का कुल दाब 25 bar हो, तो मिश्रण में नीअॉन तथा डाइअॉक्सीजन का आंशिक दाब क्या होगा?
हल
डाइअॉक्सीजन के मोलों की संख्या 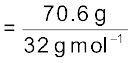
= 2.21 mol
नीअॉन के मोलों की संख्या 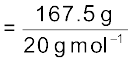
= 8.375 mol
डाइअॉक्सीजन के मोल अंश 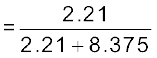
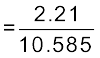 = 0.21
= 0.21
नीअॉन के मोल अंश 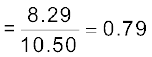
अन्य रूप में नीअॉन का मोल अंश = 1 – 0.21 = 0.79
गैस का आंशिक दाब = मोल अंश × कुल दाब
अॉक्सीजन का आंशिक दाब
= 0.21 × 25 (bar) = 5.25 (bar)
नीअॉन का आंशिक दाब
= 0.79 × 25 (bar) = 19.75 (bar)
5.7 गतिज ऊर्जा एवं अणुक गति
गैसों के अणु निरंतर गति करते रहते हैं। गति करते समय यह आपस में और पात्र की दीवारों के साथ टकराते हैं। इसके कारण अणुओं की गति और ऊर्जा परिवर्तित होती रहती है। इसलिए किसी भी क्षण सभी अणुओं की गति और ऊर्जा एक समान नहीं होती। अतः हम अणुओं की गति का केवल औसत मान ही ज्ञात कर सकते हैं। यदि नमूने में n अणु, हों जिनकी गतियाँ u1,u2,u3, …….un, हों तो अणुओं की औसत गति, uav का परिकलन निम्न प्रकार से किया जा सकता है।
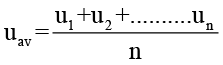
मैक्सवैल और बोल्ट्ज़मान ने प्रदर्शित किया कि गतियों का वास्तविक वितरण गैस के आण्विक द्रव्यमान और ताप पर निर्भर करता है। मैक्सवैल ने कोई भी विशेष गति प्राप्त अणुओं की संख्या ज्ञात करने के लिए एक सूत्र का सृजन किया- चित्र-5.8 में दो भिन्न तापों T1 और T2 पर अणुओं की संख्या और आण्विक गति के मध्य ग्राफ दर्शाया गया हे। ग्राफ में दिखाए गए गतियों के वितरण को गतियों का मैक्सवैल-बोल्टज़मान वितरण कहते हैं।
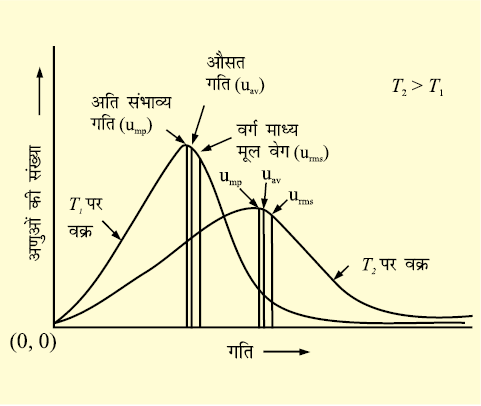
चित्र 5-8 गतियों का मैक्सवैल-बोल्ट्जमान वितरण
ग्राफ़ से पता चलता है कि बहुत अधिक और बहुत कम गति वाले अणुओं की संख्या बहुत कम होती है। ग्राफ़ का शीर्ष बिन्दु वह गति प्रदर्शित करता है जो अधिकतर अणुओं की होती है। इस गति को अति संभाव्य गति, ump. कहते हैं। यह अणुओं की औसत गति के बहुत निकट होती है। ताप बढ़ाने से अति संभाव्य गति बढ़ जाती है। इसके अतिरक्ति उच्च ताप पर गति वितरण वक्र चौड़ा हो जाता है। वक्र का चौड़ा होना दिखाता है कि अधिक गति से गतिमान अणुओं की संख्या बढ़ जाती है। गति का वितरण अणुओं के द्रव्यमान पर भी निर्भर करता है। समान ताप पर अधिक द्रव्यमान वाले अणुओं की गति हल्के अणुओं की तुलना में धीमी होती है। उदाहरणार्थ, समान ताप पर हल्के नाइट्रोजन अणु भारी क्लोरीन अणुओं से तेज़ गति करते हैं। अतः किसी भी दिए गए ताप पर नाइट्रोजन के अणुओं की अति संभाव्य गति क्लोरीन के अणुओं से अधिक होती है। क्लोरीन और नाइट्रोजन के अणुओं की गतियों के वितरण को चित्र-5.9 में देखिए। यद्यपि किसी भी ताप पर अणुओं की निजी गति परिवर्तित होती रहती है पर गतियों का वितरण वही रहता है।
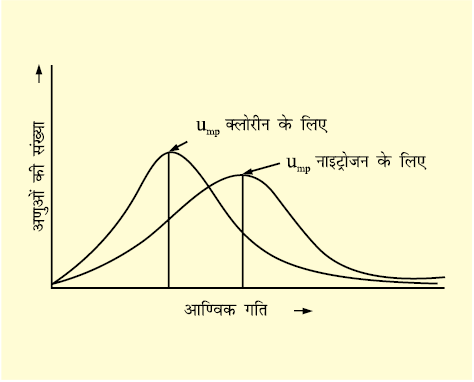
चित्र 5-9 300 ज्ञ ताप पर क्लोरीन और नाइटंोजन के अणुओं की गतियों का वितरण
हम जानते हैं कि किसी कण की गतिज ऊर्जा को निम्नलिखित व्यंजक द्वारा दिया जाता है'–
गतिज ऊर्जा = 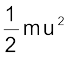
इसलिए यदि हम गैस के कण की सीधी रेखा में चलने पर औसत स्थानांतरण ऊर्जा, 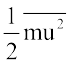 , जानना चाहें तो हमें सभी अणुओं की गतियों के वर्ग के औसत,
, जानना चाहें तो हमें सभी अणुओं की गतियों के वर्ग के औसत, 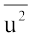 की आवश्यकता होगी। इसे निम्न प्रकार से प्रदर्शित किया जाता है।
की आवश्यकता होगी। इसे निम्न प्रकार से प्रदर्शित किया जाता है।
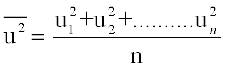
गतियों के वर्ग का औसत गैस के अणुओं की औसत गतिज ऊर्जा का सीधा माप होता है। यदि हम गतियों के वर्ग के औसत मान का वर्गमूल लें तो हमें गति का जो मान प्राप्त होता है वह अति संभाव्य गति और औसत गति से भिन्न होता है। इस गति को वर्ग माध्य मूल वेग (Root mean square speed) कहते हैं और इसे निम्नलिखित व्यंजक द्वारा दिया जाता है।
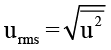
वर्ग माध्य मूल वेग, औसत गति और अति संभाव्य गति में निम्नलिखित संबंध होता है-
urms > uav > ump
तीनों गतियों का अनुपात निम्नलिखित होता है।
ump: uav :urms : : 1:1.128 : 1.224
5.8 गैसों का अणुगतिक सिद्धांत
यहाँ हमने अनेक नियमों (बॉयल नियम, चार्ल्स नियम आदि) का अध्ययन किया जो वैज्ञानिकों द्वारा दिए गए प्रायोगिक तथ्यों का संक्षिप्त कथन है। इन वैज्ञानिक विधियों का प्रयोग सावधानीपूर्वक करने पर हम पाते हैं कि कोई निकाय विभिन्न परिस्थितियों में कैसे व्यवहार करता है। जब प्रायोगिक तथ्य स्थापित हो जाते हैं, तब वैज्ञानिक यह जानने के लिए उत्सुक रहते हैं कि निकाय इस प्रकार का व्यवहार क्यों करता है? उदाहरणार्थ — गैस नियम बताते हैं कि जब दाब बढ़ाया जाता है, तब गैस संपीडित होती हैं, परंतु हमें यह भी जानना चाहिए कि जब गैस संपीडित की जाती है, तब उसके आण्विक स्तर पर क्या होता है? इन प्रश्नों के उत्तर देने के लिए एक सिद्धांत बनाया गया। यह सिद्धांत हमारे अवलोकनों को अच्छी तरह समझने में एक मॉडल का कार्य करता है। वह सिद्धांत, जो गैसों के व्यवहार का स्पष्टीकरण देता है, ‘गैसों का अणुगति सिद्धांत’ कहलाता है। यह परमाण्वीय तथा आण्विक सिद्धांत का प्रसार है।
गैसों के अणुगति सिद्धांत के प्रमुख अभिगृहीत नीचे दिए गए हैं। ये अभिगृहीत उन अणु तथा परमाणुओं से संबंधित हैं, जिनको देखा नहीं जा सकता है। अतः ये सिद्धांत गैसों के सूक्ष्मदर्शी प्रतिरूप हैं। गैसों के अणुगति सिद्धांत पर आधारित गणनाएँ तथा अनुमान इनके प्रायोगिक प्रेक्षणों के अनुरूप होते हैं तथा इस मॉडल के संशुद्ध रूप को स्थापित करते हैं —
सामान्य ताप एवं दाब पर गैस-कणों के मध्य कोई आकर्षण बल नहीं होता है। इस अभिगृहीत का आधार यह है कि गैस प्रसारित होकर उनके लिए उपलब्ध स्थान को पूर्णतः घेर लेती है तथा सामान्य ताप एवं दाब पर द्रवीकृत नहीं होती है।
गैस के कण लगातार गतिक अवस्था में रहते हैं। यदि वे कण स्थिर अवस्था में होते, तो गैसें एक निश्चित आकृति ग्रहण कर लेतीं, परंतु एेसा प्रेक्षित होता नहीं है।
गैस के कण प्रत्येक संभव दिशा में सीधी रेखा में गमन करते रहते हैं। अपनी गति के दौरान ये आपस में अथवा पात्र की दीवार से टकराते रहते हैं। गैस के द्वारा उत्पन्न दाब, पात्र की दीवारों पर गैस के अणुओं द्वारा किए गए प्रहारों का परिणाम होता है।
गैस के अणुओं के मध्य संघट्ट पूर्णतः प्रत्यास्थ होती है। इसका तात्पर्य यह है कि संघट्ट के पूर्व एवं पश्चात् अणुओं की ऊर्जा समान रहती है। संघट्ट में अणुओं के मध्य ऊर्जा का विनिमय हो सकता है, अर्थात् विशिष्ट अणु की ऊर्जा में परिवर्तन हो सकता है, परंतु कुल ऊर्जा स्थिर बनी रहती है। यह अभिगृहीत इस तथ्य पर आधारित है कि गैस का स्वतः शीतलन या ऊष्मन नहीं होता है। यदि गैस के अणुओं की गति रुक जाए, तो वे एकत्र हो जाएँगे, जो वास्तविक प्रेक्षण के विपरीत या प्रतिकूल होगा।
किसी भी समय गैस के विभिन्न कणों का वेग भिन्न-भिन्न होता है। फलस्वरूप विभिन्न गतिज ऊर्जाएँ होती हैं। यह तथ्य सही प्रतीत होता है, क्योंकि जैसे ही अणु संघट्ट करते हैं, वैसे ही उनके वेगों में परिवर्तन हो जाता है। यदि सभी अणुओं के प्रारंभिक वेग समान हों, तो भी संघट्ट के उपरांत उनकी एकरूपता समाप्त हो जाती है। परिणामतः उनके वेग भिन्न-भिन्न हो जाते हैं। यह वेग लगातार परिवर्तित होता रहता है। इसके बावजूद निश्चित ताप पर वेगों का वितरण समान बना रहता है।
यदि एक अणु में विभिन्न वेग होते हैं, तो उसकी विभिन्न गतिज ऊर्जाएँ होंगी। एेसी परिस्थितियों में हम केवल औसत गतिज ऊर्जा की बात कर सकते हैं। अणुगति सिद्धांत में एेसा माना गया है कि गैस के अणुओं की औसत गतिज ऊर्जा उसके परम ताप के समानुपाती होती है। एेसा देखा गया है कि ताप बढ़ाने पर गैस का प्रसार होता है एवं यदि आयतन स्थिर रखा जाए, तो दाब बढ़ता है (चार्ल्स तथा गै-लुसैक का नियम)। गैस को गरम किए जाने पर कणों की गतिज ऊर्जा बढ़ जाती है, जिससे ये पात्र की दीवार पर अधिक तेजी से प्रहार करते हैं। फलतः अधिक दाब उत्पन्न होता है।
गैसों का अणुगति सिद्धांत सैद्धांतिक रूप से दाब-आयतन के मध्य संबंध तथा गैसों के नियम (जिनका अध्ययन हम पूर्व खंडों में कर चुके हैं) को प्रतिपादित करता है।
5.9 आदर्श व्यवहार से विचलन
गैसों का सैद्धांतिक प्रतिरूप प्रायोगिक अवलोकनों के संगत है। कठिनाई तब उत्पन्न होती है, जब हम यह जानने का प्रयास करते हैं कि pV = nRT का संबंध कब तक गैसों के ताप- दाब-आयतन के मध्य संबंध को बनाए रखता है। इस तथ्य का पता लगाने के लिए हम गैसों के pV को p के विरुद्ध आरेख खींचते हैं। बॉयल के नियमानुसार, स्थिर ताप पर pV स्थिर होना चाहिए तथा pV और p के मध्य आरेख में सीधी रेखा (जो अक्ष के समानांतर है) प्राप्त होनी चाहिए। (चित्र 5.10,) 273 K पर विभिन्न गैसों के वास्तविक आँकड़ों चित्र 5.13: विभिन्न तापों पर कार्बन डाइअॉक्साइड के समतापी आरेख पर आधारित इस प्रकार के आरेख को दर्शाता है।
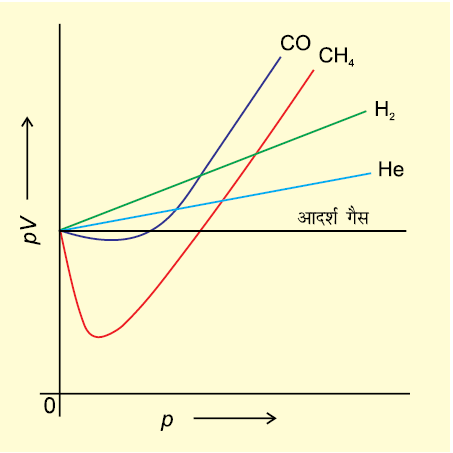
चित्र 5.10 आदर्श गैस तथा वास्तविक गैस के लिए pV तथा p के मध्य आरेख
यह आसानी से देखा जा सकता है कि स्थिर ताप पर वास्तविक गैसों के लिए pV तथा p के मध्य आरेख में सीधी रेखा प्राप्त नहीं होती है। इसमें आदर्श व्यवहार से स्पष्ट विचलन दिखाई देता है तथा दो प्रकार के वक्र दिखाई देते हैं। इस वक्र में डाइहाइड्रोजन तथा हीलियम के लिए दाब बढ़ाने पर pV का मान भी बढ़ता जाता है। कार्बन मोनोअॉक्साइड तथा मेथेन के लिए द्वितीय प्रकार का वक्र मिलता है। इस प्रकार के वक्र में प्रारंभ में आदर्श व्यवहार से ऋणात्मक विचलन मिलता है। दाब बढ़ाने पर प्रारंभ में pV का मान कम होकर, न्यूनतम स्तर तक पहुँचता है, फिर बढ़ता है और आदर्श गैस की रेखा को पार करके लगातार धनात्मक विचलन दर्शाता है। अतः प्रेक्षित होता है कि वास्तविक गैसें बॉयल नियम, चार्ल्स नियम तथा आवोगाद्रो नियम का पूर्णः पालन सभी स्थितियों में नहीं करती हैं।
जब दाब-आयतन आरेख खींचा जाता है, तब आदर्श व्यवहार से विचलन आभासी हो जाता है। वास्तविक गैसों के लिए दाब-आयतन आरेख के प्रायोगिक आँकड़े तथा आदर्श गैस के लिए बॉयल के नियमानुसार सैद्धांतिक रूप की गणनाएँ संपाती होनी चाहिए। चित्र 5.11 में यह आरेख दिखाए हैं। उच्च दाब पर मापित आयतन परिकलित आयतन से अधिक होता है, जबकि निम्न दाब पर मापित तथा परिकलित आयतन एक-दूसरे के समीप होते हैं।
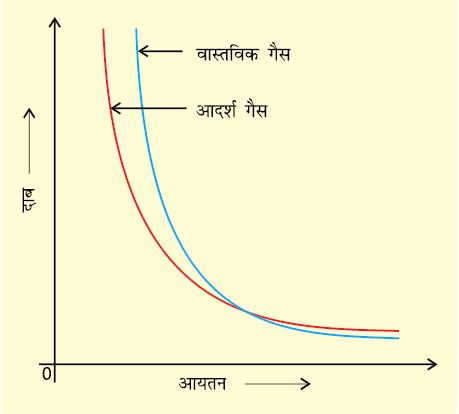
चित्र 5.11 आदर्श गैस तथा वास्तविक गैस के लिए दाब-आयतन के मध्य आरेख
एेसा देखा गया कि वास्तविक गैसें सभी परिस्थितियों में बॉयल, चार्ल्स तथा आवोगाद्रो के नियम का पूर्ण पालन नहीं करती हैं। अब दो प्रश्न उभरते हैं–
(i) गैस आदर्श व्यवहार से विचलन क्यों दर्शाती है?
(ii) वे कौन सी परिस्थितियाँ हैं, जो गैस को आदर्शत्व से विचलित करती हैं?
यदि हम गैसों के अणु-गति सिद्धांत की अभिधारणा पर पुनर्विचार करें, तो हमें इन प्रश्नों का उत्तर मिल जाएगा। हम पाते हैं कि अणु-गति सिद्धांत की दो कल्पनाएँ सही नहीं हैं। वे हैं– (क) गैस के अणुओं के मध्य कोई आकर्षण-बल नहीं होता।
(ख) गैस के अणुओं का आयतन गैस द्वारा घेरे गए आयतन की तुलना में बहुत कम होता है।
अभिधारणा (क) केवल तब सही है, जब गैस कभी भी द्रवीकृत न हो, लेकिन हम जानते हैं कि ठंडी करने पर तथा संपीडित करने पर गैस को द्रवीकृत किया जा सकता है तथा द्रव के अणुओं को संपीडित करना कठिन होता है, अर्थात् प्रतिकर्षण बल इतने प्रभावी होते हैं कि सूक्ष्म आयतन में अणुओं के अपमर्दन का विरोध करते हैं। यदि अभिगृहीत (ख) सही है, तो दाब-आयतन आरेख में वास्तविक गैस के प्रायोगिक आँकड़े तथा बॉयल के नियम पर आधारित सैद्धांतिक परिकलन एक-दूसरे के संपाती होने चाहिए।
वास्तविक गैस आदर्श व्यवहार से विचलन इसलिए दर्शाती हैं, क्योंकि अणु आपस में अन्योन्य क्रिया करते हैं। आकर्षण बल अणुओं को पास-पास लाने का प्रयास करते हैं, जबकि प्रतिकर्षण बल अणुओं को एक-दूसरे से दूर करने का प्रयास करते हैं। उच्च दाब पर गैस के अणु पूर्ण प्रतिघात के साथ पात्र की दीवार से नहीं टकराते हैं, क्योंकि आण्विक आकर्षण बल के कारण वे पीछे की ओर अन्य अणुओं के साथ आकर्षण बल महसूस करते हैं। यह गैस के अणुओं द्वारा पात्र की दीवार पर उत्पन्न दाब को प्रभावित करता है। अतः वास्तविक गैस के द्वारा उत्पन्न दाब आदर्श गैस के दाब से कम होता है।
 ...............(5.30)
...............(5.30)
यहाँ a एक स्थिरांक है।
इस स्थिति में प्रतिकर्षण बल भी सार्थक हो जाते हैं। प्रतिकर्षण अन्योन्य क्रियाएँ लघु मात्रा में होती हैं तथा जब अणु एक-दूसरे के लगभग संपर्क में होते हैं, तब ये सार्थक हो जाती हैं। यह स्थिति उच्च दाब पर उत्पन्न होती है। प्रतिकर्षण बल अणुओं को सूक्ष्म, परंतु अभेद्य गोले की भाँति व्यवहार करने के लिए प्रेरित करते हैं। अणुओं के द्वारा घेरा गया आयतन भी सार्थक हो जाता है, क्योंकि अणु V आयतन में विचरण के स्थान पर (V – nb) आयतन में विचरण करने के लिए प्रतिबंधित हो जाते हैं, जहाँ nb गैस के अणुओं द्वारा घेरे गए वास्तविक आयतन के लगभग बराबर है। b एक स्थिरांक हैै। दाब आयतन के इन संशोधनों को ध्यान में रखते हुए हम समीकरण 5.17 को इस प्रकार लिख सकते हैं–
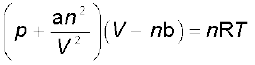 ................(5.31)
................(5.31)
समीकरण 5.31 को ‘वांडरवाल समीकरण’ कहते हैं। n गैस के मोलों की संख्या है। a तथा b वांडरवाल स्थिरांक हैं, जिनका मान गैस के चारित्रिक गुणों पर निर्भर करता है। a का मान गैस के अणुओं में अंतरा-अणुक आकर्षण बल का परिमाण है, जो ताप एवं दाब पर निर्भर नहीं करता है।
कम ताप पर भी अंतरा-अणुक बल सार्थक हो जाते हैं, क्योंकि अणु कम ऊर्जा से गमन करते हैं, जिससे ये अणु एक-दूसरे से आकर्षण बल से बंधे होते हैं। वास्तविक गैस तब आदर्श व्यवहार प्रदर्शित करती है, जब अंतर-अणुक बल प्रायोगिक रूप से नगण्य हो जाए। वास्तविक गैस तब भी आदर्श व्यवहार प्रदर्शित करती है, जब दाब शून्य हो जाए।
आदर्श व्यवहार से विचलन को संपीड्यता कारक Z द्वारा मापा जा सकता है, जो p, V तथा nRT के गुणनफल का अनुपात होता है। गणितीय रूप में
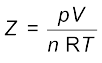 .............(5.32)
.............(5.32)
आदर्श गैसों के लिए Z = 1 होता है, क्योंकि सभी ताप एवं दाब पर pV = nRT होता है। Z एवं p के मध्य आरेख खींचने पर सीधी रेखा प्राप्त होती है, जो दाब अक्ष के समानांतर होती है। (चित्र 5.12)।
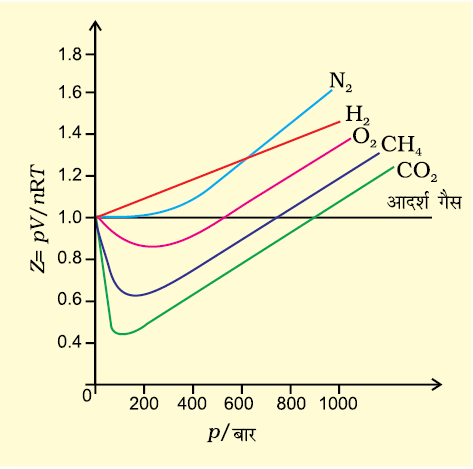
चित्र 5.12 कुछ गैसों के संपीड्यता कारक में परिवर्तन
इन गैसों में Z का मान इकाई से विचलित हो जाता है, जो आदर्शत्व से विचलन दर्शाती हैं। निम्नत्व दाब पर लगभग सभी गैसों के लिए Z 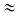 1 होता है। वे आदर्श गैस की भाँति व्यवहार करती हैं, परंतु उच्च दाब पर सभी गैसों के लिए Z > 1 होता है। अर्थात् इन्हें संपीडित करना कठिन होता है। मध्यवर्ती दाब पर Z < 1 होता है। अतः जब गैस द्वारा घेरा गया आयतन बहुत अधिक हो, तो वास्तविक गैस आदर्श गैस की भाँति व्यवहार दर्शाती है, क्योंकि एेसी स्थिति में अणुओं का आयतन नगण्य माना जा सकता है। अन्य शब्दों में — जब दाब बहुत निम्न होता है, तो गैस का व्यवहार अधिक आदर्श हो जाता है। किस दाब तक गैस आदर्श नियमों का पालन करेगी, यह गैसों की प्रकृति तथा ताप पर निर्भर करता है। वह ताप, जिसपर कोई वास्तविक गैस पर्याप्त दाब की मात्रा में आदर्श गैस की भाँति व्यवहार करती है, बॉयल ताप या बॉयल बिंदु कहलाता है। एक गैस का बॉयल बिंदु गैस की प्रकृति पर निर्भर करता है। बॉयल बिंदु से ऊपर वास्तविक गैस आदर्शता से धनात्मक विचलन दर्शाती है तथा Z का मान एक से अधिक होता है। अणुओं के मध्य आकर्षण बल बहुत क्षीण होते हैं। बॉयल बिंदु से नीचे दाब बढ़ाने पर वास्तविक गैसों का Z का मान प्रारंभ में कम होता है तथा पुनः दाब बढ़ाने पर Z का मान लगातार बढ़ता चला जाता है। उपरोक्त व्याख्या से यह स्पष्ट होता है कि उच्च ताप तथा निम्न दाब पर वास्तविक गैस आदर्श व्यवहार दर्शाती है। विभिन्न गैसों के लिए ये परिस्थितियाँ भिन्न-भिन्न होती हैं।
1 होता है। वे आदर्श गैस की भाँति व्यवहार करती हैं, परंतु उच्च दाब पर सभी गैसों के लिए Z > 1 होता है। अर्थात् इन्हें संपीडित करना कठिन होता है। मध्यवर्ती दाब पर Z < 1 होता है। अतः जब गैस द्वारा घेरा गया आयतन बहुत अधिक हो, तो वास्तविक गैस आदर्श गैस की भाँति व्यवहार दर्शाती है, क्योंकि एेसी स्थिति में अणुओं का आयतन नगण्य माना जा सकता है। अन्य शब्दों में — जब दाब बहुत निम्न होता है, तो गैस का व्यवहार अधिक आदर्श हो जाता है। किस दाब तक गैस आदर्श नियमों का पालन करेगी, यह गैसों की प्रकृति तथा ताप पर निर्भर करता है। वह ताप, जिसपर कोई वास्तविक गैस पर्याप्त दाब की मात्रा में आदर्श गैस की भाँति व्यवहार करती है, बॉयल ताप या बॉयल बिंदु कहलाता है। एक गैस का बॉयल बिंदु गैस की प्रकृति पर निर्भर करता है। बॉयल बिंदु से ऊपर वास्तविक गैस आदर्शता से धनात्मक विचलन दर्शाती है तथा Z का मान एक से अधिक होता है। अणुओं के मध्य आकर्षण बल बहुत क्षीण होते हैं। बॉयल बिंदु से नीचे दाब बढ़ाने पर वास्तविक गैसों का Z का मान प्रारंभ में कम होता है तथा पुनः दाब बढ़ाने पर Z का मान लगातार बढ़ता चला जाता है। उपरोक्त व्याख्या से यह स्पष्ट होता है कि उच्च ताप तथा निम्न दाब पर वास्तविक गैस आदर्श व्यवहार दर्शाती है। विभिन्न गैसों के लिए ये परिस्थितियाँ भिन्न-भिन्न होती हैं।
यदि हम निम्नलिखित व्युत्पन्न को देखें, तो Z के संदर्भ में हमें और अधिक जानकारी प्राप्त होती है।

समीकरण 5.34 से स्पष्ट है कि संपीड्यता गुणांक गैस के वास्तविक मोलर आयतन तथा उसी ताप एवं दाब पर आदर्श गैस के मोलर आयतन का अनुपात होता है। इस खंड में हम अध्ययन करेंगे कि गैसीय तथा द्रव अवस्था में विभेद करना संभव नहीं है तथा कम आयतन और उच्च आण्विक आकर्षण के क्षेत्र में द्रव को गैस की नैरंतर्य अवस्था माना जा सकता है। हम यह भी देखेंगे कि गैसों के द्रवीकरण के लिए उपयुक्त परिस्थितियों के लिए समतापी वक्रों का उपयोग किस प्रकार किया जाता है।
5.10 गैसों का द्रवीकरण
किसी पदार्थ की गैस तथा द्रव अवस्था के लिए दाब-आयतन-ताप संबंधों के पूर्ण आँकड़े प्रथम बार थॉमस एेन्ड्रन्न्ज ने कार्बन डाइअॉक्साइड के लिए दिए। उन्होंने विभिन्न तापों पर कार्बन डाइअॉक्साइड के समतापी आरेख खींचे (चित्र 5.13)।
चत्र 5-13ः विभिÂ तापों पर कार्बन डाइऑक्साइड के समतापी आरेख
बाद में यह पाया गया कि वास्तविक गैसें कार्बन डाइअॉक्साइड के समान व्यवहार दर्शाती हैं। एेन्ड्रन्न्ज ने देखा कि उच्च ताप पर समतापी आरेख आदर्श गैस के समतापी आरेख के समान होते हैं। उन्होंने यह भी पाया कि उच्च दाब पर भी गैस को द्रवित नहीं किया जा सकता है। जब ताप कम किया जाता है, तो वक्र की आकृति परिवर्तित हो जाती है तथा आँकड़े आदर्श व्यवहार से विचलन दर्शाते हैं। 30.98°C पर 73 वायुमंडलीय दाब से पूर्व कार्बन डाइअॉक्साइड गैस द्रव अवस्था में रहती है (चित्र 5.13 में बिंदु E)। 73 वायुमंडलीय दाब पर कार्बन डाइअॉक्साइड पहली बार द्रव अवस्था में प्रकट होती है। 30.98°C ताप कार्बन डाइअॉक्साइड का क्रांतिक ताप (Tc) कहलाता है। यह वह अधिकतम ताप है, जिसपर द्रव कार्बन डाइअॉक्साइड प्राप्त होती है तथा अधिक ताप पर यह गैस होती है।
क्रांतिक ताप पर एक मोल गैस का आयतन क्रांतिक आयतन (Vc) तथा इस ताप पर दाब क्रांतिक दाब (pc) कहलाता है।
क्रांतिक ताप, क्रांतिक दाब तथा क्रांतिक आयतन को ‘क्रांतिक स्थिरांक’ कहते हैं। पुनः दाब बढ़ाने पर द्रव कार्बन डाइअॉक्साइड संपीडित हो जाती है। खड़ी रेखा द्रव कार्बन डाइअॉक्साइड के समतापी आरेख को प्रदर्शित करती है। अत्यधिक दाब बढ़ाने पर संपीड्यता में सूक्ष्म न्यूनता द्रवों की कम संपीड्यता को प्रदर्शित करती है। 21.5°C पर बिंदु B तक कार्बन डाइअॉक्साइड गैस अवस्था में रहती है। बिंदु B पर विशिष्ट आयतन का द्रव प्राप्त होता है। इसके उपरांत संपीडन पर दाब परिवर्तित नहीं होता है। द्रव तथा गैस कार्बन डाइअॉक्साइड साथ-साथ रहती है। दाब पुनः बढ़ाने पर गैस का संघनन अधिक होता है तथा बिंदु C प्राप्त होता है। बिंदु C पर पूरी गैस संघनित हो जाती है। तत्पश्चात् पुनः दाब बढ़ाने पर द्रव बहुत कम संपीडित होता है तथा एक अतिप्रवण रेखा मिलती है। V2 से V3 तक आयतन में सूक्ष्म संपीडन p2 से p3 दाब को अतिप्रवण बनाता है (चित्र 5.13)। 30.98°C (क्रांतिक ताप) से नीचे प्रत्येक वक्र इसी प्रकार की प्रवृत्ति प्रदर्शित करता है। कम ताप पर केवल क्षैतिज रेखा की लंबाई में वृद्धि होती है। क्रांतिक बिंदु पर क्षैतिज भाग एक बिंदु में विलीन हो जाता है। अतः हम देखते हैं कि चित्र 5.13 में बिंदु A गैसीय अवस्था को प्रदर्शित करता है। D बिंदु द्रव अवस्था को प्रदर्शित करता है, जबकि इस बिंदु से नीचे गुंबदनुमा आकृति में कार्बन डाइअॉक्साइड की द्रव तथा गैसीय अवस्था साम्यावस्था में होती है। सभी गैसें स्थिर ताप पर संपीडन (समतापी संपीडन) पर कार्बन डाइअॉक्साइड के समान व्यवहार प्रदर्शित करती हैं। उपरोक्त व्याख्या यह भी दर्शाती है कि द्रवीकरण के लिए गैसों को क्रांतिक ताप से नीचे ठंडा किया जा सकता है। क्रांतिक ताप वह अधिकतम ताप होता है, जिसपर द्रवीकृत गैस प्रथम बार दिखाई देती है। स्थायी गैसों (अर्थात् वे गैसें, जो Z के मान में लगातार धनात्मक विचलन प्रदर्शित करती हैं) के द्रवीकरण के लिए ताप में कमी के साथ-साथ पर्याप्त संपीडन आवश्यक होता है। संपीडन, गैस के अणुओं को पास-पास लाता है, जबकि ताप कम करने से अणुओं का गमन कम हो जाता है, अर्थात् अंतराणुक अन्योन्य क्रिया ही कम गतिशील अणुओं को पास-पास करती है तथा गैस द्रवीकृत हो जाती है। एक गैस को द्रव में तथा द्रव को गैस में एक प्रावस्था में रहते हुए परिवर्तित किया जा सकता है। उदारणार्थ– चित्र 5.13 में ताप बढ़ाने पर जब हम बिंदु A से F की ओर जाते हैं, तब इस समतापी वक्र (31.1°C) के सहारे स्थिर ताप पर गैस को संपीडित करने पर बिंदु G मिलता है। इसके पश्चात् हम ताप कम करके ऊर्ध्वाधर नीचे की ओर बिंदु D पर जाते हैं। जैसे ही हम बिंदु H को पार करते हैं, वैसे ही हमें द्रव प्राप्त होता है, परंतु कहीं भी दो प्रावस्थाएँ उपस्थित नहीं होती हैं। यदि यह प्रक्रिया क्रांतिक ताप पर संपन्न होती है, तो पदार्थ केवल एक ही प्रावस्था में रहता है।
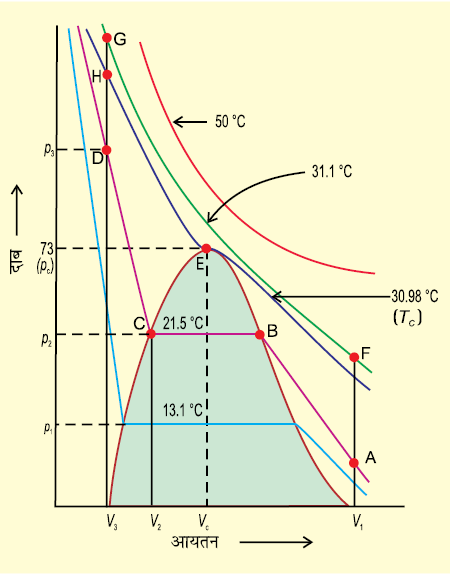
अतः द्रव तथा गैसीय अवस्था में सातत्य (निरंतरता) है इस सातत्य अवस्था को पहचानने के लिए गैस तथा द्रव के लिए तरल पद को प्रयोग में लाया जाता है। अतः द्रव को गैस के संघनित रूप में देखा जा सकता है। जब तरल, क्रांतिक ताप से कम ताप पर होता है (तथा उसका आयतन गुंबदनुमा आकृति में हो) तो द्रव तथा गैस में विभेद किया जा सकता है, क्योंकि इस परिस्थिति में द्रव तथा गैस साम्यावस्था में होते हैं और दो प्रावस्थाओं के मध्य विभेदकारी परत दिखाई देती है। इस विभेदी परत की अनुपस्थिति में हम किसी भी विधि द्वारा इन दो अवस्थाओं में विभेद नहीं कर सकते हैं। क्रांतिक ताप पर गैस में द्रव का परिवर्तन अप्रत्यक्ष तथा सतत होता है, दो परतों को पृथक् करनेवाली सतह अदृश्य हो जाती है (खंड 5.11.1)। क्रांतिक ताप से नीचे किसी भी गैस को केवल दाब बढ़ाकर द्रवीकृत किया जा सकता है। इसे उस पदार्थ की वाष्प कहते हैं। क्रांतिक ताप से नीचे कार्बन डाइअॉक्साइड को ‘कार्बन डाइअॉक्साइड वाष्प’ कहते हैं। कुछ पदार्थों के क्रांतिक स्थिरांकों के मान सारणी 5.4 में दिए गए हैं।
सारणी 5.4 कुछ पदार्थाें के क्रांतिक स्थिरांक
उदाहरण 5.5
एक गैस चारित्रिक क्रांतिक ताप रखती है, जिसके परिमाण गैस के अणुओं के मध्य अंतराणुक बलों पर निर्भर करता है। अमोनिया तथा कार्बन डाइअॉक्साइड के क्रांतिक ताप क्रमशः 405.5K तथा 304.10K है। यदि ताप को 500K से समातापी ताप तक कम करें, तो कौन सी गैस पहले द्रवीकृत होगी?
हल
अमोनिया का द्रवीकरण पहले होगा, क्योंकि इसका क्रांतिक ताप पहले प्राप्त हो जाएगा। कार्बन डाइअॉक्साइड के द्रवीकरण के लिए और अधिक शीतलन करना होगा।
5.11 द्रव अवस्था
गैस अवस्था की तुलना में, द्रव अवस्था में अंतराअणुक बल अधिक प्रबल होते हैं। उनके अणु इतने पास-पास होते हैं कि उनके मध्य रिक्त स्थान बहुत कम होता है। सामान्य परिस्थितियों में गैस की तुलना में द्रव अधिक सघन होते हैं।
द्रवों के अणु अंतराअणुक आकर्षण बलों द्वारा बंधे रहते हैं द्रवों का आयतन निश्चित होता है। क्योंकि अणु एक-दूसरे से पृथक् नहीं होते हैं, जबकि द्रव के अणु मुक्त रूप से गमन करते रहते हैं, जिससे द्रव प्रवाहित होते हैं। द्रव को एक पात्र से दूसरे पात्र में डाला जा सकता है तथा जिस पात्र में उसे रखा जाता है, उसी की आकृति ग्रहण कर लेता है। इस खंड में हम द्रव के कुछ गुणों, जैसे– वाष्पदाब, पृष्ठतनाव तथा श्यानता का अध्ययन करेंगे।
5.11.1 वाष्पदाब
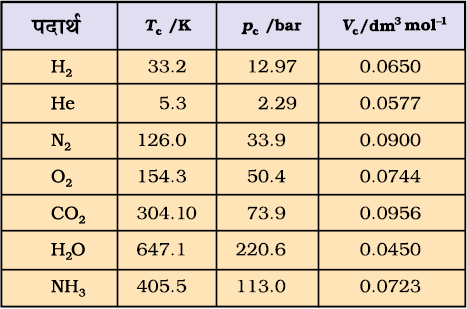
यदि एक निर्वातित पात्र को द्रव से आंशिक रूप से भरा जाता है, तो द्रव का कुछ भाग वाष्पीकृत होकर पात्र के शेष आयतन को भर देता है। प्रारंभ में द्रव वाष्पित होता है तथा वाष्प के द्वारा द्रव की सतह पर लगाए गए दाब (वाष्प दाब) में वृद्धि होती जाती है। कुछ समय पश्चात् यह स्थिर हो जाता है तथा द्रव-अवस्था एवं वाष्प-अवस्था के मध्य साम्य स्थापित हो जाता है। इस अवस्था में वाष्पदाब साम्य वाष्पदाब अथवा संतृप्त वाष्पदाब कहलाता है। चूँकि वाष्पन की प्रक्रिया ताप पर आधारित होती है, अतः किसी द्रव के वाष्पदाब की चर्चा करते समय ताप का उल्लेख करना आवश्यक होता है।
जब द्रव को खुले पात्र में गरम किया जाता है, तब वह अपनी सतह से वाष्पीकृत होता है। जब द्रव का वाष्पदाब बाह्य दाब के समान हो जाता है, तब पूरे द्रव का वाष्पीकरण होने लगता है तथा वाष्प अपने परिवेश में मुक्त रूप से प्रसारित होती है। संपूर्ण द्रव के मुक्त वाष्पीकरण की स्थिति को ‘उबलना’ कहते हैं। वह ताप, जिसपर किसी द्रव का वाष्पदाब बाह्य दाब के समान हो जाता है, यह उस दाब पर द्रव का ‘क्वथनांक’ कहलाता है। कुछ सामान्य द्रवों के वाष्पदाब चित्र 5.14 में दर्शाए गए हैं। एक वायुमंडलीय दाब पर क्वथनांक को सामान्य क्वथनांक कहते हैं। यदि दाब एक bar हो, तो क्वथनांक को मानक क्वथनांक कहते हैं। किसी द्रव का मानक क्वथनांक सामान्य क्वथनांक से कुछ कम होता है। चूँकि एक bar दाब एक वायुमंडलीय दाब से कुछ कम होता है, अतः जल का सामान्य क्वथनांक 100°C (373K) है, जबकि मानक क्वथनांक 99.6°C (372.6K) है।
चित्र 5.14
उच्च उन्नतांश पर वायुमंडलीय दाब कम होता है, अतः समुद्रतल की तुलना में उच्च उन्नतांश पर द्रव कम ताप पर उबलता है। चूँकि पहाड़ों पर जल कम ताप पर उबलता है, अतः भोजन को पकाने के लिए प्रेशर कुकर का इस्तेमाल करना पड़ता है। चिकित्सालयों में शल्य-क्रिया में काम आनेवाले उपकरणों को अॉटोक्लेव में उबालकर रोगाणुरहित किया जाता है, क्योंकि अॉटोक्लेव के मुख पर भार रखकर दाब बढ़ाने से उसमें निहित जल का क्वथनांक बढ़ जाता है।
जब हम द्रव को बंद पात्र में उबालते हैं, तब क्वथन नहीं होता है। सतत् गरम किए जाने पर वाष्पदाब बढ़ता है। प्रारंभ में द्रव तथा वाष्प के मध्य एक स्पष्ट सीमा-रेखा दिखाई देती है, क्योंकि द्रव वाष्प की तुलना में अधिक सघन होता है। जैसे-जैसे ताप बढ़ाया जाता है, वैसे-वैसे अधिकाधिक अणु वाष्प प्रावस्था में परिवर्तित होते हैं तथा वाष्प का घनत्व बढ़ता जाता है। चूँकि अणु दूर-दूर होते हैं, अतः ये प्रसारित होते हैं। जब द्रव तथा वाष्प का घनत्व समान हो जाता है, तब द्रव तथा वाष्प के मध्य की सीमा-रेखा अदृश्य हो जाती है। यह ताप ‘क्रांतिक ताप’ कहलाता है, जिसकी व्याख्या हम खंड 5.10 में कर चुके हैं।
5.11.2 पृष्ठ तनाव (Surface Tension)
यह सर्वविदित तथ्य है कि द्रव पात्र का आकार ग्रहण कर लेते हैं। मर्करी की बूँदें सतह पर फैलने की बजाय गोलाकार मणिका के रूप में क्यों होती हैं? नदी के तल में मृदा के कण पृथक्-पृथक् क्यों होते हैं तथा बाहर निकाले जाने पर साथ चिपक क्यों जाते हैं? केशिका नली को द्रव तल के संपर्क में लाने पर केशिका नली में द्रव चढ़ता अथवा उतरता क्यों है? ये सभी प्रघटनाएँ द्रव के विशिष्ट गुण, जिसे ‘पृष्ठ-तनाव’ कहते हैं, के कारण होती हैं। द्रव के एक पुंज में एक अणु सभी दिशाओं से समान आकर्षण बल अनुभव करता है तथा परिणामी आकर्षण बल शून्य होता है, परंतु सतह पर विद्यमान अणु अपने नीचे के अणुओं के कारण द्रव के अंदर की ओर आकर्षण बल अनुभव करता है (चित्र 5.15) क्योंकि इसके ऊपर अणु नहीं होते।
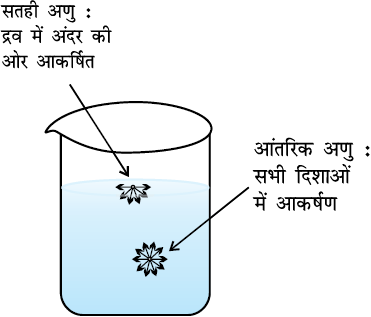
द्रव अपनी सतह को न्यूनतम करने का प्रयास करता है, सतह के अणुओं पर नेट बल नीचे की ओर होता है और उनकी ऊर्जा पुंज में उपस्थित अणुओं की ऊर्जा से अधिक होती है क्योंकि पुंज के अणुओं पर नेट बल नहीं होता। इसलिए द्रवों की प्रवृति सतह पर कम अणु रखने की होती है। यदि पुंज में से अणु सतह पर लाकर सतह को बढ़ाया जाए तो आकर्षण बलों को पार करना होगा। इसके लिए ऊर्जा व्यय होती है। किसी द्रव की सतह में एकांक वृद्धि के लिए आवश्यक ऊर्जा को ‘पृष्ठीय ऊर्जा’ कहते हैं। इसकी इकाई Jm–2 होती है। सतह पर खींची गई एक रेखा की एकांक लंबाई पर लगने वाले लंबवत बल को ‘पृष्ठ-तनाव’ कहते हैं। इसे ग्रीक शब्द γ (गामा) से प्रदर्शित करते हैं। इसकी इकाई kgs–2 तथा SI इकाई में Nm–1 होता है। किसी द्रव का निम्नतम ऊर्जास्तर तब होता है, जब उसका पृष्ठ क्षेत्रफल निम्नतम हो। इस स्थिति को गोलाकृति संतुष्ट करती है। यही कारण है कि वर्षा की बूँदें तथा मर्करी की बूँदें गोलाकार होती हैं तथा काँच के तीक्ष्ण किनारे को गरम करके चिकना बनाया जा सकता है। गरम किए जाने पर काँच पिघलता है तथा द्रव का किनारा गोल आकृति लेने का प्रयास करता है, जिससे किनारा चिकना बन जाता है। इसे ‘काँच की अग्नि-पॉलिश’ (Fire-polishing) कहते हैं।
पृष्ठ-तनाव के कारण एक केशनलिका में द्रव चढ़ता या उतरता है। द्रव वस्तुओं को नम कर देता है, क्योंकि वह पतली परत के रूप में वस्तु की सतह पर फैल जाता है। मृदा के नम कण पास-पास होते हैं, क्योंकि जल की पतली परत का पृष्ठ-तनाव कम हो जाता है। यह पृष्ठ तनाव ही है जो द्रव की सतह को तनन का गुण देता है। गुरुत्व-प्रभाव के कारण पृथ्वी पर छोटी-छोटी बूँदें आंशिक चपटी हो जाती हैं, परंतु गुरुत्वविहीन वातावरण में बूँदें पूर्ण गोलाकार होती हैं।
पृष्ठ-तनाव का परिमाण द्रव के अणुओं के मध्य आकर्षण बलों पर निर्भर करता है। जब आकर्षण-बल अधिक होता है, तब पृष्ठ-तनाव अधिक होता है। ताप बढ़ाने पर अणुओं की गतिज-ऊर्जा बढ़ जाती है तथा अंतर अणुक क्रिया की प्रभाविता कम हो जाती है। अतः ताप बढ़ाने पर पृष्ठ-तनाव कम हो जाता है।
5.11.3 श्यानता
यह द्रवों का अभिलाक्षणिक गुण है। द्रव के प्रवाह की अवस्था में जब तरल की परतें एक-दूसरे के ऊपर गुजरती हैं, तब उनके मध्य उत्पन्न घर्षण बल के माप को ‘श्यानता’ कहते हैं। घर्षण अणुओं के मध्य प्रबल अंतरा आण्विक बलों के कारण होता है जो परतों को एक साथ बांधे रखते हैं और उनके एक–दूसरे पर संचलन का प्रतिरोध करते हैं।
जब द्रव का प्रवाह किसी स्थिर सतह पर होता है, तब उस (द्रव) की वह परत, जो सतह के संपर्क में होती है, स्थायी हो जाती है। जैसे-जैसे स्थायी परत से ऊपरी परतों की दूरी बढ़ती जाती है, वैसे-वैसे परत का वेग बढ़ता जाता है। अतः इस प्रकार का प्रवाह, जिसमें एक परत से दूसरी परत का वेग क्रमशः बढ़ता चला जाता है, ‘स्तरीय प्रवाह’ कहलाती है। यदि हम प्रवाहित द्रव में किसी भी परत को चुनें (चित्र 5.16) तो उससे ऊपरी परत इसका वेग बढ़ाती है, जबकि निचली परत वेग को कम करती है।
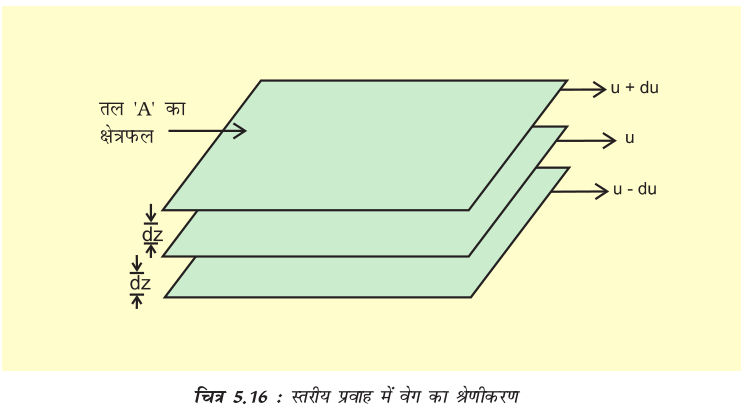
यदि दूरी dz पर परत का वेग du परिवर्तित होता है, तो वेग प्रवणता को 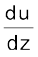 से प्रदर्शित किया जाता है। परतों के प्रवाह को बनाए रखने के लिए एक बल की आवश्यकता होती है। यह बल संपर्कयुक्त परतों के क्षेत्रफल तथा वेग-प्रवणता के समानुपाती होता है।
से प्रदर्शित किया जाता है। परतों के प्रवाह को बनाए रखने के लिए एक बल की आवश्यकता होती है। यह बल संपर्कयुक्त परतों के क्षेत्रफल तथा वेग-प्रवणता के समानुपाती होता है।
अतः F ∝ A (A संपर्क का क्षेत्रफल है)
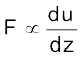
(यहाँ 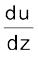 वेग-प्रवणता है, अर्थात् दूरी के साथ वेग में परिवर्तन है।)
वेग-प्रवणता है, अर्थात् दूरी के साथ वेग में परिवर्तन है।)
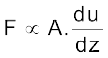
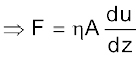
यहाँ 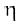 एक समानुपातिक स्थिरांक है, जिसे ‘श्यानता गुणांक’ कहते हैं। श्यानता गुणांक वह बल है, जब वेग-प्रवणता तथा संपर्क का क्षेत्रफल इकाई हो। इस प्रकार
एक समानुपातिक स्थिरांक है, जिसे ‘श्यानता गुणांक’ कहते हैं। श्यानता गुणांक वह बल है, जब वेग-प्रवणता तथा संपर्क का क्षेत्रफल इकाई हो। इस प्रकार 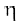 विस्कासिता की माप है। विस्कासिता गुणांक की SI इकाई 1 न्यूटन सेकंड प्रति वर्गमीटर, (Nsm–2), अर्थात् पास्कल सेकंड Pas = 1kg m-1 s-1 है। cgs पद्धति में श्यानता गुणांक की इकाई पॉइज (महान वैज्ञानिक जीन लूइस पाइज्जले के नाम पर) है।
विस्कासिता की माप है। विस्कासिता गुणांक की SI इकाई 1 न्यूटन सेकंड प्रति वर्गमीटर, (Nsm–2), अर्थात् पास्कल सेकंड Pas = 1kg m-1 s-1 है। cgs पद्धति में श्यानता गुणांक की इकाई पॉइज (महान वैज्ञानिक जीन लूइस पाइज्जले के नाम पर) है।
1 poise = 1 g cm–1s–1 = 10–1kg m–1s–1
श्यानता अधिक होने पर द्रव का प्रवाह बहुत धीरे होता है। हाइड्रोजन बंध तथा वांडरवाल्स बल के कारण विस्कासिता बढ़ जाती है। काँच एक अति चिपचिपा द्रव है। यह इतना श्यान होता है कि इसके अधिकांश गुण ठोसों से मिलते हैं।
ताप बढ़ाने पर श्यानता का गुण कम होता जाता है, क्योंकि अधिक ताप पर अणुओं की गतिज ऊर्जा अधिक होती है, जिससे अंतराणुक बलों को पराभूत कर एक-दूसरे पर फिसलती है।
सारांश
द्रव्य के कणों के मध्य अंतराणुक बल होते हैं। ये बल दो विपरीत आवेशित आयनों के मध्य उत्पन्न होने वाले स्थिर वैद्युत बलों से भिन्न होते हैं। साथ ही ये उन बलों को भी समाहित नहीं करते हैं, जो सहसंयोजक बंध में दो परमाणुओं को थामे रखता है। उष्मीय ऊर्जा तथा अंतराणुक अन्योन्य क्रिया के मध्य प्रतिंद्वद्विता द्रव्य की अवस्था को निर्धारित करती है। द्रव्य के स्थूल गुण (जैसे– गैसों का व्यवहार, द्रवों तथा ठोसों के गुण और उनकी अवस्था में परिवर्तन, अवयवी कणों तथा उनके मध्य अन्योन्य क्रिया पर निर्भर करते हैं। पदार्थ के रासायनिक गुण उसकी अवस्था के परिवर्तन से प्रभावित नहीं होते हैं, परंतु उनकी क्रियाशीलता भौतिक अवस्था पर निर्भर करती है।
गैस के अणुओं के मध्य आकर्षण-बल अति न्यून होते हैं तथा उनकी रासायनिक प्रकृति पर लगभग निर्भर नहीं करते हैं। कुछ प्रेक्षणीय गुण (जैसे– दाब, आयतन, ताप तथा द्रव्यमान) की अंतनिर्भरता ने गैसों के प्रायोगिक अध्ययनों के उपरांत विभिन्न गैस नियम दिए। बॉयल के नियमानुसार समतापी परिस्थितियों में एक निश्चित संहति वाली गैस का दाब उसके आयतन के व्युत्क्रमानुपाती होता है। चार्ल्स का नियम समदाबी परिस्थितियों में आयतन तथा परम ताप के मध्य संबंध को दर्शाता है। इसके अनुसार, किसी निश्चित संहति वाली गैस का आयतन उसके परम ताप के समानुपाती होता है। यदि गैस की प्रारंभिक अवस्था p1, V1 तथा T1 से प्रदर्शित की जाए तथा परिवर्तन को p2, V2 और T2 से दर्शाया जाए, तो इन दो अवस्थाओं के मध्य संबंधों को संयुक्त गैस नियम द्वारा प्रदर्शित कर सकते हैं, जो 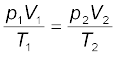 है। इनमें से यदि पाँच अन्य चर ज्ञात हों, तो छठवाँ चर ज्ञात किया जा सकता है। आवोगाद्रो के अनुसार, ताप एवं दाब की समान परिस्थितियों में गैसों के समान आयतन में अणुओं की संख्या भी समान होती है। डाल्टन के आंशिक दाब के नियमानुसार, अक्रियाशील गैसों के मिश्रण का कुल दाब उनके आंशिक दाब के योग के बराबर होता है, अर्थात् ताप, दाब, आयतन तथा मोलों की संख्या के मध्य अंतर्संबंध गैस की अवस्था को निर्धारित करता है। इसे ‘गैस की अवस्था समीकरण’ कहते हैं। आदर्श गैस के लिए अवस्था समीकरण pV = nRT होती है, जहाँ R गैस स्थिरांक है। दाब, आयतन तथा ताप की चुनी गई इकाई पर इसका मान निर्भर करता है।
है। इनमें से यदि पाँच अन्य चर ज्ञात हों, तो छठवाँ चर ज्ञात किया जा सकता है। आवोगाद्रो के अनुसार, ताप एवं दाब की समान परिस्थितियों में गैसों के समान आयतन में अणुओं की संख्या भी समान होती है। डाल्टन के आंशिक दाब के नियमानुसार, अक्रियाशील गैसों के मिश्रण का कुल दाब उनके आंशिक दाब के योग के बराबर होता है, अर्थात् ताप, दाब, आयतन तथा मोलों की संख्या के मध्य अंतर्संबंध गैस की अवस्था को निर्धारित करता है। इसे ‘गैस की अवस्था समीकरण’ कहते हैं। आदर्श गैस के लिए अवस्था समीकरण pV = nRT होती है, जहाँ R गैस स्थिरांक है। दाब, आयतन तथा ताप की चुनी गई इकाई पर इसका मान निर्भर करता है।
उच्च दाब तथा कम ताप पर गैसों के अणुओं के मध्य अंतराणुक-बल प्रबल हो जाते हैं, क्योंकि ये अणु पास-पास आ जाते हैं। ताप एवं दाब की उपयुक्त परिस्थितियों में गैस को द्रवीकृत किया जा सकता है। द्रव को कम आयतन क्षेत्र में गैस की संपीडन अवस्था माना जा सकता है। प्रबल अंतराणुक आकर्षण-बलों के कारण द्रव के कुछ गुण पृष्ठ-तनाव, श्यानता आदि हैं।
अभ्यास
5.1 30° से. तथा 1 bar दाब पर वायु के 500 dm3 आयतन को 200 dm3 तक संपीडित करने के लिए कितने न्यूनतम दाब की आवश्यकता होगी?
5.2 35° से. ताप तथा 1.2 bar दाब पर 120 mL धारिता वाले पात्र में गैस की निश्चित मात्रा भरी है। यदि 35° से. पर गैस को 180 mL धारिता वाले फ्लास्क में स्थानांतरित किया जाता है, तो गैस का दाब क्या होगा?
5.3 अवस्था-समीकरण का उपयोग करते हुए स्पष्ट कीजिए कि दिए गए ताप पर गैस का घनत्व गैस के दाब के समानुपाती होता है।
5.4 0°C पर तथा 2 bar दाब पर किसी गैस के अॉक्साइड का घनत्व 5 bar दाब पर डाइनाइट्रोजन के घनत्व के समान है, तो अॉक्साइड का अणु-भार क्या है?
5.5 27° से. पर एक ग्राम आदर्श गैस का दाब 2 bar है। जब समान ताप एवं दाब पर इसमें दो ग्राम आदर्श गैस मिलाई जाती है, तो दाब 3 bar हो जाता है। इन गैसों के अणु-भार में संबंध स्थापित कीजिए।
5.6 नाली साफ करने वाले ड्रेनेक्स में सूक्ष्म मात्रा में एेलुमिनियम होता है। यह कास्टिक सोडा से क्रिया पर डाइहाइड्रोजन गैस देता है। यदि 1 bar तथा 20°C ताप पर 0.15 ग्राम एेलुमिनियम अभिक्रिया करेगा, तो निर्गमित डाइहाइड्रोजन का आयतन क्या होगा?
5.7 यदि 27°C. पर 9 dm3 धारितावाले फ्लास्क में 3.2 ग्राम मेथेन तथा 4.4 ग्राम कार्बन डाइअॉक्साइड का मिश्रण हो, तो इसका दाब क्या होगा?
5.8 27°C ताप पर जब 1 लिटर के फ्लास्क में 0.7 bar पर 2.0 लिटर डाइअॉक्सीजन तथा 0.8 bar पर 0.5 L डाइहाइड्रोजन को भरा जाता है, तो गैसीय मिश्रण का दाब क्या होगा?
5.9 यदि 27°C ताप तथा 2 bar दाब पर एक गैस का घनत्व 5.46 g dm3 है, तो STP पर इसका घनत्व क्या होगा?
5.10 यदि 546°C तथा 0.1 bar दाब पर 34.05 mL फॉस्फोरस वाष्प का भार 0.0625 g है, तो फॉस्फोरस का मोलर द्रव्यमान क्या होगा?
5.11 एक विद्यार्थी 27°C पर गोल पेंदे के फ्लास्क में अभिक्रिया-मिश्रण डालना भूल गया तथा उस फ्लास्क को ज्वाला पर रख दिया। कुछ समय पश्चात् उसे अपनी भूल का अहसास हुआ। उसने उत्तापमापी की सहायता से फ्लास्क का ताप 477°C पाया। आप बताइए कि वायु का कितना भाग फ्लास्क से बाहर निकला।
5.12 3.32 bar पर 5 dm3 आयतन घेरनेवाली 4.0 mol गैस के ताप की गणना कीजिए।
(R = 0.83 bar dm3 mol-1)
5.13 1.4 g डाइनाइट्रोजन गैस में उपस्थित कुल इलेक्ट्रॉनों की संख्या की गणना कीजिए।
5.14 यदि एक सेकंड में 1010 गेहूँ के दाने वितरित किए जाएँ, तो आवोग्रादों-संख्या के बराबर दाने वितरित करने में कितना समय लगेगा?
5.15 27°C ताप पर 1 dm3 आयतनवाले फ्लास्क में 8 ग्राम डाइअॉक्सीजन तथा 4 ग्राम डाइहाइड्रोजन के मिश्रण का कुल दाब कितना होगा?
5.16 गुब्बारे के भार तथा विस्थापित वायु के भार के अंतर को ‘पेलोड’ कहते हैं। यदि 27°C पर 10m त्रिज्यावाले गुब्बारे में 1.66 bar पर 100 kg हीलियम भरी जाए, तो पेलोड की गणना कीजिए। (वायु का घनत्व
= 1.2 gm m-3 तथा R = 0.083 bar dm3 mol-1)
5.17 31.1 C तथा 1 bar दाब पर 8.8 ग्राम CO2 द्वारा घेरे गए आयतन की गणना कीजिए।
R = 0.083 bar L mol–1
5.18 समान दाब पर किसी गैस के 2.9 g द्रव्यमान का 95°C तथा 0.184 g डाइहाइड्रोजन का 17°C पर आयतन समान है। बताइए कि गैसें का मोलर द्रव्यमान क्या होगा?
5.19 एक bar दाब पर डाइहाइड्रोजन तथा डाइअॉक्सीजन के मिश्रण में 20% डाइहाइड्रोजन (भार से) रखा जाता है, तो डाइहाइड्रोजन का आंशिक दाब क्या होगा?
5.20 pV 2 T 2/n राशि के लिए SI इकाई क्या होगी?
5.21 चार्ल्स के नियम के आधार पर समझाइए कि न्यूनतम संभव ताप -273°C होता है।
5.22 कार्बन डाइअॉक्साइड तथा मेथेन का क्रांतिक ताप क्रमशः 31.1°C एवं -81.9°C है। इनमें से किसमें प्रबल अंतर आण्विक बल है तथा क्यों?
5.23 वॉन्डरवाल्स प्राचल की भौतिक सार्थकता को समझाइए।
