Table of Contents
एकक 6
ऊष्मागतिकी
Thermodynamics
" यह सार्वत्रिक अंतर्वस्तु का केवल भौतिक सिद्धांत है, जिसके लिए मैं संतुष्ट हूँ कि इसके मौलिक सिद्धांतों को उनकी उपयुक्तता के प्राधार में कभी नकारा नहीं जा सकता है। "
अल्बर्ट आइन्स्टीन
उद्देश्य
इस एकक के अध्ययन के बाद आप–
• निकाय एवं परिवेश पदोें को समझा सकेंगे;
• बंद, खुला एवं वियुक्त निकाय में अंतर कर सकेंगे;
• आंतरिक ऊर्जा
, कार्य एवं ऊष्मा को समझा सकेंगे;
• ऊष्मागतिकी के प्रथम नियम को व्यक्त कर सकेंगे एवं इसका गणितीय रूप लिख सकेंगे;
• रासायनिक निकायों में ऊर्जा-परिवर्तन को कार्य एवं ऊष्मा के योगदान के रूप में परिकलित कर सकेंगे;
• अवस्था-फलन U, H को समझ सकेंगे;
• ∆U एवं ∆H में संबंध स्थापित कर सकेेंगे;
• ∆U एवं ∆H का प्रायोगिक मापन कर सकेंगे;
• ∆H के लिए मानक अवस्था को परिभाषित कर सकेंगे;
• विभिन्न प्रकार की अभिक्रियाओं के लिए एन्थैल्पी परिवर्तन की गणना कर सकेंगे।
• हेस के स्थिर-ऊष्मा संकलन नियम को व्यक्त और अनुप्रयोग कर सकेंगे;
• विस्तीर्ण एवं गहन गुणों में अंतर कर सकेंगे;
• स्वतः तथा अस्वत: प्रवर्तित प्रक्रमों को परिभाषित कर सकेंगे;
• एन्ट्रापी को ऊष्मागतिकी अवस्था-फलन के रूप में परिभाषित और इसका अनुप्रयोग कर सकेंगे;
• मुक्त-ऊर्जा परिवर्तन (∆G) को समझ सकेंगे;
• स्वत: प्रवर्तिता और ∆G तथा ∆G और साम्य स्थिरांक में संबंध स्थापित कर सकेंगे।
जब ईंधन जैसे मेथेन गैस, रसोई गैस या कोयला हवा में जलते हैं, तो रासायनिक अभिक्रिया के दौरान अणुओं में संग्रहीत रासायनिक ऊर्जा ऊष्मा के रूप में निर्मुक्त होती है। जब एक इंजन में ईंधन जलता है, तब रासायनिक ऊर्जा यांत्रिक कार्य करने में प्रयुक्त हो सकती है या गैल्वनी सेल (शुष्क सेल) विद्युत् ऊर्जा प्रदान करती है। इस प्रकार ऊर्जा के विभिन्न रूप विशेष परिस्थितयों में एक- दूसरे से परस्पर संबंधित होते हैं एवं एक रूप से दूसरे रूप में बदले जा सकते हैं। इन ऊर्जा-रूपांतरणों का अध्ययन ही ऊष्मागतिकी की विषय-वस्तु है। ऊष्मागतिकी के नियम स्थूल निकायों, जिनमें बहुत-से अणु होते हैं, से संबंधित होते हैं, न कि सूक्ष्म निकायों से, जिनमें बहुत कम अणु होते हैं। ऊष्मागतिकी इस बात से संबंधित नहीं है कि ये परिवर्तन कैसे एवं किस दर से कार्यान्वित होते हैं। यह परिवर्तनकारी निकाय की प्रारंभिक एवं अन्तिम अवस्था से संबंधित हैं। ऊष्मागतिकी के नियम तभी लागू होते हैं, जब निकाय साम्यावस्था में होता है या एक साम्यावस्था से दूसरी साम्यावस्था में जाता है। किसी निकाय के स्थूल गुण (जैसे– दाब एवं ताप) साम्यावस्था में समय के साथ परिवर्तित नहीं होते हैं। इस एकक में हम ऊष्मागतिकी के माध्यम से कुछ महत्वपूर्ण प्रश्नों के उत्तर देने का प्रयास करेंगे। जैसे–
एक रासायनिक अभिक्रिया/प्रक्रम में हम ऊर्जा-परिर्वतन कैसे निर्धारित करते हैं ? यह परिवर्तन होगा अथवा नहीं? एक रासायनिक अभिक्रिया/प्रक्रम कैसे प्रेरित होता है? रासायनिक अभिक्रिया किस सीमा तक चलती है?
6.1 ऊष्मागतिकी के तकनीकी शब्द
हमारी उत्सुकता रासायनिक अभिक्रियाओं एवं उनमें होनेवाले ऊर्जा-परिवर्तनों को जानने की होती है इसके लिए हमें उष्मागतिकी में प्रयुक्त होने वाले कुछ तकनीकी शब्दों को जानना होगा इनका वर्णन नीचे दिया गया है–
6.1.1 निकाय एवं परिवेश
ऊष्मागतिकी में निकाय का अर्थ ब्रह्मांड के उस भाग से है, जिसपर प्रेक्षण किए जाते हैं तथा इसका शेष भाग ‘परिवेश’ कहलाता है। परिवेश में निकाय को छोड़कर सब कुछ सम्मिलित है। निकाय एवं परिवेश– दोनों मिलकर ब्रह्मांड बनता है।
निकाय + परिवेश = ब्रह्मांड
निकाय से अतिरिक्त संपूर्ण ब्रह्मांड निकाय में होनेवाले परिवर्तनों से प्रभावित नहीं होता है। इसीलिए प्रायोगिक कार्याें के लिए ब्रह्मांड का वही भाग, जो निकाय से अंतर्क्रिया करता है, परिवेश के रूप में लिया जाता है।
सामान्यतः समष्टि का वह क्षेत्र, जो निकाय के आसपास होता है, परिवेश के अंतर्गत लिया जाता है।
उदाहरण के लिए– यदि हम एक बीकर में उपस्थित दो पदार्थों A एवं B की अभिक्रिया का अध्ययन कर रहे हों, तो बीकर (जिसमें अभिक्रिया-मिश्रण है) निकाय* होगा एवं कमरा (जिसमें बीकर है) परिवेश का कार्य करेगा (चित्र 6.1)।

चित्र 6.1 ः परिवेश एवं निकाय
ध्यान रहे कि निकाय भौतिक सीमाओं (जैसे–बीकर या परखनली) से परिभाषित किया जा सकता है या समष्टि में एक निश्चित आयतन के कार्तीय निर्देशांकों (Cartesian coordinates) के समुच्चय (set) से परिभाषित किया जा सकता है। यह आवश्यक है कि निकाय को वास्तविक या काल्पनिक दीवार या सीमा के द्वारा परिवेश से पृथक् सोचा जाए। वह दीवार, जो निकाय एवं परिवेश को पृथक् करती है, ‘परिसीमा’ (Boundary) कहलाती है। परिसीमा द्वारा हम निकाय के अंदर और बाहर द्रव्य तथा ऊर्जा के संचरण को नियंत्रित एवं प्रेक्षित कर सकते हैं।
6.1.2 निकाय के प्रकार
अब हम द्रव्य एवं ऊर्जा के संचरण के आधार पर निकाय को वर्गीकृत करते हैं–
1. खुला निकाय (Open System)
एक खुले निकाय में ऊर्जा एवं द्रव्य–दोनों का निकाय एवं परिवेश के मध्य विनिमय (Exchange) हो सकता है।
2. बंद निकाय (Closed system)
बंद निकाय में निकाय एवं परिवेश के मध्य द्रव्य का विनिमय संभव नहीं है, परंतु ऊर्जा का विनिमय हो सकता है। जैसे– अभिकारक बंद बीकर में लिये जाएँ।
3. विलगित निकाय (Isolated system)
एक विलगित निकाय में निकाय एवं परिवेश के मध्य द्रव्य एवं ऊर्जा– दोनों का ही विनिमय संभव नहीं होता है। उदाहरणार्थ– अभिकारक एक थर्मस फ्लास्क में लिये जाएँ। चित्र 6.2 में विभिन्न प्रकार के निकाय दर्शाए गए हैं।
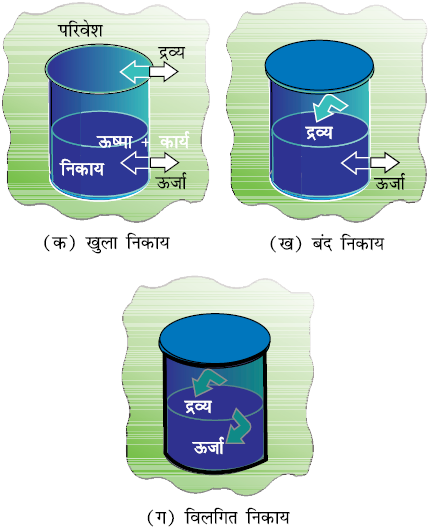
चित्र 6.2 : खुला, बंद एवं विलगित निकाय

* यदि हम केवल अभिक्रिया मिश्रण को निकाय मानें, तो बीकर की दीवार परिवेश का कार्य करेगी।

6.1.3 निकाय की अवस्था
किसी भी ऊष्मागतिकी निकाय का वर्णन कुछ गुणों, जैसे– दाब (p), आयतन (V), ताप (T) एवं निकाय के संघटन (Composition) को निर्दिष्ट (Specify) करके किया जाता है। हमें निकाय को वर्णित करने के लिए इन गुणों को परिवर्तन से पूर्व एवं पश्चात् निर्दिष्ट करना पड़ता है। आपने भौतिक शास्त्र में पढ़ा होगा कि यांत्रिकी में किसी निकाय की क्षणिक अवस्था की व्याख्या निकाय के सभी द्रव्य-बिंदुओं के उस क्षण पर स्थिति एवं वेग के आधार पर की जाती है। ऊष्मागतिकी में अवस्था का एक अलग एवं सरल रूप प्रस्तावित किया गया है। इससे प्रत्येक कण की गति के विस्तृत ज्ञान की आवश्यकता नहीं है, क्याेंकि यहाँ हम निकाय के औसत मापन योग्य गुणों का प्रयोग करते हैं हम निकाय की अवस्था को ‘अवस्था-फलनों’ या ‘अवस्था-चरों’ के द्वारा व्यक्त करते हैं।
ऊष्मागतिकीय में निकाय की अवस्था का वर्णन उसके मापनयोग्य अथवा स्थूल गुणों के द्वारा किया जाता है। हम एक गैस की अवस्था का उसके दाब (p), आयतन (V), ताप (T), मात्रा (n) आदि से वर्णन कर सकते हैं। p, V, T को अवस्था चर अथवा फलन कहते हैं, क्योंकि इनका मान निकाय की अवस्था पर निर्भर करता है, न कि इसको प्राप्त करने के तरीके पर। किसी निकाय की अवस्था को पूर्ण रूप से परिभाषित करने के लिए निकाय के सभी गुणों का वर्णन करने की आवश्यकता नहीं होती, क्योंकि कुछ गुण ही स्वतंत्र रूप में परिवर्तित हो सकते हैं। इन गुणों की संख्या निकाय की प्रकृति पर निर्भर करती है। एक बार कम से कम संख्या में इन स्थूल गुणों को तय कर दिया जाए, तो बाकी सारे गुणों का मान स्वतः निश्चित हो जाता है।
6.1.4 आंतरिक ऊर्जा ः एक अवस्था-फलन
जब हम उन रासायनिक निकायों की चर्चा करते हैं, जिनमें ऊर्जा का निकास या प्रवेश होता है, तब हमें एक एेसे गुण की आवश्यकता होती है, जो निकाय की ऊर्जा का प्रतिनिधित्व करता हो। यह ऊर्जा रासायनिक, वैद्युत या यांत्रिक ऊर्जा हो सकती है। इन सबका योग ही निकाय की ऊर्जा होती है। ऊष्मागतिकी में इसे आंतरिक ऊर्जा U कहते हैं। यह परिवर्तित होती है, जबकि
• ऊष्मा का निकाय में प्रवेश या निकास होता हो,
• निकाय पर या निकाय द्वारा कार्य किया गया हो,
• निकाय में द्रव्य का प्रवेश या निकास होता हो।
(क) कार्य
सबसे पहले हम कार्य करने पर निकाय की आंतरिक ऊर्जा में होने वाले परिवर्तन की जाँच करेंगे। हम एक एेसा निकाय लेते हैं, जिसमें एक थर्मस फ्लास्क या ऊष्मारोधी बीकर में जल की कुछ मात्रा है। इसमें निकाय एवं परिवेश के मध्य ऊष्मा का प्रवाह नहीं है, एेसे निकाय को हम रुद्धोष्म (Adiabatic) निकाय कहते हैं। एेसे निकाय में अवस्था-परिवर्तन को रुद्धोष्म प्रक्रम कहते हैं। इसमें निकाय एवं परिवेश के मध्य कोई ऊष्मा-विनिमय नहीं होती। यहाँ पर निकाय एवं परिवेश को पृथक् करनेवाली दीवार ‘रुद्धोष्म दीवार’ कहलाती है (चित्र 6.3)।
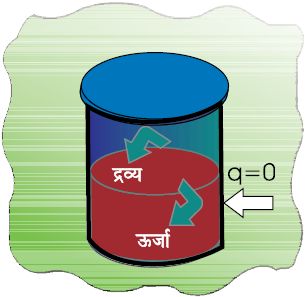
चित्र 6.3: एक रुद्धोष्म निकाय, जिसमें परिसीमा से ऊष्मा-विनिमय संभव नहीं है।
अब हम निकाय पर कुछ कार्य करके इसकी आंतरिक ऊर्जा में परिवर्तन करते हैं। माना कि निकाय की प्रांरभिक अवस्था A है एवं इसका ताप TA तथा आंतरिक ऊर्जा UA है। निकाय की अवस्था को दो प्रकार से परिवर्तित कर सकते हैं–
प्रथम प्रकार–माना कि छोटे पैडल से जल को मथकर हम 1kJ कार्य करते हैं, जिससे निकाय की नई अवस्था माना B एवं उसका ताप TB हो जाता है। यह देखा गया कि TB > TA अतः ताप में परिवर्तन ∆T = TB–TA । माना अवस्था B में आंतरिक ऊर्जा UB है, तो आंतरिकऊर्जा में परिवर्तन,
∆U= UB–UA
द्वितीय प्रकार–अब हम जल में एक निमज्जन छड़ (Immersion Rod) डालकर उतना ही वैद्युत कार्य (1kJ) करते हैं एवं निकाय में ताप-परिवर्तन नोट करते हैं। हम देखते हैं कि ताप-परितर्वन पूर्व के समान TB–TA ही रहता है।
यथार्थ में उपरोक्त प्रयोग जे.पी. जूल द्वारा सन् 1845 के आसपास किया गया था। उन्होंने पाया कि निकाय पर किया गया निश्चित कार्य निकाय की अवस्था में समान परिवर्तन लाता है, चाहे कार्य किसी भी प्रकार (प्रक्रम) द्वारा किया जाए, जैसा यहाँ पर ताप के परिवर्तन द्वारा देखा गया है।
अतः यह उपयुक्त दिखता है कि एक एेसी राशि, आंतरिक ऊर्जा U, को परिभाषित किया जाए, जिसका मान निकाय की अवस्था का अभिलाक्षणिक हो, जहाँ रुद्धोष्म प्रक्रम में किया गया कार्य wad दो अवस्थाओं में U परिवर्तन के तुल्य, अर्थात् ∆U = U2 – U1 = wad है।
अतः निकाय की आंतरिक ऊर्जा एक अवस्था-फलन है।
रासायनिक ऊष्मागतिकी में IUPAC परंपरा के अनुसार धनात्मक चिह्न* बताता है कि कार्य wad निकाय पर किया गया है तथा निकाय की आंतरिक ऊर्जा बढ़ जाती है। इसी प्रकार से यदि निकाय द्वारा कार्य किया जाए, तो wad ऋणात्मक होगा क्योंकि निकाय की आंतरिक ऊर्जा कम हो जाती है।
क्या आप किन्हीं अन्य परिचित अवस्था-फलनों के नाम बता सकते हैं? V, p एवं T कुछ अन्य परिचित अवस्था-फलन हैं। उदाहरण के लिए– यदि हम किसी निकाय के ताप में 25°C से 35°C तक परिवर्तन करें, तो ताप-परिवर्तन 35°C–25°C = +10°C होगा। चाहे हम सीधे ही 35°C तक जाएँ या निकाय को पहले कुछ अंशों (Degree) तक ठंडा करें और फिर निकाय को अंतिम ताप (35°C) तक ले जाएँ। इस प्रकार T एक अवस्था-फलन है। ताप में परिवर्तन पथ पर निर्भर नहीं करता है। एक तालाब में पानी का आयतन एक अवस्था-फलन है, क्योंकि इसके जल के आयतन में परिवर्तन इस बात पर निर्भर नहीं करता है कि तालाब कैसे भरा गया है– बारिश द्वारा, नलकूप द्वारा या दोनों द्वारा।
(ख) ऊष्मा
हम बिना कार्य किए भी परिवेश से ऊष्मा लेकर या परिवेश को ऊष्मा देकर एक निकाय की आंतरिक ऊर्जा में परिवर्तन कर सकते हैं। यह ऊर्जा-विनिमय, जो तापांतर का परिणाम है, ऊष्मा q कहलाता है। अब हम समान तापांतर लाने के लिए [पूर्व में खंड 6.14 (क) में बताए अनुसार वही प्रारंभिक एवं अंतिम ताप] जो रूद्धोष्म दीवारों की अपेक्षा ऊष्मीय चालक दीवारों (चित्र 6.4) द्वारा ऊष्मा के चालन से होता है, पर विचार करेंगे।
माना कि ताँबे का एक पात्र (जिसकी दीवारें ऊष्मीय चालक हैं) में TA ताप पर जल लिया गया है। इसे एक बड़े कुंड, जिसका ताप TB है। में रखते हैं। निकाय (जल) द्वारा अवशोषित ऊष्मा q को ताप-परिवर्तन TB–TA द्वारा मापा जा सकता है। यहाँ पर भी आंतरिक ऊर्जा में परिवर्तन, ∆U = q है, जबकि स्थिर आयतन पर कोई कार्य नहीं किया गया है।
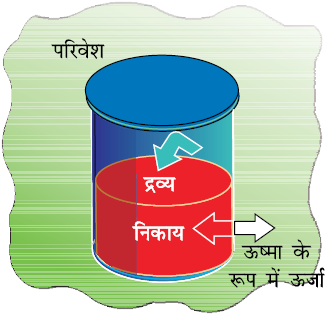
चित्र 6.4 : एक निकाय, जिसमें परिसीमा के आर-पार ऊष्मा का प्रवाह संभव है।
रासायनिक ऊष्मागतिकी में IUPAC परंपरा के अनुसार परिवेश से ऊष्मा का स्थानांतरण निकाय में होने पर q धनात्मक होता है और निकाय की ऊर्जा बढ़ती है एवं ऊष्मा के निकाय से परिवेश की ओर स्थानांतिरित होने पर q ऋणात्मक होता है परिणामतः निकाय की ऊर्जा कम हो जाती है।
(ग) सामान्य स्थिति
हम एक सामान्य स्थिति पर विचार करें, जबकि आंतरिक ऊर्जा में परिवर्तन दोनों ही प्रकारों (कार्य करके एवं ऊष्मा-स्थानांतरण) द्वारा हो। उस स्थिति में हम आंतरिक ऊर्जा में परिवर्तन को इस प्रकार लिख सकते हैं–
∆U = q + w (6.1)
एक विशिष्ट अवस्था-परिवर्तन में परिवर्तन के प्रकार के अनुसार q एवं w के मान भिन्न हो सकते हैं, परंतु q + w = ∆U केवल प्रारंभिक एवं अंतिम अवस्था पर निर्भर करेगा। यह परिवर्तन के प्रकार से स्वतंत्र है। यदि ऊष्मा या कार्य के रूप में ऊर्जा-परिवर्तन न हो (विलगित निकाय) अर्थात् यदि
w = 0 एवं q = 0, तब ∆U = 0 है।
पहले निकाय पर किए जाने वाले कार्य को ऋणात्मक समीकरण 6.1 अर्थात् ∆U = q + w, ऊष्मागतिकी के प्रथम नियम का गणितीय कथन है। प्रथम नियम के अनुसार,
"एक विलगित निकाय की ऊर्जा अपरिवर्तनीय होती है।"
बह्मांड भी एक विलगित निकाय है अत: नियम को निम्न प्रकार से भी कहा जा सकता है–‘बह्मांड की ऊर्जा अपरिवर्तनीय है।’ सामान्यतया इसे ‘ऊर्जा के संरक्षण का सिद्धांत’ कहते हैं, अर्थात् ऊर्जा न तो नष्ट की जा सकती है और न ही इसका सृजन किया जा सकता है।
नोट: एक ऊष्मागतिकीय गुण (जैसे–ऊर्जा) एवं एक यांत्रिक गुण (जैसे–आयतन) में अंतर होता है। हम किसी विशेष अवस्था में आयतन का तो निरपेक्ष (Absolute) मान निर्दिष्ट कर सकते हैं, परंतु आंतरिक ऊर्जा का निरपेक्ष मान निर्दिष्ट नहीं कर सकते हैं, यद्यपि आंतरिक ऊर्जा में परिवर्तन ∆U ज्ञात किया जा सकता है।
उदाहरण 6.1
एक निकाय की आंतरिक ऊर्जा में परिवर्तन बताइए, यदि–
(i) निकाय द्वारा परिवेश से ऊष्मा अवशोषित नहीं हो, परंतु निकाय पर (w) कार्य किया जाए। निकाय की दीवारें किस प्रकार की होंगी?
(ii) निकाय पर कोई कार्य नहीं किया जाए, परंतु ऊष्मा की मात्रा q निकाय से परिवेश को दे दी जाए। निकाय की दीवारें किस प्रकार की होंगी?
(iii) निकाय द्वारा w मात्रा का कार्य किया जाए एवं q मात्रा की ऊष्मा निकाय को दी जाए। यह किस प्रकार का निकाय होगा?
हल
(i) ∆U = wad' दीवारें रुद्धोष्म होंगी।
(ii) ∆U = - q, दीवारें ऊष्मीय सुचालक होंगी।
(iii) ∆U = q - w यह बंद निकाय है।
6.2 अनुप्रयोग
कई रासायनिक अभिक्रियाओं में गैसें उत्पन्न होती हैं, जो यांत्रिक कार्य करने या ऊष्मा उत्पन्न करने में सक्षम होती हैं। इन परिवर्तनों के परिमाण की गणना एवं इन्हें आंतरिक ऊर्जा-परिवर्तनों से संबद्ध करना महत्त्वपूर्ण है। देखें कि यह कैसे होता है।
6.2.1 कार्य
सर्वप्रथम एक निकाय द्वारा किए गए कार्य की प्रकृति पर हम प्रकाश डालते हैं। हम केवल यांत्रिक कार्य, अर्थात् दाब-आयतन कार्य पर विचार करेंगे।
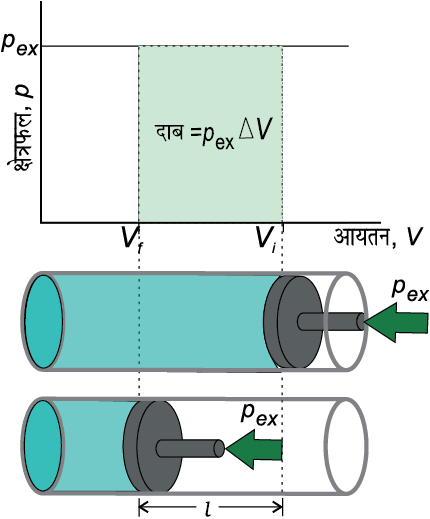
दाब-आयतन कार्य को समझने के लिए हम घर्षणरहित पिस्टनयुक्त सिलिंडर पर विचार करते हैं, जिसमें एक मोल आदर्श गैस भरी हुई है। गैस का कुल आयतन Vi एवं सिलिंडर में गैस का दाब p है। यदि बाह्य दाब pex है, जो p से अधिक हो, तो पिस्टन अंदर की ओर तब तक गति करेगा, जब तक आंतरिक दाब pex के बराबर हो जाए। माना कि यह परिवर्तन एक पद में होता है तथा अंतिम आयतन Vf है। माना कि इस संकुचन में पिस्टन l दूरी तय करता है एवं पिस्टन का अनुप्रस्थ क्षेत्रफल A है (चित्र 6.5 क)।
तब आयतन में परिवर्तन = l × A = ∆V = (Vf – Vi )
हम यह भी जानते हैं कि दाब 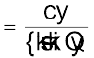
अतः पिस्टन पर बल = pex . A
यदि पिस्टन चलाने से निकाय पर किया गया कार्य w हो, तो
w = बल x विस्थापन = pex.A.l
= pex . (–∆V ) = – pex ∆V = – pex (Vf – Vi ) (6.2)
यहाँ ऋणात्मक चिह्न देना इसलिए आवश्यक है कि परिपाटी (Convention) के अनुसार संपीडन में निकाय पर कार्य हो रहा है, जो धनात्मक होगा। यहाँ (Vf – Vi ) का मान ऋणात्मक होगा। जब ऋणात्मक से ऋणात्मक का गुणा होगा, तो w का मान धनात्मक हो जाएगा।
यदि संकुचन के प्रत्येक पद पर दाब स्थिर न हो एवं कई परिमित पदों में बदलता रहे, तो कुल कार्य समस्त पदों में हुए कार्याें का योग होगा एवं 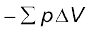 के तुल्य होगा [चित्र 6.5(ख)]।
के तुल्य होगा [चित्र 6.5(ख)]।
यदि दाब स्थिर न हो एवं इस प्रकार बदलता हो कि यह हमेशा ही गैस के दाब से अनंतसूक्ष्म अधिक हो, तब संकुचन के प्रत्येक पद में आयतन अनंतसूक्ष्म मात्रा dV घटेगा। इस स्थिति में गैस द्वारा किए गए कार्य की गणना हम निम्नलिखित संबंध से ज्ञात कर सकते हैं–
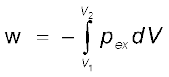 ( 6.3)
( 6.3)
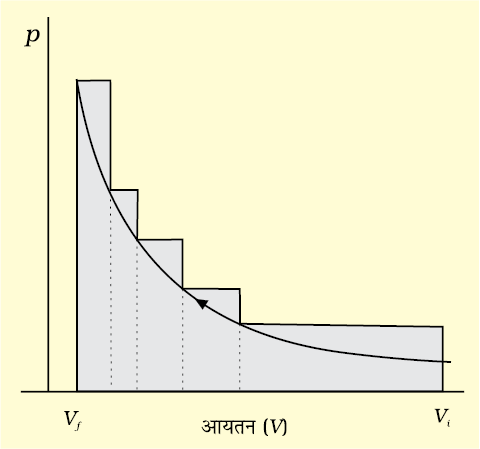
चित्र 6.5 (ख) छायादार क्षेत्र परिमित पदों में बदलते हुए अस्थिर दाब पर प्रारंभिक आयतन से अंतिम आयतन तक संकुचन में किया गया कार्य दर्शाता है।
संकुचन में pex प्रत्येक पद पर (pin + dp) के तुल्य होगा [चित्र 6.5-ग]। समान परिस्थितियों में प्रसरण में बाह्य दाब आंतरिक दाब से हमेशा कम होगा, अर्थात् pex = pin – dp व्यापक रूप में हम लिख सकते हैं कि pex = (pin + dp) एेसे प्रक्रम ‘उत्क्रमणीय प्रक्रम’ कहलाते हैं।
एक प्रक्रम या परिवर्तन तभी ‘उत्क्रमणीय प्रक्रम’ कहलाता है, जब इसे किसी भी क्षण अनंतसूक्ष्म परिवर्तन के द्वारा उत्क्रमित (Reversed) किया जा सके। एक उत्क्रमणीय प्रक्रम कई साम्यावस्थाओं में अनंतसूक्ष्म गति से इस प्रकार आगे बढ़ता है कि निकाय एवं परिवेश हमेशा लगभग साम्यावस्था में रहते हैं। उत्क्रमणीय प्रक्रम के अतिरिक्त अन्य सारे प्रक्रमों को अनुत्क्रमणीय प्रक्रम कहते हैं।
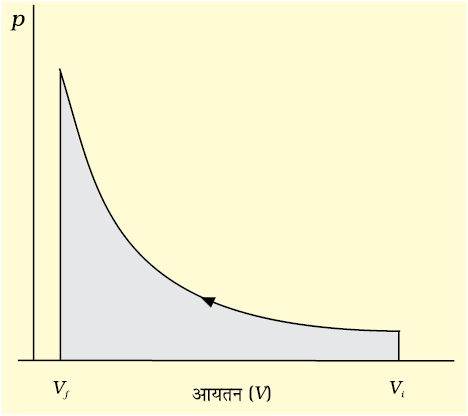
चित्र 6.5 (ग) pV वक्र जब प्रारंभिक आयतन Vi से Vf तक पहुँचने के लिए उत्क्रमणीय परिस्थितियों में लगातार बदलते हुए अस्थिर दाब पर अनंत पदों में किया गया कार्य छायादार क्षेत्र से दर्शाया गया है।
रसायन शास्त्र में बहुत सी एेसी समस्याएँ आती हैं, जिन्हें हल करने के लिए कार्य, पद और निकाय के आंतरिक दाब के पारस्परिक संबंध की आवश्यक्ता पड़ती है।
हम समीकरण 6.3 को निम्नलिखित प्रकार से लिखकर उत्क्रमणीय परिस्थितियों में कार्य को आंतरिक दाब से संबद्ध कर सकते हैं–
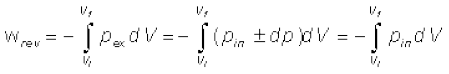
(चूँकि dp × dV का मान नगण्य है)
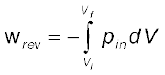 (6.4)
(6.4)
अब गैस के दाब pin को आदर्श गैस समीकरण द्वारा इसके आयतन के पदों में व्यक्त किया जा सकता है। किसी आदर्श गैस के n मोल के लिए (pV = RT)
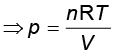
अतः एक स्थिर ताप (समतापीय प्रक्रम) पर
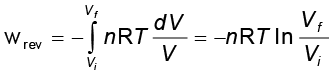
= –2.303 nRT log 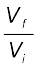 (6.5)
(6.5)
मुक्तप्रसरण : गैस का निर्वात में प्रसरण (pex = 0) मुक्त प्रसरण कहलाता है। आदर्श गैसों के मुक्त प्रसरण में कोई कार्य नहीं होता भले ही प्रक्रिया उत्क्रमणीय हो या अनुत्क्रमणीय, (समीकरण 6.2 एवं 6.3)।
अब हम समीकरण 6.1 को विभिन्न प्रक्रमों के अनुसार कई प्रकार से लिख सकते हैं–
w = –pex∆V (समीकरण 6.2) को समीकरण 6.1 में स्थापित करने पर
∆U = q - pex∆V
यदि प्रक्रम स्थिर आयतन पर होता है (∆V = 0), तब ∆U = qV, qV में पादांक V (Subscript V ) दर्शाता है कि ऊष्मा स्थिर आयतन पर प्रदान की गई है।
आदर्श गैस का मुक्त एवं समतापीय प्रसरण
एक आदर्श गैस का मुक्त एवं समतापीय प्रसरण एक
(T = स्थिरांक) में, w = 0 है, क्योंकि pex= 0 है। जूल ने प्रयोगों द्वारा निर्धारित किया कि q = 0 है, इसलिए ∆U = 0 होगा।
समीकरण 6.1, (∆U = q + w), को समतापीय उत्क्रमणीय एवं अनुत्क्रमणीय प्रक्रमों के लिए इस प्रकार व्यक्त किया जा सकता है–
1. समतापीय अनुत्क्रमणीय प्रक्रम के लिए
q = – w = pex (Vf – Vi )
2. समतापीय उत्क्रमणीय प्रक्रम के लिए
q = – w = nRT ln 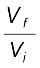 = 2.303 nRT log
= 2.303 nRT log 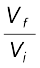
3. रुद्धोष्म प्रक्रम के लिए, q = 0
∆U = wad
उदाहरण 6.2
10 atm दाब और 25°C ताप पर किसी आदर्श गैस के दो लिटर समतापीय रूप से निर्वात में तब तक प्रसरित होते हैं, जब तक इसका कुल आयतन 10 लिटर न हो जाए। इस प्रसरण में कितनी ऊष्मा अवशोषित होती है एवं कितना कार्य किया जाता है?
हल
हम जानते हैं कि q = – w = pex (10 – 2) = 0(8) = 0 कोई कार्य नहीं होता है एवं कोई ऊष्मा अवशोषित नहीं होती है।
उदाहरण 6.3
यदि इसी प्रसरण में स्थिर बाह्य दाब 1 atm हो, तो क्या होगा?
हल
हम जानते हैं कि q = – w = pex (8) = 1 × 8
= 8 L atm
उदाहरण 6.4
यदि उदाहरण 6.2 में दिया प्रसरण उत्क्रमणीय रूप से हो तो क्या होगा?
हल
हम जानते हैं कि q = – w = 2.303 × nRT 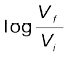

6.2.2 एन्थैल्पी Enthalpy (H)
(क) एक उपयोगी नया अवस्था-फलन
हम जानते हैं कि स्थिर आयतन पर अवशोषित ऊष्मा आंतरिक ऊर्जा में परिवर्तन के तुल्य, अर्थात् ∆U = qV होती है, परंतु अधिकांश रासायनिक अभिक्रियाएं स्थिर आयतन पर न होकर फ्लास्क, परखनली आदि में स्थिर वायुमंडलीय दाब पर होती हैं। इन परिस्थितियों के लिए हमें एक नए अवस्था-फलन की आवश्यकता होगी।
हम समीकरण (6.1) को स्थिर दाब पर ∆U = qp-p∆V के रूप में लिख सकते हैं, जहाँ qp निकाय द्वारा अवशोषित ऊष्मा एवं -p∆V निकाय द्वारा किया गया प्रसरण-कार्य है।
प्रारंभिक अवस्था को पादांक 1 से एवं अंतिम अवस्था को 2 से दर्शाते हैं।
हम उपरोक्त समीकरण को इस प्रकार लिख सकते हैं–
U2–U1 = qp – p (V2 – V1)
पुनः व्यवस्थित करने पर
qp = (U2 + pV2) – (U1 + pV1) (6.6)
अब हम एक और ऊष्मागतिकी फलन को परिभाषित कर सकते हैं, जिसे एन्थैल्पी (ग्रीक शब्द ‘एन्थैल्पियन’, जिसका अर्थ ‘गरम करना’ या ‘अंतर्निहित ऊष्मा’ होता है) कहते हैं।
H = U + pV (6.7)
अतः समीकरण (6.6) हो जाती हैः
qp= H2 – H1 = ∆H
यद्यपि q एक पथ आश्रित फलन है, तथापि qp पथ से स्वतंत्र है। स्पष्टतः H एक अवस्था-फलन है (H.U, p एवं V का फलन है। ये सभी अवस्था-फलन है)। इस प्रकार ∆H पथ स्वतंत्र राशि है।
स्थिर दाब पर परिमित परिवर्तनों के लिए समीकरण 6.7 को लिखा जा सकता है।
∆H = ∆U + ∆pV क्योंकि p स्थिरांक है, अतः हम लिख सकते हैं–
∆H = ∆U + p∆V (6.8)
उल्लेखनीय है कि जब स्थिर दाब पर ऊष्मा अवशोषित होती है, तो यथार्थ में हम एन्थैल्पी में परिवर्तन माप रहे होते हैं।
याद रखें कि ∆H = qp स्थिर दाब पर अवशोषित ऊष्मा है।
ऊष्माक्षेपी अभिक्रियाओं के लिए ∆H ऋणात्मक होता है, जहाँ अभिक्रिया के दौरान ऊष्मा उत्सर्जित होती है एवं ऊष्माशोषी अभिक्रियाओं के लिए ∆H धनात्मक होता है, जहाँ परिवेश से ऊष्मा का अवशोषण होता है।
स्थिर आयतन (∆V = 0) पर ∆U = qV, अतः समीकरण 6.8 हो जाती है। ∆H = ∆U = qV
वे निकाय, जिनमें केवल ठोस या द्रव प्रावस्थाएँ होती हैं में ∆H एवं ∆U के मध्य अंतर सार्थक नहीं होता, क्योंकि ठोस एवं द्रवों में गरम करने पर आयतन में कोई विशेष परिवर्तन नहीं होता। यदि गैसीय अवस्था हो, तो इनमें अंतर सार्थक हो जाता है। हम एक एेसी अभिक्रिया पर विचार करते हैं, जिसमें गैसें शामिल हैं। स्थिर दाब एवं ताप पर VA गैसीय अभिक्रियकों का एवं VB गैसीय उत्पादों का कुल आयतन हो तथा nA गैसीय अभिक्रियकों एवं nB गैसीय उत्पादों के मोलों की संख्या हो, तो आदर्श गैस समीकरण के अनुसार–
pVA = nART
इस प्रकार pVB = nBRT
या pVB – pVA = nBRT – nART = (nB–nA)RT
p (VB – VA) = (nB – nA) RT
p ∆V = ∆ngRT (6.9)
यहाँ ∆ng गैसीय उत्पादों के मोलों की संख्या एवं गैसीय अभिक्रियकों के मोलों की संख्या का अंतर है।
समीकरण (6.9) से p ∆V का मान समीकरण (6.8) में रखने पर
समीकरण 6.10 का उपयोग ∆H से ∆U या ∆U से ∆H का मान ज्ञात करने में किया जाता है।
उदाहरण 6.5
जलवाष्प को आदर्श गैस मानने पर 100°C एवं 1 bar दाब पर एक मोल जल के वाष्पीकरण में परिवर्तन 41kJ mol–1 पाया गया। आंतरिक ऊर्जा-परिवर्तन की गणना कीजिए, जब 1 मोल जल को 1 bar दाब एवं 100°C पर वाष्पीकृत किया जाए।
हल
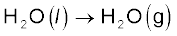 परिवर्तन के लिए
परिवर्तन के लिए
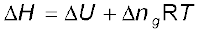
या ∆U = ∆H – 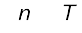
मान रखने पर


= 37.904 kJ mol–1
(ख) विस्तीर्ण एवं गहन गुण
विस्तीर्ण एवं गहन गुणों में भेद किया गया है। विस्तीर्ण गुण वह गुण है, जिसका मान निकाय में उपस्थित द्रव्य की मात्रा/आमाप (साइज़) पर निर्भर करता है। उदाहरण के लिए–द्रव्यमान, आयतन, आंतरिक ऊर्जा, एन्थैल्पी, ऊष्माधारिता आदि विस्तीर्ण गुण हैं।
वे गुण, जो निकाय में उपस्थित द्रव्य की मात्रा/आकार (साइज़) पर निर्भर नहीं करते हैं, गहन गुण कहलाते हैं। उदाहरण के लिए– ताप, घनत्व, दाब आदि गहन गुण हैं। मोलर गुण Cm किसी निकाय के एक मोल के गुण के मान के तुल्य होती है। यदि द्रव्य की मात्रा n हो, तो 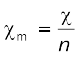 , जो द्रव्य की मात्रा से स्वतंत्र है। अन्य उदाहरण मोलर आयतन Vm एवं मोलर ऊष्माधारिता Cm है। विस्तीर्ण एवं गहन गुणों में अंतर हम एक गैस को आयतन V के पात्र में T ताप पर लेकर कर सकते हैं (चित्र 6.6 क)।
, जो द्रव्य की मात्रा से स्वतंत्र है। अन्य उदाहरण मोलर आयतन Vm एवं मोलर ऊष्माधारिता Cm है। विस्तीर्ण एवं गहन गुणों में अंतर हम एक गैस को आयतन V के पात्र में T ताप पर लेकर कर सकते हैं (चित्र 6.6 क)।
अब यदि विभाजक के द्वारा आयतन आधा कर दिया जाए (चित्र 6.6-ख), जिससे अब आयतन V/2 हो जाता है, परंतु यह ताप समान ही रहता है। अतः स्पष्ट है कि आयतन विस्तीर्ण गुण है, जबकि ताप गहन गुण है।

(क)
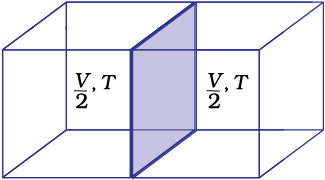
चित्र 6.6 (क) आयतन V एवं ताप T पर एक गैस, (ख) विभाजक के द्वारा आयतन का आधा होना
(ग) ऊष्माधारिता
इस उपखंड में हम देखते हैं कि निकाय को अंतरित ऊष्मा कैसे मापी जाती है। यदि निकाय द्वारा ऊष्मा ग्रहण की जाए, तो यह ताप में वृद्धि के रूप में परिलक्षित होती है।
ताप में वृद्धि अंतरित ऊष्मा के समानुपाती होती है।
q = गुणांक x ∆T
गुणांक का मान निकाय के आकार, संघटन एवं प्रकृति पर निर्भर करता है। इसे हम इस प्रकार भी लिख सकते हैं, 'q = C ∆T
यहाँ गुणांक C को ‘ऊष्माधारिता’ कहते हैं।
इस प्रकार ऊष्माधारिता ज्ञात होने पर हम तापीय वृद्धि को नाप कर प्रदत्त ऊष्मा ज्ञात कर सकते हैं।
यदि C ज्यादा है, तो ऊष्मा से तापीय वृद्धि अल्प होती है। जल की ऊष्माधारिता अधिक है, इसका अर्थ यह है कि इसका ताप बढ़ाने के लिए बहुत अधिक ऊर्जा चाहिए।
C पदार्थ की मात्रा के समानुपाती होती है। किसी पदार्थ की मोलर ऊष्माधारिता Cm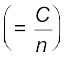 एक मोल की ऊष्माधारिता है। यह ऊष्मा की वह मात्रा है, जो एक मोल पदार्थ का ताप एक डिग्री सेल्सियस (या एक केल्विन) बढ़ाने के लिए आवश्यक होती है। विशिष्ट ऊष्मा, जिसे ‘विशिष्ट ऊष्माधारिता’ भी कहते हैं, वह ऊष्मा है, जो इकाई द्रव्यमान के किसी पदार्थ का ताप एक डिग्री सेल्सियस (या एक केल्विन) बढ़ाने के लिए आवश्यक होती है। किसी पदार्थ का ताप बढ़ाने के उद्देश्य से आवश्यक ऊष्मा q ज्ञात करने के लिए पदार्थ की विशिष्ट ऊष्मा C को हम द्रव्यमान m एवं ताप-परिवर्तन ∆T से गुणा करते हैं, अर्थात्
एक मोल की ऊष्माधारिता है। यह ऊष्मा की वह मात्रा है, जो एक मोल पदार्थ का ताप एक डिग्री सेल्सियस (या एक केल्विन) बढ़ाने के लिए आवश्यक होती है। विशिष्ट ऊष्मा, जिसे ‘विशिष्ट ऊष्माधारिता’ भी कहते हैं, वह ऊष्मा है, जो इकाई द्रव्यमान के किसी पदार्थ का ताप एक डिग्री सेल्सियस (या एक केल्विन) बढ़ाने के लिए आवश्यक होती है। किसी पदार्थ का ताप बढ़ाने के उद्देश्य से आवश्यक ऊष्मा q ज्ञात करने के लिए पदार्थ की विशिष्ट ऊष्मा C को हम द्रव्यमान m एवं ताप-परिवर्तन ∆T से गुणा करते हैं, अर्थात्
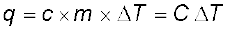 (6.11)
(6.11)
(घ) एक आदर्श गैस के लिए Cp एवं CV में संबंध
ऊष्माधारिता को स्थिर आयतन पर CV से एवं स्थिर दाब पर Cp से अंकित करते हैं। अब हम दोनों में संबंध ज्ञात करते हैं।
q के लिए स्थिर आयतन पर समीकरण लिख सकते हैं–
qV = 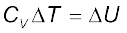
एवं स्थिर दाब पर qp = 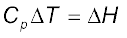
आदर्श गैस के लिए Cp एवं CV के बीच अंतर इस प्रकार ज्ञात किया जा सकता है–
एक मोल आदर्श गैस के लिए ∆H = ∆U + ∆(pV )
= ∆U + ∆(RT )
= ∆U + R∆T
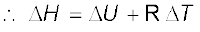 (6.12)
(6.12)
∆H एवं ∆U के मान रखने पर
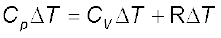
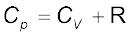
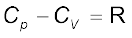 (6.13)
(6.13)
6.3 ∆U एवं ∆H का मापन कैलोरीमिति
रासायनिक एवं भौतिक प्रक्रमों से संबंधित ऊर्जा, परिवर्तन को जिस प्रायोगिक तकनीक द्वारा ज्ञात करते हैं, उसे ‘कैलोरीमीटर’ (Calorimetry) कहते हैं। कैलोरीमिति में प्रक्रम एक पात्र में किया जाता है, जिसे ‘कैलोरीमीटर’ कहते हैं। कैलोरीमीटर एक द्रव के ज्ञात आयतन में डूबा रहता है। द्रव की ऊष्माधारिता एवं कैलोरीमीटर की ऊष्माधारिता ज्ञात होने पर ताप-परिवर्तन के आधार पर प्रक्रम में उत्पन्न ऊष्मा ज्ञात की जा सकती है। मापन दो स्थितियों में किए जाते हैं–
(i) स्थिर-आयतन पर, qV (ii) स्थिर दाब पर, qp
(क) ∆U का मापन
रासायनिक अभिक्रियाओं के लिए स्थिर आयतन पर अवशोषित ऊष्मा का मापन बम कैलोरीमीटर (Bomb calorimeter) में किया जाता है (चित्र 6.7) यहाँ एक स्टील का पात्र (बम कैलोरीमीटर) जल में डुबोया जाता है। स्टील बम में अॉक्सीजन प्रवाहित कर ज्वलनशील प्रतिदर्श (Sample) को जलाया जाता है। अभिक्रिया में उत्पन्न ऊष्मा जल को अंतरित हो जाती है। उसके बाद जल का ताप ज्ञात कर लिया जाता है। चूँकि बम कैलोरीमीटर पूर्णतया बंद, है अतः इसके आयतन में कोई परिवर्तन नहीं होता। और कोई कार्य नहीं किया जाता है। यहाँ तक कि गैसों से संबंधित रासायनिक अभिक्रियाओं में भी कोई कार्य नहीं होता क्योंकि ∆V = 0 होता है। समीकरण 6.11 की सहायता से कैलोरीमीटर की ऊष्माधारिता ज्ञात होने पर ताप-परिवर्तन को qV में परिवर्तित कर लिया जाता है।
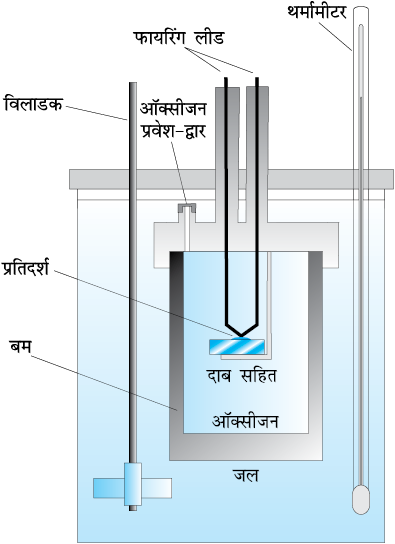
चित्र 6.7ः बम कैलोरीमीटर
(ख) ∆H का मापन
स्थिर दाब (सामान्यतया वायुमंडलीय दाब) पर ऊष्मा-परिवर्तन चित्र 6.8 में दर्शाए गए कैलोरीमीटर द्वारा मापा जा सकता है। हम जानते हैं कि ∆H = qp (स्थिर दाब पर)। अतः स्थिर दाब पर उत्सर्जित अथवा अवशोषित ऊष्मा qp अभिक्रिया ऊष्मा अथवा अभिक्रिया एन्थैल्पी ∆rH कहलाती है।
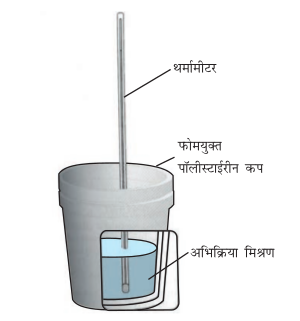
ऊष्माक्षेपी अभिक्रियाओं में ऊष्मा निर्मुक्त होती है तथा निकाय से परिवेश में ऊष्मा का प्रवाह होता है।
इसलिए qp ऋणात्मक होगा तथा ∆rH भी ऋणात्मक होगा। इसी तरह ऊष्माशोषी अभिक्रियाओं में ऊष्मा अवशोषित होगी। अत: qp और ∆rH दोनों धनात्मक होंगे।
उदाहरण 6.6
निम्नलिखित समीकरण के अनुसार, 1g ग्रैफाइट को अॉक्सीजन की अधिकता में 1atm दाब एवं 298 K पर बम कैलोरीमीटर में दहन करवाया जाता है।
C ( ग्रैफाइट ) + O2 (g)  CO2 (g)
CO2 (g)
अभिक्रिया के दौरान ताप 298 K से 299 K तक बढ़ता है। यदि बम कैलोरीमीटर की ऊष्माधारिता 20.7 kJ/K हो, तो उपरोक्त अभिक्रिया के लिए 1 atm दाब एवं 298 K पर एन्थैल्पी परिवर्तन क्या होगा?
हल
माना अभिक्रिया से प्राप्त ऊष्मा q एवं कैलोरीमीटर की ऊष्माधारिता CV है, तब कैलोरीमीटर द्वारा अवशोषित ऊष्मा,
q = CV × ∆T
अभिक्रिया से प्राप्त ऊष्मा का मान समान होगा, परंतु चिह्न ऋणात्मक होगा, क्योंकि निकाय (अभिक्रिया-मिश्रण) द्वारा प्रदत्त ऊष्मा कैलोरीमीटर द्वारा ग्रहण की गई ऊष्मा के तुल्य होगी।
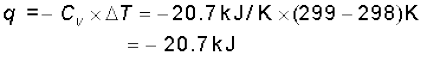
(यहाँ ऋणात्मक चिह्न अभिक्रिया के ऊष्माक्षेपी होने को इंगित करता है)
अतः 1 g ग्रैफाइट के दहन के लिए ∆U = -20.7 kJK–1
1 मोल ग्रैफाइट के दहन के लिए
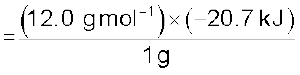
= – 2.48 ×102 kJ mol–1
यहाँ ∆ng = 0
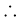 ∆Η – ∆u = –2.48 × 102kJ mol–1
∆Η – ∆u = –2.48 × 102kJ mol–1
6.4 अभिक्रिया के लिए एन्थैल्पी परिवर्तन, ∆rH अभिक्रिया एन्थैल्पी
रासायनिक अभिक्रिया में अभिक्रियक उत्पाद में बदलते हैं। इस प्रक्रिया को इस प्रकार दर्शाते हैं– अभिक्रियक → उत्पाद अभिक्रिया के दौरान एन्थैल्पी-परिवर्तन अभिक्रिया-एन्थैल्पी कहलाता है। रासायनिक अभिक्रिया में एन्थैल्पी-परिवर्तन ∆rH चिह्न से दर्शाया जाता है।
∆rH = (उत्पादों की एन्थैल्पियों का योग) – (अभिक्रियकों की एन्थैल्पियों का योग)

यहाँ 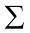 (सिग्मा) चिह्न का उपयोग जोड़ने के लिए किया जाता है एवं ai तथा bi संतुलित समीकरण में क्रमशः अभिक्रियकों एवं उत्पादों के स्टाइकियोमीट्री गुणांक हैं। उदाहरण के लिए– निम्नलिखित अभिक्रिया में–
(सिग्मा) चिह्न का उपयोग जोड़ने के लिए किया जाता है एवं ai तथा bi संतुलित समीकरण में क्रमशः अभिक्रियकों एवं उत्पादों के स्टाइकियोमीट्री गुणांक हैं। उदाहरण के लिए– निम्नलिखित अभिक्रिया में–
CH4 (g) + 2O2 (g) → CO2 (g) + 2H2O (l)
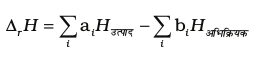
= [Hm (CO2 ,g) + 2Hm (H2O, l)]– [Hm (CH4 , g) +
2Hm (O2, g)]
जहाँ Hm मोलर एन्थैल्पी है। एन्थैल्पी-परिवर्तन एक बहुत उपयोगी राशि है। इसका ज्ञान स्थिर ताप पर किसी औद्योगिक रासायनिक अभिक्रिया में ऊष्मन या शीतलन की योजना बनाने में आवश्यक है। इसकी आवश्यकता साम्य स्थिरांक की तापीय निर्भरता की गणना करने में भी पड़ती है।
(क) अभिक्रिया की मानक एन्थैल्पी
किसी रासायनिक अभिक्रिया की एन्थैल्पी परिस्थितियों पर निर्भर करती है। अतः यह आवश्यक है कि हम कुछ मानक परिस्थितियों को निर्दिष्ट करें। किसी रासायनिक अभिक्रिया की मानक एन्थैल्पी वह एन्थैल्पी परिवर्तन है, जब अभिक्रिया में भाग लेनेवाले सभी पदार्थ अपनी मानक अवस्थाओं में हों।
किसी पदार्थ की मानक अवस्था किसी निर्दिष्ट ताप पर उसका वह शुद्ध रूप है, जो 298 K 1 bar दाब पर पाया जाता है। उदाहरण के लिए– द्रव एथेनॉल की मानक अवस्था 298 K एवं 1 bar पर शुद्ध द्रव होती है। लोहे की मानक-अवस्था 500 K एवं 1 बार (bar) पर शुद्ध ठोस होती है। आँकड़े प्रायः 298 K पर लिए जाते हैं। मानक परिस्थितियों को ∆H पर मूर्धांक 0 (Superscript) रखकर व्यक्त किया जाता है। उदाहरण के लिए–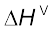
(ख) प्रावस्था रूपांतरण में एन्थैल्पी-परिवर्तन
प्रावस्था परिवर्तन में ऊर्जा-परिवर्तन भी होता है। उदाहरण के लिए बर्फ़ को पिघलाने के लिए ऊष्मा की आवश्यकता होती है। साधारणतया बर्फ़ का पिघलना स्थिर दाब (वायुमंडलीय दाब) पर होता है तथा प्रावस्था-परिर्वतन होते समय ताप स्थिर रहता है।
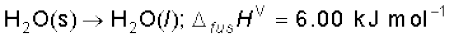
यहाँ ∆fusΗ ⊖ मानक अवस्था में गलन एन्थैल्पी है। यदि जल बर्फ़ में बदलता है, तो इसके विपरीत प्रक्रम होता है तथा उतनी ही मात्रा में ऊष्मा परिवेश में चली जाती है।
प्रति मोल ठोस पदार्थ के गलन में होनेवाले एन्थैल्पी परिवर्तन को पदार्थ की गलन एन्थैल्पी या मोलर गलन एन्थैल्पी ∆fusΗ ⊖ कहा जाता है।
ठोसों का गलन ऊष्माशोषी होता है, अतः सभी गलन एन्थैल्पियाँ धनात्मक होती हैं। जल के वाष्पीकरण में ऊष्मा की आवश्यकता होती है। इसके क्वथनांक Tb एवं स्थिर दाब परः
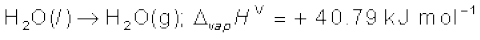
∆vapΗ ⊖ वाष्पीकरण की मानक एन्थैल्पी है।
(Tf और Tb क्रमशः गलनांक एवं क्वथनांक है।)
किसी द्रव के एक मोल को स्थिर ताप एवं मानक दाब
(1 बार) पर वाष्पीकृत करने के लिए आवश्यक ऊष्मा को उसकी वाष्पन एन्थैल्पी या मोलर वाष्पन एन्थैल्पी ∆vapΗ ⊖ कहते हैं।
ऊर्ध्वपातन में ठोस सीधे ही गैस में बदल जाता है। ठोस कार्बन डाइअॉक्साइड या शुष्क बर्फ (dry ice) ∆subΗ ⊖ = 25.2kJ mol -1 के साथ 195 Κ पर ऊर्ध्वपातित होती है। नेफ्थलीन वायु में धीरे-धीरे ऊर्ध्वपातित होती है, जिसके लिए ∆subΗ ⊖ = 73.0 kJ mol -1
किसी ठोस के एक मोल को स्थिर ताप एवं मानक दाब (1 बार) पर ऊर्ध्वपातन में होने वाली एन्थैल्पी परिवर्तन को उसकी मानक ऊर्ध्वपातन एन्थैल्पी कहते हैं।
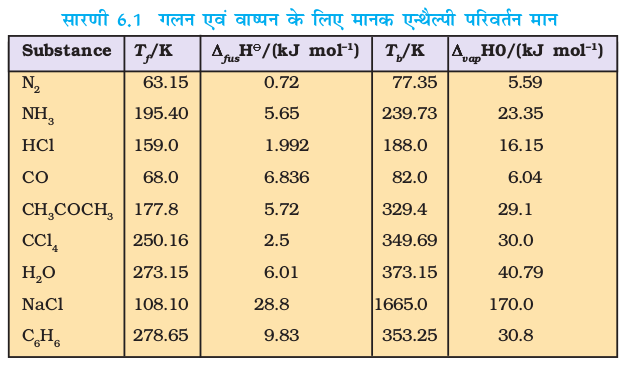
एन्थैल्पी-परिवर्तन का मान उस पदार्थ के अंतर-आण्विक बलों की क्षमता पर निर्भर करता है, जिसका प्रावस्था-परिवर्तन हो रहा है। उदाहरण के लिए– जल के अणुओं के मध्य उपस्थित प्रबल हाइड्रोजन बंध इसकी द्रव अवस्था में जल के अणुओं को प्रबलता से बांधेे रहते हैं। कार्बनिक द्रव (जैसे– एेसीटोन) में अंतर-आण्विक द्विध्रुव-द्विध्रुव अन्योन्य क्रिया विशेष रूप से दुर्बल होती है। इस प्रकार इसके 1 मोल के वाष्पीकृत होने में जल के 1 मोल को वाष्पीकृत होने की अपेक्षा कम ऊष्मा की आवश्यकता होती है। सारणी 6.1 में कुछ पदार्थों की गलन एवं वाष्पीकरण की मानक एन्थैल्पी दी गई है।
उदाहरण 6.7
एक ताल (Pool) से निकला तैराक करीब 18 g पानी की परत से ढका (गीला) है। इस पानी को 298 K पर वाष्पित होने के लिए कितनी ऊष्मा आवश्यक होगी? 298 K पर वाष्पीकरण की आंतरिक ऊर्जा की गणना कीजिए।
जल के लिए 298 K पर ∆VapΗ 0= 44.01 kJ mol-1
हल
वाष्पीकरण के प्रक्रम को हम इस प्रकार प्रदर्शित कर सकते हैं–

18g H2O (1) में मोलों की संख्या 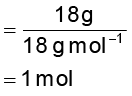
1 mol जल के 298 K पर वाष्पन के लिए दी जाने वाली ऊर्जा = n ∆vap Η 0 =1 mol×44.01 kJ Mol -1
= 44.01 kJ
(यह मानते हुए कि वाष्प आदर्श गैस के समान व्यवहार करती है।)
∆vap U⊖ = ∆vap H⊖_∆ngRT
1 mol वाष्प के लिए
∆vap H⊖ = (1 mol) (44.01 kJ mol-1)
= 44.01 kJ
∆ng = (1 mol — 0 mol) = 1 mol
‹∆vap U0 = ∆vap H0_∆ngRT
= 44.01 kJ - (1 mol) (8.314 JK-1 mol-1)(298 K)
= 44.01 kJ - (8.314 JK-1)(298 K)
= 44.01 kJ - (0.008314 kJK-1)(298 K)
= 44.01 kJ - 2.48 kJ
= 41.53 kJ
उदाहरण 6.8
जल वाष्प को आदर्श गैस मानते हुए गणना कीजिए कि
100°C ताप और 1 bar दाब पर 1 mol जल-वाष्प को 0°C ताप की बर्फ में बदलने में आन्तरिक ऊर्जा में कितना परिवर्तन होगा? दिया है कि बर्फ की गलन एन्थैल्पी
6.00 kJ mol-1 और जल की ऊष्माधारिता 4.2J/g °C है।
हल
परिवर्तन निम्न प्रकार से होता है-
चरण - 1
1 mol H2O (g, 0°C)  1 mol H2O (l, 0°C)
1 mol H2O (l, 0°C)
एन्थैल्पी परिवर्तन ∆Η1
चरण - 2
1 mol H2O (l, 0°C)  1 mol H2O (s, 0°C)
1 mol H2O (s, 0°C)
एन्थैल्पी परिवर्तन ∆Η2
कुल एन्थैल्पी परिवर्तन होगा
∆H = ∆H1 + ∆H2
∆H 1 = -(18 × 4.2 × 100) J mol-1
= -7560 J mol-1
= -7.56 kJ mol-1
∆H 2 = 6.00 kJ mol-1
‹ ∆H = ∆H1 + ∆H2
= -7.56 kJ mol-1+ (-6.00 kJ mol-1)
= -13.56 kJ mol-1
द्रव अवस्था से ठोस अवस्था में परिवर्तन होने पर
आयतन में नगण्य परिवर्तन होता है अत:–
p ∆ V = ∆ng RT = 0
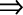 ∆U = ∆H
∆U = ∆H
= -13.56 kJ mol-1
(ग) मानक विरचन एन्थैल्पी ∆f Η 0
किसी यौगिक के एक मोल को उसके ही तत्त्वों, जो अपने सबसे स्थायी रूपों में लिये गए हों (एेसे रूप को ‘संदर्भ-अवस्था’ भी कहतेे हैं), में से विरचित करने पर होनेवाले मानक एन्थैल्पी परिवर्तन को उसकी मानक मोलर विरचन एन्थैल्पी ∆f Η ⊖ कहा जाता है।
जहाँ पादांक ‘f’ बताता है कि संबंधित यौगिक का 1 मोल उसके तत्त्वों, जो अपने सबसे स्थायी रूप में हैं, से प्राप्त किया जाता है। नीचे कुछ अभिक्रियाएं उनकी मानक विरचन मोलर एन्थैल्पी के साथ दी गई हैं–
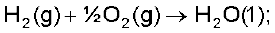
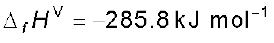
C (ग्रैफाइट, s) 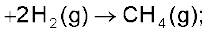
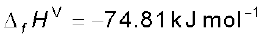
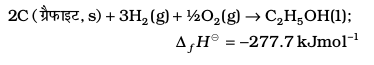
यहाँ यह समझना महत्त्वपूर्ण है कि मानक विरचन एन्थैल्पी, ∆f Η ⊖, ∆r Η ⊖ की एक विशेष स्थिति है, जिसमें 1 मोल यौगिक अपने तत्त्वों से बनता है। जैसे उपरोक्त तीन अभिक्रियाओं में जल, मेथेन एवं एथेनॉल में से प्रत्येक का 1 मोल बनता है।
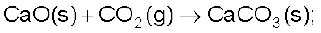
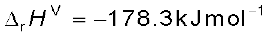
इसके विपरीत एक ऊष्माक्षेपी अभिक्रिया में एन्थैल्पी-परिवर्तन कैल्सियम कार्बोनेट की विरचन एन्थैल्पी नहीं है, क्योंकि इसमें कैल्सियम कार्बोनेट अपने तत्त्वों से न बनकर दूसरे यौगिकों से बना है। निम्नलिखित अभिक्रिया के लिए भी एन्थैल्पी-परिवर्तन HBr (g) की मानक एन्थैल्पी विरचन एन्थैलपी ∆f Η ⊖ नहीं है, बल्कि मानक अभिक्रिया एन्थैल्पी है।
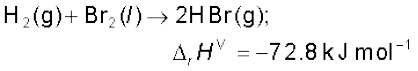
यहाँ पर उत्पाद के एक मोल की अपेक्षा दो मोल अपने तत्त्वों से बनते हैं, 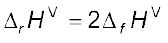
संतुलित समीकरण में समस्त गुणांकों को 2 से विभाजित कर HBr(g) के विरचन एन्थैल्पी के लिए समीकरण इस प्रकार लिखा जा सकता है–
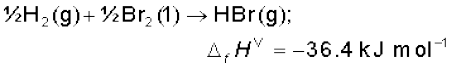
सारणी 6.2 कुछ चुने हुए पदार्थों की 298 Κ पर मानक मोलर विरचन एन्थैल्पी, ∆f Η ⊖
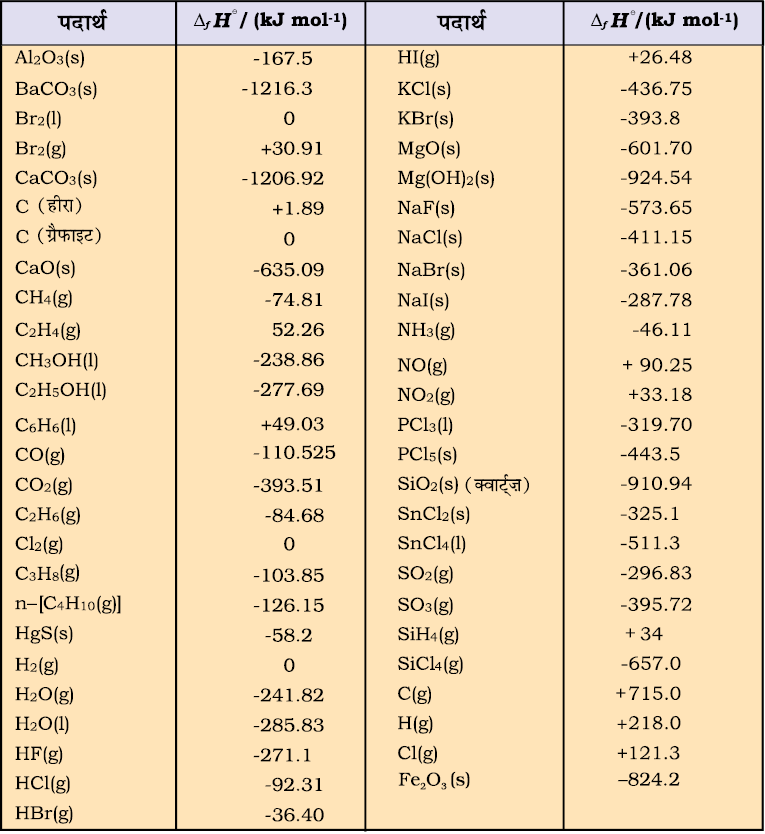
कुछ पदार्थों की 298 K पर मानक मोलर विरचन एन्थैल्पी ∆f Η ⊖ सारणी 6.2 में दी गई है।
परिपाटी के अनुसार, एक तत्त्व के सबसे अधिक स्थायित्व की अवस्था में (संदर्भ-अवस्था) मानक विरचन एन्थैल्पी ∆f Η ⊖ का मान शून्य लिया जाता है।
मान लीजिए कि आप एक केमिकल इंजीनियर हैं और जानना चाहते हैं कि यदि सारे पदार्थ अपनी मानक अवस्था में हैं तो कैल्सियम कार्बोनेट को चूना एवं कार्बन डाइअॉक्साइड में विघटित करने के लिए कितनी ऊष्मा की आवश्यकता होगी, 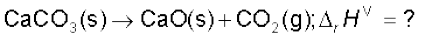
यहाँ हम मानक विरचन एन्थैल्पी का उपयोग कर सकते हैं एवं अभिक्रिया का एन्थैल्पी परिवर्तन परिकलित कर सकते हैं। एन्थैल्पी परिवर्तन की गणना करने के लिए हम निम्नलिखित सामान्य समीकरण का उपयोग कर सकते हैं–
 ................(6.15)
................(6.15)
जहाँ संतुलित समीकरण मे a एवं b क्रमशः अभिक्रियकों एवं उत्पादों कें गुणांक है। उपरोक्त समीकरण को कैल्सियम कार्बोनेट के विघटन पर लागू करते हैं। यहाँ a एवं b दोनों 1 हैं। अतः
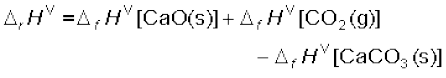
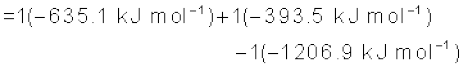
= 178.3kJ mol–1
अतः CaCO3(s) का विघटन ऊष्माशोषी अभिक्रिया है। अतः इच्छित उत्पाद प्राप्त करने के लिए आपको इसे गरम करना होगा।
(घ) ऊष्मरासायनिक समीकरण
एक संतुलित रासायनिक समीकरण, जिसमें उसके ∆rH का मान भी दिया गया हो, ‘ऊष्मरासायनिक समीकरण’ कहलाता है। हम एक समीकरण में पदार्थों की भौतिक अवस्थाएँ (अपररूप अवस्था के साथ) भी निर्दिष्ट करते हैं।
उदाहरण के लिए–
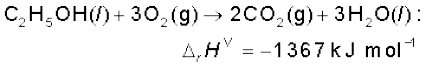
उपरोक्त समीकरण निश्चित ताप एवं दाब पर द्रव एथेनॉल का दहन दर्शाता है। एन्थैल्पी परिवर्तन का ऋणात्मक चिह्न दर्शाता है कि यह एक ऊष्माक्षेपी अभिक्रिया है।
ऊष्मरासायनिक समीकरणों के संदर्भ में निम्नलिखित परिपाटियों को याद रखना आवश्यक है–
1. संतुलित रासायनिक समीकरण में गुणांक अभिक्रियकों एवं उत्पादों के मोलों (अणुओं को नहीं) को निर्देशित करते हैं।
2. ∆r Η 0 का गणितीय मान समीकरण द्वारा पदार्थों के मोलों की संख्या के संदर्भ में होता है। मानक एन्थैल्पी परिवर्तन ∆rΗ 0 की इकाई kJ mol-1 होती है।
उपरोक्त धारणा को समझाने के लिए हम निम्नलिखित अभिक्रिया के लिए अभिक्रिया-ऊष्मा की गणना करते हैं–
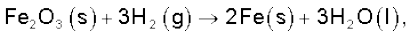
मानक विरचन एन्थैल्पी की सारणी (6.2) से हम पाते हैं–
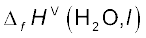 = –285.83 kJ mol–1;
= –285.83 kJ mol–1;
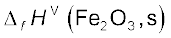 = – 824.2 kJ mol–1;
= – 824.2 kJ mol–1;
∆f H 0 (Fe, s) = 0 एवं
∆f H 0 (H2, g) = 0, परिपाटी के अनुसार
तब,
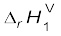 = 3(–285.83 kJ mol–1)
= 3(–285.83 kJ mol–1)
– 1(– 824.2 kJ mol–1)
= (–857.5 + 824.2) kJ mol–1
= –33.3 kJ mol–1
ध्यान रहे कि इन गणनाओं में प्रयुक्त गुणांक शुद्ध संख्याएं हैं, जो उचित स्टोकियोमिति गुणांकों (Stoichiometric coefficients) के तुल्य हैं। ∆f Η ⊖ की इकाई kJ mol-1 है, जिसका अर्थ अभिक्रिया का प्रति मोल है। जब हम उपरोक्त प्रकार से रासायनिक समीकरण को संतुलित कर लेते हैं, तब यह अभिक्रिया के एक मोल को परिभाषित करता है। हम समीकरण को भिन्न प्रकार से संतुलित करते हैं। उदाहरणार्थ–
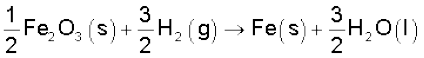
तब अभिक्रिया की यह मात्रा एक मोल अभिक्रिया होगी एवं 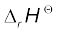 होगा
होगा
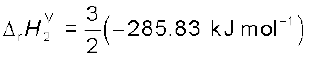
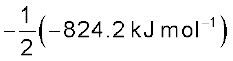
= (– 428.7 + 412.1) kJ mol–1
= –16.6 kJ mol–1 = ½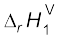
इससे स्पष्ट होता है कि एन्थैल्पी एक विस्तीर्ण राशि है।
3. जब किसी रासायनिक समीकरण को उलटा लिखा जाता है, तब 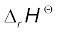 के मान का चिह्न भी बदल जाता है। उदाहरण के लिए–
के मान का चिह्न भी बदल जाता है। उदाहरण के लिए–
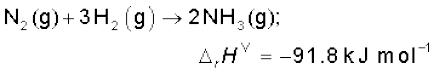
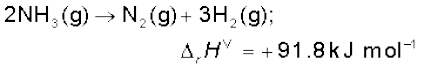
(च) हेस का नियम
चूँकि एन्थैल्पी एक अवस्था-फलन है, अतः एन्थैल्पी परिवर्तन प्रारंभिक अवस्था (अभिकारकों) अंतिम अवस्था (उत्पादों) को प्राप्त करने के पथ से स्वतंत्र होती है। दूसरे शब्दों में– एक अभिक्रिया चाहे एक पद में हो या कई पदों की शृंखला में, एन्थैल्पी परिवर्तन समान रहता है। इसे ‘हेस नियम’ के रूप में इस प्रकार कह सकते हैं–
अनेक पदों में होने वाली किसी रासायनिक अभिक्रिया की मानक एन्थैल्पी उन सभी अभिक्रियाओं की समान ताप पर मानक एन्थैल्पियों का योग होती है, जिनमें इस संपूर्ण अभिक्रिया को विभाजित किया जा सकता है।
आइए, हम इस नियम का महत्त्व एक उदाहरण के द्वारा समझें। निम्नलिखित अभिक्रिया में एन्थैल्पी-परिवर्तन पर विचार करिये करें–
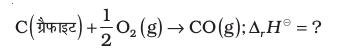
यद्यपि CO (g) प्रमुख उत्पाद है, परंतु इस अभिक्रिया में कुछ CO2 गैस हमेशा उत्पन्न होती है। अतः उपरोक्त अभिक्रिया के लिए हम एन्थैल्पी-परिवर्तन को सीधे माप कर ज्ञात् नहीं कर सकते। यदि हम अन्य एेसी अभिक्रियाएं ढूँढ सकें, जिनमें संबंधित स्पशीज हों, तो उपरोक्त समीकरण में एन्थैल्पी-परिवर्तन का परिकलन किया जा सकता है।
अब हम निम्नलिखित अभिक्रियाओं पर विचार करते हैं–
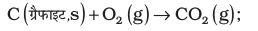
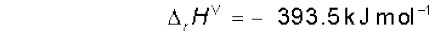 (i)
(i)
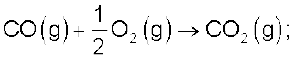
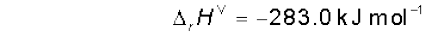 (ii)
(ii)
हम उपरोक्त समीकरणों को इस प्रकार संयुक्त करते हैं कि इच्छित अभिक्रिया प्राप्त हो जाए। दाईं ओर एक मोल CO(g) प्राप्त करने के लिए समीकरण (ii) को हम उल्टा करते हैं, जिसमें ऊर्जा निर्मुक्त होने की बजाय अवशोषित होती है। अतः हम 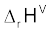 के मान का चिह्न बदल देते हैं।
के मान का चिह्न बदल देते हैं।
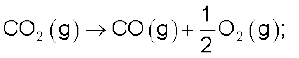
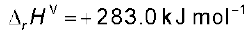 (iii)
(iii)
समीकरण (i) एवं (iii) को जोड़कर हम इच्छित समीकरण प्राप्त करते हैं।
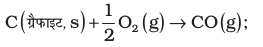
इसके लिए 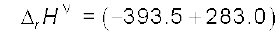
= – 110.5 kJ mol–1
व्यापक रूप में यदि एक अभिक्रिया 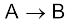 के लिए एक मार्ग से कुल एन्थैल्पी परिवर्तन
के लिए एक मार्ग से कुल एन्थैल्पी परिवर्तन 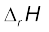 हो एवं दूसरे मार्ग से
हो एवं दूसरे मार्ग से 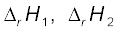 ,
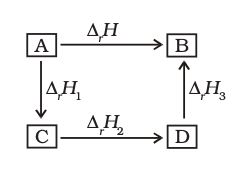
, 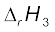 ... समान उत्पाद B के बनने में विभिन्न एन्थैल्पी-परिवर्तनों का प्रतिनिधित्व करते हों, तो
... समान उत्पाद B के बनने में विभिन्न एन्थैल्पी-परिवर्तनों का प्रतिनिधित्व करते हों, तो
∆rH = ∆rH1 + ∆rH2 + ∆rH3 ... (6.16)
इसे इस रूप में प्रदर्शित किया जा सकता है–
6.5 विभिन्न प्रकार की अभिक्रियाओं के लिए एन्थैल्पी
अभिक्रियाओं के प्रकार को निर्दिष्ट करते हुए एन्थैल्पी का नामकरण करना सुविधाजनक होता है।
(क) मानक दहन एन्थैल्पी ∆c Η ⊖
दहन अभिक्रियाएं प्रकृति से ऊष्माक्षेपी होती हैं। ये उद्योग, रॉकेट, विमान एवं जीवन के अन्य पहलुओं में महत्त्वपूर्ण होती हैं। मानक दहन एन्थैल्पी को इस प्रकार परिभाषित किया जाता है कि यह किसी पदार्थ की प्रति मोल वह एन्थैल्पी परिवर्तन है, जो इसके दहन के फलस्वरूप होता है, जब समस्त अभिक्रियक एवं उत्पाद एक विशिष्ट ताप पर अपनी मानक अवस्थाओं में होते हैं।
खाना पकाने वाली गैस के सिलिंडर में मुख्यतः ब्यूटेन (C4H10) गैस होती है। ब्यूटेन के एक मोल के दहन से 2658 kJ ऊष्मा निर्मुक्त होती है। इसके लिए हम ऊष्मरासायनिक अभिक्रिया को इस प्रकार लिख सकते हैं–
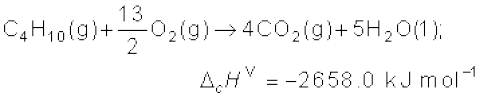
इसी प्रकार ग्लूकोस के दहन से 2802.0 kJ/mol ऊष्मा निर्मुक्त होती है, जिसके लिए समीकरण है–
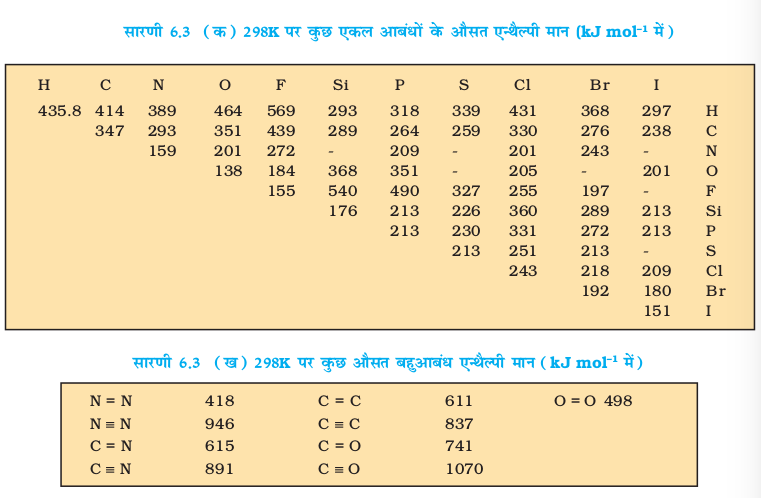
सारणी 6.3 (क) 298K पर कुछ एकल आबंधों के औसत एन्थैल्पी मान (kJ mol–1 में)
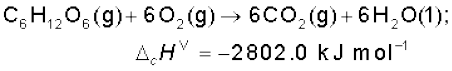
हमारे शरीर में भी दहन के प्रक्रम की तरह भोजन से ऊर्जा उत्पन्न होती है, यद्यपि अंतिम उत्पाद कई प्रकार के जटिल जैव-रासायनिक अभिक्रियाओं की श्रेणी से बनते हैं, जिनमें एन्ज़ाइम का उपयोग होता है।
उदाहरण 6.9
बेन्ज़ीन के 1 मोल का दहन 298 K एवं 1 atm पर होता है। दहन के उपरांत CO2(g) एवं H2O (1) बनते हैं तथा 3267.0 kJ ऊष्मा निर्मुक्त होती है। बेन्ज़ीन के लिए मानक विरचन एन्थैल्पी की गणना कीजिए। CO2(g) एवं H2O (1) के लिए मानक विरचन एन्थैल्पी के
मान क्रमशः –393.5 kJ mol–1 एवं –285.83 kJ mol–1 हैं।
हल
बेन्ज़ीन का विरचन निम्नलिखित समीकरण से दिया जाता है–
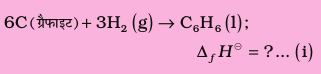
1 मोल बेन्ज़ीन के लिए दहन एन्थैल्पी है–
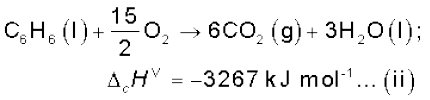
1 मोल CO2(g) के लिए विरचन एन्थैल्पी है–
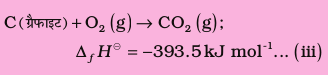
1 मोल H2O (1) के लिए विरचन एन्थैल्पी है–
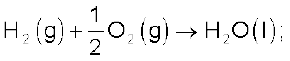
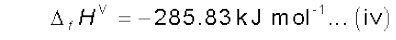
समीकरण iii को 6 से एवं iv को 3 से गुणा करने पर
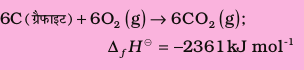
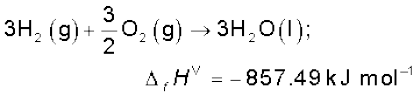
उपरोक्त दोनों समीकरणों को जोड़ने पर
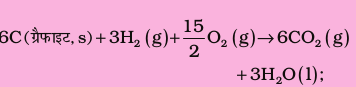
समीकरण ii को उलटा करने पर
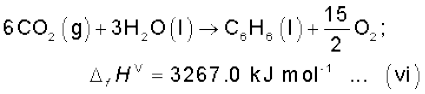
समीकरणों v एवं vi को जोड़ने पर हम पाते हैं ः
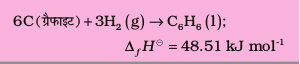
(ख) कणन एन्थैल्पी ∆a Η ⊖
आइए, डाइहाइड्रोजन के कणन के इस उदाहरण पर विचार करें–
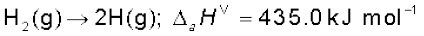
आप देख सकते हैं कि इस प्रक्रिया में डाइहाइड्रोजन के H – H बंधों के टूटने से H परमाणु प्राप्त होते हैं। इस प्रक्रिया में होने वाले एन्थैल्पी-परिवर्तन को कणन एन्थैल्पी, ∆aH⊖ कहते हैं। यह गैसीय अवस्था में किसी भी पदार्थ के एक मोल में उपस्थित आबंधों को पूर्णतः तोड़कर परमाणुओं में बदलने पर होने वाला एन्थैल्पी-परिवर्तन है। ऊपर दर्शाए गए डाइहाइड्रोजन जैसे द्विपरमाणुक अणुओं की कणन एन्थैल्पी इनकी आबंध वियोजन एन्थैल्पी भी होती है। कणन एन्थैल्पी के कुछ अन्य उदाहरण निम्नलिखित हैं–
CH4(g) → C(g) + 4H(g); ∆aH⊖ = 1665 kJ mol–1
यह ध्यान देने योग्य बात है कि यहाँ उत्पाद केवल गैसीय अवस्था में C और H परमाणु हैं।
Na(s) → Na(g) ; ∆aH⊖ = 108.4 kJ mol–1
इस उदाहरण में कणन एन्थैल्पी और ऊर्ध्वपातन एन्थैल्पी एक समान हैं।
(ग) आबंध एन्थैल्पी ∆bond H⊖
सामान्य अभिक्रियाओं में रासायनिक आबंध टूटते एवं बनते हैं। आबंध टूटने के लिए ऊर्जा की आवश्यकता होती है और आबंध बनने में ऊर्जा निर्मुक्त होती है। किसी भी अभिक्रिया की ऊष्मा को रासायनिक आबंधों के टूटने एवं बनने में होने वाले ऊर्जा- परिवर्तनों से जोड़ा जा सकता है। रासायनिक आबंधों से जुड़े एन्थैल्पी-परिवर्तनों के लिए ऊष्मागतिकी में दो अलग पद प्रयुक्त होते हैं–
(i) आबंध वियोजन एन्थैल्पी
(ii) माध्य आबंध एन्थैल्पी
आइए हम उनकी चर्चा द्विपरमाणुक एवं बहुपरमाणुक अणुओं के संदर्भ में करें।
द्विपरमाणुक अणु : में निम्नलिखित प्रक्रिया पर विचार करें एक मोल डाइहाइड्रोजन में विद्यमान सभी आबंध टूटते हैं–
H2(g) → 2H(g) ; ∆H–HH⊖ = 435.0 kJ mol–1
इस प्रक्रिया में होने वाला एन्थैल्पी-परिवर्तन H – H आबंध की आबंध वियोजन एन्थैल्पी (Bond Dissociation Enthalpy) है।
आबंध वियोजन एन्थैल्पी उस प्रक्रिया में होने वाला एन्थैल्पी-परिवर्तन है, जिसमें किसी गैसीय सहसंयोजक यौगिक के एक मोल आबंध टूटकर गैसीय उत्पाद बनें।
ध्यान दें कि यह एन्थैल्पी-परिवर्तन और डाइहाड्रोजन की कणन एन्थैल्पी एक समान हैं। अन्य सभी द्विपरमाणुक अणुओं के लिए भी यह सत्य है। उदाहरणार्थ–
Cl2(g) → 2Cl(g) ; ∆Cl–ClH⊖ = 242 kJ mol–1
O2(g) → 2O(g) ; ∆O=OH⊖ = 428 kJ mol–1
बहुपरमाणुक अणु में आबंध वियोजन ऊर्जा का मान एक अणु में भिन्न बंधों के लिए भिन्न होता है।
बहुपरमाणुक अणु (Polyatomic Molecules) : हम
एक बहुपरमाणुक अणु (जैसे– CH4) पर विचार करते हैं। इसके कणन के लिए ऊष्मरासायनिक अभिक्रिया इस प्रकार दी जाती है–
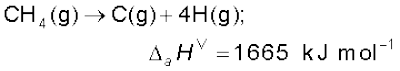
मेथेन में चारों C-H आबंध समान हैं। इसलिए मेथेन अणु में सभी C-H आबंधों की आबंध-दूरी एवं आबंध-ऊर्जा भी एक समान है, तथापि प्रत्येक C-H आबंध को तोड़ने के लिए आवश्यक ऊर्जा भिन्न-भिन्न हैं, जो नीचे दी गई हैं–
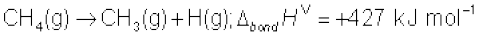
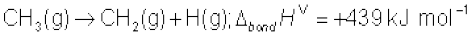
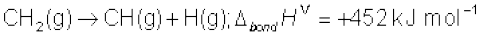
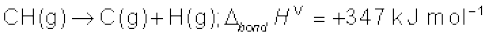
अतः
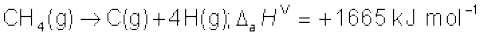
अब हम CH4 में C-H बंध की औसत आबंध एन्थैल्पी परिभाषित करते हैं–
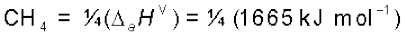
= 416 kJ mol–1
हम देखते हैं कि मेथेन में C-H बंध की औसत आबंध एन्थैल्पी 416 KJ/mol है। यह पाया गया कि विभिन्न यौगिकों, जैसे– CH3CH2Cl, CH3NO2 आदि में C-H बंध का औसत आबंध एन्थैल्पी मान एक-दूसरे से थोड़ा भिन्न होता है।* परंतु इन मानों में अधिक अंतर नहीं होता। हेस के नियम का उपयोग कर के आबंध एन्थैल्पी की गणना की जा सकती है। कुछ एकल और बहुआबंधों की एन्थैल्पी सारणी 6.3 में उपलब्ध है। अभिक्रिया एन्थैल्पी बहुत महत्त्वपूर्ण होती है, क्योंकि यह पुराने आबंधों के टूटने एवं नए आबंधों के बनने के कारण ही उत्पन्न होती है। यदि हमें विभिन्न आबंध एन्थैल्पियाँ ज्ञात हों तो गैसीय अवस्था में किसी भी अभिक्रिया की एन्थैल्पी ज्ञात की जा सकती है। गैसीय अवस्था में अभिक्रिया की मानक एन्थैल्पी 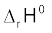 उत्पादों एवं अभिक्रियकों की आबंध एन्थैल्पियों से इस प्रकार संबंधित होती है–
उत्पादों एवं अभिक्रियकों की आबंध एन्थैल्पियों से इस प्रकार संबंधित होती है–

यह संबंध उस समय विशेष उपयोगी होता है, जब 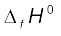 का मान ज्ञात न हो। किसी अभिक्रिया का कुल एन्थैल्पी-परिवर्तन उस अभिक्रिया में अभिक्रियक अणुओं के सभी आबंधों को तोड़ने के लिए आवश्यक ऊर्जा एवं उत्पादों के अणुओं के सभी आबंधों को तोड़ने के लिए आवश्यक ऊर्जा का अंतर होता है। ध्यान रहे कि यह संबंध लगभग सही है। यह उसी समय लागू होगा, जब अभिक्रिया में सभी पदार्थ (अभिक्रियक एवं उत्पाद) गैसीय अवस्था में हों।
का मान ज्ञात न हो। किसी अभिक्रिया का कुल एन्थैल्पी-परिवर्तन उस अभिक्रिया में अभिक्रियक अणुओं के सभी आबंधों को तोड़ने के लिए आवश्यक ऊर्जा एवं उत्पादों के अणुओं के सभी आबंधों को तोड़ने के लिए आवश्यक ऊर्जा का अंतर होता है। ध्यान रहे कि यह संबंध लगभग सही है। यह उसी समय लागू होगा, जब अभिक्रिया में सभी पदार्थ (अभिक्रियक एवं उत्पाद) गैसीय अवस्था में हों।
(घ) जालक एन्थैल्पी
एक आयनिक यौगिक की जालक एन्थैल्पी वह एन्थैल्पी परिवर्तन है, जब एक मोल आयनिक यौगिक गैसीय अवस्था में अपने आयनों में वियोजित होता है।
चूँकि जालक एन्थैल्पी को प्रयोगों द्वारा सीधे ज्ञात करना असंभव है, अतः हम एक परोक्ष विधि का उपयोग करते हैं, जहाँ एक एन्थैल्पी आरेख बनाते हैं। उसे बॉर्न-हेबर चक्र (Born-Haber cycle) कहा जाता है (चित्र 6.9)।
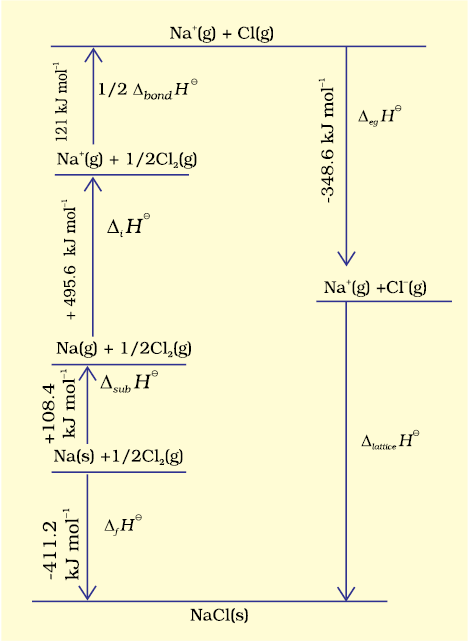
चित्र 6.9 NaCl की जालक एन्थैल्पी के लिए एन्थैल्पी आरेख
आइए, हम निम्नलिखित पदों में Na+Cl– की जालक एन्थैल्पी की गणना करते हैं–
1.  सोडियम धातु का ऊर्ध्वपातन,
सोडियम धातु का ऊर्ध्वपातन, 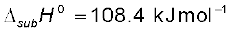
2. 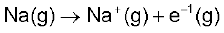 सोडियम परमाणु का आयनन एन्थैल्पी
सोडियम परमाणु का आयनन एन्थैल्पी
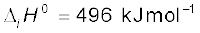
3. 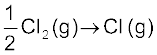 क्लोरीन का वियोजन। इस अभिक्रिया की एन्थैल्पी आबंध वियोजन एन्थैल्पी की आधी है।
क्लोरीन का वियोजन। इस अभिक्रिया की एन्थैल्पी आबंध वियोजन एन्थैल्पी की आधी है।
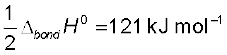
4. 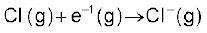 क्लोरीन परमाणुओं द्वारा ग्राह्य इलेक्ट्रॉन लब्धि। इस प्रक्रिया में इलेक्टॉन लब्धि एन्थैल्पी
क्लोरीन परमाणुओं द्वारा ग्राह्य इलेक्ट्रॉन लब्धि। इस प्रक्रिया में इलेक्टॉन लब्धि एन्थैल्पी
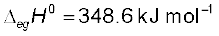
आपने एकक 3 में आयनन
एन्थैल्पी तथा इलेक्ट्रॉन लब्धि एन्थैल्पी के बारे में पढ़ा है। वास्तव में ये पद ऊष्मागतिकी से ही लिये गए हैं। पहले इन पदों की जगह आयनन ऊर्जा एवं इलेक्ट्रॉन बंधुता पदों का प्रयोग किया जाता था। (बॉक्स देखिए)

5. 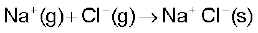
इन विभिन्न पदों का क्रम चित्र 6.9 में दर्शाया गया है। इस क्रम को ‘बॉर्न-हेबर चक्र’ कहते हैं। इस चक्र का महत्त्व यह है कि इस पूरे चक्र में एन्थैल्पी-परिवर्तन शून्य होता है।
हेस नियम के अनुसार
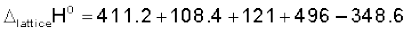
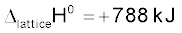
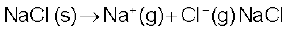 के लिए,
के लिए,
इस प्रक्रिया के लिए आंतरिक ऊर्जा इससे 2 RT कम होगी (क्योकि 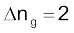 ), जो + 783 kJ mol–1. के बराबर होगी।
), जो + 783 kJ mol–1. के बराबर होगी।
अब हम इस जालक एन्थैल्पी के मान की सहायता से विलयन एन्थैल्पी का परिकलन कर सकते हैं।
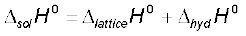
NaCl(s) के एक मोल के लिए जालक एन्थैल्पी 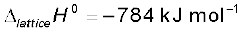 (संदर्भ-पुस्तक से)
(संदर्भ-पुस्तक से)
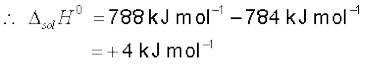
इस प्रकार NaCl(s) की विलय-प्रक्रिया में बहुत कम ऊर्जा-परिवर्तन होता है।
(च) विलयन-एन्थैल्पी ∆So1 H⊖
किसी पदार्थ की विलयन-एन्थैल्पी वह एन्थैल्पी-परिवर्तन है, जो इसके एक मोल को विलायक की निर्दिष्ट मात्रा में घोलने पर होता है। अनंत तनुता पर विलयन-एन्थैल्पी वह एन्थैल्पी-परिवर्तन है, जब पदार्थ को विलायक की अनंत मात्रा में घोला जाता है, जबकि आयनों के (या विलेय के अणुओं के) मध्य अन्योन्य क्रिया नगण्य हो।
जब एक आयनिक यौगिक को विलायक में घोला जाता है, तब इसके आयन क्रिस्टल जालक में अपनी नियमित स्थिति को छोड़ देते हैं। तब ये विलयन में अधिक स्वतंत्र होते हैं, परंतु उसी समय इन आयनों का विलायकीकरण (विलायक जल में जलीयकरण) भी होता है। इसे एक आयनिक यौगिक AB (s) के लिए आरेखीय रूप में दर्शाया गया है।
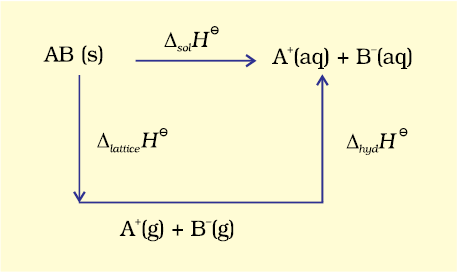
अतः जल में AB(s) की विलयन एन्थैल्पी 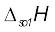 एवं जलीयकरण एन्थैल्पी,
एवं जलीयकरण एन्थैल्पी, 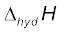 के मानों द्वारा इस प्रकार ज्ञात की जा सकती है–
के मानों द्वारा इस प्रकार ज्ञात की जा सकती है–
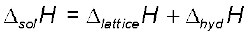
अधिकांश आयनिक यौगिकों के लिए 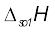 धनात्मक होता है। इसीलिए अधिकांश यौगिकों की जल में विलेयता ताप बढ़ाने पर बढ़ती है। यदि जालक एन्थैल्पी बहुत ज्यादा है, तो यौगिक का विलयन नहीं बनता है। बहुत से फ्लुओराइड क्लोराइडों की अपेक्षा कम विलेय क्यों होते हैं? एन्थैल्पी परिवर्तनों के अनुमान आबंध ऊर्जाओं (एन्थैल्पियों) एवं जालक ऊर्जाओं (एन्थैल्पियों) की सारणियों के उपयोग द्वारा किए जा सकते हैं।
धनात्मक होता है। इसीलिए अधिकांश यौगिकों की जल में विलेयता ताप बढ़ाने पर बढ़ती है। यदि जालक एन्थैल्पी बहुत ज्यादा है, तो यौगिक का विलयन नहीं बनता है। बहुत से फ्लुओराइड क्लोराइडों की अपेक्षा कम विलेय क्यों होते हैं? एन्थैल्पी परिवर्तनों के अनुमान आबंध ऊर्जाओं (एन्थैल्पियों) एवं जालक ऊर्जाओं (एन्थैल्पियों) की सारणियों के उपयोग द्वारा किए जा सकते हैं।
(छ) तनुकरण की एन्थैल्पी
यह ज्ञात है कि विलयन-एन्थैल्पी, स्थिर ताप व दाब पर विलेय की किसी विशिष्ट मात्रा को विलायक की किसी विशिष्ट मात्रा में घोलने से होने वाला एन्थैल्पी परिवर्तन होता है। यह कथन थोड़े से संशोधन के बाद किसी भी विलायक के लिए लागू किया जा सकता है। गैसीय हाइड्रोजन के 10 mol को 10 mol जल में घोलने से होने वाला एन्थैल्पी परितर्वन निम्नलिखित समीकरण द्वारा लिखा जा सकता है। सुविधा के लिए हम जल को aq. से प्रदर्शित करेंगे।
HCl(g) + 10 aq. → HCl.10 aq.
VH = – 69.01 kJ / mol
आइए हम निम्नलिखित एन्थैल्पी परिवर्तनों के समूह की ओर ध्यान दें।
(S-1) HCl(g) + 25 aq. → HCl.25 aq.
∆H = –72.03 kJ / mol
(S-2) HCl(g) + 40 aq. → HCl.40 aq.
∆H = –72.79 kJ / mol
(S-3) HCl(g) + ¥ aq. → HCl. ¥ aq.
∆H = –74.85 kJ / mol
∆H के मान यह प्रदर्शित करते हैं कि विलयन-एन्थैल्पी की सामान्य निर्भरता विलयन की मात्रा होती है। जैसे-जैसे विलयन की अधिक मात्रा इस्तेमाल की जाती है, विलयन-एन्थैल्पी सीमान्त मान तक पहुँचती जाती है यानि अनन्त मात्रा तक तनुकरण वाला मान। हाइड्रोक्लोरिक अम्ल के लिए यह उपरोक्त समीकरण (S-3) में दिया गया ∆H का मान है।
यदि हम दूसरे समीकरण (S-2) में से पहला समीकरण (S-1) घटा दें तो हमें प्राप्त होता है–
HCl.25 aq. + 15 aq. → HCl.40 aq.
VH = [ –72.79 – (–72.03)] kJ / mol
= – 0.76 kJ / mol
∆H का यह मान (– 0.76 kJ/mol) तनुकरण की एन्थैल्पी है। यह वह ऊष्मा है जो विलयन में और अधिक विलायक मिलने पर वातावरण से ली जाती है। विलयन के तनुकरण की एन्थैल्पी विलयन की मूल सांद्रता और मिलाई गई विलायक की मात्रा पर निर्भर करती है।
6.6 स्वतःप्रवर्तिता
ऊष्मागतिकी का प्रथम नियम हमें किसी निकाय द्वारा अवशोषित ऊष्मा एवं उस पर अथवा उसके द्वारा किए गए कार्य में संबंध बताता है। यह ऊष्मा के प्रवाह की दिशा पर कोई प्रतिबंध नहीं लगाता है, बल्कि ऊष्मा का प्रवाह उच्च ताप से निम्न ताप की ओर एकदिशीय होता है। वास्तव में प्राकृतिक रूप से होनेवाले सभी रासायनिक या भौतिक प्रक्रम एक ही दिशा की ओर जिसमें साम्य स्थापित हो, स्वतःप्रवर्तित होंगे। उदाहरण के लिए– एक गैस का उपलब्ध स्थान को भरने के लिए प्रसरण, कार्बन का अॉक्सीजन में जलकर कार्बन डाइअॉक्साइड बनना आदि।
परंतु ऊष्मा ठंडी वस्तु से गरम वस्तु की ओर स्वतः नहीं बहेगी। एक पात्र में रखी गैस किसी कोने में स्वतः संकुचित नहीं होगी या कार्बन डाइअॉक्साइड स्वतः कार्बन और अॉक्सीजन में परिवर्तित नहीं होगी। इसी प्रकार के अन्य स्वतःप्रक्रम एकदिशीय परिवर्तन दर्शाते हैं। अब प्रश्न उठता है कि स्वतः होनेवाले परिवर्तनों के लिए प्रेरक बल (Driving Force) क्या है? एक स्वतः प्रक्रम की दिशा कैसे निर्धारित होती है? इस खंड में हम इन प्रक्रमों के लिए मापदंड निर्धारित करेंगे कि ये संभव हो सकते हैं या नहीं।
पहले हमें समझना चाहिए कि स्वतःप्रवर्तित प्रक्रम क्या है? आप सामान्य रूप से सोच सकते हैं कि स्वतःप्रवर्तित रासायनिक अभिक्रिया वह है, जो अभिकारकों के संपर्क से तुरंत ही होने लगती है। हम अॉक्सीजन एवं हाइड्रोजन के संयोग की स्थिति को लेते हैं। इन गैसों को कमरे के ताप पर मिश्रित करके अनेक वर्षों तक बिना किसी उल्लेखनीय परिवर्तन के रखा जा सकता है। यद्यपि इनके मध्य अभिक्रिया हो रही है, परंतु बहुत ही धीमी गति से। इसे तब भी ‘स्वतःप्रवर्तित अभिक्रिया’ ही कहते हैं। अतः स्वतःप्रवर्तित प्रक्रम का अर्थ है किसी बाह्य साधन (Agency) की बिना सहायता के किसी प्रक्रम के होने की प्रवृत्ति होना। यद्यपि इससे अभिक्रिया या प्रक्रम के होने की दर का पता नहीं चलता है। स्वतःप्रवर्तित प्रक्रमों के दूसरे पहलू में हम देखते हैं कि ये स्वतः अपनी दिशा से उत्क्रमित नहीं हो सकते हैं। स्वतःप्रवर्तित प्रक्रमों के लिए हम संक्षेप में कह सकते हैं कि –
स्वतःप्रवर्तित प्रक्रम एक अनुत्क्रमणीय प्रक्रम होता है। यह किसी बाह्य साधन (Agency) के द्वारा ही उत्क्रमित किया जा सकता है।
(क) क्या एन्थैल्पी का कम होना स्वतःप्रवर्तिता की कसौटी है?
यदि हम एेसी घटनाओं जैसे – पहाड़ी से जल गिरने या जमीन पर पत्थर गिरने की प्रक्रियाओं पर विचार करें, तब देखेंगे कि प्रक्रम की दिशा में निकाय की स्थितिज ऊर्जा में कमी होती है। इस प्रकार हम कह सकते हैं कि एक रासायनिक अभिक्रिया उस दिशा में स्वतःप्रवर्तित होगी, जिस दिशा में ऊर्जा में कमी हो, जैसा ऊष्माक्षेपी अभिक्रियाओं में होता है।
उदाहरण के लिए–
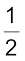 N2(g) +
N2(g) + 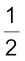 H2(g) → NH3(g) ;
H2(g) → NH3(g) ;
∆r H0 = – 46.1 kJ mol–1
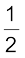 H2(g) +
H2(g) + 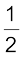 Cl2(g) → HCl (g) ;
Cl2(g) → HCl (g) ;
∆r H0 = – 92.32 kJ mol–1
H2(g) + 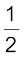 O2(g) → H2O(l) ;
O2(g) → H2O(l) ;
∆r H0 = –285.8 kJ mol–1
किसी भी ऊष्माक्षेपी अभिक्रिया के लिए अभिकारकों से उत्पादों के बनने पर एन्थैल्पी में आई कमी को एक एन्थैल्पी आरेख (चित्र 6.10 (क)) से दर्शाया जा सकता है।
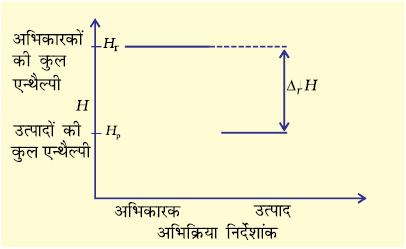
अब तक प्राप्त प्रमाणों के आधार पर हम यह अवधारणा बना सकते हैं कि किसी रासायनिक अभिक्रिया के लिए एन्थैल्पी में आई कमी उसका प्रेरक बल (Driving force) है।
अब हम निम्नलिखित अभिक्रियाओं पर विचार करते हैं–
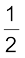 N2(g) + O2(g) → NO2(g);
N2(g) + O2(g) → NO2(g);
∆r H = +33.2 kJ mol–1
C(ग्रैफ़ाइट, s) + 2 S(l) → CS2 (l);
∆r H0 +128.5 kJ mol–1
ये अभिक्रियाएं स्वतःप्रवर्तित प्रक्रम एवं ऊष्माशोषी हैं। एन्थैल्पी में वृद्धि को एक एन्थैल्पी-आरेख द्वारा दर्शाया गया है (चित्र 6.10 (ख))
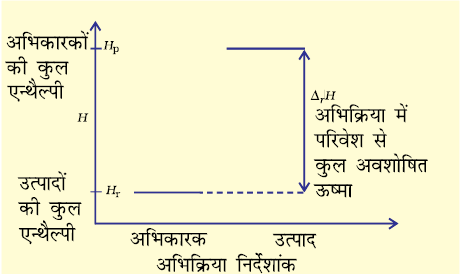
इन उदाहरणों से यह स्पष्ट होता है कि एन्थैल्पी में कमी स्वतःप्रवर्तिता के लिए एक प्रतिसहायक कारक है, परंतु यह सभी प्रक्रमों के लिए सत्य नहीं है।
(ख) एन्ट्रॉपी एवं स्वतःप्रवर्तिता
एक स्वतःप्रवर्तिता प्रक्रम दी गई दिशा में कैसे प्रेरित होती है? आइए, हम एक एेसी स्थिति का अध्ययन करें, जिसमें 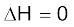 , अर्थात् एन्थैल्पी में कोई परिवर्तन नहीं है, फिर भी अभिक्रिया या प्रक्रम स्वतःप्रेरित है।
, अर्थात् एन्थैल्पी में कोई परिवर्तन नहीं है, फिर भी अभिक्रिया या प्रक्रम स्वतःप्रेरित है।
हम एक बंद पात्र जो परिवेश से विलगित (Isolated) है, में दो गैसों को विसरित करते हैं, जैसा चित्र 6.11 में दर्शाया गया है।
दो गैसें A एवं B, जिन्हें क्रमशः काले एवं श्वेत बिंदुओं से दर्शाया गया है तथा एक विभाजक से पृथक् किया गया है (चित्र 6.11 क)। जब विभाजक हटाया जाता है (चित्र 6.11 ख), तब गैसें आपस में विसरित होने लगती हैं। कुछ समय पश्चात् विसरण पूर्ण हो जाता है।
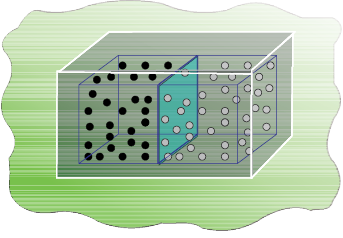
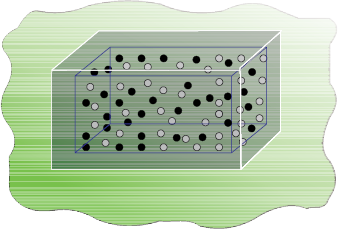
अब हम इस प्रक्रम का अध्ययन करते हैं। विसरण से पूर्व यदि हम बाईं ओर के हिस्से से गैस के अणुओं को निकालते, तो निश्चित रूप से ये गैस A के होंगे। इसी प्रकार यदि हम दाईं ओर के हिस्से से अणु निकालते, तो ये गैस B के अणु होंगे। परंतु यदि विभाजक हटाने के बाद अणु निकाले जाएं, तो हम निश्चित तौर पर नहीं कह सकते हैं कि निकाला गया अणु गैस A का है या गैस B का। हम कह सकते हैं कि निकाय कम प्रागुक्त या अधिक अव्यवस्थित हो गया है।
अब हम दूसरी अवधारणा बनाते हैंः एक विलगित निकाय में निकाय की ऊर्जा में हमेशा अधिक अव्यवस्थित होने की प्रवृत्ति होती है। यह स्वतःप्रवर्तिता की एक कसौटी हो सकती है।
यहाँ हम एक अन्य ऊष्मागतिकी फलन की बात करते हैं, जिसे ‘एन्ट्रॉपी S’ कहते हैं। उपरोक्त अव्यवस्था एन्ट्रॉपी की अभिव्यक्ति है। एक मानसिक दृश्य बनाने के लिए एक व्यक्ति सोच सकता है कि एन्ट्रॉपी किसी निकाय में अव्यवस्था का मापन है। एक विलगित निकाय में जितनी अधिक अव्यवस्था होगी, उतनी ही अधिक उसकी एन्ट्रॉपी होगी। जहाँ तक एक रासायनिक अभिक्रिया का प्रश्न है, एन्ट्रॉपी परिवर्तन परमाणुओं अथवा आयनों के एक पैटर्न (अभिक्रियक) में से दूसरे (उत्पाद) में पुनः व्यवस्थित होना है। यदि उत्पादों की संरचना क्रियाकारकों की संरचना से अधिक अव्यवस्थित होगी, तो एन्ट्रॉपी में परिणामतः वृद्धि होगी। एक रासायनिक अभिक्रिया में एन्ट्रॉपी में गुणात्मक परिवर्तन अभिक्रिया में प्रयुक्त पदार्थों की संरचना के आधार पर अनुमानित किया जाता है। संरचना में नियमितता के घटने का अर्थ है एन्ट्रॉपी का बढ़ना। एक पदार्थ के लिए ठोस अवस्था न्यूनतम एन्ट्रॉपी (सर्वाधिक नियमित) की अवस्था है, जबकि गैस अवस्था अधिकतम एन्ट्रॉपी की अवस्था है।
अब हम एन्ट्रॉपी को मात्रात्मक (Quantify) रूप देते हैं। अणुओं में ऊर्जा के वितरण से अव्यवस्था की गणना करने के लिए एक विधि सांख्यिकी है, जो इस पुस्तक की सीमा से परे हैं। दूसरी विधि इस अभिक्रिया में होने वाले ऊष्मा-परिवर्तनों से जोड़ने की विधि है, जो एन्ट्रॉपी को ऊष्मागतिकी फलन बनाती है। अन्य ऊष्मागतिकी फलनों, जैसे–आंतरिक ऊर्जा U या एन्थैल्पी H की तरह एन्ट्रॉपी भी एक ऊष्मागतिकी अवस्था फलन है। वह ∆S प्रक्रिया के पथ पर निर्भर नहीं होता।
जब भी किसी निकाय को ऊष्मा दी जाती है, तब यह आणविक गति को बढ़ाकर निकाय की अव्यवस्था बढ़ा देती है। इस प्रकार ऊष्मा (q) निकाय में अव्यवस्था बढ़ाने का प्रभाव रखती है। क्या हम ∆S को q से संबंधित सकते हैं? अनुभव दर्शाता है कि ऊर्जा का वितरण उस ताप पर निर्भर करता है, जिसपर ऊष्मा दी जाती है। एक उच्च ताप के निकाय में निम्न ताप के निकाय की तुलना में अधिक अव्यवस्था होती है। अतः किसी निकाय का ताप उसके कणों की अनियमित गति का मापन है। निम्न ताप पर किसी निकाय को दी गई ऊष्मा उसी निकाय को उच्च ताप पर दी गई उतनी ही ऊष्मा की तुलना में अधिक अव्यवस्था का कारण बनती है। इससे पता चलता है कि एन्ट्रॉपी परिवर्तन ताप के व्युत्क्रमानुपाती होता है।
उत्क्रमणीय प्रक्रमों के लिए हम ∆S को q एवं ताप T से इस प्रकार संबंधित कर सकते हैंः
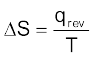 (6.18)
(6.18)
किसी स्वतः प्रवर्तित प्रक्रम के लिए निकाय एवं परिवेश का कुल एन्ट्रॉपी परिवर्तन (∆Stotal) निम्नलिखित समीकरण द्वारा दिया जा सकता है।
 (6.19)
(6.19)
जब एक निकाय साम्यावस्था में हो, तो एन्ट्रॉपी अधिकतम होती है एवं एन्ट्रॉपी में परिवर्तन ∆S = 0 है।
हम कह सकते हैं कि एक स्वतःप्रवर्तित प्रक्रम की एन्ट्रॉपी में वृद्धि तब तक होती रहती है, जब तक यह अधिकतम न हो जाए साम्यावस्था पर एन्ट्रॉपी में परिवर्तन शून्य होता है। चूँकि एन्ट्रॉपी एक अवस्था गुण है, अतः एक उत्क्रमणीय प्रक्रम के दौरान हम एन्ट्रॉपी-परिवर्तन की गणना निम्नलिखित समीकरण से हम कर सकते हैं–
∆Ssys = 
हम जानते हैं कि समतापीय परिस्थितियों में उत्क्रमणीय एवं अनुत्क्रमणीय–दोनों प्रक्रमों के लिए 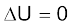 होता है, परंतु
होता है, परंतु 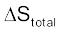 अर्थात्
अर्थात् 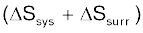 अनुत्क्रमणीय प्रक्रम के लिए शून्य नहीं है। इस प्रकार
अनुत्क्रमणीय प्रक्रम के लिए शून्य नहीं है। इस प्रकार  , अनुत्क्रमणीय एवं उत्क्रमणीय प्रक्रम में विभेद नहीं करती है, जबकि
, अनुत्क्रमणीय एवं उत्क्रमणीय प्रक्रम में विभेद नहीं करती है, जबकि 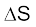 विभेद करती है।
विभेद करती है।
उदाहरण 6.10
बताइए कि निम्नलिखित में से किसमें एन्ट्रॉपी बढ़ती / घटती है–
(i) एक द्रव का ठोस अवस्था में परिवर्तन होता है।
(ii) एक क्रिस्टलीय ठोस का ताप 0 K से 115 K तक
बढ़ाया जाता है।
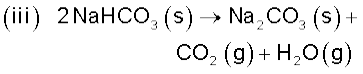
हल
(i) ठोस अवस्था में परिवर्तन होने के बाद अणु व्यवस्थित अवस्था प्राप्त करते हैं, अतः एन्ट्रॉपी घटती है।
(ii) ताप 0 K पर सभी अणु स्थिर होते हैं। अतः एन्ट्रॉपी न्यूनतम होती है। यदि ताप 115 K तक बढ़ाया जाए, तब अणु गति करना आरंभ कर देते हैं एवं अपनी साम्यावस्था से दोलन करते हैं और निकाय अधिक अव्यवस्थित हो जाता है। अतः एन्ट्रॉपी बढ़ जाती है।
(iii) अभिकारक NaHCO3 ठोस है एवं इसकी एन्ट्रॉपी कम है। उत्पादों में एक ठोस और दो गैसें हैं। अतः उत्पाद उच्च एन्ट्रॉपी की स्थिति का प्रतिनिधित्व करते हैं।
(iv) यहाँ एक अणु दो परमाणु देता है, अर्थात् कणों की संख्या बढ़ती है, जो अधिक अव्यवस्था की ओर ले जाती है। H परमाणुओं के दो मोल हाइड्रोजन अणु के एक मोल की तुलना में अधिक एन्ट्रॉपी रखते हैं।
उदाहरण 6.11
लोहे के अॉक्सीकरण
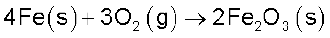
एन्ट्रॉपी परिवर्तन –549.4 JK–1 mol–1 है (298 K ताप पर)
इस अभिक्रिया में एन्ट्रॉपी परिवर्तन ऋणात्मक होने के उपरांत भी अभिक्रिया स्वतः प्रवर्तित क्यों है?
(इस अभिक्रिया के लिए 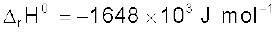 )
)
हल
एक अभिक्रिया की स्वतःप्रवर्तिता
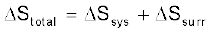 के आधार पर होती है।
के आधार पर होती है। 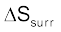 की गणना करने के लिए हमें परिवेश द्वारा अवशोषित ऊष्मा पर विचार करना होगा, जो
की गणना करने के लिए हमें परिवेश द्वारा अवशोषित ऊष्मा पर विचार करना होगा, जो  के तुल्य है। T ताप पर परिवेश की एन्ट्रॉपी में परिवर्तन है
के तुल्य है। T ताप पर परिवेश की एन्ट्रॉपी में परिवर्तन है 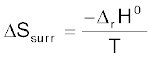 (स्थिर दाब पर)
(स्थिर दाब पर)
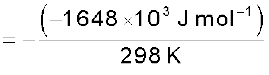
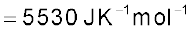
अतः अभिक्रिया के लिए कुल एन्ट्रॉपी-परिवर्तन
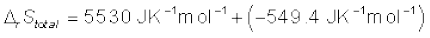
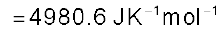
इससे प्रकट होता है कि अभिक्रिया स्वतःप्रवर्तित है।
(ग) गिब्ज़ ऊर्जा एवं स्वतःप्रवर्तिता
हम देख चुके हैं कि किसी निकाय के लिए एन्ट्रॉपी में कुल परिवर्तन 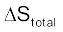 किसी प्रक्रम की स्वतःप्रवर्तिता का निर्णय करता है। परंतु अधिकांश रासायनिक अभिक्रियाएँ बंद निकाय या खुले निकाय की श्रेणी में आती हैं। अतः अधिकांश अभिक्रियाओं में एन्ट्रॉपी एवं एन्थैल्पी – दोनों में परिवर्तन आते हैं। पूर्व खंड में की गई विवेचना से यह स्पष्ट है कि न तो केवल एन्थैल्पी में कमी और न ही एन्ट्रॉपी में वृद्धि स्वतः प्रवर्तित प्रक्रमों की दिशा निर्धारित कर सकती है।
किसी प्रक्रम की स्वतःप्रवर्तिता का निर्णय करता है। परंतु अधिकांश रासायनिक अभिक्रियाएँ बंद निकाय या खुले निकाय की श्रेणी में आती हैं। अतः अधिकांश अभिक्रियाओं में एन्ट्रॉपी एवं एन्थैल्पी – दोनों में परिवर्तन आते हैं। पूर्व खंड में की गई विवेचना से यह स्पष्ट है कि न तो केवल एन्थैल्पी में कमी और न ही एन्ट्रॉपी में वृद्धि स्वतः प्रवर्तित प्रक्रमों की दिशा निर्धारित कर सकती है।
इस प्रयोजन हेतु हम एक नए ऊष्मागतिकी फलन गिब्ज़ ऊर्जा या गिब्ज़ फलन G को इस प्रकार परिभाषित करते हैं–
G = H - TS (6.20)
गिब्ज़ ऊर्जा, G एक विस्तीर्ण एवं अवस्था गुण है।
निकाय की गिब्ज़ ऊर्जा में परिवर्तन 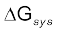 को इस प्रकार लिखा जा सकता है–
को इस प्रकार लिखा जा सकता है–
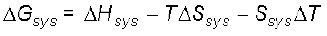
स्थिर ताप पर 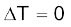
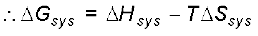
सामान्यतया पादांक (subscript) निकाय को छोड़ते हुए समीकरण को इस प्रकार लिखते हैं–
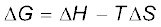 (6.21)
(6.21)
इस प्रकार गिब्ज़ ऊर्जा में परिवर्तन = एन्थैल्पी में परिवर्तन - तापमान × एन्ट्रॉपी में परिवर्तन यह समीकरण ‘गिब्ज़ समीकरण’ के रूप में जाना जाता है, जो रसायन शास्त्र के अति महत्त्वपूर्ण समीकरणों में से एक है। यहाँ हमने स्वतःप्रवर्तिता के लिए दोनों पदों को साथ-साथ लिया है : ऊर्जा (∆H के पदों में) एवं एन्ट्रॉपी ∆S (अव्यवस्था का मापन)। जैसा पूर्व में बताया गया है। विमीय आधार पर विश्लेषण करने पर हम पाते हैं कि ∆G की इकाई ऊर्जा की इकाई होती है, क्योंकि ∆H एवं T∆S दोनों ऊर्जा पद हैं [चूँकि T∆S = (K) (J/K) = J]
अब हम विचार करते हैं कि 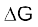 किस प्रकार अभिक्रिया की स्वतःप्रवर्तिता से संबंधित है।
किस प्रकार अभिक्रिया की स्वतःप्रवर्तिता से संबंधित है।
हम जानते हैं कि ∆Stotal = ∆Ssys + ∆Ssurr
यदि निकाय, परिवेश के साथ तापीय साम्य में है, तो परिवेश का ताप, निकाय के ताप के समान ही होगा। अतः परिवेश की एन्थैल्पी में वृद्धि निकाय की एन्थैल्पी में कमी के तुल्य होगी।
अत ः परिवेश की एन्ट्रॉपी में परिवर्तन
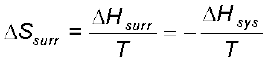
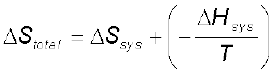
उपरोक्त समीकरण को पुनः व्यवस्थित करने पर
T∆Stotal = T∆Ssys – ∆Hsys
स्वतः प्रक्रम के लिए 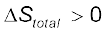 vr%
vr%
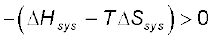
समीकरण 6.21 का उपयोग करने पर उपरोक्त समीकरण इस प्रकार लिखी जा सकती है–
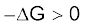
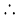
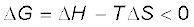 (6.22)
(6.22)
∆Hsys अभिक्रिया की एन्थैल्पी में परिवर्तन है  वह ऊर्जा है, जो उपयोगी कार्य के लिए उपलब्ध नहीं है। इस प्रकार ∆G उपयोगी कार्य के लिए नेट ऊर्जा है एवं इस प्रकार ‘मुक्त ऊर्जा’ का मापन है। इस कारण इसे अभिक्रिया की मुक्त ऊर्जा भी कहा जाता है।
वह ऊर्जा है, जो उपयोगी कार्य के लिए उपलब्ध नहीं है। इस प्रकार ∆G उपयोगी कार्य के लिए नेट ऊर्जा है एवं इस प्रकार ‘मुक्त ऊर्जा’ का मापन है। इस कारण इसे अभिक्रिया की मुक्त ऊर्जा भी कहा जाता है।
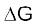 स्थिर दाब एवं ताप पर स्वतःप्रवर्तिता की कसौटी है।
स्थिर दाब एवं ताप पर स्वतःप्रवर्तिता की कसौटी है।
(i) यदि 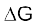 ऋणात्मक (< 0) है, तब प्रक्रम स्वतः प्रवर्तित होता है।
ऋणात्मक (< 0) है, तब प्रक्रम स्वतः प्रवर्तित होता है।
(ii) यदि 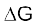 धनात्मक (> 0) तब प्रक्रम अस्वतः प्रवर्तित होगा।
धनात्मक (> 0) तब प्रक्रम अस्वतः प्रवर्तित होगा।
टिप्पणी– यदि अभिक्रिया के लिए एन्थैल्पी परिवर्तन धनात्मक हो एवं एन्ट्रॉपी परिवर्तन भी धनात्मक हो, तो अभिक्रिया तभी स्वतः होगी, जब T∆S का मान ∆H के मान से अधिक हो जाए। यह दो प्रकार से हो सकता है–
(क) धनात्मक एन्ट्रॉपी परिवर्तन कम हो, तो इस स्थिति में T अधिक होना चाहिए। (ख) धनात्मक एन्ट्रॉपी परिवर्तन अधिक हो, तो इस स्थिति में T कम होना चाहिए। पहले वाला कारण यह बताता है कि अधिकांश अभिक्रियाएं उच्च ताप पर क्यों संपादित की जाती हैं। सारणी 6.4 में अभिक्रियाओं की स्वतः प्रवर्तिता पर ताप के प्रभाव को संक्षेपित (Summarise) किया गया है।
(घ) एन्ट्रॉपी और ऊष्मागतिकी का दूसरा नियम
हम जानते हैं कि किसी विलगित निकाय के लिए ऊर्जा परिवर्तन निश्चित रहता है। इसलिए, इस प्रकार के निकाय में एन्ट्रॉपी का बढ़ना स्वतः परिवर्तन की स्वाभाविक दिशा बतलता है। वास्तव में यह ऊष्मागतिकी का दूसरा नियम है। प्रथम नियम के समान दूसरे नियम को भी विभिन्न प्रकार से लिखा जा सकता है। ऊष्मागतिकी का दूसरा नियम स्पष्ट करता है कि स्वतः प्रवर्ती ऊष्माक्षेपी अभिक्रियाएँ इतनी आम क्यों होती हैं। ऊष्माक्षेपी अभिक्रियाओं से निकली ऊर्जा वातवरण में अव्यवस्था बढ़ा देती है और कुल मिलाकर एन्ट्रॉपी परिवर्तन धनात्मक होता है जो अभिक्रिया को स्वतः प्रवर्तित बना देता है।
(च) निरपेक्ष एन्ट्रॉपी और ऊष्मागतिकी का तीसरा नियम
किसी पदार्थ के अणु सीधी रेखा में किसी भी ओर गति कर सकते हैं, वह लट्टू की तरह घूर्णन कर सकते हैं और अणुओं के आबंध खिंच और सिकुड़ सकते हैं। अणुओं की यह गतियाँ क्रमशः स्थानान्तरण गति, घूर्णनी गति एवं कंपमान गति कहलाती हैं। जब निकाय का तापमान बढ़ता है तो यह गतियाँ अधिक उग्र हो जाती हैं और एन्ट्रॉपी बढ़ जाती है। दूसरी ओर जब ताप घटाया जाता है तो एन्ट्रॉपी कम हो जाती है। किसी शुद्ध क्रिस्टलित पदार्थ का ताप जैसे-जैसे परम शून्य की ओर बढ़ता है वैसे-वैसे एन्ट्रॉपी भी शून्य की ओर बढ़ती है। इसे ऊष्मागतिकी का तीसरा नियम कहते हैं। एेसा इसलिए होता है क्योंकि परम शून्य पर क्रिस्टल में संपूर्ण क्रम होता है। यह कथन केवल शुद्ध क्रिस्टलित ठोसों तक सीमित है क्योंकि सैद्धांतिक तर्क और प्रायोगिक प्रमाण दर्शाते हैं कि विलयनों और अतिशीतलित द्रवों की एन्ट्रॉपी 0 K पर शून्य नहीं होती। तीसरे नियम का महत्व इसलिए है कि यह केवल ऊष्मीय आंकड़ों के आधार पर शुद्ध पदार्थों के निरपेक्ष एन्ट्रॉपी मान परिकलित करने में सहायक होता है। शुद्ध पदार्थ के लिए यह 0 K से 298 K तक  वृद्धियों को जोड़ कर प्राप्त किया जा सकता है। मानक एन्ट्रॉपियाँ हेस-नियम प्रकार के परिकलन द्वारा मानक एन्ट्रॉपी परिवर्तन परिकलित करने के लिए इस्तेमाल की जा सकती हैं।
वृद्धियों को जोड़ कर प्राप्त किया जा सकता है। मानक एन्ट्रॉपियाँ हेस-नियम प्रकार के परिकलन द्वारा मानक एन्ट्रॉपी परिवर्तन परिकलित करने के लिए इस्तेमाल की जा सकती हैं।
6.7 गिब्ज़ ऊर्जा-परिवर्तन एवं साम्यावस्था
हम देख चुके हैं कि इस प्रकार मुक्त ऊर्जा का चिह्र एवं परिमाण-अभिक्रिया के बारे में निम्नलिखित जानकारी देता है-
(i) रासायनिक अभिक्रिया की स्वतःप्रवर्तिता का पूर्वानुमान।
(ii) रासायनिक अभिक्रिया से प्राप्त हो सकने वाले उपयोगी कार्य का पूर्वानुमान।
अब तक हम अनुत्क्रमणीय अभिक्रियाओं में मुक्त ऊर्जा परिवर्तनों पर विचार कर चुके हैं। अब हम उत्क्रमणीय अभिक्रियाओं में मुक्त ऊर्जा-परिवर्तन की जाँच करते हैं।
‘उत्क्रमणीयता’ में ऊष्मागतिकी एक विशेष परिस्थिति है, जिसमें एक प्रक्रम को इस प्रकार किया जाता है कि निकाय हमेशा अपने परिवेश से पूर्णतः साम्य में रहे। रासायनिक अभिक्रियाओं के संदर्भ में ‘उत्क्रमणीयता’ का अर्थ है कि एक रासायनिक अभिक्रिया दोनों दिशाओं में साथ-साथ चल सकती है, जिससे कि साम्य स्थापित हो सके। इससे प्रतीत होता है कि अभिक्रिया दोनों दिशाओं में मुक्त ऊर्जा में कमी के साथ चल सके, जो असंभव प्रतीत होता है। यह तभी संभव है, जब साम्यावस्था में निकाय की मुक्त ऊर्जा न्यूनतम हो। यदि एेसा नहीं हो, तो निकाय स्वतः ही कम मुक्त ऊर्जा की स्थिति में परिवर्तित हो जाएगा।
अतः साम्य के लिए कसौटी है– 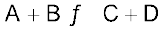
∆rG = 0
किसी अभिक्रिया, जिसमें सभी अभिकारक एवं उत्पाद मानक अवस्था में हों, तो गिब्ज़ ऊर्जा ∆rG⊖, साम्यावस्था स्थिरांक से निम्नलिखित समीकरण द्वारा संबंधित होती है–
0 = ∆rG0 + RT ln K
अथवा ∆rG0 = – RT ln K
अथवा ∆rG0 = – 2.303 RT log K (6.23)
हम यह भी जानते हैं कि
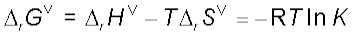 (6.24)
(6.24)
प्रबल ऊष्माशोषी अभिक्रियाओं के लिए ∆rH⊖ का मान अधिक एवं धनात्मक होता है। इन परिस्थितियों में K का मान 1 से बहुत कम होगा एवं अभिक्रिया में अधिक उत्पाद बनाने की प्रवृत्ति नहीं होगी। ऊष्माक्षेपी अभिक्रियाओं में 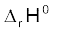 का मान अधिक ज्यादा एवं ऋणात्मक होगा तथा ∆rG⊖ का मान अधिक एवं ऋणात्मक संभावित है। इन परिस्थितियों में K का मान 1 से बहुत अधिक होगा। हम प्रबल ऊष्माक्षेपी अभिक्रियाओं के लिए उच्च K की आशा कर सकते हैं एवं अभिक्रिया लगभग पूर्ण हो सकती है। ∆rG⊖ का मान ∆rS⊖ के मान पर भी निर्भर करता है। यदि अभिक्रिया में एन्ट्रॉपी परिवर्तन को भी ध्यान में रखा जाए, तब K का मान या अभिक्रिया की सीमा इस बात से प्रभावित होगी कि ∆rS⊖ का मान धनात्मक या ऋणात्मक है।
का मान अधिक ज्यादा एवं ऋणात्मक होगा तथा ∆rG⊖ का मान अधिक एवं ऋणात्मक संभावित है। इन परिस्थितियों में K का मान 1 से बहुत अधिक होगा। हम प्रबल ऊष्माक्षेपी अभिक्रियाओं के लिए उच्च K की आशा कर सकते हैं एवं अभिक्रिया लगभग पूर्ण हो सकती है। ∆rG⊖ का मान ∆rS⊖ के मान पर भी निर्भर करता है। यदि अभिक्रिया में एन्ट्रॉपी परिवर्तन को भी ध्यान में रखा जाए, तब K का मान या अभिक्रिया की सीमा इस बात से प्रभावित होगी कि ∆rS⊖ का मान धनात्मक या ऋणात्मक है।
समीकरण (6.24) का प्रयोग करने पर
(i) ∆H0 एवं ∆S0 के मापन से ∆G0 का मान अनुमानित करके, किसी भी ताप पर किफायती रूप से उत्पादों की प्राप्ति के लिए K के मान की गणना की जा सकती है।
(ii) यदि प्रयोगशाला में K सीधा ही माप लिया जाए, तो किसी भी अन्य ताप पर ∆G0 के मान की गणना की जा सकती है।
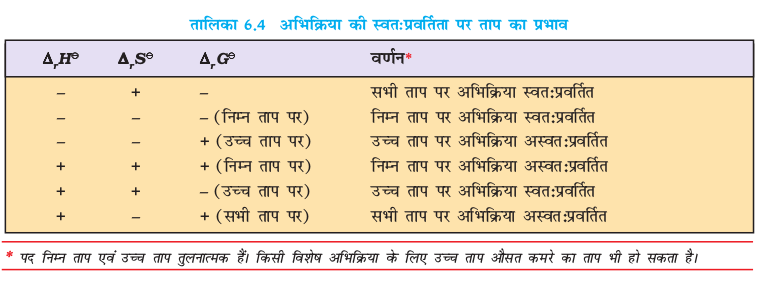
उदाहरण 6.12
298 K पर अॉक्सीजन के ओज़ोन में रूपांतरण 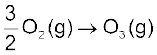 के लिए ∆rG0 के मान की
के लिए ∆rG0 के मान की
गणना कीजिए। इस अभिक्रिया के लिए Kp का मान 2.47×10–29 है।
हल
हम जानते हैं कि ∆rG0 = –2.303 RT log Kp एवं R = 8.314 JK–1 mol–1
अतः
∆rG0 =
– 2.303 (8.314 J K–1 mol–1) × (298 K) (log 2.47 × 10–29)
= 163000 J mol–1
= 163 kJ mol–1
उदाहरण 6.13
निम्नलिखित अभिक्रिया के लिए 298 K पर साम्य स्थिरांक का मान ज्ञात कीजिए–
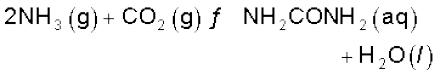
दिए गए ताप पर मानक गिब्ज़ ऊर्जा 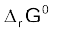 का मान
का मान
–13.6 kJ mol-1 है।
हल
हम जानते हैं कि 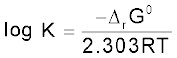
= 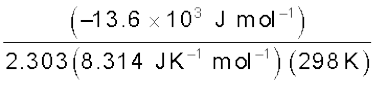
= 2.38
K = antilog 2.38 = 2.4 × 102
उदाहरण 6.14
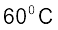 ताप पर डाइनाइट्रोजन टेट्राक्साइड 50% वियोजित होता है। एक वायुमंडलीय दाब एवं इस ताप पर मानक मुक्त ऊर्जा-परिवर्तन की गणना कीजिए।
ताप पर डाइनाइट्रोजन टेट्राक्साइड 50% वियोजित होता है। एक वायुमंडलीय दाब एवं इस ताप पर मानक मुक्त ऊर्जा-परिवर्तन की गणना कीजिए।
हल
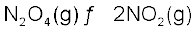
यदि 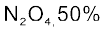 वियोजित होता है, तो दोनों पदार्थों का मोल अंश होगा–
वियोजित होता है, तो दोनों पदार्थों का मोल अंश होगा–
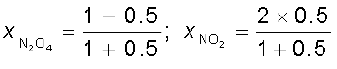
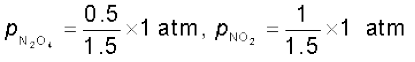
साम्य स्थिरांक
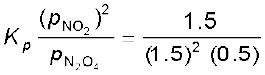
= 1.33 atm.
चूँकि
∆rG0 = –RT ln Kp
∆rG0 = (–8.314 JK–1 mol–1) × (333 K) × (2.303) × (0.1239) = – 763.8 kJ mol–1
सारांश
ऊष्मागतिकी रासायनिक एवं भौतिक प्रक्रमों में ऊर्जा-परिवर्तन से संबंध रखती है। यह इन परिवर्तनों का मात्रात्मक अध्ययन करने तथा उपयोगी अनुमान लगाने में हमें सहायता करती है। इन कार्यों के लिए हम ब्रह्मांड को निकाय एवं परिवेश में विभाजित करते हैं। रासायनिक एवं भौतिक प्रक्रम ऊष्मा (q) उत्सर्जन या अवशोषण के साथ होते हैं, जिसका कुछ भाग कार्य (w) में बदला जा सकता है। ये राशियाँ ऊष्मागतिक के प्रथम नियम ∆U = q + w द्वारा संबंधित होती हैं। ∆U प्रारंभिक एवं अंतिम अवस्था पर निर्भर करता है तथा U अवस्था फलन है, जबकि q एवं w पथ पर निर्भर करते हैं तथा अवस्था फलन नहीं है। हम q एवं w के लिए चिह्न परिपाटी का पालन करते हैं, यदि इन्हें निकाय को दिया जाए तो इन्हें धनात्मक चिह्न देते हैं,हम ऊष्मा के एक निकाय से दूसरे निकाय में स्थानांतरण का मापन कर सकते हैं, जिससे ताप में परिवर्तन होता है। तापमान में वृद्धि का मान पदार्थ की ऊष्माधारिता (C) पर निर्भर करता है। अतः अवशोषित या उत्सर्जित ऊष्मा q = C∆T होता है। यदि गैस का प्रसरण होता हो, तो कार्य का मापन W = –pex∆V से करते हैं। उत्क्रमणीय प्रक्रम में आयतन के अत्यणु परिवर्तन के लिए pex = p का मान रख सकते हैं। अतः W rev = –pdV इस अवस्था में हम गैस समीकरण pV = nRT का प्रयोग कर सकते हैं।
स्थिर आयतन पर w = 0 तब ∆U = qv अर्थात् यह स्थिर आयतन पर स्थानांतरित ऊष्मा है। परंतु रासायनिक अभिक्रियाओं के अध्ययन के लिए हम सामान्यतया स्थिर दाब लेते हैं। हम एक ओर अवस्था-फलन एन्थैल्पी को परिभाषित करते हैं। एन्थैल्पी-परिवर्तन 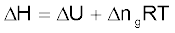 का मापन सीधे स्थिर दाब पर ऊष्मा-परिवर्तन से किया जा सकता है, यहाँ
का मापन सीधे स्थिर दाब पर ऊष्मा-परिवर्तन से किया जा सकता है, यहाँ 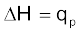 है।
है।
एन्थैल्पी-परिवर्तनों के कई प्रकार हैं। प्रावस्था परिवर्तन (जैसे–गलन, वाष्पीकरण एवं ऊर्ध्वपातन) सामान्यतया स्थिर ताप पर होते हैं, जिन्हें धनात्मक एन्थैल्पी-परिवर्तन से अभिलक्षित किया जाता है। विरचन एन्थैल्पी, दहन एन्थैल्पी एवं अन्य एन्थैल्पियों में परिवर्तन हेस के नियम का उपयोग करके ज्ञात किए जा सकते हैं। रासायनिक अभिक्रियाओं में एन्थैल्पी-परिवर्तन
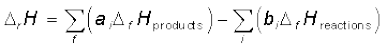
गैसीय अवस्था में  (अभिकारकों की आबंध ऊर्जा)
(अभिकारकों की आबंध ऊर्जा) 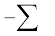 (उत्पादों की आबंध ऊर्जा)
(उत्पादों की आबंध ऊर्जा)
ऊष्मागतिकी का प्रथम नियम रासायनिक अभिक्रिया की दिशा के बारे में हमें निर्देशित नहीं करता, अर्थात् यह नहीं बताता कि रासायनिक अभिक्रिया का प्रेरक बल क्या है। विलगित निकाय के लिए 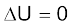 है। अतः हम इस कार्य के लिए दूसरा अवस्था-फलन, S, एन्ट्रॉपी परिभाषित करते हैं। एन्ट्रॉपी अव्यवस्था का मापन है। एक स्वतः प्रवर्तित प्रक्रम के लिए कुल एन्ट्रॉपी परिवर्तन धनात्मक होता है। एक विलगित निकाय के लिए
है। अतः हम इस कार्य के लिए दूसरा अवस्था-फलन, S, एन्ट्रॉपी परिभाषित करते हैं। एन्ट्रॉपी अव्यवस्था का मापन है। एक स्वतः प्रवर्तित प्रक्रम के लिए कुल एन्ट्रॉपी परिवर्तन धनात्मक होता है। एक विलगित निकाय के लिए 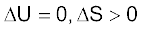 है। अतः एन्ट्रॉपी परिवर्तन स्वतः प्रवर्तित प्रक्रम को विभेदित करता है, जबकि ऊर्जा परिवर्तन नहीं करता। उत्क्रमणीय प्रक्रम के लिए एन्ट्रॉपी परिवर्तन-समीकरण
है। अतः एन्ट्रॉपी परिवर्तन स्वतः प्रवर्तित प्रक्रम को विभेदित करता है, जबकि ऊर्जा परिवर्तन नहीं करता। उत्क्रमणीय प्रक्रम के लिए एन्ट्रॉपी परिवर्तन-समीकरण 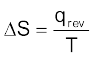 से ज्ञात किया जा सकता है।
से ज्ञात किया जा सकता है।  पथ पर निर्भर नहीं करता है।
पथ पर निर्भर नहीं करता है।
चूँकि अधिकांश रासायनिक अभिक्रियाएं स्थिर दाब पर होती हैं, अतः हम दूसरा अवस्था-फलन गिब्ज़ ऊर्जा G परिभाषित करते हैं, जो निकाय के एन्ट्रॉपी एवं एन्थैल्पी परिवर्तनों से समीकरण 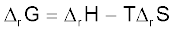 द्वारा संबंधित है।
द्वारा संबंधित है।
स्वतःप्रवर्तित प्रक्रम के लिए 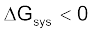 एवं साम्यावस्था पर
एवं साम्यावस्था पर 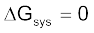
मानक गिब्ज़ ऊर्जा-परिवर्तन साम्य स्थिरांक से 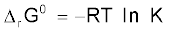 समीकरण से संबंधित है।
समीकरण से संबंधित है।
इसकी सहायता से 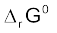 ज्ञात होने पर K का मान ज्ञात किया जा सकता है।
ज्ञात होने पर K का मान ज्ञात किया जा सकता है। 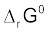 का मान समीकरण
का मान समीकरण 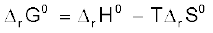 से ज्ञात किया जा सकता है। समीकरण में ताप एक महत्त्वपूर्ण कारक है। धनात्मक एन्ट्रॉपी परिवर्तनवाली कई अभिक्रियाएं, जो कम ताप पर अस्वतः प्रवर्तित हों, उन्हें उच्च ताप पर स्वतःप्रवर्तित बनाया जा सकता है।
से ज्ञात किया जा सकता है। समीकरण में ताप एक महत्त्वपूर्ण कारक है। धनात्मक एन्ट्रॉपी परिवर्तनवाली कई अभिक्रियाएं, जो कम ताप पर अस्वतः प्रवर्तित हों, उन्हें उच्च ताप पर स्वतःप्रवर्तित बनाया जा सकता है।
अभ्यास
6.1 सही उत्तर चुनिए–
ऊष्मागतिकी अवस्था फलन एक राशि है,
(i) जो ऊष्मा-परिवर्तनों के लिए प्रयुक्त होती है।
(ii) जिसका मान पथ पर निर्भर नहीं करता है।
(iii) जो दाब-आयतन कार्य की गणना करने में प्रयुक्त होती है।
(iv) जिसका मान केवल ताप पर निर्भर करता है।
6.2 एक प्रक्रम के रूद्वोष्म परिस्थितियों में होने के लिए–
(i) ∆T = 0
(ii) ∆p = 0
(iii) q = 0
(iv) w = 0
6.3 सभी तत्त्वों की एन्थैल्पी उनकी संदर्भ-अवस्था में होती है–
(i) इकाई
(ii) शून्य
(iii) < 0
(iv) सभी तत्त्वों के लिए भिन्न होती है।
6.4 मेथेन के दहन के लिए ∆U0 का मान –X kJ mol–1 है। इसके लिए ∆H0 का मान होगा–
(i) = ∆U0
(ii) > ∆U0
(iii) < ∆U0
(iv) = 0
6.5 मेथेन, ग्रैफाइट एवं डाइहाइड्रोजन के लिए 298 K पर दहन एन्थैल्पी के मान क्रमशः –890.3 kJ mol–1, –393.5kJ mol–1 एवं –285.8 kJ mol–1 हैं। CH4(g) की विरचन एन्थैल्पी क्या होगी?
(i) –74.8 kJ mol–1
(ii) –52.27 kJ mol–1
(iii) +74.8 kJ mol–1
(iv) +52.26 kJ mol–1.
6.6 एक अभिक्रिया 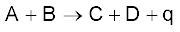 के लिए एन्ट्रॉपी परिवर्तन धनात्मक पाया गया। यह अभिक्रिया संभव होगी–
के लिए एन्ट्रॉपी परिवर्तन धनात्मक पाया गया। यह अभिक्रिया संभव होगी–
(i) उच्च ताप पर
(ii) केवल निम्न ताप पर
(iii) किसी भी ताप पर नहीं
(iv) किसी भी ताप पर
6.7 एक प्रक्रम में निकाय द्वारा 701 J ऊष्मा अवशोषित होती है एवं 394 J कार्य किया जाता है। इस प्रक्रम में आंतरिक ऊर्जा में कितना परिवर्तन होगा?
6.8 एक बम कैलोरीमीटर में NH2CN(s) की अभिक्रिया डाइअॉक्सीजन के साथ की गई एवं ∆U का मान –742.7 KJ mol–1 पाया गया (298 K पर)। इस अभिक्रिया के लिए 298 K पर एन्थैल्पी परिवर्तन ज्ञात कीजिए–
NH2CN(g) + 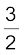 O2(g) → N2(g) + CO2(g) + H2O(l)
O2(g) → N2(g) + CO2(g) + H2O(l)
6.9 60.0 g एेलुमिनियम का ताप 35°C से 55° C करने के लिए कितने किलो जूल ऊष्मा की आवश्यकता होगी? Al की मोलर ऊष्माधारिता 24 J mol–1 K–1 है।
6.10 10.0°C पर 1 मोल जल की बर्फ –10°C पर जमाने पर एन्थैल्पी-परिवर्तन की गणना कीजिए।
∆fusH = 6.03 kJ mol–1 0°C पर,
Cp [H2O(l)] = 75.3 J mol–1 K–1
Cp [H2O(s)] = 36.8 J mol–1 K–1
6.11 CO2 की दहन एन्थैल्पी –393.5 kJ mol–1 है। कार्बन एवं अॉक्सीजन से 35.2 g CO2 बनने पर उत्सर्जित ऊष्मा की गणना कीजिए।
6.12 CO(g), CO2 (g), N2O(g) एवं N2O4(g) की विरचन एन्थैल्पी क्रमशः -110,-393, 81 एवं 9.7 kJ mol–1हैं। अभिक्रिया N2O4(g) + 3CO(g)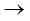 N2O(g) + 3CO2(g) के लिए
N2O(g) + 3CO2(g) के लिए 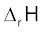 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
6.13 N2(g) + 3H2(g)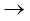 2NH3(g);
2NH3(g); 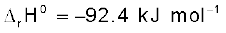 NH3 गैस की मानक विरचन एन्थैल्पी क्या है?
NH3 गैस की मानक विरचन एन्थैल्पी क्या है?
6.14 निम्नलिखित आँकड़ों से CH3OH(l) की मानक-विरचन एन्थैल्पी ज्ञात कीजिए–
CH3OH (l) + 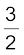 O2(g) → CO2(g) + 2H2O(l) ; ∆rH0 = –726 kJ mol–1
O2(g) → CO2(g) + 2H2O(l) ; ∆rH0 = –726 kJ mol–1
C(ग्रैफाइट) + O2(g) → CO2(g) ; ∆cH0 = –393 kJ mol–1
H2(g) + 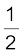 O2(g) → H2O(l) ; ∆f H0 = –286 kJ mol–1.
O2(g) → H2O(l) ; ∆f H0 = –286 kJ mol–1.
6.15 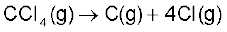 अभिक्रिया के लिए एन्थैल्पी-परिवर्तन ज्ञात कीजिए एवं
अभिक्रिया के लिए एन्थैल्पी-परिवर्तन ज्ञात कीजिए एवं 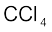 में C – Cl की आबंध एन्थैल्पी की गणना कीजिए–
में C – Cl की आबंध एन्थैल्पी की गणना कीजिए–
∆vapH0(CCl4) = 30.5 kJ mol–1.
∆fH0 (CCl4) = –135.5 kJ mol–1.
∆aH0 (C) = 715.0 kJ mol–1 , यहाँ ∆aH0 कणन एन्थैल्पी है।
∆aH0 (Cl2) = 242 kJ mol–1
6.16 एक विलगित निकाय के लिए ∆U = 0, इसके लिए ∆S क्या होगा?
6.17 298 K पर अभिक्रिया 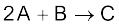 के लिए
के लिए
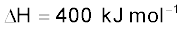 एवं
एवं 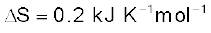
 एवं
एवं 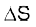 को ताप-विस्तार में स्थिर मानते हुए बताइए कि किस ताप पर अभिक्रिया स्वतः होगी?
को ताप-विस्तार में स्थिर मानते हुए बताइए कि किस ताप पर अभिक्रिया स्वतः होगी?
6.18 अभिक्रिया 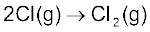 के लिए ∆H एवं ΟSQ के चिह्न क्या होंगे?
के लिए ∆H एवं ΟSQ के चिह्न क्या होंगे?
6.19 अभिक्रिया 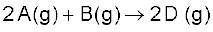 के लिए
के लिए 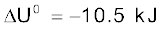 एवं
एवं 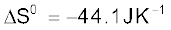 अभिक्रिया के लिए
अभिक्रिया के लिए 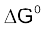 की गणना कीजिए और बताइए कि क्या अभिक्रिया स्वतः प्रवर्तित हो
की गणना कीजिए और बताइए कि क्या अभिक्रिया स्वतः प्रवर्तित हो
सकती है?
6.20 300 पर एक अभिक्रिया के लिए साम्य स्थिरांक 10 है। ∆G0 का मान क्या होगा?
R = 8.314 JK–1 mol–1
6.21 निम्नलिखित अभिक्रियाओं के आधार पर 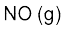 के ऊष्मागतिकी स्थायित्व पर टिप्पणी कीजिए–
के ऊष्मागतिकी स्थायित्व पर टिप्पणी कीजिए–
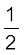 N2(g) +
N2(g) + 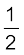 O2(g) → NO(g); ∆rH0 = 90 kJ mol–1
O2(g) → NO(g); ∆rH0 = 90 kJ mol–1
NO(g) + 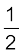 O2(g) → NO2(g): ∆rH0= –74 kJ mol–1
O2(g) → NO2(g): ∆rH0= –74 kJ mol–1
6.22 जब 1.00 मोल H2O(l) को मानक परिस्थितियों में विरचित जाता है, तब परिवेश के एन्ट्रॉपी-परिवर्तन की गणना कीजिए–