Table of Contents
समुच्चय (Sets)
"In these days of conflict between ancient and modern studies; there must purely be something to be said for a study which did not begin with Pythagoras and will not end with Einstein; but is the oldest and the youngest — G.H.Hardy "
1.1 भूमिका (Introduction)

वर्तमान समय में गणित के अध्ययन में समुच्चय की परिकल्पना आधारभूत है। आजकल इस परिकल्पना का प्रयोग गणित की प्रायः सभी शाखाओं में होता है। समुच्चय का प्रयोग संबंध एवं फलन को परिभाषित करने के लिए किया जाता है। ज्यामितीय, अनुक्रम, प्रायिकता आदि के अध्ययन में समुच्चय के ज्ञान की आवश्यकता पड़ती है।
समुच्चय सिद्धांत का विकास जर्मन गणितज्ञ Georg Cantor (1845-1918) द्वारा किया गया था। त्रिकोणमितीय श्रेणी के प्रश्नों को सरल करते समय उनका समुच्चय से पहली बार परिचय हुआ था। इस अध्याय में हम समुच्चय से संबंधित कुछ मूलभूत परिभाषाओं और संक्रियाओं पर विचार करेंगे।
1.2 समुच्चय और उनका निरूपण (Sets and their Representations)
दैनिक जीवन में हम बहुधा वस्तुओं के संग्रह की चर्चा करते हैं, जैसे ताश की गड्डी, व्यक्तियों की भीड़, क्रिकेट टीम आदि। गणित में भी हम विभिन्न संग्रहों, की चर्चा करते हैं, उदाहरणार्थ, प्राकृत संख्याओं का संग्रह बिंदुओं का संग्रह, अभाज्य संख्याओं का संग्रह आदि। विशेषतः, हम निम्नलिखित संग्रह पर विचार करेंगेः
(i) 10 से कम विषम प्राकृत संख्याएँ, अर्थात् 1, 3, 5, 7, 9
(ii) भारत की नदियाँ,
(iii) अंग्रेज़ी वर्णमाला के स्वर, यानी, a, e, i, o, u,
(iv) विभिन्न प्रकार के त्रिभुज,
(v) संख्या 210 के अभाज्य गुणनखंड, अर्थात्, 2, 3, 5 तथा 7,
(vi) समीकरण x2 – 5x + 6 = 0, के मूल अर्थात्, 2 तथा 3
यहाँ हम यह देखते हैं कि उपर्युक्त प्रत्येक उदाहरणों में से वस्तुओं का एक सुपरिभाषित संग्रह इस अर्थ में है कि किसी वस्तु के संबंध में हम यह निर्णय निश्चित रूप से ले सकते हैं कि वह वस्तु एक प्रदत्त संग्रह में है अथवा नहीं है। उदाहरणतः हम यह निश्चित रूप से कह सकते हैं कि ‘नील नदी’, भारत की नदियों के संग्रह में नहीं है। इसके विपरीत गंगा नदी इस संग्रह में निश्चितरूप से है।
हम नीचे एेसे समुच्चय के कुछ और उदाहरण दे रहे हैं, जिनका प्रयोग गणित में विशेषरूप से किया जाता है;
N : प्राकृत संख्याओं का समुच्चय
ρ रू पूर्णांकों का समुच्चय
η रू परिमेय संख्याओं का समुच्चय
त् रू वास्तविक संख्याओं का समुच्चय
Z+ : धन पूर्णांकों का समुच्चय
Q+ : धन परिमेय संख्याओं का समुच्चय
R+ : धन वास्तविक संख्याओं का समुच्चय
इन विशेष समुच्चयों के लिए निर्धारित उपर्युक्त प्रतीकों का प्रयोग हम इस पुस्तक में निरंतर करते रहेंगे।
इसके अतिरिक्त विश्व के पाँच सर्वाधिक विख्यात गणितज्ञों का संग्रह एक सुपरिभाषित समुच्चय नहीं है, क्योंकि सर्वाधिक विख्यात गणितज्ञों के निर्णय करने का मापदंड एक व्यक्ति से दूसरे व्यक्ति के लिए भिन्न-भिन्न हो सकता है। अतः यह एक सुपरिभाषित संग्रह नहीं है।
अतः ‘वस्तुओं के सुपरिभाषित संग्रह’ को हम एक समुच्चय कहते हैं। यहाँ पर हमें निम्नलिखित बिंदुओं पर ध्यान देना हैः
(i) समुच्यय के लिए वस्तुएँ, अवयव तथा सदस्य पर्यायवाची पद हैं।
(ii) समुच्यय को प्रायः अंग्रेज़ी वर्णमाला के बड़े अक्षरों से निरूपित करते हैं, जैसे A, B, C, X, Y, Z आदि
(iii) समुच्चय के अवयवों को अंग्रेज़ी वर्णमाला के छोटे अक्षरों द्वारा प्रदर्शित करते हैं, जैसे a, b, c, x, y, z आदि
यदि a, समुच्चय A का एक अवयव है, तो हम कहते हैं कि ‘a समुच्चय A में है’। वाक्यांश ‘अवयव है’ ‘सदस्य है’ या ‘में है’ को सूचित करने के लिए यूनानी प्रतीक ‘‘∈ (epsilon)’’ का प्रयोग किया जाता है। अतः हम ‘a ∈ A’ लिखते हैं। यदि b, समुच्चय A का अवयव नहीं है, तो हम ‘b ∉ A’ लिखते हैं और इसे ‘‘b समुच्चय A में नहीं है’’ पढ़ते हैं।
इस प्रकार अंग्रेज़ी वर्णमाला के स्वरों के समुच्चय V के सम्बंध में a ∈ V किंतु b ∉ V. इसी प्रकार संख्या 30 के अभाज्य गुणनखंडों के समुच्चय P के लिए, 3 ∈ P किंतु 15 ∉ P.
किसी समुच्चय को निरूपित करने की दो विधियाँ हैंः
(i) रोस्टर या सारणीबद्ध रूप
(ii) समुच्चय निर्माण रूप
(i) रोस्टर रूप में, समुच्चय के सभी अवयवों को सूचीबद्ध किया जाता है, अवयवों को, एक दूसरे से, अर्ध-विराम द्वारा पृथक किया जाता है और उन सभी को एक मझले कोष्ठक के भीतर लिखते हैं। उदाहरणार्थ, 7 से कम सभी सम धन पूर्णांकों के समुच्चय का वर्णन रोस्टर रूप में {2, 4, 6} द्वारा किया जाता है। किसी समुच्चय को रोस्टर रूप में प्रदर्शित करने के कुछ और उदाहरण नीचे दिए हैंः
(a) संख्या 42 को विभाजित करने वाली सभी प्राकृत संख्याओं का समुच्चय {1, 2, 3, 6, 7, 14, 21, 42} है।
(b) अंग्रेज़ी वर्णमाला के सभी स्वरों का समुच्चय {a, e, i, o, u} है।
(c) विषम प्राकृत संख्याओं का समुच्चय {1, 3, 5, . . .} है। अंत के बिंदु, जिनकी संख्या तीन होती है, यह बतलाते हैं कि इन विषम संख्याओं की सूची अंतहीन है।
नोट कीजिए कि रोस्टर रूप में अवयवों को सूचीबद्ध करने में उनके क्रम का महत्व नहीं होता है। इस प्रकार उपर्युक्त समुच्चय को {1, 3, 7, 21, 2, 6, 14, 42}प्रकार भी प्रदर्शित कर सकते हैं।
टिप्पणी यह ध्यान रखना चाहिए कि समुच्चय को रोस्टर रूप में लिखते समय किसी अवयव को सामान्यतः दोबारा नहीं लिखते हैं, अर्थात्, प्रत्येक अवयव दूसरे से भिन्न होता है। उदाहरण के लिए शब्द ‘School’ में प्रयुक्त अक्षरों का समुच्चय { S, C, H, O, L} है।
(ii) समुच्चय निर्माण रूप में, किसी समुच्चय के सभी अवयवों में एक सर्वनिष्ठ गुणधर्म होता है जो समुच्चय से बाहर के किसी अवयव में नहीं होता है। उदाहरर्णाथ समुच्चय {a, e, i, o, u} के सभी अवयवों में एक सर्वनिष्ठ गुणधर्म है कि इनमें से प्रत्येक अवयव अंग्रेज़ी वर्णमाला का एक स्वर है और इस गुणधर्म वाला कोई अन्य अक्षर नहीं है।
इस समुच्चय को V से निरूपित करते हुए हम लिखते हैं कि,
V = {x : x अंग्रेज़ी वर्णमाला का एक स्वर है}।
यहाँ ध्यान देना चाहिए कि किसी समुच्चय के अवयवों का वर्णन करने के लिए हम प्रतीक ‘x’ का प्रयोग करते हैं, (x के स्थान पर किसी अन्य प्रतीक का भी प्रयोग किया जा सकता है, जैसे, अक्षर y, z आदि।) जिसके उपरांत कोलन का चिह्न "ः" लिखते हैं। कोलन के चिह्न के बाद समुच्चय के अवयवों के विशिष्ट गुणधर्म को लिखते हैं और फिर संपूर्ण कथन को मझले कोष्ठक { } के भीतर लिखते हैं। समुच्चय V के उपर्युक्त वर्णन को निम्नलिखित प्रकार से पढ़ा जाता है, "सभी x का समुच्चय जहाँ x अंग्रेज़ी वर्णमाला का एक स्वर है।"
इस वर्णन में कोष्ठक का प्रयोग "सभी x का समुच्चय" के लिए और कोलन का प्रयोग ‘जहाँ x’ के लिए किया जाता है। उदाहरण के लिए
A = {x : x एक प्राकृत संख्या है और 3 < x < 10} को निम्नलिखित प्रकार से पढ़ते हैं:
‘‘सभी x का समुच्चय, जहाँ x एक प्राकृत संख्या है और x,3 और 10 के बीच में हैं। अतः संख्याएं 4,5,6,7,8 और 9 समुच्चय A के अवयव हैं।
यदि हम ऊपर (a), (b) और (c) में रोस्टर रूप में वर्णित समुच्चयों को क्रमशः A, B, C से प्रकट करें, तो A, B और C को समुच्चय निर्माण रूप में, निम्नलिखित प्रकार से भी निरूपित किया जा सकता है।
A = {x : x एक प्राकृत संख्या है जो संख्या 42 को विभाजित करती है}
B = {y : y अंग्रेज़ी वर्णमाला का एक स्वर है}
C = {z : z एक विषम प्राकृत संख्या है}
उदाहरण 1 समीकरण x2 + x – 2 = 0 का हल समुच्चय रोस्टर रूप में लिखिए।
हल प्रदत्त समीकरण इस प्रकार लिखा जा सकता है,
(x – 1) (x + 2) = 0, अर्थात् x = 1, – 2
अतः प्रदत्त समीकरण का हल समुच्चय रोस्टर रूप में इस प्रकार लिखा जा सकता है {1, – 2}.
उदाहरण 2 समुच्चय {x : x एक धन पूर्णांक है और x2 < 40} को रोस्टर रूप में लिखिए।
हल 1, 2, 3, 4, 5, और 6 अभीष्ट संख्याएँ हैं। अतः {1, 2, 3, 4, 5, 6} प्रदत्त समुच्चय का रोस्टर रूप है।
उदाहरण 3 समुच्चय A = {1, 4, 9, 16, 25, . . . } को समुच्चय निर्माण रूप में लिखिए।
हल समुच्चय A को हम इस प्रकार लिख सकते हैं,
A = {x : x एक प्राकृत संख्या का वर्ग है}
विकल्पतः हम इस प्रकार भी लिख सकते हैं,
A = {x : x = n2, जहाँ n ∈ N}
उदाहरण 4 समुच्चय 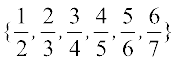 को समुच्चय निर्माण रूप में लिखिए।
को समुच्चय निर्माण रूप में लिखिए।
हल हम देखते हैं कि दिए गए समुच्चय के प्रत्येक अवयव का अंश उसके हर से 1 कम है। यह भी कि अंश एक प्राकृत संख्या है जो 1 से प्रारंभ होकर उत्तरोत्तर एक से अधिक होती जाती है और 6 से अधिक नहीं है। अतः समुच्चय निर्माण रूप में इसे इस प्रकार लिखते हैं,
{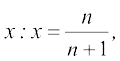 n, एक प्राकृत संख्या है और 1 ≤ n ≤ 6}
n, एक प्राकृत संख्या है और 1 ≤ n ≤ 6}
उदाहरण 5 बाईं ओर रोस्टर रूप में वर्णित प्रत्येक समुच्चय का दाईं ओर समुच्चय निर्माण रूप में वर्णित समुच्चय से सही मिलान कीजिएः
(i) {P, R, I, N, C, A, L} (a) { x : x एक धन पूर्णांक है तथा 18 का भाजक है}
(ii) { 0 } (b) { x : x एक पूर्णांक है और x2 – 9 = 0}
(iii) {1, 2, 3, 6, 9, 18} (c) {x : x एक पूर्णांक है और x + 1= 1}
(iv) {3, –3} (d) {x : x शब्द PRINCIPAL का एक अक्षर है}
हल चूँकि (d) में, शब्द PRINCIPAL में 9 अक्षर हैं और दो अक्षर P और I की पुनरावृत्ति हुई है, अतः (i) का सही मिलान (d) से होता है। इसी प्रकार (ii) का सही मिलान (c) से होता है, क्योंकि x + 1 = 1 का तात्पर्य है कि x = 0. यह भी कि, 1, 2, 3, 6, 9 और 18 में से प्रत्येक 18 का भाजक है, इसलिए (iii) का सही मिलान (a) से होता है। अंत में x2 – 9 = 0 अर्थात् x = 3, –3 और इसलिए (iv) का सही मिलान (b) से होता है।
प्रश्नावली 1.1
1. निम्नलिखित में कौन से समुच्चय हैं? अपने उत्तर का औचित्य बताइए।
(i) J अक्षर से प्रारंभ होने वाले वर्ष के सभी महीनों का संग्रह।
(ii) भारत के दस सबसे अधिक प्रतिभाशाली लेखकों का संग्रह।
(iii) विश्व के सर्वश्रेष्ठ ग्यारह बल्लेवाजों का संग्रह।
(iv) आपकी कक्षा के सभी बालकों का संग्रह।
(v) 100 से कम सभी प्राकृत संख्याओं का संग्रह।
(vi) लेखक प्रेमचंद द्वारा लिखित उपन्यासों का संग्रह।
(vii) सभी सम पूर्णांकों का संग्रह।
(viii) इस अध्याय में आने वाले प्रश्नों का संग्रह।
(ix) विश्व के सबसे अधिक खतरनाक जानवरों का संग्रह।
2. मान लीजिए A = {1, 2, 3, 4, 5, 6}, रिक्त स्थानों में उपयुक्त प्रतीक ∈ अथवा ∉ भरिए।
(i) 5. . .A (ii) 8 . . . A (iii) 0. . .A
(iv) 4. . . A (v) 2. . .A (vi) 10. . .A
3. निम्नलिखित समुच्चयों को रोस्टर रूप में लिखिएः
(i) A = {x : x एक पूर्णांक है और –3 < x < 7}
(ii) B = {x : x संख्या 6 से कम एक प्राकृत संख्या है}
(iii) C = {x : x दो अंकों की एेसी प्राकृत संख्या है जिसके अंकों का योगफल 8 है}
(iv) D = {x : x एक अभाज्य संख्या है जो संख्या 60 की भाजक है}
(v) E = TRIGONOMETRY शब्द के सभी अक्षरों का समुच्चय
(vi) F = BETTER शब्द के सभी अक्ष्ारों का समुच्चय
4. निम्नलिखित समुच्चयों को समुच्चय निर्माण रूप में व्यक्त कीजिएः
(i) (3, 6, 9, 12} (ii) {2,4,8,16,32} (iii) {5, 25, 125, 625}
(iv) {2, 4, 6, . . .} (v) {1,4,9, . . .,100}
5. निम्नलिखित समुच्चयों के सभी अवयवों (सदस्यों) को सूचीबद्ध कीजिएः
(i) A = {x : x एक विषम प्राकृत संख्या है}
(ii) B = {x : x एक पूर्णांक है, 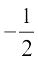 < x <
< x < }
}
(iii) C = {x : x एक पूर्णांक है, x2 ≤ 4}
(iv) D = {x : x, LOYAL शब्द का एक अक्षर है}
(v) E = {x : x वर्ष का एक एेसा महीना है, जिसमें 31 दिन नहीं होते हैं}
(vi) F = {x : x अंग्रेज़ी वर्णमाला का एक व्यंजन है, जो k से पहले आता है}।
6. बाईं ओर रोस्टर रूप में लिखित और दाईं ओर समुच्चय निर्माण रूप में वर्णित समुच्चयों का सही मिलान कीजिएः
(i) {1, 2, 3, 6} (a) {x : x एक अभाज्य संख्या है और 6 की भाजक है}
(ii) {2, 3} (b) {x : x संख्या 10 से कम एक विषम प्राकृत संख्या है}
(iii) {M,A,T,H,E,I,C,S} (c) {x : x एक प्राकृत संख्या है और 6 की भाजक है}
(iv) {1, 3, 5, 7, 9} (d) {x : x MATHEMATICS शब्द का एक अक्षर है}।
1.3 रिक्त समुच्चय (The Empty Set)
समुच्चय A = { x : x किसी स्कूल की कक्षा XI में अध्ययनरत एक विद्यार्थी है }
हम उस स्कूल में जा कर कक्षा XI में अध्ययनरत विद्यार्थियों को गिन कर उनकी संख्या ज्ञात कर सकते हैं। अतः समुच्चय A के अवयवयों की संख्या सीमित है।
अब नीचे लिखे समुच्चय B पर विचार कीजिएः
B = { x : x वर्तमान में कक्षा X तथा XI दोनों में अध्ययनरत विद्यार्थी हैं}
हम देखते हैं कि एक विद्यार्थी एक साथ दोनों कक्षाओं X तथा XI में अध्ययन नहीं कर सकता है। अतः समुच्चय B में कोई भी अवयव नहीं है।
परिभाषा 1 एक समुच्चय जिसमें एक भी अवयव नहीं होता है, εरक्त समुच्चय या शून्य समुच्चय कहलाता है। इस परिभाषा के अनुसार B एक रिक्त समुच्चय है जब कि A एक रिक्त समुच्चय नहीं है। रिक्त समुच्चय को प्रतीक φ अथवा { } से प्रदर्शित करते हैं।
हम नीचे रिक्त समुच्चयों के कुछ उदाहरण दे रहे हैंः
(i) मान लीजिए कि A = {x : 1 < x < 2, x एक प्राकृत संख्या है}.यहाँ A रिक्त समुच्चय है, क्योंकि 1 और 2 के मध्य कोई प्राकृत संख्या नहीं होती है।
(ii) B = {x : x2 – 2 = 0 और x एक परिमेय संख्या है}. यहाँ B रिक्त समुच्चय है, क्योंकि समीकरण x2 – 2 = 0, x के किसी भी परिमेय मान से संतुष्ट नहीं होता है।
(iii) C = {x : x संख्या 2 से अधिक एक सम अभाज्य संख्या है} तो C रिक्त समुच्चय है, क्योंकि केवल संख्या 2 ही सम अभाज्य संख्या है।
(iv) D = { x : x2 = 4, x विषम है}. तो D रिक्त समुच्चय है, क्योंकि समीकरण
x2 = 4, x के किसी विषम मान से संतुष्ट नहीं होता है।
1.4 परिमित और अपरिमित समुच्चय (Finite and Infinite Sets)
मान लीजिए कि A = {1, 2, 3, 4, 5}, B = {a, b, c, d, e, g}
तथा C = { इस समय विश्व के विभिन्न भागों में रहने वाले पुरुष}
हम देखते हैं कि A में 5 अवयव हैं और B में 6 अवयव हैं। C में कितने अवयव हैं? जैसा कि स्पष्ट है कि C के अवयवों की संख्या हमें ज्ञात नहीं है, किंतु यह एक प्राकृत संख्या है, जो बहुत बड़ी हो सकती है। किसी समुच्चय S के अवयवों की संख्या से हमारा अभिप्राय समुच्चय के भिन्न अवयवों की संख्या से है और इसे हम प्रतीक n (S) द्वारा प्रदर्शित करते हैं। यदि n (S) एक प्राकृत संख्या है, तो S एक आरिक्त परिमित समुच्चय होता है।
आइए प्राकृत संख्याओं के समुच्चय N पर विचार करें। हम देखते हैं इस समुच्चय के अवयवों की संख्या सीमित नहीं है, क्योंकि प्राकृत संख्याओं की संख्या असीमित होती है। इस प्रकार हम कहते हैं कि प्राकृत संख्याओं का समुच्चय एक अपरिमित समुच्चय होता है। उपर्युक्त समुच्चय A, B तथा C परिमित समुच्चय हैं और n(A) = 5, n(B) = 5 और n(C) = कोई सीमित संख्या।
परिभाषा 2 एक समुच्चय, जो रिक्त है अथवा जिसके अवयवों की संख्या निश्चित होती है, परिमित समुच्चय कहलाता है, अन्यथा समुच्चय अपरिमित समुच्चय कहलाता है।
आइए कुछ उदाहरणों पर विचार करेंः
(i) यदि W सप्ताह के दिनों का समुच्चय है, तो W परिमित है।
(ii) मान लीजिए कि S, समीकरण x2 –16 = 0 के हलों का समुच्चय है, तो S परिमित है।
(iii) मान लीजिए कि G, किसी रेखा पर स्थित सभी बिंदुओं का समुच्चय है, तो G
अपरिमित है।
जब हम किसी समुच्चय को रोस्टर रूप में निरूपित करते हैं, तो हम उस समुच्चय के सभी अवयवों को कोष्ठक { } के भीतर लिखते हैं। किसी अपरिमित समुच्चय के सभी अवयवों को कोष्ठक { } के भीतर लिखना संभव नहीं है, क्योंकि एेसे समुच्चय के अवयवों की संख्या सीमित नहीं होती है। अतः हम किसी अपरिमित समुच्चय को रोस्टर रूप में प्रकट करने के लिए उसके कम से कम इतने अवयवों को लिखते है, जिससे उस समुच्चय की संरचना स्पष्ट हो सके और तदोपरांत तीन बिंदु लगाते हैं।
उदाहरणार्थ, {1, 2, 3 . . .} प्राकृत संख्याओं का समुच्चय है, {1, 3, 5, 7, . . .} विषम प्राकृत संख्याओं का समुच्चय है और {. . .,–3, –2, –1, 0,1, 2 ,3, . . .} पूर्णांकों का समुच्चय है। ये सभी समुच्चय अपरिमित हैं।
टिप्पणी सभी अपरिमित समुच्चय का वर्णन रोस्टर रूप में नहीं किया जा सकता है। उदाहरण के लिए वास्तविक संख्याओं के समुच्चय का वर्णन इस रूप में नहीं किया जा सकता है, क्योंकि इस समुच्चय के अवयवों का कोई विशेष पैटर्न (प्रतिमान) नहीं होता है।
उदाहरण 6 बतलाइए कि निम्नलिखित समुच्चयों में कौन परिमित है और कौन अपरिमित हैः
(i) {x : x ∈ N और (x – 1) (x –2) = 0}
(ii) {x : x ∈ N और x2 = 4}
(iii) {x : x ∈ N और 2x –1 = 0}
(iv) {x : x ∈ N और x एक अभाज्य संख्या है}
(v) {x : x ∈ N और x विषम है}
हल (i) प्रदत्त समुच्चय = {1, 2}. अतः यह परिमित है।
(ii) प्रदत्त समुच्चय = {2}. अतः यह परिमित है।
(iii) प्रदत्त समुच्चय = φ. अतः यह परिमित है।
(iv) दिया हुआ समुच्चय सभी अभाज्य संख्याओं का समुच्चय है और क्योंकि अभाज्य संख्याओं का समुच्चय अनंत है; अतः प्रदत्त समुच्चय अपरिमित है।
(v) क्योंकि विषम प्राकृत संख्याएँ अनंत हैं, अतः प्रदत्त समुच्चय अपरिमित है।
1.5 समान समुच्चय (Equal Sets)
दो दिए गए समुच्चयों A और B, में, यदि A का प्रत्येक अवयव B का भी अवयव है तथा B का प्रत्येक अवयव A का भी अवयव है, तो समुच्चय A और B, समान कहलाते हैं। स्पष्टतया दोनों समुच्चयों में तथ्यतः समान अवयव होते हैं।
परिभाषा 3 दो समुच्चय A और B समान कहलाते हैं, यदि उनमें तथ्यतः समान अवयव हों और हम लिखते हैं A = B, अन्यथा समुच्चय असमान कहलाते हैं और हम लिखते हैं A ≠ B.
आइए हम निम्नलिखित उदाहरणों पर विचार करेंः
(i) मान लीजिए कि A = {1, 2, 3, 4} और B = {3, 1, 4, 2}. तो A = B.
(ii) मान लीजिए कि A, 6 से कम अभाज्य संख्याओं तथा P, 30 के अभाज्य गुणनखंडों के समुच्चय हैं। स्पष्ट है कि समुच्चय A और P समान हैं, क्योंकि केवल 2, 3 और 5 ही संख्या 30 के अभाज्य गुणनखंड हैं और 6 से कम भी हैं।
टिप्पणी यदि किसी समुच्चय के एक या एक से अधिक अवयवों की पुनरावृत्ति होती है, तो समुच्चय बदलता नहीं है। उदाहरण के लिए समुच्चय A = {1, 2, 3} और B = {2, 2, 1, 3, 3} समान हैं, क्योंकि A का प्रत्येक अवयव B में हैं और इसका विलोम भी सत्य है। इसी कारण हम प्रायः किसी समुच्चय का वर्णन करते समय उसके अवयवों की पुनरावृत्ति नहीं करते हैं।
उदाहरण 7 समान समुच्चयों के युग्म छाँटिए, यदि एेसा कोई युग्म है, और कारण भी बतलाइएः
A = {0}, B = {x : x > 15 और x < 5},
C = {x : x – 5 = 0 }, D = {x : x2 = 25},
E = {x : x समीकरण x2 – 2x –15 = 0 का एक धन पूर्णांक मूल है}.
हल यहाँ 0 ∈ A और 0 समुच्चयों B, C, D और E, में से किसी में भी नहीं है, अतः A ≠ B, A ≠ C, A ≠ D, A ≠ E.
क्योंकि B = φ किंतु और कोई समुच्चय रिक्त नहीं है।
अतः B ≠ C, B ≠ D तथा B ≠ E.
C = {5} परंतु –5 ∈ D, इसलिए C ≠ D
यहाँ क्योंकि E = {5}, C = E , D = {–5, 5} और E = {5}, अतः D ≠ E.
इस प्रकार समान समुच्चयों का युग्म केवल C तथा E है।
उदाहरण 8 निम्नलिखित समुच्चय युग्मों में से कौन से समान हैं? अपने उत्तर का औचित्य बताइए।
(i) X, शब्द “ALLOY” के अक्षरों का समुच्चय तथा B, शब्द “LOYAL” के अक्षरों का समुच्चय।
(ii) A = {n : n ∈ Z तथा n2 ≤ 4} और B = {x : x ∈ R तथा x2 – 3x + 2 = 0}.
हल (i) यहाँ X = {A, L, L, O, Y}, B = {L, O, Y, A, L}. अतः X और B समान समुच्चय हैं, क्योंकि किसी समुच्चय के अवयवों की पुनरावृत्ति से समुच्चय बदलता नहीं है। अतः
X = {A, L, O, Y} = B
(ii) A = {–2, –1, 0, 1, 2}, B = {1, 2}. क्योंकि 0 ∈ A और 0 ∉ B, इसलिए A और B समान नहीं हैं।
प्रश्नावली 1.2
1. निम्नलिखित में से कौन से रिक्त समुच्चय के उदाहरण हैं?
(i) 2 से भाज्य विषम प्राकृत संख्याओं का समुच्चय।
(ii) सम अभाज्य संख्याओं का समुच्चय।
(iii) { x : x एक प्राकृत संख्या है, x < 5 और साथ ही साथ x > 7 }
(iv) { y : y किन्हीं भी दो समांतर रेखाओं का उभयनिष्ठ बिंदु है}
2. निम्नलिखित समुच्चयों में से कौन परिमित और कौन अपरिमित हैं?
(i) वर्ष के महीनों का समुच्चय।
(ii) {1, 2, 3, . . .}
(iii) {1, 2, 3, . . .99, 100}
(iv) 100 से बड़े धन पूर्णांकों का समुच्चय।
(v) 99 से छोटे अभाज्य पूर्णांकों का समुच्चय।
3. निम्नलिखित समुच्चयों में से प्रत्येक के लिए बताइए कि कौन परिमित है और कौन अपरिमित है?
(i) x-अक्ष के समांतर रेखाओं का समुच्चय।
(ii) अंग्रेज़ी वर्णमाला के अक्षरों का समुच्चय।
(iii) उन संख्याओं का समुच्चय जो 5 के गुणज हैं।
(iv) पृथ्वी पर रहने वाले जानवरों का समुच्चय।
(v) मूल बिंदु (0,0) से हो कर जाने वाले वृत्तों का समुच्चय।
4. निम्नलिखित में बतलाइए कि A = B है अथवा नहीं हैः
(i) A = { a, b, c, d } B = { d, c, b, a }
(ii) A = { 4, 8, 12, 16 } B = { 8, 4, 16, 18}
(iii) A = {2, 4, 6, 8, 10} B = { x : x सम धन पूर्णांक है और x ≤ 10}
(iv) A = {x : x संख्या 10 का एक गुणज है}, B = { 10, 15, 20, 25, 30, . . . }
5. क्या निम्नलिखित समुच्चय युग्म समान हैं? कारण सहित बताइए।
(i) A = {2, 3}, B = {x : x समीकरण x2 + 5x + 6 = 0 का एक हल है}
(ii) A = { x : x शब्द ‘FOLLOW’ का एक अक्षर है}
B = { y : y शब्द ‘WOLF’ का एक अक्षर है}
6. नीचे दिए हुए समुच्चयों में से समान समुच्चयों का चयन कीजिएः
A = { 2, 4, 8, 12}, B = { 1, 2, 3, 4}, C = { 4, 8, 12, 14}, D = { 3, 1, 4, 2},
E = {–1, 1}, F = { 0, a}, G = {1, –1}, H = { 0, 1}
1.6 उपसमुच्चय (Subsets)
नीचे दिए समुच्चयों पर विचार कीजिएः
X = आपके विद्यालय के सभी विद्यार्थियों का समुच्चय,
Y = आपकी कक्षा के सभी विद्यार्थियों का समुच्चय।
हम देखते हैं कि Y का प्रत्येक अवयव, X का भी एक अवयव है, हम कहते हैं कि Y, X का एक उपसमुच्चय हैं X का एक उपसमुच्चय है, प्रतीकों में X ⊂ Y द्वारा प्रकट करते हैं। प्रतीक ⊂ , कथन ‘एक उपसमुच्चय है’, अथवा ‘अंतर्विष्ट है’ के लिए प्रयुक्त होता है।
परिभाषा 4 यदि समुच्चय A का प्रत्येक अवयव, समुच्चय B का भी एक अवयव है, तो A, B का उपसमुच्चय कहलाता है।
दूसरे शब्दों में, A ⊂ B, यदि जब कभी a ∈ A, तो a ∈ B. बहुधा प्रतीक ‘⇒’, जिसका अर्थ ‘तात्पर्य है’ होता है, का प्रयोग सुविधाजनक होता है। इस प्रतीक का प्रयोग कर के, हम उपसमुच्चय की परिभाषा इस प्रकार लिख सकते हैंः
A ⊂ B, यदि a ∈ A ⇒ a ∈ B
हम उपर्युक्त कथन को इस प्रकार पढ़ते हैं, “A, B का एक उपसमुच्चय है, यदि इस तथ्य का, कि a, A का एक अवयव है तात्पर्य है कि a, B का भी एक अवयव है’’। यदि A, B का एक उपसमुच्चय नहीं है, तो हम लिखते हैं कि A ⊄ B ।
हमें ध्यान देना चाहिए कि A को B, का समुच्चय होने के लिए केवल मात्र यह आवश्यक है कि A का प्रत्येक अवयव B में है। यह संभव है कि B का प्रत्येक अवयव A में हो या न हो। यदि एेसा होता है कि B का प्रत्येक अवयव A में भी है, तो B ⊂ A. इस दशा में, A और B समान समुच्चय हैं और इस प्रकार A ⊂ B और B ⊂ A ⇔ A = B, जहाँ ‘⇔’ द्विधा तात्पर्य (two way implications) के लिए प्रतीक है और जिसे प्रायः ‘यदि और केवल यदि’ पढ़ते हैं तथा संक्षेप में ‘iff’ लिखते हैं।
परिभाषा से निष्कर्ष निकलता है कि प्रत्येक समुच्चय स्वयम् का उपसमुच्चय है, अर्थात्
A ⊂ A । चूँकि रिक्त समुच्चय φ में कोई अवयव नहीं होता है अतः हम इस बात से सहमत हैं कि φ प्रत्येक समुच्चय का एक उपसमुच्चय है। अब हम कुछ उदाहरणों पर विचार करते हैंः
(i) परिमेय संख्याओं का समुच्चय Q, वास्तविक संख्याओं के समुच्चय R का एक उपसमुच्चय है और हम लिखते हैं कि Q ⊂ R.
(ii) यदि A, संख्या 56 के सभी भाजकों का समुच्चय है और B, संख्या 56 के सभी अभाज्य भाजकों का समुच्चय है, तो B, A का एक उपसमुच्चय है और हम लिखते हैं कि B ⊂ A.
(iii) मान लीजिए कि A = {1, 3, 5} और B = {x : x संख्या 6 से कम एक विषम प्राकृत संख्या है} तो A ⊂ B तथा B ⊂ A, अतः A = B
(iv) मान लीजिए कि A = { a, e, i, o, u} और B = { a, b, c, d}. तो A, B का एक उपसमुच्चय नहीं है तथा B भी A का उपसमुच्चय नहीं है।
मान लीजिए कि A और B दो समुच्चय हैं। यदि A ⊂ B तथा A ≠ B , तो A, B का उचित उपसमुच्चय कहलाता है और B, A का अधिसमुच्चय कहलाता है। उदाहरणार्थ, -
A = {1, 2, 3}, B = {1, 2, 3, 4} का एक उचित उपसमुच्चय है।
यदि समुच्चय A में केवल एक अवयव हो, तो हम इसे एक एकल समुच्चय कहते हैं। अतः { a } एक एकल समुच्चय है।
उदाहरण 9 नीचे लिखे समुच्चयों पर विचार कीजिएः
φ, A = { 1, 3 }, B = {1, 5, 9}, C = {1, 3, 5, 7, 9}.
प्रत्येक समुच्चय युग्म के बीच सही प्रतीक ⊂ अथवा ⊄ भरिए;
(i) φ . . . B (ii) A . . . B (iii) A . . . C (iv) B . . . C
हल (i) φ ⊂ B, क्योंकि φ प्रत्येक समुच्चय का उपसमुच्चय होता है।
(ii) A ⊄ B क्योंकि 3 ∈ A और 3 ∉ B
(iii) A ⊂ C क्योंकि 1, 3 ∈ A तथा 1, 3 ∈ C
(iv) B ⊂ C क्योंकि B का प्रत्येक अवयव C में भी है।
उदाहरण 10 मान लीजिए A = { a, e, i, o, u}, B = { a, b, c, d}. क्या A, B का एक उपसमुच्चय है? नहीं (क्यों?)। क्या A, B का उप समुच्चय हैं? नहीं (क्यों?)
उदाहरण 11 मान लीजिए A, B और C तीन समुच्चय हैं। यदि A ∈ B तथा B ⊂ C, तो क्या यह सत्य है कि A ⊂ C? यदि नहीं तो एक उदाहरण दीजिए।
हल मान लीजिए कि A = {1}, B = {{1}, 2} और C = {{1}, 2, 3} स्पष्टतया यहाँ
A ∈ B क्योंकि A = {1) तथा B ⊂ C सत्य है। परंतु A ⊄ C क्योंकि 1 ∈ A और 1 ∉ C.
नोट कीजिए कि किसी समुच्चय का एक अवयव उस समुच्चय का उपसमुच्चय नहीं हो सकता है।
1.6.1 वास्तविक संख्याओं के समुच्चय के उपसमुच्चय
जैसा कि अनुच्छेद 1.6 से स्पष्ट होता है कि समुच्चय R के बहुत से महत्वपूर्ण उपसमुच्चय हैं। इनमें से कुछ के नाम हम नीचे दे रहे हैंः
प्राकृत सख्याओं का समुच्चय छ = {1, 2, 3, 4, 5, . . .}
पूर्णांकों का समुच्चय ρ = {. . ., –3, –2, –1, 0, 1, 2, 3, . . .}
परिमेय संख्याओं का समुच्चय η = { x : x =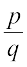 , p, q ∈ ρ तथा q ≠ 0}, जिनको इस प्रकार पढ़ते हैंः
, p, q ∈ ρ तथा q ≠ 0}, जिनको इस प्रकार पढ़ते हैंः
“Q उन सभी संख्याओं x का समुच्चय इस प्रकार है, कि x भागफल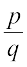 , के बराबर है, जहाँ p और q पूर्णांक है और q शून्य नहीं है।’’ Q के अवयवों में –5 (जिसे
, के बराबर है, जहाँ p और q पूर्णांक है और q शून्य नहीं है।’’ Q के अवयवों में –5 (जिसे 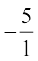 से भी प्रदर्शित किया जा सकता है)ए
से भी प्रदर्शित किया जा सकता है)ए 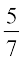 ,
,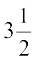 (जिसे
(जिसे 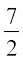 से भी प्रदर्शित किया जा सकता है) और
से भी प्रदर्शित किया जा सकता है) और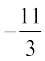 आदि सम्मिलित हैं।
आदि सम्मिलित हैं।
अपεरमेय संख्याओं का समुच्चय, जिसे T, से निरूपित करते हैं, शेष अन्य वास्तविक संख्याओं (परिमेय संख्याओं को छोड़कर) से मिलकर बनता है।
अतः T = {x : x ∈ R और x ∉ Q} = R – Q अर्थात् वह सभी वास्तविक संख्याएँ जो परिमेय नहीं है। T के सदस्यों में 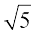 , और π आदि सम्मिलित हैं।
, और π आदि सम्मिलित हैं।
इन समुच्चयों के मध्य कुछ स्पष्ट संबंध इस प्रकार हैं;
N ⊂ Z ⊂ Q, Q ⊂ R, T ⊂ R, N ⊄ T.
1.6.2 अंतराल R के उपसमुच्चय के रूप में (Interval as subsets of R)
मान लीजिए कि a, b ∈ R और a < b. तब वास्तविक संख्याओं का समुच्चय { y : a < y < b} एक विवृत अंतराल कहलाता है और प्रतीक (a, b) द्वारा निरूपित होता है। a और b के बीच स्थित सभी बिंदु इस अंतराल में होते हैं परंतु a और b स्वयं इस अंतराल में नहीं होते हैं।
वह अंतराल जिसमें अंत्य बिंदु भी होते हैं, संवृत (बंद) अंतराल कहलाता है और प्रतीक [ a, b ] द्वारा निरूपित होता है। अतः [ a, b ] = {x : a ≤ x ≤ b}
एेसे अंतराल भी हैं जो एक अंत्य बिंदु पर बंद और दूसरे पर खुले होते हैं
[ a, b ) = {x : a ≤ x < b}, a से b, तक एक खुला अंतराल है, जिसमें a अंतर्विष्ट है किंतु b अपवर्जित है।
( a, b ] = { x : a < x ≤ b } a से b, तक एक खुला अंतराल है, जिसमें b सम्मिलित है किंतु a अपवर्जित है।
इन संकेतों द्वारा वास्तविक संख्याओं के समुच्चय के उपसमुच्चयों के उल्लेख करने की एक वैकल्पिक विधि मिलती है। उदाहरण के लिए, यदि A = (–3, 5) और B = [–7, 9], तो A ⊂ B. समुच्चय [ 0, ∞) ऋणेतर वास्तविक संख्याओं के समुच्चय को दर्शाता है, जबकि ( – ∞, 0 ) ऋण वास्तविक संख्याओं के समुच्चय को दर्शाता है। ( – ∞, ∞ ), – ∞ से ∞ तक विस्तृत रेखा से संबंधित वास्तविक संख्याओं के समुच्चय को प्रदर्शित करता है।
वास्तविक रेखा पर R के उपसमुच्चयों के रूप में वर्णित उपर्युक्त अंतरालों को आकृति 1.1 में दर्शाया गया हैः
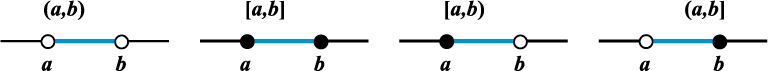
यहाँ हम ध्यान देते हैं कि एक अंतराल में असंख्य असीम मात्रा में अनेक बिंदु होते हैं। उदाहरणार्थ, समुच्चय समुच्चय {x : x ∈ त् : –5 < x ≤ 7} को अंतराल (–5, 7] रूप में लिख सकते हैं तथा अंतराल [–3, 5) को समुच्चय निर्माण रूप में {x : –3 ≤ x < 5} द्वारा लिख सकते हैं। संख्या (b – a) को अंतराल (a, b), [a, b], [a, b) तथा (a, b] में से किसी की भी लंबाई कहते हैं।
1.7 घात समुच्चय (Power Set)
समुच्चय {1, 2} पर विचार कीजिए। समुच्चय {1, 2} के सभी उपसमुच्चयों को लिखिए। हमें ज्ञात है कि φ सभी समुच्चयों का उपसमुच्चय होता है। इसलिए φ, समुच्चय {1, 2} का एक उपसमुच्चय है। हम देखते हैं कि {1} और { 2 } भी समुच्चय {1, 2}के उपसमुच्चय हैं। हमें यह भी ज्ञात है कि प्रत्येक समुच्चय स्वयं का उपसमुच्चय होता है। इसलिए { 1, 2 } भी समुच्चय {1, 2} का एक उपसमुच्चय है। अतः समुच्चय { 1, 2 } के कुल मिला कर चार उपसमुच्चय हैं, नामतः φ, { 1 }, { 2 } और { 1, 2 }. इन सभी उपसमुच्चयों के समुच्चय को समुच्चय { 1, 2 } का घात समुच्चय कहते हैं।
परिभाषा 5 समुच्चय A के उपसमुच्चयों के संग्रह को A का घात समुच्चय कहते हैं। इसे P(A) से निरूपित करते है। P(A) का प्रत्येक अवयव एक समुच्चय होता है।
अतः उपर्युक्त विवरण में, यदि A = { 1, 2 }, तो
P( A ) = { φ,{ 1 }, { 2 }, { 1,2 }}
यह भी नोट कीजिए कि n [ P (A) ] = 4 = 22
व्यापकरूप से, यदि A एक एेसा समुच्चय है कि n(A) = m, तो यह सिद्ध किया जा सकता है कि n [ P(A)] = 2m.
1.8 सार्वत्रिक समुच्चय (Universal Set)
सामान्यतः किसी विशेष संदर्भ में हमें एक आधारभूत समुच्चय के अवयवों और उपसमुच्चयों पर विचार करना पड़ता है, जो कि उस विशेष संदर्भ में प्रासंगिक होते हैं। उदाहरण के लिए, संख्या-प्रणाली का अध्ययन करते समय हमें प्राकृत संख्याओं के समुच्चय और उसके उपसमुच्चयों में रुचि होती है, जैसे अभाज्य संख्याओं का समुच्चय, सम संख्याओं का समुच्चय इत्यादि। यह आधारभूत समुच्चय ‘सार्वत्रिक समुच्चय’ कहलाता है। सार्वत्रिक समुच्चय को सामान्यतः प्रतीक U से निरूपित करते हैं और इसके उपसमुच्चयों को अक्षर A, B, C, आदि द्वारा।
उदाहरणार्थ, पूर्णांकों के समुच्चय Z के लिए, परिमेय संख्याओं का समुच्चय Q, एक सार्वत्रिक समुच्चय हो सकता है, या वास्तविक संख्याओं का समुच्चय R भी एक सार्वत्रिक समुच्चय हो सकता है। एक अन्य उदाहरण में मानव जनसंख्या अध्ययन के लिए विश्व के समस्त मानव का समुच्चय, सार्वत्रिक समुच्चय होगा।
प्रश्नावली 1.3
1. रिक्त स्थानों में प्रतीक ⊂ या ⊄ को भर कर सही कथन बनाइएः
(i) { 2, 3, 4 } . . . { 1, 2, 3, 4,5 } (ii) { a, b, c } . . . { b, c, d }
(iii) {x : x आपके विद्यालय की कक्षा XI का एक विद्यार्थी है}. . .{x : x आपके विद्यालय का एक विद्यार्थी है}
(iv) {x : x किसी समतल में स्थित एक वृत्त है} . . .{x : x एक समान समतल में वृत्त है जिसकी त्रिज्या 1 इकाई है।}
(v) {x : x किसी समतल में स्थित एक त्रिभुज है} . . . {x : x किसी समतल में स्थित एक आयत है}
(vi) {x : x किसी समतल में स्थित एक समबाहु त्रिभुज है} . . . {x : x किसी समतल में स्थित एक त्रिभुज है}
(vii) {x : x एक सम प्राकृत संख्या है} . . . {x : x एक पूर्णांक है}
2. जाँचिए कि निम्नलिखित कथन सत्य हैं अथवा असत्य हैंः
(i) { a, b } ⊄ { b, c, a }
(ii) { a, e } ⊂ { x : x अंग्रेज़ी वर्णमाला का एक स्वर है}
(iii) { 1, 2, 3 } ⊂ { 1, 3, 5 }
(iv) { a } ⊂ { a, b, c }
(v) { a } ∈ { a, b, c }
(vi) { x : x संख्या 6 से कम एक सम प्राकृत संख्या है} ⊂ { x : x एक प्राकृत संख्या है, जो संख्या 36 को विभाजित करती है}
3. मान लीजिए कि A = { 1, 2, { 3, 4 }, 5 } । निम्नलिखित में से कौन सा कथन सही नहीं है और क्यों?
(i) {3, 4} ⊂ A (ii) {3, 4} ∈ A (iii) {{3, 4}} ⊂ A
(iv) 1 ∈ A (v) 1 ⊂ A (vi) {1, 2, 5} ⊂ A
(vii) {1, 2, 5} ∈ A (viii) {1, 2, 3} ⊂ A
(ix) φ ∈ A (x) φ ⊂ A (xi) {φ} ⊂ A
4. निम्नलिखित समुच्चयों के सभी उपसमुच्चय लिखिएः
(i) {a} (ii) {a, b} (iii) {1, 2, 3} (iv) φ
5. P(A) के कितने अवयव हैं, यदि A = φ?
6. निम्नलिखित को अंतराल रूप में लिखिएः
(i) {x : x ∈ R, – 4 < x ≤ 6} (ii) {x : x ∈ R, – 12 < x < –10}
(iii) {x : x ∈ R, 0 ≤ x < 7} (iv) {x : x ∈ R, 3 ≤ x ≤ 4}
7. निम्नलिखित अंतरालों को समुच्चय निर्माण रूप में लिखिएः
(i) (– 3, 0) (ii) [6 , 12] (iii) (6, 12] (iv) [–23, 5)
8. निम्नलिखित में से प्रत्येक के लिए आप कौन-सा सार्वत्रिक समुच्चय प्रस्तावित करेंगे?
(i) समकोण त्रिभुजों का समुच्चय। (ii) समद्विबाहु त्रिभुजों का समुच्चय।
9. समुच्चय A = {1, 3, 5}, B = {2, 4, 6} और C = {0, 2, 4, 6, 8} प्रदत्त हैं। इन तीनों समुच्चय A, B और C के लिए निम्नलिखित में से कौन सा (से) सार्वत्रिक समुच्चय लिए जा सकते हैं?
(i) {0, 1, 2, 3, 4, 5, 6} (ii) φ
(iii) {0,1,2,3,4,5,6,7,8,9,10} (iv) {1,2,3,4,5,6,7,8}
1.9 वेन आरेख (Venn Diagrams)
समुच्चयों के बीच अधिकांश संबंधों को आरेखों द्वारा निरूपित किया जा सकता है जिन्हें वेन आरेख कहते हैं। वेन आरेख का नाम अंग्रेज तर्कशास्त्री John Venn (1834 ई॰– 1883 ई॰) के नाम पर रखा गया है। इन आरेखों में आयत और बंद वक्र सामान्यतः वृत्त होते हैं। किसी सार्वत्रिक समुच्चय को प्रायः एक आयत द्वारा और उसके उपसमुच्चयों को एक वृत्त द्वारा प्रदर्शित करते हैं।
किसी वेन आरेख में समुच्चयों के अवयवों को उनके विशेष समुच्चय में लिखा जाता है जैसे आकृति 1.2 और 1.3 में
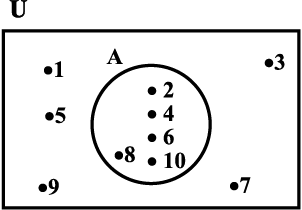
आकृति 1.2
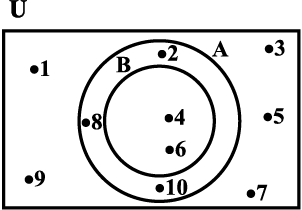
आकृति 1.3
दृष्टांत 1 आकृति 1.2 में, U = {1,2,3, ..., 10} एक सार्वत्रिक समुच्चय है और A = {2,4,6,8,10} उसका एक उपसमुच्चय है,
दृष्टांत 2 आकृति 1.3 में, U = {1,2,3, ..., 10} एक सार्वत्रिक समुच्चय है, जिसके A = {2,4,6,8,10} और B = {4, 6} उपसमुच्चय हैं और B ⊂ A.
पाठक वेन आरेखों का विस्तृत प्रयोग देखेंगे जब हम समुच्चयों के सम्मिलन, सर्वनिष्ठ और अंतर पर विचार करेंगे।
1.10 समुच्चयों पर संεक्रयाएँ (Operations on Sets)
पिछली कक्षाओं में हम सीख चुके हैं कि संख्याओं पर योग, अंतर, गुणा और भाग की संक्रियाएँ किस प्रकार संपन्न की जाती हैं। इनमें से प्रत्येक संक्रिया को दो संख्याओं पर संपन्न किया गया था, जिससे एक अन्य संख्या प्राप्त हुई थी। उदाहरण के लिए दो संख्याओं 5 और 13 पर योग की संक्रिया संपन्न करने से हमें संख्या 18 प्राप्त होती है। पुनः संख्याओं 5 और 13 पर गुणा की संक्रिया संपन्न करने पर हमें संख्या 65 प्राप्त होती है। इसी प्रकार, कुछ एेसी संक्रियाएँ है, जिनको दो समुच्चयों पर संपन्न करने से, एक अन्य समुच्चय बन जाता है। अब हम समुच्चयों पर होने वाली कुछ संक्रियाओं को परिभाषित करेंगे और उनके गुणधर्मों की जाँच करेंगे। यहाँ से आगे हम समुच्चयों का उल्लेख किसी सार्वत्रिक समुच्चय के उपसमुच्चयों के रूप में करेंगे।
1.10.1 समुच्चयों का सम्मिलन (Union of sets)
मान लीजिए कि A और B कोई दो समुच्चय हैं। A और B का सम्मिलन वह समुच्चय है जिसमें A के सभी अवयवों के साथ B के भी सभी अवयव हों, तथा उभयनिष्ठ अवयवों को केवल एक बार लिया गया हो। प्रतीक ‘∪’ का प्रयोग सम्मिलन को निरूपित करने के लिए किया जाता है। प्रतीकात्मक रूप में हम A ∪ B लिखते हैं और इसे ‘A सम्मिलन B’ पढ़ते हैं।
उदाहरण 12 मान लीजिए कि A = {2, 4, 6, 8} और B = { 6, 8, 10, 12}. A ∪ B ज्ञात कीजिए।
हल हम देखते हैं कि A ∪ B = { 2, 4, 6, 8, 10, 12}
नोट कीजिए कि A ∪ B लिखते समय उभयनिष्ठ अवयव 6 और 8 को केवल एक बार लिखते हैं।
उदाहरण 13 मान लीजिए कि A = { a, e, i, o, u } और B = { a, i, u }. दर्शाइए कि A ∪ B = A.
हल स्पष्टतया A ∪ B = { a, e, i, o, u } = A.
इस उदाहरण से स्पष्ट होता है कि किसी समुच्चय A और उसके उपसमुच्चय B का सम्मिलन समुच्चय A स्वयं होता है, अर्थात् यदि B ⊂ A, तो A ∪ B = A.
उदाहरण 14 मान लीजिए कि X = {राम, गीता, अकबर} कक्षा XI के विद्यार्थियों का जो विद्यालय की हाकी टीम में हैं, एक समुच्चय है। मान लीजिए कि Y = {गीता, डेविड, अशोक} कक्षा XI के विद्यार्थियों का, जो विद्यालय की फुटबाल टीम में हैं, एक समुच्चय है। X ∪ Y ज्ञात कीजिए और इस समुच्चय की व्याख्या कीजिए।
हल यहाँ X ∪ Y = {राम, गीता, अकबर, डेविड, अशोक}. यह कक्षा XI के उन विद्यार्थियों का समुच्चय है, जो या तो विद्यालय की हाकी टीम में हैं या फुटबाल टीम में हैं या दोनों टीमों में हैं।
अतः हम दो समुच्चयों के सम्मिलन की परिभाषा इस प्रकार कर सकते हैंः
परिभाषा 6 दो समुच्चयों A और B का सम्मिलन समुच्चय, वह समुच्चय है जिसमें वे सभी अवयव हैं, जो या तो A में हैं या B में हैं (उन अवयवों को सम्मिलित करते हुए जो दोनों में हैं)। प्रतीकात्मक रूप में हम लिखते हैं कि A ∪ B = { x : x ∈A या x ∈B } है।
दो समुच्चयों के सम्मिलन को आकृति 1.4 में दिखाए गए वेन आरेख से प्रदर्शित किया जा सकता है।
आकृति 1.4 में छायांकित भाग A ∪ B को प्रदर्शित करता है।
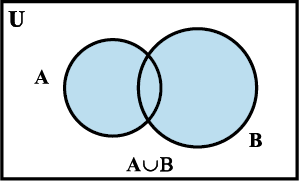
आकृति 1.4
सम्मिलन की संक्रिया के कुछ गुणधर्मः
(i) A ∪ B = B ∪ A (क्रम विनिमय नियम)
(ii) ( A ∪ B ) ∪ C = A ∪ ( B ∪ C)
(साहचर्य नियम)
(iii) A ∪ φ = A (तत्समक नियम, φ संक्रिया ∪ का तत्समक अवयव है)
(iv) A ∪ A = A (वर्गसम नियम)
(v) U ∪ A = U (U का नियम)
1.10.2 समुच्चयों का सर्वनिष्ठ (Intersection of sets)
समुच्चय A और B का सर्वनिष्ठ उन सभी अवयवों का समुच्चय है, जो A और B दोनों में उभयनिष्ठ है। प्रतीक ‘∩’ का प्रयोग सर्वनिष्ठ को निरूपित करने के लिए किया जाता है। समुच्चय A और B का सर्वनिष्ठ उन सभी अवयवों का समुच्चय है, जो A और B दोनों में हों। प्रतीकात्मक रूप में हम लिखते हैं कि
A ∩ B = {x : x ∈ A और x ∈ B}
उदाहरण 15 उदाहरण 12 के समुच्चय A और B पर विचार कीजिए। A ∩ B ज्ञात कीजिए।
हल हम देखते हैं कि केवल 6 और 8 ही एेसे अवयव हैं जो A और B दोनों में उभयनिष्ठ हैं। अतः A ∩ B = { 6, 8 }
उदाहरण 16 उदाहरण 14 के समुच्चय X और Y पर विचार कीजिए। X ∩ Y ज्ञात कीजिए।
हल हम देखते हैं केवल ‘गीता’ ही एक मात्र एेसा अवयव है, जो दोनों में उभयनिष्ठ है। अतः X ∩ Y = {गीता}
उदाहरण 17 मान लीजिए कि A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} और B = { 2, 3, 5, 7 } A ∩ B ज्ञात कीजिए और इस प्रकार दिखाइए कि A ∩ B = B.
हल हम देखते हैं कि A ∩ B = { 2, 3, 5, 7 } = B हम ध्यान देते हैं कि B ⊂ A और A ∩ B = B
परिभाषा 7 समुच्चय A और B का सर्वनिष्ठ उन सभी अवयवों का समुच्चय है, जो A और B दोनों में हो। प्रतीकात्मक रूप में, हम लिखते हैं कि
A ∩ B = {x : x ∈ A और x ∈ B}
आकृति 1.5 में छायांकित भाग, A और B के सर्वनिष्ठ को प्रदर्शित करता है।

आकृति 1.5
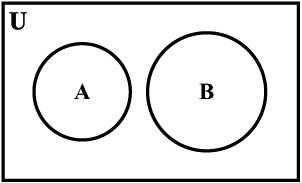
यदि A और B एेसे दो समुच्चय हों कि A ∩ B = φ, तो A और B असंयुक्त समुच्चय कहलाते हैं। उदाहरण के लिए मान लीजिए कि A = { 2, 4, 6, 8 } और
B = { 1, 3, 5, 7 }, तो A और B असंयुक्त समुच्चय हैं, क्योंकि A और B में कोई भी अवयव उभयनिष्ठ नहीं है।
असंयुक्त समुच्चयों को वेन आरेख द्वारा निरूपित किया जा सकता है, जैसा आकृति 1.6 में प्रदर्शित है।
उपर्युक्त आरेख में A और B असंयुक्त समुच्चय हैं।
सर्वनिष्ठ संक्रिय के कुछ गुणधर्म
(i) A ∩ B = B ∩ A (क्रम विनिमय नियम)
(ii) ( A ∩ B ) ∩ C = A ∩ ( B ∩ C ) (साहचर्य नियम)
(iii) φ ∩ A = φ, U ∩ A = A (φ और U के नियम)।
(iv) A ∩ A = A (वर्गसम नियम)
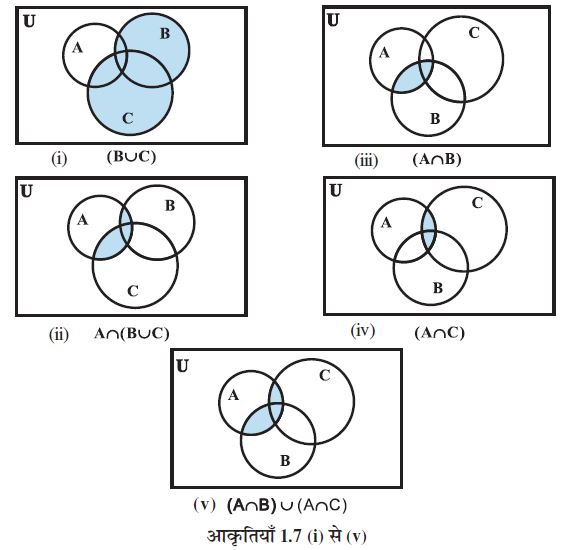
(v) A ∩ (B ∪ C) = ( A ∩ B ) ∪ ( A ∩ C ) (वितरण या बंटन नियम)
अर्थात् ∩ वितरित होता है ∪ पर।
आकृति 1.6
नीचे बने वेन आरेखों [आवृηतियों 1.7 (i)-(v)] द्वारा इस बात को सरलता से देख सकते हैं।
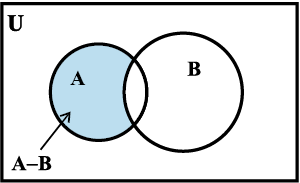
1.10.3 समुच्चयों का अंतर (Difference of sets)
समुच्चयों A और B का अंतर उन अवयवों का समुच्चय है जो A में हैं किंतु B में नहीं हैं, जब कि A और B को इसी क्रम में लिया जाए। प्रतीतात्मक रूप में इसे A–B लिखते हैं और “ A अंतर B” पढ़ते हैं।
उदाहरण 18 मान लीजिए कि A = { 1, 2, 3, 4, 5, 6}, B = { 2, 4, 6, 8 } A – B और B – A ज्ञात कीजिए ।
हल हम प्राप्त करते हैं कि, A – B = { 1, 3, 5 }, क्योंकि अवयव 1, 3, 5 समुच्चय A में हैं
किंतु B में नहीं हैं तथा B – A = { 8 }, क्योंकि अवयव 8, B में है किंतु A में नहीं है।
हम देखते हैं कि A – B ≠ B – A
उदाहरण 19 मान लीजिए कि V = { a, e, i, o, u } तो B = { a, i, k, u}, तो V – B और B – V ज्ञात कीजिए।
हल यहाँ, V – B = { e, o }, क्योंकि अवयव e, o समुच्चय V में हैं किंतु B में नहीं है तथा B – V = { k }, क्योंकि अवयव k समुच्चय B में है परंतु V में नहीं है।
आकृति 1.8
हम नोट करते हैं कि V – B ≠ B – V समुच्चय निर्माण संकेतन का प्रयोग करते हुए हम समुच्चयों के अंतर की परिभाषा को पुनः इस प्रकार लिख सकते हैंः
A – B = { x : x ∈ A और x ∉ B }
दो समुच्चयों A और B के अंतर को वेन आरेख द्वारा दर्शाया जा सकता है जैसा कि आकृति 1.8 में प्रदर्शित है।
छायांकित भाग दो समुच्चय A और B के अंतर को दर्शाता है।
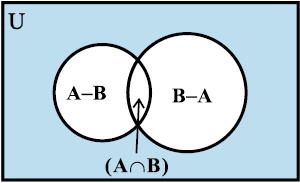
आकृति 1.9
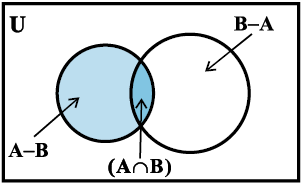
टिप्पणी समुच्चय A – B, A ∩ B और B – A परस्पर असंयुक्त होते हैं अर्थात् इनमें से किसी दो समुच्चयों का सर्वनिष्ठ समुच्चय एक रिक्त समुच्चय होता है जैसा कि आकृति 1.9 में प्रदर्शित है।
प्रश्नावली 1.4
1. निम्नलिखित में से प्रत्येक समुच्चय युग्म का सम्मिलन ज्ञात कीजिएः
(i) X = {1, 3, 5}, Y = {1, 2, 3}
(ii) A = [ a, e, i, o, u}, B = {a, b, c}
(iii) A = {x : x एक प्राकृत संख्या है और 3 का गुणज है}
B = {x : x संख्या 6 से कम एक प्राकृत संख्या है}
(iv) A = {x : x एक प्राकृत संख्या है और 1 < x ≤ 6 }
B = {x : x एक प्राकृत संख्या है और 6 < x < 10 }
(v) A = {1, 2, 3}, B = φ
2. मान लीजिए कि A = { a, b }, B = {a, b, c}. क्या A ⊂ B ? A ∪ B ज्ञात कीजिए।
3. यदि A और B दो एेसे समुच्चय हैं कि A ⊂ B, तो A ∪ B क्या है ?
4. यदि A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 } और D = { 7, 8, 9, 10}, तो निम्नलिखित ज्ञात कीजिएः
(i) A ∪ B (ii) A ∪ C (iii) B ∪ C (iv) B ∪ D
(v) A ∪ B ∪ C (vi) A ∪ B ∪ D (vii) B ∪ C ∪ D
5. प्रश्न 1 में दिए प्रत्येक समुच्चय युग्म का सर्वनिष्ठ समुच्चय ज्ञात कीजिए।
6. यदि A = { 3, 5, 7, 9, 11 }, B = {7, 9, 11, 13}, C = {11, 13, 15}और D = {15, 17}; तो निम्नलिखित ज्ञात कीजिएः
(i) A ∩ B (ii) B ∩ C (iii) A ∩ C ∩ D
(iv) A ∩ C (v) B ∩ D (vi) A ∩ (B ∪ C)
(vii) A ∩ D (viii) A ∩ (B ∪ D) (ix) ( A ∩ B ) ∩ ( B ∪ C ) (x) ( A ∪ D) ∩ ( B ∪ C)
7. यदि A = {x : x एक प्राकृत संख्या है}, B = {x : x एक सम प्राकृत संख्या है}
C = {x : x एक विषम प्राकृत संख्या है} D = {x : x एक अभाज्य संख्या है}, तो निम्नलिखित ज्ञात कीजिएः
(i) A ∩ B (ii) A ∩ C (iii) A ∩ D
(iv) B ∩ C (v) B ∩ D (vi) C ∩ D
8. निम्नलिखित समुच्चय युग्मों में से कौन से युग्म असंयुक्त हैं?
(i) {1, 2, 3, 4} तथा {x : x एक प्राकृत संख्या है और 4 ≤ x ≤ 6 }
(ii) { a, e, i, o, u } तथा { c, d, e, f }
(iii) {x : x एक सम पूर्णांक है} और {x : x एक विषम पूर्णांक है}
9. यदि A = {3, 6, 9, 12, 15, 18, 21}, B = { 4, 8, 12, 16, 20 },
C = { 2, 4, 6, 8, 10, 12, 14, 16 }, D = {5, 10, 15, 20 }; तो निम्नलिखित को ज्ञात कीजिएः
(i) A – B (ii) A – C (iii) A – D (iv) B – A
(v) C – A (vi) D – A (vii) B – C (viii) B – D
(ix) C – B (x) D – B (xi) C – D (xii) D – C
10. यदि X= { a, b, c, d } और Y = { f, b, d, g}, तो निम्नलिखित को ज्ञात कीजिएः
(i) X – Y (ii) Y – X (iii) X ∩ Y
11. यदि R वास्तविक संख्याओं और Q परिमेय संख्याओं के समुच्चय हैं, तो R – Q क्या होगा ?
12. बताइए कि निम्नलिखित कथनों में से प्रत्येक सत्य है या असत्य? अपने उत्तर का औचित्य भी बताइएः
(i) { 2, 3, 4, 5 } तथा { 3, 6} असंयुक्त समुच्चय हैं।
(ii) { a, e, i, o, u } तथा { a, b, c, d }असंयुक्त समुच्चय हैं।
(iii) { 2, 6, 10, 14 } तथा { 3, 7, 11, 15} असंयुक्त समुच्चय हैं।
(iv) { 2, 6, 10 } तथा { 3, 7, 11} असंयुक्त समुच्चय हैं।
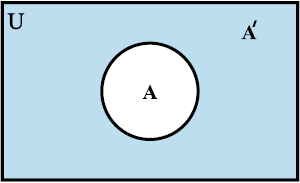
1.11 समुच्चय का पूरक (Complement of a Set)
मान लीजिए कि सभी अभाज्य संख्याओं का सार्वत्रिक समुच्चय U है तथा A, U का वह उपसमुच्चय है, जिसमें वे सभी अभाज्य संख्याएँ हैं जो 42 की भाजक नहीं हैं। इस प्रकार A = {x : x ∈ U और x संख्या 42 का भाजक नहीं है}। हम देखते हैं कि 2 ∈ U किंतु 2 ∉ A, क्योंकि 2 संख्या 42 का एक भाजक है। इसी प्रकार 3 ∈ U किंतु 3 ∉ A, तथा 7 ∈ U किंतु 7 ∉ A अब केवल 2, 3 तथा 7 ही U के एेसे अवयव हैं जो Aमें नहीं हैं। इन तीन अभाज्य संख्याओं का समुच्चय अर्थात् समुच्चय {2, 3, 7}, U के सापेक्ष A का पूरक समुच्चय कहलाता है और इसे प्रतीक A′ से निरूपित किया जाता है। अतः A′ = {2, 3, 7} इस प्रकार हम देखते हैं कि A′ = {x : x ∈ U और x ∉ A } है। इससे निम्नलिखित परिभाषा प्राप्त होती हैः
परिभाषा 8 मान लीजिए कि U एक सार्वत्रिक समुच्चय है और A, U का एक उपसमुच्चय है, तो A का पूरक समुच्चय U के उन अवयवों का समुच्चय है, जो A के अवयव नहीं हैं। प्रतीकात्मक रूप में हम U के सापेक्ष A के पूरक को प्रतीक A′ से निरूपित करते हैं। अतः A′ = {x : x ∈ U और x ∉ A } हम लिख सकते हैं। A = U – A
ध्यान दीजिए कि A के पूरक समुच्चय को, विकल्पतः, सार्वत्रिक समुच्चय U तथा समुच्चय A के अंतर के रूप में देखा जा सकता है।
उदाहरण 20 मान लीजिए कि U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} और A = {1, 3, 5, 7, 9} है तो A′ ज्ञात कीजिए।
हल हम नोट करते हैं केवल 2, 4, 6, 8, 10 ही U के एेसे अवयव हैं जो A में नहीं हैं।
अतः A′ = { 2, 4, 6, 8,10 }.
उदाहरण 21 मान लीजिए कि U एक सह शिक्षा विद्यालय के कक्षा XI के सभी विद्यार्थियों का सार्वत्रिक समुच्चय है और A, कक्षा XI की सभी लड़कियों का समुच्चय है तो A′ ज्ञात कीजिए।
हल क्योंकि A, कक्षा XI की सभी लड़कियों का समुच्चय है, अतः A′ स्पष्टतया कक्षा के सभी लड़कों का समुच्चय है।
टिप्पणी यदि A सार्वत्रिक समुच्चय U का एक उपसमुच्चय है, तो इसका पूरक A′ भी U का एक उपसमुच्चय होता है।
पुनः उपर्युक्त उदाहरण 20 में,
A′ = { 2, 4, 6, 8, 10 }
अतः (A′)′ = {x : x ∈ U और x ∉ A′}
= {1, 3, 5, 7, 9} = A
पूरक समुच्चय की परिभाषा से स्पष्ट है कि सार्वत्रिक समुच्चय U के किसी उपसमुच्चय A′ के लिए (A′)′ = A
अब निम्नलिखित उदाहरण में हम ( A ∪ B)′ तथा A′ ∩ B′ के हल निकालेंगे।
उदाहरण 22 मान लीजिए कि U = {1, 2, 3, 4, 5, 6}, A = {2, 3} और B = {3, 4, 5},
A′, B′ , A′ ∩ B′, A ∪ B ज्ञात कीजिए और फिर सिद्ध कीजिए कि ( A ∪ B)′ = A′ ∩ B′.
हल स्पष्टतया A′ = {1, 4, 5, 6}, B′ = { 1, 2, 6 }। अतः A′ ∩ B′ = { 1, 6 }
पुनः A ∪ B = { 2, 3, 4, 5 } है। इसलिए (A ∪ B)′ = { 1, 6 }
( A ∪ B)′ = { 1, 6 } = A′ ∩ B′
इस प्रकार हम देखते हैं कि ( A ∪ B)′ = A′ ∩ B′. यह सिद्ध किया जा सकता है कि उपर्युक्त परिणाम व्यापक रूप से सत्य होता है यदि A और B सार्वजनिक समुच्चय U के कोई दो उपसमुच्चय हैं, तो ( A ∪ B)′ = A′ ∩ B′. इसी प्रकार ( A ∩ B)′ = A′ ∪ B′ इन परिणामों को शब्दों में इस प्रकार व्यक्त करते हैंः
‘‘दो समुच्चयों के सम्मिलन का पूरक उनके पूरक समुच्चयों का सार्वनिष्ठ होता है तथा दोनों समुच्चयों के सार्वनिष्ठ का पूरक उनके पूरक समुच्चयों का सम्मिलन होता है।’’ इनको De Morgan के नियम कहते हैं।
आकृति 1.10
यह नाम गणितज्ञ De Morgan के नाम पर रखा गया है।
किसी समुच्चय A के पूरक A′ को वेन आरेख द्वारा निरूपित किया जा सकता है जैसा कि आकृति 1.10 में प्रदर्शित है।
छायांकित भाग समुच्चय A के पूरक A′ को दर्शाता है।
पूरकों के कुछ गुणधर्म
1. पूरक नियम : (i) A ∪ A′ = U (ii) A ∩ A′ = φ
2. De Morgan का नियम : (i) (A ∪ B)´ = A′ ∩ B′ (ii) (A ∩ B = A′ ∪ B′
3. द्वि-पूरक नियम : (A′)′ = A
4. φ′ और U के नियम: φ′ = U और U′ = φ.
इन नियमों का सत्यापन वेन आरेखों द्वारा किया जा सकता है।
प्रश्नावली 1.5
1. मान लीजिए कि U = {1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = {1, 2, 3, 4}, B = {2, 4, 6, 8 } और C = { 3, 4, 5, 6 } तो निम्नलिखित ज्ञात कीजिएः
(i) A′ (ii) B′ (iii) (A ∪ C)′ (iv) (A ∪ B)′ (v) (A′)′ (vi) (B – C)′
2. If U = { a, b, c, d, e, f, g, h}, तो निम्नलिखित समुच्चयों के पूरक ज्ञात कीजिएः
(i) A = {a, b, c} (ii) B = {d, e, f, g}
(iii) C = {a, c, e, g} (iv) D = { f, g, h, a}
3. प्राकृत संख्याओं के समुच्चय को सार्वत्रिक समुच्चय मानते हुए, निम्नलिखित समुच्चयों के पूरक लिखिएः
(i) {x : x एक प्राकृत सम संख्या है} (ii) { x : x एक प्राकृत विषम संख्या है}
(iii) {x : x संख्या 3 का एक धन गुणज है} (iv) { x : x एक अभाज्य संख्या है}
(v) {x : x, 3 और 5 से विभाजित होने वाली एक संख्या है}
(vi) { x : x एक पूर्ण वर्ग संख्या है} (vii) { x : x एक पूर्ण घन संख्या है}
(viii) { x : x + 5 = 8 } (ix) { x : 2x + 5 = 9}
(x) { x : x ≥ 7 } (xi) { x : x ∈ N और 2x + 1 > 10 }
4. यदि U = {1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = {2, 4, 6, 8} और B = { 2, 3, 5, 7}, तो सत्यापित कीजिए किः
(i) (A ∪ B)′ = A′ ∩ B′ (ii) (A ∩ B)′ = A′ ∪ B′
5. निम्नलिखित में से प्रत्येक के लिए उपर्युक्त वेन आरेख खींचिएः
(i) (A ∪ B)′ (ii) A′ ∩ B′ (iii) (A ∩ B)′ (iv) A′ ∪ B′
6. मान लीजिए कि किसी समतल में स्थित सभी त्रिभुजों का समुच्चय सार्वत्रिक समुच्चय U है। यदि A उन सभी त्रिभुजों का समुच्चय है जिनमें कम से कम एक कोण 600 से भिन्न है, तो A′ क्या है?
7. निम्नलिखित कथनों को सत्य बनाने के लिए रिक्त स्थानों को भरिएः
(i) A ∪ A′ = . . . (ii) φ′ ∩ A = . . .
(iii) A ∩ A′ = . . . (iv) U′ ∩ A = . . .
1.12 दो समुच्चयों के सम्मिलन और सर्वनिष्ठ पर आधारित व्यावहारिक प्रश्न Practical Problems on Union and Intersection of Two Sets
पहले के अनुच्छेदों में हम दो समुच्चयों के सम्मिलन, सर्वनिष्ठ तथा अंतर के बारे में सीख चुके हैं। इस अनुच्छेद में हम अपने प्रतिदिन के जीवन से सम्बन्धित कुछ प्रश्नों को सरल करेंगे। इस अनुच्छेद में प्राप्त सूत्रों का प्रयोग आगे आने वाले अध्यायों, जैसे प्रायिकता (अध्याय 16) में भी किया जाएगा।
आकृति 1.11
(i) मान लीजिए कि A और B परिमित समुच्चय हैं। यदि A ∩ B = φ, तो
n ( A ∪ B ) = n ( A ) + n ( B ) ... (1)
A ∪ B के अवयव या तो A में हैं या B में हैं परंतु दोनों में नहीं हैं, क्योंकि A ∩ B = φ. अतः परिणाम (1) तत्काल प्राप्त होता है।
(ii) व्यापक रूप से यदि A और B परिमित समुच्चय है, तो n ( A ∪ B ) = n ( A ) + n ( B )
– n ( A ∩ B ) ... (2)
नोट कीजिए कि समुच्चय A – B, A ∩ B तथा B – A असंयुक्त हैं और इनका सम्मिलन A ∪B है (आकृति 1.11)। इसलिए
n ( A ∪ B) = n ( A – B) + n ( A ∩ B ) + n ( B – A )
= n ( A – B) + n ( A ∩B ) + n ( B – A ) + n ( A ∩ B ) – n ( A ∩ B)
= n ( A ) + n ( B ) – n ( A ∩ B), जो परिणाम (2) को सत्यापित करता है।
(iii) पुनः यदि A, B और C परिमित समुच्चय हैं, तो
n ( A ∪ B ∪ C ) = n ( A ) + n ( B ) + n ( C ) – n ( A ∩ B ) – n ( B ∩ C)
– n ( A ∩ C ) + n ( A ∩ B ∩ C ) ... (3)
वास्तव में हम देखते हैं कि
n ( A ∪ B ∪ C ) = n (A) + n ( B ∪ C ) – n [ A ∩ ( B ∪ C ) ] [ (2) द्वारा ]
= n (A) + n ( B ) + n ( C ) – n ( B ∩ C ) – n [ A ∩ ( B ∪ C ) ] [ (2) द्वारा ]
क्योंकि A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C ), हमें प्राप्त होता है कि
n [ A ∩ ( B ∪ C ) ] = n ( A ∩ B ) + n ( A ∩ C ) – n [ ( A ∩ B) ∩ (A ∩ C)]
= n ( A ∩ B ) + n ( A ∩ C ) – n (A ∩ B ∩ C)
अतः n ( A ∪ B ∪ C ) = n (A) + n ( B ) + n ( C ) – n ( A ∩ B ) – n ( B ∩ C)
– n ( A ∩ C ) + n ( A ∩ B ∩ C )
इस प्रकार परिणाम (3) सिद्ध हुआ।
उदाहरण 23 यदि X और Y दो एेसे समुच्चय हैं कि X ∪ Y में 50 अवयव हैं, X में
28 अवयव हैं और Y में 32 अवयव हैं, तो X ∩ Y में कितने अवयव हैं?
हल दिया है कि n (X ∪ Y) = 50, n (X) = 28,
n (Y) = 32, n (x ∩ Y) = ?
आकृति 1.12
सूत्र n (X ∪ Y) = n (X) + n (Y) – n (X ∩ Y) के प्रयोग द्वारा हम देखते हैं कि
n (X ∩ Y) = n (X) + n (Y) – n (X ∪ Y)
= 28 + 32 – 50 = 10
विकल्पतः मान लीजिए कि n ( X ∩ Y ) = k, तो
n (X – Y) = 28 – k , n (Y – X) = 32 – k (आकृति 1.12 के वेन आरेख द्वारा)
इससे मिलता है कि 50 = n (X ∪ Y) = n (X – Y) + n (X ∩ Y) + n (Y – X)
= (28 – k) + k + (32 – k)
अतः k = 10.
उदाहरण 24 एक विद्यालय में 20 अध्यापक हैं जो गणित या भौतिकी पढ़ाते हैं। इनमें से 12 गणित पढ़ाते हैं और 4 भौतिकी और गणित दोनों को पढ़ाते हैं। कितने अध्यापक भौतिकी पढ़ाते हैं?
हल मान लीजिए कि M उन अध्यापकों का समुच्चय निरूपित करता है, जो गणित पढ़ाते हैं और P उन अध्यापकों का समुच्चय निरूपित करता है, जो भौतिकी पढ़ाते हैं। हमें प्रश्न के कथन में आने वाले शब्द ‘या’ से सम्मिलन तथा शब्द ‘और’ से सर्वनिष्ठ का संकेत मिलता है। इसलिए
n ( M ∪ P ) = 20 , n ( M ) = 12 और n ( M ∩ P ) = 4
हम n ( P ) ज्ञात करना चाहते हैं।
परिणाम n ( M ∪ P ) = n ( M ) + n ( P ) – n ( M ∩ P ), के प्रयोग द्वारा,
20 = 12 + n ( P ) – 4
अतः n ( P ) = 12
अतएव 12 अध्यापक भौतिकी पढ़ाते हैं।
उदाहरण 25 35 विद्यार्थियों की एक कक्षा में, 24 क्रिकेट खेलना पसंद करते हैं और 16 फुटबाल खेलना पसंद करते हैं। इसके अतिरिक्त प्रत्येक विद्यार्थी कम से कम एक खेल अवश्य खेलना पसंद करता है। कितने विद्यार्थी क्रिकेट और फुटबाल दोनों खेलना पसंद करते हैं?
हल मान लीजिए कि क्रिकेट खेलना पसंद करने वाले विद्यार्थियों का समुच्चय X है। मान लीजिए कि फुटबाल खेलना पसंद करने वाले विद्यार्थियों का समुच्चय Y है। इस प्रकार X ∪ Y उन विद्यार्थियों का समुच्चय है, जो कम से कम एक खेलना पसंद करते हैं और X ∩ Y उन विद्यार्थियों का समुच्चय है, जो दोनों ही खेल खेलना पसंद करते हैं।
दिया है कि n (X) = 24, n (Y) = 16, n (X ∪ Y) = 35, n (X ∩ Y) = ?
सूत्र n (X ∪ Y) = n (X) + n (Y) – n (X ∩ Y), के प्रयोग द्वारा, हम प्राप्त करते हैं।
35 = 24 + 16 – n (X ∩ Y)
इसलिए, n (X ∩ Y) = 5
अर्थात् 5 विद्यार्थी दोनों खेल खेलना पसंद करते हैं।
उदाहरण 26 किसी स्कूल के 400 विद्यार्थियों के सर्वेक्षण में 100 विद्यार्थी सेब का रस, 150 विद्यार्थी संतरे का रस और 75 विद्यार्थी सेब तथा संतरे दोनों का रस पीने वाले पाए जाते हैं। ज्ञात कीजिए कि कितने विद्यार्थी न तो सेब का रस पीते हैं और न संतरे का ही?
हल मान लीजिए कि U सर्वेक्षण किए गए विद्यार्थियों के समुच्चय को निरूपित करता है। तथा A सेब का रस पीने वाले और B संतरे का रस पीने वाले विद्यार्थियों के समुच्चयों को निरूपित करते है। इस प्रकार n (U) = 400, n (A) = 100, n (B) = 150 और n (A ∩ B) = 75.
अब n (A′ ∩ B′) = n (A ∪ B)′
= n (U) – n (A ∪ B)
= n (U) – n (A) – n (B) + n (A ∩ B)
= 400 – 100 – 150 + 75 = 225
अतः 225 विद्यार्थी न तो सेब का और न संतरे का रस पीते हैं।
उदाहरण 27 200 व्यक्ति किसी चर्म रोग से पीड़ित हैं, इनमें 120 व्यक्ति रसायन C1, 50 व्यक्ति रसायन C2, और 30 व्यक्ति रसायन C1 और C2 दोनों ही से प्रभावित हुए हैं, तो एेसे व्यक्तियों की संख्या ज्ञात कीजिए जो प्रभावित हुए हों:
(i) रसायन C1 किंतु रसायन C2 से नहीं,
(ii) रसायन C2 किंतु रसायन C1 से नहीं,
(iii) रसायन C1 अथवा रसायन C2 से प्रभावित हुए हैं।
हल मान लीजिए कि U, चर्म रोग से पीड़ित व्यक्तियों के सार्वत्रिक समुच्चय को निरूपित करता है, A, रसायन C1 से प्रभावित व्यक्तियों के समुच्चय को तथा B, रसायन C2 से प्रभावित व्यक्तियों के समुच्चय को निरूपित करते हैं।
यहाँ पर n ( U) = 200, n ( A ) = 120, n ( B ) = 50 तथा n ( A ∩ B ) = 30
(i) दिए हुए वेन आरेख (आकृति 1.13) में हम देखते हैं कि
A = ( A – B ) ∪ ( A ∩ B ).
अतः n (A) = n( A – B ) + n( A ∩ B )
(क्योंकि A – B) और A ∩ B असंयुक्त हैं)
अथवा n ( A – B ) = n ( A ) – n ( A ∩ B ) =
120 –30 = 90

आकृति 1.13
अतः रसायन C1 किंतु रसायन C2 से नहीं प्रभावित व्यक्तियों की संख्या 90 है।
(ii) आकृति 1.13 से B = ( B – A) ∪ ( A ∩ B).
इसलिए n (B) = n (B – A) + n ( A ∩ B) (क्योंकि A – B तथा A – B अंसयुक्त हैं।)
अथवा n ( B – A ) = n ( B ) – n ( A ∩ B
= 50 – 30 = 20
अतः रसायन C2 किंतु रसायन C1 से नहीं प्रभावित व्यक्तियों की संख्या 20 है।
(iii) रसयान C1 अथवा रसायन C2 से प्रभावित व्यक्तियों की संख्या अर्थात्
n ( A ∪ B ) = n ( A ) + n ( B ) – n ( A ∩ B )
= 120 + 50 – 30 = 140.
प्रश्नावली 1.6
1. यदि X और Y दो एेसे समुच्चय हैं कि n ( X ) = 17, n ( Y ) = 23 तथा n ( X ∪ Y ) = 38, तो n ( X ∩ Y ) ज्ञात कीजिए।
2. यदि X और Y दो एेसे समुच्चय हैं कि X ∪ Y में 18, X में 8 और Y में 15 अवयव हों, तो X ∩ Y में कितने अवयव होंगे?
3. 400 व्यक्तियों के समूह में, 250 हिंदी तथा 200 अंग्रेज़ी बोल सकते हैं। कितने व्यक्ति हिंदी तथा अंग्रेज़ी दोनों बोल सकते हैं?
4. यदि S और T दो एेसे समुच्चय हैं कि S में 21, T में 32 और S ∩ T में 11 अवयव हों, तो S ∪ T में कितने अवयव होंगे?
5. यदि X और Y दो एेसे समुच्चय हैं कि X में 40, X ∪ Y में 60 और X ∩ Y में 10 अवयव हों, तो Y में कितने अवयव होंगे?
6. 70 व्यक्तियों के समूह में, 37 कॉप़ηी, 52 चाय पसंद करते हैं और प्रत्येक व्यक्ति दोनों में से कम से कम एक पेय पसंद करता है, तो कितने व्यक्ति कॉप़ηी और चाय दोनों को पसंद
करते हैं?
7. 65 व्यक्तियों के समूह में, 40 व्यक्ति क्रिकेट, और 10 व्यक्ति क्रिकेट तथा टेनिस दोनों को पसंद करते हैं, तो कितने व्यक्ति केवल टेनिस को पसंद करते हैं किंतु क्रिकेट को नहीं? कितने व्यक्ति टेनिस को पसंद करते हैं?
8. एक कमेटी में, 50 व्यक्ति फ्रेंच, 20 व्यक्ति स्पेनिश और 10 व्यक्ति स्पेनिश और फ्रेंच दोनों ही भाषाओं को बोल सकते हैं। कितने व्यक्ति इन दोनों ही भाषाओं में से कम से कम एक भाषा बोल सकते हैं?
विविध उदाहरण
उदाहरण 28 दिखाइए कि शब्द “ CATARACT ” के वर्ण विन्यास के अक्षरों का समुच्चय तथा शब्द “ TRACT” के वर्णविन्यास के अक्षरों का समुच्चय समान है।
हल मान लीजिए कि X “CATARACT” के अक्षरों का समुच्चय है, तो
X = { C, A, T, A, R, A, C, T } = { C, A, T, R }
मान लीजिए कि Y “ TRACT” के अक्षरों का समुच्चय है, तो
Y = { T, R, A, C }
क्योंकि X का प्रत्येक अवयव Y में है तथा Y का प्रत्येक अवयव X में है, अतः X = Y
उदाहरण 29 समुच्चय { –1, 0, 1 } के सभी उपसमुच्चयों की सूची बनाइए।
हल माना A = {–1, 0, 1} है। समुच्चय A का वह उपसमुच्चय जिसमें कोई भी अवयव नहीं है रिक्त समुच्चय φ है। A के एक अवयव वाले उपसमुच्चय { –1 }, { 0 }, { 1 } हैं। A के दो अवयव वाले समुच्चय { –1, 0 }, {–1, 1} ,{0, 1} हैं। A के तीन अवयव वाला उपसमुच्चय A स्वयं है। इस प्रकार A के सभी उपसमुच्चय φ, { –1 }, { 0 }, { 1 }, {–1, 0}, {–1, 1} ,{0, 1} तथा {–1, 0, 1} हैं।
उदाहरण 30 सिद्ध कीजिए कि A ∪ B = A ∩ B का तात्पर्य है कि A = B
हल यदि कोई अवयव a ∈ A, तो a ∈ A ∪ B. क्योंकि A ∪ B = A ∩ B , इसलिए
a ∈ A ∩ B. अतः a ∈ B. इस प्रकार A ⊂ B. इसी प्रकार यदि b ∈ B, तो b ∈ A ∪ B. क्योंεक
A ∪ B = A ∩ B इसलिए, b ∈ A ∩ B. इस प्रकार b ∈ A. अतः B ⊂ A अतएव A = B.
उदाहरण 31 समुच्चयों A, B के लिए सिद्ध कीजिए कि
P ( A ∩ B ) = P ( A ) ∩ P ( B ).
हल मान लीजिए कि X ∈ P (A ∩ B), तो X ⊂ A ∩ B. इसलिए X ∈ P (A) तथा X ∈ P (B), जिसका तात्पर्य हुआ कि X ∈ [P ( A ) ∩ P (B)]. इस प्रकार P ( A ∩ B ) ⊂ [P ( A ) ∩ P ( B )]. मान लीजिए कि Y ∈ [P ( A ) ∩ P ( B )], तो Y ∈ P ( A ) तथा Y ∈ P ( B ), इस प्रकार Y ⊂ A और Y ⊂ B. इसलिए Y ⊂ A ∩ B, जिसका तात्पर्य है कि Y ∈ P ( A ∩ B ), अतएव [P ( A ) ∩ P ( B )]
⊂ P ( A ∩ B), अतः P ( A ∩ B ) = P ( A ) ∩ P ( B ).
उदाहरण 32 एक बाजार अनुसंधान समूह ने 1000 उपभोक्ताओं का सर्वेक्षण किया और सूचित किया कि 720 उपभोक्ताओं ने उत्पाद A तथा 450 उपभोक्ताओं ने उत्पाद B पसंद किया। दोनों उत्पादों को पसंद करने वाले उपभोक्ताओं की न्यूनतम संख्या क्या है?
हल मान लीजिए कि U सर्वेक्षण उपभोक्ताओं का समुच्चय है, S उन उपभोक्ताओं का समुच्चय है जिन्होनें उत्पाद A पसंद किया और T उन उपभोक्ताओं का समुच्चय है जिन्होंने उत्पाद B पसंद किया। दिया है कि,
n ( U ) = 1000, n ( S ) = 720, n ( T ) = 450
इस प्रकार n ( S ∪ T ) = n ( S ) + n ( T ) – n ( S ∩ T )
= 720 + 450 – n (S ∩ T) = 1170 – n ( S ∩ T )
स्पष्ट है कि n ( S ∪ T ) अधिकतम तब होगा जब n ( S ∩ T ) न्यूनतम है, किंतु S ∪ T ⊂ U, जिसका तात्पर्य है कि n ( S ∪ T ) ≤ n ( U ) = 1000 । इस प्रकार n ( S ∪ T ) का अधिकतम मान 1000 है। इसलिए n ( S ∩ T ) का न्यूनतम मान 170 है। अतः दोनों उत्पादों को पसंद करने वाले उपभोक्ताओं की न्यूनतम संख्या 170 है।
उदाहरण 33 500 कार मालिकों से पूछताछ करनें पर पाया गया कि 400 लोग A प्रकार की कार के, 200 लोग B प्रकार की कार के तथा 500 लोग A और B दोनों प्रकार की कारों के मालिक थे। क्या ये आँकड़े सही हैं?
हल मान लीजिए कि पूछताछ किए गए कार मालिकों का समुच्चय U है, A प्रकार की कार के मालिकों का समुच्चय M है और B प्रकार की कार के मालिकों का समुच्चय S है।
दिया है कि n ( U ) = 500, n (M ) = 400, n ( S ) = 200 और n ( S ∩ M ) = 50.
इस प्रकार n ( S ∪ M ) = n ( S ) + n ( M ) – n ( S ∩ M ) = 200 + 400 – 50 = 550
किंतु S ∪ M ⊂ U जिसका तात्पर्य है कि n ( S ∪ M ) ≤ n ( U ).
यह एक विरोधोक्ति है। अतः प्रदत्त आँकड़े सही नहीं है।
उदाहरण 34 एक महाविद्यालय में फुटबाल के लिए 38, बास्केट बाल के लिए 15 और क्रिकेट के लिए 20 पदक प्रदान किए गए। यदि ये पदक कुल 58 लोगों को मिले और केवल तीन लोगों को तीनों खेलों के लिए मिले, तो कितने लोगों को तीन में से ठीक-ठीक दो खेलों के लिए मिले?
हल मान लीजिए कि F, B तथा C उन लोगों के समुच्चय निरूपित करते हैं जिन्हें क्रमशः फुटबाल, बास्केटबाल तथा क्रिकेट के लिए पदक मिले।
यहाँ n ( F ) = 38, n ( B ) = 15, n ( C ) = 20, n (F ∪ B ∪ C ) = 58 और n (F ∩ B ∩ C ) = 3
पुनः n (F ∪ B ∪ C ) = n ( F ) + n ( B ) + n ( C ) – n (F ∩ B ) – n (F ∩ C ) – n (B ∩ C )
+ n ( F ∩ B ∩ C ),
इस प्रकार n ( F ∩ B ) + n ( F ∩ C ) + n ( B ∩ C ) = 18
आकृति 1.14 में दिए वेन आरेख पर विचार कीजिएः
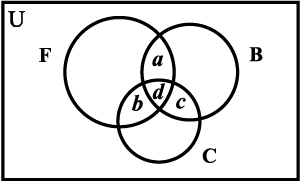
आकृति 1.14
यहाँ a उन लोगों की संख्या है, जिनको केवल फुटबाल तथा बास्केटबाल के लिए पदक मिले, b उन लोगों की संख्या है, जिनको केवल फुटबाल तथा क्रिकेट के लिए पदक मिले और c उन लोगों की संख्या है, जिनको केवल बास्केटबाल तथा क्रिकेट के लिए पदक मिले। d उन लोगों की संख्या है जिनको तीनो ही खेलों के लिए पदक मिले। इस प्रकार d = n ( F ∩ B ∩ C ) = 3 और
a + d + b + d + c + d = 18
अतः a + b + c = 9, जोकि उन लोगों की संख्या है, जिनकों तीनों खेलों में से दो खेलों के लिए
पदक मिले।
अध्याय 1 पर विविध प्रश्नावली
1. निम्नलिखित समुच्चयों में से कौन किसका उपसमुच्चय है, इसका निर्णय कीजिएः
A = {x : x ∈ R तथा x2 – 8x + 12 = 0 को संतुष्ट करने वाली सभी वास्तविक
संख्याएँ x }, B = {2, 4, 6}, C = { 2, 4, 6, 8, . . . }, D = { 6 }.
2. ज्ञात कीजिए कि निम्नलिखित में से प्रत्येक कथन सत्य है या असत्य है। यदि सत्य है, तो उसे सिद्ध कीजिए। यदि असत्य है, तो एक उदाहरण दीजिए।
(i) यदि x ∈ A तथा A ∈ B , तो x ∈ B
(ii) यदि A ⊂ B तथा B ∈ C , तो A ∈ C
(iii) यदि A ⊂ B तथा B ⊂ C , तो A ⊂ C
(iv) यदि A ⊄ B तथा B ⊄ C , तो A ⊄ C
(v) यदि x ∈ A तथा A ⊄ B , तो x ∈ B
(vi) यदि A ⊂ B तथा x ∉ B , तो x ∉ A
3. मान लीजिए A, B, और C एेसे समुच्चय हैं कि A ∪ B = A ∪ C तथा A ∩ B = A ∩ C, तो दर्शाइए कि B = C.
4. दिखाइए कि निम्नलिखित चार प्रतिबंध तुल्य हैंः
(i) A ⊂ B (ii) A – B = φ (iii) A ∪ B = B (iv) A ∩ B = A
5. दिखाइए कि यदि A ⊂ B, तो C – B ⊂ C – A.
6. मान लीजिए कि P ( A ) = P ( B ), सिद्ध कीजिए कि A = B
7. किन्हीं भी समुच्चयों A तथा B के लिए, क्या यह सत्य है कि
P ( A ) ∪ P ( B ) = P ( A ∪ B )? अपने उत्तर का औचित्य बताइए।
8. किन्हीं दो समुच्चयों A तथा B के लिए सिद्ध कीजिए कि,
A = ( A ∩ B ) ∪ ( A – B ) और A ∪ ( B – A ) = ( A ∪ B )
9. समुच्चयों के गुणधर्मों का प्रयोग करके सिद्ध कीजिए किः
(i) A ∪ ( A ∩ B ) = A (ii) A ∩ ( A ∪ B ) = A.
10. दिखलाइए कि A ∩ B = A ∩ C का तात्पर्य B = C आवश्यक रूप से नहीं होता है।
11. मान लीजिए कि A और B समुच्चय हैं। यदि किसी समुच्चय X के लिए
A ∩ X = B ∩ X = φ तथा A ∪ X = B ∪ X, तो सिद्ध कीजिए कि A = B.
(संकेतः A = A ∩ ( A ∪ X ) , B = B ∩ ( B ∪ X ) और वितरण नियम का प्रयोग कीजिए)
12. एेसे समुच्चय A, B और C ज्ञात कीजिए ताकि A ∩ B, B ∩ C तथा A ∩ C आरिक्त समुच्चय हों और A ∩ B ∩ C = φ.
13. किसी विद्यालय के 600 विद्यार्थियों के सर्वेक्षण से ज्ञात हुआ कि 150 विद्यार्थी चाय, 225 विद्यार्थी कॉफ़ी तथा 100 विद्यार्थी चाय और कॉफ़ी दोनों पीते हैं। ज्ञात कीजिए कि कितने विद्यार्थी न तो चाय पीते हैं और न कॉफ़ी पीते हैं।
14. विद्यार्थियों के एक समूह में, 100 विद्यार्थी हिंदी, 50 विद्यार्थी अंग्रेज़ी तथा 25 विद्यार्थी दोनों भाषाओं को जानते हैं। विद्यार्थियों में से प्रत्येक या तो हिंदी या अंग्रेज़ी जानता है। समूह में कुल कितने विद्यार्थी हैं?
15. 60 लोगों के सर्वेक्षण में पाया गया कि 25 लोग समाचार पत्र H, 26 लोग समाचार पत्र T, 26 लोग समाचार पत्र I, 9 लोग H तथा I दोनों, 11 लोग H तथा T दोनों, 8 लोग T तथा I दोनों और 3 लोग तीनों ही समाचार पत्र पढ़ते हैं, तो निम्नलिखित ज्ञात कीजिएः
(i) कम से कम एक समाचार पत्र पढ़ने वालों की संख्या।
(ii) ठीक-ठीक केवल एक समाचार पत्र पढ़ने वालों की संख्या।
16. एक सर्वेक्षण में पाया गया कि 21 लोग उत्पाद A, 26 लोग उत्पाद B, 29 लोग उत्पाद C पसंद करते हैं। यदि 14 लोग उत्पाद A तथा B, 12 लोग उत्पाद C तथा A, 14 लोग उत्पाद B तथा C और 8 लोग तीनो ही उत्पादों को पसंद करते हैं। ज्ञात कीजिए कि कितने लोग केवल उत्पाद C को पसंद करते हैं।
सारांश
इस अध्याय में समुच्चयों से संबंधित कुछ मूलभूत परिभाषाओं और संक्रियाओं पर विचार किया गया है। जिसका सार नीचे दिया है।
- एक समुच्चय वस्तुओं का सुपरिभाषित संग्रह होता है।
- एक समुच्चय जिसमें एक भी अवयव नहीं होता है, रिक्त समुच्चय कहलाता है।
- एक समुच्चय जिसमें अवयवों की संख्या निश्चित होती है परिमित समुच्चय कहलाता है अन्यथा अपरिमित समुच्चय कहलाता है।
- दो समुच्चय A और B समान कहलाते हैं यदि उनमें तथ्यतः समान अवयव हों।
- एक समुच्चय A किसी समुच्चय B का उपसमुच्चय कहलाता है, यदि A का प्रत्येक अवयव B का भी अवयव हो। अंतराल समुच्चय R के उपसमुच्चय होते हैं।
- किसी समुच्चय A का घात समुच्चय A के सभी उपसमुच्चयों का संग्रह होता है।
- दो समुच्चय A और B का सम्मिलन उन सभी अवयवों का समुच्चय होता है जो या तो A में हों या B में हों।
- दो समुच्चय A और B का सर्वनिष्ठ उन सभी अवयवों का समुच्चय होता है जो A और B दोनों में उभयनिष्ठ हों। दो समुच्चय A और B का अंतर, जब A तथा B इसी क्रम में हो, उन सभी अवयवों का समुच्चय है, जो A में हों किंतु B में नहीं हों।
- किन्हीं दो समुच्चय A तथा B के लिए, (A ∪ B)′ = A′ ∩ B′ तथा (A ∩ B)′ = A′ ∪ B′
- यदि A और B एेसे परिमित समुच्चय हैं कि A ∩ B = φ, तो,
n (A ∪ B) = n (A) + n (B) और
यदि A ∩ B ≠ φ, तो
n (A ∪ B) = n (A) + n (B) – n (A ∩ B)
एेतिहासिक पृष्ठभूमि
जर्मन गणित Georg Cantor (1845 ई॰ - 1918 ई॰ ) को आधुनिक समुच्चय सिद्धांत के अधिकांश भाग का जन्मदाता माना जाता है। समुच्चय सिद्धांत पर उनके शोध पत्र 1874 ई॰ से 1897 ई॰ के बीच के किसी समय में प्रकाश में आए। उनका समुच्चय सिद्धांत का अध्ययन उस समय हुआ जब वे a1 sin x + a2 sin 2x + a3 sin 3x + ... के रूप की त्रिकोणमितीय श्रेणी का अध्ययन कर रहे थे।
1874 ई॰ में अपने एक शोध पत्र में यह प्रकाशित किया कि वास्तविक संख्याओं को पूर्णांकों के साथ एक-एक संगतता में नहीं रखा जा सकता है। 1879 ई॰ के उत्तरार्ध में अमूर्त समुच्चयों के विभिन्न गुणधर्मों को दर्शाने वाले उनके अनेक शोध पत्र प्रकाεशत हुए।
Cantor के शोध को एक अन्य विख्यात गणितज्ञ Richard Dedekind (1831ई॰-1916ई॰) ने प्रशंसनीय ढंग से स्वीकार किया। लेकिन Kronecker (1810-1893 ई॰) ने अपरिमित समुच्चयों को, उसी प्रकार से लेने के लिए जिस प्रकार परिमित समुच्चयों को लिया जाता है, उनकी भर्त्सना की। एक दूसरे जर्मन गणितज्ञ Gottlob Frege ने शताब्दी की समाप्ति पर समुच्चय सिद्धांत को तर्कशास्त्र के नियमों के रूप में प्रस्तुत किया। उस समय तक संपूर्ण समुच्चय सिद्धांत सभी समुच्चयों के समुच्चय के अस्तित्व की कल्पना पर आधारित था। यह विख्यात अंग्रेज दार्शिनिक Bertand Russell (1872 ई.-1970 ई॰) थे जिन्होंने 1902 ई॰ में बतलाया कि सभी समुच्चयों के समुच्चय के अस्तित्व की कल्पना एक विरोधोक्ति को जन्म देती है। इस प्रकार Russell की विख्यात विरोधोक्ति मिली। Paul R.Halmos ने इसके बारे में अपनी पुस्तक ‘Naïve Set Theory’ में लिखा है कि ‘‘कुछ नहीं में सब कुछ समाहित है’’।
इन सभी विरोधोक्तियों के परिणामस्वरूप समुच्चय सिद्धांत का पहला अभिगृहीतीकरण 1908 ई॰ में Ernst Zermelo द्वारा प्रकाशित किया गया। 1922 ई॰ में Abraham Fraenkel ने एक दूसरा प्रस्ताव भी दिया। 1925 ई॰ में John Von Neumann ने नियमितीकरण का अभिगृहीत स्पष्ट रूप से प्रस्तुत किया। इसके बाद 1937 ई॰ में Paul Bernays ने सन्तोषजनक अभिगृहीतिकरण प्रस्तुत किया। इन अभिगृहीतों में सुधार, Kurt Gödel द्वारा 1940 ई॰ में अपने मोनोग्राफ में प्रस्तुत किया गया। इस सुधार को Von Neumann-Bernays (VNB) अथवा Gödel-Bernays (GB) का समुच्चय सिद्धांत कहते हैं।
इन सभी कठिनाइयों के बावजूद, Cantor के समुच्चय सिद्धांत को वर्तमान काल के गणित में प्रयोग किया जाता है। वास्तव में आजकल गणित के अधिकांश संकल्पनाएँ तथा परिणामों को समुच्चय सैद्धांतिक भाषा में प्रस्तुत करते हैं।