Table of Contents
"Mathematics is the indispensable instrument of all physical research.– BERTHELOT"
2.1 भूमिका (Introduction)
गणित का अधिकांश भाग पैटर्न अर्थात् परिवर्तनशील राशियों के बीच अभिज्ञेय (पहचान योग्य)कड़ियों को ज्ञात
2.2 समुच्चयों का कार्तीय गुणन (Cartesian Product of Sets)
मान लीजिए कि A, दो प्रकार के रंगों का और B, तीन वस्तुओं का समुच्चय है, अर्थात् A = {लाल, नीला}और B = {b, c, s},
जहाँ b, c और s क्रमशः किसी विशेष बैग, कोट और कमीज को निरूपित करते हैं। इन दोनों समुच्चयों से कितने प्रकार की रंगीन वस्तुओं के युग्म बनाए जा सकते हैं? क्रमबद्ध तरीके से प्रगति करते हुए हम देखते हैं कि निम्नलिखित 6 भिन्न-भिन्न युग्म प्राप्त होते हैं। (लाल, b), (लाल, c), (लाल, s), (नीला, b), (नीला, c), (नीला, s)। इस प्रकार हमें 6 भिन्न-भिन्न वस्तुएँ प्राप्त होती हैं (आकृति 2.1)।
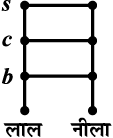
आकृति 2.1
पिछली कक्षाओं से स्मरण कीजिए कि, एक क्रमित युग्म, अवयवों का वह युग्म है, जिसे वक्र कोष्ठक में लिखते हैं और जिनको एक दूसरे से किसी विशेष क्रम में समूहित किया जाता है अर्थात् (p,q), p ∈ P और q ∈ Q। इसे निम्नलिखित परिभाषा से स्पष्ट किया जा सकता है।
परिभाषा 1 दो अरिक्त समुच्चयों P तथा Q का कार्तीय गुणन P × Q उन सभी क्रमित युग्मों का समुच्चय है, जिनको प्रथम घटक P से तथा द्वितीय घटक Q, से लेकर बनाया जा सकता है। अतः
P × Q = { (p,q) : p ∈ P, q ∈ Q }
यदि P या Q में से कोई भी रिक्त समुच्चय है, तो उनका कार्तीय गुणन भी रिक्त समुच्चय होता है, अर्थात् P × Q = φ
उपरोक्त दृष्टांत से हम जानते हैं कि
A × B = {(लाल,b), (लाल,c), (लाल,s), (नीला,b), (नीला,c), (नीला,s)}।
पुनः निम्नलिखित दो समुच्चयों पर विचार कीजिए।
A = {DL, MP, KA}, जहाँ DL, MP, KA दिल्ली, मध्य प्रदेश, तथा कर्नाटक को निरूपित करते हैं और B = {01,02, 03}क्रमशः दिल्ली, मध्य प्रदेश और कर्नाटक द्वारा गाड़ियों के लिए जारी लाइसेंस प्लेट की सांकेतिक संख्याएँ प्रकट करते हैं।
यदि तीन राज्य दिल्ली, मध्य प्रदेश और कर्नाटक, गाड़ियों के लाइसेंस प्लेट के लिए संकेत पद्धति (संकेतिकी) इस प्रतिबंध के साथ बना रहे हों कि संकेत पद्धति, समुच्चय A के अवयव से प्रारंभ हो, तो इन समुच्चयों से प्राप्त होने वाले युग्म कौन से हैं तथा इन युग्मों की कुल संख्या कितनी है (आकृति 2.2)?
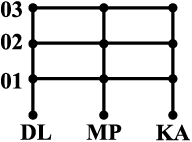
आकृति 2.2
प्राप्त होने वाले युग्म इस प्रकार हैं, (DL,01), (DL,02), (DL,03), (MP,01), (MP,02), (MP,03), (KA,01), (KA,02), (KA,03) और समुच्चय A तथा समुच्चय B का कार्तीय गुणन इस प्रकार होगा,
A × B = {(DL,01), (DL,02), (DL,03), (MP,01), (MP,02), (MP,03), (KA,01), (KA,02),(ज्ञ।ए03)द्व.
यह सरलता से देखा जा सकता है कि कार्तीय गुणन में इस प्रकार 9 युग्म हैं क्योंकि समुच्चय A और B में से प्रत्येक में 3 अवयव हैं। इससे हमें 9 संभव संकेत पद्धतियाँ मिलती हैं। यह भी नोट कीजिए कि इन अवयवों के युग्म बनाने का क्रम महत्त्वपूर्ण (निर्णायक) है। उदाहरण के लिए सांकेतिक संख्या (DL, 01) वही नहीं है जो सांकेतिक संख्या (01, DL) है।
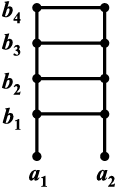
आकृति 2.3
अंत में स्पष्टीकरण के लिए समुच्चय A= {a1, a2} और
B = {b1, b2, b3, b4} पर विचार कीजिए (आकृति 2.3)। यहाँ
A × B = {( a1, b1), (a1, b2), (a1, b3), (a1, b4), (a2, b1), (a2, b2), (a2, b3), (a2, b4)}.
यदि A और B, वास्तविक संख्याओं के समुच्चय के उपसमुच्चय हों, तो इस प्रकार प्राप्त 8 क्रमित युग्म किसी समतल के बिंदुओं की स्थिति निरूपित करते हैं तथा यह स्पष्ट है कि (a1, b2) पर स्थित बिंदु, (b2, a1) पर स्थित बिंदु से भिन्न हैं।
टिप्पणी
(i) दो क्रमित युग्म समान होते हैं, यदि और केवल यदि उनके संगत प्रथम घटक समान हों और संगत द्वितीय घटक भी समान हों।
(ii) यदि A में p अवयव तथा B में q अवयव हैं, तो A × B में pq अवयव होते हैं अर्थात् यदि n(A) = p तथा n(B) = q, तो n(A × B) = pq.
(iii) यदि A तथा B अरिक्त समुच्चय हैं और A या B में से कोई अपरिमित है, तो A × B भी अपरिमित समुच्चय होता है।
(iv) A × A × A = {(a, b, c) : a, b, c ∈ A}. यहाँ (a, b, c) एक क्रमित त्रिक कहलाता है।
उदाहरण 1 यदि (x + 1, y – 2) = (3,1), तो x और y के मान ज्ञात कीजिए।
हल क्योंकि क्रमित युग्म समान है, इसलिए संगत घटक भी समान होंगे।
अतः x + 1 = 3 और y – 2 = 1.
सरल करने पर x = 2 और y = 3.
उदाहरण 2 यदि P = {a, b, c} और Q = {r}, तो P × Q तथा Q × P ज्ञात कीजिए। क्या दोनों कार्तीय गुणन समान हैं?
हल कार्तीय गुणन की परिभाषा से
P × Q = {(a, r), (b, r), (c, r)} और Q × P = {(r, a), (r, b), (r, c)}
क्योंकि, क्रमित युग्मों की समानता की परिभाषा से, युग्म (a, r) युग्म (r, a), के समान नहीं है और यह बात कार्तीय गुणन के प्रत्येक युग्म के लिए लागू होती है, जिससे हम निष्कर्ष निकालते हैं कि P × Q ≠ Q × P.
तथापि, प्रत्येक समुच्चय में अवयवों की संख्या समान है।
उदाहरण 3 मान लीजिए कि A = {1,2,3}, B = {3,4} और C = {4,5,6}. निम्नलिखित ज्ञात कीजिएः
(i) A × (B ∩ C) (ii) (A × B) ∩ (A × C)
(iii) A × (B ∪ C) (iv) (A × B) ∪ (A × C)
हल (i) दो समुच्चयों के सर्वनिष्ठ की परिभाषा से (B ∩ C) = {4}.
अतः A × (B ∩ C) = {(1,4), (2,4), (3,4)}.
(ii) अब (A × B) = {(1,3), (1,4), (2,3), (2,4), (3,3), (3,4)}
और (A × C) = {(1,4), (1,5), (1,6), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6)}
इसलिए (A × B) ∩ (A × C) = {(1, 4), (2, 4), (3, 4)}.
(iii) क्योंकि (B ∪ C) = {3, 4, 5, 6}
अतः A × (B ∪ C) = {(1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (2,5), (2,6), (3,3),
(3,4), (3,5), (3,6)}.
(iv) भाग (ii) से A × B तथा A × C समुच्चयों के प्रयोग से हमें निम्नलिखित प्राप्त होता हैः
(A × B) ∪ (A × C) = {(1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (2,5), (2,6),
(3,3), (3,4), (3,5), (3,6)}.
उदाहरण 4 यदि P = {1, 2}, तो समुच्चय P × P × P ज्ञात कीजिए।
हल P × P × P = {(1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2)}.
उदाहरण 5 यदि R समस्त वास्तविक संख्याओं का समुच्चय है, तो कार्तीय गुणन R × R और R × R × R क्या निरूपित करते हैं?
हल कार्तीय गुणन R × R समुच्चय R × R={(x, y) : x, y ∈ R}
को निरूपित करता है, जिसका प्रयोग द्विविम समष्टि के बिंदुओं के निर्देशांकों को प्रकट करने के लिए किया जाता है। R × R × R समुच्चय R × R × R ={(x, y, z) : x, y, z ∈ R} को निरूपित करता है, जिसका प्रयोग त्रिविमीय आकाश के बिंदुओं के निर्देशांकों को प्रकट करने के लिए किया जाता है।
उदाहरण 6 यदि A × B ={(p, q),(p, r), (m, q), (m, r)}, तो A और B को ज्ञात कीजिए।
हल A = प्रथम घटकों का समुच्चय = {p, m}
B = द्वितीय घटकों का समुच्चय = {q, r}.
प्रश्नावली 2.1
1. यदि 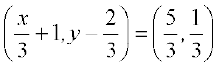 , तो x तथा y ज्ञात कीजिए।
, तो x तथा y ज्ञात कीजिए।
2. यदि समुच्चय A में 3 अवयव हैं तथा समुच्चय B = {3, 4, 5}, तो (A×B) में अवयवों की संख्या ज्ञात कीजिए।
3. यदि G = {7, 8} और H = {5, 4, 2}, तो G × H और H × G ज्ञात कीजिए।
4. बतलाइए कि निम्नलिखित कथनों में से प्रत्येक सत्य है अथवा असत्य है। यदि कथन असत्य है, तो दिए गए कथन को सही बना कर लिखिए।
(i) यदि P = {m, n} और Q = { n, m}, तो P × Q = {(m, n),(n, m)}.
(ii) यदि A और B अरिक्त समुच्चय हैं, तो A × B क्रमित युग्मों (x, y) का एक अरिक्त समुच्चय है, इस प्रकार कि x ∈ A तथा y ∈ B.
(iii) यदि A = {1, 2}, B = {3, 4}, तो A × (B ∩ φ) = φ.
5. यदि A = {–1, 1}, तो A × A × A ज्ञात कीजिए।
6. यदि A × B = {(a, x),(a , y), (b, x), (b, y)} तो A तथा B ज्ञात कीजिए।
7. मान लीजिए कि A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} तथा D = {5, 6, 7, 8}. सत्यापित कीजिए कि
(i) A × (B ∩ C) = (A × B) ∩ (A × C). (ii) A × C, B × D का एक उपसमुच्चय है।
8. मान लीजिए कि A = {1, 2} और B = {3, 4}. A × B लिखिए। A × B के कितने उपसमुच्चय होंगे? उनकी सूची बनाइए।
9. मान लीजिए कि A और B दो समुच्चय हैं, जहाँ n(A) = 3 और n(B) = 2. यदि (x, 1), (y, 2), (z, 1), A × B में हैं, तो A और B, को ज्ञात कीजिए, जहाँ x, y और z भिन्न-भिन्न अवयव हैं।
10. कार्तीय गुणन A × A में 9 अवयव हैं, जिनमें (–1,0) तथा (0,1) भी है। समुच्चय A ज्ञात कीजिए तथा A × A के शेष अवयव भी ज्ञात कीजिए।
2.3 संबंध (Relation)
दो समुच्चयों P = {a,b,c} तथा Q = {Ali, Bhanu, Binoy, Chandra, Divya} पर विचार कीजिए। P तथा Q के कार्तीय गुणन में 15 क्रमित युग्म हैं, जिन्हें इस प्रकार सूचीबद्ध किया जा सकता है,
P × Q = {(a, Ali), (a,Bhanu), (a, Binoy), ..., (c, Divya)}.
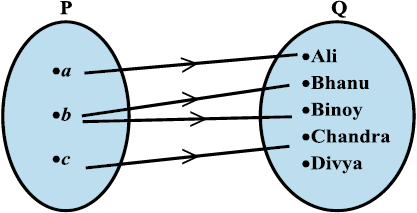
आकृति 2.4
अब हम प्रत्येक क्रमित युग्म (x, y) के प्रथम घटक x तथा द्वितीय घटक y के बीच एक संबंध R स्थापित कर P × Q का एक उपसमुच्चय इस प्रकार प्राप्त कर सकते हैं।
R = { (x,y): x, नाम y का प्रथम अक्षर है, x ∈ P, y ∈ Q} इस प्रकार
R = {(a, Ali), (b, Bhanu), (b, Binoy), (c, Chandra)}
संबंध R का एक दृष्टि-चित्रण, जिसे तीर आरेख कहते हैं, आकृति 2.4 में प्रदर्शित है।
परिभाषा 2 किसी अरिक्त समुच्चय A से अरिक्त समुच्चय B में संबंध कार्तीय गुणन A × B का एक उपसमुच्चय होता है यह उपसमुच्चय A × B के क्रमति युग्मों के प्रथम तथा द्वितीय घटकों के मध्य एक संबंध स्थापित करने से प्राप्त होता है। द्वितीय घटक, प्रथम घटक का प्रतिबिंब कहलाता है।
परिभाषा 3 समुच्चय A से समुच्चय B में संबंध R के क्रमित युग्मों के सभी प्रथम घटकों के समुच्चय को संबंध R का प्रांत कहते हैं।
परिभाषा 4 समुच्चय A से समुच्चय B में संबंध R के क्रमित युग्मों के सभी द्वितीय घटकों के समुच्चय को संबंध R का परिसर कहते हैं। समुच्चय B संबंध R का सह-प्रांत कहलाता है। नोट कीजिए कि, परिसर ⊆ सहप्रांत
टिप्पणी (i) एक संबंध का बीजीय निरूपण या तो रोस्टर विधि या समुच्चय निर्माण विधि द्वारा किया जा सकता है।
(ii) एक तीर आरेख किसी संबंध का एक दृष्टि चित्रण है।
उदाहरण 7 मान लीजिए कि A = {1, 2, 3, 4, 5, 6}. R = {(x, y) : y = x + 1 } द्वारा A से A में एक संबंध परिभाषित कीजिए।
(i) इस संबंध को एक तीर आरेख द्वारा दर्शाइए।
(ii) R के प्रांत, सहप्रांत तथा परिसर लिखिए।
हल (i) परिभाषा द्वारा
R = {(1,2), (2,3), (3,4), (4,5), (5,6)}.
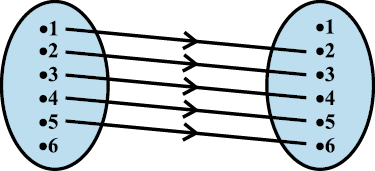
आकृति 2.5
संगत तीर आरेख आकृति 2.5 में प्रदर्शित है।
(ii) हम देख सकते हैं कि प्रथम घटकों का समुच्चय अर्थात् प्रांत={1, 2, 3, 4, 5,} इसी प्रकार, द्वितीय घटकों का समुच्चय अर्थात् परिसर = {2, 3, 4, 5, 6}तथा सहप्रांत = {1, 2, 3, 4, 5, 6}.
उदाहरण 8 नीचे आकृति 2.6 में समुच्चय P और Q के बीच एक संबंध दर्शाया गया है। इस संबंध को (i) समुच्चय निर्माण रूप में (ii) रोस्टर रूप में लिखिए। इसके प्रांत तथा परिसर क्या हैं?
हल स्पष्टतः संबंध R, “x, y का वर्ग है”
(i) समुच्चय निर्माण रूप में, R = {(x, y): x, y का वर्ग है, x ∈ P, y ∈ Q}
(ii) रोस्टर रूप में, R = {(9, 3), (9, –3), (4, 2), (4, –2), (25, 5), (25, –5)}
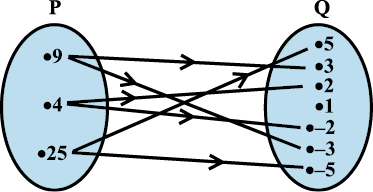
आकृति 2.6
इस संबंध का प्रांत {4, 9, 25} है।
इस संबंध का परिसर {– 2, 2, –3, 3, –5, 5}.
नोट कीजिए कि अवयव 1, P के किसी भी अवयव से संबंधित नहीं है तथा समुच्चय Q इस संबंध का सहप्रांत है।
टिप्पणी किसी समुच्चय A से समुच्चय B में संबंधों की कुल संख्या, A × B के संभव उपसमुच्चयों की संख्या के बराबर होती है। यदि n(A ) = p और n(B) = q, तो n(A × B) = pq और संबंधों की कुल संख्या 2pq होती है।
उदाहरण 9 मान लीजिए कि A = {1, 2} और B = {3, 4}. A से B में संबंधों की संख्या ज्ञात कीजिए।
हल यहाँ A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}.
क्योंकि n (A×B ) = 4, इसलिए A×B के उपसमुच्चयों की संख्या 24 है। इसलिए A से B के संबंधों की संख्या 24 है।
टिप्पणी A से A के संबंध को ‘A पर संबंध भी कहते हैं।
प्रश्नवाली 2.2
1. मान लीजिए कि A = {1, 2, 3,...,14}.R = {(x, y) : 3x – y = 0, जहाँ x, y ∈ A} द्वारा, A से A का एक संबंध R लिखिए। इसके प्रांत, सहप्रांत और परिसर लिखिए।
2. प्राकृत संख्याओं के समुच्चय पर R = {(x, y) : y = x + 5, x संख्या 4 से कम, एक प्राकृत संख्या है, x, y ∈N }द्वारा एक संबंध R परिभाषित कीजिए। इस संबंध को (i) रोस्टर रूप में इसके प्रांत और परिसर लिखिए।
3. A = {1, 2, 3, 5} और B = {4, 6, 9}. A से B में एक संबंध R = {(x, y): x और y का अंतर विषम है, x ∈ A, y ∈ B} द्वारा परिभाषित कीजिए। R को रोस्टर रूप में लिखिए।
4. आकृति 2.7, समुच्चय P से Q का एक संबंध दर्शाती है। इस संबंध को
(i) समुच्चय निर्माण रूप (ii) रोस्टर रूप में लिखिए। इसके प्रांत तथा परिसर क्या हैं?
5. मान लीजिए कि A = {1, 2, 3, 4, 6}. मान लीजिए कि R, A पर {(a, b): a , b ∈A, संख्या a संख्या b को यथावथ विभाजित करती है}द्वारा परिभाषित एक संबंध है।
(i) R को रोस्टर रूप में लिखिए
(ii) R का प्रांत ज्ञात कीजिए
(iii) R का परिसर ज्ञात कीजिए।
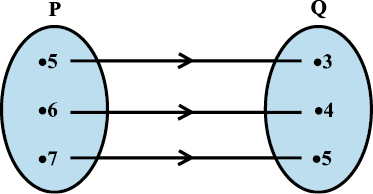
आकृति 2.7
6. R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}द्वारा परिभाषित संबंध R के प्रांत और परिसर ज्ञात कीजिए।
7. संबंध R = {(x, x3) : x संख्या 10 से कम एक अभाज्य संख्या है} को रोस्टर रूप में लिखिए।
8. मान लीजिए कि A = {x, y, z} और B = {1, 2}, A से B के संबंधों की संख्या ज्ञात कीजिए।
9. मान लीजिए कि R, Z पर, R = {(a,b): a, b ∈ Z, a – b एक पूर्णांक है}, द्वारा परिभाषित एक संबंध है। R के प्रांत तथा परिसर ज्ञात कीजिए।
2.4 फलन (Function)
इस अनुच्छेद में, हम एक विशेष प्रकार के संबंध का अध्ययन करेंगे, जिसे फलन कहते हैं। हम फलन को एक नियम के रूप में देख सकते हैं, जिससे कुछ दिए हुए अवयवों से नए अवयव उत्पन्न होते हैं। फलन को सूचित करने के लिए अनेक पद प्रयुक्त किए जाते हैं, जैसे ‘प्रतिचित्र’ अथवा ‘प्रतिचित्रण’
दूसरे शब्दों में, फलन f, किसी अरिक्त समुच्चय A से एक अरिक्त समुच्चय B का है, इस प्रकार का संबंध कि f का प्रांत A है तथा f के किसी भी दो भिन्न क्रमित युग्मों के प्रथम घटक समान नहीं हैं।
यदि f, A से B का एक फलन है तथा (a, b) ∈ f, तो f (a) = b, जहाँ b को f के अंतर्गत a का प्रतिबम्ब तथा a को b का ‘पूर्व प्रतिबिंब’ कहते हैं।
A से B के फलन f को प्रतीकात्मक रूप में f: A →B से निरूपित करते हैं।
पिछले उदाहरणों पर ध्यान देने से हम सरलता से देखते हैं कि उदाहरण 7 में दिया संबंध एक फलन नहीं है, कयोंकि अवयव 6 का कोई प्रतिबिंब नहीं है।
पुनः उदाहरण 8 में दिया संबंध एक फलन नहीं है क्येांकि इसके प्रांत के कुछ अवयवों के एक से अधिक प्रतिबिंब हैं। उदहारण 9 भी फलन नहीं है (क्यों?)। नीचे दिए उदाहरणों में बहुत से संबंधों पर विचार करेंगे, जिनमें से कुछ फलन हैं और दूसरे फलन नहीं हैं।
उदाहरण 10 मान लीजिए कि N प्राकृत संख्याओं का समुच्चय हे और N पर परिभाषित एक संबंधR इस प्रकार है कि R = {(x, y) : y = 2x, x, y ∈ N}.
R के प्रांत, सहप्रांत तथा परिसर क्या हैं? क्या यह संबंध, एक फलन है?
हल R का प्रांत, प्राकृत संख्याओं का समुच्चय N है। इसका सहप्रांत भी N है। इसका परिसर सम प्राकृत संख्याओं का समुच्चय है।
क्योंकि प्रत्येक प्राकृत संख्या n का एक और केवल एक ही प्रतिबिंब है, इसलिए यह संबंध एक फलन है।
उदाहरण 11 नीचे दिए संबंधों में से प्रत्येक का निरीक्षण कीजिए और प्रत्येक दशा में कारण सहित बतलाइए कि क्या यह फलन है अथवा नहीं?
(i) R = {(2,1),(3,1), (4,2)}, (ii) R = {(2,2),(2,4),(3,3), (4,4)}
(iii) R = {(1,2),(2,3),(3,4), (4,5), (5,6), (6,7)}
हल (i) क्योंकि R के प्रांत के प्रत्येक अवयव 2, 3, 4 के प्रतिबिंब अद्वितीय हैं, इसलिए यह संबंध एक फलन है।
(ii) क्यांकि एक ही प्रथम अवयव 2, दो भिन्न-भिन्न प्रतिबिंबों 2 और 4 से संबंधित है, इसलिए यह संबंध एक फलन नहीं हैं।
(iii) क्योंकि प्रत्येक अवयव का एक और केवल एक प्रतिबिंब है, इसलिए यह संबंध एक फलन है।
परिभाषा 6 एक एेसे फलन को जिसका परिसर वास्तविक संख्याओं का समुच्चय या उसका कोई उपसमुच्चय हो, वास्तविक मान फलन कहते हैं। यदि वास्तविक चर वाले किसी वास्तविक मान फलन का प्रांत भी वास्तविक संख्याओं का समुच्चय अथवा उसका कोई उपसमुच्चय हो तो इसे वास्तविक फलन भी कहते हैं।
उदाहरण 12 मान लीजिए कि N वास्तविक संख्याओं का समुच्चय है। f : N N, f (x) = 2x + 1, द्वारा परिभाषित एक वास्तविक मान फलन है। इस परिभाषा का प्रयोग करके, नीचे दी गई सारणी को पूर्ण कीजिए।
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | f (1) = ..... | f (2) = ...... | f (3) = ...... | f (4) = .... | f (5) = ...... | f (6) = ..... | f (7) =...... |
हल पूर्ण की हुई सारणी नीचे दी गई हैः
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | f (1) = 3 | f (2) = 5 | f (3) = 7 | f (4) = 9 | f (5) = 11 | f (6) = 13 | f (7) =15 |
2.4.1 कुछ फलन और उनके आलेख (Some functions and their graphs)
(i) तत्समक फलन (Identity function) मान लीजिए R वास्तविक संख्याओं का समुच्चय है। y = f(x), प्रत्येक x ∈ R द्वारा परिभाषित वास्तविक मान फलन f : R → R है। इस प्रकार के फलन को तत्समक फलन कहते हैं। यहाँ पर f के प्रांत तथा परिसर R हैं। इसका आलेख एक सरल रेखा होता है (आकृति 2.8)। यह रेखा मूल बिंदु से हो कर जाती है।
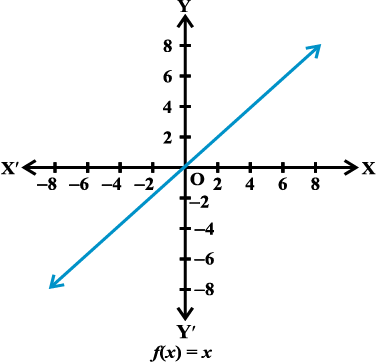
आकृति 2.8
(ii) अचर फलन (Constant function) y = f (x) = c जहाँ c एक अचर है और प्रत्येक x ∈ R द्वारा परिभाषित एक वास्तविक मान फलन f: R → R है। यहाँ पर f का प्रांत R है और उसका परिसर {c} है। f का आलेख x-अक्ष के समांतर एक रेखा है, उदाहरण के लिए यदि f(x)=3 प्रत्येक x ∈ R है, तो इसका आलेख आकृति 2.9 में दर्शाई रेखा है।
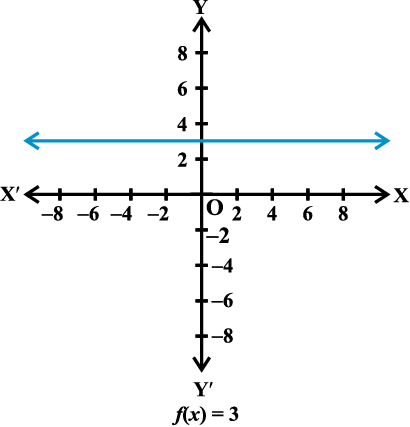
आकृति 2.9
(iii) बहुपद फलन या बहुपदीय फलन (Polynomial function) फलन f : R → R, एक बहुपदीय फलन कहलाता है, यदि R के प्रत्येक x के लिए, y = f (x) = a0 + a1x + a2x2 + ...+ an xn, जहाँ n एक ऋणेतर पूर्णांक है तथा a0, a1, a2,...,an∈R.
f(x) = x3 – x2 + 2, और g(x) = x4 + 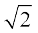 x, द्वारा परिभाषित फलन एक बहुपदीय फलन है जब कि h(x) =
x, द्वारा परिभाषित फलन एक बहुपदीय फलन है जब कि h(x) = 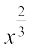 + 2x द्वारा परिभाषित फलन h, बहुपदीय फलन नहीं है। (क्यों?)
+ 2x द्वारा परिभाषित फलन h, बहुपदीय फलन नहीं है। (क्यों?)
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 1 | 2 |
| y = f(x) = x2 |
हल पूरी की हुई तालिका नीचे दी गई हैः
| ग | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 1 | 2 |
| y = f(x) = x2 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
f का प्रांत = {x : x∈R}, f का परिसर = {x2: x ∈ R}. f का आलेख आकृति 2.10 में प्रदर्शित है।

आकृति 2.10
उदाहरण 14 f (x) = x3, x∈R द्वारा परिभाषित फलन f :R → R का आलेख खींचिए।
हल यहाँ पर
f(0) = 0, f(1) = 1, f(–1) = –1, f(2) = 8, f(–2) = –8, f(3) = 27; f(–3) = –27, इत्यादि।
f = {(x,x3): x∈R} f का आलेख आकृति 2.11 में खींचा गया है।
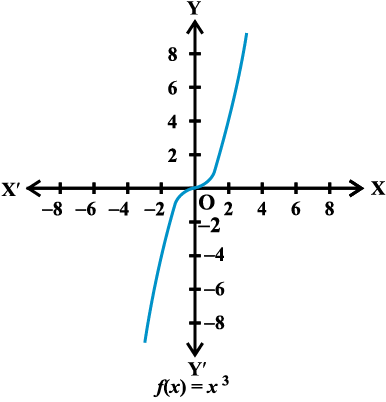
आकृति 2.11
(iv) परिमेय फलन (Rational functions) 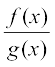 , के प्रकार के फलन जहाँ f(x) तथा g(x) एक प्रांत में, x के परिभाषित बहुपदीय फलन हैं, जिसमें g(x) ≠ 0 परिमेय फलन कहलाते हैं।
, के प्रकार के फलन जहाँ f(x) तथा g(x) एक प्रांत में, x के परिभाषित बहुपदीय फलन हैं, जिसमें g(x) ≠ 0 परिमेय फलन कहलाते हैं।
उदाहरण 15 एक वास्तविक मान फलन f : R – {0} → R की परिभाषा 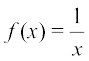 , x ∈ R –{0} द्वारा कीजिए। इस परिभाषा का प्रयोग करके निम्नलिखित तालिका को पूर्ण कीजिए। इस फलन का प्रांत तथा परिसर क्या हैं?
, x ∈ R –{0} द्वारा कीजिए। इस परिभाषा का प्रयोग करके निम्नलिखित तालिका को पूर्ण कीजिए। इस फलन का प्रांत तथा परिसर क्या हैं?
| x | -2 | -1.5 | -1 | -0.5 | 0.25 | 0.5 | 1 | 1.5 | 2 |
y =  | .... | ..... | .... | .... | .... | ... | ... | .... | .... |
हल पूर्ण की गई तालिका इस प्रकार हैः
| x | -2 | -1.5 | -1 | -0.5 | 0.25 | 0.5 | 1 | 1.5 | 2 |
y =  | – 0.5 | – 0.67 | –1 | – 2 | 4 | 2 | 1 | 0.67 | 0.5 |
इसका प्रांत, शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं तथा इसका परिसर भी शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं। f का आलेख आकृति 2.12 में प्रदर्शित है।
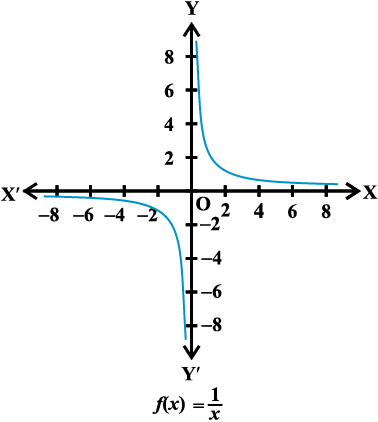
आकृति 2.12
(v) मापांक फलन (Modulus functions) f(x) = |x| प्रत्येक x ∈ R द्वारा परिभाषित फलन f: R→R, मापांक फलन कहलाता है। x के प्रत्येक ऋणेत्तर मान के लिए f(x), x के बराबर होता है। परंतु x के ऋण मानों के लिए, f(x) का मान x, के मान के ऋण के बराबर होता है, अर्थात्
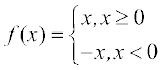
मापांक फलन का आलेख आकृति 2.13 में दिया है। मापांक फलन को निरपेक्ष मान फलन भी कहते हैं।

आकृति 2.13
(vi) चिह्न फलन (Signum functions) प्रत्येक x ∈R, के लिए
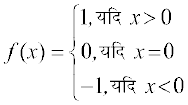
द्वारा परिभाषित फलन f:R→R चिह्न फलन कहलाता है। चिह्न फलन का प्रांत R है। परिसर समुच्चय {–1, 0, 1}है। आकृति 2.14 में चिह्न फलन का आलेख दर्शाया गया है।
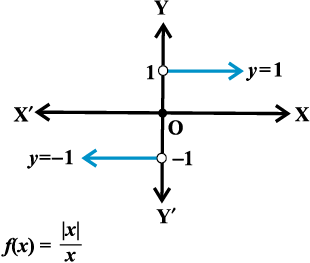
आकृति 2.14
(vii) महत्तम पूर्णांक फलन (Greatest integer functions) f(x) = [x], x ∈R द्वारा परिभाषित फलन f: R → R, x से कम या x के बराबर महत्तम पूर्णांक का मान ग्रहण (धारण) करता है एेसा फलन महत्तम पूर्णांक फलन कहलाता है।
[x], की परिभाषा से हम देख सकते हैं कि
[x] = –1 यदि –1 ≤ x < 0
[x] = 0 यदि 0 ≤ x < 1
[x] = 1 यदि 1 ≤ x < 2
[x] = 2 यदि 2 ≤ x < 3 इत्यदि
इस फलन का आलेख आकृति 2.15 में दर्शाया गया है।
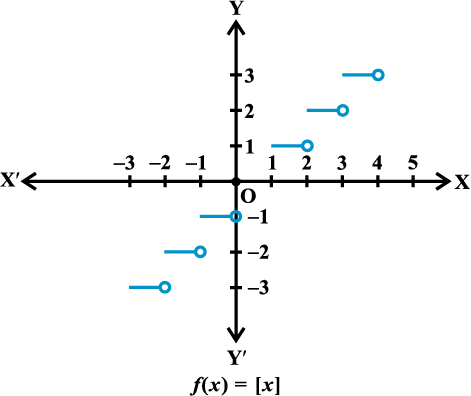
आकृति 2.15
2.4.2 वास्तविक फलनों का बीजगणित (Algebra of real functions)
इस अनुच्छेद में, हम सीखेंगे कि किस प्रकार दो वास्तविक फलनों को जोड़ा जाता है, एक वास्तविक फलन को दूसरे में से घटाया जाता है, एक वास्तविक फलन को किसी अदिश (यहाँ आदिश का अभिप्राय वास्तविक संख्या से है) से गुणा किया जाता है, दो वास्तविक फलनों का गुणा किया जाता है तथा एक वास्तविक फलन को दूसरे से भाग दिया जाता है।
(i) दो वास्तविक फलनों का योग मान लीजिए कि f : X → R तथा g : X → R कोई दो वास्तविक फलन हैं, जहाँ X ⊂ R. तब हम (f + g): X → R को, सभी x ∈ X के लिए, (f + g) (x) = f (x) + g (x), द्वारा परिभाषित करते हैं।
(iii) एक अदिश से गुणा मान लीजिए कि f : X→R एक वास्तविक मान फलन है तथा α एक अदिश है। यहाँ अदिश से हमारा अभिप्राय किसी वास्तविक संख्या से है। तब गुणनफल α f , X से R में एक फलन है, जो (α f ) (x) = α f (x), x ∈X से परिभाषित होता है।
(iv) दो वास्तविक फलनों का गुणन दो वास्तविक फलनों f: X → R तथा g: X→R का गुणनफल (या गुणा) एक फलन fg: X→R है, जो सभी (fg) (x) = f(x) g(x), x ∈ X द्वारा परिभाषित है। इसे बिंदुशः गुणन भी कहते हैं।
(v) दो वास्तविक फलनों का भागफल मान लीजिए कि f तथा g, X→R द्वारा परिभाषित, दो वास्तविक फलन हैं, जहाँ X R. f का g से भागफल, जिसे
R. f का g से भागफल, जिसे 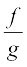 से निरूपित करते हैं, एक फलन है, जो सभी x ∈ X जहाँ g(x)
से निरूपित करते हैं, एक फलन है, जो सभी x ∈ X जहाँ g(x)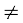 0, के लिए,
0, के लिए, 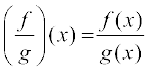 , द्वारा परिभाषित है।
, द्वारा परिभाषित है।
उदाहरण 16 मान लीजिए कि f(x) = x2 तथा g(x) = 2x + 1 दो वास्तविक फलन हैं।
(f + g) (x), (f –g) (x), (fg) (x),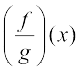 ज्ञात कीजिए।
ज्ञात कीजिए।
हल स्पष्टतः
(f + g) (x) = x2 + 2x + 1, (f –g) (x) = x2 – 2x – 1,
(fg) (x) = x2 (2x + 1) = 2x3 + x2, 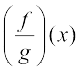 =
= 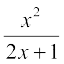 , x ≠
, x ≠ 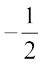
उदाहरण 17 मान लीजिए कि f(x) = 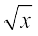 तथा g(x) = x ऋणेत्तर वास्तविक संख्याओं के लिए परिभाषित दो फलन हैं, तो (f + g) (x), (f – g) (x) (fg) (x) और
तथा g(x) = x ऋणेत्तर वास्तविक संख्याओं के लिए परिभाषित दो फलन हैं, तो (f + g) (x), (f – g) (x) (fg) (x) और 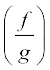 (x) ज्ञात कीजिए।
(x) ज्ञात कीजिए।
हल यहाँ हमें निम्नलिखित परिणाम मिलते हैंः
(f + g) (x) = 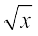 + x, (f – g) (x) =
+ x, (f – g) (x) = 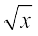 – x ,
– x ,
(fg) x = 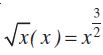
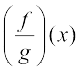
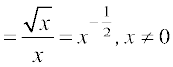
प्रश्नावली 2.3
1. निम्नलिखित संबंधों में कौन से फलन हैं? कारण का उल्लेख कीजिए। यदि संबंध एक फलन है, तो उसका परिसर निर्धारित कीजिएः
(i) {(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)}
(ii) {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)}
(iii) {(1,3), (1,5), (2,5)}.
2. निम्नलिखित वास्तविक फलनों के प्रांत तथा परिसर ज्ञात कीजिएः
(i) f(x) = – 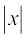 (ii) f(x) =
(ii) f(x) = 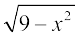 .
.
3. एक फलन f(x) = 2x –5 द्वारा परिभाषित है। निम्नलिखित के मान लिखिएः
(i) f (0), (ii) f (7), (iii) f (–3).
4. फलन ‘t’ सेल्सियस तापमान का फारेनहाइट तापमान में प्रतिचित्रण करता है, जो
t(C) = 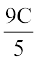 + 32 द्वारा परिभाषित हैं निम्नलिखित को ज्ञात कीजिएः
+ 32 द्वारा परिभाषित हैं निम्नलिखित को ज्ञात कीजिएः
(i) t (0) (ii) t (28) (iii) t (–10) (iv) C का मान, जब t (C) = 212.
5. निम्नलिखित में से प्रत्येक फलन का परिसर ज्ञात कीजिएः
(i) f (x) = 2 – 3x, x ∈ R, x > 0.
(ii) f (x) = x2 + 2, x एक वास्तविक संख्या है।
(iii) f (x) = x, x एक वास्तविक संख्या है।
विविध उदाहरण
उदाहरण 18 मान लीजिए कि R वास्तविक संख्याओं का समुच्चय है। एक वास्तविक फलन f: R→R को f(x) = x + 10
द्वारा परिभाषित कीजिए ओर इस फलन का आलेख खींचिए।
हल यहाँ, हम देखते हैं कि f(0) = 10, f(1) = 11,
f(2) = 12, ..., f(10) = 20, आदि और f(–1) = 9,
f(–2) = 8, ..., f(–10) = 0, इत्यादि।
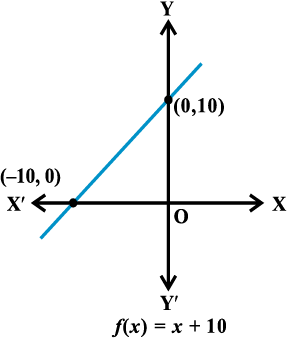
आकृति 2.16
अतः दिए हुए फलन के आलेख का आकार आकृति 2.16 में दर्शाए गए रूप का होगा।
टिप्पणी f(x) = mx + c , x ∈ R, एक रैखिक फलन कहलाता है, जहाँ m एवं c अचर हैं। उपरोक्त फलन रैखिक फलन का एक उदाहरण है।
उदाहरण 19 मान लीजिए कि R, Q से Q में R = {(a,b): a,b ∈ Q तथा a – b ∈ Z}. द्वारा परिभाषित, एक संबंध है। सिद्ध कीजिए कि
(i) (a,a) ∈ R सभी a ∈ Q के लिए
(ii) (a,b) ∈ R का तात्पर्य है कि (b, a) ∈ R
(iii) (a,b) ∈ R और (b,c) ∈ R का तात्पर्य है कि (a,c) ∈R
हल (i) क्योंकि a – a = 0 ∈ Z, जिससे निष्कर्ष निकलता है कि (a, a) ∈ R.
(ii) (a,b) ∈ R का तात्पर्य है कि a – b ∈ Z. इसलिए, b – a ∈ Z. अतः, (b, a) ∈ R
(iii) (a, b) तथा (b, c) ∈ R तात्पर्य है कि a – b ∈ Z. b – c ∈ Z. इसलिए, a – c = (a – b) + (b – c) ∈ Z. अतः, (a,c) ∈ R
उदाहरण 20 यदि f = {(1,1), (2,3), (0, –1), (–1, –3)}, Z से Z.में एक ‘रैखिक फलन है, तो f(x) ज्ञात कीजिए।
हल क्योंकि f एक रैखिक फलन है, इसलिए f (x) = mx + c. पुनः क्योंकि (1, 1), (0, – 1) ∈ R है। इसलिए, f (1) = m + c = 1 तथा f (0) = c = –1. इससे हमें m = 2 मिलता है और इस प्रकार
f(x) = 2x – 1.
उदाहरण 21 फलन 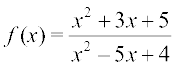 का प्रांत ज्ञात कीजिए।
का प्रांत ज्ञात कीजिए।
हल क्योंकि x2 –5x + 4 = (x – 4) (x –1), इसलिए फलन f, x = 4 और x = 1 के अतिरिक्त अन्य सभी वास्तविक संख्याओं के लिए परिभाषित है। अतः f का प्रांत R – {1, 4} है।
उदाहरण 22 फलन f ,
f (x) = 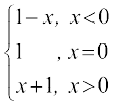
द्वारा परिभाषित है। f (x) का आलेख खींचिए।
हल यहाँ f(x) = 1 – x, x < 0, से
f(– 4) = 1 – (– 4) = 5;
f(– 3) = 1 – (– 3) = 4,
f(– 2) = 1 – (– 2) = 3
f(–1) = 1 – (–1) = 2; इत्यादि
और f(1) = 2, f (2) = 3, f (3) = 4
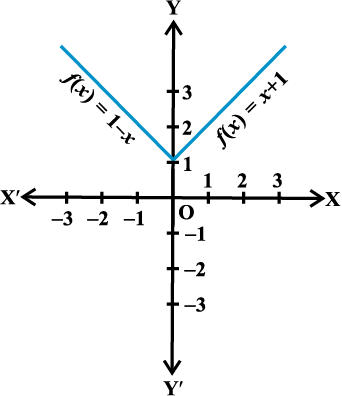
आकृति 2.17
f(4) = 5 इत्यादि, क्योंकि f(x) = x + 1, x > 0.
अतः f का आलेख आकृति 2.17 में दर्शाए रूप का होगा।
अध्याय 2 पर विविध प्रश्नावली
1. संबंध f , 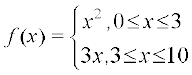 द्वारा परिभाषित है।
द्वारा परिभाषित है।
संबंध g, 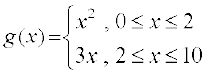 द्वारा परिभाषित है।
द्वारा परिभाषित है।
दर्शाइए कि क्यों f एक फलन है और g फलन नहीं है।
2. यदि f (x) = x2, तो 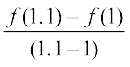 ज्ञात कीजिए।
ज्ञात कीजिए।
3. फलन f (x) 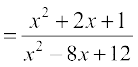 का प्रांत ज्ञात कीजिए।
का प्रांत ज्ञात कीजिए।
4. f (x) = 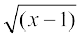 द्वारा परिभाषित वास्तविक फलन f का प्रांत तथा परिसर ज्ञात कीजिए।
द्वारा परिभाषित वास्तविक फलन f का प्रांत तथा परिसर ज्ञात कीजिए।
5. f (x) = 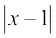 द्वारा परिभाषित वास्तविक फलन f का प्रांत तथा परिसर ज्ञात कीजिए।
द्वारा परिभाषित वास्तविक फलन f का प्रांत तथा परिसर ज्ञात कीजिए।
6. मान लीजिए कि 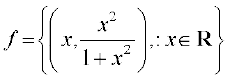 R से R में एक फलन है। f का परिसर निर्धारित कीजिए।
R से R में एक फलन है। f का परिसर निर्धारित कीजिए।
7. मान लीजिए कि f, g : R→R क्रमशः f(x) = x + 1, g(x) = 2x – 3. द्वारा परिभाषित है।
f + g, f – g और 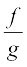 ज्ञात कीजिए।
ज्ञात कीजिए।
9. R = {(a, b) : a, b ∈N तथा a = b2} द्वारा परिभाषित N से N में, एक संबंध R है। क्या निम्नलिखित कथन सत्य हैं?
(i) (a,a) ∈ R, सभी a ∈ N, (ii) (a,b) ∈ R, का तात्पर्य है कि (b,a) ∈ R
(iii) (a,b) ∈ R, (b,c) ∈ R का तात्पर्य है कि (a,c) ∈ R?
प्रत्येक दशा में अपने उत्तर का औचित्य भी बतलाइए।
10. मान लीजिए कि A ={1,2,3,4}, B = {1,5,9,11,15,16} और f = {(1,5), (2,9), (3,1), (4,5), (2,11)}. क्या निम्नलिखित कथन सत्य हैं?
(i) f , A से B में एक संबंध है। (ii) f , A से B में एक फलन है।
प्रत्येक दशा में अपने उत्तर का औचित्य बतलाइए।
11. मान लीजिए कि f , f = {(ab, a + b) : a, b ∈ Z} द्वारा परिभाषित Z × Z का एक उपसमुच्चय है। क्या f, Z से Z में एक फलन है? अपने उत्तर का औचित्य भी स्पष्ट कीजिए।
12. मान लीजिए कि A = {9,10,11,12,13}तथा f : A→N, f (n) = n का महत्तम अभाज्य गुणक द्वारा, परिभाषित है। ε का परिसर ज्ञात कीजिए।
सारांश
इस अध्याय में हमनें संबंध तथा फलन का अध्ययन किया है। इस अध्याय की मुख्य बातों को नीचे दिया जा रहा है।
- क्रमित युग्म किसी विशेष क्रम में समूहित अवयवों का एक युग्म।
- कार्तीय गुणन समुच्चयों A तथा B का कार्तीय गुणन, समुच्चय
A × B = {(a,b): a ∈ A, b ∈ B} होता है। विशेष रूप से
R × R = {(x, y): x, y ∈ R} और R × R × R = (x, y, z): x, y, z ∈ R}
- यदि (a, b) = (x, y), तो a = x तथा b = y.
- यदि n(A) = p तथा n(B) = q, तो n(A × B) = pq.
- A × φ = φ
- सामान्यतः A × B ≠ B × A.
- संबंध समुच्चय A से समुच्चय B में संबंध R, कार्तीय गुणन A × B का एक उपसमुच्चय होता है, जिसे A × B के क्रमित युग्मों के प्रथम घटक x तथा द्वितीय घटक y के बीच किसी संबंध को वर्णित करके प्राप्त किया जाता है।
- किसी अवयव x का, संबंध R के अंतर्गत, प्रतिबिंब y होता है, जहाँ (x, y) ∈ R,
- संबंध R के क्रमित युग्मों के प्रथम घटकों का समुच्चय, संबंध R का प्रांत होता है।
- संबंध R के क्रमित युग्मों के द्वितीय घटकों का समुच्चय, संबंध R का परिसर होता है।
- फलन समुच्चय A से समुच्चय B में फलन f एक विशिष्ट प्रकार का संबंध होता है, जिसमें समुच्चय A के प्रत्येक अवयव x का समुच्चय B में एक और केवल एक प्रतिबिंब y होता है इस बात को हम f: A→B जहाँ f(x) = y लिखते हैं। ।
- A फलन f का प्रांत तथा B उसका सहप्रांत होता है।
- फलन f का परिसर, f के प्रतिबिंबों का समुच्चय होता है।
- किसी वास्तविक फलन के प्रांत तथा परिसर दोनों ही वास्तविक संख्याओं का समुच्चय अथवा उसका एक उपसमुच्चय होता हैः
- फलनों का बीजगणित फलन f : X → R तथा g : X → R, के लिए हम निम्नलिखित परिभाषाएँ देते हैं।
(f + g) (x) = f(x) + g(x), x ∈ X
(f – g) (x) = f (x) – g(x), x ∈ X
(f.g) (x) = f (x) .g (x), x ∈ X, k कोई अचर है।
(kf) (x) = k ( f (x) ), x ∈ X
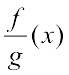 =
= 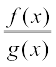 , x ∈ X, g(x) ≠ 0
, x ∈ X, g(x) ≠ 0
एेतिहासिक पृष्ठभूमि
फलन शब्द सर्वप्रथम Gottfried Wilhelm Leibnitz (1646-1716 ई०) द्वारा सन् 1673 में लिखित लैटिन पा.डुलिपि "Methodus tangentium inversa, seu de fuctionibus" में परिलक्षित हुआ है। Leibnitz ने इस शब्द का प्रयोग अविश्लेषणात्मक भाव में किया है। उन्होंने फलन को ‘गणितीय कार्य’ तथा ‘कर्मचारी’ के पदों द्वारा उत्पन्न मात्र एक वक्र के रूप में
अधिकल्पित किया है।
जुलाई 5, सन् 1698 में John Bernoulli नें Leibnitz को लिखे एक प्रत्र में पहली बार सुविचारित रूप से फलन शब्द का विश्लेषणात्मक भाव में विशिष्ट प्रयोग निर्धारित किया है। उसी माह में Leibnitz ने अपनी सहमति दर्शाते हुए उत्तर भी दे दिया था।
अंग्रेज़ी भाषा में फलन (Function) शब्द सन् 1779 के Chamber's Cyclopaedia में पाया जाता है। बीजगणित में फलन शब्द का प्रयोग चर राशियों और संख्याओं अथवा स्थिर राशियों द्वारा संयुक्त रूप से बने विश्लेषणात्मक व्यंजको के लिए किया गया है।
