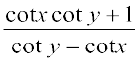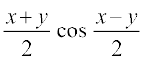Table of Contents
"A mathematician knows how to solve a problem, he can not solve it. – Milne "
3.1 भूमिका (Introduction)
शब्द ‘ट्रिगोनोमेट्री’ की व्युत्पत्ति ग्रीक शब्दों ‘ट्रिगोन’ तथा ‘मेट्रोन’ से हुई है तथा इसका अर्थ ‘त्रिभुज की
पिछली कक्षाओं में हमने न्यून कोणों के त्रिकोणमितीय अनुपात के विषय में अध्ययन किया है, जिसे समकोणीय त्रिभुजों की भुजाओं के अनुपात के रूप में बताया गया है। हमने त्रिकोणमितीय सर्वसमिकाओं तथा उनके त्रिकोणमितीय अनुपातों के अनुप्रयोगों को ऊँचाई तथा दूरी के प्रश्नों को हल करने में किया है। इस अध्याय में, हम त्रिकोणमितीय अनुपातों के संबंधों का त्रिकोणमितीय फलनों के रूप में व्यापकीकरण करेंगे तथा उनके गुणधर्मों का अध्ययन करेंगे।
3.2 कोण (Angles)
एक कोण वह माप हेै जो एक किरण के उसके प्रारंभिक बिंदु के परित: घूमने पर बनता है। किरण के घूर्णन की मूल स्थिति को प्रारंभिक भुजा तथा घूर्णन के अंतिम स्थिति को कोण की अंतिम भुजा कहते हैं। घूर्णन बिंदु को शीर्ष कहते हैं। यदि घूर्णन वामावर्त्त है तो कोण धनात्मक तथा यदि घूर्णन दक्षिणावर्त्त है तो कोण ऋणात्मक कहलाता है (आकृत्ति 3.1)। किसी कोण का माप, घूर्णन (घुमाव) की वह मात्रा है जो भुजा को प्रारंभिक स्थिति से अंतिम स्थिति तक घुमाने पर प्राप्त होता है। कोण को मापने के लिए अनेक इकाइयाँ हैं। कोण की परिभाषा इसकी इकाई का संकेत देती है, उदाहरण के लिए पΡारंभिक रेखा की स्थिति से एक पूर्ण घुमाव को कोंण की एक इकाई लिया जा सकता है जैसा, आकृति 3.2 में दर्शाया गया है।
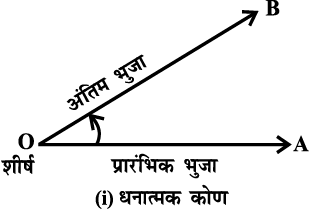
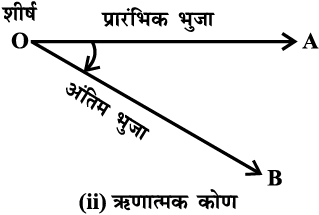
आकृति 3.1

आकृति 3.2
3.2.1 डिग्री माप (Degree measure)
यदि प्रारंभिक भुजा से अंतिम भुजा का घुमाव एक पूर्ण परिक्रमण का (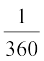 )वाँ भाग हो तो हम कोण का माप एक डिग्री कहते हैं, इसे 1° से लिखते हैं। एक डिग्री को मिनट में तथा एक मिनट को सेकंड में विभाजित किया जाता है। एक डिग्री का साठवाँ भाग एक मिनट कहलाता है, इसे 1′ से लिखते हैं तथा एक मिनट का साठवाँ भाग एक सेकंड कहलाता है, इसे 1′′ से लिखते हैं। अर्थात् 1° = 60′, 1′ = 60″
)वाँ भाग हो तो हम कोण का माप एक डिग्री कहते हैं, इसे 1° से लिखते हैं। एक डिग्री को मिनट में तथा एक मिनट को सेकंड में विभाजित किया जाता है। एक डिग्री का साठवाँ भाग एक मिनट कहलाता है, इसे 1′ से लिखते हैं तथा एक मिनट का साठवाँ भाग एक सेकंड कहलाता है, इसे 1′′ से लिखते हैं। अर्थात् 1° = 60′, 1′ = 60″
कुछ कोण जिनका माप 360°, 180°, 270°, 420°, – 30°, – 420° है उन्हें आकृति 3.3 में दर्शाया गया है।
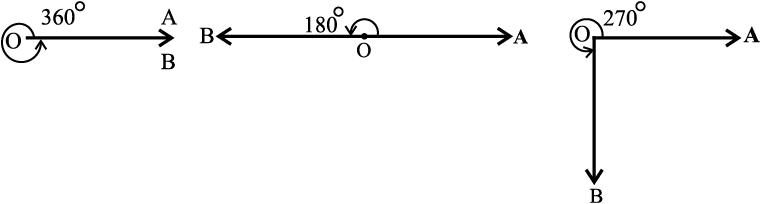
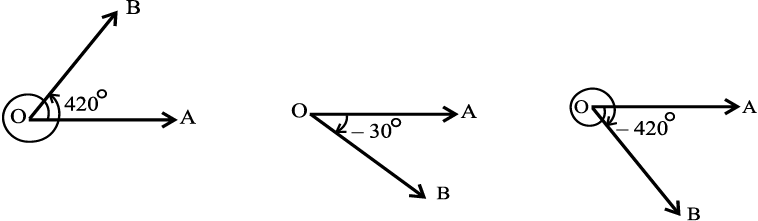
आकृति 3.3
3.2.2 रेडियन माप (Radian measure)
कोण को मापने के लिए एक दूसरी इकाई भी है, जिसे रेडियन माप कहते हैं। इकाई वृत्त (वृत्त की त्रिज्या एक इकाई हो) के केंद्र पर एक इकाई लंबाई के चाप द्वारा बने कोण को एक रेडियन माप कहते हैं। आकृति 3.4 (i)-(iv) में, OA प्रारंभिक भुजा है तथा OB अंतिम भुजा है। आकृतियों में कोण दिखाए गए हैं जिनके माप 1 रेडियन, –1 रेडियन,  रेडियन तथा
रेडियन तथा 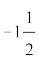 रेडियन हैं।
रेडियन हैं।
हम जानते हैं कि इकाई त्रिज्या के वृत्त की परिधि 2π होती है। अत: प्रारंभिक भुजा की एक पूर्ण परिक्रमा केंद्र पर 2π रेडियन का कोण अंतरित करती है।
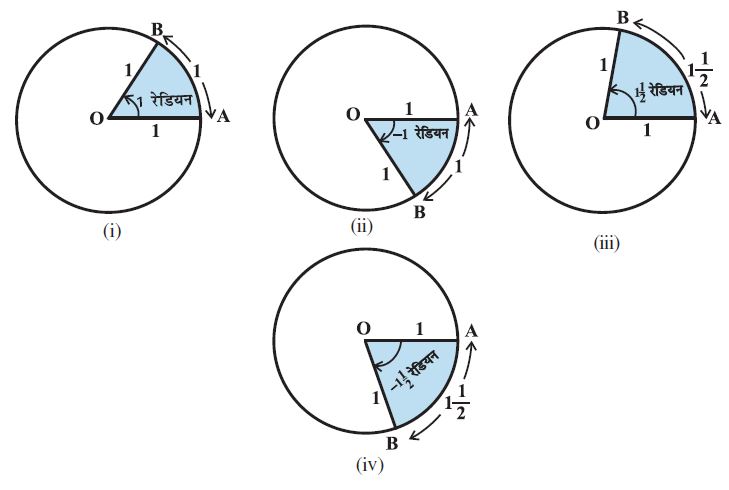
आकृति 3.4 (i) – (iv)
यह सर्वविदित है कि r त्रिज्या वाले एक वृत्त में, r लंबाई का चाप केंद्र पर एक रेडियन का कोण अंतरित करता है। हम जानते हैं कि वृत्त के समान चाप केंद्र पर समान कोण अंतरित करते हैं। चूंकि r त्रिज्या के वृत्ता में r लंबाई का चाप केंद्र पर एक रेडियन का कोण अंतरित करता है, इसलिए l लंबाई का चाप केंद्र पर  रेडियन का कोण अंतरित करेगा। अत: यदि एक वृत्त, जिसकी त्रिज्या r है, चाप की लंबाई l तथा केंद्र पर अंतरित कोण θ रेडियन है, तो हम पाते हैं कि θ =
रेडियन का कोण अंतरित करेगा। अत: यदि एक वृत्त, जिसकी त्रिज्या r है, चाप की लंबाई l तथा केंद्र पर अंतरित कोण θ रेडियन है, तो हम पाते हैं कि θ =  या l = r θ.
या l = r θ.
3.2.3 रेडियन तथा वास्तविक संख्याओं के मध्य संबंध (Relation between radian and real numbers)
माना कि इकाई वृत्त का केंद्र, O पर हैं तथा वृत्त पर कोई बिंदु A है। माना कोण की प्रारंभिक भुजा OA है, तो वृत्त के चाप की लंबाई से वृत्त के केंद्र पर चाप द्वारा अंतरित कोण की माप रेडियन में प्राप्त होती है। मान लीजिए वृत्त के बिंदु A पर स्पर्श रेखा PAQ है। माना बिंदु A वास्तविक संख्या शून्य प्रदर्शित करता है, AP धनात्मक वास्तविक संख्या दर्शाता है तथा AQ ऋणात्मक वास्तविक संख्या दर्शाता है (आकृत्ति 3.5)। यदि हम वृत्त की ओर रेखा AP को घड़ी की विपरीत दिशा में घुमाने पर तथा रेखा AQ को घड़ी की दिशा में घुमाएँ तो प्रत्येक वास्तविक संख्या के संगत रेडियन माप होगा तथा विलोमत:। इस प्रकार रेडियन माप तथा वास्तविक संख्याओं को एक तथा समान मान सकते हैं।
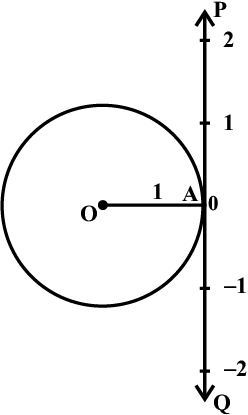
आकृति 3.5
3.2.4 डिग्री तथा रेडियन के मध्य संबंध (Relation between degree and radian)
क्योंकि वृत्त, केंद्र पर एक कोण बनाता है जिसकी माप 2π रेडियन है तथा यह 360° डिग्री माप है, इसलिए
2π रेडियन = 360° या π रेडियन = 180°
उपर्युक्त संबंध हमें रेडियन माप को डिग्री माप तथा डिग्री माप को रेडियन माप में व्यक्त करते हैं। π का निकटतम मान  का उपयोग करके, हम पाते हैं कि
का उपयोग करके, हम पाते हैं कि
1 रेडियन = 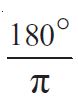
पुन: 1° = 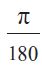
कुछ सामान्य कोणों के डिग्री माप तथा रेडियन माप के संबंध निम्नलिखित सारणी में दिए गए हैं:
| डिग्री | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| रेडियन | 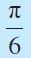 | 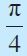 | 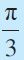 | 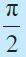 | π | 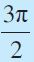 | 2π |
सांकेतिक प्रचलन
चूँकि कोणों की माप या तो डिग्री में या रेडियन में होती है, अत: प्रचलित परिपाटी के अनुसार जब हम कोण θ° लिखते हैं, हम समझते हैं कि कोण का माप θ डिग्री है तथा जब हम कोण β लिखते हैं, हम समझते हैं कि कोण का माप β रेडियन हैै।
ध्यान दीजिए जब कोण को रेडियन माप में व्यक्त करते हैं, तो प्राय: रेडियन लिखना छोड़ देते हैं अर्थात् πX180° 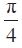
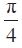
रेडियन माप = 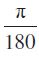
 डिग्री माप
डिग्री माप
डिग्री माप =  रेडियन माप
रेडियन माप
उदाहरण 1 40° 20′ को रेडियन माप में बदलिए।
हल हम जानते हैं कि 180° = π रेडियन
इसलिए, 40° 20′ = 40  डिग्री =
डिग्री =
इसलिए 40° 20′ =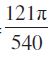
उदाहरण 2 6 रेडियन को डिग्री माप में बदलिए।
हल हम जानते हैं कि π रेडियन = 180°
इसलिए 6 रेडियन =  6 डिग्री =
6 डिग्री = 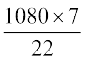 डिग्री
डिग्री
= 343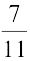 डिग्री = 343° +
डिग्री = 343° + 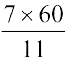 मिनट [क्योंकि 1° = 60′]
मिनट [क्योंकि 1° = 60′]
= 343° + 38′ + 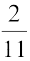 मिनट [क्योंकि 1′ = 60″]
मिनट [क्योंकि 1′ = 60″]
= 343° + 38′ + 10.9″ = 343°38′ 11″ निकटतम
इसलिए 6 रेडियन = 343° 38′ 11″ निकटतम
उदाहरण 3 उस वृत्त की त्रिज्या ज्ञात कीजिए जिसमें 60° का केंद्रीय कोण परिधि पर 37.4 सेमी लंबाई का चाप काटता है (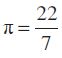
हल यहाँ l = 37.4 सेमी तथा θ = 60° = 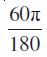
अत: r = 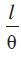
r = 
उदाहरण 4 एक घड़ी में मिनट की सुई 1.5 सेमी लंबी है। इसकी नोक 40 मिनट में कितनी दूर जा सकती हैं (π = 3.14 का प्रयोग करें)?
हल 60 मिनट में घड़ी की मिनट वाली सुई एक परिक्रमण पूर्ण करती है, अत: 40 मिनट में मिनट की सुई एक परिक्रमण का  भाग पूरा करती है। इसलिए
भाग पूरा करती है। इसलिए
0त्र्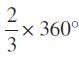
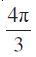
अत: तय की गई वांछित दूरी
l = r θ = 1.5 
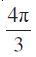
 3.14 सेमी = 6.28 सेमी
3.14 सेमी = 6.28 सेमी
उदाहरण 5 यदि दो वृत्तों के चापों की लंबाई समान हो और वे अपने केंद्र पर क्रमश: 65° तथा 110° का कोण बनाते हैं, तो उनकी त्रिज्याओं का अनुपात ज्ञात कीजिए।
हल माना दो वृत्तों की त्रिज्याएँ क्रमश: r1 तथा r2 हैं तो
θ1 = 65° =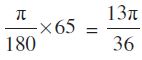
तथा θ2 = 110° = 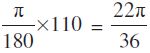
माना कि प्रत्येक चाप की लंबाई l है, तो l = r1θ1 = r2θ2, जिससे

 r2 , अर्थात्,
r2 , अर्थात्, 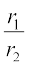 =
= 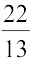
इसलिए r1 : r2 = 22 : 13.
प्रश्नावली 3.1
1. निम्नलिखित डिग्री माप के संगत रेडियन माप ज्ञात कीजिए:
(i) 25° (ii) – 47°30′ (iii) 240° (iv) 520°
2. निम्नलिखित रेडियन माप के संगत डिग्री माप ज्ञात कीजिए (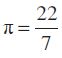
(i) 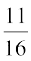 (ii) – 4 (iii)
(ii) – 4 (iii) 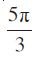
3. एक पहिया एक मिनट में 360° परिक्रमण करता है तो एक सेकंड में कितने रेडियन माप का कोण बनाएगा?
4. एक वृत्त, जिसकी त्रिज्या 100 सेमी है, की 22 सेमी लंबाई की चाप वृत्त के केंद्र पर कितने डिग्री माप का कोण बनाएगी (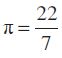
5. एक वृत्त, जिसका व्यास 40 सेमी है, की एक जीवा 20 सेमी लंबाई की है तो इसके संगत छोटे चाप की लंबाई ज्ञात कीजिए।
6. यदि दो वृत्तों के समान लंबाई वाले चाप अपने केंद्रों पर क्रमश: 60° तथा 75° के कोण बनाते हों, तो उनकी त्रिज्याओं का अनुपात ज्ञात कीजिए।
7. 75 सेमी लंबाई वाले एक दोलायमान दोलक का एक सिरे से दूसरे सिरे तक दोलन करने से जो कोण बनता है, उसका माप रेडियन में ज्ञात कीजिए, जबकि उसके नोक द्वारा बनाए गए चाप की लंबाई निम्नलिखित हैं:
(i) 10 सेमी
(ii) 15 सेमी
(iii) 21 सेमी
3.3 त्रिकोणमितीय फलन (Trigonometric Function)
पूर्व कक्षाओं में, हमने न्यून कोणों के त्रिकोणमितीय अनुपातों को समकोण त्रिभुज की भुजाओं के रूप में अध्ययन किया है। अब हम किसी कोण के त्रिकोणमितीय अनुपात की परिभाषा को रेडियन माप के पदों में तथा त्रिकोणमितीय फलन के रूप में अध्ययन करेंगे।

आकृति 3.6
मान लीजिए कि एक इकाई वृत्त, जिसका केंद्र निर्देशांक अक्षों का मूल बिंदु हो। माना कि P (a, b) वृत्त पर कोई बिंदु है तथा कोण AOP = x रेडियन अर्थात् चाप की लंबाई AP = x (आकृति 3.6) है। हम परिभाषित करते हैं:
cos x = a तथा sin x = b
चूँकि ∆OMP समकोण त्रिभुज है, हम पाते हैं,
OM2 + MP2 = OP2 या a2 + b2 = 1
इस प्रकार इकाई वृत्त पर प्रत्येक बिंदु के लिए, हम पाते हैं कि
a2 + b2 = 1 या cos2 x + sin2 x = 1
क्योंकि एक पूर्ण परिक्रमा (घूर्णन) द्वारा वृत्त के केंद्र पर 2π रेडियन का कोण अंतरित होता है, इसलिए ∠AOB = 


बिंदुओं A, B, C तथा D के निर्देशांक क्रमश: (1, 0), (0, 1), (–1, 0) तथा (0, –1) हैं,
इसलिए चतुर्थांशीय काेणों के लिए हम पाते हैं,
cos 0° = 1 sin 0° = 0
cos 

cosπ =- 1 sinπ = 0
cos 

cos 2π = 1 sin 2π = 0
इस प्रकार sin (2nπ + x) = sin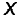 , n ∈ Z
, n ∈ Z
cos (2nπ + x) = cos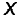 , n ∈ Z
, n ∈ Z
पुन: sin x = 0, यदि x = 0, ± π, ± 2π , ± 3π, ...अर्थात् x, π का पूर्णांक गुणज है।
तथा cos x = 0, यदि 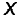 = ±
= ± 

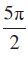

sin x = 0 से प्राप्त होता है कि x = nπ, जहाँ n कोई पूर्णांक है।
cos x = 0 से प्राप्त होता है कि x = (2n + 1) 
अब हम अन्य त्रिकोणमितीय फलनों को sine तथा cosine के पदों में परिभाषित करते हैं:
cosec x = 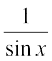 , x ≠ nπ, जहाँ n कोई पूर्णांक है।
, x ≠ nπ, जहाँ n कोई पूर्णांक है।
sec x = 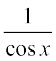 , x ≠ (2n + 1)
, x ≠ (2n + 1) 
tan x = 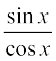 , x ≠ (2n +1)
, x ≠ (2n +1)
cot x = 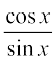 , x ≠ n π, जहाँ n कोई पूर्णांक है।
, x ≠ n π, जहाँ n कोई पूर्णांक है।
हम सभी वास्तविक x के लिए देखते हैं कि sin2 x + cos2 x = 1
इस प्रकार 1 + tan2 x = sec2 x (क्यों?)
1 + cot2 x = cosec2 x (क्यों?)
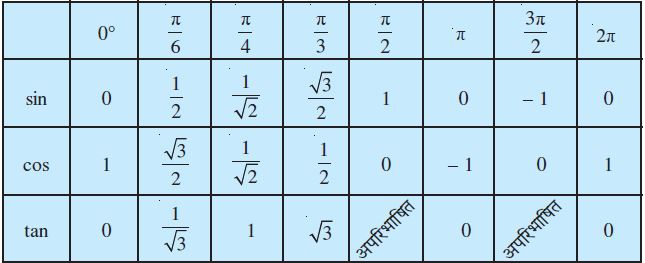
पूर्व कक्षाओं में, हम 0°, 30°, 45°, 60° तथा 90° के त्रिकोणमितीय अनुपातों के मानों की चर्चा कर चुके हैं। इन कोणों के त्रिकोणमितीय फलनों के मान वही हैं जो पिछली कक्षाओं में पढ़ चुके त्रिकोणमितीय अनुपातों के हैं। इस प्रकार, हम निम्नलिखित सारणी पाते हैं:
cosec x, sec x तथा cot x का मान क्रमश: sin x, cos x तथा tan x के मान से उल्टा (विलोम) है।
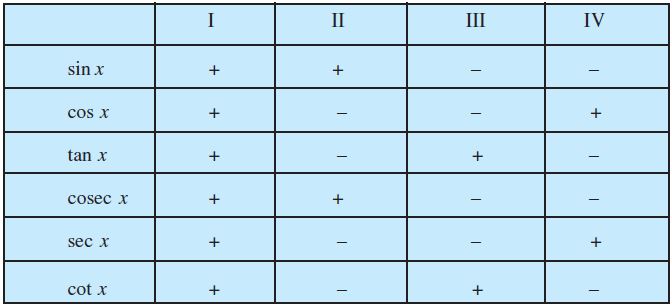
3.3.1 त्रिकोणमितीय फलनों के चिह्न (Signs of trigonometric functions)
माना कि इकाई वृत्त पर P (a, b) कोई बिंदु हैं, जिसका केंद्र मूल बिंदु हैं, तथा ∠AOP = x, यदि ∠AOQ = – x, तो बिंदु Q के निर्देशांक (a, – b) होंगे (आकृति 3.7)। इसलिए cos (– x) = cos x तथा sin (– x) = – sin x
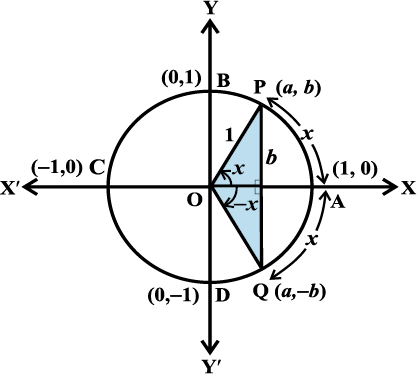
आकृति 3.7
चूँकि इकाई वृत्त के प्रत्येक बिंदु P (a, b) के लिए – 1 ≤ a ≤ 1 तथा – 1 ≤ b ≤ 1, अत:, हम x के सभी मानों के लिए – 1 ≤ cos x ≤ 1 तथा –1 ≤ sin x ≤ 1, पाते हैं। पिछली कक्षाओं से हमको ज्ञात है कि प्रथम चतुर्थांश (0 < x < 







3.3.2 त्रिकाेणमितीय फलनों का प्रांत तथा परिसर (Domain and range of trigonometric functions)
sine तथा cosine फलनों की परिभाषा से, हम यह पाते हैं कि वे सभी वास्तविक संख्याओं के लिए परिभाषित हैं। पुन:, हम यह भी पाते हैं कि प्रत्येक वास्तविक संख्या x के लिए,
– 1 ≤ sin x ≤ 1 तथा – 1 ≤ cos x ≤ 1
अत: y = sin x तथा y = cos x का प्रांत सभी वास्तविक संख्याओं का समुच्चय है तथा परिसर अंतराल [–1, 1], अर्थात्, – 1 ≤ y ≤ 1 है।
चूँकि, cosec x = 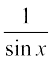 , y = cosec x का प्रांत, समुच्चय { x : x ∈ R तथा x ≠ n π, n ∈ Z} तथा परिसर समुच्चय {y : y ∈ R, y ≥ 1 या y ≤ – 1} है। इसी प्रकार, y = secx का प्रांत, समुच्चय {x : x ∈ R तथा x ≠ (2n + 1)
, y = cosec x का प्रांत, समुच्चय { x : x ∈ R तथा x ≠ n π, n ∈ Z} तथा परिसर समुच्चय {y : y ∈ R, y ≥ 1 या y ≤ – 1} है। इसी प्रकार, y = secx का प्रांत, समुच्चय {x : x ∈ R तथा x ≠ (2n + 1) 

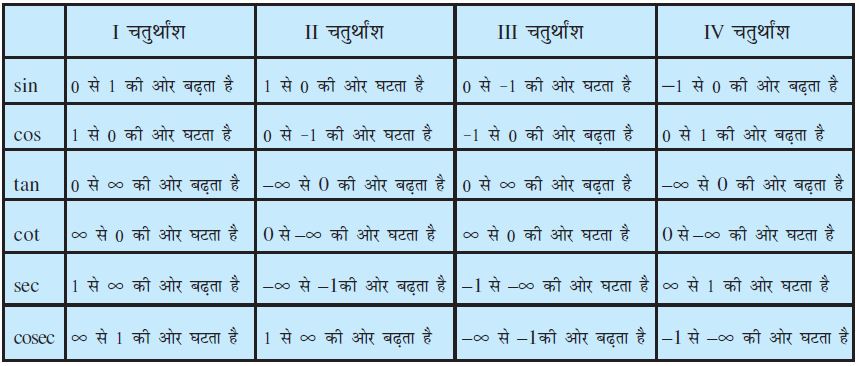
हम देखते हैं कि प्रथम चतुर्थांश में, जब x, 0 से 



टिप्पणी उपर्युक्त सारणी में, यह कथन कि अंतराल 0 < x < 


हमने देखा कि sin x तथा cos x के मानों का अंतराल 2π के पश्चात् पुनरावृत्ति होती है। जैसे, cosec x तथा sec x के मानों की भी अंतराल 2π के बाद पुनरावृत्ति होती है। हम अगले अनुच्छेद में tan (π + x) = tan x देखते हैं। जैसे, tan x के मानों में अंतराल π के पश्चात् पुनरावृत्ति होती है, क्योंकि cot x, tan x का पूरक है, इसके मानो में भी अंतराल π के पश्चात् पुनरावृत्ति होती है। त्रिकोणमितीय फलनों में इस ज्ञान (गुणधर्म) तथा व्यवहार का उपयोग करने पर, हम फलनों का आलेख खींच सकते हैं। इन फलनों का आलेख नीचे दिए गए हैं:

आकृति 3.8

आकृति 3.9

आकृति 3.10

आकृति 3.11
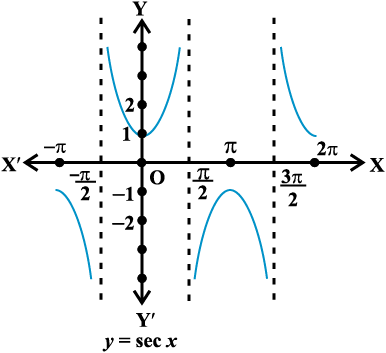
आकृति 3.12

आकृति 3.13
उदाहरण 6 यदि cos x = – 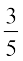 हो और x तृतीय चतुर्थांश में स्थित है, तो अन्य पाँच त्रिकोणमितीय फलनों के मानों को ज्ञात कीजिए।
हो और x तृतीय चतुर्थांश में स्थित है, तो अन्य पाँच त्रिकोणमितीय फलनों के मानों को ज्ञात कीजिए।
हल क्योंकि cos x = –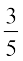 , हम पाते हैं कि sec x =
, हम पाते हैं कि sec x = 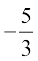
अब sin2 x + cos2 x = 1 या sin2 x = 1 – cos2 x
या sin2 x = 1 – 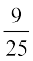 =
= 
अत: sin x = ± 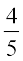
चूँकि x तृतीय चतुर्थांशमें है, तो sin x का मान ऋणात्मक होगा। इसलिए
sin x = – 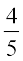
इससे यह भी प्राप्त होता है कि
cosec x = – 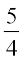
पुन:, हम पाते हैं
tan x = 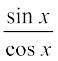 =
= 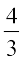 तथा cot x =
तथा cot x = 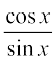 =
= 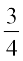
उदाहरण 7 यदि cot x = – 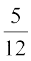 हो और x द्वितीय चतुर्थांश में स्थित हैं, तो अन्य पाँच त्रिकोणमितीय फलनों को ज्ञात कीजिए।
हो और x द्वितीय चतुर्थांश में स्थित हैं, तो अन्य पाँच त्रिकोणमितीय फलनों को ज्ञात कीजिए।
हल क्योंकि cot x = – 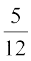 , हम पाते हैं tan x = –
, हम पाते हैं tan x = – 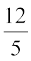
अब sec2 x = 1 + tan2 x = 1 + 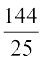 =
= 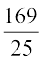
अत: sec x = ± 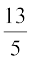
चूँकि x द्वितीय चतुर्थांश में स्थित है, sec x का मान ऋणात्मक होगा। इसलिए
sec x = – 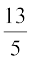
इससे यह भी प्राप्त होता है कि
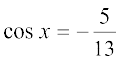
पुन: हम पाते हैं
sin x = tan x cos x = (– 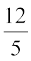 )
)  (–
(– 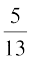 ) =
) = 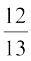
तथा cosec x = 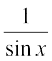 =
= 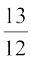
उदाहरण 8 sin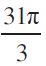
हल हम जानते हैं कि sin x के मानों में अंतराल 2π के पश्चात् पुनरावृत्ति होती है। इसलिए
sin 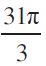
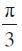
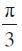
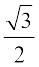 .
.
उदाहरण 9 cos (–1710°) का मान ज्ञात कीजिए।
हल हम जानते हैं कि cos x के मानों में अंतराल 2π या 360° के पश्चात् पुनरावृत्ति होती है। इसलिए cos (–1710°) = cos (–1710° + 5  360°)
360°)
= cos (–1710° + 1800°) = cos 90° = 0
प्रश्नावली 3.2
निम्नलिखित प्रश्नों में पाँच अन्य त्रिकोणमितीय फलनों का मान ज्ञात कीजिए:
1. cos x = –  , x तीसरे चतुर्थांश में स्थित है।
, x तीसरे चतुर्थांश में स्थित है।
2. sin x = 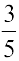 , x दूसरे चतुर्थांश में स्थित है।
, x दूसरे चतुर्थांश में स्थित है।
3. cot x =  , x तृतीय चतुर्थांश में स्थित है।
, x तृतीय चतुर्थांश में स्थित है।
4. sec x = 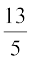 , x चतुर्थ चतुर्थांश में स्थित है।
, x चतुर्थ चतुर्थांश में स्थित है।
5. tan x = – 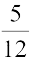 , x दूसरे चतुर्थांश में स्थित है।
, x दूसरे चतुर्थांश में स्थित है।
प्रश्न संख्या 6 से 10 के मान ज्ञात कीजिए:
6. sin 765° 7. cosec (– 1410°)
8. tan 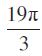
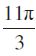
10. cot (– 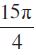
3.4 दो कोणों के योग और अंतर का त्रिकोणमितीय फलन (TrigonometricFunctions of Sum and Difference of two Angles)
इस भाग में हम दो संख्याओं (कोणों) के योग एवं अंतर के लिए त्रिकोणमितीय फलनों तथा उनसे संबंधित व्यंजकों को व्युत्पन्न करेंगे। इस संबंध में इन मूल परिणामों को हम त्रिकोणमितीय सर्वसमिकाएँ कहेंगे। हम देखते हैं कि
1. sin (– x) = – sin x
2. cos (– x) = cos x
अब हम कुछ और परिणाम सिद्ध करेंगे:
3. cos (x + y) = cos x cos y – sin x sin y
इकाई वृत्त पर विचार कीजिए, जिसका केंद्र मूल बिंदु पर हो। माना कि कोण P4OP1, x तथा कोण P1OP2, y हैं तो कोण P4OP2, (x + y) होगा। पुन: माना कोण P4OP3, (– y) हैं। अत: P1, P2, P3 तथा P4 के निर्देशांक P1(cos x, sin x), P2 [cos (x + y), sin (x + y)], P3 [cos (– y), sin (– y)] और P4 (1, 0) होंगे (आकृति 3.14)।
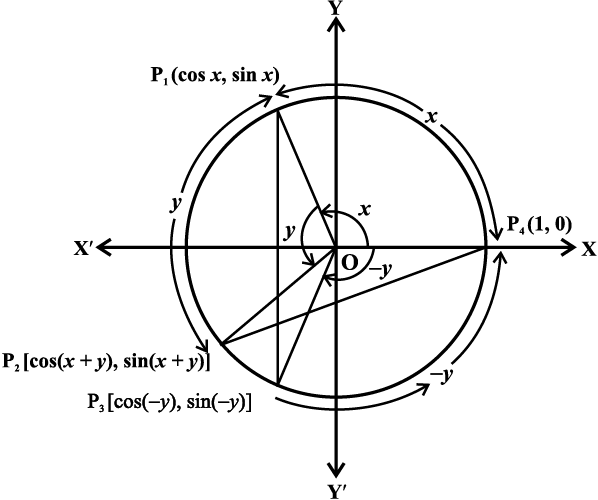
आकृति 3.14
त्रिभुजों P1OP3 तथा P2OP4 पर विचार कीजिए। वे सर्वांगासम हैं (क्यों)। इसलिए P1P3 और P2P4 बराबर हैं। दूरी सूत्र का उपयोग करने पर
P1P32 = [cos x – cos (– y)]2 + [sin x – sin(–y)]2
= (cos x – cos y)2 + (sin x + sin y)2
= cos2x + cos2 y – 2 cos x cos y + sin2 x + sin2 y + 2sin x sin y
= 2 – 2 (cos x cos y – sin x sin y) (क्यों?)
पुन: P2P42 = [1 – cos (x + y)] 2 + [0 – sin (x + y)]2
= 1 – 2cos (x + y) + cos2 (x + y) + sin2 (x + y)
= 2 – 2 cos (x + y)
क्योंकि P1P3 = P2P4, हम पाते हैं; P1P32 = P2P42
इसलिए, 2 –2 (cos x cos y – sin x sin y) = 2 – 2 cos (x + y)
अत: cos (x + y) = cos x cos y – sin x sin y
4. cos (x – y) = cos x cos y + sin x sin y
सर्वसमिका 3 में y के स्थान पर – y रखने पर
cos (x + (– y)) = cos x cos (– y) – sin x sin (– y)
या cos (x – y) = cos x cos y + sin x sin y
5. cos (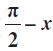
सर्वसमिका 4 में x के स्थान पर 
cos (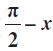


6. sin (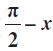
सर्वसमिका 5 का उपयोग करने पर हम पाते हैं
sin (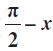
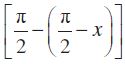
7. sin (x + y) = sin x cos y + cos x sin y
हम जानते हैं कि
sin (x + y) = cos 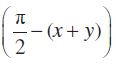
= cos (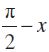
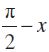
= sin x cos y + cos x sin y
8. sin (x – y) = sin x cos y – cos x sin y
यदि हम सर्वसमिका 7 में y के स्थान पर – y रखें तो उपरोक्त परिणाम पाते हैं।
9. x और y के उपर्युक्त मानों को सर्वसमिकाओं 3, 4, 7 और 8 में रखने पर हम निम्नलिखित परिणाम निकाल सकते हैं:
cos 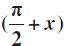
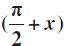
cos (π – x) = – cos x sin (π – x) = sin x
cos (π + x) = – cos x sin (π + x) = – sin x
cos (2π – x) = cos x sin (2π – x) = – sin x
इसी प्रकार के संगत परिणाम tan x, cot x, sec x एवं cosec x के लिए sin x और cos x के फलनों के परिणामों से आसानी से निकाले जा सकते हैं।
10. यदि x, y और (x + y) में से कोई 
tan (x + y) = 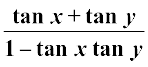
क्योंकि x, y तथा (x + y) में से कोई 
cos y तथा cos (x + y) शून्य नहीं हैं। अब
tan (x + y) = 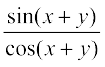 =
= 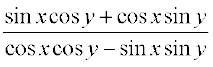
अंश और हर में cos x cos y, से विभाजित करने पर हम पाते हैं।
tan (x + y) = 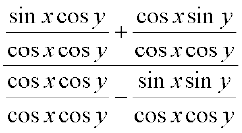
= 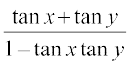
11. tan ( x – y) = 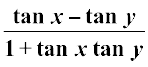
यदि सर्वसमिका 10 में y के स्थान पर – y रखने पर, हम पाते हैं
tan (x – y) = tan [x + (– y)]
= 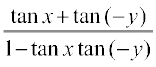 =
= 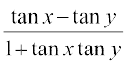
12. यदि x, y तथा (x + y) में से कोई भी कोण π, का गुणांक नहीं हैं, तो
cot ( x + y) = 
क्योंकि x, y तथा (x + y) कोणों में से कोई भी π, का गुणांक नहीं हैं, इसलिए sin x, sin y तथा sin (x + y) शून्य नहीं हैं। अब
cot ( x + y) = 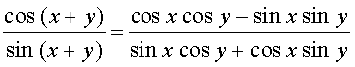
अंश और हर को sin x sin y, से विभाजित करने पर, हम पाते हैं
cot (x + y) = 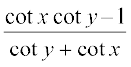
13. cot (x – y) = 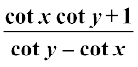 जहाँ x, y तथा x – y; π के गणांक नहीं हैं।
जहाँ x, y तथा x – y; π के गणांक नहीं हैं।
यदि सर्वसमिका 12 में y के स्थान पर –y रखते हैं तो हम उपरोक्त परिणाम पाते हैं।
14. cos 2x = cos2x – sin2 x = 2 cos2 x – 1 = 1 – 2 sin2 x = 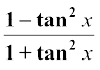
हम जानते हैं कि
cos (x + y) = cos x cos y – sin x sin y
y के स्थान पर x, रखें तो, हम पाते हैं
cos 2x = cos2x – sin2 x
= cos2 x – (1 – cos2 x) = 2 cos2x – 1
पुन: cos 2x = cos2 x – sin2 x
= 1 – sin2 x – sin2 x = 1 – 2 sin2 x.
अत: हम पाते हैं cos 2x = cos2 x – sin 2 x = 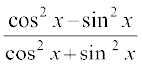
अंश और हर को cos2 x से विभाजित करने पर, हम पाते हैं
cos 2x =  x ≠ nπ +
x ≠ nπ + 
15. sin 2x = 2 sinx cos x = 
हम जानते हैं कि
sin (x + y) = sin x cos y + cos x sin y
y के स्थान पर x रखने पर, हम पाते हैं:
sin 2x = 2 sin x cos x.
पुन: sin 2x =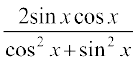
प्रत्येक पद को cos2 x से विभाजित करने पर, हम पाते हैं:
sin 2x =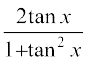
16. tan 2x =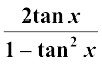 , 2x ≠ nπ +
, 2x ≠ nπ +
हम जानते हैं कि
tan (x + y) =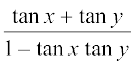
y के स्थान पर x रखने पर, हम पाते हैं, 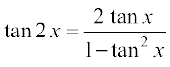
17. sin 3x = 3 sin x – 4 sin3 x
हम पाते हैं,
sin 3x = sin (2x + x)
= sin 2x cos x + cos 2x sin x
= 2 sin x cos x cos x + (1 – 2sin2 x) sin x
= 2 sin x (1 – sin2 x) + sin x – 2 sin3 x
= 2 sin x – 2 sin3 x + sin x – 2 sin3 x
= 3 sin x – 4 sin3 x
18. cos 3x = 4 cos3 x – 3 cos x
हम पाते हैं,
cos 3x = cos (2x +x)
= cos 2x cos x – sin 2x sin x
= (2cos2 x – 1) cos x – 2sin x cos x sin x
= (2cos2 x – 1) cos x – 2cos x (1 – cos2 x)
= 2cos3 x – cos x – 2cos x + 2 cos3 x
= 4cos3 x – 3cos x
19.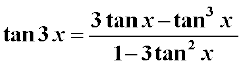 3x ≠ nπ +
3x ≠ nπ +
हम पाते हैं, tan 3x = tan (2x + x)
= 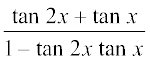
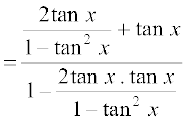
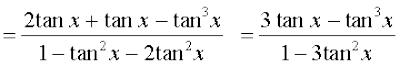
20. (i) cos x + cos y =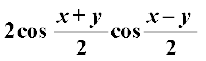
(ii) cos x – cos y = –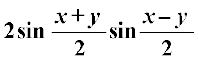
(iii) sin x + sin y =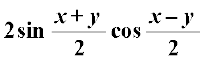
(iv) sin x – sin y =
हम जानते हैं कि
cos (x + y) = cos x cos y – sin x sin y ... (1)
और cos (x – y) = cos x cos y + sin x sin y ... (2)
(1) और (2) को जोड़ने एवं घटाने पर, हम पाते हैं,
cos (x + y) + cos(x – y) = 2 cos x cos y ... (3)
और cos (x + y) – cos (x – y) = – 2 sin x sin y ... (4)
और भी sin (x + y) = sin x cos y + cos x sin y ... (5)
और sin (x – y) = sin x cos y – cos x sin y ... (6)
(5) और (6) को जोड़ने एवं घटाने पर, हम पाते हैं,
sin (x + y) + sin (x – y) = 2 sin x cos y ... (7)
sin (x + y) – sin (x – y) = 2cos x sin y ... (8)
माना कि x + y = θ तथा x – y = φ, इसलिए
(3), (4), (7) तथा (8) में x और y के मान रखने पर, हम पाते हैं,
cos θ + cos φ = 2 cos
cos θ – cos φ = – 2 sin
sin θ + sin φ = 2 sin
sin θ – sin φ = 2 cos
क्योंकि θ तथा φ को कोई वास्तविक संख्या मान सकते हैं। हम θ के स्थान पर x तथा φ के स्थान पर y रखने पर, हम पाते हैं:
cos x + cos y = 2 cos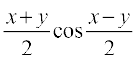 ; cos x – cos y = – 2 sin
; cos x – cos y = – 2 sin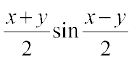 , sin x + sin y = 2 sin
, sin x + sin y = 2 sin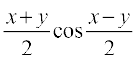 ; sin x – sin y = 2 cos
; sin x – sin y = 2 cos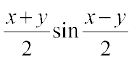
टिप्पणी सर्वसमिका 20 से हम निम्न परिणाम पाते हैं:
21. (i) 2 cos x cos y = cos (x + y) + cos (x – y)
(ii) –2 sin x sin y = cos (x + y) – cos (x – y)
(iii) 2 sin x cos y = sin (x + y) + sin (x – y)
(iv) 2 cos x sin y = sin (x + y) – sin (x – y)
उदाहरण 10 सिद्ध कीजिए: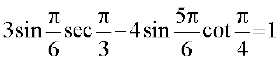
हल बायाँ पक्ष =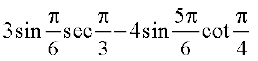
= 3 × × 2 – 4 sin
× 2 – 4 sin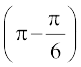 × 1 = 3 – 4 sin
× 1 = 3 – 4 sin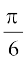
= 3 – 4 × = 1 = दायाँ पक्ष
= 1 = दायाँ पक्ष
उदाहरण 11 sin 15° का मान ज्ञात कीजिए।
हल sin 15° = sin (45° – 30°)
= sin 45° cos 30° – cos 45° sin 30°
=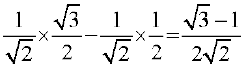
उदाहरण 12 tan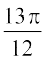 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
हल tan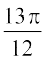 = tan
= tan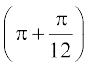 = tan
= tan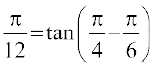
=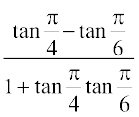 =
=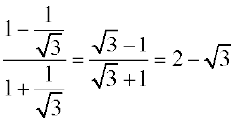
उदाहरण 13 सिद्ध कीजिए:
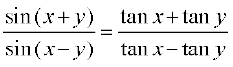 .
.
हल हम पाते हैं,
बायाँ पक्ष
अंश और हर को cos x cos y से विभाजित करने पर, हम पाते हैं,
बायाँ पक्ष =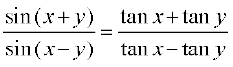 = दायाँ पक्ष
= दायाँ पक्ष
उदाहरण 14 दिखाइए
tan 3 x tan 2 x tan x = tan 3x – tan 2 x – tan x
हल हम जानते हैं कि 3x = 2x + x
इसलिए tan 3x = tan (2x + x)
या 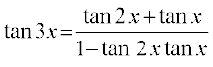
या tan 3x – tan 3x tan 2x tan x = tan 2x + tan x
या tan 3x – tan 2x – tan x = tan 3x tan 2x tan x
या tan 3x tan 2x tan x = tan 3x – tan 2x – tan x
उदाहरण 15 सिद्ध कीजिए:

हल सर्वसमिका 20(i) का उपयोग करने पर, हम पाते हैं,
बायाँ पक्ष =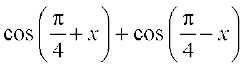
=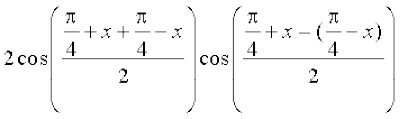
= 2 cos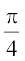 cos x = 2 ×
cos x = 2 ×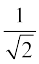 cos x =
cos x = cos x = दायाँ पक्ष
cos x = दायाँ पक्ष
उदाहरण 16 सिद्ध कीजिए 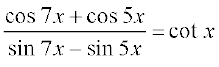
हल सर्वसमिकाओं 20(i) तथा 20(iv) का उपयोग करने पर, हम पाते हैं,
बायाँ पक्ष =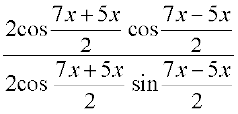 =
= = दायाँ पक्ष
= दायाँ पक्ष
उदाहरण 17 सिद्ध कीजिए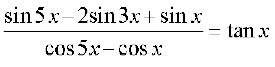
हल हम पाते हैं,
बायाँ पक्ष =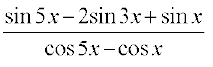
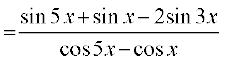
=
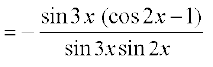
=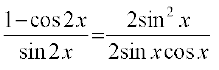 = tan x = दायाँ पक्ष
= tan x = दायाँ पक्ष
प्रश्नावली 3.3
सिद्ध कीजिए:
1. sin2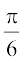 + cos2
+ cos2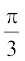 – tan2
– tan2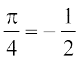
2. 2sin2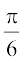 + cosec2
+ cosec2 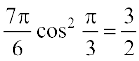
3.
4.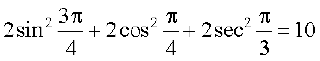
5. मान ज्ञात कीजिए:
(i) sin 75° (ii) tan 15°
निम्नलिखित को सिद्ध कीजिए:
6.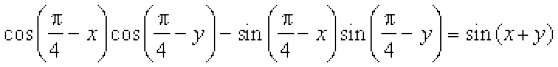
7.
8.
9.
10. sin (n + 1)x sin (n + 2)x + cos (n + 1)x cos (n + 2)x = cos x
11. 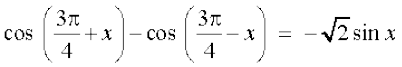
12. sin2 6x – sin2 4x = sin 2x sin 10x
13. cos2 2x – cos2 6x = sin 4x sin 8x
14. sin2 x + 2 sin 4x + sin 6x = 4 cos2 x sin 4x
15. cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
16. 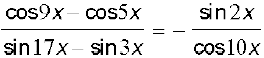
17.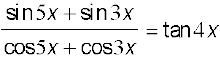
18. 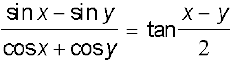
19.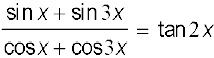
20.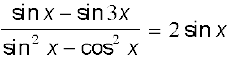
21.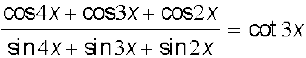
22. cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1
23.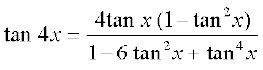
24. cos 4x = 1 – 8sin2 x cos2 x
25. cos 6x = 32 cos6 x – 48cos4 x + 18 cos2 x – 1
3.5 त्रिकोणमितीय समीकरण (Trigonometric Equations)
एक चर राशि में εत्रकोणमितीय फलनों वाले समीकरण को त्रिकोणमितीय समीकरण कहते हैं। इस अनुच्छेद में, हम एेसे समीकरणों के हल ज्ञात करेंगे। हम पहले पढ़ चुके हैं कि sin x तथा cos x के मानों में 2π अंतराल के पश्चात् पुनरावृत्ति होती है तथा tan के मानों में π अंतराल के पश्चात् पुनरावृत्ति होती है। त्रिकोणमितीय समीकरण के एेसे हल जहाँ 0 ≤ x < 2π होता है, मुख्य हल (principal solution) कहलाते हैं। पूर्णांक ‘n’ से युक्त व्यंजक जो किसी त्रिकोणमितीय समीकरण के सभी हल व्यक्त करता है, उसे व्यापक हल (general solution) कहते हैं। हम पूर्णांकों के समुच्चय को ‘Z’ से प्रदर्शित करेंगे।
के मानों में π अंतराल के पश्चात् पुनरावृत्ति होती है। त्रिकोणमितीय समीकरण के एेसे हल जहाँ 0 ≤ x < 2π होता है, मुख्य हल (principal solution) कहलाते हैं। पूर्णांक ‘n’ से युक्त व्यंजक जो किसी त्रिकोणमितीय समीकरण के सभी हल व्यक्त करता है, उसे व्यापक हल (general solution) कहते हैं। हम पूर्णांकों के समुच्चय को ‘Z’ से प्रदर्शित करेंगे।
निम्नलिखित उदाहरण त्रिकोणमितीय समीकरणों को हल करने में सहायक होंगे:
उदाहरण 18 समीकरण का मुख्य हल ज्ञात कीजिए।
का मुख्य हल ज्ञात कीजिए।
हल हम जानते हैं कि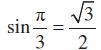
इसलिए, मुख्य हल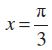
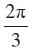
उदाहरण 19 समीकरण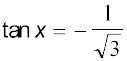 का मुख्य हल ज्ञात कीजिए।
का मुख्य हल ज्ञात कीजिए।
हल हम जानते हैं कि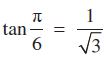
तथा
इस प्रकार
इसलिए, मुख्य हल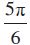
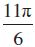
अब, हम त्रिकोणमितीय समीकरणों का व्यापक हल ज्ञात करेंगे। हम देखते हैं कि
sin = 0 तो
= 0 तो = nπ, जहाँ n ∈ Z
= nπ, जहाँ n ∈ Z
cos = 0 तो
= 0 तो = (2n + 1)
= (2n + 1)
अब हम निम्न परिणाम सिद्ध करेंगे:
प्रमेय 1 किन्हीं वास्तविक संख्याएँ x तथा y के लिए
sin x = sin y सेे x = nπ + (–1)n y, जहाँ n ∈ Z प्राप्त होता है।
उपपत्ति यदि sin x = sin y, तो
sin x – sin y = 0 या 2cos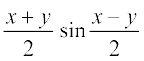 = 0
= 0
अर्थात् cos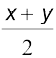 = 0 या sin
= 0 या sin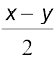 = 0
= 0
इसलिए  = (2n + 1
= (2n + 1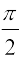 या
या 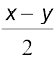 = nπ, जहाँ n ∈ Z
= nπ, जहाँ n ∈ Z
अर्थात् x = (2n + 1) π – y या x = 2nπ + y, जहाँ n∈Z
अत: x = (2n + 1)π + (–1)2n + 1 y या x = 2nπ +(–1)2n y, जहाँ n ∈ Z
उपर्युक्त दोनों परिणामों को मिलाने पर, हम पाते हैं: x = nπ + (–1)n y, जहाँ n ∈ Z
प्रमेय 2 कोई वास्तविक संख्याएँ x तथा y के लिए, cos x = cos y से = 2nπ ± y, जहाँ n ∈ Z प्राप्त होता है।
= 2nπ ± y, जहाँ n ∈ Z प्राप्त होता है।
उपपत्ति यदि cos x = cos y, तो
cos x – cos y = 0 अर्थात् –2 sin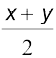 sin
sin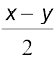 = 0
= 0
इस प्रकार sin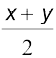 = 0 या sin
= 0 या sin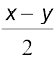 = 0
= 0
इसलिए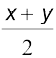 = nπ या
= nπ या 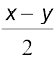 = nπ, जहाँ n ∈ Z
= nπ, जहाँ n ∈ Z
अर्थात् x = 2nπ – y या x = 2nπ + y, जहाँ n ∈ Z
अत: x = 2nπ ± y, जहाँ n ∈ Z
प्रमेय 3 सिद्ध कीजिए कि यदि x तथा y का 
tan x = tan y से x = nπ + y, जहाँ n ∈ Z प्राप्त होता है।
उपपत्ति यदि tan x = tan y, तो tan x – tan y = 0
या 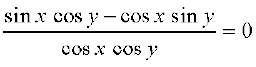
या sin (x – y) = 0 (क्यों?)
इसलिए x – y = nπ अर्थात् x = nπ + y, जहाँ n ∈ Z
उदाहरण 20 si = –
= –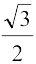 का हल ज्ञात कीजिए।
का हल ज्ञात कीजिए।
हल हम पाते हैं si = –
= –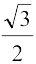 =
=
अत: sin x =
इसलिए 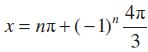
टिप्पणी 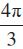
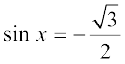 है। x का कोई भी अन्य मान लेकर समीकरण हल किया जा सकता है, जिसके लिए
है। x का कोई भी अन्य मान लेकर समीकरण हल किया जा सकता है, जिसके लिए 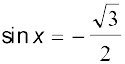 हो, यह सभी विधियों से प्राप्त हल एक ही होंगे यद्यपि वे प्रत्यक्षत: विभिन्न दिखाई पड़ सकते हैं।
हो, यह सभी विधियों से प्राप्त हल एक ही होंगे यद्यपि वे प्रत्यक्षत: विभिन्न दिखाई पड़ सकते हैं।
उदाहरण 21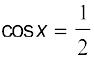 को हल कीजिए।
को हल कीजिए।
हल हम पाते हैं
इसलिए 
उदाहरण 22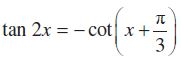
हल हम पाते हैं,
या 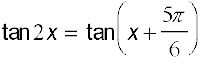
इसलिए 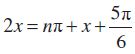
या 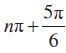
उदाहरण 23 हल कीजिए sin 2x – sin 4x + sin 6x = 0
हल समीकरण को लिख सकते हैं,

या 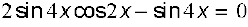
अर्थात् 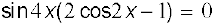
इसलिए sin 4x = 0 या 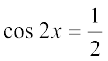
अर्थात्  य
य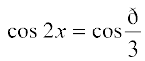
अत: 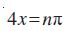

अर्थात् 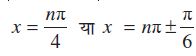
उदाहरण 24 हल कीजिए 2 cos2 x + 3 sin x = 0
हल समीकरण को इस प्रकार लिख सकते हैं
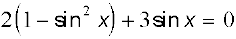
या 
या 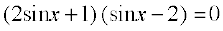
अत: sin x =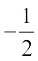 या sin x = 2
या sin x = 2
परंतु sin x = 2 असंभव है (क्यों?)
इसलिए sin x = 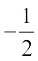 =
=
अत:, हल: 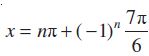
प्रश्नावली 3.4
निम्नलिखित समीकरणों का मुख्य तथा व्यापक हल ज्ञात कीजिए:
1.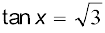 2. sec x = 2
2. sec x = 2
3.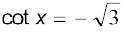 4. cosec x = – 2
4. cosec x = – 2
निम्नलिखि्ात प्रत्येक समीकरणों का व्यापक हल ज्ञात कीजिए:
5. cos 4 x = cos  6. cos 3x + co
6. cos 3x + co – cos 2x = 0
– cos 2x = 0
7. sin 2x + co = 0 8. sec2 2x = 1– tan 2x
= 0 8. sec2 2x = 1– tan 2x
9. sin x + sin 3x + sin 5x = 0
विविध उदाहरण
उदाहरण 25 यदि sin x = , cos y =
, cos y =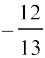 हैै, जहाँ x तथा y दोनों द्वितीय चतुर्थांश में स्थित हों तो sin (x + y) का मान ज्ञात कीजिए।
हैै, जहाँ x तथा y दोनों द्वितीय चतुर्थांश में स्थित हों तो sin (x + y) का मान ज्ञात कीजिए।
हल हम जानते हैं कि
sin (x + y) = sin x cos y + cos x sin y ... (1)
अब cos2 = 1 – sin2 x = 1 –
= 1 – sin2 x = 1 –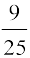 =
=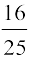
इसलिए cos x =
क्योंकि x द्वितीय चतुर्थांश में स्थित है, अत: cos x ऋणात्मक है।
अत: cos x =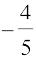
अब sin2y = 1 – cos2y = 1 –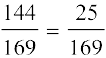
अर्थात् sin y =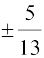
क्योंकि y द्वितीय चतुर्थांश में स्थित है, sin y धनात्मक है। इसलिए sin y = है। sin x, sin y,
है। sin x, sin y,
cos x तथा cos y का मान समीकरण (1) में रखने पर, हम पाते हैं,
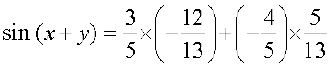 =
=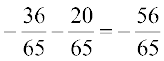
उदाहरण 26 सिद्ध कीजिए: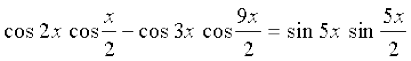
हल हम पाते हैं,
बायाँ पक्ष = 
=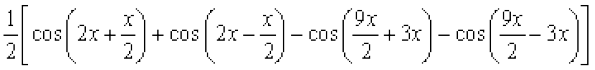
=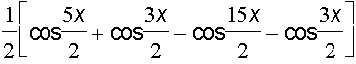 =
=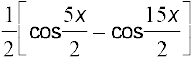
=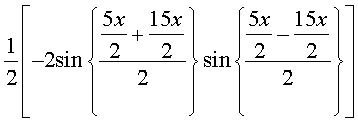
=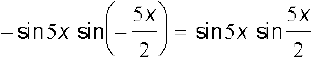 = दायाँ पक्ष
= दायाँ पक्ष
उदाहरण 27 tan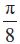
हल मान लीजिए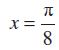
अब 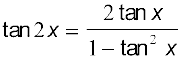
या
मान लीजिए y = tan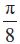
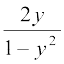
या y2 + 2y – 1 = 0
इसलिए y =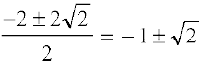
क्योंकि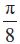
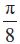
उदाहरण 28 यदि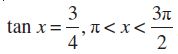
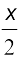 , cos
, cos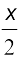 तथा tan
तथा tan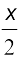 के मान ज्ञात कीजिए।
के मान ज्ञात कीजिए।
हल क्योंकि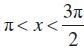
 ऋणात्मक है।
ऋणात्मक है।
पुन: 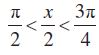
इसलिए sin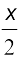 धनात्मक होगा तथा cos
धनात्मक होगा तथा cos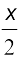 ऋणात्मक होगा।
ऋणात्मक होगा।
अब sec2 x = 1 + tan2 x = 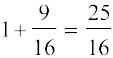
इसलिए cos2 x =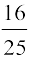 या cos x =
या cos x =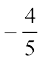 (क्यों?)
(क्यों?)
अब 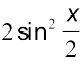 = 1 – cos x =
= 1 – cos x =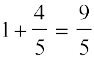
इसलिए sin2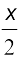 =
=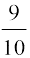
या sin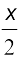 =
= 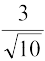 (क्यों?)
(क्यों?)
पुन: 2cos2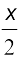 = 1+ co
= 1+ co =
=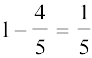
इसलिए cos2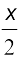 =
=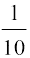 या cos
या cos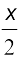 =
=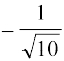 (क्यों?)
(क्यों?)
अत: tan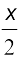 =
=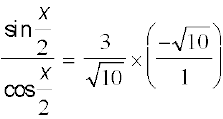 = – 3
= – 3
उदाहरण 29 सिद्ध कीजिए: cos2 x + cos
हल हम पाते हैं,
बायाँ पक्ष =
=
=
=
=
=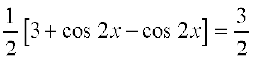 = दायाँ पक्ष
= दायाँ पक्ष
अध्याय 3 पर विविध प्रश्नावली
सिद्ध कीजिए:
1.
2. (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0
3. (cos x + cos y)2 + (sin x – sin y)2 = 4 cos2 
4. (co – cos y)2 + (si
– cos y)2 + (si – sin y)2 = 4 sin2
– sin y)2 = 4 sin2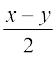
5. sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x
6.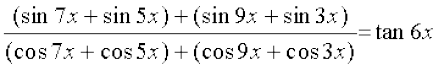
7. sin 3x + sin 2x – sin x = 4sin x cos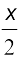 cos
cos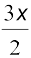
निम्नलिखित प्रत्येक प्रश्न में sin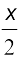 , cos
, cos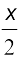 तथा tan
तथा tan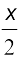 ज्ञात कीजिए:
ज्ञात कीजिए:
8. tan =
= 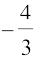 , x द्वितीय चतुर्थांश में है।
, x द्वितीय चतुर्थांश में है।
9. cos =
=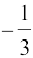 ,
, तृतीय चतुर्थांश में है।
तृतीय चतुर्थांश में है।
10. sin =
=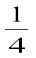 ,
, द्वितीय चतुर्थांश में है।
द्वितीय चतुर्थांश में है।
सारांश
- यदि एक वृत्त, जिसकी त्रिज्या r, चाप की लंबाई l तथा केंद्र पर अंतरित कोण θ रेडियन हैं, तो l = r θ
- रेडियन माप =
डिग्री माप
- डिग्री माप =
रेडियन माप
- cos2 x + sin2 x = 1
- 1 + tan2 x = sec2 x
- 1 + cot2 x = cosec2 x
- cos (2nπ + x) = cos x
- sin (2nπ + x) = sin x
- sin (– x) = – sin x
- cos (– x) = cos x
- cos (x + y) = cos x cos y – sin x sin y
- cos (x – y) = cos x cos y + sin x sin y
- cos
) = sin x
- sin
) = cos x
- sin (x + y) = sin x cos y + cos x sin y
- sin (x – y) = sin x cos y – cos x sin y
- cos
= – sin x sin
= cos x
cos (π – x) = – cos x sin (π – x) = sin x
cos (π + x) = – cos x sin (π + x) = – sin x
cos (2π – x) = cos x sin (2π – x) = – sin x
- यदि x, y और (x
![]() y) में से कोई कोण
y) में से कोई कोणका विषम गुणांक नहीं हैं, तो
tan (x + y) =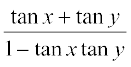
- tan (x – y) =
![]()
- यदि x, y और (x
![]() y) में से कोई कोण π का विषम गुणांक नहीं हैं, तो
y) में से कोई कोण π का विषम गुणांक नहीं हैं, तो
cot (x + y) =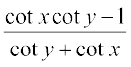
- cot (x – y) =
![]()
- cos 2x = cos2 x – sin2 x = 2cos2 x – 1 = 1 – 2 sin2 x
![]()
- sin 2x = 2 sin
![]() cos x
cos x![]()
- tan 2x =
![]()
- sin 3x = 3sin
![]() – 4sin
– 4sin![]()
- cos 3x = 4cos
![]() – 3cos
– 3cos![]()
- tan 3x =
![]()
- (i) cos x + cos y = 2cos
![]()
(ii) cos x – cos y = – 2sin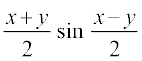
(iii) sin x + sin y = 2 si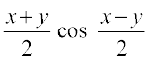
(iv) sin x – sin y = 2cos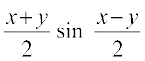
- (i) 2cos x cos y = cos
![]() + y) + cos
+ y) + cos ![]() – y)
– y)
(ii) – 2sin x sin y = cos (x + y) – cos (x – y)
(iii) 2sin x cos y = sin (x + y) + sin (x – y)
(iv) 2 cos x sin y = sin (x + y) – sin (x – y)
- sin
![]() = 0 हो तो x = nπ, जहाँ n ∈ Z
= 0 हो तो x = nπ, जहाँ n ∈ Z - cos x = 0 हो तो x = (2n + 1)
, जहाँ n ∈ Z
- sin x = sin y हो तो x = nπ + (– 1)n y, जहाँ n ∈ Z
- cos x = cos y, हो तो x = 2nπ ± y, जहाँ n ∈ Z
- tan x = tan y हो तो x = nπ + y, जहाँ n ∈ Z
एेतिहासिक पृष्ठभूमि
एेसा विश्वास किया जाता है कि त्रिकोणमिती का अध्ययन सर्वप्रथम भारत में आरंभ हुआ था। आर्यभट्ट (476 ईण्), ब्रह्मगुप्त (598 ईण्) भास्कर प्रथम (600 ईण्) तथा भास्कर द्वितीय (1114 ईण्)ने प्रमुख परिणामों को प्राप्त किया था। यह संपूर्ण ज्ञान भारत से मध्यपूर्व और पुन: वहाँ से यूरोप गया। यूनानियों ने भी त्रिकोणमिति का अध्ययन आरंभ किया परंतु उनकी कार्य विधि इतनी अनुपयुक्त थी, कि भारतीय विधि के ज्ञात हो जाने पर यह संपूर्ण विश्व द्वारा अपनाई गई।
भारत में आधुनिक त्रिकोणमितीय फलन जैसे किसी कोण की ज्या (sine) और फलन के परिचय का पूर्व विवरण सिद्धांत (संस्कृत भाषा में लिखा गया ज्योतिषीय कार्य) में दिया गया है जिसका योगदान गणित के इतिहास में प्रमुख है।
भास्कर प्रथम (600 ईण्) ने 90° से अधिक, कोणों के sine के मान के लए सूत्र दिया था। सोलहवीं शताब्दी का मलयालम भाषा में कार्य युक्ति भाषा में sin (A + B) के प्रसार की एक उपपत्ति है। 18°, 36°, 54°, 72°, आदि के sine तथा cosine के विशुद्ध मान भास्कर द्वितीय द्वारा दिए गए हैं।
sin–1 x, cos–1 x, आदि को चाप sin x, चाप cos x, आदि के स्थान पर प्रयोग करने का सुझाव ज्योतिषविद Sir John F.W. Hersehel (1813 ईण्) द्वारा दिए गए थे। ऊँचाई और दूरी संबंधित प्रश्नों के साथ Thales (600 ईण् पूर्व) का नाम अपरिहाय रूप से जुड़ा हुआ है। उन्हें मिश्र के महान पिरामिड की ऊँचाई के मापन का श्रेय प्राप्त है। इसके लिए उन्होंने एक ज्ञात ऊँचाई के सहायक दंड तथा पिरामिड की परछाइयों को नापकर उनके अनुपातों की तुलना का प्रयोग किया था। ये अनुपात हैं
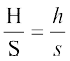 = tan (सूर्य का उन्नतांश)
= tan (सूर्य का उन्नतांश)
Thales को समुद्री जहा”ा की दूरी की गणना करने का भी श्रेय दिया जाता है। इसके लिए उन्होंने समरूप त्रिभुजों के अनुपात का प्रयोग किया था। ऊँचाई और दूरी संबधी प्रश्नों का हल समरूप त्रिभुजों की सहायता से प्राचीन भारतीय कार्यों में मिलते हैं।

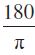
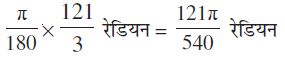
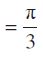
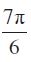
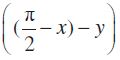
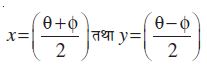
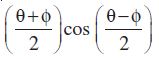
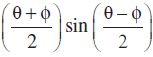
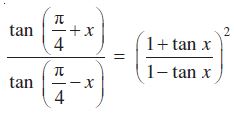
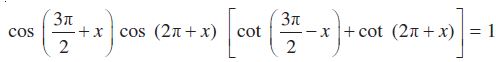
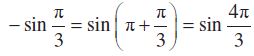
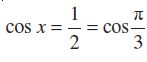
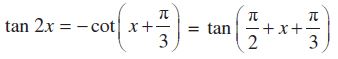

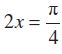

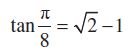

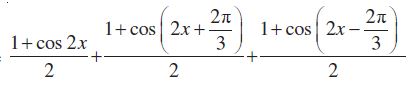
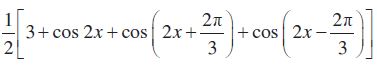
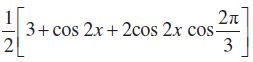
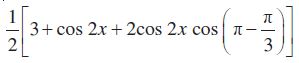


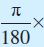
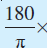
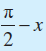 )
)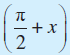 = – sin
= – sin