4.1 भूमिका (Introduction)

गणितीय चिंतन का एक आधारभूत सिद्धांत निगमनिक तर्क है। तर्कशास्त्र के अध्ययन से उद्धृत एक अनौपचारिक और निगमनिक तर्क का उदाहरण तीन कथनों में व्यक्त तर्क हैः-

(a) सुकरात एक मनुष्य है।

(b) सभी मनुष्य मरणशील हैं, इसलिए,

(c) सुकरात मरणशील है।

यदि कथन (a) और (b) सत्य हैं, तो (c) की सत्यता स्थापित है। इस सरल उदाहरण को गणितीय बनाने के लिए हम लिख सकते हैं।

(i) आठ दो से भाज्य है।

(ii) दो से भाज्य कोई संख्या सम संख्या है, इसलिए,

(iii) आठ एक सम संख्या है।

इस प्रकार संक्षेप में निगमन एक प्रक्रिया है जिसमें एक कथन सिद्ध करने को दिया जाता है, जिसे गणित में प्रायः एक अनुमानित कथन (conjecture) अथवा प्रमेय कहते हैं, तर्क संगत निगमन के चरण प्राप्त किए जाते हैं और एक उपपत्ति स्थापित की जा सकती है, अथवा नहीं की जा सकती है, अर्थात् निगमन व्यापक स्थिति से विशेष स्थिति प्राप्त करने का अनुप्रयोग है।

निगमन के विपरीत, आगमन तर्क प्रत्येक स्थिति के अध्ययन पर आधारित होता है तथा इसमें प्रत्येक एवं हर संभव स्थिति को ध्यान में रखते हुए घटनाओं के निरीक्षण द्वारा एक अनुमानित कथन विकसित किया जाता है। इसको गणित में प्रायः प्रयोग किया जाता है तथा वैज्ञानिक चिंतन, जहाँ आँकड़ों का संग्रह तथा विशलेषण मानक होता है, का यह मुख्य आधार है। इस प्रकार, सरल भाषा में हम कह सकते हैं कि आगमन शब्द का अर्थ विशिष्ट स्थितियों या तथ्यों से व्यापकीकरण करने से है।

बीजगणित में या गणित की अन्य शाखाओं में, कुछ एेसे परिणाम या कथन होते हैं जिन्हें एक धन पूर्णांक n के पदों में व्यक्त किया जाता है। एेसे कथनों को सिद्ध करने के लिए विशिष्ट तकनीक पर आधारित समुचित सिद्धांत है जो गणितीय आगमन का सिद्धांत (Principle of Mathematical Induction) कहलाता है।

4.2 प्रेरणा (Motivation)

गणित में, हम सम्पूर्ण आगमन का एक रूप जिसे गणितीय आगमन कहते हैं, प्रयुक्त करते हैं। गणितीय आगमन सिद्धांत के मूल को समझने के लिए, कल्पना कीजिए कि एक पतली आयताकार टाइलों का समूह एक सिरे पर रखा है, जैसे आकृति 4:1 में प्रदर्शित है।

जब प्रथम टाइल को निर्दिष्ट दिशा में धक्का दिया जाता है तो सभी टाइलें गिर जाएँगी। पूर्णतः सुनिश्चित होने के लिए कि सभी टाइलें गिर जाएँगी, इतना जानना पर्याप्त है कि

(a) प्रथम टाइल गिरती है, और

(b) उस घटना में जब कोई टाइल गिरती है, उसकी उत्तरवर्त्ती अनिवार्यतः गिरती है।

यही गणितीय आगमन सिद्धांत का आधार है।

हम जानते हैं कि प्राकृत संख्याओं का समुच्चय N वास्तविक संख्याओं का विशेष क्रमित उपसमुच्चय है। वास्तव में, R का सबसे छोटा उपसमुच्चय N है, जिसमें निम्नलिखित गुण हैंः

एक समुच्चय S आगमनिक समुच्चय (Inductive set) कहलाता है यदि 1∈ S और  x + 1 ∈ S जब कभी x ∈ S. क्योंकि N, जो कि एक आगमनिक समुच्चय है, R का सबसे छोटा उपसमुच्चय है, परिणामतः R के किसी भी एेसे उपसमुच्चय में जो आगमनिक है, N अनिवार्य रूप से समाहित होता है।

दृष्टांत

मान लीजिए कि हम प्राकृत संख्याओं 1, 2, 3,...,n, के योग के लिए सूत्र प्राप्त करना चाहते हैं अर्थात् एक सूत्र जो कि n = 3 के लिए 1 + 2 + 3 का मान देता है, n = 4 के लिए 1 + 2 + 3 + 4 का मान देता है इत्यादि। और मान लीजिए कि हम किसी प्रकार से यह विश्वास करने के लिए प्रेरित होते हैं कि सूत्र 1 + 2 + 3+...+ n = 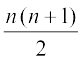सही है।

यह सूत्र वास्तव में कैसे सिद्ध किया जा सकता है? हम, निश्चित ही n के इच्छानुसार चाहे गए, धन पूर्णांक मानों के लिए कथन को सत्यापित कर सकते हैं, किंतु इस प्रक्रिया का मान n के सभी मानों के लिए सूत्र को सिद्ध नहीं कर सकती है। इसके लिए एक एेसी क्रिया शृंखला की आवश्यकता है, जिसका प्रभाव इस प्रकार का हो कि एक बार किसी धन पूर्णांक के लिए सूत्र के सिद्ध हो जाने के बाद आगामी धन पूर्णांकों के लिए सूत्र निरंतर अपने आप सिद्ध हो जाता है। इस प्रकार की क्रिया शृंखला को गणितीय आगमन विधि द्वारा उत्पन्न समझा जा सकता है।

4.3 गणितीय आगमन का सिद्धांत (The Principle of Mathematical Induction)

कल्पना कीजिए धन पूर्णांक P(n) से संबद्ध एक दिया कथन इस प्रकार है कि

(i) n = 1, के लिए कथन सत्य है अर्थात् P(1) सत्य है और

(ii) यदि n = k, एक प्राकृत संख्या, के लिए कथन सत्य है तो n = k + 1, के लिए भी कथन सत्य है अर्थात् P(k) की सत्यता का तात्पर्य है P (k + 1) की सत्यता।

अतः सभी प्राकृत संख्या n के लिए P(n) सत्य है।

गुण (i) मात्र तथ्य का कथन है। एेसी परिस्थितियाँ भी हो सकती हैं जब n ≥ 4 के सभी मानों के लिए कथन सत्य हो। इस स्थिति में, प्रथम चरण n = 4 से प्रारंभ होगा और हम परिणाम को n = 4 के लिए अर्थात् P(4) सत्यापित करेंगे।

गुण (ii) प्रतिबंधित गुणधर्म है। यह निश्चयपूर्वक नहीं कहता कि दिया कथन n = k के लिए सत्य है, परंतु केवल इतना कहता है कि यदि यह n = k के लिए कथन सत्य है, तो n = k + 1 के लिए भी सत्य है। इस प्रकार गुणधर्म की सत्यता सिद्ध करने के लिए केवल प्रतिबंधित साध्य (conditional proposition) को सिद्ध करते हैंः "यदि n = k के लिए कथन सत्य है तो यह n = k + 1 के लिए भी सत्य है"। इसे कभी-कभी आगमन का चरण (Induction step) कहा जाता है। इस आगमन चरण में ‘n = k के लिए कथन सत्य है’ की अभिधारणा (assumption) आगमन परिकल्पना (Induction hypothesis) कहलाती है।

उदाहरणार्थः गणित में बहुधा एक सूत्र खोजा जा सकता है जो किसी पैटर्न के अनुरूप होता है, जैसे

1 = 12 =1

4 = 22 = 1 + 3

9 = 32 = 1 + 3 + 5

16 = 42 = 1 + 3 + 5 + 7, इत्यादि।

ध्यान दीजिए कि प्रथम दो विषम प्राकृत संख्याओं का योग द्वितीय प्राकृत संख्या का वर्ग है, प्रथम तीन विषम प्राकृत संख्याओं का योग तृतीय प्राकृत संख्या का वर्ग है, इत्यादि। अतः इस पैटर्न से प्रतीत होता है कि

1 + 3 + 5 + 7 + ... + (2n – 1) = n2 , अर्थात्

प्रथम n विषम प्राकृत संख्याओं का योग n का वर्ग है।

मान लीजिए कि

P(n): 1 + 3 + 5 + 7 + ... + (2n – 1) = n2

हम सिद्ध करना चाहते हैं कि P(n), n के सभी मानों के लिए सत्य है। गणितीय आगमन के प्रयोग वाली उपपत्ति के प्रथम चरण में P(1) को सत्य सिद्ध करते हैं। इस चरण को मूल चरण कहते हैं। प्रत्यक्षतः

1 = 12 अर्थात् P(1) सत्य है।

अगला चरण आगमन चरण (Induction step) कहलाता है। यहाँ हम कल्पना करते हैं कि P (k) सत्य है जहाँ k ,एक प्राकृत संख्या है और हमें P (k + 1) की सत्यता सिद्ध करने की आवश्यकता है क्योंकि P (k) सत्य है, अतः

P (k) : 1 + 3 + 5 + 7 + ... + (2k – 1) = k2 ... (1)

P (k+1) पर विचार कीजिए

P (k + 1) : 1 + 3 + 5 + 7 + ... + (2k – 1) + {2(k +1) – 1} ... (2)

= k2 + (2k + 1) [(1) के प्रयोग से]

= (k + 1)2

इसलिए, P (k + 1) सत्य है और अब आगमनिक उपपत्ति पूर्ण हुई।

अतः सभी प्राकृत संख्याओं n के लिए P(n) सत्य है।

उदाहरण 1 सभी n ≥ 1 के लिए, सिद्ध कीजिए

12 + 22 + 32 + 42 +…+ n2 = .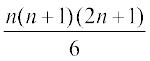

हल मान लीजिए कि दिया कथन P(n) है, अर्थात्

P(n) : 12 + 22 + 32 + 42 +…+ n2 =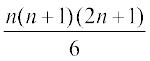

n = 1 के लिए, P(1): 1 = 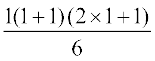= 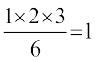जोकि सत्य है।

किसी धन पूूर्णांक k के लिए कल्पना कीजिए कि P(k) सत्य है, अर्थात्

12 + 22 + 32 + 42 +…+ k2 = 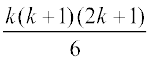...(1)

अब हम सिद्ध करेंगे कि P(k + 1) भी सत्य है,

(12 +22 +32 +42 +…+k2 ) + (k + 1) 2

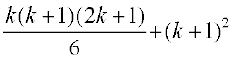= [(1) के प्रयोग से]

=

=

=

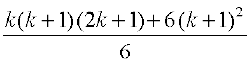
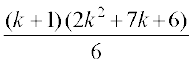
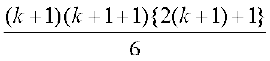
इस प्रकार, P(k + 1) सत्य है जब कभी P (k) सत्य है।

अतः गणितीय आगमन सिद्धांत से सभी प्राकृत संख्याओं N के लिए कथन P(n) सत्य है।

उदहारण 2 सभी धन पूर्णांक n के लिए सिद्ध कीजिए कि 2n > n.

हल मान लीजिए कि P(n): 2n > n

जब n=1, 21>1. अतः P(1) सत्य है।

कल्पना कीजिए कि किसी धन पूर्णांक k के लिए P(k) सत्य है अर्थात्

P(k) : 2k > k ... (1)

अब हम सिद्ध करेंगे कि P(k +1) सत्य है जब कभी P(k) सत्य है।

(1) के दोनों पक्षों में 2 का गुणा करने पर हम

2. 2k > 2k प्राप्त करते हैं।

अर्थात् 2 k + 1 > 2k = k + k > k + 1

इसलिए, P(k + 1) सत्य है जब कभी P(k) सत्य है। अतः गणितीय आगमन द्वारा, प्रत्येक धन पूर्णाक n के लिए P(n) सत्य है।

उदाहरण 3 सभी पूर्णांक n ≥ 1 के लिए, सिद्ध कीजिएः

.

हल मान लीजिए कि दिया कथन P(n) है तथा हम

P(n): लिखते हैं

इस प्रकार P(1):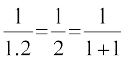, जोकि सत्य है। अतः P(n), n = 1 के लिए सत्य है।

कल्पना कीजिए कि पूर्णांक k के लिए P(k) सत्य है

अर्थात् ... (1)

हमें P(k + 1) को सत्य सिद्ध करना है जब P(k) सत्य है। इस हेतु निम्नलिखित पर विचार कीजिए।

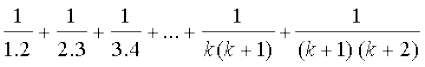
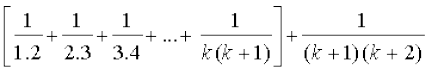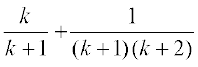= = [(1) के प्रयोग से]

= = = =

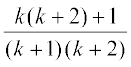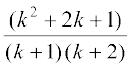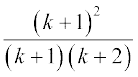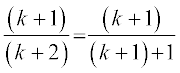
इस प्रकार कथन P(k + 1) सत्य है जब कभी P(k) सत्य है। अतः गणितीय आगमन सिद्धांत द्वारा सभी पूर्णांकों n ≥ 1 के लिए P(n) सत्य है।

उदाहरण 4 प्रत्येक धन पूर्णांक n के लिए, सिद्ध कीजिए कि 7n – 3n, 4 से विभाजित होता है।

हल मान लीजिए दिया कथन P(n) है अर्थात्

P(n) : 7n – 3n, 4 से विभाजित है।

हम पाते हैं

P(1): 71 – 31 = 4 जो कि 4 से विभाजित होता है। इस प्रकार P(n), n = 1 के लिए सत्य है।

कल्पना कीजिए कि एक धन पूर्णांक k के लिए P(k) सत्य है,

अर्थात, P(k) : 7k – 3k, 4 से विभाजित होता है।

अतः हम लिख सकते हैं 7k – 3k = 4d, जहाँ d ∈ N.

अब, हम सिद्ध करना चाहते हैं कि P(k + 1) सत्य है, जब कभी P(k ) सत्य है।

अब 7(k+1)– 3(k + 1) = 7(k + 1) – 7.3k + 7.3k – 3(k + 1)

= 7(7k – 3k) + (7 – 3)3k

= 7(4d) + (7 – 3)3k

= 7(4d) + 4.3k = 4(7d + 3k)

अंतिम पंक्ति से हम देखते हैं कि 7(k + 1) – 3(k + 1), 4 से विभाजित होता है। इस प्रकार, P(k + 1) सत्य है जब कभी P(k) सत्य है। इसलिए, गणितीय आगमन सिद्धांत से प्रत्येक धन पूर्णांक n के लिए कथन P(n) सत्य है।

उदाहरण 5 सभी प्राकृत संख्याओं n के लिए सिद्ध कीजिए कि (1 + x)n ≥ (1 + nx), जहाँ x > – 1.

हल मान लीजिए कि दिया कथन P(n) है

अर्थात् P(n): (1 + x)n ≥ (1 + nx), x > – 1 के लिए

जब n = 1, P(n) सत्य है क्योंकि ( 1+x) ≥ (1 + x) जो x > –1 के लिए सत्य है

कल्पना कीजिए कि

P(k): (1 + x)k ≥ (1 + kx), x > – 1 सत्य है। ... (1)

अब हम सिद्ध करना चाहते हैं कि P(k + 1) सत्य हैं, x > –1 के लिए, जब कभी P(k) सत्य है। ... (2)

सर्वसमिका (1 + x)k + 1 = (1 + x)k (1 + x) पर विचार कीजिए।

दिया है कि x > –1, इस प्रकार (1+x) > 0.

इसलिए (1 + x)k ≥ (1 + kx), का प्रयोग कर हम पाते हैं,

(1 + x) k + 1 ≥ (1 + kx)(1 + x)

अर्थात् (1 + x)k + 1 ≥ (1 + x + kx + kx2). ... (3)

यहाँ k एक प्राकृत संख्या है और x2 ≥ 0 इस प्रकार kx2 ≥ 0. इसलिए,

(1 + x + kx + kx2) ≥ (1 + x + kx),

और इस प्रकार, हम प्राप्त करते हैं

(1 + x)k + 1 ≥ (1 + x + kx)

अर्थात् (1 + x)k + 1 ≥ [1 + (1 + k)x]

इस प्रकार, कथन (2) सिद्ध होता है। अतः गणितीय आगमन सिद्धांत से सभी प्राकृत संख्याओं n के लिए P(n) सत्य है।

उदाहरण 6 सिद्ध कीजिए कि सभी n ∈ N के लिए 2.7n + 3.5n – 5, 24 से भाज्य है।

हल मान लीजिए कि कथन P(n) इस प्रकार परिभषित है कि

P(n) : 2.7n + 3.5n – 5, 24 से भाज्य है

जब n = 1 के लिए P(n) सत्य है। हम पाते हैं

2.7 + 3.5 – 5 = 24 जो कि 24 से भाज्य है।

कल्पना कीजिए कि P(k) सत्य है।

अर्थात् 2.7k + 3.5k – 5 = 24q, जबकि q ∈ छ ... (1)

अब हम सिद्ध करना चाहते हैं कि P(k + 1) सत्य है। जब कभी P(k) सत्य है।

हम पाते हैं,

2.7k+1 + 3.5k+1 – 5 = 2.7k . 71 + 3.5k . 51 – 5

= 7 [2.7k + 3.5k – 5 – 3.5k + 5] + 3.5k . 5 – 5

= 7 [24q – 3.5k + 5] + 15.5k –5

= 7 × 24q – 21.5k + 35 + 15.5k – 5

= 7 × 24q – 6.5k + 30

= 7 × 24q – 6 (5k – 5)

= 7 × 24q – 6 (4p) [(5k – 5), 4 का गुणज है (क्यों?), p ∈ N

= 7 × 24q – 24p

= 24 (7q – p)

= 24 × r, r = 7q – p, कोई प्राकृत संख्या है। ... (2)

व्यंजक (1) का दायाँ पक्ष 24 से भाज्य है।

इस प्रकार, P(k + 1) सत्य है, जब कभी P(k) सत्य है। अतः गणितीय आगमन सिद्धांत से, सभी
n ∈ N के लिए P(n) सत्य है।

उदाहरण 7 सिद्ध कीजिए किः

12 + 22 + ... + n2 > 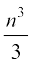, n ∈ N

हल मान लीजिए कि दिया कथन P(n) है,

अर्थात् , P(n) : 12 + 22 + ... + n2 > 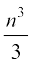, n ∈ N

हम ध्यान देते हैं कि n = 1 के लिए, P(n) सत्य है क्योंकि P(1) :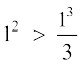

कल्पना कीजिए कि P(k) सत्य है,

अर्थात् , P(k) : 12 + 22 + ... + k2 > 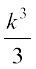... (1)

अब हम सिद्ध करेंगे कि P(k + 1) सत्य है जब कभी P(k) सत्य है।

हम पाते हैं, 12 + 22 + 32 + ... + k2 + (k + 1)2

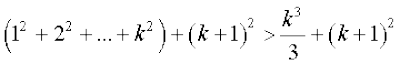= [(1)के प्रयोग से]

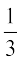= [k3 + 3k2 + 6k + 3]

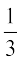= [(k + 1)3 + 3k + 2] > (k + 1)3

इस प्रकार, P(k + 1) सत्य हुआ जब कभी P(k) सत्य है। अतः गणितीय आगमन द्वारा n ∈ N के लिए P(n) सत्य है।

उदाहरण 8 प्रत्येक प्राकृत संख्या n के लिए गणितीय आगमन सिद्धांत द्वारा घातांकों का नियम
(ab)n = anbn सिद्ध कीजिए।

हल मान लीजिए दिया कथन P(n) है।

अर्थात् P(n) : (ab)n = anbn.

हम ध्यान देते हैं कि n = 1 के लिए P(n) सत्य है, चूँकि (ab)1 = a1b1.

कल्पना कीजिए P(k) सत्य है

अर्थात् (ab)k = akbk ... (1)

हम सिद्ध करेंगे कि P(k + 1) सत्य है जब कि P(k) सत्य है।

अब, हम पाते हैं,

(ab)k + 1 = (ab)k (ab)

= (ak bk) (ab) [(1) से]

= (ak . a1) (bk . b1)

= ak+1 . bk+1

इसलिए, P(k + 1) सत्य है जब कभी P(k) सत्य है। अतः गणितीय आगमन सिद्धांत द्वारा प्रत्येक प्राकृत संख्या n के लिए P(n) सत्य है।

प्रश्नावली 4.1

सभी n ∈ N के लिए गणितीय आगमन सिद्धांत के प्रयोग द्वारा सिद्ध कीजिए किः

1: 1 + 3 + 32 + ... + 3n – 1 = .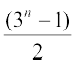

2: 13 + 23 + 33 + … +n3 = .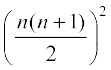

3: .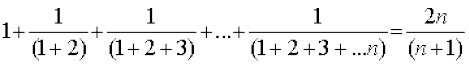

4: 1.2.3 + 2.3.4 +…+ n(n+1) (n+2) =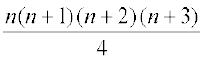

5: 1.3 + 2.32 + 3.33 +…+ n.3n =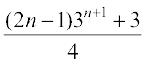

6: 1.2 + 2.3 + 3.4 +…+ n (n+1) =

7: 1.3 + 3.5 + 5.7 +…+ (2n–1) (2n+1) =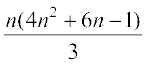

8: 1.2 + 2.22 + 3.22 + ...+n.2n = (n–1) 2n + 1 + 2

9: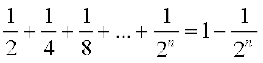

10: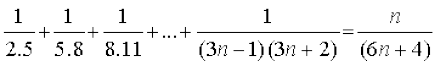

11: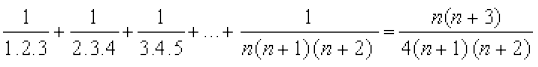

12: a + ar + ar2 +…+ arn-1 =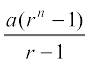

13: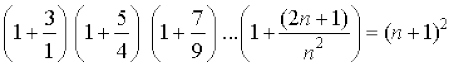

14: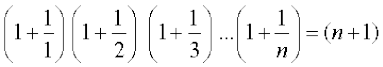

15: 12 + 32 + 52 + …+ (2n–1)2 =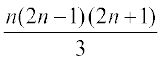

16: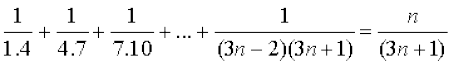

17: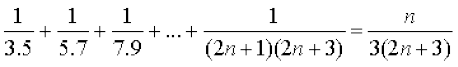

18: 1 + 2 + 3 +…+ n < 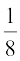(2n + 1)2

19: n (n + 1) (n + 5), संख्या 3 का एक गुणज है।

20: 102n – 1 + 1 संख्या 11 से भाज्य है।

21: x2n – y2n, ( x + y ) से भाज्य है।

22: 32n+2 – 8n – 9, संख्या 8 से भाज्य है।

23: 41n – 14n, संख्या 27 का एक गुणज है।

24: (2n + 7) < (n + 3)2