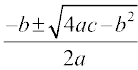Table of Contents
सम्मिश्र संख्याएँ और द्विघातीय समीकरण (Complex Numbers and Quadratic Equations)
"Mathematics is the Queen of Sciences and Arithmetic is the Queen of Mathematics. – Gauss "
5.1 भूमिका (Introduction)
पिछली कक्षाओं में हमने एक और दो चर की एक घातीय समीकरणों का तथा एक चर की द्विघातीय समीकरणों का अध्ययन किया है। हमने देखा है कि समीकरण x2 + 1 = 0 का कोई वास्तविक हल नहीं है क्योंकि x2 + 1 = 0 से हमें x2 = – 1 प्राप्त होता है और प्रत्येक वास्तविक संख्या का वर्ग श्रेणेतर होता है इसलिए वास्तविक संख्या प्रणाली को बृहद प्रणाली के रूप में बढ़ाने की आवश्यकता है जिससे कि हम समीकरण x2 = – 1 का हल प्राप्त कर सकें। वास्तव में, मुख्य उद्देश्य समीकरण ax2 + bx + c = 0 का हल प्राप्त करना है, जहाँ
D = b2 – 4ac < 0 है, जोकि वास्तविक संख्याओं की प्रणाली में संभव नहीं है।
5.2 सम्मिश्र संख्याएँ (Complex Numbers)
हम कल्पना करें कि 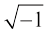 संकेतन i से निरूपित है। तब हमें
संकेतन i से निरूपित है। तब हमें  प्राप्त होता है। इसका तात्पर्य है कि i, समीकरण x2 + 1 = 0 का एक हल है।
प्राप्त होता है। इसका तात्पर्य है कि i, समीकरण x2 + 1 = 0 का एक हल है।
a + ib के प्रारूप की एक संख्या जहाँ a और b वास्तविक संख्याएँ हैं, एक सम्मिश्र संख्या परिभाषित करती है। उदाहरण के लिए, 2 + i3, (– 1) + 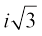 ,
, 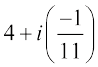 सम्मिश्र संख्याएँ हैं।
सम्मिश्र संख्याएँ हैं।
सम्मिश्र संख्या z = a + ib के लिए, a वास्तविक भाग कहलाता है तथा Rez द्वारा निरूपित किया जाता है और b काल्पनिक भाग कहलाता है तथा Imz द्वारा निरूपित किया जाता है। उदाहरण के लिए, यदि z = 2 + i5, तब Rez = 2 और Imz = 5 दो सम्मिश्र संख्याएँ z1 = a + ib तथा z2 = c + id समान होंगी यदि a = c और b = d.
उदाहरण 1 यदि 4x + i(3x – y) = 3 + i (– 6), जहाँ x और y वास्तविक संख्याएँ हैं, तब x और y ज्ञात कीजिए।
हल हमें दिया है
4x + i (3x – y) = 3 + i (– 6) ... (i)
दोनों ओर के वास्तविक तथा काल्पनिक भागों को समान लेते हुए, हमें प्राप्त होता है,
4x = 3, 3x – y = – 6,
जिन्हें युगपत् हल करने पर, 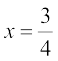 और
और 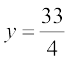
5.3 सम्मिश्र संख्याओं का बीजगणित (Algebra of Complex Numbers)
इस भाग में, हम सम्मिश्र संख्याओं के बीजगणित का विकास करेंगे।
5.3.1 दो सम्मिश्र, संख्याओं का योग (Addition of two complex numbers)
यदि z1 = a + ib और z2 = c + id कोई दो सम्मिश्र संख्याएँ हैं। तब z1 + z2 के योग को निम्नलिखित रूप से परिभाषित किया जाता हैः
z1 + z2 = (a + c) + i (b + d), जो कि पुनः एक सम्मिश्र संख्या है।
उदाहरण के लिए, (2 + i3) + (– 6 +i5) = (2 – 6) + i (3 + 5) = – 4 + i 8
सम्मिश्र संख्याओं के योग निम्नलिखित प्रगुणों को संतुष्ट करते हैं।
(i) संवरक नियम दो सम्मिश्र संख्याओं का योगफल एक सम्मिश्र संख्या होती है, अर्थात सारी सम्मिश्र सख्याओं z1 तथा z2 के लिए, z1 + z2 एक सम्मिश्र संख्या है।
(ii) क्रम विनिमय नियम किन्हीं दो सम्मिश्र संख्याओं z1 तथा z2 के लिए
(iii) साहचर्य नियम किन्हीं तीन सम्मिश्र संख्याओं z1, z2 तथा z3 के लिए
(iv) योगात्मक तत्समक का अस्तित्व सम्मिश्र संख्या 0 + i 0 (0 के द्वारा दर्शाया जाता है), योगात्मक तत्समक अथवा शून्य सम्मिश्र संख्या कहलाता है जिससे कि प्रत्येक सम्मिश्र संख्या z, z + 0 = z.
(v) योगात्मक प्रतिलोम का अस्तित्व प्रत्येक सम्मिश्र संख्या z = a + ib, के लिए हमें सम्मिश्र संख्या – a + i(– b) (– z के द्वारा दर्शाया जाता है) प्राप्त होती है, जोकि योगात्मक प्रतिलोम अथवा z का ऋण कहलाता है। हम प्रेक्षित करते हैं कि z + (–z) = 0 (योगात्मक तत्समक)।
5.3.2 दाे सम्मिश्र संख्याओं का अंतर (Difference of two complex numbers)
किन्हीं दी गई सम्मिश्र संख्याओं z1 और z2 का अंतर z1 – z2 निम्न प्रकार से परिभाषित किया जाता हैः
z1 – z2 = z1 + (–z2) उदाहरणार्थ (6 + 3i) – (2 – i) = (6 + 3 i) + (–2 + i) और (2 – i) + (– 6 – 3 i) = – 4 – 4 i
5.3.3 सम्मिश्र संख्याओं का गुणन (Multiplication of two complex numbers)
मान लीजिए z1 = a + ib तथा z2 = c + id कोई दो सम्मिश्र संख्याएँ हैं। तब गुणनफल z1.z2 निम्नलिखित रूप से परिभाषित किया जाता हैः
z1 z2 = (ac – bd) + i(ad + bc)
उदाहरण के लिए, (3 + i5) (2 + i6) = (3 × 2 – 5 × 6) + i(3 × 6 + 5 × 2) = – 24 + i28
सम्मिश्र संख्याओं के गुणन की संक्रिया में निम्नलिखित प्रगुण होते हैंः
(i) संवरक नियम दो सम्मिश्र संख्याओं का गुणनफल, एक सम्मिश्र संख्या होती है, सारी सम्मिश्र संख्याओं z1 तथा z2 के लिए, गुणनफल z1, z2 एक सम्मिश्र संख्या होती है।
(ii) क्रम विनिमय नियम किन्हीं दो सम्मिश्र संख्याओं z1 तथा z2 के लिए,
z1 z2 = z2 z1
(iii) साहचर्य नियम किन्हीं तीन सम्मिश्र संख्याओं z1, z2 तथा z3 के लिए
(z1 z2) z3 = z1 (z2 z3)
(iv) गुणात्मक तत्समक का आस्तित्व सम्मिश्र संख्या 1 + i 0 (1 के द्वारा दर्शाया जाता है), गुणात्मक तत्समक अथवा एकल सम्मिश्र संख्या कहलाता है जिससे कि प्रत्येक सम्मिश्र संख्या z के लिए z.1 = z
(v) गुणात्मक प्रतिलोम का अस्तित्व प्रत्येक शून्येत्तर सम्मिश्र संख्या z = a + ib (a ≠ 0, b ≠ 0) के लिए, हमें सम्मिश्र संख्या 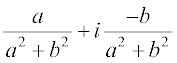 (
( अथवा z–1 के द्वारा दर्शाया जाता है) प्राप्त होती है, z की गुणात्मक प्रतिलोम कहलाती है जिससे कि
अथवा z–1 के द्वारा दर्शाया जाता है) प्राप्त होती है, z की गुणात्मक प्रतिलोम कहलाती है जिससे कि 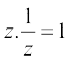 (गुणात्मक तत्समक)
(गुणात्मक तत्समक)
(vi) बंटन नियम किन्हीं तीन सम्मिश्र संख्याओं z1, z2, z3 के लिए
(a) z1 (z2 + z3) = z1 z2 + z1 z3
(b) (z1 + z2) z3 = z1 z3 + z2 z3
5.3.4 दो सम्मिश्र संख्याओं का भागफल (Division of two complex numbers)
किन्हीं दो दी हुई सम्मिश्र संख्याओं z1 तथा z2 के लिए, जहाँ z2 ≠ 0, भागफल 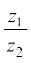 निम्नलिखित प्रकार से परिभाषित किया जाता है
निम्नलिखित प्रकार से परिभाषित किया जाता है 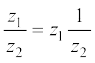
उदाहरण के लिए, मान लिया z1 = 6 + 3i और z2 = 2 – i
तब 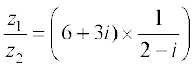 =
= 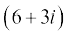
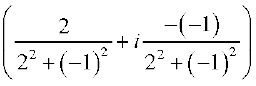
= 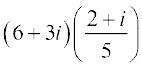
= 
5.3.5 i की घात (Power of i ) हमें ज्ञात हैं:
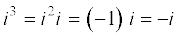 ,
, 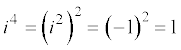
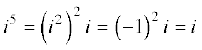 ,
, 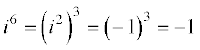 इत्यादि,
इत्यादि,
इसी प्रकार हम और भी प्राप्त करते हैंः
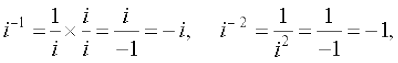
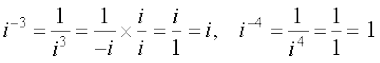
सामान्य रूप से, किसी पूर्णांक k के लिए, i4ा = 1, i4ा + 1 = i, i4ा + 2 = –1, i4ा + 3 = – i
5.3.6 एक ऋण वास्तविक संख्या के वर्गमूल (The square roots of a negative real number)
ज्ञात हैः i2 = –1 और ( – i)2 = i2 = – 1. इसलिए – 1 के वर्गमूल i और – i हैं।
यद्यपि चिह्न 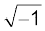 , का अर्थ हमारे लिए केवल i होगा।
, का अर्थ हमारे लिए केवल i होगा।
अब हम देख सकते हैं कि i और –i दोनों समीकरण x2 + 1 = 0 अथवा x2 = –1 के हल हैं।
इसी प्रकार, 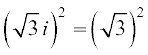 i2 = 3 (– 1) = – 3
i2 = 3 (– 1) = – 3
और 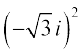 =
= 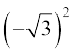 i2 = – 3
i2 = – 3
इसलिए – 3 के वर्गमूल 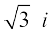 और
और 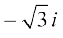 हैं।
हैं।
फिर से केवल 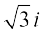 को दर्शाने के लिए ही प्रतीक
को दर्शाने के लिए ही प्रतीक 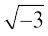 का प्रयोग किया जाता है, अर्थात्
का प्रयोग किया जाता है, अर्थात् 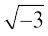 =
= 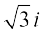 .
.
सामान्यतया यदि a एक धनात्मक वास्तविक संख्या है, तब 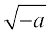 =
= 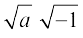 =
= 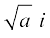 ,
,
हम जानते हैं कि सभी धनात्मक वास्तविक संख्याओं a और b के लिए 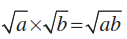
क्या होगा ? यदि a < 0, b < 0, हम इसकी जाँच करते हैं
नोट कीजिए कि i2 = 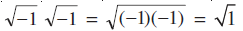
इसलिए,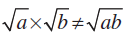
आगे यदि a और b दोनों में से कोई भी शून्य है, तब स्पष्ट रूप से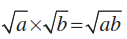
5.3.7 तत्समक (Identities)
हम निम्नलिखित तत्समक को सिद्ध करते हैंः
किन्हीं सम्मिश्र संख्याओं z1 और z2 के लिए
( z1 + z2 )2 = z12 + z22 + 2z1z2
उपपεत्त हमें प्राप्त होता है, ( z1 + z2 )2 = ( z1 + z2 ) ( z1 + z2 )
= (z1 + z2) z1+ (z1 + z2) z2 (बंटन नियम)
=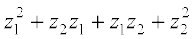 (बंटन नियम)
(बंटन नियम)
=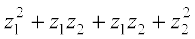 (गुणन का क्रम विनिमय नियम)
(गुणन का क्रम विनिमय नियम)
=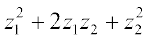
इसी भाँति हम निम्नलिखित तत्समकों को सिद्ध कर सकते हैंः
(i)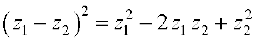
(ii)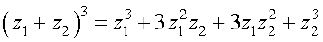
(iii)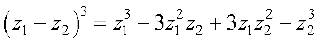
(iv)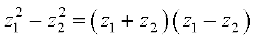
वास्तव में बहुत से दूसरे तत्समकों को जोकि सभी वास्तविक संख्याओं के लिए सत्य हैं, सभी सम्मिश्र संख्याओं की सत्यता के लिए सिद्ध किया जा सकता है।
उदाहरण 2 निम्नलिखित को a + ib के रूप में व्यक्त करेंः
(i)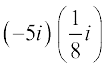 (ii)
(ii)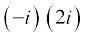
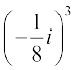
हल (i)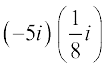 =
=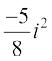 =
=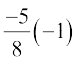 =
=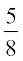 =
=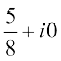
(ii)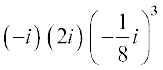 =
=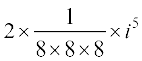 =
=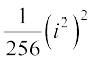
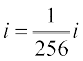
उदाहरण 3 (5 – 3i)3 को a + bi के रूप में व्यक्त करेंः
हल हमें प्राप्त है, (5 – 3i)3 = 53 – 3 × 52 × (3i) + 3 × 5 (3i)2 – (3i)3
= 125 – 225i – 135 + 27i = – 10 – 198i
उदाहरण 4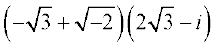 को a + ib के रूप में व्यक्त करें।
को a + ib के रूप में व्यक्त करें।
हल हमें प्राप्त है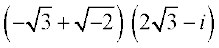 =
=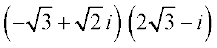
=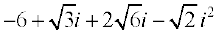 =
=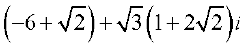
5.4 सम्मिश्र संख्या का मापांक और संयुग्मी (The Modulus and the Conjugate of a Complex Number)
मान लीजिए z = a + ib एक सम्मिश्र संख्या है। तब z का मापांक, जो | z | द्वारा दर्शाया जाता है, को ऋणेत्तर वास्तविक संख्या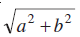
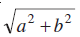
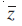
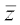 = a – ib
= a – ib
उदाहरण के लिए,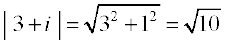 ,
,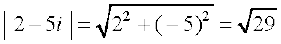 ,
,
और 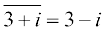 ,
, 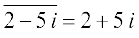 ,
,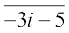 = 3i – 5
= 3i – 5
हम प्रेक्षित करते हैं कि ऋणेत्तर सम्मिश्र संख्या z = a + ib का गुणात्मक प्रतिलोम
z–1 =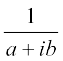 =
=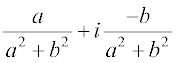 =
=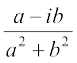 =
= 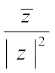 , होता है
, होता है
अर्थात् z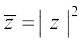
अग्रतः किन्हीं दो सम्मिश्र संख्याओं z1 एवं z2 के लिए निम्नलिखित निष्कर्षों को सुगमता से व्युत्पन्न किया जा सकता हैः
(i)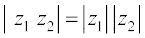
(ii)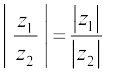 , यदि
, यदि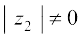
(iii)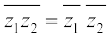
(iv)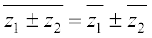
(v)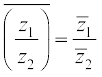 यदि z2 ≠ 0.
यदि z2 ≠ 0.
उदाहरण 5 2 – 3i का गुणात्मक प्रतिलोम ज्ञात कीजिए।
हल मान लिया z = 2 – 3i
तब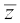 = 2 + 3i और
= 2 + 3i और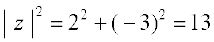
इसलिए, 2 – 3i का गुणात्मक प्रतिलोम
z–1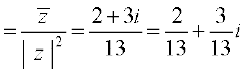 प्राप्त होता है।
प्राप्त होता है।
ऊपर दिया गया सारा हल निम्नलिखित ढंग से भी दिखाया जा सकता हैः
z–1 =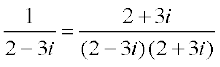 =
=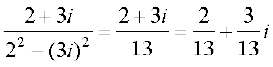
उदाहरण 6 निम्नलिखित को a + ib के रूप में व्यक्त करें।
(i)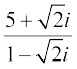
(ii) i–35
हल (i)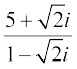 =
= 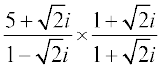 =
=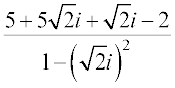
=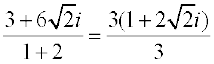 =
=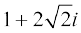
(ii)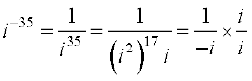 =
=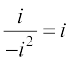
प्रश्नावली 5.1
प्रश्न 1 से 10 तक की सम्मिश्र संख्याओं में प्रत्येक को a + ib के रूप में व्यक्त कीजिए।
1.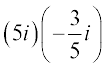
2.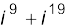
3.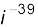
4. 3(7 + i7) + i (7 + i7)
5. (1 – i) – ( –1 + i6)
6. 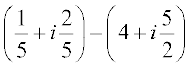
7.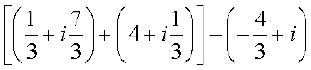
8. (1 – i)4
9.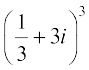
10.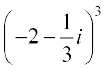
प्रश्न 11 से 13 की सम्मिश्र संख्याओं में प्रत्येक का गुणात्मक प्रतिलोम ज्ञात कीजिए।
11. 4 – 3i
12.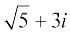
13. – i
14. निम्नलिखित व्यंजक को a + ib के रूप में व्यक्त कीजिएः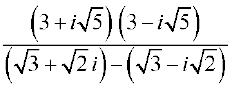
5.5 आर्गंड तल और ध्रुवीय निरूपण (Argand Plane and Polar Representation)
जैसा कि हम पहले से ही जानते हैं कि वास्तविक संख्याओं (x, y) के प्रत्येक क्रमित युग्म के संगत, हमें X Y तल में दो पारस्परिक लंब रेखाओं के संदर्भ में जिन्हें x– अक्ष y – अक्ष द्वारा जाना जाता है, एक अद्वितीय बिंदु प्राप्त होता है। अर्थात् सम्मिश्र संख्या x + iy का जो क्रमित युग्म (x,y) के संगत है, तल में एक अद्वितीय बिंदु (x, y) के रूप में ज्यामितीय निरूपण किया जा सकता है। यह कथन विलोमतः सत्य है।
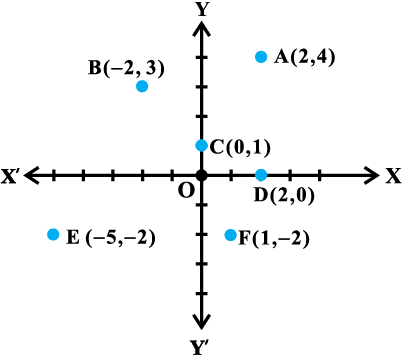
आकृति 5.1
कुछ सम्मिश्र संख्याओं जैसे 2 + 4i,–2 + 3i, 0 + 1i, 2 + 0i, –5 –2i और 1–2i को जोकि क्रमित युग्मों (2, 4), (–2,3), (0,1), (2,0), (–5,–2) और (1, –2) के संगत हैं, आकृति 5.1 में बिंदुओं A, B, C, D, E और F द्वारा ज्यामितीय निरूपण किया गया है।
तल, जिसमें प्रत्येक बिंदु को एक सम्मिश्र संख्या द्वारा निर्दिष्ट किया गया है, सम्मिश्र तल या आर्गंड तल कहलाता है।

आकृति 5.2
x–अक्ष पर बिंदु, सम्मिश्र संख्याओं a + i0 रूप के संगत होते हैं और y–अक्ष पर बिंदु, सम्मिश्र संख्याओं 0 + ib रूप के संगत होते हैं। आर्गंड तल में x–अक्ष और y–अक्ष क्रमशः वास्तविक अक्ष और काल्पनिक अक्ष कहलाते हैं।
आर्गंड तल में सम्मिश्र संख्या z = x + iy और इसकी संयुग्मी
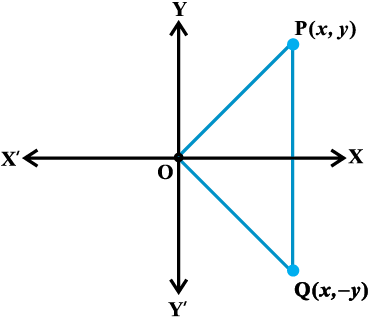
आकृति 5.3
5.5.1 एक सम्मिश्र संख्या का ध्रुवीय निरूपण (Polar representation of a complex number)
माना कि बिंदु P. ऋणेत्तर सम्मिश्र संख्या z = x + iy का निरूपण करता है। माना कि दिष्ट रेखाखंड OP की लंबाई r है और θ वह कोण है जो OP, x–अक्ष की धनात्मक दिशा के साथ बनाता है।
हम ध्यान दें कि P वास्तविक संख्याओं के क्रमित युग्म ( r, θ ) से अद्वितीय रूप से निर्धारित किया जाता है। ( r, θ ) बिंदु P के ध्रुवीय निर्देशांक कहलाते हैं आकृति 5.4 देखिए।

आकृति 5.4
हम मूल बिंदु को ध्रुव तथा x –अक्ष की धन दिशा को प्रारंभिक रेखा मानते हैं।
यहाँ x = r cos θ, y = r sin θ और इसलिए z = r (cos θ + i sin θ), सम्मिश्र संख्या का ध्रुवीय रूप कहलाता है। यहाँ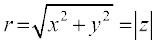 को z का मापांक कहते हैं और θ, सम्मिश्र संख्या का कोणांक या आयाम कहलाता है तथा कोणांक z से निरूपित होता है।
को z का मापांक कहते हैं और θ, सम्मिश्र संख्या का कोणांक या आयाम कहलाता है तथा कोणांक z से निरूपित होता है।
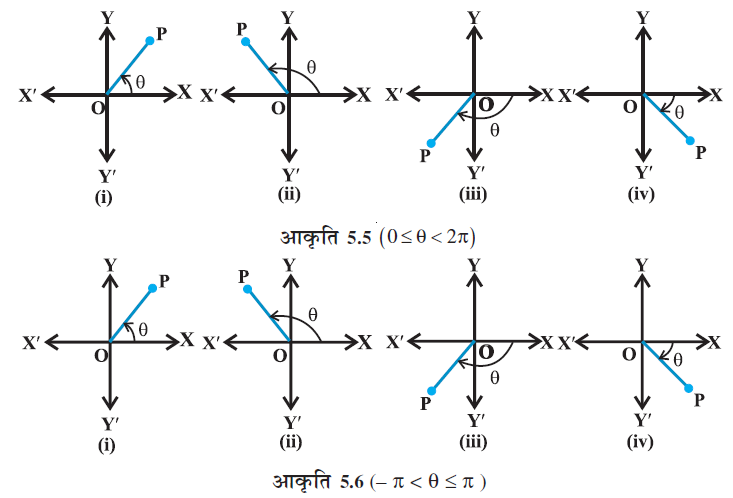
किसी सम्मिश्र संख्या z ≠ 0, 0 ≥ θ < 2π में θ का केवल मान संगत हैं। फिर भी, 2π की लंबाई के किसी दूसरे, अंतराल के लिए, उदाहरण के तौर पर – π < θ ≤ π इस प्रकार का एक अंतराल हो सकता है। हम θ का एेसा मान, जिसमें की – π < θ ≤ π, z का मुख्य आयाम कहलाता है और arg z से निरूपित किया जाता है। आकृति 5.5 और 5.6 देखिए।
उदाहरण 7 सम्मिश्र संख्या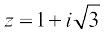 को ध्रुवीय रूप में निरूपित कीजिए।
को ध्रुवीय रूप में निरूपित कीजिए।
हल माना 1 = r cos θ,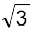 = r sin θ
= r sin θ
दोनों तरफ का वर्ग करके और जोड़ने पर हमें प्राप्त है,

आकृति 5.7
अर्थात् 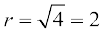 (प्रतिदर्श रूप से, r >0)
(प्रतिदर्श रूप से, r >0)
इसलिए
इनसे प्राप्त होता है 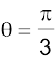
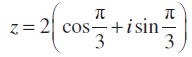
सम्मिश्र संख्या संख्या को आकृति 5.7 में दर्शाया गया है।
उदाहरण 8 सम्मिश्र संख्या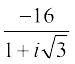 को ध्रुवीय रूप में रूपांतरित कीजिए।
को ध्रुवीय रूप में रूपांतरित कीजिए।
हल दी हुई सम्मिश्र संख्या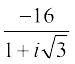 =
=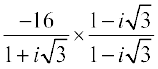

आकृति 5. 8
=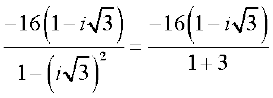
=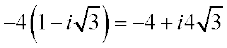 (आकृति 5.8)
(आकृति 5.8)
माना – 4 = r cos θ,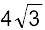 = r sin θ
= r sin θ
दोनों ओर वर्ग करके और जोड़ने पर हमें प्राप्त होता है 16 + 48 =
जिससे हमें प्राप्त होता है, r2 = 64, अर्थात् r = 8
इसलिए, cos θ =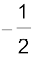 , sin θ =
, sin θ =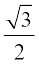
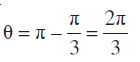
इसलिए, आवश्यक ध्रुवीय रूप =
प्रश्नावली 5.2
प्रश्न 1 से 2 तक सम्मिश्र संख्याओं में प्रत्येक का मापांक और कोणांक ज्ञात कीजिएः
1. z = – 1 – 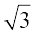
2. z = –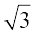 + i
+ i
प्रश्न 3 से 8 तक सम्मिश्र संख्याओं में प्रत्येक को ध्रुवीय रूप में रूपांतरित कीजिएः
3. 1 – i
4. – 1 + i
5. – 1 – i
6. – 3
7.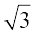 + i
+ i
8. i
5.6 द्विघातीय समीकरण (Quadratic Equations)
ax2 + bx + c = 0 जिसमें a, b, c वास्तविक गुणांक हैं और a ≠ 0
मान लीजिए कि b2 – 4ac < 0
हम जानते हैं कि हम सम्मिश्र संख्याओं के समुच्चय में ऋणात्मक वास्तविक संख्याओं के वर्गमूल निकाल सकते हैं। इसलिए उपर्युक्त समीकरण के हल सम्मिश्र संख्याओं के समुच्चय में हैं जोकि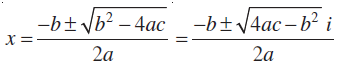
टिप्पणी यहाँ पर, कुछ लोग यह जानने के लिए उत्सुक होंगे, कि किसी समीकरण में कितने मूल होंगे? इस संदर्भ में, निम्नलिखित प्रमेय को उल्लेख (बिना उपपत्ति) के किया गया है जिसे ‘बीजगणित की मूल प्रमेय’ के रूप में जाना जाता है।
"एक बहुपद समीकरण का कम से कम एक मूल होता है"।
इस प्रमेय के फलस्वरूप हम निम्नलिखित महत्त्वपूर्ण परिणाम पर पहँचते हैं।
"n घात की एक बहुपद समीकरण में n मूल होते हैं।"
उदाहरण 9 x2 + 2 = 0 को हल कीजिए।
हल: हमें दिया है x2 + 2 = 0
या x2 = – 2
अर्थात् x =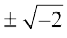 =
=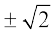 i
i
उदाहरण 10 x2 + x + 1= 0 को हल कीजिए।
हल यहाँ b2 – 4ac = 12 – 4 × 1 × 1 = 1 – 4 = – 3
इसलिए, इसके हल x =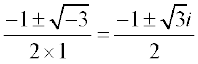 हैं
हैं
उदाहरण 11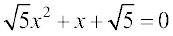 को हल कीजिए।
को हल कीजिए।
हल यहाँ, समीकरण का विविक्तकर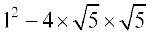 = 1 – 20 = – 19 है।
= 1 – 20 = – 19 है।
इसलिए हल 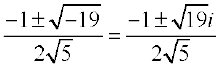 है।
है।
प्रश्नावली 5.3
निम्नलिखित समीकरणों में से प्रत्येक को हल कीजिएः
1. x2 + 3 = 0
2. 2x2 + x + 1 = 0
3. x2 + 3x + 9 = 0
4. – x2 + x – 2 = 0
5. x2 + 3x + 5 = 0
6. x2 – x + 2 = 0
7.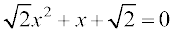
8.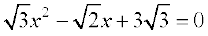
9.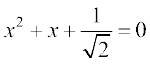
10.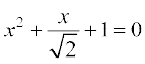
विविध उदाहरण
उदाहरण 12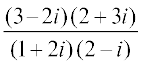 का संयुग्मी ज्ञात कीजिए।
का संयुग्मी ज्ञात कीजिए।
हल यहाँ 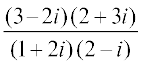 =
=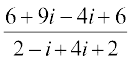 =
=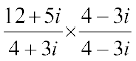
=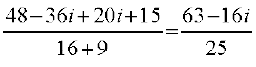 =
=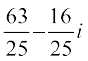
इसलिए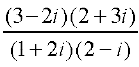 का संयुग्मी,
का संयुग्मी,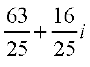 है।
है।
उदाहरण 13 निम्नलिखित सम्मिश्र संख्याओं का मापांक एवं कोणांक ज्ञात कीजिए।
(i)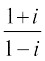 (ii)
(ii)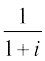
हल हमें प्राप्त है,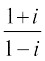 =
=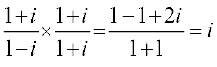 = 0 + i
= 0 + i
अब, 0 = r cos θ, 1 = r sin θ
दोनों ओर वर्ग करके जोड़ते हुए हमें प्राप्त होता है, r2 = 1 अर्थात् r = 1 तथा
cos θ = 0, sin θ = 1
इसलिए,
इस प्रकार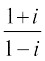 का मापांक 1 है तथा कोणांक
का मापांक 1 है तथा कोणांक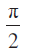
(ii)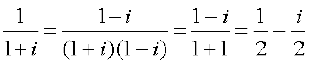
मान लीजिए  = r cos θ, –
= r cos θ, – = r sin θ
= r sin θ
भाग (i) की तरह हम प्राप्त करते हैं,
r =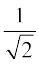 , cos θ =
, cos θ = , sin θ =
, sin θ = 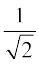
इसलिए
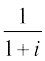 का मापांक
का मापांक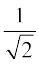 तथा कोणांक
तथा कोणांक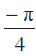
उदाहरण 14 यदि x + iy =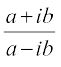 है तो, सिद्ध कीजिए कि x2 + y2 = 1
है तो, सिद्ध कीजिए कि x2 + y2 = 1
हल हमें प्राप्त है, x + iy =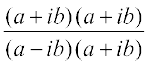 =
=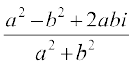 =
=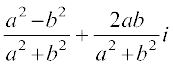
इसलिए, x – iy =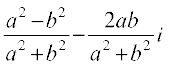
इस प्रकार x2 + y2 = (x + iy) (x – iy) =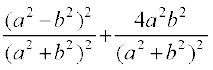
=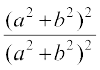 = 1
= 1
उदाहरण 15 θ का वास्तविक मान बताइए, जबकि
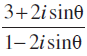
हल हमें प्राप्त है,
दिया हुआ है कि सम्मिश्र संख्या वास्तविक है।
इसलिए 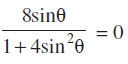
अत θ = nπ, n ∈ Z.
उदाहरण 16 सम्मिश्र संख्या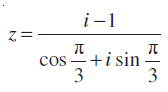
हल हमें प्राप्त है, z = 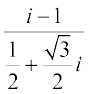
=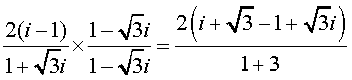 =
=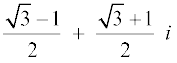
मान लीजिए
दोनों ओर वर्ग करके, जोड़ते हुए हमें प्राप्त होता है,
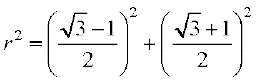 =
=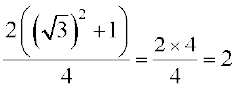
अर्थात् r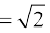 इससे
इससे
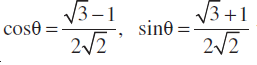
इसलिए 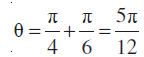
अर्थात्, 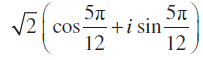
अध्याय 5 पर विविध प्रश्नावली
1. 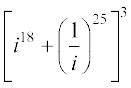 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
2. किन्हीं दो सम्मिश्र संख्याओं z1 और z2 के लिए, सिद्ध कीजिएः
Re (z1 z2) = Rez1 Rez2 – Imz1 Imz2.
3. 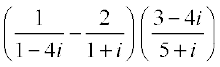 को मानक रूप में परिवर्तित कीजिए।
को मानक रूप में परिवर्तित कीजिए।
4. यदि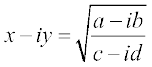 , तो सिद्ध कीजिए कि
, तो सिद्ध कीजिए कि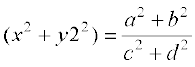
5. निम्नलिखित को ध्रुवीय रूप में परिवर्तित कीजिएः
(i)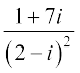 (ii)
(ii)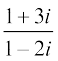
प्रश्न 6 से 9 में दिए गए प्रत्येक समीकरण को हल कीजिएः
6. 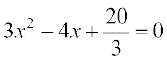
7.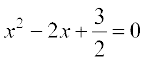
8. 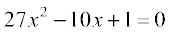
9.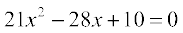
10. यदि z1 = 2 – i, z2 = 1 + i,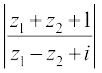 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
11. यदि a + ib =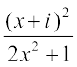 , सिद्ध कीजिए कि, a2 + b2 =
, सिद्ध कीजिए कि, a2 + b2 =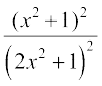
12. माना z1 = 2 – i, z2 = –2 + i, निम्न का मान निकालिए।
(i)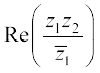 (ii)
(ii)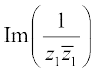
13. सम्मिश्र संख्या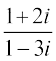 का मापांक और कोणांक ज्ञात कीजिए।
का मापांक और कोणांक ज्ञात कीजिए।
14. यदि (x – iy) (3 + 5i), –6 – 24i की संयुग्मी है तो वास्तविक संख्याएँ x और y ज्ञात कीजिए।
15.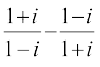 का मापांक ज्ञात कीजिए।
का मापांक ज्ञात कीजिए।
16. यदि (x + iy)3 = u + iv, तो दशाईए कि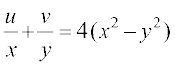
17. यदि α और β भिन्न सम्मिश्र संख्याएँ हैं जहाँ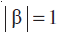
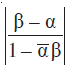
18. समीकरण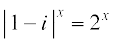 के शून्येत्तर पूर्णांक मूलों की संख्या ज्ञात कीजिए।
के शून्येत्तर पूर्णांक मूलों की संख्या ज्ञात कीजिए।
19. यदि (a + ib) (c + id) (e + if) (g + ih) = A + iB है
तो दर्शाइए कि (a2 + b2) (c2 + d2) (e2 + f 2) (g2 + h2) = A2 + B2
20. यदि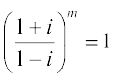 , तो m का न्यूनतम पूर्णांक मान ज्ञात कीजिए।
, तो m का न्यूनतम पूर्णांक मान ज्ञात कीजिए।
सारांश
- a + ib के प्रारूप की एक संख्या, जहाँ a और b वास्तविक संख्याएँ हैं, एक सम्मिश्र संख्या कहलाती है, a सम्मिश्र संख्या का वास्तविक भाग और b इसका काल्पनिक भाग कहलाता है।
- माना z1 = a + ib और z2 = c + id, तब
(i) z1 + z2 = (a + c) + i (b + d)
(ii) z1 z2 = (ac – bd) + i (ad + bc)
- किसी शून्येत्तर सम्मिश्र संख्या z = a + ib (a ≠ 0, b ≠ 0) के लिए, एक सम्मिश्र संख्या
![]() , का अस्तित्व होता है, इसे
, का अस्तित्व होता है, इसे![]() या z–1 द्वारा निर्दिष्ट किया जाता है और z का गुणात्मक प्रतिलोम कहलाता है जिससे कि (a + ib)
या z–1 द्वारा निर्दिष्ट किया जाता है और z का गुणात्मक प्रतिलोम कहलाता है जिससे कि (a + ib)![]() = 1 + i0 =1 प्राप्त होता है।
= 1 + i0 =1 प्राप्त होता है। - किसी पूर्णांक k के लिए, i4ा = 1, i4ा + 1 = i, i4ा + 2 = – 1, i4ा + 3 = – i
- सम्मिश्र संख्या z = a + ib का संयुग्मी
![]() द्वारा निर्दिष्ट किया जाता है और
द्वारा निर्दिष्ट किया जाता है और![]() = a – ib द्वारा दर्शाया जाता है।
= a – ib द्वारा दर्शाया जाता है। - सम्मिश्र संख्या z = x + iy का ध्रुवीय रूप r (cos θ + i sin θ), है, जहाँ r =
![]() (z का मापांक) और cosθ =
(z का मापांक) और cosθ =![]() , sinθ =
, sinθ =![]() (θ, z का कोणांक कहलाता है।) θ का मान, जिससे कि – π < θ ≤ π, z का प्रमुख कोणांक कहलाता है।
(θ, z का कोणांक कहलाता है।) θ का मान, जिससे कि – π < θ ≤ π, z का प्रमुख कोणांक कहलाता है। - एक n घातवाले बहुपद समीकरण के n मूल होते हैं।
- एक द्विघातीय समीकरण ax2 + bx + c = 0, जहाँ a, b, c ∈ R, a ≠ 0, b2 – 4ac < 0, के हल x =
![]() i के द्वारा प्राप्त होते हैं।
i के द्वारा प्राप्त होते हैं।
एेतिहासिक पृष्ठभूमि
यूनानियों ने इस तथ्य को पहचाना था कि एक ऋण संख्या के वर्गमूल का वास्तविक संख्या पद्धति में कोई अस्तित्व नहीं है परंतु इसका श्रेय भारतीय गणितज्ञ Mahavira (850 ई॰) को जाता है जिन्होंने सर्वप्रथम इस कठिनाई का स्पष्टतः उल्लेख किया। "उन्होंने अपनी कृति ‘गणित सार संग्रह’ में बताया कि ऋण (राशि) एक पूर्णवर्ग (राशि) नहीं है, अतः इसका वर्गमूल नहीं होता है।’’ एक दूसरे भारतीय गणितज्ञ Bhaskara ने 1150 ई॰ में अपनी कृति ‘बीजगणित’ में भी लिखा है, "ऋण राशि का कोई वर्गमूल नहीं होता है क्योंकि यह एक वर्ग नहीं है।" Cardan (1545 इ॰) ने x + y = 10, xy = 40 को हल करने में उत्पन्न समस्या पर ध्यान दिया। उन्होंने x = 5 +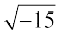 तथा y = 5 –
तथा y = 5 –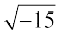 इसके हल के रूप में ज्ञात किया जिसे उन्होंने स्वयं अमान्यकर दिया कि ये संख्याएँ व्यर्थ (useless) हैं। Albert Girard (लगभग 1625 ई॰) ने ऋण संख्याओं के वर्गमूल को स्वीकार किया और कहा कि, इससे हम बहुपदीय समीकरण की जितनी घात होगी, उतने मूल प्राप्त कराने में सक्षम होंगे। Euler ने सर्वप्रथम
इसके हल के रूप में ज्ञात किया जिसे उन्होंने स्वयं अमान्यकर दिया कि ये संख्याएँ व्यर्थ (useless) हैं। Albert Girard (लगभग 1625 ई॰) ने ऋण संख्याओं के वर्गमूल को स्वीकार किया और कहा कि, इससे हम बहुपदीय समीकरण की जितनी घात होगी, उतने मूल प्राप्त कराने में सक्षम होंगे। Euler ने सर्वप्रथम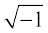 को i संकेतन प्रदान किया तथा W.R. Hamilton (लगभग 1830 ई॰) ने एक शुद्ध गणितीय परिभाषा देकर और तथाकथित ‘काल्पनिक संख्या’ के प्रयोग को छोड़ते हुए सम्मिश्र संख्या a + ib को वास्तविक संख्याओं के क्रमित युग्म (a, b) के रूप में प्रस्तुत किया।
को i संकेतन प्रदान किया तथा W.R. Hamilton (लगभग 1830 ई॰) ने एक शुद्ध गणितीय परिभाषा देकर और तथाकथित ‘काल्पनिक संख्या’ के प्रयोग को छोड़ते हुए सम्मिश्र संख्या a + ib को वास्तविक संख्याओं के क्रमित युग्म (a, b) के रूप में प्रस्तुत किया।


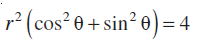
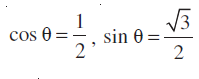
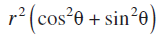
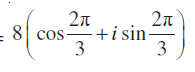
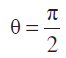
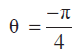
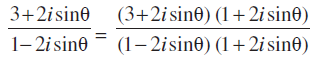
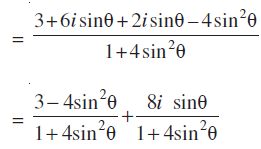
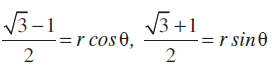
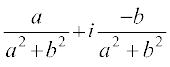
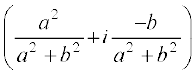 = 1 +
= 1 +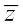
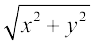
 , sin
, sin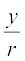 (
(