Table of Contents
"Mathematics is the art of saying many things in many different ways. — Maxwell"
6.1 भूमिका (Introduction)
पिछली कक्षाओं में हम एक चर और दो चर राशियों के समीकरणों तथा शाब्दिक प्रश्नों को समीकरणों में परिवर्तित करके हल करना सीख चुके हैं। अब हमारे मस्तिष्क में स्वभावतः यह प्रश्न उठता है कि "क्या शाब्दिक प्रश्नों को सदैव एक समीकरण के रूप में परिवर्तित करना संभव है?" उदाहरणतः आपकी कक्षा के सभी विद्यार्थियों की ऊँचाई 106 सेमी. से कम है, आपकी कक्षा में अधिकतम 60 मेज़ें या कुर्सियाँ या दोनों समा सकती हैं। यहाँ हमें एेसे कथन मिलते हैं जिनमें ‘<’ (से कम), ‘>’ (से अधिक), ‘≤’ (से कम या बराबर) ‘≥’ (से अधिक या बराबर) चिह्न प्रयुक्त होते हैं। इन्हें हम असमिकाएँ (Inequalities) कहते हैं।
इस अध्याय में, हम एक या दो चर राशियों की रैखिक असमिकाओं का अध्ययन करेंगे। असमिकाओं का अध्ययन विज्ञान, गणित, सांख्यिकी, इष्टतमकारी समस्याओं (optimisation problems), अर्थशास्त्र, मनोविज्ञान इत्यादि से संबंधित समस्याओं को हल करने में अत्यंत उपयोगी है।
6.2 असमिकाएँ (Inequalities)
हम निम्नलिखित स्थितियों पर विचार करते हैंः
(i) रवि 200 रुपये लेकर चावल खरीदने के लिए बाज़ार जाता है, चावल 1 किग्रा॰ के पैकेटों में उपलब्ध हैं। एक किलो चावल के पैकेट का मूल्य 30 रुपये है। यदि x उसके द्वारा खरीदे गए चावल के पैकेटों की संख्या को व्यक्त करता हो, तो उसके द्वारा खर्च की गई धनराशि 30 x रुपये होगी। क्योंकि उसे चावल को पैकेटों में ही खरीदना है इसलिए वह 200 रुपये की पूरी धनराशि को खर्च नहीं कर पाएगा (क्यों?)। अतः
30x < 200 ... (1)
स्पष्टतः कथन (i) समीकरण नहीं है, क्योंकि इसमें समता (equality) का चिह्न (=) नहीं है।
(ii) रेशमा के पास 120 रुपये हैं जिससे वह कुछ रजिस्टर व पेन खरीदना चाहती है। रजिस्टर का मूल्य 40 रुपये और पेन का मूल्य 20 रुपये है। इस स्थिति में यदि रेशमा द्वारा खरीदे गए रजिस्टर की संख्या x तथा पेन की संख्या y हो तो उसके द्वारा व्यय की गयी कुल धनराशि (40x +20y) रुपये है। इस प्रकार हम पाते हैं कि
40x + 20y ≤ 120 ... (2)
क्योंकि इस स्थिति में खर्च की गयी कुल धनराशि अधिकतम 120 रुपये है। ध्यान दीजिए कथन (2) के दो भाग हैं।
40x + 20y < 120 ... (3)
और 40x + 20y = 120 ... (4)
कथन (3) समीकरण नहीं है, जबकि कथन (4) समीकरण है। उपरोक्त कथन जैसे (1), (2) तथा (3) असमिका कहलाते हैं।
परिभाषा 1 एक असमिका, दो वास्तविक संख्याओं या दो बीजीय व्यंजकों में ‘<’, ‘>’, ‘≤’ या ‘≥’ के चिह्न के प्रयोग से बनती हैं।
3 < 5; 7 > 5 आदि संख्यांक असमिका के उदाहरण हैं। जबकि
x < 5; y > 2; x ≥ 3, y ≤ 4 इत्यादि शाब्दिक (चरांक) असमिका के उदाहरण हैं।
3 < 5 < 7 (इसे पढ़ते हैं 5, 3 से बड़ा व 7 से छोटा है), 3 < x < 5 (इसे पढ़ते हैं x, 3 से बड़ा या बराबर है व 5 से छोटा है) और 2 < y < 4 द्वि-असमिका के उदाहरण हैं।
असमिकाओं के कुछ अन्य उदाहरण निम्नलिखित हैं:
ax + b < 0 ... (5)
ax + b > 0 ... (6)
ax + b ≤ 0 ... (7)
ax + b ≥ 0 ... (8)
ax + by < c ... (9)
ax + by > c ... (10)
ax + by ≤ c ... (11)
ax + by ≥ c ... (12)
ax2 + bx + c ≤ 0 ... (13)
ax2 + bx + c > 0 ... (14)
क्रमांक (5), (6), (9), (10) और (14) सुनिश्चित असमिकाएँ तथा क्रमांक (7), (8), (11), (12) और (13) असमिकाएँ कहलाती हैं। यदि a 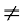 0 हो तो क्रमांक (5) से (8) तक की असमिकाएँ एक चर राशि x के रैखिक असमिकाएँ हैं और यदि a
0 हो तो क्रमांक (5) से (8) तक की असमिकाएँ एक चर राशि x के रैखिक असमिकाएँ हैं और यदि a 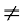 0 तथा b
0 तथा b 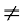 0 हो तो क्रमांक (9) से (12) तक की असमिकाएँ दो चर राशियों x तथा y के रैखिक असमिकाएंँ हैं।
0 हो तो क्रमांक (9) से (12) तक की असमिकाएँ दो चर राशियों x तथा y के रैखिक असमिकाएंँ हैं।
क्रमांक (13) और (14) की असमिकाएँ रैखिक नहीं हैं। वास्तव में यह एक चर राशि x के द्विघातीय असमिकाएँ हैं, जब a ≠ 0.
इस अध्याय में हम केवल एक चर और दो चर राशियों के रैखिक असमिकाओं का अध्ययन करेंगे।
6.3 एक चर राशि के रैखिक असमिकाओं का बीजगणितीय हल और उनका आलेखीय निरूपण (Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation)
अनुभाग 6.2 के असमिका (1) अर्थात् 30x < 200 पर विचार कीजिए। ध्यान दें, कि यहाँ x चावल के पैकेटों की संख्या को व्यक्त करता है।
स्पष्टतः x एक ऋणात्मक पूर्णांक अथवा भिन्न नहीं हो सकता है।
इस असमिका का बायाँ पक्ष 30x और दायाँ पक्ष 200 है।
x = 0 के लिए, बायाँ पक्ष = 30 (0) = 0 < 200 (दायाँ पक्ष), जोकि सत्य है।
x = 1 के लिए, बायाँ पक्ष = 30 (1) = 30 < 200 दायाँ पक्ष), जोकि सत्य है।
x = 2 के लिए, बायाँ पक्ष = 30 (2) = 60 < 200, जो कि सत्य है।
x = 3 के लिए, बायाँ पक्ष = 30 (3) = 90 < 200, जो कि सत्य है।
x = 4 के लिए, बायाँ पक्ष = 30 (4) = 120 < 200, जो कि सत्य है।
x = 5 के लिए, बायाँ पक्ष = 30 (5) = 150 < 200, जो कि सत्य है।
x = 6 के लिए, बायाँ पक्ष = 30 (6) = 180 < 200, जो कि सत्य है।
x = 7 के लिए, बायाँ पक्ष = 30 (7) = 210 < 200, जो कि असत्य है।
उपर्युक्त स्थिति में हम पाते हैं कि उपर्युक्त असमिका को सत्य कथन करने वाले x के मान केवल 0, 1, 2, 3, 4, 5 और 6 हैं। x के उन मानों को जो दिए असमिका को एक सत्य कथन बनाते हों, उन्हें असमिका का हल कहते हैं। और समुच्चय {0, 1, 2, 3, 4, 5, 6} को हल समुच्चय कहते हैं।
इस प्रकार, एक चर राशि के किसी असमिका का हल, चर राशि का वह मान है, जो इसे एक सत्य कथन बनाता हो।
हमने उपर्युक्त असमिका का हल ‘प्रयास और भूल विधि’ (trial and error method) से प्राप्त किया है। जो अधिक सुविधाजनक नहीं है। स्पष्टतः यह विधि अधिक समय लेने वाली तथा कभी-कभी संभाव्य नहीं होती है। हमें असमिकाओं के हल के लिए अधिक अच्छी या क्रमबद्ध तकनीक की आवश्यकता है। इससे पहले हमें संख्यांक असमिकाओं के कुछ और गुणधर्म सीखने चाहिए और असमिकाओं को हल करते समय उनका नियमों की तरह पालन करना चाहिए।
आपको स्मरण होगा कि रैखिक समीकरणों को हल करते समय हम निम्नलिखित नियमों का पालन करते हैंः
नियम 1 एक समीकरण के दोनों पक्षों में समान संख्याएँ जोड़ी (अथवा घटाई) जा सकती हैं।
नियम 2 एक समीकरण के दोनों पक्षों में समान शून्येतर संख्याओं से गुणा (अथवा भाग) किया जा सकता है।
असमिकाओं को हल करते समय हम पुनः इन्हीं नियमों का पालन तथा नियम 2 में कुछ संशोधन के साथ करते हैं। अंतर मात्र इतना है कि ऋणात्मक संख्याओं से असमिका के दोनों पक्षों को गुणा (या भाग) करने पर असमिका के चिह्न विपरीत हो जाते हैं (अर्थात् ‘<’ को >, ‘≤’ को ‘≥’ इत्यादि कर दिया जाता है)। इसका कारण निम्नलिखित तथ्यों से स्पष्ट हैः
3 > 2 जबकि – 3 < – 2
– 8 < – 7 जबकि (–8) (–2) > (–7) (–2), अर्थात् 16 > 14
इस प्रकार असमिकाओं को हल करने के लिए हम निम्नलिखित नियमों का उल्लेख करते हैंः
नियम 1 एक असमिका के दोनों पक्षों में, असमिका के चिह्नों को प्रभावित किए बिना समान संख्याएँ जोड़ी (अथवा घटाई) जा सकती हैं।
नियम 2 किसी असमिका के दोनों पक्षों को समान धनात्मक संख्याओं से गुणा (या भाग) किया जा सकता है। परंतु दोनों पक्षों को समान ऋणात्मक संख्याओं से गुणा (या भाग, करते समय असमिका के चिह्न तदनुसार परिवर्तित कर दिए जाते हैं।
आइए अब हम कुछ उदाहरणों पर विचार करते हैं।
उदाहरण 1 30 x < 200, को हल ज्ञात कीजिए जब
(i) x एक प्राकृत संख्या है।
(ii) x एक पूर्णांक है।
हल ज्ञात है कि 30 x < 200
अथवा 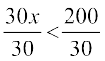 (नियम 2)
(नियम 2)
अथवा x < 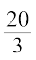
(i) जब x एक प्राकृत संख्या है।
स्पष्टतः इस स्थिति में x के निम्नलिखित मान कथन को सत्य करते हैं।
x = 1, 2, 3, 4, 5, 6
असमिका का हल समुच्चय {1, 2, 3, 4, 5, 6} है
(ii) जब x एक पूर्णांक है
स्पष्टतः इस स्थिति में दिए गए असमिका के हल हैंः
..., – 3, –2, –1, 0, 1, 2, 3, 4, 5, 6
असमिका का हल समुच्चय {...,–3, –2,–1, 0, 1, 2, 3, 4, 5, 6} है
उदाहरण 2 हल कीजिएः 5x-3< 3x+1, जब
(i) x एक पूर्णांक है। (ii) x एक वास्तविक संख्या है।
हल दिया है, कि 5x –3 < 3x + 1
अथवा 5x –3 + 3 < 3x +1 +3 (नियम 1)
अथवा 5x < 3x +4
अथवा 5x – 3x < 3x + 4 – 3x (नियम 1)
अथवा 2x < 4
अथवा x < 2 (नियम 2)
(i) जब x एक पूर्णांक है। इस स्थिति में दिए गए असमिका के हल
..., – 4, – 3, – 2, – 1, 0, 1
अतः हल समुच्चय {..., -4, -3, -2, -1, 0, 1}
(ii) जब x एक वास्तविक संख्या है। इस स्थिति में असमिका का हल x < 2 से व्यक्त है। इसका अर्थ है कि 2 से छोटी समस्त वास्तविक संख्याएँ असमिका के हल हैं। अतः असमिका का हल समुच्चय (– ∞, 2). है।
हमने असमिकाओं के हल प्राकृत संख्याओं, पूर्णाकों तथा वास्तविक संख्याओं के समुच्चयों पर विचार करके ज्ञात किए हैं। आगे जब तक अन्यथा वर्णित न हो, हम इस अध्याय में असमिकाओं का हल वास्तविक संख्याओं के समुच्चय में ही ज्ञात करेंगे।
उदाहरण 3 हल कीजिए 4x + 3 < 6x +7.
हल ज्ञात है कि 4x + 3 < 6x + 7
अथवा 4x – 6x < 6x + 4 – 6x
अथवा – 2x < 4 अथवा x > – 2
अर्थात् –2 से बड़ी समस्त वास्तविक संख्याएँ, दिए गए असमिका के हल हैं। अतः हल समुच्चय
(–2, ∞) है।
उदाहरण 4 हल कीजिए 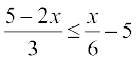
हल हमें ज्ञात है कि 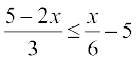
या 2 (5 – 2x) ≤ x – 30
या 10 – 4x ≤ x – 30
या – 5x ≤ – 40,
या x ≥ 8
अर्थात् एेसी समस्त वास्तविक संख्याएँ जो 8 से बड़ी या बराबर है। अतः इस असमिका के हल
x ∈ [8, ∞)
उदाहरण 5 हल कीजिए 7x + 3 < 5x + 9 तथा इस हल को संख्या रेखा पर आलेखित कीजिए।
हल हमें ज्ञात है 7x + 3 < 5x + 9
या 2x < 6 या x < 3
संख्या रेखा पर इन्हें हम निम्नलिखित प्रकार से प्रदर्शित कर सकते हैं (आकृति 6.1)।

आकृति 6.1
उदाहरण 6 हल कीजिए  तथा इस हल को संख्या रेखा पर आलेखित कीजिए।
तथा इस हल को संख्या रेखा पर आलेखित कीजिए।
हल 
या 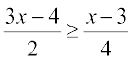
या 2 (3x – 4) ≥ (x – 3)
या 6x – 8 ≥ x – 3
या 5x ≥ 5 or x ≥ 1
संख्या रेखा पर इन्हें हम निम्नलिखित प्रकार से प्रदर्शित कर सकते हैं (आकृति 6.2)ः

आकृति 6.2
उदाहरण 7 कक्षा XI के प्रथम सत्र व द्वितीय सत्र की परीक्षाओं में एक छात्र के प्राप्तांक 62 और 48 हैं। वह न्यूनतम अंक ज्ञात कीजिए, जिसे वार्षिक परीक्षा में पाकर वह छात्र 60 अंक का न्यूनतम औसत प्राप्त कर सके।
हल मान लीजिए कि छात्र वार्षिक परीक्षा में x अंक प्राप्त करता है।
तब 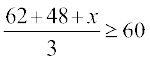
या 110 + x ≥ 180 या x ≥ 70
इस प्रकार उस छात्र को वार्षिक परीक्षा में न्यूनतम 70 अंक प्राप्त करने चाहिए।
उदाहरण 8 क्रमागत विषम संख्याओं के एेसे युग्म ज्ञात कीजिए, जिनमें दोनों संख्याएँ 10 से बड़ी हों, और उनका योगफल 40 से कम हों।
हल मान लिया कि दो क्रमागत विषम प्राकृत संख्याओं में छोटी विषम संख्या x है। इस प्रकार दूसरी विषम संख्या x + 2 है। प्रश्नानुसार
x > 10 ... (1)
तथा x + ( x + 2) < 40 ... (2)
(2) को हल करने पर हम पाते हैं कि
2 x + 2 < 40
या x < 19 ... (3)
(1) और (3) से निष्कर्ष यह है कि
10< x <19
इस प्रकार विषम संख्या x के अभीष्ट मान 10 और 19 के बीच हैं। इसलिए सभी संभव अभीष्ट जोड़े
(11, 13), (13, 15) (15, 17), (17, 19) होंगे।
प्रश्नावली 6.1
1. हल कीजिए: 24x < 100, जब
(i) x एक प्राकृत संख्या है। (ii) x एक पूर्णांक है।
2. हल कीजिएः -12x > 30, जब
(i) x एक प्राकृत संख्या है। (ii) x एक पूर्णांक है।
3. हल कीजिएः 5x-3 < 7, जब
(i) x एक पूर्णांक (ii) x एक वास्तविक संख्या है।
4. हल कीजिए: 3x + 8 > 2, जब
(i) x एक पूर्णांक (ii) x एक वास्तविक संख्या है।
निम्नलिखित प्रश्न 5 से 16 तक वास्तविक संख्या x के लिए हल कीजिएः
5. 4x + 3 < 6x + 7
6. 3x – 7 > 5x – 1
7. 3(x – 1) ≤ 2 (x – 3)
8. 3 (2 – x) ≥ 2 (1 – x)
9. 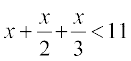
10. 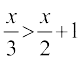
11. 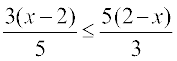
12. 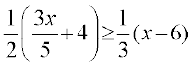
13. 2 (2x + 3) – 10 < 6 (x – 2)
14. 37 – (3x + 5) > 9x – 8 (x – 3)
15. 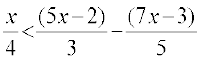
16. 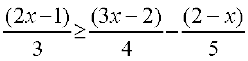
प्रश्न 17 से 20 तक की असमिकाओं का हल ज्ञात कीजिए तथा उन्हें संख्या रेखा पर आलेखित कीजिए।
17. 3x – 2 < 2x + 1
18. 5x – 3 > 3x – 5
19. 3 (1 – x) < 2 (x + 4)
20. 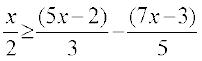
21. रवि ने पहली दो एकक परीक्षा में 70 और 75 अंक प्राप्त किए हैं। वह न्यूनतम अंक ज्ञात कीजिए, जिसे वह तीसरी एकक परीक्षा में पाकर 60 अंक का न्यूनतम औसत प्राप्त कर सके।
22. किसी पाठ्यक्रम में ग्रेड 'A' पाने के लिए एक व्यक्ति को सभी पाँच परीक्षाओं (प्रत्येक 100 में से) में 90 अंक या अधिक अंक का औसत प्राप्त करना चाहिए। यदि सुनीता के प्रथम चार परीक्षाओं के प्राप्तांक 87, 92, 94 और 95 हों तो वह न्यूनतम अंक ज्ञात कीजिए जिसें पांचवीं परीक्षा में प्राप्त करके सुनीता उस पाठ्यक्रम में ग्रेड 'A' पाएगी।
23. 10 से कम क्रमागत विषम संख्याओं के एेसे युग्म ज्ञात कीजिए जिनके योगफल 11 से अधिक हों।
24. क्रमागत सम संख्याओं के एेसे युग्म ज्ञात कीजिए, जिनमें से प्रत्येक 5 से बड़े हों, तथा उनका योगफल 23 से कम हो।
25. एक त्रिभुज की सबसे बड़ी भुजा सबसे छोटी भुजा की तीन गुनी है तथा त्रिभुज की तीसरी भुजा सबसे बड़ी भुजा से 2 सेमी कम है। तीसरी भुजा की न्यूनतम लंबाई ज्ञात कीजिए जबकि त्रिभुज का परिमाप न्यूनतम 61 सेमी है।
26. एक व्यक्ति 91 सेमी लंबे बोर्ड में से तीन लंबाईयाँ काटना चाहता है। दूसरी लंबाई सबसे छोटी लंबाई से 3 सेमी अधिक और तीसरी लंबाई सबसे छोटी लंबाई की दूनी है। सबसे छोटे बोर्ड की संभावित लंबाईयाँ क्या हैं, यदि तीसरा टुकड़ा दूसरे टुकड़े से कम से कम 5 सेमी अधिक लंबा हो?
[संकेत यदि सबसे छोटे बोर्ड की लंबाई x सेमी हो, तब (x + 3) सेमी और 2x सेमी क्रमशः दूसरे और तीसरे टुकड़ों की लंबाईयाँ हैं। इस प्रकार x + (x + 3) + 2x ≤ 91 और 2x ≥ (x + 3) + 5]
6.4 दो चर राशियों के रैखिक असमिकाओं का आलेखीय हल (Graphical Solution of Linear Inequalities in Two Variables)
पहले अनुभाग में हमने देखा है कि एक चर राशि के रैखिक असमिका का आलेख एक चित्रीय निरूपण है और असमिका के हल का वर्णन करने की एक सरल विधि है। अब हम दो चर राशियों की रैखिक असमिका के आलेखन का वर्णन करेंगे।
हम जानते हैं कि एक रेखा कार्तीय तल को रेखा के अतिरिक्त दो भागों में बाँटती है। प्रत्येक भाग को अर्ध-तल कहते हैं। एक ऊर्ध्वाधर रेखा तल को बायाँ अर्ध-तल व दायाँ अर्ध-तल में विभाजित करती है और एक ऊर्ध्वेतर (non-vertical) रेखा एक तल को निचला अर्ध-तल व ऊपरी अर्ध-तल में विभाजित करती है। आकृति 6.3 व आकृति 6.4)।
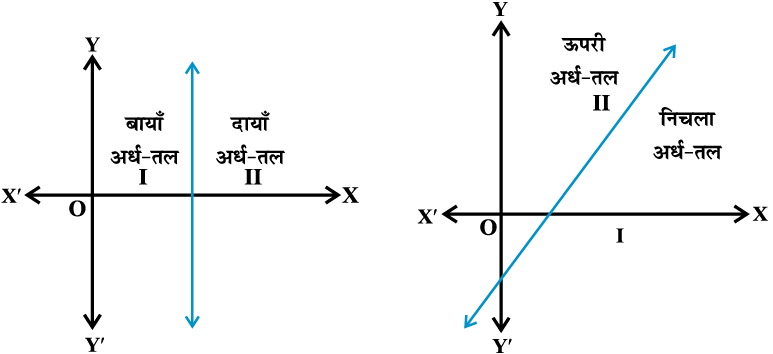
आकृति 6.3 आकृति 6.4
आइए हम मान लें ax + by = c, ... (1)
एक रेखा है जहाँ a ≠ 0 तथा b ≠ 0 है।
अब यहाँ तीन संभावनाएँ हैंः
(i) ax + by = c (ii) ax + by > c (iii) ax + by < c.
स्पष्टतः स्थिति (i) में (i) को संतुष्ट करने वाले सभी बिंदु (x, y) (i) द्वारा निरूपित रेखा पर स्थित हैं और विलोमतः।
स्थिति (ii) में पहले हम मान लेते हैं कि b > 0 और रेखा ax + by = c, b > 0, पर एक बिंदु P (α,β) लेते हैं ताकि aα + bβ = c.
माना अर्ध-तल II में कोई बिंदु Q (α , γ) है (आकृति 6.5)।
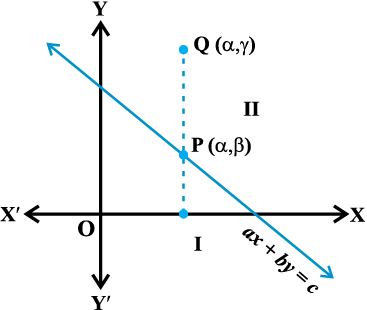
आकृति 6.5
अब आकृति 6.5 से हम निष्कर्ष निकालते है कि
γ > β (क्यों?)
या b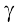 > bβ
> bβ
या aα + b γ > aα + bβ
या aα + b γ > c (क्यों?)
या, Q(α,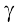 ), असमिका ax + by > c को संतुष्ट करती है।
), असमिका ax + by > c को संतुष्ट करती है।
अर्थात्, रेखा ax + by = c के ऊपर अर्ध-तल II में स्थित सभी बिंदु असमिका ax + by > c को संतुष्ट करते हैं।
विलोमतः माना रेखा ax + by = c पर एक बिंदु P (α, β) है और Q(α, γ) कोई बिंदु, असमिका
ax + by > c को संतुष्ट करता है।
ताकि aα + bγ > c
 aα + b γ > aα + bβ
aα + b γ > aα + bβ
 γ > β (क्योंकि b > 0)
γ > β (क्योंकि b > 0)
अर्थात् Q(α,  ) अर्ध-तल II में स्थित है
) अर्ध-तल II में स्थित है
अतः अर्ध-तल II का कोई भी बिंदु असमिका ax + by > c को संतुष्ट करता है और विलोमतः कोई बिंदु जो असमिका ax + by > c को संतुष्ट करता है, अर्ध-तल II में स्थित होता है।
इसी प्रकार हम सिद्ध कर सकते हैं कि b < 0 के लिए वे सभी बिंदु जो असमिका ax + by > c को संतुष्ट करते हैं, अर्ध-तल I में स्थित होते हैं और विलोमतः
अतः हम इस निष्कर्ष पर आते हैं कि वे सभी बिंदु जो असमिका ax + by > c ; b > 0 या b < 0 के अनुसार, को संतुष्ट करते हैं वे अर्ध-तल II या I में से किसी एक तल में स्थित होते हैं और विलोमतः।
असमिका ax + by > c का आलेखन इन अर्ध-तलों में से एक अर्ध-तल होगा [(जिसे हल-क्षेत्र (Solution region) कहते हैं] और इस अर्ध-तल को छायांकित क्षेत्र (Shaded region) द्वारा निरूपित करते हैं।
टिप्पणी 1 वह क्षेत्र जिसमें किसी असमिका के संपूर्ण हल स्थित हों, उसे असमिका का हल-क्षेत्र (Solution region) कहते हैं।
2. किसी असमिका द्वारा निरूपित क्षेत्र को पहचानने के लिए, किसी अर्ध-तल में केवल एक बिंदु (a, b) (जो रेखा पर स्थित न हो) लेकर जाँचना ही पर्याप्त है कि वह उस असमिका को संतुष्ट करता है अथवा नहीं। यदि यह बिंदु असमिका को संतुष्ट करता है तो असमिका उस अर्ध-तल को निरूपित करती है और उस अर्ध-तल को छायांकित कर देते हैं जिसमें यह बिंदु है। अन्यथा यह असमिका उस अर्ध-तल को निरूपित करेगी जिसमें यह बिंदु नहीं है। अपनी सुविधा की दृष्टि से बिंदु (0, 0) को प्राथमिकता दी जाती है।
3. यदि एक असमिका ax + by ≥ c या ax + by ≤ c के स्वरूप की है तो रेखा ax + by = c पर स्थित सभी बिंदु भी उसके हल-क्षेत्र में सम्मिलत होते हैं। इसलिए हल क्षेत्र पर गहरी काली रेखा खींचते हैं।
4. यदि असमिका ax + by > c या ax + by < c के स्वरूप की है तो रेखा ax + by = c पर स्थित सभी बिंदु उसके हल-क्षेत्र में सम्मिलित नहीं होते हैं। इसलिए हल क्षेत्र पर रेखा को बिंदुवत् या खंडित खींचते हैं।
अनुभाग 6.2 में हमें दो चर राशियों x तथा y का निम्नलिखित रैखिक असमिका प्राप्त हुई थी।
40x + 20y ≤ 120 ... (1)
जब रेशमा द्वारा रजिस्टर और पेन के खरीदने संबंधी शाब्दिक प्रश्न को गणितीय रूप में परिवर्तित करने से प्राप्त हुई थी।
चूँकि वस्तुओं की संख्या एक ऋणात्मक और भिन्नात्मक संख्या नहीं हो सकती है, अतः हम इस असमिका का हल x तथा y को केवल पूर्ण संख्या के रूप में ध्यान रखते हुए करते है। इस अवस्था में हम x तथा y के मानों के एेसे जोड़े ज्ञात करते हैं जिनके संगत कथन (1) सत्य है। वास्तव में एेसे युग्मों का समुच्चय असमिका (1) का हल समुच्चय (Solution set) होगा। x = 0 लेकर प्रारंभ करने पर हम पाते हैं कि (1) का
बायाँ पक्ष = 40x + 20y = 40 (0) + 20y = 20y.
इस प्रकार
20y ≤ 120 या y ≤ 6 ... (2)
आकृति 6.6
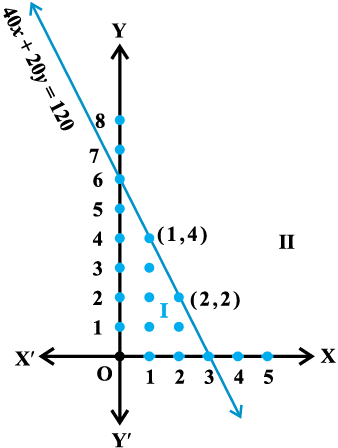
अतः x = 0 के संगत y के मान 0, 1, 2, 3, 4, 5, 6 मात्र हो सकते हैं।
इस स्थिति में (1) के हल (0, 0), (0,1), (0,2), (0,3), (0,4), (0,5) और (0,6) हैं।
इसी प्रकार जब x = 1, 2, 3 हैं तो (1) के अन्य हल निम्नलिखित हैंः
(1, 0), (1, 1), (1, 2), (1, 3), (1, 4)
(2, 0), (2, 1), (2, 2), (3, 0)
यह आकृति 6.6 में दिखाया गया है।
अब हम x तथा y के प्रांत (domain) को पूर्ण संख्याओं से विस्तारित करके वास्तविक संख्याएँ करते हैं, और देखते हैं कि इस अवस्था में असमिका (1) के क्या हल होते हैं। आप देखेंगे कि हल करने की आलेखित-विधि (Graphical method) इस स्थिति में अधिक सुविधाजनक है। इस उद्देश्य से, हम (1) के संगत समीकरण
40x + 20y = 120 ... (3)
पर विचार करते हैं और इसका आलेख खींचते हैं।
यह एक सरल रेखा है जो कार्तीय तल को अर्ध-तल I व अर्ध-तल II में विभाजित करती है
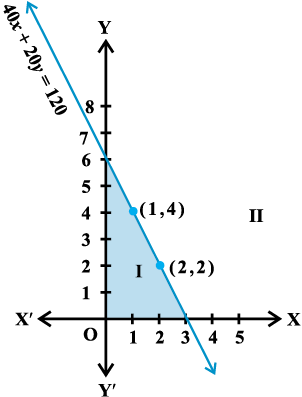
असमिका (1) का आलेख खींचने के लिए, हम अर्ध-तल-I में एक बिंदुु (0, 0) मान लेते हैं और यह जाँचते हैं कि
x और y के मान असमिका को संतुष्ट करते हैं या नहीं।
आकृति 6.7
आप यह देखेंगे कि x = 0, y = 0 असमिका को संतुष्ट करते हैं। इस प्रकार हम कहते हैं कि असमिका का आलेख, अर्ध-तल I है (आकृति 6.7 में दिखाया गया है)। चूँकि रेखा के सभी बिंदु असमिका (1) को संतुष्ट करते हैं। अतः रेखा भी आलेख का एक भाग है।
इस प्रकार दिए गए असमिका का आलेख, रेखा सहित अर्ध-तल I है। स्पष्टतः अर्ध-तल II आलेख का भाग नहीं है। इस प्रकार असमिका (1) का हल इसके आलेख (रेखा सहित, अर्ध-तल I) के समस्त बिंदु है।
अब हम कुछ उदाहरणों की सहायता से दो चर राशियों के रैखिक असमिकाओं के हल करने की विधि स्पष्ट करते हैं।
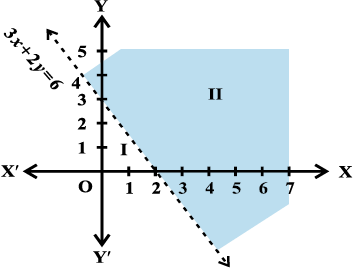
हल सर्वप्रथम हम समीकरण 3x + 2y = 6 का ग्राफ खांडित रेखा के रूप में खींचते हैं (आकृति 6.8)।
आकृति 6.8
यह रेखा xy- - तल को दो अर्ध-तल I तथा II में विभाजित करती है हम एक बिंदु (जो रेखा पर स्थित नहीं है) जैसे (0, 0) का चयन करते हैं जो अर्ध-तल I में स्थित है (आकृति 6.8)। अब जाँच करते हैं कि यह बिंदु दी गई असमिका को संतुष्ट करता है
अथवा नहीं।
हम पाते हैं कि 3 (0) + 2 (0) > 6
या 0 > 6 , जो असत्य है।
अतः अर्ध-तल I, दिए हुए असमिका का हल-क्षेत्र नहीं है। स्पष्टतः रेखा पर स्थित कोई भी बिंदु, दी गई असमिका को संतुष्ट नहीं करता है। दूसरे शब्दों में, छायांकित अर्ध-तल II, रेखा के बिंदुओं को छोड़कर, दी गई असमिका का हल क्षेत्र है।
उदाहरण 10 द्विविमीय तल में असमिका 3x – 6 ≥ 0 का आलेखन-विधि से हल कीजिए।
हल 3x – 6 = 0 का आलेख आकृति 6.9 में दिया गया है।
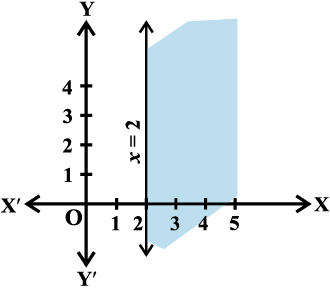
आकृति 6.9
हम एक बिंदु (0, 0) का चयन करते हैं और इसे दी गई असमिका में रखने पर हम पाते हैं कि
3 (0) – 6 ≥ 0 या – 6 ≥ 0 जो कि असत्य है।
इस प्रकार दी गई असमिका का हल-क्षेत्र रेखा x = 2 के दाहिनी ओर छायांकित भाग है।
उदाहरण 11 y < 2 को आलेखन-विधि से हल कीजिए।
हल y = 2 का आलेख 6.10 में दिया गया है।
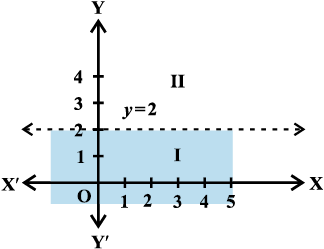
आकृति 6.10
हम निचले अर्ध-तल I में एक बिंदु जैसे (0, 0) का चयन करते हैं और दी गई असमिका में y = 0 रखने पर हम पाते हैं कि
1 × 0 < 2 या 0 < 2 जोकि सत्य है।
इस प्रकार रेखा y = 2 के नीचे का क्षेत्र जिसमें मूल बिंदु (0, 0) स्थित है, दी गई असमिका का हल-क्षेत्र है। अतः रेखा y = 2 के नीचे के समस्त बिंदु (जिसमें रेखा के बिंदु सम्मिलित नहीं हैं) दी गई असमिका के हल हैं।
प्रश्नावली 6.2
निम्नलिखित असमिकाओं को आलेखन-विधि से द्विविमीय तल में निरूपित कीजिए।
1. x + y < 5
2. 2x + y ≥ 6
3. 3x + 4y ≤ 12
4. y + 8 ≥ 2x
5. x – y ≤ 2
6. 2x – 3y > 6
7. – 3x + 2y ≥ – 6
8. 3y – 5x < 30
9. y < – 2
10. x > – 3.
6.5 दो चर राशियों की असमिका निकाय का हल (Solution of System of Linear Inequalities in Two Variables)
पिछले अनुभाग में हम दो चर राशियों के रैखिक असमिकाओं का आलेखन-विधि से हल करना सीख गए हैं। अब हम कुछ उदाहरणों की सहायता से दो चर राशियों की असमिका निकाय को हल करने की विधि स्पष्ट करेंगे।
उदाहरण 12 निम्नलिखित असमिका निकाय
x + y ≥ 5 ... (1)
x – y ≤ 3 ... (2)
को आलेखीय विधि से हल कीजिएः
हल रैखिक असमिका x + y = 5 का आलेख आकृति 6.11 में खींचा गया है।
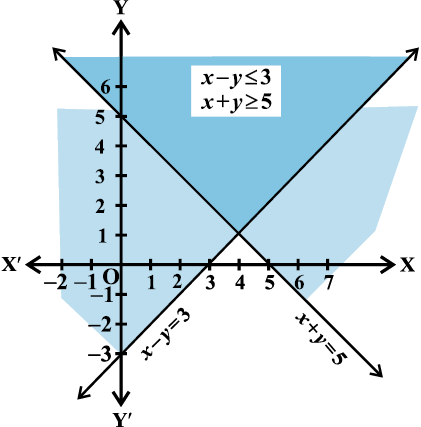
आकृति 6.11
हम देखते हैं कि असमिका (1) का हल, रेखा x + y = 5 के ऊपरी छायांकित क्षेत्र द्वारा निरूपित होता है जिसमें रेखा पर स्थित सभी बिंदुु भी सम्मिलित हैं।
उन्हीं निर्देशांक्षों पर हम समीकरण का भी आलेख खींचते है जैसा कि (आकृति 6.11) में दिखाया गया है। तब असमिका (2) का हल रेखा x – y = 3 के ऊपरी छायांकित क्षेत्र द्वारा निरूपित होता है, जिसमें रेखा पर सभी बिंदु भी सम्मिलित हैं।
स्पष्टतः द्विछायांकित क्षेत्र (double shaded region) जो उपर्युक्त दोनों छायांकित क्षेत्रों में उभयनिष्ठ हैं, वही दिए हुए असमिका निकाय (1) व (2) का वांछित हल क्षेत्र है।
उदाहरण 13 निम्नलिखित रैखिक असमिका निकाय को आलेखन विधि द्वारा हल कीजिए।
5x + 4y ≤ 40 ... (1)
x ≥ 2 ... (2)
y ≥ 3 ... (3)
हल सर्वप्रथम हम समीकरणों 5x + 4y = 40, x = 2 और = 3 द्वारा निरूपित रेखाओं के आलेख
खींचते हैं।
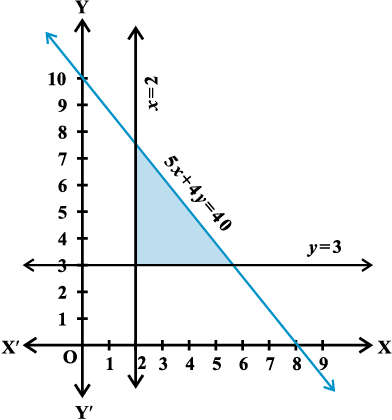
आकृति 6.12
तब हम देखते हैं कि असमिका (1), रेखा 5x + 4y = 40 के नीचे छायांकित क्षेत्र को निरूपित करता है जिसमें रेखा के सभी बिंदुु भी सम्मिलित हैं असमिका (2), रेखा x = 2 के दाहिनी ओर का छायांकित क्षेत्र और असमिका (3), रेखा y = 3 के ऊपरी छायांकित क्षेत्र जिनमें इन रेखाओं के सभी बिंदुु भी सम्मिलित हैं, को निरूपित करता है। अतः सर्वनिष्ठ छायांकित क्षेत्र और रेखाओं पर सभी बिंदुु (आकृति 6.12) दिए हुए रैखिक असमिका निकाय के हल हैं।
बहुत सी व्यावहारिक स्थितियों में जो असमिका निकाय से युक्त हैं, चर राशियाँ x और y प्रायः एेसी राशियाँ होती हैं, जो ऋणात्मक नहीं हो सकती हैं। उदाहरणतः उत्पादित इकाइयों की संख्या, क्रय की गई वस्तुओं की संख्या, काम करने में लगे घंटों की संख्या आदि। स्पष्टतः एेसी परिस्थिति में x ≥ 0 और y ≥ 0 हल क्षेत्र प्रथम चतुर्थांश में ही होता है।
आइए अब हम कुछ एेसे असमिका निकाय पर विचार करते हैं, जिनमें x ≥ 0, y ≥ 0 हैं।
उदाहरण 14 निम्नलिखित असमिका निकाय को आलेखीय विधि से हल कीजिएः
8x + 3y ≤ 100 ... (1)
x ≥ 0 ... (2)
y ≥ 0 ... (3)
हल हम रेखा 8x + 3y = 100 का आलेख खींचते हैं।
असमिका 8x + 3y ≤ 100 इस रेखा के नीचे के छायांकित क्षेत्र को निरूपित करता है, जिसमें रेखा 8x +3y =100 के सभी बिंदुु सम्मिलित हैं (आकृति 6.13)।
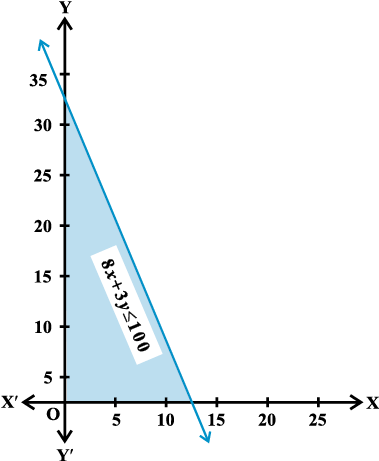
आकृति 6.13
चूंकि 8x + 3y ≤ 100, अतः त्रिविध छायांकित (Triple shaded) क्षेत्र का प्रत्येक बिंदुु जो प्रथम चतुर्थांश में है, तथा जिसमें रेखाओं के बिंदुु भी सम्मिलित हैं, दिए हुए असमिका निकाय का हल निरूपित करता है।
उदाहरण 15 निम्नलिखित असमिका निकाय को आलेखीय विधि से हल कीजिए।
x + 2y ≤ 8 ... (1)
2x + y ≤ 8 ... (2)
x > 0 ... (3)
y > 0 ... (4)
हल हम रेखाओं x + 2y = 8 और 2x + y = 8 का आलेख खींचते हैं। असमिका (1) और (2) दोनों संगत रेखाओं के बिंदुुओं सहित अपने से नीचे स्थित क्षेत्रों को निरूपित करते हैं।
चूंकि x ≥ 0, y ≥ 0 अतः प्रथम चतुर्थांश में स्थित सर्वनिष्ठ छायांकित क्षेत्र के प्रत्येक बिंदुु दिए हुए असमिका निकाय के हल को निरूपित करता है आकृति (6.14)।
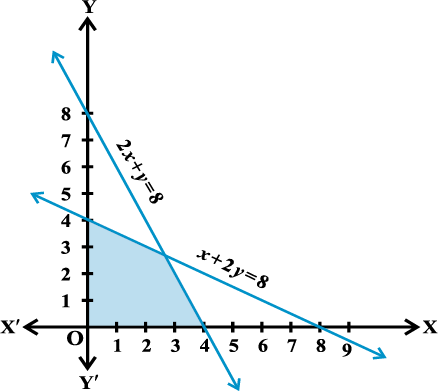
आकृति 6.14
प्रश्नावली 6.3
प्रश्न 1 से 15 तक निम्नलिखित असमिका निकाय को आलेखीय विधि से हल कीजिएः graphically:
1. x ≥ 3, y ≥ 2
2. 3x + 2y ≤ 12, x ≥ 1, y ≥ 2
3. 2x + y ≥ 6, 3x + 4y < 12
4. x + y ≥ 4, 2x – y < 0
5. 2x – y >1, x – 2y < – 1
6. x + y ≤ 6, x + y ≥ 4
7. 2x + y ≥ 8, x + 2y ≥ 10
8. x + y ≤ 9, y > x, x ≥ 0
9. 5x + 4y ≤ 20, x ≥ 1, y ≥ 2
10. 3x + 4y ≤ 60, x +3y ≤ 30, x ≥ 0, y ≥ 0
11. 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
12. x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0 , y ≥ 1.
13. 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
14. 3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0, x ≥ 0
15. x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
विविध उदाहरण
उदाहरण 16 हल कीजिए – 8 ≤ 5x – 3 < 7.
हल इस स्थिति में हमारे पास दो असमिकाएँ – 8 ≤ 5x – 3 और 5x – 3 < 7 हैं। इन्हें हम साथ-साथ हल करना चाहते हैं। हम दिए गए असमिका के मध्य में चर राशि x का गुणांक एक बनाना चाहते हैं।
हमें ज्ञात है कि – 8 ≤ 5x –3 < 7
या –5 ≤ 5x < 10 या –1 ≤ x < 2
उदाहरण 17 हल कीजिए – 5 ≤ 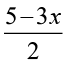 ≤ 8.
≤ 8.
हल ज्ञात है कि – 5 ≤ 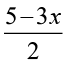 ≤ 8
≤ 8
या –10 ≤ 5 – 3x ≤ 16 या – 15 ≤ – 3x ≤ 11
या 5 ≥ x ≥ – 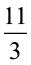
जिसे हम 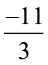 ≤ x ≤ 5 के रूप में भी लिख सकते हैं।
≤ x ≤ 5 के रूप में भी लिख सकते हैं।
उदाहरण 18 निम्नलिखित असमिका-निकाय को हल कीजिएः
3x – 7 < 5 + x ... (1)
11 – 5 x ≤ 1 ... (2)
और उन्हें संख्या रेखा पर आलेखित कीजिए।
हल असमिका (1) से हम प्राप्त करते हैं
3x – 7 < 5 + x
या x < 6 ... (3)
असमिका (2) से भी हम प्राप्त करते हैं
11 – 5 x ≤ 1
या – 5 x ≤ – 10
या x ≥ 2 ... (4)
यदि संख्या रेखा पर (3) तथा (4) को आलेखित करें तो हम पाते हैं कि x के उभयनिष्ठ मान 2 के बराबर या 2 से बड़े व 6 से छोटे हैं जो आकृति 6.16 में गहरी काली रेखा द्वारा प्रदर्शित किए गए हैं।

आकृति 6.16
अतः असमिका निकाय का हल वास्तविक संख्या x, 2 के बराबर या 2 से बड़ा और 6 से छोटी है। इस प्रकार 2 ≤ x < 6.
उदाहरण 19 किसी प्रयोग में नमक के अम्ल के एक विलयन का तापमान 30° सेल्सियस और 35° सेल्सियस के बीच ही रखना है। फारेनहाइट पैमाने पर तापमान का परिसर ज्ञात कीजिए, यदि सेंटीग्रेड से फारेनहाइट पैमाने पर परिवर्तन सूत्र
C = 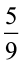 (F – 32)
(F – 32)
है, जहाँ C और F क्रमशः तापमान को अंश सेल्सियस तथा अंश फारेनहाइट में निरूपित करते हैं।
हल ज्ञात है कि 30 < C < 35
C = 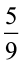 (F – 32), रखने पर हम पाते हैं,
(F – 32), रखने पर हम पाते हैं,
30 < 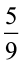 (F – 32) < 35,
(F – 32) < 35,
या 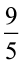 × 30 < (F – 32) <
× 30 < (F – 32) < 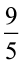 × 35
× 35
या 54 < (F – 32) < 63
या 86 < F < 95.
इस प्रकार तापमान का अभीष्ट परिसर 86° F से 95° F है।
उदाहरण 20 एक निर्माता के पास अम्ल के 12% विलयन के 600 लिटर हैं। ज्ञात कीजिए कि 30% अम्ल वाले विलयन के कितने लिटर उसमें मिलाए जाएँ ताकि परिणामी मिश्रण में अम्ल की मात्रा 15% से अधिक परंतु 18% से कम हो।
हल मान लीजिए कि 30% अम्ल के विलयन की मात्रा x लिटर है।
तब संपूर्ण मिश्रण = (x + 600) लिटर
इसलिए 30% x + 12% का 600 > 15% का (x + 600)
और 30% x + 12% का 600 < 18% का (x + 600)
या  +
+ 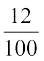 (600) >
(600) >  (x + 600)
(x + 600)
और  +
+ 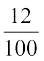 (600) <
(600) < 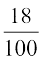 (x + 600)
(x + 600)
या 30x + 7200 > 15x + 9000
और 30x + 7200 < 18x + 10800
या 15x > 1800 और 12x < 3600
या x > 120 और x < 300,
अर्थात 120 < x < 300
इस प्रकार 30% अम्ल के विलयन की अभीष्ट मात्रा 120 लिटर से अधिक तथा 300 लिटर से कम होनी चाहिए।
अध्याय 6 पर विविध प्रश्नावली
प्रश्न 1 से 6 तक की असमिकाओं को हल कीजिएः
1. 2 ≤ 3x – 4 ≤ 5
2. 6 ≤ – 3 (2x – 4) < 12
3. 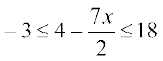
4. 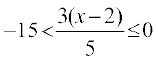
5. 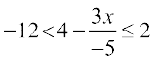
6. 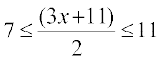 .
.
प्रश्न 7 से 10 तक की असमिकाओं को हल कीजिए और उनके हल को संख्या रेखा पर निरूपित कीजिए।
7. 5x + 1 > – 24, 5x – 1 < 24
8. 2 (x – 1) < x + 5, 3 (x + 2) > 2 – x
9. 3x – 7 > 2 (x – 6) , 6 – x > 11 – 2x
10. 5 (2x – 7) – 3 (2x + 3) ≤ 0 , 2x + 19 ≤ 6x + 47 .
11. एक विलयन को 68° F और 77° F के मध्य रखना है। सेल्सियस पैमाने पर विलयन के तापमान का परिसर ज्ञात कीजिए, जहाँ सेल्सियस फारेनहाइट परिवर्तन सूत्र F = 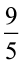 C + 32 है।
C + 32 है।
12. 8% बोरिक एसिड के विलयन में 2% बोरिक एसिड का विलयन मिलाकर तनु (dilute) किया जाता है। परिणामी मिश्रण में बोरिक एसिड 4% से अधिक तथा 6% से कम होना चाहिए। यदि हमारे पास 8% विलयन की मात्रा 640 लिटर हो तो ज्ञात कीजिए कि 2% विलयन के कितने लिटर इसमें मिलाने होंगे?
13. 45% अम्ल के 1125 लिटर विलयन में कितना पानी मिलाया जाए कि परिणामी मिश्रण में अम्ल 25% से अधिक परंतु 30% से कम हो जाए?
14. एक व्यक्ति के बौद्धिक-लब्धि (IQ) मापन का सूत्र निम्नलिखित हैः
IQ = 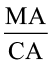 × 100,
× 100,
जहाँ MA मानसिक आयु और CA कालानुक्रमी आयु है। यदि 12 वर्ष की आयु के बच्चों के एक समूह की IQ, असमिका 80 ≤ IQ ≤ 140 द्वारा व्यक्त हो, तो उस समूह के बच्चों की मानसिक आयु का परिसर ज्ञात कीजिए।
सारांश
- एक असमिका, दो वास्तविक संख्याओं या दो बीजीय व्यंजकों में <, >, ≤ या ≥ के चिह्न के प्रयोग से बनती है।
- एक असमिका के दोनों पक्षों में समान संख्या जोड़ी या घटायी जा सकती है।
- किसी असमिका के दोनों पक्षों को समान धनात्मक, संख्या से गुणा (या भाग) किया जा सकता है। परंतु दोनों पक्षों को समान ऋणात्मक संख्याओं से गुणा (या भाग) करने पर असमिका के चिह्न तदनुसार बदल जाते हैं।
- x के उन मानों (Values) को जो दिएे गए असमिका को एक सत्य कथन बनाते हों, उन्हें असमिका का हल कहते हैं।
- x < a (या x > a) का संख्या रेखा पर आलेख खींचने के लिए संख्या रेखा पर संख्या a पर एक छोटा सा वृत्त बनाकर, a से बाईं (या दाईं) ओर की संख्या रेखा को गहरा काला कर देते हैं।
- x ≤ a (या x ≥ a) का संख्या रेखा पर आलेख खींचने के लिए संख्या रेखा पर संख्या a पर एक छोटा काला वृत्त बनाकर a से बाईं (या दाईं) ओर की संख्या रेखा को गहरा काला कर देते हैं।
- यदि दो चरांकों की एक असमिका के चिह्न ≤ या ≥ हों तो रेखा पर स्थित बिंदु, असमिका के हल में सम्मिलित होते हैं और असमिका का आलेख, समता द्वारा निरूपित गहरी मोटी रेखा के बाईं (नीचे) या दाईं (ऊपर) होता है जो उस क्षेत्र का कोई भी बिंदु असमिका को संतुष्ट करता है।
- यदि दो चरांकों की एक असमिका के चिह्न < या > हों तो रेखा पर स्थित बिंदु, असमिका के हल में सम्मिलित नहीं होते हैं और असमिका का आलेख, समता द्वारा निरूपित दानेदार रेखा के बाईं (नीचे) या दाईं (ऊपर) होता है जो उस क्षेत्र का कोई भी बिंदु, असमिका को संतुष्ट करता है।
- असमिकाओं के निकाय का हल क्षेत्र, वह उभयनिष्ठ क्षेत्र है जो निकाय में सभी दी गई असमिकाओं को संतुष्ट करता है।
