Table of Contents
Every body of discovery is mathematical in form because there is no other guidance we can have – DARWIN
7.1 भूमिक (Introduction)
मान लीजिए कि आपके पास नंबर वाले ताले का एक सूटकेस है। माना उस ताले में 4 चक्र लगे हैं और प्रत्येक चक्र 0 से 9 तक के 10 अंकों द्वारा चिह्नित है। ताले को खोला जा सकता है यदि 4 विशिष्ट अंको को, बिना दोहराए, एक निश्चित क्रम में व्यवस्थित किया जाए। माना किसी कारण आप अंकों के इस निश्चित क्रम को भूल गए हैं। आपकों केवल पहला अंक याद है जो कि 7 है। ताले को खोलने के लिए, आपको 3 अंकों के कितने अनुक्रमों की जाँच करनी पड़ेगी? इस प्रश्न के उत्तर के लिए, आप संभवतः शेष 9 अंकों में से एक समय में 3 अंकों को लेकर, सभी संभव क्रमों को अविलंब सूचीबद्ध करना प्रारंभ कर दें। परंतु यह विधि थकाने वाली और नीरस होगी, क्योंकि संभव क्रमों की संख्या बड़ी हो सकती है। इस अध्याय में, हम कुछ एेसी मौलिक गणन तकनीक सीखेंगे जिनसे हम, 3 अंकों के क्रमों को सूचीबद्ध किए बिना ही, इस प्रश्न का उत्तर दे सकेंगे। वस्तुतः ये तकनीक, वस्तुओं के चयन तथा उनको क्रमबद्ध करने के भिन्न-भिन्न तरीकों की संख्या निर्धारित करने में उपयोगी होती हैं। प्रथम चरण में, हम उस सिद्धांत पर विचार करेंगे, जो कि इन तकनीकों को सीखनें के लिए अत्यधिक मौलिक है।
7.2 गणना का आधारभूत सिद्धांत (Fundamental Principle of Counting)
आइए हम निम्नलिखित समस्या पर विचार करेंः मोहन के पास P1, P2 , P3 तीन पैंट तथा S1, S2 दो क़मीज़ो है।
उसके पास पहनने के लिए पैंट तथा कमीज़ के कितने भिन्न-भिन्न जोड़े (युग्म) हैं? एक पैंट चुनने के लिए 3 तरीके हैं, क्योंकि चयन के लिए 3 पैंट उपलब्ध हैं। इसी प्रकार एक कमीज़ का चयन 2 तरह से किया जा सकता है। पैंट के प्रत्येक चयन के लिए कमीज़ के चयन के 2 विकल्प संभव हैं। अतः पैंट तथा कमीज़ के जोड़ों के चयन की संख्या 3 × 2 = 6 है। इस तथ्य को आकृति 7:1 में स्पष्ट किया गया है।
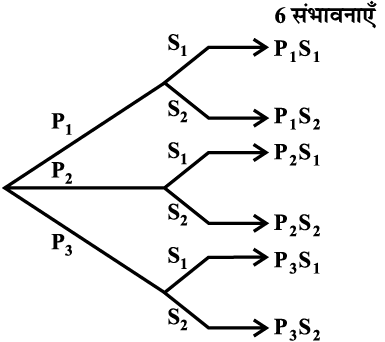
आकृति 7:1
आइए हम इसी प्रकार की एक दूसरी समस्या पर विचार करेंः
शबनम के पास 2 बस्ते, 3 खाने के डिब्बे तथा 2 पानी की बोतलें हैं। वह इन वस्तुओं को किस प्रकार से ले जा सकती है (प्रत्येक में से एक चुन कर)।
एक बस्ते को 2 भिन्न तरीकों से चुना जा सकता है। एक बस्ते के चुने जाने के बाद, एक खाने के डिब्बे को चुनने के 3 भिन्न तरीके हैं। इस प्रकार बस्ते और खाने के डिब्बे के जोड़ों की संख्या 2 × 3 = 6 है। इनमें से प्रत्येक जोड़े के लिए, एक पानी की बोतल को चुनने के 2 भिन्न तरीके हैं। अतः शबनम द्वारा इन वस्तुओं को स्कूल ले जाने के कुल 6 × 2 = 12 भिन्न तरीके हैं। यदि हम दो बस्तों को B1, B2, तीन खाने के डिब्बों को T1, T2, T3 तथा दो पानी की बोतलों को W1, W2, नाम दें, तो इन संभावनाओं को नीचे बनी आकृति द्वारा स्पष्ट किया जा सकता है (आकृति 7.2.)।
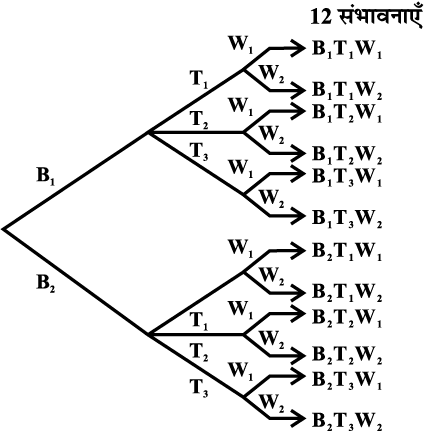
आकृति 7:2
वस्तुतः उपर्युक्त प्रकार की समस्याओं को निम्नलिखित सिद्धांत के प्रयोग द्वारा सरल किया जाता है, जिसे गणना का आधारभूत सिद्धांत अथवा केवल गणन सिद्धांत कहते हैं और जिसका कथन इस प्रकार है,
"यदि एक घटना m,n, तो दिए हुए क्रम में दोनों घटनाओं के भिन्न तरीकों के घटित होने की कुल भिन्न संख्या m×n है।”
ऊपर वर्णित सिद्धांत का घटनाओं की सीमित संख्या के लिए व्यापकीकरण किया जा सकता है। उदाहरणार्थ, 3 घटनाओं के लिए, यह सिद्धांत निम्नलिखित प्रकार से होगाः
‘यदि एक घटना m भिन्न तरीकों से घटित हो सकती है, इसके उपरांत एक दूसरी घटना n भिन्न तरीकों से घटित हो सकती है, तदोपरांत एक तीसरी घटना p भिन्न तरीकों से घटित हो सकती है, तो तीनों घटनाओं के घटित होने के भिन्न तरीकों की कुल संख्या, दिए हुए क्रम में, m × n × p है।”
प्रथम प्रश्न में, पैंट तथा कमीज़ के जोड़ों को पहनने की अभीष्ट संख्या, निम्नलिखित घटनाओं के उत्तरोत्तर घटित होने के विभिन्न विन्यासों की संख्या के तुल्य हैः
(i) एक पैंट के चयन की घटना
(ii) एक कमीज़ के चयन की घटना
दूसरे प्रश्न में विन्यासों की अभीष्ट संख्या, निम्नलिखित घटनाओं के उत्तरोत्तर घटित होने के विभिन्न विन्यासों की संख्या के बराबर हैः
(i) एक बस्ते के चयन की घटना,
(ii) एक खाने के डिब्बे के चयन की घटना,
(iii) एक पानी की बोतल के चयन की घटना।
यहाँ दोनों में से प्रत्येक प्रश्न में घटनाएँ अनेक संभव क्रमों में घटित हो सकती हैं परंतु हम इन संभव क्रमों में से किसी एक का चयन करते हैं और इस चयनित क्रम में घटनाओं के घटित होने के विभिन्न विन्यासों की गणना करते हैं।
उदाहरण 1 शब्द ROSE, के अक्षरों से बनने वाले 4 अक्षरों वाले, अर्थपूर्ण या अर्थहीन, शब्दों की संख्या ज्ञात कीजिए, जबकि अक्षरों के पुनरावृत्ति की अनुमति नहीं है।
हल रचित शब्दों की संख्या, 4 रिक्त स्थानों 


 को 4 अक्षरों से उत्तरोत्तर भरने के तरीकों की संख्या के बराबर है, जबकि इस बात का ध्यान रखा जाए कि पुनरावृत्ति की अनुमति नहीं है। पहले स्थान को, 4 अक्षर R, O, S, और E में से किसी एक द्वारा 4 विभिन्न तरीकों से भरा जा सकता है। इसके बाद, दूसरे स्थान को शेष तीन अक्षरों में से किसी एक द्वारा 3 विभिन्न तरीकों से भरा जा सकता हैं इसके उपरांत तीसरे स्थान को 2 विभिन्न तरीकों से भरा जा सकता है और अंत में चौथे स्थान को केवल 1 तरीके से भरा जा सकता है इस प्रकार गुणन सिद्धांत द्वारा चारों स्थानों को भरने के तरीकों की संख्या 4 × 3 × 2 × 1 = 24 है। अतः शब्दों की अभीष्ट संख्या 24 है।
को 4 अक्षरों से उत्तरोत्तर भरने के तरीकों की संख्या के बराबर है, जबकि इस बात का ध्यान रखा जाए कि पुनरावृत्ति की अनुमति नहीं है। पहले स्थान को, 4 अक्षर R, O, S, और E में से किसी एक द्वारा 4 विभिन्न तरीकों से भरा जा सकता है। इसके बाद, दूसरे स्थान को शेष तीन अक्षरों में से किसी एक द्वारा 3 विभिन्न तरीकों से भरा जा सकता हैं इसके उपरांत तीसरे स्थान को 2 विभिन्न तरीकों से भरा जा सकता है और अंत में चौथे स्थान को केवल 1 तरीके से भरा जा सकता है इस प्रकार गुणन सिद्धांत द्वारा चारों स्थानों को भरने के तरीकों की संख्या 4 × 3 × 2 × 1 = 24 है। अतः शब्दों की अभीष्ट संख्या 24 है।
टिप्पणी यदि अक्षरों की पुनरावृत्ति की अनुमति होती, तो कितने शब्द बन सकते हैं? यह बात सरलता से समझी जा सकती है कि 4 रिक्त स्थानों में से प्रत्येक उत्तरोत्तर 4 विभिन्न तरीकों से भरा जा सकता है। अतः शब्दों की अभीष्ट संख्या = 4 × 4 × 4 × 4 = 256.
उदाहरण 2 भिन्न-भिन्न रंगों के दिए हुए 4 झंडों से, कितने भिन्न-भिन्न संकेत उत्पन्न किए जा सकते हैं, यदि एक संकेत के लिए, एक दूसरे के नीचे, 2 झंडों की आवश्यकता पड़ती है?
हल उत्पादित संकेतों की संख्या 2 रिक्त स्थानों  को भिन्न-भिन्न रंगों के 4 झंडों से उत्तरोत्तर भरने के तरीकों की संख्या के बराबर है। ऊपर के रिक्त स्थान को 4 झंडों में से किसी एक द्वारा 4 विभिन्न तरीकों से भरा जा सकता है। इसके बाद, नीचे के रिक्त स्थान को शेष 3 झंडों में से किसी एक द्वारा 3 विभिन्न तरीकों से भरा जा सकता है। अतः गुणन सिद्धांत द्वारा संकेतों की अभीष्ट संख्या = 4 × 3 = 12.
को भिन्न-भिन्न रंगों के 4 झंडों से उत्तरोत्तर भरने के तरीकों की संख्या के बराबर है। ऊपर के रिक्त स्थान को 4 झंडों में से किसी एक द्वारा 4 विभिन्न तरीकों से भरा जा सकता है। इसके बाद, नीचे के रिक्त स्थान को शेष 3 झंडों में से किसी एक द्वारा 3 विभिन्न तरीकों से भरा जा सकता है। अतः गुणन सिद्धांत द्वारा संकेतों की अभीष्ट संख्या = 4 × 3 = 12.
उदाहरण 3 अंकों 1, 2, 3, 4, 5 से कितनी 2 अंकीय सम संख्याएँ बन सकती हैं, यदि अंकों की पुनरावृत्ति की जा सकती है?
हल संख्याओं को बनाने के तरीके, 2 रिक्त स्थानों  को उत्तरोत्तर उचित प्रकार से भरने के तरीको की संख्या के बराबर है। यहाँ इकाई स्थान को भरने के लिए केवल 2 विकल्प हैंः अंक 2 या 4, और यह 2 तरीकों से किया जा सकता है। इसके पश्चात् दहाई स्थान को 5 अंकों में से किसी एक द्वारा भरा जा सकता है (क्योंकि अंकों की पुनरावृत्ति की जा सकती है)। अतः इसके 5 विकल्प हैं। अतएव गुणन सिद्धांत द्वारा दो अंकों वाली सम संख्याओं की अभीष्ट संख्या = 2 × 5, अर्थात् 10 है।
को उत्तरोत्तर उचित प्रकार से भरने के तरीको की संख्या के बराबर है। यहाँ इकाई स्थान को भरने के लिए केवल 2 विकल्प हैंः अंक 2 या 4, और यह 2 तरीकों से किया जा सकता है। इसके पश्चात् दहाई स्थान को 5 अंकों में से किसी एक द्वारा भरा जा सकता है (क्योंकि अंकों की पुनरावृत्ति की जा सकती है)। अतः इसके 5 विकल्प हैं। अतएव गुणन सिद्धांत द्वारा दो अंकों वाली सम संख्याओं की अभीष्ट संख्या = 2 × 5, अर्थात् 10 है।
उदाहरण 4 यदि पाँच विभिन्न झंडे उपलब्ध हैं, तो उन विभिन्न संकेतों की संख्या ज्ञात कीजिए जिन्हें कम से कम दो झंडों को एक ऊर्ध्व दंड पर क्रमवत एक को दूसरे के नीचे रखकर उत्पन्न किया जा सकता है?
हल एक संकेत या तो 2 या 3 या 4 या 5 झंडों से बनाया जा सकता है। अब हम 2, 3, 4 या 5 झंडों से बनने वाले संकेतों की संभव संख्याओं की अलग-अलग गणना करेंगे और फिर इन संख्याओं को जोड़ देंगे।
2 झंडों द्वारा बनने वाले संकेतों की संख्या, 5 उपलब्ध झंडों से 2 रिक्त स्थानों  को उत्तरोत्तर भरने की संख्या के बराबर है। गुणन नियम के अनुसार इसकी संख्या = 5 × 4 = 20 है।
को उत्तरोत्तर भरने की संख्या के बराबर है। गुणन नियम के अनुसार इसकी संख्या = 5 × 4 = 20 है।
इसी प्रकार 3 झंडों द्वारा बनने वाले संकेतों की संख्या, 5 झंडों से 3 रिक्त स्थानों  को उत्तरोत्तर भरने की संख्या के बराबर है इसकी संख्या 5 × 4 × 3 = 60 है।
को उत्तरोत्तर भरने की संख्या के बराबर है इसकी संख्या 5 × 4 × 3 = 60 है।
इसी प्रकार 4 झंडों वाले संकेतों की संख्या = 5 × 4 × 3 × 2 = 120
और 5 झंडों वाले संकेतों की संख्या = 5 × 4 × 3 × 2 × 1 = 120
अतः संकेतो की अभीष्ट संख्या = 20 + 60 + 120 + 120 = 320.
प्रश्नावली 7.1
1. अंक 1, 2, 3, 4 और 5 से कितनी 3 अंकीय संख्याएँ बनाई जा सकती हैं, यदि
(i) अंकों की पुनरावृत्ति की अनुमति हो ?
(ii) अंकों की पुनरावृत्ति की अनुमति नहीं हो ?
2. अंक 1, 2, 3, 4, 5, 6 से कितनी 3 अंकीय सम संख्याएँ बनाई जा सकती हैं, यदि अंकों की पुनरावृत्ति की जा सकती है ?
3. अंग्रेज़ी वर्णमाला के प्रथम 10 अक्षरों से कितने 4 अक्षर के कोड बनाए जा सकते हैं, यदि किसी भी अक्षर की पुनरावृत्ति नहीं की जा सकती है?
4. 0 से 9 तक के अंकों का प्रयोग करके कितने 5 अंकीय टेलीफोन नंबर बनाए जा सकते हैं, यदि प्रत्येक नंबर 67 से प्रारंभ होता है और कोई अंक एक बार से अधिक नहीं आता है?
5. एक सिक्का तीन बार उछाला जाता है और परिणाम अंकित कर लिए जाते हैं। परिणामों की संभव संख्या क्या है?
6. भिन्न-भिन्न रंगों के 5 झंडे दिए हुए हैं। इनसे कितने विभिन्न संकेत बनाए जा सकते हैं, यदि प्रत्येक संकेत में 2 झंडों, एक के नीचे दूसरे, के प्रयोग की आवश्यकता पड़ती है?
7.3 क्रमचय (Permutations)
पिछले अनुच्छेद के उदाहरण 1 में, हम वास्तव में अक्षरों के विभिन्न विन्यासों, जैसे ROSE, REOS, ..., इत्यादि, की संभव संख्या की गणना करते हैं। इस सूची में प्रत्येक विन्यास दूसरे से भिन्न हैं। दूसरे शब्दों में अक्षरों के लिखने का क्रम महत्वपूर्ण है इनमें से प्रत्येक विन्यास, 4 विभिन्न अक्षरों में से एक समय में सभी को साथ लेकर बनाया गया, क्रमचय कहलाता है अब यदि हमें शब्द NUMBER, के अक्षरों में से 3 अक्षरीय, अर्थपूर्ण या अर्थहीन रचित शब्दों की संख्या निर्धारित करनी है, जबकि अक्षरों की पुनरावृत्ति की अनुमति नहीं हो, तो हमें NUM, NMU,MUN,NUB, ...इत्यादि विन्यासों की गणना की आवश्यकता है। यहाँ पर हम 6 विभिन्न अक्षरों में से एक समय में 3 अक्षरों को लेकर बनने वाले क्रमचयों की गणना कर रहे हैं। इस प्रकार के शब्दों की अभीष्ट संख्या = 6 × 5 × 4 = 120 (गुणन सिद्धांत के प्रयोग द्वारा) हैं।
यदि अक्षरों की पुनरावृत्ति की अनुमति होती, तो शब्दों की अभीष्ट संख्या 6 × 6 × 6 = 216 होगी।
परिभाषा 1 क्रमचय एक निश्चित क्रम में बना विन्यास है, जिसको दी हुई वस्तुओं में से एक समय में कुछ या सभी को लेकर बनाया गया है।
नीचे दिए उप-अनुच्छेद में हम उस सूत्र को निर्धारित करेंगे जिसकी आवश्यकता इस प्रकार के प्रश्नों के उत्तर देने के लिए पड़ती है।
7.3.1 क्रमचय, जब सभी वस्तुएँ भिन्न-भिन्न हैं (Permutations when all the objects are distinct)
प्रमेय 1 n विभिन्न वस्तुओं में से एक समय में r वस्तुओं को लेकर बनाए गए क्रमचयों की संख्या को प्रतीक nPr से निरूपित करते हैं, जहाँ 0 < r ≤ n तथा किसी भी क्रमचय में वस्तुओं की पुनरावृत्ति की अनुमति नहीं है, nPr. = n ( n – 1) ( n – 2). . .( n – r + 1)
उपपत्ति क्रमचयों की संख्या, r रिक्त स्थानों को 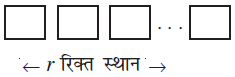
n वस्तुओं से भरने के तरीकों की संख्या के बराबर है। पहला स्थान n तरीकों से भरा जा सकता है। इसके बाद दूसरा स्थान (n – 1) तरीकों से भरा जा सकता है। इसके उपरांत तीसरा स्थान [n – 2)तरीकों से भरा जा सकता है ::::::::: और r वाँ स्थान (n – (r – 1)] तरीकों से भरा जा सकता है। अतः r रिक्त स्थानों को उत्तरोत्तर भरने के तरीकों की संख्या = n(n – 1) (n – 2) . . . (n – (r – 1)) या n ( n – 1) (n – 2) ... (n – r + 1)
nPr के लिए यह एक बोझिल व्यंजक है और हमें एक एेसे संकेतन की आवश्यकता है, जिसकी सहायता से इस व्यंजक के विस्तार को घटाया जा सके। प्रतीक n! (जिसे n क्रमगुणित पढ़ते हैं)इसमें हमारी सहायता करता है। निम्नलिखित विवरण में हम सीखेंगे कि वास्तव में n! का क्या अर्थ है?
7.3.2 क्रमगुणित संकेतन (Factorial notation)
संकेतन n! प्रथम n प्राकृत संख्याओं के गुणनफल को व्यक्त करता है अर्थात् 1 × 2 × 3 × . . . × (n – 1) × n को n! द्वारा निरूपित किया जाता है। हम इस प्रतीक को ‘n क्रमगुणित पढ़ते हैं। इस प्रकार 1 × 2 × 3 × 4 . . . × (n – 1) × n = n ! तदनुसार
1 = 1 !
1 × 2 = 2 !
1× 2 × 3 = 3 !
1 × 2 × 3 × 4 = 4 ! इत्यादि
हम परिभाषित करते हैं, कि 0 ! = 1
इस प्रकार हम लिख सकते हैं, कि 5 ! = 5 × 4 ! = 5 × 4 × 3 ! = 5 × 4 × 3 × 2 !
= 5 × 4 × 3 × 2 × 1!
स्पष्टतया सभी प्राकृत संख्या n के लिए
n ! = n (n – 1) !
= n (n – 1) (n – 2) ! [ यदि n ≥ 2]
= n (n – 1) (n – 2) (n – 3) ! [ यदि n ≥ 3]
इत्यादि
उदाहरण 5 मान निकालिए (i) 5 ! (ii) 7 ! (iii) 7 ! – 5!
हल (i) 5 ! = 1 × 2 × 3 × 4 × 5 = 120
(ii) 7 ! = 1 × 2 × 3 × 4 × 5 × 6 ×7 = 5040
और (iii) 7 ! – 5! = 5040 – 120 = 4920
उदहारण 6 परिकलन कीजिए (i) 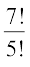 (ii)
(ii) 
हल (i) हम प्राप्त करते हैं,  =
= 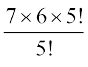 = 7 × 6 = 42
= 7 × 6 = 42
और (ii)  =
= 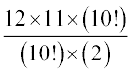 = 6 × 11 = 66
= 6 × 11 = 66
उदाहरण 7 मान निकालिए  , जहाँ n = 5, r = 2
, जहाँ n = 5, r = 2
हल हमें निम्नलिखित का मान निकालना है
 (क्योंकि n = 5, r = 2)
(क्योंकि n = 5, r = 2)
यहाँ पर  =
= 
उदाहरण 8 यदि  , तो x ज्ञात कीजिए।
, तो x ज्ञात कीजिए।
हल यहाँ पर 
अतएव 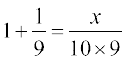 या
या 
अतः x = 100
प्र'नावाली 7.2
1. मान निकालिएः
(i) 8 ! (ii) 4 ! – 3 !
2. क्या 3 ! + 4 ! = 7 ! ?
3. 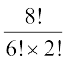 का परिकलन कीजिए
का परिकलन कीजिए
4 यदि  , तो x का मान ज्ञात कीजिए।
, तो x का मान ज्ञात कीजिए।
5.  , का मान निकालिए जब
, का मान निकालिए जब
(i) n = 6, r = 2 (ii) n = 9, r = 5.
7.3.3 nPr के लिए सूत्र की व्युत्पत्ति ( Derivation of the formula for nPr )
 , 0 ≤ r ≤ n
, 0 ≤ r ≤ n
आइए हम उस अवस्था पर वापस चलें जहाँ हमने निम्नलिखित ज्ञात किया थाः
nPr = n (n – 1) (n – 2) . . . (n – r + 1)
इसके अंश और हर को (n – r) (n – r – 1) . . . 3 × 2 × 1, से गुणा करने पर, हमें प्राप्त होता है कि
 =
=  ,
,
इस प्रकार  , जहाँ 0 < r
, जहाँ 0 < r  n
n
यह nPr पहले से अधिक सुविधाजनक व्यंजक है।
विशेष रूप से जब r = n, तो 
क्रमचयों की गणना, केवल उन तरीकों की गणना है, जिनमें एक समय में कुछ या सभी वस्तुओं का विन्यास किया गया हो। एक भी वस्तु के बिना विन्यास की संख्या बराबर है उस संख्या के जिसमें सभी वस्तुओं को छोड़कर विन्यास किया गया हो और हमें ज्ञात है कि एेसा करने का केवल एक तरीका है। इसी कारण से हमने n P0 = 1 परिभाषित किया है।
nP0 = 1 = 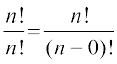 ... (1)
... (1)
अतः सूत्र (1), r = 0 के लिए भी लागू है।
अतः 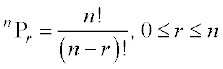 .
.
प्रमेय 2 n विभिन्न वस्तुओं में से एक समय में r वस्तुओं को लेकर बने क्रमचयों की संख्या, जबकि वस्तुओं के पुनरावृत्ति की अनुमति हो, nr होती है।
इसकी उपपत्ति पिछले प्रमेय की उपपत्ति के समान है, अतः इसको पाठक के लिए छोड़ दिया गया है।
अब हम nPr के सूत्र की उपयोगिता को स्पष्ट करने के लिए पिछले अनुच्छेद के कुछ प्रश्नों को इस सूत्र के प्रयोग द्वारा सरल कर रहे हैं।
उदाहरण 1 में शब्दों की अभीष्ट संख्या = 4P4 = 4! = 24 जब पुनरावृत्ति की अनुमति नहीं हैं। यदि पुनरावृत्ति की अनुमति हो, तो शब्दों की अभीष्ट संख्या 44 = 256 होगी।
NUMBER शब्द के अक्षरों में से 3 अक्षरों वाले चयनित शब्दों की संख्या =  = 4 × 5 × 6 = 120, यहाँ इस प्रश्न में भी पुनरावृत्ति की अनुमति नहीं है। यदि पुनरावृत्ति की अनुमति हो, तो शब्दों की अभीष्ट संख्या 63 = 216 होगी।
= 4 × 5 × 6 = 120, यहाँ इस प्रश्न में भी पुनरावृत्ति की अनुमति नहीं है। यदि पुनरावृत्ति की अनुमति हो, तो शब्दों की अभीष्ट संख्या 63 = 216 होगी।
12 व्यक्तियों के एक समुदाय से एक अध्यक्ष और एक उपाध्यक्ष के चयन के तरीकों की संख्या, यह मानकर कि एक व्यक्ति एक से अधिक पद पर नहीं रह सकता है, स्पष्टतया
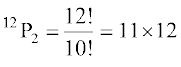 = 132.
= 132.
7.3.4 क्रमचय, जब सभी वस्तुएँ भिन्न-भिन्न नहीं हैं (Permutations when all the objects are not distinct objects)
मान लीजिए कि हमें शब्द ROOT के अक्षरों के पुनर्विन्यास के तरीकों की संख्या ज्ञात करनी है। इस दशा में, सभी अक्षर भिन्न-भिन्न नहीं है। यहाँ 2 O हैं जो समान प्रकार के अक्षर हैं। हम इन दोनों O को अस्थाई रूप से भिन्न-भिन्न मान लेते हैं जैसे O1 और O2. अब इस दशा में 4 विभिन्न अक्षरों में से एक समय में सभी को लेकर बनने वाले क्रमचयों की संख्या 4! है। इन क्रमचयों में से एक क्रमचय RO1O2T पर विचार कीजिए। इसके संगत, यहाँ पर 2! क्रमचय RO1O2T तथा RO2O1T एेसे हैं जो कि समान क्रमचय होते यदि O1 तथा O2 को भिन्न-भिन्न नहीं माना गया होता अर्थात् यदि O1 तथा O2 दोनों क्रमचय में O होते। अतएव, क्रमचयों की अभीष्ट संख्या = 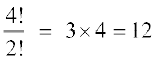
इस बात को नीचे स्पष्ट किया गया हैः
क्रमचय जब O1, O2 क्रमचय जब O1, O2 दोनों
भिन्न-भिन्न हैं। O के समान हैं

 R O O T
R O O T

 T O O R
T O O R
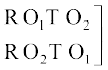
 R O T O
R O T O
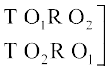
 T O R O
T O R O
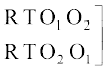
 R T O O
R T O O
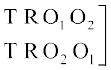
 T R O O
T R O O

 O O R T
O O R T
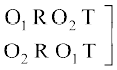
 O R O T
O R O T
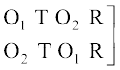
 O T O R
O T O R
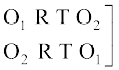
 O R T O
O R T O
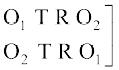
 O T R O
O T R O

 O O T R
O O T R
आइए अब हम शब्द INSTITUTE के अक्षरों के पुनर्विन्यास के तरीकों की संख्या ज्ञात करें। इस दशा में 9 अक्षर हैं, जिनमें I दो बार तथा T तीन बार आता है।
अस्थाई रूप से, हम इन समान अक्षरों को भिन्न-भिन्न मान लेते हैं जैसे I1, I2, T1, T2, T3. 9 विभिन्न अक्षरों में से एक समय में सभी को लेने से बने क्रमचयों की संख्या 9! है। इनमें से एक क्रमचय माना कि I1 NT1 SI2 T2 U E T3 पर विचार कीजिए। यदि I1, I2 समान नहीं हों और T1, T2, T3 एक जैसे न हों तो I1, I2 का 2! तरीकों से तथा T1, T2, T3 का 3! तरीकों से विन्यास किया जा सकता है। यदि I1, I2 समान हों तथा T1, T2, T3 समान हो, तो 2! × 3! क्रमचय समान होगें। इस प्रकार पूछे गए विभिन्न क्रमचयों की कुल संख्या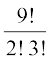 है। हम निम्नलिखित प्रमेय का कथन (बिना उपपत्ति) व्यक्त कर सकते हैं।
है। हम निम्नलिखित प्रमेय का कथन (बिना उपपत्ति) व्यक्त कर सकते हैं।
प्रमेय 3 n वस्तुओं के क्रमचयों की संख्या, जहाँ p वस्तुएँ समान प्रकार की और शेष भिन्न प्रकार
की हैं = 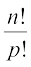 .
.
वस्तुतः इस संबंध में एक अधिक व्यापक प्रमेय हेै जो नीचे वर्णित हैः
प्रमेय 4 n वस्तुओं के क्रमचयों की संख्या 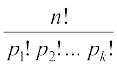 है।, जहाँ p1 वस्तुएँ एक प्रकार की, p2 वस्तुएँ दूसरे प्रकार की , ..., pk वस्तुएँ kवाँ प्रकार की और शेष (यदि कोई है) विभिन्न प्रकार की हैं।
है।, जहाँ p1 वस्तुएँ एक प्रकार की, p2 वस्तुएँ दूसरे प्रकार की , ..., pk वस्तुएँ kवाँ प्रकार की और शेष (यदि कोई है) विभिन्न प्रकार की हैं।
उदाहरण 9 ALLAHABAD शब्द के अक्षरों से बनने वाले क्रमचयों की संख्या ज्ञात कीजिए।
हल यहाँ पर 9 अक्षर हैं, जिनमें A, 4 बार आया है, 2 बार L आया है तथा शेष विभिन्न प्रकार के हैं। अतएव विन्यासों की अभीष्ट संख्या
= 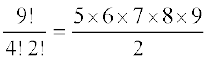 = 7560
= 7560
उदाहरण 10 1 से 9 तक के अंकों का प्रयोग करके कितनी 4 अंकीय संख्याएँ बनाई जा सकती हैं, यदि अंकों की पुनरावृत्ति की अनुमति नहीं है?
हल यहाँ पर अंकों का क्रम महत्वपूर्ण है, उदाहरण के लिए 1234 तथा 1324 दो भिन्न-भिन्न संख्याएँ हैं। अतः 4-अंकीय संख्याओं की संख्या 9 विभिन्न अंकों में से एक समय में 4 अंकों को लेकर बनने वाले क्रमचयों की संख्या के बराबर है। इस प्रकार 4-अंकीय संख्याओं की अभीष्ट संख्या 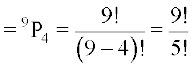 = 9 × 8 × 7 × 6 = 3024.
= 9 × 8 × 7 × 6 = 3024.
उदाहरण 11 100 से 1000 के बीच स्थित कितनी संख्याएँ हैं, जिन्हें अंक 0, 1, 2, 3, 4, 5 से बनाया जा सकता है, यदि अंकों के पुनरावृत्ति की अनुमति नहीं है।
हल 100 से 1000 के बीच स्थित प्रत्येक संख्या एक 3 अंकीय संख्या है। प्रथम हम 6 अंकों में से एक समय में 3 अंकों को लेकर बनने वाले क्रमचयों की संख्या की गणना करते हैं। यह संख्या 6P3 है परंतु इन क्रमचयों में वे भी सम्मिलित हैं, जिनमें 0, सैकड़े के स्थान पर है। उदाहरण के लिए 092, 042 :::: इत्यादि और ये एेसी संख्याएँ है जो वास्तव में 2 अंकीय हैं। अतः अभीष्ट संख्या को ज्ञात करने के लिए, इस प्रकार की 2 अंकीय संख्याओं के 6P3 में से घटाना पड़ेगा। अब इन 2-अंकीय संख्याओं की संख्या ज्ञात करने के लिए, हम 0 को सैकड़े के स्थान पर स्थिर कर देते हैं और शेष 5 अंको से एक समय में दो अंकों को लेकर बनने वाले पुनर्विन्यासों की संख्या ज्ञात करते हैं। यह संख्या 5P2 है। अतः अभीष्ट संख्या = 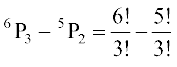
= 4 × 5 × 6 – 4 ×5 = 100
उदाहरण 12 n का मान ज्ञात कीजिए, इस प्रकार कि
(i) 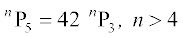 (ii)
(ii) 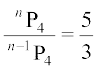 , n > 4
, n > 4
हल (i) दिया है कि
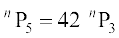
या n (n – 1) (n – 2) (n – 3) (n – 4) = 42 n(n – 1) (n – 2)
क्योंकि n > 4 इसलिए n(n – 1) (n – 2) ≠ 0
अतएव, दोनों पक्षों को n(n – 1) (n – 2), से भाग देने पर
(n – 3) (n – 4) = 42
या n2 – 7n – 30 = 0
या n2 – 10n + 3n – 30 = 0
या (n – 10) (n + 3) = 0
या n – 10 = 0 या n + 3 = 0
या n = 10 या n = – 3
क्योंकि n ऋण संख्या नहीं हो सकती है अतः n = 10
(ii) दिया है कि 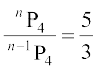
इस प्रकार 3n (n – 1) (n – 2) (n – 3) = 5(n – 1) (n – 2) (n – 3) (n – 4)
या 3n = 5 (n – 4) [ क्योंकि (n – 1) (n – 2) (n – 3) ≠ 0, n > 4]
या n = 10
उदाहरण 13 ज्ञात कीजिए r, यदि 5 4Pr = 6 5Pr–1 .
हल यहाँ पर

या 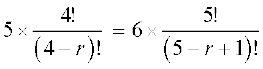
या 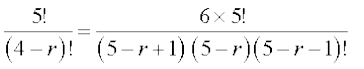
या (6 – r) (5 – r) = 6
या r2 – 11r + 24 = 0
या r2 – 8r – 3r + 24 = 0
या (r – 8) (r – 3) = 0
या r = 8 or r = 3.
अतः r = 8, 3.
उदाहरण 14 DAUGHTER शब्द के अक्षरों से 8 अक्षर वाले विन्यासों की संख्या ज्ञात कीजिए, यदि
(i) सब स्वर एक साथ रहें। (ii) सब स्वर एक साथ नहीं रहें।
हल (i) DAUGHTER शब्द में 8 विभिन्न अक्षर हैं, जिनमें से 3 स्वर हैं, अर्थात् A, U तथा E क्योंकि सभी स्वरों को एक साथ रहना है इसलिए हम कुछ समय के लिए उनको सम्मिलित रूप से एक वस्तु (AUE) मान लेते हैं। यह अकेली वस्तु शेष 5 वस्तुओं (अक्षरों) के साथ मिलकर 6 वस्तुएँ हो जाती हैं। फिर हम 6 वस्तुओं में से एक समय में सभी को लेकर बनने वाले क्रमचयों की संख्या की गणना करते हैं। यह संख्या 6P6 = 6! है। इनमें से प्रत्येक क्रमचय के संगत हमें तीन स्वरों A, U, E में से सभी को एक समय में लेकर 3! क्रमचय बनते हैं। अतएव गुणन सिद्धांत से क्रमचयों की अभीष्ट संख्या = 6 ! × 3 ! = 4320.
(ii) यदि हमें उन क्रमचयों की संख्या ज्ञात करनी है, जिनमें सभी स्वर एक साथ नहीं हैं, तो हमें पहले 8 अक्षरों में से एक समय में सभी को साथ लेकर बनने वाले विन्यासों की संभव संख्या ज्ञात करनी होगी, जो 8! है। फिर इस संख्या से हमें सब स्वरों के एक साथ रहने वाली क्रमचयों की संख्या घटानी पड़ेगी।
अतः अभीष्ट संख्या 8 ! – 6 ! × 3 ! = 6 ! (7×8 – 6)
= 2 × 6 ! (28 – 3)
= 50 × 6 ! = 50 × 720 = 36000
उदाहरण 15 4 लाल, 3 पीली तथा 2 हरी डिस्कों को एक पंक्ति में कितने प्रकार से व्यवस्थित किया जा सकता है, यदि एक ही रंग की डिस्कों में कोई अंतर नहीं है ?
हल डिस्कों की कुल संख्या 4 + 3 + 2 = 9 है। इन 9 डिस्कों में से 4 डिस्कें एक प्रकार की (लाल), 3 डिस्कें दूसरे प्रकार की (पीली) तथा 2 डिस्कें तीसरे प्रकार की (हरी) हैं।
इस प्रकार डिस्कों को व्यवस्थित करने की संख्या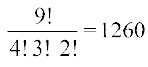 .
.
उदाहरण 16 INDEPENDENCE शब्द के अक्षरों से बनने वाले विन्यासों की संख्या ज्ञात कीजिए। इन विन्यासों में से कितने विन्यासों में,
(i) शब्द P से प्रारंभ होते हैं?
(ii) सभी स्वर सदैव एक साथ रहते हैं?
(iii) स्वर कभी भी एक साथ नहीं रहते हैं?
(iv) शब्द I से प्रारंभ होते हैं और उनका अंत P से होता है ?
हल यहाँ पर 12 अक्षर है, जिनमें से N तीन बार, E चार बार D, दो बार आता है और शेष अक्षरों में सभी भिन्न-भिन्न हैं।
इसलिए विन्यासों की अभीष्ट संख्या 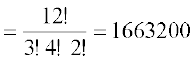
(i) हम P को सबसे बाएँ स्थान पर स्थिर कर देते हैं और फिर शेष 11 अक्षरों के विन्यास की गणना करते हैं। अतएव P से प्रारंभ होने वाले शब्दों की अभीष्ट संख्या
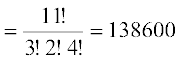 .
.
(ii) प्रदत्त शब्द में 5 स्वर हैं, जो कि 4 बार E है तथा 1 बार I है क्योंकि कि इनको सदैव एक साथ रहना है, इसलिए इनको कुछ समय के लिए एक अकेली वस्तु  समझ लेते हैं। यह अकेली वस्तु शेष 7 वस्तुओं के साथ मिलकर कुल 8 वस्तुएँ हो जाती हैं। इन 8 वस्तुओं जिनमें 3 बार N है, तथा दो बार D है के विन्यासों की संख्या
समझ लेते हैं। यह अकेली वस्तु शेष 7 वस्तुओं के साथ मिलकर कुल 8 वस्तुएँ हो जाती हैं। इन 8 वस्तुओं जिनमें 3 बार N है, तथा दो बार D है के विन्यासों की संख्या 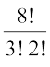 है। इनमें से प्रत्येक विन्यास के संगत 5 स्वर E, E, E, E तथा I के विन्यासों की संख्या
है। इनमें से प्रत्येक विन्यास के संगत 5 स्वर E, E, E, E तथा I के विन्यासों की संख्या 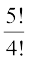 है। इसलिए गुणन सिद्धांत द्वारा विन्यासों की अभीष्ट संख्या
है। इसलिए गुणन सिद्धांत द्वारा विन्यासों की अभीष्ट संख्या 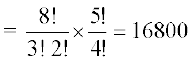
(iii) विन्यासों की अभीष्ट संख्या
= विन्यासों की कुल संख्या (बिना किसी प्रतिबंध के) - विन्यासों की संख्या, जिनमें सभी स्वर एक साथ रहते हैं
= 1663200 – 16800 = 1646400
(iv) हम I तथा P को दोनों सिरों पर स्थिर कर देते हैं (I बाएँ सिरे पर और P दाएँ सिरे पर).
इस प्रकार हमारे पास 10 अक्षर शेष रहते हैं।
अतः विन्यासों की अभीष्ट संख्या =  = 12600
= 12600
प्रश्नावली 7.3
1. 1 से 9 तक के अंकों को प्रयोग करके कितने 3 अंकीय संख्याएँ बन सकती हैं, यदि किसी भी अंक को दोहराया नहीं गया है?
2. किसी भी अंक को दोहराए बिना कितनी 4 अंकीय संख्याएँ होती हैं?
3. अंक 1, 2, 3, 4, 6, 7 को प्रयुक्त करने से कितनी 3 अंकीय सम संख्याएँ बनाई जा सकती हैं, यदि कोई भी अंक दोहराया नहीं गया है?
4. अंक 1, 2, 3, 4, 5 के उपयोग द्वारा कितनी 4 अंकीय संख्याएँ बनाई जा सकती है, यदि कोई भी अंक दोहराया नहीं गया है? इनमें से कितनी सम संख्याएँ होंगीं?
5. 8 व्यक्तियों की समिति में, हम कितने प्रकार से एक अध्यक्ष और एक उपाध्यक्ष चुन सकते हैं, यह मानते हुए कि एक व्यक्ति एक से अधिक पद पर नहीं रह सकता है?
6. यदि n – 1P3 : nP4 = 1 : 9 तो n ज्ञात कीजिए।
7. r ज्ञात कीजिए, यदि (i) 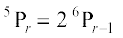 (ii)
(ii) 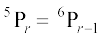 .
.
8. EQUATION शब्द के अक्षरों में से प्रत्येक को तथ्यतः केवल एक बार उपयोग करके कितने अर्थपूर्ण या अर्थहीन, शब्द बन सकते हैं?
9. MONDAY शब्द के अक्षरों से कितने, अर्थपूर्ण या अर्थहीन, शब्द बन सकते हैं, यह मानते हुए कि किसी भी अक्षर की पुनरावृत्ति नहीं की जाती है, यदि
(i) एक समय में 4 अक्षर लिए जाते हैं? (ii) एक समय में सभी अक्षर लिए जाते हैं?
(iii) सभी अक्षरों का प्रयोग किया जाता है, किंतु प्रथम अक्षर एक स्वर है?
10. MISSISSIPPI शब्द के अक्षरों से बने भिन्न-भिन्न क्रमचयों में से कितनों में चारों I एक साथ नहीं आते हैं ?
11. PERMUTATIONS शब्द के अक्षरों को कितने तरीकों से व्यवस्थित किया जा सकता है, यदि
(i) चयनित शब्द का प्रारंभ P से तथा अंत S से होता है।
(ii) चयनित शब्द में सभी स्वर एक साथ हैं?
(iii) चयनित शब्द में P तथा S के मध्य सदैव 4 अक्षर हों ?
7.4 संचय (Combinations)
मान लीजिए कि 3 लॉन टेनिस खिलाड़ियों X, Y, Z का एक समूह है। 2 खिलाड़ियों की एक टीम बनानी है। इसको हम कितने प्रकार से कर सकते हैं? क्या X और Y की टीम, Y तथा X की टीम से भिन्न है ? यहाँ पर खिलाड़ियों का क्रम महत्त्वपूर्ण नहीं है। वास्तव में टीम बनाने के केवल तीन ही संभव तरीके हैं। यह XY, YZ तथा ZX हैं (आकृति 7:3)।

आकृति 7:3
यहाँ पर, प्रत्येक चयन, 3 विभिन्न वस्तुओं में से एक समय में 2 को लेकर बना हुआ, संचय कहलाता है।
किसी संचय में चयनित वस्तुओं का क्रम महत्वपूर्ण नहीं है। अब कुछ और उदाहरणों पर विचार करते हैं।
बारह व्यक्ति एक कमरे में मिलते हैं और प्रत्येक व्यक्ति अन्य सभी व्यक्तियों से हाथ मिलाता है। ‘हाथ मिलाने’ की कुल संख्या का निर्धारण हम किस प्रकार करते हैं। X का Y से हाथ मिलाना तथा Y का X से हाथ मिलाना दो भिन्न हाथ मिलाना नहीं हैं। यहाँ क्रम महत्वपूर्ण नहीं है। ‘हाथ मिलाने’ की कुल संख्या उतनी ही है, जितनी 12 विभिन्न वस्तुओं में से एक समय में 2 वस्तुओं को लेकर बनने वाले संचयों की संख्या है।
सात बिंदु एक वृत्त पर स्थित हैं। इन बिंदुओं में से किन्हीं भी दो को मिलाकर कितनी जीवाएँ खींची जा सकती हैं। यहाँ जीवाओं की कुल संख्या उतनी ही है, जितनी 7 विभिन्न वस्तुओं में से एक समय में 2 वस्तुओं को लेकर बनने वाले संचयों की संख्या है।
अब हम n विभिन्न वस्तुओं में से एक समय में r वस्तुओं को लेकर बनने वाले संचयों की संख्या, जिसे प्रतीक 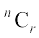 से प्रकट करते हैं, ज्ञात करने के लिए सूत्र प्राप्त करते हैं।
से प्रकट करते हैं, ज्ञात करने के लिए सूत्र प्राप्त करते हैं।
मान लीजिए कि हमारे पास 4 भिन्न-भिन्न वस्तुएँ A, B, C और D हैं। इनमें से एक समय में 2 वस्तुओं को लेकर यदि इसे संचय बनाना चाहें, तो ये संचय AB, AC, AD, BC, BD, CD हैं। यहाँ पर AB तथा BA एक ही संचय है, क्योंकि वस्तुओं का क्रम संचय को परिवर्तित नहीं करता है। इसी कारण से हमने BA, CA, DA, CB, DB तथा DC को इस सूची में सम्मिलित नहीं किया है। इस प्रकार 4 विभिन्न वस्तुओं में से एक समय में 2 वस्तुओं को लेकर बनने वाले संचयों की संख्या 6 है, अर्थात् 4C2 = 6.
इस सूची के प्रत्येक संचय के संगत, हमें 2! क्रमचय मिल सकते हैं, क्योंकि प्रत्येक संचय की 2 वस्तुओं को 2! तरीकों से पुनर्व्यवस्थित किया जा सकता है। इसलिए, क्रमचयों की संख्या= 4C2 × 2!, दूसरी तरफ 4 विभिन्न वस्तुओं में से एक समय में 2 वस्तुओं को लेकर बनने वाले क्रमचयों की संख्या = 4P2.
अतएव 4P2 = 4C2 × 2! या 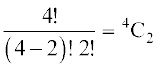
अब, मान लीजिए कि हमारे पास 5 विभिन्न वस्तुएँ A, B, C, D, E हैं। इनमें से एक समय में 3 वस्तुओं को लेकर, यदि हम संचय बनाते हैं, तो ये ABC, ABD, ABE, BCD, BCE, CDE, ACE, ACD, ADE, BDE इन 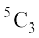 संचयों में से प्रत्येक के संगत 3! क्रमचय हैं, क्योंकि प्रत्येक संचय की तीन वस्तुओं को 3! तरीकों से पुनर्व्यवस्थित किया जा सकता है। इसलिए क्रमचयों की कुल संख्या =
संचयों में से प्रत्येक के संगत 3! क्रमचय हैं, क्योंकि प्रत्येक संचय की तीन वस्तुओं को 3! तरीकों से पुनर्व्यवस्थित किया जा सकता है। इसलिए क्रमचयों की कुल संख्या = 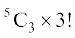
अतः 5P3 = 5C3 × 3! या 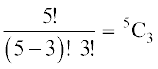
ये उदाहरण, क्रमचय तथा संचय के बीच संबंध दर्शाने वाली, निम्नलिखित प्रमेय की ओर संकेत करते हैंः
प्रमेय 5 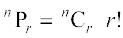 , 0 < r ≤ n.
, 0 < r ≤ n.
उपपत्ति nCr संचयों में से प्रत्येक के संगत r ! क्रमचय हैं, क्योंकि प्रत्येक संचय के r वस्तुओं को r ! तरीकों से पुनर्व्यवस्थित किया जा सकता है।
अतः n विभिन्न वस्तुओं में से, एक समय में r वस्तुओं को लेकर बनने वाले क्रमचयों की कुल संख्या nCr × r!. है। दूसरी ओर यह संख्या 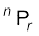 है।
है।
इस प्रकार 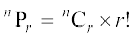 ,
, 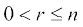 .
.
टिप्पणी 1.उपर्युक्त परिणाम से 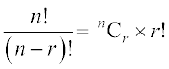 ,अर्थात्
,अर्थात् 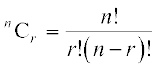 .
.
विशेष रूप से, यदि 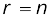 , तो
, तो 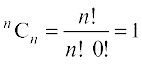 .
.
2: हम परिभाषित करते हैं कि nC0 = 1, अर्थात् n विभिन्न वस्तुओं में से केवल उन तरीकों की संख्या की गणना करना है जहाँ कुछ भी वस्तु लिए बिना बनाए गए संचयों की संख्या 1 मानी जाती है। संचयों की गणना करना, जिनमें एक समय में कुछ या सभी वस्तुओं का चयन किया जाता है। कुछ भी वस्तु लिए बिना चयन करना, इस बात के समान है कि सभी वस्तुओं को छोड़ दिया गया है और हमें ज्ञात है कि एेसा करने का केवल मात्र एक तरीका है। इसी प्रकार, हम परिभाषित करते हैं कि nC0 = 1.
3: क्योंकि  , इसलिए, सूत्र
, इसलिए, सूत्र  , r = 0 के लिए भी
, r = 0 के लिए भी
उपयुक्त है। अतः
 , 0 ≤ r ≤ n.
, 0 ≤ r ≤ n.
4:  =
= 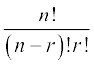 =
= 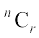 ,
,
अर्थात्, n वस्तुओं में से r वस्तुओं का चयन करना, (n – r) वस्तुओं को अस्वीकार करने के
समान है।
5: nCa = nCb ⇒ a = b या a = n – b, अर्थात् n = a + b
प्रमेय 6 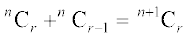
उपपत्ति हम जानते हैं 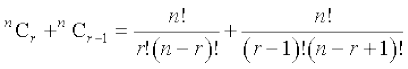
= 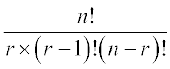 +
+ 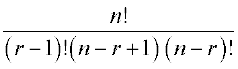
= 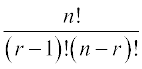

=  =
= 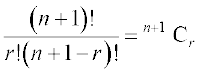
उदाहरण 17 यदि 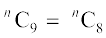 , तो
, तो 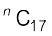 ज्ञात कीजिए।
ज्ञात कीजिए।
हल हम जानते हैं कि 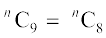
अर्थात् 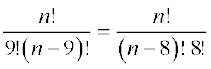
या  या n – 8 = 9 या n = 17
या n – 8 = 9 या n = 17
इसलिए  .
.
उदाहरण 18 2 पुरुषों और 3 महिलाओं के एक समूह से 3 व्यक्तियों की एक समिति बनानी है। यह कितने प्रकार से किया जा सकता है? इनमें से कितनी समितियाँ एेसी हैं, जिनमें 1 पुरुष तथा 2 महिलाएँ हैं?
हल यहाँ क्रम का महत्व नहीं है। अतः हमें संचयों की गणना करनी है। यहाँ पर समितियों की संख्या उतनी ही है, जितनी 5 विभिन्न व्यक्तियों में से एक समय में 3 को लेकर बनने वाले संचयों की संख्या है। इसलिए समिति बनाने के तरीकों की अभीष्ट संख्या = 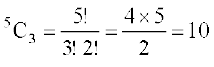 .
.
पुनः 2 पुरुषों में से 1 को चुनने के 2C1 तरीके हैं तथा 3 महिलाओं में से 2 चुनने के 3C2 तरीके हैं। इसलिए, इस प्रकार की समितियों की अभीष्ट संख्या
= 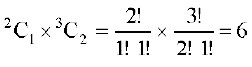 .
.
उदाहरण 19 52 ताशों की एक गड्डी से 4 पत्तों को चुनने के तरीकों की संख्या क्या है? इन तरीकों में से कितनों में
(i) चार पत्ते एक ही प्रकार (suit) के हैं?
(ii) चार पत्ते चार, भिन्न प्रकार (suit) के हैं?
(iii) तस्वीरें हैं?
(iv) दो पत्ते लाल रंग के और दो काले रंग के हैं?
(v) सभी पत्ते एक ही रंग के हैं?
हल 52 पत्तों में से 4 पत्तों को चुनने के उतने ही तरीके हैं, जितने 52 विभिन्न वस्तुओं में से एक समय में 4 वस्तुओं को ले कर बनने वाले संचय हैं। इसलिए, तरीकों की अभीष्ट संख्या
= 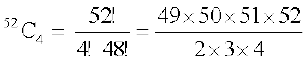 = 270725
= 270725
(i) गड्डी में पत्ते चार प्रकार के हैं ईंट, चिड़ी, हुकुम, पान और प्रत्येक के 13 पत्ते हैं। इसलिए
4 ईंट के पत्ते चुनने के 13C4 तरीके हैं। इसी प्रकार 4 चिड़ी के पत्ते चुनने के 13C4 4 हुकुम के पत्ते चुनने के 13C4 तथा 4 पान के पत्ते चुनने के 13C4 तरीके हैं। इसलिए तरीकों की अभीष्ट संख्या = 13C4 + 13C4 + 13C4 + 13C4
= 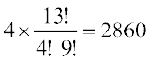
(ii) प्रत्येक प्रकार के 13 पत्ते हैं। इसलिए ईंट के 13 पत्तों में से 1 चुनने के 13C1 तरीके हैं, पान के 13 पत्तों में से 1 चुनने के 13C1, चिड़ी के 13 पत्तों में से 1 चुनने के 13C1 तरीके हैं। अतः गुणन सिद्धांत द्वारा, तरीकों की अभीष्ट संख्या
= 13C1 × 13C1 × 13C1× 13C1 = 134
(iii) गड्डी में कुल 12 तस्वीरें हैं और इन 12 पत्तों में से 4 पत्ते चुनने हैं। इसे 12C4 तरीकों से किया जा सकता है। इसलिए तरीकों की अभीष्ट संख्या = 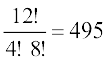 .
.
(iv) गड्डी में 26 लाल रंग के और 26 काले रंग के पत्ते हैं। अतः तरीकों की अभीष्ट संख्या
= 26C2 × 26C2
=  = 105625
= 105625
(v) 26 लाल रंग के पत्तों में से 4 पत्ते 26C4 तरीकों से चुने जा सकते हैं। 26 काले रंगे के पत्तों में से 4 पत्ते 26C4 तरीकों से चुने जा सकते हैं।
अतः तरीकों की अभीष्ट संख्या = 26C4 + 26C4 = 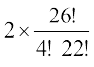 = 29900.
= 29900.
प्रश्नावली 7.4
1. यदि nC8 = nC2, तो nC2 ज्ञात कीजिए।
2. n का मान निकालिए, यदि
(i) 2nC2 : nC2 = 12 : 1 (ii) 2nC3 : nC3 = 11 : 1
3. किसी वृत्त पर स्थित 21 बिंदुओं से होकर जाने वाली कितनी जीवाएँ खींची जा सकती हैं?
4. 5 लड़के और 4 लड़कियों में से 3 लड़के और 3 लड़कियों की टीमें बनाने के कितने तरीके हैं?
5. 6 लाल रंग की, 5 सफेद रंग की और 5 नीले रंग की गेंदों में से 9 गेंदों के चुनने के तरीकों की संख्या ज्ञात कीजिए, यदि प्रत्येक संग्रह में प्रत्येक रंग की 3 गेंदें हैं।
6. 52 पत्तों की एक गड्डी में से 5 पत्तों को लेकर बनने वाले संचयों की संख्या निर्धारित कीजिए, यदि प्रत्येक संचय में तथ्यतः एक इक्का है।
7. 17 खिलाड़ियों में से, जिनमें केवल 5 खिलाड़ी गेंदबा”ाी कर सकते हैं, एक क्रिकेट टीम के 11 खिलाड़ियों का चयन कितने प्रकार से किया जा सकता है, यदि प्रत्येक टीम में तथ्यतः 4 गेंदबा”ा हैं?
8. एक थैली में 5 काली तथा 6 लाल गेंद हैं। 2 काली तथा 3 लाल गेदों के चयन के तरीकों की संख्या निर्धारित कीजिए।
9. 9 उपलब्ध पाठ्यक्रमों में से, एक विद्यार्थी 5 पाठ्यक्रमों का चयन कितने प्रकार से कर सकता है, यदि प्रत्येक विद्यार्थी के लिए 2 विशिष्ट पाठ्यक्रम अनिवार्य हैं?
विविध उदाहरण
उदाहरण 20 INVOLUTE शब्द के अक्षरों से, अर्थपूर्ण या अर्थहीन प्रत्येक 3 स्वरों तथा 2 व्यंजनों वाले, कितने शब्दों की रचना की जा सकती है?
हल शब्द INVOLUTE, में I,O,E, तथा U, 4 स्वर और N, V, L तथा T, 4 व्यंजन हैं
4 में से 3 स्वरों के चयन के तरीकों की संख्या = 4C3 = 4.
4 में से 2 व्यंजनों के चयन के तरीकों की संख्या = 4C2 = 6.
अतः 3 स्वरों तथा 2 व्यंजनों के संचय की संख्या 4 × 6 = 24.
अब, इन 24 संचयों में से प्रतयेक में 5 अक्षर हैं, जिन्हें परस्पर एक दूसरे के साथ 5! प्रकार से विन्यासित किया जा सकता है। अतएव विभिन्न शब्दों की अभीष्ट संख्या 24 × 5 ! = 2880.
उदाहरण 21 किसी समूह में 4 लड़कियाँ और 7 लड़के हैं। इनमें से 5 सदस्यों की एक टीम का चयन कितने प्रकार से किया जा सकता है, यदि टीम में (i) एक भी लड़की नहीं है ? (ii) कम से कम एक लड़का तथा एक लड़की है? (iii) कम से कम 3 लड़कियाँ हैं ?
हल (i) क्योंकि टीम में कोई भी लड़की सम्मिलित नहीं है, इसलिए केवल लड़कों का चयन करना है। 7 लड़कों में से 5 लड़कों का चयन 7C5 प्रकार से किया जा सकता है। अतः अभीष्ट संख्या
= 
(ii) क्योंकि प्रत्येक टीम में कम से कम एक लड़की तथा एक लड़का है, इसलिए टीम निम्नलिखित प्रकार से चयनित होगीः
(a) 1 लड़का तथा 4 लड़कियाँ (b) 2 लड़के तथा 3 लड़कियाँ
(c) 3 लड़के तथा 2 लड़कियाँ (d) 4 लड़के तथा 1 लड़की
1 लड़का तथा 4 लड़कियों का चयन 7C1 × 4C4 प्रकार से किया जा सकता है।
2 लड़के तथा 3 लड़कियों का चयन 7C2 × 4C3 प्रकार से किया जा सकता है।
3 लड़के तथा 2 लड़कियों का चयन 7C3 × 4C2 प्रकार से किया जा सकता है।
4 लड़के तथा 1 लड़की का चयन 7C4 × 4C1 प्रकार से किया जा सकता है।
अतः अभीष्ट संख्या = 7C1 × 4C4 + 7C2 × 4C3 + 7C3 × 4C2 + 7C4 × 4C1
= 7 + 84 + 210 + 140 = 441
(iii) क्योंकि टीम में कम से कम 3 लड़कियाँ हैं, इसलिए टीम की रचना निम्नलिखित प्रकार से हो सकती हैः
(a) 3 लड़कियाँ तथा 2 लड़के अथवा (b) 4 लड़कियाँ तथा 1 लड़का।
नोट कीजिए कि टीम में सभी 5 लड़कियाँ नहीं हो सकतीं, क्योंकि समूह में केवल
4 लड़कियाँ हैं।
3 लड़कियों तथा 2 लड़कों का चयन 4C3 × 7C2 प्रकार से किया जा सकता है।
4 लड़कियों तथा 1 लड़के का चयन 4C4 × 7C1 प्रकार से किया जा सकता है।
इसलिए अभीष्ट संख्या
= 4C3 × 7C2 + 4C4 × 7C1 = 84 + 7 = 91
उदाहरण 22 AGAIN शब्द के अक्षरों से बनने वाले, अर्थपूर्ण या अर्थहीन, शब्दों की संख्या ज्ञात कीजिए। यदि इन शब्दों को इस प्रकार लिखा जाए जिस प्रकार किसी शब्दकोश में लिखा जाता है, तो 50वाँ शब्द क्या है?
हल AGAIN शब्द में 5 अक्षर हैं, जिनमें A दो बार आता है। इसलिए शब्दों की अभीष्ट संख्या
= 
A से प्रारंभ होने वाले शब्दों की संख्या ज्ञात करने के लिए, हम A को सबसे बाएँ स्थान पर स्थिर कर देते हैं, और फिर शेष 4 भिन्न अक्षरों का, एक समय में सभी को लेकर पुनर्विन्यासित करते हैं। इन विन्यासों की संख्या उतनी ही है, जितनी 4 विभिन्न वस्तुओं से, एक समय में सभी को लेकर बनने वाले क्रमचयों की संख्या है। अतएव A से प्रारंभ होने वाले शब्दों की संख्या = 4! = 24 फिर G से प्रारंभ होने वाले शब्दों की संख्या 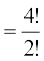 = 12 क्योंकि G को सबसे बाएँ स्थान पर स्थापित करने के बाद हमारे पास अक्षर A, A, I तथा N शेष रहते हैं। इसी प्रकार I से प्रारंभ होने वाले शब्दों की संख्या 12 है। इस प्रकार अभी तक प्राप्त शब्दों की संख्या = 24 + 12 + 12 = 48
= 12 क्योंकि G को सबसे बाएँ स्थान पर स्थापित करने के बाद हमारे पास अक्षर A, A, I तथा N शेष रहते हैं। इसी प्रकार I से प्रारंभ होने वाले शब्दों की संख्या 12 है। इस प्रकार अभी तक प्राप्त शब्दों की संख्या = 24 + 12 + 12 = 48
अब 49वाँ शब्द NAAGI है। अतः 50 वाँ शब्द NAAIG है।
उदाहरण 23 1, 2, 0, 2, 4, 2, 4 अंकों के प्रयोग द्वारा 1000000 से बड़ी कितनी संख्याएँ बन सकती हैं?
हल क्योंकि 1000000 एक 7 अंकीय संख्या है और प्रयोग किए जाने वाले अंकों की भी संख्या 7 है, इसलिए केवल 7 अंकीय संख्याओं की ही गणना उत्तर में की जाएगी। इसके अतिरिक्त क्योंकि रचित संख्याओं को 1000000 से बड़ा होना चाहिए, अतः उन संख्याओं को 1, 2 या 4 से प्रारंभ होना चाहिए।
1 से प्रारंभ होने वाली संख्याओं की संख्या = 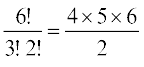 = 60, क्योंकि जब 1 को सबसे बाएँ स्थान पर स्थाεपत कर देते हैं, तो फिर शेष अंक 0, 2, 2, 2, 4, 4, को पुनर्विन्यासित करते हैं, जिनमें 2, तीन बार तथाा 4, दो बार आते हैं।
= 60, क्योंकि जब 1 को सबसे बाएँ स्थान पर स्थाεपत कर देते हैं, तो फिर शेष अंक 0, 2, 2, 2, 4, 4, को पुनर्विन्यासित करते हैं, जिनमें 2, तीन बार तथाा 4, दो बार आते हैं।
2 से प्रारंभ होने वाली संख्याओं की कुल संख्या =  = 180
= 180
4 से प्रारंभ होने वाली संख्याओं की कुल संख्या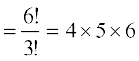 = 120
= 120
अतः रचित संख्याओं की अभीष्ट संख्या = 60 + 180 + 120 = 360
वैकल्पिक विधि
7 अंकीय संख्याओं का विन्यास स्पष्टतया 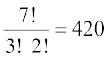 है किंतु इनमें वे संख्याएँ भी सम्मिलित हैं, जिनमें 0 सबसे बाएँ स्थान पर है। इस प्रकार के विन्यासों की संख्या
है किंतु इनमें वे संख्याएँ भी सम्मिलित हैं, जिनमें 0 सबसे बाएँ स्थान पर है। इस प्रकार के विन्यासों की संख्या  = 60 (0 के सबसे बाएँ स्थान पर स्थिर करके)।
= 60 (0 के सबसे बाएँ स्थान पर स्थिर करके)।
अतएव, संख्याओं की अभीष्ट संख्या = 420 – 60 = 360
टिप्पणी यदि प्रदत्त सूची के एक या एक से अधिक अंकों की पुनरावृत्ति होती है, तो यह मान लेते हैं, कि किसी भी संख्या में अंकों को उतनी ही बार प्रयोग किया जा सकता है जितनी बार वे सूची में दिए गए हैं, अर्थात्, उपर्युक्त प्रश्न में 1 तथा 0 केवल एक बार प्रयोग किए जा सकते हैं, जबकि 2 तथा 4, क्रमशः 3 तथा 2 बार प्रयोग किए जा सकते हैं।
उदाहरण 24 5 लड़कियों और 3 लड़कों को एक पंक्ति में कितने प्रकार से बैठा सकते हैं, जब कि कोई भी दो लड़के एक साथ नहीं बैठते हैं?
हल हम पहले 5 लड़कियों को बैठा देते हैं। इसे 5! प्रकार से कर सकते हैं। इस प्रकार के प्रत्येक विन्यास में, तीन लड़कों को केवल गुणा से चिह्नित स्थानों पर बैठाया जा सकता है।
× G × G × G × G × G ×.
गुणा से चिह्नित 6 स्थानों पर 3 लड़को को 6P3 तरीकों से बैठाया जा सकता है। अतः गुणन सिद्धांत से, इन तरीकों की कुल संख्या
= 5! × 6P3 = 
= 4 × 5 × 2 × 3 × 4 × 5 × 6 = 14400
अध्याय 7 पर विविध प्रश्नावली
1. DAUGHTER शब्द के अक्षरों से, कितने अर्थपूर्ण या अर्थहीन शब्दों की रचना की जा सकती है, जबकि प्रत्येक शब्द में 2 स्वर तथा 3 व्यंजन हों ?
2. EQUATION शब्द के अक्षरों से कितने, अर्थपूर्ण या अर्थहीन, शब्दों की रचना की जा सकती है, जबकि स्वर तथा व्यंजक एक साथ रहते हैं ?
3. 9 लड़के और 4 लड़कियों से 7 सदस्यों की एक समिति बनानी हैं यह कितने प्रकार से किया जा सकता है, जबकि समिति में,
(i) तथ्यतः 3 लड़कियाँ हैं ? (ii) न्यूनतम 3 लड़कियाँ हैं? (iii) अधिकतम 3 लड़कियाँ हैं?
4. यदि शब्द EXAMINATION के सभी अक्षरों से बने विभिन्न क्रमचयों को शब्दकोष की तरह सूचीबद्ध किया जाता है, तो E से प्रारंभ होने वाले प्रथम शब्द से पूर्व कितने शब्द हैं ?
5. 0, 1, 3, 5, 7 तथा 9 अंकों से, 10 से विभाजित होने वाली और बिना पुनरावृत्ति किए कितनी 6 अंकीय संख्याएँ बनाई जा सकती हैं ?
6. अंग्रेज़ी वर्णमाला में 5 स्वर तथा 21 व्यंजन हैं। इस वर्णमाला से 2 भिन्न स्वरों और 2 भिन्न व्यंजनो वाले कितने शब्दों की रचना की जा सकती है ?
7. किसी परीक्षा के एक प्रश्नपत्र में 12 प्रश्न हैं जो क्रमशः 5 तथा 7 प्रश्नों वाले दो खंडों में विभक्त हैं अर्थात् खंड I और खंड II. एक विद्यार्थी को प्रत्येक खंड से न्यूनतम 3 प्रश्नों का चयन करते हुए कुल 8 प्रश्नों को हल करना है। एक विद्यार्थी कितने प्रकार से प्रश्नों का चयन कर
सकता है?
8. 52 पत्तों की एक गड्डी में से 5 पत्तों के संचय की संख्या निर्धारित कीजिए, यदि 5 पत्तों के प्रत्येक चयन (संचय) में तथ्यतः एक बादशाह है।
9. 5 पुरुषों और 4 महिलाओं को एक पंक्ति में इस प्रकार बैठाया जाता है कि महिलाएँ सम स्थानों पर बैठती हैं। इस प्रकार के कितने विन्यास संभव हैं?
10. 25 विद्यार्थियों की एक कक्षा से, 10 का चयन एक भ्रमण-दल के लिए किया जाता है।
3 विद्यार्थी एेसे हैं, जिन्होंने यह निर्णय लिया है कि या तो वे तीनों दल में शमिल होंगे या उनमें से कोई भी दल में शामिल नहीं होगा। भ्रमण-दल का चयन कितने प्रकार से किया जा सकता है?
11. ASSASSINATION शब्द के अक्षरों के कितने विन्यास बनाए जा सकते हैं, जबकि सभी 'S' एक साथ रहें ?
सारांश
- गणना का आधारभूत सिद्धांतः यदि एक घटना m विभिन्न तरीकों से घटित हो सकती है, तदेपरांत एक दूसरी घटना n विभिन्न तरीकों से घटित हो सकती है, तो प्रदत्त क्रम में घटनाओं के घटित होने की संख्या m × n है।
- n विभिन्न वस्तुओं में से एक समय में r को लेकर बनने वाले क्रमचयों की संख्या, जबकि पुनरावृत्ति की अनुमति नहीं है, nPr द्वारा प्रकट की जाती है और nPr =
![]() , जहाँ 0 ≤ r ≤ n.
, जहाँ 0 ≤ r ≤ n. - n! = 1 × 2 × 3 × ...×n
- n! = n × (n – 1) !
- n विभिन्न वस्तुओं में से एक समय में r को लेकर बनने वाले क्रमचयों की संख्या, जबकि पुनरावृत्ति की अनुमति है, nr है।
- n वस्तुओं में से एक समय में सभी को लेकर बनने वाले क्रमचयों की संख्या
![]() है जहाँ p1 वस्तुएँ एक प्रकार की, p2 वस्तुएँ दूसरे प्रकार की, ..., pk वस्तुएँ k वें प्रकार की और शेष सभी वस्तुए, यदि कोई हैं तो विभिन्न प्रकार की हैंः
है जहाँ p1 वस्तुएँ एक प्रकार की, p2 वस्तुएँ दूसरे प्रकार की, ..., pk वस्तुएँ k वें प्रकार की और शेष सभी वस्तुए, यदि कोई हैं तो विभिन्न प्रकार की हैंः - n विभिन्न वस्तुओं में से एक समय में r को लेकर बनने वाले संचयों की संख्या को nCr से प्रकट करते हैं और nCr =
![]() , 0 ≤ r ≤ n.
, 0 ≤ r ≤ n.
एेतिहासिक पृष्ठभूमि
भारत में क्रमचय और संचय की संकल्पना की अवधारणा जैन धर्म के अभ्युदय और संभवतः और पहले हुई है। तथापि इसका श्रेय जैनियों को ही प्राप्त है, जिन्होंने ‘विकल्प’ शीर्षक के अंतर्गत इस विषय को गणित के स्वसंपन्न प्रकरण के रूप में विकसित किया।
जैनियों में महावीर (सन् 850 ई: के लगभग) संभवतः विश्व के प्रथम गणितज्ञ हैं, जिन्होंने क्रमचय और संचय के सूत्रों को देकर श्रेयस्कर कार्य किया।
ईसा के पूर्व छठी शताव्दी में सुश्रुत ने अपने औषधि विज्ञान की सुप्रसिद्ध पुस्तक सुश्रुत-संहिता में उद्घोषित किया कि 6 विभिन्न रसों से एक साथ एक, दो, :::, आदि लेकर 63 संचय बनाए जा सकते हैं। ईसा से तीसरी शताब्दी पूर्व संस्कृतविद् पिंगल ने दिए गए अक्षरों के समूह से एक, दो, :::, इत्यादि लेकर बनाए गए संचयों की संख्या ज्ञात करने की विधि का वर्णन अपने सुप्रसिद्ध ग्रंथ छंद सूत्र में किया है। भास्कराचार्य (जन्म 1114 ई:) ने अपनी प्रसिद्ध पुस्तक लीलावती में अंकपाश शीर्षक के अंतर्गत क्रमचय और संचय प्रकरण पर उत्कृष्ट कार्य किया है। महावीर द्वारा प्रदत्त nCr और nPr के सूत्रों के अतिरिक्त भास्कराचार्य ने विषय संबंधी अनेक प्रमेयों और परिणामों का उल्लेख किया है।
भारत के बाहर क्रमचय और संचय संबंधी प्रकरणों पर कार्य का शुभारंभ चीनी गणितज्ञों द्वारा उनकी सुप्रसिद्ध पुस्तक आई किंग (I-King ) में वर्णित है। इस कार्य के सन्निकट काल को बता पाना कठिन है, क्योंकि 213 ई: पूर्व में तत्कालीन सम्राट ने आदेश दिया था कि सभी पुस्तकें तथा हस्तलिखित पा:डुलिपियाँ जला दी जाएं। सौभाग्यवश इसका पूर्ण रूप से पालन नहीं हुआ। यूनानी और बाद में लैटिन गणितज्ञों ने भी क्रमचय और संचय के सिद्धांत पर कुछ छिटपुट कार्य किये हैं।
कुछ अरबी और हेब्रो लेखकों ने भी क्रमचय औीर संचय की संकल्पनाओं का प्रयोग ज्योतिष के अध्ययन के लिए किया। उदाहरणतः Rabbi ben Ezra ने ज्ञात ग्रहों की संख्या से एक बार में एक, दो, :::, आदि लेकर बनाए संचयों की संख्या ज्ञात की। यह कार्य 1140 ई: पूर्व में हुआ एेसा प्रतीत होता है कि Rabbi ben Ezra को nCr का सूत्र ज्ञात नहीं था, तथापि वे इससे परचित थे कि n और r के कुछ विशेष मानों के लिए nCr= nCn–r होता है। सन 1321 ई: में हीब्रु लेखक, Levi Ben Gerson ने nPr, nPn के सूत्रों के साथ nCr के व्यापक सूत्रों को बतलाया।
प्रथम ग्रंथ जिसमें क्रमचय और संचय विषय पर पूर्ण और क्रमबद्ध कार्य Ars Conjectandi है जिसका लेखन स्विस गणितज्ञ Jacob Bernoulli (1654-1705 ई:) ने किया। इसका प्रकाशन उनके मरणोपरांत 1713 ई: में हुआ। इस पुस्तक में मुख्यतः क्रमचय और संचय के सिद्धांतों का ठीक उसी प्रकार वर्णन है जैसा कि हम आजकल करते हैं।


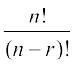 ,
,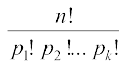
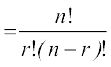 ,
,