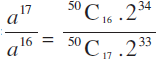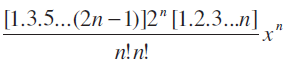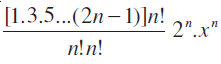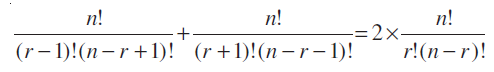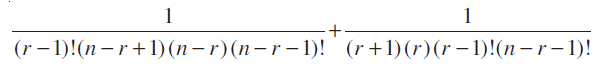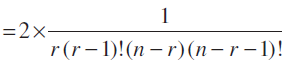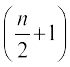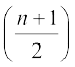Table of Contents
" Mathematics is a most exact science and its conclusions are capable of absolute proofs. – C.P. Steinmetz "
8.1 भूमिका (Introduction)
पिछली कक्षाओं में हमने सीखा है कि किस प्रकार a + b तथा a – b जैसे द्विपदों का वर्ग व घन ज्ञात करते हैं। इनके सूत्रों का प्रयोग करके हम संख्याओं के वर्गों व घनों का मान ज्ञात कर सकते हैं जैसे (98)2 = [(100 – 2)]2, (999)3 = [(1000 – 1)3], इत्यादि।
फिर भी, अधिक घात वाली संख्याओं जैसे (98)5, (101)6 इत्यादि की गणना, क्रमिक गुणनफल द्वारा अधिक जटिल हो जाती है। इस जटिलता को द्विपद प्रमेय द्वारा दूर किया गया।
इससे हमें (a + b)n के प्रसार की आसान विधि प्राप्त होती है जहाँ घातांक n एक पूर्णांक या परिमेय संख्या है। इस अध्याय में हम केवल धन पूर्णांकों के लिए द्विपद प्रमेय का अध्ययन करेंगें।
8.2 धन पूर्णांकों के लिए द्विपद प्रमेय (Binomial Theorem for Positive Integral Indices)
आइए पूर्व में की गई निम्नलिखित सर्वसमिकाओं पर हम विचार करेंः
(a + b)0 = 1; a + b  0
0
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = (a + b)3 (a + b) = a4 + 4a3b + 6a2b2 + 4ab3 + b4
इन प्रसारों में हम देखते हैं कि
(i) प्रसार में पदों की कुल संख्या, घातांक से 1 अधिक है। उदाहरणतः (a+ b)2 के प्रसार में (a + b)2 का घात 2 है जबकि प्रसार में कुल पदों की संख्या 3 है।
(ii) प्रसार के उत्तरोत्तर पदों में प्रथम a की घातें एक के क्रम से घट रही हैं जबकि द्वितीय राशि b की घातें एक के क्रम से बढ़ रही हैं।
(iii) प्रसार के प्रत्येक पद में a तथा b की घातों का योग समान है और a + b की घात के बराबर है।
अब हम a + b के उपरोक्त विस्तारों में विभिन्न पदों के गुणांकों को निम्न प्रकार व्यवस्थित करते हैं (आकृति 8.1)
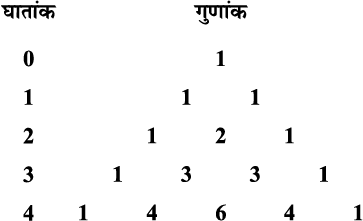
आकृति 8-1
क्या हम इस सारणी में अगली पंक्ति लिखने के लिए किसी प्रतिरूप का अवलोकन करते हैं? हाँ। यह देखा जा सकता है कि घात 1 की पंक्ति में लिखे 1 और 1 का योग घात 2 की पंक्ति के लिए 2 देता है। घात 2 की पंक्ति में लिखे 1 और 2 तथा 2 और 1 का योग घात 3 की पंक्ति के लिए 3 और 3 देता है और आगे भी इसी प्रकार 1 पुनः प्रत्येक पंक्ति के प्रारंभ व अंत में स्थित है। इस प्रक्रिया को किसी भी इच्छित घात तक के लिए लिखा जा सकता है।
हम आकृति 8.2 में दिए गए प्रतिरूप को कुछ और पंक्तियाँ लिखकर आगे बढ़ा सकते हैं।
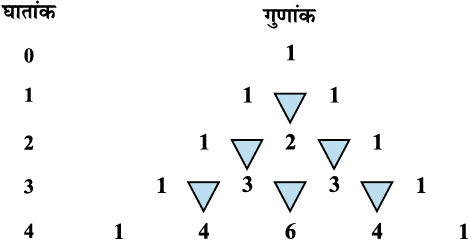
आकृति 8ण्2 पास्कल त्रिभुज
पास्कल त्रिभुज
आकृति 8.2 में दी गई सारणी को अपनी रूचि के अनुसार किसी भी घात तक बढ़ा सकते हैं। यह संरचना एक एेसे त्रिभुज की तरह लगती है जिसके शीर्ष पर 1 लिखा है और दो तिरछी भुजाएं नीचे की ओर जा रही हैं। संख्याओं का व्यूह फ्रांसीसी गणितज्ञ Blaise Pascal के नाम पर पास्कल त्रिभुज के नाम से प्रसिद्ध है। इसे पिंगल के मेरुप्रस्त्र के नाम से भी जाना जाता है।
एक द्विपद की उच्च घातों का प्रसार भी पास्कल के त्रिभुज के प्रयोग द्वारा संभव है। आइए हम पास्कल त्रिभुज का प्रयोग कर के (2x+3y)5 का विस्तार करें। घात 5 की पंक्ति हैः
1 5 10 10 5 1
इस पंक्ति का, और हमारे परीक्षणों (i), (ii), (iii), का प्रयोग करते हुए हम पाते हैं कि
(2x+3y)5 = (2x)5 + 5(2x)4 (3y) + 10(2x)3 (3y)2 +10 (2x)2 (3y)3 + 5(2x)(3y)4 + (3y)5
= 32x5 + 240x4y + 720x3y2 + 1080x2y3 + 810xy4 + 243y5.
अब यदि हम (2x+3y)12, का प्रसार ज्ञात करना चाहें तो पहले हमें घात 12 की पंक्ति ज्ञात करनी होगी। इसे पास्कल त्रिभुज की पंक्तियों को घात 12 तक की सभी पंक्तियाँ लिख कर प्राप्त किया जा सकता है। यह थोड़ी सी लंबी विधि है। जैसा कि आप देखते हैं कि और भी उच्च घातों का विस्तार करने के लिए विधि और अधिक कठिन हो जाएगी।
अतः हम एक एेसा नियम ढूँढने का प्रयत्न करते हैं जिससे पास्कल त्रिभुज की एेच्छिक पंक्ति से पहले की सारी पंक्तियों को लिखे बिना ही, द्विपद के किसी भी घात का विस्तार ज्ञात कर सकें।
इसके लिए हम पहले पढ़ चुके ‘संचय’ के सूत्रों का प्रयोग करके, पास्कल त्रिभुज में लिखी संख्याओं को पुनः लिखते हैं। हम जानते हैं कि
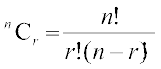 , 0
, 0 r
r  n जहाँ n ऋणेतर पूर्णांक है।
n जहाँ n ऋणेतर पूर्णांक है। 
अब पास्कल त्रिभुज को पुनः इस प्रकार लिख सकते हैं (आकृति 8ण्3)
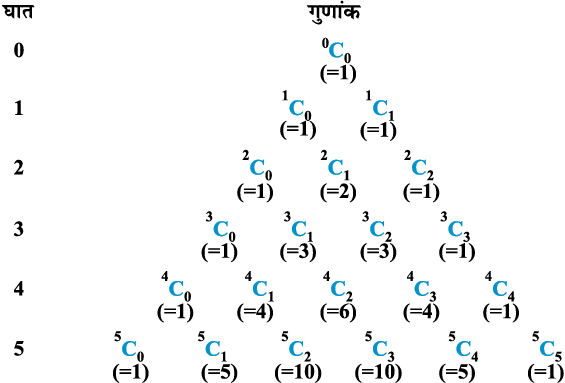
आकृति 8.3 पास्कल त्रिभुज
उपरोक्त प्रतिरूप (pattern) को देखकर, पूर्व पंक्तियों को लिखे बिना हम पास्कल त्रिभुज की किसी भी घात के लिए पंक्ति को लिख सकते हैं। उदाहरणतः घात 7 के लिए पंक्ति होगीः
7C0 7C1 7C2 7C3 7C4 7C5 7C6 7C7
इस प्रकार, इस पंक्ति और प्रेक्षण (i), (ii) व (iii), का प्रयोग करके हम पाते हैं,
(a+b)7 = 7C0 a7 + 7C1a6b + 7C2a5b2 + 7C3a4b3 + 7C4a3b4 + 7C5a2b5 + 7C6ab6 + 7C7b7
इन प्रेक्षणों का उपयोग करके एक द्विपद के किसी ऋणेतर पूर्णांक n के लिए प्रसार दिखाया जा सकता है। अब हम एक द्विपद के किसी भी (ऋणेतर पूर्णांक) घात के प्रसार को लिखने की अवस्था में हैं।
8.2.1 द्विपद प्रमेय किसी धन पूर्णांक n के लिए (Binomial theorem for any positive integer n)
(a + b)n = nC0an + nC1an-1b + nC2an-2 b2 + ...+ nCn-1a.bn-1 + nCnbn
उपपत्ति इस प्रमेय की उपपत्ति गणितीय आगमन सिद्धांत द्वारा प्राप्त की जाती है।
मान लीजिए कथन P(n) निम्नलिखित हैः
P(n) : (a + b)n = nC0an + nC1an-1b + nC2an-2b2 + ...+ nCn-1a.bn-1 + nCnbn
n = 1 लेने पर
P (1) : (a + b)1 = 1C0a1 + 1C1b1 = a + b
अतः P (1) सत्य है।
मान लीजिए कि P (k), किसी धन पूर्णांक k के लिए सत्य है, अर्थात्
(a+b)k = kC0ak + kC1ak-1b + kC2ak-2b2 + ...+ kCkbk ... (1)
हम सिद्ध करेंगें कि P(k+1) भी सत्य है अर्थात्,
(a+b)k+1 = k+1C0ak+1 + k+1C1akb + k+1C2ak-1b2 + ...+ k+1Ck+1bk+1
अब,
(a+b)k+1 = (a+b) (a+b)k
= (a+b) (kC0ak + kC1ak-1b + kC2ak–2b2+... +kCk-1abk-1 + kCkbk) [(1) से]
= kC0ak+1 + kC1akb + kC2ak–1b2 +...+ kCk–1a2bk–1 + kCkabk + kC0akb
+ kC1ak-1b2 + kC2ak–2b3+ ... + kCk-1abk + kCkbk+1 [वास्त्विक गुणा द्वारा]
= kC0ak+1 + (kC1+kC0)akb + (kC2+kC1)ak-1b2 + ...
+ (kCk+kCk-1) abk + kCkbk+1 (समान पदों के समूह बनाकर)
= k+1C0ak+1 + k+1C1akb + k+1C2 ak–1b2 + ...+ k+1Ckabk + k+1Ck+1 bk+1
(k+1C0= 1, kCr + kCr-1= k+1Cr और kCk = 1= k+1Ck+1 का प्रयोग करके)
इससे सिद्ध होता है कि यदि P(k) भी सत्य है तो P (k+1) सत्य है। इसलिए, गणितीय आगमन सिद्धांत द्वारा, प्रत्येक धन पूर्णांक n के लिए P(n) सत्य है।
हम इस प्रमेय को (x + 2)6 के प्रसार का उदाहरण लेकर समझते हैं।
(x+2)6 = 6C0x6 + 6C1x5.2 + 6C2x422 + 6C3x3.23 + 6C4x2.24 + 6C5x.25 + 6C6.26
= x6 + 12x5 +60x4 + 160x3 + 240x2 + 192x + 64
इस प्रकार, (x+2)6 = x6 + 12x5 +60x4 + 160x3 + 240x2 + 192x + 64.
प्रेक्षण
1. nC0anb0 + nC1an-1b1 + ...+ nCran–rbr + ...+nCnan–nbn, जहाँ b0 = 1 = an–n
का संकेतन 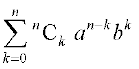 है।
है।
अतः इस प्रमेय को इस प्रकार भी लिख सकते हैं।

2. द्विपद प्रमेय में आने वाले गुणांक nCr को द्विपद गुणांक कहते हैं।
3. (a+b)n के प्रसार में पदों की संख्या (n+1) है अर्थात्् घातांक से 1 अधिक है।
4. प्रसार के उत्तरोत्तर पदों में, a की घातें एक के क्रम से घट रही हैं। यह पहले पद में n, दूसरे पद में (n–1) और फिर इसी प्रकार अंतिम पद में शून्य है। ठीक उसी प्रकार b की घातें एक के क्रम से बढ़ रही हैं, पहले पद में शून्य से शुरू होकर, दूसरे पद में 1 और फिर इसी प्रकार अंतिम पद में n पर समाप्त होती हैं।
5. (a+b)n, के प्रसार में, a तथा b की घातों का योग, पहले पद में n + 0 = n, दूसरे पद में (n – 1) + 1 = n और इसी प्रकार अंतिम पद में 0 + n = n है। अतः यह देखा जा सकता है कि प्रसार के प्रत्येक पद में a तथा b की घातों का योग n है।
8.2.2 (a + b)n के प्रसार की कुछ विशिष्ट स्थितियाँ (Some special cases)
(i) a = x तथा b = –y, लेकर हम पाते हैं;
(x – y)n = [x + (–y)]n
= nC0xn + nC1xn-1(–y) + nC2xn–2(–y)2 + nC3xn–3(–y)3 + ... + nCn (–y)n
= nC0xn – nC1xn–1y + nC2xn–2y2 – nC3xn-3y3 + ... + (–1)n nCn yn
इस प्रकार (x–y)n = nC0xn – nC1xn–1 y + nC2xn–2 y2 + ... + (–1)n nCn yn
इसका प्रयोग करके हम पाते हैं,
(x–2y)5 = 5C0x5 – 5C1x4 (2y) + 5C2x3 (2y2)
– 5C3x2 (2y)3 + 5C4 x(2y)4 – 5C5(2y)5
= x5 –10x4y + 40x3y2 – 80x2y3 + 80xy4 – 32y5
(ii) a = 1 तथा b = x, लेकर हम पाते हैं कि,
(1+x)n = nC0(1)n + nC1(1)n-1x + nC2(1)n-2x2 + ... + nCnxn
= nC0 + nC1x + nC2x2 + nC3x3 + ... + nCnxn
इस प्रकार, (1+x)n = nC0 + nC1x + nC2x2 + nC3x3 + ... + nCnxn
विशेषत x = 1, के लिए हम पाते हैं,
2n = nC0 + nC1 + nC2 + ... + nCn.
(iii) a = 1 तथा b = – x, लेकर हम पाते हैं,
(1– x)n = nC0 – nC1x + nC2x2 – ... + (–1)n nCnxn
विशेषत x = 1, के लिए हम पाते हैं,
0 = nC0 – nC1 + nC2 – ... + (–1)n nCn
उदाहरण 1 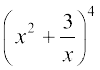 , x ≠ 0 का प्रसार ज्ञात कीजिएः
, x ≠ 0 का प्रसार ज्ञात कीजिएः
हल द्विपद प्रमेय का प्रयोग करके हमें प्राप्त होता है,
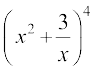 = 4C0(x2)4 + 4C1(x2)3
= 4C0(x2)4 + 4C1(x2)3  + 4C2(x2)2
+ 4C2(x2)2  + 4C3(x2)
+ 4C3(x2) 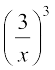 + 4C4
+ 4C4 
= x8 + 4.x6 .  + 6.x4 .
+ 6.x4 . 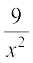 + 4.x2.
+ 4.x2.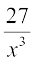 +
+ 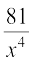
= x8 + 12x5 + 54x2 + 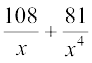
उदाहरण 2 (98)5 की गणना कीजिए।
हल हम 98 को दो संख्याओं के योग या अंतर में व्यक्त करते हैं जिनकी घात ज्ञात करना सरल हो, फिर द्विपद प्रमेय का प्रयोग करते हैं।
98 को 100 – 2 लिखने पर,
(98)5 = (100 – 2)5
= 5C0 (100)5 – 5C1 (100)4.2 + 5C2 (100)322 – 5C3 (100)2 (2)3
+ 5C4 (100) (2)4 – 5C5 (2)5
= 10000000000 – 5 × 100000000 × 2 + 10 × 1000000 × 4 – 10 ×10000
× 8 + 5 × 100 × 16 – 32
= 10040008000 – 1000800032
= 9039207968
उदाहरण 3 (1.01)1000000 और 10,000 में से कौन सी संख्या बड़ी है?
हल 1.01 को दो पदों में व्यक्त करके द्विपद प्रमेय के पहले कुछ पदों को लिखकर हम पाते हैं
(1.01)1000000 = (1 + 0.01)1000000
= 1000000C0 + 1000000C1(0.01) + अन्य धनात्मक पद
= 1 + 1000000 × 0.01 + अन्य धनात्मक पद
= 1 + 10000 + अन्य धनात्मक पद
> 10000
अतः (1.01)1000000 > 10000
उदाहरण 4 द्विपद प्रमेय का प्रयोग करके सिद्ध कीजिए कि 6n–5n को जब 25 से भाग दिया जाए तो सदैव 1 शेष बचता है।
हल दो सख्याओं a तथा b के लिए यदि हम संख्याएँ q तथा r प्राप्त कर सकें ताकि a = bq + r तो हम कह सकते हैं कि a को b से भाग करने पर q भजनफल तथा r शेषफल प्राप्त होता है। इसी प्रकार यह दर्शाने के लिए कि 6n–5n को 25 से भाग करने पर 1 शेष बचता है, हमें सिद्ध करना हैः 6n–5n = 25k+1 जहाँ k एक प्राकृत संख्या है।
हम जानते हैंः (1 + a)n = nC0 + nC1a + nC2a2 + ... + nCnan
a = 5, के लिए हमें प्राप्त होता है,
(1 + 5)n = nC0 + nC15 + nC252 + ... + nCn5n
या (6)n = 1+5n + 52.nC2 + 53.nC3 + ... + 5n
या 6n – 5n = 1+52 (nC2 + nC35 + ... + 5n-2)
या 6n – 5n = 1+ 25 (nC2 + 5 .nC3 + ... + 5n-2)
या 6n – 5n = 25k+1 जहाँ k= nC2 + 5 .nC3 + ... + 5n–2.
यह दर्शाता है कि जब 6n – 5n को 25 से भाग किया जाता है तो शेष 1 बचता है।
प्रश्नावली 8.1
प्रश्न 1 से 5 तक प्रत्येक व्यंजक का प्रसार कीजिएः 5.
1. (1–2x)5
2. 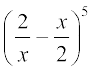
3. (2x – 3)6
4. 
5. 
द्विपद प्रमेय का प्रयोग करके निम्नलिखित का मान ज्ञात कीजिए
6. (96)3
7. (102)5
8. (101)4
9. (99)5
10. द्विपद प्रमेय का प्रयोग करते हुए बताइए कौन-सी संख्या बड़ी है (1.1)10000 या 1000.
11. (a+b)4 – (a–b)4 का विस्तार कीजिए। इसका प्रयोग करके  –
– 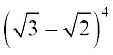 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
12. (x+1)6 + (x–1)6 का मान ज्ञात कीजिए। इसका प्रयोग करके या अन्यथा (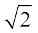 +1)6 + (
+1)6 + (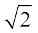 –1)6 का मान ज्ञात कीजिए।
–1)6 का मान ज्ञात कीजिए।
13. दिखाइए कि 9n+1 – 8n – 9, 64 से विभाज्य है जहाँ n एक धन पूर्णांक है।
14. सिद्ध कीजिए कि 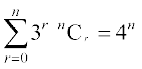
8.3 व्यापक एवं मध्य पद (General and Middle Terms)
1. (a + b)n के द्विपद प्रसार में हमने देखा है कि पहला पद nC0an है, दूसरा पद nC1an–1b है, तीसरा पद nC2an–2b2 है और आगे इसी प्रकार। इन उत्तरोत्तर पदों के प्रतिरूपों में हम कह सकते हैं कि (r + 1)वां पद nCran–rbr है। (a + b)n का (r + 1)वां पद, व्यापक पद (General term) कहलाता है। इसे Tr+1 द्वारा लिखते हैं। अतः Tr+1 = nCr an – rbr
2. (a + b)n के प्रसार के मध्य पद के बारे में हम पाते हैं
(i) यदि n सम (Even) संख्या है तो प्रसार के पदों की संख्या (n+1) होगी। क्योंकि n एक सम संख्या हैं इसलिए n + 1 एक विषम संख्या होगी। इसलिए मध्य पद  वाँ अर्थात्
वाँ अर्थात् 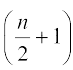 वाँ पद है।
वाँ पद है।
उदाहरणार्थ, (x + 2y)8 के प्रसार में मध्य पद 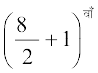 अर्थात् 5वाँ पद है।
अर्थात् 5वाँ पद है।
(ii) यदि n विषम संख्या (odd) है तो (n+1) सम संख्या है। इसलिए, प्रसार के दो मध्य पद 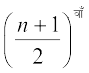 तथा
तथा  होंगे। अतः (2x–y)7 के प्रसार में मध्य पद
होंगे। अतः (2x–y)7 के प्रसार में मध्य पद 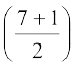 वाँ अर्थात्् चौथा और
वाँ अर्थात्् चौथा और 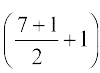 वाँ अर्थात् पाँचवाँ पद है।
वाँ अर्थात् पाँचवाँ पद है।
3. 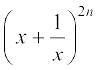 , जहाँ x
, जहाँ x 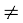 0 है, के प्रसार में मध्य पद
0 है, के प्रसार में मध्य पद 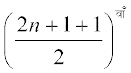 अर्थात् (n+1)वाँ पद है, क्योंकि 2n सम संख्या है।
अर्थात् (n+1)वाँ पद है, क्योंकि 2n सम संख्या है।
यह 2nCnxn  = 2nCn (अचर) द्वारा दिया जाता है।
= 2nCn (अचर) द्वारा दिया जाता है।
यह पद x से स्वतंत्र पद (Independent Term) या अचर पद (Constant term) कहलाता है।
उदाहरण 5 यदि (2+a)50 के द्विपद प्रसार का सत्रहवाँ और अट्ठारहवाँ पद समान हो तो a का मान ज्ञात कीजिए।
हल (x+y)n के द्विपद प्रसार में (r+1)वाँ पद हैः Tr+1 = nCrxn–ryr
सत्रहवें पद के लिए, r + 1 = 17, या r = 16
इसलिए T17 = T16+! = 50C16 (2)50–16 a16
= 50C16 234 a16.
इसी प्रकार T18 = 50C17 233 a17
हमें ज्ञात है कि T17 = T18
इसलिए, 50C16 (2)34 a16 = 50C17 (2)33 a17
या
या a =  =
= 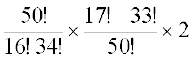 = 1
= 1
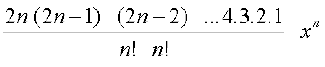
उदाहरण 6 दिखाइए कि (1+x)2n के प्रसार में मध्य पद  है, जहाँ n एक धन पूर्णांक है।
है, जहाँ n एक धन पूर्णांक है।
हल क्योंकि 2n एक सम संख्या है, इसलिए (1+x)2n का मध्य पद  वाँ अर्थात्् (n+1)वाँ पद है।
वाँ अर्थात्् (n+1)वाँ पद है।
इस प्रकार, मध्य पद Tn+1 = 2nCn(1)2n–n(x)n = 2nCnxn = 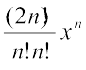
= 
= 
= 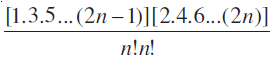
=
=
= 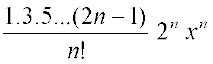
उदाहरण 7 (x+2y)9 के प्रसार में x6y3 का गुणांक ज्ञात कीजिए।
हल मान लीजिए (x+2y)9 के प्रसार में x6y3, (r+1)वें पद में आता है।
अब Tr+1 = 9Cr x9– r (2y)r = 9Cr 2 r . x9 – r . y r
Tr+1 तथा x6y3 में x और y के घातांकों की तुलना करने पर हमें प्राप्त होता है, r = 3.
इसलिए, x6y3 का गुणांक = 9C3 2 3 =  =
= 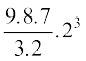 = 672.
= 672.
उदाहरण 8 (x + a)n के द्विपद प्रसार के दूसरे, तीसरे और चौथे पद क्रमशः 240, 720 और 1080 हैं। x, a तथा n ज्ञात कीजिए।
हल हमें ज्ञात है कि दूसरा पद T2 = 240
परंतु T2 = nC1xn–1 . a
इसलिए nC1xn–1 . a = 240 ... (1)
इसी प्रकार nC2xn–2 a2 = 720 ... (2)
और nC3xn–3 a3 = 1080 ... (3)
(2) को (1) से भाग करने पर हमें प्राप्त होता है,
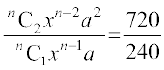 या
या 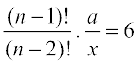
या 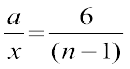 ... (4)
... (4)
(3) को (2), से भाग करने पर,
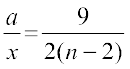 ... (5)
... (5)
(4) व (5) से, 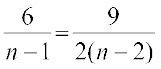 या n = 5
या n = 5
अब (1) से, 5x4a = 240 और (4) से, 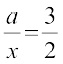
इन समीकरणों को हल करने से हम x = 2 और a = 3 प्राप्त करते हैं।
उदाहरण 9 यदि (1+a)n के प्रसार में तीन क्रमागत पदों के गुणांक 1: 7: 42 के अनुपात में हैं तो n का मान ज्ञात कीजिए।
हल मान लीजिए (1 + a)n के प्रसार में (r – 1)वाँ, rवाँ तथा (r + 1)वाँ पद, तीन क्रमागत पद हैं।
(r – 1)वाँ पद nCr–2ar–2 है तथा इसका गुणांक nCr–2 है। इसी प्रकार rवें तथा (r + 1)वें पदों के गुणांक क्रमशः nCr–1 व nCr हैं। क्योंकि गुणांको का अनुपात 1: 7: 42 है इसलिए हमें प्राप्त होता है,
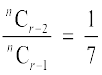 अर्थात् n – 8r + 9 = 0 ... (1)
अर्थात् n – 8r + 9 = 0 ... (1)
और 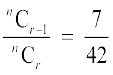 अर्थात् n – 7r + 1 = 0 ... (2)
अर्थात् n – 7r + 1 = 0 ... (2)
समीकरण (1) व (2) को हल करने पर हमें n = 55 प्राप्त होता है।
प्रश्नावली 8.2
गुणांक ज्ञात कीजिएः
1. (x + 3)8 में x5 का
2. (a – 2b)12 में a5b7 का
निम्नलिखित के प्रसार में व्यापक पद लिखिएः
3. (x2 – y)6
4. (x2 – yx)12, x 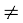 0
0
5. (x – 2y)12 के प्रसार में चौथा पद ज्ञात कीजिए।
6. 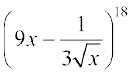 के प्रसार में 13वाँ पद ज्ञात कीजिए।
के प्रसार में 13वाँ पद ज्ञात कीजिए।
निम्नलिखित प्रसारों में मध्य पद ज्ञात कीजिएः
7. 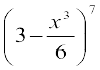
8. 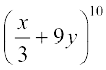
9. (1 + a)m+n के प्रसार में सिद्ध कीजिए कि am तथा an के गुणांक बराबर हैं।
10. यदि (x + 1)n के प्रसार में (r – 1)वाँ , rवाँ और (r + 1)वाँ पदों के गुणांकों में 1: 3: 5 का अनुपात हो, तो n तथा r का मान ज्ञात कीजिए।
11. सिद्ध कीजिए कि (1 + x)2n के प्रसार में xn का गुणांक, (1 + x)2n–1 के प्रसार में xn के गुणांक का दुगना होता है।
12. m का धनात्मक मान ज्ञात कीजिए जिसके लिए (1 + x)m के प्रसार में x2 का गुणांक 6 हो।
विविध उदाहरण
उदाहरण 10  के प्रसार में x से स्वतंत्र पद ज्ञात कीजिए।
के प्रसार में x से स्वतंत्र पद ज्ञात कीजिए।
हल हम पाते हैं कि Tr+1 = 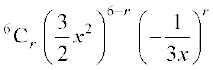
= 
= 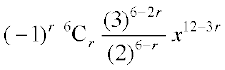
x से स्वतंत्र पद के लिए, पद में x का घातांक 0 (होना चाहिए)। अतः 12 – 3r = 0 या r = 4
इस प्रकार 5वाँ पद x से स्वतंत्र है। इसलिए अभीष्ट पद = (–1)4 6C4 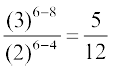
उदाहरण 11 यदि (1 + a)n के प्रसार में ar-1, ar तथा ar+1 के गुणांक समांतर श्रेणी में हों तो सिद्ध कीजिए कि n2 – n(4r + 1) + 4r2–2 = 0
हल हम जानते हैं कि (1 + a)n के प्रसार में (r + 1)वाँ पद nCrar है। इस प्रकार यह देखा जा सकता है कि ar, (r + 1)वें पद में आता है। और इसका गुणांक nCr है। इसलिए ar–1, ar तथा ar+1 के गुणांक क्रमशः nCr–1 , nCr तथा nCr+1 हैं। परंतु ये गुणांक समांतर श्रेणी में हैं। इसलिए
nCr–1+ nCr+1 = 2nCr
या
या
या 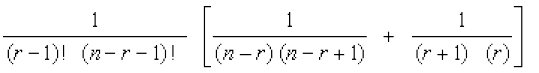
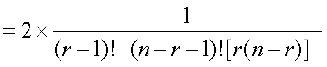
या 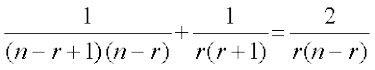
या 
या r(r + 1) + (n – r) (n – r + 1) = 2 (r + 1) (n – r + 1)
या r2 + r + n2 – nr + n – nr + r2 – r = 2(nr – r2 + r + n – r + 1)
या n2 – 4nr – n + 4r2 – 2 = 0
या n2 – n (4r + 1) + 4r2 – 2 = 0
उदाहरण 12 दिखाइए कि (1 + x)2n के प्रसार में मध्य पद का गुणांक, (1 + x)2n–1 के प्रसार में दोनों मध्य पदों के गुणांकों के योग के बराबर होता है।
हल क्योंकि 2n एक सम संख्या है इसलिए (1+x)2n के प्रसार में केवल एक मध्य पद है जो कि 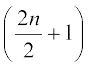 वाँ अर्थात् (n + 1)वाँ पद है।
वाँ अर्थात् (n + 1)वाँ पद है।
अब (n+1)वाँ पद 2nCnxn है जिसका गुणांक 2nCn है।
इसी प्रकार, (2n–1) एक विषम संख्या है इसलिए (1 + x)2n–1 के प्रसार के दो मध्य पद 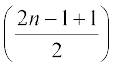 वाँ और
वाँ और  वाँ अर्थात् nवाँ और (n + 1) वाँ पद है।
वाँ अर्थात् nवाँ और (n + 1) वाँ पद है।
इन पदों के गुणांक क्रमशः 2n–1Cn–1 और 2n–1Cn हैं।
इस प्रकार 2n–1Cn–1 + 2n–1Cn= 2nCn [क्योंकि nCr–1+ nCr = n+1Cr]
यही अभीष्ट है।
उदाहरण 13 द्विपद प्रमेय का उपयोग करते हुए गुणनफल (1 + 2a)4 (2 – a)5 में a4 का गुणांक ज्ञात कीजिए।
हल सबसे पहले हम गुणनफल के प्रत्येक में द्विपद प्रमेय गुणनखंड प्रयोग कर प्रसारण करते हैं। इस प्रकार
(1+2a)4 = 4C0+4C1 (2a) + 4C2 (2a)2 + 4C3 (2a)3+ 4C4 (2a)4
= 1+4 (2a)+6 (4a2) + 4 (8a3) + 16a4.
= 1+8 a+24a2+3 2a3 + 16a4
और (2–a)5 = 5C0 (2)5 – 5C1 (2)4 (a) + 5C2 (2)3 (a)2 – 5C3 (2)2 (a)3
+ 5C4 (2) (a)4 – 5C5 (a)5
= 32 – 80a + 80a2 – 40a3+10a4 – a5
इस प्रकार, (1+2a)4 (2–a)5
= (1+8a + 24a2 + 32a3 + 16a4) (32–80a + 80a2 – 40a3 + 10a4 – a5)
हमें संपूर्ण गुणा करने तथा सभी पदों के लिखने की आवश्यकता नहीं है। हम केवल वही पद लिखते हैं जिनमें a4 आता है। यदि ar.a4–r = a4 तो यह किया जा सकता है। जिन पदों में a4 आता है, वे हैंः
1.10a4 + (8a) (–40a3) + (24a2) (80a2) + (32a3) (–80a) + (16a4) (32) = – 438a4
अतः गुणनफल में a4 का गुणांक – 438 है।
उदाहरण 14 (x+a)n के प्रसार में अंत से rवाँ पद ज्ञात कीजिए।
हल (x + a)n के प्रसार में (n + 1) पद हैं। पदों का अवलोकन करते हुए हम कह सकते हैं कि अंत में पहला पद प्रसार का अंतिम पद हैं अर्थात् (n + 1)वाँ पद (n + 1) – (1–1) है। अंत से दूसरा पद, प्रसार का nवाँ पद n=(n + 1) – (2 – 1) है। अंत से तीसरा पद, प्रसार का (n–1)वाँ पद है और
n–1 = (n+1) – (3 – 1). इसी प्रकार, अंत से rवाँ पद, प्रसार का [(n+1) – (r – 1)]वाँ पद अर्थात्् (n– r + 2)वाँ पद होगा।
और प्रसार का (n–r+2)वाँ पद nCn–r+1 xr–1 an–r+1 है।
उदाहरण 15 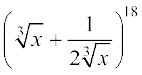 , x > 0 के प्रसार में x से स्वतंत्र पद ज्ञात कीजिए।
, x > 0 के प्रसार में x से स्वतंत्र पद ज्ञात कीजिए।
हल प्रसार का व्यापक पद
Tr+1 = 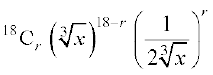
= 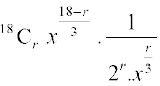 =
= 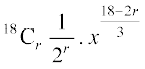
क्योंकि हमें x से स्वतंत्र पद ज्ञात करना है अर्थात् उस पद में x नहीं है।
इसलिए 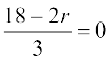 या r = 9
या r = 9
अतः अभीष्ट पद 18C9 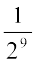 है।
है।
उदाहरण 16 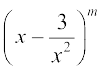 , x ≠ 0, जहाँ m एक प्राकृत संख्या है, के प्रसार में पहले तीन पदों के गुणांकों का योग 559 है। प्रसार में x3 वाला पद ज्ञात कीजिए।
, x ≠ 0, जहाँ m एक प्राकृत संख्या है, के प्रसार में पहले तीन पदों के गुणांकों का योग 559 है। प्रसार में x3 वाला पद ज्ञात कीजिए।
हल 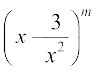 के प्रसार के पहले तीन पदों के गुणांक mC0 , (–3) mC1 और 9 mC2 हैं।
के प्रसार के पहले तीन पदों के गुणांक mC0 , (–3) mC1 और 9 mC2 हैं।
इसलिए दिए गए प्रतिबंध के अनुसार mC0 –3 mC1+ 9 mC2= 559.
या 1 – 3m +  इससे हमें m = 12 (m एक प्राकृत संख्या है) प्राप्त होता है।
इससे हमें m = 12 (m एक प्राकृत संख्या है) प्राप्त होता है।
अब Tr+1 = 12Cr x12–r  = 12Cr (–3)r . x12–3r
= 12Cr (–3)r . x12–3r
क्योंकि हमें x3 वाला पद चाहिए। अतः 12 – 3r = 3 या r = 3.
इस प्रकार, अभीष्ट पद = 12C3 (–3)3 x3 अर्थात् – 5940 x3 है।
उदाहरण 17 यदि (1+x)34 के प्रसार में (r–5)वें और (2r–1)वें पदों के गुणांक समान हों r ज्ञात कीजिए।
हल (1+x)34 के प्रसार में (r–5)वें तथा (2r–1)वें पदों के गुणांक क्रमशः 34Cr–6 और 34C2r–2 हैं। क्योंकि वे समान हैं, इसलिए
34Cr–6 = 34C2r–2
यह तभी संभव है जबकि या r – 6 = 2r – 2 या r–6 = 34 – (2r – 2) हो।
[इस तथ्य का प्रयोग करके कि यदि nCr=nCp हो तो r = p या r = n–p]
इसलिए, हमें r = – 4 या r = 14 प्राप्त हुआ परंतु r प्राकृत संख्या है और r = –4 संभव नहीं है।
अतः r = 14
अध्याय 8 पर विविध प्रश्नावली
1. यदि (a + b)n के प्रसार में प्रथम तीन पद क्रमशः 729, 7290 तथा 30375 हों तो a, b, और n ज्ञात कीजिए।
2. यदि (3 + ax)9 के प्रसार में x2 तथा x3 के गुणांक समान हों, तो a का मान ज्ञात कीजिए।
3. द्विपद प्रमेय का उपयोग करते हुए गुणनफल (1+2x)6 (1–x)7 में x5 का गुणांक ज्ञात कीजिए।
4. यदि a और b भिन्न-भिन्न पूर्णांक हों, तो सिद्ध कीजिए कि (an – bn) का एक गुणनखंड
(a – b)है, जबकि n एक धन पूर्णांक है।
[ संकेत an = (a – b + b)n लिखकर प्रसार कीजिए।]
5.  का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
6.  का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
7. (0.99)5 के प्रसार के पहले तीन पदों का प्रयोग करते हुए इसका निकटतम मान ज्ञात कीजिए।
8. यदि 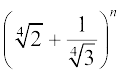 के प्रसार में आरंभ से 5वें और अंत से 5वें पद का अनुपात
के प्रसार में आरंभ से 5वें और अंत से 5वें पद का अनुपात 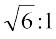 हो तो n ज्ञात कीजिए।
हो तो n ज्ञात कीजिए।
9. 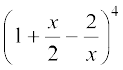 x ≠ 0 का द्विपद प्रमेय द्वारा प्रसार ज्ञात कीजिए।
x ≠ 0 का द्विपद प्रमेय द्वारा प्रसार ज्ञात कीजिए।
10. (3x2 – 2ax + 3a2)3 का द्विपद प्रमेय से प्रसार ज्ञात कीजिए।
सारांश
- एक द्विपद का किसी भी धन पूर्णांक n के लिए प्रसार द्विपद प्रमेय द्वारा किया जाता है। इस प्रमेय के अनुसार (a + b)n = nC0an + nC1an–1b + nC2an–2b2 + ...+ nCn–1a.bn–1 + nCnbn
- प्रसार के पदों के गुणांकों का व्यवस्थित क्रम पास्कल त्रिभुज कहलाता है।
- (a + b)n के प्रसार का व्यापक पद Tr+1 = nCran–r.br है।
- (a+b)n के प्रसार में, यदि n सम संख्या हो तो मध्य पद
![]() वाँ पद है और यदि n विषम संख्या है तो दो मध्य पद
वाँ पद है और यदि n विषम संख्या है तो दो मध्य पद ![]() वाँ तथा
वाँ तथा ![]() वाँ हैं।
वाँ हैं।
एेतिहासिक पृष्ठभूमि
प्राचीन भारतीय गणितज्ञ (x+y)n, 0 ≤ n ≤ 7, के प्रसार में गुणांकों को जानते थे। ईसा पूर्व दूसरी शताब्दी में पिंगल ने अपनी पुस्तक छंद शास्त्र (200ई॰ पू॰) में इन गुणांकों को एक आकृति, जिसे मेरुप्रस्त्र कहते हैं, के रूप में दिया था। 1303ई॰ में चीनी गणितज्ञ Chu-shi-kie के कार्य में भी यह त्रिभुजाकार विन्यास पाया गया। 1544 के लगभग जर्मन गणितज्ञ Michael Stipel (1486-1567 ई॰) ने सर्वप्रथम ‘द्विपद गुणांक’ शब्द को प्रारंभ किया। Bombelli (1572 ई॰) ने भी, n = 1,2, ..., 7 के लिए तथा Oughtred (1631 ई॰) ने n = 1, 2,..., 10 के लिए, (a + b)n के प्रसार में गुणांकों को बताया। पिंगल के मेरुप्रस्त्र के समान थोड़े परिवर्तन के साथ लिखा हुआ अंकगणितीय त्रिभुज जो पास्कल त्रिभुज के नाम से प्रचलित है, यद्यपि बहुत बाद में फ्रांसीसी मूल के गणितज्ञ Blaise Pascal
(1623–1662 ई॰) ने बनाया। उन्होंने द्विपद प्रसार के गुणांकों को निकालने के लिए त्रिभुज का प्रयोग किया।
n के पूर्णांक मानों के लिए द्विपद प्रमेय का वर्तमान स्वरूप पास्कल द्वारा लिखित पुस्तक Trate du triange arithmetic में प्रस्तुत हुआ जो 1665 में उनकी मृत्यु के बाद प्रकाशित हुई।