Table of Contents
“Natural numbers are the product of human spirit” – Dedekind
9.1 भूमिका (Introduction)
गणित में, शब्द ‘अनुक्रम’ का उपयोग साधारण अँग्रेाी के समान किया जाता है। जब हम कहते हैं कि समूह के अवयवों को अनुक्रम में सूचीबद्ध किया गया है तब हमारा तात्पर्य है कि समूह को इस प्रकार क्रमिक किया गया है कि हम उसके सदस्यों को प्रथम, द्वितीय, तृतीय संख्या तथा आदि से पहचान सकते हैं। उदाहरणत:, विभिन्न समयों में मानव की जनसंख्या अथवा बैक्टीरिया अनुक्रम की रचना करते हैं। कोई धनराशि जो बैंक खातें में जमा कर दी जाती है, विभिन्न वर्षों में एक अनुक्रम का निर्माण करती है। किसी सामान की अवमूल्यित कीमतें एक अनुक्रम बनाती हैं मानव क्रियाओं के कई क्षेत्रों में अनुक्रमों का बहुत महत्त्वपूर्ण उपयोग है। विशिष्ट पैटर्नों का अनुसरण करने वाले अनुक्रम Js.kh (Progression) कहलाते हैं। पिछली कक्षा में, हम समांतर श्रेणी के संबंध में पढ़ चुके हैं। इस अध्याय में समांतर श्रेणी के बारे में और अधिक चर्चा करने के साथ-साथ हम समांतर माध्य, गुणोत्तर माध्य, समांतर माध्य तथा गुणोत्तर माध्य में संबंध, विशेष अनुक्रमों के क्रमागत n प्राकृत संख्याओं का योग, n प्राकृत संख्याआं के वगाेρं का योग तथा n प्राकृत संख्याओं के घनों के योग का भी अध्ययन करेंगे।

(1175-1250 A.D.)
9.2 अनुक्रम (Sequence)
आइए हम निम्नलिखित उदाहरणों पर विचार करें:
माना कि पीढ़ियों का अंतर 30 वर्ष है और व्यक्ति के 300 वर्षाें में पूर्वजों अर्थात् माता-पिता दादा-दादी, परदादा-परदादी अादि की संख्या ज्ञात कीजिए।
यहाँ पीढ़ियों की कुल संख्या = 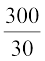 = 10.
= 10.
प्रथम, द्वितीय, तृतीय, ... दसवीं पीढ़ी के लिए व्यक्ति के पूर्वजों की संख्या क्रमश: 2ए 4ए 8ए 16ए 32ए ...ए 1024 है। ये संख्याएँ एक अनुक्रम का निर्माण करती हैं, एेसा हम कहते हैं।
10 को 3 से भाग देते समय विभिन्न चरणाें के बाद प्राप्त क्रमिक भागफलों पर विचार कीजिए। इस प्रक्रिया में हम क्रमश: 3,3.3,3.33,3.333... आदि पाते हैं ये भागफल भी एक अनुक्रम का निर्माण करते हैं। एक अनुक्रम में जो संख्याएँ आती हैं उन्हें हम उसका in कहते हैं। अनुक्रम के पदों को हम a1, a2, a3,…, an, …, आदि द्वारा निरूपित करते हैं। प्रत्येक पद के साथ लगी संख्या जिसे inkad कहते हैं, उसका स्थान बताती है। अनुक्रम का nवाँ पद nवें स्थान को निरूपित करता है और इसे an द्वारा निरूपित करते हैं, इसे अनुक्रम का व्यापक पद भी कहते हैं।
इस प्रकार, व्यक्ति के पूर्वजों (पुर्वजों) के अनुक्रम के पदों को निम्न प्रकार से निरूपित करते हैं:
a1 = 2, a2 = 4, a3 = 8, …, a10 = 1024.
इसी प्रकार क्रमिक भागफलों वाले उदाहरण में:
a1 = 3, a2 = 3.3, a3 = 3.33, … a6 = 3.33333, आदि।
वे अनुक्रम, जिनमें पदों की संख्या सीमित होती हैं, उसे ‘परिमित अनुक्रम’ कहते हैं। उदाहरणत: पूर्वजों का अनुक्रम परिमित अनुक्रम है, क्योंकि उसमें 10 पद हैं (सीमित संख्या)।
एक अनुक्रम, ‘‘अपरिमित अनुक्रम कहा जाता है, जिसमें पदों की संख्या सीमित नहीं होती है।’’ उदाहरणत: पूर्वोक्त क्रमागत भागफलों का अनुक्रम एक ‘अपरिमित अनुक्रम’ है। अपरिमित कहने का अर्थ है, जो कभी समाप्त नहीं होता।
प्राय: यह संभव है कि अनुक्रम के विभिन्न पदों को व्यक्त करने के नियम को एक बीज गणितीय सूत्र द्वारा व्यक्त किया जा सकता है। उदाहरणार्थ, प्राकृत सम संख्याओं के अनुक्रम 2, 4, 6, … पर विचार कीजिए।
यहाँ a1 = 2 = 2 × 1 a2 = 4 = 2 × 2
a3 = 6 = 2 × 3 a4 = 8 = 2 × 4
.... .... .... .... .... ....
.... .... .... .... .... ....
a23 = 46 = 2 × 23 a24 = 48 = 2 = 2 × 24, और इसी प्रकार अन्य।
वस्तुत:, हम देखते हैं कि अनुक्रम का nवाँ पद aद = 2n, लिखा जा सकता हैं, जबकि n एक प्राकृत संख्या है। इसी प्रकार, विषम प्राकृत संख्याओं के अनुक्रम 1,3,5,7,…, में nवें पद के सूत्र को an = 2n – 1, के रूप में निरूपित किया जा सकता है, जबकि n एक प्राकृत संख्या है।
व्यवस्थित संख्याओं 1, 1, 2, 3, 5, 8,.. का कोई स्पष्ट पैटर्न नहीं है, किंतु अनुक्रम की रचना पुनरावृत्ति संबंध द्वारा व्यक्त की जा सकती हैं। उदाहरणत:
a1 = a2 = 1
a3 = a1 + a2
an = an–2 + an–1, n > 2
इस अनुक्रम को Fibonacci अनुक्रम कहते हैं।
अभाज्य संख्याओं के अनुक्रम 2,3,5,7… में nवीं अभाज्य संख्या का कोई सूत्र नहीं हैं। एेसे वर्णित अनुक्रम को केवल मौखिक निरूपित किया जा सकता हैं।
प्रत्येक अनुक्रम में यह अपेक्षा नहीं की जानी चाहिए कि उसके लिए विशेष सूत्र होगा। किंतु फिर भी एेसे अनुक्रम के निर्माण के लिए कोई न कोई सैद्धांतिक योजना अथवा नियम की आशा तो की जा सकती है, जो पदों a1, a2, a3,…,an,… का क्रमागत रूप दे सके।
उपर्युक्त तथ्यों के आधार पर, एक अनुक्रम को हम एक फलन के रूप में ले सकते हैं जिसका प्रांत प्राकृत संख्याओं का समुच्चय हो अथवा उसका उपसमुच्चय हो। कभी-कभी हम फलन के संकेत an के लिए a(n) का उपयोग करते हैं।
9.3 श्रेणी (Series)
माना कि यदि a1, a2, a3,…,aद अनुक्रम है, तो व्यंजक a1 + a2 + a3 +,…+ an संबंधित अनुक्रम से बनी श्रेणी कहलाती हैं। श्रेणी परिमित अथवा अपरिमित होगी, यदि अनुक्रम क्रमश: परिमित अथवा अपरिमित है। श्रेणी को संधि रीति में प्रदर्शित करते हैं, जिसे सिग्मा संकेत कहते हैं। इसके लिए ग्रीक अक्षर संकेत 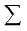 (सिग्मा) का उपयोग करते हैं, जिसका अर्थ होता हैं जोड़ना। इस प्रकार, श्रेणी
(सिग्मा) का उपयोग करते हैं, जिसका अर्थ होता हैं जोड़ना। इस प्रकार, श्रेणी
a1 + a2 + a3 + ... + an का संक्षिप्त रूप, 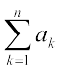 . है।
. है।
टिप्पणी श्रेणी का उपयोग, योग के लिए नहीं, बल्कि निरूपित योग के लिए किया जाता है।
उदाहरणत: 1 + 3 + 5 + 7 चार पदों वाली एक परिमित श्रेणी है। जब हम ‘श्रेणी का योग’ मुहावरे का उपयोग करते हैं, तब उसका तात्पर्य उस संख्या से है जो पदों के जोड़ने से परिणित होती है। अत: श्रेणी का योग 16 है।
अब हम कुछ उदाहरणों पर विचार करते हैं।
उदाहरण 1 दी गई परिभाषाओं के आधार पर निम्नलिखित प्रत्येक अनुक्रम के प्रथम तीन पद बताइए:
(i) an = 2n + 5
(ii) an = 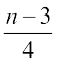 .
.
हल (1) यहाँ an = 2n + 5,
n=1,2,3, रखने पर, हम पाते हैं:
a1 = 2(1) + 5 = 7, a2 = 9, a3 = 11
इसलिए, वांछित पद 7, 9 तथा 11 हैं।
(ii) यहाँ an = 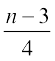
इस प्रकार 
अत: प्रथम तीन पद 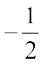 ,
, 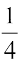 तथा 0 हैं।
तथा 0 हैं।
उदाहरण 2 an = (n – 1) (2 – n) (3 + n) द्वारा परिभाषित अनुक्रम का 20वाँ पद क्या हैं?
हल हम n = 20 रखने पर, पाते हैं
a20 = (20 – 1) (2 – 20) (3 + 20)
= 19 * (– 18) * (23)
= – 7866.
उदाहरण 3 माना कि अनुक्रम an निम्नलिखित रूप में परिभाषित है:
a1 = 1,
an = an–1 + 2 for n  2.
2.
तो अनुक्रम के पाँच पद ज्ञात कीजिए तथा संगत श्रेणी लिखिए।
हल हम पाते हैं:
a1 = 1, a2 = a1 + 2 = 1 + 2 = 3, a3 = a2 + 2 = 3 + 2 = 5,
a4 = a3 + 2 = 5 + 2 = 7, a5 = a4 + 2 = 7 + 2 = 9.
अत: अनुक्रम के प्रथम पाँच पद 1,3,5,7 तथा 9 हैं।
संगत श्रेणी 1 + 3 + 5 + 7 + 9 +... है।
प्रश्नावली 9.1
प्रश्न 1 से 6 तक के अनुक्रमों में प्रत्येक के प्रथम पाँच पद लिखिये, जिनका nवाँ पद दिया गया है:
1. an = n (n + 2) 2. an = 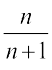 3. an = 2द
3. an = 2द
4. an = 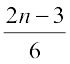 5. an = (–1)n–1 5n+1 6. an
5. an = (–1)n–1 5n+1 6. an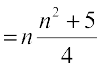 .
.
निम्नलिखित प्रश्न 7 से 10 तक के अनुक्रमों में प्रत्येक का वांछित पद ज्ञात कीजिए, जिनका nवाँ पर दिया गया है:
7. an = 4n – 3; a17, a24 8. an = 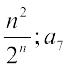
9. an = (–1)n – 1n3; a9 10. 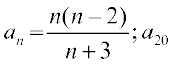 .
.
प्रश्न 11 से 13 तक प्रत्येक अनुक्रम के पाँच पद लिखिए तथा संगत श्रेणी ज्ञात कीजिए:
11. a1 = 3, an = 3an–1 + 2 सभी n > 1 के लिए
12. a1 = –1, an = 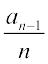 , जहाँ n
, जहाँ n 2
2
13. a1 = a2 = 2, an = aद–1–1, जहाँ n 2
2
14. Fibonacci अनुक्रम निम्नलिखित रूप में परिभाषित है:
1 = a1 = a2 तथा an = an–1 + an–2, n.>2 तो
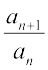 ज्ञात कीजिए, जबकि n = 1, 2, 3, 4, 5
ज्ञात कीजिए, जबकि n = 1, 2, 3, 4, 5
9.4 समांतर श्रेणी [Arithmetic Progression (A.P.)]
पूर्व में अध्ययन किए कुछ सूत्रों तथा गुणों का पुन: स्मरण करते हैं।
एक अनुक्रम a1, a2 a3,…,an… को समांतर अनुक्रम या समांतर श्रेणी कहते हैं, यदि
an+1 = an + d, n  N
N
a1 को प्रथम पद कहते हैं तथा अचर पद d को समांतर श्रेणी का सार्व अंतर कहते हैं।
मान लीजिए एक समांतर श्रेणी (प्रमाणित रूप में) पर विचार करें, जिसका प्रथम पद a, तथा सार्व अंतर d है, अर्थात् a, a + d, a + 2d, ...समांतर श्रेणी का nवाँ पद (व्यापक पद) an = a + (n – 1)d है।
हम समांतर श्रेणी की सामान्य विशेषताओं का परीक्षण कर सकते हैं:
(1) यदि समांतर श्रेणी के प्रत्येक पद में एक अचर जोड़ा जाए, तो इस प्रकार प्राप्त अनुक्रम भी समांतर श्रेणी होता है।
(ii) यदि किसी समांतर श्रेणी के प्रत्येक पद में से एक अचर घटाया जाए तो, इस प्रकार प्राप्त अनुक्रम भी समांतर श्रेणी होता है।
(iii) यदि किसी समांतर श्रेणी के प्रत्येक पद में एक अचर से गुणा किया जाए तो, इस प्रकार प्राप्त अनुक्रम भी समांतर श्रेणी होता है।
(iv) यदि किसी समांतर श्रेणी के प्रत्येक पद को एक अशून्य अचर से भाग दिया जाए तो इस प्रकार प्राप्त अनुक्रम भी एक समांतर श्रेणी होगा।
यहाँ इसके बाद, हम समांतर श्रेणी के लिए निम्नलिखित संकेतों का उपयोग करेंगे:
a = प्रथम पद, l = अंतिम पद, d = सार्व अंतर
n = पदों की संख्या, Sn = समांतर श्रेणी के n पदों का योगफल
माना a, a + d, a + 2d, …, a + (n – 1) d एक समांतर श्रेणी है, तो
l = a + (n – 1) d
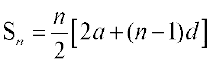
हम इस प्रकार भी लिख सकते हैं:
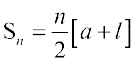
आइए कुछ उदाहरण लेते हैं।
उदाहरण 4 यदि किसी समांतर श्रेणी का mवाँ पद n तथा nवाँ पद m, जहाँ m 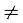 n, हो तो pवाँ पद ज्ञात कीजिए।
n, हो तो pवाँ पद ज्ञात कीजिए।
हल हम पाते हैं:
am = a + (m – 1) d = n, ... (1)
तथा an = a + (n – 1) d = m, ... (2)
(1) और (2) को हल करने पर, हम पाते हैं:
(m – n) d = n – m, या d = –1, ... (3)
तथा a = n + m –1 ... (4)
इसलिए
ap = a + (p – 1)d
= n + m – 1 +( p – 1) (–1) = n + m – p
अत: , p वाँ पद n + m – p. है।
उदाहरण 5 यदि किसी समांतर श्रेणी के n पदों का योग 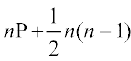 Q, है, जहाँ P तथा Q अचर हो तो सार्व अंतर ज्ञात कीजिए।
Q, है, जहाँ P तथा Q अचर हो तो सार्व अंतर ज्ञात कीजिए।
हल माना कि a1, a2, …, an दी गई समांतर श्रेणी है, तो
Sn = a1 + a2 + a3 +...+ an–1 + an = nP +  n(n – 1)Q
n(n – 1)Q
इसलिए S1 = a1 = P, S2 = a1 + a2 = 2P + Q
इसलिए a2 = S2 – S1 = P + Q
अत: सार्व अंतर है: d = a2 – a1 = (P + Q) – P = Q
उदाहरण 6 दाे समांतर श्रेढ़ियों के n पदों के योगफल का अनुपात (3n + 8) : (7n + 15) है। 12 वें पद का अनुपात ज्ञात कीजिए।
हल माना कि a1, a2, तथा d1, d2, क्रमश: प्रथम एवं द्वितीय समांतर श्रेढ़ियों के प्रथम पद तथा सार्व अंतर हैं, तो दी हुई शर्त के अनुसार, हम पाते हैं:

या 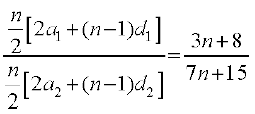
या 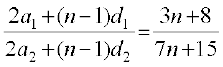 ... (1)
... (1)
अब 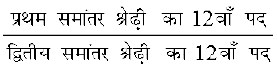
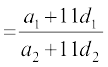
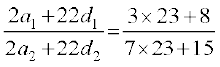 [(1) में n = 23 रखने पर]
[(1) में n = 23 रखने पर]
या 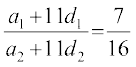
अत: वांछित अनुपात 7 : 16 है।
उदाहरण 7 एक व्यक्ति की प्रथम वर्ष में आय 3,00,000 रुपये है तथा उसकी आय 10,000 रुपये प्रति वर्ष, उन्नीस वर्षों तक बढ़ती है, तो उसके द्वारा 20 वर्षों में प्राप्त आय ज्ञात कीजिए।
हल यहाँ, हम पाते हैं, समांतर श्रेणी जिसका
a = 3,00,000, d = 10,000, तथा n = 20
योग सूत्र का उपयोग करने पर, हम पातें हैं,
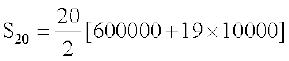 = 10 (790000) = 79,00,000
= 10 (790000) = 79,00,000
वह व्यक्ति 20 वर्ष के अंत में 79,00,000 रुपये प्राप्त करता है।
9.4.1 समांतर माध्य (Arithmetic mean)
दिया है दो संख्याएँ a तथा b. हम इन संख्याओं के बीच में एक संख्या A ले सकते हैं ताकि a, A, b समांतर श्रेणी में हों, तो संख्या A को a और b का समांतर माध्य (A.M.) कहते हैं।
A – a = b – A अर्थात् A =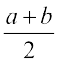
दो संख्याओं a तथा b के मध्य समांतर माध्य को इनके औसत 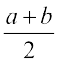 के रूप में व्याख्यित किया जा सकता है।
के रूप में व्याख्यित किया जा सकता है।
उदाहरण के लिए, दो संख्याओं 4 तथा 16 का समांतर माध्य 10 है। इस तरह हम एक संख्या 10 को 4 तथा 16 के मध्य रखकर एक समांतर श्रेणी 4, 10, 16 की रचना करते हैं। अब एक स्वाभाविक प्रश्न उठता हैं। क्या दिए गए किन्हीं दो संख्याओं के बीच दो या अधिक संख्याओं को रखने से समांतर श्रेणी (A.P.) तैयार हो सकेगी? अवलोकन कीजिए कि संख्याओं 4 तथा 16 के बीच 8 और 12 रखा जाए तो 4ए 8ए 12ए 16 समांतर श्रेणी (A.P.) हो जाती है।
सामान्यत: किन्हीं दो संख्याओं a तथा b के बीच कितनी भी संख्याओं को रखकर समांतर श्रेणी A.P. में परिणित किया जा सकता है।
माना कि A1, A2, A3, …An a तथा के मध्य संख्याएँ इस प्रकार हैं, कि a, A1, A2, A3, …An, b समांतर श्रेणी में है।
यहाँ b, (n + 2) वाँ पद हैं,
अथााρत्
b = a + [(n + 2) – 1]d
= a + (n + 1)d
इससे पाते हैं 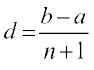 .
.
इस प्रकार, a तथा b के मध्य n संख्याएँ निम्नलिखित हैं:
A1 = a + d = a + 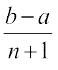
A2 = a + 2d = a + 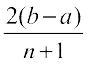
A3 = a + 3d = a + 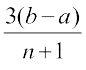
.... . ..... ..... .....
..... ..... ..... .....
An = a + nd = a + 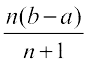
उदाहरण 8 एेसी 6 संख्याएँ ज्ञात कीजिए जिनको 3 और 24 के बीच रखने पर प्राप्त अनुक्रम एक समांतर श्रेणी बन जाए।
हल माना कि A1, A2, A3, A4, A5 तथा A6,3 तथा 24 के मध्य 6 संख्याएँ हैं, इसलिए 3, A1, A2, A3, A4, A5, A6 24 समांतर श्रेणी में हैं।
यहाँ a = 3, b = 24, n = 8.
इसलिए 24 = 3 + (8 –1) d, इससे प्राप्त होता है d = 3.
इस प्रकार
A1 = a + d = 3 + 3 = 6; A2 = a + 2d = 3 + 2 × 3 = 9;
A3 = a + 3d = 3 + 3 × 3 = 12; A4 = a + 4d = 3 + 4 × 3 = 15;
A5 = a + 5d = 3 + 5 × 3 = 18; A6 = a + 6d = 3 + 6 × 3 = 21.
अत:, संख्याएँ 3 तथा 24 के मध्य 6 संख्याएँ 6, 9, 12, 15, 18 तथा 21 हैं।
प्रश्नावली 9.2
1. 1 से 2001 तक के विषम पूर्णांकों का योग ज्ञात कीजिए।
2. 100 तथा 1000 के मध्य उन सभी प्राकृत संख्याओं का योगफल ज्ञात कीजिए जो 5 के गुणज हों।
3. किसी समांतर श्रेणी में प्रथम पद 2 है तथा प्रथम पाँच पदों का योगफल, अगले पाँच पदों के योगफल का एक चौथाई है। दर्शाइए कि 20वाँ पद –112 है।
4. समांतर श्रेणी – 6, 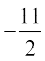 , – 5, … के कितने पदों का योगफल –25 है?
, – 5, … के कितने पदों का योगफल –25 है?
5. किसी समांतर श्रेणी का pवाँ पद  तथा qवाँ पद
तथा qवाँ पद  , हो तो सिद्ध कीजिए कि प्रथम pq पदों का योग
, हो तो सिद्ध कीजिए कि प्रथम pq पदों का योग  (pq +1) होगा जहाँ p
(pq +1) होगा जहाँ p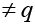 .
.
6. यदि किसी समांतर श्रेणी 25, 22, 19, … के कुछ पदों का योगफल 116 है तो अंतिम पद ज्ञात कीजिए।
7. उस समांतर श्रेणी के n पदों का योगफल ज्ञात कीजिए, जिसका k वाँ पद 5 k + 1 है।
8. यदि किसी समांतर श्रेणी के n पदों का योगफल (pn + qn2), है, जहाँ p तथा q अचर हों तो सार्व अंतर ज्ञात कीजिए।
9. दो समांतर श्रेढ़ियों के n पदों के योगफल का अनुपात 5n + 4 : 9n + 6. हो, तो उनके 18 वें पदों का अनुपात ज्ञात कीजिए।
10. यदि किसी समांतर श्रेणी के प्रथम p पदों का योग, प्रथम q पदों के योगफल के बराबर हो तो प्रथम (p + q) पदों का योगफल ज्ञात कीजिए।
11. यदि किसी समांतर श्रेणी के प्रथम p, q, r पदों का योगफल क्रमश: a, b तथा c हो तो सिद्ध कीजिए कि 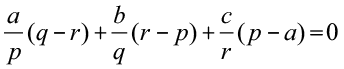
12. किसी समांतर श्रेणी के m तथा n पदों के योगफलों का अनुपात m2 : n2 है तो दर्शाइए कि m वें तथा nवें पदों का अनुपात (2m–1) : (2n–1) है।
13. यदि किसी समांतर श्रेणी के nवें पद का योगफल 3n2 + 5n हैं तथा इसका mवाँ पद 164 है, तो m का मान ज्ञात कीजिए।
14. 5 और 26 के बीच एेसी 5 संख्याएँ डालिए ताकि प्राप्त अनुक्रम समांतर श्रेणी बन जाए।
15. यदि 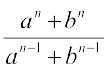 , a तथा b के मध्य समांतर माध्य हो तो n का मान ज्ञात कीजिए।
, a तथा b के मध्य समांतर माध्य हो तो n का मान ज्ञात कीजिए।
16. m संख्याओं को 1 तथा 31 के रखने पर प्राप्त अनुक्रम एक समांतर श्रेणी है और 7वीं एवं (m –1) वीं संख्याओं का अनुपात 5 : 9 है। तो m का मान ज्ञात कीजिए।
17. एक व्यक्ति ऋण का भुगतान 100 रुपये की प्रथम किश्त से शुरू करता है। यदि वह प्रत्येक किश्त में 5 रुपये प्रति माह बढ़ता है तो 30 वीं किश्त की राशि क्या होगी?
18. एक बहुभुज के दो क्रमिक अंत:कोणों का अंतर 50 है। यदि सबसे छोटा कोण 1200 हो, तो बहुभुज की भुजाओं की संख्या ज्ञात कीजिए।
9.5 गुणोत्तर श्रेणी [Geometric Progression (G . P.)]
आइए निम्नलिखित अनुक्रमों पर विचार करें:
(i) 2,4,8,16,....
(ii) 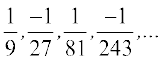
(iii) .01,0001,.000001,...
इनमे से प्रत्येक अनुक्रम के पद किस प्रकार बढ़ते हैं?
उपर्युक्त प्रत्येक अनुक्रम में हम पाते हैं कि प्रथम पद को छोड़, सभी पद एक विशेष क्रम में बढ़ते हैं।
(i) में हम पाते हैं:
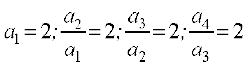 और इस प्रकार
और इस प्रकार
(ii) में हम पाते हैं:
 इत्यादि।
इत्यादि।
इसी प्रकार (iii) में पद कैसे अग्रसर होते हैं बताइए? निरीक्षण से यह ज्ञात हो जाता है कि प्रत्येक स्थिति में, प्रथम पद को छोड़, हर अगला पद अपने पिछले पद से अचर अनुपात में बढ़ता है। (i) में यह अचर अनुपात 2 है, (ii) में यह 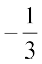 है (iii) में यह अचर अनुपात 0.01 है। एेसे अनुक्रमों को गुणोत्तर अनुक्रम या गुणोत्तर श्रेणी या संक्षेप में G.P. कहते हैं।
है (iii) में यह अचर अनुपात 0.01 है। एेसे अनुक्रमों को गुणोत्तर अनुक्रम या गुणोत्तर श्रेणी या संक्षेप में G.P. कहते हैं।
अनुक्रम a1, a2, a3, …, aद, … को गुणोत्तर श्रेणी कहा जाता है, यदि प्रत्येक पद अशून्य हो तथा 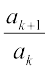 = r (अचर), k ≥ 1 के लिए।
= r (अचर), k ≥ 1 के लिए।
a1 = a, लिखने पर हम गुणोत्तर श्रेणी पाते हैं : a, ar, ar2, ar3, +…., जहाँ a को प्रथम पद कहते हैं तथा r को गुणोत्तर श्रेणी का
सार्व अनुपात कहते हैं। (i), (ii) तथा (iii) में दी गई गुणोत्तर श्रेढ़ियों का सार्व अनुपात क्रमश: 2, 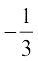 तथा 0.01 है।
तथा 0.01 है।
जैसा कि समांतर श्रेणी के संदर्भ में, वैसे ही पद गुणोत्तर श्रेणी का nवाँ खोजने की समस्या या गुणोत्तर श्रेणी के n पदों का योग जिसमें बहुत संख्याओं का समावेश हो तो इन्हें बिना सूत्र के हल करना कठिन है। इन सूत्रों को हम अगले अनुच्छेद में विकसित करेंगे:
हम इन सूत्रों के साथ निम्नलिखित संकेत का उपयोग करेंगे।
a = प्रथम पद, r = सार्व अनुपात, l = अंतिम पद,
n = पदों की संख्या, Sn = प्रथम n पदों का योगफल
9.5.1 गुणोत्तर श्रेणी का व्यापक पद (General term of a G.P.)
आइए एक गुणोत्तर श्रेणी G.P. जिसका प्रथम अशून्य पद ‘a’ तथा सार्व अनुपात ‘r’ है, पर विचार करें। इसके कुछ पदों को लिखिए। दूसरा पद, प्रथम पद a को सार्व अनुपात r से गुणा करने पर प्राप्त होता है, अर्थात् a2 = ar, इसी प्रकार तीसरा पद a3 को r से गुणा करने पर प्राप्त होता है अर्थात् a3 = a2r = ar2, आदि। हम इन्हें तथा कुछ और पद नीचे लिखते हैं:
प्रथम पद = a1 = a = ar1–1ए द्वितीय पद = a2 = ar = ar2–1ए तृतीय पद = a3 = ar2 = ar3–1
चतुर्थ पद = a4 = ar3 = ar4–1ए पाँचवाँँ पद= a5 = ar4 = ar5–1
क्या आप कोई पैटर्न देखते हैं? 16वाँ पद क्या होगा?
a16 = ar16–1 = ar15
इसलिए यह प्रतिरूप बताता है कि गुणोत्तर श्रेणी का n वाँ पद 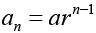 .
.
अर्थात् गुणोत्तर श्रेणी इस रूप में लिखी जा सकती हैं : a, ar, ar2, ar3 ,… arn–1; a, ar, ar2...,
arn–1... क्रमश: जब श्रेणी परिमित हो या जब श्रेणी अपरिमित हो।
श्रेणी a + ar + ar2 + ... + arn–1 अथवा a + ar + ar2 + ... + arn–1 +... क्रमश: परिमित या अपरिमित गुणोत्तर श्रेणी कहलाते हैं।
9.5.2. गुणोत्तर श्रेणी के द पदोें का योगफल (Sum to n terms of a G.P.)

उदाहरण 12 गुणोत्तर श्रेणी 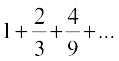 के प्रथम n पदों का योग तथा प्रथम 5 पदों का योगफल ज्ञात कीजिए।
के प्रथम n पदों का योग तथा प्रथम 5 पदों का योगफल ज्ञात कीजिए।
हल यहाँ a = 1, तथा r =  . इसलिए
. इसलिए
Sn = 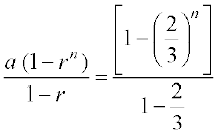 =
= 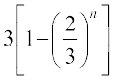
विशेषत: S5 =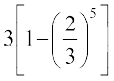 =
= 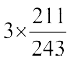 =
= 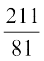
उदाहरण 13 गुणोत्तर श्रेणी 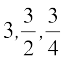 ... के कितने पद आवश्यक हैं ताकि उनका योगफल
... के कितने पद आवश्यक हैं ताकि उनका योगफल 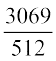 हो जाए?
हो जाए?
हल माना कि n आवश्यक पदों की संख्या हैं। दिया है a = 3, r =  तथा
तथा 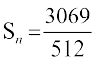
क्योंकि 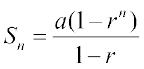
इसलिए 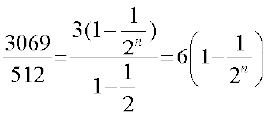
या 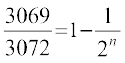
या 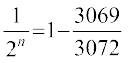
या 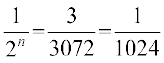
या 2n = 1024 = 210, या n = 10
उदाहरण 14 एक गुणोत्तर श्रेणी के प्रथम तीन पदों का योगफल 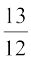 है तथा उनका गुणानफल 1 है, तो सार्व अनुपात तथा पदों को ज्ञात कीजिए?
है तथा उनका गुणानफल 1 है, तो सार्व अनुपात तथा पदों को ज्ञात कीजिए?
हल माना 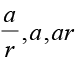 गुणोत्तर श्रेणी के तीन पद हैं तो
गुणोत्तर श्रेणी के तीन पद हैं तो
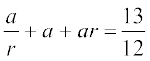 ... (1)
... (1)
तथा 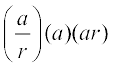 = – 1 ... (2)
= – 1 ... (2)
(2) से हम पाते हैं a3 = –1 अर्थात् a = -–1 (केवल वास्तविक मूल पर विचार करने से)
(1) में a = –1 रखने पर हम पाते है 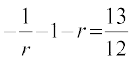 या 12r2 + 25r + 12 = 0.
या 12r2 + 25r + 12 = 0.
यह r में द्विघात समीकरण है, जिसे हल करने पर हम पाते हैं: 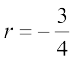 या
या 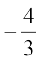
अत: गुणोत्तर श्रेणी के तीन पद हैं
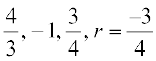 के लिए तथा
के लिए तथा 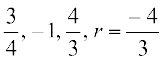 के लिए
के लिए
उदाहरण 15 अनुक्रम 7, 77, 777, 7777,... के nपदों का योग ज्ञात कीजिए।
हल इस रूप में यह गुणोत्तर श्रेणी नहीं हैं। तथापि इसे निम्नलिखित रूप में लिखकर गुणोत्तर श्रेणी से संबंध निरूपित किया जा सकता है:
Sn = 7 + 77 + 777 + 7777 + ... to n पदों तक
= 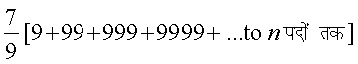
= 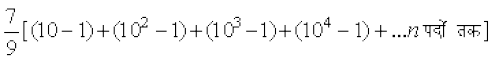
= 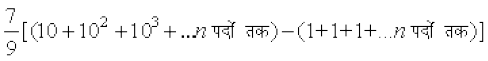
= 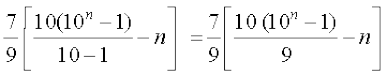 .
.
उदाहरण 16 एक व्यक्ति की दसवीं पीढ़ी तक पूर्वजों की संख्या कितनी होगी, जबकि उसके 2 माता-पिता, 4 दादा-दादी, 8 पर दादा, पर दादी तथा आदि हैं।
हल यहाँ a = 2, r = 2 तथा n = 10,
योगफल का सूत्र उपयोग करने पर 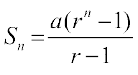
हम पाते हैं S10 = 2(210 – 1) = 2046
अत: व्यक्ति के पूर्वजों की संख्या 2046 है।
9.5.3 गुणोत्तर माध्य (Geometric Mean G .M.) ,
दो धनात्मक संख्याओं a तथा b का गुणोत्तर माध्य संख्या 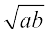 है। इसलिए 2 तथा 8 का गुणोत्तर माध्य 4 है। हम देखते हैं कि तीन संख्याओं 2, 4, 8 गुणोत्तर श्रेणी के क्रमागत पद हैं। यह दो संख्याओं के गुणोत्तर माध्य की धारणा के व्यापकीकरण की ओर अग्रसर करता है।
है। इसलिए 2 तथा 8 का गुणोत्तर माध्य 4 है। हम देखते हैं कि तीन संख्याओं 2, 4, 8 गुणोत्तर श्रेणी के क्रमागत पद हैं। यह दो संख्याओं के गुणोत्तर माध्य की धारणा के व्यापकीकरण की ओर अग्रसर करता है।
यदि दो धनात्मक संख्याएँ a तथा b दी गई हो तो उनके बीच इच्छित संख्याएँ रखी जा सकती हैं ताकि प्राप्त अनुक्रम एक गुणोत्तर श्रेणी बन जाए।
मान लीजिए a तथा b के बीच n संख्याएँ G1, G2, G3 ,…,Gn, इस प्रकार हैं कि a,G1,G2,G3,…,Gn,b
गुणोत्तर श्रेणी है। इस प्रकार b गुणोत्तर श्रेणी का (n + 2) वाँ पद है।
हम पाते हैं:
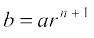 , या
, या 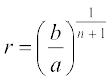
अत: 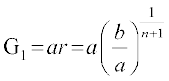 ,
, 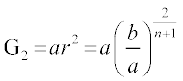 ,
, 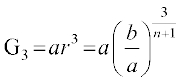 ,
, 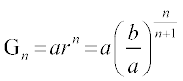
उदाहरण 17 एेसी 3 संख्याएँ ज्ञात कीजिए जिनको 1 तथा 256 के बीच रखने पर प्राप्त अनुक्रम एक गुणोत्तर श्रेणी बन जाए।
हल माना कि G1, G2,G3 तीन गुणोत्तर माध्य 1 तथा 256 के बीच में है।
1, G1,G2,G3 ,256 गुणोत्तर श्रेणी में हैं।
इसलिए 256 = r4 जिससे r =  4 (केवल वास्तविक मूल लेने पर) r = 4 के लिए हम पाते हैं ़G1 = ar = 4, G2 = ar2 = 16, G3 = ar3 = 64
4 (केवल वास्तविक मूल लेने पर) r = 4 के लिए हम पाते हैं ़G1 = ar = 4, G2 = ar2 = 16, G3 = ar3 = 64
इसी प्रकार r = – 4, के लिए संख्याएँ – 4,16 तथा – 64 हैं।
अत: 1 तथा 256 के बीच तीन संख्याएँ 4, 16, 64 हैं।
9.6 समांतर माध्य तथा गुणोत्तर माध्य के बीच संबंध (Relationship between A.M. and G.M.)
माना कि A तथा G दी गई दो धनात्मक वास्तविक संख्याओं a तथा b के बीच क्रमश: समांतर माध्य (A.M.) तथा गुणोत्तर माध्य (A.M.) हैं। तो
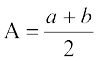 तथा
तथा 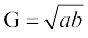
इस प्रकार
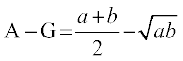 =
= 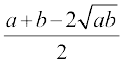 =
= 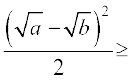 0 ... (1)
0 ... (1)
(1) से हम A ≥ G संबंध पाते हैं।
उदाहरण 18 यदि दो धनात्मक संख्याओं a तथा b के बीच समांतर माध्य तथा गुणोत्तर माध्य क्रमश: 10 तथा 8 हैं, तो संख्याएँ ज्ञात कीजिए।
हल दिया है 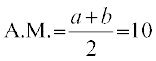 ... (1)
... (1)
तथा 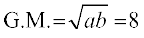 ... (2)
... (2)
(1) तथा (2) से हम पाते हैं
a + b = 20 ... .............(3)
ab = 64 ...................... (4)
(3), (4) से a तथा b का मान सर्वसमिका (a – b)2 = (a + b)2 – 4ab में रखने पर हम पाते हैं
(a – b)2 = 400 – 256 = 144 या a – b =  12
12
(3) तथा (5) को हल करने पर, हम पाते हैं
a = 4, b = 16 या a = 16, b = 4
अत: संख्याएँ a तथा b क्रमश: 4, 16 या 16, 4 हैं।
प्रश्नावली 9.3
1. गुणोत्तर श्रेणी 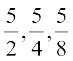 , ... का 20वाँ तथा nवाँ पद ज्ञात कीजिए।
, ... का 20वाँ तथा nवाँ पद ज्ञात कीजिए।
2. उस गुणोत्तर श्रेणी का 12वाँ पद ज्ञात कीजिए, जिसका 8वाँ पद 192 तथा सार्व अनुपात 2 है।
3. किसी गुणोत्तर श्रेणी का 5वाँ, 8वाँ तथा 11वाँ पद क्रमश: p, q तथा s हैं तो दिखाइए
कि q2 = ps.
4. किसी गुणोत्तर श्रेणी का चौथा पद उसके दूसरे पद का वर्ग है तथा प्रथम पद –3 है तो 7वाँ पद ज्ञात कीजिए।
5. अनुक्रम का कौन सा पद:
(a) 2, 2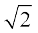 , 4, ...; 128 है?
, 4, ...; 128 है?
(b) 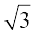 ,3 3
,3 3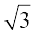 , ... ; 729 है?
, ... ; 729 है?
(c) 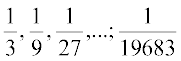 है?
है?
6. x के किस मान के लिए संख्याएँ 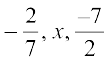 गुणोत्तर श्रेणी में हैं?
गुणोत्तर श्रेणी में हैं?
प्रश्न 7 से 10 तक प्रत्येक गुणोत्तर श्रेणी का योगफल निर्दिष्ट पदों तक ज्ञात कीजिए।
7. 0.15, 0.015, 0.0015, ... 20 पदों तक
8. 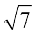 ,
, 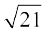 , 3
, 3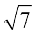 , ... n पदों तक
, ... n पदों तक
9. 1, – a, a2, – a3, ... n पदों तक (यदि a ≠ –1)
10. x3, x5, x7, ... n पदों तक (यदि x 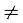
 1)
1)
11. मान ज्ञात कीजिए 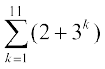
12. एक गुणोत्तर श्रेणी के तीन पदों का योगफल 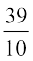 हैं तथा उनका गुणनफल 1 है। सार्व अनुपात तथा पदों को ज्ञात कीजिए।
हैं तथा उनका गुणनफल 1 है। सार्व अनुपात तथा पदों को ज्ञात कीजिए।
13. गुणोत्तर श्रेणी 3, 32, 33, … के कितने पद आवश्यक हैं ताकि उनका योगफल 120 हो जाए।
14. किसी गुणोत्तर श्रेणी के प्रथम तीन पदों का योगफल 16 है तथा अगले तीन पदों का योग 128 है तो गुणोत्तर श्रेणी का प्रथम पद, सार्व अनुपात तथा n पदों का योगफल ज्ञात कीजिए।
15. एक गुणोत्तर श्रेणी का प्रथम पद a = 729 तथा 7वाँ पद 64 है तो S7 ज्ञात कीजिए?
16. एक गुणोत्तर श्रेणी को ज्ञात कीजिए, जिसके प्रथम दो पदों का योगफल – 4 है तथा 5वाँ पद तृतीय पद का 4 गुना है।
17. यदि किसी गुणोत्तर श्रेणी का 4 वाँ, 10वाँ तथा 16वाँ पद क्रमश: x, y तथा z हैं, तो सिद्ध कीजिए कि x, y, z गुणोत्तर श्रेणी में हैं।
18. अनुक्रम 8, 88, 888, 8888… के n पदों का योग ज्ञात कीजिए।
19. अनुक्रम 2, 4, 8, 16, 32 तथा 128, 32, 8, 2,  के संगत पदों के गुणनफल से बने अनुक्रम का योगफल ज्ञात कीजिए।
के संगत पदों के गुणनफल से बने अनुक्रम का योगफल ज्ञात कीजिए।
20. दिखाइए कि अनुक्रम a, ar, ar2, … arn-1 तथा A, AR, AR2, ...ARn-1 के संगत पदों के गुणनफल से बना अनुक्रम गुणोत्तर श्रेणी होती है तथा सार्व अनुपात ज्ञात कीजिए।
21. एेसे चार पद ज्ञात कीजिए जो गुणोत्तर श्रेणी में हो, जिसका तीसरा पद प्रथम पद से 9 अधिक हो तथा दूसरा पद चौथे पद से 18 अधिक हो।
22. यदि किसी गुणोत्तर श्रेणी का pवाँ, qवाँ तथा r वाँ पद क्रमश: a, b तथा c हो, तो सिद्ध कीजिए कि aq–r br-pcचp-q= 1
23. यदि किसी गुणोत्तर श्रेणी का प्रथम तथा n वाँ पद क्रमश: a तथा b हैं, एवं P, n पदों का गुणनफल हो, तो सिद्ध कीजिए कि P2 = (ab)n
24. दिखाइए कि एक गुणोत्तर श्रेणी के प्रथम n पदों के योगफल तथा (n + 1) वें पद से (2n)वें पद तक के पदों के योगफल का अनुपात 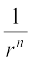 है।
है।
25. यदि a, b, c तथा d गुणोत्तर श्रेणी में हैं तो दिखाइए कि (a2 + b2 + c2) (b2 + c2 + d2) = (ab + bc + cd)2 .
26. एेसी दो संख्याएँ ज्ञात कीजिए जिनको 3 तथा 81 के बीच रखने पर प्राप्त अनुक्रम एक गुणोत्तर श्रेणी बन जाय।
27. n का मान ज्ञात कीजिए ताकि 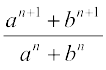 , a तथा b के बीच गुणोत्तर माध्य हो।
, a तथा b के बीच गुणोत्तर माध्य हो।
28. दो संख्याओं का योगफल उनके गुणोत्तर माध्य का 6 गुना है तो दिखाइए कि संख्याएँ 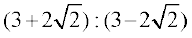 के अनुपात में हैं।
के अनुपात में हैं।
29. यदि A तथा G दो धनात्मक संख्याओं के बीच क्रमश: समांतर माध्य तथा गुणोत्तर माध्य हों, तो सिद्ध कीजिए कि संख्याएँ 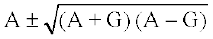 हैं।
हैं।
30. किसी कल्चर में बैक्टीरिया की संख्या प्रत्येक घंटे पश्चात् दुगुनी हो जाती है। यदि प्रारंभ में उसमें 30 बैक्टीरिया उपस्थित थे, तो बैक्टीरिया की संख्या दूसरे, चौथे तथा nवें घंटों बाद
क्या होगी?
31. 500 रुपये धनराशि 10: वार्षिक चक्रवृद्धि ब्याज पर 10 वर्षों बाद क्या हो जाएगी, ज्ञात कीजिए?
32. यदि किसी द्विघात समीकरण के मूलों के समांतर माध्य एवं गुणोत्तर माध्य क्रमश: 8 तथा 5 हैं, तो द्विघात समीकरण ज्ञात कीजिए।
9.7 विशेष अनुक्रमों के द पदों का योगफल (Sum to n Terms of Special Series)
अब हम कुछ विशेष अनुक्रमों के n पदों का योग ज्ञात करेंगे: वे निम्नलिखित हैं।
(i) 1 + 2 + 3 +… + n (प्रथम n प्राकृत संख्याओं का योग)
(ii) 12 + 22 + 32+… + n2 (प्रथम n प्राकृत संख्याओं के वर्गों का योग)
(iii) 13 + 23 + 33+… + n3 (प्रथम n प्राकृत संख्याओं के घनों का योग)
आइए हम इन पर एक के बाद दूसरे पर विचार करें:
(i) Sn=1+ 2 + 3 + … + n, तो = 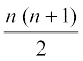 (भाग 9.4 देखें)
(भाग 9.4 देखें)
(ii) यहाँ Sn=12+22+32+ … +n2
हम सर्वसमिका 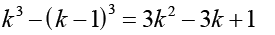 पर विचार करते हैं
पर विचार करते हैं
क्रमश: k = 1, 2… , n रखने पर, हम पाते हैं
13 – 03 = 3 (1)2 – 3 (1) + 1
23 – 13 = 3 (2)2 + 1
33 – 23 = 3(3)2 – 3 (3) + 1
.......................................
.......................................
......................................
n3 – (n – 1)3 = 3 (n)2 – 3 (n) + 1
दोनों पक्षों को जोड़ने पर हम पाते हैं
n3 – 03 = 3 (12 + 22 + 32 + ... + n2) – 3 (1 +2 +3 + ... + n) + n
या 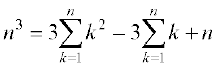
(i) से हम जानते हैं
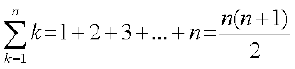
अत: Sn = 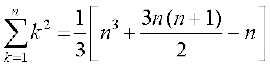 =
=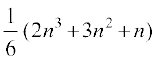 =
= 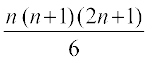
(iii) यहाँ Sn = 13 + 23 + ...+n3
हम सर्वसमिका (k + 1)4 – k4 = 4k3 + 6k2 + 4k + 1 पर विचार करते हैं
क्रमश: k = 1, 2, 3… n, रखने पर, हम पाते हैं
24 – 14 = 4(1)3 + 6(1)2 + 4(1) + 1
34 – 24 = 4(2)3 + 6(2)2 + 4(2) + 1
44 – 34 = 4(3)3 + 6(3)2 + 4(3) + 1
..................................................
..................................................
..................................................
(n – 1)4 – (n – 2)4 = 4(n – 2)3 + 6(n – 2)2 + 4(n – 2) + 1
n4 – (n – 1)4 = 4(n – 1)3 + 6(n – 1)2 + 4(n – 1) + 1
(n + 1)4 – n4 = 4n3 + 6n2 + 4n + 1
दोनों पक्षों को जोड़ने पर, हम पाते हैं
(n + 1)4 – 14 = 4(13 + 23 + 33 +...+ n3) + 6(12 + 22 + 32 + ...+ n2) +
4(1 + 2 + 3 +...+ n) + n
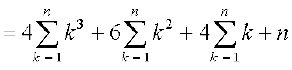 , ... (1)
, ... (1)
(i) तथा (ii) से, हम जानते हैं
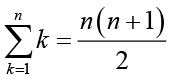 तथा
तथा 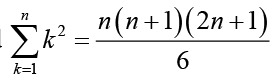
इन मानों को (1) में रखने पर, हम पाते हैं
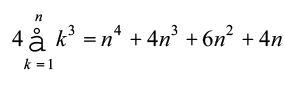
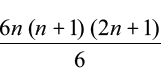
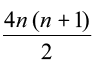 n
n
or 4Sn = n4 + 4n3 + 6n2 + 4n – n (2n2 + 3n + 1) – 2n (n + 1) – n
= n4 + 2n3 + n2
= n2(n + 1)2.
अत: Sn = 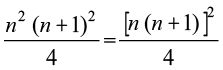
उदाहरण 19 श्रेणी 5 + 11 + 19 + 29 + 41… के nपदों का योगफल ज्ञात कीजिए।
हल आइए लिखें
Sn = 5 + 11 + 19 + 29 + ... + an–1 + an
अथवा Sn = 5 + 11 + 19 + ... + an–2 + an–1 + an
घटाने पर हम पाते हैं
0 = 5 + [6 + 8 + 10 + 12 + ...(n – 1) पदों ] – an
अथवा an = 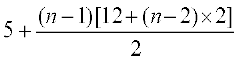
= 5 + (n – 1) (n + 4) = n2 + 3n + 1
इस प्रकार Sn = 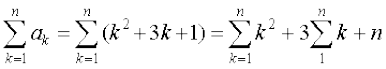
= 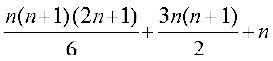 =
= 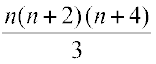 .
.
उदाहरण 20 उस श्रेणी के n पदों का योग ज्ञात कीजिए जिसका nवाँ पद n (n + 3) है।
हल दिया गया है
an = n (n + 3) = n2 + 3n
इस प्रकार n पदों का योगफल
Sn = 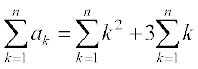
= 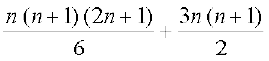
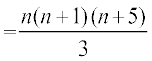 .
.
प्रश्नावली 9.4
प्रश्न 1 से 7 तक प्रत्येक श्रेणी के nपदों का योग ज्ञात कीजिए।
1. 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 +... 2. 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + ...
3. 3 × 12 + 5 × 22 + 7 × 32 + ... 4. 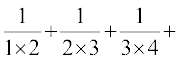 ...
...
5. 52 + 62 + 72 + ... + 202 6. 3 × 8 + 6 × 11 + 9 × 14 + ...
7. 12 + (12 + 22) + (12 + 22 + 32) + ...
प्रश्न 8 से 10 तक प्रत्येक श्रेणी के n पदों का योग ज्ञात कीजिए जिसका n वाँ पद दिया है:
8. n (n+1) (n+4).
9. n2 + 2द.
10. 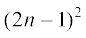
विविध उदाहरण
उदाहरण 21 यदि किसी समांतर श्रेणी का p वाँ, q वाँ, r वाँ तथा s वाँ पद गुणोत्तर श्रेणी में हैं, तो दिखाइए कि (p – q), (q – r), (r-s) भी गुणोत्तर श्रेणी में होगें।
हल यहाँ ap = a + (p –1) d ............. (1)
aq = a + (q –1) d ......................... (2)
ar = a + (r –1) d .......................... (3)
as = a + (s –1) d ... ......................(4)
दिया गया है कि ap, aq, ar तथा as गुणोत्तर श्रेणी में हैं। इसलिए
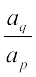 =
= 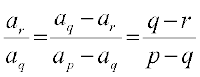 (क्यों?) … (5)
(क्यों?) … (5)
इसी प्रकार 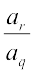 =
= 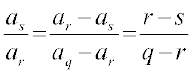 ; (क्यों?) … (6)
; (क्यों?) … (6)
अत: (5) तथा (6) से
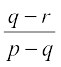 =
= 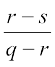 अर्थात् p – q, q – r तथा r – s गुणोत्तर श्रेणी में हैं।
अर्थात् p – q, q – r तथा r – s गुणोत्तर श्रेणी में हैं।
उदाहरण 22 यदि a, b, c गुणोत्तर श्रेणी में हैं तथा 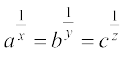 हैं तो सिद्ध कीजिए x, y, z समांतर श्रेणी में हैं।
हैं तो सिद्ध कीजिए x, y, z समांतर श्रेणी में हैं।
हल माना कि a1/x = b1/y = c1/z= k. हैं तो
a = kx , b = ky तथा c = kΡ. … (1)
क्योंकि a, b, c गुणोत्तर श्रेणी में हैं
b2 = ac … (2)
(1) तथा (2) के उपयोग से हम पाते हैं
k2y = kx+z
इससे हमें मिलता है 2y = x + z.
अत: x, y तथा z समांतर श्रेणी में हैं।
उदाहरण 23 यदि a, b, c, d तथा p विभिन्न वास्तविक संख्याएँ इस प्रकार हैं कि (a2 + b2 + c2)p2 – 2(ab + bc + cd)p + (b2 + c2 + d2) ≤ 0 तो दर्शाइए कि a, b, c तथा d गुणोत्तर श्रेणी में हैं।
हल दिया हैं
(a2 + b2 + c2) p2 – 2 (ab + bc + cd)p + (b2 + c2 + d2) ≤ 0 .................... (1)
परंतु बायाँ पक्ष
= (a2p2 – 2abp+b2) + (b2p2 – 2bcp+c2) + (c2p2 – 2cdp + d2),
इससे हमें मिलता है
(ap – b)2 + (bp – c)2 + (cp – d)2 ≥ 0 ................. (2)
क्योंकि वास्तविक संख्याओं के वर्गों का योग ऋणेतर है, इसलिए (1) तथा (2) से, हम पाते हैं
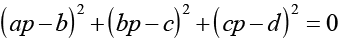
अथवा ap – b = 0, bp – c = 0, cp – d = 0 इससे हमें मिलता है
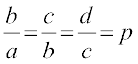
अत: a, b, c तथा d गुणोत्तर श्रेणी में हैं।
उदाहरण 24 यदि p,q,r गुणोत्तर श्रेणी में हैं तथा समीकरणों px2 + 2qx + r = 0 और dx2 + 2ex + f = 0 एक उभयनिष्ठ मूल रखते हों, तो दर्शाइए कि 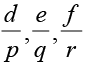 समांतर श्रेणी में हैं।
समांतर श्रेणी में हैं।
हल समीकरण px2 + 2qx + r = 0 के मूल निम्नलिखित हैं:
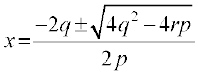
क्योंकि p ,q, r गुणोत्तर श्रेणी में हैं, इसलिए q2 = pr, अर्थात् 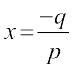 परंतु
परंतु 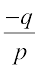 समीकरण
समीकरण
dx2 + 2ex + f = 0 का भी मूल है, (क्यों?)
इसलिए
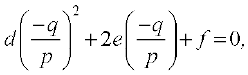
या oqQ2 – 2eqp + fp2 = 0 ................ (1)
(1) को pq2 से भाग देने पर तथा q2 = pr का उपयोग करने से, हम पाते हैं
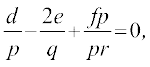 या
या 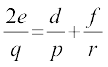
अत: 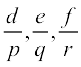 समांतर श्रेणी में हैं।
समांतर श्रेणी में हैं।
अध्याय 9 पर विविध प्रश्नावली
1. दर्शाइए कि किसी समांतर श्रेणी के (m + n)वें तथा (m – n)वें पदों का योग mवें पद का दुगुना है।
2. यदि किसी समांतर श्रेणी की तीन संख्याओं का योग 24 है तथा उनका गुणनफल 440 है, तो संख्याएँ ज्ञात कीजिए।
3. माना कि किसी समांतर श्रेणी के n, 2n, तथा 3n पदों का योगफल क्रमश: S1, S2 तथा S3 है तो दिखाइए कि S3 = 3(S2 –S1)
4. 200 तथा 400 के मध्य आने वाली उन सभी संख्याओं का योगफल ज्ञात कीजिए जो 7 से विभाजित हों।
5. 1 से 100 तक आने वाले उन सभी पूर्णांकों का योगफल ज्ञात कीजिए जो 2 या 5 से विभाजित हों।
6. दो अंकों की उन सभी संख्याओं का योगफल ज्ञात कीजिए, जिनको 4 से विभजित करने पर शेषफल 1 हो।
7. सभी x , y ∈N के लिए f (x + y) = f (x). f (y) को संतुष्ट करता हुआ f एक एेसा फलन है कि f (1) = 3 एवं 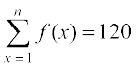 तो n का मान ज्ञात कीजिए।
तो n का मान ज्ञात कीजिए।
8. गुणोत्तर श्रेणी के कुछ पदों का योग 315 है, उसका प्रथम पद तथा सार्व अनुपात क्रमश: 5 तथा 2 हैं। अंतिम पद तथा पदों की संख्या ज्ञात कीजिए।
9. किसी गुणोत्तर श्रेणी का प्रथम पद 1 है। तीसरे एवं पाँचवें पदों का योग 90 हो तो गुणोत्तर श्रेणी का सार्व अनुपात ज्ञात कीजिए।
10. किसी गुणोत्तर श्रेणी के तीन पदों का योग 56 है। यदि हम क्रम से इन संख्याओं में से 1, 7, 21 घटाएँ तो हमें एक समांतर श्रेणी प्राप्त होती है। संख्याएँ ज्ञात कीजिए।
11. किसी गुणोत्तर श्रेणी के पदों की संख्या सम है। यदि उसके सभी पदों का योगफल, विषम स्थान पर रखे पदों के योगफल का 5 गुना है, तो सार्व अनुपात ज्ञात कीजिए।
12. एक समांतर श्रेणी के प्रथम चार पदों का योगफल 56 है। अंतिम चार पदों का योगफल 112 है। यदि इसका प्रथम पद 11 है, तो पदों की संख्या ज्ञात कीजिए।
13. यदि 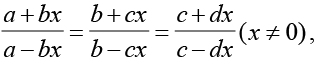 हो तो दिखाइए कि a, b, c तथा d गुणोत्तर श्रेणी में हैं।
हो तो दिखाइए कि a, b, c तथा d गुणोत्तर श्रेणी में हैं।
14. किसी गुणोत्तर श्रेणी में S, n पदों का योग, P उनका गुणनफल तथा R उनके व्युत्क्रमों का योग हो तो सिद्ध कीजिए कि P2Rn = Sn.
15. किसी समांतर श्रेणी का pवाँ, qवाँ rवाँ पद क्रमश: a, b, c हैं, तो सिद्ध कीजिए
(q – r )a + (r – p )b + (p – q )c = 0
16. यदि 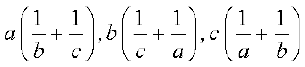 समांतर श्रेणी में हैं, तो सिद्ध कीजिए कि a, b, c समांतर श्रेणी में हैं।
समांतर श्रेणी में हैं, तो सिद्ध कीजिए कि a, b, c समांतर श्रेणी में हैं।
17. यदि a, b, c, d गुणोत्तर श्रेणी में हैं, तो सिद्ध कीजिए कि
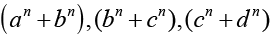 गुणोत्तर श्रेणी में हैं।
गुणोत्तर श्रेणी में हैं।
18. यदि x2 – 3x +p = 0 के मूल a तथा b हैं तथा x2 –12x +q = 0, के मूल c तथा d हैं, जहाँ a, b, c, d गुणोत्तर श्रेणी के रूप में हैं। सिद्ध कीजिए कि (q + p) : (q – p) = 17:15
19.दो धनात्मक संख्याओं a तथा b के बीच समांतर माध्य तथा गुणोत्तर माध्य का अनुपात m:n. है। दर्शाइए कि 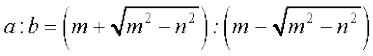
20. यदि a, b, c समांतर श्रेणी में हैं b, c, d गुणोत्तर श्रेणी में हैं तथा 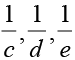 समांतर श्रेणी में हैं, तो सिद्ध कीजिए कि a, c, e गुणोत्तर श्रेणी में हैं।
समांतर श्रेणी में हैं, तो सिद्ध कीजिए कि a, c, e गुणोत्तर श्रेणी में हैं।
21. निम्नलिखित श्रेणियों के n पदों का योग ज्ञात कीजिए।
(i) 5 + 55 +555 + …
(ii) .6 +. 66 +. 666+…
22. श्रेणी का 20वाँ पद ज्ञात कीजिए:
2 × 4 + 4 × 6 + 6 × 8 + ... + n पदों तक
23. श्रेणी 3+ 7 +13 +21 +31 +… के n पदों का योग ज्ञात कीजिए।
24. यदि S1, S2, S3 क्रमश: प्रथम n प्राकृत संख्याओं का योग, उनके वर्गों का योग तथा घनों का योग है तो सिद्ध कीजिए कि 9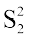 = S3 (1 + 8S1).
= S3 (1 + 8S1).
25.निम्नलिखित श्रेणियों के n पदों तक योग ज्ञात कीजिएं: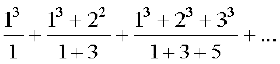
26. दर्शाइए कि: 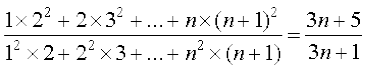 .
.
27. कोई किसान एक पुराने ट्रैक्टर को 12000 रुपये में खरीदता है। वह Rs 6000 रुपये नकद भुगतान करता है और शेष राशि को Rs 500 रुपये की वार्षिक किस्त के अतिरिक्त उस धन पर जिसका भुगतान न किया गया हो 12% वार्षिक ब्याज भी देता है। किसान को ट्रैक्टर की कुल कितनी कीमत देनी पड़ेगी?
28. शमशाद अली 22000 रुपये में एक स्कूटर खरीदता है। वह 4000 रुपये नकद देता है तथा शेष राशि को 1000 रुपयें वार्षिक किश्त के अतिरिक्त उस धन पर जिसका भुगतान न किया गया हो 10% वार्षिक ब्याज भी देता है। उसे स्कूटर के लिए कुल कितनी राशि चुकानी पड़ेगी?
29. एक व्यक्ति अपने चार मित्रों को पत्र लिखता है। वह प्रत्येक को उसकी नकल करके चार दूसरे व्यक्तियों को भेजने का निर्देश देता है, तथा उनसे यह भी करने को कहता हैं कि प्रत्येक पत्र प्राप्त करने वाला व्यक्ति इस शाृंखला को जारी रखे। यह कल्पना करके कि शाृंखला न टूटे तो 8 वें पत्रों के समूह भेजे जाने तक कितना डाक खर्च होगा जबकि एक पत्र का डाक खर्च 50 पैसे है।
30. एक आदमी ने एक बैंक में 10000 रुपये 5% वार्षिक साधारण ब्याज पर जमा किया। जब से रकम बैंक में जमा की गई तब से, 15 वें वर्ष में उसके खातें में कितनी रकम हो गई, तथा 20 वर्षों बाद कुल कितनी रकम हो गई, ज्ञात कीजिए।
31. एक निर्माता घोषित करता है कि उसकी मशीन जिसका मूल्य 15625 रुपये है, हर वर्ष 20% की दर से उसका अवमूल्यन होता है। 5 वर्ष बाद मशीन का अनुमानित मूल्य ज्ञात कीजिए।
32. किसी कार्य को कुछ दिनों में पूरा करने के लिए 150 कर्मचारी लगाए गए। दूसरे दिन 4 कर्मचारियों ने काम छोड़ दिया, तीसरे दिन 4 और कर्मचारियों ने काम छोड़ दिया तथा इस प्रकार अन्य। अब कार्य पूर्ण करने में 8 दिन अधिक लगते हैं, तो दिनों की संख्या ज्ञात कीजिए, जिनमें कार्य पूर्ण किया गया।
सारांश
अनुक्रम से हमारा तात्पर्य है, "किसी नियम के अनुसार एक परिभाषित (निश्चित) क्रम में संख्याओं की व्यवस्था"। पुन: हम एक अनुक्रम को एक फलन के रूप में परिभाषित कर सकते हैं, जिसका प्रांत प्राकृत संख्याओं का समुच्चय हो अथवा उसका उपसमुच्चय
{1, 2, 3, ..., k} के प्रकार का हो। वे अनुक्रम, जिनमें पदों की संख्या सीमित होती है, "परिमित अनुक्रम" कहलाते हैं। यदि कोई अनुक्रम परिमित नहीं है तो उसे अपरिमित अनुक्रम कहते हैं।
मान लीजिए a1,a2,a3, ... एक अनुक्रम हैं ता a1 +a2+a3 + ... के रूप में व्यक्त किया गया योग श्रेणी कहलाता है जिस श्रेणी के पदों की संख्या सीमित होती है उसे परिमित श्रेणी कहते हैं।
किसी अनुक्रम में पद समान नियतांक से लगातार बढ़ते या घटते हैं, समांतर श्रेणी होती हैं। नियतांक को समांतर श्रेणी का सार्व अंतर कहते हैं। सामान्यत: हम समांतर श्रेणी का प्रथम पद a, सार्व अंतर d तथा अंतिम पद l से प्रदर्शित करते हैं। समांतर श्रेणी का व्यापक पद या n वाँ पद an = a + (n – 1) d है।
समांतर श्रेणी के n पदों का योग Sn निम्नलिखित सूत्र द्वारा प्राप्त होता है:
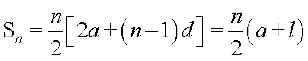 .
.
कोई दो संख्याओं a तथा b का समांतर माध्य A, 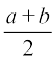 होता है अर्थात् अनुक्रम a, A, b समांतर श्रेणी (A.P.) में है।
होता है अर्थात् अनुक्रम a, A, b समांतर श्रेणी (A.P.) में है।
किसी अनुक्रम को गुणोत्तर श्रेणी या G.P. कहते हैं, यदि कोई पद, अपने पिछले पद से एक अचर अनुपात में बढ़ता है। इस अचर गुणांक को सार्व अनुपात कहते हैं। साधारणत: हम गुणोत्तर श्रेणी के प्रथम पद को a तथा सार्व अनुपात r से सांकेतिक करते हैं। गुणोत्तर श्रेणी का व्यापक पद या nवाँ पद an= arn – 1 होता है।
गुणोत्तर श्रेणी के प्रथम द पदों का योग  या
या 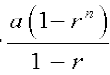 यदि त ≠1
यदि त ≠1
होता है।
कोई दो धनात्मक संख्याएँ तथा इ का गुणोत्तर माध्य 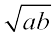 है अर्थात् अनुक्रम a, G, b गुणोत्तर श्रेणी में हैं।
है अर्थात् अनुक्रम a, G, b गुणोत्तर श्रेणी में हैं।
एेतिहासिक पृष्ठभूमि
इस बात के प्रमाण मिलते हैं कि 4000 वर्ष पूर्व बेबीलोनिया के निवासियों को समांतर तथा गुणोत्तर अनुक्रमों का ज्ञान था। Boethius (510 A.D.) के अनुसार समांतर तथा गुणोत्तर अनुक्रमों की जानकारी प्रारंभिक यूनानी (ग्रीक) लेखकों को थी। भारतीय गणितज्ञों में से आर्यभट (476 A.D.) ने पहली बार प्राकृत संख्याओं के वर्गों तथा घनों का योग अपनी प्रसिद्ध पुस्तक ‘आर्यभटीयम्’ जो लगभग 499 A.D. में लिखी गई थी, में दिया। उन्होंने p वाँ पद से आरंभ, समांतर अनुक्रम के n पदों के योग का सूत्र भी दिया। अन्य महान भारतीय गणितज्ञ ब्रह्मगुप्त (598 A.D.), महावीर (850 A.D.) तथा भास्कर (1114–1185 A.D.) ने संख्याओं के वर्गों एवं घनों के योग पर विचार किया। एक दूसरे विशिष्ट प्रकार का अनुक्रम जिसका गणित में महत्त्वपूर्ण गुणधर्म है जो Fibonacci sequence कहलाता है, का आविष्कार इटली के महान गणितज्ञ Leonardo Fibonacci (1170–1250 A.D.) ने किया। सत्रहवीं शताब्दी में श्रेणियों का वर्गीकरण विशिष्ट रूप से हुआ। 1671 ई. में James Gregory ने अपरिमित अनुक्रम के संदर्भ में अपरिमित श्रेणी शब्द का उपयोग किया। बीजगणितीय तथा समुच्चय सिद्धांतों के समुचित विकास के उपरांत ही अनुक्रम तथा श्रेणियों से संबंधित जानकारी अच्छे ढ़ंग से प्रस्तुत हो सकी।
