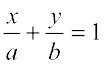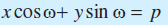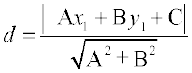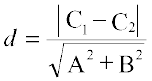Table of Contents
10.1 भूमिका (Introduction)
हम अपनी पूर्ववर्ती कक्षाओं में द्विविमीय निर्देशांक ज्यामिति से परिचित हो चुके हैं। मुख्यतः यह बीजगणित और ज्यामिति का संयोजन है। बीजगणित के प्रयोग से ज्यामिति का क्रमबद्ध अध्ययन सर्वप्रथम प्रख्यात फ्रांसीसी दार्शनिक एवं गणितज्ञ Rene Descartes ने 1637 में प्रकाशित अपनी पुस्तक La Gemoetry में किया था। इस पुस्तक से ज्यामिति के अध्ययन में वक्र के समीकरण का विचार तथा संबंधित वैश्लेषिक विधियों का प्रारंभ हुआ। ज्यामिति एवं विश्लेष. कापरिणामी संयोजन अब वैश्लेषिक ज्यामिति (Analytical Geometry) के रूप में उल्लेखित होता है। पूर्ववर्ती कक्षाओं में हमने निर्देशांक ज्यामिति का अध्ययन प्रारंभ किया है, जिसमें हमने निर्देशांक अक्षों, निर्देशांक तल, तल में बिंदुओं को आलेखित करना, दो बिंदुओं के बीच की दूरी, विभाजन सूत्र इत्यादि के बारे में अध्ययन किया है। ये सभी संकल्पनाएँ निर्देशांक ज्यामिति के आधार (basics) हैं। आइए हम, पूर्ववर्ती कक्षाओं में अध्ययन की गई निर्देशांक ज्यामिति का स्मर. करें। स्मर. के लिए, xy-तल में (6, – 4) और (3, 0) बिंदुओं के संक्षेप में दोहराने को आकृति 10.1 में प्रदर्शित किया गया है।
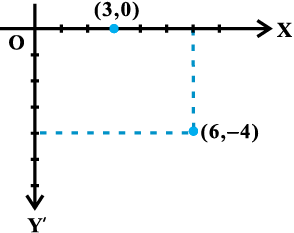
आकृति 10.1
ध्यान दीजिए कि बिंदु (6, – 4) धन x-अक्ष के अनुदिश y-अक्ष से 6 इकाई दूरी पर और ऋ. y-अक्ष के अनुदिश x-अक्ष से 4 इकाई दूरी पर है। इसी प्रकार बिंदु (3,0) धन x-अक्ष के अनुदिश y-अक्ष से 3 इकाई दूरी पर और x-अक्ष से शून्य दूरी पर है।
हमने निम्नलिखित महत्वपूर्. सूत्रों का भी अध्ययन किया हैः
I. P (x1, y1) और Q (x2, y2) बिंदुओं के बीच की दूरी
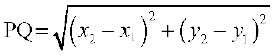 है।
है।
उदाहरणार्थ , (6, – 4) और (3, 0) बिंदुओं के बीच की दूरी
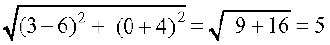 इकाई है।
इकाई है।
II. (x1, y1) और (x2, y2) बिंदुओं को मिलाने वाले रेखाखंड को m: n में अंतःविभाजित करने वाले बिंदु के निर्देशांक 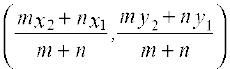 हैं।
हैं।
उदाहरणार्थ , उस बिंदु के निर्देशांक जो A(1, – 3) और B (–3, 9) को मिलाने वाले रेखाखंड को 1: 3 में अंतःविभाजित करता है, इसलिए 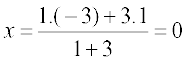 और
और 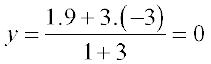 हैं।
हैं।
III. विशेष रूप में यदि m = n, तो (x1, y1) और (x2, y2) बिंदुओं को मिलाने वाले रेखाखंड के मध्य बिंदु के निर्देशांक 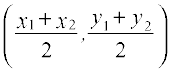 हैं।
हैं।
IV. (x1, y1), (x2, y2) और (x3, y3) शीर्षों से बने त्रिभुुज का क्षेत्रफल
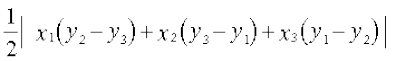 वर्ग इकाई है।
वर्ग इकाई है।
उदाहरणार्थ , एक त्रिभुज जिसके शीर्ष (4, 4), (3, – 2) और (– 3, 16) हैं,
उसका क्षेत्रफल = 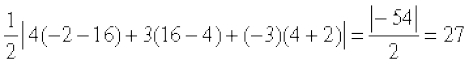 वर्ग इकाई है।
वर्ग इकाई है।
टिप्पणी यदि त्रिभुज ।ठब् का क्षेत्रफल शून्य है, तो तीन बिंदु A,B और C एक रेखा पर होते हैं अर्थात् वे सांरेख ( collinear ) हैं।
इस अध्याय में, हम निर्देशांक ज्यामिति के अध्ययन को सरलतम ज्यामितीय आकृति-सरल रेखा के गुणधर्मो के अध्ययन हेतु सतत करते रहेंगे। इसकी सरलता के होते हुए भी रेखा, ज्यामिति की एक अत्यावश्यक संकल्पना है और हमारे दैनिक जीवन के अनुभव में बहुत रोचक एवं उपयोगी ढंग से सम्मिलित हैं। यहाँ मुख्य उद्देश्य रेखा का बीजगणितीय निरूप. है जिसके लिए ढाल (slope ) की संकल्पना अत्यंत आवश्यक है।
10.2 रेखा की ढाल (Slope of a line)
निर्देशांक तल में एक रेखा x- अक्ष , के साथ दो कोण बनाती है, जो परस्पर संपूरक होते हैं। कोण θ(मान लीजिए) जो रेखा l,x- अक्ष की धनात्मक दिशा के साथ बनाती है, रेखा L, का झुकाव ( Inclination of the line l ) कहलाता है। स्पष्टतया 0° ≤ θ <180° ( आकृति 10.2) ।
हम देखते हैं कि x- अक्ष पर संपाती रेखाओं का झुकाव 0° होता है। एक ऊर्ध्व रेखा (y- अक्ष के समांतर या y- अक्ष पर संपाती) का झुकाव 90° है।
परिभाषा 1 यदि θ किसी रेखा स का झुकाव है, तो tan θ को रेखा स की ढाल कहते हैं।
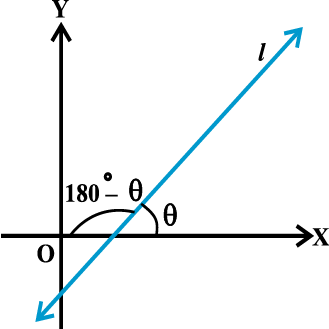
आकृति 10.2
वह रेखा जिसका झुकाव 90° है, उसकी ढाल परिभाषित नहीं है। एक रेखा की ढाल को उ से व्यक्त करते हैं। इस
प्रकार m = tan θ, θ ≠ 90° यह देखा जा सकता है कि x अक्ष की ढाल शून्य है और y अक्ष की ढाल परिभाषित नहीं है।
10.2.1 रेखा की ढाल, जब उस पर दो बिंदु दिए गए हों (Slope of a line when
coordinates of any two points on the line are given)
हम जानते हैं, कि यदि एक रेखा पर दो बिंदु ज्ञात हो , तो वह पूर्णतया परिभाषित होती है। अतः हम रेखा की ढाल को उस पर दिए दो बिंदअु के निर्देशांकाें के पद में ज्ञात करते हैं।
मान लीजिए कि एक ऊर्ध्वेत्तर ( non vertical ) रेखा l, जिसका झुकाव θ है, पर दो बिं द p (x 1 , y 1 ) औ र Q(x 2, y 2 ) है । स्पष्टतया x1 ≠ x 2 , अन्यथा रेखा ग- अक्ष पर लंब होगी, जिसकी ढाल परिभाषित नहीं है। रेखा l का झुकाव θ, न्यूनकोण या अधिक कोण हो सकता है। हम दोनों स्थितियों पर विचार करते हैं।
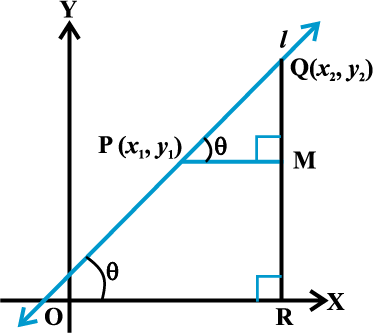
आकृति 10. 3 (i)
x- अक्ष पर QR तथा RQ पर PM लंब खींचिए (आकृति 10.3 (i) और (ii) में दर्शाया गया है
दशा 1 जब θ न्यूनकोण है आकृति 10.3 (i), में ∠ MPQ= θ
इसलिए रेखा l की ढाल = m = tan θ
परंतु त्रिभुज ∆ MPQ में, tan θ = 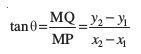 ... (1)
... (1)
समीकरण (1) तथा (2) से, हम पाते हैं कि m =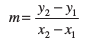 ... (2)
... (2)
दशा II जब θ अधिक कोण है:
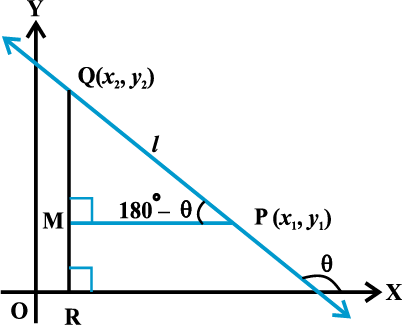
आकृति 10. 3 (ii)
आकृति 10.3 (ii) में , ∠ MPQ= 180° - θ.
इसलिए, θ = 180° - ∠MPQ
अब, रेखा l की ढाल =m = tan θ
= tan ( 180° - ∠ MPQ)
= - tan ∠ MPQ
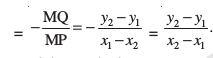
फलतः दोनों दशाओं में बिंदु (x 1 ,y 1 ) और
(x 2 , y 2 ) से जाने वाली रेखा की ढाल
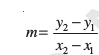
10.2.2 दो रेखाओं के समांतर और परस्पर लंब होने का प्रतिबंध (Conditions for parallelism and perpendicularity of lines)
मान लीजिए कि ऊर्ध्वेतर रेखाओं l 1 और l 2 की ढालें, जो एक निर्देशांक तल में हैं क्रमशः m1 तथा m 2 हैं। मान लीजिए कि इनके झुकाव क्रमशः α और β हैं। यदि l 1 और l 2 समांतर रेखाएँहैं (आकृति 10-4) तब उनके झुकाव समान होंगे
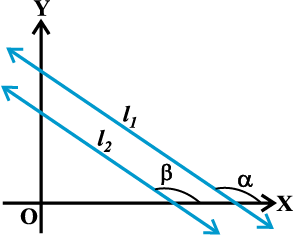
आकृति 10. 4
अर्थात्
α = β, और tan α = tan β
इसलिए
m1 = m2 , अर्थात् उनके ढाल बराबर हैं।
विलोमतः यदि दो रेखाओं l 1 और l 2 के ढाल बराबर हैं
अर्थात्
m1 = m2
तब
tan α = tan β
स्पर्शज्या (tangent) फलन के गु.धर्म से (0° और 180° के बीच ), α = β
अतः रेखाएँ समांतर हैं।
अतः दो ऊर्ध्वेत्तर रेखाएँ l 1 और l 2 समांतर होती हैं, यदि और
केवल यदि उनके ढाल समान हैं।
यदि रेखाएँ l 1 और l 2 परस्पर लंब हैं (आकृति 10-5), तब
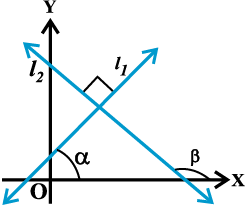
आकृति 10. 5
β = α + 90°.
इसलिए
tan β = tan (α + 90°)
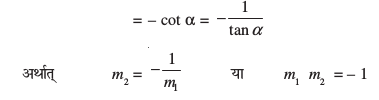
विलोमतः यदि m 1 m 2 = - 1, अर्थात् tan α tan β = - 1.
तब, tan α = - cot β = tan (β + 90°) या tan (β - 90°)
इसलिए, α और β का अंतर 90° है।
अतः, रेखाएँ l 1 और l 2 परस्पर लंब हैं।
अतः दो ऊर्ध्वेत्तर रेखाएँ l 1 और l 2 परस्पर लंब होती हैं यदि और केवल यदि उनकी ढाल परस्पर
ऋणात्मक व्युत्क्रम है।
आइए, निम्नलिखित उदाहरण पर विचार करेंः
उदाहरण 1 उन रेखाओं के ढाल ज्ञात कीजिए जो
(a) (3, – 2) और (–1, 4) बिंदुओं से होकर जाती है,
(b) (3, – 2) और (7, –2) बिंदुओं से होकर जाती है,
(c) (3, – 2) और (3, 4) बिंदुओं से होकर जाती है,
(d) धन x–अक्ष से 60° का कोण बनाती है।
हल (a) (3, – 2) और (–1, 4) बिंदुओं से जाने वाली रेखा की ढाल
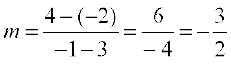 है
है
(b) (3, – 2) और (7, –2) बिंदुओं से जाने वाली रेखा का ढाल
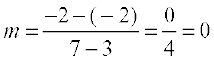 है
है
(c) (3, – 2) और (3, 4) बिंदुओं से जाने वाली रेखा का ढाल 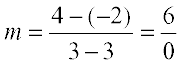 , जो कि परिभाषित नहीं है।
, जो कि परिभाषित नहीं है।
(d) यहाँ रेखा का झुकाव α= 60° । इसलिए, रेखा का ढाल
m = tan 60° = 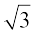 है।
है।
10.2.3 दो रेखाओं के बीच का कोण (Angle between two line)
जब हम एक तल में स्थित एक से अधिक रेखाओं के बारे में विचार करते हैं तब देखते हैं कि या तो ये रेखाएँ प्रतिच्छेद
करती हैंं या समांतर होती हैं। यहाँ हम दो रेखाओं के बीच के कोण पर, उनके ढालों के पदों में विचार करेंगे।
मान लीजिए दो ऊर्ध्वत्त्र रेखाओं L 1 और L 2 के ढाल क्रमशः m 1 और m 2 है। यदि L 1 और L 2 के झुकाव क्रमशः α 1 और α 2 हों तो
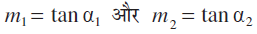
हम जानते हैं कि जब दो रेखाएँ परस्पर प्रतिच्छेद करती हैं तब वे दो शीर्षाभिमुख कोणों के युग्म बनाती हैं जो एेसे हैं कि किन्हीं दो संलग्न कोणों का योग 180° है। मान लीजिए कि रेखाओं L1और L2 के बीच संलग्न कोण θ और φ हैं (आकृति 10.6)। तब
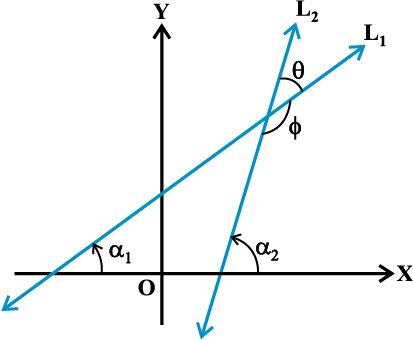
आकृति 10. 6
θ = α2 – α1 और α1, α2 ≠ 90°
इसलिए, tan θ = tan (α2 – α1) 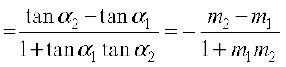 (क्योंकि 1 + m1m2 ≠ 0)
(क्योंकि 1 + m1m2 ≠ 0)
और φ = 180° – θ
इस प्रकार tan φ = tan (180° – θ ) = – tan θ = 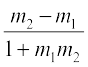 , क्योंकि 1 + m1m2 ≠ 0
, क्योंकि 1 + m1m2 ≠ 0
अब, दो स्थितियाँ उत्पन्न होती हैंः
स्थिति I यदि 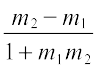 धनात्मक है, तब tan θ धनात्मक होगा और tan φ ऋणात्मक होगा जिसका अर्थ है θ न्यूनकोण होगा और φ अधिक कोण होगा।
धनात्मक है, तब tan θ धनात्मक होगा और tan φ ऋणात्मक होगा जिसका अर्थ है θ न्यूनकोण होगा और φ अधिक कोण होगा।
स्थिति II यदि 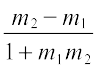 ऋणात्मक है, तब tan θ ऋणात्मक होगा और tan φ धनात्मक होगा जिसका अर्थ है θ अधिक कोण होगा और φ न्यून कोण होगा।
ऋणात्मक है, तब tan θ ऋणात्मक होगा और tan φ धनात्मक होगा जिसका अर्थ है θ अधिक कोण होगा और φ न्यून कोण होगा।
इस प्रकार, m1 और m2, ढाल वाली रेखाओं L1 और L2 के बीच का न्यून कोण (माना कि θ) इस प्रकार है,
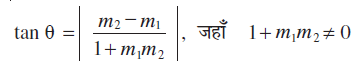
अधिक कोण (माना कि φ) φ =180° – θ के प्रयोग से प्राप्त किया जा सकता है।
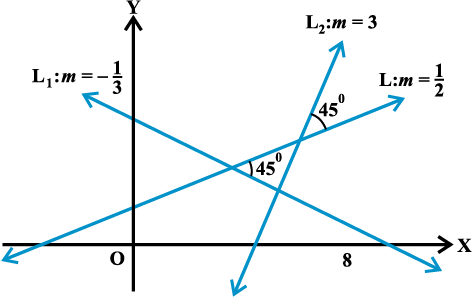
उदाहर. 2 यदि दो रेखाओं के बीच का कोण 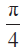
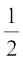 है तो दूसरी रेखा की ढाल ज्ञात कीजिए।
है तो दूसरी रेखा की ढाल ज्ञात कीजिए।
हल हम जानते हैं कि m1 और m2 ढाल वाली दो रेखाओं के बीच न्यूनकोण θ इस प्रकार है कि
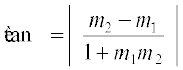 ... (1)
... (1)
यहाँ m1 = 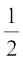 , m2 = m और θ =
, m2 = m और θ =
अब (1) में इन मानों को रखने पर
जिससे प्राप्त होता है 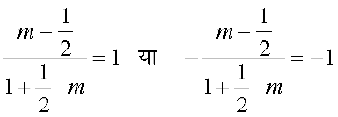
इसलिए, 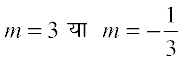
आकृति 10. 7
अतः दूसरी रेखा की ढाल 3 या है। आकृति 10.7 में दो उत्तर का कार. स्पष्ट किया गया है।
उदाहरण 3 (-2, 6) और (4, 8) बिंदुओं को मिलाने वाली रेखा, (8, 12) और (x, 24) बिंदुओं को
मिलाने वाली रेखा पर लंब है। x का मान ज्ञात कीजिए।
हल (- 2, 6) और (4, 8) बिंदुओं से जाने वाली रेखा की ढाल m 1 =8-6/ 4 − ( − 2 ) = 2/6 = 1/3
(8, 12) और (x, 24) बिंदुओं से जाने वाली रेखा की ढाल m 2 =24 − 12/x-8 = 12/x-8
क्योंकि दोनों रेखाएँ लंब हैं इसलिए, m1 m2 = –1, जिससे प्राप्त होता है
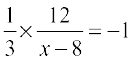 या
या 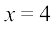 .
.
10.2.4 तीन बिंदुओं की संरेखता (Collinearity of three points)
हम जानते हैं कि दो समांतर रेखाओं के ढाल समान होते हैं। यदि समान ढाल वाली दो रेखाएँ एक ही बिंदु से होकर जाती हैं, तो आवश्यक रूप से वे संपाती (coincident) होती हैं। अतः यदि XY- तल में A,B और C तीन बिंदु हैं, तब वे एक रेखा पर होंगे अर्थात् तीनों बिंदु संरेख होंगे (आकृति 10-8) यदि और केवल यदि AB की ढाल = BC की ढाल।
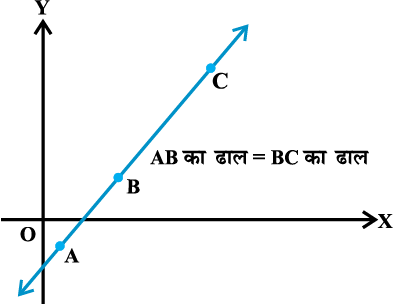
आकृति 10. 8
उदाहरण 4 तीन बिंदु P (h, k), Q (x 1 , y 1 ) और तR (x 2 , y 2 ) एक रेखा पर हैं। दिखाइए (h - x 1 ) (y 2 - y 1 ) = (k -y 1 ) (x 2 - x 1 )
हल क्योंकि बिंदु P,Q और R संरेख हैं, हम पाते है
PQ की ढाल = QR की ढाल अर्थात्

उदाहरण 5 आकृति 10.9, में एक रैखिक गति का समय और दूरी का लेखाचित्र दिया है। समय और दूरी की दो स्थितियाँ, जब T= 0 ,D = 2 और जब T= 3, D = 8 अंकित की गईं हैं। ढाल की संकल्पना का प्रयोग करके गति का नियम ज्ञात कीजिए अर्थात् दूरी, समय पर किस प्रकार आश्रित है?

आकृति 10. 9
हल मान लीजिए कि रेखा पर कोई बिंदु (T,D) है जहाँ T समय पर क् दूरी निरूपित है।
इसलिए, बिंदु (0, 2), (3, 8) और (T,D) संरेख है। इस प्रकार
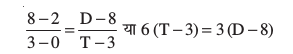
या D = 2(T+ 1), जो कि अभीष्ट संबंध है।
प्रश्नावली 10-1
1. कार्तीय तल में एक चतुर्भुज खींचिए जिसके शीर्ष (- 4, 5), (0, 7), (5, - 5) और (- 4, -2) हैं। इसका क्षेत्रफल भी ज्ञात कीजिए।
2. 2a भुजा के समबाहु त्रिभुज का आधार y- अक्ष के अनुदिश इस प्रकार है कि आधार का मध्य बिंदु मूल बिंदु पर है। त्रिभुज के शीर्ष ज्ञात कीजिए।
3. P (x 1 , y 1 ) और Q (x 2 , y 2 ) के बीच की दूरी ज्ञात कीजिए जब : (i)PQ, y- अक्ष के समांतर
है, (ii) PQ, x- अक्ष के समांतर है।
4. x- अक्ष पर एक बिंदु ज्ञात कीजिए जो (7, 6) और (3, 4) बिंदुओं से समान दूरी पर है।
5. रेखा की ढाल ज्ञात कीजिए जो मूल बिंदु और P (0, - 4) तथा B (8, 0) बिंदुओं को मिलाने वाले रेखाखंड के मध्य बिंदु से जाती हैं।
6. पाइथागोरस प्रमेय के प्रयोग बिना दिखलाइए कि बिंदु (4, 4), (3, 5) और (-1, -1) एक समकोण त्रिभुज के शीर्ष हैं।
7. उस रेखा का समीकरण ज्ञात कीजिए जो y -अक्ष की धन दिशा से वामावर्त्त मापा गया 30 ° का कोण बनाती है।
8. x का वह मान ज्ञात कीजिए जिसके लिए बिंदु (x, - 1), (2,1) और (4, 5) संरेख हैं।
9. दूरी सूत्र का प्रयोग किए बिना दिखलाइए कि बिंदु (- 2, - 1), (4, 0), (3, 3) और (-3, 2) एक समांतर चतुर्भुज के शीर्ष हैं।
10. x-अक्ष और (3,–1) और (4,–2) बिंदुओं को मिलाने वाली रेखा के बीच का कोण ज्ञात कीजिए।
11. एक रेखा की ढाल दूसरी रेखा की ढाल का दुगुना है। यदि दोनों के बीच के कोण की स्पर्शज्या (tangent)  है तो रेखाओं की ढाल ज्ञात कीजिए।
है तो रेखाओं की ढाल ज्ञात कीजिए।
12. एक रेखा (x1, y1) और (h, k) से जाती है। यदि रेखा की ढाल m है तो दिखाइए
k – y1 = m (h – x1).
13. यदि तीन बिंदु (h, 0), (a, b) और (0, k) एक रेखा पर हैं तो दिखाइए कि 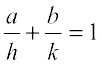 .
.
10.3 रेखा के समीकरण के विविध रूप (Various Forms of the Equation
of a Line))
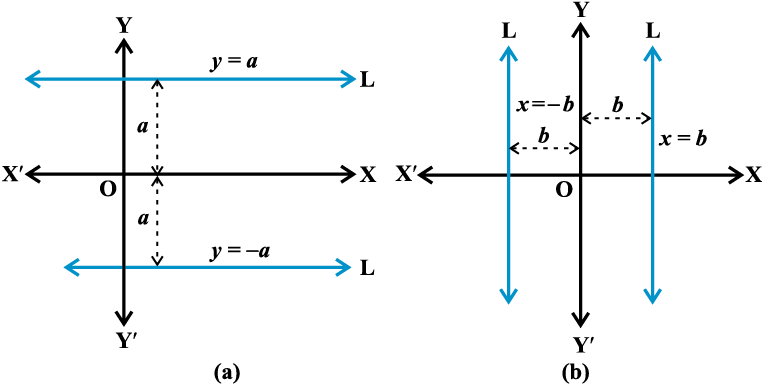
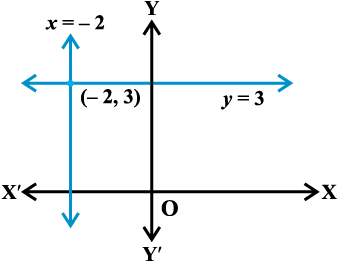
10.3.11 क्षैतिज एवंऊर्ध्वाधर रेखाएँ (Horizontal and vertical lines)
10.3.2 बिंदु-ढाल रूप (Point-slope form)
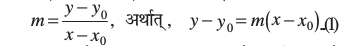
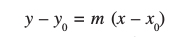
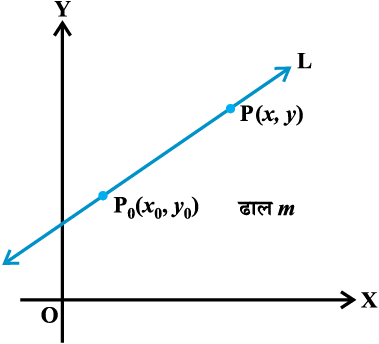
उपर्युक्त बिंदु-ढाल रूप सूत्र (1) से दी रेखा का समीकरण y – 3 = – 4 (x + 2) या 4x + y + 5 = 0, है जो अभीष्ट समीकरण है।
10.3.3 दो बिंदु रूप (Two -point form)
मान लीजिए रेखा L दो दिए बिंदुओं p 1 (x 1 , y 1 ) और p 2 (x 2 , x 2 ) से जाती है और L पर व्यापक बिंदु P (x, y) है (आकृति 10-14)।
तीन बिंदु P 1 , P 2 और P संरेख हैं, इसलिए,
P 1 P की ढाल = P 1 P 2 की ढाल

अर्थात् 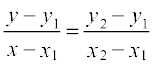
या 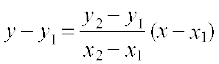
इस प्रकार, (x1, y 1 ) और (x 2 , y 2 )
बिंदुओं से जाने वाली रेखा का
समीकरण
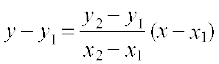
उदाहरण 8 बिंदुओं (1, -1) और (3, 5) से होकर जाने वाली रेखा का समीकरण लिखिए।
हल यहाँ x1 = 1, y1 = –1, x2 = 3 और y2 = 5, दो बिंदु रूप सूत्र (2) के प्रयोग से रेखा का समीकरण , हम पाते हैं
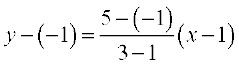
या -3x+y+4=0, जो अभीष्ट समीकरण है।
10.3.4 ढाल अंतःखंड रूप (Slope-intercept form)
कभी-कभी हमें एक रेखा का मान उसकी ढाल तथा उसके द्वारा किसी एक अक्ष पर काटे गए अंतःखंड द्वारा होता है।
स्थिति I कल्पना कीजिए कि ढाल m की रेखा L, y- अक्ष पर मूल बिंदु से ब दूरी पर प्रतिच्छेद करती है (आकृति 10-15)। दूरी c रेखा L का y- अंतःखंड कहलाती है। स्पष्ट रूप से उस बिंदु के निर्देशांक जहाँ यह रेखा y- अक्ष से मिलती है, (0, c) हैं। इस प्रकार L की ढाल m है और यह एक स्थिर बिंदु (0,c) से होकर जाती है। इसलिए, बिंदु-ढाल रूप से, L का समीकरण
y-c=m(x-0)

आकृति 10. 15
y-c=m(x-0)
या y=mx+c
इस प्रकार, ढाल m तथा y - अंतःखंड c वाली रेखा पर बिंदु (x, y) केवल और केवल तभी होगी
यदि
y=mx+c
ध्यान दीजिए कि c का मान धनात्मक या ऋणात्मक होगा यदि y -अक्ष से अंतःखंड क्रमशः धन या ऋण भाग से बना हो।
स्थिति II कल्पना कीजिए ढाल m वाली रेखा x- अक्ष से d अंतःखंड बनाती है। तब रेखा L का
समीकरण है। y = m ( x − d ) ..... (4)
स्थिति (1) में कही वर्णित से विद्यार्थी स्वयं इस समीकरण को प्राप्त कर सकते हैं।
उदाहरण 9 उन रेखाओं के समीकरण लिखिए जिनके लिए tan θ = 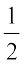 , जहाँ θ रेखा का झुकाव है और (i) y-अंतःखंड –
, जहाँ θ रेखा का झुकाव है और (i) y-अंतःखंड – 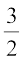 है, (ii) x-अंतःखंड 4 है।
है, (ii) x-अंतःखंड 4 है।
हल (i) यहाँ रेखा की ढाल = m = tan θ = 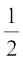 और y - अंतःखंड c = –
और y - अंतःखंड c = – 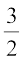 . इसलिए, ढाल-अंतःखंड रूप उपर्युक्त सूत्र (3) से रेखा का समीकरण
. इसलिए, ढाल-अंतःखंड रूप उपर्युक्त सूत्र (3) से रेखा का समीकरण 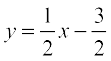 या
या 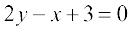 है, जो अभीष्ट समीकरण है।
है, जो अभीष्ट समीकरण है।
(ii) यहाँ, m = tan θ = 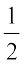 और d = 4
और d = 4
इसलिए, ढाल-अंतःखंड रूप उपर्युक्त सूत्र (4) से रेखा का समीकरण
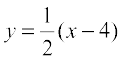 या
या 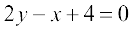 ,
,
है, जो अभीष्ट समीकरण है।
10.3.5 अंतःखंड-रूप (Intercept - form)
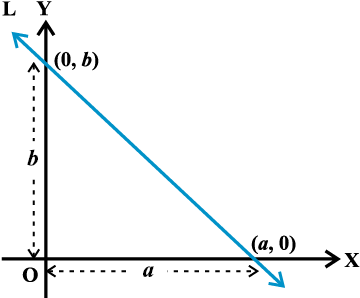
कल्पना कीजिए कि एक रेखा L, x- अंतःखंडं और y- अंतःखंड b बनाती है। स्पष्टतया L,x- अक्ष से बिंदु (a, 0) और y- अक्ष से बिंदु (0,b) पर मिलती है (आकृति 10.16) ।
रेखा के दो बिंदु रूप समीकरण से
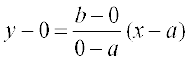 या
या 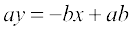 ,
,
अर्थात् 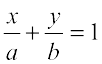
इस प्रकार, x-अक्ष और y-अक्ष से क्रमशः a और b अंतःखंड बनाने वाली रेखा का समीकरण निम्नलिखित है: 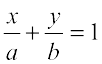 ... (5)
... (5)
उदाहरण 10 एक रेखा का समीकरण ज्ञात कीजिए जो x- और y- अक्ष से क्रमशः -3 और 2 के अंतःखंड बनाती है।
हल यहाँ a= -3 और b = 2. उपयुर्क् अं त:खंड रूप (5) से रे ख का समीकरण
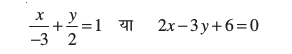
10.3.6 लंब रूप (Normal form)
कल्पना कीजिए कि निम्नलिखित आँकड़ों सहित हमको एक ऊर्ध्वेतर रेखा ज्ञात है।
(प) मूल बिंदु से रेखा पर लंब की लंबाई।
(पप) लंब एवं धन ग -अक्ष के बीच का कोण।
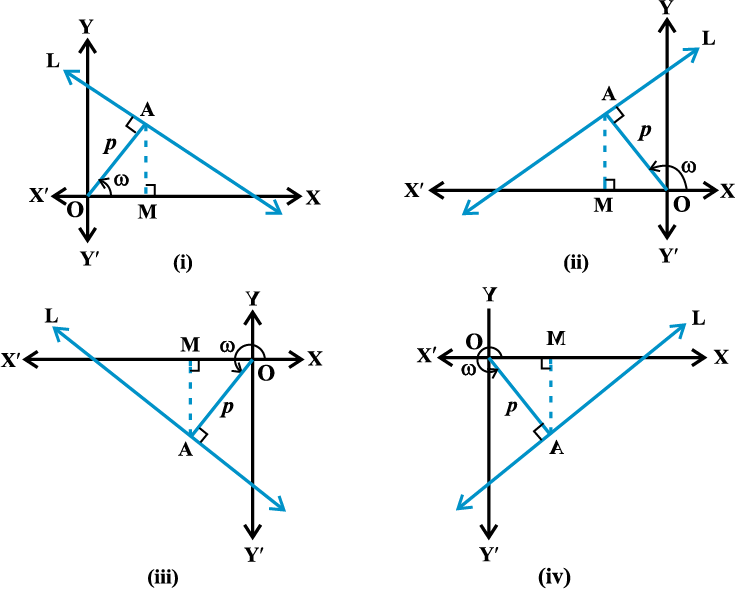
आकृति 10. 17
मान लीजिए कि L एक रेखा है जिसकी मूल बिंदु O से लांबिक दूरी OA = p और धन x- अक्ष और OA के बीच का कोण ∠ XOA = ω. कार्त्तीय तल में रेखा L की संभव स्थितियाँ आकृति 10.17 में दर्शाई गयी हैं। अब, हमारा उद्देश्य L का ढाल और इस पर एक बिंदु ज्ञात करना है। प्रत्येक स्थिति में x- अक्ष पर AM लंब डाला गया है।
प्रत्येक स्थिति में, OM = p cos ω और MA = p sin ω, इस प्रकार बिंदु A के निर्देशांक (p cos ω, p sin ω) हैं।
इसके अतिरिक्त रेखा L, OA पर लंब है।
रेखा L की ढाल =
इस प्रकार, रेखा L की ढाल 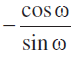
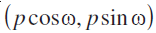
या x cos ω + y sin ω = p.
अतः, मूल बिंदु से लांबिक दूरी p और धन x-अक्ष तथा लंब के बीच कोण ω वाली रेखा का समीकरण इस प्रकार है x cos ω + y sin ω = p ... (6)
उदाहरण 11 रेखा का समीकरण ज्ञात कीजिए जिसकी मूल बिंदु से लांबिक दूरी 4 इकाई और धन x- अक्ष तथा लंब के
बीच कोण 15° है।
हल यहाँ हमें दिया है च = 4 और ω = 15 0 (आकृति 10.18).
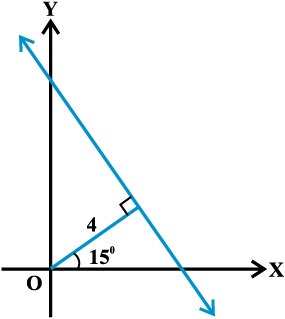
अब, cos 15° = 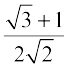 और
और
sin 15º = 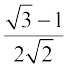 (क्यों?)
(क्यों?)
उपर्युक्त लंब रूप (6) से रेखा का समीकरण
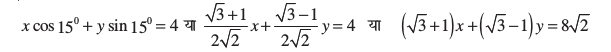
है। यही अभीष्ट समीकरण है।
उदाहरण 12 फारेनहाइट ताप F और परम ताम K एक रैखिक समीकरण को संतुष्ट करते हैं। दिया है कि K = 273 जब F= 32 और K = 373 जब F = 212 तो K को F के पदों में व्यक्त कीजिए और F का मान ज्ञात कीजिए जबकि K= 0
हल कल्पना कीजिए कि F, x - अक्ष के अनुदिश और K, y- अक्ष अनुदिश है तो XY- तल में हमें दो बिंदु (32,273) और (212, 373) स्थित हैं। दो बिंदु रूप सूत्र से बिंदु (F, K) के द्वारा संतुष्ट होने वाला
समीकरण निम्नलिखित है:
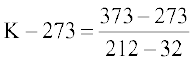
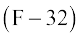 या
या 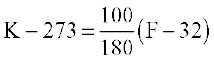
या 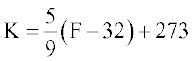 ... (1)
... (1)
यही अभीष्ट संबंध है। जब K= 0, समीकरण (1) से,

टिप्पणी हम जानते हैं कि समीकरण y = mx+c, में दो अचर, नामतः m और c हैं। इन दो अचरों को ज्ञात करने के लिए हमें रेखा के समीकरण को संतुष्ट करने के लिए दो प्रतिबंध चाहिए।उपर्युक्त सभी उदाहरणों में हमें रेखा का समीकरण ज्ञात करने के लिए दो प्रतिबंध दिये गये हैं।
प्रश्नावली 10.2
प्रश्न 1 से 8 तक, रेखा का समीकरण ज्ञात कीजिए जो दिये गये प्रतिबंधों को संतुष्ट करता है:
1. x- और y- अक्षों के समीकरण लिखिए।
2. ढाल 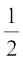 और बिंदु (– 4, 3) से जाने वाली ।
और बिंदु (– 4, 3) से जाने वाली ।
3. बिंदु (0, 0) से जाने वाली और ढाल m वाली।
4. बिंदु 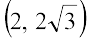 से जाने वाली और x-अक्ष से 75° के कोण पर झुकी हुई।
से जाने वाली और x-अक्ष से 75° के कोण पर झुकी हुई।
15. मूल बिंदु से किसी रेखा पर डाला गया लंब रेखा से बिंदु (-2, 9) पर मिलता है, रेखा का समीकरण ज्ञात कीजिए।
16. ताँबे की छड़ की लंबाई L (सेमी में) सेल्सियस ताप C का रैखिक फलन है। एक प्रयोग में यदि L = 124.942 जब C=20 और L= 125.134 जब C = 110 हो, तो L को C के पदों में व्यक्त कीजिए।
17. किसी दूध भंडार का स्वामी प्रति सप्ताह 980 लिटर दूध, 14 रु. प्रति लिटर के भाव से और 1220 लीटर दूध 16 रु. प्रति लिटर के भाव से बेच सकता है। विक्रय मूल्य तथा मांग के मध्य के संबंध को रैखिक मानते हुए यह ज्ञात कीजिए कि प्रति सप्ताह वह कितना दूध 17 रु. प्रति लिटर के भाव से बेच सकता है?
18. अक्षों के बीच रेखाखंड का मध्य बिंदु P (a, b) है। दिखाइए कि रेखा का समीकरण 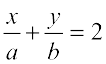 है।
है।
19. अक्षों के बीच रेखाखंड को बिंदु R (h, k), 1:2 के अनुपात में विभक्त करता है। रेखा का समीकरण ज्ञात कीजिए।
20. रेखा के समीकरण की संकल्पना का प्रयोग करते हुए सिद्ध कीजिए कि तीन बिंदु (3,0), (-2, -2) और (8, 2) संरेख हैं।
10.4 रेखा का व्यापक समीकरण (General Equation of a Line)
पूर्ववर्ती कक्षाओं में हमने दो चर राशियों के एक घातीय व्यापक समीकरण Ax + By + C = 0, का अध्ययन किया जहाँ A, B और C , एेसे वास्तविक अचर हैं कि A और B एक साथ शून्य नहीं हैं। समीकरण Ax + By + C = 0 का लेखाचित्र सदैव एक सरल रेखा होता है। इसलिए, जब A और B एक साथ शून्य नहीं हैं तो Ax + By + C = 0, के रूप का कोई समीकरण रेखा का व्यापक रैखिक समीकरण (General linear equation) या रेखा का व्यापक समीकरण (General equation) कहलाता है।
10.4.1 Ax + By + C = 0 के विभिन्न रूप (Different forms of Ax + By + C = 0) समीकरण को निम्नलिखित प्रक्रियाओं द्वारा रेखा के समीकरण के विभिन्न रूपों में रूपांतरित किया जा सकता है।
(a) ढाल-अंतःखंड रूप (Slope-intercept form) यदि B ≠ 0ए तो Ax+By+C = 0 को

हम जानते हैं कि समीकरण (1) उस रेखा की ढाल-अंतःखंड रूप है जिसकी ढाल 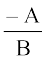 , और y-अंतःखंड
, और y-अंतःखंड 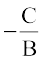 है। यदि B = 0, तो x =
है। यदि B = 0, तो x = 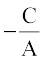 , जो कि एक ऊर्ध्वाधर रेखा का समीकरण है जिसकी ढाल अपरिभाषित और x-अंतःखंड
, जो कि एक ऊर्ध्वाधर रेखा का समीकरण है जिसकी ढाल अपरिभाषित और x-अंतःखंड 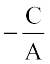 है।
है।
(इ) अंतःखंड-रूप (Intercept form) यदि C ≠ 0, तो Ax+By+C=0 को
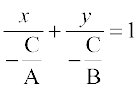 या
या 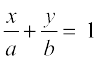 ... (1)
... (1)
जहाँ a = 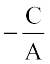 और b =
और b = 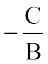

जिससे 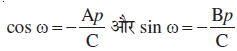
अब
अथवा 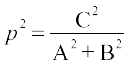 या
या 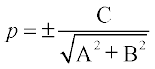
इसलिए 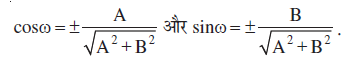
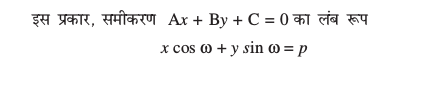

लिखा जा सकता है। (1) की तुलना y = mx + c, से करने पर हम पाते हैं कि दी हुई रेखा की ढाल m =  है।
है।

(2) की तुलना 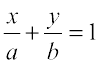 , से करने पर हम पाते हैं कि x-अंतःखंड
, से करने पर हम पाते हैं कि x-अंतःखंड
a = 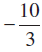
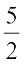 है।
है।
उदाहरण 14 समीकरण 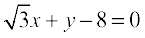 को लंब रूप में रूपांतरित कीजिए और p तथा ω के मान ज्ञात कीजिए।
को लंब रूप में रूपांतरित कीजिए और p तथा ω के मान ज्ञात कीजिए।
हल दिया समीकरण
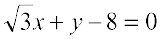 ... (1)
... (1)
है। (1) को 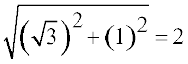 , से भाग देने पर
, से भाग देने पर
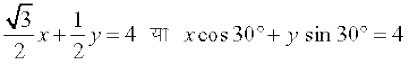 ... (2)
... (2)
(2) की तुलना x cos α + y sin α = p, से करने पर, हम p = 4 और α = 30° पाते हैं।
उदाहरण 15 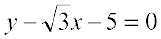 और
और 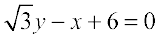 रेखाओं के बीच का कोण ज्ञात कीजिए।
रेखाओं के बीच का कोण ज्ञात कीजिए।
हल दी हुई रेखाएँ
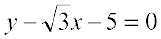 या
या 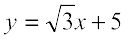 ... (1)
... (1)
और 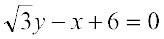 या
या 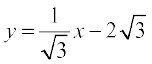 ... (2)
... (2)
रेखा (1) की ढाल m1 = 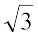 और रेखा (2) की ढाल m2 =
और रेखा (2) की ढाल m2 = 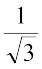 है।
है।
दोनों रेखाओं के बीच न्यूनकोण (माना कि θ) इस प्रकार है
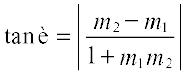 ... (3)
... (3)
m1 और m2 के मान (3) में रखने पर,
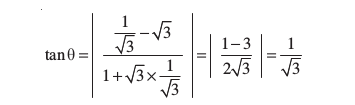
जिससे θ = 30°. प्राप्त होता है। अतः दोनों रेखाओं के बीच कोण या तो 30° या
180° – 30° = 150° है।
उदाहरण 16 दर्शाइए कि दो रेखाएँ 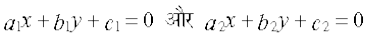 , जहाँ b1, b2 ≠ 0
, जहाँ b1, b2 ≠ 0
(i) समांतर हैं यदि 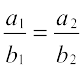 और (ii) लंब है यदि
और (ii) लंब है यदि 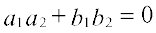 .
.
हल दी गई रेखाएँ एेसे लिखी जा सकती हैं
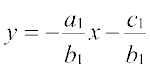 ... (1)
... (1)
और 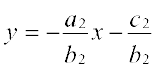 ... (2)
... (2)
रेखाओं (1) और (2) की ढाल क्रमशः m1 = 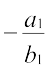 और m2 =
और m2 = 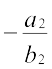 हैं।
हैं।
अब (i) रेखाएँ समांतर होंगी, यदि m1 = m2, जिससे प्राप्त होता है 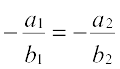 या
या 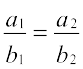
(ii) रेखाएँ लंब होंगी, यदि m1.m2 = – 1, जिससे प्राप्त होता है
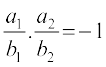 या a1a2 + b1b2 = 0
या a1a2 + b1b2 = 0
उदाहरण 17 रेखा  पर लंब और बिंदु (1, -2) से जाने वाली रेखा का समीकरण ज्ञात कीजिए।
पर लंब और बिंदु (1, -2) से जाने वाली रेखा का समीकरण ज्ञात कीजिए।
हल दी हुई रेखा 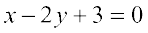 को
को
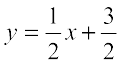 लिखा जा सकता है। ... (1)
लिखा जा सकता है। ... (1)
रेखा (1) की ढाल m1 = 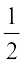 . है। इसलिए, रेखा (1) के लंब रेखा की ढाल
. है। इसलिए, रेखा (1) के लंब रेखा की ढाल 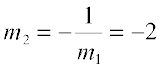 है।
है।
ढाल -2 वाली और बिंदु (1, – 2) से जाने वाली रेखा का समीकरण
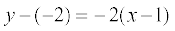 या
या  ,
,
है, जो अभीष्ट समीकरण है।
10.5 एक बिंदु की रेखा से दूरी (Distance of a Point From a Line)
एक बिंदु की किसी रेखा से दूरी बिंदु से रेखा पर डाले लंब की लंबाई है। मान लीजिए कि L : Ax + By + C = 0 एक रेखा है, जिसकी बिंदु P (x1, y1) से दूरी d है। बिंदु P से रेखा पर लंब PL खींचिए (आकृति 10.19) यदि रेखा x-अक्ष और y-अक्ष को क्रमशः Q और R, पर मिलती है तो इन बिंदुओं के निर्देशांक Q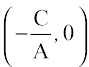 और R
और R 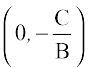 हैं।
हैं।
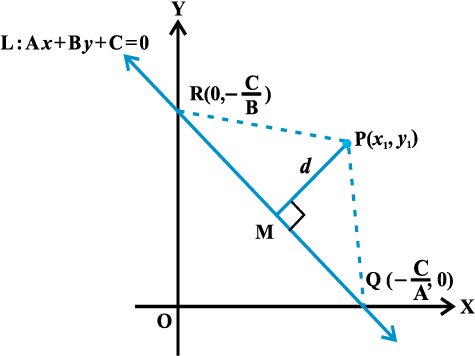
त्रिभुज PQR का क्षेत्रफल निम्नलिखित प्रकार से किया जा सकता हैः
क्षेत्रफल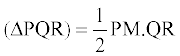 जिससे
जिससे 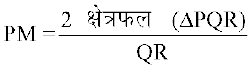 ... (1)
... (1)
साथ ही ∆PQR का क्षेत्रफल = 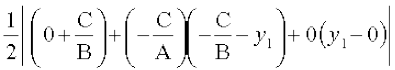
= 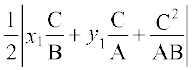
या, 2 ∆PQR का क्षेत्रफल = 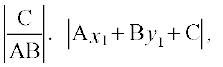 और
और
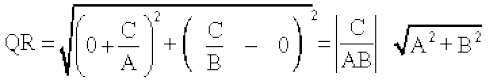
∆PQR के क्षेत्रफल और QR के मान (1) में रखने पर,
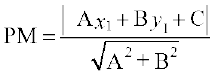
या 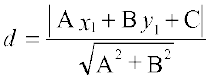 .
.
इस प्रकार, बिंदु (x1, y1) से रेखा Ax + By+ C = 0 की लांबिक दूरी (d) इस प्रकार है:
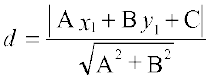

रेखा (1) x-अक्ष पर बिंदु A 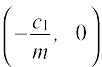 में प्रतिच्छेद करेगी जैसा आकृति 10.20 में दिखाया गया है। दो रेखाओं के बीच की दूरी, बिंदु A से रेखा (2) पर लंब की लंबाई है। इसलिए, रेखाओं (1) और (2) के बीच की दूरी
में प्रतिच्छेद करेगी जैसा आकृति 10.20 में दिखाया गया है। दो रेखाओं के बीच की दूरी, बिंदु A से रेखा (2) पर लंब की लंबाई है। इसलिए, रेखाओं (1) और (2) के बीच की दूरी
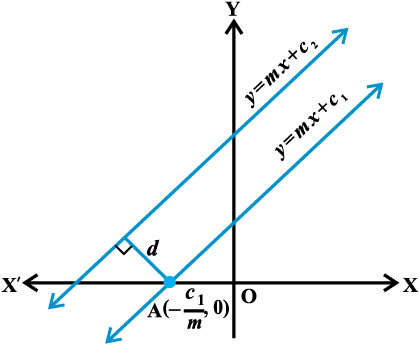
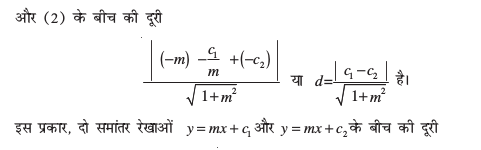
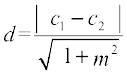
यदि रेखाएँ व्यापक रूप में दी गई हैं अर्थात् Ax + By + C1 = 0 और Ax + By + C2 = 0, तो उपर्युक्त सूत्र 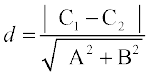 का रूप ले लेता है।
का रूप ले लेता है।
उदाहरण 18 बिंदु (3, – 5) की रेखा 3x – 4y –26 = 0 से दूरी ज्ञात कीजिए।
हल दी हुई रेखा 3x – 4y –26 = 0 ...(1)
(1) की तुलना रेखा के व्यापक समीकरण Ax + By + C = 0, से करने पर, हम पाते हैंः
A = 3, B = – 4 और C = – 26
दिया हुआ बिंदु (x1, y1) = (3, –5) है। दिए बिंदु की रेखा से दूरी 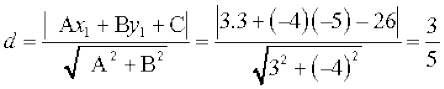 इकाई है।
इकाई है।
उदाहरण 19 समांतर रेखाओं 3x – 4y +7 = 0 और 3x – 4y + 5 = 0 के बीच की दूरी ज्ञात कीजिए।
हल यहाँ A = 3, B = –4, C1 = 7 और C2 = 5. इसलिए, अभीष्ट दूरी
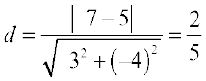
प्रश्नावली 10.3
1. निम्नलिखित समीकरणों को ढाल-अंतःखंड रूप में रूपांतरित कीजिए और उनके ढाल तथा y-अंतःखंड ज्ञात कीजिएः
(i) x + 7y = 0 (ii) 6x + 3y – 5 = 0 (iii) y = 0
2. निम्नलिखित समीकरणों को अंतःखंड रूप में रूपांतरित कीजिए और अक्षों पर इनके द्वारा काटे गए अंतःखंड ज्ञात कीजिएः
(i) 3x + 2y – 12 = 0 (ii) 4x – 3y = 6 (iii) 3y + 2 = 0.
3. निम्नलिखित समीकरणों को लंब रूप में रूपांतरित कीजिए। उनकी मूल बिंदु से लांबिक दूरियाँ और लंब तथा धन x-अक्ष के बीच का कोण ज्ञात कीजिए:
(i) x –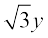 + 8 = 0 (ii) y – 2 = 0 (iii) x – y = 4.
+ 8 = 0 (ii) y – 2 = 0 (iii) x – y = 4.
4. बिंदु (-1, 1) की रेखा 12(x + 6) = 5(y – 2) से दूरी ज्ञात कीजिए।
5. x-अक्ष पर बिंदुओं को ज्ञात कीजिए जिनकी रेखा 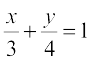 से दूरीयाँ 4 इकाई हैं।
से दूरीयाँ 4 इकाई हैं।
6. समांतर रेखाओं के बीच की दूरी ज्ञात कीजिएः
(i) 15x + 8y – 34 = 0 और 15x + 8y + 31 = 0 (ii) l(x + y) + p = 0 और l (x + y) – r = 0
7. रेखा 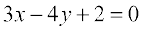 के समांतर और बिंदु (–2, 3) से जाने वाली रेखा का समीकरण ज्ञात कीजिए।
के समांतर और बिंदु (–2, 3) से जाने वाली रेखा का समीकरण ज्ञात कीजिए।
8. रेखा x – 7y + 5 = 0 पर लंब और x-अंतःखंड 3 वाली रेखा का समीकरण ज्ञात कीजिए।
9. रेखाओं 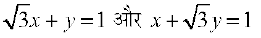 के बीच का कोण ज्ञात कीजिए।
के बीच का कोण ज्ञात कीजिए।
10. बिंदुओं (h, 3) और (4, 1) से जाने वाली रेखा, रेखा 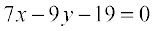 को समकोण पर प्रतिच्छेद करती है। h का मान ज्ञात कीजिए।
को समकोण पर प्रतिच्छेद करती है। h का मान ज्ञात कीजिए।
14. बिंदु (-1, 3) से रेखा 3x + 4y + 16 = 0 पर डाले गये लंबपाद के निर्देशांक ज्ञात कीजिए।
16. यदि p और q क्रमशः मूल बिंदु से रेखाओं 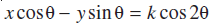
18. यदि p मूल बिंदु से उस रेखा पर डाले लंब की लंबाई हो जिस पर अक्षों पर कटे अंतः खंड a और b हों, तो दिखाइए कि 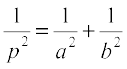
विविध उदाहर.
उदाहरण. 20 यदि रेखााएँ 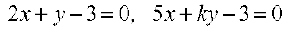 अाैर
अाैर 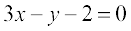 संगामी (concurrent) हैं, तो k का मान ज्ञात कीजिए।
संगामी (concurrent) हैं, तो k का मान ज्ञात कीजिए।

(1) और (3) को वज्र गु.न विधि से हल करने पर,
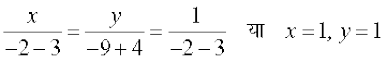
इसलिए, दो रेखाओं का प्रतिच्छेद बिंदु (1, 1) है। चूँकि उपर्युक्त तीनों रेखाएँ संगामी हैं, बिंदु
(1, 1) समीकरण (2) को संतुष्ट करेगा जिससे
 या
या 
उदाहरण 21 बिंदु P(4, 1) से रेखा 4x-y = 0 की दूरी उस रेखा के अनुदिश ज्ञात कीजिए जो धन x- अक्ष से 135° का कोण बनाती है।
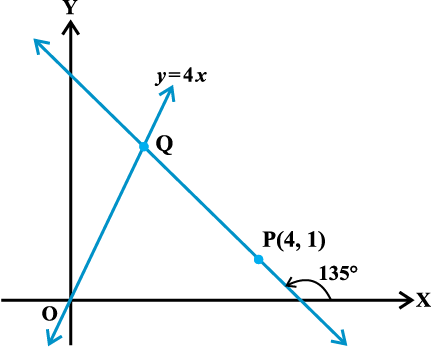
हल दी हुई रेखा 4x-y = 0 ......(1)
रेखा (1) की बिंदु P (4, 1) से दूरी, किसी अन्य रेखा के अनुदिश, ज्ञात करने के लिए हमें दोनों रेखाओं के प्रतिच्छेद
बिंदु को ज्ञात करना पड़ेगा। इसके लिए हम पहले दूसरी रेखा का समीकरण प्राप्त करेंगे (आकृति 10.21) । दूसरी रेखा की ढाल स्पर्शज्या (tangent) 135° = -1
ढाल -1 वाली और बिंदु P (4, 1) से जाने वाली रेखा का समीकरण

उदाहरण 22 कल्पना करते हुए कि सरल रेखाएँ बिंदु के लिए दर्पण की तरह कार्य करती है, बिंदु (1, 2) का रेखा
x − 3 y + 4 = 0 मे a प्रतिबिम्ब ज्ञात कीजिए।
हल मान लीजिए Q (h, k) बिंदु P (1, 2) का रेखा x – 3y + 4 = 0 ... (1)
में प्रतिबिंब है।
इसलिए, रेखा (1) रेखाखंड PQ का लंब समद्विभाजक है
(आकृति 10.22) ।
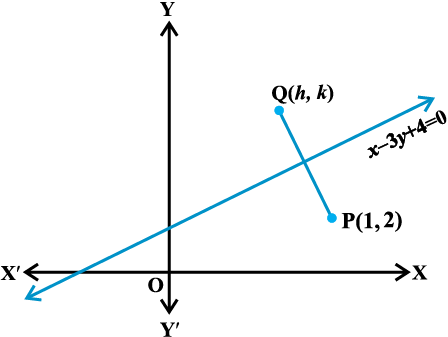
अतः PQ की ढाल = 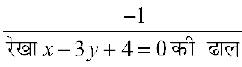 ,
,
जिससे 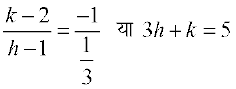 ... (2)
... (2)
और PQ का मध्य बिंदु अर्थात् बिंदु 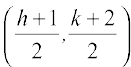 समीकरण (1) को संतुष्ट करेगा जिससे
समीकरण (1) को संतुष्ट करेगा जिससे
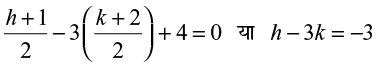 ... (3)
... (3)
(2) और (3) को हल करने पर, हम पाते हैं h =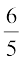 और k =
और k =  .
.
अतः बिंदु (1, 2) का रेखा (1) में प्रतिबिंब 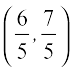 है।
है।
उदाहरण 23 दर्शाइए कि रेखाओं
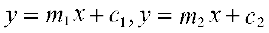 और x = 0 से बने त्रिभुज का क्षेत्रफल
और x = 0 से बने त्रिभुज का क्षेत्रफल 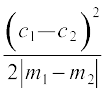 है।
है।
हल दी रेखाएँ हैं
y = m1 x + c1 ... (1)
y = m2 x + c2 ... (2)
x = 0 ... (3)
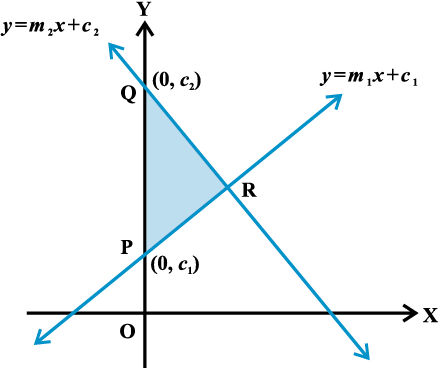
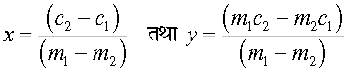
इसलिए, त्रिभुज का तीसरा शीर्ष R 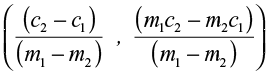 है।
है।
अब, त्रिभुज का क्षेत्रफल
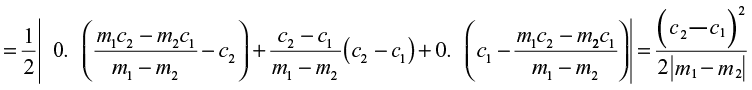 है
है
उदाहरण 24 एक रेखा इस प्रकार है कि इसका रेखाओं 5x – y + 4 = 0 और 3x + 4y – 4 = 0 के बीच का रेखाखंड बिंदु (1, 5) पर समद्विभाजित होता है इसका समीकरण प्राप्त कीजिए।
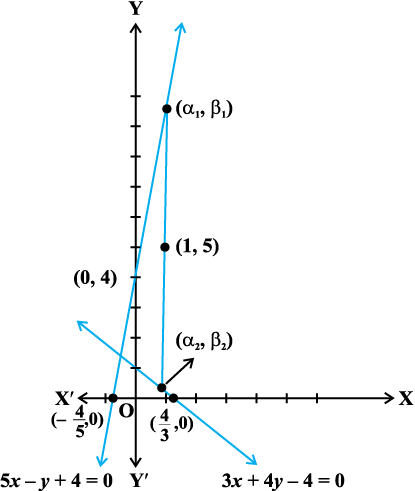
इसलिए
या
हमें दिया है कि अभीष्ट रेखा का (α1, β1) और (α2, β2) के बीच के खंड का मध्य बिंदु (1, 5) है।
इसलिए,
या α1 + α2 = 2 और
या α1 + α2 = 2 और 20 α1 – 3 α2 = 20 ... (3)
α1 और α2, के मानों के लिए (3) के समीकरणों को हल करने पर, हम पाते हैं
(1,5) और (α1, β1) से जाने वाली अभीष्ट रेखा का समीकरण
या 107x – 3y – 92 = 0, जो कि अभीष्ट रेखा का समीकरण है।

 या
या  ,
,
इन दोनों संबंधों को हल करने पर हम पाते हैं , k = 0 या h =  . इस प्रकार, बिंदु (h, k) समीकरणों y = 0 या x =
. इस प्रकार, बिंदु (h, k) समीकरणों y = 0 या x = 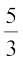 , जो कि सरल रेखाएँ निरूपित करते हैं, को संतुष्ट करता है। अतः रेखाओं (1) और (2) से समान दूरी पर रहने वाले बिंदु का पथ एक सरल रेखा है।
, जो कि सरल रेखाएँ निरूपित करते हैं, को संतुष्ट करता है। अतः रेखाओं (1) और (2) से समान दूरी पर रहने वाले बिंदु का पथ एक सरल रेखा है।

4. y-अक्ष पर कौन से बिंदु एेसे हैं, जिनकी रेखा 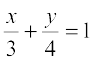 से दूरी 4 इकाई है।
से दूरी 4 इकाई है।
5. मूल बिंदु से बिंदुओं (cosθ, sin θ) और (cos φ, sin φ) को मिलाने वाली रेखा की लांबिक दूरी ज्ञात कीजिए।
6. रेखाओं x – 7y + 5 = 0 और 3x + y = 0 के प्रतिच्छेद बिंदु से खींची गई और y-अक्ष के समांतर रेखा का समीकरण ज्ञात कीजिए।
7. रेखा 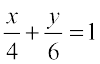 पर लंब उस बिंदु से खींची गई रेखा का समीकरण ज्ञात कीजिए जहाँ यह रेखा y-अक्ष से मिलती है।
पर लंब उस बिंदु से खींची गई रेखा का समीकरण ज्ञात कीजिए जहाँ यह रेखा y-अक्ष से मिलती है।
16. बिंदु (–1, 2) से खींची जा सकने वाली उस रेखा की दिशा ज्ञात कीजिए जिसका रेखा x + y =4 से प्रतिच्छेद बिंदु दिए बिंदु से 3 इकाई की दूरी पर है।

सारांश
- (x1, y1) और (x2, y2) बिंदुओं से जाने वाली ऊर्ध्वेत्तर रेखा की ढाल m इस प्रकार है
![]()
- यदि एक रेखा x-अक्ष की धन दिशा से α कोण बनाती है तो रेखा की ढाल m = tan α, α ≠ 90°है।
- क्षैतिज रेखा की ढाल शून्य है और ऊर्ध्वाधर रेखा की ढाल अपरिभाषित है।
- m1 और m2 ढालों वाली रेखाओं L1 और L2 के बीच का न्यून कोण θ (मान लिया) हो तो
- दो रेखाएँ समांतर होती हैं यदि और केवल यदि उनके ढाल समान हैं।
- दो रेखाएँ लंब होती हैं यदि और केवल यदि उनके ढालों का गु.नफल -1 है।
- तीन बिंदु A, B और C संरेख होते हैं यदि और केवल यदि AB की ढाल = BC की ढाल।
- x-अक्ष से a दूरी पर स्थित क्षैतिज रेखा का समीकरण या तो y = a या y = – a है।
- y-अक्ष से b दूरी पर स्थित ऊर्ध्वाधर रेखा का समीकरण या तो x = b या x = – b
- स्थिर बिंदु (xo, yo) से जाने वाली और ढाल m वाली रेखा पर बिंदु (x, y) स्थित होगा यदि और केवल यदि इसके निर्देशांक समीकरण y – yo = m (x – xo) को संतुष्ट करते हैं।
- बिंदुओं (x1, y1) और (x2, y2) से जाने वाली रेखा का समीकरण इस पΡकार है,
![]()
- ढाल m और y-अंतःखंड c वाली रेखा पर बिंदु (x, y) होगा यदि और केवल यदि
![]() .
. - यदि ढाल m वाली रेखा x-अंतःखंड d बनाती है तो रेखा का समीकरण y = m (x – d) है।
- x- और y-अक्षों से क्रमशः a और b अंतःखंड बनाने वाली रेखा का समीकरण
![]()
- मूल बिंदु से लांबिक दूरी p और इस लंब तथा धन x-अक्ष के बीच ω कोण बनाने वाली रेखा का समीकरण
- यदि A और B एक साथ शून्य न हों तो Ax + By + C = 0 के रूप का कोई समीकरण रेखा का व्यापक रैखिक समीकरण या रेखा का व्यापक समीकरण कहलाता है।
- एक बिंदु (x1, y1) से रेखा Ax + By+ C = 0 की लांबिक दूरी (d) इस प्रकार है
![]()
- समांतर रेखाओं Ax + By + C1 = 0 और Ax + By + C2 = 0, के बीच की दूरी
![]() है।
है।


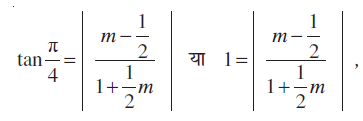
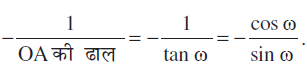
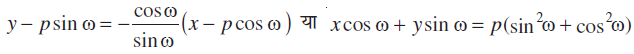
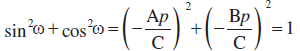
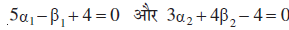
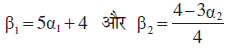
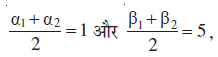
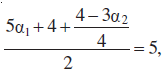

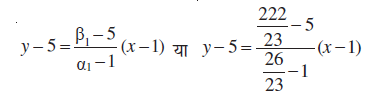
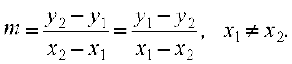
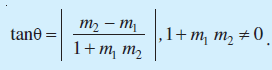
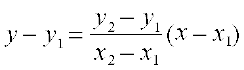
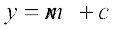 .
.