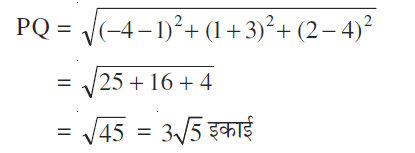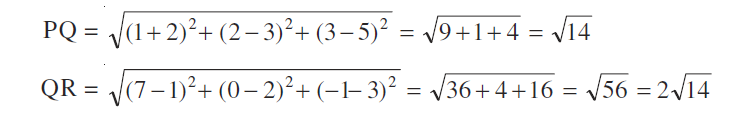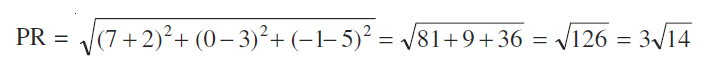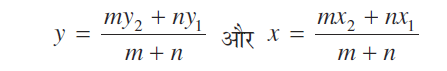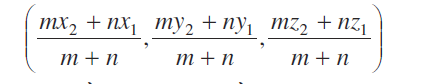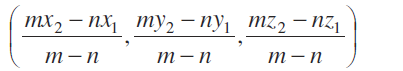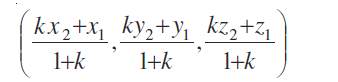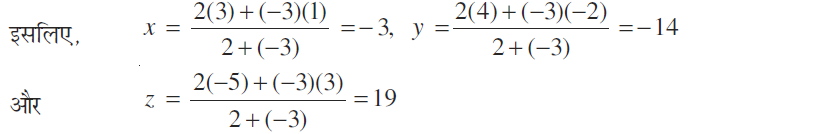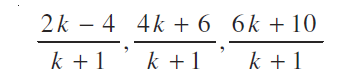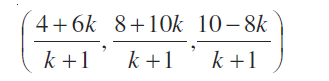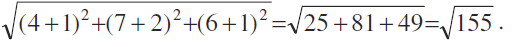Table of Contents
"Mathematics is both the queen and the hand-maiden of all sciences"
-E.T.Bell
12.1 भूमिका (Introduction)
हम जानते हैं, कि किसी तल में स्थित एक बिंदु की स्थिति निर्धारण के लिए हमें उस तल में दो परस्पर लंब एवं प्रतिच्छेदित रेखाओं से लांबिक दूरियों की आवश्यकता होती है। इन रेखाओं को निर्देशांक्ष और उन दो लांबिक दूरियों को अक्षोें के सापेक्ष उस बिंदु के निर्देशांक (coordinate) कहते हैं। वास्तविक जीवन में हमारा केवल एक तल में स्थित बिंदुओं से ही संबंध नहीं रह जाता है। उदाहरणत: अंतरिक्ष में फेंके गए एक गेंद की विभिन्न समय में स्थिति अथवा एक स्थान से दूसरे स्थान तक जाने के दौरान वायुयान की एक विशिष्ट समय में स्थिति आदि, को भी जानने की आवश्यकता पड़ती है।

इसी प्रकार एक कमरे की छत से लटकते हुए एक विद्युत बल्ब की निचली नोक अथवा छत के पंखे की नोक की स्थिति का निर्धारण करने के लिए हमें उन बिंदुओं की दो परस्पर लंब दीवारों से दूरियाँ मात्र ही पर्याप्त नहीं है बल्कि उस बिंदु की, कमरे के फर्श से ऊँचाई, की भी आवश्यकता पड़ती है। अत: हमें केवल दो नहीं बल्कि तीन परस्पर लांबिक तलों से लंबवत् दूरियों को निरूपित करने के लिए तीन संख्याओं की आवश्यकता होती है, जो बिंदु की दो परस्पर लंब दीवारों से दूरियाँ, तथा उस कमरे के फर्श से ऊँचाई को व्यक्त करती हैं। कमरे की परस्पर लंब दीवारों तथा उस क्षैतिज का फर्श तीन परस्पर प्रतिच्छेदित करने वाले तल हैं। इन परस्पर प्रतिच्छेदित करने वाले तलों से लंब दूरियों को व्यक्त करने वाली तीन संख्याएँ उस बिंदु के तीन निर्देशांक तलों के सापेक्ष निर्देशांक कहलाते हैं। इस प्रकार अंतरिक्ष (space) में स्थित एक बिंदु के तीन निर्देशांक होते हैं। इस अध्याय में हम त्रिविमीय अंतरिक्ष में ज्यामिति की मूलभूत संकल्पनाओं का अध्ययन करेंगे।
12.2 त्रिविमीय अंतरिक्ष में निर्देशांक्ष और निर्देशांक-तल (Coordinate Axes and Coordinate Planes in Three Dimensional Space)
बिंदु O पर प्रतिच्छेदित करने वाले तीन परस्पर लंब तलों की कल्पना कीजिए (आकृति 12.1)। ये तीनों तल रेखाओं X'OX, Y'OY और Z'OZ पर प्रतिच्छेदित करते हैं जिन्हें क्रमश: x-अक्ष, y-अक्ष और z-अक्ष कहते हैं। हम स्पष्टत: देखते हैं कि ये तीनों रेखाएँ परस्पर लंब हैं। इन्हें हम समकोणिक निर्देशांक निकाय कहते हैं। XOY, YOZ और ZOX, तलों को क्रमश: XY-तल, YZ-तल, तथा ZX-तल, कहते हैं। ये तीनों तल निर्देशांक तल कहलाते हैं।

आकृति 12.1
हम कागज के तल को XOY तल लेते हैं। और Z'OZ रेखा को तल XOY पर लंबवत लेते हैं। यदि कागज के तल को क्षैतिजत: रखें तो Z'OZ रेखा ऊर्ध्वारत: होती है। XY-तल से OZ की दिशा में ऊपर की ओर नापी गई दूरियाँ धनात्मक और OZ' की दिशा में नीचे की ओर नापी गई दूरियाँ ऋणात्मक होती हैं। ठीक उसी प्रकार ZX-तल के दाहिने OY दिशा में नापी गई दूरियाँ धनात्मक और ZX तल के बाएँ OY' की दिशा में नापी गई दूरियाँ ऋणात्मक होती हैं। YZ-तल के सम्मुख OX दिशा में नापी गई दूरियाँ धनात्मक तथा इसके पीछे OX' की दिशा में नापी गई दूरियाँ ऋणात्मक होती हैं। बिंदु O को निर्देशांक निकाय का मूल बिंदु कहते हैं। तीन निर्देशांक तल अंतरिक्ष को आठ भागों में बांटते हैं, इन अष्टाशों के नाम XOYZ, X'OYZ, X'OY'Z, XOY'Z, XOYZ', X'OY'Z', X'OY'Z' और XOY'Z' हैं। और जिन्हें क्रमश: I, II, III, ...., VIII द्वारा प्रदर्शित करते हैं।
12.3 अंतरिक्ष में एक बिंदु के निर्देशांक (Coordinates of a Point in Space)
अंतरिक्ष में निश्चित निर्देशांक्षों, निर्देशांक तलों और मूल बिंदु सहित निर्देशांक्ष निकाय के चयन के पश्चात् दिए बिंदु के तीन निर्देशांक (x , y, z) को ज्ञात करने की विधि तथा विलोमत: तीन संख्याओं के त्रिदिक (Triplet) दिए जाने पर अंतरिक्ष में संगत बिंदु (x, y, z) के निर्धारण करने की विधि की अब हम विस्तार से व्याख्या करते हैं।
अंतरिक्ष में दिए गए बिंदु P से XY-तल पर PM लंब खींचते हैं जिसका पाद M है (आकृति 12.2)। तब M से x–अक्ष पर ML लंब खींचिए, जो उससे L पर मिलता है। मान लीजिए OL=x, LM = y और PM = z तब (x, y, z) बिंदु P के निर्देशांक कहलाते हैं। इसमें x,y, z को क्रमश: बिंदु P के x-निर्देशांक, y-निर्देशांक, तथा z-निर्देशांक कहते हैं। आकृति 12.2 में हम देखते हैं कि बिंदु P(x, y, z) अष्टांश XOYZ में स्थित है, अत: x, y और z सभी धनात्मक हैं।
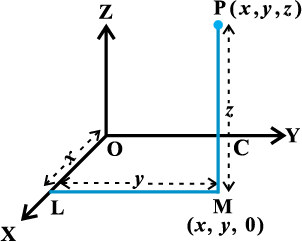
आकृति 12.2
यदि P किसी अन्य अष्टांश में हो तो x, y और z के चिह्न तदनुसार परिवर्तित हो जाते हैं। इस प्रकार अंतरिक्ष में स्थित किसी बिंदु P की संगतता वास्तविक संख्याओं के क्रमित त्रिदिक (x, y, z) से किया जाता है।
विलोमत:, किसी त्रिदिक (x, y, z) के दिए जाने पर हम x के संगत x-अक्ष पर बिंदु L निर्धारित करते हैं। पुन: XY-तल में बिंदु M निर्धारित करते हैं, जहाँ इसके निर्देशांक (x, y) हैं। ध्यान दीजिए कि LM या तो x-अक्ष पर लंब है अथवा y-अक्ष के समांतर है। बिंदु M पर पहुँचने के पश्चात्् हम XY-तल पर MP लंब खींचते हैं, इसपर बिंदु P को z के संगत निर्धारण करते हैं। इस प्रकार निर्धारित बिंदु P के निर्देशांक (x, y, z) हैं। अत: अंतरिक्ष में स्थित बिंदुओं की वास्तविक संख्याओं के क्रमित त्रिदिक (x, y, z) से सदैव एकेक-संगतता रखते हैं।
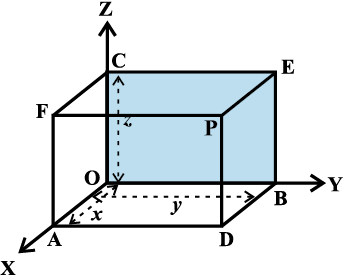
आकृति 12.3
विकल्पत:, अंतरिक्ष में स्थित बिंदु P से हम निर्देशांक तलों के समांतर तीन तल खींचते हैं, जो x-अक्ष, y-अक्ष और z-अक्ष को क्रमश: A, B तथा C बिंदुओं पर प्रतिच्छेदित करते हैं
(आकृति 12.3)। यदि OA=x, OB=y तथा OC=z हो तो बिंदु P के निर्देशांक x, y और z होते हैं और इसे हम P(x, y, z,) के रूप में लिखते हैं। विलोमत: x, y और z के दिए जाने पर हम निर्देशांक्षों पर बिंदु A, B तथा C निर्धारित करते हैं। बिंदु A, B तथा C से हम क्रमश: YZ-तल, ZX-तल तथा XY-तल के समांतर तीन तल खींचते हैं। इन तीनों तलों को ADPF, BDPE तथा CEPF का प्रतिच्छेदन बिंदु स्पष्टत: P है, जो क्रमित-त्रिदिक ( x, y z) के संगत है।
हम देखते हैं कि यदि अंतरिक्ष में कोई बिंदु P (x, y, z) है, तो YZ, ZX तथा XY तलों से लंबवत् दूरियाँ क्रमश: x, y तथा z हैं।
टिप्पणी बिंदु O के निर्देशांक (0, 0, 0) हैं। x-अक्ष पर स्थित किसी बिंदु के निर्देशांक (x, 0, 0) और YZ तल में स्थित किसी बिंदु के निर्देशांक (0, y, z) होते हैं।
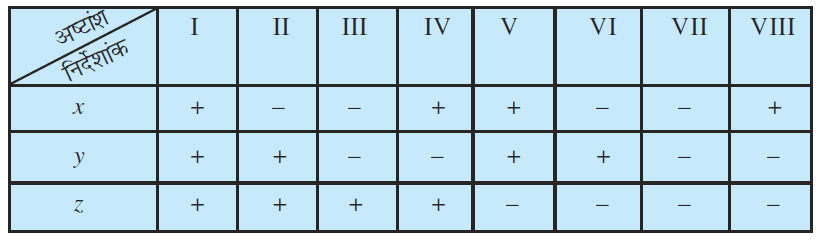
टिप्पणी एक बिंदु के निर्देशांकों के चिह्न उस अष्टांश को निर्धारित करते हैं जिसमें बिंदु स्थित होता है। निम्नलिखित सारणी आठों अष्टांशों में निर्देशांकों के εचह्न दर्शाती है।
सारणी 12.1
उदाहरण 1 आकृति 12.3 में, यदि P के निर्देशांक (2, 4, 5) हैं तो F के निर्देशांक ज्ञात कीजिए।
हल बिंदु F के लिए OY के अनुदिश नापी गयी दूरी शून्य है। अत: F के निर्देशांक (2, 0, 5) हैं।
उदाहरण 2 वे अष्टांश ज्ञात कीजिए जिसमें बिंदु (-3, 1, 2) और (-3, 1, -2) स्थित हैं।
हल सारणी 12.1 से, बिंदु (-3, 1, 2) दूसरे अष्टांश में तथा बिंदु (-3, 1, -2) छठे अष्टांश में स्थित हैं।
प्रश्नावली 12.1
1. एक बिंदु x–अक्ष पर स्थित है। इसके y-निर्देशांक तथा z-निर्देशांक क्या हैं?
2. एक बिंदु XZ–तल में है। इसके y-निर्देशांक के बारे में आप क्या कह सकते हैं?
3. उन अष्टांशों के नाम बताइए, जिनमें निम्नलिखित बिंदु स्थित हैं।
(1, 2, 3), (4, –2, 3), (4, –2, –5), (4, 2, –5), (– 4, 2, –5), (– 4, 2, 5), (–3, –1, 6) (–2, – 4, –7)
4. रिक्त स्थान की पूर्ति कीजिए:
(i) x-अक्ष और y-अक्ष दोनों एक साथ मिल कर एक तल बनाते हैं, उस तल को _______ कहते हैं।
(ii) XY-तल में एक बिंदु के निर्देशांक _______ रूप के होते हैं।
(iii) निर्देशांक तल अंतरिक्ष को _______ अष्टांश में विभाजित करते हैं।
12.4 दो बिंदुओं के बीच की दूरी (Distance between Two Points)
द्विविमीय निर्देशांक निकाय में हमने दो बिंदुओं के बीच की दूरी का अध्ययन कर चुके हैं। आइए अब हम अपने अध्ययन का विस्तार त्रिविमीय निकाय के लिए करते हैं।
मान लीजिए, समकोणिक अक्ष OX, OY तथा OZ के सापेक्ष दो बिंदु P(x1, y1, z1) तथा Q (x2, y2, z2) हैं।
P तथा Q बिंदुओं से निर्देशांक तलों के समांतर तल खींचिए, जिससे हमें एेसा घनाभ मिलता है जिसका विकर्ण PQ है (देखिए आकृति 12.4)
क्योंकि ∠PAQ एक समकोण है अत:  PAQ में,
PAQ में,
PQ2 = PA2 + AQ2 ... (1)
पुन: क्योंकि ∠ANQ = एक समकोण, इसलिए  ANQ में,
ANQ में,
AQ2 = AN2 + NQ2 ... (2)
(1) और (2) से हमें प्राप्त होता है, कि
PQ2 = PA2 + AN2 + NQ2
अब, PA = y2 – y1, AN = x2 – x1 और NQ = z2 – z1
इस प्रकार, PQ2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
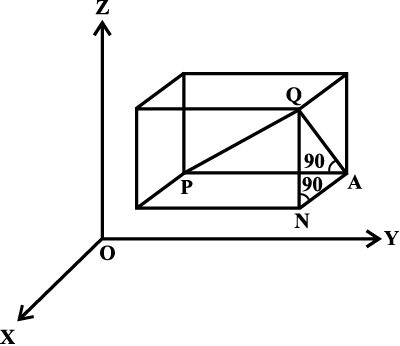
आकृति 12.4
अत: PQ = 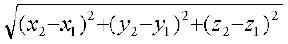
यह दो बिंदुओं P(x1, y1, z1) और Q(x2, y2, z2) के बीच की दूरी PQ के लिए सूत्र है।
विशेषत: यदि x1 = y1 = z1 = 0, अर्थात् बिंदु P, मूल बिंदु O हो तो
OQ = 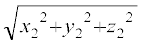 ,
,
जिससे हमें मूल बिंदु O और किसी बिंदु Q (x2, y2, z2) के बीच की दूरी प्राप्त होती है।
उदाहरण 3 बिंदुओं P (1, -3, 4) और Q (-4, 1, 2) के बीच की दूरी ज्ञात कीजिए।
हल PQ बिंदुओं P (1,–3, 4) और Q (– 4, 1, 2) के बीच की दूरी है।
उदाहरण 4 दर्शाइए कि P (–2, 3, 5), Q (1, 2, 3) और R (7, 0, –1) संरेख हैं।
हल हम जानते हैं कि संरेख बिंदु, एक ही रेखा पर स्थित होते हैं।
यहाँ
और
इस प्रकार PQ + QR = PR
अत: बिंदु P, Q और R संरेख हैं।
उदाहरण 5 क्या बिंदु A (3, 6, 9), B (10, 20, 30) और C (25, – 41, 5) एक समकोण त्रिभुज के शीर्ष हैं?
हल दूरी-सूत्र से हमें प्राप्त होता है कि
AB2 = (10 – 3)2 + (20 – 6)2 + (30 – 9)2
= 49 + 196 + 441 = 686
BC2 = (25 – 10)2 + (– 41 – 20)2 + (5 – 30)2
= 225 + 3721 + 625 = 4571
CA2 = (3 – 25)2 + (6 + 41)2 + (9 – 5)2
= 484 + 2209 + 16 = 2709
हम पाते हैं कि CA2 + AB2 ≠ BC2
अत: ∆ABC एक समकोण त्रिभुज नहीं है।
उदाहरण 6 दो बिंदुओं A तथा B के निर्देशांक क्रमश: (3, 4, 5) और (-1, 3, -7) हैं। गतिशील बिंदु P के पथ का समीकरण ज्ञात कीजिए, जबकि PA2 + PB2 = 2k2.
हल माना गतिशील बिंदु P के निर्देशांक (x, y, z) हैं।
अब PA2 = (x – 3)2 + (y – 4)2 + ( z – 5)2
PB2 = (x + 1)2 + (y – 3)2 + (z + 7)2
दिए गए प्रतिबन्ध के अनुसार, PA2 + PB2 = 2k2, हमें प्राप्त होता है:
(x – 3)2 + (y – 4)2 + (z – 5)2 + (x + 1)2 + (y – 3)2 + (z + 7)2 = 2k2
या 2x2 + 2y2 + 2z2 – 4x – 14y + 4z = 2k2 – 109.
प्रश्नावली 12.2
1. निम्नलिखित बिंदु-युग्मों के बीच की दूरी ज्ञात कीजिए:
(i) (2, 3, 5) और (4, 3, 1) (ii) (–3, 7, 2) और (2, 4, –1)
(iii) (–1, 3, – 4) और (1, –3, 4) (iv) (2, –1, 3) और (–2, 1, 3)
2. दर्शाइए कि बिंदु (-2, 3, 5) (1, 2, 3) और (7, 0, -1) संरेख हैं।
3. निम्नलिखित को सत्यापित कीजिए:
(i) (0, 7, –10), (1, 6, – 6) और (4, 9, – 6) एक समद्विबाहु त्रिभुज के शीर्ष हैं।
(ii) (0, 7, 10), (–1, 6, 6) और (– 4, 9, 6) एक समकोण त्रिभुज के शीर्ष हैं।
(iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8) और (2, –3, 4) एक समांतर चतुर्भुज के शीर्ष हैं।
4. एेसे बिंदुओं के समुच्चय का समीकरण ज्ञात कीजिए जो बिंदु (1, 2, 3) और
(3, 2, -1) से समदूरस्थ हैं।
5. बिंदुओं P से बने समुच्चय का समीकरण ज्ञात कीजिए जिनकी बिंदुओं A (4, 0, 0) और B (-4, 0, 0) से दूरियों का योगफल 10 है।
12.5 विभाजन सूत्र (Section Formula)
स्मरण कीजिए द्विविमीय ज्यामिति में हमने सीखा है कि किस प्रकार समकोणिक कार्तीय निकाय में एक रेखा खंड को दिए अनुपात में अंत: विभाजित करने वाले बिंदु के निर्देशांक ज्ञात करते हैं। अब हम इस संकल्पना का विस्तार त्रिविमीय ज्यामिति के लिए करते हैं।
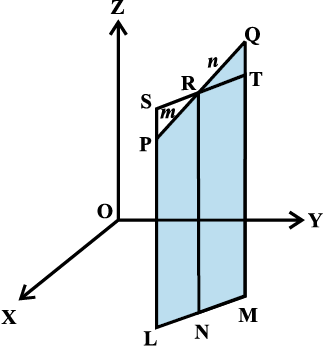
आकृति 12.5
मान लीजिए अंतरिक्ष में दो बिंदु P(x1, y1, z1) व Q (x2, y2, z2) हैं। माना R (x, y, z) रेखा खंड PQ को m : n अनुपात में अंत: विभाजित करता है। XY-तल पर PL, QM और RN लंब खींचिए। स्पष्टत: PL 11 QM 11 RN हैं तथा इन तीन लंबों के पाद XY–तल में स्थित हैं बिंदु L, M और N उस रेखा पर स्थित हैं जो उस तल और XY-तल के प्रतिच्छेदन से बनती है। बिंदु R से रेखा LM के समांतर रेखा ST खींचिए। ST रेखा खींचे गए लंब के तल में स्थित है तथा रेखा LP (विस्तारित) को S और MQ को T पर प्रतिच्छेदित करती है। जैसा आकृति 12.5 में प्रदर्शित है।
स्पष्टत: चर्तुभुज LNRS और NMTR समांतर चर्तुभुज हैं। त्रिभुजों PSR और QTR स्पष्टत: समरूप हैं। इसलिए
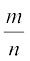 =
= 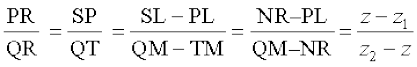
इस प्रकार z = 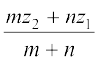
ठीक इसी प्रकार XZ-तल और YZ-तल पर लंब खींचने पर हमें प्राप्त होता है,
अत: बिंदु R जो बिंदु P (x1, y1, z1) और Q (x2, y2, z2) को मिलाने वाले रेखा खंड को
m : n के अनुपात में अंत: विभाजित करता है, के निर्देशांक हैं,
यदि εबंदु R, रेखा खंड PQ को m : n अनुपात में बाह्य विभाजित करता हो तो इसके निर्देशांक उपर्युक्त सूत्र में n को -n से विस्थापित करके प्राप्त किए जाते हैं। इस प्रकार R के निर्देशांक होंगें,
स्थिति 1 मध्य-बिंदु के निर्देशांक यदि R, रेखाखंड PQ का मध्य-बिंदु है तो m : n = 1:1 रखने पर
x = 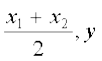 =
= 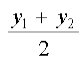 और z =
और z =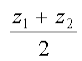
ये P (x1, y1, z1) और Q (x2, y2, z2) को मिलाने वाली रेखा खंड के मध्य-बिंदु के निर्देशांक हैं।
स्थिति 2 रेखा खंड PQ को k : 1 के अनुपात में अंत: विभाजित करने वाले बिंदु R के निर्देशांक 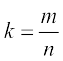 रखने पर प्राप्त किए जा सकते हैं:
रखने पर प्राप्त किए जा सकते हैं:
यह परिणाम प्राय: दो बिंदुओं को मिलाने वाली रेखा पर व्यापक बिंदु संबंधी प्रश्नों के हल करने में प्रयुक्त होता है।
उदाहरण 7 बिंदुओं (1, -2, 3) और (3, 4, -5) को मिलाने से बने रेखा खंड को अनुपात 2:3 में (i) अंत: (ii) बाह्य विभाजित करने वाले बिंदु के निर्देशांक ज्ञात कीजिए।
हल (i) मान लीजिए P (x, y, z), A (1, –2, 3) और B(3, 4, –5) को मिलाने वाले रेखा खंड को अंत: 2:3 में विभक्त करता है।
इसलिए, 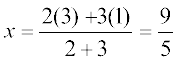 ,
, 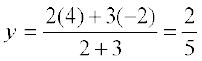 , और
, और 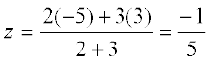
अत: अभीष्ट बिंदु 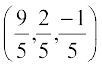 है।
है।
(ii) मान लीजिए P (x, y, z), A (1, –2, 3) और B(3, 4, –5) को मिलाने वाले रेखा खंड को बाह्य अनुपात 2 : 3 में बाह्य विभक्त करता है।
अत: अभीष्ट बिंदु (–3, –14, 19). है।
उदाहरण 8 विभाजन सूत्र का प्रयोग करके सिद्ध कीजिए कि बिंदु (-4, 6, 10), (2, 4, 6) और
(14, 0, –2) संरेख हैं।
हल मान लीजिए A (– 4, 6, 10), B (2, 4, 6) और C(14, 0, – 2) दिए गए बिंदु हैं। मान लीजिए बिंदु P, AB को k : 1 में विभाजित करता है। तो P के निर्देशांक हैं:
आइये अब हम जाँच करें कि k के किसी मान के लिए बिंदु P, बिंदु C के संपाती हैं।
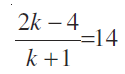
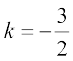
जब 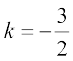 हो तो
हो तो 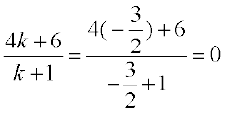
और 
इसलिए C (14, 0, –2) वह बिंदु है जो AB को 3 : 2 अनुपात में बाह्य विभक्त करता है और वही P है। अत: A, B व C संरेख है।
उदाहरण 9 त्रिभुज जिसके शीर्ष (x1, y1, z1), (x2, y2, z2) तथा (x3, y3, z3) हैं। इसके केंद्रक (Centroid) के निर्देशांक ज्ञात कीजिए।
हल मान लीजिए ABC एक त्रिभुज है जिसके शीर्ष A, B, C के निर्देशांक क्रमश: (x1, y1, z1),
(x2, y2, z2) तथा (x3, y3, z3), हैं।
मान लीजिए BC का मध्य-बिंदु D है। इसलिए D के निदेशांक हैं:
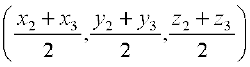
माना त्रिभुज का केंद्रक G है जो मध्यिका AD को अंत 2 : 1 में विभाजन करता है। इसलिए G के निर्देशांक हैं:
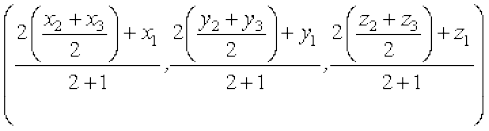
या 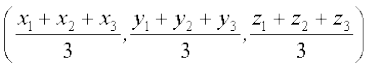
उदाहरण 10 बिंदुओं (4, 8, 10) और (6, 10, -8) को मिलाने वाले रेखा खंड, YZ-तल द्वारा जिस अनुपात में विभक्त होता है, उसे ज्ञात कीजिए।
हल मान लीजिए YZ-तल बिंदु P(x, y, z) पर, A (4, 8, 10) और B (6, 10, –8) को मिलाने वाला रेखा खंड को k :1 में विभक्त करता है। तो बिंदु P के निर्देशांक हैं;
क्योंकि P, YZ-तल पर स्थित है इसलिए इसका x-निर्देशांक शून्य है।
अत: 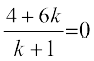
या 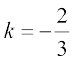
इसलिए YZ-तल AB को 2 : 3 के अनुपात में बाह्य विभाजित करता है।
प्रश्नावली 12.3
1. बिंदुओं (-2, 3, 5) और (1, -4, 6) को मिलाने से बने रेखा खंड को अनुपात (i) 2:3 में अंत: (ii) 2: 3 में बाह्यत: विभाजित करने वाले बिंदु के निर्देशांक ज्ञात कीजिए।
2. दिया गया है कि बिंदु P(3, 2, -4), Q(5, 4, -6) और R(9, 8, -10) संरेख हैं। वह अनुपात ज्ञात कीजिए जिसमें Q, PR को विभाजित करता है।
3. बिंदुओं (-2, 4, 7) और (3, -5, 8) को मिलाने वाली रेखा खंड, YZ-तल द्वारा जिस अनुपात में विभक्त होता है, उसे ज्ञात कीजिए।
4. विभाजन सूत्र का प्रयोग करके दिखाइए कि बिंदु A(2, -3, 4), B(-1, 2, 1) तथा 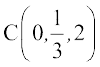 संरेख हैं।
संरेख हैं।
5. P(4, 2, -6) और Q(10, -16, 6) के मिलाने वाली रेखा खंड PQ को सम त्रि-भाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
विविध उदाहरण
उदाहरण 11 दर्शाइए कि बिंदु A (1, 2, 3), B (–1, –2, –1), C (2, 3, 2) और D (4, 7, 6) एक समांतर चतुर्भुज के शीर्ष हैं परंतु यह एक आयत नहीं है।
हल यह दर्शाने के लिए कि ABCD एक समांतर चतुर्भुज है, हमें सम्मुख भुजाओं को समान दिखाने की आवश्यकता है।
AB = 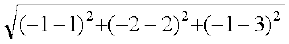 =
= 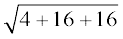 = 6
= 6
BC = 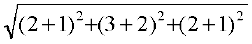 =
= 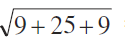
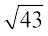
CD = 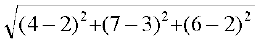 =
= 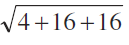
DA = 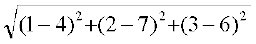 =
= 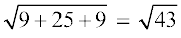
क्योंकि AB = CD और BC = AD, इसलिए ABCD एक समांतर चतुर्भुज है।
अब यह सिद्ध करने के लिए कि ABCD आयत नहीं है, हमें दिखाना है कि इसके विकर्ण AC और BD समान नहीं हैं, हम पाते हैं :
AC = 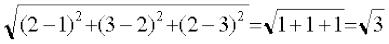
BD =
क्योंकि AC ≠ BD । अत: ABCD एक आयत नहीं है।
टिप्पणी विकर्ण AC तथा BD परस्पर समद्विभाजित करते हैं, के गुण का प्रयोग करके भी ABCD को समांतर चतुर्भुज सिद्ध किया जा सकता है।
उदाहरण 12 बिंदु P से बने समुच्चय का समीकरण ज्ञात कीजिए जो इस प्रकार चलता है कि उसकी बिंदुओं A(3, 4, -5) व B(-2, 1, 4) से दूरी समान है।
हल कोई बिंदु P (x, y, z) इस प्रकार है कि PA = PB
अत: 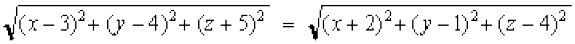
या 
या 10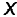 + 6y – 18z – 29 = 0.
+ 6y – 18z – 29 = 0.
उदाहरण 13 एक त्रिभुज ABC का केंद्रक (1, 1, 1) है। यदि A और B के निर्देशांक क्रमश: (3, –5, 7) व (–1, 7, –6) हैं। बिंदु C के निर्देशांक ज्ञात कीजिए।
हल माना C के निर्देशांक (x, y, z) है और केंद्रक G के निर्देशांक (1, 1, 1) दिए हैं।
इसलिए 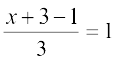 , या x = 1
, या x = 1
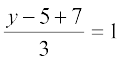 , या y = 1
, या y = 1
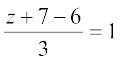 , या z = 2.
, या z = 2.
अत: C के निर्देशांक (1, 1, 2) हैं।
अध्याय 12 पर विविध प्रश्नावली
1. समांतर चतुर्भुज के तीन शीर्ष A(3, -1, 2) B(1, 2, -4) व C(-1, 1, 2) है। चौथे शीर्ष D के निर्देशांक ज्ञात कीजिए।
2. एक त्रिभुज ABC के शीर्षों के निर्देशांक क्रमश: A(0, 0, 6) B(0, 4, 0) तथा
C(6, 0, 0) हैं। त्रिभुज की माध्यिकाओं की लंबाई ज्ञात कीजिए।
3. यदि त्रिभुज PQR का केंद्रक मूल बिंदु है और शीर्ष P(2a, 2, 6), Q(-4, 3b -10) और R(8, 14, 2c) हैं तो a, b और c का मान ज्ञात कीजिए।
4. y-अक्ष पर उस बिंदु के निर्देशांक ज्ञात कीजिए जिसकी बिंदु P(3, -2, 5) से दूरी
5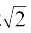 है।
है।
5. P(2, -3, 4) और Q(8, 0, 10) को मिलाने वाली रेखाखंड पर स्थित एक बिंदु R का
x-निर्देशांक 4 है। बिंदु R के निर्देशांक ज्ञात कीजिए।
(संकेत मान लीजिए R, PQ को k : 1 में विभाजित करता है। बिंदु R के निर्देशांक 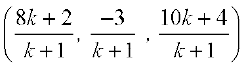 हैं।)
हैं।)
6. यदि बिंदु A और B क्रमश: (3, 4, 5) तथा (-1, 3, -7) हैं। चर बिंदु P द्वारा निर्मित समुच्चय से संबधित समीकरण ज्ञात कीजिए, जहाँ PA2 + PB2 = k2 जहाँ k अचर है।
सारांश
त्रिविमीय ज्यामिति के समकोणिक कार्तीय निर्देशांक निकाय में निर्देशांक्ष तीन परस्पर लंबवत् रेखाएँ होती हैं।
निर्देशांक्षों के युग्म, तीन तल निर्धारित करते हैं जिन्हें निर्देशांक्ष तल XY-तल, YZ-तल व ZX-तल कहते हैं।
तीन निर्देशांक्ष तल अंतरिक्ष को आठ भागों में बाँटते हैं जिन्हें अष्टांश कहते हैं।
त्रिविमीय ज्यामिति में किसी बिंदु P के निर्देशांकों को सदैव एक त्रिदिक (x, y, z) के रूप में लिखा जाता है। यहाँ x, YZ-तल से, y, ZX तल से व z, XY तल से दूरी है।
(i) x-अक्ष पर किसी बिंदु के निर्देशांक (x, 0, 0) हैं।
(ii) y-अक्ष पर किसी बिंदु के निर्देशांक (0, y, 0) हैं।
(iii) z-अक्ष पर किसी बिंदु के निर्देशांक (0, 0, z) हैं।
दो बिंदुओं P(x1, y1, z1) तथा Q (x2, y2, z2) के बीच का दूरी सूत्र है:
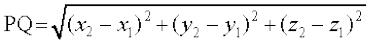
दो बिंदुओं P (x1 y1 z1) तथा Q (x2, y2, z2) को मिलाने वाले रेखा खंड को m : n अनुपात में अंत: और बाह्य: विभाजित करने वाले बिंदु R के निर्देशांक क्रमश: 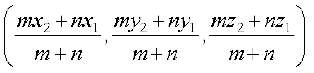
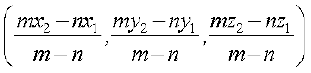 हैं।
हैं।
दो बिंदुओं P(x1, y1, z1) और Q(x2, y2, z2) को मिलाने वाले रेखा खंड PQ के मध्य-बिंदु के निर्देशांक हैं:
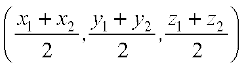
एक त्रिभुज जिसके शीर्षों के निर्देशांक (x1, y1, z1), (x2, y2, z2) और (x3, y3, z3) हैं, के केंद्रक के निर्देशांक है:
 .
.
एेतिहासिक पृष्ठभूमि
1637 ई॰ में वैश्लेषिक ज्यामिति के जनक Rene' Descartes (1596—1650 A.D.) ने तलीय ज्यामिति के क्षेत्र में उल्लेखनीय कार्य किया, इनके सहआविष्कारक Piarre Fermat
(1601—1665 A.D.) और La Hire (1640—1718 A.D.) ने भी इस क्षेत्र में कार्य किया। यद्यपि इन लोगों के कार्यों में त्रिविमीय ज्यामिति के संबंध में सुझाव है, परंतु विशद विवेचन नहीं है। Descartes को त्रिविमीय अंतरिक्ष में बिंदु के निर्देशांको के विषय में जानकारी थी परंतु उन्होंने इसे विकसित नहीं किया।
1715 ई॰ में J. Bernoulli (1667—1748 A.D.) ने Leibnitz को लिखे पत्र में तीन निर्देशांक तलों का परिचय उल्लेखित है जिसे हम आज प्रयोग कर रहे हैं।
सर्वप्रथम सन 1700 ई॰ में फ्रेंच एेकेडमी को प्रस्तुत किए गए Antoinne Parent (1666—1716 A.D.) के लेख में वैश्लेषिक ठोस ज्यामिति के विषय में विस्तृत विवेचन है।
L. Euler, (1707—1783 A.D.) ने सन् 1748 में प्रकाशित अपनी पुस्तक ‘ज्यामिति का परिचय’ के दूसरे खंड के परिशिष्ट के 5वें अध्याय में त्रिविमीय निर्देशांक ज्यामिति का सुव्यवस्थित एंव क्रमबद्ध वर्णन प्रस्तुत किया।
उन्नीसवीं शताब्दी के मध्य के बाद ही ज्यामिति का तीन से अधिक आयामों में विस्तार किया गया, जिसका सर्वोत्तम प्रयोग Einstein के सापेक्षवाद के सिद्धांत में स्थान-समय अनुक्रमण (Space-Time Continuum) में द्रष्टव्य है।