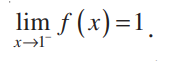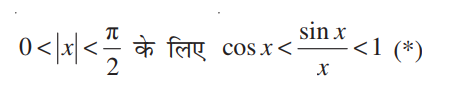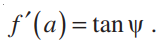Table of Contents
"With the Calculus as a key, Mathematics can be successfully applied to the explanation of the course of Nature- Whitehead"
13.1 भूमिका (Introduction)
यह अध्याय कलन की एक भूमिका है। कलन गणित की वह शाखा है जिसमें मुख्यतः प्रांत में बिंदुओं के परिवर्तन से फलन के मान में होने वाले परिवर्तन का अध्ययन किया जाता है। पहले हम अवकलज का (वास्तविक रूप से परिभाषित किए बिना) सहजानुभूत बोध (Intuitive idea) कराते हैं। तदेपरांत हम सीमा की सहज परिभाषा देंगे और सीमा के बीजगणित का कुछ अध्ययन करेंगे। इसके बाद हम अवकलज की परिभाषा करने के लिए वापस आएँगे और अवकलज के बीजगणित का कुछ अध्ययन करेंगे। हम कुछ विशेष मानक फलनों के अवकलज भी प्राप्त करेंगे।

Sir Issac Newton
(1642-1727 A.D.)
13.2 अवकलजों का सहजानुभूत बोध (Intuitive Idea of Derivatives)
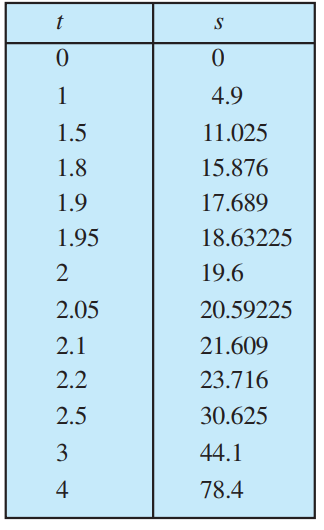
भौतिक प्रयोगों ने अनुमोदित किया है कि पिंड एक खड़ी/ऊँची चट्टान से गिरकर t सेकंडों में 4.9t2 मीटर दूरी तय करता है अर्थात् पिंड द्वारा मीटर में तय की गई दूरी (s) सेकंडों में मापे गए समय (t) के एक फलन के रूप में s = 4.9t2 से दी गई है।
संलग्न सारणी 13.1 में एक खड़ी/ऊँची चट्टान से गिराए गए एक पिंड के सेकंडों में विभिन्न समय (t) पर मीटर में तय की दूरी (s) दी गई है।
इन आँकड़ों से समय t = 2 सेकंड पर पिंड का वेग ज्ञात करना ही उद्देश्य है। इस समस्या तक पहुँचने के लिए t = 2 सेकंड पर समाप्त होने बाले विविध समयांतरालों पर माध्य वेग ज्ञात करना एक ढंग है और आशा करते हैं कि इससे t = 2 सेकंड पर वेग के बारे में कुछ प्रकाश पड़ेगा।
t = t1 और t = t2 के बीच माध्य वेग t = t1 और t = t2 सेकंडों के बीच तय की गई दूरी को (t2– t1) से भाग देने पर प्राप्त होता है। अतः प्रथम 2 सेकंडों में माध्य वेग
सारणी 13.1

= 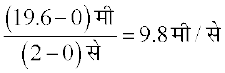
इसी प्रकार, t = 1 और t = 2 के बीच माध्य वेग
= 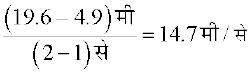
इसी प्रकार विविध के लिए t = t1 और t = 2 के बीच हम माध्य वेग का परिकलन करते हैं। निम्नलिखित सारणी 13.2,
t = t1 सेकंडों और t = 2 सेकंडों के बीच मीटर प्रति सेकंड में माध्य वेग (v) देती है।
सारणी 13.2
इस सारणी से हम अवलोकन करते हैं कि माध्य वेग धीरे-धीरे बढ़ रहा है। जैसे-जैसे t = 2 पर समाप्त होने वाले समयांतरालोंको लघुत्तर बनाते जाते हैं हम देखते हैं कि t = 2 पर हम वेग का एक बहुत अच्छा बोध कर पाते हैं। आशा करते हैं कि 1.99 सेकंड और 2 सेकंड के बीच कुछ अप्रत्याशित घटना न घटे तो हम निष्कर्ष निकालते हैं कि t = 2 सेकंड पर माध्य वेग 19.55 मी/से से थोड़ा अधिक है।
इस निष्कर्ष को निम्नलिखित अभिकलनों के समुच्चय से किंचित बल मिलता है। t = 2 सेकंड से प्रारंभ करते हुए विविध समयांतरालों पर माध्य वेग का परिकलन कीजिए। पूर्व की भाँति t = 2 सेकंड और t = t2 सेकंड के बीच माध्य वेग (v)
= 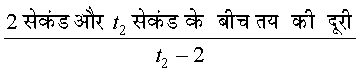
= 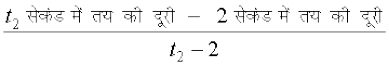
= 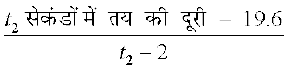
निम्नलिखित सारणी 13.3, t = 2 सेकंडों और t2 सेकंड के बीच मीटर प्रति सेकंड में माध्य वेग v देती हैः
सारणी 13.3
यहाँ पुनः हम ध्यान देते हैं कि यदि हम t = 2, से प्रारंभ करते हुए लघुत्तर समयान्तरालों को लेते जाते हैं तो हमें t = 2 पर वेग का अधिक अच्छा बोध होता है।
अभिकलनों के प्रथम समुच्चय में हमने t = 2 पर समाप्त होने वाले बढ़ते समयान्तरालों में माध्य वेग ज्ञात किया है और तब आशा की है कि t = 2 से किंचित पूर्व कुछ अप्रत्याशित घटना न घटे। अभिकलनों के द्वितीय समुच्चय में t = 2 पर अंत होने वाले घटते समयांतरालोें में माध्य वेग ज्ञात किया है और तब आशा की है कि t = 2 के किंचित बाद कुछ अप्रत्याशित घटना न घटे। विशुद्ध रूप से भौतिकीय आधार पर माध्य वेग के ये दोनों अनुक्रम एक समान सीमा पर पहुँचने चाहिए हम निश्चित रूप से निष्कर्ष निकालते हैं कि t = 2 पर पिंड का वेग 19.551 मी/से और 19.649 मी/से के बीच है। तकनीकी रूप से हम कह सकते हैं कि t = 2 पर तात्कालिक वेग 19.551 मी/से. और 19.649 मी/से. के बीच है। जैसा कि भली प्रकार ज्ञात है कि वेग दूरी के परिवर्तन की दर है। अतः हमने जो निष्पादित किया, वह निम्नलिखित है। "विविध क्षण पर दूरी में परिवर्तन की दर का अनुमान लगाया है। हम कहते हैं कि दूरी फलन s = 4.9t2 का t = 2 पर अवकलज 19.551 और 19.649 के बीच में है।"

आकृति 13.1
इस सीमा की प्रक्रिया की एक विकल्प विधि आकृति 13.1 में दर्शाई गई है। यह बीते समय (t) और चट्टान के शिखर से पिंड की दूरी (s) का आलेख है। जैसे-जैसे समयांतरालों के अनुक्रम h1, h2, ..., की सीमा शून्य की ओर अग्रसर होती है वैसे ही माध्य वेगों के अग्रसर होने की वही सीमा होती है जो
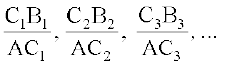
के अनुपातों के अनुक्रम की होती है, जहाँ C1B1 = s1 – s0 वह दूरी है जो पिंड समयांतरालों
h1 = AC1 में तय करता है, इत्यादि। आकृति 13.1 से यह निष्कर्ष निकलना सुनिश्चित है कि यह बाद की अनुक्रम वक्र के बिंदु A पर स्पर्शरेखा के ढाल की ओर अग्रसर होती है। दूसरे शब्दों में, t = 2 समय पर पिंड का तात्कालिक वेग वक्र s = 4.9t2 के t = 2 पर स्पर्शी के ढाल के समान है।
13.3 सीमाएँ (Limits)
उपर्युक्त विवेचन इस तथ्य की ओर स्पष्टतया निर्दिष्ट करता है कि हमें सीमा की प्रक्रिया और अधिक स्पष्ट रूप से समझने की आवश्यकता है। हम सीमा की संकल्पना से परिचित होने के लिए कुछ दृष्टांतों (illustrations) का अध्ययन करते हैं।
फलन f(x) = x2 पर विचार कीजिए। अवलोकन कीजिए कि जैसे-जैसे x को शून्य के
अधिक निकट मान देते हैं, f(x) का मान भी 0 की ओर अग्रसर होता जाता है। (देखें आकृति 2.10 अध्याय 2) हम कहते है 
(इसे f (x) की सीमा शून्य है, जब x शून्य की ओर अग्रसर होता है, पढ़ा जाता है) f (x) की सीमा, जब x शून्य की ओर अग्रसर होता है, को एेसे समझा जाए जैसे x = 0 पर f (x) का मान होना चाहिए।
व्यापक रूप से जब x → a, f (x) → l, तब l को फलन f (x) की सीमा कहा जाता है और इसे इस प्रकार लिखा जाता है  .
.
फलन g(x) = |x|, x  0 पर विचार कीजिए। ध्यान दीजिए कि g(0) परिभाषित नहीं है। x के 0 के अत्यधिक निकट मानों के लिए g(x) के मान का परिकलन करने के लिए हम देखते हैं कि g(x) का मान 0 की ओर अग्रसर करता है। इसलिए
0 पर विचार कीजिए। ध्यान दीजिए कि g(0) परिभाषित नहीं है। x के 0 के अत्यधिक निकट मानों के लिए g(x) के मान का परिकलन करने के लिए हम देखते हैं कि g(x) का मान 0 की ओर अग्रसर करता है। इसलिए 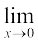 g(x) = 0. x
g(x) = 0. x 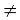 0 के लिए y = |x| के आलेख से यह सहजता से स्पष्ट होता है। (देखें आकृति 2.13 अध्याय 2)
0 के लिए y = |x| के आलेख से यह सहजता से स्पष्ट होता है। (देखें आकृति 2.13 अध्याय 2)
निम्नलिखित फलन पर विचार कीजिएः  .
.
x के 2 के अत्यधिक निकट मानों (लेकिन 2 नहीं) के लिए h(x) के मान का परिकलन कीजिए। आप स्वयं को स्वीकार कराइए कि सभी मान 4 के निकट हैं। यहाँ (आकृति 13.2) में दिए फलन
y = h(x) के आलेख पर विचार करने से इसको किंचित बल मिलता है।
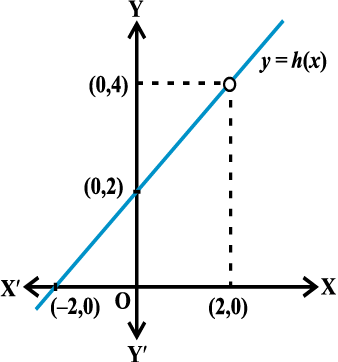
आकृति 13.2
इन सभी दृष्टांतों से एक दिए मान x = a पर फलन के जो मान ग्रहण कर ने चाहिए वे वास्तव में इस पर
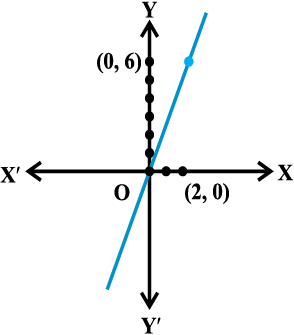
आधारित नहीं हैं कि x कैसे a की ओर अग्रसर होता है। ध्यान दीजिए कि x के संख्या a की ओर अग्रसर होने के लिए या तो बाईं ओर या दाईं ओर है, अर्थात् x के निकट सभी मान या तो a से कम हो सकते हैं या a से अधिक हो सकते हैं। इससे स्वाभाविक रूप से दो सीमाएँ - बाएँ पक्ष की सीमा और दाएँ पक्ष की सीमा प्रेरित होती है। फलन f के दाएँ पक्ष की सीमा f(x) का वह मान है जो f(x) के मान से आदेशित होता है जब x, a के दाईं ओर अग्रसर होता है। इसी प्रकार बाएँ पक्ष की सीमा। इसके दृष्टांत के लिए, फलन पर विचार कीजिए
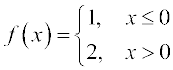
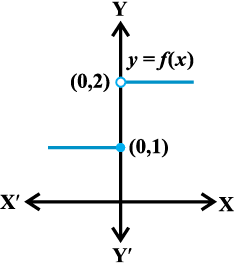
आकृति 13.3
आकृति 13.3 में इस फलन का आलेख दर्शाया गया है यह स्पष्ट है कि 0 पर f का मान x ≤ 0 के लिए f (x) के मान से पर निर्भर करता है जो कि 1 के समान है अर्थात् शून्य पर f (x) के बाएँ पक्ष की सीमा  है। इसी प्रकार 0 पर f का मान x > 0 के लिए f (x) के मान पर निर्भर करता है, 2 है अर्थात् 0 के दाएँ पक्ष की सीमा
है। इसी प्रकार 0 पर f का मान x > 0 के लिए f (x) के मान पर निर्भर करता है, 2 है अर्थात् 0 के दाएँ पक्ष की सीमा  है। इस स्थिति में बाएँ और दाएँ पक्ष की सीमाएँ भिन्न-भिन्न हैं और अतः हम कह सकते हैं कि जब x शून्य की ओर अग्रसर होता है तब f (x) की सीमा अस्तित्वहीन है। (भले ही फलन 0 पर परिभाषित है।)
है। इस स्थिति में बाएँ और दाएँ पक्ष की सीमाएँ भिन्न-भिन्न हैं और अतः हम कह सकते हैं कि जब x शून्य की ओर अग्रसर होता है तब f (x) की सीमा अस्तित्वहीन है। (भले ही फलन 0 पर परिभाषित है।)
सारांश
हम कहते हैं कि 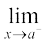 f(x), x = a पर f (x) का अपेक्षित (expected) मान हैं, जिसने x के बाईं अोर निकट मानों के लिए f (x) को मान दिए हैं। इस मान को a पर f (x) की बाएँ पक्ष की सीमा कहते हैं।
f(x), x = a पर f (x) का अपेक्षित (expected) मान हैं, जिसने x के बाईं अोर निकट मानों के लिए f (x) को मान दिए हैं। इस मान को a पर f (x) की बाएँ पक्ष की सीमा कहते हैं।
हम कहते हैं कि , x = a पर f (x) का अपेक्षित मान है जिसमें x के a के दाईं ओर के निकट मानों के लिए f(x) के मान दिए हैं। इस मान को a पर f (x) की दाएँ पक्ष की सीमा कहते हैं।
, x = a पर f (x) का अपेक्षित मान है जिसमें x के a के दाईं ओर के निकट मानों के लिए f(x) के मान दिए हैं। इस मान को a पर f (x) की दाएँ पक्ष की सीमा कहते हैं।
यदि दाएँ और बाएँ पक्ष की सीमाएँ संपाती हों तो हम इस उभयनिष्ठ मान को x = a पर f(x) की सीमा कहते हैं और इसे  f(x) से निरूपित करते हैं।
f(x) से निरूपित करते हैं।
दृष्टांत 1 (Illustration 1) फलन f(x) = x + 10 पर विचार कीजिए। हम x = 5 पर फलन की सीमा ज्ञात करना चाहेंगे। आइए, हम 5 के अत्यंत निकट x के मानों के लिए f के मान का परिकलन करें। 5 के अत्यंत निकट बाईं ओर कुछ बिंदु 4.9, 4.95, 4.994, 4.995... इत्यादि हैं। इन बिंदुओं पर f(x) के मान नीचे सारणीबद्ध हैं। इसी प्रकार, 5 के अत्यंत निकट और दाईं ओर वास्तविक संख्याएँ 5.001, 5.01, 5.1 भी हैं। इन बिंदुओं पर भी फलन के मान सारणी 13.4 में दिए हैं।
सारणी 13.4
सारणी 13.4 से हम निगमित करते हैं कि f(x) का मान 14.995 से बड़ा और 15.001 से छोटा है, यह कल्पना करते हुए कि x = 4.995 और 5.001 के बीच कुछ अप्रत्याशित घटना घटित न हो। यह कल्पना करना तर्कसंगत है कि 5 के बाईं ओर की संख्याओं के लिए x = 5 पर f (x) का मान 15 है अर्थात् 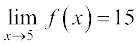
इसी प्रकार, जब x, 5 के दाईं ओर अग्रसर होता है, f का मान 15 होना चाहिए अर्थात्
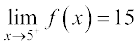
अतः यह संभाव्य है कि f के बाएँ पक्ष की सीमा और दाएँ पक्ष की सीमा, दोनों 15 के बराबर हैं। इस प्रकार
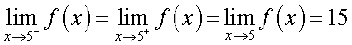
सीमा 15 के बराबर होने के बारे में यह निष्कर्ष फलन के आलेख जो आकृति 2.9(ii) अध्याय 2 में दिया है, को देखकर किंचित बल देता है। इस आकृति में हम ध्यान देते हैं कि जैसे-जैसे x, 5 के या तो दाईं ओर या बाईं ओर अग्रसर हो, फलन f (x) = x + 10 का आलेख बिंदु (5, 15) की ओर अग्रसर होता जाता हैं। हम देखते हैं कि x = 5 पर भी फलन का मान 15 के बराबर
होता है।
दृष्टांत 2 फलन f(x) = x3 पर विचार कीजिए। आइए हम x = 1 पर इस फलन की सीमा ज्ञात करने का प्रयास करें। पूर्ववर्ती स्थिति की तरह बढ़ते हुए हम x के 1 के निकट मानों के लिए f(x) के मानों को सारणीबद्ध करते हैं। इसे सारणी 13.5 में दिया गया हैः
सारणी 13.5
इस सारणी से हम निगमन करते हैं कि x = 1 पर f का मान 0.997002999 से अधिक और 1.003003001 से कम है, यह कल्पना करते हुए कि x = 0.999 और 1.001. के बीच कुछ अप्रत्याशित घटना घटित न हो। यह मानना तर्कसंगत है कि x = 1 का मान 1 के बाईं ओर की संख्याओं पर निर्भर करता है अथ्ााρत्
इसी प्रकार, जब x, 1 के दाईं ओर अग्रसर होता है, तो f का मान 1 होना चाहिए अर्थात्
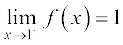 .
.
अतः, यह संभाव्य है कि बाएँ पक्ष की सीमा और दाएँ पक्ष की सीमा दोनों 1 के बराबर हों। इस प्रकार
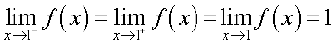 .
.
सीमा 1 के बराबर होने का यह निष्कर्ष फलन के आलेख जो आकृति 2.11, अध्याय 2 में दिया है, को देखकर किंचित बल देता है। इस आकृति में हम ध्यान देते हैं कि जैसे-जैसे x, 1 के या तो दाईं ओर या बाईं ओर अग्रसर हो, फलन f(x) = x3 का आलेख बिंदु (1, 1) की ओर अग्रसर होता जाता है।
हम पुनः अवलोकन करते हैं कि x = 1 पर फलन का मान भी 1 के बराबर है।
दृष्टांत 3 फलन f(x) = 3x पर विचार कीजिए। आइए, x = 2 पर इस फलन की सीमा ज्ञात करने का प्रयास करें। निम्नलिखित सारणी 13.6 स्वतः स्पष्ट करती है।
सारणी 13.6
पूर्ववत हम अवलोकन करते हैं कि x या तो बाएँ या दाएँ 2 की ओर अग्रसर होता है, f(x) का मान 6 की ओर अग्रसर होता हुआ प्रतीत होता है। हम इसे, इस प्रकार अभिलेखित कर सकते
हैं कि
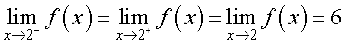
आकृति 13.4 में प्रदर्शित इसका आलेख इस तथ्य को बल देता है।
यहाँ पुनः हम ध्यान देते हैं कि x = 2 पर फलन का मान x = 2 पर सीमा के संपाती है।
आकृति 13.4
दृष्टांत 4 अचर फलन f(x) = 3 पर विचार कीजिए। आइए हम x = 2 पर इसकी सीमा ज्ञात करने का प्रयास करें। यह फलन अचर फलन होने के कारण सर्वत्र एक ही मान (इस स्थिति में 3) प्राप्त करता है अर्थात् 2 के अत्यंत निकट बिंदुओं के लिए इसका मान 3 है। अतः 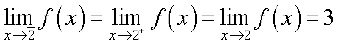
f(x) = 3 का आलेख हर हालत में (0, 3) से जाने वाली x-अक्ष के समांतर रेखा है और आकृति 2.9, अध्याय 2 में दर्शाया गया है। इससे यह भी स्पष्ट है कि अभीष्ट सीमा 3 है तथ्यतः यह सरलता से अवलोकित होता है कि किसी वास्तविक संख्या a के लिए 
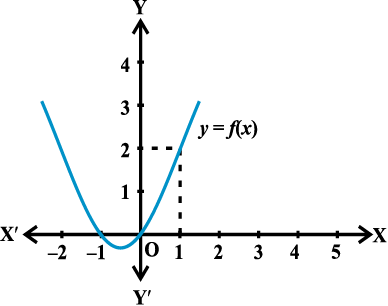
दृष्टांत 5 फलन f(x) = x2 + x पर विचार कीजिए। हम  ज्ञात करना चाहते हैं। हम
ज्ञात करना चाहते हैं। हम
x = 1 के निकट f(x) के मान सारणी 13.7 में सारणीबद्ध करते हैंः
सारणी 13.7
इससे यह तर्कसंगत निगमित होता है कि
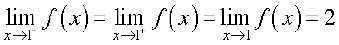 .
.
आकृεत 13.5 में दर्शाए f(x) = x2 + x के आलेख से यह स्पष्ट है कि जैसे-जैसे x, 1 की ओर अग्रसर होता है, आलेख (1, 2) की ओर अग्रसर होता जाता है।
आकृति 13.5
अतः हम पुनः प्रेक्षण करते हैं कि
 f (x) = f (1)
f (x) = f (1)
अब, निम्नलिखित तीन तथ्यों को आप स्वयं को स्वीकार कराएँ

तब 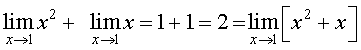 .
.
तथा  .
.
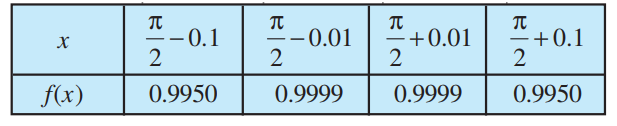
दृष्टांत 6 फलन f(x) = sin x पर विचार कीजिए। हमारी 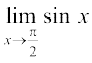 में रुचि है जहाँ कोण रेडियन में मापा गया है। यहाँ, हमने
में रुचि है जहाँ कोण रेडियन में मापा गया है। यहाँ, हमने 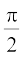 के निकट f(x) के मानों (निकटतम) को सारणीबद्ध किया है।
के निकट f(x) के मानों (निकटतम) को सारणीबद्ध किया है।
सारणी 13.8
इससे हम निगमन कर सकते हैं कि 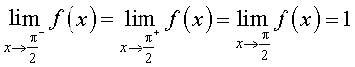
इसके अतिरिक्त, यह f(x) = sin x के आलेख से पुष्ट होता है जो आकृति 3.8 अध्याय 3 में दिया है। इस स्थिति में भी हम देखते हैं कि 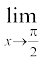 sin x = 1.
sin x = 1.
दृष्टांत 7 फलन f(x) = x + cos x पर विचार कीजिए। हम 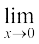 f (x) ज्ञात करना चाहते हैं।
f (x) ज्ञात करना चाहते हैं।
यहाँ हमने 0 के निकट f(x) के मान (निकटतम) सारणीबद्ध किए हैंः (सारणी 13.9).
सारणी 13.9
सारणी 13.9, से हम निगमन कर सकते हैं कि
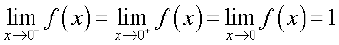
इस स्थिति में भी हम प्रेक्षण करते हैं कि 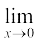 f (x) = f (0) = 1.
f (x) = f (0) = 1.
अब, क्या आप स्वयं को स्वीकार करा सकते हैं कि
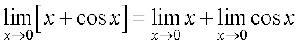 वास्तव में सत्य है?
वास्तव में सत्य है?
दृष्टांत 8  के लिए, फलन
के लिए, फलन 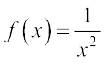 पर विचार कीजिए। हम
पर विचार कीजिए। हम  f (x) ज्ञात करना चाहते हैं।
f (x) ज्ञात करना चाहते हैं।
यहाँ, हम अवलोकन करते हैं कि फलन का प्रांत सभी धनात्मक वास्तविक संख्याएँ हैं। अतः जब हम f(x) के मान सारणीबद्ध करते हैं, x शून्य के बाईं ओर अग्रसर होता है, का कोई अर्थ नहीं है। नीचे हम 0 के निकट x के धनात्मक मानों के लिए फलन के मानों को सारणीबद्ध करते हैं (इस सारणी में n किसी धन पूर्णांक को निरूपित करता है।
नीचे दी गई सारणी 13.10 से, हम देखते हैं कि जब x, 0 की ओर अग्रसर होता है, f(x) बड़ा और बड़ा होता जाता है। यहाँ इसका अर्थ है कि, f(x) का मान किसी दी संख्या से भी बड़ा किया जा सकता है।
सारणी 13.10
गणितीय रूप से, हम कह सकते हैं 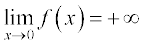
हम टिप्पणी भी करते हैं कि इस पाठ्यक्रम में हम इस प्रकार की सीमाओं की चर्चा नहीं करेंगे।
दृष्टांत 9 हम 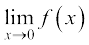 , ज्ञात करना चाहते हैं, जहाँ
, ज्ञात करना चाहते हैं, जहाँ
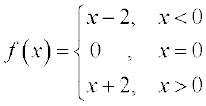
पहले की तरह हम 0 के निकट x के लिए f(x) की सारणी बनाते हैं। प्रेक्षण करते हैं कि x के ऋणात्मक मानों के लिए हमें x – 2 का मान निकालने की आवश्यकता है और x के धनात्मक मानों के लिए x + 2 का मान निकालने की आवश्यकता होती है।
सारणी 13.11
सारणी 13.11 की प्रथम तीन प्रविष्टियों से, हम निगमन करते हैं कि फलन का मान –2 तक घट रहा है और
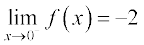
सारणी की अंतिम तीन प्रविष्टियों से, हम निगमन करते हैं कि फलन का मान 2 तक बढ़ रहा है और अतः
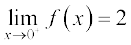
क्योंεक 0 पर बाएँ और दाएँ पक्षों की सीमाएँ संपाती नहीं हैं, हम कहते हैं कि 0 पर फलन की सीमा अस्तित्वहीन है।
इस फलन का आलेख आकृति 13.6 में दिया है यहाँ, हम टिप्पणी करते हैं कि x = 0 पर फलन का मान पूर्णतः परिभाषित है और, वास्तव में, 0 के बराबर है, परंतु x = 0 पर फलन की सीमा परिभाषित भी नहीं है।
आकृति 13.6
दृष्टांत 10 एक अंतिम दृष्टांत के रूप में, हम 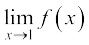 , ज्ञात करते हैं जबकि
, ज्ञात करते हैं जबकि
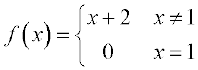
सारणी 13.12
पहले की तरह, 1 के निकट x के लिए हम f(x) के मानों को सारणीबद्ध करते हैं। 1 से कम x के लिए f(x) में मानों से, यह प्रतीत होता है कि x = 1 पर फलन का मान 3 होना चाहिए अर्थात्
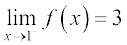
इसी प्रकार, 1 से बड़े x के लिए f(x) के मानों से आदेशित f(x) का मान 3 होना चाहिए, अर्थात्
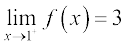 .
.
परंतु तब बाएँ और दाएँ पक्षों की सीमाएँ संपाती हैं और अतः 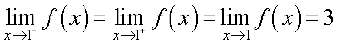 .
.
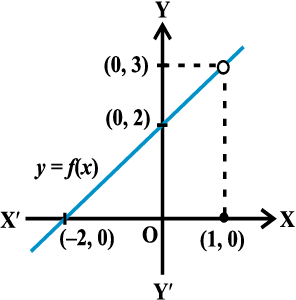
आकृति 13.7
आकृति 13.7 में फलन का आलेख सीमा के बारे में हमारे निगमन को बल देता है। यहाँ, हम ध्यान देते हैं कि व्यापक रूप से, एक दिए बिंदु पर फलन का मान और इसकी सीमा भिन्न-भिन्न हो सकते हैं (भले ही दोनों परिभाषित हों।)
13.3.1 सीमाओं का बीजगणित (Algebra of limits)
उपर्युक्त दृष्टांतों से, हम अवलोकन कर चुके हैं कि सीमा प्रक्रिया योग, व्यवकलन, गुणा और भाग का पालन करती है जब तक कि
विचाराधीन फलन और सीमाएँ सुपरिभाषित हैं। यह संयोग नहीं है। वास्तव में, हम इनको बिना उपपत्ति के प्रमेय के रूप में अौपचारिक रूप देते हैं।
प्रमेय 1 मान लीजिए कि f और g दो फलन एेसे हैं कि  f (x) और
f (x) और  g(x) दोनों का अस्तित्व है। तब
g(x) दोनों का अस्तित्व है। तब
(i) दो फलनों के योग की सीमा फलनों की सीमाओं का योग होता है, अर्थात्
 [f(x) + g (x)] =
[f(x) + g (x)] =  f(x) +
f(x) +  g(x).
g(x).
(ii) दो फलनों के अंतर की सीमा फलनों की सीमाओं का अंतर होता है, अर्थात्
 [f(x) – g(x)] =
[f(x) – g(x)] =  f(x) –
f(x) –  g(x).
g(x).
(iii) दो फलनों के गुणन की सीमा फलनों की सीमाओं का गुणन होता है, अर्थात्
 [f(x) . g(x)] =
[f(x) . g(x)] =  f(x).
f(x).  g(x).
g(x).
(iv) दो फलनों के भागफल की सीमा फलनों की सीमाओं का भागफल होता है, (जबकि हर शून्येतर होता है), अर्थात्
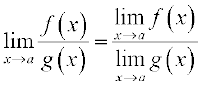
टिप्पणी विशेष रूप से स्थिति (iii) की एक विशिष्ट स्थिति में जब g(x) एक एेसा अचर फलन है कि किसी वास्तविक संख्या  के लिए g(x) =
के लिए g(x) =  हम पाते हैं
हम पाते हैं
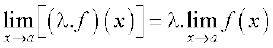 .
.
अगले दो अनुच्छेदों में, हम दृष्टांत देंगे कि इस प्रमेय को विशिष्ट प्रकार के फलनों की सीमाओं के मान प्राप्त करने में कैसे प्रयोग किया जाता है।
13.3.2 बहुपदों और परिमेय फलनों की सीमाएँ (Limits of polynomials and rational functions)
n घात का एक फलन f(x) बहुपदीय फलन कहलाता है, यदि f(x) = a0 + a1x + a2x2 +. . . + anxn, जहाँ ais एेसी वास्तविक संख्याएँ हैं कि किसी प्राकृत संख्या n के लिए an ≠ 0
हम जानते हैं कि  x = a. अतः
x = a. अतः
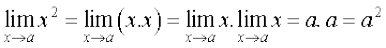
n पर आगमन का सरल अभ्यास हमको बताता है कि
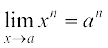
अब, मान लीजिए  एक बहुपदीय फलन है।
एक बहुपदीय फलन है।  प्रत्येक को एक फलन जैसा विचारते हुए, हम पाते हैं कि
प्रत्येक को एक फलन जैसा विचारते हुए, हम पाते हैं कि
 =
= 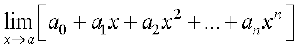
= 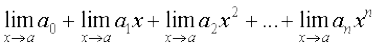
= 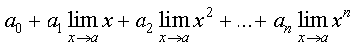
= 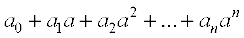
= 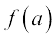
(सुनिश्चित करें कि आपने उपर्युक्त में प्रत्येक चरण का औचित्य समझ लिया है।)
एक फलन f एक परिमेय फलन कहलाता है यदि f(x) = 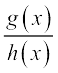 , जहाँ g(x) और h(x) एेसे बहुपद हैं कि h(x) ≠ 0. तो
, जहाँ g(x) और h(x) एेसे बहुपद हैं कि h(x) ≠ 0. तो
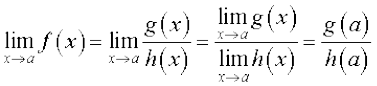
यद्यपि, यदि h(a) = 0, दो स्थितियाँ हैं – (i) जब g(a) ≠ 0 और (ii) जब g(a) = 0. पूर्व की स्थिति में हम कहते हैं कि सीमा का अस्तित्व नहीं है। बाद की स्थिति में हम
g(x) = (x – a)k g1 (x), जहाँ k, g(x) में (x – a) की महत्तम घात है। इसी प्रकार
h(x) = (x – a) lh1 (x) क्योंकि h (a) = 0. अब, यदि k > l, हम पाते हैं
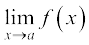 =
= 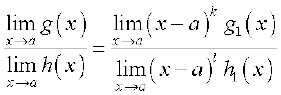
= 
यदि k < l, तो सीमा परिभाषित नहीं है।
उदाहरण 1 सीमाएँ ज्ञात कीजिएः
(i) 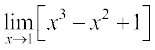 (ii)
(ii) 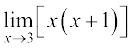
(iii) 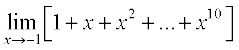 .
.
हल अभीष्ट सभी सीमाएँ कुछ बहुपदीय फलनों की सीमाएँ हैं। अतः सीमाएँ प्रदत्त बिंदुओं पर फलनों के मान हैं। हम पाते हैं
(i)  [x3 – x2 + 1] = 13 – 12 + 1 = 1
[x3 – x2 + 1] = 13 – 12 + 1 = 1
(ii) 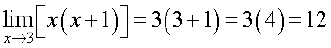
(iii) 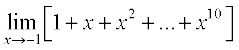 = 1 + (–1) + (–1)2 + ... + (–1)10
= 1 + (–1) + (–1)2 + ... + (–1)10
= 1 – 1 + 1 + ... + 1 = 1.
उदाहरण 2 सीमाएँ ज्ञात कीजिएः
(i) 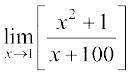 (ii)
(ii) 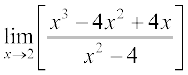
(iii) 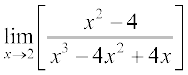 (iv)
(iv) 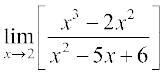
(v) 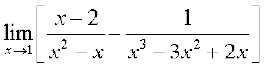 .
.
हल सभी विचाराधीन फलन परिमेय फलन हैं। अतः, हम पहले प्रदत्त बिंदुओं पर इन फलनों के मान प्राप्त करते हैं। यदि यह 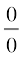 , के रूप का है, हम गुणनखंडों, जो सीमा के
, के रूप का है, हम गुणनखंडों, जो सीमा के 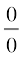 का रूप होने का कारण है, को निरस्त करते हुए फलनों को पुनः लिखते हैं।
का रूप होने का कारण है, को निरस्त करते हुए फलनों को पुनः लिखते हैं।
(i) हम पाते हैं 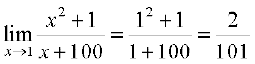
(ii) 2 पर फलन का मान प्राप्त करने पर हम इसे 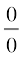 का रूप में पाते हैं। अतः
का रूप में पाते हैं। अतः
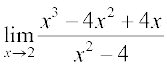 =
= 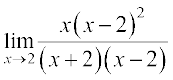 =
= 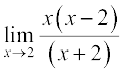 क्योंकि x ≠ 2
क्योंकि x ≠ 2
= 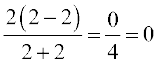 .
.
(iii) 2 पर फलन का मान प्राप्त करने पर, हम इसे 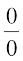 के रूप में पाते हैं, अतः
के रूप में पाते हैं, अतः
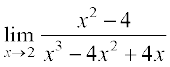 =
= 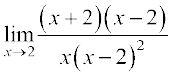
= 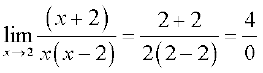
जोकि परिभाषित नहीं है।
(iv) 2 पर फलन का मान प्राप्त करने पर, हम इसे 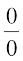 के रूप में पाते है। अतः
के रूप में पाते है। अतः
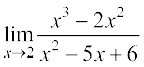 =
= 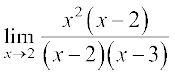
=  .
.
(v) पहले हम फलन को परिमेय फलन जैसा पुनः लिखते हैं।
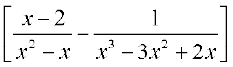 =
= 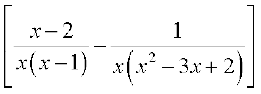
= 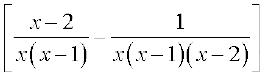
= 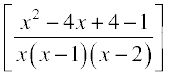
= 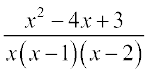
1 पर फलन का मान प्राप्त करने पर हम 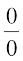 का रूप पाते हैं। अतः
का रूप पाते हैं। अतः
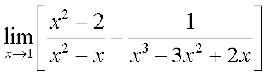 =
= 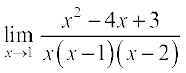
= 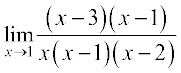
= 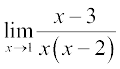 =
= 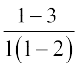 = 2.
= 2.
हम टिप्पणी करते हैं कि उपर्युक्त मान प्राप्त करने में हमने पद (x – 1) को निरस्त किया क्योंकि 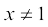 .
.
एक महत्वपूर्ण सीमा का मान प्राप्त करना, जो कि आगे परिणामों में प्रयुक्त होगी, नीचे एक प्रमेय के रूप में प्रस्तुत है।
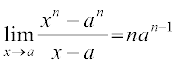
प्रमेय 2 किसी धन पूर्णांक n के लिए,
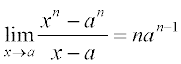 .
.
टिप्पणी उपर्युक्त प्रमेय में सीमा हेतु व्यंजक सत्य है जबकि n कोई परिमेय संख्या है और
a धनात्मक है।
उपपत्ति (xn – an) को (x – a), से भाग देने पर, हम देखते हैं कि
xn – an = (x–a) (xn–1 + xn–2 a + xn–3 a2 + ... + x an–2 + an–1)
इस प्रकार 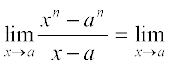 (xn–1 + xn–2 a + xn–3 a2 + ... + x an–2 + an–1)
(xn–1 + xn–2 a + xn–3 a2 + ... + x an–2 + an–1)
= an – l + a an–2 +. . . + an–2 (a) +an–l
= an–1 + an – 1 +...+an–1 + an–1 (n पद)
= 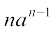
उदाहरण 3 मान ज्ञात कीजिए
(i) 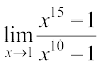 (ii)
(ii) 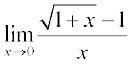
हल (i) हमारे पास है
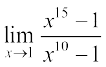 =
= 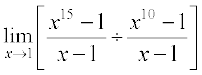
= 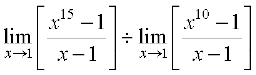
= 15 (1)14 ÷ 10(1)9 (उपर्युक्त प्रमेय से)
= 15 ÷ 10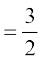
(ii) y = 1 + x, जिससे 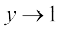 जैसे
जैसे 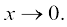 तब
तब
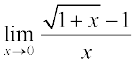 =
= 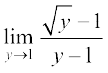
= 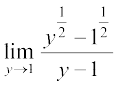
= 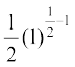 (उपर्युक्त टिप्पणी से) =
(उपर्युक्त टिप्पणी से) = 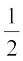
13.4. त्रिकोणमितीय फलनों की सीमाएँ (Limits of Trigonometric Functions)
व्यापक रूप से, फलनों के बारे में निम्नलिखित तथ्य (प्रमेयों के रूप में कहे गए) कुछ त्रिकोणमितीय फलनों की सीमाओं का परिकलन करने में सुलभ हो जाते हैं।
प्रमेय 3 मान लीजिए समान प्रांत वाले दो वास्तविक मानीय फलन f और 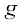 एेसे हैं कि परिभाषा के प्रांत में सभी x के लिए f (x) ≤ g( x) किसी a के लिए यदि
एेसे हैं कि परिभाषा के प्रांत में सभी x के लिए f (x) ≤ g( x) किसी a के लिए यदि  f(x) और
f(x) और  g(x) दोनों का अस्तित्व है तो
g(x) दोनों का अस्तित्व है तो  f(x) ≤
f(x) ≤  g(x) इसे आकृति 13.8 में चित्र से स्पष्ट किया गया है।
g(x) इसे आकृति 13.8 में चित्र से स्पष्ट किया गया है।

आकृति 13.8
प्रमेय 4 सैंडविच प्रमेय (Sandwich Theorem) मान लीजिए f, g और h वास्तविक मानीय फलन एेसे हैं कि परिभाषा के सर्वनिष्ठ प्रांतों के सभी x के लिए f (x) ≤ g( x) ≤ h(x). किसी वास्तविक संख्या a के लिए यदि 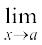 f(x) = l
f(x) = l
= 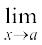 h(x), तो
h(x), तो 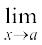 g(x) = l. इसे
g(x) = l. इसे
आकृति 13.9 में चित्र से स्पष्ट किया गया है।
त्रिकोणमितीय फलनों से संबंधित निम्नलिखित महत्वपूर्ण असमिका की एक सुंदर ज्यामितीय उपपत्ति नीचे प्रस्तुत हैः

आकृति 13.9
उपपत्ति हम जानते हैं कि sin (– x) = – sin x और cos( – x) = cos x. अतः 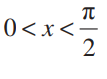
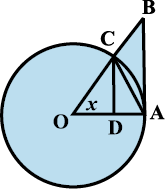
आकृति 13.10
आकृति 13.10, में एेसे इकाई वृत्त का केंद्र O है। कोण AOC, x रेडियन का है और 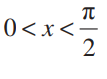
 क्षेत्रफल < ∆OAB का क्षेत्रफल
क्षेत्रफल < ∆OAB का क्षेत्रफल
अर्थात् 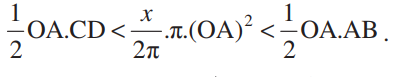
अर्थात् CD < x . OA < AB.  OCD में
OCD में
sin x = 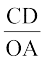 (चूँकि OC = OA) और अतः CD = OA sin x. इसके अतिरिक्त
(चूँकि OC = OA) और अतः CD = OA sin x. इसके अतिरिक्त
tan x =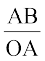 और अतः AB = OA tan x. इस प्रकार
और अतः AB = OA tan x. इस प्रकार
OA sin x < OA x < OA. tan x.
क्योंकि लंबाई OA धनात्मक है, हम पाते हैं
sin x < x < tan x.
क्योंकि 0 < x <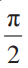
1<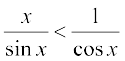 सभी का व्युत्क्रम करने पर, हम पाते हैं
सभी का व्युत्क्रम करने पर, हम पाते हैं
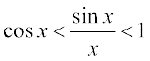 उपपत्ति पूर्ण हुई।
उपपत्ति पूर्ण हुई।
प्रमेय 5 निम्नलिखित दो महत्वपूर्ण सीमाएँ हैंः
(i) 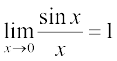 (ii)
(ii) 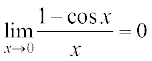
उपपत्ति (i) (*) में असमिका (Inequality) के अनुसार फलन  , फलन cos x और अचर फलन जिसका मान 1 हो जाता है, के बीच में स्थित है।
, फलन cos x और अचर फलन जिसका मान 1 हो जाता है, के बीच में स्थित है।
इसके अतिरिक्त क्योंकि 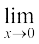 cos x = 1, हम देखते हैं कि प्रमेय के (i) की उपपत्ति सैंडविच प्रमेय से पूर्ण है।
cos x = 1, हम देखते हैं कि प्रमेय के (i) की उपपत्ति सैंडविच प्रमेय से पूर्ण है।
(ii) को सिद्ध करने के लिए, हम त्रिकोणमिति सर्वसमिका 1 – cos x = 2 sin2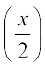 का प्रयोग करते हैं, तब
का प्रयोग करते हैं, तब 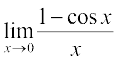 =
= 
= 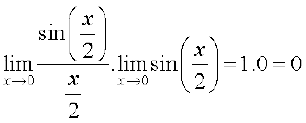
अवलोकन कीजिए कि हमने अस्पष्ट रूप से इस तथ्य का प्रयोग किया है कि  ,
,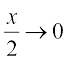 के तुल्य है। इसको y =
के तुल्य है। इसको y =  रखकर प्रमाणित किया जा सकता है।
रखकर प्रमाणित किया जा सकता है।
उदाहरण 4 मान ज्ञात कीजिएः (i) 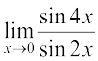 (ii)
(ii) 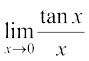
हल (i) 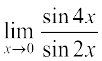 =
= 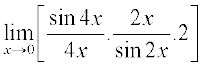
= 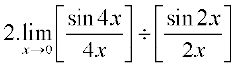
= 
= 2.1.1 = 2 (जब x → 0, 4x → 0 तथा 2x → 0)
हमारे पास है (ii) 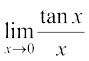 =
= 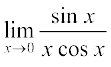 =
= 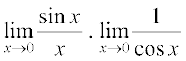 = 1.1 = 1
= 1.1 = 1
एक सामान्य नियम, जिसको सीमाओं का मान निकालते समय ध्यान में रखने की आवश्यकता है, निम्नलिखित हैः
माना कि सीमा 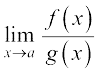 का अस्तित्व है और हम इसका मान ज्ञात करना चाहते हैं। पहले हम f (a) और g(a) के मानों को जाँचें। यदि दोनों शून्य हैं, तो हम देखते हैं कि यदि हम उस गुणनखंड को प्राप्त कर सकते हैं जो पद समाप्त होने का कारण है, अर्थात् देखें यदि हम
का अस्तित्व है और हम इसका मान ज्ञात करना चाहते हैं। पहले हम f (a) और g(a) के मानों को जाँचें। यदि दोनों शून्य हैं, तो हम देखते हैं कि यदि हम उस गुणनखंड को प्राप्त कर सकते हैं जो पद समाप्त होने का कारण है, अर्थात् देखें यदि हम
f(x) = f1 (x) f2(x) लिख सकें जिससे f1 (a) = 0 और f2 (a) ≠ 0 । इसी प्रकार g(x) = g1 (x) g2(x),लिखते हैं जहाँ g1(a) = 0 और g2(a) ≠ 0. f(x) और g(x) में से उभयनिष्ठ गुणनखंड (यदि संभव है) तो निरस्त कर देते हैं और
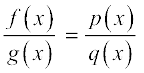 , जहाँ q(x) ≠ 0 लिखते हैं ,
, जहाँ q(x) ≠ 0 लिखते हैं ,
तब 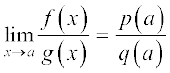
प्रश्नावली 13.1
प्रश्न 1 से 22 तक निम्नलिखित सीमाओं के मान प्राप्त कीजिएः
1.  2.
2. 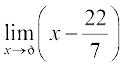 3.
3. 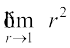
4. 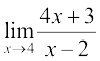 5.
5. 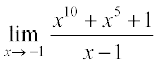 6.
6. 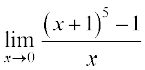
7. 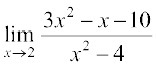 8.
8.  9.
9. 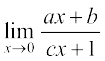
10. 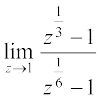 11.
11. 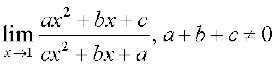
12. 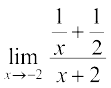 13.
13. 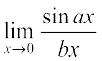 14.
14. 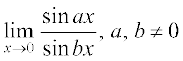
15. 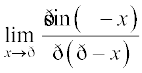 16.
16.  17.
17. 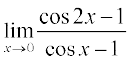
18. 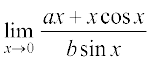 19.
19. 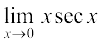
20. 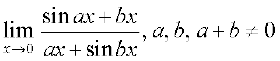 ,
,
21. 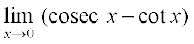 22.
22. 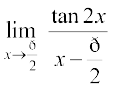
23. 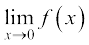 और
और 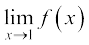 , ज्ञात कीजिए, जहाँ
, ज्ञात कीजिए, जहाँ 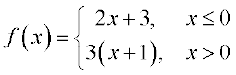
24. 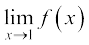 , ज्ञात कीजिए, जहाँ
, ज्ञात कीजिए, जहाँ 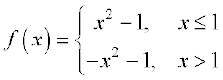
25. 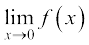 , का मान प्राप्त कीजिए, जहाँ
, का मान प्राप्त कीजिए, जहाँ 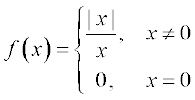
26. 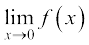 , ज्ञात कीजिए, जहाँ
, ज्ञात कीजिए, जहाँ 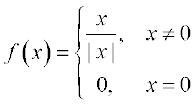
27. 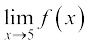 , ज्ञात कीजिए, जहाँ
, ज्ञात कीजिए, जहाँ 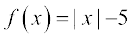
28. मान लीजिए 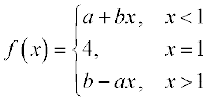
और यदि  f (x) = f (1) तो a और b के संभव मान क्या हैं?
f (x) = f (1) तो a और b के संभव मान क्या हैं?
29. मान लीजिए a1, a2, . . ., an अचर वास्तविक संख्याएँ हैं आैर एक पηलन  से परिभाषित है।
से परिभाषित है। 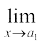 f (x) क्या है?
f (x) क्या है?
किसी a ≠ a1, a2, ..., an, के लिए 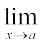 f (x) का परिकलन कीजिए।
f (x) का परिकलन कीजिए।
30. यदि  .
.
तो a के किन मानों के लिए  f (x) का अस्तित्व है?
f (x) का अस्तित्व है?
31. यदि फलन f(x), 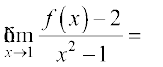 , को संतुष्ट करता है, तो
, को संतुष्ट करता है, तो 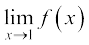 का मान प्राप्त कीजिए।
का मान प्राप्त कीजिए।
32. किन पूर्णांकों m और n के लिए 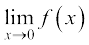 और
और 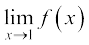 दोनों का अस्तित्व है, यदि
दोनों का अस्तित्व है, यदि 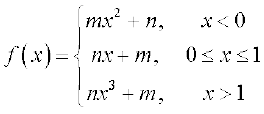
13.5 अवकलज (Derivatives)
हम अनुच्छेद 13.2, में देख चुके हैं कि विविध समयांतरालों पर पिंड की स्थिति को जानकर उस दर को ज्ञात करना संभव है जिससे पिंड की स्थिति परिवर्तित हो रही है। समय के विविध क्षणों पर एक निश्चित प्राचल (parameter) का जानना और उस दर को ज्ञात करने का प्रयास करना जिससे इसमें परिवर्तन हो रहा है, अत्यंत व्यापक रुचि का विषय है। वास्तविक जीवन की अनेक स्थितियाँ होती हैं जिनमें एेसी प्रक्रिया कार्यान्वित करने की आवश्यकता होती है। उदाहरणतः एक टंकी के रख-रखाव करने वाले व्यक्ति के लिए समय के अनेक क्षणों पर पानी की गहराई जानकर यह जानना आवश्यक होता है कि टंकी कब छलकने लगेगी, विविध समयों पर राकेट की ऊँचाई जानकर राकेट वैज्ञानिकों को उस यथार्थ वेग के परिकलन की आवश्यकता होती है जिससे उपग्रह का राकेट से प्रक्षेपण आवश्यक हो। वित्तीय संस्थानों को किसी विशेष स्टाक के वर्तमान मूल्य जानकर इसके मूल्यों में परिवर्तन की भविष्यवाणी करनी आवश्यक होती है। इनमें और एेसी अनेक अन्य स्थितियों में यह जानना अभीष्ट होता है कि एक प्राचल में दूसरे किसी प्राचल के सापेक्ष परिवर्तन किस प्रकार होता है? परिभाषा के प्रांत के प्रदत्त बिंदु पर फलन का अवकलज इस विषय का मुख्य उद्देश्य है।
परिभाषा 1 मान लीजिए f एक वास्तविक मानीय फलन है और इसकी परिभाषा के प्रांत में एक बिंदु a है। a पर f का अवकलज
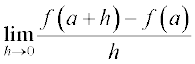
से परिभाषित है बशर्ते कि इस सीमा का अस्तित्व हो। a पर f(x) का अवकलज f’ (a) से निरूपित होता है।
अवलोकन कीजिए कि f′ (a), a पर x के सापेक्ष परिवर्तन का परिमाण बताता है।
उदाहरण 5 x = 2 पर फलन f(x) = 3x का अवकलज ज्ञात कीजिए।
हल हम पाते हैं 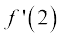 =
= 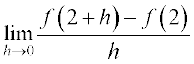 =
= 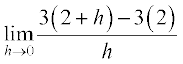
= 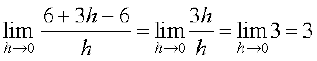 .
.
अतः x = 2 पर फलन 3x का अवकलज 3 है।
उदाहरण 6 x = –1 पर फलन f(x) = 2x2 + 3x – 5 का अवकलज ज्ञात कीजिए। यह भी सिद्ध कीजिए कि f ′ (0) + 3f ′ ( –1) = 0.
हल हम पहले x = 0 और x = –1 पर f(x) का अवकलज ज्ञात करते हैं। हम पाते हैं कि
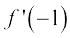 =
= 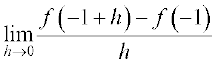
= 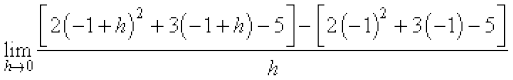
= 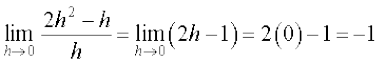
और 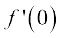 =
= 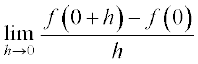
= 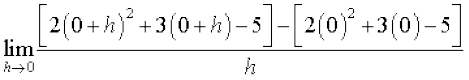
= 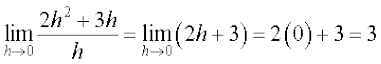
स्पष्टतः 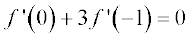
टिप्पणी इस स्थिति में ध्यान दीजिए कि एक बिंदु पर अवकलज का मान प्राप्त करने में सीमा ज्ञात करने के विविध नियमों का प्रभावकारी प्रयोग सम्मिलित है। निम्नलिखित इसको स्पष्ट करता हैः
उदाहरण 7 x = 0 पर sin x का अवकलज ज्ञात कीजिए।
हल मान लीजिए f(x) = sin x. तब
f′(0) = 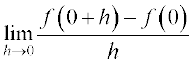 =
= 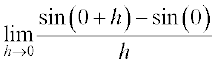 =
= 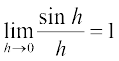
उदाहरण 8 x = 0 और x = 3 पर फलन f(x) = 3 का अवकलज ज्ञात कीजिए।
हल क्योंकि अवकलज फलन में परिवर्तन को मापता है, सहजरूप से यह स्पष्ट है कि अचर फलन का प्रत्येक बिंदु पर अवकलन शून्य होना चाहिए। इसे, वास्तव में, निम्नलिखित परिकलन से बल मिलता है।
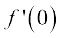 =
= 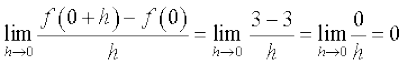 .
.
इसी प्रकार 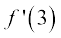 =
=  .
.
अब हम एक बिंदु पर फलन के अवकलज की ज्यामितीय व्याख्या प्रस्तुत करते हैं।

आकृति 13.11
मान लीजिए y = f(x) एक फलन है और मान लीजिए इस फलन के आलेख पर P = (a, f(a)) और
Q = (a + h, f(a + h) दो परस्पर निकट बिंदु हैं। आकृति 13.11 अब स्वयं व्याख्यात्मक है। हम जानते हैं कि 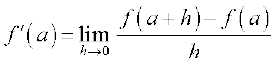
त्रिभुज PQR, से यह स्पष्ट है कि वह अनुपात जिसकी सीमा हम ले रहे हैं, यथार्थता से
tan (QPR) के बराबर है जो कि जीवा PQ का ढाल है। सीमा लेने की प्रक्रिया में, जब h, 0 की ओर अग्रसर होता है, बिंदु Q, P की ओर अग्रसर होता है और हम पाते हैं अर्थात्
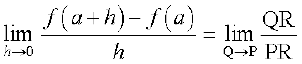
यह इस तथ्य के तुल्य है कि जीवा PQ, वक्र y = f(x) के बिंदु P पर स्पर्शी की ओर अग्रसर होती है। अतः
एक दिए फलन f के लिए हम प्रत्येक बिंदु पर अवकलज ज्ञात कर सकते हैं। यदि प्रत्येक बिंदु पर अवकलज का अस्तित्व है तो यह एक नये फलन को परिभाषित करता है जिसे फलन f का अवकलज कहा जाता है औपचारिक रूप से हम एक फलन के अवकलज को निम्नलिखित प्रकार परिभाषित करते हैं।
परिभाषा 2 मान लीजिए कि f एक वास्तविक मानीय फलन है, तो
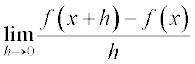
से परिभाषित फलन, जहाँ कहीं सीमा का अस्तित्व है, को x पर f का अवकलज परिभाषित किया जाता है और f′(x) से निरूपित किया जाता है। अवकलज की इस परिभाषा को अवकलज का प्रथम सिद्धांत भी कहा जाता है।
इस प्रकार f′ (x) = 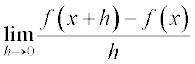
स्पष्टतः f′ (x) की परिभाषा का प्रांत वही है जहाँ कहीं उपर्युक्त सीमा का अस्तित्व है। एक फलन के अवकलज के विभिन्न संकेतन हैं। कभी-कभी f′(x) को  से निरूपित किया जाता है यदि y = f(x), तो यह
से निरूपित किया जाता है यदि y = f(x), तो यह 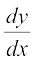 से निरूपित किया जाता है। इसे y या f(x) के सापेक्ष अवकलज के रूप में उल्लेखित किया जाता है इसे D (f (x) ) से भी निरूपित किया जाता है।
से निरूपित किया जाता है। इसे y या f(x) के सापेक्ष अवकलज के रूप में उल्लेखित किया जाता है इसे D (f (x) ) से भी निरूपित किया जाता है।
इसके अतिरिक्त x = a पर f के अवकलज को 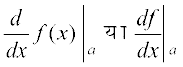 या
या 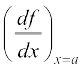 से भी निरूपित किया जाता है।
से भी निरूपित किया जाता है।
उदाहरण 9 f(x) = 10 x का अवकलज ज्ञात कीजिए।
हल हम पाते हैं f′ (x) = 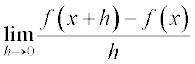 =
= 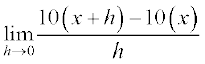
= 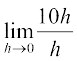 =
= 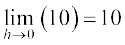
उदाहरण 10 f(x) = x2 का अवकलज ज्ञात कीजिए।
हल हम पाते हैं f′(x) = 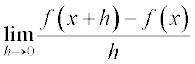
= 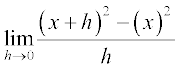 =
= 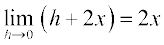
उदाहाण 11 एक अचर वास्तविक संख्या a के लिए, अचर फलन f(x) = a का अवकलज ज्ञात कीजिए।
हल हम पाते हैं f′(x) = 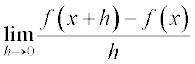
= 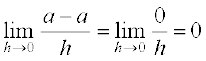 क्योंकि
क्योंकि 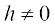
उदाहरण 12 f(x) =  का अवकलज ज्ञात कीजिए।
का अवकलज ज्ञात कीजिए।
हल हम पाते हैं f′(x) = 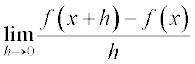
= 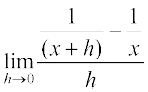
= 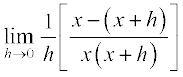
=  =
= 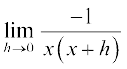 =
= 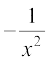
13.5.1 फलनों के अवकलज का बीजगणित (Algebra of derivative of functions)
क्योंकि अवकलज की यथार्थ परिभाषा में सीमा निश्चय ही सीधे रूप में सम्मिलित है, हम अवकलज के नियमों के निकटता से सीमा के नियमों के अनुगमन की आशा करते हैं। हम इनको निम्नलिखित प्रमेयों में पाते हैंः
प्रमेय 5 मान लीजिए f और g दो एेसे फलन हैं कि उनके उभयनिष्ठ प्रांत में उनके अवकलन परिभाεषत हैं, तब
(i) दो फलनों के योग का अवकलज उन फलनों के अवकलजों का योग है।
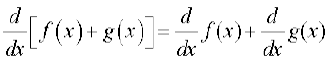
(ii) दो फलनों के अंतर का अवकलज उन फलनों के अवकलजों का अंतर है।
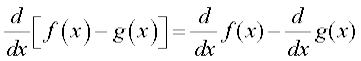
(iii) दो फलनों के गुणन का अवकलज निम्नलिखित गुणन नियम (product rule) से दिया गया हैः
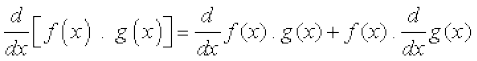
(iv) दो फलनों के भागफल का अवकलज निम्नलिखित भागफल नियम (quotient rule) से दिया गया है (जहाँ कहीं हर शून्येतर है)
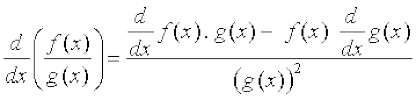
इनकी उपपत्ति सीमाओं की तुल्य रूप प्रमेयों से आवश्यकीय रूप से अनुसरण करती हैं। हम इन्हें यहाँ सिद्ध नहीं करेंगे। सीमाओं की स्थिति की तरह यह प्रमेय बतलाता है कि विशेष प्रकार के फलनों के अवकलज कैसे परिकलित किए जाते हैं। प्रमेय के अंतिम दो कथनों को निम्नलिखित ढंग से पुनः कहा जा सकता है जिससे उनके पुनर्स्मरण करने में आसानी से सहायता मिलती है।
मान लीजिए 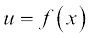 और
और 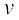 = g (x) तब
= g (x) तब
 =
= 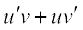
यह फलनों के गुणन के अवकलन के लिए Leibnitz नियम या गुणन नियम उल्लेखित होता है। इसी प्रकार, भागफल नियम है
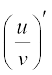 =
= 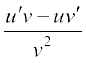
अब, आइए हम कुछ मानक फलनों के अवकलनों को लें। यह देखना सरल है कि फलन
f(x) = x का अवकलज अचर फलन 1 है। यह है क्योंकि
f (x) =
(x) = 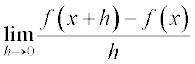 =
= 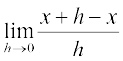
= 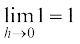
हम इसका और उपर्युक्त प्रमेय का प्रयोग f(x) = 10x = x + x + ... + x (10 पद)
(उपर्युक्त प्रमेय के (i) से) के अवकलज के परिकलन में करते हैं
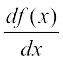 =
= 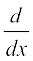
 (10 पद)
(10 पद)
=  (10 पद)
(10 पद)
=  (10 पद) = 10.
(10 पद) = 10.
हम ध्यान देते हैं कि इस सीमा का मान गुणन सूत्र के प्रयोग से भी प्राप्त किया जा सकता है। हम लिखते हैं, f(x) = 10x = uv, जहाँ u लिखते हैं जहाँ u प्रत्येक जगह मान 10 लेकर अचर फलन है और v(x) = x. यहाँ हम जानते हैं कि u का अवकलज 0 के बराबर है साथ ही v(x) = x का अवकलज 1 के बराबर है। इस प्रकार गुणन नियम से, हम पाते हैं
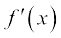 =
= 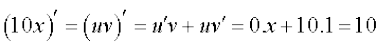
इसी आधार पर f(x) = x2 के अवकलज का मान प्राप्त किया जा सकता है। हम पाते हैं
f(x) = x2 = x .x और अतः
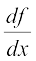 =
= 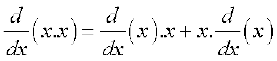
= 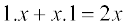
अधिक व्यापक रूप से हम निम्नलिखित प्रमेय पाते हैंः
प्रमेय 6 किसी धन पूर्णांक n के लिए f(x) = xn का अवकलज nxn – 1 है।
उपपत्ति अवकलज फलन की परिभाषा से, हम पाते हैं
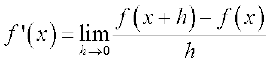 =
=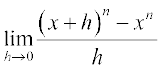 .
.
द्विपद प्रमेय कहता है कि (x + h)n =  और
और
(x + h)n – xn = h(nxn – 1 +... + hn – 1) इस प्रकार
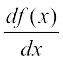 =
= 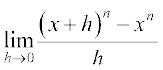 =
= 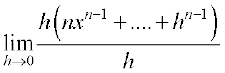
= 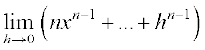 , =
, = 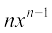
विकल्पतः हम इसको n पर आगमन और गुणन सूत्र से भी निम्न प्रकार सिद्ध कर सकते हैंः n = 1 के लिए यह सत्य है जैसा कि पहले दिखाया जा चुका है
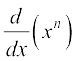 =
= 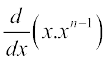
= 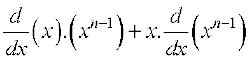 (गुणन सूत्र से)
(गुणन सूत्र से)
=  (आगमन परिकल्पना से)
(आगमन परिकल्पना से)
= 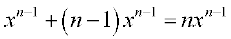
टिप्पणी उपर्युक्त प्रमेय x,की सभी घातों के लिए सत्य है अर्थात् n कोई भी वास्तविक संख्या हो सकती है। (लेकिन हम इसको यहाँ सिद्ध नहीं करेंगे)
13.5.2 बहुपदों और त्रिकोणमितीय फलनों के अवकलज (Derivative of polynomials and trigonometric functions)
हम निम्नलिखित प्रमेय से प्रारंभ करेंगे जो हमको बहुपदीय फलनों के अवकलज बतलाती है।
प्रमेय 7 मान लीजिए 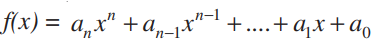
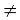 0 तब अवकलज फलन इस प्रकार दिया जाता हैः
0 तब अवकलज फलन इस प्रकार दिया जाता हैः

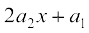
इस प्रमेय की उपपत्ति प्रमेय 5 और प्रमेय 6 के भाग (i) को मात्र साथ रखने से प्राप्त की जा सकती है।
उदाहरण 13 6x100 – x55 + x के अवकलज का परिकलन कीजिए।
हल उपर्युक्त प्रमेय का सीधा अनुप्रयोग बतलाता है कि उपर्युक्त फलन का अवकलज 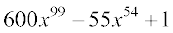 है।
है।
उदाहरण 14 x = 1 पर f(x) = 1 + x + x2 + x3 +... + x50 का अवकलज ज्ञात कीजिए। .
हल उपर्युक्त प्रमेय 6 का सीधा अनुप्रयोग बतलाता है कि उपर्युक्त फलन का अवकलज
1 + 2x + 3x2 + . . . + 50x49 है। x = 1 पर इस फलन का मान 1 + 2(1) + 3(1)2 + .. . + 50(1)49 = 1 + 2 + 3 + . . . + 50 = 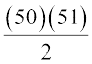 = 1275 है।
= 1275 है।
उदाहरण 15 f(x) =  का अवकलज ज्ञात कीजिए।
का अवकलज ज्ञात कीजिए।
हल यह पηलन x = 0 के अतिरिक्त प्रत्येक के लिए परिभाषित है। हम यहाँ u = x + 1 और v = x लेकर भागफल नियम का प्रयोग करते हैं। अतः u´ = 1 और v´ = 1 इसलिए
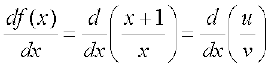

उदाहरण 16 sin x के अवकलज का परिकलन कीजिए।
हल मान लीजिए f(x) = sin x, तब
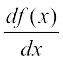 =
= 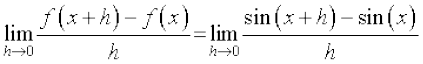
=  ( sin A – sin B के सूत्र का प्रयोग करके)
( sin A – sin B के सूत्र का प्रयोग करके)
=  .
.
उदाहरण 17 tan x के अवकलज का परिकलन कीजिए।
हल मान लीजिए f(x) = tan x, तब
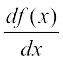 =
= 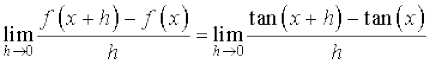
= 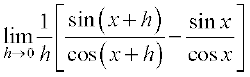
= 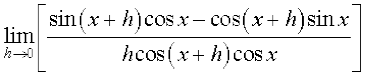
= 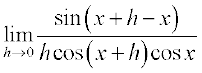 (sin (A + B) के सूत्र का प्रयोग करके)
(sin (A + B) के सूत्र का प्रयोग करके)
= 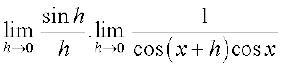
= 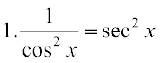
उदाहरण 18 f(x) = sin2 x के अवकलज का परिकलन कीजिए।
हल हम इसका मान प्राप्त करने के लिए Leibnitz गुणन सूत्र का प्रयोग करते हैं।
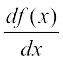 =
= 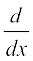 (sin x sin x)
(sin x sin x)
= (sin x)′ sin x + sin x (sin x)′
= (cos x) sin x + sin x (cos x)
= 2sin x cos x = sin 2x.
प्रश्नावली 13.2
1. x = 10 पर x2 – 2 का अवकलज ज्ञात कीजिए।
2. x = 1 पर x का अवकलज ज्ञात कीजिए।
3. x = l00 पर 99x का अवकलज ज्ञात कीजिए।
4. प्रथम सिद्धांत से निम्नलिखित फलनों के अवकलज ज्ञात कीजिएः
(i) 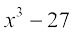 (ii)
(ii) 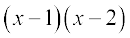
(iii) 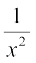 (iv)
(iv) 
5. फलन 
के लिए सिद्ध कीजिए कि 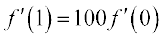 .
.
6. किसी अचर वास्तविक संख्या a के लिए  का अवकलज ज्ञात कीजिए
का अवकलज ज्ञात कीजिए
7. किन्हीं अचरों a और b, वेη लिए,
(i) 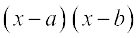 (ii)
(ii) 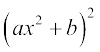 (iii)
(iii) 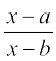
के अवकलज ज्ञात कीजिए।
8. किसी अचर a के लिए 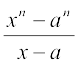 का अवकलज ज्ञात कीजिए।
का अवकलज ज्ञात कीजिए।
9. निम्नलिखित के अवकलज ज्ञात कीजिएः
(i)  (ii)
(ii) 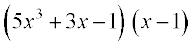
(iii) 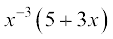 (iv)
(iv) 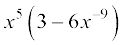
(v) 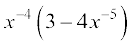 (vi)
(vi) 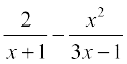
10. प्रथम सिद्धांत से cos x का अवकलज ज्ञात कीजिए।
11. निम्नलिखित फलनों के अवकलज ज्ञात कीजिए।
(i) 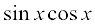 (ii)
(ii)  (iii)
(iii) 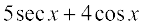
(iv) cosec x (v) 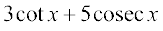
(vi)  (vii)
(vii) 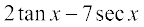
विविध उदाहरण
उदाहरण 19 प्रथम सिद्धांत से f का अवकलज ज्ञात कीजिए जहाँ f इस प्रकार प्रदत्त हैः
(i) f (x) = 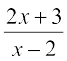 (ii) f (x) =
(ii) f (x) = 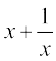
हल (i) ध्यान दीजिए कि फलन x = 2 पर परिभाषित नहीं है। लेकिन, हम पाते हैं
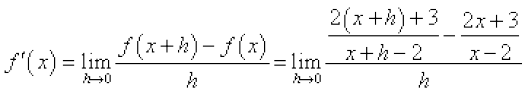
= 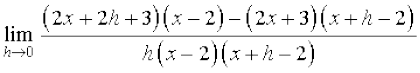
= 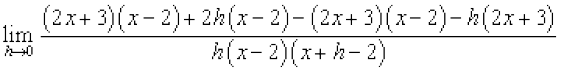
= 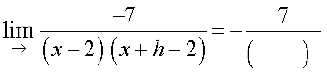
पुनः ध्यान दीजिए कि x = 2 पर फलन 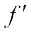 भी परिभाषित नहीं है।
भी परिभाषित नहीं है।
(ii) x = 0 पर फलन परिभाषित नहीं है। लेकिन, हम पाते हैं
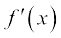 =
= 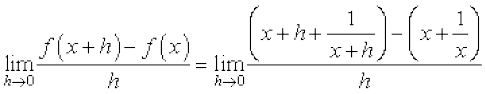
= 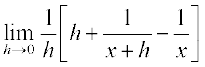
= 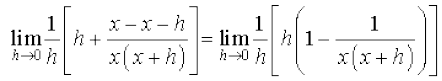
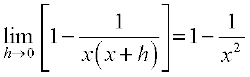 =
= 
पुनः ध्यान दीजिए कि x = 0 पर फलन  परिभाषित नहीं है।
परिभाषित नहीं है।
उदाहरण 20 प्रथम सिद्धांत से फलन f(x) का अवकलज ज्ञात कीजिए जहाँ f(x)
(i)  (ii)
(ii) 
हल (i) हम पाते हैं,  =
=
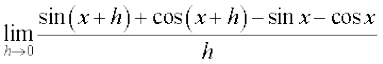
= 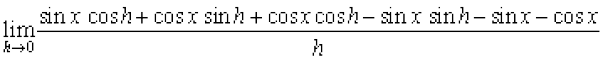
= 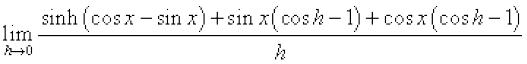
= 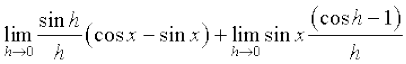
= 
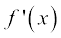
= cos x – sin x
(ii) 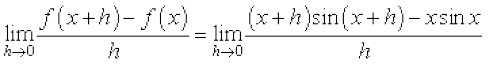 =
= 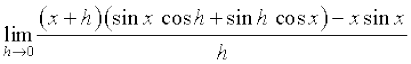
= 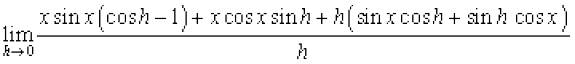
= 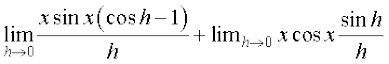
= 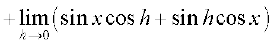
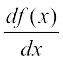
= x cos x + sin x
उदाहरण 21 (i) f(x) = sin 2x (ii) g(x) = cot x
के अवकलज का परिकलन कीजिए।
हल (i) त्रिकोणमिति सूत्र sin 2x = 2 sin x cos x का पुनर्स्मरण कीजिए। इस प्रकार
 =
= 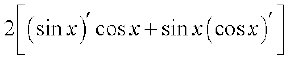
= 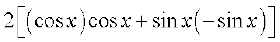
= 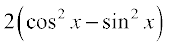 =
= 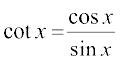
(ii) परिभाषा से, g(x) = 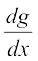 हम भागफल सूत्र का प्रयोग इस फलन पर करेंगे, जहाँ कहीं यह परिभाषित है।
हम भागफल सूत्र का प्रयोग इस फलन पर करेंगे, जहाँ कहीं यह परिभाषित है। 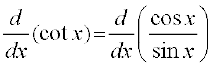 =
=  =
= 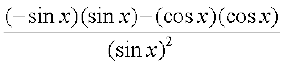
= 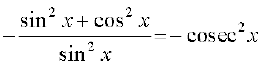
=
विकल्पतः इसको ध्यान देकर कि  , परिकलित किया जा सकता है। यहाँ हम इस तथ्य का प्रयोग करते हैं कि tan x का अवकलज sec2 x है जो हमने उदाहरण 17 में देखा है और साथ ही अचर फलन का अवकलज 0 होता है।
, परिकलित किया जा सकता है। यहाँ हम इस तथ्य का प्रयोग करते हैं कि tan x का अवकलज sec2 x है जो हमने उदाहरण 17 में देखा है और साथ ही अचर फलन का अवकलज 0 होता है।
 =
=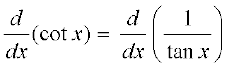
=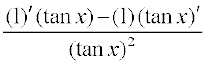
= 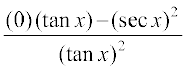
= 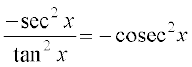
=
उदाहरण 22 (i) 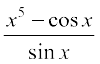 (ii)
(ii) 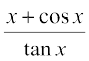
का अवकलज ज्ञात कीजिए।
हल (i) मान लीजिए 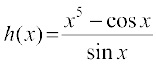 जहाँ कहीं भी यह परिभाषित है, हम इस फलन पर भागफल नियम का प्रयोग करेंगे।
जहाँ कहीं भी यह परिभाषित है, हम इस फलन पर भागफल नियम का प्रयोग करेंगे।
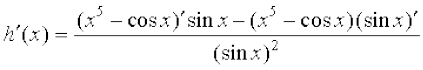 .
.

= 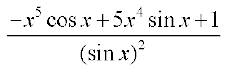
(ii) हम फलन 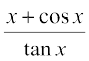 पर भागफल नियम का प्रयोग करेंगे जहाँ कहीं भी यह परिभाषित है।
पर भागफल नियम का प्रयोग करेंगे जहाँ कहीं भी यह परिभाषित है।
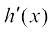 =
=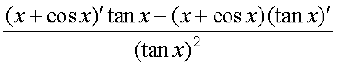

अध्याय 13 पर विविध प्रश्नावली
1. प्रथम सिद्धांत से निम्नलिखित फलनों का अवकलज ज्ञात कीजिएः
(i) (ii)
(ii) (iii)sin (x + 1) (iv) cos (x –
(iii)sin (x + 1) (iv) cos (x –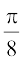 )
)
निम्नलिखित फलनों के अवकलज ज्ञात कीजिए (यह समझा जाय कि a, b, c, d, p, q, r और s निश्चित शून्येतर अचर हैं और m तथा n पूर्णांक हैं।):
2. (x + a) 3. (px + q) 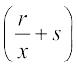 4.
4. 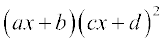
5. 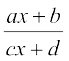 6.
6. 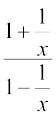 7.
7. 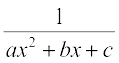
8. 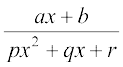 9.
9.  10.
10.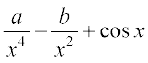
11.  12.
12. 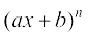 13.
13. 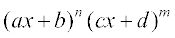
14. sin (x + a) 15. cosec x cot x 16. 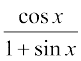
17. 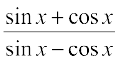 18.
18. 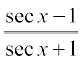 19.
19. 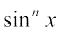
20. 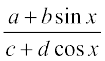 21.
21. 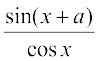 22.
22.  23.
23.  24.
24.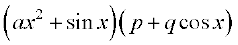
25. 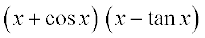 26.
26. 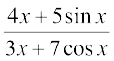 27.
27. 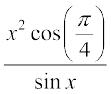
28. 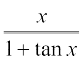 29.
29.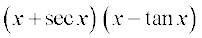 30.
30. 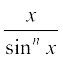
सारांश
- फलन का अपेक्षित मान जो एक बिंदु के बाईं ओर के बिंदुओं पर निर्भर करता है, बिंदु पर फलन के बाएँ पक्ष की सीमा (Left handed limit) को परिभाषित करता है। इसी प्रकार दाएँ पक्ष की सीमा (Right handed limit)।
- एक बिंदु पर फलन की सीमा बाएँ पक्ष और दाएँ पक्ष की सीमाओं से प्राप्त उभयनिष्ठ मान हैं यदि वे संपाती हों।
- यदि किसी बिंदु पर बाएँ पक्ष और दाएँ पक्ष की सीमाएँ संपाती न हों तो यह कहा जाता है कि उस बिंदु पर फलन की सीमा का अस्तित्व नहीं है।
- एक वास्तविक संख्या a और एक फलन f के लिए
![]() f(x) और f (a) समान नहीं भी हो सकते (वास्तव में, एक परिभाषित हो और दूसरा नहीं)
f(x) और f (a) समान नहीं भी हो सकते (वास्तव में, एक परिभाषित हो और दूसरा नहीं) - फलनाें f और g के लिए निम्नलिखित लागू होते हैंः

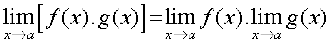
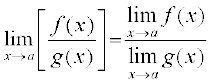
- निम्नलिखित कुछ मानक सीमाएँ हैं।
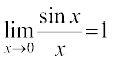
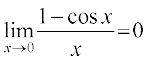
- a पर फलन f का अवकलज
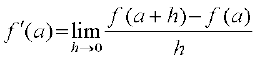 से परिभाषित होता है।
से परिभाषित होता है।
- प्रत्येक बिंदु पर अवकलज, अवकलज फलन
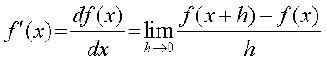
से परिभाषित होता है।
- फलनों u और v के लिए निम्नलिखित लागू होता हैः
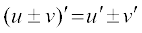
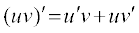
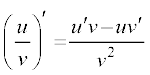
बशर्ते सभी परिभाषित हैं।
निम्नलिखित कुछ मानक अवकलज हैंः
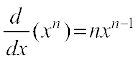
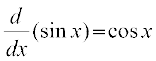
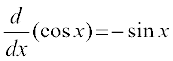
एेतिहासिक पृष्ठभूमि
गणित के इतिहास में कलन के अन्वेषण के श्रेय की भागीदारी हेतु दो नाम प्रमुख हैं Issac Newton (1642 – 1727) और G.W. Leibnitz (1646 – 1717). सत्रहवीं शताब्दी में दोनों ने स्वतंत्रता पूर्वक कलन का अन्वेषण किया। कलन के आगमन के बाद इसके आगामी विकास हेतु अनेक गणितज्ञों ने योगदान किया। परिशुद्ध संकल्पना का मुख्य श्रेय महान गणितज्ञों A.L.Cauchy, J.L.Lagrange और Karl Weier strass को प्राप्त है। Cauchy ने कलन को आधार दिया जिसको अब हम व्यापकतः पाठ््य पुस्तकों में स्वीकार कर चुके हैं। Cauchy ने D'Almbert की सीमा संकल्पना के प्रयोग के द्वारा अवकलज की परिभाषा दी। सीमा की परिभाषा से प्रारंभ करते हुए 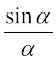 = 0 के लिए
= 0 के लिए 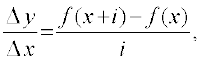 की सीमा जैसे उदाहरण दिए। उन्होंने
की सीमा जैसे उदाहरण दिए। उन्होंने 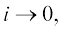 लिखा और के लिए सीमा को 'f "(x) के लिए y’, "function derive’e" नाम दिया।
लिखा और के लिए सीमा को 'f "(x) के लिए y’, "function derive’e" नाम दिया।
1900 से पूर्व यह सोचा जाता था कि कलन को पढ़ाना बहुत कठिन है, इसलिए कलन युवाओं की पहुँच से बाहर थी। लेकिन ठीक 1900 में इंगलैंड में John Perry एवं अन्य ने इस विचार का प्रचार करना प्रारंभ किया कि कलन की मुख्य विधियाँ और धारणाएँ सरल हैं और स्कूल स्तर पर भी पढ़ाया जा सकता है। F.L. Griffin ने कलन के अध्ययन को प्रथम वर्ष के छात्रों से प्रारंभ करके नेतृत्व प्रदान किया। उन दिनों यह बहुत चुनौतीपूर्ण कार्य था।
आज न केवल गणित अपितु अनेक अन्य विषयों जैसे भौतिकी, रसायन विज्ञान, अर्थशास्त्र, जीवविज्ञान में कलन की उपयोगिता महत्वपूर्ण है।