"There are few things which we know which are not capable of mathematical reasoning and when these can not, it is a sign that our knowledge of them is very small and confused and where a mathematical reasoning can be had, it is as great a folly to make use of another, as to grope for a thing in the dark when you have a candle stick standing by you. – Arthenbot"

14.1 भूमिका (Introduction)

इस अध्याय में हम गणितीय विवेचन से संबंधित कुछ मौलिक धारणाओं पर चर्चा करेंगे। हमें ज्ञात है कि मनुष्य, अनेकों सहस्त्राब्दियों में, निम्न स्तर की प्रजातियों से, विकसित हुआ है। मनुष्य में विवेचन करने के गुण ने उसे अन्य प्रजातियों से श्रेष्ठ बनाया है। एक व्यक्ति इस गुण को कितनी अच्छी तरह प्रयोग कर सकता है, उसके विवेचन क्षमता पर निर्भर करता है। इस क्षमता को केसे विकसित किया जाए? यहाँ पर हम विवेचन की प्रक्रिया की चर्चा विशेष रूप से गणित के संदर्भ में करेंगे। गणितीय भाषा में विवेचन दो प्रकार के होते हैं- आगमनात्मक (आगमिक) विवेचन तथा निगमनात्मक (निगमनिक) विवेचन। गणितीय आगमन (Mathematical Induction) के संदर्भ में हम आगमनात्मक विवेचन की चर्चा पहले कर चुके हैं। इस अध्याय में हम कुछ मूलभूत निगमनात्मक विवेचन पर चर्चा करेंगे।

14.2 कथन (Statements)

गणितीय विवेचन की मौलिक इकाई गणितीय कथन की संकल्पना है।

हम निम्नलिखित दो वाक्यों में प्रारंभ करेंगे।

"सन् 2003 में भारत की राष्ट्रपति एक महिला थीं।"

"किसी हाथी का भार एक मनुष्य के भार से अधिक होता है।"

इन वाक्यों को पढ़ते ही हम तुरन्त निर्णय ले सकते हैं कि प्रथम वाक्य गलत (असत्य) तथा दूसरा वाक्य सही (सत्य) है। इस संबंध में कोई भ्रांति नहीं है। गणित में एेसे वाक्यों को कथन
कहते हैं।

इसके विपरीत निम्नलिखित वाक्य पर विचार कीजिएः

"महिलाएँ, पुरुषों से अधिक बुद्धिमान होती हैं।"

कुछ लोगों के विचार से यह वाक्य सत्य हो सकता है परंतु कुछ अन्य इससे असहमत हो सकते हैं। इस वाक्य के बारे में हम यह नहीं कह सकते कि यह सत्य या असत्य है। इसका तात्पर्य है कि यह वाक्य द्वयर्थक है।

इस प्रकार का वाक्य गणित में कथन के रूप में स्वीकार्य नहीं है।

‘एक वाक्य गणितानुसार कथन कहलाता है। यदि वह या तो सत्य हो अथवा असत्य हो परंतु दोनों (सत्य और असत्य) न हो।’ अब जब भी हम कथन का उल्लेख करेंगे हमारा तात्पर्य "गणितानुसार स्वीकार्य" कथन से होगा।

गणित के अध्ययन के दौरान हमें इस प्रकार के अनेक वाक्य मिलते हैं। कुछ उदाहरण इस
प्रकार हैंः

दो धन दो बराबर चार।

दो धन संख्याओं का योगफल धन होता है।

सभी अभाज्य संख्याएँ विषम संख्याएं होती हैं।

इनमें से प्रथम दो वाक्य सत्य हैं और तीसरा वाक्य असत्य है। इन वाक्यों के बारे में कोई भी संदिग्धता नहीं है। अत:ये (वाक्य) कथन हैं।

क्या आप किसी एेसे वाक्य का उदाहरण सोच सकते हैं जो अस्पष्ट हो? निम्नलिखित वाक्य पर विचार कीजिएः

x और y का योगफल 0 से अधिक है।

यहाँ हम यह सुनिश्चित नहीं कर सकते कि वाक्य सत्य है अथवा असत्य है, जब तक हमें यह ज्ञात न हो कि x और y क्या हैं। उदाहरणार्थ, x = 1, y = –3 के लिए यह असत्य है तथा
x = 1, y = 0 के लिए यह सत्य है। अत:यह वाक्य एक कथन नहीं है। किंतु निम्नलिखित वाक्य एक कथन है

प्रत्येक प्राकृत संख्याओं x और y का योगफल 0 से अधिक है, एक कथन है।

अब निम्नलिखित वाक्यों पर विचार कीजिएः

आहा, कितना सुंदर!

द्वार (दरवाजा) खोलिए।

आप कहाँ जा रहे हैं?

क्या ये कथन हैं? नहीं, क्योंकि पहला विस्मयादिबोधक (विस्मयबोधक) वाक्य है, दूसरा एक आदेश है तथा तीसरा एक प्रश्न है। गणितीय भाषा में इनमें से किसी को भी कथन नहीं माना जाता है। एेसे वाक्य जिनमें चर (अनिश्चित) समय हो जैसे "आज", "कल" "बीता हुआ कल", कथन नहीं होते हैं। यह इसलिए कि हमें यह ज्ञात नहीं होता कि किसी समय की चर्चा हो रही है।
उदाहरणार्थ, वाक्य

‘कल शुक्रवार है।’

एक कथन नहीं है।

यह वाक्य किसी बृहस्पतिवार के लिए तो सत्य होगा परंतु अन्य दिनों के लिए सत्य नहीं होगा। यह बात उन वाक्यों के लिए भी लागू होती है जिनमें सर्वनाम का प्रयोग बिना संबंधित संज्ञा को बताए किया गया हो और एेसे वाक्यों के लिए भी जिनमें चर (अनिश्चित) स्थानों का प्रयोग किया गया हो, जैसे ‘यहाँ’, ‘वहाँ’ आदि। तात्पर्य यह हुआ कि वाक्य

वह गणित की एक स्नातक है

कश्मीर यहाँ से बहुत दूर है।

कथन नहीं है।

यहाँ एक अन्य वाक्य पर विचार कीजिएः

एक महीने (माह) में 40 दिन होते हैं।

क्या आप इसे एक कथन कहेंगे? नोट कीजिए कि यहाँ पर उल्लिखित समय "अनिश्चित (चर)" है अर्थात्् 12 महीनों में से कोई एक। किंतु हमें ज्ञात है कि यह वाक्य सदैव (महीने का ध्यान किए बिना) असत्य होता है क्योंकि एक महीने में दिनों की संख्या 31 से अधिक नहीं हो सकती है। अत:यह वाक्य एक कथन है। इसलिए यह तथ्य कि एक वाक्य या तो सत्य हो या असत्य हो किंतु दोनों न हो सके एक कथन बनाता है।

सामान्यत:हम कथनों को छोटे अक्षर p, q, r, ... से निरूपित (निर्दिष्ट) करते हैं

उदाहरण के लिए, कथन "आग सदैव गर्म होती है" को हम p द्वारा दर्शाते हैं। इस बात को निम्नलिखित प्रकार से भी दर्शाते हैंः

p :आग सदैव गर्म होती है।

उदाहरण 1 जाँचिए कि क्या निम्नलिखित वाक्य कथन हैं। अपने उत्तर को कारण सहित लिखिए।

(i) 8, 6 से कम है।

(ii) प्रत्येक समुच्चय एक परिमित समुच्चय होता है।

(iii) सूर्य एक तारा है।

(iv) गणित एक कौतुक है।

(v) बिना बादल के वर्षा नहीं होती।

(vi) यहाँ से चेन्नई कितनी दूर है?

हल (i) यह वाक्य असत्य है क्योंकि 8 अधिक होता है 6 से। अत:यह एक कथन है।

(ii) यह वाक्य भी सदैव असत्य है क्योंकि एेसे भी समुच्चय हैं जो कि परिमित नहीं होते हैं अत:यह एक कथन है।

(iii) यह वैज्ञानिक रूप से प्रमाणित है कि सूर्य एक तारा है और इसलिए यह वाक्य सत्य है। अत:यह एक कथन है।

(iv) यह वाक्य व्यक्तिनिष्ठ है क्योंकि जिन्हें गणित में रुचि है उनके लिए यह कौतुक हो सकता है किंतु अन्य के लिए एेसा नहीं हो सकता है। इसका अर्थ हुआ कि यह वाक्य सत्य या असत्य नहीं है। अत:यह एक कथन नहीं है।

(v) यह वैज्ञानिक रूप से प्रमाणित प्राकृतिक तथ्य है कि वर्षा होने से पहले बादल बनते हैं। इसलिए यह सदैव सत्य है। अत:यह एक कथन है।

(vi) यह एक प्रश्न है, जिसमें शब्द ‘यहाँ’ भी आता है। अत:यह एक कथन नहीं है।

उपरोक्त उदाहरण यह दर्शाते हैं कि जब कभी हम किसी वाक्य को कथन कहते हैं तो हमें यह भी बतलाना चाहिए कि एेसा क्यों है प्रश्न के उत्तर की अपेक्षा यह ‘क्यों’ अधिक महत्वपूर्ण है।

14.3 पूर्व ज्ञात कथनों से नए कथन बनाना (New Statements from Old)

अब हम पूर्व ज्ञात कथानों से नए कथन बनाने की विधि पर विचार करेंगे। सन् 1854 में एक अँगरेज़  गणितज्ञ Georg Boole ने अपनी पुस्तक The laws of Thoughts में इन विधियों पर विचार-विमर्श किया है। यहाँ, हम दो तकनीकों पर विचार-विमर्श करेंगे।

कथन के अध्ययन में प्रथम चरण के रूप में हम एक महत्वपूर्ण तकनीक पर दृष्टि डालेंगे जिसके प्रयोग से हम गणितीय वाक्यों की अपनी समझ को गहन कर सकेंगे। इस तकनीक में हम अपने आप से न केवल यह प्रश्न पूछेंगे कि एक दिए हुए वाक्य के सत्य होने का क्या अर्थ होता है बल्कि यह भी कि उस वाक्य के सत्य नहीं होने का क्या अर्थ होता है।

14.3.1 किसी कथन का निषेधन (Negation of a statement)

किसी कथन का नकारना उस कथन का निषेधन कहलाता है।

वाक्य ‘नई दिल्ली एक नगर है।’

इसका निषेधन निम्नलिखित प्रकार से लिखा जा सकता है।

यह वस्तुस्थिति नहीं है कि नई दिल्ली एक नगर है।’ इसे इस प्रकार भी लिख सकते हैं। कि

‘यह असत्य है कि नई दिल्ली एक नगर है।’

सरलता से यह भी कह सकते हैं कि

‘नई दिल्ली एक नगर नहीं है।’

परिभाषा 1 यदि p एक कथन है, तो p का निषेधन वह कथन है जो p को नकारता है और इसे प्रतीक ~p से दर्शाते (निर्दिष्ट करते) हैं जिसे "p-नहीं" पढ़ते हैं।

टिप्पणी किसी कथन के निषेधन की रचना करते समय ‘यह वस्तु स्थिति नहीं है’ अथवा ‘यह असत्य है कि’ यहाँ एक उदाहरण से यह स्पष्ट किया गया है कि किस प्रकार एक कथन के निषेधन का अवलोकन करके, हम उसके संबंध में अपनी समझ सुधार सकते हैं।

वाक्य ‘जर्मनी में हर कोई (प्रत्येक व्यक्ति) जर्मन भाषा बोलता है।’ पर विचार करें।

इस वाक्य को नकारने से हमें वाक्य ‘जर्मनी में हर कोई जर्मन भाषा नहीं बोलता है।’ इसका यह तात्पर्य नहीं हुआ कि ‘जर्मनी में कोई भी व्यक्ति जर्मन भाषा नहीं बोलता है।’ यह केवल यह बतलाता है कि ‘जर्मनी में कम से कम एक व्यक्ति एेसा है जो जर्मन भाषा नहीं बोलता है।

हम कुछ और उदाहरणों पर विचार करेंगे।

उदाहरण 2 निम्नलिखित कथनों का निषेधन लिखिए।

(i) किसी आयत के दोनों विकर्णों की लंबाई समान होती है।

(ii) एक परिमेय संख्या है।

हल (i) यह कथन यह बतलाता है कि सभी आयतों में दोनों विकर्णों की लंबाई समान होती है। इसका तत्पर्य यह हुआ कि यदि हम कोई आयत लें तो इसके दोनों विकर्णे की लंबाई समान होगी। इस कथन का निषेधन, "यह असत्य है कि किसी आयत के दोनों विकर्णों की लंबाई समान होती है" है। अर्थात्् ‘कम से कम एक आयत एेसा है, जिसके दोनाें विकर्णों की लंबाई समान नहीं है।’

(ii) इस कथन का निषेधन निम्नलिखित प्रकार लिखा जा सकता है

‘यह वस्तुस्थिति नहीं है कि एक परिमेय संख्या है।’

इसे निम्नलिखित प्रकार से भी लिख सकते हैंः

‘ एक परिमेय संख्या नहीं है।’

उदाहरण 3 निम्नलिखित कथन के निषेधन लिखिए और जाँचिए कि क्या परिणामी कथन सत्य है?

(i) अास्ट्रेलिया एक महाद्वीप है।

(ii) एेसे किसी चतुर्भुज का अस्तित्व नहीं है जिसकी चारों भुजाएँ बराबर हों।

(iii) प्रत्येक प्राकृत संख्या 0 से अधिक होती है।

(iv) 3 और 4 का योगफल 9 है।

हल (i) ‘यह असत्य है कि आस्ट्रेलिया एक महाद्वीप है’, दिये हुए कथन का निषेधन है। इसे इस प्रकार भी लिख सकते हैं कि ‘आस्ट्रेलिया एक महाद्वीप नहीं है।’ हमें ज्ञात है कि यह कथन असत्य है।

(ii) इस कथन का निषेधन इस प्रकार है, ‘यह वस्तुस्थिति नहीं है कि किसी चतुर्भुज का अस्तित्व नहीं है जिसकी चारों भुजाएँ बराबर हैं।’

इसका तात्पर्य हुआ कि ‘एक एेसे चतुर्भुज का अस्तित्व है, जिसकी चारों भुजाएँ बराबर होती हैं। यह कथन सत्य है क्योंकि हमें ज्ञात है कि वर्ग एक एेसा चतुर्भुज होता है, जिसकी चारों भुजाएँ बराबर होती हैं।

(iii) इस कथन का निषेधन इस प्रकार है, ‘यह असत्य है कि प्रत्येक प्राकृत संख्या 0 से
अधिक होती हैं।

इसको इस प्रकार भी लिख सकते हैं कि ‘एक एेसी प्राकृत संख्या का अस्तित्व है जो 0 से अधिक नहीं है।’ यह कथन असत्य है।

(iv) अभीष्ट निषेधन इस प्रकार है, ‘यह असत्य है कि 3 और 4 का योगफल 9 है।’

इसे इस प्रकार भी लिखा जा सकता है कि, ‘3 और 4 का योगफल 9 नहीं हेाता है।’ यह कथन सत्य है।

14.3.2 मिश्र कथन (संयुक्त कथन) 

(Compound statements) ‘और (तथा)’, ‘या (अथवा)’ आदि प्रकार के संयोजक शब्दों द्वारा एक या एक से अधिक कथन को जोड़ कर अनेक गणितीय कथन प्राप्त किए जा सकते हैं। निम्नलिखित कथन पर विचार कीजिएः

‘बल्ब या बिजली के तार में कुछ खराबी है’ यह कथन बतलाता है कि बल्ब में कुछ खराबी है या बिजली के तार में कुछ खराबी है। इसका तात्पर्य यह है कि प्रदत्त कथन वास्तव में दो संक्षिप्त (छोटे) कथन से मिल कर बना है, जो इस प्रकार हैंः

q: ‘बल्ब में कुछ खराबी है’

r: बिजली के तार में कुछ खराबी है’ और

जिनको शब्द ‘या’ द्वारा जोड़ा गया है।

अब मान लीजिए कि निम्नलिखित दो कथन दिए हैं,

p: ‘7 एक विषम संख्या है।’

q: ‘7 एक अभाज्य संख्या है।’

इन दोनों को शब्द ‘और’ द्वारा जोड़ने से निम्नलिखित कथन प्राप्त होगा

r: ‘7 विषम और अभाज्य, दोनों ही प्रकार की संख्या है।’

यह एक मिश्र कथन है।

उपरोक्त परिचर्चा से निम्नलिखित परिभाषा प्राप्त होती हैः

परिभाषा 2 एक मिश्र कथन वह है, जो दो या दो से अधिक एेसे कथनों द्वारा बना हो, इस स्थिति में प्रत्येक कथन को घटक कथन कहते हैं।

आइए अब हम कुछ उदाहरणों पर विचार करें।

उदाहरण 4 निम्नलिखित मिश्र कथन के घटक कथन ज्ञात कीजिए।

(i) आकाश नीला है और घास हरी है।

(ii) वर्षा हो रही है और ठ.डक है।

(iii) सभी परिमेय संख्याएँ, वास्तविक संख्याएँ होती हैं और सभी वास्तविक संख्याएँ, सम्मिश्र संख्याएँ होती हैं।

(iv) 0 एक धन संख्या है या एक ऋण संख्या है।

हल इनमें से प्रत्येक पर हम बारी-बारी से विचार करेंगे।

(i) घटक कथन इस प्रकार हैं

p: आकाश नीला है।

q: घास हरी है।

संयोजक शब्द ‘और’ है।

(ii) घटक कथन नीचे दिए गए हैं,

p: वर्षा हो रही है।

q: ठंडक है।

संयोजक शब्द ‘और’ है।

(iii) घटक कथन नीचे लिखे हैं,

p: सभी परिमेय संख्याएँ वास्तविक संख्याएँ होती हैं।

q: सभी वास्तविक संख्याएँ सम्मिश्र संख्याएँ होती हैं।

संयोजक शब्द ‘और’ है।

(iv) घटक कथन इस प्रकार हैं।

p:  एक धन संख्या हैं।

q:  एक ऋण संख्या है।

संयोजक शब्द ‘या’ है।

उदाहरण 5 निम्नलिखित कथन के घटक कथन ज्ञात कीजिए और जाँचिए कि वे सत्य हैं या नहीं।

(i) एक वर्ग एक चतुर्भुज होता है और इसकी चारों भुजाएँ बराबर होती हैं।

(ii) सभी अभाज्य संख्याएँ या तो सम या विषम होती हैं।

(iii) एक व्यक्ति, जिसने गणित या कंप्यूटर विज्ञान का चयन किया है, कंप्यूटर अनुप्रयोग में स्नाकोत्तर डिग्री पाठ्यक्रम (MCA) में प्रवेश ले सकता है।

(iv) चंडीगढ़ हरिणाणा और उत्तर प्रदेश की राजधानी है।

(v एक परिमेय संख्या या एक अपरिमेय संख्या है।

(vi) 2, 4, और 8 का एक गुणज 24 है।

हल (i) यहाँ घटक कथन इस प्रकार हैं,

p: ‘एक वर्ग एक चतुर्भुज होता है।

q: एक वर्ग की चारों भुजाएँ बराबर होती हैं।

हमें ज्ञात है कि दोनों कथन सत्य हैं। यहाँ पर संयोजक शब्द ‘और’ है।

(ii) यहाँ घटक कथन इस प्रकार हैं,

p: सभी अभाज्य संख्याएँ सम होती हैं।

q: सभी अभाज्य संख्याएँ विषम होती हैं।

यह दोनाें कथन असत्य हैं। यहाँ संयोजक शब्द ‘या’ है।

(iii) यहाँ घटक कथन नीचे लिखे हैं,

p: एक व्यक्ति, जिसने गणित का चयन किया है, एम.सी.ए. में प्रवेश ले सकता है।

q: एक व्यक्ति, जिसने कंप्यूटर विज्ञान का चयन किया है, एम॰सी॰ए॰ में प्रवेश ले सकता है।

यह दोनों ही कथन सत्य हैं। यहाँ संयोजक शब्द ‘या’ है।

(iv) यहाँ घटक कथन इस प्रकार हैं,

p: चंडीगढ़ हरियाणा की राजधानी है।’

q: चंडीगढ़ उत्तर प्रदेश की राजधानी है।’

इस प्रश्न में प्रथम घटक कथन सत्य है और दूसरा असत्य है। यहाँ संयोजक शब्द ‘और’ है।

(v) अभीष्ट घटक कथन नीचे लिख हैं,

p:एक परिमेय संख्या है।

q:एक अपरिमेय संख्या है।

यहाँ प्रथम घटक कथन असत्य है और दूसरा सत्य है। यहाँ संयोजक शब्द ‘या’ है।

(vi) इसमें घटक कथन नीचे लिखे हैं,

p: 2 का एक गुणज 24 है।

q: 4 का एक गुणज 24 है।

r: 8 का एक गुणज 24 है।

यह तीनों ही घटक कथन सत्य है। यहाँ संयोजक शब्द ‘और’ है।

अत:हम देखते हैं कि मिश्र कथन वास्तव में दो या दो से अधिक कथनों को ‘और’, ‘या’ प्रकार के शब्दों द्वारा जोड़ने से बनते हैं। ये शब्द गणित में विशिष्ट महत्व रखते हैं। अगले अनुच्छेद में हम इनके बारे में परिचर्चा करेंगे।

14.4 विशेष शब्द/वाक्यांश (Special WordsQ/Phrases)

मिश्र कथन में प्रयुक्त ‘और’, ‘या’ प्रकार के कुछ संयोजक शब्दों का प्रयोग बहुधा गणितीय कथन में होता है। इन्हें ‘संयोजक’ कहते हैं। जब कभी हम मिश्र कथन का प्रयोग करते हैं तब यह आवश्यक हो जाता है कि हम इन शब्दों की भूमिका समझ सकें।

यहाँ हम इस पर परिचर्चा करेंगे।

14.4.1 संयोजक ‘और’ (The word 'And') 

संयोजक ‘और’ के प्रयोग द्वारा बने निम्नलिखित मिश्र कथन पर विचार करते हैंः

p: किसी बिंदु का एक स्थान होता है और उसकी स्थिति निर्धारित की जा सकती है।

इस कथन को निम्नलिखित दो घटक कथन में विघटित किया जा सकता हैः

q: किसी बिंदु का एक स्थान होता है।

r: उसकी स्थिति निर्धारित की जा सकती है।

उपरोक्त दोनों कथन सत्य हैं।

एक अन्य कथन पर विचार कीजिए।

p: संख्या 42 संख्याओं 5, 6 और 7 से भाज्य है।

इस कथन का विघटन इस प्रकार है,

q: संख्या 42 संख्या 5 से भाज्य है।

r: संख्या 42 संख्या 6 से भाज्य है।

s: संख्या 42 संख्या 7 से भाज्य है।

यहाँ हमें ज्ञात है कि प्रथम कथन असत्य है और शेष दो सत्य हैं।

अत:हमें निम्नलिखित नियम प्राप्त होता है

उदाहरण 6 निम्नलिखित मिश्र कथन के घटक कथन लिखिए और जाँचिए कि मिश्र कथन सत्य है अथवा असत्य है।

(i) एक रेखा सीधी होती है और दोनों दिशाओं में अनंत तक विस्तृत होती है।

(ii) 0 प्रत्येक धन पूर्णांक और प्रत्येक ऋण पूर्णांक से कम होता है।

(iii) प्रत्येक सजीव के दो पैर और दो आँखें होती हैं।

हल (i) घटक कथन निम्नलिखित हैं,

p: एक रेखा सीधी होती हैं।’

q: एक रेखा दोनों दिशाओं में अनंत तक विस्तृत होती है।

उपरोक्त दोनों कथन सत्य हैं और इसलिए मिश्र कथन भी सत्य है।

(ii) यहाँ घटक कथन इस प्रकार हैं,

p:  प्रत्येक धन पूर्णांक से कम होता है।

q:  प्रत्येक ऋण पूर्णांक से कम होता है।

इनमें से दूसरा कथन असत्य है। अत:मिश्र कथन भी असत्य है।

(iii) अभीष्ट घटक कथन नीचे लिखे हैं,

‘प्रत्येक सजीव के दो पैर होते हैं।’

‘प्रत्येक सजीव की दो आँखें होती हैं।’

ये दोनों ही कथन असत्य हैं। अत:मिश्र कथन भी असत्य है।

अब निम्नलिखित कथन पर विचार कीजिएः

p: एेलकोहॉल और पानी के मिश्रण को रासायनिक विधियों द्वारा अलग-अलग किया जा सकता है।’

इस कथन को शब्द "और" से प्रयुक्त मिश्र कथन नहीं माना जा सकता है। यहाँ पर शब्द "और" दो वस्तुओं, एेलकोहॉल तथा पानी का उल्लेख करता है।

इससे हम एक महत्वपूर्ण निष्कर्ष निकालते हैं जो नीचे लिखी टिप्पणी में दिया हैः

टिप्पणी यह नहीं समझना चाहिए कि शब्द ‘और’ से प्रयुक्त वाक्य सदैव एक मिश्र कथन होता है जैसा कि उपरोक्त उदाहरण में स्पष्ट किया गया है। यहाँ पर शब्द ‘और’, दो वाक्यों के संयोजन के लिए प्रयुक्त नहीं है।

14.4.2 शब्द ‘या’ से प्रयुक्त वाक्य 

(The word 'Or') नीचे लिखे कथन पर विचार कीजिए।

वे समांतर होती हैं।

हमें ज्ञात है कि यह एक सत्य कथन है। इसका क्या अर्थ है? इसका अर्थ यह है कि एक समतल पर स्थित दो रेखाएँ यदि एक दूसरे को काटती हैं, तो वे समांतर नहीं हैं। इसके विपरीत यदि एेसी दोनों रेखाएँ समांतर नहीं हैं, तो वे एक दूसरे को एक बिंदु पर काटती है’, अर्थात  यह कथन दोनों ही स्थितियों में सत्य है।

शब्द ‘या’ से प्रयुक्त कथन समझने के लिए हम पहले यह देखते हैं कि अंग्रेजी  भाषा में ‘या’ का प्रयोग दो प्रकार से किया जाता है।

पहले हम निम्नलिखित कथन पर विचार करेंगेः

‘किसी आहार गृह (रेस्ताराँ) में एक ‘थाली’ के साथ आइसक्रीम या पेप्सी भी उपलब्ध की
जाती है।’

इसका अर्थ यह हुआ कि एक व्यक्ति जो आइसक्रीम नहीं चाहता वह ‘थाली’ के साथ पेप्सी ले सकता है अन्यथा वह ‘थाली’ के साथ आइसक्रीम ले सकता है। अर्थात् यदि जो पेप्सी नहीं चाहते वे आइसक्रीम ले सकते हैं। किंतु एक व्यक्ति दोनों वस्तुएँ अर्थात् आइसक्रीम और पेप्सी नहीं ले सकता। यह ‘अपवर्जित’ ‘या’ कहलाता है। यहाँ एक अन्य कथन पर विचार कीजिए।

‘एक विद्यार्थी, जिसने जीवविज्ञान या रसायन विज्ञान विषयों का चयन किया है वह सूक्ष्म जीवविज्ञान के स्नाकोत्तर पाठ्यक्रम में प्रवेश के लिए आवेदन कर सकता है।’

यहाँ पर हम यह मानते हैं कि वे विद्यार्थी जिन्होंने जीवविज्ञान और रसायन विज्ञान दोनों ही विषयों का चयन किया है। वे सूक्ष्म जीवविज्ञान पाठ्यक्रम में प्रवेश ले सकते हैं, साथ ही साथ वे विद्यार्थी जिन्होंने इन विषयों में से केवल एक विषय का चयन किया है वे भी इस पाठ्यक्रम में प्रवेश ले सकते हैं। इस स्थिति में हम अंतर्विष्ट ‘या’ का प्रयोग कर रहे हैं।

उपरोक्त दो प्रयोगों का अंतर जान लेना महत्वपूर्ण है क्योंकि हम इसकी आवश्यकता उस समय जब हम यह जाँचेंगे कि कोई कथन सत्य है अथवा नहीं।

आइए हम एक उदाहरण पर विचार करें।

उदाहरण 7 निम्नलिखित प्रत्येक कथन में ज्ञात कीजिए क्या ‘अंतर्विष्ट’ ‘या’ अथवा ‘अपवर्जित’ ‘या’ का प्रयोग किया गया है। अपना उत्तर कारण सहित बतलाइए।

(i) किसी देश में प्रवेश करने के लिए आपको पासपोर्ट या मतदाता पहचानपत्र की आवश्यकता पड़ती है।

(ii) अवकाश या रविवार के दिन विद्यालय बंद रहता है।

(iii) दो रेखाएँ एक दूसरे को एक बिंदु पर काटती हैं या समांतर होती हैं।

(iv) तृतीय भाषा के रूप में कोई विद्यार्थी फ्रेंच (फ्रांसीसी) भाषा या संस्कृत भाषा का चयन कर सकता है।

हल (i) यहाँ पर ‘या’ अंतर्विष्ट है, क्योंकि किसी देश में प्रवेश करने के लिए एक व्यक्ति के पास पासपोर्ट और मतदाता पहचान पत्र दोनों ही हो सकते हैं।

(ii) यहाँ पर भी ‘या’ अंतर्विष्ट है, क्योंकि विद्यालय अवकाश के दिन और साथ ही साथ रविवार को बंद रहता है।

(iii) यहाँ पर ‘या’ अपवर्जित है क्योंकि कि दोनों रेखाओं के लिए यह संभव नहीं है कि वे एक दूसरे को काटें और साथ ही साथ समांतर भी हों।

(iv) यहाँ भी ‘या’ अपवर्जित है क्योंकि कोई विद्यार्थी तृतीय भाषा के रूप में फ्रेंच और संस्कृत दोनों नहीं ले सकता है।

उपरोक्त उदाहरण के सूक्ष्म निरीक्षण से निम्नलिखित नियम प्राप्त होता है।

संयोजक "या" प्रयुक्त मिश्र कथन के लिए नियम

उदाहरण के लिए नीचे लिखे कथन पर विचार कीजिए, ‘दो रेखाएँ एक दूसरे को एक बिंदु पर काटती हैं या वे समांतर हैंः

इसके घटक कथन निम्नलिखित हैंः

p : दो रेखाएँ एक दूसरे को एक बिंदु पर काटती हैं।

q : वे (दो रेखाएँ) समांतर हैं।

यहाँ यदि p सत्य हैं तो q असत्य है और यदि p असत्य है तो q सत्य है। अत:मिश्र कथन सत्य है।

एक अन्य कथन पर विचार कीजिए।

‘संख्या 125, संख्या 7 या संख्या 8 का गुणज है।’

इसके घटक कथन इस प्रकार हैं,

p : संख्या 125, संख्या 7 का गुणज है।

q : संख्या 125, संख्या 8 का गुणज है।

यहाँ p और q दोनों ही असत्य हैं। अत:मिश्र कथन भी असत्य है।

एक और कथन पर विचार कीजिए जो नीचे दिया है,

‘विद्यालय बंद है, यदि आज अवकाश का दिन है या रविवार है।’

इसके घटक कथन नीचे दिए हैं,

p : विद्यालय बंद है, यदि आज अवकाश का दिन है।

q : विद्यालय बंद है, यदि आज रविवार है।

p और q दोनों ही सत्य हैं। अत:मिश्र कथन सत्य है।

एक और कथन पर विचार कीजिए,

‘मुंबई कोलकाता या कर्नाटक की राजधानी है।’

इसके घटक नीचे लिखे हैं,

p : मुंबई, कोलकाता की राजधानी है।

q : मुंबई, कर्नाटक की राजधानी है।

उपरोक्त दोनों ही कथन असत्य हैं। अत:मिश्र कथन भी असत्य है।

आइए अब हम कुछ उदाहरणों पर विचार करेंः

उदाहरण 8 निम्नलिखित कथनों में पहचानिए कि किस प्रकार के ‘या’ का प्रयोग किया गया है और जाँचिए कि कथन सत्यै अथवा असत्य है।

(i) एक परिमेय संख्या है या अपरिमेय संख्या है।

(ii) किसी सार्वजनिक पुस्तकालय में प्रवेश हेतु बच्चों को विद्यालय द्वारा प्रदत्त पहचान पत्र या विद्यालय अधिकारियों द्वारा लिखित पत्र की आवश्यकता पड़ती है।

(iii) आयत एक चतुर्भुज या एक पाँच भुजीय बहुभुज होता है।

हल (i) घटक कथन नीचे दिए हैं।

p : एक परिमेय संख्या है।

q : एक अपरिमेय संख्या है।

यहाँ हमें ज्ञात है कि प्रथम कथन असत्य है और द्वितीय कथन सत्य है और इस प्रकार ‘या’ अपवर्जित है।

(ii) घटक कथन निम्नलिखित हैं

p : किसी सार्वजनिक पुस्तकालय में प्रवेश हेतु बच्चों को विद्यालय द्वारा प्रदत्त पहचान पत्र की आवश्यकता पड़ती है।

q : किसी सार्वजनिक पुस्तकालय में प्रवेश हेतु बच्चों को विद्यालय अधिकारियों द्वारा लिखित पत्र की आवश्यकता पड़ती है।

यहाँ पुस्तकालय में प्रवेश के लिए बच्चों के पास या तो पहचान पत्र होना चाहिए अथवा विद्यालय के अधिकारियों द्वारा लिखित पत्र होना चाहिए अथवा दोनों की प्रलेख (कागज़ात) हो सकते हैं। अत:यहाँ पर ‘या’ अंतर्विष्ट है।

(iii) यहाँ ‘या’ अपवर्जित है। घटक कथनों के आधार पर यह कथन सत्य है।

14.4.3 परिमाणवाचक वाक्यांश (सूक्ति)

(Quantifiers Phrases) "एक एेसे का अस्तित्व है" और "सभी के लिए/प्रत्येक के लिए" इन दोनों विशेष वाक्यांशों को ‘परिमाणवाचक वाक्यांश कहते है।

गणितीय कथन में बहुधा आने वाले वाक्यांशाें में एक वाक्यांश ‘एक एेसे का अस्तित्व है’ है। उदाहरण के लिए कथन ‘एक एेसे आयत का अस्तित्व है जिसकी भुजाएँ समान लंबाई की हैं।’ पर विचार कीजिए। इस कथन का तात्पर्य है कि कम से कम एक एेसा आयत है जिसकी सभी भुजाओं की लंबाई समान है।

वाक्यांश ‘एक एेसे का अस्तित्व’ से निकटस्थ वाक्यांश ‘प्रत्येक के लिए (या सभी कि लिए)’ है।

आइए इस प्रकार के एक कथन पर विचार करें,

‘प्रत्येक अभाज्य संख्या p के लिए, एक अपरिमेय संख्या है।’

इसका अर्थ हुआ कि यदि S अभाज्य संख्याओं का समुच्चय है, तो समुच्चS के सभी अवयव p के लिए, एक अपरिमेय संख्या है।

व्यापक रूप से किसी गणतीय कथन में ‘प्रत्येक के लिए’ वाक्यांश के प्रयोग से यह अर्थ होता है कि यदि किसी समुच्चय में कोई विशेषता है तो उस समुच्चय के सभी अवयवों में वह विशेषता होनी चाहिए।

हमें यह भी ध्यान देना चाहिए कि इस बात का जानना भी महत्वपूर्ण है कि किसी वाक्य में संयोजक को ठीक-ठीक किस स्थान पर लिखना चाहिए। उदाहरण के लिए निम्नलिखित दो वाक्यों की तुलना कीजिएः

1. प्रत्येक धन पूर्णांक x के लिए एक एेसे धन पूर्णांक y का अस्तित्व है कि y < x

2. एक धन पूर्णांक y का एेसा अस्तित्व है कि प्रत्येक धन पूर्णांक x के लिए y < x.

यद्यपि एेसा प्रतीत होता है कि दोनों वाक्यों का एक ही अर्थ है किंतु एेसा नहीं है। वास्तविकता तो यह है। कि कथन (1) सत्य है जबकि (2) असत्य है। किसी गणितीय वाक्य (कथन) के अर्थपूर्ण होने के लिए प्रतीकों (वाक्याशों, संयोजकों) का सही स्थान पर ठीक-ठीक प्रयोग किया जाना आवश्यक है।

शब्द "और" तथा ‘या’ संयोजक कहलाते है तथा "एक एेसा का अस्तित्व है" और "प्रत्येक के लिए" को परिमाणवाचक वाक्यांश कहते हैं।

इस प्रकार हमने देखा कि अनेकों गणितीय कथनों में कुछ विशिष्ट शब्दों/वाक्यांशों का प्रयोग होता है जिनके अर्थ को समझना महत्वपूर्ण है, विशेष रूप से जब हमें विभिन्न कथनों की वैधता की जाँच करनी है।

14.5 अंतर्भाव/सप्रतिबंध कथन (Implications/Conditional Statements)

इस अनुच्छेद हम अंतर्भाव "यदि-तो", "केवल यदि" और "यदि और केवल यदि" पर विचार-विमर्श करेंगे।

"यदि-तो" से युक्त कथनों का प्रयोग बहुत सामान्य है। उदाहरण के लिए नीचे लिखे कथन पर विचार कीजिए

r: यदि आपका जन्म किसी देश में हुआ है, तो आप उस देश के नागरिक हैं। हम देखते हैं कि यह निम्नलिखित दो कथनों p और q के सदृश है,

p :आपका जन्म किसी देश में हुआ है।

q :आप उस देश के नागरिक हैं।

तब कथन "यदि p तो q" यह बतलाता है कि उस दशा में जब p सत्य हो, तो q अनिवार्य रूप से सत्य होगा।

कथन ‘यदि p तो q’ से संबंधित एक सबसे महत्वपूर्ण तथ्य यह है कि यदि p असत्य है तो यह q के बारे में कुछ नहीं कहता। उदाहरणार्थ उपरोक्त कथन में यदि आपका जन्म किसी देश में नहीं हुआ है तो आप q के संबंध में कुछ नहीं कह सकते हैं। दूसरे शब्दों में p के घटित नहीं होने का q के घटित होने पर कोई प्रभाव नहीं पड़ता है।

कथन "यदि p, तो q’’ के बारे में एक अन्य तथ्य भी नोट कीजिए कि इस कथन में यह अंतर्निहित नहीं है कि p घटित होता है।

कथन "यदि p, तो q" को समझने के अनेक तरीके हैं। हम इन तरीकों को निम्नलिखित कथन के माध्यम से स्पष्ट करेंगे।

यदि कोई संख्या 9 की गुणज है, तो वह 3 की भी गुणज है।

मान लीजिए कि p और q निम्नलिखित कथनों को प्रगट करते हैं,

p : कोई संख्या 9 की गुणज है।

q : वह संख्या 3 की भी गुणज है।

इस प्रकार कथन ‘यदि p, तो q’ निम्नलिखित कथनों के सान हैः

1. ‘p अंतर्भाव q’ को p q से प्रकट किया जाता है। प्रतीक ‘’ अंतर्भाव (सप्रतिबंध कथन) के लिए प्रयोग किया जाता है। इसका अर्थ यह कि कथन ‘कोई संख्या 9 की गुणज है’ में यह कथन अंतर्निहित है कि ‘वह संख्या 3 की भी गुणज है’।

2. ‘p पर्याप्त प्रतिबंध है q के लिए’। इसका अर्थ हुआ कि यह ज्ञात होना कि संख्या 9 की गुणज है, पर्याप्त है यह निष्कर्ष निकालने के लिए कि वह संख्या 3 की भी गुणज है।

3. ‘p केवल यदि q’

इसका अर्थ हुआ कि कोई संख्या 9 की गुणज है, केवल यदि वह संख्या 3 की भी गुणज है।

4. ‘q अनिवार्य प्रतिबंध है p के लिए।’

इसका अर्थ हुआ कि जब कोई संख्या 9 की गुणज है, तो वह संख्या अनिवार्य रूप से 3 की भी गुणज है।

5. ‘~ q अंतर्भाव ~ p’

इसका अर्थ हुआ कि यदि कोई संख्या 3 की गुणज नहीं है, तो वह संख्या 9 की भी गुणज नहीं है।

14.5.1 प्रतिधनात्मक और विलोम (Contrapositive and Converse) 

प्रतिधनात्मक और विलोम निश्चित रूप से कुछ अन्य कथन हैं, जिन्हें वाक्यांश ‘यदि-तो’ से प्रयुक्त कथन से (द्वारा) रचित किया जा सकता है।

उदाहरणार्थ नीचे दिए वाक्यांश ‘यदि-तो’ वाले कथन पर विचार कीजिए,

यदि भौतिक वातावरण में परिवर्तन होता है तब जैविक वातावरण परिवर्तित हो जाता है।

इस कथन का प्रतिधनात्मक कथन

‘‘यदि जैविक वातावरण में परिवर्तन नहीं होता है तब भौतिक वातावरण परिवर्तित नहीं होता है।’’

नोट कीजिए कि ये दोनों कथन एक ही (समान) अर्थ व्यक्त करते हैं।

इस बात को समझने के लिए आइए कुछ और उदाहरणों पर विचार करें।

उदाहरण 9 निम्नलिखित कथनों के प्रतिधनात्मक कथन लिखिएः

(i) यदि एक संख्या 9 से भाज्य है, तो वह 3 से भी भाज्य है।

(ii) यदि आप भारत में जन्मे हैं, तो आप भारत के एक नागरिक हैं।

(iii) यदि एक त्रिभुज समबाहु है, तो समद्विबाहु भी है।

हल उपरोक्त तीन कथनों के प्रतिधनात्मक कथन इस प्रकार है,

(i) यदि एक संख्या 3 से भाज्य नहीं है, तो वह 9 से भी भाज्य नहीं है।

(ii) यदि आप भारत के नागरिक नहीं हैं, तो आप भारत में नहीं जन्मे हैं।

(iii) यदि एक त्रिभुज समद्विबाहु नहीं है, तो वह समबाहु भी नहीं है।

उपरोक्त उदाहरण दर्शाते हैं कि कथन ‘यदि p, तो q’ का प्रतिधनात्मक कथन ‘यदि q-नहीं, तो
p-नहीं’ अर्थात् ‘यदि ~ q, तो ~ p’ है। इसके बाद हम ‘विलोम’ कहलाने वाले एक और पद पर विचार करेंगे।

दिए हुए कथन ‘यदि p, तो q’ का विलोम कथन, यदि q तब p है।

उदाहरण के लिए कथन p‘यदि एक संख्या 10 से भाज्य है तो वह (संख्या) 5 से भी भाज्य है।’ का विलोम कथन q’ यदि एक संख्या 5 से भाज्य है, तो वह (संख्या) 10 से भी भाज्य है।’

उदाहरण 10 निम्नलिखित कथनों के विलोम लिखिएः

(i) यदि एक संख्या n सम है, तो n2 भी सम है।

(ii) यदि आप सभी प्रश्नों को पुस्तिका में हल करें, तो आपको कक्षा में A-ग्रेड मिलेगा।

(iii) यदि दो पूर्णांक a और b इस प्रकार हैं कि a > b, तो (a – b) सदैव एक धन पूर्णांक है।

हल इन कथनों के विलोम नीचे लिखे हैं,

(i) यदि संख्या n2 सम है, तो n भी सम है।

(ii) यदि आपको कक्षा में A-ग्रेड मिला है, तो आपने सभी प्रश्नों को पुस्तिका में हल किया है।

(iii) यदि दो पूर्णांक a और b इस प्रकार हैं कि (a – b) सदैव एक धन पूर्णांक है, तो a > b. आइए कुछ और उदाहरणों पर विचार करें।

उदाहरण 11 निम्नलिखित मिश्र कथनों में से प्रत्येक के लिए पहले संगत घटक कथनों को पहचानिए और फिर जाँचिए कि क्या कथन सत्य है अथवा नहीं।

(i) यदि त्रिभुज ABC समबाहु है, तो वह (त्रिभुज) समद्विबाहु है।

(ii) यदि a और b पूर्णांक हैं, तो ab एक परिमेय संख्या है।

हल (i) घटक कथन नीचे लिखें हैं,

p : त्रिभुज ABC समबाहु है।

q : त्रिभुज समद्विबाहु है।

क्योंकि एक समबाहु त्रिभुज समद्विबाहु भी होता है, अत:दिया हुआ कथन सत्य है।

(ii) यहाँ घटक कथन इस प्रकार है,

p : a और b पूर्णांक हैं।

q : ab एक परिमेय संख्या है।

क्योंकि दो पूर्णांकों का गुणनफल एक पूर्णांक होता है और इसलिए एक परिमेय संख्या भी होता है, अत:मिश्र कथन सत्य है।

वाक्य।ंश ‘यदि और केवल यदि’, प्रतीक द्वारा प्रकट किया जाता है और दिए हुए कथन p और q के लिए इसके निम्नलिखित समतुल्य रूप हैं।

(i) ‘p यदि और केवल यदि q’

(ii) ‘q यदि और केवल यदि p’

(iii) ‘p अनिवार्य और पर्याप्त प्रतिबंध है q के लिए’और इसका विलोम (उलटा)

(iv) p q

यहाँ निम्नलिखित उदाहरण पर विचार करते हैं।

उदाहरण 12 नीचे दो कथन युग्म दिए हैं। प्रत्येक कथन युग्म वाक्यांश ‘यदि और केवल यदि’ के प्रयोग द्वारा सम्मिलित कीजिए।

(i) p: यदि कोई आयत एक वर्ग है, तो उसकी चारों भुजाएँ बराबर लंबाई की हैं।

यदि किसी आयत की चारों भुजाएँ बराबर लंबाई की है, तो आयत एक वर्ग है।

(ii) q: यदि किसी संख्या के अंकों का योगफल 3 से भाज्य है, तो वह संख्या भी 3 से भाज्य है।

q: यदि एक संख्या 3 से भाज्य है, तो उस संख्या के अंकों का योगफल भी 3 से भाज्य है।

हल (i) कोई आयत एक वर्ग है यदि और केवल यदि उसकी चारों भुजाओं की लंबाई बराबर है।

(ii) एक संख्या 3 से भाज्य है यदि और केवल यदि उस संख्या के अंकों का योगफल 3 से भाज्य है।

14.6 कथनों की वैधता को प्रमाणित (सत्यापित) करना (Validating Statements)

इस अनुच्छेद में हम इस बात पर विचार करेंगे कि एक कथन किन स्थितियों में सत्य होता है। उपरोक्त प्रश्न का उत्तर जानने के लिए हमें निम्नलिखित प्रश्नों का उत्तर जानना आवश्यक है।

प्रदत्त कथन का अर्थ क्या हैं? यह कहने का क्या अर्थ है कि कब कथन सत्य है और कब असत्य है?

ऊपर लिखे प्रश्नों के उत्तर इस बात पर निर्भर करते हैं कि प्रदत्त कथन में "और" तथा ‘या’ में से संयोजक शब्द का अथवा "यदि और केवल यदि" तथा "यदि-तो" में से किस प्रतिबंध का अथवा "प्रत्येक के लिए" तथा "एक एेसा का अस्तित्व है" में से किस परिमाणवाचक वाक्यांश का प्रयोग किया गया है।

यहाँ पर इन किसी कथन की वैधता ज्ञात करने के लिए कुछ प्रक्रियाओं पर विचार करेंगे।

अब हम यह जाँचने के लिए कि कोई कथन सत्य है या नहीं, कुछ सामान्य नियमों की सूची बनाते हैं।

नियम 1 यदि p तथा q गणितीय कथन हैं, तो यह सिद्ध करने के लिए कि कथन "p और q" सत्य है, हम निम्नलिखित चरणों का अनुसरण करते हैं।

चरण 1 दर्शाइए कि कथन p सत्य है

चरण 2 दर्शाइए कि कथन q सत्य है

नियम 2 ‘संयोजक ‘या’ से प्रयुक्त कथन’

यदि p तथा q गणितीय कथन हैं, तो कथन "p या q" को सत्य सिद्ध करने के लिए हम निम्नलिखित स्थितियों में से किसी एक को सत्य प्रमाणित करते हैं।

स्थिति 1 यह मानते हुए कि p असत्य है, q को अनिवार्यत:सत्य प्रमाणित कीजिए।

स्थिति 2 यह मानते हुए कि q असत्य है, p को अनिवार्यत:सत्य प्रमाणित कीजिए।

नियम 3 वाक्यांश ‘‘यदि-तो’’ से प्रयुक्त कथन

कथन ‘यदि p, तो q’ को सत्य सिद्ध करने के लिए हम निम्नलिखित स्थितियों में से किसी एक को सत्य प्रमाणित करते हैं।

स्थिति 1 यह मानते हुए कि p सत्य है, q को अनिवार्यत:सत्य प्रमाणित कीजिए
(प्रत्यक्ष विधि)।

स्थिति 2 यह मानते हुए कि q असत्य है, p को भी अनिवार्यत:असत्य प्रमाणित कीजिए (प्रतिधनात्मक विधि)।

नियम 4 वाक्यांश (प्रतिबंध) "यदि और केवल यदि" से प्रयुक्त कथन

कथन "p, यदि और केवल यदि q" को सत्य सिद्ध करने के लिए हमें यह प्रमाणित करने की आवश्यकता है कि,

(i) यदि p सत्य है तो q सत्य है और (ii) यदि q सत्य है, तो p सत्य है।

आइए हम कुछ उदाहरणों पर विचार करेंः

उदाहरण 13 जाँचिए कि नीचे दिया गया कथन सत्य हैं अथवा नहीं।

यदि x, y ∈ Zρ इस प्रकार हैं कि x तथा y विषम हैं, तो xy भी विषम है।

हल यहाँ p : x, y ∈ Z, इस प्रकार हैं कि x तथा y विषम हैं।

q : xy विषम हैं।

प्रदत्त कथन की वैधता को जाँचने के लिए हम नियम 3 की स्थिति 1 का प्रयोग करते हैं अर्थात्् यह मानते हुए कि p सत्य है हम q को अनिवार्यत:सत्य प्रमाणित करते हैं।

p सत्य है अर्थात् x तथा y विषम पूर्णांक हैं। अतः

x = 2m + 1 किसी पूर्णांक m के लिए।

y = 2m + 1 किसी पूर्णांक n के लिए।

अतः

xy = (2m + 1) (2n + 1)

= 2(2mn + m + n) + 1

इससे स्पष्ट है कि xy भी विषम है। इसलिए प्रदत्त कथन सत्य है।

मान लीजिए कि हम नियम 3 की स्थिति 2 के प्रयोग द्वारा जाँच करना चाहते हैं, तो हमें, निम्नलिखित विधि का प्रयोग करना चाहिए।

हम मानते हैं कि q सत्य नहीं है। इसका तात्पर्य है कि हमें कथन q के निषेधन पर विचार करना चाहिए।

इस प्रकार निम्नलिखित कथन प्राप्त होता है,

~ q : गुणनफल x y सम है।

यह केवल तभी संभव है जब x अथवा y सम हों जिससे यह प्रमाणित होता है कि p सत्य नहीं है। अत:हमने यह दर्शा दिया कि

~ q ⇒ ~ p

टिप्पणी उपरोक्त उदाहरण यह स्पष्ट करता है कि कथन p ⇒ q को सिद्ध करने के लिए कथन ~ q ⇒ ~ p सिद्ध कर देना पर्याप्त है, जो कि प्रदत्त कथन का प्रतिधनात्मक कथन है।

उदाहरण 14 निम्नलिखित कथन के प्रतिधनात्मक कथन का जाँच कर यह ज्ञात कीजिए कि प्रदत्त कथन सत्य है अथवा असत्य है;

‘यदि x, y ∈ Z इस प्रकार कि xy विषम हैं, तो x तथा y भी विषम है।’

हल आइए हम कथनों को नीचे दिए नाम से संबोधित करें,

p : x y विषम हैं।

q : x तथा y दोनों ही विषम हैं।

हमें प्रतिधनात्मक कथन ~ q ⇒ ~ p को जाँच कर ज्ञात करना है कि कथन p ⇒ q सत्य है अथवा नहीं।

अब, ~ q = यह असत्य है कि x तथा y दोनों विषम है।

इसका अर्थ यही हुआ कि x (अथवा y) सम है।

तो, x = 2n जहाँ n एक पूर्णांक है।

अत: xy = 2ny, यह दर्शाता है कि xy सम है। अर्थात्् ~ p सत्य है।

इस प्रकार हमने ~ q ⇒ ~ p को सिद्ध कर दिया है, अत:प्रदत्त कथन सत्य है।

अब हम विचार करते हैं कि जब एक सप्रतिबंध कथन और उसके विलोम कथन को मिलाते हैं तो क्या होता है।

निम्नलिखित कथनों पर विचार कीजिए

p : एक गिलास आधा खाली है।

q : एक गिलास आधा भरा है।

हमें ज्ञात है कि यदि पहला कथन घटित होगा तो दूसरा भी घटित होगा। इस तथ्य को निम्नलिखित प्रकार से व्यक्त कर सकते हैं।

यदि एक गिलास आधा खाली है, तो वह आधा भरा है, यदि एक गिलास आधा भरा है, तो वह आधा खाली है। हम इन दोनों कथनों को मिलाते हैं और निम्नलिखित कथन प्राप्त करते हैं।

एक गिलास आधा खाली है यदि और केवल यदि यह आधा भरा है।

इसके बाद हम एक अन्य विधि पर विचार करेंगे।

14.6.1 विरोधोक्ति द्वारा (By Contradiction)

इस विधि में यह सिद्ध करने के लिए कि कोई (प्रदत्त) कथन p सत्य है हम यह मान लेते हैं कि p सत्य नहीं है। अर्थात ~ p सत्य है। इस प्रकार हम एक एेसे निष्कर्ष पर पहुँचते हैं जो हमारी मान्यता (पूर्वधारणा) का खंडन करता है। परिणामत:p को सत्य होना चाहिए।

नीचे सरल किए उदाहरण को देखिए :

उदाहरण 15 विरोधोक्ति द्वारानिम्नलिखित कथन को सत्यापित कीजिए,

‘एक अपरिमेय संख्या है।’

हल इस विधि में हम यह मान लेतेैं कि प्रदत्त कथन असत्य है। अर्थात एक अपरिमेसंख्या नहीं है।’ तात्पर्य यह हुआ कि ‘परिमेय है।’

अत:दो एसे पूर्णांक a तथा b का अस्तित्व है कि, जहाँ a तथा b में कोई समापवर्तक (उभयनिष्ठ गुणनखंड) नहीहै।

उपरोक्समीकरण का वर्ग करने पर

a2 = 7b2 संख्या 7, संख्या a को विभाजित करती है। इसलिए एक एेसे पूर्णांक c का अस्तित्व है कि a = 7c

इस प्रकार a2 = 49c2 औ a2 = 7b2

अत:7b2 = 49c2 b2 = 7c2 संख्या 7, संख्या b को विभाजित करती है। किंतु हमें ज्ञात है कि संख्या 7, संख्या a को भी विभाजित करती है। इसका तात्पर्य हुआ कि संख्या 7, संख्याओं a तथा b का समापवर्तक है, जो हमारी मान्यता कि ‘a तथा b में कोई समापर्वतक नहीं है’ का खंडन है।इससे स्पष्ट होता है कि यह मान्यता कि ‘पमिेय है’ असत्य है। अत:प्रदत्त कथन कि ‘एक अपरिमेय संख्या है’ सत्य है।

इसके उपरांत हम एक और विधि पर विचार करेंगे, जिसके द्वारा हम सिद्ध कर सकते हैं कि एक प्रदत्त कथन असत्य है। इस विधि में हम एक एेसी दशा (स्थिति) का उदाहरण प्रस्तुत करते हैं, जिसमें प्रदत्त कथन वैध नहीं होता है। इस प्रकार के उदाहरण को ‘‘प्रत्युदाहर.ा’’ कहते है। यह नाम स्वयं ही संकेत करता है कि यह उदाहरण प्रदत्त कथन का खंडन करता है।

उदाहरण 16 एक प्रत्युदाहरण द्वारा सिद्ध कीजिए कि निम्नलिखित कथन असत्य है,

‘यदि n एक विषम पूर्णांक है, तो n एक अभाज्य संख्या है।’

हल प्रदत्त कथन ‘यदि p, तो q’ के रूप का है। हमें इसे असत्य सिद्ध करना है जिसके लिए हमें यह दर्शाना है कि ‘यदि p, तो ~ q’ है। इसके लिए हमें किसी एक एेसे विषम पूर्णांक को खोजना है, जो अभाज्य नहीं हो। संख्या 9 इस प्रकार का एक विषम पूर्णांक है। अत:संख्या 9 एक प्रत्युदाहरण है और हम निष्कर्ष निकालते हैं कि प्रदत्त कथन असत्य है।

इस प्रकार हमनें कुछ विधियों पर विचार किया जिनके प्रयोग द्वारा हम यह ज्ञात करते हैं कि एक प्रदत्त कथन सत्य है अथवा नहीं।

टिप्पणी गणित में प्रत्युदाहरणों का प्रयोग किसी कथन को अस्वीकार करने के लिए किया जाता है। तथापि किसी कथन के अनुमोदन में उदाहरणों को प्रस्तुत करने से कथन की वैधता प्रमाणित नहीं होती है।

प्रश्नावली 14.5

1. सिद्ध कीजिए कि कथन यदि x एक एेसी वास्तविक संख्या है कि x3 + 4x = 0, तो x = 0

(i) प्रत्यक्ष विधि द्वारा (ii) विरोधोक्ति द्वारा (iii) प्रतिधनात्मक कथन द्वारा।

2. प्रत्युदाहरण द्वारा सिद्ध कीजिए कि कथन "किसी भी एेसी वास्तविक संख्याओं ंऔर b के लिए, जहाँ a2 = b2, का तात्पर्य है कि a = b" सत्य नहीं है।

3. प्रतिधनात्मक विधि द्वारा सिद्ध कीजिए कि निम्नलिखित कथन सत्य है,

p: यदि x एक पूर्णांक है और x2 सम है, तो x भी सम है।’

4. प्रत्युदाहरण द्वारा सिद्ध कीजिए कि निम्नलिखित कथन सत्य नहीं है,

(i) p: यदि किसी त्रिभुज के कोण समान हैं, तो त्रिभुज एक अधिक कोण त्रिभुज है।

(ii) q: समीकरण x2 – 1 = 0 वेη मूल 0 और 2 के बीच स्थित नहीं है।

5. निम्नलिखित कथनों में से कौन से सत्य हैं और कौन से असत्य हैं? प्रत्येक दशा में अपने उत्तर के लिए वैध कारण बतलाइएः

(i) p: किसी वृत्त की प्रत्येक त्रिज्या वृत्त की जीवा होती है।

(ii) q: किसी वृत्त का केंद्र वृत्त की प्रत्येक जीवा को समद्विभाजित करता है।

(iii) r: एक वृत्त, किसी दीर्घवृत्त की एक विशेष स्थिति है।

(iv) s: यदि x और y एेसे पूर्णांकहै कि x > y, तो –x < –y है।

(v) t: 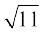एक परिमेय संख्या है।

विविध उदाहरण

उदाहरण 17 जाँचिए कि निम्नलिखित मिश्र कथन में प्रयुक्त ‘या’ अपवर्जित है अथवा अंतर्विष्ट है। अपने उत्तर को तर्क संगत (उचित) सिद्ध कीजिएः

t: जब वर्षा होती है, आप भीग जाते हैं, या जब आप नदी में होते हैं, आप भीग जाते हैं।’

तदोपरांत मिश्र कथन के घटक कथन लिखिए और उनका प्रयोग यह जाँचने के लिए कीजिए कि मिश्र कथन सत्य है अथवा नहीं।

हल प्रदत्त कथन में प्रयुक्त ‘या’ अंतर्विष्ट है, क्योंकि यह संभव है कि वर्षा हो रही है और आप नदी में हों।

प्रदत्त कथन के घटक कथन नीचे दिए हैं,

p : जब वर्षा होती है आप भीग जाते हैं।

q : जब आप नदी में होते हैं आप भीग जाते हैं।

यहाँ दोनों घटक कथन सत्य हैं और इसलिए मिश्र कथन भी सत्य है।

उदाहरण 18 निम्नलिखित कथनों के निषेधन लिखिएः

(i) p: प्रत्येक वास्तविक संख्या x के लिए, x2 > x

(ii) q: एक एेसी परिमेय संख्या x का अस्तित्व है ताकि x2 = 2

(iii) r: प्रत्येक पक्षी के पंख होते हैं।

(iv) s: प्रारंभिक स्तर पर प्रत्येक विद्यार्थी गणित का अध्ययन करता है।

हल मान लीजिए कि दिए गए कथन को p निरूपित किया जाता है। तब p का निषेधन ‘‘यह असत्य है कि p सत्य है’’ होगा, अर्थात्् प्रतिबंध x2 > x प्रत्येक वास्तविक संख्या के लिए लागू नहीं होता है। इस बात को इस प्रकार व्यक्त कर सकते हैं,

~p: एक एेसी वास्तविक संख्या x का अस्तित्व है ताकि x2 < x है।

(ii) मान लीजिए कि

q = एक एेसी परिमेय संख्या x का अस्तित्व है कि x2 = 2

अत:∼q = एेसी (किसी) परिमेय संख्या x का अस्तित्व नहीं है कि x2 = 2

जिसे इस प्रकार भी लिखा जा सकता है,

~p प्रत्येक (सभी) परिमेय संख्या x के लिए x2 2

(iii) प्रदत्त कथन का निषेधन नीचे लिखा है,

~r: एक एेसे पक्षी का अस्तित्व है, जिसके पंख नहीं होते हैं।’

(iv) प्रदत्त कथन का निषेधन इस प्रकार है,

~s: एक एेसे विद्यार्थी का अस्तित्व है जो प्रारंभिक स्तर पर गणित का अध्ययन नहीं
करता है।’

उदाहरण 19 वाक्यांश ‘‘अनिवार्य और पर्याप्त’’ का प्रयोग करके निम्नलिखित कथन को पुन:लिखिए। तथा इसकी वैधता की जाँच भी कीजिए।

‘‘पूर्णांक n विषम है यदि और केवल यदि n2 विषम है।’’

हल पूर्णांक n के विषम होने के लिए अनिवार्य और पर्याप्त प्रतिबंध है कि n2 अनिवार्यत:विषम हो।

मान लीजिए कि p तथा q निम्नलिखित कथनों को निरूपित करते हैं,

p : पूर्णांक n विषम है।

q : n2 विषम है।

तो ‘p यदि और केवल यदि q’ प्रदत्त कथन को निरूपित करता है और जिसकी वैधता जाँचने के लिए हमें यह जाँचना पड़ेगा कि क्या कथन ‘‘यदि p, तो q’’ तथा ‘‘यदि q, तो p’’ सत्य है।

स्थिति 1 ‘यदि p, तो q’

यदि p, तो q कथन ‘यदि पूर्णांक n विषम है, तो n2 विषम है।’ को निरूपित करता है। हमें ज्ञात करना है कि क्या यह कथन सत्य है।

मान लीजिए कि n विषम है। तब n = 2k + 1 जहाँ k एक पूर्णांक है।

इस प्रकार n2 = (2k + 1)2

= 4k2 + 4k + 1 = 2(2k2 + 2k) + 1

अत: n2 विषम है।

स्थिति 2 यदि q, तो p

कथन ‘यदि n एक पूर्णांक है और n2 विषम है, तो n विषम है।’ यदि q, तो p द्वारा निरूपित होता है। हमें ज्ञात करना है कि क्या यह कथन सत्य है। इसे ज्ञात करने के लिए हम प्रतिधनामक विधि का प्रयोग करेंगे। (अर्थात् ~ p ~ q)

उपरोक्त कथन का प्रतिधनात्मक कथन नीचे लिखा है,

‘यदि n एक सम पूर्णांक है, तो n2 भी एक सम पूर्णांक है।’

n एक सम पूर्णांक है इसलिए n = 2k, जहाँ k एक पूर्णांक है। अत:n2 = 4k2 = 2(2k2) निष्कर्षत:n2 सम है।

उदाहरण 20 निम्नलिखित कथन के लिए अनिवार्य तथा पर्याप्त प्रतिबंधों को ज्ञात कीजिए।

t: यदि आप 80 km प्रति घंटा की अधिक गति से गाड़ी चलाते हैं तो आपको जुर्माना लगेगा।

हल मान लीजिए कि p और q निम्नलिखित कथनों को प्रकट करते हैं।

p: यदि आप 80 km प्रति घंटा की अधिक गति से गाड़ी चलाते हैं।

q: आपको जुर्माना होगा।

प्रतिबंध यदि p तो q दर्शाता है कि p, q के लिए पर्याप्त प्रतिबंध है। अर्थात्् जुर्माना होने के लिए, 80 कि.मी. प्रति घंटा की अधिक गति से गाड़ी चलाना पर्याप्त कथन है।

यहाँ “80 km प्रतिघंटा की अधिक गति से गाड़ी चलाना” पर्याप्त प्रतिबंध है।

इसी प्रकार, यदि p तब q दर्शाता है कि q, p के लिए अनिवार्य प्रतिबंध है। अर्थात्् “जब आप 80 km प्रतिघंटा की अधिक गति से गाड़ी चलाते हैं तो अनिवार्य रूप से आपको जुर्माना होगा।” यहाँ “जुर्माना होना” अनिवार्य प्रतिबंध है।