Table of Contents
"Where a mathematical reasoning can be had, it is as great a folly to make use of any other, as to grope for a thing in the dark, when you have a candle in your hand.– John Arbuthnot "
16.1 भूमिका (Introduction)
पहले की कक्षाओं में हमने प्रायिकता की संकल्पना को विभिन्न परिस्थितियों की अनिश्चितता की माप के रूप में पढ़ा है। हमने किसी पासे केे फेंकने पर एक सम संख्या प्राप्त होने की प्रायिकता  अर्थात्
अर्थात्  ज्ञात की थी। यहाँ कुल संभावित परिणाम (outcomes)1, 2, 3, 4, 5 और 6 हैं (जिनकी संख्या छ: है)। घटना ‘एक सम संख्या प्राप्त होना’ के अनुकूल परिणाम 2, 4, 6 (अर्थात् तीन संख्याएँ) हैं। व्यापक रूप से किसी घटना की प्रायिकता ज्ञात करने के लिए हम घटना के अनुकूल परिणामों की संख्या का कुल परिणामों की संख्या के साथ अनुपात ज्ञात करते हैं। प्रायिकता के इस सिद्धांत को प्रायिकता का पुरातन सिद्धांत (Classical theory of probability) कहा जाता है।
ज्ञात की थी। यहाँ कुल संभावित परिणाम (outcomes)1, 2, 3, 4, 5 और 6 हैं (जिनकी संख्या छ: है)। घटना ‘एक सम संख्या प्राप्त होना’ के अनुकूल परिणाम 2, 4, 6 (अर्थात् तीन संख्याएँ) हैं। व्यापक रूप से किसी घटना की प्रायिकता ज्ञात करने के लिए हम घटना के अनुकूल परिणामों की संख्या का कुल परिणामों की संख्या के साथ अनुपात ज्ञात करते हैं। प्रायिकता के इस सिद्धांत को प्रायिकता का पुरातन सिद्धांत (Classical theory of probability) कहा जाता है।

Kolmogorove
(1903-1987 A.D.)
कक्षा नवीं में हमने प्रायिकता को प्रेक्षण और संकलित आँकड़ों के आधार पर ज्ञात करना सीखा है। इसे प्रायिकता का सांख्यिकीय दृष्टिकोण (Statistical approach) कहते हैं।
इन दोनों सिद्धांतों में कुछ गंभीर समस्याएँ हैं। उदाहरणत: इन सिद्धांतों को उन क्रियाकलापों/ प्रयोगों पर नहीं लगाया जा सकता है जिनमें संभावित परिणामों की संख्या अपरिमित होती है। पुरातन सिद्धांत में हम सभी संभावित परिणामों को सम संभाव्य मानते हैं। स्मरण कीजिए कि परिणामों को सम संभाव्य कहा जाता है जब हमें यह विश्वास करने का कोई कारण न हो कि एक परिणाम के घटित होने की संभावना दूसरे से अधिक है। दूसरे शब्दों में, हम यह मानते हैं कि सभी परिणामों के घटित होने की संभावना (प्रायिकता) समान है। अत: हमने प्रायिकता को परिभाषित करने के लिए सम प्रायिकता या सम संभाव्य परिणामों का उपयोग किया है। यह तार्किक दृष्टि से ठीक परिभाषा नहीं है। इसलिए रूस के गणितज्ञ A.N.Kolomogrove ने एक अन्य प्रायिकता सिद्धांत का विकास किया। उन्हाेंने 1933 में प्रकाशित अपनी पुस्तक ‘प्रायिकता का आधार’ (Foundation of Probability) में प्रायिकता की व्याख्या के लिए कुछ स्वत: प्रमाणित तथ्य (अभिगृहीत) निर्धारित किए। इस अध्याय में हम प्रायिकता के इसी दृष्टिकोण, जिसे प्रायिकता का अभिगृहीतीय दृष्टिकोण (Axiomatic approach of probability) कहते हैं, का अध्ययन करेगें। इस दृष्टिकोण को समझने के लिए कुछ मूल शब्दों को जानना आवश्यक है, जैसे कि यादृच्छिक परीक्षण (Random experiment), प्रतिदर्श समष्टि (Sample space), घटनाएँ (events) इत्यादि। आइए इनके बारे में आगे आने वाले अनुभागों में अध्ययन करेें।
16.2 यादृच्छिक परीक्षण (Random Experiment)
दैनिक जीवन में हम एेसे कई क्रियाकलाप करते हैं जिनके परिणाम सदैव एक ही होते हैं चाहे उन्हें कितनी बार भी दोहराया जाए। उदाहरण के लिए, किसी दिए गए त्रिभुज के कोणों का मान न जानते हुए भी हम निश्चित रूप से कह सकते हैं कि कोणों का योग 180° होगा।
हम इस प्रकार के भी कई प्रायोगिक क्रियाकलाप करते हैं जिन्हें समान परिस्थितियों में दोहराने पर भी परिणाम सदैव एक सा नहीं होता है। उदाहरण के लिए जब एक सिक्के को उछाला जाता है तो चित्त (head) आ सकता है या पट् (tail) आ सकता है लेकिन हम यह निश्चित नहीं कर सकते हैं कि वास्तविक परिणाम इन दोनों में से क्या होगा? इस प्रकार के परीक्षण को यादृच्छिक परीक्षण कहा जाता है। अत: एक परीक्षण को यादृच्छिक परीक्षण कहा जाता है यदि यह निम्नलिखित दो प्रतिबंधों को संतुष्ट करता है:
(i) इसके एक से अधिक संभावित परिणाम हों।
(ii) परीक्षण के पूर्ण होने से पहले परिणाम बताना संभव न हो।
जाँच कीजिए कि एक पासा को फेंकने का परीक्षण यादृच्छिक है या नहीं?
इस अध्याय में एक यादृच्छिक परीक्षण को केवल परीक्षण कहा गया है जब तक कि अन्यथा व्यक्त न किया गया हो।
16.2.1 परिणाम और प्रतिदर्श समष्टि (Outcomes and sample space) किसी यादृच्छिक परीक्षण के किसी सभांवित नतीजे को परिणाम कहते हैं।
एक पासा फेकनें के परीक्षण पर विचार करें। यदि हम पासे के ऊपरी फलक पर अंकित बिंदुओं की संख्या में रुचि रखते हैं तो इस परीक्षण के परिणाम 1, 2, 3, 4, 5 या 6 हैं। सभी परिणामों का समुच्चय {1, 2, 3, 4, 5, 6} इस परीक्षण का प्रतिदर्श समष्टि कहलाता है।
अत: किसी यादृच्छिक परीक्षण के सभी संभावित परिणामों का समुच्चय उस परीक्षण का प्रतिदर्श समष्टि कहलाता है। प्रतिदर्श समष्टि को संकेत S द्वारा प्रकट किया जाता है।
प्रतिदर्श समष्टि का प्रत्येक अवयव एक प्रतिदर्श बिंदु कहलाता है। दूसरे शब्दों में, यादृच्छिक परीक्षण का प्रत्येक परिणाम भी प्रतिदर्श बिंदु कहलाता है।
आइए कुछ उदाहरणों पर विचार करें।
उदाहरण 1 दो सिक्कों (एक 1 रु का तथा दूसरा 2 रु का) को एक बार उछाला गया है। प्रतिदर्श समष्टि ज्ञात कीजिए।
हल स्पष्टत: सिक्के इस अर्थ में विभेद्य हैं कि हम उनको पहला सिक्का और दूसरा सिक्का
संबोधित कर सकते हैं क्योंकि दोनों सिक्कों में से किसी पर चित्त (H) या पट् (T) प्रकट हो सकते हैं, इसलिए संभव परिणाम निम्नलिखित हो सकते हैं:
दोनों सिक्कों पर चित्त = (H,H) = HH
पहले सिक्के पर चित्त और दूसरे पर पट् = (H,T) = HT
पहले सिक्के पर पट् और दूसरे पर चित्त = (T,H) = TH
दोनों सिक्कों पर पट् = (T,T) = TT
अतएव, दिए हुए परीक्षण का प्रतिदर्श समष्टि
S = {HH, HT, TH, TT}है।
टिप्पणी परीक्षण के परिणाम H तथा T के क्रमित युग्म हैं। सरलता के लिए क्रमित युग्म में स्थित अर्द्ध-विराम (comma) को छोड़ दिया गया है।
उदाहरण 2 पासों के जोड़े (जिसमें एक लाल रंग का और दूसरा नीले रंग का है) को एक बार फेंकने के परीक्षण का प्रतिदर्श समष्टि ज्ञात कीजिए। प्रतिदर्श समष्टि के अवयवों की संख्या भी
ज्ञात कीजिए।
हल मान लीजिए कि नीले रंग के पासे पर 1 और लाल रंग पर 2 प्रकट होता है। हम इस परिणाम को क्रमित युग्म (1, 2) द्वारा निरूपित करते हैं। इसी प्रकार, यदि नीले पासे पर 3 और लाल पर 5 प्रकट होता है, तो इस परिणाम को (3, 5) द्वारा निरूपित करते हैं।
व्यापक रूप से प्रत्येक परिणाम को क्रमित युग्म (ग, ल), द्वारा निरूपित किया जा सकता है जहाँ ग नीले रंग के पासे पर और ल लाल पासे पर प्रकट होने वाली संख्याएँ हैं। अतएव, प्रतिदर्श समष्टि निम्नलिखित है:
S = {(x, y): x नीले पासे पर प्रकट संख्या और y लाल पासे पर प्रकट संख्या है }
इस प्रतिदर्श समष्टि के अवयवों की संख्या 6 × 6 = 36 है ओर प्रतिदर्श समष्टि नीचे प्रदत्त है:
{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}
उदाहरण 3 निम्नलिखित प्रत्येक परीक्षण के लिए उपयुक्त प्रतिदर्श समष्टि का उल्लेख कीजिए
(i) एक बालक की जेब में एक 1 रु, एक 2 रु व एक 5 रु के सिक्के हैं। वह अपनी जेब से एक के बाद एक दो सिक्केे निकालता है।
(ii) एक व्यक्ति किसी व्यस्त राजमार्ग पर एक वर्ष में होने वाली दुर्घटनाओं की संख्या
लिखता है।
हल (i) मान लीजिए 1 रु का सिक्का Q से, 2 रु का सिक्का H से तथा 5 रु का सिक्का R से निरूपित होते हैं। उसके द्वारा जेब से निकाला गया पहला सिक्का तीन सिक्कों में से कोई भी एक सिक्का Q, H या R हो सकता है। पहले सिक्के Q के संगत दूसरी बार निकाला गया सिक्का H या R हो सकता है। अत: दो सिक्के निकालने का परिणाम QH या QR हो सकता है। इसी प्रकार, H के संगत दूसरी बार निकाला गया सिक्का Q या R हो सकता है। इसलिए, परिणाम HQ या HR हो सकता है। अंतत: R के संगत दूसरी बार निकाला गया सिक्का H या Q हो सकता है। इसलिए परिणाम RH या RQ होगा।
अत: प्रतिदर्श समष्टि S={QH, QR, HQ, HR, RH, RQ}है।
(ii) किसी व्यस्त राजमार्ग पर दुर्घटनाओं की संख्या 0 (किसी दुर्घटना के न होने पर) या 1 या 2, या कोई भी धन पूर्णांक हो सकता है।
अत: इस परीक्षण के लिए प्रतिदर्श समष्टि S = {0,1,2,...} है:
उदाहरण 4 एक सिक्का उछाला जाता है। यदि उस पर चित्त प्रकट हो तो हम एक थैली, जिसमें
3 नीली एवं 4 सफ़ेद गेंद हैं, में से एक गेंद निकालते हैं। यदि सिक्के पर पट् प्रकट होता है तो हम एक पासा फेंकते हैं। इस परीक्षण के प्रतिदर्श समष्टि का वर्णन कीजिए।
हल मान लीजिए हम नीली गेंदों को B1, B2, B3 और सफ़ेद गेंदों को W1, W2, W3, W4 से निरूपित करते हैं। इस परीक्षण का प्रतिदर्श समष्टि
S = { HB1, HB2, HB3, HW1, HW2, HW3, HW4, T1, T2, T3, T4, T5, T6}है।
यहाँ HBi का अर्थ है कि सिक्के पर चित्त है और गेंद Bi निकाली गई है। HWi का अर्थ है कि सिक्के पर चित्त है और गेंद Wi निकाली गई है। इसी प्रकार Ti का अर्थ है कि सिक्के पर पट् और पासे पर संख्या प प्रकट हुई है।
उदाहरण 5 एक एेसे परीक्षण पर विचार कीजिए जिसमें एक सिक्के को बार-बार तब तक उछालते रहते हैं जब तक उस पर चित्त प्रकट न हो जाए। इसकी प्रतिदर्श समष्टि का वर्णन कीजिए।
हल इस परीक्षण में चित्त प्रथम उछाल या द्वितीय उछाल या तृतीय उछाल इत्यादि में से किसी में भी प्रकट हो सकता है।
अत:, वांछित प्रतिदर्श समष्टि S = {H, TH, TTH, TTTH, TTTTH,...} है।
प्रश्नावली 16.1
निम्नलिखित प्रश्नों 1 से 7, में प्रत्येक में निर्दिष्ट परीक्षण का प्रतिदर्श समष्टि ज्ञात कीजिए।
1. एक सिक्के को तीन बार उछाला गया है।
2. एक पासा दो बार फेंका गया है।
3. एक सिक्का चार बार उछाला गया है।
4. एक सिक्का उछाला गया है और एक पासा फेंका गया है।
5. एक सिक्का उछाला गया है और केवल उस दशा में, जब सिक्के पर चित्त प्रकट होता है एक पासा फेंका जाता है।
6. X कमरे में 2 लड़के और 2 लड़कियाँ हैं तथा Y कमरे में 1 लड़का और 3 लड़कियाँ हैं। उस परीक्षण का प्रतिदर्श समष्टि ज्ञात कीजिए जिसमें पहले एक कमरा चुना जाता है फिर एक बच्चा चुना जाता है।
7. एक पासा लाल रंग का, एक सफ़ेद रंग का और एक अन्य पासा नीले रंग का एक थैले में रखे हैं। एक पासा यादृच्छया चुना गया और उसे फेंका गया है, पासे का रंग और इसके ऊपर के फलक पर प्राप्त संख्या को लिखा गया है। प्रतिदर्श समष्टि का वर्णन कीजिए।
8. एक परीक्षण में 2 बच्चों वाले परिवारों में से प्रत्येक में लड़के-लड़कियों की संख्याओं को लिखा जाता है।
(i) यदि हमारी रुचि इस बात को जानने में है कि जन्म के क्रम में बच्चा लड़का या लड़की है तो प्रतिदर्श समष्टि क्या होगी?
(ii) यदि हमारी रुचि किसी परिवार में लड़कियों की संख्या जानने में है तो प्रतिदर्श समष्टि क्या होगी?
9. एक डिब्बे में 1 लाल और एक जैसी 3 सफ़ेद गेंद रखी गई हैं। दो गेंद उत्तरोतर (in succession) बिना प्रतिस्थापित किए यादृच्छया निकाली जाती है। इस परीक्षण का प्रतिदर्श समष्टि ज्ञात कीजिए।
10. एक परीक्षण में एक सिक्के को उछाला जाता है और यदि उस पर चित्त प्रकट होता है तो उसे पुन: उछाला जाता है। यदि पहली बार उछालने पर पट् प्राप्त होता है तो एक पासा फेंका जाता है। प्रतिदर्श समष्टि ज्ञात कीजिए।
11. मान लीजिए कि बल्बों के एक ढेर में से 3 बल्ब यादृच्छया निकाले जाते हैं। प्रत्येक बल्ब कोे जाँचा जाता है और उसे खराब (D) या ठीक (N) में वर्गीकृत करते हैं। इस परीक्षण का प्रतिदर्श समष्टि ज्ञात कीजिए।
12. एक सिक्का उछाला जाता है। यदि परिणाम चित्त हो तो एक पासा फेंका जाता है। यदि पासे पर एक सम संख्या प्रकट होती है तो पासे को पुन: फेंका जाता है। इस परीक्षण का प्रतिदर्श समष्टि ज्ञात कीजिए।
13. कागज़ की चार पर्चियों पर संख्याएँ 1, 2, 3 और 4 अलग-अलग लिखी गई हैं। इन पर्चियों को एक डिब्बे में रख कर भली-भाँति मिलाया गया है। एक व्यक्ति डिब्बे में से दो पर्चियाँ एक के बाद दूसरी बिना प्रतिस्थापित किए निकालता है। इस परीक्षण का प्रतिदर्श समष्टि ज्ञात कीजिए।
14. एक परीक्षण में एक पासा फेंका जाता है और यदि पासे पर प्राप्त संख्या सम है तो एक सिक्का एक बार उछाला जाता है। यदि पासे पर प्राप्त संख्या विषम है, तो सिक्के को दो बार उछालते हैं। प्रतिदर्श समष्टि लिखिए।
15. एक सिक्का उछाला गया। यदि उस पर पट् प्रकट होता है तो एक डिब्बे में से जिसमें 2 लाल और 3 काली गेंदें रखी हैं, एक गेंद निकालते हैं। यदि सिक्के पर चित्त प्रकट होता है तो एक पासा फेंका जाता है। इस परीक्षण का प्रतिदर्श समष्टि लिखिए।
16. एक पासा को बार-बार तब तक फेंका जाता है जब तक उस पर 6 प्रकट न हो जाए। इस परीक्षण का प्रतिदर्श समष्टि क्या है?
16.3 घटना (Event)
हमने यादृच्छिक परीक्षण और उसके प्रतिदर्श समष्टि के बारे में पढ़ा है। किसी परीक्षण का प्रतिदर्श समष्टि उस परीक्षण से संबंधित सभी प्रश्नों के लिए सार्वत्रिक समुच्चय (Universal set) होता है।
एक सिक्के को दो बार उछालने के परीक्षण पर विचार कीजिए। संबंधित प्रतिदर्श समष्टि S = {HH, HT, TH, TT} है।
अब, मान लीजिए कि हमारी रुचि उन परिणामों में है जो तथ्यत: एक चित्त प्रकट होने के अनुकूल होते हैं। हम पाते हैं कि इस घटना के होने के अनुकूल S के अवयव केवल HT और TH हैं। यह दो अवयव एक समुच्चय E = {HT, TH} बनाते हैं।
हम जानते हैं कि समुच्चय E प्रतिदर्श समष्टि S का उपसमुच्चय है। इसी प्रकार हम पाते हैं कि विभिन्न घटनाओं और S के उपसमुच्चयों में निम्नलिखित संगतता है:

उपर्युक्त चर्चा से यह स्पष्ट है कि प्रतिदर्श समष्टि के किसी उपसमुच्चय के संगत एक घटना होती है और किसी घटना के संगत प्रतिदर्श समष्टि का एक उपसमुच्चय होता है। इसके संदर्भ में एक घटना को निम्नलिखित प्रकार से परिभाषित किया जाता है:
परिभाषा प्रतिदर्श समष्टि S का कोई उपसमुच्चय एक घटना कही जाती है।
16.3.1 एक घटना का घटित होना (Occurrence of an event)
एक पासा को फेंकने के परीक्षण पर विचार कीजिए। मान लीजिए कि घटना ‘पासा पर 4 से छोटी संख्या प्रकट होना’ को E से निरूपित किया जाता है। यदि पासा पर वास्तव में ‘1’ प्रकट होता है तो हम कह सकते हैं कि घटना E घटित हुई है। वस्तुत: यदि परिणाम 2 या 3 हैं तो हम कहते हैं कि घटना E घटित हुई है।
अत: किसी परीक्षण के प्रतिदर्श समष्टि S की घटना E घटित हुई कही जाती है यदि परीक्षण का परिणाम ω इस प्रकार है कि ω ∈ E. यदि परिणाम ω एेसा है कि ω ∉ E,तो हम कहते हैं कि घटना E घटित नहीं हुई है।
16.3.2 घटनाओं के प्रकार (Types of events)
घटनाओं को उनके अवयवों के आधार पर विभिन्न प्रकारों में वर्गीकृत किया जा सकता है।
1. असंभव व निश्चित घटनाएँ (Impossible and Sure Events) रिक्त समुच्चय φ और प्रतिदर्श समष्टि S भी घटनाओं को व्यक्त करते हैं। वास्तव में φ को असंभव घटना और S अर्थात् पूर्ण प्रतिदर्श समष्टि को निश्चित घटना कहते हैं।
इन्हें समझने के लिए आइए पासा फेंकने के परीक्षण पर विचार करें। इस परीक्षण का प्रतिदर्श समष्टि S = {1,2,3,4,5,6} है।
मान लीजिए E घटना ‘पासे पर प्रकट संख्या 7 का गुणज है’ को निरूपित करता है। क्या आप घटना E के संगत उपसमुच्चय लिख सकते हैं?
स्पष्टतया परीक्षण का कोई भी परिणाम घटना E के प्रतिबंध को संतुष्ट नहीं करता है अर्थात् प्रतिदर्श समष्टि का कोई भी अवयव घटना E का घटित होने को निश्चित नहीं करता हैं। अत: हम कह सकते हैं कि केवल रिक्त समुच्चय ही घटना E के संगत समुच्चय है। दूसरे शब्दों में, हम कह सकते हैं कि पासे के ऊपरी फलक पर 7 का गुणज प्रकट होना असंभव है।
इस प्रकार घटना E = φ एक असंभव घटना है।
आइए अब हम एक अन्य घटना F ‘पासा पर प्राप्त संख्या या तो सम है या विषम’ पर विचार करें। स्पष्टतया F = {1,2,3,4,5,6,} = S.
अर्थात् सभी परिणाम घटना F के घटित होने को निश्चित करते हैं। अत: F = S एक निश्चित घटना है।
2. सरल घटना (Simple Event) यदि किसी घटना E में केवल एक ही प्रतिदर्श बिंदु हो, तो घटना E को सरल या प्रारम्भिक घटना कहते हैं। एेसा परीक्षण जिसके प्रतिदर्श समष्टि जिसमें द पृथक अवयव हों, में द सरल घटनाएँ विद्यमान होती हैं।
उदाहरण के लिए, एक सिक्का के दो उछालों वाले परीक्षण का प्रतिदर्श समष्टि
S={HH, HT, TH, TT} है।
यहाँ इस प्रतिदर्श समष्टि की चार सरल घटनाएँ हैं, जो निम्नलिखित हैं:
E1= {HH}, E2={HT}, E3= { TH} और E4={TT}.
3. मिश्र घटना (Compound Events) यदि किसी घटना में एक से अधिक प्रतिदर्श बिंदु होते हैं, तो उसे मिश्र घटना कहते हैं। उदाहरण के लिए एक सिक्के की तीन उछालों के परीक्षण में निम्नलिखित घटनाएँ मिश्र घटनाएँ हैं:
E: तथ्यत: एक चित्त प्रकट होना
F: न्यूनतम एक चित्त प्रकट होना
G: अधिकतम एक चित्त प्रकट होना, इत्यादि।
इन घटनाओं के संगत S के उपसमुच्चय निम्नलिखित हैं:
E={HTT,THT,TTH}
F={HTT,THT, TTH, HHT, HTH, THH, HHH}
G= {TTT, THT, HTT, TTH}
उपर्युक्त प्रत्येक उपसमुच्चय में एक से अधिक प्रतिदर्श बिंदु हैं इसलिए यह सब मिश्र
घटनाएँ हैं।
16.3.3 घटनाओं का बीजगणित (Algebra of Events)
समुच्चयों के अध्याय में हमने दो या अधिक समुच्चयों के संयोजन के विभिन्न तरीकों के बारे में पढ़ा था अर्थात् सम्मिलन (union), सर्वनिष्ठ (intersection), अंतर (difference), समुच्चय का पूरक (Complement of a set), इत्यादि के बारे में समझा था। इसी प्रकार हम घटनाओं का संयोजन समुच्चय संकेतनों के सदृश उपयोग द्वारा कर सकते हैं।
मान लीजिए A,B,C एेसे प्रयोग से संबद्ध घटनाएँ हैं जिसकी प्रतिदर्श समष्टि S है।
1. पूरक घटना (Complementary Event) प्रत्येक घटना A के सापेक्ष एक अन्य घटना 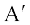 होती है जिसे घटना A की पूरक घटना कहते हैं। A′ को घटना ‘A–नहीं’ भी कहा जाता है।
होती है जिसे घटना A की पूरक घटना कहते हैं। A′ को घटना ‘A–नहीं’ भी कहा जाता है।
उदाहरण के लिए ‘एक सिक्के की तीन उछालों’ के परीक्षण को लें। इसका प्रतिदर्श समष्टि
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} है।
मान लीजिए A={HTH, HHT, THH} घटना ‘केवल एक पट का प्रकट होना’ को दर्शाता है। परिणाम HTT के होने पर घटना A घटित नहीं हुई है। किंतु हम कह सकते हैं कि घटना ‘A–नहीं’ घटित हुई है। इस प्रकार, प्रत्येक परिणाम के लिए जो A में नहीं हैं हम कहते हैं कि ‘A-नहीं’ घटित हुई है। इस प्रकार घटना A के लिए पूरक घटना ‘A–नहीं’ अर्थात्
A′= {HHH, HTT, THT, TTH, TTT}
या A′= {ω : ω ∈ S और ω ∉ A} = S – A है।
2. घटना ‘A या B’ (Event A or B) स्मरण कीजिए कि दो समुच्चयों A और B का सम्मिलन
A ∪ B द्वारा निरूपित किया जाता है जिसमें वह सब अवयव सम्मिलित होते हैं जो या तो A में हैं या B में है या दोनों में हैं।
जब समुच्चय A और B किसी प्रतिदर्श समष्टि से संबंधित दो घटनाएँ हों तो ‘A ∪ B’ घटना A या B या दोनों को निरूपित करता है। घटना ‘A ∪ B’ को ‘A या B’ भी कहा जाता है।
इसलिए घटना ‘A या B’ = A ∪ B = {ω: ω∈A या  ∈ B}
∈ B}
3. घटना 'A और B' (Event A and B) हम जानते हैं कि दो समुच्चयों का सर्वनिष्ठ
A ∩ B वह समुच्चय होता है जिसमें वे अवयव होते हैं जो A और B दोनों में उभयनिष्ठ होते हैं अर्थात् जो A और B दोनों में होते हैं।
यदि ‘A और B’ दो घटनाएँ हों तो समुच्चय A ∩ B घटना ‘A और B’ को दर्शाता है।
इस प्रकार, A ∩ B = {ω : ω ∈ A और ω ∈ B}
उदाहरण के लिए एक पासा को दो बार फेंकने के परीक्षण में मान लीजिए घटना A ‘पहली फेंक में संख्या 6 प्रकट होती है’ और घटना B ‘दो फेंकों पर प्रकट संख्याओं का योग न्यूनतम 11 होता है’ को व्यक्त करती हैं। तब
A = {(6,1), (6,2}, (6,3), (6,4), (6,5), (6,6)} और B = {(5,6), (6,5), (6,6)}
इसलिए A ∩ B = {(6,5), (6,6)}
नोट कीजिए कि समुच्चय A ∩ B = {(6,5), (6,6)}, घटना ‘पहली फेंक पर 6 प्रकट होता है और दोनों फेंकों पर प्रकट संख्याओं का योग न्यूनतम 11 होता है’ को व्यक्त करता है।
4. घटना ‘A किंतु B नहीं’ (Event A but not B) हम जानते हैं कि A – B उन सभी अवयवों का समुच्चय होता है जो A में तो हैं लेकिन B में नहीं हैं। इसलिए, समुच्चय 'A – B' घटना ‘A किंतु B नहीं’ को व्यक्त कर सकता है। हम जानते हैं कि A – B = A ∩ B′
उदाहरण 6 एक पासा फेंकने के परीक्षण पर विचार कीजिए। घटना ‘एक अभाज्य संख्या प्राप्त होना’ को A से और घटना ‘एक विषम संख्या प्राप्त होना’ को B से निरूपित किया गया है। निम्नलिखित घटनाओं (i) A या B (ii) A और B (iii) A किंतु B नहीं (iv) ‘A–नहीं’ को निरूपित करने वाले समुच्चय लिखिए।
हल यहाँ S = {1,2,3,4,5,6}, A = {2,3,5} और B = {1,3,5}
प्रत्यक्षत:
(i) ‘A या B’ = A ∪ B = {1,2,3,5}
(ii) ‘A और B’ = A ∩ B = {3,5}
(iii) ‘A किंतु B नहीं’ = A – B = {2}
(iv) ‘A–नहीं’ = A´ = {1,4,6}
16.3.4 परस्पर अपवर्जी घटनाएँ (Mutually exclusive events)
पासा फेंकने के परीक्षण का प्रतिदर्श समष्टि S = {1, 2, 3, 4, 5, 6} है। मान लीजिए घटना A ‘एक विषम संख्या का प्रकट होना’ और घटना B ‘एक सम संख्या का प्रकट होना’ को व्यक्त करते हैं।
स्पष्टतया घटना A, घटना B को अपवर्जित कर रही है तथा इसका विलोम भी सत्य है। दूसरे शब्दों में, एेसा कोई परिणाम नहीं है जो घटना A और B के एक साथ घटित होने को निश्चित करता है यहाँ
A = {1, 3, 5} और B = {2, 4, 6}
स्पष्टतया A ∩ B = φ अर्थात् A और B असंयुक्त समुच्चय हैं।
व्यापकत: दो घटनाएँ A और B परस्पर अपवर्जी घटनाएँ कही जाती हैं, यदि इनमें से किसी एक का घटित होना दूसरी के घटित होने को अपवर्जित करता है अर्थात् वे एक साथ घटित नहीं हो सकती हैं। इस दशा में समुच्चय A और B असंयुक्त होते हैं।
पुन: एक पासे को फेंकने के परीक्षण में घटना A ‘एक विषम संख्या प्रकट होना’ और घटना B ‘4 से छोटी संख्या प्रकट होना’ पर विचार कीजिए।
प्रत्यक्षत: A = {1, 3, 5} और B = {1, 2, 3}
अब 3 ∈ A तथा साथ ही 3 ∈ B
इसलिए A और B असंयुक्त नहीं है। अत: A और B परस्पर अपवर्जी घटनाएँ नहीं हैं।
टिपप्णी एक प्रतिदर्श समष्टि की सरल घटनाएँ सदैव परस्पर अपवर्जी होती हैं।
16.3.5 नि:शेष घटनाएँ (Exhaustive events)
एक पासे को फेंकने के परीक्षण पर विचार कीजिए। हम पाते हैं S = {1, 2, 3, 4, 5, 6}.
आइए निम्नलिखित घटनाओं को परिभाषित करें:
A: ‘4 से छोटी संख्या प्रकट होना’,
B: ‘2 से बड़ी किंतु 5 से छोटी संख्या प्रकट होना’
और C:‘4 से बड़ी संख्या प्रकट होना’.
तब A = {1, 2, 3}, B = {3,4} और C = {5, 6}. हम देखते हैं कि
A ∪ B ∪ C = {1,2,3} ∪ {3,4} ∪ {5, 6} = S.
एेसी घटनाओं A, B और C को नि:शेष घटनाएँ कहते हैं। व्यापक रूप से यदि E1, E2, ..., En किसी प्रतिदर्श समष्टि S की n घटनाएँ हैं और यदि
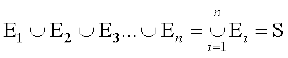
तब E1, E2, ..., En को नि:शेष घटनाएँ कहते हैं। दूसरे शब्दों में, घटनाएँ E1, E2, ..., En नि:शेष कहलाती हैं यदि परीक्षण के करने पर इनमें से कम से कम एक घटना अवश्य ही घटित हो।
इसके अतिरिक्त यदि सभी i ≠ j के लिए Ei ∩ Ej = φ अग्रत: यदि Ei ∩ Ej = φए i ≠ j अर्थात् Ei और Ej परस्पर अपवर्जी हैं, और  हो, तो घटनाएँ E1, E2, ..., En परस्पर अपवर्जी नि:शेष घटनाएँ कहलाती हैं।
हो, तो घटनाएँ E1, E2, ..., En परस्पर अपवर्जी नि:शेष घटनाएँ कहलाती हैं।
आइए अब कुछ उदाहरणों पर विचार करें।
उदाहरण 7 दो पासे फेंके जाते हैं और पासों पर प्राप्त संख्याओं का योग लिखा जाता है। आइए अब हम इस प्रयोग से संबंधित निम्नलिखित घटनाओं पर विचार करें:
A: ‘प्राप्त योग सम संख्या है’।
B: ‘प्राप्त योग 3 का गुणज है’।
C: ‘प्राप्त योग 4 से कम है’।
D: ‘प्राप्त योग 11 से अधिक है’।
इन घटनाओं में से कौन से युग्म परस्पर अपवर्जी हैं?
हल प्रतिदर्श समष्टि S = {(x, y): x, y = 1, 2, 3, 4, 5, 6} में 36 अवयव हैं।
तब A = {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6), (3, 1), (3, 3), (3, 5), (4, 2), (4, 4),
(4, 6), (5, 1), (5, 3), (5, 5), (6, 2), (6, 4), (6, 6)}
B = {(1, 2), (2, 1), (1, 5), (5, 1), (3, 3), (2, 4), (4, 2), (3, 6), (6, 3), (4, 5), (5, 4),
(6, 6)}
C = {(1, 1), (2, 1), (1, 2)} और D = {(6, 6)}
हमें प्राप्त होता है
A ∩ B = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1), (6, 6)} ≠ φ
इसलिए, A और B परस्पर अपवर्जी नहीं हैं।
इसी प्रकार A ∩ C ≠ φए A ∩ D ≠ φए B ∩ C ≠ φए और B ∩ D ≠ φए
इस प्रकार युग्म (A, C), (A, D), (B, C), (B, D) परस्पर अपवर्जी नहीं है।
साथ ही C ∩ D ≠ φ इसलिए, C और D परस्पर अपवर्जी घटनाएँ हैं।
उदाहरण 8 एक सिक्के को तीन बार उछाला गया है। निम्नलिखित घटनाओं पर विचार कीजिए:
A: ‘कोई चित्त प्रकट नहीं होता है’ ,
B: ‘तथ्यत: एक चित्त प्रकट होता है’ और
C: ‘कम से कम दो चित्त प्रकट होते हैं’।
क्या यह परस्पर अपवर्जी और नि:शेष घटनाओं का समुच्चय है?
हल परिणाम का प्रतिदर्श समष्टि
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} है
और A = {TTT}, B = {HTT, THT, TTH}तथा C = {HHT, HTH, THH, HHH}
अब A ∪ B ∪ C = {TTT, HTT, THT, TTH, HHT, HTH, THH, HHH} = S
इसलिए, A, B और C नि:शेष घटनाएँ हैं।
साथ ही A ∩ B = φ, A ∩ C = φ और B ∩ C = φ
इसलिए, घटनाएँ युग्म के अनुसार असंयुक्त हैं अर्थात् वे परस्पर अपवर्जी हैं।
अत: A, B और C परस्पर अपवर्जी व नि:शेष घटनाओं का समुच्चय बनाते हैं।
प्रश्नावली 16.2
1. एक पासा फेंका जाता है। मान लीजिए घटना E ‘पासे पर संख्या 4 दर्शाता’ है और घटना F ‘पासे पर सम संख्या दर्शाता’ है। क्या E और F परस्पर अपवर्जी हैं?
2. एक पासा फेंका जाता है। निम्नलिखित घटनाओं का वर्णन कीजिए:
(i) A: संख्या 7 से कम है। (ii) B: संख्या 7 से बड़ी है।
(iii) C: संख्या 3 का गुणज है। (iv) D: संख्या 4 से कम है।
(v) E: 4 से बड़ी सम संख्या है। (vi) F: संख्या 3 से कम नहीं है।
A ∪ B, A ∩ B, B ∪ C, E ∩ F, D ∩ E, A – C, D – E, E ∩ F′, F´ भी ज्ञात कीजिए।
3. एक परीक्षण में पासें केे एक जोड़े को फेंकते हैं और उन पर प्रकट संख्याओं को लिखते हैं। निम्नलिखित घटनाओं का वर्णन कीजिए:
A: प्राप्त संख्याओं का योग 8 से अधिक है।
B: दोनों पासों पर संख्या 2 प्रकट होती है।
C: प्रकट संख्याओं का योग कम से कम 7 है और 3 का गुणज है।
इन घटनाओं केे कौन-कौन से युग्म परस्पर अपवर्जी हैं?
4. तीन सिक्कों को एक बार उछाला जाता है। मान लीजिए कि घटना ’तीन चित्त दिखना’ को A से, घटना ‘दो चित्त और एक पट् दिखना’ को B से, घटना ‘तीन पट् दिखना’ को C और घटना ’पहले सिक्के पर चित्त दिखना’ को D से निरूपित किया गया है। बताइए कि इनमें से कौन सी घटनाएँ (i) परस्पर अपवर्जी हैं? (ii) सरल हैं ? (iii) मिश्र हैं ?
5. तीन सिक्के एक बार उछाले जाते हैं। वर्णन कीजिए।
(i) दो घटनाएँ जो परस्पर अपवर्जी हैं।
(ii) तीन घटनाएँ जो परस्पर अपवर्जी और नि:शेष हैं।
(iii) दो घटनाएँ जो परस्पर अपवर्जी नहीं हैं।
(iv) दो घटनाएँ जो परस्पर अपवर्जी हैं किंतु नि:शेष नहीं हैं।
(v) तीन घटनाएँ जो परस्पर अपवर्जी हैं किंतु नि:शेष नहीं हैं।
6. दो पासे फेंके जाते हैं। घटनाएँ A, B और C निम्नलिखित प्रकार से हैं:
A: पहले पासे पर सम संख्या प्राप्त होना
B: पहले पासे पर विषम संख्या प्राप्त होना
C: पासों पर प्राप्त संख्याओं का योग  5 होना
5 होना
निम्नलिखित घटनाओं का वर्णन कीजिए:
(i) A′ (ii) B-नहीं (iii) A या B
(iv) A और B (v) A किंतु C नहीं (vi) B या C
(vii) B और C (viii) A ∩ B′ ∩ C′
7. उपर्युक्त प्रश्न 6 को देखिए और निम्नलिखित में सत्य या असत्य बताइए (अपने उत्तर का कारण दीजिए):
(i) A और B परस्पर अपवर्जी हैं।
(ii) A और B परस्पर अपवर्जी और नि:शेष हैं।
(iii) A = B′
(iv) A और C परस्पर अपवर्जी हैं।
(v) A और B′ परस्पर अपवर्जी हैं।
(vi) A′, B′, C परस्पर अपवर्जी और नि:शेष घटनाएँ हैं।
16.4 प्रायिकता की अभिगृहीतीय दृष्टिकोण (Axiomatic Approach to Probability)
इस अध्याय के पहले अनुच्छेदों में हमने यादृच्छिक परीक्षण, प्रतिदर्श समष्टि तथा इन परीक्षणों से संबंधित घटनाओं पर विचार किया है। हम अपने दैनिक जीवन में किसी घटना के घटित होने की संभावना के लिए अनेक शब्दों का उपयोग करते हैं। प्रायिकता सिद्धांत किसी घटना के घटित होने या न होने की संभावना को एक माप देने का प्रयास है।
पिछली कक्षाओं में हमने किसी परीक्षण में कुल संभावित परिणामों की संख्या ज्ञात होने पर, किसी घटना की प्रायिकता ज्ञात करने की कुछ विधियों के बारे में पढ़ा है।
किसी घटना की प्रायिकता ज्ञात करने की एक और विधि अभिगृहीतीय दृष्टिकोण है। इस तरीका में प्रायिकताएँ निर्धारित करने के लिए अभिगृहीतियों या नियमों को बर्णित (depict) किया गया है।
मान लें कि किसी यादृच्छिक परीक्षण का प्रतिदर्श समष्टि S है। प्रायिकता P एक वास्तविक मानीय फलन है जिसका प्रांत S का घात समुच्चय है, और परिसर अंतराल [0,1] है जो निम्नलिखित अभिगृहीतियों को संतुष्ट करता है:
(i) किसी घटना E, के लिए, P (E) ≥ 0
(ii) P (S) = 1
(iii) यदि E और F परस्पर अपवर्जी घटनाएँ हैं तो P(E ∪ F) = P(E) + P(F).
अभिगृहित (iii) से यह अनुसरित होता है कि P(φ) = 0. इसे सिद्ध करने के लिए हम F = φ लेते हैं और देखते हैं कि E और φ परस्पर अपवर्जी घटनाएँ है, इसलिए अभिगृहीत (iii) से हम पाते हैं कि
P (E ∪ φ) = P (E) + P ( φ ) या P(E) = P(E) + P (φ) अर्थात् P(φ) = 0
मान लीजिए कि ω1, ω2, ...,ωn प्रतिदर्श समष्टि S के परिणाम हैं अर्थात्
S = {ω1, ω2, ...,ωn}है।
प्रायिकता की अभिगृहीतीय परिभाषा से यह निष्कर्ष निकलता है कि
(i) प्रत्येक ωi ∈ S के लिए 0  P (ωi)
P (ωi)  1
1
(ii) P (ω1) + P (ω2) + ... + P (ωn) = 1
(iii) किसी घटना ωi के लिए P(A) = Σ P (ωi), ωi ∈ A
टिप्पणी ध्यान दीजिए कि एकल समुच्चय {ωi} को सरल घटना कहते हैं और संकेतन की सुविधा के लिए हम P(क्ष्ωi}) को P(ωi) लिखते हैं।
उदाहरण के लिए एक सिक्के को उछालने के परीक्षण में हम प्रत्येक परिणाम H और T के साथ संख्या  निर्धारित कर सकते हैं
निर्धारित कर सकते हैं
अर्थात् P(H) =  और P(T) =
और P(T) =  ... (1)
... (1)
स्पष्टतया यह निर्धारण दोनों प्रतिबंधों को संतुष्ट करता है अर्थात् प्रत्येक संख्या न तो शून्य से छोटी है और न ही एक से बड़ी है
और P(H) + P(T) =  +
+  = 1
= 1
इसलिए इस दशा में हम कह सकते हैं कि
H की प्रायिकता =  और T की प्रायिकता =
और T की प्रायिकता =  .
.
आइए हम P(H) =  और P(T) =
और P(T) = 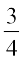 लेते हैं। ... (2)
लेते हैं। ... (2)
क्या यह निर्धारण अभिगृहीतीय तरीका के प्रतिबंधों को संतुष्ट करता है?
हाँ, इस दशा में H की प्रायिकता =  और T की प्रायिकता =
और T की प्रायिकता =  है।
है।
हम पाते हैं कि दोनाें प्रायिकता निर्धारण (1) और (2), H और T की प्रायिकताओं के लिए वैध हैं।
वास्तव में दोनों परिणामों H तथा T की प्रायिकताओं के लिए संख्याएँ क्रमश: च तथा
(1 – च) निर्धारित कर सकते हैं, जबकि 0 ≤ च ≤ 1 और P(H) + P(T) = च + (1 – च) = 1
यह प्रायिकता निर्धारण भी अभिगृहीतीय दृष्टिकोण के प्रतिबंधों को संतुष्ट करते हैं। अत: हम कह सकते हैं कि किसी परीक्षण के परिणामों के साथ प्रायिकता वितरण अनेक (या यह कहना अधिक उचित्त होगा कि अनंत) प्रकार से किया जा सकता है।
आइए अब कुछ उदाहरणों पर विचार करें।
उदाहरण 9 मान लीजिए एक प्रतिदर्श समष्टि S = {ω1, ω2, ...एω6}है। निम्नलिखित में से प्रत्येक परिणाम के लिए कौन-कौन से प्रायिकता निर्धारण वैध हैं?
परिणाम ω1 ω2 ω3 ω4 ω5 ω6
(a) 





(b) 1 0 0 0 0 0
(c) 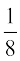

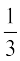
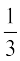

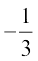
(d) 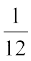
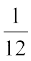




(e) 0.1 0.2 0.3 0.4 0.5 0.6
हल (a) प्रतिबंध (i): प्रत्येक संख्या p (ωi) धनात्मक है और एक से छोटी है।
प्रतिबंध (ii): प्रायिकताओं का योग
= 
इसलिए यह प्रायिकता निर्धारण वैध है।
(b) प्रतिबंध (i): प्रत्येक संख्या p(ωi) या तो 0 है या 1 है।
प्रतिबंध (ii): प्रायिकताओं का योग = 1 + 0 + 0 + 0 + 0 + 0 = 1
इसलिए यह निर्धारण वैध है।
(c) प्रतिबंध (i): दो प्रायिकताएँ च (ω5) और च(ω6) ऋणात्मक हैं। इसलिए यह निर्धारण वैध
नहीं है।
(d) क्याेंकि p (ω6) =  > 1, इसलिए यह प्रायिकता निर्धारण वैध नहीं है।
> 1, इसलिए यह प्रायिकता निर्धारण वैध नहीं है।
(e) क्याेंकि प्रायिकताओं का योग = 0.1 + 0.2 + 0.3 + 0.4 + 0.5 + 0.6 = 2.1 है इसलिए , यह प्रायिकता निर्धारण वैध नहीं है।
16.4.1 घटना की प्रायिकता (Probability of an event)
एक मशीन द्वारा निर्मित कलमों में से तीन का परीक्षण उन्हें अच्छा (त्रुटिरहित) और खराब (त्रुटियुक्त) में वर्गीकृत करने के लिए किया गया। मान लीजिए कि इस परीक्षण का प्रतिदर्श समष्टि S है। इस परीक्षण के पलस्वरूप हमें 0, 1, 2 या 3 खराब कलमें मिल सकती हैं।
इस प्रयोग के संगत प्रतिदर्श समष्टि
S = {BBB, BBG, BGB, GBB, BGG, GBG, GGB, GGG}है।
जहाँ B एक त्रुटियुक्त या खराब कलम को और G एक अच्छे या त्रुटिरहित कलम को प्रकट करता है।
मान लीजिए, कि परिणामों के लिए निम्नलिखित प्रायिकताएँ निर्धारित की गई हैं:
प्रतिदर्श बिंदु: BBB BBG BGB GBB BGG GBG GGB GGG
प्रायिकता: 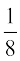
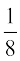
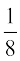
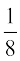
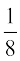
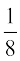
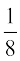
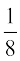
मान लीजिए घटना ‘तथ्यत: एक त्रुटियुक्त कलम का निकलना’ को A से व घटना ‘न्यूनतम दो त्रुटियुक्त कलमों का निकलना’ को B से प्रकट करते हैं।
स्पष्टत : A = {BGG, GBG, GGB} और B = {BBG, BGB, GBB, BBB}
अब P(A) = 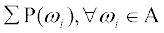
= P(BGG) + P(GBG) + P(GGB) = 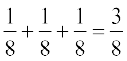
और P(B) = 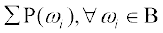
= P(BBG) + P(BGB) + P(GBB) + P(BBB) = 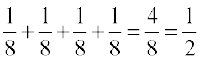
आइए एक अन्य परीक्षण ‘एक सिक्के को दो बार उछालना’ पर विचार करें।
इस परीक्षण का प्रतिदर्श समष्टि S = {HH, HT, TH, TT} है।
मान लीजिए कि विभिन्न परिणामों के लिए निम्नलिखित प्रायिकताएँ निर्धारित की गई हैं:
P(HH) =  , P(HT) =
, P(HT) =  , P(TH) =
, P(TH) = 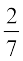 , P(TT) =
, P(TT) = 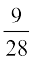
स्पष्टतया यह प्रायिकता निर्धारण अभिगृहीतीय अभिगम के प्रतिबंधों को संतुष्ट करता है। आइए अब हम घटना E ‘दोनों उछालों में एक सा ही परिणाम है’ की प्रायिकता ज्ञात करें।
यहाँ E = {HH, TT}
अब सभी ωi ∈ E के लिए P(E) = 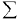 P(ωi), = P(HH) + P(TT) =
P(ωi), = P(HH) + P(TT) = 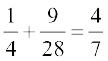
घटना F: ‘तथ्यत: दो चित्त’ के लिए, हम पाते हैं F = {HH}
और P(F) = P(HH) = 
16.4.2 सम सम्भाव्य परिणामों की प्रायिकता (Probability of equally likely outcomes)
मान लीजिए कि एक परीक्षण का प्रतिदर्श समष्टि
S = {ω1, ω2, ..., ωn} है
मान लें कि सभी परिणाम सम संभाव्य हैं, अर्थात् प्रत्येक सरल घटना के घटित होने की संभावना समान है।
अर्थात् सभी ωi ∈ S के लिए, P(ωi) = p, जहाँ 0 ≤ p ≤ 1
क्योंकि 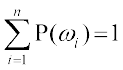 इसलिए च + च + ... + च (द बार) = 1
इसलिए च + च + ... + च (द बार) = 1
या दच = 1 या च = 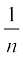
मान लीजिए कि प्रतिदर्श समष्टि S की कोई एक घटना E, इस प्रकार है कि n(S) = n और n(E) = m. यदि प्रत्येक परिणाम सम संभाव्य है तो यह अनुसरित होता है कि
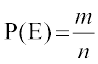 =
= 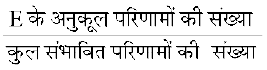
16.4.3 घटना 'A या B' की प्रायिकता (Probability of the event ‘A or B’)
आइए अब हम घटना ‘A या B’, की प्रायिकता अर्थात् P (A ∪ B) ज्ञात करें।
मान लीजिए, A = {HHT, HTH, THH} और B = {HTH, THH, HHH}, ‘एक सिक्के की तीन उछालों के परीक्षण की दो घटनाएँ हैं।
स्पष्टतया A ∪ B = {HHT, HTH, THH, HHH}
अब P (A ∪ B) = P(HHT) + P(HTH) + P(THH) + P(HHH)
यदि सभी परिणाम सम संभाव्य हों तो
P (A ∪ B) 
साथ ही P(A) = P(HHT) + P(HTH) + P(THH) = 
और P(B) = P(HTH) + P(THH) + P(HHH) = 
इसलिए P(A) + P(B) = 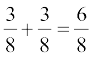
यह स्पष्ट है कि P(A ∪ B) ≠ P(A) + P(B)
बिंदुओं HTH और THH, A तथा B में उभयनिष्ठ अवयव हैं। P(A) + P(B) के परिकलन में HTH और THH, (अर्थात् A ∩ B के अवयव) की प्रायिकता को दो बार सम्मिलित किया गया है। अत: P(A ∪ B) को ज्ञात करने के लिए हमें A ∩ B के प्रतिदर्श बिंदुओं की प्रायिकताओं को
P(A) + P(B) में से घटाना होगा।
अर्थात् 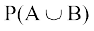 =
= 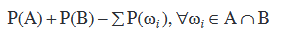
= 
अत: 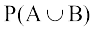 =
= 
व्यापकत: यदि A और B किसी परीक्षण की कोई दो घटनाएँ हैं तब किसी घटना की प्रायिकता की परिभाषा के अनुसार हमें प्राप्त होता है कि
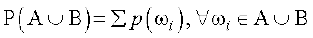 .
.
क्योंकि  , इसलिए
, इसलिए
P(A ∪ B)= 
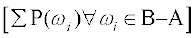
(क्योंकि A–B, A ∩ B और B – A परस्पर अपवर्जी हैं। ... (1)
साथ ही 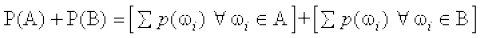
= 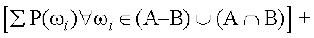
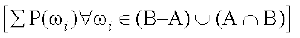
= 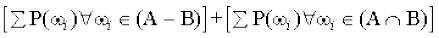 +
+ 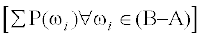
+ 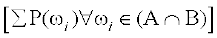
=  [(1) के प्रयोग से]
[(1) के प्रयोग से]
= 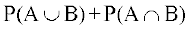 .
.
अत: 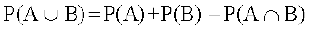 .
.
इस सूत्र का वैकल्पिक प्रमाण निम्नलिखित प्रकार से भी दिया जा सकता है।
A ∪ B = A ∪ (B – A) जहाँ A और B – A परस्पर अपवर्जी हैं।
और B = (A ∩ B) ∪ (B – A) जहाँ A ∩ B और B – A परस्पर अपवर्जी हैं।
प्रायिकता की अभिगृहीत (iii) द्वारा, हमें प्राप्त होता है कि
P (A ∪ B) = P (A) + P (B – A) ... (2)
और P(B) = P ( A ∩ B) + P (B – A) ... (3)
(2) में से (3) घटाने पर,
P (A ∪ B) – P(B) = P(A) – P (A ∩ B)
या P(A ∪ B) = P(A) + P (B) – P (A ∩ B)
उपर्युक्त परिणाम को वेन्-आरेख (आकृति 16.1) का अवलोकन करके भी पुन: सत्यापित किया जा सकता है।
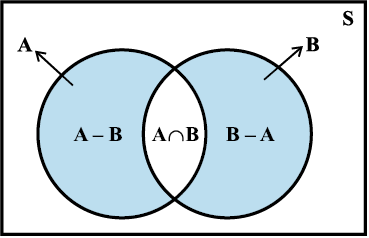
आकृति 16.1
यदि A और B असंयुक्त समुच्चय हों अर्थात् ये दोनों परस्पर अपवर्जी घटनाएँ हों तो (A ∩ B) = φ
इसलिए, P (A ∩ B) = P (φ) = 0
अत: परस्पर अपवर्जी घटनाओं A और B, के लिए, हम पाते हैं
P (A ∪ B) = P (A) + P (B), जो कि प्रायिकता की अभिगृहीत (iii) ही है।
16.4.4 घटना ‘A-नहीं’ की प्रायिकता (Probability of event 'not A')
1 से 10 तक अंकित पूर्णांकों वाले दस पत्तों के डेक में से एक पत्ता निकालने के परीक्षण की घटना A = {2, 4, 6, 8} पर विचार कीजिए। स्पष्टतया प्रतिदर्श समष्टि S = {1, 2, 3, ...,10} है।
यदि सभी परिणामों 1, 2, 3,...,10 को सम संभाव्य मान लें तो प्रत्येक परिणाम की प्रायिकता  होगी।
होगी।
अब P(A) = P(2) + P(4) + P(6) + P(8)
= 
साथ ही घटना ‘A-नहीं’ = A′ = {1, 3, 5, 7, 9, 10}
अब P(A′) = P(1) + P(3) + P(5) + P(7) + P(9) + P(10)
= 
इस प्रकार P(A′) = 
साथ ही हमें यह भी पता है कि A′ तथा A परस्पर अपवर्जी और नि:शेष घटनाएँ हैं। अत: A ∩ A′ = φ और A ∪ A′ = S
या P(A ∪ A′) = P(S)
अब P(A) + P(A′) = 1, अभिगृहीतों (ii) और (iii) के प्रयोग द्वारा
या P(A′) = P(A नहीं) = 1 – P(A)
आइए सम संभावित परिणामों वाले परीक्षणों के लिए कुछ उदाहरणों व प्रश्नों पर विचार करें, जब तक कि अन्यथा न कहा गया हो।
उदाहरण 10 ताश के 52 पत्तों की एक भली-भाँति फेंटी गई गड्डी में से एक पत्ता निकाला गया है। निकाले गए पत्ते की प्रायिकता ज्ञात कीजिए यदि
(i) पत्ता ईंट का है। (ii) पत्ता इक्का नहीं है।
(iii) पत्ता काले रंग का है (अर्थात् चिड़ी या हुकुम का),
(iv) पत्ता ईंट का नहीं है। (v) पत्ता काले रंग का नहीं है।
हल जब 52 पत्तों की भली-भाँति फेंटी गई गड्डी में एक पत्ता निकाला जाता है तो संभव परिणामों की संख्या 52 है।
(i) मान लीजिए घटना ‘निकाला गया पत्ता ईंट का है, को A से दर्शाया गया है।
स्पष्टतया A में अवयवों की संख्या 13 है।
इसलिए, P(A) = 
अर्थात्, एक ईंट का पत्ता निकालने की प्रायिकता = 
(ii) मान लीजिए कि घटना ‘निकाला गया पत्ता इक्का है’ को B से दर्शाते हैं।
इसलिए ‘निकाला गया पत्ता इक्का नहीं है’ को B′ से दर्शाया जाएगा।
अब P(B′) = 1 – P(B) = 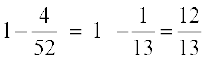
(iii) मान लीजिए घटना ‘निकाला गया पत्ता काले रंग का है’ को C से दर्शाते हैं।
इसलिए समुच्चय C में अवयवों की संख्या = 26
अर्थात् P(C) = 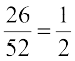
इस प्रकार काले रंग का पत्ता निकालने की प्रायिकता = 
(iv) हमने उपर्युक्त (i) में माना है कि घटना ‘निकाला गया पत्ता ईंट का है’ को A से दर्शाते हैं। इसलिए घटना ‘निकाला गया पत्ता ईंट का नहीं है’ को A′ या ‘A-नहीं’ से दर्शाएंगे।
अब P(A-नहीं) = 1 – P(A) = 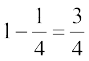
(v) घटना ‘निकाला गया पत्ता काले रंग का नहीं है’ को C′ या ‘C-नहीं’ से दर्शाया जा सकता है।
अब हमें ज्ञात है कि P(C-नहीं) = 1 – P(C) = 
इसलिए, पत्ता काले रंग का न होने की प्रायिकता = 
उदाहरण 11 एक थैले में 9 डिस्क हैं जिनमें से 4 लाल रंग की, 3 नीले रंग की और 2 पीले रंग की हैं। डिस्क आकार एवं माप में समरूप हैं। थैले में से एक डिस्क यादृच्छया निकाली जाती है। प्रायकिता ज्ञात कीजिए कि निकाली गई डिस्क (i) लाल रंग की है (ii) पीले रंग की है (iii) नीले रंग की है (iv) नीले रंग की नहीं है, (v) लाल रंग की है या नीले रंग की है।
हल डिस्काें की कुल संख्या 9 है। इसलिए संभव परिणामों की कुल संख्या 9 हुई।
मान लीजिए घटनाओं A, B व C को इस प्रकार से परिभाषित किया गया है।
A: निकाली गई डिस्क लाल रंग की है।
B: निकाली गई डिस्क पीले रंग की है।
C: निकाली गई डिस्क नीले रंग की है।
(i) लाल रंग की डिस्कों की संख्या = 4 अर्थात् द (A) = 4
अत: P(A) = 
(ii) पीले रंग की डिस्कों की संख्या = 2, अर्थात् n (B) = 2
इसलिए, P(B) = 
(iii) नीले रंग की डिस्कों की संख्या = 3, अर्थात् n(C) = 3
इसलिए, P(C) = 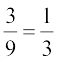
(iv) स्पष्टतया घटना ‘डिस्क नीले रंग की नहीं है’ 'C-नहीं' ही है हम जानते हैं कि
P(C-नहीं) = 1 – P(C)
इसलिए P(C-नहीं) = 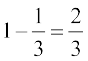
(v) घटना ‘लाल रंग की डिस्क या नीले रंग की डिस्क’ का समुच्चय ‘A ∪ C’ से वर्णित किया जा सकता है।
क्योंकि, A और C परस्पर अपवर्जी घटनाएँ हैं, इसलिए
P(A या C) = P (A ∪ C) = P(A) + P(C) = 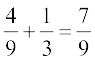
उदाहरण 12 दो विद्यार्थियों अनिल और आशिमा एक परीक्षा में प्रविष्ट हुए। अनिल के परीक्षा में उत्तीर्ण होने की प्रायिकता 0.05 है और आशिमा के परीक्षा में उत्तीर्ण होने की प्रायिकता 0.10 है। दोनों के परीक्षा में उत्तीर्ण होने की प्रायिकता 0.02 है। प्रायिकता ज्ञात कीजिए कि
(a) अनिल और आशिमा दोनों परीक्षा में उत्तीर्ण नहीं हो पाएगें।
(b) दोनों में से कम से कम एक परीक्षा में उत्तीर्ण नहीं होगा।
(c) दोनों में से केवल एक परीक्षा में उत्तीर्ण होगा।
हल मान लीजिए E तथा F घटनाओं ‘अनिल परीक्षा उत्तीर्ण कर लेगा’ और ‘आशिमा परीक्षा उत्तीर्ण कर लेगी’ को क्रमश: दर्शाते हैं।
इसलिए P(E) = 0.05, P(F) = 0.10 और P(E ∩ F) = 0.02.
तब
(a) घटना ’दोनों परीक्षा उर्त्तीण नहीं हाेंगे’ को E' ∩ F' से दर्शाया जा सकता है।
क्योंकि E' घटना ‘E-नहीं’, अर्थात् ‘अनिल परीक्षा उत्तीर्ण नहीं करेगा’ तथा F' घटना ‘F-नहीं’, अर्थात् ‘आशिमा परीक्षा उत्तीर्ण नहीं करेगी’ दर्शाते हैं।
साथ ही E' ∩ F' = (E ∪ F)' (डी-मोरगन् नियम द्वारा)
अब P(E ∪ F) = P(E) + P(F) – P(E ∩ F)
या P(E ∪ F) = 0.05 + 0.10 – 0.02 = 0.13
इसलिए P(E' ∩ F') = P(E ∪ F)' = 1 – P(E ∪ F) = 1 – 0.13 = 0.87
(b) P(दोनों में से कम से कम एक उत्तीर्ण नहीं होगा)
= 1 – P(दोनों उत्तीर्ण होंगे)
= 1 – 0.02 = 0.98
(c) घटना ‘दोनों मे से केवल एक उत्तीर्ण होगा’ निम्नलिखित घटना के समरूप है:
‘अनिल उत्तीर्ण होगा और आशिमा उत्तीर्ण नहीं होगी’
या ‘अनिल उत्तीर्ण नहीं होगा और आशिमा उत्तीर्ण होगी’
अर्थात् E ∩ F' या E' ∩ F जहाँ E ∩ F´ और E´ ∩ F परस्पर अपवर्जी हैं।
इसलिए, P (दोनों में से केवल एक उत्तीर्ण होगा)
= P(E ∩ F' या E' ∩ F)
= P(E ∩ F') + P(E' ∩ F) = P (E) – P(E ∩ F) + P(F) – P (E ∩ F)
= 0.05 – 0.02 + 0.10 – 0.02 = 0.11
उदाहरण 13 दो पुरुषों व दो स्त्रियों के समूह में से दो व्यक्तियों की एक समिति का गठन करना है। प्रायिकता क्या है कि गठित समिति में (a) कोई पुरुष न हो? (b) एक पुरुष हो ? (c) दोनों ही पुरुष हों?
हल समूह में व्यक्तियों की कुल संख्या = 2 + 2 = 4. इन चार व्यक्तियों में से दो को 4C2 तरीके से चुना जा सकता है।
(a) समिति में कोई पुरुष न होने का अर्थ है कि समिति में दो स्त्रियाँ हैं। दो स्त्रियों में से दोनों के चुनने के 2C2 = 1तरीका है।
इसलिए P(कोई पुरुष नहीं)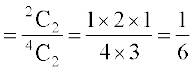
(b) समिति में एक पुरुष होने का तात्पर्य है कि इसमें एक स्त्री है 2 पुरुषों में से एक पुरुष चुनने के 2C1 तरीके हैं तथा दो स्त्रियों में से एक चुनने के भी 2C1 तरीके हैं। दोनों चुनावों को एक साथ करने के 2C1 ञ् 2C1 तरीके हैं।
इसलिए P(एक पुरूष)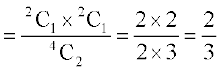
(c) दो पुरुषों को 2C2 तरीकों से चुना जा सकता है।
अत: P(दो पुरुष) 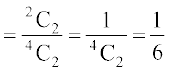
प्रश्नावली 16.3
1. प्रतिदर्श समष्टि S = {ω1, ω2, ω3, ω4, ω5, ω6, ω7}के परिणामों के लिए निम्नलिखित में से कौन से प्रायिकता निर्धारण वैध नहीं है:
परिणाम ω 1 ω 2 ω 3 ω 4 ω 5 ω 6 ω 7
(a) 0.1 0.01 0.05 0.03 0.01 0.2 0.6
(b) 






(c) 0.1 0.2 0.3 0.4 0.5 0.6 0.7
(d) – 0.1 0.2 0.3 0.4 – 0.2 0.1 0.3
(e) 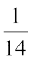
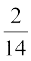
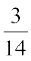
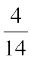
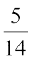


2. एक सिक्का दो बार उछाला जाता है। कम से कम एक पट् प्राप्त होने की क्या प्रायिकता है?
3. एक पासा फेंका जाता है। निम्नलिखित घटनाओं की प्रायिकता ज्ञात कीजिए:
(i) एक अभाज्य संख्या प्रकट होना
(ii) 3 या 3 से बड़ी संख्या प्रकट होना
(iii) 1 या 1 से छोटी संख्या प्रकट होना
(iv) छ: से बड़ी संख्या प्रकट होना
(v) छ: से छोटी संख्या प्रकट होना
4. ताश की गड्डी के 52 पत्तों में से एक पत्ता यादृच्छया निकाला गया है।
(a) प्रतिदर्श समष्टि में कितने बिंदु हैं?
(b) पत्ते का हुकुम का इक्का होने की प्रायिकता क्या है?
(c) प्रायिकता ज्ञात कीजिए कि पत्ता (i) इक्का है (ii) काले रंग का है।
5. एक अनभिनत (unbiased) सिक्का जिसके एक तल पर 1 और दूसरे तल पर 6 अंकित है तथा एक अनभिनत पासा दोनों को उछाला जाता है। प्रायिकता ज्ञात कीजिए कि प्रकट संख्याओं का योग (i) 3 है। (ii) 12 है।
6. नगर परिषद् में चार पुरुष व छ: स्त्रियाँ हैं। यदि एक समिति के लिए यादृच्छया एक परिषद् सदस्य चुना गया है तो एक स्त्री के चुने जाने की कितनी संभावना है?
7. एक अनभिनत सिक्के को चार बार उछाला जाता है और एक व्यक्ति प्रत्येक चित्त पर एक रू जीतता है और प्रत्येक पट् पर 1ण्50रू हारता है। इस परीक्षण के प्रतिदर्श समष्टि से ज्ञात कीजिए कि आप चार उछालों में कितनी विभिन्न राशियाँ प्राप्त कर सकते हैं। साथ ही इन राशियों में से प्रत्येक की प्रायिकता भी ज्ञात कीजिए?
8. तीन सिक्के एक बार उछाले जाते हैं। निम्नलिखित की प्रायिकता ज्ञात कीजिए:
(i) तीन चित्त प्रकट होना (ii) 2 चित्त प्रकट होना
(iii) न्यूनतम 2 चित्त प्रकट होना (iv) अधिकतम 2 चित्त प्रकट होना
(v) एक भी चित्त प्रकट न होना (vi) 3 पट् प्रकट होना
(vii) तथ्यत: 2 पट् प्रकट होना (viii) कोई भी पट् न प्रकट होना
(ix) अधिकतम 2 पट् प्रकट होना
9. यदि किसी घटना A की प्रायिकता  है तो घटना ‘A-नहीं’ की प्रायिकता ज्ञात कीजिए।
है तो घटना ‘A-नहीं’ की प्रायिकता ज्ञात कीजिए।
10. शब्द 'ASSASSINATION' से एक अक्षर यादृच्छया चुना जाता है। प्रायिकता ज्ञात कीजिए कि चुना गया अक्षर (i) एक स्वर (vowel) है (ii) एक व्यंजन (consonant) है।
11. एक लाटरी में एक व्यक्ति 1 से 20 तक की संख्याओं में से छ: भिन्न-भिन्न संख्याएँ यादृच्छया चुनता है और यदि ये चुनी गई छ: संख्याएँ उन छ: संख्याओं से मेल खाती हैं, जिन्हें लाटरी समिति ने पूर्वनिर्धारित कर रखा है, तो वह व्यक्ति इनाम जीत जाता है। लाटरी के खेल में इनाम जीतने की प्रायिकता क्या है? [संकेत: संख्याओं के प्राप्त होने का क्रम महत्वपूर्ण नहीं है]
12. जाँच कीजिए कि निम्न प्रायिकताएँ P(A) और P(B) युक्ति संगत (consistently) परिभाषित की गई हैं:
(i) P(A) = 0.5, P(B) = 0.7, P(A B) = 0.6
B) = 0.6
(ii) P(A) = 0.5, P(B) = 0.4, P(A B) = 0.8
B) = 0.8
13. निम्नलिखित सारणी में खाली स्थान भरिए:

14. P(A) = 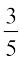 और P(B) =
और P(B) = 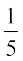 , दिया गया है। यदि A और B परस्पर अपवर्जी घटनाएँ हैं, तो
, दिया गया है। यदि A और B परस्पर अपवर्जी घटनाएँ हैं, तो
P(A या B), ज्ञात कीजिए।
15. यदि E और F घटनाएँ इस प्रकार हैं कि P(E) =  , P(F) =
, P(F) =  और P(E और F) =
और P(E और F) = 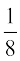 , तो ज्ञात कीजिए (i) P(E या F) (ii) P(E-नहीं और F-नहीं)।
, तो ज्ञात कीजिए (i) P(E या F) (ii) P(E-नहीं और F-नहीं)।
16. घटनाएँ E और F इस प्रकार हैं कि P(E -नहीं और F-नहीं) = 0.25, बताइए कि E और F परस्पर अपवर्जी हैं या नहीं?
17. घटनाएँ A और B इस प्रकार हैं कि P(A) = 0.42, P(B) = 0.48 और P(A और B) = 0.16. ज्ञात कीजिए:
(i) P(A-नहीं) (ii) P(B-नहीं) (iii) P(A या B)
18. एक पाठशाला की कक्षा XI के 40% विद्यार्थी गणित पढ़ते हैं और 30% जीव विज्ञान पढ़ते हैं। कक्षा के 10% विद्यार्थी गणित और जीव विज्ञान दोनों पढ़ते हैं। यदि कक्षा का एक विद्यार्थी यादृच्छया चुना जाता है, तो प्रायिकता ज्ञात कीजिए कि वह गणित या जीव विज्ञान पढ़ता होगा।
19. एक प्रवेश परीक्षा को दो परीक्षणों (Tests)के आधार पर श्रेणीबद्ध किया जाता है। किसी यादृच्छया चुने गए विद्यार्थी की पहले परीक्षण में उत्तीर्ण होने की प्रायकिता 0.8 है और दूसरे परीक्षण में उत्तीर्ण होने की प्रायिकता 0.7 है। दोनों में से कम से कम एक परीक्षण उत्तीर्ण करने की प्रायिकता 0.95 है। दोनों परीक्षणों को उत्तीर्ण करने की प्रायिकता क्या है?
20. एक विद्यार्थी के अंतिम परीक्षा के अंग्रेजी और हिंदी दोनों विषयों को उत्तीर्ण करने की प्रायिकता 0.5 है और दोनों में से कोई भी विषय उत्तीर्ण न करने की प्रायिकता 0.1 है। यदि अंग्रेजी की परीक्षा उत्तीर्ण करने की प्रायिकता 0.75 हो तो हिंदी की परीक्षा उत्तीर्ण करने की प्रायिकता क्या है?
21. एक कक्षा के 60 विद्यार्थियों में से 30 ने एनण् सीण् सीण् (NCC), 32 ने एनण् एसण् एसण् (NSS) और 24 ने दोनों को चुना है। यदि इनमें से एक विद्यार्थी यादृच्छया चुना गया है तो प्रायिकता ज्ञात कीजिए कि
(i) विद्यार्थी ने एन.सी.सी. या एन.एस.एस. को चुना है।
(ii) विद्यार्थी ने न तो एन.सी.सी. और न ही एन.एस.एस. को चुना है।
(iii) विद्यार्थी ने एन.एस.एस. को चुना है किंतु एन.सी.सी. को नहीं चुना है।
विविध उदाहरण
उदाहरण 14 छुट्टियों में वीना ने चार शहरों A, B, C और D की यादृच्छया क्रम में यात्रा की। क्या प्रायिकता है कि उसने
(i) A की यात्रा B से पहले की?
(ii) A की यात्रा B से पहले और B की C से पहले की?
(iii) A की सबसे पहले और B की सबसे अंत में यात्रा की?
(iv) A की या तो सबसे पहले या दूसरे स्थान पर यात्रा की?
(v) A की यात्रा B से एकदम पहले की?
हल वीना द्वारा चार शहरों A, B, C, और D की यात्रा के विभिन्न ढंगों की संख्या 4! अर्थात् 24 है। इसलिए n (S) = 24 क्योंकि प्रयोग की प्रतिदर्श समष्टि के अवयवों की संख्या 24 है। ये सभी परिणाम सम संभाव्य माने गए हैं। इस परीक्षण का प्रतिदर्श समष्टि
S = {ABCD, ABDC, ACBD, ACDB, ADBC, ADCB
BACD, BADC, BDAC, BDCA, BCAD, BCDA
CABD, CADB, CBDA, CBAD, CDAB, CDBA
DABC, DACB, DBCA, DBAC, DCAB, DCBA} है।
(i) मान लीजिए घटना ‘वीना A की यात्रा B से पहले करती है,’ को E से दर्शाते हैं।
इसलिए E = {ABCD, CABD, DABC, ABDC, CADB, DACB
ACBD, ACDB, ADBC, CDAB, DCAB, ADCB}
इस प्रकार 
(ii) मान लीजिए घटना ‘वीना ने A की यात्रा B से पहले और B की यात्रा C से पहले की’ को F से दर्शाते हैं।
यहाँ F = {ABCD, DABC, ABDC, ADBC}
इसलिए 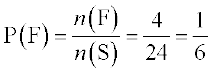
विद्यार्थियों को सलाह दी जाती है कि (iii), (iv) व (v) की प्रायिकता स्वयं ज्ञात करें।
उदाहरण 15 जब ताश के 52 पत्तों की गड्डी से 7 पत्तों का एक समूह बनाया जाता है तो इस बात की प्रायिकता ज्ञात कीजिए कि इसमें (i) सारे बादशाह शामिल हैं (ii) तथ्यत: 3 बादशाह हैं (iii) न्यूनतम 3 बादशाह हैं।
हल समूहों की कुल संभव संख्या = 52C7
(i) 4 बादशाहों सहित समूहों की संख्या = 4C4 × 48C3 (अन्य 3 पत्ते शेष 48 पत्तों में से चुने
जाते हैं)
अत: P (समूह में चार बादशाह) = 
(ii) 3 बादशाह और 4 अन्य पत्तों वाले समूहों की संख्या = 4
इसलिए P (तथ्यत: 3 बादशाह) = 
(iii) P(न्यूनतम 3 बादशाह)
= P(तथ्यत: 3 बादशाह) + P(4 बादशाह)
= 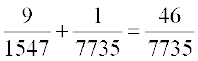
उदाहरण 16 यदि A, B, C किसी यादृच्छिक प्रयोग के संगत तीन घटनाएँ हों तो सिद्ध कीजिए कि


हल विचारिए E = B ∪ C तब
P(A ∪ B ∪ C ) = P(A ∪ E)
=  ... (1)
... (1)
अब P(E) = P(B ∪ C)
= 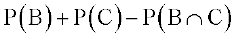 ... (2)
... (2)
साथ ही  =
= 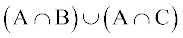 [समुच्चयों के संघ पर सर्वनिष्ठ के वितरण नियम द्वारा]
[समुच्चयों के संघ पर सर्वनिष्ठ के वितरण नियम द्वारा]
अत:  =
= 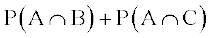 –
– 
= 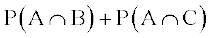 –
– 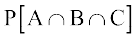 ... (3)
... (3)
(2) और (3) को (1) में प्रयोग करने पर
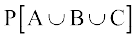 =
= 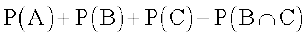 –
–
P(A ∩ B) – P(A ∩ C) – P(A ∩ B ∩ C)
उदाहरण 17 एक रिले दौड़ (relay race) में पाँच टीमों A, B, C, D और E ने भाग लिया।
(a) A, B और C के क्रमश: पहला, दूसरा व तीसरा स्थान पाने की क्या प्रायिकता है?
(b) A, B और C के पहले तीन स्थानों (किसी भी क्रम) पर रहने की क्या प्रायिकता है?
(मान लीजिए कि सभी अंतिम क्रम सम संभाव्य हैं।)
हल यदि हम पहले तीन स्थानों के लिए अंतिम क्रमों के प्रतिदर्श समष्टि पर विचार करें तो पाएँगे कि इसमें  , i.e.,
, i.e.,  = 5 × 4 × 3 = 60 प्रतिदर्श बिंदु हैं और प्रत्येक की प्रायिकता
= 5 × 4 × 3 = 60 प्रतिदर्श बिंदु हैं और प्रत्येक की प्रायिकता 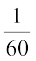 है।
है।
(a) A,B और C क्रमश: प्रथम, दूसरे व तीसरे स्थान पर रहते हैं। इसके लिए एक ही अंतिम क्रम है अर्थात् ABC
अत: P(A, B और C क्रमश: प्रथम, दूसरे व तीसरे स्थान पर रहते हैं) = 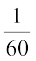
(b) A, B और C पहले तीन स्थानों पर हैं। इसके लिए A, B और C के लिए 3! तरीके हैं। इसलिए इस घटना के संगत 3! प्रतिदर्श बिंदु होंगे।
अत: P (A, B और C पहले तीन स्थानों पर रहते हैं) 
विविध प्रश्नावली
1. एक डिब्बे में 10 लाल, 20 नीली व 30 हरी गोलियाँ रखी हैं। डिब्बे से 5 गोलियाँ यादृच्छया निकाली जाती हैं। प्रायिकता क्या है कि
(i) सभी गोलियाँ नीली हैं ? (ii) कम से कम एक गोली हरी है?
2. ताश के 52 पत्तों की एक अच्छी तरह फेंटी गई गड्डी से 4 पत्ते निकाले जाते हैं। इस बात की क्या प्रायिकता है कि निकाले गए पत्तों में 3 ईंट और एक हुकुम का पत्ता है?
3. एक पासे के दो फलकों में से प्रत्येक पर संख्या ‘1’ अंकित है, तीन फलकों में प्रत्येक पर संख्या ‘2’ अंकित है और एक फलक पर संख्या ‘3’ अंकित है। यदि पासा एक बार फेंका जाता है, तो निम्नलिखित ज्ञात कीजिए:
(i) P(2) (ii) P(1 या 3) (iii) P(3-नहीं)
4. एक लाटरी में 10000 टिकट बेचे गए जिनमें दस समान इनाम दिए जाने हैं। कोई भी ईनाम न मिलने की प्रायिकता क्या है यदि आप (a) एक टिकट खरीदते हैं (b) दो टिकट खरीदते हैं
(c) 10 टिकट खरीदते हैं?
5. 100 विद्यार्थियों में से 40 और 60 विद्यार्थियों के दो वर्ग बनाए गए हैं। यदि आप और आपका एक मित्र 100 विद्यार्थियों में हैं तो प्रायिकता क्या है कि
(a) आप दोनों एक ही वर्ग में हों?
(b) आप दोनों अलग-अलग वर्गों में हों?
6. तीन व्यक्तियों के लिए तीन पत्र लिखवाए गए हैं और प्रत्येक के लिए पता लिखा एक लिफाफा है। पत्रों को लिफाफों में यादृच्छया इस प्रकार डाला गया कि प्रत्येक लिफाफे में एक ही पत्र है। प्रायिकता ज्ञात कीजिए कि कम से कम एक पत्र अपने सही लिफाफे में डाला गया है।
7. A और B दो घटनाएँ इस प्रकार हैं कि P(A) = 0.54, P(B) = 0.69 और P(A ∩ B) = 0.35.
ज्ञात कीजिए:
(i) P(A ∪ B) (ii) P(A' ∩ B') (iii) P(A ∩ B') (iv) P(B ∩ A')
8. एक संस्था के कर्मचारियों में से 5 कर्मचारियों का चयन प्रबंध समिति के लिए किया गया है। पाँच कर्मचारियों का ब्योरा निम्नलिखित है:

इस समूह से प्रवक्ता पद के लिए यादृच्छया एक व्यक्ति का चयन किया गया। प्रवक्ता के पुरुष या 35 वर्ष से अधिक आयु का होने की क्या प्रायिकता है?
9. यदि 0, 1, 3, 5 और 7 अंकों द्वारा 5000 से बड़ी चार अंकों की संख्या का यादृच्छया निर्माण किया गया हो तो पाँच से भाज्य संख्या के निर्माण की क्या प्रायिकता है जब,
(i) अंकों की पुनरावृत्ति नहीं की जाए? (ii) अंकों की पुनरावृत्ति की जाए?
10. किसी अटैची के ताले में चार चक्र लगे हैं जिनमें प्रत्येक पर 0 से 9 तक 10 अंक अंकित हैं। ताला चार अंकों के एक विशेष क्रम (अंकों की पुनरावृत्ति नहीं) द्वारा ही खुलता है। इस बात की क्या प्रायिकता है कि कोई व्यक्ति अटैची खोलने के लिए सही क्रम का पता लगा ले?
सारांश
इस अध्याय में हमने प्रायिकता की अभिगृहीतीय तरीका के विषय में पढ़ा है। इस अध्याय की मुख्य विशेषताएँ निम्नलिखित हैं:
प्रतिदर्श समष्टि: सभी संभावित परिणामों का समुच्चय
प्रतिदर्श बिंदु: प्रतिदर्श समष्टि के अवयव
घटना: प्रतिदर्श समष्टि का एक उपसमुच्चय
असंभव घटना: रिक्त समुच्चय
निश्चित घटना: पूर्ण प्रतिदर्श समष्टि
पूरक घटना या नहीं-घटना : समुच्चय A′ या S – A
घटना A या B: समुच्चय A ∪ B
घटना A और B: समुच्चय A ∩ B
घटना A किंतु B नहीं: समुच्चय A – B
परस्पर अपवर्जी घटनाएँ: A और B परस्पर अपवर्जी होती हैं यदि A  B =
B =
नि:शेष व परस्पर अपवर्जी घटनाएँ : घटनाएँ E1, E2,..., En परस्पर अपवर्जी व नि:शेष हैं यदि E1 ∪ E2 ∪ ... ∪ En = S और Ei ∩ Ej = φ ट प ≠ र
प्रायिकता : प्रत्येक प्रतिदर्श बिंदु ωi के संगत एक संख्या P (ωi) एेसी है कि
(i) 0 ≤ P (ωi) ≤ 1 (ii)  सभी ωi
सभी ωi  S = 1
S = 1
(iii) P(A) =  सभी
सभी  i ∈ A
i ∈ A
संख्या P(ωi) परिणाम ωiण् की प्रायिकता कहा जाता है।
सम संभावित परिणाम : समान प्रायिकता वाले सभी परिणाम
घटना की प्रायिकता : एक सम संभावित परिणामों वाले परिमित प्रतिदर्श समष्टि के लिए घटना A की प्रायिकता  ,जहाँ द(A) = समुच्चय A में अवयवों की संख्या और द(S) = समुच्चय S में अवयवों की संख्या
,जहाँ द(A) = समुच्चय A में अवयवों की संख्या और द(S) = समुच्चय S में अवयवों की संख्या
यदि A और B कोई दो घटनाएँ हैं, तो
P(A या B) = P (A) + P(B) – P (A और B)
समतुल्यत: P (A  B) = P (A) + P (B) – P (A
B) = P (A) + P (B) – P (A  B)
B)
यदि A और B परस्पर अपवर्जी हैं, तो P (A या B) = P(A) + P(B)
किसी घटना A के लिए
P(A–नहीं) = 1 – P(A)
एेतिहासिक पृष्ठभूामि
प्रायिकता सिद्धांत का विकास, गणित की अन्य शाखाओं की भाँति, व्यावहारिक कारणों से हुआ है। इसकी उत्पत्ति 16वीं शताब्दी में हुई थी जब इटली ने एक चिकित्सक तथा गणितज्ञ Jerome Cardan (1501-1576) ने इस विषय पर पहली पुस्तक ‘संयोग के खेलों पर, (Biber de Ludo Aleae) लिखी। यह पुस्तक उनके मरणोपरांत सन् 1633 में प्रकाशित हुई।
सन् 1654 में, Chevaliar de Mere नामक जुआरी ने, पासे से संबधित कुछ समस्याओं को लेकर सुप्रसिद्ध फ्रांसीसी दार्शनिक एवं गणितज्ञ Blaise Pascal (1623-1662) से संपर्क किया। Pascal इस प्रकार की समस्याओं में रुचि लेने लगे और उन्होंने इसकी चर्चा विख्यात फ्रांसीसी गणितज्ञ Pierre de Fermat (1601-1665) से की। Pascal और Fermat दोनों ने स्वतंत्र रूप से समस्याओं को हल किया।
Pascal और Fermat के अतिरिक्त एक डच निवासी Christian Huygenes (1929-1695), एक स्विस निवासी J.Bernoulli (1651-1705), एक फ्रांसीसी A.De Moivre (1667-1754), एक अन्य फ्रांस निवासी Pierre Laplace (1749-1827) तथा रूसी P.L.Chebyechav (1821-1894), A.A.Morkov (1856-1922) और A.N.Kolmogorove ने भी प्रायिकता सिद्धांत में विशिष्ट योगदान दिया। प्रायिकता सिद्धांत के अभिगृहीतिकरण का श्रेय Kolmogorove को मिला है। सन 1933 में प्रकाशित उनकी पुस्तक ‘प्रायिकता के आधार’ (Foundation of Probability) में प्रायिकता को समुच्चय फलन के रूप में प्रस्तुत किया गया है और यह पुस्तक एक क्लासिक (Classic) मानी जाती है।
