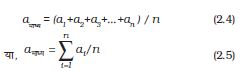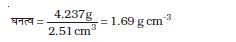Table of Contents

अध्याय 2
मात्रक एवं मापन
2.1 भूमिका
2.2 मात्रकों की अंतर्राष्ट्रीय प्रणाली
2.3 लम्बाई का मापन
2.4 द्रव्यमान का मापन
2.5 समय का मापन
2.6 यथार्थता, यंत्रों की परिशुद्धता एवं मापन में त्रुटि
2.7 सार्थक अंक
2.8 भौतिक राशियों की विमाएँ
2.9 विमीय सूत्र एवं विमीय समीकरणें
2.10 विमीय विश्लेषण एवं इसके अनुप्रयोग
सारांश
अभ्यास
अतिरिक्त अभ्यास
2.1 भूमिका
किसी भौतिक राशि का मापन, एक निश्चित, आधारभूत, यादृच्छिक रूप से चुने गए मान्यताप्राप्त, संदर्भ-मानक से इस राशि की तुलना करना है। यह संदर्भ-मानक मात्रक कहलाता है। किसी भी भौतिक राशि की माप को मात्रक के आगे एक संख्या (आंकिक संख्या) लिखकर व्यक्त किया जाता है। यद्यपि हमारे द्वारा मापी जाने वाली भौतिक राशियों की संख्या बहुत अधिक है, फिर भी, हमें इन सब भौतिक राशियों को व्यक्त करने के लिए, मात्रकों की सीमित संख्या की ही आवश्यकता होती है, क्योंकि, ये राशियाँ एक दूसरे से परस्पर संबंधित हैं। मूल राशियों को व्यक्त करने के लिए प्रयुक्त मात्रकों को मूल मात्रक कहते हैं। इनके अतिरिक्त अन्य सभी भौतिक राशियोें के मात्रकों को मूल मात्रकों के संयोजन द्वारा व्यक्त किया जा सकता है। इस प्रकार प्राप्त किए गए व्युत्पन्न राशियों के मात्रकों को व्युत्पन्न मात्रक कहते हैं। मूल-मात्रकों और व्युत्पन्न मात्रकों के सम्पूर्ण समुच्चय को मात्रकों की प्रणाली (या पद्धति) कहते हैं।
2.2 मात्रकों की अंतर्राष्ट्रीय प्रणाली
बहुत वर्षों तक मापन के लिए, विभिन्न देशों के वैज्ञानिक, अलग-अलग मापन प्रणालियों का उपयोग करते थे। अब से कुछ समय-पूर्व तक एेसी तीन प्रणालियाँ - CGS प्रणाली, FPS ddd(या ब्रिटिश) प्रणाली एवं MKS प्रणाली, प्रमुखता से प्रयोग में लाई जाती थीं।
इन प्रणालियों में लम्बाई, द्रव्यमान एवं समय के मूल मात्रक क्रमशः इस प्रकार हैं :
• CGS प्रणाली में, सेन्टीमीटर, ग्राम एवं सेकन्ड।
• FPS प्रणाली में, फुट, पाउन्ड एवं सेकन्ड।
• MKS प्रणाली में, मीटर, किलोग्राम एवं सेकन्ड।
आजकल अंतर्राष्ट्रीय स्तर पर मान्य प्रणाली "सिस्टम इन्टरनेशनल डि यूनिट्स" है (जो फ्रेंच भाषा में "मात्रकों की अंतर्राष्ट्रीय प्रणाली" कहना है)। इसे संकेताक्षर में SI लिखा जाता है। SI प्रतीकों, मात्रकों और उनके संकेताक्षरों की योजना अंतरराष्ट्रीय माप-तोल ब्यूरो (बी.आई.पी.एम.) द्वारा 1971 में विकसित की गई थी एवं नवंबर, 2018 में आयोजित माप-तोल के महासम्मेलन में संशोधित की गई। यह योजना अब वैज्ञानिक, तकनीकी, औद्योगिक एवं व्यापारिक कार्यों में अंतर्राष्ट्रीय स्तर पर उपयोग हेतु अनुमोदित की गई। SI मात्रकों की 10 की घातों पर आधारित (दाश्मिक) प्रकृति के कारण, इस प्रणाली के अंतर्गत रूपांतरण अत्यंत सुगम एवं सुविधाजनक है। हम इस पुस्तक में SI मात्रकों का ही प्रयोग करेंगे।
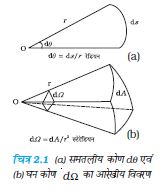
SI में सात मूल मात्रक हैं, जो सारणी 2.1 में दिए गए हैं। इन सात मूल मात्रकों के अतिरिक्त दो पूरक मात्रक भी हैं जिनको हम इस प्रकार परिभाषित कर सकते हैं : (i) समतलीय कोण, dθ चित्र 2.1(a) में दर्शाए अनुसार वृत्त के चाप की लम्बाई ds और इसकी त्रिज्या r का अनुपात होता है। तथा (ii) घन-कोण,  चित्र 2.1(b) में दर्शाए अनुसार शीर्ष O को केन्द्र की भांति प्रयुक्त करके उसके परितः निर्मित गोलीय पृष्ठ के अपरोधन क्षेत्र dA तथा त्रिज्या r के वर्ग का अनुपात होता है। समतलीय कोण का मात्रक रेडियन है जिसका प्रतीक rad है एवं घन कोण का मात्रक स्टेरेडियन है जिसका प्रतीक sr है। ये दोनों ही विमाविहीन राशियाँ हैं।
चित्र 2.1(b) में दर्शाए अनुसार शीर्ष O को केन्द्र की भांति प्रयुक्त करके उसके परितः निर्मित गोलीय पृष्ठ के अपरोधन क्षेत्र dA तथा त्रिज्या r के वर्ग का अनुपात होता है। समतलीय कोण का मात्रक रेडियन है जिसका प्रतीक rad है एवं घन कोण का मात्रक स्टेरेडियन है जिसका प्रतीक sr है। ये दोनों ही विमाविहीन राशियाँ हैं।
* इन परिभाषाओं में प्रयुक्त संख्याओं के मान, न तो याद रखने की आवश्यकता है, न परीक्षा में पूछे जाने की। ये यहाँ पर केवल इनके मापन की यथार्थता की सीमा का संकेत देने के लिए दिए गए हैं। प्रौद्योगिकी के विकास के साथ मापन की तकनीकों में भी सुधार होता है, परिणामस्वरूप, मापन अधिक परिशुद्धता से होता है। इस प्रगति के साथ तालमेल बनाए रखने के लिए मूल मात्रकों को संशोधित किया जाता है।
ध्यान दीजिए, मोल का उपयोग करते समय मूल सत्ताओं का विशेष रूप से उल्लेख किया जाना चाहिए। ये मूल सत्ताएँ परमाणु, अणु, आयन, इलेक्ट्रॉन, अन्य कोई कण अथवा इसी प्रकार के कणों का विशिष्ट समूह हो सकता है।
SI मात्रकों के सामान्य गुणज और अपवर्तकों को व्यक्त करने वाले उपसर्ग और उनके प्रतीक परिशिष्ट (A2) में दिए गएहैं। भौतिक राशियों, रासायनिक तत्वों और नाभिकों के संकेतों के उपयोग संबंधी सामान्य निर्देश परिशिष्ट (A7) में दिए गए हैं और आपके मार्गदर्शन तथा तात्कालिक संदर्भ के लिए SI मात्रकों एवं अन्य मात्रकों संबंधी निर्देश परिशिष्ट (A8)में दिए गए हैं।
2.3 लम्बाई का मापन
लम्बाई मापन की कुछ प्रत्यक्ष विधियों से आप पहले ही से परिचित हैं। उदाहरण के लिए, आप जानते हैं कि 10–3 m से 102 m तक की लम्बाइयाँ मीटर पैमाने का उपयोग करके ज्ञात की जाती हैं। 10–4 m की लम्बाई को यथार्थता से मापने के लिए हम वर्नियर कैलिपर्स का उपयोग करते हैं। स्क्रू-गेज (पेंचमापी) और गोलाईमापी (स्फेरोमीटर) का उपयोग 10–5 m तक की लम्बाइयों को मापने में किया जाता है। इन परिसरों से बाहर की लम्बाइयों को मापने के लिए हमें कुछ परोक्ष विधियों का सहारा लेना होता है।
2.3.1 बड़ी दूरियों का मापन
बहुत बड़ी दूरियाँ, जैसे किसी ग्रह अथवा तारे की पृथ्वी से दूरी, प्रत्यक्ष-रूप से किसी मीटर पैमाने की सहायता से ज्ञात नहीं की जा सकती है। एेसी दशाओं में महत्वपूर्ण विधि जिसे लम्बन-विधि कहते हैं, का उपयोग किया जाता है।
जब आप किसी पेंसिल को अपने सामने पकड़ ते हैं और पृष्ठभूमि (माना दीवार) के किसी विशिष्ट बिन्दु के सापेक्ष पेंसिल को पहले अपनी बायीं आँख A से (दायीं आँख बंद रखते हुए) देखते हैं, और फिर दायीं आँख B से (बायीं आँख बंद रखते हुए), तो आप पाते हैं, कि दीवार के उस बिन्दु के सापेक्ष पेंसिल की स्थिति परिवर्तित होती प्रतीत होती है। इसे लम्बन कहा जाता है। दो प्रेक्षण बिन्दुओं (A एवं B) के बीच की दूरी को आधारक कहा जाता है। इस उदाहरण में दोनों आँखों के बीच की दूरी आधारक है।
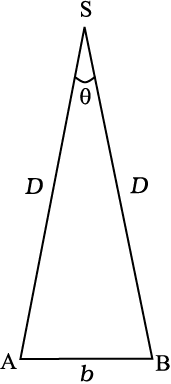
लम्बन विधि द्वारा किसी दूरस्थ ग्रह S की दूरी D ज्ञात करने के लिए, हम इसको, पृथ्वी पर दो विभिन्न स्थितियों (वेधशालाओं) A एवं B से, एक ही समय पर देखते हैं। A एवं B के बीच की दूरी AB = b है। चित्र 2.2 देखिए। इन दो स्थितियों से ग्रह की प्रेक्षण दिशाओं के बीच का कोण माप लिया जाता है। चित्र 2.2 में θ द्वारा दर्शाया गया यह कोण ∠ASB लम्बन कोण या लम्बनिक कोण कहलाता है।
क्योंकि, ग्रह की पृथ्वी से दूरी बहुत अधिक है  और, इसलिए, कोण θ बहुत ही छोटा है। एेसी दशा में हम AB को, केन्द्र S और त्रिज्या D वाले वृत्त का, लम्बाई b का चाप मान सकते हैं।
और, इसलिए, कोण θ बहुत ही छोटा है। एेसी दशा में हम AB को, केन्द्र S और त्रिज्या D वाले वृत्त का, लम्बाई b का चाप मान सकते हैं।  त्रिज्या AS = BS, ∴ AB = b = D θ
त्रिज्या AS = BS, ∴ AB = b = D θ
जहाँ θ रेडियन में है।
अतः 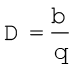
D के निर्धारण के पश्चात् हम इसी विधि द्वारा ग्रह का आमाप अथवा कोणीय व्यास भी निर्धारित कर सकते हैं। यदि d ग्रह का व्यास और α उसका कोणीय आमाप (d द्वारा पृथ्वी के किसी बिन्दु पर अंतरित कोण) हो, तो
α = d/D (2.2)
कोण α को, पृथ्वी की उसी अवस्थिति से मापा जा सकता है। यह ग्रह के दो व्यासतः विपरीत (व्यास के विपरीत सिरों पर स्थित) बिन्दुओं को दूरदर्शक द्वारा देखने पर प्राप्त दो दिशाओं के बीच बना कोण है। क्योंकि D का मान ज्ञात है, अतः ग्रह के व्यास d का मान समीकरण (2.2) की सहायता से ज्ञात किया जा सकता है।
उदाहरण 2.1 (a) 10 (डिग्री) (b) 1′ (1 आर्क मिनट) एवं (c) 1″ (1आर्क सेकंड) के कोणों के मान रेडियन में परिकलित कीजिए (3600 =2π rad, 10=60′ एवं 1′ = 60 ″ लीजिए)।
हल (a) हमें ज्ञात है 3600 = 2π rad
10 = (π /180) rad = 1.745×10–2 rad
(b) 10 = 60′ = 1.745×10–2 rad
1′ = 2.908×10–4 rad = 2.91×10–4 rad
(c) 1′ = 60″ = 2.908×10–4 rad
1″ = 4.847×10–4 rad = 4.85×10–6 rad
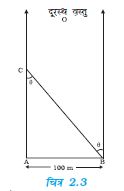
उदाहरण 2.2 एक व्यक्ति अपने पास की किसी मीनार की अपने से दूरी का आकलन करना चाहता है। वह मीनार C के सामने किसी बिन्दु A पर खड़ ा होता है और AC की सीध में बहुत दूर स्थित किसी बिन्दु O को देखता है। फिर वह, AC के लम्बवत् 100 m दूर स्थित बिन्दु B तक चलता है और वहाँ से O एवं C को फिर देखता है। क्योंकि O बहुत अधिक दूरी पर है, BO एवं AO की दिशाएँ व्यावहारिक रूप में एक ही हैं, लेकिन वह पाता है कि C की दृष्टि रेखा मूल दृष्टि रेखा के सापेक्ष θ = 400 पर घूम गई है (θ को लम्बन कहा जाता है)। उसकी मूल स्थिति A से मीनार C की दूरी का आकलन कीजिए।
चित्र 2.3
हल दिया गया है, लम्बन कोण θ =400
चित्र 2.3 से, AB = AC tan θ
AC = AB/tanθ = 100 m/tan 400
= 100 m/0.8391 = 119 m
उदाहरण 2.3 पृथ्वी के दो व्यासतः विपरीत बिन्दुओं A एवं B से चन्द्रमा का प्रेक्षण किया गया। प्रेक्षण की दो दिशाओं के बीच, चन्द्रमा पर अंतरित कोण θ की माप
1o 54′ है। पृथ्वी का व्यास लगभग 1.276 × 107 m, है। पृथ्वी से चन्द्रमा की दूरी का अभिकलन कीजिए।
हल ज्ञात है θ = 1° 54′ = 114′
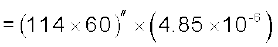 rad
rad 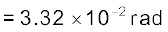
2.3.2 अति सूक्ष्म दूरियों का मापन : अणु का आकार
अणु के व्यास (10–8 m से 10–10 m) जैसी अत्यंत सूक्ष्म दूरियों के मापन के लिए हमें विशिष्ट विधियों का अनुसरण करना होता है। इनके लिए हम पेंचमापी जैसे मापक-यंत्रों का उपयोग नहीं कर सकते। यहाँ तक कि सूक्ष्मदर्शी की भी अपनी कुछ सीमाएँ हैं। एक प्रकाशीय सूक्ष्मदर्शी द्वारा किसी निकाय की जाँच के लिए दृश्य-प्रकाश का उपयोग किया जाता है। प्रकाश के लक्षण तरंग जैसे होने के कारण, प्रकाशीय सूक्ष्मदर्शी को,
अधिक से अधिक, प्रयुक्त प्रकाश के तरंगदैर्घ्य के बराबर विभेदन के लिए ही प्रयोग में लाया जा सकता है। (इस विषय में विस्तृत विवेचन आपको कक्षा XII की भौतिकी की पाठ्य पुस्तक में मिलेगा)। दृश्य प्रकाश की तरंगदैर्घ्य का परिसर 4000 Å से 7000 Å है। (1 Å = 10-10 m)। अतः प्रकाशीय सूक्ष्मदर्शी इससे छोटे आकार के कणों का विभेदन नहीं कर सकता। दृश्य प्रकाश के स्थान पर हम, इलेक्ट्रॉन-पुंज का उपयोग कर सकते हैं। इलेक्ट्रॉन पुंजों को उचित रीति से अभिकल्पित वैद्युत एवं चुम्बकीय क्षेत्रों द्वारा फोकसित किया जा सकता है। इस प्रकार के इलेक्ट्रॉन-सूक्ष्मदर्शी का विभेदन भी अंततः इसी तथ्य द्वारा सीमित होता है कि इलेक्ट्रॉन भी तरंगों की तरह व्यवहार कर सकते हैं (इस विषय में विस्तार से आप कक्षा XII में पढ़ेंगे)। किसी इलेक्ट्रॉन की तरंगदैर्घ्य 1 Å के अंश के बराबर कम हो सकती है। 0.6 Å विभेदन क्षमता तक के इलेक्ट्रॉन सूक्ष्मदर्शी विकसित किए जा चुके हैं। इनके द्वारा, लगभग, पदार्थों के अणुओं और परमाणुओं का विभेदन संभव हो गया है। हाल ही में विकसित सुरंगन सूक्ष्मदर्शिकी द्वारा भी 1Å से सूक्ष्मतर विभेदन प्राप्त कर लिया गया है। इनके द्वारा अब अणुओं की आमाप का आकलन संभव है।
ओलीक अम्ल अणु के साइज़ का आकलन करने की एक सरल विधि नीचे दी गई है। ओलीक अम्ल एक साबुनी द्रव है जिसके अणु का साइज़ 10–9 m कोटि का है।
इस विधि का मूल आधार, जल के पृष्ठ पर ओलीक अम्ल की एक एकाण्विक परत बनाना है।
इसके लिए, पहले हम 1 cm3 ओलीक अम्ल को एेल्कोहॉल में घोल कर 20 cm3 घोल बनाते हैं। इस घोल का 1 cm3 लेकर एेल्कोहॉल में पुनः 20 cm3 घोल बनाते हैं। अब इस घोल की सांद्रता 1/20*20 cm3 ओलीक अम्ल/ cm3 घोल हुई। इसके बाद एक बड़ े नांद में पानी लेकर, उसके ऊपर लायकोपोडियम पाउडर छिड़ क कर, लाइकोपोडियम पाउडर की एक पतली फिल्म जल के पृष्ठ के ऊपर बनाते हैं। फिर ओलीक अम्ल के पहले बनाए गए घोल की एक बूंद इसके ऊपर रखते हैं। ओलीक अम्ल की यह बूंद जल के पृष्ठ के ऊपर लगभग वृत्ताकार, एक अणु मोटाई की फिल्म के रूप में फैल जाती है। इस प्रकार बनी तनु फिल्म का व्यास माप कर इसका क्षेत्रफल A ज्ञात किया जा सकता है। माना कि हमने जल के पृष्ठ पर n बूंदें ओलीक अम्ल घोल की डालीं। यदि प्रारंभ में ही हम एक बूंद का अनुमानित आयतन (V cm3) ज्ञात कर लें,
तो घोल की n बूंदों का आयतन = nV cm3
इस घोल में विद्यमान ओलीक अम्ल का आयतन nv(1/20*20)cm3
ओलीक अम्ल का यह घोल तेजी से जल के पृष्ठ पर फैल कर t मोटाई की पतली फिल्म बना लेता है। यदि इस फिल्म का क्षेत्रफल A cm2 है, तो फिल्म की मोटाई
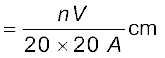 (2.3)
(2.3)
यदि हम यह मान लें कि फिल्म एक एकाण्विक मोटाई की है तो 't' ओलीक अम्ल के अणु की आमाप अथवा व्यास बन जाता है। इस मोटाई का मान 10–9 m की कोटि का आता है।
उदाहरण 2.5 यदि किसी नाभिक का आमाप (जो वास्तव में 10–15 से 10–14 m के परिसर में है) बढ़ाकर एक तीक्ष्ण पिन की नोक (10–5m से 10–4m के परिसर में) के बराबर कर दिया जाए, तो परमाणु का लगभग आमाप क्या है?
हल नाभिक की आमाप 10–15 m से 10–14 m के परिसर में है तीक्ष्ण पिन की नोक 10–5 m से 10–4 m के परिसर में ले सकते हैं। इस तरह, हमने नाभिक की आमाप को 1010 गुणा बढ़ा दिया है। परमाणु का सामान्य आकार 10–10 m की कोटि का है। अतः उसी अनुपात में बढ़ाने पर इसकी आमाप 1m हो जाएगी। अतः किसी परमाणु में नाभिक आमाप में उतना ही छोटा है जितनी छोटी लगभग 1m व्यास के गोले के केन्द्र पर रखे गए तीक्ष्ण पिन की नोक होती है।
2.3.3 लम्बाइयों का परिसर
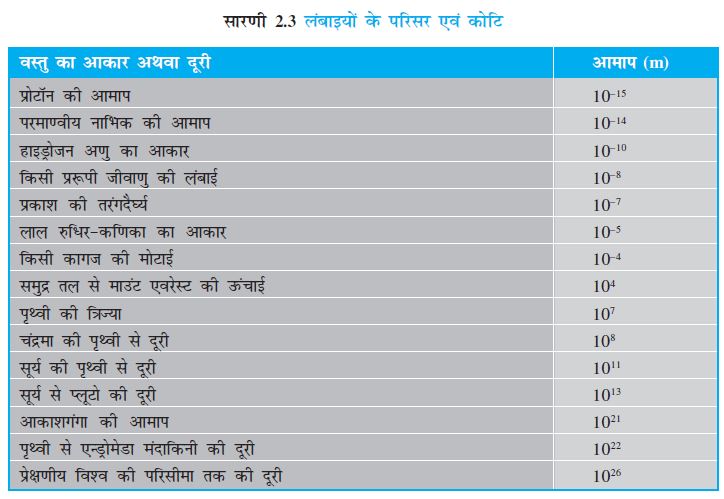
हमें विश्व में जो पिण्ड दिखाई देते हैं उन पिण्डों की आमापों में अंतर का एक विस्तृत परिसर है। जिसमें एक ओर 10–14 m कोटि की आमाप का किसी परमाणु का सूक्ष्म नाभिक है, तो दूसरी ओर 1026 m कोटि की आमाप का दृश्यमान विश्व का परिसर है। सारणी 2.3 में इनमें से कुछ पिण्डों की आमापों और दूरियों की कोटि और परास दिए गए हैं।
अत्यंत सूक्ष्म और बहुत बड़ ी दूरियों के मापन के लिए हम लम्बाई के कुछ विशिष्ट मात्रक भी प्रयोग में लाते हैं। ये हैं,
1 फर्मी = 1 f = 10–15 m
1 एंग्सट्रम = 1 Å = 10–10 m
1 खगोलीय मात्रक = 1 AU (सूर्य से पृथ्वी की औसत दूरी)
= 1.496 × 1011 m
1 प्रकाश वर्ष = 1 ly = 9.46 × 1015 m
(3 × 108 m s–1 के वेग से प्रकाश
द्वारा 1 सेकंड में चली गई दूरी में 1 वर्ष)
1 पारसेक = 3.08 × 1016 m
(वह दूरी जिस पर पृथ्वी की कक्षा की औसत त्रिज्या 1 आर्क सेकण्ड का कोण अंतरित करे, 1 पारसेक कहलाती है।)
2.4 द्रव्यमान का मापन
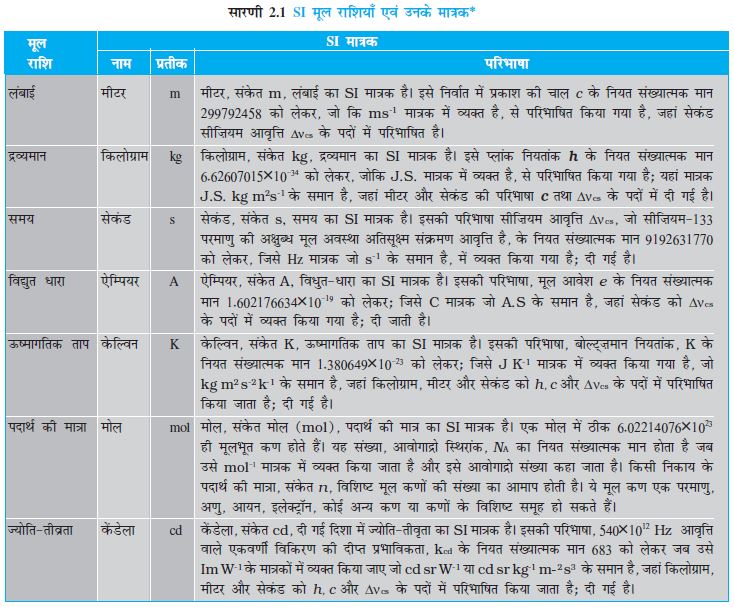
द्रव्यमान पदार्थ का एक आधारभूत गुण है। यदि पिण्ड के ताप, दाब या दिक्काल में उसकी अवस्थिति पर निर्भर नहीं करता। द्रव्यमान का SI मात्रक किलोग्राम (kg) है। इसे प्लांक नियतांक h के नियत संख्यात्मक मान 6.62607015×10-34 को लेकर जो कि J.S मात्रक में व्यक्त है, से परिभाषित किया गया है; मात्रक J.S kg m2 s-1 के समान है, जहाँ मीटर और सेकंड को c और ∆νcs के पदों में परिभाषित किया गया है।
परमाणुओं और अणुओं के द्रव्यमानों के संबंध में किलोग्राम एक सुविधाजनक मात्रक नहीं है। अतः अणुओं, परमाणुओं के द्रव्यमान व्यक्त करने के लिए द्रव्यमान के एक महत्वपूर्ण मानक मात्रक, जिसे एकीकृत परमाणु संहति मात्रक (u) कहते हैं, का प्रयोग करते हैं, जिसकी स्थापना परमाणुओं के द्रव्यमानों को इस प्रकार, व्यक्त करने के लिए की गई है:
सामान्य वस्तुओं के द्रव्यमान मापन के लिए हम उसी तरह की सामान्य तुला का उपयोग करते हैं जैसी परचून की दुकान में पाई जाती है। विश्व में पाए जाने वाले विशाल पिण्डों जैसे ग्रहों, तारों आदि के द्रव्यमान ज्ञात करने के लिए हम न्यूटन के गुरुत्वाकर्षण के नियम का उपयोग करते हैं (देखिए अध्याय 8)। अति सूक्ष्म कणों, जैसे परमाणुओं, अवपरमाणुक कणों आदि के लघु द्रव्यमानों के मापन के लिए हम द्रव्यमान-स्पेक्ट्रमलेखी का प्रयोग करते हैं, जिसमें, एकसमान विद्युत एवं चुम्बकीय क्षेत्र में गतिमान, आवेशित कणों के प्रक्षेप-पथ की त्रिज्या उस कण के द्रव्यमान के अनुक्रमानुपाती होती है।
2.4.1 द्रव्यमानों के परास
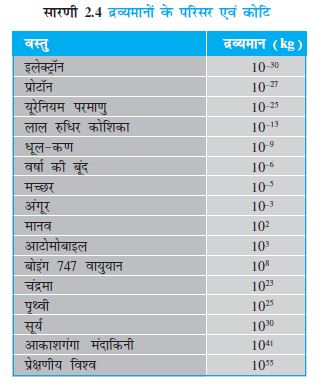
विश्व में हम जो पिण्ड देखते हैं, उनके द्रव्यमानों में अंतर का एक अत्यंत विस्तृत परिसर है। एक ओर इलेक्ट्रॉन जैसा सूक्ष्म कण है जिसका द्रव्यमान 10-30 kg कोटि का है, तो दूसरी ओर लगभग 1055 kg का ज्ञात विश्व है। सारणी (2.4) में विभिन्न द्रव्यमानों के कोटि और परास दिए गए हैं।
2.5 समय का मापन
किसी भी समय-अंतराल को मापने के लिए हमें घड़ ी की आवश्यकता होती है। अब हम समय-मापन हेतु समय का परमाण्वीय मानक प्रयोग करते हैं जो सीज़ियम परमाणु में उत्पन्न आवर्त कम्पनों पर आधारित है। यही राष्ट्रीय मानक के रूप में प्रयुक्त सीज़ियम घड़ ी, जिसे परमाणु घड़ ी भी कहते हैं, का आधार है। एेसे मानक अनेक प्रयोगशालाओं में उपलब्ध हैं। सीज़ियम परमाणु घड़ ी में एक सेकन्ड, सीज़ियम-133 परमाणु के निम्नतम ऊर्जा स्तर के दो अतिसूक्ष्म स्तरों के मध्य संक्रमण के तदनुरूपी विकिरणों के 9,192,631,770 कम्पनों के लिए आवश्यक है। इस सीज़ियम परमाणु घड़ ी की समय दर को, सीज़ियम परमाणु के कम्पन ठीक उसी प्रकार नियंत्रित करते हैं जैसे संतुलन चक्र के कम्पन सामान्य कलाई घड़ ी को अथवा छोटे क्वाट्ρज़ क्रिस्टल के कम्पन किसी क्वाट्ρज़ कलाई घड़ ी को करते हैं।
सीज़ियम परमाणु घड़ियाँ अत्यंत यथार्थ होती हैं। सिद्धान्ततः वे एक सुबाह्य मानक उपलब्ध कराती हैं। चार सीज़ियम परमाणु घड़ ियों के माध्यम से, समय-अंतराल के राष्ट्रीय मानक ‘सेकन्ड’ का अनुरक्षण किया जाता है। समय के भारतीय मानक के अनुरक्षण के लिए नयी दिल्ली की राष्ट्रीय भौतिकी प्रयोगशाला में एक सीज़ियम घड़ ी लगाई गई है।
हमारे देश में, सभी भौतिक मानकों (जिनमें समय और आवृत्ति आदि के मानक भी शामिल हैं) के अनुरक्षण और
सुधार का दायित्व NPL का है। ध्यान दें कि भारतीय मानक समय (IST), इन चार घड़ियों के समुच्चय से जुड़ ा है। दक्ष सीज़ियम परमाणु घड़ ियाँ इतनी अधिक यथार्थ हैं कि इनके द्वारा समय बोध में अनिश्चितता ± 1 × 10–15, अर्थात् 1015 सेकन्ड में एक सेकन्ड से भी कम की त्रुटि होने की रहती है। ये एक वर्ष में 3 नैनो सेकंड से ज्यादा इधर-उधर नहीं होती। समय मापन की इस आश्चर्यजनक यथार्थता को ध्यान में रखकर ही लम्बाई के SI मात्रक को प्रकाश द्वारा (1/299, 792, 458) सेकंड में चलित दूरी के रूप में व्यक्त किया गया है (सारणी 2.1)।
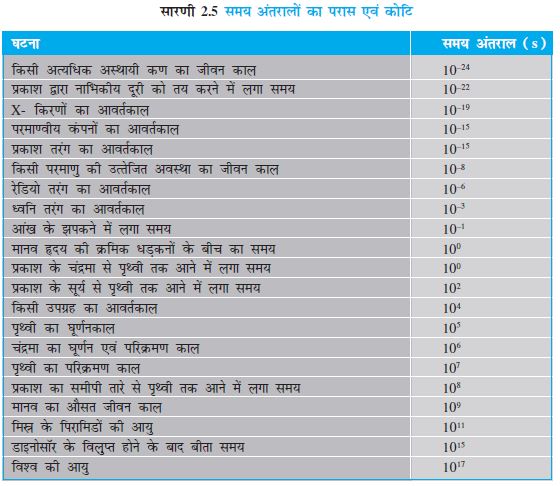
विश्व में होने वाली घटनाओं के समय-अंतरालों में अंतर का परिसर बहुत व्यापक है। सारणी 2.5, कुछ प्रारूपिक समय-अंतरालों के परास और कोटि दर्शाती है।
सारणी 2.3 एवं 2.5 में दर्शायी गई संख्याओं में आश्चर्यजनक अनुरूपता है। इनका ध्यानपूर्वक अवलोकन करने पर आप देख सकते हैं कि हमारे विश्व में विशालतम और लघुतम पिण्डों की लम्बाइयों का अनुपात लगभग 1041 है तथा यह भी कम रुचिकर नहीं है कि विश्व की घटनाओं से संबद्ध सबसे बड़ े और सबसे छोटे समय-अंतरालों का अनुपात भी 1041 ही है। यह संख्या 1041, सारणी 2.4 में फिर से प्रकट होती है, जिसमें कुछ पिण्डों के प्रारूपिक द्रव्यमानों को सूचीबद्ध किया गया है। हमारे विश्व के विशालतम एवं लघुतम पिण्डों के द्रव्यमानों का अनुपात लगभग (1041)2 है। क्या इन विशाल संख्याओं की यह आश्चर्यजनक, अनुरूपता मात्र संयोग है?
2.6 यथार्थता, यंत्रों की परिशुद्धता एवं मापन में त्रुटि
मापन, समस्त प्रायोगिक विज्ञान एवं प्रौद्योगिकी का मूलाधार है। किसी भी मापन-यंत्र के सभी मापन के परिणामों में कुछ न कुछ अनिश्चितता रहती ही है। यह अनिश्चितता ही त्रुटि कहलाती है। प्रत्येक परिकलित राशि, जो मापित मानों पर
आधारित होती है, में भी कुछ त्रुटि होती है। यहाँ हम दो तकनीकी शब्दों ः यथार्थता और परिशुद्धता में प्रभेद करेंगे। किसी माप की यथार्थता वह मान है जो हमें यह बताता है कि किसी राशि का मापित मान, उसके वास्तविक मान के कितना निकट है जबकि परिशुद्धता यह बताती है कि वह राशि किस विभेदन या सीमा तक मापी गई है।
मापन की यथार्थता कई कारकों पर निर्भर कर सकती है जिनमें मापक यंत्रों का विभेदन या सीमा भी सम्मिलित है। उदाहरण के लिए, माना कि किसी लम्बाई का वास्तविक मान 3.678 cm है। एक प्रयोग में 0.1 cm विभेदन का मापक-यंत्र प्रयोग करके इसका मान 3.5 cm मापा गया, जबकि, दूसरे प्रयोग में अधिक विभेदन वाला (माना 0.01 cm) मापक यंत्र प्रयोग करके उसी लंबाई को 3.38 cm मापा गया। यहाँ पहला माप अधिक यथार्थ है (क्योंकि वास्तविक मान के निकट है) परन्तु कम परिशुद्ध है (क्योंकि इसका विभेदन केवल 0.1 cm है।) जबकि, दूसरा माप कम यथार्थ परन्तु अधिक परिशुद्ध है। अतः मापन में त्रुटियों के कारण हर माप एक सन्निकट माप है। सामान्यतः, मापन में आई त्रुटियों को मुख्य रूप से निम्नलिखित दो श्रेणियों में वर्गीकृत किया जा सकता है ः (a) क्रमबद्ध त्रुटियाँ एवं (b) यादृच्छिक त्रुटियाँ।
क्रमबद्ध त्रुटियाँ
क्रमबद्ध त्रुटियाँ वे त्रुटियाँ हैं जो किसी एक दिशा धनात्मक या फिर ऋणात्मक में प्रवृत्त होती हैं। क्रमबद्ध त्रुटियों के कुछ स्रोत निम्नलिखित हैं :
(b) प्रायोगिक तकनीक या कार्यविधि में अपूर्णता ः
मानव शरीर का ताप ज्ञात करने के लिए यदि आप तापमापी को बगल में लगाकर ताप ज्ञात करेंगे तो यह ताप शरीर के वास्तविक ताप से सदैव ही कुछ कम आएगा। प्रयोग के दौरान बाह्य परिस्थितियाँ (ताप, दाब, वायु वेग, आर्द्रता आदि में परिवर्तन) मापन में क्रमबद्ध त्रुटियाँ प्रस्तुत कर सकती हैं।
सुधरी हुई प्रायोगिकी तकनीकों के उपयोग, प्रयोग के लिए अपेक्षाकृत अच्छे मापन यंत्रों का चयन एवं यथासंभव व्यक्तिगत पूर्वाग्रहों को दूर करके क्रमबद्ध त्रुटियों को कम किया जा सकता है। किसी भी दी गई व्यवस्था के लिए, इन त्रुटियों का कुछ निश्चित सीमाओं तक आकलन किया जा सकता है और पाठ्यांकों को तदनुसार संशोधित किया जा सकता है।
यादृच्छिक त्रुटियाँ
मापन में अनियमित रूप से होने वाली त्रुटियों को यादृच्छिक त्रुटियाँ कहते हैं और इसलिए ये चिह्न और परिमाण में यादृच्छिक हैं। यादृच्छिक त्रुटियाँ, प्रायोगिक अवस्थाओं (ताप, वोल्टता प्रदाय, प्रयोग व्यवस्था के यांत्रिक कम्पन आदि) में होने वाले यादृच्छिक तथा अननुमेय उतार-चढ़ाव के कारण तथा पाठ्यांक के समय प्रेक्षक द्वारा की गई (पूर्वाग्रह रहित) व्यक्तिगत त्रुटियों आदि के कारण होती हैं। उदाहरण के लिए, कोई व्यक्ति एक ही प्रेक्षण को बार-बार दोहराये तो संभव है कि हर बार उसका पाठ्यांक भिन्न हो।
अल्पतमांक त्रुटि
किसी मापक यंत्र द्वारा मापा जा सकने वाला छोटे से छोटा मान उस मापक यंत्र का अल्पतमांक कहलाता है। किसी मापक यंत्र द्वारा लिए गए सभी पाठ्यांक या मापित मान उसके अल्पतमांक तक ही सही होते हैं।
अल्पतमांक त्रुटि एक एेसी त्रुटि होती है जो मापक यंत्र के विभेदन से संबद्ध होती है। उदाहरण के लिए, किसी वर्नियर कैलिपर्स का अल्पतमांक 0.01cm है; किसी गोलाईमापी का अल्पतमांक 0.001 cm हो सकता है। अल्पतमांक त्रुटि को यादृच्छिक त्रुटियों की श्रेणी में एक सीमित परिमाण तक ही रखा जा सकता है; यह त्रुटि क्रमबद्ध और यादृच्छिक दोनों ही के साथ होती है। यदि हम लंबाई मापने के लिए मीटर स्केल का उपयोग करते हैं तो मीटर स्केल में अंकन 1 mm अंतराल पर होता है।
अधिक परिशुद्ध मापन यंत्रों के प्रयोग करके, प्रायोगिक तकनीकों में सुधार, आदि के द्वारा, हम अल्पतमांक त्रुटि को कम कर सकते हैं। प्रेक्षणों को कई बार दोहराने पर प्राप्त सभी प्रेक्षणों के मानों का औसत प्राप्त होता है। यह माध्य मान मापित राशि के वास्तविक मान के अत्यधिक निकट होगा।
2.6.1 निरपेक्ष त्रुटि, आपेक्षिक त्रुटि एवं प्रतिशत त्रुटि
(a) माना कि किसी राशि के कई मापनों के मान a1, a2, a3...., an हैं। प्रायोगिक परिस्थितियों में, इस राशि का सर्वाधिक संभव मान, इन सभी मानों के समांतर माध्य को माना जा सकता है।
क्योंकि जैसा पहले स्पष्ट किया जा चुका है कि यह मानना युक्तिसंगत है कि किसी राशि की व्यष्टिगत माप उस राशि के वास्तविक मान से उतनी ही अधिआकलित हो सकती है, जितनी उसके अवआकलित होने की संभावना होती है।
राशि के व्यष्टिगत और वास्तविक माप के बीच के अंतर के परिमाण को मापन की निरपेक्ष त्रुटि कहते हैं। इसको |∆a | द्वारा निर्दिष्ट किया जाता है। क्योंकि, हमें किसी राशि का वास्तविक मान ज्ञात करने की कोई विधि पता नहीं है, इसलिए हम समांतर माध्य को ही राशि का वास्तविक मान स्वीकार कर लेते हैं। तब हमारी व्यष्टिगत माप में वास्तविक माप से निरपेक्ष त्रुटियाँ इस प्रकार हैं,
∆a1 = a1 – aमाध्य,
∆a2 = a2– aमाध्य,
.... .... ....
.... .... ....
∆a n = an – aमाध्य
ऊपर परिकलित∆a का मान कुछ प्रकरणों के लिए धनात्मक हो सकता है जबकि दूसरे कुछ अन्य प्रकरणों के लिए यह ऋणात्मक हो सकता है। परन्तु निरपेक्ष त्रुटि |∆a| सदैव ही धनात्मक होगी।
(b) भौतिक राशि की निरपेक्ष त्रुटियों के परिमाणों के समांतर माध्य को भौतिक राशि a के मान की अंतिम या माध्य निरपेक्ष त्रुटि कहा जाता है। इसको ∆aमाध्य से निरूपित करते हैं।
अतः,
यदि हम कोई एकल माप लें, तो हमें इसका मान aमाध्य ± ∆aमाध्य के परिसर में कहीं प्राप्त होगा।
अर्थात् a = aमाध्य ± ∆aमाध्य
या,
aमाध्य – ∆aमाध्य ≤ a ≤ aमाध्य + ∆aमाध्य (2.8)
इसका अर्थ यह हुआ कि भौतिक राशि की किसी माप a का मान (aमाध्य+ ∆aमाध्य) तथा (aमाध्य− ∆aमाध्य) के बीच होने की संभावना है।
(c) निरपेक्ष त्रुटि के स्थान पर, हम प्रायः आपेक्षिक त्रुटि या प्रतिशत त्रुटि (δa) का प्रयोग करते हैं। आपेक्षिक त्रुटि, मापित राशि की माध्य निरपेक्ष त्रुटि ∆aमाध्य एवं इसके माध्य मान aमाध्य का अनुपात है।
आपेक्षिक त्रुटि = ∆aमाध्य/aमाध्य (2.9)
जब आपेक्षिक त्रुटि को प्रतिशत में व्यक्त करते हैं, तो इसे प्रतिशत त्रुटि कहा जाता है।
अतः प्रतिशत त्रुटि, δa = (∆aमाध्य/aमाध्य) × 100% (2.10)
आइये, अब हम एक उदाहरण पर विचार करते हैं।

हल
सात दिन के घड़ ी 1 के प्रेक्षणों में अंतर का परिसर 162s है जबकि घड़ ी 2 में यह परिसर 31s का है। घड़ ी 1 द्वारा लिए गए समय के पाठ्यांक, घड़ ी 2 द्वारा लिए गए समय के पाठ्यांकों की तुलना में, मानक समय के अधिक निकट है। महत्वपूर्ण बात यह है कि घड़ ी की शून्यांक त्रुटि, परिशुद्ध कार्य के लिए उतनी महत्वपूर्ण नहीं है जितना इसके समय में होने वाला परिवर्तन है, क्योंकि, शून्यांक त्रुटि को तो कभी भी सरलता से दूर किया जा सकता है। अतः घड़ ी 1 की तुलना में घड़ ी 2 को वरीयता दी जाएगी।
उदाहरण 2.7 हम एक सरल लोलक का दोलन-काल ज्ञात करते हैं। प्रयोग के क्रमिक मापनों में लिए गए पाठ्यांक हैं ः 2.63 s, 2.56s, 2.42 s, 2.71s एवं 2.80 s । निरपेक्ष त्रुटि, सापेक्ष त्रुटि एवं प्रतिशत त्रुटि परिकलित कीजिए।
हल लोलक का औसत दोलन काल,
क्योंकि, सभी काल 0.01 s के विभेदन तक मापे गए हैं, इसलिए समय की सभी मापें दूसरे दशमलव स्थान तक हैं। इस औसत काल को भी दूसरे दशमलव स्थान तक लिखना उचित है।
मापन में त्रुटियाँ हैं :
2.63 s – 2.62 s = 0.01 s
2.56 s – 2.62 s = – 0.06 s
2.42 s – 2.62 s = – 0.20 s
2.71 s – 2.62 s = 0.09 s
2.80 s – 2.62 s = 0.18 s
ध्यान दीजिए, त्रुटियों के भी वही मात्रक हैं जो मापी जाने वाली राशियों के हैं।
सभी निरपेक्ष त्रुटियों का समांतर माध्य (समांतर माध्य के लिए हम केवल परिमाण लेते हैं) हैं :
∆Τमाध्य = [(0.01+ 0.06+0.20+0.09+0.18)s]/5
= 0.54 s/5
= 0.11 s
इसका अर्थ है कि सरल लोलक का दोलन काल (2.62 ± 0.11) s है। अर्थात् इसका मान (2.62 + 0.11) s एवं (2.62 – 0.11) s, अथवा 2.73 s एवं 2.51 s के बीच है। क्योंकि सभी निरपेक्ष त्रुटियों का समांतर माध्य 0.11 s है, अतः इस मान में सेकंड के दसवें अंश में पहले से ही त्रुटि है। इसलिए दोलन काल का मान सेकंड के सौवें भाग तक व्यक्त करने का कोई अर्थ नहीं है। इसको व्यक्त करने का अधिक सही ढंग इस प्रकार है :
T = 2.6 ± 0.1 s
किसी रेखा की लंबाई आप कैसे मापेंगे?
आप कह सकते हैं, इस स्तर तक आने के बाद यह कैसा अटपटा प्रश्न है? लेकिन जरा सोचिए कि यदि यह रेखा सरल-रेखा न हो, तो? अपनी अभ्यास पुस्तिका में या श्याम-पट पर एक टेढ़ी-मेढ़ी रेखा खींचिए। ठीक है, इसकी लंबाई मापना भी कोई बहुत कठिन कार्य नहीं है। आप एक धागा लेंगे, इसे रेखा के ऊपर सावधानीपूर्वक रखेंगे, फिर धागे को फैला कर इसकी लंबाई माप लेंगे।
अब कल्पना कीजिए कि आपको राष्ट्रीय राजमार्ग की या किसी नदी की, या दो रेलवे स्टेशनों के बीच रेल की पटरियों की, या दो राज्यों अथवा देशों के बीच की सीमा रेखा की लंबाई मापनी है। तो इसके लिए, यदि आप 1m या 100m की रस्सी लें, इसे रेखा के अनुदिश रखें, बार-बार इसकी स्थिति बदल कर आगे ले जाएं, तो इसमें जो मानवीय श्रम, समय और खर्च आएगा वह उपलब्धि के अनुपात में बहुत अधिक होगा। इसके अतिरिक्त इस महत्कार्य में त्रुटियाँ अवश्यमेव आ जाएंगी। इस सिलसिले में एक रोचक तथ्य आपको बताएँ। फ्रांस और बेल्जियम की उभयनिष्ठ अंतर्राष्ट्रीय सीमा रेखा है। दोनों देशों के राजकीय दस्तावेजों में दर्ज उसकी लंबाई में बहुत अंतर है।
एक कदम और आगे बढ़ें और समुद्र की तट रेखा अर्थात् वह रेखा जिस पर समुद्र और जमीन एक दूसरे से मिलते हैं, के बारे में विचार करें। इसकी तुलना में तो सड़कों और नदियों में काफी हलके मोड़ होते हैं। इस सबके बावजूद, सभी दस्तावेजों में, जिनमें हमारी स्कूल की पुस्तकें भी शामिल हैं, गुजरात या आंध्रप्रदेश के समुद्र तट की लंबाई या दो राज्यों के बीच की सीमा रेखा की लंबाई आदि के बारे में सूचनाएं दर्ज हैं। रेल के टिकटों पर स्टेशनों के साथ, उनके बीच की दूरी भी छपी रहती है। आपने सड़कों के किनारे-किनारे लगे मील के पत्थर देखे होंगे। ये विभिन्न शहरों की दूरियाँ बताते हैं।आखिर, यह सब किया कैसे जाता है?
आपको यह तय करना होता है कि किस सीमा तक त्रुटि सहन की जा सकती है और मापने के प्रक्रम पर अधिकतम खर्च कितना करना है। अगर आपको कम त्रुटियाँ चाहिए तो इसके लिए उच्च तकनीकी और अधिक खर्च की आवश्यकता होगी। यह कहना पर्याप्त होगा कि इसके लिए काफी उच्च स्तर की भौतिकी, गणित, अभियांत्रिकी और प्रौद्योगिकी की आवश्यकता होगी। इसका संबंध फ्रेक्टलों(Fractals) के क्षेत्र से है जो सैद्धांतिक भौतिकी में कुछ समय से काफी लोकप्रिय है। इस सबके बावजूद जो आंकड़े प्राप्त होते हैं उन पर कितना विश्वास किया जाए यह कहना कठिन होता है जैसा फ्रांस और बेल्जियम के दृष्टांत से स्पष्ट ही है। बात चल रही है तो आपको बता दें कि बेल्जियम और फ्रांस की यह विसंगति, फ्रेक्टलों (Fractals) एवं केअॉस (Chaos) विषय से संबंधित उच्च भौतिकी की एक पुस्तक के प्रथम पृष्ठ पर प्रस्तुत की गई है।
ध्यान दीजिए, अंतिम संख्यांक 6 विश्वसनीय नहीं है, क्योंकि यह 5 एवं 7 के बीच कुछ भी हो सकता है। इस तथ्य को संकेत के रूप में हम इस प्रकार कहते हैं कि माप में दो सार्थक अंक हैं। इस प्रकरण में दो सार्थक अंक 2 तथा 6 हैं जिनमें 2 विश्वसनीय है और 6 में त्रुटि संबद्ध है। अनुभाग 2.7 में आप सार्थक अंकों के विषय में और विस्तार से सीखेंगे।

2.6.2 त्रुटियों का संयोजन
यदि हम कोई एेसा प्रयोग करें जिसमें कई माप सम्मिलित हों, तो हमें यह भी जानना चाहिए कि इन मापनों में त्रुटियाँ किस प्रकार संयोजित होती हैं। उदाहरण के लिए, किसी पदार्थ का घनत्व उसके द्रव्यमान और आयतन के अनुपात द्वारा प्राप्त किया जाता है। यदि हम किसी वस्तु के द्रव्यमान और उसकी आमापों या विमाओं के मापने में त्रुटि करते हैं तो हमें यह ज्ञात होना चाहिए कि उस वस्तु के पदार्थ के घनत्व में भी त्रुटि आएगी। यह आकलन करने के लिए कि यह त्रुटि कितनी होगी हमें यह सीखना होगा कि विभिन्न गणितीय संक्रियाओं में त्रुटियाँ किस प्रकार संयोजित होती हैं। इसके लिए हम निम्नलिखित कार्यविधि का अनुसरण करते हैं।
(a) किसी संकलन या व्यवकलन की त्रुटि
मान लीजिए, कि दो भौतिक राशियों A एवं B के मापित मान क्रमशः A ± ∆A, B ± ∆B हैं। जहाँ, ∆A एवं ∆B क्रमशः इन राशियों की निरपेक्ष त्रुटियाँ हैं। हम संकलन Z = A + B में त्रुटि ∆Z ज्ञात करना चाहते हैं। संकलित करने पर
Z ± ∆Z = (A ± ∆A) + (B ± ∆B)
Z में अधिकतम संभावित त्रुटि
∆Z = ∆A + ∆B
व्यकलित करने पर Z = A – B के लिए हमेें प्राप्त होता है
Z ± ∆ Z = (A ± ∆A) – (B ± ∆B)
= (A – B) ± ∆A ± ∆B
अथवा ± ∆Z = ± ∆A ± ∆B
यहाँ फिर अधिकतम संभावित त्रुटि ∆Z = ∆A ± ∆B
अतः, नियम यह है ः जब दो राशियों को संकलित या व्यवकलित किया जाता है, तो अंतिम परिणाम में निरपेक्ष त्रुटि उन राशियों की निरपेक्ष त्रुटियों के योग के बराबर होती है।
उदाहरण 2.8 किसी तापमापी द्वारा मापे गए दो पिण्डों के ताप क्रमशः t1 = 20 0C ± 0.5 0C एवं t2 = 50 0C ± 0.5 0C हैं। इन पिण्डों का तापान्तर और उसमें आई त्रुटि परिकलित कीजिए।
हल t′ = t2–t1 = (50 0C±0.5 0C)– (200C±0.5 0C)
t′ = 30 0C ± 1 0C
(b) गुणनफल या भागफल की त्रुटि
मान लीजिए, कि Z = AB और A एवं B के मापित मान
A ± ∆A एवं B ± ∆B हैं, तब,
Z ± ∆Z = (A ± ∆A) (B ± ∆B)
= AB ± B ∆A ± A ∆B ± ∆A ∆B.
वाम पक्ष को Z से एवं दक्षिण पक्ष को AB से भाग करने पर,
1±(∆Z/Z) = 1 ± (∆A/A) ± (∆B/B) ± (∆A/A)(∆B/B)
चूंकि ∆A एवं ∆B बहुत छोटे हैं उनके गुणनफल को हम उपेक्षणीय मान सकते हैं।
अतः अधिकतम आपेक्षिक त्रुटि
∆Z/ Z = (∆A/A) + (∆B/B)
आप यह आसानी से जाँच सकते हैं कि यह तथ्य भागफल पर भी लागू होता है।
अतः, नियम यह है : जब दो राशियों को गुणा या भाग किया जाता है तो प्राप्त परिणाम में आपेक्षिक त्रुटि, उन गुणकों अथवा भाजकोें में आपेक्षिक त्रुटियों का योग होती हैं।
उदाहरण 2.9 प्रतिरोध R = V/I, जहाँ V =
(100 ± 5)V एवं I = (10 ± 0.2)A है। R में प्रतिशत त्रुटि ज्ञात कीजिए।
हल V में प्रतिशत त्रुटि 5% और I में प्रतिशत त्रुटि 2% है
∴ R में कुल प्रतिशत त्रुटि = 5% + 2% = 7%
उदाहरण 2.10 R1 = 100±3 ओम व R2 = 200 ± 4 ओम के दो प्रतिरोधकों को (a) श्रेणी क्रम में, (b) पार्श्व क्रम में संयोजित किया गया है। (a) श्रेणी क्रम संयोजन तथा (b) पार्श्व क्रम संयोजन में तुल्य प्रतिरोध ज्ञात कीजिए। (a) के लिए संबंध R =R1 + R2 एवं (b)
हल
(a) श्रेणी क्रम संयोजन का तुल्य प्रतिरोध,
R =R1 + R2 = (100 ± 3) ohm + (200 ± 4) ohm
= 300 ± 7 ohm.
(b) पार्श्व क्रम संयोजन का तुल्य प्रतिरोध,
(यहाँ सार्थक अंकों के नियमों को प्रमाणित करने की दृष्टि से ΔR' का मान 2 के स्थान पर 1.8 के रूप में व्यक्त किया गया है।
(c) मापित राशि की घातों के प्रकरण में त्रुटि
मान लीजिए Z = A2,
तब,
∆Z/Z = (∆A/A) + (∆A/A) = 2 (∆A/A)
अतः A2 में आपेक्षिक त्रुटि, A में आपेक्षिक त्रुटि की दो गुनी है। व्यापकीकरण करने पर, यदि Z = Ap Bq/Cr
तो, ∆Z/Z = p (∆A/A) + q (∆B/B) + r (∆C/C).
अतः, नियम यह है : किसी भौतिक राशि जिस पर k घात चढ़ाई गई है, की आपेक्षिक त्रुटि उस व्यष्टिगत राशि की आपेक्षिक त्रुटि की k गुनी होती है।
उदाहरण 2.11 यदि Z = A4B1/3/CD3/2 हो तो Z की आपेक्षिक त्रुटि ज्ञात कीजिए।
हल Z में आपेक्षिक त्रुटि ∆Z/Z = 4(∆A/A) +(1/3)
(∆B/B) + (∆C/C) + (3/2) (∆D/D)
उदाहरण 2.12 किसी सरल लोलक का दोलनकाल 
2.7 सार्थक अंक
जैसा कि ऊपर वर्णन किया जा चुका है, हर मापन में त्रुटियाँ सम्मिलित होती हैं। अतः मापन के परिणामों को इस प्रकार प्रस्तुत किया जाना चाहिए कि मापन की परिशुद्धता स्पष्ट हो जाए। साधारणतः, मापन के परिणामों को एक संख्या के रूप में प्रस्तुत करते हैं जिसमें वह सभी अंक सम्मिलित होते हैं जो विश्वसनीय हैं, तथा वह प्रथम अंक भी सम्मिलित किया जाता है जो अनिश्चित है। विश्वसनीय अंकों और पहले अनिश्चित अंक को संख्या के सार्थक-अंक माना जाता है। यदि हम कहें कि किसी सरल लोलक का दोलन काल 1.62 s है, तो इसमें अंक 1 एवं 6 तो विश्वसनीय एवं निश्चित हैं, जबकि अंक 2 अनिश्चित है; इस प्रकार मापित मान में 3 सार्थक अंक हैं। यदि मापन के बाद किसी वस्तु की लम्बाई, 287.5 cm व्यक्त की जाए तो इसमें चार सार्थक अंक हैं, जिनमें 2, 8, 7 तो निश्चित हैं परन्तु अंक 5 अनिश्चित है। अतः राशि के मापन के परिणाम में सार्थक अंकों से अधिक अंक लिखना अनावश्यक एवं भ्रामक होगा, क्योंकि, यह माप की परिशुद्धता के विषय में गलत धारणा देगा।
किसी संख्या में सार्थक अंकों की संख्या ज्ञात करने के नियम निम्नलिखित उदाहरणों द्वारा समझे जा सकते हैं। जैसा पहले वर्णन किया जा चुका है कि सार्थक अंक मापन की परिशुद्धता इंगित करते हैं जो मापक यंत्र के अल्पतमांक पर निर्भर करती है। किसी मापन में विभिन्न मात्रकों के परिवर्तन के चयन से सार्थक अंकों की संख्या परिवर्तित नहीं होती। यह महत्वपूर्ण टिप्पणी निम्नलिखित में से अधिक प्रेक्षणों को स्पष्ट कर देती है ः
(1) उदाहरण के लिए, लम्बाई 2.308 cm में चार सार्थक अंक हैं। परन्तु विभिन्न मात्रकों में इसी लम्बाई को हम 0.02308 m या 23.08 mm या 23080 µm भी लिख सकते हैं।
इन सभी संख्याओं में सार्थक अंकों की संख्या वही अर्थात चार (अंक 2, 3, 0, 8) है। यह दर्शाता है कि सार्थक अंकों की संख्या निर्धारित करने में, दशमलव कहाँ लगा है इसका कोई महत्व नहीं होता। उपरोक्त उदाहरण से निम्नलिखित नियम प्राप्त होते हैं ः
• सभी शून्येतर अंक सार्थक अंक होते हैं।
• यदि किसी संख्या में दशमलव बिन्दु है, तो उसकी स्थिति का ध्यान रखे बिना, किन्हीं दो शून्येतर अंकों के बीच के सभी शून्य सार्थक अंक होते हैं।
• यदि कोई संख्या 1 से छोटी है तो वे शून्य जो दशमलव के दाईं ओर पर प्रथम शून्येतर अंक के बाईं ओर हों, सार्थक अंक नहीं होते। ( 0.00 2308 में
अधोरेखांकित शून्य सार्थक अंक नहीं हैं)।
• एेसी संख्या जिसमें दशमलव नहीं है के अंतिम अथवा अनुगामी शून्य सार्थक अंक नहीं होते।
(अतः 123 m = 12300 cm = 123000 mm में तीन ही सार्थक अंक हैं, संख्या में अनुगामी शून्य सार्थक अंक नहीं हैं)। तथापि, आप अगले प्रेक्षण पर भी ध्यान दे सकते हैं।
• एक एेसी संख्या, जिसमें दशमलव बिन्दु हो, के अनुगामी शून्य सार्थक अंक होते हैं।
(संख्या 3.500 या 0.06900 में चार सार्थक अंक हैं)।
(2) अनुगामी शून्य सार्थक अंक हैं या नहीं इस विषय में भ्रांति हो सकती है। मान लीजिए किसी वस्तु की लम्बाई 4.700 m लिखी गई है। इस प्रेक्षण से यह स्पष्ट है कि यहाँ शून्यों का उद्देश्य माप की परिशुद्धता को बतलाना है अतः यहाँ सभी शून्य सार्थक अंक हैं। (यदि ये सार्थक न होते तो इनको स्पष्ट रूप से लिखने की आवश्यकता न होती। तब सीधे-सीधे हम अपनी माप को 4.7 m लिख सकते थे।) अब मान लीजिए हम अपना मात्रक बदल लेते हैं तो
4.700 m = 470.0 cm = 0.004700 km = 4700 mm
क्योंकि, अंतिम संख्या में दो शून्य, बिना दशमलव वाली संख्या में अनुगामी शून्य हैं, अतः प्रेक्षण (1) के अनुसार हम इस गलत निष्कर्ष पर पहुँच सकते हैं कि इस संख्या में 2 सार्थक अंक हैं जबकि वास्तव में इसमें चार सार्थक अंक हैं, मात्र मात्रकों के परिवर्तन से सार्थक अंकों की संख्या में परिवर्तन नहीं होता।
(3) सार्थक अंकों के निर्धारण में इस प्रकार की संदिग्धता को दूर करने के लिए सर्वोत्तम उपाय यह है कि प्रत्येक माप को वैज्ञानिक संकेत (10 की घातों के रूप में) में प्रस्तुत किया जाए। इस संकेत पद्धति में प्रत्येक संख्या को
a × 10b के रूप में लिखा जाता है, जहाँ a, 1 से 10 के बीच की कोई संख्या है और b, 10 की कोई धनात्मक या ऋणात्मक घात है। संख्या की सन्निकट अवधारणा बनाने के लिए हम इसका पूर्णांकन कर सकते हैं, यानि (a  5) होने पर इसे 1 और (5<a
5) होने पर इसे 1 और (5<a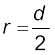 10) होने पर 10 मान सकते हैं। तब, इस संख्या को लगभग 10b के रूप में व्यक्त कर सकते हैं जिसमें 10 की घात b भौतिक राशि के परिमाण की कोटि कहलाती है। जब केवल एक अनुमान की आवश्यकता हो तो यह कहने से काम चलेगा कि राशि 10b की कोटि की है। उदाहरण के लिए पृथ्वी का व्यास (1.28×107m), 107m की कोटि का है, इसके परिमाण की कोटि 7 है। हाइड्रोजन परमाणु का व्यास
10) होने पर 10 मान सकते हैं। तब, इस संख्या को लगभग 10b के रूप में व्यक्त कर सकते हैं जिसमें 10 की घात b भौतिक राशि के परिमाण की कोटि कहलाती है। जब केवल एक अनुमान की आवश्यकता हो तो यह कहने से काम चलेगा कि राशि 10b की कोटि की है। उदाहरण के लिए पृथ्वी का व्यास (1.28×107m), 107m की कोटि का है, इसके परिमाण की कोटि 7 है। हाइड्रोजन परमाणु का व्यास
(1.06×10–10m), 10–10m की कोटि का है। इसके परिमाण की कोटि –10 है। अतः, पृथ्वी का व्यास, हाइड्रोजन परमाणु के व्यास से 17 परिमाण कोटि बड़ा है।
प्रायः एक अंक के बाद दशमलव लगाने की प्रथा है। इससे ऊपर प्रेक्षण(a) में उल्लिखित भ्रांति लुप्त हो जाता है ः
4.700 m = 4.700 × 102 cm
= 4.700 × 103 mm = 4.700 × 10–3 km
यहाँ सार्थक अंकों की संख्या ज्ञात करने में 10 की घात असंगत है। तथापि, वैज्ञानिक संकेत में आधार संख्या के सभी शून्य सार्थक अंक होते हैं। इस प्रकरण में सभी संख्याओं में 4 सार्थक अंक हैं।
इस प्रकार, वैज्ञानिक संकेत में आधार संख्या a के अनुगामी शून्यों के बारे में कोई भ्रांति नहीं रह जाती। वे सदैव सार्थक अंक होते हैं।
(4) किसी भी मापन के प्रस्तुतिकरण की वैज्ञानिक संकेत विधि एक आदर्श विधि है। परन्तु यदि यह विधि नहीं अपनायी जाती, तो हम पूर्वगामी उदाहरण में उल्लिखित नियमों का पालन करते हैं ः
• एक से बड़ ी, बिना दशमलव वाली संख्या के लिए, अनुगामी शून्य सार्थक-अंक नहीं हैं।
• दशमलव वाली संख्या के लिए अनुगामी शून्य सार्थक अंक हैं।
(5) 1 से छोटी संख्या में, पारस्परिक रूप से, दशमलव के बाईं ओर लिखा शून्य (जैसे 0.1250) कभी भी सार्थक अंक नहीं होता। तथापि, किसी माप में एेसी संख्या के अंत में आने वाले शून्य सार्थक अंक होते हैं।
(6) गुणक या विभाजी कारक जो न तो पूर्णांकित संख्याएँ होती हैं और न ही किसी मापित मान को निरूपित करती हैं, यथार्थ होती हैं और उनमें अनन्त सार्थक-अंक होते हैं। उदाहरण के लिए r=d/2 अथवा s = 2πr में गुणांक 2 एक यथार्थ संख्या है और इसे 2.0, 2.00 या 2.0000, जो भी आवश्यक हो लिखा जा सकता है। इसी प्रकार T=t/n, में n एक पूर्णांक है।
2.7.1 सार्थक अंकों से संबंधित अंकीय संक्रियाओं के नियम
किसी परिकलन का परिणाम, जिसमें राशियों के सन्निकट मापे गए मान सम्मिलित हैं (अर्थात् वे मान जिनमें सार्थक अंकों की संख्या सीमित है) व्यक्त करते समय, मूल रूप से मापे गए मानों की अनिश्चितता भी प्रतिबिम्बित होनी चाहिए। यह परिणाम, उन मापित मानों से अधिक यथार्थ नहीं हो सकता जिन पर यह आधारित है। अतः, व्यापक रूप से, किसी भी परिणाम में सार्थक अंकों की संख्या, उन मूल आंकड़ ों से अधिक नहीं हो सकती जिनसे इसे प्राप्त किया गया है। इस प्रकार, यदि किसी पिण्ड का मापित द्रव्यमान मान लीजिए 4.237 g है
(4 सार्थक अंक), और इसका मापित आयतन 2.51 cm3 है, तो मात्र अंकीय विभाजन द्वारा इसका घनत्व दशमलव के 11 स्थानों तक 1.68804780876 g/cm3 आता है। स्पष्टतः घनत्व के इस परिकलित मान को इतनी परिशुद्धता के साथ लिखना पूर्णतः हास्यास्पद तथा असंगत होगा, क्योंकि जिन मापों पर यह मान आधारित है उनकी परिशुद्धता काफी कम है। सार्थक अंकों के साथ अंकीय संक्रियाओं के निम्नलिखित नियम यह सुनिश्चित करते हैं कि किसी परिकलन का अंतिम परिणाम उतनी ही परिशुद्धता के साथ दर्शाया जाता है जो निवेशित मापित मानों की परिशुद्धता के संगत हो
(1) संख्याओं को गुणा या भाग करने से प्राप्त परिणाम में केवल उतने ही सार्थक अंक रहने देना चाहिए जितने कि सबसे कम सार्थक अंकों वाली मूल संख्या में है।
अतः उपरोक्त उदाहरण में घनत्व को तीन सार्थक अंकों तक ही लिखा जाना चाहिए,
इसी प्रकार, यदि दी गई प्रकाश की चाल 3 × 108 m/s-1 (एक सार्थक अंक) और एक वर्ष (1 y = 365.25 d) में 3.1557×107 s (पांच सार्थक अंक) हों, तो एक प्रकाश वर्ष में 9.47×1015 m (तीन सार्थक अंक) होंगे।
(2) संख्याओं के संकलन अथवा व्यवकलन से प्राप्त अंतिम परिणाम में दशमलव के बाद उतने ही सार्थक अंक रहने देने चाहिए जितने कि संकलित या व्यवकलित की जाने वाली किसी राशि में दशमलव के बाद कम से
कम हैं।
उदाहरणार्थ, संख्याओं 436.32 g, 227.2 g एवं 0.301 g का योग 663.821 g है। दी गई संख्याओं में सबसे कम परिशुद्ध (227.2 g) माप दशमलव के एक स्थान तक ही यथार्थ है। इसलिए, अंतिम परिणाम को 663.8 g तक पूर्णांकित कर दिया जाना चाहिए।
इसी प्रकार, लम्बाइयों में अंतर को निम्न प्रकार से व्यक्त कर सकते हैं,
0.307 m – 0.304 m = 0.003 m = 3 × 10–3 m
ध्यान दीजिए, हमें नियम (1) जो गुणा और भाग के लिए लागू होता है, उसे संकलन (योग) के उदाहरण में प्रयोग करके परिणाम को 664 g नहीं लिखना चाहिए और व्यवकलन के उदाहरण में 3.00 × 10–3 m नहीं लिखना चाहिए। ये माप की परिशुद्धता को उचित रूप से व्यक्त नहीं करते हैं। संकलन और व्यवकलन के लिए यह नियम दशमलव स्थान के पदों में है।
2.7.2 अनिश्चित अंकों का पूर्णांकन
जिन संख्याओं में एक से अधिक अनिश्चित अंक होते हैं, उनके अभिकलन के परिणाम का पूर्णांकन किया जाना चाहिए।
अधिकांश प्रकरणों में, संख्याओं को उचित सार्थक अंकों तक पूर्णांकित करने के नियम स्पष्ट ही हैं। संख्या 2.746 को तीन सार्थक अंकों तक पूर्णांकित करने पर 2.75 प्राप्त होता है, जबकि 2.743 के पूर्णांकन से 2.74 मिलता है। परिपाटी के अनुसार नियम यह है कि यदि उपेक्षणीय अंक (पूर्वोक्त संख्या में अधोरेखांकित अंक) 5 से अधिक है तो पूर्ववर्ती अंक में एक की वृद्धि कर दी जाती है, और यदि यह उपेक्षणीय अंक 5 से कम होता है, तो पूर्ववर्ती अंक अपरिवर्तित रखा जाता है। लेकिन यदि संख्या 2.745 है, जिसमें उपेक्षणीय अंक 5 है, तो क्या होता है? यहाँ परिपाटी यह है कि यदि पूर्ववर्ती अंक सम है तो उपेक्षणीय अंक को छोड़ दिया जाता है और यदि यह विषम है, तो पूर्ववर्ती अंक में 1 की वृद्धि कर देते हैं। तब संख्या 2.745, तीन सार्थक अंकों तक पूर्णांकन करने पर 2.74 हो जाती है। दूसरी ओर, संख्या 2.735 तीन सार्थक अंकों तक पूर्णांकित करने के पश्चात् 2.74 हो जाती है, क्योंकि पूर्ववर्ती अंक विषम है।
किसी भी उलझन वाले अथवा बहुपदी जटिल परिकलन में, मध्यवर्ती पदों में सार्थक अंकों से एक अंक अधिक रहने देना चाहिए, जिसे परिकलन के अंत में उचित सार्थक अंकों तक पूर्णांकित कर देना चाहिए। इसी प्रकार, एक संख्या जो कई सार्थक अंकों तक ज्ञात है, जैसे निर्वात में प्रकाश का वेग, जिसके लिए, प्रायः 2.99792458 × 108 m/s को सन्निकट मान 3 × 108 m/s में पूर्णांकित कर परिकलनों में उपयोग करते हैं। अंत में ध्यान रखिये कि सूत्रों में उपयोग होने वाली यथार्थ संख्याएं, जैसे 
उदाहरण 2.13 किसी घन की प्रत्येक भुजा की माप 7.203 m है। उचित सार्थक अंकों तक घन का कुल पृष्ठ क्षेत्रफल एवं आयतन ज्ञात कीजिए।
हल
मापी गई लम्बाई में सार्थक अंकों की संख्या 4 है। इसलिए, परिकलित क्षेत्रफल एवं आयतन के मानों को भी 4 सार्थक अंकों तक पूर्णांकित किया जाना चाहिए।
घन का पृष्ठ क्षेत्रफल = 6(7.203)2 m2
= 311.299254 m2
= 311.3 m2
घन का आयतन = (7.203)3 m3
= 373.714754 m3
= 373.7 m3
उदाहरण 2.14 किसी पदार्थ के 5.74 g का आयतन 1.2 cm3 है। सार्थक अंकों को ध्यान में रखते हुए इसका घनत्व व्यक्त कीजिए।
हल
द्रव्यमान में 3 सार्थक अंक हैं, जबकि आयतन के मापित मान में केवल दो सार्थक अंक हैं। अतः घनत्व को केवल दो सार्थक अंकों तक व्यक्त किया जाना चाहिए।
2.7.3 अंकगणितीय परिकलनों के परिणामों में अनिश्चितता निर्धारित करने के नियम
अंकीय संक्रियाओं में संख्याओं/ मापित राशियों में अनिश्चितता या त्रुटि निर्धारित करने संबंधी नियमों को निम्नलिखित उदाहरणों के द्वारा समझा जा सकता है।
(1) यदि किसी पतली, आयताकार शीट की लम्बाई और चौड़ ाई, किसी मीटर पैमाने से मापने पर क्रमशः 16.2 cm एवं
10.1 cm हैं, तो यहाँ प्रत्येक माप में तीन सार्थक अंक हैं। इसका अर्थ है कि लम्बाई को हम इस प्रकार लिख सकते हैं
l = 16.2 ± 0.1 cm
= 16.2 cm ± 0.6 %.
इसी प्रकार, चौड़ ाई को इस प्रकार लिखा जा सकता है
b = 10.1 ± 0.1 cm
= 10.1 cm ± 1 %
तब, त्रुटि संयोजन के नियम का उपयोग करने पर, दो (या अधिक) प्रायोगिक मापों के गुणनफल की त्रुटि
lb = 163.62 cm2 + 1.6%
= 163.62 + 2.6 cm2
इस उदाहरण के अनुसार हम अंतिम परिणाम को इस प्रकार लिखेंगे
l b = 164 + 3 cm2
यहाँ, 3 cm2 आयताकार शीट के क्षेत्रफल के आकलन में की गई त्रुटि अथवा अनिश्चितता है।
(2) यदि किसी प्रायोगिक आंकड़ े के समुच्चय में n सार्थक अंकों का उल्लेख है, तो आंकड़ े के संयोजन से प्राप्त परिणाम भी n सार्थक अंकों तक वैध होगा।
तथापि, यदि आंकड़ े घटाये जाते हैं तो सार्थक अंकों की संख्या कम की जा सकती है। उदाहरणार्थ, 12.9 g – 7.06 g दोनों तीन सार्थक अंकों तक विनिर्दिष्ट हैं, परन्तु इसे 5.84 g के रूप में मूल्यांकित नहीं किया जा सकता है बल्कि केवल 5.8 g लिखा जाएगा, क्योंकि संकलन या व्यवकलन में अनिश्चितताएँ एक भिन्न प्रकार से संयोजित होती हैं। (संकलित या व्यवकलित की जाने वाली संख्याओं में दशमलव के बाद कम से कम अंकों वाली संख्या न कि कम से कम सार्थक अंकों वाली संख्या निर्णय का आधार होती है।)
(3) किसी संख्या के मान में आपेक्षिक त्रुटि, जो विनिर्दिष्ट सार्थक अंकों तक दी गई है, न केवल n पर, वरन, दी गई संख्या पर भी निर्भर करती है।
उदाहरणार्थ, द्रव्यमान 1.02 g के मापन में यथार्थता ± 0.01 g है, जबकि दूसरी माप 9.89 g भी ± 0.01 g तक ही
यथार्थ है।
1.02 में आपेक्षिक त्रुटि
= (± 0.01/1.02) × 100 %
= ± 1%
इसी प्रकार 9.89 g में आपेक्षिक त्रुटि
= (± 0.01/9.89) × 100 %
= ± 0.1 %
अंत में, याद रखिए कि बहुपदीय अभिकलन के मध्यवर्ती परिणाम को परिकलित करने में प्रत्येक माप को, अल्पतम परिशुद्ध माप से एक सार्थक अंक अधिक रखना चाहिए। आंकड़ ों के अनुसार इसे तर्कसंगत करने के बाद ही इनकी अंकीय संक्रियाएँ करना चाहिए अन्यथा पूर्णांकन की त्रुटियाँ उत्पन्न हो जाएंगी। उदाहरणार्थ, 9.58 के व्युत्क्रम का तीन सार्थक अंकों तक पूर्णांकन करने पर मान 0.104 है, परन्तु 0.104 का व्युत्क्रम करने पर तीन सार्थक अंकों तक प्राप्त मान 9.62 है। पर यदि हमने 1/9.58 = 0.1044 लिखा होता तो उसके व्युत्क्रम को तीन सार्थक अंकों तक पूर्णांकित करने पर हमें मूल मान 9.58 प्राप्त होगा।
उपरोक्त उदाहरण, जटिल बहुपदी परिकलन के मध्यवर्ती पदों में (कम से कम परिशुद्ध माप में अंकों की संख्या की अपेक्षा) एक अतिरिक्त अंक रखने की धारणा को न्यायसंगत ठहराता है, जिससे कि संख्याओं की पूर्णांकन प्रक्रिया में अतिरिक्त त्रुटि से बचा जा सके।
2.8 भौतिक राशियों की विमाएँ
किसी भौतिक राशि की प्रकृति की व्याख्या उसकी विमाओं द्वारा की जाती है। व्युत्पन्न मात्रकों द्वारा व्यक्त होने वाली सभी भौतिक राशियाँ, सात मूल राशियों के संयोजन के पदों में प्रस्तुत की जा सकती हैं। इन मूल राशियों को हम भौतिक संसार की सात विमाएँ कह सकते हैं और इन्हें गुरु कोष्ठक के साथ निर्दिष्ट किया जाता है। इस प्रकार, लम्बाई की विमा [L], विद्युत धारा की [A], ऊष्मागतिकीय ताप की [K], ज्योति तीव्रता की [cd], और पदार्थ की मात्रा की [mol] है। किसी भौतिक राशि की विमाएँ उन घातों (या घातांकों) को कहते हैं, जिन्हें उस राशि को व्यक्त करने के लिए मूल राशियों पर चढ़ाना पड़ ता है। ध्यान दीजिए किसी राशि को गुरु कोष्ठक
[ ] से घेरने का यह अर्थ है कि हम उस राशि की विमा पर विचार कर रहे हैं।
यांत्रिकी में, सभी भौतिक राशियों को विमाओं [L], [M] और [T] के पदों में व्यक्त किया जा सकता है। उदाहरणार्थ, किसी वस्तु द्वारा घेरा गया आयतन उसकी लम्बाई, चौड़ ाई और ऊँचाई अथवा तीन लम्बाइयों के गुणन द्वारा व्यक्त किया जाता है। इसलिए, आयतन का विमीय सूत्र = [L] × [L] × [L] = [L]3 = [L3]। क्योंकि, आयतन, द्रव्यमान और समय पर निर्भर नहीं करता, इसलिए यह कहा जाता है कि आयतन में द्रव्यमान की शून्य विमा, [M°], समय की शून्य विमा [T°] तथा लम्बाई की 3 विमाएँ [L3] हैं।
इसी प्रकार, बल को द्रव्यमान और त्वरण के गुणनफल के रूप में इस प्रकार व्यक्त कर सकते हैं,
बल = द्रव्यमान × त्वरण
= द्रव्यमान × (लम्बाई)/(समय)2
बल की विमाएँ [M] [L]/[T]2 = [M L T–2] हैं । अतः बल में, द्रव्यमान की 1, लम्बाई की 1 और समय की –2 विमाएँ हैं। यहाँ अन्य सभी मूल राशियों की विमाएँ शून्य हैं।
ध्यान दीजिए, इस प्रकार के प्रस्तुतीकरण में परिमाणों पर विचार नहीं किया जाता। इसमें भौतिक राशियों के प्रकार की गुणता का समावेश होता है। इस प्रकार, इस संदर्भ में वेग परिवर्तन, प्रारंभिक वेग, औसत वेग, अंतिम वेग और चाल, ये सभी तुल्य राशियाँ हैं, क्योंकि ये सभी राशियाँ लम्बाई/समय के रूप में व्यक्त की जा सकती हैं और इनकी विमाएँ [L]/[T] या [L T–1] हैं।
2.9 विमीय सूत्र एवं विमीय समीकरणें
किसी दी हुई भौतिक राशि का विमीय सूत्र वह व्यंजक है जो यह दर्शाता है कि किसी भौतिक राशि में किस मूल राशि की कितनी विमाएँ हैं। उदाहरणार्थ, आयतन का विमीय सूत्र
[M° L3 T°] और वेग या चाल का [M° L T-1] है। इसी प्रकार, [M° L T–2], त्वरण का तथा [M L–3 T°] द्रव्यमान घनत्व का विमीय सूत्र है।
किसी भौतिक राशि को उसके विमीय सूत्र के बराबर लिखने पर प्राप्त समीकरण को उस राशि का विमीय समीकरण कहते हैं। अतः विमीय समीकरण वह समीकरण है जिसमें किसी भौतिक राशि को मूल राशियों और उनकी विमाओं के पदों में निरूपित किया जाता है। उदाहरण के लिए, आयतन [V], चाल [v], बल [F] और द्रव्यमान घनत्व [ρ] की विमीय समीकरण को इस प्रकार व्यक्त किया जा सकता है :
[V] = [M0 L3 T0]
[v] = [M0 L T–1]
[F] = [M L T–2]
[ρ] = [M L–3 T0]
भौतिक राशियों के बीच संबंध निरूपित करने वाले समीकरण के आधार पर विमीय समीकरण, व्युत्पन्न की जा सकती है। विविध प्रकार की बहुत सी भौतिक राशियों के विमीय सूत्र, जिन्हें अन्य भौतिक राशियों के मध्य संबंधों को निरूपित करने वाले समीकरणों से व्युत्पन्न तथा मूल राशियों के पदों में व्यक्त किया गया है, आपके मार्गदर्शन एवं तात्कालिक संदर्भ के लिए परिशिष्ट-9 में दिए गए हैं।
2.10 विमीय विश्लेषण एवं इसके अनुप्रयोग
विमाओं की संकल्पना की स्वीकृति, जो भौतिक व्यवहार के वर्णन में मार्गदर्शन करती है, अपना एक आधारिक महत्व रखती है क्योंकि इसके अनुसार केवल वही भौतिक राशियाँ संकलित या व्यवकलित की जा सकती हैं जिनकी विमाएँ समान हैं। विमीय विश्लेषण का व्यापक ज्ञान, विभिन्न भौतिक राशियों के बीच संबंधों के निगमन में सहायता करता है और विभिन्न गणितीय व्यंजकों की व्युत्पत्ति, यथार्थता तथा विमीय संगतता की जाँच करने में सहायक है। जब दो या अधिक भौतिक राशियों के परिमाणों को गुणा (या भाग) किया जाता है, तो उनके मात्रकों के साथ उस प्रकार का व्यवहार किया जाना चाहिए जैसा हम सामान्य बीज-गणितीय प्रतीकों के साथ करते हैं। अंश और हर से सर्वसम मात्रकों को हम निरसित कर सकते हैं। यही बात भौतिक राशि की विमाओं के साथ भी लागू होती है। इसी प्रकार, किसी गणितीय समीकरण में पक्षों में प्रतीकों द्वारा निरूपित भौतिक राशियों की विमाएँ समान होनी चाहिए।
2.10.1 समीकरणों की विमीय संगति की जाँच
भौतिक राशियों के परिमाण केवल तभी संकलित या व्यवकलित किए जा सकते हैं यदि उनकी विमाएँ समान हों। दूसरे शब्दों में, हम केवल एक ही प्रकार की राशियों का संकलन या व्यवकलन कर सकते हैं। अतः बल को वेग के साथ संकलित या ऊष्मा गतिक ताप में से विद्युत धारा को व्यवकलित नहीं किया जा सकता। इस सरल सिद्धांत को विमाओं की समघातता सिद्धांत कहते हैं और इसकी सहायता से किसी समीकरण की संशुद्धि की जाँच कर सकते हैं। यदि किसी समीकरण के सभी पदों की विमाएँ समान नहीं हैं तो वह समीकरण गलत होती है। अतः यदि हम किसी पिण्ड की लम्बाई (या दूरी) के लिए व्यंजक व्युत्पन्न करें, तो चाहे उसमें सम्मिलित प्रतीक कुछ भी हों, उनकी विमाओं को सरल करने पर अंत में प्रत्येक पद में लम्बाई की विमा ही शेष रहनी चाहिए। इसी प्रकार, यदि हम चाल के लिए समीकरण व्युत्पन्न करें, तो इसके दोनों पक्षों के पदों का विमीय-सूत्र सरलीकरण के बाद [L T–1] ही पाया जाना चाहिए।
यदि किसी समीकरण की संशुद्धि में संदेह हो तो उस समीकरण की संगति की प्राथमिक जांच के लिए मान्य प्रथा के अनुसार विमाओं का उपयोग किया जाता है। किन्तु, विमीय संगति किसी समीकरण के सही होने की गारंटी नहीं है। यह अविम राशियों या फलनों की अनिश्चितता सीमा तक अनिश्चित होती है। त्रिकोणमितीय, लघुगणकीय और चरघातांकी फलनों जैसे विशिष्ट फलनों के कोणांक अविम होने चाहिए। एक शुद्ध संख्या, समान भौतिक राशियों का अनुपात, जैसे अनुपात के रूप में कोण (लम्बाई/लम्बाई), अनुपात के रूप में अपवर्तनांक (निर्वात में प्रकाश का वेग/माध्यम में प्रकाश का वेग) आदि की कोई विमाएँ नहीं होतीं।
अब, हम निम्नलिखित समीकरण की विमीय संगति या समांगता की जाँच कर सकते हैं
जहाँ x किसी कण अथवा पिण्ड द्वारा t सेकंड में चलित वह दूरी है, जो कण या पिण्ड समय t = 0 पर स्थिति x0 से प्रारंभिक वेग v0 से आरम्भ करके तय करता है, और इसका गति की दिशा में एकसमान त्वरण a रहता है।
प्रत्येक पद के लिए विमीय समीकरण लिखने पर,
[x] = [L]
[x0 ] = [L]
[v0 t] = [L T–1] [T]
= [L]
[1/2 a t2] = [L T–2] [T2]
= [L]
क्योंकि इस समीकरण के सभी पदों की विमाएँ समान (लम्बाई की) हैं, इसलिए यह विमीय दृष्टि से संगत समीकरण है।
यहाँ ध्यान देने योग्य तथ्य यह है, कि विमीय संगति परीक्षण, मात्रकों की संगति से कम या अधिक कुछ नहीं बताता। लेकिन, इसका लाभ यह है कि हम मात्रकों के किसी विशेष चयन के लिए बाध्य नहीं हैं और न ही हमें मात्रकों के पारस्परिक गुणजों या अपवर्तकों में रूपांतरण की चिन्ता करने की आवश्यकता है। यह बात भी हमें स्पष्ट करनी चाहिए कि यदि कोई समीकरण संगति परीक्षण में असफल हो जाती है तो वह गलत सिद्ध हो जाती है, परन्तु यदि वह परीक्षण में सफल हो जाती है तो इससे वह सही सिद्ध नहीं हो जाती। इस प्रकार कोई विमीय रूप से सही समीकरण आवश्यक रूप से यथार्थ (सही) समीकरण नहीं होती, जबकि विमीय रूप से गलत या असंगत समीकरण गलत होनी चाहिए।
उदाहरण 2.15 आइए निम्नलिखित समीकरण पर विचार करें
1/2 mv2=mghयहाँ m वस्तु का द्रव्यमान, v इसका वेग है, g गुरुत्वीय त्वरण और h ऊँचाई है। जाँचिए कि क्या यह समीकरण विमीय दृष्टि से सही है।
हल यहाँ वाम पक्ष की विमाएँ
[M] [L T–1 ]2 = [M] [ L2 T–2]
तथा = [M L2 T–2]
दक्षिण पक्ष की विमाएँ
[M][L T–2] [L] = [M][L2 T–2]
= [M L2 T–2]
चूँकि, दोनों पक्षों की विमाएँ समान हैं, इसलिए यह समीकरण विमीय दृष्टि से सही है।
उदाहरण 2.16 ऊर्जा का SI मात्रक J = kg m2 s–2; है, चाल v का m s–1 और त्वरण a का m s–2 है। गतिज ऊर्जा (k) के लिए निम्नलिखित सूत्रों में आप किस-किस को विमीय दृष्टि से गलत बताएँगे? (m पिण्ड का द्रव्यमान है)।
(a) K = m2 v3
(b) K = (1/2)mv2
(c) K = ma
(d) K = (3/16)mv2
(e) K = (1/2)mv2 + ma
हल प्रत्येक सही समीकरण में दोनों पक्षों का विमीय सूत्र समान होना चाहिए। यह भी कि केवल समान विमाओं वाली राशियों का ही संकलन या व्यवकलन किया जा सकता है। दक्षिण पक्ष की राशि की विमाएँ (a) के लिए [M2 L3 T–3]; (b) तथा (d) के लिए [M L2 T–2]; (c) के लिए [M L T–2] है। समीकरण (e) के दक्षिण पक्ष की राशि की कोई उचित विमाएँ नहीं हैं क्योंकि इसमें भिन्न विमाओं वाली दो राशियों को संकलित किया गया है। अब क्योंकि K की विमाएँ [M L2 T–2] है, इसलिए सूत्र (a), (c) एवं (e) विमीय रूप से संगत नहीं हैं। ध्यान दें, कि विमीय तर्कों से यह पता नहीं चलता कि (b) व (d) में कौन सा सूत्र सही है। इसके लिए गतिज ऊर्जा की वास्तविक परिभाषा को देखना पड़ ेगा (देखें अध्याय 6)। गतिज ऊर्जा के लिए सही सूत्र (b) में दिया गया है।
2.10.2 विभिन्न भौतिक राशियों के मध्य संबंध व्युत्पन्न करना
कभी-कभी विभिन्न भौतिक राशियों के बीच संबंध व्युत्पन्न करने के लिए विमाओं की विधि का उपयोग किया जा सकता है। इसके लिए हमें यह ज्ञात होना चाहिए कि एक भौतिक राशि किन-किन दूसरी भौतिक राशियों पर निर्भर करती है (तीन भौतिक राशियों या एकघाततः स्वतंत्र चरों तक)। इसके लिए, हम दी गई राशि को निर्भर राशियों की विभिन्न घातों के गुणनफल के रूप में लिखते हैं। आइये, एक उदाहरण द्वारा इस प्रक्रिया को समझें।
उदाहरण 2.17 एक सरल लोलक पर विचार कीजिए, जिसमें गोलक को एक धागे से बाँध कर लटकाया गया है और जो गुरुत्व बल के अधीन दोलन कर रहा है। मान लीजिए कि इस लोलक का दोलन काल इसकी लम्बाई (l), गोलक के द्रव्यमान (m) और गुरुत्वीय त्वरण (g) पर निर्भर करता है। विमाओं की विधि का उपयोग करके इसके दोलन-काल के लिए सूत्र व्युत्पन्न कीजिए।
T =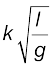
ध्यान दीजिए, यहाँ स्थिरांक k का मान विमीय विधि से ज्ञात नहीं किया जा सकता है। यहाँ इसका कोई अर्थ नहीं है कि सूत्र के दक्षिण पक्ष को किसी संख्या से गुणा किया गया है, क्योंकि एेसा करने से विमाएँ प्रभावित नहीं होतीं।
वास्तव में, k = 2π, अतः T =
परस्पर संबंधित राशियों के बीच संबंध व्युत्पन्न करने के लिए विमीय विश्लेषण काफी उपयोगी है। तथापि विमाहीन स्थिरांकों के मान इस विधि द्वारा ज्ञात नहीं किए जा सकते। विमीय विधि द्वारा किसी समीकरण की केवल विमीय वैधता ही जांची जा सकती है, किसी समीकरण में विभिन्न भौतिक राशियों के बीच यथार्थ संबंध नहीं जांचे जा सकते। यह समान विमा वाली राशियों में विभेद नहीं कर सकती।
इस अध्याय के अंत में दिए गए कई अभ्यास प्रश्न, आपकी विमीय विश्लेषण की कुशलता विकसित करने में सहायक होंगे।
सारांश
1. भौतिक विज्ञान भौतिक राशियों के मापन पर आधारित एक परिमाणात्मक विज्ञान है । कुछ भौतिक राशियां जैसे लंबाई, द्रव्यमान, समय, विद्युत धारा, ऊष्मागतिक ताप, पदार्थ की मात्रा और ज्योति-तीव्रता, मूल राशियों के रूप में चुनी गई हैं।
2. प्रत्येक मूल राशि किसी मूल मात्रक (जैसे मीटर, किलोग्राम, सेकंड, एेम्पियर, केल्विन, मोल और कैंडेला) के पद में परिभाषित है । मूल मात्रक स्वेच्छा से चयनित परंतु समुचित रूप से मानकीकृत निर्देश मानक होते हैं । मूल राशियों के मात्रकों को मूल मात्रक कहते हैं।
3. मूल राशियों से व्युत्पन्न अन्य भौतिक राशियों को मूल मात्रकाें के संयोजन के रूप में व्यक्त कर सकते हैं, जिन्हेंव्युत्पन्न मात्रक कहते हैं । मूल और व्युत्पन्न दोनों मात्रकों के पूर्ण समुच्चय को, मात्रक प्रणाली कहते हैं ।
4. सात मूल मात्रकों पर आधारित मात्रकों की अंतर्राष्ट्रीय प्रणाली (SI) वर्तमान में अंतर्राष्ट्रीय स्तर पर स्वीकृत प्रणाली है । यह प्रणाली समस्त संसार में व्यापक रूप से प्रयोग मेें लाई जाती है ।
5. मूल राशियों और व्युत्पन्न राशियों से प्राप्त सभी भौतिक मापों में SI मात्रकों का प्रयोग किया जाता है। कुछ व्युत्पन्न मात्रकों को SI मात्रकों में विशेष नामों (जैसे जूल, न्यूटन, वाट आदि) से व्यक्त किया जाता है ।
6. SI मात्रकों के सुपरिभाषित एवं अंतर्राष्ट्रीय स्तर पर स्वीकृत मात्रक प्रतीक हैं (जैसे मीटर के लिए m, किलोग्राम के लिए kg, सेकंड के लिए s, एेम्पियर के लिए A, न्यूटन के लिए N, इत्यादि)।
7. प्रायः छोटी एवं बड़ ी राशियों की भौतिक मापों को वैज्ञानिक संकेत में 10 की घातों में व्यक्त किया जाता है । माप संकेतों तथा आंकिक अभिकलनों की सरलता हेतु संख्याओं की परिशुद्धता का संकेत करते हुए वैज्ञानिक संकेत एवं पूर्वलग्नों का प्रयोग किया जाता है ।
8. भौतिक राशियों के संकेतन और SI मात्रकों के प्रतीकों, कुछ अन्य मात्रकों, भौतिक राशियों और मापों को उचित रूप से व्यक्त करने हेतु पूर्वलग्न के लिए कुछ सामान्य नियमों और निर्देशों का पालन करना चाहिए ।
9. किसी भी भौतिक राशि के अभिकलन में उसके मात्रक की प्राप्ति हेतु संबंध (संबंधों) में सम्मिलित व्युत्पन्न राशियों के मात्रकों को वांछित मात्रकों की प्राप्ति तक बीजगणितीय राशियों की भांति समझना चाहिए ।
10. भौतिक राशियों के मापन हेतु प्रत्यक्ष एवं अप्रत्यक्ष विधियों का प्रयोग किया जा सकता है । मापित राशियों में परिणाम को व्यक्त करते समय मापक यंत्रों की यथार्थता (accuracy) और परिशुद्धता (precision)के साथ मापन में त्रुटियों को भी दर्शाया जाना चाहिए ।
11. मापित एवं अभिकलित राशियों में केवल उचित सार्थक अंकों को ही रखा रहने देना चाहिए । किसी भी संख्या में सार्थक अंकों की संख्या का निर्धारण, उनके साथ अंकीय संक्रियाओं को करने और अनिश्चित अंकों का निकटन करने में इनके लिए बनाए गए नियमों का पालन करना चाहिए ।
12. मूल राशियों की विमाओं और इन विमाओं का संयोजन भौतिक राशियों की प्रकृति का वर्णन करता है । समीकरणों की विमीय संगति की जांच और भौतिक राशियों में संबंध व्युत्पन्न करने में विमीय विश्लेषण का प्रयोग किया जा सकता है। कोई विमीय संगत समीकरण वास्तव में सही हो, यह आवश्यक नहीं है परंतु विमीय रूप से गलत या असंगत समीकरण गलत ही होगी ।
अभ्यास
टिप्पणी : संख्यात्मक उत्तरों को लिखते समय, सार्थक अंकों का ध्यान रखिये।
2.1 रिक्त स्थान भरिए
(a) किसी 1 cm भुजा वाले घन का आयतन.........m3 के बराबर है ।
(b) किसी 2 cm त्रिज्या व 10 cm ऊंचाई वाले सिलिंडर का पृष्ठ क्षेत्रफल.........(mm)2 के बराबर है।
(c) कोई गाड़ ी 18 km/h की चाल से चल रही है तो यह l s में.........m चलती है ।
(d) सीसे का आपेक्षिक घनत्व 11.3 है । इसका घनत्व.......g cm–3 या......kg m–3 है ।
2.2 रिक्त स्थानों को मात्रकों के उचित परिर्वतन द्वारा भरिए
(a) 1 kg m2 s–2 =............ g cm2 s–2
(b) 1 m =................. ly
(c) 3.0 m s–2 =................. km h–2
(d) G = 6.67 × 10–11 Nm2 (kg)–2 =................. (cm)3 s–2 g–1
2.3 ऊष्मा (परागमन में ऊर्जा) का मात्रक कैलोरी है और यह लगभग 4.2 J के बराबर है, जहां 1 J = 1 kg m2 s–2। मान लीजिए कि हम मात्रकों की कोई एेसी प्रणाली उपयोग करते हैं जिससे द्रव्यमान का मात्रक α kg के बराबर है, लंबाई का मात्रक β m के बराबर है, समय का मात्रक γ s के बराबर है । यह प्रदर्शित कीजिए कि नए मात्रकों के पदों में कैलोरी का परिमाण 4.2 α−1 β−2 γ2 है ।
2.4 इस कथन की स्पष्ट व्याख्या कीजिए ः तुलना के मानक का विशेष उल्लेख किए बिना "किसी विमीय राशि को ‘बड़ा’ या ‘छोटा’ कहना अर्थहीन है" । इसे ध्यान में रखते हुए नीचे दिए गए कथनों को जहां कहीं भी आवश्यक हो, दूसरे शब्दों में व्यक्त कीजिए ः
(a) परमाणु बहुत छोटे पिण्ड होते हैं ।
(b) जेट वायुयान अत्यधिक गति से चलता है ।
(c) बृहस्पति का द्रव्यमान बहुत ही अधिक है ।
(d) इस कमरे के अंदर वायु में अणुओं की संख्या बहुत अधिक है ।
(e) इलेक्ट्रॉन, प्रोटॉन से बहुत भारी होता है ।
(f) ध्वनि की गति प्रकाश की गति से बहुत ही कम होती है ।
2.5 लंबाई का कोई एेसा नया मात्रक चुना गया है जिसके अनुसार निर्वात में प्रकाश की चाल 1 है । लम्बाई के नए मात्रक के पदों में सूर्य तथा पृथ्वी के बीच की दूरी कितनी है, प्रकाश इस दूरी को तय करने में
8 min और 20 s लगाता है ।
2.6 लंबाई मापने के लिए निम्नलिखित में से कौन-सा सबसे परिशुद्ध यंत्र है ः
(a) एक वर्नियर केलिपर्स जिसके वर्नियर पैमाने पर 20 विभाजन हैं ।
(b) एक स्क्रूगेज जिसका चूड़ ी अंतराल 1 mm और वृत्तीय पैमाने पर 100 विभाजन हैं ।
(c) कोई प्रकाशिक यंत्र जो प्रकाश की तरंगदैर्घ्य की सीमा के अंदर लंबाई माप सकता है ।
2.7 कोई छात्र 100 आवर्धन के एक सूक्ष्मदर्शी के द्वारा देखकर मनुष्य के बाल की मोटाई मापता है । वह 20 बार प्रेक्षण करता है और उसे ज्ञात होता है कि सूक्ष्मदर्शी के दृश्य क्षेत्र में बाल की औसत मोटाई 3.5 mm है । बाल की मोटाई का अनुमान क्या है?
2.8 निम्नलिखित के उत्तर दीजिए ः
(a) आपको एक धागा और मीटर पैमाना दिया जाता है । आप धागे के व्यास का अनुमान किस प्रकार लगाएंगे ?
(b) एक स्क्रूगेज का चूड़ ी अंतराल 1.0 mm है और उसके वृत्तीय पैमाने पर 200 विभाजन हैं । क्या आप यह सोचते हैं कि वृत्तीय पैमाने पर विभाजनों की संख्या स्वेच्छा से बढ़ा देने पर स्क्रूगेज की यथार्थता में वृद्धि करना संभव है ?
(c) वर्नियर केलिपर्स द्वारा पीतल की किसी पतली छड़ का माध्य व्यास मापा जाना है । केवल 5 मापनों के समुच्चय की तुलना में व्यास के 100 मापनों के समुच्चय के द्वारा अधिक विश्वसनीय अनुमान प्राप्त होने की संभावना क्यों है ?
2.9 किसी मकान का फोटोग्राफ 35 mm स्लाइड पर 1.75 cm2 क्षेत्र घेरता है । स्लाइड को किसी स्क्रीन पर प्रक्षेपित किया जाता है और स्क्रीन पर मकान का क्षेत्रफल 1.55 m2 है । प्रक्षेपित्र-परदा व्यवस्था का रेखीय आवर्धन क्या है ?
2.10 निम्नलिखित में सार्थक अंकों की संख्या लिखिए ः
(a) 0.007 m2 (b) 2.64 × 1024 kg (c) 0.2370 g cm-3
(d) 6.320 J (e) 6.032 N m–2 (f) 0.0006032 m2
2.11 धातु की किसी आयताकार शीट की लंबाई, चौड़ ाई व मोटाई क्रमशः 4.234 m, 1.005 m व 2.01 cm है । उचित सार्थक अंकों तक इस शीट का क्षेत्रफल व आयतन ज्ञात कीजिए ।
2.12 पंसारी की तुला द्वारा मापे गए डिब्बे का द्रव्यमान 2.30 kg है । सोने के दो टुकड़ े जिनका द्रव्यमान
20.15 g व 20.17 g है, डिब्बे में रखे जाते हैं । (a) डिब्बे का कुल द्रव्यमान कितना है, (b) उचित सार्थक अंकों तक टुकड़ ों के द्रव्यमानों में कितना अंतर है ?
2.13 कोई भौतिक राशि P, चार प्रेक्षण-योग्य राशियों a, b, c तथा d से इस प्रकार संबधित है :

a,b, c तथा d के मापने में प्रतिशत त्रुटियां क्रमशः 1%, 3%, 4%, तथा 2%, हैं । राशि P में प्रतिशत त्रुटि कितनी है ? यदि उपर्युक्त संबंध का उपयोग करके P का परिकलित मान 3.763 आता है, तो आप परिणाम का किस मान तक निकटन करेंगे ?
2.14 किसी पुस्तक में, जिसमें छपाई की अनेक त्रुटियां हैं, आवर्त गति कर रहे किसी कण के विस्थापन के चार भिन्न सूत्र दिए गए हैं

(a = कण का अधिकतम विस्थापन, v = कण की चाल, T = गति का आवर्त काल) । विमीय आधारों पर गलत सूत्रों को निकाल दीजिए ।
2.15 भौतिकी का एक प्रसिद्ध संबंध किसी कण के ‘चल द्रव्यमान (moving mass)’ m, ‘विराम द्रव्यमान (rest mass)’ m0 , इसकी चाल v, और प्रकाश की चाल c के बीच है । (यह संबंध सबसे पहले अल्बर्ट आइंस्टाइन के विशेष आपेक्षिकता के सिद्धांत के परिणामस्वरूप उत्पन्न हुआ था ।) कोई छात्र इस संबंध को लगभग सही याद करता है लेकिन स्थिरांक c को लगाना भूल जाता है । वह लिखता है। 
2.16 परमाण्विक पैमाने पर लंबाई का सुविधाजनक मात्रक एंगस्ट्रम है और इसे Å :1Å = 10–10 m द्वारा निर्दिष्ट किया जाता है । हाइड्रोजन के परमाणु का आमाप लगभग 0.5Å है । हाइड्रोजन परमाणुओं के एक मोल का m3 में कुल आण्विक आयतन कितना होगा?
2.17 किसी आदर्श गैस का एक मोल (ग्राम अणुक) मानक ताप व दाब पर 22.4 L आयतन (ग्राम अणुक आयतन) घेरता है । हाइड्रोजन के ग्राम अणुक आयतन तथा उसके एक मोल के परमाण्विक आयतन का अनुपात क्या है? (हाइड्रोजन के अणु की आमाप लगभग 1Å मानिए) । यह अनुपात इतना अधिक क्यों है?
2.18 इस सामान्य प्रेक्षण की स्पष्ट व्याख्या कीजिए ः यदि आप तीव्र गति से गतिमान किसी रेलगाड़ ी की खिड़ की से बाहर देखें तो समीप के पेड़ , मकान आदि रेलगाड़ ी की गति की विपरीत दिशा में तेजी से गति करते प्रतीत होते हैं, परन्तु दूरस्थ पिण्ड (पहाड़ ियां, चंद्रमा, तारे आदि) स्थिर प्रतीत होते हैं । (वास्तव में, क्योंकि आपको ज्ञात है कि आप चल रहे हैं, इसलिए, ये दूरस्थ वस्तुएं आपको अपने साथ चलती हुई प्रतीत होती हैं)।
2.19 समीपी तारों की दूरियां ज्ञात करने के लिए अनुभाग 2.3.1 में दिए गए ‘लंबन’ के सिद्धांत का प्रयोग किया जाता है । सूर्य के परितः अपनी कक्षा में छः महीनों के अंतराल पर पृथ्वी की अपनी, दो स्थानों को मिलानेवाली, आधार रेखा AB है। अर्थात् आधार रेखा पृथ्वी की कक्षा के व्यास 3 × 1011m के लगभग बराबर है । लेकिन, चूंकि निकटतम तारे भी इतने अधिक दूर हैं कि इतनी लंबी आधार रेखा होने पर भी वे चाप के केवल 1" (सेकंड, चाप का) की कोटि का लंबन प्रदर्शित करते हैं । खगोलीय पैमाने पर लंबाई का सुविधाजनक मात्रक पारसेक है । यह किसी पिण्ड की वह दूरी है जो पृथ्वी से सूर्य तक की दूरी के बराबर आधार रेखा के दो विपरीत किनारों से चाप के 1" का लंबन प्रदर्शित करती है । मीटरों में एक पारसेक कितना होता है ?
2.20 हमारे सौर परिवार से निकटतम तारा 4.29 प्रकाश वर्ष दूर है । पारसेक में यह दूरी कितनी है ? यह तारा (एेल्फा सेंटौरी नामक) तब कितना लंबन प्रदर्शित करेगा जब इसे सूर्य के परितः अपनी कक्षा में पृथ्वी के दो स्थानों से जो छः महीने के अन्तराल पर हैं, देखा जाएगा ?
2.21 भौतिक राशियों का परिशुद्ध मापन विज्ञान की आवश्यकताएं हैं। उदाहरण के लिए, किसी शत्रु के लड़ ाकू जहाज की चाल सुनिश्चित करने के लिए बहुत ही छोटे समय-अंतरालों पर इसकी स्थिति का पता लगाने की कोई यथार्थ विधि होनी चाहिए । द्वितीय विश्व युद्ध में रेडार की खोज के पीछे वास्तविक प्रयोजन यही था । आधुनिक विज्ञान के उन भिन्न उदाहरणों को सोचिए जिनमें लंबाई, समय, द्रव्यमान आदि के परिशुद्ध मापन की आवश्यकता होती है । अन्य जिस किसी विषय में भी आप बता सकते हैं, परिशुद्धता की मात्रात्मक धारणा दीजिए ।
2.22 जिस प्रकार विज्ञान में परिशुद्ध मापन आवश्यक है, उसी प्रकार अल्पविकसित विचारों तथा सामान्य प्रेक्षणों को उपयोग करने वाली राशियों के स्थूल आकलन कर सकना भी उतना ही महत्त्वपूर्ण है । उन उपायों को सोचिए जिनके द्वारा आप निम्नलिखित का अनुमान लगा सकते हैं ः (जहां अनुमान लगाना कठिन है वहां राशि की उपरिसीमा पता लगाने का प्रयास कीजिए) ।
(a) मानसून की अवधि में भारत के ऊपर वर्षाधारी मेघों का कुल द्रव्यमान ।
(b) किसी हाथी का द्रव्यमान ।
(c) किसी तूफान की अवधि में वायु की चाल ।
(d) आपके सिर के बालों की संख्या ।
(e) आपकी कक्षा के कमरे में वायु के अणुओं की संख्या ।
2.23 सूर्य एक ऊष्म प्लै\ज़्मा (आयनीकृत पदार्थ) है जिसके आंतरिक क्रोड का ताप 107 K से अधिक और बाह्य पृष्ठ का ताप लगभग 6000 K है । इतने अधिक ताप पर कोई भी पदार्थ ठोस या तरल प्रावस्था में नहीं रह सकता। आपको सूर्य का द्रव्यमान घनत्व किस परिसर में होने की आशा है ? क्या यह ठोसों, तरलों या गैसों के घनत्वों के परिसर में है ? क्या आपका अनुमान सही है, इसकी जांच आप निम्नलिखित आंकड़ ों के आधार पर कर सकते हैं ः सूर्य का द्रव्यमान = 2.0 × 1030 kg; सूर्य की त्रिज्या = 7.0 × 108 m ।
2.24 जब बृहस्पति ग्रह पृथ्वी से 8247 लाख किलोमीटर दूर होता है, तो इसके व्यास की कोणीय माप 35.72" का चाप है । बृहस्पति का व्यास परिकलित कीजिए ।
अतिरिक्त अभ्यास
2.25 वर्षा के समय में कोई व्यक्ति चाल v के साथ तेजी से चला जा रहा है । उसे अपने छाते को टेढ़ा करके ऊर्ध्व के साथ θ कोण बनाना पड़ ता है । कोई विद्यार्थी कोण θ व v के बीच निम्नलिखित संबंध व्युत्पन्न करता है ः
tan θ = v;
और वह इस संबंध के औचित्य की सीमा पता लगाता हैः जैसी कि आशा की जाती है यदि v → 0 तो
θ → 0। (हम यह मान रहे हैं कि तेज हवा नहीं चल रही है और किसी खड़ े व्यक्ति के लिए वर्षा ऊर्ध्वाधरतः पड़ रही है) । क्या आप सोचते हैं कि यह संबंध सही हो सकता है? यदि एेसा नहीं है तो सही संबंध का अनुमान लगाइए ।
2.26 यह दावा किया जाता है कि यदि बिना किसी बाधा के 100 वर्षों तक दो सी\ज़ियम घड़ ियों को चलने दिया जाए, तो उनके समयों में केवल 0.02 s का अंतर हो सकता है । मानक सी\ज़ियम घड़ ी द्वारा 1 s के समय अंतराल को मापने में यथार्थता के लिए इसका क्या अभिप्राय है?
2.27 एक सोडियम परमाणु का आमाप लगभग 2.5Å मानते हुए उसके माध्य द्रव्यमान घनत्व का अनुमान लगाइए। (सोडियम के परमाण्वीय द्रव्यमान तथा आवोगाद्रो संख्या के ज्ञात मान का प्रयोग कीजिए ।) इस घनत्व की क्रिस्टलीय प्रावस्था में सोडियम के घनत्व 970 kg m–3 के साथ तुलना कीजिए । क्या इन दोनों घनत्वों के परिमाण की कोटि समान है? यदि हां, तो क्यों?
2.28 नाभिकीय पैमाने पर लंबाई का सुविधाजनक मात्रक फर्मी है ः (1 f =10–15m) । नाभिकीय आमाप लगभग निम्नलिखित आनुभविक संबंध का पालन करते हैं ः
r=r0 A1/3
जहां r नाभिक की त्रिज्या, A इसकी द्रव्यमान संख्या और r0 कोई स्थिरांक है जो लगभग 1.2 f के बराबर है । यह प्रदर्शित कीजिए कि इस नियम का अर्थ है कि विभिन्न नाभिकों के लिए नाभिकीय द्रव्यमान घनत्व लगभग स्थिर है । सोडियम नाभिक के द्रव्यमान घनत्व का आकलन कीजिए । प्रश्न 2.27 में ज्ञात किए गए सोडियम परमाणु के माध्य द्रव्यमान घनत्व के साथ इसकी तुलना कीजिए ।
2.29 लेसर (LASER), प्रकाश के अत्यधिक तीव्र, एकवर्णी तथा एकदिश किरण-पुंज का स्रोत है । लेसर के इन गुणों का लंबी दूरियां मापने में उपयोग किया जाता है । लेसर को प्रकाश के स्रोत के रूप में उपयोग करते हुए पहले ही चंद्रमा की पृथ्वी से दूरी परिशुद्धता के साथ ज्ञात की जा चुकी है । कोई लेसर प्रकाश किरण-पुंज चंद्रमा के पृष्ठ से परावर्तित होकर 2.56 s में वापस आ जाता है । पृथ्वी के परितः चंद्रमा की कक्षा की त्रिज्या कितनी है ?
2.30 जल के नीचे वस्तुओं को ढूंढ़ने व उनके स्थान का पता लगाने के लिए सोनार (SONAR) में पराश्रव्य तरंगों का प्रयोग होता है । कोई पनडुब्बी सोनार से सुसज्जित है । इसके द्वारा जनित अन्वेषी तरंग और शत्रु की पनडुब्बी से परावर्तित इसकी प्रतिध्वनि की प्राप्ति के बीच काल विलंब 77.0 s है । शत्रु की पनडुब्बी कितनी दूर है ? (जल में ध्वनि की चाल = 1450 m s–1) ।
2.31 हमारे विश्व में आधुनिक खगोलविदों द्वारा खोजे गए सर्वाधिक दूरस्थ पिण्ड इतनी दूर हैं कि उनके द्वारा उत्सर्जित प्रकाश को पृथ्वी तक पहुंचने में अरबों वर्ष लगते हैं । इन पिंडों (जिन्हें क्वासर ‘Quasar’ कहा जाता है) के कई रहस्यमय लक्षण हैं जिनकी अभी तक संतोषजनक व्याख्या नहीं की जा सकी है । किसी एेसे क्वासर की km में दूरी ज्ञात कीजिए जिससे उत्सर्जित प्रकाश को हम तक पहुंचने में 300 करोड़ वर्ष लगते हों ।
2.32 यह एक विख्यात तथ्य है कि पूर्ण सूर्यग्रहण की अवधि में चंद्रमा की चक्रिका सूर्य की चक्रिका को पूरी तरह ढक लेती है । इस तथ्य और उदाहरण 2.3 और 2.4 से एकत्र सूचनाओं के आधार पर चंद्रमा का लगभग व्यास ज्ञात कीजिए ।
2.33 इस शताब्दी के एक महान भौतिकविद् (पी.ए.एम. डिरैक) प्रकृति के मूल स्थिरांकों (नियतांकों) के आंकिक मानों के साथ क्रीड़ ा में आनंद लेते थे । इससे उन्होंने एक बहुत ही रोचक प्रेक्षण किया । परमाण्वीय भौतिकी के मूल नियतांकों (जैसे इलेक्ट्रॉन का द्रव्यमान, प्रोटॉन का द्रव्यमान तथा गुरुत्वीय नियतांक G) से उन्हें पता लगा कि वे एक एेसी संख्या पर पहुंच गए हैं जिसकी विमा समय की विमा है । साथ ही, यह एक बहुत ही बड़ ी संख्या थी और इसका परिमाण विश्व की वर्तमान आकलित आयु