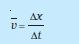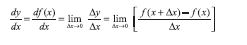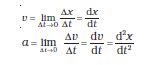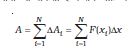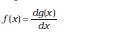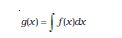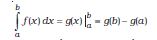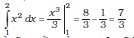Table of Contents

अध्याय 3
सरल रेखा में गति
3.2 स्थिति, पथ-लंबाई एवं विस्थापन
3.3 औसत वेग तथा औसत चाल
3.4 तात्क्षणिक वेग एवं चाल
3.5 त्वरण
3.6 एकसमान त्वरण से गतिमान वस्तु का शुद्धगतिकी संबंधी समीकरण
3.7 आपेक्षिक वेग
सारांश
विचारणीय विषय
अभ्यास
अतिरिक्त अभ्यास
परिशिष्ट 3.1
3.1 भूमिका
विश्व की प्रत्येक वस्तु प्रत्यक्ष या अप्रत्यक्ष रूप से गतिमान रहती है । हमारा चलना, दौड़ ना, साइकिल सवारी आदि दैनिक जीवन में दिखाई देने वाली क्रियाएँ गति के कुछ उदाहरण हैं । इतना ही नहीं, निद्रावस्था में भी हमारे फेफड़ ों में वायु का प्रवेश एवं निष्कासन तथा हमारी धमनियों एवं शिराओें में रुधिर का संचरण होता रहता है । हम पेड़ ों से गिरते हुए पत्तों को तथा बाँध से बहते हुए पानी को देखते हैं । मोटरगाड़ ी और वायुयान यात्रियों को एक स्थान से दूसरे स्थान को ले जाते हैं । पृथ्वी 24 घंटे में एक बार अपनी अक्ष के परितः घूर्णन करती है तथा वर्ष में एक बार सूर्य की परिक्रमा पूरी करती है । सूर्य अपने ग्रहों सहित हमारी आकाशगंगा नामक मंदाकिनी में विचरण करता है, तथा जो स्वयं भी स्थानीय मंदाकिनियों के समूह में गति करती है ।
इस प्रकार समय के सापेक्ष वस्तु की स्थिति में परिवर्तन को गति कहते हैं । समय के साथ स्थिति कैसे परिवर्तित होती है ? इस अध्याय में हम गति के बारे में पढ़ेंगे । इसके लिए हमें वेग तथा त्वरण की धारणा को समझना होगा । इस अध्याय में हम अपना अध्ययन वस्तु के एक सरल रेखा के अनुदिश गति तक ही सीमित रखेंगे । इस प्रकार की गति को सरल रेखीय गति भी कहते हैं । एकसमान त्वरित सरल रेखीय गति के लिए कुछ सरल समीकरण प्राप्त किए जा सकते हैं। अंततः गति की आपेक्षिक प्रकृति को समझने के लिए हम आपेक्षिक गति की धारणा प्रस्तुत करेंगे ।
इस अध्ययन में हम सभी गतिमान वस्तुओं को अतिसूक्ष्म मानकर बिंदु रूप में निरूपित करेंगे । यह सन्निकटन तब तक मान्य होता है जब तक वस्तु का आकार निश्चित समय अंतराल में वस्तु द्वारा चली गई दूरी की अपेक्षा पर्याप्त रूप से कम होता है । वास्तविक जीवन में बहुत-सी स्थितियाें में वस्तुओं के आमाप (साइज़) की उपेक्षा की जा सकती है और बिना अधिक त्रुटि के उन्हें एक बिंदु-वस्तु माना जा सकता है ।
शुद्धगतिकी में, हम वस्तु की गति के कारणोें पर ध्यान न देकर केवल उसकी गति का ही अध्ययन करते हैं । इस अध्याय एवं अगले अध्याय में विभिन्न प्रकार की गतियाें का वर्णन किया गया है । इन गतियाें के कारणों का अध्ययन हम पाँचवें अध्याय में करेंगे ।
3.2 स्थिति, पथ-लंबाई एवं विस्थापन
पहले आपने पढ़ा है कि किसी वस्तु की स्थिति में परिवर्तन को गति कहते हैं। स्थिति के निर्धारण के लिए एक संदर्भ बिंदु तथा अक्षों के एक समुच्चय की आवश्यकता होती है। इसके लिए एक समकोणिक निर्देशांक-निकाय का चुनाव सुविधाजनक होता है। इस निकाय में तीन परस्पर लम्बवत अक्ष होते हैं जिन्हें x-, y- तथा z-अक्ष कहते हैं। इन अक्षों के प्रतिच्छेद बिंदु को मूल बिंदु (O) कहते हैं तथा यह संदर्भ बिंदु होता है। किसी वस्तु के निर्देशांक (x, y, z) इस निर्देशांक निकाय के सापेक्ष उस वस्तु की स्थिति निरूपित करते हैं। समय नापने के लिए इस निकाय में एक घड़ ी रख देते हैं। घड़ ी सहित इस निर्देशांक-निकाय को निर्देश तंत्र (frame of reference) कहते हैं।
जब किसी वस्तु के एक या अधिक निर्देशांक समय के साथ परिवर्तित होते हैं तो वस्तु को गतिमान कहते हैं। अन्यथा वस्तु को उस निर्देश तंत्र के सापेक्ष विरामावस्था में मानते हैें।
किसी निर्देश तंत्र में अक्षों का चुनाव स्थिति विशेष पर निर्भर करता है। उदाहरण के लिए, एक विमा में गति के निरूपण के लिए हमें केवल एक अक्ष की आवश्यकता होती है। दो/तीन विमाओं में गति के निरूपण के लिए दो/तीन अक्षों की आवश्यकता होती है।
किसी घटना का वर्णन इसके लिए चुने गए निर्देश-तंत्र पर निर्भर करता है। उदाहरण के लिए, जब हम कहते हैं कि सड़ क पर कार चल रही है तो वास्तव में ‘कार की गति’ का वर्णन हम स्वयं से या जमीन से संलग्न निर्देश तंत्र के सापेक्ष करते हैं। यदि हम कार में बैठे किसी व्यक्ति से संलग्न निर्देश तंत्र के सापेक्ष कार की स्थिति का वर्णन करें तो कार विरामावस्था में होगी।
एक सरल रेखा में किसी वस्तु की गति के विवरण हेतु हम एक अक्ष (मान लीजिए x-अक्ष) को इस प्रकार चुन सकते हैं कि वह वस्तु के पथ के संपाती हो । इस प्रकार वस्तु की स्थिति को हम अपनी सुविधानुसार चुने गए किसी मूल बिंदु (मान लीजिए चित्र 3.1 में दर्शाए गए बिंदु O) के सापेक्ष निरूपित करते हैं । बिंदु O के दायीं ओर के निर्देशांक को हम धनात्मक तथा बायीं ओर के स्थिति-निर्देशांक को ऋणात्मक कहेंगे । इस पद्धति के अनुसार चित्र 3.1 में बिंदु P और Q के स्थिति-निर्देशांक क्रमशः +360 m और +240 m हैं । इसी प्रकार बिंदु R का स्थिति-निर्देशांक -120 m है ।
पथ-लंबाई
कल्पना कीजिए कि कोई कार एक सरल रेखा के अनुदिश गतिमान है । हम x-अक्ष इस प्रकार चुनते हैं कि यह गतिमान कार के पथ के संपाती हो । अक्ष का मूल बिंदु वह है जहाँ से कार चलना शुरू करती है अर्थात समय t =0 पर कार x = 0
पर थी (चित्र 3.1) । मान लीजिए कि भिन्न-भिन्न क्षणों पर कार की स्थिति बिंदुओं P, Q तथा R से व्यक्त होती है । यहाँ हम गति की दो स्थितियाें पर विचार करेंगे । पहली में कार O से P तक जाती है । अतः कार द्वारा चली गई दूरी OP = +360 m है । इस दूरी को कार द्वारा चली गई पथ-लंबाई कहते हैं । दूसरी स्थिति में कार पहले O से P तक जाती है और फिर P से Q पर वापस आ जाती है । गति की इस अवधि में कार द्वारा चली गई पथ-लंबाई = OP + PQ = 360 m + (+120 m) = +480 m होगी। क्योंकि पथ-लंबाई में केवल परिमाण होता है दिशा नहीं, अतः यह एक अदिश राशि है (अध्याय 4 देखिए) ।
विस्थापन
यहाँ यह प्रासंगिक होगा कि हम एक दूसरी उपयोगी भौतिक राशि विस्थापन को वस्तु की स्थिति में परिवर्तन के रूप में परिभाषित करें । कल्पना कीजिए कि समय t1 व t2 पर वस्तु की स्थिति क्रमशः x1 व x2 है । तब समय ∆t (=t2–t1) में उसका विस्थापन, जिसे हम ∆x से व्यक्त करते हैं, अंतिम तथा प्रारंभिक स्थितियाें के अंतर द्वारा व्यक्त किया जाता है ः
∆x =x2–x1
(यहाँ हम ग्रीक अक्षर डेल्टा (∆) का प्रयोग किसी राशि में परिवर्तन को व्यक्त करने के लिए करते हैं)।
यदि x2 > x1 तो ∆x धनात्मक होगा, परंतु यदि x2 < x1 तो ∆x ऋणात्मक होगा । विस्थापन में परिमाण व दिशा दोनों होते
हैं, एेसी राशियों को सदिशों द्वारा निरूपित किया जाता है । आप सदिशों के विषय में अगले अध्याय में पढ़ेंगे । इस अध्याय में हम एक सरल रेखा के अनुदिश सरल गति (जिसे हम रेखीय गति कहते हैं) के विषय में ही पढ़ेंगे । एक-विमीय गति में केवल दो ही दिशायें होती हैं (अग्रवर्ती एवं पश्चगामी अथवा अधोगामी एवं ऊर्ध्वगामी) जिनमें वस्तु गति करती है । इन दोनाें दिशाओं को हम सुगमता के लिए + और - संकेताें से व्यक्त कर सकते हैं । उदाहरण के लिए, यदि कार स्थिति O से P पर पहुँचती है, तो उसका विस्थापन
∆x = x2 – x1 = (+360 m) – 0 m = +360 m
होगा । इस विस्थापन का परिमाण 360 m है तथा इसकी दिशा x की धनात्मक दिशा में होगी जिसे हम + संकेत से चिह्नित करेंगे । इसी प्रकार कार का P से Q तक का विस्थापन 240 m –
360 m = –120 m होगा । ऋणात्मक चिह्न विस्थापन की दिशा को इंगित करता है । अतएव, वस्तु की एक-विमीय गति के विवरण के लिए सदिश संकेत का उपयोग आवश्यक नहीं होता है ।
विस्थापन का परिमाण गतिमान वस्तु द्वारा चली गई पथ-लंबाई के बराबर हो भी सकता है और नहीं भी हो सकता है । उदाहरण के लिए, यदि कार स्थिति O से चल कर P पर पहुँच जाए, तो पथ-लंबाई = +360 m तथा विस्थापन = +360 m होगा । यहाँ विस्थापन का परिमाण (360 m) पथ-लंबाई (360 m) के बराबर है । परंतु यदि कार O से चलकर P तक जाए और फिर Q पर वापस आ जाए तो, पथ-लंबाई = (+360 m) + (+120 m) = +480 m होगी परंतु विस्थापन = (+240 m) – (0 m) = +240 m होगा । इस बार विस्थापन का परिमाण (240 m) कार द्वारा चली गई पथ-लंबाई (480 m) के बराबर नहीं (वास्तव में कम) है ।
विस्थापन का परिमाण गति की किसी अवधि के लिए शून्य भी हो सकता है जबकि तदनुरूप पथ-लंबाई शून्य नहीं है। उदाहरण के लिए, चित्र 3.1 में यदि कार O से चल कर P तक जाए और पुनः O पर वापस आ जाए तो कार की अंतिम स्थिति प्रारंभिक स्थिति के संपाती हो जाती है और विस्थापन शून्य हो जाता है । परंतु कार की इस पूरी यात्रा के लिए कुल पथ-लंबाई OP + PO = +360 m + 360 m = +720 m होगी ।

चित्र 3.2 स्थिति-समय ग्राफ, जब (a) वस्तु स्थिर है, तथा (b) जब वस्तु एकसमान गति से चल रही है ।
जैसा कि आप पहले पढ़ चुके हैं किसी भी वस्तु की गति को स्थिति-समय ग्राफ द्वारा व्यक्त किया जा सकता है । इस प्रकार के ग्राफ एेसे सशक्त साधन होते हैं, जिनके माध्यम से वस्तु की गति के विभिन्न पहलुआें का निरूपण एवं विश्लेषण आसानी से किया जा सकता है । किसी सरल रेखा (जैसे- x-अक्ष) के अनुदिश गतिमान वस्तु के लिए समय के साथ केवल x-निर्देशांक ही परिवर्तित होता है । इस प्रकार हमें
x - t ग्राफ प्राप्त होता है । हम सर्वप्रथम एक सरल स्थिति पर विचार करेंगे, जिसमें वस्तु उदाहरणार्थ, एक कार x = 40 m पर स्थित है । एेसी वस्तु के लिए स्थिति-समय (x- t) ग्राफ समय-अक्ष के समांतर एक सीधी सरल रेखा होता है जैसा कि चित्र 3.2(a) में दिखाया गया है ।
यदि कोई वस्तु समान समय अंतराल में समान दूरी तय करती है, तो उस वस्तु की गति एकसमान गति कहलाती है । इस प्रकार की गति का स्थिति-समय ग्राफ चित्र 3.2(b) में दिखलाया गया है ।
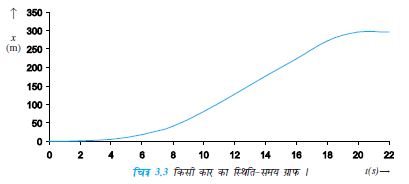
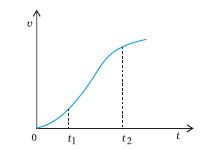
अब हम उस कार की गति पर विचार करेंगे जो मूल बिंदु O से t = 0 s पर विरामावस्था से चलना प्रारंभ करती है । इसकी चाल उत्तरोत्तर t = 10 s तक बढ़ती जाती है । इसके बाद वह
t = 18 s तक एकसमान चाल से चलती है । इस समय इसमें ब्रेक लगाया जाता है जिसके परिणामस्वरूप वह t = 20 s पर और x = 296 m पर रुक जाती है । एेसी कार का स्थिति-समय ग्राफ चित्र 3.3 में दिखाया गया है । हम इस ग्राफ की चर्चा इसी अध्याय में आगे आने वाले कुछ खंडों में पुनः करेंगे ।
3.3 औसत वेग तथा औसत चाल
जब कोई वस्तु गतिमान होती है तो समय के साथ-साथ उसकी स्थिति परिवर्तित होती है । प्रश्न उठता है कि समय के साथ कितनी तेजी से वस्तु की स्थिति परिवर्तित होती है तथा यह परिवर्तन किस दिशा में होता है ? इसके विवरण के लिए हम एक राशि परिभाषित करते हैं जिसे औसत वेेग कहा जाता है । किसी वस्तु की स्थिति में परिवर्तन अथवा विस्थापन (∆x) को समय अंतराल (∆t) द्वारा विभाजित करने पर औसत वेग प्राप्त होता है । इसे v-- से चिह्नित करते हैं :
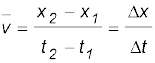 (3.1)
(3.1)
यहां x1, आरंभिक समय t1 पर तथा x2 अंतिम समय t2 पर, वस्तु की स्थिति को व्यक्त करता है । यहाँ वेग के प्रतीक (v) के ऊपर लगाई गई ‘रेखा’ वेग के औसत मान को व्यक्त करती है। किसी राशि के औसत मान को दर्शाने की यह एक मानक
पद्धति है । वेग का SI मात्रक m/s अथवा m s–1 है यद्यपि दैनिक उपयोगों में उसके लिए km/h का भी प्रयोग होता है।
विस्थापन की भाँति माध्य-वेग भी एक सदिश राशि है । इसमें दिशा एवं परिमाण दोनों समाहित होते हैं । परंतु जैसा कि हम पीछे स्पष्ट कर चुके हैं, यदि वस्तु एक सरल रेखा में गतिमान हो तो उसके दिशात्मक पक्ष को + या - चिह्नों द्वारा प्रकट कर सकते हैं । इसलिए इस अध्याय में वेग के लिए हम सदिश संकेतन का उपयोग नहीं करेंगे ।
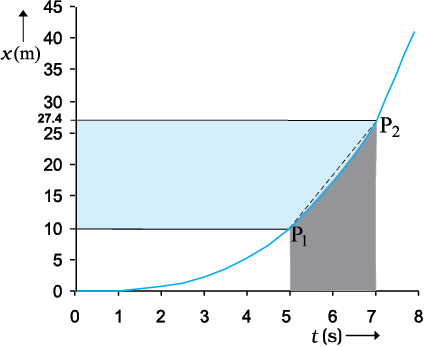
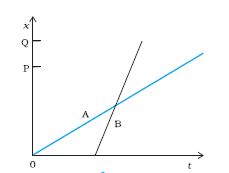
चित्र 3.4 औसत चाल सरल रेखा P1 P2 की प्रवणता है ।
चित्र 3.3 में दर्शाई गई कार की गति के लिए x-t ग्राफ का t = 0 s तथा t=8 s के बीच के भाग को बड़ ा करके चित्र
3.4 में दिखाया गया है । जैसा कि आलेख से स्पष्ट है,
t = 5 s तथा t =7 s के मध्य समय अंतराल में कार का औसत-वेग होगाः
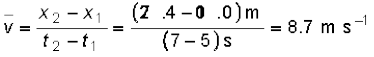
यह मान चित्र 3.4 में दर्शाई गई सरल रेखा p1 p2 की प्रवणता के बराबर होगा । यह सरल रेखा कार की प्रारंभिक स्थिति p1 को उसकी अंतिम स्थिति p2 से मिलाती है ।
औसत वेग का ऋणात्मक या धनात्मक होना विस्थापन के चिह्न पर निर्भर करता है । यदि विस्थापन शून्य होगा तो औसत वेग का मान भी शून्य होगा । धनात्मक तथा ऋणात्मक वेग से चलती हुई वस्तु के लिए x–t ग्राफ क्रमशः चित्र 3.5(a) तथा चित्र 3.5(b) में दर्शाए गए हैं । किसी स्थिर वस्तु के लिए
x-t ग्राफ चित्र 3.5(c) में दर्शाया गया है ।

(a) (b) (c)
चित्र 3.5 स्थिति-समय ग्राफ उस वस्तु के लिए जो (a) धनात्मक वेग से गतिमान है, (b) ऋणात्मक वेग से गतिमान है, तथा (c) विरामावस्था में है ।
औसत वेग को परिभाषित करने के लिए केवल विस्थापन का ज्ञान ही आवश्यक होता है । हम यह देख चुके हैं कि विस्थापन का परिमाण वास्तविक पथ-लंबाई से भिन्न हो सकता है । वास्तविक पथ पर वस्तु की गति की दर के लिए हम एक दूसरी राशि को प्रयुक्त करते हैं जिसे औसत चाल कहते हैं ।
वस्तु की यात्रा की अवधि में चली गई कुल पथ-लंबाई एवं इसमें लगे समय के भागफल को औसत चाल कहते हैं ।

औसत चाल का वही मात्रक (m s–1) होता है जो वेग का होता है । परंतु औसत चाल से यह पता नहीं चल पाता कि वस्तु किस दिशा में गतिमान है । इस दृष्टिकोण से औसत चाल सदैव धनात्मक ही होती है (जबकि औसत वेग धनात्मक या ऋणात्मक कुछ भी हो सकता है)। यदि वस्तु एक सरल रेखा के अनुदिश गतिमान है और केवल एक ही दिशा में चलती है तो विस्थापन का परिमाण कुल पथ-लंबाई के बराबर होगा । एेसी परिस्थितियाें में वस्तु के औसत वेग का परिमाण उसकी औसत चाल के बराबर होगा । परंतु यह बात हमेशा सही नहीं होगी । यह आप उदाहरण 3.1 में देखेंगे ।
¯ उदाहरण 3.1 कोई कार एक सरल रेखा (मान लीजिए चित्र 3.1 में रेखा op) के अनुदिश गतिमान है । कार O से चलकर 18 s में P तक पहुंचती है, फिर 6.0 s में स्थिति Q पर वापस आ जाती है । कार के औसत वेग एवं औसत चाल की गणना कीजिए, जब (a) कार O से P तक जाती है, और (b) जब वह O से P तक जा कर पुनः Q पर वापस आ जाती है ।
अतः इस स्थिति में औसत चाल का मान औसत वेग के परिमाण के बराबर नहीं है । इसका कारण कार की गति के दौरान गति में दिशा परिवर्तन है जिसके फलस्वरूप पथ-लंबाई विस्थापन के परिमाण से अधिक है । इससे स्पष्ट है कि वस्तु की चाल सामान्यतया वेग के परिमाण से अधिक होती है । °
यदि उदाहरण 3.1 में कार स्थिति O से P बिंदु तक जाए तथा उसी समय अंतराल में वह O स्थिति पर वापस आ जाए तो कार की माध्य चाल 20 m s–1 होगी, परंतु उसका औसत वेग
शून्य होगा!
3.4 तात्क्षणिक वेग एवं चाल
जैसा कि हम पढ़ चुके हैं कि औसत वेग से हमें यह ज्ञात होता है कि कोई वस्तु किसी दिए गए समय अंतराल में किस गति से चल रही है, किन्तु इससे यह पता नहीं चल पाता कि इस समय अंतराल के भिन्न-भिन्न क्षणों पर वह किस गति से चल रही है। अतः किसी क्षण t पर वेग के लिए हम तात्क्षणिक वेग या केवल वेग v को परिभाषित करते हैं ।
गतिमान वस्तु का तात्क्षणिक वेग उसके औसत वेग के बराबर होगा यदि उसके दो समयों (t तथा t + ∆t) के बीच का अंतराल (∆t) अनन्तः सूक्ष्म हो । गणितीय विधि से हम इस कथन को निम्न प्रकार से व्यक्त करते हैं-
यहाँ प्रतीक 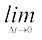 का तात्पर्य उसके दायीं ओर स्थित राशि
का तात्पर्य उसके दायीं ओर स्थित राशि
(जैसे 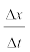 ) का वह मान है जो ∆t के मान को शून्य की ओर (∆t→0) प्रवृत्त करने पर प्राप्त होगा । कलन गणित की भाषा में समीकरण (3.3a) में दायीं ओर की राशि
) का वह मान है जो ∆t के मान को शून्य की ओर (∆t→0) प्रवृत्त करने पर प्राप्त होगा । कलन गणित की भाषा में समीकरण (3.3a) में दायीं ओर की राशि 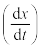 x का t
x का t
के सापेक्ष अवकलन गुणांक है। (परिशिष्ट 3.1 देखिए)। यह गुणांक उस क्षण पर वस्तु की स्थिति परिवर्तन की दर
होती है ।
किसी क्षण पर वस्तु का वेग निकालने के लिए हम समीकरण (3.3a) का उपयोग कर सकते हैं । इसके लिए ग्राफिक या गणितीय विधि को प्रयोग में लाते हैं । मान लीजिए कि हम चित्र (3.3) में निरूपित गतिमान कार का वेग t = 4 s (बिंदु P) पर निकालना चाहते हैं । गणना की आसानी के लिए इस चित्र को चित्र 3.6 में अलग पैमाना लेकर पुनः खींचा गया है। पहले हम t = 4 s को केंद्र में रखकर ∆t को 2 s लें । औसत वेग की परिभाषा के अनुसार सरल रेखा p1p2 (चित्र 3.6) की प्रवणता 3 s से 5 s के अंतराल में वस्तु के औसत वेग को व्यक्त करेगी । अब हम ∆t का मान 2 s से घटाकर 1 s कर देते हैं तो P1P2 रेखा Q1Q2 हो जाती है और इसकी प्रवणता 3.5 s से 4.5 s अंतराल में औसत वेग का मान देगी । अंततः सीमांत मान ∆t→0 की परिस्थिति में रेखा P1P2 स्थिति-समय वक्र के बिंदु P पर स्पर्श रेखा हो जाती है ।
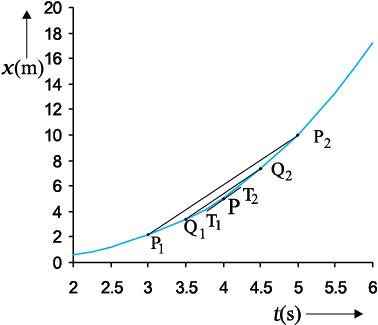
चित्र 3.6 स्थिति-समय ग्राफ से वेग ज्ञात करना । t = 4 s पर वेग उस क्षण पर ग्राफ की स्पर्श रेखा की प्रवणता है ।
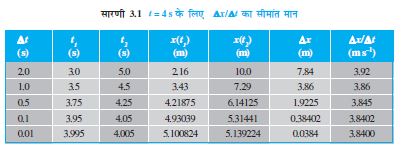
इस प्रकार t = 4 s क्षण पर कार का वेग उस बिंदु पर खींची गई स्पर्श रेखा की प्रवणता के बराबर होगा । यद्यपि ग्राफिक विधि से इसे प्रदर्शित करना कुछ कठिन है तथापि यदि इसके लिए हम गणितीय विधि का उपयोग करेें तो सीमांत प्रक्रिया आसानी से समझी जा सकती है । चित्र 3.6 में खींचे गए ग्राफ के लिए x = 0.8 t3 है । सारणी 3.1 में t=4 s को केंद्र मेें रखकर ∆t = 2.0 s, 1.0 s, 0.5 s, 0.1 s तथा 0.01 s के लिए ∆x/∆t के मूल्यों को दर्शाया गया है । दूसरे और तीसरे कॉलम में t1(=t–∆t/2) तथा t2(=t–∆t/2) और चौथे एवं पाँचवें कॉलम में x के तदनुरूप मानोें अर्थात x(t1) = 0.08 t31 तथा x(t2) = 0.03 t32 को दिखलाया गया है । छठे कॉलम में अंतर ∆x = x(t2)–x(t1) को तथा अंतिम कॉलम में ∆x व ∆t के अनुपात को व्यक्त किया गया है । यह अनुपात प्रथम कॉलम में अंकित ∆t के भिन्न-भिन्न मानों के संगत औसत वेग का मान है ।
सारणी 3.1 से स्पष्ट है कि जैसे-जैसे ∆t का मान 2.0 s से घटाते-घटाते 0.01 s करते हैं तो औसत वेग अंततः सीमांत मान 3.84 ms-1 के बराबर हो जाता है जो t=4 s पर कार का वेग है अर्थात t=4 s पर dx/dt का मान । इस प्रकार चित्र 3.3 में दर्शाई गई गति के हर क्षण के लिए हम कार का वेग निकाल सकते हैं । इस उदाहरण के लिए समय के सापेक्ष वेग में परिवर्तन चित्र 3.7 में दर्शाया गया है ।
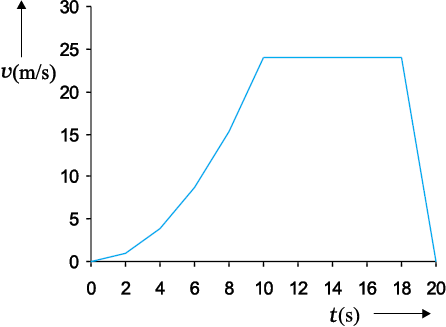
चित्र 3.7 चित्र 3.3 में दर्शाई गई वस्तु की गति के तदनुरूप वेग-समय ग्राफ ।
यहाँ यह बात ध्यान देने योग्य है कि वस्तु का तात्क्षणिक वेग निकालने के लिए ग्राफिक विधि सदैव सुविधाजनक नहीं होती है । इस विधि (ग्राफिक विधि) में हम गतिमान वस्तु के स्थिति-समय ग्राफ को सावधानीपूर्वक खींचते हैं तथा ∆t को उत्तरोत्तर कम करते हुए वस्तु के औसत वेग (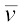 ) की गणना करते जाते हैं । भिन्न-भिन्न क्षणों पर वस्तु का वेग निकालना तब बहुत आसान हो जाता है जब विभिन्न समयों पर हमारे पास वस्तु की स्थिति के पर्याप्त आँकड़ े उपलब्ध हों अथवा वस्तु की स्थिति का समय के फलन के रूप में हमारे पास यथार्थ व्यंजक उपलब्ध हो । एेसी स्थिति में उपलब्ध आँकड़ ों का उपयोग करते हुए समय अंतराल ∆t को क्रमशः सूक्ष्म करते हुए ∆x/∆t का मान निकालते जाएँगे और अंततः सारणी 3.1 में दर्शाई गई विधि के अनुसार ∆x/∆t का सीमांत मान प्राप्त कर लेंगे । अन्यथा किसी दिए गए व्यंजक के लिए अवकल गणित का प्रयोग करके गतिमान वस्तु के भिन्न-भिन्न क्षणों के लिए dx/dt की गणना कर लेंगे जैसा कि उदाहरण 3.2 में बताया गया है ।
) की गणना करते जाते हैं । भिन्न-भिन्न क्षणों पर वस्तु का वेग निकालना तब बहुत आसान हो जाता है जब विभिन्न समयों पर हमारे पास वस्तु की स्थिति के पर्याप्त आँकड़ े उपलब्ध हों अथवा वस्तु की स्थिति का समय के फलन के रूप में हमारे पास यथार्थ व्यंजक उपलब्ध हो । एेसी स्थिति में उपलब्ध आँकड़ ों का उपयोग करते हुए समय अंतराल ∆t को क्रमशः सूक्ष्म करते हुए ∆x/∆t का मान निकालते जाएँगे और अंततः सारणी 3.1 में दर्शाई गई विधि के अनुसार ∆x/∆t का सीमांत मान प्राप्त कर लेंगे । अन्यथा किसी दिए गए व्यंजक के लिए अवकल गणित का प्रयोग करके गतिमान वस्तु के भिन्न-भिन्न क्षणों के लिए dx/dt की गणना कर लेंगे जैसा कि उदाहरण 3.2 में बताया गया है ।
उदाहरण 3.2 x-अक्ष के अनुदिश किसी गतिमान वस्तु की स्थिति निम्नलिखित सूत्र से व्यक्त की जाती है ः x=a+bt2 । यहाँ a = 8.5 m, b = 2.5 m s–2 तथा समय t को सेकंड में व्यक्त किया गया है । t=0 s तथा t=2.0 s क्षणों पर वस्तु का वेग क्या होगा ? t=2.0 s तथा t=4.0 s के मध्य के समय अंतराल में वस्तु का औसत वेग क्या होगा ?
हल अवकल गणित की पद्धति के अनुसार वस्तु का वेग
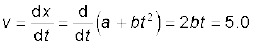 t m s–1
t m s–1
t =0 s क्षण के लिए v = 0 m/s, तथा t =2.0 s समय पर,
v =10 m s–1
औसत वेग =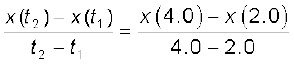
= 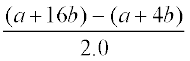 = 6.0b
= 6.0b
= 6.0 ×2.5 = 15 m s–1 °
चित्र 3.7 से यह स्पष्ट है कि t=10 s से 18 s के मध्य वेग स्थिर रहता है । t=18 s से t=20 s के मध्य यह एकसमान रूप से घटता जाता है जबकि t=0 s से t=10 s के बीच यह बढ़ता जाता है । ध्यान दीजिए कि एकसमान गति में हर समय (तात्क्षणिक) वेग का वही मान होता है जो औसत वेग का होता है।
तात्क्षणिक चाल या केवल चाल गतिमान वस्तु के वेग का परिमाण है । उदाहरण के तौर पर, वेग + 24.0 m s–1 तथा –24.0 m s–1 दोनों में प्रत्येक का परिमाण 24.0 m s–1 होगा। यहाँ यह तथ्य ध्यान में रखना है कि जहाँ किसी सीमित समय अंतराल में वस्तु की औसत चाल उसके औसत वेग के परिमाण के या तो बराबर होती है या उससे अधिक होती है वहीं किसी क्षण पर वस्तु की तात्क्षणिक चाल उस क्षण पर उसके तात्क्षणिक वेग के परिमाण के बराबर होती है । एेसा क्यों होता है ?
3.5 त्वरण
सामान्यतः वस्तु की गति की अवधि में उसके वेग में परिवर्तन होता रहता है । वेग में हो रहे इस परिवर्तन को कैसे व्यक्त करें । वेग में हो रहे इस परिवर्तन को समय के सापेक्ष व्यक्त करना चाहिए या दूरी के सापेक्ष ? यह समस्या गैलीलियो के समय भी थी । गैलीलियो ने पहले सोचा कि वेग में हो रहे परिवर्तन की इस दर को दूरी के सापेक्ष व्यक्त किया जा सकता है परंतु जब उन्होंने मुक्त रूप से गिरती हुई तथा नत समतल पर गतिमान वस्तुओं की गति का विधिवत् अध्ययन किया तो उन्होंने पाया कि समय के सापेक्ष वेग परिवर्तन की दर का मान मुक्त रूप से गिरती हुई वस्तुओं के लिए, स्थिर रहता है जबकि दूरी के सापेक्ष वस्तु का वेग परिवर्तन स्थिर नहीं रहता वरन जैसे-जैसे गिरती हुई वस्तु की दूरी बढ़ती जाती है वैसे-वैसे यह मान घटता जाता है। इस अध्ययन ने त्वरण की वर्तमान धारणा को जन्म दिया जिसके अनुसार त्वरण को हम समय के सापेक्ष वेग परिवर्तन के रूप में परिभाषित करते हैं ।
जब किसी वस्तु का वेग समय के सापेक्ष बदलता है तो हम कहते हैं कि उसमें त्वरण हो रहा है । वेग में परिवर्तन तथा तत्संबंधित समय अंतराल के अनुपात को हम औसत त्वरण कहते हैं । इसे a- से प्रदर्शित करते हैं ः
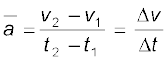 (3.4)
(3.4)
यहां t1, t2क्षणों पर वस्तु का वेग क्रमशः v1 तथा v2 है । यह एकांक समय में वेग में औसत परिवर्तन होता है । त्वरण का
SI मात्रक m s–2 है ।
वेग-समय (v-t) ग्राफ से हम वस्तु का औसत त्वरण निकाल सकते हैं । यह इस प्रकार के ग्राफ में उस सरल रेखा की प्रवणता के बराबर होता है जो बिंदु (v2, t2) को बिंदु (v1, t1) से जोड़ ती है । नीचे के उदाहरण में चित्र 3.7 में दर्शाई गई गति के भिन्न-भिन्न समय अंतरालों में हमने वस्तु का औसत त्वरण निकाला है :
0 s - 10 s 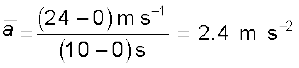
10 s - 18 s 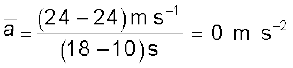
18 s - 20 s 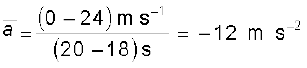
तात्क्षणिक त्वरण ः जिस प्रकार हमने पूर्व में तात्क्षणिक वेग की व्याख्या की है, उसी प्रकार हम तात्क्षणिक त्वरण को भी परिभाषित करते हैं । वस्तु के तात्क्षणिक त्वरण को a से चिह्नित करते हैं, अर्थात
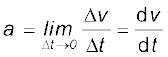 (3.5)
(3.5)
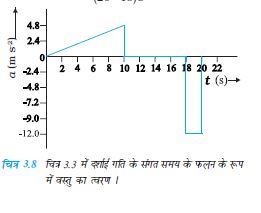
v–t ग्राफ में किसी क्षण वस्तु का त्वरण उस क्षण वक्र पर खींची गई स्पर्श रेखा की प्रवणता के बराबर होता है । चित्र 3.7 में दर्शाए गए v–t वक्र में प्रत्येक क्षण के लिए त्वरण प्राप्त कर सकते हैं । परिणामस्वरूप उपलब्ध a–t वक्र चित्र 3.8 में दिखाया गया है । चित्र से स्पष्ट है कि 0 s से 10 s की अवधि में त्वरण असमान है । 10 s–18 s के मध्य यह शून्य है जबकि 18 s तथा 20 s के बीच यह स्थिर है तथा इसका मान -12 m s–2 है । जब त्वरण एकसमान होता है तो यह स्पष्ट है कि वह उस अवधि में औसत त्वरण के बराबर होता है।
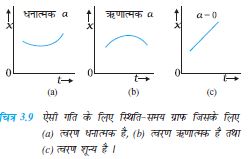
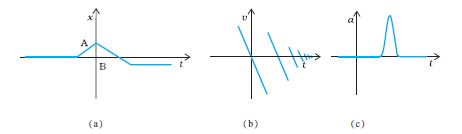
चूँकि वेग एक सदिश राशि है जिसमें दिशा एवं परिमाण दोनों होते हैं अतएव वेग परिवर्तन में इनमें से कोई एक अथवा दोनों निहित हो सकते हैं । अतः या तो चाल (परिमाण) में परिवर्तन, दिशा में परिवर्तन अथवा इन दोनों में परिवर्तन से त्वरण का उद्भव हो सकता है । वेग के समान ही त्वरण भी धनात्मक, ऋणात्मक अथवा शून्य हो सकता है । इसी प्रकार के त्वरण संबंधी स्थिति-समय ग्राफों को चित्रों 3.9 (a), 3.9 (b) तथा 3.9 (c) में दर्शाया गया है । चित्रों से स्पष्ट है कि धनात्मक त्वरण के लिए x–t ग्राफ ऊपर की ओर वक्रित है किन्तु ऋणात्मक त्वरण के लिए ग्राफ नीचे की ओर वक्रित है । शून्य त्वरण के लिए x–t ग्राफ एक सरल रेखा है । अभ्यास के लिए चित्र 3.3 में दर्शाई गई गति के उन तीनों भागों को पहचानिए जिनके लिए त्वरण +a, –a अथवा शून्य है ।
यद्यपि गतिमान वस्तु का त्वरण समय के साथ-साथ बदल सकता है, परंतु सुविधा के लिए इस अध्याय में गति संबंधी
हमारा अध्ययन मात्र स्थिर त्वरण तक ही सीमित रहेगा । एेसी स्थिति में औसत त्वरण 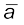 का मान गति की अवधि में स्थिर त्वरण के मान के बराबर होगा ।
का मान गति की अवधि में स्थिर त्वरण के मान के बराबर होगा ।
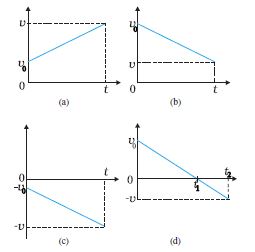
चित्र 3.10 स्थिर त्वरण के साथ गतिमान वस्तु का वेग-समय ग्राफ
(a) धनात्मक त्वरण से धनात्मक दिशा में गति,
(b) ऋणात्मक त्वरण से धनात्मक दिशा में गति,
(c) ऋणात्मक त्वरण से ऋणात्मक दिशा में गति,
(d) ऋणात्मक त्वरण के साथ वस्तु की गति जो समय t1 पर दिशा बदलती है । 0 से t1 समयावधि में यह धनात्मक x की दिशा में गति करती है जबकि t1 व t2 के मध्य वह विपरीत दिशा में गतिमान है ।
यदि क्षण t=0 पर वस्तु का वेग v॰ तथा t क्षण पर उसका वेग v हो, तो त्वरण a =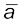 =
=  होगा ।
होगा ।
अतएव, v= v॰+at (3.6)
अब हम यह देखेंगे कि कुछ सरल उदाहरणों में वेग-समय ग्राफ कैसा दिखलाई देता है । चित्र 3.10 में स्थिर त्वरण के लिए चार अलग-अलग स्थितियों में v – t ग्राफ दिखाए गए हैंः
(a) कोई वस्तु धनात्मक दिशा में धनात्मक त्वरण से गतिमान है । उदाहरणार्थ, चित्र 3.3 में t = 0 s से t = 10 s के बीच की अवधि में कार की गति ।
(b) कोई वस्तु धनात्मक दिशा में ऋणात्मक त्वरण से गतिमान है । उदाहरणार्थ, चित्र 3.3 में t = 18 s से t = 20 s के बीच की अवधि में कार की गति ।
(c) कोई वस्तु ऋणात्मक दिशा में ऋणात्मक त्वरण से गतिमान है । उदाहरणार्थ, चित्र 3.1 में O से x की ऋण दिशा में त्वरित होती कार ।
(d) कोई वस्तु पहले t1 समय तक धनात्मक दिशा में चलती है और फिर ऋणात्मक दिशा में ऋणात्मक त्वरण के साथ गतिमान है । उदाहरण के लिए, चित्र 3.1 में कार का t1 समय तक O से बिंदु Q तक मंदन के साथ जाना, फिर, मुड़ कर उसी ऋणात्मक त्वरण के साथ t2 समय तक चलते रहना है ।
किसी गतिमान वस्तु के वेग-समय ग्राफ का एक महत्त्वपूर्ण लक्षण है कि v–t ग्राफ के अंतर्गत आने वाला क्षेत्रफल वस्तु का विस्थापन व्यक्त करता है। इस कथन की सामान्य उपपत्ति के लिए अवकल गणित की आवश्यकता पड़ ती है तथापि सुगमता के लिए एक स्थिर वेग u से गतिमान वस्तु पर विचार करके इस कथन की सत्यता प्रमाणित कर सकते हैं । इसका वेग-समय ग्राफ चित्र 3.11 में दिखाया गया है ।

चित्र 3.11 v-t ग्राफ के अंतर्गत आने वाला क्षेत्रफल वस्तु द्वारा निश्चित समय अंतराल में विस्थापन व्यक्त करता है ।
चित्र में v-t वक्र समय अक्ष के समांतर एक सरल रेखा है । t=0 से t=T के मध्य इस रेखा के अंतर्गत आने वाला क्षेत्रफल उस आयत के क्षेत्रफल के बराबर है जिसकी ऊँचाई u तथा आधार T है । अतएव क्षेत्रफल = u × T = uT, जो इस समय में वस्तु के विस्थापन को व्यक्त करता है । कोई क्षेत्रफल दूरी के बराबर कैसे हो सकता है ? सोचिए ! दोनों निर्देशांक अक्षों के अनुदिश जो राशियाँ अंकित की गई हैं, यदि आप उनकी विमाओं पर ध्यान देंगे तो आपको इस प्रश्न का उत्तर मिल
जाएगा।
ध्यान दीजिए कि इस अध्याय में अनेक स्थानों पर खींचे गए x–t, v–t तथा a–t ग्राफों में कुछ बिंदुओें पर तीक्ष्ण मोड़ हैं । इसका आशय यह है कि दिए गए फलनों का इन बिंदुओं पर अवकलन नहीं निकाला जा सकता । परंतु किसी वास्तविक परिस्थिति में सभी ग्राफ निष्कोण वक्र होंगे और उनके सभी बिंदुओं पर फलनों का अवकलन प्राप्त किया जा सकता है।
इसका अभिप्राय है कि वेग तथा त्वरण किसी क्षण सहसा नहीं बदल सकते। परिवर्तन सदैव सतत होता है।
3.6 एकसमान त्वरण से गतिमान वस्तु का शुद्धगतिकी संबंधी समीकरण
अब हम एकसमान त्वरण ‘a’ से गतिमान वस्तु के लिए कुछ गणितीय समीकरण व्युत्पन्न कर सकते हैं जो पाँचों राशियों को किसी प्रकार एक दूसरे से संबंधित करते हैं । ये राशियाँ हैंः विस्थापन (x), लिया गया समय (t), t = 0 समय पर वस्तु का प्रारंभिक वेग (vo ), समय t बीत जाने पर अंतिम वेग (v), तथा त्वरण (a) । हम पहले ही vo और v के मध्य एक समीकरण (3.6) प्राप्त कर चुके हैं जिसमें एकसमान त्वरण a तथा समय t निहित हैं । यह समीकरण है :
v = vo + at (3.6)
इस समीकरण को चित्र 3.12 में ग्राफ के रूप में निरूपित किया गया है ।
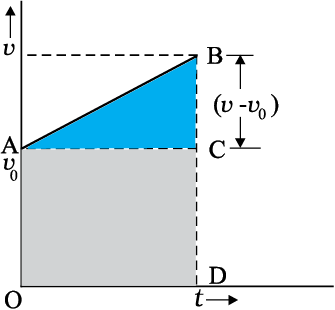
चित्र 3.12 एकसमान त्वरण से गतिमान वस्तु के लिए v-t वक्र के नीचे का क्षेत्रफल ।
इस वक्र के अंतर्गत आने वाला क्षेत्रफल :
0 से t समय के बीच का क्षेत्रफल = त्रिभुज ABC का क्षेत्रफल + आयत OACD का क्षेत्रफल
= 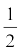 (v–v0 ) t + v0 t
(v–v0 ) t + v0 t
जैसे कि पहले स्पष्ट किया जा चुका है, v-t ग्राफ के अंतर्गत आने वाला क्षेत्रफल वस्तु का विस्थापन होता है। अतः वस्तु का विस्थापन x होगा:
समीकरण (3.9a) तथा (3.9b) का अभिप्राय है कि वस्तु का विस्थापन x माध्य वेग - v से होता है जो प्रारंभिक एवं अंतिम वेगों के समांतर माध्य के बराबर होता है ।
समीकरण (3.6) से t = (v–v0)/a । यह मान समीकरण (3.9a) में रखने पर
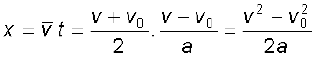
 (3.10)
(3.10)
यदि हम समीकरण (3.6) से t का मान समीकरण (3.8) में रख दें तो भी उपरोक्त समीकरण को प्राप्त किया जा सकता है। इस प्रकार पांचों राशियों v0, v, a, t तथा x के बीच संबंध स्थापित करनेवाले हमें तीन महत्त्वपूर्ण समीकरण प्राप्त हुए-
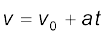
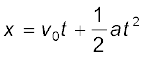
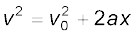 (3.11a)
(3.11a)
ये सभी एकसमान त्वरित सरल रेखीय गति के शुद्धगतिक समीकरण हैं ।
व्यंजक (3.11a) में जो समीकरण दिए गए हैं, उसकी व्युत्पत्ति के लिए हमने माना है कि क्षण t = 0 पर वस्तु की स्थिति 0 है (अर्थात् x = 0) । परंतु यदि हम यह मान लें कि क्षण t = 0 पर वस्तु की स्थिति शून्य न हो, वरन् अशून्य यानी x0 हो तो समीकरण (3.11a) और व्यापक समीकरण में रूपांतरित हो जाएगी (यदि हम x के स्थान पर x–x0 लिखें)ः
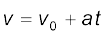
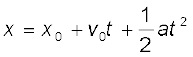 (3.11b)
(3.11b)
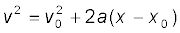 (3.11c)
(3.11c)
¯ उदाहरण 3.3 कलन-विधि का उपयोग कर एकसमान त्वरण के लिए शुद्धगतिक समीकरण प्राप्त कीजिए।
हल परिभाषा से
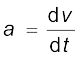
dv = a dt
दोनों पक्षों के समाकलन से
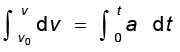
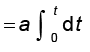 (a अचर है)
(a अचर है)
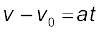
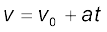
पुनः 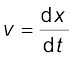
dx = v dt
दोनों पक्षों के समाकलन से
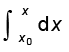
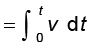
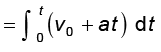
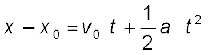
x = 
हम लिख सकते हैं :
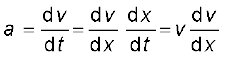
अथवा, v dv = a dx
दोनों पक्षों के समाकलन से
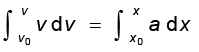
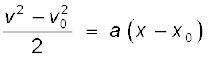
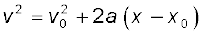
इस विधि का लाभ यह है कि इसका प्रयोग असमान त्वरण वाले गति के लिए भी कर सकते हैं।
अब हम उपरोक्त समीकरणों का उपयोग कुछ महत्त्वपूर्ण उदाहरणों में करेंगे ।
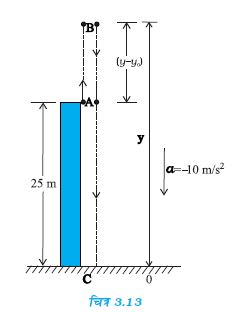
¯ उदाहरण 3.4 किसी बहुमंजिले भवन की ऊपरी छत से कोई गेंद 20 m s–1 के वेग से ऊपर की ओर ऊर्ध्वाधर दिशा में फेंकी गई है । जिस बिंदु से गेंद फेंकी गई
है धरती से उसकी ऊँचाई 25.0 m है । (a) गेंद कितनी ऊपर जाएगी ?, तथा (b) गेंद धरती से टकराने के पहले कितना समय लेगी? g = 10 m s–2 ।
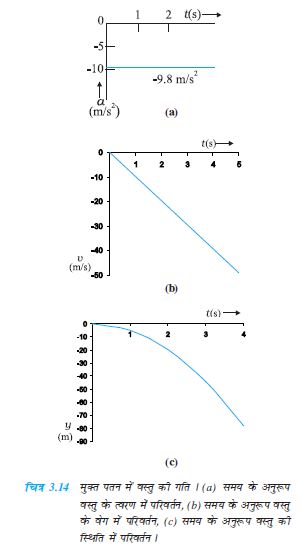
चित्र 3.14 मुक्त पतन में वस्तु की गति । (a) समय के अनुरूप वस्तु के त्वरण में परिवर्तन, (b) समय के अनुरूप वस्तु के वेग में परिवर्तन, (c) समय के अनुरूप वस्तु की स्थिति में परिवर्तन ।
हल (a) y – अक्ष को चित्र 3.13 में दिखाए गए अनुसार ऊर्ध्वाधर दिशा में ऊपर की ओर इस प्रकार चुनते हैं कि अक्ष का शून्य बिंदु धरती पर हो ।
अब, vo = + 20 m s–1,
a = – g = –10 m s–2,
v = 0 m s–1
यदि फेंके गए बिंदु से गेंद y ऊँचाई तक जाती है तो समीकरण
v2 = 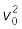 + 2a(y – y0) से हमें निम्नलिखित परिणाम मिलेगा-
+ 2a(y – y0) से हमें निम्नलिखित परिणाम मिलेगा-
0 = (20)2 + 2(–10)(y – y0), हल करने पर,
∴ y – y0 = 20 m
(b) इस खण्ड का उत्तर हम दो प्रकार से प्राप्त कर सकते हैं । इन दोनों विधियों को ध्यानपूर्वक समझें ।
पहली विधि : इसमें, हम गेंद के मार्ग को दो भागों में विभाजित करते हैं ः ऊपर की ओर गति (A से B) तथा नीचे की ओर गति (B से C) तथा संगत समय t1 व t2 निकाल लेते हैं । क्योंकि B पर वेग शून्य है, इसलिए :
v =v0 + at
0 =20 – 10 t1
या t1 =2 s
इस समय में गेंद बिंदु A से B पर पहुंचती है । B अर्थात अधिकतम ऊँचाई से गेंद गुरुत्वजनित त्वरण से मुक्त रूप से नीचे की ओर गिरती है । क्योंकि गेंद y की ऋणात्मक दिशा के अनुदिश चलती है, इसलिए निम्नलिखित समीकरण का उपयोग करके हम t2 का मान निकाल लेते हैं-
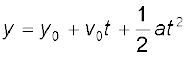
हमें y0 = 45 m दिया है तथा y = 0, v0= 0, a = –g =
–10 m s–2
∴ 0 = 45 +(1/2) (–10) t22
अतः t2 = 3 s
इसलिए धरती पर टकराने के पहले गेंद द्वारा लिया गया कुल समय t1 + t2 = 2 s + 3 s = 5 s होगा ।
दूसरी विधि : मूल बिंदु के सापेक्ष गेंद के प्रारंभिक तथा अंतिम स्थितियों के निर्देशांकों को निम्नलिखित समीकरण में उपयोग करके हम गेंद द्वारा लिए गए कुल समय की गणना कर सकते हैं :
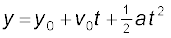
y = 0 m, y0 = 25 m, v0 = 20 m s–1, a = –10 m s–2, t = ?
0 = 25 + 20 t + (1/2) (–10)t2
या 5t2– 20t – 25 = 0
t के लिए यदि इस द्विघाती समीकरण को हल करें, तो
t = 5 s
ध्यान दीजिए कि दूसरी विधि पहली से श्रेष्ठ है क्योंकि इसमें हमें गति के पथ की चिंता नहीं करनी है क्योंकि वस्तु स्थिर त्वरण से गतिमान है ।
उदाहरण 3.5 मुक्त पतन :
स्वतंत्रतापूर्वक नीचे की ओर गिरती हुई वस्तु की गति का वर्णन कीजिए । वायुजनित प्रतिरोध की उपेक्षा की जा सकती है ।
हल
यदि धरती की सतह से थोड़ ी ऊंचाई पर से कोई वस्तु छोड़ दी जाए तो वह पृथ्वी की ओर गुरुत्व बल के कारण त्वरित होगी। गुरुत्वजनित त्वरण को हम g से व्यक्त करते हैं । यदि वस्तु पर वायु के प्रतिरोध को हम नगण्य मानें तो हम कहेंगे कि वस्तु का पतन मुक्त रूप से हो रहा है । यदि गिरती हुई वस्तु द्वारा चली गई दूरी पृथ्वी की त्रिज्या की तुलना में बहुत कम है, तो हम g के मान को स्थिर अर्थात 9.8 m s–2 ले सकते हैं।
इस प्रकार मुक्त पतन एकसमान त्वरण वाली गति का एक उदाहरण है ।
चित्र 3.15 प्रतिक्रिया काल का मापन ।
हम यह मानेंगे कि वस्तु की गति -y दिशा में है, क्योंकि ऊपर की दिशा को हम धनात्मक मानते हैं । गुरुत्वीय त्वरण की दिशा सदैव नीचे की ओर होती है, इसलिए इसे हम ऋणात्मक दिशा में लेेते हैं ।
अतएव, a = –g = – 9.8 m s–2
वस्तु को y = 0 स्थिति में विरामावस्था से गिराते हैं । इसलिए v0=0 और वस्तु के लिए गति संबंधी (3.11a) में दिए गए समीकरण निम्नलिखित प्रकार से व्यक्त किए जा सकते हैं-
v = 0 – g t = –9.8 t m s–1
y = 0 – ½ g t2 = –4.9 t2 m
v2 = 0 – 2 g y = –19.6 y m2 s–2
ये समीकरण वस्तु के वेग, और उसके द्वारा चली गई दूरी को समय के फलन के रूप में तथा दूरी के सापेक्ष उसके वेग में परिवर्तन को व्यक्त करते हैं । समय के सापेक्ष त्वरण, वेग तथा दूरी के परिवर्तन को चित्र 3.14(a), (b) तथा (c) में दिखलाया गया है । °
उदाहरण 3.6
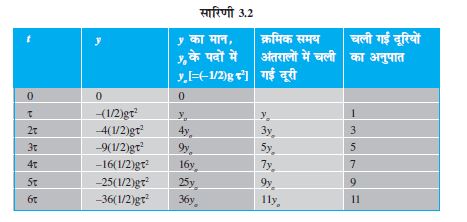
गैलीलियो का विषम अंक संबंधित नियम ः इस नियम के अनुसार ‘‘विरामावस्था से गिरती हुई किसी वस्तु द्वारा समान समय अंतरालों में चली गई दूरियाँ एक दूसरे से उसी अनुपात में होती हैं जिस अनुपात में एक से प्रारंभ होने वाले विषम अंक [अर्थात 1: 3: 5: 7,.......]’’। इस कथन को सिद्ध कीजिए ।
हल
हम विरामावस्था से गिरती हुई किसी वस्तु के समय अंतराल को बहुत-से समान समय अंतरालों τ में विभक्त कर लेते हैं तथा क्रमशः इन समय अंतरालों में वस्तु द्वारा चली गई दूरी निकालते जाते हैं । इस स्थिति में वस्तु का प्रारंभिक वेग शून्य है, अतः
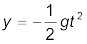
इस समीकरण की सहायता से हम भिन्न-भिन्न समय अंतरालों 0, τ, 2τ, 3τ, ...... में वस्तु की स्थितियों की गणना कर सकते हैं जिन्हें सारणी 3.2 के दूसरे कॉलम में दिखाया है । यदि प्रथम समय अंतराल τ पर वस्तु का स्थिति निर्देशांक y0 लें (y0 = (–1/2)gτ2) तो आगे के समय अंतरालों के बाद वस्तु की स्थितियों को y0 के मात्रक में कॉलम तीन में दिए गए तरीके से व्यक्त कर सकते हैं । क्रमिक समय अंतरालों (प्रत्येक τ) में चली गई दूरियों को कॉलम चार में व्यक्त किया गया है । स्पष्ट है कि क्रमशः समय अंतरालों में वस्तु द्वारा चली गई दूरियाँ 1:3:5:7:9:11...... के सरल अनुपात में हैं जैसा कि अंतिम कॉलम में दिखाया गया है ।
इस नियम को सर्वप्रथम गैलीलियो गैलिली (1564-1642) ने प्रतिपादित किया था जिन्होंने मुक्त रूप से गिरती हुई वस्तु का पहली बार विधिवत परिमाणात्मक अध्ययन किया था ।
चित्र 3.17 असमान वेगों से गतिमान वस्तुओं के स्थिति-समय ग्राफ जिसमें मिलने का समय दर्शाया गया है ।
उदाहरण 3.7
वाहनों की अवरोधन दूरी ः अवरोधन दूरी से हमारा अभिप्राय उस दूरी से है जो गतिमान वस्तु ब्रेक लगाने के कारण रुकने से पहले चल चुकी होती है । सड़ क पर गतिमान वाहनों की सुरक्षा के संबंध में यह एक महत्त्वपूर्ण कारक है । यह दूरी वाहन के प्रारंभिक वेग (vo) तथा उसके ब्रेक की क्षमता या ब्रेक लगाए जाने के परिणामस्वरूप वाहन में उत्पन्न मंदन –a पर निर्भर करती है। किसी वाहन की अवरोधन दूरी के लिए vo तथा a के पदों में व्यंजक निकालिए ।
हल
मान लीजिए कि वाहन रुकने के पूर्व ds दूरी चल चुका है । गति संबंधी समीकरण v2 = v02 + 2ax में यदि अंतिम वेग
v = 0 तो अवरोधन दूरी
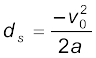
होगी। अतः अवरोधन दूरी वाहन के प्रारंभिक वेग के वर्ग के समानुपाती होती है । यदि प्रारंभिक वेग को दूना कर दिया जाए तो उसी मंदन के लिए अवरोधन दूरी चार गुनी हो जाएगी।
कार के किसी विशिष्ट मॉडल के लिए विभिन्न वेगों 11, 15, 20 तथा 25 m s–1 के संगत अवरोधन दूरियाँ क्रमशः
10 m, 20 m, 34 m तथा 50 m पाई गई हैं जो उपरोक्त समीकरण से प्राप्त मानों के लगभग संगत हैं ।
कुछ क्षेत्रों, जैसे किसी विद्यालय के निकट वाहनों की चाल की सीमा के निर्धारण में अवरोधन दूरी का ज्ञान एक महत्त्वपूर्ण कारक होता है । °
उदाहरण 3.8 प्रतिक्रिया काल :
कभी-कभी हमारे सामने एेसी परिस्थिति पैदा हो जाती है कि हमसे तत्क्षण कार्यवाही की अपेक्षा की जाती है किंतु अनुक्रिया व्यक्त करने में हमसे कुछ समय लग जाता है । प्रतिक्रिया काल किसी व्यक्ति को कोई घटनाक्रम देखने में, उसके विषय में सोचने में तथा कार्यवाही करने में लगने वाला समय है । उदाहरणस्वरूप, मान लीजिए कि कोई व्यक्ति सड़ क पर कार चला रहा है और अचानक रास्ते में एक लड़ का सामने आ जाता है तो कार में तेजी से ब्रेक लगाने के पहले व्यक्ति को जो समय लग जाता है, उसे प्रतिक्रिया काल कहेंगे । प्रतिक्रिया काल परिस्थिति की जटिलता एवं व्यक्ति विशेष पर निर्भर करता है ।
आप स्वयं का प्रतिक्रिया काल एक साधारण प्रयोग द्वारा माप सकते हैं । आप अपने मित्र को एक रूलर दें और उससे कहें कि वह आपके हाथ के अंगूठे और तर्जनी के बीच की खाली जगह से रूलर ऊर्ध्वाधर दिशा में गिरा दे (चित्र 3.15) । ज्योंही रूलर को छोड़ ा जाए आप उसे पकड़ लें । इन दोनों घटनाओं (रूलर को छोड़ ने तथा आपके द्वारा पकड़ ने) के बीच लगे समय tr तथा रूलर द्वारा चली गई दूरी d को नाप लें । किसी विशेष उदाहरण में d = 21.0 cm है तो प्रतिक्रिया काल की गणना कीजिए ।
हल
रूलर मुक्त रूप से गिरता है, अतः v0 = 0, a = – g = –9.8 ms–2 प्रतिक्रिया काल tr तथा तय की गई दूरी (d) में संबंध है,
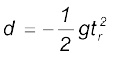
या 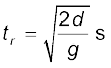
यदि d = 21.0 cm और g = 9.8 ms–2 है, तो
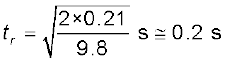
3.7 आपेक्षिक वेग
आपको रेलगाड़ी में यात्रा करने तथा यात्रा के दौरान यह देखने का अवसर मिला होगा कि एक दूसरी रेलगाड़ी जो आपकी ही दिशा में गतिमान है, आपसे आगे निकल जाती है । क्योंकि यह रेलगाड़ी आपसे आगे निकल जाती है इसलिए यह आपकी रेलगाड़ी से अधिक तीव्र गति से चल रही है । परंतु यह आपको उस व्यक्ति की अपेक्षा धीमी चलती दिखाई दे रही होगी, जो धरती पर खड़ा होकर दोनों रेलगाड़ियों को देख रहा है । यदि धरती के सापेक्ष दोनों रेलगाड़ियों का वेग समान है तो आपको एेसा लगेगा कि दूसरी गाड़ी बिलकुल भी नहीं चल रही है । इन अनुभवों को समझने के लिए अब हम आपेक्षिक वेग की संकल्पना को प्रस्तुत करते हैं ।
एेसी दो वस्तुओं A व B पर विचार कीजिए जो एक-विमा (मान लीजिए कि x-अक्ष) के अनुदिश औसत वेगों vA तथा vB से गतिमान हैं । (जब तक विशेष रूप से उल्लेेखित न हो इस अध्याय में वेगों को धरती के सापेक्ष व्यक्त किया गया है) । यदि t=0 क्षण पर वस्तु A व B की स्थितियाँ क्रमशः xA(0) तथा xB(0) हों, तो किसी अन्य क्षण t पर ये स्थितियाँ निम्नवत होंगी:
xA(t) = xA(0) + vAt (3.12a)
xB(t) = xB(0) + vBt (3.12b)
वस्तु A तथा वस्तु B के मध्य विस्थापन
xBA(t) = xB(t) – xA(t)
= [xB(0) – xA(0)] + (vB–vA)t (3.13)
होगा । समीकरण (3.13) की हम आसानी से व्याख्या कर सकते हैं । इस समीकरण से यह मालूम पड़ता है कि जब वस्तु A से देखते हैं तो वस्तु B का वेग vB–vA होता है क्योंकि A से B तक विस्थापन एकांक समय में vB–vA की दर से अनवरत बदलता जाता है । अतः हम यह कहते हैं कि वस्तु B का वेग वस्तु A के सापेक्ष vB–vA होता हैः
vBA = vB–vA (3.14a)
इसी प्रकार वस्तु A का वेग वस्तु B के सापेक्ष
vAB = vA–vB (3.14b)
होगा । इससे यह निकलता है कि,
vBA = –vAB 3.14c)
चित्र 3.16 समान वेग से गतिमान वस्तुओं A व B के लिए स्थिति-समय ग्राफ ।
अब हम कुछ विशेष परिस्थितियों पर विचार करेंगे:
(a) यदि vB = vA, vB– vA= 0, तो समीकरण (3.13) से xB(t)–xA(t) = xB(0) – xA(0) । इसका आशय यह है कि दोनों वस्तुएँ एक दूसरे से सदैव स्थिर दूरी (xB(0) – xA(0)) पर हैं और उनके स्थिति-समय ग्राफ परस्पर समांतर सरल रेखाएँ होती हैं, जैसा चित्र 3.16 से दर्शाया गया है । इस उदाहरण में आपेक्षिक वेग vAB या vBA शून्य है ।
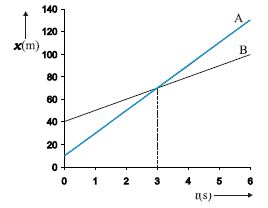
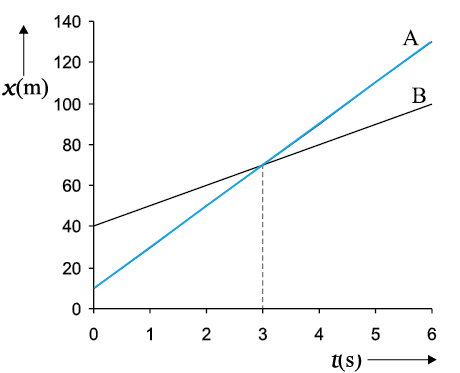
(b) यदि vA > vB, vB – vA ऋणात्मक है । एक वस्तु के ग्राफ का ढाल दूसरी वस्तु के ग्राफ के ढाल की अपेक्षा अधिक है । दोनों ग्राफ एक उभयनिष्ठ बिंदु पर मिलते हैं । उदाहरण के तौर पर यदि vA = 20 m s–1 एवं xA(0) = 10 m; तथा vB = 10 m s-1 और xB(0) = 40 m हों तो जिस क्षण पर दोनों वस्तु एक दूसरे से मिलती हैं वह t = 3 s होगा (चित्र 3.17) । इस क्षण वे दोनों वस्तुएँ xA(t) = xB(t) = 70 m पर होंगी । इस प्रकार इस क्षण पर वस्तु A वस्तु B से आगे निकल जाएगी । इस उदाहरण में vBA = 10 m s–1 – 20 m s–1 = –10 m s–1 = –vAB
चित्र 3.17 असमान वेगों से गतिमान वस्तुओं के स्थिति-समय ग्राफ जिसमें मिलने का समय दर्शाया गया है ।
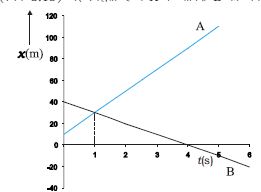
(c) मान लीजिए कि vA व vB विपरीत चिह्नों के हैं । उदाहरणस्वरूप, उपरोक्त उदाहरण में यदि वस्तु A स्थिति xA(0)=10 m से 20 m s–1 के वेग से तथा वस्तु B स्थिति xB(0) = 40 m से –10 m s–1 वेग से चलना प्रारंभ करती हैं तो वे t=1 s (चित्र 3.18) पर मिलती हैं । A के सापेक्ष B का वेग, vBA = [–10–(20)] m s–1 = –30 m s–1= –vAB होगा । इस उदाहरण में, vBA या vAB का परिमाण (=30 m s–1) वस्तु A या B के वेग के परिमाण से अधिक है । यदि विचाराधीन वस्तुएंँ दो रेलगाड़ियाँ हैं तो उस व्यक्ति के लिए जो किसी एक रेलगाड़ी में बैठा है, दूसरी रेलगाड़ी बहुत तेज चलती हुई प्रतीत होती है।
ध्यान दीजिए कि समीकरण (3.14) तब भी सही होगी जब vA और vB तात्क्षणिक वेगों को व्यक्त करते हैं ।
चित्र 3.18 परस्पर विपरीत दिशाओं में गतिमान दो वस्तुओं के स्थिति-समय ग्राफ जिसमें दोनों के मिलने का समय दर्शाया गया है ।
उदाहरण 3.9
दो समांतर रेल पटरियाँ उत्तर-दक्षिण दिशा में हैं । एक रेलगाड़ी A उत्तर दिशा में 54 km/h की चाल से गतिमान है तथा दूसरी रेलगाड़ी B दक्षिण दिशा में 90 km/h की चाल से चल रही है ।
(a) A के सापेक्ष B का आपेक्षिक वेग निकालिए,
(b) B के सापेक्ष पृथ्वी का आपेक्षिक वेग निकालिए,
(c) रेलगाड़ी A की छत पर गति की विपरीत दिशा में (रेलगाड़ी A के सापेक्ष 18 km/h–1 के वेग से) दौड़ते हुए उस बंदर के वेग की गणना कीजिए जो पृथ्वी पर खड़े व्यक्ति द्वारा देखा जा रहा है ।
हल (a)
x-अक्ष की धनात्मक दिशा को दक्षिण से उत्तर की ओर चुनिए । तब,
vA = +54 km/h–1 = 15 m s–1
vB = –90 km/h–1 = –25 m s–1
A के सापेक्ष B का आपेक्षिक वेग vB–vA = – 40 m s-1 होगा । इसका अभिप्राय यह है कि रेलगाड़ी B रेलगाड़ी A के सापेक्ष उत्तर से दक्षिण दिशा में 40 m s–1 की गति से चलती प्रतीत होगी ।
(b) B के सापेक्ष पृथ्वी का आपेक्षिक वेग = 0 – vB = 25 m s–1
(c) मान लीजिए कि पृथ्वी के सापेक्ष बंदर का वेग vM है । इसलिए A के सापेक्ष बंदर का वेग vMA = vM–vA = –18km h–1
= –5 m s–1। फलस्वरूप, vM = (15–5) m s–1 = 10m s–1 °
सारांश
1. यदि किसी वस्तु की स्थिति समय के साथ बदलती है तो हम कहते हैं कि वस्तु गतिमान है। एक सरल रैखिक गति में वस्तु की स्थिति को सुगमता के दृष्टिकोण से चुने गए किसी मूल बिंदु के सापेक्ष निर्दिष्ट किया जा सकता है । मूल बिंदु के दायीं ओर की स्थितियों को धनात्मक तथा बायीं ओर की स्थितियों को ऋणात्मक कहा जाता है ।
2. किसी वस्तु द्वारा चली गई दूरी की लंबाई को पथ-लंबाई के रूप में परिभाषित करते हैं ।
3. वस्तु की स्थिति में परिवर्तन को हम विस्थापन कहते हैं और इसे ∆x से निरूपित करते हैं;
∆x = x2 – x1
x1 और x2 वस्तु की क्रमशः प्रारंभिक तथा अंतिम स्थितियाँ हैं ।
पथ-लंबाई उन्हीं दो बिंदुओं के बीच विस्थापन के परिणाम के बराबर या उससे अधिक हो सकती है ।
4. जब कोई वस्तु समान समय अंतराल में समान दूरियाँ तय करती है तो एेसी गति को एकसमान गति कहते हैं । यदि एेसा नहीं है तो गति असमान होती है ।
5. विस्थापन की अवधि के समय अंतराल द्वारा विस्थापन को विभाजित करने पर जो राशि प्राप्त होती है, उसे औसत वेग कहते हैं तथा इसे 2924.png द्वारा चिह्नित करते हैं;
x – t ग्राफ में किसी दिए गए अंतराल की अवधि में औसत वेग उस सरल रेखा की प्रवणता है जो समय अंतराल की प्रांरभिक एवं अंतिम स्थितियों को जोड़ती है ।
6. वस्तु की यात्रा की अवधि में चली गई कुल पथ-लंबाई एवं इसमें लगे समय अंतराल अनुपात को औसत चाल कहते हैं । किसी वस्तु की औसत चाल किसी दिए गए समय अन्तराल में उसके औसत वेेग के परिणाम के बराबर अथवा अधिक होती है ।
7. जब समय अतंराल ∆t अत्यल्प हो तो वस्तु के औसत वेग के सीमान्त मान को तात्क्षणिक वेग या केवल वेग कहते हैं:
किसी क्षण वस्तु का वेग उस क्षण स्थान समय-ग्राफ की प्रवणता के बराबर होता है ।
8. वस्तु के वेग में परिवर्तन को संगत समय अंतराल से विभाजित करने पर जो राशि प्राप्त होती है, उसे औसत त्वरण कहते हैं:
9. जब समय अंतराल अत्यल्प ∆t→0 हो तो, वस्तु के औसत त्वरण के सीमान्त मान को तात्क्षणिक त्वरण या केवल त्वरण कहते हैं:
किसी क्षण वस्तु का त्वरण उस क्षण वेग-समय ग्राफ की प्रवणता के बराबर होता है । एकसमान गति के लिए त्वरण शून्य होता है तथा x - t ग्राफ समय-अक्ष पर आनत एक सरल रेखा होती है । इसी प्रकार एकसमान गति के लिए v - t ग्राफ समय-अक्ष के समांतर सरल रेखा होती है । एकसमान त्वरण के लिए x - t ग्राफ परवलय होता है जबकि v - t ग्राफ समय-अक्ष के आनत एक सरल रेखा होती है ।
10. किन्हीं दो क्षणों t1 तथा t2 के मध्य खींचे गए वेग-समय वक्र के अंतर्गत आने वाला क्षेत्रफल वस्तु के विस्थापन के बराबर होता है ।
11. एकसमान त्वरण से गतिमान वस्तु के लिए कुछ सामान्य समीकरणों का एक समूह होता है जिससे पाँच राशियाँ यथा विस्थापन x, तत्संबंधित समय t, प्रारंभिक वेग vo, अंतिम वेग v तथा त्वरण a एक दूसरे से संबंधित होते हैं । इन समीकरणों को वस्तु के शुद्धगतिक समीकरणों के नाम से जाना जाता है ः
v = v0 + at
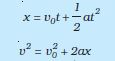
इन समीकरणों में क्षण t = 0 पर वस्तु की स्थिति x = 0 ली गई है । यदि वस्तु x = xo से चलना प्रारंभ करे तो उपर्युक्त समीकरणों में x के स्थान पर (x – xo) लिखेंगे ।
विचारणीय विषय
1. सामान्यतया दो बिंदुओं के मध्य किसी वस्तु द्वारा चली गई पथ-लंबाई विस्थापन के परिमाण के बराबर नहीं होती । विस्थापन छोर के बिंदुओं पर निर्भर करता है जबकि पथ-लंबाई (जैसा नाम से पता चलता है) वास्तविक पथ पर निर्भर करती है। एक विमा में दोनों राशियाँ तभी बराबर होती हैं जब वस्तु गति की अवधि में अपनी दिशा नहीं बदलती है । अन्य सभी उदाहरणों में पथ-लंबाई विस्थापन के परिमाण से अधिक होती है ।
2. उपरोक्त बिंदु 1 के अनुसार किसी दिए गए समय अंतराल के लिए वस्तु की औसत चाल का मान या तो औसत वेग के परिमाण के बराबर होता है या उससे अधिक होता है । दोनों तभी बराबर होंगे जब पथ-लंबाई विस्थापन के परिमाण के बराबर होगी।
3. मूल बिंदु तथा किसी अक्ष की धनात्मक दिशा का चयन अपनी रुचि का विषय है । आपको सबसे पहले इस चयन का उल्लेख कर देना चाहिए और इसी के बाद राशियों; जैसे- विस्थापन, वेग तथा त्वरण के चिह्नों का निर्धारण करना चाहिए ।
4. यदि किसी वस्तु की चाल बढ़ती जा रही है तो त्वरण वेग की दिशा में होगा परंतु यदि चाल घटती जाती है तो त्वरण वेग की विपरीत दिशा में होगा । यह कथन मूल बिंदु तथा अक्ष के चुनाव पर निर्भर नहीं करता ।
5. त्वरण के चिह्न से हमें यह पता नहीं चलता कि वस्तु की चाल बढ़ रही है या घट रही है । त्वरण का चिह्न (जैसा कि उपरोक्त बिंदु 3 में बतलाया गया है) अक्ष के धनात्मक दिशा के चयन पर निर्भर करता है । उदाहरण के तौर पर यदि ऊपर की ओर ऊर्ध्वाधर दिशा को अक्ष की धनात्मक दिशा माना जाए तो गुरुत्वजनित त्वरण ऋणात्मक होगा । यदि कोई वस्तु गुरुत्व के कारण नीचे की ओर गिर रही है तो भी वस्तु की चाल बढ़ती जाएगी यद्यपि त्वरण का मान ऋणात्मक है। वस्तु ऊपर की दिशा में फेंकी जाए तो उसी ऋणात्मक (गुरुत्वजनित) त्वरण के कारण वस्तु की चाल में कमी आती जाएगी।
6. यदि किसी क्षण वस्तु का वेग शून्य है तो यह आवश्यक नहीं है कि उस क्षण उसका त्वरण भी शून्य हो । कोई वस्तु क्षणिक रूप से विरामावस्था में हो सकती है तथापि उस क्षण उसका त्वरण शून्य नहीं होगा । उदाहरणस्वरूप, यदि किसी वस्तु को ऊपर की ओर फेंका जाए तो शीर्षस्थ बिंदु पर उसका वेग तोे शून्य होगा परंतु इस अवसर पर उसका त्वरण गुरुत्वजनित त्वरण ही होगा ।
7. गति संबंधी शुद्धगतिक समीकरणों [समीकरण (3.11)] की विभिन्न राशियाँ बीजगणितीय हैं अर्थात वे धनात्मक या ऋणात्मक हो सकती हैं । ये समीकरण सभी परिस्थितियों (स्थिर त्वरण वाली एकविमीय गति) के लिए उपयुक्त होते हैं बशर्ते समीकरणों में विभिन्न राशियों के मान उपयुक्त चिह्नों के साथ रखे जाएँ ।
8. तात्क्षणिक वेग तथा त्वरण की परिभाषाएँ [समीकरण (3.3) तथा समीकरण (3.5)] यथार्थ हैं और सदैव सही हैं जबकि शुद्धगतिक समीकरण [समीकरण (3.11)] उन्हीं गतियों के लिए सही है जिनमें गति की अवधि में त्वरण का परिमाण और दिशा स्थिर रहते हैं ।
अभ्यास
3.1 नीचे दिए गए गति के कौन से उदाहरणों में वस्तु को लगभग बिंदु वस्तु माना जा सकता है:
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी ।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बंदर ।
(c) जमीन से टकरा कर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद ।
(d) किसी मेज के किनारे से फिसल कर गिरा कोई बीकर ।
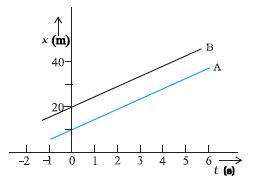
3.2 दो बच्चे A व B अपने विद्यालय O से लौट कर अपने-अपने घर क्रमशः P तथा Q को जा रहे हैं । उनके स्थिति-समय (x - t ) ग्राफ चित्र 3.19 में दिखाए गए हैं । नीचे लिखे कोष्ठकों में सही प्रविष्टियों को चुनिए:
(a) B/A की तुलना में A/B विद्यालय से निकट रहता है ।
(b) B/A की तुलना में A/B विद्यालय से पहले चलता है ।
(c) B/A की तुलना A/B तेज चलता है ।
(d) A और B घर (एक ही/भिन्न) समय पर पहुँचते हैं ।
(e) A/B सड़क पर B/A से (एक बार/दो बार) आगे हो जाते हैं ।
चित्र 3.19
3.3 एक महिला अपने घर से प्रातः 9.00 बजे 2.5 km दूर अपने कार्यालय के लिए सीधी सड़क पर 5 km h–1 चाल से चलती है । वहाँ वह सायं 5.00 बजे तक रहती है और 25 km h–1 की चाल से चल रही किसी अॉटो रिक्शा द्वारा अपने घर लौट आती है । उपयुक्त पैमाना चुनिए तथा उसकी गति का x - t ग्राफ खींचिए ।
3.4 कोई शराबी किसी तंग गली में 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, उसके बाद फिर 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, और इसी तरह वह चलता रहता है । उसका हर कदम 1m लंबा है और 1s समय लगता है । उसकी गति का x - t ग्राफ खींचिए । ग्राफ से तथा किसी अन्य विधि से यह ज्ञात कीजिए कि वह जहां से चलना प्रारंभ करता है वहाँ से 13 m दूर किसी गड्ढे में कितने समय पश्चात गिरता है ।
3.5 कोई जेट वायुयान 500 km h–1 की चाल से चल रहा है और यह जेट यान के सापेक्ष 1500 km h–1 की चाल से अपने दहन उत्पादों को बाहर निकालता है । जमीन पर खड़े किसी प्रेक्षक के सापेक्ष इन दहन उत्पादों की चाल क्या होगी ?
3.6 सीधे राजमार्ग पर कोई कार 126 km h–1 की चाल से चल रही है । इसे 200 m की दूरी पर रोक दिया जाता है । कार के मंदन को एकसमान मानिए और इसका मान निकालिए । कार को रुकने में कितना समय लगा ?
3.7 दो रेलगाड़ियाँ A व B दो समांतर पटरियों पर 72 km h–1 की एकसमान चाल से एक ही दिशा में चल रही हैं । प्रत्येक गाड़ी 400 m लंबी है और गाड़ी A गाड़ी B से आगे है । B का चालक A से आगे निकलना चाहता है तथा 1m s–2 से इसे त्वरित करता है । यदि 50 s के बाद B का गार्ड A के चालक से आगे हो जाता है तो दोनों के बीच आरंभिक दूरी कितनी थी ?
3.8 दो-लेन वाली किसी सड़क पर कार A 36 km h–1 की चाल से चल रही है । एक दूसरे की विपरीत दिशाओं में चलती दो कारें B व C जिनमें से प्रत्येक की चाल 54 km h–1 है, कार A तक पहुँचना चाहती हैं । किसी क्षण जब दूरी AB दूरी AC के बराबर है तथा दोनों 1km है, कार B का चालक यह निर्णय करता है कि कार C के कार A तक पहुँचने के पहले ही वह कार A से आगे निकल जाए । किसी दुर्घटना से बचने के लिए कार B का कितना न्यूनतम त्वरण जरूरी है ?
3.9 दो नगर A व B नियमित बस सेवा द्वारा एक दूसरे से जुड़े हैं और प्रत्येक T मिनट के बाद दोनों तरफ बसें चलती हैं । कोई व्यक्ति साइकिल से 20 km h–1 की चाल से A से B की तरफ जा रहा है और यह नोट करता है कि प्रत्येक 18 मिनट के बाद एक बस उसकी गति की दिशा में तथा प्रत्येक 6 मिनट बाद उसके विपरीत दिशा में गुजरती है । बस सेवाकाल T कितना है और बसें सड़क पर किस चाल (स्थिर मानिए) से चलती हैं ?
3.10 कोई खिलाड़ी एक गेंद को ऊपर की ओर आरंभिक चाल 29 m s–1 से फेंकता है,
(i) गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी ?
(ii) इसकी गति के उच्चतम बिंदु पर गेंद के वेेग व त्वरण क्या होंगे ?
(iii) गेंद के उच्चतम बिंदु पर स्थान व समय को x = 0 व t = 0 चुनिए, ऊर्ध्वाधर नीचे की ओर की दिशा को x-अक्ष की धनात्मक दिशा मानिए । गेंद की ऊपर की व नीचे की ओर गति के दौरान स्थिति, वेग व त्वरण के चिह्न बताइए ।
(iv) किस ऊँचाई तक गेंद ऊपर जाती है और कितनी देर के बाद गेंद खिलाड़ी के हाथों में आ जाती है ?
[g = 9.8 m s–2 तथा वायु का प्रतिरोध नगण्य है ।]
3.11 नीचे दिए गए कथनों को ध्यान से पढ़िए और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य हैं या असत्य,
एकविमीय गति में किसी कण की
(a) किसी क्षण चाल शून्य होने पर भी उसका त्वरण अशून्य हो सकता है ।
(b) चाल शून्य होने पर भी उसका वेग अशून्य हो सकता है ।
(c) चाल स्थिर हो तो त्वरण अवश्य ही शून्य होना चाहिए ।
(d) चाल अवश्य ही बढ़ती रहेगी, यदि उसका त्वरण धनात्मक हो ।
3.12 किसी गेंद को 90 m की ऊँचाई से फर्श पर गिराया जाता है । फर्श के साथ प्रत्येक टक्कर में गेंद की चाल 1/10 कम हो जाती है । इसकी गति का t = 0 से 12 s के बीच चाल-समय ग्राफ खींचिए ।
3.13 उदाहरण सहित निम्नलिखित के बीच के अंतर को स्पष्ट कीजिए:
(a) किसी समय अंतराल में विस्थापन के परिमाण (जिसे कभी-कभी दूरी भी कहा जाता है) और किसी कण द्वारा उसी अंतराल के दौरान तय किए गए पथ की कुल लंबाई ।
(b) किसी समय अंतराल में औसत वेग के परिमाण और उसी अंतराल में औसत चाल (किसी समय अंतराल में किसी कण की औसत चाल को समय अंतराल द्वारा विभाजित की गई कुल पथ-लंबाई के रूप में परिभाषित किया जाता है) । प्रदर्शित कीजिए कि (a) व (b) दोनों में ही दूसरी राशि पहली से अधिक या उसके बराबर है । समता का चिह्न कब सत्य होता है ? (सरलता के लिए केवल एकविमीय गति पर विचार कीजिए ।)
3.14 कोई व्यक्ति अपने घर से सीधी सड़क पर 5 km h–1 की चाल से 2.5 km दूर बाजार तक पैदल चलता है । परंतु बाजार बंद देखकर वह उसी क्षण वापस मुड़ जाता है तथा 7.5 km h–1 की चाल से घर लौट आता है । समय अंतराल (i) 0 - 30 मिनट, (ii) 0 - 50 मिनट, (iii) 0 - 40 मिनट की अवधि में उस व्यक्ति (a) के माध्य वेग का परिमाण, तथा (b) का माध्य चाल क्या है? (नोट: आप इस उदाहरण से समझ सकेंगे कि औसत चाल को औसत-वेग के परिमाण के रूप में परिभाषित करने की अपेक्षा समय द्वारा विभाजित कुल पथ-लंबाई के रूप में परिभाषित करना अधिक अच्छा क्यों है । आप थक कर घर लौटे उस व्यक्ति को यह बताना नहीं चाहेंगे कि उसकी औसत चाल शून्य थी ।)
3.15 हमने अभ्यास 3.13 तथा 3.14 में औसत चाल व औसत वेग के परिमाण के बीच के अंतर को स्पष्ट किया है । यदि हम तात्क्षणिक चाल व वेग के परिमाण पर विचार करते हैं तो इस तरह का अंतर करना आवश्यक नहीं होता । तात्क्षणिक चाल हमेशा तात्क्षणिक वेग के बराबर होती है । क्यों ?
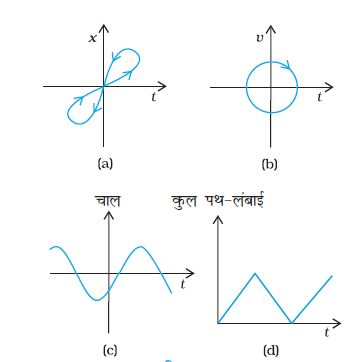
3.16 चित्र 3.20 में (a) से (d) तक के ग्राफों को ध्यान से देखिए और देखकर बताइए कि इनमें से कौन-सा ग्राफ एकविमीय गति को संभवतः नहीं दर्शा सकता ।
चित्र 3.20
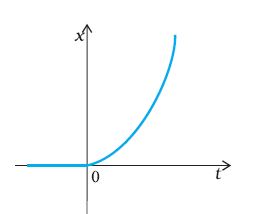
3.17 चित्र 3.21 में किसी कण की एकविमीय गति का x - t ग्राफ दिखाया गया है । ग्राफ से क्या यह कहना ठीक होगा कि यह कण t < 0 के लिए किसी सरल रेखा में और t > 0 के लिए किसी परवलीय पथ में गति करता है । यदि नहीं, तो ग्राफ के संगत किसी उचित भौतिक संदर्भ का सुझाव दीजिए ।
चित्र 3.21
3.18 किसी राजमार्ग पर पुलिस की कोई गाड़ी 30 km/h की चाल से चल रही है और यह उसी दिशा में 192 km/h की चाल से जा रही किसी चोर की कार पर गोली चलाती है । यदि गोली की नाल मुखी चाल 150 m s-1 है तो चोर की कार को गोली किस चाल के साथ आघात करेगी ?
(नोट: उस चाल को ज्ञात कीजिए जो चोर की कार को हानि पहुँचाने में प्रासंगिक हो) ।
3.19 चित्र 3.22 में दिखाए गए प्रत्येक ग्राफ के लिए किसी उचित भौतिक स्थिति का सुझाव दीजिए:
चित्र 3.22
3.20 चित्र 3.23 में किसी कण की एकविमीय सरल आवर्ती गति के लिए x - t ग्राफ दिखाया गया है । (इस गति के बारे में आप अध्याय 14 में पढ़ेंगे) समय t = 0.3 s, 1.2 s, –1.2 s पर कण के स्थिति, वेग व त्वरण के चिह्न क्या होंगे ?
चित्र 3.23
3.21 चित्र 3.24 किसी कण की एकविमीय गति का x - t ग्राफ
चित्र 3.25
दर्शाता है । इसमें तीन समान अंतराल दिखाए गए हैं । किस अंतराल में औसत चाल अधिकतम है और किसमें न्यूनतम है ? प्रत्येक अंतराल के लिए औसत वेग का चिह्न बताइए ।
3.22 चित्र 3.25 में किसी नियत (स्थिर) दिशा के अनुदिश चल रहे कण का चाल-समय ग्राफ दिखाया गया है । इसमें तीन समान समय अंतराल दिखाए गए हैं । किस अंतराल में औसत त्वरण का परिमाण अधिकतम होगा ? किस अंतराल में औसत चाल अधिकतम होगी ?
धनात्मक दिशा को गति की स्थिर दिशा चुनते हुए तीनों अंतरालों में v तथा a के चिह्न बताइए । A, B, C, व D बिंदुओं पर त्वरण क्या होंगे ?
अतिरिक्त अभ्यास
3.23 कोई तीन पहिये वाला स्कूटर अपनी विरामावस्था से गति प्रारंभ करता है । फिर 10 s तक किसी सीधी सड़क पर 1m s-2 के एकसमान त्वरण से चलता है । इसके बाद वह एकसमान वेग से चलता है । स्कूटर द्वारा nवें सेकंड (n = 1, 2, 3........) में तय की गई दूरी को n के सापेेक्ष आलेखित कीजिए । आप क्या आशा करते हैं कि त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा ?
3.24 किसी स्थिर लिफ्ट में (जो ऊपर से खुली है) कोई बालक खड़ा है । वह अपने पूरे जोर से एक गेंद ऊपर की ओर फेंकता है जिसकी प्रारंभिक चाल 49 m s–1 है । उसके हाथों में गेंद के वापिस आने में कितना समय लगेगा ? यदि लिफ्ट ऊपर की ओर 5 m s-1 की एकसमान चाल से गति करना प्रारंभ कर दे और वह बालक फिर गेंद को अपने पूरे जोर से फेंकता तो कितनी देर में गेंद उसके हाथों में लौट आएगी ?
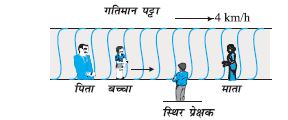
3.25 क्षैतिज में गतिमान कोई लंबा पट्टा (चित्र 3.26) 4 km/h की चाल से चल रहा है । एक बालक इस पर (पट्टेे के सापेक्ष) 9 km/h की चाल से कभी आगे कभी पीछे अपने माता-पिता के बीच दौड़ रहा है । माता व पिता के बीच 50 m की दूरी है । बाहर किसी स्थिर प्लेटफार्म पर खड़े एक प्रेक्षक के लिए, निम्नलिखित का मान प्राप्त करिए ।
(a) पट्टे की गति की दिशा में दौड़ रहे बालक की चाल,
(b) पट्टे की गति की दिशा के विपरीत दौड़ रहे बालक की चाल,
(c) बच्चे द्वारा (a) व (b) में लिया गया समय यदि बालक की गति का प्रेक्षण उसके माता या पिता करें तो कौन- सा उत्तर बदल जाएगा ?
चित्र 3.26
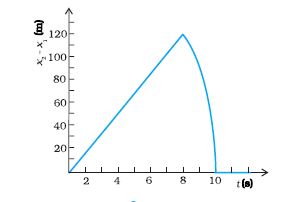
3.26 किसी 200 m ऊँची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओर 15 m s–1 तथा 30 m s–1 की प्रारंभिक चाल से फेंका जाता है । इसका सत्यापन कीजिए कि नीचे दिखाया गया ग्राफ (चित्र 3.27) पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है । वायु के प्रतिरोध को नगण्य मानिए और यह मानिए कि जमीन से टकराने के बाद पत्थर ऊपर की ओर उछलते नहीं । मान लिजिए g = 10 m s–2 । ग्राफ के रेखीय व वक्रीय भागों के लिए समीकरण लिखिए ।
चित्र 3.27
3.27 किसी निश्चित दिशा के अनुदिश चल रहे किसी कण का चाल-समय ग्राफ चित्र 3.28 में दिखाया गया है । कण द्वारा
(a) t = 0 s से t = 10 s, (b) t = 2 s से 6 s के बीच तय की गई दूरी ज्ञात कीजिए ।
चित्र 3.28
(a) तथा (b) में दिए गए अंतरालों की अवधि में कण की औसत चाल क्या है ?
3.28 एकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र 3.29 में दिखाया गया है:
चित्र 3.29
नीचे दिए सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही हैं:
(i) x (t2) = x (t1) + v (t1)(t2 – t1) + (1/2) a(t2 – t1)2
(ii) v(t2) = v(t1) + a(t2 – t1)
(iii) vaverage = [x(t2) – x (t1)]/(t2 – t1)
(iv) aaverage = [v(t2) – v (t1)]/(t2 – t1)
(v) x(t2) = x(t1) + vaverage (t2 – t1) + (1/2) aaverage (t2 – t1)2
(vi) x (t2) – x (t1) = t- अक्ष तथा दिखाई गई बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल ।
परिशिष्ट 3.1
कलन के अवयव
अवकल गणित
‘अवकल गुणांक’ अथवा ‘अवकलज’ की संकल्पना का उपयोग करके हम आसानी से वेग तथा त्वरण को परिभाषित कर सकते हैं । यद्यपि आप अवकलजों के विषय में विस्तार से गणित में अध्ययन करेेंगे, तथापि इस परिशिष्ट में हम संक्षेप मेें इस संकल्पना से आपको परिचित कराएँगे, ताकि आपको गति से संबद्ध भौतिक राशियों के वर्णन करने में सुविधा हो जाए ।
मान लीजिए हमारे पास कोई राशि y है जिसका मान किसी एकल चर x पर निर्भर करता है, तथा इस राशि को एक समीकरण द्वारा व्यक्त किया जाता है जो y को x के किसी विशिष्ट फलन के रूप मेें परिभाषित करती है । इसे इस प्रकार निरूपित करते हैं:
y = f (x) (1)
इस संबंध को फलन y = f(x) का ग्राफ खींचकर चित्र 3.30 (a) में दर्शाए अनुसार y तथा x को कार्तीय निर्देशांक (Cartesian coordinates) मानते हुए स्पष्ट रूप से देख सकते हैं ।
चित्र 3.30
वक्र y = f(x) पर एक बिंदु P जिसके निर्देशांक (x, y) हैं तथा अन्य बिंदु जिसके निर्देशांक (x + ∆ x, y + ∆ y) हैं मान लीजिए । P तथा Q को मिलाने वाली सरल रेखा के ढाल को इस प्रकार दर्शाया जाता है,
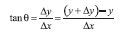
अब अगर बिंदु Q को वक्र के अनुदिश बिंदु P की ओर लाया जाता है । इस प्रक्रिया में ∆y तथा ∆x घटते जाते हैं तथा शून्य की ओर अग्रसर होते जाते हैं, यद्यपि इनका अनुपात2994.pngअनिवार्य रूप से लुप्त नहीं होगा । जब ∆y→0, ∆x→0 है, तब रेखा PQ का क्या होगा ? आप यह देख सकते हैं कि यह रेखा चित्र 3.30 (b) में दर्शाए अनुसार वक्र के बिंदु P पर स्पर्श रेखा बन जाती है । इसका यह अर्थ हुआ कि tan θ बिंदु P पर स्पर्श रेखा के ढाल के सदृश होता जाता है । इसे m द्वारा निर्दिष्ट किया जाता है,

अनुपात ∆y/∆x की सीमा, जैसे-जैसे ∆x शून्य की ओर बढ़ता जाता है, x के सापेक्ष y का अवकलज कहलाता है तथा इसे dy/dx लिखते हैं । यह वक्र y = f(x) के बिंदु (x, y) पर स्पर्श रेखा के ढाल को निरूपित करता है ।
चूँकि y = f(x) तथा y + ∆ y = f (x + ∆x), हम अवकलज की परिभाषा इस प्रकार लिख सकते हैं:
नीचे फलनों के अवकलजों के लिए कुछ प्राथमिक सूत्र दिए गए हैं । इनमें u (x) तथा v (x), x के यादृच्छिक फलनों का निरूपण करते हैं तथा a और b नियत राशियों को निर्दिष्ट करते हैं, जो x पर निर्भर नहीं करतीं । कुल सामान्य फलनों के अवकलजों की सूची भी दी गई है ।
अवकलनों के पदों में तात्क्षणिक वेग तथा त्वरण की परिभाषा इस प्रकार करते हैं–
समाकलन-गणित
क्षेत्रफल की धारणा से आप भलीभाँति परिचित हैं । कुछ सरल ज्यामितीय आकृतियों के क्षेत्रफल के लिए सूत्र भी आपको ज्ञात हैं । उदाहरण के लिए, किसी आयत का क्षेत्रफल उसकी लंबाई और चौड़ाई का गुणनफल, तथा त्रिभुज का क्षेत्रफल उसके आधार तथा शीर्षलंब के गुणनफल का आधा होता है । परंतु किसी अनियमित आकृति का क्षेत्रफल ज्ञात करने की समस्या पर कैसे विचार किया जाए ? एेसी समस्याओं को हल करने के लिए समाकलन की गणितीय धारणा आवश्यक है ।
आइए, अब हम एक प्रत्यक्ष उदाहरण लेेते हैं। मान लीजिए गति करते किसी कण पर x-अक्ष के अनुदिश x= a से x = b तक कोई चर बल f (x) कार्य करता है । हमारी समस्या यह है कि इस बल द्वारा कण की गति की अवधि में किया गया कार्य (W) कैसे ज्ञात किया जाए । इस समस्या पर अध्याय 6 में विस्तार से चर्चा की गई है ।
चित्र 3.31 में x के साथ f (x) मेें परिवर्तन दर्शाया गया है । यदि बल अचर होता, तो किया गया कार्य चित्र 3.31 (i) में दर्शाए अनुसार मात्र क्षेत्रफल f (b-a) होगा । परंतु व्यापक प्रकरणों में, बल चर होता है ।
चित्र 3.31
इस वक्र [चित्र 3.31 (ii)] के नीचे के क्षेत्रफल का परिकलन करने के लिए एक युक्ति करते हैं जो निम्नलिखित है । x-अक्ष पर a से b तक के अंतराल को संख्या में बहुत अधिक (N) लघु-अंतरालों में विभाजित कर लेते हैं, जो इस प्रकार हैं: x0 (=a) से x1 तक, x1 से x2 तक, x2 से x3 तक,.......x N-1 से xN (=b) तक । इस प्रकार वक्र के नीचे का कुल क्षेत्रफल N पट्टियों में विभाजित हो जाता है । प्रत्येक पट्टी सन्निकटतः आयताकार है, चूँकि किसी पट्टी पर F(x) में परिवर्तन नगण्य है । चित्र 3.31 (ii) मेें दर्शायी गई iवीं पट्टी का सन्निकटतः क्षेत्रफल तब होगा,
यहाँ ∆x पट्टी की चौड़ाई है जो हमने सभी पट्टियों के लिए समान ली है । आप उलझन में पड़ सकते हैं कि इस व्यंजक में हमें F(xi-1) लिखना चाहिए अथवा F(xi) तथा F(xi-1) का माध्य लिखना चाहिए । यदि संख्या N को बहुत-बहुत बड़ी (N→∞) लें, तो फिर इसका कोई महत्त्व नहीं रहेगा । क्योंकि तब पट्टियाँ इतनी पतली होंगी कि F(xi) तथा F(xi-1) के बीच का अंतर इतना कम होगा कि उसे नगण्य माना जा सकता है । तब वक्र के नीचे का कुल क्षेत्रफल,
इस योग की सीमा को, जब N→∞ हो, a से b तक F(x) का x पर समाकलन कहते हैं । इसे एक विशेष प्रतीक दिया गया है जिसे नीचे दर्शाया गया है–
समाकलन-चिह्न ∫ विस्तारित S जैसा दिखाई देता है । यह हमें याद दिलाता है कि मूल रूप से यह असंख्य पदों के योग की सीमा है ।
एक अत्यंत महत्त्वपूर्ण गणितीय तथ्य यह है कि समाकलन, कुछ अर्थो मेें अवकलन का व्युत्क्रम है । मान लीजिए हमारे पास कोई फलन g (x) है जिसका अवकलन f (x) है, तब
फलन g (x) को f (x) का अनिश्चित समाकल कहते हैं तथा इसे इस प्रकार निर्दिष्ट किया जाता है
कोई समाकल जिसकी निम्न सीमा तथा उच्च सीमा ज्ञात हो, निश्चित समाकल कहलाता है । यह कोई संख्या होती है । अनिश्चित समाकल की कोई सीमा नहीं होती । यह एक फलन होता है । उपरोक्त प्रकरण के लिए गणित की एक मूल प्रमेय बताती है कि
उदाहरण के लिए, मान लीजिए f (x) = x2, तथा हम x = 1 से x = 2 तक इसके निश्चित समाकल का मान ज्ञात करना चाहते हैं। वह फलन f (x) जिसका अवकलन x2 होता है, x3/3 है। अतः
स्पष्ट है कि निश्चित समाकलों का मूल्यांकन करने के लिए हमें उसके तदनुरूपी अनिश्चित समाकलों को जानना आवश्यक है। कुछ सामान्य अनिश्चित समाकल इस प्रकार हैं–
अवकल गणित तथा समाकलन गणित का आरंभिक ज्ञान कठिन नहीं है तथा यहाँ आपको कलन की मूल धारणाओें से परिचित कराने का प्रयास किया गया है ।