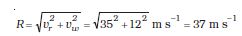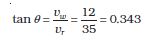Table of Contents

अध्याय 4
समतल में गति
4.1 भूमिका
4.2 अदिश एवं सदिश
4.3 सदिशों की वास्तविक संख्या से गुणा
4.4 सदिशों का संकलन व व्यवकलन - ग्राफी विधि
4.5 सदिशों का वियोजन
4.6 सदिशों का योग - विश्लेषणात्मक विधि
4.7 किसी समतल में गति
4.8 किसी समतल में एकसमान त्वरण से गति
4.9 दो विमाओं में आपेक्षिक वेग
4.10 प्रक्षेप्य गति
4.11 एकसमान वृत्तीय गति
सारांश
विचारणीय विषय
अभ्यास
अतिरिक्त अभ्यास
4.1 भूमिका
पिछले अध्याय में हमने स्थिति, विस्थापन, वेग एवं त्वरण की धारणाओं को विकसित किया था, जिनकी किसी वस्तु की सरल रेखीय गति का वर्णन करने के लिए आवश्यकता पड़ती है । क्योंकि एकविमीय गति में मात्र दो ही दिशाएँ संभव हैं, इसलिए इन राशियों के दिशात्मक पक्ष को + और - चिह्नों से व्यक्त कर सकते हैं । परंतु जब हम वस्तुओं की गति का द्विविमीय (एक समतल) या त्रिविमीय (दिक्स्थान) वर्णन करना चाहते हैं, तब हमें उपर्युक्त भौतिक राशियों का अध्ययन करने के लिए सदिशों की आवश्यकता पड़ती है । अतएव सर्वप्रथम हम सदिशों की भाषा (अर्थात सदिशों के गुणों एवं उन्हें उपयोग में लाने की विधियाँ) सीखेंगे । सदिश क्या है ? सदिशों को कैसे जोड़ा, घटाया या गुणा किया जाता है ? सदिशों को किसी वास्तविक संख्या से गुणा करें तो हमें क्या परिणाम मिलेगा ? यह सब हम इसलिए सीखेंगे जिससे किसी समतल में वस्तु के वेग एवं त्वरण को परिभाषित करने के लिए हम सदिशों का उपयोग कर सकें । इसके बाद हम किसी समतल में वस्तु की गति पर परिचर्चा करेंगे । किसी समतल में गति के सरल उदाहरण के रूप में हम एकसमान त्वरित गति का अध्ययन करेंगे तथा एक प्रक्षेप्य की गति के विषय में विस्तार से पढ़ेंगे । वृत्तीय गति से हम भलीभाँति परिचित हैं जिसका हमारे दैनिक जीवन में विशेष महत्त्व है । हम एकसमान वृत्तीय गति की कुछ विस्तार से चर्चा करेंगे ।
हम इस अध्याय में जिन समीकरणों को प्राप्त करेंगे उन्हें आसानी से त्रिविमीय गति के लिए विस्तारित किया जा सकता है ।
4.2 अदिश एवं सदिश
हम भौतिक राशियों को अदिशों एवं सदिशों में वर्गीकृत करते हैं । दोनों में मूल अंतर यह है कि सदिश के साथ दिशा को संबद्ध करते हैं वहीं अदिश के साथ एेसा नहीं करते । एक अदिश राशि वह राशि है जिसमें मात्र परिमाण होता है । इसे केवल एक संख्या एवं उचित मात्रक द्वारा पूर्ण रूप से व्यक्त किया जा सकता है । इसके उदाहरण हैं: दो बिंदुओं के बीच की दूरी, किसी वस्तु की संहति (द्रव्यमान), किसी वस्तु का तापक्रम, तथा वह समय जिस पर
कोई घटना घटती है । अदिशों के जोड़ में वही नियम लागू होते हैं जो सामान्यतया बीजगणित में । अदिशों को हम ठीक वैसे ही जोड़ सकते हैं, घटा सकते हैं, गुणा या भाग कर सकते हैं जैसा कि हम सामान्य संख्याओं के साथ करते हैं * । उदाहरण के लिए, यदि किसी आयत की लंबाई और चौड़ाई क्रमशः 1.0 m तथा ddd 0.5 m है तो उसकी परिमाप चारों भुजाओं के योग, 1.0 m + 0.5 m + 1.0 m + 0.5 m =
3.0 m होगा। हर भुजा की लंबाई एक अदिश है तथा परिमाप भी एक अदिश है । हम एक दूसरे उदाहरण पर विचार करेंगे: यदि किसी एक दिन का अधिकतम एवं न्यूनतम ताप क्रमशः
35.6 °C तथा 24.2 °C है तो इन दोनों का अंतर 11.4 °C होगा । इसी प्रकार यदि एल्युमिनियम के किसी एकसमान ठोस घन की भुजा 10 cm है और उसका द्रव्यमान 2.7 kg है तो उसका आयतन 10–3 m3 (एक अदिश) होगा तथा घनत्व 2.7×103 kg/m3 भी एक अदिश है ।
एक सदिश राशि वह राशि है जिसमें परिमाण तथा दिशा दोनों होते हैं तथा वह योग संबंधी त्रिभुज के नियम अथवा समानान्तर चतुर्भुज के योग संबंधी नियम का पालन करती है । इस प्रकार, एक सदिश को उसके परिमाण की संख्या तथा दिशा द्वारा व्यक्त करते हैं । कुछ भौतिक राशियाँ जिन्हें सदिशों द्वारा व्यक्त करते हैं, वे हैं विस्थापन, वेग, त्वरण तथा बल ।
सदिश को व्यक्त करने के लिए इस पुस्तक में हम मोटे अक्षरों का प्रयोग करेंगे । जैसे कि वेग सदिश को व्यक्त करने के लिए v चिह्न का प्रयोग करेंगे । परंतु हाथ से लिखते समय क्योंकि मोटे अक्षरों का लिखना थोड़ा मुश्किल होता है, इसलिए एक सदिश को अक्षर के ऊपर तीर लगाकर व्यक्त करते हैं, जैसे →v । इस प्रकार v तथा →v दोनों ही वेग सदिश को व्यक्त करते हैं । किसी सदिश के परिमाण को प्रायः हम उसका ‘परम मान’ कहते हैं और उसे |v| = v द्वारा व्यक्त करते हैं । इस प्रकार एक सदिश को हम मोटे अक्षर यथा A या a, p, q, r, ..... x, y से व्यक्त करते हैं जबकि इनके परिमाणों को क्रमशः हम A या a, p, q, r, .... x, y द्वारा व्यक्त करते हैं ।
4.2.1 स्थिति एवं विस्थापन सदिश
* केवल समान मात्रक वाली राशियों का जोड़ व घटाना सार्थक होता है । जबकि आप भिन्न मात्रकों वाले अदिशों का गुणा या भाग कर सकते हैं ।
** हमारे अध्ययन में सदिशों की स्थितियां निर्धारित नहीं हैं । इसलिए जब एक सदिश को स्वयं के समांतर विस्थापित करते हैं तो सदिश अपरिवर्तित रहता है । इस प्रकार के सदिशों को हम ‘मुक्त सदिश’ कहते हैं । हालांकि कुछ भौतिक उपयोगों में सदिश की स्थिति या उसकी क्रिया रेखा महत्त्वपूर्ण होती है । एेसे सदिशों को हम ‘स्थानगत सदिश’ कहते हैं।
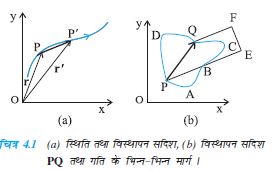
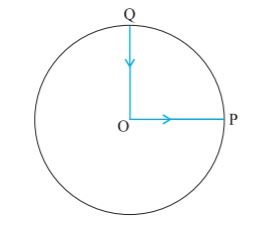
किसी समतल में गतिमान वस्तु की स्थिति व्यक्त करने के लिए हम सुविधानुसार किसी बिंदु O को मूल बिंदु के रूप में चुनते हैं । कल्पना कीजिए कि दो भिन्न-भिन्न समयों t और t' पर वस्तु की स्थिति क्रमशः P और P' है (चित्र 4.1a) । हम P को O से एक सरल रेखा से जोड़ देते हैं । इस प्रकार OP समय t पर वस्तु की स्थिति सदिश होगी । इस रेखा के सिरे पर एक तीर का निशान लगा देते हैं । इसे किसी चिह्न (मान लीजिए) r से निरूपित करते हैं, अर्थात् OP = r । इसी प्रकार बिंदु P' को एक दूसरे स्थिति सदिश OP' यानी r' से निरूपित करते हैं। सदिश r की लंबाई उसके परिमाण को निरूपित करती है तथा सदिश की दिशा वह होगी जिसके अनुदिश P (बिंदु O से देखने पर) स्थित होगा । यदि वस्तु P से चलकर P' पर पहुंच जाती है तो सदिश PP' (जिसकी पुच्छ P पर तथा शीर्ष P' पर है) बिंदु P (समय t) से P' (समय t') तक गति के संगत विस्थापन सदिश कहलाता है ।
यहाँ यह बात महत्वपूर्ण है कि ‘विस्थापन सदिश’ को एक सरल रेखा से व्यक्त करते हैं जो वस्तु की अंतिम स्थिति को उसकी प्रारम्भिक स्थिति से जोड़ती है तथा यह उस वास्तविक पथ पर निर्भर नहीं करता जो वस्तु द्वारा बिंदुओं के मध्य चला जाता है । उदाहरणस्वरूप, जैसा कि चित्र 4.1b में दिखाया गया है, प्रारम्भिक स्थिति P तथा अंतिम स्थिति Q के मध्य विस्थापन सदिश PQ यद्यपि वही है परंतु दोनों स्थितियों के बीच चली गई दूरियां जैसे PABCQ, PDQ तथा PBEFQ अलग-अलग हैं । इसी प्रकार, किन्हीं दो बिंदुओं के मध्य विस्थापन सदिश का परिमाण या तो गतिमान वस्तु की पथ-लंबाई से कम होता है या उसके बराबर होता है। पिछले अध्याय में भी एक सरल रेखा के अनुदिश गतिमान वस्तु के लिए इस तथ्य को भलीभांति समझाया गया था ।
4.2.2 सदिशों की समता
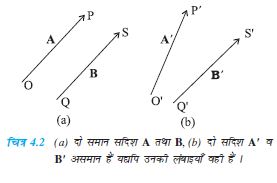
दो सदिशों A तथा B को केवल तभी बराबर कहा जा सकता है जब उनके परिमाण बराबर हों तथा उनकी दिशा समान हो** ।
चित्र 4.2(a) में दो समान सदिशों A तथा B को दर्शाया गया है । हम इनकी समानता की परख आसानी से कर सकते हैं । B को स्वयं के समांतर खिसकाइये ताकि उसकी पुच्छ Q सदिश A की पुच्छ O के संपाती हो जाए । फिर क्योंकि उनके शीर्ष S एवं P भी संपाती हैं अतः दोनोें सदिश बराबर कहलाएंगे । सामान्यतया इस समानता को A = B के रूप में लिखते हैं । इस बात की ओर ध्यान दीजिए कि चित्र 4.2(b) में यद्यपि सदिशों A' तथा B' के परिमाण समान हैं फिर भी दोनों सदिश समान नहीं हैं क्योंकि उनकी दिशायें अलग-अलग हैं । यदि हम B' को उसके ही समांतर खिसकाएं जिससे उसकी पुच्छ Q', A' की पुच्छ O' से संपाती हो जाए तो भी B' का शीर्ष S', A' के शीर्ष P' का संपाती नहीं होगा ।
4.3 सदिशों की वास्तविक संख्या से गुणा
यदि एक सदिश A को किसी धनात्मक संख्या λ से गुणा करें तो हमें एक सदिश ही मिलता है जिसका परिमाण सदिश A के परिमाण का λ गुना हो जाता है तथा जिसकी दिशा वही है जो A की है । इस गुणनफल को हम λA से लिखते हैं ।
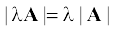 यदि
यदि 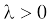
उदाहरणस्वरूप, यदि A को 2 से गुणा किया जाए, तो परिणामी सदिश 2A होगा (चित्र 4.3a) जिसकी दिशा A की दिशा होगी तथा परिमाण 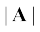 का दोगुना होगा । सदिश A को यदि एक ऋणात्मक संख्या –λ से गुणा करें तो एक अन्य सदिश प्राप्त होता है जिसकी दिशा A की दिशा के विपरीत है और जिसका परिमाण
का दोगुना होगा । सदिश A को यदि एक ऋणात्मक संख्या –λ से गुणा करें तो एक अन्य सदिश प्राप्त होता है जिसकी दिशा A की दिशा के विपरीत है और जिसका परिमाण 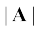 का λ गुना होता है ।
का λ गुना होता है ।
यदि किसी सदिश A को ऋणात्मक संख्याओं -1 व -1.5 से गुणा करें तो परिणामी सदिश चित्र 4.3(b) जैसे होंगे ।
भौतिकी में जिस घटक λ द्वारा सदिश A को गुणा किया जाता है वह कोई अदिश हो सकता है जिसकी स्वयं की विमाएँ होती हैं । अतएव λΑ की विमाएँ λ व A की विमाओं के गुणनफल के बराबर होंगी । उदाहरणस्वरूप, यदि हम किसी अचर वेग सदिश को किसी (समय) अंतराल से गुणा करें तो हमें एक विस्थापन सदिश प्राप्त होगा ।
4.4 सदिशों का संकलन व व्यवकलन : ग्राफी विधि
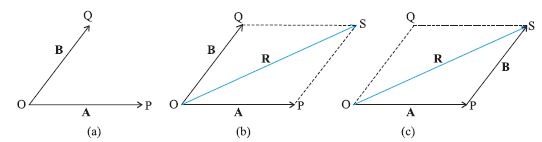
जैसा कि खण्ड 4.2 में बतलाया जा चुका है कि सदिश योग के त्रिभुज नियम या समान्तर चतुर्भुज के योग के नियम का पालन करते हैं । अब हम ग्राफी विधि द्वारा योग के इस नियम को समझाएंगे । हम चित्र 4.4 (a) में दर्शाए अनुसार किसी समतल में स्थित दो सदिशों A तथा B पर विचार करते हैं । इन सदिशों को व्यक्त करने वाली रेखा-खण्डों की लंबाइयाँ सदिशों के परिमाण के समानुपाती हैं ।
चित्र 4.4 (a) सदिश A तथा B, (b) सदिशों A व B का ग्राफी विधि द्वारा जोड़ना, (c) सदिशों B व A का ग्राफी विधि द्वारा जोड़ना,(d) सदिशों के जोड़ से संबंधित साहचर्य नियम का प्रदर्शन ।
योग A + B प्राप्त करने के लिए चित्र 4.4(b) के अनुसार हम सदिश B इस प्रकार रखते हैं कि उसकी पुच्छ सदिश A के शीर्ष पर हो । फिर हम A की पुच्छ को B के सिरे से जोड़ देते हैं । यह रेखा OQ परिणामी सदिश R को व्यक्त करती है जो सदिशों A तथा B का योग है। क्योंकि सदिशों के जोड़ने की इस विधि में सदिशों में से किसी एक के शीर्ष को दूसरे की पुच्छ से जोड़ते हैं, इसलिए इस ग्राफी विधि को शीर्ष व पुच्छ विधि के नाम से जाना जाता है । दोनों सदिश तथा उनका परिणामी सदिश किसी त्रिभुज की तीन भुजाएं बनाते हैं । इसलिए इस विधि को सदिश योग के त्रिभुज नियम भी कहते हैं । यदि हम B+A का परिणामी सदिश प्राप्त करें तो भी हमें वही सदिश R प्राप्त होता है (चित्र 4.4c)। इस प्रकार सदिशों का योग ‘क्रम विनिमेय’ (सदिशों के जोड़ने में यदि उनका क्रम बदल दें तो भी परिणामी सदिश नहीं बदलता) है ।
A + B = B + A (4.1)
सदिशों का योग साहचर्य नियम का भी पालन करता है जैसा कि चित्र 4.4 (d) में दर्शाया गया है । सदिशों A व B को पहले जोड़कर और फिर सदिश C को जोड़ने पर जो परिणाम प्राप्त होता है वह वही है जो सदिशों B और C को पहले जोड़कर फिर A को जोड़ने पर मिलता है, अर्थात्
(A + B) + C = A + (B + C) (4.2)
दो समान और विपरीत सदिशों को जोड़ने पर क्या परिणाम मिलता है ? हम दो सदिशों A और –A जिन्हें चित्र 4.3(b) में दिखलाया है, पर विचार करते हैं । इनका योग A + (–A) है। क्योंकि दो सदिशों का परिमाण वही है किन्तु दिशा विपरीत है, इसलिए परिणामी सदिश का परिमाण शून्य होगा और इसे 0 से व्यक्त करते हैं।
A – A = 0 |0| = 0 (4.3)
0 को हम शून्य सदिश कहते हैं । क्योंकि शून्य सदिश का परिमाण शून्य होता है, इसलिए इसकी दिशा का निर्धारण नहीं किया जा सकता है । दरअसल जब हम एक सदिश A को संख्या शून्य से गुणा करते हैं तो भी परिणामस्वरूप हमें एक सदिश ही मिलेगा किन्तु उसका परिमाण शून्य होगा । O सदिश के मुख्य गुण निम्न हैंः
A + 0 = A
λ 0 = 0
0 A = 0 (4.4)
शून्य सदिश का भौतिक अर्थ क्या है ? जैसाकि चित्र 4.1(a) में दिखाया गया है हम किसी समतल में स्थिति एवं विस्थापन सदिशों पर विचार करते हैं । मान लीजिए कि किसी क्षण t पर कोई वस्तु P पर है । वह P' तक जाकर पुनः P पर वापस आ जाती है । इस स्थिति में वस्तु का विस्थापन क्या होगा ? चूंकि प्रारंभिक एवं अंतिम स्थितियां संपाती हो जाती हैं, इसलिए विस्थापन "शून्य सदिश" होगा ।
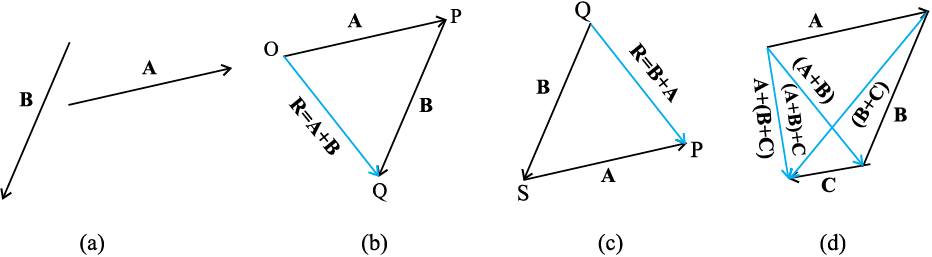
सदिशों का व्यवकलन सदिशों के योग के रूप में भी परिभाषित किया जा सकता है । दो सदिशों A व B के अंतर को हम दो सदिशों A व –B के योग के रूप में निम्न प्रकार से व्यक्त करते हैं:
A – B = A + (–B) (4.5)
इसे चित्र 4.5 में दर्शाया गया है । सदिश –B को सदिश A में जोड़कर R2 = (A – B) प्राप्त होता है । तुलना के लिए इसी चित्र में सदिश R1 = A + B को भी दिखाया गया है । समान्तर चतुर्भुज विधि को प्रयुक्त करके भी हम दो सदिशों का योग ज्ञात कर सकते हैं । मान लीजिए हमारे पास दो सदिश A व B हैं। इन सदिशों को जोड़ने के लिए उनकी पुच्छ को एक उभयनिष्ठ मूल बिंदु O पर लाते हैं जैसा चित्र 4.6(a) में दिखाया गया है। फिर हम A के शीर्ष से B के समांतर एक रेखा खींचते हैं और B के शीर्ष से A के समांतर एक दूसरी रेखा खींचकर समांतर चतुर्भुज OQSP पूरा करते हैं । जिस बिंदु पर यह दोनों रेखाएं एक दूसरे को काटती हैं, उसे मूल बिंदु O से जोड़ देते हैं। परिणामी सदिश R की दिशा समान्तर चतुर्भुज के मूल बिंदु O से कटान बिंदु S की ओर खींचे गए विकर्ण OS के अनुदिश होगी [चित्र 4.6 (b)]। चित्र 4.6 (c) में सदिशों A व B का परिणामी निकालने के लिए त्रिभुज नियम का उपयोग दिखाया गया है । दोनों चित्रों से स्पष्ट है कि दोनों विधियों से एक ही परिणाम निकलता है । इस प्रकार दोनों विधियाँ समतुल्य हैं।
चित्र 4.6 (a) एक ही उभयनिष्ठ बिंदु वाले दो सदिश A व B पर, (b) समान्तर चतुर्भुज विधि द्वारा A+B योग प्राप्त करना, (c) दो सदिशों को जोड़ने की समान्तर चतुर्भुज विधि त्रिभुज विधि के समतुल्य है ।
उदाहरण 4.1 किसी दिन वर्षा 35 ms-1 की चाल से ऊर्ध्वाधर नीचे की ओर हो रही है । कुछ देर बाद हवा
12 ms-1 की चाल से पूर्व से पश्चिम दिशा की ओरचलने लगती है । बस स्टाप पर खड़े किसी लड़के को
अपना छाता किस दिशा में करना चाहिए ?
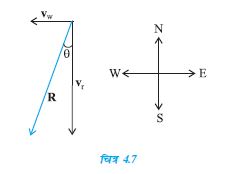
हल: वर्षा एवं हवा के वेगों को सदिशों vr तथा vw से चित्र 4.7 में दर्शाया गया है। इनकी दिशाएं प्रश्न के अनुसार प्रदर्शित की गई हैं । सदिशों के योग के नियम के अनुसार vr तथा vw का परिणामी R चित्र में खींचा गया है । R का परिमाण होगा-
ऊर्ध्वाधर से R की दिशा θ होगी-
या θ = tan–1 (0.343) = 19°
अतएव लड़के को अपना छाता ऊर्ध्वाधर तल में ऊर्ध्वाधर से 19° का कोण बनाते हुए पूर्व दिशा की ओर रखना
चाहिए ।
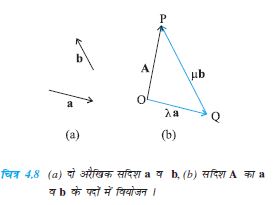
4.5 सदिशों का वियोजन
मान लीजिए कि a व b किसी समतल में भिन्न दिशाओं वाले दो शून्येतर (शून्य नहीं) सदिश हैं तथा A इसी समतल में कोई अन्य सदिश है । (चित्र 4.8) तब A को दो सदिशों के योग के रूप में वियोजित किया जा सकता है । एक सदिश a के किसी वास्तविक संख्या के गुणनफल के रूप में और इसी प्रकार दूसरा सदिश b के गुणनफल के रूप में है । एेसा करने के लिए पहले A खींचिए जिसका पुच्छ O तथा शीर्ष P है । फिर O से a के समांतर एक सरल रेखा खींचिए तथा P से एक सरल रेखा b के समांतर खींचिए । मान लीजिए वे एक दूसरे को Q पर काटती हैं । तब,
A = OP = OQ + QP (4.6)
परंतु क्योंकि OQ, a के समांतर है तथा Q P, b के समांतर है इसलिए
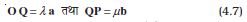
जहां λ तथा µ कोई वास्तविक संख्याएँ हैं ।
अतः 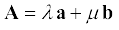 (4.8)
(4.8)
हम कह सकते हैं कि A को a व b के अनुदिश दो सदिश-घटकों क्रमशः λa तथा µb में वियोजित कर दिया गया है । इस विधि का उपयोग करके हम किसी सदिश को उसी समतल के दो सदिश-घटकों में वियोजित कर सकते हैं । एकांक परिमाण के सदिशों की सहायता से समकोणिक निर्देशांक निकाय के अनुदिश किसी सदिश का वियोजन सुविधाजनक होता है । एेसे सदिशों को एकांक सदिश कहते हैं जिस पर अब हम परिचर्चा करेंगे ।
एकांक सदिश :
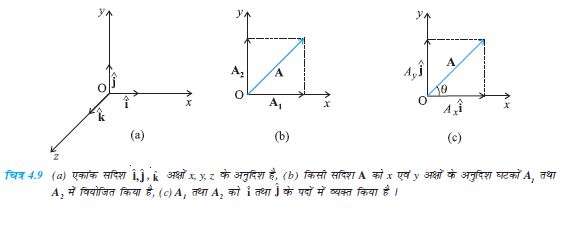
एकांक सदिश वह सदिश होता है जिसका परिमाण एक हो तथा जो किसी विशेष दिशा के अनुदिश हो । न तो इसकी कोई विमा होती है और न ही कोई मात्रक । मात्र दिशा व्यक्त करने के लिए इसका उपयोग होता है । चित्र 4.9a में प्रदर्शित एक ‘आयतीय निर्देशांक निकाय’ की x, y तथा z अक्षों के अनुदिश एकांक सदिशों को हम क्रमशः 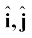 तथा
तथा 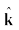 द्वारा व्यक्त करते हैं । क्योंकि ये सभी एकांक सदिश हैं, इसलिए
द्वारा व्यक्त करते हैं । क्योंकि ये सभी एकांक सदिश हैं, इसलिए
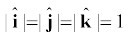 (4.9)
(4.9)
ये एकांक सदिश एक दूसरे के लंबवत् हैं । दूसरे सदिशों से इनकी अलग पहचान के लिए हमने इस पुस्तक में मोटे टाइप i, j, k के ऊपर एक कैप (^) लगा दिया है । क्याेंकि इस अध्याय में हम केवल द्विविमीय गति का ही अध्ययन कर रहे हैं अतः हमें केवल दो एकांक सदिशों की आवश्यकता होगी ।
यदि किसी एकांक सदिश 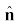 को एक अदिश λ से गुणा करें तो परिणामी एक सदिश λ
को एक अदिश λ से गुणा करें तो परिणामी एक सदिश λ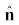 होगा । सामान्यतया किसी सदिश A को निम्न प्रकार से व्यक्त कर सकते हैं:
होगा । सामान्यतया किसी सदिश A को निम्न प्रकार से व्यक्त कर सकते हैं:
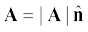 (4.10)
(4.10)
यहाँ A के अनुदिश 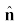 एकांक सदिश है ।
एकांक सदिश है ।
हम किसी सदिश A को एकांक सदिशों  तथा
तथा  के पदों में वियोजित कर सकते हैं । मान लीजिए कि चित्र (4.9b) के अनुसार सदिश A समतल x-y मेें स्थित है । चित्र 4.9(b) के अनुसार A के शीर्ष से हम निर्देशांक अक्षों पर लंब खींचते हैं । इससे हमें दो सदिश A1 व A2 इस प्रकार प्राप्त हैं कि
के पदों में वियोजित कर सकते हैं । मान लीजिए कि चित्र (4.9b) के अनुसार सदिश A समतल x-y मेें स्थित है । चित्र 4.9(b) के अनुसार A के शीर्ष से हम निर्देशांक अक्षों पर लंब खींचते हैं । इससे हमें दो सदिश A1 व A2 इस प्रकार प्राप्त हैं कि
A1 + A2 = A । क्योंकि A1 एकांक सदिश  के समान्तर है तथा A2 एकांक सदिश
के समान्तर है तथा A2 एकांक सदिश  के समान्तर है,
के समान्तर है,
अतः A1 = Ax  , A2 = Ay
, A2 = Ay  (4.11)
(4.11)
यहाँ Ax तथा Ay वास्तविक संख्याएँ हैें ।
इस प्रकार A = Ax  + Ay
+ Ay  (4.12)
(4.12)
इसे चित्र (4.9c) में दर्शाया गया है । राशियों Ax व Ay को हम सदिश A के x- व y- घटक कहते हैं । यहाँ यह बात ध्यान देने योग्य है कि Ax सदिश नहीं है, वरन् Ax  एक सदिश है । इसी प्रकार Ay
एक सदिश है । इसी प्रकार Ay  एक सदिश है ।
एक सदिश है ।
त्रिकोणमिति का उपयोग करके Ax व Ay को A के परिमाण तथा उसके द्वारा x-अक्ष के साथ बनने वाले कोण θ के पदों में व्यक्त कर सकते हैं :
Ax = A cos θ
Ay = A sin θ (4.13)
समीकरण (4.13) से स्पष्ट है कि किसी सदिश का घटक कोण θ पर निर्भर करता है तथा वह धनात्मक, ऋणात्मक या शून्य हो सकता है ।
किसी समतल में एक सदिश A को व्यक्त करने के लिए अब हमारे पास दो विधियाँ हैं:
(i) उसके परिमाण A तथा उसके द्वारा x-अक्ष के साथ बनाए गए कोण θ द्वारा, अथवा
(ii) उसके घटकों Ax तथा Ay द्वारा ।
यदि A तथा θ हमें ज्ञात हैं तो Ax और Ay का मान समीकरण (4.13) से ज्ञात किया जा सकता है । यदि Ax एवं Ay ज्ञात हों तो A तथा θ का मान निम्न प्रकार से ज्ञात किया जा सकता है :
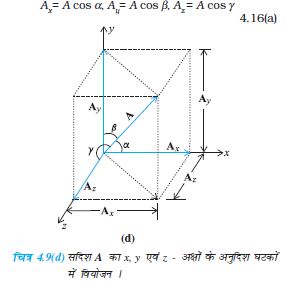
अभी तक इस विधि में हमने एक (x-y)समतल में किसी सदिश को उसके घटकों में वियोजित किया है किन्तु इसी विधि द्वारा किसी सदिश A को तीन विमाओं में x, y तथा z अक्षों के अनुदिश तीन घटकों में वियोजित किया जा सकता है । यदि A व x-, y-, व z- अक्षों के मध्य
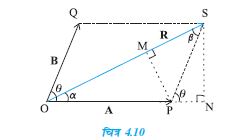
¯ उदाहरण 4.2 चित्र 4.10 में दिखाए गए दो सदिशों A तथा B के बीच का कोण θ है । इनके परिणामी सदिश का परिमाण तथा दिशा उनके परिमाणों तथा θ के पद में निकालिए ।
कोण क्रमशः α, β तथा γ हो* [चित्र 4.9 (d)] तो
सामान्य रूप से,
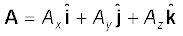 (4.16b)
(4.16b)
सदिश A का परिमाण
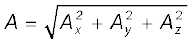 (4.16c)
(4.16c)
होगा ।
एक स्थिति सदिश r को निम्नलिखित प्रकार से व्यक्त किया जा सकता है |
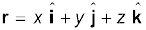 (4.17)
(4.17)
यहां x, y तथा z सदिश r के अक्षों x-, y-, z- के अनुदिश घटक हैं ।
4.6 सदिशों का योग : विश्लेषणात्मक विधि
यद्यपि सदिशों को जोड़ने की ग्राफी विधि हमें सदिशों तथा उनके परिणामी सदिश को स्पष्ट रूप से समझने में सहायक होती है, परन्तु कभी-कभी यह विधि जटिल होती है और इसकी शुद्धता भी सीमित होती है । भिन्न-भिन्न सदिशों को उनके संगत घटकों को मिलाकर जोड़ना अधिक आसान होता है। मान लीजिए कि किसी समतल में दो सदिश A तथा B हैं जिनके घटक क्रमशः Ax, Ay तथा Bx, By हैं तो
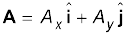
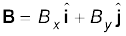 (4.18)
(4.18)
मान लीजिए कि R इनका योग है, तो
R= A+B
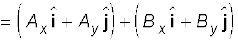 (4.19)
(4.19)
क्योंकि सदिश क्रमविनिमेय तथा साहचर्य नियमों का पालन करते हैं, इसलिए समीकरण (4.19) में व्यक्त किए गए सदिशों को निम्न प्रकार से पुनः व्यवस्थित कर सकते हैं :
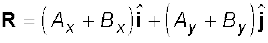 (4.19a)
(4.19a)
क्योंकि 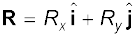 (4.20)
(4.20)
इसलिए Rx = Ax + Bx, Ry= Ay+ By (4.21)
इस प्रकार परिणामी सदिश R का प्रत्येक घटक सदिशों A और B के संगत घटकों के योग के बराबर होता है ।
तीन विमाओं के लिए सदिशों A और B को हम निम्न प्रकार से व्यक्त करते हैं:
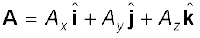
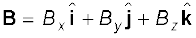
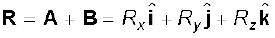
जहाँ घटकों Rx, Ry तथा Rz के मान निम्न प्रकार से हैंः
Rx = Ax + Bx
Ry = Ay + By
Rz = Az + Bz (4.22)
इस विधि को अनेक सदिशों को जोड़ने व घटाने के लिए उपयोग में ला सकते हैं । उदाहरणार्थ, यदि a, b तथा c तीनों सदिश निम्न प्रकार से दिए गए हों :
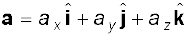
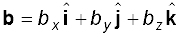
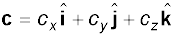 (4.23a)
(4.23a)
तो सदिश T = a + b – c के घटक निम्नलिखित होंगेः
Tx = ax + bx – cx
Ty = ay + by – cy
Tz = az + bz – cz (4.23b)
हल चित्र 4.10 के अनुसार मान लीजिए कि OP तथा OQ दो सदिशों A तथा B को व्यक्त करते हैं, जिनके बीच का कोण θ है । तब सदिश योग के समान्तर चर्तुभुज नियम द्वारा हमें परिणामी सदिश R प्राप्त होगा जिसे चित्र में OS द्वारा दिखाया गया है । इस प्रकार
R = A + B
चित्र में SN, OP के लंबवत् है तथा PM, OS के लंबवत् है ।
∴ OS2= ON2 + SN2
किन्तु ON = OP + PN = A + B cos θ
SN = B sin θ
OS2 = (A+B cos θ)2 + (B sin θ)2
अथवा R2 = A2 + B2 + 2AB cos θ
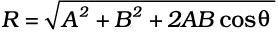 (4.24a)
(4.24a)
त्रिभुज OSN में, SN = OS sin α = R sin α
एवं त्रिभुज PSN में, SN = PS sin θ = B sin θ
अतएव R sin α = B sin θ
अथवा 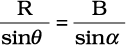 (4.24b)
(4.24b)
इसी प्रकार, PM = A sin α = B sin β
अथवा 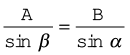 (4.24c)
(4.24c)
समीकरणों (4.24b) तथा (4.24c) से हमें प्राप्त होता है-
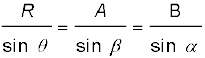 (4.24d)
(4.24d)
समीकरण (4.24d) के द्वारा हम निम्नांकित सूत्र प्राप्त करते हैं-
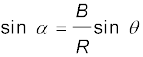 (4.24e)
(4.24e)
यहाँ R का मान समीकरण (4.24a) में दिया गया है ।
या, 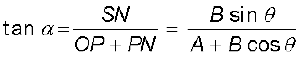 (4.24f)
(4.24f)
समीकरण (4.24a) से परिणामी R का परिमाण तथा समीकरण (4.24e) से इसकी दिशा मालूम की जा सकती है । समीकरण (4.24a) को कोज्या-नियम तथा समीकरण (4.24d) को ज्या-नियम कहते हैं । °
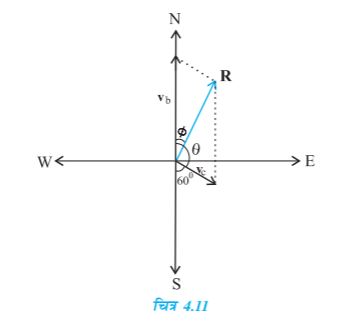
हल चित्र 4.11 में सदिश vb मोटरबोट के वेग को तथा vc जल धारा के वेग को व्यक्त करते हैं । प्रश्न के अनुसार चित्र में इनकी दिशायें दर्शाई गई हैं । सदिश योग के समांतर चतुर्भुज नियम के अनुसार प्राप्त परिणामी R की दिशा चित्र में दर्शाई
गई है । कोज्या-नियम का उपयोग करके हम R का परिमाण निकाल सकते हैं ।
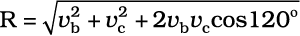
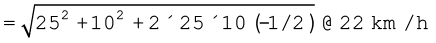
R की दिशा ज्ञात करने के लिए हम ‘ज्या-नियम’ का उपयोग करते हैं--
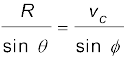 या,
या, 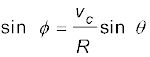
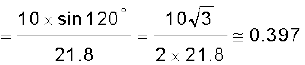
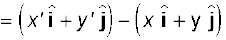
4.7 किसी समतल में गति
इस खण्ड में हम सदिशो का उपयोग कर दो या तीन विमाओं में का वर्णन करेंगे ।
4.7.1 स्थिति सदिश तथा विस्थापन
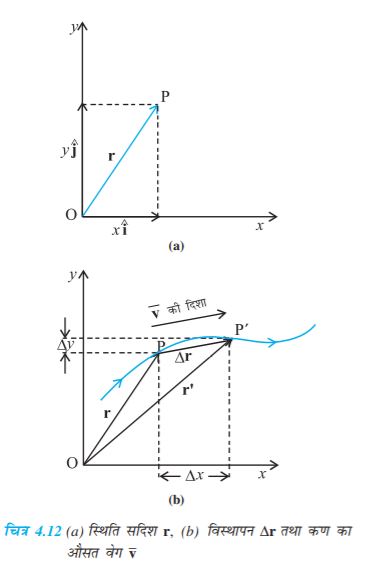
किसी समतल में स्थित कण P का x-y निर्देशतंत्र के मूल बिंदु के सापेक्ष स्थिति सदिश r [चित्र (4.12)] को निम्नलिखित समीकरण से व्यक्त करते हैं :
r = x i^ + y j^
यहाँ x तथा y अक्षों x-तथा y- के अनुदिश r के घटक हैं । इन्हें हम कण के निर्देशांक भी कह सकते हैं ।
मान लीजिए कि चित्र (4.12b) के अनुसार कोई कण मोटी रेखा से व्यक्त वक्र के अनुदिश चलता है । किसी क्षण t पर इसकी स्थिति P है तथा दूसरे अन्य क्षण t' पर इसकी स्थिति P' है । कण के विस्थापन को हम निम्नलिखित प्रकार से लिखेंगे,
∆r = r' – r (4.25)
इसकी दिशा P से P' की ओर है ।
समीकरण (4.25) को हम सदिशों के घटक के रूप में निम्नांकित प्रकार से व्यक्त करेंगे,
∆r 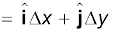

यहाँ ∆x = x ′ – x, ∆y = y′ – y (4.26)
वेग
वस्तु के विस्थापन और संगत समय अंतराल के अनुपात को हम औसत वेग (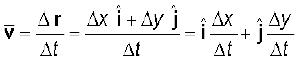 ) कहते हैं, अतः
) कहते हैं, अतः
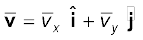 (4.27)
(4.27)
अथवा, 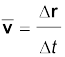
क्योंकि 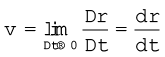 , इसलिए चित्र (4.12) के अनुसार औसत वेग की दिशा वही होगी, जो ∆r की है ।
, इसलिए चित्र (4.12) के अनुसार औसत वेग की दिशा वही होगी, जो ∆r की है ।
गतिमान वस्तु का वेग (तात्क्षणिक वेग) अति सूक्ष्म समयान्तराल (∆t→0 की सीमा में)विस्थापन ∆r का समय अन्तराल ∆t से अनुपात है । इसे हम v से व्यक्त करेंगे, अतः
* x व y के पदों में ax तथा ay को हम निम्न प्रकार से व्यक्त करते हैं:
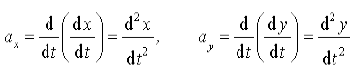
 (4.28)
(4.28)
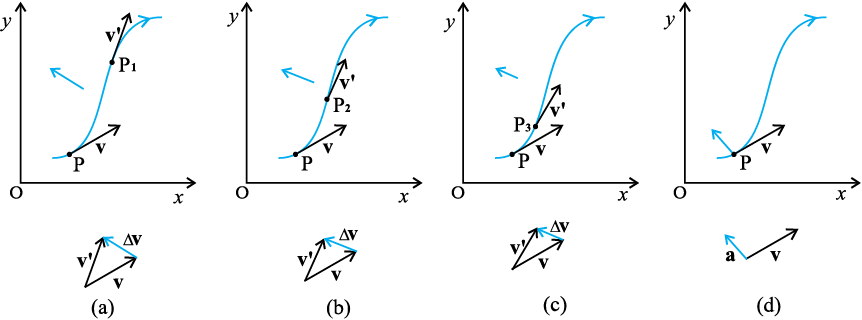
चित्रों 4.13(a) से लेकर 4.13(d) की सहायता से इस सीमान्त प्रक्रम को आसानी से समझा जा सकता है । इन चित्रों में मोटी रेखा उस पथ को दर्शाती है जिस पर कोई वस्तु क्षण t पर बिंदु P से चलना प्रारम्भ करती है । वस्तु की स्थिति ∆t1, ∆t2, ∆t3, समयों के उपरांत क्रमशः P1, P2, P3, से व्यक्त होती है । इन समयों में कण का विस्थापन क्रमशः ∆r1, ∆r2, ∆r3, है । चित्रों
(a), (b) तथा (c) में क्रमशः घटते हुए ∆t के मानों अर्थात् ∆t1, ∆t2, ∆t3, (∆t1> ∆t2> ∆t3) के लिए कण के औसत वेग  की दिशा को दिखाया गया है । जैसे ही ∆t →0 तो ∆r→0 एवं ∆r पथ की स्पर्श रेखा के अनुदिश हो जाता है (चित्र 4.13d)। इस प्रकार पथ के किसी बिंदु पर वेग उस बिंदु पर खींची गई स्पर्श रेखा द्वारा व्यक्त होता है जिसकी दिशा वस्तु की गति के अनुदिश होती है।
की दिशा को दिखाया गया है । जैसे ही ∆t →0 तो ∆r→0 एवं ∆r पथ की स्पर्श रेखा के अनुदिश हो जाता है (चित्र 4.13d)। इस प्रकार पथ के किसी बिंदु पर वेग उस बिंदु पर खींची गई स्पर्श रेखा द्वारा व्यक्त होता है जिसकी दिशा वस्तु की गति के अनुदिश होती है।
चित्र 4.15 तीन समय अंतरालों (a) ∆t1, (b) ∆t2, (c) ∆t3, (∆t1>∆t2>∆t3) के लिए औसत त्वरण 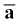 (d) ∆t→0 सीमा के अंतर्गत औसत त्वरण वस्तु के त्वरण के बराबर होता है ।
(d) ∆t→0 सीमा के अंतर्गत औसत त्वरण वस्तु के त्वरण के बराबर होता है ।
सुविधा के लिए v को हम प्रायः घटक के रूप में निम्नलिखित प्रकार से व्यक्त करते हैं :
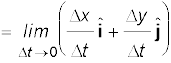
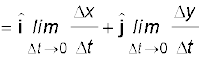 (4.29)
(4.29)
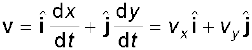
या, 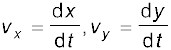 . यहाँ
. यहाँ 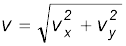 (4.30a)
(4.30a)
अतः यदि समय के फलन के रूप मे हमें निर्देशांक x और y ज्ञात हैं तो हम उपरोक्त समीकरणों का उपयोग vx और vy निकालने में कर सकते है I
सदिश v का परिमाण निम्नलिखित होगा,
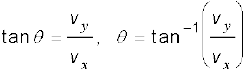 (4.30b)
(4.30b)
तथा इसकी दिशा कोण θ द्वारा निम्न प्रकार से व्यक्त
होगी:
 (4.30c)
(4.30c)
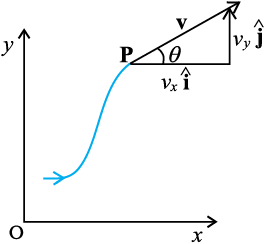
चित्र 4.14 में बिन्दु P पर किसी वेग सदिश v के लिए vx, vy तथा कोण θ को दर्शाया गया है ।
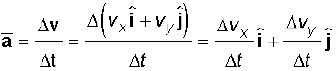
चित्र 4.14 वेग v के घटक vx, vy तथा कोण θ जो x-अक्ष से बनाता है । चित्र में vx = v cos θ, vy = v sin θ
त्वरण
x-y समतल में गतिमान वस्तु का औसत त्वरण (_a) उसके वेग में परिवर्तन तथा संगत समय अंतराल ∆t के अनुपात के बराबर होता है :
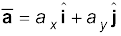 (4.31a)
(4.31a)
अथवा 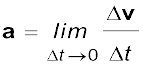 . (4.31b)
. (4.31b)
त्वरण (तात्क्षणिक त्वरण) औसत त्वरण के सीमान्त मान के बराबर होता है जब समय अंतराल शून्य हो जाता है:
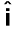 (4.32a)
(4.32a)
क्योंकि ∆v =  ∆vx +
∆vx + 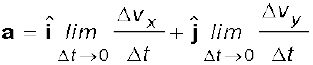 ∆vy, इसलिए
∆vy, इसलिए
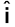
अथवा a =  ax +
ax + 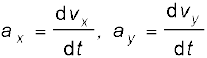 ay (4.32b)
ay (4.32b)
जहाँ  (4.32c)*
(4.32c)*
वेग की भाँति यहाँ भी वस्तु के पथ को प्रदर्शित करने वाले किसी आलेख में त्वरण की परिभाषा के लिए हम ग्राफी विधि से सीमान्त प्रक्रम को समझ सकते हैं । इसे चित्रों (4.15a) से (4.15d) तक में समझाया गया है । किसी क्षण t पर कण की स्थिति बिंदु P द्वारा दर्शाई गई है । ∆t1, ∆t2, ∆t3, (∆t1>∆t2>∆t3) समय के बाद कण की स्थिति क्रमशः बिंदुओं P1, P2, P3 द्वारा व्यक्त की गई है । चित्रों (4.15) a, b और c में इन सभी बिंदुओं P, P1, P2, P3 पर वेग सदिशों को भी दिखाया गया है । प्रत्येक ∆t के लिए सदिश योग के त्रिभुज नियम का उपयोग करके ∆v का मान निकालते हैं । परिभाषा के अनुसार औसत त्वरण की दिशा वही है जो ∆v की होती है । हम देखते हैं कि जैसे-जैसे ∆t का मान घटता जाता है वैसे-वैसे ∆v की दिशा भी बदलती जाती है और इसके परिणामस्वरूप त्वरण की भी दिशा बदलती है । अंततः ∆t →0 सीमा में [चित्र 4.15 (d)] औसत त्वरण, तात्क्षणिक त्वरण के बराबर हो जाता है और इसकी दिशा चित्र में दर्शाए अनुसार होती है ।
ध्यान दें कि एक विमा में वस्तु का वेग एवं त्वरण सदैव एक सरल रेखा में होते हैं (वे या तो एक ही दिशा में होते हैं अथवा विपरीत दिशा में) । परंतु दो या तीन विमाओं में गति के लिए वेग एवं त्वरण सदिशों के बीच 0॰ से 180॰ के बीच कोई भी कोण हो सकता है।
उदाहरण 4.4 किसी कण की स्थिति
r = 3.0 t$i + 2.0 t2$j + 5.0$ k है ।
जहां t सेकंड में व्यक्त किया गया है । अन्य गुणकों के मात्रक इस प्रकार हैं कि r मीटर में व्यक्त हो जाएँ।
(a) कण का v(t) व a(t) ज्ञात कीजिए; (b) t = 1.0 s पर v(t) का परिमाण व दिशा ज्ञात कीजिए ।
dr d
हल v(t) =  =
=  (3.0 t$i + 2.0 t2$j + 5.0$k)
(3.0 t$i + 2.0 t2$j + 5.0$k)
dt dt
= 3.0 $i + 4.0 t$j
dv
a(t) = 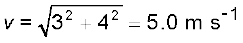 = 4.0 $j
= 4.0 $j
dt
a = 4.0 m s–2 y- दिशा में
t = 1.0 s पर v = 3.0$i + 4.0$j
इसका परिमाण 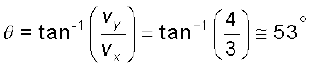 है, तथा
है, तथा
इसकी दिशा  °
°
4.8 किसी समतल में एकसमान त्वरण से गति
मान लीजिए कि कोई वस्तु एक समतल x-y में एक समान त्वरण a से गति कर रही है अर्थात् a का मान नियत है । किसी समय अंतराल में औसत त्वरण इस स्थिर त्वरण
के मान 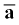 के बराबर होगा
के बराबर होगा 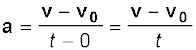 = a । अब मान लीजिए किसी
= a । अब मान लीजिए किसी
क्षण t = 0 पर वस्तु का वेग v0 तथा दूसरे अन्य क्षण t पर उसका वेग v है ।
तब परिभाषा के अनुसार
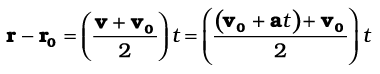
अथवा v = v0 + a t (4.33a)
उपर्युक्त समीकरण को सदिशों के घटक के रूप में निम्नलिखित प्रकार से व्यक्त करते हैं-
vx = v0x+axt
vy = v0y + ayt (4.33b)
अब हम देखेंगे कि समय के साथ स्थिति सदिश r किस प्रकार बदलता है । यहाँ एकविमीय गति के लिए बताई गई विधि
का उपयोग करेंगे । मान लीजिए कि t = 0 तथा t = t क्षणों पर कण के स्थिति के सदिश क्रमशः r0 तथा r हैं तथा इन क्षणों पर कण के वेग v0 तथा v हैं । तब समय अंतराल t – 0 = t में कण का औसत वेग (vo + v)/2 तथा विस्थापन r – r0 होगा । क्योंकि विस्थापन औसत तथा समय अंतराल का गुणनफल होता है,
अर्थात्
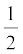
= v0 + 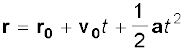 at2
at2
अतएव,
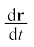 (4.34a)
(4.34a)
यह बात आसानी से सत्यापित की जा सकती है कि समीकरण (4.34a)का अवकलन 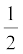 समीकरण (4.33a) है तथा साथ ही t = 0 क्षण पर r = r0 की शर्त को भी पूरी करता है । समीकरण (4.34a) को घटकों के रूप में निम्नलिखित प्रकार से व्यक्त कर सकते हैं:
समीकरण (4.33a) है तथा साथ ही t = 0 क्षण पर r = r0 की शर्त को भी पूरी करता है । समीकरण (4.34a) को घटकों के रूप में निम्नलिखित प्रकार से व्यक्त कर सकते हैं:
x = x0 + vox t + 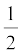 ax t2
ax t2
y = y0 + voy t + 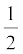 ay t2 (4.34b)
ay t2 (4.34b)
समीकरण (4.34b) की सीधी व्याख्या यह है कि x व y दिशाओं में गतियाँ एक दूसरे पर निर्भर नहीं करती हैं । अर्थात्, किसी समतल (दो विमा) में गति को दो अलग-अलग समकालिक एकविमीय एकसमान त्वरित गतियों के रूप
मेें समझ सकते हैं जो परस्पर लंबवत् दिशाओं के अनुदिश हों। यह महत्वपूर्ण परिणाम है जो दो विमाओं में वस्तु की
गति के विश्लेषण में उपयोगी होता है । यहाँ परिणाम त्रिविमीय गति के लिए भी है । बहुत-सी भौतिक स्थितियों में दो लंबवत् दिशाओं का चुनाव सुविधाजनक होता है जैसा कि हम प्रक्षेप्य गति के लिए खण्ड (4.10) में देखेंगे ।
उदाहरण 4.5 t = 0 क्षण पर कोई कण मूल बिंदु से 5.0$i m/s के वेग से चलना शुरू करता है । x - y समतल में उस पर एक एेसा बल लगता है जो उसमें एकसमान त्वरण (3.0$i + 2.0$j) m/s2 उत्पन्न करता है । (a) जिस क्षण पर कण का x निर्देशांक 84 m हो उस क्षण उसका y निर्देशांक कितना होगा ? (b) इस क्षण कण की चाल क्या होगी?
हल समीकरण (4.34 a) से r0= 0 पर प्रश्नानुसार कण की स्थिति निम्नांकित समीकरण से व्यक्त होगी,
r(t) = v0 t + 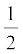 a t2
a t2
= 5.0i t + 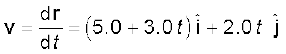 (3.0i + 2.0$j)t2
(3.0i + 2.0$j)t2
= (5.0t + 1.5t2)$i + 1.0t2$j
अतएव, x(t) = 5.0 t + 1.5 t2
y(t) = 1.0 t2
जब x(t) = 84 m तब t = ?
∴ 84 = 5.0 t + 1.5 t2
हल करने पर
t = 6.0 s पर y = 1.0(6)2 = 36.0 m
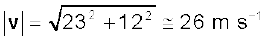
t = 6 s के लिए, v = 23.0$i + 12.0$j
अतः कण की चाल, 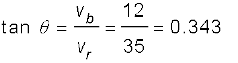 °
°
4.9 दो विमाओं में आपेक्षिक वेग
खण्ड 3.7 में किसी सरल रेखा के अनुदिश जिस आपेक्षिक वेग की धारणा से हम परिचित हुए हैं, उसे किसी समतल में या त्रिविमीय गति के लिए आसानी से विस्तारित कर सकते हैं । माना कि दो वस्तुएँ A व B वेगों vA तथा vB से गतिमान हैं (प्रत्येक गति किसी सामान्य निर्देश तंत्र जैसे धरती के सापेक्ष है)।
अतः वस्तु A का B के सापेक्ष वेग :
vAB= va – vb (4.35a)
होगा । इसी प्रकार, वस्तु B का A के सापेक्ष वेग निम्न होगा:
vBA= vB – vA
अतएव, vAB= – vbA (4.35b)
तथा |vAB| = |vba| (4.35c)
उदाहरण 4.6 : ऊर्ध्वाधर दिशा में 35 m s–1 की चाल से वर्षा हो रही है । कोई महिला पूर्व से पश्चिम दिशा में 12 m s–1 की चाल से साइकिल चला रही है । वर्षा से बचने के लिए उसे छाता किस दिशा में लगाना चाहिए ?
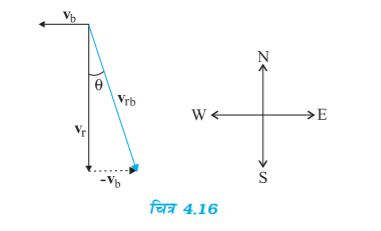
हल चित्र 4.16 में vr वर्षा के वेग को तथा vb महिला द्वारा चलाई जा रही साइकिल के वेग को व्यक्त करते हैं । ये दोनों वेग धरती के सापेक्ष हैं । क्योंकि महिला साइकिल चला रही है इसलिए वर्षा के जिस वेग का उसे आभास होगा वह साइकिल के सापेक्ष वर्षा का वेग होगा । अर्थात्
vrb = vr - vb
चित्र 4.16 के अनुसार यह सापेक्ष वेग सदिश ऊर्ध्वाधर से θ कोण बनाएगा जिसका मान
होगा । अर्थात् θ ≅ 190
अतः महिला को अपना छाता ऊर्ध्वाधर दिशा से 190 का कोण बनाते हुए पश्चिम की ओर रखना चाहिए ।
आप इस प्रश्न तथा उदाहरण 4.1 के अंतर पर ध्यान दीजिए । उदाहरण 4.1 में बालक को दो वेगों के परिणामी
(सदिश योग) का आभास होता है जबकि इस उदाहरण में महिला को साइकिल के सापेक्ष वर्षा के वेग (दोनों वेगों के सदिश अंतर) का आभास होता है । °
4.10 प्रक्षेप्य गति
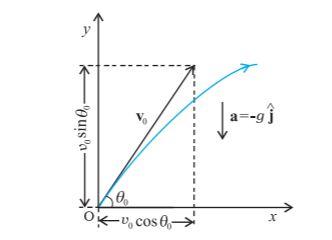
इससे पहले खण्ड में हमने जो विचार विकसित किए हैं, उदाहरणस्वरूप उनका उपयोग हम प्रक्षेप्य की गति के अध्ययन के लिए करेंगे । जब कोई वस्तु उछालने के बाद उड़ान में हो या प्रक्षेपित की गई हो तो उसे प्रक्षेप्य कहते हैं । एेसा प्रक्षेप्य फुटबॉल, क्रिकेट की बॉल, बेस-बॉल या अन्य कोई भी वस्तु हो सकती है । किसी प्रक्षेप्य की गति को दो अलग-अलग समकालिक गतियों के घटक के परिणाम के रूप में लिया जा सकता है । इनमें से एक घटक बिना किसी त्वरण के क्षैतिज दिशा में होता है तथा दूसरा गुरुत्वीय बल के कारण एकसमान त्वरण से ऊर्ध्वाधर दिशा में होता है ।
सर्वप्रथम गैलीलियो ने अपने लेख डायलॉग आन दि ग्रेट वर्ल्ड सिस्टम्स (1632) में प्रक्षेप्य गति के क्षैतिज एवं ऊर्ध्वाधर घटकों की स्वतंत्र प्रकृति का उल्लेख किया था ।
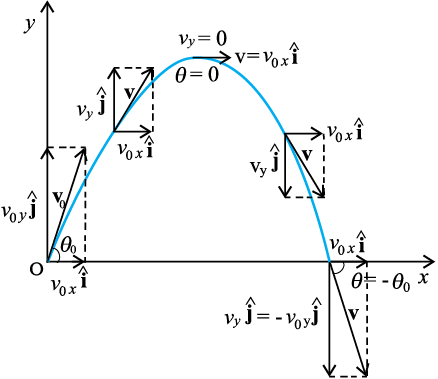
इस अध्ययन में हम यह मानेंगे कि प्रक्षेप्य की गति पर वायु का प्रतिरोध नगण्य प्रभाव डालता है । माना कि प्रक्षेप्य को एेसी दिशा की ओर v0 वेग से फेंका गया है जो x- अक्ष से
(चित्र 4.17 के अनुसार) θ0 कोण बनाता है ।
फेंकी गई वस्तु को प्रक्षेपित करने के बाद उस पर गुरुत्व के कारण लगने वाले त्वरण की दिशा नीचे की ओर होती है:
a = –g$j
अर्थात् ax = 0, तथा ay = –g (4.36)
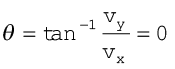
चित्र 4.17 v0 वेग से θ0 कोण पर प्रक्षेपित किसी वस्तु की गति ।
प्रारंम्भिक वेग v0 के घटक निम्न प्रकार होंगे:
vox = v0 cos θ0
voy = v0 sin θ0 (4.37)
यदि चित्र 4.17 के अनुसार वस्तु की प्रारंभिक स्थिति निर्देश तंत्र के मूल बिंदु पर हो, तो
x0 = 0, y0 = 0
इस प्रकार समीकरण (4.34b) को निम्न प्रकार से लिखेंगे:
x = vox t = (v0cos θ0)t
तथा, y = (v0sin θ0) t – 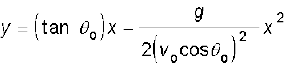 g t2 (4.38)
g t2 (4.38)
समीकरण (4.33b) का उपयोग करके किसी समय t के लिए वेग के घटकों को नीचे लिखे गए समीकरणों से व्यक्त करेंगे:
vx = vox = v0 cos θ0
vy = v0 sin θ0 – g t (4.39)
समीकरण (4.38) से हमें किसी क्षण t पर प्रारंभिक वेग v0 तथा प्रक्षेप्य कोण θ0 के पदों में प्रक्षेप्य के निर्देशांक x- और y- प्राप्त हो जाएँगे । इस बात पर ध्यान दीजिए कि x व y दिशाओं के परस्पर लंबवत् होने के चुनाव से प्रक्षेप्य गति के विश्लेषण में पर्याप्त सरलता हो गई है । वेग के दो घटकों में से एक x- घटक गति की पूरी अवधि में स्थिर रहता है जबकि दूसरा y- घटक इस प्रकार परिवर्तित होता है मानो प्रक्षेप्य स्वतंत्रतापूर्वक नीचे गिर रहा हो । चित्र 4.18 में विभिन्न क्षणों के लिए इसे आलेखी विधि से दर्शाया गया है । ध्यान दीजिए कि अधिकतम ऊँचाई वाले बिंदु के लिए vy = 0 तथा
प्रक्षेपक के पथ का समीकरण
प्रक्षेप्य द्वारा चले गए पथ की आकृति क्या होती है ? इसके लिए हमें पथ का समीकरण निकालना होगा । समीकरण (4.38) में दिए गए x व y व्यंजकों से t को विलुप्त करने से निम्नलिखित समीकरण प्राप्त होता है:
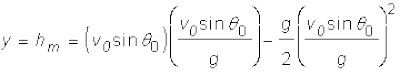 (4.40)
(4.40)
यह प्रक्षेप्य के पथ का समीकरण है और इसे चित्र 4.18 में दिखाया गया है । क्योंकि g, θ0 तथा v0 अचर हैं, समीकरण (4.40) को निम्न प्रकार से व्यक्त कर सकते हैं:
y = ax + bx2
इसमेें a तथा b नियतांक हैं । यह एक परवलय का समीकरण है, अर्थात् प्रक्षेप्य का पथ परवलयिक होता है ।
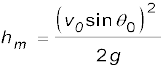
चित्र 4.18 प्रक्षेप्य का पथ परवलयाकार होता है ।
अधिकतम ऊँचाई का समय
प्रक्षेप्य अधिकतम ऊँचाई तक पहुँचने के लिए कितना समय लेता है? मान लीजिए कि यह समय tm है । क्योंकि इस बिंदु पर vy = 0 इसलिए समीकरण (4.39) से हम tm का मान निकाल सकते हैं:
vy = v0 sin θ0 – gtm = 0
अथवा tm = vo sinθo /g (4.41a)
प्रक्षेप्य की उड़ान की अवधि में लगा कुल समय Tf हम समीकरण (4.38) में y = 0 रखकर निकाल लेते हैं । इसलिए,
Tf = 2 (vo sin θo )/g (4.41b)
Tf को प्रक्षेप्य का उड्डयन काल कहते हैं । यह ध्यान देने की बात है कि Tf = 2tm । पथ की सममिति से हम एेसे ही परिणाम की आशा करते हैं ।
प्रक्षेप्य की अधिकतम ऊँचाई
समीकरण (4.38) में t = tm रखकर प्रक्षेप्य द्वारा प्राप्त अधिकतम ऊँचाई hm की गणना की जा सकती है ।
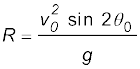
या 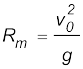 (4.42)
(4.42)
प्रक्षेप्य का क्षैतिज परास
प्रारंभिक स्थिति (x = y = 0) से चलकर उस स्थिति तक जब y = 0 हो प्रक्षेप्य द्वारा चली गई दूरी को क्षैतिज परास, R, कहते हैं। क्षैतिज परास उड्डयन काल Tf में चली गई दूरी है । इसलिए, परास R होगा:
R = (v0cos θ0)(Tf)
=(vo cos θo) (2 vo sin θo)/g
अथवा 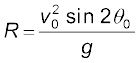 (4.43)
(4.43)
समीकरण (4.43) से स्पष्ट है कि किसी प्रक्षेप्य के वेग v0 लिए R अधिकतम तब होगा जब θ0 = 450 क्योंकि sin 900 = 1 (जो sin 2θ0 का अधिकतम मान है) । इस प्रकार अधिकतम क्षैतिज परास होगा
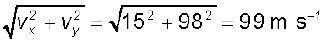
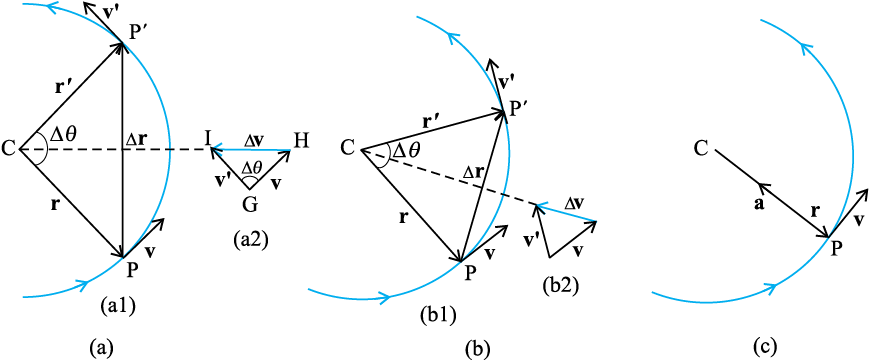
चित्र 4.19 किसी वस्तु की एकसमान वृत्तीय गति के लिए वेग तथा त्वरण । चित्र (a) से (c) तक ∆t घटता जाता है (चित्र c में शून्य हो जाता है) । वृत्ताकार पथ के प्रत्येक बिंदु पर त्वरण वृत्त के केंद्र की ओर होता है ।
∗∆t→0 सीमा में ∆r, r के लंबवत् हो जाता है । इस सीमा में क्योंकि ∆v→ 0 होता है, फलस्वरूप यह भी v के लंबवत् होगा । अतः वृत्तीय पथ के प्रत्येक बिंदु पर त्वरण की दिशा केंद्र की ओर होती है।
उदाहरण 4.7 : गैलीलियो ने अपनी पुस्तक "टू न्यू साइंसेज़" में कहा है कि "उन उन्नयनो के लिए जिनके मान 45॰ से बराबर मात्रा द्वारा अधिक या कम हैं, क्षैतिज परास बराबर होते हैं" । इस कथन को सिद्ध कीजिए ।
हल यदि कोई प्रक्षेप्य θ0 कोण पर प्रांरभिक वेग v0 से फेंका जाए, तो उसका परास  होगा।
होगा।
अब कोणों (450 + α) तथा (450 - α) के लिए 2θ0 का मान क्रमशः (900 + 2α) तथा (900 - 2α) होगा । sin(900 + 2α) तथा sin(9002α) दोनों का मान समान अर्थात् cos 2α होता है । अतः उन उन्नयनों के लिए जिनके मान 450 से बराबर मात्रा द्वारा कम या अधिक हैं, क्षैतिज परास बराबर होते हैं । °
उदाहरण 4.8 : एक पैदल यात्री किसी खड़ी चट्टान के कोने पर खड़ा है । चट्टान जमीन से 490 m ऊंची है । वह एक पत्थर को क्षैतिज दिशा में 15 m s–1 की आरंभिक चाल से फेंकता है । वायु के प्रतिरोध को नगण्य मानते हुए यह ज्ञात कीजिए कि पत्थर को जमीन तक पहुँचने में कितना समय लगा तथा जमीन से टकराते समय उसकी चाल कितनी थी? (g = 9.8 m s–2)।
हल हम खड़ी चट्टान के कोने को x- तथा y- अक्ष का मूल बिंदु तथा पत्थर फेंके जाने के समय को t = 0 मानेंगे । x- अक्ष की धनात्मक दिशा आरंभिक वेग के अनुदिश तथा y-अक्ष की धनात्मक दिशा ऊर्ध्वाधर ऊपर की ओर चुनते हैं । जैसा कि हम पहले कह चुके हैं कि गति के x- व y- घटक एक दूसरे पर निर्भर नहीं करते, इसलिए
x(t) = x0 + vox t
y(t) = y0 + voy t + (1/2) ay t2
यहाँ xo = yo = 0, voy = 0, ay = –g = –9.8 m s-2
vox = 15 m s-1.
पत्थर उस समय जमीन से टकराता है जब y(t) = – 490 m
∴ – 490 m = – (1/2) (9.8)t2
अर्थात् t = 10 s
वेग घटक vx = vox तथा vy = voy– g t होंगे ।
अतः, जब पत्थर जमीन से टकराता है, तब
vox = 15 m s–1
voy = 0 – 9.8 × 10 = –98 m s–1
इसलिए पत्थर की चाल होगी । °
होगी । °
उदाहरण 4.9 : क्षैतिज से ऊपर की ओर 30॰ का कोण बनाते हुए एक क्रिकेट गेंद 28 m s–1 की चाल से फेंकी जाती है । (a) अधिकतम ऊँचाई की गणना कीजिए,
(b) उसी स्तर पर वापस पहुँचने में लगे समय की गणना कीजिए, तथा (c) फेंकने वाले बिंदु से उस बिंदु की दूरी जहाँ गेंद उसी स्तर पर पहुँची है, की गणना कीजिए ।
हल (a) अधिकतम ऊँचाई
(v0sin θ0)2 (28 sin 300)2
hm = 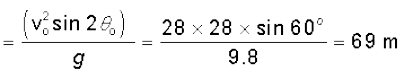 =
=  m
m
2 g 2(9.8)
= 10.0 m होगी ।
(b) उसी धरातल पर वापस आने में लगा समय
Tf = (2 vo sin θo )/g = (2 × 28 × sin 30° )/9.8 = 28/9.8 s = 2.9 s होगा ।
(c) फेंकने वाले बिंदु से उस बिंदु की दूरी जहाँ गेंद उसी स्तर पर पहुँचती हैः R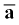 होगी।
होगी।
°वायु प्रतिरोध की उपेक्षा करना - इस अभिधारणा का वास्तविक अर्थ क्या है?
प्रक्षेप्य गति के विषय में बात करते समय, हमने कहा है, कि हमने यह मान रखा है, कि वायु के प्रतिरोध का प्रक्षेप्य की गति पर कोई प्रभाव नहीं होता। आपको यह समझना चाहिए, कि इस कथन का वास्तविक अर्थ क्या है? घर्षण, श्यानता बल, वायु प्रतिरोध ये सभी क्षयकारी बल हैं। गति का विरोध करते एेसे बलों की उपस्थिति के कारण गतिमान पिंड की मूल ऊर्जा, और परिणामतः इसके संवेग, में कमी आएगी। अतः अपने परवलयाकार पथ पर गतिमान कोई प्रक्षेप्य वायु प्रतिरोध की उपस्थिति में निश्चित रूप से, अपने आदर्श गमन-पथ से विचलित हो जाएगा। यह धरातल से उसी वेग से आकर नहीं टकराएगा जिससे यह फेंका गया था। वायु प्रतिरोध की अनुपस्थिति में वेग का x-अवयव अचर रहता है और केवल y-अवयव में ही सतत परिवर्तन होता है। तथापि, वायु प्रतिरोध की उपस्थिति में, ये दोनों ही अवयव प्रभावित होंगे। इसका अर्थ यह होगा कि प्रक्षेप्य का क्षैतिज परास समीकरण (4.43) द्वारा प्राप्त मान से कम होगा। अधिकतम ऊँचाई भी समीकरण (4.42) द्वारा प्रागुक्त मान से कम होगी। तब, क्या आप अनुमान लगा सकते हैं, कि उड्डयन काल में क्या परिवर्तन होगा?
वायु-प्रतिरोध से बचना हो, तो हमें प्रयोग, निर्वात में, या बहुत कम दाब की स्थिति में करना होगा जो आसान कार्य नहीं है। जब हम ‘वायु प्रतिरोध को नगण्य मान लीजिए’ जैसे वाक्यांशों का प्रयोग करते हैं, तो हम यह कहना चाहते हैं, कि परास, ऊँचाई जैसे प्राचलों में, इसके कारण होने वाला परिवर्तन, वायुविहीन स्थिति में ज्ञात इनके मानों की तुलना में बहुत कम है। बिना वायु-प्रतिरोध को विचार में लाए गणना करना आसान होता है बनिस्बत उस स्थिति के जब हम वायु प्रतिरोध को गणना में लाते हैं।
4.11 एकसमान वृत्तीय गति
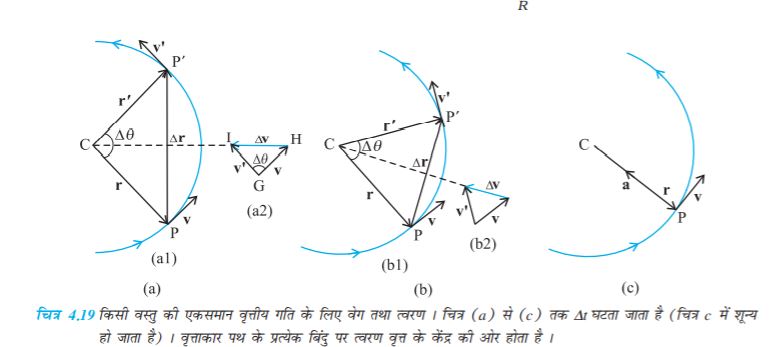
जब कोई वस्तु एकसमान चाल से एक वृत्ताकार पथ पर चलती है, तो वस्तु की गति को एकसमान वृत्तीय गति कहते हैं । शब्द "एकसमान" उस चाल के संदर्भ में प्रयुक्त हुआ है जो वस्तु की गति की अवधि में एकसमान (नियत) रहती है । माना कि चित्र 4.19 के अनुसार कोई वस्तु एकसमान चाल v से R त्रिज्या वाले वृत्त के अनुदिश गतिमान है । क्योंकि वस्तु के वेग की दिशा में निरन्तर परिवर्तन हो रहा है, अतः उसमें त्वरण उत्पन्न हो रहा है। हमें त्वरण का परिमाण तथा उसकी दिशा ज्ञात करनी है ।
माना r व r' तथा v व v' कण की स्थिति तथा गति सदिश हैं जब वह गति के दौरान क्रमशः बिंदुओं P व P' पर है
(चित्र 4.19a) । परिभाषा के अनुसार, किसी बिंदु पर कण का वेग उस बिंदु पर स्पर्श रेखा के अनुदिश गति की दिशा में होता है । चित्र 4.19(a1) में वेग सदिशों v व v' को दिखाया गया है। चित्र 4.19(a2) में सदिश योग के त्रिभुज नियम का उपयोग करके ∆v निकाल लेते हैं । क्योंकि पथ वृत्तीय है, इसलिए चित्र में, ज्यामिति से स्पष्ट है कि v, r के तथा v', r' के लंबवत् हैं । इसलिए, ∆v, ∆r के लंबवत् होगा । पुनः क्योंकि औसत त्वरण  के अनुदिश है, इसलिए
के अनुदिश है, इसलिए  भी ∆r के लंबवत् होगा । अब यदि हम ∆v को उस रेखा पर रखें जो r व r' के बीच के कोण को द्विभाजित करती है तो हम देखेंगे कि इसकी दिशा वृत्त के केंद्र की ओर होगी । इन्हीे राशियों को चित्र 4.19(b) में छोटे समय अंतराल के लिए दिखाया गया है । ∆v, अतः
भी ∆r के लंबवत् होगा । अब यदि हम ∆v को उस रेखा पर रखें जो r व r' के बीच के कोण को द्विभाजित करती है तो हम देखेंगे कि इसकी दिशा वृत्त के केंद्र की ओर होगी । इन्हीे राशियों को चित्र 4.19(b) में छोटे समय अंतराल के लिए दिखाया गया है । ∆v, अतः 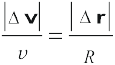 की दिशा पुनः केंद्र की ओर होगी । चित्र (4.19c) में ∆t→0 है, इसलिए औसत त्वरण, तात्क्षणिक त्वरण के बराबर हो जाता है । इसकी दिशा केंद्र की ओर होती है* । इस प्रकार, यह निष्कर्ष निकलता है कि एकसमान वृत्तीय गति के लिए वस्तु के त्वरण की दिशा वृत्त के केंद्र की ओर होती है । अब हम इस त्वरण का परिमाण निकालेंगे।
की दिशा पुनः केंद्र की ओर होगी । चित्र (4.19c) में ∆t→0 है, इसलिए औसत त्वरण, तात्क्षणिक त्वरण के बराबर हो जाता है । इसकी दिशा केंद्र की ओर होती है* । इस प्रकार, यह निष्कर्ष निकलता है कि एकसमान वृत्तीय गति के लिए वस्तु के त्वरण की दिशा वृत्त के केंद्र की ओर होती है । अब हम इस त्वरण का परिमाण निकालेंगे।
परिभाषा के अनुसार, a का परिमाण निम्नलिखित सूत्र से व्यक्त होता है,
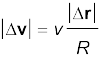
मान लीजिए r व r' के बीच का कोण ∆θ है । क्योंकि वेग सदिश v व v' सदैव स्थिति सदिशों के लंबवत् होते हैं, इसलिए उनके बीच का कोण भी ∆θ होगा । अतएव स्थिति सदिशों द्वारा निर्मित त्रिभुज (∆CPP') तथा वेग सदिशों v, v' व ∆v द्वारा निर्मित त्रिभुज (∆GHI) समरूप हैं (चित्र 4.19a) । इस प्रकार एक त्रिभुज के आधार की लंबाई व किनारे की भुजा की लंबाई का अनुपात दूसरे त्रिभुज की तदनुरूप लंबाइयों के अनुपात के बराबर होगा, अर्थात्
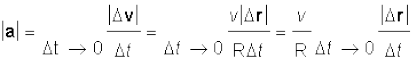
या 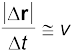
इसलिए,
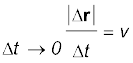
यदि ∆t छोटा है, तो ∆θ भी छोटा होगा । एेसी स्थिति में चाप PP' को लगभग |∆r| के बराबर ले सकते हैं ।
अर्थात्, |∆r| ≅ v ∆t
या  अथवा
अथवा 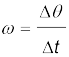
इस प्रकार, अभिकेंद्र त्वरण ac का मान निम्नलिखित होगा,
ac = 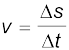 v = v2/R (4.44)
v = v2/R (4.44)
इस प्रकार किसी R त्रिज्या वाले वृत्तीय पथ के अनुदिश v चाल से गतिमान वस्तु के त्वरण का परिमाण v2/R होता है जिसकी दिशा सदैव वृत्त के केंद्र की ओर होती है । इसी कारण इस प्रकार के त्वरण को अभिकेंद्र त्वरण कहते हैं (यह पद न्यूटन ने सुझाया था) । अभिकेंद्र त्वरण से संबंधित संपूर्ण विश्लेषणात्मक लेख सर्वप्रथम 1673 में एक डच वैज्ञानिक क्रिस्चियान हाइगेन्स (1629-1695) ने प्रकाशित करवाया था, किन्तु संभवतया न्यूटन को भी कुछ वर्षों पूर्व ही इसका ज्ञान हो चुका था । अभिकेंद्र को अंग्रेजी में सेंट्रीपीटल कहते हैं जो एक ग्रीक शब्द है जिसका अभिप्राय केंद्र-अभिमुख (केंद्र की ओर) है । क्योंकि v तथा R दोनों अचर हैं इसलिए अभिकेंद्र त्वरण का परिमाण भी अचर होता है। परंतु दिशा बदलती रहती है और सदैव केंद्र की ओर होती है। इस प्रकार निष्कर्ष निकलता है कि अभिकेंद्र त्वरण एकसमान सदिश नहीं होता है ।
किसी वस्तु के एकसमान वृत्तीय गति के वेग तथा त्वरण को हम एक दूसरे प्रकार से भी समझ सकते हैं । चित्र 4.19 में दिखाए गए अनुसार ∆t (=t'–t) समय अंतराल में जब कण P से P' पर पहुँच जाता है तो रेखा CP कोण ∆θ से घूम जाती है । ∆θ को हम कोणीय दूरी कहते हैं । कोणीय वेग ω (ग्रीक अक्षर ‘ओमेगा’) को हम कोणीय दूरी के समय परिवर्तन की दर के रूप में परिभाषित करते हैं । इस प्रकार,
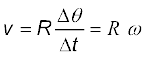 (4.45)
(4.45)
अब यदि ∆t समय में कण द्वारा चली दूरी को ∆s से व्यक्त करें (अर्थात् PP'=∆s) तो,
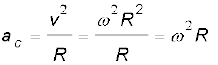
किंतु ∆s = R∆θ, इसलिए 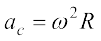
अतः v = ωR (4.46)
अभिकेंद्र त्वरण को हम कोणीय चाल के रूप में भी व्यक्त कर सकते हैं । अर्थात्,
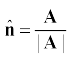
या  (4.47)
(4.47)
वृत्त का एक चक्कर लगाने में वस्तु को जो समय लगता है उसे हम आवर्तकाल T कहते हैं । एक सेकंड में वस्तु जितने चक्कर लगाती है, उसे हम वस्तु की आवृत्ति ν कहते हैं । परंतु इतने समय में वस्तु द्वारा चली गई दूरी s = 2πR होती है, इसलिए
v = 2πR/T = 2πRν (4.48)
इस प्रकार ω, v तथा ac को हम आवृति ν के पद में व्यक्त कर सकते हैं, अर्थात्
ω = 2πν
v = 2πνR
ac = 4π2ν2R (4.49)
¯ उदाहरण 4.10 : कोई कीड़ा एक वृत्तीय खाँचे में जिसकी त्रिज्या 12cm है, फँस गया है । वह खाँचे के अनुदिश स्थिर चाल से चलता है और 100 सेकंड में 7 चक्कर लगा लेता है। (a) कीड़े की कोणीय चाल व रैखिक चाल कितनी होगी? (b) क्या त्वरण सदिश एक अचर सदिश है। इसका परिणाम कितना होगा?
हल यह एकसमान वृत्तीय गति का एक उदाहरण है । यहाँ R = 12 cm है । कोणीय चाल ω का मान
ω = 2π/T = 2π × 7/100 = 0.44 rad/s
है तथा रैखिक चाल v का मान
v = ω R = 0.44 × 12 cm = 5.3 cm s–1
होगा । वृत्त के हर बिंदु पर वेग v की दिशा उस बिंदु पर स्पर्श रेखा के अनुदिश होगी तथा त्वरण की दिशा वृत्त के केंद्र की ओर होगी । क्योंकि यह दिशा लगातार बदलती रहती है, इसलिए त्वरण एक अचर सदिश नहीं है । परंतु त्वरण का परिमाण अचर है, जिसका मान
a = ω2 R = (0.44 s–1)2 (12 cm) = 2.3 cm s–2 होगा। °
सारांश
1. अदिश राशियाँ वे राशियाँ हैं जिनमेें केवल परिमाण होता है । दूरी, चाल, संहति (द्रव्यमान) तथा ताप अदिश राशियों के कुछ उदाहरण हैं ।
2. सदिश राशियाँ वे राशियाँ हैं जिनमेें परिमाण तथा दिशा दोनों होते हैं । विस्थापन, वेग तथा त्वरण आदि इस प्रकार की राशि के कुछ उदाहरण हैं । ये राशियाँ सदिश बीजगणित के विशिष्ट नियमों का पालन करती हैं ।
3. यदि किसी सदिश A को किसी वास्तविक संख्या λ से गुणा करें तो हमें एक दूसरा सदिश B प्राप्त होता है जिसका परिमाण A के परिमाण का λ गुना होता है । नए सदिश की दिशा या तो A के अनुदिश होती है या इसके विपरीत । दिशा इस बात पर निर्भर करती है कि λ धनात्मक है या ऋणात्मक ।
4. दो सदिशों A व B को जोड़ने के लिए या तो शीर्ष व पुच्छ की ग्राफी विधि का या समान्तर चतुर्भुज विधि का उपयोग करते हैं ।
5. सदिश योग क्रम-विनिमेय नियम का पालन करता है-
A + B = B + A
साथ ही यह साहचर्य के नियम का भी पालन करता है अर्थात् (A + B) + C = A + (B + C)
6. शून्य सदिश एक एेसा सदिश होता है जिसका परिमाण शून्य होता है । क्योंकि परिमाण शून्य होता है इसलिए इसके साथ दिशा बतलाना आवश्यक नहीं है ।
इसके निम्नलिखित गुण होते हैं:
A + 0 = A
λ0 = 0
0A = 0
7. सदिश B को A से घटाने की क्रिया को हम A व –B को जोड़ने के रूप में परिभाषित करते हैं-
A – B = A + (–B)
8. किसी सदिश A को उसी समतल में स्थित दो सदिशों a तथा b के अनुदिश दो घटक सदिशों में वियोजित कर सकते हैंः
A = λa + µb
यहाँ λ व µ वास्तविक संख्याएँ हैं ।
9. किसी सदिश A से संबंधित एकांक सदिश वह सदिश है जिसका परिमाण एक होता है और जिसकी दिशा सदिश A के अनुदिश होती है । एकांक सदिश 
एकांक सदिश 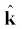 ,
,  ,
,  इकाई परिमाण वाले वे सदिश हैं जिनकी दिशाएँ दक्षिणावर्ती निकाय की अक्षों क्रमशः x-, y-
इकाई परिमाण वाले वे सदिश हैं जिनकी दिशाएँ दक्षिणावर्ती निकाय की अक्षों क्रमशः x-, y-
व z- के अनुदिश होती हैं ।
10. दो विमा के लिए सदिश A को हम निम्न प्रकार से व्यक्त करते हैं-
A = Ax 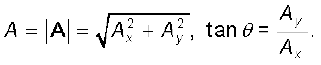 + Ay
+ Ay 
यहाँ Ax तथा Ay क्रमशः x-, y-अक्षों के अनुदिश A के घटक हैं । यदि सदिश A, x-अक्ष के साथ θ कोण बनाता है, तो Ax = A cos θ,Ay = A sin θ तथा

11. विश्लेषणात्मक विधि से भी सदिशों को आसानी से जोड़ा जा सकता है । यदि x-y समतल में दो सदिशों A व B का योग R हो, तो
R = Rx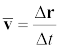 + Ry
+ Ry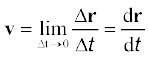 जहाँ Rx = Ax + Bx तथा Ry = Ay + By
जहाँ Rx = Ax + Bx तथा Ry = Ay + By
12. समतल में किसी वस्तु की स्थिति सदिश r को प्रायः निम्न प्रकार से व्यक्त करते हैं:
r = x i^ + yj^
स्थिति सदिशों r व r' के बीच के विस्थापन को निम्न प्रकार से लिखते हैं:
∆r = r' – r
= (x' – x) i^ + (y' – y) j^
=∆x i^ +∆y j^
13. यदि कोई वस्तु समय अंतराल ∆t में ∆r से विस्थापित होती है तो उसका औसत वेग 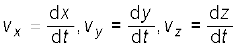 होगा । किसी क्षण t पर वस्तु का वेग उसके औसत वेग के सीमान्त मान के बराबर होता है जब ∆t शून्य के सन्निकट हो जाता है । अर्थात्
होगा । किसी क्षण t पर वस्तु का वेग उसके औसत वेग के सीमान्त मान के बराबर होता है जब ∆t शून्य के सन्निकट हो जाता है । अर्थात्
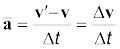
इसे एकांक सदिशों के रूप में भी व्यक्त करते हैं:
v = vxi^+ vy j^+vz k^
जहाँ 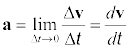
जब किसी निर्देशांक निकाय में कण की स्थिति को दर्शाते हैं, तो v की दिशा कण के पथ के वक्र की उस बिंदु पर खींची गई स्पर्श रेखा के अनुदिश होती है ।
14. यदि वस्तु का वेग ∆t समय अंतराल में v से v' में बदल जाता है, तो उसका औसत त्वरण 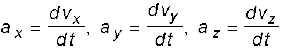 होगा । जब ∆t का सीमान्त मान शून्य हो जाता है तो किसी क्षण t पर वस्तु का त्वरण
होगा । जब ∆t का सीमान्त मान शून्य हो जाता है तो किसी क्षण t पर वस्तु का त्वरण 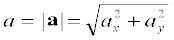 होगा ।
होगा ।
घटक के पदों में इसे निम्न प्रकार से व्यक्त किया जा सकता है:
a = axi^+ ay j^ + az k^
यहाँ,
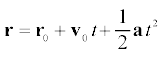
15. यदि एक वस्तु किसी समतल में एकसमान त्वरण 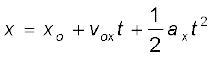 से गतिमान है तथा क्षण t=0 पर उसका स्थिति सदिश ro है, तो किसी अन्य क्षण t पर उसका स्थिति सदिश
से गतिमान है तथा क्षण t=0 पर उसका स्थिति सदिश ro है, तो किसी अन्य क्षण t पर उसका स्थिति सदिश 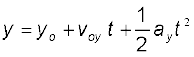 होगा तथा उसका वेग v = v0+ at होगा ।
होगा तथा उसका वेग v = v0+ at होगा ।
यहाँ v0, t = 0 क्षण पर वस्तु के वेग को व्यक्त करता है ।
घटक के रूप में
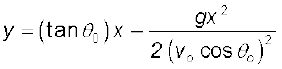
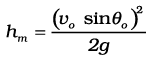
vx = v0x + ax t
vy = v0y + ay t
किसी समतल में एकसमान त्वरण की गति को दो अलग-अलग समकालिक एकविमीय व परस्पर लंबवत् गतियों के अध्यारोपण के रूप में मान सकते हैं ।
16. प्रक्षेपित होने के उपरांत जब कोई वस्तु उड़ान में होती है तो उसे प्रक्षेप्य कहते हैं । यदि x-अक्ष से θ0 कोण पर वस्तु का प्रारंभिक वेग v0 है तो t क्षण के उपरांत प्रक्षेप्य के स्थिति एवं वेग संबंधी समीकरण निम्नवत् होंगे-
x = (v0cos θ0) t
y = (v0sin θ0) t− (1/2) g t2
vx = v0x= v0cos θ0
vy = v0 sin θ0 –gt
प्रक्षेप्य का पथ परवलयिक होता है जिसका समीकरण
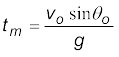 होगा ।
होगा ।
प्रक्षेप्य की अधिकतम ऊँचाई 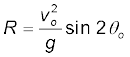 , तथा
, तथा
इस ऊँचाई तक पहुंचने में लगा समय  होगा ।
होगा ।
प्रक्षेप्य द्वारा अपनी प्रारंभिक स्थिति से उस स्थिति तक, जिसके लिए नीचे उतरते समय y = 0 हो, चली गई क्षैतिज दूरी को प्रक्षेप्य का परास R कहते हैं ।
अतः प्रक्षेप्य का परास 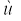 होगा ।
होगा ।
17. जब कोई वस्तु एकसमान चाल से एक वृत्तीय मार्ग में चलती है तो इसे एकसमान वृत्तीय गति कहते हैं । यदि वस्तु की चाल v हो तथा इसकी त्रिज्या R हो, तो अभिकेंद्र त्वरण, ac= v2/R होगा तथा इसकी दिशा सदैव वृत्त के केंद्र की ओर होगी । कोणीय चाल 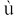 कोणीय दूरी के समान परिवर्तन की दर होता है । रैखिक वेग v =
कोणीय दूरी के समान परिवर्तन की दर होता है । रैखिक वेग v =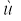 R होगा तथा त्वरण ac =
R होगा तथा त्वरण ac = 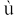 2R होगा ।
2R होगा ।
यदि वस्तु का आवर्तकाल T तथा,v तथा ac के मान निम्नवत् होंगे ।
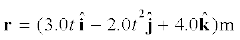 = 2πν, v = 2πνR, ac = 4π2ν2R
= 2πν, v = 2πνR, ac = 4π2ν2R
विचारणीय विषय
1. किसी वस्तु द्वारा दो बिंदुओं के बीच की पथ-लंबाई सामान्यतया, विस्थापन के परिमाण के बराबर नहीं होती । विस्थापन केवल पथ के अंतिम बिंदुओं पर निर्भर करता है जबकि पथ-लंबाई (जैसाकि नाम से ही स्पष्ट है) वास्तविक पथ पर निर्भर करती है । दोनों राशियां तभी बराबर होंगी जब वस्तु गति मार्ग में अपनी दिशा नहीं बदलती । अन्य दूसरी परिस्थितियों में पथ-लंबाई विस्थापन के परिमाण से अधिक होती है ।
2. उपरोक्त बिंदु 1 की दृष्टि से वस्तु की औसत चाल किसी दिए समय अंतराल में या तो उसके औसत वेग के परिमाण के बराबर होगी या उससे अधिक होगी । दोनों बराबर तब होंगी जब पथ-लंबाई विस्थापन के परिमाण के बराबर हो ।
3. सदिश समीकरण (4.3a) तथा (4.34a) अक्षों के चुनाव पर निर्भर नहीं करते हैं । निःसंदेह आप उन्हें दो स्वतंत्र अक्षों के अनुदिश वियोजित कर सकते हैं ।
4. एकसमान त्वरण के लिए शुद्धगतिकी के समीकरण एकसमान वृत्तीय गति में लागू नहीं होते क्योंकि इसमेें त्वरण का परिमाण तो स्थिर रहता है परंतु उसकी दिशा निरंतर बदलती रहती है ।
5. यदि किसी वस्तु के दो वेग v1 तथा v2 हों तो उनका परिणामी वेग v =v1+ v2 होगा । उपरोक्त सूत्र तथा वस्तु 2 के सापेक्ष वस्तु का1 के वेग अर्थात्ः v12 = v1- v2 के बीच भेद को भलीभांति जानिए । यहां v1तथा v2 किसी उभयनिष्ठ निर्देश तन्त्र के सापेक्ष वस्तु की गतियां हैं ।
6. वृत्तीय गति में किसी कण का परिणामी त्वरण वृत्त के केंद्र की ओर होता है यदि उसकी चाल एकसमान है ।
7. किसी वस्तु की गति के मार्ग की आकृति केवल त्वरण से ही निर्धारित नहीं होती बल्कि वह गति की प्रारंभिक दशाओं (प्रारंभिक स्थिति व प्रारंभिक वेग) पर भी निर्भर करती है । उदाहरणस्वरूप, एक ही गुरुत्वीय त्वरण से गतिमान किसी वस्तु का मार्ग एक सरल रेखा भी हो सकता है या कोई परवलय भी, एेसा प्रारंभिक दशाओं पर निर्भर करेगा ।
अभ्यास
4.1 निम्नलिखित भौतिक राशियों में से बतलाइए कि कौन-सी सदिश हैं और कौन-सी अदिश:
आयतन, द्रव्यमान, चाल, त्वरण, घनत्व, मोल संख्या, वेग, कोणीय आवृत्ति, विस्थापन, कोणीय वेग।
4.2 निम्नांकित सूची में से दो अदिश राशियों को छाँटिए-
बल, कोणीय संवेग, कार्य, धारा, रैखिक संवेग, विद्युत क्षेत्र, औसत वेग, चुंबकीय आघूर्ण, आपेक्षिक वेग।
4.3 निम्नलिखित सूची में से एकमात्र सदिश राशि को छाँटिए-
ताप, दाब, आवेग, समय, शक्ति, पूरी पथ-लंबाई, ऊर्जा, गुरुत्वीय विभव, घर्षण गुणांक, आवेश।
4.4 कारण सहित बताइए कि अदिश तथा सदिश राशियों के साथ क्या निम्नलिखित बीजगणितीय संक्रियाएँ अर्थपूर्ण हैं?
(a) दो अदिशों को जोड़ना, (b) एक ही विमाओं के एक सदिश व एक अदिश को जोड़ना, (c) एक सदिश को एक अदिश से गुणा करना, (d) दो अदिशों का गुणन, (e) दो सदिशों को जोड़ना, (f) एक सदिश के घटक को उसी सदिश से जोड़ना ।
4.5 निम्नलिखित में से प्रत्येक कथन को ध्यानपूर्वक पढ़िए और कारण सहित बताइए कि यह सत्य है या असत्य:
(a) किसी सदिश का परिमाण सदैव एक अदिश होता है, (b) किसी सदिश का प्रत्येक घटक सदैव अदिश होता है,
(c) किसी कण द्वारा चली गई पथ की कुल लंबाई सदैव विस्थापन सदिश के परिमाण के बराबर होती है, (d) किसी कण की औसत चाल (पथ तय करने में लगे समय द्वारा विभाजित कुल पथ-लंबाई) समय के समान-अंतराल में कण के औसत वेग के परिमाण से अधिक या उसके बराबर होती है । (e) उन तीन सदिशों का योग जो एक समतल में नहीं हैं, कभी भी शून्य सदिश नहीं होता ।
4.6 निम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिए:
(a) |a+b| ≤ |a| + |b|
(b) |a+b| ≥ ||a| – |b||
(c) |a–b| ≤ |a| + |b|
(d) |a–b| ≥ ||a| – |b||
इनमें समिका (समता) का चिह्न कब लागू होता है ?
4.7 दिया है a + b + c + d = 0, नीचे दिए गए कथनों में से कौन-सा सही है ः
(a) a, b, c तथा d में से प्रत्येक शून्य सदिश है,
(b) (a + c) का परिमाण (b + d) के परिमाण के बराबर है,
(c) a का परिमाण b, c तथा d के परिमाणों के योग से कभी भी अधिक नहीं हो सकता,
(d) यदि a तथा d संरेखीय नहीं हैं तो b + c अवश्य ही a तथा d के समतल में होगा, और यह a तथा d के अनुदिश होगा यदि वे संरेखीय हैं ।
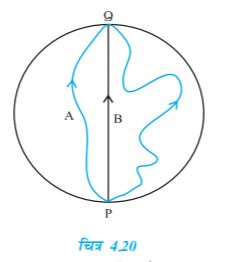
4.8 तीन लड़कियाँ 200 m त्रिज्या वाली वृत्तीय बर्फीली सतह पर स्केटिंग कर रही हैं । वे सतह के किनारे के बिंदु P से स्केटिंग शुरू करती हैं तथा P के व्यासीय विपरीत बिंदु Q पर विभिन्न पथों से होकर पहुँचती हैं जैसा कि चित्र 4.20 में दिखाया गया है । प्रत्येक लड़की के विस्थापन सदिश का परिमाण कितना है ? किस लड़की के लिए यह वास्तव में स्केट किए गए पथ की लंबाई के बराबर है ।
4.9 कोई साइकिल सवार किसी वृत्तीय पार्कं के केंद्र O से चलना शुरू करता है तथा पार्क के किनारे P पर पहुँचता है। पुनः वह पार्क की परिधि के अनुदिश साइकिल चलाता हुआ QO के रास्ते (जैसा चित्र 4.21 में दिखाया गया है) केंद्र पर वापस आ जाता है । पार्क की त्रिज्या 1 km है । यदि पूरे चक्कर में 10 मिनट लगते हों तो साइकिल सवार का (a) कुल विस्थापन, (b) औसत वेग, तथा (c) औसत चाल क्या होगी?
चित्र 4.21
4.10 किसी खुले मैदान में कोई मोटर चालक एक एेसा रास्ता अपनाता है जो प्रत्येक 500 m के बाद उसके बाईं ओर 60॰ के कोण पर मुड़ जाता है। किसी दिए मोड़ से शुरू होकर मोटर चालक का तीसरे, छठे व आठवें मोड़ पर विस्थापन बताइए। प्रत्येक स्थिति में मोटर चालक द्वारा इन मोड़ों पर तय की गई कुल पथ-लंबाई के साथ विस्थापन के परिमाण की तुलना कीजिए।
4.11 कोई यात्री किसी नए शहर में आया है और वह स्टेशन से किसी सीधी सड़क पर स्थित किसी होटल तक जो 10 km दूर है, जाना चाहता है। कोई बेईमान टैक्सी चालक 23 km के चक्करदार रास्ते से उसे ले जाता है और 28 मिनट में होटल में पहुँचता है।
(a) टैक्सी की औसत चाल, और (b) औसत वेग का परिमाण क्या होगा? क्या वे बराबर हैं?
4.12 वर्षा का पानी 30 m s–1 की चाल से ऊर्ध्वाधर नीचे गिर रहा है। कोई महिला उत्तर से दक्षिण की ओर 10 m s–1 की चाल से साइकिल चला रही है। उसे अपना छाता किस दिशा में रखना चाहिए।
4.13 कोई व्यक्ति स्थिर पानी में 4.0 km/h की चाल से तैर सकता है । उसे 1.0 km चौड़ी नदी को पार करने में कितना समय लगेगा यदि नदी 3.0 km/h की स्थिर चाल से बह रही हो और वह नदी के बहाव के लंब तैर रहा हो । जब वह नदी के दूसरे किनारे पहुँचता है तो वह नदी के बहाव की ओर कितनी दूर पहुँचेगा?
4.14 किसी बंदरगाह में 72 km/h की चाल से हवा चल रही है और बंदरगाह में खड़ी किसी नौका के ऊपर लगा झंडा
N-E दिशा में लहरा रहा है । यदि वह नौका उत्तर की ओर 51 km/h चाल से गति करना प्रारंभ कर दे तो नौका पर लगा झंडा किस दिशा में लहराएगा ?
4.15 किसी लंबे हाल की छत 25 m ऊंची है । वह अधिकतम क्षैतिज दूरी कितनी होगी जिसमें 40 m s–1 की चाल से फेंकी गई कोई गेंद छत से टकराए बिना गुजर जाए ?
4.16 क्रिकेट का कोई खिलाड़ी किसी गेंद को 100 m की अधिकतम क्षैतिज दूरी तक फेंक सकता है । वह खिलाड़ी उसी गेंद को जमीन से ऊपर कितनी ऊंचाई तक फेंक सकता है ?
4.17 80 cm लंबे धागे के एक सिरे पर एक पत्थर बाँधा गया है और इसे किसी एकसमान चाल के साथ किसी क्षैतिज वृत्त में घुमाया जाता है । यदि पत्थर 25 s में 14 चक्कर लगाता है तो पत्थर के त्वरण का परिमाण और उसकी दिशा क्या होगी ?
4.18 कोई वायुयान 900 km h–1 की एकसमान चाल से उड़ रहा है और 1.00 km त्रिज्या का कोई क्षैतिज लूप बनाता है । इसके अभिकेंद्र त्वरण की गुरुत्वीय त्वरण के साथ तुलना कीजिए ।
4.19 नीचे दिए गए कथनों को ध्यानपूर्वक पढ़िए और कारण देकर बताइए कि वे सत्य हैं या असत्य:
(a) वृत्तीय गति में किसी कण का नेट त्वरण हमेशा वृत्त की त्रिज्या के अनुदिश केंद्र की ओर होता है ।
(b) किस बिंदु पर किसी कण का वेग सदिश सदैव उस बिंदु पर कण के पथ की स्पर्श रेखा के अनुदिश होता है।
(c) किसी कण का एकसमान वृत्तीय गति में एक चक्र में लिया गया औसत त्वरण सदिश एक शून्य सदिश होता है।
4.20 किसी कण की स्थिति सदिश निम्नलिखित है:
समय t सेकंड में है तथा सभी गुणकों के मात्रक इस प्रकार से हैं कि r में मीटर में व्यक्त हो जाए ।
(a) कण का v तथा a निकालिए,
(b) t = 2.0 s पर कण के वेग का परिमाण तथा दिशा कितनी होगी ?
4.21 कोई कण t = 0 क्षण पर मूल बिंदु से  के वेग से चलना प्रांरभ करता है तथा x-y समतल में एकसमान त्वरण (8.0 ^i + 2.0 ^j)m s-2 से गति करता है ।
के वेग से चलना प्रांरभ करता है तथा x-y समतल में एकसमान त्वरण (8.0 ^i + 2.0 ^j)m s-2 से गति करता है ।
(a) किस क्षण कण का x-निर्देशांक 16 m होगा ? इसी समय इसका y-निर्देशांक कितना होगा ?
(b) इस क्षण कण की चाल कितनी होगी ?
4.22 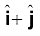 व
व 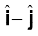 क्रमशः x- व y-अक्षों के अनुदिश एकांक सदिश हैं । सदिशों
क्रमशः x- व y-अक्षों के अनुदिश एकांक सदिश हैं । सदिशों 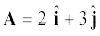 तथा
तथा 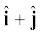 का परिमाण तथा दिशा क्या होगा ? सदिश
का परिमाण तथा दिशा क्या होगा ? सदिश 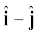 के
के 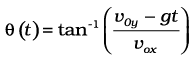 व
व 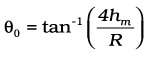 के दिशाओं के अनुदिश घटक निकालिए। [ आप ग्राफी विधि का उपयोग कर सकते हैं ]
के दिशाओं के अनुदिश घटक निकालिए। [ आप ग्राफी विधि का उपयोग कर सकते हैं ]
4.23 किसी दिक्स्थान पर एक स्वेच्छ गति के लिए निम्नलिखित संबंधाें में से कौन-सा सत्य है ?
(a) vऔसत = (1/2) (v (t1) + v (t2))
(b) v औसत = [r(t2) - r(t1) ] /(t2 – t1)
(c) v (t) = v (0) + a t
(d) r (t) = r (0) + v (0) t + (1/2) a t2
(e) a औसत =[ v (t2) - v (t1 )] /( t2 – t1)
यहाँ ‘औसत’ का आशय समय अंतराल t2 व t1 से संबंधित भौतिक राशि के औसत मान से है ।
4.24 निम्नलिखित में से प्रत्येक कथन को ध्यानपूर्वक पढ़िए तथा कारण एवं उदाहरण सहित बताइए कि क्या यह सत्य है या असत्य:
अदिश वह राशि है जो
(a) किसी प्रक्रिया में संरक्षित रहती है,
(b) कभी ऋणात्मक नहीं होती,
(c) विमाहीन होती है,
(d) किसी स्थान पर एक बिंदु से दूसरे बिंदु के बीच नहीं बदलती,
(e) उन सभी दर्शकों के लिए एक ही मान रखती है चाहे अक्षों से उनके अभिविन्यास भिन्न-भिन्न क्यों न हों ।
4.25 कोई वायुयान पृथ्वी से 3400 m की ऊंचाई पर उड़ रहा है । यदि पृथ्वी पर किसी अवलोकन बिंदु पर वायुयान की
10.0 s की दूरी की स्थितियां 30॰ का कोण बनाती हैं तो वायुमान की चाल क्या होगी ?
अतिरिक्त अभ्यास
4.26 किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या दिक्स्थान में इसकी कोई स्थिति होती है? क्या यह समय के साथ परिवर्तित हो सकता है। क्या दिक्स्थान में भिन्न स्थानों पर दो बराबर सदिशों a व b का समान भौतिक प्रभाव अवश्य पड़ेगा? अपने उत्तर के समर्थन में उदाहरण दीजिए।
4.27 किसी सदिश में परिणाम व दिशा दोनों होते हैं। क्या इसका यह अर्थ है कि कोई राशि जिसका परिमाण व दिशा हो, वह अवश्य ही सदिश होगी? किसी वस्तु के घूर्णन की व्याख्या घूर्णन-अक्ष की दिशा और अक्ष के परितः घूर्णन-कोण द्वारा की जा सकती है। क्या इसका यह अर्थ है कि कोई भी घूर्णन एक सदिश है?
4.28 क्या आप निम्नलिखित के साथ कोई सदिश संबद्ध कर सकते हैं: (a) किसी लूप में मोड़ी गई तार की लंबाई, (b) किसी समतल क्षेत्र, (c) किसी गोले के साथ? व्याख्या कीजिए।
4.29 कोई गोली क्षैतिज से 30॰ के कोण पर दागी गई है और वह धरातल पर 3.0 km दूर गिरती है । इसके प्रक्षेप्य के कोण का समायोजन करके क्या 5.0 km दूर स्थित किसी लक्ष्य का भेद किया जा सकता है ? गोली की नालमुख चाल को नियत तथा वायु के प्रतिरोेध को नगण्य मानिए ।
4.30 कोई लड़ाकू जहाज 1.5 km की ऊंचाई पर 720 km/h की चाल से क्षैतिज दिशा में उड़ रहा है और किसी वायुयान भेदी तोप के ठीक ऊपर से गुजरता है । ऊर्ध्वाधर से तोप की नाल का क्या कोण हो जिससे 600 m s–1 की चाल से दागा गया गोला वायुमान पर वार कर सके । वायुयान के चालक को किस न्यूनतम ऊंचाई पर जहाज को उड़ाना चाहिए जिससे गोला लगने से बच सके। (g = 10 ms–2)
4.31 एक साइकिल सवार 27 km/h की चाल से साइकिल चला रहा है। जैसे ही सड़क पर वह 80 m त्रिज्या के वृत्तीय मोड़ पर पहुंचता है, वह ब्रेक लगाता है और अपनी चाल को 0.5 m/s की एकसमान दर से कम कर लेता है। वृत्तीय मोड़ पर साइकिल सवार के नेट त्वरण का परिमाण और उसकी दिशा निकालिए।
4.32 (a) सिद्ध कीजिए कि किसी प्रक्षेप्य के x-अक्ष तथा उसके वेग के बीच के कोण को समय के फलन के रूप में निम्न प्रकार से व्यक्त कर सकते हैं
(b) सिद्ध कीजिए कि मूल बिंदु से फेंके गए प्रक्षेप्य कोण का मान होगा। यहाँ प्रयुक्त प्रतीकों के अर्थ सामान्य हैं।