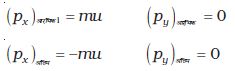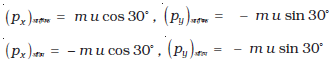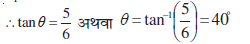Table of Contents
अध्याय 5
गति के नियम
5.1 भूमिका
5.2 अरस्तू की भ्रामकता
5.3 जड़त्व का नियम
5.4 न्यूटन का गति का प्रथम नियम
5.5 न्यूटन का गति का द्वितीय नियम
5.6 न्यूटन का गति का तृतीय नियम
5.7 संवेग-संरक्षण
5.8 किसी कण की साम्यावस्था
5.9 यांत्रिकी में सामान्य बल
5.10 वर्तुल (वृत्तीय) गति
5.11 यांत्रिकी में समस्याओं को हल करना
सारांश
विचारणीय विषय
अभ्यास
अतिरिक्त अभ्यास
5.1 भूमिका
पिछले अध्याय में हमारा संबंध दिक्स्थान में किसी कण की गति का मात्रात्मक वर्णन करने से था। हमने देखा कि एकसमान गति में मात्र वेग की संकल्पना की आवश्यकता थी जबकि असमान गति में त्वरण की अवधारणा की अतिरिक्त आवश्यकता पड़ी। अब तक हमने यह प्रश्न नहीं पूछा है कि पिण्डों की गति का क्या कारण है ? इस अध्याय में हम अपना ध्यान भौतिकी के इस मूल प्रश्न पर केंद्रित करेंगे।
आइए, सबसे पहले हम अपने सामान्य अनुभवों के आधार पर इस प्रश्न के उत्तर का अनुमान लगाएँ। विरामावस्था में पड़ी फुटबाल को गति प्रदान करने के लिए किसी न किसी को उस पर अवश्य ठोकर मारनी होती है । किसी पत्थर को ऊपर की ओर फेंकने के लिए, हमें उसे ऊपर की ओर प्रक्षेपित करना पड़ता है। मंद पवन पेड़ की शाखाओं को झुला देती है; प्रबल वायु का झोंका तो भारी पिण्डों तक को भी लुढ़का सकता है ! बहती नदी किसी के न खेने पर भी नाव को गतिमान कर देती है। स्पष्टतः किसी पिण्ड को विराम से गति में लाने के लिए किसी बाह्य साधन द्वारा बल लगाने की आवश्यकता होती है। इसी प्रकार गति को रोकने अथवा मंद करने के लिए भी बाह्य बल की आवश्यकता होती है। किसी आनत तल पर नीचे की ओर लुढ़कती किसी गेंद को उसकी गति की विपरीत दिशा में बल लगाकर रोका जा सकता है।
इन उदाहरणों में, बल का बाह्य साधन (हाथ, वायु, जलधारा, आदि) पिण्ड के संपर्क में है। परंतु यह सदैव आवश्यक नहीं है। किसी भवन के शिखर से बिना अधोमुखी धक्का दिये मुक्त किया गया पत्थर पृथ्वी के गुरुत्वीय खिंचाव के कारण त्वरित हो जाता है। कोई छड़ चुंबक लोहे की कीलों को दूर से ही, अपनी ओर आकर्षित कर लेता है। यह दर्शाता है कि बाह्य साधन (इन उदाहरणों में गुरुत्वीय एवं चुंबकीय बल) एक दूरी से भी किसी पिण्ड पर बल लगा सकता है।
संक्षेप में, किसी रुके हुए पिण्ड को गति प्रदान करने तथा गतिमान पिण्ड को रोकने के लिए बल की आवश्यकता होती है, तथा इस बल को प्रदान करने के लिए किसी बाह्य साधन की आवश्यकता होती है। यह बाह्य साधन उस पिण्ड के संपर्क में भी हो सकता है, और नहीं भी।
यहाँ तक तो सब सही है। परंतु तब क्या होता है जब कोई पिण्ड एकसमान गति से चलता है (उदाहरण के लिए, बर्फ के क्षैतिज फर्श पर एकसमान चाल से सीधी रेखा में गतिमान कोई स्केटर) ? क्या किसी पिण्ड की एकसमान गति बनाए रखने के लिए कोई बाह्य बल आवश्यक है ?
5.2 अरस्तू की भ्रामकता
उपरोक्त प्रश्न सरल प्रतीत होता है। तथापि इसका उत्तर देने में कई युग लग गए थे। वस्तुतः सत्रहवीं शताब्दी में गैलीलियो द्वारा दिए गए इस प्रश्न का सही उत्तर न्यूटनी यांत्रिकी का आधार बना जिसने आधुनिक विज्ञान के जन्म का संकेत दिया ।
महान ग्रीक विचारक, अरस्तू (384 ई.पू. - 322 ई.पू.) ने यह विचार रखा कि यदि कोई पिण्ड गतिमान है, तो उसे उसी अवस्था में बनाए रखने के लिए कोई न कोई बाह्य साधन अवश्य चाहिए। उदाहरण के लिए, इस विचार के अनुसार किसी धनुष से छोड़ा गया तीर उड़ता रहता है, क्योंकि तीर के पीछे की वायु उसे धकेलती रहती है । यह अरस्तू द्वारा विकसित विश्व में पिण्डों की गतियों से संबंधित विचारों के विस्तृत ढाँचे का एक भाग था। गति के विषय में अरस्तू के अधिकांश विचार अब गलत माने जाते हैं, और उनकी अब चिंता करने की आवश्यकता नहीं है। अपने काम के लिए हम यहाँ अरस्तू के गति के नियम को इस प्रकार लिख सकते हैं: किसी पिण्ड को गतिशील रखने के लिए बाह्य बल की आवश्यकता होती है।
जैसा कि हम आगे देखेंगे, अरस्तू का गति का नियम दोषयुक्त है। तथापि, यह एक स्वाभाविक विचार है, जो कोई भी व्यक्ति अपने सामान्य अनुभवों से रख सकता है। अपनी सामान्य खिलौना कार (अवैद्युत) से फर्श पर खेलती छोटी बालिका भी अपने अंतर्ज्ञान से यह जानती है कि कार को चलती रखने के लिए उस पर बंधी डोरी का स्थायी रूप से कुछ बल लगाकर बराबर खींचना होगा । यदि वह डोरी को छोड़ देती है तो कुछ क्षण बाद कार रुक जाती है। अधिकांश स्थलीय गतियों में यही सामान्य अनुभव होता है। पिण्डों को गतिशील बनाए रखने के लिए बाह्य बलों की आवश्यकता प्रतीत होती है। स्वतंत्र छोड़ देने पर सभी वस्तुएं अंततः रुक जाती हैं।
फिर अरस्तू के तर्क में क्या दोष है ? इसका उत्तर है: गतिशील खिलौना कार इसलिए रुक जाती है कि फर्श द्वारा कार पर लगने वाला बाह्य घर्षण बल इसकी गति का विरोध करता है। इस बल को निष्फल करने के लिए बालिका को कार पर गति की दिशा में बाह्य बल लगाना पड़ता है। जब कार एकसमान गति में होती है तब उस पर कोई नेट बाह्य बल कार्य नहीं करता; बालिका द्वारा लगाया गया बल फर्श के बल (घर्षण बल) को निरस्त कर देता है। इसका उपप्रमेय है: यदि कोई घर्षण न हो, तो बालिका को खिलौना कार की एकसमान गति बनाए रखने के लिए, कोई भी बल लगाने की आवश्यकता नहीं पड़ती ।
प्रकृति में सदैव ही विरोधी घर्षण बल (ठोसों के बीच) अथवा श्यान बल (तरलों के बीच) आदि उपस्थित रहते हैं । यह उन व्यावहारिक अनुभवों से स्पष्ट है जिनके अनुसार वस्तुओं में एकसमान गति बनाए रखने के लिए घर्षण बलों को निष्फल करने हेतु बाह्य साधनों द्वारा बल लगाना आवश्यक होता है। अब हम समझ सकते हैं कि अरस्तू से त्रुटि कहां हुई । उसने अपने इस व्यावहारिक अनुभव को एक मौलिक तर्क का रूप दिया । गति तथा बलों के लिए प्रकृति के यथार्थ नियम को जानने के लिए हमें एक एेसे आदर्श संसार की कल्पना करनी होगी जिसमें बिना किसी विरोधी घर्षण बल लगे एकसमान गति का निष्पादन होता है। यही गैलीलियो ने किया था।
5.3 जड़त्व का नियम
गैलीलियो ने वस्तुओं की गति का अध्ययन एक आनत समतल पर किया था। किसी (i) आनत समतल पर नीचे की ओर गतिमान वस्तुएं त्वरित होती हैं जबकि (ii) तल पर ऊपर की ओर जाने वाली वस्तुओं में मंदन होता है। क्षैतिज समतल पर गति (iii) इन दोनों के बीच की स्थिति है। गैलीलियो ने यह निष्कर्ष निकाला कि किसी घर्षण रहित क्षैतिज समतल पर गतिशील किसी वस्तु में न तो त्वरण होना चाहिए और न ही मंदन, अर्थात् इसे एकसमान वेग से गति करनी चाहिए (चित्र 5.1 (a))।
गैलीलियो के एक अन्य प्रयोग जिसमें उन्होंने द्विआनत समतल का उपयोग किया, से भी यही निष्कर्ष निकलता है। एक आनत समतल पर विरामावस्था से छोड़ी गई गेंद नीचे लुढ़कती है और दूसरे आनत समतल पर ऊपर चढ़ती है। यदि दोनों आनत समतलों के पृष्ठ अधिक रुक्ष नहीं हैं तो गेंद की अंतिम ऊंचाई उसकी आरंभिक ऊंचाई के लगभग समान (कुछ कम, परंतु अधिक कभी नहीं) होती है। आदर्श स्थिति में, जब घर्षण बल पूर्णतः विलुप्त कर दिया जाता है, तब गेंद की अंतिम ऊंचाई उसकी आरंभिक ऊंचाई के समान होनी चाहिए।

चित्र 5.1 (a)
अब यदि दूसरे समतल के ढाल को घटाकर प्रयोग को दोहराएं, तो फिर भी गेंद उसी ऊंचाई तक पहुंचेगी, परंतु एेसा करने पर वह अधिक दूरी चलेगी। सीमान्त स्थिति में, जब दूसरे समतल का ढाल शून्य है (अर्थात् वह क्षैतिज समतल है) तब गेंद अनन्त दूरी तक चलती है। दूसरे शब्दों में इसकी गति कभी नहीं रुकेगी । निःसंदेह यह एक आदर्श स्थिति है (चित्र 5.1 (b))। व्यवहार में गेंद क्षैतिज समतल पर एक परिमित दूरी तक चलने के बाद बाह्य विरोधी घर्षण बल जिसे पूर्ण रूप से विलुप्त नहीं किया जा सकता, के कारण विराम में आ जाती है। तथापि निष्कर्ष स्पष्ट है: यदि घर्षण न होता तो गेंद क्षैतिज समतल पर एकसमान वेग से निरंतर चलती रहती।
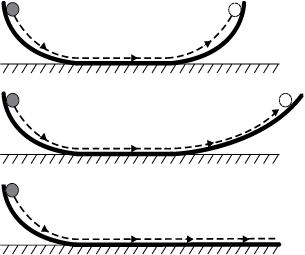
चित्र 5.1 (b) द्विआनत समतल पर गति के प्रेक्षणों से गैलीलियो ने जड़त्व का नियम अनुमानित किया ।
इस प्रकार गैलीलियो को गति के संबंध में एक नई अंतर्दृष्टि प्राप्त हुई, जो अरस्तू तथा उनके अनुयायिओं को समझ में नहीं आई । गतिकी में विरामावस्था तथा एकसमान रैखिक गति की अवस्था (अर्थात् एकसमान वेग से गति) तुल्य होती हैं। दोनों ही प्रकरणों में पिण्ड पर कोई नेट बल नहीं लगता। यह सोचना त्रुटिपूर्ण है कि किसी पिण्ड की एकसमान गति के लिए उस पर कोई नेट बल लगाना आवश्यक है। किसी पिण्ड को एकसमान गति में बनाए रखने के लिए हमें घर्षण बल को निष्फल करने के लिए एक बाह्य बल लगाने की आवश्यकता होती है ताकि पिण्ड पर लगे दोनों बाह्य बलों का नेट बाह्य बल शून्य हो जाए।
प्राचीन भारतीय विज्ञान में गति संबंधी धारणाएँ
प्राचीन भारतीय विचारकों ने भी गति संबंधी धारणाओं की एक विस्तृत प्रणाली विकसित कर ली थी । बल जो गति का कारण है, भिन्न प्रकार का माना गया: सतत दाब के कारण बल (जिसे नोदन कहा गया) जैसे जल-यात्राकरते पाल-यानों पर लगने वाला पवन का बल; संघट्ट (अभिघात) जो कुम्भकार द्वारा चाक को छड़ से घुमाने पर लगता है; सरल रैखिक गति (वेग) के लिए अथवा प्रत्यास्थ पिण्डों में आकृति के प्रत्यानयन की दीर्घस्थायी प्रवृत्ति (संस्कार); डोरी, छड़ आदि से संचारित बल। गति के ‘वैशेषिका’ सिद्धांत में वेगों की संकल्पना कदाचित जड़त्व की संकल्पना के समीपस्थ है । वेग, सरल रेखा में चलने की प्रवृत्ति का विरोध संपर्क में आने वाली वस्तुओं जिनमें वायुमण्डल भी शामिल है, के द्वारा होता है एेसा माना गया । यह घर्षण तथा वायु-प्रतिरोध के विचार के समान विचार है । उनका यह अनुमान सही था कि पिण्डों की विभिन्न प्रकार की गतियां (स्थानांतरीय, घूर्णी तथा कंपन) उस पिण्ड के अवयवी कणों की केवल स्थानांतरीय गति के कारण ही उत्पन्न होती हैं । पवन में गिरती किसी पत्ती की कुल मिलाकर अधोमुखी गति (पतन) हो सकती है और साथ ही उसमें घूर्णी तथा कंपन गति (भ्रमण, स्पंदन) भी हो सकती हैं, परंतु किसी क्षण उस पत्ती के प्रत्येक कण में केवल एक निश्चित (लघु) विस्थापन होता है । गति की माप तथा लंबाई एवं समय के मात्रकों के विषय में भारतीय चिन्तन में यथेष्ट बल दिया गया । यह ज्ञात था कि दिक्स्थान में किसी कण की स्थिति को उसकी तीन अक्षों से दूरियां मापकर निर्दिष्ट किया जा सकता था । भास्कर (1150 ई.) ने तात्क्षणिक गति (तात्कालिकी गति) की अवधारणा प्रस्तावित की जिससे अवकल गणित के प्रयोग द्वारा तात्क्षणिक वेग की आधुनिक संकल्पना का पूर्वज्ञान हुआ । तरंग तथा धारा (जल की) के बीच अंतर को भली-भांति समझा जा चुका था; धारा गुरुत्व तथा तरलता के अंतर्गत जल कणों की गति है जबकि तरंग जल कणों के कंपन के संचरण का परिणाम है ।
सारांश में, यदि नेट बाह्य बल शून्य है तो विराम अवस्था में रह रहा पिण्ड विरामावस्था में ही रहता है और गतिशील पिण्ड निरंतर एकसमान वेग से गतिशील रहता है। वस्तु के इस गुण को जड़त्व कहते हैं। जड़त्व से तात्पर्य है "परिवर्तन के प्रति प्रतिरोध"। कोई पिण्ड अपनी विरामावस्था अथवा एकसमान गति की अवस्था में तब तक कोई परिवर्तन नहीं करता जब तक कोई बाह्य बल उसे एेसा करने के लिए विवश नहीं करता।
5.4 न्यूटन का गति का प्रथम नियम
गैलीलियो की सरल परंतु क्रांतिकारी धारणाओं ने अरस्तू की यांत्रिकी को पूर्णतया नकार दिया। अब एक नई यांत्रिकी का विकास किया जाना था। विशिष्ट रूप से, इस कार्य को सर आइजक न्यूटन ने जिन्हें सभी युगों का महानतम वैज्ञानिक माना जाता है, लगभग अकेले ही संपन्न किया।
न्यूटन ने गैलीलियो की धारणाओं के आधार पर गति के तीन नियमों जो उनके नाम से जाने जाते हैं, के रूप में एक यांत्रिकी की आधारशिला रखी। गैलीलियो का जड़त्व का नियम उसका आरंभ बिंदु था जिसका न्यूटन ने ‘गति के प्रथम नियम’ के रूप में संरूपण किया:
"प्रत्येक पिण्ड तब तक अपनी विरामावस्था अथवा सरल रेखा में एकसमान गति की अवस्था में रहता है जब तक कोई बाह्य बल उसे अन्यथा व्यवहार करने के लिए विवश नहीं करता।"
अब विरामावस्था अथवा एकसमान रैखिक गति दोनों ही में "शून्य त्वरण" समाविष्ट है। अतः गति के प्रथम नियम को, सरल शब्दों में, इस प्रकार भी व्यक्त किया जा सकता है:
यदि किसी पिण्ड पर लगने वाला नेट बाह्य बल शून्य है, तो उसका त्वरण शून्य होता है। शून्येतर त्वरण केवल तभी हो सकता है जब पिण्ड पर कोई नेट बाह्य बल लगता हो।
व्यवहार में इस नियम के अनुप्रयोग से हमें दो प्रकार की स्थितियों से सामना करना होता है। कुछ उदाहरणों में तो हम यह जानते हैं कि वस्तु पर नेट बाह्य बल शून्य होता है। उसमें हम यह निष्कर्ष निकाल सकते हैं कि वस्तु का त्वरण शून्य है। उदाहरण के लिए, अंतरा तारकीय आकाश में सभी गुरुत्वीय वस्तुओं से बहुत दूर किसी अंतरिक्षयान, जिसके सभी राकेट बंद किए जा चुके हों, पर कोई नेट बाह्य बल कार्यरत नहीं होता। गति के प्रथम नियम के अनुसार इसका त्वरण शून्य होना चाहिए। यदि यह गति में है, तो इसे एकसमान वेग से गतिशील रहना चाहिए।
गैलीलियो गैलिली (1564-1642)

इटली के पीसा नामक शहर में 1564 ई. में जन्मे गैलीलियो गैलिली लगभग चार शताब्दी पूर्व यूरोप में हुई वैज्ञानिक क्रांति के सूत्रधार थे । उन्होंने त्वरण की संकल्पना की । पिण्डों की आनत समतलों पर गति अथवा मुक्त रूप से गिरते पिण्डों की गतियों के प्रयोगों द्वारा उन्होंने अरस्तू की धारणा कि किसी पिण्ड को गतिमान रखने के लिए किसी बल की आवश्यकता होती है तथा भारी पिण्ड हल्के पिण्डों की तुलना में गुरुत्व बल के प्रभाव में तीव्रतर गति से गिरते हैं, का खंडन किया । इस प्रकार, उन्होंने जड़त्व के नियम की खोज की जो आइजक न्यूटन के युगांतरीय कार्य का आरम्भ बिंदु था ।
गैलीलियो के खगोलिकी के क्षेत्र में आविष्कार भी उतने ही क्रांतिकारी थे । 1609 ई. में उन्होंने अपना दूरदर्शी (जिसकी खोज पहले हॉलैण्ड में हुई थी) स्वयं बनाया तथा उसका उपयोग उन्होंने अपने कई चौंकाने वाले प्रेक्षणों: चंद्रमा के पृष्ठ पर पर्वत तथा गर्त; सूर्य पर काले धब्बे; बृहस्पति के उपग्रह, तथा शुक्र की कलाओं के लिए किया । उन्होंने यह निष्कर्ष निकाला कि आकाशगंगा अपनी ज्योति नंगी आंखों से न दिखाई दे सकने वाले असंख्य तारों से प्राप्त करती है । अपने वैज्ञानिक तर्क की अति उत्तम रचना "डायलॉग अॉन दि टू चीफ वर्ल्ड सिस्टम्स" में गैलीलियो ने कॉपरनिकस द्वारा प्रस्तावित सौर परिवार के "सूर्य केंद्रीय सिद्धांत" का समर्थन किया और अंततः इसी सिद्धांत को सार्वजनिक मान्यता प्राप्त हुई ।
गैलीलियो के साथ ही वैज्ञानिक जांच (खोजबीन) की विधि में एक मोड़ आया । अब विज्ञान मात्र प्रकृति का प्रेक्षण तथा उन प्रेक्षणों के आधार पर तार्किक अनुमान लगाना ही नहीं रह गया था । अब विज्ञान से तात्पर्य नई-नई युक्तियां बनाकर प्रयोगों द्वारा सिद्धांतों को प्रतिपादित अथवा तिरस्कृत करना बन गया था । विज्ञान का अर्थ भौतिक राशियों की माप और उनके बीच गणितीय संबंधों की खोज बन गया था । उनकी इसी विलक्षण योग्यता के कारण ही गैलीलियो का आधुनिक विज्ञान का जनक माना जाता है ।
तथापि, बहुधा हमें आरम्भ में सभी बलों का ज्ञान नहीं होता । उस अवस्था में, यदि हमें यह ज्ञात हो कि कोई वस्तु अत्वरित है (अर्थात् वह वस्तु या तो विरामावस्था में है अथवा एकसमान रैखिक गति में है) तब हम गति के प्रथम नियम के आधार पर यह निष्कर्ष निकाल सकते हैं कि उस वस्तु पर नेट बाह्य बल शून्य होना चाहिए। गुरुत्व हर स्थान पर है। विशेष रूप से, पार्थिव परिघटनाओं में, पृथ्वी पर स्थित सभी वस्तुएं पृथ्वी के गुरुत्वाकर्षण का अनुभव करती हैं। साथ ही, गतिशील वस्तुएं सदैव ही घर्षण बल, श्यान कर्षण आदि का अनुभव करती हैं । तब यदि पृथ्वी पर स्थित कोई वस्तु विरामावस्था अथवा एकसमान रैखिक गति में हो, तब एेसा होने का कारण यह नहीं है कि उस पर कोई बल कार्यरत नहीं है, वरन् उस पर कार्यरत विभिन्न बाह्य बल एक दूसरे को निरस्त करके सभी बलों के योग को ‘शून्य नेट बाह्य बल’ बनाते हैं।
अब मेज पर विराम अवस्था में रखी एक पुस्तक पर विचार करते हैं (चित्र 5.2(a))। इस पुस्तक पर दो बाह्य बल कार्यरत हैं: गुरुत्वीय बल (अर्थात् पुस्तक का भार W) नीचे की दिशा में कार्यरत है तथा मेज द्वारा पुस्तक पर ऊपर की दिशा में अभिलंब बल R कार्यरत है। R स्वयं समायोजित होने वाला बल है । यह ऊपर वर्णित दूसरी प्रकार की स्थिति का उदाहरण है। बलों के बारे में तो पूर्ण ज्ञान नहीं है परंतु गति की अवस्था ज्ञात है। हम पुस्तक को विराम की स्थिति में देखते हैं। अतः गति के प्रथम नियम के आधार पर हम यह निष्कर्ष निकाल सकते हैं कि R का परिमाण W के परिमाण के समान है। हमारा प्रायः इस प्रकथन से समागम होता है ; "चूंकि W = R, बल एक दूसरे को निरस्त करते हैं, इसीलिए पुस्तक विराम की स्थिति में है"। यह विवेक के विपरीत है। सही प्रकथन यह होना चाहिएः "चूंकि पुस्तक विराम में दिखाई देती है"; गति के प्रथम नियम के अनुसार इस पर नेट बाह्य बल शून्य होना चाहिए। इसका तात्पर्य है कि अभिलंब R पुस्तक के भार W के समान तथा विपरीत होना चाहिए।

चित्र 5.2 (a) मेज पर विराम में रखी पुस्तक तथा (b) एकसमान वेग से गतिमान कार, इन दोनों ही प्रकरणों में नेट बाह्य बल शून्य है ।
अब हम एक कार की गति पर विचार करते हैं जिसमें वह कार विराम से गति आरंभ करके अपनी चाल में वृद्धि करती है और फिर चिकनी सीधी सड़क पर पहुंचकर एकसमान वेग से गति करती है (चित्र 5.2 (b))। जब यह विराम में होती है तब उस पर कोई नेट बल नहीं होता। चाल में वृद्धि के समय इसमें त्वरण होता है। एेसा नेट बाह्य बल के कारण होना चाहिए। ध्यान दें, यह एक बाह्य बल ही होना चाहिए। कार के त्वरण के लिए किसी भी आंतरिक बल को उत्तरदायी नहीं माना जा सकता। सुनने में यह अद्भुत लग सकता है, परंतु यह सत्य है। सड़क के अनुदिश विचारणीय बल घर्षण बल ही है। सब बातों पर विचार करने के उपरांत यही निष्कर्ष निकलता है कि कार की गति में त्वरण का कारण घर्षण बल ही है (घर्षण के विषय में आप अनुभाग 5.9 में पढ़ेंगे)। जब कार एक समान वेग से गति करती है तब उस पर कोई नेट बाह्य बल नहीं होता ।
गति के प्रथम नियम में निहित जड़त्व का गुण बहुत-सी स्थितियों में प्रत्यक्ष दिखाई पड़ता है। मान लीजिए हम किसी रुकी हुई बस में असावधानी से खड़े हैं और यकायक ड्राइवर बस को चला देता है। हम झटके के साथ पीछे की ओर गिर पड़ते हैं। क्यों ? हमारे पैर बस के फर्श को स्पर्श कर रहे होते हैं। यदि घर्षण न होता, तो हम वहीं रहते जहां पहले थे जबकि हमारे पैरों के नीचे बस का फर्श केवल आगे की दिशा में सरकता और बस का पीछे का भाग हमसे आकर टकराता। परंतु सौभाग्यवश, हमारे पैर और फर्श के बीच कुछ घर्षण होता है। यदि बस की पिक-अप अति आकस्मिक नहीं है, अर्थात् त्वरण साधारण है तो घर्षण बल हमारे पैरों को बस के साथ त्वरित करने के लिए पर्याप्त होगा। परंतु वस्तुतः हमारा शरीर एक दृढ़ पिण्ड नहीं है। इसमें विरूपण हो सकता है, अर्थात् इसके विभिन्न भागों के बीच आपेक्ष विस्थापन संभव है । इसका तात्पर्य यह हुआ कि जब हमारे पैर बस के साथ आगे बढ़ते हैं, तो शरीर का शेष भाग जड़त्व के कारण वहीं रहता है। इसीलिए, बस के आपेक्ष हम पीछे की ओर फेंक दिए जाते हैं। जैसे ही यह घटना घटती है, शरीर के शेष भागों पर पेशीय बल (पैरों के द्वारा) कार्य करने लगते हैं, जो शरीर के शेष भाग को पैरों के साथ गति कराते हैं। इसी प्रकार की घटना तीव्र गति से चलती बस के यकायक रुकने पर घटती है। हमारे पैर घर्षण के कारण रुक जाते हैं, क्योंकि घर्षण बल पैरों तथा बस के फर्श के बीच आपेक्ष गति नहीं होने देता। परंतु शरीर का शेष भाग, जड़त्व के कारण, आगे की ओर गति करता रहता है। परिणामस्वरूप हम आगे की ओर फेंक दिए जाते हैं। प्रत्यानयनी पेशीय बलों के कार्यरत होने के कारण शरीर विराम अवस्था में आ जाती है।
¯ उदाहरण 5.1 कोई अंतरिक्षयात्री अंतरातारकीय आकाश में 100 m s-2 की एकसमान दर से त्वरित अपने अंतरिक्षयान से दुर्घटनावश बाहर फेेेंक दिया जाता है । जिस क्षण अंतरिक्षयात्री अंतरिक्षयान से बाहर आ जाता है, उसके तुरंत पश्चात् अंतरिक्षयात्री का त्वरण क्या है ? (मान लीजिए कि यात्री पर गुरुत्वाकर्षण बल आरोपित करने के लिए उसके निकट कोई तारा नहीं है)।
हल जिस क्षण वह यात्री यान से बाहर आता है, उसी क्षण से अंतरिक्षयात्री पर कोई बाह्य बल कार्यरत नहीं रहता क्योंकि हमने यह माना है कि यात्री पर गुरुत्वाकर्षण बल आरोपित करने के लिए उसके निकट कोई तारा नहीं हैं तथा अंतरिक्ष यान छोटा होने के कारण इसके द्वारा यात्री पर लग रहा गुरुत्वाकर्षण बल उपेक्षणीय है। गति के प्रथम नियम के अनुसार अंतरिक्षयात्री का त्वरण शून्य है।
5.5 न्यूटन का गति का द्वितीय नियम
गति का प्रथम नियम उस साधारण प्रकरण से संबंध रखता है जिसमें किसी पिण्ड पर नेट बाह्य बल शून्य है। गति का द्वितीय नियम उन व्यापक स्थितियों से संबंध रखता है, जिनमें पिण्ड पर कोई नेट बाह्य बल लग रहा हो। यह नियम नेट बाह्य बल और पिण्ड के त्वरण में संबंध दर्शाता है।
संवेग
किसी पिण्ड के संवेग को उसकी संहति m तथा वेग v के गुणनफल द्वारा पारिभाषित किया जाता है। इसे p द्वारा निर्दिष्ट किया जाता है:
p = mv (5.1)
स्पष्ट रूप से संवेग एक सदिश राशि है। दैनिक जीवन के निम्नलिखित साधारण अनुभवों में पिण्डों की गतियों पर बलों के प्रभाव पर विचार करते समय हमें संवेग के महत्त्व का पता चलता है।
» मान लीजिए एक कम भार का वाहन (जैसे छोटी कार) तथा एक अधिक भार का वाहन (जैसे सामान से लदा ट्रक) दोनों ही किसी क्षैतिज सड़क पर खड़े हैं। हम सभी भलीभांति जानते हैं कि समान समय अंतराल में दोनों वाहनों को समान चाल से गति कराने में कार की तुलना में ट्रक को धकेलने के लिए अपेक्षाकृत अधिक बल की आवश्यकता होती है। इसी प्रकार, यदि एक हलका पिण्ड तथा एक भारी पिण्ड दोनों समान चाल से गतिमान हैं, तो समान समय अंतराल में दोनों पिण्डों को रोकने में हलके पिण्ड की तुलना में भारी पिण्ड में अपेक्षाकृत अधिक परिमाण के विरोधी बल की आवश्यकता होती है ।
» यदि दो पत्थर, एक हलका तथा दूसरा भारी, एक ही भवन के शिखर से गिराए जाते हैं, तो धरती पर खड़े किसी व्यक्ति के लिए भारी पत्थर की तुलना में हलके पत्थर को लपकना आसान होता है। इस प्रकार किसी पिण्ड की संहति एक महत्त्वपूर्ण प्राचल है जो गति पर बल के प्रभाव को निर्धारित करता है।
» विचार करने योग्य एक अन्य महत्त्वपूर्ण प्राचल है– चाल । बंदूक से छोड़ी गई कोई गोली रुकने से पूर्व मानव ऊतक को आसानी से वेध सकती है, फलस्वरूप दुर्घटना हो जाती है। यदि उसी गोली को साधारण चाल से फेंकेें तो अधिक क्षति नहीं होती। अतः किसी दी गई संहति के लिए यदि चाल अधिक हो तो उसे एक निश्चित समय अंतराल में रोकने के लिए अधिक परिमाण के विरोधी बल की आवश्यकता होती है। साथ-साथ लेने पर, संहति और वेग का गुणनफल, अर्थात संवेग, प्रत्यक्ष रूप से गति का एक प्रासंगिक चर है । यदि अधिक संवेग परिवर्तन की आवश्यकता है तो लगाने के लिए अधिक परिमाण के बल की आवश्यकता होगी।
» क्रिकेट का कोई अभ्यस्त खिलाड़ी तीव्र गति से आती गेंद को एक नौसिखिया खिलाड़ी की तुलना में कहीं अधिक आसानी से लपक लेता है जबकि नौसिखिया खिलाड़ी उसी गेंद को लपकने में हाथों में चोट खा लेता है। इसका एक कारण यह है कि अभ्यस्त खिलाड़ी, अपने हाथों से गेंद को लपक कर, उसे रोकने में अधिक समय लगाता है । आपने ध्यान दिया होगा कि अभ्यस्त खिलाड़ी गेंद को लपकने की क्रिया में अपने हाथों को पीछे की ओर खींचता है (चित्र 5.3)। जबकि नौसिखिया खिलाड़ी अपने हाथों को स्थिर रखता है तथा गेंद को लगभग तत्क्षण ही लपकने का प्रयास करता है। गेंद को तत्क्षण रोकने के लिए उसे अपेक्षाकृत काफी अधिक बल लगाना पड़ता है फलस्वरूप उसके हाथों में चोट लग जाती है। इससे निष्कर्ष निकलता है: बल केवल संवेग परिवर्तन पर ही निर्भर नहीं करता, वह इस बात पर भी निर्भर करता है कि कितनी तीव्रता से यह परिवर्तन किया जाता है। समान संवेग परिवर्तन यदि अपेक्षाकृत कम समय में किया जाता है, तो अपेक्षाकृत अधिक बल लगाने की आवश्यकता होती है । संक्षेप में, संवेग परिवर्तन की दर अधिक है, तो बल अधिक होता है ।

चित्र 5.3 बल केवल संवेग परिवर्तन पर ही निर्भर नहीं करता, वरन् वह इस बात पर भी निर्भर करता है कि यह परिवर्तन कितनी तीव्रता से किया जाता है । एक अभ्यस्त खिलाड़ी गेंद लपकते समय अपने हाथों को पीछे की ओर खींचता है जिससे गेंद को रोकने में अधिक समय लगता है, जिसके लिए अपेक्षाकृत कम बल की आवश्यकता होती है ।
» एक अत्यंत महत्त्वपूर्ण प्रेक्षण इस तथ्य की पुष्टि करता है कि संहति तथा वेग का गुणनफल (अर्थात् संवेग) ही गति पर बल के प्रभाव का मूल है। मान लीजिए, विभिन्न संहतियों के दो पिण्डों, जो आरंभ में विराम में हैं, पर कोई निश्चित बल एक निश्चित समय अंतराल के लिए लगाया जाता है। हलका पिण्ड, अपेक्षानुसार, भारी पिण्ड की तुलना में अधिक चाल ग्रहण कर लेता है। परंतु, समय अंतराल के अंत में, प्रेक्षण यह दर्शाते हैं कि, प्रत्येक पिण्ड समान संवेग उपार्जित करता है। इस प्रकार, समान समय के लिए लगाया गया समान बल विभिन्न पिण्डों में समान संवेग परिवर्तन करता है। यह गति के द्वितीय नियम का प्रामाणिक मार्गदर्शक सिद्धांत है।
» पिछले प्रेक्षणों में संवेग का सदिश चरित्र अर्थपूर्ण नहीं रहा है। अब तक के उदाहरणों में, संवेग परिवर्तन तथा संवेग समान्तर दिशाओं में हैं। परंतु सदैव एेसा नहीं होता। मान लीजिए, किसी डोरी द्वारा एक पत्थर को क्षैतिज समतल में एकसमान चाल से घुमाया जाता है । इसमें संवेग का परिमाण स्थिर रहता है, परंतु इसकी दिशा निरन्तर परिवर्तित होती है (चित्र 5.4)। संवेग सदिश में यह परिवर्तन करने के लिए बल की आवश्यकता होती है। यह बल डोरी से होकर पत्थर को हमारे हाथों द्वारा प्रदान किया जाता है। अनुभवों से यह संकेत मिलता है कि यदि पत्थर को अपेक्षाकृत अधिक चाल तथा/अथवा छोटी त्रिज्या के वृत्त में घुमाया जाए तो हमारे हाथों द्वारा अधिक बल लगाने की आवश्यकता होती है। यह अधिक त्वरण अथवा संवेग सदिश में तुल्यांकी अधिक परिवर्तन के तदनुरूपी होता है। इससे यह संकेत मिलता है कि संवेग सदिश में अधिक परिवर्तन के लिए अधिक बल लगाना होता है।

चित्र 5.4 संवेग का परिमाण स्थिर रहने पर भी संवेग की दिशा में परिवर्तन केे लिए बल आवश्यक है । इसका अनुभव हम डोरी द्वारा किसी पत्थर को एकसमान चाल से वृत्त में घुमाकर कर सकते हैं ।
ये गुणात्मक प्रेक्षण हमें गति के द्वितीय नियम की ओर ले जाते हैं, जिसे न्यूटन ने इस प्रकार व्यक्त किया था:
किसी पिण्ड के संवेग परिवर्तन की दर आरोपित बल के अनुक्रमानुपाती होती है तथा उसी दिशा में होती है जिस दिशा में बल कार्य करता है।
इस प्रकार यदि m संहति के किसी पिण्ड पर कोई बल F समय अंतराल ∆t तक लगाने पर उस पिण्ड के वेग में v से v + ∆v का परिवर्तन हो जाता है, अर्थात् पिण्ड के प्रारंभिक संवेग mv में ∆(mv) का परिवर्तन हो जाता है। तब गति के द्वितीय
नियम के अनुसार,

यहाँ k आनुपातिकता स्थिरांक है। यदि 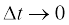 , पद
, पद  ,
,
t के आपेक्ष p का अवकलज अथवा अवकल गुणांक बन जाता है, जिसे 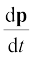 द्वारा निर्दिष्ट किया जाता है। इस प्रकार,
द्वारा निर्दिष्ट किया जाता है। इस प्रकार,
F = k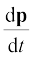 (5.2)
(5.2)
किसी स्थिर संहति m के पिण्ड के लिए
 (5.3)
(5.3)
अर्थात्, द्वितीय नियम को इस प्रकार भी लिख सकते हैं,
F = k m a (5.4)
जो यह दर्शाता है कि बल F, संहति m तथा त्वरण a के गुणनफल के अनुक्रमानुपाती होता है।
हमने बल के मात्रक की अब तक परिभाषा नहीं दी है । वास्तव में, बल के मात्रक की परिभाषा देने के लिए हम समीकरण (5.4) का उपयोग करते हैं। अतः हम k के लिए कोई भी नियत मान चुनने के लिए स्वतंत्र हैं। सरलता के लिए, हम k = 1 चुनते हैं। तब द्वितीय नियम हो जाता है,
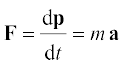 (5.5)
(5.5)
SI मात्रकों में, एक मात्रक बल वह होता है जो 1kg के पिण्ड में 1m s-2 का त्वरण उत्पन्न कर देता है। इस मात्रक बल को न्यूटन कहते हैं। इसका प्रतीक N है। 1N = 1kg m s-2।
इस स्थिति में हमें गति के द्वितीय नियम के कुछ महत्त्वपूर्ण बिंदुओं पर ध्यान देना है:
1. गति के द्वितीय नियम में F = 0 से यह उपलक्षित होता है कि a = 0। प्रत्यक्ष रूप से द्वितीय नियम प्रथम नियम के अनुरूप है।
2. गति का द्वितीय नियम एक सदिश नियम है। यह, वास्तव में, तीन समीकरणों के तुल्य है, सदिशों के प्रत्येक घटक के लिए एक समीकरण:

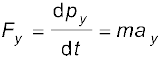
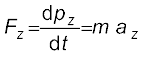 (5.6)
(5.6)
इसका अर्थ यह हुआ कि यदि कोई बल पिण्ड के वेग के समान्तर नहीं है, वरन् उससे कोई कोण बनाता है, तब वह केवल बल की दिशा में वेग के घटक को परिवर्तित करता है। बल के अभिलंबवत् वेग का घटक अपरिवर्तित रहता है। उदाहरण के लिए, ऊर्ध्वाधर गुरुत्वाकर्षण बल के अधीन किसी प्रक्षेप्य की गति में वेग का क्षैतिज घटक अपरिवर्तित रहता है (चित्र 5.5)।
3. समीकरण (5.5) से प्राप्त गति का द्वितीय नियम वस्तुतः, एकल बिंदु कण पर लागू होता है। नियम में F कण पर लगे नेट बाह्य बल तथा a कण के त्वरण के लिए प्रयुक्त हुआ है । तथापि इस नियम को इसी रूप में दृढ़ पिण्डों अथवा, यहाँ तक कि व्यापक रूप में कणों के निकाय पर भी लागू किया जाता है। उस अवस्था में, F का उल्लेख निकाय पर लगे कुल बल तथा a का उल्लेख समस्त निकाय के त्वरण के लिए होता है। अधिक यथार्थता से, a निकाय के संहति केंद्र का त्वरण है जिसके बारे में हम अध्याय 7 में विस्तार से पढ़ेंगे। निकाय में किन्हीं भी आंतरिक बलों को F में सम्मिलित नहीं किया जाता है।
4. गति का द्वितीय नियम एक स्थानीय संबंध है। इसका यह अर्थ है कि समय के किसी निश्चित क्षण पर समष्टि में किसी बिंदु (कण की अवस्थिति) पर लगा बल F उसी क्षण उसी बिंदु पर त्वरण a से संबंधित है। अर्थात् ‘किसी कण के त्वरण का निर्धारण उसी समय उस पर लगे बल द्वारा किया जाता है, कण की गति के किसी भी इतिहास द्वारा नहीं (चित्र 5.5 देखें)।
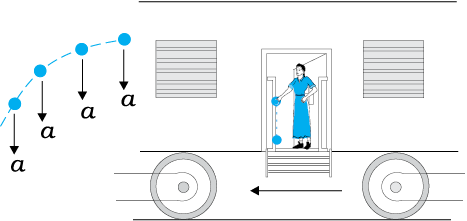
चित्र 5-5 किसी क्षण पर त्वरण का निर्धारण उसी क्षण के बल द्वारा किया जाता है । किसी त्वरित रेलगाड़ी से कोई पत्थर बाहर डालने के क्षण के तुरंत पश्चात्, यदि वायु के प्रतिरोध को नगण्य मानें तो, उस पत्थर पर कोई क्षैतिज त्वरण अथवा बल कार्यरत नहीं होता । कुछ क्षण पूर्व पत्थर पर रेलगाड़ी के त्वरण का प्रभाव अब पूर्णतया समाप्त हो जाता है।
¯ उदाहरण 5.2 90 m s-1 चाल से गतिमान 0.04 kg संहति की कोई गोली लकड़ी के भारी गुटके में धँसकर 60 cm दूरी चलकर रुक जाती है । गुटके द्वारा गोली पर लगने वाला औसत अवरोधी बल क्या है ?
हल गोली का मंदन (नियत मानते हुए)
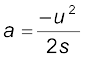 =
= 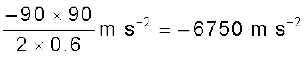
गति के द्वितीय नियम के द्वारा, मंदन बल
= 0.04 kg × 6750 m s–2 = 270 N
इस प्रकरण में, वास्तविक अवरोधी बल और इसीलिए, गोली का मंदन एकसमान नहीं होता। इसीलिए, उत्तर केवल औसत अवरोधी बल को व्यक्त करता है। °
उदाहरण 5.3 द्रव्यमान m के एक कण की गति,
y = 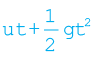 से वर्णित है। उस कण पर लगने वाले बल को ज्ञात करो।
से वर्णित है। उस कण पर लगने वाले बल को ज्ञात करो।
हल: हम जानते हैं
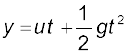
अब,
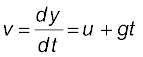
त्वरण, 
समीकरण (5.5) से बल,
F = ma = mg
अतः दिए गए समीकरण से गुरुत्वीय त्वरण के अधीन कण की गति का वर्णन होता है तथा y गुरुत्वीय त्वरण g की दिशा में स्थान निर्देशांक है। t
आवेग
कभी-कभी हमारा सामना एेसे दृष्टांतों से होता है जिनमें किसी पिण्ड पर कोई बड़ा बल, बहुत कम समय के लिए कार्यरत रहकर, उस पिण्ड के संवेग में परिमित परिर्वतन उत्पन्न करता है। उदाहरण के लिए, जब कोई गेंद किसी दीवार से टकराकर वापस परावर्तित होती है, तब दीवार द्वारा गेंद पर लगने वाला बल बहुत कम समय के लिए (जितने समय तक दोनों संपर्क में होते हैं) कार्यरत रहता है तो भी यह बल गेंद के संवेग को उत्क्रमित करने के लिए पर्याप्त होता है। प्रायः इन स्थितियों में, बल तथा समयावधि को पृथक-पृथक सुनिश्चित करना कठिन होता है। परंतु बल तथा समय का गुणनफल, जो कि पिण्ड का संवेग परिवर्तन है, एक मापने योग्य राशि है। इस गुणनफल को आवेग कहते हैं:
आवेग = बल × समयावधि
= संवेग में परिवर्तन (5.7)
परिमित संवेग परिवर्तन उत्पन्न करने के लिए, कम समय के लिए कार्यरत रहने वाले बड़े बल को आवेगी बल कहते हैं। यद्यपि विज्ञान के इतिहास में आवेगी बलों को संकल्पनात्मक रूप से सामान्य बलों से अलग श्रेणी में रखा गया, न्यूटनी यांत्रिकी में एेसा कोई विभेदन नहीं किया गया है। अन्य बलों की भांति आवेगी बल भी बल ही है–केवल यह बड़ा है और कम समय के लिए कार्यरत रहता है।
¯ उदाहरण 5.4 कोई बल्लेबाज किसी गेंद की आरंभिक चाल जो 12 m s-1 है, में बिना परिवर्तन किए उस पर हिट लगाकर सीधे गेंदबाज की दिशा में वापस भेज देता है । यदि गेंद की संहति 0.15 kg है, तो गेंद को दिया गया आवेग ज्ञात कीजिए । (गेंद की गति रैखिक मानिए) ।
हल: संवेग परिवर्तन =0.15×12–(–0.15×12) = 3.6 N s
आवेग = 3.6 N s बल्लेबाज से गेंदबाज की दिशा में
यह एक एेसा उदाहरण है जिसमें बल्लेबाज द्वारा गेंद पर लगा बल तथा गेंद और बल्ले के बीच संपर्क का समय ज्ञात करना एक कठिन कार्य है जबकि आवेग का परिकलन तुरंत किया जा सकता है।
5.6 न्यूटन का गति का तृतीय नियम
गति का द्वितीय नियम किसी पिण्ड पर लगे बाह्य बल तथा उसमें उत्पन्न त्वरण में संबंध बताता है। पिण्ड पर लगे बाह्य बल का उद्गम क्या है ? कौन साधन बाह्य बल प्रदान करता है ? न्यूटनी यांत्रिकी में इन प्रश्नों का सरल उत्तर यह है कि किसी पिण्ड पर लगने वाला बाह्य बल सदैव ही किसी अन्य पिण्ड के कारण होता है। दो पिण्डों A और B के युगल पर विचार कीजिए। मान लीजिए पिण्ड B पिण्ड A पर कोई बाह्य बल लगाता है, तब यह प्रश्न भी स्वाभाविक है: क्या पिण्ड A भी पिण्ड B पर कोई बाह्य बल लगाता है ? कुछ उदाहरणों में उत्तर स्पष्ट जान पड़ता है। यदि आप किसी कुण्डलित कमानी को अपने हाथों से दबाएँ तो वह कमानी आपके हाथों के बल से संपीडित हो जाती है। संपीडित कमानी भी प्रत्युत्तर में आपके हाथों पर बल आरोपित करती है: आप इस बल का अनुभव करते हैं। परंतु तब क्या होता है जब पिण्ड संपर्क में नहीं होते ? पृथ्वी गुरुत्वीय बल के कारण किसी पत्थर को अधोमुखी दिशा में खींचती है। क्या पत्थर पृथ्वी पर कोई बल लगाता है ? इसका उत्तर स्पष्ट नहीं है, क्योंकि हम पत्थर द्वारा पृथ्वी पर लगे बल के प्रभाव को नहीं देख सकते हैं। परंतु न्यूटन के अनुसार इस प्रश्न का उत्तर है: हाँ, पत्थर भी पृथ्वी पर परिमाण में समान तथा दिशा में विपरीत बल लगाता है। हमें इस बल की जानकारी नहीं हो पाती, इसका कारण यह है कि अत्यधिक भारी होने के कारण पृथ्वी की गति पर पत्थर द्वारा लगने वाले कम बल का प्रभाव नगण्य होता है।
इस प्रकार, न्यूटनी यांत्रिकी के अनुसार, प्रकृति में बल कभी भी अकेला नहीं पाया जाता। दो पिण्डों के बीच परस्पर अन्योन्य क्रिया बल है। बल सदैव युगल में पाए जाते हैं। साथ ही, दो पिण्डों के बीच परस्पर बल सदैव समान और विपरीत दिशा में होते हैं। न्यूटन ने इस धारणा को गति के तृतीय नियम के रूप में व्यक्त किया।
प्रत्येक क्रिया की सदैव समान एवं विपरीत दिशा में प्रतिक्रिया होती है।
न्यूटन की गति के तृतीय नियम की भाषा इतनी सुस्पष्ट और रोचक है कि यह सामान्य भाषा का अंग बन गई है। कदाचित इसी कारणवश गति के तृतीय नियम के बारे मेें काफी भ्रांतियाँ हैं । आइए, गति के तृतीय नियम के बारे में कुछ महत्त्वपूर्ण बिंदुओं पर ध्यान दें, विशेषकर क्रिया तथा प्रतिक्रिया पदों के प्रयोग के संदर्भ में।
1. गति के तृतीय नियम में पदों - क्रिया तथा प्रतिक्रिया का अर्थ ‘बल’ के अतिरिक्त अन्य कुछ नहीं है। एक ही भौतिक राशि के लिए विभिन्न पदों का प्रयोग कभी-कभी भ्रमित कर सकता है। तृतीय नियम को सरल तथा स्पष्ट शब्दों में इस प्रकार लिखा जाता है:
बल सदैव युगलों में पाए जाते हैं। पिण्ड A पर B द्वारा आरोपित बल पिण्ड B पर A द्वारा आरोपित बल के समान एवं विपरीत होता है।
2. तृतीय नियम के पदों क्रिया तथा प्रतिक्रिया से यह भ्रम उत्पन्न हो सकता है कि क्रिया प्रतिक्रिया से पहले आती है, अर्थात् क्रिया कारण है तथा निहित प्रतिक्रिया उसका प्रभाव। तृतीय नियम में एेसा कोई कारण-प्रभाव संबंध नहीं है। A पर B द्वारा आरोपित बल तथा B पर A द्वारा आरोपित बल एक ही क्षण कार्यरत होते हैं। इसी संकेत के आधार पर इनमें से किसी भी एक को क्रिया तथा दूसरे को प्रतिक्रिया कहा जा सकता है।
3. क्रिया तथा प्रतिक्रिया बल दो भिन्न पिण्डों पर कार्य करते हैं, एक ही वस्तु पर नहीं। दो पिण्डों A तथा B के युगल पर विचार कीजिए। तृतीय नियम के अनुसार,
FAB = – F BA (5.8)
(A पर B द्वारा बल) = - (B पर A द्वारा बल)
इस प्रकार, यदि हम किसी एक पिण्ड (A अथवा B) की गति पर विचार करते हैं तो दो बलों में से केवल एक ही प्रासंगिक है। दोनों बलों का योग करके दृढ़तापूर्वक यह कहना कि नेट बल शून्य है, यह त्रुटिपूर्ण है। फिर भी, यदि आप दो पिण्डों के किसी निकाय को एक पिण्ड मानकर उस पर विचार करते हैं, तो FAB तथा FBA उस निकाय (A + B) के आंतरिक बल हैं। ये दोनों मिलकर एक शून्य बल देते हैं । इस प्रकार किसी पिण्ड अथवा कणों के निकाय में आंतरिक बल युगलों में निरस्त हो जाते हैं। यह एक महत्त्वपूर्ण तथ्य है जो द्वितीय नियम को किसी पिण्ड अथवा कणों के निकाय पर अनुप्रयोज्य होने योग्य बनाता है (देखिए अध्याय 7)।
आइजक न्यूटन (1642-1727)

आइजक न्यूटन का जन्म सन् 1642 ई. में इंग्लैण्ड के वूल्सथॉर्पे नामक शहर में हुआ, संयोगवश इसी वर्ष गैलीलियो का देहांत हुआ । विद्यालयी जीवन में उनकी अद्भुत गणितीय प्रतिभा तथा यांत्रिक अभिरुचि अन्य लोगों से छिपी रही । सन् 1662 में स्नातक पूर्व अध्ययन के लिए वे कैम्ब्रिज गए । सन् 1669 में प्लेग-महामारी फैलने के कारण विश्वविद्यालय बंद करना पड़ा और न्यूटन अपनी मातृभूमि वापस लौट आए । इन दो वर्षों के एकाकी जीवन में उनकी प्रसुप्त सृजनात्मक शक्ति विस्फुटित हुई । गणित तथा भौतिकी के मूल आविष्कारोंः ऋणात्मक तथा भिन्नात्मक घातांकों के लिए द्विपदी प्रमेय, अवकल गणित का आरंभ, गुरुत्वाकर्षण का व्युत्क्रम वर्ग नियम, श्वेत प्रकाश का स्पेक्ट्रम आदि की बाढ़-सी आ गई । वापस कैम्ब्रिज लौटने पर उन्होंने प्रकाशिकी में अपने आविष्कारों को आगे बढ़ाया तथा परावर्ती दूरदर्शक की रचना की ।
सन् 1684 ई. में अपने मित्र एडमण्ड हेली के उत्साहित करने पर न्यूटन ने अपने वैज्ञानिक आविष्कारों को लिखना आरंभ किया और ‘‘दि प्रिंसीपिया मैथेमेटिका’’ नामक महान ग्रंथ की रचना की जो किसी भी काल में रचे गए महानतम ग्रंथों में से एक माना जाता है । इसी ग्रंथ में उन्होंने गति के तीनों नियमों तथा गुरुत्वाकर्षण के सार्वत्रिक नियम का प्रतिपादन किया है जो केप्लर के ग्रह गति के तीनों नियमों की विधिवत व्याख्या करते हैं । इस ग्रंथ में नयी-नयी पथ प्रदर्शक उपलब्धियाँ कूट-कूट कर भरी थीं जिनमें से कुछ प्रमुख इस प्रकार हैं: तरल यांत्रिकी के मूल सिद्धांत, तरंग गति का गणित, पृथ्वी, सूर्य तथा अन्य ग्रहों की संहतियों का परिकलन, विषुवों के पुरस्सरण की व्याख्या, ज्वार-भाटों का सिद्धांत, आदि । सन् 1704 ई. में न्यूटन ने एक अन्य उत्कृष्ट ग्रंथ ‘‘अॉप्टिक्स’’ प्रकाशित किया जिसमें उन्होंने अपने प्रकाश तथा वर्ण संबंधी कार्य का सार प्रस्तुत किया ।
कॉपरनिकस ने जिस वैज्ञानिक क्रांति को प्ररित किया और जिसे केप्लर तथा गैलीलियो ने प्रवलता से आगे प्रचलित किया उसी का भव्य संपूरण न्यूटन द्वारा हुआ । न्यूटनी यांत्रिकी ने पार्थिव तथा आकाशीय परिघटनाओं को एकीकृत किया । एक ही समीकरण पृथ्वी पर सेव के गिरने तथा पृथ्वी के चारों ओर चंद्रमा की परिक्रमा करने को नियंत्रित कर सकती थी । विवेक के युग का उदय हो चुका था ।
¯ उदाहरण 5.5 दो सर्वसम बिलियर्ड गेंदें किसी दृढ़ दीवार से समान चाल से, परंतु भिन्न कोणों पर, टकराती हैं तथा नीचे दर्शाए चित्र 5.6 की भांति चाल में बिना क्षय हुए परावर्तित हो जाती हैं । (i) प्रत्येक गेंद के कारण दीवार पर बल की दिशा क्या है ? तथा (ii) दीवार द्वारा दोनों गेंदों पर लगे आवेगों का अनुपात क्या है ?
हल स्वाभाविक रूप में इन प्रश्नों के उत्तर इस प्रकार होंगे- (i) यह हो सकता है कि (a) में गेंद के कारण दीवार पर लगा बल दीवार के अभिलंबवत् हो जबकि (b) में गेंद के कारण दीवार पर लगा बल दीवार पर अभिलंब के साथ 30॰ का कोण बनाता है। यह उत्तर सही नहीं है। दोनों ही प्रकरणों में दीवार पर लगा बल दीवार के अभिलंबवत् है।
दीवार पर लगे बल को कैसे ज्ञात करें ? इसकी गति के बारे में हमें कोई जानकारी नहीं है। इसके लिए एक युक्ति अपनाते हैं जिसमें पहले हम द्वितीय नियम का उपयोग करके दीवार के कारण गेंद पर लगे बल (अथवा आवेग) पर विचार करते हैं और तत्पश्चात् (i) का उत्तर देने के लिए तृतीय नियम का उपयोग करते हैं। मान लीजिए प्रत्येक गेंद की संहति m है तथा दीवार से टकराने से पूर्व और टकराने के पश्चात् दोनों गेंदों की चाल u है। चित्र में दर्शाए गये के अनुसार x- तथा y- अक्षों का चुनाव कीजिए, तथा प्रत्येक प्रकरण में गेंद के संवेग में परिवर्तन पर विचार कीजिए:
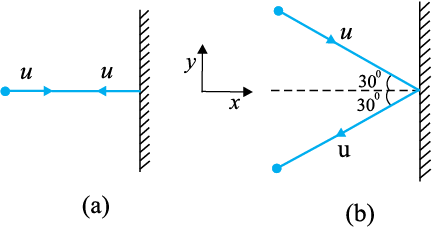
चित्र 5.6
प्रकरण (a)
संवेग, आवेग सदिश में परिवर्तन होता है, अतः
आवेग का x-घटक = –2 mu
आवेग का y-घटक = 0
आवेग तथा बल समान दिशा में हैं उपरोक्त चर्चा से यह स्पष्ट है कि दीवार के कारण गेंद पर लगा बल दीवार के अभिलंबवत्, तथा गति की ऋणात्मक x-दिशा के अनुदिश है। न्यूटन के गति के तृतीय नियम का उपयोग करने पर गेंद के कारण दीवार पर लगा बल दीवार के अभिलंबवत्, तथा गति की धनात्मक x-दिशा के अनुदिश है। चूंकि इस समस्या में यह नहीं बताया गया है कि दीवार से टक्कर में लगा अल्प समय कितना है, अतः बल के परिमाण को सुनिश्चित नहीं किया जा सकता।
प्रकरण (b)
ध्यान दीजिए, टकराने के पश्चात् px का चिह्न परिवर्तित हो जाता है, जबकि py का नहीं होता। अतः
आवेग का x-घटक = –2 mu cos 30॰
आवेग का y-घटक = 0
आवेग (तथा बल) की दिशा वही है जो (a) में थीः यह दीवार के अभिलंबवत् ऋणात्मक x- दिशा के अनुदिश है। पहले की ही भांति, न्यूटन के तृतीय नियम का उपयोग करने पर गेंद के कारण दीवार पर बल दीवार के अभिलंबवत् धनात्मक x-दिशा के अनुदिश है।
प्रकरण (a) व प्रकरण (b) में गेंद को दीवार द्वारा प्रदान किए गए आवेगों के परिमाणों का अनुपात है:
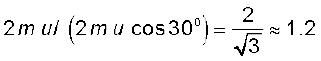
5.7 संवेग-संरक्षण
न्यूटन के गति के द्वितीय तथा तृतीय नियम एक अत्यन्त महत्त्वपूर्ण परिणाम: संवेग-संरक्षण नियम की ओर अग्रसर करते हैं। एक परिचित उदाहरण पर विचार कीजिए। किसी बंदूक से एक गोली छोड़ी जाती है। यदि बंदूक द्वारा गोली पर लगा बल F है, तो न्यूटन के तृतीय नियम के अनुसार गोली द्वारा बंदूक पर लगने वाला बल –F है। दोनों बल समान समय अंतराल ∆t तक कार्य करते हैं। द्वितीय नियम के अनुसार गोली का संवेग परिवर्तन F ∆t है तथा बंदूक का संवेग परिवर्तन –F ∆t है। चूंकि आरंभ में दोनों विराम में हैं, अतः संवेग परिवर्तन अंतिम संवेग के बराबर है। इस प्रकार यदि छोड़ने के पश्चात् गोली का संवेग, pB है तथा बंदूक का प्रतिक्षेप संवेग, pg है, तो pg = – pb अर्थात् pg + pb = 0 अर्थात्, गोली बंदूक निकाय का कुल संवेग संरक्षित रहता है।
इस प्रकार, किसी वियुक्त निकाय (अर्थात् कोई निकाय जिस पर कोई बाह्य बल नहीं लगता है।) में, निकाय के कणों के युगलों के बीच पारस्परिक बल व्यष्टि कणों में संवेग परिवर्तन कर सकते हैं, परंतु चूंकि प्रत्येक युगल के लिए पारस्परिक बल समान एवं विपरीत हैं संवेग परिवर्तन युगलों में निरस्त हो जाते हैं तथा कुल संवेग अपरिवर्तित रहता है। इस तथ्य को संवेग- संरक्षण नियम कहते हैं। इस नियम के अनुसार:
अन्योन्य क्रिया करने वाले कणों के किसी वियुक्त निकाय का कुल संवेग संरक्षित रहता है।
संवेग-संरक्षण नियम के अनुप्रयोग का एक महत्त्वपूर्ण उदाहरण दो पिण्डों में संघट्टन है। दो पिण्डों A व B पर विचार कीजिए जिनके आरंभिक संवेग pA तथा pB हैं। दोनों टकराते हैं और पृथक हो जाते हैं। यदि पृथक होने के पश्चात् उनके अंतिम संवेग क्रमशः P'A तथा P'B हैं; तो द्वितीय नियम के द्वारा
FAB ∆t = p'A – pA
तथा, FBA ∆t = p'B – pB
(यहाँ हमने दोनों बलों के लिए समान समय अंतराल ∆t लिया है, जो वह समय है जिसमें दोनों पिण्ड संपर्क में रहते हैं।)
चूंकि FAB = - FBA तृतीय नियम द्वारा,
p'A – pA = – (p'B – pB )
अर्थात् p'A + p'B = (pA + pB ) (5.9)
जो यह दर्शाता है कि वियुक्त निकाय (A + B) का कुल अंतिम संवेग उसके आरंभिक संवेग के बराबर है। ध्यान रहे कि, यह नियम दोनों प्रकार के संघट्टों - प्रत्यास्थ तथा अप्रत्यास्थ, पर लागू होता है। प्रत्यास्थ संघट्ट में दूसरी शर्त है कि निकाय की कुल आरंभिक गतिज ऊर्जा निकाय की कुल अंतिम गतिज ऊर्जा के बराबर होती है (देखिए अध्याय 6)।
5.8 किसी कण की साम्यावस्था
यांत्रिकी में किसी कण की साम्यावस्था का उल्लेख उन स्थितियों के लिए किया जाता है जिनमें कण पर नेट बाह्य बल शून्य* हो। प्रथम नियम के अनुसार, इसका यह अर्थ है कि या तो कण विराम में है अथवा एक समान गति में है। यदि किसी कण पर दो बल F1 तथा F2 कार्यरत हैं, तो साम्यावस्था के लिए आवश्यक है कि,
F1 = – F2 (5.10)
* किसी पिण्ड की साम्यावस्था के लिए केवल स्थानान्तरीय साम्यावस्था (शून्य नेट बाह्य बल) ही आवश्यक नहीं है वरन् घूर्णी साम्यावस्था (शून्य नेट बाह्य बल आघूर्ण) भी आवश्यक है, यह हम अध्याय 7 में देखेंगे ।
अर्थात् कण पर कार्यरत दोनों बल समान एवं विपरीत होनेे चाहिए । तीन संगामी बलों, F1, F2 तथा F3 के अधीन साम्यावस्था (अथवा संतुलन) के लिए इन तीनों बलों का सदिश योग शून्य होना चाहिए:
F1 + F2 + F3 = 0 (5.11)
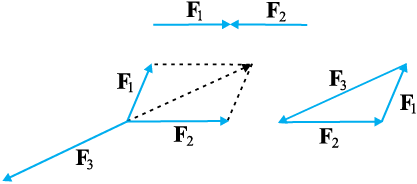
चित्र 5.7 संगामी बलों के अधीन संतुलन
दूसरे शब्दों में, बलों के समान्तर चतुर्भुज नियम द्वारा प्राप्त किन्हीं दो बलों, मान लीजिए F1 तथा F2 , का परिणामी तीसरे बल F3 , के समान एवं विपरीत होना चाहिए। चित्र 5.7 के अनुसार साम्यावस्था में तीनों बलों को किसी त्रिभुज की भुजाओं, जिस पर चक्रीय क्रम में सदिश तीर बने हों, द्वारा निरूपित किया जा सकता है। इस परिणाम का व्यापीकरण बलों की किसी भी संख्या के लिए किया जा सकता है। आरोपित बलों F1 , F2 , F3 .... Fn के अधीन कोई कण साम्यावस्था में होगा यदि उन बलों को n-भुजा के बंद चक्रीय बहुभुज की भुजाओं द्वारा निरूपित किया जा सके ।
समीकरण (5.11) से
F1x + F2x + F3x = 0
F1y + F2y + F3y = 0
F1z + F2z + F3z = 0 (5.12)
जहाँ पर F1x, F1y तथा F1z क्रमशः F1 के x, y तथा z दिशा में घटक है।
¯ उदाहरण 5.6 6 kg संहति के किसी पिण्ड को छत से 2 m लंबाई की डोरी द्वारा लटकाया गया है । डोरी के मध्य-बिंदु पर चित्र 5.8 में दर्शाए अनुसार क्षैतिज दिशा में 50 N बल लगाया जाता है । साम्यावस्था में डोरी ऊर्ध्वाधर से कितना कोण बनाती है ? (g = 10 m s-2 लीजिए)। डोरी की संहति को नगण्य मानिए ।
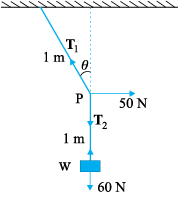
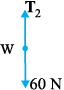
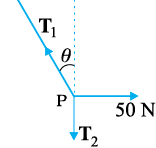
चित्र 5.8
हल चित्र 5.8(b) तथा 5.8(c) बल निर्देशक आरेख कहलाते हैं। चित्र 5.8(b) भार W का बल निर्देशक आरेख है तथा 5.8(c) बिन्दु P का बल निर्देशक आरेख है। सर्वप्रथम भार W की साम्यावस्था पर विचार कीजिए। स्पष्ट है, T2 = 6×10 = 60N। अब तीन बलों - तनाव T1 तथा T2, तथा क्षैतिज बल 50 N की क्रियाओं के अधीन संहति बिंदु P की साम्यावस्था पर विचार कीजिए। परिणामी बल के क्षैतिज तथा ऊर्ध्वाधर घटकों को पृथक-पृथक शून्य होना चाहिएः
T1 cos θ = T2 = 60 N
T1 sin θ = 50 N
ध्यान दीजिए, उत्तर न तो डोरी (जिसका द्रव्यमान नगण्य माना है) की लंबाई पर निर्भर करता है और न ही उस बिंदु की स्थिति पर निर्भर करता है जिस पर क्षैतिज बल लगाया गया है ।
5.9 यांत्रिकी में सामान्य बल
यांत्रिकी में हमारा सामना कई प्रकार के बलों से होता है। वास्तव में, गुरुत्वाकर्षण बल सर्वव्यापक है। पृथ्वी पर स्थित सभी वस्तुएँ पृथ्वी के गुरुत्व बल का अनुभव करती हैं। गुरुत्वाकर्षण बल आकाशीय पिण्डों की गतियों को नियंत्रित करता है। गुरुत्वाकर्षण बल किसी दूरी पर बिना मध्यवर्ती माध्यम के कार्य कर सकता है।
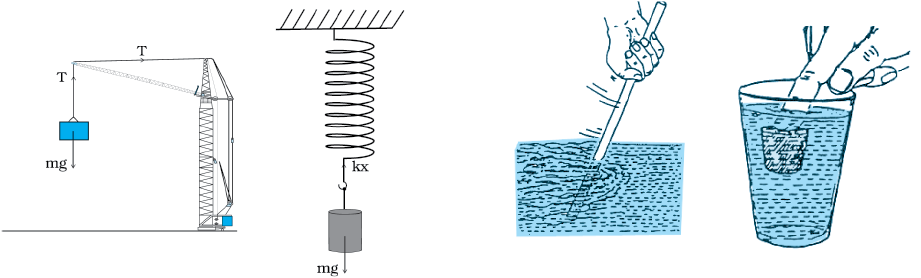
चित्र 5.9 यांत्रिकी में संपर्क बलों के कुछ उदाहरण ।
* सुगमता के लिए यहाँ हम आवेशित तथा चुंबकीय पिण्डों पर विचार नहीं कर रहे हैं । इनके लिए, गुरुत्वाकर्षण के अतिरिक्त, यहाँ वैद्युत तथा चुंबकीय असंपर्क बल हैं ।
यांत्रिकी में सामान्यतः आने वाले सभी बल संपर्क बल* हैं। जैसा कि नाम से संकेत मिलता है, किसी पिण्ड पर संपर्क बल किसी अन्य पिण्ड ठोस अथवा तरल के संपर्क द्वारा उत्पन्न होता है। जब कई पिण्ड संपर्क में होते हैं, (उदाहरणार्थ, मेज पर रखी कोई पुस्तक, छड़ों, कब्जों तथा अन्य प्रकार के आधारों से संबद्ध दृढ़ पिण्डों का कोई निकाय), तब वहाँ तृतीय नियम को संतुष्ट करने वाले (पिण्डों के प्रत्येक युगल के लिए) पारस्परिक संपर्क बल होते हैं। संपर्क-पृष्ठों के अभिलंबवत् संपर्क बल के घटक को अभिलंब बल (अथवा अभिलंब प्रतिक्रिया) कहते हैं। संपर्क-पृष्ठों के समान्तर घटक को घर्षण बल कहते हैं। संपर्क बल तब भी उत्पन्न होते हैं जब ठोस तरलों के संपर्क में आते हैं। उदाहरण के लिए, जब किसी ठोस को किसी तरल में डुबाते हैं, तो एक उपरिमुखी बल (उत्प्लावन बल) होता है जो उस ठोस द्वारा विस्थापित तरल के भार के बराबर होता है। श्यान बल, वायु-प्रतिरोध, आदि भी संपर्क बलों के उदाहरण हैं (चित्र 5.9)।
दो सामान्य बल कमानी बल तथा डोरी में तनाव हैं। जब किसी कमानी को किसी बाह्य बल द्वारा संपीडित अथवा विस्तारित किया जाता है, तब एक प्रत्यानयन बल उत्पन्न होता है। यह बल प्रायः संपीडन अथवा दैर्घ्यवृद्धि के अनुक्रमानुपाती होता है (छोटे विस्थापनों के लिए)। कमानी बल F को, F = – kx द्वारा व्यक्त किया जाता है, यहाँ x विस्थापन है तथा k को कमानी-स्थिरांक या बल-स्थिरांक कहते हैं। यहाँ ऋणात्मक चिह्न यह दर्शाता है कि बल अतानित अवस्था से विस्थापन के विपरीत है। किसी अवितान्य डोरी के लिए, बल नियतांक बहुत अधिक होता है। किसी डोरी के प्रत्यानयन बल को तनाव कहते हैं। परंपरा के अनुसार समस्त डोरी के अनुदिश एक समान तनाव T मान लेते हैं। नगण्य संहति की डोरी के लिए, डोरी के प्रत्येक भाग पर समान तनाव मानने की परंपरा सही है।
अध्याय 1 में हमने यह सीखा कि प्रकृति में केवल चार मूल बल हैं। इनमें दुर्बल तथा प्रबल बल एेसे प्रभाव क्षेत्र में प्रकट होते हैं, जिनका यहां हमसे संबंध नहीं है। यांत्रिकी के संदर्भ में केवल गुरुत्वाकर्षण तथा वैद्युत बल ही प्रासंगित होते हैं। यांत्रिकी के विभिन्न संपर्क बल जिनका हमने अभी वर्णन किया है, मूल रूप से वैद्युत बलों से ही उत्पन्न होते हैं। यह बात आश्चर्यजनक प्रतीत हो सकती है क्योंकि यांत्रिकी में हम अनावेशित तथा अचुंबकीय पिण्डों की चर्चा कर रहे हैं। परंतु सूक्ष्म स्तर पर, सभी पिण्ड आवेशित अवयवों (नाभिकों तथा इलेक्ट्रॉनों) से मिलकर बने हैं तथा आण्विक संघट्टाें प्रतिघातों तथा पिण्डों की प्रत्यास्थता आदि के कारण उत्पन्न विभिन्न संपर्क बलों की खोजबीन से ज्ञात होता है कि अंततः ये विभिन्न पिण्डों के आवेशित अवयवों के बीच वैद्युत बल ही हैं। इन बलों की विस्तृत सूक्ष्म उत्पत्ति के विषय में जानकारी जटिल है तथा स्थूल स्तर पर यांत्रिकी की समस्याओं को हल करने की दृष्टि से उपयोगी नहीं है । यही कारण है कि उन्हें विभिन्न प्रकार के बलों के रूप माना जाता है तथा उनके अभिलाक्षणिक गुणों का आनुभविक निर्धारण किया जाता है।
5.9.1 घर्षण
आइए, फिर से क्षैतिज मेज पर रखे m संहति के पिण्ड वाले उदाहरण पर विचार करें। गुरुत्व बल (mg) को मेज का अभिलंब बल (N) निरस्त कर देता है। अब मानिए कि पिण्ड पर कोई बाह्य बल F क्षैतिजतः आरोपित किया जाता है । अनुभव से हमें यह ज्ञात है कि परिमाण में छोटा बल आरोपित करने पर पिण्ड को गतिशील करने में अपर्याप्त हो सकता है। परंतु यदि आरोपित बल ही पिण्ड पर लगा एक मात्र बाह्य बल है, तो यह बल परिमाण में चाहे कितना भी छोटा क्यों न हो, पिण्ड को F/m त्वरण से गतिशील होना चाहिए। स्पष्ट है, कि अगर पिण्ड विराम में है तो पिण्ड पर कोई अन्य बाह्य बल क्षैतिज दिशा में कार्य करने लगा है, जो अरोपित बल F का विरोध करता है, फलस्वरूप पिण्ड पर नेट बल शून्य हो जाता है। यह विरोधी बल fs, जो मेज के संपर्क में पिण्ड के पृष्ठ के समान्तर लगता है , घषर्ण बल अथवा केवल घर्षण कहलाता है (चित्र 5.10(a))। यहाँ पादाक्षर s को स्थैतिक घर्षण के लिए प्रयोग किया गया है, ताकि हम इसकी गतिज घर्षण fk जिसके विषय में बाद में विचार करेंगे (चित्र 5.10(b)), से भिन्न पहचान कर सकें। ध्यान दीजिए, स्थैतिक घर्षण का अपना कोई आस्तित्व नहीं होता। जब तक कोई बाह्य बल आरोपित नहीं होता, तब तक स्थैतिक घर्षण भी नहीं होता । जिस क्षण कोई बल आरोपित होता है, उसी क्षण घर्षण बल भी लगने लगता है। पिंड को विराम में रखते हुए जब आरोपित बल F बढ़ता है, आरोपित बल के समान व विपरीत दिशा में रहते हुए fs भी एक सीमा तक बढ़ता है। अतः इसे स्थैतिक घर्षण कहते हैं। स्थैतिक घर्षण समुपस्थित गति का विरोध करता है । समुपस्थित गति का तात्पर्य एेसी गति से है जो तभी होगी जब (परंतु वास्तव में होती नहीं) किसी आरोपित बल के अंतर्गत घर्षण अनुपस्थित हो।
हम अनुभव से यह जानते हैं कि, जैसे आरोपित बल एक निश्चित सीमा से बढ़ता है, तो पिण्ड गति आरंभ कर देता है। प्रयोगों द्वारा यह पाया गया है कि स्थैतिक घर्षण का सीमान्त मान 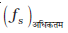

यहाँ µs आनुपातिकता स्थिरांक है, जो केवल संपर्क-पृष्ठों के युगल की प्रकृति पर ही निर्भर करता है। इस स्थिरांक µs को स्थैतिक घर्षण गुणांक कहते हैं। स्थैतिक घर्षण नियम को इस प्रकार लिखा जा सकता हैः
fs ≤ µs N (5.14)

चित्र 5.10 स्थैतिक तथा सर्पी घर्षणः (a) स्थैतिक घर्षण पिण्ड की समुपस्थित गति का विरोध करता है । जब बाह्य बल स्थैतिक घर्षण की अधिकतम सीमा से बढ़ जाता है, तो गति आरंभ होती है । (b) एक बार जब पिण्ड गतिशील हो जाता है तो उस पर सर्पी अथवा गतिज घर्षण कार्य करने लगता है जो संपर्क पृष्ठों के बीच आपेक्ष गति का विरोध करता है । गतिज घर्षण प्रायः स्थैतिक घर्षण के अधिकतम मान से कम होता है ।
यदि आरोपित बल F का मान से अधिक हो जाता है, तो पिण्ड पृष्ठ पर सरकना आरंभ कर देता है। प्रयोगों द्वारा यह पाया गया है कि जब आपेक्ष गति आरंभ हो जाती है, तब घर्षण बल, अधिकतम स्थैतिक घर्षण बल 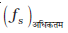
fk = µkN (5.15)
यहाँ µk, गतिज घर्षण गुणांक हैं जो केवल संपर्क पृष्ठों के युगल की प्रकृति पर निर्भर करता है। जैसा कि ऊपर वर्णन किया जा चुका है, प्रयोग यह दर्शाते हैं कि µk, µs से कम होता है । जब आपेक्ष गति आरंभ हो जाती है तो, द्वितीय नियम के अनुसार, गतिमान पिण्ड का त्वरण (F–fk)/m होता है। एकसमान वेग से गतिमान पिण्ड के लिए, F = fk। यदि पिण्ड से आरोपित बल को हटा लें तो उसका त्वरण –fk/m होता है और अंतिमतः पिण्ड रुक जाता है।
ऊपर वर्णन किए गए घर्षण के नियमाें को मूल नियमों की उस श्रेणी में नहीं माना जाता जिसमें गुरुत्वाकर्षण, वैद्युत तथा चुंबकीय बलों को माना जाता है। ये आनुभविक संबंध हैं, जो केवल सीमित प्रभाव क्षेत्रों में ही सन्निकटतः सही हैं। फिर भी ये नियम यांत्रिकी में व्यावहारिक परिकलनों में बहुत लाभप्रद हैं ।
इस प्रकार, जब दो पिण्ड संपर्क में होते हैं तब प्रत्येेक पिण्ड अन्य पिण्ड के द्वारा संपर्क बल का अनुभव करता है । परिभाषा के अनुसार, घर्षण बल संपर्क बल का संपर्क पृष्ठों के समान्तर घटक होता है, जो दो पृष्ठों के बीच समुपस्थित अथवा वास्तविक आपेक्ष गति का विरोध करता है। ध्यान दीजिए, घर्षण बल गति का नहीं वरन् आपेक्ष गति का विरोध करता है। त्वरित गति से गतिमान रेलगाड़ी के किसी डिब्बे में रखे बॉक्स पर विचार कीजिए। यदि बॉक्स रेलगाड़ी के आपेक्ष स्थिर है, तो वास्तव में वह रेलगाड़ी के साथ त्वरित हो रहा है। वह कौन-सा बल है जो बॉक्स को त्वरित कर रहा है ? स्पष्ट है कि क्षैतिज दिशा में एक ही कल्पनीय बल है, और वह है घर्षण बल। यदि कोई घर्षण नहीं है तो रेलगाड़ी के डिब्बे का फर्श तो आगे की ओर सरकेगा तथा जड़त्व के कारण बॉक्स अपनी आरंभिक स्थिति पर ही रहेगा (तथा रेलगाड़ी के डिब्बे की पिछली दीवार से टकराएगा)। इस समुपस्थित आपेक्ष गति का स्थैतिक घर्षण fs द्वारा विरोध किया जाता है। यहाँ स्थैतिक घर्षण, बॉक्स को रेलगाड़ी के आपेक्ष स्थित रखते हुए, रेलगाड़ी के समान त्वरण प्रदान करता है।
¯ उदाहरण 5.7 कोई बॉक्स रेलगाड़ी के फर्श पर स्थिर रखा है । यदि बॉक्स तथा रेलगाड़ी के फर्श के बीच स्थैतिक, घर्षण गुणांक 0.15 है, तो रेलगाड़ी का वह अधिकतम त्वरण ज्ञात कीजिए जो बॉक्स को रेलगाड़ी के फर्श पर स्थिर रखने के लिए आवश्यक है ।
हल चूंकि बॉक्स में त्वरण स्थैतिक घर्षण के कारण ही है, अतः
ma = fs ≤ µs N = µs m g
अर्थात् a ≤ µs g
∴ aअधिकतम = µsg = 0.15 × 10 m s-2 = 1.5 m s-2
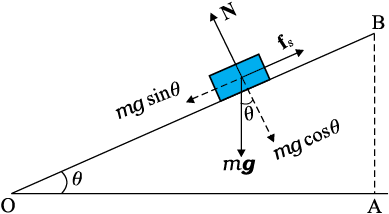
¯ उदाहरण 5.8 4 kg का कोई गुटका एक क्षैतिज समतल पर रखा है (चित्र 5.11)। समतल को धीरे-धीरे तब तक आनत किया जाता है जब तक क्षैतिज से किसी कोण
θ =15° पर वह गुटका सरकना आरंभ नहीं कर देता । पृष्ठ और गुटके के बीच स्थैतिक घर्षण गुणांक क्या है ?
चित्र 5.11
हल आनत समतल पर विरामावस्था में रखे m संहति के गुटके पर कार्यरत बल है (i) गुटके का भार mg ऊर्ध्वाधर नीचे की ओर, (ii) समतल द्वारा गुटके पर लगाया गया अभिलंब बल N, तथा (iii) समुपस्थित गति का विरोध करने वाला स्थैतिक घर्षण बल fs । गुटके की साम्यावस्था में इन बलों का परिणामी शून्य बल होना चाहिए। भार mg को चित्र में दर्शाए अनुसार दो दिशाओं में अपघटित करने पर
mg sin θ = fs mg cos θ = N
जैसे-जैसे θ बढ़ता है, स्वसमायोजी घर्षण बल fs तब तक बढ़ता है जब तक, θ = θअधिकतम पर यह अपना अधिकतम मान प्राप्त नहीं कर लेता, 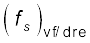 = µs N, जहाँ µs गुटके तथा समतल के बीच स्थैतिक घर्षण गुणांक है।
= µs N, जहाँ µs गुटके तथा समतल के बीच स्थैतिक घर्षण गुणांक है।
अतः
tanθअधिकतम = µs अथवा θअधिकतम = tan-1 µs
जब θ का मान θअधिकतम से केवल कुछ ही अधिक होता है, तो गुटके पर एक लघु नेेट बल लगता है और गुटका सरकना आरंभ कर देता है। ध्यान दीजिए, θअधिकतम केवल µs पर ही निर्भर करता है, यह गुटके की संहति पर निर्भर नहीं करता।
θअधिकतम = 15° केे लिए,
µs = tan 15°
= 0.27
¯ उदाहरण 5.9 चित्र 5.12(a) में दर्शाए ब्लॉक-ट्राली निकाय का त्वरण क्या है, यदि ट्राली और पृष्ठ के बीच गतिज घर्षण गुणांक 0.04 है? डोरी में तनाव क्या है ?
(g = 10 m s-2 लीजिए), डोरी की संहति नगण्य मानिए ।
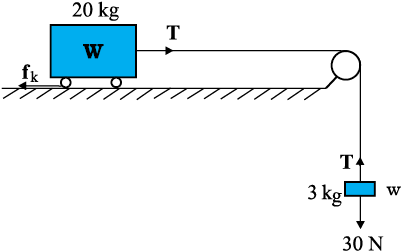
(a)


(b) (c)
चित्र 5.12
हल: चूंकि डोरी की लंबाई नियत है तथा घिरनी चिकनी है, 3 kg के ब्लॉक तथा 20 kg की ट्राली दोनों के त्वरणों के परिमाण समान हैं। ब्लॉक की गति पर द्वितीय नियम का अनुप्रयोग करने पर (चित्र 5.12(b)),
30 – T = 3a
ट्राली की गति पर द्वितीय नियम का अनुप्रयोग करने पर (चित्र 5.12(c)),
T – fk = 20a
अब fk = µkN, जहाँ µk गतिज घर्षण गुणांक है तथा N अभिलंब बल है । यहाँ µk = 0.04, तथा N = 20 × 10 = 200 N
इस प्रकार, ट्राली की गति के लिए समीकरण
T – 0.04 × 200 = 20a अथवा T – 8 = 20a
इस समीकरणों से हमें प्राप्त होता है,
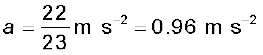
तथा T = 27.1 N
लोटनिक घर्षण
सिद्धांत रूप से क्षैतिज समतल पर एक वलय (रिंग) के समान वस्तु अथवा गोल गेंद जैसे पिण्ड जो बिना सरके केवल लोटन कर रहा (लुढ़क) है, पर किसी भी प्रकार का कोई घर्षण बल नहीं लगेगा । लोटनिक गति करते किसी पिण्ड का हर क्षण समतल तथा पिण्ड के बीच केवल एक ही संपर्क बिंदु होता है तथा यदि कोई सरकन नहीं है तो इस तात्क्षणिक संपर्क बिंदु की समतल के आपेक्ष कोई गति नहीं होती। इस आदर्श स्थिति में गतिज अथवा स्थैतिक घर्षण शून्य होता है तथा पिण्ड को एकसमान वेग से निरंतर लोटनिक गति करते रहना चाहिए। हम जानते हैं कि व्यवहार में एेसा नहीं होगा, तथा गति में कुछ न कुछ अवरोध (लोटनिक घर्षण) अवश्य रहता है, अर्थात्, पिण्ड को निरंतर लोटनिक गति करते रहने के लिए उस पर कुछ बल लगाने की आवश्यकता होती है। समान भार के पिण्ड के लिए लोटनिक घर्षण सदैव ही सर्पी अथवा स्थैतिक घर्षण की तुलना में बहुत कम (यहाँ तक कि परिमाण की 2 अथवा 3 कोटि तक) होता है। यही कारण है कि मानव सभ्यता के इतिहास में भारी बोझों के परिवहन के लिए पहिए की खोज एक बड़ा मील का पत्थर माना गया है।
लोटनिक घर्षण का उद्गम जटिल है यद्यपि यह स्थैतिक तथा सर्पी घर्षण के उद्गम से कुछ भिन्न है। लोटनिक गति के समय संपर्क पृष्ठों में क्षणमात्र के लिए विरूपण होता है, तथा इसके फलस्वरूप पिण्ड का कुछ परिमित क्षेत्रफल (कोई बिंदु नहीं), लोटनिक गति के समय पृष्ठ के संपर्क में होता है। इसका नेट प्रभाव यह होता है कि संपर्क बल का एक घटक पृष्ठ के समान्तर प्रकट होता है जो गति का अवरोध करता है।
हम प्रायः घर्षण को एक अवांछनीय बल मानते हैं। बहुत सी स्थितियों में, जैसे किसी मशीन, जिसमें विभिन्न कल पुर्जे गति करते हों, में घर्षण की ऋणात्मक भूमिका होती है। यह आपेक्ष गतियों का विरोध करता है जिसके फलस्वरूप ऊष्मा, आदि के रूप में ऊर्जा-क्षय होता है। मशीनों में स्नेहक गतिज घर्षण को कम करने का एक साधन होता है। घर्षण को कम करने का एक अन्य उपाय मशीन के दो गतिशील भागों के बीच, बॉल-बेयरिंग लगाना है चित्र 5.13(a)। (क्योंकि दो संपर्क पृष्ठों तथा बाल बेयरिगों के बीच लोटनिक घर्षण बहुत कम होता है, अतः ऊर्जा-क्षय घट जाता है । सापेक्ष गति करते दो ठोस पृष्ठों के बीच वायु की पतली परत बनाए रखकर भी प्रभावी ढंग से घर्षण को घटाया जा सकता है (चित्र 5.13(b))।

चित्र 5.13 घर्षण को घटाने के कुछ उपाय । (a) मशीन के गतिशील भागों के बीच बॉल-बेयरिंग लगाकर, (b) आपेक्षिक गति करने वाले पृष्ठों के बीच वायु का संपीडित गद्दा ।
तथापि, बहुत-सी व्यावहारिक स्थितियों में, घर्षण अत्यन्त आवश्यक होता है । गतिज घर्षण में ऊर्जा-क्षय होता है, फिर भी आपेक्षिक गति को शीघ्र समाप्त करने में इसकी महत्त्वपूर्ण भूमिका है। मशीनों तथा यंत्रों में ब्रेक की भांति इसका उपयोग किया जाता है। इसी प्रकार स्थैतिक घर्षण भी हमारे दैनिक जीवन में अत्यन्त महत्त्वपूर्ण है। हम घर्षण के कारण ही फर्श पर चल पाते हैं । अत्यधिक फिसलन वाली सड़क पर कार को चला पाना असंभव होता है। किसी साधारण सड़क पर, टायरों और सड़क के बीच घर्षण पहिए की घूर्णी गति को लोटनिक गति में रूपांतरित करके कार को त्वरित करने के लिए आवश्यक बाह्य बल प्रदान करता है ।
5.10 वर्तुल (वृतीय) गति
हमने अध्याय 4 में यह देखा कि R त्रिज्या के किसी वृत्त में एकसमान चाल v से गतिमान किसी पिण्ड का त्वरण v2/R वृत्त के केंद्र की ओर निर्दिष्ट होता है। द्वितीय नियम के अनुसार इस त्वरण को प्रदान करने वाला बल है:
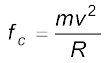 (5.16)
(5.16)
जहाँ m पिण्ड की संहति है। केंद्र की ओर निर्दिष्ट इस बल को अभिकेंद्र बल कहते हैं। डोरी की सहायता से वृत्त में घूर्णन करने वाले पत्थर को डोरी में तनाव अभिकेंद्र बल प्रदान करता है। सूर्य के चारों ओर किसी ग्रह की गति के लिए आवश्यक अभिकेंद्र बल सूर्य के कारण उस ग्रह पर लगे गुरुत्वाकर्षण से मिलता है। किसी क्षैतिज सड़क पर कार को वृत्तीय मोड़ लेने के लिए आवश्यक अभिकेंद्र बल घर्षण बल प्रदान करता है ।

चित्र 5.14 कार की (a) समतल सड़क, तथा (b) ढालू सड़क पर वर्तुल गति ।
![1302.png]()
किसी सपाट सड़क तथा किसी ढालू सड़क पर कार की वर्तुल गति, गति के नियमों के रोचक उदाहरण हैं।
समतल सड़क पर कार की गति-
कार पर तीन बल आरोपित हैं [चित्र 5.14(a)]
(i) कार का भार, mg
(ii) अभिलम्ब प्रतिक्रिया, N
(iii) घर्षण बल, f
क्योंकि यहाँ ऊर्ध्वाधर दिशा में कोई त्वरण नहीं है, अतः
N – mg = 0
N = mg (5.17)
वर्तुल गति के लिए आवश्यक अभिकेंद्र बल सड़क के पृष्ठ के अनुदिश है । यह बल कार के टायरों तथा सड़क के पृष्ठ के बीच पृष्ठ के अनुदिश संपर्क बल के घटक, जो परिभाषा के अनुसार घर्षण बल ही है, द्वारा प्रदान किया जाना चाहिए। ध्यान दीजिए, यहाँ स्थैतिक घर्षण ही अभिकेंद्र त्वरण प्रदान करता है। स्थैतिक घर्षण, घर्षण की अनुपस्थिति में वृत्त से दूर जाती गतिमान कार की समुपस्थित गति का विरोध करता है।
समीकरण (5.14) तथा (5.16) से हमें प्राप्त होता है

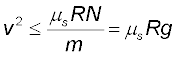 [therefore, N = mg ]
[therefore, N = mg ]
यह संबंध कार की संहति पर निर्भर नहीं करता। इससे यह प्रदर्शित होता है कि µs तथा R के किसी दिए हुए मान के लिए कार की वर्तुल गति की कोई संभावित अधिकतम चाल होती है, जिसे इस प्रकार व्यक्त किया जा सकता है,
vअधिकतम = 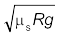 (5.18)
(5.18)
ढालू सड़क पर कार की गति
यदि सड़क ढालू है (चित्र 5.14b), तो हम कार की वर्तुल गति में घर्षण के योगदान को घटा सकते हैं। क्योंकि यहाँ फिर ऊर्ध्वाधर दिशा में कोई त्वरण नहीं है, इसलिए नेट बल शून्य होगा। अतः
N cos θ = mg + f sin θ (5.19a)
N तथा f के घटकों द्वारा अभिकेंद्र बल प्राप्त किया जाता है:
N sin 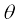 + f cos
+ f cos 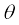 =
= 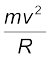 (5.19b)
(5.19b)
यहाँ, पहले कि भाँति, 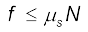
vअधिकतम के लिए हम 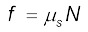 लेते हैं।
लेते हैं।
समीकरण (5.19a) तथा (5.19b) को लिखा जा सकता है
N cos 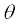 = mg +
= mg + 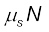 sin
sin 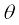 (5.20a)
(5.20a)
N sin  +
+ 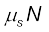 cos
cos 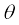 = mv2/R (5.20b)
= mv2/R (5.20b)
अतः समीकरण (5.20a) से 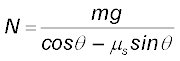
समीकरण (5.20b) में N का मान रखने पर
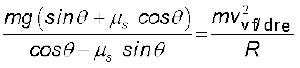
या 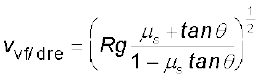 (5.21)
(5.21)
समीकरण (5.18) से तुलना करने पर हम देखते हैं कि ढालू सड़क पर कार की अधिकतम चाल समतल सड़क पर कार की अधिकतम संभव चाल से अधिक है। समीकरण (5.21) में
µs = 0 के लिए,
v0 = (Rg tan θ)1/2 (5.22)
इस चाल पर आवश्यक अभिकेंद्र बल प्रदान करने के लिए घर्षण बल की कोई आवश्यकता नहीं होती। इस चाल से ढालू सड़क पर कार चलाने पर कार के टायरों की कम घिसाई होती है। इसी समीकरण से यह भी ज्ञात होता है कि v < v0 के लिए घर्षण बल उपरिमुखी होगा तथा किसी कार को स्थिर स्थिति में केवल तभी पार्क किया जा सकता है जब tan θ  µs हो।
µs हो।
¯ उदाहरण 5.10 18 km/h की चाल से समतल सड़क पर गतिमान कोई साइकिल सवार बिना चाल को कम किए 3 m त्रिज्या का तीव्र वर्तुल मोड़ लेता है । टायरों तथा सड़क के बीच स्थैतिक घर्षण गुणांक 0.1 है । क्या साइकिल सवार मोड़ लेते समय फिसल कर गिर जाएगा ?
हल सपाट सड़क पर अकेला घर्षण बल ही साइकिल सवार को बिना फिसले वर्तुल मोड़ लेने के लिए आवश्यक अभिकेंद्र बल प्रदान कर सकता है। यदि चाल बहुत अधिक है, तथा/अथवा मोड़ अत्यधिक तीव्र है (अर्थात् त्रिज्या बहुत कम है), तब घर्षण बल इन स्थितियों में आवश्यक अभिकेंद्र बल प्रदान करने के लिए पर्याप्त नहीं होता और साइकिल सवार मोड़ लेते समय फिसल कर गिर जाता है। साइकिल सवार के न फिसलने की शर्त समीकरण (5.18) द्वारा इस प्रकार है:
v2  µs Rg
µs Rg
अब, यहाँ इस प्रश्न में R = 3 m, g = 9.8 m s-2 तथा µs = 0.1 अर्थात् µsRg = 2.94 m2s–2; तथा v = 18 km/h = 5 m s-1; अर्थात् v2 = 25 m2s-2 अर्थात्, शर्त v2  µs Rg का पालन नहीं होता। अतः, साइकिल सवार तीव्र वर्तुल मोड़ लेते समय फिसलकर गिरेगा। °
µs Rg का पालन नहीं होता। अतः, साइकिल सवार तीव्र वर्तुल मोड़ लेते समय फिसलकर गिरेगा। °
¯ उदाहरण 5.11 300 m त्रिज्या वाले किसी वृत्ताकार दौड़ के मैदान का ढाल 15॰ है । यदि मैदान और रेसकार के पट्टियों के बीच घर्षण गुणांक 0.2 है, तो (a) टायरों को घिसने से बचाने के लिए रेसकार की अनुकूलतम चाल, तथा (b) फिसलने से बचने के लिए अधिकतम अनुमेय चाल क्या है ?
हल ढालू मैदान पर बिना फिसले गतिशील रेसकार को वर्तुल मोड़ लेने के लिए आवश्यक अभिकेंद्र बल प्रदान करने में घर्षण बल तथा अभिलंब बल के क्षैतिज घटक का योगदान होता है । रेसकार की अनुकूलतम चाल पर गति के लिए अभिलंब बल का घटक ही आवश्यक अभिकेंद्र बल प्रदान करने के लिए पर्याप्त होता है तथा घर्षण बल की कोई आवश्यकता नहीं होती। समीकरण (5.22) द्वारा रेसकार की अनुकूलतम चाल v0 को इस प्रकार व्यक्त करते हैं:
v0 = (Rg tan θ)1/2
यहां R = 300 m, θ = 150, g = 9.8 m s-2; अतः
v0 = 28.1 m s-1
समीकरण (5.21) द्वारा रेसकार की अधिकतम अनुमेय चाल को इस प्रकार व्यक्त करते हैं:
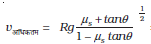
5.11 यांत्रिकी में समस्याओं को हल करना
गति के जिन तीन नियमों के विषय में आपने इस अध्याय में अध्ययन किया है वे यांत्रिकी की आधारशिला हैं। अब आप यांत्रिकी की विविध प्रकार की समस्याओं को हल करने में सक्षम हैं। आमतौर पर यांत्रिकी की किसी प्ररूपी समस्या में बलों की क्रिया के अधीन केवल एक पिण्ड का ही समावेश नहीं होता । अधिकांश प्रकरणों में हम विभिन्न पिण्डों के एेसे संयोजन पर विचार करते हैं जिनमें पिण्ड परस्पर एक दूसरे पर बल लगाते हैं। इसके अतिरिक्त संयोजन का प्रत्येक पिण्ड गुरुत्व बल का भी अनुभव करता है । इस प्रकार की किसी समस्या को हल करने का प्रयास करते समय हमें एक स्पष्ट तथ्य याद रखना परमावश्यक है कि समस्या का हल करने के लिए उस संयोजन के किसी भी भाग को चुना जा सकता है तथा उस भाग पर गति के नियमों को इस शर्त के साथ लागू किया जा सकता है कि चुने गए भाग पर संयोजन के शेष भागों द्वारा आरोपित सभी बलों को सम्मिलित करना सुनिश्चित कर लिया गया है। संयोजन के चुने गए भाग को हम निकाय कह सकते हैं तथा संयोजन के शेष भाग (निकाय पर आरोपित बलों के अन्य साधनों को सम्मिलित करते हुए) को वातावरण कह सकते हैं। इस विधि को वास्तव में हमने पहले भी कई उदाहरणों में अपनाया है। यांत्रिकी की किसी प्ररूपी समस्या को सुव्यवस्थित ढंग से हल करने के लिए हमें निम्नलिखित चरणों को अपनाना चाहिए:
(i) पिण्डों के संयोजन के विभिन्न भागों – संबंधों, टेकों, आदि को दर्शाने वाला संक्षिप्त योजनाबद्ध आरेख खींचिए।
(ii) संयोजन के किसी सुविधाजनक भाग को निकाय के रूप में चुनिए ।
(iii) एक पृथक आरेख खींचिए जिसमें केवल निकाय तथा पिण्डों के संयोजन के शेष भागों द्वारा निकाय पर आरोपित सभी बलों को सम्मिलित करके दर्शाया गया हो । निकाय पर सभी अन्य साधनों द्वारा आरोपित बलों को भी सम्मिलित कीजिए। निकाय द्वारा वातावरण पर आरोपित बलों को इसमें सम्मिलित नहीं कीजिए। इस प्रकार के आरेख को "बल-निर्देशक आरेख" कहते हैं । (ध्यान दीजिए, इसका यह अर्थ नहीं है कि विचाराधीन निकाय पर कोई नेट बल नहीं है ।)
(iv) किसी बल निर्देशक आरेख में बलों से संबंधित केवल वही सूचनाएँ (बलों के परिमाण तथा दिशाएँ) सम्मिलित कीजिए जो या तो आपको दी गई हैं अथवा जो निर्विवाद निश्चित हैं। (उदाहरण के लिए, किसी पतली डोरी में तनाव की दिशा सदैव डोरी की लंबाई के अनुदिश होती है।) शेष उन सभी को अज्ञात माना जाना चाहिए जिन्हें गति के नियमों के अनुप्रयोगों द्वारा ज्ञात किया जाना है ।
(v) यदि आवश्यक हो, तो संयोजन से किसी अन्य निकाय के लिए भी यही विधि अपनाइए। एेसा करने के लिए न्यूटन का तृतीय नियम प्रयोग कीजिए। अर्थात्, यदि A के बल निर्देशक आरेख में B के कारण A पर बल को F द्वारा दर्शाया गया है, तो B के बल निर्देशक आरेख में A के कारण B पर बल को –F द्वारा दर्शाया जाना चाहिए ।
निम्नलिखित उदाहरण में उपरोक्त विधि का स्पष्टीकरण किया गया है:
¯ उदाहरण 5.12 किसी कोमल क्षैतिज फर्श पर 2 kg संहति का लकड़ी का गुटका रखा है (चित्र 5.15)। जब इस गुटके के ऊपर 25 kg संहति का लोहे का बेलन रखा जाता है तो फर्श स्थिर गति से नीचे धँसता है तथा गुटका व बेलन एक साथ 0.1 m s-2 त्वरण से नीचे जाते हैं । गुटके की फर्श पर क्रिया (a) फर्श के धँसने से पूर्व तथा (b) फर्श के धँसने के पश्चात् क्या है ? g = 10 m s-2 लीजिए । समस्या में क्रिया-प्रतिक्रिया युगलों को पहचानिए ।
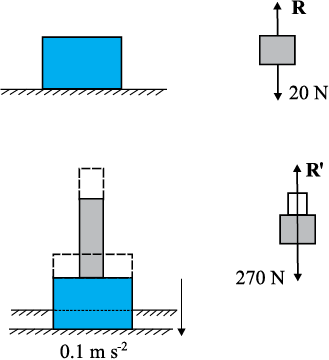
चित्र 5.15
हल
(a) फर्श पर गुटका विरामावस्था में है। इसका बल निर्देशक आरेख गुटके पर दो बलों को दर्शाता है, पृथ्वी द्वारा आरोपित गुरुत्वाकर्षण बल = 2 × 10 = 20 N; तथा गुटके पर फर्श का अभिलंब बल R। प्रथम नियम के द्वारा गुटके पर आरोपित नेट बल शून्य होना चाहिए, अर्थात्, R = 20 N। तीसरे नियम का उपयोग करने पर गुटके की क्रिया अर्थात् गुटके द्वारा फर्श पर आरोपित बल परिमाण में 20 N के बराबर है तथा इसकी दिशा ऊर्ध्वाधरतः अधोमुखी है।
(b) निकाय (गुटका + बेलन) नीचे की ओर 0.1 m s–2 त्वरण से धँस रहा है। इसका बल निर्देशक आरेख निकाय पर दो बलों को दर्शाता है। पृथ्वी के कारण गुरुत्व बल
(270 N); तथा फर्श का अभिलंब बल R'। ध्यान दीजिए, निकाय का बल निर्देशक आरेख गुटके और बेलन के बीच आंतरिक बलों को नहीं दर्शाता। निकाय पर द्वितीय नियम का अनुप्रयोग करने पर,
270 – R' = 27 × 0.1
अर्थात् R' = 267.3 N
तृतीय नियम के अनुसार फर्श पर निकाय की क्रिया 267.3 N के बराबर है तथा यह ऊर्ध्वाधरतः अधोमुखी है।
क्रिया-प्रतिक्रिया युगल
(a) के लिए: (i) पृथ्वी द्वारा गुटके पर आरोपित गुरुत्व बल (20 N) (क्रिया) तथा गुटके द्वारा पृथ्वी पर आरोपित गुरुत्व बल (प्रतिक्रिया) 20 N के बराबर उपरिमुखी निदेशित (आरेख में नहीं दर्शाया गया है)।
(ii) गुटके द्वारा फर्श पर आरोपित बल (क्रिया); फर्श द्वारा गुटके पर आरोपित बल (प्रतिक्रिया)
(b) के लिए (i) पृथ्वी द्वारा निकाय पर आरोपित गुरुत्व बल (270 N) (क्रिया); निकाय द्वारा पृथ्वी पर आरोपित गुरुत्व बल (प्रतिक्रिया) 270 N के बराबर उपरिमुखी निदेशित (आरेख में नहीं दर्शाया गया है ।)
(ii) निकाय द्वारा फर्श पर आरोपित बल (क्रिया); फर्श द्वारा निकाय पर आरोपित बल (प्रतिक्रिया)
इसके अतिरिक्त (b) के लिए बेलन द्वारा गुटके पर आरोपित बल तथा गुटके द्वारा बेलन पर आरोपित बल भी क्रिया-प्रतिक्रिया का एक युगल बनाते हैं।
याद रखने योग्य एक महत्त्वपूर्ण तथ्य यह है कि किसी क्रिया-प्रतिक्रिया युगल की रचना दो पिण्डों के बीच पारस्परिक बलों, जो सदैव परिमाण में समान तथा दिशा में विपरीत होते हैं, से होती है। एक ही पिण्ड पर दो बलों, जो किसी विशेष परिस्थिति में परिमाण में समान व दिशा में विपरीत हो सकते हैं, से किसी क्रिया-प्रतिक्रिया युगल की रचना नहीं हो सकती। उदाहरण के लिए (a) अथवा (b) में पिण्ड पर गुरुत्व बल तथा फर्श द्वारा पिण्ड पर आरोपित अभिलंब बल कोई क्रिया-प्रतिक्रिया युगल नहीं है। ये बल संयोगवश (a) के लिए समान एवं विपरीत हैं क्योंकि पिण्ड विरामावस्था में है । परंतु प्रकरण (b) के लिए वे एेसे नहीं हैं जैसा कि हमने पहले ही देख लिया है। निकाय का भार 270 N है जबकि अभिलंब बल R' = 267.3 N है।
यांत्रिकी की समस्याओं को हल करने में बल निर्देशक आरेख खींचने की प्रथा अत्यंत सहायक है। यह आपको, अपने निकाय को स्पष्ट रूप से परिभाषित करने तथा उन सभी पिण्डों के कारण, जो स्वयं निकाय के भाग नहीं हैं, निकाय पर आरोपित सभी विभिन्न बलों पर विचार करने के लिए विवश करता है। इस अध्याय तथा आगामी अध्यायों में दिए गए अभ्यास-प्रश्नों द्वारा इस प्रथा के पोषण में आपको सहायता मिलेगी।
सारांश
1. अरस्तू का यह दृष्टिकोण, कि किसी पिण्ड की एकसमान गति रखने के लिए बल आवश्यक है, गलत है। व्यवहार में विरोधी घर्षण बल को प्रभावहीन करने के लिए कोई बल आवश्यक होता है ।
2. गैलीलियो ने आनत समतलों पर पिण्डों की गतियों का बहिर्वेशन करके जड़त्व के नियम की खोज की। न्यूटन का गति का प्रथम नियम वही नियम है, जिसे फिर से शब्दों में इस प्रकार व्यक्त किया गया है:
"प्रत्येक पिण्ड तब तक अपनी विरामावस्था अथवा किसी सरल रेखा में एकसमान गति की अवस्था में रहता है, जब तक कोई बाह्य बल उसे अन्यथा व्यवहार करने के लिए विवश नहीं करता ।" सरल पदों में, प्रथम नियम इस प्रकार है "यदि किसी पिण्ड पर बाह्य बल शून्य है तो उसका त्वरण शून्य होता है ।"
3. किसी पिण्ड का संवेग (p) उसकी संहति (m) तथा वेग (v) का गुणनफल होता है:
p = m v
4. न्यूटन का गति का द्वितीय नियम:
किसी पिण्ड के संवेग परिवर्तन की दर आरोपित बल के अनुक्रमानुपाती होती है तथा संवेग परिवर्तन आरोपित बल की दिशा में होता है। इस प्रकार:
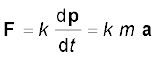
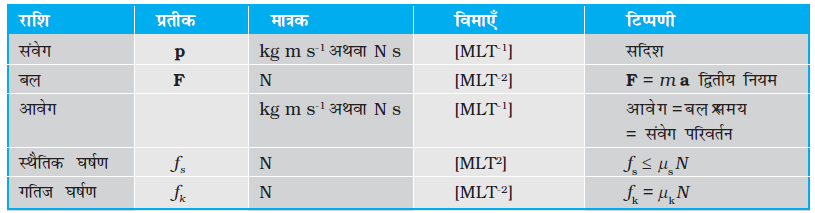
यहाँ F पिण्ड पर आरोपित नेट बाह्य बल है, तथा a पिण्ड में उत्पन्न त्वरण है। SI मात्रकों में राशियों के मात्रकों का चयन करने पर आनुपातिकता स्थिरांक k = 1 आता है। तब
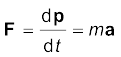
बल का S.I. मात्रक न्यूटन (प्रतीक N) है: 1 N = 1 kg m s-2
(a) द्वितीय नियम तथा प्रथम नियम में सामंजस्य है (F = 0 का अर्थ है a = 0)
(b) यह एक सदिश समीकरण है।
(c) सही अर्थों में तो यह किसी बिंदु कण पर लागू होती है । फिर भी किसी पिण्ड अथवा कणों के निकाय पर भी इसे लागू किया जा सकता है, परंतु शर्त यह है कि हम F को निकाय पर कुल आरोपित बाह्य बल तथा a को समस्त निकाय का त्वरण मानें।
(d) किसी निश्चित क्षण पर किसी बिंदु पर आरोपित बल F उसी क्षण उसी बिंदु पर a का निर्धारण करता है । अर्थात् द्वितीय नियम एक स्थानीय नियम है। किसी क्षण पर a गति के इतिहास पर निर्भर नहीं करता।
5. बल तथा समय का गुणनफल आवेग कहलाता है जो संवेग परिवर्तन के बराबर होता है।
आवेग की धारणा उस स्थिति में लाभदायक होती है जब कोई बृह्त बल अल्प काल के लिए कार्य करके संवेग में मापने योग्य परिवर्तन उत्पन्न कर देता है। क्योंकि बल का क्रिया समय अत्यंत अल्प है इसलिए यह माना जा सकता है कि आवेगी बल लगने के समय वस्तु की स्थिति में पर्याप्त परिवर्तन नहीं होगा।
6. न्यूटन का गति का तृतीय नियम:
प्रत्येक क्रिया की समान तथा विपरीत प्रतिक्रिया होती है।
सरल पदों में इस नियम को इस प्रकार भी अभिव्यक्त किया जा सकता है:
प्रकृति में बल सदैव ही पिण्डों के युगलों के बीच पाए जाते हैं । किसी पिण्ड A पर पिण्ड B द्वारा आरोपित बल पिण्ड B पर पिण्ड A द्वारा आरोपित बल के समान तथा विपरीत होता है।
क्रिया तथा प्रतिक्रिया समक्षणिक बल हैं। क्रिया तथा प्रतिक्रिया के बीच कारण-प्रभाव संबंध नहीं होता। इन दो पारस्परिक बलों में से किसी भी एक को क्रिया तथा अन्य को प्रतिक्रिया कहा जा सकता है। क्रिया तथा प्रतिक्रिया बल दो भिन्न पिण्डों पर कार्य करते हैं। अतः ये बल एक दूसरे को निरस्त नहीं कर सकते। तथापि, किसी पिण्ड में आंतरिक क्रिया तथा प्रतिक्रिया बलों का योग अवश्य ही शून्य होता है।
7. संवेग संरक्षण नियम
कणों के किसी वियुक्त निकाय का कुल संवेग संरक्षित रहता है। यह नियम गति के द्वितीय तथा तृतीय नियमों से व्युत्पन्न हुआ है।
8. घर्षण
घर्षण बल दो संपर्क पृष्ठों के बीच आपेक्षिक गति (समुपस्थित अथवा वास्तविक) का विरोध करता है। यह संपर्क बल का संपर्क पृष्ठाें के अनुदिश घटक है। स्थैतिक घर्षण ƒs समुपस्थित आपेक्ष गति का विरोध करता है ; गतिज घर्षण ƒk वास्तविक आपेक्ष गति का विरोध करता है। घर्षण बल संपर्क पृष्ठों के क्षेत्रफल पर निर्भर नहीं करते तथा निम्नलिखित सन्निकट नियम की तुष्टि करते हैं:
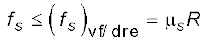
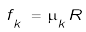
µs (स्थैतिक घर्षण गुणांक) तथा µk (गतिज घर्षण गुणांक) संपर्क पृष्ठों के युगल के अभिलक्षणों के स्थिरांक हैं। प्रयोगों द्वारा यह पाया गया है कि µk , µs से तुलना में बहुत कम होता है।
विचारणीय विषय
1. बल सदैव गति की दिशा में नहीं होता। परिस्थितियों पर निर्भर करते हए, F, v के अनुदिश, v के विपरीत, v के अभिलंबवत् अथवा v से कोई अन्य कोण बनाते हुए हो सकता है। प्रत्येक स्थिति में, यह त्वरण के समान्तर होता है।
2. यदि किसी क्षण v = 0 है, अर्थात् यदि कोई पिण्ड क्षणिक विराम में है, तो इसका यह अर्थ नहीं होता कि उस क्षण पर बल अथवा त्वरण अवश्य ही शून्य हों। उदाहरण के लिए, जब ऊर्ध्वाधर ऊपर फेंकी गई कोई गेंद अपनी अधिकतम ऊँचाई पर पहुँचती है, तो v = 0 होता है, परंतु उस गेंद पर गेंद के भार mg के बराबर बल निरंतर लगा रहता है तथा त्वरण शून्य नहीं होता, यह g ही होता है।
3. किसी दिए गए समय पर किसी पिण्ड पर आरोपित बल उस समय उस पिण्ड के स्थान की अवस्थिति द्वारा ज्ञात किया जाता है। कोई पिण्ड बल का वहन अपनी गति के पूर्व इतिहास से नहीं करता। जिस क्षण कोई पत्थर किसी त्वरित रेलगाड़ी से बाहर गिरा दिया जाता है, उस क्षण के तुरंत पश्चात्, यदि चारों ओर की वायु के प्रभाव अपेक्षणीय हैं तो उस पत्थर पर कोई क्षैतिज बल (अथवा त्वरण) कार्यरत नहीं रहता। तब उस पत्थर पर केवल पृथ्वी का ऊर्ध्वाधर गुरुत्व बल ही कार्य करता है ।
4. गति के द्वितीय नियम F = m a में F पिण्ड के बाहर के सभी भौतिक साधनों द्वारा आरोपित नेट बल है। a बल का प्रभाव है। m a को F के अतिरिक्त अन्य कोई बल नहीं समझा जाना चाहिए।
5. अभिकेंद्र बल को कोई अन्य प्रकार का बल नहीं समझना चाहिए। यह मात्र एक नाम है जो उस बल को दिया गया है जो वर्तुल मार्ग पर गतिमान किसी पिण्ड को त्रिज्यतः केंद्र की ओर त्वरण प्रदान करता है। हमें वृत्तीय गतियों में सदैव ही अभिकेंद्र बल के रूप में कुछ भौतिक बलों; जैसे- तनाव, गुरुत्वाकर्षण बल, वैद्युत बल, घर्षण बल आदि को खोजना चाहिए।
6. स्थैतिक घर्षण बल अपनी सीमा µsN (ƒs≤ µsN) तक एक स्वयं समायोजी बल है। बिना यह सुनिश्चित किए कि स्थैतिक घर्षण का अधिकतम मान कार्यरत हो गया है ƒs= µsN कदापि मत रखिए।
7. मेज पर रखे पिण्ड के लिए सुपरिचित समीकरण mg = R केवल तभी सही है, जब पिण्ड साम्यावस्था में हो। ये दोनों बल, mg तथा R भिन्न भी हो सकते हैं (जैसा कि त्वरित लिफ्ट में रखे पिण्ड के उदाहरण में)। mg और R में समानता का तृतीय नियम से कोई संबंध नहीं है।
8. गति के तृतीय नियम में पद ‘क्रिया’ तथा ‘प्रतिक्रिया’ का अर्थ किसी पिण्डों के युगल के बीच समक्षणिक पारस्परिक बलों से है। भाषा के अर्थ के विपरीत, क्रिया न तो प्रतिक्रिया से पहले घटित होती है और न ही प्रतिक्रिया का कारण होती है । क्रिया तथा प्रतिक्रिया भिन्न पिण्डों पर कार्य करती हैं।
9. विभिन्न पद जैसे ‘घर्षण’, ‘अभिलंब प्रतिक्रिया’, ‘तनाव’, वायु-प्रतिरोध’ ‘श्यान कर्षण’, ‘प्रणोद’, ‘उत्प्लावन बल’, ‘भार’, ‘अभिकेंद्र बल’ इन सभी का तात्पर्य विभिन्न संदर्भों में ‘बल’ ही होता है। स्पष्टता के लिए, यांत्रिकी में मिलने वाले प्रत्येक बल तथा उसके तुल्य पदों को इस वाक्यांश में रूपान्तरित करना चाहिए ‘A पर B द्वारा बल’।
10. गति के द्वितीय नियम को लागू करने के लिए, सजीव तथा निर्जीव पिण्डों के बीच कोई वैचारिक भिन्नता नहीं होती। किसी सजीव पिण्ड, जैसे किसी मानव को भी त्वरित करने के लिए बाह्य बल चाहिए। उदाहरण के लिए, बाह्य घर्षण बल के बिना हम धरती पर चल ही नहीं सकते।
11. भौतिकी में ‘बल’ की वस्तुनिष्ठ संकल्पना तथा ‘बल का अनुभव’ की व्यक्तिनिष्ठ संकल्पना के बीच कोई भ्रम नहीं होना चाहिए। किसी ‘मेरी-गो-राउण्ड’ में हमारे शरीर के सभी अंगों पर अंदर की ओर बल लगता है। परंतु हमें बाहर की ओर धकेले जाने का अनुभव होता है जो समुपस्थित गति की दिशा है।
अभ्यास
(सरलता के लिए आंकिक परिकलनाओं में g = 10 m s–2 लीजिए)
5.1 निम्नलिखित पर कार्यरत नेट बल का परिमाण व उसकी दिशा लिखिए:
(a) एकसमान चाल से नीचे गिरती वर्षा की कोई बूंद,
(b) जल में तैरता 10 g संहति का कोई कार्क,
(c) कुशलता से आकाश में स्थिर रोकी गई कोई पतंग,
(d) 30 km h-1 के एकसमान वेग से ऊबड़-खाबड़ सड़क पर गतिशील कोई कार,
(e) सभी गुरुत्वीय पिण्डों से दूर तथा वैद्युत और चुंबकीय क्षेत्रों से मुक्त, अंतरिक्ष में तीव्र चाल वाला इलेक्ट्रॉन।
5.2 0.05 kg संहति का कोई कंकड़ ऊर्ध्वाधर ऊपर फेंका गया है। नीचे दी गई प्रत्येक परिस्थिति में कंकड़ पर लग रहे नेट बल का परिमाण व उसकी दिशा लिखिए:
(a) उपरिमुखी गति के समय ।
(b) अधोमुखी गति के समय ।
(c) उच्चतम बिंदु पर जहाँ क्षण भर के लिए यह विराम में रहता है। यदि कंकड़ को क्षैतिज दिशा से 45॰ कोण पर फेेंका जाए, तो क्या आपके उत्तर में कोई परिवर्तन होगा ?
वायु-प्रतिरोध को उपेक्षणीय मानिए।
5.3 0.1 kg संहति के पत्थर पर कार्यरत नेट बल का परिमाण व उसकी दिशा निम्नलिखित परिस्थितियों में ज्ञात कीजिए:
(a) पत्थर को स्थिर रेलगाड़ी की खिड़की से गिराने के तुरंत पश्चात्,
(b) पत्थर को 36 km h–1 के एकसमान वेग से गतिशील किसी रेलगाड़ी की खिड़की से गिराने के तुरंत पश्चात्,
(c) पत्थर को 1 m s–2 के त्वरण से गतिशील किसी रेलगाड़ी की खिड़की से गिराने के तुरंत पश्चात्,
(d) पत्थर 1 m s–2 के त्वरण से गतिशील किसी रेलगाड़ी के फर्श पर पड़ा है तथा वह रेलगाड़ी के सापेक्ष विराम में है।
उपरोक्त सभी स्थितियों में वायु का प्रतिरोध उपेक्षणीय मानिए।
5.4 l लंबाई की एक डोरी का एक सिरा m संहति के किसी कण से तथा दूसरा सिरा चिकनी क्षैतिज मेज पर लगी खूँटी से बँधा है । यदि कण v चाल से वृत्त में गति करता है तो कण पर (केंद्र की ओर निदेशित) नेट बल है:
(i) T, (ii) T-mv2/l, (iii) T+mv2/l, (iv) 0
T डोरी में तनाव है। [सही विकल्प चुनिए]
5.5 15 m s–1 की आरंभिक चाल से गतिशील 20 kg संहति के किसी पिण्ड पर 50 N का स्थाई मंदन बल आरोपित किया गया है । पिण्ड को रुकने में कितना समय लगेगा ?
5.6 3.0 kg संहति के किसी पिण्ड पर आरोपित कोई बल 25 s में उसकी चाल को 2.0 m s–1 से 3.5 m s–1 कर देता है। पिण्ड की गति की दिशा अपरिवर्तित रहती है। बल का परिमाण व दिशा क्या है ?
5.7 5.0 kg संहति के किसी पिण्ड पर 8 N व 6 N के दो लंबवत् बल आरोपित हैं। पिण्ड के त्वरण का परिमाण व दिशा ज्ञात कीजिए।
5.8 36 km h-1 की चाल से गतिमान किसी आटो रिक्शा का चालक सड़क के बीच एक बच्चे को खड़ा देखकर अपने वाहन को ठीक 4.0 s में रोककर उस बच्चे को बचा लेता है। यदि आटो रिक्शा बच्चे के ठीक निकट रुकता है, तो वाहन पर लगा औसत मंदन बल क्या है ? आटोरिक्शा तथा चालक की संहतियाँ क्रमशः 400 kg और 65 kg हैं।
5.9 20,000 kg उत्थापन संहति के किसी राकेट में 5 m s–2 के आरंभिक त्वरण के साथ ऊपर की ओर स्फोट किया जाता है। स्फोट का आरंभिक प्रणोद (बल) परिकलित कीजिए।
5.10 उत्तर की ओर 10 m s–1 की एकसमान आरंभिक चाल से गतिमान 0.40 kg संहति के किसी पिण्ड पर दक्षिण दिशा के अनुदिश 8.0 N का स्थाई बल 30 s के लिए आरोपित किया गया है। जिस क्षण बल आरोपित किया गया उसे t = 0, तथा उस समय पिण्ड की स्थिति x = 0 लीजिए। t = –5 s, 25 s, 100 s पर इस कण की स्थिति क्या होगी?
5.11 कोई ट्रक विरामावस्था से गति आरंभ करके 2.0 m s–2 के समान त्वरण से गतिशील रहता है। t = 10 s पर, ट्रक के ऊपर खड़ा एक व्यक्ति धरती से 6 m की ऊँचाई से कोई पत्थर बाहर गिराता है। t = 11 s पर, पत्थर का (a) वेग, तथा (b) त्वरण क्या है ? (वायु का प्रतिरोध उपेक्षणीय मानिए ।)
5.12 किसी कमरे की छत से 2 m लंबी डोरी द्वारा 0.1 kg संहति के गोलक को लटकाकर दोलन आरंभ किए गए। अपनी माध्य स्थिति पर गोलक की चाल 1 m s–1 है। गोलक का प्रक्षेप-पथ क्या होगा यदि डोरी को उस समय काट दिया जाता है जब गोेलक अपनी (a) चरम स्थितियों में से किसी एक पर है, तथा (b) माध्य स्थिति पर है ?
5.13 किसी व्यक्ति की संहति 70 kg है। वह एक गतिमान लिफ्ट में तुला पर खड़ा है जो
(a) 10 m s–1 की एकसमान चाल से ऊपर जा रही है,
(b) 5 m s–2 के एकसमान त्वरण से नीचे जा रही है,
(c) 5 m s–2 के एकसमान त्वरण से ऊपर जा रही है,
तो प्रत्येक प्रकरण में तुला के पैमाने का पाठ्यांक क्या होगा ?
(d) यदि लिफ्ट की मशीन में खराबी आ जाए और वह गुरुत्वीय प्रभाव में मुक्त रूप से नीचे गिरे तो पाठ्यांक क्या होगा?
5.14 चित्र 5.16 में 4 kg संहति के किसी पिण्ड का स्थिति-समय ग्राफ दर्शाया गया है।
(a) t < 0; t > 4 s; 0 < t < 4 s के लिए पिण्ड पर आरोपित बल क्या है ?
(b) t = 0 तथा t = 4 s पर आवेग क्या है ?
(केवल एकविमीय गति पर विचार कीजिए)

चित्र 5.16
5.15 किसी घर्षणरहित मेज पर रखे 10 kg तथा 20 kg के दो पिण्ड किसी पतली डोरी द्वारा आपस में जुड़े हैं। 600N का कोई क्षैतिज बल (i) A पर, (ii) B पर डोरी के अनुदिश लगाया जाता है। प्रत्येक स्थिति में डोरी में तनाव क्या है ?
5.16 8 kg तथा 12 kg के दो पिण्डों को किसी हलकी अवितान्य डोरी, जो घर्षणरहित घिरनी पर चढ़ी है, के दो सिरों से बाँधा गया है । पिण्डों को मुक्त छोड़ने पर उनके त्वरण तथा डोरी में तनाव ज्ञात कीजिए।
5.17 प्रयोगशाला के निर्देश फ्रेम में कोई नाभिक विराम में है। यदि यह नाभिक दो छोटे नाभिकों में विघटित हो जाता है, तो यह दर्शाइए कि उत्पाद विपरीत दिशाओं में गति करने चाहिए।
5.18 दो बिलियर्ड गेंद जिनमें प्रत्येक की संहति 0.05 kg है, 6 m s–1 की चाल से विपरीत दिशाओं में गति करती हुई संघट्ट करती है और संघट्ट के पश्चात् उसी चाल से वापस लौटती हैं। प्रत्येक गेंद पर दूसरी गेंद कितना आवेग लगाती है ?
5.19 100 kg संहति की किसी तोप द्वारा 0.020 kg का गोला दागा जाता है। यदि गोले की नालमुखी चाल 80 m s–1 है, तो तोप की प्रतिक्षेप चाल क्या है ?
5.20 कोई बल्लेबाज किसी गेंद को 45॰ के कोण पर विक्षेपित कर देता है । एेसा करने में वह गेंद की आरंभिक चाल, जो 54 km/h–1 है, में कोई परिवर्तन नहीं करता। गेंद को कितना आवेग दिया जाता है ? (गेंद की संहति 0.15 kg है।)
5.21 किसी डोरी के एक सिरे से बँधा 0.25 kg संहति का कोई पत्थर क्षैतिज तल में 1.5 m त्रिज्या के वृत्त पर 40 rev/min की चाल से चक्कर लगाता है? डोरी में तनाव कितना है ? यदि डोरी 200 N के अधिकतम तनाव को सहन कर सकती है, तो वह अधिकतम चाल ज्ञात कीजिए जिससे पत्थर को घुमाया जा सकता है।
5.22 यदि अभ्यास 5.21 में पत्थर की चाल को अधिकतम निर्धारित सीमा से भी अधिक कर दिया जाए, तथा डोरी यकायक टूट जाए, तो डोरी के टूटने के पश्चात् पत्थर के प्रक्षेप का सही वर्णन निम्नलिखित में से कौन करता है:
(a) वह पत्थर झटके के साथ त्रिज्यतः बाहर की ओर जाता है ।
(b) डोरी टूटने के क्षण पत्थर स्पर्शरेखीय पथ पर उड़ जाता है ।
(c) पत्थर स्पर्शी से किसी कोण पर, जिसका परिमाण पत्थर की चाल पर निर्भर करता है, उड़ जाता है।
5.23 स्पष्ट कीजिए कि क्यों:
(a) कोई घोड़ा रिक्त दिक्स्थान में किसी गाड़ी को खींचते हुए दौड़ नहीं सकता।
(b) किसी तीव्र गति से चल रही बस के यकायक रुकने पर यात्री आगे की ओर गिरते हैं।
(c) लान मूवर को धकेलने की तुलना में खींचना आसान होता है।
(d) क्रिकेट का खिलाड़ी गेंद को लपकते समय अपने हाथ गेंद के साथ पीछे को खींचता है।
अतिरिक्त अभ्यास
5.24 चित्र 5.17 में 0.04 kg संहति के किसी पिण्ड का स्थिति-समय ग्राफ दर्शाया गया है। इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिए। पिण्ड द्वारा प्राप्त दो क्रमिक आवेगों के बीच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?
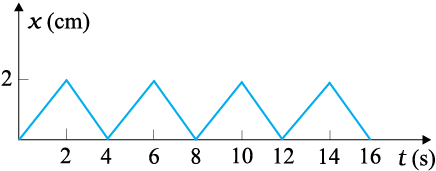
चित्र 5.17
5.25 चित्र 5.18 में कोई व्यक्ति 1 m s–2 त्वरण से गतिशील क्षैतिज संवाहक पट्टे पर स्थिर खड़ा है। उस व्यक्ति पर आरोपित नेट बल क्या है ? यदि व्यक्ति के जूतों और पट्टे के बीच स्थैतिक घर्षण गुणांक 0.2 है, तो पट्टे के कितने त्वरण तक वह व्यक्ति उस पट्टे के सापेक्ष स्थिर रह सकता है ? (व्यक्ति की संहति = 65 kg)
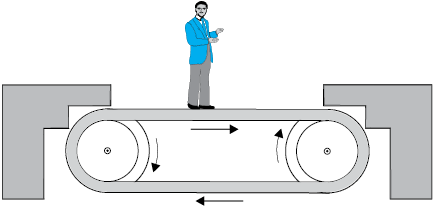
चित्र 5.18
5.26 m संहति के पत्थर को किसी डोरी के एक सिरे से बाँधकर R त्रिज्या के ऊर्ध्वाधर वृत्त में घुमाया जाता है। वृत्त के निम्नतम तथा उच्चतम बिंदुओं पर ऊर्ध्वाधरतः अधोमुखी दिशा में नेट बल हैं: (सही विकल्प चुनिए)
यहाँ T1 तथा v1 निम्नतम बिन्दु पर तनाव तथा चाल दर्शाते हैं। T2 तथा v2 इनके उच्चतम बिन्दु पर तदनुरूपी मान हैं।
5.27 1000 kg संहति का कोई हेलीकॉप्टर 15 m s–2 के ऊर्ध्वाधर त्वरण से ऊपर उठता है। चालक दल तथा यात्रियों की संहति 300 kg है। निम्नलिखित बलों का परिमाण व दिशा लिखिएः
(a) चालक दल तथा यात्रियों द्वारा फर्श पर आरोपित बल,
(b) चारों ओर की वायु पर हेलीकॉप्टर के रोटर की क्रिया, तथा
(c) चारों ओर की वायु के कारण हेलीकॉप्टर पर आरोपित बल ।
5.28 15 m s–1 चाल से क्षैतिजतः प्रवाहित कोई जलधारा 10-2 m2 अनुप्रस्थ काट की किसी नली से बाहर निकलती है तथा समीप की किसी ऊर्ध्वाधर दीवार से टकराती है। जल की टक्कर द्वारा, यह मानते हुए कि जलधारा टकराने पर वापस नहीं लौटती, दीवार पर आरोपित बल ज्ञात कीजिए।
5.29 किसी मेज पर एक-एक रुपये के दस सिक्कों को एक के ऊपर एक करके रखा गया है। प्रत्येक सिक्के की संहति m है। निम्नलिखित प्रत्येक स्थिति में बल का परिमाण एवं दिशा लिखिएः
(a) सातवें सिक्के (नीचे से गिनने पर) पर उसके ऊपर रखे सभी सिक्कों के कारण बल,
(b) सातवें सिक्के पर आठवें सिक्के द्वारा आरोपित बल, तथा
(c) छठे सिक्के की सातवें सिक्के पर प्रतिक्रिया।
5.30 कोई वायुयान अपने पंखों को क्षैतिज से 15॰ के झुकाव पर रखते हुए 720 km h-1 की चाल से एक क्षैतिज लूप पूरा करता है। लूप की त्रिज्या क्या है ?
5.31 कोई रेलगाड़ी बिना ढाल वाले 30 m त्रिज्या के वृत्तीय मोड़ पर 54 km h-1 चाल से चलती है। रेलगाड़ी की संहति 106 kg है। इस कार्य को करने के लिए आवश्यक अभिकेंद्र बल कौन प्रदान करता है ? इंजन अथवा पटरियाँ ? पटरियाें को क्षतिग्रस्त होने से बचाने के लिए मोड़ का ढाल-कोण कितना होना चाहिए ?
5.32 चित्र 5.19 में दर्शाए अनुसार 50 kg संहति का कोई व्यक्ति 25 kg संहति के किसी गुटके को दो भिन्न ढंग से उठाता है । दोनों स्थितियों में उस व्यक्ति द्वारा फर्श पर आरोपित क्रिया-बल कितना है ? यदि 700 N अभिलंब बल से फर्श धँसने लगता है, तो फर्श को धँसने से बचाने के लिए उस व्यक्ति को, गुटके को उठाने के लिए, कौन-सा ढंग अपनाना चाहिए ?
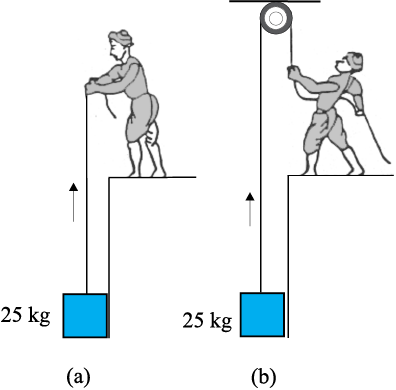
चित्र 5.19
5.33 40 kg संहति का कोई बंदर 600 N का अधिकतम तनाव सह सकने योग्य किसी रस्सी पर चढ़ता है (चित्र 5.20)। नीचे दी गई स्थितियों में से किसमें रस्सी टूट जाएगी:
(a) बंदर 6 m s–2 त्वरण से ऊपर चढ़ता है,
(b) बंदर 4 m s–2 त्वरण से नीचे उतरता है,
(c) बंदर 5 m s–1 की एकसमान चाल से ऊपर चढ़ता है,
(d) बंदर लगभग मुक्त रूप से गुरुत्व बल के प्रभाव में रस्सी से गिरता है।
(रस्सी की संहति उपेक्षणीय मानिए।)

चित्र 5.20
5.34 दो पिण्ड A तथा B, जिनकी संहति क्रमशः 5 kg तथा 10 kg हैं, एक दूसरे के संपर्क में एक मेज पर किसी दृढ़ विभाजक दीवार के सामने विराम में रखे हैं (चित्र 5.21)। पिण्डों तथा मेज के बीच घर्षण गुणांक 0.15 है। 200 N का कोई बल क्षैतिजतः A पर आरोपित किया जाता है। (a) विभाजक दीवार की प्रतिक्रिया, तथा (b)A तथा B के बीच क्रिया-प्रतिक्रिया बल क्या हैं ? विभाजक दीवार को हटाने पर क्या होता है ? यदि पिण्ड गतिशील हैं तो क्या (b) का उत्तर बदल जाएगा ? µs तथा µk के बीच अंतर की उपेक्षा कीजिए।

चित्र 5.21
5.35 15 kg संहति का कोई गुटका किसी लंबी ट्राली पर रखा है। गुटके तथा ट्राली के बीच स्थैतिक घर्षण गुणांक 0.18 है। ट्राली विरामावस्था से 20 s तक 0.5 m s–2 के त्वरण से त्वरित होकर एकसमान वेग से गति करने लगती है। (a) धरती पर स्थिर खड़े किसी प्रेक्षक को, तथा (b) ट्राली के साथ गतिमान किसी अन्य प्रेक्षक को, गुटके की गति कैसी प्रतीत होगी, इसकी विवेचना कीजिए ।
5.36 चित्र 5.22 में दर्शाए अनुसार किसी ट्रक का पिछला भाग खुला है तथा 40 kg संहति का एक संदूक खुले सिरे से 5 m दूरी पर रखा है। ट्रक के फर्श तथा संदूक के बीच घर्षण गुणांक 0.15 है। किसी सीधी सड़क पर ट्रक विरामावस्था से गति प्रारंभ करके 2 m s–2 से त्वरित होता है। आरंभ बिंदु से कितनी दूरी चलने पर वह संदूक ट्रक से नीचे गिर जाएगा? (संदूक के आमाप की उपेक्षा कीजिए।)
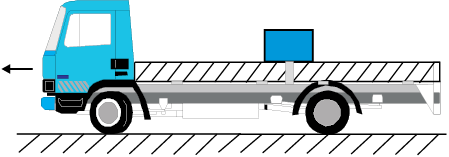
चित्र 5.22
5.37 15 cm त्रिज्या का कोई बड़ा ग्रामोफोन रिकार्ड 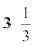 rev/min की चाल से घूर्णन कर रहा है। रिकार्ड पर उसके केंद्र से 4 cm तथा 14 cm की दूरियों पर दो सिक्के रखे गए हैं। यदि सिक्के तथा रिकार्ड के बीच घर्षण गुणांक 0.15 है तो कौन सा सिक्का रिकार्ड के साथ परिक्रमा करेगा ?
rev/min की चाल से घूर्णन कर रहा है। रिकार्ड पर उसके केंद्र से 4 cm तथा 14 cm की दूरियों पर दो सिक्के रखे गए हैं। यदि सिक्के तथा रिकार्ड के बीच घर्षण गुणांक 0.15 है तो कौन सा सिक्का रिकार्ड के साथ परिक्रमा करेगा ?
5.38 आपने सरकस में ‘मौत के कुएँ’ (एक खोखला जालयुक्त गोलीय चैम्बर ताकि उसके भीतर के क्रियाकलापों को दर्शक देख सकें) में मोटरसाइकिल सवार को ऊर्ध्वाधर लूप में मोटरसाइकिल चलाते हुए देखा होगा। स्पष्ट कीजिए कि वह मोटरसाइकिल सवार नीचे से कोई सहारा न होने पर भी गोले के उच्चतम बिंदु से नीचे क्यों नहीं गिरता? यदि चैम्बर की त्रिज्या 25 m है, तो ऊर्ध्वाधर लूप को पूरा करने के लिए मोटरसाइकिल की न्यूनतम चाल कितनी होनी चाहिए ?
5.39 70 kg संहति का कोई व्यक्ति अपने ऊर्ध्वाधर अक्ष पर 200 rev/min की चाल से घूर्णन करती 3 m त्रिज्या की किसी बेलनाकार दीवार के साथ उसके संपर्क में खड़ा है। दीवार तथा उसके कपड़ों के बीच घर्षण गुणांक 0.15 है। दीवार की वह न्यूनतम घूर्णन चाल ज्ञात कीजिए, जिससे फर्श को यकायक हटा लेने पर भी, वह व्यक्ति बिना गिरे दीवार से चिपका रह सके।
5.40 R त्रिज्या का पतला वृत्तीय तार अपने ऊर्ध्वाधर व्यास के परितः कोणीय आवृत्ति ω से घूर्णन कर रहा है। यह दर्शाइए कि इस तार में डली कोई मणिका  के लिए अपने निम्नतम बिंदु पर रहती है।
के लिए अपने निम्नतम बिंदु पर रहती है। 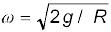 के लिए, केंद्र से मनके को जोड़ने वाला त्रिज्य सदिश ऊर्ध्वाधर अधोमुखी दिशा से कितना कोण बनाता है। (घर्षण को उपेक्षणीय मानिए।)
के लिए, केंद्र से मनके को जोड़ने वाला त्रिज्य सदिश ऊर्ध्वाधर अधोमुखी दिशा से कितना कोण बनाता है। (घर्षण को उपेक्षणीय मानिए।)