Table of Contents

अध्याय 6
कार्य, ऊर्जा और शक्ति
6.1 भूमिका
6.2 कार्य और गतिज ऊर्जा की धारणा : कार्य-ऊर्जा प्रमेय
6.3 कार्य
6.4 गतिज ऊर्जा
6.5 परिवर्ती बल द्वारा किया गया कार्य
6.6 परिवर्ती बल के लिए कार्य-ऊर्जा प्रमेय
6.7 स्थितिज ऊर्जा की अभिधारणा
6.8 यांत्रिक ऊर्जा का संरक्षण
6.9 किसी स्प्रिंग की स्थितिज ऊर्जा
6.10 ऊर्जा के विभिन्न रूप : ऊर्जा-संरक्षण का नियम
6.11 शक्ति
6.12 संघट्ट
6.1 भूमिका
दैनिक बोल चाल की भाषा में हम प्राय: ‘कार्य’, ‘ऊर्जा’, और ‘शक्ति’ शब्दों का प्रयोग करते हैं| यदि कोई किसान खेत जोतता है, कोई मिस्त्री ईंट ढोता है, कोई छात्र परीक्षा के लिए पढ़ता है या कोई चित्रकार सुन्दर दृश्यभूमि का चित्र बनाता है तो हम कहते हैं कि सभी कार्य कर रहे हैं परन्तु भौतिकी में कार्य शब्द को परिशुद्ध रूप से परिभाषित करते हैं| जिस व्यक्ति में प्रतिदिन चौदह से सोलह घण्टें कार्य करने की क्षमता होती है, उसे अधिक शक्ति या ऊर्जा वाला कहते हैं| हम लंबी दूरी वाले घातक को उसकी शक्ति या ऊर्जा के लिए प्रशंसा करते हैं| इस प्रकार ऊर्जा कार्य करने की क्षमता है| भौतिकी में भी ऊर्जा कार्य से इसी प्रकार सम्बन्धित है परन्तु जैसा ऊपर बताया गया है शब्द कार्य को और अधिक परिशुद्ध रूप से परिभाषित करते हैं| शक्ति शब्द का दैनिक जीवन में प्रयोग विभिन्न अर्थों में होता है| कराटे या बॉक्सिंग में शक्तिशाली मुक्का वही माना जाता है जो तेज गति से मारा जाता है| शब्द ‘शक्ति’ का यह अर्थ भौतिकी में इस शब्द के अर्थ के निकट है| हम यह देखेंगे कि इन पदों की भौतिक परिभाषाओं तथा इनके द्वारा मस्तिष्क में बने कार्यकीय चित्रणों के बीच अधिक से अधिक यह सम्बन्ध अल्प ही होता है| इस पाठ का लक्ष्य इन तीन भौतिक राशियों की धारणाओं का विकास करना है लेकिन इसके पहले हमें आवश्यक गणितीय भाषा मुख्यत: दो सदिशों के अदिश गुणनफल को समझना होगा|
6.1.1 अदिश गुणनफल
अध्याय 4 में हम लोगों ने सदिश राशियों और उनके प्रयोगों के बारे में पढ़ा है| कई भौतिक राशियाँ; जैसे-विस्थापन, वेग, त्वरण, बल आदि सदिश हैं| हम लोगों ने सदिशों को जोड़ना और घटाना भी सीखा है| अब हम लोग सदिशों के गुणन के बारे में अध्ययन करेंगे| सदिशों को गुणा करने की दो विधियाँ हैं| प्रथम विधि से दो सदिशों के गुणनफल से अदिश गुणनफल प्राप्त होता है और इसे अदिश गुणनफल कहते हैं| दूसरी विधि में दो सदिशों के गुणनफल से एक सदिश प्राप्त होता है और इसे सदिश गुणनफल कहते हैं| सदिश गुणनफल के बारे में हम लोग अध्याय 7 में पढ़ेंगे| इस अध्याय में हम लोग अदिश गुणनफल की विवेचना करेंगे|
किन्हीं दो सदिशों A तथा B के अदिश या बिंदु-गुणनफल (डॉट गुणनफल) को हम [A.B (A डॅाट B)] के रूप में लिखते हैं और निम्न प्रकार से परिभाषित करते हैं :
A.B = AB cos θ (6.1a)
यहाँ θ दो सदिशों A तथा B के बीच का कोण है| इसे चित्र 6.1a में दिखाया गया है| क्योंकि, B तथा cos θ सभी अदिश हैं इसलिए A तथा B का बिंदु गुणनफल भी अदिश राशि है | A व B में से प्रत्येक की अपनी-अपनी दिशा है किन्तु उनके अदिश गुणनफल की कोई दिशा नहीं है|
समीकरण (6.1a) से हमें निम्नलिखित परिणाम मिलता है :
A.B = A (B cos θ )
= B (A cos θ )
ज्यामिति के अनुसार B cos θ सदिश B का सदिश A पर प्रक्षेप है (चित्र 6.1b)| इसी प्रकार A cos θ सदिश A का सदिश B पर प्रक्षेप है (देखिए चित्र 6.1c)| इस प्रकार A.B सदिश A के परिमाण तथा B के अनुदिश A के घटक के गुणनफल के बराबर होता है| दूसरे तरीके से यह B के परिमाण तथा A का सदिश B के अनुदिश घटक के गुणनफल के बराबर है|
समीकरण (6.1a) से यह संकेत भी मिलता है कि अदिश गुण्नफल क्रम विनिमेय नियम का पालन करता है-
A.B = B.A
अदिश गुणनफल वितरण-नियम का भी पालन करते हैं :
A.(B + C) =A.B +A.C
तथा,
A.(λ B) = λ(A.B)
यहाँ λ एक वास्तविक संख्या है|
उपरोक्त समीकरणों की व्युत्पत्ति आपके लिए अभ्यास हेतु छोड़ी जा रही है|
अब हम एकांक सदिशों 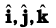 का अदिश गुणनफल निकालेेंगे| क्योंकि वे एक दूसरे के लंबवत् हैं, इसलिए
का अदिश गुणनफल निकालेेंगे| क्योंकि वे एक दूसरे के लंबवत् हैं, इसलिए
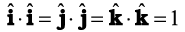
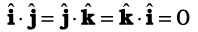

चित्र 6.1 (a) दो सदिशों A व B का अदिश गुणनफल एक अदिश होता है अर्थात् A.B = AB cos θ, (b) B cos θसदिश B का सदिश A पर प्रक्षेप है, (c) A cos θ सदिश A का B पर प्रक्षेप है|
दो सदिशों
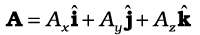
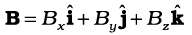
का अदिश गुणनफल होगा : 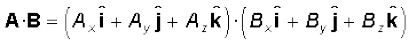
=AxBx +AyBy +AzBz (6.1b)
अदिश गुणनफल परिभाषा तथा समीकरण (6.1b) से हमें निम्न प्राप्त होता है :
(i) A.A =AxAx+AyAy +AzAz
अथवा A2 =A2x +A2y +A2z (6.1c)
क्योंकि A.A = AAcos 0 =A2
(ii) A.B = 0 यदि| A व B एक दूसरे के लंबवत् हैं|
उदाहरण 6.1 बल F = 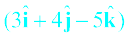 तथा विस्थापन
तथा विस्थापन
d = 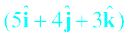 के बीच का कोण ज्ञात करें| F का d पर प्रक्षेप भी ज्ञात करें|
के बीच का कोण ज्ञात करें| F का d पर प्रक्षेप भी ज्ञात करें|
हल F.d = Fxdx + Fydy + Fzdz
= 3(5) + 4(4) + (– 5) (3)
= 16 unit
अत: F.d = Fd cosθ = 16 unit
अब F.F = F2 = 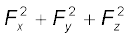
= 9 + 16 + 25
= 50 unit
तथा d.d = d2 = 
= 25 + 16 + 9
= 50 unit
∴ cos θ = 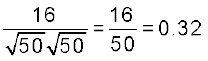
θ = cos– 1 0.32
6.2 कार्य और गतिज ऊर्जा की धारणा : कार्य-ऊर्जा प्रमेय
अध्याय 3 में, नियत त्वरण a के अंतर्गत सरल रेखीय गति के लिए आप निम्न भौतिक संबंध पढ़ चुके हैं;
v2 – u2 = 2as (6.2)
जहाँ u तथा v क्रमश: आरंभिक व अंतिम चाल और s वस्तु द्वारा चली गई दूरी है| दोनों पक्षों को m/2 से गुणा करने पर
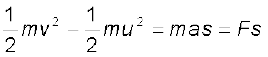 (6.2a)
(6.2a)
जहाँ आखिरी चरण न्यूटन के द्वितीय नियमानुसार है| इस प्रकार सदिशों के प्रयोग द्वारा सहज ही समीकरण (6.2) का त्रिविमीय व्यापकीकरण कर सकते हैं
v2 − u2 = 2 a.d
यहाँ a और b पिंड के क्रमश: त्वरण और विस्थापन सदिश हैं| एक बार फिर दोनों पक्षों को m/2 से गुणा करने पर हम प्राप्त करते हैं
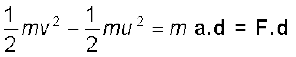 (6.2b)
(6.2b)
उपरोक्त समीकरण कार्य एवं गतिज ऊर्जा को परिभाषित करने के लिए प्रेरित करता है| समीकरण (6.2 b) में बायाँ पक्ष वस्तु के द्रव्यमान के आधे और उसकी चाल के वर्ग के गुणनफल के अंतिम और आरंभिक मान का अंतर है| हम इनमें से प्रत्येक राशि को ‘गतिज ऊर्जा’ कहते हैं और संकेत K से निर्दिष्ट करते हैं| समीकरण का दायाँ पक्ष वस्तु पर आरोपित बल का विस्थापन के अनुदिश घटक और वस्तु के विस्थापन का गुणनफल है| इस राशि को ‘कार्य’ कहते हैं और इसे संकेत W से निर्दिष्ट करते हैं| अत: समीकरण (6.2 b) को निम्न प्रकार लिख सकते हैं :
Kf – Ki = W (6.3)
जहाँ Ki तथा Kf वस्तु की आरंभिक एवं अंतिम गतिज ऊर्जा हैं| कार्य किसी वस्तु पर लगने वाले बल और इसके विस्थापन के संबंध को बताता है| अत: किसी निश्चित विस्थापन के दौरान वस्तु पर लगाया गया बल कार्य करता है|
समीकरण (6.3) कार्य-ऊर्जा प्रमेय की एक विशेष स्थिति है जो यह प्रदर्शित करती है कि किसी वस्तु पर लगाए गए कुुल बल द्वारा किया गया कार्य उस वस्तु की गतिज ऊर्जा में परिवर्तन के बराबर होता है| परिवर्ती बल के लिए उपरोक्त व्युत्पत्ति का व्यापकीकरण हम अनुभाग 6.6 में करेंगे |
उदाहरण 6.2 हम अच्छी तरह जानते हैं कि वर्षा की बूँद नीचे की ओर लगने वाले गुरुत्वाकर्षण बल और बूँद के गिरने की दिशा के विपरीत लगने वाले प्रतिरोधी बल के प्रभाव के अधीन गिरती है| प्रतिरोधी बल बूँद की चाल के अनुक्रमानुपाती, परंतु अनिर्धारित होता है| माना कि
1.00 g द्रव्यमान की वर्षा की बूँद 1.00 km ऊँचाई से गिर रही है| यह धरातल पर 50.00 m s–1 की चाल से संघट्ट करती है| (a) गुरुत्वीय बल द्वारा किया गया कार्य क्या है? (b) अज्ञात प्रतिरोधी बल द्वारा किया गया कार्य क्या है ?
हल (a) बूँद की गतिज ऊर्जा में परिवर्तन
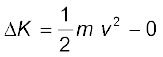
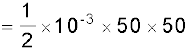
= 1.25 J
यहाँ हमने यह मान लिया है कि बूँद विरामावस्था से गिरना आरंभ करती है|
गुरुत्वाकर्षण बल द्वारा किया गया कार्य Wg = m g h
मान लीजिए कि g = 10 m s–2 है|
अत: Wg = m g h
= 10–3 × 10 × 103
= 10 J
(b) कार्य-ऊर्जा प्रमेय से, ∆K = Wg + Wr
जहाँ Wr प्रतिरोधी बल द्वारा किया गया कार्य है| अत:
Wr = ∆K – Wg
= 1.25 – 10
= – 8.75 J
ऋणात्मक है| °
6.3 कार्य
उपरोक्त अनुभाग में आपने देखा कि कार्य, बल और उसके द्वारा वस्तु के विस्थापन से संबंधित होता है| माना कि एक अचर बल F, किसी m द्रव्यमान के पिंड पर लग रहा है जिसके कारण पिंड का धनात्मक x-दिशा में होने वाला विस्थापन d है जैसा कि चित्र 6.2 में दर्शाया गया है|
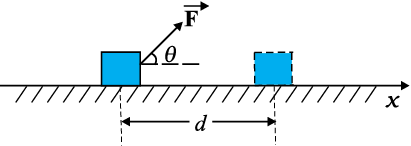
चित्र 6.2 किसी पिंड का आरोपित बल F के कारण विस्थापन d |
अत: किसी बल द्वारा किया गया कार्य "बल के विस्थापन की दिशा के अनुदिश घटक और विस्थापन के परिमाण के गुणनफल" के रूप में परिभाषित किया जाता है| अत:
W = ( F cos θ) d = F . d (6.4)
हम देखते हैं कि यदि वस्तु का विस्थापन शून्य है तो बल का परिमाण कितना ही अधिक क्यों न हो, वस्तु द्वारा किया गया कार्य शून्य होता है| जब कभी आप किसी ईंटों की दृढ़ दीवार को धक्का देते हैं तो कोई कार्य नहीं होता है| इस प्रक्रिया में आपकी मांसपेशियों का बारी-बारी से संकुचन और शिथिलीकरण हो रहा है और आंतरिक ऊर्जा लगातार व्यय हो रही है और आप थक जाते हैं| भौतिक विज्ञान में कार्य का अर्थ इसके दैनिक भाषा में प्रयोग के अर्थ से भिन्न है|
कोई भी कार्य संपन्न हुआ नहीं माना जाता है यदि :
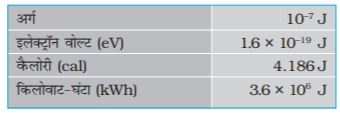
सारणी 6.1 : कार्य/ऊर्जा के वैकल्पिक मात्रक (जूल में)
(i) वस्तु का विस्थापन शून्य है, जैसा कि पूर्ववर्ती उदाहरण में आपने देखा| कोई भारोत्तोलक 150 kg द्रव्यमान के भार को 30 s तक अपने कंधे पर लगातार उठाए हुए खड़ा है तो वह कोई कार्य नहीं कर रहा है |
(ii) बल शून्य है| किसी चिकनी क्षैतिज मेज पर गतिमान पिंड पर कोई क्षैतिज बल कार्य नहीं करता है, (क्योंकि घर्षण नहीं है) परंतु पिंड का विस्थापन काफी अधिक हो सकता है|
(iii) बल और विस्थापन परस्पर लंबवत् हैं क्योंकि θ = π/2 rad ( = 90°), cos (π/2) = 0| किसी चिकनी क्षैतिज मेज पर गतिमान पिंड के लिए गुरुत्वाकर्षण बल m g कोई कार्य नहीं करता है क्योंकि यह विस्थापन के लंबवत् कार्य कर रहा है| पृथ्वी के परित: चंद्रमा की कक्षा लगभग वृत्ताकार है| यदि हम चंद्रमा की कक्षा को पूर्ण रूप से वृत्ताकार मान लें, तो पृथ्वी का गुरुत्वाकर्षण बल कोई कार्य नहीं करता है क्योंकि चंद्रमा का तात्कालिक विस्थापन स्पर्शरेखीय है जबकि पृथ्वी का बल त्रिज्यीय (केंद्र की ओर) है, अर्थात् θ = π/2 |
कार्य धनात्मक व ऋणात्मक दोनों प्रकार का हो सकता है| यदि θ, 0° और 90° के मध्य है तो समीकरण (6.4) में cos θ का मान धनात्मक होगा| यदि θ, 90° और 180° के मध्य है तो cos θ का मान ऋणात्मक होगा| अनेक उदाहरणों में घर्षण बल, विस्थापन का विरोध करता है और θ = 180° होता है| एेसी दशा में घर्षण बल द्वारा किया गया कार्य ऋणात्मक होता है (cos 180° = –1)|
समीकरण (6.4) से स्पष्ट है कि कार्य और ऊर्जा की विमाएँ समान [M L2 T–2] हैं | ब्रिटिश भौतिकविद जेम्स प्रेसकॉट जूल (1818-1869) के सम्मान में इनका SI मात्रक ‘जूल’ कहलाता है| चूंकि कार्य एवं ऊर्जा व्यापक रूप से
भौतिक धारणाओं के रूप में प्रयोग किए जाते हैं, अत: ये वैकल्पिक मात्रकों से भरपूर हैं और उनमें से कुछ सारणी 6.1 में सूचीबद्ध हैं|
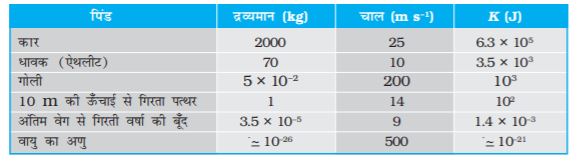
सारणी 6.2 विशिष्ट गतिज ऊर्जाएँ (K)
¯ उदाहरण 6.3 कोई साइकिल सवार ब्रेक लगाने पर फिसलता हुआ 10 m दूर जाकर रुकता है| इस प्रक्रिया की अवधि में, सड़क द्वारा साइकिल पर लगाया गया बल 200 N है जो उसकी गति के विपरीत है| (a) सड़क द्वारा साइकिल पर कितना कार्य किया गया?
(b) साइकिल द्वारा सड़क पर कितना कार्य किया गया?
हल सड़क द्वारा साइकिल पर किया गया कार्य सड़क द्वारा साइकिल पर लगाए गए विरोधी (घर्षण बल) द्वारा किया किया कार्य है|
(a) यहाँ विरोधी बल और साइकिल के विस्थापन के मध्य कोण 180° (या π rad) है| अत: सड़क द्वारा किया गया कार्य
Wr = Fd cos θ
= 200 × 10 × cos π
= –2000 J
कार्य-ऊर्जा प्रमेय के अनुसार, इस ऋणात्मक कार्य के कारण ही साइकिल रुक जाती है|
(b) न्यूटन के गति के तृतीय नियमानुसार साइकिल द्वारा सड़क पर लगाया गया बल सड़क द्वारा साइकिल पर लगाए बल के बराबर परंतु विपरीत दिशा में होगा| इसका परिमाण 200N है | तथापि, सड़क का विस्थापन नहीं होता है | अत: साइकिल द्वारा सड़क पर किया गया कार्य शून्य होगा|
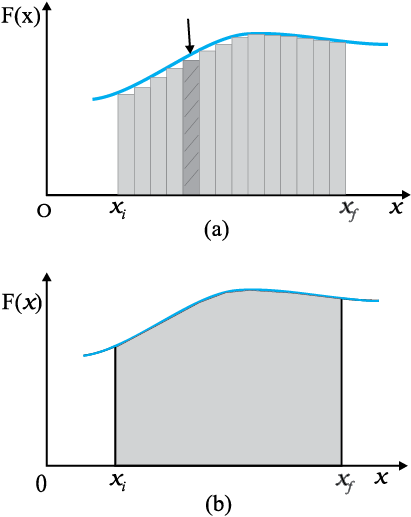
चित्र 6.3 (a) परिवर्ती बल F(x) द्वारा सूक्ष्म विस्थापन ∆x में किया गया कार्य ∆W = F(x)∆x छायांकित आयत से निरूपित है | (b) ∆x → 0 के लिए सभी आयतों के क्षेत्रफलों को जोड़ने पर, वक्र द्वारा आच्छादित क्षेत्रफल, बल F(x) द्वारा किए गए कार्य के ठीक बराबर है |
इस उदाहरण से हमें यह पता चलता है कि यद्यपि पिंड B द्वारा A पर लगाया गया बल, पिंड A द्वारा पिंड B पर लगाए गए बल के बराबर तथा विपरीत दिशा में है (न्यूटन का गति का तीसरा नियम) तथापि यह आवश्यक नहीं है कि पिंड B द्वारा A पर किया गया कार्य, पिंड A द्वारा B पर किए गए कार्य के बराबर तथा विपरीत दिशा में हो|
6.4 गतिज ऊर्जा
जैसा कि पहले उल्लेख किया गया है, यदि किसी पिंड का द्रव्यमान m और वेग v है तो इसकी गतिज ऊर्जा,
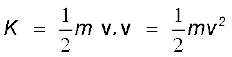 (6.5)
(6.5)
गतिज ऊर्जा एक अदिश राशि है|
किसी पिंड की गतिज ऊर्जा, उस पिंड द्वारा किए गए कार्य की माप होती है जो वह अपनी गति के कारण कर सकता है| इस धारणा का अंतर्ज्ञान काफी समय से है| तीव्र गति से बहने वाली जल की धारा की गतिज ऊर्जा का उपयोग अनाज पीसने के लिए किया जाता है| पाल जलयान पवन की गतिज ऊर्जा का प्रयोग करते हैं| सारणी 6.2 में विभिन्न पिंडों की गतिज ऊर्जाएँ सूचीबद्ध हैं|
उदाहरण 6.4 किसी प्राक्षेपिक प्रदर्शन में एक पुलिस अधिकारी 50 g द्रव्यमान की गोली को 2cm मोटी नरम परतदार लकड़ी (प्लाइवुड) पर 200 m s–1 की चाल से फायर करता है| नरम लकड़ी को भेदने के पश्चात् गोली की गतिज ऊर्जा प्रारंभिक ऊर्जा की 10% रह जाती है| लकड़ी से निकलते समय गोली की चाल क्या होगी?
हल चित्र 6.4 में आरोपित बल का आलेख प्रदर्शित किया गया है |
हल गोली की प्रारंभिक गतिज ऊर्जा mv2/2 = 1000 J
गोली की अंतिम गतिज ऊर्जा = 0.1 × 1000 = 100 J| यदि गोली की नरम लकड़ी को भेदने के पश्चात् चाल vf है तो,
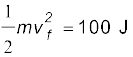
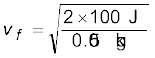
= 63.2 m s–1
नरम लकड़ी को भेदने के पश्चात् गोली की चाल लगभग 68% कम हो गई है (90% नहीं)| °
6.5 परिवर्ती बल द्वारा किया गया कार्य
अचर बल दुष्प्राप्य है| अधिकतर परिवर्ती बल के उदाहरण ही देखने को मिलते हैं| चित्र 6.3 एकविमीय परिवर्ती बल का आलेख है|
यदि विस्थापन ∆x सूक्ष्म है तब हम बल F(x) को भी लगभग नियत ले सकते हैं और तब किया गया कार्य
∆W = F(x) ∆x
इसे चित्र 6.3(a) में समझाया गया है| चित्र 6.3 (a) में क्रमिक आयताकार क्षेत्रफलों का योग करने पर हमें कुल किया गया कार्य प्राप्त होता है जिसे इस प्रकार लिखा जाता है :
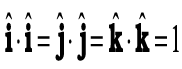 (6.6)
(6.6)
जहाँ संकेत ‘∑’ का अर्थ है संकलन-फल (योगफल), जबकि 'xi' वस्तु की आरंभिक स्थिति और 'xf' वस्तु की अंतिम स्थिति को निरूपित करता है|
यदि विस्थापनों को अतिसूक्ष्म मान लिया जाए तब योगफल में पदों की संख्या असीमित रूप से बढ़ जाती है लेकिन योगफल एक निश्चित मान के समीप पहुंच जाता है जो
चित्र 6.3(b) में वक्र के नीचे के क्षेत्रफल के समान होता है | अत: किया गया कार्य
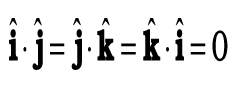
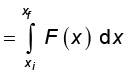
 (6.7)
(6.7)
जहाँ 'lim' का अर्थ है ‘योगफल की सीमा’ जबकि ∆x नगण्य रूप से सूक्ष्म मानों की ओर अग्रसर है| इस प्रकार परिवर्ती बल के लिए किए गए कार्य को बल का विस्थापन पर सीमांकित समाकलन, के रूप में व्यक्त कर सकते हैं (परिशिष्ट 3.1 भी देखें)
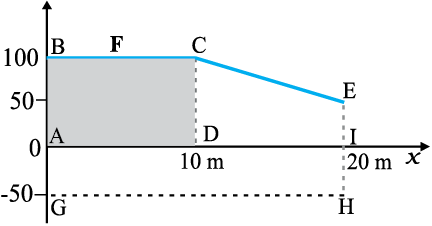
¯ उदाहरण 6.4 कोई स्त्री खुरदरी सतह वाले रेलवे प्लेटफार्म पर संदूक को खिसकाती है| वह 10 m की दूरी तक 100 N का बल आरोपित करती है| उसके पश्चात्, उत्तरोत्तर वह थक जाती है और उसके द्वारा आरोपित बल रेखीय रूप से घटकर 50 N हो जाता है| संदूक को कुल 20 m की दूरी तक खिसकाया जाता है| स्त्री द्वारा संदूक पर आरोपित बल और घर्षण बल जो कि 50 N है, तथा विस्थापन के बीच ग्राफ खींचिए| दोनों बलों द्वारा 20 m तक किए गए कार्य का परिकलन कीजिए |
चित्र 6.4 किसी स्त्री द्वारा आरोपित बल F और विरोधी घर्षण बल f तथा विस्थापन के बीच ग्राफ|
x = 20 m पर F = 50 N(≠ 0) है| हमें घर्षण बल f दिया गया है जिसका परिमाण है
| f | = 50 N
यह गति का विरोध करता है और आरोपित बल F के विपरीत दिशा में कार्य करता है| इसलिए, इसे बल-अक्ष की ऋणात्मक दिशा की ओर प्रदर्शित किया गया है|
स्त्री द्वारा किया गया कार्य WF→(आयत ABCD + समलंब CEID) का क्षेत्रफल
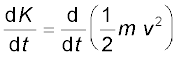
= 1000 + 750
= 1750 J
घर्षण बल द्वारा किया गया कार्य WF→आयत AGHI का क्षेत्रफल
Wf = (–50) × 20
= – 1000J
यहाँ क्षेत्रफल का बल-अक्ष के ऋणात्मक दिशा की ओर होने से, क्षेत्रफल का चिह्न ऋणात्मक है| °
6.6 परिवर्ती बल के लिए कार्य-ऊर्जा प्रमेय
हम परिवर्ती बल के लिए कार्य-ऊर्जा प्रमेय को सिद्ध करने के लिए कार्य और गतिज ऊर्जा की धारणाओं से भलीभांति परिचित हैं| यहाँ हम कार्य-ऊर्जा प्रमेय के एकविमीय पक्ष तक ही विचार को सीमित करेंगे| गतिज ऊर्जा परिवर्तन की दर है :
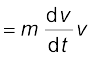

= Fv (न्यूटन के दूसरे नियमानुसार 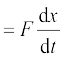 = F )
= F )
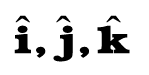
अत: dK = Fdx
प्रारंभिक स्थिति xi से अंतिम स्थिति xf तक समाकलन करने पर,
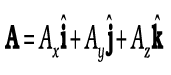
जहाँ xi और xf के संगत Ki और Kf क्रमश: प्रारंभिक एवं अंतिम गतिज ऊर्जाएँ हैं|
या 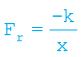 (6.8 a)
(6.8 a)
समीकरण (6.7) से प्राप्त होता है
Kf – Ki = W (6.8 b)
इस प्रकार परिवर्ती बल के लिए कार्य-ऊर्जा प्रमेय सिद्ध होती है|
हालांकि कार्य-ऊर्जा प्रमेय अनेक प्रकार के प्रश्नों को हल करने में उपयोगी है परंतु यह न्यूटन के द्वितीय नियम की पूर्णरूपेण गतिकीय सूचना का समावेश नहीं करती है| वास्तव में यह न्यूटन के द्वितीय नियम का समाकल रूप है| न्यूटन का द्वितीय नियम किसी क्षण, त्वरण तथा बल के बीच संबंध दर्शाता है| कार्य-ऊर्जा प्रमेय में एक काल के लिए समाकल निहित है| इस दृष्टि से न्यूटन के द्वितीय नियम में निहित कालिक सूचना कार्य ऊर्जा प्रमेय में स्पष्ट रूप से प्रकट नहीं होता| बल्कि एक निश्चित काल के लिए समाकलन के रूप में होता है| दूसरी ध्यान देने की बात यह है कि दो या तीन विमाओं में न्यूटन का द्वितीय नियम सदिश रूप में होता है जबकि कार्य-ऊर्जा प्रमेय अदिश रूप में होता है| न्यूटन के द्वितीय नियम में दिशा संबंधित निहित ज्ञान भी कार्य ऊर्जा प्रमेय जैसे- अदिश संबंध निहित नहीं है|
¯ उदाहरण 6.6 m (=1kg) द्रव्यमान का एक गुटका क्षैतिज सतह पर vi = 2 m s–1 की चाल से चलते हुए
x = 0.10 m से x = 2.01m के खुरदरे हिस्से प्रवेश करता है| गुटके पर लगने वाला मंदक बल (Fr) इस क्षेत्र में x के व्युत्क्रमानुपाती है,
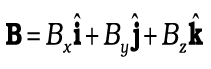 0.1< x < 2.01m
0.1< x < 2.01m
= 0 x < 0.1m और x > 2.01m के लिए
जहाँ k = 0.5J| गुटका जैसे ही खुरदरे हिस्से को पार करता है, इसकी अंतिम गतिज ऊर्जा और चाल vf की गणना कीजिए|
हल समीकरण (6.8 a) से
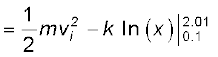
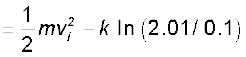
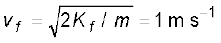
= 2 − 0.5 ln (20.1)
= 2 − 1.5 = 0.5 J
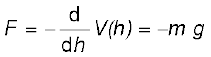
ध्यान दीजिए कि ln आधार e पर किसी संख्या का प्राकृतिक लघुगणक है, न कि आधार 10 पर किसी संख्या का
[ln X = loge X = 2.303 log10 X] °
6.7 स्थितिज ऊर्जा की अभिधारणा
यहाँ ‘स्थितिज’ शब्द किसी कार्य को करने की संभावना या क्षमता को व्यक्त करता है| स्थितिज ऊर्जा की धारणा ‘संग्रहित’ ऊर्जा से संबंधित है| किसी खि्ांचे हुए तीर-कमान के तार (डोरी) की ऊर्जा स्थितिज ऊर्जा होती है| जब इसे ढीला छोड़ा जाता है तो तीर तीव्र चाल से दूर चला जाता है| पृथ्वी के भूपृष्ठ पर भ्रंश रेखाएँ संपीडित कमानियों के सदृश होती हैं| उनकी स्थितिज ऊर्जा बहुत अधिक होती है| जब ये भ्रंश रेखाएँ फिर से समायोजित हो जाती हैं तो भूकंप आता है| किसी भी पिंड की स्थितिज ऊर्जा (संचित ऊर्जा) उसकी स्थिति या अभिविन्यास के कारण होती है| पिंड को मुक्त रूप से छोड़ने पर इसमें संचित ऊर्जा, गतिज ऊर्जा के रूप में निर्मुक्त होती है| आइए, अब हम स्थितिज ऊर्जा की धारणा को एक निश्चित रूप देते हैं|
पृथ्वी की सतह के समीप m द्रव्यमान की एक गेंद पर आरोपित गुरुत्वाकर्षण बल m g है| g को पृथ्वी की सतह के समीप अचर माना जा सकता है | यहाँ समीपता से तात्पर्य यह है कि गेंद की पृथ्वी की सतह से ऊँचाई h, पृथ्वी की त्रिज्या RE की तुलना में अति सूक्ष्म है (h << RE), अत: हम पृथ्वी के पृष्ठ पर g के मान में परिवर्तन की उपेक्षा कर सकते हैं|* माना कि गेंद को बिना कोई गति प्रदान किए h ऊँचाई तक ऊपर उठाया जाता है| अत: बाह्य कारक द्वारा गुरुत्वाकर्षण बल के विरुद्ध किया गया कार्य m g h होगा| यह कार्य, स्थितिज ऊर्जा के रूप में संचित हो जाता है| किसी पिण्ड की h ऊँचाई पर गुरुत्वीय स्थितिज ऊर्जा उसी पिण्ड को उसी ऊँचाई तक उठाने में गुरुत्वाकर्षण बल द्वारा किए गए कार्य के ऋणात्मक मान के बराबर होता है|
V(h) = m g h
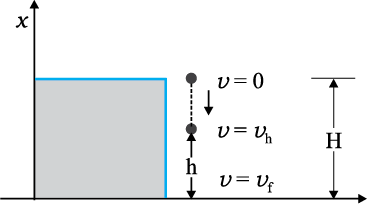
चित्र 6.5 H ऊँचाई की किसी चट्टान से गिराई गई, m द्रव्यमान की गेंद की स्थितिज ऊर्जा का गतिज ऊर्जा में रूपांतरण|
यदि h को परिवर्ती लिया जाता है तो यह सरलता से देखा जा सकता है कि गुरुत्वाकर्षण बल F, h के सापेक्ष V(h) के ऋणात्मक अवकलज के समान है
यहाँ ऋणात्मक चिह्न प्रदर्शित करता है कि गुरुत्वाकर्षण बल नीचे की ओर है| जब गेंद को छोड़ा जाता है तो यह बढ़ती हुई चाल से नीचे आती है | पृथ्वी की सतह से संघट्ट से पूर्व इसकी चाल शुद्धगतिकी संबंध द्वारा निम्न प्रकार दी जाती है
v2 = 2 g h
इसी समीकरण को निम्न प्रकार से भी लिखा जा सकता है :
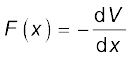 m v2 = m g h
m v2 = m g h
जो यह प्रदर्शित करता है कि जब पिण्ड को मुक्त रूप से छोड़ा जाता है तो पिंड की h ऊँचाई पर गुरुत्वीय स्थितिज ऊर्जा पृथ्वी पर पहुंचने तक स्वत: ही गतिज ऊर्जा में परिवर्तित हो जाती है |
प्राकृतिक नियमानुसार, स्थितिज ऊर्जा की धारणा केवल उन्हीं बलों की श्रेणी में लागू होती है जहाँ बल के विरुद्ध किया गया कार्य, ऊर्जा के रूप में संचित हो जाता है और जो बाह्य कारक के हट जाने पर स्वत: गतिज ऊर्जा के रूप में दिखाई पड़ती है| गणितानुसार स्थितिज ऊर्जा V (x) को (सरलता के लिए एक-विमा में)
परिभाषित किया जाता है यदि F(x) बल को निम्न रूप में लिखा जाता है :
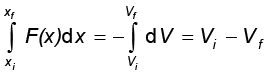
यह निरूपित करता है कि
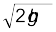
किसी संरक्षी बल जैसे गुरुत्वाकर्षण बल द्वारा किया गया कार्य पिण्ड की केवल आरंभिक तथा अंतिम स्थिति पर निर्भर करता है| पिछले अध्याय में हमने आनत समतल से संबंधित उदाहरणों का अध्ययन किया | यदि m द्रव्यमान का कोई पिण्ड h ऊंचाई के चिकने (घर्षणरहित) आनत तल के शीर्ष से विरामावस्था से छोड़ा जाता है तो आनत समतल के अधस्तल (तली) पर इसकी चाल, आनति (झुकाव) कोण का ध्यान रखे बिना 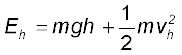 होती है| इस प्रकार यहां पर पिण्ड m g h गतिज ऊर्जा प्राप्त कर लेता है| यदि किया गया कार्य या गतिज ऊर्जा दूसरे कारकों, जैसे पिण्ड के वेग या उसके द्वारा चले गए विशेष पथ की लंबाई पर निर्भर करता है तब यह बल असंरक्षी होता है|
होती है| इस प्रकार यहां पर पिण्ड m g h गतिज ऊर्जा प्राप्त कर लेता है| यदि किया गया कार्य या गतिज ऊर्जा दूसरे कारकों, जैसे पिण्ड के वेग या उसके द्वारा चले गए विशेष पथ की लंबाई पर निर्भर करता है तब यह बल असंरक्षी होता है|
कार्य या गतिज ऊर्जा के सदृश स्थितिज ऊर्जा की विमा
[ML2T–2] और SI मात्रक जूल (J) है| याद रखिए कि संरक्षी बल के लिए, स्थितिज ऊर्जा में परिवर्तन ∆V बल द्वारा किए गए ऋणात्मक कार्य के बराबर होता है|
∆V = –F(x) ∆x (6.9)
इस अनुभाग में गिरती हुई गेंद के उदाहरण में हमने देखा कि किस प्रकार गेंद की स्थितिज ऊर्जा उसकी गतिज ऊर्जा में परिवर्तित हो गई थी| यह यांत्रिकी में संरक्षण के महत्त्वपूर्ण सिद्धांत की ओर संकेत करता है जिसे हम अब परखेंगे|
6.8 यांत्रिक ऊर्जा का संरक्षण
सरलता के लिए, हम इस महत्त्वपूर्ण सिद्धांत का एकविमीय गति के लिए निदर्शन कर रहे हैं| मान लीजिए कि किसी पिण्ड का संरक्षी बल F के कारण विस्थापन ∆x होता है| कार्य-ऊर्जा प्रमेय से, किसी बल F के लिए
∆K = F(x) ∆x
संरक्षी बल के लिए स्थितिज ऊर्जा फलन V(x) को निम्न रूप से परिभाषित किया जा सकता है :
−∆V = F(x)∆x
उपरोक्त समीकरण निरूपित करती है कि
∆K + ∆V = 0
∆(K + V) = 0 (6.10)
इसका अर्थ है कि किसी पिण्ड की गतिज और स्थितिज ऊर्जाओं का योगफल, K + V अचर होता है| इससे तात्पर्य है कि संपूर्ण पथ xi से xf के लिए
Ki + V (xi) = Kf + V (xf) (6.11)
यहाँ राशि K + V(x), निकाय की कुल यांत्रिक ऊर्जा कहलाती है| पृथक रूप से, गतिज ऊर्जा K और स्थितिज ऊर्जा V(x) एक स्थिति से दूसरी स्थिति तक परिवर्तित हो सकती है परंतु इनका योगफल अचर रहता है| उपरोक्त विवेचन से शब्द ‘संरक्षी बल’ की उपयुक्तता स्पष्ट होती है|
आइए, अब हम संक्षेप में संरक्षी बल की विभिन्न परिभाषाओं पर विचार करते हैं|
कोई बल F(x) संरक्षी है यदि इसे समीकरण (6.9) के प्रयोग द्वारा अदिश राशि V(x) से प्राप्त कर सकते हैं| त्रिविमीय व्यापकीकरण के लिए सदिश अवकलज विधि का प्रयोग करना पड़ता है जो इस पुस्तक के विवेचना क्षेत्र से बाहर है|
स्ांरक्षी बल द्वारा किया गया कार्य केवल सिरे के बिंदुओं पर निर्भर करता है जो निम्न संबंध से स्पष्ट है :
चित्र 6.7 किसी स्प्रिंग के मुक्त सिरे से जुड़े हुए गुटके पर स्प्रिंग-बल का निदर्शन
(a) जब माध्य स्थिति से विस्थापन x शून्य है तो स्प्रिंग बल Fs भी शून्य है |
(b) खिंचे हुए स्प्रिंग के लिए x > 0 और Fs < 0
(c) संपीडित स्प्रिंग के लिए x < 0 और Fs > 0
(d) Fs तथा x के बीच खींचा गया आलेख | छायांकित त्रिभुज का क्षेत्रफल स्प्रिंग-बल द्वारा किए गए कार्य को निरूपित करता है| Fs और x के विपरीत चिह्नों के कारण, किया गया कार्य ऋणात्मक है, 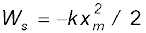
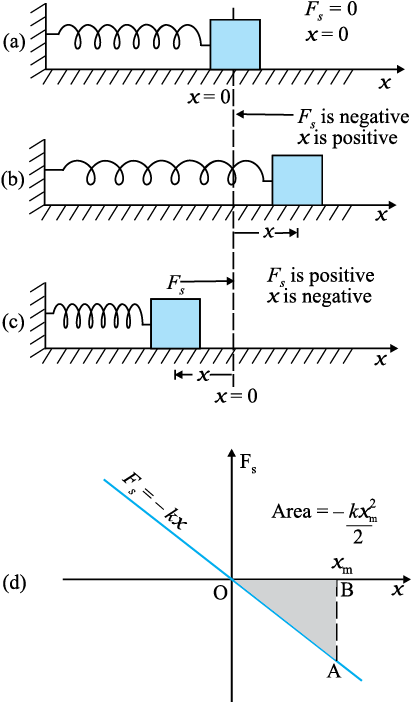

क्षेत्रफल =
W = Kf – Ki = V(xi) – V(xf)
तीसरी परिभाषा के अनुसार, इस बल द्वारा बंद पथ में किया गया कार्य शून्य होता है|
यह एक बार फिर समीकरण (6.11) से स्पष्ट है, क्योंकि
xi = xf है|
अत: यांत्रिक ऊर्जा-संरक्षण नियम के अनुसार किसी भी निकाय की कुल यान्त्रिक ऊर्जा अचर रहती है यदि उस पर कार्य करने वाले बल संरक्षी हैं|
उपरोक्त विवेचना को अधिक मूर्त बनाने के लिए, एक बार फिर गुरुत्वाकर्षण बल के उदाहरण पर विचार करते हैं और स्प्रिंग बल के उदाहरण पर अगले अनुभाग में विचार करेंगे | चित्र
6.5 H ऊँचाई की किसी चट्टान से गिराई, m द्रव्यमान की गेंद का चित्रण करता है|
गेंद की निदर्शित ऊँचाई, शून्य (भूमितल), h और H के संगत कुल यांत्रिक ऊर्जाएँ क्रमश: Eo, Eh और EH हैं
EH = m g H (6.11a)
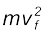 (6.11b)
(6.11b)
E0 = (1/2) (6.11c)
(6.11c)
अचर बल, त्रिविम-निर्भर बल F(x) का एक विशेष उदाहरण है | अत: यांत्रिक ऊर्जा संरक्षित है| इस प्रकार
EH = E0
अथवा, 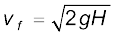
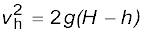
उपरोक्त परिणाम अनुभाग 6.7 में मुक्त रूप से गिरते हुए पिण्ड के वेग के लिए प्राप्त किया गया था|
इसके अतिरिक्त
EH = Eh
जो इंगित करता है कि
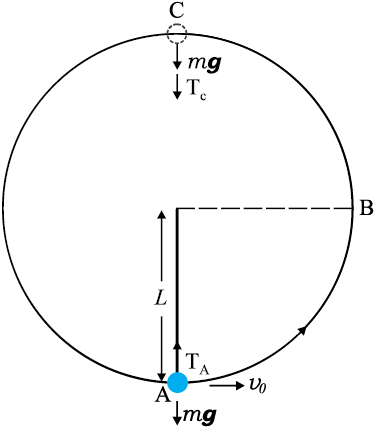 (6.11d)
(6.11d)
उपरोक्त परिणाम, शुद्धगतिकी का एक सुविदित परिणाम है|
H ऊँचाई पर, पिण्ड की ऊर्जा केवल स्थितिज ऊर्जा है| यह h ऊँचाई पर आंशिक रूप से गतिज ऊर्जा में रूपांतरित हो जाती है तथा भूमि तल पर पूर्णरूपेण गतिज ऊर्जा में रूपांतरित हो जाती है| इस प्रकार उपरोक्त उदाहरण, यांत्रिक ऊर्जा के संरक्षण के सिद्धांत को स्पष्ट करता है|
उदाहरण 6.7m द्रव्यमान का एक गोलक L लंबाई की हलकी डोरी से लटका हुआ है| इसके निम्नतम बिंदु A पर क्षैतिज वेग vo इस प्रकार लगाया जाता है कि यह ऊर्ध्वाधर तल में अर्धवृत्ताकार प्रक्षेप्य पथ को इस प्रकार तय करता है कि डोरी केवल उच्चतम बिंदु C पर ढीली होती है जैसा कि चित्र 6.6 में दिखाया गया है| निम्न राशियों के लिए व्यंजक प्राप्त कीजिए : (a) v0, (b) बिंदुओं B तथा C पर गोलक की चाल, तथा (c) बिंदु B तथा C पर गतिज ऊर्जाओं का अनुपात (KB/KC)| गोलक के बिंदु C पर पहुंचने के बाद पथ की प्रकृति पर टिप्पणी कीजिए |
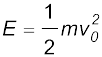
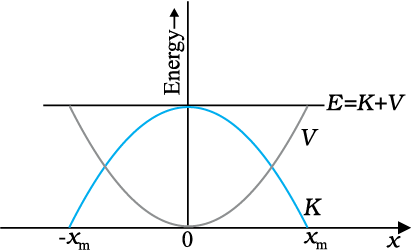
चित्र 6.6
हल (a) यहाँ गोलक पर लगने वाले दो बाह्य बल हैं-गुरुत्व बल और डोरी में तनाव ( T )| बाद वाला बल (तनाव) कोई कार्य नहीं करता है क्योंकि गोलक का विस्थापन हमेशा डोरी के लंबवत् है| अत: गोलक की स्थितिज ऊर्जा केवल गुरुत्वाकर्षण बल से संबंधित है| निकाय की संपूर्ण यांत्रिक ऊर्जा E अचर है | हम निकाय की स्थितिज ऊर्जा निम्नतम बिंदु A पर शून्य ले लेते हैं| अत: बिंदु A पर ऊर्जा
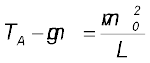 (6.12)
(6.12)
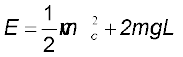 [न्यूटन के गति के द्वितीय नियमानुसार]
[न्यूटन के गति के द्वितीय नियमानुसार]
यहाँ TA, बिंदु A पर डोरी का तनाव है| उच्चतम बिंदु C पर डोरी ढीली हो जाती है; अत: यहाँ बिंदु C पर डोरी का तनाव
TC = 0| अत: बिंदु C पर हमें प्राप्त होता है
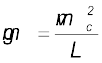 (6.13)
(6.13)
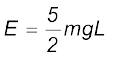 [न्यूटन के द्वितीय नियमानुसार] (6.14)
[न्यूटन के द्वितीय नियमानुसार] (6.14)
जहाँ vc बिंदु C पर गोलक की चाल है| समीकरण (6.13) व (6.14) से प्राप्त होता है
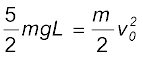
इसे बिंदु A पर ऊर्जा से समीकृत करने पर
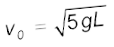
अथवा 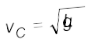
(b) समीकरण (6.14) से यह स्पष्ट है कि
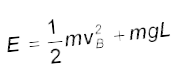
अत: बिंदु B पर ऊर्जा है
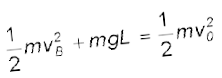
इसे बिंदु A पर ऊर्जा के व्यंजक के बराबर रखने पर और (a) के परिणाम v20 = 5gL प्रयोग में लाने पर हमें प्राप्त
होता है|
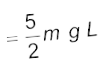
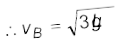
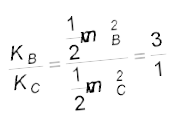
(c) बिंदु B व C पर गतिज ऊर्जाओं का अनुपात
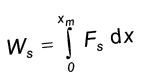
बिंदु C पर डोरी ढीली हो जाती है और गोलक का वेग बाईं ओर को एवं क्षैतिज हो जाता है| यदि इस क्षण पर डोरी को काट दिया जाए तो गोलक एक क्षैतिज प्रक्षेप की भांति प्रक्षेप्य गति ठीक उसी प्रकार दर्शाएगा जैसा कि खड़ी चट्टान से क्षैतिज दिशा में किसी पत्थर को फेंकने पर होता है| अन्यथा गोलक लगातार अपने वृत्ताकार पथ पर गति करता रहेगा और परिक्रमण को पूर्ण करेगा| °
6.9 किसी स्प्रिंग की स्थितिज ऊर्जा
कोई स्प्रिंग-बल एक परिवर्ती-बल का उदाहरण है जो संरक्षी होता है |
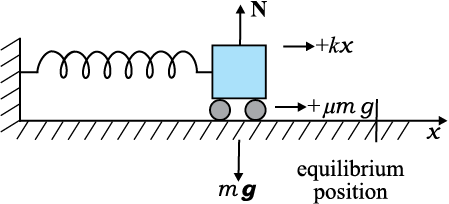
चित्र 6.7 स्प्रिंग से संलग्न किसी गुटके को दर्शाता है जो किसी चिकने क्षैतिज पृष्ठ पर विरामावस्था में है| स्प्रिंग का दूसरा सिरा किसी दृढ़ दीवार से जुड़ा है| स्प्रिंग हलका है और द्रव्यमान-रहित माना जा सकता है| किसी आदर्श स्प्रिंग में, स्प्रिंग-बल Fs, गुटके का अपनी साम्यावस्था स्थिति से विस्थापन x के समानुपाती होता है| गुटके का साम्यावस्था से विस्थापन धनात्मक (चित्र 6.7b) या ऋणात्मक (चित्र 6.7c) हो सकता है| स्प्रिंग के लिए बल का नियम, हुक का नियम कहलाता है और गणितीय रूप में इस प्रकार व्यक्त किया जा सकता है :
साम्यावस्था स्थिति
Fs = – k x
जहाँ नियतांक k एक स्प्रिंग नियतांक है जिसका मात्रक N m–1 है| यदि k का मान बहुत अधिक है, तब स्प्रिंग को दृढ़ कहा जाता है| यदि k का मान कम है, तब इसे नर्म (मृदु) कहा जाता है|
मान लीजिए कि हम गुटके को बाहर की तरफ, जैसा कि चित्र 6.7(b) में दिखाया गया है, धीमी अचर चाल से खींचते हैं | यदि स्प्रिंग का खिंचाव xm है तो स्प्रिंग-बल द्वारा किया कार्य

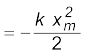
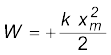 (6.15)
(6.15)
इस व्यंजक को हम चित्र 6.7(d) में दिखाए गए त्रिभुज के क्षेत्रफल से भी प्राप्त कर सकते हैं| ध्यान दीजिए कि बाह्य खिंचाव बल द्वारा किया गया कार्य धनात्मक है|
 (6.16)
(6.16)
यदि स्प्रिंग का विस्थापन xc (<0) से संपीडित किया जाता है तब भी उपरोक्त व्यंजक सत्य है| स्प्रिंग-बल 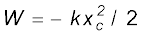 कार्य करता है जबकि बाह्य बल
कार्य करता है जबकि बाह्य बल 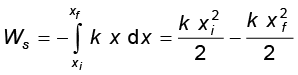 कार्य करता है|
कार्य करता है|
यदि गुटके को इसके आरंभिक विस्थापन xi से अंतिम विस्थापन xf तक विस्थापित किया जाता है तो स्प्रिंग-बल द्वारा किया गया कार्य
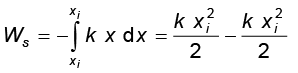 (6.17)
(6.17)
अत: स्प्रिंग-बल द्वारा किया गया कार्य केवल सिरे के बिंदुओं पर निर्भर करता है| विशेष रूप से जब गुटके को स्थिति xi से खीचा गया हो और वापस xi स्थिति तक आने दिया गया हो तो
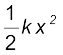 = 0 (6.18)
= 0 (6.18)
अत: स्प्रिंग बल द्वारा किसी चक्रीय प्रक्रम में किया गया कार्य शून्य होता है| हमने यहां स्पष्ट कर दिया है कि (i) स्प्रिंग बल केवल स्थिति पर निर्भर करता है जैसा कि हुक द्वारा पहले कहा गया है (Fs = –k x); (ii) यह बल कार्य करता है जो किसी पिण्ड की आरंभिक एवं अंतिम स्थितियों पर निर्भर करता है; उदाहरणार्थ, समीकरण (6.17) | अत: स्प्रिंग बल एक संरक्षी बल है|
जब गुटका साम्यावस्था में है अर्थात् माध्य स्थिति से उसका विस्थापन शून्य है तब स्प्रिंग की स्थितिज ऊर्जा V(x) को हम शून्य मानते हैं| किसी खिंचाव (या संपीडन) x के लिए उपरोक्त विश्लेषण सुझाता है कि
V(x) = 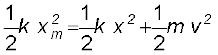 (6.19)
(6.19)
इसे सुविधापूर्वक सत्यापित किया जा सकता है कि
− dV/dx = − k x जो कि स्प्रिंग बल है| जब m द्रव्यमान के गुटके को चित्र 6.7 के अनुसार xm तक खींचा जाता है और फिर विरामावस्था से छोड़ा जाता है, तब इसकी समूची यांत्रिक ऊर्जा स्वेच्छा से चुनी गई किसी भी स्थिति x पर निम्नलिखित रूप में दी जाएगी, जहाँ x का मान –xm से + xm के बीच है:
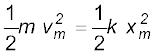
जहाँ हमने यांत्रिक ऊर्जा के संरक्षण नियम का उपयोग किया है | इसके अनुसार गुटके की चाल vm और गतिज ऊर्जा साम्यावस्था x = 0 पर अधिकतम होगी, अर्थात्
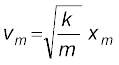
या, 
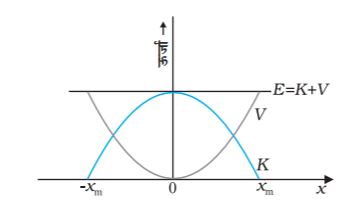
ध्यान दीजिए कि k/m की विमा [T–2] है और यह समीकरण विमीय रूप से सही है| यहाँ निकाय की गतिज ऊर्जा, स्थितिज ऊर्जा में, और स्थितिज ऊर्जा, गतिज ऊर्जा में परिवर्तित हो जाती है, तथापि कुल यांत्रिक ऊर्जा नियत रहती है | चित्र 6.8 में इसका ग्राफीय निरूपण किया गया है|
चित्र 6.8 किसी स्प्रिंग से जुड़े हुए गुटके की स्थितिज ऊर्जा V और गतिज ऊर्जा K के परवलयिक आलेख जो हुक के नियम का पालन करते हैं| ये एक-दूसरे के पूरक हैं अर्थात् इनमें जब एक घटता है तो दूसरा बढ़ता है, परंतु कुल यांत्रिक ऊर्जा E = K + V हमेशा अचर रहती है|
उदाहरण 6.8 कार दुर्घटना को दिखाने के लिए (अनुकार) मोटरकार निर्माता विभिन्न स्प्रिंग नियतांकों के स्प्रिंगों का फ्रेम चढ़ाकर चलती हुई कारों के संघट्ट का अध्ययन करते हैं| मान लीजिए किसी प्रतीकात्मक अनुरूपण में कोई 1000kg द्रव्यमान की कार एक चिकनी सड़क पर 18 km/h की चाल से चलते हुए, क्षैतिज फ्रेम पर चढ़ाए गए स्प्रिंग से संघट्ट करती है जिसका स्प्रिंग नियतांक 6.25 × 103 N m–1 है| स्प्रिंग का अधिकतम संपीडन क्या होगा?
जहाँ कार की चाल 18 km h–1 को इसके SI मान 5 m s–1 में परिवर्तित कर दिया गया है | [यहाँ यह ध्यान रखने योग्य है कि 36 km h–1 = 10 m s–1] | यांत्रिक ऊर्जा-संरक्षण नियम के अनुसार अधिकतम संपीडन xm पर स्प्रिंग की स्थितिज ऊर्जा (V), गतिशील कार की गतिज ऊर्जा (K) के बराबर होती है|
अत: 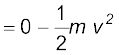
= 1.25 × 104 J
हल करने पर हम प्राप्त करते हैं कि xm = 2.00 m
ध्यान दें कि यहाँ इस स्थिति को हमने आदर्श रूप में प्रस्तुत किया है| यहाँ स्प्रिंग को द्रव्यमानरहित माना है और सड़क का घर्षण नगण्य लिया है| °
हम संरक्षी बलों पर कुछ टिप्पणी करते हुए इस अनुभाग का समापन करते हैं :
(i) उपरोक्त विवेचना में समय के विषय में कोई सूचना नहीं है| इस उदाहरण में हम संपीडन का परिकलन कर सकते हैं लेकिन उस समय अंतराल का परिकलन नहीं कर सकते जिसमें यह संपीडन हुआ है| अत: कालिक सूचना प्राप्त करने के लिए, इस निकाय के लिए न्यूटन के द्वितीय नियम के हल की आवश्यकता है|
(ii) सभी बल संरक्षी नहीं हैं| उदाहरणार्थ, घर्षण एक असंरक्षी बल है| इस स्थिति में, ऊर्जा-सरंक्षण नियम में किंचित परिवर्तन करना पड़ेगा| इसे उदाहरण 6.9 में स्पष्ट किया
गया है|
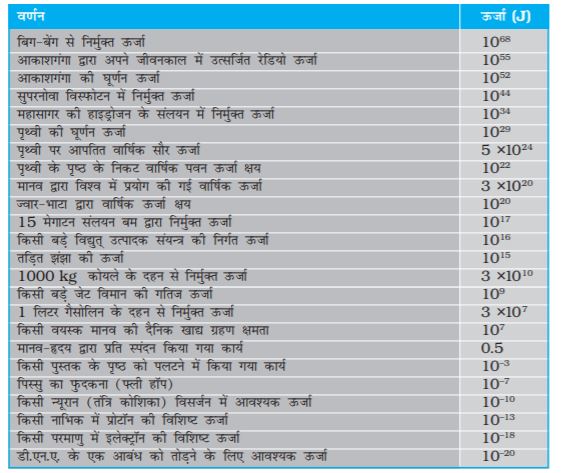
सारणी 6.3 विभिन्न परिघटनाओं से संबद्ध सन्निकट ऊर्जा
(iii) स्थितिज ऊर्जा का शून्य स्वेच्छा से लिया गया है जिसे सुविधानुसार निश्चित कर लिया जाता है| स्प्रिंग-बल के लिए, x = 0 पर हम V = 0 लेते हैं, अर्थात् बिना खिंचे स्प्रिंग की स्थितिज ऊर्जा शून्य थी| नियत गुरुत्वाकर्षण बल m g के लिए हमने पृथ्वी की सतह पर V = 0 लिया था| अगले अध्याय में हम देखेंगे कि गुरुत्वाकर्षण के सार्वत्रिक नियमानुसार बल के लिए, गुरुत्वाकर्षण स्रोत से अनन्त दूरी पर शून्य सर्वोत्तम रूप से परिभाषित होती है तथापि, किसी विवेचना में स्थितिज ऊर्जा के लिए एक बार शून्य की स्थिति निश्चित करने के पश्चात्, शुरू से अंत तक विवेचना में उसी नियम का पालन करना चाहिए|
उदाहरण 6.9 उदाहरण 6.8 में घर्षण गुणांक µ का मान 0.5 लेकर कमानी के अधिकतम संपीडन का परिकलन कीजिए|
हल : स्प्रिंग बल और घर्षण बल, दोनों ही संपीडन का विरोध करने में संयुक्त रूप से कार्य करते हैं, जैसा कि चित्र 6.9 में दिखाया गया है|
यहाँ हम यांत्रिक ऊर्जा-संरक्षण के सिद्धांत के बजाय कार्य-ऊर्जा प्रमेय का प्रयोग करते हैं|
गतिज ऊर्जा में परिवर्तन है :
∆K = Kf − Ki 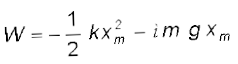
कुुल बल द्वारा किया गया कार्य :
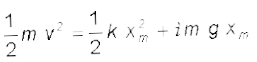
∆K और W को समीकृत करने पर हम प्राप्त करते हैं
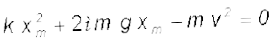
यहाँ µ mg = 0.5 × 103 × 10 = 5 × 103 N (g = 10 m s–2 लेने पर) | उपरोक्त समीकरण को व्यवस्थित करने पर हमें अज्ञात xm के लिए निम्न द्विघातीय समीकरण प्राप्त होती है :
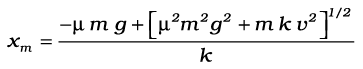
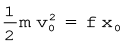
जहाँ हमने xm धनात्मक होने के कारण इसका धनात्मक वर्गमूल ले लिया है| आंकिक मानों को समीकरण में प्रतिस्थापित करने पर हम प्राप्त करते हैं
xm = 1.35 m
जो आशानुसार उदाहरण 6.8 में प्राप्त परिणाम से कम है| °
यदि मान लें कि पिंड पर लगने वाले दोनों बलों में एक संरक्षी बल Fc और दूसरा असंरक्षी बल Fnc है तो यांत्रिक ऊर्जा-संरक्षण के सूत्र में किंचित् परिवर्तन करना पड़ेगा| कार्य-ऊर्जा प्रमेय से :
(Fc + Fnc) ∆x = ∆K
परंतु Fc ∆x = – ∆V
अत: ∆(K + V) = Fnc ∆x
∆E = Fnc ∆x
जहाँ E कुल यांत्रिक ऊर्जा है| समस्त पथ पर यह निम्न रूप ले लेती है
Ef – Ei = Wnc
जहाँ Wnc असंरक्षी बल द्वारा किसी पथ पर किया गया कुल कार्य है| ध्यान दीजिए कि Wnc i से f तक एक विशेष पथ पर निर्भर करता है जैसा कि संरक्षी बल में नहीं है|
6.10 ऊर्जा के विभिन्न रूप : ऊर्जा-संरक्षण का नियम
पिछले अनुभाग में हमने यांत्रिक ऊर्जा की विवेचना की और यह पाया कि इसे दो भिन्न श्रेणियों में विभाजित किया जा सकता है| पहली गति पर आधारित है अर्थात् गतिज ऊर्जा, और दूसरी संरूपण अथवा स्थिति पर आधारित अर्थात् स्थितिज ऊर्जा| ऊर्जा बहुत से रूपों में प्राप्त होती है जिनको एक रूप से दूसरे रूप में कई विधियों द्वारा रूपान्तरित किया जाता है जो प्राय: हमें भी कभी-कभी स्पष्ट नहीं होते|
6.10.1 ऊष्मा
हम पहले ही देख चुके हैं कि घर्षण बल संरक्षी बल नहीं है| लेकिन कार्य, घर्षण बल से संबंधित है (उदाहरण 6.5)| कोई m द्रव्यमान का गुटका रूक्ष क्षैतिज पृष्ठ पर v0 चाल से फिसलता हुआ x0 दूरी चलकर रुक जाता है| x0 पर गतिज घर्षण बल f द्वारा किया गया कार्य –f x0 है | कार्य-ऊर्जा प्रमेय से 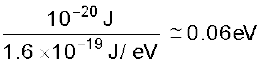 प्राप्त होता है| यदि हम अपने विषय-क्षेत्र को यांत्रिकी तक ही सीमित रखें तो हम कहेंगे कि गुटके की गतिज ऊर्जा, घर्षण बल के कारण क्षयित हो गई है| मेज और गुटके का परीक्षण करने पर हमें पता चलेगा कि इनका ताप मामूली-सा बढ़ गया है| घर्षण बल द्वारा किया गया कार्य क्षयित नहीं हुआ है अपितु ऊष्मीय ऊर्जा के रूप में मेज और गुटके को स्थानान्तरित हो गया है जो गुटके और मेज की आंतरिक ऊर्जा को बढ़ा देता है| शीतकाल में हम अपनी हथेलियों को आपस में जोर से रगड़कर ऊष्मा उत्पन्न करते हैं| हम बाद में देखेंगे कि आंतरिक ऊर्जा प्राय: अणुओं की निरंतर यादृच्छिक गति से संबंधित है | ऊष्मीय ऊर्जा के स्थानान्तरण की परिमाणात्मक धारणा इस लक्षण से प्राप्त की जा सकती है कि 1 kg जल 10° C ठंडा होने पर 42000 J ऊर्जा मुक्त करता है|
प्राप्त होता है| यदि हम अपने विषय-क्षेत्र को यांत्रिकी तक ही सीमित रखें तो हम कहेंगे कि गुटके की गतिज ऊर्जा, घर्षण बल के कारण क्षयित हो गई है| मेज और गुटके का परीक्षण करने पर हमें पता चलेगा कि इनका ताप मामूली-सा बढ़ गया है| घर्षण बल द्वारा किया गया कार्य क्षयित नहीं हुआ है अपितु ऊष्मीय ऊर्जा के रूप में मेज और गुटके को स्थानान्तरित हो गया है जो गुटके और मेज की आंतरिक ऊर्जा को बढ़ा देता है| शीतकाल में हम अपनी हथेलियों को आपस में जोर से रगड़कर ऊष्मा उत्पन्न करते हैं| हम बाद में देखेंगे कि आंतरिक ऊर्जा प्राय: अणुओं की निरंतर यादृच्छिक गति से संबंधित है | ऊष्मीय ऊर्जा के स्थानान्तरण की परिमाणात्मक धारणा इस लक्षण से प्राप्त की जा सकती है कि 1 kg जल 10° C ठंडा होने पर 42000 J ऊर्जा मुक्त करता है|
6.10.2 रासायनिक ऊर्जा
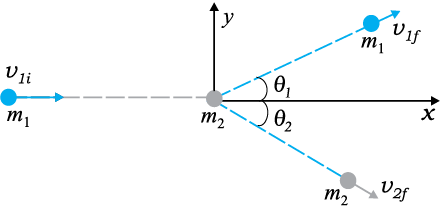
चित्र 6.10 किसी द्रव्यमान m1 का अन्य स्थिर द्रव्यमान m2 से संघट्ट|
मानव जाति ने महानतम् तकनीकी सफलता प्राप्त की जब यह पता लगा कि अग्नि को कैसे प्रज्वलित और नियंत्रित किया जाता है| हमने दो फ्लिन्ट पत्थरों को आपस में रगड़ना (यांत्रिक ऊर्जा), उन्हें गर्म होने देना और पत्तियों के ढेर को सुलगाना (रासायनिक ऊर्जा) सीखा जिसके कारण हम सतत् ऊष्मा प्राप्त कर पाए | माचिस की एक तीली जब विशेष रूप से तैयार की गई रासायनिक सतह पर रगड़ी जाती है तो एक चमकीली ज्वाला के रूप में प्रज्वलित होती है| जब सुलगाई गई माचिस की तीली पटाखे में लगाई जाती है तो उसके परिणामस्वरूप ध्वनि एवं प्रकाश ऊर्जाओं का भव्य प्रदर्शन होता है|
रासायनिक ऊर्जा, रासायनिक अभिक्रिया में भाग लेने वाले अणुओं की भिन्न-भिन्न बंधन ऊर्जाओं के कारण उत्पन्न होती है| एक स्थिर रासायनिक यौगिक की ऊर्जा इसके पृथक-पृथक अंशों की अपेक्षा कम होती है| रासायनिक अभिक्रिया मुख्यत: परमाणुओं की पुन: व्यवस्था है | यदि अभिकारकों की कुल ऊर्जा, उत्पादों की ऊर्जा से अधिक है तो ऊष्मा मुक्त होती है अर्थात् अभिक्रिया ऊष्माक्षेपी होती है| यदि इसके विपरीत सत्य है तो ऊष्मा अवशोषित होगी अर्थात् अभिक्रिया ऊष्माशोषी होगी | कोयले में कार्बन होता है और इसके 1 kg के दहन से 3 × 107 J ऊर्जा मुक्त होती है|
रासायनिक ऊर्जा उन बलों से संबंधित होती है जो पदार्थों को स्थायित्व प्रदान करते है| ये बल परमाणुओं को अणुओं में और अणुओं को पॉलीमेरिक शृृंखला इत्यादि में बाँध देते हैं| कोयला, कुकिंग गैस, लकड़ी और पैट्रोलियम के दहन से उत्पन्न रासायनिक ऊर्जा हमारे दैनिक अस्तित्व के लिए अनिवार्य है|
6.10.3 विद्युत-ऊर्जा
विद्युत धारा के प्रवाह के कारण विद्युत बल्ब उद्दीप्त होते हैं, पंखे घूमते हैं और घंटियां बजती हैं| आवेशों के आकर्षण- प्रतिकर्षण संबंधी नियमों और विद्युत धारा के विषय में हम बाद में सीखेंगे | ऊर्जा विद्युत धारा से भी संबद्ध है| एक भारतीय शहरी परिवार औसतन 200 J/s ऊर्जा का उपभोग करता है|
6.10.4 द्रव्यमान-ऊर्जा तुल्यता
उन्नीसवीं शताब्दी के अंत तक भौतिक विज्ञानी का विश्वास था कि प्रत्येक भौतिक एवं रासायनिक प्रक्रम में, विलगित निकाय का द्रव्यमान संरक्षित रहता है| द्रव्य अपनी प्रावस्था परिवर्तित कर सकता है| उदाहरणार्थ, हिमानी बर्फ पिघलकर एक प्रवाही नदी के रूप में बह सकती है लेकिन द्रव्य न तो उत्पन्न किया जा सकता है और न ही नष्ट| तथापि अल्बर्ट आइंस्टाइन (1879-1955) ने प्रदर्शित किया कि द्रव्यमान और ऊर्जा एक-दूसरे के तुल्य होते हैं और निम्नलिखित समीकरण द्वारा संबंधित होते हैं :
E = m c2 (6.20)
जहां c, निर्वात में प्रकाश की चाल है जो लगभग 3 × 108 m s–1 के बराबर है| अत: मात्र एक किलोग्राम द्रव्य के ऊर्जा में परिवर्तन से संबंधित एक आश्चर्यचकित कर देने वाली ऊर्जा की मात्रा है
E = 1 × (3 × 108)2 J = 9 × 1016 J
यह एक बहुत बड़े पैमाने पर विद्युत उत्पन्न करने वाले बिजली घर के वार्षिक उत्पादन (3000 MW) के तुल्य है|
6.10.5 नाभिकीय ऊर्जा
एक ओर जहाँ मानव जाति द्वारा निर्मित अत्यन्त विनाशकारी नाभिकीय आयुध, विखंडन एवं संलयन बम उपरोक्त तुल्यता [समीकरण (6.20)] संबंध की अभिव्यक्ति है, वहीं दूसरी ओर सूर्य द्वारा उत्पादित जीवन-पोषण करने वाली ऊर्जा की व्याख्या भी उपरोक्त समीकरण पर ही आधारित है| इसमें हाइड्रोजन के चार हलके नाभिकों के संलयन द्वारा एक हीलियम नाभिक बनता है जिसका द्रव्यमान हाइड्रोजन के चारों नाभिकों के कुल द्रव्यमानों से कम होता है| यह द्रव्यमान-अंतर ∆m, जिसे द्रव्यमान क्षति कहते हैं, ऊर्जा (∆m) c2 का स्रोत है | विखंडन में एक भारी अस्थायी नाभिक, जैसे यूरेनियम (23592U), एक न्यूट्रॉन की बमबारी द्वारा हलके नाभिकों में विभक्त हो जाता है | इस प्रक्रम में भी अंतिम द्रव्यमान, आरंभिक द्रव्यमान से कम होता है और यह द्रव्यमान-क्षति ऊर्जा में रूपांतरित हो जाती है| इस ऊर्जा का उपयोग नियंत्रित नाभिकीय विखंडन अभिक्रिया पर आधारित नाभिकीय शक्ति संयंत्रों द्वारा विद्युत ऊर्जा उपलब्ध कराने में किया जाता है| वहीं दूसरी ओर, इसे अनियंत्रित नाभिकीय विखंडन अभिक्रिया पर आधारित विनाशकारी नाभिकीय आयुधों के निर्माण में भी प्रयोग किया जा सकता है | सही अर्थ में किसी रासायनिक अभिक्रिया में मुक्त ऊर्जा ∆E को द्रव्यमान-क्षति ∆m = ∆E/c2 से भी संबद्ध किया जा सकता है | तथापि, किसी रासायनिक अभिक्रिया में द्रव्यमान-क्षति, नाभिकीय अभिक्रिया में होने वाली द्रव्यमान-क्षति से काफी कम होती है | सारणी 6.3 में भिन्न-भिन्न घटनाओं और परिघटनाओं से संबद्ध कुल ऊर्जाओं को सूचीबद्ध किया गया है|
उदाहरण 6.10 सारणी 6.1 से 6.3 तक का परीक्षण कीजिए और बताइए (a) डी.एन.ए. के एक आबंध को तोड़ने के लिए आवश्यक ऊर्जा (इलेक्ट्रॉन-वोल्ट में); (b) वायु के एक अणु की गतिज ऊर्जा (10–21J) इलेक्ट्रॉन-वोल्ट में (c) किसी वयस्क मानव का दैनिक आहार (किलो कैलोरी में)|
हल (a) डी.एन.ए. के एक आबंध को तोड़ने के लिए आवश्यक ऊर्जा है :
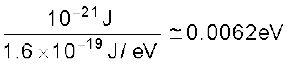
ध्यान दीजिए 0.1eV = 100 meV (100 मिलि इलेक्ट्रॉन-वोल्ट)
(b) वायु के अणु की गतिज ऊर्जा है :
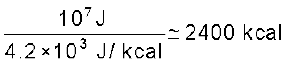
यह 6.2 meV के सदृश है|
(c) वयस्क मानव की औसत दैनिक भोजन की खपत है :
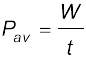
यहाँ हम समाचार-पत्रों और पत्रिकाओं की सामान्य भ्रांति की ओर ध्यान दिलाते हैं| ये भोजन की मात्रा का कैलोरी में उल्लेख करते हैं और हमें 2400 कैलोरी से कम खुराक लेने का सुझाव देते हैं| जो उन्हें कहना चाहिए वह किलो कैलोरी (kcal) है, न कि कैलोरी| 2400 कैलोरी प्रतिदिन उपभोग करने वाला व्यक्ति शीघ्र भूखों मर जाएगा! 1 भोजन कैलोरी सामान्यत: 1 किलो-कैलोरी ही है| °
6.10.6 ऊर्जा-संरक्षण का सिद्धांत
हमने यह देखा है कि किसी भी निकाय की कुल यांत्रिक ऊर्जा संरक्षित रहती है यदि इस पर कार्य करने वाले बल संरक्षी हैं | यदि कार्यरत कुछ बल असंरक्षी हैं तो यांत्रिक ऊर्जा का कुछ अंश दूसरे रूपों; जैसे–ऊष्मा, प्रकाश और ध्वनि ऊर्जाओं में रूपान्तरित हो जाता है| तथापि ऊर्जा के सभी रूपों का ध्यान रखने पर हम पाते हैं कि विलगित निकाय की कुल ऊर्जा परिवर्तित नहीं होती| ऊर्जा एक रूप से दूसरे रूप में रूपांतरित हो सकती है परंतु किसी विलगित निकाय की कुल ऊर्जा नियत रहती है | ऊर्जा न तो उत्पन्न की जा सकती है और न ही नष्ट|
चूंकि संपूर्ण विश्व को एक विलगित निकाय के रूप में देखा जा सकता है अत: विश्व की कुल ऊर्जा अचर है | यदि विश्व के एक हिस्से में ऊर्जा की क्षति होती है तो दूसरे हिस्से में समान मात्रा में ऊर्जा वृद्धि होनी चाहिए|
ऊर्जा-संरक्षण सिद्धांत को सिद्ध नहीं किया जा सकता है| तथापि, इस सिद्धांत के उल्लंघन की कोई स्थिति सामने नहीं आई है| संरक्षण की अभिधारणा और विभिन्न रूपों में ऊर्जा का रूपांतरण भौतिकी, रसायन विज्ञान और जीवन विज्ञान आदि, विज्ञान की विभिन्न शाखाओं को आपस में संबद्ध कर देती है | यह वैज्ञानिक खोजों में एकीकरण और स्थायित्व के तत्व को प्रदान करता है | अभियांत्रिकी (इंजीनियरी) की दृष्टि से सभी इलेक्ट्रॉनिक, संप्रेषण और यांत्रिकी आधारित यंत्र, ऊर्जा-रूपांतरण के किसी न किसी रूप पर निर्भर करते हैं|
6.11 शक्ति
बहुधा केवल यह जानना ही पर्याप्त नहीं है कि किसी पिंड पर कितना कार्य किया गया अपितु यह जानना भी आवश्यक है कि यह कार्य किस दर से किया गया है| हम कहते हैं कि व्यक्ति शारीरिक रूप से स्वस्थ है यदि वह केवल किसी भवन के चार तल तक चढ़ ही नहीं जाता है अपितु वह इन पर तेजी से चढ़ जाता है | अत: शक्ति को उस समय-दर से परिभाषित करते हैं जिससे कार्य किया गया या ऊर्जा स्थानांतरित हुई| किसी बल की औसत शक्ति उस बल द्वारा किए गए कार्य W और उसमें लगे समय t के अनुपात से परिभाषित करते हैं| अत:
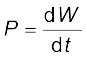
तात्क्षणिक शक्ति को औसत शक्ति के सीमान्त मान के रूप में परिभाषित करते हैैं जबकि समय शून्य की ओर अग्रसर हो रहा होता है, अर्थात्
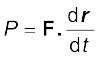 (6.21)
(6.21)
जहाँ विस्थापन dr में बल F द्वारा किया गया कार्य dW = F.dr होता है| अत: तात्क्षणिक शक्ति को निम्नलिखित प्रकार से भी व्यक्त कर सकते हैं :
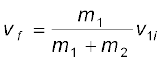
= F.v (6.22)
जहाँ v तात्क्षणिक वेग है जबकि बल F है|
कार्य और ऊर्जा की भांति शक्ति भी एक अदिश राशि है| इसका SI मात्रक वाट (W) और विमा [ML2T–3] है| 1W का मान 1J s–1 के बराबर होता है| अठारहवीं शताब्दी में भाप इंजन के प्रवर्तकों में से एक प्रवर्तक जेम्स वॉट के नाम पर शक्ति का मात्रक वाट (W) रखा गया है|
शक्ति का बहुत पुराना मात्रक अश्व शक्ति है|
1 अश्व शक्ति (hp) = 746 W
यह मात्रक आज भी कार, मोटरबाईक इत्यादि की निर्गत क्षमता को व्यक्त करने के लिए प्रयुक्त होता है|
जब हम विद्युत उपकरण; जैसे–विद्युत बल्ब, हीटर और प्रशीतक आदि खरीदते हैं तो हमें मात्रक वाट से व्यवहार करना होता है | एक 100 वाट का बल्ब 10 घंटे में एक किलोवाट-घंटा विद्युत ऊर्जा की खपत करता है|
अर्थात् 100 (वाट) × 10 (घंटा)
=1000 वाट-घंटा
= 1 किलोवाट घंटा (k Wh)
= 103 (W) × 3600 (s)
= 3.6 × 106 J
विद्युत-ऊर्जा की खपत के लिए मूल्य, मात्रक kW h में चुकाया जाता है जिसे साधारणतया ‘यूनिट’ के नाम से पुकारते हैं| ध्यान दें कि kWh ऊर्जा का मात्रक है, न कि शक्ति का|
उदाहरण 6.11 कोई लिफ्ट जिसका कुल द्रव्यमान
(लिफ्ट + यात्रियों का) 1800 kg है, ऊपर की ओर 2 m s–1 की अचर चाल से गतिमान है| 4000 N का घर्षण बल इसकी गति का विरोध करता है| लिफ्ट को मोटर द्वारा प्रदत्त न्यूनतम शक्ति का आकलन वाट और अश्व शक्ति में कीजिए |
हल लिफ्ट पर लगने वाला अधोमुखी बल
F = mg + Ff = (1800 × 10) + 4000 = 22000 N
इस बल को संतुलित करने के लिए मोटर द्वारा पर्याप्त शक्ति की आपूर्ति की जानी चाहिए|
अत: P = F.v = 22000 × 2 = 44000 W = 59 hp °
6.12 संघट्ट
भौतिकी में हम गति (स्थान में परिवर्तन) का अध्ययन करते हैं| साथ ही साथ हम एेसी भौतिक राशियों की खोज करते हैं जो किसी भौतिक प्रक्रम में परिवर्तित नहीं होती हैं| ऊर्जा-संरक्षण एवं संवेग-संरक्षण के नियम इसके अच्छे उदाहरण हैं| इस अनुभाग में, हम इन नियमों का बहुधा सामने आने वाली परिघटनाओं, जिन्हें संघट्ट कहते हैं, में प्रयोग करेंगे| विभिन्न खेलों; जैसे–बिलियर्ड, मारबल या कैरम आदि में संघट्ट एक अनिवार्य घटक है| अब हम किन्हीं दो द्रव्यमानों का आदर्श रूप में प्रस्तुत संघट्ट का अध्ययन करेंगे|
मान लीजिए कि दो द्रव्यमान m1 व m2 हैं जिसमें कण m1 चाल vli से गतिमान है जहाँ अधोलिखित ‘i’ आरंभिक चाल को निरूपित करता है| दूसरा द्रव्यमान m2 स्थिर है| इस निर्देश फ्रेम का चयन करने में व्यापकता में कोई कमी नहीं आती| इस फ्रेम में द्रव्यमान m1, दूसरे द्रव्यमान m2 से जो विरामावस्था में है, संघट्ट करता है जो चित्र 6.10 में चित्रित किया गया है |
संघट्ट के पश्चात् द्रव्यमान m1 व m2 विभिन्न दिशाओं में गति करते हैं| हम देखेंगे कि द्रव्यमानों, उनके वेगों और कोणों में निश्चित संबंध है|
6.12.1 प्रत्यास्थ एवं अप्रत्यास्थ संघट्ट
सभी संघट्टों में निकाय का कुल रेखीय संवेग नियत रहता है अर्थात् निकाय का आरंभिक संवेग उसके अंतिम संवेग के बराबर होता है| इसे निम्न प्रकार से सिद्ध किया जा सकता है | जब दो पिंड संघट्ट करते हैं तो संघट्ट समय ∆t में कार्यरत परस्पर आवेगी बल, उनके परस्पर संवेगों में परिवर्तन लाने का कारण होते हैं| अर्थात्
∆p1 = F12 ∆t
∆p2 = F21 ∆t
जहाँ F12 दूसरे पिंड द्वारा पहले पिंड पर आरोपित बल है| इसी तरह F21 पहले पिंड द्वारा दूसरे पिंड पर आरोपित बल है| न्यूटन के गति के तृतीय नियमानुसार F12 = –F21 होता है | यह दर्शाता है कि
∆p1 + ∆p2 = 0
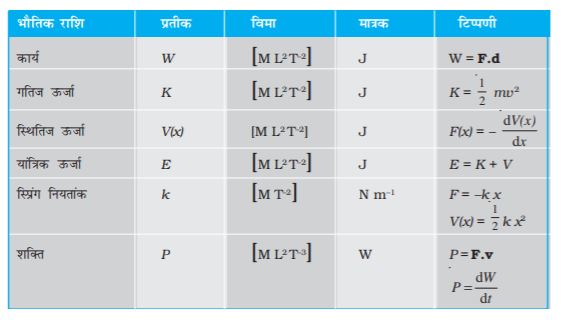
भौतिक राशि प्रतीक विमा मात्रक टिप्पणी
कार्य W [M L2 T–2] J W = F.d
गतिज ऊर्जा K [M L2 T–2] J K =  mv2
mv2
स्थितिज ऊर्जा V(x) [M L2 T–2] J F(x) = – 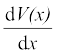
यांत्रिक ऊर्जा E [M L2 T–2] J E = K + V
स्प्रिंग नियतांक k [M T–2] N m–1 F = –k x V(x) = 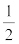 k x2
k x2
शक्ति P [M L2 T–3] W P = F.v
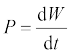

यदि बल संघट्ट समय ∆t के दौरान जटिल रूप से परिवर्तित हो रहे हों तो भी उपरोक्त परिणाम सत्य हैं| चूंकि न्यूटन का तृतीय नियम प्रत्येक क्षण पर सत्य है अत: पहले पिंड पर आरोपित कुल आवेग, दूसरे पिंड पर आरोपित आवेग के बराबर परंतु विपरीत दिशा में होगा|
दूसरी ओर निकाय की कुल गतिज ऊर्जा आवश्यक रूप से संरक्षित नहीं रहती है| संघट्ट के दौरान टक्कर और विकृति, ऊष्मा और ध्वनि उत्पन्न करते हैं| आरंभिक गतिज ऊर्जा का कुछ अंश ऊर्जा के दूसरे रूपों में रूपान्तरित हो जाता है| यदि उपरोक्त दोनों द्रव्यमानों को जोड़ने वाली ‘स्प्रिंग’ बिना किसी ऊर्जा-क्षति के अपनी मूल आकृति प्राप्त कर लेती है, जो पिंडों की आरंभिक गतिज ऊर्जा उनकी अंतिम गतिज ऊर्जा के बराबर होगी परंतु संघट्ट काल ∆t के दौरान अचर नहीं रहती| इस प्रकार के संघट्ट को प्रत्यास्थ संघट्ट कहते हैं | दूसरी ओर यदि विकृति दूर नहीं होती है और दोनों पिंड संघट्ट के पश्चात् आपस में सटे रहकर गति करें तो इस प्रकार के संघट्ट को पूर्णत: अप्रत्यास्थ संघट्ट कहते हैं| इसके अतिरिक्त मध्यवर्ती स्थिति आमतौर पर देखने को मिलती है जब विकृति आंशिक रूप से कम हो जाती है और प्रारंभिक गतिज ऊर्जा की आंशिक रूप से क्षति हो जाती है| इसे समुचित रूप से अप्रत्यास्थ संघट्ट कहते हैं|
6.12.2 एकविमीय संघट्ट
सर्वप्रथम हम किसी पूर्णत: अप्रत्यास्थ संघट्ट की स्थिति का अध्ययन करते हैं| चित्र 6.10 में
θ1 = θ2 = 0
mlvli = (m1+m2)vf (संवेग संरक्षण के नियम से)
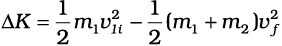 (6.23)
(6.23)
संघट्ट में गतिज ऊर्जा की क्षति:
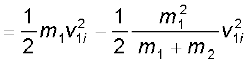
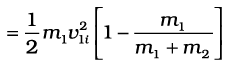 [समीकरण (6.23) द्वारा]
[समीकरण (6.23) द्वारा]
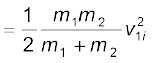
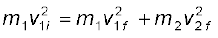
जो कि अपेक्षानुसार एक धनात्मक राशि है|
आइए, अब प्रत्यास्थ संघट्ट की स्थिति का अध्ययन करते हैं | उपरोक्त नामावली के प्रयोग के साथ θ1 = θ2 = 0 लेने पर, रेखीय संवेग एवं गतिज ऊर्जा के संरक्षण की समीकरण
निम्न है :
m1v1i = m1v1f + m2v2f (6.24)
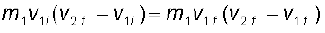 (6.25)
(6.25)
समीकरण (6.24) और समीकरण (6.25) से हम प्राप्त करते हैं
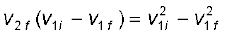
अथवा,
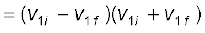
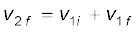
अत: 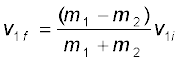 (6.26)
(6.26)
इसे समीकरण (6.24) में प्रतिस्थापित करने पर हम प्राप्त करते हैं
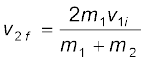 (6.27)
(6.27)
तथा 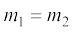 (6.28)
(6.28)
इस प्रकार ‘अज्ञात राशियाँ’ {v1f, v2f} ज्ञात राशियों {m1, m2, v1i} के पदों में प्राप्त हो गई हैं| आइए, अब उपरोक्त विश्लेषण से विशेष दशाओं में रुचिकर निष्कर्ष प्राप्त करते हैं |
दशा I : यदि दोनों द्रव्यमान समान हैं, अर्थात् 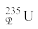 , तब
, तब
v1f = 0, v2f = v1i
अर्थात् प्रथम द्रव्यमान विरामावस्था में आ जाता है और संघट्ट के पश्चात् दूसरा द्रव्यमान, प्रथम द्रव्यमान का आरंभिक वेग प्राप्त कर लेता है|
दशा II : यदि एक पिंड का द्रव्यमान दूसरे पिंड के द्रव्यमान से बहुत अधिक है, अर्थात् m2 >> m1, तब
v1f ~ − v1i v2f ~ 0
भारी द्रव्यमान स्थिर रहता है जबकि हलके द्रव्यमान का वेग उत्क्रमित हो जाता है|
चित्र 6.11
उदाहरण 6.12 गतिशील न्यूट्रॉनों का मंदन : किसी नाभिकीय रिएेक्टर में तीव्रगामी न्यूट्रॉन (विशिष्ट रूप से वेग 107 m s–1) को 103 m s–1 के वेग तक मंदित कर दिया जाना चाहिए ताकि नाभिकीय विखंडन अभिक्रिया में न्यूट्रॉन की यूरेनियम के समस्थानिक 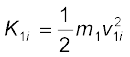 से अन्योन्यक्रिया करने की प्रायिकता उच्च हो जाए| सिद्ध कीजिए कि न्यूट्रॉन एक हलके नाभिक, जैसे ड्यूटीरियम या कार्बन जिसका द्रव्यमान न्यूट्रॉन के द्रव्यमान का मात्र कुछ गुना है, से प्रत्यास्थ संघट्ट करने में अपनी अधिकांश गतिज ऊर्जा की क्षति कर देता है| एेसे पदार्थ प्राय: भारी जल (D2O) अथवा ग्रेफाइट, जो न्यूट्रॉनों की गति को मंद कर देते हैं, ‘मंदक’ कहलाते हैं |
से अन्योन्यक्रिया करने की प्रायिकता उच्च हो जाए| सिद्ध कीजिए कि न्यूट्रॉन एक हलके नाभिक, जैसे ड्यूटीरियम या कार्बन जिसका द्रव्यमान न्यूट्रॉन के द्रव्यमान का मात्र कुछ गुना है, से प्रत्यास्थ संघट्ट करने में अपनी अधिकांश गतिज ऊर्जा की क्षति कर देता है| एेसे पदार्थ प्राय: भारी जल (D2O) अथवा ग्रेफाइट, जो न्यूट्रॉनों की गति को मंद कर देते हैं, ‘मंदक’ कहलाते हैं |
हल न्यूट्रॉन की प्रारंभिक गतिज ऊर्जा है
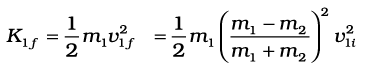
जबकि समीकरण (6.27) से इसकी अंतिम गतिज ऊर्जा है
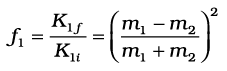
क्षयित आंशिक गतिज ऊर्जा है
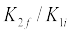
जबकि विमंदक नाभिक 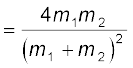 द्वारा भिन्नात्मक गतिज ऊर्जा वृद्धि है |
द्वारा भिन्नात्मक गतिज ऊर्जा वृद्धि है |
f2 = 1 − f1 (प्रत्यास्थ संघट्ट)
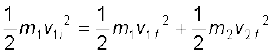
उपरोक्त परिणाम को समीकरण (6.28) से प्रतिस्थापित करके भी सत्यापित किया जा सकता है|
ड्यूटीरियम के लिए, m2 = 2 m1 और हम प्राप्त करते हैं
f1 = 1/9, जबकि f2 = 8/9 है| अत: न्यूट्रॉन की लगभग 90% ऊर्जा ड्यूटीरियम को हस्तांतरित हो जाती है| कार्बन के लिए,
f1 = 71.6% और f2 = 28.4% है| हालांकि, व्यवहार में, सीधा संघट्ट विरले ही होने के कारण यह संख्या काफी कम होती है| °
यदि दोनों पिंडों के आरंभिक तथा अंतिम वेग एक ही सरल रेखा के अनुदिश कार्य करते हैं तो एेसे संघट्ट को एकविमीय संघट्ट अथवा सीधा संघट्ट कहते हैं| छोटे गोलीय पिंडों के लिए यह संभव है कि पिंड 1 की गति की दिशा विरामावस्था में रखे पिंड 2 के केन्द्र से होकर गुजरे| सामान्यत:, यदि आरंभिक वेग तथा अंतिम वेग एक ही तल में हों तो संघट्ट द्विविमीय कहलाता है|
6.12.3 द्विविमीय संघट्ट
चित्र 6.10 स्थिर द्रव्यमान m2 से गतिमान द्रव्यमान m1 का संघट्ट का चित्रण करता है| इस प्रकार के संघट्ट में रेखीय संवेग संरक्षित रहता है| चूंकि संवेग एक सदिश राशि है, अत: यह तीन दिशाओं {x, y, z} के लिए तीन समीकरण प्रदर्शित करता है| संघट्ट के पश्चात् m1 तथा m2 के अंतिम वेग की दिशाओं के आधार पर समतल का निर्धारण कीजिए और मान लीजिए कि यह x-y समतल है| रेखीय संवेग के z- घटक का संरक्षण यह दर्शाता है कि संपूर्ण संघट्ट x-y समतल में है| x-घटक और y-घटक के समीकरण निम्न हैं :
m1v1i = m1v1f cos θ1 + m2 v2f cos θ2 (6.29)
0 = m1v1f sin θ1 – m2v2f sin θ2 (6.30)
अधिकतर स्थितियों में यह माना जाता है कि {m1, m2, v1i}
ज्ञात है| अत: संघट्ट के पश्चात्, हमें चार अज्ञात राशियाँ
{v1f, v2f, θ1 और θ2} प्राप्त होती हैं जबकि हमारे पास मात्र दो समीकरण हैं| यदि θ1 = θ2 = 0, हम पुन: एकविमीय संघट्ट के लिए समीकरण (6.24) प्राप्त कर लेते हैं|
अब यदि संघट्ट प्रत्यास्थ है तो,
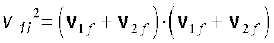 (6.31)
(6.31)
यह हमें समीकरण (6.29) व (6.30) के अलावा एक और समीकरण देता है लेकिन अभी भी हमारे पास सभी अज्ञात राशियों का पता लगाने के लिए एक समीकरण कम है| अत: प्रश्न को हल करने के लिए, चार अज्ञात राशियों में से कम से कम एक और राशि, मान लीजिए θ1, ज्ञात होनी चाहिए| उदाहरणार्थ, कोण θ1 का निर्धारण संसूचक को कोणीय रीति में x-अक्ष से y-अक्ष तक घुमा कर किया जा सकता है| राशियों {m1, m2, v1i, θ1} के ज्ञात मान से हम समीकरण (6.29)-(6.31) का प्रयोग करके {v1f, v2f, θ2} का निर्धारण कर सकते हैं|
उदाहरण 6.13 मान लीजिए कि चित्र 6.10 में चित्रित संघट्ट बिलियर्ड की समान द्रव्यमान (m1 = m2) वाली दो गेंदों के मध्य हुआ है जिसमें प्रथम गेंद क्यू (डण्डा) कहलाती है और द्वितीय गेंद ‘लक्ष्य’ कहलाती है| खिलाड़ी लक्ष्य गेंद को θ2 = 37° के कोण पर कोने में लगी थैली में गिराना चाहता है| यहाँ मान लीजिए कि संघट्ट प्रत्यास्थ है तथा घर्षण और घूर्णन गति महत्त्वपूर्ण नहीं हैं | कोण θ1 ज्ञात कीजिए|
हल चूंकि द्रव्यमान समान हैं अत: संवेग संरक्षण के नियमानुसार,
v1i = v1f + v2f
समीकरण के दोनों पक्षों का वर्ग करने पर प्राप्त होता है
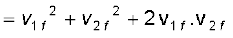
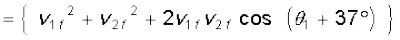
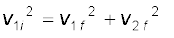 (6.32)
(6.32)
चूंकि संघट्ट प्रत्यास्थ है और द्रव्यमान m1 = m2 है, गतिज ऊर्जा के सरंक्षण, समीकरण (6.31) से हमें प्राप्त होता है
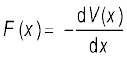 (6.33)
(6.33)
उपरोक्त दोनों समीकरणों (6.32) और (6.33) की तुलना करने पर,
cos (θ1+ 37°) = 0
अत: θ1+ 37° = 90°
अथवा, θ1 = 53°
इससे सिद्ध होता है कि जब समान द्रव्यमान के दो पिंड जिनमें से एक स्थिर है, पृष्ठसर्पी प्रत्यास्थ संघट्ट करते हैं तो
संघट्ट के पश्चात्, दोनों एक-दूसरे से समकोण बनाते हुए गति करेंगे|
°
यदि हम चिकने पृष्ठ वाले गोलीय द्रव्यमानों पर विचार करें और मान लें कि संघट्ट तभी होता है जब पिंड एक दूसरे को स्पर्श करे तो विषय अत्यंत सरल हो जाता है| मारबल, कैरम तथा बिलियार्ड के खेल में ठीक एेसा ही होता है|
हमारे दैनिक जीवन में संघट्ट तभी होता है जब दो वस्तुएँ एक दूसरे को स्पर्श करें| लेकिन विचार कीजिए कि कोई धूमकेतु दूरस्थ स्थान से सूर्य की ओर आ रहा है अथवा अल्फा कण किसी नाभिक की ओर आता हुआ किसी दिशा में चला जाता है| यहाँ पर हमारी दूरी पर कार्यरत बलों से सामना होता है| इस प्रकार की घटना को प्रकीर्णन कहते हैं| जिस वेग तथा दिशाओं में दोनों कण गतिमान होंगे वह उनके आरंभिक वेग, उनके द्रव्यमान, आकार तथा आमाप तथा उनके बीच होने वाली अन्योन्य क्रिया के प्रकार पर निर्भर है|
सारांश
1. कार्य-ऊर्जा प्रमेय के अनुसार, किसी पिंड की गतिज ऊर्जा में परिवर्तन उस पर आरोपित कुल बल द्वारा किया गया
कार्य है |
Kf - Ki = Wnet
2. कोई बल संरक्षी कहलाता है यदि (i) उसके द्वारा किसी पिंड पर किया गया कार्य पथ पर निर्भर न करके केवल सिरे के बिंदुओं {xi , xj} पर निर्भर करता है, अथवा (ii) बल द्वारा किया गया कार्य शून्य होता है, जब पिंड के लिए जो स्वेच्छा से किसी एेसे बंद पथ में स्वत: अपनी प्रारंभिक स्थिति पर वापस आ जाता है|
3. एकविमीय संरक्षी बल के लिए हम स्थितिज ऊर्जा फलन V(x) को इस प्रकार परिभाषित सकते हैं
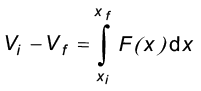
अथवा, 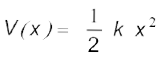
4. यांत्रिक ऊर्जा-संरक्षण के सिद्धांत के अनुसार, यदि किसी पिंड पर कार्यरत बल संरक्षी हैं तो पिंड की कुुल यांत्रिक ऊर्जा अचर रहती हैं|
5. m द्रव्यमान के किसी कण की पृथ्वी की सतह से x ऊँचाई पर गुरुत्वीय स्थितिज ऊर्जा V(x) = m g x होती है, जहाँ ऊँचाई के साथ g के मान में परिवर्तन उपेक्षणीय है|
6. k बल-नियतांक वाले स्प्रिंग, जिसमें खि्ांचाव x है, की प्रत्यास्थ स्थितिज ऊर्जा होती है :
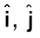
7. दो सदिशों के अदिश अथवा बिंदु गुणनफल को हम A.B लिखते हैं (इसे A डॉट B के रूप में पढ़ते हैं)A.B एक अदिश राशि है जिसका मान AB cosθ होता है| θ सदिशाें A व B के बीच का कोण है| A.B का मान चूंकि θ पर निर्भर करता है इसलिए यह धनात्मक, त्रृणात्मक अथवा शुन्य हो सकता है| दो सदिशों के अदिश गुणनफल की व्याख्याएक सदिश के परिमाण तथा दूसरे सदिश के पहले घटक के अनुदिश घटक के गुणनफल के रूप में भी कर सकते हैं| एकांक सदिशों 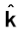 व
व 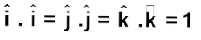 के लिए हमें निम्नलिखित तथ्य याद रखने चाहिए :
के लिए हमें निम्नलिखित तथ्य याद रखने चाहिए :
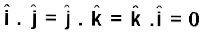
तथा 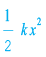
अदिश गुणनफल क्रम-विनिमेय तथा वितरण नियमों का पालन करते हैं|
विचारणीय विषय
1. वाक्यांश "किए गए कार्य का परिकलन कीजिए" अधूरा है| हमें विशेष बल या बलों के समूह द्वारा किसी पिंड का निश्चित विस्थापन करने में किए गए कार्य का स्पष्ट उल्लेख करना चाहिए (अथवा संदर्भ देते हुए स्पष्टतया इंगित करना चाहिए)|
2. किया गया कार्य एक अदिश राशि है| यह भौतिक राशि धनात्मक या ऋणात्मक हो सकती है, जबकि द्रव्यमान और गतिज ऊर्जा धनात्मक अदिश राशियाँ हैं| किसी पिंड पर घर्षण या श्यान बल द्वारा किया गया कार्य ऋणात्मक होता है|
3. न्यूटन के तृतीय नियमानुसार, किन्हीं दो पिंडों के मध्य परस्पर एक-दूसरे पर आरोपित बलों का योग शून्य होता है |
F12 + F21 = 0
परंतु दो बलों द्वारा किए गए कार्य का योग सदैव शून्य नहीं होता है, अर्थात्
W12 + W21 ≠ 0
तथापि, कभी-कभी यह सत्य भी हो सकता है |
4. कभी-कभी किसी बल द्वारा किए गए कार्य की गणना तब भी की जा सकती है जबकि बल की ठीक-ठीक प्रकृति का ज्ञान न भी हो| उदाहरण 6.2 से यह स्पष्ट है, जहाँ कार्य-ऊर्जा प्रमेय का एेसी स्थिति में प्रयोग किया गया है |
5. कार्य-ऊर्जा प्रमेय न्यूटन के द्वितीय नियम से स्वतन्त्र नहीं है| कार्य-ऊर्जा प्रमेय को न्यूटन के द्वितीय नियम के अदिश रूप में देखा जा सकता है| यांत्रिक ऊर्जा के संरक्षण के सिद्धांत को, संरक्षी बलों के लिए कार्य-ऊर्जा प्रमेय के एक महत्त्वपूर्ण परिणाम के रूप में समझा जा सकता है|
6. कार्य-ऊर्जा प्रमेय सभी जड़त्वीय फ्रेमों में लागू होती है| इसे अजड़त्वीय फ्रेमों में भी लागू किया जा सकता है यदि विचारणीय पिंड पर आरोपित कुल बलों के परिकलन में छद्म बल के प्रभाव को भी सम्मिलित कर लिया जाए|
7. संरक्षी बलों के अधीन किसी पिंड की स्थितिज ऊर्जा हमेशा किसी नियतांक तक अनिश्चित रहती है| उदाहरणार्थ, किसी पिंड की स्थितिज ऊर्जा किस बिंदु पर शून्य लेनी है, यह केवल स्वेच्छा से चयन किए गए बिंदु पर निर्भर करता है| जैसे गुरुत्वीय स्थितिज ऊर्जा m g h की स्थिति में स्थितिज ऊर्जा के लिए शून्य बिंदु पृथ्वी के पृष्ठ पर लिया गया है| स्प्रिंग के लिए जिसकी ऊर्जा 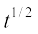 है, स्थितिज ऊर्जा के लिए शून्य बिंदु, दोलायमान द्रव्यमान की माध्य स्थिति पर लिया गया है |
है, स्थितिज ऊर्जा के लिए शून्य बिंदु, दोलायमान द्रव्यमान की माध्य स्थिति पर लिया गया है |
8. यांत्रिकी में प्रत्येक बल स्थितिज ऊर्जा से संबद्ध नहीं होता है| उदाहरणार्थ, घर्षण बल द्वारा किसी बंद पथ में किया गया कार्य शून्य नहीं है और न ही घर्षण से स्थितिज ऊर्जा को संबद्ध किया जा सकता है|
9. किसी संघट्ट के दौरान (a) संघट्ट के प्रत्येक क्षण में पिंड का कुल रेखीय संवेग संरक्षित रहता है, (b) गतिज ऊर्जा संरक्षण (चाहे संघट्ट प्रत्यास्थ ही हो) संघट्ट की समाप्ति के पश्चात् ही लागू होता है और संघट्ट के प्रत्येक क्षण के लिए लागू नहीं होता है| वास्तव में, संघट्ट करने वाले दोनों पिंड विकृत हो जाते हैं और क्षण भर के लिए एक दूसरे के सापेक्ष विरामावस्था में आ जाते हैं|
अभ्यास
6.1 किसी वस्तु पर किसी बल द्वारा किए गए कार्य का चिह्न समझना महत्त्वपूर्ण है| सावधानीपूर्वक बताइए कि निम्नलिखित राशियाँ धनात्मक हैं या ऋणात्मक :
(a) किसी व्यक्ति द्वारा किसी कुएँ में से रस्सी से बँधी बाल्टी को रस्सी द्वारा बाहर निकालने में किया गया कार्य |
(b) उपर्युक्त स्थिति में गुरुत्वीय बल द्वारा किया गया कार्य|
(c) किसी आनत तल पर फिसलती हुई किसी वस्तु पर घर्षण द्वारा किया गया कार्य|
(d) किसी खुरदरे क्षैतिज तल पर एकसमान वेग से गतिमान किसी वस्तु पर लगाए गए बल द्वारा किया गया कार्य |
(e) किसी दोलायमान लोलक को विरामावस्था में लाने के लिए वायु के प्रतिरोधी बल द्वारा किया गया कार्य|
6.2 2 kg द्रव्यमान की कोई वस्तु जो आरंभ में विरामावस्था में है, 7N के किसी क्षैतिज बल के प्रभाव से एक मेज पर गति करती है| मेज का गतिज-घर्षण गुणांक 0.1 है| निम्नलिखित का परिकलन कीजिए और अपने परिणामों की व्याख्या कीजिए |
(a) लगाए गए बल द्वारा 10 s में किया गया कार्य|
(b) घर्षण द्वारा 10 s में किया गया कार्य|
(c) वस्तु पर कुल बल द्वारा 10 s में किया गया कार्य |
(d) वस्तु की गतिज ऊर्जा में 10 s में परिवर्तन|
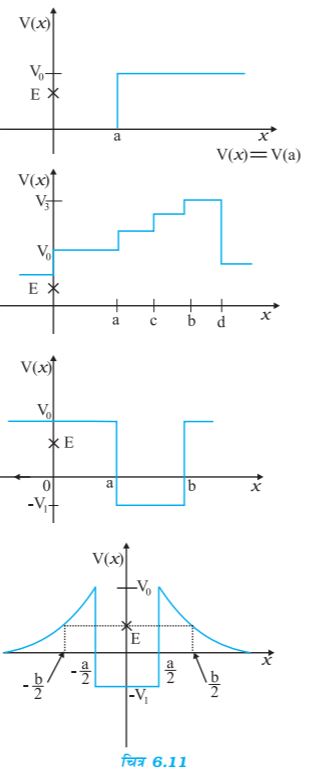
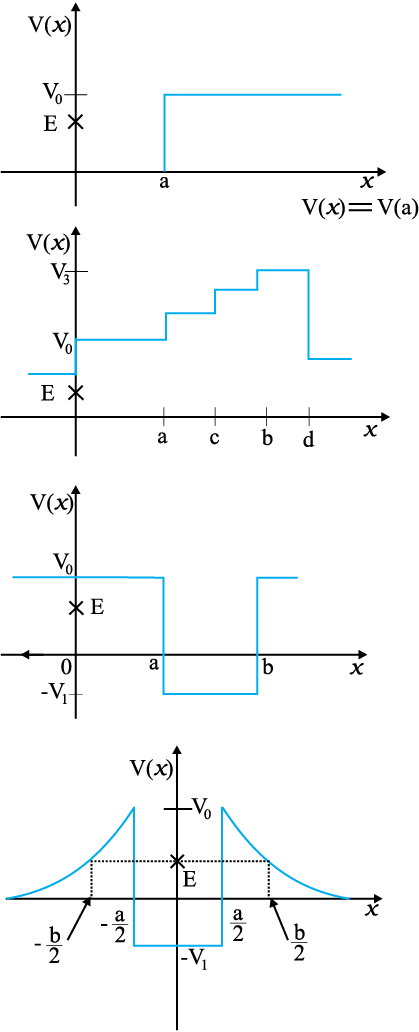
6.3 चित्र 6.11 में कुछ एकविमीय स्थितिज ऊर्जा-फलनों के उदाहरण दिए गए हैं| कण की कुल ऊर्जा कोटि-अक्ष पर क्रॅास द्वारा निर्देशित की गई है| प्रत्येक स्थिति में, कोई एेसे क्षेत्र बताइए, यदि कोई हैं तो, जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता| इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए| कुछ एेसे भौतिक संदर्भो के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों|
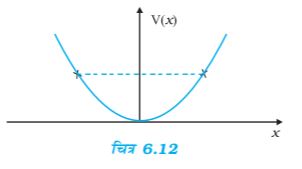
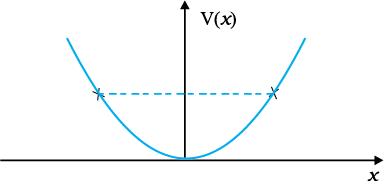
6.4 रेखीय सरल आवर्त गति कर रहे किसी कण का स्थितिज ऊर्जा फलन V(x) = kx2/2 है, जहां k दोलक का बल नियतांक है | k = 0.5 N m–1 के लिए V(x) व x के मध्य ग्राफ चित्र 6.12 में दिखाया गया है| यह दिखाइए कि इस विभव के अंतर्गत गतिमान कुल 1J ऊर्जा वाले कण को अवश्य ही ‘वापिस आना’ चाहिए जब यह x = ± 2 m पर पहुंचता है|
6.5 निम्नलिखित का उत्तर दीजिए:
(a) किसी राकेट का बाह्य आवरण उड़ान के दौरान घर्षण के कारण जल जाता है| जलने के लिए आवश्यक ऊष्मीय ऊर्जा किसके व्यय पर प्राप्त की गई--राकेट या वातावरण ?
(b) धूमकेतु सूर्य के चारों ओर बहुत ही दीर्घवृत्तीय कक्षाओं में घूमते हैं| साधारणतया धूमकेतु पर सूर्य का गुरुत्वीय बल धूमकेतु के लंबवत् नहीं होता है| फिर भी धूमकेतु की संपूर्ण कक्षा में गुरुत्वीय बल द्वारा किया गया कार्य शून्य होता है| क्यों ?
(c) पृथ्वी के चारों ओर बहुत ही क्षीण वायुमण्डल में घूमते हुए किसी कृत्रिम उपग्रह की ऊर्जा धीरे-धीरे वायुमण्डलीय प्रतिरोध (चाहे यह कितना ही कम क्यों न हो) के विरुद्ध क्षय के कारण कम होती जाती है फिर भी जैसे-जैसे कृत्रिम उपग्रह पृथ्वी के समीप आता है तो उसकी चाल में लगातार वृद्धि क्यों होती है ?
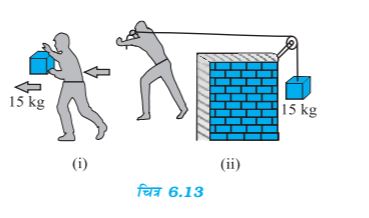
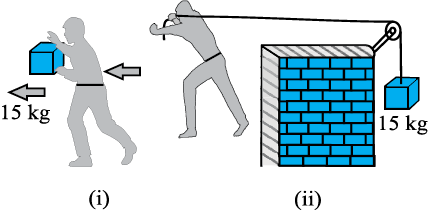
(d) चित्र 6.13(i) में एक व्यक्ति अपने हाथों में 15kg का कोई द्रव्यमान लेकर 2 m चलता है| चित्र 6.13(ii) में वह उतनी ही दूरी अपने पीछे रस्सी को खींचते हुए चलता है| रस्सी घिरनी पर चढ़ी हुई है और उसके दूसरे सिरे पर 15 kg का द्रव्यमान लटका हुआ है | परिकलन कीजिए कि किस स्थिति में किया गया कार्य अधिक है ?
6.6 सही विकल्प को रेखांकित कीजिए :
(a) जब कोई संरक्षी बल किसी वस्तु पर धनात्मक कार्य करता है तो वस्तु की स्थितिज ऊर्जा बढ़ती है/घटती है/अपरिवर्ती रहती है|
(b) किसी वस्तु द्वारा घर्षण के विरुद्ध किए गए कार्य का परिणाम हमेशा इसकी गतिज/स्थितिज ऊर्जा में क्षय होता है|
(c) किसी बहुकण निकाय के कुल संवेग-परिवर्तन की दर निकाय के बाह्य बल/आंतरिक बलों के जोड़ के अनुक्रमानुपाती होती है|
(d) किन्हीं दो पिंडों के अप्रत्यास्थ संघट्ट में वे राशियाँ, जो संघट्ट के बाद नहीं बदलती हैं; निकाय की कुल गतिज ऊर्जा/कुल रेखीय संवेग/कुल ऊर्जा हैं|
6.7 बतलाइए कि निम्नलिखित कथन सत्य हैं या असत्य| अपने उत्तर के लिए कारण भी दीजिए|
(a) किन्हीं दो पिंडों के प्रत्यास्थ संघट्ट में, प्रत्येक पिंड का संवेग व ऊर्जा संरक्षित रहती है|
(b) किसी पिंड पर चाहे कोई भी आंतरिक व बाह्य बल क्यों न लग रहा हो, निकाय की कुल ऊर्जा सर्वदा संरक्षित
रहती है|
(c) प्रकृति में प्रत्येक बल के लिए किसी बंद लूप में, किसी पिंड की गति में किया गया कार्य शून्य होता है|
(d) किसी अप्रत्यास्थ संघट्ट में, किसी निकाय की अंतिम गतिज ऊर्जा, आरंभिक गतिज ऊर्जा से हमेशा कम होती है |
6.8 निम्नलिखित का उत्तर ध्यानपूर्वक, कारण सहित दीजिए :
(a) किन्हीं दो बिलियर्ड-गेंदों के प्रत्यास्थ संघट्ट में, क्या गेंदों के संघट्ट की अल्पावधि में (जब वे संपर्क में होती हैं) कुल गतिज ऊर्जा संरक्षित रहती है?
(b) दो गेंदों के किसी प्रत्यास्थ संघट्ट की लघु अवधि में क्या कुल रेखीय संवेग संरक्षित रहता है?
(c) किसी अप्रत्यास्थ संघट्ट के लिए प्रश्न (a) व (b) के लिए आपके उत्तर क्या हैं?
(d) यदि दो बिलियर्ड-गेंदों की स्थितिज ऊर्जा केवल उनके केंद्रों के मध्य, पृथक्करण-दूरी पर निर्भर करती है तो संघट्ट प्रत्यास्थ होगा या अप्रत्यास्थ ? (ध्यान दीजिए कि यहाँ हम संघट्ट के दौरान बल के संगत स्थितिज ऊर्जा की बात कर रहे हैं, ना कि गुरुत्वीय स्थितिज ऊर्जा की)
6.9 कोई पिंड जो विरामावस्था में है, अचर त्वरण से एकविमीय गति करता है| इसको किसी t समय पर दी गई शक्ति अनुक्रमानुपाती है
(i) 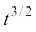 (ii) t (iii)
(ii) t (iii) 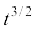 (iv) t2
(iv) t2
6.10 एक पिंड अचर शक्ति के स्रोत के प्रभाव में एक ही दिशा में गतिमान है| इसका t समय में विस्थापन,
अनुक्रमानुपाती है
(i) t1/2 (ii) t (iii)  (iv) t2
(iv) t2
6.11 किसी पिंड पर नियत बल लगाकर उसे किसी निर्देशांक प्रणाली के अनुसार z - अक्ष के अनुदिश गति करने के लिए बाध्य किया गया है जो इस प्रकार है
F = (– + 2
+ 2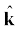 + 3
+ 3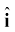 ) N
) N
जहां 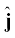 ,
, 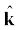 ,
, 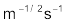 क्रमश: x-, y- एवं z- अक्ष के अनुदिश एकांक सदिश हैं| इस वस्तु को z-अक्ष के अनुदिश4 m की दूरी तक गति कराने के लिए आरोपित बल द्वारा किया गया कार्य कितना होगा ?
क्रमश: x-, y- एवं z- अक्ष के अनुदिश एकांक सदिश हैं| इस वस्तु को z-अक्ष के अनुदिश4 m की दूरी तक गति कराने के लिए आरोपित बल द्वारा किया गया कार्य कितना होगा ?
6.12 किसी अंतरिक्ष किरण प्रयोग में एक इलेक्ट्रॉन और एक प्रोटॉन का संसूचन होता है जिसमें पहले कण की गतिज ऊर्जा 10 keV है और दूसरे कण की गतिज ऊर्जा 100 keV है| इनमें कौन-सा तीव्रगामी है, इलेक्ट्रॉन या प्रोटॉन ? इनकी चालों का अनुपात ज्ञात कीजिए| (इलेक्ट्रॉन का द्रव्यमान = 9.11× 10–31 kg, प्रोटॉन का द्रव्यमान = 1.67 ×10–27 kg, l eV = 1.60 × 10–19J)
6.13 2 mm त्रिज्या की वर्षा की कोई बूंद 500 m की ऊंचाई से पृथ्वी पर गिरती है| यह अपनी आरंभिक ऊंचाई के आधे हिस्से तक (वायु के श्यान प्रतिरोध के कारण) घटते त्वरण के साथ गिरती है और अपनी अधिकतम (सीमान्त) चाल प्राप्त कर लेती है, और उसके बाद एकसमान चाल से गति करती है| वर्षा की बूंद पर उसकी यात्रा के पहले व दूसरे अर्ध भागों में गुरुत्वीय बल द्वारा किया गया कार्य कितना होगा ? यदि बूंद की चाल पृथ्वी तक पहुंचने पर 10 ms–1 हो तो संपूर्ण यात्रा में प्रतिरोधी बल द्वारा किया गया कार्य कितना होगा ?
6.14 किसी गैस-पात्र में कोई अणु 200 m s–1 की चाल से अभिलंब के साथ 30° का कोण बनाता हुआ क्षैतिज दीवार से टकराकर पुन: उसी चाल से वापस लौट जाता है| क्या इस संघट्ट में संवेग संरक्षित है? यह संघट्ट प्रत्यास्थ है या अप्रत्यास्थ ?
6.15 किसी भवन के भूतल पर लगा कोई पंप 30 m3 आयतन की पानी की टंकी को 15 मिनट में भर देता है| यदि टंकी पृथ्वी तल से 40 m ऊपर हो और पंप की दक्षता 30% हो तो पंप द्वारा कितनी विद्युत शक्ति का उपयोग किया गया ?
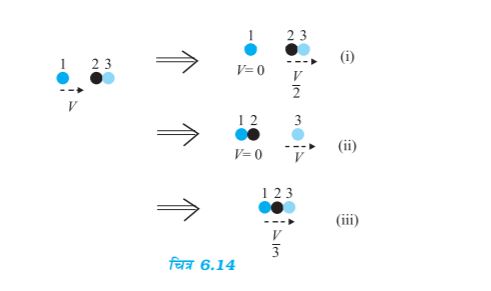
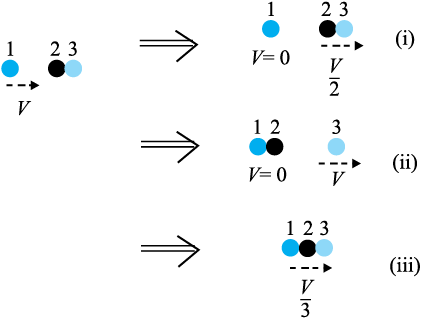
6.16 दो समरूपी बॉल-बियरिंग एक-दूसरे के संपर्क में हैं और किसी घर्षणरहित मेज पर विरामावस्था में हैं| इनके साथ समान द्रव्यमान का कोई दूसरा बॉल-बियरिंग, जो आरंभ में V चाल से गतिमान है, सम्मुख संघट्ट करता है| यदि संघट्ट प्रत्यास्थ है तो संघट्ट के पश्चात् निम्नलिखित (चित्र 6.14) में से कौन-सा परिणाम संभव है?
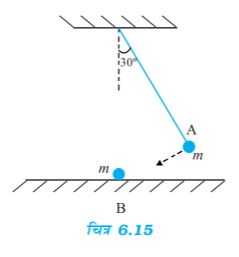
6.17 किसी लोलक के गोलक A को, जो ऊर्ध्वाधर से 30° का कोण बनाता है, छोड़े जाने पर मेज पर, विरामावस्था में रखे दूसरे गोलक B से टकराता है जैसा कि चित्र 6.15 में प्रदर्शित है| ज्ञात कीजिए कि संघट्ट के पश्चात् गोलक A कितना ऊंचा उठता है? गोलकों के आकारों की उपेक्षा कीजिए और मान लीजिए कि संघट्ट प्रत्यास्थ है|
6.18 किसी लोलक के गोलक को क्षैतिज अवस्था से छोड़ा गया है| यदि लोलक की लंबाई 1.5 m है तो निम्नतम बिंदु पर आने पर गोलक की चाल क्या होगी? यह दिया गया है कि इसकी आरंभिक ऊर्जा का 5% अंश वायु प्रतिरोध के विरुद्ध क्षय हो जाता है|
6.19 300 kg द्रव्यमान की कोई ट्रॉली, 25 kg रेत का बोरा लिए हुए किसी घर्षणरहित पथ पर 27 km h–1 की एकसमान चाल से गतिमान है| कुछ समय पश्चात् बोरे में किसी छिद्र से रेत 0.05 kg s–1 की दर से निकलकर ट्राली के फर्श पर रिसने लगती है| रेत का बोरा खाली होने के पश्चात ट्रॉली की चाल क्या होगी ?
6.20 0.5 kg द्रव्यमान का एक कण v =a x3/2 वेग से सरल रेखीय गति करता है जहां a = 5 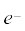 है | x = 0 से
है | x = 0 से
x = 2 m तक इसके विस्थापन में कुल बल द्वारा किया गया कार्य कितना होगा ?
6.21 किसी पवनचक्की के ब्लेड, क्षेत्रफल A के वृत्त जितना क्षेत्रफल प्रसर्प करते हैं| (a) यदि हवा v वेग से वृत्त के लंबवत् दिशा में बहती है तो t समय में इससे गुजरने वाली वायु का द्रव्यमान क्या होगा ? (b) वायु की गतिज ऊर्जा क्या होगी ?
(c) मान लीजिए कि पवनचक्की हवा की 25% ऊर्जा को विद्युत ऊर्जा में रूपान्तरित कर देती है| यदि A = 30 m2,और
v = 36 km h–1 और वायु का घनत्व 1.2 kg m–3 है तो उत्पन्न विद्युत शक्ति का परिकलन कीजिए|
6.22 कोई व्यक्ति वजन कम करने के लिए 10 kg द्रव्यमान को 0.5 m की ऊंचाई तक 1000 बार उठाता है| मान लीजिए कि प्रत्येक बार द्रव्यमान को नीचे लाने में खोई हुई ऊर्जा क्षयित हो जाती है| (a) वह गुरुत्वाकर्षण बल के विरुद्ध कितना कार्य करता है ? (b) यदि वसा 3.8 × 107 J ऊर्जा प्रति किलोग्राम आपूर्ति करता हो जो कि 20%दक्षता की दर से यांत्रिक ऊर्जा में परिवर्तित हो जाती है तो वह कितनी वसा खर्च कर डालेगा?
6.23 कोई परिवार 8 kW विद्युत-शक्ति का उपभोग करता है| (a) किसी क्षैतिज सतह पर सीधे आपतित होने वाली सौर ऊर्जा की औसत दर 200 W m–2 है| यदि इस ऊर्जा का 20% भाग लाभदायक विद्युत ऊर्जा में रूपान्तरित किया जा सकता है तो 8 kW की विद्युत आपूर्ति के लिए कितने क्षेत्रफल की आवश्यकता होगी ? (b) इस क्षेत्रफल की तुलना किसी विशिष्ट भवन की छत के क्षेत्रफल से कीजिए|
अतिरिक्त अभ्यास
6.24 0.012 kg द्रव्यमान की कोई गोली 70 ms–1 की क्षैतिज चाल से चलते हुए 0.4 kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरंत ही विरामावस्था में आ जाती है| गुटके को छत से पतली तारों द्वारा लटकाया गया है| परिकलन कीजिए कि गुटका किस ऊंचाई तक ऊपर उठता है ? गुटके में पैदा हुई ऊष्मा की मात्रा का भी अनुमान लगाइए|
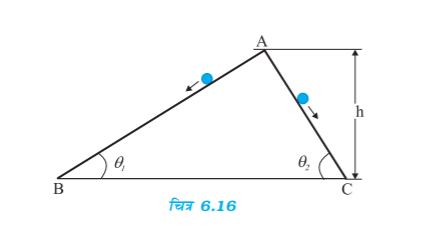
6.25 दो घर्षणरहित आनत पथ, जिनमें से एक की ढाल अधिक है और दूसरे की ढाल कम है, बिंदु A पर मिलते हैं| बिंदु A से प्रत्येक पथ पर एक-एक पत्थर को विरामावस्था से नीचे सरकाया जाता है (चित्र 6.16)| क्या ये पत्थर एक ही समय पर नीचे पहुंचेंगे ? क्या वे वहां एक ही चाल से पहुंचेंगे? व्याख्या कीजिए| यदि θ1 = 30°, θ2 = 60° और h =10 m दिया है तो दोनों पत्थरों की चाल एवं उनके द्वारा नीचे पहुंचने में लिए गए समय क्या हैं ?
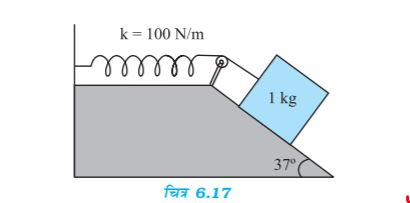
6.26 किसी रूक्ष आनत तल पर रखा हुआ 1 kg द्रव्यमान का गुटका किसी 100 N m–1 स्प्रिंग नियतांक वाले स्प्रिंग से दिए गए चित्र 6.17 के अनुसार जुड़ा है| गुटके को स्प्रिंग की बिना खि्ांची स्थिति में, विरामावस्था से छोड़ा जाता है| गुटका विरामावस्था में आने से पहले आनत तल पर 10 cm नीचे खिसक जाता है| गुटके और आनत तल के मध्य घर्षण गुणांक ज्ञात कीजिए | मान लीजिए कि स्प्रिंग का द्रव्यमान उपेक्षणीय है और घिरनी घर्षणरहित है|
6.27 0.3 kg द्रव्यमान का कोई बोल्ट 7 m s–1 की एकसमान चाल से नीचे आ रही किसी लिफ्ट की छत से गिरता है| यह लिफ्ट के फर्श से टकराता है (लिफ्ट की लंबाई = 3 m) और वापस नहीं लौटता है | टक्कर द्वारा कितनी ऊष्मा उत्पन्न हुई ? यदि लिफ्ट स्थिर होती तो क्या आपका उत्तर इससे भिन्न होता?
6.28 200 kg द्रव्यमान की कोई ट्रॉली किसी घर्षणरहित पथ पर 36 km h–1 की एकसमान चाल से गतिमान है| 20kg द्रव्यमान का कोई बच्चा ट्रॉली के एक सिरे से दूसरे सिरे तक (10 m दूर) ट्रॉली के सापेक्ष 4 m s–1 की चाल से ट्रॉली की गति की विपरीत दिशा में दौड़ता है और ट्रॉली से बाहर कूद जाता है| ट्रॉली की अंतिम चाल क्या है ? बच्चे के दौड़ना आरंभ करने के समय से ट्रॉली ने कितनी दूरी तय की?
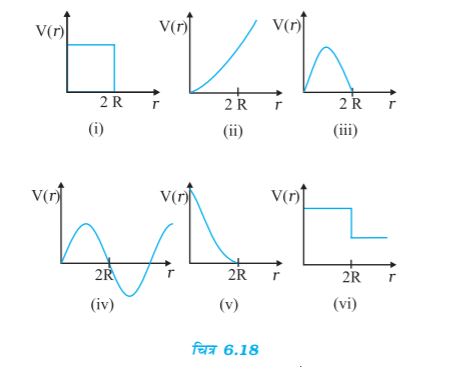
6.29 नीचे दिए गए चित्र 6.18 में दिए गए स्थितिज ऊर्जा वक्रों में से कौन-सा वक्र संभवत: दो बिलियर्ड-गेंदों के प्रत्यास्थ संघट्ट का वर्णन नहीं करेगा? यहां r गेंदों के केंद्रों के मध्य की दूरी है और प्रत्येक गेंद का अर्धव्यास R है|
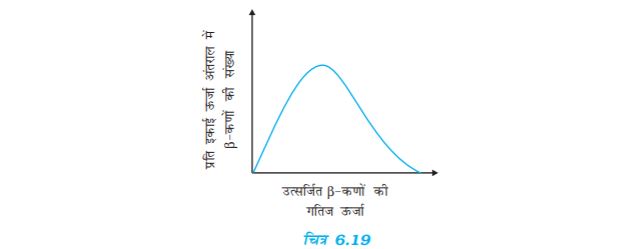
6.30 विरामावस्था में किसी मुक्त न्यूट्रॉन के क्षय पर विचार कीजिए n→p +प्रदर्शित कीजिए कि इस प्रकार के द्विपिंड क्षय से नियत ऊर्जा का कोई इलेक्ट्रॉन अवश्य उत्सर्जित होना चाहिए, और इसलिए यह किसी न्यूट्रॉन या किसी नाभिक के β- क्षय में प्रेक्षित सतत ऊर्जा वितरण का स्पष्टीकरण नहीं दे सकता (चित्र 6.19) |
[नोट: इस अभ्यास का हल उन कई तर्कों में से एक है जिन्हें डब्ल्यु पॉली द्वारा β-क्षय के क्षय उत्पादों में किसी तीसरे कण के अस्तित्व का पूर्वानुमान करने के लिए दिया गया था| यह कण न्यूट्रिनो के नाम से जाना जाता है| अब हम जानते हैं कि यह निजी प्रचक्रण 1/2 (जैसे e–, p या n) का कोई कण है| लेकिन यह उदासीन है या द्रव्यमानरहित या (इलेक्ट्रॉन के द्रव्यमान की तुलना में) इसका द्रव्यमान अत्यधिक कम है और जो द्रव्य के साथ दुर्बलता से परस्पर क्रिया करता है| न्यूट्रॉन की उचित क्षय-प्रक्रिया इस प्रकार है : n p + e– + ν ]
परिशिष्ट 6.1 पैदल सैर में व्यय की गई शक्ति
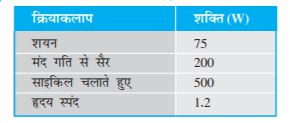
नीचे दी गई सारणी में 60 kg द्रव्यमान के वयस्क मानव द्वारा विभिन्न दैनिक क्रियाकलापों में व्यय की गई शक्ति (लगभग) सूचीबद्ध की गई है |
सारणी 6.4 कुछ क्रियाकलापों में व्यय की गई शक्ति (लगभग)
‘यान्त्रिक कार्य का अर्थ दैनिक बोलचाल में प्रचलित शब्द ‘कार्य’ के अर्थ से भिन्न है | यदि कोई महिला सिर पर भारी बोझा लिए खड़ी है तोे वह थक जाएगी परंतु इस प्रक्रिया में महिला ने कोई ‘यांत्रिक कार्य’ नहीं किया है | इसका अर्थ यह बिलकुल नहीं है कि मानव द्वारा साधारण क्रियाकलापों में किए गए कार्य का आकलन कर पाना संभव नहीं है |
विचार कीजिए कि कोई व्यक्ति अचर चाल v0 से पैदल सैर कर रहा है | उसके द्वारा किए गए यांत्रिक कार्य का आकलन, कार्य-ऊर्जा प्रमेय द्वारा सरलता से किया जा सकता है | मान लीजिए
(i) गमन पाद (पैदल सैर) में किया गया मुख्य कार्य प्रत्येक कदम के साथ टांगों के त्वरण और मंदन का है (चित्र 6.20 देखिए) |
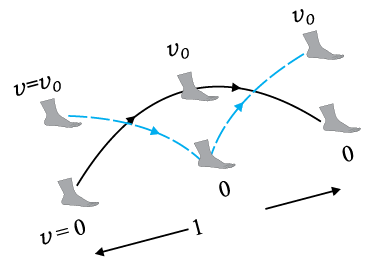
 चित्र 6.20 गमन पाद में किसी एक लंबे डग (कदम) का निदर्शन जबकि एक टांग पृथ्वी की सतह से अधिकतम दूर और दूसरी टांग पृथ्वी पर है और विलोमत: |कदम
चित्र 6.20 गमन पाद में किसी एक लंबे डग (कदम) का निदर्शन जबकि एक टांग पृथ्वी की सतह से अधिकतम दूर और दूसरी टांग पृथ्वी पर है और विलोमत: |कदम
(ii) वायु प्रतिरोध नगण्य है |
(iii) टांगों को गुरुत्व बल के विरुद्ध उठाने में किया गया थोड़ा-सा कार्य नगण्य है |
(iv) गमन पाद (सैर) में हाथों का हिलाना जो एक आम बात है, न के बराबर है |
जैसा कि हम चित्र 6.20 में देख सकते हैं कि प्रत्येक कदम भरने में टांग विरामावस्था से किसी चाल v = v0 (जो गमन पाद की चाल के लगभग समान है) तक लाई जाती है और फिर विरामावस्था में लाई जाती है |
अत: कार्य-ऊर्जा प्रमेय से प्रत्येक लंबा डग (कदम) भरने में प्रत्येक टांग द्वारा किया गया कार्य ml v20 होगा | यहां ml टांग का द्रव्यमान है| टांग की मांसपेशियों द्वारा पैर को विरामावस्था से चाल v0 तक लाने में व्यय की गई ऊर्जा ml v20 /2 है जबकि पूरक टांग की मांसपेशियों द्वारा दूसरे पैर को चाल v0 से विरामावस्था में लाने में व्यय की गई अतिरिक्त ऊर्जा mlv20/2 है | अत: दोनों टांगों द्वारा एक कदम भरने में किया गया कार्य है (चित्र 6.20 का सावधानीपूर्वक अध्ययन करें)
Ws = 2mlv20 (6.34)
मान लीजिए टांग का द्रव्यमान ml = 10 kg और धीमी गति से एक घंटे में 10 km की चाल से दौड़ना, अर्थात् v0 = 3 m s–1 लगभग| अत:
Ws = 180 जूल/कदम
यदि हम एक कदम में तय किए गए पथ की लंबाई 2 m लेते हैं तब कोई व्यक्ति 3 m s–1 की चाल से 1.5 कदम प्रति सेकंड भरता है | इस प्रकार व्यय शक्ति
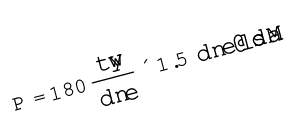
= 270 W
यहाँ हमें ध्यान रखना चाहिए कि व्यय शक्ति का आकलन वास्तविक मान से काफी कम है क्योंकि इस विधि में शक्ति-हानि के विभिन्न कारकों, जैसे हाथों का हिलना, वायु प्रतिरोध आदि, की उपेक्षा कर दी गई है | इसके अतिरिक्त एक दिलचस्प बात यह है कि हमने अपेक्षित विभिन्न बलों को भी गणना में कोई महत्त्व नहीं दिया है | बलों मेें से मुख्यत: घर्षण बल और शरीर की अन्य मांसपेशियों द्वारा टांग पर लगने वाले बलों का आकलन कर पाना कठिन है | घर्षण यहाँ ‘कोई’ कार्य नहीं करता है और हम कार्य-ऊर्जा प्रमेय का प्रयोग करके मांसपेशियों द्वारा किए गए ‘कार्य’ के आकलन के अत्यंत कठिन कार्य से बाहर निकल आए | इसी प्रकार, हम पहिये के लाभ भी देख सकते हैं | पहिया मानव को बिना किसी शुरुआत और विराम के निर्विघ्न गति प्रदान करता है |