Table of Contents

अध्याय 7
कणों के निकाय तथा घूर्णी गति
7.1 भूमिका
7.2 द्रव्यमान केन्द्र
7.3 द्रव्यमान केन्द्र की गति
7.4 कणों के निकाय का रेखीय संवेग
7.5 दो सदिशों का सदिश गुणनफल
7.6 कोणीय वेग और इसका रेखीय वेग से संबंध
7.7 बल आघूर्ण एवं कोणीय संवेग
7.8 दृढ़ पिंडों का संतुलन
7.9 जड़त्व आघूर्ण
7.10 लम्बवत् एवं समानान्तर अक्षों के प्रमेय
7.11 अचल अक्ष के परित: शुद्ध घूर्णी गतिकी
7.12 अचल अक्ष के परित: घूर्णी गतिकी
7.13 अचल अक्ष के परित: घूर्णी गति का कोणीय संवेग
7.14 लोटनिक गति
सारांश
विचारणीय विषय
अभ्यास
अतिरिक्त अभ्यास
7.1 भूमिका
पिछले अध्यायों में हमने मुख्य रूप से आदर्श बिन्दु कण (एक कण जिसे द्रव्यमान युक्त बिन्दु के रूप में व्यक्त किया जाए तथा इसका कोई आकार नहीं हो) की गति का अध्ययन किया था| फिर, यह मानते हुए कि परिमित आकार के पिण्डों की गति को बिन्दु कण की गति के पदों में व्यक्त किया जा सकता है, हमने उस अध्ययन के परिणामों को परिमित आकार के पिण्डों पर भी लागू कर दिया था|
दैनिक जीवन में जितने पिण्ड हमारे संपर्क में आते हैं वे सभी परिमित आकार के होते हैं| एक विस्तृत पिण्ड (परिमित आकार के पिण्ड) की गति को पूरे तौर पर समझने के लिए आमतौर पर उसका बिन्दुवत् आदर्श अपर्याप्त रहता है| इस अध्याय में हम इस प्रतिबंध के परे जाने की चेष्टा करेेंगे और विस्तृत, पर परिमित पिण्डों की गति को समझने का प्रयास करेंगे| एक विस्तृत पिण्ड प्रथमतया कणों का एक निकाय है| अत: हम अपना विवेचन एक निकाय की गति से ही शुरू करना चाहेंगे| यहाँ कणों के निकाय का द्रव्यमान केन्द्र एक मुख्य अवधारणा होगी| हम कणों के निकाय के द्रव्यमान केन्द्र की गति का वर्णन करेंगे और फिर, परिमित आकार के पिण्डों की गति को समझने में इस अवधारणा की उपयोगिता बतायेंगे|
बड़े पिण्डों से जुड़ी बहुत सी समस्याएं उनको दृढ़ पिण्ड मानकर हल की जा सकती हैं| आदर्श दृढ़ पिण्ड एक एेसा पिण्ड है जिसकी एक सुनिश्चित और अपरिवर्तनीय आकृति होती है| इस प्रकार के ठोस के सभी कण युग्मों के बीच की दूरियाँ परिवर्तित नहीं होती| दृढ़ पिण्ड की इस परिभाषा से यह स्पष्ट है कि कोई भी वास्तविक पिण्ड पूरी तरह दृढ़ नहीं होता, क्योंकि सभी व्यावहारिक पिण्ड बलों के प्रभाव से विकृत हो जाते हैं|
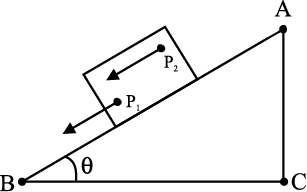
Fig 7.1 नत-तल पर एक ब्लॉक की अधोमुखी स्थानांतरण (फिसलन) गति (ब्लॉक का प्रत्येक बिंदु यथा P1, P2.... किसी भी क्षण समान गति में हैं)
परन्तु एेसी बहुत सी स्थितियाँ होती हैं जिनमें विकृतियाँ नगण्य होती हैं| अत: कई प्रकार की स्थितियों में यथा पहिये, लट्टू, स्टील के शहतीर और यहाँ तक कि अणु, ग्रह जैसे पिण्डों की गति का अध्ययन करते समय, हम ध्यान न देंगे कि उनमें विकृति आती है, वे मुड़ते हैं या कम्पन करते हैं| हम उन्हें दृढ़ पिण्ड मान कर उनकी गति का अध्ययन करेंगे|
7.1.1 एक दृढ़ पिण्ड में किस प्रकार की गतियाँ हो सकती हैं?
आइये, दृढ़ पिण्डों की गति के कुछ उदाहरणों से इस प्रश्न का उत्तर ढूंढ़ने की कोशिश करें| प्रथम एक आयताकार ब्लॉक पर विचार करें जो एक नत तल पर सीधा (बिना इधर-उधर हटे) नीचे की ओर फिसल रहा है| ब्लॉक एक दृढ़ पिण्ड लिया है| नत तल पर नीचे की ओर इसकी गति एेसी है कि इसके सभी कण साथ-साथ चल रहे हैं, अर्थात् किसी क्षण सभी कण समान वेग से चलते हैं (चित्र 7.1)| यहाँ यह दृढ़ पिंड शुद्ध स्थानांतरण गति में है|
शुद्ध स्थानांतरण गति में किसी क्षण विशेष पर पिण्ड का प्रत्येक कण समान वेग से चलता है|
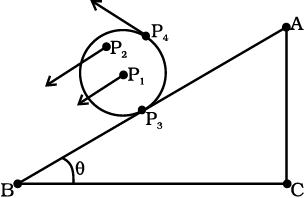
चित्र 7.2 नत तल पर नीचे की ओर लुढ़कता सिलिंडर (बेलन)| यह शुद्ध स्थानांतरण गति नहीं है| किसी क्षण पर बिन्दु P1, P2, P3 एवं P4 के अलग-अलग वेग हैं (जैसा कि तीर दर्शाते हैं)| वास्तव में सम्पर्क बिन्दु P3 का वेग किसी भी क्षण शून्य है यदि बेलन बिना फिसले हुए लुढ़कता है|
आइये, अब उसी नत तल पर नीचे की ओर लुढ़कते हुए एक धातु या लकड़ी के बेलन की गति पर विचार करते हैं (चित्र 7.2)| यह दृढ़ पिण्ड (बेलन) नत तल के शीर्ष से उसकी तली तक स्थानांतरित होता है, अत: इसमें स्थानांतरण गति प्रतीत होती है| लेकिन चित्र 7.2 यह भी दर्शाता है कि इसके सभी कण क्षण विशेष पर एक ही वेग से नहीं चल रहे हैं| अत: पिण्ड शुद्ध स्थानांतरण गति में नहीं है| अत: इसकी गति स्थानांतरीय होने के साथ-साथ ‘कुछ और अलग’ भी है|
यह ‘कुछ और अलग’ भी क्या है? यह समझने के लिए, आइये, हम एक एेसा दृढ़ पिंड लें जिसको इस प्रकार व्यवरुद्ध कर दिया गया है कि यह स्थानांतरण गति न कर सके| किसी दृढ़ पिण्ड की स्थानांतरण गति को निरुद्ध करने की सर्व सामान्य विधि यह है कि उसे एक सरल रेखा के अनुदिश स्थिर कर दिया जाए| तब इस दृढ़ पिण्ड की एकमात्र संभावित गति घूर्णी गति होगी| वह सरल रेखा जिसके अनुदिश इस दृढ़ पिण्ड को स्थिर बनाया गया है इसकी घूर्णन-अक्ष कहलाती है| यदि आप अपने चारों ओर देखें तो आपको छत का पंखा, कुम्हार का चाक (चित्र 7.3(a) एवं (b)), विशाल चक्री-झूला (जॉयन्ट व्हील), मेरी-गो-राउण्ड जैसे अनेक एेसे उदाहरण मिल जायेंगे जहाँ किसी अक्ष के परित: घूर्णन हो रहा हो|

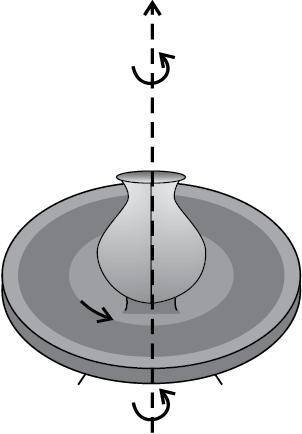
चित्र 7.3 एक स्थिर अक्ष के परित: घूर्णन
(a) छत का पंखा
(b) कुम्हार का चाक
आइये, अब हम यह समझने की चेष्टा करें कि घूर्णन क्या है, और इसके क्या अभिलक्षण हैं? आप देख सकते हैं कि एक दृढ़ पिण्ड के एक स्थिर अक्ष के परित: घूर्णन में, पिण्ड का हर कण एक वृत्त में घूमता है| यह वृत्त अक्ष के लम्बवत् तल में है और इनका केन्द्र अक्ष पर अवस्थित है|
चित्र 7.4 में एक स्थिर अक्ष (निर्देश फ्रेम की z-अक्ष) के परित: किसी दृढ़ पिण्ड की घूर्णन गति दर्शायी है| हम अक्ष से r1 दूरी पर स्थित दृढ़ पिण्ड का कोई स्वेच्छ कण P1 लें| यह कण अक्ष के परित: r1 त्रिज्या के वृत्त पर घूमता है जिसका केन्द्र C1 अक्ष पर स्थित है| यह वृत्त अक्ष के लम्बवत् तल में अवस्थित है| चित्र में एक दूसरा कण P2 भी दर्शाया गया है जो स्थिर अक्ष से r2 दूरी पर है| कण P2 , r2 त्रिज्या के वृत्ताकार पथ पर चलता है जिसका केन्द्र अक्ष पर C2 है| यह वृत्त भी अक्ष के लम्बवत् तल में है| ध्यान दें कि P1 एवं P2 द्वारा बनाये गए वृत्त अलग-अलग तलों में हैं पर ये दोनों तल स्थिर अक्ष के लम्बवत् हैं| अक्ष पर स्थित किसी बिन्दु, जैसे P3 के लिए, r = 0 | ये कण, पिण्ड के घूमते समय भी स्थित रहते हैं| यह अपेक्षित भी है क्योंकि घूर्णन अक्ष स्थिर है|
तथापि, घूर्णन के कुछ उदाहरणों में, अक्ष स्थिर नहीं भी रहती| इस प्रकार के घूर्णन के मुख्य उदाहरणों में एक है, एक ही स्थान पर घूमता लट्टू (चित्र 7.5(a))| (लट्टू की गति के संबंध में हमने यह मान लिया है कि यह एक स्थान से दूसरे स्थान पर स्थानांतरित नहीं होता और इसलिए इसमें स्थानांतरण गति नहीं है|) अपने अनुभव के आधार पर हम यह जानते हैं कि इस प्रकार घूमते लट्टू की अक्ष, भूमि पर इसके सम्पर्क-बिन्दु से गुजरते अभिलम्ब के परित: एक शंकु बनाती है जैसा कि चित्र 7.5(a) में दर्शाया गया है| (ऊर्ध्वाधर के परित: लट्टू की अक्ष का इस प्रकार घूमना पुरस्सरण कहलाता है )| ध्यान दें कि लट्टू का वह बिन्दु जहाँ यह धरातल को छूता है, स्थिर है| किसी भी क्षण, लट्टू की घूर्णन-अक्ष, इसके सम्पर्क बिन्दु से गुजरती है| इस प्रकार की घूर्णन गति का दूसरा सरल उदाहरण घूमने वाला मेज का पंखा या पीठिका-पंखा है| आपने देखा होगा कि इस प्रकार के पंखे की अक्ष, क्षैतिज तल में, दोलन गति (इधर से उधर घूमने की) करती है और यह गति ऊर्ध्वाधर रेखा के परित: होती है जो उस बिन्दु से गुजरती है जिस पर अक्ष की धुरी टिकी होती है (चित्र 7.5(b) में बिन्दु O)|
चित्र 7.5 (b) दोलन करता हुआ मेज का पंखा जिसकी पंखुड़ियाँ घूर्णन गति में हैं| (पंखे की धुरी, बिन्दु O, स्थिर है )
जब पंखा घूमता है और इसकी अक्ष इधर से उधर दोलन करती है तब भी यह बिन्दु स्थिर रहता है| घूर्णन गति के
अधिक सार्विक मामलों में, जैसे कि लट्टू या पीठिका-पंखे के घूमने में, दृढ़ पिण्ड का एक बिन्दु स्थिर रहता है, न कि एक रेखा| इस मामले में अक्ष तो स्थिर नहीं है पर यह हमेशा एक स्थिर बिन्दु से गुजरती है| तथापि, अपने अध्ययन में,
अधिकांशत:, हम एेसी सरल एवं विशिष्ट घूर्णन गतियों तक सीमित रहेंगे जिनमें एक रेखा (यानि अक्ष) स्थिर रहती है| अत: जब तक अन्यथा न कहा जाय, हमारे लिए घूर्णी गति एक स्थिर अक्ष के परित: ही होगी|
एक नत तल पर नीचे की ओर बेलन का लुढ़कना दो तरह की गतियों का संयोजन है- स्थानांतरण गति और एक स्थिर अक्ष के परित: घूर्णी गति| अत:, लुढ़कन गति के संदर्भ में जिस ‘कुछ और अलग’ का जिक्र पहले हमने किया था वह घूर्णी गति है| इस दृष्टिकोण से चित्र 7.6(a) एवं (b) को आप पर्याप्त शिक्षाप्रद पायेंगे| इन दोनों चित्रों में एक ही पिण्ड की गति, समान स्थानांतरीय गमन-पथ के अनुदिश दर्शाई गई है| चित्र 7.6(a) में दर्शाई गई गति शुद्ध स्थानांतरीय है, जबकि चित्र 7.6(b) में दर्शाई गई गति स्थानांतरण एवं घूर्णी दोनों प्रकार की गतियों का संयोजन है| (आप स्वयं भारी पुस्तक जैसा एक दृढ़ पिण्ड फेंक कर दर्शाई गई दोनों प्रकार की गतियाँ उत्पन्न करने की कोशिश कर सकते हैं|)
आइये अब हम प्रस्तुत खण्ड में वर्णित महत्वपूर्ण तथ्यों का सार फिर से आपको बतायें| एक एेसा दृढ़ पिण्ड जो न तो किसी चूल पर टिका हो और न ही किसी रूप में स्थिर हो, दो प्रकार की गति कर सकता है - या तो शुद्ध स्थानांतरण या स्थानांतरण एवं घूर्णन गति का संयोजन| एक एेसे दृढ़ पिण्ड की गति जो या तो चूल पर टिका हो या किसी न किसी रूप में स्थिर हो, घूर्णी गति होती है| घूर्णन किसी एेसी अक्ष के परित: हो सकता है जो स्थिर हो (जैसे छत के पंखे में) या फिर एक एेसी अक्ष के परित: जो स्वयं घूमती हो (जैसे इधर से उधर घूमते मेज के पंखे में)| इस अध्याय में हम एक स्थिर अक्ष के परित: होने वाली घूर्णी गति का ही अध्ययन करेंगे|
7.2 द्रव्यमान केन्द्र
पहले हम यह देखेंगे कि द्रव्यमान केन्द्र क्या है और फिर इसके महत्व पर प्रकाश डालेंगे| सरलता की दृष्टि से हम दो कणों के निकाय से शुरुआत करेंगे| दोनों कणों की स्थितियों को मिलाने वाली रेखा को हम x- अक्ष मानेंगे| (चित्र 7.7)

चित्र 7.7 दो कणों और उनके द्रव्यमान केन्द्र की स्थिति
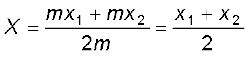 (7.1)
(7.1)
समीकरण (7.1) में X को हम x1 एवं x2 का द्रव्यमान भारित माध्य मान सकते हैं| यदि दोनों कणों का द्रव्यमान बराबर हो तो m1 = m2 = m, तब
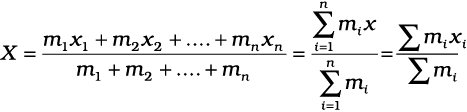
इस प्रकार समान द्रव्यमान के दो कणों का द्रव्यमान केन्द्र ठीक उनके बीचोंबीच है|
अगर हमारे पास n कण हों, जिनके द्रव्यमान क्रमश: m1, m2, ...mn हों और सबको x- अक्ष के अनुदिश रखा गया हो, तो परिभाषा के अनुसार इन सब कणों का द्रव्यमान केन्द्र होगा
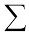 (7.2)
(7.2)
जहाँ x1, x2,...xn कणों की क्रमश: मूलबिन्दु से दूरियाँ हैं; X भी उसी मूलबिन्दु से मापा गया है| संकेत (यूनानी भाषा का अक्षर सिग्मा) संकलन को व्यक्त करता है जो इस मामले में n कणों के लिए किया गया है| संकलन फल
कणों के लिए किया गया है| संकलन फल
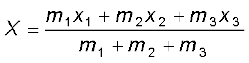
निकाय का कुल द्रव्यमान है|
माना हमारे पास तीन कण हैं जो एक सरल रेखा में तो नहीं, पर एक समतल में रखे गए हैं| तब हम उस तल में जिसमें ये तीन कण रखे गए हैं x- एवं y-अक्ष निर्धारित कर सकते हैं, और इन तीन कणों की स्थितियों को क्रमश: निर्देशांकों (x1,y1), (x2,y2) एवं (x3,y3) द्वारा व्यक्त कर सकते हैं| मान लीजिए कि इन तीन कणों के द्रव्यमान क्रमश: m1, m2 एवं m3 हैं| इन तीन कणों के निकाय का द्रव्यमान केन्द्र C निर्देशांकों (X, Y) द्वारा व्यक्त किया जायेगा जिनके मान हैं
- 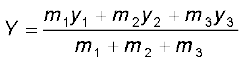 (7.3a)
(7.3a)
 (7.3b)
(7.3b)
समान द्रव्यमान वाले कणों के लिए m = m1 = m2 = m3,


अर्थात् समान द्रव्यमान वाले कणों के लिए तीन कणों का द्रव्यमान केन्द्र उनकी स्थिति बिन्दुओं को मिलाने से बने त्रिभुज के केन्द्रक पर होगा|
समीकरण (7.3a,b) के परिणामों को, सरलतापूर्वक, एेसे n कणों के एक निकाय के लिए सार्विक किया जा सकता है जो एक समतल में न होकर, अंतरिक्ष में फैले हों| इस तरह के निकाय का द्रव्यमान केन्द्र (X, Y, Z) है, जहाँ
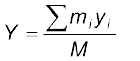 (7.4a)
(7.4a)
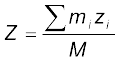 (7.4b)
(7.4b)
और  (7.4c)
(7.4c)
यहाँ M = 2552.pngनिकाय का कुल द्रव्यमान है| सूचक i का मान 1 से n तक बदलता है, mi i वें कण का द्रव्यमान है, और i वें कण की स्थिति (xi, yi, zi) से व्यक्त की गई है|
यदि हम स्थिति-सदिश की अवधारणा का उपयोग करें तो समीकरण (7.4a, b, c) को संयोजित करके एकल समीकरण के रूप में लिखा जा सकता है| यदि 2557.png, i वें कण का स्थिति-वेक्टर है और R द्रव्यमान केन्द्र का स्थिति-सदिश है:

एवं 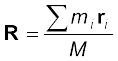
तब 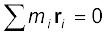 (7.4d)
(7.4d)
समीकरण के दाहिनी ओर लिखा गया योग सदिश-योग है|
सदिशों के इस्तेमाल से समीकरणों की संक्षिप्तता पर ध्यान दीजिए| यदि संदर्भ-फ्रेम (निर्देशांक निकाय) के मूल बिन्दु को, दिए गए कण-निकाय के द्रव्यमान केन्द्र में लिया जाए तो 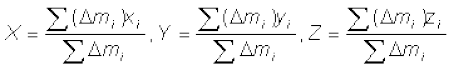 |
|
एक दृढ़ पिण्ड, जैसे कि मीटर-छड़ या फ्लाइ व्हील, बहुत पास-पास रखे गए कणों का निकाय है; अत: समीकरण (7.4a, b, c, d) दृढ़ पिण्ड के लिए भी लागू होते हैं| इस प्रकार के पिण्डों में कणों (परमाणुओं या अणुओं) की संख्या इतनी अधिक होती है, कि इन समीकरणों में, सभी पृथक-पृथक कणों को लेकर संयुक्त प्रभाव ज्ञात करना असंभव कार्य है| पर, क्योंकि कणों के बीच की दूरी बहुत कम है, हम पिण्ड में द्रव्यमान का सतत वितरण मान सकते हैं| यदि पिण्ड को n छोटे द्रव्यमान खण्डों में विभाजित करें जिनके द्रव्यमान ∆m1, ∆m2... ∆mn हैं तथा i-वाँ खण्ड ∆mi बिन्दु (xi, yi, zi) पर अवस्थित है एेसा सोचें तो द्रव्यमान केन्द्र के निर्देशांकों के लगभग मान इस प्रकार व्यक्त करेंगे -
यदि हम n को वृहत्तर करें अर्थात् ∆mi को और छोटा करें तो ये समीकरण काफी यथार्थ मान बताने लगेंगे| उस स्थिति में i-कणों के योग को हम समाकल से व्यक्त करेंगे|
और 
यहाँ M पिण्ड का कुल द्रव्यमान है| द्रव्यमान केन्द्र के निर्देशांकों को अब हम इस प्रकार लिख सकते हैं

(7.5a)
इन तीन अदिश व्यंजकों के तुल्य सदिश व्यंजक इस प्रकार लिख सकते हैं-
 (7.5b)
(7.5b)
यदि हम द्रव्यमान केन्द्र को अपने निर्देशांक निकाय का मूल-बिन्दु चुनें तो
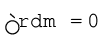
अर्थात्, 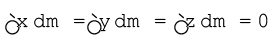
प्राय: हमें नियमित आकार के समांग पिण्डों; जैसे – वलयों, गोल-चकतियों, गोलों, छड़ों इत्यादि के द्रव्यमान केन्द्रों की गणना करनी पड़ती है| (समांग पिण्ड से हमारा तात्पर्य एक एेसी वस्तु से है जिसमें द्रव्यमान का समान रूप से वितरण हो)| सममिति का विचार करके हम सरलता से यह दर्शा सकते हैं कि इन पिण्डों के द्रव्यमान केन्द्र उनके ज्यामितीय केन्द्र ही होते हैं|

आइये, एक पतली छड़ पर विचार करें, जिसकी चौड़ाई और मोटाई (यदि इसकी अनुप्रस्थ काट आयताकार है) अथवा त्रिज्या (यदि छड़ बेलनाकार है), इसकी लम्बाई की तुलना में बहुत छोटी है| छड़ की लम्बाई x-अक्ष के अनुदिश रखें और मूल बिन्दु इसके ज्यामितीय केन्द्र पर ले लें तो परावर्तन सममिति की दृष्टि से हम कह सकते हैं कि प्रत्येक x पर स्थित प्रत्येक dm घटक के समान dm का घटक –x पर भी स्थित होगा (चित्र 7.8)|
समाकल में हर जोड़े का योगदान शून्य है और इस कारण स्वयं 2713.png का मान शून्य हो जाता है| समीकरण (7.6) बताती है कि जिस बिन्दु के लिए समाकल शून्य हो वह पिण्ड का द्रव्यमान केन्द्र है| अत: समांग छड़ का ज्यामितीय केन्द्र इसका द्रव्यमान केन्द्र है| इसे परावर्तन सममिति के प्रयोग से समझ सकते हैं|
सममिति का यही तर्क, समांग वलयों, चकतियों, गोलों और यहाँ तक कि वृत्ताकार या आयताकार अनुप्रस्थ काट वाली मोटी छड़ों के लिए भी लागू होगा| एेसे सभी पिण्डों के लिए आप पायेंगे कि बिन्दु (x,y,z) पर स्थित हर द्रव्यमान घटक के लिए बिन्दु (-x,-y,-z) पर भी उसी द्रव्यमान का घटक लिया जा सकता है| (दूसरे शब्दों में कहें तो इन सभी पिण्डों के लिए मूल बिन्दु परावर्तन-सममिति का बिन्दु है)| परिणामत:, समीकरण (7.5 a) में दिए गए सभी समाकल शून्य हो जाते हैं| इसका अर्थ यह हुआ कि उपरोक्त सभी पिण्डों का द्रव्यमान केन्द्र उनके ज्यामितीय केन्द्र पर ही पड़ता है|
उदाहरण 7.1 एक समबाहु त्रिभुज के शीर्षों पर रखे गए तीन कणों का द्रव्यमान केन्द्र ज्ञात कीजिए| कणों के द्रव्यमान क्रमश: 100g, 150g, एवं 200g हैं| त्रिभुज की प्रत्येक भुजा की लम्बाई 0.5 m है|
हल

चित्र 7.9
x एवं y- अक्ष चित्र 7.9 में दर्शाये अनुसार चुनें तो समबाहु त्रिभुज के शीर्ष बिन्दुओं O, A एवं B के निर्देशांक क्रमश: (0,0), (0.5,0) एवं (0.25,0.25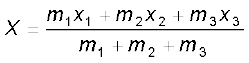 ) होंगे| माना कि 100g, 150g एवं 200g के द्रव्यमान क्रमश: O, A एवं B पर अवस्थित हैं| तब
) होंगे| माना कि 100g, 150g एवं 200g के द्रव्यमान क्रमश: O, A एवं B पर अवस्थित हैं| तब
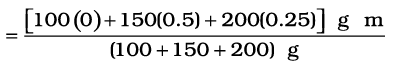
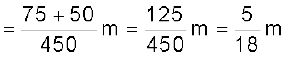
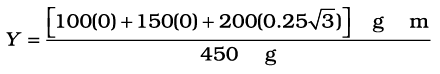
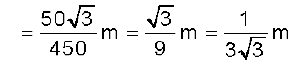
द्रव्यमान केन्द्र C चित्र में दर्शाया गया है| ध्यान दें कि यह त्रिभुज OAB का ज्यामितीय केन्द्र नहीं है| क्या आप बता सकते हैं कि एेसा क्यों नही है?
उदाहरण 7.2: एक त्रिभुजाकार फलक का द्रव्यमान केन्द्र ज्ञात कीजिए|
हल फलक (∆LMN) को आधार (MN) के समान्तर पतली पट्टियों में बांटा जा सकता है जैसा चित्र 7.10 में दर्शाया
गया है|
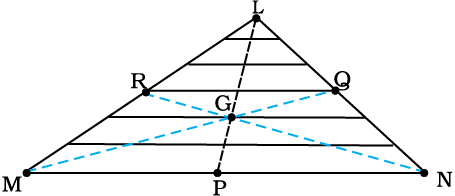
चित्र 7.10
सममिति के आधार पर हम कह सकते हैं कि हर पट्टी का द्रव्यमान केन्द्र उसका मध्य बिन्दु है| अगर हम सभी पट्टियों के मध्य बिन्दुओं को मिलाते हैं तो हमें माध्यिका LP प्राप्त होती है| इसलिए, पूरे त्रिभुज का द्रव्यमान केन्द्र इस माध्यिका LP पर कहीं अवस्थित होगा| इसी प्रकार हम तर्क कर सकते हैं कि यह माध्यिका MQ और NR पर भी अवस्थित होगा| अत: यह द्रव्यमान केन्द्र तीनों माध्यिकाओं का संगामी बिन्दु गति त्रिभुज का केन्द्रक G है|
उदाहरण 7.3: एक दिए गए L-आकृति के फलक (एक पतली चपटी प्लेट) का द्रव्यमान केन्द्र ज्ञात कीजिए, जिसका विभिन्न भुजाओं को चित्र 7.11 में दर्शाया है| फलक का द्रव्यमान 3 kg है|
हल चित्र 7.11 के अनुसार X एवं Y अक्षाें को चुनें तो L-आकृति फलक के विभिन्न शीर्षों के निर्देशांक वही प्राप्त होते हैं जो चित्र में अंकित किए गए हैं| हम L-आकृति को तीन वर्गों से मिलकर बना हुआ मान सकते हैं जिनमें से प्रत्येक वर्ग की भुजा 1m है| प्रत्येक वर्ग का द्रव्यमान 1kg है, क्योंकि फलक समांग हैं| इन तीन वर्गों के द्रव्यमान केन्द्र C1, C2 और C3 हैं, जो सममिति के विचार से उनके ज्यामितीय केन्द्र हैं और इनके निर्देशांक क्रमश: (1/2,1/2), (3/2,1/2), (1/2,3/2) हैं| हम कह सकते हैं कि L-आकृति का द्रव्यमान केन्द्र (X, Y) इन द्रव्यमान बिन्दुओं का द्रव्यमान केन्द्र हैं|
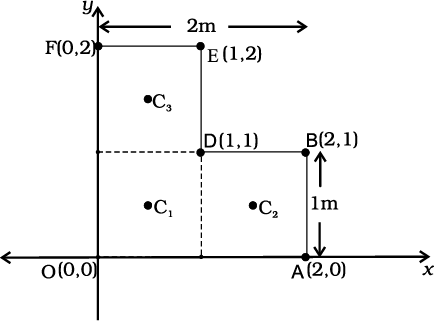
चित्र 7.11
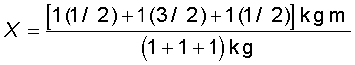
चित्र 7.11
अत:
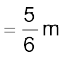

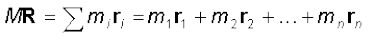
L-आकृति का द्रव्यमान केन्द्र रेखा OD पर पड़ता है| इस बात का अंदाजा हम बिना किसी गणना के लगा सकते थे| क्या आप बता सकते हैं, कैसे? यदि यह मानें कि चित्र 7.11 में दर्शाये गए L आकृति फलक के तीन वर्गों के द्रव्यमान अलग-अलग होते तब आप इस फलक का द्रव्यमान केन्द्र कैसे ज्ञात करेंगे?
7.3 द्रव्यमान केन्द्र की गति
द्रव्यमान केन्द्र की परिभाषा जानने के बाद, अब हम इस स्थिति में हैं कि n कणों के एक निकाय के लिए इसके भौतिक महत्व की विवेचना कर सकें| समीकरण (7.4d) को हम फिर से इस प्रकार लिख सकते हैं-
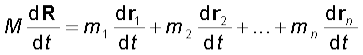 (7.7)
(7.7)
समीकरण के दोनों पक्षों को समय के सापेक्ष अवकलित करने पर-
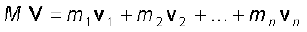
या
 (7.8)
(7.8)
जहाँ,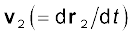 प्रथम कण का वेग है,
प्रथम कण का वेग है,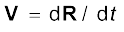
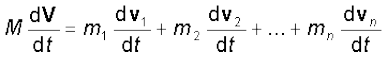 कणों के निकाय के द्रव्यमान केन्द्र का वेग है| ध्यान दें, कि हमने यह मान लिया है कि m1, m2, ... आदि के मान समय के साथ बदलते नहीं हैं| इसलिए, समय के सापेक्ष समीकरणों को अवकलित करते समय हमने उनके साथ अचरांकों जैसा व्यवहार किया है|
कणों के निकाय के द्रव्यमान केन्द्र का वेग है| ध्यान दें, कि हमने यह मान लिया है कि m1, m2, ... आदि के मान समय के साथ बदलते नहीं हैं| इसलिए, समय के सापेक्ष समीकरणों को अवकलित करते समय हमने उनके साथ अचरांकों जैसा व्यवहार किया है|
समीकरण (7.8) को समय के सापेक्ष अवकलित करने पर-
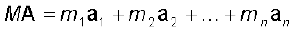
या
 (7.9)
(7.9)
जहाँ 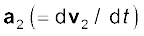 प्रथम कण का त्वरण है,
प्रथम कण का त्वरण है, 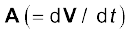 दूसरे कण का त्वरण है, इत्यादि और
दूसरे कण का त्वरण है, इत्यादि और 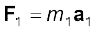 कणों के निकाय के द्रव्यमान केन्द्र का त्वरण है|
कणों के निकाय के द्रव्यमान केन्द्र का त्वरण है|
अब, न्यूटन के द्वितीय नियमानुसार, पहले कण पर लगने वाला बल है 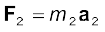 , दूसरे कण पर लगने वाला बल है , आदि| तब समीकरण
, दूसरे कण पर लगने वाला बल है , आदि| तब समीकरण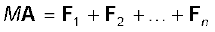 (7.9) को हम इस प्रकार भी लिख सकते हैं-
(7.9) को हम इस प्रकार भी लिख सकते हैं-
 (7.10)
(7.10)
अत: कणों के निकाय के कुल द्रव्यमान को द्रव्यमान केन्द्र के त्वरण से गुणा करने पर हमें उस कण-निकाय पर लगने वाले सभी बलों का सदिश योग प्राप्त होता है|
ध्यान दें कि जब हम पहले कण पर लगने वाले बल 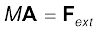 की बात करते हैं, तो यह कोई एकल बल नहीं है, बल्कि, इस कण पर लगने वाले सभी बलों का सदिश योग है| यही बात हम अन्य कणों के विषय में भी कह सकते हैं| प्रत्येक कण पर लगने वाले उन बलों में कुछ बाह्य बल होंगे जो निकाय से बाहर के पिण्डों द्वारा आरोपित होंगे और कुछ आंतरिक बल होंगे जो निकाय के अंदर के कण एक दूसरे पर आरोपित करते हैं| न्यूटन के तृतीय नियम से हम जानते हैं कि ये आंतरिक बल सदैव बराबर परिमाण के और विपरीत दिशा में काम करने वाले जोड़ों के रूप में पाए जाते हैं और इसलिए समीकरण (7.10) में बलों को जोड़ने में इनका योग शून्य हो जाता है| समीकरण में केवल बाह्य बलों का योगदान रह जाता है| समीकरण (7.10) को फिर इस प्रकार लिख सकते हैं
की बात करते हैं, तो यह कोई एकल बल नहीं है, बल्कि, इस कण पर लगने वाले सभी बलों का सदिश योग है| यही बात हम अन्य कणों के विषय में भी कह सकते हैं| प्रत्येक कण पर लगने वाले उन बलों में कुछ बाह्य बल होंगे जो निकाय से बाहर के पिण्डों द्वारा आरोपित होंगे और कुछ आंतरिक बल होंगे जो निकाय के अंदर के कण एक दूसरे पर आरोपित करते हैं| न्यूटन के तृतीय नियम से हम जानते हैं कि ये आंतरिक बल सदैव बराबर परिमाण के और विपरीत दिशा में काम करने वाले जोड़ों के रूप में पाए जाते हैं और इसलिए समीकरण (7.10) में बलों को जोड़ने में इनका योग शून्य हो जाता है| समीकरण में केवल बाह्य बलों का योगदान रह जाता है| समीकरण (7.10) को फिर इस प्रकार लिख सकते हैं
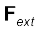 (7.11)
(7.11)
जहाँ निकाय के कणों पर प्रभावी सभी बाह्य बलों का सदिश योग है|
समीकरण (7.11) बताती है कि कणों के किसी निकाय का द्रव्यमान केन्द्र इस प्रकार गति करता है मानो निकाय का संपूर्ण द्रव्यमान उसमें संकेन्द्रित हो और सभी बाह्य बल उसी पर आरोपित हों|
ध्यान दें कि द्रव्यमान केन्द्र की गति के विषय में जानने के लिए, कणों के निकाय के आंतरिक बलों के विषय में कोई जानकारी नहीं चाहिए, इस उद्देश्य के लिए हमें केवल बाह्य बलों को ही जानने की आवश्यकता है|
समीकरण (7.11) व्युत्पन्न करने के लिए हमें कणों के निकाय की प्रकृति सुनिश्चित नहीं करनी पड़ी| निकाय कणों का एेसा संग्रह भी हो सकता है जिसमें तरह-तरह की आंतरिक गतियाँ हों, और शुद्ध स्थानांतरण गति करता हुआ, अथवा, स्थानांतरण एवं घूर्णी गति के संयोजन युक्त एक दृढ़ पिण्ड भी हो सकता है| निकाय कैसा भी हो और इसके अवयवी कणों में किसी भी प्रकार की गतियाँ हों, इसका द्रव्यमान केन्द्र समीकरण (7.11) के अनुसार ही गति करेगा|
परिमित आकार के पिण्डों को एकल कणों की तरह व्यवहार में लाने के बजाय अब हम उनको कणों के निकाय की तरह व्यवहार में ला सकते हैं| हम उनकी गति का शुद्ध स्थानांतरीय अवयव यानि निकाय के द्रव्यमान केन्द्र की गति ज्ञात कर सकते हैं| इसके लिए, बस, पूरे निकाय का कुल द्रव्यमान और निकाय पर लगे सभी बाह्य बलों को निकाय के द्रव्यमान केन्द्र पर प्रभावी मानना होगा|
यही कार्यविधि हमने पिण्डों पर लगे बलों के विश्लेषण और उनसे जुड़ी समस्या के हल के लिए अपनाई थी| हालांकि, इसके लिए कोई स्पष्ट कारण नहीं बताया गया था| अब हम यह समझ सकते हैं, कि पूर्व के अध्ययनों में, हमने बिन कहे ही यह मान लिया था कि निकाय में घूर्णी गति, एवं कणों में आंतरिक गति या तो थी ही नहीं और यदि थी तो नगण्य थी| आगे से हमें यह मानने की आवश्यकता नहीं रहेगी| न केवल हमें अपनी पहले अपनाई गई पद्धति का औचित्य समझ में आ गया है, वरन्, हमने वह विधि भी ज्ञात कर ली है जिसके द्वारा (i) एेसे दृढ़ पिण्ड की जिसमें घूर्णी गति भी हो, (ii) एक एेसे निकाय की जिसके कणों में तरह-तरह की आंतरिक गतियाँ हों, स्थानांतरण गति को अलग करके समझा समझाया जा सकता है|
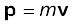
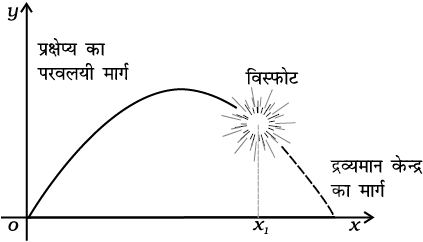
चित्र 7.12 किसी प्रक्षेप्य के खण्डों का द्रव्यमान केन्द्र विस्फोट के बाद भी उसी परवलयाकार पथ पर चलता हुआ पाया जायेगा जिस पर यह विस्फोट न होने पर चलता|
चित्र 7.12 समीकरण (7.11) को स्पष्ट करने वाला एक अच्छा उदाहरण है| अपने निर्धारित परवलयाकार पथ पर चलता हुआ एक प्रक्षेप्य हवा में फट कर टुकड़ों में बिखर जाता है| विस्फोट कारक बल आंतरिक बल है इसलिए उनका द्रव्यमान केन्द्र की गति पर कोई प्रभाव नहीं होता| प्रक्षेप्य और उसके खण्डों पर लगने वाला कुल बाह्य बल विस्फोट के बाद भी वही है जो विस्फोट से पहले था, यानि पृथ्वी का गुरुत्वाकर्षण बल| अत:, बाह्य बल के अंतर्गत प्रक्षेप्य के द्रव्यमान केन्द्र का परवलयाकार पथ विस्फोट के बाद भी वही बना रहता जो विस्फोट न होने की स्थिति में होता|
7.4 कणों के निकाय का रेखीय संवेग
आपको याद होगा कि रेखीय संवेग की परिभाषा करने वाला व्यंजक है
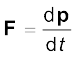 (7.12)
(7.12)
और, एकल कण के लिए न्यूटन के द्वितीय नियम को हम सांकेतिक भाषा में लिख सकते हैं
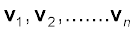 (7.13)
(7.13)
जहाँ F कण पर आरोपित बल है| आइये, अब हम n कणों के एक निकाय पर विचार करें जिनके द्रव्यमान क्रमश: m1, m2,...mn है और वेग क्रमश: 2911.png हैं| कण, परस्पर अन्योन्य क्रियारत हो सकते हैं और उन पर बाह्य बल भी लगे हो सकते हैं| पहले कण का रेखीय संवेग 2916.png, दूसरे कण का रेखीय संवेग 2921.png और इसी प्रकार अन्य कणों के रेखीय संवेग भी हैं|
n कणों के इस निकाय का कुल रेखीय संवेग, एकल कणों के रेखीय संवेगों के सदिश योग के बराबर है|
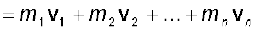
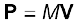 (7.14)
(7.14)
इस समीकरण की समीकरण (7.8) से तुलना करने पर,
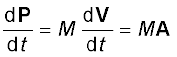 (7.15)
(7.15)
अत: कणों के एक निकाय का कुल रेखीय संवेग, निकाय के कुल द्रव्यमान तथा इसके द्रव्यमान केन्द्र के वेग के गुणनफल के बराबर होता है| समीकरण (7.15) का समय के सापेक्ष अवकलन करने पर,
 (7.16)
(7.16)
समीकरण (7.16) एवं समीकरण (7.11) की तुलना करने पर
 (7.17)
(7.17)
यह गति के न्यूटन के द्वितीय नियम का कथन है जो कणों के निकाय के लिए लागू किया गया है|
यदि कणों के किसी निकाय पर लगे बाह्य बलों का योग शून्य हो, तो समीकरण (7.17) के आधार पर,
 = अचरांक (7.18a)
= अचरांक (7.18a)
चित्र 7.13 (a) एक भारी नाभिक रेडियम (Ra) एक अपेक्षाकृत हलके नाभिक रेडॉन (Rn) एवं एक अल्फा-कण (हीलियम परमाणु का नाभिक, He) में विखंडित होता है| निकाय का द्रव्यमान केन्द्र समगति में है|
अत: जब कणों के किसी निकाय पर लगे बाह्य बलों का योग शून्य होता है तो उस निकाय का कुल रेखीय संवेग अचर रहता है| यह कणों के एक निकाय के लिए लागू होने वाला रेखीय संवेग के संरक्षण का नियम है| समीकरण (7.15) के कारण, इसका अर्थ यह भी होता है कि जब निकाय पर लगने वाला कुल बाह्य बल शून्य होता है तो इसके द्रव्यमान केन्द्र का वेग परिवर्तित नहीं होता| (इस अध्याय में कणों के निकाय का अध्ययन करते समय हम हमेशा यह मान कर चलेंगे कि निकाय का कुल द्रव्यमान अचर रहता है|)
ध्यान दें, कि आंतरिक बलों के कारण, यानि उन बलों के कारण जो कण एक दूसरे पर आरोपित करते हैं, किसी विशिष्ट कण का गमन-पथ काफी जटिल हो सकता है| फिर भी, यदि निकाय पर लगने वाला कुल बाह्य बल शून्य हो तो द्रव्यमान केन्द्र अचर-वेग से ही चलता है, अर्थात्, मुक्त कण की तरह समगति से सरल रेखीय पथ पर चलता है|
सदिश समीकरण (7.18a) जिन अदिश समीकरणों के तुल्य है, वे हैं-
Px = C1, Py = C2 तथा Pz = C3 (7.18 b)
यहाँ Px, Py, Pz कुल रेखीय संवेग सदिश P के, क्रमश: x, y एवं z दिशा में अवयव हैं और C1, C2, C3 अचरांक हैं|
(a) (b)
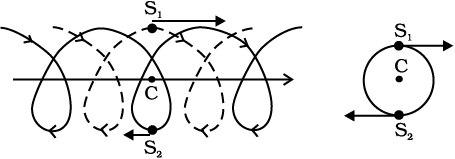
चित्र 7.14 (a) बायनरी निकाय बनाते दो नक्षत्रों S1 एवं S2 के गमन पथ, जो क्रमश: बिन्दु रेखा एवं सतत रेखा द्वारा दर्शाये गए हैं| इनका द्रव्यमान केन्द्र C समगति में है|
(b) द्रव्यमान केन्द्र की स्थिर अवस्था में उसी भारी कण रेडियम (Ra) का विखंडन| दोनों उत्पन्न हुए कण एक दूसरे की विपरीत दिशा में गतिमान होते हैं|
एक उदाहरण के रूप में, आइये, रेडियम के नाभिक जैसे किसी गतिमान अस्थायी नाभिक के रेडियोएक्टिव क्षय पर विचार करें| रेडियम का नाभिक एक रेडन के नाभिक और एक अल्फा कण में विखंडित होता है| क्षय-कारक बल निकाय के आंतरिक बल हैं और उस पर प्रभावी बाह्य बल नगण्य हैं| अत: निकाय का कुल रेखीय संवेग, क्षय से पहले और क्षय के बाद समान रहता है| विखंडन में उत्पन्न हुए दोनों कण, रेडन का नाभिक एवं अल्फा-कण, विभिन्न दिशाओं में इस प्रकार चलते हैं कि उनके द्रव्यमान केन्द्र का गमन-पथ वही बना रहता है जिस पर क्षयित होने से पहले मूल रेडियम नाभिक गतिमान था (चित्र 7.13(a))|
यदि हम एक एेसे संदर्भ फ्रेम से इस क्षय प्रक्रिया को देखें जिसमें द्रव्यमान केन्द्र स्थिर हो, तो इसमें शामिल कणों की गति विशेषकर सरल दिखाई पड़ती है; उत्पन्न हुए दोनों कण एक दूसरे की विपरीत दिशा में इस प्रकार गतिमान होते हैं कि उनका द्रव्यमान केन्द्र स्थिर रहे, जैसा चित्र 7.13 (b) में दर्शाया गया है|
(b) उसी बायनरी निकाय की गति जब द्रव्यमान केन्द्र C स्थिर है|
कणों की निकाय संबंधी बहुत सी समस्याओं में जैसा ऊपर बताई गई रेडियोएक्टिव क्षय संबंधी समस्या में दर्शाया है, प्रयोगशाला के संदर्भ-फ्रेम की अपेक्षा, द्रव्यमान-केन्द्र के फ्रेम में कार्य करना आसान होता है|
खगोलिकी में युग्मित (बायनरी) नक्षत्रों का पाया जाना एक आम बात है| यदि कोई बाह्य बल न लगा हो तो किसी युग्मित नक्षत्र का द्रव्यमान केन्द्र एक मुक्त-कण की तरह चलता है जैसा चित्र 7.14 (a) में दर्शाया गया है| चित्र में समान द्रव्यमान वाले दोनों नक्षत्रों के गमन पथ भी दर्शाये गए हैं; वे काफी जटिल दिखाई पड़ते हैं| यदि हम द्रव्यमान केन्द्र के फ्रेम से देखें तो हम पाते हैं कि ये दोनों नक्षत्र द्रव्यमान केन्द्र के परित: एक वृत्ताकार पथ पर गतिमान हैं जबकि द्रव्यमान केन्द्र स्थिर है| ध्यान दें, कि दोनों नक्षत्रों को वृत्ताकार पथ के व्यास के विपरीत सिरों पर बने रहना है (चित्र 7.14(b))| इस प्रकार इन नक्षत्रों का गमन पथ दो गतियों के संयोजन से निर्मित होता है (i) द्रव्यमान केन्द्र की सरल रेखा में समांग गति (ii) द्रव्यमान केन्द्र के परित: नक्षत्रों की वृत्ताकार कक्षाएँ|
उपरोक्त दो उदाहरणों से दृष्टव्य है, कि निकाय के एकल कणों की गति को द्रव्यमान केन्द्र की गति और द्रव्यमान केन्द्र के परित: गति में अलग करके देखना एक अत्यंत उपयोगी तकनीक है जिससे निकाय की गति को समझने में सहायता मिलती है|
7.5 दो सदिशों का सदिश गुणन
हम सदिशों एवं भौतिकी में उनके उपयोग के विषय में पहले से ही जानते हैं| अध्याय 6 (कार्य, ऊर्जा, शक्ति) में हमने दो सदिशों के अदिश गुणन की परिभाषा की थी| एक महत्वपूर्ण भौतिक राशि, कार्य, दो सदिश राशियों, बल एवं विस्थापन के अदिश गुणनफल द्वारा परिभाषित की जाती है|
अब हम दो सदिशों का एक अन्य प्रकार का गुणन परिभाषित करेंगे| यह सदिश गुणन है| घूर्णी गति से संबंधित दो महत्वपूर्ण राशियाँ, बल आघूर्ण एवं कोणीय संवेग, सदिश गुणन के रूप में परिभाषित की जाती हैं|
सदिश गुणन की परिभाषा
दो सदिशों a एवं b का सदिश गुणनफल एक एेसा सदिश c है
(i) जिसका परिमाण c है, जहाँ a एवं b क्रमश: a एवं b के परिमाण हैं और θ दो सदिशों के बीच का कोण है|
(ii) c उस तल के अभिलम्बवत् है जिसमें a एवं b अवस्थित हैं|
(iii) यदि हम एक दक्षिणावर्त्त पेंच लें और इसको इस प्रकार रखें कि इसका शीर्ष a एवं b के तल में हो और लम्बाई इस तल के अभिलम्बवत् हो और फिर शीर्ष को a से b की ओर घुमायें, तो पेंच की नाेंक c की दिशा में आगे बढ़ेगा| दक्षिणावर्त पेंच का नियम चित्र 7.15a में दर्शाया गया है|
यदि आप सदिशों a एवं b के तल के अभिलम्बवत् रेखा के परित: अपने दाहिने हाथ की उंगलियों को इस प्रकार मोड़ें कि उनके सिरे a से b की ओर इंगित करें, तब इस हाथ का फैला हुआ अंगूठा c की दिशा बतायेगा जैसा चित्र 7.15b में दर्शाया गया है|
दाहिने हाथ के नियम को सरल रूप में इस प्रकार व्यक्त कर सकते हैं: अपने दाहिने हाथ की हथेली को a से b की ओर संकेत करते हुए खोलो| आपके फैले हुए अंगूठे का सिरा c की दिशा बतायेगा|
यह याद रखना चाहिए कि a और b के बीच दो कोण बनते हैं| चित्र 7.15 (a) एवं (b) में इनमें से कोण θ दर्शाया गया है, स्पष्टत: दूसरा (3600– θ) है| उपरोक्त नियमों में से कोई भी नियम लगाते समय a एवं b के बीच का छोटा कोण (<1800) लेकर नियम लगाना चाहिए| यहाँ यह θ है|
क्योंकि सदिश गुणन में, गुणा व्यक्त करने के लिए क्रॉस (×) चिह्न का उपयोग किया जाता है इसलिए इस गुणन को क्रॉस गुणन भी कहते हैं|
• ध्यान दें कि दो सदिशों का अदिश गुणन क्रमविनियम नियम का पालन करता है जैसा पहले बताया गया है a.b = b.a
परन्तु, सदिश गुणन क्रमविनिमय नियम का पालन नहीं करता, अर्थात् a × b 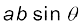 b × a
b × a
a × b एवं b × a के परिमाण समान ( ) हैं ; और ये दोनों ही उस तल के अभिलम्बवत् हैं जिसमें a एवं b विद्यमान है| लेकिन, a × b के लिए दक्षिणावर्त पेंच को a से b की ओर घुमाना होता है जबकि b × a के लिए b से a की ओर| परिणामत: ये दो सदिश विपरीत दिशा में होते हैं
) हैं ; और ये दोनों ही उस तल के अभिलम्बवत् हैं जिसमें a एवं b विद्यमान है| लेकिन, a × b के लिए दक्षिणावर्त पेंच को a से b की ओर घुमाना होता है जबकि b × a के लिए b से a की ओर| परिणामत: ये दो सदिश विपरीत दिशा में होते हैं

• सदिश गुणन का दूसरा रोचक गुण है इसका परावर्तन-गत व्यवहार| परावर्तन के अंतर्गत (यानि दर्पण में प्रतिबिम्ब
लेने पर) हमें 
a × b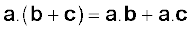
अत: परावर्तन से a × b का चिह्न नहीं बदलता|
• अदिश एवं सदिश दोनों ही गुणन सदिश-योग पर वितरणशील होते हैं| अत:


• हम c = a × b को अवयवों के रूप में भी लिख सकते हैं| इसके लिए हमें कुछ सदिश गुणनफलों की जानकारी आवश्यक होगी :
(i) a × a = 0 (0 एक शून्य सदिश है, यानि शून्य परिमाण वाला सदिश )
स्पष्टत: एेसा इसलिए है क्योंकि a × a का परिमाण 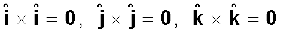 |
|
इससे हम इस परिणाम पर पहुँचते हैं कि
(i) 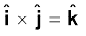
(ii) 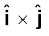
ध्यान दें, कि 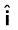 का परिमाण sin 900 या 1 है, चूंकि
का परिमाण sin 900 या 1 है, चूंकि  और
और  दोनों का परिमाण 1 है और उनके बीच 900 का कोण है| अत:
दोनों का परिमाण 1 है और उनके बीच 900 का कोण है| अत: 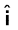 एक एकांक सदिश है|
एक एकांक सदिश है|  और
और 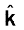 के तल के अभिलम्बवत् दक्षिणावर्त पेंच के नियमानुसार ज्ञात करें तो इनसे संबंधित यह एकांक सदिश
के तल के अभिलम्बवत् दक्षिणावर्त पेंच के नियमानुसार ज्ञात करें तो इनसे संबंधित यह एकांक सदिश 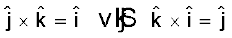
 है| इसी प्रकार आप यह भी पुष्ट कर सकते हैं कि
है| इसी प्रकार आप यह भी पुष्ट कर सकते हैं कि
सदिश गुणन के क्रम विनिमेयता गुण के आधार पर हम कह सकते हैं-
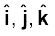
ध्यान दें कि उपरोक्त सदिश गुणन व्यंजकों में यदि 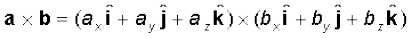
चक्रीय क्रम में आते हैं तो सदिश गुणन धनात्मक है और यदि चक्रीय क्रम में नहीं आते हैं तो सदिश गुणन ऋणात्मक है|अब,
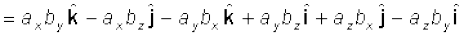
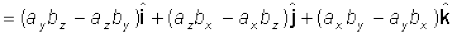

उपरोक्त व्यंजक प्राप्त करने में हमने सरल सदिश गुणनफलों का उपयोग किया है| a × b को व्यक्त करने वाले व्यंजक को हम एक डिटरमिनेंट (सारणिक) के रूप में लिख सकते हैं जो याद रखने में आसान है|
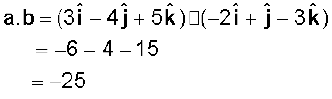
उदाहरण 7.4: दो सदिशों a = (3iˆ – 4jˆ + 5kˆ ) एवं b = (– 2iˆ + jˆ – 3kˆ ) के अदिश एवं सदिश गुणनफल ज्ञात कीजिए|
हल

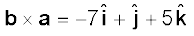
ध्यान दें कि, 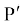
7.6 कोणीय वेग और इसक रेखीय वेग से संबंध
इस अनुभाग में हम अध्ययन करेंगे कि कोणीय वेग क्या है, और घूर्णी गति में इसकी क्या भूमिका है? हम यह समझ चुके हैं कि घूर्णी गति में पिण्ड का प्रत्येक कण एक वृत्ताकार पथ पर चलता है| किसी कण का रेखीय वेग उसके कोणीय वेग से संबंधित होता है| इन दो राशियों के बीच का संबंध एक सदिश गुणन से व्यक्त होता है| सदिश गुणन के विषय में आपने पिछले अनुभाग में पढ़ा है|
आइये चित्र 7.4 पुन: देंखे| जैसा ऊपर बताया गया है, किसी दृढ़ पिण्ड की एक स्थिर अक्ष के परित: घूर्णी गति में, पिण्ड का प्रत्येक कण एक वृत्त में गति करता है| ये वृत्त अक्ष के लम्बवत् समतल में होते हैं जिनके केन्द्र अक्ष के ऊपर अवस्थित होते हैं| चित्र 7.16 में हमने चित्र 7.4 को फिर से बनाया है और इसमें स्थिर (z-) अक्ष के परित: घूमते, दृढ़ पिण्ड के, एक विशिष्ट कण को बिन्दु P पर दर्शाया है| यह कण एक वृत्त बनाता है जिसका केन्द्र C, अक्ष पर स्थित है| वृत्त की त्रिज्या r है, जो बिन्दु P की अक्ष से लम्बवत् दूरी है| चित्र में हमने P बिन्दु पर कण का रेखीय वेग सदिश v भी दर्शाया है| इसकी दिशा वृत्त के P बिन्दु पर खींची गई स्पर्श रेखा के अनुदिश है|
माना कि ∆t समय अंतराल के बाद कण की स्थिति P' है (चित्र 7.16)| कोण PC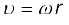 , ∆t समय में कण के कोणीय विस्थापन ∆θ का माप है| ∆t समय में कण का औसत कोणीय वेग ∆θ/∆t है| जैसे-जैसे ∆t का मान घटाते हुए शून्योन्मुख करते हैं, अनुपात ∆θ/∆t का मान एक सीमांत मान प्राप्त करता है जो P बिन्दु पर कण का तात्क्षणिक कोणीय वेग dθ/dt है| तात्क्षणिक कोणीय वेग को हम ω से व्यक्त करते हैं| वृत्तीय गति के अध्ययन से हम जानते हैं कि रेखीय वेग सदिश का परिमाण v एवं कोणीय वेग ω के बीच संबंध एक सरल समीकरण द्वारा प्रस्तुत किया जा सकता है, जहाँ r वृत्त की
, ∆t समय में कण के कोणीय विस्थापन ∆θ का माप है| ∆t समय में कण का औसत कोणीय वेग ∆θ/∆t है| जैसे-जैसे ∆t का मान घटाते हुए शून्योन्मुख करते हैं, अनुपात ∆θ/∆t का मान एक सीमांत मान प्राप्त करता है जो P बिन्दु पर कण का तात्क्षणिक कोणीय वेग dθ/dt है| तात्क्षणिक कोणीय वेग को हम ω से व्यक्त करते हैं| वृत्तीय गति के अध्ययन से हम जानते हैं कि रेखीय वेग सदिश का परिमाण v एवं कोणीय वेग ω के बीच संबंध एक सरल समीकरण द्वारा प्रस्तुत किया जा सकता है, जहाँ r वृत्त की  त्रिज्या है|
त्रिज्या है|
हमने देखा कि किसी दिए गए क्षण पर समीकरण 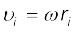 दृढ़ पिण्ड के सभी कणों पर लागू होती है| अत: स्थिर अक्ष से ri दूरी पर स्थित किसी कण का, किसी क्षण पर, रेखीय वेग vi होगा
दृढ़ पिण्ड के सभी कणों पर लागू होती है| अत: स्थिर अक्ष से ri दूरी पर स्थित किसी कण का, किसी क्षण पर, रेखीय वेग vi होगा
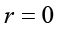 (7.19)
(7.19)
यहाँ भी सूचकांक i का मान 1 से n तक बदलता है, जहाँ n पिण्ड के कुल कणों की संख्या है|
अक्ष पर स्थित कणों के लिए 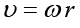 , और इसलिए
, और इसलिए 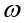 = 0| अत: अक्ष पर स्थित कण रेखीय गति नहीं करते| इससे यह पुष्ट होता है कि अक्ष स्थिर है|
= 0| अत: अक्ष पर स्थित कण रेखीय गति नहीं करते| इससे यह पुष्ट होता है कि अक्ष स्थिर है|
ध्यान दें कि हमने सभी कणों का समान कोणीय वेग 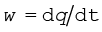 लिया है| इसलिए हम ω को पूरे पिण्ड का कोणीय वेग कह सकते हैं|
लिया है| इसलिए हम ω को पूरे पिण्ड का कोणीय वेग कह सकते हैं|
किसी पिण्ड की शुद्ध स्थानांतरण गति का अभिलक्षण हमने यह बताया कि इसके सभी कण, किसी दिए गए क्षण पर समान वेग से चलते हैं| इसी प्रकार, शुद्ध घूर्णी गति के लिए हम कह सकते हैं कि किसी दिए गए क्षण पर पिण्ड के सभी कण समान कोणीय वेग से घूमते हैं| ध्यान दें कि स्थिर अक्ष के परित: घूमते दृढ़ पिण्ड की घूर्णी गति का यह अभिलक्षण, दूसरे शब्दों में (जैसा अनुभाग 7.1 में बताया गया है) पिण्ड का हर कण एक वृत्त में गति करता है और यह वृत्त अक्ष के अभिलम्बवत् तल में स्थित होता है जिसका केन्द्र अक्ष पर होता है|
हमारे अभी तक के विवेचन से एेसा लगता है कि कोणीय वेग एक अदिश राशि है| किंतु तथ्य यह है, कि यह एक सदिश राशि है| हम इस तथ्य के समर्थन या पुष्टि के लिए कोई तर्क नहीं देंगे, बस यह मान कर चलेंगे| एक स्थिर अक्ष के परित: घूर्णन में, कोणीय वेग सदिश, घूर्णन अक्ष के अनुदिश होता है, और उस दिशा में संकेत करता है जिसमें एक दक्षिणावर्त पेंच आगे बढ़ेगा जब उसके शीर्ष को पिण्ड के घूर्णन की दिशा में घुमाया जाएगा| देखिए चित्र 7.17(a)| इस सदिश का परिमाण, जैसा ऊपर बताया गया है|
 ,
,
चित्र 7.17(a) यदि दक्षिणावर्त्त पेंच के शीर्ष को पिण्ड के घूर्णन की दिशा में घुमाया जाए तो पेंच कोणीय वेग ω की दिशा में आगे बढ़ेगा| यदि पिण्ड के घूर्णन की दिशा (वामावर्त या दक्षिणावर्त) बदलेगी तो ω की दिशा भी बदल जाएगी|

चित्र 7.17 (b) कोणीय वेग सदिश ω की दिशा स्थिर घूर्णन अक्ष के अनुदिश है| P बिन्दु पर स्थित कण का रेखीय वेग v = ω × r है| यह ω एवं r दोनों के लम्बवत् है और कण जिस वृत्त पर चलता है उसके ऊपर खींची गई स्पर्श रेखा के
अनुदिश है|
आइये, अब हम सदिश गुणनफल ω × r को ठीक से समझें और जानें कि यह क्या व्यक्त करता है| चित्र 7.17(b) को देखें, जो वैसे तो चित्र 7.16 का ही भाग है पर, यहाँ इसे कण P का पथ दर्शाने के लिए दोबारा बनाया गया है| चित्र में, स्थिर (z-) अक्ष के अनुदिश सदिश ω और मूल बिन्दु O के सापेक्ष दृढ़ पिण्ड के बिन्दु P का स्थिति-सदिश r = OP दर्शाया गया है| ध्यान दें कि मूल बिन्दु को घूर्णन अक्ष के ऊपर ही रखा गया है|
अब 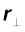
लेकिन ω × OC = 0 क्योंकि के अनुदिश ω OC है|
अत: ω × r = ω × CP
सदिश ω × CP, ω के लम्बवत् है, यानि z-अक्ष पर भी तथा कण P द्वारा बनाये गए वृत्त की त्रिज्या CP पर भी| अत: यह वृत्त के P बिन्दु पर खींची गई स्पर्श रेखा के अनुदिश है| ω × CP का परिमाण ω (CP) है, क्योंकि ω एवं CP एक दूसरे के लम्बवत् हैं| हमें CP को 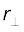 से प्रदर्शित करना चाहिए ताकि इसके और OP = r के परिमाण में संभ्रम की स्थिति से बचा जा सके|
से प्रदर्शित करना चाहिए ताकि इसके और OP = r के परिमाण में संभ्रम की स्थिति से बचा जा सके|
अत: ω × r एक एेसा सदिश है जिसका परिमाण ω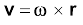 है और जिसकी दिशा कण P द्वारा बनाये गए वृत्त पर खींची गई स्पर्श रेखा के अनुदिश है| यही बिन्दु P पर रेखीय वेग सदिश का परिमाण और दिशा है| अत:
है और जिसकी दिशा कण P द्वारा बनाये गए वृत्त पर खींची गई स्पर्श रेखा के अनुदिश है| यही बिन्दु P पर रेखीय वेग सदिश का परिमाण और दिशा है| अत:
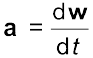 (7.20)
(7.20)
वास्तव में, समीकरण (7.20) उन दृढ़ पिण्डों की घूर्णन गति पर भी लागू होती है जो एक बिन्दु के परित: घूमते हैं, जैसे लट्टू का घूमना (चित्र 7.6(a))| इस तरह के मामलों में, r कण का स्थिति सदिश प्रदर्शित करता है जो स्थिर बिन्दु को मूल बिन्दु लेकर मापा गया हो|
ध्यान दें, कि जब कोई वस्तु एक स्थिर अक्ष के परित: घूर्णन करती है तो समय के साथ सदिश ω की दिशा नहीं बदलती| हाँ, इसका परिमाण क्षण-क्षण पर बदलता रहता है| अधिक व्यापक घूर्णन के मामलों में ω के परिमाण और दिशा दोनों समय के साथ बदलते रह सकते हैं|
7.6.1 कोणीय त्वरण
आपने ध्यान दिया होगा कि हम घूर्णी गति संबंधी अध्ययन को भी उसी तरह आगे बढ़ा रहे हैं जिस तरह हमने अपने स्थानांतरण गति संबंधी अध्ययन को आगे बढ़ाया था और जिसके बारे में अब हम भली-भाँति परिचित हैं| स्थानांतरण गति की गतिज चर राशियों यथा रेखीय विस्थापन (∆r) और रेखीय वेग (v) के सदृश ही घूर्णी गति में कोणीय विस्थापन (θ) एवं कोणीय वेग (ω) की अवधारणाएं हैं| तब यह स्वाभाविक ही है कि जैसे हमने स्थानांतरीय गति में रेखीय त्वरण को वेग परिवर्तन की दर के रूप में परिभाषित किया था वैसे ही घूर्णी गति में कोणीय त्वरण को भी परिभाषित करें| अत: कोणीय त्वरण α की परिभाषा, समय के सापेक्ष कोणीय वेग परिवर्तन की दर के रूप में कर सकते हैं| यानि,
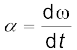 (7.21)
(7.21)
यदि घूर्णन अक्ष स्थिर है तो ω की दिशा और इसलिए α की दिशा भी स्थिर होगी| इस स्थिति में तब सदिश समीकरण अदिश समीकरण में बदल जाती है और हम लिख सकते हैं-
7.7 बल आघूर्ण एवं कोणीय संवेग
इस अनुभाग में, हम आपको एेसी दो राशियों से अवगत करायेंगे जिनको दो सदिशों के सदिश गुणन के रूप में परिभाषित किया जाता है| ये राशियाँ, जैसा हम देखेंगे, कणों के निकायों, विशेषकर दृढ़ पिण्डों की गति का विवेचन करने में बहुत महत्वपूर्ण भूमिका अदा करती हैं|
7.7.1 एक कण पर आरोपित बल का आघूर्ण
हमने सीेखा है, कि किसी दृढ़ पिण्ड की गति, व्यापक रूप में, घूर्णन एवं स्थानांतरण का संयोजन होती है| यदि पिण्ड किसी बिन्दु या किसी रेखा के अनुदिश स्थिर है तो इसमें केवल घूर्णी गति होती है| हम जानते हैं कि किसी वस्तु की स्थानांतरीय गत्यावस्था में परिवर्तन लाने के लिए (यानि इसमें रेखीय त्वरण पैदा करने के लिए) बल की आवश्यकता होती है| तब स्वाभाविक प्रश्न यह उठता है कि घूर्णी गति में बल के तुल्य रूप कौन सी राशि है? एक समग्र स्थिति द्वारा इस प्रश्न का उत्तर तलाशने के लिए आइये किसी द्वार को खोलने या बंद करने का उदाहरण लें| द्वार एक दृढ़ पिण्ड है जो कब्ज़ों से होकर गुजरने वाली ऊर्ध्वाधर अक्ष के परित: घूम सकता है| द्वार को कौन घुमाता है? यह तो स्पष्ट ही है कि जब तक दरवाजे पर बल नहीं लगाया जायेगा यह नहीं घूम सकता| किन्तु, किसी भी बल द्वारा यह कार्य किया जा
सकता हो, एेसा नहीं है| कब्जों से गुजरने वाली ऊर्ध्वाधर रेखा पर लगने वाला बल, द्वार में कोई भी घूर्णन गति उत्पन्न नहीं कर सकता किंतु किसी दिए गए परिमाण का द्वार को घुमाने में सबसे अधिक प्रभावी होता है| घूर्णी गति में बल का परिमाण ही नहीं, बल्कि, यह कहाँ और कैसे लगाया जाता है यह भी महत्वपूर्ण होता है|
घूर्णी गति मेें बल के समतुल्य राशि बल आघूर्ण है| इसको एेंठन (टॉर्क) अथवा बल युग्म भी कहा जाता है| (हम बल आघूर्ण और टॉर्क शब्दों का इस्तेमाल एकार्थी मानकर करेंगे| पहले हम एकल कण के विशिष्ट मामले में बल आघूर्ण की परिभाषा देंगे| बाद में इस अवधारणा को आगे बढ़ाकर कणों के निकाय और दृढ़ पिण्डों के लिए लागू करेंगे| हम, घूर्णन गति में इसके कारण होने वाले परिवर्तन यानि दृढ़ पिण्ड के कोणीय त्वरण से इसका संबंध भी जानेंगे|
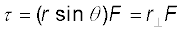
चित्र 7.18 τ = r × F, τ उस तल के लम्बवत् है जिसमें r एवं F हैं, और इसकी दिशा दक्षिणावर्त पेंच के नियम द्वारा जानी जा सकती है|
यदि, P बिन्दु पर स्थित किसी कण पर बल F लगा हो और मूल बिन्दु O के सापेक्ष बिन्दु P का स्थिति सदिश r हो (चित्र 7.18), तो मूल बिन्दु के सापेक्ष कण पर लगने वाले बल का आघूर्ण निम्नलिखित सदिश गुणनफल के रूप में परिभाषित किया जायेगा-
τ = r × F (7.23)
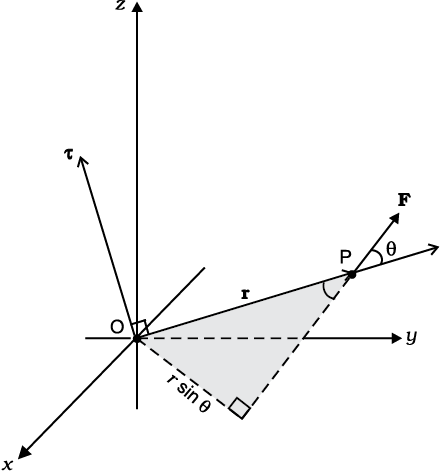
बल आघूर्ण एक सदिश राशि है| इसका संकेत चिह्न ग्रीक वर्णमाला का एक अक्षर τ टॉव है| τ का परिमाण है
τ = rF sinθ (7.24a)
जहाँ r स्थिति सदिश r का परिमाण यानि OP की लंबाई है,
F, बल F का परिमाण है तथा θ, r एवं F के बीच का लघु कोण है, जैसा चित्र में दर्शाया गया है|
बल आघूर्ण का विमीय सूत्र M L2 T -2 है | इसकी विमायें वही हैं जो कार्य और ऊर्जा की| तथापि, यह कार्य से बिलकुल अलग भौतिक राशि है| बल आघूर्ण एक सदिश राशि है, जबकि, कार्य एक अदिश राशि है| बल आघूर्ण का S.I मात्रक न्यूटन मीटर (Nm) है| चित्र से स्पष्ट है कि बल आघूर्ण के परिमाण को हम लिख सकते हैं-
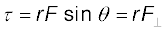 (7.24b)
(7.24b)
या 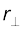 (7.24c)
(7.24c)
जहाँ 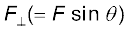 = r sinθ बल की क्रिया-रेखा की मूल बिन्दु से लम्बवत् दूरी है और
= r sinθ बल की क्रिया-रेखा की मूल बिन्दु से लम्बवत् दूरी है और 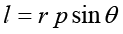 , r के लम्बवत् दिशा में F का अवयव है| ध्यान दें कि जब r = 0 या F = 0 या θ = 00 अथवा 1800 तब τ = 0 | अत: यदि बल का परिमाण शून्य हो या बल मूल बिन्दु पर प्रभावी हो या बल की क्रिया रेखा मूल बिन्दु से गुजरती हो तो बल आघूर्ण शून्य हो जाता है|
, r के लम्बवत् दिशा में F का अवयव है| ध्यान दें कि जब r = 0 या F = 0 या θ = 00 अथवा 1800 तब τ = 0 | अत: यदि बल का परिमाण शून्य हो या बल मूल बिन्दु पर प्रभावी हो या बल की क्रिया रेखा मूल बिन्दु से गुजरती हो तो बल आघूर्ण शून्य हो जाता है|
आपका ध्यान इस बात की ओर जाना चाहिए कि r × F सदिश गुणन होने के कारण दो सदिशों के सदिश गुणनफल के सभी गुण इस पर भी लागू होते हैं| अत: यदि बल की दिशा उलट दी जायेगी तो बल आघूर्ण की दिशा भी उलटी हो जायेगी| परन्तु यदि r और F दोनों की दिशा उलट दी जाए तो बल आघूर्ण की दिशा में कोई परिवर्तन नहीं होगा|
7.7.2 किसी कण का कोणीय संवेग
जैसे बल आघूर्ण, रेखीय गति में बल का घूर्णी समतुल्य है, ठीक वैसे ही कोणीय संवेग, रेखीय संवेग का घूर्णी समतुल्य है| पहले हम एकल कण के विशिष्ट मामले में कोणीय संवेग को परिभाषित करंेंगे और एकल कण की गति के संदर्भ में इसकी उपयोगिता देखेंगे| तब, कोणीय संवेग की परिभाषा को दृढ़ पिण्डों सहित कणों के निकायों के लिए लागू करेंगे|
बल आघूर्ण की तरह ही कोणीय संवेग भी एक सदिश गुणन है| इसको हम (रेखीय) संवेग का आघूर्ण कह सकते हैं| इस नाम से कोणीय संवेग की परिभाषा का अनुमान लगाया जा सकता है|
m द्रव्यमान और p रेखीय संवेग का एक कण लीजिए, मूल बिन्दु O के सापेक्ष, जिसका स्थिति सदिश r हो| तब मूल बिन्दु O के सापेक्ष इस कण का कोणीय संवेग l निम्नलिखित समीकरण द्वारा परिभाषित होगा-
l = r × p (7.25a)
कोणीय संवेग सदिश की परिमाण है
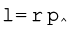 (7.26a)
(7.26a)
जहाँ p सदिश p का परिमाण है तथा θ r एवं p के बीच का लघु कोण है| इस समीकरण को हम लिख सकते हैं-
 या
या  (7.26b)
(7.26b)
जहाँ 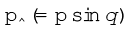 (= r sinθ) सदिश p की दिशा रेखा की मूल बिन्दु से लम्बवत् दूरी है और
(= r sinθ) सदिश p की दिशा रेखा की मूल बिन्दु से लम्बवत् दूरी है और 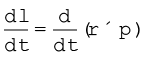 , r की लम्बवत् दिशा में p का अवयव है| जब या तो रेखीय संवेग शून्य हो (p = 0) या कण मूल बिन्दु पर हो (r = 0) या फिर p की दिशा रेखा मूल बिन्दु से गुजरती हो θ = 00 या 1800) तब हम अपेक्षा कर सकते हैं कि कोणीय संवेग शून्य होगा (l = 0)|
, r की लम्बवत् दिशा में p का अवयव है| जब या तो रेखीय संवेग शून्य हो (p = 0) या कण मूल बिन्दु पर हो (r = 0) या फिर p की दिशा रेखा मूल बिन्दु से गुजरती हो θ = 00 या 1800) तब हम अपेक्षा कर सकते हैं कि कोणीय संवेग शून्य होगा (l = 0)|
भौतिक राशियों, बल आघूर्ण एवं कोणीय संवेग में एक महत्वपूर्ण पारस्परिक संबंध है| यह संबंध भी बल एवं रेखीय संवेग के बीच के संबंध का घूर्णी समतुल्य है| एकल कण के संदर्भ में यह संबंध व्युत्पन्न करने के लिए हम l = r × p को समय के आधार पर अवकलित करते हैं,
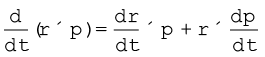
दाईं ओर के व्यंजक पर गुणन के अवकलन का नियम लागू करें, तो
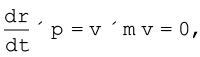
अब, कण का वेग v = dr/dt एवं p = mv लिखें, तो
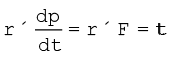
क्योंकि दो समान्तर सदिशों का सदिश गुणनफल शून्य होता है| तथा, चूंकि dp / dt = F,
∴ 
अत: 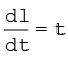
या,  (7.27)
(7.27)
अतएव, किसी कण के कोणीय संवेग में समय के साथ होने वाले परिवर्तन की दर इस पर प्रभावी बल आघूर्ण के बराबर होती है| यह समीकरण F = dp/dt , जो एकल कण की स्थानांतरीय गति के लिए न्यूटन के द्वितीय नियम को व्यक्त करता है, का घूर्णी समतुल्य है|
कणों के निकाय का बल आघूर्ण एवं कोणीय संवेग
कणों के किसी निकाय का, किसी दिए गए बिन्दु के परित: कुल कोणीय संवेग ज्ञात करने के लिए हमें एकल कणों के कोणीय संवेगों के सदिश योग की गणना करनी होगी| अत: n कणों के निकाय के लिए,
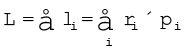
i वें कण का कोणीय संवेग होगा,
li = ri × pi
जहाँ, ri दिए गए मूल बिन्दु के सापेक्ष i वें कण का स्थिति सदिश है और p = (mivi) उस कण का रेखीय संवेग है| (कण का द्रव्यमान mi एवं वेग vi है)| कणों के निकाय के कुल कोणीय संवेग को हम निम्नवत् लिख सकते हैं-
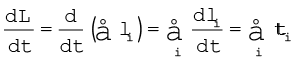 (7.25b)
(7.25b)
यह समीकरण (7.25a) में दी गई एकाकी कण के संवेग की परिभाषा का कणों के निकाय के लिए किया गया व्यापकीकरण है|
समीकरणों (7.23) और (7.25b)का उपयोग करें तो
 (7.28a)
(7.28a)
जहाँ τi , i वें कण पर प्रभावी बल आघूर्ण है;
τi = ri × Fi
i वें कण पर लगने वाला बल Fi , इस पर लगने वाले सभी बाह्य बलों Fi ext एवं निकाय के दूसरे कणों द्वारा इस कण पर लगने वाले आंतरिक बलों Fi int का सदिश योग है| इसलिए, हम कुल बल आघूर्ण में बाह्य एवं आंतरिक बलों के योगदान को अलग-अलग कर सकते हैं|
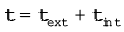 अर्थात्
अर्थात्
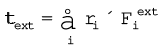 ,
,
जहाँ 
और 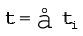
हम, न सिर्फ न्यूटन के गति का तृतीय नियम यानि यह तथ्य कि निकाय के किन्हीं दो कणों के बीच लगने वाले बल बराबर होते हैं और विपरीत दिशा में लगते हैं, बल्कि यह भी मानकर चलेंगे कि ये बल दोनों कणों को मिलाने वाली रेखा के अनुदिश लगते हैं| इस स्थिति में आंतरिक बलों का, निकाय के कुल बल आघूर्ण में योगदान शून्य होगा| क्योंकि, प्रत्येक क्रिया-प्रतिक्रिया युग्म का परिणामी बल आघूर्ण शून्य है|
अत: τint = 0 और इसलिए τ = τext
चूंकि 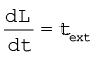 , समीकरण (7.28a) से निष्कर्ष निकलता है, कि
, समीकरण (7.28a) से निष्कर्ष निकलता है, कि
 (7.28 b)
(7.28 b)
अत:, कणों के किसी निकाय के कुल कोणीय संवेग में समय के अनुसार होने वाले परिवर्तन की दर उस पर आरोपित बाह्य बल आघूर्णों (यानि बाह्य बलो के आघूर्णों) के सदिश योग के बराबर होती है| ध्यान रहे कि जिस बिन्दु (यहाँ हमारे संदर्भ-फ्रेम का मूल बिन्दु) के परित: कुल कोणीय संवेग लिया जाता है उसी के परित: बाह्य बल आघूर्णों की गणना की जाती है| समीकरण (7.28 b), कणों के निकाय के व्यापकीकृत कण की समीकरण (7.27) ही है| यह भी ध्यान देने की बात है कि एक कण के मामले में आंतरिक बलों या आंतरिक बल आघूर्णों का कोई अस्तित्व नहीं होता| समीकरण
(7.28 b) निम्नलिखित समीकरण (7.17) का घूर्णी समतुल्य है|
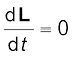 (7.17)
(7.17)
ध्यान दें कि समीकरण (7.17) की तरह ही, समीकरण (7.28b) भी कणों के सभी निकायों के लिए लागू होती है चाहे वह पिण्ड दृढ़ हो या विभिन्न प्रकार की गतियों से युक्त पृथक पृथक कणों का निकाय|
कोणीय संवेग का संरक्षण
यदि τext = 0, तो समीकरण (7.28b) रह जाती है
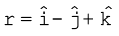
∴ L = अचरांक (7.29a)
अत:, कणों के किसी निकाय पर आरोपित कुुल बाह्य बल आघूर्ण यदि शून्य हो तो उस निकाय का कुल कोणीय संवेग संरक्षित होता है अर्थात् अचर रहता है| समीकरण (7.29a) तीन अदिश समीकरणों के समतुल्य है|
Lx = K1, Ly = K2 एवं Lz = K3 (7.29 b )
यहाँ K1, K2 एवं K3 अचरांक हैं तथा Lx, Ly और Lz कुल कोणीय संवेग सदिश L के क्रमश: x, y एवं z दिशाओं में वियोजित अवयव हैं| यह कथन कि कुुल कोणीय संवेग संरक्षित है, इसका यह भी अर्थ है कि ये तीनों अवयव भी संरक्षित हैं|
समीकरण (7.29a), समीकरण (7.18a) यानि कणों के निकाय के कुल रेखीय संवेग के संरक्षण के नियम, का घूर्णी समतुल्य है| समीकरण (7.18a) की तरह ही अनेक व्यावहारिक स्थितियों में इसके अनुप्रयोग हैं| इस अध्याय में कुछ रोचक अनुप्रयोगों की हम चर्चा करेंगे|
उदाहरण 7.5: मूल बिन्दु के परित:, बल 7iˆ + 3jˆ – 5kˆ का बल आघूर्ण ज्ञात कीजिए| बल जिस कण पर लगता है उसका स्थिति सदिश iˆ – jˆ + kˆ है|
हल : यहाँ 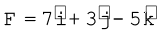
एवं  .
.
बलाघूर्ण τ = r × F ज्ञात करने के लिए हम डिटरमिनेंट हल करेंगे
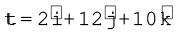
उदाहरण 7.6: दर्शाइये, कि अचर-वेग से चलते एकल कण का किसी बिन्दु के परित: कोणीय संवेग उसकी समस्त गति के दौरान अचर रहता है|
हल : माना कि कोई कण P किसी कण t पर, v वेग से चल रहा है| हम, इस कण का कोणीय संवेग, स्वेच्छ बिन्दु O के परित: ज्ञात करना चाहते हैं|
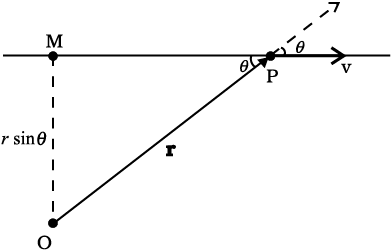
चित्र 7.19
कोणीय संवेग l = r × mv है| इसका परिमाण mvr sinθ है, जहाँ θ , r और v के बीच का कोण है (देखिए चित्र 7.19)| यद्यपि कण समय के साथ अपनी स्थिति बदल रहा है, फिर भी, v की दिशा रेखा वही बनी रहती है और इसलिए
OM = r sin θ अचर है|
l की दिशा, r एवं v के तल के अभिलम्बवत्, पृष्ठ के अंदर की ओर जाती हुई है| यह दिशा भी नहीं बदलती|
अत:, l का परिमाण एवं दिशा वही रहती है और इसलिए यह संरक्षित है| क्या कण पर कोई बाह्य बल आरोपित है?
7.8 दृढ़ पिण्डों का संतुलन
अब हम व्यापक कण-निकायों के बजाय दृढ़ पिण्डों की गति पर अपना ध्यान केंद्रित करेंगे|
आइये, स्मरण करें कि दृढ़ पिण्डों पर बाह्य बलों के क्या प्रभाव होते हैं? (आगे से हम विशेषण ‘बाह्य’ का प्रयोग नहीं करेंगे| जब तक अन्यथा न कहा जाय, हम केवल बाह्य बलों और बल आघूर्णों से ही व्यवहार करेंगे)| बल, किसी दृढ़ पिण्ड की स्थानांतरीय गत्यावस्था में परिवर्तन लाते हैं, अर्थात् वे समीकरण (7.17) के अनुसार, इसके कुल रेखीय संवेग को परिवर्तित करते हैं| लेकिन, बलों का यह एकमात्र प्रभाव नहीं है| यदि पिण्ड पर लगने वाला कुल बल आघूर्ण शून्य न हो तो इसके कारण, दृढ़ पिण्ड की घूर्णी गति में परिवर्तन होगा अर्थात् पिण्ड का कुल कोणीय संवेग समीकरण (7.28b) के अनुसार बदलेगा|
किसी दृढ़ पिण्ड को यांत्रिक संतुलन की अवस्था में तब कहा जाएगा जब इसके रेखीय संवेग और कोणीय संवेग दोनों का ही मान समय के साथ न बदलता हो यानि उस पिण्ड में न रेखीय त्वरण हो न कोणीय त्वरण| इसका अर्थ होगा कि
(1) पिण्ड पर लगने वाला कुल बल यानि बलों का सदिश योग शून्य हो :
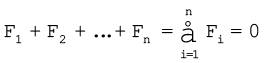 (7.30a)
(7.30a)
यदि पिण्ड पर लगने वाला कुल बल शून्य होगा तो उस पिण्ड के रेखीय संवेग में समय के साथ कोई परिवर्तन नहीं होगा| समीकरण (7.30a) पिण्ड के स्थानांतरीय संतुलन की शर्त है|
(2) कुल बल आघूर्ण, यानि दृढ़-पिण्ड पर लगने वाले बल-आघूर्णों का सदिश योग शून्य होगा :
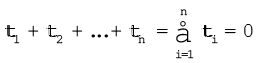
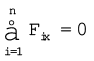 (7.30b)
(7.30b)
यदि दृढ़ पिण्ड पर आरोपित कुल बल आघूर्ण शून्य हो तो इसका कुल कोणीय संवेग समय के साथ नहीं बदलेगा| समीकरण (7.30b) पिण्ड के घूर्णी संतुलन की शर्त है|
अब यह प्रश्न उठ सकता है, कि यदि वह मूल बिन्दु जिसके परित: आघूर्णों की गणना की गई है बदल जाए, तो क्या घूर्णी संतुलन की शर्त बदलेगी? यह दिखाया जा सकता है कि यदि किसी दृढ़ पिण्ड के लिए स्थानांतरीय संतुलन की शर्त समीकरण (7.30b) लागू होती है तो इस पर मूल बिन्दु के स्थानांतरण का कोई प्रभाव नहीं होगा अर्थात् घूर्णी संतुलन की शर्त उस मूल बिन्दु की स्थिति के ऊपर निर्भर नहीं करती जिसके परित: आघूर्ण लिए गए हैं| उदाहरण 7.7, में बलयुग्म (यानि स्थानांतरीय संतुलन में, किसी पिण्ड के ऊपर लगने वाले बलों का एक जोड़ा) के विशिष्ट मामले में इस तथ्य की पुष्टि की जाएगी| n बलों के लिए इस परिणाम का व्यापक व्यंजक प्राप्त करना आपके अभ्यास के लिए छोड़ दिया गया है|
समीकरण (7.30a) एवं समीकरण (7.30b) दोनों ही सदिश समीकरणें हैं| इनमें से प्रत्येक तीन अदिश समीकरणों के समतुल्य हैं| समीकरण (7.30a) के संगत ये समीकरणें हैं
 ,
, 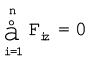 एवं
एवं 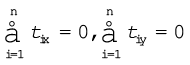 (7.31a)
(7.31a)
जहाँ Fix, Fiy एवं Fiz बल Fi के क्रमश: x, y एवं z दिशा में वियोजित अवयव हैं| इसी प्रकार, समीकरण (7.30b) जिन तीन अदिश समीकरणों के समतुल्य हैं, वे हैं
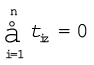 एवं
एवं  (7.31b)
(7.31b)
जहाँ τix, τiy एवं τiz क्रमश: x, y एवं z दिशा में बल आघूर्ण τi के अवयव हैं|
समीकरण (7.31a) एवं (7.31b), हमें किसी दृढ़ पिण्ड के यांत्रिक संतुलन के लिए आवश्यक छ: एेसी शर्तें बताते हैं जो एक दूसरे के ऊपर निर्भर नहीं करतीं| बहुत सी समस्याओं में किसी पिण्ड पर लगने वाले सभी बल एक ही तल में होते हैं| इस स्थिति में यांत्रिक संतुलन के लिए केवल तीन शर्तों को पूरी किए जाने की आवश्यकता होगी| इनमें से दो शर्तें स्थानांतरीय संतुलन के संगत होंगी, जिनके अनुसार, सभी बलों के, इस तल में स्वेच्छ चुनी गई दो परस्पर लम्बवत् अक्षों के अनुदिश, अवयवों का सदिश योग अलग-अलग शून्य होगा| तीसरी शर्त घूर्णी-संतुलन के संगत है| बलों के तल के अभिलम्बवत् अक्ष के अनुदिश बल आघूर्ण के अवयवों का योग शून्य होना चाहिए|
एक दृढ़ पिण्ड के संतुलन की शर्तों की तुलना, एकल कण के संतुलन की शर्तों से की जा सकती है| इस विषय में हमने पहले के अध्यायों में बात की है| कण पर घूर्णी गति का कोई विचार आवश्यक नहीं होता| इसके संतुलन के लिए केवल स्थानांतरीय संतुलन की शर्तें (समीकरण 7.30 a) ही पर्याप्त हैं| अत: किसी कण के संतुलन के लिए इस पर आरोपित सभी बलों का सदिश योग शून्य होना चाहिए| क्योंकि ये सब बल एक ही कण पर कार्य करते हैं इसलिए संगामी भी होते हैं| संगामी बलों के तहत संतुलन का विवेचन पहले के अध्यायों में किया जा चुका है|
ज्ञातव्य है कि एक पिण्ड आंशिक संतुलन में हो सकता है यानि यह हो सकता है कि यह स्थानांतरीय संतुलन में हो परन्तु घूर्णी संतुलन में न हो या फिर घूर्णी संतुलन में तो हो पर स्थानांतरीय संतुलन में ना हो|
एक हलकी (यानि नगण्य द्रव्यमान वाली) स्वतंत्र छड़ (AB) पर विचार कीजिए, जिसके दो सिरों (A एवं B) पर, बराबर परिमाण वाले दो समांतर बल, (जो समान दिशा में लगे हों) F, चित्र 7.20(a) में दर्शाये अनुसार, छड़ के लम्बवत् लगे हों|
 |
|
चित्र 7.20(a)
माना कि छड़ AB का मध्य बिन्दु C है और CA = CB = a है| A एवं B पर लगे बलों के C के परित: आघूर्ण, परिमाण में समान (aF) हैं, पर जैसा चित्र में दिखाया गया है, विपरीत दिशाओं में प्रभावकारी हैं| छड़ पर कुल बल आघूर्ण शून्य होगा| निकाय घूर्णी संतुलन में है, पर यह स्थानांतरीय संतुलन में नहीं है, क्योंकि
चित्र 7.20(b)
चित्र 7.20(b) में, चित्र (7.20a) में B सिरे पर लगाए गए बल की दिशा उलट दी गई है| अब उसी छड़ पर किसी क्षण पर बराबर परिमाण के दो बल, विपरीत दिशाओं में, छड़ के लम्बवत् लगे हैं एक A सिरे पर और दूसरा B सिरे पर| यहाँ दोनों बलों के आघूर्ण बराबर तो हैं पर वे विपरीत दिशा में नहीं हैं; वे एक ही दिशा में हैं और छड़ में वामावर्त घूर्णन की प्रवृत्ति लाते हैं| छड़ पर लगने वाला कुल बल शून्य है| अत: छड़ स्थानांतरीय संतुलन में है, लेकिन यह घूर्णी संतुलन में नहीं है| यद्यपि यह छड़ किसी भी तरह से स्थिर नहीं की गई है, इसमें शुद्ध घूर्णी संभव होती है (यानि स्थानांतरण रहित घूर्णन गति)|
दो बराबर परिमाण के, विपरीत दिशाओं में लगे बलों का जोड़ा जिनकी क्रिया रेखाएँ एक न हों बलयुग्म अथवा एेंठन (टॉर्क) कहलाता है| बलयुग्म बिना स्थानांतरण के घूर्णन पैदा करता है|
जब हम घुमाकर किसी बोतल का ढक्कन खोलते हैं तो हमारी उंगलियाँ ढक्कन पर एक बलयुग्म आरोपित करती हैं| [चित्र 7.21(a)]| इसका दूसरा उदाहरण पृथ्वी के चुम्बकीय क्षेत्र में रखी चुम्बकीय सुई है [चित्र 7.21(b)]| पृथ्वी का चुम्बकीय क्षेत्र, चुम्बकीय सुई के उत्तरी और दक्षिणी ध्रुवों पर बराबर बल लगाता है| उत्तरी ध्रुव पर लगा बल उत्तर दिशा की ओर एवं दक्षिणी ध्रुव पर लगा बल दक्षिणी दिशा की ओर होता है| उस अवस्था के अतिरिक्त जब सुई उत्तर-दक्षिण दिशा में संकेत करती हो, दोनों बलों की क्रिया रेखा एक नहीं होती| अत: उस पर, पृथ्वी के चुम्बकीय क्षेत्र के कारण, एक बलयुग्म प्रभावी होता है|
उदाहरण 7.7: दर्शाइये कि किसी बलयुग्म का आघूर्ण उस बिन्दु के ऊपर निर्भर नहीं करता जिसके परित: आप आघूर्ण ज्ञात करते हैं|
हल
चित्र 7.22
एक दृढ़ पिण्ड लीजिए जिस पर चित्र 7.22 में दिखाये अनुसार बलयुग्म लगा है| बल F एवं -F क्रमश: बिन्दु B और A पर लगे हैं| मूल बिन्दु O के सापेक्ष इन बिन्दुओं के स्थिति सदिश क्रमश: r2 एवं r1 हैं| आइये, मूल बिन्दु के परित: बलों के आघूर्ण ज्ञात करें|
बलयुग्म का आघूर्ण = युग्म बनाने वाले बलों के आघूर्णों का योग
= r1 × (–F) + r2 × F
= r2 × F – r1 × F
= (r2–r1) × F
लेकिन r1 + AB = r2, ∴ AB = r2 –r1.
बलयुग्म का आघूर्ण = AB × F
स्पष्टत:, यह मान मूल बिन्दु यानि वह बिन्दु जिसके परित: हमने बलों के आघूर्ण लिए हैं उसकी स्थिति पर निर्भर नहीं करता|
7.8.1 आघूर्णों का सिद्धांत
एक आदर्श उत्तोलक, अनिवार्य रूप से, एक एेसी हलकी (यानि नगण्य द्रव्यमान वाली) छड़ है जो अपनी लम्बाई के अनुदिश लिए गए किसी बिन्दु के परित: घूम सकती हो| यह बिन्दु आलम्ब कहलाता है| बच्चों के खेल के मैदान में लगा सी-सा, उत्तोलक का एक प्रतिनिधिक उदाहरण है| दो बल F1 एवं F2, जो एक दूसरे के समांतर हैं उत्तोलक के सिरों पर, इसके लम्बवत् तथा आलम्ब से क्रमश: d1 एवं d2 दूरियों पर लगाये गए हैं जैसा चित्र 7.23 में दर्शाया गया है|
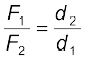
चित्र 7.23
यह उत्तोलक यांत्रिक रूप से एक संतुलित निकाय है| माना कि आलम्ब पर बलों का प्रतिक्रिया बल R है| यह बलों F1 एवं F2 की विपरीत दिशा में प्रभावी है| स्थानांतरीय संतुलन के लिए,
R – F1 – F2 = 0 (i)
और घूर्णी संतुलन में, आलम्ब के परित: आघूर्ण लेने पर, इन आघूर्णों का योग शून्य होगा| अत:
d1F1–d2F2 = 0 (ii)
सामान्यत: वामावर्त आघूर्णों को धनात्मक एवं दक्षिणावर्त आघूर्णों को ऋणात्मक लिया जाता है| ध्यान दें कि R आलम्ब, पर ही कार्यरत है और इसका आघूर्ण शून्य है|
उत्तोलक के मामले में, F1 प्राय: कोई लोड होता है जिसे उठाना होता है इसे भार कहते हैं| आलम्ब से इसकी दूरी d1 भार की भुजा कहलाती है| बल F2, लोड को उठाने के लिए लगाया गया बल, प्रयास है| आलम्ब से इसकी दूरी प्रयास भुजा कहलाती है|
समीकरण (ii) को हम इस प्रकार भी लिख सकते हैं
d1F1 = d2 F2 (7.32a)
या, भार × भार की भुजा = प्रयास × प्रयास की भुजा
उपरोक्त समीकरण, किसी उत्तोलक के लिए आघूर्णों का नियम व्यक्त करती है| अनुपात F1/F2 यांत्रिक लाभ (M.A) कहलाता है|
अत: M.A. = 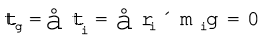 (7.32b)
(7.32b)
यदि प्रयास भुजा d2 की लम्बाई, भार-भुजा d1 से अधिक हो, तो यांत्रिक लाभ एक से अधिक होता है| यांत्रिक लाभ एक से अधिक होने का अर्थ होता है कि कम प्रयास से अधिक भार उठाया जा सकता है| सी-सा के अतिरिक्त भी आपके इर्द-गिर्द उत्तोलकों के बहुत से उदाहरण आपको मिल जायेंगे| तुलादण्ड भी एक उत्तोलक ही है| कुछ अन्य उत्तोलकों के उदाहरण अपने परिवेश से ढूँढ़िए| प्रत्येक के लिए उनके आलम्ब, भार, भार-भुजा, प्रयास और प्रयास-भुजा की पहचान कीजिए|
आप यह सरलता से दर्शा सकते हैं कि यदि समांतर बल F1 और F2 उत्तोलक के लम्बवत् न हों बल्कि कोई कोण बनाते हुए लगे हों तब भी आघूर्णों का नियम लागू होता है|
7.8.2 गुरुत्व केन्द्र
आपमें से कई लोगों ने अपनी नोट बुक को अपनी उंगली की नोक पर संतुलित किया होगा| चित्र 7.24 उसी तरह का एक क्रियाकलाप है जो आप आसानी से कर सकते हैं| एक अनियमित आकार का M द्रव्यमान वाला गत्ते का टुकड़ा और पेंसिल जैसी कोई बारीक नोक वाली वस्तु लो| कुछ बार प्रयास करके आप गत्ते के टुकड़े में एक एेसा बिन्दु G ढूँढ़ सकते हैं जिसके नीचे पेंसिल की नोक रखने पर गत्ते का टुकड़ा उस नोक पर संतुलित हो जाएगा| (इस स्थिति में गत्ते का टुकड़ा पूर्णत: क्षैतिज अवस्था में रहना चाहिए)| यह संतुलन बिन्दु गत्ते के टुकड़े का गुरुत्व केन्द्र (CG) है| पेंसिल की नोक ऊर्ध्वाधरत: ऊपर की ओर लगने वाला एक बल प्रदान करती है जिसके कारण गत्ते का टुकड़ा यांत्रिक संतुलन में आ जाता है| जैसा चित्र 7.24 में दर्शाया गया है, पेंसिल की नोक का प्रतिक्रिया बल R गत्ते के टुकड़े के कुल भार M g के बराबर और विपरीत है और इसलिए यह स्थानांतरीय संतुलनावस्था में है| साथ ही यह घूर्णी संतुलन में भी है| क्योंकि, अगर एेसा न होता तो असंतुलित बल आघूर्ण के कारण यह एक ओर झुक जाता और गिर जाता| गुरुत्व बल के कारण गत्ते के टुकड़े पर बहुत से बल आघूर्ण प्रभावी हैं क्योंकि एकाकी कणों के भार m1g, m2g …. आदि G से विभिन्न दूरियों पर कार्य कर रहे हैं|
चित्र 7.24 गत्ते के टुकड़े को पेंसिल की नोक पर संतुलित करना| पेंसिल की नोक गत्ते के टुकड़े का गुरुत्व केन्द्र निर्धारित करती है|
गत्ते के टुकड़े का गुरुत्व केन्द्र इस प्रकार निर्धारित किया गया है कि m1g, m2g …. आदि बलों का इसके परित: लिया गया आघूर्ण शून्य है|
यदि ri गुरुत्व केन्द्र के सापेक्ष किसी पिण्ड के i-वें कण का स्थिति सदिश हो, तो इस पर लगने वाले गुरुत्व बल का गुरुत्व केन्द्र के परित: बल आघूर्ण τi = ri × mi g| गुरुत्व केन्द्र के परित: कुल गुरुत्वीय बल आघूर्ण शून्य होने के कारण
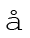 (7.33)
(7.33)
इसलिए, किसी पिण्ड के गुरुत्व-केन्द्र को हम एक एेसे बिन्दु के रूप में परिभाषित कर सकते हैं जिसके परित: पिण्ड का कुल गुरुत्वीय बल आघूर्ण शून्य हो|
हम देखते हैं कि समीरकण (7.33) में g सभी कणों के लिए समान है अत: यह योग-चिन्ह  से बाहर आ सकता है| अत:,
से बाहर आ सकता है| अत:, 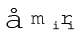 = 0 | याद रखिए कि स्थिति सदिश (ri) गुरुत्व केन्द्र के सापेक्ष नापे गए हैं| अब अनुभाग 7.2 की समीकरण (7.4a) के अनुसार यदि
= 0 | याद रखिए कि स्थिति सदिश (ri) गुरुत्व केन्द्र के सापेक्ष नापे गए हैं| अब अनुभाग 7.2 की समीकरण (7.4a) के अनुसार यदि  = 0, तो मूल बिन्दु पिण्ड का द्रव्यमान केन्द्र होना चाहिए| अत: पिण्ड का गुरुत्व केन्द्र एवं द्रव्यमान केन्द्र एक ही है| हमारे ध्यान में यह बात आनी चाहिए कि एेसा इसलिए है, क्योंकि, वस्तु का आकार इतना छोटा है कि इसके सभी बिन्दुओं के लिए g का मान समान है| यदि पिण्ड इतना बड़ा हो जाए कि इसके एक भाग की तुलना में दूसरे भाग के लिए g का मान बदल जाए तब गुरुत्व केन्द्र एवं द्रव्यमान केन्द सम्पाती नहीं होंगे| मूल रूप में, ये दो अलग-अलग अवधारणाएँ हैं| द्रव्यमान केन्द्र का गुरुत्व से कुछ लेना देना नहीं है| यह केवल पिण्ड में द्रव्यमान के वितरण पर निर्भर करता है|
= 0, तो मूल बिन्दु पिण्ड का द्रव्यमान केन्द्र होना चाहिए| अत: पिण्ड का गुरुत्व केन्द्र एवं द्रव्यमान केन्द्र एक ही है| हमारे ध्यान में यह बात आनी चाहिए कि एेसा इसलिए है, क्योंकि, वस्तु का आकार इतना छोटा है कि इसके सभी बिन्दुओं के लिए g का मान समान है| यदि पिण्ड इतना बड़ा हो जाए कि इसके एक भाग की तुलना में दूसरे भाग के लिए g का मान बदल जाए तब गुरुत्व केन्द्र एवं द्रव्यमान केन्द सम्पाती नहीं होंगे| मूल रूप में, ये दो अलग-अलग अवधारणाएँ हैं| द्रव्यमान केन्द्र का गुरुत्व से कुछ लेना देना नहीं है| यह केवल पिण्ड में द्रव्यमान के वितरण पर निर्भर करता है|
चित्र 7.25 अनियमित आकार के फलक का गुरुत्व केन्द्र ज्ञात करना| फलक का गुरुत्व केन्द्र G इसको A कोने से लटकाने पर इससे होकर गुजरने वाली ऊर्ध्वाधर रेखा पर पड़ता है|
अनुभाग 7.2 में हमने कई नियमित, समांग, पिण्डों के द्रव्यमान केन्द्र की स्थिति ज्ञात की थी| स्पष्टत:, यदि पिण्ड विशालकाय नहीं है, तो उसी विधि से हम उनके गुरुत्व केन्द्र ज्ञात कर सकते हैं|
चित्र 7.25, गत्ते के टुकड़े जैसे किसी अनियमित आकार के फलक का गुरुत्व केन्द्र ज्ञात करने की एक अन्य विधि दर्शाता है| यदि आप इस फलक को किसी बिन्दु जैसे A से लटकायें तो A से गुजरने वाली ऊर्ध्वाधर रेखा गुरुत्व केन्द्र से गुजरेगी| हम इस ऊर्ध्वाधर रेखा AA1, को अंकित कर लेते हैं| अब हम फलक को किसी दूसरे बिन्दु जैसे B या C से लटकाते हैं| इन दो ऊर्ध्वाधर रेखाओं का कटान बिन्दु गुरुत्व केन्द्र है| समझाइये कि यह विधि क्यों प्रभावी होती है? चूंकि यहाँ पिण्ड छोटा सा ही है अत: इस विधि से इसका द्रव्यमान केन्द्र भी ज्ञात किया जा सकता है|
उदाहरण 7.8: 70 सेंटीमीटर लंबी और 4.00 kg द्रव्यमान की धातु की छड़ के दोनों सिरों से 10 सेंटीमीटर दूर रखे दो क्षुर-धारों पर टिकी है| इसके एक सिरे से 40 सेंटीमीटर की दूरी पर 6.00 kg द्रव्यमान का एक भार लटकाया गया है| क्षुर-धारों पर लगने वाले प्रतिक्रिया बलों की गणना कीजिए| (छड़ को समांग और समान अनुप्रस्थ काट वाली मान सकते हैं|)
हल :
चित्र 7.26
चित्र 7.26 में छड़ को AB से दर्शाया गया है| K1 एवं K2 क्षुर-धारों की स्थिति दर्शाते हैं| G एवं P क्रमश: गुरुत्व केन्द्र एवं लटकाये गए बल की स्थितियाँ हैं|
ध्यान दें कि छड़ का भार W इसके गुरुत्व केन्द्र G पर कार्य करता है| छड़ समान अनुप्रस्थ काट वाली और समांग द्रव्य से बनी है इसलिए G इसका केन्द्र है| AB = 70 cm. AG = 35 cm, AP = 30 cm, PG = 5 cm, AK1= BK2 = 10 cm और K1G = K2G = 25 cm एवं W = छड़ का भार = 4.00 kg तथा W1= लटकाया गया भार = 6.00 kg; R1 एवं R2 क्षुर-धारों के आधारों के अभिलम्बवत् प्रतिक्रिया बल हैं|
छड़ के स्थानांतरीय संतुलन के लिए
R1+R2 -W1 - W = 0 (i)
ध्यान दें कि W1 एवं W ऊर्ध्वाधरत: नीचे की ओर तथा R1 एवं R2 ऊर्ध्वाधरत: ऊपर की ओर लगते हैं|
घूर्णी संतुलन की दृष्टि से हम बलों के आघूर्ण ज्ञात करते हैं| एक एेसा बिन्दु जिसके परित: आघूर्ण ज्ञात करने से
सुविधा रहेगी G है| R2 और W1 के आघूर्ण वामावर्त (धनात्मक) हैं, जबकि R1 का आघूर्ण दक्षिणावर्त (ऋणात्मक) है|
अत: घूर्णी संतुलन के लिए
–R1 (K1G) + W1 (PG) + R2 (K2G) = 0 (ii)
यह दिया गया है कि W = 4.00g N, W1 = 6.00g N, जहाँ g = गुरुत्व के कारण त्वरण g = 9.8 m/s2.
समीकरण (i) में आंकिक मान प्रतिस्थापित करने पर,
R1 + R2 – 4.00g – 6.00g =0
या R1 + R2 = 10.00g N (iii)
= 98.00 N
समीकरण (ii) से –0.25 R1 + 0.05 W1 + 0.25 R2 = 0
या R1 – R2 = 1.2g N = 11.76 N (iv)
समीकरण (iii) and (iv) से R1 = 54.88 N,
R2 = 43.12 N
अत: क्षुर-धारों के आधारों के प्रतिक्रिया बल हैं-
K1 पर 55 N तथा K2 पर 43 N
उदाहरण 7.9: 20 kg द्रव्यमान की एक 3 m लंबी सीढ़ी एक घर्षणविहीन दीवार के साथ झुका कर टिकाई गई है| जैसा चित्र 7.27 में दर्शाया गया है, इसका निचला सिरा फर्श पर दीवार से 1 m की दूरी पर है| दीवार और फर्श के प्रतिक्रिया बल ज्ञात कीजिए|
हल
सीढ़ी AB की लंबाई = 3 m, इसके पैरों की दीवार से दूरी AC = 1 m, पाइथागोरस प्रमेय के अनुसार BC = 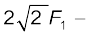 m | सीढ़ी पर लगने वाले बल हैं - इसके गुरुत्व केन्द्र D पर प्रभावी इसका भार W| दीवार और फर्श के प्रतिक्रिया बल F1 एवं F2| बल F1 दीवार पर अभिलम्बवत् है, क्योंकि, दीवार घर्षणविहीन है| बल F2 को दो अवयवों में वियोजित किया जा सकता
m | सीढ़ी पर लगने वाले बल हैं - इसके गुरुत्व केन्द्र D पर प्रभावी इसका भार W| दीवार और फर्श के प्रतिक्रिया बल F1 एवं F2| बल F1 दीवार पर अभिलम्बवत् है, क्योंकि, दीवार घर्षणविहीन है| बल F2 को दो अवयवों में वियोजित किया जा सकता
है -अभिलम्बवत् प्रतिक्रिया बल N एवं घर्षण बल F | ध्यान दें कि F सीढ़ी को दीवार से दूर फिसलने से रोकता है इसलिए इसकी दिशा दीवार की ओर है|
स्थानांतरीय संतुलन के लिए, ऊर्ध्वाधर बलों का योग शून्य करने पर
N – W = 0 (i)
इसी प्रकार क्षैतिज बल लें तो,
F –F1 = 0 (ii)
घूर्णी संतुलन के कारण बिन्दु A के परित: आघूर्ण लेने पर
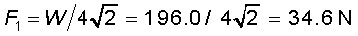 (1/2) W = 0 (iii)
(1/2) W = 0 (iii)
अब, W = 20 g = 20 × 9.8 N = 196.0 N
(g = 9.8 m/s2)
समीकरण (i) से N = 196.0 N
समीकरण (iii) से
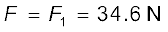
समीकरण (ii) से 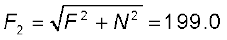
अत: 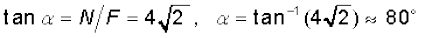 N
N
बल F2 , क्षैतिज से α कोण बनाता है

7.9 जड़त्व आघूर्ण
हम पहले ही यह उल्लेख कर चुके हैं कि घूर्णी गति का अध्ययन हम स्थानांतरण गति के समांतर ही चलायेंगे| इस विषय में आप पहले से ही सुपरिचित हैं| इस संबंध में एक मुख्य प्रश्न का उत्तर देना अभी शेष है कि घूर्णी गति में द्रव्यमान के समतुल्य राशि क्या है? इस प्रश्न का उत्तर हम प्रस्तुत अनुभाग में देंगे| विवेचना को सरल बनाए रखने के लिए हम केवल स्थिर अक्ष के परित: घूर्णन पर ही विचार करेंगे| आइये, घूर्णन करते पिण्ड की गतिज ऊर्जा के लिए व्यंजक प्राप्त करें| हम जानते हैं कि स्थिर अक्ष के परित: घूर्णन करते पिण्ड का प्रत्येक कण, एक वृत्ताकार पथ पर चलता है (देखें चित्र 7.16)| और अक्ष से ri दूरी पर स्थित कण का रेखीय वेग, जैसा समीकरण (7.19) दर्शाती है,
 है| इस कण की गतिज ऊर्जा है
है| इस कण की गतिज ऊर्जा है
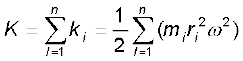
जहाँ mi कण का द्रव्यमान है| पिण्ड की कुल गतिज ऊर्जा K इसके पृथक-पृथक कणों की गतिज ऊर्जाओं का योग है|
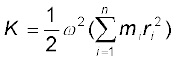
यहाँ n पिण्ड के कुल कणों की संख्या है| ज्ञातव्य है कि ω सभी कणों के लिए समान है अत: ω2 को योग-चिह्न के बाहर निकाल सकते हैं| तब,
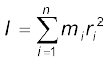
हम दृढ़ पिण्ड को अभिलक्षित करने वाला एक नया प्राचल परिभाषित करते हैं जिसका नाम जड़त्त्व आघूर्ण है और जिसका व्यक्तिकरण है
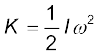 (7.34)
(7.34)
इस परिभाषा के साथ
 (7.35)
(7.35)
ध्यान दें कि प्राचल I कोणीय वेग के परिमाण पर निर्भर नहीं करता| यह दृढ़ पिण्ड और उस अक्ष का अभिलक्षण है जिसके परित: पिण्ड घूर्णन करता है|
समीकरण (7.35) द्वारा व्यक्त घूर्णन करते पिण्ड की गतिज ऊर्जा की रेखीय (स्थानांतरीय) गति करते पिण्ड की गतिज ऊर्जा  से तुलना कीजिए| यहाँ m पिण्ड का द्रव्यमान और v उसका वेग है| कोणीय वेग ω (किसी स्थिर अक्ष के घूर्णन के संदर्भ में) और रेखीय वेग v (रेखीय गति के संदर्भ में) की समतुल्यता हम पहले से ही जानते हैं| अत: यह स्पष्ट है कि जड़त्व आघूर्ण I, प्राचल द्रव्यमान का घूर्णी समतुल्य है| (स्थिर अक्ष के परित:) घूर्णन में जड़त्व आघूर्ण वही भूमिका अदा करता है जो रेखीय गति में द्रव्यमान|
से तुलना कीजिए| यहाँ m पिण्ड का द्रव्यमान और v उसका वेग है| कोणीय वेग ω (किसी स्थिर अक्ष के घूर्णन के संदर्भ में) और रेखीय वेग v (रेखीय गति के संदर्भ में) की समतुल्यता हम पहले से ही जानते हैं| अत: यह स्पष्ट है कि जड़त्व आघूर्ण I, प्राचल द्रव्यमान का घूर्णी समतुल्य है| (स्थिर अक्ष के परित:) घूर्णन में जड़त्व आघूर्ण वही भूमिका अदा करता है जो रेखीय गति में द्रव्यमान|
अब हम समीकरण (7.34) में दी गई परिभाषा का उपयोग दो सरल स्थितियों में जड़त्व आघूर्ण ज्ञात करने के लिए करेंगे|
a) त्रिज्या R और द्रव्यमान M के एक पतले वलय पर विचार कीजिए जो अपने तल में, अपने केन्द्र के परित: ω कोणीय वेग से घूर्णन कर रहा है| वलय का प्रत्येक द्रव्यमान घटक इसकी अक्ष से R दूरी पर है और v = Rω चाल से चलता है| इसलिए इसकी गतिज ऊर्जा है-
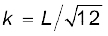
समीकरण (7.35) से तुलना करने पर हम पाते हैं कि वलय के लिए I = MR2
चित्र 7.28 द्रव्यमान के एक जोड़े से युक्त, l लंबाई की छड़, जो निकाय के द्रव्यमान केन्द्र से गुजरने वाली इसकी लंबाई के लम्बवत् अक्ष के परित: घूम रही है| निकाय का कुल द्रव्यमान M है|
b) अब, हम l लंबाई की दृढ़, नगण्य द्रव्यमान की छड़ के सिरों पर लगे दो द्रव्यमानों से बने एक निकाय पर विचार करेंगे| यह निकाय इसके द्रव्यमान केन्द्र से गुजरती छड़ के लम्बवत् अक्ष के परित: घूम रहा है (चित्र 7.28)| प्रत्येक द्रव्यमान M/2 अक्ष से l/2 दूरी पर है| इसलिए, इन द्रव्यमानों का जड़त्व आघूर्ण होगा,
(M/2) (l/2)2 + (M/2)(l/2)2
अत:, द्रव्यमानों के इस जोड़े का, द्रव्यमान केन्द्र से गुजरती छड़ के लम्बवत् अक्ष के परित: जड़त्व आघूर्ण
I = Ml2 / 4
सारिणी 7.1 में कुछ सुपरिचित नियमित आकार के पिंडों के विशिष्ट अक्षों के परित: जड़त्व आघूर्ण केवल दिए गए हैं| (इन सूत्रों के व्युत्पन्न इस पाठ्यपुस्तक के क्षेत्र से बाहर हैं| आगे आप इनके विषय में उच्च कक्षाओं में पढ़ेेंगे|)
क्याेंकि, किसी पिण्ड का द्रव्यमान, उसकी रेखीय गत्यावस्था में परिवर्तन का प्रतिरोध करता है, वह उसकी रेखीय गति के जड़त्व का माप है| उसी प्रकार, दी गई अक्ष के परित: जड़त्त्व आघूर्ण, घूर्णी गति में परिवर्तन का प्रतिरोध करता है, अत: इसको पिण्ड के घूर्णी जड़त्व का माप माना जा सकता है| इस माप से यह बोध होता है कि किसी पिण्ड में पिण्ड के विभिन्न कण घूर्णन अक्ष के आपेक्ष किस प्रकार अवस्थित हैं| द्रव्यमान की तरह जड़त्व आघूर्ण एक नियत राशि नहीं होती, बल्कि, इसका मान पिण्ड के सापेक्ष इसकी अक्ष की स्थिति और दिग्विन्यास के ऊपर निर्भर करता है| किसी घूर्णन अक्ष के सापेक्ष घूर्णन करते दृढ़ पिण्ड का द्रव्यमान किस प्रकार वितरित है इसके एक माप के रूप में हम एक नया प्राचल परिभाषित करते हैं, जिसे परिभ्रमण त्रिज्या कहते हैं| यह पिण्ड के जड़त्व आघूर्ण और कुल द्रव्यमान से संबंधित है|
सारणी 7.1 से हम देख सकते हैं कि सभी पिण्डों के लिए, I = Mk2, जहाँ k की विमा वही है जो लंबाई की| मध्य बिन्दु से गुजरती छड़ के लम्बवत् अक्ष के लिए k2 = L2/12, अर्थात् 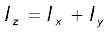 | इसी प्रकार वृत्ताकार चकती के उसके व्यास के परित: जड़त्व आघूर्ण के लिए k = R/2| k पिण्ड और घूर्णन अक्ष का एक ज्यामितीय गुण है| इसे परिभ्रमण त्रिज्या कहा जाता है| किसी अक्ष के परित: किसी पिण्ड की परिभ्रमण त्रिज्या अक्ष से एक एेसे कण की दूरी है जिसका द्रव्यमान सम्पूर्ण पिण्ड के द्रव्यमान के बराबर है| फलत: जिसका जड़त्व आघूर्ण, दी गई अक्ष के परित: पिण्ड के वास्तविक जड़त्व आघूर्ण के बराबर है|
| इसी प्रकार वृत्ताकार चकती के उसके व्यास के परित: जड़त्व आघूर्ण के लिए k = R/2| k पिण्ड और घूर्णन अक्ष का एक ज्यामितीय गुण है| इसे परिभ्रमण त्रिज्या कहा जाता है| किसी अक्ष के परित: किसी पिण्ड की परिभ्रमण त्रिज्या अक्ष से एक एेसे कण की दूरी है जिसका द्रव्यमान सम्पूर्ण पिण्ड के द्रव्यमान के बराबर है| फलत: जिसका जड़त्व आघूर्ण, दी गई अक्ष के परित: पिण्ड के वास्तविक जड़त्व आघूर्ण के बराबर है|
अत:, किसी दृढ़ पिण्ड का जड़त्व आघूर्ण, उसके द्रव्यमान, उसके आकार एवं आकृति, घूर्णन-अक्ष के परित: इसके द्रव्यमान के वितरण और इस अक्ष की स्थिति एवं दिग्विन्यास पर निर्भर करता है| समीकरण (7.34), में दी गई परिभाषा
के आधार पर हम तुरन्त इस निष्कर्ष पर पहुँच सकते हैं कि जड़त्व आघूर्ण का विमीय सूत्र ML2 एवं इसके SI मात्रक
kg m2 हैं|
किसी पिण्ड के घूर्णन के जड़त्व के माप के रूप में इस अत्यंत महत्वपूर्ण राशि I के बहुत से व्यावहारिक उपयोग हैं| वाष्प इंजन और अॉटोमोबाइल इंजन जैसी मशीनें जो घूर्णी गति पैदा करती हैं, इनमें बहुत अधिक जड़त्व आघूर्ण वाली एक चकती लगी रहती है जिसे गतिपालक चक्र कहते हैं| अपने विशाल जड़त्व आघूर्ण के कारण यह चक्र वाहन की गति में अचानक परिवर्तन नहीं होने देता| इससे गति धीरे-धीरे परिवर्तित होती है, गाड़ी झटके खा-खाकर नहीं चलती
और वाहन पर सवार यात्रियों के लिए सवारी आरामदेह हो जाती है|
7.10 लम्बवत् एवं समांतर अक्षों के प्रमेय
जड़त्व आघूर्ण से जुड़ी ये दो उपयोगी प्रमेय हैं| पहले हम लम्बवत् अक्षों का प्रमेय बतायेंगे और कुछ नियमित आकार के पिण्डों के जड़त्व आघूर्ण ज्ञात करने के लिए इसके कुछ सरल उपयोग सीखेंगे|
लम्बवत् अक्षों का प्रमेय
यह प्रमेय फलकाकार पिण्डों पर लागू होता है| व्यवहार में इसका अर्थ हुआ कि यह उन पिण्डों पर लागू होता है जिनकी मोटाई अन्य विमाओं (यानि लंबाई, चौड़ाई या त्रिज्या) की तुलना में बहुत कम हो| चित्र 7.29 में इस प्रमेय को दर्शाया गया है| इसका कथन है कि इसके तल के लम्बवत् अक्ष के परित: किसी फलक का जड़त्व आघूर्ण फलक के तल में स्थित दो लम्बवत् संगामी अक्षों के परित: ज्ञात जड़त्व आघूर्णों के योग के बराबर होगा|
चित्र 7.29 में एक फलकाकार पिण्ड दर्शाया गया है| इसके तल में स्थित किसी बिन्दु O पर तल के लम्बवत्,
z-अक्ष है| फलक के तल में, और z-अक्ष से संगामी, यानि O, से गुजरती हुई, दो परस्पर लम्बवत् अक्षें हैं जिनमें एक को
x -अक्ष और दूसरी को y-अक्ष लिया गया है| प्रमेय यह कहता है कि,
 (7.36)
(7.36)
आइये, प्रमेय की एक उदाहरण द्वारा उपयोगिता समझते हैं|
उदाहरण 7.10: एक वृत्ताकार चकती का जड़त्व आघूर्ण इसके किसी व्यास के परित: क्या होगा?
चित्र 7.30 व्यास के परित: चकती का जड़त्व आघूर्ण इसके द्रव्यमान केन्द्र से गुजरती, तल के लम्बवत् अक्ष के परित: जड़त्व आघूर्ण के पदों में|
हल हम जानते हैं कि किसी चकती का जड़त्व आघूर्ण, उसके केन्द्र से गुजरती और इसके तल के लम्बवत् अक्ष के परित: I = MR2/2 होता है, जहाँ M चकती का द्रव्यमान और R इसकी त्रिज्या है (सारणी 7.1)
चकती को हम फलकाकार पिण्ड समझ सकते हैं| इसलिए लम्बवत् अक्षों का प्रमेय इसके लिए लागू किया जा सकता है जैसा चित्र 7.30 में दर्शाया गया है, हम चकती के केन्द्र O से संगामी तीन परस्पर लम्बवत् अक्षें x,y,z लेते हैं| इनमें x एवं y चकती के तल में हैं और z इसके लम्बवत् है| लम्बवत् अक्षों के प्रमेय के अनुसार

अब, x और y अक्षें चकती के दो व्यासों के अनुदिश हैं और सममिति के विचार से प्रत्येक व्यास के परित: जड़त्व आघूर्ण का मान समान होना चाहिए| अत:
 Ix = Iy
Ix = Iy
अत: Iz = 2Ix
परन्तु Iz = MR2/2
∴ Ix = Iz/2 = MR2/4
अत:, किसी व्यास के परित: चकती का जड़त्व आघूर्ण MR2/4 है|
इसी प्रकार आप किसी वलय का जड़त्व आघूर्ण भी इसके किसी व्यास के परित: ज्ञात कर सकते हैं| क्या यह सिद्धांत किसी ठोस बेलनाकार पिण्ड के लिए भी लागू हो सकता है?
समानान्तर अक्षों का प्रमेय
यह प्रमेय, प्रत्येक पिण्ड पर लागू होता है, चाहे वह किसी भी आकृति का क्यों न हो| यदि किसी पिण्ड का जड़त्व आघूर्ण उसके गुरुत्व केन्द्र से गुजरने वाली अक्ष के परित: ज्ञात हो, तो उस अक्ष के सामानान्तर किसी दूसरी अक्ष के परित: जड़त्व आघूर्ण हम इस प्रमेय की सहायता से ज्ञात कर सकते हैं| हम इस प्रमेय का कथन मात्र देंगे, इसकी उपपत्ति नही करेंगे| तदपि, हम इसको कुछ सरल स्थितियों में लागू करके देखेंगे और उसी से इसकी उपयोगिता स्पष्ट हो जाएगी| प्रमेय का कथन इस प्रकार है :
किसी पिण्ड का, किसी अक्ष के परित: जड़त्व आघूर्ण, उस योग के बराबर है जो पिण्ड के द्रव्यमान केन्द्र से गुजरने वाली सामानान्तर अक्ष के परित: लिए गए जड़त्व आघूर्ण और पिण्ड के द्रव्यमान तथा दोनों अक्षों के बीच की दूरी के वर्ग के गुणनफल को जोड़ने से प्राप्त होता है| जैसा कि चित्र 7.31 में दर्शाया गया है z एवं z′ दो सामानान्तर अक्षें हैं जिनके बीच की दूरी a है| z-अक्ष पिण्ड के द्रव्यमान केन्द्र O से गुजरती है| तब सामानान्तर अक्षों के प्रमेय के अनुसार
चित्र 7.31 समानान्तर अक्षों का प्रमेय| z एवं z' दो समानान्तर अक्ष हैं जिनके बीच की दूरी a है, O पिण्ड का द्रव्यमान केन्द्र है, OO’ = a
Iz′ = Iz + Ma2 (7.37)
जहाँ Iz एवं Iz′ क्रमश: z एवं z′ अक्ष के परित: जड़त्व आघूर्ण हैं, M पिण्ड का द्रव्यमान है और a दोनों अक्षों के बीच की लम्बवत् दूरी है|
उदाहरण 7.11: द्रव्यमान M, और लंबाई l वाली छड़ का, उस अक्ष के परित: जड़त्व आघूर्ण क्या होगा जो इसके लम्बवत् किसी एक सिरे से गुजरती हो?
हल M द्रव्यमान और l लंबाई की छड़ का, इसके द्रव्यमान केन्द्र से लंबाई के लम्बवत् गुजरने वाली अक्ष के परित: जड़त्व आघूर्ण, I = Ml2/12 हैं| समानान्तर अक्षों का प्रमेय लगाने पर,
I′ = I + Ma2
a = l/2 रखें, तो
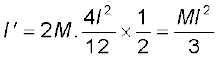
हम स्वतंत्र रूप से इसको एक दूसरी विधि से भी जाँच सकते हैं, यदि हम I' को उस छड़ के मध्य बिन्दु के परित: जड़त्व आघूर्ण का आधा लें जिसका द्रव्यमान 2M और लंबाई 2l हो| इस प्रकार,

उदाहरण 7.12: किसी पतले वलय की परिधि पर स्पर्श रेखा बनाती हुई और इसके तल में ही स्थित अक्ष के परित: इसका जड़त्व आघूर्ण क्या है?
हल
वलय के तल में इसके ऊपर खींची गई स्पर्श रेखा इसके व्यास के समान्तर है| इन दो समानांतर अक्षों के बीच की दूरी R यानि वलय की त्रिज्या है| समानान्तर अक्षों का प्रमेय लगायें तो
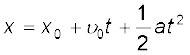
चित्र 7.32
7.11 अचल अक्ष के परित: शुद्ध घूर्णी गतिकी
हमने पहले भी स्थानांतरण गति और घूर्णी गति के बीच समतुल्यता के संकेत दिए हैं| उदारहण के लिए यह कि कोणीय वेग ω का घूर्णी गति में वही भूमिका है जो रेखीय वेग v का स्थानांतरण गति में| हम इस समतुल्यता को आगे बढ़ाना चाहते हैं| एेसा करते समय हम अपना विवेचन अचर (स्थिर) अक्ष के परित: घूर्णन तक ही सीमित रखेंगे| एेसी गति के लिए केवल एक स्वातंत्र्य-कोटि की आवश्यकता होगी अर्थात् इसका वर्णन करने के लिए केवल एक स्वतंत्र चर कोणीय विस्थापन चाहिए| यह रेखीय गति में स्थानांतरण के संगत है| यह अनुभाग केवल शुद्ध गतिकी से संबंधित है| गति विज्ञान की ओर हम अगले अनुभाग में मुखातिब होंगे|
याद करें, कि किसी घूर्णन करते हुए पिण्ड का कोणीय विस्थापन बताने के लिए हमने इस पिण्ड पर कोई कण P ले लिया था (चित्र 7.33)| जिस तल में यह कण गति करता है उसमें इसका कोणीय विस्थापन θ ही सम्पूर्ण पिण्ड का कोणीय विस्थापन है; θ एक नियत दिशा से मापा जाता है, जिसको यहाँ हम x′ - अक्ष ले लेते हैं जो बिन्दु P के गति के तल में स्थित x-अक्ष के समानांतर रेखा है| ध्यान दें कि z – अक्ष घूर्णन-अक्ष है और कण P की गति का तल x - y तल के समानांतर है| चित्र 7.33 में θ0, भी दर्शाया गया है जो t = 0 पर कोणीय विस्थापन है|
हम यह भी याद करें कि कोणीय वेग, समय के साथ कोणीय विस्थापन में होने वाले परिवर्तन की दर है| यानि,
ω = dθ/dt | ध्यान दें, कि चूंकि घूर्णन अक्ष अचल है, कोणीय वेग के साथ सदिश की तरह व्यवहार करने की आवश्यकता नहीं है| कोणीय त्वरण, α = dω/dt है|
शुद्ध घूर्णी गतिकी में प्रयुक्त होने वाली राशियाँ, कोणीय विस्थापन (θ), कोणीय वेग (ω) एवं कोणीय त्वरण (α) क्रमश: स्थानांतरीय शुद्ध गतिकी की राशियों रेखीय विस्थापन (x), रेखीय वेग (v) एवं रेखीय त्वरण (a) के समतुल्य हैं| सम (यानि अचर) त्वरण के तहत स्थानांतरीय शुद्ध गतिकी के समीकरण हम जानते हैं| वे हैं :
v = v0 + at (a)
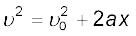 (b)
(b)
 (c)
(c)
जहाँ x0 = प्रारंभिक विस्थापन एवं v0= प्रारंभिक वेग है| शब्द ‘प्रारंभिक’ का अर्थ है t = 0 पर राशि का मान|
इनके संगत, अचर त्वरण से घूर्णी गति करती हुई वस्तु के लिए शुद्ध घूर्णी गतिकी के समीकरण होंगे :
 (7.38)
(7.38)
 (7.39)
(7.39)
और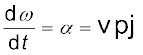 (7.40)
(7.40)
जहाँ θ0= घूर्णन करते पिण्ड का प्रारंभिक कोणीय विस्थापन है एवं ω0 = इस पिण्ड का प्रारंभिक कोणीय वेग है|
चित्र 7.33 किसी दृढ़ पिण्ड की कोणीय स्थिति बताना
उदाहरण 7.13: मूल सिद्धांत के आधार पर समीकरण (7.38) व्युत्पन्न कीजिए|
हल : कोणीय त्वरण समान है, अत:
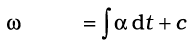 (i)
(i)
इस समीकरण का समाकलन करने पर

t = 0, ω = ω0 (दिया है)
समीकरण (i) से, t = 0 पर
ω = c = ω0
अत: ω = αt + ω0 , जो वांछित समीकरण है|
परिभाषा ω = dθ/dt (7.38 )का इस्तेमाल करके हम समीकरण का समाकलन कर समीकरण (7.39) प्राप्त कर सकते हैं| यह व्युत्पत्ति एवं समीकरण (7.40) की व्युत्पत्ति हम आपके अभ्यास के लिए छोड़ते हैं|
उदाहरण 7.14: अॉटोमोबाइल इंजन का कोणीय वेग 16 सेकेंड में 1200 rpm से बढ़कर 3120 rpm हो जाता है| (i) यह मानते हुए कि कोणीय त्वरण समान रहता है, इसका मान ज्ञात कीजिए| (ii) इस समय में इंजन कितने चक्कर लगाता है?
हल :
(i) ω = ω0 + αt , जहाँ ω0 = rad/s में व्यक्त इसका प्रारंभिक कोणीय वेग है
ω0 = 2π × rev/s में प्रारंभिक कोणीय वेग
= 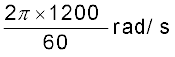
= 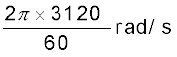
= 40π rad/s
इसी प्रकार, ω = rad/s में अंतिम कोणीय वेग
= 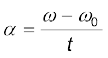
= 2π × 52 rad/s
= 104 π rad/s
∴ कोणीय त्वरण,  = 4π rad/s2
= 4π rad/s2
इंजन का कोणीय त्वरण 4π rad/s2 है|
(ii) t समय में कोणीय विस्थापन,

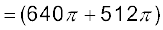 rad
rad
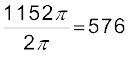 rad
rad
= 1152π rad
चक्करों की संख्या = 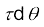
7.12 अचल अक्ष के परित: घूर्णी गतिकी
सारणी 7.2 में रेखीय गति से संबंधी राशियों और उनके संगत घूर्णी गति की समतुल्य राशियों की सूची दी गई है| पिछले अनुभाग में हमने इन दोनों प्रकार की गतियों की शुद्ध गतिकी से तुलना की है| हमें यह भी पता है कि घूर्णी गति में जड़त्व आघूर्ण एवं बल आघूर्ण, रेखीय गति के क्रमश: द्रव्यमान एवं बलों का प्रतिनिधित्व करते हैं| यह सब जानने के बाद सारणी में दिए गए अन्य समतुल्यों के विषय में अनुमान लगा लेना अधिक कठिन नहीं है| उदाहरण के लिए, रेखीय गति में
कार्य = F dx | अत: एक अचल अक्ष के परित: घूर्णी गति में कार्य 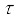 होना चाहिए क्योंकि हम पहले से ही यह जानते हैं कि dx के संगत राशि है dθ एवं F के संगत राशि
होना चाहिए क्योंकि हम पहले से ही यह जानते हैं कि dx के संगत राशि है dθ एवं F के संगत राशि 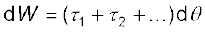 है| तथापि यह आवश्यक है कि राशियों की यह संगतता, गति विज्ञान के मजबूत आधार पर प्रतिष्ठापित की जाए| आगे हम यही करने जा रहे हैं|
है| तथापि यह आवश्यक है कि राशियों की यह संगतता, गति विज्ञान के मजबूत आधार पर प्रतिष्ठापित की जाए| आगे हम यही करने जा रहे हैं|
इससे पहले कि हम अपनी बात शुरू करें, एक अचल अक्ष के परित: घूर्णी गति में एक सरलीकरण की ओर ध्यान दिलाना आवश्यक है| क्योंकि अक्ष स्थिर है, हमें अपने विवेचन में बल आघूर्णों एवं कोणीय संवेगों के इसके अनुदिश अवयवों पर ही विचार करने की आवश्यकता होगी| केवल यही घटक पिण्ड को घूर्णन कराते हैं| बल आघूर्ण का अक्ष से अभिलंबवत घटक अक्ष को उसकी स्थिति से घुमाने का प्रयास करता है| हालांकि हम मानकर चलेंगे कि बल आघूर्ण के इस घटक को संतुलित करने हेतु आवश्यक बल आघूर्ण उत्पन्न होंगे जो अक्ष की स्थिति बनाए रखने के लिए उत्तरदायी होंगे| अत: इन अभिलंबवत् बल आघूर्ण के घटकों पर विचार में करने की आवश्यकता नहीं है| पर्याय में हमें निम्न विचार में लाने की आवश्यकता है:
(1) पिण्ड पर कार्य करने वाले वे बल जो घूर्णन अक्ष के लम्बवत् तल में हैं|
(2) पिण्ड के कणों की स्थिति-सदिशों के केवल वे अवयव जो घूर्णन अक्ष के लम्बवत् हैं|
या यूँ कहें कि बलों और स्थिति सदिशों के अक्ष के अनुदिश लिए गए अवयवों को हमें गणना में लाने की आवश्यकता नहीं है|
बल आघूर्ण द्वारा किया गया कार्य
चित्र 7.34 एक अचल अक्ष के परित: घूमते पिण्ड के किसी कण पर लगे बल F1 द्वारा किया गया कार्य| कण, अक्ष पर स्थित केन्द्र C वाले वृत्त पर चलता है| चाप P1P′1(ds1) कण का विस्थापन बताता है|
चित्र 7.34 में एक अचल अक्ष के परित: घूर्णन करता एक दृढ़ पिण्ड दर्शाया गया है| घूर्णन अक्ष, z-अक्ष है, जो पृष्ठ के अभिलम्बवत् है| जैसा ऊपर बताया गया है हमें केवल उन्हीं बलों पर विचार करने की आवश्यकता है जो अक्ष के अभिलंबवत् तल में अवस्थित है| पिण्ड के किसी कण पर, जिसकी स्थिति P1, से दर्शाई गई है, एक बल F1 लगता है जिसकी क्रिया रेखा, अक्ष के अभिलम्बवत् तल में है| सुविधा के लिए हम इसको
x′–y′ तल कहते हैं (यह हमारे पृष्ठ का तल ही है)| P1 पर स्थित कण r1 त्रिज्या के वृत्त पर चलता है जिसका केन्द्र अक्ष पर है; CP1 = r1|
∆t समय में, कण, P1′ पर पहुँच जाता है| इसलिए कण के विस्थापन ds1 का परिमाण ds1 = r1dθ है| जैसा कि चित्र में दिखाया गया है| इसकी दिशा वृत्त के स्पर्श रेखा के अनुदिश हैं| कण पर बल द्वारा किया गया कार्य -
dW1 = F1. ds1= F1ds1 cosφ1= F1(r1 dθ)sinα1
जहाँ φ1 , F1 और P1, पर खींची गई स्पर्श रेखा के बीच बना कोण है, और α1, F1 एवं त्रिज्या OP1 के मध्य कोण हैं|
φ1 + α1 = 90°|
मूल बिन्दु के परित: F1 के कारण बल आघूर्ण OP1 × F1 है| OP1 = OC + CP1 [चित्र 7.17(b) देखें] चूंकि OC अक्ष के अनुदिश है इसके कारण बल आघूर्ण पर विचार करने की आवश्यकता नहीं है| F1 के कारण प्रभाव बल आघूर्ण है :
τ1= CP1 × F1; यह घूर्णी अक्ष के अनुदिश है तथा इसका परिमाण τ1= r1F1 sin α है| अत:
dW1 = τ1dθ
यदि पिण्ड पर एक से अधिक बल कार्य कर रहे हों, तो उन सबके द्वारा किए गए कार्यों को जोड़ने से पिण्ड पर किया गया कुल कार्य प्राप्त होगा| विभिन्न बलों के कारण लगे बल आघूर्णों के परिमाणों को τ1, τ2, … इत्यादि से दर्शाएँ तो

याद रहे, कि बल आघूर्णों को जन्म देने वाले बल तो अलग-अलग कणों पर लग रहे हैं, मगर कोणीय विस्थापन dθ सभी कणों के लिए समान है| अब जैसा कि इस अनुभाग के प्रारंभ में कहा गया था, हमारे लिए सभी बल आघूर्ण z-अक्ष के अनुदिश प्रभावी हैं| अत: कुल बल आघूर्ण का परिमाण τ , प्रत्येक बल आघूर्णों के परिमाणों τ1 , τ2 ..... के बीजगणितीय योग के बराबर है| अर्थात् τ = τ1 + τ2 + ....., अत: हम कह
सकते हैं
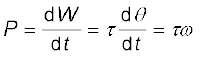 (7.41)
(7.41)
यह समीकरण एक अचल अक्ष के परित: घूमते पिण्ड पर लगे कुल बाह्य बल आघूर्ण τ के द्वारा किया गया कार्य बताता है| रेखीय गति के संगत समीकरण
dW= F ds
से इसकी तुल्यता स्पष्ट ही है| समीकरण (7.41) के दोनों पक्षों को dt से विभाजित करने पर

या 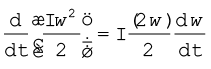 (7.42)
(7.42)
यह तात्क्षणिक शक्ति के लिए समीकरण है| अचल अक्ष के परित: घूर्णी गति में शक्ति के इस समीकरण की तुलना रेखीय गति में शक्ति की समीकरण P = Fv से कर सकते हैं|
एक पूर्णत: दृढ़ पिण्ड में विभिन्न कणों की कोई आंतरिक गति नहीं होती| अत:, बाह्य बल आघूर्णों द्वारा किया गया कार्य विसरित नहीं होता| परिणामस्वरूप पिण्ड की गतिज ऊर्जा बढ़ती चली जाती है| पिण्ड पर किए गए कार्य की दर, समीकरण (7.42) द्वारा प्राप्त होती है| इसी दर से पिण्ड की गतिज ऊर्जा बढ़ती है| गतिज ऊर्जा की वृद्धि की दर
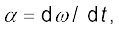
हम मानते हैं कि समय के साथ पिण्ड का जड़त्व आघूर्ण नहीं बदलता| यानि कि पिण्ड का द्रव्यमान स्थिर रहता है तथा पिण्ड दृढ़ बना रहता है और इसके सापेक्ष घूर्णन अक्ष की स्थिति नहीं बदलती|
तब, चूंकि 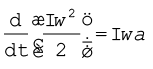 अत:
अत:

कार्य करने की दर को गतिज ऊर्जा में वृद्धि की दर के बराबर रखने पर

 (7.43)
(7.43)
समीकरण (7.43) सरल रेखीय गति के लिए न्यूटन के द्वितीय नियम F = ma से मिलती जुलती है|
ठीक वैसे ही जैसे बल पिण्ड में रेखीय त्वरण उत्पन्न करता है, बल आघूर्ण इसमें कोणीय त्वरण पैदा करता है| कोणीय त्वरण, आरोपित बल आघूर्ण के समानुपाती और पिण्ड के जड़त्व आघूर्ण के व्युत्क्रमानुपाती होता है| इस संदर्भ में समीकरण (7.43) को, एक अचल अक्ष के परित: घूर्णन के लिए लागू होने वाला न्यूटन का द्वितीय नियम, कह सकते हैं|
उदाहरण 7.15: नगण्य द्रव्यामन वाली एक रस्सी, 20 kg द्रव्यमान एवं 20 cm त्रिज्या के गतिपालक पहिये के रिम पर लपेटी हुई है| रस्सी पर 25 N का एकसमान कर्षण बल लगाया जाता है जैसा कि चित्र 7.35 में दर्शाया गया है| गतिपालक पहिया एक क्षैतिज धुरी पर लगाया गया है जिसके वियरिंगों में कोई घर्षण नहीं है|
(a) पहिये के कोणीय त्वरण की गणना कीजिए|
(b) 2 m रस्सी खुलने तक कर्षण बल द्वारा किया गया कार्य ज्ञात कीजिए|
(c) इस क्षण पर पहिये की गतिज ऊर्जा ज्ञात कीजिए| यह मानिए कि पहिया शून्य से गति प्रारंभ करता है|
(d) भाग (b) एवं (c) के उत्तरों की तुलना कीजिए|
हल
चित्र 7.35
(a) इसके लिए I α = τ
बल आघूर्ण τ = F R
= 25 × 0.20 Nm (R = 0.20m)
= 5.0 Nm
और I = अपनी अक्ष के परित: पहिये का जड़त्व आघूर्ण 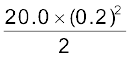
= 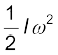 = 0.4 kg m2
= 0.4 kg m2
कोणीय त्वरण α = 5.0 N m/0.4 kg m2 = 12.5 s–2
(b) 2 m रस्सी खोलने में किया गया कार्य
= 25 N × 2 m = 50 J
(c) माना कि ω अंतिम कोणीय वेग है| तब पहिये की गतिज ऊर्जा में हुई वृद्धि = 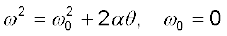
चूंकि पहिया विरामावस्था से गति प्रारंभ करता है

तथा कोणीय विस्थापन θ = खोली गई रस्सी की लंबाई/पहिये की त्रिज्या
= 2 m/0.2 m = 10 rad

(d) दोनों उत्तर समान हैं, अर्थात् पहिये द्वारा प्राप्त गतिज ऊर्जा = बल द्वारा किया गया कार्य| यहाँ घर्षण के कारण ऊर्जा का बिलकुल क्षय नहीं हुआ है|
7.13 अचल अक्ष के परित: घूर्णी गति का कोणीय संवेग
अनुभाग 7.7 में, हमने कणों के निकाय के कोणीय संवेग के विषय में पढ़ा था| उससे हम यह जानते हैं, कि किसी बिन्दु के परित:, कणों के निकाय के कुल कोणीय संवेग में समय के साथ होने वाले परिवर्तन की दर, उस निकाय पर उसी बिन्दु के परित: लिए गए कुल बाह्य बल आघूर्ण के बराबर होती है| जब कुल बाह्य बल आघूर्ण शून्य हो, तो निकाय का कुल कोणीय संवेग संरक्षित रहता है|
अब हम कोणीय संवेग का अध्ययन, एक अचल अक्ष के परित: घूर्णन के विशिष्ट मामलों में करना चाहते हैं| n-कणों के निकाय के कुल कोणीय संवेग की व्यापक समीकरण है,
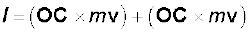 (7.25b)
(7.25b)
अब हम पहले, एक अचल अक्ष के परित: किसी दृढ़ पिण्ड के कोणीय संवेग पर विचार करेंगे| प्राप्त समीकरण को सरलतम पदों में लाकर फिर पिण्ड के सभी कणों के लिए इसका जोड़ निकालेंगे तथा पूरे पिण्ड के लिए L प्राप्त करेंगे|
एकाकी कण के लिए, l = r × p.
चित्र (7.17b) देखिए| घूर्णन करती वस्तु के किसी विशिष्ट कण का स्थिति सदिश OP = r है| चित्र में
r = OC + CP (क्योंकि p = mv)

P पर कण के रेखीय वेग v का परिमाण v = ωr⊥ है जहाँ r⊥ CP की लम्बाई या P की घूर्णी अक्ष के लम्बवत् दूरी है| v कण द्वारा बनाए गए वृत्त के बिन्दु P पर स्पर्श रेखा के अनुदिश है| दाहिने हाथ के नियम द्वारा ज्ञात कर सकते हैं कि CP × v अचल अक्ष के अनुदिश है| घूर्णन अक्ष (जो यहाँ z-अक्ष है) को इकाई सदिश 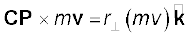 के अनुदिश व्यक्त करने पर
के अनुदिश व्यक्त करने पर
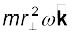
= 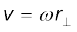 (
(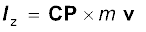 )
)
इसी प्रकार हम जाँच सकते हैं कि OC × v अचर अक्ष के लम्बवत् हैं| अचर अक्ष (यानि z-अक्ष) के अनुदिश l के घटक से lz से दर्शाने पर
 =
=



























