Table of Contents

अध्याय 8
गुरुत्वाकर्षण
8.1 भूमिका
8.2 केप्लर के नियम
8.3 गुरुत्वाकर्षण का सार्वत्रिक नियम
8.4 गुरुत्वीय नियतांक
8.5 पृथ्वी का गुरुत्वीय त्वरण
8.6 पृथ्वी के पृष्ठ के नीचे तथा ऊपर गुरुत्वीय त्वरण
8.7 गुरुत्वीय स्थितिज ऊर्जा
8.8 पलायन चाल
8.9 भू उपग्रह
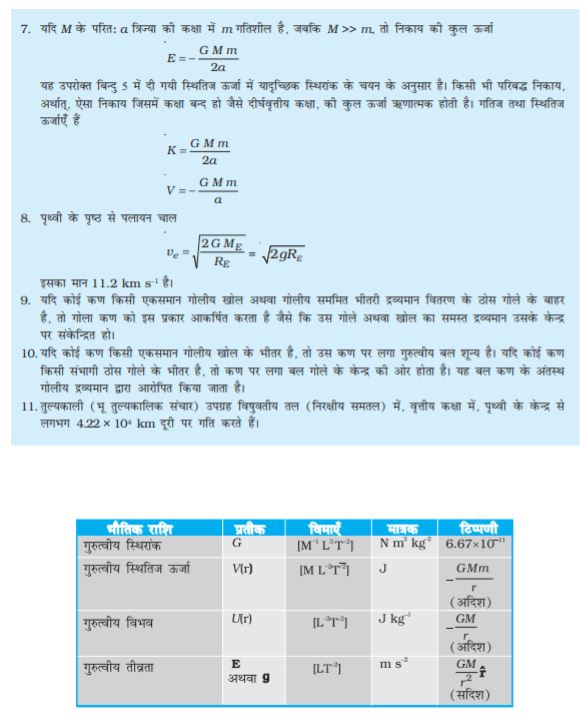
8.10 कक्षा में गतिशील उपग्रह की ऊर्जा
8.11 तुल्यकाली तथा ध्रुवीय उपग्रह
8.12 भारहीनता
सारांश
विचारणीय विषय
अभ्यास
अतिरिक्त अभ्यास
8.1 भूमिका
हम अपने आरंभिक जीवन में ही, सभी पदार्थों के पृथ्वी की ओर आकर्षित होने की प्रकृति को जान लेते हैं| जो भी वस्तु ऊपर फेंकी जाती है वह पृथ्वी की ओर गिरती है, पहाड़ से नीचे उतरने की तुलना में पहाड़ पर ऊपर जाने में कहीं अधिक थकान होती है, ऊपर बादलों से वर्षा की बूँदें पृथ्वी की ओर गिरती हैं, तथा अन्य एेसी ही बहुत सी परिघटनाएँ हैं| इतिहास के अनुसार इटली के भौतिक विज्ञानी गैलीलियो (1564-1642) ने इस तथ्य को मान्यता प्रदान की कि सभी पिण्ड, चाहे उनके द्रव्यमान कुछ भी हों, एकसमान त्वरण से पृथ्वी की ओर त्वरित होते हैं| एेसा कहा जाता है कि उन्होंने इस तथ्य का सार्वजनिक निदर्शन किया था| यह कहना, चाहे सत्य भी न हो, परंतु यह निश्चित है कि उन्होंने आनत समतल पर लोटनी पिण्डों के साथ कुछ प्रयोग करके गुरुत्वीय त्वरण का एक मान प्राप्त किया था, जो बाद में किए गए प्रयोगों द्वारा प्राप्त अधिक यथार्थ मानों के काफी निकट था|
आद्य काल से ही बहुत से देशों में तारों, ग्रहों तथा उनकी गतियों के प्रेक्षण जैसी असंबद्ध प्रतीत होने वाली परिघटनाएँ ध्यानाकर्षण का विषय रही हैं| आद्य काल के प्रेक्षणों द्वारा आकाश में दिखाई देने वाले तारों की पहचान की गई, जिनकी स्थिति में सालोंसाल कोई परिवर्तन नहीं होता है| प्राचीन काल से देखे जाने वाले पिण्डों में कुछ अधिक रोचक पिण्ड भी देखे गए, जिन्हें ग्रह कहते हैं, और जो तारों की पृष्ठभूमि में नियमित गति करते प्रतीत होते हैं| ग्रहीय गतियों के सबसे प्राचीन प्रमाणित मॉडल को अब से लगभग 2000 वर्ष पूर्व टॉलमी ने प्रस्तावित किया था| यह ‘भूकेन्द्री’ मॉडल था, जिसके अनुसार सभी आकाशीय पिण्ड तारे, सूर्य तथा ग्रह पृथ्वी की परिक्रमा करते हैं| इस मॉडल की धारणा के अनुसार आकाशीय पिण्डों की संभावित गति केवल वृत्तीय गति ही हो सकती थी| ग्रहों की प्रेक्षित गतियों का वर्णन करने के लिए टॉलमी ने गतियों के जिस विन्यास को प्रतिपादित किया वह बहुत जटिल था| इसके अनुसार ग्रहों को वृत्तों में परिक्रमा करने वाला तथा इन वृत्तों के केन्द्रों को स्वयं एक बड़े वृत्त में गतिशील बताया गया था| लगभग 400 वर्ष के पश्चात भारतीय खगोलज्ञों ने भी इसी प्रकार के सिद्धांत प्रतिपादित किए| तथापि, आर्यभट्ट (5 वीं शताब्दी में) ने पहले से ही अपने शोध प्रबन्ध में एक अधिक परिष्कृत मॉडल का वर्णन किया था, जिसे सूर्य केन्द्री मॉडल कहते हैं जिसके अनुसार सूर्य को सभी ग्रहों की गतियों का केन्द्र माना गया है| एक हजार वर्ष के पश्चात पोलैण्ड के एक ईसाई भिक्षु, जिनका नाम निकोलस कोपरनिकस (1473-1543) था, ने एक पूर्ण विकसित मॉडल प्रस्तावित किया जिसके अनुसार सभी ग्रह, केन्द्रीय स्थान पर स्थित स्थिर सूर्य, के परितः वृत्तों में परिक्रमा करते हैं| गिरजाघर ने इस सिद्धांत पर संदेह प्रकट किया| परन्तु इस सिद्धांत के लब्ध प्रतिष्ठित समर्थकों में एक गैलीलियो थे, जिनपर शासन के द्वारा, आस्था के विरुद्ध होने के कारण, मुकदमा चलाया गया|
लगभग गैलीलियो के ही काल में डेनमार्क के एक कुलीन पुरुष टायको ब्रेह (1546-1601) ने अपना समस्त जीवन काल अपनी नंगी आंखों से सीधे ही ग्रहों के प्रेक्षणों का अभिलेखन करने में लगा दिया| उनके द्वारा संकलित आँकड़ों का बाद में उसके सहायक जोहान्नेस केप्लर (1571-1640) द्वारा विश्लेषण किया गया| उन्होंने इन आँकड़ों को सार के रूप में तीन परिष्कृत नियमों द्वारा प्रतिपादित किया, जिन्हें अब केप्लर के नियमों के नाम से जाना जाता है| ये नियम न्यूटन को ज्ञात थे| इन उत्कृष्ट नियमों ने न्यूटन को अपना गुरुत्वाकर्षण का सार्वत्रिक नियम प्रस्तावित करके असाधारण वैज्ञानिकों की पंक्ति में शामिल होने योग्य बनाया|
8.2 केप्लर के नियम
केप्लर के तीन नियमों का उल्लेख इस प्रकार किया जा सकता हैः
1. कक्षाओं का नियम : सभी ग्रह दीर्घवृत्तीय कक्षाओं में गति करते हैं तथा सूर्य इसकी, एक नाभि पर स्थित होता है (चित्र 8.1a)|
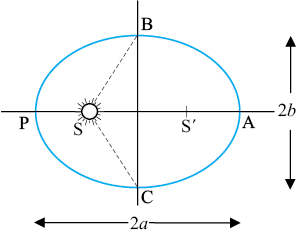
चित्र 8.1(a) सूर्य के परितः किसी ग्रह द्वारा अनुरेखित दीर्घवृत्त| सूर्य का निकटतम बिन्दु P तथा दूरस्थ बिन्दु A है| P को उपसौर तथा A को अपसौर कहते हैं| अर्ध दीर्घ अक्ष दूरी AP का आधा है|
यह नियम कोपरनिकस के मॉडल से हटकर था जिसके अनुसार ग्रह केवल वृत्तीय कक्षाओं में ही गति कर सकते हैं| दीर्घवृत्त, जिसका वृत्त एक विशिष्ट प्रकरण होता है, एक बन्द वक्र होता है, जिसे बहुत सरलता से इस प्रकार खींचा जा सकता है:
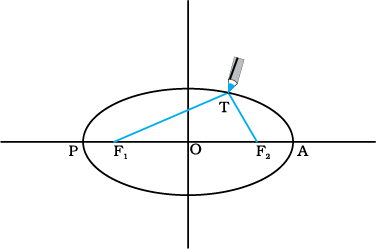
चित्र 8.1(b) एक दीर्घवृत खींचना| एक डोरी के दो सिरे F1 तथा F2 स्थिर हैं| पेंसिल की नोंक डोरी को तनी रखते हुए इन सिरों के परितः चलायी जाती है|
दो बिन्दुओं F1 तथा F2 का चयन कीजिए| एक डोरी लेकर इसके सिरों को F1 तथा F2 पर पिनों द्वारा जड़िए| पेंसिल की नोंक से डोरी को तानिए और फिर डोरी को तनी हुई रखते हुए पेंसिल को चलाते हुए बन्द वक्र खींचिए (चित्र 8.1 (b)) इस प्रकार प्राप्त बन्द वक्र को दीर्घवृत्त कहते हैं| स्पष्ट है कि दीर्घवृत्त के किसी भी बिन्दु T पर F1 तथा F2 से दूरियों का योग अपरिवर्तित (नियत) है| बिन्दु F1 तथा F2 दीर्घवृत्त की नाभि कहलाती है| बिन्दु F1 तथा F2 को मिलाइए और इस रेखा को आगे बढ़ाइए जिससे यह दीर्घवृत्त को चित्र 8.1 (b) में दर्शाए अनुसार बिन्दुओं P तथा A पर प्रतिच्छेद करती है| रेखा PA का मध्यबिन्दु दीर्घवृत्त का केन्द्र है तथा लम्बाई
PO = AO दीर्घवृत्त का अर्ध दीर्घ अक्ष कहलाती है| किसी वृत्त के लिए दोनों नाभियाँ एक दूसरे में विलीन होकर एक हो जाती हैं तथा अर्ध दीर्घ अक्ष वृत्त की त्रिज्या बन जाती है|
2. क्षेत्रफलों का नियम : सूर्य से किसी ग्रह को मिलाने वाली रेखा समान समय अंतरालों में समान क्षेत्रफल प्रसर्प करती है (चित्र 8.2)| यह नियम इस प्रेक्षण से प्रकट होता है कि ग्रह उस समय धीमी गति करते प्रतीत होते हैं जब वे सूर्य से अधिक दूरी पर होते हैं| सूर्य के निकट होने पर ग्रहों की गति अपेक्षाकृत तीव्र होती है|
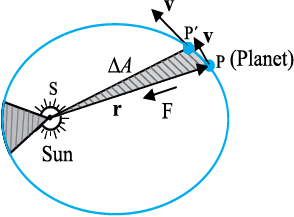
चित्र 8.2 ग्रह P सूर्य के परितः दीर्घवृत्तीय कक्षा में गति करता है| किसी छोटे समय अंतराल ∆t में ग्रह द्वारा प्रसर्पित क्षेत्रफल ∆A को छायांकित क्षेत्र द्वारा दर्शाया गया है|
3. आवर्त कालों का नियम
किसी ग्रह के परिक्रमण काल का वर्ग उस ग्रह द्वारा अनुरेखित दीर्घवृत्त के अर्ध-दीर्घ अक्ष के घन के अनुक्रमानुपाती होता है|
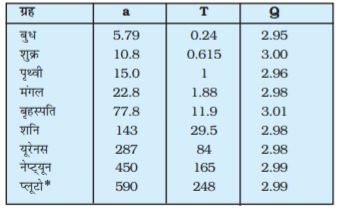
नीचे दी गयी सारणी (8.1) में सूर्य के परितः आठ* ग्रहों के सन्निकट परिक्रमण-काल उनके अर्ध-दीर्घ अक्षों के मानों सहित दर्शाए गए हैं
सारणी 8.1
नीचे दिए गए ग्रहीय गतियों की माप के आँकड़े केप्लर के आवर्तकालों के नियम की पुष्टि करते हैं|
a ≡ अर्ध-दीर्घ अक्ष 1010 m के मात्रकों में
T ≡ ग्रह का परिक्रमण-काल वर्षों (y) में
Q ≡ भागफल ( T2 / a 3 )
10 -34 y2 m-3 मात्रकों में
जोहान्नेस केप्लर (1571- 1630) जर्मन मूल के वैज्ञानिक थे| उन्होंने टायको ब्रेह और उनके सहयोगियों द्वारा बहुत परिश्रमपूर्वक लिए गए प्रेक्षणों के आधार पर ग्रहों की गति के तीन नियमों का प्रतिपादन किया| केप्लर स्वयं ब्रेह के सहायक थे और उनको ग्रहों के तीन नियमों तक पहुँचने में 16 वर्षों का लंबा समय लगा| वह पहले व्यक्ति थे जिन्होंने यह बताया कि दूरदर्शी में प्रवेश करने पर प्रकाश का क्या होता है, इसलिए, वह ज्यामितीय प्रकाशिकी के संस्थापक के रूप में भी जाने जाते हैं|
क्षेत्रफलों के नियम को कोणीय संवेग संरक्षण का निष्कर्ष माना जा सकता है जो सभी केन्द्रीय बलों के लिए मान्य है| किसी ग्रह पर लगने वाला केन्द्रीय बल, केन्द्रीय सूर्य तथा ग्रह को मिलाने वाले सदिश के अनुदिश कार्य करता है| मान लीजिए सूर्य मूल बिन्दु पर है और यह भी मानिए कि ग्रह की स्थिति तथा संवेग को क्रमशः r तथा  से दर्शाया जाता है, तब m द्रव्यमान के ग्रह द्वारा ∆t समय में प्रसर्पित क्षेत्रफल ∆A (चित्र 8.2) इस प्रकार व्यक्त किया जाता है
से दर्शाया जाता है, तब m द्रव्यमान के ग्रह द्वारा ∆t समय में प्रसर्पित क्षेत्रफल ∆A (चित्र 8.2) इस प्रकार व्यक्त किया जाता है
 = ½ (r × v∆t) (8.1)
= ½ (r × v∆t) (8.1)
अतः
 /∆t = ½ (r × p)/m, (चूँकि v = p/m)
/∆t = ½ (r × p)/m, (चूँकि v = p/m)
= L / (2 m) (8.2)
यहाँ v वेग है तथा L कोणीय संवेग है जो (r × p) के तुल्य है| किसी केन्द्रीय बल के लिए, जो r के अनुदिश निर्देशित है, L एक नियतांक होता है, जबकि ग्रह परिक्रमा कर रहा होता है| अतः अंतिम समीकरण के अनुसार  /∆t एक नियतांक है| यही क्षेत्रफलों का नियम है| गुरुत्वाकर्षण का बल भी केन्द्रीय बल ही है और इसलिए क्षेत्रफलों का नियम न्यूटन के नियमों के इसी लक्षण का पालन/अनुगमन करता है|
/∆t एक नियतांक है| यही क्षेत्रफलों का नियम है| गुरुत्वाकर्षण का बल भी केन्द्रीय बल ही है और इसलिए क्षेत्रफलों का नियम न्यूटन के नियमों के इसी लक्षण का पालन/अनुगमन करता है|
केन्द्रीय बल
हमें ज्ञात है, कि मूल बिन्दु के परितः किसी एकल कण के कोणीय संवेग में, समय के साथ होने वाले परिवर्तन की दर
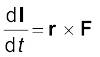
यदि उस पर लगे बल का आघूर्ण 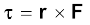 शून्य हो, तो कण का कोणीय संवेग संरक्षित रहता है, यह तभी होता है जब या तो F शून्य हो या बल r के अनुदिश हो| हम उन बलों की चर्चा करेंगे जो दूसरी शर्त पूरी करते हैं| केन्द्रीय बल उन बलों के उदाहरण हैं जो यह शर्त पूरी करते हैं|
शून्य हो, तो कण का कोणीय संवेग संरक्षित रहता है, यह तभी होता है जब या तो F शून्य हो या बल r के अनुदिश हो| हम उन बलों की चर्चा करेंगे जो दूसरी शर्त पूरी करते हैं| केन्द्रीय बल उन बलों के उदाहरण हैं जो यह शर्त पूरी करते हैं|
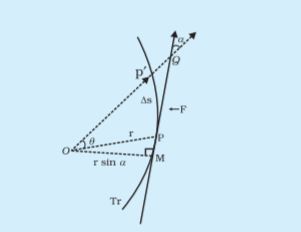
केन्द्रीय बल, सदैव या तो एक नियत बिन्दु की ओर या इससे दूर दिशा में लगे होते हैं, यानि, नियत बिन्दु से बलारोपण बिन्दु के संगत स्थिति सदिश के अनुदिश होते हैं| (देखिए चित्र)| केन्द्रीय बल का परिमाण F , केवल नियत बिन्दु से बलारोपण बिन्दु की दूरी, r, के ऊपर निर्भर करता है F=F(r)|
केन्द्रीय बल के तहत गति में कोणीय संवेग सदैव संरक्षित रहता है| इससे दो महत्त्वपूर्ण परिणाम सीधे प्राप्त होते हैं ः
(1) केन्द्रीय बल के तहत किसी कण की गति सदैव एक समतल में सीमित रहती है|
(2) बल के केन्द्र (यानि नियत बिन्दु) से, लिए गए कण के स्थिति सदिश का क्षेत्रफलीय वेग अचर रहता है| दूसरे शब्दों में कहें तो केन्द्रीय बल के तहत गतिमान कण का स्थिति सदिश बराबर समय में बराबर क्षेत्रफल बुहारता है|
इन दोनों कथनों की उप्पत्ति की चेष्टा करें| आपके लिए शायद यह जानना जरूरी होगा कि क्षेत्रफल वेग,
dA/dt = ½ r v sin α.
उपरोक्त विवेचन का उपयोग हम सूर्य के आकर्षण बल से इसके इर्द-गिर्द घूमते किसी ग्रह की गति के संदर्भ में कर सकते हैं| सुविधा के लिए हम सूर्य को इतना भारी मान सकते हैं कि इसकी स्थिति नियत रहे| ग्रह पर सूर्य का आकर्षण बल सदैव सूर्य की दिशा में लगता है| यह बल शर्त F = F(r), भी पूरी करता है, क्योंकि, F = G m1m2/r2 जहाँ m1 एवं m2 क्रमशः ग्रह और सूर्य के द्रव्यमान हैं, और G गुरुत्वाकर्षण का वैश्विक अचरांक| अतः ऊपर दिए गए दोनो कथन, (1) एवं (2) ग्रहों की गति के लिए लागू होते हैं| वास्तव में कथन (2) केप्लर का सुप्रसिद्ध द्वितीय नियम है|
Tr केन्द्रीय बल के तहत, कण का गमन-पथ है| कण की किसी स्थिति P, पर बल OP के अनुदिश होता है| O बल का केन्द्र है जिसे मूलबिन्दु ले लिया गया है| ∆t समय में कण P से 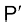 तक चाप ∆s = v ∆t के ऊपर चलता है| गमन पथ के बिन्दु P पर खींची गई स्पर्श रेखा PQ इस बिन्दु पर वेग की दिशा दर्शाती है| ∆t समय में, r, वृत्तखण्ड
तक चाप ∆s = v ∆t के ऊपर चलता है| गमन पथ के बिन्दु P पर खींची गई स्पर्श रेखा PQ इस बिन्दु पर वेग की दिशा दर्शाती है| ∆t समय में, r, वृत्तखण्ड  के क्षेत्र से गुजरता है जो
के क्षेत्र से गुजरता है जो 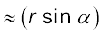
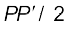 = (r v sin a) ∆t/2) है|
= (r v sin a) ∆t/2) है|
उदाहरण 8.1 मान लीजिए किसी ग्रह की उपसौर P पर (चित्र 8.1a) चाल vP है, तथा सूर्य व ग्रह की दूरी SP = rP है| {rP, vP} तथा अपसौर पर इन राशियो के तदनुरूपी मान {rA, vA} में संबंध स्थापित कीजिए|
क्या ग्रह BAC तथा CPB पथ तय करने में समान समय लेगा?
हल कोणीय संवेग का परिमाण P पर है Lp = mp rp vp, क्योंकि निरीक्षण द्वारा यह ज्ञात होता है कि rp तथा vp परस्पर लम्बवत हैं| इसी प्रकार, LA = mp rA vA. तब कोणीय संवेग संरक्षण से
mp rp vp = mp rA vA
अथवा 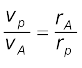
चूँकि rA > rp, vp > vA .
दीर्घवृत्त तथा त्रिज्या सदिशों SB एवं SC द्वारा घेरा गया क्षेत्रफल SBPC की तुलना में अधिक है (चित्र 8.1a)| केप्लर के दूसरे नियम के अनुसार, समान समय अंतरालों में समान क्षेत्रफल प्रसर्प होते हैं| अतः ग्रह पथ CPB को तय करने की अपेक्षा पथ BAC को तय करने में अधिक समय लेगा|
8.3 गुरुत्वाकर्षण का सार्वत्रिक नियम
एक दंत कथा में लिखा है पेड़ से गिरते हुए सेब का प्रेक्षण करते हुए न्यूटन को गुरुत्वाकर्षण के सार्वत्रिक नियम तक पहुँचने की प्रेरणा मिली जिससे केप्लर के नियमों तथा पार्थिव गुरुत्वाकर्षण के स्पष्टीकरण का मार्ग प्रशस्त हुआ| न्यूटन ने अपने विवेक के आधार पर यह स्पष्ट अनुभव किया कि Rm त्रिज्या की कक्षा में परिक्रमा करने वाले चन्द्रमा पर पृथ्वी के गुरुत्व के कारण एक अभिकेन्द्र त्वरण आरोपित होता है जिसका परिमाण
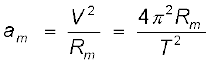 (8.3)
(8.3)
यहाँ V चन्द्रमा की चाल है जो आवर्तकाल T से इस प्रकार
संबंधित है, 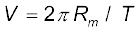 | आवर्त काल T का मान लगभग 27.3 दिन है तथा उस समय तक Rm का मान लगभग 3.84×108m ज्ञात हो चुका था| यदि हम इन संख्याओं को समीकरण (8.3) में प्रतिस्थापित करें, तो हमें am का जो मान प्राप्त होता है, वह पृथ्वी के गुरुत्व बल के कारण उत्पन्न पृथ्वी के पृष्ठ पर गुरुत्वीय त्वरण g के मान से काफी कम होता है| यह स्पष्ट रूप से इस तथ्य को दर्शाता है कि पृथ्वी के गुरुत्व बल का मान दूरी के साथ घट जाता है| यदि हम यह मान लें कि पृथ्वी के कारण गुरुत्वाकर्षण का मान पृथ्वी के केन्द्र से दूरी के वर्ग के व्युत्क्रमानुपाती होता है, तो हमें
| आवर्त काल T का मान लगभग 27.3 दिन है तथा उस समय तक Rm का मान लगभग 3.84×108m ज्ञात हो चुका था| यदि हम इन संख्याओं को समीकरण (8.3) में प्रतिस्थापित करें, तो हमें am का जो मान प्राप्त होता है, वह पृथ्वी के गुरुत्व बल के कारण उत्पन्न पृथ्वी के पृष्ठ पर गुरुत्वीय त्वरण g के मान से काफी कम होता है| यह स्पष्ट रूप से इस तथ्य को दर्शाता है कि पृथ्वी के गुरुत्व बल का मान दूरी के साथ घट जाता है| यदि हम यह मान लें कि पृथ्वी के कारण गुरुत्वाकर्षण का मान पृथ्वी के केन्द्र से दूरी के वर्ग के व्युत्क्रमानुपाती होता है, तो हमें 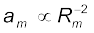 और
और 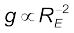 प्राप्त होगा (यहाँ RE पृथ्वी की त्रिज्या है), जिससे हमें निम्नलिखित संबंध प्राप्त होता है :
प्राप्त होगा (यहाँ RE पृथ्वी की त्रिज्या है), जिससे हमें निम्नलिखित संबंध प्राप्त होता है :
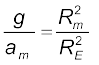
 3600 (8.4)
3600 (8.4)
जो g  9.8 m s-2 तथा समीकरण (8.3) से am के मान के साथ मेल खाता है| इस प्रेक्षण ने न्यूटन को नीचे दिए गए गुरुत्वाकर्षण के सार्वत्रिक नियम को प्रतिपादित करने में मार्गदर्शन दिया :
9.8 m s-2 तथा समीकरण (8.3) से am के मान के साथ मेल खाता है| इस प्रेक्षण ने न्यूटन को नीचे दिए गए गुरुत्वाकर्षण के सार्वत्रिक नियम को प्रतिपादित करने में मार्गदर्शन दिया :
"इस विश्व में प्रत्येक पिण्ड हर दूसरे पिण्ड को एक बल द्वारा आकर्षित करता है जिसका परिमाण दोनों पिण्डों के द्रव्यमानों के गुणनफल के अनुक्रमानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है|"
यह उद्धरण तत्वतः न्यूटन के प्रसिद्ध शोध प्रबन्ध "प्राकृतिक दर्शन के गणितीय सिद्धांत" (Mathematical Principles of Natural Philosophy) जिसे संक्षेप में प्रिंसिपिया (Principia) कहते हैं, से प्राप्त होता है|
गणितीय रूप में न्यूटन के गुरुत्वाकर्षण नियम को इस प्रकार कहा जा सकता है ः किसी बिंदु द्रव्यमान m2 पर किसी अन्य बिंदु द्रव्यमान m1 के कारण बल F का परिमाण
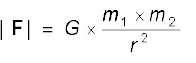 (8.5)
(8.5)
सदिश रूप में समीकरण (8.5) को इस प्रकार व्यक्त किया जा सकता है
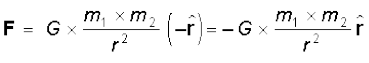
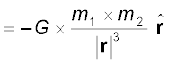
यहाँ G सार्वत्रिक गुरुत्वीय नियतांक, 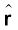 m1 से m2 तक एकांक सदिश तथा r = r2 – r1 है जैसा कि चित्र 8.3 में दर्शाया गया है|
m1 से m2 तक एकांक सदिश तथा r = r2 – r1 है जैसा कि चित्र 8.3 में दर्शाया गया है|
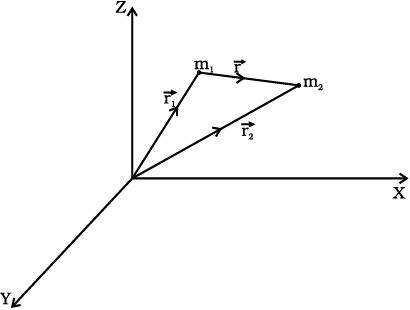
चित्र 8.3 m2 के कारण m1 पर गुरुत्वीय बल r के अनुदिश है, यहाँ r, (r2– r1) है|
गुरुत्वीय बल आकर्षी बल है, अर्थात् m2 पर m1 के कारण लगने वाला बल F, – r के अनुदिश है| न्यूटन के गति के तीसरे नियम के अनुसार, वास्तव में बिन्दु द्रव्यमान m1 पर m2 के कारण बल – F है| इस प्रकार m1 पर m2 के कारण लगने वाले गुरुत्वाकर्षण बल F12 एवं m2 पर m1 के कारण लगने वाले बल F21 का परस्पर संबंध है,
F12 = –F21
समीकरण (8.5) का अनुप्रयोग, अपने पास उपलब्ध पिण्डों पर कर सकने से पूर्व हमें सावधान रहना होगा, क्योंकि यह नियम बिन्दु द्रव्यमानों से संबंधित है, जबकि हमें विस्तारित पिण्डों, जिनका परिमित आमाप होता है, पर विचार करना है| यदि हमारे पास बिन्दु द्रव्यमानों का कोई संचयन है, तो उनमें से किसी एक पर बल अन्य बिन्दु द्रव्यमानों के कारण गुरुत्वाकर्षण बलों के सदिश योग के बराबर होता है जैसा कि चित्र 8.4 में दर्शाया गया है|
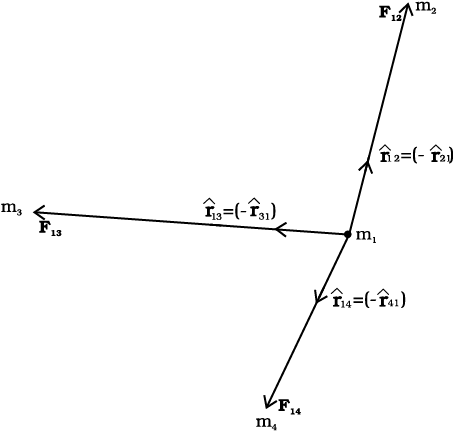
चित्र 8.4 बिन्दु द्रव्यमान m1 पर बिन्दु द्रव्यमानों m2, m3 और m4 के द्वारा आरोपित कुल गुरुत्वाकर्षण बल इन द्रव्यमानों द्वारा m1 पर लगाए गए व्यष्टिगत बलों के सदिश योग के बराबर है|
m1 पर कुल बल है
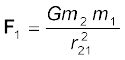
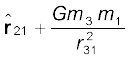
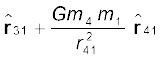
न्यूटन की प्रिंसिपिया
सन् 1619 तक केप्लर अपना तृतीय नियम प्रतिपादित कर चुके थे| उनमें अंतर्निहित गुरुत्वाकर्षण के सार्वत्रिक नियम की घोषणा, 1687 में, इसके लगभग 70 वर्ष बाद हुई, जब न्यूटन ने अपनी श्रेष्ठ कृति ‘फिलोसिफिया नेचुरलिस प्रिंसिपिया मैथेमेटिका’ जिसे आमतौर पर ‘प्रिंसिपिया’ कहा जाता है, प्रकाशित की|
सन् 1685 के लगभग, एडमण्ड हेली (जिनके नाम के आधार पर प्रसिद्ध हेली धूमकेतु का नाम रखा गया है) कैम्ब्रिज में न्यूटन से मिलने आए और उन्होंने प्रतिलोम वर्ग नियम प्रभाव के तहत गतिमान किसी पिण्ड के गमन पथ की प्रकृति के बारे में पूछा| न्यूटन ने बिना झिझक तुरंत उत्तर दिया कि यह दीर्घवृत्ताकार होना चाहिए और बताया कि इस तथ्य का पता उन्होंने बहुत पहले 1665 में ही उस समय लगा लिया था जब उन्हें प्लेग फैलने के कारण कैम्ब्रिज से वापस अपने फार्म हाउस पर आकर रहना पड़ा था| दुर्भाग्य से न्यूटन ने अपने तत्संबंधी कागजात खो दिए थे| हेली ने न्यूटन को पुस्तक के रूप में उनकी धारणाओं को प्रस्तुत करने के लिए मना लिया और उसके प्रकाशन पर होने वाले कुल खर्च को स्वयं वहन करने की सहमति दी| न्यूटन ने अतिमानवीय प्रयत्नों द्वारा 18 महीने के अल्पकाल में यह महान कार्य पूरा कर दिखाया| प्रिंसिपिया, विशिष्ट वैज्ञानिक कृति है और लैग्रेंजे के शब्दों में कहें तो, "मानवीय मस्तिष्क का सर्वश्रेष्ठ उत्पादन है"| भारतीय मूल के, नोबेल पुरस्कार विजेता खगोल-भौतिकीविद् डा. एस. चंद्रशेखर ने दस वर्ष की मेहनत से ‘प्रिंसिपिया’ की टीका लिखी| उनकी पुस्तक, "आम आदमी के लिए प्रिंसिपिया" न्यूटन की विधियों के सौंदर्य, स्पष्टता एवं अदभुत संक्षिप्तता को बहुत अच्छी तरह उभार कर प्रस्तुत करती है|
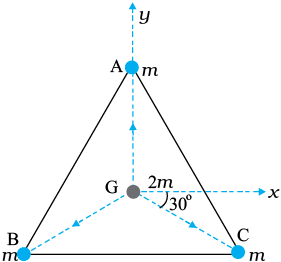
उदाहरण 8.2 किसी समबाहु त्रिभुज ABC के प्रत्येक शीर्ष पर m kg के तीन समान द्रव्यमान रखे हैं|
(a) इस त्रिभुज के केन्द्रक G पर रखे 2m kg के द्रव्यमान पर कितना बल आरोपित हो रहा है?
(b) यदि शीर्ष A पर रखे द्रव्यमान को दो गुना कर दिया जाए, तो कितना बल आरोपित होगा?
AG = BG = CG = 1m लीजिए (देखिए चित्र 8.5)
हल (a) धनात्मक x-अक्ष तथा GC के बीच का कोण 30° है और इतना ही कोण ऋणात्मक x-अक्ष तथा GB के बीच बनता है| सदिश संकेत पद्धति में व्यष्टिगत बल इस प्रकार हैं
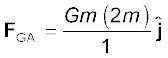
चित्र 8.5 तीन समान द्रव्यमान त्रिभुज ABC के तीन शीर्षों पर स्थित हैं| इसके केंद्रक G पर कोई द्रव्यमान 2m रखा गया है|
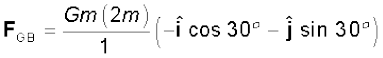
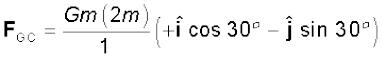 .
.
अध्यारोपण सिद्धांत तथा सदिश योग नियम के अनुसार (2m) पर परिणामी गुरुत्वाकर्षण बल
FR = FGA + FGB + FGC
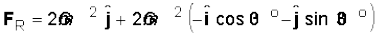
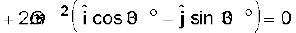
विकल्प के रूप में, सममिति के आधार पर यह अपेक्षा की जा सकती है कि परिणामी बल शून्य होना चाहिए|
(b) यदि शीर्ष A पर द्रव्यमान 2m हो तो,
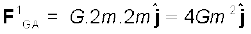
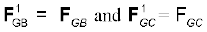
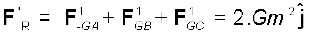
किसी विस्तारित पिण्ड (जैसे पृथ्वी) तथा बिन्दु द्रव्यमान के बीच गुरुत्वाकर्षण बल के लिए समीकरण (8.5) का सीधे ही अनुप्रयोग नहीं किया जा सकता| विस्तारित पिण्ड का प्रत्येक बिन्दु द्रव्यमान दिए गए बिन्दु द्रव्यमान पर बल आरोपित करता है तथा इन सभी बलों की दिशा समान नहीं होती| हमें इन बलों का सदिश रीति द्वारा योग करना होता है ताकि विस्तारित पिण्ड के प्रत्येक बिन्दु द्रव्यमान के कारण आरोपित कुल बल प्राप्त हो जाए| एेसा हम आसानी से कलन (कैलकुलस) के उपयोग द्वारा कर सकते हैं| जब हम एेसा करते हैं तो हमे दो विशिष्ट प्रकरणों में सरल परिणाम प्राप्त होते हैं
(1) किसी एकसमान घनत्व के खोखले गोलीय खोल तथा खोल के बाहर स्थित किसी बिन्दु द्रव्यमान के बीच आकर्षण बल ठीक-ठाक उतना ही होता है जैसा कि खोल के समस्त द्रव्यमान को उसके केन्द्र पर संकेन्द्रित मान कर ज्ञात किया जाता है|
गुणात्मक रूप से इसे इस प्रकार समझा जा सकता है| खोल के विभिन्न क्षेत्रों के कारण गुरुत्वीय बलों के, खोल के केन्द्र को बिन्दु द्रव्यमान से मिलाने वाली रेखा के अनुदिश तथा इसके लंबवत्, दोनों दिशाओं में घटक होते हैं| खोल के सभी क्षेत्रों के बलों के घटकों का योग करते समय इस रेखा के लंबवत् दिशा के घटक निरस्त हो जाते हैं तथा केवल खोल के केन्द्र से बिन्दु द्रव्यमान को मिलाने वाली रेखा के अनुदिश परिणामी बल बचा रहता है| इस परिणामी बल का परिमाण भी ऊपर वर्णन की गई विधि द्वारा ज्ञात किया जा सकता है|
(2) एकसमान घनत्व के किसी खोखले गोले के कारण उसके भीतर स्थित किसी बिन्दु द्रव्यमान पर आकर्षण बल शून्य होता है|
गुणात्मक रूप में, हम फिर से इस परिणाम को समझ सकते हैं| गोलीय खोल के विभिन्न क्षेत्र खोल के भीतर स्थित बिन्दु द्रव्यमान को विभिन्न दिशाओं में आकर्षित करते हैं| ये बल परस्पर एक दूसरे को पूर्णतः निरस्त कर देते हैं|
8.4 गुरुत्वीय नियतांक
गुरुत्वाकर्षण के सार्वत्रिक नियम में प्रयुक्त गुरुत्वीय स्थिरांक G के मान को प्रायोगिक आधार पर ज्ञात किया जा सकता है तथा इस प्रकार के प्रयोग को सर्वप्रथम अंग्रेज वैज्ञानिक हेनरी कैवेन्डिश ने 1798 में किया था| उनके द्वारा उपयोग किए गए उपकरण को व्यवस्था चित्र 8.6 में दर्शाया गया है|
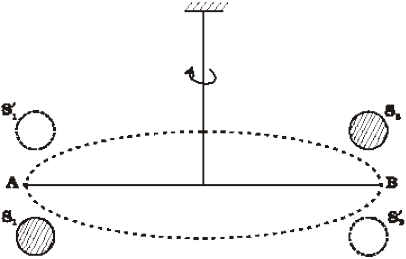
चित्र 8.6 कैवेन्डिश प्रयोग का योजनावत आरेखन| S1 तथा S2 दो विशाल गोले हैं (छायांकित दर्शाए गए हैं) जिन्हें A और B पर स्थिति द्रव्यमानों के दोनों ओर रखा जाता है| जब विशाल द्रव्यमानों (बिन्दुकित वृत्तों द्वारा दर्शाए) को दूसरी ओर ले जाते हैं, तो छड़ AB थोड़ा घूर्णन करती है, क्योंकि अब बल आघूर्ण की दिशा व्युत्क्रमित हो जाती है| घूर्णन कोण को प्रयोगों द्वारा ज्ञात किया जा सकता है|
छड़ AB के दोनों सिरों पर दो छोटे सीसे के गोले जुड़े होते हैं| इस छड़ को एक पतले तार द्वारा किसी दृढ़ टेक से निलंबित किया जाता है| सीसे के दो विशाल गोलों को चित्र में दर्शाए अनुसार छोटे गोलों के निकट परन्तु विपरीत दिशाओं में लाया जाता है| बड़े गोले चित्र में दर्शाए अनुसार अपने निकट के छोटे गोलों को समान तथा विपरीत बलों से आकर्षित करते हैं| छड़ पर कोई नेट बल नहीं लगता, परन्तु केवल एक बल आघूर्ण कार्य करता है जो स्पष्ट रूप से छड़ की लम्बाई का F-गुना होता है, जबकि यहाँ F विशाल गोले तथा उसके निकट वाले छोटे गोले के बीच परस्पर आकर्षण बल है| इस बल आघूर्ण के कारण, निलंबन तार में तब तक एेंठन आती है जब तक प्रत्यानयन बल आघूर्ण गुरुत्वीय बल आघूर्ण के बराबर नहीं होता| यदि निलंबन तार का व्यावर्तन कोण θ है, तो प्रत्यानयन बल आघूर्ण θ के अनुक्रमानुपाती तथा 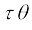 के बराबर हुआ, यहाँ
के बराबर हुआ, यहाँ 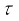 प्रत्यानयन बल युग्म प्रति एकांक व्यावर्तन कोण है|
प्रत्यानयन बल युग्म प्रति एकांक व्यावर्तन कोण है| 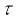 की माप अलग प्रयोग द्वारा की जा सकती है, जैसे कि ज्ञात बल आघूर्ण का अनुप्रयोग करके तथा व्यावर्तन कोण मापकर| गोल गेदों के बीच गुरुत्वाकर्षण बल उतना ही होता है जितना कि गेदों के द्रव्यमानों को उनके केन्द्रों पर संकेंन्द्रित मान कर ज्ञात किया जाता है| इस प्रकार यदि विशाल गोले तथा उसके निकट के छोटे गोले के केन्द्रों के बीच की दूरी d है, M तथा m इन गोलों के द्रव्यमान हैं, तो बड़े गोले तथा उसके निकट के छोटे गोले के बीच गुरुत्वाकर्षण बल
की माप अलग प्रयोग द्वारा की जा सकती है, जैसे कि ज्ञात बल आघूर्ण का अनुप्रयोग करके तथा व्यावर्तन कोण मापकर| गोल गेदों के बीच गुरुत्वाकर्षण बल उतना ही होता है जितना कि गेदों के द्रव्यमानों को उनके केन्द्रों पर संकेंन्द्रित मान कर ज्ञात किया जाता है| इस प्रकार यदि विशाल गोले तथा उसके निकट के छोटे गोले के केन्द्रों के बीच की दूरी d है, M तथा m इन गोलों के द्रव्यमान हैं, तो बड़े गोले तथा उसके निकट के छोटे गोले के बीच गुरुत्वाकर्षण बल
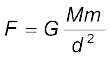 (8.6)
(8.6)
यदि छड़ AB की लम्बाई L है, तो F के कारण उत्पन्न बल आघूर्ण F तथा L का गुणनफल होगा| संतुलन के समय यह बल आघूर्ण प्रत्यानयन बल आघूर्ण के बराबर होता है| अतः
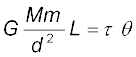 (8.7)
(8.7)
इस प्रकार θ का प्रेक्षण करके इस समीकरण की सहायता से G का मान परिकलित किया जा सकता है|
कैवेन्डिश प्रयोग के बाद G के मापन में परिष्करण हुए तथा अब G का प्रचलित मान इस प्रकार है
G = 6.67x10-11 N m2/kg2 (8.8)
8.5 पृथ्वी का गुरुत्वीय त्वरण
पृथ्वी को गोल होने के कारण बहुत से संकेन्द्री गोलीय खोलों का मिलकर बना माना जा सकता है जिनमें सबसे छोटा खोल केन्द्र पर तथा सबसे बड़ा खोल इसके पृष्ठ पर है| पृथ्वी के बाहर का कोई भी बिन्दु स्पष्ट रूप से इन सभी खोलों के बाहर हुआ| इस प्रकार सभी खोल पृथ्वी के बाहर किसी बिन्दु पर इस प्रकार गुरुत्वाकर्षण बल आरोपित करेंगे जैसे कि इन सभी खोलों के द्रव्यमान पिछले अनुभाग में वर्णित परिणाम के अनुसार उनके उभयनिष्ठ केन्द्र पर संकेन्द्रित हैं| सभी खोलों के संयोजन का कुल द्रव्यमान पृथ्वी का ही द्रव्यमान हुआ| अतः, पृथ्वी के बाहर किसी बिन्दु पर, गुरुत्वाकर्षण बल को यही मानकर ज्ञात किया जाता है कि पृथ्वी का समस्त द्रव्यमान उसके केन्द्र पर संकेन्द्रित है|
पृथ्वी के भीतर स्थित बिन्दुओं के लिए स्थिति भिन्न होती है| इसे चित्र 8.7 में स्पष्ट किया गया है|
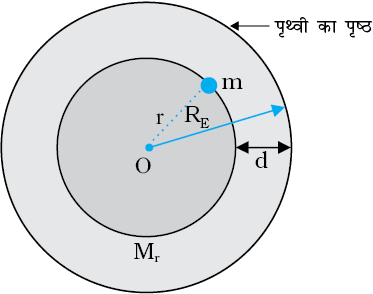
चित्र 8.7 ME पृथ्वी का द्रव्यमान तथा RE पृथ्वी की त्रिज्या है, पृथ्वी के पृष्ठ के नीचे d गहराई पर स्थित किसी खान में कोई द्रव्यमान m रखा है| हम पृथ्वी को गोलतः सममित मानते हैं|
पहले की ही भांति अब फिर पृथ्वी को संकेन्द्री खोलों से मिलकर बनी मानिए और यह विचार कीजिए कि पृथ्वी के केन्द्र से r दूरी पर कोई द्रव्यमान m रखा गया है| बिन्दु P, r त्रिज्या के गोले के बाहर है| उन सभी खोलों के लिए जिनकी त्रिज्या r से अधिक है, बिन्दु P उनके भीतर है| अतः पिछले भाग में वर्णित परिणाम के अनुसार ये सभी खोल P पर रखे द्रव्यमानों पर कोई गुरुत्वाकर्षण बल आरोपित नहीं करते| त्रिज्या  r के खोल मिलकर r त्रिज्या का गोला निर्मित करते हैं तथा बिन्दु P इस गोले के पृष्ठ पर स्थित है| अतः r त्रिज्या का यह छोटा गोला P पर स्थित द्रव्यमान m पर इस प्रकार गुरुत्वाकर्षण बल आरोपित करता है जैसे इसका समस्त द्रव्यमान mr इसके केन्द्र पर संकेन्द्रित है| इस प्रकार P पर स्थित द्रव्यमान m पर आरोपित बल का परिमाण
r के खोल मिलकर r त्रिज्या का गोला निर्मित करते हैं तथा बिन्दु P इस गोले के पृष्ठ पर स्थित है| अतः r त्रिज्या का यह छोटा गोला P पर स्थित द्रव्यमान m पर इस प्रकार गुरुत्वाकर्षण बल आरोपित करता है जैसे इसका समस्त द्रव्यमान mr इसके केन्द्र पर संकेन्द्रित है| इस प्रकार P पर स्थित द्रव्यमान m पर आरोपित बल का परिमाण
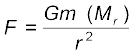 (8.9)
(8.9)
हम यह मानते हैं कि समस्त पृथ्वी का घनत्व एकसमान है अतः इसका द्रव्यमान 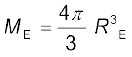 ρ है| यहाँ RE पृथ्वी की त्रिज्या तथा ρ इसका घनत्व है| इसके विपरीत r त्रिज्या के गोले का द्रव्यमान
ρ है| यहाँ RE पृथ्वी की त्रिज्या तथा ρ इसका घनत्व है| इसके विपरीत r त्रिज्या के गोले का द्रव्यमान 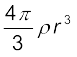 होता है| इसलिए
होता है| इसलिए
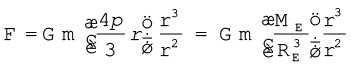
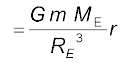 (8.10)
(8.10)
यदि द्रव्यमान m पृथ्वी के पृष्ठ पर स्थित है, तो r = RE तथा समीकरण (8.10) से इस पर गुरुत्वाकर्षण बल
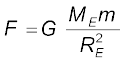 (8.11)
(8.11)
यहाँ ME तथा RE क्रमशः पृथ्वी का द्रव्यमान तथा त्रिज्या है| द्रव्यमान m द्वारा अनुभव किया जाने वाला त्वरण जिसे प्रायः प्रतीक g द्वारा निर्दिष्ट किया जाता है, न्यूटन के द्वितीय नियम द्वारा बल F से संबंध F = mg द्वारा संबंधित होता है| इस
प्रकार
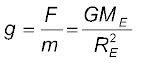 (8.12)
(8.12)
g सहज ही मापन योग्य है| RE एक ज्ञात राशि है| कैवेन्डिश-प्रयोग द्वारा अथवा दूसरी विधि से प्राप्त G की माप g तथा RE के ज्ञान को सम्मिलित करने पर ME का आकलन समीकरण (8.12) की सहायता से किया जा सकता है| यही कारण है कि कैवेन्डिश के बारे में एक प्रचलित कथन यह है कि "कैवेन्डिश ने पृथ्वी को तोला"|
8.6 पृथ्वी के पृष्ठ के नीचे तथा ऊपर गुरुत्वीय त्वरण
चित्र में दर्शाए अनुसार पृथ्वी के पृष्ठ से ऊँचाई h पर स्थित किसी बिन्दु द्रव्यमान m पर विचार कीजिए (चित्र 8.8(a))|
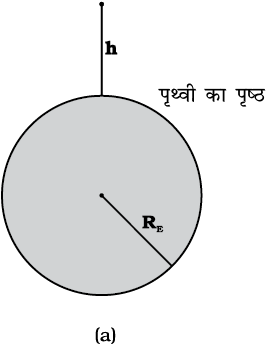
चित्र 8.8(a) पृथ्वी के पृष्ठ से किसी ऊँचाई h पर g
पृथ्वी की त्रिज्या को R E द्वारा निर्दिष्ट किया जाता है| चूंकि यह बिन्दु पृथ्वी से बाहर है, इसकी पृथ्वी के केन्द्र से दूरी
(RE + h ) है| यदि बिन्दु द्रव्यमान m पर बल के परिमाण को F (h) द्वारा निर्दिष्ट किया गया है, तो समीकरण (8.5) से हमें निम्नलिखित संबंध प्राप्त होता है
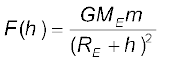 (8.13)
(8.13)
बिन्दु द्रव्यमान द्वारा अनुभव किया जाने वाला त्वरण 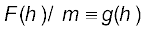 तथा इस प्रकार हमें प्राप्त होता है
तथा इस प्रकार हमें प्राप्त होता है
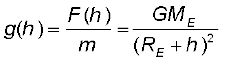 (8.14)
(8.14)
स्पष्ट रूप से यह मान पृथ्वी के पृष्ठ पर g के मान से कम है : 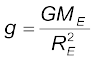 जबकि
जबकि 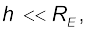 हम समीकरण (8.14) के दक्षिण पक्ष को इस प्रकार भी लिख सकते हैं :
हम समीकरण (8.14) के दक्षिण पक्ष को इस प्रकार भी लिख सकते हैं :
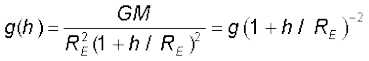
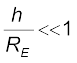 के लिए द्विपद व्यंजक का उपयोग करने पर
के लिए द्विपद व्यंजक का उपयोग करने पर
 (8.15)
(8.15)
इस प्रकार समीकरण (8.15) से हमें प्राप्त होता है कि कम ऊँचाई h के लिए g का मान गुणक 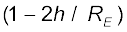 द्वारा घटता है|
द्वारा घटता है|
अब हम पृथ्वी के पृष्ठ के नीचे गहराई d पर स्थित किसी बिन्दु द्रव्यमान m के विषय मेें विचार करते हैं| एेसा होने पर चित्र 8.8(b) में दर्शाए अनुसार इस द्रव्यमान की पृथ्वी के केन्द्र से दूरी 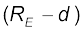 त्रिज्या के छोटे गोले तथा d मोटाई के एक गोलीय खोल से मिलकर बनी मान सकते हैं| तब द्रव्यमान m पर d मोटाई की बाह्य खोल के कारण आरोपित बल पिछले अनुभाग में वर्णित परिणाम के कारण शून्य होगा| जहाँ तक
त्रिज्या के छोटे गोले तथा d मोटाई के एक गोलीय खोल से मिलकर बनी मान सकते हैं| तब द्रव्यमान m पर d मोटाई की बाह्य खोल के कारण आरोपित बल पिछले अनुभाग में वर्णित परिणाम के कारण शून्य होगा| जहाँ तक
(R E – d ) त्रिज्या के छोटे गोले के कारण आरोपित बल का संबंध है तो पिछले अनुभाग में वर्णित परिणाम के अनुसार, इस छोटे गोले के कारण बल इस प्रकार लगेगा जैसे कि छोटे गोले का समस्त द्रव्यमान उसके केन्द्र पर संकेन्द्रित है| यदि छोटे गोले का द्रव्यमान Ms है, तो Ms / ME = ( RE – d ) 3 / RE 3 ( 8.16)
क्योंकि, किसी गोले का द्रव्यमान उसकी त्रिज्या के घन के अनुक्रमानुपाती होता है|
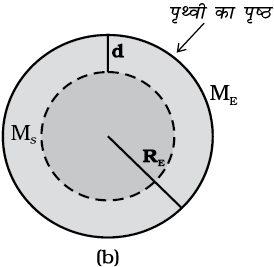
चित्र 8.8 (b) किसी गहराई d पर g इस प्रकरण में केवल (RE– d) त्रिज्या का छोटा गोला ही g के लिए योगदान देता है|
अतः बिन्दु द्रव्यमान पर आरोपित बल
F ( d ) = G Ms m / ( RE – d ) 2 (8.17)
ऊपर से Ms का मान प्रतिस्थापित करने पर, हमें प्राप्त होता है
F ( d) = G ME m ( RE – d ) / RE 3 (8.18)
और इस प्रकार गहराई d पर गुरुत्वीय त्वरण,
g(d) = 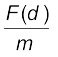
अर्थात् 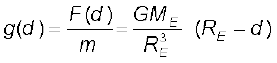
= 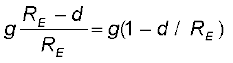 (8.19)
(8.19)
इस प्रकार जैसे-जैसे हम पृथ्वी से नीचे अधिक गहराई तक जाते हैं, गुरुत्वीय त्वरण का मान गुणक 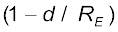 द्वारा घटता जाता है| पृथ्वी के गुरुत्वीय त्वरण से संबंधित यह एक आश्चर्यजनक तथ्य है कि पृष्ठ पर इसका मान अधिकतम है तथा चाहे हम पृष्ठ से ऊपर जाएँ अथवा नीचे यह मान सदैव घटता है|
द्वारा घटता जाता है| पृथ्वी के गुरुत्वीय त्वरण से संबंधित यह एक आश्चर्यजनक तथ्य है कि पृष्ठ पर इसका मान अधिकतम है तथा चाहे हम पृष्ठ से ऊपर जाएँ अथवा नीचे यह मान सदैव घटता है|
8.7 गुरुत्वीय स्थितिज ऊर्जा
पहले हमने स्थितिज ऊर्जा की धारणा की चर्चा किसी वस्तु की दी हुई स्थिति पर उसमें संचित ऊर्जा के रूप में दी थी| यदि किसी कण की स्थिति उस पर कार्यरत बल के कारण परिवर्तित हो जाती है तो उस कण की स्थितिज ऊर्जा में परिवर्तन आरोपित बल द्वारा उस कण पर किए गए कार्य के परिमाण के ठीक-ठीक बराबर होगा| जैसा कि हम पहले चर्चा कर चुके हैं जिन बलों द्वारा किया गया कार्य चले गए पथों पर निर्भर नहीं करता, वे बल संरक्षी बल होते हैं तथा केवल एेसे बलों के लिए ही किसी पिण्ड की स्थितिज ऊर्जा की कोई सार्थकता होती है|
गुरुत्व बल एक संरक्षी बल है तथा हम किसी पिण्ड में इस बल के कारण उत्पन्न स्थितिज ऊर्जा, जिसे गुरुत्वीय स्थितिज ऊर्जा कहते हैं, का परिकलन कर सकते हैं| पहले पृथ्वी के पृष्ठ के निकट के उन बिन्दुओं पर विचार कीजिए जिनकी पृष्ठ से दूरियाँ पृथ्वी की त्रिज्या की तुलना में बहुत कम हैं| जैसा कि हम देख चुके हैं एेसे प्रकरणों में गुरुत्वीय बल व्यावहारिक दृष्टि से नियत रहता है तथा यह mg होता है तथा इसकी दिशा पृथ्वी के केन्द्र की ओर होती है| यदि हम पृथ्वी के पृष्ठ से h1 ऊँचाई पर स्थित किसी बिन्दु तथा इसी बिन्दु के ठीक ऊर्ध्वाधर ऊपर h2 ऊँचाई पर स्थित किसी अन्य बिन्दु पर विचार करें तो m द्रव्यमान के किसी कण को पहली स्थिति से दूसरी स्थिति तक ऊपर उठाने में किया गया कार्य, जिसे W12 द्वारा निर्दिष्ट करते हैं,
W12 = बल × विस्थापन
= mg (h2 – h1) . (8.20)
यदि हम पृथ्वी के पृष्ठ से h ऊँचाई के बिन्दु से कोई स्थितिज ऊर्जा W(h) संबद्ध करें जो इस प्रकार है कि
W(h) = mg h + Wo (8.21)
(यहाँ Wo = नियतांक) ;
तब यह स्पष्ट है कि
W12 = W(h2) – W(h1) (8.22)
कण को स्थानांतरित करने में किया गया कार्य ठीक इस कण की अंतिम तथा आरंभिक स्थितियों की स्थितिज ऊर्जाओं के अंतर के बराबर है| ध्यान दीजिए कि समीकरण (8.22) में Wo निरस्त हो जाता है| समीकरण (8.21) में h = 0 रखने पर हमें W ( h = 0 ) = Wo प्राप्त होता है| h = 0 का अर्थ यह है कि दोनों बिन्दु पृथ्वी के पृष्ठ पर स्थित हैं| इस प्रकार Wo कण की पृथ्वी के पृष्ठ पर स्थितिज ऊर्जा हुई|
यदि हम पृथ्वी के पृष्ठ से यादृच्छिक दूरियों के बिन्दुओं पर विचार करें तो उपरोक्त परिणाम प्रामाणिक नहीं होते क्योंकि तब यह मान्यता कि गुरुत्वाकर्षण बल mg अपरिवर्तित रहता है वैध नहीं है| तथापि, अपनी अब तक की चर्चा के आधार पर हम जानते हैं कि पृथ्वी के बाहर के किसी बिन्दु पर स्थित किसी कण पर लगे गुरुत्वीय बल की दिशा पृथ्वी के केन्द्र की ओर निदेशित होती है तथा इस बल का परिमाण है,
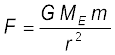 (8.23)
(8.23)
यहाँ ME = पृथ्वी का द्रव्यमान, m = कण का द्रव्यमान तथा r इस कण की पृथ्वी के केन्द्र से दूरी है| यदि हम किसी कण को r = r1 से r = r2 तक (जबकि r2 > r1) ऊर्ध्वाधर पथ के अनुदिश ऊपर उठाने में किए गए कार्य का परिकलन करें तो हमें समीकरण (8.20) के स्थान पर यह संबंध प्राप्त होता है
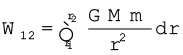
 (8.24)
(8.24)
इस प्रकार समीकरण (8.21) के बजाय, हम किसी दूरी r पर स्थितिज ऊर्जा W(r) को इस प्रकार संबद्ध कर सकते हैं :
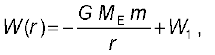 (8.25)
(8.25)
जो कि r > R के लिए वैध है|
अतः एक बार फिर W12 = W(r2) – W(r1) | अंतिम समीकरण में r = 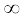 रखने पर हमें W(r =
रखने पर हमें W(r = 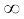 ) = W1 प्राप्त होता है| इस प्रकार W1 अनन्त पर स्थितिज ऊर्जा हुई| हमें यह ध्यान देना चाहिए कि समीकरणों (8.22) तथा (8.24) के अनुसार केवल दो बिन्दुओं के बीच स्थितिज ऊर्जाओं में अंतर की ही कोई निश्चित सार्थकता है| हम प्रचलित मान्य परिपाटी के अनुसार W1 को शून्य मान लेते हैं जिसके कारण किसी बिन्दु पर किसी कण को स्थितिज ऊर्जा उस कण को अनन्त से उस बिन्दु तक लाने में किए जाने वाले कार्य के ठीक बराबर होती है|
) = W1 प्राप्त होता है| इस प्रकार W1 अनन्त पर स्थितिज ऊर्जा हुई| हमें यह ध्यान देना चाहिए कि समीकरणों (8.22) तथा (8.24) के अनुसार केवल दो बिन्दुओं के बीच स्थितिज ऊर्जाओं में अंतर की ही कोई निश्चित सार्थकता है| हम प्रचलित मान्य परिपाटी के अनुसार W1 को शून्य मान लेते हैं जिसके कारण किसी बिन्दु पर किसी कण को स्थितिज ऊर्जा उस कण को अनन्त से उस बिन्दु तक लाने में किए जाने वाले कार्य के ठीक बराबर होती है|
हमने, किसी बिन्दु पर किसी कण की स्थितिज ऊर्जा का परिकलन उस कण पर लगे पृथ्वी के गुरुत्वीय बलों के कारण, जो कि कण के द्रव्यमान के अनुक्रमानुपाती होता है, किया है| पृथ्वी के गुरुत्वीय बल के कारण किसी बिन्दु पर गुरुत्वीय विभव की परिभाषा "उस बिन्दु पर किसी कण के एकांक द्रव्यमान की स्थितिज ऊर्जा" के रूप में की जाती है|
पूर्व विवेचन के आधार पर, हम जानते हैं कि m1 एवं m2 द्रव्यमान के एक दूसरे से r दूरी पर रखे दो कणों की गुरुत्वीय स्थितिज ऊर्जा है,
V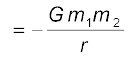 (यदि हम r =
(यदि हम r = 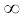 पर V = 0 लें)
पर V = 0 लें)
यह भी ध्यान दिया जाना चाहिए कि कणों के किसी सभी वियुक्त निकाय की कुल स्थितिज ऊर्जा, अवयवों/कणों के सभी संभावित युग्मों की ऊर्जाओं (उपरोक्त समीकरण द्वारा परिकलित) के योग के बराबर होती है| यह अध्यारोपण सिद्धांत के एक अनुप्रयोग का उदाहरण है|
उदाहरण 8.3 l भुजा के किसी वर्ग के शीर्षों पर स्थित चार कणों के निकाय की स्थितिज ऊर्जा ज्ञात कीजिए| वर्ग के केन्द्र पर विभव भी ज्ञात कीजिए|
उत्तर मान लीजिए प्रत्येक कण का द्रव्यमान m है, तथा वर्ग की भुजा l है| हमारे पास l दूरी वाले 4 द्रव्यमान युगल तथा 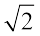 l दूरी वाले 2 द्रव्यमान युगल हैं| अतः निकाय की स्थितिज ऊर्जा
l दूरी वाले 2 द्रव्यमान युगल हैं| अतः निकाय की स्थितिज ऊर्जा
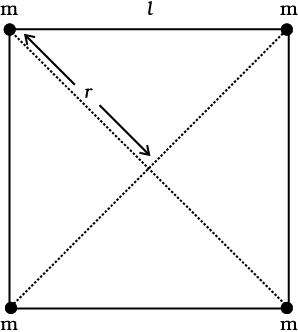
चित्र 8.9

वर्ग के केन्द्र 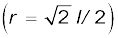 पर गुरुत्वीय विभव,
पर गुरुत्वीय विभव,
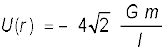
8.8 पलायन चाल
यदि हम अपने हाथों से किसी पत्थर को फेंकते हैं, तो हम यह पाते हैं कि वह फिर वापस पृथ्वी पर गिर जाता है| निस्संदेह मशीनों का उपयोग करके हम किसी पिण्ड को अधिकाधिक तीव्रता तथा प्रारंभिक वेगों से शूट कर सकते हैं जिसके कारण पिण्ड अधिकाधिक ऊँचाइयों तक पहुँच जाते हैं| तब स्वाभाविक रूप से हमारे मस्तिष्क में यह विचार उत्पन्न होता है "क्या हम किसी पिण्ड को इतने अधिक आरंभिक चाल से ऊपर फेंक सकते हैं कि वह फिर पृथ्वी पर वापस न गिरे?"
इस प्रश्न का उत्तर देने में ऊर्जा संरक्षण नियम हमारी सहायता करता है| मान लीजिए फेंका गया पिण्ड अनन्त तक पहुंचता है और वहाँ उसकी चाल Vf है| किसी पिण्ड की ऊर्जा स्थितिज तथा गतिज ऊर्जाओं का योग होती है| पहले की ही भांति W1 पिण्ड की अनन्त पर गुरुत्वीय स्थितिज ऊर्जा को निर्दिष्ट करता है| तब प्रक्षेप्य की अनन्त पर कुल ऊर्जा
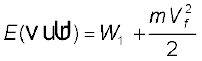 (8.26)
(8.26)
यदि पिण्ड को पृथ्वी (RE = पृथ्वी की त्रिज्या) के केन्द्र से (h + RE) ऊँचाई पर स्थित किसी बिन्दु से आरंभ में चाल
Vi से फेंका गया था, तो इस पिण्ड की आरंभिक ऊर्जा थी
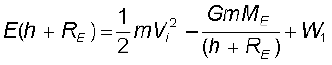 (8.27)
(8.27)
ऊर्जा संरक्षण नियम के अनुसार समीकरण (8.26) तथा (8.27) बराबर होने चाहिए| अतः
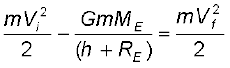 (8.28)
(8.28)
समीकरण (8.28) का दक्षिण पक्ष एक धनात्मक राशि है जिसका न्यूनतम मान शून्य है, अतः वाम पक्ष भी एेसा ही होना चाहिए| अतः कोई पिण्ड अनन्त तक पहुंच सकता है जब Vi इतना हो कि
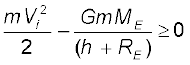 (8.29)
(8.29)
Vi का न्यूनतम मान उस प्रकरण के तदनुरूपी है जिसमें समीकरण (8.29) का वाम पक्ष शून्य के बराबर है| इस प्रकार, किसी पिण्ड को अनन्त तक पहुंचने के लिए (अर्थात् पृथ्वी से पलायन के लिए) आवश्यक न्यूनतम चाल इस संबंध के तदनुरूपी होती है
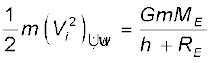 (8.30)
(8.30)
यदि पिण्ड को पृथ्वी के पृष्ठ से छोड़ा जाता है, तो
h = 0 और हमें प्राप्त होता है
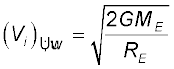 (8.31)
(8.31)
संबंध 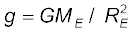 का उपयोग करने पर हमें निम्न मान प्राप्त होता है
का उपयोग करने पर हमें निम्न मान प्राप्त होता है
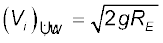 (8.32)
(8.32)
समीकरण (8.32) में g और RE के आंकिक मान रखने पर हमें (Vi)न्यून ≈11.2 km/s प्राप्त होता है| उसे पलायन चाल कहते हैं| कभी-कभी लापरवाही में इसे हम पलायन वेग भी कह देते हैं|
समीकरण (8.32) का उपयोग भली भांति समान रूप से चन्द्रमा से फेंके जाने वाले पिण्डों के लिए भी किया जा सकता है, एेसा करते समय हम g के स्थान पर चन्द्रमा के पृष्ठ पर चन्द्रमा के गुरुत्वीय त्वरण तथा RE के स्थान पर चन्द्रमा की त्रिज्या का मान रखते हैं| इन दोनों ही राशियों के चन्द्रमा के लिए मान पृथ्वी पर इनके मानों से कम हैं तथा चन्द्रमा के लिए पलायन चाल का मान 2.3 km/s प्राप्त होता है| यह मान पृथ्वी की तुलना में लगभग 1/5 गुना है| यही कारण है कि चन्द्रमा पर कोई वातावरण नहीं है| यदि चन्द्रमा के पृष्ठ पर गैसीय अणु बनें, तो उनकी चाल इस पलायन चाल से अधिक होगी तथा वे चन्द्रमा के गुरुत्वीय खिंचाव के बाहर पलायन कर जाएंगे|
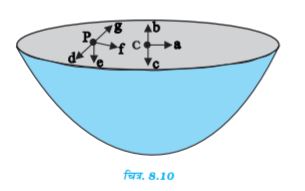
उदाहरण 8.4 समान त्रिज्या R परन्तु M तथा 4 M द्रव्यमान के दो एकसमान ठोस गोले इस प्रकार रखे हैं कि इनके केन्द्रों के बीच पृथकन (चित्र 8.10 में दर्शाए अनुसार) 6 R है| दोनों गोले स्थिर रखे गए हैं|
m द्रव्यमान के किसी प्रक्षेप्य को M द्रव्यमान के गोले के पृष्ठ से 4M द्रव्यमान के गोले के केन्द्र की ओर सीधे प्रक्षेपित किया जाता है| प्रक्षेप्य की उस न्यूनतम चाल के लिए व्यंजक प्राप्त कीजिए जिससे फेंके जाने पर वह दूसरे गोले के पृष्ठ पर पहुंच जाए|
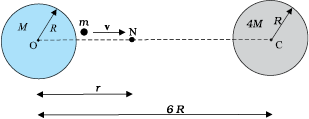
चित्र 8.10
हल प्रक्षेप्य पर दो गोलों के परस्पर विरोधी गुरुत्वीय बल कार्य करते हैं| उदासीन बिन्दु N (चित्र 8.10 देखिए) की परिभाषा एक एेसे बिन्दु (स्थिति) के रूप में की जाती है जहाँ दो बल यथार्थतः एक दूसरे को निरस्त करते हैं| यदि ON = r है, तो
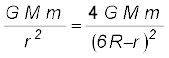
(6R – r)2 = 4r2
6R – r = ±2r
r = 2R या – 6R
इस उदाहरण में उदासीन बिन्दु r = – 6R हमसे संबंधित नहीं है| इस प्रकार, ON = r = 2R| कण को उस चाल से प्रक्षेपित करना पर्याप्त है जो उसे N तक पहुंचने योग्य बना दे| इसके पश्चात् वहाँ पहुंचने पर 4 M द्रव्यमान के गोले का गुरुत्वीय बल कण को अपनी ओर खींचने के लिए पर्याप्त होगा| M द्रव्यमान के गोले के पृष्ठ पर यांत्रिक ऊर्जा
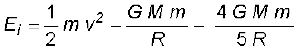
उदासीन बिन्दु N पर कण की चाल शून्य मान की ओर प्रवृत्त होती है| अतः N पर यांत्रिक ऊर्जा शुद्ध रूप से स्थितिज ऊर्जा होती है| अतः
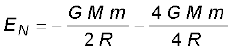
यांत्रिक ऊर्जा संरक्षण नियम के अनुसार

अथवा 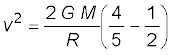
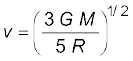
यहाँ यह ध्यान देने का विषय है कि N पर प्रक्षेप्य की चाल शून्य है, परन्तु जब यह 4 M द्रव्यमान के गोले से टकराता तब इसकी चाल शून्येत्तर होती है| जिस चाल से प्रक्षेप्य 4M द्रव्यमान के गोले से टकराता है, उसे ज्ञात करना छात्रों के अभ्यास के लिए छोड़ा जा रहा है|
8.9 भू उपग्रह
भू उपग्रह वह पिण्ड है जो पृथ्वी के परितः परिक्रमण करते हैं| इनकी गतियां, ग्रहों की सूर्य के परितः गतियों के बहुत समान होती हैं, अतः केप्लर के ग्रहीय गति नियम इन पर भी समान रूप से लागू होते हैं| विशेष बात यह है कि इन उपग्रहों की पृथ्वी के परितः कक्षाएं वृत्ताकार अथवा दीर्घवृत्ताकार है| पृथ्वी का एकमात्र प्राकृतिक उपग्रह चन्द्रमा है जिसकी लगभग वृत्ताकार कक्षा है और लगभग 27.3 दिन का परिक्रमण काल है जो चन्द्रमा के अपनी अक्ष के परितः घूर्णन काल के लगभग समान है| वर्ष 1957 के पश्चात् विज्ञान तथा प्रौद्योगिकी में उन्नति के फलस्वरूप भारत सहित कई देश दूर संचार, भू भौतिकी, मौसम विज्ञान के क्षेत्र में व्यावहारिक उपयोगों के लिए मानव-निर्मित भू उपग्रहों को कक्षाओं में प्रमोचित करने योग्य बन गए हैं|
अब हम पृथ्वी के केन्द्र से (RE + h) दूरी पर स्थित वृत्तीय कक्षा में गतिमान उपग्रह पर विचार करेंगे, यहाँ RE = पृथ्वी की त्रिज्या है| यदि उपग्रह का द्रव्यमान m तथा V इसकी चाल है, तो इस कक्षा के लिए आवश्यक अभिकेन्द्र बल
F(अभिकेन्द्र) = 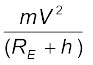 (8.33)
(8.33)
तथा यह बल कक्षा के केन्द्र की ओर निदेशित है| अभिकेन्द्र बल गुरुत्वाकर्षण बल द्वारा प्रदान किया जाता है, जिसका
मान
F(गुरुत्वाकर्षण) = 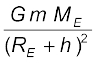 (8.34)
(8.34)
यहाँ ME पृथ्वी का द्रव्यमान है|
समीकरणों (8.33) तथा (8.34) के दक्षिण पक्षों को समीकृत तथा m का निरसन करने पर हमें प्राप्त होता है
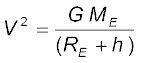 (8.35)
(8.35)
इस प्रकार h के बढ़ने पर V घटता है| समीकरण (8.35) के अनुसार जब h = 0 है, तो उपग्रह की चाल V है
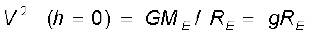 (8.36)
(8.36)
यहाँ हमने संबंध g =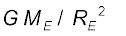 का उपयोग किया है| प्रत्येक कक्षा में उपग्रह 2π(RE + h) दूरी चाल V से तय करता है| अतः इसका आवर्तकाल T है
का उपयोग किया है| प्रत्येक कक्षा में उपग्रह 2π(RE + h) दूरी चाल V से तय करता है| अतः इसका आवर्तकाल T है
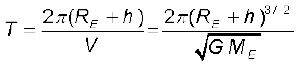 (8.37)
(8.37)
यहाँ हमने समीकरण (8.35) से V का मान प्रतिस्थापित किया है| समीकरण (8.37) के दोनों पक्षों का वर्ग करने पर हमें प्राप्त होता है
T 2 = k ( RE + h )3 ( जहाँ k = 4 π2 / G ME), (8.38)
और यही केप्लर का आवर्तकालों का नियम है जिसका अनुप्रयोग पृथ्वी के परितः उपग्रहों की गतियों के लिए किया जाता है|
उन भू उपग्रहों के लिए, जो पृथ्वी के पृष्ठ के अति निकट होते हैं, h के मान को पृथ्वी की त्रिज्या RE की तुलना में समीकरण (8.38) में नगण्य मान लेते हैं| अतः इस प्रकार के
भू उपग्रहों के लिए T ही To होता है, यहाँ
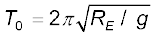 (8.39)
(8.39)
यदि हम समीकरण (8.39) में g तथा RE के आंकिक मानों (g  9.8 ms-2 तथा RE = 6400 km.) को प्रतिस्थापित करें, तो हमें प्राप्त होता है
9.8 ms-2 तथा RE = 6400 km.) को प्रतिस्थापित करें, तो हमें प्राप्त होता है
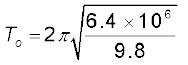 s
s
जो लगभग 85 मिनट के बराबर हैं|
उत्तर 8.5 मंगल ग्रह के फोबोस तथा डेल्मोस नामक दो चन्द्रमा हैं| (i) यदि फोबोस का आवर्तकाल 7 घंटे 39 मिनट तथा कक्षीय त्रिज्या 9.4 ×103 km है तो मंगल का द्रव्यमान परिकलित कीजिए| (ii) यह मानते हुए कि पृथ्वी तथा मंगल सूर्य के परितः वृत्तीय कक्षाओं में परिक्रमण कर रहे हैं तथा मंगल की कक्षा की त्रिज्या पृथ्वी की कक्षा की त्रिज्या की 1.52 गुनी है तो मंगल-वर्ष की अवधि दिनों में क्या है?
हल (i) यहाँ पर समीकरण (8.38) का उपयोग पृथ्वी के द्रव्यमान ME को मंगल के द्रव्यमान Mm से प्रतिस्थापित करके करते हैं
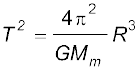
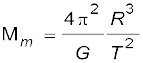
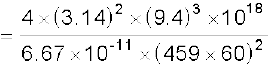
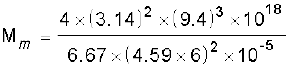
= 6.48 × 1023 kg
(ii) केप्लर के आवर्तकालों के नियम का उपयोग करने पर
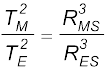
यहाँ RMS एवं RES क्रमशः मंगल-सूर्य तथा पृथ्वी-सूर्य के बीच की दूरियां हैं|
TM = (1.52)3/2 × 365
= 684 दिन
ध्यान देने योग्य तथ्य यह है कि बुध, मंगल तथा प्लूटो* के अतिरिक्त सभी ग्रहों की कक्षाएं लगभग वृत्ताकार हैं| उदाहरण के लिए, हमारी पृथ्वी के अर्ध लघु अक्ष तथा अर्ध दीर्घ अक्ष का अनुपात b/a = 0.99986 है|
उत्तर 8.6 पृथ्वी को तोलना : आपको निम्नलिखित आंकड़े दिए गए हैं: g = 9.81 m s–2, RE = 6.37×106m, पृथ्वी से चन्द्रमा की दूरी R = 3.84×108 m पृथ्वी के परितः चन्द्रमा के परिक्रमण का आवर्त काल = 27.3 दिन| दो भिन्न विधियों द्वारा पृथ्वी का द्रव्यमान प्राप्त कीजिए|
हल (i) पहली विधि : समीकरण (8.12) से
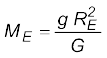
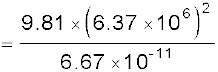
= 5.97× 1024 kg
(ii) दूसरी विधि : चन्द्रमा पृथ्वी का उपग्रह है| केप्लर के आवर्तकालों के नियम की व्युत्पत्ति में (समीकरण (8.38) देखिए)]
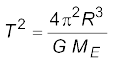
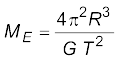
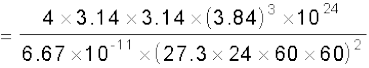
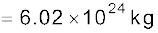
दोनों विधियों द्वारा लगभग समान उत्तर प्राप्त होते हैं, जिनमें 1% से भी कम का अंतर है|
उदाहरण 8.7 समीकरण (8.38) में स्थिरांक k को दिनों तथा किलोमीटरों में व्यक्त कीजिए| k = 10–13 s2 m–3 है| चन्द्रमा पृथ्वी से 3.84 × 105 km दूर है| चन्द्रमा के परिक्रमण के आवर्तकाल को दिनों में प्राप्त कीजिए|
हल हम जानते हैं कि
k = 10–13 s2 m–3
= 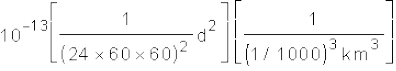
= 1.33 ×10–14 d2 km–3
समीकरणों (8.38) तथा k के दिए गए मान का उपयोग करने पर चन्द्रमा के परिक्रमण का आवर्तकाल
T2 = (1.33 × 10-14)(3.84 × 105)3
T = 27.3 d
ध्यान दीजिए, यदि हम (RE+h) को दीर्घवृत्त के अर्ध दीर्घ अक्ष (a) द्वारा प्रतिस्थापित करें तो समीकरण (8.38) को दीर्घवृत्तीय कक्षाओं पर भी लागू किया जा सकता है, तब पृथ्वी इस दीर्घवृत्त की एक नाभि पर होगी|
8.10 कक्षा में गतिशील उपग्रह की ऊर्जा
समीकरण (8.35) का उपयोग करने पर वृत्ताकार कक्षा में चाल v से गतिशील उपग्रह की गतिज ऊर्जा
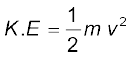 ;
;
v2 का मान समीकरण (8.35) से रखने पर
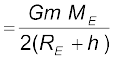 , (8.40)
, (8.40)
एेसा मानें कि अनन्त पर गुरुत्वीय स्थितिज ऊर्जा शून्य है तब पृथ्वी के केन्द्र से (Re+h) दूरी पर उपग्रह की स्थितिज
ऊर्जा
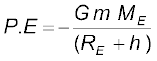 (8.41)
(8.41)
K.E धनात्मक है जबकि P.E ऋणात्मक होती है| तथापि परिमाण में K.E = 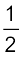 P.E, अतः उपग्रह की कुल ऊर्जा
P.E, अतः उपग्रह की कुल ऊर्जा
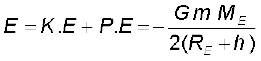 (8.42)
(8.42)
इस प्रकार वृत्ताकार कक्षा में गतिशील किसी उपग्रह की कुल ऊर्जा ऋणात्मक होती है, स्थितिज ऊर्जा का ऋणात्मक तथा परिमाण में धनात्मक गतिज ऊर्जा का दो गुना होता है|
जब किसी उपग्रह की कक्षा दीर्घवृत्तीय होती है तो उसकी K.E तथा P.E दोनों ही पथ के हर बिन्दु पर भिन्न होती हैं| वृत्तीय कक्षा के प्रकरण की भांति ही उपग्रह की कुल ऊर्जा नियत रहती है तथा यह ऋणात्मक होती है और यही हम अपेक्षा भी करते हैं क्योंकि जैसा हम पहले चर्चा कर चुके हैं कि यदि कुल ऊर्जा धनात्मक अथवा शून्य हो तो पिण्ड अनन्त की ओर पलायन कर जाता है| उपग्रह सदैव पृथ्वी से परिमित दूरियों पर परिक्रमण करते हैं, अतः उनकी ऊर्जाएँ धनात्मक अथवा शून्य नहीं हो सकतीं|
उदाहरण 8.8 400 kg द्रव्यमान का कोई उपग्रह पृथ्वी के परित 2RE त्रिज्या की वृत्तीय कक्षा में परिक्रमण कर रहा है| इसे 4RE की वृत्तीय कक्षा में स्थानांतरित करने के लिए आवश्यक ऊर्जा परिकलित कीजिए| इसकी गतिज तथा स्थितिज ऊर्जा में कितने परिवर्तन होंगे?
हल आरंभ में
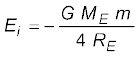
जबकि, अंत में
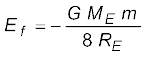
कुल ऊर्जा में परिवर्तन
∆E = Ef – Ei
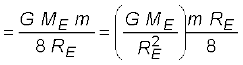
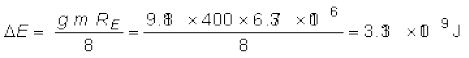
गतिज ऊर्जा घट जाती है और यह ∆E की अनुहारक है, अर्थात् ∆K = Kf – Ki = – 3.13 × 109 J |
स्थितिज ऊर्जा में होने वाला परिवर्तन कुल ऊर्जा का दो गुना है, अर्थात्
∆V = Vf – Vi = – 6.25 × 109 J
अंतरिक्ष में भारत की छलाँग
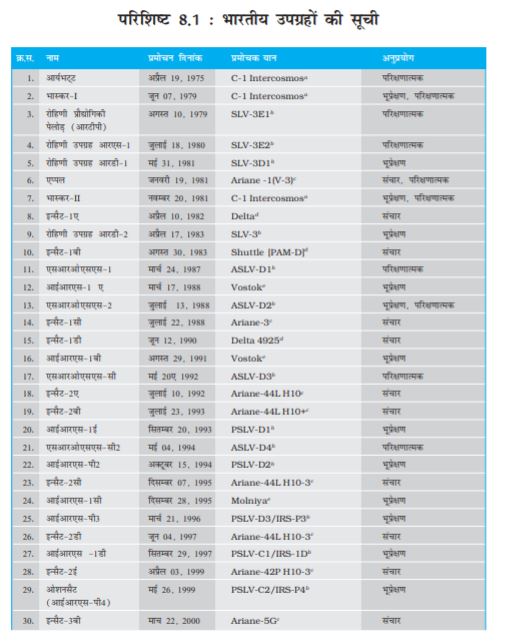
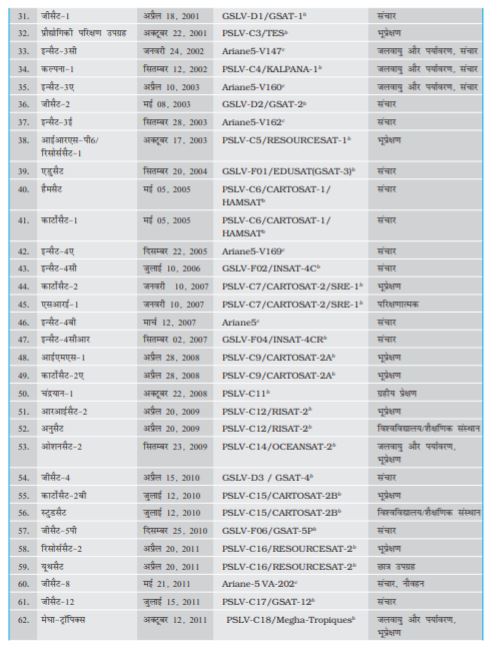
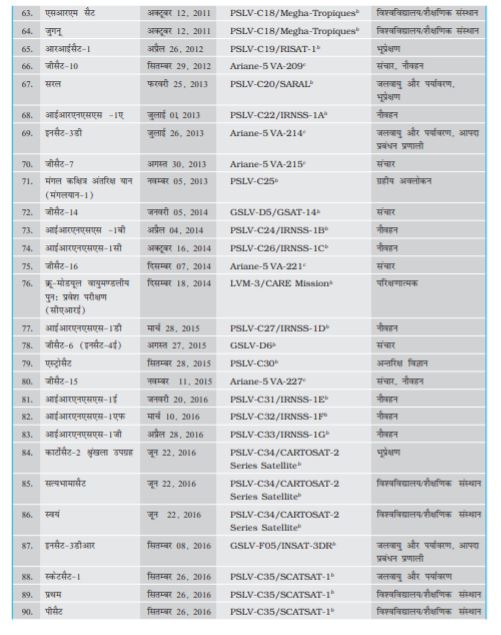
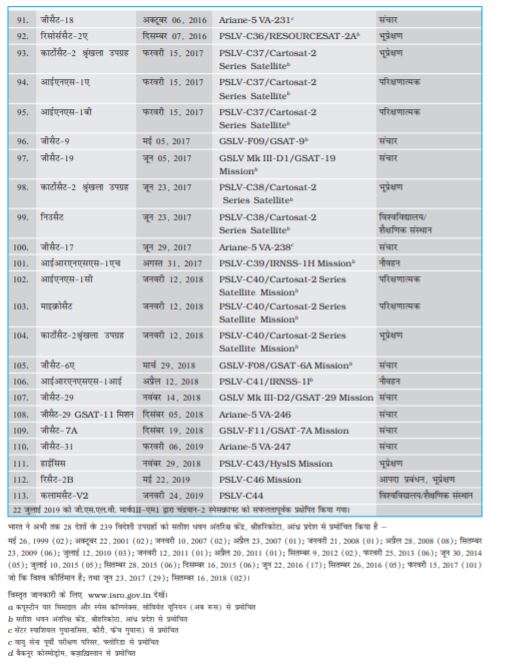
सन् 1962 में भारत सरकार द्वारा भारतीय राष्ट्रीय अंतरिक्ष अनुसंधान समिति (INCOSPAR) के गठन के साथ भारत के अंतरिक्ष कार्यक्रम प्रारम्भ हुए| सन् 1969 में गठित भारतीय अंतरिक्ष अनुसंधान संगठन (ISRO) ने तत्कालीनINCOSPAR का अधिक्रमण किया| इसरो ने देश के विकास में अंतरिक्ष प्रौद्योगिकी की भूमिका और महत्व को पहचानते हुए आम जनता के लिए अंतरिक्ष विज्ञान के उपयोग का ध्येय बनाए रखा है| भारत ने अपना पहला निम्न-कक्षा उपग्रह आर्यभट्ट 1975 में तत्कालीन सोवियत संघ के प्रमोचक रॉकेट द्वारा प्रक्षेपित किया| सन् 1979 में, रोहिणी शृंखला के उपग्रहों को अंतरिक्ष में भेजने के साथ ही इसरो ने अपने मुख्य प्रक्षेपण स्थल सतीश धवन अंतरिक्ष केन्द्र, श्रीहरिकोटा, आंध्र प्रदेश से देशज प्रमोचक रॉकेटों का उपयोग प्रारम्भ किया| भारत के अंतरिक्ष कार्यक्रम में अपनी अद्भुत सफलताओं से इसरो विश्व की छठी वृहत्तम अंतरिक्ष एजेंसी बन गई है| इसरो प्रसारण, संचार, मौसम पूर्वानुमान, आपदा प्रबंधन उपकरण, भौगोलिक सूचना प्रणाली, मानचित्र कला, नौवहन, टेलीचिकित्सा, समर्पित दूरस्थ शिक्षा संबधी उपग्रह आदि के लिए विशिष्ट उपग्रह उत्पादों और उपकरणों का विकास करती है| इन उपयोगों के संबंध में सम्पूर्ण आत्मनिर्भरता प्राप्त करने के लिए लागत प्रभावी एवम् विश्वसनीय ध्रुवीय उपग्रह प्रमोचक प्रणाली(पी.एस.एल.वी.) का विकास 1990 के दशक के प्रारम्भ में हुआ| इन विशेषताओं के कारण पी.एस.एल.वी. विभिन्न देशों के उपग्रहों के लिए सबसे प्रिय वाहक बन गया है| इससे अंतराष्ट्रीय सहयोग में भी अभूर्तपूर्व रूप से वृद्धि हुई है| सन् 2001 में अधिक भारी और अधिक माँग वाले भूतुल्यकाली संचार उपग्रहों के लिए भूतुल्यकाली उपग्रह प्रमोचक रॉकेट (जी.एस.एल.वी.) को विकसित किया गया| भारत सरकार के अंतरिक्ष विभाग के तत्वाधान में सुदूर संवेदन, खगोलिकी और खगोल भौतिकी, वायुमंडलीय विज्ञान और अंतरिक्ष अनुसंधान के क्षेत्रों में विभिन्न अनुसंधान केन्द्र और स्वायत्त संस्थान कार्यरत हैं| वैज्ञानिक परियोजनाओं सहित चन्द्र (चन्द्रयान) तथा अंतरग्रहीय (मंगलयान) मिशनों की सफलताएँ इसरो की उल्लेखनीय उपलब्धियाँ है| इसरो के भविष्य के प्रयासों में समानव अंतरिक्ष उड़ान परियोजनाएँ, भारी वाहक प्रमोचकों, पुनरूपयोगी प्रमोचक रॉकेटों, सेमी-क्रायोजेनिक इंजन, एकल तथा द्वि-चरणी कक्षा (SSTOतथा TSTO) रॉकेटों, अंतरिक्ष उपयोगों के लिए सम्मिश्र सामग्री का विकास एवम् उपयोग इत्यादि शामिल हैं| 1984 में राकेश शर्मा सोवियत अंतरिक्षयान में जाने वाले प्रथम भारतीय अंतरिक्ष यात्री बने|
8.11 तुल्यकाली तथा ध्रुवीय उपग्रह
यदि हम समीकरण (8.37) में (RE+ h) के मान में इस तरह समायोजन करें कि आवर्तकाल T का मान 24 घन्टे हो जाए, तो एक अत्यन्त रोचक परिघटना उत्पन्न हो जाती है| यदि वृत्तीय कक्षा पृथ्वी के विषुवत वृत्त के तल में है, तो इस प्रकार का उपग्रह, जिसका आवर्तकाल पृथ्वी के अपने अक्ष पर घूर्णन करने के आवर्तकाल के बराबर हो, पृथ्वी के किसी बिन्दु से देखने पर स्थिर प्रतीत होगा| इस उद्देश्य के लिए परिकलन करने पर (RE + h) का मान RE की तुलना में काफी अधिक आता है :

चित्र 8.11 ध्रुवीय उपग्रह| एक चक्कर में उपग्रह से दिखाई देने वाली पृथ्वी के पृष्ठ की एक पट्टी (छायांकित दर्शायी गयी है)| उपग्रह के अगले परिक्रमण के लिए पृथ्वी अपने अक्ष पर कुछ घूर्णन कर गयी है, जिससे संलग्न पट्टी दिखाई देने
लगती है|
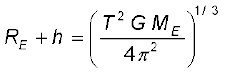 (8.43)
(8.43)
T = 24 घन्टे के लिए, परिकलन करने पर, RE+ h = 35800 km, जो कि पृथ्वी की त्रिज्या RE से काफी अधिक है| वे उपग्रह जो पृथ्वी के विषुवत वृत्त के तल (अर्थात निरक्षीय समतल) में पृथ्वी के परितः वृत्तीय कक्षा में, T = 24 घन्टे के आवर्तकाल से, परिक्रमण करते हैं, तुल्यकाली उपग्रह कहलाते हैं| स्पष्ट है कि क्योंकि पृथ्वी समान आवर्तकाल से अपने अक्ष पर घूर्णन करती है अतः यह उपग्रह पृथ्वी के किसी भी बिन्दु से स्थिर प्रतीत होगा| पृथ्वी के पृष्ठ से इतनी अधिक ऊँचाई तक ऊपर फेंकने के लिए अत्यन्त शक्तिशाली रॉकेटों की आवश्यकता होती है| परन्तु, बहुत से व्यावहारिक अनुप्रयोगों को ध्यान में रखकर इनका प्रबन्ध किया गया है|
हम जानते हैं कि एक निश्चित आवृत्ति से अधिक आवृत्ति की विद्युत चुम्बकीय तरंगें आयनमंडल द्वारा परावर्तित नहीं होतीं| रेडियो-प्रसारण में उपयोग होने वाली रेडियो तरंगें जिनका आवृत्ति परिसर 2MHZ से 10MHZ है क्रांतिक आवृत्ति से कम है, इसलिए ये तरंगें आयनमंडल से परिवर्तित हो जाती हैं| इस प्रकार किसी एेन्टेना द्वारा किया गया रेडियो तरंग प्रसारण उन स्थानों पर भी ग्रहण किया जा सकता है जो बहुत दूर है तथा पृथ्वी की वक्रता के कारण जहाँ तरंगें सीधे नहीं पहुँच पातीं| दूरदर्शन-प्रसारण अथवा अन्य प्रकार के संचार में उपयोग होने वाली तरंगों की आवृत्तियाँ अत्यधिक उच्च होती हैं, अतः इन्हें सीधे ही दृष्टि-रेखा से बाहर ग्रहण नहीं किया जा सकता| प्रसारण केन्द्र के ऊपर स्थापित कोई तुल्यकाली उपग्रह जो स्थिर प्रतीत होता है, इन सिगनलों को ग्रहण करके उन्हें, पृथ्वी के बड़े क्षेत्र पर वापस प्रसारित कर सकता है| भारत द्वारा अन्तरिक्ष में भेजा गया इनसैट उपग्रह समूह एेसा ही तुल्यकाली उपग्रह समूह है जिसका विस्तृत उपयोग दूरसंचार के लिए भारत में किया जा रहा है|
उपग्रह की अन्य श्रेणी को ध्रुवीय उपग्रह कहते हैं| ये निम्न तुंगता (h ≈ 500 से 800 km) उपग्रह हैं| परन्तु ये पृथ्वी के ध्रुवों के परितः उत्तर दक्षिण दिशा में गमन करते हैं जबकि पृथ्वी अपने अक्ष पर पश्चिम से पूर्व की ओर घूर्णन करती है| (देखिए चित्र 8.11)| चूंकि इन उपग्रहों का आवर्तकाल लगभग 100 मिनट होता है, अतः ये किसी भी अक्षांश से दिन में कई बार गुजरते हैं| तथापि, क्योंकि इन उपग्रहों की पृथ्वी के पृष्ठ से ऊँचाई h लगभग 500-800 km होती है, अतः इस पर लगे किसी कैमरे द्वारा किसी एक कक्षा में केवल पृथ्वी की एक छोटी पट्टी का ही दृश्य लिया जा सकता है| संलग्न पट्टियों को अगली कक्षा में देखा जाता है| इस प्रकार प्रभावी रूप में पूरे एक दिन में पट्टी दर पट्टी पूरी पृथ्वी का सर्वेक्षण किया जा सकता है| ये उपग्रह निकट से, अच्छे विभेदन के साथ, विषुवतीय तथा ध्रुवीय क्षेत्रों का सर्वेक्षण कर सकते हैं| इस प्रकार के उपग्रहों द्वारा एकत्र सूचनाएँ सुदूर संवेदन, मौसम विज्ञान के साथ पृथ्वी के पर्यावरणीय अध्ययनों के लिए भी अत्यन्त उपयोगी हैं|
8.12 भारहीनता
किसी पिण्ड का भार वह बल है जिससे पृथ्वी उसे अपने केन्द्र की और आकर्षित करती है| जब हम किसी पृष्ठ पर खड़े होते हैं तो हमें अपने भार का बोध होता है क्योंकि वह पृष्ठ हमारे भार के विपरीत बल आरोपित करके हमें विराम की स्थिति में रखता है| यही सिद्धान्त उस समय लागू होता है जब हम किसी स्थिर बिन्दु, जैसे छत से लटकी किसी कमानीदार तुला से किसी पिण्ड का भार मापते हैं| यदि गुरुत्व बल के विरुद्ध पिण्ड पर कोई बल आरोपित न हो तो वह नीचे गिर जाएगा| कमानी भी यथार्थ रूप में पिण्ड पर इसी प्रकार बल आरोपित करती है| एेसा इसलिए है क्योंकि पिण्ड के गुरुत्वीय खिंचाव के कारण कमानी नीचे की ओर कुछ खिंच जाती है और क्रम से ऊर्ध्वाधर ऊपर दिशा में कमानी पिण्ड पर एक बल आरोपित करती है|
अब कल्पना कीजिए कि कमानीदार तुला का ऊपरी सिरा कमरे की छत से जुड़ कर स्थिर नहीं है| तब कमानी के दोनों सिरों के साथ-साथ पिण्ड भी सर्वसम त्वरण g से गति करेंगे| इस स्थिति में कमानी में कोई खिंचाव नहीं होगा तथा वह उस पिण्ड पर, जो गुरुत्व बल के कारण g त्वरण से नीचे की ओर गतिशील है, कोई बल आरोपित नहीं करेगी| कमानीदार तुला का इस स्थिति में पाठ्यांक कमानी में कोई खिंचाव न होने के कारण शून्य होगा| यदि उस पिण्ड के रूप में कोई स्त्री अथवा पुरुष है, तो वह इस स्थिति में अपने भार का अनुभव नहीं करेगी/ करेगा, क्योंकि उस पर ऊपर की दिशा में कोई बल नहीं लग रहा है| इस प्रकार, जब कोई पिण्ड स्वतंत्रतापूर्वक गिरता है, तो वह भारहीन होता है, तथा इस परिघटना को प्रायः भारहीनता की परिघटना कहते हैं|
पृथ्वी के परितः परिक्रमण करने वाले किसी उपग्रह में, उपग्रह का हर छोटे से छोटा टुकड़ा तथा उसके भीतर की प्रत्येक वस्तु पृथ्वी के केन्द्र की ओर त्वरित गति से गतिशील है, तथा इस गति का त्वरण, यथार्थ रूप से, उस स्थिति में पृथ्वी के गुरुत्वीय त्वरण के बराबर है| अतः उपग्रह के भीतर की प्रत्येक वस्तु स्वतंत्रतापूर्वक गिरती है| यह ठीक एेसा ही है जैसा कि हम किसी ऊंचाई से पृथ्वी की ओर गिर रहे हों| अतः किसी उपग्रह के भीतर बैठे व्यक्ति किसी प्रकार के गुरुत्व बल का अनुभव नहीं करते| गुरुत्व बल हमें उर्ध्वाधर दिशा की परिभाषा का ज्ञान कराता है, अतः उपग्रह के भीतर बैठे व्यक्तियों के लिए क्षैतिज अथवा ऊर्ध्वाधर दिशाओं का कोई महत्व नहीं होता, उनके लिए सभी दिशाएँ समान होती हैं| वायु में तैरते अंतरिक्षयात्रियों के चित्र ठीक इसी तथ्य को दर्शाते हैं|
सारांश
अभ्यास
8.1 निम्नलिखित के उत्तर दीजिएः
(a) आप किसी आवेश का वैद्युत बलों से परिरक्षण उस आवेश को किसी खोखले चालक के भीतर रखकर कर सकते हैं| क्या आप किसी पिण्ड का परिरक्षण, निकट में रखे पदार्थ के गुरुत्वीय प्रभाव से, उसे खोखले गोले में रखकर अथवा किसी अन्य साधनों द्वारा कर सकते हैं?
(b) पृथ्वी के परितः परिक्रमण करने वाले छोटे अन्तरिक्षयान में बैठा कोई अन्तरिक्ष यात्री गुरुत्व बल का संसूचन नहीं कर सकता| यदि पृथ्वी के परितः परिक्रमण करने वाला अन्तरिक्ष स्टेशन आकार में बड़ा है, तब क्या वह गुरुत्व बल के संसूचन की आशा कर सकता है?
(c) यदि आप पृथ्वी पर सूर्य के कारण गुरुत्वीय बल की तुलना पृथ्वी पर चन्द्रमा के कारण गुरुत्व बल से करें, तो आपयह पाएंगे कि सूर्य का खिंचाव चन्द्रमा के खिचाव की तुलना में अधिक है (इसकी जाँच आप स्वयं आगामी अभ्यासों में दिए गए आंकड़ों की सहायता से कर सकते हैं|) तथापि चन्द्रमा के खिंचाव का ज्वारीय प्रभाव सूर्य के ज्वारीय प्रभाव से अधिक है| क्यों?
8.2 सही विकल्प का चयन कीजिए ः
(a) बढ़ती तुंगता के साथ गुरुत्वीय त्वरण बढ़ता/घटता है|
(b) बढ़ती गहराई के साथ (पृथ्वी को एकसमान घनत्व को गोला मानकर) गुरुत्वीय त्वरण बढ़ता/घटता है|
(c) गुरुत्चीय त्वरण पृथ्वी के द्रव्यमान/पिण्ड के द्रव्यमान पर निर्भर नहीं करता|
(d) पृथ्वी के केन्द्र से r2 तथा r1 दूरियों के दो बिन्दुओं के बीच स्थितिज ऊर्जा-अन्तर के लिए सूत्र
–G Mm(1/r2 – 1/r1) सूत्र mg(r2 – r1) से अधिक/कम यथार्थ है|
8.3 मान लीजिए एक एेसा ग्रह है जो सूर्य के परितः पृथ्वी की तुलना में दो गुनी चाल से गति करता है, तब पृथ्वी कीकक्षा की तुलना में इसका कक्षीय आमाप क्या है?
8.4 बृहस्पति के एक उपग्रह, आयो (Io), की कक्षीय अवधि 1.769 दिन तथा कक्षा की त्रिज्या 4.22 × 108 m है| यह दर्शाइए कि बृहस्पति का द्रव्यमान सूर्य के द्रव्यमान का लगभग 1/1000 गुना है|
8.5 मान लीजिए कि हमारी आकाशगंगा में एक सौर द्रव्यमान के 2.5 × 1011 तारे हैं| मंदाकिनीय केन्द्र से50,000 ly दूरी पर स्थित कोई तारा अपनी एक परिक्रमा पूरी करने में कितना समय लेगा? आकाशगंगा का व्यास105 ly लीजिए|
8.6 सही विकल्प का चयन कीजिए ः
(a) यदि स्थितिज ऊर्जा का शून्य अनन्त पर है, तो कक्षा में परिक्रमा करते किसी उपग्रह की कुल ऊर्जा इसकी गतिज/स्थितिज ऊर्जा का ऋणात्मक है|
(b) कक्षा में परिक्रमा करने वाले किसी उपग्रह को पृथ्वी के गुरुत्वीय प्रभाव से बाहर निकालने के लिए आवश्यक ऊर्जा समान ऊंचाई (जितनी उपग्रह की है) के किसी स्थिर पिण्ड को पृथ्वी के प्रभाव से बाहर प्रक्षेपित करने के लिए आवश्यक ऊर्जा से अधिक/कम होती है|
8.7 क्या किसी पिण्ड की पृथ्वी से पलायन चाल (a) पिण्ड के द्रव्यमान, (b) प्रक्षेपण बिन्दु की अवस्थिति, (c) प्रक्षेपण की दिशा, (d) पिण्ड के प्रमोचन की अवस्थिति की ऊंचाई पर निर्भर करती है?
8.8 कोई धूमकेतु सूर्य की परिक्रमा अत्यधिक दीर्घवृत्तीय कक्षा में कर रहा है| क्या अपनी कक्षा में धूमकेतु की शुरू सेअन्त तक (a) रैखिक चाल, (b) कोणीय चाल, (c) कोणीय संवेग, (d) गतिज ऊर्जा, (e) स्थितिज ऊर्जा (f) कुल ऊर्जानियत रहती है| सूर्य के अति निकट आने पर धूमकेतु के द्रव्यमान में ह्रास को नगण्य मानिये|
8.9 निम्नलिखित में से कौन से लक्षण अन्तरिक्ष में अन्तरिक्ष यात्री के लिए दुखःदायी हो सकते हैं? (a) पैरों में सूजन,
(b) चेहरे पर सूजन, (c) सिरदर्द, (d) दिक्विन्यास समस्या|
8.10 एकसमान द्रव्यमान घनत्व की अर्धगोलीय खोलों द्वारा परिभाषित ढोल के पृष्ठ के केन्द्र पर गुरुत्वीय तीव्रता की दिशा [देखिए चित्र 8.10] (i) a, (ii) b,(iii)c, (iv) 0 में किस तीर द्वारा दर्शायी जाएगी?
चित्र. 8.10
8.11 उपरोक्त समस्या में किसी यादृच्छिक बिन्दु P पर गुरुत्वीय तीव्रता किस तीर (i) d, (ii) e, (iii) f, (iv) g द्वारा व्यक्त की जाएगी?
8.12 पृथ्वी से किसी रॉकेट को सूर्य की ओर दागा गया है| पृथ्वी के केन्द्र से किस दूरी पर रॉकेट पर गुरुत्वाकर्षण बल शून्य है? सूर्य का द्रव्यमान = 2×1030 kg, पृथ्वी का द्रव्यमान = 6×1024 kg| अन्य ग्रहों आदि के प्रभावों की उपेक्षा कीजिए (कक्षीय त्रिज्या = 1.5 × 1011 m)|
8.13 आप सूर्य को कैसे तोलेंगे, अर्थात् उसके द्रव्यमान का आकलन कैसे करेंग? सूर्य के परितः पृथ्वी की कक्षा की औसत त्रिज्या 1.5 × 108 km है|
8.14 एक शनि वर्ष एक पृथ्वी-वर्ष का 29.5 गुना है| यदि पृथ्वी सूर्य से 1.5 × 108 km दूरी पर है, तो शनि सूर्य से कितनी दूरी पर है?
8.15 पृथ्वी के पृष्ठ पर किसी वस्तु का भार 63 N है| पृथ्वी की त्रिज्या की आधी ऊंचाई पर पृथ्वी के कारण इस वस्तु परगुरुत्वीय बल कितना है?
8.16 यह मानते हुए कि पृथ्वी एकसमान घनत्व का एक गोला है तथा इसके पृष्ठ पर किसी वस्तु का भार 250 N है, यह ज्ञात कीजिए कि पृथ्वी के केन्द्र की ओर आधी दूरी पर इस वस्तु का भार क्या होगा?
8.17 पृथ्वी के पृष्ठ से उर्ध्वाधरतः ऊपर की ओर कोई रॉकेट 5 km s-1 की चाल से दागा जाता है| पृथ्वी पर वापस लौटने से पूर्व यह रॉकेट पृथ्वी से कितनी दूरी तक जाएगा? पृथ्वी का द्रव्यमान = 6.0 × 1024 kg; पृथ्वी की माध्य
त्रिज्या = 6.4 × 106 m तथा G = 6.67 × 10–11 N m2 kg–2|
8.18 पृथ्वी के पृष्ठ पर किसी प्रक्षेप्य की पलायन चाल 11.2 km s–1 है| किसी वस्तु को इस चाल की तीन गुनी चाल से प्रक्षेपित किया जाता है| पृथ्वी से अत्यधिक दूर जाने पर इस वस्तु की चाल क्या होगी? सूर्य तथा अन्य ग्रहों की उपस्थिति की उपेक्षा कीजिए|
8.19 कोई उपग्रह पृथ्वी के पृष्ठ से 400 km ऊंचाई पर पृथ्वी की परिक्रमा कर रहा है| इस उपग्रह को पृथ्वी के गुरुत्वीय प्रभाव से बाहर निकालने में कितनी ऊर्जा खर्च होगी? उपग्रह का द्रव्यमान = 200 kg; पृथ्वी का द्रव्यमान =6.0×1024 kg; पृथ्वी की त्रिज्या = 6.4 × 106 m तथा G = 6.67 × 10–11 N m2 kg–2|
8.20 दो तारे, जिनमें प्रत्येक का द्रव्यमान सूर्य के द्रव्यमान (2×1030 kg) के बराबर है, एक दूसरे की ओर सम्मुखटक्कर के लिए आ रहे हैं| जब वे 109 km दूरी पर हैं तब इनकी चाल उपेक्षणीय हैं| ये तारे किस चाल से टकराएंगे? प्रत्येक तारे की त्रिज्या 104 km है| यह मानिए कि टकराने के पूर्व तक तारों में कोई विरूपण नहीं होता (G के ज्ञात मान का उपयोग कीजिए)|
8.21 दो भारी गोले जिनमें प्रत्येक का द्रव्यमान 100 kg त्रिज्या 0.10 m है किसी क्षैतिज मेज पर एक दूसरे से 1.0 mदूरी पर स्थित हैं| दोनों गोलों के केन्द्रों को मिलाने वाली रेखा के मध्य बिन्दु पर गुरुत्वीय बल तथा विभव क्या है? क्या इस बिन्दु पर रखा कोई पिण्ड संतुलन में होगा? यदि हां, तो यह संतुलन स्थायी होगा अथवा अस्थायी?
अतिरिक्त अभ्यास
8.22 जैसा कि आपने इस अध्याय में सीखा है कि कोई तुल्यकाली उपग्रह पृथ्वी के पृष्ठ से लगभग 36,000 kmऊंचाई पर पृथ्वी की परिक्रमा करता है| इस उपग्रह के निर्धारित स्थल पर पृथ्वी के गुरुत्व बल के कारण विभव क्या है? (अनन्त पर स्थितिज ऊर्जा शून्य लीजिए|) पृथ्वी का द्रव्यमान = 6.0×1024 kg; पृथ्वी की त्रिज्या = 6400 km.
8.23 सूर्य के द्रव्यमान से 2.5 गुने द्रव्यमान का कोई तारा 12 km आमाप से निपात होकर 1.2 परिक्रमण प्रति सेकण्ड से घूर्णन कर रहा है (इसी प्रकार के संहत तारे को न्यूट्रॉन तारा कहते है| कुछ प्रेक्षित तारकीय पिण्ड, जिन्हें पल्सार कहते हैं, इसी श्रेणी में आते हैं|)| इसके विषुवत् वृत्त पर रखा कोई पिण्ड, गुरुत्व बल के कारण, क्या इसके पृष्ठ से चिपका रहेगा? (सूर्य का द्रव्यमान = 2 × 1030kg )
8.24 कोई अन्तरिक्षयान मंगल पर ठहरा हुआ है| इस अन्तरिक्षयान पर कितनी ऊर्जा खर्च की जाए कि इसे सौरमण्डल से बाहर धकेला जा सके| अन्तरिक्षयान का द्रव्यमान = 1000 kg; सूर्य का द्रव्यमान = 2×1030 kg; मंगल का द्रव्यमान = 6.4×1023 kg; मंगल की त्रिज्या = 3395 km; मंगल की कक्षा की त्रिज्या = 2.28 ×108 km तथा
G = 6.67×10-11 N m2 kg–2|
8.25 किसी राकेट को मंगल के पृष्ठ से 2 km s–1 की चाल से ऊर्ध्वाधर ऊपर दागा जाता है| यदि मंगल के वातावरणीय प्रतिरोध के कारण इसकी 20% आरंभिक ऊर्जा नष्ट हो जाती है, तो मंगल के पृष्ठ पर वापस लौटने से पूर्व यह रॉकेट मंगल से कितनी दूरी तक जाएगा? मंगल का द्रव्यमान = 6.4×1023 kg; मंगल की त्रिज्या = 3395 kmतथा
G = 6.67×10-11 N m2 kg–2|