Table of Contents
9.1 भूमिका
9.2 ठोसों का प्रत्यास्थ व्यवहार
9.3 प्रतिबल तथा विकृति
9.4 हुक का नियम
9.5 प्रतिबल-विकृति वक्र
9.6 प्रत्यास्थता गुणांक
9.7 द्रव्यों के प्रत्यास्थ व्यवहार के अनुप्रयोग
सारांश
विचारणीय बिंदु
अभ्यास
अतिरिक्त अभ्यास
9.1 भूमिका
अध्याय 7 में हमने पिण्डों के घूर्णन के बारे में पढ़ा और यह समझा कि किसी पिण्ड की गति इस बात पर कैसे निर्भर करती है कि पिण्ड के अंदर द्रव्यमान किस प्रकार वितरित है। हमने अपने अध्ययन को केवल दृढ़ पिण्डों की सरल स्थितियों तक ही सीमित रखा था। साधारणतया दृढ़ पिण्ड का अर्थ होता है एक एेसा कठोर ठोस पदार्थ जिसकी कोई निश्चित आकृति तथा आकार हो। परन्तु वास्तव में पिण्डों को तनित, संपीडित अथवा बंकित किया जा सकता है। यहाँ तक कि किसी काफी दृढ़ इस्पात की छड़ को भी एक पर्याप्त बाह्य बल लगाकर विरूपित किया जा सकता है। इससे यह अर्थ निकलता है कि ठोस पिण्ड पूर्ण रूप से दृढ़ नहीं होते हैं।
किसी ठोस की एक निश्चित आकृति तथा आकार होता है। किसी पिण्ड की आकृति अथवा आकार को बदलने (या विरूपित करने) के लिए एक बल की आवश्यकता होती है। यदि किसी कुण्डलित सि्ंप्रग के सिरों को धीरे से खींचकर विस्तारित किया जाए तो सि्ंप्रग की लंबाई थोड़ी बढ़ जाती है। अब यदि सि्ंप्रग के सिरों को छोड़ दें तो वह अपनी प्रारंभिक आकृति एवं आकार को पुन: प्राप्त कर लेगी। किसी पिण्ड का वह गुण, जिससे वह प्रत्यारोपित बल को हटाने पर अपनी प्रारंभिक आकृति एवं आकार को पुन: प्राप्त कर लेता है, प्रत्यास्थता कहलाता है तथा उत्पन्न विरूपण प्रत्यास्थ विरूपण कहलाता है। जब एक पंक पिण्ड पर बल लगाते हैं तो पिण्डक में अपना प्रारंभिक आकार प्राप्त करने की प्रवृत्ति नहीं होती है और यह स्थायी रूप से विरूपित हो जाता है। इस प्रकार के पदार्थ को प्लास्टिक तथा पदार्थ के इस गुण को प्लास्टिकता कहते हैं। पंक और पुटी लगभग आदर्श प्लैस्टिक हैं।
अभियांत्रिकी डिज़ाइन में द्रव्यों के प्रत्यास्थ व्यवहार की अहम भूमिका होती है। उदाहरण के लिए, किसी भवन को डिज़ाइन करते समय इस्पात, कांक्रीट आदि द्रव्यों की प्रत्यास्थ प्रकृति का ज्ञान आवश्यक है। पुल, स्वचालित वाहन, रज्जुमार्ग आदि की डिज़ाइन के लिए भी यही बात सत्य है। यह प्रश्न भी पूछा जा सकता है कि क्या हम एेसा वायुयान डिज़ाइन कर सकते हैं जो बहुत हलका फिर भी बहुत मजबूत हो? क्या हम एक एेसा कृत्रिम अंग डिज़ाइन कर सकते हैं जो अपेक्षाकृत हलका किन्तु अधिक मजबूत हो? रेल पटरी की आकृति I के समान क्यों होती है? काँच क्यों भंगुर होता है जबकि पीतल एेसा नहीं होता? इस प्रकार के प्रश्नों का उत्तर इस अध्ययन से प्रारंभ होगा कि अपेक्षाकृत साधारण प्रकार के लोड या बल भिन्न-भिन्न ठोस पिण्डों को किस प्रकार विरूपित करने का कार्य करते हैं। इस अध्याय में हम ठोसों के प्रत्यास्थ व्यवहार और यांत्रिक गुणों का अध्ययन करेंगे जो एेसे बहुत से प्रश्नों का उत्तर देगा।
9.2 ठोसों का प्रत्यास्थ व्यवहार
हम जानते हैं कि किसी ठोस में प्रत्येक परमाणु या अणु पास वाले परमाणुओं या अणुओं से घिरा होता है। यह अंतरा-परमाणविक या अंतरा-आणविक बलों द्वारा आपस में बँधे होते हैं और एक स्थिर साम्य अवस्था में रहते हैं। जब कोई ठोस विरूपित किया जाता है तो परमाणु/अणु अपनी साम्य स्थिति से विस्थापित हो जाते हैं जिससे उनकी अंतरा-परमाणविक (अंतरा-आणविक) दूरी में अंतर आ जाता है। जब विरूपक बल को हटा लिया जाता है तो अंतरा-परमाणविक बल उन्हें वापस अपनी प्रारंभिक स्थितियों में ले जाते हैं। इस प्रकार पिण्ड अपनी प्रारंभिक आकृति तथा आकार को पुन: प्राप्त कर लेता है। प्रत्यानयन क्रियाविधि को समझने के लिए चित्र 9.1 में दिखाए गए सि्ंप्रग गेंद निकाय के मॉडल पर विचार करें। इसमें गेंदें परमाणुओं को तथा सि्ंप्रग अंतरा-परमाणविक बलों को निरूपित करती हैं।

चित्र 9.1 ठोसों के प्रत्यास्थ व्यवहार के दृष्टांत के लिए सि्ंप्रग-गेंद मॉडल।
यदि आप किसी गेंद को अपनी साम्य स्थिति से विस्थापित करने का प्रयास करेंगे तो सि्ंप्रग तंत्र उस गेंद को वापस अपनी प्रारंभिक स्थिति में लाने का प्रयास करेगा। इस प्रकार ठोसों का प्रत्यास्थ व्यवहार ठोस की सूक्ष्मीय प्रकृति के आधार पर समझाया जा सकता है। एक अंग्रेज़ भौतिक शास्त्री राबर्ट हुक (सन् 1635 - 1703) ने सि्ंप्रगों पर प्रयोग किए और यह पाया कि किसी पिण्ड मेें उत्पन्न विस्तार (लंबाई में वृद्धि) प्रत्यारोपित बल या लोड के अनुक्रमानुपाती होता है। उन्होंने सन् 1676 में प्रत्यास्थता का नियम प्रस्तुत किया जो अब हुक का नियम कहलाता है। हम इसके बारे में खण्ड 9.4 में अध्ययन करेंगे। बॉयल के नियम की ही तरह यह नियम भी विज्ञान के आरंभिक परिमाणात्मक संबंधों में से एक है। अभियांत्रिकी डिज़ाइन के संदर्भ में विभिन्न प्रकार के लोडों के लिए द्रव्यों के व्यवहार को जानना बहुत महत्त्वपूर्ण होता है।
9.3 प्रतिबल तथा विकृति
जब किसी पिण्ड पर एक बल लगाया जाता है तो उसमें थोड़ा या अधिक विरूपण हो जाता है जो पिण्ड के द्रव्य की प्रकृति तथा विरूपक बल के मान पर निर्भर करता है। हो सकता है कि बहुत से द्रव्यों में यह विरूपण बेशक दिखाई नहीं पड़ता, फिर भी यह होता है। जब किसी पिण्ड पर एक विरूपक बल लगाया जाता है तो उसमें एक प्रत्यानयन बल विकसित हो जाता है, जैसा कि पहले कहा जा चुका है। यह प्रत्यानयन बल मान में प्रत्यारोपित बल के बराबर तथा दिशा में उसके विपरीत होता है। एकांक क्षेत्रफल पर लगने वाले प्रत्यानयन बल को प्रतिबल कहते हैं। यदि पिण्ड के क्षेत्रफल A वाले किसी अनुप्रस्थ काट की लंबवत् दिशा में लगाए गए बल का मान F हो तो
प्रतिबल = F/A (9.1)
प्रतिबल की SI इकाई N m–2 तथा इसका विमीय सूत्र
[ML–1T–2 ] होता है।
जब किसी ठोस पर कोई बाहृा बल कार्य करता है तो इसकी विमाएँ तीन प्रकार से बदल सकती हैं। ये चित्र 9.2 में दिखाए गए हैं। चित्र 9.2(a) में, एक बेलन को उसके अनुप्रस्थ परिच्छेद की लंबवत् दिशा में दो समान बल लगाकर तानित किया गया है। इस स्थिति में, एकांक क्षेत्रफल पर प्रत्यानयन बल को तनन प्रतिबल कहते हैं। यदि प्रत्यारोपित बलों के कार्य से बेलन संपीडित हो जाए तो एकांक क्षेत्रफल पर प्रत्यानयन बल को संपीडन प्रतिबल कहते हैं। तनन या संपीडन प्रतिबल को अनुदैर्घ्य प्रतिबल भी कहा जा सकता है।
दोनों ही स्थितियों में बेलन की लंबाई में अंतर हो जाता है। पिण्ड (यहाँ बेलन) की लंबाई में परिवर्तन ∆L तथा उसकी प्रारंभिक लंबाई L के अनुपात को अनुदैर्घ्य विकृति कहते हैं।
अनुदैर्घ्य विकृति 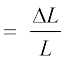 (9.2)
(9.2)
राबर्ट हुक
(1635 – 1703)
राबर्ट हुक का जन्म फ्रेशवाटर, आइल अॉफ वाइट में 18 जुलाई, सन् 1635 को हुआ था। वे सत्रहवीं शताब्दी के सबसे मेधावी और बहुमुखी प्रतिभा वाले अंग्रेज़ वैज्ञानिकों में से एक थे। उन्होंने अॉक्सफोर्ड विश्वविद्यालय में पढ़ाई की परन्तु ग्रेजुएशन (स्नातक) नहीं कर पाए। फिर भी वह एक अत्यधिक प्रतिभाशाली आविष्कारक, यंत्र बनाने वाले तथा भवन डिज़ाइन करने वाले थे। उन्होंने राबर्ट बॉयल की बॉयल वायु पम्पकी संरचना करने में सहायता की। सन् 1662 में वे नयी संस्थापित ‘रॉयल सोसाइटी’ के ‘प्रयोगों के क्यूरेटर’ नियुक्त किए गए। सन् 1665 में वे ग्रेशमकॉलेज में ज्यामिति के प्रोफेसर बने, जहाँ उन्होंने अपने खगोलीय प्रेक्षण पूरे किए। उन्होंने एक ग्रेगोरियन परावर्ती दूरदर्शी की रचना की; ट्रैपीज़ियम में पाँचवें सितारे तथा ओरॉयन तारामण्डल में एक तारापुन्ज की खोज की; जुपिटर के अपने अक्ष पर घूर्णन का सुझाव रखा; मंगलग्रह के विस्तृत रेखाचित्र तैयार किए जो बाद में उन्नीसवीं शताब्दी में इस ग्रह की घूर्णन दर निकालने के लिए इस्तेमाल किए गए; ग्रहों की गति का वर्णन करने के लिए व्युत्क्रम वर्ग नियम का वक्तव्य दिया जिसे बाद मेंन्यूटन ने संशोधित किया, आदि। वे रॉयल सोसाइटी के फैलो चुने गए और सन् 1667 से 1682 तक इस सोसाइटी के सचिव के रूप में भी कार्य किया। "माइक्रोग्रैफिया" में प्रस्तुत प्रेक्षणमाला में उन्होंने प्रकाश के तरंग सिद्धांत का सुझाव रखा तथा कार्क के अध्ययन के परिणामस्वरूप जीव विज्ञान केसंदर्भ में पहली बार ‘सेल (कोशिका)’ शब्द का इस्तेमाल किया।

भौतिक शास्त्रियों द्वारा राबर्ट हुक प्रत्यास्थता के नियम की खोज के लिए सबसे अधिक जाने जाते हैं: ‘उट टेन्सियो सिक विस’ (यह एक लैटिन वाक्यांश है और इसका अर्थ है: ‘जैसा बल, वैसा विरूपण’)। इस नियम ने प्रतिबल तथा विकृति के अध्ययन और प्रत्यास्थ द्रव्यों की समझ के लिए आधार रखा।
अपरूपण विकृति 
= tan θ (9.3)
जहाँ θ ऊर्ध्वाधर (बेलन की प्रारंभिक स्थिति) से बेलन का कोणीय विस्थापन है। चूंकि θ बहुत कम होता है, tan θ लगभग कोण θ के बराबर ही होता है, (उदाहरण के लिए यदि θ = 10° तो θ और tanθ के मान में केवल 1% का अंतर होता है)। यदि किसी पुस्तक को हाथ से दबाकर क्षैतिज दिशा में ढकेलें, जैसा चित्र 9.2(c) में दिखाया गया है, तब भी एेसी विकृति को देखा जा सकता है। इस प्रकार,
अपरूपण विकृति = tan θ ≈ θ (9.4)
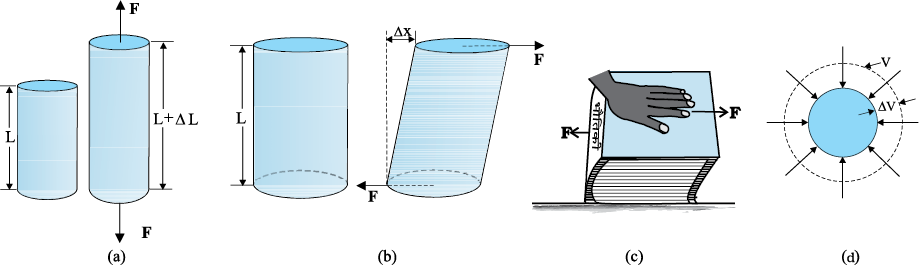
चित्र 9.2 (a) तनन प्रतिबल के प्रभाव में एक बेलन ∆L मान से विस्तरित हो जाता है, (b) अपरूपण (स्पर्शी) प्रतिबल के प्रभाव में एक बेलन कोण θ से विरूपित हो जाता है, (c) अपरूपण प्रतिबल के प्रभाव में एक पुस्तक,(d) समान जलीय प्रतिबल के प्रभाव में एक ठोस गोला ∆V मान से आयतन में संकुचित हो जाता है।
चित्र 9.2(d) में, अधिक दाब के किसी द्रव के अंदर रखा एक ठोस गोला सभी ओर से समान रूप से संपीडित हो जाता है। द्रव द्वारा लगाया गया बल पिण्ड के पृष्ठ के प्रत्येक बिंदु पर लंबवत् दिशा में कार्य करता है; एेसी स्थिति में पिण्ड को जलीय संपीडन की स्थिति में कहा जाता है। इससे ज्यामितीय आकृति में किसी परिवर्तन के बिना ही आयतन में कमी हो जाती है। पिण्ड के अंदर आंतरिक प्रत्यानयन बल उत्पन्न हो जाते हैं जो द्रव द्वारा लगाए गए बलों के बराबर तथा विरोधी होते हैं (द्रव से बाहर निकालने पर पिण्ड अपनी प्रारंभिक आकृति तथा आकार को पुन: प्राप्त कर लेता है)। इस स्थिति में एकांक क्षेत्रफल पर आंतरिक प्रत्यानयन बल को जलीय प्रतिबल कहते हैं और इसका मान जलीय दाब (एकांक क्षेत्रफल पर लगने वाला बल) के बराबर होता है।
जलीय दाब के कारण उत्पन्न विकृति को आयतन विकृति कहते हैं। इसे आयतन में परिवर्तन (∆V) तथा प्रारंभिक आयतन (V) के अनुपात से परिभाषित करते हैं:
आयतन विकृति 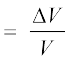 (9.5)
(9.5)
चूंकि विकृत प्रारंभिक विमा तथा विमा में अंतर का अनुपात होता है, इसलिए इसका कोई इकाई या विमीय सूत्र नहीं होता है।
9.4 हुक का नियम
चित्र 9.2 में दिखाई गई विभिन्न स्थितियों में प्रतिबल तथा विकृति के अलग-अलग रूप हो जाते हैं। कम विरूपण के लिए प्रतिबल तथा विकृति एक दूसरे के अनुक्रमानुपाती होते हैं। यही हुक का नियम कहलाता है। इस प्रकार
प्रतिबल α विकृति
प्रतिबल = k × विकृति (9.6)
जहाँ k अनुक्रमानुपातिकता स्थिरांक है और इसे प्रत्यास्थता गुणांक कहते हैं।
हुक का नियम एक आनुभाविक नियम है तथा अधिकतर पदार्थों के लिए वैध होता है। तथापि कुछ पदार्थ इस प्रकार रैखिक संबंध नहीं दर्शाते।
9.5 प्रतिबल-विकृति वक्र
तनन प्रतिबल के अंतर्गत किसी दिए गए द्रव्य के लिए प्रतिबल तथा विकृति के बीच संबंध प्रयोग द्वारा जाना जा सकता है। तनन गुणों की मानक जाँच में, किसी परीक्षण बेलन या तार को एक प्रत्यारोपित बल द्वारा विस्तारित किया जाता है। लंबाई में भिन्नात्मक अन्तर (विकृति) तथा इस विकृति को उत्पन्न करने के लिए आवश्यक प्रत्यारोपित बल को रिकार्ड करते हैं। प्रत्यारोपित बल को धीरे-धीरे क्रमबद्ध चरणों में बढ़ाते हैं और लंबाई में परिवर्तन को नोट करते जाते हैं। प्रतिबल (जिसका मान एकांक क्षेत्रफल पर लगाए गए बल के मान के बराबर होता है) और उससे उत्पन्न विकृति के बीच एक ग्राफ खींचते हैं। किसी धातु के लिए एेसा एक प्रारूपिक ग्राफ चित्र 9.3 में दिखाया गया है। संपीडन तथा अपरूपण प्रतिबल के लिए भी सदृश ग्राफ प्राप्त किए जा सकते हैं। भिन्न-भिन्न द्रव्यों के लिए प्रतिबल-विकृति वक्र भिन्न-भिन्न होते हैं। इन वक्रों की सहायता से हम यह समझ सकते हैं कि कोई दिया हुआ द्रव्य बढ़ते हुए लोड के साथ कैसे विरूपित होता है। ग्राफ से हम यह देख सकते हैं कि O से A के बीच में वक्र रैखिक है। इस क्षेत्र में हुक के नियम का पालन होता है। जब प्रत्यारोपित बल को हटा लिया जाता है तो पिण्ड अपनी प्रारंभिक विमाओं को पुन: प्राप्त कर लेता है। इस क्षेत्र में ठोस एक प्रत्यास्थ पिण्ड जैसा आचरण करता है।
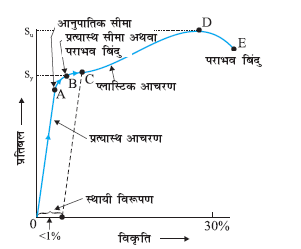
चित्र 9.3 किसी धातु के लिए एक प्रारूपिक प्रतिबल-विकृति वक्र।
A से B के बीच के क्षेत्र में प्रतिबल तथा विकृति अनुक्रमानुपाती नहीं है। फिर भी भार हटाने पर पिण्ड अभी भी अपनी प्रारंभिक विमाओं पर वापस आ जाता है। वक्र में बिंदु B पराभव बिंदु (अथवा प्रत्यास्थ सीमा) कहलाता है और संगत प्रतिबल को द्रव्य का पराभव सामर्थ्य (σy) कहते हैं।
जैसा पहले कहा जा चुका है, प्रतिबल-विकृति व्यवहार में एक द्रव्य से दूसरे द्रव्य में अंतर हो जाता है। उदाहरण के लिए, रबड़ को अपनी प्रारंभिक लंबाई के कई गुने तक खींचा जा सकता है, फिर भी वह अपनी प्रारंभिक आकृति में वापस आ जाता है। चित्र 9.4 में रबड़ जैसे द्रव्य, महाधमनी का प्रत्यास्थ
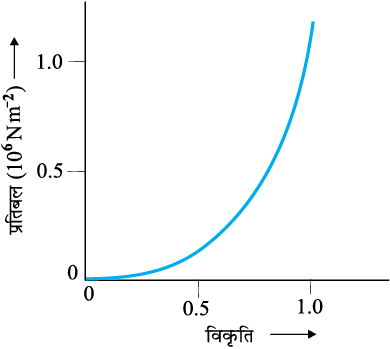
चित्र 9.4 महाधमनी, हृदय से रक्त को ले जाने वाली वृहत नलिका (वाहिका), के प्रत्यास्थ ऊतक के लिए प्रतिबल-विकृति वक्र।
ऊतक, के लिए प्रतिबल-विकृति वक्र दिखाया गया है। ध्यान दें कि यद्यपि प्रत्यास्थ क्षेत्र बहुत अधिक है फिर भी यह द्रव्य हुक के नियम का बिलकुल भी पालन नहीं करता है। इसमें कोई सुस्पष्ट प्लैस्टिक क्षेत्र भी नहीं है। महाधमनी, रबड़ जैसे पदार्थ जिन्हें तनित करके अत्यधिक विकृति पैदा की जा सकती है, प्रत्यस्थालक कहलाते हैं।
9.6 प्रत्यास्थता गुणांक
संरचनात्मक तथा निर्माण अभियांत्रिकी डिज़ाइन के लिए प्रतिबल-विकृति वक्र में प्रत्यास्थ सीमा के अंदर का अनुक्रमानुपाती क्षेत्र (चित्र 9.3 में क्षेत्र OA) बहुत महत्वपूर्ण होता है। प्रतिबल तथा विकृति के अनुपात को प्रत्यास्थता गुणांक कहते हैं और किसी दिए हुए द्रव्य के लिए इसका एक विशिष्ट मान होता है।
9.6.1 यंग गुणांक
प्रायोगिक प्रेक्षण यह दर्शाते हैं कि प्रतिबल चाहे तनक हो या चाहे संपीडक, उत्पन्न विकृति का मान समान होता है। तनक (या संपीडक) प्रतिबल (σ) तथा अनुदैर्घ्य विकृति (ε) के अनुपात से यंग गुणांक को परिभाषित करते हैं तथा इसे प्रतीक 'Y' द्वारा निरूपित करते हैं:
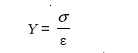 (9.7)
(9.7)
समीकरणों (9.1) और (9.2) से
Y = (F/A)/(∆L/L)
= (F × L) /(A × ∆L) (9.8)
चूंकि विकृति एक विमाविहीन राशि है, यंग गुणांक की इकाई वही होती है जो प्रतिबल की, अर्थात्, N m–2 या पास्कल (Pa) । सारणी 9.1 में कुछ द्रव्यों के यंग गुणांक तथा पराभव सामर्थ्य के मान दिए गए हैं।
सारणी 9.1 में दिए गए आँकड़ों से यह पता चलता है कि धातुओं के लिए यंग गुणांक अधिक होता है। इसलिए इन पदार्थों में लंबाई में थोड़ा ही अंतर उत्पन्न करने के लिए बहुत अधिक बल की आवश्यकता होती है। 0.1 cm2 अनुप्रस्थ परिच्छेद के एक पतले इस्पात के तार की लंबाई को 0.1% से बढ़ाने के लिए 2000 N के बल की आवश्यकता होती है। उसी अनुप्रस्थ परिच्छेद के एेलुमिनियम, पीतल तथा ताँबे के तारों में उतनी ही विकृति उत्पन्न करने के लिए आवश्यक बल क्रमश: 690 N, 900 N तथा 1100 N होते हैं। इसका अर्थ यह है कि ताँबा, पीतल तथा एेलुमिनियम से इस्पात अधिक प्रत्यास्थ होता है। इसी कारण से अधिक काम ली जाने वाली मशीनों और संरचनात्मक डिज़ाइनों में इस्पात को अधिक वरीयता दी जाती है। लकड़ी, अस्थि, कंक्रीट तथा काँच के यंग गुणांक कम होते हैं।
सारणी 9.1 कुछ द्रव्यों के यंग गुणांक तथा पराभव सामर्थ्य
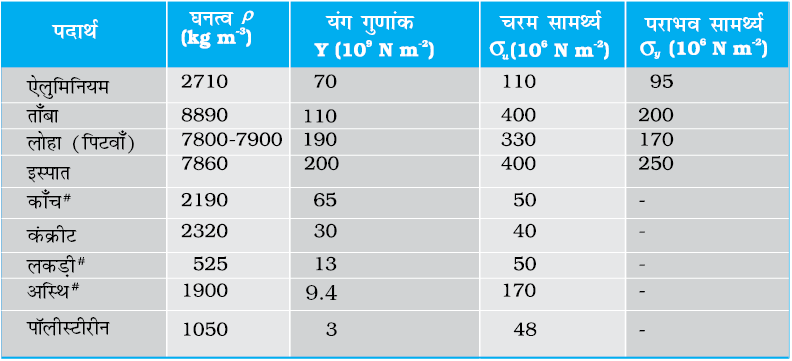
# पदार्थ का परीक्षण संपीडन के अंतर्गत किया गया
उदाहरण 9.1 एक संरचनात्मक इस्पात की छड़ की त्रिज्या 10 mm तथा लंबाई 1 m है। 100 kN का एक बल F इसको लंबाई की दिशा में तनित करता है। छड़ में (a) प्रतिबल, (b) विस्तार, तथा (c) विकृति की गणना कीजिए। संरचनात्मक इस्पात का यंग गुणांक 2.0×1011 N m–2है।
हल हम यह मान लेंगे कि छड़ को एक सिरे पर क्लैम्प करके रखा गया है और बल को दूसरे सिरे पर छड़ की लंबाई की दिशा में लगाया गया है तोछड़ पर प्रतिबल होगा
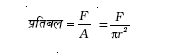
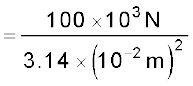
= 3.18 × 108 N m–2
विस्तार होगा,
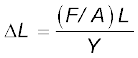
= 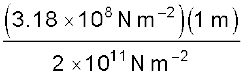
= 1.59 × 10–3 m
= 1.59 mm
विकृति होगी
विकृति = ∆L/L
= (1.59 × 10–3 m )/(1 m)
= 1.59 × 10–3
= 0.16 % t
उदाहरण 9.2 ताँबे का एक 2.2 m लंबा तार तथा इस्पात का एक 1.6 m लंबा तार, जिनमें दोनों के व्यास 3.0 mm हैं, सिरे से जुड़े हुए हैं। जब इसे एक भार से तनित किया गया तो कुल विस्तार 0.7 mm हुआ। लगाए गए भार का मान प्राप्त कीजिए।
हल ताँबे और इस्पात के तार उतने ही तनक प्रतिबल के अंतर्गत हैं क्योंकि उन पर समान तनाव (भार W के बराबर) लगा है तथा उनके अनुप्रस्थ परिच्छेद के क्षेत्रफल A बराबर हैं। समीकरण (9.7) से हम जानते हैं कि प्रतिबल = विकृति × यंग गुणांक, इसलिए
W/A = Yc × (∆Lc/Lc) = Ys × (∆Ls/Ls)
जहाँ पादाक्षर c तथा s क्रमश: ताँबे तथा इस्पात को संदर्भित करते हैं। अथवा,
∆Lc/∆Ls = (Ys/Yc) × (Lc/Ls)
दिया है, Lc = 2.2 m, Ls = 1.6 m
सारणी 9.1 से Yc = 1.1 × 1011 N m–2 और
Ys = 2.0 × 1011 N m–2। इसलिए
∆Lc/∆Ls = (2.0 × 1011/1.1 × 1011) × (2.2/1.6) = 2.5
कुल विस्तार दिया हुआ है
∆Lc + ∆Ls = 7.0 × 10-4 m
ऊपर दिए गए समीकरणों को हल करने पर
∆Lc = 5.0 × 10-4 m, तथा ∆Ls = 2.0 × 10-4 m
इसलिए,
W = (A × Yc × ∆Lc)/Lc
= π (1.5 × 10-3)2 × [1.1 × 1011 × (5.0 × 10-4 )/2.2]
= 1.8 × 102 N t
उदाहरण 9.3 किसी सर्कस में एक मानवीय पिरैमिड में एक संतुलित ग्रुप का सारा भार एक व्यक्ति, जो अपनी पीठ के बल लेटा हुआ है, के पैरों पर आधारित है (जैसा चित्र 9.5 में दिखाया गया है)। इस कार्य का निष्पादन करने वाले सभी व्यक्तियों, मेजों, प्लाकों आदि का कुल द्रव्यमान 280 kg है। पिरैमिड की तली पर अपनी पीठ के बल लेटे हुए व्यक्ति का द्रव्यमान 60 kg है। इस व्यक्ति की प्रत्येक उर्वस्थि (फीमर) की लंबाई 50 cm तथा प्रभावी त्रिज्या 2.0 cm है। निकालिए कि अतिरिक्त भार के कारण प्रत्येक उर्वस्थि कितनी मात्रा से संपीडित हो जाती है।

चित्र 9.5 सर्कस में एक मानवीय पिरैमिड।
हल सभी निष्पादकों, मेजों, प्लाकों आदि का कुल द्रव्यमान = 280 kg
आधार देने वाले निष्पादक का द्रव्यमान = 60 kg
पिरैमिड की तली के निष्पादक के पैरों पर आधारित द्रव्यमान = 280 – 60 = 220 kg
इस आधारित द्रव्यमान का भार
= 220 kg wt = 220 × 9.8 N = 2156 N
निष्पादक की प्रत्येक उर्वस्थि पर आधारित भार
= – (2156) N = 1078 N
सारणी 9.1 से अस्थि का यंग गुणांक,
Y = 9.4 × 109 N m–2
प्रत्येक उर्वस्थि की लंबाई L = 0.5 m तथा त्रिज्या = 2.0 cm
इस प्रकार उर्वस्थि के अनुप्रस्थ काट का क्षेत्रफल
A = π × (2 × 10-2)2 m2 = 1.26 × 10-3 m2
प्रत्येक उर्वस्थि में संपीडन (∆L) की गणना समीकरण (9.8) का इस्तेमाल करके की जा सकती है:
∆L = [(F × L)/(Y × A)]
= [(1078 × 0.5)/(9.4 × 109 × 1.26 × 10-3)]
= 4.55 × 10-5 m या 4.55 × 10-3 cm
यह बहुत कम अंतर है। उर्वस्थि में भिन्नात्मक कमी होगी ∆L/L = 0.000091 या 0.0091% t
9.6.2 किसी तार के द्रव्य के यंग गुणांक का मापन
तनाव के अंतर्गत किसी तार के द्रव्य के यंग गुणांक का मापन करने के लिए एक प्रारूपिक प्रायोगिक व्यवस्था चित्र 9.6 में दिखाई गई है। इसमें दो लंबे सीधे तार, जिनकी लंबाई तथा त्रिज्या बराबर हों, किसी स्थिर दृढ़ आधार से अगल-बगल लटके होते हैं। तार A (संदर्भ तार कहलाता है) में मिलीमीटर की एक मुख्य स्केल M तथा एक भार रखने के लिए एक पलड़ा लगा होता है। तार B (प्रायोगिक तार कहलाता है) समान अनुप्रस्थ परिच्छेद का होता है और इसमें भी एक पलड़ा लगा होता है जिसमें ज्ञात भारों को रखा जा सकता है। प्रायोगिक तार B की तली पर एक संकेतक में एक वर्नियर स्केल V जोड़ दिया जाता है तथा मुख्य स्केल M संदर्भ तार A से जोड़ा जाता है। पलड़े में रखे भार नीचे की ओर एक बल लगाते हैं और प्रायोगिक तार को तनक प्रतिबल के अंतर्गत विस्तारित कर देते हैं। तार में विस्तार (लंबाई में वृद्धि) को वर्नियर व्यवस्था से नाप लिया जाता है। कमरे के ताप में अंतर के कारण होने वाली लंबाई में किसी परिवर्तन की प्रतिपूर्ति करने के लिए संदर्भ तार का इस्तेमाल किया जाता है क्योंकि प्रायोगिक तार की लंबाई में ताप के कारण किसी परिवर्तन के साथ-साथ संदर्भ तार की लंबाई में भी उतना ही परिवर्तन होगा। (ताप के इन प्रभावों को हम अध्याय 11 में विस्तार से पढ़ेंगे)।
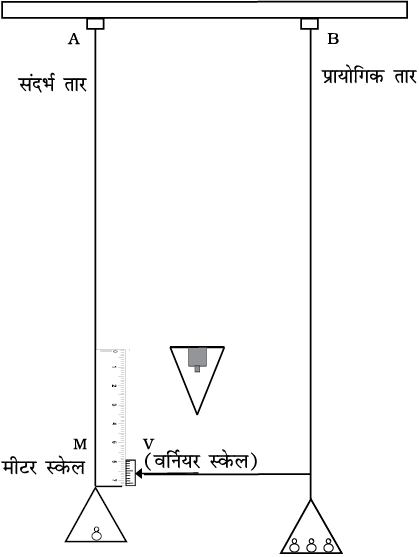
चित्र 9.6 किसी तार के द्रव्य के यंग गुणांक के मापन के लिए एक व्यवस्था।
आरंभ में संदर्भ तथा प्रायोगिक, दोनों तारों पर एक छोटा-सा भार रख देते हैं ताकि तार सीधे रहें और फिर वर्नियर का पाठ्यांक नोट कर लेते हैं। अब प्रायोगिक तार को तनक प्रतिबल के अंतर्गत लाने के लिए उस पर धीरे-धीरे और भार चढ़ाते जाते हैं तथा वर्नियर का पाठ्यांक नोट करते जाते हैं। दो वर्नियर पाठ्यांकों में अंतर तार में उत्पन्न विस्तार बताता है। मान लें कि प्रायोगिक तार की प्रारंभिक त्रिज्या तथा लंबाई क्रमश: r तथा L है तो तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल πr2 होगा। मान लें कि द्रव्यमान M से तार में उत्पन्न विस्तार ∆L है। इस प्रकार, प्रत्यारोपित बल Mg के बराबर हुआ, जहाँ g गुरुत्वीय त्वरण है। समीकरण (9.8) से प्रायोगिक तार के द्रव्य का यंग गुणांक होगा
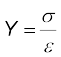 =
= 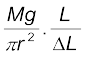
= Mg × L/(πr2 × ∆L) (9.9)
9.6.3 अपरूपण गुणांक
अपरूपण प्रतिबल तथा संगत अपरूपण विकृति का अनुपात द्रव्य का अपरूपण गुणांक कहलाता है तथा इसे G से निरूपित करते हैं। इसे दृढ़ता गुणांक भी कहते हैं:
G = अपरूपण प्रतिबल (σs)/अपरूपण विकृति
G = (F/A)/(∆x/L)
= (F × L)/(A × ∆x) (9.10)
इसी प्रकार समीकरण (9.4) से
G = (F/A)/θ
= F/(A × θ) (9.11)
अपरूपण प्रतिबल σs को एेसे भी व्यक्त किया जा सकता है
σs = G × θ (9.12)
अपरूपण गुणांक की SI इकाई N m–2 या Pa होती है। सारणी 9.2 में कुछ साधारण द्रव्यों के अपरूपण गुणांक दिए गए हैं। यह देखा जा सकता है कि अपरूपण गुणांक (या दृढ़ता गुणांक) आमतौर पर यंग गुणांक (सारणी 9.1) से कम होता है। अधिकतर द्रव्यों के लिए G ≈ Y/3 ।
सारणी 9.2 कुछ सामान्य द्रव्यों के अपरूपण गुणांक (G)
| द्रव्य | G (109 Nm–2 या GPa) |
| एेलुमिनियम पीतल ताँबा काँच लोहा सीसा निकिल इस्पात टंगस्टन लकड़ी | 25 36 42 23 70 5.6 77 84 150 10 |
उदाहरण 9.4 सीसे के 50 cm भुजा के एक वर्गाकार स्लैब, जिसकी मोटाई 10 cm है, की पतली फलक पर 9.0 × 104 N का एक अपरूपक बल लगा है। दूसरा पतला फलक फर्श से रिवेट किया हुआ है। ऊपरी फलक कितनी विस्थापित हो जाएगी?
हल सीसे का स्लैब स्थिर है तथा बल को पतली फलक के समांतर लगाया गया है, जैसा चित्र 9.7 में दिखाया गया है। इस फलक का क्षेत्रफल है
A = 50 cm × 10 cm
= 0.5 m × 0.1 m
= 0.05 m2
इसलिए
प्रतिबल = (9.4 × 104 N/0.05 m2)
= 1.80 × 106 N m–2
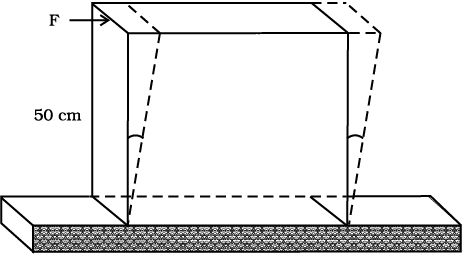
चित्र 9.7
हम जानते हैं कि अपरूपण विकृति = (∆x/L)= प्रतिबल /G
इसलिए, विस्थापन ∆x = (प्रतिबल × L)/G
= (1.8 × 106 N m–2 × 0.5 m)/(5.6 ×109 N m–2)
= 1.6 × 10–4 m = 0.16 mm t
9.6.4 आयतन गुणांक
पहले के खंड (9.3) में हम यह देख चुके हैं कि जब किसी पिण्ड को अधिक दाब के एक द्रव में डुबोया जाता है [चित्र 9.2(d)] तो वह जलीय प्रतिबल (जलीय दाब के मान के बराबर) के अंतर्गत चला जाता है। यह पिण्ड के आयतन में कमी उत्पन्न करता है, इस प्रकार एक विकृति, जिसे आयतन विकृति कहते हैं, उत्पन्न होती है (समीकरण 9.5)। जलीय प्रतिबल तथा संगत आयतन विकृति के अनुपात को आयतन गुणांक कहते हैं। यह प्रतीक B से निरूपित किया जाता है:
B = – p/(∆V/V) (9.13)
ऋण चिह्न इस तथ्य की ओर संकेत करता है कि दाब में वृद्धि करने पर आयतन में कमी होती है। अर्थात्, यदि p धनात्मक है तो ∆V ऋणात्मक होगा। इस प्रकार साम्यावस्था में किसी निकाय के लिए आयतन गुणांक B का मान सदा धनात्मक होगा। आयतन गुणांक की SI इकाई वही होती है जो दाब की, अर्थात्, N m–2 या Pa। कुछ सामान्य द्रव्यों के आयतन गुणांक सारणी 9.3 में दिए गए हैं।
सारणी 9.3 कुछ सामान्य द्रव्यों के आयतन गुणांक (B)
| द्रव्य | B (109 N m–2 या GPa) |
| ठोस | |
| एेलुमिनियम | 72 |
| पीतल | 61 |
| ताँबा | 140 |
| काँच | 37 |
| लोहा | 100 |
| निकिल | 260 |
| इस्पात | 160 |
| द्रव | |
| 22 | |
| इथेनाल | 0.9 |
| कार्बन डाइसल्फाइड | 1.56 |
| ग्लिसरीन | 4.76 |
| पारा | 25 |
| गैस | |
| वायु मानक (मानक ताप एवं दाब पर) | 1.0 × 10–4 |
आयतन गुणांक के व्युत्क्रम को संपीड्यता कहते हैं तथा इसे k से निरूपित करते हैं। दाब में एकांक वृद्धि पर आयतन में भिन्नात्मक अंतर से इसे परिभाषित करते हैं:
k = (1/B) = – (1/∆p) × (∆V/V) (9.14)
सारणी 9.3 मेें दिए गए आँकड़ों से यह देख सकते हैं कि ठोसों के आयतन गुणांक द्रवों से कहीं अधिक हैं और द्रवों के लिए इसका मान गैसों (वायु) की तुलना में कहीं अधिक है। इस प्रकार ठोस पदार्थ सबसे कम संपीड्य होते हैं जबकि गैसें सबसे अधिक संपीड्य होती हैं। गैसें ठोसों की अपेक्षा लगभग दस लाख गुनी अधिक संपीड्य होती हैं। गैसों की संपीड्यता
अधिक होती है जो ताप तथा दाब के साथ बदलती है। ठोसों की असंपीड्यता मुख्यतया आस-पास के परमाणुओं के बीच दृढ़ युग्मन के कारण होती है। द्रवों के अणु भी अपने पास के अणुओं से बँधे होते हैं लेकिन उतने मजबूती से नहीं जितने ठोसों में। गैसों के अणु अपने पास के अणुओं से बहुत हलके से युग्मित होते हैं।
सारणी 9.4 में विभिन्न प्रकार के प्रतिबल, विकृति, प्रत्यास्थ गुणांक तथा द्रव्यों की वह अवस्था जिसमें यह लागू होते हों, को एक दृष्टि में दिखाया गया है।
उदाहरण 9.5 हिन्द महासागर की औसत गहराई लगभग 3000 m है। महासागर की तली में पानी के भिन्नात्मक संपीडन ∆V/V की गणना कीजिए, दिया है कि पानी का आयतन गुणांक 2.2 × 109 N m–2 है
(g = 10 m s–2 लीजिए)।
हल तली की परत पर पानी के 3000 m ऊँचे स्तंभ द्वारा लगने वाला दाब
p = hρ g = 3000 m × 1000 kg m–3 × 10 m s–2
= 3 × 107 kg m–1 s-2 = 3 × 107 N m–2
भिन्नात्मक संपीडन ∆V/V होगा
∆V/V = प्रतिबल/B
= (3 × 107 N m-2)/(2.2 × 109 N m–2)
= 1.36 × 10-2 या 1.36 % t
9.6.5 प्वासो अनुपात
अनुभााग 9.6.2 में वर्णित यंग गुणाांक प्रयोग में सावधानीपूर्वक किए गए परीक्षाण्ाों से ज्ञात होता है कि तनाव के अन्तर्गत किसी तार के अनुप्रस्था परिच्छेद (अथावा उसके व्यास) में कुछ कमी होती है। प्रयुक्त बल के लम्बवत दिश्ाा में होने वाली विकृति को पश्चिवर्क विकृति कहते हैं। सिमोन प्वासों ने यह निर्धारित किया थाा कि प्रत्यास्थाता सीमा में पार्श्विक विकृति अनुदैर्घ्य विकृति के समानुपाती होती है। किसी तानित तार में पार्श्विक विकृति तथा अनुदैर्घ्य विकृति का अनुपात प्वासों अनुपात कहलाता है। यदि किसी तार का मwy व्यास d तथा पzयुक्त पzतिबy की दशा में व्यास में संकुचu ∆d है, तो पार्श्विक विकृति ∆d/d होगी। यदि इस तार की मूल लंबाई L तथा प्रयुक्त प्रतिबल की स्थिति में लंबाई में वृद्धि ∆L है, तो अनुदैर्घ्य विकृति ∆L/L है। अत: प्वासों अनुपात (∆d/d)/(∆L/L) अथवा (∆d/∆L) × (L/d) होगा। प्वासों अनुपात दो विकृतियों का अनुपात है। अत: यह एक संख्या है तथा इसकी कोई विमा अथवा मात्रक नहीं होता। इसका मान पदार्थ की प्रकृति पर ही निर्भर करता है। स्टील के लिए इस अनुपात का मान 0.28 तथा 0.30 के मध्य होता है। एल्युमीनियम की मिश्रधातुओं के लिए इसका मान लगभग 0.33 होता है।
9.6.6 तानित तार में प्रत्यास्थ स्थैतिक ऊर्जा
जब किसी तार पर तनन प्रतिबल आक्षेपित किया जाता है, ताे अंत:परमाण्विक बलाें के विरुद्ध कार्य किया जाता है। यह कार्य तार में प्रत्यास्थ स्थैतिक ऊर्जा के रूप में संग्रहित हाे जाता है। काेई L मूल लंबाई तथा A अनुप्रस्थ परिच्छेद क्षेत्रफल के एक तार की लंबाई के परित: किसी विकृतकारी बल F लगाने पर माना कि लंबाई में l वृद्धि हाे जाती है, तब समीकरण (9.8) से हमें F = YA × (l/L) प्राप्त हाेता है। यहाँ Y तार के पदार्थ का यंग गुणांक है। अब इस तार की लंबाई में अत्यन्त सूक्ष्म dl मात्रा से पुन: वृद्धि कराने के लिए प्रयुक्त कार्य dW का मान F × dl अथवा YAldl/L हाेगा। अत: किसी तार को उसकी मूल लंबाई L से L + l तक अर्थात् l = 0 से l = l तक बढ़ाने में किया गया कार्य (W) –
W = 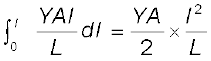
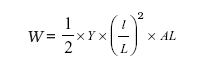
= 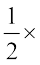 यंग गुणांक × विकृति × तार का अायतन
यंग गुणांक × विकृति × तार का अायतन
= 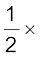 प्रतिबल × विकृति × तार का अायतन
प्रतिबल × विकृति × तार का अायतन
यह कार्य तार में प्रत्यास्थ स्थैतिक ऊजाρ (U) वेη रूप में संग्रहित हो जाती है। अत: तार में पदार्थ की प्रति एकांक आयतन प्रत्यास्थ स्थैतिक ऊर्जा (u) निम्न है –
u = 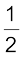 ×
×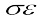 (19.15)
(19.15)
9.7 द्रव्यों के प्रत्यास्थ व्यवहार के अनुप्रयोग
दैनिक जीवन में द्रव्यों के प्रत्यास्थ व्यवहार की अहम भूमिका होती है। सभी अभियांत्रिकी डिज़ाइनों में द्रव्यों के प्रत्यास्थ व्यवहार के परिशुद्ध ज्ञान की आवश्यकता होती है। उदाहरण के लिए किसी भवन की डिज़ाइन करते समय स्तंभों, दंडों तथा आधारों की संरचनात्मक डिज़ाइन के लिए उपयुक्त द्रव्यों की प्रबलता का ज्ञान आवश्यक है। क्या आपने कभी इस पर विचार किया है कि पुलों की संरचना में आधार के रूप में प्रयुक्त दंडों का अनुप्रस्थ परिच्छेद I की तरह का क्यों होता है? बालू का एक ढेर या एक पहाड़ी पिरैमिड की आकृति का क्यों होता है? इन प्रश्नों के उत्तर संरचनात्मक अभियांत्रिकी के अध्ययन से पाए जा सकते हैं।
भारी भारों को उठाने तथा एक स्थान से दूसरे स्थान तक ले जाने के लिए प्रयुक्त क्रेनों में धातु का एक मोटा रस्सा होता है जिससे भार को जोड़ दिया जाता है। रस्से को मोटरों तथा घिरनियों की मदद से खींचा जाता है। मान लें कि हमें एक एेसा क्रेन बनाना है जिसको उठा सकने की सामर्थ्य 10 मीट्रिक टन (1metric ton = 1000 kg) हो। इस्पात का रस्सा कितना मोटा होना चाहिए? स्पष्टतया, हम यह चाहते हैं कि भार रस्से को स्थायी रूप से विरूपित न कर दे। इसलिए विस्तार प्रत्यास्थ सीमा से अधिक नहीं होना चाहिए। सारणी 9.1 से हमें पता चलता है कि मृदु इस्पात का पराभव सामर्थ्य (σy) लगभग 300 × 106 N m-2 है। इस प्रकार रस्से के अनुप्रस्थ परिच्छेद का क्षेत्रफल का न्यूनतम मान है:
A ≥ W/σy = Mg/σy (9.16)
= (104 kg × 10 m s-2)/(300 × 106 N m-2)
= 3.3 × 10-4 m2
जो वृत्ताकार परिच्छेद के रस्से के लिए लगभग 1 cm त्रिज्या के संगत बनता है। साधारणतया, सुरक्षा के लिए भार में एक बड़ा मार्जिन (लगभग दस के गुणक का) दिया जाता है। इस तरह लगभग 3 cm त्रिज्या का एक मोटा रस्सा संस्तुत किया जाता है। इस त्रिज्या का एकल तार व्यावहारिक रूप से एक दृढ़ छड़ हो जाएगा। इसलिए व्यापारिक निर्माण में लचक तथा प्रबलता के लिए एेसे रस्सों को हमेशा वेणी की तरह बहुत से पतले तारों को गुम्फित करके आसानी से बनाया जाता है।
सारणी 9.4 प्रतिबल, विकृति तथा विभिन्न प्रत्यास्थ गुणांक
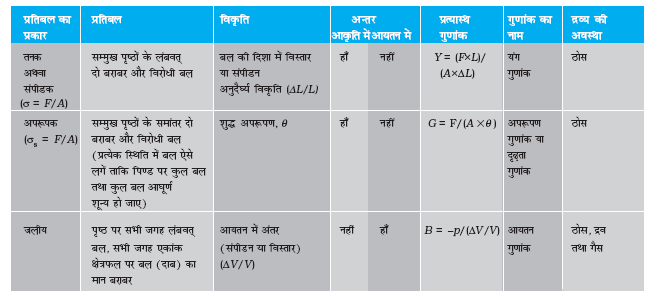
किसी पुल को इस प्रकार डिज़ाइन करना होता है जिससे यह चलते हुए यातायात के भार को, पवन बल को तथा अपने भार को वहन कर सके। इसी प्रकार, भवनों की डिज़ाइन में दण्डों एवं स्तंभों का उपयोग बहुत प्रचलित है। दोनों ही स्थितियों में, भार के अंतर्गत दण्ड के बंकन की समस्या से छुटकारा पाना बहुत ही महत्वपूर्ण होता है। दण्ड को अत्यधिक बंकित होना या टूटना नहीं चाहिए। हम किसी एेसे दण्ड के बारे में विचार करें जो सिरों के पास आधारित हो तथा जिसके मध्य बिंदु पर भार लगा हो, जैसा चित्र 9.8 में दिखाया गया है। लंबाई l, चौड़ाई b तथा मोटाई d की एक पट्टी के मध्य बिंदु पर भार W का भार लगाने से इसमें एक झोल आएगा जिसकी मात्रा होगी
δ = W l3/(4bd3Y) (9.17)
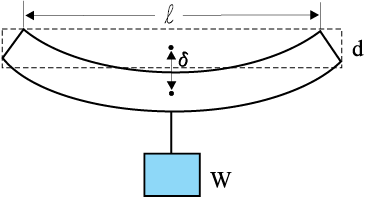
चित्र 9.8 सिरों पर आधारित तथा केन्द्र पर भारित एक दण्ड।
थोड़ा सा कैलकुलस और जितना आप पहले ही पढ़ चुके हैं, उसका उपयोग करके इस संबंध का निगमन किया जा सकता है। समीकरण (9.16) से हम देखते हैं कि किसी दिये हुए भार के लिए बंकन कम करने के लिए एेसे द्रव्य का उपयोग करना चाहिए जिसका यंग गुणांक Y अधिक हो। किसी दिये हुए द्रव्य के लिए बंकन कम करने के लिए चौड़ाई b की बजाय मोटाई d को बढ़ाना अधिक प्रभावी होता है क्योंकि δ , d -3 लेकिन b-1 के अनुक्रमानुपाती होता है (यद्यपि दण्ड की लंबाई यथासम्भव कम होनी ही चाहिए)। लेकिन जब तक एेसा न हो कि भार बिलकुल ठीक स्थान पर लगा हो (पर चलते हुए यातायात वाले पुल पर एेसा व्यवस्थित करना कठिन है), मोटाई बढ़ाने पर पट्टी एेसे बंकित हो सकती है जैसा चित्र 9.9(b) में दिखाया गया है। इसे आकुंचन कहते हैं। इससे बचने के लिए साधारणतया चित्र 9.9(c) में दिखाई गई आकृति का अनुप्रस्थ परिच्छेद लिया जाता है। एेसे परिच्छेद से भार वहन करने के लिए बड़ा पृष्ठ तथा बंकन रोकने के लिए पर्याप्त मोटाई मिलती है। इस प्रकार की आकृति से प्रबलता को न्योछावर किये बिना ही दण्ड के भार को कम किया जा सकता है, अत: लागत भी कम हो जाती है।
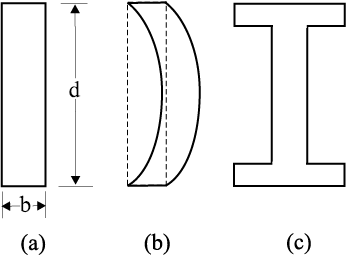
चित्र 9.9 किसी दण्ड की विभिन्न अनुप्रस्थ परिच्छेद आकृतियाँ (a) एक पट्टी का आयताकार परिच्छेद, (b) एक पतली पट्टी और कैसे आकुंचित हो सकती है, (c) भार वहन करने वाली पट्टी के लिए साधारणतया प्रयुक्त परिच्छेद।
भवनों तथा पुलों में खम्भों या स्तम्भों का उपयोग भी बहुत प्रचलित है। गोल सिरों वाले खम्भे जैसा चित्र 9.10(a) में दिखाये गये हैं, फैलावदार आकृति चित्र 9.10(b) वाले खम्भों की अपेक्षा कम भार वहन कर सकते हैं। किसी पुल या भवन की परिशुद्ध डिज़ाइन करते समय उन बातों का ध्यान रखना पड़ता है कि वह किन परिस्थितियों में काम करता है, लागत क्या होगी और संभावित द्रव्यों आदि की दीर्घकालीन विश्वसनीयता आदि क्या है?
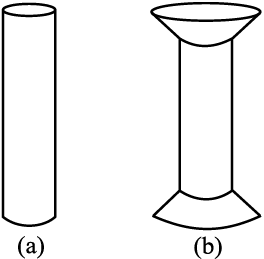
चित्र 9.10 खम्भे या स्तम्भ: (a) गोलीय सिरों का खम्भा,
(b) फैलावदार सिरों का खम्भा।
पृथ्वी पर किसी पर्वत की अधिकतम ऊँचाई लगभग 10 km होती है, इस प्रश्न का उत्तर भी चट्टानों के प्रत्यास्थ गुणों पर विचार करने से मिल सकता है। एक पर्वत का आधार समान संपीडन के अन्तर्गत नहीं होता है, यह चट्टानों को कुछ अपरूपक प्रतिबल प्रदान करता है जिसके अन्तर्गत वे प्रवाहित (खिसक) हो सकती हैं। ऊपर के सारे द्रव्य के कारण प्रतिबल उस क्रान्तिक अपरूपक प्रतिबल से कम होना चाहिए जिस पर चट्टानें प्रवाहित हों (खिसकें)।
hρg = 30 × 107 N m–2
या, h = 30 × 107 N m–2/(3 × 103 kg m–3 × 10 m s–2)
~ 10 km
जो माउन्ट एवरेस्ट की ऊँचाई से ज़्यादा है।
सारांश
1. एकांक क्षेत्रफल पर प्रत्यानयन बल प्रतिबल होता है तथा विमा में भिन्नात्मक अन्तर विकृति होता है। आम तौर पर तीन प्रकार के प्रतिबल होते हैं (a) तनक प्रतिबल--अनुदैर्घ्य प्रतिबल (तनन से संबद्ध) या संपीडक प्रतिबल (संपीडन से संबद्ध), (b) अपरूपक प्रतिबल, तथा (c) जलीय प्रतिबल।
2. कम विरूपण के लिए अधिकतर पदार्थों में प्रतिबल विकृति के अनुक्रमानुपाती होता है। इसे हुक का नियम कहते हैं। अनुक्रमानुपातिकता का स्थिरांक प्रत्यास्थता गुणांक कहलाता है। विरूपण बलों के लगने पर पिण्डों की प्रतिक्रिया और प्रत्यास्थ व्यवहार का वर्णन करने के लिए तीन प्रत्यास्थता गुणांकों - यंग गुणांक, अपरूपण गुणांक तथा आयतन गुणांक का उपयोग किया जाता है।
ठोसों का एक वर्ग, जो प्रत्यास्थलक कहलाता है, हुक के नियम का पालन नहीं करता है।
3. जब कोई पिण्ड तनाव या संपीडन के अंतर्गत होता है तो हुक के नियम का रूप होता है
F/A = Y∆L/L,
जहाँ ∆L/L पिण्ड की तनन या संपीडन विकृति है, F विकृति उत्पन्न करने वाले प्रत्यारोपित बल का मान है, A अनुप्रस्थ परिच्छेद का वह वह क्षेत्रफल है जिस पर F प्रत्यारोपित होता है (A के लंबवत) और Y पिण्ड के द्रव्य का यंग गुणांक है। प्रतिबल F/A है।
4. जब दो बल ऊपरी और निचली फलकों के समान्तर लगाये जाते हैं तो ठोस पिण्ड इस प्रकार विरूपित होता है कि ऊपरी फलक निचली फलक के सापेक्ष बगल की ओर विस्थापित होती है। ऊपरी फलक का क्षैतिज विस्थापन ∆L ऊर्ध्वाधर ऊँचाई L के लंबवत होता है। इस प्रकार का विरूपण अपरूपण कहलाता है और संगत प्रतिबल अपरूपण प्रतिबल होता है। इस प्रकार का प्रतिबल केवल ठोसों में ही संभव है।
इस प्रकार के विरूपण के लिए हुक के नियम का रूप हो जाता है
F/A = G × ∆L/L
जहाँ ∆L पिण्ड के एक सिरे का प्रत्यारोपित बल F की दिशा में विस्थापित है और G अपरूपण गुणांक है।
5. जब कोई पिण्ड परिवर्ती द्रव द्वारा लगाये गये प्रतिबल के कारण जलीय संपीडन में जाता है तो हुक के नियम का रूप निम्न हो जाता है
p = B (∆V/V),
जहाँ p पिण्ड पर द्रव के कारण दाब (जलीय प्रतिबल) है, ∆V/V (आयतन विकृति) उस दाब के कारण पिण्ड के आयतन में भिन्नात्मक अन्तर और B पिण्ड का आयतन गुणांक होता है।
विचारणीय विषय
1. किसी तार को एक छत से लटकाया गया है तथा उसे दूसरे सिरे पर भार (F) लगाकर तनित किया गया है। छत द्वारा इस तार पर आरोपित बल भार के बराबर और विपरीत होता है। परन्तु तार के किसी परिच्छेद A पर तनाव F होता है ना कि 2F । अत: तनन प्रतिबल, जो प्रति इकाई क्षेत्रफल पर तनाव है, F/A होता है।
2. हुक का नियम प्रतिबल-विकृति वक्र के केवल रैखिक भाग में ही वैध है।
3. यंग प्रत्यास्थता गुणांक तथा अपरूपण गुणांक केवल ठोसों के लिए ही प्रासंगिक होते हैं, इसका कारण यह है कि केवल ठोसों की ही लंबाई तथा आकृति होती है ।
4. आयतन प्रत्यास्थता गुणांक ठोसों, द्रवों तथा गैसों सभी के लिए प्रासंगिक होता है। यह उस स्थिति में आयतन में परिवर्तन से संबंधित है जब पिण्ड का प्रत्येक भाग समान प्रतिबल के अंतर्गत होता है ताकि पिण्ड की आकृति ज्यों की त्यों बनी रहे।
5. धातुओं के लिए यंग गुणांक का मान मिश्र धातुओं और प्रत्यास्थलकों की अपेक्षा अधिक होता है। यंग गुणांक के अधिक मान वाले द्रव्यों में लंबाई में थोड़ा परिवर्तन करने के लिए अधिक बल की आवश्यकता होती है।
6. दैनिक जीवन में हमारी यह धारणा होती है कि जो द्रव्य अधिक तनित होते हैं, वे अधिक प्रत्यास्थ होते हैं, लेकिन यह मिथ्या है। वास्तव में वे द्रव्य जो दिए हुए भार के लिए कम तनित होते हैं, अधिक प्रत्यास्थ समझे जाते हैं।
7. व्यापक रूप में, किसी एक दिशा में आरोपित विरूपक बल अन्य दिशाओं में भी विकृति उत्पन्न कर सकता है। एेसी परिस्थितियों में प्रतिबल एवं विकृति के बीच आनुपातिकता का वर्णन केवल एक प्रत्यास्थता नियतांक द्वारा नहीं किया जा सकता। उदाहरण के लिए, अनुदैर्घ्य विकृति के अंतर्गत, अनुप्रस्थ विमा (परिच्छेद की त्रिज्या) में भी थोड़ा अंतर हो जाएगा जिसका वर्णन द्रव्य के दूसरे प्रत्यास्थता नियतांक से करते हैं (जिसे प्वायसां अनुपात कहते हैं)।
8. प्रतिबल एक सदिश राशि नहीं है क्योंकि बल की तरह प्रतिबल किसी विशेष दिशा से निर्धारित नहीं किया जा सकता। किसी पिण्ड के एक भाग पर किसी काट की निश्चित ओर कार्यरत बल की एक निश्चित दिशा
होती है।
अभ्यास
9.1 4.7 m लंबे व 3.0 × 10–5 m2 अनुप्रस्थ काट के स्टील के तार तथा 3.5 m लंबे व 4.0 × 10–5 m2 अनुप्रस्थ काट के ताँबे के तार पर दिए गए समान परिमाण के भारों को लटकाने पर उनकी लंबाइयों में समान वृद्धि होती है । स्टील तथा ताँबे के यंग प्रत्यास्थता गुणांकों में क्या अनुपात है?
9.2 नीचे चित्र 9.11 में किसी दिए गए पदार्थ के लिए प्रतिबल-विकृति वक्र दर्शाया गया है। इस पदार्थ के लिए
(a) यंग प्रत्यास्थता गुणांक, तथा (b) सन्निकट पराभव सामर्थ्य क्या है?
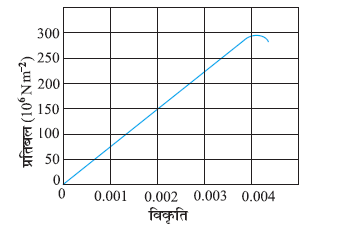
चित्र 9.11
9.3 दो पदार्थों A और B के लिए प्रतिबल-विकृति ग्राफ चित्र 9.12 में दर्शाए गए हैं।
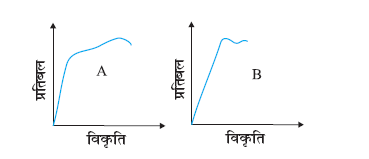
चित्र 9.12
इन ग्राफों को एक ही पैमाना मानकर खींचा गया है।
(a) किसी पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है?
(b) दोनों पदार्थों में कौन अधिक मजबूत है?
9.4 निम्नलिखित दो कथनों को ध्यान से पढ़िये और कारण सहित बताइये कि वे सत्य हैं या असत्य :
(a) इस्पात की अपेक्षा रबड़ का यंग गुणांक अधिक है;
(b) किसी कुण्डली का तनन उसके अपरूपण गुणांक से निर्धारित होता है।
9.5 0.25 cm व्यास के दो तार, जिनमें एक इस्पात का तथा दूसरा पीतल का है, चित्र 9.13 के अनुसार भारित हैं। बिना भार लटकाये इस्पात तथा पीतल के तारों की लंबाइयाँ क्रमश: 1.5 m तथा 1.0 m हैं। यदि इस्पात तथा पीतल के यंग गुणांक क्रमश: 2.0 × 1011 Pa तथा 0.91 × 1011 Pa हों तो इस्पात तथा पीतल के तारों में विस्तार की गणना कीजिए।

चित्र 9.13
9.6 एेलुमिनियम के किसी घन के किनारे 10 cm लंबे हैं। इसकी एक फलक किसी ऊर्ध्वाधर दीवार से कसकर जड़ी हुई है। इस घन के सम्मुख फलक से 100 kg का एक द्रव्यमान जोड़ दिया गया है। एलुमिनियम का अपरूपण गुणांक 25 GPa है। इस फलक का ऊर्ध्वाधर विस्थापन कितना होगा?
9.7 मृदु इस्पात के चार समरूप खोखले बेलनाकार स्तम्भ 50,000 kg द्रव्यमान के किसी बड़े ढाँचे को आधार दिये हुए हैं। प्रत्येक स्तम्भ की भीतरी तथा बाहरी त्रिज्याएँ क्रमश: 30 तथा 60 cm हैं। भार वितरण को एकसमान मानते हुए प्रत्येक स्तम्भ की संपीडन विकृति की गणना कीजिये।
9.8 ताँबे का एक टुकड़ा, जिसका अनुप्रस्थ परिच्छेद 15.2 mm × 19.1 mm का है, 44,500 N बल के तनाव से खींचा जाता है, जिससे केवल प्रत्यास्थ विरूपण उत्पन्न हो। उत्पन्न विकृति की गणना कीजिये।
9.9 1.5 cm त्रिज्या का एक इस्पात का केबिल भार उठाने के लिए इस्तेमाल किया जाता है। यदि इस्पात के लिए अधिकतम अनुज्ञेय प्रतिबल 108 N m–2 है तो उस अधिकतम भार की गणना कीजिए जिसे केबिल उठा सकता है।
9.10 15 kg द्रव्यमान की एक दृढ़ पट्टी को तीन तारों, जिनमें प्रत्येक की लंबाई 2 m है, से सममित लटकाया गया है। सिरों के दोनों तार ताँबे के हैं तथा बीच वाला लोहे का है। तारों के व्यासों के अनुपात निकालिए, प्रत्येक पर तनाव उतना ही रहना चाहिए।
9.11 एक मीटर अतानित लंबाई के इस्पात के तार के एक सिरे से 14.5 kg का द्रव्यमान बाँध कर उसे एक ऊर्ध्वाधर वृत्त में घुमाया जाता है, वृत्त की तली पर उसका कोणीय वेग 2rev/s है। तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.065 cm2 है। तार में विस्तार की गणना कीजिए जब द्रव्यमान अपने पथ के निम्नतम बिंदु पर है।
9.12 नीचे दिये गये आँकड़ों से जल के आयतन प्रत्यास्था गुणांक की गणना कीजिए; प्रारंभिक आयतन = 100.0 L दाब में वृद्धि = 100.0 atm (1 atm = 1.013 × 105 Pa), अंतिम आयतन = 100.5 L । नियत ताप पर जल तथा वायु के आयतन प्रत्यास्थता गुणांकों की तुलना कीजिए। सरल शब्दों में समझाइये कि यह अनुपात इतना अधिक क्यों है।
9.13 जल का घनत्व उस गहराई पर, जहाँ दाब 80.0 atm हो, कितना होगा? दिया गया है कि पृष्ठ पर जल का घनत्व 1.03 × 103 kg m–3, जल की संपीडता 45.8 × 10–11 Pa–1 (1 Pa = 1 N m–2)
9.14 काँच के स्लेब पर 10 atm का जलीय दाब लगाने पर उसके आयतन में भिन्नात्मक अंतर की गणना कीजिए।
9.15 ताँबे के एक ठोस घन का एक किनारा 10 cm का है। इस पर 7.0 × 106 Pa का जलीय दाब लगाने पर इसके आयतन में संकुचन निकालिए।
9.16 एक लीटर जल पर दाब में कितना अंतर किया जाए कि वह 0.10% से संपीडित हो जाए?
अतिरिक्त अभ्यास
9.17 हीरे के एकल क्रिस्टलों से बनी निहाइयों, जिनकी आकृति चित्र 9.14 में दिखाई गयी है, का उपयोग अति उच्च दाब के अंतर्गत द्रव्यों के व्यवहार की जाँच के लिए किया जाता है। निहाई के संकीर्ण सिरों पर सपाट फलकों का व्यास 0.50 mm है। यदि निहाई के चौड़े सिरों पर 50,000 N का बल लगा हो तो उसकी नोंक पर दाब ज्ञात कीजिए।
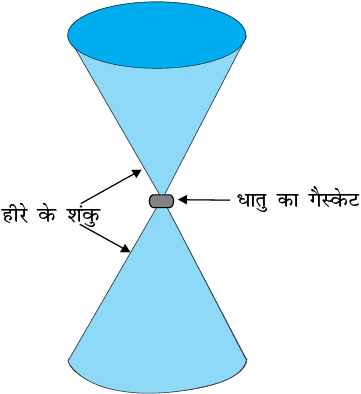
चित्र 9.14
9.18 1.05 m लंबाई तथा नगण्य द्रव्यमान की एक छड़ को बराबर लंबाई के दो तारों, एक इस्पात का (तार A) तथा दूसरा एेलुमिनियम का तार (तार B) द्वारा सिरों से लटका दिया गया है, जैसा कि चित्र 9.15 में दिखाया गया है। A तथा B के तारों के अनुप्रस्थ परिच्छेद के क्षेत्रफल क्रमश: 1.0 mm2 और 2.0 mm2 हैं। छड़ के किसी बिंदु से एक द्रव्यमान m को लटका दिया जाए ताकि इस्पात तथा एेलुमिनियम के तारों में (a) समान प्रतिबल तथा (b) समान विकृति उत्पन्न हो।
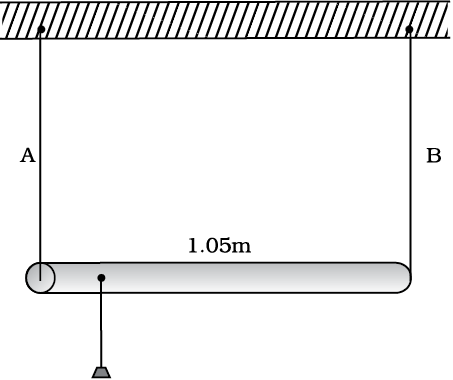
चित्र 9. 15
9.19 मृदु इस्पात के एक तार, जिसकी लंबाई 1.0 m तथा अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.50 × 10-2 cm2 है, को दो खम्बों के बीच क्षैतिज दिशा में प्रत्यास्थ सीमा के अंदर ही तनित किया जाता है। तार के मध्य बिंदु से 100 g का एक द्रव्यमान लटका दिया जाता है। मध्य बिंदु पर अवनमन की गणना कीजिए।
9.21 प्रशांत महासागर में स्थित मैरिना नामक खाई एक स्थान पर पानी की सतह से 11 km नीचे चली जाती है और उस खाई में नीचे तक 0.32 m3 आयतन का इस्पात का एक गोला गिराया जाता है तो गोले के आयतन में परिवर्तन की गणना करें। खाई के तल पर जल का दाब 1.1 × 108 Pa है और इस्पात का आयतन गुणांक 160 GPa है।
