Table of Contents
11.1 भूमिका
11.2 ताप तथा ऊष्मा
11.3 ताप मापन
11.4 आदर्श गैस समीकरण तथा परम ताप
11.5 तापीय प्रसार
11.6 विशिष्ट ऊष्मा धारिता
11.7 ऊष्मामिति
11.8 अवस्था परिवर्तन
11.9 ऊष्मा स्थानांतरण
11.10 न्यूटन का शीतलन नियम
सारांश
विचारणीय विषय
अभ्यास
11.1 भूमिका
हम सभी में ताप तथा ऊष्मा की सहज बोध धारणा होती है। ताप किसी वस्तु की तप्तता (ऊष्णता) की माप होती है। उबलते जल से भरी केतली बर्फ से भरे बॉक्स से अधिक तप्त होती है। भौतिकी में हमें ऊष्मा, ताप, आदि धारणाओं को अधिक सावधानीपूर्वक परिभाषित करने की आवश्यकता होती है। इस अध्याय में आप यह जानेंगे कि ऊष्मा क्या है और इसे कैसे मापते हैं, तथा एक वस्तु से दूसरी वस्तु में ऊष्मा प्रवाह की विभिन्न प्रक्रियाओं का अध्ययन करेंगे। अध्ययन करते आप यह भी ज्ञात करेंगे कि किसी घोड़ागाड़ी के लकड़ी के पहिए की नेमि पर लोहे की रिंग चढ़ाने से पहले लोहार इसे तप्त क्यों करते हैं, तथा सूर्य छिपने के पश्चात् समुद्र तटों पर पवन प्रायः अपनी दिशा उत्क्रमित क्यों कर लेती हैं? आप यह भी जानेंगे कि क्या होता है जब जल उबलता अथवा जमता है तथा इन प्रक्रियाओं की अवधि में इसके ताप में परिवर्तन नहीं होता, यद्यपि काफी मात्रा में ऊष्मा इनके भीतर/इनसे बाहर प्रवाहित होती है।
11.2 ताप तथा ऊष्मा
हम द्रव्य के तापीय गुणों के अध्ययन का आरंभ ताप तथा ऊष्मा की परिभाषा से कर सकते हैं। ताप तप्तता अथवा शीतलता की आपेक्षिक माप अथवा सूचन होता है। किसी तप्त बर्तन के ताप को उच्च ताप तथा बर्फ के घन के ताप को निम्न ताप कहते हैं। एक पिण्ड जिसका ताप दूसरे पिण्ड की अपेक्षा अधिक है, अपेक्षाकृत अधिक तप्त कहा जाता है। ध्यान दीजिए, कि लंबे और ठिगने की भांति तप्त तथा शीत भी आपेक्षिक पद हैं। हम स्पर्श द्वारा ताप का अनुभव कर सकते हैं। परन्तु यह ताप बोध कुछ-कुछ अविश्वसनीय होता है तथा इसका परिसर इतना सीमित है कि किसी वैज्ञानिक कार्यों के लिए इसका कोई उपयोग नहीं किया जा सकता।
अपने अनुभवों से हम यह जानते हैं कि किसी तप्त गर्मी के दिन एक मेज पर रखा बर्फ के शीतल जल से भरा गिलास अंततोगत्वा गर्म हो जाता है जबकि तप्त चाय से भरा प्याला उसी मेज पर ठंडा हो जाता है। इसका अर्थ यह हुआ कि जब भी किसी वस्तु (निकाय), इस प्रकरण में बर्फ का शीतल जल अथवा गर्म चाय, तथा उसके परिवेशी माध्यम के तापों में अंतर होगा तो वस्तु तथा उसके परिवेशी माध्यम के बीच उस समय तक ऊष्मा स्थानांतरण होता है जब तक वस्तु तथा इसका परिवेशी माध्यम समान ताप पर नहीं आ जाते। हम यह भी जानते हैं कि गिलास में भरे शीतल जल के प्रकरण में ऊष्मा पर्यावरण से गिलास में प्रवाहित होती है, जबकि गर्म चाय के प्रकरण में ऊष्मा गर्म चाय के प्याले से पर्यावरण में प्रवाहित होती है। अतः हम यह कह सकते हैं कि ऊष्मा ऊर्जा का एक रूप है जिसका स्थानांतरण दो (अथवा अधिक) निकायों के बीच अथवा किसी निकाय तथा उसके परिवेश के बीच ताप में अंतर के कारण होता है। स्थानांतरित ऊष्मा ऊर्जा के SI मात्रक को जूल (J) में व्यक्त किया जाता है जबकि ताप का SI मात्रक केल्विन (K) है तथा °C सामान्य उपयोग में आने वाला ताप का मात्रक है। जब किसी वस्तु को गर्म करते हैं तो उसमें बहुत से परिवर्तन हो सकते हैं। इसके ताप में वृद्धि हो सकती है, इसमें प्रसार हो सकता है अथवा अवस्था परिवर्तन हो सकता है। अनुवर्ती अनुभागों में हम विभिन्न वस्तुओं पर ऊष्मा के प्रभाव का अध्ययन करेंगे।
11.3 ताप मापन
तापमापी (थर्मामीटर) का उपयोग करके ताप की एक माप प्राप्त होती है। पदार्थों के बहुत से भौतिक गुणों में ताप के साथ पर्याप्त परिवर्तन होते हैं। एेसे कुछ गुणों को तापमापी की रचना का आधार मानकर उपयोग किया जाता है। सामान्य उपयोग में आने वाला गुण "ताप के साथ किसी द्रव के आयतन में परिवर्तन" होता है। उदाहरण के लिए, सामान्य काँच-में-द्रव प्रकार के तापमापियों में पारा, एेल्कोहॉल आदि का उपयोग किया जाता है, जिनका एक बड़े परिसर में आयतन तापीय प्रसार रेखीय होता है। जिससे आप परिचित हैं। पारा तथा एल्कोहॉल एेसे द्रव हैं जिनका उपयोग अधिकांश काँच-में-द्रव तापमापियों में किया जाता है।
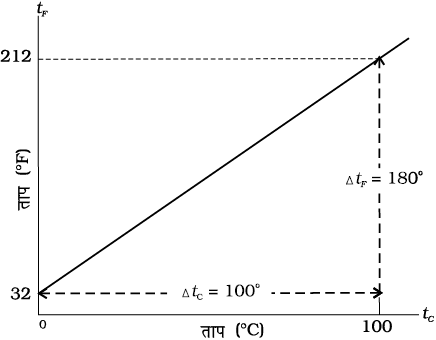
चित्र 11.1 फारेनहाइट ताप (tF) प्रति सेल्सियस ताप (tc ) का आलेखन।
दो मापक्रमों में रूपांतरण के लिए आवश्यक संबंध को फारेनहाइट ताप (tF) तथा सेल्सियस ताप (tC) के बीच ग्राफ से प्राप्त किया जा सकता है। यह एक सरल रेखा (चित्र 11.1) है जिसका समीकरण इस प्रकार है:
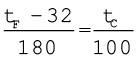 (11.1)
(11.1)
11.4 आदर्श-गैस समीकरण तथा परम ताप
काँच-में-द्रव तापमापी, प्रसार गुणों में अंतर के कारण नियत बिंदुओं से अन्य तापों के भिन्न पाठ्यांक दर्शाते हैं। परन्तु एेसे तापमापी जिनमें गैस का उपयोग होता है, चाहे उनमें किसी भी गैस का उपयोग किया जाए, सदैव एक ही पाठ्यांक प्रदर्शित करते हैं। प्रयोग यह दर्शाते हैं कि सभी गैसें कम घनत्व होने पर समान प्रसार-आचरण दर्शाती हैं। वे चर राशियाँ, जो किसी दी गई मात्रा (द्रव्यमान) की गैस के आचरण की व्याख्या करते हैं, दाब, आयतन तथा ताप (P, V, तथा T) (यहाँ T = t+273.15;t सेल्सियस मापक्रम °C में ताप है)। जब ताप को नियत रखा जाता है, तो किसी गैस की निश्चित मात्रा का दाब तथा आयतन pv = नियतांक के रूप में संबंधित होते हैं। इस संबंध को, एक अंग्रेज रसायनज्ञ रॉबर्ट बॉयल (1627-1691) जिन्होंने इस संबंध की खोज की थी, के नाम पर बॉयल-नियम कहते हैं। जब दाब को नियत रखते हैं, तो किसी निश्चित परिमाण की गैस का आयतन उसके ताप से इस प्रकार संबंधित है:
V/T = नियतांक। यह संबंध फ्रेंच वैज्ञानिक जैक्स चार्ल्स (1747-1823) के नाम पर चार्ल्स के नियम से जाना जाता है। कम घनत्व पर गैसें इन नियमों का पालन करती हैं जिन्हें एकल संबंध में समायोजित किया जा सकता है। ध्यान दीजिये कि चूंकि गैस की दी हुई मात्रा के लिए PV = नियतांक तथा V/T = नियतांक, इसलिए pV/T भी एक नियतांक होना चाहिए। इस संबंध को आदर्श गैस नियम कहते हैं। इसे और अधिक व्यापक रूप में लिखा जा सकता है जिसका अनुप्रयोग केवल किसी एकल गैस की दी गई मात्रा पर ही नहीं होता, वरन् किसी भी कम घनत्व की गैस की किसी मात्रा के लिए किया जा सकता है। इस संबंध को आदर्श गैस समीकरण कहते हैं।
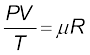
अथवा PV = µRT (11.2)
यहाँ, µ गैस के प्रतिदर्श में मोल की संख्या है तथा R को सार्वत्रिक गैस नियतांक कहते हैं ः
R = 8.31 J mol–1 K–1
समीकरण 11.2 से हमने जाना है कि दाब तथा आयतन (का गुणनफल) ताप के अनुक्रमानुपाती है: PV α T । यह संबंध किसी नियत आयतन गैस तापमापी में ताप मापन के लिए गैस के उपयोग को स्वीकार करते हैं। किसी गैस का आयतन नियत रखने पर, P αT प्राप्त होता है। इस प्रकार, किसी नियत आयतन गैस तापमापी में ताप को दाब के पदों में मापा जाता है।
चित्र 11.2 नियत आयतन पर रखी किसी कम घनत्व की गैस के दाब तथा आयतन के बीच ग्राफ।
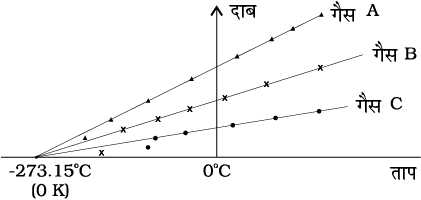
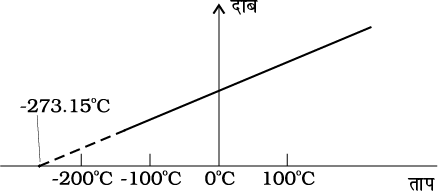
चित्र 11.3 दाब तथा ताप के बीच ग्राफ का आलेखन तथा कम घनत्व की गैसों के लिए रेखाओं का बहिर्वेशन समान परम शून्य ताप को संकेत करता है।
तथापि, निम्न ताप पर वास्तविक गैसों पर ली गई मापों तथा आदर्श गैस नियम द्वारा प्रागुक्त मानों में अंतर पाया गया है। परन्तु एक विस्तृत ताप परिसर में यह संबंध रैखिक है तथा एेसा प्रतीत होता है कि यदि गैस गैसीय अवस्था में ही बनी रहे तो ताप घटाने पर दाब शून्य हो जाएगा। चित्र 11.3 में दर्शाए अनुसार, सरल रेखा को बहिर्वेशित करके किसी आदर्श गैस के लिए परम निम्निष्ठ ताप प्राप्त किया जा सकता है। इस ताप का मान – 273.150C पाया गया तथा इसे परम शून्य कहा जाता है। परम शून्य ब्रिटिश वैज्ञानिक लॉर्ड केल्विन के नाम पर केल्विन ताप मापक्रम अथवा परम ताप मापक्रम का आधार है। इस मापक्रम पर – 273.15°C को शून्य बिंदु के रूप में, अर्थात् 0 K लिया जाता है (चित्र 11.4)।

चित्र 11.4 केल्विन, सेल्सियस तथा फारेनहाइट ताप मापक्रमों में तुलना।
केल्विन तथा सेल्सियस मापक्रमों के लिए मात्रक की आमाप अंश समान होते हैं, अतः इन मापक्रमों के तापों में संबंध इस प्रकार है:
T = tC + 273.15 (11.3)
11.5 तापीय प्रसार
यह हमारा सामान्य अनुभव है कि अधिकांश पदार्थ तप्त होने पर प्रसारित होते हैं तथा शीतलन पर सिकुड़ते हैं। किसी वस्तु के ताप में परिवर्तन होने पर उसकी विमाओं में अंतर हो जाता है। किसी वस्तु के ताप में वृद्धि होने पर उसकी विमाओं में वृद्धि होने को तापीय प्रसार कहते हैं। लंबाई में प्रसार को रैखिक प्रसार कहते हैं। क्षेत्रफल में प्रसार को क्षेत्र प्रसार कहते हैं। आयतन में प्रसार को आयतन प्रसार कहते हैं (चित्र 11.5)।
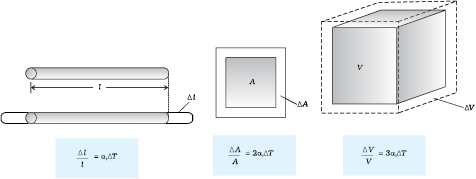
(a) रैखिक प्रसार (b) क्षेत्र प्रसार (c) आयतन प्रसार
चित्र 11.5 तापीय प्रसार।
यदि पदार्थ किसी लंबी छड़ के रूप में है, तो ताप में अल्प परिवर्तन, ∆T, के लिए लंबाई में भिन्नात्मक परिवर्तन, ∆l/l, ∆T के अनुक्रमानुपाती होता है।
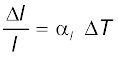 (11.4)
(11.4)
जहाँ αl को रैखिक प्रसार गुणांक (अथवा रैखिक प्रसारता) कहते हैं तथा यह छड़ के पदार्थ का अभिलक्षण होता है। सारणी 11.1 में ताप परिसर 0 °C से 100 °C में कुछ पदार्थों के रैखिक प्रसार गुणांकों के प्रतिरूपी माध्य मान दिए गए हैं। इस सारणी से काँच तथा ताँबे के लिए αl के मानों की तुलना कीजिए। हम यह पाते हैं कि समान ताप वृद्धि के लिए ताँबे में काँच की तुलना में पाँच गुना अधिक प्रसार होता है। सामान्यतः, धातुओं में अधिक प्रसार होता है तथा इनके लिए αl के मान अपेक्षाकृत अधिक होते हैं।
सारणी 11.1 कुछ पदार्थों के लिए रैखिक प्रसार गुणांकों के मान
| पदार्थ | αl (10–5 K–1) |
| एलुमिनियम पीतल लोहा ताँबा चाँदी सोना काँच (पायरेक्स) लैड | 2.5 1.8 1.2 1.7 1.9 1.4 0.32 0.29 |
इसी प्रकार, हम किसी ताप परिवर्तन, ∆T के लिए किसी पदार्थ के भिन्नात्मक आयतन परिवर्तन, पर विचार करते हैं तथा आयतन प्रसार गुणांक (अथवा आयतन प्रसारता), αV को इस प्रकार परिभाषित करते हैं
αV=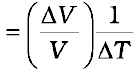 , (11.5)
, (11.5)
यहाँ भी αV पदार्थ का अभिलक्षण है, परन्तु सही अर्थ में यह नियतांक नहीं है। व्यापक रूप में यह ताप पर निर्भर करता है (चित्र 11.6)। यह पाया गया है कि केवल उच्च ताप पर αV नियतांक बन जाता है।
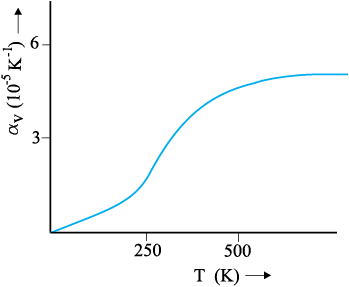
चित्र 11.6 ताप के फलन के रूप में ताँबे का आयतन प्रसार गुणांक।
सारणी 11.2 में 0-100 °C ताप परिसर में कुछ सामान्य पदार्थों के आयतन प्रसार गुणांकों के मान दिए गए हैं। आप यह देख सकते हैं कि इन पदार्थों (ठोस तथा द्रव) के तापीय प्रसार कम हैं, तथा पायरेक्स काँच तथा इनवार (लोहे तथा निकेल की विशिष्ट मिश्र धातु) जैसे पदार्थों के αV के मान विशेषकर निम्न हैं। इस सारणी से हम यह पाते हैं कि एल्कोहॉल (एेथिल) के लिए αv का मान पारे की तुलना में अधिक है, तथा समान ताप वृद्धि के लिए इसमें पारे की तुलना में अधिक वृद्धि होती है।
सारणी 11.2 कुछ पदार्थों के आयतन प्रसार गुणांक के मान
| पदार्थ | αv ( K–1) |
| एलुमिनियम पीतल लोहा पैराफीन काँच (सामान्य) काँच (पायरेक्स) कठोर रबड़ इनवार पारा जल एल्कोहॉल (इथैनॉल) | 7 × 10–5 6 × 10–5 3.55 × 10–5 58.8 × 10–5 2.5 × 10–5 1 × 10–5 2.4 × 10–4 2 × 10–6 18.2 × 10–5 20.7 × 10–5 110×10–5 |
जल असंगत व्यवहार प्रदर्शित करता है; यह 0°C से 4°C के बीच गर्म किए जाने पर सिकुड़ता है। किसी दिए गए परिमाण के जल का आयतन, कक्ष ताप से 4°C तक ठंडा किए जाने पर, घटता है [चित्र 11.7(a)]। 4°C से कम ताप पर आयतन बढ़ता है अतः घनत्व घटता है [चित्र 11.7(b)]।
इसका अर्थ यह हुआ कि जल का घनत्व 4°C पर अधिकतम होता है। जल के इस गुण का एक महत्त्वपूर्ण पर्यावरणीय प्रभाव है: तालाबों तथा झीलों जैसे जलाशयों का शीर्ष भाग पहले जमता है। जैसे-जैसे झील 4°C तक ठंडी होती जाती है, पृष्ठ के समीप का जल अपनी ऊर्जा वातावरण को देता जाता है और संघनित होकर डूबता जाता है। तली का उष्ण, अपेक्षाकृत कम संघनित जल ऊपर उठता है। परन्तु, एक बार शीर्षभाग के ठंडे जल का ताप 4°C से नीचे पहुँच जाता है, यह जल कम संघनित बन जाता है, और पृष्ठ पर ही रहता है, जहाँ यह जम जाता है। यदि जल में यह गुण न होता, तो झील तथा तालाब तली से ऊपर की ओर जमते जिससे उसका अधिकांश जलीय जीवन (जल जीव-जन्तु तथा पौधे) नष्ट हो जाता।

चित्र 11.7 जल का तापीय प्रसार।
सामान्य ताप पर ठोसों तथा द्रवों की अपेक्षा गैसों में अपेक्षाकृत अधिक प्रसार होता है। द्रवों के लिए, आयतन प्रसार गुणांक अपेक्षाकृत ताप पर निर्भर नहीं करता। परन्तु गैसों के लिए यह ताप पर निर्भर करता है। किसी आदर्श गैस के लिए किसी नियत दाब पर आयतन प्रसार गुणांक का मान आदर्श गैस समीकरण से प्राप्त किया जा सकता है:
PV = µRT
नियत ताप पर
P∆V = µR∆T
 (11.6)
(11.6)
0°C, αv = 3.7 × 10–3 K–1, जो ठोसों तथा द्रवों की अपेक्षा अत्यधिक बड़ा है। समीकरण (11.6) αv की ताप पर निर्भरता को दर्शाती है। इसका मान ताप में वृद्धि के साथ कम हो जाता है। नियत दाब तथा कक्ष ताप पर किसी गैस के लिए αv का मान लगभग 3300×10–6K–1 है, जो कि प्रतिरूपी द्रवों के आयतन प्रसार गुणांक की तुलना में कई कोटि गुना बड़ा है।
∆l = αl l ∆T
इसीलिए, ∆V = (l+∆l)3 – l3 3l2 ∆l (11.7)
समीकरण 11.7 में हमने (∆l) को l की तुलना में छोटा होने के कारण (∆l)2 तथा (∆l)3 के पदों को उपेक्षणीय मान लिया है। अतः

इससे हमें प्राप्त होता है
αv = 3αl (11.9)
क्या होता है, जब किसी छड़ के दोनों सिरों को दृढ़ता से जड़कर इसके तापीय प्रसार को रोका जाता है। स्पष्ट है कि सिरों के दृढ़ अवलंबों द्वारा प्रदत्त बाह्य बलों के कारण छड़ में संपीडन विकृति उत्पन्न हो जाती है जिसके तदनुरूपी छड़ में एक प्रतिबल उत्पन्न होता है जिसे तापीय प्रतिबल कहते हैं। उदाहरण के लिए 40 cm2 अनुप्रस्थ काट के क्षेत्रफल की 5m लंबी स्टील की एेसी छड़ के बारे में विचार कीजिए जिसके तापीय प्रसार को रोका जाता है, जबकि उसके ताप में 10°C की वृद्धि की गई है। स्टील का रैखिक प्रसार गुणांक αl(स्टील) = 1.2 × 10–5 K–1 है। अतः यहाँ संपीडन विकृति

यदि बाह्य सिरों पर आबद्ध इस प्रकार की स्टील की दो पटरियों के भीतरी सिरे संपर्क में हैं तो इस परिमाण के बल पटरियों को सरलता से मोड़ सकते हैं।
उदाहरण 11.1यह दर्शाइए कि किसी ठोस की आयताकार शीट का क्षेत्र प्रसार गुणांक, (∆A/A)/∆T, इसके रैखिक प्रसार गुणांक αl का दो गुना होता है।
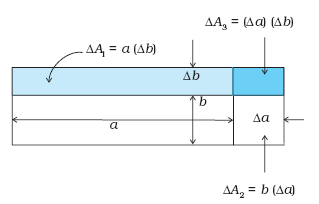
चित्र 11.8
हल किसी ठोस पदार्थ की आयताकार शीट जिसकी लंबाई a तथा चौड़ाई b (चित्र 11.8 ) है, पर विचार कीजिए। जब ताप में ∆T की वृद्धि की जाती है तो a में ∆a = αl a∆T तथा b में ∆b = αlb ∆T की वृद्धि होती है। चित्र 11.8 के अनुसार क्षेत्रफल में वृद्धि
∆A = ∆A1 +∆A2 + ∆A3
∆A = a ∆b + b∆a + (∆a) (∆b)
= aαlb ∆T + bαl a ∆T + (αl)2 ab (∆T)2
= αl ab ∆T (2 + αl ∆T) = αl A ∆T (2 + αl ∆T)
चूंकि αl 10–5 K–1, तब सारणी 11.1 के अनुसार 2 की तुलना में गुणनफल, αl ∆T का मान बहुत छोटा है, अतः इसे उपेक्षणीय माना जा सकता है। अतः
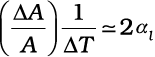
उदाहरण 11.2 कोई लोहार किसी घोड़ागाड़ी के लकड़ी के पहिए की नेमी पर लोहे की रिंग जड़ता है। 27°C पर नेमी तथा लोहे की रिंग के व्यास क्रमशः 5.243m तथा 5.231 m हैं। लोहे की रिंग को किस ताप तक तप्त किया जाए कि वह पहिए की नेमी पर ठीक बैठ जाए।
हल
दिया गया है कि, T1 = 27°C
LT1 = 5.231 m
LT2 = 5.243 m
अतः
LT2 =LT1 [1+αl (T2–T1)]
5.243m = 5.231m [1 + 1.20 × 10–5 K–1 (T2 – 27°C]
अथवा T2 = 218°C t
11.6 विशिष्ट ऊष्मा धारिता
किसी बर्तन में जल लेकर उसे किसी बर्नर पर गर्म करना आरंभ कीजिए। शीघ्र ही आप जल में बुलबुले ऊपर उठते देखेंगे। जैसे ही ताप में वृद्धि की जाती है, तो जल के कणों की गति में विक्षोभ होने तक वृद्धि होती जाती है और जल उबलने लगता है। वे कौन से कारक हैं जिन पर किसी पदार्थ का ताप बढ़ाने के लिए आवश्यक ऊष्मा की मात्रा निर्भर करती है? इस प्रश्न का उत्तर देने के लिए प्रथम चरण में, जल की कुछ मात्रा को गर्म करके उसके ताप में कुछ वृद्धि, जैसे 20°C कीजिए और उसमें लगा समय नोट कीजिए। पुनः इतना ही जल लेकर अब इसके ताप में ऊष्मा के उसी स्रोत द्वारा 40°C की ताप वृद्धि कीजिए और विराम घड़ी से समय नोट कीजिए। आप यह पाएंगे कि इस बार लगभग दो गुना समय लगता है। अतः समान मात्रा के जल के ताप में दो गुनी वृद्धि करने के लिए दो गुनी ऊष्मा की मात्रा की आवश्यकता होती है।
दूसरे चरण में, अब मान लीजिए आप दो गुना जल लेकर इसे गर्म करने के लिए उसी स्रोत का उपयोग करके इसके ताप में 20°C की ताप-वृद्धि करते हैं। आप यह पाएँगे कि इस बार फिर गर्म करने में पहले चरण की अपेक्षा लगभग दो गुना समय लगा है।
तीसरे चरण में, जल के स्थान पर, अब किसी तेल, जैसे सरसों का तेल, की समान मात्रा लेकर इसके ताप में भी 20°C की वृद्धि कीजिए। अब उसी विराम घड़ी द्वारा समय नोट कीजिए। आप यह पाएँगे कि इस बार पहले की अपेक्षा कम समय लगा है। अतः आवश्यक ऊष्मा की मात्रा समान मात्रा के जल के ताप में समान वृद्धि के लिए आवश्यक ऊष्मा की मात्रा से कम है।
उपरोक्त प्रेक्षण यह दर्शाते हैं कि किसी दिए गए पदार्थ को उष्ण करने के लिए आवश्यक ऊष्मा की मात्रा इसके द्रव्यमान m , ताप में परिवर्तन ∆T, तथा पदार्थ की प्रकृति पर निर्भर करती है। किसी पदार्थ के ताप में परिवर्तन, जबकि ऊष्मा की एक दी गई मात्रा को वह पदार्थ अवशोषित करता है अथवा बहिष्कृत करता है, एक राशि, जिसे उस पदार्थ की ऊष्मा धारिता कहते हैं, द्वारा अभिलक्षित की जाती है। किसी पदार्थ की ऊष्मा धारिता S को हम इस प्रकार परिभाषित करते हैं:
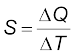 (11.10)
(11.10)
यहाँ ∆Q पदार्थ के ताप में T से T + ∆T तक परिवर्तन करने के लिए आवश्यक ऊष्मा की मात्रा है।
आपने यह प्रेक्षण किया है कि जब विभिन्न पदार्थों के समान द्रव्यमानों को समान मात्रा में ऊष्मा प्रदान की जाती है, तो उनमें होने वाले परिणामी ताप परिवर्तन समान नहीं होते। इससे यह निष्कर्ष निकलता है कि किसी पदार्थ के एकांक द्रव्यमान में एकांक ताप-परिवर्तन के लिए वह पदार्थ ऊष्मा की एक निश्चित व अनन्य मात्रा का अवशोषण अथवा बहिष्करण करता है, इस मात्रा को पदार्थ की विशिष्ट ऊष्मा धारिता कहते हैं।
यदि m द्रव्यमान के किसी पदार्थ द्वारा ∆T ताप परिवर्तन के लिए ∆Q ऊष्मा की मात्रा अवशोषित अथवा बहिष्कृत करनी होती है तो उस पदार्थ की विशिष्ट ऊष्मा धारिता s को इस प्रकार व्यक्त किया जाता है
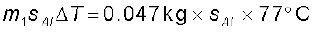
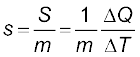 (11.11)
(11.11)
विशिष्ट ऊष्मा धारिता किसी पदार्थ का वह गुण होता है जो इस पदार्थ द्वारा एक दिए गए परिमाण की ऊष्मा को अवशोषित (अथवा बहिष्कृत) करने पर (यदि प्रावस्था परिवर्तन नहीं है) उस पदार्थ के ताप में होने वाले परिवर्तन को निर्धारित करता है। इसे "ऊष्मा की वह मात्रा जो किसी पदार्थ का एकांक द्रव्यमान अपने ताप में एकांक परिवर्तन के लिए अवशोषित अथवा बहिष्कृत करता है" के रूप में परिभाषित किया जाता है। विशिष्ट ऊष्मा धारिता का SI मात्रक J kg–1 K–1 है।
यदि पदार्थ की मात्रा का उल्लेख "द्रव्यमान m किलोग्रामों" में न करके मोल µ के पदाें में किया जाता है तो हम किसी पदार्थ की ऊष्मा धारिता प्रति मोल को इस प्रकार व्यक्त
करते हैं
(11.12)
जहाँ C मोलर विशिष्ट ऊष्मा धारिता कहलाती है। S की भांति C भी पदार्थ की प्रकृति तथा इसके ताप पर निर्भर करता है। मोलर विशिष्ट ऊष्मा धारिता का SI मात्रक J mol–1 K–1 है।
परन्तु, गैसों की विशिष्ट ऊष्मा धारिता के संबंध में C को परिभाषित करने के लिए अतिरिक्त प्रतिबंधों की आवश्यकता होती है। इस प्रकरण में दाब अथवा आयतन को नियत रखकर भी ऊष्मा स्थानांतर किया जा सकता है। यदि ऊष्मा स्थानांतरण के समय गैस का दाब नियत रखा जाता है, तो इसे नियत दाब पर मोलर विशिष्ट ऊष्मा धारिता कहते हैं और इसे Cp द्वारा निर्दिष्ट किया जाता है। इसके विपरीत, यदि ऊष्मा स्थानांतरण के समय गैस का आयतन नियत रखते हैं, तो इसे नियत आयतन पर मोलर विशिष्ट ऊष्मा धारिता कहते हैं और इसे Cv द्वारा निर्दिष्ट करते हैं। इसके विस्तृत वर्णन के लिए
सारणी 11.3 वायुमण्डलीय दाब तथा कक्ष ताप पर कुछ पदार्थों की विशिष्ट ऊष्मा धारिताएँ
| पदार्थ | विशिष्ट ऊष्मा धारिता (J kg–1 K–1) | पदार्थ | विशिष्ट ऊष्मा धारिता (J kg–1 K–1) |
| एलुमिनियम कार्बन ताँबा लैड चाँदी टंग्सटन जल | 900.0 506.5 386.4 127.7 236.1 134.1 4186.0 | बर्फ काँच आयरन कैरोसीन खाद्य तेल पारा | 2060 840 450 2118 1965 140 |
अध्याय 12 देखिए। सारणी 11.3 में वायुमण्डलीय दाब तथा कक्ष ताप पर कुछ पदार्थों की विशिष्ट ऊष्मा धारिता के मापे हुए मानों की सूची दी गई है जबकि सारणी 11.4 में कुछ गैसों की
सारणी 11.4 कुछ गैसों की मोलर विशिष्ट ऊष्मा धारिताएँ
| गैस | Cp (J mol–1K–1) | Cv(J mol–1K–1) |
| He H2 N2 O2 CO2 | 20.8 28.8 29.1 29.4 37.0 | 12.5 20.4 20.8 21.1 28.5 |
मोलर विशिष्ट ऊष्मा धारिता की सूची दी गई है। सारणी 11.3 से आप यह ध्यान में रख सकते हैं कि अन्य पदार्थों की तुलना में जल की विशिष्ट ऊष्मा धारिता उच्चतम होती है। यही कारण है कि स्वचालित वाहनों के रैडिएटरों में जल का उपयोग शीतलक के रूप में किया जाता है तथा सिकाई के लिए उपयोग होने वाली तप्त जल थैलियों में जल का उपयोग तापक के रूप में किया जाता है। उच्च विशिष्ट ऊष्मा धारिता होने के कारण गर्मियों में थल की अपेक्षा जल बहुत धीमी गति से गर्म होता है फलस्वरूप समुद्र की ओर से आने वाली पवनें शीतल होती हैं। अब आप यह बता सकते हैं कि मरुक्षेत्रों में पृथ्वी का पृष्ठ दिन के समय शीघ्र उष्ण तथा रात्रि के समय शीघ्र शीतल क्यों हो जाता है।
11.7 ऊष्मामिति
किसी निकाय को वियुक्त निकाय तब कहा जाता है जब उस निकाय तथा उसके परिवेश के बीच कोई ऊष्मा विनिमय अथवा ऊष्मा स्थानांतर नहीं होता। जब किसी वियुक्त निकाय के विभिन्न भाग भिन्न-भिन्न ताप पर होते हैं, तब ऊष्मा की कुछ मात्रा उच्च ताप के भाग से निम्न ताप वाले भाग को स्थानांतरित हो जाती है। उच्च ताप के भाग द्वारा लुप्त ऊष्मा निम्न ताप के भाग द्वारा ऊष्मा लब्धि के बराबर होती है।
ऊष्मामिति का अर्थ ऊष्मा मापन है। जब कोई उच्च ताप की वस्तु किसी निम्न ताप की वस्तु के संपर्क में लाई जाती है, तो उच्च ताप की वस्तु द्वारा लुप्त ऊष्मा निम्न ताप की वस्तु द्वारा ऊष्मा लब्धि के बराबर होती है, बशर्ते कि निकाय से ऊष्मा का कोई भाग भी परिवेश में पलायन न करे। एेसी युक्ति जिसमें ऊष्मा मापन किया जा सके उसे ऊष्मामापी कहते हैं (चित्र 11.20)। यह धातु के एक बर्तन तथा उसी पदार्थ जैसे ताँबा अथवा एल्युमिनियम के विडोलक से मिलकर बना होता है। इस बर्तन को एक लकड़ी के आवरण के भीतर, जिसमें ऊष्मारोधी पदार्थ जैसे काँच तंतु भरा होता है, रखा जाता है। बाहरी आवरण ऊष्मा कवच की भांति कार्य करता है तथा यह भीतरी बर्तन से ऊष्मा-हानि को कम कर देता है। बाहरी आवरण में एक छिद्र बनाया जाता है जिससे होते हुए पारे का तापमापी बर्तन के भीतर पहुँचता है। निम्नलिखित उदाहरण द्वारा आपको किसी दिए गए ठोस पदार्थ की विशिष्ट ऊष्मा धारिता ज्ञात करने की एेसी विधि मिल जाएगी जिसमें लुप्त ऊष्मा = ऊष्मा लब्धि के सिद्धांत का उपयोग किया जाता है।
उदाहरण 11.3 0.047 kg द्रव्यमान के किसी एेलुमिनियम के गोले को काफी समय के लिए उबलते जल से भरे बर्तन में रखा गया है ताकि गोले का ताप 100°C हो जाए। इसके पश्चात् गोले को तुरन्त 0.14 kg द्रव्यमान के ताँबे के ऊष्मामापी, जिसमें 20°C का 0.25 kg जल भरा है, में स्थानांतरित किया जाता है। जल के ताप में वृद्धि होती है तथा यह 23°C पर स्थायी अवस्था ग्रहण कर लेता है। एेलुमिनियम की विशिष्ट ऊष्मा
धारिता परिकलित कीजिए।
हल इस उदाहरण को हल करते समय हम इस तथ्य का उपयोग करेंगे कि स्थायी अवस्था में एेलुमिनियम के गोले द्वारा दी गई ऊष्मा जल तथा ऊष्मामापी द्वारा अवशोषित ऊष्मा के बराबर होती है।
एेलुमिनियम के गोले का द्रव्यमान (m1) = 0.047 kg
एेलुमिनियम के गोले का आरंभिक ताप = 100ºC
अंतिम ताप = 23ºC
ताप में परिवर्तन (∆T) = (100ºC - 23ºC) = 77ºC
मान लीजिए, एेलुमिनियम की विशिष्ट ऊष्मा धारिता = sAl
एेलुमिनियम के गोले द्वारा लुप्त ऊष्मा की मात्रा =
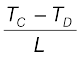
जल का द्रव्यमान (m2) = 0.25 kg
ऊष्मामापी का द्रव्यमान (m3) = 0.14 kg
जल तथा ऊष्मामापी का आरंभिक ताप = 20ºC
मिश्रण का अंतिम ताप = 23ºC
ताप में परिवर्तन (∆T2) = 23ºC–20ºC = 3ºC
जल की विशिष्ट ऊष्मा धारिता (sw)
= 4.18×103 J kg–1 ºC–1
ताँबे के ऊष्मामापी की विशिष्ट ऊष्मा धारिता
= 0.386×103 J kg–1 ºC–1
जल तथा ऊष्मामापी द्वारा ऊष्मालब्धि की मात्रा
= m2 sw ∆T2 + m3scu∆T2
= (m2sw + m3scu) (∆T2)
= 0.25 kg ×4.18 × 103 J kg–1 ºC–1 + 0.14 kg ×
0.386 × 103 J kg–1 ºC–1) (23ºC – 20ºC)
स्थायी अवस्था में एेलुमिनियम के गोले द्वारा लुप्त ऊष्मा = जल द्वारा ऊष्मा लब्धि + ऊष्मामापी द्वारा ऊष्मा लब्धि
0.047 kg × sAl × 77ºC
= (0.25 kg × 4.18 × 103 J kg–1 ºC–1+ 0.14 kg ×
0.386 × 103 J kg–1 ºC–1)(3ºC)
sAl = 0.911 kJ kg–1 ºC–1 t
11.8 अवस्था परिवर्तन
सामान्य रूप में द्रव्य की तीन अवस्थाएँ हैं: ठोस, द्रव तथा गैस। इन अवस्थाओं में से किसी एक अवस्था से दूसरी अवस्था में संक्रमण को अवस्था परिवर्तन कहते हैं। दो सामान्य अवस्था परिवर्तन ठोस से द्रव तथा द्रव से गैस (तथा विलोमतः) हैं। ये परिवर्तन तब ही हो सकते हैं जबकि पदार्थ तथा उसके परिवेश के बीच ऊष्मा का विनिमय होता है। तापन अथवा शीतलन पर अवस्था परिवर्तन का अध्ययन करने के लिए आइए निम्नलिखित क्रियाकलाप करते हैं।
क्रियाकलाप 11.1
एक बीकर में कुछ हिम क्यूब लीजिए। हिम का ताप नोट कीजिए। इसे धीरे-धीरे किसी अचल ऊष्मा स्रोत पर गर्म करना आरंभ कीजिए। हर एक मिनट के पश्चात् ताप नोट कीजिए। जल तथा हिम के मिश्रण को निरंतर विडोलित करते
रहिए। समय और ताप के बीच ग्राफ आलेखित कीजिए
(चित्र 11.9)। आप यह पाएँगे कि जब तक बीकर में हिम उपस्थित है तब तक ताप में कोई परिवर्तन नहीं होता। उपरोक्त प्रक्रिया में, निकाय को ऊष्मा की सतत आपूर्ति होने पर भी उसके ताप में कोई परिवर्तन नहीं होता। यहाँ संभरण की जा रही ऊष्मा का उपयोग ठोस (हिम) से द्रव (जल) में अवस्था परिवर्तन किए जाने में हो रहा है।
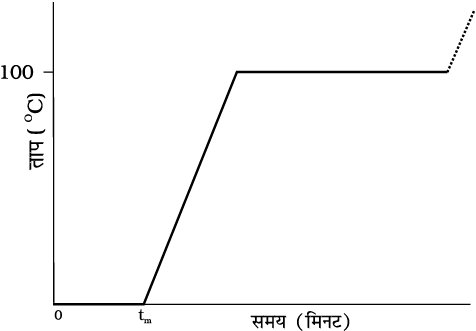
चित्र 11.9 हिम को गर्म करने पर अवस्था में हुए परिवर्तनों को ताप और समय के बीच ग्राफ आलेखित करके दर्शाना (पैमाने के अनुसार नहीं)।
त्रिक बिंदु
किसी पदार्थ का ताप उसकी अवस्था परिवर्तन (प्रावस्था परिवर्तन) की अवधि में नियत रहता है। किसी पदार्थ के ताप T तथा दाब P के बीच आलेखित ग्राफ को प्रावस्था आरेख अथवा P – T आरेख कहते हैं। नीचे दिखाए गए चित्र में जल तथा CO2 के प्रावस्था आरेख दर्शाए गए हैं। इस प्रकार का प्रावस्था आरेख P – T तल को ठोस क्षेत्र, वाष्प क्षेत्र तथा द्रव क्षेत्र में विभाजित करता है। इन क्षेत्रों को वक्रों जैसे ऊर्ध्वपातन वक्र (BO), संगलन वक्र (AO) तथा वाष्पन वक्र (CO) द्वारा पृथक किया जाता है। ऊर्ध्वपातन वक्र BO के बिंदु उस अवस्था को निरूपित करते हैं जिस पर ठोस तथा वाष्प प्रावस्थाएँ सहवर्ती होती हैं। संगलन वक्र AO के बिंदु उस अवस्था का निरूपण करते हैं जिसमें ठोस तथा द्रव प्रावस्थाएँ सहवर्ती होती हैं। वाष्पन वक्र CO के बिंदु उस अवस्था को निरूपित करते हैं जिसमें द्रव तथा वाष्प प्रावस्थाएँ सहवर्ती होती हैं। वह ताप तथा दाब जिस पर संगलन वक्र, वाष्पन वक्र तथा ऊर्ध्वपातन वक्र मिलते हैं तथा किसी पदार्थ की तीनों प्रावस्थाएँ सहवर्ती होती हैं उस पदार्थ का त्रिक बिंदु कहलाता है। उदाहरण के लिए, जल के त्रिक बिंदु को ताप 273.16K तथा दाब 6.11×10–3 Pa द्वारा निरूपित करते हैं।
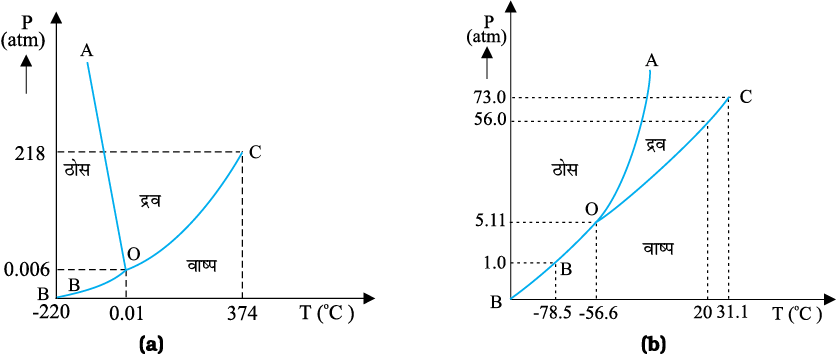
(a) जल तथा (b) CO2 के लिए दाब-ताप प्रावस्था आरेख (पैमाने के अनुसार नहीं)
ठोस से द्रव में अवस्था परिवर्तन को गलन (अथवा पिघलना) तथा द्रव से ठोस में अवस्था परिवर्तन को संगलन कहते हैं। यह पाया गया है कि ठोस पदार्थ की समस्त मात्रा के पिघलने तक ताप नियत रहता है अर्थात् ठोस से द्रव में अवस्था परिवर्तन की अवधि में पदार्थ की दोनों अवस्थाएँ ठोस तथा द्रव तापीय साम्य में सहवर्ती होती हैं। वह ताप जिस पर किसी पदार्थ की ठोस तथा द्रव अवस्थाएँ परस्पर तापीय साम्य में होती हैं उसे उस पदार्थ का गलनांक कहते हैं। यह किसी पदार्थ का अभिलक्षण होता है। यह दाब पर भी निर्भर करता है। मानक वायुमण्डलीय दाब पर किसी पदार्थ के गलनांक को प्रसामान्य गलनांक कहते हैं। हिम के गलने की प्रक्रिया को समझने के लिए आइए निम्नलिखित क्रियाकलाप करें।
क्रियाकलाप 11.2
एक हिम शिला लीजिए। एक धातु का तार लेकर उसके दोनों सिरों से समान भार जैसे 5 kg के बाट बाँधिए। चित्र 11.10 में दर्शाए अनुसार इस तार को हिम शिला के ऊपर रखिए। आप यह देखेंगे कि तार हिमशिला में से पार हो जाता है। एेसा होने का कारण यह है कि तार के ठीक नीचे दाब में वृद्धि के कारण हिम निम्न ताप पर पिघल जाता है। जब तार वहाँ से गुजर जाता है, तो तार के ऊपर का जल पुनः हिमीभूत हो जाता है। इस प्रकार तार हिम शिला से पार हो जाता है तथा शिला विभक्त नहीं होती। पुनर्हिमीभवन की इस परिघटना को पुनर्हिमायन कहते हैं। हिम पर ‘स्केट’ के नीचे जल बनने के कारण ही ‘स्केटिंग’ करना संभव हो पाता है। दाब में वृद्धि के कारण जल बनता है जो स्नेहक की भांति कार्य करता है।
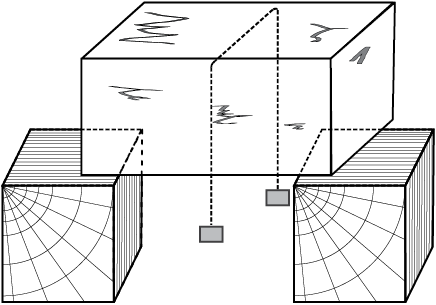
चित्र 11.10
जब समस्त हिम जल में रूपांतरित हो जाता है और इसके पश्चात् जैसे ही हम और आगे गर्म करना चालू रखते हैं तो हम यह पाते हैं कि ताप में वृद्धि होनी आरंभ हो जाती है
चित्र 11.9। ताप में यह वृद्धि निरंतर लगभग 100 °C तक होती है और यहाँ फिर ताप स्थिर हो जाता है। अब फिर जल को आपूर्त ऊष्मा का उपयोग जल को द्रव अवस्था से वाष्प अथवा गैसीय अवस्था में रूपांतरित करने में होता है।
द्रव से वाष्प (अथवा गैस) में अवस्था परिवर्तन को वाष्पन कहते हैं। यह पाया गया है कि समस्त द्रव के वाष्प में रूपांतरित होने तक ताप नियत रहता है। अर्थात्, ठोस से वाष्प में अवस्था परिवर्तन की अवधि में पदार्थ की दोनों अवस्थाएँ द्रव तथा गैस तापीय साम्य में सहवर्ती होती हैं। वह ताप जिस पर किसी पदार्थ की द्रव तथा वाष्प दोनों अवस्थाएँ तापीय साम्य में परस्पर सहवर्ती होती हैं उसे उस पदार्थ का क्वथनांक कहते हैं। जल के क्वथन की प्रक्रिया को समझने के लिए आइए निम्नलिखित क्रियाकलाप करें।
क्रियाकलाप 11.3
आधे से अधिक जल से भरा एक गोल पेंदी का फ्लास्क लीजिए। चित्र 11.11 में दर्शाए अनुसार फ्लास्क के मुख पर लगी कार्क के वेधों से होकर भीतर जाते हुए एक तापमापी तथा एक भाप निकास कार्क में लगाइए और फ्लास्क को बर्नर के ऊपर रखिए। जैसे ही जल गर्म होता है, तो पहले यह देखिए कि वह वायु, जो जल में विलीन थी, छोटे-छोटे बुलबुलों के रूप में बाहर आएगी। तत्पश्चात् भाप के बुलबुले फ्लास्क की तली में बनेंगे, परन्तु जैसे ही वे शीर्षभाग के पास के शीतल जल की ओर ऊपर उठते हैं, संघनित होकर अदृश्य हो जाते हैं। अंततः जैसे ही समस्त जल का ताप 100°C पर पहुँचता है, भाप के बुलबुले पृष्ठ पर पहुँचते हैं और क्वथन होने लगता है। फ्लास्क के भीतर भाप दिखाई नहीं देती, परन्तु जैसे ही फ्लास्क से बाहर निकलती है, यह जल की अत्यंत छोटी बूँदों के रूप में संघनित होकर धुंध के रूप में प्रकट होती है।
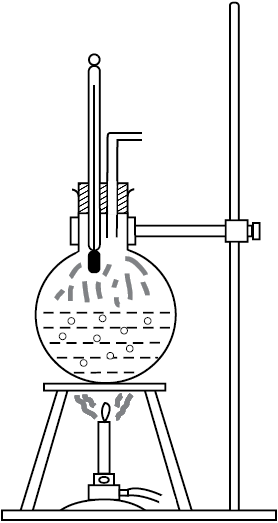
चित्र 11.11 क्वथन प्रक्रिया।
अब यदि कुछ सेकंडों के लिए भाप निकास को बंद कर दें, ताकि फ्लास्क के भीतर दाब में वृद्धि हो, तब आप यह देखेंगे कि क्वथन रुक जाता है। जल में क्वथन प्रक्रिया पुनः आरंभ होने तक जल के ताप में वृद्धि करने के लिए (दाब पर निर्भर करते हुए) और ऊष्मा की आवश्यकता होती है। इस प्रकार दाब में वृद्धि के साथ क्वथनांक में वृद्धि हो जाती है।
आइए अब हम बर्नर को हटा लेते हैं तथा जल को लगभग 80°C तक ठंडा होने देते हैं। फ्लास्क से तापमापी तथा भाप निकास हटाकर फ्लास्क के मुँह को वायुरुद्ध कर्क से कस कर बंद कर देते हैं। अब फ्लास्क को स्टैंड पर उलटा करके रखते हैं और फ्लास्क पर हिमशीतित जल उड़ेलते हैं। एेसा करने पर फ्लास्क के भीतर की जलवाष्प संघनित होकर फ्लास्क के भीतर जल के पृष्ठ पर दाब को कम कर देती है। अब निम्न ताप पर जल में पुनः क्वथन आरंभ हो जाता है। इस प्रकार दाब में कमी होने पर क्वथनांक घट जाता है।
इससे यह स्पष्ट हो जाता है कि पहाड़ी क्षेत्रों में भोजन पकाना क्यों कठिन होता है। उच्च तुंगता पर वायुमण्डलीय दाब निम्न होता है, जिसके कारण वहाँ पर समुद्र तट की तुलना में जल का क्वथनांक घट जाता है। इसके विपरीत, दाब कुकर के भीतर दाब में वृद्धि करके क्वथनांक बढ़ाया जाता है। इसीलिए पाकक्रिया तेज होती है। मानक वायुमण्डलीय दाब पर किसी पदार्थ के क्वथनांक को प्रसामान्य क्वथनांक कहते हैं।
परन्तु, सभी पदार्थ इन तीनों अवस्थाओं - ठोस, द्रव तथा गैस से नहीं गुजरते। कुछ पदार्थ एेसे भी हैं जो सामान्यतः सीधे ठोस से वाष्प अवस्था में और विलोमतः पहुँच जाते हैं। किसी पदार्थ का ठोस अवस्था से वाष्प अवस्था मेें, बिना द्रव अवस्था से गुजरे, पहुँचना ऊर्ध्वपातन कहलाता है तथा एेसे पदार्थ को ऊर्ध्वपातन पदार्थ कहते हैं। शुष्क हिम (ठोस CO2) का ऊर्ध्वपातन होता है, आयोडीन भी इसी प्रकार का पदार्थ है। ऊर्ध्वपातन की प्रक्रिया के समय किसी पदार्थ की दोनों अवस्थाएँ - ठोस तथा वाष्प अवस्था तापीय साम्य में सहवर्ती होती हैं।
11.8.1 गुप्त ऊष्मा
अनुभाग 11.8 में हमने यह सीखा है कि जब कोई पदार्थ अवस्था परिवर्तन की स्थिति में होता है तो पदार्थ तथा उसके परिवेश के बीच ऊष्मा की एक निश्चित मात्रा स्थानांतरित होती है। किसी पदार्थ की अवस्था परिवर्तन की अवधि में, ऊष्मा की मात्रा का प्रति एकांक द्रव्यमान स्थानांतरण, उस पदार्थ की इस प्रक्रिया के लिए गुप्त ऊष्मा कहलाती है। उदाहरण के लिए, यदि –10°C के किसी दिए गए परिमाण के हिम को गर्म किया जाए तो उसका ताप इसके गलनांक (0°C) तक बढ़ता है। इस ताप पर और ऊष्मा देने पर ताप में वृद्धि नहीं होती, परन्तु हिम पिघलने लगती है अर्थात् अवस्था परिवर्तन होता है। जब समस्त हिम पिघल जाती है, तो और ऊष्मा देने पर जल के ताप में वृद्धि होती है। इसी प्रकार की स्थिति क्वथनांक पर द्रव-गैस अवस्था परिवर्तन के समय होती है। उबलते जल को और ऊष्मा प्रदान करने पर ताप में वृद्धि नहीं होती; वाष्पन हो जाता है।
सारणी 11.4 1 atm दाब पर विभिन्न पदार्थों के अवस्था परिवर्तन के ताप तथा गुप्त ऊष्माएँ
| पदार्थ | गलनांक (0C) | Lf (105J kg–1) | क्वथनांक (0C) | Lv (105J kg–1) |
| इथैनॉल सोना लैड पारा नाइट्रोजन अॉक्सीजन जल | –114 1063 328 -39 -210 -219 0 | 1.0 0.645 0.25 0.12 0.26 0.14 3.33 | 78 2660 1744 357 -196 -183 100 | 8.5 15.8 8.67 2.7 2.0 2.1 22.6 |
अवस्था परिवर्तन के समय आवश्यक ऊष्मा का परिमाण जिस पदार्थ की अवस्था में परिवर्तन हो रहा है उसके द्रव्यमान तथा रूपांतरण-ऊष्मा पर निर्भर करता है। इस प्रकार, यदि m उस पदार्थ का द्रव्यमान है जिसका एक अवस्था से दूसरी अवस्था में परिवर्तन हो रहा है, तब आवश्यक ऊष्मा का परिमाण
Q = mL
अथवा L = Q/m (11.13)
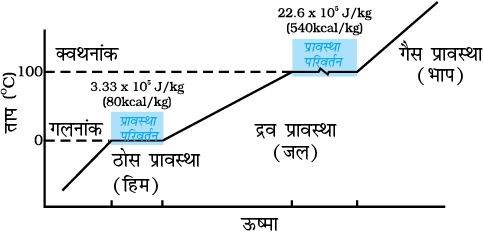
यहाँ L को गुप्त ऊष्मा कहते हैं तथा यह पदार्थ का अभिलक्षण है। इसका SI मात्रक J kg–1 है। L का मान दाब पर भी निर्भर करता है। प्रायः इसके मान का उद्धरण मानक वायुमण्डलीय दाब पर किया जाता है। ठोस-द्रव अवस्था परिवर्तन के लिए गुप्त ऊष्मा को संगलन की गुप्त ऊष्मा (Lf) कहते हैं, तथा द्रव-गैस अवस्था परिवर्तन के लिए गुप्त ऊष्मा को वाष्पन की गुप्त ऊष्मा (Lv) कहते हैं। इसे हम प्रायः संगलन ऊष्मा तथा वाष्पन ऊष्मा कहते हैं। चित्र 11.12 में जल के किसी परिमाण के लिए ताप तथा ऊष्मा के बीच ग्राफ का आलेख दर्शाया गया है। सारणी 11.4 में कुछ पदार्थों की गुप्त ऊष्मा, गलनांक तथा क्वथनांक दिए गए हैं।
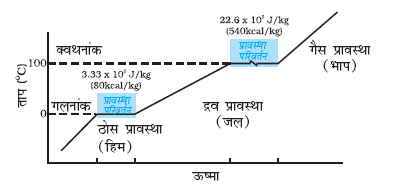
चित्र 11.12 जल के लिए ताप तथा ऊष्मा के बीच ग्राफ आलेखन (पैमाने के अनुसार नहीं)।
ध्यान दीजिए कि जब अवस्था परिवर्तन के समय ऊष्मा दी (अथवा ली) जाती है, तो ताप नियत रहता है। ध्यान से देखिए कि चित्र 11.12 में प्रावस्था रेखाओं की प्रवणताएँ समान नहीं हैं जो यह संकेत देता है कि विभिन्न अवस्थाओं की विशिष्ट ऊष्मा धारिताएँ समान नहीं हैं। जल के लिए, संगलन तथा वाष्पन की गुप्त ऊष्माएँ क्रमशः Lf = 3.33×105 J kg–1 तथा Lv = 22.6×105 J kg–1 हैं। अर्थात् 1 kg हिम को 0°C पर गलन के लिए 3.33×105 J ऊष्मा चाहिए तथा 1 kg जल को 100°C पर भाप में परिवर्तन होने के लिए 22.6×105 J ऊष्मा चाहिए। अतः 100°C के जल की अपेक्षा 100°C की भाप में 22.6 ´ 105 J kg–1 ऊष्मा अधिक होती है। यही कारण है कि उबलते जल की तुलना में उसी ताप की भाप प्रायः अधिक गंभीर जलन देती है।
उदाहरण 11.4 जब 0°C पर रखे 0.15 kg हिम को किसी पात्र में भरे 50°C के 0.30 kg जल में मिलाया जाता है तो मिश्रण का परिणामी ताप 6.7°C हो जाता है। हिम के संगलन की ऊष्मा परिकलित कीजिए।
(sजल = 4186 J kg–1 0C–1)
हल :
जल द्वारा लुप्त ऊष्मा = msw (θf–θi)w
= (0.30 kg) (4186 J kg–1 °C–1) (50.0°C – 6.7°C)
= 54376.14 J
हिम के गलन के लिए आवश्यक ऊष्मा
= m2Lf = (0.15 kg) Lf
हिम जल के ताप को अंतिम ताप तक बढ़ाने के लिए आवश्यक ऊष्मा = mIsw (θf–θi)I
= (0.15 kg) (4186 J kg–1 °C –1) (6.7°C – 0°C)
= 4206.93 J
लुप्त ऊष्मा = ऊष्मा लब्धि
54376.14 J = (0.15 kg) Lf + 4206.93 J
Lf = 3.34×105 J kg–1 t
उदाहरण 11.5 किसी ऊष्मामापी में भरे –12°C के 3 kg हिम को वायुमण्डलीय दाब पर 100°C की भाप में परिवर्तित करने के लिए आवश्यक ऊष्मा परिकलित कीजिए। दिया गया है हिम की विशिष्ट ऊष्मा धारिता = 2100 J kg–1 0C–1, जल की विशिष्ट ऊष्मा धारिता = 4186 J kg– 1 0C–1, हिम के संगलन की गुप्त ऊष्मा = 3.35×105 J kg–1 तथा भाप की गुप्त ऊष्मा = 2.256×106 J kg–1.
हल : दिया है
हिम का द्रव्यमान m = 3 kg
हिम की विशिष्ट ऊष्मा धारिता, sहिम
= 2100 J kg–1 0C–1
जल की विशिष्ट ऊष्मा धारिता, sजल
= 4186 J kg–1 0C–1
हिम के संगलन की गुप्त ऊष्मा, Lf हिम
= 3.35×105 J kg–1
भाप की गुप्त ऊष्मा, Lभाप
= 2.256×106 J kg–1
अब, Q = –12°C के 3 kg हिम को 100°C की भाप में परिवर्तित करने के लिए आवश्यक ऊष्मा
Q1 = –12°C के 3 kg हिम को 0°C के हिम में परिवर्तित करने के लिए आवश्यक ऊष्मा
= m sहिम ∆T1 = (3 kg) (2100 J kg–1. °C–1) [0–(–12)]°C = 75600 J
Q2 = 0°C के 3 kg हिम को 0°C के जल में संगलित करने के लिए आवश्यक ऊष्मा
= m Lf हिम = (3 kg) (3.35×105 J kg–1)
= 1005000 J
Q3 = 0°C के 3 kg जल को 100°C के जल में परिवर्तित करने के लिए आवश्यक ऊष्मा
= msw ∆T2
= (3kg) (4186J kg–1 °C–1) (100°C)
= 1255800 J
Q4 = 100°C के 3 kg जल को 100°C की भाप में परिवर्तित करने के लिए आवश्यक ऊष्मा
= m Lभाप = (3 kg) (2.256×106 J kg–1)
= 6768000 J
अतः, Q = Q1+Q2+Q3+Q4
= 75600 J + 1005000J
+ 1255800 J + 6768000 J
= 9.1×106 J t
11.9 ऊष्मा स्थानांतरण
हमने देखा है कि ताप में अंतर के कारण एक निकाय से दूसरे निकाय में अथवा किसी निकाय के एक भाग से उसके दूसरे भाग में ऊर्जा के स्थानांतरण को ऊष्मा कहते हैं। इस ऊर्जा स्थानांतर के विविध साधन क्या हैं? ऊष्मा स्थानांतरण
की सुस्पष्ट तीन विधियाँ हैंः चालन, संवहन तथा विकिरण (चित्र 11.13)।

चित्र 11.13 चालन, संवहन तथा विकिरण द्वारा तापन।
11.9.1 चालन
किसी वस्तु के दो संलग्न भागों के बीच उनके तापों में अंतर के कारण ऊष्मा स्थानांतरण की क्रियाविधि को चालन कहते हैं। मान लीजिए किसी धातु की छड़ का एक सिरा आग की ज्वाला में रखा है। शीघ्र ही छड़ का दूसरा सिरा इतना गर्म हो जाएगा कि आप उसे अपने नंगे हाथों से पकड़ नहीं सकेंगे। यहाँ छड़ में ऊष्मा स्थानांतरण चालन द्वारा छड़ के तप्त सिरे से छड़ के विभिन्न भागों से होकर दूसरे सिरे तक होता है। गैसें हीन ऊष्मा चालक होती हैं तथा द्रवों की चालकता ठोसों तथा गैसों के बीच की होती है।
मात्रात्मक रूप में, ऊष्मा चालन का वर्णन "किसी पदार्थ में किसी दिए गए तापांतर के लिए ऊष्मा प्रवाह की दर" द्वारा किया जाता है। L लंबाई तथा A एकसमान अनुप्रस्थ काट क्षेत्रफल की धातु की किसी एेसी छड़ पर विचार कीजिए जिसके दोनों सिरों के बीच तापांतर स्थापित किया गया है। उदाहरण के लिए, एेसा छड़ के सिरों को क्रमशः TC तथा TD ताप के ऊष्मा भंडारों के संपर्क में रखकर किया जा सकता है (चित्र 11.14)। अब हम एक एेसी आदर्श स्थिति की कल्पना करते हैं जिसमें छड़ के पार्श्व पूर्णतः ऊष्मारोधी हैं ताकि पार्श्वों तथा परिवेश के बीच ऊष्मा का विनिमय नहीं होता।
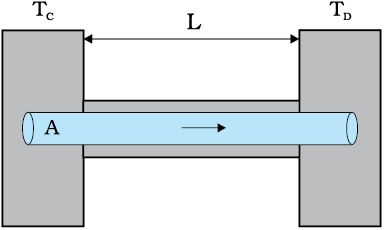
चित्र 11.14 किसी छड़ जिसके दो सिरों को TC तथा TD तापों पर (TC > TD) स्थापित किया गया है, में चालन द्वारा स्थायी अवस्था ऊष्मा प्रवाह।
कुछ समय के पश्चात् स्थायी अवस्था आ जाती है; छड़ का ताप दूरी के साथ एकसमान रूप से TC से TD तक घटता है; (TC>TD)। C पर ऊष्मा भण्डार एक नियत दर पर ऊष्मा की आपूर्ति करता है, जो छड़ से स्थानांतरित होकर उसी दर से D पर स्थित ऊष्मा भंडार में पहुँच जाती है। प्रयोगों द्वारा यह पाया जाता है कि इस स्थायी अवस्था में, ऊष्मा प्रवाह की दर H तापांतर (TC – TD) तथा अनुप्रस्थ काट क्षेत्रफल, A के अनुक्रमानुपाती और छड़ की लंबाई L के व्युत्क्रमानुपाती होती हैः
H = KA Tc-TD/L (11.14)
आनुपातिकता स्थिरांक K को पदार्थ की ऊष्मा चालकता कहते हैं। किसी पदार्थ के लिए K का मान जितना अधिक होता है उतनी ही शीघ्रता से वह ऊष्मा चालन करता है। K का SI मात्रक J s–1 m–1 K–1 अथवा W m–1 K–1 है। सारणी 11.6 में विभिन्न पदार्थों की ऊष्मा चालकता के मान दिए गए हैं। इन मानों में ताप के साथ अल्प अंतर होता है, परन्तु सामान्य ताप परिसर में इन मानों को अचर मान सकते हैं।
अच्छे ऊष्मा चालकों (धातुओं) की अपेक्षाकृत अधिक ऊष्मा चालकताओं की तुलना कुछ अच्छे ऊष्मारोधी पदार्थों, जैसे लकड़ी तथा काँच तंतु, की अपेक्षाकृत कम ऊष्मा चालकताओं से कीजिए। आपने यह पाया होगा कि खाना पकाने के कुछ बर्तनों की पेंदी पर ताँबे का विलेपन होता है। ऊष्मा का अच्छा चालक होने के कारण ताँबा बर्तन की पेंदी पर ऊष्मा वितरण को उन्नत करता है जिससे भोजन समान रूप से पकता है। इसके विपरीत, प्लास्टिक फेन, मुख्यतः वायु की कोटरिका होने के कारण, अच्छे ऊष्मारोधी होते हैं। याद कीजिए गैसें अल्प चालक होती हैं तथा सारणी 11.5 से वायु की निम्न ऊष्मा चालकता नोट कीजिए। बहुत से अन्य अनुप्रयोगों में ऊष्मा धारण तथा स्थानांतरण महत्वपूर्ण होते हैं। हमारे देश में, कंक्रीट की छतों वाले घर गर्मियों में बहुत गर्म हो जाते हैं, इसका कारण यह है कि कंक्रीट की ऊष्मा चालकता (यद्यपि धातुओं की तुलना काफी कम है।) फिर भी बहुत कम नहीं है। इसीलिए, प्रायः लोग छतों पर फोन-रोधन कराना पसंद करते हैं ताकि ऊष्मा स्थानांतरण को रोककर कमरे को शीतल रखा जा सके। कुछ स्थितियों में ऊष्मा स्थानांतरण क्रांतिक होता है। उदाहरण के लिए नाभिकीय रिएक्टरों में सुविस्तृत ऊष्मा-स्थानांतर निकायों को स्थापित करने की आवश्यकता होती है ताकि नाभिकीय रिएक्टर के क्रोड में नाभिकीय विखंडन द्वारा उत्पन्न विशाल ऊर्जा का काफी तेज़ी से बाहर पारगमन किया जा सके तथा क्रोड अतितप्त होने से बचा रहे।
सारणी 11.5 कुछ पदार्थों की ऊष्मा चालकताएँ
| पदार्थ | ऊष्मा चालकता (J s–1 m–1 K–1 ) |
| धातुएँ | |
| चाँदी ताँबा एेलुमिनियम पीतल स्टील लैड पारा | 406 365 205 109 50.2 34.7 8.3 |
| अधातुएँ | |
| ऊष्मारोधी ईंट कंक्रीट शरीर-वसा नमदा काँच हिम काँच तंतु लकड़ी जल | 0.15 0.8 0.20 0.04 0.8 1.6 0.04 0.12 0.8 |
| गैसें | |
| वायु अॉर्गन हाइड्रोजन | 0.024 0.016 0.14 |
उदाहरण 11.6 चित्र 11.15 में दर्शाए गए निकाय की स्थायी अवस्था में स्टील-ताँबा संधि का ताप क्या है? स्टील छड़ की लंबाई = 15.0 cm, ताँबे की छड़ की लंबाई = 10.0 cm, भट्ठी का ताप = 300°C, दूसरे सिरे का ताप = 0°C; स्टील की छड़ की अनुप्रस्थ काट का क्षेत्रफल ताँबे की छड़ की अनुप्रस्थ काट के क्षेत्रफल का दो गुना है। (स्टील की ऊष्मा चालकता = 50.2 J s–1 m–1 K–1; ताँबे की ऊष्मा चालकता =
385 J s–1m–1 K–1)
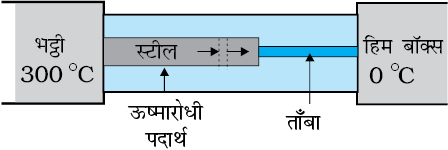
चित्र 11.15
हल : छड़ों को चारों ओर से घेरे रखने वाले ऊष्मारोधी पदार्थ छड़ों के पार्श्व से होने वाली ऊष्मा क्षति को कम कर देते हैं। इसीलिए, ऊष्मा केवल छड़ की लंबाई के अनुदिश ही प्रवाहित होती है। छड़ की किसी भी अनुप्रस्थ काट पर विचार कीजिए। स्थायी अवस्था में छड़ के किसी अवयव में प्रवेश करने वाली ऊष्मा उससे बाहर निष्कासित होने वाली ऊष्मा के बराबर होनी चाहिए, वरना अवयव द्वारा ऊष्मा की नेट लब्धि अथवा हानि होगी तथा इसका ताप स्थायी नहीं रहेगा। इस प्रकार स्थायी अवस्था में छड़ की किसी अनुप्रस्थ काट से प्रवाहित होने वाली ऊष्मा की दर संयुक्त स्टील-ताँबा छड़ की लंबाई के अनुदिश सभी बिंदुओं पर समान है। मान लीजिए स्टील-ताँबा संधि का स्थायी अवस्था में ताप T है, तब
यहाँ, 1 तथा 2 क्रमशः स्टील तथा ताँबे को संदर्भित करते हैं।
A1 = 2 A2, L1 = 15.0 cm, L2 = 10.0 cm, K1 = 50.2 J s–1 m–1 K –1, K2 = 385 J s–1 m–1 K –1, के लिए
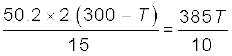
अर्थात् T = 44.4 °C t
उदाहरण 11.7 चित्र 11.16 में दर्शाए अनुसार लोहे की किसी छड़ (L1 = 0.1m, A1 = 0.02 m2, K1 = 79 W m–1 K–1) को किसी पीतल की छड़ (L2 = 0.1m, A2 = 0.02 m2, K2 = 109 W m–1 K–1) के साथ सिरे से सिरे को मिलाकर डाला गया है। लोहे की छड़ तथा पीतल की छड़ के स्वतंत्र सिरों को क्रमशः 373 K तथा 273 K पर स्थापित किया गया है। (i) दोनों छड़ों की संधि पर ताप, (ii) संयुक्त छड़ की तुल्य ऊष्मा चालकता, तथा (iii) संयुक्त छड़ में ऊष्मा प्रवाह की दर के लिए व्यंजक निकालिए तथा परिकलित कीजिए।
हल

चित्र 11.16
दिया गया है,
L1 = L2= L = 0.1m, A1 = A2= A= 0.02 m2
K1 = 79 W m–1 K–1, K2 = 109 W m–1 K–1,
T1 = 373 K, और T2 = 273 K
स्थायी अवस्था की शर्तों के अधीन, लोहे की छड़ से ऊष्मा प्रवाह की दर (H1) ताँबे की छड़ से ऊष्मा प्रवाह की दर (H2) के समान है।
अतः, H = H1 = H2
=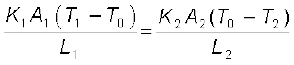
चूंकि A1 = A2 = A तथा L1 = L2 = L
अतः उपरोक्त समीकरण होगा
K1 (T1 – T0) = K2 (T0 – T2)
अतः दोनों छड़ों की संधि का ताप T0 होगा
T0 = = 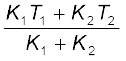
T0 के इस मान का प्रतिस्थापन करने से किसी भी छड़ से ऊष्मा प्रवाह की दर H का मान प्राप्त होता हैः

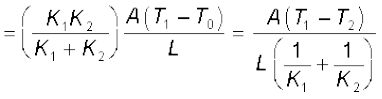
यदि लंबाई L1 + L2 = 2L की संयुक्त छड़ की तुल्य ऊष्मा चालकता K है तथा इससे होकर जाने वाली ऊष्मा प्रवाह की दर H′ हो, तो उपरोक्त समीकरण का उपयोग करने पर
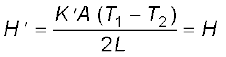
तथा K' = 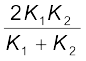
इस प्रकार,
(i)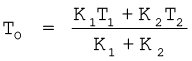
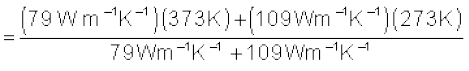
= 315 K
(ii)
=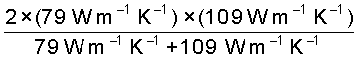
=
= 91.6 W m–1K–1
(iii) H′ = H = 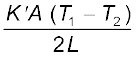
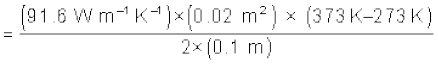
= 916.1 W t
11.9.2 संवहन
संवहन वह विधि है जिसमें पदार्थ की वास्तविक गति द्वारा ऊष्मा स्थानांतरण होता है। यह केवल तरलों में ही संभव है। संवहन प्राकृतिक हो सकता है अथवा प्रणोदित भी हो सकता है। प्राकृतिक संवहन में गुरुत्व एक महत्वपूर्ण भूमिका निभाती है। जब किसी तरल को नीचे से गर्म किया जाता है, तो गर्म भाग में प्रसार होता है, फलस्वरूप उसका घनत्व घट जाता है। उत्प्लावना के कारण यह ऊपर उठता है तथा ऊपरी शीतल भाग इसे प्रतिस्थापित कर देता है। यह पुनः तप्त होता है, ऊपर उठता है तथा तरल के अपेक्षाकृत शीतल भाग द्वारा प्रतिस्थापित होता है। यह प्रक्रिया चलती रहती है। स्पष्ट रूप से ऊष्मा स्थानांतर की यह विधि चालन से भिन्न होती है। संवहन में तरल के विभिन्न भागों का स्थूल अभिगमन होता है।
प्रणोदित संवहन में पदार्थ को किसी पम्प अथवा किसी अन्य भौतिक साधन द्वारा गति करने के लिए विवश किया जाता है। घरों में प्रणोदित वायु तापन निकाय, मानव परिसंचरण तंत्र तथा स्वचालित वाहनों के इंजनों के शीतलन निकाय प्रणोदित संवहन निकायों के सामान्य उदाहरण हैं। मानव शरीर में हृदय एक पम्प की भांति कार्य करता है जो रुधिर का शरीर के विभिन्न भागों में संचरण करता है, तथा इस प्रकार प्रणोदित संवहन द्वारा ऊष्मा स्थानांतरित करके शरीर में एकसमान ताप स्थापित करता है।
प्राकृतिक संवहन बहुत सी सुपरिचित परिघटनाओं के लिए उत्तरदायी है। दिन के समय बड़े जलाशयों की तुलना में थल शीघ्र तप्त हो जाता है। एेसा दो कारणों से होता है - पहला जल की विशिष्ट ऊष्मा धारिता उच्च है तथा दूसरा मिश्रित धाराएँ अवशोषित ऊष्मा को विशाल आयतन के जल के सब भागों में विसारित कर देती हैं। तप्त थल के संपर्क वाली वायु चालन द्वारा गर्म होती है तथा तप्त होकर वायु फैलती है, जिससे परिवेश की शीतल वायु की तुलना में इसका घनत्व कम हो जाता है। फलस्वरूप उष्ण वायु ऊपर उठती है (वायु धाराएँ), तथा रिक्त स्थान को भरने के लिए अन्य वायु गति करती हैं (पवनें) - जिससे बड़े जलाशयों के निकट समुद्र समीर उत्पन्न हो जाती हैं। ठंडी वायु नीचे आती हैं तथा एक तापीय संवहन चक्र बन जाता है, जो ऊष्मा को थल से दूर स्थानांतरित कर देता है। रात्रि में थल की ऊष्मा का ह्रास अधिक शीघ्रता से होता है तथा जलीय पृष्ठ थल की तुलना में उष्ण होती है। परिणामस्वरूप चक्र उत्क्रमित हो जाता है (चित्र 11.17)।
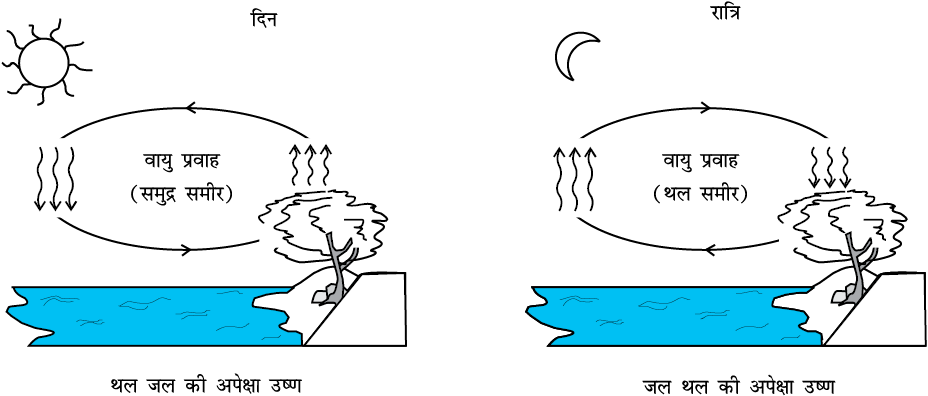
चित्र 11.17 संवहन चक्र।
प्राकृतिक संवहन का एक अन्य उदाहरण उत्तर पूर्व से विषुवत् वृत्त की ओर पृथ्वी पर बहने वाली स्थायी पृष्ठीय पवनें हैं, जिन्हें व्यापारिक पवनें कहते हैं। इनके बहने की यथोचित व्याख्या इस प्रकार है: पृथ्वी के विषुवतीय क्षेत्रों तथा ध्रुवीय क्षेत्रों को सूर्य की ऊष्मा समान मात्रा में प्राप्त नहीं होती। विषुवत वृत्त के समीप पृथ्वी के पृष्ठ पर वायु तप्त होती है जबकि ध्रुवों के ऊपरी वायुमण्डलीय वायु शीतल होती है। किसी अन्य कारक की अनुपस्थिति में, संवहन धाराएँ प्रवाहित होने लगेंगी जिसमें वायु विषुवतीय पृष्ठ से ऊपर उठकर ध्रुवों की ओर बहेगी, फिर नीचे की ओर जाएगी तथा बहती हुई पुनः विषुवत वृत्त की ओर जाएगी। परन्तु, पृथ्वी की घूर्णन गति इस संवहन धारा में संशोधन कर देती है जिसके कारण विषुवत वृत्त के समीप की वायु की पूर्व की ओर चाल 1600 km/h होती है जबकि ध्रुवों के समीप यह चाल शून्य होती है। परिणामस्वरूप यह वायु ध्रुवों पर नीचे की ओर न फैलकर 30°N (उत्तर) अक्षांश पर फैलती है और विषुवत वृत्त पर लौट आती है। इसे व्यापारिक पवनें कहते हैं।
11.9.3 विकिरण
चालन तथा संवहन को परिवहन माध्यम के रूप में किसी पदार्थ की आवश्यकता होती है। ऊष्मा स्थानांतरण की ये विधियाँ निर्वात से पृथक दो वस्तुओं के बीच क्रियाशील नहीं हो सकतीं। परन्तु विशाल दूरी होने पर भी पृथ्वी सूर्य से ऊष्मा प्राप्त कर लेती है। इसी प्रकार, हम पास की आग की उष्णता शीघ्र ही अनुभव कर लेते हैं, यद्यपि वायु अल्प चालक है तथा इतने कम समय में संवहन धाराएँ भी स्थापित नहीं हो पातीं। ऊष्मा स्थानांतरण की तीसरी विधि को किसी माध्यम की आवश्यकता नहीं होती। इस विधि को विकिरण कहते हैं, तथा विद्युत चुंबकीय तरंगों द्वारा इस प्रकार विकरित ऊर्जा को विकिरण ऊर्जा कहते हैं। किसी विद्युत चुंबकीय तरंग में वैद्युत तथा चुंबकीय क्षेत्र दिक तथा काल में दोलन करते हैं। अन्य किसी तरंग की भांति विद्युत चुंबकीय तरंगों की विभिन्न तरंगदैर्घ्य हो सकती हैं तथा वे निर्वात में समान चाल, जिसे प्रकाश की चाल कहते हैं अर्थात् 3×108 m s–1 से चल सकती हैं। इन तथ्यों के बारे में विस्तार से आप बाद में फिर कभी सीखेंगे, परन्तु अब आप यह जान गए हैं कि विकिरण द्वारा ऊष्मा स्थानांतरण के लिए माध्यम का होना क्यों आवश्यक नहीं है तथा यह इतनी तीव्र गति से क्यों होता है। विकिरण द्वारा ही सूर्य से ऊष्मा निर्वात (शून्य अंतरिक्ष) से होकर पृथ्वी तक पहुँचती है। सभी तप्त पिण्ड चाहे वे ठोस, द्रव अथवा गैस हों, विकिरण ऊर्जा उत्सर्जित करते हैं। किसी पिण्ड द्वारा उसके ताप के कारण उत्सर्जित विद्युत चुंबकीय विकिरणों जैसे लाल तप्त लोहा से विकिरण अथवा तंतु लैम्प से प्रकाश को ऊष्मा विकिरण कहते हैं।
जब यह ऊष्मा विकिरण अन्य पिण्डों पर पड़ता है तो इसका आंशिक परावर्तन तथा आंशिक अवशोषण होता है। ऊष्मा का वह परिमाण जिसे कोई पिण्ड विकिरण द्वारा अवशोषित कर सकता है, उस पिण्ड के वर्ण (रंग) पर निर्भर करता है।
हम यह पाते हैं कि कृष्ण पिण्ड विकिरण ऊर्जा का अवशोषण तथा उत्सर्जन हलके वर्णों के पिण्डों की अपेक्षा अधिक करते हैं। इस तथ्य के हमारे दैनिक जीवन में अनेक अनुप्रयोग हैं। हम गर्मियों में श्वेत अथवा हलके वर्णों के वस्त्र पहनते हैं ताकि वे सूर्य की कम से कम ऊष्मा अवशोषित करें। परन्तु सर्दियों में हम गहरे वर्ण के वस्त्र पहनते हैं जो सूर्य की अधिक ऊष्मा को अवशोषित करके हमें उष्ण रखते हैं। खाना पकाने के बर्तनों की पेंदी को काला पोत दिया जाता है ताकि आग से वह अधिकतम ऊष्मा अवशोषित करके पकाई जाने वाली सब्जी को दें।
इसी प्रकार, ड्यूआर फ्लास्क अथवा थर्मस बोतल एक एेसी युक्ति है जो बोतल की अंतर्वस्तु तथा बाहरी परिवेश के बीच ऊष्मा स्थानांतरण को निम्नतम कर देती है। यह दोहरी दीवारों का काँच का बर्तन होता है जिसकी भीतरी तथा बाहरी दीवारों पर चाँदी का लेप होता है। भीतरी दीवार से विकिरण परावर्तित होकर बोतल की अंतर्वस्तु में वापस लौट जाते हैं। इसी प्रकार बाहरी दीवार भी बाहर से आने वाले किन्हीं भी विकिरणों को वापस परावर्तित कर देती है। दीवारों के बीच के स्थान को निर्वातित करके चालन तथा संवहन द्वारा होने वाले ऊष्मा क्षय को घटाया जाता है तथा फ्लास्क को ऊष्मा रोधी जैसे कार्क पर टिकाया जाता है। इसीलिए यह युक्ति तप्त अंतर्वस्तु (जैसे दूध) को ठंडा होने से बचाने में उपयोगी है, अथवा वैकल्पिक रूप से ठंडी अंतर्वस्तुओं (जैसे हिम) का भंडारण करने में भी उपयोगी है।
11.9.4 कृष्णिका विकिरण
अब तक हमने उष्मा विकिरण के तरंगदैर्घ्य के पक्ष का उल्लेख नहीं किया है। किसी ताप पर उष्मा विकिरण के विषय में महत्त्वपूर्ण बात यह है कि विकिरण में मात्र एक ही (या कतिपय) तरंगदैर्घ्य नहीं होते हैं, बल्कि इसमें कम तरंगदैर्घ्य से लेकर अधिक तरंगदैर्घ्य के बीच उसका सतत् स्पैक्ट्रम होता है। तथापि विभिन्न तरंगदैर्घ्याें के लिए विकिरित उष्मा की ऊर्जा की मात्रा भिन्न-भिन्न होती है। चित्र 11.8 विभिन्न तापों पर किसी कृष्णिका के एकांक क्षेत्र द्वारा एकांक तरंगदैर्घ्य पर उत्सर्जित विकिरित ऊर्जा तथा तरंगदैर्घ्य के मध्य प्रायोगिक वक्र दर्शाता है।
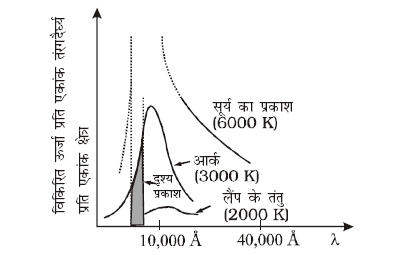
चित्र 11.8: कृष्णिका द्वारा विभिन्न तापों पर उत्सर्जित ऊर्जा तथा तंरगदैर्घ्य के मध्य खींचे गए वक्र।
इस बात पर गौर कीजिए कि तरंगदैर्घ्य λm जिसके लिए विकिरित ऊर्जा सर्वाधिक है, ताप बढ़ने पर घटती है। λm तथा T के मध्य संबंध को वीन-विस्थापन नियम कहते हैं-
λm T = नियतांक (11.15)
नियतांक (वीन नियतांक) का मान 2.9 × 10–3 m K होता है। यह नियम इस बात की व्याख्या करता है कि जब लोहे के किसी टुकड़े को अग्नि में गर्म करते हैं, तो उसका रंग पहले हलका लाल, फिर रक्ताभ पीला और अंत में सफेद क्यों हो जाता है। वीन-नियम का उपयोग खगोलीय पिंडों, जैसे- चाँद, सूर्य या अन्य तारों की सतह के ताप का अनुमान लगाने में करते हैं। चंद्रमा से प्रकाश की सबसे अधिक तीव्रता 14 µm तरंगदैर्घ्य के आसपास होती है। वीन-नियम से चन्द्रमा की सतह का ताप 200 K अनुमानित किया गया है। सौर विकिरण की अधिकतम तीव्रता λm = 4753 Å पर होती है। इसके अनुसार
T = 6060 K । याद रखिए कि यह ताप सूर्य की सतह का है न कि उसके आंतरिक (भीतरी) भाग का।
चित्र 11.18 में दर्शाए गए कृष्णिका विकिरण वक्रों से संबंधित सर्वाधिक विशिष्ट बात यह है कि ये वक्र सार्वत्रिक होते हैं। ये कृष्णिका के केवल ताप पर निर्भर करते हैं न कि उसके आकार, आकृति या पदार्थ पर। बीसवीं शताब्दी के प्रारंभ में कृष्णिका के विकिरण को सैद्धांतिक रूप से व्याख्या करने के लिए जो प्रयास किए गए उन्हाेंने भौतिकी में क्वांटम क्रांति की प्रेरणा दी। इसके विषय में आप आगे अपने पाठ्यक्रम
में पढ़ेंगे।
विकिरण द्वारा ऊर्जा बिना माध्यम के (अर्थात् निर्वात में) बहुत दूरियों तक स्थानान्तरित की जा सकती है। परम ताप T पर किसी वस्तु द्वारा उत्सर्जित कुल विद्युत चुम्बकीय ऊर्जा उसके आकार, उसकी उत्सर्जित करने की क्षमता (जिसे उत्सर्जकता कहते हैं) और विशेष रूप से उसके ताप के समानुपाती होती है। एक वस्तु के लिए जो पूर्ण उत्सर्जक है, प्रति इकाई समय में उत्सर्जित ऊर्जा (H) होगी-
H = AσT4 (11.16)
जहाँ A वस्तु का क्षेत्रफल है तथा T उसका परमताप है। इस सम्बन्ध को पहले स्टेफॉन ने प्रयोगों से निकाला तथा बाद में बोल्ट्समान ने सैद्धांतिक रूप से सिद्ध किया। इसे स्टेफॉन बोल्ट्समान नियम तथा नियतांक σ को स्टेफॉन-बोल्टसमान नियतांक कहते हैं। SI मात्रक पद्धति में इसका मान 5.67 × 10–8 W m–2 K–4 होता है। अधिकतर वस्तुएँ समीकरण (A2) में दी गई उष्मा की दर का कुछ अंश ही उत्सर्जित करती हैं। दीप कज्जल जैसे पदार्थाें द्वारा उत्सर्जित उष्मा की दर ही इस सीमा के करीब होती है। इस कारण ‘एक’ विमाहीन अंश e जिसे वस्तु की उत्सर्जकता कहते हैं, को परिभाषित करते हैं और समीकरण (11.16) को निम्न प्रकार से व्यक्त करते हैं–
H = AeσT4 (11.17)
किसी आदर्श विकिरक के लिए e = 1 होता है। उदाहरण के तौर पर टंगस्टन लैम्प के लिए e का मान लगभग 0.4 होता है। इस तरह 0.3 cm2 पृष्ठ क्षेत्रफल तथा 3000K ताप वाला टंगस्टन लैम्प निम्नलिखित दर से उष्मा विकिरित करेगा-
H = 0.3 × 10–4 × 0.4 × 5.67 × 10–8 (3000)4 = 60 W
T ताप वाली कोई वस्तु जिसके चारों ओर के वातावरण का ताप TS है, ऊर्जा का अवशोषण तथा उत्सर्जन दोनों करती है। अतः किसी आदर्श विकिरक से विकिरित उष्मा के क्षय (हानि) की नेट दर निम्नलिखित सूत्र से व्यक्त की जाएगी –
H = σA (T4 – Ts4)
उस वस्तु के लिए जिसकी उत्सर्जकता e है, उपरोक्त सूत्र निम्न प्रकार से रूपांतरित हो जाएगा –
H = eσ A (T4 – Ts4) (11.18)
उदाहरणार्थ, आइए, हम अपने शरीर से उत्सर्जित उष्मा की गणना करें। मान लीजिए किसी व्यक्ति के शरीर का पृष्ठ क्षेत्रफल लगभग 1.9 m2 है तथा कमरे का ताप 22°C है। जैसाकि हम जानते हैं, शरीर का आंतरिक ताप 37°C होता है। माना, त्वचा का ताप 20°C है। प्रासंगिक विद्युत चुम्बकीय विकिरण क्षेत्र में त्वचा की उत्सर्जकता 'e' लगभग 0.97 है। इस उदाहरण से उष्मा हानि की दर–
H = 5.67 × 10–8 × 1.9 × 0.97 × {(301)4 – (295)4}
= 66.4 W
जो विराम अवस्था में शरीर द्वारा उत्पन्न ऊर्जा की दर (120 W) के आधे से थोड़ा अधिक है। उष्मा के इस क्षय को कारगर तरीके से रोकने के लिए आधुनिक आर्कटिक कपड़े (आम कपड़ों से अच्छे) इस प्रकार बनाए जाते हैं कि शरीर की त्वचा के साथ एक अतिरिक्त पतली चमकदार धातुई परत होती है, जो शरीर के विकिरण को परावर्तित कर देती है।
11.9.5 ग्रीनहाउस प्रभाव
पृथ्वी की सतह उष्मा विकिरण का स्रोत है, क्योंकि यह सूर्य से प्राप्त ऊर्जा अवशोषित करती है। इस विकिरण का तरंगदैर्घ्य, दीर्घ तरंगदैर्घ्य (अवरक्त) क्षेत्र में होता है, पंरतु इस विकिरण का अधिकतम अंश ग्रीनहाउस गैसों द्वारा अवशोषित हो जाता है। ये गैस हैं-कार्बन डाइअॉक्साइड (CO2), मेथैन (CH4), नाइट्रसअॉक्साइड (N2O), क्लोरोफ्लोरोकार्बन (CFxClx) तथा क्षोभमंडलीय ओज़ोन (O3)। इसके फलस्वरूप वायुमण्डल गर्म हो जाता है, जो पृथ्वी को और अधिक ऊर्जा देती है और पृथ्वी की सतह और गर्म हो जाती है। इससे पृथ्वी की सतह से विकिरण की तीव्रता बढ़ जाती है। उपरोक्त वर्णित प्रक्रियाओं का चक्र तब तक चलता है, जब तक अवशोषण के लिए कोई ऊर्जा शेष न हो। नेट प्रभाव, पृथ्वी की सतह तथा वायुमण्डल का और गर्म होना है। इसे ग्रीनहाउस प्रभाव कहते हैं। यदि यह प्रभाव नहीं होता तो पृथ्वी का ताप –18°C होता।
मानविक गतिविधियों के कारण वायुमंडल में ग्रीनहाउस गैसों की सांद्रता बढ़ गई है, जिससे पृथ्वी और गर्म हो जाती है। एक अनुमान के अनुसार सांद्रता में इस वृद्धि से इस शताब्दी के आंरभ से अब तक पृथ्वी का ताप औसतन 0.3°C से 0.6°C बढ़ गया है। अगली शताब्दी के मध्य तक भूमण्डलीय ताप वर्तमान की तुलना में 1°C से 3°C अधिक होगा। इस विश्वव्यापी उष्णता से मानव जीवन, पौधों तथा जानवरों को खतरा है। इस उष्णता से बर्फ़ छत्रक तेज़ी से पिघल रहे हैं, समुद्र तल ऊपर जा रहा है तथा मौसम का पैटर्न बदल रहा है। कई तटीय शहरों पर डूबने का खतरा मंडरा रहा है। ग्रीनहाउस प्रभाव से रेगिस्तान का प्रसार हो सकता है। पूरे विश्व में विश्वव्यापी उष्णता के प्रभाव को कम करने के प्रयास किए जा रहे हैं।
11.10 न्यूटन का शीतलन नियम
हम सभी यह जानते हैं कि तप्त जल अथवा दूध मेज पर यदि रखा छोड़ दें तो वह धीरे-धीरे शीतल होना आरंभ कर देता है। अंततः वह परिवेश के ताप पर पहुँच जाता है। कोई दी गई वस्तु अपने परिवेश से ऊष्मा का विनिमय करके कैसे शीतल हो सकती है, इसका अध्ययन करने के लिए आइए निम्नलिखित क्रियाकलाप करें।
क्रियाकलाप 11.4
एक विडोलक सहित ऊष्मामापी में कुछ जल, मान लें 300 mL लीजिए और इसे दो छिद्र वाले ढक्कन से ढक दीजिए। ढक्कन के एक छिद्र में विडोलक तथा दूसरे छिद्र में तापमापी लगाइए तथा यह सुनिश्चित कीजिए कि तापमापी का बल्ब जल में डूब जाए। तापमापी का पाठ्यांक नोट कीजिए। यह पाठ्यांक T1 परिवेश का ताप है। ऊष्मामापी के जल को इतना गर्म कीजिए कि इसका ताप कक्ष ताप (अर्थात् परिवेश के ताप) से लगभग 40 °C अधिक तक पहुँच जाए। तत्पश्चात् ऊष्मा स्रोत को हटाकर जल को गर्म करना बंद कीजिए। विराम घड़ी चलाइए तथा प्रत्येक नियत समय अंतराल जैसे 1 मिनट के पश्चात् विडोलक से धीरे-धीरे विडोलित करते हुए तापमापी के पाठ्यांक नोट कीजिए। जल का ताप परिवेश के ताप से लगभग 5 °C अधिक रहने तक पाठ्यांक नोट करते रहिए। मान लीजिए यह पाठ्यांक (T2) है। तत्पश्चात् ताप ∆T = T2 – T1 को y–अक्ष के अनुदिश लेकर इसके प्रत्येक मान के लिए तदनुरूपी t के मान को x-अक्ष के अनुदिश लेकर ग्राफ आलेखित करिए
(चित्र 11.19)।
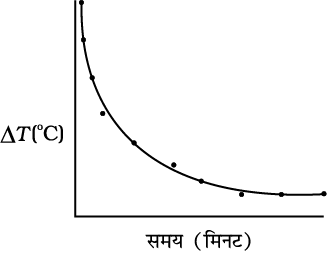
चित्र 11.19 समय के साथ तप्त जल के शीतलन को दर्शाने वाला वक्र।
ग्राफ से आप यह निष्कर्ष निकाल सकते हैं कि किस प्रकार तप्त जल का शीतलन उसके अपने तथा अपने परिवेश के तापों के बीच अंतर पर निर्भर करता है। आप यह भी नोट करेंगे कि आरंभ में शीतलन की दर उच्च है तथा वस्तु के ताप में कमी होने पर यह दर घट जाती है।
उपरोक्त क्रियाकलाप यह दर्शाता है कि कोई तप्त पिण्ड ऊष्मा विकिरण के रूप में अपने परिवेश को ऊष्मा खो देता है। यह ऊष्मा-क्षय की दर पिण्ड तथा उसके परिवेश के तापों के अंतर पर निर्भर करती है। न्यूटन एेसे पहले वैज्ञानिक थे जिन्होंने किसी दिए गए अंतःक्षेत्र के भीतर रखे किसी पिण्ड द्वारा लुप्त ऊष्मा तथा उसके ताप के बीच संबंध का योजनाबद्ध अध्ययन किया।
न्यूटन के शीतलन नियम के अनुसार किसी पिण्ड के ऊष्मा क्षय की दर, – dQ/dt पिण्ड तथा उसके परिवेश के तापों के अंतर ∆T = (T2–T1) के अनुक्रमानुपाती होती है। यह नियम केवल लघु तापांतर के लिए ही वैध है। विकिरण द्वारा ऊष्मा-क्षय पिण्ड के पृष्ठ की प्रकृति तथा खुले पृष्ठ के क्षेत्रफल पर भी निर्भर करता है। अतः हम लिख सकते हैं कि
 (11.19)
(11.19)
यहाँ k एक धनात्मक नियतांक है जो पिण्ड के पृष्ठ के क्षेत्रफल तथा उसकी प्रकृति पर निर्भर करता है। मान लीजिए m द्रव्यमान तथा विशिष्ट ऊष्मा धारिता s का कोई पिण्ड T2 ताप पर है। मान लीजिए परिवेश का ताप T1 है। मान लीजिए पिण्ड का ताप एक लघु समय अंतराल dt में dT2 कम हो जाता है, तब लुप्त ऊष्मा का परिमाण
dQ = ms dT2
∴ ऊष्मा क्षय की दर
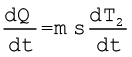 (11.20)
(11.20)
समीकरणों (11.15) तथा (11.16) से हमें प्राप्त होता है
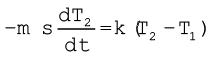
 (11.21)
(11.21)
यहाँ K = k/(ms)
समाकलित करने पर
loge (T2 – T1) = – Kt + c (11.22)
अथवा T2 = T1 + C′ e–Kt; यहाँ C′ = ec (11.23)
समीकरण (11.23) की सहायता से एक विशिष्ट ताप परिसर के आद्योपांत शीतलन का समय परिकलित किया जा सकता है।
लघु तापांतरों के लिए, चालन, संवहन तथा विकिरण के संयुक्त प्रभाव के कारण शीतलन की दर तापांतर के अनुक्रमानुपाती होती है। किसी विकिरक से कमरे में ऊष्मा स्थानांतरण, कमरे की दीवारों से पार होकर ऊष्मा-क्षति अथवा मेज पर प्याले में रखी चाय के शीतलन में यह एक वैध सन्निकटन है।
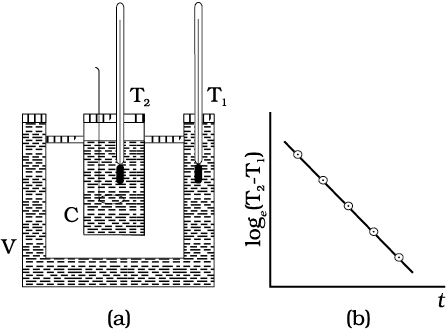
चित्र 11.20 न्यूटन के शीतलन नियम का सत्यापन।
चित्र 11.20(a) में दर्शायी गई प्रायोगिक व्यवस्था की सहायता से न्यूटन के शीतलन नियम का सत्यापन किया जा सकता है। इसमें दोहरी दीवारों वाला एक बर्तन (V) जिसकी दीवारों के बीच जल भरा होता है, लिया जाता है। इस दोहरी दीवारों वाले बर्तन में तप्त जल से भरा ताँबे का ऊष्मामापी (C) रखते हैं। इसमें दो तापमापियों का उपयोग किया जाता है, जिसमें तापमापी T1 के द्वारा दोहरी दीवारों के बीच भरे उष्ण जल का ताप, तथा तापमापी T2 के द्वारा ऊष्मामापी में भरे जल का ताप मापते हैं। ऊष्मामापी के तप्त जल का ताप एक नियमित अंतराल के पश्चात् मापा जाता है। समय t तथा loge (T2–T1) [या ln
(T2–T1 )] के बीच ग्राफ आलेखित किया जाता है जिसकी प्रकृति चित्र 11.19(b) में दर्शाए अनुसार ऋणात्मक प्रवणता की एक सरल रेखा होती है। यह समीकरण 11.22 की पुष्टि करती है।
उदाहरण 11.8 किसी बर्तन में भरे तप्त भोजन का ताप 2 मिनट में 94 °C से 86 °C हो जाता है जबकि कक्ष-ताप 20 °C है। 71 °C से 69 °C तक ताप के गिरने में कितना समय लगेगा?

सारांश
1. ऊष्मा ऊर्जा का एक रूप है जो किसी पिण्ड तथा उसके परिवर्ती माध्यम के बीच उनमें तापांतर के कारण प्रवाहित होती है। किसी पिण्ड की तप्तता की कोटि मात्रात्मक रूप में ताप द्वारा निरूपित होती है।
2. किसी ताप मापन युक्ति (तापमापी) में मापन योग्य किसी एेसे गुण (जिसे तापमापीय गुण कहते हैं) का उपयोग किया जाता है, जिसमें ताप के साथ परिवर्तन होता है। विभिन्न तापमापी में भिन्न-भिन्न ताप मापक्रम बनते हैं। कोई ताप मापक्रम बनाने के लिए दो नियत बिंदुओं का चयन किया जाता है तथा उन्हें कुछ यादृच्छिक ताप मान दिए जाते हैं। ये दो संख्याएँ मापक्रम के मूल बिंदु तथा उसके मात्रक की आमाप को निश्चित करती हैं।
3. सेल्सियस ताप (tC) तथा फारेनहाइट ताप (tF) में यह संबंध होता है: tF = (9/5) tC + 32
4. दाब (P), आयतन (V) तथा परम ताप (T) में संबंध दर्शाने वाली आदर्श गैस समीकरण इस प्रकार व्यक्त की जाती हैः
PV = µRT
यहाँ µ मोल की संख्या तथा R सार्वत्रिक गैस नियतांक है।
5. परम ताप मापक्रम में, मापक्रम का शून्य, ताप के परम शून्य को व्यक्त करता है। यह वह ताप है जिस पर प्रत्येक पदार्थ में न्यूनतम संभावित आण्विक सक्रियता होती है। केल्विन परम ताप मापक्रम (T ) के मात्रक का आकार सेल्सियस ताप मापक्रम (tc ) के मात्रक के आकार के बराबर होता है परन्तु इनके मूल बिंदुओं में अंतर होता हैः
tC = T – 273.15
6. रैखिक प्रसार गुणांक (αl ) तथा आयतन प्रसार गुणांक (αv ) को इस प्रकार परिभाषित किया जाता हैः
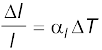
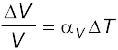
यहाँ ∆l तथा ∆V ताप में ∆T का परिवर्तन होने पर क्रमशः लंबाई l तथा आयतन V में परिवर्तन को निर्दिष्ट करते हैं। इनमें निम्नलिखित संबंध हैः
αv = 3 αl
7. किसी पदार्थ की विशिष्ट ऊष्मा धारिता को इस प्रकार परिभाषित किया जाता हैः
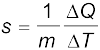
यहाँ m पदार्थ का द्रव्यमान तथा ∆Q पदार्थ के ताप में ∆T का परिवर्तन करने के लिए आवश्यक ऊर्जा की मात्रा है। किसी पदार्थ की मोलर विशिष्ट ऊष्मा धारिता को इस प्रकार परिभाषित किया जाता हैः
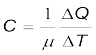
यहाँ µ पदार्थ के मोल की संख्या है।
8. संगलन की गुप्त ऊष्मा (Lf) ऊष्मा की वह मात्रा है जो किसी पदार्थ के एकांक द्रव्यमान को समान ताप तथा दाब पर ठोस अवस्था से द्रव अवस्था में परिवर्तित करने के लिए आवश्यक होती है। वाष्पन की गुप्त ऊष्मा (Lv) ऊष्मा की वह मात्रा है जो किसी पदार्थ के एकांक द्रव्यमान को ताप व दाब में बिना कोई परिवर्तन किए द्रव अवस्था से वाष्प अवस्था में परिवर्तित करने के लिए आवश्यक होती है।
9. ऊष्मा-स्थानांतरण की तीन विधियाँ हैं - चालन, संवहन तथा विकिरण।
10. चालन में किसी पिण्ड के आस-पास के भागों के बीच ऊष्मा का स्थानांतरण आण्विक संघट्टनों द्वारा संपन्न होता है परन्तु इसमें द्रव्य का प्रवाह नहीं होता। किसी L लंबाई तथा Aअनुप्रस्थ काट क्षेत्रफल की छड़, जिसके दोनों सिरों के तापों को TC तथा TD पर स्थापित किया गया है, द्वारा प्रवाहित ऊष्मा की दर
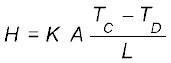
यहाँ K छड़ के पदार्थ की ऊष्मा चालकता है।
11. न्यूटन के शीतलन नियम के अनुसार किसी पिण्ड के शीतलन की दर परिवेश के ऊपर वस्तु के ताप-आधिक्य के अनुक्रमानुपाती होती है
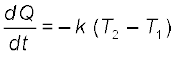
यहाँ T1 परिवेशी माध्यम का ताप तथा T2 पिण्ड का ताप है।

विचारणीय विषय
1. केल्विन ताप (T ) तथा सेल्सियस ताप tc को जोड़ने वाला संबंध इस प्रकार हैः
T = tc + 273.15
तथा जल के त्रिक बिंदु के लिए (चयन द्वारा) T = 273.16 K का निर्धारण यथार्थ संबंध है। इस चयन के साथ सेल्सियस मापक्रम पर हिम का गलनांक तथा जल का क्वथनांक (दोनाें 1 atm दाब पर) क्रमशः 0 °C तथा 100 °C के अत्यधिक निकट हैं परन्तु यथार्थ रूप से इनके बराबर नहीं हैं। मूल सेल्सियस ताप मापक्रम में पिछले नियत बिंदु (चयन द्वारा) तथ्यतः 0 °C तथा 100 °C थे, परन्तु अब नियत बिंदुओं के चयन के लिए जल के त्रिक बिंदु को अच्छा माना जाता है क्योंकि इसका ताप अद्वितीय है।
2. जब कोई द्रव वाष्प के साथ साम्य में होता है तो समस्त निकाय का दाब तथा ताप समान होता है तथा साम्यावस्था में दोनों प्रावस्थाओं के मोलर आयतनों में अंतर (घनत्वों में अंतर) होता है। यह सभी निकायों पर लागू होता है चाहे उसमें कितनी भी प्रावस्थाएँ साम्य में हों।
3. ऊष्मा स्थानांतरण में सदैव दो निकायों अथवा एक ही निकाय के दो भागों के बीच तापांतर सम्मिलित होता है। एेसा ऊर्जा स्थानांतरण जिसमें किसी भी रूप में तापांतर सम्मिलित नहीं होता, वह ऊष्मा नहीं है।
4. संवहन में किसी तरल के भीतर उसके भागों में असमान ताप होने के कारण द्रव्य का प्रवाह सम्मिलित होता है। किसी टोंटी से गिरते जल के नीचे रखी किसी तप्त छड़ की ऊष्मा का क्षय छड़ के पृष्ठ तथा जल के बीच चालन के कारण होता है जल के भीतर संवहन द्वारा नहीं होता।
अभ्यास
11.1 निअॉन तथा CO2 के त्रिक बिंदु क्रमशः 24.57 K तथा 216.55 K हैं। इन तापों को सेल्सियस तथा फारेनहाइट मापक्रमों में व्यक्त कीजिए।
11.2 दो परम ताप मापक्रमों A तथा B पर जल के त्रिक बिंदु को 200 A तथा 350 B द्वारा परिभाषित किया गया है। TA तथा TB में क्या संबंध है?
11.3 किसी तापमापी का ओम में विद्युत प्रतिरोध ताप के साथ निम्नलिखित सन्निकट नियम के अनुसार परिवर्तित होता है
R = Ro [1 + α (T – To )]
यदि तापमापी का जल के त्रिक बिंदु 273.16 K पर प्रतिरोध 101.6 Ω तथा लैड के सामान्य संगलन बिंदु (600.5 K) पर प्रतिरोध 165.5 Ω है तो वह ताप ज्ञात कीजिए जिस पर तापमापी का प्रतिरोध 123.4 Ω है।
11.4 निम्नलिखित के उत्तर दीजिएः
(a) आधुनिक तापमिति में जल का त्रिक बिंदु एक मानक नियत बिंदु है, क्यों? हिम के गलनांक तथा जल के क्वथनांक को मानक नियत बिंदु मानने में (जैसा कि मूल सेल्सियस मापक्रम में किया गया था।) क्या दोष है?
(b) जैसा कि ऊपर वर्णन किया जा चुका है कि मूल सेल्सियस मापक्रम में दो नियत बिंदु थे जिनको क्रमशः 0 °C तथा 100 °C संख्याएँ निर्धारित की गई थीं। परम ताप मापक्रम पर दो में से एक नियत बिंदु जल का त्रिक बिंदु लिया गया है जिसे केल्विन परम ताप मापक्रम पर संख्या 273.16 K निर्धारित की गई है। इस मापक्रम (केल्विन परम ताप) पर अन्य नियत बिंदु क्या है?
(c) परम ताप (केल्विन मापक्रम) T तथा सेल्सियस मापक्रम पर ताप tc में संबंध इस प्रकार हैः
tc = T – 273.15
इस संबंध में हमने 273.15 लिखा है 273.16 क्यों नहीं लिखा?
(d) उस परम ताप मापक्रम पर, जिसके एकांक अंतराल का आमाप फारेनहाइट के एकांक अंतराल की आमाप के बराबर है, जल के त्रिक बिंदु का ताप क्या होगा?
11.5 दो आदर्श गैस तापमापियों A तथा B में क्रमशः अॉक्सीजन तथा हाइड्रोजन प्रयोग की गई है। इनके प्रेक्षण निम्नलिखित है:
ताप दाब दाब
तापमापी A में तापमापी B में
जल का त्रिक बिंदु 1.250 × 105 Pa 0.200 × 105 Pa
सल्फर का सामान्य गलनांक 1.797 × 105 Pa 0.287 × 105 Pa
(a) तापमापियों A तथा B के द्वारा लिए गए पाठ्यांकों के अनुसार सल्फर के सामान्य गलनांक के परमताप क्या हैं?
(b) आपके विचार से तापमापियों A तथा B के उत्तरों में थोड़ा अंतर होने का क्या कारण है? (दोनों तापमापियों में कोई दोष नहीं है)। दो पाठ्यांकों के बीच की विसंगति को कम करने के लिए इस प्रयोग में और क्या प्रावधान आवश्यक हैं?
11.6 किसी 1m लंबे स्टील के फीते का यथार्थ अंशांकन 27.0 °C पर किया गया है। किसी तप्त दिन जब ताप 45°C था तब इस फीते से किसी स्टील की छड़ की लंबाई 63.0 cm मापी गई। उस दिन स्टील की छड़ की वास्तविक लंबाई क्या थी? जिस दिन ताप 27.0 °C होगा उस दिन इसी छड़ की लंबाई क्या होगी? स्टील का रेखीय प्रसार गुणांक = 1.20 × 10–5 K–1 ।
11.7 किसी बड़े स्टील के पहिए को उसी पदार्थ की किसी धुरी पर ठीक बैठाना है। 27°C पर धुरी का बाहरी व्यास 8.70 cm तथा पहिए के केंद्रीय छिद्र का व्यास 8.69 cm है। सूखी बर्फ द्वारा धुरी को ठंडा किया गया है। धुरी के किस ताप पर पहिया धुरी पर चढ़ेगा? यह मानिए कि आवश्यक ताप परिसर में स्टील का रैखिक प्रसार गुणांक नियत रहता हैः αस्टील = 1.20×10–5K–1।
11.8 ताँबे की चादर में एक छिद्र किया गया है। 27.0 °C पर छिद्र का व्यास 4.24 cm है। इस धातु की चादर को 227 °C तक तप्त करने पर छिद्र के व्यास में क्या परिवर्तन होगा? ताँबे का रेखीय प्रसार गुणांक
= 1.70 × 10–5 K–1।
11.9 27°C पर 1.8 cm लंबे किसी ताँबे के तार को दो दृढ़ टेकों के बीच अल्प तनाव रखकर थोड़ा कसा गया है। यदि तार को –39 °C ताप तक शीतित करें तो तार में कितना तनाव उत्पन्न हो जाएगा? तार का व्यास 2.0 mm है। पीतल का रेखीय प्रसार गुणांक = 2.0 × 10–5 K–1, पीतल का यंग प्रत्यास्थता
गुणांक = 0.91 × 1011 Pa।
11.10 50 cm लंबी तथा 3.0 mm व्यास की किसी पीतल की छड़ को उसी लंबाई तथा व्यास की किसी स्टील की छड़ से जोड़ा गया है। यदि ये मूल लंबाइयाँ 40°C पर हैं, तो 250 °C पर संयुक्त छड़ की लंबाई में क्या परिवर्तन होगा? क्या संधि पर कोई तापीय प्रतिबल उत्पन्न होगा? छड़ के सिरों को प्रसार के लिए मुक्त रखा गया है।
(ताँबे तथा स्टील के रेखीय प्रसार गुणांक क्रमशः = 2.0 × 10–5 K–1, स्टील = 1.2 × 10–5 K–1 हैं।)
11.11 ग्लिसरीन का आयतन प्रसार गुणांक 49 × 10–5 K–1 है। ताप में 30 °C की वृद्धि होने पर इसके घनत्व में क्या आंशिक परिवर्तन होगा?
11.12 8.0 kg द्रव्यमान के किसी एेलुमिनियम के छोटे ब्लॉक में छिद्र करने के लिए किसी 10 kW की बरमी का उपयोग किया गया है। 2.5 मिनट में ब्लॉक के ताप में कितनी वृद्धि हो जाएगी। यह मानिए कि 50% शक्ति तो स्वयं बरमी को गर्म करने में खर्च हो जाती है अथवा परिवेश में लुप्त हो जाती है। एेलुमिनियम की विशिष्ट ऊष्मा धारिता = 0.91 J g–1 K–1 है।
11.13 2.5 kg द्रव्यमान के ताँबे के गुटके को किसी भट्ठी में 500 °C तक तप्त करने के पश्चात् किसी बड़े हिम-ब्लॉक पर रख दिया जाता है। गलित हो सकने वाली हिम की अधिकतम मात्रा क्या है? ताँबे की विशिष्ट ऊष्मा धारिता = 0.39 J g–1 K–1; बर्फ की संगलन ऊष्मा = 335 J g–1 ।
11.14 किसी धातु की विशिष्ट ऊष्मा धारिता के प्रयोग में 0.20 kg के धातु के गुटके को 150 °C पर तप्त करके, किसी ताँबे के ऊष्मामापी (जल तुल्यांक = 0.025 kg), जिसमें 27 °C का 150 cm3 जल भरा है, में गिराया जाता है। अंतिम ताप 40 °C है। धातु की विशिष्ट ऊष्मा धारिता परिकलित कीजिए। यदि परिवेश में क्षय ऊष्मा उपेक्षणीय न मानकर परिकलन किया जाता है, तब क्या आपका उत्तर धातु की विशिष्ट ऊष्मा धारिता के वास्तविक मान से अधिक मान दर्शाएगा अथवा कम?
11.15 कुछ सामान्य गैसों के कक्ष ताप पर मोलर विशिष्ट ऊष्मा धारिताओं के प्रेक्षण नीचे दिए गए हैंः
गैस मोलर विशिष्ट ऊष्मा धारिता (Cv )
(cal mo1–1 K–1)
हाइड्रोजन 4.87
नाइट्रोजन 4.97
अॉक्सीजन 5.02
नाइट्रिक अॉक्साइड 4.99
कार्बन मोनोक्साइड 5.01
क्लोरीन 6.17
इन गैसों की मापी गई मोलर विशिष्ट ऊष्मा धारिताएँ एक परमाणुक गैसों की मोलर विशिष्ट ऊष्मा धारिताओं से सुस्पष्ट रूप से भिन्न हैं। प्रतीकात्मक रूप में किसी एक परमाणुक गैस की मोलर विशिष्ट ऊष्मा धारिता 2.92 cal/mol K होती है। इस अंतर का स्पष्टीकरण कीजिए। क्लोरीन के लिए कुछ अधिक मान (शेष की अपेक्षा) होने से आप क्या निष्कर्ष निकालते हैं?
11.16 101°F ताप ज्वर से पीड़ित किसी बच्चे को एन्टीपायरिन (ज्वर कम करने की दवा) दी गई जिसके कारण उसके शरीर से पसीने के वाष्पन की दर में वृद्धि हो गई। यदि 20 मिनट में ज्वर 98 °F तक गिर जाता है तो दवा द्वारा होने वाले अतिरिक्त वाष्पन की औसत दर क्या है? यह मानिए कि ऊष्मा ह्रास का एकमात्र उपाय वाष्पन ही है। बच्चे का द्रव्यमान 30 kg है। मानव शरीर की विशिष्ट ऊष्मा धारिता जल की विशिष्ट ऊष्मा धारिता के लगभग बराबर है तथा उस ताप पर जल के वाष्पन की गुप्त ऊष्मा 580 cal g–1 है।
11.17 थर्मोकोल का बना ‘हिम बॉक्स’ विशेषकर गर्मियों में कम मात्रा के पके भोजन के भंडारण का सस्ता तथा दक्ष साधन है। 30 cm भुजा के किसी हिम बॉक्स की मोटाई 5.0 cm है। यदि इस बॉक्स में 4.0 kg हिम रखा है तो 6 h के पश्चात् बचे हिम की मात्रा का आकलन कीजिए। बाहरी ताप 45 °C है तथा थर्मोकोल की ऊष्मा चालकता 0.01 J s–1 m–1 K–1 है। (हिम की संगलन ऊष्मा = 335 × 103 J kg–1)
11.18 किसी पीतल के बॉयलर की पेंदी का क्षेत्रफल 0.15 m2 तथा मोटाई 1.0 cm है। किसी गैस स्टोव पर रखने पर इसमें 6.0 kg/min की दर से जल उबलता है। बॉयलर के संपर्क की ज्वाला के भाग का ताप आकलित कीजिए। पीतल की ऊष्मा चालकता = 109 J s–1 m–1 K–1; जल की वाष्पन ऊष्मा = 2256 × 103 J kg–1 है।
11.19 स्पष्ट कीजिए कि क्यों -
(a) अधिक परावर्तकता वाले पिण्ड अल्प उत्सर्जक होते हैं।
(b) कंपकंपी वाले दिन लकड़ी की ट्रे की अपेक्षा पीतल का गिलास कहीं अधिक शीतल प्रतीत होता है।
(c) कोई प्रकाशिक उत्तापमापी (उच्च तापों को मापने की युक्ति), जिसका अंशांकन किसी आदर्श कृष्णिका के विकिरणों के लिए किया गया है, खुले में रखे किसी लाल तप्त लोहे के टुकड़े का ताप काफी कम मापता है, परन्तु जब उसी लोहे के टुकड़े को भट्ठी में रखते हैं, तो वह ताप का सही मान मापता है।
(d) बिना वातावरण के पृथ्वी अशरणीय शीतल हो जाएगी।
(e) भाप के परिचालन पर आधारित तापन निकाय तप्त जल के परिचालन पर आधारित निकायों की अपेक्षा भवनों को उष्ण बनाने में अधिक दक्ष होते हैं।
11.20 किसी पिण्ड का ताप 5 मिनट में 80 °C से 50 °C हो जाता है। यदि परिवेश का ताप 20°C है, तो उस समय का परिकलन कीजिए जिसमें उसका ताप 60 °C से 30 °C हो जाएगा।
अतिरिक्त अभ्यास
11.21 CO2 के P-T प्रावस्था आरेख पर आधारित निम्नलिखित प्रश्नों के उत्तर दीजिए:
(a) किस ताप व दाब पर CO2 की ठोस, द्रव तथा वाष्प प्रावस्थाएँ साम्य में सहवर्ती हो सकती हैं?
(b) CO2 के गलनांक तथा क्वथनांक पर दाब में कमी का क्या प्रभाव पड़ता है?
(c) CO2 के लिए क्रांतिक ताप तथा दाब क्या हैं? इनका क्या महत्त्व है?
(d) (a) –70 °C ताप व 1 atm दाब, (b) –60 °C ताप व 10 atm दाब, (c) 15 °C ताप व 56 atm दाब पर CO2 ठोस, द्रव अथवा गैस में से किस अवस्था में होती है?
11.22 CO2 के P – T प्रावस्था आरेख पर आधारित निम्नलिखित प्रश्नों के उत्तर दीजिए:
(a) 1 atm दाब तथा –60 °C ताप पर CO2 का समतापी संपीडन किया जाता है? क्या यह द्रव प्रावस्था में जाएगी?
(b) क्या होता है जब 4 atm दाब पर CO2 का दाब नियत रखकर कक्ष ताप पर शीतन किया जाता है?
(c) 10 atm दाब तथा –65 °C ताप पर किसी दिए गए द्रव्यमान की ठोस CO2 को दाब नियत रखकर कक्ष ताप तक तप्त करते समय होने वाले गुणात्मक परिवर्तनों का वर्णन कीजिए।
(d) CO2 को 70 °C तक तप्त तथा समतापी संपीडित किया जाता है। आप प्रेक्षण के लिए इसके किन गुणों में अंतर की अपेक्षा करते हैं?
