Table of Contents
तरलों के यांत्रिकी गुण
10.1 भूमिका
10.2 दाब
10.3 धारारेखी प्रवाह
10.4 बर्नूली का सिद्धांत
10.5 श्यानता
10.6 पृष्ठ तनाव
सारांश
विचारणीय विषय
अभ्यास
10.1 भूमिका
इस अध्याय में हम द्रवों तथा गैसों के कुछ सामान्य भौतिक गुणों का अध्ययन करेंगे। द्रव तथा गैस प्रवाहित होती हैं अतः तरल कहलाती है। मूल रूप में इस गुण के आधार पर हम द्रवों एवं गैसों का ठोसों से विभेद करते हैं।
हमारे चारों ओर हर स्थान पर तरल हैं। पृथ्वी के ऊपर वायु का आवरण है और इसके पृष्ठ का दो-तिहाई भाग जल से आच्छादित है। जल केवल हमारे जीवन के अस्तित्व के लिए ही आवश्यक नहीं है वरन् सभी स्तनपायी जंतुओं के शरीर का अधिकांश भाग जल है। पौधों सहित सभी सजीवों में होने वाली समस्त प्रक्रियाओं में तरलों की परोक्ष भूमिका होती है। अतः तरलों के व्यवहार व गुणों को समझना बहुत महत्त्वपूर्ण है।
तरल ठोसों से कैसे भिन्न हैं? द्रवों तथा गैसों में क्या-क्या समानता है? ठोसों के विपरीत तरल की अपनी कोई निश्चित आकृति नहीं होती। ठोसों एवं द्रवों का निश्चित आयतन होता है जबकि गैस पात्र के कुल आयतन को भर देती है। पिछले अध्याय में हमने पढ़ा है कि प्रतिबल द्वारा ठोसों के आयतन में परिवर्तन किया जा सकता है। ठोस, द्रव अथवा गैस का आयतन इस पर लगने वाले प्रतिबल अथवा दाब पर निर्भर है। जब हम ठोस या द्रव के निश्चित आयतन की बात करते हैं, तब हमारा तात्पर्य वायुमंडलीय दाब के अधीन आयतन से होता है। गैसों की तुलना में बाह्य दाबांतर से ठोस या द्रव के आयतन में परिवर्तन बहुत कम होता है। दूसरे शब्दों में गैसों की अपेक्षा ठोस एवं द्रवों की संपीड्यता काफी कम होती है।
अपरूपण (विरूपण) प्रतिबल ठोस के आयतन में परिवर्तन किए बिना उसकी आकृति बदल सकता है। तरलों का मूल गुण यह है कि वह विरूपण प्रतिबल का बहुत ही न्यून प्रतिरोध करते हैं। फलतः थोड़े से विरूपण प्रतिबल लगाने से भी उनकी आकृति बदल जाती है। ठोसों की अपेक्षा तरलों का अपरूपक प्रतिबल लगभग दस लाखवाँ कम होता है।
10.2 दाब
जब एक नुकीली सुई हमारी त्वचा में दाब लगाकर रखी जाती है, तो वह त्वचा को बेध देती है। परन्तु किसी अधिक संपर्क क्षेत्र की वस्तु (जैसे चम्मच का पिछला भाग) को उतने ही बल से दबाएँ तो हमारी त्वचा अपरिवर्तित रहती है। यदि किसी व्यक्ति की छाती पर कोई हाथी अपना पैर रख दे तो उसकी पसलियाँ टूट जाएँगी। सर्कस में यह करतब दिखाने वाले की छाती पर मजबूत लकड़ी का तख्ता रखा जाता है अतः वह इस दुर्घटना से बच जाता है। दैनिक जीवन के इस प्रकार के अनुभवों से हमें विश्वास हो जाता है कि बल के साथ-साथ जिस क्षेत्र पर वह बल आरोपित किया जाता है उसका क्षेत्रफल भी महत्त्वपूर्ण होता है। वह क्षेत्र जिस पर बल कार्य कर रहा है जितना छोटा होगा उसका प्रतिघात उतना ही अधिक होगा। यह प्रतिघात ‘दाब’ कहलाता है।
जब कोई पिण्ड किसी शांत तरल में डूबा हुआ है, तो तरल उस पिण्ड पर बल आरोपित करता है। यह बल सदैव पिण्ड के पृष्ठों के अभिलंबवत् होता है। एेसा इसलिए है कि, यदि बल का अवयव पिण्ड के पृष्ठ के समांतर होता है तो न्यूटन के तृतीय नियमानुसार, पिण्ड भी अपने सतह के समांतर तरल पर बल आरोपित करता है। यह बल तरल को पृष्ठ के समांतर बहने के लिए बाध्य करता है। यह संभव नहीं है, क्योंकि तरल विश्रामावस्था में है। अतः विरामावस्था में तरल द्वारा लगने वाला बल पिण्ड के संपर्क पृष्ठ के अभिलंब ही आरोपित हो सकता है। इसे चित्र 10.1(a) में दर्शाया गया है।
तरल द्वारा किसी बिंदु पर कार्यरत इस अभिलंब बल को मापा जा सकता है। एेसा ही एक दाब मापक युक्ति के आदर्श रूप को चित्र 10.1(b) में दर्शाया गया है। इस युक्ति में एक निर्वातित चैम्बर होता है, जिससे एक कमानी जुड़ी होती है। इस कमानी का अंशांकन पहले से ही इसके पिस्टन पर लगे बल को मापने के लिए कर लिया जाता है। इस युक्ति को तरल के अंदर के किसी बिंदु पर रखा जाता है। पिस्टन पर तरल द्वारा आरोपित बल को कमानी द्वारा पिस्टन पर आरोपित बल से संतुलित करके तरल द्वारा पिस्टन पर आरोपित बल को माप लेते हैं। यदि तरल द्वारा A क्षेत्रफल के पिस्टन पर आरोपित अभिलंब बल का परिमाण F है, तो औसत दाब Pav को बल तथा क्षेत्रफल के अनुपात के रूप में परिभाषित किया जाता है
अतः
 (10.1)
(10.1)
सैद्धांतिक रूप में पिस्टन के क्षेत्रफल को मनमाने ढंग से छोटा किया जा सकता है। तब सीमित अर्थों में दाब को इस प्रकार परिभाषित करते हैं:
P = 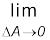
 (10.2)
(10.2)
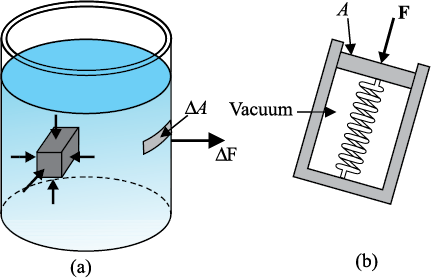
चित्र 10.1 (a) बीकर के द्रव में डूबे पिण्ड अथवा उसकी दीवारों पर द्रव द्वारा आरोपित बल पिण्ड के पृष्ठ के हर बिंदु के लंबवत् कार्य करता है। (b) दाब मापने के लिए युक्ति का आदर्श रूप।
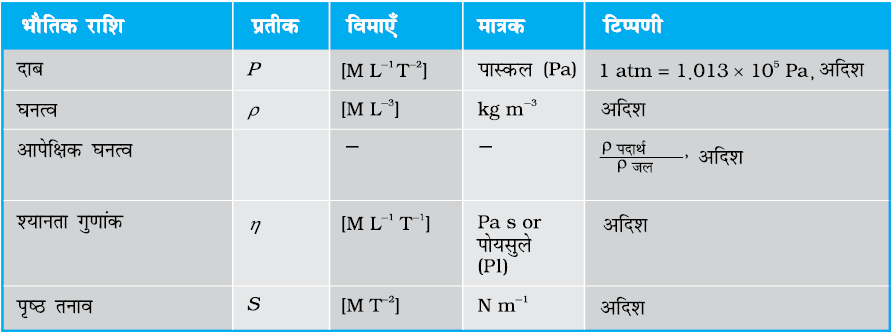
दाब एक अदिश राशि है। यहाँ हम आपको यह याद दिलाना चाहते हैं कि समीकरणों (10.1) तथा (10.2) के अंश में दृष्टिगोचर होने वाली राशि संबंधित क्षेत्र के अभिलंबवत् बल का अवयव है न कि (सदिश) बल। इसकी विमाएँ [ML–1T–2] हैं। दाब का मात्रक N m–2 है। फ्रांसीसी वैज्ञानिक ब्लेजी पास्कल (1623-1662) ने तरल दाब क्षेत्र में पुरोगामी अध्ययन किया। इसलिए उनके सम्मान में दाब के SI मात्रक का नाम पास्कल (pascal, प्रतीक Pa) रखा गया है। दाब का एक अन्य सामान्य मात्रक वायुमण्डल (atmosphere, प्रतीक atm) अर्थात् समुद्र तल पर वायुमंडल द्वारा आरोपित दाब, है
(1 atm = 1.013 × 105 Pa)।
तरलों का वर्णन करने के लिए घनत्व (ρ) एक एेसी भौतिक राशि है जिसके विषय में चर्चा करना अनिवार्य है। V आयतन वाले m संहति के किसी तरल का घनत्व
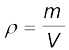 (10.3)
(10.3)
घनत्व की विमाएँ [ML–3] हैं। इसका SI मात्रक kg m–3 है। यह एक धनात्मक अदिश राशि है। द्रव असंपीड्य होते हैं, अतः किसी द्रव का घनत्व सभी दाबों पर लगभग अचर रहता है। इसके विपरित, गैसें दाब में परिवर्तन के साथ घनत्व में अत्यधिक परिवर्तन दर्शाती हैं।
4 oC (277 K) पर जल का घनत्व 1.0 × 103 kg m–3 है। किसी पदार्थ का आपेक्षिक घनत्व (विशिष्ट गुरुत्व) उस पदार्थ के घनत्व तथा जल के 4 oC पर घनत्व का अनुपात होता है। यह विमाहीन धनात्मक अदिश भौतिक राशि है। उदाहरण के लिए एेलुमिनियम का आपेक्षिक घनत्व 2.7 है। जबकि इसका घनत्व 2.7 × 103 kg m–3 है। सारणी 10.1 में कुछ सामान्य तरलों के घनत्व दर्शाए गए हैं।
सारणी 10.1 कुछ सामान्य तरलों के घनत्व मानक ताप तथा वायुमंडलीय दाब (STP) पर*
| तरल | घनत्व ρ (kg m–3) |
| जल | 1.00 × 103 |
| समुद्र जल | 1.03 × 103 |
| पारा | 13.6 × 103 |
| एेथिल एल्कोहॉल | 0.806 × 103 |
| संपूर्ण रक्त | 1.06 × 103 |
| वायु | 1.29 |
| अॉक्सीजन | 1.43 |
| हाइड्रोजन | 9.0 × 10–2 |
| अंतरातारकीय आकाश | ≈10–20 |
उदाहरण 10.1 दो उर्वस्थितियाँ (फीमर) जिनमें प्रत्येक की अनुप्रस्थ काट का क्षेत्रफल 10 cm2 है, 40 kg संहति के मानव शरीर के ऊपरी भाग को सँभालती हैं। उर्वस्थितियों द्वारा सहन किए जाने वाले औसत दाब का आकलन कीजिए।
हल उर्वस्थियों की कुल अनुप्रस्थ काट का क्षेत्रफल A = 2 × 10 cm2 = 20 × 10–4 m2। उर्वस्थियों पर कार्यरत बल F = 40 kg wt = 400 N (g = 10 m s–2 लेने पर)।
यह बल ऊर्ध्वाधर नीचे की दिशा में कार्य करता है, अतःयह उर्वस्थियों पर अभिलंबवत् लगता है। इसीलिए औसत दाब
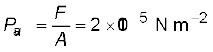 t
t
10.2.1 पास्कल का नियम
फ्रांसीसी वैज्ञानिक ब्लेज पास्कल ने पाया कि यदि सभी बिंदु एक ही ऊँचाई पर हों तो विराम स्थिति के तरल के सभी बिंदुओं पर दाब समान होगा। इस सत्य को भली भाँति सरल रूप में दर्शाया जा सकता है।
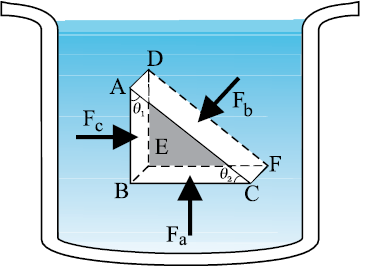
चित्र 10.2 पास्कल के नियम का परीक्षण। ABC-DEF विराम स्थिति के किसी तरल के अभ्यन्तर का कोई अवयव है। यह अवयव इतना छोटा है कि गुरुत्व के प्रभाव की उपेक्षा की जा सकती है, परन्तु स्पष्टता के लिए इसे प्रवर्धित दर्शाया गया है।
चित्र 10.2 में विराम स्थिति के किसी तरल के अभ्यन्तर में कोई अवयव दर्शाया गया है। यह अवयव ABC-DEF एक समकोण प्रिज़्म के रूप में है। प्रिज़्मीय अवयव आकार में बहुत छोटा है इसलिए इसका प्रत्येक बिंदु तरल के पृष्ठ के समान गहराई पर माना जा सकता है और इसलिए प्रत्येक बिंदु पर गुरुत्व का प्रभाव समान होगा। परन्तु इस सिद्धान्त को स्पष्ट करने के लिए हमने इस अवयव को बड़ा करके दर्शाया है। इस अवयव पर आपतित बल शेष तरल के कारण है और जैसा कि ऊपर दर्शाया गया है तरल के कारण आरोपित बल पृष्ठों के अभिलंब कार्य करते हैं। अतः चित्र में दर्शाये अनुसार तरल द्वारा इस अवयव पर आरोपित दाबों Pa, Pb तथा Pc के तदनरूपी बल Fa, Fb तथा Fc क्रमशः फलकों BEFC, ADFC तथा ADEB पर अभिलंबवत् आपतित होते हैं जैसा कि चित्र 10.2 में दर्शाया गया है। फलकों BEFC, ADFC तथा ADEB को Aa, Ab तथा Ac से क्रमशः व्यक्त करते हैं। तब
Fb sinθ = Fc, Fb cosθ = Fa (साम्यावस्था से)
Ab sinθ = Ac, Ab cosθ = Aa (ज्यामिती से)
इस प्रकार
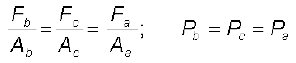 (10.4)
(10.4)
अतः विरामावस्था में द्रव के अभ्यन्तर में सभी दिशाओं में दाब समान रूप से कार्य करता है। हमें यह पुनः याद दिलाता है कि अन्य प्रकार के प्रतिबलों की भाँति ही दाब सदिश नहीं है। इसे कोई दिशा नहीं दी जा सकती। विरामावस्था में दाब, तरल के भीतर के किसी क्षेत्रफल (अथवा परिबद्ध तरल) पर अभिलंबवत् होता है चाहे क्षेत्रफल किसी भी अवस्थिति में हो।
10.2.2 गहराई के साथ दाब में परिवर्तन
एक पात्र में द्रव की विरामावस्था पर विचार करें। चित्र 10.3 में बिंदु 1 बिंदु 2 से h ऊँचाई पर है। बिंदु 1 व 2 पर दाब क्रमशः P1 तथा P2 हैं। A आधार क्षेत्रफल तथा h ऊँचाई के तरल के एक बेलनाकार अवयव को लें। चूँकि तरल विरामावस्था में है अतः परिणामी क्षैतिज बल शून्य होना चाहिए। परिणामी ऊर्ध्वाधर दिशा में कार्यरत बल तरल अवयव के भार के तुल्य होना चाहिए। नीचे की ओर कार्य करने वाला ऊपरी सिरे पर तरल के दाब द्वारा बल (P1A) तथा पैंदी पर ऊपर की ओर कार्य करने वाला बल (P2A) है। यदि बेलन में तरल का भार mg है तो
(P2 − P1) A = mg (10.5)
अब यदि ρ तरल का घनत्व है तो उसकी संहति
m = ρV= ρhA होगी, इसलिए
P2 − P1= ρgh (10.6)
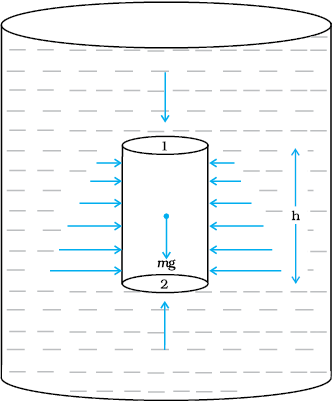
चित्र 10.3 तरल के ऊर्ध्वाधर बेलनी स्तंभ पर दाब के द्वारा गुरुत्व का प्रभाव दिखाया गया है।
बिन्दु 1 व 2 में दाबांतर उनके बीच ऊर्ध्वाधर दूरी h, तरल के घनत्व ρ तथा गुरुत्वीय जनित त्वरण g पर निर्भर है। यदि विचारणीय बिंदु 1 को तरल (माना पानी) के शीर्ष फलक पर स्थानांतरित कर दिया जाए जो वायुमण्डल के लिए खुला है तो P1 को वायुमंडलीय दाब (Pa) द्वारा तथा P2 को P से प्रतिस्थापित किया जा सकता है। तब समीकरण (10.6) से
P = Pa + ρgh (10.7)
इस प्रकार, वायुमण्डल के लिए खुले पृष्ठ के नीचे दाब P वायुमण्डलीय दाब की अपेक्षा ρgh परिमाण से अधिक होगा। h गहराई पर स्थित किसी बिंदु पर अतिरिक्त दाब P − Pa उस बिंदु पर गेज़ दाब कहलाता है।
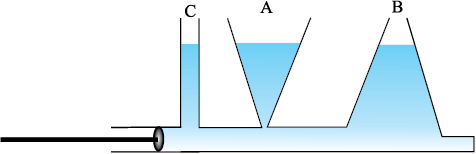
निरपेक्ष (परम) दाब के समीकरण (10.7) में बेलन का क्षेत्रफल नहीं आ रहा। अतः, दाब परिकलन के लिए तरल के स्तंभ की ऊँचाई महत्त्वपूर्ण है न कि पात्र की आकृति, आधार या अनुप्रस्थ काट। समान क्षैतिज तल (समान गहराई) के सभी बिंदुओं पर द्रव का दाब समान होता है। द्रवस्थैतिक विरोधोक्ति के उदाहरण से इस परिणाम को भलीभांति समझा जा सकता है। A, B तथा C विभिन्न आकृतियों के पात्र लें (चित्र 10.4)। पैंदी में एक क्षैतिज पाइप द्वारा इनको जोड़ा जाता है। पानी भरने पर इन तीनों पात्रों में उसका तल समान रहता है यद्यपि इनमें पानी भिन्न-भिन्न मात्रा में होता है। यह इसलिए है कि इनकी तली पर दाब समान रहता है।
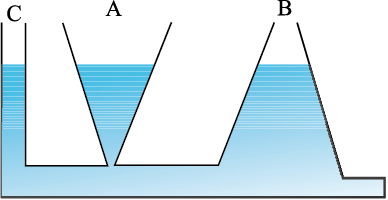
चित्र 10.4 द्रवस्थैतिक विरोधोक्ति की व्याख्या। तीन पात्रों A, B और C में समान ऊँचाई तक जल भरा है परन्तु सभी में जल का परिमाण भिन्न-भिन्न है।
उदाहरण 10.2 किसी झील के पृष्ठ से 10 m गहराई पर किसी तैराक पर दाब ज्ञात कीजिए।
हल यहाँ h = 10 m तथा ρ = 1000 kg m-3
g = 10 m s–2 लें
समीकरण (10.7) से,
10.2.3 वायुमण्डलीय दाब तथा गेज दाब
किसी बिंदु पर वायुमण्डलीय दाब उस बिंदु के एकांक अनुप्रस्थ काट वाले क्षेत्रफल पर उस बिंदु से वायुमण्डल के शीर्ष तक की वायु के स्तंभ के भार के बराबर होता है। समुद्र तल पर यह 1.013 × 105 Pa है (1 atm)। वायुमण्डलीय दाब की यथार्थ माप के लिए सर्वप्रथम इटली के वैज्ञानिक इवेंगलिस्टा टॉरिसेली (1608-1647) ने एक युक्ति की रचना की तथा वायुमण्डल दाब को मापा। जैसा कि चित्र 10.5 (a) में दर्शाया गया है, एक सिरे से बंद लंबी काँच की नली लेकर उसमें पारा भरा गया और फिर उसे पारे से आंशिक भरे पात्र में ऊर्ध्वाधर उलटा खड़ा किया गया। इस युक्ति को पारे का बैरोमीटर कहते हैं। नली में पारे से ऊपर का स्थान पारे की वाष्प जिसका दाब P बहुत अल्प होता है, भरा रहता है, यह दाब इतना कम होता है कि इसे नगण्य मान सकते हैं। अतः बिन्दु A पर दाब शून्य होगा। स्तंभ के अन्दर बिंदु B पर दाब समान तल वाले बिंदु C पर दाब के तुल्य होना चाहिए 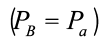 ।
।
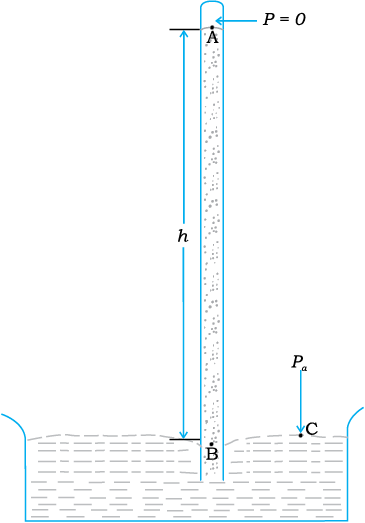
(a) पारद वायुदाब मापी
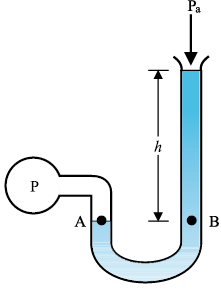
(b) खुली-नली मैनोमीटर (दाबांतर मापी)
चित्र 10.5 दाब मापने की दो युक्तियाँ।
B पर दाब = वायुमण्डल दाब Pa
Pa = ρgh (10.8)
जहाँ ρ पारे का घनत्व तथा h नली में पारे के स्तंभ की ऊँचाई है।
प्रयोग में पाया गया कि समुद्र तल पर बैरोमीटर में पारे के स्तंभ की ऊँचाई 76 cm के लगभग होती है जो एक वायुमण्डलीय दाब (1 atm) के तुल्य है। समीकरण (10.8) में ρ का मान भरकर भी इसे प्राप्त किया जा सकता है। सामान्यतः दाब का वर्णन cm अथवा mm (पारा स्तंभ) के पदों में किया जाता है। 1 mm (Hg) दाब का तुल्यांकी दाब 1 टॉर (torr) कहलाता है (टॉरिसेली के सम्मान में)।
1 torr = 133 Pa
औषध विज्ञान तथा शरीर क्रिया विज्ञान (फ़िजिओलॉजी) में दाब के मात्रक के रूप में mm (Hg) तथा टॉर (torr) का उपयोग किया जाता है। मौसम विज्ञान में दाब का सामान्य मात्रक बार (bar) तथा मिलिबार (millibar) लिया जाता है।
1 bar = 105 Pa
दाबांतर को मापने के लिए खुली-नली मैनोमीटर एक लाभप्रद उपकरण है। इस युक्ति में एक U आकार की नली होती है जिसमें उपयुक्त द्रव भरा होता है अर्थात् कम दाबांतर मापने के लिए कम घनत्व का द्रव (जैसे तेल) तथा अधिक दाबांतर के लिए अधिक घनत्व का द्रव (जैसे पारा) भरा जाता है। नली का एक सिरा वायुमंडल में खुला छोड़ दिया जाता है तथा दूसरा सिरा जिस निकाय का दाब ज्ञात करना है, उससे जोड़ दिया जाता है। [देखिए चित्र 10.5 (b)]। बिंदु A पर दाब बिंदु B पर दाब के बराबर है। जिस दाब को हम सामान्यतः मापते हैं वह वास्तव में प्रमापी अथवा गेज़ दाब होता है। यह P − Pa के बराबर होता है जो समीकरण (10.8) द्वारा दिया जाता है तथा मैनोमीटर की ऊँचाई h के अनुपाती होता है।
U नली में भरे द्रव के तलों में दोनों ओर समान दाब होता है। दाब तथा ताप के विस्तृत परिसर में द्रव के घनत्व में बहुत कम परिवर्तन होता है। हम प्रस्तुत विवेचन के लिए इसे स्थिर मान सकते हैं। दूसरी ओर दाब तथा ताप परिवर्तन के साथ गैसों के घनत्व में बहुत अधिक परिवर्तन परिलक्षित होता है। अतः गैसों की तुलना में विपरीत द्रवों को अधिकांश रूप से असंपीड्य माना जाता है।
उदाहरण 10.3 समुद्र तल पर वायुमंडल का घनत्व 1.29 kg/m3 है। यह मानते हुए कि ऊँचाई के साथ घनत्व में कोई परिवर्तन नहीं होता, ज्ञात कीजिए कि वायुमंडल का विस्तार कितनी ऊँचाई तक है?
हल: हम समीकरण (10.8) का उपयोग करते हैं
ρgh = 1.29 kg m–3 × 9.8 m s–2 × h m = 1.01 × 105 Pa
h = 7989 m ≈ 8 km
वास्तव में, ऊँचाई के साथ वायु के घनत्व में कमी होती जाती है। एेसा ही गुरुत्वीय त्वरण g के साथ भी होता है। वायुमण्डलीय आवरण का विस्तार घटते दाब के साथ लगभग 100 km ऊँचाई तक है। हमें यह ध्यान रखना चाहिए कि समुद्र तल पर वायुमंडलीय दाब सदैव ही 760 mm (Hg) नहीं होता। इसमें 10 mm (Hg) अथवा अधिक की कमी तूफान के आने की सूचक होती है।
उदाहरण 10.4 समुद्र के नीचे 1000 m गहराई पर (a) परम दाब कितना है? (b) गेज़ दाब कितना है? (c) इस गहराई पर पनडुब्बी की 20 cm × 20 cm क्षेत्रफल वाली खिड़की (जिसके आंतरिक भाग का दाब समुद्र तल पर वायुमण्डलीय दाब के बराबर रखा गया है) पर आरोपित बल का आकलन कीजिए। (समुद्र जल का घनत्व 1.03 × 103 kg m-3, g = 10 m s–2 )
हल: यहाँ h = 1000 m तथा ρ = 1.03 × 103 kg m-3
(a) समीकरण (10.7) से परम दाब
P = Pa + ρgh
= 1.01 × 105 Pa + 1.03 × 103 kg m–3
× 10 m s–2 × 1000 m
= 104.01 × 105 Pa
≈ 104 atm
(b) गेज़ दाब = P − Pa = ρgh ≈ Pg
Pg = 1.03 × 103 kg m–3 × 10 m s–2 × 1000 m
= 103 × 105 Pa
≈ 103 atm
(c) पनडुब्बी के बाहर दाब P = Pa + ρgh और अंदर दाब Pa है। इसलिए खिड़की पर आपतित कुल दाब गेज़ दाब Pg = ρgh है। चूँकि खिड़की का क्षेत्रफल A = 0.04 m2 है अतः आपतित बल
F = Pg A = 103 × 105 Pa × 0.04 m2 = 4.12 × 105 N t
आर्किमिडीज का सिद्धांत
एेसा प्रतीत होता है कि तरल में रखे किसी पिण्ड को तरल आंशिक सहारा प्रदान करता है। विराम स्थिति के किसी तरल में जब किसी पिण्ड को पूर्ण या आंशिक रूप से डुबोया जाता है तो तरल पिण्ड के सम्पर्क पृष्ठ पर दाब डालता है। पिण्ड के निचले पृष्ठ पर ऊपरी पृष्ठ की अपेक्षा दाब अधिक होता है क्योंकि तरल में दाब गहराई बढ़ने के साथ-साथ बढ़ता है। सभी बलों का परिणामी बल उपरमुखी बल है जिसे उत्प्लावन बल कहते हैं। माना कि किसी तरल में एक बेलनाकार पिण्ड को डुबोया जाता है। पिण्ड की तली पर ऊर्ध्वमुखी बल उसके शीर्ष पर लगने वाले अधोमुखी बल से अधिक है। तरल पिण्ड पर एक परिणामी बल या उत्प्लावन बल (P2 – P1) A
(चित्र 10.3) लगाता है। समीकरण (10.4) में हमने देखा कि (P2 – P1) A = ρgh A। h A पिण्ड का आयतन है तथा ρhA तरल के तुल्य आयतन का भार है। (P2 – P1)A = mg । इस प्रकार आरोपित ऊर्ध्वबल विस्थापित तरल के भार के बराबर है।
यह परिणाम पिण्ड की आकृति पर निर्भर नहीं करता है, यह सभी आकृति के पिण्डों के लिए सत्य है। बेलनाकार पिण्ड केवल सुविधा के लिए लिया गया था। यह आर्किमिडीज का सिद्धांत है। पूर्ण डूबे पिण्ड द्वारा विस्थापित तरल का आयतन उसके अपने आयतन के तुल्य होता है। यदि डूबे हुए पिण्ड का घनत्व तरल के घनत्व से अधिक है तो पिण्ड डूब जाएगा क्योंकि पिण्ड का भार ऊर्ध्वमुखी प्रणोद से अधिक होगा। यदि ठोस का घनत्व तरल से कम है वह आंशिक रूप से डूबा हुआ तैरेगा। डूबे हुए भाग के आयतन का आकलन करने के लिए माना कि पिण्ड का कुल आयतन Vs है तथा इसका अंश आयतन Vp तरल में डूबा है। तो ऊर्ध्वमुखी बल जो विस्थापित तरल के भार ρlgVp के तुल्य है, पिण्ड के भार के तुल्य होना चाहिए। ρsgVs = ρlgVp अथवा ρs/ρl = Vp/Vs तैरते पिण्ड का आभासी भार शून्य है।
संक्षिप्त में यह सिद्धांत है ‘किसी तरल में (आंशिक या पूर्ण रूप से) डूबे पिण्ड के भार में कमी पिण्ड द्वारा विस्थापित तरल के भार के तुल्य होती है।’
10.2.4 द्रव चालित मशीन
आइये अब हम देखते हैं कि पात्र में रखे तरल पर जब दाब परिवर्तन करते हैं तो क्या होता है? एक क्षैतिज बेलन पर विचार करें जिसमें पिस्टन लगा है तथा उसके विभिन्न बिंदुओं पर तीन ऊर्ध्व ट्यूब लगी हैं [चित्र 10.6(a)] ऊर्ध्व ट्यूब में द्रव स्तंभ की ऊँचाई क्षैतिज बेलन में तरल का दाब दर्शाती है। यह सभी ऊर्ध्व ट्यूबों में अनिवार्यतः समान होती है। यदि पिस्टन को धकेलते हैं तो सभी ट्यूबों में तरल का स्तर उठ जाता है, तथा पुनः यह सभी में समान हो जाता है।
चित्र 10.6 (a) पात्र में रखे तरल के किसी भाग पर जब बाहय दाब आपतित होता है, तो यह सभी दिशाओं में समान रूप से संचरित हो जाता है।
यह दर्शाता है कि जब बेलन पर दाब बढ़ाया जाता है तो यह पूर्ण तरल से समान रूप में वितरित हो जाता है। हम कह सकते हैं कि पात्र में रखे तरल के किसी भाग पर जब बाह्य दाब आपतित होता है, तो यह बिना ह्रास के सभी दिशाओं में समान रूप से संचरित हो जाता है। यह "पास्कल के नियम का अन्य रूप" है तथा दैनिक जीवन में इसके कई उपयोग हैं।
कईं युक्तियाँ जैसे द्रव चालित उत्थापक और द्रव चालित ब्रेक इस नियम पर आधारित हैं। इन युक्तियों में दाब संचरण के लिए तरलों का उपयोग किया जाता है। चित्र 10.6 (b) के अनुसार द्रव चालित उत्थापक में तरल द्वारा भरे स्थान से विलगित दो पिस्टन हैं। अनुप्रस्थ काट A1 का छोटा पिस्टन द्रव पर सीधा बल F1 आरोपित करता है। P = दाब पूर्ण द्रव में संचरित होता है तथा अनुप्रस्थ काट A2 के बड़े बेलन जिसमें पिस्टन लगा है पर ऊर्ध्वमुखी बल P×A2 के रूप में प्राप्त होता है। अतएव, पिस्टन अधिक बल को संतुलित (जैसे प्लेटफॉर्म पर रखे कार या ट्रक के अधिक भार) कर सकता है
दाब पूर्ण द्रव में संचरित होता है तथा अनुप्रस्थ काट A2 के बड़े बेलन जिसमें पिस्टन लगा है पर ऊर्ध्वमुखी बल P×A2 के रूप में प्राप्त होता है। अतएव, पिस्टन अधिक बल को संतुलित (जैसे प्लेटफॉर्म पर रखे कार या ट्रक के अधिक भार) कर सकता है
F2 = PA2 =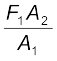 । A1 पर बल बदलकर प्लेटफॉर्म को ऊपर या नीचे लाया जा सकता है। इस प्रकार प्रयुक्त बल
। A1 पर बल बदलकर प्लेटफॉर्म को ऊपर या नीचे लाया जा सकता है। इस प्रकार प्रयुक्त बल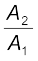 गुणक से बढ़ जाता है। यह गुणक युक्ति का यांत्रिक लाभ कहलाता है। निम्न उदाहरण इसे स्पष्ट करता है।
गुणक से बढ़ जाता है। यह गुणक युक्ति का यांत्रिक लाभ कहलाता है। निम्न उदाहरण इसे स्पष्ट करता है।
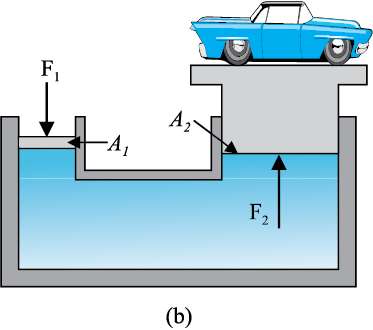
चित्र 10.6 (b) द्रव चालित उत्थापक, भारी बोझ उठाने की एक युक्ति के कार्य करने के सिद्धांत की व्याख्या का योजनाबद्ध आरेख।
उदाहरण 10.5 भिन्न-भिन्न अनुप्रस्थ काट वाली दो पिचकारियों में (बिना सुई के) पानी भरा है और इन्हें पानी से भरी रबर नली से कसकर जोड़ दिया गया है। छोटे तथा बड़े पिस्टन के व्यास क्रमशः 1 cm तथा 3 cm हैं। (a) जब छोटे पिस्टन पर 10 N का बल लगाया जाता है तो बड़े पिस्टन पर लगे बल का आकलन कीजिए। (b) यदि छोटे पिस्टन की 6 cm अंदर धक्का दिया जाता है तो बड़ा पिस्टन कितना
बाहर चलेगा?
हल: (a) चूँकि बिना ह्रास के दाब संपूर्ण द्रव में संचरित होता है,
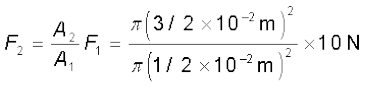
= 90 N
आर्किमिडीज (287-212 ई. पू.)

ग्रीस के दार्शनिक, गणितज्ञ, वैज्ञानिक तथा अभियंता थे । उन्होंने गुलेल की खोज की तथा घिरनियों एवं उत्तोलकों के संयोजन से भारी बोझों के संचालन के लिए एक तंत्र का आविष्कार किया । उनके अपने देश साइराक्यूज के राजा हीरो II ने आर्किमिडीज को सोने का ठोस मुकुट देकर यह कहा कि मुकुट को बिना तोड़े ही वह यह निर्धारित करे कि मुकुट शुद्ध सोने का बना है, अथवा उसमें कोई सस्ती धातु; जैसे–चाँदी मिलाई गई है । पानी से लबालब भरे टब में लेटते समय उन्होंने अपने भार में अांशिक कमी अनुभव की, जिससे उन्हें अपनी समस्या का हल मिल गया । जिसे पाकर आर्किमिडीज इतने उत्तेजित हो गए कि, दंतकथा के अनुसार, टब से बाहर निकलकर, साइराक्यूज की गलियों में "यूरेका" - यूरेका (अर्थात् "मैंने पा लिया" - "मैंने पा लिया") चिल्लाते हुए दौड़ पड़े । उस समय वह यह भी भूल गए कि उनके शरीर पर कोई वस्त्र नहीं है ।
(b) पानी पूरा असंपीड्य माना जाता है। छोटे पिस्टन के अन्दर चलने से तुल्य आयतन बड़े पिस्टन द्वारा बाहर की ओर चलने को बाध्य करता है।
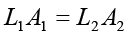
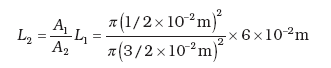
≅ 0.67 × 10-2 m = 0.67 cm
नोट: दोनों पिस्टनों के लिए वायुमण्डलीय दाब उभयनिष्ठ है अतः इसे छोड़ दिया गया है। t
उदाहरण 10.6 एक कार उत्थापक में छोटे पिस्टन जिसकी त्रिज्या 5 cm है पर F1 बल संपीड्य वायु लगाती है। यह दाब 15 cm त्रिज्या वाले दूसरे पिस्टन पर संचरित होता है (चित्र 10.6)। यदि उठाई जाने वाली कार की संहति 1350 kg हो तो F1 का आकलन कीजिए। इस कार्य को संपन्न करने के लिए आवश्यक दाब क्या है? (g = 9.8 ms-2)
= 1470 N
≈ 1.5 × 103 N
इस बल के संगत वायु दाब
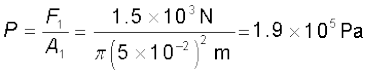
यह वायुमण्डलीय दाब का लगभग दुगुना है। t
मोटर कार में द्रव चालित ब्रेक भी इसी सिद्धांत पर कार्य करते हैं। जब हम अपने पैर से थोड़ा सा बल पैडल पर लगाते हैं तो पिस्टन मास्टर बेलन के अंदर जाता है और उत्पन्न दाब ब्रेक तेल द्वारा पिस्टन के बड़े क्षेत्रफल पर संचरित होता है। पिस्टन पर एक बड़ा बल कार्य करता है। इसके नीचे की ओर ढकेले जाने पर ब्रेक शू फैल कर ब्रेक लाइन को दबाता है। इस प्रकार पैडल पर थोड़ा सा बल पहिए पर अधिक बल मंदन उत्पन्न करता है। इस निकाय का एक प्रमुख लाभ यह है कि पैडल को दबाने से उत्पन्न दाब चारों पहियों से संलग्न बेलनों में समान रूप से संचरित होता है जिससे ब्रेकों का प्रभाव सभी पहियों पर बराबर पड़ता है।
10.3 धारारेखी प्रभाव
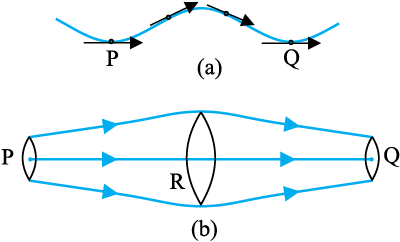
चित्र 10.7 धारारेखाओं का अर्थ (a) किसी तरल का प्ररूपी प्रपथ (b) धारारेखी प्रभाव का क्षेत्र।
किसी तरल अपरिवर्ती प्रवाह में जिस पथ पर कण गमन करता है उसे धारारेखा कहते हैं। किसी बिंदु पर तरल कण का वेग सदैव ही धारारेखा के उसी बिंदु पर खींची गई स्पर्श रेखा के अनुदिश होता है जो धारारेखा प्रवाह को परिभाषित करता है। जैसा कि चित्र 10.7 (a) में दर्शाया गया है, किसी कण के पथ को लेते है। वक्र यह दर्शाता है कि तरल का कण समय के साथ किस प्रकार गति करता है। वक्र PQ तरल प्रवाह का स्थायी प्रतिचित्र है जो यह दर्शाता है कि तरल किस प्रकार धारारेखा में प्रवाहित होता है। कोई भी दो धारारेखाएँ एक दूसरे को नहीं काटतीं यदि वह एेसा करती हैं (अर्थात् काटती हैं) तो किसी बिंदु पर तरल का प्रवाह स्थिर नहीं होता तथा एक तरल कण किसी भी दिशा में गति करने लगेगा और प्रवाह अपरिवर्ती नहीं रहेगा। इसलिए अपरिवर्ती प्रवाह में प्रवाह का मानचित्र समय में स्थिर रहता है। हम निकटवर्ती धारारेखाओं को कैसे खींचते हैं? यदि हम प्रत्येक प्रभावित कण की धारारेखा को प्रदर्शित करने की इच्छा रखते हैं तो हम रेखाओं के सांतत्य में सिमट जाएँगे। तरल प्रवाह की दिशा में लंबवत समतलों पर विचार कीजिए अर्थात चित्र 10.7 (b) में तीन बिंदु P, R तथा Q पर। इन समतल खंडों का चुनाव इस प्रकार किया जाता है कि इनकी सीमाएँ धारारेखाओं के समान समूह द्वारा निर्धारित हो जाएँ। इसका अर्थ है कि P, R तथा Q पर दर्शाये गये लंबवत समतल पृष्ठों से प्रवाहित होने वाले तरल कणों की संख्या समान है। इस प्रकार यदि P, R, तथा Q पर तरल कणों के वेग परिमाण क्रमशः vP, vR तथा vQ हैं तथा इन तलों के क्षेत्रफल क्रमशः AP,AR और AQ हैं तो छोटे से समय अंतराल ∆t में Ap से गुज़रने वाले तरल की संहति ρPAPvP ∆t है। इसी प्रकार AR से होकर प्रवाहित तरल की संहति ∆mR = ρRARvR ∆t और ∆mQ = ρQAQvQ ∆t होगी। सभी मामलों में तरल के बाहर निकलने की संहति उस स्थान में आने वाले तरल की संहति के बराबर होगी।
अतएव,
ρPAPvP∆t = ρRARvR∆t = ρQAQvQ∆t (10.9)
असंपीड्य तरल के प्रवाह के लिए
ρP = ρR = ρQ
तब समीकरण (10.9)
APvP = ARvR = AQvQ (10.10)
में बदल जाता है। जिसे सांतत्य-समीकरण कहते हैं तथा असंपीड्य तरल प्रभाव में यह संहति संरक्षण का कथन है। सामान्यतः Av = स्थिरांक (10.11)
Av आयतन अभिवाह या प्रवाह दर देता है। यह नली प्रवाह में सर्वत्र स्थिर रहता है अतः संकरे स्थानों पर जहाँ धारा रेखाएँ पास-पास हैं वहाँ वेग बढ़ जाता है तथा इसका विलोमतः चित्र 10.7b से स्पष्ट है कि AR > AQ या vR < vQ R से Q को प्रवाहित तरल त्वरित होता है। क्षैतिज पाइप में यह तरल दाब में परिवर्तन से संबद्ध है।
डेनियल बर्नूली (1700-1782)

स्विटज़रलैंड के एक वैज्ञानिक तथा गणितज्ञ थे जिन्होंने लिओनार्ड अॉयलर के साथमिलकर गणित का फ्रेंच अकादमी पुरस्कार दस बार जीतने का कीर्तिमान स्थापित किया । उन्होंने चिकित्सा शास्त्र का भी अध्ययन किया तथा कुछ समय के लिए वे बैस्ले, स्विटज़रलैंड में शरीर रचना विज्ञान तथा वनस्पति शास्त्र के प्रोफेसर के पद पर भी रहे । उनका अत्यधिक सुविख्यात कार्य द्रवगतिकी, एक विषय जिसे उन्होंने स्वयं एकलसिद्धांतः ऊर्जा संरक्षण से विकसित किया, के क्षेत्र में है । उनके कार्यों में कैलकुलस,प्रायिकता, कंपायमान डोरी का सिद्धांत, तथा अनुप्रयुक्त गणित सम्मिलित हैं । उन्हें गणितीय भौतिकी का संस्थापक कहा जाता है ।
तरल के कम वेग से धारा प्रवाह प्राप्त होता है। एक सीमांत मान के पश्चात जिसे क्रांतिक वेग कहते हैं, यह धारा प्रवाह प्रक्षुद्ध प्रवाह में बदल जाता है। जब एक तेज़ प्रवाही
धारा चट्टान से टकराती है तो हम देख सकते हैं कि कैसेे छोटे-छोटे फेन (foam) भँवर जैसे बनते हैं जिन्हें दूध-धारा (white water rapids) कहते हैं।
चित्र 10.8 कुछ प्ररूपी प्रवाह की धारारेखाएँ दर्शायी गई हैं। उदाहरण के लिए चित्र 10.8(a) में स्तरीय प्रवाह दर्शाया गया है जहाँ तरल के विभिन्न बिंदुओं पर वेगों के परिमाण भिन्न-भिन्न हो सकते हैं, परन्तु उनकी दिशाएँ एक दूसरे से समानांतर हैं। चित्र 10.8 (b) में प्रक्षुब्ध प्रवाह आलेखित किया गया है।

चित्र 10.8 (a) तरल प्रवाह की कुछ धारारेखाएँ (b) प्रवाह के लंबवत् रखी चपटी प्लेट से टकराता वायु जेट। यह प्रक्षुब्ध प्रवाह का एक उदाहरण है।
10.4 बर्नूली का सिद्धांत
तरल प्रवाह एक जटिल परिघटना है। परन्तु ऊर्जा संरक्षण का उपयोग करते हुए हम अपरिवर्ती अथवा धारा-प्रवाह के कुछ विशिष्ट गुणों को प्राप्त कर सकते हैं।
परिवर्ती अनुप्रस्थ काट के पाइप में तरल प्रवाह पर विचार कीजिए। माना कि पाइप परिवर्ती ऊँचाइयों पर है जैसा कि चित्र 10.9 में दर्शाया गया है। अब माना कि पाइप में एक असंपीड्य तरल अपरिवर्ती प्रवाह से प्रवाहित है। सांतत्य समीकरण के अनुसार इसके वेग में परिवर्तन होना चाहिए। त्वरण उत्पन्न करने के लिए एक बल की आवश्यकता है जो इसे घेरे हुए तरल से उत्पन्न होता है। भिन्न-भिन्न भागों में दाब भिन्न होना चाहिए। पाइप के दो बिंदुओं के बीच दाबांतर का संबंध वेग परिवर्तन (गति ऊर्जा परिवर्तन) तथा उन्नयन (ऊँचाई) में परिवर्तन (स्थिति ऊर्जा में परिवर्तन) दोनों में प्रदर्शित करने वाला सामान्य व्यंजक, बर्नूली का समीकरण है। इस संबंध को स्विस भौतिकविद् डेनियल बर्नूली ने विकसित किया था।
दो क्षेत्रों 1 (अर्थात् BC) तथा 2 (अर्थात् DE) क्षेत्रों में प्रवाह को लें। आरंभ में B तथा D के बीच तरल को लें। अत्यंत अल्प अंतराल ∆t में यह तरल प्रवाहित होगा। माना कि B पर चाल v1 तथा D पर v2 हैं। तब B पर तरल v1∆t, C की ओर प्रवाहित होगा (v1∆t इतना छोटा है कि हम BC का समान अनुप्रस्थ काट ले सकते हैं)। इसी समय अंतराल ∆t में तरल जो आरंभ में D पर है E की ओर प्रवाहित होगा तथा v2∆t दूरी तय करेगा। दो क्षेत्रों के बाँधने वाले A1, A2 क्षेत्रफल वाले समतल फलकों पर, जैसा दिखाया गया है, दाब P1, P2 कार्य करते हैं। बाएँ सिरे (BC) पर तरल पर किया गया कार्य
W1 = P1A1(v1Dt) = P1DV है। क्योंकि दोनों क्षेत्रों से समान आयतन का तरल प्रवाहित होता है (सांतत्य समीकरण से) दूसरे सिरे (DE) पर तरल द्वारा किया गया कार्य W2 = P2A2(v2Dt) = P2∆V है। अथवा तरल पर किया गया कार्य –P2∆V है। अतः द्रव पर किया गया कुल कार्य
W1 – W2 = (P1− P2) ∆V है।
इस कार्य का कुछ भाग तरल की गतिज ऊर्जा परिवर्तित करने में चला जाता है, तथा शेष भाग तरल की गुरुत्वीय स्थितिज ऊर्जा परिवर्तित करने में चला जाता है। यदि पाइप प्रवाहित तरल का घनत्व ρ तथा ∆m = ρA1v1∆t = ρ∆V की संहति ∆t समय में पाइप से प्रवाहित है तो गुरुत्वीय स्थितिज ऊर्जा में परिवर्तन
∆U = ρg∆V (h2 − h1)
गतिज ऊर्जा में परिवर्तन
∆K =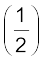 ρ ∆V (v22 − v12)
ρ ∆V (v22 − v12)
तरल के इस आयतन पर हम कार्य-ऊर्जा प्रमेय (अध्याय 6) का उपयोग कर सकते हैं जिससे हमें निम्नलिखित संबंध प्राप्त होता है।
(P1− P2) ∆V =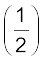 ρ ∆V (v22 − v12) + ρg∆V (h2 − h1)
ρ ∆V (v22 − v12) + ρg∆V (h2 − h1)
प्रत्येक पद को ∆V से विभाजित करने पर
(P1− P2) =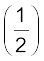 ρ (v22 − v12) + ρg (h2 − h1)
ρ (v22 − v12) + ρg (h2 − h1)
उपरोक्त पदों को पुनः व्यवस्थित करने पर हम प्राप्त करते हैं:
P1+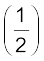 ρv12 + ρgh1 = P2+
ρv12 + ρgh1 = P2+ ρv22 + ρgh2 (10.12)
ρv22 + ρgh2 (10.12)
यह बर्नूली समीकरण है। चूंकि पाइपलाइन की लंबाई में 1 व 2 किन्हीं दो स्थितियों को दर्शाते हैं अतः हम सामान्य रूप में व्यक्त कर सकते हैं कि
P+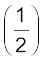 ρv2 + ρgh = स्थिरांक (10.13)
ρv2 + ρgh = स्थिरांक (10.13)
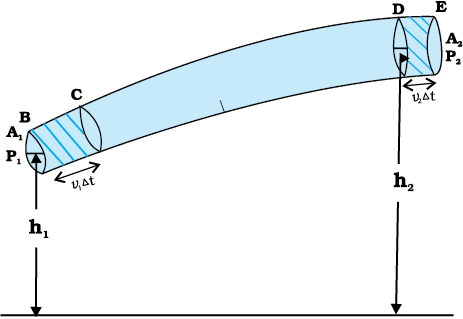
चित्र 10.9 परिवर्ती अनुप्रस्थकाट के किसी पाइप में किसी आदर्श तरल का प्रवाह, v1∆t लंबाई के खंड में भरा तरल समय ∆t में v2∆t लंबाई के खंड तक गति कर लेता है।
दूसरे शब्दों में, बर्नूली के कथन को हम निम्न प्रकार लिख सकते हैंः "जब हम किसी धारा रेखा के अनुदिश गति करते हैं, तो दाब P प्रति एकांक आयतन गतिज ऊर्जा तथा प्रति एकांक आयतन गुरुत्वीय स्थितिज ऊर्जा (ρgh) का योग अचर रहता है।"
तथा प्रति एकांक आयतन गुरुत्वीय स्थितिज ऊर्जा (ρgh) का योग अचर रहता है।"
नोट करें कि ऊर्जा संरक्षण के नियम का उपयोग करते समय यह माना गया है कि घर्षण के कारण कोई ऊर्जा क्षति नहीं होती। परन्तु वास्तव में, जब तरल प्रवाह होता है, तो आंतरिक घर्षण के कारण कुछ ऊर्जा की हानि हो जाती है। इसकी व्युत्पत्ति तरल की विभिन्न सतहों के भिन्न-भिन्न वेगों से प्रवाह के कारण होती है। यह सतहें एक दूसरे पर घर्षण बल लगाती हैं और परिणामस्वरूप ऊर्जा का ह्रास होता है। तरलों के इस गुण को श्यानता कहते हैं जिसकी विस्तार से व्याख्या बाद के खंड में की गई है। तरल की क्षय गतिज ऊर्जा ऊष्मा ऊर्जा में परिवर्तित हो जाती है। अतः बर्नूली का समीकरण शून्य श्यानता अथवा असान्य तरलों पर लागू होता है। बर्नूली प्रमेय पर एक और प्रतिबंध है कि यह असंपीड्य तरलों पर ही लागू होता है, क्योंकि तरलों की प्रत्यास्थ ऊर्जा को नहीं लिया गया है। वास्तव में इसके कई उपयोग हैं जो कम श्यानता तथा असंपीड्य तरलों की बहुत सी घटनाओं की व्याख्या कर सकते हैं। अस्थिर अथवा विक्षोभ प्रवाह में भी बर्नूली समीकरण काम नहीं आता क्योंकि इसमें वेग तथा दाब समय में लगातार अस्थिर रहते हैं।
जब तरल विरामावस्था में होता है अर्थात् प्रत्येक स्थान पर इसके कणों का वेग शून्य है, बर्नूली समीकरण निम्न प्रकार हो जाता हैः
P1 + ρgh1 = P2 + ρgh2
(P1− P2) = ρg (h2 − h1)
जो समीकरण (10.6) के ही समान है।
10.4.1 चाल का बहिर्वाह: टोरिसेली का नियम
बहिर्वाह शब्द का अर्थ है तरल का बहिर्गमन। टोरिसेली ने यह पता लगाया कि किसी खुली टंकी से तरल के बहिर्वाह की चाल को मुक्त रूप से गिरते पिण्ड की चाल के सूत्र के समरूप सूत्र द्वारा प्रदर्शित किया जा सकता है। ρ घनत्व के द्रव से भरी किसी एेसी टंकी पर विचार कीजिए जिसमें टंकी की तली से y1 ऊँचाई पर एक छोटा छिद्र है (देखिए चित्र 10.10)। द्रव के ऊपर, जिसका पृष्ठ y2 ऊँचाई पर है, वायु है जिसका दाब P है। सांतत्य समीकरण (समीकरण 10.9) से
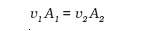
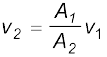
यदि टंकी की अनुप्रस्थ काट का क्षेत्रफल A2 छिद्र की अनुप्रस्थ का क्षेत्रफल A1 की तुलना में काफी अधिक है (A2 >>A1), तब हम शीर्ष भाग पर तरल को सन्निकटतः विराम में मान सकते हैं, अर्थात् v2 = 0। तब बिंदु 1 तथा 2 पर बर्नूली का समीकरण लागू करते हुए तथा यह लेते हुए कि छिद्र पर दाब P1 वायुमण्डलीय दाब के बराबर है, अर्थात् P1 = Pa, समीकरण (10.12) से हमें यह संबंध प्राप्त होता है।

y2 – y1 = h लेने पर
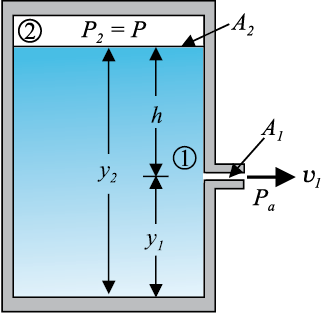
चित्र 10.10 टॉरिसेली नियम। पात्र के पार्श्व से बहिर्वाह की चाल v1 बर्नूली समीकरण द्वारा प्राप्त होती है। यदि पात्र का शीर्ष भाग खुला है तथा वायुमण्डल के संपर्क में है तब 2763.png
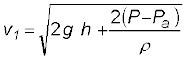 (10.14)
(10.14)
जब P >>Pa है तथा 2 g h की उपेक्षा की जा सकती है, तब बहिर्वाह की चाल का निर्धारण पात्र-दाब द्वारा किया जाता है। एेसी ही स्थिति रॉकेट-नोदन में होती है। इसके विपरीत यदि टंकी का ऊपरी भाग खुला होने के कारण वायुमण्डल के संपर्क में है तो P = Pa तब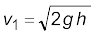 (10.15)
(10.15)
यह किसी मुक्त रूप से गिरते पिण्ड की चाल है। समीकरण (10.14) टॉरिसेली के सिद्धांत को इंगित करता है।
10.4.2 वैंटुरीमापी
वैंटुरीमापी किसी असंपीड्य तरल में प्रवाह-वेगों को मापने की एक युक्ति है। इसमें एक चौड़े व्यास वाली नली होती है जिसके मध्य में छोटा संकीर्णन होता है जैसा (चित्र 10.11) में दर्शाया गया है। इसमें U-नली के रूप में एक मैनोमीटर, जिसकी एक भुजा चौड़ी गर्दन के बिंदु तथा दूसरी संकुचित गर्दन से जुड़ी होती है जैसा कि (चित्र 10.11) में दर्शाया गया है। मैनोमीटर में ρm घनत्व का द्रव भरा होता है। इस युक्ति द्वारा नली की
चौड़ी गर्दन जिसका क्षेत्रफल A है, से प्रवाहित द्रव की चाल v1 मापनी होती है। संकुचित भाग पर, समीकरण (10.10) से,
चाल । तब बर्नूली समीकरण [h1= h2 के लिए, समीकरण (10.12)] का उपयोग करके हमें प्राप्त होता है:
। तब बर्नूली समीकरण [h1= h2 के लिए, समीकरण (10.12)] का उपयोग करके हमें प्राप्त होता है:
P1+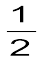 ρv12 = P2
ρv12 = P2 ρv12 (A/a)2
ρv12 (A/a)2
जिससे
P1- P2 =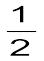 ρv12
ρv12 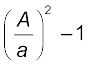 ] (10.16)
] (10.16)

चित्र 10.11 वैंटुरीमापी का व्यवस्था आरेख।
यह दाबांतर U नली की संकुचित भुजा में दूसरी भुजा की तुलना में तरल के उच्चतर स्तर का कारण है। भुजाओं की ऊँचाई में अंतर h दाबांतर की माप है।
P1– P2 = ρmgh =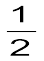 ρv12
ρv12
जिससे चौड़ी गर्दन पर तरल का वेग
v1= (10.17)
(10.17)
इस सिद्धांत के बहुत से अनुप्रयोग हैं। मोटर वाहन अथवा स्वचालित वाहन में कार्बूरेटर में वैंटुरीवाहिका (नोज़ल) होती है जिसमें से तीव्र गति से वायु प्रवाहित होती है। संकरी गर्दन पर दाब कम होता है इसलिए पैट्रोल (गैसोलीन) भीतर की ओर चैम्बर में चूस लिया जाता है ताकि दहन के लिए वायु तथा ईंधन का सही मिश्रण प्राप्त हो सके। फिल्टर पम्प या चूषित्र, बुनसन बर्नर, कणित्र तथा स्प्रेयर (देखिए चित्र 10.12) इत्र के लिए अथवा कीटनाशकों के छिड़काव के लिए प्रयोग में लाये जाने वाले इसी सिद्धांत पर कार्य करते हैं।
उदाहरण 10.7 रक्त वेग : किसी मूर्च्छित कुत्ते की बड़ी धमनी में रक्त का प्रवाह किसी वैंटुरीमापी से होकर परिवर्तित किया जाता है। इस युक्ति के चौड़े भाग की अनुप्रस्थ काट का क्षेत्रफल धमनी की अनुप्रस्थ काट के क्षेत्रफल, A = 8 mm2 के बराबर है। युक्ति के संकरे भाग का क्षेत्रफल a = 4 mm2 है। धमनी में दाब ह्रास
24 Pa है। धमनी रक्त के प्रवाह की चाल क्या है?
हल सारणी 10.1 से रक्त का घनत्व 1.06 × 103 kg m-3 लेते हैं। क्षेत्रफलों का अनुपात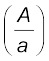 = 2 है। समीकरण (10.17) का उपयोग करके
= 2 है। समीकरण (10.17) का उपयोग करके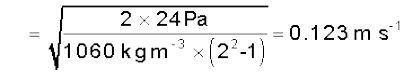 t
t
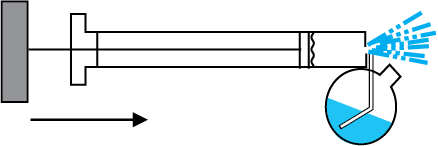
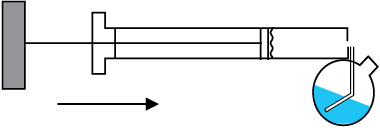
चित्र 10.12 स्प्रेगन। पिस्टन उच्च ताप पर वायु निकालता है जिसके फलस्वरूप पात्र की गर्दन पर दाब कम हो जाता है।
10.4.3 रक्त प्रवाह और हार्टअटैक (दिल का दौरा)
धमनी में बर्नूली सिद्धांत से रक्त प्रवाह को समझने में सहायता मिलती है। इसकी भीतरी दीवार पर प्लाक (Pluque) का जमाव होने के कारण धमनी भीतर से संकीर्ण हो जाती है। इन संकरी धमनियों से रक्त प्रवाहित कराने के लिए हृदय की गतिविधि पर अधिक बोझ पड़ जाता है। इस क्षेत्र में रक्त के प्रवाह की चाल बढ़ जाती है और भीतरी दाब घट जाता है तथा बाह्य दाब के कारण धमनी दब जाती है। हृदय इस धमनी को खोलने के लिए रक्त को धक्का देता है। जैसे ही रक्त इसे खोलकर बाहर की ओर तीव्र गति से प्रवाहित होता है, आंतरिक दाब पुनः गिर जाता है, और धमनी पुनः दब जाती है। इससे हार्ट अटैक हो सकता है।
10.4.4 गतिक उत्थापक (लिफ्ट)
किसी पिण्ड पर गतिक उत्थापक एक बल है। जैसे निम्न के तरल में गति के कारण वायुयान के पंख पर, जलपर्णी या एक घूमती गेंद पर। कई खेल जैसे क्रिकेट, टेनिस, बेसबॉल या गोलक में हम देखते हैं कि वायु में जाती हुई बॉल अपने परवलीय पथ से हट जाती है। इस हटाव को आंशिक रूप से बर्नूली सिद्धांत से समझाया जा सकता है।
(i) बिना घूमे गेंद का चलना : तरल के सापेक्ष बिना घूमती गतिमान गेंद के चारों ओर चित्र 10.13(a) में धारारेखाएँ प्रदर्शित हैं। धारारेखाओं की सममिती से यह स्पष्ट है कि तरल में गेंद के ऊपर तथा नीचे संगत बिंदुओं पर उसका वेग समान है, जिससे दाबांतर शून्य होता है। अतः गेंद पर वायु कोई ऊर्ध्वमुखी अथवा अधोमुखी बल नहीं लगाती।
(ii) घूमती हुई गेंद की चाल : चक्रण करती हुई गेंद अपने साथ वायु को घसीटती है। यदि फलक खुरदुरा हो तो अधिक वायु घसीटी जाएगी। किसी घूमती हुई गतिमान गेंद की धारारेखाएँ [चित्र 10.13(b)] दर्शायी गई हैं। गेंद आगे की ओर चलती है तथा इसके सापेक्ष वायु पीछे की ओर चलती है। इसलिए, गेंद के ऊपर वायु का वेग बढ़ जाता है और नीचे घट जाता है (खण्ड 10.3 देखें)। धारा रेखायें ऊपर की ओर संघन हो जाती हैं और नीचे की ओर विरल हो जाती हैं।
वेगों में अंतर के कारण ऊपरी तथा निचले पृष्ठों पर दाबांतर उत्पन्न हो जाते हैं जिससे गेंद पर एक नेट ऊर्ध्वमुखी बल कार्य करता है। प्रचक्रण के कारण उत्पन्न इस गतिक उत्थापक को मेगनस प्रभाव (Magnus Effect) कहते हैं।
वायुयान के पंख या एेयरोफॉयल पर उत्थापक : जब एेयरोफॉयल वायु में क्षैतिज दिशा में चलता है तो चित्र 10.13 (c) में दिखाए अनुसार विशिष्ट आकार के ठोस एेयरोफॉयल पर गतिक उत्थापक ऊपर की ओर लगता है। चित्र 10.13 (c) के अनुसार वायुयान के पंख की अनुप्रस्थ काट एेयरोफॉयल जैसी प्रतीत होती है जिसके परितः धारारेखाएँ प्रदर्शित हैं। जब एेयरोफॉइल हवा के विपरीत चलता है तब पंखों का तरल प्रवाह के सापेक्ष दिक्विन्यास धारारेखाओं को पंख के ऊपर-नीचे की अपेक्षा समीप कर देता है। प्रवाह की गति शीर्ष पर अधिक और नीचे कम होती है। इसके कारण ऊर्ध्वमुखी बल से पंख पर गतिक उत्थापक उत्पन्न होता है और यह वायुयान के भार को संतुलित करता है। निम्न उदाहरण इसे दर्शाता है।
उदाहरण 10.8 किसी पूर्णतः भारित बोइंग विमान की संहति 3.3 × 105 kg है। इसका कुल पंख क्षेत्रफल 500 m2 । यह एक निश्चित ऊँचाई पर 960 km/h की चाल से उड़ रहा है। (a) पंख के ऊपरी तथा निचले पृष्ठों के बीच दाबांतर आकलित कीजिए। (b) निचले पृष्ठ की तुलना में ऊपरी पृष्ठ पर वायु की चाल में आंशिक वृद्धि आकलित कीजिए। [वायु का घनत्व ρ = 1.2 kg m-3]
(a)
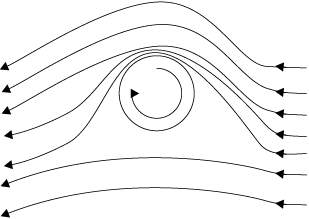

चित्र 10.13 ( a) अघूर्णी गतिमान गोले के समीप तरल (b) एक घूमते गतिमान गोले के निकट से गुज़रने वाले तरल का धाराप्रवाह (c) एेयरोफॉयल के समीप से गुज़रने वाली वायु में धारारेखाएँ।
हल (a) दाबान्तर से ऊर्ध्वमुखी बल से संतुलित बोइंग विमान का भार है
∆P × A = 3.3 × 105 kg × 9.8
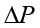 = (3.3 × 105 kg × 9.8 m s–2) / 500 m2
= (3.3 × 105 kg × 9.8 m s–2) / 500 m2
= 6.5 ×103 N m-2
(b) समीकरण (10.12) में हम वायुयान के ऊपरी पृष्ठ तथा निचले पृष्ठ की ऊँचाइयों के थोड़े अंतर की उपेक्षा कर देते हैं। तब इनके बीच दाबांतर

यहाँ v2 वायु की ऊपरी पृष्ठ के ऊपर चाल तथा v1 वायु की निचले पृष्ठ के नीचे चाल है।
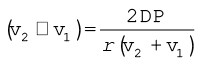
औसत चाल
vav = (v2 + v1)/2 = 960 km/h = 267 m s-1 लेने पर
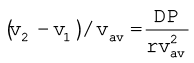 ≈ 0.08
≈ 0.08
पंखों के ऊपर वायु की चाल पंखों के नीचे वायु की चाल की तुलना में केवल 8 % अधिक होनी चाहिए। t
10.5 श्यानता
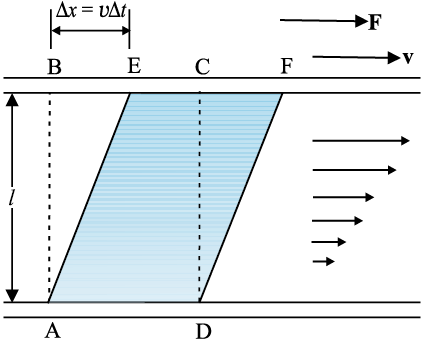
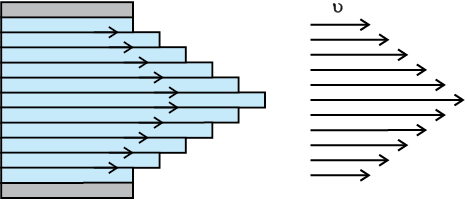
सभी तरल आदर्श तरल नहीं होते तथा वह गति में कुुछ प्रतिरोध डालते हैं। तरल गति में इस प्रतिरोध को आंतरिक घर्षण के रूप में देखा जा सकता है जो ठोसों में पृष्ठ पर गति से उत्पन्न घर्षण जैसा होता है। इसे श्यानता कहते हैं। जब द्रव की सतहों में सापेक्ष गति होती है तब यह बल उपस्थित होता है। चित्र 10.14 (a) में दर्शाये अनुसार यदि काँच की दो प्लेटों के बीच एक द्रव जैसे तेल को लेते हैं, निचली प्लेट को स्थिर रखा जाए जबकि ऊपरी प्लेट को समान गति से निचली प्लेट की अपेक्षा चलाते हैं। यदि तेल को शहद से विस्थापित कर दें तो उसी वेग से प्लेट को चलाने के लिए अधिक बल की आवश्यकता होगी। इससे हम यह निष्कर्ष निकालते हैं कि तेल की तुलना में शहद की श्यानता अधिक है। पृष्ठ के संपर्क में तरल का वेग पृष्ठ के वेग के समान होता है। अतः, द्रव की ऊपरी सतह के संपर्क में द्रव v वेग से चलता है और निचली स्थिर सतह के संपर्क में तरल की सतह स्थिर होगी। निचली स्थिर सतह से (शून्य वेग) जैसे-जैसे ऊपर जाते हैं सतहों का वेग समान रूप से बढ़ता जाता है तथा सबसे ऊपरी सतह का वेग v होता है। किसी भी द्रव सतह के लिए, इससे ऊपर की सतह इसे आगे की ओर खींचती है जबकि नीचे की सतह पीछे की ओर खींचती है। इसके कारण सतहों के बीच में बल उत्पन्न हो जाता है। इस प्रकार के प्रवाह को परत प्रवाह कहते हैं। जैसे मेज़ पर रखी चपटी किताब पर क्षैतिज बल लगाने पर उसके पन्ने फिसलते हैं इसी प्रकार द्रव की परतें एक दूसरे पर फिसलती हैं। किसी पाइप या ट्यूब में जब एक तरल बहता है तो ट्यूब के अक्ष के अनुदिश द्रव की परत का वेग अधिकतम होता है और शनैः शनैः जैसे हम दीवारों की ओर चलते हैं यह कम होता जाता है और अंत में शून्य हो जाता है [ चित्र 10.14 (b)]। एक ट्यूब में बेलनाकार पृष्ठ पर वेग स्थिर रहता है।
(a)
(b)
चित्र 10.14 (a) दो समांतर काँच की प्लेटों के बीच रखे द्रव की एक परत जिसमें काँच की निचली प्लेट स्थिर है तथा ऊपरी प्लेट v वेग से दाहिनी ओर गतिमान है। (b)पाइप में श्यान प्रवाह के लिए वेग वितरण।
इस गति के कारण द्रव के एक भाग जो किसी समय ABCD के रूप में था कुछ समय अंतराल (∆t) में AEFD का स्वरूप ले लेता है। इस समय अंतराल में द्रव मेें एक अवरूपण विकृति ∆x/l उत्पन्न हो जाती है। चूंकि प्रवाहित द्रव में समय के बढ़ने के अनुसार विकृति बढ़ती जाती है। ठोसों के विपरीत प्रयोगों द्वारा पाया गया है कि प्रतिबल विकृति की अपेक्षा ‘विकृति परिवर्तन की दर’ या ‘विकृति दर’ अर्थात् ∆x/(l ∆t) या v/l द्वारा प्रतिबल को प्राप्त किया जाता है। श्यानता गुणांक (उच्चारण ‘इटा’) की परिभाषा अवरूपण प्रतिबल तथा विकृतिदर के रूप में की जाती है,
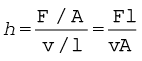 (10.18)
(10.18)
श्यानता का SI मात्र प्वाज (Pl) है। इसके दूसरे मात्रक N s m-2 या Pa s हैं। श्यानता की विमाएँ [ML-1T-1] हैं। आमतौर पर पतले द्रवों जैसे पानी, एल्कोहल आदि गाढ़े तरलों जैसे कोलतार, रक्त, ग्लिसरीन आदि की अपेक्षा कम श्यान होते हैं। कुछ सामान्य तरलों के श्यानता गुणांक सारणी 10.2 में सूचीबद्ध हैं। हम रक्त तथा जल के विषय में दो तथ्यों को बताते हैं, जो आपके लिए रोचक हो सकते हैं। सारणी 10.2 में इंगित सूचना के आधार पर जल की तुलना में रक्त अधिक गाढ़ा (अधिक श्यान) है। साथ ही रक्त की आपेक्षिक श्यानता (η/ηजल) ताप-परिसर 0 oC से 37 oC के बीच अचर रहती है।
द्रव की श्यानता ताप बढ़ने पर घटती है, जबकि गैसों की श्यानता ताप बढ़ने पर बढ़ती है।
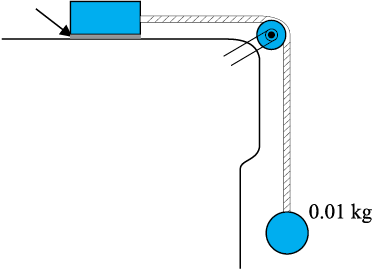
उदाहरण 10.9 0.10 m2 क्षेत्रफल की कोई धातु की प्लेट किसी डोरी की सहायता से जो एक आदर्श घिरनी (जिसे संहति रहित, तथा घर्षण रहित माना गया है) के ऊपर से होकर जाती है, 0.010 kg संहति से चित्र 10.15 की भांति जुड़ी है। कोई द्रव जिसकी फिल्म 0.30 mm मोटाई की है, मेज़ तथा प्लेट के बीच रखी हुई है। मुक्त किए जाने पर प्लेट 0.085 m s-1 की अचर चाल से दाईं ओर गति करने लगती है। द्रव का श्यानता गुणांक ज्ञात कीजिए।
फिल्म
चित्र 10.15 द्रव के श्यानता गुणांक का मापन।
हल डोरी में तनाव के कारण धातु की प्लेट दाईं ओर गति करती है। डोरी में यह तनाव T परिमाण में डोरी से निलम्बित पिण्ड के भार mg के बराबर है। अतः अवरूपण
F = T = mg = 0.010 kg × 9.8 m s–2 = 9.8 × 10-2 N
द्रव पर अवरूपण प्रतिबल = F/A =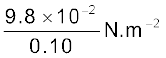
विकृति दर =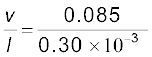

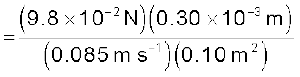
= 3.46 ×10-3 Pa s t
सारणी 10.2 कुछ तरलों की श्यानता
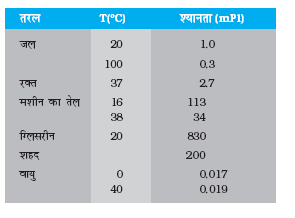
10.5.1 स्टोक का नियम
सामान्यतः जब एक पिण्ड किसी तरल से गिरता है तो वह अपने संपर्क में तरल की परतों को भी खींचता है। तरल की विभिन्न परतों में आपेक्ष गति उत्पन्न हो जाती है और परिणामस्वरूप पिण्ड एक परिणामी मंदक बल अनुभव करता है। स्वतंत्रतापूर्वक गिरती हुई पानी की बूंदें तथा दोलन गति करता हुआ लोलक एेसी गति के कुछ सामान्य उदाहरण हैं। यह देखा गया है कि श्यानता बल पिण्ड की गति के अनुपाती तथा उसकी दिशा के विपरीत कार्य करता है। दूसरी अन्य राशियाँ जिस पर बल F निर्भर है तरल की श्यानता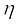 तथा गोल की त्रिज्या a है। एक अंग्रेज़ी वैज्ञानिक सर जॉर्ज जी. स्टोक्स (1819-1903) ने श्यान कर्षण बल F निम्न संबंध द्वारा निरूपित किया हैः
तथा गोल की त्रिज्या a है। एक अंग्रेज़ी वैज्ञानिक सर जॉर्ज जी. स्टोक्स (1819-1903) ने श्यान कर्षण बल F निम्न संबंध द्वारा निरूपित किया हैः
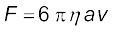 (10.19)
(10.19)
इसे स्टोक का नियम कहते हैं। हम स्टोक के नियम की व्युत्पत्ति नहीं करेंगे।
अवमंदन बल का यह नियम एक रोचक उदाहरण है जो वेग के अनुपाती है। किसी श्यान माध्यम में गिरते पिण्ड का अध्ययन करके हम इसका महत्त्व ज्ञात कर सकते हैं। हम वायु में गिरती एक वर्षा की बूँद पर ध्यान केंद्रित करते हैं। आरंभ में यह गुरुत्व बल के कारण त्वरित होती है। जैसे-जैसे इसका वेग बढ़ता जाता है, मंदक श्यान बल भी बढ़ता जाता है। अंत में जब इस पर कार्यरत श्यान बल तथा उत्प्लावन बल, गुरुत्व बल के तुल्य हो जाता है, तो नेट बल तथा त्वरण शून्य हो जाता है। तब वर्षा की बूँद अचर वेग से नीचे की ओर गिरती है। साम्य अवस्था में सीमांत वेग vt निम्न द्वारा दिया जाता है:
6πηavt = (4π/3) a3 (ρ-σ)g
जहाँ ρ तथा σ बूँद तथा तरल के क्रमशः संहति घनत्व हैं। हमें प्राप्त होता है:
vt = 2a2 (ρ-σ)g / (9η) (10.20)
अतः सीमांत वेग vt गोले के आकार के वर्ग के ऊपर निर्भर करता है तथा माध्यम के श्यानता के व्युत्क्रमानुपाती होता है।
इस संदर्भ में आप उदाहरण 6.2 पर पुनः ध्यान दे सकते हैं।
उदाहरण 10.10 2.0 mm त्रिज्या वाली एक ताँबे की गेंद 20oC पर 6.5 cm s-1 सीमांत वेग से तेल के टेंक में गिर रही है। 20oC पर तेल की श्यानता का आकलन कीजिए। तेल का घनत्व 1.5 ×103 kg m-3 तथा ताँबे का घनत्व 8.9 × 103 kg m-3 है।
हल यहाँ vt = 6.5 × 10-2 m s-1, a = 2 × 10-3 m, g = 9.8 m s-2, ρ = 8.9 × 103 kg m-3,
σ =1.5 ×103 kg m-3। समीकरण (10.20) से
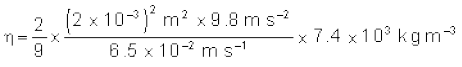
= 9.9 × 10-1 kg m–1 s–1 t
10.6 पृष्ठ तनाव
आपने देखा होगा कि तेल तथा जल आपस में नहीं मिलते; जल आपको और मुझे गीला कर देता है परन्तु बतख को नहीं; पारा काँच से नहीं चिपकता किन्तु जल चिपक जाता है; गुरुत्व बल की उपस्थिति में भी तेल रुई की बत्ती से ऊपर चढ़ जाता है। रस तथा पानी पेड़ के शीर्ष की पत्तियों तक ऊपर उठ जाता है, रंग के ब्रुश के बाल सूखे होने पर और पानी में डुबोने पर भी एक दूसरे से नहीं चिपकते लेकिन जब उसके बाहर होते हैं तो एक उत्तम नोक बनाते हैं। ये और एेसे ही अनेक अनुभव द्रवों की स्वतंत्र सतहों से संबंधित हैं। द्रवों की कोई निश्चित आकृति नहीं होती, परन्तु उनका अपना एक निश्चित आयतन होता है। जब उन्हें किसी पात्र में उड़ेलते हैं तो उनका एक स्वतंत्र पृष्ठ होगा। इन पृष्ठों की कुछ अतिरिक्त ऊर्जा होती है। इस परिघटना को पृष्ठ तनाव कहते हैं। यह केवल द्रवों में हो सकती है क्योंकि गैसों के कोई स्वतंत्र पृष्ठ नहीं होते। अब हम इस परिघटना को समझने का प्रयत्न करते हैं।
10.6.1 पृष्ठीय ऊर्जा
कोई द्रव अपने अणुओं के बीच आकर्षण के कारण स्थायी है। द्रव के भीतर एक अणु लीजिए। अंतरापरमाणुक दूरियाँ इस प्रकार की होती हैं कि यह अपने घेरने वाले सभी परमाणुओं की ओर आकर्षित होता है [चित्र 10.16(a)]। इस आकर्षण के परिणामस्वरूप अणुओं के लिए ऋणात्मक स्थितिज ऊर्जा उत्पन्न होती है। स्थितिज ऊर्जा का परिमाण इस बात पर निर्भर है कि इस चुने हुए अणु के चारों ओर अणु विन्यास किस प्रकार वितरित है तथा उनकी संख्या क्या है। परन्तु सभी अणुओं की औसत स्थितिज ऊर्जा समान होती है। यह इस तथ्य से स्पष्ट है कि इस प्रकार के अणुओं के किसी संचयन (द्रव) को लेने की अपेक्षा उन्हें एक दूसरे से दूर बिखेरने (वाष्पन या वाष्पीकृत करने) के लिए ऊर्जा की आवश्यकता होती है। यह वाष्पन ऊर्जा काफी अधिक होती है। पानी के लिए यह ऊर्जा 40 kJ/mol के आसपास होती है।
अब द्रव के पृष्ठ के समीप किसी अणु पर हम विचार करते हैं [ चित्र 10.16(b)]। द्रव के भीतर के अणु की तुलना में द्रव के आधे अणु ही इस अणु को घेरते हैं। इन अणुओं के कारण कुछ ऋणात्मक स्थितिज ऊर्जा होती है। परन्तु स्पष्ट रूप से यह द्रव के भीतर के अणु से अपेक्षाकृत कम होती है अर्थात् जो पूर्णरूप से अंदर है। यह लगभग बाद वाले के अपेक्षा आधी होती है। इस प्रकार किसी द्रव के पृष्ठ के अणु की ऊर्जा द्रव के भीतरी अणुओं की ऊर्जा से कुछ अधिक होती है। अतः कोई द्रव बाह्य स्थितियों के अनुसार, कम से कम अनुमत पृष्ठ क्षेत्रफल करने का प्रयास करता है। पृष्ठ के क्षेत्रफल में वृद्धि करने के लिए ऊर्जा खर्च करनी पड़ती है। अधिकांश पृष्ठीय परिघटनाओं को हम इसी तथ्य के पदों में समझ सकते हैं। किसी अणु को पृष्ठ पर रखने में कितनी ऊर्जा आवश्यक होती है? जैसा कि ऊपर वर्णन किया जा चुका है यह लगभग अणु को पूर्ण रूप से द्रव से बाहर निकालने की ऊर्जा के आधी होती है अर्थात् वाष्पन की ऊष्मा की आधी ऊर्जा चाहिए।
अंत में देखें पृष्ठ क्या है? चूँकि द्रव अनियमित गतिशील अणुओं से बना है अतः पूर्ण रूप से स्पष्ट पृष्ठ नहीं हो सकता। [चित्र 10.16(c)] द्रव अणुओं का घनत्व z = 0 पर कुछ ही अणु आकार की दूरी पर तेज़ी से घटकर शून्य हो जाता है।
10.6.2 पृष्ठीय ऊर्जा तथा पृष्ठ तनाव
अन्य सभी कारकों, जैसे आयतन आदि को स्थिर रखते हुए जैसा हमने पहले विचार किया है कि द्रव के पृष्ठ के साथ ऊर्जा संबद्ध होती है और अधिक पृष्ठ उत्पन्न करना चाहें तो हमें और अधिक ऊर्जा खर्च करनी होगी। इस तथ्य को ठीक प्रकार समझने के लिए द्रव की एक एेसी क्षैतिज फिल्म पर विचार कीजिए जो किसी एेसी छड़ पर समाप्त होती है जो समांतर निर्देशकों पर सरकने के लिए स्वतंत्र है [चित्र (10.17)]।
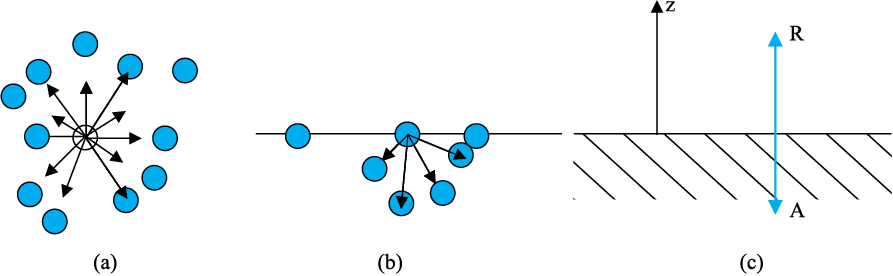
चित्र 10.16 किसी द्रव में पृष्ठ पर अणुओं का व्यवस्था आरेख तथा बलों का संतुलन (a)किसी द्रव के भीतर अणु। अणु पर अन्य अणुओं के कारण बलों को दर्शाया गया है। तीरों की दिशाएँ आकर्षण अथवा प्रतिकर्षण को दर्शाती हैं। (b) यही घटनाएँ द्रव के पृष्ठ के लिए। (c) आकर्षी (A) तथा प्रतिकर्षी (R) बलों की संतुलन।
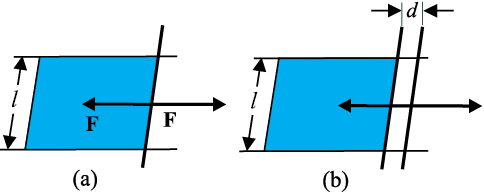
चित्र 10.17 किसी फिल्म को तानना। (a) संतुलन में कोई फिल्म (b) किसी अतिरिक्त दूरी तक तानित फिल्म।
मान लीजिए साम्यावस्था में हम चित्र में दर्शाये अनुसार छड़ को किसी छोटी दूरी d तक हटाते हैं। चूंकि फिल्म का क्षेत्रफल (अथवा पृष्ठ का क्षेत्रफल) बढ़ गया है अतः अब निकाय में अधिक ऊर्जा होगी। इसका अर्थ है कि आंतरिक बल के विपरीत कार्य किया गया है। माना यह आंतरिक बल F है तो आरोपित बल द्वारा किया गया कार्य F.d = Fd है। ऊर्जा संरक्षण के अनुसार यह अब फिल्म में संचित अतिरिक्त आंतरिक ऊर्जा है। माना कि फिल्म की प्रति एकांक क्षेत्रफल पृष्ठ ऊर्जा S है, और अतिरिक्त क्षेत्रफल 2dl है। किसी फिल्म के दो पार्श्व होते हैं जिनके बीच में द्रव होता है अतः फिल्म के दो पृष्ठ होते हैं। अतः अतिरिक्त ऊर्जा
S (2dl ) = Fd (10.21)
अथवा S=Fd/2dl = F/2l (10.22)
राशि S पृष्ठ तनाव का परिमाण है। यह द्रव के प्रति एकांक क्षेत्रफल की पृष्ठीय ऊर्जा है। यह चालित छड़ की प्रति एकांक लंबाई पर तरल द्वारा आरोपित बल है।
अभी तक हमने केवल एक द्रव के पृष्ठ की चर्चा की है। अधिक सामान्य रूप से हमें तरल के द्रवों या ठोस पृष्ठों पर विचार करना चाहिए। इन स्थितियों में पृष्ठीय ऊर्जा पृष्ठ के दोनों ओर के पदार्थों पर निर्भर होती है। उदाहरणस्वरूप यदि पदार्थों के अणु आपस में एक दूसरे को आकर्षित करते हैं तो पृष्ठीय ऊर्जा कम हो जाएगी परन्तु यदि वह एक दूसरे को प्रतिकर्षित करते हैं तो पृष्ठीय ऊर्जा बढ़ जाएगी। इस प्रकार और अधिक उपयुक्त रूप से हम कह सकते हैं कि पृष्ठीय ऊर्जा दोनों पदार्थों के मध्य अंतरापृष्ठ की ऊर्जा है तथा यह दोनों पर ही निर्भर है।
उपरोक्त चर्चा के आधार पर निम्नलिखित प्रेक्षण प्राप्त करते हैं:
(i) पृष्ठ तनाव द्रव तथा अन्य किसी पदार्थ के बीच अंतरापृष्ठ के तल में प्रति एकांक लंबाई पर कार्यरत बल (अथवा प्रति एकांक क्षेत्रफल की पृष्ठीय ऊर्जा) है। यह द्रव के भीतर के अणुओं की तुलना में अंतरापृष्ठ के अणुओं की अतिरिक्त ऊर्जा है।
(ii) अंतरापृष्ठ के किसी भी बिंदु पर हम पृष्ठ तल (सीमा के अतिरिक्त) में एक रेखा खींच सकते हैं तथा इस रेखा की प्रति एकांक लंबाई पर रेखा के लंबवत् परिमाण में समान तथा दिशा में विपरीत पृष्ठ तनाव बलों S की कल्पना कर सकते हैं। यह रेखा साम्यावस्था में है और अधिक स्पष्टता के लिए पृष्ठ पर परमाणुओं अथवा अणुओं की एक रेखा की कल्पना कीजिए। इस रेखा के बाईं ओर परमाणु रेखा को अपनी ओर खींचते हैं तथा जो इस रेखा के दाईं ओर हैं वह इसे अपनी ओर खींचते हैं। तनाव की स्थिति में यह परमाणुओं की रेखा साम्यावस्था में होती है। यदि वास्तव में, रेखा अंतरापृष्ठ की सीमांत रेखा को निर्दिष्ट करती है जैसा कि चित्र 10.16 (a) तथा (b) में दर्शाया गया है तो केवल अंदर की ओर प्रति एकांक लंबाई में लगने वाला बल S है।
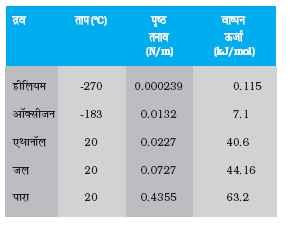
सारणी 10.3 में विभिन्न द्रवों के लिए पृष्ठ तनाव के मान दिए गए हैं। पृष्ठ तनाव का मान ताप पर निर्भर करता है। श्यानता के समान पृष्ठ तनाव का मान तापवृद्धि के साथ कम होता जाता है।
सारणी 10.3 दिए गए तापों पर कुछ द्रवों के पृष्ठ तनाव तथा वाष्पन ऊष्मा
यदि ठोस-वायु तथा तरल-वायु पृष्ठीय ऊर्जाओं के योग से तरल तथा ठोस की पृष्ठीय ऊर्जा कम है तो तरल ठोस से चिपकेगा। ठोस तथा द्रव पृष्ठों में आर्कषण बल होता है।
चित्र 10.18 में उपकरण के आरेख के अनुसार हम इसे सीधे ही माप सकते हैं। एक चपटी क्षैतिज काँच की प्लेट जिसके नीचे किसी पात्र में द्रव भरा है, तुला की एक भुजा कार्य करती है। प्लेट के क्षैतिज निचले किनारे को पानी से थोड़ा ऊपर रखकर, तुला के दूसरी ओर बाट रखकर संतुलित कर लेते हैं। द्रव से भरे पात्र को थोड़ा ऊपर उठाते हैं ताकि यह काँच की प्लेट के क्षैतिज किनारों को छूने भर लगे और पृष्ठ तनाव के कारण प्लेट को नीचे की ओर खींचने लगे। अब दूसरी ओर कुछ बाट रखते हैं जब तक कि प्लेट द्रव से कुछ अलग न हो जाए।
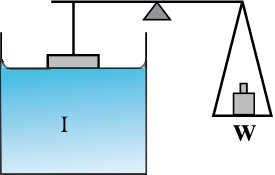
चित्र 10.18 पृष्ठ तनाव मापना।
मान लीजिए आवश्यक अतिरिक्त भार W है। तब समीकरण 10.22 तथा वहाँ की गई चर्चा से, द्रव-वायु अंतरापृष्ठ का पृष्ठ तनाव
Sla = (W/2l) = (mg/2l) (10.23)
जहाँ m अतिरिक्त संहति तथा l काँच की प्लेट के निचले किनारे की लंबाई है, पादाक्षर (la) इस तथ्य को स्पष्ट करता है कि यहाँ द्रव-वायु अंतरापृष्ठ तनाव सम्मिलित है।
10.6.3 संपर्क कोण
किसी अन्य माध्यम के संपर्क तल के निकट द्रव का पृष्ठ, आमतौर पर वक्रीय होता है। संपर्क बिंदु पर द्रव पृष्ठ पर स्पर्शज्या तथा द्रव के अंदर ठोस पृष्ठ पर स्पर्शज्या के बीच कोण को संपर्क कोण कहते हैं। इसे θ से प्रदर्शित करते हैं। द्रवों तथा ठोसों के विभिन्न युग्मों के अंतरापृष्ठों पर यह भिन्न-भिन्न होता है। संपर्क कोण का मान यह दर्शाता है कि कोई द्रव किसी ठोस के पृष्ठ पर फैलेगा अथवा इस पर बूंदें बनाएगा। उदाहरणस्वरूप जैसा चित्र 10.19 (a) में दर्शाया गया है, कमल के पत्ते पर पानी की बूंदें बनती हैं परन्तु स्वच्छ प्लास्टिक प्लेट पर यह फैल जाती है [चित्र 10.19(b)]।
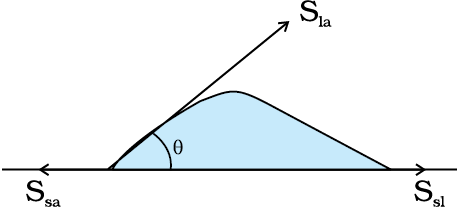
चित्र 10.19 अंतरापृष्ठों में तनाव के साथ पानी की बूँदों के विभिन्न आकार (a) कमल के एक पत्ते पर (b) एक स्वच्छ प्लास्टिक प्लेट पर।
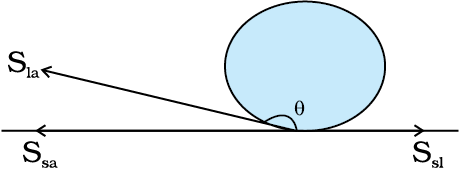
अब हम तीन अंतरापृष्ठीय तनावों का तीन अंतरापृष्ठों पर विचार करते हैं। जैसा कि चित्र 10.19(a) तथा (b) में दर्शाया गया है कि हम द्रव-वायु, ठोस-वायु तथा ठोस-द्रव के पृष्ठ तनाव Sla, Ssa, Ssl से दर्शाते हैं। तीनों माध्यमों के पृष्ठों पर लगे बल संपर्क रेखा पर साम्यावस्था में होने चाहिए। चित्र 10.19 (b) से हम निम्न संबंध व्युत्पन्न कर सकते हैं
Sla cos θ + Ssl = Ssa (10.24)
यदि Ssl > Sla तो संपर्क कोण बृहद कोण होगा जैसा कि पानी तथा पत्ते का अंतरापृष्ठ। जब θ बृहद कोण है तो द्रव के अणु एक दूसरे की ओर मजबूती से आकर्षित होते हैं तथा ठोस के अणुओं के साथ दुर्बल रूप से। द्रव-ठोस अंतरापृष्ठ को बनाने में बहुत ऊर्जा व्यय होती है, और तब द्रव ठोस को नहीं भिगोता। एेसा मोम या तेल लगे पृष्ठ पर पानी के साथ होता है एवं पारे के साथ किसी भी तल पर। दूसरी ओर, यदि द्रव के अणु ठोस के अणुओं की ओर अधिक शक्ति से आकर्षित होते हैं, तो यह Ssl को कम कर देगा। इसलिए, cos θ बढ़ सकता है या θ कम हो सकता है। तब θ न्यूनकोण होगा, एेसा पानी के काँच या प्लास्टिक पर होने से होता है या मिट्टी के तेल का किसी भी वस्तु पर (यह केवल फैल जाता है)। साबुन, अपमार्जक तथा रँगने वाली वस्तुएँ, गीले कर्मक हैं। जब इन्हें मिलाया जाता है तो संपर्क कोण छोटा हो जाता है जिससे यह भलीभांति अंदर घुसकर प्रभावी हो जाते हैं। पानी तथा रेशों के बीच संपर्क कोण बड़ा करने के लिए पानी में जल सहकारक को मिलाया जाता है।
10.6.4 बूँद तथा बुलबुले
पृष्ठ तनाव का एक महत्त्व यह भी है कि यदि गुरुत्व बल के प्रभाव की उपेक्षा की जा सके तो द्रव की मुक्त बूँदें तथा बुलबुले गोलाकार होते हैं। आपने इस तथ्य को अवश्य देखा होगाः विशेषकर स्पष्ट रूप से उच्च वेग वाले स्प्रे अथवा जेट से द्रुत बनने वाली छोटी बूँदों में, अथवा अपने बचपन के समय बनाए साबुन के बुलबुलों में। बूँदें तथा बुलबुले गोल ही क्यों होते हैं? साबुन के बुलबुले किस कारण स्थायी हैं? जैसा कि हम बार-बार चर्चा कर रहे हैं कि किसी द्रव-वायु अंतरापृष्ठ में ऊर्जा होती है। अतः किसी दिए गए आयतन के लिए सर्वाधिक स्थायी पृष्ठ वही है जिसका पृष्ठ क्षेत्रफल सबसे कम हो। गोले में यह गुण होता है। हम इस तथ्य को इस पुस्तक में सत्यापित नहीं कर सकते परन्तु आप स्वयं यह जाँच कर सकते हैं कि इस संदर्भ में गोला कम से कम एक घन की तुलना में बेहतर है। अतः यदि गुरुत्व बल तथा अन्य बल (उदाहरणार्थ वायु-प्रतिरोध) निष्प्रभावी हों तो द्रव की बूँदें गोल होती हैं।
पृष्ठ तनाव का एक अन्य रोचक परिणाम यह है कि बूँद के भीतर का दाब बूँद के बाहर के दाब से अधिक होता है। [चित्र 10.20(a)]। मान लीजिए r त्रिज्या की कोई गोल बूँद साम्यावस्था में है। यदि इस बूँद की त्रिज्या में ∆r की वृद्धि की जाए, तो बूँद में अतिरिक्त ऊर्जा होगी,
[4π(r + ∆r) 2- 4πr2] Sla = 8πr ∆r Sla (10.25)
यदि बूँद साम्यावस्था में है तो खर्च की गई यह ऊर्जा बूँद के भीतर तथा बाहर के दाबांतर (Pi – Po) के प्रभाव में प्रसार के कारण बूँद द्वारा प्राप्त की गई ऊर्जा से संतुलित होती है। यहाँ कृत कार्य
W = (Pi – Po) 4πr2∆r (10.26)
जिससे
(Pi – Po) = (2 Sla/ r) (10.27)
व्यापक रूप में, किसी द्रव-गैस अंतरापृष्ठ के लिए, उत्तल पार्श्व की ओर दाब का मान अवतल पार्श्व की ओर के दाब के मान से अधिक होता है। उदाहरण के लिए, यदि किसी द्रव के भीतर कोई वायु का बुलबुला है, तो यह वायु का बुलबुला
अधिक दाब पर होगा [चित्र 10.20 (b)]।
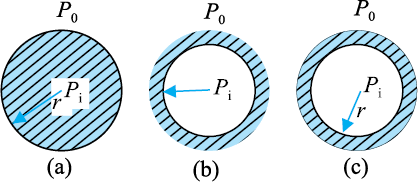
चित्र 10.20 r त्रिज्या की बूँद, गुहिका तथा बुलबुला।
किसी बुलबुले [ चित्र10.20 (c)] की बनावट किसी बूँद अथवा किसी गुहिका से भिन्न होती है। बुलबुले में दो अंतरापृष्ठ होते हैं। उपरोक्त तर्क के आधार पर किसी बुलबुले के लिए
(Pi – Po) = (4 Sla/ r) (10.28)
कदाचित् इसी कारण साबुन का बुलबुला बनाने के लिए आपको कुछ तेज़ी से फूँकना पड़ता है, परन्तु बहुत अधिक नहीं। अंदर थोड़ा अधिक दाब आवश्यक है।
10.6.5 केशिकीय उन्नयन
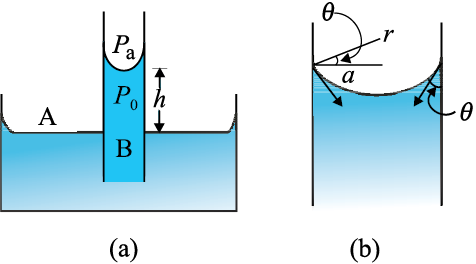
चित्र 10.21 केशिकीय उन्नयन (a) जल से भरे खुले बर्तन में डूबी किसी पतली नली का व्यवस्था आरेख।
(b) अंतरापृष्ठ के निकट का आवर्धित आरेख।
= (2S/a) cos θ (10.29)
इस प्रकार, नली के भीतर नवचंद्रक (वायु-जल अंतरापृष्ठ) पर जल का दाब वायुमण्डलीय दाब से कम है। चित्र 10.21(a) में दो बिंदुओं A तथा B पर ध्यान केंद्रित कीजिए, इन दोनों पर समान दाब होना चाहिए, अर्थात्
P0 + h ρ g = Pi = PA (10.30)
जहाँ ρ जल का घनत्व तथा h को केशिकीय उन्नयन कहते हैं [चित्र 10.21(a)]। समीकरण (10.29) तथा (10.30) का उपयोग करके हम प्राप्त करते हैं
h ρ g = (Pi – P0) = (2S cos θ )/a (10.31)
यहाँ की गई इस विवेचना तथा समीकरण (10.26) एवं (10.27) से यह स्पष्ट हो जाता है कि केशिकीय उन्नयन का कारण पृष्ठ तनाव ही है। a के लघुमानों के लिए यह अधिक होगा। बारीक या अत्यधिक पतली केशिका में प्रतिरूपी तौर से यह कुछ cm की कोटि का होता है। उदाहरण के लिए यदि
a = 0.05 cm है तो पानी के पृष्ठ तनाव (सारणी 10.3) का उपयोग करके हम पाते हैं
h = 2S/(ρ g a)
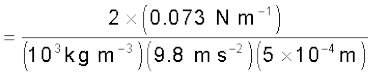
= 2.98 × 10–2 m = 2.98 cm
ध्यान दीजिए, यदि द्रव-नवचंद्रक (मेनिस्कस) उत्तल है जैसा कि पारे में होता है अर्थात् cos θ ऋणात्मक है तो समीकरण (10.30) से यह स्पष्ट है कि केशनली में द्रव का तल नीचे गिर जाता है अर्थात् केशिकीय अपनयन होता है।
10.6.6 अपमार्जक तथा पृष्ठ तनाव
हम अपने ग्रीज़ तथा तेल के दाग-धब्बे लगे गंदे सूती अथवा रेशों से बने कपड़ों को जल में अपमार्जक अथवा साबुन घोलकर, इसमें कपड़ों को डुबोकर तथा हिलाकर साफ़ करते हैं। आइए इस प्रक्रिया को भली भाँति समझें।
जल से धोने पर ग्रीज़ के दाग दूर नहीं होते। इसका कारण यह है कि जल ग्रीज़ लगी धूल को गीला नहीं करता; अर्थात् इन दोनों के बीच संपर्क पृष्ठ का क्षेत्रफल बहुत कम होता है। यदि जल ग्रीज़ को गीला कर सकता होता, तो जल का प्रवाह ग्रीज़ को हटा सकता था। कुछ इसी प्रकार की स्थिति अपमार्जक द्वारा प्राप्त की जाती है। अपमार्जकों के अणु ‘हेयरपिन’ की आकृति के होते हैं, जिनका एक सिरा जल से आकर्षित रहता है तथा दूसरा सिरा ग्रीज़, तेल अथवा मोम से, और इस प्रकार ये अणु जल-तेल अंतरापृष्ठ बनाने का प्रयास करते हैं। इसके परिणाम को चित्र 10.22 में चित्रों के क्रम के रूप में दर्शाया गया है।
अपनी भाषा में, इसे हम इस प्रकार कहेंगे कि अपमार्जक, जिसके अणु एक सिरे पर जल को तथा दूसरे सिरे पर मान लीजिए तेल को आकर्षित करते हैं जो पानी के साथ मिलकर पृष्ठ तनाव अत्यधिक कम कर देते हैं। यह अंतरापृष्ठ बनाना ऊर्जा की दृष्टि से भी अनुकूल हो सकता है जिनमें अपमार्जक से घिरे गंदगी के गोले पुनः जल से घिरे हों। पृष्ठ क्रियाशील अपमार्जकों अथवा केवल सफ़ाई के लिए ही नहीं वरन् तेल तथा खनिज अयस्कों की प्रतिप्राप्ति में भी महत्त्वपूर्ण होता है।

चित्र 10.22 अपमार्जक की कार्यप्रणाली - ‘अपमार्जक अणु क्या करते हैं’ के पदों में।
उदाहरण 10.11 2.00 mm व्यास की किसी केशनली का निचला सिरा बीकर में भरे जल के पृष्ठ से 8.00 cm नीचे तक डुबोया जाता है। नली के जल में डूबे सिरे पर अर्धगोलीय बुलबुला फुलाने के लिए नली के भीतर आवश्यक दाब ज्ञात कीजिए। प्रयोग के ताप पर जल का पृष्ठ तनाव 7.30 ×10-2 Nm-1 है। जल का घनत्व = 1000 kg/m3, वायुमण्डलीय दाब = 1.01 × 105 Pa तथा g = 9.80 m s-2 । दाब आधिक्य भी परिकलित कीजिए।
हल किसी तरल के भीतर गैस के बुलबुले के अंदर दाब आधिक्य = 2S/r, यहाँ S द्रव-गैस अंतरापृष्ठ का पृष्ठतनाव तथा r बुलबुले की त्रिज्या है। यहाँ ध्यान दीजिए, इसमें केवल एक ही द्रव पृष्ठ है। (किसी गैस में द्रव की बूँद के लिए दो द्रव अंतरापृष्ठ होते हैं, अतः उस प्रकरण में दाब आधिक्य = 4S/r लागू होता है)। बुलबुले के बाहर दाब Po = वायुमण्डलीय दाब + 8 cm जल स्तंभ का दाब। अर्थात्
Po = (1.01 × 105 Pa + 0.08 m × 1000 kg m–3
× 9.80 m s–2)
= 1.01784 × 105 Pa
अतः बुलबुले के भीतर दाब
Pi = Po + 2S/r
= 1.01784 × 105 Pa + (2 × 7.3 × 10-2 Pa m/10-3 m)
= (1.01784 + 0.00146) × 105 Pa
= 1.02 × 105 Pa चूँकि बुलबुला अर्धगोलीय है, अतः यहाँ केशनली की त्रिज्या को ही बुलबुले की त्रिज्या माना गया है। (उत्तर का निकटन तीन सार्थक अंकों तक किया गया है।) बुलबुले के भीतर दाब
आधिक्य 146 Pa है। t
सारांश
1. तरलों का मूलभूत गुण यह है कि वह प्रवाहित होते (बहते) हैं। अपनी आकृति में परिवर्तन के प्रति तरलों में कोई प्रतिरोध नहीं होता। अतः पात्र की आकृति तरल की आकृति को निर्धारित करती है।
2. द्रव असंपीड्य होता है तथा इसका अपना स्वतंत्र पृष्ठ होता है। गैस संपीड्य होती है तथा यह फैलकर समस्त उपलब्ध आयतन (स्थान) को भर देती है।
3. यदि किसी तरल द्वारा किसी क्षेत्रफल A पर आरोपित अभिलंब बल F है तो औसत दाब Pav को बल तथा क्षेत्रफल के अनुपात के रूप में इस प्रकार परिभाषित किया जाता है:
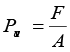
4. दाब का मात्रक पास्कल (Pa) है। यह वास्तव में N m-2 ही है। दाब के अन्य सामान्य मात्रक इस प्रकार हैं:
1 atm = 1.01×105 Pa
1 bar = 105 Pa
1 torr = 133 Pa = 0.133 kPa
1 mm of Hg = 1 torr = 133 Pa
5. पास्कल का नियम: इसके अनुसार विरामावस्था में तरल का दाब उन सभी बिंदुओं पर जो समान ऊँचाई पर स्थित हैं, समान होता है। किसी परिबद्ध तरल पर आरोपित दाब बिना घटे उस तरल के सभी बिंदुओं तथा पात्र की दीवारों पर संचरित हो जाता है।
6. किसी तरल के भीतर दाब गहराई h के साथ इस व्यंजक के अनुसार परिवर्तित होता है
P = Pa + ρgh
यहाँ ρ तरल का घनत्व है जिसे एकसमान माना गया है।
7. किसी असमान अनुप्रस्थ काट वाले पाइप में अपरिवर्ती प्रवाहरत, असंपीड्य तरल के प्रत्येक बिंदु से एक सेकंड में प्रवाहित होने वाले आयतन का परिमाण समान रहता है।
v A = नियतांक ( v वेग तथा A अनुप्रस्थ काट का क्षेत्रफल)
असंपीड्य तरलों के बहाव में यह समीकरण संहति संरक्षण के नियम के कारण है।
8. बर्नूली का सिद्धांत: इस सिद्धांत के अनुसार जब हम किसी धारा रेखा के अनुदिश गमन करते हैं, तो दाब (P), प्रति एकांक आयतन गतिज ऊर्जा (ρv2/2), तथा प्रति एकांक आयतन स्थितिज ऊर्जा (ρgy) का योग अचर
रहता है
P + ρv2/2 + ρgy = नियतांक
यह समीकरण, मूलतः अपरिवर्ती प्रवाहरत, शून्य श्यानता वाले तरल के लिए लागू होने वाला ऊर्जा संरक्षण नियम है। शून्य श्यानता का कोई द्रव नहीं होता अतः उपरोक्त कथन लगभग सत्य है। श्यानता घर्षण की भांति होती है और वह गतिज ऊर्जा को ऊष्मा ऊर्जा में बदल देती है।
9. यद्यपि तरल में अपरूपण विकृति के लिए अपरूपक प्रतिबल की आवश्यकता नहीं होती, परन्तु जब किसी तरल पर अपरूपण प्रतिबल लगाया जाता है तो उसमें गति आ जाती है, जिसके कारण इसमें एक अपरूपण विकृति उत्पन्न हो जाती है जो समय के बढ़ने के साथ बढ़ती है। अपरूपण प्रतिबल एवं अपरूपण विकृति की समय दर के अनुपात को श्यानता गुणांकη कहते हैं।
यहाँ प्रतीकों के अपने सामान्य अर्थ हैं जो पाठ्य सामग्री में दिए गए हैं।
10. स्टोक का नियम: इस नियम के अनुसार a त्रिज्या का गोला, जो श्यानता η के तरल में, v वेग से गतिमान है, द्रव की श्यानता के कारण एक श्यान कर्षण बल F अनुभव करता है जो F = –6πηav द्वारा व्यक्त किया जा सकता है।
11. किसी द्रव का पृष्ठ तनाव प्रति एकांक लंबाई पर आरोपित बल (अथवा प्रति एकांक क्षेत्रफल की पृष्ठीय ऊर्जा होता है), जो द्रव तथा सीमांत पृष्ठ के बीच अंतरापृष्ठ के तल में कार्य करता है। यह वह अतिरिक्त ऊर्जा है जो द्रव के अभ्यंतर (आंतरिक) के अणुओं की अपेक्षा इसके अंतरापृष्ठ के अणुओं में होती है।
विचारणीय विषय
1. दाब एक अदिश राशि है। दाब की परिभाषा "प्रति एकांक क्षेत्रफल पर आरोपित बल" से हमारे मन में एेसी
धारणा बनती है कि दाब सदिश राशि है जो कि वास्तव में असत्य है। परिभाषा के अंश में जिस ‘बल’ का प्रयोग किया गया है वह वास्तव में बल का एक घटक है जो पृष्ठ के क्षेत्रफल पर अभिलंबवत् आरोपित होता है। तरलों का वर्णन करते समय कण तथा दृढ़ पिण्ड यांत्रिकी की तुलना में संकल्पनात्मक बदलाव की आवश्यकता होती है। यहाँ हमारी रुचि तरल के उन-उन धर्मों में है जो तरल के एक बिंदु से दूसरे बिंदु में परिवर्तित हो जाते हैं।
2. हमें यह कदापि नहीं सोचना चाहिए कि तरल केवल ठोसों, जैसे किसी पात्र की दीवारें अथवा तरल में डूबा ठोस पदार्थ, पर ही दाब डालते हैं। वास्तव में तरल में हर बिंदु पर दाब होता है। तरल का कोई अवयव (जैसा कि चित्र 10.2 (a)] में दर्शाया गया है, उसके विभिन्न फलकों पर सामान्य दाब आरोपित होने के कारण साम्यावस्था में होता है।
3. दाब के लिए व्यंजक
P = Pa + ρgh
तभी सत्य होता है, जब तरल असंपीड्य हो। व्यावहारिक रूप से कहें तो यह द्रवों पर जो अधिकतर असंपीड्य हैं, लागू होता है और इसीलिए एक नियत ऊँचाई के लिए अपरिवर्तनीय रहता है।
4. गेज़ दाब (या प्रमापी दाब) वास्तविक दाब तथा वायुमण्डलीय दाब का अंतर होता है।
P – Pa = Pg
बहुत सी दाब मापक युक्तियाँ गेज़ दाब ही मापती हैं। इनमें टायरों के दाब गेज़ तथा रक्तचाप गेज़ (स्फाइग्मौमैनोमीटर) सम्मिलित हैं।
5. धारारेखा किसी तरल प्रवाह का मानचित्र होती है। स्थायी प्रवाह में दो धारारेखाएँ एक दूसरे को नहीं काटतीं। यदि एेसा होता, तो जिस बिंदु पर दो धारारेखाएँ एक दूसरे को काटती हैं वहाँ तरल कण के दो संभव वेग होते।
6. जिन तरलों में श्यान कर्षण होता है उन पर बर्नूली-सिद्धांत लागू नहीं होता। इस प्रकरण में क्षयकारी श्यान बल द्वारा किया गया कार्य भी गणना में लेना चाहिए तथा P2 [चित्र 10.9] का मान समीकरण (10.12) में दिए गए मान से कम होगा।
7. ताप बढ़ने पर द्रव के परमाणु और अधिक गतिशील हो जाते हैं तथा श्यानता गुणांक η का मान घट जाता है। किसी गैस में ताप बढ़ने पर उसके परमाणुओं की यादृच्छिक गति बढ़ जाती है और η भी बढ़ जाता है।
8. पृष्ठ पर अणुओं की स्थितिज ऊर्जा अभ्यंतर के अणुओं की स्थितिज ऊर्जा की अपेक्षा अधिक होने के कारण पृष्ठ तनाव होता है। दो पदार्थों जिनमें कम से कम एक तरल है, के अंतरापृष्ठ पर (जो दोनों को पृथक करता है) पृष्ठ ऊर्जा होती है। यह केवल एक तरल का ही गुण नहीं है।
अभ्यास
10.1 स्पष्ट कीजिए क्यों
(a) मस्तिष्क की अपेक्षा मानव का पैरों पर रक्त चाप अधिक होता है।
(b) 6 km ऊँचाई पर वायुमण्डलीय दाब समुद्र तल पर वायुमण्डलीय दाब का लगभग आधा हो जाता है, यद्यपि वायुमण्डल का विस्तार 100 km से भी अधिक ऊँचाई तक है।
(c) यद्यपि दाब, प्रति एकांक क्षेत्रफल पर लगने वाला बल होता है तथापि द्रवस्थैतिक दाब एक अदिश राशि है।
10.2 स्पष्ट कीजिए क्यों
(a) पारे का काँच के साथ स्पर्श कोण अधिक कोण होता है जबकि जल का काँच के साथ स्पर्श कोण न्यून कोण होता है।
(b) काँच के स्वच्छ समतल पृष्ठ पर जल फैलने का प्रयास करता है जबकि पारा उसी पृष्ठ पर बूँदें बनाने का प्रयास करता है। (दूसरे शब्दों में जल काँच को गीला कर देता है जबकि पारा एेसा नहीं करता है।)
(c) किसी द्रव का पृष्ठ तनाव पृष्ठ के क्षेत्रफल पर निर्भर नहीं करता है।
(d) जल में घुले अपमार्जकों के स्पर्श कोणों का मान कम होना चाहिए।
(e) यदि किसी बाह्य बल का प्रभाव न हो, तो द्रव बूँद की आकृति सदैव गोलाकार होती है।
10.3 प्रत्येक प्रकथन के साथ संलग्न सूची में से उपयुक्त शब्द छाँटकर उस प्रकथन के रिक्त स्थान की पूर्ति कीजिएः
(a) व्यापक रूप में द्रवों का पृष्ठ तनाव ताप बढ़ने पर .……… है। (बढ़ता/घटता)
(b) गैसों की श्यानता ताप बढ़ने पर ……… है, जबकि द्रवों की श्यानता ताप बढ़ने पर ………… है। (बढ़ती/घटती)
(c) दृढ़ता प्रत्यास्थ्ता गुणांक वाले ठोसों के लिए अपरूपण प्रतिबल………….., के अनुक्रमानुपाती होता है, जबकि द्रवों के लिए वह …………….. के अनुक्रमानुपाती होता है। (अपरूपण विकृति/अपरूपण विकृति की दर)
(d) किसी तरल के अपरिवर्ती प्रवाह में आए किसी संकीर्णन पर प्रवाह की चाल में वृद्धि में .......... का अनुसरण होता है। (संहति का संरक्षण/बर्नूली सिद्धांत)
(e) किसी वायु सुरंग में किसी वायुयान के मॉडल में प्रक्षोभ की चाल वास्तविक वायुयान के प्रक्षोभ के लिए क्रांतिक चाल की तुलना में……… होती है। (अधिक/कम)
10.4 निम्नलिखित के कारण स्पष्ट कीजिए:
(a) किसी कागज़ की पट्टी को क्षैतिज रखने के लिए आपको उस कागज़ पर ऊपर की ओर हवा फूँकनी चाहिए, नीचे की ओर नहीं।
(b) जब हम किसी जल टोंटी को अपनी उँगलियों द्वारा बंद करने का प्रयास करते हैं, तो उँगलियों के बीच की खाली जगह से तीव्र जल धाराएँ फूट निकलती हैं।
(c) इंजक्शन लगाते समय डॉक्टर के अँगूठे द्वारा आरोपित दाब की अपेक्षा सुई का आकार दवाई की बहिःप्रवाही धारा को अधिक अच्छा नियंत्रित करता है।
(d) किसी पात्र के बारीक छिद्र से निकलने वाला तरल उस पर पीछे की ओर प्रणोद आरोपित करता है।
(e) कोई प्रचक्रमान क्रिकेट की गेंद वायु में परवलीय प्रपथ का अनुसरण नहीं करती।
10.5 ऊँची एड़ी के जूते पहने 50 kg संहति की कोई बालिका अपने शरीर को 1.0 cm व्यास की एक ही वृत्ताकार एड़ी पर संतुलित किए हुए है । क्षैतिज फर्श पर एड़ी द्वारा आरोपित दाब ज्ञात कीजिए ।
10.6 टॉरिसिली के वायुदाब मापी में पारे का उपयोग किया गया था। पास्कल ने एेसा ही वायुदाब मापी
984 kg m–3 घनत्व की फ्रेंच शराब का उपयोग करके बनाया। सामान्य वायुमंडलीय दाब के लिए शराब-स्तंभ की ऊँचाई ज्ञात कीजिए ।
10.7 समुद्र तट से दूर कोई ऊर्ध्वाधर संरचना 109 Pa के अधिकतम प्रतिबल को सहन करने के लिए बनाई गई है । क्या यह संरचना किसी महासागर के भीतर किसी तेल कूप के शिखर पर रखे जाने के लिए उपयुक्त है ? महासागर की गहराई लगभग 3 km है । समुद्री धाराओं की उपेक्षा कीजिए ।
10.8 किसी द्रवचालित आटोमोबाइल लिफ्ट की संरचना अधिकतम 3000 kg संहति की कारों को उठाने के लिए की गई है । बोझ को उठाने वाले पिस्टन की अनुप्रस्थ काट का क्षेत्रफल 425 cm2 है । छोटे पिस्टन को कितना अधिकतम दाब सहन करना होगा ?
10.9 किसी U-नली की दोनों भुजाओं में भरे जल तथा मेथेलेटिड स्पिरिट को पारा एक-दूसरे से पृथक् करता है । जब जल तथा पारे के स्तंभ क्रमशः 10 cm तथा 12.5 cm ऊँचे हैं, तो दोनों भुजाओं में पारे का स्तर समान है । स्पिरिट का आपेक्षिक घनत्व ज्ञात कीजिए ।
10.10 यदि प्रश्न 10.9 की समस्या में, U-नली की दोनों भुजाओं में इन्हीं दोनों द्रवों को और उड़ेल कर दोनों द्रवों के स्तंभों की ऊँचाई 15 cm और बढ़ा दी जाएँ, तो दोनों भुजाओं में पारे के स्तरों में क्या अंतर होगा । (पारे का आपेक्षिक घनत्व = 13.6) ।
10.11 क्या बर्नूली समीकरण का उपयोग किसी नदी की किसी क्षिप्रिका के जल-प्रवाह का विवरण देने के लिए किया जा सकता है ? स्पष्ट कीजिए ।
10.12 बर्नूली समीकरण के अनुप्रयोग में यदि निरपेक्ष दाब के स्थान पर प्रमापी दाब (गेज़ दाब) का प्रयोग करें तो क्या इससे कोई अंतर पड़ेगा ? स्पष्ट कीजिए ।
10.13 किसी 1.5 m लंबी 1.0 cm त्रिज्या की क्षैतिज नली से ग्लिसरीन का अपरिवर्ती प्रवाह हो रहा है । यदि नली के एक सिरे पर प्रति सेकंड एकत्र होने वाली ग्लिसरीन का परिमाण 4.0 × 10–3 kg s–1 है, तो नली के दोनों सिरों के बीच दाबांतर ज्ञात कीजिए । (ग्लिसरीन का घनत्व = 1.3 × 103 kg m–3 तथा ग्लिसरीन की श्यानता = 0.83 Pa s)
[आप यह भी जाँच करना चाहेंगे कि क्या इस नली में स्तरीय प्रवाह की परिकल्पना सही है ।]
10.14 किसी आदर्श वायुयान के परीक्षण प्रयोग में वायु-सुरंग के भीतर पंखों के ऊपर और नीचे के पृष्ठों पर वायु-प्रवाह की गतियाँ क्रमशः 70 m s–1 तथा 63 m s–1 हैं । यदि पंख का क्षेत्रफल 2.5 m2 है, तो उस पर आरोपित उत्थापक बल परिकलित कीजिए । वायु का घनत्व 1.3 kg m–3 लीजिए ।
10.15 चित्र 10.23(a) तथा (b) किसी द्रव (श्यानताहीन) का अपरिवर्ती प्रवाह दर्शाते हैं । इन दोनों चित्रों में से कौन सही नहीं है ? कारण स्पष्ट कीजिए ।

चित्र 10.23
10.16 किसी स्प्रे पंप की बेलनाकार नली की अनुप्रस्थ काट का क्षेत्रफल 8.0 cm2 है । इस नली के एक सिरे पर 1.0 mm व्यास के 40 सूक्ष्म छिद्र हैं । यदि इस नली के भीतर द्रव के प्रवाहित होने की दर
1.5 m min–1 है, तो छिद्रों से होकर जाने वाले द्रव की निष्कासन-चाल ज्ञात कीजिए ।
10.17 U-आकार के किसी तार को साबुन के विलयन में डुबो कर बाहर निकाला गया जिससे उस पर एक पतली साबुन की फिल्म बन गई । इस तार के दूसरे सिरे पर फिल्म के संपर्क में एक फिसलने वाला हलका तार लगा है जो 1.5 × 10–2 N भार (जिसमें इसका अपना भार भी सम्मिलित है) को सँभालता है । फिसलने वाले तार की लंबाई 30 cm है । साबुन की फिल्म का पृष्ठ तनाव कितना है ?
10.18 निम्नांकित चित्र 10.24(a) में किसी पतली द्रव-फिल्म को 4.5 × 10–2 N का छोटा भार सँभाले दर्शाया गया है । चित्र (b) तथा (c) में बनी इसी द्रव की फिल्में इसी ताप पर कितना भार सँभाल सकती हैं ? अपने उत्तर को प्राकृतिक नियमों के अनुसार स्पष्ट कीजिए ।
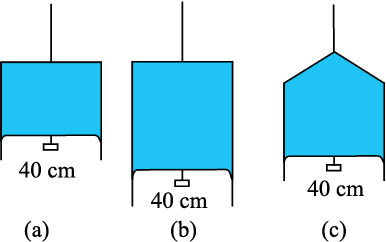
चित्र 10.24
10.19 3.00 mm त्रिज्या की किसी पारे की बूँद के भीतर कमरे के ताप पर दाब क्या है? 20 °C ताप पर पारे का पृष्ठ तनाव 4.65 × 10–1 N m–1 है । यदि वायुमंडलीय दाब 1.01 × 105 Pa है, तो पारे की बूँद के भीतर दाब-अधिक्य भी ज्ञात कीजिए ।
10.20 5.00 mm त्रिज्या के किसी साबुन के विलयन के बुलबुले के भीतर दाब-आधिक्य क्या है? 20 °C ताप पर साबुन के विलयन का पृष्ठ तनाव 2.50 × 10–2 N m–1 है । यदि इसी विमा का कोई वायु का बुलबुला 1.20 आपेक्षिक घनत्व के साबुन के विलयन से भरे किसी पात्र में 40.0 cm गहराई पर बनता, तो इस बुलबुले के भीतर क्या दाब होता, ज्ञात कीजिए। (1 वायुमंडलीय दाब = 1.01 × 105 Pa) ।
अतिरिक्त अभ्यास
10.21 1.0 m2 क्षेत्रफल के वर्गाकार आधार वाले किसी टैंक को बीच में ऊर्ध्वाधर विभाजक दीवार द्वारा दो भागों में बाँटा गया है । विभाजक दीवार में नीचे 20 cm2 क्षेत्रफल का कब्ज़ेदार दरवाज़ा है । टैंक का एक भाग जल से भरा है तथा दूसरा भाग 1.7 आपेक्षिक घनत्व के अम्ल से भरा है । दोनों भाग 4.0 m ऊँचाई तक भरे गए हैं । दरवाज़े को बंद रखने के आवश्यक बल परिकलित कीजिए ।
10.22 चित्र 10.25(a) में दर्शाए अनुसार कोई मैनोमीटर किसी बर्तन में भरी गैस के दाब का पाठ्यांक लेता है । पंप द्वारा कुछ गैस बाहर निकालने के पश्चात् मैनोमीटर चित्र 10.25(b) में दर्शाए अनुसार पाठ्यांक लेता है । मैनोमीटर में पारा भरा है तथा वायुमंडलीय दाब का मान 76 cm (Hg) है ।
(i) प्रकरणों (a) तथा (b) में बर्तन में भरी गैस के निरपेक्ष दाब तथा प्रमापी दाब cm (Hg) के मात्रक में लिखिए ।
(ii) यदि मैनोमीटर की दाहिनी भुजा में 13.6 cm ऊँचाई तक जल (पारे के साथ अमिश्रणीय) उड़ेल दिया जाए तो प्रकरण (b) में स्तर में क्या परिवर्तन होगा ? (गैस के आयतन में हुए थोड़े परिवर्तन की उपेक्षा कीजिए ।)
पंप को
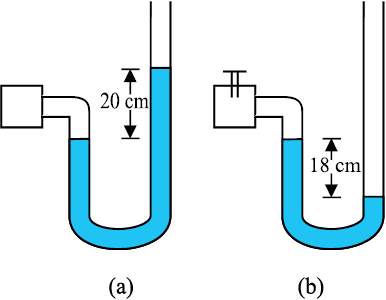
चित्र 10.25
10.23 दो पात्रों के आधारों के क्षेत्रफल समान हैं परंतु आकृतियाँ भिन्न-भिन्न हैं । पहले पात्र में दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दो गुना जल आता है । क्या दोनों प्रकरणों में पात्रों के आधारों पर आरोपित बल समान हैं । यदि एेसा है तो भार मापने की मशीन पर रखे एक ही ऊँचाई तक जल से भरे दोनों पात्रों के पाठ्यांक भिन्न-भिन्न क्यों होते हैं ?
10.24 रुधिर-आधान के समय किसी शिरा में, जहाँ दाब 2000 Pa है, एक सुई धँसाई जाती है । रुधिर के पात्र को किस ऊँचाई पर रखा जाना चाहिए ताकि शिरा में रक्त ठीक-ठीक प्रवेश कर सके । (संपूर्ण रुधिर का घनत्व सारणी 10.1 में दिया गया है।)
10.25 बर्नूली समीकरण व्युत्पन्न करने में हमने नली में भरे तरल पर किए गए कार्य को तरल की गतिज तथा स्थितिज ऊर्जाओं में परिवर्तन के बराबर माना था । (a) यदि क्षयकारी बल उपस्थित है, तब नली के अनुदिश तरल में गति करने पर दाब में परिवर्तन किस प्रकार होता है ? (b) क्या तरल का वेग बढ़ने पर क्षयकारी बल अधिक महत्त्वपूर्ण हो जाते हैं ? गुणात्मक रूप में चर्चा कीजिए ।
10.26 (a) यदि किसी धमनी में रुधिर का प्रवाह पटलीय प्रवाह ही बनाए रखना है तो 2 × 10–3 m त्रिज्या की किसी धमनी में रुधिर-प्रवाह की अधिकतम चाल क्या होनी चाहिए ? (b) तदनुरूपी प्रवाह-दर क्या है ? (रुधिर की श्यानता 2.084 × 10-3 Pa s लीजिए) ।
10.28 मिलिकन तेल बूँद प्रयोग में, 2.0 × 10–5 m त्रिज्या तथा 1.2 × 103 kg m–3 घनत्व की किसी बूँद की सीमांत चाल क्या है? प्रयोग के ताप पर वायु की श्यानता 1.8 × 10–5 Pa s लीजिए । इस चाल पर बूँद पर श्यान बल कितना है ? (वायु के कारण बूँद पर उत्प्लावन बल की उपेक्षा कीजिए) ।
10.29 सोडा काँच के साथ पारे का स्पर्श कोण 140o है । यदि पारे से भरी द्रोणिका में 1.00 mm त्रिज्या की काँच की किसी नली का एक सिरा डुबोया जाता है, तो पारे के बाहरी पृष्ठ के स्तर की तुलना में नली के भीतर पारे का स्तर कितना नीचे चला जाता है ? (पारे का घनत्व = 13.6