Table of Contents
अध्याय 12
ऊष्मागतिकी
12.1 भूमिका
12.2 तापीय साम्य
12.3 ऊष्मागतिकी का शून्य कोटि नियम
12.4 ऊष्मा, आंतरिक ऊर्जा तथा कार्य
12.5 ऊष्मागतिकी का प्रथम नियम
12.6 विशिष्ट ऊष्मा धारिता
12.7 ऊष्मागतिकीय अवस्था चर तथा अवस्था का समीकरण
12.8 ऊष्मागतिकीय प्रक्रम
12.9 ऊष्मा इंजन
12.10 प्रशीतक/ऊष्मा पंप
12.11 ऊष्मागतिकी का द्वितीय नियम
12.12 उत्क्रमणीय व अनुत्क्रमणीय प्रक्रम
12.13 कार्नो इंजन
सारांश
विचारणीय विषय
अभ्यास
12.1 भूमिका
पिछले अध्याय में हमने द्रव्यों के तापीय गुणों का अध्ययन किया। इस अध्याय में हम उन नियमों का अध्ययन करेंगे जो ऊष्मीय ऊर्जा को निर्धारित करते हैं। हम उन प्रक्रियाओं का अध्ययन करेंगे जिनमें कार्य ऊष्मा में परिवर्तित होता है, तथा विलोमतः ऊष्मा भी कार्य में परिवर्तित होती है । शीत ऋतु में जब हम हथेलियों को परस्पर रगड़ते हैं तो हमें गरमी की अनुभूति होती है क्योंकि इस प्रक्रिया में किया गया कार्य ऊष्मा उत्पन्न करता है । इसके विपरीत, भाप इंजन में वाष्प की ऊष्मा का उपयोग लाभप्रद कार्य को संपन्न करने में अर्थात् पिस्टन को गति देने में होता है जिसके परिणामस्वरूप रेलगाड़ी के पहिए घूमते हैं।
भौतिकी में ऊष्मा, ताप, कार्य आदि की अवधारणाओं को अधिक सावधानीपूर्वक परिभाषित करने की आवश्यकता पड़ती है । एेतिहासिक रूप से ऊष्मा की सटीक अवधारणा तक पहुँचने के लिए पर्याप्त समय लगा । आधुनिक अवधारणा के पूर्व ऊष्मा को एेसे सूक्ष्म अदृश्य तरल के रूप में समझा गया जो किसी पदार्थ के रंध्रों में भरा रहता है । गरम व ठंडे पिंडों के पारस्परिक संपर्क में आने पर यह तरल (जिसे कैलॉरिक कहते थे) ठंडे पिंड से अपेक्षाकृत गरम पिंड में बहने लगता है ! यह बिलकुल वैसा ही है जैसा उस समय होता है जब भिन्न-भिन्न ऊँचाइयों तक पानी से भरी दो टंकियों को एक क्षैतिज नल से जोड़ दिया जाता है । जल का बहाव उस समय तक निरंतर बना रहता है जब तक दोनों टंकियों में जल के तल समान न हो जाएँ। इसी के समान ऊष्मा की ‘कैलॉरिक’ धारणा में ऊष्मा उस समय तक प्रवाहित होती रहती है जब तक कि ‘कैलॉरिक तल’ (अर्थात् ताप) समान नहीं हो जाते ।
इसी बीच, ऊष्मा को ऊर्जा के रूप में कल्पित करने की आधुनिक अवधारणा के कारण इसके (ऊष्मा के) तरल स्वरूप को नकार दिया गया । इस संबंध में 1798 में बेंजामिन थॉमसन (जिन्हें काउन्ट रम्फोर्ड भी कहते हैं) ने एक महत्वपूर्ण प्रयोग भी किया । इन्होंने पाया कि पीतल की तोप में छेद करते समय इतनी अधिक ऊष्मा उत्पन्न होती है कि उससे पानी उबल सकता है । इससे अधिक महत्वपूर्ण तथ्य यह प्राप्त हुआ कि प्रयोग में उत्पन्न ऊष्मा का परिमाण उस कार्य पर निर्भर करता था जो घोड़े ड्रिल को घुमाने में करते थे न कि ड्रिल के पैनेपन पर । कैलॉरिक स्वरूप के अनुसार अधिक पैनी ड्रिल को रंध्रों से अधिक ऊष्मा तरल बाहर निकालना चाहिए, किंतु प्रयोग में यह सही नहीं पाया गया । प्रेक्षणों की सबसे अधिक स्वाभाविक व्याख्या यह थी कि ऊष्मा ऊर्जा का ही एक रूप है तथा प्रयोग से भी यह प्रमाणित हो गया कि ऊर्जा एक रूप से दूसरे रूप में अर्थात् कार्य से ऊष्मा में रूपांतारित हो जाती है ।
ऊष्मागतिकी भौतिकी की वह शाखा है जो ऊष्मा तथा ताप की अवधारणा एवं ऊष्मा के अन्य प्रकार की ऊर्जाओं में अंतरा- रूपान्तरण का विवेचन करती है । ऊष्मागतिकी एक स्थूल विज्ञान है, क्योंकि यह किसी निकाय की स्थूल प्रकृति पर विचार करती है न कि द्रव्य की आण्विक संरचना पर । वास्तव में, इससे संबंधित अवधारणाओं तथा नियमों का प्रतिपादन 19वीं शताब्दी में उस समय हुआ था जब द्रव्य के आण्विक स्वरूप को दृढ़तापूर्वक प्रमाणित नहीं किया गया था । ऊष्मागतिकी के वर्णन में निकाय के अपेक्षाकृत कुछ ही स्थूल चर समाहित होते हैं जो सामान्य अनुभव पर आधारित हैं तथा जिन्हें प्रत्यक्ष रूप में मापा जा सकता है । उदाहरणार्थ, किसी गैस के सूक्ष्म वर्णन में उसकी रचना करने वाले अगणित अणुओं के निर्देशांकों एवं वेगों का निर्धारण आवश्यक होता है । हालांकि गैसों के अणुगति सिद्धांत का विवरण बहुत विस्तृत नहीं है फिर भी इसमें अणुओं के वेर्गों का विवरण समाहित है । इसके विपरीत किसी गैस के ऊष्मागतिकीय विवरण में आण्विक वर्णन पूर्ण रूप से नकार दिया जाता है । ऊष्मागतिकी में किसी गैस की अवस्था दाब, आयतन, ताप, द्रव्यमान तथा संगठन जैसे एेसे स्थूल चरों द्वारा निर्धारित होती है जिन्हें हम अपनी इंद्रियों से अनुभव करते हैं और माप सकते हैं*।
यांत्रिकी एवं ऊष्मागतिकी के बीच भेद आपके मस्तिष्क में भलीभांति आ जाना चाहिए । यांत्रिकी में हमारी रुचि बलों तथा बल आघूर्णों के प्रभाव में गति कर रहे कणों एवं पिण्डों में होती है । ऊष्मागतिकी में संपूर्ण निकाय की गति पर विचार नहीं किया जाता । इसकी रुचि पिण्ड की आंतिरक स्थूल अवस्था में होती है । जब बंदूक से गोली दागते हैं तब जो परिवर्तन होता है वह गोली की यांत्रिक अवस्था (विशेषकर गतिज ऊर्जा) में परिवर्तन होता है, उसके ताप में नहीं । जब गोली लकड़ी में धँसकर रुक जाती है तो गोली की गतिज ऊर्जा ऊष्मा में रूपांतरित हो जाती है जिससे गोली तथा उसके चारों ओर की लकड़ी की सतहों का ताप परिवर्तित हो जाता है । ताप गोली की आंतरिक गति (जो अव्यवस्थित है) की ऊर्जा से संबंधित होता है न कि गोली की संपूर्ण गति से ।
12.2 तापीय साम्य
यांत्रिकी में साम्यावस्था से तात्पर्य है कि निकाय पर नेट बाह्य बल व बल आघूर्ण शून्य हैं । ऊष्मागतिकी में साम्यावस्था का अर्थ भिन्न संदर्भ में दृष्टिगोचर होता है: निकाय की अवस्था को हम उस समय साम्यावस्था में कहते हैं जब निकाय को अभिलक्षणित करने वाले स्थूल चर समय के साथ परिवर्तित नहीं होते । उदाहरणार्थ, किसी पर्यावरण से पूर्णतः ऊष्मारोधी बंद दृढ़ पात्र में भरी कोई गैस ऊष्मागतिक रूप से तब साम्यावस्था में होगी जब उसके दाब, आयतन, ताप, द्रव्यमान के परिमाण तथा संगठन समय के साथ परिवर्तित न हों ।
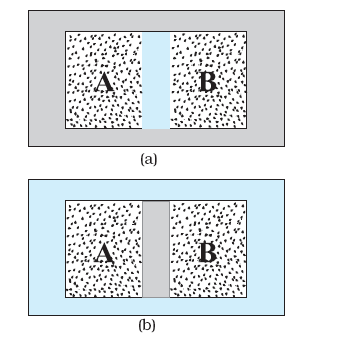
चित्र 12.1 (a) (दो गैसों के) निकाय A व B एक रुद्धोष्म दीवार से पृथक् हैं: इस दीवार से ऊष्मा आर-पार नहीं जा पाती । (b) यही निकाय A व B एक ऊष्मा-पार्थ दीवार से पृथक् दर्शाए गए हैं । यह एक चालक दीवार होती है जिससे ऊष्मा एक निकाय से दूसरे में चली जाती है । इस उदाहरण में तापीय साम्य यथोचित समय में प्राप्त हो जाता है ।
कोई निकाय साम्यावस्था में है कि नहीं व्यापक रूप में यह चारों ओर के परिवेश तथा उस दीवार की प्रकृति पर निर्भर करता है जो निकाय को परिवेश से पृथक् करती है । कल्पना कीजिए कि दो गैसें A व B दो भिन्न-भिन्न पात्रों में भरी हैं । प्रयोग द्वारा हमें पता है कि किसी गैस के दिए हुए द्रव्यमान के दाब व ताप को उसके दो स्वतंत्र चरों के रूप में चुना जा सकता है । मान लीजिए कि गैसों के दाब व आयतन क्रमशः (PA, VA) तथा (PB, VB) हैं । कल्पना कीजिए कि पहले दोनों निकाय पास-पास हैं परंतु उन्हें किसी रुद्धोष्म दीवार (एक ऊष्मारोधी दीवार) द्वारा एक दूसरे से पृथक् रखा गया है । इस दीवार के कारण ऊर्जा (ऊष्मा) एक पात्र से दूसरे पात्र में नहीं जा पाती है । निकायों को भी शेष परिवेश से इसी प्रकार की रुद्धोष्म दीवार से पृथक् रखते हैं । इस व्यवस्था का आरेखीय चित्रण [12.1(a)] में दिया गया है । यहाँ यह पाया गया है कि (PA, VA) के किसी भी संभावित युग्म का मान (PB, VB) के किसी भी संभव युग्म के मान के साथ साम्यावस्था में होगा । पुनः कल्पना कीजिए कि रुद्धोष्म दीवार को एक ऊष्मा-पार्थ-दीवार से प्रतिस्थापित कर दिया गया है - यह दीवार (ऊष्मा) ऊर्जा को एक निकाय से दूसरे निकाय में जाने देती है । एेसा करने में यह देखा गया है कि निकायों A व B के स्थूल चर स्वतः उस समय तक परिवर्तित होते हैं जब तक कि दोनों निकाय साम्यावस्था की स्थिति प्राप्त नहीं कर लेते । इसके पश्चात् उनकी अवस्था में कोई परिवर्तन नहीं होता है । इस स्थिति को चित्र [12.1(b)] में दर्शाया गया है । मान लीजिए कि दोनों गैसों के दाब व आयतन संबंधी चर परिवर्तित होकर क्रमशः (PA′, V′A) तथा (PB′, V′B) हो जाते हैं ताकि A व B की नयी अवस्थाएँ पुनः एक-दूसरे की साम्यावस्था में हो जाती हैं** । एक निकाय से दूसरे निकाय में अब और ऊर्जा का प्रवाह नहीं होता । एेसी स्थिति में हम कहते हैं कि निकाय A, निकाय B के साथ तापीय साम्य में है ।
* ऊष्मागतिकी में अन्य एेसे चर भी निहित होते हैं जो हमारी इंद्रियों को इतने सुस्पष्ट नहीं होते (उदाहरणार्थ, एंट्रॉपी, एंथाल्पी (संपूर्ण ऊष्मा), आदि जिनके विषय में आप उच्च कक्षाओं में पढ़ेंगे), किंतु ये सभी स्थूल चर हैं । यद्यपि किसी उष्मागतिकीय अवस्था को पाँच अवस्था चरों, जैसे दाब, आयतन, ताप, आंतरिक ऊर्जा और एंट्रॉपी के रूप में निरूपित किया जाता है । किसीनिकाय की एंट्रॉपी उसकी अव्यवस्था का माप होता है ।
दो निकायों के मध्य की साम्यावस्था की स्थिति को क्या अभिलक्षित करती है ? आप अपने अनुभव से उत्तर का अनुमान लगा सकते हैं । तापीय साम्य में, दो निकायों के ताप समान होते हैं । हम जानेंगे कि ऊष्मागतिकी में ताप की अवधारणा तक कैसे पहुँचते हैं ? ऊष्मागतिकी का शून्य कोटि का नियम इसकी ओर संकेत करता है ।
12.3 ऊष्मागतिकी का शून्य कोटि नियम
कल्पना कीजिए कि दो निकाय A व B एक रुद्धोष्म दीवार से पृथक् हैं । इनमें से प्रत्येक एक तीसरे निकाय C से एक सुचालक दीवार द्वारा संपर्क में हैं [चित्र 12.2(a)] । निकायों की अवस्थाएँ (अर्थात् उनके स्थूल चर) तब तक परिवर्तित होंगी जब तक A व B दोनों निकाय C के साथ तापीय साम्य में नहीं आ जाते हैं । जब एेसा हो जाए तो कल्पना कीजिए कि A व B के मध्य की रुद्धोष्म दीवार एक सुचालक दीवार से प्रतिस्थापित कर दी जाती है तथा C को A व B से किसी रुद्धोष्म दीवार से पृथक् कर दिया जाता है [चित्र 12.2(b)] । एेसा देखा जाता है कि A व B की अवस्थाएँ अब और नहीं बदलतीं अर्थात् वे दोनों अब तापीय साम्य में होती हैं । यह प्रेक्षण ऊष्मागतिकी के शून्य कोटि नियम का आधार बना । यह नियम बतलाता है कि यदि दो निकाय किसी तीसरे निकाय के साथ पृथक्-पृथक् रूप से तापीय साम्य में हैं तो वे परस्पर भी तापीय साम्य में होते हैं । यहाँ यह बात ध्यान में रखनी चाहिए कि ऊष्मागतिकी के प्रथम व द्वितीय नियम की अभिव्यक्ति तथा उनके क्रमांकन के बहुत समय बाद 1931 में आर.एच. फाउलर ने शून्य कोटि नियम का प्रतिपादन किया था।
शून्य कोटि नियम से यह संकेत मिलता है कि जब दो निकाय A व B परस्पर तापीय साम्य में होते हैं, तो एेसी कोई भौतिक राशि है जो दोनों निकायों के लिए समान मान रखती है । यह ऊष्मागतिक चर, जिसका मान तापीय साम्य वाले निकायों के लिए समान होता है, ताप (T) कहलाता है । अतः यदि A व B साम्यावस्था में तीसरे निकाय C से पृथक् हैं तो TA = TC तथा TB = TC । इसका तात्पर्य यह है कि TA = TB अर्थात् निकाय A व B स्वयं भी तापीय साम्य में हैं ।
शून्य कोटि नियम के माध्यम से हमने विधिवत ताप की अवधारणा विकसित की है । हमारे सामने पुनः एक प्रश्न उत्पन्न होता है: भिन्न-भिन्न पिंडों के ताप के लिए हम अंकिक मानों का निर्धारण कैसे करें? दूसरे शब्दों में, हम ताप मापक्रम कैसे बनाएँ? तापमिति इस मौलिक प्रश्न से संबंध रखती है जिसके विषय में हम अगले अनुभाग में अध्ययन करेंगे ।
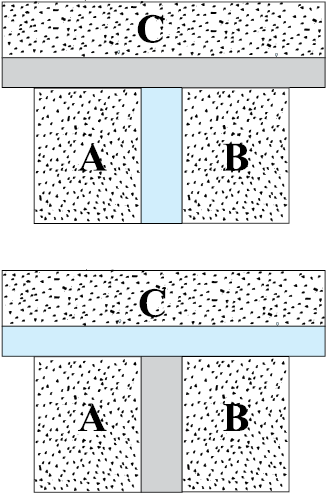
चित्र 12.2 (a) निकाय A व B जो एक रुद्धोष्म दीवार से पृथक हैं जबकि इनमें से प्रत्येक एक तीसरे निकाय C से एक सुचालक दीवार द्वारा संपर्क में है । (b) A व B के मध्य की रुद्धोष्म दीवार को किसी सुचालक दीवार से प्रतिस्थापित किया गया है जबकि C को A व B से रुद्धोष्म दीवार से पृथक दर्शाया गया है ।
** यह आवश्यक नहीं है कि दोनों चर बदलें । एेसा प्रतिबंधों पर निर्भर करता है । उदाहरण के लिए, यदि गैस स्थिर आयतन वाले पात्र में भरी हो तो तापीय साम्य के लिए केवल गैसों के दाब को परिवर्तित होना चाहिए ।
12.4 ऊष्मा, आंतरिक ऊर्जा तथा कार्य
ऊष्मागतिकी के शून्य कोटि नियम से ताप की अवधारणा की उत्पत्ति हुई जो हमारे सामान्य ज्ञान के अनुकूल है । ताप किसी पिण्ड की उष्णता का द्योतक है । जब दो पिण्ड ऊष्मीय संपर्क में लाए जाते हैं तो इससे ऊष्मा के प्रवाह की दिशा निर्धारित होती है । ऊष्मा उच्च ताप वाले पिण्ड से निम्न ताप वाले पिण्ड की ओर प्रवाहित होती है । जब ताप समान हो जाते हैं तो प्रवाह रुक जाता है । एेसी स्थिति में दोनों पिण्ड तापीय साम्य में होते हैं । हम यह विस्तार से पढ़ चुके हैं कि भांति-भांति के पिण्डों के ताप के निर्धारण के लिए ताप मापक्रम कैसे बनाए जाते हैं । अब हम ऊष्मा तथा तत्संबंधित राशियों; जैसे–आंतरिक ऊर्जा तथा कार्य की अवधारणाओं का वर्णन करेंगे ।
किसी निकाय की आंतरिक ऊर्जा की अवधारणा को समझना कठिन नहीं है । हम जानते हैं कि प्रत्येक स्थूल निकाय असंख्य अणुओं से निर्मित है । आंतरिक ऊर्जा इन अणुओं की स्थितिज व गतिज ऊर्जाओं का योग है । हमने यह टिप्पणी की है कि ऊष्मागतिकी में निकाय की समग्र रूप से गतिज ऊर्जा प्रासंगिक नहीं होती । इस प्रकार, निर्देश फ्रेम में आंतरिक ऊर्जा अणु की गतिज व स्थितिज ऊर्जा के योग के बराबर होती है जिसके सापेक्ष निकाय का द्रव्यमान-केंद्र विरामावस्था में होता है । इस प्रकार, इसमें केवल निकाय के अणुओं की यादृच्छिक गति से संबंधित (अव्यवस्थित) ऊर्जा ही समाहित होती है । निकाय की आंतरिक ऊर्जा को U से चिह्नित करते हैं ।
यद्यपि हमने आंतरिक ऊर्जा के अर्थ को समझने के लिए आण्विक चित्र प्रस्तुत किया है तथापि जहाँ तक ऊष्मागतिकी का संबंध है, U निकाय का केवल एक स्थूल चर ही है । आंतरिक ऊर्जा के संबंध में एक महत्वपूर्ण तथ्य यह है कि यह केवल निकाय की अवस्था पर निर्भर करती है न कि इस बात पर कि यह अवस्था किस प्रकार प्राप्त हुई । निकाय की आंतरिक ऊर्जा U ऊष्मागतिकीय ‘अवस्था चर’ का एक उदाहरण है । इसका मान निकाय की दी हुई अवस्था पर निर्भर करता है न कि उसके इतिवृत्ति (History) (अर्थात् उस स्थिति तक पहुँचने के लिए अनुसरण किए गए पथ) पर। अतः किसी गैस के दिए गए द्रव्यमान के लिए आंतरिक ऊर्जा उसकी स्थिति पर निर्भर करती है । यह स्थिति दाब, आयतन व ताप के विशिष्ट मानों से वर्णित होती है । यह इस बात पर निर्भर नहीं करती कि गैस की यह स्थिति किस प्रकार प्राप्त हुई । दाब, आयतन, ताप तथा आंतरिक ऊर्जा निकाय (गैस) के ऊष्मागतिकीय अवस्था चर कहलाते हैं (अनुभाग 12.7 देखें) । यदि गैस के अल्पप्रभावी अंतराण्विक बलों की उपेक्षा कर दें तो गैस की आंतरिक ऊर्जा उसके अणुओं की अनेक यादृच्छिक गतियों से संबद्ध गतिज ऊर्जाओं के योग के ठीक बराबर होती है । अगले अध्याय में हम पढ़ेंगे कि किसी गैस में यह गति केवल स्थानांतरीय ही नहीं होती (इसमें गति पात्र के आयतन में एक बिंदु से दूसरे बिंदु के मध्य होती है), वरन् इसमें अणु की घूर्णी तथा कंपन गति भी होती है (चित्र 12.3) ।
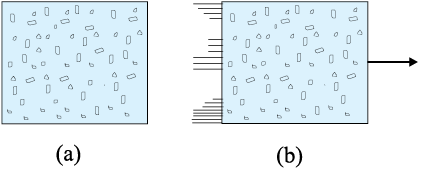
चित्र 12.3 (a) जब बॉक्स विरामावस्था में है तो गैस की आंतरिक ऊर्जा U उसके अणुओं की गतिज व स्थितिज ऊर्जा के योग के बराबर होती है । विभिन्न प्रकार की गतियों (स्थानांतरीय,घूर्णी, कंपन) के कारण गतिज ऊर्जा को U में समाहित किया जाता है । (b) यदि यही समग्र बॉक्स कुछ वेग से गतिमान है, तो बॉक्स की गतिज ऊर्जा को U में सम्मिलित नहीं करना है ।
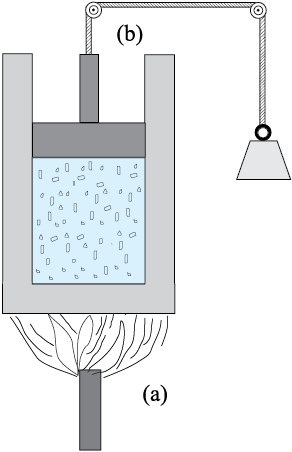
चित्र 12.4 ऊष्मा व कार्य किसी निकाय में ऊर्जा स्थानांतरण की दो विभिन्न विधियाँ हैं जिनसे उसकी आंतरिक ऊर्जा में परिवर्तन होता है । (a) निकाय तथा परिवेश के बीच तापांतर के कारणऊष्मा को ऊर्जा के स्थानांतरण के रूप में परिभाषित करते हैं । (b) कार्य उन साधनों (उदाहरणार्थ, पिस्टन से जुड़े भारों को ऊपर नीचे करके पिस्टन को गति देना) द्वारा उत्पन्न ऊर्जा का स्थानांतरण है जिनमें तापांतर समाहित नहीं होता ।
किसी निकाय की आंतरिक ऊर्जा में किन उपायों से परिवर्तन किए जा सकते हैं ? सुविधा की दृष्टि से पुनः कल्पना कीजिए कि चित्र 12.4 के अनुसार निकाय किसी दिए गए द्रव्यमान की एक गैस है जो एक सिलिंडर में भरी है जिसमें गतिशील पिस्टन लगा है । अनुभव यह बताता है कि गैस की अवस्था (तथा इस प्रकार उसकी आंतरिक ऊर्जा) परिवर्तित करने के दो उपाय होते हैं । एक उपाय है कि सिलिंडर को उस पिण्ड के संपर्क में रखें जो गैस की अपेक्षा उच्च ताप पर है । तापांतर के कारण ऊर्जा (ऊष्मा) गरम पिण्ड से गैस में प्रवाहित होगी । इससे गैस की आंतरिक ऊर्जा बढ़ जाएगी । दूसरा उपाय है कि पिस्टन को नीचे की ओर दबाया जाए (अर्थात् निकाय पर कार्य किया जाए) । इसमें भी गैस की आंतरिक ऊर्जा बढ़ जाती है । निःसंदेह ये दोनों बातें विपरीत दिशा में भी संभव होती हैं । यदि चारों ओर के परिवेश का ताप कम है तो ऊष्मा गैस से परिवेश में प्रवाहित होगी । इसी प्रकार, गैस पिस्टन को ऊपर की ओर धक्का दे सकती है और परिवेश पर कार्य कर सकती है । संक्षेप में, ऊष्मा और कार्य दो भिन्न-भिन्न विधियाँ हैं जिनसे ऊष्मीय निकाय की स्थिति परिवर्तित होती है तथा उसकी आंतरिक ऊर्जा में परिवर्तन होता है ।
ऊष्मा एवं आंतरिक ऊर्जा की धारणाओं में अंतर को सावधानीपूर्वक समझना आवश्यक है । ऊष्मा निश्चित रूप से ऊर्जा है परंतु यह ऊर्जा पारगमन में है । यह मात्र शब्दों का खेल नहीं है । दोनों में अंतर मूल महत्त्व का है । किसी ऊष्मागतिकी निकाय की स्थिति उसकी आंतरिक ऊर्जा से अभिलक्षित होती है न कि ऊष्मा से । इस प्रकार का प्रकथन कि ‘किसी दी
हुई अवस्था में गैस में ऊष्मा की कुछ मात्रा होती है’ उतना ही निरर्थक है जितना कि यह प्रकथन कि ‘किसी दी हुई स्थिति में गैस में कुछ कार्य निहित होता है ।’ इसके विपरीत, ‘किसी दी हुई अवस्था में गैस में आंतरिक ऊर्जा की कुछ मात्रा होती है’ पूरी तरह से एक सार्थक प्रकथन है । इसी प्रकार से, एेसे प्रकथन जैसे ‘निकाय को एक निश्चित मात्रा की ऊष्मा दी गई है’ या ‘निकाय द्वारा एक निश्चित मात्रा का कार्य किया गया’ पूर्णतः अर्थपूर्ण सार्थक प्रकथन हैं ।
संक्षेप में, ऊष्मा व कार्य ऊष्मागतिकी में स्थिति चर नहीं होते । ये किसी निकाय में ऊर्जा स्थानांतरण की विधियाँ होती हैं जिससे उसकी आंतरिक ऊर्जा परिवर्तित होती है। जो, जैसा कि पहले वर्णन कर चुके हैं, एक अवस्था चर होता है ।
साधारण भाषा में हमें प्रायः ऊष्मा तथा आंतरिक ऊर्जा में भ्रम बना रहता है । कुछ प्राथमिक भौतिकी की पुस्तकों में कभी-कभी इस भेद की उपेक्षा कर दी जाती है । तथापि ऊष्मागतिकी को भलीभांति समझने के लिए यह विभेद आवश्यक है ।
12.5 ऊष्मागतिकी का प्रथम नियम
हम यह देख चुके हैं कि किसी निकाय की आंतरिक ऊर्जा U दो विधियों से ऊर्जा स्थानांतरण के कारण परिवर्तित हो सकती है । ये विधियाँ हैं: ऊष्मा तथा कार्य । कल्पना कीजिए कि
∆Q = परिवेश द्वारा निकाय को दी गई ऊष्मा
∆W = निकाय द्वारा परिवेश पर किया गया कार्य
∆U = निकाय की आंतरिक ऊर्जा में परिवर्तन
ऊर्जा संरक्षण के सामान्य नियम में यह अंतर्निहित है कि
∆Q = ∆U + ∆W (12.1)
इसका तात्पर्य यह है कि जो ऊर्जा (∆Q) निकाय को दी जाती है, उसका कुछ अंश निकाय की आंतरिक ऊर्जा में वृद्धि करता है (∆U) तथा शेष परिवेश पर किया गया कार्य (∆W) है । समीकरण (12.1) को ऊष्मागतिकी के प्रथम नियम के रूप में जाना जाता है । यह ऊर्जा संरक्षण का केवल सामान्य नियम है जिसे किसी भी उस निकाय पर लागू किया जा सकता है जिसमें परिवेश को अथवा परिवेश से ऊष्मा स्थानांतरण पर ध्यान दिया जाता है ।
मान लीजिए कि हम समीकरण (12.1) को वैकल्पिक रूप में प्रस्तुत करते हैं,
∆Q – ∆W = ∆U (12.2)
अब मान लीजिए कि निकाय किसी आरंभिक अवस्था से अंतिम अवस्था में कई प्रकार से आता है । उदाहरणार्थ, गैस की अवस्था (P1, V1) से परिवर्तित करके (P2, V2) कर दी जाए तो हम पहले गैस के दाब को स्थिर रखकर उसके आयतन को V1 से V2 में परिवर्तित करते हैं अर्थात् पहले हम अवस्था (P1, V2) में जा सकते हैं और फिर गैस के आयतन को स्थिर रखते हुए इसके दाब को P1 से P2 में परिवर्तित करते हैं । इससे गैस (P2, V2) अवस्था में पहुँच जाती है । विकल्पतः हम पहले आयतन को स्थिर रख सकते हैं और फिर दबाव स्थिर रखते हैं। चूंकि U एक अवस्था चर है, ∆U केवल प्रारंभिक व अंतिम अवस्थाओं पर निर्भर करेगा न कि उस पथ पर जिससे गैस एक अवस्था से दूसरी अवस्था में पहुँचती है । यद्यपि, ∆Q तथा ∆W दोनों, सामान्यतया, उस पथ पर निर्भर करते हैं जिससे गैस प्रारंभिक अवस्था से अंतिम अवस्था में जाती है । ऊष्मागतिकी के प्रथम नियम, समीकरण (12.2), से यह स्पष्ट है कि संयोजन ∆Q – ∆W पथ पर निर्भर नहीं करता । इससे पता चलता है कि यदि कोई निकाय एेसी प्रक्रिया अपनाता है जिसमें ∆U = 0 (उदाहरणार्थ, आदर्श गैस का समतापीय प्रसार, अनुभाग 12.8 देखिए), तो
∆Q = ∆W
अर्थात् निकाय को दी गई ऊष्मा निकाय द्वारा परिवेश पर कार्य करने में पूर्ण रूप से उपयोग में आ जाती है ।
यदि निकाय सिलिंडर में भरी गैस है तथा सिलिंडर में गतिशील पिस्टन लगा है तो पिस्टन को गति देने में गैस को कार्य करना पड़ता है । चूंकि बल को दाब × क्षेत्रफल के रूप में परिभाषित करते हैं तथा क्षेत्रफल × विस्थापन को आयतन कहते हैं तो स्थिर दाब P के विरुद्ध निकाय द्वारा संपादित कार्य निम्नलिखित होगा,
∆W = P∆V
यहाँ ∆V गैस में आयतन के परिवर्तन को व्यक्त करता है । अतः इस उदाहरण के लिए, समीकरण (12.20) निम्न प्रकार से लिखी जाएगी
∆Q = ∆U + P∆V (12.3)
समीकरण (12.3) के अनुप्रयोग के रूप में हमें 1g जल की आंतरिक ऊर्जा के परिवर्तन पर विचार करना होगा जब यह अपनी द्रव प्रावस्था से वाष्प प्रावस्था में परिवर्तित होता है । जल की मापी गई गुप्त ऊष्मा 2256 J/g है अर्थात् जल के 1 ग्राम के लिए ∆Q = 2256 J होता है । वायुमंडलीय दाब पर, 1 g जल का आयतन द्रव प्रावस्था में 1 cm3 तथा वाष्प प्रावस्था में 1671 cm3 होता है । अतः
समीकरण (12.3) से हमें आंतरिक ऊर्जा का मान प्राप्त होता है,
∆U = 2256 – 169.2 = 2086.8 J
इस प्रकार, हम देखते हैं कि ऊष्मा का अधिकांश भाग जल की आंतरिक ऊर्जा में वृद्धि करने में व्यय होता है । इस प्रक्रिया में जल द्रव से वाष्प प्रावस्था में परिवर्तित होता है ।
12.6 विशिष्ट ऊष्मा धारिता
कल्पना कीजिए कि किसी पदार्थ को दी गई ऊष्मा की मात्रा ∆Q उसके ताप को T से बढ़ाकर T + ∆T कर देती है । हम पदार्थ की ऊष्मा धारिता को निम्नलिखित प्रकार से परिभाषित करते हैं ।
S = 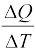 (12.4)
(12.4)
हम आशा करते हैं कि ∆Q और इस प्रकार से ऊष्मा धारिता S पदार्थ के द्रव्यमान के अनुक्रमानुपाती होती है । इसके अतिरिक्त यह ताप पर भी निर्भर कर सकती है । अर्थात् भिन्न-भिन्न तापों पर पदार्थ के ताप में एकांक वृद्धि के लिए ऊष्मा के भिन्न-भिन्न परिमाणों की आवश्यकता पड़ सकती है । पदार्थ के किसी नियत अभिलक्षण को परिभाषित करने तथा उसे उसके परिमाण से स्वतंत्र रखने के लिए हम S को पदार्थ के द्रव्यमान m (kg में) से विभाजित कर देते हैं:
s = 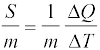 (12.5)
(12.5)
s को पदार्थ की विशिष्ट ऊष्मा धारिता कहते हैं । यह पदार्थ की प्रकृति और उसके ताप पर निर्भर करती है । विशिष्ट ऊष्मा का मात्रक J kg-1 K-1 है।
यदि पदार्थ के परिमाण का निर्धारण µ मोल (द्रव्यमान m को kg में व्यक्त करने के स्थान पर) के पदों में करें तो हम पदार्थ की ऊष्मा धारिता प्रति मोल को इस प्रकार से व्यक्त कर
सकते हैं
C = 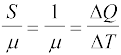 (12.6)
(12.6)
C को पदार्थ की मोलर विशिष्ट ऊष्मा धारिता कहते हैं । s की भांति C भी पदार्थ के परिमाण पर निर्भर नहीं करता तथा प्रदत्त ऊष्मा की परिस्थितियों, पदार्थ की प्रकृति, उसके ताप पर निर्भर करता है । C का मात्रक J mol-1 K-1 है । जैसा कि हम बाद में देखेंगे (गैस की विशिष्ट ऊष्मा के संबंध में) C या s को परिभाषित करने के लिए अतिरिक्त शर्तो की आवश्यकता पड़ सकती है । C को परिभाषित करने के पीछे यह विचार है कि मोलर विशिष्ट ऊष्माओं के संबंध में सरल भविष्यवाणियाँ की जा सकती हैं।
सारणी 12.1 में कमरे के ताप तथा वायुमंडलीय दाब पर कुछ ठोसों की विशिष्ट ऊष्मा धारिता तथा मोलर विशिष्ट ऊष्मा धारिता दी गई हैं।
हम अध्याय 13 में पढ़ेंगे कि गैसों की विशिष्ट ऊष्माओं के संबंध में की गई भविष्यवाणियाँ सामान्यतया प्रयोग से मेल खाती हैं । हम उसी ऊर्जा सम विभाजन नियम का उपयोग कर सकते हैं । जैसा कि हमने वहाँ ठोसों की मोलर विशिष्ट ऊष्मा की भविष्यवाणी में किया है (खंड 13.5 और 13.6 देखें)। N परमाणुओं वाले किसी ठोस पर विचार करें । प्रत्येक परमाणु अपनी माध्य स्थिति के दोनों ओर कंपन करता है । एक विमा में किसी दोलक की माध्य ऊर्जा 2 × ½ kBT = kBT होगी । तीन विमाओं में माध्य ऊर्जा 3 kBT होगी । ठोस के एक मोल के लिए कुल ऊर्जा
U = 3 kBT × NA = 3 RT ( kB NA = R )
अब स्थिर दाब पर, ∆Q = ∆U + P∆ V ≅ ∆U होगा, क्योंकि किसी ठोस के लिए ∆V नगण्य होगा । अतः
∆ Q ∆ U
C = ∆T = ∆T = 3 R (12.7)
सारणी 12.1 कमरे के ताप तथा वायुमंडलीय दाब पर कुछ ठोसों की विशिष्ट ऊष्मा धारिता तथा मोलर विशिष्ट ऊष्मा धारिता
| पदार्थ | विशिष्ट ऊष्मा धारिता (Jkg-1K-1) | मोलर विशिष्ट ऊष्मा धारिता (J mol-1K-1) |
| एेलुमिनियम | 900.0 | 24.4 |
| कार्बन | 506.5 | 6.1 |
| ताँबा | 386.4 | 24.5 |
| सीसा | 127.7 | 26.5 |
| चाँदी | 236.1 | 25.5 |
| टंगस्टन | 134.4 | 24.9 |
जैसा कि सारणी से स्पष्ट है कि भविष्यवाणियाँ सामान्यतया साधारण तापों पर प्रायोगिक मानों से मेल खाती हैं (कार्बन एक अपवाद है) । यह ज्ञात है कि यह मेल निम्न तापों पर भंग हो जाता है ।
जल की विशिष्ट ऊष्मा धारिता
ऊष्मा का पुराना मात्रक कैलोरी था। 1 कैलोरी को ऊष्मा के उस परिमाण के रूप में परिभाषित करते थे जो 1g जल के ताप में 1°C की वृद्धि कर दे । अधिक परिशुद्ध मापों से यह पाया गया है कि जल की विशिष्ट ऊष्मा में ताप के साथ किंचितमात्र परिवर्तन होता है । चित्र 12.5 में ताप परिसर 0-100 °C में यह परिवर्तन दर्शाया गया है ।
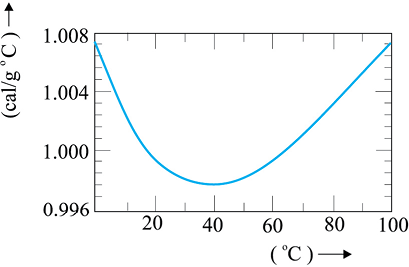
चित्र 12.5 ताप के साथ जल की विशिष्ट ऊष्मा धारिता में परिवर्तन
इसलिए कैलोरी की यथार्थ परिभाषा के लिए यह आवश्यक समझा गया कि एकांक ताप अंतराल को निर्धारित किया जाए । ऊष्मा का वह परिमाण जो 1 g जल के ताप में 1 °C (14.5 °C से 15.5 °C) की वृद्धि कर दे, उसे 1 कैलोरी के रूप में परिभाषित किया गया । चूंकि ऊष्मा ऊर्जा का ही एक रूप है, इसलिए मात्रक जूल, J के उपयोग को प्राथमिकता देना अधिक उपयुक्त है । SI मात्रकों में, जल की विशिष्ट ऊष्मा धारिता 4186 J kg-1K-1 अर्थात् 4.186 J g-1 K-1 है । तथाकथित ऊष्मा का यांत्रिक तुल्यांक, जिसे 1 कैलोरी ऊष्मा उत्पन्न करने के लिए आवश्यक कार्य के रूप में परिभाषित करते हैं, वास्तव में ऊर्जा के दो भिन्न मात्रकों (कैलोरी से जूल) के मध्य एक परिवर्तन गुणक है । चूंकि SI मात्रक पद्धति में ऊष्मा कार्य या ऊर्जा के किसी अन्य रूप के लिए जूल मात्रक का उपयोग करते हैं, अतः ‘यांत्रिक तुल्यांक’ पद अब निरर्थक हो गया है और इसे उपयोग में लाने की आवश्यकता नहीं है ।
* जैसा पहले भी दर्शाया गया है Q अवस्था चर नहीं है किन्तु DQ निकाय की कुल मात्रा समानुपातिक है। अतः यह विस्तीर्ण चर है।
जैसा कि पहले वर्णन किया जा चुका है कि विशिष्ट ऊष्मा धारिता, प्रक्रिया या उन परिस्थितियों पर निर्भर करती है जिनके अंतर्गत ऊष्मा का स्थानांतरण होता है । उदाहरणार्थ, गैसों के लिए हम दो विशिष्ट ऊष्माओं को परिभाषित करते हैं: स्थिर आयतन पर विशिष्ट ऊष्मा धारिता तथा स्थिर दाब पर विशिष्ट ऊष्मा धारिता। किसी आदर्श गैस के लिए हमारे पास एक सरल संबंध होता है जिसे हम निम्नलिखित प्रकार से व्यक्त करते हैं:
CP – CV = R (12.8)
यहाँ CP व CV आदर्श गैस की क्रमशः स्थिर दाब व स्थिर आयतन पर मोलर विशिष्ट ऊष्मा धारिताएँ हैं तथा R सार्वत्रिक गैस नियतांक है । इसे सिद्ध करने के लिए हम 1 मोल गैस के लिए समीकरण (12.3) पर विचार करते हैं:
∆Q = ∆U + P∆V
यदि ∆Q का स्थिर आयतन पर अवशोषण होता है तो
∆V = 0 होगा ।
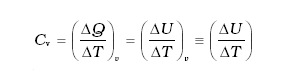 (12.9)
(12.9)
यहाँ अधोलिखित V को अंतिम पद में छोड़ दिया गया है क्योंकि आदर्श गैस के लिए U का मान मात्र ताप पर निर्भर करता है । (अधोलिखित यह व्यक्त करता है कि तत्संबंधित राशि स्थिर है ।) इसके विपरीत, यदि ∆Q का स्थिर दाब पर अवशोषण होता है तो
 (12.10)
(12.10)
अधोलिखित P को प्रथम पद में छोड़ा जा सकता है क्योंकि आदर्श गैस के लिए U का मान मात्र T पर निर्भर करता है । आदर्श गैस के 1 मोल के लिए
PV = RT
जो निम्नलिखित परिणाम देता है:
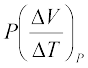 = R (12.11)
= R (12.11)
समीकरणों (12.9) से (12.11) तक के उपयोग से हमें वांछित संबंध (12.8) प्राप्त होता है ।
12.7 ऊष्मागतिकीय अवस्था चर तथा अवस्था का समीकरण
किसी भी ऊष्मागतिकीय निकाय की प्रत्येक साम्य अवस्था को कुछ स्थूल चरों के विशिष्ट मानों के उपयोग द्वारा पूरी तरह से वर्णित कर सकते हैं । उदाहरणार्थ, किसी गैस की साम्य अवस्था उसके दाब, आयतन, ताप व द्रव्यमान (तथा संगठन यदि गैसों का सम्मिश्रण है) के मानों द्वारा पूरी तरह से निर्धारित होती है । कोई ऊष्मागतिक निकाय सदैव साम्य स्थिति में नहीं होता । उदाहरणार्थ, किसी गैस को निर्वात के विरुद्ध यदि फैलने दिया जाता है तो यह साम्य अवस्था नहीं होती [चित्र 12.6(a)] । द्रुत्र प्रसरण की अवधि में गैस का दाब संभव है कि सभी स्थानों पर एकसमान न हो । इसी प्रकार, गैसों का वह सम्मिश्रण जिसमें विस्फोटक रासायनिक अभिक्रिया होती है (उदाहरणार्थ, पेट्रोल की वाष्प तथा वायु का मिश्रण जिसे एक चिंगारी से प्रज्ज्वलित किया जाता है) एक साम्य अवस्था नहीं है; इसके अतिरिक्त इसके ताप व दाब एकसमान नहीं हैं [चित्र 12.6(b)]। अंततः, गैस का ताप व दाब एकसमान हो जाता है तथा वह परिवेश के साथ तापीय व यांत्रिक साम्य में आ जाती है ।
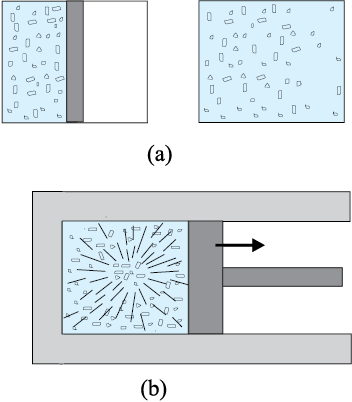
चित्र 12.6 (a) बॉक्स के विभाजक को अचानक हटा दिया गया है जिससे गैस का मुक्त प्रसरण होता है। (b) गैसों का मिश्रण जिसमें विस्फोटक रासायनिक अभिक्रिया संपन्न होती है । दोनों स्थितियों में गैस साम्यावस्था में नहीं है तथा चरों से इसका विवरण नहीं दिया जा सकता ।
संक्षेप में, ऊष्मागतिकीय अवस्था चर निकायों की साम्यावस्था का विवरण देते हैं । यह आवश्यक नहीं है कि विभिन्न अवस्था चर स्वतंत्र हों । अवस्था चरों के पारस्परिक संबंध को अवस्था का समीकरण कहते हैं । उदाहरणार्थ, किसी आदर्श गैस के लिए अवस्था का समीकरण आदर्श गैस संबंध होता है,
P V = µ R T
गैस की निश्चित मात्रा के लिए अर्थात् दिए गए µ के लिए इस प्रकार से केवल दो ही स्वतंत्र चर होते हैं । मान लीजिए कि वे P और V या T और V हैं । निश्चित ताप पर दाब आयतन वक्र को समतापी कहते हैं । वास्तविक गैसों के लिए अवस्था का समीकरण अधिक जटिल हो सकता है ।
ऊष्मागतिकीय अवस्था चर दो प्रकार के होते हैं: विस्तीर्ण तथा गहन। विस्तीर्ण चर निकाय के आकार का संकेत देते हैं जबकि गहन चर जैसे दाब तथा ताप से एेसा नहीं करते । यह निर्णय लेने के लिए कि कौन-सा चर विस्तीर्ण है तथा कौन-सा गहन है, किसी प्रासंगिक निकाय पर विचार कीजिए तथा कल्पना कीजिए कि उसे दो समान भागों में बाँट दिया गया है । वे चर जो हर भाग में अपरिवर्तित रहते हैं गहन चर कहलाते हैं किंतु जिन चरों का मान हर भाग में आधा हो जाता है, उन्हें विस्तीर्ण चर कहते हैं । उदाहरणार्थ, यह आसानी से देखा जा सकता है कि आंतरिक ऊर्जा U, आयतन V, कुल द्रव्यमान M विस्तीर्ण चर हैं जबकि दाब P, ताप T व घनत्व ρ गहन चर हैं । यह एक अच्छी आदत होगी यदि चरों के इस प्रकार के वर्गीकरण के द्वारा ऊष्मागतिकीय समीकरणों की प्रासंगिकता का परीक्षण कर लिया जाए । उदाहरणार्थ, समीकरण,
∆Q = ∆U + P∆V
में दोनों ओर की राशियाँ विस्तीर्ण है* (किसी गहन चर जैसे P तथा विस्तीर्ण राशि ∆V का गुणनफल विस्तीर्ण राशि है) ।
12.8 ऊष्मागतिकीय प्रक्रम
12.8.1 स्थैतिककल्प प्रक्रम
एेसी गैस पर विचार कीजिए जो अपने परिवेश से तापीय तथा यांत्रिक रूप से साम्य में हो । एेसी स्थिति में गैस का दाब बाह्य दाब के बराबर होगा तथा इसका ताप वही होगा जो परिवेश का है । कल्पना कीजिए कि बाह्य दाब को यकायक कम कर देते हैं (मान लीजिए कि बर्तन में लगे गतिशील पिस्टन से भार हटा लेते हैं) । पिस्टन बाहर की ओर त्वरित होगा । प्रक्रम की अवधि में गैस उन अवस्थाओं से गुजरती है जो साम्यावस्थाएँ नहीं हैं । असाम्य अवसथाओं का सुनिश्चित दाब व ताप नहीं होता । इसी प्रकार, यदि गैस व उसके परिवेश के मध्य सीमित तापांतर है, तो ऊष्मा का विनिमय द्रुत गति से होता है । इस प्रक्रम में गैस असाम्यावस्था से गुजरती है । यथासमय, गैस संतुलन की अवस्था में पहुँच जाएगी जिसमें सुुनिश्चित ताप व दाब परिवेश के ताप व दाब के बराबर हो जाएगा । निर्वात में गैस का स्वतंत्र प्रसार तथा विस्फोटक रासायनिक अभिक्रिया प्रदर्शित करने वाली गैसों का सम्मिश्रण (जिसका खंड (12.7) में वर्णन किया गया है) भी एेसे उदाहरण हैं जिसमें निकाय असाम्यावस्था से गुजरता है।
स्पष्ट रूप से, स्थैतिककल्प प्रक्रम काल्पनिक रचना है। व्यवहार रूप से उन प्रक्रमों को, जो बहुत ही धीमे हैं, जिनके पिस्टन में त्वरित गति नहीं होती तथा जिनमें अधिक ताप प्रवणता नहीं होती, इन्हें आदर्श स्थैतिककल्प प्रक्रम मानना तर्कसंगत है। यदि अन्य बात का वर्णन न किया जाए तो हम अब स्थैतिककल्प प्रक्रमों के विषय में ही अध्ययन करेंगे।
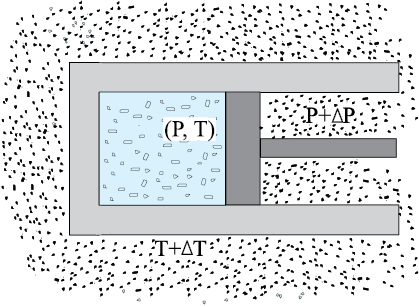
चित्र 12.7 स्थैतिककल्प प्रक्रम में परिवेश के पात्र का ताप तथा बाह्य दाब एवं निकाय के ताप व दाब का अंतर अत्यल्प है ।
वह प्रक्रम जिसकी पूरी अवधि में निकाय का ताप स्थिर रखा जाता है, समतापीय प्रक्रम कहलाता है । स्थिर ताप के किसी विशाल ऊष्मा भंडार में रखे धात्विक सिलिंडर में प्रसरित हो रही गैस समतापीय प्रक्रम का एक उदाहरण है । (ऊष्मा भंडार से निकाय में ऊष्मा के स्थानांतरण से ऊष्माशय का ताप यथार्थ रूप से प्रभावित नहीं होता, क्योंकि उसकी ऊष्माधारिता अत्यधिक होती है) । समदाबीय प्रक्रम में दाब स्थिर रहता है जबकि समआयतनिक प्रक्रम में आयतन स्थिर रहता है । अंततः, यदि निकाय को परिवेश से ऊष्मारुद्ध कर दिया जाए तथा निकाय व परिवेश के मध्य ऊष्मा प्रवाहित न हो, तो प्रक्रम रुद्धोष्म होता है । इन विशेष प्रक्रमों की परिभाषाओं का सार सारणी 12.2 में प्रस्तुत किया गया है ।
सारणी 12.2 कुछ विशिष्ट ऊष्मागतिकीय प्रक्रम
| प्रक्रमों का प्रकार | विशेषता |
| समतापीय | स्थिर ताप |
| समदाबीय | स्थिर दाब |
| समआयतनिक | स्थिर आयतन |
| रुद्धोष्म | निकाय व परिवेश के मध्य ऊष्मा प्रवाह नहीें (∆ Q = 0) |
अब हम इन प्रक्रमों के विषय में विस्तार से अध्ययन करेंगे।
12.8.2 समतापीय प्रक्रम
किसी समतापीय प्रक्रम में (जिसमें T स्थिर है) आदर्श गैस समीकरण से निम्नलिखित सूत्र प्राप्त होता है
PV = नियतांक
अर्थात् किसी निश्चित द्रव्यमान की गैस का दाब उसके आयतन का व्युत्क्रमानुपाती होता है । यह और कुछ नहीं वरन् बॉयल का नियम है ।
कल्पना कीजिए कि कोई आदर्श गैस समतापीय (ताप T पर) रूप से अपनी प्रारंभिक (P1, V1) से अंतिम अवस्था
(P2, V2) में पहुँचती है । बीच के किसी चरण में जब दाब P हो तथा आयतन में परिवर्तन V से V + ∆V (∆V कम) हो, तो
∆W = P∆V
∆V→0 लेते हुए राशि ∆W को संपूर्ण प्रक्रम में जोड़कर कार्य की कुल मात्रा निम्नलिखित रूप से ज्ञात कर लेते हैं,
W = 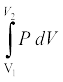
= µRT 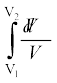 = µRT ln
= µRT ln 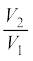 (12.12)
(12.12)
दूसरे चरण में हमने आदर्श गैस समीकरण PV = µRT का उपयोग किया है तथा अचरों को समाकलन से बाहर ले लिया है । आदर्श गैस के लिए आंतरिक ऊर्जा ताप पर निर्भर करती है । इस प्रकार, किसी आदर्श गैस के समतापीय प्रक्रम में आंतरिक ऊर्जा में कोई परिवर्तन नहीं होता । इसलिए ऊष्मागतिकी के प्रथम नियम के अनुसार, गैस को दी गई ऊष्मा की मात्रा गैस द्वारा संपादित किए गए कार्य के बराबर होती है: Q=W । समीकरण (12.12) में ध्यान दीजिए कि जब V2 > V1 तो W > 0; तथा V2 < V1 के लिए W < 0 होता है । इसका तात्पर्य यह है कि समतापीय प्रसार में गैस ऊष्मा अवशोषित करके कुछ कार्य संपादित करती है जबकि समतापीय संपीडन में गैस पर परिवेश द्वारा कार्य होता है तथा ऊष्मा का निष्कासन होता है ।
12.8.3 रुद्धोष्म प्रक्रम
रुद्धोष्म प्रक्रम में निकाय को परिवेश से ऊष्मारुद्ध कर देते हैं फलस्वरूप अवशोषित या निष्कासित ऊष्मा शून्य होती है । समीकरण (12.1) से पता चलता है कि गैस द्वारा संपादित कार्य के फलस्वरूप आंतरिक ऊर्जा कम हो जाती है (और इस प्रकार आदर्श गैस के लिए उसका ताप) । यहाँ हम बिना उपपत्ति के इस तथ्य का उल्लेख कर रहे हैं (जिसका आप उच्च कक्षाओं में अध्ययन करेंगे) कि आदर्श गैस के लिए रुद्धोष्म प्रक्रम में
PVγ = नियतांक (12.13)
जहाँ γ गैस की दो विशिष्ट ऊष्माओं (सामान्य अथवा मोलर), स्थिर दाब पर विशिष्ट ऊष्मा Cp तथा स्थिर आयतन पर विशिष्ट ऊष्मा Cv का अनुपात है । अर्थात्

अतः यदि कोई आदर्श गैस रुद्धोष्म ढंग से (P1, V1) अवस्था से (P2, V2) अवस्था में पहुँच जाती है, तो
P1V1γ = P2V2γ (12.14)
चित्र 12.8 मेें आदर्श गैस के लिए P-V वक्रों को दो रुद्धोष्म से जोड़ने वाले दो समतापीय को दर्शाया गया है ।
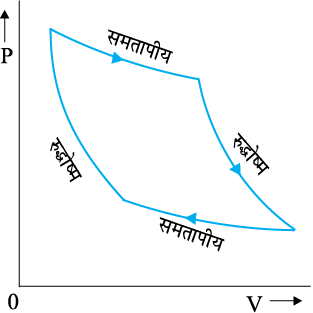
चित्र 12.8 आदर्श गैस के समतापीय व रुद्धोष्म प्रक्रमों के लिए P-V वक्र ।
किसी आदर्श गैस की अवस्था (P1, V1, T1) से अवस्था (P2, V2, T2) में रुद्धोष्म परिवर्तन में होने वाले कार्य को हम पहले ही की भांति परिकलित कर सकते हैं । अर्थात्,

जैसा अपेक्षित है, यदि रुद्धोष्म प्रक्रम में कार्य गैस द्वारा संपन्न होता है (W > 0), तब समीकरण (12.16) से T2>T1 । इसके विपरीत, यदि कार्य गैस पर संपादित होता है (W < 0) तो, हमें T2 > T1 प्राप्त होता है, अर्थात् गैस का ताप बढ़ता है ।
12.8.4 समआयतनिक प्रक्रम
किसी समआयतनिक प्रक्रम में V नियत रहता है । इस प्रक्रम में न तो गैस पर कोई कार्य होता है और न ही गैस द्वारा कोई कार्य संपादित होता है । समीकरण (12.1) से गैस द्वारा अवशोषित ऊष्मा पूर्ण रूप से उसकी आंतरिक ऊर्जा तथा उसके ताप को परिवर्तित करने में व्यय होती है । किसी दी गई ऊष्मा की मात्रा के लिए ताप में परिवर्तन नियत आयतन पर गैस की विशिष्ट ऊष्मा द्वारा निर्धारित की जाती है।
12.8.5 समदाबीय प्रक्रम
समदाबीय प्रक्रम में दाब P नियत रहता है । गैस द्वारा किया गया कार्य
W = P (V2–V1) = µR (T2–T1) (12.17)
चूंकि ताप परिवर्तित होता है, अतः आंतरिक ऊर्जा भी परिवर्तित होती है । अवशोषित ऊष्मा आंशिक रूप से आंतरिक ऊर्जा में वृद्धि करने में तथा आंशिक रूप से कार्य करने में व्यय होती है । किसी नियत ऊष्मा की मात्रा के लिए ताप में परिवर्तन नियत दाब पर गैस की विशिष्ट ऊष्मा द्वारा निर्धारित किया जाता है ।
12.8.6 चक्रीय प्रक्रम
चक्रीय प्रक्रम में निकाय अपनी प्रारंभिक अवस्था में वापस लौट आता है । चूंकि आंतरिक ऊर्जा अवस्था चर है, चक्रीय प्रक्रम के लिए ∆U=0 । समीकरण (12.1) से, अवशोषित ऊष्मा की कुल मात्रा निकाय द्वारा किए गए कार्य के बराबर होती है ।
12.9 ऊष्मा इंजन
ऊष्मा इंजन एक एेसी युक्ति है, जिसमें निकाय द्वारा चक्रीय प्रक्रम पूरा कराया जाता है जिसके फलस्वरूप ऊष्मा कार्य में रूपांतरित होती है ।
(1) इसमें एक कार्यकारी पदार्थ होता है। उदाहरणार्थ, किसी गैसोलीन अथवा डीजल इंजन में ईंधन वाष्प तथा वायु का मिश्रण, अथवा किसी भाप इंजन में भाप कार्यकारी पदार्थ हैं।
(2) कार्यकारी पदार्थ एक चक्र से गुजरता है जिसमें कई प्रक्रम होते हैं। एक प्रक्रम में यह पदार्थ किसी उच्च ताप T1 पर किसी बाह्य ऊष्मा भंडार से ऊष्मा की कुल मात्रा Q1 अवशोषित करता है ।
(3) चक्र के द्वितीय प्रक्रम में कार्यकारी पदार्थ किसी अपेक्षाकृत कम ताप T2 पर किसी बाह्य ऊष्मा भंडार को कुल ऊष्मा की मात्रा Q2 मुक्त करता है ।
(4) एक चक्र में निकाय द्वारा संपादित कार्य W किसी
विधा द्वारा परिवेश में स्थानांतरित किया जाता है (उदाहरणार्थ, कार्यकारी पदार्थ गतिशील पिस्टन लगे किसी सिलिंडर में भरा हो सकता है जो पिस्टन द्वारा यांत्रिक ऊर्जा को शाफ्ट के माध्यम से वाहन के पहियों को स्थनांतरित कर देता है )।
किसी ऊष्मा इंजन के मौलिक लक्षणों का योजनाबद्ध निरूपण चित्र 12.9 में किया गया है ।
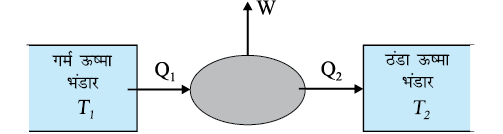
चित्र 12.9 ऊष्मा इंजन का योजनाबद्ध निरूपण । इंजन ताप T1 पर गरम ऊष्मा भंडार से Q1ऊष्मा ग्रहण करता है, ताप T2 पर एक ठंडे ऊष्मा भंडार को Q2 ऊष्मा मुक्त करता है तथा परिवेश को कार्य W प्रदान करता है ।
चक्र बार-बार दोहराया जाता है ताकि किसी प्रयोजन के लिए उपयोगी कार्य संपादित हो सके । ऊष्मागतिकी विषय की जड़ें ऊष्मा इंजनों के अध्ययन में हैं । किसी ऊष्मा इंजन की दक्षता से एक मौलिक प्रश्न संबंधित होता है । किसी ऊष्मा इंजन की दक्षता (η) को इस प्रकार परिभाषित करते हैं
η = 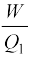 (12.18)
(12.18)
यहाँ Q1 ऊष्मा निवेश है, अर्थात् निकाय द्वारा एक पूरे चक्र में अवशोषित ऊष्मा की मात्रा है तथा W एक चक्र में परिवेश पर किया गया कार्य है । एक चक्र में ऊष्मा की कुछ निश्चित मात्रा [Q2] परिवेश में निष्कासित भी हो सकती है । एेसी परिस्थिति में ऊष्मागतिकी के प्रथम नियम के अनुसार एक पूरे चक्र के लिए किया गया कार्य
W = Q1 – Q2 (12.19)
अर्थात्
η = 1 – 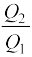 (12.20)
(12.20)
यदि Q2 = 0 है, तो η = 1, अर्थात् ऊष्मा को कार्य में परिवर्तित करने में इंजन की दक्षता 100% होगी । इस बात पर ध्यान दीजिए कि ऊष्मागतिकी का प्रथम नियम अर्थात् ऊर्जा संरक्षण का नियम इस प्रकार के इंजन की संभावना से इनकार नहीं करता । परंतु अनुभव यह दर्शाता है कि चाहे हम वास्तविक इंजन से संबंधित विभिन्न प्रकार की हानियों को कितना भी कम क्यों न कर दें, एेसा आदर्श इंजन होना जिसके लिए η = 1 हो, कदापि संभव नहीं है। इससे यह निष्कर्ष निकलता है कि ऊष्मा इंजन की दक्षता की एक मौलिक सीमा होती है जिसका निर्धारण प्रकृति के एक स्वतंत्र नियम, जिसे ऊष्मागतिकी का द्वितीय नियम कहते हैं (खंड
12.11) द्वारा होता है ।
ऊष्मा को कार्य में परिवर्तित करने की प्रक्रिया विभिन्न प्रकार के ऊष्मा इंजनों के लिए भिन्न है । मौलिक रूप से इसके दो प्रकार हैंः निकाय (जैसे कोई गैस या गैसों के मिश्रण) को किसी बाह्य भट्ठी द्वारा गरम किया जाए, जैसा कि भाप इंजन में होता है, अथवा इसके आंतरिक रूप से ऊष्मान्मोची (ऊष्माक्षेपी) रासायनिक अभिक्रिया द्वारा गरम किया जाए, जैसा कि आंतरिक दहन इंजन में होता है । किसी चक्र में निहित विभिन्न चरण भी विभिन्न इंजनों के लिए अलग-अलग होते हैं ।
12.10 प्रशीतक/ऊष्मा पंप
प्रशीतक या ऊष्मा पंप ऊष्मा इंजन के ठीक विपरीत होता है । इसमें कार्यकारी पदार्थ किसी निम्न ताप T2 के ऊष्मा भंडार से Q2 ऊष्मा ग्रहण करता है, तत्पश्चात उस पर कुछ बाह्य कार्य W किया जाता है तथा ऊष्मा Q1 किसी उच्च ताप T1 के ऊष्मा भंडार को मुक्त कर दी जाती है (चित्र 12.10)।
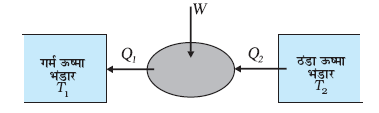
चित्र 12.10 प्रशीतक या ऊष्मा पंप का योजनाबद्ध निरूपण । यह ऊष्मा इंजन का उत्क्रमणीय होता है ।
ऊष्मा पंप प्रशीतक के समान होता है । हम किस शब्द का उपयोग करते हैं, यह युक्ति के प्रयोजन पर निर्भर करता है। यदि प्रयोजन किसी स्थान के कुछ भाग, जैसे कि किसी प्रकोष्ठ के भीतरी भाग को ठंडा करना है, तो युक्ति को हम प्रशीतक कहते हैं । किंतु यदि प्रयोजन किसी स्थान के किसी भाग में ऊष्मा को पंप करना है, तो युक्ति को ऊष्मा पंप कहते हैं । एेसा भवन के किसी कमरे को गरम करने के लिए उस समय किया जाता है जब बाहरी वातावरण ठंडा होता है ।
प्रशीतक में कार्यकारी पदार्थ (प्रायः, फ्रीअॉन गैस) निम्नलिखित चरणों से गुजरती है: (a) उच्च दाब से निम्न दाब के क्षेत्र में गैस में अचानक प्रसार होता है जिसके कारण वह (फ्रीअॉन) ठंडी हो जाती है तथा वाष्प-द्रव मिश्रण में रूपांतरित हो जाती है। (b) ठंडे तरल द्वारा उस भाग से ऊष्मा का अवशोषण जिसे ठंडा करना है, होता है। इससे तरल वाष्प में रूपांतरित हो जाता है। (c) निकाय पर किए गए बाह्य कार्य द्वारा वाष्प का गरम होना, तथा (d) वाष्प द्वारा परिवेश में ऊष्मा मुक्त करके कार्यकारी पदार्थ को एक चक्र पूरा कर पुनः अपनी आरंभिक अवस्था में वापस लाना है । इस प्रकार प्रशीतक का निष्पादन गुणांक
α =  (12.21)
(12.21)
यहाँ Q2 ठंडे ऊष्मा भंडार से अवशोषित ऊष्मा की मात्रा तथा W निकाय – प्रशीतक पर किया गया कार्य है । ध्यान दीजिए, परिभाषा के अनुसार η का मान 1 से अधिक नहीं हो सकता, जबकि α का मान 1 से अधिक हो सकता है । ऊष्मा संरक्षण द्वारा गरम ऊष्मा भंडार को मुक्त की गई ऊष्मा
Q1 = W + Q2
अर्थात्
α = 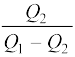 (12.22)
(12.22)
होती है ।
ऊष्मा इंजन में ऊष्मा को पूर्ण रूप से कार्य में रूपांतरित नहीं किया जा सकता: उसी प्रकार से निकाय पर बिना कुछ बाह्य कार्य किए कोई प्रशीतक कार्य नहीं कर सकता, अर्थात् समीकरण (12.21) में निष्पादन गुणांक अनंत नहीं हो सकता ।
12.11 ऊष्मागतिकी का द्वितीय नियम
ऊष्मागतिकी का प्रथम नियम ऊर्जा संरक्षण नियम है । सामान्य अनुभव यह बतलाता है कि एेसे बहुत से मनोगम्य प्रक्रम हैं जो ऊष्मागतिकी के प्रथम नियम से पूर्णतया अनुमत हैं तथापि कभी भी होते हुए दिखाई नहीं देते । उदाहरणार्थ, एेेसा किसी ने कभी नहीं देखा कि मेज पर पड़ी कोई पुस्तक स्वतः उछलकर किसी ऊँचाई पर पहुँच जाए । किंतु एेसी बात तभी संभव हो सकती है यदि केवल ऊर्जा संरक्षण नियम का ही नियंत्रण हो । मेज स्वतः ठंडी होकर अपनी आंतरिक ऊर्जा का कुछ अंश पुस्तक की समान मात्रा की यांत्रिक ऊर्जा में रूपांतरित करने में करे और इस यांत्रिक ऊर्जा के कारण पुस्तक उस ऊँचाई तक उछले जिसकी स्थितिज ऊर्जा पुस्तक द्वारा प्राप्त यांत्रिक ऊर्जा के बराबर हो । परंतु एेसा कदापि नहीं होता । स्पष्ट है कि प्रकृति के किसी आंतरिक मूल नियम के कारण यह निषेध है । यद्यपि यह ऊर्जा संरक्षण नियम का अनुपालन करता है । वह नियम जो ऊष्मागतिकी के प्रथम नियम से संगत अनेक परिघटनाओं को स्वीकृति नहीं देता, ऊष्मागतिकी का द्वितीय नियम कहलाता है ।
ऊष्मागतिकी के पथ-प्रदर्शक

लार्ड केल्विन (विलियम थॉमसन) (1824-1907), बेल्फास्ट, आयरलैंड में जन्मे 19वीं शती के ब्रिटिश वैज्ञानिकों में से एक हैं । जेम्स जूल (1818-1889), जूलियस मेयर (1814-1878) तथा हरमैन हेल्महॉल्ट्ज़ (1821-1894) द्वारा प्रस्तावित ऊर्जा के संरक्षण नियम के विकास में थॉमसन ने प्रमुख भूमिका अदा की । उन्होंने सुविख्यात ‘‘जूल-थॉमसन प्रभाव’’: निर्वात में प्रसारित होने पर किसी गैस का ठंडा होना, की खोज में जूल के सहयोगी के रूप में कार्य किया । इन्होंने ताप के परम शून्य की धारणा से परिचय कराया । परम त0ाप मापक्रम को प्रस्तावित किया, जिसे उनके सम्मान में केल्विन तापक्रम कहते हैं । साडी कार्नो (1796-1832) के कार्य से थॉमसन ऊष्मागतिकी के द्वितीय नियम के एक स्वरूप तक पहुंँचे । थॉमसन एक बहुमुखी प्रतिभा के भौतिकविद थे जिन्होंने वैद्युतचुंबकीय सिद्धांत तथा द्रव्यगतिकी में महत्वपूर्ण योगदान दिया ।

रूडोल्फ क्लासियस (1822-1888), पोलैण्ड में जन्मे इस भौतिकविद को प्रमुख रूप से ऊष्मागतिकी के दूसरे नियम का आविष्कारक माना जाता है । कार्नो तथा थॉमसन के कार्य के आधार पर क्लासियस एंट्रॉपी जैसी महत्वपूर्ण धारणा पर पहुँचे जिसने ऊष्मागतिकी के द्वितीय नियम के मूल स्वरूप की खोज का मार्ग प्रशस्त किया जिसका कथन है कि किसी वियुक्त निकाय की एंट्रॉपी कभी भी घट नहीं सकती । क्लासियस ने गैसों के अणुगति सिद्धांत पर भी कार्य किया तथा प्रथम आण्विक अमाप, चाल तथा माध्य मुक्त पथ का विश्वसनीय आकलन प्राप्त किया ।
ऊष्मागतिकी का द्वितीय नियम किसी ऊष्मा इंजन की दक्षता तथा किसी प्रशीतक के निष्पादन गुणांक की मूल सीमा निर्धारित करता है । सरल भाषा में, यह नियम बताता है कि ऊष्मा इंजन की दक्षता कदापि 1 नहीं हो सकती । समीकरण (12.20) के अनुसार, इसका तात्पर्य यह है कि ठंडे ऊष्मा भंडार की मुक्त ऊष्मा को कभी भी शून्य नहीं किया जा सकता । प्रशीतक के लिए द्वितीय नियम यह बताता है कि निष्पादन गुणांक कदापि अनंत नहीं हो सकता । समीकरण (12.21) से यह भी निष्कर्ष निकलता है कि प्रशीतक पर बाह्य कार्य (W) कभी भी शून्य नहीं हो सकता । अधोलिखित दोनों प्रकथन, इन प्रेक्षणों का एक संक्षिप्त सार है। उनमें से एक केल्विन तथा प्लैंक के द्वारा दिया गया है जिसके अनुसार, किसी आदर्श ऊष्मा इंजन की संभावना का खंडन किया गया है, तथा दूसरा क्लासियस द्वारा दिया गया है जिसके अनुसार, किसी आदर्श प्रशीतक अथवा ऊष्मा पंप की संभावना का खंडन किया गया है।
केल्विन-प्लैंक का प्रकथन
एेसा कोई प्रक्रम संभव नहीं है जिसका एकमात्र परिणाम किसी ऊष्मा भंडार से ऊष्मा का अवशोषण करना तथा उस ऊष्मा को पूर्णतया कार्य में रूपांतरित करना हो ।
क्लासियस का प्रकथन
एेसा कोई भी प्रक्रम संभव नहीं है जिसका एकमात्र परिणाम किसी ठंडे पिंड से किसी गर्म पिंड में ऊष्मा स्थानांतरण हो ।
उच्च कक्षाओं के पाठ्यक्रमों में आप इसकी उपपत्ति पढ़ेंगे कि दोनों प्रकथन पूर्णतया समतुल्य हैं ।
12.12 उत्क्रमणीय व अनुत्क्रमणीय प्रक्रम
किसी एेसे प्रक्रम की कल्पना कीजिए जिसमें कोई ऊष्मागतिकीय निकाय आरंभिक अवस्था i से अंतिम अवस्था f में पहुँचता है । प्रक्रम में निकाय परिवेश से Q ऊष्मा अवशोषित करता है तथा उस पर W कार्य संपादित करता है । क्या हम इस प्रक्रम को उलट सकते हैं तथा निकाय व परिवेश दोनों को, कहीं भी कोई अन्य प्रभाव पड़े बिना, आरंभिक अवस्था में वापस ला सकते हैं? अनुभव बताता है कि प्रकृति के अधिकांश प्रक्रमों में एेसा होना संभव नहीं है । प्रकृति में सभी नैसर्गिक प्रक्रम अनुत्क्रमणीय हैं । इनके अनेक उदाहरण गिनाये जा सकते हैं। चूल्हे पर रखे बर्तन का आधार दूसरे भागों की अपेक्षा अधिक गरम होता है । जब बर्तन को हटाते हैं तो ऊष्मा आधार से दूसरे भागों में स्थानांतरित होती है जिससे बर्तन का ताप एकसमान हो जाता है (यथोचित समय में यह परिवेश के ताप के बराबर ठंडा हो जाता है) । इस प्रक्रम को उत्क्रमित नहीं किया जा सकता, बर्तन का कोई भाग स्वतः ठंडा होकर आधार को गर्म नहीं करेगा । यदि एेसा होता है तो ऊष्मागतिकी के द्वितीय नियम का उल्लंघन होगा । गैस का मुक्त प्रसार अनुत्क्रमणीय होता है । वायु तथा पेट्रोल के मिश्रण में स्फुलिंग द्वारा प्रज्वलित दहन अभिक्रिया को उत्क्रमित नहीं किया जा सकता । रसोईघर में किसी गैस सिलिंडर से रिस रही भोजन पकाने की गैस पूरे कमरे में विसरित हो जाती है । विसरण प्रक्रम स्वतः उत्क्रमित नहीं होगा जिससे गैस वापस सिलिंडर में भर जाए । किसी ऊष्मा भंडार के ऊष्मीय संपर्क में आने वाले द्रव का विलोड़न संपादित हो रहे कार्य को ऊष्मा में रूपांतरित कर देगा जिससे उष्माशय की आंतरिक ऊर्जा बढ़ जाती है । प्रक्रम को पूर्णतया उत्क्रमित नहीं कर सकते, अन्यथा इसका अर्थ होगा कि ऊष्मा पूर्णतया कार्य में परिवर्तित हो गई है । यह ऊष्मागतिकी के दूसरे नियम का उल्लंघन है । अनुत्क्रमणीयता एक नियम है न कि प्रकृति में कोई अपवाद ।
अनुत्क्रमणीयता मुख्यतः दो कारणों से उत्पन्न होती है ः पहला, अनेक प्रक्रम (जैसे मुक्त प्रसरण या विस्फोटक रासायनिक अभिक्रिया) निकाय को असंतुलन की अवस्थाओं में ले जाते हैं; दूसरा, अनेक प्रक्रमों में घर्षण, श्यानता तथा अन्य क्षय संबंधी प्रभाव निहित होते हैं (इसके उदाहरण हैं – किसी गतिमान पिंड का रुकना जिसमें पिंड अपनी यांत्रिक ऊर्जा को फर्श व स्वयं अपनी ऊष्मा के रूप में दे देता है; द्रव में घूमते हुए ब्लेड का श्यानता के कारण रुक जाना जिसमें यह अपनी यांत्रिक ऊर्जा को द्रव की आंतरिक ऊर्जा के रूप में दे देता है) । चूंकि क्षयकारी प्रभाव सभी स्थानों पर उपस्थित रहते हैं । इन्हें कम तो किया जा सकता है पर पूर्णतया समाप्त नहीं किया जा सकता । जिन प्रक्रमों से हमारा अधिकतर सामना होता है वे सभी अनुत्क्रमणीय होते हैं ।
कोई ऊष्मागतिकीय प्रक्रम (अवस्था i 6 अवस्था f ) तभी उत्क्रमणीय होता है यदि उसे इस प्रकार वापस लौटाया जा सके कि निकाय व परिवेश दोनों अपनी प्रारंभिक अवस्थाओं में वापस आ जाएँ तथा परिवेश में कहीं भी किसी भी प्रकार का अन्य परिवर्तन न हो । पूर्व विवेचना के अनुसार कोई उत्क्रमणीय प्रक्रम एक आदर्श धारणा है । कोई प्रक्रम उत्क्रमणीय तभी होता है जब वह स्थैतिककल्प होता है (परिवेश के साथ प्रत्येक चरण पर साम्य निकाय) तथा निकाय में कोई क्षयकारी प्रभाव नहीं होते हैं । उदाहरणार्थ, घर्षणहीन गतिशील पिस्टन लगे सिलिंडर भरी किसी आदर्श गैस का स्थैतिककल्प समतापीय प्रसरण उत्क्रमणीय प्रक्रम है ।
उत्क्रमणीयता ऊष्मागतिकी की एेसी मूल धारणा क्यों है ? जैसा कि हम देख चुके है, ऊष्मागतिकी के महत्त्वों में से एक महत्त्व दक्षता का है जिससे ऊष्मा कार्य में रूपांतरित की जा सकती है । ऊष्मागतिकी का दूसरा नियम 100% दक्षता के आदर्श ऊष्मा इंजन की संभावना को नियम विरुद्ध बताता है । T1 व T2 के दो ऊष्मा भंडारों के बीच कार्य करने वाले किसी ऊष्मा इंजन की संभावित अधिकतम दक्षता कितनी होगी ? यह देखा जाता है कि आदर्श उत्क्रमणीय प्रक्रमों पर आधारित ऊष्मा इंजन अधिकतम संभावित दक्षता प्राप्त करता है । अन्य दूसरे इंजनों जिनमें किसी न किसी रूप में अनुत्क्रमणीयता निहित होती है (जैसा कि व्यावहारिक इंजनों में होता है) की दक्षता इस सीमांत दक्षता से कम होती है ।
12.13 कार्नो इंजन
कल्पना कीजिए कि हमारे पास ताप T1 पर एक उष्ण ऊष्मा भंडार व ताप T2 पर एक ठंडा ऊष्मा भंडार है । इन दोनों ऊष्मा भंडारों के बीच कार्य करने वाले किसी ऊष्मा इंजन की अधिकतम दक्षता कितनी होगी तथा सर्वाधिक दक्षता प्राप्त करने के लिए प्रकर्मों के किस चक्र को अपनाना चाहिए ? फ्रेंच इंजीनियर, साडी कार्नो ने 1824 में सर्वप्रथम इस प्रश्न पर विचार किया । दिलचस्प बात यह है कि कार्नो ने इस प्रश्न का सही उत्तर पा लिया था यद्यपि ऊष्मा और ऊष्मागतिकी की मौलिक अवधारणा को तब तक दृढ़तापूर्वक स्थापित नहीं किया जा सका था ।
हम यह आशा करते हैं कि दो तापों के बीच कार्य करने वाला आदर्श इंजन उत्क्रमणीय इंजन है । जैसा कि पहले अनुभागों में बताया जा चुका है, अनुत्क्रमणीयता से दक्षता को कम करने वाले क्षयकारी प्रभाव संबद्ध होते हैं । कोई प्रक्रम तभी उत्क्रमणीय होता है यदि वह स्थैतिककल्प तथा ऊर्जा-संरक्षी हो । हम यह देख चुके हैं कि वह प्रक्रम स्थैतिककल्प नहीं होता है जिसमें निकाय व ऊष्मा भंडार के बीच तापांतर पर्याप्त हो । इसका तात्पर्य यह है कि दो तापों के मध्य कार्य कर रहे किसी उत्क्रमणीय ऊष्मा इंजन में ऊष्मा का अवशोषण (गरम ऊष्मा भंडार से) समतापीय विधि द्वारा होना चाहिए तथा (अपेक्षाकृत ठंडे ऊष्मा भंडार को) समतापीय विधि द्वारा ऊष्मा मुक्त होनी चाहिए । इस प्रकार, हमने उत्क्रमणीय इंजन के दो चरणों की पहचान की: ताप T1 पर समतापीय प्रक्रम जिसमें गरम ऊष्मा भंडार से Q1 ऊष्मा अवशोषित होती है तथा ताप T2 पर दूसरा समतापीय प्रक्रम जिसमें ठंडे ऊष्मा भंडार को Q2 ऊष्मा मुक्त होती है । चक्र पूरा होने के लिए इस बात की आवश्यकता है कि हम निकाय को ताप T1 से T2 तक ले जाएँ फिर उसे ताप T2 से T1 पर वापस ले जाएँ । प्रश्न यह है कि इस उद्देश्य के लिए हमें किन प्रक्रमों का उपयोग करना चाहिए जो उत्क्रमणीय हों ? थोड़े चिंतन से यह पता चल जाता है कि उस उद्देश्य के लिए हम केवल उत्क्रमणीय रुद्धोष्म प्रक्रम ही अपना सकते हैं जिसमें किसी भी ऊष्मा भंडार से ऊष्मा का प्रवाह सम्मिलित नहीं होता । निकाय को एक ताप से दूसरे ताप तक ले जाने के लिए यदि हम कोई अन्य प्रक्रम अपनाते हैं जो रुद्धोष्म नहीं है, मान लीजिए समआयतनिक प्रक्रम, तो हमें ताप परिसर T2 से T1 में ऊष्मा भंडार की एक शृंखला की आवश्यकता होगी ताकि यह निश्चित किया जा सके कि हर चरण में प्रक्रम स्थैतिककल्प में है । (हम आपको पुनः याद दिलाते हैं कि किसी स्थैतिककल्प व उत्क्रमणीय प्रक्रम में निकाय व ऊष्मा भंडार के बीच बहुत तापांतर नहीं होना चाहिए) । परंतु हम यहाँ एक एेसे उत्क्रमणीय इंजन पर विचार कर रहे हैं जो केवल दो तापों के बीच कार्य करता है । इस प्रकार, रुद्धोष्म प्रक्रमों द्वारा निकाय के ताप में T1 से T2 तथा इस इंजन के ताप में T2 से T1 का परिवर्तन लाना चाहिए ।

चित्र 12.11 किसी ऊष्मा इंजन के लिए कार्नो चक्र जिसमें कार्यकारी पदार्थ के रूप में आदर्श गैस का उपयोग होता है ।
दो तापों के मध्य कार्य करने वाला कोई उत्क्रमणीय ऊष्मा इंजन कार्नो इंजन कहलाता है । हमने अभी विवेचना की है कि इस इंजन में चरणों का क्रम निम्नलिखित होना चाहिए, जो चित्र 12.11 में दर्शाए अनुसार एक चक्र का निर्माण करते हैं, जिसे कार्नो चक्र कहते हैं । हमने कार्नो इंजन का कार्यकारी पदार्थ एक आदर्श गैस लिया है ।
(a) चरण 1→2 गैस का समतापी प्रसार जिसमें गैस अवस्था (P1, V1, T1) से (P2, V2, T1) में पहुँच जाती है ।
ताप T1 पर ऊष्माशय से अवशोषित ऊष्मा (Q1) का मान समीकरण (12.12) से दिया जाता है । यह गैस द्वारा परिवेश पर संपादित किए गए कार्य W 1→2 के बराबर होता है ।
W1→2 = Q1=µRT1 ln 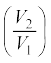 (12.23)
(12.23)
(b) चरण 2→3 (P2, V2, T1) से (P3, V3, T2) अवस्था में गैस का रुद्धोष्म प्रसार । समीकरण (12.16) से गैस द्वारा संपादित हुआ कार्य होगा
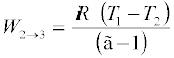 (12.24)
(12.24)
(c) चरण 3→ 4 गैस की अवस्था (P3, V3, T2) से (P4, V4, T2) में समतापी संपीडन ।
ताप T2 पर गैस द्वारा ऊष्माशय को मुक्त की गई ऊष्मा की मात्रा समीकरण (12.12) से प्राप्त होती है । यह परिवेश द्वारा गैस पर संपादित कार्य W3→ 4 के भी बराबर होती है
W3→ 4 = Q2 = µRT2 ln 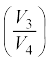 (12.25)
(12.25)
(d) चरण 4→ 1 गैस की अवस्था (P4, V4, T2) से (P1, V1, T1) में रुद्धोष्म संपीडन । समीकरण
(12.16) से गैस पर किया गया कार्य
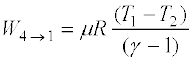 (12.26)
(12.26)
समीकरणों (12.23)से (12.26) के उपयोग से एक पूरे चक्र में गैस द्वारा संपादित कुल कार्य की मात्रा,
W = W1→ 2 + W2→ 3 – W3→ 4 – W4→ 1
= µ RT1 ln 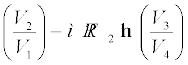 (12.27)
(12.27)
कार्नो इंजन की दक्षता
η = 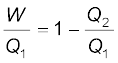
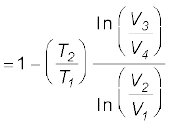 (12.28)
(12.28)
अब चूंकि चरण 2→3 एक रुद्धोष्म प्रक्रम है, इसलिए
T1 V2γ -1 = T2 V3γ -1
अथवा 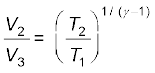 (12.29)
(12.29)
इसी प्रकार, चूंकि चरण 4→1 भी एक रुद्धोष्म प्रक्रम है, इसलिए
T2 V4γ -1 = T1 V1γ -1
अथवा 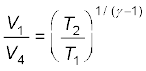 (12.30)
(12.30)
समीकरणों (12.29) तथा (12.30) से,
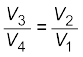 (12.31)
(12.31)
समीकरण (12.31) के उपयोग से समीकरण (12.28) से η का निम्नलिखित सूत्र प्राप्त होता है:
 (कार्नो इंजन) (12.32)
(कार्नो इंजन) (12.32)
हम जानते हैं कि कार्नो इंजन एक उत्क्रमणीय इंजन है । वास्तव में यही एकमात्र एेसा इंजन संभव है जो भिन्न तापों के दो ऊष्मा भंडारों के मध्य कार्य करता है । चित्र 12.11 मेें दर्शाए कार्नो चक्र का हर चरण उत्क्रमित किया जा सकता है । यह उस प्रक्रम के समान होता है, जिसमें T2 ताप पर ठंडे ऊष्मा भंडार से Q2 ऊष्मा ली जाती है, निकाय पर W कार्य किया जाता है, तथा गरम ऊष्मा भंडार को Q1 ऊष्मा स्थानांतरित कर दी जाती है । यह युक्ति एक उत्क्रमणीय प्रशीतक होगी ।
अब हम महत्वपूर्ण परिणाम सिद्ध करेंगे (जिसे कभी-कभी कार्नो प्रमेय कहते हैं) (a) दिए हुए गरम तथा ठंडे ऊष्माशयों के क्रमशः दो तापों T1 तथा T2 के बीच कार्यरत किसी भी इंजन की दक्षता कार्नो इंजन की दक्षता से अधिक नहीं हो सकती है तथा (b) कार्नो इंजन की दक्षता कार्यकारी पदार्थ की प्रकृति पर निर्भर नहीं करती ।
परिणाम (a) को सिद्ध करने के लिए हम कल्पना करते हैं कि एक उत्क्रमणीय (कार्नो) इंजन R तथा एक अनुत्क्रमणीय इंजन I एक ही स्रोत (गरम ऊष्मा भंडार) तथा अभिगम (Sink) (ठंडा ऊष्मा भंडार) के बीच कार्यरत हैं । अब हम इन दोनों इंजनों को इस प्रकार संयोजित करते हैं कि I ऊष्मा इंजन की भांति तथा R प्रशीतक की भांति कार्य करें । कल्पना कीजिए कि I स्रोत से Q1 ऊष्मा अवशोषित करता है, W′ कार्य प्रदान करता है तथा Q1 – W′ ऊष्मा अभिगम को मुक्त करता है । हम एेसा समायोजन करते हैं कि R अधिगम से Q2 ऊष्मा लेकर तथा उस पर जो कार्य W = Q1 – Q2 किया जाना है, उसे कराकर उतनी ही ऊष्मा Q1 स्रोत को वापस करता है । मान लीजिए कि ηR < ηI है । अर्थात् यदि R इंजन की भांति कार्य करता तो वह I की अपेक्षा कम कार्य निर्गत करता। अर्थात् किसी दी गई ऊष्मा Q1 के लिए W < W ′ । यदि R प्रशीतक के रूप में कार्य करता, तो इसका तात्पर्य यह होता कि Q2 = Q1 – W > Q1 – W ′ । इस प्रकार, युक्तिपूर्ण संयोजित I – R निकाय ठंडे ऊष्मा भंडार से (Q1 – W) – (Q1 – W ′) = W ′ – W ऊष्मा निकालता है तथा एक चक्र में इतनी ही मात्रा का कार्य उसे सौंप देता है (इस पूरे चक्र में स्रोत या अन्यत्र कोई परिवर्तन नहीं होता)। यह ऊष्मागतिकी के द्वितीय नियम से संबंधित केल्विन-प्लैंक के प्रकथन से सर्वथा विपरीत है । इसलिए यह निश्चयपूर्वक कहना कि ηI > ηR अनुचित है । अतः समान तापों के मध्य कार्यरत किसी भी इंजन की दक्षता कार्नो इंजन की दक्षता से अधिक नहीं हो सकती । इसी प्रकार के एक तर्क की रचना यह दर्शाने के लिए भी की जा सकती है कि एेसे उत्क्रमणीय इंजन की दक्षता जिसमें एक विशेष कार्यकारी पदार्थ है, उस इंजन की दक्षता से अधिक नहीं हो सकती जिसमें कोई अन्य पदार्थ उपयोग होता है । कार्नो इंजन की अधिकतम दक्षता जो समीकरण (12.32) से दी जाती है, कार्नो चक्र की प्रक्रिया को संपादित करने वाले निकाय की प्रकृति पर निर्भर नहीं करती है । अतः हमारे लिए कार्नो इंजन की दक्षता η के परिकलन के लिए कार्यकारी पदार्थ के रूप में आदर्श गैस का उपयोग न्यायसंगत है । आदर्श गैस की अवस्था समीकरण सरल होती है जिसके कारण η का परिकलन सरल हो जाता है, किंतु η के लिए अंतिम परिणाम, समीकरण (12.32), किसी भी कार्नो इंजन के लिए सही है ।
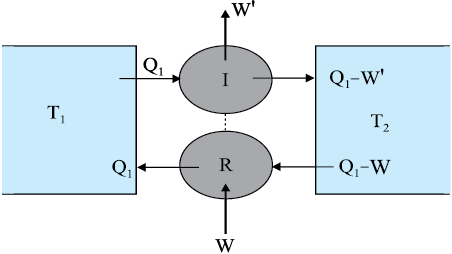
यह अंतिम टिप्पणी दर्शाती है कि कार्नो इंजन के लिए,
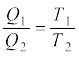 (12.33)
(12.33)
एक व्यापक संबंध है जो निकाय की प्रकृति पर निर्भर नहीं करता। यहाँ Q1 व Q2 कार्नो इंजन में क्रमशः गरम व ठंडे ऊष्मा भंडारों द्वारा समतापीय ढंग से अवशोषित व मुक्त की गई ऊष्माएँ हैं । किसी वास्तविक सर्वव्यापक ऊष्मागतिकीय ताप मापक्रम को परिभाषित करने के लिए हम समीकरण (12.33) का एक सूत्र के रूप में उपयोग कर सकते हैं । यह तापक्रम कार्नो चक्र में प्रयुक्त निकाय के किन्हीं विशेष गुणधर्मों पर निर्भर नहीं करता। वास्तव में, कार्यकारी पदार्थ के रूप में किसी आदर्श गैस के लिए इस ताप का मान वही है जो खंड 12.11 में उल्लेखित आदर्श गैस ताप का है ।
सारांश
1. ऊष्मागतिकी का शून्यवाँ नियम यह अभिव्यक्त करता है कि "दो निकाय जो किसी तीसरे निकाय के साथ स्वतंत्र रूप से तापीय साम्य में हैं, वे एक-दूसरे के साथ भी तापीय साम्य में होते हैं"। शून्यवाँ नियम ताप की अवधारणा का सूत्रपात करता है ।
2. निकाय की आंतरिक ऊर्जा उसके आण्विक घटकों की गतिज एवं स्थितिज ऊर्जाओं के योग के बराबर होती है । इसमें
निकाय की संपूर्ण गतिज ऊर्जा सम्मिलित नहीं होती । ऊष्मा और कार्य किसी निकाय में ऊर्जा स्थानांतरण के दो रूप हैं । निकाय व उसके परिवेश के बीच तापांतर के कारण ऊर्जा का स्थानांतरण ऊष्मा के रूप में होता है । कार्य अन्य साधनों (जैसे गैस भरे सिलिंडर के पिस्टन जिससे कुछ भार संबद्ध है, को ऊपर नीचे करने में) द्वारा उत्पन्न ऊर्जा का
स्थानांतरण है । इसमें तापांतर समाहित नहीं होता है ।
3. ऊष्मागतिकी का प्रथम नियम ऊर्जा संरक्षण का व्यापक नियम है, जो उस निकाय में लागू होता है जिसमें परिवेश को या परिवेश से (ऊष्मा व कार्य द्वारा) ऊर्जा स्थानांतरण हो । यह बताता है कि
∆Q = ∆U + ∆W
यहाँ ∆Q निकाय को दी गई ऊष्मा है, ∆W निकाय पर किया गया कार्य है तथा ∆U निकाय की आंतरिक ऊर्जा में
परिवर्तन है ।
4. पदार्थ की विशिष्ट ऊष्मा धारिता को हम निम्नलिखित सूत्र द्वारा परिभाषित करते हैं
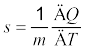
यहाँ m पदार्थ का द्रव्यमान है तथा ∆Q वह ऊष्मा है जिसके द्वारा पदार्थ के ताप में ∆T की वृद्धि हो जाती है । पदार्थ की मोलीय विशिष्ट ऊष्मा धारिता निम्नांकित सूत्र से परिभाषित की जाती है
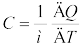
µ पदार्थ के मोल की संख्या को व्यक्त करता है । किसी ठोस के लिए ऊर्जा के सम विभाजन के नियम से
C = 3 R
जो सामान्यतया साधारण तापों पर किए जाने वाले प्रयोगों से प्राप्त परिणामों से मेल खाता है ।
कैलोरी ऊष्मा का पुराना मात्रक है । 1 कैलोरी ऊष्मा की वह मात्रा है जो 1g जल के ताप में 14.5 °C से 15.5 °C तक वृृद्धि कर देती है । 1 cal = 4.186 J
5. किसी आदर्श गैस के लिए स्थिर ताप तथा स्थिर दाब पर मोलीय विशिष्ट ऊष्मा धारिताएँ निम्नलिखित संबंध का पालन करती हैं
CP – CV = R
यहाँ R गैस का सार्वत्रिक नियतांक है ।
6. किसी ऊष्मागतिकीय निकाय की साम्यावस्था का विवरण अवस्था चरों द्वारा होता है । किसी अवस्था चर का मान
केवल उसकी किसी विशेष अवस्था पर निर्भर करता है न कि उस पथ पर जिससे यह अवस्था प्राप्त होती है । अवस्था चरों के उदाहरण हैं: दाब (P), आयतन (V), ताप (T), तथा द्रव्यमान(m)। ऊष्मा और कार्य अवस्था चर नहीं हैं । कोई
अवस्था समीकरण (जैसे आदर्श गैस समीकरण PV = µ RT) विभिन्न अवस्था चरों के मध्य एक संबंध को व्यक्त
करता है ।
7. कोई स्थैतिककल्प प्रक्रम अत्यंत धीमी गति से संपन्न होने वाला प्रक्रम है जिसमें निकायपरिवेश के साथ पूरे समय तापीय व यांत्रिक साम्य में रहता हैं । स्थैतिककल्प प्रक्रम में परिवेश के दाब व ताप तथा निकाय के दाब व ताप में अनंत सूक्ष्म अंतर हो सकता है ।
8. किसी आदर्श गैस के ताप T पर आयतन V1 से V2 तक होने वाले किसी समतापीय प्रसार में अवशोषित ऊष्मा (Q) का मान गैस द्वारा किए गए कार्य (W) के बराबर होता है । प्रत्येक का मान निम्नलिखित है:
Q = W = µ RT ln 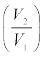
9. किसी आदर्श गैस के रुद्धोष्म प्रक्रम में
PV γ = नियतांक
किसी आदर्श गैस द्वारा अवस्था (P1, V1, T1) से अवस्था (P2, V2, T2) में रुद्धोष्म प्रक्रम से परिवर्तन में संपादित
कार्य है:
µ R(T1–T2)
W = 
γ – 1
10. ऊष्मा इंजन एक एेसी युक्ति है जिसमें निकाय एक चक्रीय प्रक्रम में चलता है जिसके परिणामस्वरूप ऊष्मा कार्य में परिवर्तित होती है । यदि एक चक्र में स्रोत से अवशोषित ऊष्माQ1, अभिगम को मुक्त की गई ऊष्मा Q2 तथा W निर्गत कार्य है, तो इंजन की दक्षता
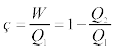
11. प्रशीतक या ऊष्मा पंप में निकाय ठंडे ऊष्माशय से Q2 ऊष्मा ग्रहण करता है तथा Q1मात्रा गरम ऊष्मा भंडार को मुक्त
करता है । इस प्रक्रिया में निकाय पर W कार्य संपन्न होता है । प्रशीतक का निष्पादन गुणांक निम्न प्रकार से परिभाषित
होता है,
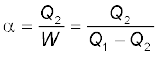
12. ऊष्मागतिकी का द्वितीय नियम कुछ उन प्रक्रमों की स्वीकृति नहीं देता जो ऊष्मागतिकी केप्रथम नियम के अनुकूल हैं । इसके दो प्रकथन इस प्रकार हैं:
केल्विन-प्लैंक का प्रकथन
एेसा कोई प्रक्रम संभव नहीं है जिसका मात्र परिणाम केवल किसी ऊष्मा भंडार से ऊष्मा काअवशोषण करके उसे पूर्णतया कार्य में रूपांतरित करना हो ।
क्लॉसियस का प्रकथन
एेसा कोई प्रक्रम संभव नहीं है जिसका मात्र परिणाम ऊष्मा का किसी ठंडे पिंड से अपेक्षाकृत गरम पिंड में स्थानांतरण हो ।
इसे सरल ढंग से कहा जाए तो द्वितीय नियम यह बताता है कि किसी भी ऊष्मा इंजन की दक्षताη = 1 नहीं हो
सकती अथवा किसी प्रशीतक का निष्पादन गुणांक α अनंत के बराबर नहीं हो सकता ।
13. कोई प्रक्रम उत्क्रमणीय होता है यदि उसे इस प्रकार उत्क्रमित किया जाए कि निकाय व परिवेश दोनों अपनी प्रारंभिक अवस्थाओं में वापस पहुँच जाएँ और परिवेश में कहीं भी कोई परिवर्तन न हो । प्रकृति के नैसर्गिक प्रक्रम अनुत्क्रमणीय होते हैं । आदर्शीकृत उत्क्रमणीय प्रक्रम स्थैतिककल्प प्रक्रम होता है जिसमें कोई भी क्षयकारी घटक; जैसे – घर्षण, श्यानता आदि विद्यमान नहीं रहते ।
14. किन्हीं दो तापों T1 (स्रोत) तथा T2 (अभिगम) के मध्य कार्य करने वाला कार्नो इंजन उत्क्रमणीय इंजन है । दो रुद्धोष्म प्रक्रमों से संयुक्त दो समतापी प्रक्रम कार्नो चक्र का निर्माण करते हैं । कार्नो इंजन की दक्षता निम्नलिखित सूत्र से व्यक्त की जाती है:
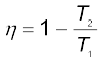 (कार्नो इंजन)
(कार्नो इंजन)
किन्हीं दो तापों के मध्य कार्य करने वाले इंजन की दक्षता कार्नो इंजन की दक्षता से अधिक नहीं हो सकती ।
15. यदि Q > 0, निकाय को ऊष्मा दी गई।
यदि Q < 0, निकाय से ऊष्मा निकाली गई।
यदि W > 0, निकाय द्वारा कार्य किया गया।
यदि W < 0, निकाय पर कार्य किया गया।
विचारणीय विषय
1. किसी पिंड का ताप उसकी माध्य अांतरिक ऊर्जा से संबंधित है न कि उसके द्रव्यमान केंद्र की गतिज ऊर्जा से । बंदूक से दागी गई किसी गोली का उच्च ताप उसकी अधिक चाल के कारण नहीं होता ।
2. ऊष्मागतिकी में साम्य उस परिस्थिति की ओर निर्देश करता है जब निकाय की ऊष्मागतिकीय अवस्था का वर्णन करने वाले स्थूल चर, समय पर निर्भर नहीं करते । यांत्रिकी में किसी निकाय की साम्यावस्था से अभिप्राय है कि निकाय पर कार्य करने वाले नेट बल तथा बल आघूर्ण दोनों शून्य होते हैं ।
3. ऊष्मागतिकीय साम्य में निकाय के सूक्ष्म संघटक साम्यावस्था में नहीं होते (यांत्रिकी के प्रसंग में)।
4. ऊष्माधारिता, व्यापक रूप में उस प्रक्रम पर निर्भर करती है जिससे निकाय तब गुजरता है जब वह ऊष्मा ग्रहण करता है ।
5. समतापीय स्थैतिककल्प प्रक्रमों में, निकाय द्वारा ऊष्मा अवशोषित या निर्गत होती है यद्यपि हर चरण में गैस का ताप वही होता है जो परिवेशीय ऊष्मा भंडार होता है । निकाय तथा ऊष्मा भंडार के मध्य अत्यंत सूक्ष्म तापांतर के कारण एेसा संभव हो पाता है ।
अभ्यास
12.1 कोई गीज़र 3.0 लीटर प्रति मिनट की दर से बहते हुए जल को 27 ºC से 77 ºC तक गर्म करता है । यदि
गीज़र का परिचालन गैस बर्नर द्वारा किया जाए तो ईधन के व्यय की क्या दर होगी ? बर्नर के ईंधन की दहन-ऊष्मा
4.0×104 J g-1 है ?
12.2 स्थिर दाब पर 2.0×10–2 kg नाइट्रोजन (कमरे के ताप पर) के ताप में 45 ºC वृद्धि करने के लिए कितनी ऊष्मा की आपूर्ति की जानी चाहिए ? (N2 का अणुभार = 28; R = 8.3 J mol-1 K-1) ।
12.3 व्याख्या कीजिए कि एेसा क्यों होता है:
(a) भिन्न-भिन्न तापों T1 व T2 के दो पिण्डों को यदि ऊष्मीय संपर्क में लाया जाए तो यह आवश्यक नहीं कि उनका अंतिम ताप (T1 + T2)/2 ही हो।
(b) रासायनिक या नाभिकीय संयत्रों में शीतलक (अर्थात् द्रव जो संयत्र के भिन्न-भिन्न भागों को अधिक गर्म होने से रोकता है) की विशिष्ट ऊष्मा अधिक होनी चाहिए।
(c) कार को चलाते-चलाते उसके टायरों में वायुदाब बढ़ जाता है।
(d) किसी बंदरगाह के समीप के शहर की जलवायु, समान अक्षांश के किसी रेगिस्तानी शहर की जलवायु से अधिक शीतोष्ण होती है।
12.4 गतिशील पिस्टन लगे किसी सिलिंडर में मानक ताप व दाब पर 3 मोल हाइड्रोजन भरी है । सिलिंडर की दीवारें ऊष्मारोधी पदार्थ की बनी हैं तथा पिस्टन को उस पर बालू की परत लगाकर ऊष्मारोधी बनाया गया है । यदि गैस को उसके आरंभिक आयतन के आधे आयतन तक संपीडित किया जाए तो गैस का दाब कितना बढ़ेगा ?
12.5 रुद्धोष्म विधि द्वारा किसी गैस की अवस्था परिवर्तन करते समय उसकी एक साम्यावस्था A से दूसरी साम्यावस्था B तक ले जाने में निकाय पर 22.3 J कार्य किया जाता है । यदि गैस को दूसरी प्रक्रिया द्वारा अवस्था A से अवस्था B में लाने में निकाय द्वारा अवशोषित नेट ऊष्मा 9.35 cal है तो बाद के प्रकरण में निकाय द्वारा किया गया नेट कार्य कितना है? (1 cal = 4.19 J)।
12.6 समान धारिता वाले दो सिलिंडर A तथा B एक-दूसरे से स्टॉपकॉक के द्वारा जुड़े हैं । A में मानक ताप व दाब पर गैस भरी है जबकि B पूर्णतः निर्वातित है । स्टॉपकॉक यकायक खोल दी जाती है । निम्नलिखित का उत्तर दीजिए:
(a) सिलिंडर A तथा B में अंतिम दाब क्या होगा ?
(b) गैस की अांतरिक ऊर्जा में कितना परिवर्तन होगा ?
(c) गैस के ताप में क्या परिवर्तन होगा ?
(d) क्या निकाय की माध्यमिक अवस्थाएँ (अंतिम साम्यावस्था प्राप्त करने के पूर्व) इसके P-V-T पृष्ठ पर होंगी ?
12.7 एक वाष्प इंजन अपने बॉयलर से प्रति मिनट 3.6 × 109J ऊर्जा प्रदान करता है जो प्रति मिनट 5.4 × 108J कार्य देता है। इंजन की दक्षता कितनी है? प्रति मिनट कितनी ऊष्मा अपशिष्ट होगी?
12.8 एक हीटर किसी निकाय को 100 W की दर से ऊष्मा प्रदान करता है। यदि निकाय 75 J s–1 की दर से कार्य करता है, तो आंतरिक ऊर्जा की वृद्धि किस दर से होगी?
12.9 किसी ऊष्मागतिकीय निकाय को मूल अवस्था से मध्यवर्ती अवस्था तक चित्र (12.13) में दर्शाये अनुसार एक रेखीय प्रक्रम द्वारा ले जाया गया है।
दाब (N/m2)
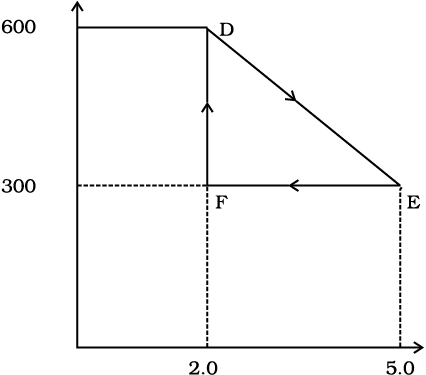
आयतन (m3)
चित्र 12.13
एक समदाबी प्रक्रम द्वारा इसके आयतन को E से F तक ले जाकर मूल मान तक कम कर देते हैं। गैस द्वारा D से E तथा वहाँ से F तक कुल किए गए कार्य का आकलन कीजिए।
12.10 खाद्य पदार्थ को एक प्रशीतक के अंदर रखने पर वह उसे 9°C पर बनाए रखता है। यदि कमरे का ताप 36°C है तो प्रशीतक के निष्पादन गुणांक का आकलन कीजिए।
