Table of Contents
13.1 भूमिका
13.2 द्रव्य की आण्विक प्रकृति
13.3 गैसों का व्यवहार
13.4 आदर्श गैसों का अणुगति सिद्धांत
13.5 ऊर्जा के समविभाजन का नियम
13.6 विशिष्ट ऊष्मा धारिता
13.7 माध्य मुक्त पथ
सारांश
विचारणीय विषय
अभ्यास
अतिरिक्त अभ्यास
13.1 भूमिका
बॉयल ने 1661 में एक नियम की खोज की, जिसे उनके नाम से जाना जाता है। बॉयल, न्यूटन एवं अन्य कई वैज्ञानिकों ने गैसों के व्यवहार को यह मानकर समझाने की चेष्टा की कि गैसें अत्यंत सूक्ष्म परमाण्वीय कणों से बनी हैं। वास्तविक परमाणु सिद्धांत तो इसके 150 से भी अधिक वर्ष बाद ही स्थापित हो पाया। अणुगति सिद्धांत इस धारणा के आधार पर गैसों के व्यवहार की व्याख्या करता है कि गैसों में अत्यंत तीव्र गति से गतिमान परमाणु अथवा अणु होते हैं। यह संभव भी है, क्योंकि ठोसों तथा द्रवों के परमाणुओं के बीच अंतरापरमाणुक बल, जो कि लघु परासी बल है, एक महत्वपूर्ण भूमिका निभाता है जबकि गैसों में इस बल को उपेक्षणीय माना जा सकता है। अणुगति सिद्धांत, 19वीं शताब्दी में, मैक्सवेल, बोल्ट्ज़मान और अन्य वैज्ञानिकों द्वारा विकसित किया गया था। यह असाधारण रूप से सफल सिद्धांत रहा है। यह दाब एवं ताप की एक आण्विक व्याख्या प्रस्तुत करता है तथा आवोगाद्रो की परिकल्पना और गैस नियमों के अनुरूप है। यह बहुत सी गैसों की विशिष्ट ऊष्मा धारिता की ठीक-ठीक व्याख्या करता है। यह श्यानता, चालकता, विसरण जैसे गैसों के मापनीय गुणों को आण्विक प्राचलों से जोड़ता है और अणुओं की आमापों एवं द्रव्यमानों का आकलन संभव बनाता है। इस अध्याय में अणुगति सिद्धांत का आरंभिक ज्ञान दिया गया है।
13.2 द्रव्य की आण्विक प्रकृति
बीसवीं शताब्दी के महान वैज्ञानिकों में एक रिचर्ड फीनमेन, इस खोज को कि ‘द्रव्य परमाणुओं से बना है’ अत्यंत महत्वपूर्ण मानते हैं। यदि हम विवेक से काम नहीं लेंगे, तो (नाभिकीय विध्वंस के कारण) मानवता का विनाश हो सकता है, या फिर वह (पर्यावरणीय विपदाओं के कारण) विलुप्त हो सकती है। यदि वैसा होता है और संपूर्ण वैज्ञानिक ज्ञान के नष्ट होने की स्थिति उत्पन्न हो जाती है तो फीनमेन विश्व की अगली पीढ़ी के प्राणियों को परमाणु परिकल्पना संप्रेषित करना चाहेंगे। परमाणु परिकल्पना: सभी वस्तुएँ परमाणुओं से बनी हैं, जो अनवरत गतिमान अत्यंत सूक्ष्म कण हैं, बीच में अल्प दूरी होने पर ये एक दूसरे को आकर्षित करते हैं पर एक दूसरे में निष्पीडित किए जाने पर प्रतिकर्षित करने लगते हैं।
प्राचीन भारत एवं यूनान में परमाण्वीय परिकल्पना
यद्यपि, आधुनिक विज्ञान से परमाण्वीय दृष्टिकोण का परिचय कराने का श्रेय जॉन डाल्टन को दिया जाता है, तथापि, प्राचीन भारत और यूनान के विद्वानों ने बहुत पहले ही परमाणुओं और अणुओं के अस्तित्व का अनुमान लगा लिया था। भारत में वैशेषिक दर्शन, जिसके प्रणेता कणाद थे (छठी शताब्दी ई.पू.), में परमाण्वीय प्रारूप का विस्तृत विकास हुआ । उन्होंने परमाणुओं को अविभाज्य, सूक्ष्म तथा द्रव्य का अविभाज्य अंश माना । यह भी तर्क दिया गया कि यदि द्रव्य को विभाजित करने के क्रम का कोई अन्त न हो तो किसी सरसों के दाने तथा मेरु पर्वत में कोई अंतर नहीं रहेगा । चार प्रकार के परमाणुओं (संस्कृत में सूक्ष्मतम कण को परमाणु कहते हैं) की कल्पना की गई जिनकी अपनी अभिलाक्षणिक संहति तथा अन्य विशेषताएँ थीं जो इस प्रकार हैं: भूमि (पृथ्वी), अप् (जल), तेज (अग्नि) तथा वायु (हवा) । उन्होंने आकाश (अंतरिक्ष) को सतत् तथा अक्रिय माना और यह बताया कि इसकी कोई परमाण्वीय संरचना नहीं है । परमाणु संयोग करके विभिन्न अणुओं का निर्माण करते हैं (जैसे दो परमाणु संयोग करके एक द्विपरमाणुक अणु ‘द्वैणुक’, तीन परमाणुओं के संयोग से ‘त्रसरेणु’ अथवा त्रिपरमाणुक अणु बनाते हैं), इनके गुण संघटक अणुओं की प्रकृति एवं अनुपात पर निर्भर करते हैं । अनुमानों द्वारा अथवा उन विधियों द्वारा जो हमें ज्ञात नहीं हैं, उन्होंने परमाणुओं के आकार का आकलन भी किया । इन आकलनों में विविधता है । ललित विस्तार - बुद्ध की एक प्रसिद्ध जीवनी जिसे मुख्य रूप से ईसा पूर्व द्वितीय शताब्दी में लिखा गया, में परमाणु का आकार 10-10 m की कोटि का बताया गया है । यह आकलन परमाणु के आकार के आधुनिक आकलनों के निकट है ।
पुरातन ग्रीस में, डेमोक्रिटस (चतुर्थ शताब्दी ई.पू.) को उनकी परमाण्वीय परिकल्पना के लिए सर्वश्रेष्ठ माना जाता है। ग्रीक भाषा में 'Atom' शब्द का अर्थ है ‘अविभाज्य’ । उनके अनुसार परमाणु एक दूसरे से भौतिक रूप में, आकृति में, आकार में तथा अन्य गुणों में भिन्न होते हैं तथा इसी के परिणामस्वरूप उनके संयोग द्वारा निर्मित पदार्थों के भिन्न-भिन्न गुण होते हैं। उनके विचारों के अनुसार जल के अणु चिकने तथा गोल होते हैं तथा वे एक दूसरे के साथ जुड़ने योग्य नहीं होते, यही कारण है कि जल आसानी से प्रवाहित होने लगता है। भूमि के परमाणु खुरदरे तथा काँटेदार होते हैं जिसके कारण वे एक दूसरे को जकड़े रहते हैं तथा कठोर पदार्थ निर्मित करते हैं । उनके विचार से अग्नि के परमाणु कँटीले होते हैं जिसके कारण वे पीड़ादायक जलन उत्पन्न करते हैं। ये धारणाएँ चित्ताकर्षक होते हुए भी, और आगे विकसित न हो सकीं। इसका कदाचित यह कारण हो सकता है कि ये विचार उन दार्शनिकों की अंतर्दर्शी कल्पनाएं एवं अनुमान मात्र थे, जिनका न तो परीक्षण किया गया था और न ही मात्रात्मक प्रयोगों (जो कि आधुनिक विज्ञान का प्रमाण-चिह्न हैं) द्वारा संशोधन ।
यह चिंतन कि द्रव्य सतत नहीं हो सकता, कई स्थानों और संस्कृतियों में विद्यमान था। भारत में कणाद और यूनान में डेमोक्रिटस ने यह सुझाव दिया था कि द्रव्य अविभाज्य अवयवों का बना हो सकता हैै। प्राय: वैज्ञानिक आण्विक सिद्धांत की खोज का श्रेय डाल्टन को देते हैं। तत्वों के संयोजन द्वारा यौगिक बनने की प्रक्रिया में पालन किए जाने वाले निश्चित अनुपात और बहुगुणक अनुपात के नियमों की व्याख्या करने के लिए डाल्टन ने यह सिद्धांत प्रस्तावित किया था। पहला नियम बताता है कि किसी यौगिक में अवयवों के द्रव्यमानों का अनुपात नियत रहता है। दूसरे नियम का कथन है कि जब दो तत्व मिलकर दो या अधिक यौगिक बनाते हैं तो एक तत्व के निश्चित द्रव्यमान से संयोजित होने वाले दूसरे तत्व के द्रव्यमानों में एक सरल पूर्णांकीय अनुपात होता है।
इन नियमों की व्याख्या करने के लिए, लगभग 200 वर्ष पूर्व डाल्टन ने सुझाया कि किसी तत्व के सूक्ष्मतम अवयव परमाणु हैं। एक तत्व के सभी परमाणु सर्वसम होते हैं पर ये दूसरे तत्वों के परमाणुओं से भिन्न होते हैं। अल्प संख्या में तत्वों के परमाणु संयोग करके यौगिक का अणु बनाते ह। 19वीं शताब्दी के आरंभ में दिए गए गै-लुसैक के नियम के अनुसार: जब गैसें रासायनिक रूप से संयोजन करके कोई अन्य गैस बनाती हैं, तो उनके आयतन लघु पूर्णांकों के अनुपात में होते हैं। आवोगाद्रो का नियम (या परिकल्पना) बताता है कि समान ताप और दाब पर गैसों के समान आयतनों में अणुओं की संख्या समान होती है। आवोगाद्रो नियम को डाल्टन के सिद्धांत से जोड़ने पर गै-लुसैक के नियम की व्याख्या की जा सकती है। क्योंकि, तत्व प्राय: अणुओं के रूप में होते हैं, डाल्टन के परमाणु सिद्धांत को द्रव्य का आण्विक सिद्धांत भी कहा जा सकता है। इस सिद्धांत को अब वैज्ञानिकों द्वारा मान्यता है। तथापि, उन्नीसवीं शताब्दी के अंत तक भी एेसे कई प्रसिद्ध वैज्ञानिक थे जो परमाणु सिद्धांत में विश्वास नहीं करते थे।
आधुनिक काल में, बहुत से प्रेक्षणों से, अब हम यह जानते हैं कि पदार्थ अणुओं (एक या अधिक परमाणुओं से बने) से मिलकर बना होता है। इलेक्ट्रॉन सूक्ष्मदर्शी एवं क्रमवीक्षण सुरंगक सूक्ष्मदर्शी की सहायता से अब हम उनको देख सकते हैं। परमाणु का आमाप लगभग एक एेंग्स्ट्रॉम (1Å) (10–10m) है। ठोसों में, जहाँ कण कसकर एक दूसरे से जुड़े हैं, परमाणुओं के बीच कुछ एेंग्स्ट्रॉम (2 Å) की दूरी है। द्रवों में भी परमाणुओं के बीच इतनी ही दूरी है। द्रवों में परमाणु एक दूसरे के साथ उतनी दृढ़ता से नहीं बँधे होते जितने ठोसों में, और, इसलिए इधर-उधर गति कर सकते ह। इसीलिए, द्रवों में प्रवाह होता है। गैसों में अंतरपरमाणुक दूरी दसों एंग्स्ट्रॉम में होती है। वह औसत दूरी जो कोई अणु बिना संघट्ट किए चल सकता है उसकी औसत मुक्त पथ कहलाती है। गैसों में औसत मुक्त पथ हजारों एंग्स्ट्रॉम की कोटि का होता है। अत: गैसों में परमाणु अत्यधिक स्वतंत्र होते हैं और बड़ी-बड़ी दूरियों तक बिना संघट्ट किए जा सकते हैं। यदि बंद करके न रखा जाए, तो गैसें विसरित हो जाती हैं। ठोसों और द्रवों में पास-पास होने के कारण परमाणुओं के बीच के अंतर परमाणुक बल महत्वपूर्ण हो जाते हैं। ये बल अधिक दूरियों पर आकर्षण और अल्प दूरी पर प्रतिकर्षण बल होते हैं। जब परमाणु एक दूसरे से कुछ एंग्स्ट्रॉम की दूरी पर होते हैं तो वे एक दूसरे को आकर्षित करते हैं पर बहुत पास लाए जाने पर प्रतिकर्षित करने लगते हैं। गैस का स्थैतिक दिखाई पड़ना भ्रामक है। गैस सक्रियता से भरपूर है और इनका संतुलन गतिक संतुलन है। गतिक संतुलन में अणु एक दूसरे से संघट्ट करते हैं और संघट्ट की अवधि में उनकी चालों में परिवर्तन होता है। केवल औसत गुण नियत रहते हैं।
परमाणु सिद्धांत हमारी खोजों का अंत नहीं है बल्कि यह तो इसका एक आरंभ है। अब हम जानते हैं कि परमाणु अविभाज्य या मूल कण नहीं हैं। उनमें एक नाभिक और इलेक्ट्रॉनहोते हैं। नाभिक स्वयं प्रोटॉनों और न्यूट्रॉनों से बने होते हैं। यही नहीं प्रोटॉन तथा न्यूट्रॉन क्वार्कों से मिलकर बने होते हैं। हो सकता है कि क्वार्क भी इस कहानी का अंत न हों। यह भी हो सकता है कि स्ट्रिंग (तंतु) जैसी कोई प्राथमिक सत्ता हो। प्रकृति हमारे लिए सदैव ही विलक्षण भरी है, पर, सत्य की खोज आनंददायक होती है और हर आविष्कार में अपना सौंदर्य होता है। इस अध्याय में हम अपना अध्ययन गैसों के (और थोड़ा बहुत ठोसों के) व्यवहार तक ही सीमित रखेंगे। इसके लिए हम उन्हें अनवरत गति करते गतिमान कणों का समूह मानेंगे।
13.3 गैसों का व्यवहार
ठोसों एवं द्रवों की तुलना में गैसों के गुणों को समझना आसान है। यह मुख्यत: इस कारण होता है, क्योंकि, गैस में अणु एक दूसरे से दूर-दूर होते हैं और दो अणुओं के संघट्ट की स्थिति को छोड़कर उनके बीच पारस्परिक अन्योन्य क्रियाएँ उपेक्षणीय होती हैं जैसे निम्न दाब व उनके द्रवित (या घनीभूत) होने के तापों की अपेक्षा अत्यधिक उच्च ताप पर अपने ताप, दाब और आयतन में लगभग निम्नलिखित संबंध दर्शाती हैं (देखिए अध्याय 11)
PV = KT (13.1)
जॉन डाल्टन (1766-1844)

जॉन डाल्टन (1766-1844)
वह एक अंग्रेज रसायनज्ञ थे। जब अलग-अलग तरह के परमाणु संयोजित होते हैं तो वे कुछ सरल नियमों का पालन करते हैं। डाल्टन का परमाणु सिद्धांत इन नियमों की सरल व्याख्या करता है। डाल्टन में वर्णांधता संबंधी एक सिद्धांत भी प्रस्तुत किया।
एमेदियो आवोगाद्रो (1776-1856)
एमेदियो आवोगाद्रो (1776 – 1856)
उन्होंने एक अत्यंत बुद्धिमत्तापूर्ण अनुमान लगाया कि समान ताप और दाब पर सभी गैसों के समान आयतनों में अणुओं की संख्या समान होती है। इससे गैसों की संयोजन प्रक्रिया को एक सरल ढंग से समझने में सहायता मिली। यह कथन अब आवोगाद्रो की परिकल्पना (या नियम) कहलाता है। उन्होंने यह भी प्रस्तावित किया कि हाइड्रोजन, अॉक्सीजन, नाइट्रोजन जैसी गैसों के सूक्ष्मतम संघटक कण परमाणु नहीं बल्कि द्विपरमाणुक अणु हैं।
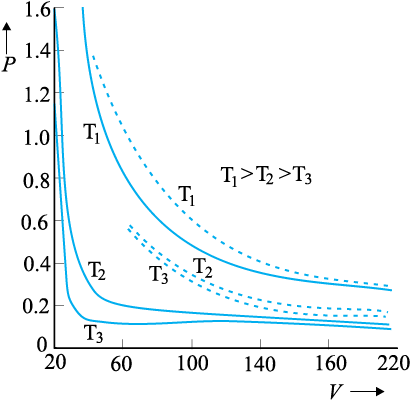
चित्र 13.2 भाप के लिए, तीन भिन्न तापों पर प्रायोगिक P-V वक्रों (ठोस रेखाएँ) की बॉयल के नियम (बिंदुकित रेखाएँ) से तुलना। P का मान 22 atm के मात्रकों में है और V का मान 0.09 लीटर के मात्रकों में है।
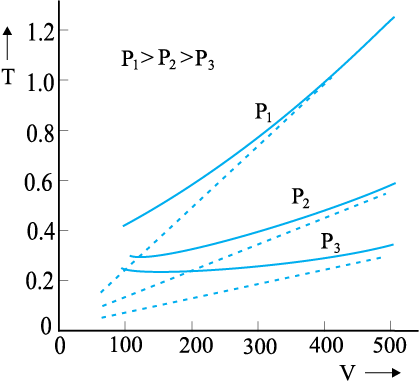
चित्र 13.3 तीन भिन्न दाबों के लिए CO2 के प्रायोगिक T-V वक्रों की (पूर्ण रेखाओं द्वारा प्रदर्शित) चार्ल्स नियमानुसार प्राप्त सैद्धांतिक वक्रों से (बिंदुकित रेखाओं द्वारा प्रदर्शित) तुलना। T , 300 K के मात्रकों में एवं V, 0.13 लीटर के मात्रकों में है।
दीवार पर आरोपित बल (एवं दाब) का परिकलन करने के लिए, हमें प्रति एकांक समय में दीवार पर प्रदान किए जाने वाले संवेग का परिकलन करना होगा। एक अल्प काल-अंतराल ∆t में कोई अणु जिसके वेग का x-अवयव vx है दीवार से संघट्ट करेगा यदि यह दीवार से vx ∆t दूरी के भीतर है। अर्थात् वह सभी अणु, जो दीवार के पास Avx ∆t आयतन में हैं; ∆t समय में केवल वही दीवार से संघात कर सकेंगे। परंतु औसतन इन अणुओं में से आधे दीवार की ओर गति करते हैं और आधे दीवार से दूर गति करते हैं। अत: (vx, vy, vz ) वेग से चलते हुए अणुओं में से ½A vx ∆t n अणु ∆t समय में दीवार से संघात करेंगे, यहाँ n प्रति एकांक आयतन में अणुओं की संख्या है। तब ∆t समय में अणुओं द्वारा दीवार को प्रदान किया गया संवेग होगा,
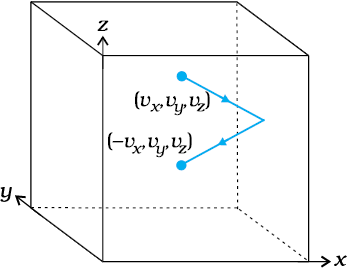
चित्र 13.4 गैस के एक अणु का धारक की दीवार से प्रत्यास्थ संघट्ट।
अणुगति सिद्धांत के संस्थापक

जेम्स क्लॉर्क मैक्सवेल (1831 – 1879)
स्कॉटलैंड के एडिनबर्ग में जन्मे जेम्स क्लॉर्क मैक्सवेल, उन्नीसवीं शताब्दी के महानतम भौतिक विज्ञानियों में से थे। उन्होंने, गैस में अणुओं के तापीय वेग वितरण के लिए सूत्र व्युत्पन्न किया और वे उन वैज्ञानिकों में से थे जिन्होंने सर्वप्रथम श्यानता जैसी मेय राशियों से आण्विक प्राचलों का विश्वसनीय आकलन किया। मैक्सवेल की सबसे बड़ी उपलब्धि (कूलॉम, अॉर्स्टेड, एम्पियर एवं फैराडे द्वारा खोजे गए) विद्युत एवं चुंबकत्व के नियमों का एकीकरण और उनको समीकरणों के एक संगत समुच्चय के रूप में प्रस्तुत करना था जिन्हें आज हम मैक्सवेल समीकरणों के नाम से जानते हैं। इनके आधार पर वह इस अत्यंत महत्वपूर्ण निष्कर्ष पर पहुँचे कि प्रकाश एक विद्युत चुंबकीय तरंग है। यहाँ यह वर्णन करना रुचिकर है कि मैक्सवेल, विद्युत की कणीय प्रकृति (जो फैराडे के विद्युत अपघटन के नियमों से बिलकुल स्पष्ट होती है) की धारणा से कभी सहमत नहीं हो पाए।

लुडविग बोल्ट्ज़मान (1844 – 1906) अॉस्ट्रिया के वियना शहर में जन्मे लुडविग बोल्ट्ज़मान ने, मैक्सवेल से अलग, स्वतंत्र रूप से गैसों के अणुगति सिद्धांत पर कार्य किया। परमाणुकता जो अणुगति सिद्धांत का मुख्य आधार है, के प्रबल पक्षधर, बोल्ट्ज़मान ने ऊष्मागतिकी के द्वितीय नियम एवं एंट्रॉपी की एक सांख्यिकीय व्याख्या प्रस्तुत की। उनकोचिरप्रतिष्ठित सांख्यिकीय यांत्रिकी के संस्थापकों में से एक माना जाता है। अणुगति सिद्धांत में ताप और ऊर्जा में संबंध बताने वाले संबंध में उपयोग किए जाने वाले आनुपातिकतानियतांक को उन्हीं के सम्मान में बोल्ट्ज़मान नियंताक कहा जाता है।
अक्रिय आदर्श गैसों के मिश्रण के लिए कुल दाब मिश्रण की प्रत्येक गैस के दाब का योगदान होता है। समीकरण (13.14) को नए रूप में इस प्रकार लिख सकते हैं,
मैक्सवेल बंटन फलन
गैस के दिए गए द्रव्यमान में, दाब, ताप, आयतन जैसे स्थूल प्राचलों के नियत होने पर भी, इसके सब अणुओं के वेग समान नहीं होते। संघट्टों के कारण अणुओं की चाल और गति की दिशा परिवर्तित होती रहती है। तथापि, साम्यावस्था में चालों का वितरण स्थायी या नियत रहता है।
बहुत से पिंडों के निकाय के व्यवहार का अध्ययन करते समय चालों के ये वितरण बहुत महत्वपूर्ण एवं उपयोगी हो जाते हैं। एक उदाहरण के रूप में, आइये किसी शहर में लोगोें की आयु पर विचार करें। प्रत्येक व्यक्ति की आयु को परिकलन में सम्मिलित करना हो - व्यावहारिक नहीं है। हम लोगोें को समूहों में बाँट सकते हैं: 20 वर्ष तक की आयु के बच्चे, 20 से 60 वर्ष तक की आयु के वयस्क, 60 वर्ष से अधिक आयु के वृद्ध। यदि हमें अधिक विस्तृत जानकारी चाहिए तो हम आयु के और छोटे अंतराल वाले समूह ले सकते हैं: 0-1, 1-2,.... 99-100 वर्ष आयु के समूह। जब आयु का अंतराल कम करते हैं तो उस आयु-अंतराल में आने वाले लोगों की संख्या भी कम हो जाती है। उदाहरणार्थ, आधा वर्ष अंतराल में लोगों की संख्या एक वर्ष अंतराल में लोगों की संख्या की लगभग आधी होगी। आयु अंतराल x एवं x + dx में लोगों की संख्या dN(x) अंतराल dx के अनुक्रमानुपाती होगी। अर्थात्, dN(x) = nx dx, यहाँ nx का उपयोग हमने x एवं x + dx के बीच के अंतराल में लोगों की संख्या को निर्दिष्ट करने में किया है।
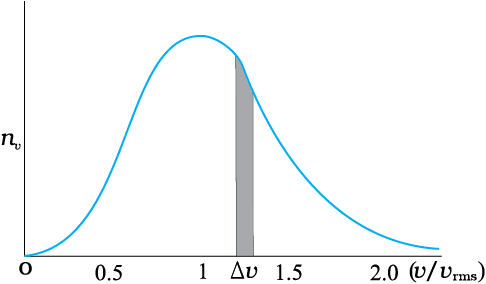
आण्विक चालों का मैक्सवेल बंटन
इसी प्रकार, आण्विक गतियों के बंटन पर विचार करें तो चालों v एवं v + dv के बीच अणुओं की संख्या
dN(v) = 4p N a3e–bv2 v2 dv = nvdv । यह मैक्सवेल बंटन कहलाता है। nv और vके बीच ग्राफ ऊपर चित्र में दर्शाया गया है। उन अणुओं की संख्या जिनकी चाल v एवंv+dv के बीच है ग्राफ में दर्शायी पट्टी के क्षेत्रफल के बराबर होती है। v2 जैसी किसी राशि का औसत, समाकलन <v2> = (1/N ) ∫ v2 dN(v) = Å(3kB T/m) द्वारा परिभाषित किया जाता है जो अधिक प्राथमिक धारणाओं के आधार पर व्युत्पन्न परिणामों से मिलता है।
समीकरण (13.19) से हम किसी गैस में अणुओं की प्रारूपिक चाल का अनुमान लगा सकते हैं। नाइट्रोजन के एक अणु की T = 300 K, ताप पर माध्य वर्ग चाल होगी:
यहाँ, 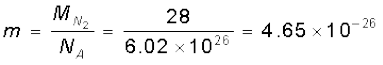 kg
kg
 = 3 kB T / m = (516)2 m2s-2
= 3 kB T / m = (516)2 m2s-2
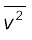 का वर्गमूल इसकी वर्ग माध्य मूल (rms) चाल कहलाती है और इसे vrms द्वारा निर्दिष्ट करते हैं।
का वर्गमूल इसकी वर्ग माध्य मूल (rms) चाल कहलाती है और इसे vrms द्वारा निर्दिष्ट करते हैं।
(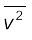 को हम < v2 > भी लिख सकते हैं )
को हम < v2 > भी लिख सकते हैं )
vrms = 516 m s-1
इस चाल की कोटि वायु में ध्वनि के वेग के समान है। समीकरण (13.19) से हम इस निष्कर्ष पर पहुँचते हैं कि समान ताप पर हलके अणुओं की rms चाल अधिक होती है।
उदाहरण 13.5 किसी फ्लास्क में आर्गन एवं क्लोरीन गैस भरी है जिनके द्रव्यमान 2: 1 के अनुपात में हैं। मिश्रण का ताप 27°C है। दोनों गैसों के (i) प्रति अणु की औसत गतिज ऊर्जा का अनुपात (ii) दोनों गैसों के अणुओं की वर्ग माध्य मूल चालों vrms का अनुपात ज्ञात कीजिए। आर्गन का परमाणु द्रव्यमान = 39.9 u, क्लोरीन का अणु द्रव्यमान = 70.9u
हल यहाँ याद रखने योग्य महत्वपूर्ण बात यह है कि किसी (आदर्श) गैस की (प्रति अणु) औसत गतिज ऊर्जा (चाहे वह आर्गन की तरह एक परमाणुक हो, क्लोरीन की तरह द्विपरमाणुक हो, अथवा बहुपरमाणुक भी क्यों न हो) सदैव ही (3/2) kBT के बराबर होती है, गैस के ताप पर निर्भर करती है और गैस की प्रकृति पर निर्भर नहीं करती।
(i) चूंकि फ्लास्क में आर्गन और क्लोरीन दोनों का ताप समान है, अत: इन दो गैसों की (प्रति अणु) औसत गतिज ऊर्जाओं का अनुपात 1: 1 है।
(ii) अब – m vrms2 = प्रति अणु औसत गतिज ऊर्जा =
(3/2) ) kBT यहाँ m गैस के एक अणु का द्रव्यमान है।
 =
= 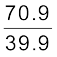 =1.77
=1.77
यहाँ M गैस का अणु-द्रव्यमान है (आर्गन का परमाणु ही उसका अणु है।) दोनों पक्षों का वर्गमूल लेने पर
 = 1.33
= 1.33
आपने इस तथ्य पर ध्यान दिया होगा कि उपरोक्त परिकलनों में मिश्रण के द्रव्यमानों के आधार पर संघटन की कोई प्रासंगिकता नहीं है। यदि ताप का मान अपरिवर्तित रहता है तो आर्गन और क्लोरीन के द्रव्यमान किसी अन्य अनुपात में होते, तब भी
(i) एवं (ii) के उत्तर यही होते। t
उदाहरण 13.6 यूरेनियम के दो समस्थानिकों के द्रव्यमान 235 u एवं 238 u हैं। यदि यूरेनियम हेक्साफ्लोराइड गैस में ये दोनों समस्थानिक विद्यमान हों, तो किसकी औसत चाल अधिक होगी? यदि फ्लोरीन का परमाणु द्रव्यमान 19 u हो, तो किसी भी ताप पर, इनकी चालों में प्रतिशत अंतर आकलित कीजिए।
हल: किसी नियत ताप पर औसत ऊर्जा = ½ m <v2 > नियत रहती है। अत: अणु का द्रव्यमान जितना कम होगा, उतनी ही अधिक तीव्र उसकी गति होगी। चालों का अनुपात, द्रव्यमानों के अनुपात के वर्गमूल के व्युत्क्रमानुपाती है। चूंकि यहाँ द्रव्यमान 349u एवं 352 इकाइयाँ हैं, इसलिए
v349 / v352 = ( 352/ 349)1/2 = 1.0044
चालों के अंतर का प्रतिशत 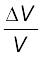 = 0.44 %
= 0.44 %
235U वह समस्थानिक है जिसकी आवश्यकता नाभिकीय विखंडन में होती है। इसको अधिक मात्रा में पाए जाने वाले समस्थानिक 238U से पृथक करने के लिए मिश्रण को एक सरंध्र सिलिंडर द्वारा चारों ओर से घेर देते हैं। सरंध्र सिलिंडर मोटी दीवार का लेकिन संकरा होना चाहिए ताकि अणु लंबे रंध्रों की दीवारों से संघट्ट करते हुए एक एक कर जा सकें। धीमे अणुओं की तुलना में तीव्रगति से चलने वाले अणु अधिक संख्या में रिस कर बाहर आएंगे और इस प्रकार सरंध्र सिलिंडर के बाहर हलके अणु अधिक मात्रा में पाए जाएँगे (संवर्धन) (देखिए चित्र 13.5)। यह विधि अत्यंत प्रभावी नहीं है और पर्याप्त संवर्धन के लिए इसे कई बार दोहराना पड़ता है।
जब गैसें विसरित होती हैं, तो उनके विसरण की दर उनके अणुओं के द्रव्यमान के वर्गमूल के व्युत्क्रमानुपाती होती है (देखिए अभ्यास 13.12)। क्या उपरोक्त उत्तर के आधार पर आप इस तथ्य की व्याख्या का अनुमान लगा सकते हैं?
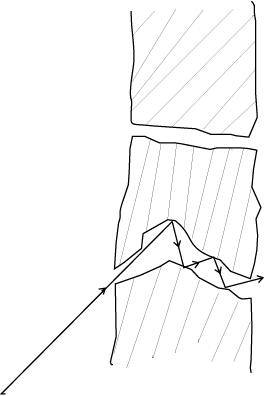
चित्र 13.5 एक सरंध्र दीवार से गुज़रते हुए अणु।
उदाहरण 13.7 (a) जब कोई अणु (या प्रत्यास्थ गेंद) किसी (भारी) दीवार से टकराता है, तो टकराने के पश्चात् यह उसी चाल से विपरीत दिशा में वापस लौटता है। जब कोई गेंद दृढ़तापूर्वक पकड़े गए भारी बल्ले से टकराती है, तो भी एेसा ही होता है। तथापि, जब गेंद अपनी ओर आते हुए बल्ले से टकराती है, तो यह भिन्न चाल से वापस लौटती है। उस स्थिति में गेंद की चाल अपेक्षाकृत कम होती है या अधिक? (अध्याय 6 प्रत्यास्थ संघट्टों से संबंधित आपकी याद ताजा कर सकेगा)। (b) पिस्टन लगे सिलिंडर में पिस्टन को अंदर की ओर धकेल कर जब किसी गैस को संपीडित किया जाता है, तो उस गैस का ताप बढ़ जाता है। ऊपर (a) में प्रयुक्त अणुगति सिद्धांत के आधार पर इस प्रेक्षण की व्याख्या कीजिए। (c) पिस्टन लगे सिलिंडर में संपीडित गैस जब पिस्टन को बाहर धकेलकर फैलती है तो क्या होता है? तब आप क्या प्रेक्षण करेंगे? (d) खेलते समय सचिन तेंदुलकर एक भारी बल्ले का उपयोग करते हैं। इससे क्या उनको किसी प्रकार की कोई सहायता मिलती है?
हल (a) माना कि बल्ले के पीछे लगे विकिटों के सापेक्ष गेंद की चाल u है। यदि विकिटों के सापेक्ष बल्ला V चाल से गेंद की ओर आ रहा हो तो बल्ले के सापेक्ष गेंद की चाल V + u होगी, जो बल्ले की ओर प्रभावी होगी। भारी बल्ले से टकराकर जब गेंद वापस लौटती है तो बल्ले के सापेक्ष इसकी चाल
V + u बल्ले से दूर की ओर होगी। अत: विकिट के सापेक्ष, लौटती हुई गेंद की चाल, V + (V + u) = 2V + u, विकिट से परे जाती हुई होगी। अत: इस प्रकार गतिमान बल्ले से संघट्ट के पश्चात् गेंद की चाल बढ़ जाती है। यदि बल्ला भारी नहीं है तो प्रतिपेक्ष चाल u से कम होगी। अणु के लिए इसका अर्थ ताप में वृद्धि होगा।
(a) के उत्तर के आधार पर, अब आप, (b) (c), (d) के उत्तर दे सकते हैं।
(संकेत: इस संगतता पर ध्यान दें, पिस्टन बल्ला, सिलिंडर विकिट, अणु गेंद )। t
13.5 ऊर्जा के समविभाजन का नियम
किसी एकल अणु की गतिज ऊर्जा होती है :
 (13.22)
(13.22)
T ताप पर, तापीय साम्य में किसी गैस की औसत ऊर्जा का मान < > द्वारा निर्दिष्ट किया जाता है, अत:
> द्वारा निर्दिष्ट किया जाता है, अत:
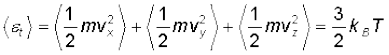 (13.23)
(13.23)
क्योंकि यहाँ कोई वरीय दिशा नहीं है, अत: समीकरण (13.23) से इंगित होता है कि
 ;
;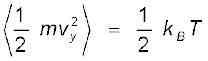 ;
;
 (13.24)
(13.24)
दिक्स्थान में गति के लिए स्वतंत्र किसी अणु की स्थिति दर्शाने के लिए हमें तीन निर्देशांकों की आवश्यकता होती है। यदि इसकी गति किसी एक समतल में बाध्य कर दी जाए, तो दो निर्देशांकों की, और यदि इसे किसी सरल रेखा के अनुदिश गति के लिए बाध्य कर दिया जाए, तो केवल एक निर्देशांक की आवश्यकता होगी। इसे एक दूसरे ढंग से भी व्यक्त किया जा सकता है। हम कहते हैं कि सरल रेखीय गति के लिए इसकी स्वातंत्र्य कोटि एक है, समतल गति की स्वातंत्र्य कोटि दो तथा दिक्स्थान में गति के लिए स्वातंत्र्य कोटि तीन है। किसी संपूर्ण पिण्ड की एक बिंदु से दूसरे बिंदु तक गति को स्थानांतरीय गति कहते हैं। अत:, दिक्स्थान में गति के लिए स्वतंत्र अणु की तीन स्वातंत्र्य कोटि होती हैं। प्रत्येक स्थानांतरीय स्वतंत्रता की एक स्वातंत्र्य कोटि होती है, जिसमें गति के किसी चर का वर्ग सम्मिलित होता है, उदारहणार्थ यहाँ – mvx2 और इसी के सदृश पद vy एवं vz हैं। समीकरण (13.24) में हम देखते हैं कि तापीय साम्य में इस प्रकार के प्रत्येक पद का औसत मान – kBT है।
आर्गन जैसी एकपरमाणुक गैस के अणुओं में केवल स्थानांतरीय स्वातंत्र्य कोटि होती है। लेकिन O2 या N2 जैसी द्विपरमाणुक गैसों के विषय में क्या कह सकते हैं? O2 के अणु में 3 स्थानांतरीय स्वातंत्र्य कोटि तो होती ही हैं, पर, इनके अतिरिक्त यह अणु अपने द्रव्यमान केंद्र के परित: घूर्णन गति भी कर सकते हैं। चित्र 13.6 में, अॉक्सीजन के दो परमाणुओं को जोड़ने वाली रेखा के लंबवत् दो स्वतंत्र घूर्णन अक्ष 1 एवं 2 दर्शाए गए हैं जिनके परित: अणु घूर्णन गति कर सकता है*। अत: इन अणुओं में प्रत्येक की दो घूर्णी स्वातंत्र्य कोटि होती हैं। इस प्रकार कुल ऊर्जा में स्थानांतरीय ऊर्जा 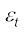 एवं घूर्णी ऊर्जा
एवं घूर्णी ऊर्जा  r दोनों का योगदान होता है।
r दोनों का योगदान होता है।
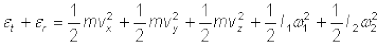 (13.25)
(13.25)
* परमाणुओं को मिलाने वाली रेखा के परित: घूर्णन का जड़त्व आघूर्ण बहुत कम होता है और क्वांटम यांत्रिकीय कारणों से प्रभावी नहीं हो पाता। अनुभाग 13.6 का अंतिम भाग देखिए।
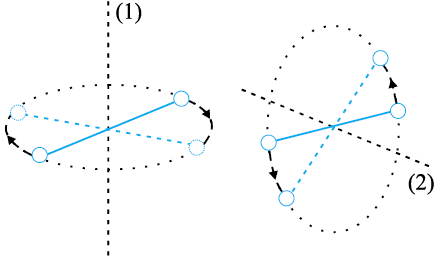
चित्र 13.6 द्विपरमाणुक अणु के दो स्वतंत्रूर्णन अक्ष।
यहाँ ω1 एवं ω2 क्रमश: अक्षों 1 एवं 2 के परित: कोणीय चाल तथा I1 एवं I2 उनके संगत जड़त्व-आघूर्ण हैं। ध्यान दीजिए, प्रत्येक घूर्णी स्वातंत्र्य कोटि ऊर्जा में एक पद का योगदान करती है जिसमें घूर्णी गति के किसी चर का वर्ग सम्मिलित होता है।
ऊपर हमने यह मान लिया है, कि O2 अणु एक "दृढ़ घूर्णी" है, अर्थात्, यह अणु कंपन नहीं करता। O2 के लिए यह
पूर्वधारणा, यद्यपि (सामान्य ताप पर) सही पाई गई है, पर सदैव मान्य नहीं होती। CO जैसे कुछ अणु, सामान्य ताप पर भी कुछ कंपन करते हैं, अर्थात् इनके परमाणु, अंतरापरमाणुक अक्ष के अनुदिश एकविमीय कंपन करते हैं (ठीक वैसे ही जैसे एकविमीय लोलक) और परिणामत: कुल ऊर्जा में एक पद, εv कंपन ऊर्जा का भी होता है, यहाँ,

जहाँ k लोलक का बल नियतांक एवं y इसका कंपन निर्देशांक है। अब,
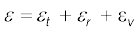 (13.26)
(13.26)
पुन: ध्यान दीजिए, समीकरण (13.26) में दिए गए कंपन-ऊर्जा पद में, गति के कंपन चरों y एवं dy/dt के वर्ग सम्मिलित हैं।
यह भी देखिए कि प्रत्येक स्थानांतरीय एवं घूर्णी स्वातंत्र्य कोटि ने तो एक ही "वर्गित पद" का योगदान किया है, पर समीकरण (13.26) में दिए गए कंपन स्वातंत्र्य कोटि के सापेक्ष पद में गतिज एवं स्थितिज ऊर्जा व्यक्त करने वाले दो वर्गित
पद हैं।
ऊर्जा के व्यंजक में प्रत्येक द्विघाती पद अणु द्वारा ऊर्जा अवशोषित करने का एक ढंग बताता है। हम देख चुके हैं कि परम ताप T पर तापीय साम्यावस्था में स्थानांतरीय गति के प्रत्येक ढंग के लिए औसत ऊर्जा ½ kBT है। सर्वप्रथम मैक्सवेल द्वारा सिद्ध किए गए चिर प्रतिष्ठित सांख्यिकीय यांत्रिकी के सर्वाधिक परिष्कृत सिद्धांत के अनुसार ऊर्जा के विभाजन के प्रत्येक ढंग में एेसा ही होता है चाहे ऊर्जा स्थानांतरीय हो, घूर्णी हो या कंपन ऊर्जा हो। अर्थात् तापीय साम्य में, ऊर्जा समान रूप से सभी संभव ऊर्जा रूपों पर बंटित होती है और प्रत्येक रूप में औसत ऊर्जा ½ kBT पाई जाती है। यही ऊर्जा का समविभाजन नियम है। तदनुसार, किसी अणु की स्थानांतरीय एवं घूर्णी स्वातंत्र्य कोटियों में प्रत्येक ½ kBT ऊर्जा का योगदान देती है जबकि प्रत्येक कंपन आवृत्ति 2 × ½ kBT = kBT ऊर्जा का योगदान देती है, क्योंकि, कंपन रूप में गतिज और स्थितिज दोनों प्रकार की ऊर्जाओं का योगदान होता है।
ऊर्जा के समविभाजन नियम की उपपत्ति इस पुस्तक की विषय वस्तु से बाहर है। यहाँ हम सैद्धांतिक रूप से गैसों की विशिष्ट ऊष्मा धारिता ज्ञात करने के लिए इस नियम का उपयोग करेंगे। बाद में ठोसों की विशिष्ट ऊष्मा धारिता के लिए भी इसके उपयोग का संक्षिप्त विवरण देंगे।
13.6 विशिष्ट ऊष्मा धारिता
13.6.1 एकपरमाणुक गैसों के लिए
एकपरमाणुक गैस के अणु में केवल तीन स्थानांतरीय स्वातंत्र्य कोटि होती हैं। अत: इनके एक अणु की T ताप पर औसत ऊर्जा (3/2)kBT होगी। इस प्रकार की गैस के 1 मोल की कुल आंतरिक ऊर्जा,
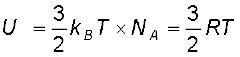 (13.27)
(13.27)
नियत आयतन पर मोलर विशिष्ट ऊष्मा धारिता Cv का मान है,
Cv (एकपरमाणुक गैस के लिए) =  =
= RT (13.28)
RT (13.28)
आदर्श गैस के लिए
Cp – Cv = R (13.29)
जहाँ, Cp नियत दाब पर मोलर विशिष्ट ऊष्माधारिता है।
अत:, Cp = 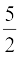 R (13.30)
R (13.30)
इन दो विशिष्ट ऊष्मा धारिताओं का अनुपात
 (13.31)
(13.31)
13.6.2 द्विपरमाणुक गैसों के लिए
जैसा पहले स्पष्ट किया जा चुका है कि द्विपरमाणुक अणु की आकृति डंबलाकार होती है और यदि इस आकृति को दृढ़ घूर्णी मानें, तो इसकी 5 स्वातंत्र्य कोटि हैं : 3 स्थानांतरीय एवं 2 घूर्णी। ऊर्जा समविभाजन के नियमानुसार इस प्रकार की गैस के एक मोल की, T ताप पर कुल आंतरिक ऊर्जा,
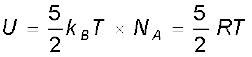 (13.32)
(13.32)
अत: मोलर विशिष्ट ऊष्मा धारिताएँ
Cv (दृढ़ द्विपरमाणुक) =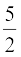 R, Cp =
R, Cp = 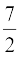 R (13.33)
R (13.33)
γ (दृढ़ द्विपरमाणुक) =  (13.34)
(13.34)
यदि द्विपरमाणुक अणु दृढ़ नहीं है, वरन् इसमें एक अतिरिक्त कंपन रूप भी सम्मिलित है, तो

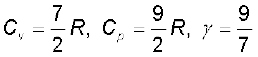 R (13.35)
R (13.35)
13.6.3 बहुपरमाणुक गैसों के लिए
व्यापक रूप में किसी बहुपरमाणुक अणु में 3 स्थानांतरीय, 3 घूर्णी स्वातंत्र्य कोटि एवं कुछ निश्चित संख्या (f ) के कंपन रूप होते हैं। ऊर्जा समविभाजन के नियमानुसार यह सुगमता से समझा जा सकता है कि इस प्रकार की गैस के 1 मोल की कुल आंतरिक ऊर्जा
U = (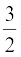 kBT +
kBT + 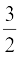 kBT + f kBT ) NA
kBT + f kBT ) NA
अर्थात् Cv = (3 + f ) R; Cp = (4 + f ) R,  (13.36)
(13.36)
ध्यान दीजिए, Cp – Cv = R सभी आदर्श गैसों के लिए सत्य है, फिर चाहे वह गैस एकपरमाणुक हो, द्विपरमाणुक हो अथवा बहुपरमाणुक भी क्यों न हो।
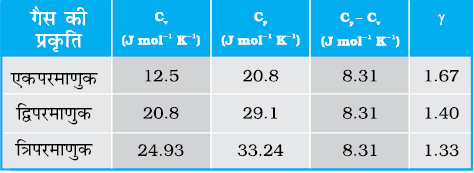
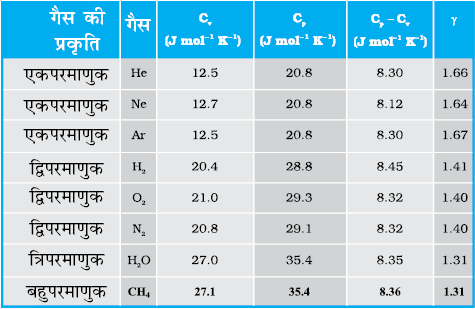
सारणी (13.1) में, गैसों में, कंपन रूपों की उपेक्षा करते हुए, उनकी विशिष्ट ऊष्मा धारिताओं के विषय में सैद्धांतिक पूर्वानुमानों को सूचीबद्ध किया गया है। ये मान सारणी (13.2) में दिए गए कई गैसों के लिए विशिष्ट ऊष्मा धारिताओं के प्रायोगिक मानों से काफी मेल खाते हैं। यह सत्य है, कि एेसी कई गैसे हैं (जो सारणी में नहीं दर्शाई गई हैं), जैसे Cl2, C2H6 और बहुत सी बहुपरमाणुक गैसें, जिनके प्रायोगिक और सैद्धांतिक मानों में बहुत अंतर पाया गया है। साधारणत: इन गैसों की विशिष्ट ऊष्मा धारिताओं के मान सारणी (13.1) में दिए गए सैद्धांतिक मानों से अधिक पाए गए हैं। इसका अर्थ यह हुआ कि यदि हम परिकलनों में कंपन रूपों के योगदान को भी सम्मिलित करें, तो प्रायोगिक एवं सैद्धांतिक मानों में अधिक संगति दृष्टिगोचर होगी। अत:, सामान्य ताप पर ऊर्जा समविभाजन का नियम, प्रायोगिक रूप से अच्छी तरह पुष्ट होता है।
सारणी 13.1 गैसों की विशिष्ट ऊष्मा धारिताओं के पूर्वानुमानित मान (कंपन रूपों की उपेक्षा करते हुए)
सारणी 13.2 कुछ गैसों की विशिष्ट ऊष्मा धारिताओं के मापित मान
उदाहरण 13.8 44.8 लीटर नियत धारिता के एक बेलनाकार बर्तन में STP पर हीलियम गैस भरी है। इस गैस के ताप में 15.0 °C वृद्धि करने के लिए कितनी ऊष्मा की आवश्यकता होगी? (R = 8.31 J mo1–1 K–1)
हल: गैस नियम PV = µRT का उपयोग करके आप यह आसानी से दर्शा सकते हैं कि किसी भी आदर्श गैस के 1 मोल का, मानक ताप (273 K) एवं दाब (1 atm = 1.01 × 105 Pa) पर आयतन 22.4 लीटर होता है। इस सार्वत्रिक आयतन को ‘मोलर आयतन’ कहते हैं। अत: इस उदाहरण में बर्तन के भीतर हीलियम के 2 मोल हैं। क्योंकि हीलियम एकपरमाणु गैस है, इसकी नियत आयतन पर विशिष्ट ऊष्मा धारिता
Cv = (3/2) R, तथा नियत दाब पर विशिष्ट ऊष्मा धारिता
CP = (5/2) R है। क्योंकि बर्तन का आयतन नियत है, आवश्यक ऊष्मा ज्ञात करने के लिए Cv का उपयोग करेंगे। अत:
आवश्यक ऊष्मा = मोलों की संख्या × मोलर विशिष्ट ऊष्मा
धारिता × तापवृद्धि
= 2 × 1.5 R × 15.0 = 45 R
= 45 × 8.31 = 374 J t
देखें, तो विश्वास करें
क्या परमाणुओं को इधर-उधर दौड़ते हुए देखा जा सकता है, ठीक-ठीक तो नहीं, पर लगभग एेसा हो सकता है। आप फूलों के परागकणों को जल के अणुओं द्वारा धकेले जाते हुए देख सकते हैं। परागकणों की आमाप ~ 10-5 m है। 1827 में, स्कॉटलैंड के वनस्पतिशास्त्री, रॉबर्ट ब्राऊन ने जल में निलंबित फूल के परागकणों का सूक्ष्मदर्शी से परीक्षण करते समय यह पाया कि वे टेढ़े-मेढ़े पथों पर निरंतर यादृच्छिक गति कर रहे हैं।
अणुगति सिद्धांत इस परिघटना की एक सरल व्याख्या प्रस्तुत करता है। जल में निलंबित किसी पिण्ड पर जल के अणु सभी दिशाओं से संघट्ट करते रहते हैं। क्योंकि अणुओं की गति यादृच्छिक है, किसी एक दिशा से संघट्ट करने वाले अणुओं की संख्या लगभग उतनी ही है जितनी विपरीत दिशा से आकर संघट्ट करने वाले परमाणुआें की संख्या होती है। सामान्य आमाप की वस्तु के लिए इन आण्विक संघट्टों की संख्या में अंतर कुल संघट्टों की संख्या की तुलना में उपेक्षणीय होने के कारण हमेें अणुओं की गति का प्रभाव दिखाई नहीं पड़ता।
यदि पिण्ड काफी छोटा हो, पर फिर भी सूक्ष्मदर्शी से दिखाई पड़ सकता हो, तो विभिन्न दिशाओं से होने वाले आण्विक संघट्टों की संख्या में अंतर पूर्णरूपेण उपेक्षणीय नहीं होता अर्थात् माध्यम (जल या अन्य तरल) के अणुओं के सतत संघट्टों द्वारा निलंबित पिण्ड पर संघट्टों के कारण आरोपित संवेगों एवं बल आघूर्णों का योग शून्य नहीं होता। किसी न किसी दिशा में कुल संवेग और बल आघूर्ण प्रभावी रह जाते हैं। इसलिए, यह पिण्ड टेढ़े-मेढ़े ढंग से गति करता है और यादृच्छिक ढंग से कलाबाजी खाता है। आजकल ब्राउनी गति कहलाने वाली अणुओं की यह गति आण्विक क्रियाशीलता का एक दृष्टव्य प्रमाण है। गत लगभग 50 वर्षों से क्रमवीक्षण सुरंगक (scanning tunneling) एवं अन्य विशिष्ट सूक्ष्मदर्शियों द्वारा, अणुओं को देखा जा रहा है।
1987 में, अमेरिका में कार्यरत मिस्र के वैज्ञानिक अहमद जेवैल ने न केवल अणुओं को देखने में सफलता पाई, वरन् वह उनकी विस्तृत पारस्परिक अन्योन्यक्रियाओं को भी देख सके। एेसा वे अति अल्प अवधि, दस फेम्टोसेकेंड की कोटि से भी कम अवधि वाले लेसर प्रकाश की क्षणदीप्ति से उनको प्रकाशित कर, और उनके फोटो लेकर संभव कर पाएं। (फेम्टो सेकंड = 10-15 s ) अब तो आप रासायनिक आबंधों के टूटने और बनने का भी अध्ययन कर सकते हैं। इसी को वास्तव में ‘देखना’ कहते हैं।
13.6.4 ठोसों की विशिष्ट ऊष्मा धारिता
ठोसों की विशिष्ट ऊष्माधारिता ज्ञात करने के लिए भी हम ऊर्जा समविभाजन का नियम लागू कर सकते हैं। किसी ठोस के विषय में विचार कीजिए, जो N परमाणुओं का बना है। प्रत्येक परमाणु अपनी माध्य स्थिति के इधर-उधर कंपन कर रहा है। किसी एकविमीय कंपन की औसत ऊर्जा 2 ×½ kBT
= kBT है। त्रिविमीय कंपनों के लिए औसत ऊर्जा 3 kBT है। ठोस के 1 मोल के लिए N = NA और इसकी कुल आंतरिक ऊर्जा
U = 3 kBT × NA = 3 RT
अब, नियत दाब पर ∆Q = ∆U + P∆V = ∆U, क्योंकि किसी ठोस के लिए ∆V उपेक्षणीय है। अत:
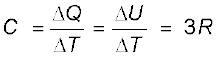 (13.37)
(13.37)
सारणी 13.3 कमरे के ताप एवं वायुमंडलीय दाब पर कुछ ठोसों की विशिष्ट ऊष्मा धारिताओं के मान
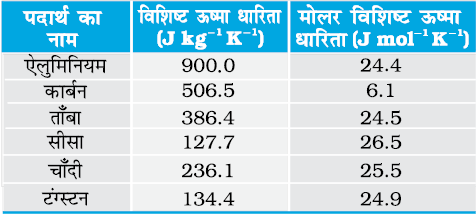
सारणी 13.3 दर्शाती है कि व्यापक रूप से, सामान्य ताप पर प्राप्त प्रायोगिक मान प्रागुक्त मानों से मेल खाते हैं। (कार्बन एक अपवाद है)।
13.6.5 जल की विशिष्ट ऊष्मा धारिता
हम जल को ठोसों की तरह ही लेते हैं। प्रत्येक परमाणु के लिए औसत ऊर्जा 3kBT है। जल के अणु में 3 परमाणु, दो हाइड्रोजन के और एक अॉक्सीजन के होते हैं। अत: इसके 1 मोल की आंतरिक ऊर्जा,
U = 3 × 3 kBT × NA = 9 RT
एवं C = ∆Q/ ∆T =∆ U / ∆T = 9R
यह इसका प्रेक्षित मान है और प्रायोगिक और सैद्धांतिक मानों में काफी समानता है। कैलॉरी, ग्राम, डिग्री मात्रक में जल की विशिष्ट ऊष्मा धारिता का मान 1 है। क्योंकि, 1 कैलॉरी = 4.179 J और जल का 1 मोल 18 ग्राम है। अत: जल की प्रति मोल विशिष्ट ऊष्मा धारिता ~ 75 J mol-1 K-1 ~ 9R है। तथापि, एेल्कोहॉल या एसिटोन जैसे अधिक जटिल अणुओं के लिए स्वातंत्र्य कोटि पर आधारित तर्क और अधिक उलझा देते हैं।
अंत में, हमें ऊर्जा समविभाजन के चिर प्रतिष्ठित नियम पर आधारित विशिष्ट ऊष्मा धारिताओं के पूर्वानुमान के एक महत्वपूर्ण पक्ष को ध्यान में रखना चाहिए। जिसके अनुसार प्रागुक्त विशिष्ट ऊष्मा धारिताएँ ताप पर निर्भर नहीं करतीं। परंतु जैसे-जैसे हम निम्न तापों की ओर बढ़ते जाते हैं, इस प्रागुक्ति में स्पष्ट विचलन दृष्टिगोचर होने लगता है। जैसे T 0। सभी पदार्थों की विशिष्ट ऊष्मा धारिताएँ शून्य की ओर अग्रसर होती जाती हैं। इसका संबंध इस तथ्य से है कि निम्न ताप पर स्वातंत्र्य कोटियाँ अनुपलभ्य और इसलिए अप्रभावी हो जाती हैं। चिरप्रतिष्ठित भौतिकी की दृष्टि से, प्रत्येक स्थिति में स्वातंत्र्य कोटियाँ अपरिवर्तित रहनी चाहिएँ। निम्न ताप पर विशिष्ट ऊष्मा
धारिताओं का व्यवहार चिरप्रतिष्ठित भौतिकी की अव्यवहार्यता दर्शाता है और यह व्यवहार केवल क्वांटम धारणाओं के
आधार पर ही स्पष्ट किया जा सकता है, जैसा कि सर्वप्रथम आइंस्टीन ने दर्शाया था। क्वांटम यांत्रिकी में स्वातंत्र्य कोटि के प्रभावी होने से पहले ही निकाय में किसी शून्येतर ऊर्जा होना आवश्यक है। यही इस बात का भी कारण है केवल कुछ ही प्रकरणों में क्यों कंपनिक स्वातंत्र्य कोटि प्रभावी होती हैं।
13.7 माध्य मुक्त पथ
गैसों में अणुओं की गति काफी अधिक, वायु में ध्वनि के वेग की कोटि के बराबर होती है। तो भी, रसोईघर में सिलिंडर से लीक हुई गैस को कमरे के दूसरे कोने तक विसरित होने में काफी अधिक समय लगता है। वायुमंडल में धुएँ का बादल घंटों तक बना रहता है। एेसा इसलिए होता है, क्योंकि, गैस के अणु एक परिमित, पर अत्यंत छोटी आमाप के होते हैं। इसीलिए वे परस्पर टकराते रहने के लिए बाध्य हैं। परिणामस्वरूप, वे अबाध्य रूप से, सरल रेखा में चलते नहीं रह सकते, उनका पथ निरंतर परिवर्तित रहता है।
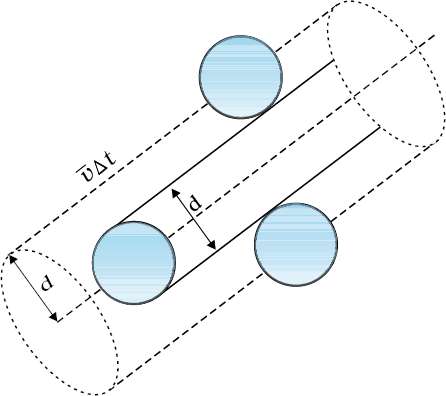
चित्र 13.7 ∆t समय में किसी अणु द्वारा प्रसर्पित आयतन जिसमें कोई दूसरा अणु इससे टकराएगा।
मान लीजिए, किसी गैस के अणु d व्यास के गोले हैं। यहाँ हम अपना ध्यान किसी एेसे गतिमान अणु पर केंद्रित करेंगे जिसकी माध्य चाल <v> है। यह किसी भी एेसे दूसरे अणु से संघट्ट करेगा जो इन दो अणुओं के केंद्रों के बीच की दूरी d के अंदर आ जाएगा। ∆t समय में यह आयतन (πd2 <v> ∆t) तय करता है जिसमें आने वाला कोई अणु इससे टकराएगा (देखें चित्र 13.7)। यदि प्रति एकांक आयतन में अणुओं की संख्या n हो तो कोई अणु ∆t समय में nπd2 <v> ∆t संघट्ट करेगा। इस प्रकार संघट्टाें की दर nπd2 <v> है। अथवा दो क्रमिक संघट्टों के बीच औसत अंतराल,
τ = 1/(nπ <v> d2 ) (13.38)
किन्हीं दो क्रमिक संघट्टों के बीच की औसत दूरी, जिसे माध्य मुक्त पथ (l ) कहते हैं, होगा :
l = <v> τ = 1/(nπd2) (13.39)
इस व्युत्पत्ति में हमने यह कल्पना की है कि दूसरे सभी अणु विरामावस्था में हैं। परंतु वास्तव में सभी अणु गतिमान हैं और संघट्ट दर अणुओं के औसत आपेक्षिक वेग द्वारा निर्धारित की जाती है। अत: हमें समीकरण (13.38) में <v> को <vr> से प्रतिस्थापित करना होगा। अत: अधिक यथार्थ व्युत्पत्ति द्वारा
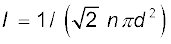 (13.40)
(13.40)
आइये, अब हम वायु के अणुओं के लिए, STP पर औसत वेग <v> = ( 485m/s) लेकर l एवं T का आकलन करते हैं।
n = 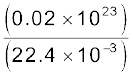
= 2.7 × 10 25 m–3
d = 2 × 10–10 m लेने पर,
τ = 6.1 × 10–10 s
तथा, l = 2.9 × 10–7 m ≈ 1500d (13.41)
जैसी अपेक्षा थी, समीकरण (13.40) द्वारा दिया गया माध्य मुक्त पथ का मान अणु की आमाप एवं संख्या घनत्व पर प्रतिलोमत: निर्भर करता है। किसी अत्यधिक निर्वातित नली में चाहे n कितना भी कम क्यों न हो, माध्य मुक्त पथ का मान नली की लंबाई के बराबर हो सकता है।
उदाहरण 13.9 373 K पर, जल वाष्प में, जल के अणु के माध्य मुक्त पथ का आकलन कीजिए। उदाहरण 13.1 और समीकरण (13.41) में दी गई सूचनाओं का उपयोग कीजिए।
हल जल वाष्प के लिए d का मान, इसका वायु के लिए मान बराबर होता है। संख्या घनत्व परम ताप के व्युत्क्रमानुपाती है।
इसलिए 
अत: माध्य मुक्त पथ  t
t
ध्यान दीजिए, माध्य मुक्त पथ, पूर्व परिकलनों द्वारा ज्ञात अंतरापरमाणुक दूरी ~ 40 Å = 4 ×10-9 m की तुलना में 100 गुनी है। माध्य मुक्त पथ का यह बड़ा मान ही गैसों के प्रारूपिक व्यवहार का मार्गदर्शक है। बिना किसी धारक पात्र के गैसों को सीमित नहीं किया जा सकता है।
अणुगति सिद्धांत का उपयोग करके, श्यानता, ऊष्मा-चालकता, एवं विसरण जैसे स्थूल मेय गुणों को आण्विक आमाप जैसे अतिसूक्ष्म प्राचलों से संबंधित किया जा सकता है। इसी तरह के संबंधों से ही सर्वप्रथम अणुओं की आमाप का आकलन किया गया था।
सारांश
1. दाब (P), आयतन (V) और परम ताप (T ) में संबंध स्थापित करने वाली आदर्श गैस समीकरण है,
PV = µ RT = kB NT
यहाँ µ गैस में मोलों की संख्या और N अणुओं की संख्या है। R तथा kB क्रमश: सार्वत्रिक गैस नियतांक एवं
बोल्ट्ज़मान नियतांक हैं।
R = 8.314 J mol–1 K–1, kB = 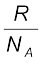 = 1.38 × 10–23 J K–1
= 1.38 × 10–23 J K–1
वास्तविक गैसें, आदर्श गैस समीकरण का अधिकाधिक पालन केवल उच्च ताप तथा निम्न दाब पर ही करती हैं।
2. आदर्श गैस के अणुगति सिद्धांत के अनुसार
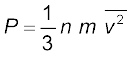
यहाँ n अणुओं का संख्या घनत्व, m अणु का द्रव्यमान एवं 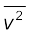 इनकी माध्य वर्ग चाल है। इसको आदर्श गैस समीकरण के साथ मिलाने से ताप की एक अणुगतिक व्याख्या प्राप्त होती है,
इनकी माध्य वर्ग चाल है। इसको आदर्श गैस समीकरण के साथ मिलाने से ताप की एक अणुगतिक व्याख्या प्राप्त होती है,
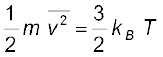 ,
, 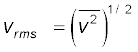
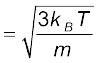
इससे हमें यह ज्ञात होता है कि किसी गैस का ताप उसके किसी अणु की औसत गतिज ऊर्जा की माप है और यह गैस या अणु की प्रकृति पर निर्भर नहीं करता। एक नियत ताप पर गैसों के मिश्रण में भारी अणु की औसत चाल अपेक्षाकृत कम होती है।
3. स्थानांतरीय गतिज ऊर्जा
E =  kB NT
kB NT
इससे हमें यह सूत्र प्राप्त होता है-
PV = 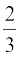 E
E
4. ऊर्जा समविभाजन का नियम बताता है कि यदि एक निकाय परमताप T पर साम्यावस्था में है तो कुल ऊर्जा समान रूप से विभिन्न ऊर्जा रूपों में बँट कर अवशोषित होती है और हर रूप के साथ जुड़ी यह ऊर्जा – kB T होती है। प्रत्येक स्थानांतरीय एवं घूर्णी स्वातंत्र्य कोटि के संगत अवशोषण का एक ऊर्जा रूप होता है और इससे जुड़ी ऊर्जा – kB T होती है। प्रत्येक कंपन आवृत्ति के साथ ऊर्जा के दो रूप (गतिज एवं स्थितिज) जुड़ते हैं इसलिए इसके संगत ऊर्जा = 2 × – kB T = kB T
5. ऊर्जा समविभाजन का नियम लागू करके हम गैसों की मोलर विशिष्ट ऊष्मा धारिता ज्ञात कर सकते हैं और इस प्रकार प्राप्त विशिष्ट ऊष्मा धारिताओं के मान कई गैसों के प्रयोगों द्वारा प्राप्त विशिष्ट ऊष्मा धारिताओं के मानों से मिलते हैं। यदि गति के कंपन रूपों को भी परिकलनों में सम्मिलित करें तो यह साम्यता और भी सटीक बैठेगी।
6. माध्य मुक्त पथ l अणु के दो क्रमिक संघट्टों के बीच उसके द्वारा चलित औसत दूरी है
1834.png
जहाँ n संख्या घनत्व एवं d अणु का व्यास है।
विचारणीय विषय
1. किसी तरल का दाब केवल धारक की दीवारों पर ही आरोपित नहीं होता, बल्कि यह तरल में हर जगह विद्यमान रहता है। बर्तन में रखे गैस के आयतन में कोई परत साम्यावस्था में होती है क्योंकि इस परत के दोनों ओर समान दाब होता है।
2. गैस में अंतरापरमाणुक दूरी के संबंध में हमें बहुत बढ़ा-चढ़ा कर कोई धारणा नहीं बनानी चाहिए। सामान्य ताप और दाब पर यह ठोसों और द्रवों में अंतरापरमाणुक दूरी के लगभग दस गुने के बराबर है। बहुत भिन्न अगर कुछ है तो वह माध्य मुक्त पथ है जो किसी गैस में अंतरापरमाणुक दूरी का 100 गुना और अणु की आमाप का
1000 गुना होता है।
3. ऊर्जा समविभाजन के नियम को हम इस प्रकार कह सकते हैं– तापीय साम्य में प्रत्येक स्वातंत्र्य कोटि के साथ ½ kB T ऊर्जा जुड़ी होती है। अणु की कुुल ऊर्जा के व्यंजक में प्रत्येक द्विघाती पद एक स्वातंत्र्य कोटि गिना जाना चाहिए। अत:, प्रत्येक कंपन-विधा में दो स्वातंत्र्य कोटि (न कि एक) होते हैं (गतिज एवं स्थितिज रूपों के संगत) जिनकी ऊर्जा 2 × ½ kB T = kB T होती है।
4. किसी कमरे में वायु के सब अणु नीचे नहीं गिर जाते (गुरुत्व के कारण) तथा फर्श पर आकर नहीं ठहर जाते क्योंकि वह बहुत वेग से गतिमान होते हैं और निरंतर संघट्ट करते रहते हैं। साम्यावस्था में कम ऊँचाइयों पर घनत्व थोड़ा अधिक होता है (जैसे वायुमण्डल में)। इसका प्रभाव कम है, क्योंकि सामान्य ऊँचाइयों के लिए स्थितिज ऊर्जा (mgh) का मान अणु की औसत गतिज ऊर्जा 1/2 mv2 की तुलना में काफी कम है।
5. < v2 > सदैव ( < v >)2 के बराबर नहीं होता। किसी राशि के वर्ग का माध्य आवश्यक नहीं है कि उस राशि के माध्य के वर्ग के बराबर हो। क्या आप इस कथन की पुष्टि के लिए उदाहरण बता सकते हैं?
अभ्यास
13.1 अॉक्सीजन के अणुओं के आयतन और STP पर इनके द्वारा घेरे गए कुल आयतन का अनुपात ज्ञात कीजिए। अॉक्सीजन के एक अणु का व्यास 3 Å लीजिए।
13.2 मोलर आयतन, STP पर किसी गैस (आदर्श) के 1 मोल द्वारा घेरा गया आयतन है। (STP : 1 atm दाब, 0 °C)। दर्शाइये कि यह 22.4 लीटर है।
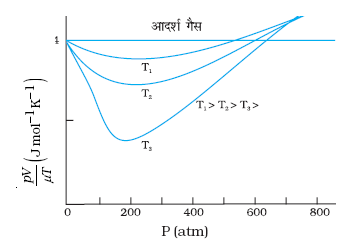
13.3 चित्र 13.8 में अॉक्सीजन के 1.00×10–3 kg द्रव्यमान के लिए PV/T एवं P में, दो अलग-अलग तापों पर ग्राफ दर्शाये गए हैं।

चित्र 13.8
(a) बिंदुकित रेखा क्या दर्शाती है?
(b) क्या सत्य है: T1 > T2 अथवा T1 < T2?
(c) y-अक्ष पर जहाँ वक्र मिलते हैं वहाँ PV/T का मान क्या है?
(d) यदि हम एेसे ही ग्राफ 1.00×10–3 kg हाइड्रोजन के लिए बनाएँ तो भी क्या उस बिंदु पर जहाँ वक्र
y-अक्ष से मिलते हैं PV/T का मान यही होगा? यदि नहीं तो हाइड्रोजन के कितने द्रव्यमान के लिए PV/T का मान (कम दाब और उच्च ताप के क्षेत्र के लिए वही होगा? H2 का अणु द्रव्यमान = 2.02 u, O2 का अणु द्रव्यमान = 32.0 u, R = 8.31 J mo1–1 K–1)
13.4 एक अॉक्सीजन सिलिंडर जिसका आयतन 30 लीटर है, में अॉक्सीजन का आरंभिक दाब 15 atm एवं ताप 27 °C है। इसमें से कुछ गैस निकाल लेने के बाद प्रमापी (गेज) दाब गिर कर 11 atm एवं ताप गिर कर 17 °C हो जाता है। ज्ञात कीजिए कि सिलिंडर से अॉक्सीजन की कितनी मात्रा निकाली गई है। (R = 8.31 J mol–1 K–1, अॉक्सीजन का अणु द्रव्यमान O2 = 32 u)।
13.5 वायु का एक बुलबुला, जिसका आयतन 1.0 cm3 है, 40 m गहरी झील की तली से जहाँ ताप 12 °C है, उठकर ऊपर पृष्ठ पर आता है जहाँ ताप 35 °C है। अब इसका आयतन क्या होगा?
13.6 एक कमरे में, जिसकी धारिता 25.0 m3 है, 27 °C ताप और 1 atm दाब पर, वायु के कुल अणुओं (जिनमें नाइट्रोजन, अॉक्सीजन, जलवाष्प और अन्य सभी अवयवों के कण सम्मिलित हैं) की संख्या ज्ञात कीजिए।
13.7 हीलियम परमाणु की औसत तापीय ऊर्जा का आकलन कीजिए (i) कमरे के ताप (27 °C) पर। (ii) सूर्य के पृष्ठीय ताप (6000 K) पर। (iii) 100 लाख केल्विन ताप (तारे के क्रोड का प्रारूपिक ताप) पर।
13.8 समान धारिता के तीन बर्तनों में एक ही ताप और दाब पर गैसें भरी हैं। पहले बर्तन में नियॉन (एकपरमाणुक) गैस है, दूसरे में क्लोरीन (द्विपरमाणुक) गैस है और तीसरे में यूरेनियम हेक्साफ्लोराइड (बहुपरमाणुक) गैस है। क्या तीनों बर्तनों में गैसों के संगत अणुओं की संख्या समान है? क्या तीनों प्रकरणाें में अणुओं की vrms (वर्ग माध्य मूल चाल) समान है।
13.9 किस ताप पर आर्गन गैस सिलिंडर में अणुओं की vrms , – 20 °C पर हीलियम गैस परमाणुओं की vrms के बराबर होगी। (Ar का परमाणु द्रव्यमान = 39.9 u, एवं हीलियम का परमाणु द्रव्यमान = 4.0 u)।
13.10 नाइट्रोजन गैस के एक सिलिंडर में, 2.0 atm दाब एवं 17 0C ताप पर, नाइट्रोजन अणुओं के माध्य मुक्त पथ एवं संघट्ट आवृत्ति का आकलन कीजिए। नाइट्रोजन अणु की त्रिज्या लगभग 1.0 Å लीजिए। संघट्ट-काल की तुलना अणुओं द्वारा दो संघट्टों के बीच स्वतंत्रतापूर्वक चलने में लगे समय से कीजिए। (नाइट्रोजन का आण्विक द्रव्यमान = 28.0 u)।
अतिरिक्त अभ्यास
13.11 1 मीटर लंबी संकरी (और एक सिरे पर बंद) नली क्षैतिज रखी गई है। इसमें 76 cm लंबाई भरा पारद सूत्र, वायु के 15 cm स्तंभ को नली में रोककर रखता है। क्या होगा यदि खुला सिरा नीचे की ओर रखते हुए नली को ऊर्ध्वाधर कर दिया जाए।
13.12 किसी उपकरण से हाइड्रोजन गैस 28.7 cm3 s–1 की दर से विसरित हो रही है। उन्हीं स्थितियों में कोई दूसरी गैस 7.2 cm3 s–1 की दर से विसरित होती है। इस दूसरी गैस को पहचानिए।
[संकेत : ग्राहम के विसरण नियम R1/R2 = ( M2 /M1 )1/2 का उपयोग कीजिए, यहाँ R1, R2 क्रमश: गैसों की विसरण दर तथा M1 एवं M2 उनके आण्विक द्रव्यमान हैं। यह नियम अणुगति सिद्धांत का एक सरल परिणाम है।
13.13 साम्यावस्था में किसी गैस का घनत्व और दाब अपने संपूर्ण आयतन में एकसमान हैं । यह पूर्णतया सत्य केवल तभी है जब कोई भी बाह्य प्रभाव न हो । उदाहरण के लिए, गुरुत्व से प्रभावित किसी गैस स्तंभ का घनत्व (और दाब) एकसमान नहीं होता है । जैसा कि आप आशा करेंगे इसका घनत्व ऊँचाई के साथ घटता है । परिशुद्ध निर्भरता ‘वातावरण के नियम’ n2 = n1 exp 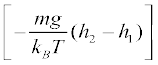 से दी जाती है, यहाँ n2, n1 क्रमश: h2 व h1ऊँचाइयों पर संख्यात्मक घनत्व को प्रदर्शित करते हैं । इस संबंध का उपयोग द्रव स्तंभ में निलंबित किसी कण के अवसादन साम्य के लिए समीकरण n2 = n1 exp
से दी जाती है, यहाँ n2, n1 क्रमश: h2 व h1ऊँचाइयों पर संख्यात्मक घनत्व को प्रदर्शित करते हैं । इस संबंध का उपयोग द्रव स्तंभ में निलंबित किसी कण के अवसादन साम्य के लिए समीकरण n2 = n1 exp 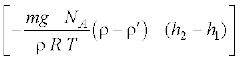 को व्युत्पन्न करने के लिए कीजिए, यहाँ ρ निलंबित कण का घनत्व तथा
को व्युत्पन्न करने के लिए कीजिए, यहाँ ρ निलंबित कण का घनत्व तथा 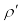 चारों तरफ के माध्यम का घनत्व है । NA आवोगाद्रो संख्या, तथा R सार्वत्रिक गैस नियतांक है । [संकेत: निलंबित कण के आभासी भार को जानने के लिए आर्किमिडीज के सिद्धांत का उपयोग कीजिए ।]
चारों तरफ के माध्यम का घनत्व है । NA आवोगाद्रो संख्या, तथा R सार्वत्रिक गैस नियतांक है । [संकेत: निलंबित कण के आभासी भार को जानने के लिए आर्किमिडीज के सिद्धांत का उपयोग कीजिए ।]
13.14 नीचे कुछ ठोसों व द्रवों के घनत्व दिए गए हैं । उनके परमाणुओं की आमापों का आकलन (लगभग) कीजिए।
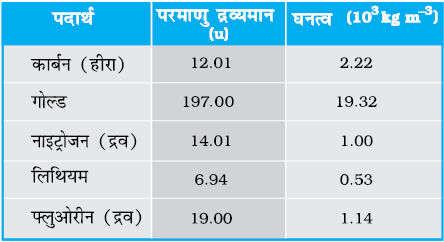
[संकेत: मान लीजिए कि परमाणु ठोस अथवा द्रव प्रावस्था में ‘दृढ़ता से बँधे’ हैं, तथा आवोगाद्रो संख्या के ज्ञात मान का उपयोग कीजिए। फिर भी आपको विभिन्न परमाण्वीय आकारों के लिए अपने द्वारा प्राप्त वास्तविक संख्याओं का बिलकुल अक्षरश: प्रयोग नहीं करना चाहिए क्योंकि दृढ़ संवेष्टन सन्निकटन की रूक्षता के परमाणवीय आकार कुछ Å के परास में हैं।]
