Table of Contents
अध्याय 14
दोलन
14.1 भूमिका
14.2 दोलन और आवर्ती गति
14.3 सरल आवर्त गति
14.4 सरल आवर्त गति तथा एकसमान वर्तुल गति
14.5 सरल आवर्त गति में वेग तथा त्वरण
14.6 सरल आवर्त गति के लिए बल नियम
14.7 सरल आवर्त गति में ऊर्जा
14.8 सरल आवर्त गति निष्पादित करने वाले कुछ निकाय
14.9 अवमंदित सरल आवर्त गति
14.10 प्रणोदित दोलन तथा अनुनाद
सारांश
विचारणीय विषय
अभ्यास
अतिरिक्त अभ्यास
अध्याय 14
दोलन
14.1 भूमिका
14.2 दोलन और आवर्ती गति
14.3 सरल आवर्त गति
14.4 सरल आवर्त गति तथा एकसमान वर्तुल गति
14.5 सरल आवर्त गति में वेग तथा त्वरण
14.6 सरल आवर्त गति के लिए बल नियम
14.7 सरल आवर्त गति में ऊर्जा
14.8 सरल आवर्त गति निष्पादित करने वाले कुछ निकाय
14.9 अवमंदित सरल आवर्त गति
14.10 प्रणोदित दोलन तथा अनुनाद
सारांश
विचारणीय विषय
अभ्यास
अतिरिक्त अभ्यास
14.1 भूमिका
हम अपने दैनिक जीवन में विभिन्न प्रकार की गतियाँ देखते हैं । इनमें से कुछ जैसे सरल रैखिक गति और किसी प्रक्षेप्य की गति के विषय में तो आप अध्ययन कर ही चुके हैं । ये दोनों ही गतियाँ अनावर्ती होती हैं । हमने एकसमान वर्तुल गति तथा सौर परिवार में ग्रहों की कक्षीय गतियों के विषय में भी अध्ययन कर लिया है। इन उदाहरणों में निश्चित समय-अंतराल के पश्चात् गति की पुनरावृत्ति होती है, अर्थात् यह आवर्ती होती है । आपने बचपन में अपने पालने अथवा झूले पर झूलने का आनन्द लिया होगा । यह दोनों गतियाँ पुनरावर्ती होती हैं, परंतु किसी ग्रह की आवर्ती गति से भिन्न होती हैं । यहाँ वस्तु किसी माध्य स्थिति के इधर-उधर गति करती है । दीवार-घड़ी का लोलक भी इसी प्रकार की गति करता है। इस प्रकार की अग्र-पश्च (आगे-पीछे) आवर्ती गति के प्रचुर उदाहरण हैं– नदी में डूबती-उतरती हुई नाव, वाष्प इंजन में अग्र और पश्च चलता हुआ पिस्टन आदि। इस प्रकार की गति को दोलन गति कहते हैं । इस अध्याय में हम इस गति के बारे में अध्ययन करेंगे ।
दोलन गति का अध्ययन भौतिकी के लिए आधारभूत है; बहुत-सी भौतिक परिघटनाओं को समझने के लिए इसकी संकल्पना की आवश्यकता होती है । वाद्य यंत्रों; जैसे-सितार, गिटार अथवा वायलिन में हम कंपायमान डोरियों द्वारा रोचक ध्वनियाँ उत्पन्न होते हुए देखते हैं । ढोलों में झिल्लियाँ तथा टेलीफोन और ध्वनि विस्तारकों के स्पीकरों में डायफ्राम अपनी माध्य स्थिति के इधर-उधर कंपन करते हैं । वायु के अणुओं के कंपनों द्वारा ही ध्वनि-संचरण संभव हो पाता है। एक ठोस पदार्थ में अणु अपनी माध्य स्थितियों के परित: कम्पन करते हैं, कम्पन की औसत ऊर्जा तापमान के समानुपाती होती है। AC पावर एेसी वोल्टता का संभरण करता है जो माध्य मान (शून्य) के धनात्मक तथा ऋणात्मक ओर एकांतर क्रम से दोलायमान रहता है।
किसी आवर्ती गति के व्यापक तथा दोलन गति के विशेष विवरण के लिए कुछ मूल संकल्पनाओं; जैसे–आवर्तकाल, आवृत्ति, विस्थापन, आयाम और कला की आवश्यकता होती है । अगले अनुभाग में इन संकल्पनाओं को विकसित किया गया है ।
14.2 दोलन और आवर्ती गति
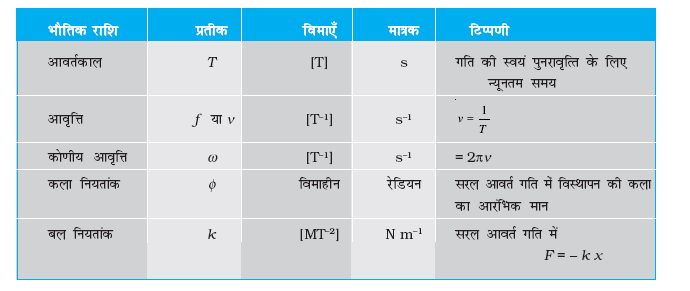
चित्र 14.1 में कुछ आवर्ती गतियाँ दर्शाई गई हैं। मान लीजिए कोई कीट किसी रैम्प पर चढ़ता है और गिर जाता है। वह अपने प्रारंभिक स्थान पर आ जाता है और इस प्रक्रिया को बार-बार दोहराता है। यदि आप जमीन से ऊपर इसकी ऊँचाई तथा समय के बीच ग्राफ खींचें तो यह चित्र 14.1(a) की तरह दिखेगा। यदि कोई बालक किसी सीढ़ी पर चढ़े और उतरे तथा इस प्रक्रिया को समान रूप से बार-बार दोहराये तो उसकी ऊँचाई तथा समय के बीच ग्राफ चित्र 14.1(b) के जैसा दिखेगा। जब आप किसी गेंद को अपनी हथेली से जमीन की तरफ बार-बार मारते हैं तो इसकी ऊँचाई और समय के बीच ग्राफ 14.3(c) के जैसा दिखेगा। ध्यान दीजिए कि चित्र 14.1(c) में दोनों वक्रीय भाग न्यूटन की गति समीकरण के अनुसार परवलय के अंश हैं, अनुभाग (3.6) देखिए।
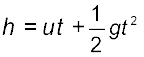 अधोमुखी गति के लिए, तथा
अधोमुखी गति के लिए, तथा
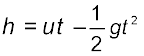 उपरिमुखी गति के लिए,
उपरिमुखी गति के लिए,
इन समीकरणों में u का मान अलग परिस्थितियों के लिए भिन्न होगा। ये सभी आवर्ती गति के उदाहरण हैं। अत: कोई गति जो निश्चित अंतराल के बाद पुनरावृत्ति करती है आवर्ती गति कहलाती है।
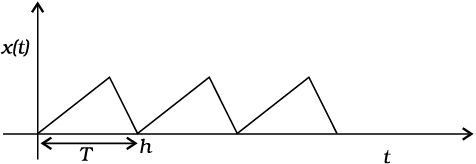
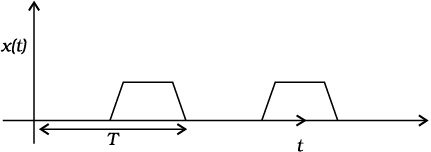

चित्र 14.1 आवृत्ति गति के उदाहरण। प्रत्येक अवस्था में आवर्तकाल T दर्शाया गया है।
सामान्यत: आवर्ती गति करने वाले पिण्ड की एक संतुलन अवस्था होती है जो उसके गति के पथ में स्थित होता है। जब पिण्ड इस संतुलन अवस्था में होता है तो उस पर लगने वाला कुल बाह्य बल शून्य होता है। अत: यदि पिण्ड को इस अवस्था में विराम की स्थिति में छोड़ दें तो यह सदैव विरामावस्था में रहेगा। यदि पिण्ड को इस अवस्था से थोड़ा सा विस्थापित करें तो पिण्ड पर एक बल कार्य करने लगता है जो पिण्ड को पुन: उसकी संतुलन-अवस्था की ओर ले जाने का प्रयास करता है और फलस्वरूप पिण्ड में दोलन या कंपन उत्पन्न हो जाता है। उदाहरण के लिए यदि किसी कटोरे में एक गेंद रख दें तो गेंद कटोरे की तली पर संतुलन अवस्था में होती है। यदि इसको इस बिंदु से थोड़ा विस्थापित करें तो गेंद कटोरे में दोलन करने लगती है। प्रत्येक दोलन गति आवर्ती होती है परंतु प्रत्येक आवर्ती गति दोलनीय नहीं होती। वर्तुल गति भी आवर्ती होती है, परंतु दोलनीय नहीं होती है।
दोलन एवं कंपन में कोई मुख्य अंतर नहीं है। साधारणत: जब आवृत्ति का मान कम होता है तो हम गति को दोलनीय कहते हैं (जैसे किसी वृक्ष की टहनी की दोलन गति)। इसके विपरीत जब गति की आवृत्ति अधिक होती है तो हम गति को कंपन कहते हैं। जैसे किसी संगीत वाद्य के तार का कंपन।
सरल आवर्ती गति दोलनीय गति का एक सरल रूप है। यह तब होता है जब किसी दोलनीय वस्तु के ऊपर लगने वाला बल संतुलन अवस्था में इसके विस्थापन के समानुपाती होता है। पुन: वस्तु के दोलन के दौरान यह बल सदैव इस संतुलन अवस्था की तरफ निदेशित होता है। यह संतुलन अवस्था वस्तु की गति की माध्य स्थिति भी होती है।
किसी भी द्रव्यात्मक माध्यम को हम युग्मित दलित्रों का एक बड़ा समूह मान सकते हैं। इन दलित्रों के सामूहिक दोलन तरंग का रूप लेते हैं। जल तरंग, भूकम्पित तरंगें, विद्युत चुंबकीय तरंगें इन तरंगों के उदाहरण हैं। तरंगीय घटनाओं के विषय में हम अगले अध्याय में अध्ययन करेंगे।
14.2.1 आवर्तकाल तथा आवृत्ति
हमने देखा है कि कोई गति जिसकी किसी नियमित समय अंतराल पर स्वयं पुनरावृत्ति होती है आवर्ती गति कहलाती है। वह न्यूनतम समय अंतराल जिसके पश्चात् गति की पुनरावृत्ति होती है, इसका आवर्तकाल कहलाता है। अत: समय को हम T द्वारा दर्शाते हैं। इसका SI मात्रक सेकंड है । उन आवर्ती गतियों के लिए, जो सेकंडों के पैमाने पर या तो बहुत तीव्र अथवा बहुत मंद होती हैं, समय के अन्य सुविधाजनक मात्रक उपयोग में लाए जाते हैं । किसी क्वार्ट्ज़ क्रिस्टल का कंपन काल माइक्रोसेकंड (10–6 s) के मात्रकों, जिसका प्रतीक µs है, में व्यक्त किया जाता है । इसके विपरीत बुध ग्रह की कक्षीय अवधि 88 भू-दिवस होती है । हेली धूमकेतु हर 76 वर्ष के पश्चात् पुन: दृष्टिगोचर होता है ।
आवर्तकाल ‘T’ के व्युत्क्रम से हमें प्रति इकाई समय में दोलनों की संख्या प्राप्त होती है । यह राशि आवर्ती गति की आवृत्ति कहलाती है । इसे प्रतीक v द्वारा निरूपित किया जाता है । n तथा T के मध्य निम्नलिखित पारस्परिक संबंध होता है:
n = 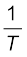 (14.1)
(14.1)
इस प्रकार n का मात्रक (s–1) है । रेडियो तरंगों के आविष्कारक हेनरिख रुडोल्फ हर्ट्स (1857-1894) के नाम पर आवृत्ति के मात्रक को एक विशेष नाम दिया गया । इसे हर्ट्स (hertz प्रतीक Hz) कहते हैं । इस प्रकार,
1 हर्ट्स = 1 Hz = 1 दोलन प्रति सेकंड = 1s–1 (14.2)
ध्यान दीजिए, आवृत्ति का सदैव ही पूर्णांक होना आवश्यक नहीं है ।
उदाहरण 14.1 कोई मानव हृदय एक मिनट में औसतन 75 बार धड़कन करता पाया जाता है । इसकी आवृत्ति तथा आवर्तकाल परिकलित कीजिए ।
हल हृदय की धड़कन की आवृत्ति = 75/(1 मिनट)
= 75/(60 s)
= 1.25 s–1
आवर्तकाल, T = 1/(1.25 s–1)
= 0.8 s °
14.2.2 विस्थापन
अनुभाग 4.2 में हमने किसी कण के विस्थापन को उसके स्थिति सदिश में परिवर्तन के रूप में परिभाषित किया था । इस अध्याय में हम विस्थापन नामक इस पद का उपयोग अधिक व्यापक अर्थों में करेंगे । यह किसी भी विचारणीय भौतिक गुण में समय के साथ परिवर्तन को निरूपित करेगा । उदाहरण के लिए, एक पृष्ठ पर किसी स्टील बॉल की सरल रेखीय गति के लिए, समय के फलन के रूप में आरंभ बिंदु से बॉल की दूरी इसका स्थिति-विस्थापन है । मूल बिंदु का चुनाव सुविधानुसार किया जा सकता है । मान लीजिए कोई गुटका किसी कमानी से जुड़ा है जिसका दूसरा सिरा किसी दृढ़ दीवार से संबद्ध है [देखिए चित्र 14.2 (a)] साधारणत: किसी पिण्ड का विस्थापन इसकी संतुलन अवस्था से मापना सरल होगा। किसी दोलायमान सरल लोलक के लिए, समय के फलन के रूप में ऊर्ध्वाधर से कोण को विस्थापन-चर के रूप में निरूपित किया जा सकता है [देखिए चित्र 14.2(b)]। ‘विस्थापन’ पद का उल्लेख सदैव स्थिति के संदर्भ में ही नहीं किया जाता । विस्थापन चर कई अन्य प्रकार के भी हो सकते हैं । किसी a.c. परिपथ में संयोजित संधारित्र के सिरों के बीच समय के साथ परिवर्तित हो रही "वोल्टता" को भी एक विस्थापन चर के रूप में लिया जा सकता है । इसी प्रकार, ध्वनि तरंगों के संचरण में समय के साथ ‘दाब’ में परिवर्तन, प्रकाश तरंगों में परिवर्तित हो रहे वैद्युत तथा चुंबकीय क्षेत्र अन्य संदर्भो में विस्थापन के उदाहरण हैं। विस्थापन चर का मान धनात्मक या ऋणात्मक हो सकता है। दोलनों के प्रयोगों में, भिन्न समयों के लिए विस्थापन चरों की माप ली जाती है ।
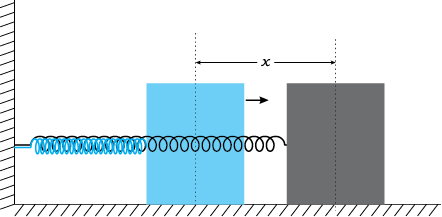
चित्र 1.4.2(a) कोई गुटका किसी कमानी से संलग्न, जिसका दूसरा सिरा किसी दृढ़ दीवार से संबद्ध है । गुटका घर्षण रहित पृष्ठ पर गति करता है । गुटके की गति को दीवार से दूरी, अथवा विस्थापन x के पदों में व्यक्त किया जा सकता है ।

चित्र 14.2(b) एक दोलायमान सरल लोलक, इसकी गति को ऊर्ध्वाधर से कोणीय विस्थापन θ के पदों में व्यक्त किया जा सकता है ।
विस्थापन को सदैव ही समय के गणितीय फलन द्वारा निरूपित किया जा सकता है । आवर्ती गतियों में यह फलन समय का आवर्ती होता है । आवर्ती फलनों में से एक सरलतम आवर्ती फलन को निम्न प्रकार से व्यक्त कर सकते हैं,
f (t) = A cos ωt (14.3a)
यदि इस फलन के कोणांक, ωt, में 2π रेडियन या इसके किसी पूर्णांक गुणज की वृद्धि कर दी जाए, तो फलन का मान
वही f रहता है । तब भी फलन f (t) आवर्ती ही रहता है जिसका आवर्तकाल, T निम्नलिखित होगा,
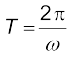 (14.3b)
(14.3b)
अत: कोई फलन f (t) काल T का आवर्ती होता है,
f (t) = f (t+T)
यदि हम ज्या (sin) फलन, f (t) = A sin ωt भी लें तो स्पष्ट रूप से यही परिणाम सही होता है । साथ ही ज्या (sin) एवं कोज्या (cos) फलनों का एक घात संचय, जैसे
f (t) = A sin ωt + B cos ωt (14.3c)
भी आवर्ती फलन होता है, जिसका आवर्तकाल T होता है । यदि हम
A = D cos φ तथा B = D sin φ
लें, तो समीकरण (14.3c) को इस प्रकार लिख सकते हैं
f (t) = D sin (ωt + φ ) , (14.3d)
यहाँ अचर D और φ दिए गए हैं
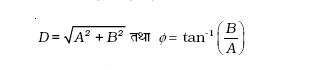
उदाहरण 14.2 निम्नलिखित समय के फलनों में कौन (a) आवर्ती तथा (b) अनावर्ती गति को निरूपित करते हैं ? प्रत्येक आवर्ती गति का आवर्तकाल लिखिए
[ω कोई धनात्मक नियतांक है] ।
(i) sin ωt + cos ωt
(ii) sin ωt + cos 2ωt + sin 4 ωt
(iii) e–ωt
(iv) log (ωt)
हल (i) sin ωt + cos ωt एक आवर्ती फलन है। इसे 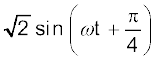 के रूप में भी व्यक्त किया जा सकता है।
के रूप में भी व्यक्त किया जा सकता है।
अब, 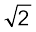 sin (ωt + π/4) =
sin (ωt + π/4) = 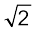 sin (ωt + π/4+2π)
sin (ωt + π/4+2π)
= 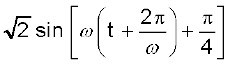
इस फलन का आवर्तकाल 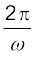 है ।
है ।
(ii) यह आवर्ती गति का एक उदाहरण है । ध्यान दीजिए, यहाँ प्रत्येक पद एक विभिन्न कोणीय आवृत्ति के आवर्ती फलन को निरूपित करता है । चूँकि आवर्तकाल वह न्यूनतम समय अंतराल होता है जिसके पश्चात् फलन अपने मान की स्वयं पुनरावृत्ति करता है, sin ωt का आवर्तकाल T0 = 2π/ω; cos 2ωt का आवर्तकाल π/ω = T0/2; तथा sin 4 ωt का आवर्तकाल 2π/4 ω = T0/4 होता है । प्रथम पद का आवर्तकाल अंतिम दो पदों के आवर्तकालों का गुणनफल होता है। अत: अंतिम समय का निम्न अंतराल जिसके उपरांत तीनों पदों का योग पुनरावृत्ति करता है T0 होता है जिसका आवर्त काल 2π/ω है।
(iii) फलन e–ωt अनावर्ती है, यह समय में वृद्धि के साथ एक दिष्टत: घटता है तथा t→∞ होने पर शून्य की ओर प्रवृत्त होता है और इस प्रकार कभी भी अपने मान की पुनरावृत्ति नहीं करता ।
(iv) फलन log (ωt) समय के साथ एकदिष्टत: बढ़ता है । अत: यह अपने मान की कभी भी पुनरावृत्ति नहीं करता और यह एक अनावर्ती फलन है । ध्यान दीजिए, t→∞ होने पर log ωt अपसारित होकर ∞ तक पहुँच जाता है। अत: यह किसी भी प्रकार के भौतिक विस्थापन को निरूपित नहीं कर सकता । °
14.3 सरल आवर्त गति
हम चित्र 14.3 के अनुसार x-अक्ष के मूल बिंदु पर +A और –A चरम सीमाओं के मध्य अग्र और पश्च कंपन करने वाले किसी कण पर विचार करें । इस दोलायमान गति को सरल आवर्त गति कहते हैं, यदि मूल बिन्दु से कण का विस्थापन x समय के साथ निम्न समीकरण के अनुसार परिवर्तित हो:

चित्र 14.3 x-अक्ष के मूल बिंदु पर +A और –A सीमाओं के भीतर अग्र और पश्च कंपन करते हुए कोई कण ।
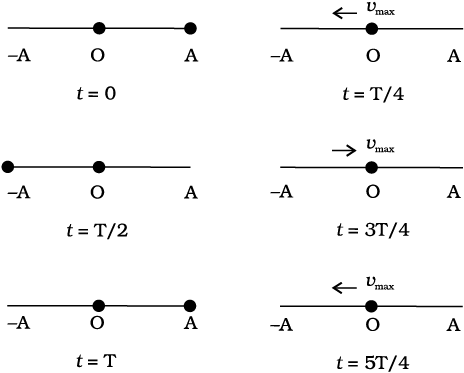
यहाँ A, ω तथा φ स्थिरांक हैं। अत: प्रत्येक आवर्त गति सरल आवर्त गति (SHM) नहीं है; केवल एेसी आवर्त गति जिसमें विस्थापन-समय का फलन ज्यावक्रीय है, सरल आवर्त गति होती है। चित्र 14.4 में सरल आवर्त गति करते हुए एक कण की समय के असतत् मानों पर स्थिति दर्शायी गई है। प्रत्येक समय अन्तराल T/4 है जहाँ T गति का आवर्तकाल है।
![1493.png]()
चित्र 14.4 सरल आवर्त गति करते हुए समय के असतत मान t = 0. T/4, T/2, 3T/4, T, 5T/4 पर कण की स्थिति। वह समय जिसके पश्चात गति की पुनरावृत्ति होती है, T कहलाती है। प्रारंभिक स्थिति (t = 0) आपकुछ भी चुनें, T का मान स्थिर रहेगा। कण की चाल शून्य विस्थापन (x = 0 पर) पर अधिकतम तथा गति की चरम स्थितियों पर शून्य होती है।
विस्थापन
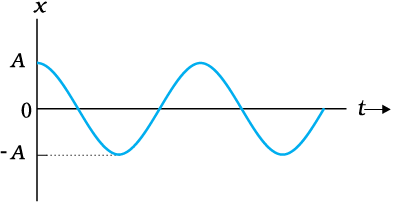
![1533.png]() चित्र 14.5 सरल आवर्त गति करते हुए कण का विस्थापन समय के सतत फलन के रूप में
चित्र 14.5 सरल आवर्त गति करते हुए कण का विस्थापन समय के सतत फलन के रूप में
चित्र 14.5 में x के साथ t का ग्राफ आलेखित है जो समय के सतत फलन के रूप में कण के विस्थापन का मान देती है। राशियाँ A, ω तथा φ जो दी गई आवर्त गति की विशेषता बताती हैं, के मानक नाम हैं, जैसा कि चित्र 14.6 में संक्षिप्त किया गया है। आइए, इन राशियों को हम समझें।
x (t) : विस्थापन x, समय t के फलन के रूप में
A : आयाम
ω : कोणीय आवृत्ति
ωt + φ : कला (समय पर आश्रित)
φ : कला स्थिरांक
विस्थापन
A : आयाम
ω : कोणीय आवृत्ति
ωt + φ : कला (समय पर आश्रित)
φ : कला स्थिरांक
चित्र 14.6 समीकरण (14.4) में दिए मानक संकेतों का अर्थ
SHM का आयाम A, कण के अधिकतम विस्थापन का परिमाण होता है। [ध्यान दें, व्यापकीकृकता के बिना किसी नुकसान के, A को धनात्मक लिया जा सकता है]। चूंकि समय का कोज्या फलन +1 से –1 के बीच विचरण करता है, इसलिए विस्थापन चरम स्थिति +A से –A के बीच विचरण करेगा। दो सरल आवर्त गतियों के ω तथा φ समान, लेकिन आयाम अलग हो सकते हैं, जैसा कि चित्र 14.7(a) में दिखाया गया है।
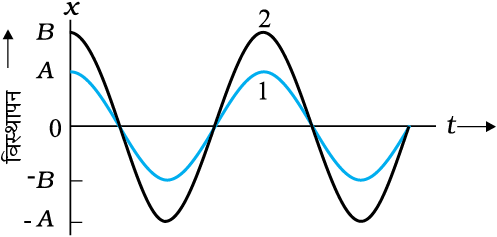
चित्र 14.7 (a) समीकरण (14.4) से प्राप्त φ = 0 पर समय के फलन के रूप में विस्थापन का आलेख । वक्र 1 और 2 दो भिन्न आयामों A तथा A के लिए हैं ।
चित्र 14.7 (a) समीकरण (14.4) से प्राप्त φ = 0 पर समय के फलन के रूप में विस्थापन का आलेख । वक्र 1 और 2 दो भिन्न आयामों A तथा A के लिए हैं ।
जब किसी दिए गए आवर्त गति का आयाम A नियत है, किसी समय t पर कण की गति की आवस्था को कोज्या फलन के कोणांक (ωt + φ) के द्वारा दर्शाया जाता है। समय पर आश्रित रहने वाली इस राशि (ωt + φ) को गति की कला कहते हैं। t = 0 पर कला का परिमाण φ होता है जिसे कला नियतांक (अथवा कला-कोण) कहते हैं। यदि आयाम ज्ञात हो तो t = 0 पर के विस्थापन मान से φ ज्ञात किया जा सकता है। दो सरल आवर्त गतियों के A तथा ω समान लेकिन कला-कोण φ विभिन्न हो सकते हैं, जैसा कि चित्र 14.7 (b) में दर्शाया गया है।
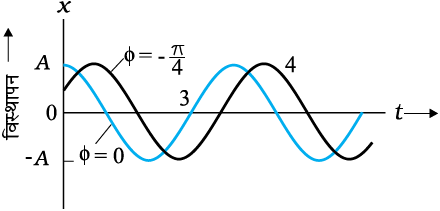
चित्र 14.7(b) समीकरण (14.4) से प्राप्त (x-t) आलेख । वक्र 3 तथा 4 क्रमश: कला कोणφ = 0 rad तथा φ = − π /4 rad के लिए हैं । दोनों आलेखों के लिए आयाम A समान है।
अंतत: राशि ω को गति के आवर्तकाल T से संबंधित देखा जा सकता है। सरलता के लिए समीकरण (14.4) में φ = 0 rad लेने पर हमें प्राप्त होता है–
x(t) = A cos ωt (14.5)
चूंकि गति का आवर्तकाल T है, x(t) का मान x(t+T) के समान होगा। अर्थात्,
A cos ωt = A cos ω(t+T) (14.6)
अब चूँकि 2π आवर्त काल वाला कोज्या फलन आवर्ती है, अर्थात् जब कोणांक 2π रेडियन से परिवर्तित होता है, यह प्रथम बार स्वयं की पुनरावृत्ति करता है। अत:
ω(t+T) = ωt + 2π
अर्थात् ω = 2π/T (14.7)
ω को SHM की कोणीय आवृत्ति कहते हैं। इसका S.I. मात्रक रेडियन प्रति सेकेंड है। चूंकि दोलन की आवृत्ति मात्र 1/T है, ω दोलन की आवृत्ति का 2π गुणा होता है। दो सरल आवर्त गति के A तथा φ समान, किन्तु ω विभिन्न हो सकते हैं, जैसा कि चित्र 11.8 में देखा जा सकता है। इस आलेख में वक्र b का आवर्त काल वक्र a के आवर्त काल का आधा है जबकि इसकी आवृत्ति वक्र a की आवृत्ति की दुगुनी है।
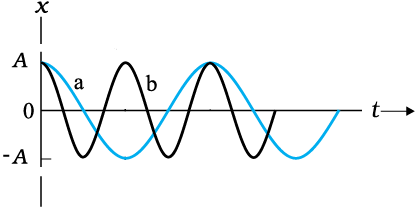
चित्र 14.8 समीकरण (14.4) के φ = 0 rad पर दो भिन्न आवर्तकालों के लिए आलेख।
उदाहरण 14.3 समय के निम्नलिखित फलनों में से कौन (a) सरल आवर्त गति तथा (b) आवर्ती गति को निरूपित करता है परंतु सरल आवर्त गति नहीं ? प्रत्येक का आवर्तकाल निकालिए ।
(a) sin ωt – cos ωt
(b) sin2 ωt
हल (a) sin ωt – cos ωt
= sin ωt – sin (π/2 – ωt)
= 2 cos (π/4) sin (ωt – π/4)
= 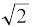 sin (ωt – π/4)
sin (ωt – π/4)
यह फलन सरल आवर्त गति का निरूपण करता है, जिसका आवर्तकाल T = 2π/ω तथा कला-कोण (–π/4) rad अथवा
(7π/4) rad है ।
(b) sin2 ωt = ½ – ½ cos 2 ωt
यह फलन आवर्ती है, जिसका आवर्तकाल T=π/ω है । ये संतुलन बिंदु शून्य के बदले ½ पर सरल आवर्त गति को भी दर्शाता है।
14.4 सरल आवर्त गति तथा एकसमान वर्तुल गति
इस अनुभाग में हम देखेंगे कि वृत्त के व्यास पर एकसमान वर्तुल गति का प्रक्षेप सरल आवर्त गति करता है। एक सरल प्रयोग (चित्र 14.9) इस संबंध की सजीव कल्पना करने में हमारी मदद करता है। एक गेंद को किसी डोरी के सिरे से बाँधकर क्षैतिज तल में उसे किसी निश्चित बिंदु के परित: अचर कोणीय चाल से गति कराइये। तब गेंद क्षैतिज तल में एकसमान वर्तुल गति करेगी। अपनी आंख को गति के तल पर केन्द्रित रखते हुए तिरछी ओर से अथवा सामने से गेंद का अवलोकन कीजिए। घूर्णन बिन्दु को यदि हम मध्य बिन्दु मानें तो यह गेंद एक क्षैतिज तल के अनुदिश इधर-उधर गति करती हुई प्रतीत होगी। विकल्पत: आप गेंद की परछाईं वृत्त के तल के लंबवत् किसी दीवार पर भी देख सकते हैं। इस प्रक्रिया में हम जो कुछ अवलोकन करते हैं, वास्तव में वह हमारी दृष्टि की दिशा के अभिलंबवत् व्यास पर बॉल की गति होती है।
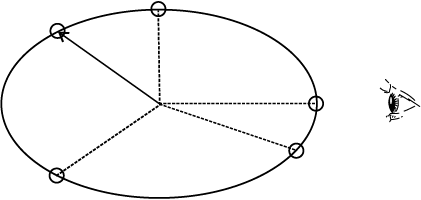
चित्र 14.9 किनारे से देखे गए एक समतल में बॉल की वृत्तीय गति सरल आवर्त गति है।
चित्र 14.10 इसी स्थिति को गणितीय रूप में वर्णन करता है। मान लीजिए कोई कण P, त्रिज्या A के एक वृत्त पर कोणीय चाल ω से एकसमानीय गति कर रहा है। घूमने की दिशा वामावर्त है। कण की प्रारंभिक ‘स्थिति सदिश’ अर्थात् t = 0 पर सदिश  , धनात्मक x अक्ष के साथ कोण φ बनाता है।
, धनात्मक x अक्ष के साथ कोण φ बनाता है।

चित्र 14.10
t समय के बाद यह अगला कोण ωt पूरा करता है और इसकी ‘स्थिति सदिश’ +ve x-अक्ष के साथ एक कोण ωt+φ बनाती है। अब x-अक्ष पर ‘स्थिति सदिश’ OP के प्रक्षेप पर विचार करें। यह OP′ होगा। जब कण P वृत्त पर गति करता है तो x-अक्ष पर P′ की स्थिति प्रदत्त की जाती है
x(t) = A cos (ωt + φ)
जो कि SHM का पारिभाषिक समीकरण है। यह दर्शाता है कि यदि P किसी वृृत्त पर एकसमानीय गति करता है तो इसका प्रक्षेप P′ वृत्त के व्यास पर सरल आवर्त गति करता है। कण P तथा वह वृत्त जिसपर यह गति करता है उसे क्रमश: संदर्भ कण तथा संदर्भ वृत्त कहते हैं।
P की गति के प्रक्षेप को हम किसी भी व्यास, जैसे कि y-अक्ष पर ले सकते हैं। इस स्थिति में y-अक्ष पर P′ का विस्थापन y(t) होगा।
y(t) = A sin (ωt + φ)
यह भी एक SHM है जिसका आयाम x-अक्ष पर प्रक्षेप के समान ही है, लेकिन इसकी कला π/2 से भिन्न है।
वर्तुल गति तथा SHM के बीच इस संबंध के बावजूद रैखिक सरल आवर्ती गति में किसी कण पर लगता हुआ बल किसी कण को एकसमान वर्तुल गति में रखने के लिए आवश्यक अभिकेन्द्रीय बल से काफी अलग है।
उदाहरण 14.4 नीचे दिये चित्र में दो वर्तुल गतियाँ दर्शायी गई हैं । इन चित्रों पर वृत्त की त्रिज्या, घूर्णन का आवर्तकाल, आरंभिक स्थिति तथा घूर्णन की दिशा अंकित की गई है । प्रत्येक स्थिति में घूर्णी कण P के त्रिज्या सदिश के x-प्रक्षेप की सरल आवर्त गति प्राप्त कीजिए ।
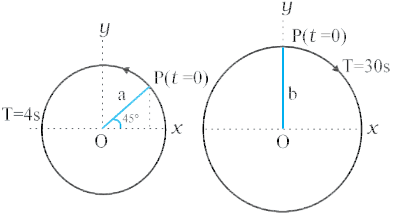
हल
(a) t = 0 पर, OP x-अक्ष (की धनात्मक दिशा) से 45° = π/4 rad का कोण बनाता है । t समय पश्चात् यह वामावर्त दिशा में 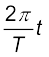 rad कोण पूरा करता है, तथा
rad कोण पूरा करता है, तथा
x-अक्ष से 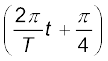 rad कोण बनाता है । समय t पर x-अक्ष पर OP के प्रक्षेप इस प्रकार व्यक्त करते हैं :
rad कोण बनाता है । समय t पर x-अक्ष पर OP के प्रक्षेप इस प्रकार व्यक्त करते हैं :
x(t) = A cos 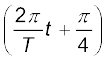
T = 4 s के लिए
x(t) = A cos 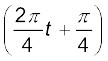
जो कि A आयाम, 4 s आवर्तकाल तथा प्रारंभिक कला* 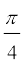 की सरल आवर्त गति है ।
की सरल आवर्त गति है ।
(b) इस स्थिति में t = 0 पर, OP x-अक्ष से 90° = π/2
का कोण बनाता है । यह दक्षिणावर्त दिशा में 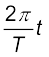 कोण पूरा करता है, तथा x-अक्ष से
कोण पूरा करता है, तथा x-अक्ष से 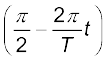 कोण बनाता है । समय t पर x-अक्ष पर OP प्रक्षेप को इस प्रकार व्यक्त करते हैं:
कोण बनाता है । समय t पर x-अक्ष पर OP प्रक्षेप को इस प्रकार व्यक्त करते हैं:
x(t) = B cos 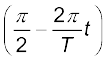
= B sin 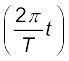
T = 30 s के लिए,
x(t) = B sin 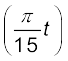
इसे इस प्रकार x(t) = B cos 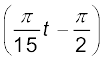 लिखकर इसकी समीकरण (14.4) से तुलना करने पर हमें यह ज्ञात होता है कि यह B आयाम, 30 s आवर्तकाल तथा
लिखकर इसकी समीकरण (14.4) से तुलना करने पर हमें यह ज्ञात होता है कि यह B आयाम, 30 s आवर्तकाल तथा
प्रारंभिक कला 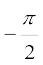 rad की सरल आवर्त गति को निरूपित करता है ।
rad की सरल आवर्त गति को निरूपित करता है ।
* कोण की प्राकृतिक इकाई रेडियन है जिसे त्रिज्या की चाप के अनुपात द्वारा परिभाषित करते हैं। कोण अदिश राशि है। जब हम π को उसके बहुगुण या अपवर्तक लिखते हैं तो रेडियन इकाई का उल्लेख करना आवश्यक नहीं है। रेडियन और डिग्री के बीच रूपांतरण, मीटर, सेंटीमीटर या मील के बीच रूपांतरण के समरूप नहीं है। यदि किसी त्रिकोणमितीय फलन के कोणांक में इकाई नहीं दिया है तो मानना चाहिए कि इकाई रेडियन है। यदि कोण की इकाई डिग्री है तो उसको स्पष्टत: दर्शाना होगा। उदाहरण के लिए sin(150) का अर्थ है 15 डिग्री का sin। परन्तु sin (15) का तात्पर्य 15 रेडियन का sin है। आगे से 'rad' इकाई नहीं दर्शाया जाएगा। जब भी कोण का अंकिक मान बिना इकाई के दिया हुआ है तो इकाई वास्तव में रेडियन है।
14.5 सरल आवर्त गति में वेग तथा त्वरण
एकसमानीय वर्तुल गति करते हुए किसी कण की चाल इसकी कोणीय चाल गुणा वृत्त की त्रिज्या A के बराबर होती है।
v = ω A (14.8)
किसी समय t पर, वेग v की दिशा वृत्त के उस बिन्दु पर स्पर्शज्या के अनुदिश होती है जहाँ कण उस क्षण पर अवस्थित रहता है। चित्र 14.11 की ज्यामिति से यह स्पष्ट है कि समय t पर प्रक्षेप कण P′ का वेग है
v(t) = –ω A sin (ωt + φ) (14.9)
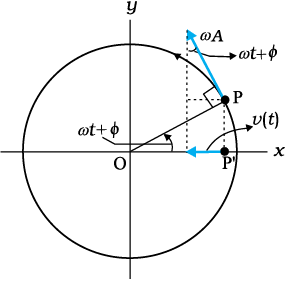
यहाँ ऋणात्मक चिह्न यह दर्शाता है कि v(t) की दिशा x-अक्ष की धनात्मक दिशा के विपरीत है। समीकरण (14.9), सरल आवर्त गति करते हुए कण की तात्क्षणिक वेग प्रदत्त करता है, जहाँ विस्थापन समीकरण (14.4) से प्राप्त होता है। निस्संदेह इस समीकरण को हम बिना ज्यामितीय कोणांक के भी प्राप्त कर सकते हैं।
इसके लिए सीधे समीकरण (14.4) को t के सापेक्ष अवकलित करते हैं:
v(t) = 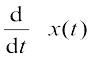 (14.10)
(14.10)
सरल आवर्त गति करते हुए कण के तात्क्षणिक त्वरण को प्राप्त करने के लिए संदर्भ वृत्त की विधि को इसी प्रकार प्रयोग में लाया जा सकता है।
हमें ज्ञात है कि एकसमानीय वर्तुल गति में कण के अभिकेन्द्रीय त्वरण का परिमाण v2/A अथवा ω2A है तथा यह केन्द्र की ओर निर्दिष्ट है, अर्थात इसकी दिशा PO की ओर है। प्रक्षेप कण P′ का तात्क्षणिक त्वरण तब होगा (चित्र 14.12 देखें)
a(t) = – ω2A cos (ωt + φ)
a(t) = – ω2x (t) (14.11)
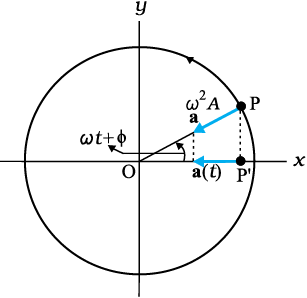
चित्र 14.12 बिंदु P' का त्वरण a(t), संदर्भ बिंदु P के त्वरण a का प्रक्षेप होता है ।
समीकरण (14.11) सरल आवर्त गति करते हुए कण का त्वरण व्यक्त करता है। इसी समीकरण को, समीकरण (14.9) से प्रदत्त वेग v(t) को समय के सापेक्ष अवकलित करके सीधे प्राप्त किया जा सकता है:
a(t) = 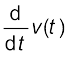 (14.12)
(14.12)
समीकरण (14.11) से हम एक महत्त्वपूर्ण परिणाम पर ध्यान देते हैं कि सरल आवर्त गति में कण का त्वरण इसके विस्थापन के अनुक्रमानुपाती होता है। x(t) > 0 के लिए a(t) < 0 तथा x(t) < 0 के लिए a(t) > 0 होता है। अत: –A तथा A के बीच x का मान कुछ भी हो, त्वरण a(t) हमेशा केन्द्र की ओर निर्दिष्ट रहता है।
सरलता के लिए हम φ = 0 रख कर x(t), v(t) और a(t) के व्यंजक को लिखते हैं
x(t)=A cos ωt, v(t)=–ωA sin ωt, a(t)=–ω2A cos ωt
संगत आलेख को चित्र 14.13 में दर्शाया गया है। सभी राशियाँ समय के साथ ज्यावक्रीय विचरण करती हैं; केवल उनकी उच्चिष्ठ (maxima) में अन्तर होता है तथा उनके आलेखों में कलाओं की भिन्नता होती है। x, –A तथा A के मध्य विचरण करता है; v(t), –ωA तथा ωA के मध्य विचरण करता है एवं
a(t), –ω2A तथा ω2A के मध्य विचरण करता है। विस्थापन आलेख के सापेक्ष, वेग आलेख की कला में π/2 का अंतर है तथा त्वरण आलेख की कला में π का अंतर है।

चित्र 14.13 सरल आवर्त गति में किसी कण का विस्थापन, वेग तथा त्वरण का आवर्तकाल T समान होता है, लेकिन उनकी कलाओं में भिन्नता होती है।
उदाहरण 14.5 : कोई पिंड निम्नलिखित समीकरण के अनुसार सरल आवर्त गति से दोलन करता है,
x = (5.0 m) cos [(2π rad/s) t + π/4]
t = 1.5 s पर, पिंड का (a) विस्थापन, (b) वेग तथा (c) त्वरण परिकलित कीजिए ।
हल पिंड की कोणीय आवृत्ति ω = 2π s–1 तथा इसका आवर्तकाल T = 1 s
t = 1.5 s पर,
(a) विस्थापन = (5.0 m) cos [(2π s–1) × 1.5 s + ]
]
= (5.0 m) cos [(3π + 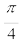 )]
)]
= – 5.0 × 0.707 m
= – 3.535 m
(b) समीकरण (14.9) का उपयोग करने पर पिंड का वेग
= – (5.0 m) (2π s–1) sin [(2π s–1) ×
(1.5 s + ) ]
) ]
= – (5.0 m) (2π s–1) sin [(3π +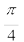 )]
)]
= 10π × 0.707 m s–1
= 22 m s–1
(c) समीकरण (14.10) का उपयोग करने पर पिंड का त्वरण
= – (2π s–1)2 × विस्थापन
= – (2π s–1)2 × (–3.535 m)
= 140 m s–2 °
14.6 सरल आवर्त गति के लिए बल का नियम
न्यूटन की गति के दूसरे नियम तथा आवर्त गति करते किसी कण के लिए त्वरण के व्यंजक (समीकरण 14.11) प्रयोग करने पर
F (t) = ma
= – mω2x (t)
अथवा, F (t) = – k x(t) (14.13)
यहाँ k = mω2 (14.14a)
अथवा, 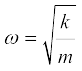 (14.14b)
(14.14b)
त्वरण की तरह, बल हमेशा माध्य स्थिति की ओर निर्दिष्ट रहता है – इसलिए यह सरल आवर्त गति में प्रत्यानयन बल कहलाता है। अब तक की गई चर्चाओं को संक्षिप्त करने पर हम पाते हैं कि सरल आवर्त गति को दो प्रकार से परिभाषित किया जा सकता है, या तो विस्थापन के लिए समीकरण (14.4) द्वारा अथवा समीकरण (14.13) द्वारा जो कि बल के नियम प्रदान करता है। समीकरण (14.4) से समीकरण (14.13) प्राप्त करने के लिए हमें इसे दो बार अवकलित करना पड़ा। इसी प्रकार बल के नियम, समीकरण (14.13) को दो बार समाकलित करने पर हमें वापस समीकरण (14.4) प्राप्त हो सकता है।
ध्यान दीजिए कि समीकरण (14.13) में बल x(t) के रैखिकीय समानुपाती है। अत: इस तरह के बल के प्रभाव से दोलन करते हुए किसी कण को रैखिक आवर्ती दोलक कहते हैं। वास्तव में, बल के व्यंजक में x2, x3 आदि के समानुपाती कुछ पद हो सकते हैं। अत: इन्हें अरैखिक दोलक कहते हैं।
उदाहरण 14.6 कमानी स्थिरांक k की दो सर्वसम कमानियाँ M संहति के किसी गुटके तथा स्थिर आधारों से चित्र 14.14 में दर्शाए गए अनुसार जुड़ी हुई हैं ।
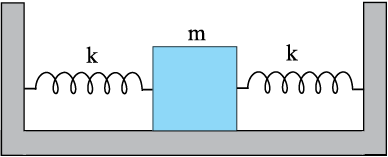
यह दर्शाइए कि जब गुटके को अपनी साम्यावस्था की स्थिति से किसी ओर विस्थापित किया जाता है, तब यह सरल आवर्त गति करता है । दोलन का आवर्तकाल ज्ञात कीजिए ।
हल मान लीजिए गुटके को अपनी साम्यावस्था की स्थिति से दाईं ओर x दूरी तक विस्थापित किया जाता है । इसे चित्र 14.15 में दिखाया गया है। इस स्थिति में बाईं ओर की कमानी x लंबाई द्वारा दीर्घित हो जाती है तथा दाईं ओर की कमानी भी उतनी ही लंबाई द्वारा संपीडित हो जाती है । तब गुटके पर कार्यरत बल
F1 = – k x (कमानी द्वारा बाईं ओर आरोपित बल, जो गुटके को माध्य स्थिति की ओर खींचने का प्रयास करता है ।)
F2 = – k x (कमानी द्वारा दाईं ओर आरोपित बल, जो गुटके को माध्य स्थिति की ओर धकेलने का प्रयास करता है ।)
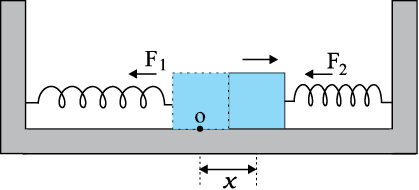
चित्र 14.15
तब गुटके पर आरोपित नेट बल,
F = –2 kx
अत:, गुटके पर आरोपित बल विस्थापन के अनुक्रमानुपाती तथा माध्य-स्थिति की ओर निर्दिष्ट होता है; इसलिए, गुटके की गति सरल आवर्त गति है । इसमें दोलन का आवर्तकाल,
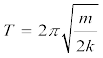 है । °
है । °
14.7 सरल आवर्त गति में ऊर्जा
सरल आवर्त गति करते हुए कण की स्थितिज तथा गतिज ऊर्जाएँ दोनों शून्य तथा अपने अधिकतम परिमाण के बीच विचरण करती हैं।
अनुभाग 14.5 में हमने देखा है कि सरल आवर्त गति करते किसी कण का वेग समय का आवर्ती फलन होता है । विस्थापन की चरम स्थितियों में यह शून्य होता है । अत: एेसे कण की गतिज ऊर्जा (K), जिसे हम इस प्रकार परिभाषित करते हैं,
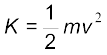
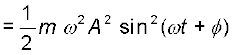
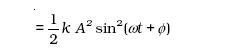 (14.15)
(14.15)
भी समय का आवर्ती फलन होती है जिसका परिमाण विस्थापन अधिकतम होने पर शून्य तथा कण के माध्य स्थिति पर होने पर अधिकतम होता है । ध्यान दीजिए, चूँकि गतिज ऊर्जा K में, v के चिह्न का कोई अर्थ नहीं होता, अत: K का आवर्तकाल T/2 है।
सरल आवर्त गति करने वाले किसी कण की स्थितिज ऊर्जा कितनी होती है ? अध्याय 6 में हमने देखा है कि स्थितिज ऊर्जा की संकल्पना केवल संरक्षी बलों के लिए ही होती है । कमानी बल F = – kx एक संरक्षी बल है जिससे स्थितिज ऊर्जा संयुक्त होती है ।
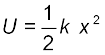 (14.16)
(14.16)
अत: सरल आवर्त गति करते किसी कण की स्थितिज ऊर्जा,
U(x) = 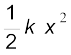
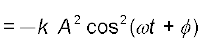 (14.17)
(14.17)
इस प्रकार, सरल आवर्त गति करते किसी कण की स्थितिज ऊर्जा भी आवर्ती होती है जिसका आवर्तकाल T/2 होता है, यह ऊर्जा माध्य स्थिति में शून्य तथा चरम विस्थापनों पर अधिकतम होती है । अत: समीकरणों (14.15) तथा (14.17) से हमेें निकाय की कुल ऊर्जा E, प्राप्त होती है,
E = U + K
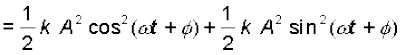
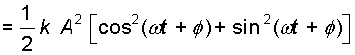
त्रिकोणमिती की सामान्य तादात्मक को प्रयोग करने पर कोष्ठक में दी गई राशि का मान एक प्राप्त होता है। अत:
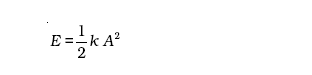 14.18)
14.18)
जैसा कि संरक्षी बलों के अधीन गतियों के लिए आशा की जाती है किसी भी सरल आवर्ती दोलक की कुल यांत्रिक ऊर्जा कालाश्रित नहीं होती । किसी रैखिक सरल आवर्ती दोलक की गतिज तथा स्थितिज ऊर्जाओं की समय और विस्थापन पर निर्भरता चित्र 14.16 में दर्शायी गई है ।
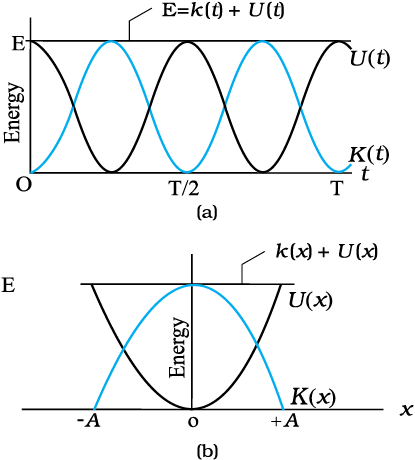
चित्र 14.16 गतिज ऊर्जा, स्थितिज ऊर्जा तथा कुल ऊर्जा समय के फलन के रूप में [(a) में दर्शित] तथा सरल आवर्त गति करते हुए कण का विस्थापन [(b) में दर्शित]। गतिज ऊर्जा तथा स्थितिज ऊर्जा दोनों आवर्तकाल T/2 के पश्चात पुनरावृत्ति करते हैं। t तथा x के सभी मानों के लिए कुल ऊर्जा नियत रहती है।
ध्यान दीजिए कि सरल आवर्त गति में स्थितिज तथा गतिज दोनों ऊर्जाएँ चित्र 14.16 में हमेशा धनात्मक मानी गई हैं। निस्सन्देह गतिज ऊर्जा कभी ऋणात्मक नहीं हो सकती, क्योंकि यह चाल के वर्ग के समानुपाती होती है। स्थितिज ऊर्जा के समीकरण में गुप्त नियतांक के चयन के कारण स्थितिज ऊर्जा धनात्मक होती है। गतिज तथा स्थितिज दोनों ऊर्जाएँ SHM के प्रत्येक आवर्तकाल में दो बार अपनी चरम स्थिति को प्राप्त करती हैं। x = 0 के लिए, ऊर्जा गतिज है; चरम स्थिति x = ± A पर यह पूरे तौर पर स्थितिज ऊर्जा है। इन सीमाओं के बीच गति करते हुए, स्थितिज ऊर्जा के घटने से गतिज ऊर्जा बढ़ती है तथा गतिज ऊर्जा के घटने से स्थितिज ऊर्जा बढ़ती है।
उदाहरण 14.7 1kg संहति के किसी गुटके को एक कमानी से बाँधा गया है । कमानी का कमानी स्थिरांक 50N m–1 है । गुटके को उसकी साम्यावस्था की स्थिति x = 0 से t = 0 पर किसी घर्षणहीन पृष्ठ पर कुछ दूरी x = 10 cm तक खींचा जाता है । जब गुटका अपनी माध्य-स्थिति से 5 cm दूर है, तब उसकी गतिज, स्थितिज तथा कुल ऊर्जाएँ परिकलित कीजिए ।
हल
गुटका सरल आवर्त गति करता है । समीकरण [14.14(b)] से इसकी कोणीय आवृत्ति
ω = 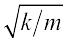
= 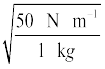
= 7.07 rad s–1 होगी,
तब किसी समय t पर इसका विस्थापन
x(t) = 0.1 cos (7.07t) होगा ।
अत:, जब कण अपनी माध्य स्थिति से 5 cm दूर है, तब
0.05 = 0.1 cos (7.07t)
अथवा cos (7.07t) = 0.5,
अत:, sin (7.07t) 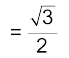 = 0.866
= 0.866
तब गुटके का x = 5 cm पर वेग = 0.1× 7.07 × 0.866m s–1
= 0.61m s–1

यह ऊर्जा 5 cm विस्थापन पर दोनों ऊर्जाओं के योग के बराबर ही है । यह ऊर्जा संरक्षण सिद्धांत के अनुकूल है। °
14.8 सरल आवर्त गति निष्पादित करने वाले कुछ निकाय
निरपेक्षत: शुद्ध सरल आवर्त गति के कोई भौतिक उदाहरण नहीं हैं । अपने व्यावहारिक जीवन में हम एेसे निकाय देखते हैं जो किन्ही निश्चित परिस्थितियों में लगभग सरल आवर्त गति करते हैं । इस अनुभाग में इसके पश्चात् हम एेसे ही कुछ निकायों की गतियों की चर्चा करेंगे ।
14.8.1 कमानी के दोलन
सरल आवर्त गति का सरलतम प्रेक्षण योग्य उदाहरण, चित्र 14.17 की भाँति, किसी कमानी के एक सिरे से जुड़े m संहति के किसी गुटके के छोटे दोलन होते हैं । कमानी का दूसरा सिरा एक दृढ़ दीवार से जुड़ा होता है । गुटके को किसी समतल घर्षणरहित पृष्ठ पर रखते हैं । यदि गुटके को एक ओर थोड़ा खींचकर छोड़ दें, तो वह किसी माध्य स्थिति पर इधर-उधर गति करने लगता है । मान लीजिए x = 0 गुटके के केंद्र की उस स्थिति को सूचित करता है जब कमानी विश्रांत अवस्था में है । चित्र में अंकित स्थितियाँ -A तथा +A माध्य स्थिति से बाईं तथा दाईं ओर के अधिकतम विस्थापनों को इंगित करती हैं । हम पहले ही पढ़ चुके हैं कि कमानियों में विशेष गुण होते हैं, जिन्हें सर्वप्रथम एक अंग्रेज भौतिकीवेत्ता रॉबर्ट हुक ने खोजा था । उन्होंने दर्शाया कि जब एेसे किसी निकाय को विरूपित किया जाता है, तो उस पर एक प्रत्यानयन बल लगता है, जिसका परिमाण विरूपण अथवा विस्थापन के अनुक्रमानुपाती होता है तथा यह विपरीत दिशा में कार्य करता है । इसे हुक का नियम (अध्याय 9) कहते हैं । यह नियम तब भलीभाँति लागू होता है जब विस्थापन कमानी की लंबाई की तुलना में काफी कम होते हैं । किसी समय t पर, यदि गुटके का उसकी माध्य स्थिति से विस्थापन x है, तो गुटके पर कार्यरत बल F इस प्रकार व्यक्त किया जाता है,
F (x) = – kx (14.19)
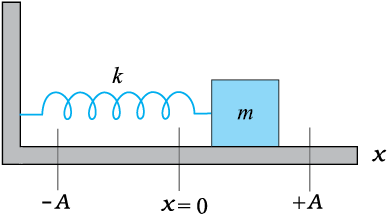
चित्र 14.17 एक रैखिक सरल आवर्ती दोलक जिसमें m संहति का एक गुटका किसी कमानी से जुड़ा है । गुटका एक घर्षणरहित पृृष्ठ पर गति करता है । एक बार किसी ओर खींचकर छोड़ने पर गुटका सरल आवर्त गति करता है ।
यहाँ k आनुपातिकता स्थिरांक है जिसे कमानी-स्थिरांक कहते हैं, तथा इसका मान कमानी के प्रत्यास्थ गुणों से ज्ञात किया जाता है । किसी दृढ़ कमानी के लिए k का मान अधिक तथा मृदु कमानी के k का मान कम होता है । समीकरण (14.19), सरल आवर्त गति के लिए बल-नियम के समान है, अत: यह निकाय सरल आवर्त गति करता है । समीकरण (14.14) से हमें यह संबंध प्राप्त होता है,
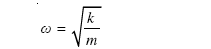 (14.20)
(14.20)
तथा दोलक का आवर्तकाल, T इस प्रकार व्यक्त किया जाता है,
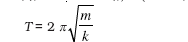 (14.21)
(14.21)
दृढ़ कमानियों के k (कमानी स्थिरांक) के मान ज्यादा होते हैं। दृढ़ कमानी से जुड़े लघु संहति के एक गुटके की दोलन आवृत्ति समीकरण (14.20) के अनुसार ज्यादा होगी, जैसा की भौतिक रूप से अपेक्षित है।
उदाहरण 14.8 500N m–1 कमानी स्थिरांक की किसी कमानी से 5 kg संहति का कोई कॉलर जुड़ा है जो एक क्षैतिज छड़ पर बिना किसी घर्षण के सरकता है । कॉलर को उसकी साम्यावस्था की स्थिति से 10.0cm विस्थापित करके छोड़ दिया जाता है । कॉलर के
(a) दोलन का आवर्तकाल (b) अधिकतम चाल तथा
(c) अधिकतम त्वरण परिकलित कीजिए ।
हल (a) समीकरण (14.21) के अनुसार दोलन का आवर्त काल होता है:
T = 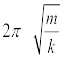
= 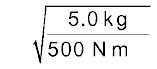 = (2π/10)s
= (2π/10)s
= 0.63 s
(b) सरल आवर्त गति करते कॉलर का वेग इस प्रकार व्यक्त किया जाता है,
v(t)= – A ω sin (ωt + φ)
अत: अधिकतम चाल,
vm = A ω
= 0.1 × 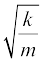
= 0.1 × 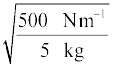
= 1ms–1
और यहाँ x = 0
(c) साम्यावस्था की स्थिति से x(t) विस्थापन पर कॉलर का त्वरण इस प्रकार व्यक्त किया जाता है,
a (t) = – ω2 x(t)
= – 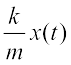
अत: अधिकतम त्वरण
amax = ω2 A
= 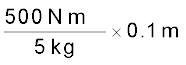
= 10 m s–2
और यह अग्रान्त पर घटित होता है।
14.8.2 सरल लोलक
यह कहा जाता है कि गैलीलियो ने किसी चर्च में एक दोलायमान झाड़फानूस का आवर्तकाल अपनी नाड़ी की स्पंद गति द्वारा मापा था । उसने यह निष्कर्ष निकाला कि झाड़फानूस की गति आवर्ती है । यह निकाय लोलक का ही एक प्रकार होता है । लगभग 1 मीटर लंबे न खिंचने वाले धागे को लेकर उसके एक सिरे से पत्थर का टुकड़ा बाँधकर आप भी अपना एक लोलक बना सकते हैं । अपने लोलक को किसी उचित टेक से बाँधकर इस प्रकार लटकाइए कि वह स्वतंत्रतापूर्वक दोलन कर सके । पत्थर के टुकड़े को कम दूरी तक विस्थापित करके छोड़ दीजिए । पत्थर इधर-उधर गति करने लगता है । पत्थर की यह गति आवर्ती होती है जिसका आवर्तकाल लगभग 2 सेकंड होता है।
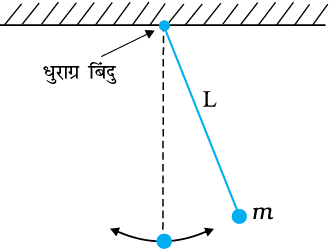
हम यह स्थापित करेंगे कि मध्यमान स्थिति से लघु विस्थापनों के लिए इस लोलक की आवर्त गति सरल आवर्त गति होती है। किसी एेसे सरल लोलक पर विचार कीजिए जिसमें m द्रव्यमान का कोई लघु आमाप का गोलक L लम्बाई के द्रव्यमानहीन तथा न खि्ांचने योग्य डोरी के एक सिरे से बंधा हो। डोरी का दूसरा सिरा किसी दृढ़ टेक से जुड़ा है। गोलक इस ऊर्ध्वाधर दृढ़ टेक से होकर जाने वाली रेखा के अनुदिश तल में दोलन करता है। यह व्यवस्था चित्र 14.18(a) द्वारा दर्शाई गई है। चित्र 14.18 (b) में दोलक पर कार्यरत बल प्रदर्शित किए गए हैं जो एक प्रकार का बल-निर्देशक आरेख है।
(a)
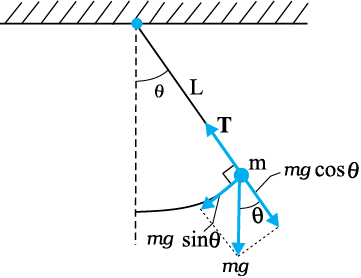
चित्र 14.18 (a) माध्य स्थिति के सापेक्ष दोलन करता कोई सरल लोलक, (b) त्रिज्य बलT–mg cosθ अभिकेन्द्र बल प्रदान करता है परंतु धुराग्र के सापेक्ष इसका कोई बल-आघूर्ण नहीं होता। स्पर्श रेखीय बल mg sinθ प्रत्यानयन बल प्रदान करता है।
माना कि डोरी ऊर्ध्वाधर से θ कोण बनाती है। जब गोलक माध्य स्थिति में होता है तो θ = 0
गोलक पर केवल दो बल कार्यरत हैं: डोरी की लंबाई के अनुदिश तनाव T तथा गुरुत्व के कारण ऊर्ध्वाधर बल (=mg)। हम बल mg का वियोजन डोरी के अनुदिश घटक mg cos θ तथा उसके लंबवत् mg sin θ के रूप में कर सकते हैं। चूँकि गोलक की गति L त्रिज्या के किसी वृत्त के अनुदिश है जिसका केन्द्र धुराग्र बिन्दु पर स्थित है, अत: गोलक का कोई त्रिज्य त्वरण (ω2L) तथा साथ ही स्पर्शरेखीय त्वरण होगा। स्पर्शरेखीय त्वरण का कारण वृत्त के चाप के अनुरूप गति का एकसमान न होना है। त्रिज्य त्वरण नेट त्रिज्य बल T – mg cosθ के कारण होता है जबकि स्पर्शरेखीय त्वरण mg sinθ के कारण उत्पन्न होता है। धुराग्र के सापेक्ष बल आघूर्ण पर विचार करना अधिक सुविधाजनक होता है क्योंकि तब त्रिज्य बल का आघूर्ण शून्य हो जाता है। इस प्रकार आधार के सापेक्ष बल आघूर्ण τ बल के स्पर्शरेखीय घटक द्वारा ही पूर्णतया प्राप्त होता है।
τ = –L (mg sin θ) (14.22)
यह एक प्रत्यानयन बल आघूर्ण है जो विस्थापन के परिणाम को कम करने का प्रयास करता है; इसी कारण इसे ऋणात्मक चिह्न द्वारा व्यक्त किया गया है। घूर्णी गति के लिए न्यूटन के नियम के अनुसार
τ = I α (14.23)
यहाँ I धुराग्र बिंदु के परित: लोलक का घूर्णी जड़त्व है तथा α उसी बिंदु के परित: कोणीय त्वरण है । इस प्रकार
Iα = –mgL sin θ (14.24)
अथवा 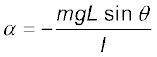 (14.25)
(14.25)
यदि हम यह मानें कि विस्थापन θ छोटा है, तो समीकरण (14.25) को सरल बना सकते हैं । हम जानते हैं कि sin θ को इस प्रकार व्यक्त किया जा सकता है,
sin θ = θ – 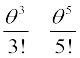 – ...... (14.26)
– ...... (14.26)
यहाँ θ रेडियन में है।
अब यदि θ छोटा है, तो sin θ का सन्निकटन θ द्वारा किया जा सकता है । एेसी परिस्थिति के समीकरण (14.25) को इस प्रकार भी लिख सकते हैं,
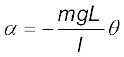 (14.27)
(14.27)
सारणी 14.1 में हमने कोण θ को अंशों में, इसके तुल्यांक रेडियनों में, तथा फलन sin θ के मान सूचीबद्ध किए हैं । सारणी से यह देखा जा सकता है कि θ के 20 अंश तक बड़े मानों के लिए sin θ के मान लगभग वही होते हैं जैसे θ को रेडियनों में व्यक्त करने पर मिलते हैं
सरल आवर्त गति–आयाम कितना छोटा होना चाहिए?
जब आप किसी सरल लोलक का आवर्त काल ज्ञात करने के लिए प्रयोग करते हैं तो आपके अध्यापक आयाम को कम रखने की सलाह देते हैं। परन्तु क्या आपने कभी सोचा है कि यह ‘कम’ कितना कम होना चाहिए? क्या आयाम 5°, 2°, 1°, या 0.5° होना चाहिए या यह 10°, 20°, या 30° भी हो सकता है।
इसकी मात्रा समझने के लिए यह अच्छा होगा कि हम लोलक का आवर्तकाल भिन्न आयामों के लिए ज्ञात करें। परंतु प्रयोग के दौरान आपको ध्यान रखना होगा कि अधिक आयामों की अवस्था में भी लोलक ऊर्ध्वाधर तल में ही दोलन करे। मान लीजिए कम आयाम वाले दोलनों के लिए आवर्तकाल T (0) है। तथा θ आयाम के लिए आवर्तकाल T(θ0) = cT (0), यहाँ c गुणककाल है। यदि आप c और θ0 में ग्राफ खींचे तो इनके विभिन्न मान इस प्रकार होंगे।
θ0 : 20° 45° 50° 70° 90°
c : 1.02 1.04 1.05 1.10 1.18
इस सारणी से स्पष्ट है कि लगभग 20° के आयाम पर आवर्तकाल में त्रुटि लगभग 2%, 50° के आयाम पर 5%, 70% के आयाम पर 10% तथा 90° के आयाम पर 18% है।
प्रयोग से आप कभी भी T (0) नहीं माप सकते। क्योंकि यह शून्य दोलन का सूचक है। सैद्धांतिक रूप से भी θ = 0 पर sin θ , θ के बराबर होता है। θ के अन्य मानों के लिए कुछ त्रुटि तो आ ही जाएगी। यह त्रुटि θ के मान में वृद्धि से बढ़ती है। अत: हमें यह पहले ही निश्चित कर लेना होगा कि त्रुटि की कितनी सीमा होनी चाहिए। वास्तव में कोई भी मापन पूर्ण रूप से त्रुटिरहित नहीं होता है। आपको निम्न प्रश्नों पर भी विचार करना होगा जैसे विराम घड़ी के मान में यथार्थता क्या है? घड़ी के शुरू करने तथा रोकने में आपकी यथार्थता क्या है? आपको पता चलेगा कि इस स्तर पर प्रयोगों में यथार्थता कभी भी 5% या 10% से अधिक नहीं होती। उपरोक्त सारणी से स्पष्ट है कि किसी दोलक के आवर्तकाल में वृद्धि 50° के आयाम पर भी 5% से अधिक नहीं होती है। अत: आप अपने प्रयोगों में लोलक का आयाम 50° या इससे कम रख सकते हैं।
सारणी 14.1 sin θ कोण θ के फलन के रूप में
| θ (अंशों में) | θ (रेडियनों में) | sin θ |
| 0 | 0 | 0 |
| 5 | 0.087 | 0.087 |
| 10 | 0.174 | 0.174 |
| 15 | 0.262 | 0.259 |
| 20 | 0.349 | 0.342 |
गणितीय रूप में समीकरण (14.27) समीकरण (14.11) के तुल्य है, अंतर केवल यह है कि यहाँ चर राशि कोणीय त्वरण है। अत: हमने यह सिद्ध कर दिया है कि θ के लघु मानों के लिए गोलक की गति सरल आवर्त गति है।
समीकरण (14.27) तथा समीकरण (14.11) से हम यह देखते हैं कि
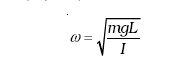
तथा लोलक का आवर्तकाल
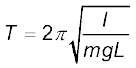 (14.28)
(14.28)
अब क्योंकि लोलक की डोरी द्रव्यहीन है, अत: जड़त्व आघूर्ण I केवल mL2 के तुल्य होगा। इससे हमें सरल लोलक के आवर्त काल के लिए सुपरिचित सूत्र मिल जाता है
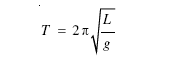 (14.29)
(14.29)
उदाहरण 14.9 उस सरल लोलक की लंबाई क्या है, जो हर सेकंड के बाद टिक करता है ?
हल समीकरण (14.29) से किसी सरल लोलक का आवर्तकाल,

14.9 अवमंदित सरल आवर्त गति
हम जानते हैं कि वायु में दोलन करने वाले किसी सरल लोलक की गति धीरे-धीरे समाप्त हो जाती है । एेसा क्यों होता है ? इसका कारण यह है कि वायु का कर्षण बल तथा टेक पर घर्षण बल लोलक की गति का विरोध करते हैं जिससे धीरे-धीरे इसका ऊर्जा-क्षय होता रहता है । लोलक के इस प्रकार के दोलनों को अवमंदित दोलन कहते हैं । अवमंदित दोलनों में यद्यपि निकाय की ऊर्जा का धीरे-धीरे क्षय होता रहता है तथापि आभासी रूप से दोलन आवर्ती रहते हैं । व्यापक रूप में क्षयकारी बल घर्षण बल ही होते हैं । इस प्रकार के बाह्य बलों का किसी दोलक की गति पर प्रभाव समझने के लिए आइए चित्र 14.19 मेें दर्शाए किसी निकाय पर विचार करें । यहाँ k कमानी-स्थिरांक की किसी प्रत्यास्थ कमानी से जुड़ा कोई गुटका ऊर्ध्वाधर दोलन करता दिखाया गया है। यदि गुटके को नीचे की ओर थोड़ा खींचकर छोड़ दिया जाए तो समीकरण (14.20) के अनुसार यह 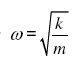 की कोणीय आवृत्ति से दोलन करने लगेगा। तथापि वास्तविक स्थिति में गुटके के परिवेश में स्थित माध्यम (वायु) उसकी गति पर कोई अवमंदन बल आरोपित करेगा तथा गुटका-कमानी निकाय की यांत्रिक ऊर्जा घटती जाएगी। ऊर्जा ह्रास परिवेश माध्यम के (तथा गुटके के भी) ताप के रूप में परिलक्षित होगा (चित्र 14.19)।
की कोणीय आवृत्ति से दोलन करने लगेगा। तथापि वास्तविक स्थिति में गुटके के परिवेश में स्थित माध्यम (वायु) उसकी गति पर कोई अवमंदन बल आरोपित करेगा तथा गुटका-कमानी निकाय की यांत्रिक ऊर्जा घटती जाएगी। ऊर्जा ह्रास परिवेश माध्यम के (तथा गुटके के भी) ताप के रूप में परिलक्षित होगा (चित्र 14.19)।
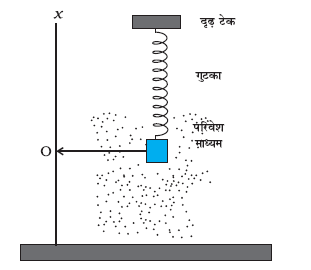
चित्र 14.19 परिवेश में उपस्थित श्यान माध्यम दोलन करते गुटके पर अवमंदन बल आरोपित करता है जिसके कारण वह अंतत: विराम स्थिति में आ जाता है।
अवमंदन बल परिवेश माध्यम की प्रकृति पर निर्भर करेगा। यदि गुटका किसी द्रव में डूबा हो तो अवमंदन बल का परिमाण उच्च होगा तथा ऊर्जा क्षय की दर भी द्रुत होगी। सामान्यत: अवमंदन बल गोलक के वेग के अनुक्रमानुपाती होता है [स्टोक्स के नियम का स्मरण कीजिए, समीकरण (10.19)] तथा यह वेग की दिशा की विपरीत दिशा में कार्यरत होता है। यदि अवमंदन बल को Fd से निरूपित किया जाए तो
Fd = – bv (14.30)
जहाँ धनात्मक स्थिरांक b माध्यम के गुणों (उदाहरण के लिए श्यानता), तथा गुटके की अमाप तथा आकृति पर निर्भर करता है। समीकरण (14.30) सामान्यत: वेग के न्यून मानों के लिए ही वैध है।
जब कमानी से कोई द्रव्यमान m से जोड़कर छोड़ते हैं तो कमानी की लंबाई में कुछ वृद्धि होती है तथा द्रव्यमान एक ऊँचाई पर आकर स्थिर हो जाता है। इस अवस्था को दव्यमान की संतुलन अवस्था कहते हैं जिसे चित्र 14.19 में o से दर्शाया गया है। जब द्रव्यमान को थोड़ा नीचे या ऊपर खींचते हैं तो इस पर एक प्रत्यावस्था (प्रत्यानयन) बल FS = –kx, कार्य करता है।
जहाँ x द्रव्यमान की संतुलन अवस्था से विस्थापन* है। इस प्रकार किसी क्षण द्रव्यमान पर कार्य करने वाला कुल बल होता है F = –kx – bv। यदि किसी क्षण t पर द्रव्यमान का त्वरण a(t) हो तो न्यूटन की गति के द्वितीय नियम को गति की दिशा में लागू करने पर हमें प्राप्त होता है
m a(t) = –k x(t) – b v(t) (14.31)
यहाँ पर हमने सदिश संकेत का प्रयोग नहीं किया है क्योंकि हम एकविमीय गति का वर्णन कर रहे हैं।
v(t) तथा a(t) के लिए x(t) के प्रथम तथा द्वितीय अवकलज क्रमश: प्रतिस्थापित करने पर हमें प्राप्त होता है
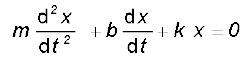 (14.32)
(14.32)
समीकरण (14.32) का हल वेग के अनुपाती अवमंदन बल के प्रभाव में गुटके की गति का वर्णन करता है। इसका हल निम्न रूप में होता है
x(t) = A e–b t/2m cos (ω′t + φ ) (14.33)
जहाँ A अवमंदित दोलन का आयाम तथा ω ′ इसकी कोणीय आवृत्ति होता है
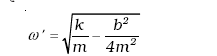 (14.34)
(14.34)
इस फलन में, कोज्या (cos) फलन का आवर्तकाल 2π/ω′ है परंतु यह फलन वस्तुत: आवर्ती नहीं है क्योंकि कारक e–bt/2m समय के साथ निरंतर घटता है । फिर भी यदि एक आवर्तकाल T में घटोतरी कम है, तो समीकरण (14.33) द्वारा निरूपित गति सन्निकट रूप से आवर्ती है ।
समीकरण (14.33) द्वारा दर्शाए गए हल को चित्र 14.20 में दिए अनुसार ग्राफीय निरूपण द्वारा दर्शाया जा सकता है । इसे हम एक कोज्या फलन की भाँति मान सकते हैं जिसका आयाम Ae–bt/2m समय के साथ धीरे-धीरे घटता है ।
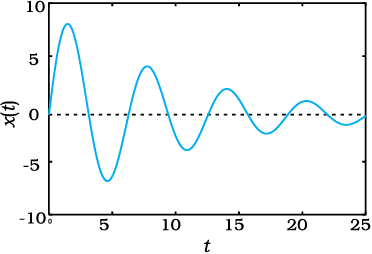
चित्र 14.20 दोलन के घटते हुए आयाम के साथ एक अवमंदित दोलक सन्निकट रूप से आवर्ती होता है। ज्यादा अवमंदन होने पर दोलन द्रुत रूप से क्षीण हो जाती है।
किसी अनवमंदित दोलक की यांत्रिक ऊर्जा 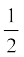 k A2 होती है। यदि दोलक में अवमंदन है, तो आयाम अचर नहीं होता, वरन समय पर निर्भर करता है। यदि अवमंदन लघु है, तो हम आयाम को Ae–bt/2m मानकर उसी व्यंजक का उपयोग कर सकते हैं ।
k A2 होती है। यदि दोलक में अवमंदन है, तो आयाम अचर नहीं होता, वरन समय पर निर्भर करता है। यदि अवमंदन लघु है, तो हम आयाम को Ae–bt/2m मानकर उसी व्यंजक का उपयोग कर सकते हैं ।
E(t) = 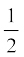 k A2e–bt/m (14.35)
k A2e–bt/m (14.35)
समीकरण (14.35) यह दर्शाता है कि निकाय की कुल ऊर्जा समय के साथ चरघातांकी रूप में घटती है । ध्यान दीजिए, लघु अवमंदन का तात्पर्य यह है कि विमाहीन अनुपात 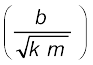 का मान 1 से बहुत कम है ।
का मान 1 से बहुत कम है ।
इस खंड में उल्लिखित समीकरणों में b का मान शून्य रखने पर अवमंदित दोलक में समीकरण आशा के अनुरुप सामान्य दोलक के लिए समीकरणों में परिवर्तित हो जाते हेैं ।
उदाहरण 14.10: चित्र 14.19 में दर्शाए अवमंदित दोलक के लिए गुटके का द्रव्यमान m = 200 g, k = 90 N m–1 तथा अवमंदन स्थिरांक b = 40 g s–1 है । (a) दोलन का आवर्तकाल, (b) वह समय जिसमें इसके कंपन का आयाम अपने आरंभिक मान का आधा रह जाता है तथा (c) वह समय जिसमें यांत्रिक ऊर्जा अपने आरंभिक मान की आधी रह जाती है, परिकलित कीजिए ।
हल (a) km = 90×0.2 = 18 kg N m–1 = 18kg2 s–2; इसलिए 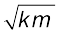 = 4.243 kg s–1 और b = 0.04 kg s–1 अत: b,
= 4.243 kg s–1 और b = 0.04 kg s–1 अत: b,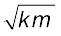 से अति निम्न है। समीकरण (14.34) से आवर्त काल T
से अति निम्न है। समीकरण (14.34) से आवर्त काल T
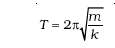
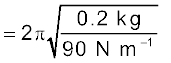
= 0.3 s
(b) अब, समीकरण (14.33) से, वह समय, T1/2 जिसमें आयाम घटकर अपने आरंभिक आयाम का आधा रह जाता है,
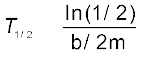
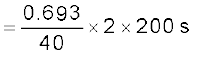
= 6.93 s
(c) वह समय t1/2, जिसमें दोलन की यंांत्रिक ऊर्जा घटकर अपने आरंभिक मान की आधी रह जाती है, परिकलित करने के लिए हमें समीकरण (14.35) की सहायता लेनी होती है । इस समीकरण से,
E (t1/2)/E (0) = exp (–bt1/2/m)
अथवा ½ = exp (–bt1/2/m)
ln (1/2) = –(bt1/2/m)
अथवा t1/2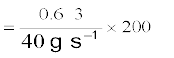 = 3.46 s
= 3.46 s
* गुरुत्व के प्रभाव में गुटका डोरी पर किसी निश्चित साम्यावस्था की स्थिति O पर होगा। यहाँ x उस भाग से विस्थापन को निरूपित करता है।
यह वास्तव में क्षय काल का आधा है। यह उचित ही है क्योंकि समीकरण (14.33) और (14.35) के अनुसार ऊर्जा आयाम के वर्ग पर निर्भर करती है। ध्यान दें कि दोनों समीकरणों के घातांकों में गुणज 2 है। t
14.10 प्रणोदित दोलन तथा अनुनाद
जब किसी निकाय (जैसे कोई सरल दोलक या कमानी से लटका हुआ कोई गुटका) को उसकी साम्यावस्था से विस्थापित कर मुक्त किया जाता है तो वह अपनी प्राकृतिक आवृत्ति ω से दोलन करने लगता है। इस प्रकार के दोलन मुक्त दोलन कहलाते हैं। सभी मुक्त दोलन सदैव उपस्थित रहने वाले क्षय बलों के कारण अंतत: रुक जाते हैं, तथापि कोई बाह्य कारक (बल) इन दोलनों को बनाए रख सकता है। एेसे दोलनों को प्रणोदित अथवा परिचालित दोलन कहते हैं। हम किसी एेसी स्थिति पर विचार करेंगे जब कार्यरत बाह्य बल की प्रकृति आवर्ती हो जिसकी प्राकृतिक आवृत्ति ωd को परिचालित आवृत्ति कहा जाता है। प्रणोदित अथवा परिचालित आवर्ती दोलनों के संदर्भ में सबसे महत्वपूर्ण तथ्य यह है कि निकाय अपनी प्राकृतिक आवृत्ति ω से दोलन नहीं करता वरन यह बाह्य बल की आवृत्ति ωd से दोलन करता है; मुक्त दोलन अवमंदन के कारण समाप्त (रुक) हो जाते हैं। इसका सबसे सामान्य उदाहरण किसी पार्क में झूले के वह प्रणोदित दोलन हैं जो बच्चे द्वारा फर्श को अपने पैरों से धक्का देकर (अथवा किसी अन्य व्यक्ति द्वारा आवर्ती रूप में धक्का देकर) आवर्ती बल आरोपित करने के फलस्वरूप स्थापित होते हैं।
मान लीजिए किसी अवमंदित दोलक पर समय के साथ विचरण करने वाले F0 आयाम का कोई आवर्ती बाह्य बल F(t) आरोपित किया जाता है । इस बल को इस प्रकार निरूपित करते हैं,
F(t) = Fo cos ωd t (14.36)
समीकरण (14.36) द्वारा निरूपित किसी कण का रैखिक प्रत्यानयन बल, अवमंदित बल तथा कालाश्रित प्रणोदित
बल के संयोजी प्रभाव के अंतर्गत गति को इस प्रकार व्यक्त करते हैं,
m a(t) = –k x(t) – bv(t) + Fo cos ωd t (14.37a)
समीकरण (14.37a) में त्वरण को d2x/dt2 द्वारा प्रतिस्थापित तथा उसे पुनर्व्यवस्थित करने पर,
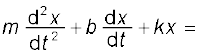 Fo cos ωd t (14.37b)
Fo cos ωd t (14.37b)
यह m द्रव्यमान वाले उस दोलित्र का गति समीकरण है जिस पर ωd (कोणीय) आवृत्ति वाला बल कार्यरत है। प्रारंभ में दोलित्र अपने प्राकृतिक आवृत्ति ω से दोलन करता है। जब हम इस पर एक बाह्य आवृत्ति बल लगाते हैं तो प्राकृतिक आवृत्ति वाला दोलन क्षीण हो जाता है और वस्तु आरोपित बाह्य बल की (कोणीय) आवृत्ति से दोलन करने लगता है। प्राकृतिक दोलन के शांत हो जाने के उपरांत दोलित्र का विस्थापन होता है
x(t) = A cos (ωdt + φ ) (14.38)
जहाँ t आवृत्ति बल के लगाए जाने के क्षण से मापा समय है।
आयाम A कोणीय आवृत्तियों ωd तथा प्राणोदित आवृत्ति ω का फलन है जिसे हम इस प्रकार व्यक्त करते हैं:
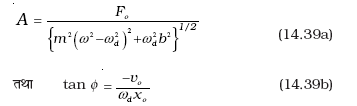
यहाँ m कण का द्रव्यमान तथा v0 और x0 समय t = 0 पर कण के क्रमश: वेग और विस्थापन हैं । यह वह क्षण है जब हम आवर्ती बल आरोपित करते हैं।
समीकरण (14.39) दर्शाता है कि आयाम परिचालन बल की (कोणीय) आवृत्ति पर निर्भर करता है। ωd के ω से अत्यधिक भिन्न होने और समीप होने की अवस्थाओं में हम दोलित्र का भिन्न-भिन्न व्यवहार देखते हैं। अब हम इन दोनों परिस्थितियों पर विचार करते हैं:
(a) अल्प अवमंदन जब परिचालक आवृत्ति प्राकृतिक आवृत्ति से अधिक भिन्न है: इस स्थिति में ωdb, m(ω2 – ωd2) से अति कम होगा। अत: समीकरण 14.39(a) में उस पद को नगण्य मान सकते हैं:
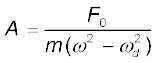 (14.40)
(14.40)
चित्र 14.21 में निकाय में उपस्थित विभिन्न सीमाओं के अवमंदक बलों के लिए किसी दोलक के विस्थापन आयाम की परिचालन बल की कोणीय आवृत्ति पर निर्भरता दर्शायी गई है । ध्यान दीजिए, तीनों परिस्थितियों मेें ωd /ω = 1 होने पर ही आयाम अधिकतम होता है। इस चित्र के वक्र यह दर्शाते हैं कि अवमंदन कम होने पर ऊँचा और संकीर्ण अनुनाद शिखर प्राप्त होता है।
यदि हम परिचालक आवृत्ति को बदलते रहें तो जब यह आवृत्ति वस्तु की प्राकृतिक आवृत्ति के बराबर हो जाती है तो दोलन का आयाम अनंत की ओर अग्रसर होता है। परन्तु यह शून्य अवमंदन की आदर्श स्थिति होती है जो किसी वास्तविक निकाय में नहीं होती है क्योंकि अवमंदन किसी भी अवस्था में पूर्ण रूप से शून्य नहीं हो सकता। आपने झूला झूलते हुए निश्चय ही अनुभव किया होगा कि जब आप झूले पर इस आवृत्ति से बल लगाते हैं कि बल का आवर्तकाल झूले के प्राकृतिक आवर्तकाल के बराबर होता है तो झूले के दोलन का आयाम अधिकतम होता है। यह आयाम अधिक तो होता है परन्तु अनंत नहीं होता है। क्योंकि झूले की दोलन गति में कुछ न कुछ अवमंदन तो होता ही है। यह अगले भाग (b) में स्पष्ट हो जाएगा।
(b) जब परिचालक आवृत्ति प्राकृतिक आवृत्ति के निकट हो : यदि ω, ωd के अति निकट हो m (ω2 –w2d), b के उचित मानों के लिए ωd b से बहुत कम होगा। इस अवस्था में समीकरण (14.39) हो जाता है।
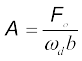 (14.41)
(14.41)
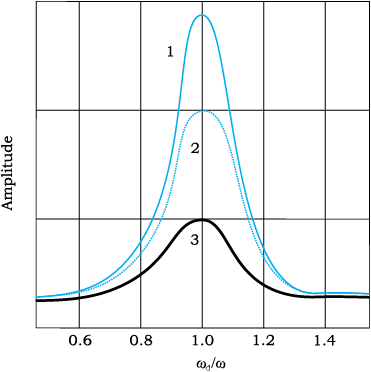
अपने दैनिक जीवन में हमें अनुनाद से संबंधित परिघटनाएँ देखने को मिलती हैं । झूलों से झूलने का हमारा अनुभव अनुनाद का अच्छा उदाहरण है । आपने यह अनुभव किया होगा कि झूले को अधिक ऊँचाई तक झुलाने की कुशलता धरती पर जोर लगाने की लय को झूले की प्राकृतिक आवृत्ति के समकालिक बनाने में है ।
इस तथ्य की और अधिक व्याख्या करने के लिए मान लीजिए चित्र 14.22 की भाँति एक ही डोरी से वर्गीकृत लंबाइयों के 5 सरल लोलक लटकाये गए हैं । लोलक 1 व 4 की लंबाइयां समान हैं तथा अन्य तीनों की लंबाइयाँ भिन्न-भिन्न हैं । अब हम लोलक 1 को गतिमान बनाते हैं । संबद्ध डोरी से होकर ऊर्जा इस लोलक से अन्य लोलकों को स्थानांतरित होती है, फलस्वरूप वे दोलन करने लगते हैं । संबद्ध डोरी द्वारा परिचालन बल प्रदान किया जाता है । इस परिचालन बल की आवृत्ति लोलक 1 के दोलन की आवृत्ति के समान होती है । यदि हम लोलकों 2, 3 तथा 5 की अनुक्रियाओं का अवलोकन करें, तो हम यह पाते हैं कि आरंभ मेें वे सभी विभिन्न आयामों से अपनी-अपनी प्राकृतिक आवृत्तियों के दोलन करते हैं, परंतु ये गतियाँ अत्यधिक अवमंदित होती हैं और कायम नहीं रह पातीं । धीरे-धीरे उनके दोलन की आवृत्तियाँ परिवर्तित होती हैं और अंत में वे लोलक 1 की आवृत्ति अर्थात् परिचालन बल की आवृत्ति से भिन्न-भिन्न आयामों से दोलन करते हैं । ये दोलन आयाम छोटे होते हैं किन्तु लोलक 4 की अनुक्रिया अन्य तीनों लोलकों से विपरीत होती है । यह लोलक 1 की ही आवृत्ति से दोलन करता है परंतु इसका आयाम धीरे-धीरे बढ़ता हुआ अत्यधिक हो जाता है । अनुनाद की भाँति अनुक्रिया दिखाई देती है । एेसा होने का कारण यह है कि यहाँ अनुनाद की शर्त, अर्थात् निकाय की प्राकृतिक आवृत्ति परिचालन बल की आवृत्ति के संपाती होनी चाहिए, संतुष्ट होती है ।
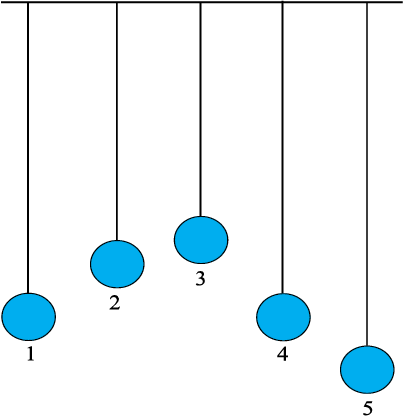
चित्र 14.22 एक ही आधार से निलंबित भिन्न-भिन्न लंबाई के 5 सरल लोलक।
अब तक हमने केवल एेसे निकायों पर विचार किया है जिनकी केवल एक प्राकृतिक आवृत्ति होती है। सामान्यत: किसी निकाय की अनेक प्राकृतिक आवृत्तियाँ हो सकती हैं। आप इस प्रकार के निकायों (कंपायमान डोरी, वायु स्तंभ आदि) के विषय में अगले अध्याय में पढ़ेंगे। किसी यांत्रिक संरचना यथा कोई भवन, कोई पुल अथवा वायुयान की अनेक प्राकृतिक आवृत्तियाँ संभव हैं। कोई बाह्य आवर्ती बल अथवा विक्षोभ निकाय को प्रणोदित दोलन प्रदान कर सकता है। यदि संयोगवश प्रणोदित बल की आवृत्ति ωd निकाय की किसी एक प्राकृतिक आवृत्ति के सन्निकट हो तो दोलन के आयाम (अनुनाद) में आशातीत वृद्धि हो सकती है जिससे विनाश की स्थिति उत्पन्न हो सकती है। इसी कारण किसी पुल से गुजरते समय सैनिकों को कदम से कदम मिलाकर न चलने की सलाह दी जाती है। किसी क्षेत्र में भूकंप के कारण सभी भवनों को एकसमान रूप से क्षति न पहुँचने का भी यही कारण है चाहे वह सभी एक ही सामग्री तथा सामान मजबूती से बने हों। किसी भवन की प्राकृतिक आवृत्ति उसकी ऊँचाई, आमाप के अन्य प्राचलों तथा उसके निर्माण में प्रयुक्त सामग्री की प्रकृति पर निर्भर करती है। जिस भवन की प्राकृतिक आवृत्ति भूकंपी तरंग की आवृत्ति के सन्निकट होती है उसे क्षति पहुँचने की आशंका सर्वाधिक होती है।
सारांश
1. वह गति जो स्वयं को दोहराती है आवर्ती गति कहलाती है,
2. एक दोलन अथवा चक्र को पूरा करने के लिए आवश्यक समय T को आवर्तकाल कहते हैं । यह आवृत्ति से इस प्रकार संबंधित है,
T=1/vकिसी आवर्ती अथवा दोलनी गति की आवृत्ति उसके द्वारा 1 सेकंड में पूरे किए गए दोलनों की संख्या होती है । SI मात्रक पद्धति में इसे हर्ट्स में मापा जाता है;
1 हर्ट्स = 1Hz = 1 दोलन प्रति सेकंड = 1s–1
3. सरल आवर्त गति में, किसी कण का उसकी साम्यावस्था की स्थिति से विस्थापन x(t) इस प्रकार व्यक्त किया जाता है,
x(t) = xm cos (ωt + φ) (विस्थापन)
यहाँ xm विस्थापन का आयाम (ωt + φ) गति की कला, तथा φ कला स्थिरांक है । कोणीय आवृत्ति ω गति के आवर्तकाल तथा आवृत्ति से इस प्रकार संबंधित होती है
ω = 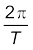 = 2πν (कोणीय आवृत्ति)
= 2πν (कोणीय आवृत्ति)
4. सरल आवर्त गति, एकसमान वर्तुल गति के उस वृत्त के व्यास पर प्रक्षेप होती है, जिस पर गति हो रही है ।
5. सरल आवर्त गति के समय कण के वेग तथा त्वरण को समय t के फलन के रूप में इस प्रकार व्यक्त करते हैं,
v (t) = –ωAm sin (ωt + φ ) (वेग)
a (t) = –ω2Am cos (ωt + φ )
= –ω2x (t) (त्वरण)
समयकालिक क्रिया और सरल आवर्त गति द्वारा हम वेग और गति को इस प्रकारदेख सकते हैं।
6. सरल आवर्त गति किसी कण की वह गति होती है जिसमें उस कण पर कोई एेसाबल आरोपित रहता है, जो कण के विस्थापन के अनुक्रमानुपाती, तथा सदैव गति के केंद्र की ओर निर्दिष्ट होता है ।
7. सरल आवर्त गति करते किसी कण में, किसी भी क्षण, गतिज ऊर्जा K =  mv2तथा स्थितिज ऊर्जा U =
mv2तथा स्थितिज ऊर्जा U =  kx2 होती है । यदि कोई घर्षण न हो, तो निकाय कीकुल यांत्रिक ऊर्जा, E = K+U सदैव ही अचर रहती है यद्यपि K और U परिवर्तित होते हैं ।
kx2 होती है । यदि कोई घर्षण न हो, तो निकाय कीकुल यांत्रिक ऊर्जा, E = K+U सदैव ही अचर रहती है यद्यपि K और U परिवर्तित होते हैं ।
8. m द्रव्यमान का कोई कण जो हुक के नियम के अनुसार लगे प्रत्यानयन बल F =– kx के प्रभाव में दोलन करता है, सरल आवर्त गति दर्शाता है जिसके लिए,
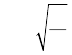 (कोणीय आवृत्ति)
(कोणीय आवृत्ति)
तथा T = 2π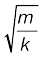 (आवर्तकाल)
(आवर्तकाल)
एेसे निकाय को रैखिक दोलक भी कहते हैं ।
9. लघु कोणों में दोलन करते सरल लोलक की गति सन्निकट सरल आवर्त गति होती है । इसका आवर्तकाल,
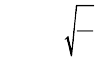
10. किसी भी वास्तविक दोलायनमान निकाय की यांत्रिक ऊर्जा दोलन करते समय घट जाती है क्योंकि बाह्य बल जैसे कर्षण दोलनों को रोकते हैं तथा यांत्रिक ऊर्जा कोऊष्मीय ऊर्जा में स्थानांतरित कर देते हैं । तब वास्तविक दोलक तथा उसकी गति कोअवमंदित गति कहते हैं । यदि अवमंदन बल Fd = –bv है, यहाँ v दोलक का वेग तथा b अवमंदन स्थिरांक है, तब दोलक का विस्थापन,
x(t) = A e–bt/2m cos (ω't + φ)
यहाँ ω', अवमंदित दोलनों की कोणीय आवृत्ति है जिसे इस प्रकार व्यक्त करते हैं,
ω′ = 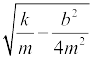
यदि अवमंदन स्थिरांक का मान कम है, तो ω′ ≈ ω, यहाँ ω अवमंदित दोलक की कोणीय आवृत्ति है । अवमंदित दोलक की यांत्रिक ऊर्जा E को इस प्रकार व्यक्त करते हैं,
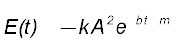
11. यदि प्राकृतिक कोणीय आवृत्ति ω के किसी दोलायमान निकाय पर ωdकोणीय आवृत्ति का कोई बाह्य आवर्ती बल आरोपित किया जाए, तो वह निकायωd कोणीय आवृत्ति से दोलन करता है । इन दोलनों का आयाम तब अधिक होता है जब,
ωd = ω
जो अनुनाद की शर्त होती है ।
विचारणीय विषय
1. आवर्तकाल T वह न्यूनतम समय होता है जिसके पश्चात् गति की स्वयं पुनरावृत्ति होती है । इस प्रकार, समय अंतराल nT के पश्चात् गति की स्वयं पुनरावृत्ति होती है, यहाँ n कोई पूर्णांक है ।
2. प्रत्येक आवर्ती गति सरल आवर्त गति नहीं होती । केवल वही आवर्ती गति जो बल-नियम F = –k x द्वारा नियंत्रित होती है, सरल आवर्त गति होती है ।
3. वर्तुल गति व्युत्क्रम-वर्ग नियम बल (जैसे ग्रहीय गति में) तथा द्विविमा में सरल आवर्त बल –mω2r के कारण उत्पन्न हो सकती है । बाद के प्रकरण में, गति की कलाएँ, दो लंबवत् दिशाओं (x तथा y) में π/2 rad द्वारा भिन्न होनी चाहिए । इस प्रकार, कोई कण जिसकी आरंभिक स्थिति (0, a) तथा वेग (ωA, 0) है –m ω2r बल आरोपित किए जाने पर A त्रिज्या के वृत्त में एकसमान वर्तुल गति करेगा ।
4. ω के किसी दिए गए मान की रैखिक सरल आवर्त गति के लिए दो आरंभिक शर्तें आवश्यक हैं और ये शर्तें गति को पूर्णत: निर्धारित करने के लिए पर्याप्त हैं । ये आवश्यक शर्तें हो सकती हैं (i) आरंभिक स्थिति तथा आरंभिक वेग, अथवा (ii) आयाम तथा कला, अथवा (iii) ऊर्जा तथा कला ।
5. उपरोक्त बिंदु (4) से, दिए गए आयाम अथवा ऊर्जा गति की कला का निर्धारण आरंभिक स्थिति अथवा आरंभिक वेग द्वारा किया जाता है ।
6. यादृच्छिक आयामों तथा कलाओं वाली दो सरल आवर्त गतियों का संयोजन व्यापक रूप में आवर्ती नहीं होता । यह केवल तभी आवर्ती होता है जब एक गति कीआवृत्ति दूसरी गति की आवृत्ति की पूर्णांक गुणज हो । तथापि, किसी आवर्ती गति को सदैव ही उपयुक्त आयामों की अनंत सरल आवर्त गतियों के रूप में व्यक्त किया जा सकता है।
7. सरल आवर्त गति का आवर्तकाल आयाम अथवा ऊर्जा अथवा कला नियतांक पर निर्भर नहीं करता । गुरुत्वाकर्षण के अधीन ग्रहीय कक्षों के आवर्तकाल इसके विपरीत हैं (केप्लर का तृतीय नियम) ।
8. किसी सरल लोलक की गति लघु कोणीय विस्थापन के लिए ही सरल आवर्त गति होती है।
9. किसी कण की गति यदि सरल आवर्त गति है, तो उसके विस्थापन को निम्न रूपों में से किसी एक रूप में व्यक्त किया जाना चाहिए:
x = A cos ωt + B sin ωt;
x = A cos (ωt + α ); x = B sin (ωt + β )
ये तीनों रूप पूर्णत: समतुल्य हैं (किसी भी एक रूप को अन्य दो रूपों के पदों में व्यक्त किया जा सकता है ।)
इस प्रकार अवमंदित सरल आवर्त गति समीकरण (14.31) सही अर्थों में सरल आवर्त गति नहीं होती । यह केवल
2m/b से बहुत छोटे समय अन्तरालों के लिए ही सन्निकटत: सरल आवर्त गति होती है, यहाँ b अवमंदन नियतांक है ।
10. प्रणोदित दोलनों में, कण की स्थायी अवस्था गति (प्रणोदित दोलनों की समाप्ति के पश्चात्) एक एेसी सरल आवर्त गति होती है जिसकी आवृत्ति उस कण की प्राकृतिक आवृत्ति ω नहीं होती वरन् प्रणोदित दोलन उत्पन्न करने वाले बाह्य बल की आवृत्ति ωd होती है ।
11. शून्य अवमंदन की आदर्श अवस्था में होने की स्थिति में अनुनाद पर सरल आवर्त गति का आयाम अनंत होता है । क्योंकि सभी वास्तविक निकायों में कुछ न कुछ अवमंदन अवश्य ही होता है, चाहे यह छोटा ही क्यों न हो, आदर्श स्थिति कभी भी आती नहीं है ।
12. प्रणोदित दोलनों के अधीन, कण की सरल आवर्त गति की कला प्रणोदित दोलन उत्पन्न करने वाले बाह्य बल की कला से भिन्न होती है ।
अभ्यास
14.1 नीचे दिए गए उदाहरणों में कौन आवर्ती गति को निरूपित करता है ?
(i) किसी तैराक द्वारा नदी के एक तट से दूसरे तट तक जाना और अपनी एक वापसी यात्रा पूरी करना ।
(ii) किसी स्वतंत्रतापूर्वक लटकाए गए दंड चुंबक को उसकी N-S दिशा से विस्थापित कर छोड़ देना ।
(iii) अपने द्रव्यमान केंद्र के परित: घूर्णी गति करता कोई हाइड्रोजन अणु ।
(iv) किसी कमान से छोड़ा गया तीर ।
14.2 नीचे दिए गए उदाहरणों में कौन (लगभग) सरल आवर्त गति को तथा कौन आवर्ती परंतु सरल आवर्त गति नहीं निरूपित करते हैं ?
(i) पृथ्वी की अपने अक्ष के परित: घूर्णन गति ।
(ii) किसी U–नली में दोलायमान पारे के स्तंभ की गति ।
(iii) किसी चिकने वक्रीय कटोरे के भीतर एक बॉल बेयरिंग की गति जब उसे निम्नतम बिंदु से कुछ ऊपर के बिंदु से मुक्त रूप से छोड़ा जाए ।
(iv) किसी बहुपरमाणुक अणु की अपनी साम्यावस्था की स्थिति के परित: व्यापक कंपन ।
14.3 चित्र 14.24 में किसी कण की रैखिक गति के लिए चार x-t आरेख दिए गए हैं । इनमें से कौन-सा आरेख आवर्ती गति का निरूपण करता है ? उस गति का आवर्तकाल क्या है (आवर्ती गति वाली गति का) ।
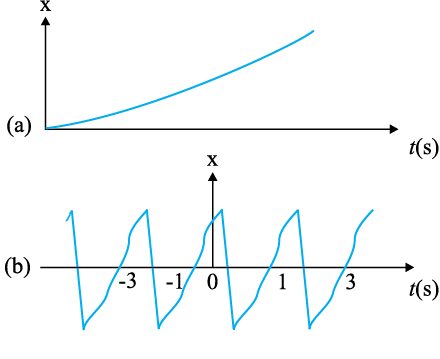
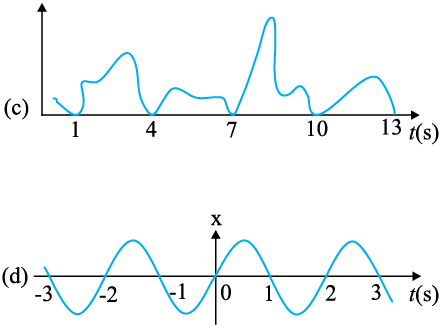
चित्र 14.28
14.4 नीचे दिए गए समय के फलनों में कौन (a) सरल आवर्त गति (b) आवर्ती परंतु सरल आवर्त गति नहीं, तथा (c) अनावर्ती गति का निरूपण करते हैं । प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिए : (ω कोई धनात्मक अचर है ।)
(a) sin ωt – cos ωt
(b) sin3 ωt
(c) 3 cos (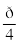 – 2 ωt)
– 2 ωt)
(d) cos ωt + cos 3 ωt + cos 5 ωt
(e) exp (–ω2t2)
(f) 1 + ωt + ω2t2
14.5 कोई कण एक दूसरे से 10 cm दूरी पर स्थित दो बिंदुओं A तथा B के बीच रैखिक सरल आवर्त गति कर रहा है । A से B की ओर की दिशा को धनात्मक दिशा मानकर वेग, त्वरण तथा कण पर लगे बल के चिह्न ज्ञात कीजिए जबकि यह कण
(a) A सिरे पर है,
(b) B सिरे पर है,
(c) A की ओर जाते हुए AB के मध्य बिंदु पर है,
(d) A की ओर जाते हुए B से 2 cm दूर है,
(e) B की ओर जाते हुए A से 3 cm दूर है, तथा
(f) A की ओर जाते हुए B से 4 cm दूर है ।
14.6 नीचे दिए गए किसी कण के त्वरण a तथा विस्थापन x के बीच संबंधों में से किससे सरल आवर्त गति संबद्ध है:
(a) a = 0.7 x
(b) a = – 200 x2
(c) a = – 10 x
(d) a = 100 x3
14.7 सरल आवर्त गति करते किसी कण की गति का वर्णन नीचे दिए गए विस्थापन फलन द्वारा किया जाता है,
x(t) = A cos (ωt + φ)
यदि कण की आरंभिक (t = 0) स्थिति 1 cm तथा उसका आरंभिक वेग π cm s–1 है, तो कण का आयाम तथा आरंभिक कला कोण क्या है ? कण की कोणीय आवृत्ति π s–1 है । यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या (cos) फलन के स्थान पर हम ज्या (sin) फलन चुनें; x = B sin (ωt + α), तो उपरोक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला कोण क्या होगा ?
14.8 किसी कमानीदार तुला का पैमाना 0 से 50 kg तक अंकित है और पैमाने की लंबाई 20 cm है । इस तुला से लटकाया गया कोई εंपण्ड, जब विस्थापित करके मुक्त किया जाता है, 0.6 s के आवर्तकाल से दोलन करता है । पिंड का भार कितना है ?
14.9 1200 N m–1 कमानी-स्थिरांक की कोई कमानी चित्र 14.25 में दर्शाए अनुसार किसी क्षैतिज मेज से जड़ी है । कमानी के मुक्त सिरे से 3 kg द्रव्यमान का कोई पिण्ड जुड़ा है । इस पिण्ड को एक ओर 2.0 cm दूरी तक खींच कर मुक्त किया जाता है,
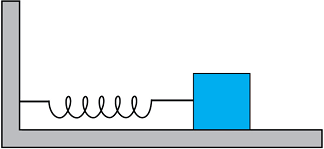
चित्र 14.25
(i) पिण्ड के दोलन की आवृत्ति,
(ii) पिण्ड का अधिकतम त्वरण, तथा
(iii) पिण्ड की अधिकतम चाल ज्ञात कीजिए ।
14.10 अभ्यास 14.9 में, मान लीजिए जब कमानी अतानित अवस्था में है तब पिण्ड की स्थिति x = 0 है तथा बाएँ से दाएँ की दिशा x-अक्ष की धनात्मक दिशा है । दोलन करते पिण्ड के विस्थापन x को समय के फलन के रूप मे दर्शाइए, जबकि विराम घड़ी को आरंभ (t = 0) करते समय पिण्ड,
(a) अपनी माध्य स्थिति,
(b) अधिकतम तानित स्थिति, तथा
(c) अधिकतम संपीडन की स्थिति पर है ।
सरल आवर्त गति के लिए ये फलन एक दूसरे से आवृत्ति में, आयाम में अथवा आरंभिक कला में किस रूप में भिन्न हैं ?
14.11 चित्र 14.26 में दिए गए दो आरेख दो वर्तुल गतियों के तदनुरूपी हैं । प्रत्येक आरेख पर वृत्त की त्रिज्य, परिक्रमण-काल, आरंभिक स्थिति और परिक्रमण की दिशा दर्शायी गई है । प्रत्येक प्रकरण में, परिक्रमण करते कण के त्रिज्य-सदिश के x-अक्ष पर प्रक्षेप की तदनुरूपी सरल आवर्त गति ज्ञात कीजिए ।
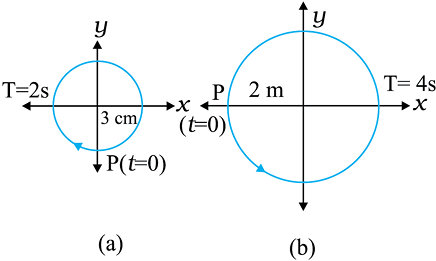
चित्र 14.26
14.12 नीचे दी गई प्रत्येक सरल आवर्त गति के लिए तदनुरूपी निर्देश वृत्त का आरेख खींचिए । घूर्णी कण की आरंभिक (t = 0) स्थिति, वृत्त की त्रिज्या तथा कोणीय चाल दर्शाइए । सुगमता के लिए प्रत्येक प्रकरण में परिक्रमण की दिशा वामावर्त लीजिए । (x को cm में तथा t को s में लीजिए ।)
(a) x = – 2 sin (3t + π/3)
(b) x = cos (π/6 – t)
(c) x = 3 sin (2πt + π/4)
(d) x = 2 cos πt
14.13 चित्र 14.27(a) में k बल-स्थिरांक की किसी कमानी के एक सिरे को किसी दृढ़ आधार से जकड़ा तथा दूसरे मुक्त सिरे से एक द्रव्यमान m जुड़ा दर्शाया गया है । कमानी के मुक्त सिरे पर बल F आरोपित करने से कमानी तन जाती है । चित्र 14.30(b) में उसी कमानी के दोनों मुक्त सिरों से द्रव्यमान m जुड़ा दर्शाया गया है । कमानी के दोनों सिरों को चित्र 14.30 में समान बल F द्वारा तानित किया गया है ।
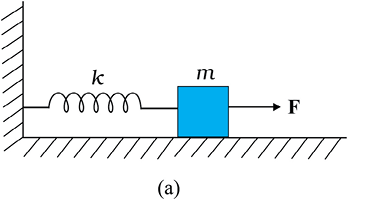
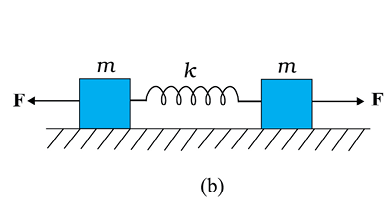
चित्र 14.27
(a) दोनों प्रकरणों में कमानी का अधिकतम विस्तार क्या है?
(b) यदि (a) का द्रव्यमान तथा (b) के दोनों द्रव्यमानों को मुक्त छोड़ दिया जाए, तो प्रत्येक प्रकरण में दोलन का आवर्तकाल ज्ञात कीजिए ।
14.14 किसी रेलगाड़ी के इंजन के सिलिंडर हैड में पिस्टन का स्ट्रोक (आयाम का दो गुना) 1.0 m का है । यदि पिस्टन 200 rad/min की कोणीय आवृत्ति से सरल आवर्त गति करता है, तो उसकी अधिकतम चाल कितनी है ?
14.15 चंद्रमा के पृष्ठ पर गुरुत्वीय त्वरण 1.7 m s–2 है । यदि किसी सरल लोलक का पृथ्वी के पृष्ठ पर आवर्तकाल 3.5s है, तो उसका चंद्रमा के पृष्ठ पर आवर्तकाल कितना होगा ? (पृथ्वी के पृष्ठ पर g = 9.8m s–2)
14.16 नीचे दिए गए प्रश्नों के उत्तर दीजिए:
(a) किसी कण की सरल आवर्त गति के आवर्तकाल का मान उस कण के द्रव्यमान तथा बल-स्थिरांक पर निर्भर
करता है: 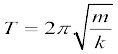 । कोई सरल लोलक सन्निकट सरल आवर्त गति करता है । तब फिर किसी लोलक का आवर्तकाल लोलक के द्रव्यमान पर निर्भर क्यों नहीं करता ?
। कोई सरल लोलक सन्निकट सरल आवर्त गति करता है । तब फिर किसी लोलक का आवर्तकाल लोलक के द्रव्यमान पर निर्भर क्यों नहीं करता ?
(b) किसी सरल लोलक की गति छोटे कोण के सभी दोलनों के लिए सन्निकट सरल आवर्त गति होती है । बड़े कोणों के दोलनों के लिए एक अधिक गूढ़ विश्लेषण यह दर्शाता है कि T का मान 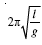 से अधिक होता है । इस परिणाम को समझने के लिए किसी गुणात्मक कारण का चिंतन कीजिए ।
से अधिक होता है । इस परिणाम को समझने के लिए किसी गुणात्मक कारण का चिंतन कीजिए ।
(c) कोई व्यक्ति कलाई घड़ी बाँधे किसी मीनार की चोटी से गिरता है । क्या मुक्त रूप से गिरते समय उसकी घड़ी यथार्थ समय बताती है ?
(d) गुरुत्व बल के अंतर्गत मुक्त रूप से गिरते किसी केबिन में लगे सरल लोलक के दोलन की आवृत्ति क्या
होती है?
14.17 किसी कार की छत से l लंबाई का कोई सरल लोलक, जिसके लोलक का द्रव्यमान M है, लटकाया गया है । कार R त्रिज्या की वृत्तीय पथ पर एकसमान चाल v से गतिमान है । यदि लोलक त्रिज्य दिशा में अपनी साम्यावस्था की स्थिति के इधर-उधर छोटे दोलन करता है, तो इसका आवर्तकाल क्या होगा ?
14.18 आधार क्षेत्रफल A तथा ऊँचाई h के एक कॉर्क का बेलनाकार टुकड़ा ρl घनत्व के किसी द्रव में तैर रहा है । कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते हैं, यह दर्शाइए कि कॉर्क ऊपर-नीचे सरल आवर्त दोलन करता है जिसका आवर्तकाल
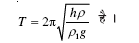
यहाँ ρ कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए) ।
14.19 पारे से भरी किसी U नली का एक सिरा किसी चूषण पंप से जुड़ा है, तथा दूसरा सिरा वायुमंडल में खुला छोड़ दिया गया है । दोनों स्तंभों में कुछ दाबांतर बनाए रखा जाता है । यह दर्शाइए कि जब चूषण पंप को हटा देते हैं, तब U नली में पारे का स्तंभ सरल आवर्त गति करता है ।
अतिरिक्त अभ्यास
14.20 चित्र 14.28 में दर्शाए अनुसार V आयतन के किसी वायु कक्ष की ग्रीवा (गर्दन) की अनुप्रस्थ काट का क्षेत्रफल a है। इस ग्रीवा में m द्रव्यमान की कोई गोली बिना किसी घर्षण के ऊपर-नीचे गति कर सकती है । यह दर्शाइए कि जब गोली को थोड़ा नीचे दबाकर मुक्त छोड़ देते हैं, तो वह सरल आवर्त गति करती है । दाब-आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए [चित्र 14.28 देखिए]।
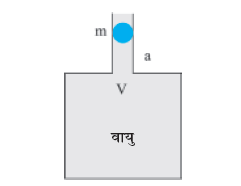
चित्र 14.28
14.21 आप किसी 3000 kg द्रव्यमान के स्वचालित वाहन पर सवार हैं । यह मानिए कि आप इस वाहन की निलंबन प्रणाली के दोलनी अभिलक्षणों का परीक्षण कर रहे हैं । जब समस्त वाहन इस पर रखा जाता है, तब निलंबन 15 cm आनमित होता है । साथ ही, एक पूर्ण दोलन की अवधि में दोलन के आयाम में 50% घटोतरी हो जाती है । निम्नलिखित के मानों का आकलन कीजिए:
(a) कमानी स्थिरांक, तथा
(b) कमानी तथा एक पहिए के प्रघात अवशोषक तंत्र के लिए अवमंदन स्थिरांक b
यह मानिए कि प्रत्येक पहिया 750 kg द्रव्यमान वहन करता है ।
14.22 यह दर्शाइए कि रैखिक सरल आवर्त गति करते किसी कण के लिए दोलन की किसी अवधि की औसत गतिज ऊर्जा उसी अवधि की औसत स्थितिज ऊर्जा के समान होती है ।
14.23 10kg द्रव्यमान की कोई वृत्तीय चक्रिका अपने केंद्र से जुड़े किसी तार से लटकी है । चक्रिका को घूर्णन देकर तार में एेंठन उत्पन्न करके मुक्त कर दिया जाता है । मरोड़ी दोलन का आवर्तकाल 1.5 s है । चक्रिका की त्रिज्या 15 cm है । तार का मरोड़ी कमानी नियतांक ज्ञात कीजिए । [मरोड़ी कमानी नियतांक α संबंध J = – α θ द्वारा परिभाषित किया जाता है, यहाँ J प्रत्यानयन बल युग्म है तथा θ एेंठन कोण है]
14.24 कोई वस्तु 5 cm के आयाम तथा 0.2 सेकंड की आवृत्ति से सरल आवृत्ति गति करती है। वस्तु का त्वरण तथा वेग ज्ञात कीजिए जब वस्तु का विस्थापन (a) 5 cm (b) 3 cm (c) 0 cm हो।
14.25 किसी कमानी से लटका एक पिण्ड एक क्षैतिज तल में कोणीय वेग ω से घर्षण या अवमंदन रहित दोलन कर सकता है। इसे जब x0 दूरी तक खींचते हैं और खींचकर छोड़ देते हैं तो यह संतुलन केन्द्र से समय t = 0 पर v0 वेग से गुजरता है। प्राचल ω, x0 तथा v0 के पदों में परिणामी दोलन का आयाम ज्ञात करिये। [संकेत: समीकरण x = a cos (ωt+θ) से प्रारंभ कीजिए। ध्यान रहे कि प्रारंभिक वेग ऋणात्मक है।]
