Table of Contents
अध्याय 15
तरंगें
15.1 भूमिका
15.2 अनुप्रस्थ तथा अनुदैर्घ्य तरंगें
15.3 प्रगामी तरंगों में विस्थापन संबंध
15.4 प्रगामी तरंग की चाल
15.5 तरंगों के अध्यारोपण का सिद्धांत
15.6 तरंगों का परावर्तन
15.7 विस्पंदें
15.8 डॉप्लर प्रभाव
सारांश
विचारणीय विषय
अभ्यास
अतिरिक्त अभ्यास
15.1 भूमिका
पिछले अध्याय में हमने एेसे पिण्डों की गति के बारे में अध्ययन किया जो एकाकी दोलन करते हैं। यदि कोई निकाय इसी प्रकार के पिण्डों का समूह है, तो उस निकाय में क्या होगा? एक द्रव्यमान युक्त माध्यम इसी प्रकार के निकाय का उदाहरण है। इस प्रकार के माध्यम में प्रत्यास्थ बल माध्यम के अवयवों को एक-दूसरे से बाँधरखते हैं जिसके कारण किसी एक अवयव की गति दूसरे अवयव की गति को प्रभावित करती है। यदि आप एक छोटे कंकड़ को किसी तालाब के शांत जल में धीरे से गिराएँ, तो जल का पृष्ठ विक्षुब्ध हो जाता है । यह विक्षोभ किसी एक स्थान तक ही सीमित नहीं रहता, वरन् एक वृत्त के अनुदिश बाहर की ओर संचरित होता है। यदि आप इसी प्रकार तालाब में निरंतर कंकड़ गिराते रहें, तो आप यह देखेंगे कि तालाब के पृष्ठ के जिस बिंदु पर विक्षोभ उत्पन्न हुआ है वहाँ से यह विक्षोभ वृत्तों के रूप में तीव्रता से बाहर की ओर गति करता है । हमें एेसा प्रतीत होता है जैसे विक्षोभ बिंदु से जल स्वयं बाहर की ओर गति कर रहा हो । यदि आप विक्षुब्ध पृष्ठ पर कुछ छोटे-छोटे कॉर्क के टुकड़े धीरे से रख दें, तो आप पाएँगे कि ये कॉर्क के टुकड़े अपने-अपने स्थानों पर ही ऊपर-नीचे गति करते हैं, परंतु विक्षोभ के केंद्र बिंदु से दूर नहीं जाते अर्थात् उनकी विक्षोभ के केंद्र से दूरी नियत बनी रहती है। इससे यह प्रदर्शित होता है कि जल का द्रव्यमान स्वयं वृत्तों के साथ बाहर की ओर गति नहीं करता, बस, एक गतिशील विक्षोभ उत्पन्न हो जाता है । इसी प्रकार जब हम बोलते हैं, तो ध्वनि हवा (माध्यम) में हमसे दूर जाती है । परंतु इस प्रक्रिया में (वायु) एक भाग से दूसरे भाग में प्रवाहित नहीं होती । वायु में उत्पन्न हुए विक्षोभ हमें स्पष्ट रूप से दिखाई नहीं देते, हमारे कानों अथवा माइक्रोफोनों द्वारा ही हम इनको जान पाते हैं। इस प्रकार के विक्षोभों के प्रतिरूप या पैटर्न जो द्रव्य के वास्तविक भौतिक स्थानांतरण अथवा समूचे द्रव्य के प्रवाह के बिना ही माध्यम के एक स्थान से दूसरे स्थान तक गति करते हैं, तरंग कहलाते हैं । इस अध्याय में हम तरंगों के विषय में अध्ययन करेंगे ।
तरंगों द्वारा एक बिंदु से दूसरे बिंदु तक ऊर्जा तथा विक्षोभ के पैटर्न की सूचना का संचरण होता है। हमारा समस्त संचार-तंत्र तरंगों द्वारा संकेतों के संचरण पर निर्भर करता है। वाक् (बातचीत) का अर्थ है वायु में ध्वनि तरंगें उत्पन्न करना तथा श्रवण उनके संसूचन को व्यक्त करता है। सूचना का आदान-प्रदान प्राय: विभिन्न प्रकार की तरंगों के माध्यम द्वारा होता है। उदाहरण के लिए ध्वनि तरंगों को सर्वप्रथम विद्युत संकेतों के रूप में परिवर्तित किया जा सकता है जिनसे विद्युत-चुंबकीय तरंगें जनित की जा सकती हैं जिनका संचरण प्रकाशिक रेशों की केबिल अथवा उपग्रह द्वारा हो सकता है। मूल संकेत के संसूचन में समान्यतया यही चरण व्युत्क्रम क्रम में अपनाए जाते हैं।
सभी तरंगों को संचरण के लिए माध्यम की आवश्यकता नहीं होती । हम जानते हैं कि प्रकाश तरंगें निर्वात से गमन कर सकती हैं । हमसे सैकड़ों प्रकाश वर्ष की दूरी पर स्थित तारों से उत्सर्जित प्रकाश अंतरतारकीय अंतरिक्ष, जो व्यावहारिक रूप से निर्वात ही है, से गमन करता हुआ हम तक पहुँचता है ।
किसी डोरी तथा जल में उत्पन्न तरंगों, ध्वनि तरंगों, भूकंपी तरंगों जैसी सुपरिचित तरंगें यांत्रिक तरंगों के रूप में जानी जाती हैं। इन सभी तरंगों के संचरण के लिए माध्यम की आवश्यकता होती है, ये बिना माध्यम के संचरित नहीं हो सकतीं। इनका संचरण माध्यम के कणों के दोलनों के कारण संभव हो पाता है तथा माध्यम के प्रत्यास्थ गुणों पर निर्भर करता है। विद्युत-चुंबकीय तरंगें सर्वथा भिन्न प्रकार की तरंगें होती हैं जिनके विषय में आप कक्षा 12 में अध्ययन करेंगे। विद्युत-चुंबकीय तरंगों के संचरण के लिए माध्यम का होना आवश्यक नहीं है– इनका संचरण निर्वात में भी होता है। प्रकाश, रेडियो तरंगें, X-किरणें सभी विद्युत-चुंबकीय किरणें हैं। निर्वात में सभी विद्युत-चुंबकीय तरंगों की चाल, c, समान होती है जिसका मान है:
c = 29,97,92,458 m s-1 (15.1)
तीसरी प्रकार की एक अन्य तरंग है जिसे द्रव्य तरंग के नाम से जाना जाता है। यह द्रव्य के इलेक्ट्रॉन, प्रोटान, न्यूट्रान, परमाणु तथा अणु जैसे घटकों से संबद्ध हैं। ये तरंगें प्रकृति के क्वांटम यांत्रिकीय विवरण में प्रकट होती हैं जिसके विषय में आप अगली कक्षाओं में पढ़ेंगे । यद्यपि ये तरंगें संकल्पनात्मक रूप में यांत्रिक तथा विद्युत चुंबकीय तरंगों की तुलना में अधिक अमूर्त हैं, तथापि इनका अनुप्रयोग आधुनिक प्रौद्योगिकी की बहुत सी मूल युक्तियों में पाया जाता है; इलेक्ट्रॉन से संबद्ध द्रव्य तरंगों का उपयोग इलेक्ट्रॅान सूक्ष्मदर्शी में किया जाता है ।
इस अध्याय में हम केवल यांत्रिक तरंगों के बारे में, जिनके संचरण के लिए द्रव्यात्मक माध्यम आवश्यक है, अध्ययन करेंगे ।
पुरातन काल से ही हमारी कला तथा साहित्य पर तरंगों का सौंदर्यबोधात्मक प्रभाव दृष्टिगोचर होता है, फिर भी तरंग गति का वैज्ञानिक विश्लेषण सर्वप्रथम सत्रहवीं शताब्दी में किया गया था । क्रिश्चियन हाइगेन्स (1629-1695), राबर्ट हुक तथा आइज़क न्यूटन कुछ एेसे प्रसिद्ध भौतिकविद हैं जिनके नाम तरंग गति की भौतिकी से संबद्ध हैं । कमानी से बँधे पिण्डों के दोलनों की भौतिकी तथा सरल लोलक की भौतिकी के पश्चात् ही तरंगों की भौतिकी को समझा गया । प्रत्यास्थ माध्यमों में तरंगों का आवर्ती दोलनों के साथ अंतरंग संबंध होता है । (तानित डोरियाँ, कुंडलित कमानियाँ, वायु आदि प्रत्यास्थ माध्यमों के उदाहरण हैं ।) इस संबंध की व्याख्या हम सरल उदाहरणों द्वारा करेंगे ।
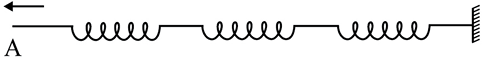
चित्र 15.1 एक-दूसरे से संबद्ध कमानियों का संग्रह । सिरे A को यकायक खींचा जाता है; तब विक्षोभ दूसरे सिरे तक संचरित हो जाता है ।
आइए, अब हम वायु में ध्वनि तरंगों के संचरण पर विचार करते हैं । जैसे ही कोई ध्वनि तरंग वायु से होकर गुजरती है, तो वह उस स्थान की वायु के छोटे से क्षेत्र को संपीडित अथवा विस्तारित करती है । इसके कारण उस छोटे क्षेत्र की वायु के घनत्व में, मान लीजिए (δρ), परिवर्तन होता है । दाब, प्रति एकांक क्षेत्रफल पर आरोपित बल होता है, अत: कमानी की ही भाँति इस स्थिति में भी विक्षोभ के अनुक्रमानुपात में ‘प्रत्यानयन बल’ उत्पन्न हो जाता है । यहाँ इस प्रकरण में, घनत्व में परिवर्तन, कमानी में उत्पन्न संपीडन अथवा विस्तारण के समरूप है । यदि किसी क्षेत्र को संपीडित किया जाता है, तो उस क्षेत्र के अणु बाहर निकलकर समीपवर्ती क्षेत्र में जाने का प्रयास करते हैं । इस प्रकार, समीपवर्ती क्षेत्र में घनत्व बढ़ता है, अथवा उस क्षेत्र में ‘संपीडन’ उत्पन्न होता है जिसके फलस्वरूप पूर्ववर्ती क्षेत्र में ‘विरलन’ उत्पन्न हो जाता है । यदि कोई क्षेत्र अपने चारों ओर के क्षेत्रों की तुलना में विरलित हो, तो उस क्षेत्र के चारों ओर के परिवेश की वायु उस क्षेत्र में प्रवेश करके विरलन को समीपवर्ती क्षेत्र की ओर धकेल देती है । इस प्रकार, संपीडन अथवा विरलन एक क्षेत्र से दूसरे क्षेत्र की ओर गति करते हैं, जिसके कारण वायु में विक्षोभ का संचरण संभव हो पाता है ।
ठोसों में भी इसी के सदृश तर्क दिया जा सकता है । क्रिस्टलीय ठोसों में परमाणु अथवा परमाणुओं के समूह आवर्ती जालकों में व्यवस्थित होते हैं । इनमें, प्रत्येक परमाणु अथवा परमाणुओं का समूह, अपने चारों ओर के परमाणुओं द्वारा आरोपित बलों के कारण, साम्यावस्था में होता है । यदि अन्य परमाणुओं को स्थिर रखते हुए किसी एक परमाणु को विस्थापित किया जाए, तो ठीक उसी प्रकार जैसा कि कमानी के प्रकरण में था, इस स्थिति में भी एक प्रत्यानयन बल उत्पन्न हो जाता है । अत: हम जालक (lattice) के परमाणुओं को अंत्य बिंदुओं की भाँति ले सकते हैं तथा परमाणु-युगलों के बीच कमानियाँ लगी मान सकते हैं ।
अब हम इस अध्याय के अगले अनुभागों में तरंगों के विभिन्न अभिलाक्षणिक गुणों की चर्चा करेंगे ।
15.2 अनुप्रस्थ तथा अनुदैर्घ्य तरंगें
हम जानते हैं कि यांत्रिक तरंगों की गति में माध्यम के घटक दोलन करते हैं। यदि माध्यम के घटक तरंग की गति की दिशा के लंबवत् दोलन करते हैं तो एेसी तरंग को हम अनुप्रस्थ तरंग कहते हैं। यदि माध्यम के घटक तरंग की गति की दिशा के अनुदिश दोलन करते हैं तो तरंग को अनुदैर्घ्य तरंग के रूप में जाना जाता है।
चित्र 15.2 में किसी डोरी के अनुदिश एक एेसे स्पंद को गति करते दिखाया गया है जिसे डोरी को एक बार ऊपर-नीचे झटकने के बाद उत्पन्न किया गया है। यदि स्पंद के आमाप की तुलना में डोरी की लंबाई अत्यधिक हो तो उसके दूसरे सिरे तक पहुँचने से पहले ही स्पंद का अवमंदन हो जाएगा। अत: दूसरे सिरे पर स्पंद के परावर्तन को अनदेखा किया जा सकता है। चित्र 15.3 में भी एेसी ही एक स्थिति प्रदर्शित की गई है अंतर केवल इतना है कि इसमें बाह्य कारक द्वारा डोरी के एक सिरे पर ऊपर-नीचे की ओर सतत आवर्ती ज्यावक्रीय झटके प्रदान किए जा रहे हैं। इस प्रकार से डोरी में उत्पन्न विक्षोभ का परिणाम उसमें प्रग्रामी ज्यावक्रीय तरंग होता है। दोनों ही परिस्थितियों में माध्यम के अवयव अपनी माध्य साम्यावस्था के इर्द-गिर्द दोलन करते हैं जबकि स्पंद अथवा तरंग उनसे संचरित होती है। दोलन डोरी में तरंग की गति की दिशा के लंबवत् हैं, अत: यह अनुप्रस्थ तरंग का एक उदाहरण है।
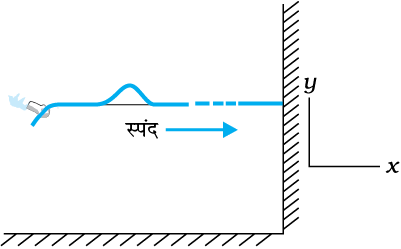
चित्र 15.2जब किसी तानित डोरी के अनुदिश (x-अक्ष) कोई एकल स्पंद गतिशील होता है तो डोरी का कोई प्रतिरूपी अवयव ऊपर-नीचे (y-अक्ष) दोलन करता है ।

चित्र15.3 किसी डोरी के अनुदिश प्रेषित कोई आवर्त (ज्यावक्रीय) तरंग अनुप्रस्थ तरंग का एक उदाहरणहै तरंग के क्षेत्र में डोरी का कोई प्रतिरूपी अवयव तरंग की गमन दिशा के लंबवत् अपनी साम्यावस्था केसापेक्ष दोलन करता है।
हम किसी तरंग पर दो प्रकार से विचार कर सकते हैं। हम किसी निश्चित काल-क्षण पर आकाश में तरंग का चित्रण कर सकते हैं। इससे हमें किसी काल-क्षण पर तरंग की आकृति मिल जाएगी। एक अन्य विधि तरंग की किसी स्थान विशेष पर विचार करना है अर्थात् हम अपना ध्यान डोरी के किसी निश्चित अवयव पर केंद्रित करें तथा समय के साथ इसके दोलनों को देखें।
चित्र 15.4 में अनुदैर्घ्य तरंगों के सबसे सामान्य उदाहरण ध्वनि तरंगों की स्थिति प्रदर्शित की गई है। वायु से भरे किसी लंबे पाइप के एक सिरे पर एक पिस्टन लगा है। पिस्टन को एक बार अंदर की ओर धकेलते और फिर बाहर की ओर खींचने से संपीडन (उच्च घनत्व) तथा विरलन (न्यून घनत्व) का स्पंद उत्पन्न हो जाएगा। यदि पिस्टन को अंदर की ओर धकेलने तथा बाहर की ओर खींचने का क्रम सतत तथा आवर्ती (ज्यावक्रीय) हो तो एक ज्यावक्रीय तरंग उत्पन्न होगी जो पाइप की लंबाई के अनुदिश वायु में गमन करेगी। स्पष्ट रूप से यह अनुदैर्घ्य तरंग का उदाहरण है।

चित्र 15.4 पिस्टन को आगे-पीछे गति कराकर वायु से भरी नली में ध्वनि तरंग उत्पन्न की जाती है । चूँकि वायु-अवयव के दोलन तरंग गति की दिशा के समांतर हैं, अत: यह अनुदैर्घ्य तरंग है ।
उपरोक्त वर्णित तरंगें, चाहे वह अनुप्रस्थ हों अथवा अनुदैर्घ्य, प्रगामी तरंगें हैं क्योंकि वह माध्यम के एक बिन्दु से दूसरे बिंदु तक गमन करती हैं। जैसा कि पहले बताया गया है, वह द्रव्य जिससे तरंग संचरित होती है, गति नहीं करता है। उदाहरणार्थ, किसी धारा में जल की पूर्ण रूप से गति होती है। परन्तु, किसी जल तरंग में विक्षोभ गति करते हैं न कि पूर्ण रूप से जल। इसी प्रकार, पवन (वायु का पूर्ण रूप से गति) तथा ध्वनि तरंग को एक नहीं समझना चाहिए– ध्वनि तरंग में विक्षोभ (दाब घनत्व में) का वायु में संचरण होता है वायु माध्यम पूर्ण रूपेण गति नहीं करता है।
अनुप्रस्थ तरंगों में कणों की गति तरंग संचरण की दिशा के लंबवत् होती है । अत: तरंग संचरण के समय माध्यम के प्रत्येक अवयव में अपरूपण विकृति होती है । अत: अनुप्रस्थ तरंगों का संचरण केवल उन्हीं माध्यमों, जैसे ठोसों में हो सकता है जो अपरूपक प्रतिबलों का परिपालन कर सकें जबकि तरलों में यह संचरण नहीं हो सकता । तरलों के साथ-साथ ठोस भी संपीडन विकृति का प्रतिपालन कर सकते हैं, अत: अनुदैर्ध्य तरंगों का संचरण सभी प्रत्यास्थ माध्यमों में कराया जा सकता है । उदाहरण के लिए, स्टील जैसे माध्यमों में अनुप्रस्थ एवं अनुदैर्ध्य दोनों प्रकार की तरंगें संचरित हो सकती हैं, जबकि वायु में केवल अनुदैर्ध्य यांत्रिक तरंगों का ही संचरण संभव है । जल के पृष्ठ पर दो प्रकार की तरंग होती हैं: केशिकात्वीच (अथवा पृष्ठ तनावी) तरंगें तथा गुरुत्व तरंगें । पहले प्रकार की तरंगें काफी कम तरंगदैर्ध्य की उर्मिकाएं होती हैं जिनकी तरंगदैर्ध्य कुछ सेंटीमीटर से अधिक नहीं होती तथा इनके बनने का कारण जल के पृष्ठ तनाव के कारण प्रत्यानयन बल होता है । गुरुत्व तरंगों की तरंगदैर्ध्य का प्रारूपिक परिसर कई मीटर से कई सौ मीटर तक होता है । ये तरंगें गुरुत्वीय खिंचाव के रूप में लगने वाले प्रत्यानयन बल द्वारा बनती हैं जो जल के पृष्ठ को अपने न्यूनतम स्तर पर रखने का प्रयास करती हैं।
इन तरंगों में कणों के दोलन पृष्ठ तक ही सीमित नहीं रहते बल्कि इनका विस्तार घटते आयाम के साथ तली तक होता है जल-तरंगों में कण-गति के साथ एक जटिल गति सम्मिलित होती है, वे न केवल ऊपर-नीचे गति करते हैं बल्कि उनकी पश्च तथा अग्र-गति भी होती है। समुद्र में उत्पन्न तरंगें अनुप्रस्थ तरंगों तथा अनुदैर्ध्य तरंगों का संयोजन होती हैं।
व्यापक रूप में यह पाया गया है कि एक ही माध्यम में अनुप्रस्थ तरंगों तथा अनुदैर्ध्य तरंगों की चाल भिन्न-भिन्न होती है।
(a) किसी लंबी कुंडलित कमानी के एक सिरे को एक ओर विस्थापित करने पर उस कमानी की किसी विभंग (एेंठन) की गति ।
(b) द्रव से भरे किसी सिलिंडर में इसके पिस्टन को आगे-पीछे करके सिलिंडर में उत्पन्न तरंगें ।
(c) जल के पृष्ठ पर चलती मोटरबोट द्वारा उत्पन्न तरंगें ।
(d) किसी कंपायमान क्वार्टा क्रिस्टल द्वारा वायु में उत्पन्न पराश्रव्य तरंगें ।
हल
(a) अनुप्रस्थ
(b) अनुदैर्घ्य
(c) अनुप्रस्थ तथा अनुदैर्घ्य
(d) अनुदैर्घ्य °
15.3 प्रगामी तरंगों में विस्थापन संबंध
किसी प्रगामी तरंग के गणितीय विवरण के लिए, हमें स्थिति x तथा समय t दोनों के किसी फलन की आवश्यकता होती है। प्रत्येक क्षण पर यह फलन तरंग की उस क्षण पर आकृति का विवरण देता है। साथ ही दी हुई प्रत्येक स्थिति पर यह फलन उस स्थिति पर माध्यम की अवयव की गति का विवरण भी देता है। यदि हम किसी ज्यावक्रीय प्रगामी तरंग (एेसी एक तरंग चित्र 15.3 में दर्शायी गई है) का वर्णन करना चाहते हैं तो संलग्न फलन भी ज्यावक्रीय होना चाहिए। सुविधा के लिए हम किसी अनुप्रस्थ तरंग पर विचार करेंगे जिससे यदि माध्यम के किसी अवयव की स्थिति को x से निरूपित करें तो अवयव की माध्य स्थिति से विस्थापन को y से निरूपित करना होगा। किसी ज्यावक्रीय प्रगामी तरंग को तब निम्न रूप से वर्णित करते हैं
y (x, t) = a sin (k x – ωt + φ) (15.2)
ज्या फलन के कोणांक में पद φ का तात्पर्य है कि हम ज्या और कोज्या फलनों के रैखिक संयोजन पर विचार कर रहे हैं:
y(x, t) = A sin (kx – ωt) + B cos (kx – ωt) (15.3)
तब समीकरण (15.2) एवं (15.3) से
a = 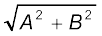 तथा φ = tan-1
तथा φ = tan-1 
समीकरण (15.2) क्यों ज्यावक्रीय प्रगामी तरंग निरूपित करता है यह समझने के लिए किसी निश्चित क्षण, मान लीजिए t = t0, पर विचार करें। तब समीकरण (15.2) में ज्या फलन का कोणांक
(kx + स्थिरांक) होगा। अत: तरंग का आकार (किसी निश्चित क्षण पर) x के फलन के रूप में ज्या तरंग है। इसी प्रकार, किसी निश्चित स्थिति x = x0 पर विचार करें। तब समीकरण (15.2) में ज्या फलन का कोणांक एक स्थिरांक –ωt है। अत: किसी निश्चित स्थिति पर विस्थापन y समय के साथ ज्यावक्रीय रूप से परिवर्तित होता है। अर्थात, विभिन्न स्थितियों पर माध्यम के अवयव सरल आवर्त गति करते हैं। ध्यान दीजिए कि जैसे t का मान बढ़ता है, x का मान भी धनात्मक दिशा में बढ़ेगा जिससे kx –ωt + φ का मान अचर रहे। अत: समीकरण (15.2) x - अक्ष के धनात्मक दिशा के अनुदिश ज्यावक्रीय (आवर्त) तरंग निरूपित करता है। इसके विपरीत, फलन
y(x, t) = a sin (kx + ωt + φ) (15.4)
y(x,t) : स्थिति x तथा समय t के फलन के रूप में विस्थापन
a : तरंग का आयाम
ω : तरंग की कोणीय आवृत्ति
k : कोणीय तरंग संख्या
kx–ωt+φ : आरंभिक कला कोण (a+x = 0, t = 0)
चित्र 15.5समीकरण (15.2) के मानक चिह्नों की परिभाषा।
x-अक्ष की ऋणात्मक दिशा के अनुदिश गतिशील तरंग को निरूपित करता है । चित्र 15.5 समीकरण (15.2) के विभिन्न भौतिक राशियों के नाम दर्शाता है जिसको हम अब परिभाषित करेंगे।
चित्र 15.6 समान अंतराल पर पाँच भिन्न मानों के लिए समीकरण (15.2) के आलेख दर्शाता है। किसी तरंग में अधिकतम धनात्मक विस्थापन वाले बिंदु को शीर्ष कहते हैं तथा अधिकतम ऋणात्मक विस्थापन वाले बिंदु को गर्त कहते हैं। यह देखने के लिए कि कोई तरंग कैसे गति करती है हम शीर्ष पर ध्यान केन्द्रित कर सकते हैं और फिर देखें कि यह शीर्ष समय के साथ कैसे गति करता है। चित्र में इसे शीर्ष पर क्रास (×) से दर्शाया गया है। इसी प्रकार हम माध्यम के किसी निश्चित स्थिति, मान लीजिए x अक्ष के मूल बिंदु पर किसी अवयव की गति पर विचार कर सकते हैं। इसे चित्र पर ठोस बिन्दु (•) से दर्शाया गया है। चित्र 15.6 के आलेख दर्शाते हैं कि मूल बिंदु पर ठोस बिंदु (•) समय के साथ आवर्ती रूप से गति करता है। अर्थात, तरंग के गति के साथ मूल बिंदु पर स्थित कण अपनी माध्य स्थिति के पारित: दोलन करता है। यह किसी अन्य स्थिति के कण के लिए भी सत्य है। हम यह भी देखते हैं कि जितने समय में ठोस बिंदु (•) एक पूर्ण दोलन करता है उतने में शीर्ष एक निश्चित दूरी चल लेता है।
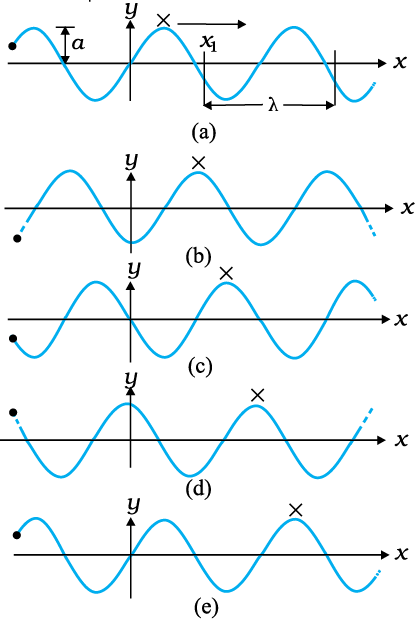
चित्र 15.6 भिन्न समयों पर x-अक्ष की धनात्मक दिशा के अनुदिश गतिशील कोई आवर्ती तरंग
चित्र 15.6 के आलेखों के आधार पर अब हम समीकरण (15.2) की विभिन्न राशियों को परिभाषित करेंगे
15.3.1 आयाम तथा कला
समीकरण (15.2) में, चूंकि ज्या फलन का मान +1 तथा –1 के बीच परिवर्तित होता है, विस्थापन y (x,t) का मान a तथा
–a के बीच परिवर्तित होता है। हम यदि a को धनात्मक अचर मानें तो व्यापकता का कोई ह्रास नहीं होता है। तब a माध्यक के किसी अवयव का अपने माध्य स्थिति से अधिकतम विस्थापन दर्शाता है। ध्यान दें कि विस्थापन y धनात्मक या ऋणात्मक हो सकता है परंतु a धनात्मक है। a को तरंग का आयाम कहते हैं।
समीकरण (15.2) के कोणांक की राशि (kx – ωt + φ) को तरंग की कला कहते हैं। दिये हुए आयाम a के लिए, किसी स्थिति एवं समय पर कला तरंग का विस्थापन निर्धारित करता है। स्पष्टत: x = 0 तथा t = 0 पर कला φ है। अत: φ को आरंभिक कला कोण कहते हैं। x- अक्ष पर मूल बिंदु तथा आरंभिक क्षण का इस प्रकार चुनाव सदैव ही संभव होता है कि φ = 0 । अत: समीकरण (15.2) में φ = 0 लेने पर व्यापकता का कोई ह्रास नहीं होता है।
15.3.2 तरंगदैर्घ्य तथा कोणीय तरंग संख्या
समान कला के दो बिंदुओं के बीच की न्यूनतम दूरी को तरंगदैर्घ्य कहते हैं और इसे सामान्यत: λ से दर्शाते हैं। सुविधा के लिए हम समान कला वाले बिंदुओं को शीर्ष या गर्त ले सकते हैं। तब तरंगदैर्घ्य दो क्रमागत शीर्षों अथवा गर्तों के बीच की दूरी है। समीकरण (15.2) में φ = 0 लेने पर, t = 0 पर विस्थापन होगा
y(x, 0) = a sin kx (15.5)
चूंकि कोण में 2π से प्रत्येक परिवर्तन पर ज्या फलन का मान वही रहता है:
sin kx = sin (kx + 2nπ) = sin k
अर्थात बिंदुओं x तथा  पर विस्थापन समान होते हैं – यहाँ n = 1, 2, 3, ..... । समान विस्थापन किसी दिये हुए क्षण पर वाले बिंदुओं के मध्य न्यूनतम दूरी n = 1 लेने पर प्राप्त होती है। λ तब दिया जाता है समीकरण
पर विस्थापन समान होते हैं – यहाँ n = 1, 2, 3, ..... । समान विस्थापन किसी दिये हुए क्षण पर वाले बिंदुओं के मध्य न्यूनतम दूरी n = 1 लेने पर प्राप्त होती है। λ तब दिया जाता है समीकरण
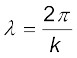 , या
, या  (15.6)
(15.6)
k को संचरण स्थिरांक अथवा कोणीय तरंग संख्या कहते हैं । इसका SI मात्रक रेडियन प्रति मीटर अथवा rad m-1 है।*
15.3.3 आवर्तकाल, कोणीय आवृत्ति तथा आवृत्ति
चित्र 15.7 में एक ज्यावक्रीय आलेख दिखाया गया है। यह किसी निश्चित क्षण पर तरंग का आकार नहीं दर्शाता है बल्कि माध्यम के एक अवयव (किसी निश्चित स्थिति पर) का समय के साथ विस्थापन दर्शाता है। सुविधा के लिए हम समीकरण (15.2) में φ =0 लेते हैं और अवयव (मान लीजिए x=0 पर) की गति पर ध्यान देते हैं। तब हमें प्राप्त होता है
y (0,t) = a sin (–ωt)
= –a sin ωt
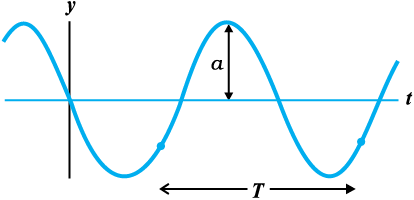
चित्र 15.7जब तरंग डोरी में से गुजरती है तो किसी निश्चित स्थिति पर डोरी का अवयव आयाम a से समय के साथ दोलन करता है।
तरंग के दोलन का आवर्त काल डोरी के किसी अवयव द्वारा एक पूर्ण दोलन में लिया गया समय है। अर्थात्
–a sin ωt = –a sin ω(t + T)
= –a sin (ωt + ωT)
चूंकि ज्या फलन प्रत्येक 2π कोण पर पुनरावृत्ति करता है,
ωΤ = 2π, या 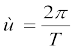 (15.7)
(15.7)
ω को तरंग की कोणीय आवृत्ति कहते हैं । इसका SI मात्रक रेडियन प्रति सेकंड अथवा rad s-1 है। किसी तरंग की आवृत्ति ν प्रति सेकंड दोलनों की संख्या है। अत:
ν =  =
= 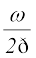 (15.8)
(15.8)
*यहाँ भी rad को छोड़ सकते हैं और मात्रक को केवल m–1 से व्यक्त कर सकते हैं। अत:, k, इकाई लंबाई में समा सकने वाली तरंगों की संख्या का 2p से गुणा करने पर प्राप्त होने वाली m–1 SI मात्रक में मापी जाने वाली राशि है।
t पर तरंग = 0
t = ∆t पर तरंग
उपर्युक्त चर्चा में सदैव ही किसी डोरी के अनुदिश गतिशील तरंग अथवा अनुप्रस्थ तरंग का संदर्भ लिया गया है । अनुदैर्घ्य तरंग में माध्यम के किसी अवयव में तरंग संचरण की दिशा के समांतर विस्थापन होता है । समीकरण (15.2) में किसी अनुदैर्घ्य तरंग के लिए विस्थापन फलन इस प्रकार लिखा जाता है,
s(x, t) = a sin (kx – ωt + φ) (15.9)
यहाँ s(x, t) स्थिति x तथा समय t पर माध्यम के किसी अवयव का तरंग संचरण की दिशा में विस्थापन है । समीकरण (15.9) में a विस्थापन आयाम है। अन्य सभी राशियों के वही अर्थ हैं जो अनुप्रस्थ तरंग के प्रकरण में थे । केवल एक ही अंतर है कि विस्थापन फलन y(x, t) के स्थान पर फलन s (x, t) लिया गया है।
उदाहरण 15.2 : किसी डोरी के अनुदिश गमन करती तरंग का विवरण इस प्रकार दिया गया है,
y(x, t) = 0.005 sin (80.0 x – 3.0 t)
यहाँ आंकिक स्थिरांक SI मात्रकों में हैं (0.005 m,
80.0 rad/m तथा 3.0 rad/s)। तरंग का
(a) आयाम, (b) तरंगदैर्घ्य (c) आवर्तकाल एवं आवृत्ति परिकलित कीजिए । दूरी x = 30.0 cm तथा समय t = 20 s पर तरंग का विस्थापन y भी परिकलित कीजिए ।
हल इस विस्थापन की तुलना समीकरण (15.2) से करने पर
y (x, t) = a sin (kx – ωt)
हमें निम्नलिखित मान प्राप्त होते हैं,
(a) तरंग का आयाम = 0.005 m = 5 mm
(b) कोणीय तरंग संख्या = 80.0 m–1 तथा कोणीय आवृत्ति
ω = 30 s–1
अब हम समीकरण (15.6) के द्वारा तरंगदैर्घ्य λ तथा k में संबंध लिखते हैं
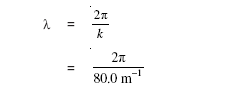
= 7.85 cm
(c) अब हम नीचे दिए गए T तथा ω में संबंध द्वारा T का मान ज्ञात करते हैं,
T = 2π/ω
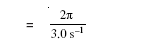
= 2.09 s
अब चूँकि आवृत्ति v = 1/T
= 0.48 Hz
दूरी x = 30.0 cm तथा समय t = 20 s पर विस्थापन
y = 0.005m sin 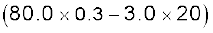
= 0.005m sin (–36 + 12p) = (0.005 m) sin (1.699)
= (0.005 m) sin (97°) ~ 5 mm °
15.4 प्रगामी तरंग की चाल
किसी प्रगामी तरंग की चाल निरूपित करने के लिए हम तरंग के किसी बिन्दु (किसी कला कोण द्वारा अभिलक्षित) पर ध्यान केंद्रित कर सकते हैं और देखते हैं कि यह बिंदु समय के साथ किस तरह गमन करता है। तरंग के शीर्ष की गति पर ध्यान देना सुविधाजनक होता है। चित्र 15.8 में दो विभिन्न समयों, जिनके बीच ∆t का लघु समय अंतराल है, पर तरंग का आकार दर्शाया गया है। समस्त तरंग पैटर्न दाईं ओर (x-अक्ष की धनात्मक दिशा) ∆x दूरी चलता है। वास्तव में, बिन्दु (•) द्वारा दर्शाया शीर्ष समय ∆t में दूरी ∆x चलता है। इस प्रकार तरंग की चाल ∆x/∆t है। किसी अन्य कला वाले बिंदु पर भी हम बिन्दु (•) लगा सकते हैं। यह उसी वेग v से गमन करेगा (अन्यथा तरंग पैटर्न अपरिवर्तित नहीं रहेगा)। तरंग पर किसी निश्चित कला बिंदु की गति को दिया जाता है
kx – ωt = नियतांक (15.10)
अत: जब समय t बदलता है, तो निश्चित कला बिंदु की स्थिति x भी इस प्रकार बदलती है कि कला कोणांक अचर रहे। अत:
kx – ωt = k (x+∆x)–ω(t + ∆t)
या k∆x – ω∆t = 0
∆x, ∆t का अल्पतम मान लेने पर
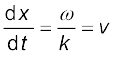 (15.11)
(15.11)
ω को T से तथा k को λ से संबंधित करने पर हमें प्राप्त होता है
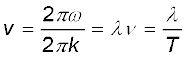 (15.12)
(15.12)
समीकरण (15.12) सभी प्रगामी तरंगों के लिए एक व्यापक संबंध है। यह बताती है कि माध्यम के किसी अवयव के एक पूर्ण दोलन काल में तरंग पैटर्न एक तरंगदैर्घ्य के बराबर दूरी तय करती है। ध्यान दीजिए कि किसी यांत्रिक तरंग की चाल माध्यम के जड़त्वीय गुणों (डोरी के लिए रैखिक द्रव्यमान घनत्व, सामान्यतया द्रव्यमान घनत्व) तथा प्रत्यास्थ गुणों (रैखिक निकायों के लिए यंग प्रत्यास्थता गुणांक/अपरूपण गुणांक, आयतन प्रत्यास्थता गुणांक) द्वारा निर्धारित होता है। माध्यम चाल निर्धारित करता है। यथा समीकरण (15.2) एक निश्चित चाल के लिए तरंगदैर्घ्य और आवृत्ति का संबंध देता है। वास्तव में, जैसा पहले बताया जा चुका है, माध्यम में अनुप्रस्थ तथा अनुदैर्घ्य दोनों तरंगें संभव हैं तथा इनकी चाल उसी माध्यम में अलग-अलग होगी। इस अध्याय के अनुवर्ती उपभागों में कुछ माध्य यांत्रिक तरंगों की चाल के लिए हम विशिष्ट व्यंजक प्राप्त करेंगे।

चित्र 15.8 समय t से t+∆t तक किसी आवृत्ति तरंग का गमन, जहाँ ∆t लघु समय अंतराल है। तरंग पैटर्न समस्त रूप से दाईं ओर स्थानांतरित हो जाता है। तरंग का शीर्ष (या निश्चित कला वाला कोई और बिंदु) समय ∆t में दूरी ∆x गमन करता है।
15.4.1 तनित डोरी पर अनुप्रस्थ तरंग की चाल
किसी यांत्रिक तरंग की चाल विक्षोभ के कारण माध्यम में उत्पन्न प्रत्यानयन बल और जड़त्वीय गुणों (द्रव्यमान घनत्व) द्वारा निर्धारित होती है। चाल प्रथम कारक से अनुलोम रूप से तथा दूसरे कारक से प्रतिलोम रूप से संबंधित होती है। किसी डोरी पर तरंग के लिए प्रत्यानयन बल डोरी में तनाव T प्रदान करता है। इस संदर्भ में जड़त्वीय गुण रैखिक द्रव्यमान घनत्व µ है जो डोरी के द्रव्यमान m को उसकी लंबाई l से विभाजित करने पर प्राप्त होता है। न्यूटन के गतिकीय नियमों का उपयोग करके किसी डोरी पर तरंग की चाल के लिए यथार्थ सूत्र प्राप्त किया जा सकता है परन्तु यह उत्पत्ति इस पुस्तक की सीमा के बाहर है। अत: हम विमीय विश्लेषण का उपयोग करेंगे। परन्तु हम यह जान चुके हैं कि केवल विमीय विश्लेषण से यथार्थ सूत्र नहीं प्राप्त हो सकता है। इस विधि से प्राप्त संबंध में स्थिरांक संबंधी अनिश्चितता रहती है। µ की विमा [ML–1] है तथा T की बल की, अर्थात [MLT–2] है। हमें इन विमाओं को इस प्रकार संयोजित करना है कि चाल की विमा [LT–1] प्राप्त हो। हम आसानी से देख सकते हैं कि अनुपात T/µ में यही विमा है
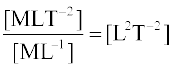
अत:, यदि T तथा µ ही प्रासंगिक भौतिक राशियाँ हैं तो
v 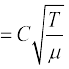 (15.13)
(15.13)
जहाँ C विमाहीन स्थिरांक है, जिसे विमीय विश्लेषण द्वारा निर्धारित करना संभव नहीं है । वास्तव में यथार्थ सूत्र में C का मान 1 है। अत: तानित डोरी में अनुप्रस्थ तरंग की चाल
 (15.14)
(15.14)
ध्यान दीजिए कि चाल v माध्यम के गुण T और µ (T बाहरी बल के कारण तानित डोरी का अभिलक्षण है) पर तरंग की तरंगदैर्घ्य या आवृत्ति पर स्वत: निर्भर नहीं करती है। आगे की कक्षाओं में आप एेसी तरंगों के बारे में पढ़ेंगे जिनकी चाल आवृत्ति से स्वतंत्र नहीं है। दो कारकों λ तथा ν उत्पन्न तरंग की आवृत्ति विक्षोभ के स्रोत पर निर्भर करता है। माध्यम में किसी निश्चित चाल तथा आवृत्ति के लिए, समीकरण (15.12) तरंगदैर्घ्य का निर्धारण करता है:
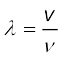 (15.15)
(15.15)
किसी रस्सी पर स्पंद का संचरण
किसी रस्सी पर एक स्पंद का संचरण आप आसानी से देख सकते हैं। आप एक दृढ़ परिसीमा से इस स्पंद का परिवर्तन होना भी देख सकते हैं और इसके गमन वेग की गणना भी कर सकते हैं। इसके लिए आपको 1 से 3 cm व्यास के एक रस्से, दो हुकों और कुछ भारों की आवश्यकता होगी। आप यह प्रयोग अपनी कक्षा में भी कर सकते हैं और प्रयोगशाला
में भी।
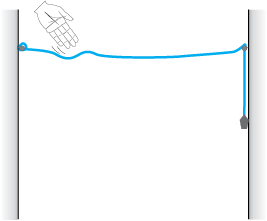
1 से 3 cm व्यास की लंबी रस्सी लीजिए। किसी सभागार या प्रयोगशाला के आमने-सामने की दीवारों पर दो हुक लगाकर इसका एक सिरा एक हुक से कस कर बाँध दीजिए और दूसरे सिरे को सामने वाले हुक से गुजार कर इस पर कोई भार (1 से 5kg) लटकाइये। दीवारों के बीच की दूरी 3 से 5 मीटर हो सकती है। एक छड़ लीजिए और रस्सी के एक सिरे के पास इस पर ज़ोर से प्रहार कीजिए। इससे रस्सी पर एक स्पंद बनेगा जो फिर इस पर दूसरे सिरे तक जाएगा। आप इसे दूसरे सिरे तक जाकर परावर्तित होता हुआ देख सकते हैं। आप आपाती स्पंद और परावर्तित स्पंद की कलाओं का संबंध भी जाँच सकते हैं। स्पंद के समाप्त होने से पहले आप इसके दो- तीन परावर्तन होते देख सकते हैं। एक स्टॉपवाच (विराम घड़ी) की सहायता से आप स्पंद द्वारा एक दीवार से दूसरी दीवार की दूरी तक चलने में लगा समय ज्ञात कर सकते हैं और फिर इसके वेग की गणना कर सकते हैं।
इसकी तुलना समीकरण (15.14) द्वारा प्राप्त मान से कीजिए।
एेसा ही किसी संगीत वाद्य के पतले धात्विक तंतु के मामले में भी होता है। मुख्य अंतर बस यह है कि तंतु का प्रति इकाई द्रव्यमान कम होने के कारण इस पर स्पंद का वेग मोटी रस्सी पर इसके वेग की तुलना में काफी अधिक होता है। रस्सी पर स्पंद का वेग कम होने के कारण इसे देखा जा सकता है और इसलिए मापन सुविधाजनक और सटीक हो जाता है।
उदाहरण 15.3 : 0.72 m लंबे किसी स्टील के तार का द्रव्यमान 5.0×10-3kg है । यदि तार पर तनाव 60N है, तो तार पर अनुप्रस्थ तरंगों की चाल क्या है ?
हल: तार की प्रति एकांक लंबाई का द्रव्यमान
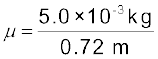
= 6.9×10-3kg m-1
तनाव, T = 60N
तार पर अनुप्रस्थ तरंगों की चाल,
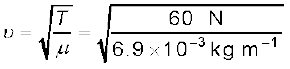 = 93 m s-1 °
= 93 m s-1 °
15.4.2 अनुदैर्घ्य तरंग की चाल - ध्वनि की चाल
किसी अनुदैर्घ्य तरंग में माध्यम के अवयव तरंग संचरण की दिशा में अपनी स्थिति के आगे-पीछे दोलन करते हैं । हम पहले भी देख चुके हैं कि ध्वनि तरंगें वायु के लघु आयतन-अवयवों के संपीडनों तथा विरलनों के रूप में गमन करती हैं । संपीडन विकृति में प्रतिबल का निर्धारण करने वाली प्रत्यास्थ गुणधर्म माध्यम का आयतन प्रत्यास्थता गुणांक है जिसे इस प्रकार परिभाषित करते हैं,
 (15.16)
(15.16)
यहाँ दाब में परिवर्तन ∆P आयतन विकृति ∆V/V उत्पन्न करता है। B की विमा वही है जो दाब की है और SI मात्रक में इसे पास्कल (Pa) में व्यक्त करते हैं। तरंग के संचरण के लिए प्रासंगिक जड़त्वीय गुण द्रव्यमान घनत्व ρ है जिसकी विमा [ML-3] है । हम आसानी से देख सकते हैं कि राशि B/ρ में उपेक्षित विमा है:
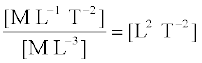 (15.17)
(15.17)
अत:, यदि B तथा ρ ही प्रासंगिक भौतिक राशियाँ हैं तो
v = C (15.18)
(15.18)
यहाँ C एक स्थिरांक है जिसे विमीय विश्लेषण द्वारा निर्धारित करना संभव नहीं है। यथार्थ उत्पत्ति से C=1 प्राप्त होता है । अत: किसी माध्यम में अनुदैर्घ्य तरंगों की चाल के लिए व्यापक सूत्र है:
v =  (15.19)
(15.19)
किसी ठोस छड़ जैसे रैखीय माध्यम के लिए, छड़ में पार्श्वीय प्रसार नगण्य होता है और हमें छड़ को केवल अनुदैर्घ्य विकृति पर विचार करने की आवश्यकता होती है। इस प्रकरण में, प्रासंगिक प्रत्यास्थता गुणांक ‘यंग गुणांक’ है जिसकी विमा आयतन-प्रत्यास्थता गुणांक की विमा है। इस प्रकरण के लिए विमीय विश्लेषण पहले जैसा है और हमें समीकरण (15.18) जैसी समीकरण प्राप्त होती है जिसमें अनिर्धारित स्थिरांक C होता है जिसका मान यथार्थ उत्पत्ति से 1 प्राप्त होता है। इस प्रकार किसी ठोस छड़ में अनुदैर्घ्य तरंग की चाल निम्नलिखित संबंध द्वारा व्यक्त की जाती है:
v =  (15.20)
(15.20)
यहाँ Y छड़ के पदार्थ का यंग प्रत्यास्थता गुणांक है । सारणी 15.1 में विभिन्न माध्यमों में ध्वनि की चाल दर्शायी
गई है।
सारणी 15.1 कुछ माध्यमों में ध्वनि की चाल
| माध्यम | चाल (ms-1) |
|---|---|
| गैसें | |
| वायु (0°C) वायु (20°C) हीलियम हाइड्रोजन | 331 343 965 1284 |
| द्रव | |
| जल (0°C) जल (20°C) समुद्र-जल | 1402 1482 1522 |
| ठोस | |
| एेलुमिनियम कॉपर (ताँबा) स्टील ग्रेनाइट वल्केनाइज्ड रबर | 6420 3560 5941 6000 54 |
द्रवों तथा ठोसों में ध्वनि की चाल गैसों की तुलना में अधिक है। [ध्यान दें कि ठोसों के प्रकरण में, प्रासंगिक चाल ठोस में अनुदैर्घ्य तरंग की चाल है]। इसका कारण यह है कि द्रवों व ठोसों को गैसों की तुलना में संपीडित करना अधिक कठिन होता है। अत: इनके आयतन प्रत्यास्थता गुणांक के मान अधिक होते हैं। समीकरण (15.19) देखें । ठोसों और द्रवों का गैसों की तुलना में द्रव्यमान घनत्व अधिक होता है । परन्तु उनमें अनुरूपी आयतन प्रत्यास्थता गुणांकों में वृद्धि कहीं अधिक होती है । यही कारण है कि ठोसों और द्रवों में ध्वनी की तीव्र गति होती है ।
किसी गैस में ध्वनि के चाल का आकलन हम आदर्श गैस सन्निकटन में कर सकते हैं। किसी आदर्श गैस (देखें अध्याय 11) के लिए दाब P, आयतन V तथा ताप T के नीचे संबंध इस प्रकार व्यक्त किया जाता है:
PV = NkBT (15.21)
यहाँ N गैस में अणुओं की संख्या, kB बोल्ट्ज़मान नियतांक तथा T गैस का केल्विन में ताप है । अत: किसी समतापी परिवर्तन के लिए समीकरण (15.21) से हमें निम्नलिखित संबंध प्राप्त होता है
V∆P + P∆V = 0
अथवा 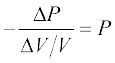
अत: समीकरण (15.16) में यह मान प्रतिस्थापित करने पर,
B = P
अत: समीकरण (15.19) से किसी आदर्श गैस में अनुदैर्घ्य तरंगों की चाल,
 (15.22)
(15.22)
इस संबंध को सर्वप्रथम न्यूटन ने स्थापित किया था, अत: इसे न्यूटन का सूत्र भी कहते हैं ।
उदाहरण 15.4 न्यूटन के सूत्र का उपयोग करके मानक ताप एवं दाब (STP) पर वायु में ध्वनि की चाल का आकलन कीजिए । वायु के 1 मोल का द्रव्यमान
29.0 × 10–3 kg है ।
हल: हम जानते हैं कि किसी भी गैस के 1 मोल का STP पर आयतन 22.4 लीटर होता है । अत: वायु का STP पर घनत्व
1 मोल वायु का द्रव्यमान
ρ0 = 
STP पर 1 मोल वायु का आयतन
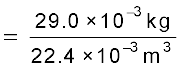
= 1.29 kg m–3
किसी माध्यम से ध्वनि की चाल के लिए न्यूटन के सूत्र के अनुसार हमें STP पर वायु मेें ध्वनि के वेग का निम्नलिखित मान प्राप्त होता है,
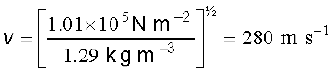 (15.23)
(15.23)
समीकरण (15.23) से प्राप्त वायु में ध्वनि की चाल का मान, सारणी 15.1 में दिए गए प्रयोगों द्वारा प्राप्त वायु में ध्वनि की चाल के मान 331 m s-1 की तुलना मेें 15% कम है। आखिर हमसे कहाँ गलती हुई? यदि हम न्यूटन की इस मूल कल्पना का परीक्षण करें जिसमें न्यूटन ने ध्वनि संचरण के समय माध्यम में दाब मेें होने वाले परिवर्तन को समतापी माना, तो हम यह पाते हैं कि उनकी यह कल्पना सही नहीं थी । लाप्लास ने यह बताया कि ध्वनि संचरण के समय माध्यम में दाब-परिवर्तन इतनी तीव्र गति से होते हैं कि ऊष्मा प्रवाह के लिए ताप को स्थायी बनाए रखने का आवश्यक समय उपलब्ध नहीं हो पाता। फलस्वरूप यह परिवर्तन समतापी नहीं होते वरन् रुद्धोष्म (adiabatic) होते हैं । रुद्धोष्म प्रक्रियाओं के लिए आदर्श गैसों पर निम्न संबंध लागू होता है (खण्ड 12.8 देखें)

न्यूटन के सूत्र में इस संशुद्धि को लाप्लास संशोधन कहते हैं । वायु के लिए γ = 7/5, अत: अब यदि हम STP पर वायु में ध्वनि की चाल के आकलन के लिए समीकरण (15.24) का प्रयोग करें तो ध्वनि की चाल का मान 331.3 m s-1 प्राप्त होता है, जो मापित चाल से मेल खाता है ।
15.5 तरंगों के अध्यारोपण का सिद्धांत
जब विपरीत दिशाओं में गमन करती दो तरंग स्पंद एक दूसरे को पार करते हैं तो क्या होता है (चित्र 15.9)? यह देखा जाता है कि पार करने के बाद भी तरंग स्पंद अपना व्यष्टित्व बनाए रखती है। परंतु, अतिव्यापन के दौरान, तरंग पैटर्न दोनों तरंग स्पंदों से भिन्न होता है। चित्र 15.9 बराबर एवं विपरीत आकारों वाले दो तरंग स्पंदों के एक दूसरे की ओर गमन की स्थिति दर्शाता है। जब स्पंद अतिव्याप्ति होते हैं तो परिणामी विस्थापन पृथक-पृथक स्पंदों के कारण विस्थापनों का बीजगणितीय योग होता है। इस प्रकार जोड़ना तरंगों का अध्यारोपण का सिद्धांत कहलाता है। इस सिद्धांत के अनुसार, प्रत्येक स्पंद इस प्रकार गमन करता है मानो दूसरे स्पंद विद्यमान नहीं हैं। अत: माध्यम के अवयव दोनों के कारण विस्थापित होते हैं और चूंकि विस्थापन धनात्मक या ऋणात्मक हो सकते हैं, नेट विस्थापन दोनों विस्थापनो का बीजगणितीय योग होता है। चित्र 15.9 विभिन्न समयों पर तरंग आकार का आलेख दर्शाता है। आलेख (c) में विशेष प्रभाव पर ध्यान दें: दोनों स्पंदों के कारण पृथक-पृथक उत्पन्न विस्थापन एक दूसरे को ठीक से निरस्त कर देते हैं तथा प्रत्येक बिंदु पर कुल विस्थापन शून्य है।
अध्यारोपण के सिद्धांत को गणितीय रूप में व्यक्त करने के लिए, मान लीजिए y1(x, t) तथा y2 (x, t) माध्यम के किसी अवयव के विस्थापन हैं, जो यदि तरंग अलग-अलग गमन करती तो उस अवयव के होते। यदि दो तरंगें किसी क्षेत्र में एक साथ पहुंचती हैं और अतिव्यापित होती हैं तो नेट विस्थापन y(x, t) होगा
y (x, t) = y1 (x, t) + y2 (x, t) (15.25)
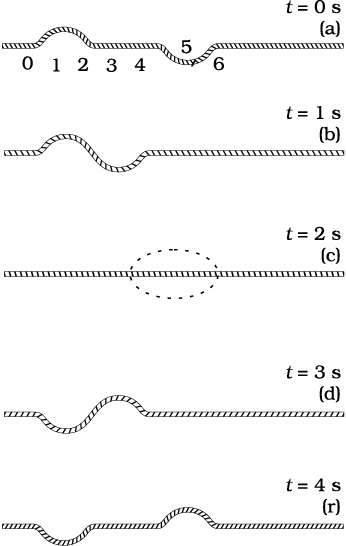
चित्र 15.9 समान एवं विपरीत विस्थापन वाली विपरीत दिशा में गमन करती दो स्पंद। आलेख (c) में दोनों स्पंदों के अतिव्यापन से शून्य विस्थापन होता है।
यदि किसी माध्यम में एक ही क्षण दो अथवा अधिक तरंगें गमन कर रहीं हैं तो उनका परिणामी तरंग रूप दोनों तरंगों के पृथक-पृथक तरंग फलनों का योग होता है । अर्थात यदि गतिशील तरंगों के तरंग फलन इस प्रकार हैं,
y1 = f1 (x – vt),
y2 = f2 (x – vt),
......................
......................
yn = fn (x – vt),
तब माध्यम मेें विक्षोभ का वर्णन करने वाला तंरग फलन इस प्रकार व्यक्त किया जाता है,
y = f1 (x – vt) + f2 (x – vt) + ............ + fn (x – vt)
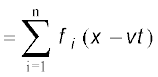 (15.26)
(15.26)
अध्यारोपण का सिद्धांत व्यतिकरण की परिघटना का मूल है।
सरलता के लिए, किसी तानित डोरी के अनुदिश गमन करती दो आवर्ती प्रगामी तरंगों पर विचार करिये। दोनों तरंगों की कोणीय आवृत्तियाँ ω समान हैं तथा कोणीय तरंग संख्या k भी समान है। अत: इनके तरंगदैर्घ्य भी समान हैं। इनकी तरंग चाल भी समान होगी। मान लीजिए कि इनके आयाम समान हैं तथा दोनों x-अक्ष के धनात्मक दिशा में गमन करती हैं। इन तरंगों में अन्तर केवल आरंभिक कला में है। समीकरण (15.2) के अनुसार इन दोनों तरंगों को इस प्रकार व्यक्त करते हैं:
y1 (x, t) = a sin (kx – ωt) (15.27)
और y2 (x, t) = a sin (kx – ωt + φ) (15.28)
अब अध्यारोपण के सिद्धांत का प्रयोग करने पर, नेट विस्थापन इस प्रकार व्यक्त किया जाता है:
y (x, t) = a sin (kx – ωt) + a sin (kx – ωt + φ) (15.29)
 (15.30)
(15.30)
यहाँ हमने (sin A + sin B) के लिए त्रिकोणमिति के सुपरिचित सूत्र का प्रयोग किया है। अत:
 (15.31)
(15.31)
समीकरण (15.31) यह दर्शाता है कि परिणामी तरंग भी, x-अक्ष की धनात्मक दिशा मेें गमन करती आवर्ती तरंग है जिसकी आवृत्ति तथा तरंगदैर्घ्य दोनों तरंगों के समान है। परन्तु इसका कलान्तर φ/2 है। महत्वपूर्ण तथ्य यह है कि इसका आयाम दोनों घटक तरंगों के बीच कलान्तर φ का फलन है:
 (15.32)
(15.32)
यदि φ = 0, अर्थात् दोनों तरंगें समान कला में हैं,
y (x,t) = 2 a sin (kx – ωt) (15.33)
अर्थात् परिणामी तरंग का आयाम 2a है, जो A के संभावित मानों में अधिकतम है। φ = π के लिए, दोनों तरंगें पूर्णत: एक दूसरे से विपरीत कलाओं में होती हैं तथा परिणामी तरंग का आयाम सर्वत्र हर क्षण शून्य होता है:
y (x, t) = 0 (15.34)
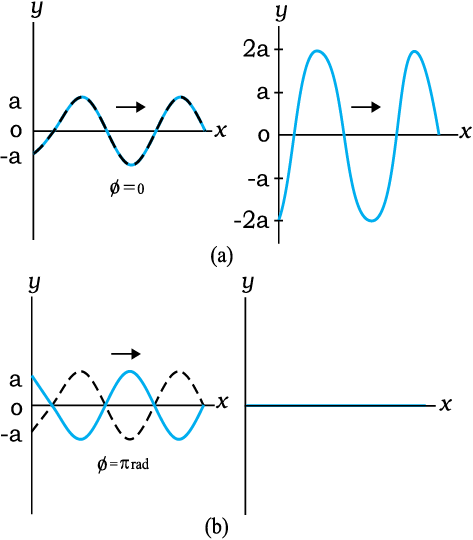
चित्र 15.10 अध्यारोपण के सिद्धांत के अनुसार समान आयाम तथा तरंगदैर्घ्य वाले दो आवृत्ति तरंगों का परिणामी तरंग। परिणामी तरंग का आयाम कलांतर φ पर निर्भर करता है। यह कलांतर (a) के लिए शून्य है तथा (b) के लिए π।
समीकरण (15.33) दो तरंगों का संपोषी व्यतिकरण दर्शाता है। इस प्रकरण में दोनों आयाम जुड़ जाते हैं। समीकरण (15.34) दो तरंगों का विनाशी व्यतिकरण दर्शाता है जिसमें परिणामी तरंग में दोनों आयाम का अंतर होता है। चित्र 15.10 व्यतिकरण के इन दोनों प्रकरणों को दर्शाता है जो अध्यारोपण के सिद्धांत का परिणाम है।
15.6 तरंगों का परावर्तन
पिछले अनुभागों में हमने अपरिबद्ध माध्यमों में तरंग संचरण की चर्चा की । क्या होता है जब कोई स्पंद अथवा तरंग किसी परिसीमा का सामना करती है ? यदि परिसीमा दृढ़ है तो स्पंद अथवा तरंग परावर्तित हो जाती है। प्रतिध्वनि की परिघटना दृढ़ परिसीमा से परावर्तन का उदाहरण है। यदि परिसीमा पूर्णत: दृढ़ नहीं है, अथवा वह किन्हीं दो भिन्न प्रत्यास्थ माध्यमों के बीच अंतरापृष्ठ है, तो स्थिति कुछ जटिल हो जाती है। इस स्थिति में आपतित तरंग का कुछ भाग परावर्तित हो जाता है तथा कुछ भाग दूसरे माध्यम में पारगमित हो जाता है। यदि कोई तरंग दो भिन्न माध्यमों की परिसीमा पर तिरछी आपतित होती है तो पारगमित तरंग को अपवर्तित तरंग कहते हैं। आपतित एवं अपवर्तित तरंगें स्नेल के अपवर्तन के नियमों का पालन करती हैं, तथा
आपतित एवं परावर्तित तरंगें परावर्तन के सामान्य नियमों का पालन करती हैं।
चित्र 15.11 किसी तानित डोरी के अनुदिश गमन करती तथा परिसीमा से परावर्तित होती तरंग दर्शाता है। यदि मान लें कि परिसीमा द्वारा ऊर्जा का कोई अवशोषण नहीं होता है तो परावर्तित तरंग का आकार वही होता है जो आपतित स्पंद का है परंतु परावर्तन से इसके कला में π या 180º का कलांतर उत्पन्न हो जाता है। इसका कारण यह है कि परिसीमा दृढ़ है तथा परिसीमा पर सभी क्षणों पर विक्षोभ का विस्थापन शून्य होना चाहिए। अध्यारोपण के सिद्धांत के अनुसार, यह तभी संभव है जब आपतित एवं परावर्तित तरंगों में π कलांतर हो ताकि परिणामी विस्थापन शून्य हो। यह तर्क दृढ़ दीवार में परिसीमा प्रतिबंध पर आधारित है। इस परिणाम को हम गतिकीय दृष्टि से भी प्राप्त कर सकते हैं। जब स्पंद दीवार पर पहुँचता है तो वह दीवार पर बल आरोपित करता है। न्यूटन के तीसरे नियम के अनुसार दीवार डोरी पर परिणाम में समान तथा दिशा में विपरीत बल आरोपित करती है। परिणामस्वरूप परावर्तित स्पंद उत्पन्न होता है जिसकी कला में π का अंतर होता है।
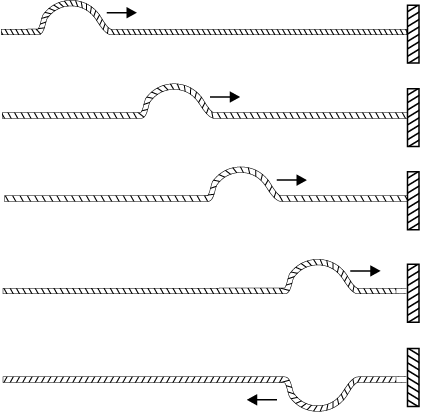
चित्र 15.11 किसी दृढ़ परिसीमा से स्पंद का परावर्तन।
इसके विपरीत, यदि परिसीमा बिंदु दृढ़ नहीं है और गति के लिए पूर्ण रूप से स्वतंत्र है (जैसे एक डोरी एक एेसे छल्ले से बंधी है जो किसी छड़ पर स्वतंत्र रूप से गति कर सके) तो परावर्तित स्पंद की कला तथा आयाम (मान लें ऊर्जा ह्रास न हो) वही हैं जो आपतित स्पंद के हैं। नेट परिसीमा पर अधिकतम विस्थापन तब प्रत्येक स्पंद के आयाम का दो गुना है। अदृढ़ परिसीमा का उदाहरण आर्गन पाइप का खुला सिरा है।
संक्षेप में, किसी प्रगामी तरंग या स्पंद की किसी दृढ़ परिसीमा से परावर्तन में π कलांतर उत्पन्न होता है तथा खुले परिसीमा से परावर्तन में कोई कलांतर उत्पन्न नहीं होता है। इस कथन को गणितीय रूप में व्यक्त करने के लिए, मान लीजिए आपतित तरंग को इस प्रकार निरूपित करते हैं:
yi (x, t) = a sin (kx – ωt)
तब, दृढ़ परिसीमा से परावर्तन के लिए, परावर्तित तरंग को इस प्रकार निरूपित करते हैं,
yr (x, t) = a sin (kx + ωt + π)
= –a sin (kx + ωt) (15.35)
किसी खुली परिसीमा से परावर्तन के लिए, परावर्तित तरंग को इस प्रकार निरूपित करते हैं,
yr (x, t) = a sin (kx + ωt ) (15.36)
स्पष्टत: दृढ़ परिसीमा पर y = yi + yr = 0 सभी बलों पर।
15.6.1 अप्रगामी तरंगें तथा प्रसामान्य विधाएँ
पिछले अनुभाग में हमने एक सिरे पर परिसीमित निकाय पर विचार किया । परंतु एेसी कई सुपरिचित स्थितियाँ हैं (जैसे दोनों सिरों पर परिबद्ध डोरी अथवा परिमित लम्बाई का वायु कॉलम) जिसमें परावर्तन दो या अधिक सिरों पर होता है। उदाहरण के लिए, किसी डोरी में एक दिशा में गमन करती तरंग एक सिरे से परावर्तित होती है। यह परावर्तित तरंग दूसरी दिशा में गमन करके दूसरे सिरे से परावर्तित होती है। यह प्रक्रिया तब तक चलती रहती है जब तक डोरी में एक अपरिवर्ती तरंग पैटर्न न बन जाय। एेसे तरंग पैटर्न अप्रगामी तरंगें कहलाते हैं। गणितीय रूप में इसे व्यक्त करने के लिए, x-अक्ष की धनात्मक दिशा में गमन करती किसी तरंग तथा x-अक्ष की ऋणात्मक दिशा में गमन करती समान आयाम एवं तरंगदैर्घ्य वाली परावर्तित तरंग पर विचार कीजिए। φ = 0 के लिए समीकरण (15.2) और (15.4) से
y1 (x, t) = a sin (kx – ωt)
y2 (x, t) = a sin (kx + ωt)
तब, अध्यारोपण के सिद्धांत के अनुसार प्राप्त परिणामी तरंग इस प्रकार व्यक्त की जाती है,
y (x, t) = y1 (x, t) + y2 (x, t)
= a [sin (kx – ωt) + sin (kx + ωt)]
सुपरिचित त्रिकोणमितीय तत्समक
sin (A + B) + sin (A – B) = 2 sin A cos B, का उपयोग करने पर
y (x,t) = 2 a sin kx cos ωt (15.37)
समीकरण (15.37) द्वारा निरूपित तरंग पैटर्न तथा समीकरण (15.2) अथवा समीकरण (15.4) द्वारा निरूपित तरंगों के बीच महत्वपूर्ण अंतर पर ध्यान दें। समीकरण (15.37) में पद kx एवं ωt अलग-अलग विद्यमान हैं, न कि (kx – ωt) के संयोजन के रूप में। इस तरंग का आयाम 2a sin kx है। अत: इस तरंग पैटर्न में, आयाम प्रत्येक बिंदु पर भिन्न होता है परन्तु डोरी का प्रत्येक अवयव समान कोणीय आवृत्ति ω या आवर्त काल से दोलन करता है। तरंग के विभिन्न अवयवों के दोलन में कोई कलांतर नहीं होता है। डोरी पूर्ण रूप से विभिन्न बिंदुओं पर विभिन्न आयामों से एक ही कला में दोलन करती है। तरंग पैटर्न न तो बाईं और और न दाईं ओर गमन करता है। अत: इन्हें अप्रगामी तरंगें कहते हैं। किसी निश्चित स्थिति पर इसका आयाम निश्चित होता है परंतु जैसा पहले बताया गया है विभिन्न स्थितियों पर आयाम भिन्न होता है। जिन बिंदुओं पर आयाम शून्य होता है उन्हें निस्पंद कहते हैं तथा जिन बिंदुओं पर अधिकतम होता है उन्हें प्रस्पंद कहते हैं। चित्र 15.12 विपरीत दिशाओं में गमन करती दो तरंगों के अध्यारोपण के फलस्वरूप परिणामी अप्रगामी तरंग दर्शाता है।
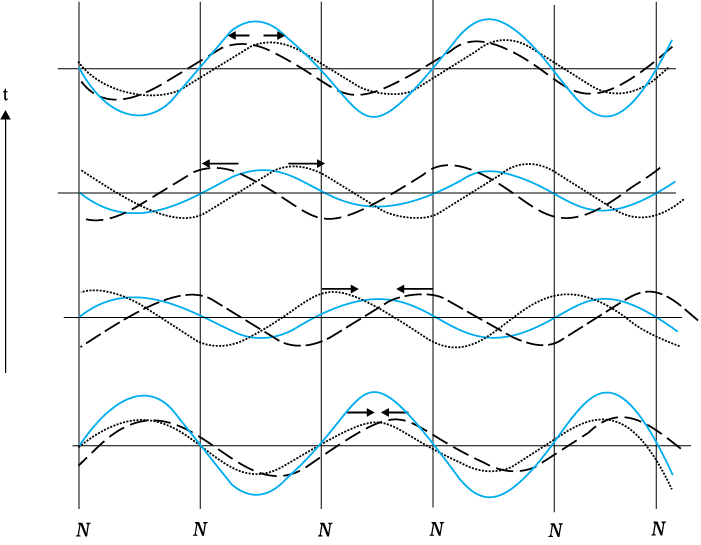
चित्र 15.12 विपरीत दिशाओं में गमन करती दो आवर्ती तरंगों के अध्यारोपण से उत्पन्न अप्रगामी तरंगें। ध्यान दें कि निस्पंदों (शून्य विस्थापन वाले बिंदु) की स्थिति सभी समयों पर अपरिवर्तित रहती है।
अप्रगामी तरंगों का सबसे महत्वपूर्ण लक्षण यह है कि निकाय के दोलन की संभावित तरंग दैर्घ्यों या आवृत्तियों के मान, परिसीमा प्रतिबंध के कारण, प्रतिबंधित होते हैं। निकाय किसी स्वेच्छ आवृत्ति से दोलन नहीं कर सकता है (इसकी तुलना आवर्ती प्रगामी तरंग से करें) वरन् इसकी दोलन की आवृत्तियाँ स्वाभाविक आवृत्तियों का एक समुच्चय होती हैं। इन आवृत्तियों को दोलन का प्रसामान्य विधा कहते हैं। अब हम दोनों सिरों पर परिबद्ध किसी तानित डोरी के लिए प्रसामान्य विधा का निर्धारण करेंगे।
समीकरण (15.37) से निस्पंद की स्थितियों (जहाँ आयाम शून्य होता है) में
sin kx = 0
अर्थात् kx = nπ, n = 0, 1, 2, 3...
चूंकि k = 2π/λ है, अत:
x = n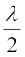 , n = 0, 1, 2, 3... (15.38)
, n = 0, 1, 2, 3... (15.38)
स्पष्टत: दो क्रमागत निस्पंदों के बीच की दूरी  होती है। उसी प्रकार स्पंदों की स्थितियों (जहाँ आयाम अधिकतम होते हैं) में sin kx का मान अधिकतम होता है:
होती है। उसी प्रकार स्पंदों की स्थितियों (जहाँ आयाम अधिकतम होते हैं) में sin kx का मान अधिकतम होता है:
|sin kx| = 1
अर्थात् kx = (n +  )π , n = 0, 1, 2, 3...
)π , n = 0, 1, 2, 3...
k = 2π/λ लेने पर
x = (n+ )
)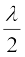 , n = 0, 1, 2, 3... (15.39)
, n = 0, 1, 2, 3... (15.39)
पुन: दो क्रमागत प्रस्पंदों के बीच की दूरी λ/2 होती है। समीकरण (15.38) का उपयोग दोनों सिरों पर परिबद्ध L लंबाई के तानित डोरी के लिए कर सकते हैं। यदि एक सिरे पर
x = 0 मान लें तो परिसीमा प्रतिबंध होंगे x = 0 तथा x = L पर निस्पंद होंगे। x = 0 प्रतिबंध की पहले से संतुष्टि होती है। x = L निस्पंद प्रतिबंध के लिए आवश्यक है कि लंबाई L तरंगदैर्घ्य λ से निम्न प्रकार से संबंधित हो
L = n  , n = 1, 2, 3... (15.40)
, n = 1, 2, 3... (15.40)
अत: L लंबाई की डोरी पर सीमित तरंगदैर्घ्य की अप्रगामी तरंगें बन सकती हैं जिनका मान निम्नलिखित संबंध द्वारा प्राप्त किया जाता है,
λ = 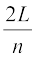 , n = 1, 2, 3... (15.41)
, n = 1, 2, 3... (15.41)
तदनुरूपी आवृत्तियों के मान होंगे
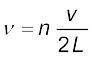 , n = 1, 2, 3... (15.42)
, n = 1, 2, 3... (15.42)
इस प्रकार हमने निकाय के दोलन की स्वाभाविक आवृत्तियाँ अथवा सामान्य विधा निर्धारित कर लिया है। किसी निकाय की न्यूनतम संभावित स्वाभाविक आवृत्ति को निकाय की मूल विधा या प्रथम गुणावृत्ति कहते हैं। दोनों सिरों पर परिबद्ध L लंबाई के तानित डोरी के लिए  जो समीकरण (15.42) में
जो समीकरण (15.42) में
n =1 के संगत है। यहाँ v माध्यम के लक्षणों पर आधारित तरंग की चाल है। n = 2 की दोलन विधा को द्वितीय गुणावृत्ति कहते हैं। n = 3 के तदनुरूपी तृतीय गुणावृत्ति होती है और इसी प्रकार अगली गुणावृत्तियाँ होती हैं । इन विधाओं से संबद्ध आवृत्तियों को νn (n = 1, 2, ...) द्वारा चिह्नित किया जाता है।
चित्र 15.13 में दोनों सिरों पर परिबद्ध तानित डोरी में प्रथम छ: गुणावृत्तियाँ दर्शायी गई हैं ।
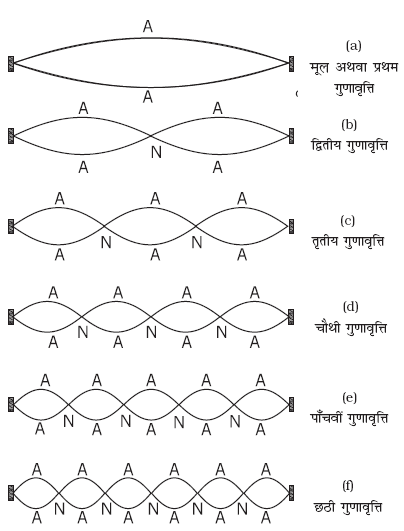
चित्र 15.13 दोनों सिरों पर परिबद्ध तानित डोरी में दोलन की प्रथम छ: गुणावृत्तियाँ।
यह आवश्यक नहीं है कि कोई तानित डोरी इन विधाओं में से किसी विधा में कंपन करे। सामान्यतया किसी डोरी का कंपन विभिन्न विधाओं का अध्यारोपण होता है। कुछ विधाएँ अधिक प्रबलता से उत्तेजित हो सकती हैं और कुछ कम प्रबलता से।सितार व वायलिन जैसे वाद्य यंत्र इस सिद्धांत पर आधारित हैं। कौन सी विधा दूसरी विधा से अधिक उत्तेजित है यह इस बात पर निर्भर करता है कि डोरी को किस बिंदु पर झंकृत किया गया है।
अब हम किसी एेसे निकाय के कंपनों की विधाओं का अध्ययन करेंगे जिनका एक सिरा बंद है जबकि दूसरा सिरा मुक्त है। अंशत: जल से भरी लम्बी काँच की नलिका का वायु कॉलम एेसे निकाय का एक उदाहरण है। वायु कॉलम में जल को छूने वाले सिरे पर निस्पंद होता है तथा खुले सिरे पर प्रस्पंद होता है। निस्पंद पर दाब में परिवर्तन अधिकतम होते हैं जबकि विस्थापन न्यूनतम (शून्य) होता है। इसके विपरीत खुले सिरे पर जहाँ प्रस्पंद होते हैं, न्यूनतम दाब परिवर्तन होते हैं तथा विस्थापन का आयाम अधिकतम होता है। जल के संपर्क वाले सिरे को x = 0 लेने पर निस्पंद प्रतिबंध (समीकरण 15.38) की स्वत: संतुष्टि होती है। यदि दूसरा सिरा x = L प्रस्पंद हो तो समीकरण (15.39) से यह परिणाम निकलता है कि
L =  , n = 0, 1, 2, 3...
, n = 0, 1, 2, 3...
संभावित तरंगदैर्घ्य निम्नलिखित संबंध से प्रतिबंधित होगी
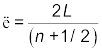 , n = 0, 1, 2, 3... (15.43)
, n = 0, 1, 2, 3... (15.43)
निकाय की सामान्य विधाएँ स्वाभाविक आवृत्तियाँ इस प्रकार व्यक्त की जाती हैं:
ν = , n = 0, 1, 2, 3... (15.44)
, n = 0, 1, 2, 3... (15.44)
मूल विधा n = 0 के संगत है और यह 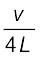 है। अन्य उच्च आवृत्तियाँ मूल आवृत्ति की विषम गुणावृत्तियाँ अर्थात्
है। अन्य उच्च आवृत्तियाँ मूल आवृत्ति की विषम गुणावृत्तियाँ अर्थात् 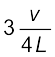 ,
, 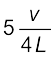 आदि होती हैं ।
आदि होती हैं ।
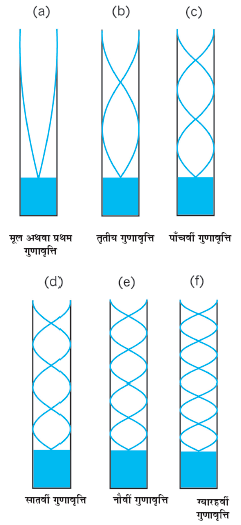
चित्र 15.14 एक सिरे से खुले तथा दूसरे सिरे पर बंद किसी वायु-कॉलम की कुछ प्रसामान्य विधाएँ। केवल विषम विधाएँ संभव हैं।
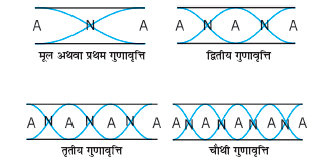
चित्र 15.15 किसी खुले पाइप में अप्रगामी तरंगें । पहली चार गुणावृत्तियाँ दर्शायी गई हैं ।
किसी पात्र की परिधि से दृढ़तापूर्वक परिबद्ध वृत्ताकार झिल्ली, उदाहरणार्थ, तबले की झिल्ली के कंपनों की प्रसामान्य विधाओं का निर्धारण इस परिसीमा शर्त के द्वारा किया जाता है कि झिल्ली की परिधि पर स्थित कोई भी बिंदु कंपन नहीं करता। इस निकाय के कंपन की प्रसामान्य विधाओं की आवृत्तियों का आकलन अधिक जटिल कार्य है । इस समस्या में दो विमाओं में तरंग संचरण सम्मिलित होता है । फिर भी इसमें अन्तर्निहित भौतिकी वही है ।
उदाहरण 15.5 दोनों सिरों से खुले किसी पाइप की लंबाई 30.0 cm है । 1.1 kHz आवृत्ति के स्रोत द्वारा इस पाइप की कौन-सी गुणावृत्ति विधा को अनुनाद द्वारा उत्तेजित किया जाता है ? यदि इस पाइप के एक सिरे को बंद कर दिया जाए तो क्या हम फिर भी इसी स्रोत द्वारा अनुनाद सुन सकते हैं ? वायु में ध्वनि की चाल
330 m s-1 है ।
हल: खुले पाइप के कंपन की पहली कुछ विधाएँ चित्र 15.15 में दर्शायी गई हैं । पहली गुणावृत्ति की आवृत्ति,
 (खुला पाइप)
(खुला पाइप)
यहाँ L पाइप की लंबाई है । n वीं गुणावृत्ति की आवृत्ति
 (n = 1, 2, 3...) (खुला पाइप)
(n = 1, 2, 3...) (खुला पाइप)
यहाँ L = 30.0 cm, v = 330 m s-1
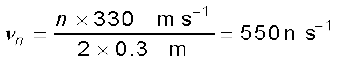
स्पष्ट है कि 1.1 kHz आवृत्ति का स्रोत, अनुनाद द्वारा ν2 आवृत्ति अर्थात् द्वितीय गुणावृत्ति को उत्तेजित करेगा ।
अब यदि पाइप का एक सिरा बंद है तब समीकरण (15.40) से यह परिणाम निकलता है कि इस पाइप की मूल आवृत्ति,
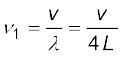 (एक सिरे पर बंद पाइप)
(एक सिरे पर बंद पाइप)
इस पाइप में केवल विषम संख्या की गुणावृत्तियाँ ही विद्यमान होती हैं:
 ,
, 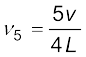 तथा इसी प्रकार आगे भी...।
तथा इसी प्रकार आगे भी...।
L = 30 cm तथा v = 300 m s-1 के लिए, एक सिरे से बंद पाइप की मूल आवृत्ति 275 Hz है तथा स्रोत की आवृत्ति चतुर्थ गुणावृत्ति के तदनुरूपी है। चूँकि यह गुणावृत्ति पाइप के कंपन की संभावित विधा नहीं है, अत: इस स्रोत के साथ पाइप का एक सिरा बंद करने पर कोई अनुनाद सुनाई नहीं देगा। °
15.7 विस्पंदें
विस्पंद तरंगों के व्यतिकरण से उत्पन्न एक रोचक परिघटना है। जब लगभग सन्निकट आवृत्ति (परंतु बराबर नहीं) वाली दो आवर्त ध्वनि तरंगें एक ही समय सुनाई देती हैं तो हमें समान आवृत्ति (दोनों सन्निकट आवृत्तियों का औसत) सुनाई देता है परन्तु हमें कुछ और भी सुनाई देता है। हमें ध्वनि की तीव्रता में धीरे-धीरे घटाव और बढ़ाव सुनाई देता है जिसकी आवृत्ति दो सन्निकट आवृत्तियों के अंतर के बराबर होती है। संगीतज्ञ इस परिघटना का उपयोग अपने वाद्यों के समस्वरण में करते हैं। वे अपने यंत्र को तब तक समस्वरक करते रहते हैं जब तक उनके सुग्राही कानों को कोई विस्पंद सुनाई न दे।
इस घटना की गणितीय विवेचना के लिए, हम दो लगभग बराबर कोणीय आवृत्तियों ω1 एवं ω2 की आवर्ती ध्वनि तरंगों पर विचार करते हैं तथा सुविधा के लिए स्थिति को x = 0 मान लें। समीकरण (15.2) में कला का एक समुचित मान (φ = π/2 प्रत्येक तरंग के लिए) तथा बराबर आयाम लेने पर हमें प्राप्त होता है:
s1 = a cos ω1t तथा s2 = a cos ω2t (15.45)
यहाँ पर हमने प्रतीक y के स्थान पर s का उपयोग किया है क्योंकि हम अनुदैर्घ्य न कि अनुप्रस्थ विस्थापन की बात कर रहे हैं। मान लीजिए कि दोनों आवृत्तियों में ω1 थोड़ी बड़ी है। अध्यारोपण के सिद्धांत के अनुसार, परिणामी विस्थापन को हम इस प्रकार व्यक्त करते हैं:
s = s1 + s2 = a (cos ω1t +cos ω2t)
cos A + cos B के सुपरिचित त्रिकोणमितीय सर्वसमिका का उपयोग करने पर
s = 2 a cos 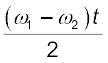 cos
cos 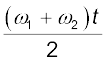 (15.46)
(15.46)
यदि हम ωb =  तथा
तथा 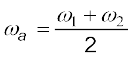 लिखें तब समीकरण (15.46) को इस प्रकार लिख सकते हैं:
लिखें तब समीकरण (15.46) को इस प्रकार लिख सकते हैं:
संगीत स्तंभ
मंदिरों में, स्तंभों पर बनी संगीत वाद्य बजाती मानवमूर्तियाँ अक्सर देखने में आती हैं, लेकिन, ये स्तंभ, स्वयं संगीत शायद ही कहीं उत्पन्न करते हों। तमिलनाडु के नेल्ल्याप्परमंदिर में एकल शिला में उत्कीर्णित एेसे स्तंभों का समूह है जिनको धीरे से टकटकाने पर, भारतीय शास्त्रीय संगीत के मूल स्वर-सा, रे, गा, मा, पा, धा, नी, सा, उत्पन्न होते हैं। इन स्तंभों के कंपन उनमें इस्तेमाल किए गए पत्थर की प्रत्यास्थता, घनत्व और स्तंभ के आकार पर निर्भर करते हैं।

पुरातत्ववेत्ता मानते हैं कि नेल्ल्याप्पर मंदिर पाण्डयन कुल के शासकों द्वारा सातवीं शताब्दी में बनवाये गए थे।
नेल्ल्याप्पर मंदिर तथा दक्षिण भारत में बने कई दूसरे मंदिरों (जैसे हम्पी (देखिये चित्र),कन्याकुमारी और तिरुअनन्तपुरम् के मंदिर) में लगे संगीत-स्तंभ हमारे देश की ही विशिष्टता है और दुनिया के किसी भी भाग में ये नहीं पाए जाते।
s = [2 a cos ωb t] cos ωa t (15.47)
यदि |ω1- ω2| << ω1, ω2; ωa >> ωb है, तब समीकरण (15.47) से निष्कर्ष निकलता है, परिणामी तरंग औसत कोणीय आवृत्ति wa से दोलन करता है परन्तु इसका आयाम समय के साथ अचर नहीं है जैसा कि एक शुद्ध आवर्त तरंग के प्रकरण में होता है। जब भी cos ωb t का मान + 1 अथवा –1 होता है आयाम अधिकतम होता है। दूसरे शब्दों में, परिणामी तरंग की तीव्रता में आवृत्ति 2 ωb = ω1 – ω2 से उतार-चढ़ाव होता है। चूंकि ω = 2πν विस्पंद νbeat को इस प्रकार व्यक्त करते हैं,
vbeat = ν1 – ν2 (15.48)
11 Hz तथा 9 Hz के दो आवृत्ति तरंगों से उत्पन्न विस्पंद की परिघटना चित्र 15.16 दर्शाता है। परिणामी तरंग का आयाम 2Hz की आवृत्ति पर विस्पंद दर्शाता है।
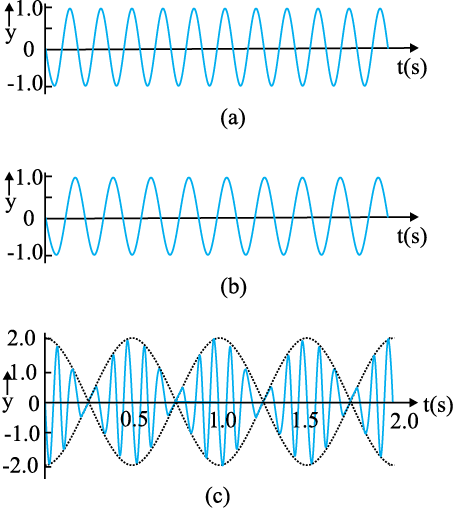
2 Hz आवृत्ति का विस्पंद दर्शाता है।
उदाहरण 15.6 दो सितारों की डोरियाँ A तथा B एक साथ ‘धा’ स्वर बजा रहीं हैं तथा स्वरों में थोड़ा अंतर होने के कारण 5 Hz आवृत्ति के विस्पंद उत्पन्न कर रही हैं । डोरी B के तनाव में कुछ वृद्धि करने पर विस्पंद की आवृत्ति घटकर 3 Hz रह जाती है । यदि A की आवृत्ति 427 Hz है, तो B की मूल आवृत्ति ज्ञात कीजिए ।
हल: डोरी में तनाव बढ़ाने पर उसकी कंपन की आवृत्ति बढ़ जाती है । यदि डोरी B की मूल आवृत्ति (νB) A की आवृत्ति (νA) से अधिक है, तब νB में और वृद्धि होने पर विस्पंदों की आवृत्ति बढ़नी चाहिए, परंतु विस्पंद-आवृत्ति में गिरावट पाई
गई । अत: यह निष्कर्ष निकलता है कि νB < νA । चूँकि
νA – νB = 5Hz, तथा νA = 427 Hz, अत: डोरी B की मूल आवृत्ति νB = 422 Hz °
15.8 डॉप्लर प्रभाव
यह हमारे दैनिक जीवन का अनुभव है कि जब कोई सीटी बजाती हुई तीव्रगामी रेलगाड़ी हमसे दूर जाती है, उस सीटी के तारत्व (अथवा आवृत्ति) में कमी होती जाती है । जब हम तीव्र गति से किसी ध्वनि-स्रोत के निकट जाते हैं, तब सुनाई देने वाली ध्वनि का तारत्व ध्वनि-स्रोत के वास्तविक तारत्व से अधिक प्रतीत होता है। इसके विपरीत जब कोई प्रेक्षक ध्वनि-स्रोत से दूर हटता जाता है, तो प्रेक्षित तारत्व ध्वनि-स्रोत के वास्तविक तारत्व से कम होता है । इस गति संबंधी आवृत्ति परिवर्तन को डॉप्लर प्रभाव कहते हैं । आस्ट्रिया के भौतिकविद जोहान क्रिश्चियन डॉप्लर ने सर्वप्रथम सन् 1842 ई. में इस प्रभाव को प्रस्तावित किया । सन् 1845 में हालैंड में बाईस बैलो ने इसका प्रायोगिक परीक्षण किया । डॉप्लर प्रभाव एक तरंग-परिघटना है, यह केवल ध्वनि तरंगों पर ही लागू नहीं होता, बल्कि यह सभी विद्युत चुंबकीय तरंगों पर भी लागू होता है । लेकिन, हम यहाँ केवल ध्वनि तरंगों पर ही विचार करेंगे ।
हम तीन विभिन्न परिस्थितियों में आवृत्ति में परिवर्तन का विश्लेषण करेंगे: (1) प्रेक्षक स्थिर है परंतु स्रोत गतिशील है,
(2) प्रेक्षक गतिशील है परंतु स्रोत स्थिर है, तथा (3) प्रेक्षक तथा स्रोत दोनाें गतिशील हैं । प्रेक्षक तथा माध्यम के बीच सापेक्ष गति होने अथवा न होने के कारण परिस्थितियाँ (1) व (2) एक दूसरे से भिन्न हैं । अधिकांश तरंगों को संचरण के लिए माध्यम की आवश्यकता होती है; फिर भी, विद्युत चुंबकीय तरंगों को संचरण के लिए माध्यम की आवश्यकता नहीं होती । यदि कोई माध्यम न हो, तो इन दोनाें परिस्थितियों में भेद करने का कोई उपाय नहीं होने के कारण, चाहे प्रेक्षक गतिशील हो अथवा स्रोत, डॉप्लर-विस्थापन समान होता है ।
15.8.1 स्रोत गतिशील; प्रेक्षक स्थिर
वेग की दिशा के संबंध में हम यह परिपाटी बना लेते हैं कि प्रेक्षक से स्रोत की ओर वेग धनात्मक है। अब हम एक स्रोत S पर विचार करते हैं जो vs वेग से गतिमान है और प्रेक्षक एक एेसे फ्रेम में स्थिर है जिसमें माध्यम भी स्थिर है। मान लीजिए कि कोई तरंग, जिसकी माध्यम के सापेक्ष विराम अवस्था स्थिति प्रेक्षक द्वारा मापी गई कोणीय आवृत्ति ω तथा आवर्तकाल T0 है, की चाल v है । हम मानते हैं कि प्रेक्षक के पास एक संसूचक (detector) है जो इसके पास पहुँचने वाले प्रत्येक तरंग-शिखर (crest) को गिनता है । समय t = 0 पर जब स्रोत बिंदु S1 पर अवस्थित है (देखें चित्र 15.17), स्रोत एक तरंग-शिखर उत्सर्जित करता है । इस समय (t = 0) पर स्रोत प्रेक्षक से L दूरी पर है । यह तरंग-शिखर प्रेक्षक के पास समय t1 = (L/v) पर पहुँचता है । समय t = T0 पर स्रोत प्रेक्षक की ओर vsT0 दूरी चल लेता है और बिंदु S2 पर पहुँच जाता है जिसकी प्रेक्षक से दूरी (L+vsT0) है।
बिंदु S2 पर स्रोत एक और (दूसरा) तरंग-शिखर उत्सर्जित करता है । यह दूसरा तरंग-शिखर प्रेक्षक तक समय t2 पर पहुँचता है,
खुले पाइप में ध्वनि का परावर्तन
जब खुले पाइप में चलता हुआ वायु का, उच्च दाब वाला कोई स्पंद इसके दूसरे सिरे पर पहुँचता है, तो इसका संवेग वायु को खुले में खींच निकालता है इसलिए यहाँ दाब तेजी से गिरकर वायुमण्डलीय दाब के बराबर हो जाता है। परिणामस्वरूप इस स्पंद के पीछे आने वाली कुछ वायु भी बाहर निकल जाती है। पाइप में इस सिरे पर कम दाब, पाइप में, इससे ऊपर की कुछ वायु को नीचे खींचता है। इससे कम दाब का यह क्षेत्र ऊपर की ओर चलता है।

परिणामत: नीचे की ओर चलता हुआ उच्च दाब का स्पंद, न्यून दाब के वायु स्पंद में बदल कर ऊपर की ओर चलता है। हम कहते हैं कि दाब तरंग खुले सिरे से परावर्तित होती है तो इसकी कला में 180° का अंतर आ जाता है। बाँसुरी जैसे खुले अॉर्गन पाइप में अप्रगामी तरंगों का बनना इसी प्रक्रम का परिणाम है।
तुलना के लिए देखें, कि जब उच्च दाब का वायु स्पंद, बंद सिरे पर पहुँचता है, तो क्या होता है: बंद सिरे से टकराकर वायु विपरीत दिशा में वापस लौटती है। यहाँ हम कहते हैं कि दाब तरंग बिना किसी कलांतर के परिवर्तित होती है।
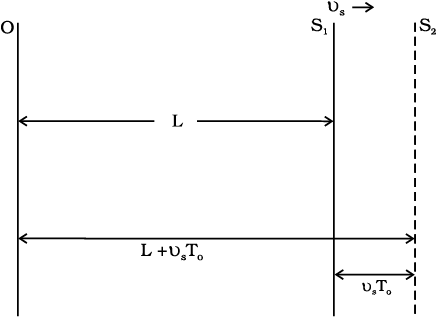
t2 = T0 + 
समय nT0 पर स्रोत (n+1) वाँ तरंग-शिखर उत्सर्जित करता है जो प्रेक्षक तक जिस समय tn पर पहुँचता है उसे इस प्रकार व्यक्त कर सकते हैं,
tn+1 = nT0 + 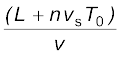
अत: समय अंतराल
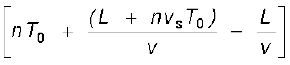
में प्रेक्षक का संसूचक n तरंग-शिखर गिनता है तथा प्रेक्षक तरंग का आवर्तकाल T नीचे दिए अनुसार रिकार्ड करता है
T = 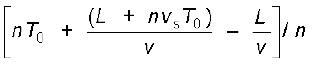
= 
=  (15.49)
(15.49)
समीकरण (15.49) को हम आवृत्ति के पदों में भी लिख सकते हैं । यदि v0 वह आवृत्ति है जो स्रोत एवं प्रेक्षक दोनों के विराम में होने पर मापी गई है तथा v वह प्रेक्षित आवृत्ति है जो स्रोत के गतिशील होने पर है, तो प्रेक्षित आवृत्ति,
ν =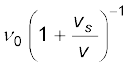 (15.50)
(15.50)
यदि तरंग चाल v की तुलना में स्रोत की चाल vs का मान कम है तो द्विपद प्रसरण के 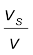 से उच्चतर घातों के पदों को न लेकर, समीकरण (15.50) को सन्निकटत: इस प्रकार लिख सकते हैं,
से उच्चतर घातों के पदों को न लेकर, समीकरण (15.50) को सन्निकटत: इस प्रकार लिख सकते हैं,
ν = 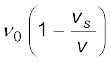 (15.51)
(15.51)
यदि स्रोत प्रेक्षक की ओर आ रहा हो तो vs को (–vs) से प्रतिस्थापित करने पर हम पाते हैं:
ν = 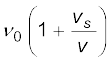 (15.52)
(15.52)
अत: जब कोई ध्वनि स्रोत किसी प्रेक्षक से दूर जाता है तब उस स्थिति की तुलना में जब यह विराम पर था, प्रेक्षक अपेक्षाकृत कम आवृत्ति मापता है। जब स्रोत उसकी ओर चलता है तो यह तरंगों की आवृत्ति अधिक मापता है।
डॉप्लर प्रभाव के अनुप्रयोग
गतिमान पिण्डों की आवृत्तियों में, डॉप्लर प्रभाव के कारण आने वाले अंतर का उपयोग, सेना, औषधि विज्ञान, खगोलिकी जैसे विविध क्षेत्रों में पिण्डों का वेग मापने के लिए किया जाता है। इसका उपयोग पुलिस यह जाँचने के लिए भी करती है कि कोई गाड़ी गतिसीमा से अधिक गति से तो नहीं चलाई जा रही।
ज्ञात आवृत्ति की ध्वनि या विद्युत चुंबकीय तरंगों को गतिमान पिण्ड की ओर भेजा जाता है। मॉनीटरिंग स्टेशन पर, पिण्ड द्वारा परावर्तित तरंगें प्राप्त करके इनकी आवृत्ति ज्ञात की जाती है। इन दो आवृत्तियों का अंतर डॉप्लर विस्थापन कहलाता है।
हवाई अड्डों पर वायुयानों के मार्गदर्शन के लिए, सेना में शत्रु यानों के संसूचन के लिए इस विधि का उपयोग किया जाता है। खगोल भौतिकीविद तारों का वेग मापने के लिए इसका उपयोग करते हैं।
डॉक्टर लोग हृदय स्पंदनों और शरीर के विभिन्न अंगों में रक्त प्रवाह का अध्ययन करने के लिए इसका उपयोग करते हैं। यहाँ वे पराध्वनि तरंगों का उपयोग करते हैं और सामान्य व्यवहार में इसे सोनोग्राफी कहा जाता है। पराध्वनि तरंगें व्यक्ति के शरीर में प्रवेश करती हैं और इनमें से कुछ परावर्तित हो जाती हैं तथा रक्त की गति और हृदय के वाल्बों के स्पंदन के विषय में जानकारी प्रदान करती है, इसमें भ्रूण के हृदय का स्पंदन भी शामिल है। हृदय से परावर्तित तरंगों से जो चित्र बनता है उसे इकोकार्डियोग्राम कहा जाता है।
15.8.2 प्रेक्षक गतिशील; स्रोत स्थिर
अब उस स्थिति में, जब प्रेक्षक स्रोत की ओर v0 चाल से गतिमान हो, तथा स्रोत विराम में हो, तो डॉप्लर विस्थापन को व्युत्पन्न करने के लिए हमें दूसरे ढंग से आगे बढ़ना होगा । हम गतिशील प्रेक्षक के निर्देश फ्रेम में कार्य करेंगे । इस निर्देश फ्रेम में स्रोत तथा प्रेक्षक चाल v0 से समीप आते हैं तथा तरंग के समीप आने की चाल v0 + v है । पिछली परिस्थिति में जो ढंग अपनाया गया था उसी को इस परिस्थिति में भी अपनाने पर हम यह पाते हैं कि पहले तरंग शिखर तथा (n+1) वें तरंग शिखर के प्रेक्षक तक पहुँचने के बीच समय अंतराल इस प्रकार व्यक्त किया जा सकता है,

अत:, प्रेक्षक द्वारा मापा गया तरंग का आवर्त काल
T 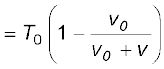

आवृत्ति के पदों में इसे इस प्रकार व्यक्त कर सकते हैं,
ν =  (15.53)
(15.53)
यदि 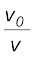 का मान कम है, तब डॉप्लर विस्थापन लगभग वही होगा, चाहे प्रेक्षक गति करे अथवा स्रोत, क्योंकि समीकरण (15.53) तथा सन्निकट संबंध (15.51) समान हैं ।
का मान कम है, तब डॉप्लर विस्थापन लगभग वही होगा, चाहे प्रेक्षक गति करे अथवा स्रोत, क्योंकि समीकरण (15.53) तथा सन्निकट संबंध (15.51) समान हैं ।
15.8.3 स्रोत तथा प्रेक्षक दोनों गतिशील हैं
अब हम डॉप्लर प्रभाव के लिए, स्रोत तथा प्रेक्षक दोनों को गतिशील लेकर व्यापक व्यंजक व्युत्पन्न करेंगे । पहले की तरह हम प्रेक्षक से स्रोत की दिशा को धनात्मक दिशा मानेंगे। मान लीजिए चित्र 15.18 की भाँति स्रोत तथा प्रेक्षक क्रमश: vs तथा v0 वेग से गतिशील हैं, माना समय t = 0 पर प्रेक्षक O1 पर तथा स्रोत S1(O) की बाईं ओर है। माध्यम के सापेक्ष स्थिर एक प्रेक्षक देखता है कि स्रोत वेग ν, आवृति ν और आवर्त काल T0 की तरंग उत्सर्जित करता है। t = 0 पर जब स्रोत पहला तरंग शिखर उत्सर्जित
करता हो उस समय प्रेक्षक O1 की स्रोत S1 से दूरी L है ।
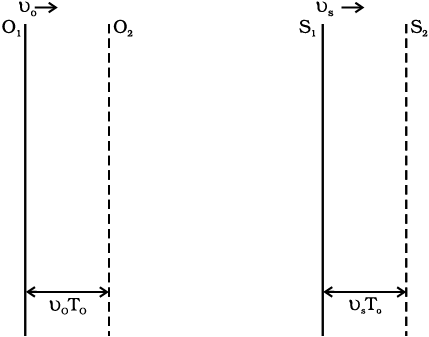
अब चूँकि प्रेक्षक गतिशील है, इसलिए तरंग की प्रेक्षक के सापेक्ष चाल (v + v0) है । अत: पहला तरंग-शिखर प्रेक्षक पर समय t1 = L/(v + v0) पर पहुँचता है । समय t = T0 पर प्रेक्षक तथा स्रोत दोनों ही अपनी नयी स्थितियों क्रमश: O2 तथा S2 पर पहुँच जाते हैं । प्रेक्षक तथा स्रोत के बीच की नयी दूरी, O2S2 = [L + (v0 – vs)/T0] है । S2 पर स्रोत दूसरा तरंग-शिखर उत्सर्जित कर देता है । यह तरंग-शिखर प्रेक्षक तक समय t2 पर पहुँचता है जिसे इस प्रकार व्यक्त किया जा सकता है,
t2 = T0 + [L – (vs – v0)T0]/(v + v0)
समय n T0 पर, स्रोत (n + 1) वाँ तरंग-शिखर उत्सर्जित कर देता है जो समय tn+1 पर प्रेक्षक पर पहुँचता है जिसे इस प्रकार व्यक्त कर सकते हैं,
tn+1 = nTo + [L – n (vs + vo)To)] /(v + vo)
अत: समय अंतराल, (tn + 1 – t)
nT0 + [L + n(vs+v0)T0]/(v+v0) – L/(v + v0)
में प्रेक्षक n तरंग-शिखर गिनता है तथा प्रेक्षक तरंग का आवर्तकाल T रिकार्ड करता है जिसे इस संबंध द्वारा व्यक्त किया जाता है
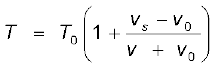
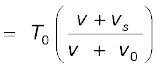 (15.54)
(15.54)
आवृत्ति के पदों में प्रेषक द्वारा प्रेक्षित आवृत्ति को इस प्रकार व्यक्त कर सकते हैं,
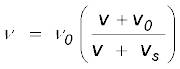 (15.55)
(15.55)
सोचिए कि सीधी पटरियों पर चलती हुई किसी रेलगाड़ी में एक महिला यात्री बैठी है। माना कि वह रेलगाड़ी के ड्राइवर द्वारा बजायी गई सीटी की ध्वनि सुनती है। वह क्या आवृत्ति सुनेगी? यहाँ स्रोत और प्रेक्षक दोनों ही समान वेग से चल रहे हैं अत: आवृत्ति में कोई अंतर नहीं आएगा और यात्री वही प्राकृतिक आवृत्ति सुनेगी जो स्रोत उत्पन्न कर रहा है। लेकिन रेल की पटरियों के पास खड़ा कोई प्रेक्षक प्राकृतिक आवृत्ति से अधिक आवृत्ति नोट करेगा जब रेलगाड़ी उसकी ओर आती है और कम आवृत्ति नोट करेगा जब रेलगाड़ी उससे दूर जाती है।
ध्यान दें कि हमने प्रेक्षक से स्रोत की दिशा को धनात्मक दिशा कहा है। इसलिए यदि प्रेक्षक स्रोत की ओर चल रहा है तो v0 का मान धनात्मक है जबकि यदि वह स्रोत S से दूर जा रहा हो तो v0 का मान ऋणात्मक है। दूसरी ओर यदि S प्रेक्षक O से दूर जा रहा है तो vs का मान धनात्मक है जबकि यदि वह O की ओर आ रहा है तो vs का मान ऋणात्मक है। स्रोत द्वारा उत्सर्जित ध्वनि सभी दिशाओं में गमन करती है। इस ध्वनि का जो भाग प्रेक्षक की ओर आता है उसको ही वह संसूचित करता है। इसी कारण प्रत्येक स्थितियों में प्रेक्षक के सापेक्ष ध्वनि का वेग (v + v0) होता है।
उदाहरण 15.7 : कोई रॉकेट 200 m s-1 की चाल से किसी लक्ष्य की ओर गतिमान है । गति करते समय यह 1000 Hz आवृत्ति की तरंग उत्सर्जित करता है । इस ध्वनि का कुछ भाग लक्ष्य पर पहुँच कर प्रतिध्वनि के रूप में वापस रॉकेट की ओर परावर्तित हो जाता है । (a) लक्ष्य द्वारा संसूचित ध्वनि की आवृत्ति, तथा (b) रॉकेट द्वारा संसूचित प्रतिध्वनि की आवृत्ति परिकलित कीजिए ।
हल: (a) इस प्रश्न में प्रेक्षक स्थिर है तथा स्रोत प्रेक्षक की ओर 200 m s-1 चाल से गतिशील है, क्योंकि यह वेग, ध्वनि वेग (= 330 ms–1) के साथ तुलनीय है। अत: हम यहाँ समीकरण (15.50) का उपयोग करेंगे न कि सन्निकट समीकरण (15.51) का। यहाँ क्योंकि स्रोत स्थिर लक्ष्य की ओर चल रहा है vs के स्थान पर (–vs) प्रतिस्थापित करेंगे। इस प्रकार समीकरण
(15.50) से
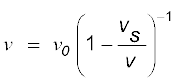
= 1000 Hz × 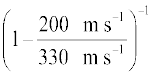
= 2540 Hz
(b) यहाँ इस प्रश्न में अब लक्ष्य स्रोत है (क्योंकि यह प्रतिध्वनि का स्रोत है) तथा रॉकेट का संसूचक अब एक संसूचक अथवा प्रेक्षक (क्योंकि यह संसूचन भी करता है) है । अत: vs = 0 एवं v0 का मान धनात्मक है। अब स्रोत (लक्ष्य) द्वारा उत्सर्जित ध्वनि की आवृत्ति v है जो कि लक्ष्य द्वारा अवरुद्ध आवृत्ति है । यहाँ हम स्रोत की मूल आवृत्ति ν0 का उपयोग नहीं कर सकते । अत: रॉकेट से जुड़े संसूचक द्वारा रिकार्ड की गई आवृत्ति
ν' = 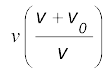
= 2540 Hz × 
= 4080 Hz
सारांश
1. यांत्रिक तरंगें द्रव्यात्मक माध्यमों में विद्यमान रह सकती हैं तथा ये न्यूटन के गति के नियमों द्वारा संनियमित होती हैं ।
2. अनुप्रस्थ तरंगें वे तरंगें होती हैं जिनमें माध्यम के कण तरंग संचरण की दिशा के लंबवत् दोलन करते हैं ।
3. अनुदैर्घ्य तरंगें वे तंरगें होती हैं जिनमें माध्यम के कण तरंग संचरण की दिशा के अनुदिश दोलन करते हैं ।
4. प्रगामी तरंग वह तरंग होती है जो माध्यम के एक बिंदु से दूसरे बिंदु तक गमन करती है ।
5. धनात्मक x-दिशा में संचरित ज्यावक्रीय तरंग का विस्थापन इस प्रकार व्यक्त किया जाता है-
y (x, t) = a sin (kx – ωt + φ)
यहाँ a तरंग का आयाम, k कोणीय तरंग संख्या, ω कोणीय आवृत्ति, (kx – ωt + φ) कला, तथा φ कला-नियतांक अथवा प्रारंभिक कला कोण है ।
6. किसी प्रगामी तरंग का तरंगदैर्घ्य λ, उसके किन्हीं एेसे दो क्रमागत बिंदुओं के बीच की दूरी के बराबर होती है जो किसी क्षण पर समान कला में होते हैं । अप्रगामी तरंगों के लिए यह दो क्रमागत निस्पंदों अथवा प्रस्पंदों के बीच की दूरी के दोगुने के बराबर होती है ।
7. किसी तरंग के आवर्तकाल T को उस समय द्वारा परिभाषित किया जाता है जिसमें माध्यम का कोई अवयव अपना एक दोलन पूर्ण करता है । यह तरंग की कोणीय आवृत्ति ωसे इस प्रकार संबधित होता है
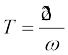
8. किसी तरंग की आवृत्ति ν को 1/T के रूप में परिभाषित किया जाता है तथा आवृत्ति व कोणीय आवृत्ति मेें निम्नलिखित संबंध होता है:

9. प्रगामी तरंग की चाल 
10. किसी तानित डोरी पर अनुप्रस्थ तरंग की चाल उस डोरी के गुणों से निर्धारित होती है । यदि किसी डोरी में तनाव T है तथा डोरी का रैखिक द्रव्यमान घनत्व µ है तो उस डोरी मेें अनुप्रस्थ तरंग की चाल,
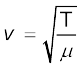
11. ध्वनि तरंगें अनुदैर्घ्य यांत्रिक तरंगें होती हैं जो ठोसों, द्रवों तथा गैसों में गमन कर सकती हैं । यदि किसी माध्यम का आयतन प्रत्यास्थता गुणांक B तथा घनत्व ρ है तो उस माध्यम में ध्वनि तरंगों की चाल
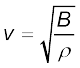
धातु की छड़ में अनुदैर्घ्य तरंगों की चाल

किसी गैस मेें, चूँकि B = γP, अत: ध्वनि की चाल
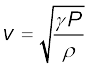
यहाँ γ गैस की दो विशिष्ट ऊष्माओं का अनुपात (γ = Cp/Cv), ρ गैस का घनत्व तथा Pगैस का दाब है ।
12. जब दो या अधिक तरंगें किसी माध्यम में एक साथ गमन करती हैं, तब माध्यम के किसी अवयव का विस्थापन प्रत्येक तरंग के विस्थापनों का बीजगणितीय योग होता है । इसे तरंगों के अध्यारोपण का सिद्धांत कहते हैं ।
भौतिक राशि प्रतीक विमाएँ मात्रक टिप्पणी
तरंगदैर्घ्य λ [ L ] m एक ही क्षण पर समान कला के दो क्रमागत बिंदुओं के बीच की दूरी
संचरण नियतांक k [ L-1 ] m-1 k = 
तरंग चाल v [LT-1] m s-1 ν = vλ
विस्पंद आवृत्ति νbeat [T-1] s-1 दो निकट आवृत्तियों की अध्यारोपित तरंगों
की आवृत्तियों का अंतर
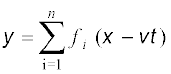
13. एक ही डोरी पर गमन करती दो ज्यावक्रीय तरंगें अध्यारोपण के सिद्धांत के अनुसार संकलन अथवा निरसन द्वारा व्यतिकरण की परिघटना प्रदर्शित करती हैं । यदि समान आयाम a तथा समान आवृत्ति वाली परंतु कला में कला-नियतांक φ के अंतर वाली दोतरंगें एक ही दिशा में गतिमान हैं तो उनके व्यतिकरण का परिणाम एक एकल तरंग होती हैं जिसकी आवृत्ति भी उनके समान होती है:
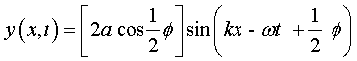
यदि φ = 0 अथवा 2π का पूर्णांक गुणज हो तो तरंगें एकदम समान कला मेें होती हैं तथा व्यतिकरण संपोषी होता है; यदि φ = π अथवा π रेडियन का विषम गुणज हो तो तरंगें एकदम विपरीत कलाओं मेें होती है तथा व्यतिकरण विनाशी
होता है ।
14. किसी प्रगामी तरंग का किसी दृढ़ परिसीमा अथवा बंद सिरे पर परावर्तन कला-उत्क्रमण के साथ होता है, परंतु किसी खुली परिसीमा पर यह परावर्तन बिना किसी कला-परिवर्तन के होता है ।
किसी आपतित तरंग के लिए
yi (x, t) = a sin (kx – ωt)
दृढ़ परिसीमा से परावर्तित तरंग के लिए
yr (x, t) = – a sin (kx + ωt)
खुली परिसीमा से परावर्तित तरंग के लिए
yr (x, t) = a sin (kx + ωt)
15. विपरीत दिशाओं में गतिशील दो सर्वसम तरंगों के व्यतिकरण से अप्रगामी तरंगें उत्पन्न होती हैं । दोनों सिरों पर परिबद्ध तानित डोरी में उत्पन्न अप्रगामी तरंगों को इस प्रकार व्यक्त किया जाता है
y (x, t) = [2 a sin kx] cos ωt
अप्रगामी तरंगों का एक अभिलक्षण यह है कि इनमें शून्य विस्थापन की निश्चित अवस्थितियाँ जिन्हें निस्पंद कहते हैं तथा अधिकतम विस्थापन की निश्चित अवस्थितियाँजिन्हें प्रस्पंद कहते हैं, होती हैं । दो क्रमागत निस्पंदों अथवा दो क्रमागत प्रस्पंदों के बीच की दूरी  होती है ।
होती है ।
L लंबाई की तानित डोरी जो दोनों सिरों पर परिबद्ध हो, निम्नलिखित आवृत्तियों से कंपन करती है:
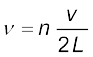 , n = 1, 2, 3....
, n = 1, 2, 3....
यहाँ v तरंग की डोरी पर गमन की चाल है । इस संबंध से प्राप्त आवृत्तियों को सेट निकाय के कंपन अथवा दोलन की प्रसामान्य विधाएँ कहते है । निम्नतम आवृत्ति से दोलन की विधामूल विधा अथवा प्रथम गुणावृत्ति कहलाती है । n = 2 की दोलन विधा को द्वितीय गुणावृत्ति कहते हैं, और इसी प्रकार क्रम बढ़ता जाता है ।
L लंबाई की कोई नली जिसका एक सिरा बंद तथा दूसरा सिरा खुला हो, जैसे वायु-कॉलम, निम्नलिखित आवृत्तियों से कंपन करता है:
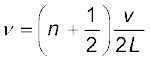 , n = 0, 1, 2, 3....
, n = 0, 1, 2, 3....
उपरोक्त संबंध द्वारा निरूपित आवृत्तियों का सेट इस प्रकार के निकाय के दोलन कीप्रसामान्य विधाएँ होती हैं । इस संबंध द्वारा n = 0 के लिए प्राप्त निम्नतम आवृत्ति 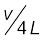 है, जो इस प्रकार के निकाय की मूल विधा अथवा प्रथम गुणावृत्ति होती है ।
है, जो इस प्रकार के निकाय की मूल विधा अथवा प्रथम गुणावृत्ति होती है ।
16. दोनों सिरों से परिबद्ध L लंबाई की तानित डोरी अथवा एक सिरे से बंद तथा दूसरे सिरे पर मुक्त अथवा दोनों सिरों पर मुक्त वायु-कॉलम जिन नियत आवृत्तियों से कंपन करते हैं उन्हें इन निकायों की प्रसामान्य विधाएँ कहते हैं । इनमें से प्रत्येक आवृत्ति निकाय कीअनुनाद आवृत्ति होती है ।
17. विस्पंद तब उत्पन्न </style>होते हैं जब बहुत कम अंतर की दो आवृत्तियों ν1तथा ν2की तरंगें एक साथ संसूचित की जाती हैं। विस्पंद आवृत्ति इस प्रकार व्यक्त की जाती है,
νbeat = ν1 ~ ν2
18. माध्यम के सापेक्ष ध्वनि स्रोत (S) अथवा प्रेक्षक O अथवा दोनों की गति के कारण किसी तरंग की प्रेक्षित आवृत्ति में परिवर्तन होना डॉप्लर प्रभाव कहलाता है। ध्वनि के लिए प्रेक्षित आवृत्ति को ध्वनि स्रोत की आवृत्ति ν0 के पदों मेें व्यक्त किया जाता है
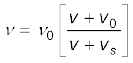
यहाँ v माध्यम में ध्वनि की चाल, v0 माध्यम के सापेक्ष प्रेक्षक की चाल तथा vs माध्यम के सापेक्ष ध्वनि-स्रोत का वेग है । इस सूत्र का उपयोग करते समय, OS की दिशा में वेग धनात्मक और विपरीत दिशा में ऋणात्मक लिए जाएँगे।
विचारणीय विषय
1. तरंग किसी माध्यम में समूचे द्रव्य की गति नहीं है । पवन वायु में ध्वनि तरंग से भिन्न होती है । पवन में एक स्थान से दूसरे स्थान तक वायु की गति सम्मिलित होती है । ध्वनि तरंग में वायु की परतों का संपीडन तथा विरलन सम्मिलित होता है ।
2. तरंग में एक स्थान से दूसरे स्थान तक ऊर्जा स्थानांतरित होती है न कि द्रव्य ।
3. किसी यांत्रिक तरंग में, माध्यम के निकटतम दोलनी भागों के बीच आद्योपांत (शुरू से अंत तक) प्रत्यास्थ बलों के युग्मन के कारण ऊर्जा स्थानांतरण होता है ।
4. अनुप्रस्थ तरंगों का संचरण केवल उन्हीं माध्यमों में हो सकता है जिनमें अपरूपण प्रत्यास्थता गुणांक हो, उदाहरणार्थ ठोस । अनुदैर्घ्य तरंगों को आयतन प्रत्यास्थता गुणांक की आवश्यकता होती है, अत: येे तरंगें सभी माध्यमों-ठोस, द्रव तथा गैस में संभव होती हैं ।
5. दी गई आवृत्ति की किसी सरल आवर्त प्रगामी तरंग में सभी कणों का आयाम समान होता है, परंतु किसी दिए गए नियत समय पर उनकी कलाएँ भिन्न होती हैं । किसी अप्रगामी तरंग मेें किसी निश्चित क्षण पर सभी कणों की कलाएँ समान होती हैं परंतु उनके आयाम भिन्न होते हैं ।
6. किसी माध्यम मेें विराम की स्थिति वाले प्रेक्षक के सापेक्ष उस माध्यम में किसी यांत्रिक तरंग की चाल (v) केवल माध्यम के प्रत्यास्थ तथा अन्य गुणों (जैसे द्रव्यमान घनत्व) पर निर्भर करती है । यह ध्वनि-स्रोत के वेग पर निर्भर नहीं करती ।
7. माध्यम के सापेक्ष v0 वेग से गतिशील किसी प्रेक्षक के लिए प्रत्यक्ष रूप से तरंग की चाल v से भिन्न होती है तथा यह चाल v ± v0 होती है ।
अभ्यास
15.1 2.50 kg द्रव्यमान की 20 cm लंबी तानित डोरी पर 200 N बल का तनाव है । यदि इस डोरी के एक सिरे को अनुप्रस्थ झटका दिया जाए तो उत्पन्न विक्षोभ कितने समय में दूसरे सिरे तक पहुँचेगा ?
15.2 300 m ऊँची मीनार के शीर्ष से गिराया गया पत्थर मीनार के आधार पर बने तालाब के पानी से टकराता है । यदि वायु मेें ध्वनि की चाल 340 m s-1 है तो पत्थर के टकराने की ध्वनि मीनार के शीर्ष पर पत्थर गिराने के कितनी देर बाद सुनाई देगी ? (g = 9.8 m s-2)
15.3 12.0 m लंबे स्टील के तार का द्रव्यमान 2.10 kg है । तार में तनाव कितना होना चाहिए ताकि उस तार पर किसी अनुप्रस्थ तरंग की चाल 20 °C पर शुष्क वायु मेें ध्वनि की चाल (343 m s-1) के बराबर हो ।
15.4 सूत्र का उपयोग करके स्पष्ट कीजिए कि वायु में ध्वनि की चाल क्यों
(a) दाब पर निर्भर नहीं करती,
(b) ताप के साथ बढ़ जाती है, तथा
(c) आर्द्रता के साथ बढ़ जाती है ?
15.5 आपने यह सीखा है कि एक विमा में कोई प्रगामी तरंग फलन y = f (x, t) द्वारा निरूपित की जाती है जिसमें x तथा t को x - vt अथवा x + vt अर्थात् y = f (x ± vt) संयोजन में प्रकट होना चाहिए । क्या इसका प्रतिलोम भी सत्य है ? नीचे दिए गए y के प्रत्येक फलन का परीक्षण करके यह बताइए कि वह किसी प्रगामी तरंग को निरूपित कर सकता है:
(a) (x - vt)2
(b) log [(x+vt)/x0]
(c) 1/(x + vt)
15.6 कोई चमगादड़ वायु मेें 1000 k Hz आवृत्ति की पराश्रव्य ध्वनि उत्सर्जित करता है । यदि यह ध्वनि जल के पृष्ठ से टकराती है, तो (a) परावर्तित ध्वनि तथा (b) पारगमित ध्वनि की तरंगदैर्घ्य ज्ञात कीजिए । वायु तथा जल में ध्वनि की चाल क्रमश: 340 m s-1 तथा 1486 m s-1 है ।
15.7 किसी अस्पताल में ऊतकों में ट्यूमरों का पता लगाने के लिए पराश्रव्य स्कैनर का प्रयोग किया जाता है । उस ऊतक में ध्वनि में तरंगदैर्घ्य कितनी है जिसमें ध्वनि की चाल 1.7 k m s-1 है ? स्कैनर की प्रचालन आवृत्ति 4.2 MHz है ।
15.8 किसी डोरी पर कोई अनुप्रस्थ गुणावृत्ति तरंग का वर्णन
y (x, t) = 3.0 sin (36 t + 0.018 x + π/4)
द्वारा किया जाता है । यहाँ x तथा y सेंटीमीटर में तथा t सेकंड मेें है । x की धनात्मक दिशा बाएँ से दाएँ है ।
(a) क्या यह प्रगामी तरंग है अथवा अप्रगामी ? यदि यह प्रगामी तरंग है तो इसकी चाल तथा संचरण की दिशा क्या है ?
(b) इसका आयाम तथा आवृत्ति क्या है ?
(c) उद्गम के समय इसकी आरंभिक कला क्या है ?
(d) इस तरंग में दो क्रमागत शिखरों के बीच की न्यूनतम दूरी क्या है ?
15.9 प्रश्न 15.8 में वर्णित तरंग के लिए x = 0 cm, 2 cm तथा 4 cm के लिए विस्थापन (y) और समय (t) के बीच ग्राफ आलेखित कीजिए । इन ग्राफाें की आकृति क्या है ? आयाम, आवृत्ति अथवा कला में से किन पहलुओं में प्रगामी तरंग में दोलनी गति एक बिंदु से दूसरे बिंदु पर भिन्न है ?
15.10 प्रगामी गुणावृत्ति तरंग
y (x, t)
