Table of Contents

अध्याय 5
केंद्रीय प्रवृत्ति की माप

इस अध्याय को पढ़ने के बाद आप इस योग्य होंगे किः
• किसी एक संख्या द्वारा आँकड़ों के समुच्चय को संक्षिप्त करने की आवश्यकता समझ सकें;
• विभिन्न प्रकार के औसतों को समझकर इनके बीच अंतर कर सकें;
• विभिन्न प्रकार के औसतों का अभिकलन सीख सकें;
• आँकड़ों के किसी समुच्चय से अर्थपूर्ण निष्कर्ष निकाल सकें;
• इसका निर्णय ले सकें कि स्थिति विशेष में कौन-सा औसत सर्वाधिक उपयोगी होगा।
1. प्रस्तावना
पिछले अध्याय में, आप आँकड़ों के सारणीबद्ध एवं आलेखी प्रस्तुतीकरण के बारे में पढ़ चुके हैं। इस अध्याय में, आप केंद्रीय प्रवृत्ति के मापों के बारे में अध्ययन करेंगे, जो आँकड़ों की संक्षिप्त रूप में व्याख्या करने की संख्यात्मक विधि है। दैनिक जीवन में आप आँकड़ों के विशाल समुच्चय के संक्षेपण के उदाहरण देख सकते हैं, जैसे किसी कक्षा में छात्रों द्वारा किसी परीक्षा में प्राप्त किए गए औसत अंक, क्षेत्र विशेष की औसत वर्षा, किसी कारखाने में औसत उत्पादन, किसी फर्म में काम करने वाले या किसी स्थान विशेष में रहने वाले लोगों की औसत आय आदि।
बैजू एक किसान है। वह बिहार के बक्सर जिले के बालापुर गाँव में अपने खेत में खाद्यान्न का उत्पादन करता है। उस गाँव में 50 छोटे कृषक हैं। बैजू के पास एक एकड़ भूमि है। आप बालापुर के किसानों की आर्थिक स्थिति जानने में रुचि रखते हैं। आप बालापुर गाँव में बैजू की आर्थिक स्थिति की तुलना करना चाहते हैं। इसके लिए आपको बालापुर गाँव के दूसरे किसानों की जोतों के आकार के साथ बैजू की जोत के आकार का तुलनात्मक मूल्यांकन करना होगा। आप यह जानना चाहेंगे कि क्या बैजू की भूमि -
1. सामान्य अर्थ में औसत से ऊपर है (देखें नीचे दिया गया माध्य)
2. आधे किसानों की जोतों के आकार से अधिक है (देखें नीचे दी गई मध्यिका)
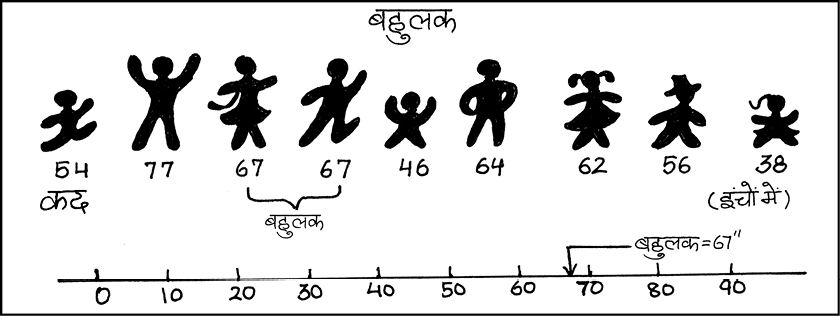
3. अधिकतर किसानों की जोत से अधिक है (देखें नीचे दिया गया बहुलक)
बैजू की तुलनात्मक आर्थिक स्थिति के मूल्यांकन के लिए, आपको बालापुर गाँव के सभी किसानों की जोतों के आँकड़ों के संपूर्ण समुच्चय का संक्षेपण करना होगा। इसे केंद्रीय प्रवृत्ति के माप द्वारा किया जा सकता है, जो आँकड़ों का संक्षेपण किसी एकल मान में इस प्रकार करता है कि यह एकल मान संपूर्ण आँकड़ों का प्रतिनिधित्व करे। केंद्रीय प्रवृत्ति की माप प्रतिनिधि या विशिष्ट मान के रूप में आँकड़ों के संक्षेपण का एक तरीका है।
केंद्रीय प्रवृत्ति या औसतों के कई सांख्यिकीय माप हैं। तीन सर्वाधिक प्रचलित औसत निम्नलिखित हैं-
• समांतर माध्य
• मध्यिका
• बहुलक
आपको यह भी ध्यान रखना चाहिए कि दो अन्य प्रकार के औसत और भी हैं, जैसे ज्यामितीय माध्य तथा हरात्मक माध्य, जो विशिष्ट परिस्थितियों में उपयुक्त होते हैं। लेकिन वर्तमान परिचर्चा उपर्युक्त तीन प्रकार के औसतों तक ही सीमित रहेगी।
2. समांतर माध्य (Arithmetic Mean)
मान लीजिए 6 परिवारों की मासिक आय (रु में) निम्नलिखित हैः
1600, 1500, 1400, 1525, 1625, 1630.
यहाँ पर परिवारों की औसत आय प्राप्त करने के लिए आय को एक साथ जोड़कर, उसे परिवारों की संख्या से विभाजित किया गया है।
= 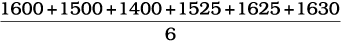
= 1,547 रु
इससे पता चलता है कि औसतन एक परिवार 1,547 रु अर्जित करता है।
समांतर माध्य केंद्रीय प्रवृत्ति का सबसे अधिक प्रयोग किया जाने वाला माप है। समांतर माध्य को, सभी प्रेक्षणों के मूल्यों के योग को उनकी कुल संख्याओं से विभाजन के रूप में परिभाषित किया जाता है और सामान्यतः 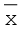 से निर्देशित किया जाता है। यदि X1, X2, X3, ..., XN, आदि N प्रेक्षण हैं, तो समांतर माध्य इस प्रकार प्राप्त होगाः
से निर्देशित किया जाता है। यदि X1, X2, X3, ..., XN, आदि N प्रेक्षण हैं, तो समांतर माध्य इस प्रकार प्राप्त होगाः
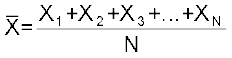
दाँए पक्ष को इस प्रकार लिखा जा सकता है 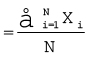
यहाँ i एक सूचक है जो क्रमबद्ध रूप से मान 1, 2, 3, ...., N धारण करता है। सुविधा के लिए, इसे सूचक i के बिना सरल रूप में लिखा जाएगा। अतः 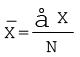 , जहाँ,
, जहाँ, 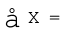 सभी मानों का योग तथा
सभी मानों का योग तथा
N = मानों की संख्या।
समांतर माध्य का परिकलन कैसे किया जाता है
समांतर माध्य के परिकलन का अध्ययन मोटे तौर पर दो श्रेणियों के अंतर्गत किया जा सकता है -
1. असमूहित आँकड़ों का समांतर माध्य
2. समूहित आँकड़ों का समांतर माध्य
असमूहित आँकड़ों की शृंखला के लिए समांतर माध्य
प्रत्यक्ष विधि
प्रत्यक्ष विधि के द्वारा समांतर माध्य निकालने के लिए किसी . ंशृखला के सभी प्रेक्षणों के योग को प्रेक्षणों की कुल संख्याओं से विभाजित किया जाता है।
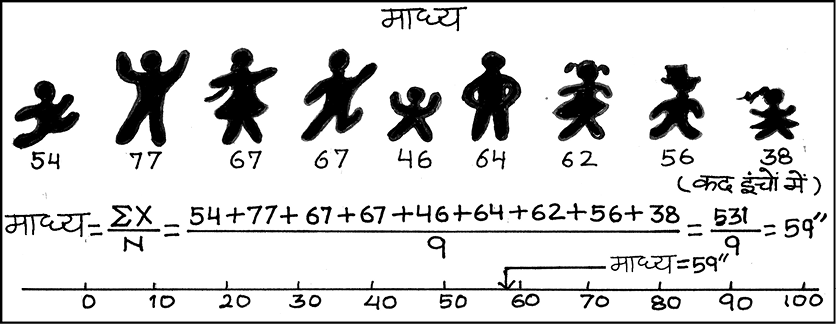
उदाहरण 1
किसी कक्षा के छात्रों के अर्थशास्त्र की परीक्षा में प्राप्तांक प्रदर्शित करने वाले आँकड़ों से समांतर माध्य का परिकलन करेंः 40, 50, 55, 78, 58,
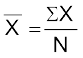
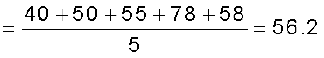
अर्थशास्त्र की परीक्षा में छात्रों के औसत अंक 56.2 हैं।
कल्पित माध्य विधि
यदि आँकड़ों में प्रेक्षणों की संख्या अधिक हो तथा संख्याएँ भी बड़ी हाें, तो प्रत्यक्ष विधि द्वारा समांतर मान को अभिकलित करना कठिन हो जाता है। अतः अभिकलन को कल्पित माध्य विधि के प्रयोग द्वारा सरल बनाया जा सकता है।
एेसे आँकड़ा-समुच्चयों में जिनमें बड़ी संख्या में प्रेक्षणों के साथ-साथ बड़े संख्यात्मक अंक भी हों, परिकलन में समय बचाने के लिए आप कल्पित माध्य विधि का प्रयोग कर सकते हैं। यहां पर आप तर्क/अनुभव के आधार पर एक विशिष्ट अंक को समांतर माध्य मान लेते हैं। इसके बाद आप प्रत्येक प्रेक्षण का इस कल्पित माध्य से विचलन ले सकते हैं। इसके बाद आप इन विचलनों के संकलन को आँकड़ों के प्रेक्षणों की संख्या से विभाजित कर सकते हैं। विचलनों के जोड़ तथा प्रेक्षणों की संख्या के अनुपात को, कल्पित माध्य में जोड़कर, वास्तविक समांतर माध्य का अनुमान लगाया जा सकता है। प्रतीकात्मक रूप में,
A = कल्पित माध्य
X = व्यष्टिगत प्रेक्षण
N = प्रेक्षणों की कुल संख्या
d = व्यष्टिगत प्रेक्षणों से कल्पित माध्य का विचलन अर्थात् d = X–A.
इसके बाद, सभी विचलनों को जोड़ लें, जैसे
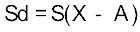
इसके बाद 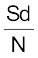 निकालें।
निकालें।
इसके बाद A तथा 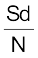 को जोड़कर
को जोड़कर 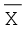 प्राप्त करें।
प्राप्त करें।
इसके बाद 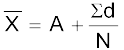
ध्यान रहे कि किसी भी मान को, चाहे वह आँकड़ों में विद्यमान हो या नहीं, कल्पित माध्य के रूप में लिया जा सकता है। फिर भी, परिकलन को सरल बनाने के लिए आँकड़ों में केंद्रीय रूप में अवस्थित मान को कल्पित माध्य के लिए चुना जा सकता है।
उदाहरण 2
निम्नलिखित आँकड़े 10 परिवारों की साप्ताहिक आय दिखाते हैंः
परिवार
क ख ग घ ङ
च छ ज झ ञ
साप्ताहिक आय (रु में)
850 700 100 750 5000 80 420 2500 400 360
परिवारों की माध्य आय का आकलन करें।
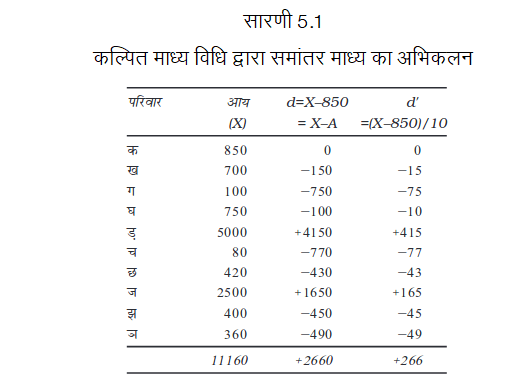
कल्पित माध्य विधि के प्रयोग द्वारा समांतर माध्य
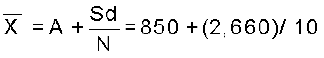
= 1,116 रु।
अतः दोनों ही विधियों से उस परिवार की औसत साप्ताहिक आय 1,116 रु है। इसे आप प्रत्यक्ष विधि के प्रयोग द्वारा भी जाँच सकते हैं।
पद विचलन विधि
कल्पित माध्य से लिए गए सभी विचलनों को समापवर्तक 'c' से विभाजित करके और भी सरल बनाया जा सकता है। इसका उद्देश्य बड़ी संख्याओं से बचना है। उदाहरण के लिए, यदि d = X – A का मान बहुत बड़ा है, तब d' को ज्ञात करें। इसे निम्नलिखित विधि से किया जा सकता हैः
d' = 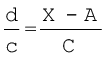 .
.
इसका सूत्र नीचे दिया गया हैः

c = समापवर्तक, N = कुल प्रेक्षणों की संख्या, A = कल्पित माध्य।
इस प्रकार, आप पद विचलन विधि द्वारा, उदाहरण 2 में दिए गए समांतर माध्य का परिकलन कर सकते हैं।
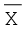 = 850 + (266)/10 × 10 = 1,116 रु
= 850 + (266)/10 × 10 = 1,116 रु
समूहित आँकड़ों के लिए समांतर माध्य का परिकलन विविक्त शृंखला
प्रत्यक्ष विधि
यदि शृंखला विविक्त है, तो प्रत्येक प्रेक्षण की बारंबारता को प्रेक्षण के मान के द्वारा गुणा किया जाता है। इससे जो मान प्राप्त होते हैं, उन्हें जोड़ा जाता है और बारंबारताओं की कुल संख्या के द्वारा विभाजित किया जाता है। प्रतीक के रूप में,
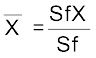
यहाँ पर 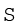 fX = चरों के उत्पाद तथा बारंबारताओं का योग।
fX = चरों के उत्पाद तथा बारंबारताओं का योग।
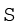 f = बारंबारताओं का योग
f = बारंबारताओं का योग
उदाहरण 3
एक आवासीय कॉलेानी में भूखंड केवल तीन आकारों में मिलते हैंः 100 वर्ग मीटर, 200 वर्ग मीटर एवं 300 वर्ग मीटर तथा भूखण्डों की संख्या क्रमशः 200, 50 एवं 10 है।
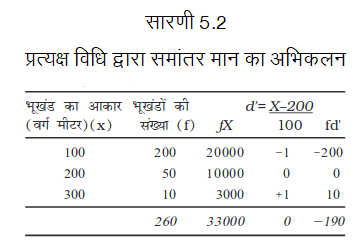
प्रत्यक्ष विधि के प्रयोग द्वारा समांतर माध्य,
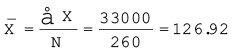 वर्ग मीटर
वर्ग मीटर
अतः आवासीय कॉलोनी का औसत भूखण्ड आकार 126.92 वर्ग मीटर है।
कल्पित माध्य विधि
जैसा पहले बताया जा चुका है व्यष्टि शृंखला में, कल्पित माध्य विधि के प्रयोग द्वारा परिकलन को थोड़ा संशोधित करके सरल बनाया जा सकता है। चूँकि यहाँ प्रत्येक मद की बारंबारता (f) दी गयी है, अतः fd को ज्ञात करने हेतु हम प्रत्येक विचलन (d) को बारंबारता से गुणा करते हैं। इससे हमें 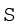 fd मिलता है। अगला चरण सभी बारंबारताओं का योग करके
fd मिलता है। अगला चरण सभी बारंबारताओं का योग करके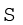 f प्राप्त करना है। इसके बाद
f प्राप्त करना है। इसके बाद 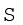 fd/
fd/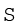 f
f
ज्ञात करें। अंत में समांतर माध्य के परिकलन 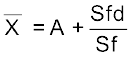 के द्वारा कल्पित माध्य विधि का प्रयोग कर किया जाता है।
के द्वारा कल्पित माध्य विधि का प्रयोग कर किया जाता है।
पद विचलन विधि
इसमें विचलनों को समापवर्तक 'c' द्वारा विभाजित किया जाता हैं, जो कि परिकलन को सरल बना देता हैं। यहां संख्यात्मक अंकों के आकार को घटा कर परिकलन को सरल बनाने के लिए d' = 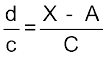 का आकलन किया जाता है। इसके बाद fd' तथा
का आकलन किया जाता है। इसके बाद fd' तथा 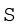 fd' प्राप्त करें। अंत में, पद विचलन विधि का सूत्र नीचे दिया गया हैः
fd' प्राप्त करें। अंत में, पद विचलन विधि का सूत्र नीचे दिया गया हैः
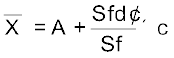
क्रियात्मक गतिविधि
• पद विचलन तथा कल्पित माध्य विधि का प्रयोग करते हुए उदाहरण 3 में दिए गए आँकड़ों के लिए जोत का माध्य आकार ज्ञात करें।
संतत शृंखला
यहाँ वर्ग अंतराल दिए गए हैं। संतत शृंखला में भी समांतर माध्य परिकलन की प्रक्रिया ठीक वैसी ही है, जैसी विविक्त शृंखला में थी। इसमें अंतर केवल इतना है कि भिन्न वर्ग अंतरालों के मध्य बिंदु लेने पड़ते हैं। आप स्वतः जानते हैं कि वर्ग अंतराल, अपवर्जी या समावेशी या असमान आकार वाले हो सकते हैं। अपवर्जी अंतराल के उदाहरण हैं, 0–10, 10–20 आदि। समावेशी अंतराल के उदाहरण हैं 0–9, 10–19 आदि। असमान वर्ग अंतराल के उदाहरण हैं, 0–20, 20–50 आदि। इन सभी स्थितियों में, समांतर माध्य का परिकलन एक ही तरीके से होता है।
उदाहरण 4
निम्नलिखित छात्रों के औसत प्राप्तांकों का परिकलन (क) प्रत्यक्ष विधि (ख) पद विचलन विधि का प्रयोग करते हुए कीजिए।
प्रत्यक्ष विधि
प्राप्तांक
0–10 10–20 20–30 30–40 40–50 50–60 60–70
छात्रों की संख्या
5 12 15 25 8 3 2
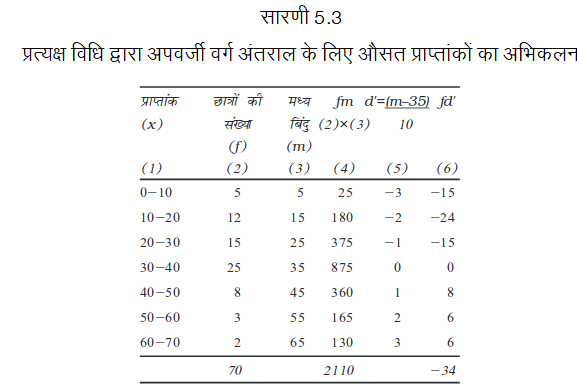
चरणः
1. प्रत्येक वर्ग के लिए मध्यमान प्राप्त करें, जिसे m द्वारा दर्शाया जाता है।
2. 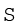 fm निकालें और प्रत्यक्ष विधि सूत्र का प्रयोग करें।
fm निकालें और प्रत्यक्ष विधि सूत्र का प्रयोग करें।
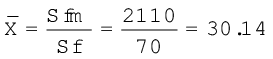 अंक
अंक
पद विचलन विधि
1. d' = 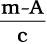 निकालें
निकालें
2. A = 35 लें (कोई स्वैच्छिक संख्या),
c = समापवर्तक

= 30.14 अंक
समांतर माध्य की दो रोचक विशेषताएँ
1. समांतर माध्य से मदों के विचलन का योग सदा शून्य के बराबर होता है। प्रतीकात्मक रूप से, 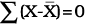
2. औसत माध्य चरम मूल्यों द्वारा प्रभावित होता है। कोई भी चरम मूल्य, किसी भी तरफ, औसत माध्य को ऊपर या नीचे धकेल सकता है।
भारित समांतर माध्य (Weighted Arithmetic Mean)
समांतर माध्य के परिकलन में कभी-कभी विभिन्न मदों के लिए, उनके महत्व के अनुसार, भार निर्धारित करना महत्वपूर्ण होता है। उदाहरण के लिए, दो खाद्य पदार्थ आम और आलू हैं। आप आम तथा आलू की औसत कीमतें (क्रमशः p1 तथा p2) जानना चाहते हैं। इनका समांतर माध्य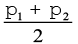 होगा। हो सकता है आप आलू की कीमत (p2) में वृद्धि को अधिक महत्व देना चाहते हों। एेसा करने के लिए, आप उपभोक्ता के बजट में आमों के भाग को भार (W1) के तौर पर प्रयोग कर सकते हैं तथा बजट में आलू के भाग को भार (W2) के तौर पर। अब बजट में भाग के द्वारा भारित समांतर माध्य
होगा। हो सकता है आप आलू की कीमत (p2) में वृद्धि को अधिक महत्व देना चाहते हों। एेसा करने के लिए, आप उपभोक्ता के बजट में आमों के भाग को भार (W1) के तौर पर प्रयोग कर सकते हैं तथा बजट में आलू के भाग को भार (W2) के तौर पर। अब बजट में भाग के द्वारा भारित समांतर माध्य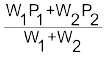 होगा।
होगा।
सामान्यतः भारित समांतर माध्य
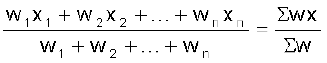 के द्वारा प्राप्त किया जाता है।
के द्वारा प्राप्त किया जाता है।
जब कीमतों में वृद्धि होती है, तब आप शायद उन वस्तुओं की कीमतों की वृद्धि में रुचि रख सकते हैं। जो आपके लिए अधिक महत्वपूर्ण हों। आप इसके बारे में, अध्याय 8 में सूचकांकों की चर्चा में अधिक विस्तार से पढ़ेंगे।
क्रियात्मक गतिविधियाँ
• निम्नलिखित उदाहरण से समांतर माध्य की उपर्युक्त विशेषता की जाँच करेंः
Xः 4 6 8 10 12
• उपर्युक्त उदाहरण में, यदि माध्य के मूल्य में 2 की वृद्धि की जाय, तब व्यष्टिगत प्रेक्षणों में क्या परिवर्तन होता है?
• यदि पहले तीन मदों में 2 की वृद्धि होती है, तब बाद के दो मदों का मान क्या होना चाहिए, ताकि माध्य पूर्ववत् बना रहे।
• यदि मान 12 के स्थान पर 96 का प्रयोग करें, तब समांतर माध्य क्या होगा? टिप्पणी करें।
3. मध्यिका (Median)
मध्यिका उस चर का स्थितिक मान है जो वितरण को दो समान भागों में बाँट देता है। एक भाग के अंतर्गत सभी मान मध्यिका मान से अधिक या उसके बराबर होते हैं तथा दूसरे भाग के सभी मान उससे कम या उसके बराबर होते हैं। जब आँकड़ों के समुच्चय को उनके परिमाण के क्रम में व्यवस्थित किया जाए, तो मध्यवर्ती मान मध्यिका होता है। क्योंकि मध्यिका का निर्धारण विभिन्न मानों की स्थिति या स्थान द्वारा होता है, यह अधिकतम मूल्य वाले मान में होने वाली वृद्धि से अप्रभावित रहता है।
मध्यिका का अभिकलन
आँकड़ों को क्रमशः सबसे छोटे से सबसे बड़े की ओर व्यवस्थित करते हए मध्यिका को मध्य मान द्वारा आसानी से अभिकलित किया जा सकता है।
उदाहरण 5
मान लीजिए, एक आँकड़ा समुच्चय में निम्नलिखित प्रेक्षण हैंः 5, 7, 6, 1, 8, 10, 12, 4, और 3.
आँकड़ों को आरोही क्रम में व्यवस्थित करते हुए आप पाते हैंः
1, 3, 4, 5, 6, 7, 8, 10, 12.

यहाँ पर ‘मध्य अंक’ 6 है। अतः मध्यिका भी 6 है। इसमें आधे अंक 6 से अधिक हैं और आधे 6 से कम।
यदि आँकड़ों में सम संख्याएँ होती हैं, तब दो प्रेक्षण होंगे, जो मध्य में होेंगे। एेसी स्थिति में मध्यिका को इन दो मध्य मानों के समांतर माध्य द्वारा अभिकलित किया जाता है।
उदाहरण 6
निम्नलिखित आँकड़ों में 20 छात्रों के प्राप्तांक दिए गए है। मध्यिका का परिकलन करेंः
25, 72, 28, 65, 29, 60, 30, 54, 32, 53, 33, 52, 35, 51, 42, 48, 45, 47, 46, 33.
आँकड़ों को आरोही क्रम में व्यवस्थित करने पर आप पाते हैं
25, 28, 29, 30, 32, 33, 33, 35, 42, 45, 46, 47, 48, 51, 52, 53, 54, 60, 65, 72.
यहाँ पर आप देख सकते हैं कि मध्य भाग में दो प्रेक्षण 45 और 46 हैं। इन दो प्रेक्षणों का समांतर माध्य निकालकर मध्यिका को प्राप्त किया जा सकता हैः
मध्यिका =
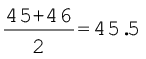 अंक
अंक
मध्यिका को परिकलित करने के लिए मध्य इकाई/इकाइयों की अवस्थिति को जान लेना महत्त्वपूर्ण है, जिस पर मध्यिका निर्भर होती है। मध्यिका की अवस्थिति को निम्नलिखित सूत्र के द्वारा परिकलित किया जा सकता हैः
मध्यिका की अवस्थिति =
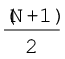 वें मद का आकार
वें मद का आकार
जहाँ, N = मदों की संख्या।
आप यह देख सकते हैं कि उपर्युक्त सूत्र आपको मध्यिका की अवस्थिति एक क्रमबद्ध सारणी के रूप में देता है, न कि मध्यिका को ही। मध्यिका इस सूत्र द्वारा अभिकलित की जाती हैः
मध्यिका =
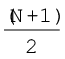 वें मद का आकार
वें मद का आकार
विविक्त या असंतत शृंखला
विविक्त शृंखला में मध्यिका की अवस्थिति अर्थात् (N+1)/2वीं इकाई को संचयी बारंबारता के माध्यम से प्राप्त किया जा सकता है। इस अवस्थिति पर संगत मान ही मध्यिका का मान होता है।
उदाहरण 7
नीचे व्यक्तियों की संख्याएँ तथा उनकी आय (रु में) का बारंबारता वितरण दिया गया है। मध्यिका आय का परिकलन कीजिए।
आय (रु में)ः 10 20 30 40
व्यक्तियों की संख्याः 2 4 10 4
मध्यिका आय को परिकलित करने के लिये, आप निम्नानुसार बारंबारता-वितरण तैयार कर सकते हैं।
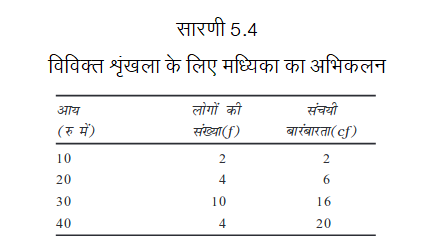
मध्यिका (N+1)/2 = (20+1)/2 = 10.5वें प्रेक्षण में अवस्थित है। इसे आसानी पूर्वक संचयी बारंबारता के माध्यम से ढूंढ़ा जा सकता है। 10.5वाँ प्रेक्षण, 16वीं संचयी बारंबारता में निहित है। इससे संगत आय 30 रु है। अतः मध्यिका आय 30 रु है।
संतत शृंखला
संतत शृंखला में आपको वह मध्य-वर्ग वहाँ ढूँढ़ना है, जहाँ N/2वाँ मद [न कि (N+1)/2वाँ मद] निहित है। तब मध्यिका को निम्न प्रकार से प्राप्त किया जा सकता हैः
मध्यिका = 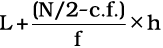
यहाँ पर, L = मध्यिका वर्ग की निम्न सीमा,
c.f. = मध्यिका वर्ग के पूर्ववर्ती वर्ग की संचयी बारंबारता,
f = मध्यवर्ग की बारंबारता,
h = मध्यिका वर्ग के अंतराल का परिमाण
उस दशा में किसी समायोजन की आवश्यकता नहीं है, जब बारंबारता का आकार या परिमाण असमान हो।
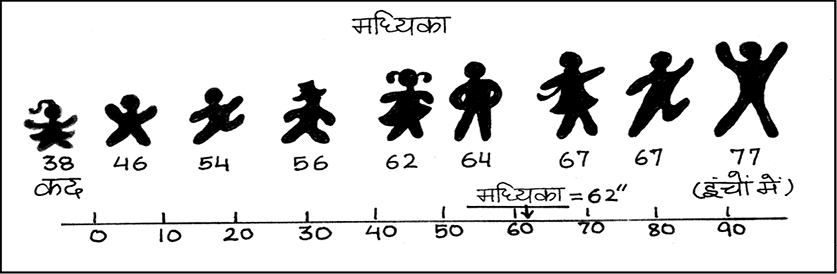
उदाहरण 8
निम्नलिखित आँकड़े किसी कारखाने में कार्यरत लोगों की दैनिक मजदूरी से संबद्ध हैं। मध्यिका दैनिक मजदूरी का अभिकलन कीजिए।
दैनिक मजदूरी (रु में)
55–60 50–55 45–50 40–45 35–40 30–35 25–30 20–25
मजदूरों की संख्या
7 13 15 20 30 33 28 14
यहाँ पर आँकड़े आरोही क्रम में व्यवस्थित हैं।
उपर्युक्त चित्र में, मध्यिका (N/2)वें मद (अर्थात् 160/2) = शृंखला के 80वें मद का मान है, जो 35–40 वर्ग-अंतराल में स्थित है। मध्यिका के सूत्र का प्रयोग करने परः
मध्यिका
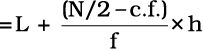
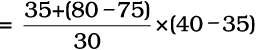
= 35.83 रु
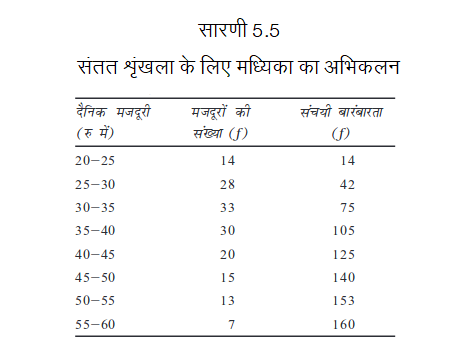
अतः मध्यिका दैनिक मजदूरी 35.83 रु है। इसका अर्थ है कि 50 प्रतिशत मजदूर 35.83 रुपये से कम या इसके बराबर मजदूरी प्राप्त करते हैं और 50 प्रतिशत मजदूर इससे अधिक या इसके बराबर मजदूरी प्राप्त करते हैं।
आपको यह ध्यान रखना चाहिए कि केंद्रीय प्रवृत्ति के माप के रूप में मध्यिका शृंखला के सभी मानों के प्रति संवेदी नहीं होता है। यह आँकड़ों के केंद्रीय मदों के मान पर संकेंद्रित होता है।
क्रियात्मक गविविधि
• श्रेणह के सभी चारों मूल्यों के लिए माध्य एवं मध्यिका ज्ञात करें। आप क्या देखते हैं?
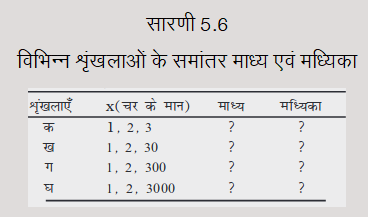
• क्या मध्यिका चरम मूल्यों द्वारा प्रभावित होती है? चरम मूल्य क्या हैं?
• क्या मध्यिका, माध्य की अपेक्षा एक बेहतर प्रणाली है?
चतुर्थक (Quartiles)
चतुर्थक वे माप हैं, जो आँकड़ों को चार बराबर भागों में विभाजित करते हैं और प्रत्येक भाग में बराबर संख्या में प्रेक्षण दिए होते हैं। अतः यहाँ पर तीन चतुर्थक प्रचलित हैं। प्रथम चतुर्थक या निम्न चतुर्थक (Q1 द्वारा निर्देशित) में वितरण के 25 प्रतिशत मद इससे कम होते हैं और 75 प्रतिशत मद इससे अधिक होते हैं। द्वितीय चतुर्थक या मध्यिका (Q2 द्वारा निर्देशित) में 50 प्रतिशत मद इसके नीचे होते है और 50 प्रतिशत मद इसके ऊपर होते हैं। तृतीय चतुर्थक या उच्च चतुर्थक (Q3 द्वारा निर्देशित) में विवरण के 75 प्रतिशत मद इसके नीचे होते हैं और 25 प्रतिशत मद इसके ऊपर होते हैं। अतः Q1 एवं Q3 दो सीमाएँ हैं जिनके बीच केन्द्रीय 50 प्रतिशत आँकड़े निहित होते हैं।
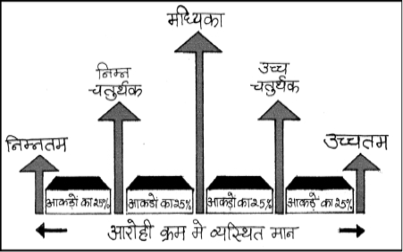
शतमक (Percentile)
शतमक वितरण को 100 बराबर भागों में विभाजित करता है। इस प्रकार आपको 99 विभाजक स्थितियाँ प्राप्त होती हैं, जिन्हें P1, P2, P3, ..., P99 द्वारा दर्शाया जाता है। इसमें P50 मध्यिका मान होता है। यदि आप एक प्रबंधन-प्रवेश परीक्षा में 82 शतमक प्राप्त करते हैं, तो इसका अर्थ है कि कुल परीक्षार्थियों से आपका स्थान 18 प्रतिशत नीचे था। यदि इस परीक्षा में कुल एक लाख परीक्षार्थी बैठते हैं तो बताएँ आपकी स्थिति कहाँ है?
चतुर्थकों का परिकलन
चतुर्थक की अवस्थिति ज्ञात करने की विधि ठीक वैसी ही है जैसी कि व्यष्टिगत एवं विविक्त शृंखलाओं में मध्यिका की थी। किसी क्रमबद्ध शृंखला में Q1 एवं Q3 के मान निम्नलिखित सूत्र (सिद्धांत) से प्राप्त किए जा सकते हैं, जिसमें N प्रेक्षणों की कुल संख्या है और
Q1 =
 वें मद का आकार और
वें मद का आकार और
Q3 =  वें मद का आकार है।
वें मद का आकार है।
उदाहरण 9
किसी परीक्षा में दस छात्रों द्वारा प्राप्त किए गए अंकों के आँकड़ों से निम्न चतुर्थक के मान का परिकलन कीजिए।
22, 26, 14, 30, 18, 11, 35, 41, 12, 32.
आँकड़ों को आरोही क्रम में व्यवस्थित करने पर11, 12, 14, 18, 22, 26, 30, 32, 35, 41.
Q1 =  वें मद का आकार =
वें मद का आकार =  वें मद का आकार = 2.75 वें मद का आकार = 2वाँ मद + .75 (3वाँ मद - 2वाँ मद) = 12 + .75 (14-12) = 13.5 अंक।
वें मद का आकार = 2.75 वें मद का आकार = 2वाँ मद + .75 (3वाँ मद - 2वाँ मद) = 12 + .75 (14-12) = 13.5 अंक।
क्रियात्मक गतिविधि
• तृतीय चतुर्थक (Q3) स्वयं ज्ञात करें।
5. बहुलक (Mode)
कभी-कभी आपको किसी शृंखला से अति प्ररूपी मान अथवा उस मान को, जिसके आस-पास मदों का संकेंद्रीकरण अधिकतम हो, जानने की उत्सुकता हो सकती है। उदाहरण के लिए, एक विनिर्माता जूते के उस आकार, जिसकी माँग अधिकतम है या किसी खास स्टाइल की शर्ट, जिसकी बहुत अधिक माँग है, के बारे में जानना चाहता है। एेसी स्थिति में बहुलक एक सर्वाधिक उपयुक्त माप है। बहुलक शब्द फ्रेंच भाषा के शब्द ‘ला मोड (La Mode)’ से व्युत्पन्न है, जो वितरण के सर्वाधिक प्रचलित मानों का द्योतक है, क्योंकि यह शृंखला में सबसे अधिक बार दोहराया जाता है। बहुलक सर्वाधिक प्रेक्षित आँकड़ा मान है। इसे M0 के द्वारा दर्शाया जाता है।
बहुलक का अभिकलन
विविक्त शृंखला
आँकड़ा समुच्चय 1, 2, 3, 4, 4, 5 को लें। यहाँ पर इस आँकड़े का बहुलक 4 है, क्योंकि यह आँकड़ा समुच्चय में सबसे अधिक बार (दो बार) आया है।
उदाहरण 10
निम्नलिखित विविक्त शृंखला को देखिएः
चर 10 20 30 40 50
बारंबारता 2 8 20 10 5
यहाँ पर आप देख सकते हैं कि अधिकतम बारंबारता 20 है, अतः बहुलक का मान 30 है। चूँकि यह मोड का एकल मान है, अतः आँकड़ा एक-बहुलकी है, लेकिन यह जरूरी नहीं है कि बहुलक समांतर माध्य एवं मध्यिका की भाँति एकल ही रहे। आपके पास एेसा आँकड़ा हो सकता है, जिसमें दो बहुलक (द्विबहुलकी) या दो से अधिक बहुलक (बहु-बहुलकी) हों। यह भी संभव है कि एक भी बहुलक न हो, यदि वितरण में कोई मान अन्य मानों की तुलना में अधिक बार प्रकट नहीं होता है। उदाहरण के लिए शृंखला 1, 1, 2, 2, 3, 3, 4, 4 लें। यहां कोई भी बहुलक नहीं है।
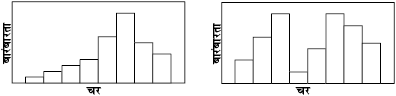
एक बहुलक आँकड़ा द्वि-बहुलक आँकड़ा
संतत शृंखला
संतत बारंबारता वितरण में, बहुलक वर्ग वह वर्ग है, जिसकी बारंबारता सबसे अधिक है। बहुलक को निम्नलिखित सूत्र के द्वारा परिकलित किया जा सकता हैः
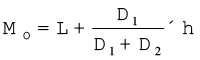
यहाँ पर,
L = बहुलक वर्ग की निम्न सीमा
D1 = बहुलक वर्ग की बारंबारता और बहुलक वर्ग के पूर्ववर्ती वर्ग (संकेतों को छोड़कर) की बारंबारता के बीच का अंतर
D2 = बहुलक वर्ग की बारंबारता और बहुलक वर्ग के परवर्ती वर्ग (संकेतों को छोड़कर) की बारंबारता के बीच का अंतर
h = वितरण का वर्ग अंतराल।
ध्यान रहे कि संतत शृंखला में वर्ग अंतराल समान होने चाहिए तथा शृंखला को बहुलक के परिकलन के लिए अपवर्जी होना चाहिए। यदि मध्य बिन्दु दिए गये हैं, तो वर्ग अंतरालों को निकालना पड़ता है।
उदाहरण 11
निम्नलिखित आँकड़ों के आधार पर श्रमिक परिवारों की बहुलक मासिक आय का परिकलन कीजिएः
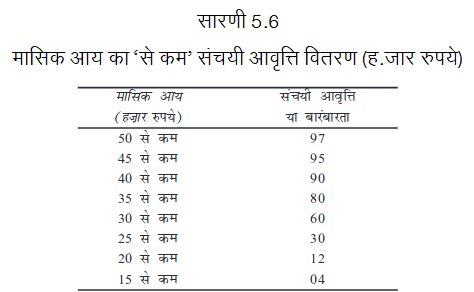
जैसा कि आप देख सकते हैं, यह संचयी आवृत्ति वितरण की स्थिति है। बहुलक को परिकलित करने के लिए आपको इसे अपवर्जी शृंखला में बदलना होगा। इस उदाहरण में, शृंखला अवरोही क्रम में है। बहुलक वर्ग को निर्धारित करने के लिए समूहन एवं विश्लेषण सारणी (सारणी 5.7) बनानी होगी।
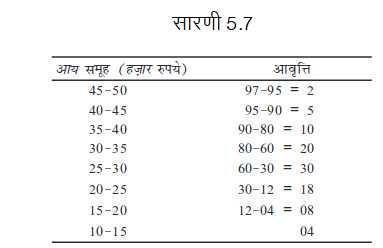
बहुलक का मूल्य 25–30 वर्ग अंतराल में पड़ता है। निरीक्षण करने पर यह देखा जा सकता है कि यह बहुलक वर्ग है।
अब L = 25, D1 = (30 – 18) = 12, D2 = (30 – 20) = 10, h = 5
सूत्र का प्रयोग करके बहुलक का मान इस प्रकार प्राप्त कर सकते हैंः
MO (ह.जार रुपये)
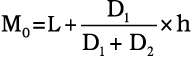
= 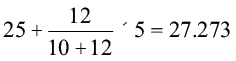
अतः श्रमिक परिवार की बहुलक आय 27.273 रु है।
क्रियात्मक गविविधियाँ
• एक जूता कंपनी, जो केवल वयस्कों के लिए जूते बनाती है, जूतों का सर्वाधिक लोकप्रिय आकार जानना चाहती है। इसके लिए कौन-सा माध्य सर्वाधिक उपयुक्त होगा?
• निम्नलिखित वस्तुओं का उत्पादन करने वाली कंपनियों के लिए कौन-सा औसत सर्वाधिक उपयुक्त रहेगा?
(1) डायरी तथा कॉपी
(2) स्कूल बैग
(3) जीन्स तथा टी शर्ट
• अपनी कक्षा में, चायनी.ज भोजन के लिए विद्यार्थियों की प्राथमिकता जानने के लिए केंद्रीय प्रवृत्ति उपयुक्त माप का उपयोग करते हुए एक संक्षिप्त सर्वेक्षण करें।
• क्या बहुलक की स्थिति ग्रा.फ द्वारा ज्ञात की जा सकती है?
6. समांतर माध्य, मध्यिका एवं बहुलक की सापेक्षिक स्थिति
मान लीजिए कि,
समांतर माध्य = Me
मध्यिका = Mi
बहुलक = Mo
इन तीनों की सापेक्षिक स्थिति Me>Mi>Mo या Me<Mi<Mo होती है। (यहाँ पादांक वर्णमाला के क्रम से आते हैं) मध्यिका सदैव समांतर माध्य और बहुलक के बीच में होती है।
7. सारांश
केंद्रीय प्रवृत्ति की माप या औसतों का प्रयोग आँकड़ों के संक्षेपण के लिए किया जाता है। यह आँकड़ा-समुच्चय का वर्णन करने के लिए एकल प्रतिनिधि मान को दर्शाता है। समांतर माध्य सर्वाधिक प्रयोग किया जाने वाला औसत है। यह परिकलन में सरल एवं सभी प्रेक्षणों पर आधारित होता है। लेकिन यह चरम मदों की उपस्थिति से अनुचित रूप से प्रभावित होता है। इस प्रकार के आँकड़ों के लिए मध्यिका अच्छा संक्षेपण है। बहुलक का प्रयोग सामान्यतः गुणात्मक आँकड़ों की व्याख्या में किया जाता है। मध्यिका एवं बहुलक को आलेखी तौर पर आसानी से अभिकलित किया जा सकता है। मुक्तांत वितरणों के लिए भी इनका अभिकलन सरलता से किया जा सकता है। इसलिए यह महत्वपूर्ण है कि हम विश्लेषण के उद्देश्य तथा वितरण की प्रकृति को देखते हुए उपयुक्त औसत का चुनाव करें।
पुनरावर्तन
• केंद्रीय प्रवृत्ति की माप एक एेसे एकल मान द्वारा आँकड़ों को संक्षिप्त करता है, जो संपूर्ण आँकड़ों का प्रतिनिधित्व कर सके।
• समांतर माध्य को प्रेक्षणों के मान के योग का प्रेक्षणों की संख्या से विभाजन के भागफल के रूप में परिभाषित करते हैं।
• समांतर माध्य से मदों के विचलनों का योग सदैव शून्य के बराबर होता है।
• कभी-कभी यह महत्त्वपूर्ण होता है कि विविध मदों के भार, उनके महत्व के अनुसार निर्दिष्ट किए जाएं।
• मध्यिका, वितरण का केंद्रीय मान है, अर्थात् मध्यिका से कम मानों की संख्या, इससे अधिक मानों की संख्या के बराबर होती है।
• चतुर्थक मानों के कुल समुच्चय को चार बराबर भागों में बाँटते हैं।
• बहुलक वह मान है, जो सबसे अधिक बार प्रकट होता है।
अभ्यास
1. निम्नलिखित स्थितियों में कौन सा औसत उपयुक्त होगा?
(क) तैयार वस्त्रों के औसत आकार।
(ख) एक कक्षा में छात्रों की औसत बौद्धिक प्रतिभा।
(ग) एक कारखाने में प्रति पाली औसत उत्पादन।
(घ) एक कारखाने में औसत मजदूरी।
(ङ) जब औसत से निरपेक्ष विचलनों का योग न्यूनतम हो।
(च) जब चरों की मात्रा अनुपात में हो।
(छ) मुक्तांत बारंबारता बंटन के मामले में।
2. प्रत्येक प्रश्न के सामने दिए गए बहु विकल्पों में से सर्वाधिक उचित विकल्प को चिह्नित करेंः
(i) गुणात्मक मापन के लिए सर्वाधिक उपयुक्त औसत हैः
(क) समांतर माध्य
(ख) मध्यिका
(ग) बहुलक
(घ) ज्यामितीय माध्य
(ङ) उपर्युक्त में से कोई नहीं
(ii) चरम मदों को उपस्थिति से कौन सा औसत सर्वाधिक प्रभावित होता हैः
(क) मध्यिका
(ख) बहुलक
(ग) समांतर माध्य
(घ) उपरोक्त में से कोई नहीं
(iii) समांतर माध्य से मूल्यों के किसी समुच्चय के विचलन का बीजगणितीय योग है-
(क) द
(ख) 0
(ग) 1
(घ) उपुर्यक्त कोई भी नहीं।
[उत्तर (1) (ख) (2) (ग) (3) (ग)]
3. बताइए कि निम्नलिखत कथन सही है या गलत-
(क) मध्यिका से मदों के विचलनों का योग शून्य होता है।
(ख) शृंखलाओं की तुलना के लिए मात्र औसत ही पर्याप्त नहीं है।
(ग) समांतर माध्य एक स्थैतिक मूल्य है।
(घ) उच्च चतुर्थक शीर्ष 25 प्रतिशत मदों का निम्नतम मान है।
(ङ) मध्यिका चरम प्रेक्षणों द्वारा अनुचित रूप से प्रभावित होती है।
[(क) गलत (ख) सही (ग) गलत (घ) सही (ङ) गलत]
4. यदि नीचे दिए गए आँकड़ों का समांतर माध्य 28 है, तो (क) लुप्त आवृत्ति का पता करें, और
(ख) शृंखला की मध्यिका ज्ञात करें।
प्रति खुदरा दुकान लाभ (रु में) 0–10 10–20 20–30 30–40 40–50 50–60
खुदरा दुकानों की संख्या 12 18 27 – 17 6
(उत्तर - लुप्त आवृत्ति का मान 20 है और मध्यिका का मान 27.41 रु है)
5. निम्नलिखित सारणी में एक कारखाने के 10 मजदूरों की दैनिक आय दी गई है। इनका समांतर माध्य ज्ञात कीजिए।
मजदूर A B C D E F G H I J
दैनिक आय (रु में) 120 150 180 200 250 300 220 350 370 260
(उत्तर - रु 240)
6. निम्नलिखित सूचना 150 परिवारों की दैनिक आय से संबद्ध है। समांतर माध्य का परिकलन कीजिए।
आय (रु में) परिवारों की संख्या
75 से अधिक 150
85 ,, 140
95 ,, 115
105 ,, 95
115 ,, 70
125 ,, 60
135 ,, 40
145 ,, 25
(उत्तर - 116.3 रु)
7. नीचे एक गाँव के 380 परिवारों की जोतों का आकार दिया गया है। जोत का मध्यिका आकार ज्ञात कीजिए।
जोतों का आकार (एकड़ में)
100 से कम 100–200 200–300 300–400 400 तथा उससे अधिक
परिवारों की संख्या
40 89 148 64 39
(उत्तर 241.22 एकड़)
8. निम्न शृंखला किसी कंपनी में नियोजित मजदूरों की दैनिक आय से संबद्ध है। अभिकलन कीजिएः (क) निम्नतम 50 प्रतिशत मजदूरों की उच्चतम आय (ख) शीर्ष 25 प्रतिशत मजदूरों द्वारा अर्जित न्यूनतम आय और (ग) निम्नतम 25 प्रतिशत मजदूरों द्वारा अर्जित अधिकतम आय।
दैनिक आय (रु में) 10–14 15–19 20–24 25–29 30–34 35–39
मजदूरों की संख्या 5 10 15 20 10 5
(संकेत - मध्य, निम्न चतुर्थक तथा उच्च चतुर्थक का अभिकलन कीजिए)
[उत्तर - (क) रु 25.11 (ख) रु 19.92 (ग) रु 29.19,
9. निम्न सारणी में किसी गाँव के 150 खेतों में गेहूँ की प्रति हेक्टेयर पैदावार दी गई है। समांतर माध्य, मध्यिका तथा बहुलक के मान की गणना कीजिए।
उत्पादित फसल (प्रति हेक्टेयर कि.ग्रा. में)
50–53 53–56 56–59 59–62 62–65 65–68 68–71 71–74 74–77
खेतों की संख्या
3 8 14 30 36 28 16 10 5
(उत्तर - माध्य = 63.83 कि.ग्रा. प्रति हेक्टेयर, मध्यिका = 63.67 कि.ग्रा. प्रति हेक्टेयर, बहुलक =
63.29 कि.ग्रा. प्रति हेक्टेयर)