Table of Contents

अध्याय 6
परिक्षेपण के माप

इस अध्याय के अध्ययन के बाद आप इस योग्य होंगे किः
• औसतों की सीमाएँ जान सकें;
• परिक्षेपण के माप की आवश्यकता को समझ सकें।
• परिक्षेपण के विभिन्न मापों का परिगणन कर सकें;
• मापों का परिकलन और उनकी तुलना कर सकें;
• निरपेक्ष एवं सापेक्ष मापों के बीच भेद कर सकें।
1. प्रस्तावना
पिछले अध्याय में आपने पढ़ा कि किस प्रकार से आँकड़ों को एक प्रतिनिधि मान के रूप में समेटा जा सकता है। लेकिन वह मान आँकड़ों में विद्यमान परिवर्तनशीलता को नहीं दर्शाता है। इस अध्याय में आप उन मापों का अध्ययन करेंगे जो आँकड़ों में परिवर्तनशीलताओं को मापने का प्रयास करते हैं।
तीन मित्र राम, रहीम और मारिया चाय पीते हुए बातचीत कर रहे हैं। उनकी आपसी बातचीत के दौरान, उनके अपने परिवारों की आय के बारे में चर्चा होने लगती है। राम बताता है कि उसके परिवार में चार सदस्य हैं और उसके परिवार के सदस्यों की औसत आय 15,000 रुपये है। रहीम बताता है कि उसके परिवार की औसम आय भी उतनी ही है, किंतु उसके परिवार में 6 सदस्य हैं। मारिया बताती है कि उसके परिवार में 5 सदस्य हैं, उनमें से एक काम नहीं करता है। वह भी परिकलन कर के बताती है कि उसके परिवार की भी औसत आय 15,000 रुपये है। वे तीनों काफी आश्चर्यचकित हुए, क्योंकि उन्हें मालूम है कि मारिया के पिता की आय बहुत अधिक है। उन्होंने विस्तार से पता किया और निम्नलिखित आँकड़ों को एकत्र कियाः
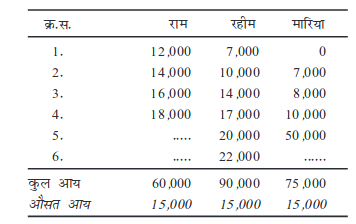
पारिवारिक आय (रुपयों में)
क्या आपने ध्यान दिया कि सब के औसत एक जैसे है, परंतु व्यक्तिगत आय में बहुत भिन्नताएँ हैं।
यह बिल्कुल स्पष्ट है कि औसत वितरण के केवल एक पहलू के बारे में बताता है, अर्थात् मानों का प्रतिनिधि आकार। इसे बेहतर ढंग से समझने के लिए आपको मानों के प्रसरण को जानने की आवश्यकता है।

आप देख सकते हैं कि राम के परिवार में आय की भिन्नता अपेक्षाकृत कम है। रहीम के परिवार में आय की यह भिन्नता काफी अधिक है, जबकि मारिया के परिवार में यह भिन्नता अधिकतम है। केवल औसत का ज्ञान अपर्याप्त है। यदि आपको किसी अन्य मान की जानकारी हो, जो मान में विचरण की मात्रा को प्रदर्शित करता है, तो उस वितरण के बारे में आपका ज्ञान बढ़ जायेगा। उदाहरण के लिए, प्रतिव्यक्ति आय केवल औसत आय को प्रदर्शित करती है। परिक्षेपण की माप आपको आय की असमानताओं के बारे में बता सकता है। इस तरह से समाज के विभिन्न वर्गों के लोगों के सापेक्ष जीवन-स्तर के बारे में आपकी जानकारी में वृद्धि होगी।
परिक्षेपण यह दर्शाता है कि वितरण का मान उसके औसत मान से कितना भिन्न है।
विचरण विभिन्नता के विस्तार को निर्धारित करने हेतु कुछ निश्चित माप हैं, जो इस प्रकार हैः
(क) परास
(ख) चतुर्थक विचलन
(ग) माध्य विचलन
(घ) मानक विचलन
इन मापों के अतिरिक्त, जो संख्यात्मक मान देते हैं, परिक्षेपण के अनुमान के लिए आरेखीय विधि भी है।
परास एवं चतुर्थक विचलन परिक्षेपण की माप उस प्रसरण के परिकलन द्वारा करते हैं, जिसमें ये मान निहित होते हैं। माध्य विचलन तथा मानक विचलन औसत से मानों के अंतर की मात्रा को मापते हैं।
2. मानों के प्रसरण पर आधारित माप परास (Range)
परास किसी वितरण में अधिकतम (L) एवं न्यूनतम (S) मानों के बीच का अंतर है। अतः, R = L - S। परास का अधिक मान अधिक परिक्षेपण दर्शाता है और, इसके विपरीत कम मान निम्न परिक्षेपण को दर्शाता है।
क्रियात्मक गतिविधियाँ
निम्नलिखित मानों को देखेंः
20, 30, 40, 50, 200
• परास का परिकलन कीजिये।
• यदि आँकड़ा समुच्चय में मान 200 नहीं हो तो परास क्या होगा?
• यदि 50 के स्थान पर 150 हो तो परास क्या होगा?
परास ः टिप्पणी
परास चरम मान के द्वारा अनुचित रूप से प्रभावित होता है। यह सभी मानों पर आधारित नहीं है। जब तक न्यूनतम एवं अधिकतम मान अपरिवर्तित रहते हैं, तब तक दूसरे मानों में कोई भी बदलाव परास को प्रभावित नहीं करता। इसे मुक्तांत बारंबारता वितरण में परिकलित नहीं किया जा सकता है।
कुछ सीमाओं के होते हुए भी परास अपनी सरलता के कारण आसानी से समझा एवं बहुधा प्रयुक्त किया जाता है। उदाहरण के लिए, हम लोग दूरदर्शन पर विभिन्न शहरों का दैनिक अधिकतम एवं न्यूनतम तापमान देखते रहते हैं और तापमान विविधता के आधार पर उनके बारे में राय बनाते हैं।
मुक्तांत वितरण वे हैं, जिनमें या तो निम्नतम वर्ग की निम्न सीमा या उच्चतम वर्ग की उच्च सीमा या दोनों ही नहीं दी होती हैं।
क्रियात्मक गतिविधि
• एक समाचार-पत्र से 10 कंपनियों के शेयर के 52 सप्ताहों के उच्च एवं निम्न मूल्यों के आँकड़े संग्रहित कीजिए। शेयर कीमतों के परास का परिकलन कीजिए। किस कंपनी का शेयर सर्वाधिक अस्थिर एवं कौन-सा सर्वाधिक स्थिर है?चतुर्थक विचलन (Quartile Deviation)
किसी वितरण में उच्च या निम्न किसी भी चरम मान की उपस्थिति परिक्षेपण के माप के रूप में परास की उपयोगिता को घटा सकती है। इसलिए, आपको एक एेसे माप की जरूरत हो सकती है, जो कि बाह्यमूल्यों से अनुचित रूप से प्रभावित न हो।
एेसी स्थिति में, यदि संपूर्ण आँकड़ों को चार बराबर भागों में विभाजित किया जाए, तो प्रत्येक में मानों का 25% भाग समाहित होगा, जिससे हमें चतुर्थकों एवं मध्यिका का मान प्राप्त होता है (जिनके बारे में आप पहले ही अध्याय 5 में पढ़ चुके हैं)। उच्च एवं निम्न चतुर्थक (क्रमशः Q3 एवं Q1) का प्रयोग अंतर-चतुर्थक परास के परिकलन में किया जाता है, जो Q3–Q1 हैं।
अंतर–चतुर्थक परास, किसी वितरण में माध्य के 50% मानों पर आधारित होता है। अतः वह चरम मान के द्वारा प्रभावित नहीं होता है। अंतर-चतुर्थक परास के आधे को चतुर्थक-विचलन (Q.D) कहा जाता है। अतः
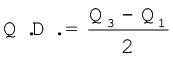 ,
,
चतुर्थक विचलन को अर्ध-अंतर-चतुर्थक परास भी कहा जाता है।
असमूहित आँकड़ों के लिए परास और चतुर्थक विचलन का परिकलन।
उदाहरण 1
निम्नलिखित प्रेक्षणों का परास और चतुर्थक विचलन परिकलित कीजिएः
20, 25, 29, 30, 35, 39, 41, 48,51, 60 और 70
स्पष्टतः परास 70 – 20 = 50 है।
चतुर्थक विचलन के लिए हमें उच्च Q3 एवं निम्न Q1 के मानों को परिकलित करने की आवश्यकता होती है।
Q1 मान 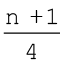 वें मद का आकार है।
वें मद का आकार है।
चूँकि n 11 है, Q1 तीसरे मद का आकार है।
क्योंकि मानों को पहले ही आरोही क्रम में व्यवस्थित किया हुआ है, यह देखा जा सकता है कि Q1 तीसरा मान 29 है। (यदि ये मान एक क्रम में नहीं हों तो आप क्या करेंगे?)
ठीक इसी तरह से, Q3 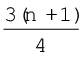 वें मद का आकार है, अर्थात 9वें मद का मान, 51 है। अतः
वें मद का आकार है, अर्थात 9वें मद का मान, 51 है। अतः
Q3 = 51
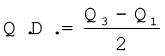 =
= 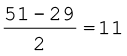
क्या आपने ध्यान दिया है कि Q.D. मध्यिका से चतुर्थकों का औसत अंतर है।
क्रियात्मक गतिविधि
• मध्यिका का परिकलन कीजिए और जाँच कीजिए कि उपर्युक्त कथन सही है या नहीं।
बारंबारता वितरण के लिए परास और चतुर्थक विचलन का परिकलन
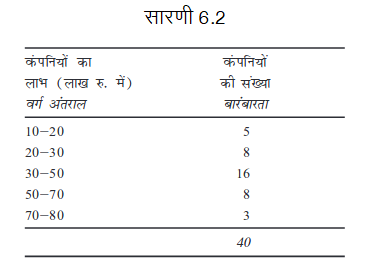
उदाहरण 2
किसी कक्षा के 40 छात्रों द्वारा प्राप्तांकों के वितरण में परास एवं चतुर्थक विचलन का परिकलन कीजिए।
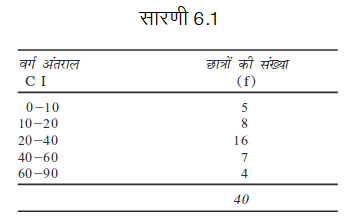
परास उच्चतम वर्ग की उच्च सीमा तथा निम्नतम वर्ग की निम्न सीमा के बीच का अंतर है। इसलिए, परास 90–0=90 है। चतुर्थक विचलन के लिए, सबसे पहले संचयी बारंबारता को निम्नानुसार परिकलित कीजिएः
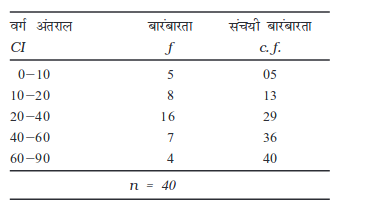
एक संतत श्रृंखला में Q1 का मान  वें मद का आकार है। अतः यह 10वें मद का आकार है, जो कि वर्ग 10–20 में निहित है। अतः Q1 वर्ग 10–20 में निहित है। Q1 का सही मान परिकलित करने हेतु, निम्नलिखित सूत्र प्रयुक्त होता हैः
वें मद का आकार है। अतः यह 10वें मद का आकार है, जो कि वर्ग 10–20 में निहित है। अतः Q1 वर्ग 10–20 में निहित है। Q1 का सही मान परिकलित करने हेतु, निम्नलिखित सूत्र प्रयुक्त होता हैः
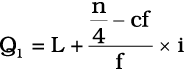
यहाँ पर L = 10 (संगत चतुर्थक वर्ग की निम्न सीमा) है।
c.f. = 5 (चतुर्थक वर्ग के पूर्ववर्ती वर्ग के लिए c.f. का मान)
i = 10 (चतुर्थक वर्ग का अंतराल)
f = 8 (चतुर्थक वर्ग की बारंबारता)
अतः
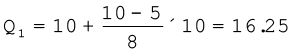
ठीक इसी तरह से, Q3 का मान 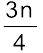
वें मद
का आकार है, अर्थात् 30वें मद का मान जो वर्ग 40–60 में निहित है। अब Q3 के सूत्र का प्रयोग करते हुए इसके मान को निम्न तरीके से परिकलित किया जा सकता हैः
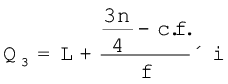
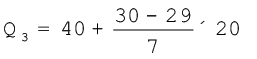
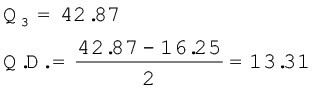
विविक्त एवं व्यष्टिगत शृंखलाओं में, Q1 का मान 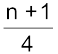 वें मद का आकार है। लेकिन संतत वितरण में, यह मान
वें मद का आकार है। लेकिन संतत वितरण में, यह मान 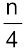 वें मद का आकार होता है। ठीक इसी प्रकार से, Q3 और मध्यिका के लिए भी n+1 की जगह में n प्रयुक्त होता है।
वें मद का आकार होता है। ठीक इसी प्रकार से, Q3 और मध्यिका के लिए भी n+1 की जगह में n प्रयुक्त होता है।
यदि समूचे समूह को दो बराबर भागों में बाँटा जाए और प्रत्येक भाग की मध्यिका परिकलित की जाए तो आपके पास बेहतर छात्रों की मध्यिका तथा कमजोर छात्रों की मध्यिका होगी। ये मध्यिकाएँ समूचे समूह की मध्यिका से औसतन 13.31 से भिन्न हैं। ठीक इसी प्रकार से, मान लीजिए, आप के पास एक कस्बे के लोगों की आय के आँकड़े हैं, तो सभी लोगों की मध्यिका आय परिकलित की जा सकती है। अब यदि सभी लोगों को दो बराबर भागों, धनी एवं निर्धन समूहों में बाँट दिया जाए तो इनकी मध्यिकाएँ परिकलित की जा सकती हैं। चतुर्थक विचलन आपको धनी समूह से संबंधित तथा निर्धन समूह से संबंधित मध्यिकाओं के, पूरे समूह की मध्यिका से, औसत अंतर को बताएगा। सामान्यतः चतुर्थक विचलन मुक्तांत वितरण के लिए परिकलित किया जा सकता है और यह चरम मानों द्वारा अनुचित रूप से प्रभावित नहीं होता है।
3. औसत से परिक्षेपण के माप
आपको याद होगा कि परिक्षेपण हमें यह बतलाता है कि किसी वितरण की विभिन्न मदों का मान वितरण के औसत मान से किस सीमा तक भिन्न है। परास और चतुर्थक विचलन माप में उपयोगी नहीं हैं कि मान अपने औसत से कितनी दूर हैं, फिर भी मानों के प्रसरण के परिकलन द्वारा वे परिक्षेपण के बारे में एक अच्छा अनुमान दे देते हैं। दो माप, जोकि मानों के अपने औसत से विचलन पर आधारित होते हैं वे हैं, माध्य विचलन और मानक विचलन।
चूँकि औसत एक केंद्रीय मान है, कुछ विचलन धनात्मक और कुछ ऋणात्मक होते हैं। अगर उन्हें एेसे ही जोड़ दिया जाए, तो जोड़ से कोई परिणाम नहीं निकलेगा। वास्तव में समांतर माध्य से विचलनों का योग सदैव शून्य होता है। मानों के निम्न दो समुच्चयों को देखेंः
समुच्चय अः 5, 9, 16
समुच्चय बः 1, 9, 20
आप देख सकते हैं कि समुच्चय ब में मान अपने औसत से अधिक दूर है और इसलिए समुच्चय अ के मानों की अपेक्षा अधिक प्रसरित है। यहाँ समांतर माध्य से विचलनों को परिकलित कीजिए और फिर उन्हें जोड़ दीजिए। आपने क्या देखा? अब यही क्रिया मध्यिका के साथ दोहराइए। क्या आप परिकलित मानों से विचरण की मात्रा पर टिप्पणी कर सकते हैं? माध्य विचलन, विचलनों के संकेतों की उपेक्षा करके इस समस्या का समाधान करने की कोशिश करता है, अर्थात् यह सभी विचलनों को धनात्मक मानता है। मानक विचलन के लिए, पहले विचलनों के वर्गाें का परिकलन करके उनका औसत निकाला जाता है। इसके बाद औसत का वर्गमूल निकाला जाता है। अब हम विस्तार से इन पर चर्चा करेंगे।
माध्य विचलन (Mean Deviation)
मान लीजिए पाँच कस्बों A, B, C, D और E के लिए एक कॅालेज प्रस्तावित किया जाता है। ये कस्बे एक सड़क के किनारे इसी क्रम से स्थित हैं। A कस्बे से दूसरे कस्बों की दूरी (किलोमीटर में) तथा छात्रों की संख्या नीचे दी जा रही है।
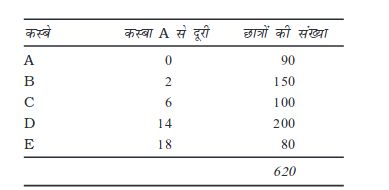
अब, यदि कॉलेज कस्बा A में स्थित होता है तो कस्बा B के 150 छात्र 2 किमी प्रति छात्र के हिसाब से (कुल 300 किमी) यात्रा करके कॉलेज पहुँचेंगे। उद्देश्य यह है कि एेसी जगह पता करें, जिससे छात्रों को कम से कम औसत दूरी की यात्रा करनी पड़े।
आप देख सकते हैं कि यदि कॉलेज A या E कस्बे में स्थित होता है तो छात्रों को औसतन अधिक यात्रा करनी होगी और यदि कॉलेज किसी मध्यवर्ती जगह पर स्थित होता है, तो उन्हें अपेक्षाकृत कम यात्रा करनी पड़ेगी। माध्य विचलन औसत से अंतरों का समांतर माध्य है। यहाँ प्रयुक्त उपयुक्त सांख्यिकी उपकरण है जिससे छात्रों द्वारा तय की गई औसत दूरी का आकलन किया जा सकता है। माध्य विचलन औसत या तो समांतर माध्य है या मध्यिका।
(चूँकि बहुलक एक स्थिर औसत नहीं है अतः माध्य विचलन के परिकलन हेतु इसका प्रयोग नहीं किया जाता है)।
क्रियात्मक गतिविधियाँ
• यदि कॉलेज कस्बा A या कस्बा C या कस्बा E में स्थापित होता है तो छात्रों द्वारा यात्रा की गई कुल दूरी को परिकलित कीजिए। इसके साथ ही यदि यह कस्बा A और E के ठीक बीच में स्थित होता है, तो भी दूरी परिकलित कीजिए।
• बताइए कि आपकी राय में यदि हर कस्बे में एक छात्र हो तो कॉलेज कहाँ पर स्थापित होना चाहिए? क्या इससे आप का उत्तर बदल जाता है?
प्रत्यक्ष विधि
इस विधि के निम्नलिखित चरण हैंः
(क) मानों का समांतर माध्य परिकलित किया जाता है।
(ख) प्रत्येक मान और समांतर माध्य के बीच के अंतर का परिकलन किया जाता है। ये सभी अंतर धनात्मक माने जाते हैं। इन्हें |d| द्वारा दर्शाया जाता है।
(ग) इन अंतरों का समांतर माध्य, माध्य विचलन है।
अर्थात्
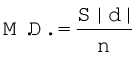
उदाहरण 3
निम्नलिखित मानों का माध्य विचलन परिकलित कीजिएः 2, 4, 7, 8 एवं 9.
समांतर माध्य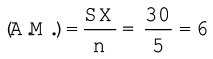
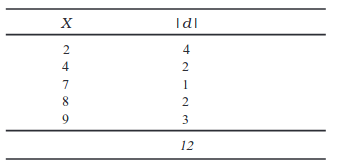
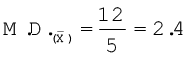
कल्पित माध्य विधि
माध्य विचलन कल्पित माध्य से परिकलित विचलनों द्वारा भी निकाला जा सकता है। यह विधि विशेष रूप से तब अपनाई जाती है, जब वास्तविक माध्य भिन्नात्मक संख्या में होता है। (यह ध्यान रखें कि कल्पित माध्य वास्तविक माध्य के निकट हो)।
उदाहरण 3 के मानों के लिए मान 7 को कल्पित माध्य लेकर माध्य विचलन निम्न तरह से परिकलित किया जा सकता हैः
उदाहरण 4

एेसे मामलों में, निम्नलिखित सूत्र प्रयुक्त होता हैः
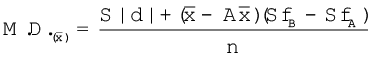
यहाँ पर 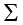 |d| कल्पित माध्य से लिए गए निरपेक्ष विचलनों का योग है।
|d| कल्पित माध्य से लिए गए निरपेक्ष विचलनों का योग है।
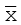 वास्तविक माध्य है।
वास्तविक माध्य है।
A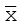 कल्पित माध्य है, जो विचलनों के परिकलन में प्रयुक्त होता है।
कल्पित माध्य है, जो विचलनों के परिकलन में प्रयुक्त होता है।
 fB वास्तविक माध्य तथा उससे नीचे के मानों की संख्या है।
fB वास्तविक माध्य तथा उससे नीचे के मानों की संख्या है।
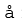 fA वास्तविक माध्य से ऊपर के मानों की संख्या है।
fA वास्तविक माध्य से ऊपर के मानों की संख्या है।
सूत्र में मानों को प्रतिस्थापित करने पर,
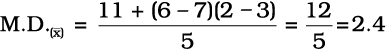
असमूहित आँकड़ों के लिए मध्यिका से माध्य विचलन
विधि
उदाहरण 3 के मानों का प्रयोग करते हुए मध्यिका से माध्य विचलनों को निम्न प्रकार से परिकलित किया जा सकता है,
(क) मध्यिका को परिकलित कीजिए जो 7 है।
(ख) मध्यिका से निरपेक्ष विचलन परिकलित कीजिए, |d| के रूप में दिखाइए।
(ग) इन निरपेक्ष विचलनों का औसत ज्ञात कीजिए। यह माध्य विचलन है।
उदाहरण 5
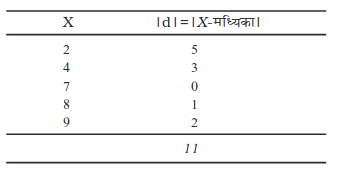
मध्यिका से माध्य विचलन इस प्रकार है
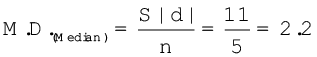
संक्षिप्त विधि
संक्षिप्त विधि द्वारा माध्य विचलन को परिकलित करने हेतु किसी मान (A) को विचलनों के परिकलन के लिए प्रयुक्त किया जाता है और इसके लिए निम्न
सूत्र है,
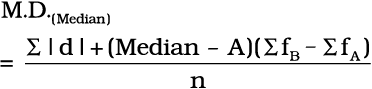
यहाँ पर A = एक स्थिरांक है, जिससे विचलनों को परिकलित करते हैं (अन्य संकेतक वैसे ही रहेंगे जैसे कि कल्पित माध्य विधि में है)।
संतत वितरण के लिए माध्य से माध्य विचलन
चरण
(क) वितरण का माध्य परिकलित कीजिए।
(ख) माध्य से वर्गाें के मध्य बिंदुओं का निरपेक्ष विचलन |d| परिकलित कीजिए।
(ग) f|d|का मान प्राप्त करने के लिए प्रत्येक |d| मान को इसकी संगत बारंबारता से गुणा कीजिए और इन्हें जोड़कर
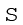 f|d| प्राप्त कीजिए।
f|d| प्राप्त कीजिए।
(घ) निम्न सूत्र का प्रयोग कीजिए
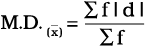
सारणी 6.2 में वितरण का माध्य विचलन निम्नानुसार भी परिकलित कर सकते हैंः
उदाहरण 6
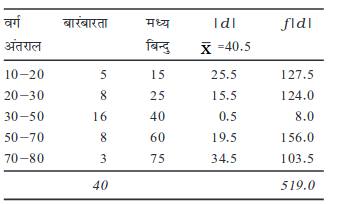
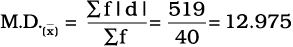
मध्यिका से माध्य विचलन
मध्यिका से माध्य विचलन परिकलित करने की प्रक्रिया ठीक वैसी ही है, जैसी कि माध्य से माध्य विचलन के लिए होती है, सिवाय इसके कि विचलन मध्यिका से लिए जायें, जैसा कि नीचे दिखाया गया हैः
उदाहरण 7
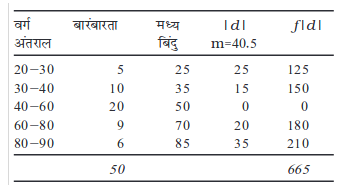
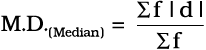
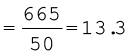
माध्य विचलन - टिप्पणी
माध्य विचलन सभी मानों पर आधारित होता है। अतः एक भी मान में परिवर्तन इस पर प्रभाव डालेगा। यदि इसे मध्यिका से परिकलित किया जाए तो माध्य विचलन निम्नतम होगा, अर्थात् यदि इसे माध्य से परिकलित किया जाए तो यह अधिक होगा। परंतु, यह विचलनों के चिह्नों की उपेक्षा करता है और मुक्तांत वितरण के लिए परिकलित नहीं किया जा सकता है।
मानक विचलन (Standard Deviation)
मानक विचलन माध्य से विचलनों के वर्गाें के माध्य का धनात्मक वर्गमूल है। इसलिए यदि पाँच मान x1, x2, x3, x4 एवं x5 हैं, तो सबसे पहले इनका माध्य परिकलित किया जाता है। इसके बाद माध्य से मानों के विचलन परिकलित किए जाते हैं। फिर इन विचलनों का वर्ग किया जाता है। इन वर्ग विचलनों का माध्य प्रसरण कहलाता है। प्रसरण का धनात्मक वर्गमूल मानक विचलन होता है। (यह ध्यान दें कि मानक विचलन का परिकलन केवल माध्य के आधार पर होता है)।
असमूहित आँकड़ों के लिए मानक विचलन का परिकलन
व्यक्तिगत मानों के मानक विचलन के परिकलन के लिए चार वैकल्पिक विधियाँ उपलब्ध हैं। इन सभी विधियों के द्वारा मानक विचलन का मान एक ही प्राप्त होता है। ये निम्न हैंः
(क) वास्तविक माध्य विधि
(ख) कल्पित माध्य विधि
(ग) प्रत्यक्ष विधि
(घ) पद विचलन विधि
वास्तविक माध्य विधि
मान लीजिए, आपको निम्नलिखित मानों का मानक विचलन परिकलित करना हैः
5, 10, 25, 30, 50
इसकी गणना के लिए प्रथम चरण यह होगा
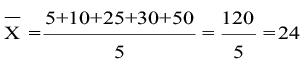
उदाहरण 8
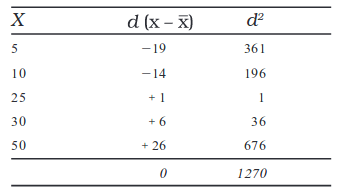
अब निम्नलिखित सूत्र प्रयुक्त होगाः
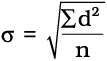
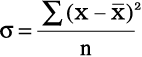
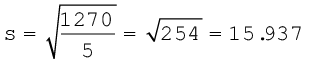
उपर्युक्त उदाहरण में जिस मान से विचलन परिकलित किए गए हैं, क्या आपने उस मान पर ध्यान दिया है? क्या यह वास्तविक माध्य है?
कल्पित माध्य विधि
इन्हीं मानों के लिए विचलन को किसी भी स्वैच्छिक
मान A से परिकलित किया जा सकता है। d = x – A
से परिकलित किया जा सकता है। d = x – A , A
, A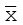 = 25 लेते हुए मानक विचलन का अभिकलन नीचे दिखाया गया है,
= 25 लेते हुए मानक विचलन का अभिकलन नीचे दिखाया गया है,
उदाहरण 9
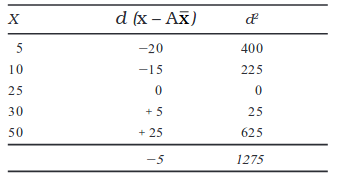
मानक विचलन के लिए सूत्र,

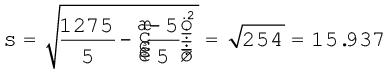
इसे जान लें कि वास्तविक माध्य के अतिरिक्त अन्य किसी मान से विचलन का योग शून्य के बराबर नहीं होगा।
प्रत्यक्ष विधि
मानक विचलन को मानों से सीधे भी, अर्थात् विचलनों को बिना लिए भी, परिकलित किया जा सकता है, जैसा कि नीचे दिखाया गया हैः
उदाहरण 10
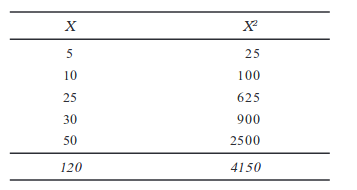
(यहाँ विचलन शून्य से लिए गए माने जा सकते हैं)।
यहाँ निम्नलिखित सूत्र प्रयुक्त किया जायगाः
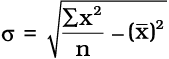
या 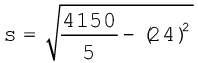
या 
पद - विचलन विधि
यदि मान किसी समापवर्तक से विभाज्य है, तो उन्हें इससे विभाजित किया जा सकता है और मानक विचलन को प्राप्त मानों से निम्नानुसार परिकलित किया जा सकता हैः
उदाहरण 11
चूँकि सभी पाँचों मान समापवर्तक 5 से विभाज्य हैं, अतः विभाजन करके हम निम्न मान प्राप्त करते हैंः
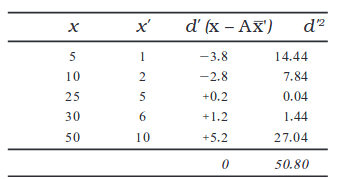
ऊपर दी गई सारणी में,
x' = 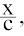 यहाँ पर C= समापवर्तक है।
यहाँ पर C= समापवर्तक है।
प्रथम परण
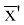 = 1+2+6+10 =
= 1+2+6+10 =  = 4.8
= 4.8
मानक विचलन के परिकलन हेतु निम्न सूत्र प्रयुक्त किया जाता हैः
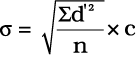
मानों को प्रतिस्थापित करने पर,

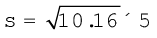
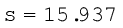
वैकल्पिक तौर पर, किसी समापवर्तक द्वारा मानों को विभाजित करने की अपेक्षा, विचलनों की गणना कर और किसी समापवर्तक से विभाजित किया जा सकता है। मानक विचलन का परिकलन निम्नानुसार किया जा सकता है।
उदाहरण 12

यहाँ विचलन को स्वैच्छिक मान 25 से परिकलित किया गया है। विचलनों को विभाजित करने के लिए समापवर्तक 5 को प्रयुक्त किया गया है।
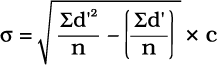

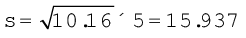
मानक विचलन पैमाने पर स्वतंत्र नहीं होता है। अतः, यदि मान या विचलन एक समापवर्तक से विभाजित होते हैं तो मानक विचलन ज्ञात करने के लिए समापवर्तक का मान सूत्र में प्रयुक्त होता है।
संतत बारंबारता वितरण में मानक विचलन
असमूहित आँकड़ों की भाँति, समूहित आँकड़ों के लिए मानक विचलन को किसी भी निम्नलिखित विधि के द्वारा परिकलित किया जा सकता हैः
(क) वास्तविक माध्य विधि
(ख) कल्पित माध्य विधि
(ग) पद-विचलन विधि
वास्तविक माध्य विधि
सारणी 6.2 में दिए मानों के लिए मानक विचलन को निम्नानुसार परिकलित किया जा सकता है।
उदाहरण 13
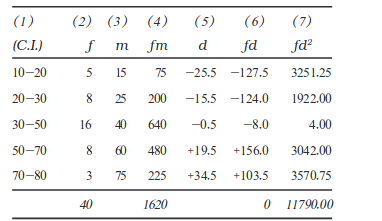
निम्नलिखित चरण अपनाए जाते हैंः
1. वितरण का माध्य परिकलित कीजिए।
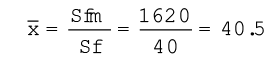
2. माध्य से मध्यबिंदुओं का विचलन परिकलित कीजिए, ताकि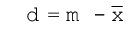 (स्तंभ 5)
(स्तंभ 5)
3. 'fd' मान (स्तंभ 6) को पाने हेतु विचलन के साथ उसकी संगत बारंबारता को गुणा कीजिए [ध्यान दें कि 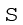 fd = 0]
fd = 0]
4. ‘fd’ मानों को ‘d’ मानों के साथ गुणा करके ‘fd2’ परिकलित कीजिए (स्तंभ 7), इन्हें जोड़कर  fd2 प्राप्त करें।
fd2 प्राप्त करें।
5. निम्न सूत्र का प्रयोग कीजिएः
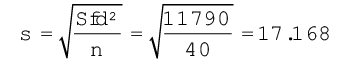
कल्पित माध्य विधि
उदाहरण 13 के मानों के लिए मानक विचलन को एक कल्पित माध्य, जैसे 40, से विचलन लेकर निम्नानुसार परिकलित किया जा सकता हैः
उदाहरण 14
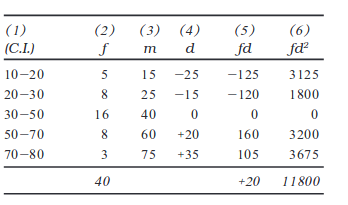
निम्नलिखित चरण आवश्यक हैंः
1. वर्गाें के मध्य बिंदु परिकलित करें। (स्तंभ 3)
2. किसी कल्पित माध्य से मध्य बिंदुओं के विचलन परिकलित कीजिए जैसे कि d = m – A (स्तंभ 4)। कल्पित माध्य = 40 है।
3. ‘fd’ मानों (स्तंभ 5) की प्राप्ति हेतु ‘d’ के मानों को संगत बारंबारताओं से गुणा कीजिए। (यह ध्यान दें कि इस स्तंभ का कुल योग शून्य नहीं है, चूँकि विचलनों को कल्पित माध्य से लिया गया है)।
4. ‘d’ (स्तंभ 4) मानों के साथ fd (स्तंभ 5) मानों को गुणा कीजिए, ताकि fd2 मान (स्तंभ 6) प्राप्त हो सकें।
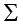 fd2 प्राप्त कीजिए।
fd2 प्राप्त कीजिए।
5. निम्नलिखित सूत्र द्वारा मानक विचलन का परिकलन किया जा सकता है।
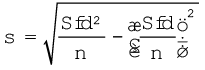
या
या 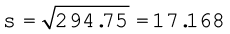
पद विचलन विधि
यदि विचलनों के मूल्य किसी समापवर्तक द्वारा विभाज्य हों तो पद विचलन विधि से परिकलनों को सरल बनाया जा सकता है, जैसा नीचे उदाहरण में दिया गया हैःउदाहरण 15
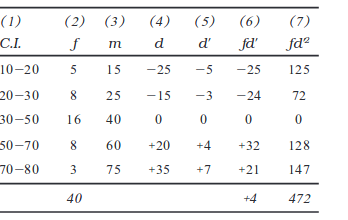 .
.निम्नलिखित चरण आवश्यक हैः
1. वर्ग के मध्य बिंदुओं का परिकलन करें (स्तंभ 3) तथा किसी भी स्वैच्छिक मूल्य से इनका विचलन निकालें, जैसा कल्पित माध्य विधि में किया जाता है। इस उदाहरण में 40 से विचलन लिए गए हैं। (कॉलम 4)
2. विचलनों को समापवर्तक C से भाग दें। उपर्युक्त उदाहरण में C = 5। इस प्रकार से प्राप्त किए गए मूल्य d' (स्तंभ 5) में दिये गये हैं।
3. d' मूल्यों को संगत f (स्तंभ 2) से गुणा करें। जिससे fd' मूल्य प्राप्त हो सके। (स्तंभ 6)
4. fd' मूल्यों को d' मूल्यों से गुणा करके fd'2 मूल्य (स्तंभ 7) प्राप्त करें।
5 स्तंभ 6 तथा स्तंभ 7 के मूल्यों को जोड़कर
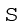 fd' तथा
fd' तथा 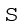 fd'2 मूल्यों को प्राप्त करें।
fd'2 मूल्यों को प्राप्त करें।
6. निम्नलिखित सूत्र का प्रयोग करेंः
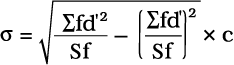
या, 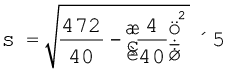
या, 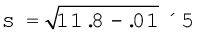
या, 
मानक विचलनः टिप्पणी
मानक विचलन परिक्षेपण के मापों में सर्वाधिक प्रचलित है, क्योंकि यह सभी मानों पर आधारित होता है। इसलिए, किसी भी मान में परिवर्तन, मानक विचलन के मान को प्रभावित करता है। यह उद्गम से स्वतंत्र है, पर स्केल से नहीं। इसके साथ ही यह कुछ उच्च सांख्यिकीय विधियों में भी प्रयुक्त होता है।
4. परिक्षेपण के निरपेक्ष तथा सापेक्ष माप
अभी तक ऊपर वर्णित सभी माप परिक्षेपण के निरपेक्ष माप हैं। वे एेसे मान का परिकलन करते हैं, जो कभी-कभी निर्वचन में कठिन होते हैं। उदाहरण के लिए, निम्नलिखित दो आँकड़ों के समुच्चय पर ध्यान दीजिएः
समुच्चय (क) 500 700 1000
समुच्चय (ख) 1,00,000 1,20,000 1,30,000
मान लीजिए समुच्चय क के मान एक आइसक्रीम विक्रेता की दैनिक बिक्री का रिकार्ड है, जबकि समुच्चय ख के मान एक बड़े डिपार्टमेंटल स्टोर की दैनिक बिक्री के हैं। समुच्चय क का परास 500 है, जबकि समुच्चय ख का परास 30,000 है। परास का मान समुच्चय ख में बहुत अधिक है। क्या आप यह कह सकते हैं कि डिपार्टमेंटल स्टोर की बिक्री में विचरण अधिक है? यह बात आसानी से देखी जा सकती है कि समुच्चय क का उच्चतम मान निम्नतम मान का दोगुना है, जबकि समुच्चय ख में यह केवल 30% अधिक है। अतः निरपेक्ष माप विचरण के प्रसरण के बारे में भ्रामक अनुमान दे सकते हैं, विशेष रूप से तब जब औसतों में महत्त्वपूर्ण अंतर हो।
निरपेक्ष मापों की एक अन्य कमजोरी यह है कि इनका उत्तर उस इकाई में आता है, जिसमें वास्तविक मान व्यक्त किए गए हों। फलस्वरूप, यदि मान को किलोमीटर में व्यक्त किया गया है, तो परिक्षेपण भी किलोमीटर में ही व्यक्त होगा। लेकिन यदि ठीक वही मान मीटर में व्यक्त किए गए हों तो निरपेक्ष माप भी मीटर में ही होंगे और परिक्षेपण का मान 1000 गुना प्रतीत होगा।
इन समस्याओं के हल के लिए, परिक्षेपण के सापेक्ष मान प्रयुक्त किए जाते हैं। प्रत्येक निरपेक्ष माप का एक संबद्ध प्रतिरूप होता है। अतः परास के लिए, परास-गुणांक है, जिसे निम्नानुसार परिकलित किया जाता है।
परास-गुणांक
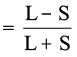
यहाँ पर L = अधिकतम मान
S = न्यूनतम मान
ठीक इसी प्रकार से, चतुर्थक विचलन के लिए चतुर्थक विचलन गुणांक है, जिसे निम्नानुसार परिकलित किया जा सकता हैः
चतुर्थक विचलन गुणांक 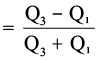 , यहाँ
, यहाँ
पर Q3 = तृतीय चतुर्थक तथा Q1 = प्रथम चतुर्थक
माध्य विचलन के लिए, यह माध्य विचलन गुणांक है।
माध्य विचलन गुणांक = 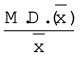 अथवा
अथवा 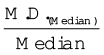
इसलिए, यदि माध्य के आधार पर माध्य विचलन का परिकलन होता है तो इसे माध्य द्वारा विभाजित करते हैं। यदि माध्य विचलन के परिकलन हेतु मध्यिका प्रयुक्त होता है तो इसे मध्यिका द्वारा विभाजित किया जाता है।
मानक विचलन के लिए सापेक्ष माप को विचरण गुणांक कहा जाता है, जिसका परिकलन आगे दिया गया है।

5. लारेंज वक्र (Lorenz Curve)
अब तक चर्चित परिक्षेपण के माप, परिक्षेपण का एक संख्यात्मक मान देते हैं। वितरण में असमानता के अनुमान के लिए एक आरेखी माप जिसे लारेंज वक्र कहा जाता है, भी उपलब्ध है। आपने एेसे वक्तव्य सुने होंगे, जैसे देश के शीर्ष 10% लोग देश की 50% राष्ट्रीय आय अर्जित करते हैं, जबकि शीर्ष 20% लोग 80% आय। इन संख्याओं से आय वितरण की असमानता के बारे में अनुमान प्राप्त होता हैैं। लारेंज वक्र का प्रयोग संचयी रूप में व्यक्त सूचनाओं की असमानता की मात्रा को दर्शाने के लिए किया जाता है। उदाहरण के लिए, आय की लारेंज वक्र आबादी के प्रतिशत और उसकी कुल आय के भाग में संबंध बताती है। यह दो या दो से अधिक वितरणों की परिवर्तनशीलता की तुलना में विशेष उपयोगी है, जिसे दो या दो से अधिक लारेंज वक्र एक ही अक्ष पर बनाकर तुलना की जा सकती है।
लारेंज वक्र का निर्माण
निम्न चरण अपनाना आवश्यक है-
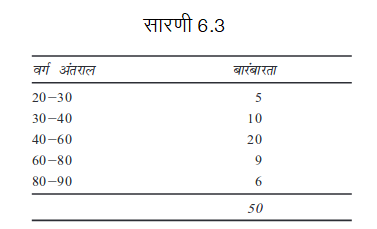
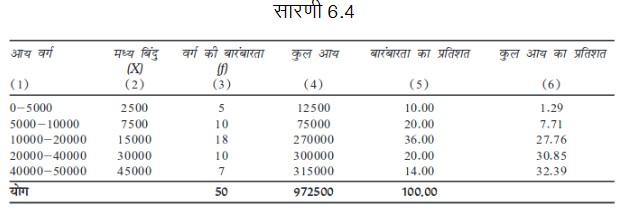
1. तालिका 6.4 के स्तंभ 2 को ज्ञात करने के लिए, वर्गों के मध्य बिंदुओं का परिकलन कीजिए।
2. प्रत्येक वर्ग के मध्य बिंदुओं को, वर्ग की बारंबारता से गुणा करके, कर्मचारियों की प्रत्येक वर्ग में अनुमानित कुल आय का परिकलन कीजिए। इस प्रकार तालिका 6.4 के कॉलम (4) को ज्ञात कीजिए।
3. प्रत्येक वर्ग की बारंबारता को, कुल बारंबारताओं के प्रतिशत में व्यक्त कीजिए। इस प्रकार तालिका 6.4 के स्तंभ (5) को ज्ञात कीजिए।
4. प्रत्येक वर्ग की कुल आय को, सभी वर्गों की कुल आय के समग्र योग के प्रतिशत में व्यक्त कीजिए। इस प्रकार तालिका 6.4 के स्तंभ (6) को ज्ञात कीजिए।
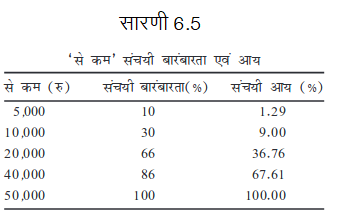
5. ‘से कम’ संचयी बारंबारता और संचयी आय ज्ञात कीजिए (तालिका 6.5)।
6. तालिका 6.5 क स्तंभ (2), कर्मचारियों की संचयी बारंबारता प्रदर्शित करता है।
7. तालिका 6.5 का स्तंभ (3) इन व्यक्तियों को प्राप्त आय को दिखाता है।
8. निर्देशांक (0,0) को (100,100) से जोड़ते हुए एक रेखा खींचिए। इसे ‘सम वितरण की रेखा’ कहा जाता है, जिसे OE रेखा द्वारा चित्र 6.1 में दिखाया गया है।
9. कर्मचारियों के संचयी प्रतिशतों को क्षैतिज अक्ष पर तथा संचयी आय को ऊर्ध्वाधर अक्ष पर दिखाइए। इस प्रकार हम इस रेखा को प्राप्त कर सकते हैं।
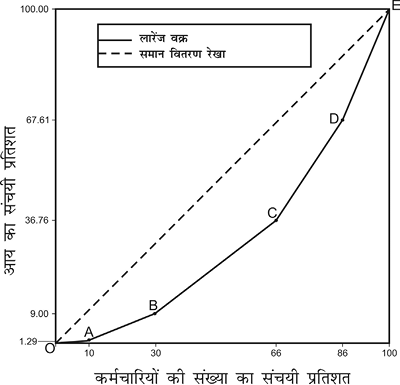
चित्र 6.1
लारेंज वक्र का अध्ययन
OE को सम वितरण की रेखा कहा जाता है, चूूँकि यह एेसी स्थिति में लागू होता है, जहाँ शीर्ष 20% लोग कुल आय का 20% अर्जित करते हैं और शीर्ष 60% कुल आय का 60% अर्जित करते हैं। OABCDE वक्र इस रेखा से जितना अधिक दूर होता है वितरण में उतनी ही अधिक असमानता होती है। यदि यहाँ पर दो या इससे अधिक वक्र हैं, तो वह वक्र जो OE रेखा से जितना अधिक दूर होगा, उसमें उतनी ही अधिक असमानता होगी।8. सारांश
यद्यपि परास समझने तथा परिकलन के लिए सबसे सरल है, लेकिन यह चरम मानों से अनुचित रूप से प्रभावित होता है। चतुर्थक विचलन चरम मानों से प्रभावित नहीं होता है, क्योंकि वह आँकड़ों के केवल मध्यवर्ती 50% आँकड़ों पर आधारित होता है। परंतु, चतुर्थक विचलन का निर्वचन बहुत कठिन होता है। माध्य विचलन और मानक विचलन दोनों ही मानों के अपने औसत से विचलनों पर आधारित होते हैं। माध्य विचलन औसत से विचलनों के औसत को परिकलित करता है, लेकिन विचलन के चिन्हों की (ऋणात्मक तथा धनात्मक) उपेक्षा करता है। इसी कारण यह अंगणितीय प्रतीत होता है। मानक विचलन माध्य से औसत विचलन के परिकलन का प्रयास करता है। माध्य विचलन की भाँति यह सभी मानों पर आधारित होता है एवं इसका प्रयोग उच्चतर सांख्यिकीय समस्याओं में भी होता है। यह परिक्षेपण के माप के लिए सामान्य रूप से प्रयुक्त होता है।
पुनरावर्तन
• परिक्षेपण का माप किसी आर्थिक चर के व्यवहार के बारे में हमारे ज्ञान में वृद्धि करता है।
• परास तथा चतुर्थक विचलन मानों के प्रसरण पर आधारित होते हैं।
• माध्य विचलन तथा मानक विचलन औसत से मानों के विचलनों पर आधारित होते हैं।
• परिक्षेपण के माप निरपेक्ष या सापेक्ष हो सकते हैं।
• निरपेक्ष मापों का उत्तर उन्हीं इकाइयों में होता है, जिसमें आँकड़ों को व्यक्त किया गया है।
• सापेक्ष माप उन इकाइयों से मुक्त होते हैं, जिनमें आँकड़े व्यक्त किए जाते हैं और इसीलिए ये विभिन्न चरों की तुलना करने के लिए प्रयुक्त किए जा सकते हैं।
• वक्र के आकार में परिक्षेपण अनुमान प्रस्तुत करने वाली आरेखीय विधि को लारेंज वक्र कहते हैं।
अभ्यास
1. ‘किसी बारंबारता वितरण के समझने में परिक्षेपण का माप केंद्रीय मान का एक अच्छा संपूरक है’, टिप्पणी करें।
2. परिक्षेपण का कौन सा माप सर्वाेत्तम है और कैसे?
3. ‘परिक्षेपण के कुछ माप मानों के प्रसरण पर निर्भर करते हैं, लेकिन कुछ, केंद्रीय मान से मानों के विचरण के आधार पर परिकलित किए जाते हैं।’ क्या आप सहमत हैं?
4. एक कस्बे में, 25% लोग रु० 45,000 से अधिक आय अर्जित करते हैं, जबकि 75% लोग 18,000 से अधिक अर्जित करते हैं। परिक्षेपण के निरपेक्ष एवं सापेक्ष मानों का परिकलन कीजिए।
5. एक राज्य के 10 जिलों की प्रति एकड़ गेहूँ व चावल फसल की उपज निम्नवत् हैः
जिले 1 2 3 4 5 6 7 8 9 10
गेहूँ 12 10 15 19 21 16 18 9 25 10
चावल 22 29 12 23 18 15 12 34 18 12
प्रत्येक फसल के लिए परिकलन करें,
(क) परास
(ख) चतुर्थक विचलन
(ग) माध्य से माध्य विचलन
(घ) मध्यिका से माध्य विचलन
(ड़) मानक विचलन
(च) किस फसल में अधिक विचरण है?
(छ) प्रत्येक फसल के लिए विभिन्न मापों के मानों की तुलना कीजिए।
6. पूर्ववर्ती प्रश्न में, विचरण के सापेक्ष मापों को परिकलित कीजिए और वह मान बताइए जो आपके विचार से सर्वाधिक विश्वसनीय हो।
7. किसी क्रिकेट टीम के लिए एक बल्लेबाज का चयन करना है। यह चयन x और y के बीच पाँच पूर्ववर्ती टेस्टों के स्कोर के आधार पर करना है, जो निम्नवत् हैंः
x 25 85 40 80 120
y 50 70 65 45 80
किस बल्लेबाज को टीम में चुना जाना चाहिए?
(क) अधिक रन स्कोर करने वाले को, या
(ख) अधिक भरोसेमंद बल्लेबाज को।
8. दो ब्रांडों के बल्बों की गुणवत्ता जाँचने के लिए, ज्वलन अवधि घंटों में उनके जीवन काल को, प्रत्येक ब्रांड के 100 बल्बों के आधार पर निम्नानुसार अनुमानित किया गया हैः
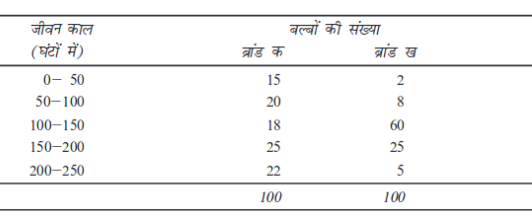
(क) किस ब्रांड का जीवन काल अधिक है?
(ख) कौन सा ब्रांड अधिक भरोसेमंद है?
9. एक कारखाने के 50 मजदूरों की औसत दैनिक मजदूरी 200 रु. तथा मानक विचलन 40 रु० था। प्रत्येक मजदूर की मजदूरी में 20 रु. की वृद्धि की गई। अब मजदूरों की औसत दैनिक मजदूरी एवं मानक विचलन क्या है? क्या मजदूरी में समानता आई है?
10. पूर्ववर्ती प्रश्न में, यदि प्रत्येक मजदूर की मजदूरी में 10% की वृद्धि की जाए, तो माध्य एवं मानक विचलन पर क्या प्रभाव पड़ेगा?
11. निम्नलिखित वितरण के लिए, माध्य से माध्य विचलन और मानक विचलन का परिकलन कीजिए।

12. 10 मानों का योग 100 है और उनके वर्गाें का योग 1090 है। विचरण गुणांक ज्ञात कीजिए।