Table of Contents
Chapter 6
Application of Derivatives
 With the Calculus as a key, Mathematics can be successfully applied
With the Calculus as a key, Mathematics can be successfully applied
to the explanation of the course of Nature.” — Whitehead
6.1 Introduction
In Chapter 5, we have learnt how to find derivative of composite functions, inverse trigonometric functions, implicit functions, exponential functions and logarithmic functions. In this chapter, we will study applications of the derivative in various disciplines, e.g., in engineering, science, social science, and many other fields. For instance, we will learn how the derivative can be used (i) to determine rate of change of quantities, (ii) to find the equations of tangent and normal to a curve at a point, (iii) to find turning points on the graph of a function which in turn will help us to locate points at which largest or smallest value (locally) of a function occurs. We will also use derivative to find intervals on which a function is increasing or decreasing. Finally, we use the derivative to find approximate value of certain quantities.
6.2 Rate of Change of Quantities
Recall that by the derivative 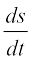 , we mean the rate of change of distance s with respect to the time t. In a similar fashion, whenever one quantity y varies with another quantity x, satisfying some rule
, we mean the rate of change of distance s with respect to the time t. In a similar fashion, whenever one quantity y varies with another quantity x, satisfying some rule 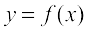 , then
, then 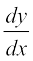 (or f′(x)) represents the rate of change of y with respect to x and
(or f′(x)) represents the rate of change of y with respect to x and  (or f′(x0)) represents the rate of change of y with respect to x at
(or f′(x0)) represents the rate of change of y with respect to x at 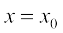 .
.
Further, if two variables x and y are varying with respect to another variable t, i.e., if 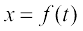 and
and 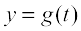 , then by Chain Rule
, then by Chain Rule
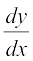 =
= 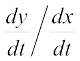 , if
, if 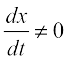
Thus, the rate of change of y with respect to x can be calculated using the rate of change of y and that of x both with respect to t.
Let us consider some examples.
Example 1 Find the rate of change of the area of a circle per second with respect to its radius r when r = 5 cm.
Solution The area A of a circle with radius r is given by A = πr2. Therefore, the rate of change of the area A with respect to its radius r is given by 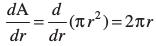 . When
. When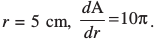 Thus, the area of the circle is changing at the rate of 10π cm2/s.
Thus, the area of the circle is changing at the rate of 10π cm2/s.
Example 2 The volume of a cube is increasing at a rate of 9 cubic centimetres per second. How fast is the surface area increasing when the length of an edge is 10 centimetres ?
Solution Let x be the length of a side, V be the volume and S be the surface area of the cube. Then, V = x3 and S = 6x2, where x is a function of time t.
Now 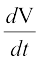 = 9cm3/s (Given)
= 9cm3/s (Given)
Therefore 9 = 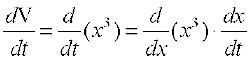 (By Chain Rule) =
(By Chain Rule) = 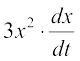
or 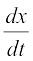 =
= 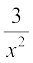 ... (1)
... (1)
Now 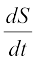 =
= 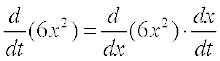 (By Chain Rule)
(By Chain Rule)
= 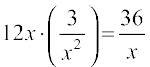 (Using (1))
(Using (1))
Hence, when x = 10 cm, 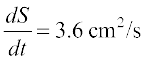
Example 3 A stone is dropped into a quiet lake and waves move in circles at a speed of 4cm per second. At the instant, when the radius of the circular wave is 10 cm, how fast is the enclosed area increasing?
Solution The area A of a circle with radius r is given by A = πr2. Therefore, the rate of change of area A with respect to time t is
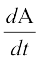 =
= 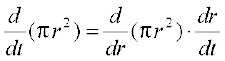 = 2π r
= 2π r 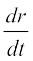 (By Chain Rule)
(By Chain Rule)
It is given that 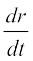 = 4cm/s
= 4cm/s
Therefore, when r = 10 cm, 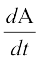 = 2π(10) (4) = 80π
= 2π(10) (4) = 80π
Thus, the enclosed area is increasing at the rate of 80π cm2/s, when r = 10 cm.
Note 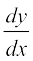 is positive if y increases as x increases and is negative if y decreases as x increases.
is positive if y increases as x increases and is negative if y decreases as x increases.
Example 4 The length x of a rectangle is decreasing at the rate of 3 cm/minute and the width y is increasing at the rate of 2cm/minute. When x =10cm and y = 6cm, find the rates of change of (a) the perimeter and (b) the area of the rectangle.
Solution Since the length x is decreasing and the width y is increasing with respect to time, we have
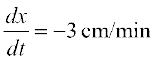 and
and 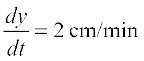
(a) The perimeter P of a rectangle is given by
P = 2(x + y)
Therefore 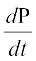 =
= 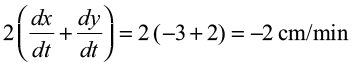
(b) The area A of the rectangle is given by
A = x . y
Therefore 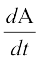 =
= 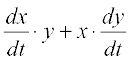
= – 3(6) + 10(2) (as x = 10 cm and y = 6 cm) = 2 cm2/min
Example 5 The total cost C(x) in Rupees, associated with the production of x units of an item is given by
C(x) = 0.005 x3 – 0.02 x2 + 30x + 5000
Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Solution Since marginal cost is the rate of change of total cost with respect to the output, we have
Marginal cost (MC) = 
When x = 3, MC = 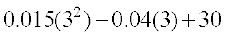
= 0.135 – 0.12 + 30 = 30.015
Hence, the required marginal cost is ` 30.02 (nearly).
Example 6 The total revenue in Rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. Find the marginal revenue, when x = 5, where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant.
Solution Since marginal revenue is the rate of change of total revenue with respect to the number of units sold, we have
Marginal Revenue (MR) = 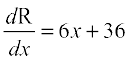
When x = 5, MR = 6(5) + 36 = 66
Hence, the required marginal revenue is ` 66.
Exercise 6.1
1. Find the rate of change of the area of a circle with respect to its radius r when
(a) r = 3 cm (b) r = 4 cm
2. The volume of a cube is increasing at the rate of 8 cm3/s. How fast is the surface area increasing when the length of an edge is 12 cm?
3. The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
4. An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
5. A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?
6. The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
7. The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8cm and y = 6cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.
8. A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.
9. A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.
10. A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall ?
11. A particle moves along the curve 6y = x3 +2. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.
12. The radius of an air bubble is increasing at the rate of  cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
13. A balloon, which always remains spherical, has a variable diameter 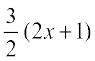 . Find the rate of change of its volume with respect to x.
. Find the rate of change of its volume with respect to x.
14. Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
15. The total cost C(x) in Rupees associated with the production of x units of an item is given by
C(x) = 0.007x3 – 0.003x2 + 15x + 4000.
Find the marginal cost when 17 units are produced.
16. The total revenue in Rupees received from the sale of x units of a product is given by
R(x) = 13x2 + 26x + 15.
Find the marginal revenue when x = 7.
Choose the correct answer for questions 17 and 18.
17. The rate of change of the area of a circle with respect to its radius r at r = 6 cm is
(A) 10π (B) 12π (C) 8π (D) 11π
18. The total revenue in Rupees received from the sale of x units of a product is given by
R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15 is
(A) 116 (B) 96 (C) 90 (D) 126
6.3 Increasing and Decreasing Functions
In this section, we will use differentiation to find out whether a function is increasing or decreasing or none.
Consider the function f given by f(x) = x2, x ∈ R. The graph of this function is a parabola as given in Fig 6.1.
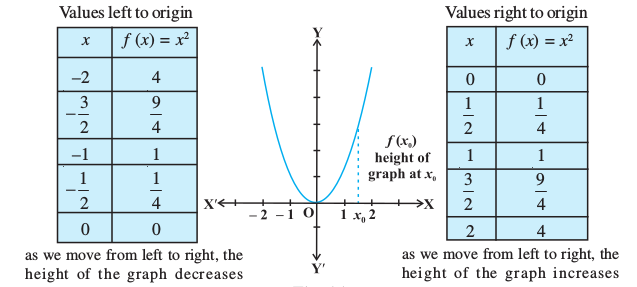
Fig 6.1.
First consider the graph (Fig 6.1) to the right of the origin. Observe that as we move from left to right along the graph, the height of the graph continuously increases. For this reason, the function is said to be increasing for the real numbers x > 0.
Now consider the graph to the left of the origin and observe here that as we move from left to right along the graph, the height of the graph continuously decreases. Consequently, the function is said to be decreasing for the real numbers x < 0.
We shall now give the following analytical definitions for a function which is increasing or decreasing on an interval.
Definition 1 Let I be an interval contained in the domain of a real valued function f. Then f is said to be
(i) increasing on I if x1 < x2 in I ⇒ f(x1) < f(x2) for all x1, x2 ∈ I.
(ii) decreasing on I, if x1, x2 in I ⇒ f(x1) < f(x2) for all x1, x2 ∈ I.
(iii) constant on I, if f(x) = c for all x ∈ I, where c is a constant.
(iv) decreasing on I if x1 < x2 in I ⇒ f(x1) ≥ f(x2) for all x1, x2 ∈ I.
(v) strictly decreasing on I if x1 < x2 in I ⇒ f(x1) > f(x2) for all x1, x2 ∈ I.
For graphical representation of such functions see Fig 6.2.
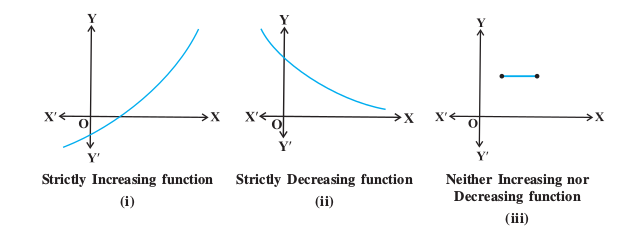
Fig 6.2
We shall now define when a function is increasing or decreasing at a point.
Definition 2 Let x0 be a point in the domain of definition of a real valued function f. Then f is said to be increasing, decreasing at x0 if there exists an open interval I containing x0 such that f is increasing, decreasing, respectively, in I.
Let us clarify this definition for the case of increasing function.
Example 7 Show that the function given by f(x) = 7x – 3 is increasing on R.
Solution Let x1 and x2 be any two numbers in R. Then
x1 < x2 ⇒ 7x1 < 7x2 ⇒ 7x1 – 3 < 7x2 – 3 ⇒ f(x1) < f(x2)
Thus, by Definition 1, it follows that f is strictly increasing on R.
We shall now give the first derivative test for increasing and decreasing functions. The proof of this test requires the Mean Value Theorem studied in Chapter 5.
Theorem 1 Let f be continuous on [a, b] and differentiable on the open interval (a,b). Then
(a) f is increasing in [a,b] if f′(x) > 0 for each x ∈ (a, b)
(b) f is decreasing in [a,b] if f′(x) < 0 for each x ∈ (a, b)
(c) f is a constant function in [a,b] if f′(x) = 0 for each x ∈ (a, b)
Proof (a) Let x1, x2 ∈ [a, b] be such that x1 < x2.
Then, by Mean Value Theorem (Theorem 8 in Chapter 5), there exists a point c between x1 and x2 such that
f(x2) – f(x1) = f′(c) (x2 – x1)
i.e. f(x2) – f(x1) > 0 (as f′(c) > 0 (given))
i.e. f(x2) > f(x1)
Thus, we have
x1 < x2 ⇒ f(x1) < f(x2) for all x1, x2 ∈ [a, b]
Hence, f is an increasing function in [a,b].
The proofs of part (b) and (c) are similar. It is left as an exercise to the reader.
Remarks
There is a more generalised theorem, which states that if f¢(x) > 0 for x in an interval excluding the end points and f is continuous in the interval, then f is increasing. Similarly, if f¢(x) < 0 for x in an interval excluding the end points and f is continuous in the interval, then f is decreasing.
Example 8 Show that the function f given by
f(x) = x3 – 3x2 + 4x, x ∈ R
is increasing on R.
Solution Note that
f′(x) = 3x2 – 6x + 4
= 3(x2 – 2x + 1) + 1
= 3(x – 1)2 + 1 > 0, in every interval of R
Therefore, the function f is increasing on R.
Example 9 Prove that the function given by f(x) = cos x is
(a) decreasing in (0, π)
(b) increasing in (π, 2π), and
(c) neither increasing nor decreasing in (0, 2π).
Solution Note that f′(x) = – sin x
(a) Since for each x ∈ (0, π), sin x > 0, we have f′(x) < 0 and so f is decreasing in
(0, π).
(b) Since for each x ∈ (π, 2π), sin x < 0, we have f′(x) > 0 and so f is increasing in (π, 2π).
(c) Clearly by (a) and (b) above, f is neither increasing nor decreasing in (0, 2π).
Example 10 Find the intervals in which the function f given by f(x) = x2 – 4x + 6 is
(a) increasing (b) decreasing

Fig 6.3
Solution We have
f(x) = x2 – 4x + 6
or f′(x) = 2x – 4
Therefore, f′(x) = 0 gives x = 2. Now the point x = 2 divides the real line into two disjoint intervals namely, (– ∞, 2) and (2, ∞) (Fig 6.3). In the interval (– ∞, 2), f′(x) = 2x – 4 < 0.
Therefore, f is decreasing in this interval. Also, in the interval 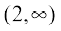 ,
, 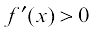 and so the function f is increasing in this interval.
and so the function f is increasing in this interval.
Example 11 Find the intervals in which the function f given by f (x) = 4x3 – 6x2 – 72x + 30 is (a) increasing (b) decreasing.
Solution We have
f(x) = 4x3 – 6x2 – 72x + 30
or f′(x) = 12x2 – 12x – 72
= 12(x2 – x – 6)
= 12(x – 3) (x + 2)
Therefore, f′(x) = 0 gives x = – 2, 3. The points x = – 2 and x = 3 divides the real line into three disjoint intervals, namely, (– ∞, – 2), (– 2, 3) and (3, ∞).

Fig 6.4
In the intervals (– ∞, – 2) and (3, ∞), f′(x) is positive while in the interval (– 2, 3), f′(x) is negative. Consequently, the function f is increasing in the intervals (– ∞, – 2) and (3, ∞) while the function is decreasing in the interval (– 2, 3). However, f is neither increasing nor decreasing in R.
| Interval | Sign of f′(x) | Nature of function f |
| (– ∞, – 2) | (–) (–) > 0 | f is increasing |
| (– 2, 3) | (–) (+) < 0 | f is decreasing |
| (3, ∞) | (+) (+) > 0 g | f is increasing |
Example 12 Find intervals in which the function given by f (x) = sin 3x,  is (a) increasing (b) decreasing.
is (a) increasing (b) decreasing.
Solution We have
f(x) = sin 3x
or f′(x) = 3cos 3x
Therefore, f′(x) = 0 gives cos 3x = 0 which in turn gives 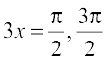 (as
(as  implies
implies 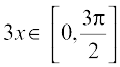 ). So
). So 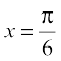 and
and 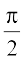 . The point
. The point 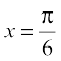 divides the interval
divides the interval  into two disjoint intervals
into two disjoint intervals 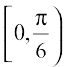 and
and  .
.
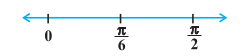
Fig 6.5
Now, 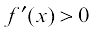 for all
for all 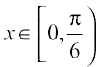 as
as 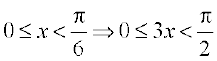 and
and 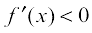 for all
for all 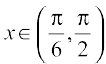 as
as 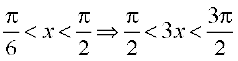 .
.
Therefore, f is increasing in 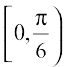 and decreasing in
and decreasing in 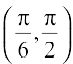 .
.
Also, the given function is continuous at x = 0 and 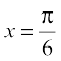 . Therefore, by Theorem 1, f is increasing on
. Therefore, by Theorem 1, f is increasing on  and decreasing on
and decreasing on  .
.
Example 13 Find the intervals in which the function f given by
f(x) = sin x + cos x, 0 ≤ x ≤ 2π
is increasing or decreasing.
Solution We have
f(x) = sin x + cos x,
or f′(x) = cos x – sin x
Now 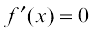 gives sin x = cos x which gives that
gives sin x = cos x which gives that 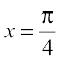 ,
, 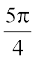 as
as 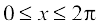
The points 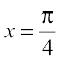 and
and 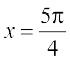 divide the interval [0, 2π] into three disjoint intervals, namely,
divide the interval [0, 2π] into three disjoint intervals, namely, 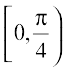 ,
, 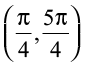 and
and 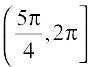 .
.
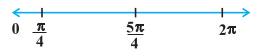
Fig 6.6
Note that 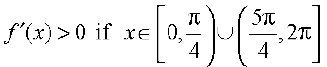
or f is increasing in the intervals 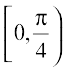 and
and 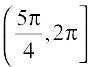
Also 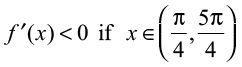
or f is decreasing in 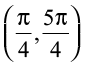
| Interval | Sign of 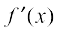 | Nature of function |
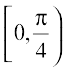 | > 0 | f is increasing |
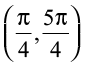 | < 0 | f is decreasing |
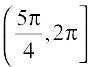 | > 0 | f is increasing |
Exercise 6.2
1. Show that the function given by f (x) = 3x + 17 is increasing on R.
2. Show that the function given by f (x) = e2x is increasing on R.
3. Show that the function given by f (x) = sin x is
(a) increasing in 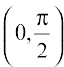 (b) decreasing in
(b) decreasing in 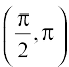
(c) neither increasing nor decreasing in (0, π)
4. Find the intervals in which the function f given by f(x) = 2x2 – 3x is
(a) increasing (b) decreasing
5. Find the intervals in which the function f given by f(x) = 2x3 – 3x2 – 36x + 7 is
(a) increasing (b) decreasing
6. Find the intervals in which the following functions are strictly increasing or decreasing:
(a) x2 + 2x – 5 (b) 10 – 6x – 2x2
(c) –2x3 – 9x2 – 12x + 1 (d) 6 – 9x – x2
(e) (x + 1)3 (x – 3)3
7. Show that 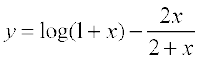 , x > – 1, is an increasing function of x throughout its domain.
, x > – 1, is an increasing function of x throughout its domain.
8. Find the values of x for which y = [x(x – 2)]2 is an increasing function.
9. Prove that 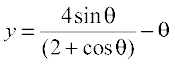 is an increasing function of
is an increasing function of  in
in  .
.
10. Prove that the logarithmic function is increasing on (0, ∞).
11. Prove that the function f given by f(x) = x2 – x + 1 is neither strictly increasing nor decreasing on (– 1, 1).
12. Which of the following functions are decreasing on 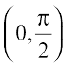 ?
?
(A) cos x (B) cos 2x (C) cos 3x (D) tan x
13. On which of the following intervals is the function f given by f(x) = x100 + sin x –1 decreasing ?
(A) (0,1) (B) 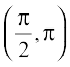 (C)
(C) 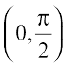 (D) None of these
(D) None of these
14. For what values of a the function f given by f(x) = x2 + ax + 1 is increasing on [1, 2]?
15. Let I be any interval disjoint from [–1, 1]. Prove that the function f given by 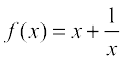 is increasing on I.
is increasing on I.
16. Prove that the function f given by f(x) = log sin x is increasing on  and decreasing on
and decreasing on  .
.
17. Prove that the function f given by f(x) = log |cos x| is decreasing on 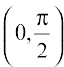 and increasing on
and increasing on 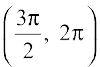 .
.
18. Prove that the function given by f(x) = x3 – 3x2 + 3x – 100 is increasing in R.
19. The interval in which y = x2 e–x is increasing is
(A) (– ∞, ∞) (B) (– 2, 0) (C) (2, ∞) (D) (0, 2)
6.4 Tangents and Normals
In this section, we shall use differentiation to find the equation of the tangent line and the normal line to a curve at a given point.
Recall that the equation of a straight line passing through a given point (x0, y0) having finite slope m is given by
y – y0 = m(x – x0)
Note that the slope of the tangent to the curve y = f(x) at the point (x0, y0) is given by 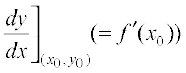 . So the equation of the tangent at (x0, y0) to the curve y = f (x) is given by
. So the equation of the tangent at (x0, y0) to the curve y = f (x) is given by
y – y0 = f′(x0)(x – x0)
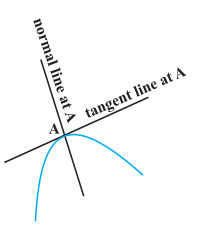
Fig 6.7
Also, since the normal is perpendicular to the tangent, the slope of the normal to the curve y = f(x) at (x0, y0) is 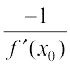 , if
, if 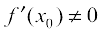 . Therefore, the equation of the normal to the curve y = f(x) at (x0, y0) is given by
. Therefore, the equation of the normal to the curve y = f(x) at (x0, y0) is given by
y – y0 = 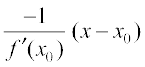
i.e. 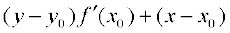 = 0
= 0
Note If a tangent line to the curve y = f(x) makes an angle θ with x-axis in the positive direction, then 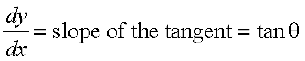 .
.
Particular cases
(i) If slope of the tangent line is zero, then tan θ = 0 and so θ = 0 which means the tangent line is parallel to the x-axis. In this case, the equation of the tangent at the point (x0, y0) is given by y = y0.
(ii) If 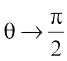 , then tan θ → ∞, which means the tangent line is perpendicular to the x-axis, i.e., parallel to the y-axis. In this case, the equation of the tangent at
, then tan θ → ∞, which means the tangent line is perpendicular to the x-axis, i.e., parallel to the y-axis. In this case, the equation of the tangent at
(x0, y0) is given by x = x0 (Why?).
Example 14 Find the slope of the tangent to the curve y = x3 – x at x = 2.
Solution The slope of the tangent at x = 2 is given by
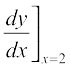 =
= 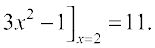
Example 15 Find the point at which the tangent to the curve 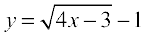 has its slope
has its slope  .
.
Solution Slope of tangent to the given curve at (x, y) is
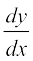 =
= 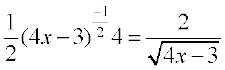
The slope is given to be  .
.
So 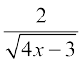 =
= 
or 4x – 3 = 9
or x = 3
Now 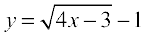 . So when x = 3,
. So when x = 3, 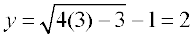 .
.
Therefore, the required point is (3, 2).
Example 16 Find the equation of all lines having slope 2 and being tangent to the curve 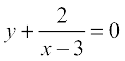 .
.
Solution Slope of the tangent to the given curve at any point (x,y) is given by
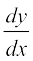 =
= 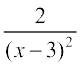
But the slope is given to be 2. Therefore
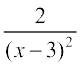 = 2
= 2
or (x – 3)2 = 1
or x – 3 = ± 1
or x = 2, 4
Now x = 2 gives y = 2 and x = 4 gives y = – 2. Thus, there are two tangents to the given curve with slope 2 and passing through the points (2, 2) and (4, – 2). The equation of tangent through (2, 2) is given by
y – 2 = 2(x – 2)
or y – 2x + 2 = 0
and the equation of the tangent through (4, – 2) is given by
y – (– 2) = 2(x – 4)
or y – 2x + 10 = 0
Example 17 Find points on the curve 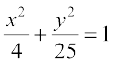 at which the tangents are (i) parallel to x-axis (ii) parallel to y-axis.
at which the tangents are (i) parallel to x-axis (ii) parallel to y-axis.
Solution Differentiating 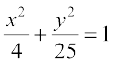 with respect to x, we get
with respect to x, we get
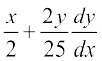 = 0
= 0
or 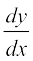 =
= 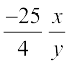
(i) Now, the tangent is parallel to the x-axis if the slope of the tangent is zero which gives 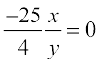 . This is possible if x = 0. Then
. This is possible if x = 0. Then 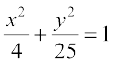 for x = 0 gives
for x = 0 gives
y2 = 25, i.e., y = ± 5.
Thus, the points at which the tangents are parallel to the x-axis are (0, 5) and
(0, – 5).
(ii) The tangent line is parallel to y-axis if the slope of the normal is 0 which gives 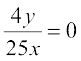 , i.e., y = 0. Therefore,
, i.e., y = 0. Therefore, 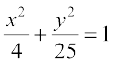 for y = 0 gives x = ± 2. Hence, the points at which the tangents are parallel to the y-axis are (2, 0) and (–2, 0).
for y = 0 gives x = ± 2. Hence, the points at which the tangents are parallel to the y-axis are (2, 0) and (–2, 0).
Example 18 Find the equation of the tangent to the curve 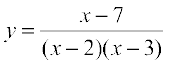 at the point where it cuts the x-axis.
at the point where it cuts the x-axis.
Solution Note that on x-axis, y = 0. So the equation of the curve, when y = 0, gives
x = 7. Thus, the curve cuts the x-axis at (7, 0). Now differentiating the equation of the curve with respect to x, we obtain
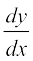 =
= 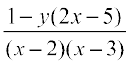 (Why?)
(Why?)
or 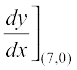 =
= 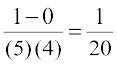
Therefore, the slope of the tangent at (7, 0) is 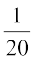 . Hence, the equation of the tangent at (7, 0) is
. Hence, the equation of the tangent at (7, 0) is
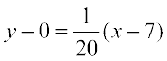 or
or 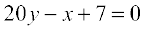
Example 19 Find the equations of the tangent and normal to the curve 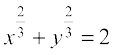
at (1, 1).
Solution Differentiating 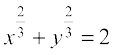 with respect to x, we get
with respect to x, we get
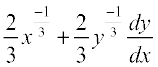 = 0
= 0
or 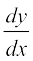 =
= 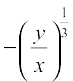
Therefore, the slope of the tangent at (1, 1) is 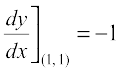 .
.
So the equation of the tangent at (1, 1) is
y – 1 = – 1 (x – 1) or y + x – 2 = 0
Also, the slope of the normal at (1, 1) is given by
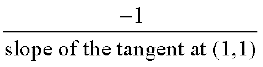 = 1
= 1
Therefore, the equation of the normal at (1, 1) is
y – 1 = 1 (x – 1) or y – x = 0
Example 20 Find the equation of tangent to the curve given by
x = a sin3 t , y = b cos3 t ... (1)
at a point where 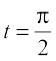 .
.
Solution Differentiating (1) with respect to t, we get
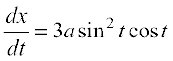 and
and 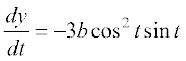
or 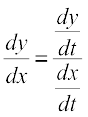 =
= 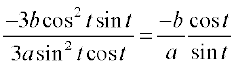
Therefore, slope of the tangent at 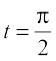 is
is
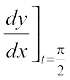 =
= 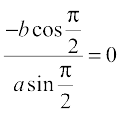
Also, when 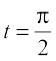 , x = a and y = 0. Hence, the equation of tangent to the given curve at
, x = a and y = 0. Hence, the equation of tangent to the given curve at 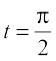 , i.e., at (a, 0) is
, i.e., at (a, 0) is
y – 0 = 0(x – a), i.e., y = 0.
Exercise 6.3
1. Find the slope of the tangent to the curve y = 3x4 – 4x at x = 4.
2. Find the slope of the tangent to the curve 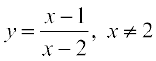 at x = 10.
at x = 10.
3. Find the slope of the tangent to curve y = x3 – x + 1 at the point whose
x-coordinate is 2.
4. Find the slope of the tangent to the curve y = x3 –3x + 2 at the point whose
x-coordinate is 3.
5. Find the slope of the normal to the curve 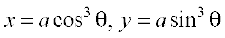 at
at 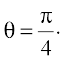
6. Find the slope of the normal to the curve 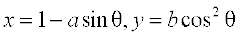 at
at 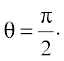
7. Find points at which the tangent to the curve y = x3 – 3x2 – 9x + 7 is parallel to the x-axis.
8. Find a point on the curve y = (x – 2)2 at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4).
9. Find the point on the curve y = x3 – 11x + 5 at which the tangent is y = x –11.
10. Find the equation of all lines having slope –1 that are tangents to the curve 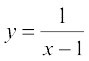 , x ≠ 1.
, x ≠ 1.
11. Find the equation of all lines having slope 2 which are tangents to the curve 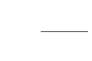 , x ≠ 3.
, x ≠ 3.
12. Find the equations of all lines having slope 0 which are tangent to the curve 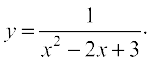
13. Find points on the curve 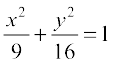 at which the tangents are
at which the tangents are
(i) parallel to x-axis (ii) parallel to y-axis.
14. Find the equations of the tangent and normal to the given curves at the indicated points:
(i) y = x4 – 6x3 + 13x2 – 10x + 5 at (0, 5)
(ii) y = x4 – 6x3 + 13x2 – 10x + 5 at (1, 3)
(iii) y = x3 at (1, 1)
(iv) y = x2 at (0, 0)
(v) x = cost, y = sint at 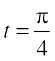
15. Find the equation of the tangent line to the curve y = x2 – 2x +7 which is
(a) parallel to the line 2x – y + 9 = 0
(b) perpendicular to the line 5y – 15x = 13.
16. Show that the tangents to the curve y = 7x3 + 11 at the points where x = 2 and
x = – 2 are parallel.
17. Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-coordinate of the point.
18. For the curve y = 4x3 – 2x5, find all the points at which the tangent passes through the origin.
19. Find the points on the curve x2 + y2 – 2x – 3 = 0 at which the tangents are parallel to the x-axis.
20. Find the equation of the normal at the point (am2,am3) for the curve ay2 = x3.
21. Find the equation of the normals to the curve y = x3 + 2x + 6 which are parallel to the line x + 14y + 4 = 0.
22. Find the equations of the tangent and normal to the parabola y2 = 4ax at the point (at2, 2at).
23. Prove that the curves x = y2 and xy = k cut at right angles* if 8k2 = 1.
24. Find the equations of the tangent and normal to the hyperbola 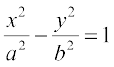 at the point (x0, y0).
at the point (x0, y0).
25. Find the equation of the tangent to the curve 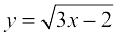 which is parallel to the line
which is parallel to the line 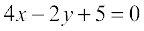 .
.
Choose the correct answer in Exercises 26 and 27.
26. The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0 is
(A) 3 (B) 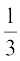 (C) –3 (D)
(C) –3 (D) 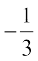
27. The line y = x + 1 is a tangent to the curve y2 = 4x at the point
(A) (1, 2) (B) (2, 1) (C) (1, – 2) (D) (– 1, 2)
6.5 Approximations
In this section, we will use differentials to approximate values of certain quantities.
Let f : D → R, D ⊂ R, be a given function and let y = f(x). Let ∆x denote a small increment in x. Recall that the increment in y corresponding to the increment in x, denoted by ∆y, is given by ∆y = f(x + ∆x) – f(x). We define the following
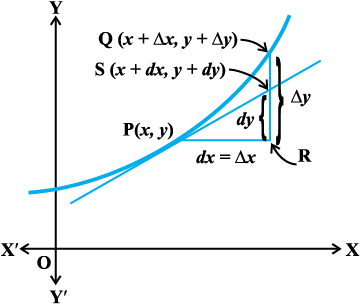
Fig 6.8
(i) The differential of x, denoted by dx, is defined by dx = ∆x.
(ii) The differential of y, denoted by dy,
is defined by dy = f′(x) dx or 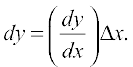
* Two curves intersect at right angle if the tangents to the curves at the point of intersection are perpendicular to each other.
In case dx = ∆x is relatively small when compared with x, dy is a good approximation of ∆y and we denote it by dy ≈ ∆y.
For geometrical meaning of ∆x, ∆y, dx and dy, one may refer to Fig 6.8.
Note In view of the above discussion and Fig 6.8, we may note that the differential of the dependent variable is not equal to the increment of the variable where as the differential of independent variable is equal to the increment of the variable.
Example 21 Use differential to approximate 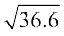 .
.
Solution Take 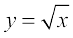 . Let x = 36 and let ∆x = 0.6. Then
. Let x = 36 and let ∆x = 0.6. Then
∆y = 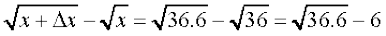
or 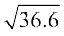 = 6 + ∆y
= 6 + ∆y
Now dy is approximately equal to ∆y and is given by
dy = 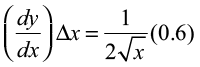 =
= 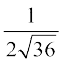 (0.6) = 0.05
(0.6) = 0.05 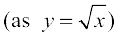
Thus, the approximate value of 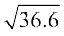 is 6 + 0.05 = 6.05.
is 6 + 0.05 = 6.05.
Example 22 Use differential to approximate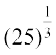 .
.
Solution Let 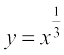 . Let x = 27 and let ∆x = – 2. Then
. Let x = 27 and let ∆x = – 2. Then
∆y = 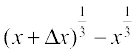 =
= 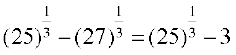
or 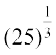 = 3 + ∆y
= 3 + ∆y
Now dy is approximately equal to ∆y and is given by
dy = 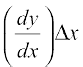 =
= 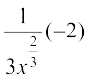
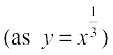
= 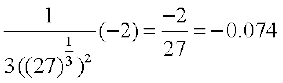
Thus, the approximate value of 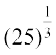 is given by
is given by
3 + (– 0. 074) = 2.926
Example 23 Find the approximate value of f(3.02), where f(x) = 3x2 + 5x + 3.
Solution Let x = 3 and ∆x = 0.02. Then
f(3. 02) = f(x + ∆x) = 3(x + ∆x)2 + 5(x + ∆x) + 3
Note that ∆y = f(x + ∆x) – f(x). Therefore
f(x + ∆x) = f(x) + ∆y
≈ f(x) + f′(x) ∆x (as dx = ∆x)
or f(3.02) ≈ (3x2 + 5x + 3) + (6x + 5) ∆x
= (3(3)2 + 5(3) + 3) + (6(3) + 5) (0.02) (as x = 3, ∆x = 0.02)
= (27 + 15 + 3) + (18 + 5) (0.02)
= 45 + 0.46 = 45.46
Hence, approximate value of f(3.02) is 45.46.
Example 24 Find the approximate change in the volume V of a cube of side x meters caused by increasing the side by 2%.
Solution Note that
V = x3
or dV = 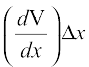 = (3x2) ∆x
= (3x2) ∆x
= (3x2) (0.02x) = 0.06x3 m3 (as 2% of x is 0.02x)
Thus, the approximate change in volume is 0.06 x3 m3.
Example 25 If the radius of a sphere is measured as 9 cm with an error of 0.03 cm, then find the approximate error in calculating its volume.
Solution Let r be the radius of the sphere and ∆r be the error in measuring the radius. Then r = 9 cm and ∆r = 0.03 cm. Now, the volume V of the sphere is given by
V = 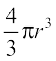
or 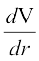 = 4πr2
= 4πr2
Therefore dV = 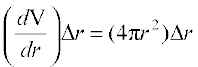
= 4π(9)2 (0.03) = 9.72πcm3
Thus, the approximate error in calculating the volume is 9.72π cm3.
Exercise 6.4
1. Using differentials, find the approximate value of each of the following up to 3 places of decimal.
(i) 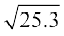 (ii)
(ii) 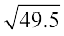 (iii)
(iii) 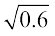
(iv) 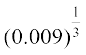 (v)
(v) 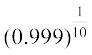 (vi)
(vi) 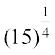
(vii) 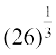 (viii)
(viii) 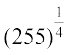 (ix)
(ix) 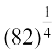
(x) 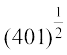 (xi)
(xi) 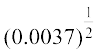 (xii)
(xii) 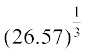
(xiii) 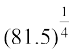 (xiv)
(xiv) 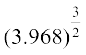 (xv)
(xv) 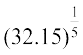
2. Find the approximate value of f(2.01), where f(x) = 4x2 + 5x + 2.
3. Find the approximate value of f(5.001), where f(x) = x3 – 7x2 + 15.
4. Find the approximate change in the volume V of a cube of side x metres caused by increasing the side by 1%.
5. Find the approximate change in the surface area of a cube of side x metres caused by decreasing the side by 1%.
6. If the radius of a sphere is measured as 7 m with an error of 0.02 m, then find the approximate error in calculating its volume.
7. If the radius of a sphere is measured as 9 m with an error of 0.03 m, then find the approximate error in calculating its surface area.
8. If f(x) = 3x2 + 15x + 5, then the approximate value of f (3.02) is
(A) 47.66 (B) 57.66 (C) 67.66 (D) 77.66
9. The approximate change in the volume of a cube of side x metres caused by increasing the side by 3% is
(A) 0.06 x3 m3 (B) 0.6 x3 m3 (C) 0.09 x3 m3 (D) 0.9 x3 m3
6.6 Maxima and Minima
In this section, we will use the concept of derivatives to calculate the maximum or minimum values of various functions. In fact, we will find the ‘turning points’ of the graph of a function and thus find points at which the graph reaches its highest (or lowest) locally. The knowledge of such points is very useful in sketching the graph of a given function. Further, we will also find the absolute maximum and absolute minimum of a function that are necessary for the solution of many applied problems.
Let us consider the following problems that arise in day to day life.
(i) The profit from a grove of orange trees is given by P(x) = ax + bx2, where a,b are constants and x is the number of orange trees per acre. How many trees per acre will maximise the profit?
(ii) A ball, thrown into the air from a building 60 metres high, travels along a path given by 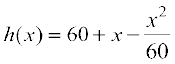 , where x is the horizontal distance from the building and h(x) is the height of the ball . What is the maximum height the ball will reach?
, where x is the horizontal distance from the building and h(x) is the height of the ball . What is the maximum height the ball will reach?
(iii) An Apache helicopter of enemy is flying along the path given by the curve
f (x) = x2 + 7. A soldier, placed at the point (1, 2), wants to shoot the helicopter when it is nearest to him. What is the nearest distance?
In each of the above problem, there is something common, i.e., we wish to find out the maximum or minimum values of the given functions. In order to tackle such problems, we first formally define maximum or minimum values of a function, points of local maxima and minima and test for determining such points.
Definition 3 Let f be a function defined on an interval I. Then
(a) f is said to have a maximum value in I, if there exists a point c in I such that 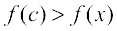 , for all x ∈ I.
, for all x ∈ I.
The number f(c) is called the maximum value of f in I and the point c is called a point of maximum value of f in I.
(b) f is said to have a minimum value in I, if there exists a point c in I such that f(c) < f(x), for all x ∈ I.
The number f(c), in this case, is called the minimum value of f in I and the point c, in this case, is called a point of minimum value of f in I.
(c) f is said to have an extreme value in I if there exists a point c in I such that
f (c) is either a maximum value or a minimum value of f in I.
The number f(c), in this case, is called an extreme value of f in I and the point c is called an extreme point.
Remark In Fig 6.9(a), (b) and (c), we have exhibited that graphs of certain particular functions help us to find maximum value and minimum value at a point. Infact, through graphs, we can even find maximum/minimum value of a function at a point at which it is not even differentiable (Example 27).
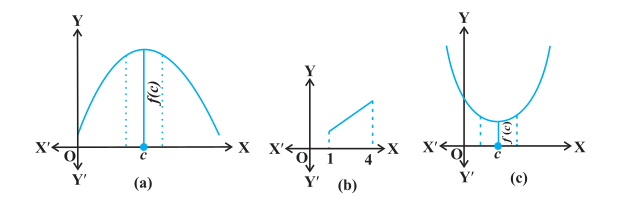
Fig 6.9
Example 26 Find the maximum and the minimum values, if any, of the function f given by
f(x) = x2, x ∈ R.
Solution From the graph of the given function (Fig 6.10), we have f(x) = 0 if x = 0. Also
f(x) ≥ 0, for all x ∈ R.
Therefore, the minimum value of f is 0 and the point of minimum value of f is x = 0. Further, it may be observed from the graph of the function that f has no maximum value and hence no point of maximum value of f in R.
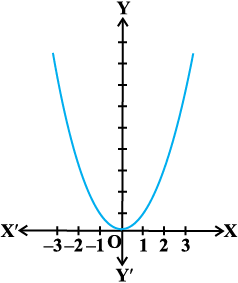
Fig 6.10
Note If we restrict the domain of f to [– 2, 1] only, then f will have maximum value(– 2)2 = 4 at x = – 2.
Example 27 Find the maximum and minimum values of f , if any, of the function given by f(x) = |x|, x ∈ R.
Solution From the graph of the given function (Fig 6.11) , note that
f(x) ≥ 0, for all x ∈ R and f(x) = 0 if x = 0.
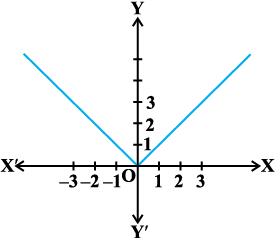
Fig 6.11
Therefore, the function f has a minimum value 0 and the point of minimum value of f is x = 0. Also, the graph clearly shows that f has no maximum value in R and hence no point of maximum value in R. 
Note
(i) If we restrict the domain of f to [– 2, 1] only, then f will have maximum value |– 2| = 2.
(ii) One may note that the function f in Example 27 is not differentiable at
x = 0.
Example 28 Find the maximum and the minimum values, if any, of the function
given by
f(x) = x, x ∈ (0, 1).
Solution The given function is an increasing (strictly) function in the given interval
(0, 1). From the graph (Fig 6.12) of the function f , it seems that, it should have the minimum value at a point closest to 0 on its right and the maximum value at a point closest to 1 on its left. Are such points available? Of course, not. It is not possible to locate such points. Infact, if a point x0 is closest to 0, then we find 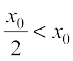 for all
for all 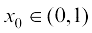 . Also, if x1 is closest to 1, then
. Also, if x1 is closest to 1, then 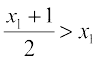 for all
for all  .
.
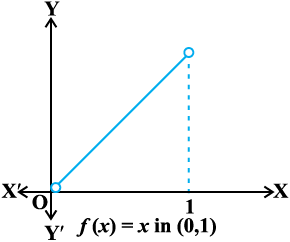
Fig 6.12
Therefore, the given function has neither the maximum value nor the minimum value in the interval (0,1).
Remark The reader may observe that in Example 28, if we include the points 0 and 1 in the domain of f , i.e., if we extend the domain of f to [0,1], then the function f has minimum value 0 at x = 0 and maximum value 1 at x = 1. Infact, we have the following results (The proof of these results are beyond the scope of the present text)
Every monotonic function assumes its maximum/minimum value at the end points of the domain of definition of the function.
A more general result is
Every continuous function on a closed interval has a maximum and a minimum value.
Note By a monotonic function f in an interval I, we mean that f is either increasing in I or decreasing in I.
Maximum and minimum values of a function defined on a closed interval will be discussed later in this section.
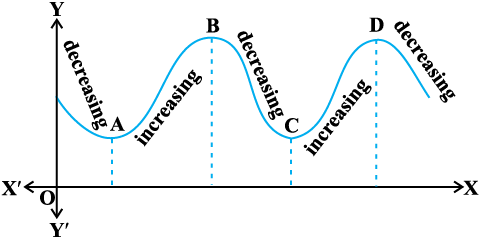
Fig 6.13
Let us now examine the graph of a function as shown in Fig 6.13. Observe that at points A, B, C and D on the graph, the function changes its nature from decreasing to increasing or vice-versa. These points may be called turning points of the given function. Further, observe that at turning points, the graph has either a little hill or a little valley. Roughly speaking, the function has minimum value in some neighbourhood (interval) of each of the points A and C which are at the bottom of their respective valleys. Similarly, the function has maximum value in some neighbourhood of points B and D which are at the top of their respective hills. For this reason, the points A and C may be regarded as points of local minimum value (or relative minimum value) and points B and D may be regarded as points of local maximum value (or relative maximum value) for the function. The local maximum value and local minimum value of the function are referred to as local maxima and local minima, respectively, of the function.
We now formally give the following definition
Definition 4 Let f be a real valued function and let c be an interior point in the domain of f. Then
(a) c is called a point of local maxima if there is an h > 0 such that
f(c) ≥ f(x), for all x in (c – h, c + h), x ≠ c
The value f(c) is called the local maximum value of f.
(b) c is called a point of local minima if there is an h > 0 such that
f(c) ≤ f(x), for all x in (c – h, c + h)
The value f(c) is called the local minimum value of f .
Geometrically, the above definition states that if x = c is a point of local maxima of f, then the graph of f around c will be as shown in Fig 6.14(a). Note that the function f is increasing (i.e., f′(x) > 0) in the interval (c – h, c) and decreasing (i.e., f′(x) < 0) in the interval (c, c + h).
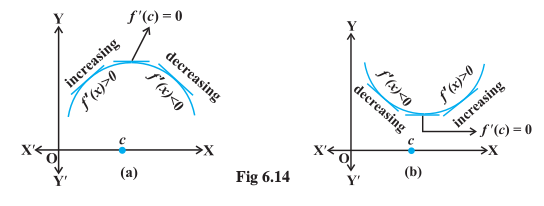
Fig 6.14
This suggests that f′(c) must be zero.
Similarly, if c is a point of local minima of f , then the graph of f around c will be as shown in Fig 6.14(b). Here f is decreasing (i.e., f′(x) < 0) in the interval (c – h, c) and increasing (i.e., f′(x) > 0) in the interval (c, c + h). This again suggest that f′(c) must be zero.
The above discussion lead us to the following theorem (without proof).
Theorem 2 Let f be a function defined on an open interval I. Suppose c ∈ I be any point. If f has a local maxima or a local minima at x = c, then either f′(c) = 0 or f is not differentiable at c.
Remark The converse of above theorem need not be true, that is, a point at which the derivative vanishes need not be a point of local maxima or local minima. For example, if f(x) = x3, then f′(x) = 3x2 and so f′(0) = 0. But 0 is neither a point of local maxima nor a point of local minima (Fig 6.15).
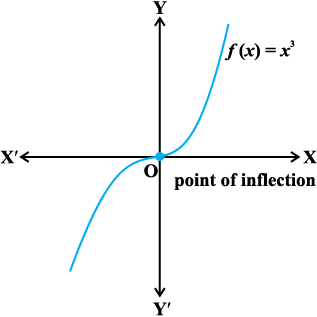
Fig 6.15
Note A point c in the domain of a function f at which either f′(c) = 0 or f is not differentiable is called a critical point of f. Note that if f is continuous at c and f′(c) = 0, then there exists an h > 0 such that f is differentiable in the interval
(c – h, c + h).
We shall now give a working rule for finding points of local maxima or points of local minima using only the first order derivatives.
Theorem 3 (First Derivative Test) Let f be a function defined on an open interval I. Let f be continuous at a critical point c in I. Then
(i) If f′(x) changes sign from positive to negative as x increases through c, i.e., if f′(x) > 0 at every point sufficiently close to and to the left of c, and f′(x) < 0 at every point sufficiently close to and to the right of c, then c is a point of local maxima.
(ii) If f′(x) changes sign from negative to positive as x increases through c, i.e., if f′(x) < 0 at every point sufficiently close to and to the left of c, and f′(x) > 0 at every point sufficiently close to and to the right of c, then c is a point of local minima.
(iii) If f′(x) does not change sign as x increases through c, then c is neither a point of local maxima nor a point of local minima. Infact, such a point is called point of inflection (Fig 6.15).
Note If c is a point of local maxima of f , then f(c) is a local maximum value of f. Similarly, if c is a point of local minima of f , then f(c) is a local minimum value of f.
Figures 6.15 and 6.16, geometrically explain Theorem 3.
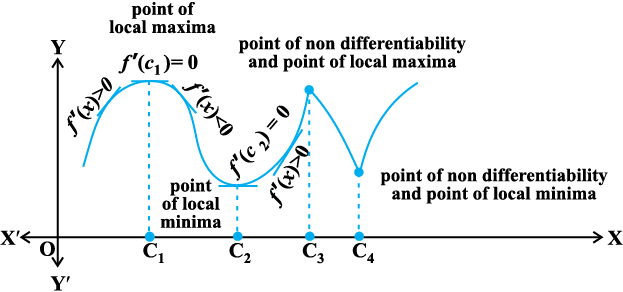
Fig 6.16
Example 29 Find all points of local maxima and local minima of the function f
given by
f(x) = x3 – 3x + 3.
Solution We have
f(x) = x3 – 3x + 3
or f′(x) = 3x2 – 3 = 3(x – 1) (x + 1)
or f′(x) = 0 at x = 1 and x = – 1
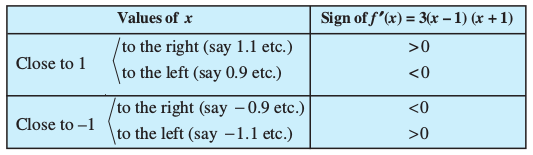
Thus, x = ± 1 are the only critical points which could possibly be the points of local maxima and/or local minima of f . Let us first examine the point x = 1.
Note that for values close to 1 and to the right of 1, f′(x) > 0 and for values close to 1 and to the left of 1, f′(x) < 0. Therefore, by first derivative test, x = 1 is a point
of local minima and local minimum value is f(1) = 1. In the case of x = –1, note that f′(x) > 0, for values close to and to the left of –1 and f′(x) < 0, for values close to and to the right of – 1. Therefore, by first derivative test, x = – 1 is a point of local maxima and local maximum value is f(–1) = 5.
Example 30 Find all the points of local maxima and local minima of the function f given by
f(x) = 2x3 – 6x2 + 6x +5.
Solution We have
f(x) = 2x3 – 6x2 + 6x + 5
or f′(x) = 6x2 – 12x + 6 = 6(x – 1)2
or f′(x) = 0 at x = 1
Thus, x = 1 is the only critical point of f . We shall now examine this point for local maxima and/or local minima of f. Observe that f′(x) ≥ 0, for all x ∈ R and in particular f′(x) > 0, for values close to 1 and to the left and to the right of 1. Therefore, by first derivative test, the point x = 1 is neither a point of local maxima nor a point of local minima. Hence x = 1 is a point of inflexion.
Remark One may note that since f′(x), in Example 30, never changes its sign on R, graph of f has no turning points and hence no point of local maxima or local minima.
We shall now give another test to examine local maxima and local minima of a given function. This test is often easier to apply than the first derivative test.
Theorem 4 (Second Derivative Test) Let f be a function defined on an interval I and c ∈ I. Let f be twice differentiable at c. Then
(i) x = c is a point of local maxima if f′(c) = 0 and f″(c) < 0
The value f (c) is local maximum value of f .
(ii) x = c is a point of local minima if 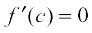 and f″(c) > 0
and f″(c) > 0
In this case, f (c) is local minimum value of f .
(iii) The test fails if f′(c) = 0 and f″(c) = 0.
In this case, we go back to the first derivative test and find whether c is a point of local maxima, local minima or a point of inflexion.
Note As f is twice differentiable at c, we mean second order derivative of f exists at c.
Example 31 Find local minimum value of the function f given by f (x) = 3 + |x|, x ∈ R.

Fig 6.1
Solution Note that the given function is not differentiable at x = 0. So, second derivative test fails. Let us try first derivative test. Note that 0 is a critical point of f . Now to the left of 0, f(x) = 3 – x and so f′(x) = – 1 < 0. Also to the right of 0, f(x) = 3 + x and so f′(x) = 1 > 0. Therefore, by first derivative test, x = 0 is a point of local minima of f and local minimum value of f is f (0) = 3.
Example 32 Find local maximum and local minimum values of the function f given by f (x) = 3x4 + 4x3 – 12x2 + 12
Solution We have
f (x) = 3x4 + 4x3 – 12x2 + 12
or f′(x) = 12x3 + 12x2 – 24x = 12x (x – 1) (x + 2)
or f′(x) = 0 at x = 0, x = 1 and x = – 2.
Now f″(x) = 36x2 + 24x – 24 = 12(3x2 + 2x – 2)
or 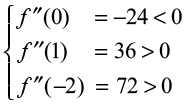
Therefore, by second derivative test, x = 0 is a point of local maxima and local maximum value of f at x = 0 is f (0) = 12 while x = 1 and x = – 2 are the points of local minima and local minimum values of f at x = – 1 and – 2 are f (1) = 7 and f (–2) = –20, respectively.
Example 33 Find all the points of local maxima and local minima of the function f given by
f(x) = 2x3 – 6x2 + 6x +5.
Solution We have
f(x) = 2x3 – 6x2 + 6x +5
or 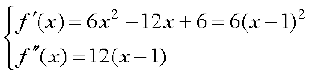
Now f′(x) = 0 gives x =1. Also f″(1) = 0. Therefore, the second derivative test fails in this case. So, we shall go back to the first derivative test.
We have already seen (Example 30) that, using first derivative test, x =1 is neither a point of local maxima nor a point of local minima and so it is a point of inflexion.
Example 34 Find two positive numbers whose sum is 15 and the sum of whose squares is minimum.
Solution Let one of the numbers be x. Then the other number is (15 – x). Let S(x) denote the sum of the squares of these numbers. Then
S(x) = x2 + (15 – x)2 = 2x2 – 30x + 225
or 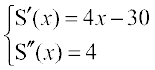
Now S′(x) = 0 gives 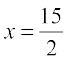 . Also
. Also 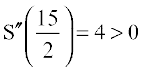 . Therefore, by second derivative test,
. Therefore, by second derivative test, 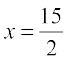 is the point of local minima of S. Hence the sum of squares of numbers is minimum when the numbers are
is the point of local minima of S. Hence the sum of squares of numbers is minimum when the numbers are 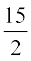 and
and 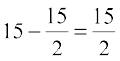 .
.
Remark Proceeding as in Example 34 one may prove that the two positive numbers, whose sum is k and the sum of whose squares is minimum, are 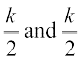 .
.
Example 35 Find the shortest distance of the point (0, c) from the parabola y = x2, where 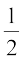 ≤ c ≤ 5.
≤ c ≤ 5.
Solution Let (h, k) be any point on the parabola y = x2. Let D be the required distance between (h, k) and (0, c). Then
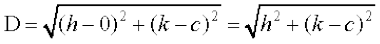 ... (1)
... (1)
Since (h, k) lies on the parabola y = x2, we have k = h2. So (1) gives
D ≡ D(k) = 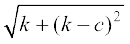
or D′(k) = 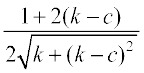
Now D′(k) = 0 gives 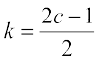
Observe that when 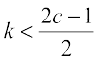 , then
, then 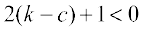 , i.e.,
, i.e., 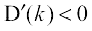 . Also when
. Also when 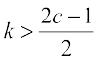 , then
, then 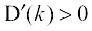 . So, by first derivative test, D(k) is minimum at
. So, by first derivative test, D(k) is minimum at 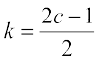 . Hence, the required shortest distance is given by
. Hence, the required shortest distance is given by
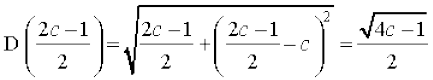
Note The reader may note that in Example 35, we have used first derivative test instead of the second derivative test as the former is easy and short.
Example 36 Let AP and BQ be two vertical poles at points A and B, respectively. If AP = 16 m, BQ = 22 m and AB = 20 m, then find the distance of a point R on AB from the point A such that RP2 + RQ2 is minimum.
Solution Let R be a point on AB such that AR = x m. Then RB = (20 – x) m (as AB = 20 m). From Fig 6.18, we have
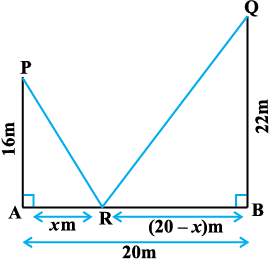
Fig 6.18
RP2 = AR2 + AP2
and RQ2 = RB2 + BQ2
Therefore RP2 + RQ2 = AR2 + AP2 + RB2 + BQ2
= x2 + (16)2 + (20 – x)2 + (22)2
= 2x2 – 40x + 1140
Let S ≡ S(x) = RP2 + RQ2 = 2x2 – 40x + 1140.
Therefore S′(x) = 4x – 40.
Now S′(x) = 0 gives x = 10. Also S″(x) = 4 > 0, for all x and so S″(10) > 0. Therefore, by second derivative test, x = 10 is the point of local minima of S. Thus, the distance of R from A on AB is AR = x =10 m.
Example 37 If length of three sides of a trapezium other than base are equal to 10cm, then find the area of the trapezium when it is maximum.
Solution The required trapezium is as given in Fig 6.19. Draw perpendiculars DP and CQ on AB. Let AP = x cm. Note that ∆APD ~ ∆BQC. Therefore, QB = x cm. Also, by Pythagoras theorem, DP = QC = 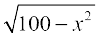 . Let A be the area of the trapezium. Then
. Let A be the area of the trapezium. Then
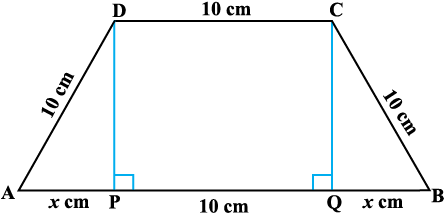
Fig 6.19
A ≡ A(x) =  (sum of parallel sides) (height)
(sum of parallel sides) (height)
= 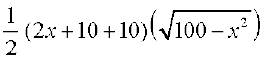
= 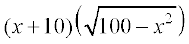
or A′(x) = 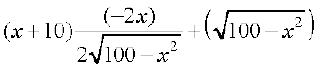
= 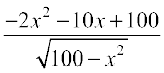
Now A′(x) = 0 gives 2x2 + 10x – 100 = 0, i.e., x = 5 and x = –10.
Since x represents distance, it can not be negative.
So, x = 5. Now
A″(x) = 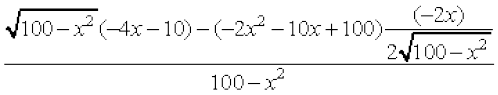
= 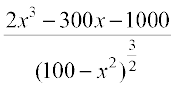 (on simplification)
(on simplification)
or A″(5) = 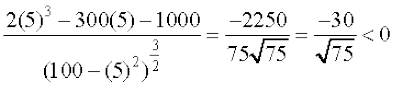
Thus, area of trapezium is maximum at x = 5 and the area is given by
A(5) = 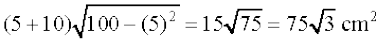
Example 38 Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.
Solution Let OC = r be the radius of the cone and OA = h be its height. Let a cylinder with radius OE = x inscribed in the given cone (Fig 6.20). The height QE of the cylinder is given by
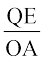 =
= 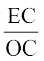 (since ∆QEC ~ ∆AOC)
(since ∆QEC ~ ∆AOC)
or 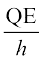 =
= 
or QE = 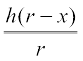
Let S be the curved surface area of the given
cylinder. Then
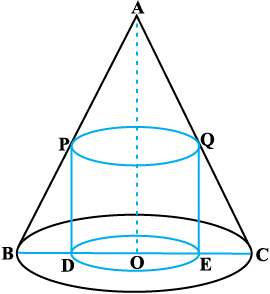
Fig 6.20
S ≡ S(x) = 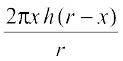 =
= 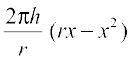
or 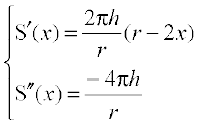
Now S′(x) = 0 gives 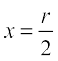 . Since S″(x) < 0 for all x,
. Since S″(x) < 0 for all x, 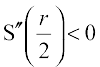 . So
. So 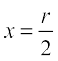 is a point of maxima of S. Hence, the radius of the cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.
is a point of maxima of S. Hence, the radius of the cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.
6.6.1 Maximum and Minimum Values of a Function in a Closed Interval
Let us consider a function f given by
f(x) = x + 2, x ∈ (0, 1)
Observe that the function is continuous on (0, 1) and neither has a maximum value nor has a minimum value. Further, we may note that the function even has neither a local maximum value nor a local minimum value.
However, if we extend the domain of f to the closed interval [0, 1], then f still may not have a local maximum (minimum) values but it certainly does have maximum value 3 = f(1) and minimum value 2 = f(0). The maximum value 3 of f at x = 1 is called absolute maximum value (global maximum or greatest value) of f on the interval
[0, 1]. Similarly, the minimum value 2 of f at x = 0 is called the absolute minimum value (global minimum or least value) of f on [0, 1].
Consider the graph given in Fig 6.21 of a continuous function defined on a closed interval [a, d]. Observe that the function f has a local minima at x = b and local minimum value is f(b). The function also has a local maxima at x = c and local maximum value is f (c).
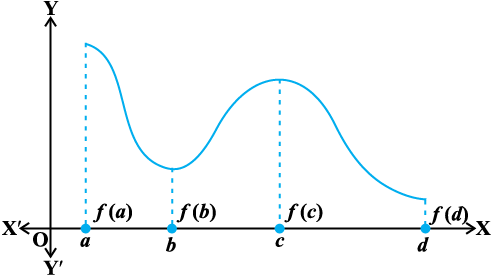
Fig 6.21
Also from the graph, it is evident that f has absolute maximum value f(a) and absolute minimum value f(d). Further note that the absolute maximum (minimum) value of f is different from local maximum (minimum) value of f.
We will now state two results (without proof) regarding absolute maximum and absolute minimum values of a function on a closed interval I.
Theorem 5 Let f be a continuous function on an interval I = [a, b]. Then f has the absolute maximum value and f attains it at least once in I. Also, f has the absolute minimum value and attains it at least once in I.
Theorem 6 Let f be a differentiable function on a closed interval I and let c be any interior point of I. Then
(i) f′(c) = 0 if f attains its absolute maximum value at c.
(ii) f′(c) = 0 if f attains its absolute minimum value at c.
In view of the above results, we have the following working rule for finding absolute maximum and/or absolute minimum values of a function in a given closed interval
[a, b].
Working Rule
Step 1: Find all critical points of f in the interval, i.e., find points x where either 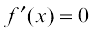 or f is not differentiable.
or f is not differentiable.
Step 2: Take the end points of the interval.
Step 3: At all these points (listed in Step 1 and 2), calculate the values of f .
Step 4: Identify the maximum and minimum values of f out of the values calculated in Step 3. This maximum value will be the absolute maximum (greatest) value of f and the minimum value will be the absolute minimum (least) value of f .
Example 39 Find the absolute maximum and minimum values of a function f given by f(x) = 2x3 – 15x2 + 36x +1 on the interval [1, 5].
Solution We have
f(x) = 2x3 – 15x2 + 36x + 1
or f′(x) = 6x2 – 30x + 36 = 6(x – 3) (x – 2)
Note that f′(x) = 0 gives x = 2 and x = 3.
We shall now evaluate the value of f at these points and at the end points of the interval [1, 5], i.e., at x = 1, x = 2, x = 3 and at x = 5. So
f(1) = 2(13) – 15(12) + 36(1) + 1 = 24
f(2) = 2(23) – 15(22) + 36(2) + 1 = 29
f(3) = 2(33) – 15(32) + 36(3) + 1 = 28
f(5) = 2(53) – 15(52) + 36(5) + 1 = 56
Thus, we conclude that absolute maximum value of f on [1, 5] is 56, occurring at
x =5, and absolute minimum value of f on [1, 5] is 24 which occurs at x = 1.
Example 40 Find absolute maximum and minimum values of a function f given by
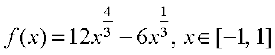
Solution We have
f(x) = 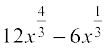
or f′(x) = 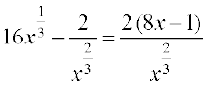
Thus, f′(x) = 0 gives 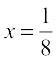 . Further note that f′(x) is not defined at x = 0. So the critical points are x = 0 and
. Further note that f′(x) is not defined at x = 0. So the critical points are x = 0 and 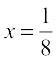 . Now evaluating the value of f at critical points
. Now evaluating the value of f at critical points
x = 0, 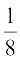 and at end points of the interval x = –1 and x = 1, we have
and at end points of the interval x = –1 and x = 1, we have
f(–1) = 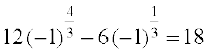
f(0) = 12(0) – 6(0) = 0
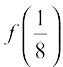 =
= 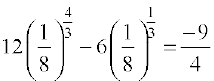
f(1) = 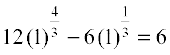
Hence, we conclude that absolute maximum value of f is 18 that occurs at x = –1 and absolute minimum value of f is 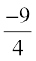 that occurs at
that occurs at 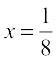 .
.
Example 41 An Apache helicopter of enemy is flying along the curve given by
y = x2 + 7. A soldier, placed at (3, 7), wants to shoot down the helicopter when it is nearest to him. Find the nearest distance.
Solution For each value of x, the helicopter’s position is at point (x, x2 + 7).
Therefore, the distance between the helicopter and the soldier placed at (3,7) is
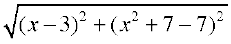 , i.e.,
, i.e., 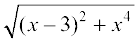 .
.
Let f(x) = (x – 3)2 + x4
or f′(x) = 2(x – 3) + 4x3 = 2(x – 1) (2x2 + 2x + 3)
Thus, f′(x) = 0 gives x = 1 or 2x2 + 2x + 3 = 0 for which there are no real roots. Also, there are no end points of the interval to be added to the set for which f′ is zero, i.e., there is only one point, namely, x = 1. The value of f at this point is given by
f (1) = (1 – 3)2 + (1)4 = 5. Thus, the distance between the solider and the helicopter is 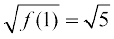 .
.
Note that 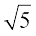 is either a maximum value or a minimum value. Since
is either a maximum value or a minimum value. Since
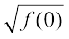 =
= 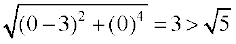 ,
,
it follows that 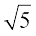 is the minimum value of
is the minimum value of 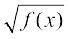 . Hence,
. Hence, 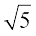 is the minimum distance between the soldier and the helicopter.
is the minimum distance between the soldier and the helicopter.
Exercise 6.5
1. Find the maximum and minimum values, if any, of the following functions
given by
(i) f(x) = (2x – 1)2 + 3 (ii) f(x) = 9x2 + 12x + 2
(iii) f(x) = – (x – 1)2 + 10 (iv) g(x) = x3 + 1
2. Find the maximum and minimum values, if any, of the following functions
given by
(i) f(x) = |x + 2| – 1 (ii) g(x) = – |x + 1| + 3
(iii) h(x) = sin(2x) + 5 (iv) f(x) = |sin 4x + 3|
(v) h(x) = x + 1, x ∈ (– 1, 1)
3. Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:
(i) f(x) = x2 (ii) g(x) = x3 – 3x
(iii) h(x) = sin x + cos x,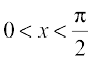
(iv) f(x) = sin x – cos x, 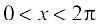
(v) f(x) = x3 – 6x2 + 9x + 15 (vi) 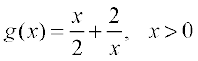
(vii) 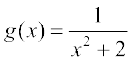 (viii)
(viii) 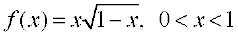
4. Prove that the following functions do not have maxima or minima:
(i) f(x) = ex (ii) g(x) = log x
(iii) h(x) = x3 + x2 + x +1
5. Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:
(i) f(x) = x3, x ∈ [– 2, 2] (ii) f(x) = sin x + cos x , x ∈ [0, π]
(iii) f(x) =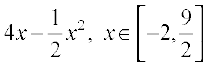 (iv)
(iv) 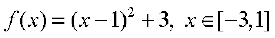
6. Find the maximum profit that a company can make, if the profit function is
given by
p(x) = 41 – 72x – 18x2
7. Find both the maximum value and the minimum value of
3x4 – 8x3 + 12x2 – 48x + 25 on the interval [0, 3].
8. At what points in the interval [0, 2π], does the function sin 2x attain its maximum value?
9. What is the maximum value of the function sin x + cos x?
10. Find the maximum value of 2x3 – 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [–3, –1].
11. It is given that at x = 1, the function x4 – 62x2 + ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.
12. Find the maximum and minimum values of x + sin 2x on [0, 2π].
13. Find two numbers whose sum is 24 and whose product is as large as possible.
14. Find two positive numbers x and y such that x + y = 60 and xy3 is maximum.
15. Find two positive numbers x and y such that their sum is 35 and the product x2 y5 is a maximum.
16. Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
17. A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible.
18. A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum ?
19. Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
20. Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.
21. Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?
22. A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
23. Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is 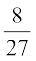 of the volume of the sphere.
of the volume of the sphere.
24. Show that the right circular cone of least curved surface and given volume has an altitude equal to 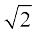 time the radius of the base.
time the radius of the base.
25. Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is 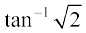 .
.
26. Show that semi-vertical angle of right circular cone of given surface area and maximum volume is  .
.
Choose the correct answer in Questions 27 and 29.
27. The point on the curve x2 = 2y which is nearest to the point (0, 5) is
(A) 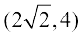 (B)
(B) 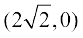 (C) (0, 0) (D) (2, 2)
(C) (0, 0) (D) (2, 2)
28. For all real values of x, the minimum value of 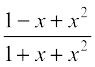 is
is
(A) 0 (B) 1 (C) 3 (D) 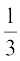
29. The maximum value of 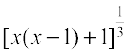 ,
, 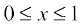 is
is
(A)  (B)
(B) 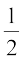 (C) 1 (D) 0
(C) 1 (D) 0
Miscellaneous Examples
Example 42 A car starts from a point P at time t = 0 seconds and stops at point Q. The distance x, in metres, covered by it, in t seconds is given by

Find the time taken by it to reach Q and also find distance between P and Q.
Solution Let v be the velocity of the car at t seconds.
Now x = 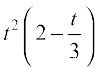
Therefore v = 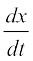 = 4t – t2 = t(4 – t)
= 4t – t2 = t(4 – t)
Thus, v = 0 gives t = 0 and/or t = 4.
Now v = 0 at P as well as at Q and at P, t = 0. So, at Q, t = 4. Thus, the car will reach the point Q after 4 seconds. Also the distance travelled in 4 seconds is given by x]t = 4 = 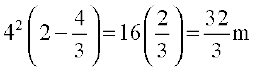
Example 43 A water tank has the shape of an inverted right circular cone with its axis vertical and vertex lowermost. Its semi-vertical angle is tan–1(0.5). Water is poured into it at a constant rate of 5 cubic metre per hour. Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 4 m.
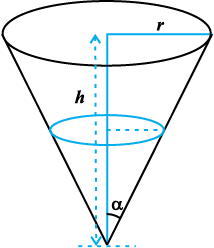
Fig 6.22
Solution Let r, h and α be as in Fig 6.22. Then 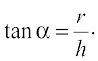
So α = 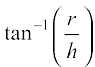 .
.
But α = tan–1(0.5) (given)
or  = 0.5
= 0.5
or r = 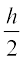
Let V be the volume of the cone. Then
V = 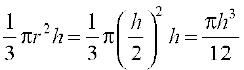
Therefore 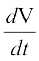 =
= 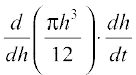 (by Chain Rule)
(by Chain Rule)
= 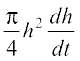
Now rate of change of volume, i.e., 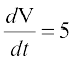 m3/h and h = 4 m.
m3/h and h = 4 m.
Therefore 5 = 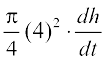
or 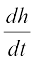 =
= 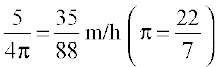
Thus, the rate of change of water level is 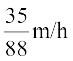 .
.
Example 44 A man of height 2 metres walks at a uniform speed of 5 km/h away from a lamp post which is 6 metres high. Find the rate at which the length of his shadow increases.
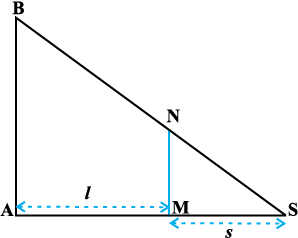
Fig 6.23
Solution In Fig 6.23, Let AB be the lamp-post, the lamp being at the position B and let MN be the man at a particular time t and let AM = l metres. Then, MS is the shadow of the man. Let MS = s metres.
Note that ∆MSN ~ ∆ASB
or 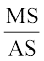 =
= 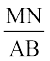
or AS = 3s (as MN = 2 and AB = 6 (given))
Thus AM = 3s – s = 2s. But AM = l
So l = 2s
Therefore 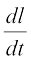 =
= 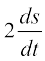
Since 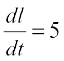 km/h. Hence, the length of the shadow increases at the rate
km/h. Hence, the length of the shadow increases at the rate 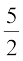 km/h.
km/h.
Example 45 Find the equation of the normal to the curve x2 = 4y which passes through the point (1, 2).
Solution Differentiating x2 = 4y with respect to x, we get
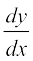 =
= 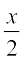
Let (h, k) be the coordinates of the point of contact of the normal to the curve
x2 = 4y. Now, slope of the tangent at (h, k) is given by
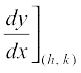 =
= 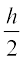
Hence, slope of the normal at (h, k) = 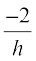
Therefore, the equation of normal at (h, k) is
y – k = 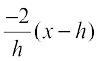 ... (1)
... (1)
Since it passes through the point (1, 2), we have
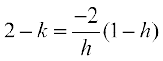 or
or 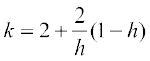 ... (2)
... (2)
Since (h, k) lies on the curve x2 = 4y, we have
h2 = 4k ... (3)
From (2) and (3), we have h = 2 and k = 1. Substituting the values of h and k in (1), we get the required equation of normal as
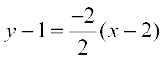 or x + y = 3
or x + y = 3
Example 46 Find the equation of tangents to the curve
y = cos(x + y), – 2π ≤ x ≤ 2π
that are parallel to the line x + 2y = 0.
Solution Differentiating y = cos(x + y) with respect to x, we have
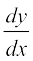 =
= 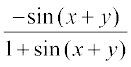
or slope of tangent at (x, y) = 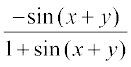
Since the tangents to the given curve are parallel to the line x + 2y = 0, whose slope is 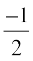 , we have
, we have
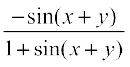 =
= 
or sin(x + y) = 1
or x + y = nπ + (– 1)n 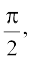 n ∈ Z
n ∈ Z
Then y = cos(x + y) = 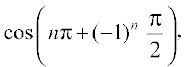 n ∈ Z
n ∈ Z
= 0, for all n ∈ Z
Also, since 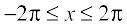 , we get
, we get 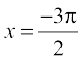 and
and 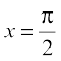 . Thus, tangents to the given curve are parallel to the line x + 2y = 0 only at points
. Thus, tangents to the given curve are parallel to the line x + 2y = 0 only at points 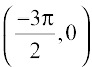 and
and  . Therefore, the required equation of tangents are
. Therefore, the required equation of tangents are
y – 0 = 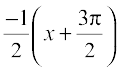 or
or 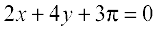
and y – 0 =  or
or 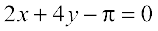
Example 47 Find intervals in which the function given by
f(x) = 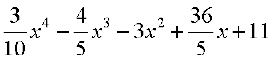
is (a) increasing (b) decreasing.
Solution We have
f(x) = 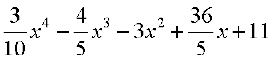
Therefore f′(x) = 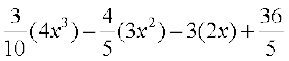
= 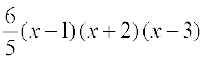 (on simplification)
(on simplification)
Now f′(x) = 0 gives x = 1, x = – 2, or x = 3. The points x = 1, – 2, and 3 divide the real line into four disjoint intervals namely, (– ∞, – 2), (– 2, 1), (1, 3) and (3, ∞) (Fig 6.24).
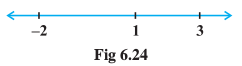
Consider the interval (– ∞, – 2), i.e., when – ∞ < x < – 2.
In this case, we have x – 1 < 0, x + 2 < 0 and x – 3 < 0.
(In particular, observe that for x = –3, f′(x) = (x – 1) (x + 2) (x – 3) = (– 4) (– 1) (– 6) < 0)
Therefore, f′(x) < 0 when – ∞ < x < – 2.
Thus, the function f is decreasing in (– ∞, – 2).
Consider the interval (– 2, 1), i.e., when – 2 < x < 1.
In this case, we have x – 1 < 0, x + 2 > 0 and x – 3 < 0
(In particular, observe that for x = 0, f′(x) = (x – 1) (x + 2) (x – 3) = (–1) (2) (–3) = 6 > 0)
So f′(x) > 0 when – 2 < x < 1.
Thus, f is increasing in (– 2, 1).
Now consider the interval (1, 3), i.e., when 1 < x < 3. In this case, we have
x – 1 > 0, x + 2 > 0 and x – 3 < 0.
So, f′(x) < 0 when 1 < x < 3.
Thus, f is decreasing in (1, 3).
Finally, consider the interval (3, ∞), i.e., when x > 3. In this case, we have x – 1 > 0, x + 2 > 0 and x – 3 > 0. So f′(x) > 0 when x > 3.
Thus, f is increasing in the interval (3, ∞).
Example 48 Show that the function f given by
f(x) = tan–1(sin x + cos x), x > 0
is always an increasing function in  .
.
Solution We have
f(x) = tan–1(sin x + cos x), x > 0
Therefore f′(x) = 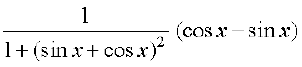
= 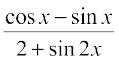 (on simplification)
(on simplification)
Note that 2 + sin 2x > 0 for all x in 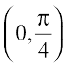 .
.
Therefore f′(x) > 0 if cos x – sin x > 0
or f′(x) > 0 if cos x > sin x or cot x > 1
Now cot x > 1 if tan x < 1, i.e., if 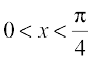
Thus f′(x) > 0 in 
Hence f is increasing function in 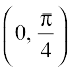 .
.
Example 49 A circular disc of radius 3 cm is being heated. Due to expansion, its radius increases at the rate of 0.05 cm/s. Find the rate at which its area is increasing when radius is 3.2 cm.
Solution Let r be the radius of the given disc and A be its area. Then
A = πr2
or 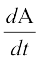 =
= 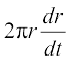 (by Chain Rule)
(by Chain Rule)
Now approximate rate of increase of radius = dr = 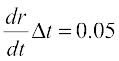 cm/s.
cm/s.
Therefore, the approximate rate of increase in area is given by
dA = 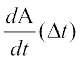 =
= 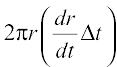
= 2π(3.2) (0.05) = 0.320π cm2/s (r = 3.2 cm)
Example 50 An open topped box is to be constructed by removing equal squares from each corner of a 3 metre by 8 metre rectangular sheet of aluminium and folding up the sides. Find the volume of the largest such box.
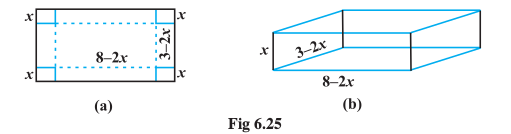
Solution Let x metre be the length of a side of the removed squares. Then, the height of the box is x, length is 8 – 2x and breadth is 3 – 2x (Fig 6.25). If V(x) is the volume of the box, then
Fig 6.25
V(x) = x(3 – 2x) (8 – 2x)
= 4x3 – 22x2 + 24x
Therefore 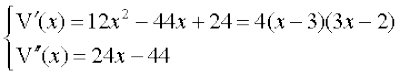
Now V′(x) = 0 gives 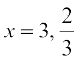 . But x ≠ 3 (Why?)
. But x ≠ 3 (Why?)
Thus, we have 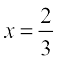 . Now
. Now 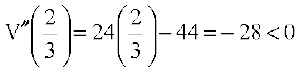 .
.
Therefore, 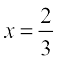 is the point of maxima, i.e., if we remove a square of side
is the point of maxima, i.e., if we remove a square of side  metre from each corner of the sheet and make a box from the remaining sheet, then the volume of the box such obtained will be the largest and it is given by
metre from each corner of the sheet and make a box from the remaining sheet, then the volume of the box such obtained will be the largest and it is given by
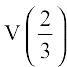 =
= 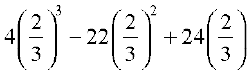
= 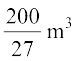
Example 51 Manufacturer can sell x items at a price of rupees 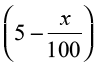 each. The cost price of x items is Rs
each. The cost price of x items is Rs 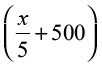 . Find the number of items he should sell to earn maximum profit.
. Find the number of items he should sell to earn maximum profit.
Solution Let S(x) be the selling price of x items and let C(x) be the cost price of x items. Then, we have
S(x) = 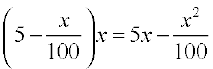
and C(x) = 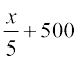
Thus, the profit function P(x) is given by
P(x) = 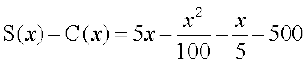
i.e. P(x) = 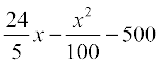
or P′(x) = 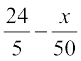
Now P′(x) = 0 gives x = 240. Also 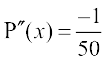 . So
. So 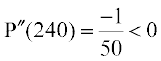
Thus, x = 240 is a point of maxima. Hence, the manufacturer can earn maximum profit, if he sells 240 items.
Miscellaneous Exercise on Chapter 6
1. Using differentials, find the approximate value of each of the following:
(a) 
(b) 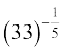
2. Show that the function given by 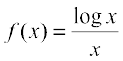 has maximum at x = e.
has maximum at x = e.
3. The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base ?
4. Find the equation of the normal to curve x2 = 4y which passes through the point (1, 2).
5. Show that the normal at any point  to the curve x = a cosθ + a θ sinθ, y = a sinθ – aθ cosθ is at a constant distance from the origin.
to the curve x = a cosθ + a θ sinθ, y = a sinθ – aθ cosθ is at a constant distance from the origin.
6. Find the intervals in which the function f given by 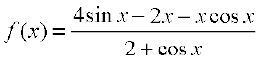 is (i) increasing (ii) decreasing.
is (i) increasing (ii) decreasing.
7. Find the intervals in which the function f given by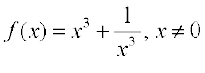 is
is
(i) increasing (ii) decreasing.
8. Find the maximum area of an isosceles triangle inscribed in the ellipse 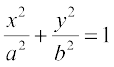 with its vertex at one end of the major axis.
with its vertex at one end of the major axis.
9. A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If building of tank costs
Rs 70 per sq metres for the base and Rs 45 per square metre for sides. What is the cost of least expensive tank?
10. The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
11. A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.
12. A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle.
Show that the minimum length of the hypotenuse is 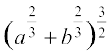 .
.
13. Find the points at which the function f given by f (x) = (x – 2)4 (x + 1)3 has
(i) local maxima (ii) local minima
(iii) point of inflexion
14. Find the absolute maximum and minimum values of the function f given by
f(x) = cos2 x + sin x, x ∈ [0, π]
15. Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 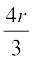 .
.
16. Let f be a function defined on [a, b] such that f′(x) > 0, for all x ∈ (a, b). Then prove that f is an increasing function on (a, b).
17. Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 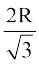 . Also find the maximum volume.
. Also find the maximum volume.
18. Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle α is one-third that of the cone and the greatest volume of cylinder is 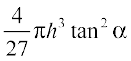 .
.
Choose the correct answer in the questions from 19 to 24.
19. A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of
(A) 1 m/h (B) 0.1 m/h
(C) 1.1 m/h (D) 0.5 m/h
20. The slope of the tangent to the curve x = t2 + 3t – 8, y = 2t2 – 2t – 5 at the point (2,– 1) is
(A) 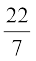 (B)
(B) 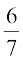 (C)
(C) 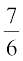 (D)
(D) 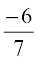
21. The line y = mx + 1 is a tangent to the curve y2 = 4x if the value of m is
(A) 1 (B) 2 (C) 3 (D) 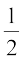
22. The normal at the point (1,1) on the curve 2y + x2 = 3 is
(A) x + y = 0 (B) x – y = 0
(C) x + y +1 = 0 (D) x – y = 1
23. The normal to the curve x2 = 4y passing (1,2) is
(A) x + y = 3 (B) x – y = 3
(C) x + y = 1 (D) x – y = 1
24. The points on the curve 9y2 = x3, where the normal to the curve makes equal intercepts with the axes are
(A) 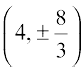 (B)
(B) 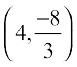
(C) 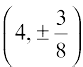 (D)
(D) 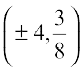
Summary
 If a quantity y varies with another quantity x, satisfying some rule
If a quantity y varies with another quantity x, satisfying some rule 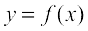 , then
, then 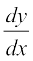 (or
(or 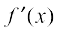 ) represents the rate of change of y with respect to x and
) represents the rate of change of y with respect to x and 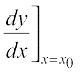 (or
(or 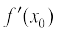 ) represents the rate of change of y with respect to x at
) represents the rate of change of y with respect to x at 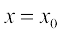 .
.
 If two variables x and y are varying with respect to another variable t, i.e., if
If two variables x and y are varying with respect to another variable t, i.e., if 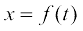 and
and 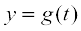 , then by Chain Rule
, then by Chain Rule
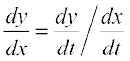 , if
, if 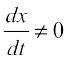 .
.
 A function f is said to be
A function f is said to be
(a) increasing on an interval (a, b) if
x1 < x2 in (a, b) ⇒ f(x1) < f(x2) for all x1, x2 ∈ (a, b).
Alternatively, if f′(x) ≥ 0 for each x in (a, b)
(b) decreasing on (a,b) if
x1 < x2 in (a, b) ⇒ f(x1) > f(x2) for all x1, x2 ∈ (a, b).
(c) constant in (a, b), if f(x) = c for all x ∈ (a, b), where c is a constant.
 The equation of the tangent at (x0, y0) to the curve y = f (x) is given by
The equation of the tangent at (x0, y0) to the curve y = f (x) is given by

 If
If 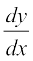 does not exist at the point
does not exist at the point 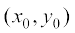 , then the tangent at this point is parallel to the y-axis and its equation is x = x0.
, then the tangent at this point is parallel to the y-axis and its equation is x = x0.
 If tangent to a curve y = f (x) at x = x0 is parallel to x-axis, then
If tangent to a curve y = f (x) at x = x0 is parallel to x-axis, then 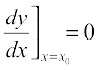 .
.
 Equation of the normal to the curve y = f (x) at a point
Equation of the normal to the curve y = f (x) at a point 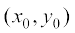 is given by
is given by

 If
If 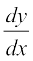 at the point
at the point 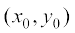 is zero, then equation of the normal is x = x0.
is zero, then equation of the normal is x = x0.
 If
If 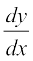 at the point
at the point 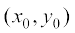 does not exist, then the normal is parallel to x-axis and its equation is y = y0.
does not exist, then the normal is parallel to x-axis and its equation is y = y0.
 Let y = f(x), ∆x be a small increment in x and ∆y be the increment in y corresponding to the increment in x, i.e., ∆y = f(x + ∆x) – f(x). Then dy given by
Let y = f(x), ∆x be a small increment in x and ∆y be the increment in y corresponding to the increment in x, i.e., ∆y = f(x + ∆x) – f(x). Then dy given by
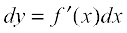 or
or  .
.
is a good approximation of ∆y when  is relatively small and we denote it by dy ≈ ∆y.
is relatively small and we denote it by dy ≈ ∆y.
 A point c in the domain of a function f at which either f′(c) = 0 or f is not differentiable is called a critical point of f.
A point c in the domain of a function f at which either f′(c) = 0 or f is not differentiable is called a critical point of f.
 First Derivative Test Let f be a function defined on an open interval I. Let f be continuous at a critical point c in I. Then
First Derivative Test Let f be a function defined on an open interval I. Let f be continuous at a critical point c in I. Then
(i) If f′(x) changes sign from positive to negative as x increases through c, i.e., if f′(x) > 0 at every point sufficiently close to and to the left of c, and f′(x) < 0 at every point sufficiently close to and to the right of c, then c is a point of local maxima.
(ii) If f′(x) changes sign from negative to positive as x increases through c, i.e., if f′(x) < 0 at every point sufficiently close to and to the left of c, and f′(x) > 0 at every point sufficiently close to and to the right of c, then c is a point of local minima.
(iii) If f′(x) does not change sign as x increases through c, then c is neither a point of local maxima nor a point of local minima. Infact, such a point is called point of inflexion.
 Second Derivative Test Let f be a function defined on an interval I and
Second Derivative Test Let f be a function defined on an interval I and
c ∈ I. Let f be twice differentiable at c. Then
(i) x = c is a point of local maxima if f′(c) = 0 and f″(c) < 0
The values f(c) is local maximum value of f .
(ii) x = c is a point of local minima if f′(c) = 0 and f″(c) > 0
In this case, f (c) is local minimum value of f .
(iii) The test fails if f′(c) = 0 and f″(c) = 0.
In this case, we go back to the first derivative test and find whether c is a point of maxima, minima or a point of inflexion.
 Working rule for finding absolute maxima and/or absolute minima
Working rule for finding absolute maxima and/or absolute minima
Step 1: Find all critical points of f in the interval, i.e., find points x where either f′(x) = 0 or f is not differentiable.
Step 2: Take the end points of the interval.
Step 3: At all these points (listed in Step 1 and 2), calculate the values of f .
Step 4: Identify the maximum and minimum values of f out of the values calculated in Step 3. This maximum value will be the absolute maximum value of f and the minimum value will be the absolute minimum value of f .
