Table of Contents
 There is no permanent place in the world for ugly mathematics ... . It may be very hard to define mathematical beauty but that is just as true of beauty of any kind, we may not know quite what we mean by a beautiful poem, but that does not prevent us from recognising one when we read it. — G. H. Hardy
There is no permanent place in the world for ugly mathematics ... . It may be very hard to define mathematical beauty but that is just as true of beauty of any kind, we may not know quite what we mean by a beautiful poem, but that does not prevent us from recognising one when we read it. — G. H. Hardy
1.1 भूमिका (Introduction)
स्मरण कीजिए कि कक्षा XI में, संबंध एवं फलन, प्रांत, सहप्रांत तथा परिसर आदि की अवधारणाओं का, विभिन्न प्रकार के वास्तविक मानीय फलनों और उनके आलेखों सहित परिचय कराया जा चुका है। गणित में शब्द ‘संबंध (Relation)’ की सकंल्पना को अंग्रेजी भाषा में इस शब्द के अर्थ से लिया गया है, जिसके अनुसार दो वस्तुएँ परस्पर संबंधित होती है, यदि उनके बीच एक अभिज्ञेय (Recognisable) कड़ी हो। मान लीजिए कि A, किसी स्कूल की कक्षा XII के विद्यार्थियों का समुच्चय है तथा B उसी स्कूल की कक्षा ग्प् के विद्यार्थियों का समुच्चय हैं। अब समुच्चय A से समुच्चय B तक के संबंधों के कुछ उदाहरण इस प्रकार हैं

स्मरमनदम क्पतपबीसमज
(1805.1859)
(i) {(a, b) ∈ A × B: a, b का भाई है},
(ii) {(a, b) ∈ A × B: a, b की बहन है},
(iii) {(a, b) ∈ A × B: a की आयु b की आयु से अधिक है},
(पअ) {(a, b) ∈ A × B: पिछली अंतिम परीक्षा में a द्वारा प्राप्त पूर्णांक b द्वारा प्राप्त पूर्णांक से कम हैै},
(अ) {(a, b) ∈ A × B: a उसी जगह रहता है जहाँ b रहता हैै},
तथापि A से ठ तक के किसी संबंध R को अमूर्तरूप (Abstracting) से हम गणित में । ञ् ठ के एक स्वेच्छ (।तइपजतंतल) उपसमुच्चय की तरह परिभाषित करते हैं।
यदि (a, b) ∈ त्ए तो हम कहते हैं कि संबंध त् के अंतर्गत a, b से संबंधित है और हम इसे a R b लिखते हैं। सामान्यतः, यदि (a, b) ∈ R, तो हम इस बात की चिंता नहीं करते हैं कि a तथा b के बीच कोई अभिज्ञेय कड़ी है अथवा नहीं है। जैसा कि कक्षा XI में देख चुके हैं, फलन एक विशेष प्रकार के संबंध होता हैं।
इस अध्याय में, हम विभिन्न प्रकार के संबंधों एवं फलनों, फलनों के संयोजन (composition), व्युत्क्रमणीय (Invertible) फलनों और द्विआधारी संक्रियाओं का अध्ययन करेंगे।
1.2 संबंधों के प्रकार (Types of Relations)
इस अनुच्छेद में हम विभिन्न प्रकार के संबंधों का अध्ययन करेंगे। हमें ज्ञात है कि किसी समुच्चय A में संबंध, A × A का एक उपसमुच्चय होता है। अतः रिक्त समुच्चय φ ⊂ A × A तथा A × A स्वयं, दो अन्त्य संबंध हैं। स्पष्टीकरण हेतु, R = {(a, b): a – b = 10} द्वारा प्रदत्त समुच्चय A = {1, 2, 3, 4} पर परिभाषित एक संबंध R पर विचार कीजिए। यह एक रिक्त समुच्चय है, क्योंकि एेसा कोई भी युग्म (pair) नहीं है जो प्रतिबंध a – b = 10 को संतुष्ट करता है। इसी प्रकार R′ = {(a, b) : | a – b | ≥ 0}, संपूर्ण समुच्चय A × A के तुल्य है, क्योंकि A × A के सभी युग्म (a, b), | a – b | ≥ 0 को संतुष्ट करते हैं। यह दोनों अन्त्य के उदाहरण हमें निम्नलिखित परिभाषाओं के लिए प्रेरित करते हैं।
परिभाषा 1 समुच्चय A पर परिभाषित संबंध R एक रिक्त संबंध कहलाता है, यदि A का कोई भी अवयव A के किसी भी अवयव से संबंधित नहीं है, अर्थात् R = φ ⊂ A × A.
परिभाषा 2 समुच्चय A पर परिभाषित संबंध R, एक सार्वत्रिक (universal) संबंध कहलाता है, यदि A का प्रत्येक अवयव A के सभी अवयवों से संबंधित है, अर्थात् R = A × A.
रिक्त संबंध तथा सार्वत्रिक संबंध को कभी-कभी तुच्छ (trivial) संबंध भी कहते हैं।
उदाहरण 1 मान लीजिए कि A किसी बालकों के स्कूल के सभी विद्यार्थियों का समुच्चय है। दर्शाइए कि R = {(a, b) : a, b की बहन है } द्वारा प्रदत्त संबंध एक रिक्त संबंध है तथा R′ = {(a, b) : a तथा b की ऊँचाईयों का अंतर 3 मीटर से कम है } द्वारा प्रदत्त संबंध एक सार्वत्रिक संबंध है।
हल प्रश्नानुसार, क्योंकि स्कूल बालकों का है, अतएव स्कूल का कोई भी विद्यार्थी, स्कूल के किसी भी विद्यार्थी की बहन नहीं हो सकता है। अतः R = φ, जिससे प्रदर्शित होता है कि R रिक्त संबंध है। यह भी स्पष्ट है कि किन्हीं भी दो विद्यार्थियों की ऊँचाइयों का अंतर 3 मीटर से कम होना ही चाहिए। इससे प्रकट होता है कि R′ = A × A सार्वत्रिक संबंध है।
टिप्पणी कक्षा XI में विद्यार्थीगण सीख चुके हैं कि किसी संबंध को दो प्रकार से निरूपित किया जा सकता है, नामतः रोस्टर विधि तथा समुच्चय निर्माण विधि। तथापि बहुत से लेखकों द्वारा समुच्चय {1, 2, 3, 4} पर परिभाषित संबंध R = {(a, b) : b = a + 1} को a R b द्वारा भी निरूपित किया जाता है, यदि और केवल यदि b = a + 1 हो। जब कभी सुविधाजनक होगा, हम भी इस संकेतन (notation) का प्रयोग करेंगे।
यदि (a, b) ∈ R, तो हम कहते हैं कि a,b से संबंधित है’ और इस बात को हम a R b द्वारा प्रकट करते हैं।
एक अत्यन्त महत्वपूर्ण संबंध, जिसकी गणित में एक सार्थक (significant) भूमिका है, तुल्यता संबंध (Equivalence Relation) कहलाता है। तुल्यता संबंध का अध्ययन करने के लिए हम पहले तीन प्रकार के संबंधों, नामतः स्वतुल्य (Reflexive), सममित (Symmetric) तथा संक्रामक (Transitive) संबंधों पर विचार करते हैं।
परिभाषा 3 समुच्चय A पर परिभाषित संबंध R;
(i) स्वतुल्य (reflexive) कहलाता है, यदि प्रत्येक a ∈ A के लिए (a, a) ∈ R,
(ii) सममित (symmetric) कहलाता है, यदि समस्त a1, a2 ∈ A के लिए (a1, a2) ∈ R से (a2, a1) ∈ R प्राप्त हो।
(iii) संक्रामक (transitive) कहलाता है, यदि समस्त, a1, a2, a3 ∈ A के लिए (a1, a2) ∈ R तथा (a2, a3) ∈ R से (a1, a3) ∈ R प्राप्त हो।
परिभाषा 4 A पर परिभाषित संबंध R एक तुल्यता संबंध कहलाता है, यदि R स्वतुल्य, सममित तथा संक्रामक है।
उदाहरण 2 मान लीजिए कि T किसी समतल में स्थित समस्त त्रिभुजों का एक समुच्चय है। समुच्चय T में R = {(T1, T2) : T1, T2के सर्वागंसम है} एक संबंध है। सिद्ध कीजिए कि R एक तुल्यता संबंध है।
हल संबंध R स्वतुल्य है, क्योंकि प्रत्येक त्रिभुज स्वयं के सवार्गंसम होता है। पुनः (T1, T2) ∈ R ⇒ T1 , T2 के सर्वागंसम है ⇒ T2 , T1 के सर्वागंसम है ⇒ (T2, T1) ∈ R. अतः संबंध R सममित है। इसके अतिरिक्त (T1, T2), (T2, T3) ∈ R ⇒ T1 , T2 के सर्वागंसम है तथा T2, T3 के सर्वागंसम है ⇒ T1, T3 के सर्वागंसम है ⇒ (T1, T3) ∈ R. अतः संबंध R संक्रामक है। इस प्रकार R एक तुल्यता संबंध है।
उदाहरण 3 मान लीजिए कि L किसी समतल में स्थित समस्त रेखाओं का एक समुच्चय है तथा R = {(L1, L2) : L1, L2 पर लंब है} समुच्चय L में परिभाषित एक संबंध है। सिद्ध कीजिए कि R सममित है किंतु यह न तो स्वतुल्य है और न संक्रामक है।
हल R स्वतुल्य नहीं है, क्योंकि कोई रेखा L1 अपने आप पर लंब नहीं हो सकती है, अर्थात्
(L1, L1) ∉ R. R सममित है, क्योंकि (L1, L2) ∈ R
⇒ L1, L2 पर लंब है
⇒ L2 , L1 पर लंब है
⇒ (L2, L1) ∈ R
R संक्रामक नहीं है। निश्चय ही, यदि L1, L2 पर लंब है तथा L2 , L3 पर लंब है, तो L1 , L3 पर कभी भी लंब नहीं हो सकती है। वास्तव में एेसी दशा में L1 , L3 के समान्तर होगी। अर्थात्, (L1, L2) ∈ R,
(L2, L3) ∈ R परंतु (L1, L3) ∉ R

आकृति 1.1
उदाहरण 4 सिद्ध कीजिए कि समुच्चय {1, 2, 3} में R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} द्वारा प्रदत्त संबंध स्वतुल्य है, परंतु न तो सममित है और न संक्रामक है।
हल R स्वतुल्य है क्योंकि (1, 1), (2, 2) और (3, 3), R के अवयव हैं। R सममित नहीं है, क्योंकि (1, 2) ∈ R किंतु (2, 1) ∉ R. इसी प्रकार R संक्रामक नहीं है, क्योंकि (1, 2) ∈ R तथा (2, 3)∈R परंतु (1, 3) ∉ R
उदाहरण 5 सिद्ध कीजिए कि पूर्णांकों के समुच्चय Z में R = {(a, b) : संख्या 2, (a – b) को विभाजित करती है} द्वारा प्रदत्त संबंध एक तुल्यता संबंध है।
हल R स्वतुल्य है, क्योंकि समस्त a ∈ Z के लिए 2, (a – a) को विभाजित करता है। अतः (a, a) ∈ R. पुनः, यदि (a, b) ∈ R, तो 2, a – b को विभाजित करता है । अतएव b – a को भी 2 विभाजित करता है। अतः (b, a) ∈ R, जिससे सिद्ध होता है कि R सममित है। इसी प्रकार, यदि (a, b) ∈ R तथा (b, c) ∈ R, तो a – b तथा b – c संख्या 2 से भाज्य है। अब, a – c = (a – b) + (b – c) सम (even) है (क्यों?)। अतः (a – c) भी 2 से भाज्य है। इससे सिद्ध होता है कि R संक्रामक है। अतः समुच्चय Z में R एक तुल्यता संबंध है।
उदाहरण 5 में, नोट कीजिए कि सभी सम पूर्णांक शून्य से संबंधित हैं, क्योंकि (0, ± 2), (0, ± 4), ...आदि R में हैं और कोई भी विषम पूर्णांक 0 से संबंधित नहीं है, क्योंकि (0, ± 1), (0, ± 3), ...आदि R में नहीं हैं। इसी प्रकार सभी विषम पूर्णांक 1 से संबंधित हैं और कोई भी सम पूर्णांक 1 से संबंधित नहीं है। अतएव, समस्त सम पूर्णांकों का समुच्चय E तथा समस्त विषम पूर्णांकों का समुच्चय O समुच्चय Z के उप समुच्चय हैं, जो निम्नलिखित प्रतिबंधों को संतुष्ट करते हैं।
(i) E के समस्त अवयव एक दूसरे से संबंधित हैं तथा O के समस्त अवयव एक दूसरे से संबंधित हैं।
(ii) E का कोई भी अवयव O के किसी भी अवयव से संबंधित नहीं है और विलोमतः O का कोई भी अवयव E के किसी भी अवयव से संबंधित नहीं है।
(iii) E तथा O असंयुक्त है और Z = E ∪ O है।
उपसमुच्चय E, शून्य को अंतर्विष्ट (contain) करने वाला तुल्यता-वर्ग (Equivalence Class) कहलाता है और जिसे प्रतीक [0] से निरूपित करते हैं। इसी प्रकार O, 1 को अंतर्विष्ट करने वाला तुल्यता-वर्ग है, जिसे [1] द्वारा निरूपित करते हैं। नोट कीजिए कि [0] ≠ [1], [0] = [2r] और [1]=[2r + 1], r ∈ Z. वास्तव में, जो कुछ हमने ऊपर देखा है, वह किसी भी समुच्चय X में एक स्वेच्छ तुल्यता संबंध R के लिए सत्य होता है। किसी प्रदत्त स्वेच्छ समुच्चय X में प्रदत्त एक स्वेच्छ (arbitrary) तुल्यता संबंध R, X को परस्पर असंयुक्त उपसमुच्चयों Ai में विभाजित कर देता है, जिन्हें X का विभाजन (Partition) कहते हैं ओर जो निम्नलिखित प्रतिबंधों को संतुष्ट करते हैंः
(i) समस्त i के लिए Ai के सभी अवयव एक दूसरे से संबंधित होते हैं।
(ii) Ai का कोई भी अवयव, Aj के किसी भी अवयव से संबंधित नहीं होता है, जहाँ i ≠ j
(iii) ∪ Aj = X तथा Ai ∩ Aj = φ, i ≠ j
उपसमुच्चय Ai तुल्यता-वर्ग कहलाते हैं। इस स्थिति का रोचक पक्ष यह है कि हम विपरीत क्रिया भी कर सकते हैं। उदाहरण के लिए Z के उन उपविभाजनों पर विचार कीजिए, जो Z के एेसे तीन परस्पर असंयुक्त उपसमुच्चयों A1, A2 तथा A3 द्वारा प्रदत्त हैं, जिनका सम्मिलन (Union) Z है,
A1 = {x ∈ Z : x संख्या 3 का गुणज है } = {..., – 6, – 3, 0, 3, 6, ...}
A2 = {x ∈ Z : x – 1 संख्या 3 का गुणज है } = {..., – 5, – 2, 1, 4, 7, ...}
A3 = {x ∈ Z : x – 2 संख्या 3 का गुणज है } = {..., – 4, – 1, 2, 5, 8, ...}
Z में एक संबंध R = {(a, b) : 3, a – b को विभाजित करता है} परिभाषित कीजिए। उदाहरण 5 में प्रयुक्त तर्क के अनुसार हम सिद्ध कर सकते हैं कि R एक तुल्यता संबंध हैं। इसके अतिरिक्त A1, Z के उन सभी पूर्णांकों के समुच्चय के बराबर है, जो शून्य से संबंधित हैं, A2, Z के उन सभी पूर्णांकों के समुच्चय के बराबर है, जो 1 से संबंधित हैं और A3 , Z के उन सभी पूर्णांकों के समुच्चय बराबर है, जो 2 से संबंधित हैं। अतः A1 = [0], A2 = [1] और A3 = [2]. वास्तव में A1 = [3r], A2 = [3r + 1] और A3 = [3r + 2], जहाँ r ∈ Z.
उदाहरण 6 मान लीजिए कि समुच्चय A = {1, 2, 3, 4, 5, 6, 7} में R = {(a, b) : a तथा b दोनों ही या तो विषम हैं या सम हैं} द्वारा परिभाषित एक संबंध है। सिद्ध कीजिए कि R एक तुल्यता संबंध है। साथ ही सिद्ध कीजिए कि उपसमुच्चय {1, 3, 5, 7} के सभी अवयव एक दूसरे से संबंधित है, और उपसमुच्चय {2, 4, 6} के सभी अवयव एक दूसरे से संबंधित है, परंतु उपसमुच्चय {1, 3, 5,7} का कोई भी अवयव उपसमुच्चय {2, 4, 6} के किसी भी अवयव से संबंधित नहीं है।
हल A का प्रदत्त कोई अवयव a या तो विषम है या सम है, अतएव (a, a) ∈ R. इसके अतिरिक्त (a, b) ∈ R ⇒ a तथा b दोनों ही, या तो विषम हैं या सम हैं ⇒ (b, a) ∈ R. इसी प्रकार (a, b) ∈ R तथा (b, c) ∈ R ⇒ अवयव a, b, c, सभी या तो विषम हैं या सम हैं ⇒ (a, c) ∈ R. अतः R एक तुल्यता संबंध है। पुनः, {1, 3, 5, 7} के सभी अवयव एक दूसरे से संबंधित हैं, क्योंकि इस उपसमुच्चय के सभी अवयव विषम हैं। इसी प्रकार {2, 4, 6,} के सभी अवयव एक दूसरे से संबंधित हैं, क्योंकि ये सभी सम हैं। साथ ही उपसमुच्चय {1, 3, 5, 7} का कोई भी अवयव {2, 4, 6} के किसी भी अवयव से संबंधित नहीं हो सकता है, क्योंकि {1, 3, 5, 7} के अवयव विषम हैं, जब कि {2, 4, 6}, के अवयव सम हैं।
प्रश्नावली 1.1
1. निर्धारित कीजिए कि क्या निम्नलिखित संबंधों में से प्रत्येक स्वतुल्य, सममित तथा संक्रामक हैंः
(i) समुच्चय A = {1, 2, 3, ..., 13, 14} में संबंध R, इस प्रकार परिभाषित है कि
R = {(x, y) : 3x – y = 0}
(ii) प्राकृत संख्याओं के समुच्चय N में R = {(x, y) : y = x + 5 तथा x < 4}द्वारा परिभाषित संबंध R.
(iii) समुच्चय A = {1, 2, 3, 4, 5, 6} में R = {(x, y) : y भाज्य है x से} द्वारा परिभाषित संबंध R है।
(iv) समस्त पूर्णांकों के समुच्चय Z में R = {(x, y) : x – y एक पूर्णांक है} द्वारा परिभाषित संबंध R.
(v) किसी विशेष समय पर किसी नगर के निवासियों के समुच्चय में निम्नलिखित संबंध R
(a) R = {(x, y) : x तथा y एक ही स्थान पर कार्य करते हैं}
(b) R = {(x, y) : x तथा y एक ही मोहल्ले में रहते हैं}
(c) R = {(x, y) : x, y से ठीक-ठीक 7 सेमी लंबा है}
(d) R = {(x, y) : x , y की पत्नी है}
(e) R = {(x, y) : x, y के पिता हैं}
2. सिद्ध कीजिए कि वास्तविक संख्याओं के समुच्चय R में R = {(a, b) : a ≤ b2}, द्वारा परिभाषित संबंध R, न तो स्वतुल्य है, न सममित हैं और न ही संक्रामक है।
3. जाँच कीजिए कि क्या समुच्चय {1, 2, 3, 4, 5, 6} में R = {(a, b) : b = a + 1} द्वारा परिभाषित संबंध R स्वतुल्य, सममित या संक्रामक है।
4. सिद्ध कीजिए कि R में R = {(a, b) : a ≤ b}, द्वारा परिभाषित संबंध R स्वतुल्य तथा संक्रामक है किंतु सममित नहीं है।
5. जाँच कीजिए कि क्या R में R = {(a, b) : a ≤ b3} द्वारा परिभाषित संबंध स्वतुल्य, सममित अथवा संक्रामक है?
6. सिद्ध कीजिए कि समुच्चय {1, 2, 3} में R = {(1, 2), (2, 1)} द्वारा प्रदत्त संबंध R सममित है किंतु न तो स्वतुल्य है और न संक्रामक है।
7. सिद्ध कीजिए कि किसी कॉलेज के पुस्तकालय की समस्त पुस्तकों के समुच्चय A में R = {(x, y) : x तथा y में पेजों की संख्या समान है} द्वारा प्रदत्त संबंध R एक तुल्यता संबंध है।
8. सिद्ध कीजिए कि A = {1, 2, 3, 4, 5} में, R = {(a, b) : |a – b| सम है} द्वारा प्रदत्त संबंध R एक तुल्यता संबंध है। प्रमाणित कीजिए कि {1, 3, 5} के सभी अवयव एक दूसरे से संबंधित हैं और समुच्चय {2, 4} के सभी अवयव एक दूसरे से संबंधित हैं परंतु {1, 3, 5} का कोई भी अवयव {2, 4} के किसी अवयव से संबंधित नहीं है।
9. सिद्ध किजिए कि समुच्चय A = {x ∈ Z : 0 ≤ x ≤ 12}, में दिए गए निम्नलिखित संबंधों R में से प्रत्येक एक तुल्यता संबंध हैः
(i) R = {(a, b) : |a – b|, 4 का एक गुणज है},
(ii) R = {(a, b) : a = b},
प्रत्येक दशा में 1 से संबंधित अवयवों को ज्ञात कीजिए।
10. एेसे संबंध का उदाहरण दीजिए, जो
(i) सममित हो परंतु न तो स्वतुल्य हो और न संक्रामक हो।
(ii) संक्रामक हो परंतु न तो स्वतुल्य हो और न सममित हो। .
(iii) स्वतुल्य तथा सममित हो किंतु संक्रामक न हो।
(iv) स्वतुल्य तथा संक्रामक हो किंतु सममित न हो।
(v) सममित तथा संक्रामक हो किंतु स्वतुल्य न हो।
11. सिद्ध कीजिए कि किसी समतल में स्थित बिंदुओं के समुच्चय में, R = {(P, Q) : बिंदु P की मूल बिंदु से दूरी, बिंदु Q की मूल बिंदु से दूरी के समान है} द्वारा प्रदत्त संबंध R एक तुल्यता संबंध है। पुनः सिद्ध कीजिए कि बिंदु P ≠ (0, 0) से संबंधित सभी बिंदुओं का समुच्चय P से होकर जाने वाले एक एेसे वृत्त को निरूपित करता है, जिसका केंद्र मूलबिंदु पर है।
12. सिद्ध कीजिए कि समस्त त्रिभुजों के समुच्चय A में, R = {(T1, T2) : T1, T2 के समरूप है} द्वारा परिभाषित संबंध R एक तुल्यता संबंध है। भुजाओं 3, 4, 5 वाले समकोण त्रिभुज T1 , भुजाओं 5, 12, 13 वाले समकोण त्रिभुज T2 तथा भुजाओं 6, 8, 10 वाले समकोण त्रिभुज T3 पर विचार कीजिए। T1, T2 और T3 में से कौन से त्रिभुज परस्पर संबंधित हैं?
13. सिद्ध कीजिए कि समस्त बहुभुजों के समुच्चय A में, R = {(P1, P2) : P1 तथा P2 की भुजाओं की संख्या समान है}प्रकार से परिभाषित संबंध R एक तुल्यता संबंध है। 3, 4, और 5 लंबाई की भुजाओं वाले समकोण त्रिभुज से संबंधित समुच्चय A के सभी अवयवों का समुच्चय ज्ञात कीजिए।
14. मान लीजिए कि XY-तल में स्थित समस्त रेखाओं का समुच्चय L है और L में R = {(L1,L2) : L1 समान्तर है L2 के} द्वारा परिभाषित संबंध R है। सिद्ध कीजिए कि R एक तुल्यता संबंध है। रेखा y = 2x + 4 से संबंधित समस्त रेखाओं का समुच्चय ज्ञात कीजिए।
15. मान लीजिए कि समुच्चय {1, 2, 3, 4} में, R = {(1, 2), (2, 2), (1, 1), (4,4), (1, 3), (3, 3), (3, 2)} द्वारा परिभाषित संबंध R है। निम्नलिखित में से सही उत्तर चुनिए।
(A) R स्वतुल्य तथा सममित है किंतु संक्रामक नहीं है।
(B) R स्वतुल्य तथा संक्रामक है किंतु सममित नहीं है।
(C) R सममित तथा संक्रामक है किंतु स्वतुल्य नहीं है।
(D) R एक तुल्यता संबंध है।
16. मान लीजिए कि समुच्चय N में, R = {(a, b) : a = b – 2, b > 6} द्वारा प्रदत्त संबंध R है। निम्नलिखित में से सही उत्तर चुनिएः
(A) (2, 4) ∈ R (B) (3, 8) ∈ R (C) (6, 8) ∈ R (D) (8, 7) ∈ R
1.3 फलनों के प्रकार (Types of Functions)
फलनों की अवधारणा, कुछ विशेष फलन जैसे तत्समक फलन, अचर फलन, बहुपद फलन, परिमेय फलन, मापांक फलन, चिह्न फलन आदि का वर्णन उनके आलेखों सहित कक्षा XI में किया जा चुका है।
दो फलनों के योग, अंतर, गुणा तथा भाग का भी अध्ययन किया जा चुका है। क्योंकि फलन की संकल्पना गणित तथा अध्ययन की अन्य शाखाओं (Disciplines) में सर्वाधिक महत्वपूर्ण है, इसलिए हम फलन के बारे में अपना अध्ययन वहाँ से आगे बढ़ाना चाहते हैं, जहाँ इसे पहले समाप्त किया था। इस अनुच्छेद में, हम विभिन्न प्रकार के फलनों का अध्ययन करेंगे।
निम्नलिखित आकृतियों द्वारा दर्शाए गए फलन f1, f2, f3 तथा f4 पर विचार कीजिए।
आकृति 1.2 में हम देखते हैं कि X1 के भिन्न (distinct) अवयवों के, फलन f1 के अंतर्गत, प्रतिबिंब भी भिन्न हैं, किंतु f2 के अंतर्गत दो भिन्न अवयवों 1 तथा 2 के प्रतिबिंब एक ही हैं नामतः b है। पुनः X2 में कुछ एेसे अवयव है जैसे e तथा f जो f1 के अंतर्गत X1 के किसी भी अवयव के प्रतिबिंब नहीं हैं, जबकि f3 के अंतर्गत X3 के सभी अवयव X1 के किसी न किसी अवयव के प्रतिबिंब हैं।
उपर्युक्त परिचर्चा से हमें निम्नलिखित परिभाषाएँ प्राप्त होती हैं।
परिभाषा 5 एक फलन f : X → Y एकैकी (one-one) अथवा एकैक (injective) फलन कहलाता है, यदि f के अंतर्गत X के भिन्न अवयवों के प्रतिबिंब भी भिन्न होते हैं, अर्थात् प्रत्येक
x1, x2 ∈ X, के लिए f(x1) = f(x2) का तात्पर्य है कि x1 = x2, अन्यथा f एक बहुएक (many-one) फलन कहलाता है।
आकृति 1.2 (i) में फलन f1 एकैकी फलन है तथा आकृति 1.2 (ii) में f2 एक बहुएक फलन है।
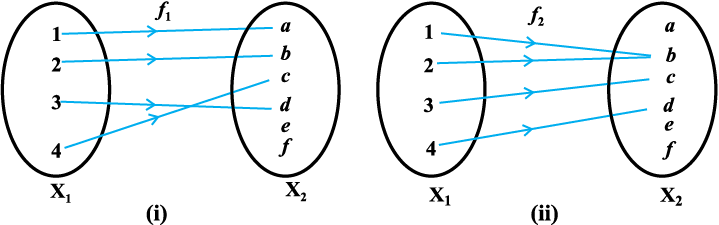

आकृति 1.2
परिभाषा 6 फलन f : X → Y आच्छादक (onto) अथवा आच्छादी (surjective) कहलाता है, यदि f के अंतर्गत Y का प्रत्येक अवयव, X के किसी न किसी अवयव का प्रतिबिंब होता है, अर्थात् प्रत्येक y ∈ Y, के लिए, X में एक एेसे अवयव x का अस्तित्व है कि f(x) = y.
आकृति 1.2 (iii) में, फलन f3 आच्छादक है तथा आकृति 1.2 (i) में, फलन f1 आच्छादक नहीं है, क्योंकि X2 के अवयव e, तथा f, f1 के अंतर्गत X1 के किसी भी अवयव के प्रतिबिंब नहीं हैं।
टिप्पणी f : X → Y एक आच्छादक फलन है, यदि और केवल यदि f का परिसर (range)= Y.
परिभाषा 7 एक फलन f : X → Y एक एकैकी तथा आच्छादक (one-one and onto) अथवा एकैकी आच्छादी (bijective) फलन कहलाता है, यदि f एकैकी तथा आच्छादक दोनों ही होता है।
आकृति 1.2 (iv) में, फलन f4 एक एकैकी तथा आच्छादी फलन है।
उदाहरण 7 मान लीजिए कि कक्षा X के सभी 50 विद्यार्थियों का समुच्चय A है। मान लीजिए f : A → N , f(x) = विद्यार्थी x का रोल नंबर, द्वारा परिभाषित एक फलन है। सिद्ध कीजिए कि f एकैकी है किंतु आच्छादक नहीं है।
हल कक्षा के दो भिन्न-भिन्न विद्यार्थियों के रोल नंबर समान नहीं हो सकते हैं। अतएव f एकैकी है। व्यापकता की बिना क्षति किए हम मान सकते हैं कि विद्यार्थियों के रोल नंबर 1 से 50 तक हैं। इसका तात्पर्य यह हुआ कि N का अवयव 51, कक्षा के किसी भी विद्यार्थी का रोल नंबर नहीं है, अतएव f के अंतर्गत 51, A के किसी भी अवयव का प्रतिबिंब नहीं है। अतः f आच्छादक नहीं है।
उदाहरण 8 सिद्ध कीजिए कि f(x) = 2x द्वारा प्रदत्त फलन f : N → N, एकैकी है किंतु आच्छादक नहीं है।
हल फलन f एकैकी है, क्योंकि f(x1) = f(x2) ⇒ 2x1 = 2x2 ⇒ x1 = x2. पुनः, f आच्छदक नहीं है, क्योंकि 1 ∈ N, के लिए N में एेसे किसी x का अस्तित्व नहीं है ताकि f(x) = 2x = 1 हो।
उदाहरण 9 सिद्ध कीजिए कि f(x) = 2x द्वारा प्रदत्त फलन f : R → R, एकैकी तथा आच्छादक है।
हल f एकैकी है, क्योंकि f(x1) = f(x2) ⇒ 2x1 = 2x2 ⇒ x1 = x2. साथ ही, R में प्रदत्त किसी भी वास्तविक संख्या y के लिए R में 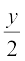 का अस्तित्व है, जहाँ f(
का अस्तित्व है, जहाँ f(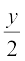 ) = 2 . (
) = 2 . (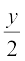 ) = y है। अतः f आच्छादक भी है।
) = y है। अतः f आच्छादक भी है।
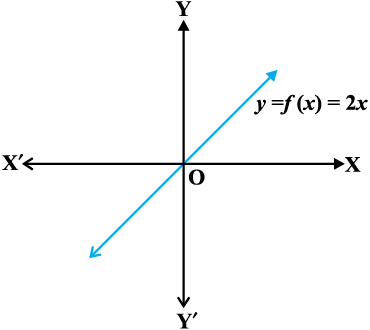
आकृति 1.3
उदाहरण 10 सिद्ध किजिए कि f(1) = f(2) = 1 तथा x > 2 के लिए f(x) = x – 1 द्वारा प्रदत्त फलन f : N → N, आच्छादक तो है किंतु एकैकी नहीं है।
हल f एकैकी नहीं है, क्याेंकि f(1) = f(2) = 1, परंतु f आच्छादक है, क्योंकि किसी प्रदत्त y ∈ N, y ≠ 1, के लिए, हम x को y + 1 चुन लेते हैं, ताकि f (y+ 1) = y + 1 – 1 = y साथ ही 1 ∈ N के लिए f (1) = 1 है।
उदाहरण 11 सिद्ध कीजिए कि f(x) = x2 द्वारा परिभाषित फलन f : R → R, न तो एकैकी है और न आच्छादक है।
हल क्योंकि f(– 1) = 1 = f(1), इसलिए f एकैकी नहीं है। पुनः सहप्रांत R का अवयव -2, प्रांत R के किसी भी अवयव x का प्रतिबिंब नहीं है (क्यों?)। अतः f आच्छादक नहीं है।
उदाहरण 12 सिद्ध कीजिए कि नीचे परिभाषित फलन f : N → N, एकैकी तथा आच्छादक दोनों ही है


आकृति 1.4
हल मान लीजिए f(x1) = f(x2) है। नोट कीजिए कि यदि x1 विषम है तथा x2 सम है, तो x1 + 1 = x2 – 1, अर्थात् x2 – x1 = 2 जो असम्भव है। इस प्रकार x1 के सम तथा x2 के विषम होने की भी संभावना नहीं है। इसलिए x1 तथा x2 दोनों ही या तो विषम होंगे या सम होंगे। मान लीजिए कि x1 तथा x2 दोनों विषम हैं, तो f(x1) = f(x2) ⇒ x1 + 1 = x2 + 1 ⇒ x1 = x2. इसी प्रकार यदि x1 तथा x2 दोनों सम हैं, तो भी f(x1) = f(x2) ⇒ x1 – 1 = x2 – 1 ⇒ x1 = x2. अतः f एकैकी है। साथ ही सहप्रांत N की कोई भी विषम संख्या 2r + 1, प्रांत N की संख्या 2r + 2 का प्रतिबिंब है और सहप्रांत N की कोई भी सम संख्या 2r, N की संख्या 2r – 1 का प्रतिबिंब है। अतः f आच्छादक है।
उदाहरण 13 सिद्ध कीजिए कि आच्छादक फलन f : {1, 2, 3} → {1, 2, 3} सदैव एकैकी फलन होता है।
हल मान लीजिए कि f एकैकी नहीं है। अतः इसके प्रांत में कम से कम दो अवयव मान लिया कि 1 तथा 2 का अस्तित्व है जिनके सहप्रांत में प्रतिबिंब समान है। साथ ही f के अंतर्गत 3 का प्रतिबिंब केवल एक ही अवयव है। अतः, परिसर में, सहप्रांत {1, 2, 3} के, अधिकतम दो ही अवयव हो सकते हैं, जिससे प्रकट होता है कि f आच्छादक नहीं है, जो कि एक विरोधोक्ति है। अतः f को एकैकी होना ही चाहिए।
उदाहरण 14 सिद्ध कीजिए कि एक एकैकी फलन f : {1, 2, 3} → {1, 2, 3}अनिवार्य रूप से आच्छादक भी है।
हल चूँकि f एकैकी है, इसलिए {1, 2, 3} के तीन अवयव f के अंतर्गत सहप्रांत {1, 2, 3} के तीन अलग-अलग अवयवों से क्रमशः संबंधित होंगे। अतः f आच्छादक भी है।
टिप्पणी उदाहरण 13 तथा 14 में प्राप्त परिणाम किसी भी स्वेच्छ परिमित (finite) समुच्चय X, के लिए सत्य है, अर्थात् एक एकैकी फलन f : X → X अनिवार्यतः आच्छादक होता है तथा प्रत्येक परिमित समुच्चय X के लिए एक आच्छादक फलन f : X → X अनिवार्यतः एकैकी होता है। इसके विपरीत उदाहरण 8 तथा 10 से स्पष्ट होता है कि किसी अपरिमित (Infinite) समुच्चय के लिए यह सही नहीं भी हो सकता है। वास्तव में यह परिमित तथा अपरिमित समुच्चयों के बीच एक अभिलक्षणिक (characteristic) अंतर है।
प्रश्नावली 1.2
1. सिद्ध कीजिए कि f(x) =  द्वारा परिभाषित फलन f : R∗ → R∗ एकैकी तथा आच्छादक है, जहाँ R∗ सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है। यदि प्रांत R∗ को N से बदल दिया जाए, जब कि सहप्रांत पूर्ववत R∗ही रहे, तो भी क्या यह परिणाम सत्य होगा?
द्वारा परिभाषित फलन f : R∗ → R∗ एकैकी तथा आच्छादक है, जहाँ R∗ सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है। यदि प्रांत R∗ को N से बदल दिया जाए, जब कि सहप्रांत पूर्ववत R∗ही रहे, तो भी क्या यह परिणाम सत्य होगा?
2. निम्नलिखित फलनों की एकैक (Injective) तथा आच्छादी (Surjective) गुणों की जाँच कीजिएः
(i) f(x) = x2 द्वारा प्रदत्त f : N → N फलन है।
(ii) f(x) = x2 द्वारा प्रदत्त f : Z → Z फलन है।
(iii) f(x) = x2 द्वारा प्रदत्त f : R → R फलन है।
(iv) f(x) = x3 द्वारा प्रदत्त f : N → N फलन है।
(v) f(x) = x3 द्वारा प्रदत्त f : Z → Z फलन है।
3. सिद्ध कीजिए कि f(x) = [x] द्वारा प्रदत्त महत्तम पूर्णांक फलन f : R → R, न तो एकैकी है और न आच्छादक है, जहाँ [x], x से कम या उसके बराबर महत्तम पूर्णांक को निरूपित करता है।
4. सिद्ध कीजिए कि f(x) = |x| द्वारा प्रदत्त मापांक फलन f : R → R, न तो एकैकी है और न आच्छादक है, जहाँ | x | बराबर x, यदि x धन या शून्य है तथा |x| बराबर – x, यदि x ऋण है।
5. सिद्ध कीजिए कि f : R → R,
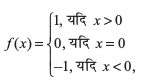
द्वारा प्रदत्त चिह्न फलन न तो एकैकी है और न आच्छादक है।
6. मान लीजिए कि A = {1, 2, 3}, B = {4, 5, 6, 7} तथा f = {(1, 4), (2, 5), (3, 6)} A से B तक एक फलन है। सिद्ध कीजिए कि f एकैकी है।
7. निम्नलिखित में से प्रत्येक स्थिति में बतलाइए कि क्या दिए हुए फलन एकैकी, आच्छादक अथवा एकैकी आच्छादी (bijective) हैं। अपने उत्तर का औचित्य भी बतलाइए।
(i) f(x) = 3 – 4x द्वारा परिभाषित फलन f : R → R है।
(ii) f(x) = 1 + x2 द्वारा परिभाषित फलन f : R → R है।
8. मान लीजिए कि A तथा B दो समुच्चय हैं। सिद्ध कीजिए कि f : A × B → B × A, इस प्रकार कि f(a, b) = (b, a) एक एकैकी आच्छादी (bijective) फलन है।
9. मान लीजिए कि समस्त n ∈ N के लिए, f(n) =
द्वारा परिभाषित एक फलन f : N → N है। बतलाइए कि क्या फलन f एकैकी आच्छादी (bijective) है। अपने उत्तर का औचित्य भी बतलाइए।
10. मान लीजिए कि A = R – {3} तथा B = R – {1} हैं। f(x) = 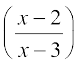 द्वारा परिभाषित फलन f : A → B पर विचार कीजिए। क्या f एकैकी तथा आच्छादक है? अपने उत्तर का औचित्य भी बतलाइए।
द्वारा परिभाषित फलन f : A → B पर विचार कीजिए। क्या f एकैकी तथा आच्छादक है? अपने उत्तर का औचित्य भी बतलाइए।
11. मान लीजिए कि f : R → R , f(x) = x4 द्वारा परिभाषित है। सही उत्तर का चयन कीजिए।
(A) f एकैकी आच्छादक है (B) f बहुएक आच्छादक है
(C) f एकैकी है किंतु आच्छादक नहीं है (D) f न तो एकैकी है और न आच्छादक है।
12. मान लीजिए कि f(x) = 3x द्वारा परिभाषित फलन f : R → R है। सही उत्तर चुनिएः
(A) f एकैकी आच्छादक है (B) f बहुएक आच्छादक है
(C) f एकैकी है परंतु आच्छादक नहीं है (D) f न तो एकैकी है और न आच्छादक है
1.4 फलनों का संयोजन तथा व्युत्क्रमणीय फलन (Composition of Functions and Invertible Function)
इस अनुच्छेद में हम दो फलनों के संयोजन तथा किसी एकैकी आच्छादी (bijective) फलन के प्रतिलोम (Inverse) का अध्ययन करेंगे। सन् 2006 की किसी बोर्ड (परिषद््) की कक्षा X की परीक्षा में बैठ चुके सभी विद्यार्थियों के समुच्चय A पर विचार कीजिए। बोर्ड की परीक्षा में बैठने वाले प्रत्येक विद्यार्थी को बोर्ड द्वारा एक रोल नंबर दिया जाता है, जिसे विद्यार्थी परीक्षा के समय अपनी उत्तर पुस्तिका पर लिखता है। गोपनीयता रखने के लिए बोर्ड विद्यार्थियों के रोल नंबरों को विरूप (deface) करके, प्रत्येक रोल नंबर को एक नकली सांकेतिक नंबर (Fake Code Number) में बदल देता हैं। मान लीजिए कि B ⊂ N समस्त रोल नंबरों का समुच्चय है, तथा C ⊂ N समस्त सांकेतिक नंबरों का समुच्चय है। इससे दो फलन f : A → B तथा g : B → C बनते हैं जो क्रमशः f(a) = विद्यार्थी a को दिया गया रोल नंबर तथा g(b) = रोल नंबर b को बदल कर दिया गया सांकेतिक नंबर, द्वारा परिभाषित हैं। इस प्रक्रिया में फलन f द्वारा प्रत्येक विद्यार्थी के लिए एक रोल नंबर निर्धारित होता है तथा फलन g द्वारा प्रत्येक रोल नंबर के लिए एक सांकेतिक नंबर निर्धारित होता है। अतः इन दोनों फलनों के संयोजन से प्रत्येक विद्यार्थी को अंततः एक सांकेतिक नंबर से संबंध कर दिया जाता हे। इससे निम्नलिखित परिभाषा प्राप्त होती है।
परिभाषा 8 मान लीजिए कि f : A → B तथा g : B → C दो फलन हैं। तब f और g का संयोजन, gof द्वारा निरूपित होता है, तथा फलन gof : A → C, gof(x) = g(f(x)),  x ∈ A द्वारा परिभाषित होता है।
x ∈ A द्वारा परिभाषित होता है।
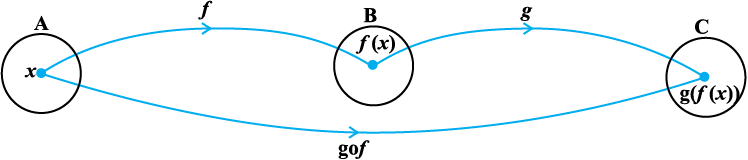
आकृति 1.5
उदाहरण 15 मान लीजिए कि f : {2, 3, 4, 5} → {3, 4, 5, 9} और g : {3, 4, 5, 9} → {7, 11, 15} दो फलन इस प्रकार हैं कि f(2) = 3, f(3) = 4, f(4) = f(5) = 5 और g(3) = g(4) = 7 तथा g(5) = g(9) = 11, तो gof ज्ञात कीजिए।
हल यहाँ gof(2) = g(f(2)) = g(3) = 7, gof(3) = g(f(3)) = g(4) = 7, gof(4) = g(f(4)) = g(5) = 11 और gof(5) = g(5) = 11.
उदाहरण 16 यदि f : R → R तथा g : R → R फलन क्रमशः f(x) = cos x तथा g(x) = 3x2 द्वारा परिभाषित है तो gof और fog ज्ञात कीजिए। सिद्ध कीजिए gof ≠ fog.
हल यहाँ gof(x) = g(f(x)) = g(cos x) = 3 (cos x)2 = 3 cos2 x. इसी प्रकार, fog(x) = f(g(x)) = f(3x2) = cos (3x2) हैं। नोट कीजिए कि x = 0 के लिए 3cos2 x ≠ cos 3x2 है। अतः gof ≠ fog.
उदाहरण 17 यदि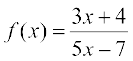 द्वारा परिभाषित फलन
द्वारा परिभाषित फलन तथा
तथा  द्वारा परिभाषित फलन
द्वारा परिभाषित फलन 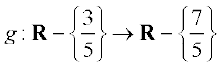 प्रदत्त हैं, तो सिद्ध कीजिए कि fog = IA तथा gof = IB, इस प्रकार कि IA (x) = x,
प्रदत्त हैं, तो सिद्ध कीजिए कि fog = IA तथा gof = IB, इस प्रकार कि IA (x) = x,  x ∈ A और IB (x) = x,
x ∈ A और IB (x) = x, 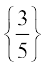 x ∈ B, जहाँ
x ∈ B, जहाँ
A = R – 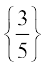 , B = R –
, B = R – 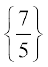 हैं। IA तथा IB को क्रमशः समुच्चय A तथा B पर तत्समक (Identity) फलन कहते हैं।
हैं। IA तथा IB को क्रमशः समुच्चय A तथा B पर तत्समक (Identity) फलन कहते हैं।
हल यहाँ पर
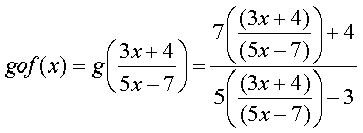 त्र्
त्र् 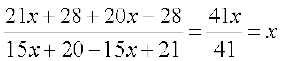
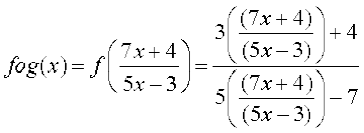 त्र्
त्र् 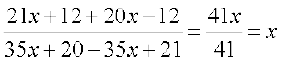
अतः gof(x) = x,  x ∈ B और fog(x) = x,
x ∈ B और fog(x) = x,  x ∈ A, जिसका तात्पर्य यह है कि gof = IB और fog = IA.
x ∈ A, जिसका तात्पर्य यह है कि gof = IB और fog = IA.
उदाहरण 18 सिद्ध कीजिए कि यदि f : A → B तथा g : B → C एकैकी हैं, तो gof : A → C भी एकैकी है।
हल gof(x1) = gof(x2)
⇒ g(f(x1)) = g(f(x2))
⇒ f(x1) = f(x2), क्योंकि g एकैकी है
⇒ x1 = x2, क्योंकि f एकैकी है
अतः gof भी एकैकी है।
उदाहरण 19 सिद्ध कीजिए कि यदि f : A → B तथा g : B → C आच्छादक हैं, तो gof : A →C भी आच्छादक है।
हल मान लीजिए कि एक स्वेच्छ अवयव z ∈ C है। g के अंतर्गत z के एक पूर्व प्रतिबिंब (Pre-image) y ∈ B का अस्तित्व इस प्रकार है कि, g(y) = z, क्योंकि g आच्छादक है। इसी प्रकार y ∈ B के लिए A में एक अवयव x का अस्तित्व इस प्रकार है कि, f(x) = y, क्योंकि f आच्छादक है। अतः gof(x) = g(f(x)) = g(y) = z, जिससे प्रमाणित होता है कि gof आच्छादक है।
उदाहरण 20 f तथा g एेसे दो फलनों पर विचार कीजिए कि gof परिभाषित है तथा एकैकी है। क्या f तथा g दोनों अनिवार्यतः एकैकी हैं?
हल फलन f : {1, 2, 3, 4} → {1, 2, 3, 4, 5, 6} f(x) = x,  x द्वारा परिभाषित और g(x) = x, x = 1, 2, 3, 4 तथा g(5) = g(6) = 5 द्वारा परिभाषित g : {1, 2, 3, 4, 5, 6} → {1, 2, 3, 4, 5, 6} पर विचार कीजिए। यहाँ gof : {1, 2, 3, 4} → {1, 2, 3, 4, 5, 6} परिभाषित है तथा gof(x) = x,
x द्वारा परिभाषित और g(x) = x, x = 1, 2, 3, 4 तथा g(5) = g(6) = 5 द्वारा परिभाषित g : {1, 2, 3, 4, 5, 6} → {1, 2, 3, 4, 5, 6} पर विचार कीजिए। यहाँ gof : {1, 2, 3, 4} → {1, 2, 3, 4, 5, 6} परिभाषित है तथा gof(x) = x, 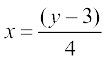 x, जिससे प्रमाणित होता है कि gof एकैकी है। किंतु g स्पष्टतया एकैकी नहीं है।
x, जिससे प्रमाणित होता है कि gof एकैकी है। किंतु g स्पष्टतया एकैकी नहीं है।
उदाहरण 21 यदि gof आच्छदक है, तो क्या f तथा g दोनों अनिवार्यतः आच्छादक हैं?ण्
हल f : {1, 2, 3, 4} → {1, 2, 3, 4} तथा g : {1, 2, 3, 4} → {1, 2, 3} पर विचार कीजिए, जो, क्रमशः f(1) = 1, f(2) = 2, f(3) = f(4) = 3, g(1) = 1, g(2) = 2 तथा g(3) = g(4) = 3. द्वारा परिभाषित हैं। यहाँ सरलता से देखा जा सकता है कि gof आच्छादक है, किंतु f आच्छादक नहीं है।
टिप्पणी यह सत्यापित किया जा सकता है कि व्यापक रूप से gof के एकैकी होने का तात्पर्य है कि f एकैकी होता है। इसी प्रकार gof आच्छादक होने का तात्पर्य है कि g आच्छादक होता है।
अब हम इस अनुच्छेद के प्रारंभ में बोर्ड की परीक्षा के संदर्भ में वर्णित फलन f और g पर बारीकी से विचार करना चाहते हैं। बोर्ड की कक्षा X की परीक्षा में बैठने वाले प्रत्येक विद्यार्थी को फलन f के अंतर्गत एक रोल नंबर प्रदान किया जाता है और प्रत्येक रोल नंबर को g के अंतर्गत एक सांकेतिक नंबर प्रदान किया जाता है। उत्तर पुस्तिकाओं के मूल्यांकन के बाद परीक्षक प्रत्येक मूल्यांकित पुस्तिका पर सांकेतिक नंबर के समक्ष प्राप्तांक लिख कर बोर्ड के कार्यालय में प्रस्तुत करता है। बोर्ड के अधिकारी, g के विपरीत प्रक्रिया द्वारा, प्रत्येक सांकेतिक नंबर को बदल कर पुनः संगत रोल नंबर प्रदान कर देते हैं और इस प्रकार प्राप्तांक सांकेतिक नंबर के बजाए सीधे रोल नंबर से संबंधित हो जाता है। पुनः, f की विपरीत प्रक्रिया द्वारा, प्रत्येक रोल नंबर को उस रोल नंबर वाले विद्यार्थी से बदल दिया जाता है। इससे प्राप्तांक सीधे संबंधित विद्यार्थी के नाम निर्धारित हो जाता है। हम देखते हैं कि f तथा g, के संयोजन द्वारा gof, प्राप्त करते समय, पहले f और फिर g को प्रयुक्त करते हैं, जब कि संयुक्त gof, की विपरीत प्रक्रिया में, पहले g की विपरीत प्रक्रिया और फिर f की विपरीत प्रक्रिया करते हैं।
उदाहरण 22 मान लीजिए कि f : {1, 2, 3} → {a, b, c} एक एकैकी तथा अच्छादक फलन इस प्रकार है कि f(1) = a, f(2) = b और f(3) = c, तो सिद्ध कीजिए कि फलन g : {a, b, c} → {1, 2, 3} का एेसा अस्तित्व है, ताकि gof = IX तथा fog = IY, जहाँ X = {1, 2, 3} तथा Y = {a, b, c} हो।
हल फलन g : {a, b, c} → {1, 2, 3} है जहाँ g(a) = 1, g(b) = 2 और g(c) = 3, पर विचार कीजिए। यह सत्यापित करना सरल है कि संयुक्त फलन gof = IX , X पर तत्समक फलन है और सयुंक्त फलन fog = IY , Y पर तत्समक फलन हैं।
टिप्पणी यह एक रोचक तथ्य है कि उपर्युक्त उदाहरण में वर्णित परिणाम किसी भी स्वेच्छ एकैकी तथा आच्छादक फलन f : X → Y के लिए सत्य होता है। केवल यही नहीं अपितु इसका विलोम (converse) भी सत्य होता है, अर्थात्, यदि f : X → Y एक एेसा फलन है कि किसी फलन g : Y → X का अस्तित्व इस प्रकार है कि gof = IX तथा fog = IY, तो f एकैकी तथा आच्छादक होता है।
उपर्युक्त परिचर्चा, उदाहरण 22 तथा टिप्पणी निम्नलिखित परिभाषा के लिए प्रेरित करते हैंः
परिभाषा 9 फलन f : X → Y व्युत्क्रमणीय (Invertible) कहलाता है, यदि एक फलन g : Y → X का अस्तित्व इस प्रकार है कि gof = IX तथा fog = IY है। फलन g को फलन f का प्रतिलोम (Inverse) कहते हैं और इसे प्रतीक f–1 द्वारा प्रकट करते हैं।
अतः, यदि f व्युत्क्रमणीय है, तो f अनिवार्यतः एकैकी तथा आच्छादक होता है और विलोमतः, यदि f एकैकी तथा आच्छादक है, तो f अनिवार्यतः व्युत्क्रमणीय होता है। यह तथ्य, f को एकैकी तथा आच्छादक सिद्ध करके, व्युत्क्रमणीय प्रमाणित करने में महत्वपूर्ण रूप से सहायक होता है, विशेष रूप से जब f का प्रतिलोम वास्तव में ज्ञात नहीं करना हो।
उदाहरण 23 मान लीजिए कि f : N → Y, f(x) = 4x + 3, द्वारा परिभाषित एक फलन है, जहाँ Y = {y ∈ N: y = 4x + 3 किसी x ∈ N के लिए}। सिद्ध कीजिए कि f व्युत्क्रमणीय है। प्रतिलोम फलन भी ज्ञात कीजिए।
हल Y के किसी स्वेच्छ अवयव y पर विचार कीजिए। Y, की परिभाषा द्वारा, प्रांत N के किसी अवयव x के लिए y = 4x + 3 है। इससे निष्कर्ष निकलता है कि है। 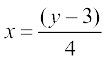 अब
अब  द्वारा g : Y → N को परिभाषित कीजिए। इस प्रकाण्र gof(x) = g(f(x)) = g(4x + 3) =
द्वारा g : Y → N को परिभाषित कीजिए। इस प्रकाण्र gof(x) = g(f(x)) = g(4x + 3) =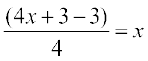 तथा fog(y) = f(g(y)) = ε
तथा fog(y) = f(g(y)) = ε = y – 3 + 3 = y है। इससे स्पष्ट होता है कि gof = IN तथा fog = IY, जिसका तात्पर्य यह हुआ कि f व्युत्क्रमणीय है और फलन g फलन f का प्रतिलोम है।ण्
= y – 3 + 3 = y है। इससे स्पष्ट होता है कि gof = IN तथा fog = IY, जिसका तात्पर्य यह हुआ कि f व्युत्क्रमणीय है और फलन g फलन f का प्रतिलोम है।ण्
उदाहरण 24 मान लीजिए कि Y = {n2 : n ∈ N} ⊂ Nहै। फलन f : N → Y जहाँ f(n) = n2 पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम भी ज्ञात कीजिए।
हल Y का एक स्वेच्छ अवयव y, n2 के रूप का है जहाँ n ∈ N. इसका तात्पर्य यह है कि n = 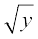 इससे g(y) =
इससे g(y) = 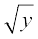 द्वारा परिभाषित एक फलन g : Y → N प्राप्त होता है। अब gof(n) = g(n2) =
द्वारा परिभाषित एक फलन g : Y → N प्राप्त होता है। अब gof(n) = g(n2) =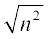 = n और fog(y) =
= n और fog(y) =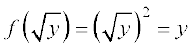 , जिससे प्रमाणित होता है कि gof = IN तथा fog = IYहै। अतः f व्युत्क्रमणीय है तथा f –1 = g.
, जिससे प्रमाणित होता है कि gof = IN तथा fog = IYहै। अतः f व्युत्क्रमणीय है तथा f –1 = g.
उदाहरण 25 मान लीजिए कि f : N → R , f(x) = 4x2 + 12x + 15 द्वारा परिभाषित एक फलन है। सिद्ध कीजिए कि f : N→ S, जहाँ S, f का परिसर है, व्युत्क्रमणीय है। f का प्रतिलोम भी ज्ञात कीजिए।
हल मान लीजिए कि f के परिसर का y एक स्वेच्छ अवयव है। इसलिए y = 4x2 + 12x + 15, जहाँ x ∈ N. इसका तात्पर्य यह है कि y = (2x + 3)2 + 6. अतएव 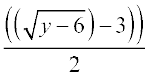 .
.
अब, एक फलन g : S → N , g(y) =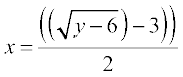 द्वारा परिभाषित कीजिए।
द्वारा परिभाषित कीजिए।
इस प्रकार gof(x) = g(f(x)) = g(4x2 + 12x + 15) = g((2x + 3)2 + 6))
= 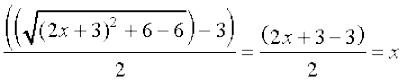
और fog (y) = 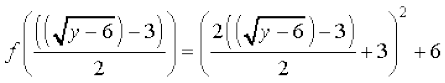
=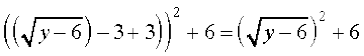 =
=  = y – 6 + 6 = y.
= y – 6 + 6 = y.
अतः gof = Iछ तथा fog =Isहै। इसका तात्पर्य यह है कि f व्युत्क्रमणीय है तथा f –1 = g है।
उदाहरण 26 तीन फलन f : N → N, g : N → N तथा h : N → R पर विचार कीजिए जहाँ f(x) = 2x, g(y) = 3y + 4 तथा h(z) = sin z, 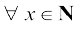 x, y तथा z ∈ N. सिद्ध कीजिए कि ho(gof) = (hog) of.
x, y तथा z ∈ N. सिद्ध कीजिए कि ho(gof) = (hog) of.
हल यहाँ
ho(gof) (x) = h(gof (x)) = h(g(f(x))) = h(g(2x))
ण्= h(3(2x) + 4) = h(6x + 4) = sin (6x + 4),  छ
छ
साथ ही, ((hog)of ) (x) = (hog) (f(x)) = (hog) (2x) = h(g(2x))
= h(3(2x) + 4) = h(6x + 4) = sin (6x + 4),  x ∈ N
x ∈ N
इससे प्रमाणित होता है कि ho(gof) = (hog)of
यह परिणाम व्यापक स्थिति में भी सत्य होता है।
प्रमेय 1 यदि f : X → Y, g : Y → Z तथाा h : Z → S तीन फलन हैं, तो ho(gof) = (hog)of
उपपत्ति यहाँ हम देखते हैं कि
ho(gof) (x) = h(gof(x)) = h(g(f(x))),  x in X
x in X
तथा (hog) of (x) = hog(f (x)) = h(g(f(x))),  x in X
x in X
अतः ho(gof) = (hog)of
उदाहरण 27 f : {1, 2, 3} → {a, b, c} तथा g : {a, b, c} → {सेब, गेंद, बिल्ली} f(1) = a, f(2) = b, f(3) = c, g(a) = सेब, g(b) = गेंद तथा g(c) = बिल्ली द्वारा परिभाषित फलनों पर विचार कीजिए। सिद्ध कीजिए कि f, g और gof व्युत्क्रमणीय हैं। f –1, g–1 तथा (gof)–1 ज्ञात कीजिए तथा प्रमाणित कीजिए कि (gof) –1 = f–1og–1 है।
हल नोट कीजिए कि परिभाषा द्वारा f और g एकैकी आच्छादी फलन हैं। मान लीजिए कि f –1: {a, b, c} → (1, 2, 3} और g–1 : {सेब, गेंद, बिल्ली} → {a, b, c} इस प्रकार परिभाषित हैं कि f –1{a} = 1, f –1{b} = 2, f –1{c} = 3, g–1{सेब} = a, g–1{गेंद} = b और g–1{बिल्ली} = c. यह सत्यापित करना सरल है कि f–1of = I{1,2,3}, fo f –1 = I{a, b, c}, g–1og = I{a, b, c} और gog–1 = ID, जहाँ D = {सेब, गेंद, बिल्ली}। अब, gof : {1, 2, 3} → {सेब, गेंद, बिल्ली} gof(1) = सेब, gof(2) = गेंद, gof(3) = बिल्ली द्वारा प्रदत्त है।
हम (gof)–1 : {सेब, गेंद, बिल्ली} → {1, 2, 3} को (gof)–1 (सेब) = 1, (gof)–1 (गेंद) = 2 तथा (gof)–1 (बिल्ली) = 3 द्वारा परिभाषित कर सकते हैं। यह सरलता से प्रमाणित किया जा सकता है कि (gof)–1 o (gof) = I{1, 2, 3} तथा (gof) o (gof)–1 = ID होगा।
इस प्रकार प्रमाणित होता है कि f, g तथा gof व्युत्क्रमणीय हैं।
अब f–1og–1 (सेब) = f –1(g–1(सेब)) = f –1(a) = 1 = (gof)–1 (सेब)
f–1og–1 (गेंद) = f –1(g–1(गेंद)) = f –1(b) = 2 = (gof)–1 (गेंद) तथा
f–1og–1 (बिल्ली) = f –1(g–1(बिल्ली)) = f –1(c) = 3 = (gof)–1 (बिल्ली)
अतः (gof)–1 = f –1og–1
उपर्युक्त परिणाम व्यापक स्थिति में भी सत्य होता है।
प्रमेय 2 मान लीजिए कि f : X → Y तथा g : Y → Z दो व्युत्क्रमणीय फलन हैं, तो gof भी व्युत्क्रमणीय होगा तथा (gof)–1 = f–1og–1
उपपत्ति gof को व्युत्क्रमणीय तथा (gof)–1 = f–1og–1, को सिद्ध करने के लिए यह प्रमाणित करना पर्याप्त है कि (f–1og–1)o(gof) = Ix तथा (gof)o(f–1og–1) = Iz है।
अब (f–1og–1)o(gof) = ((f–1og–1) og) of, प्रमेय 1 द्वारा
= (f–1o(g–1og)) of, प्रमेय 1 द्वारा
= (f–1 oIY) of, g–1 की परिभाषा द्वारा
= Ix
इसी प्रकार, यह प्रमाणित किया जा सकता है कि, (gof) (f –1 og –1) = Iz
उदाहरण 28 मान लीजिए कि S = {1, 2, 3}है। निर्धारित कीजिए कि क्या नीचे परिभाषित फलन f : S → S के प्रतिलोम फलन हैं। f–1, ज्ञात कीजिए यदि इसका अस्तित्व है।
(a) f = {(1, 1), (2, 2), (3, 3)}
(b) f = {(1, 2), (2, 1), (3, 1)}
(c) f = {(1, 3), (3, 2), (2, 1)}
हल
(a) यह सरलता से देखा जा सकता है कि f एकैकी आच्छादी है, इसलिए f व्युत्क्रमणीय है तथा f का प्रतिलोम f–1 = {(1, 1), (2, 2), (3, 3)} = f द्वारा प्राप्त होता है।
(b) क्योंकि f(2) = f(3) = 1, अतएव f एकैकी नहीं है, अतः f व्युत्क्रमणीय नहीं है।
(c) यह सरलता पूर्वक देखा जा सकता है कि f एकैकी तथा आच्छादक है, अतएव f व्युत्क्रमणीय है तथा f–1 = {(3, 1), (2, 3), (1, 2)}है।
प्रश्नावली 1.3
1. मान लीजिए कि f : {1, 3, 4} → {1, 2, 5} तथा g : {1, 2, 5} → {1, 3}, f = {(1, 2), (3, 5), (4, 1)} तथा g = {(1, 3), (2, 3), (5, 1)} द्वारा प्रदत्त हैं। gof ज्ञात कीजिए।
2. मान लीजिए कि f, g तथा h, R से R तक दिए फलन हैं। सिद्ध कीजिए कि
(f + g)oh = foh + goh
(f . g)oh = (foh) . (goh)
3. gof तथा fog ज्ञात कीजिए, यदि
(i) f(x) = | x | तथा g(x) = | 5x – 2 |
(ii) f(x) = 8x3 तथा g(x) = 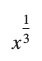
4. यदि f(x) = 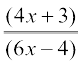 ए
ए 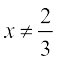 , तो सिद्ध कीजिए कि सभी
, तो सिद्ध कीजिए कि सभी  ए के लिए fof(x) = x है। f का प्रतिलोम फलन क्या है?
ए के लिए fof(x) = x है। f का प्रतिलोम फलन क्या है?
5. कारण सहित बतलाइए कि क्या निम्नलिखित फलनों के प्रतिलोम हैंः
(i) f : {1, 2, 3, 4} → {10} जहाँ
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
(ii) g : {5, 6, 7, 8} → {1, 2, 3, 4} जहाँ
g = {(5, 4), (6, 3), (7, 4), (8, 2)}
(iii) h : {2, 3, 4, 5} → {7, 9, 11, 13} जहाँ
h = {(2, 7), (3, 9), (4, 11), (5, 13)}
6. सिद्ध कीजिए कि f : [–1, 1] → R, f(x) = , द्वारा प्रदत्त फलन एकैकी है। फलन f : [–1, 1] → ( f का परिसर), का प्रतिलोम फलन ज्ञात कीजिए।
, द्वारा प्रदत्त फलन एकैकी है। फलन f : [–1, 1] → ( f का परिसर), का प्रतिलोम फलन ज्ञात कीजिए।
(संकेत y ∈ परिसर f, के लिए, [–1, 1] के किसी x के अंतर्गत y = f(x) = 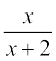 , अर्थात् x =
, अर्थात् x = 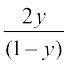
7. f(x) = 4x + 3 द्वारा प्रदत्त फलन f : R → R पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम फलन ज्ञात कीजिए।
8. f(x) = x2 + 4 द्वारा प्रदत्त फलन f : R+ → [4, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f का प्रतिलोम f–1 , f–1(y) = ), द्वारा प्राप्त होता है, जहाँ R+ सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है।
), द्वारा प्राप्त होता है, जहाँ R+ सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है।
9. f(x) = 9x2 + 6x – 5 द्वारा प्रदत्त फलन f : R+ → [– 5, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f–1(y) = है।
है।
10. मान लीजिए कि f : X → Y एक व्युत्क्रमणीय फलन है। सिद्ध कीजिए कि f का प्रतिलोम फलन अद्वितीय (unique) है। (संकेतः कल्पना कीजिए कि f के दो प्रतिलोम फलन g1 तथा g2 हैं। तब सभी y ∈ Y के लिए fog1(y) = 1Y(y) = fog2(y) है। अब f के एकैकी गुण का प्रयोग कीजिए)
11. f : {1, 2, 3} → {a, b, c}, f(1) = a, f(2) = b तथा f(3) = c. द्वारा प्रदत्त फलन f पर विचार कीजिए। f–1 ज्ञात कीजिए और सिद्ध कीजिए कि (f–1)–1 = f है।
12. मान लीजिए कि f: X → Y एक व्युत्क्रमणीय फलन हैं सिद्ध कीजिए कि f –1 का प्रतिलोम f, है अर्थात् (f–1)–1 = f है।
13. यदि f: R → R, f(x) = , द्वारा प्रदत्त है, तो fof(x) बराबर है।
, द्वारा प्रदत्त है, तो fof(x) बराबर है।
(A) 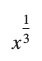 (B) x3 (C) x (D) (3 – x3)
(B) x3 (C) x (D) (3 – x3)
14. मान लीजिए कि f(x) = द्वारा परिभाषित एक फलन f : R –  → R है। f का प्रतिलोम, अर्थात् प्रतिचित्र (Map) g : परिसर f → R –
→ R है। f का प्रतिलोम, अर्थात् प्रतिचित्र (Map) g : परिसर f → R –  , निम्नलिखित में से किसके द्वारा प्राप्त होगाः
, निम्नलिखित में से किसके द्वारा प्राप्त होगाः
(A) 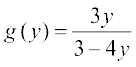 (B)
(B) 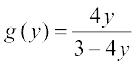
(C) 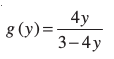 (D)
(D) 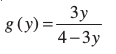
1.5 द्वि-आधारी संक्रियाएँ (Binary Operations)
अपने स्कूल के दिनों में ही आप चार मूल संक्रियाओं, नामतः योग, अंतर, गुणा तथा भाग से परिचित हो चुके हैं। इन संक्रियाओं की मुख्य विशेषता यह है कि दो दी गई संख्याओं a तथा b, से हम एक संख्या a + b या a – b या ab या  , b ≠ 0 को संबद्ध (Associate) कर देते हैं। यह बात नोट कीजिए कि, एक समय में, केवल दो संख्याएँ ही जोड़ी या गुणा की जा सकती हैं। जब हमें तीन संख्याओं को जोड़ने की आवश्यकता होती है, तो हम पहले दो संख्याओं को जोड़ते हैं और प्राप्त योगफल को फिर तीसरी संख्या में जोड़ देते हैं। अतः योग, गुणा, अंतर तथा भाग द्विआधारी संक्रिया के उदाहरण हैं, क्योंकि ‘द्विआधारी’ का अर्थ है ‘दो आधार वाली’। यदि हम एक व्यापक परिभाषा चाहते हैं, जिसमेे यह चारों संक्रियाएँ भी आ जाती हैं, तो हमें संख्याओं के समुच्चय के स्थान पर एक स्वेच्छ समुच्चय X लेना चाहिए और तब व्यापक रूप से द्विआधारी संक्रिया, कुछ अन्य नहीं अपितु, X के दो अवयवों a तथा b को X के ही किसी अवयव से संबद्ध करना है। इससे निम्नलिखित व्यापक परिभाषा प्राप्त होती हैः
, b ≠ 0 को संबद्ध (Associate) कर देते हैं। यह बात नोट कीजिए कि, एक समय में, केवल दो संख्याएँ ही जोड़ी या गुणा की जा सकती हैं। जब हमें तीन संख्याओं को जोड़ने की आवश्यकता होती है, तो हम पहले दो संख्याओं को जोड़ते हैं और प्राप्त योगफल को फिर तीसरी संख्या में जोड़ देते हैं। अतः योग, गुणा, अंतर तथा भाग द्विआधारी संक्रिया के उदाहरण हैं, क्योंकि ‘द्विआधारी’ का अर्थ है ‘दो आधार वाली’। यदि हम एक व्यापक परिभाषा चाहते हैं, जिसमेे यह चारों संक्रियाएँ भी आ जाती हैं, तो हमें संख्याओं के समुच्चय के स्थान पर एक स्वेच्छ समुच्चय X लेना चाहिए और तब व्यापक रूप से द्विआधारी संक्रिया, कुछ अन्य नहीं अपितु, X के दो अवयवों a तथा b को X के ही किसी अवयव से संबद्ध करना है। इससे निम्नलिखित व्यापक परिभाषा प्राप्त होती हैः
परिभाषा 10 किसी समुच्चय A में एक द्विआधारी संक्रिया ∗, एक फलन ∗ : A × A → A है। हम ∗ (a, b) को a ∗ b द्वारा निरूपित करते हैं।
उदाहरण 29 सिद्ध कीजिए कि R में योग, अंतर और गुणा द्विआधारी संक्रियाएँ हैं, किंतु भाग R में द्विआधारी संक्रिया नहीं है। साथ ही सिद्ध कीजिए कि भाग ऋणेतर वास्तविक संख्याओं के समुच्चय R में द्विआधारी संक्रिया है।
हल
+ : R × R → R , (a, b) → a + b द्वारा परिभाषित है
– : R × R → R, (a, b) → a – b द्वारा परिभाषित है
× : R × R → R, (a, b) → ab द्वारा परिभाषित है
क्योंकि ‘+’, ‘–’ और ‘×’ फलन हैं, अतः ये R में द्विआधारी संक्रियाएँ हैं।
परंतु ÷ : R × R → R, (a, b) →  , एक फलन नहीं है, क्योंकि b = 0 के लिए
, एक फलन नहीं है, क्योंकि b = 0 के लिए  परिभाषित नहीं है।
परिभाषित नहीं है।
तथापि ÷ : R∗ × R∗ → R∗, (a, b) →  द्वारा परिभाषित एक फलन है और इसलिए यह R∗ में एक द्विआधारी संक्रिया है।
द्वारा परिभाषित एक फलन है और इसलिए यह R∗ में एक द्विआधारी संक्रिया है।
उदाहरण 30 सिद्ध कीजिए कि अंतर (व्यवकलन) तथा भाग N में द्विआधारी संक्रिया नहीं है।
हल – : N × N → N, (a, b) → a – b, द्वारा प्रदत्त एक द्विआधारी संक्रिया नहीं है, क्योंकि ‘–’ के अंतर्गत (3, 5) का प्रतिबिंब 3 – 5 = – 2 ∉ N. इसी प्रकार, ÷ N × N → N, (a, b) →  द्वारा प्रदत्त एक द्विआधारी संक्रिया नहीं है, क्योंकि ‘÷’ के अंतर्गत (3¸5) का प्रतिबिंब 3 ÷ 5=
द्वारा प्रदत्त एक द्विआधारी संक्रिया नहीं है, क्योंकि ‘÷’ के अंतर्गत (3¸5) का प्रतिबिंब 3 ÷ 5=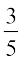 ∉ N.
∉ N.
उदाहरण 31 सिद्ध कीजिए कि ∗ : R × R → R, (a, b) → a + 4b2 द्वारा प्रदत्त एक द्विआधारी संक्रिया है।
हल चूँकि ∗ प्रत्येक युग्म (a, b) को R के एक अद्वितीय अवयव a + 4b2 तक ले जाता है, अतः ∗ R में एक द्विआधारी संक्रिया है।
उदाहरण 32 मान लीजिए कि P, किसी प्रदत्त समुच्चय X के समस्त उप समुच्चयों का, समुच्चय है। सिद्ध कीजिए कि ∪ : P × P → P, (A, B) → A ∪ B द्वारा प्रदत्त तथा ∩ : P × P → P, (A, B) → A ∩ B द्वारा परिभाषित फलन, P में द्विआधारी संक्रियाएँ हैं।
हल क्योंकि सम्मिलन संक्रिया (Union Operation) ∪, P × P के प्रत्येक युग्म (A, B) को P के एक अद्वितीय अवयव A ∪ B तक ले जाती है, इसलिए ∪, समुच्चय P में एक द्विआधारी संक्रिया है। इसी प्रकार सर्वनिष्ठ (Intersection) संक्रिया ∩ , P × P के प्रत्येक युग्म (A, B) को P के एक अद्वितीय अवयव A ∩ B तक ले जाती है, अतएव ∩, समुच्चय P में एक द्विआधारी संक्रिया है।
उदाहरण 33 सिद्ध कीजिए कि (a, b) → अधिकतम {a, b} द्वारा परिभाषित 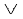 : R × R → R तथा (a, b) → निम्नतम {a, b} द्वारा परिभाषित
: R × R → R तथा (a, b) → निम्नतम {a, b} द्वारा परिभाषित  : R × R → R द्विआधारी संक्रियाएँ हैं।
: R × R → R द्विआधारी संक्रियाएँ हैं।
हल क्योंकि 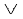 , R × R के प्रत्येक युग्म (a, b) को समुच्चय R के एक अद्वितीय अवयव, नामतः a तथा b में से अधिकतम, पर ले जाता है, अतएव
, R × R के प्रत्येक युग्म (a, b) को समुच्चय R के एक अद्वितीय अवयव, नामतः a तथा b में से अधिकतम, पर ले जाता है, अतएव  एक द्विआधारी संक्रिया हैं इसी प्रकार के तर्क द्वारा यह कहा जा सकता है कि
एक द्विआधारी संक्रिया हैं इसी प्रकार के तर्क द्वारा यह कहा जा सकता है कि 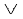 भी एक द्विआधारी संक्रिया है।
भी एक द्विआधारी संक्रिया है।
टिप्पणी 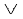 (4, 7) = 7,
(4, 7) = 7, 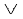 (4, – 7) = 4,
(4, – 7) = 4,  (4, 7) = 4 तथा
(4, 7) = 4 तथा  (4, – 7) = – 7 है।
(4, – 7) = – 7 है।
जब किसी समुच्चय A में अवयवों की संख्या कम होती है, तो हम समुच्चय A में एक द्विआधारी संक्रिया ∗ को एक सारणी द्वारा व्यक्त कर सकते हैं, जिसे संक्रिया ∗ की संक्रिया सारणी कहते हैं। उदाहरणार्थ A = {1, 2, 3} पर विचार कीजिए। तब उदाहरण 33 में परिभाषित A में संक्रिया 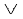 निम्नलिखित सारणी (सारणी 1.1) द्वारा व्यक्त की जा सकती है। यहाँ संक्रिया सारणी में
निम्नलिखित सारणी (सारणी 1.1) द्वारा व्यक्त की जा सकती है। यहाँ संक्रिया सारणी में 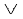 (1, 3) = 3,
(1, 3) = 3, 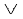 (2, 3) = 3,
(2, 3) = 3,  (1, 2) = 2.
(1, 2) = 2.
सारणी 1.1
यहाँ संक्रिया सारणी में 3 पंक्तियाँ तथा 3 स्तंभ हैं, जिसमें (i, j)वीं प्रविष्टि समुच्चय A के i वें तथा j वें अवयवों में से अधिकतम होता है। इसका व्यापकीकरण किसी भी सामान्य संक्रिया * : A × A → A के लिए किया जा सकता है। यदि A = {a1, a2, ..., an}है तो संक्रिया सारणी में n पंक्तियाँ तथा n स्तम्भ होंगे तथा (i, j)वीं प्रविष्टि ai ∗ aj होगी। विलोमतः n पंक्तियों तथा n स्तंभों वाले प्रदत्त किसी संक्रिया सारणी, जिसकी प्रत्येक प्रविष्टि A = {a1, a2, ..., an}, का एक अवयव है, के लिए हम एक द्विआधारी संक्रिया ∗ : A × A → A परिभाषित कर सकते हैं, इस प्रकार कि
ai ∗ aj = संक्रिया सारणी की iवीं पंक्ति तथा jवें स्तम्भ की प्रविष्टियाँ हैं।
परिभाषा 11 समुच्चय X में एक द्विआधारी संक्रिया ∗ क्रमविनिमेय (Commutative) कहलाती है, यदि प्रत्येक a, b ∈ X के लिए a ∗ b = b ∗ a हो।
उदाहरण 34 सिद्ध कीजिए कि + : R × R → R तथा × : R × R → R क्रमविनिमेय द्विआधारी संक्रियाएँ है, परंतु – : R × R → R तथा ÷ : R∗ × R∗ → R∗ क्रमविनिमेय नहीं हैं।
हल क्योंकि a + b = b + a तथा a × b = b × a,  a, b ∈ R, अतएव ‘+’ तथा ‘×’ क्रमविनिमेय द्विआधारी संक्रियाएँ हैं। तथापि ‘–’ क्रमविनिमेय नहीं है, क्योंकि 3 – 4 ≠ 4 – 3.
a, b ∈ R, अतएव ‘+’ तथा ‘×’ क्रमविनिमेय द्विआधारी संक्रियाएँ हैं। तथापि ‘–’ क्रमविनिमेय नहीं है, क्योंकि 3 – 4 ≠ 4 – 3.
इसी प्रकार 3 ÷ 4 ≠ 4 ÷ 3, जिससे स्पष्ट होता है कि ‘÷’ क्रमविनिमेय नहीं है।
उदाहरण 35 सिद्ध कीजिए कि a ∗ b = a + 2b द्वारा परिभाषित ∗ : R × R → R क्रमविनिमेय नहीं है।
हल क्योंकि 3 ∗ 4 = 3 + 8 = 11 और 4 ∗ 3 = 4 + 6 = 10, अतः संक्रिया ∗ क्रमविनिमेय नहीं है।
यदि हम समुच्चय X के तीन अवयवों को X में परिभाषित किसी द्विआधारी संक्रिया के द्वारा संबद्ध करना चाहते हैं तो एक स्वाभाविक समस्या उठती है। व्यंजक a ∗ b ∗ c का अर्थ (a ∗ b) ∗ c अथवा a ∗ (b ∗ c) हो सकता है और यह दोनों व्यजंक, आवश्यक नहीं है, कि समान हों। उदाहरणार्थ (8 – 5) – 2 ≠ 8 – (5 – 2). इसलिए, तीन संख्याओं 8, 5 और 3 का द्विआधारी संक्रिया ‘व्यवकलन’ के द्वारा संबंध अर्थहीन है जब तक कि कोष्ठक (Bracket) का प्रयोग नहीं किया जाए। परंतु योग की संक्रिया में, 8 + 5 + 2 का मान समान होता है, चाहे हम इसे ( 8 + 5) + 2 अथवा 8 + (5 + 2) प्रकार से लिखें। अतः तीन या तीन से अधिक संख्याओं का योग की संक्रिया द्वारा संबंध, बिना कोष्ठकों के प्रयोग किए भी, अर्थपूर्ण है। इससे निम्नलिखित परिभाषा प्राप्त होती हैः
परिभाषा 12 एक द्विआधारी संक्रिया ∗ : A × A → A साहचर्य (Associative) कहलाती है, यदि (a ∗ b) ∗ c = a ∗ (b ∗ c),  a, b, c, ∈ A.
a, b, c, ∈ A.
उदाहरण 36 सिद्ध कीजिए कि R में योग तथा गुणा साहचर्य द्विआधारी संक्रियाएँ हैं। परंतु व्यवकलन तथा भाग R में साहचर्य नहीं है।
हल योग तथा गुणा साहचर्य हैं, क्योंकि (a + b) + c = a + (b + c) तथा (a×b) × c = a × (b × c),  a, b, c ∈ R है। तथापि अंतर तथा भाग साहचर्य नहीं हैं, क्योंकि (8 – 5) – 3 ≠ 8 – (5 – 3) तथा (8 ÷ 5) ÷ 3 ≠ 8 ÷ (5 ÷ 3).
a, b, c ∈ R है। तथापि अंतर तथा भाग साहचर्य नहीं हैं, क्योंकि (8 – 5) – 3 ≠ 8 – (5 – 3) तथा (8 ÷ 5) ÷ 3 ≠ 8 ÷ (5 ÷ 3).
उदाहरण 37 सिद्ध कीजिए कि a ∗ b → a + 2b द्वारा प्रदत्त ∗ : R × R → R साहचर्य नहीं है।
हल संक्रिया ∗ साहचर्य नहीं है, क्योंकि
(8 ∗ 5) ∗ 3 = (8 + 10) ∗ 3 = (8 + 10) + 6 = 24,
जबकि 8 ∗ (5 ∗ 3) = 8 ∗ (5 + 6) = 8 ∗ 11 = 8 + 22 = 30.
टिप्पणी किसी द्विआधारी संक्रिया का साहचर्य गुणधर्म इस अर्थ में अत्यंत महत्वपूर्ण है कि हम व्यंजक a1 ∗ a2 ∗ ... ∗ an लिख सकते हैं, क्योंकि इस गुणधर्म के कारण यह संदिग्ध नहीं रह जाता है। परंतु इस गुणधर्म के अभाव में, व्यंजक a1 ∗ a2 ∗ ... ∗ an संदिग्ध (Ambiguous) रहता है, जब तक कि कोष्ठक का प्रयोग न किया जाए। स्मरण कीजिए कि पूर्ववर्ती कक्षाओं में, जब कभी अंतर या भाग की संक्रियाएँ अथवा एक से अधिक संक्रियाएँ संपन्न की गईं थीं, तब कोष्ठकों का प्रयोग किया गया था।
R में द्विआधारी संक्रिया '+'’ से संबंधित संख्या शून्य (zero) की एक रोचक विशेषता यह है कि a + 0 = a = 0 + a,  a ∈ R, अर्थात्, किसी भी संख्या में शून्य को जोड़ने पर वह संख्या अपरिवर्तित रहती है। परंतु गुणा की स्थिति में यह भूमिका (Role) संख्या 1 द्वारा अदा की जाती है, क्योंकि a × 1 = a = 1 × a,
a ∈ R, अर्थात्, किसी भी संख्या में शून्य को जोड़ने पर वह संख्या अपरिवर्तित रहती है। परंतु गुणा की स्थिति में यह भूमिका (Role) संख्या 1 द्वारा अदा की जाती है, क्योंकि a × 1 = a = 1 × a,  a ∈ R है। इससे निम्नलिखित परिभाषा प्राप्त होती है।
a ∈ R है। इससे निम्नलिखित परिभाषा प्राप्त होती है।
परिभाषा 13 किसी प्रदत्त द्विआधारी संक्रिया ∗ : A × A → A, के लिए, एक अवयव e ∈ A, यदि इसका अस्तित्व है, तत्समक (Identity) कहलाता है, यदि a ∗ e = a = e ∗ a,  a ∈ A हो।
a ∈ A हो।
उदाहरण 38 सिद्ध कीजिए कि R में शून्य (0) योग का तत्समक है तथा 1 गुणा का तत्समक है। परंतु संक्रियाओं – : R × R → R और ÷ : R∗ × R∗ → R∗ के लिए कोई तत्समक अवयव नहीं है।
हल a + 0 = 0 + a = a और a × 1 = a = 1 × a,  a ∈ R का तात्पर्य है कि 0 तथा 1 क्रमशः ‘+’ तथा ‘×’, के तत्समक अवयव हैं। साथ ही R में एेसा कोई अवयव e नहीं है कि a – e = e – a,
a ∈ R का तात्पर्य है कि 0 तथा 1 क्रमशः ‘+’ तथा ‘×’, के तत्समक अवयव हैं। साथ ही R में एेसा कोई अवयव e नहीं है कि a – e = e – a,  a ∈ R हो। इसी प्रकार हमें R∗ में कोई एेसा अवयव e नहीं मिल सकता है कि a ÷ e = e ÷ a
a ∈ R हो। इसी प्रकार हमें R∗ में कोई एेसा अवयव e नहीं मिल सकता है कि a ÷ e = e ÷ a , a ∈ R∗ हो। अतः ‘–’ तथा ‘÷’ के तत्समक अवयव नहीं होते हैं।
, a ∈ R∗ हो। अतः ‘–’ तथा ‘÷’ के तत्समक अवयव नहीं होते हैं।
टिप्पणी R में शून्य (0) धन संक्रिया का तत्समक है, किंतु यह N में धन संक्रिया का तत्समक नहीं है, क्योंकि 0 ∉ N वास्तव में N में धन संक्रिया का कोई तत्समक नहीं होता है।
हम पुनः देखते हैं कि धन संक्रिया + : R × R → R के लिए, किसी प्रदत्त a ∈ R से संबंधित R में – a का अस्तित्व इस प्रकार है कि a + (– a) = 0 (‘+’ का तत्समक) = (– a) + a. इसी प्रकार R में गुणा संक्रिया के लिए, किसी प्रदत्त a ∈ R, a ≠ 0 से संबंधित हम R में  को इस प्रकार चुन सकते हैं कि a ×
को इस प्रकार चुन सकते हैं कि a ×  = 1(‘×’ का तत्समक) =
= 1(‘×’ का तत्समक) =  × a हो। इससे निम्नलिखित परिभाषा प्राप्त होती है।
× a हो। इससे निम्नलिखित परिभाषा प्राप्त होती है।
परिभाषा 14 A में तत्समक अवयव e वाले एक प्रदत्त द्विआधारी संक्रिया ∗ : A × A → A के लिए किसी अवयव a ∈ A को संक्रिया ∗ के संदर्भ में व्युत्क्रमणीय कहते हैं, यदि A में एक एेसे अवयव b का अस्तित्व है कि a ∗ b = e = b ∗ a हो तो b को a का प्रतिलोम (Inverse) कहते हैं, जिसे प्रतीक a–1 द्वारा निरूपित करते हैं।
उदाहरण 39 सिद्ध कीजिए कि R में धन संक्रिया ‘+’ के लिए – a का प्रतिलोम a है और R में गुणा संक्रिया ‘×’ के लिए a ≠ 0 का प्रतिलोम  है।
है।
हल क्योंकि a + (– a) = a – a = 0 तथा (– a) + a = 0, इसलिए – a धन संक्रिया के लिए a का प्रतिलोम है। इसी प्रकार, a ≠ 0, के लिए a × = 1 =
= 1 =  × a, जिसका तात्पर्य यह है कि
× a, जिसका तात्पर्य यह है कि  गुणा संक्रिया के लिए a का प्रतिलोम है।
गुणा संक्रिया के लिए a का प्रतिलोम है।
उदाहरण 40 सिद्ध कीजिए कि N में धन संक्रिया '+' के लिए a ∈ N का प्रतिलोम – a नहीं है और N में गुणा संεक्रया ‘×’ के लिए a ∈ N, a ≠ 1 का प्रतिलोम  नहीं है।
नहीं है।
हल क्योंकि – a ∉ N, इसलिए N में धन संक्रिया के लिए a का प्रतिलोम – a नहीं हो सकता है यद्यपि – a, प्रतिबंध a + (– a) = 0 = (– a) + a को संतुष्ट करता है। इसी प्रकार, N में a ≠ 1 के लिए  ∉ N, जिसका अर्थ यह है कि 1 के अतिरिक्त N के किसी भी अवयव का प्रतिलोम N में गुणा संक्रिया के लिए नहीं होता है।
∉ N, जिसका अर्थ यह है कि 1 के अतिरिक्त N के किसी भी अवयव का प्रतिलोम N में गुणा संक्रिया के लिए नहीं होता है।
उदाहरण 34, 36, 38 तथा 39 से स्पष्ट होता है कि R में धन संक्रिया क्रमविनिमय तथा साहचर्य द्विआधारी संक्रिया है, जिसमें 0 तत्समक अवयव तथा a ∈ R,  a का प्रतिलोम अवयव – a होता है।
a का प्रतिलोम अवयव – a होता है।
प्रश्नावली 1.4
1. निर्धारित कीजिए कि क्या निम्नलिखित प्रकार से परिभाषित प्रत्येक संक्रिया ∗ से एक द्विआधारी संक्रिया प्राप्त होती है या नहीं। उस दशा में जब ∗ एक द्विआधारी संक्रिया नहीं है, औचित्य भी बतलाइए।
(i) Z+ में, a ∗ b = a – b द्वारा परिभाषित संक्रिया ∗
(ii) Z+ में, a ∗ b = ab द्वारा परिभाषित संक्रिया ∗
(iii) R में, संक्रिया ∗, a ∗ b = ab2 द्वारा परिभाषित
(iv) Z+ में, संक्रिया ∗, a ∗ b = |a – b| द्वारा परिभाषित
(v) Z+ में, संक्रिया ∗, a ∗ b = a द्वारा परिभाषित
2. निम्नलिखित परिभाषित प्रत्येक द्विआधारी संक्रिया ∗ के लिए निर्धारित कीजिए कि क्या ∗ द्विआधारी क्रमविनिमय है तथा क्या ∗ साहचर्य है।
(i) Z में, a ∗ b = a – b द्वारा परिभाषित
(ii) Q में, a ∗ b = ab + 1 द्वारा परिभाषित
(iii) Q में, a ∗ b = 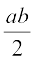 द्वारा परिभाषित
द्वारा परिभाषित
(iv) Z+ में, a ∗ b = 2ab द्वारा परिभाषित
(v) Z+ में, a ∗ b = ab द्वारा परिभाषित
(vi) R – {– 1} में, a ∗ b =  द्वारा परिभाषित
द्वारा परिभाषित
3. समुच्चय {1, 2, 3, 4, 5} में a  b = निम्नतम {a, b} द्वारा परिभाषित द्विआधारी संक्रिया पर विचार कीजिए। संक्रिया
b = निम्नतम {a, b} द्वारा परिभाषित द्विआधारी संक्रिया पर विचार कीजिए। संक्रिया  के लिए संक्रिया सारणी लिखिए।
के लिए संक्रिया सारणी लिखिए।
4. समुच्चय {1, 2, 3, 4, 5} में, निम्नलिखित संक्रिया सारणी (सारणी 1.2) द्वारा परिभाषित, द्विआधारी संक्रिया ∗ पर विचार कीजिए तथा
(i) (2 ∗ 3) ∗ 4 तथा 2 ∗ (3 ∗ 4) का परिकलन कीजिए।
(ii) क्या ∗ क्रमविनिमेय है?
(iii) (2 ∗ 3) ∗ (4 ∗ 5) का परिकलन कीजिए।
(संकेतः निम्न सारणी का प्रयोग कीजिए।)
सारणी 1.2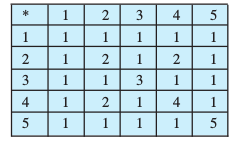
5. मान लीजिए कि समुच्चय {1, 2, 3, 4, 5} में एक द्विआधारी संक्रिया ∗′, a ∗′ b = a तथा b का HCF द्वारा परिभाषित है। क्या संक्रिया ∗′ उर्पयुक्त प्रश्न 4 में परिभाषित संक्रिया ∗ के समान है? अपने उत्तर का औचित्य भी बतलाइए।
6. मान लीजिए कि N में एक द्विआधारी संक्रिया ∗, a ∗ b = a तथा b का LCM द्वारा परिभाषित है। निम्नलिखित ज्ञात कीजिएः
(i) 5 ∗ 7, 20 ∗ 16 (ii) क्या संक्रिय ∗ क्रमविनिमेय है ?
(iii) क्या ∗ साहचर्य है? (iv) N में ∗ का तत्समक अवयव ज्ञात कीजिए
(v) N के कौन से अवयव ∗ संक्रिया के लिए व्युत्क्रमणीय हैं?
7. क्या समुच्चय {1, 2, 3, 4, 5} में a ∗ b = a तथा b का LCM द्वारा परिभाषित ∗ एक द्विआधारी संक्रिया है? अपने उत्तर का औचित्य भी बतलाइए।
8. मान लीजिए कि N में a ∗ b = a तथा b का HCF द्वारा परिभाषित एक द्विआधारी संक्रिया है। क्या ∗ क्रमविनिमेय है? क्या ∗ साहचर्य है? क्या N में इस द्विआधारी संक्रिया के तत्समक का अस्तित्व है?
9. मान लीजिए कि परिमेय संख्याओं के समुच्चय Q में निम्नलिखित प्रकार से परिभाषित ∗ एक द्विआधारी संक्रिया हैः
(i) a ∗ b = a – b (ii) a ∗ b = a2 + b2
(iii) a ∗ b = a + ab (iv) a ∗ b = (a – b)2
(v) a ∗ b = 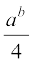 (vi) a ∗ b = ab2
(vi) a ∗ b = ab2
ज्ञात कीजिए कि इनमें से कौन सी संक्रियाएँ क्रमविनिमेय हैं और कौनसी साहचर्य हैं।
10. प्रश्न 9 में दी गई संक्रियाओं में किसी का तत्समक है, वह बतलाइए।
11. मान लीजिए कि A = N × N है तथा A में (a, b) ∗ (c, d) = (a + c, b + d) द्वारा परिभाषित एक द्विआधारी संक्रिया है। सिद्ध कीजिए कि ∗ क्रमविनिमय तथा साहचर्य है। A में ∗ का तत्समक अवयव, यदि कोई है, तो ज्ञात कीजिए।
12. बतलाइए कि क्या निम्नलिखित कथन सत्य हैं या असत्य हैं। औचित्य भी बतलाइए।
(i) समुच्चय N में किसी भी स्वेच्छ द्विआधारी संक्रिया ∗ के लिए a ∗ a = a,  a ∈ N
a ∈ N
(ii) यदि N में ∗ एक क्रमविनिमेय द्विआधारी संक्रिया है, तो a ∗ (b ∗ c) = (c ∗ b) ∗ a
13. a ∗ b = a3 + b3 प्रकार से परिभाषित N में एक द्विआधारी संक्रिया ∗ पर विचार कीजिए। अब निम्नलिखित में से सही उत्तर का चयन कीजिए
(A) ∗ साहचर्य तथा क्रमविनिमेय दोनों है
(B) ∗ क्रमविनिमेय है किंतु साहचर्य नहीं है
(C) ∗ साहचर्य है किंतु क्रमविनिमेय नहीं है
(D) ∗ न तो क्रमविनिमेय है और न साहचर्य है
विविध उदाहरण
उदाहरण 41 यदि R1 तथा R2 समुच्चय A में तुल्यता संबंध हैं, तो सिद्ध कीजिए कि R1 ∩ R2 भी एक तुल्यता संबंध है।
हल क्योंकि R1 तथा R2 तुल्यता संबंध है इसलिए (a, a) ∈ R1, तथा (a, a) ∈ R2,  a ∈ A इसका तात्पर्य है कि (a, a) ∈ R1 ∩ R2,
a ∈ A इसका तात्पर्य है कि (a, a) ∈ R1 ∩ R2, a, जिससे सिद्ध होता है कि R1 ∩ R2 स्वतुल्य है। पुनः (a, b) ∈ R1 ∩ R2 ⇒ (a, b) ∈ R1 तथा (a, b) ∈ R2 ⇒ (b, a) ∈ R1 तथा (b, a) ∈ R2 ⇒ (b, a) ∈ R1 ∩ R2, अतः R1 ∩ R2 सममित है। इसी प्रकार (a, b) ∈ R1 ∩ R2 तथा (b, c) ∈ R1 ∩ R2 ⇒ (a, c) ∈ R1 तथा (a, c) ∈ R2 ⇒ (a, c) ∈ R1 ∩ R2. इससे सिद्ध होता है कि R1 ∩ R2 संक्रामक है। अतः R1 ∩ R2 एक तुल्यता संबंध है।
a, जिससे सिद्ध होता है कि R1 ∩ R2 स्वतुल्य है। पुनः (a, b) ∈ R1 ∩ R2 ⇒ (a, b) ∈ R1 तथा (a, b) ∈ R2 ⇒ (b, a) ∈ R1 तथा (b, a) ∈ R2 ⇒ (b, a) ∈ R1 ∩ R2, अतः R1 ∩ R2 सममित है। इसी प्रकार (a, b) ∈ R1 ∩ R2 तथा (b, c) ∈ R1 ∩ R2 ⇒ (a, c) ∈ R1 तथा (a, c) ∈ R2 ⇒ (a, c) ∈ R1 ∩ R2. इससे सिद्ध होता है कि R1 ∩ R2 संक्रामक है। अतः R1 ∩ R2 एक तुल्यता संबंध है।
उदाहरण 42 मान लीजिए कि समुच्चय A में धन पूर्णांकों के क्रमित युग्मों (ordered pairs)का एक संबंध R, (x, y) R (u, v), यदि और केवल यदि, xv = yu द्वारा परिभाषित है। सिद्ध कीजिए कि R एक तुल्यता संबंध है।
हल स्पष्टतया (x, y) R (x, y), (x, y) ∈ A, क्योंकि xy = yx है। इससे स्पष्ट होता है कि R स्वतुल्य है। पुनः (x, y) R (u, v) ⇒ xv = yu ⇒ uy = vx और इसलिए (u, v) R (x, y)है। इससे स्पष्ट होता है कि R सममित है। इसी प्रकार (x, y) R (u, v) तथा (u, v) R (a, b) ⇒ xv = yu तथा ub = va ⇒
(x, y) ∈ A, क्योंकि xy = yx है। इससे स्पष्ट होता है कि R स्वतुल्य है। पुनः (x, y) R (u, v) ⇒ xv = yu ⇒ uy = vx और इसलिए (u, v) R (x, y)है। इससे स्पष्ट होता है कि R सममित है। इसी प्रकार (x, y) R (u, v) तथा (u, v) R (a, b) ⇒ xv = yu तथा ub = va ⇒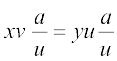
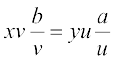 ⇒ xb = ya और इसलिए (x, y) R (a, b)है। अतएव R संक्रामक है। अतः R एक तुल्यता संबंध है।
⇒ xb = ya और इसलिए (x, y) R (a, b)है। अतएव R संक्रामक है। अतः R एक तुल्यता संबंध है।
उदाहरण 43 मान लीजिए कि X = {1, 2, 3, 4, 5, 6, 7, 8, 9}है। मान लीजिए कि X में R1 = {(x, y) : x – y संख्या 3 से भाज्य है} द्वारा प्रदत्त एक संबंध R1 है तथा R2 = {(x, y): {x, y} ⊂ {1, 4, 7} या {x, y} ⊂ {2, 5, 8} या {(x, y} ⊂ {3, 6, 9} द्वारा प्रदत्त X में एक अन्य संबंध R2 है। सिद्ध कीजिए कि R1 = R2है।
हल नोट कीजिए कि {1, 4, 7}, {2, 5, 8} तथा {3, 6, 9} समुच्चयों में से प्रत्येक का अभिलक्षण (characterstic) यह है कि इनके किसी भी दो अवयवों का अंतर 3 का एक गुणज है। इसलिए (x, y) ∈ R1 ⇒ x – y संख्या 3 का गुणज है ⇒ {x, y} ⊂ {1, 4, 7} या {x, y} ⊂ {2, 5, 8} या {x, y} ⊂ {3, 6, 9} ⇒ (x, y) ∈ R2, अतः R1 ⊂ R2. इसी प्रकार {x, y} ∈ R2 ⇒ {x, y} ⊂ {1, 4, 7} या {x, y} ⊂ {2, 5, 8} या {x, y} ⊂ {3, 6, 9} ⇒ x – y संख्या 3 से भाज्य है ⇒ {x, y} ∈ R1. इससे स्पष्ट होता है कि R2 ⊂ R1. अतः R1 = R2 है।
उदाहरण 44 मान लीजिए कि f : X → Y एक फलन है। X में R = {(a, b): f(a) = f(b)} द्वारा प्रदत्त एक संबंध R परिभाषित कीजिए। जाँचिए कि क्या R एक तुल्यता संबंध है।
हल प्रत्येक a ∈ X के लिए (a, a) ∈ R, क्योंकि f(a) = f(a), जिससे स्पष्ट होता है कि R स्वतुल्य है। इसी प्रकार, (a, b) ∈ R ⇒ f(a) = f(b) ⇒ f(b) = f(a) ⇒ (b, a) ∈ R. इसलिए R सममित है। पुनः (a, b) ∈ R तथा (b, c) ∈ R ⇒ f(a) = f(b) तथा f(b) = f(c) ⇒ f(a) = f(c) ⇒ (a, c) ∈ R, जिसका तात्पर्य है कि R संक्रामक है। अतः R एक तुल्यता संबंध है।
उदाहरण 45 निर्धारित कीजिए कि समुच्चय R में प्रदत्त निम्नलिखित द्विआधारी संक्रियाओं में से कौन सी साहचर्य हैं और कौन सी क्रमविनिमेय हैं।
(a) a ∗ b = 1,  a, b ∈ R (b) a ∗ b =
a, b ∈ R (b) a ∗ b =
 a, b ∈ R
a, b ∈ R
हल
(a) स्पष्टतया परिभाषा द्वारा a ∗ b = b ∗ a = 1,  a, b ∈ R. साथ ही (a ∗ b) ∗ c = (1 ∗ c) =1 तथा a ∗ (b ∗ c) = a ∗ (1) = 1,
a, b ∈ R. साथ ही (a ∗ b) ∗ c = (1 ∗ c) =1 तथा a ∗ (b ∗ c) = a ∗ (1) = 1,  a, b, c ∈ R अतः R साहचर्य तथा क्रमविनिमेय दोनों है।
a, b, c ∈ R अतः R साहचर्य तथा क्रमविनिमेय दोनों है।
(b) a ∗ b = 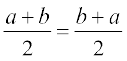 = b ∗ a, ∀ a, b ∈ R, जिससे स्पष्ट होता है कि ∗ क्रमविनिमेय है। पुनः
= b ∗ a, ∀ a, b ∈ R, जिससे स्पष्ट होता है कि ∗ क्रमविनिमेय है। पुनः
(a ∗ b) ∗ c = 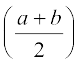 ∗ c.
∗ c.
=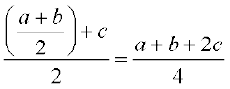 .
.
किंतु a ∗ (b ∗ c) =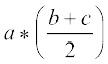
= 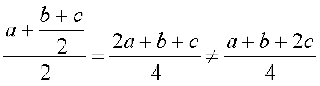 (सामान्यतः)
(सामान्यतः)
अतः ∗ साहचर्य नहीं है।
उदाहरण 46 समुच्चय A = {1, 2, 3} से स्वयं तक सभी एकैकी फलन की संख्या ज्ञात कीजिए।
हल {1, 2, 3} से स्वयं तक एकैकी फलन केवल तीन प्रतीकों 1, 2, 3 का क्रमचय है। अतः {1, 2, 3} से स्वयं तक के प्रतिचित्रों (Maps) की कुल संख्या तीन प्रतीकों 1, 2 , 3 के क्रमचयों की कुल संख्या के बराबर होगी, जो कि 3! = 6 है।
उदाहरण 47 मान लीजिए कि A = {1, 2, 3} है। तब सिद्ध कीजिए कि एेसे संबंधों की संख्या चार है, जिनमें (1, 2) तथा (2, 3) हैं और जो स्वतुल्य तथा संक्रामक तो हैं किंतु सममित नहीं हैं।
हल {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)}, (1, 2) तथा (2, 3) अवयवों वाला वह सबसे छोटा संबंध R1 है, जो स्वतुल्य तथा संक्रामक है किंतु सममित नहीं है। अब यदि R1 में युग्म (2, 1) बढ़ा दें, तो प्राप्त संबंध R2 अब भी स्वतुल्य तथा संक्रामक है परंतु सममित नहीं है। इसी प्रकार, हम R1 में (3, 2) बढ़ा कर R3 प्राप्त कर सकते हैं, जिनमें अभीष्ट गुणधर्म हैं। तथापि हम R1 में किन्हीं दो युग्मों (2, 1), (3, 2) या एक युग्म (3, 1) को नहीं बढ़ा सकते हैं, क्योंकि एेसा करने पर हम, संक्रामकता बनाए रखने के लिए, शेष युग्म को लेने के लिए बाध्य हो जाएँगे और इस प्रक्रिया द्वारा प्राप्त संबंध सममित भी हो जाएगा, जो अभीष्ट नहीं है। अतः अभीष्ट संबंधों की कुल संख्या तीन है।
उदाहरण 48 सिद्ध कीजिए कि समुच्चय {1, 2, 3} में (1, 2) तथा (2, 1) को अन्तर्विष्ट करने वाले तुल्यता संबंधों की संख्या 2 है।
हल (1, 2) तथा (2, 1) को अंतर्विष्ट करने वाला सबसे छोटा तुल्यता संबंध R1, {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)} है। अब केवल 4 युग्म, नामतः (2, 3), (3, 2), (1, 3) तथा (3, 1) शेष बचते हैं। यदि हम इनमें से किसी एक को, जैसे (2, 3) को R1 में अंतर्विष्ट करते हैं, तो सममित के लिए हमें (3, 2) को भी लेना पड़ेगा, साथ ही संक्रमकता हेतु हम (1, 3) तथा (3, 1) को लेने के लिए बाध्य होंगे। अतः R1 से बड़ा तुल्यता संबंध केवल सार्वत्रिक संबंध है। इससे स्पष्ट होता है कि (1, 2) तथा (2, 1) को अंतर्विष्ट करने वाले तुल्यता संबंधों की कुल संख्या दो है।
उदाहरण 49 सिद्ध कीजिए कि {1, 2} में एेसी द्विआधारी संक्रियाओं की संख्या केवल एक है, जिसका तत्समक 1 हैं तथा जिसके अंतर्गत 2 का प्रतिलोम 2 है।
हल {1, 2} में कोई द्विआधारी संक्रिया ∗, {1, 2} × {1, 2} से {1, 2} में एक फलन है, अर्थात् {(1, 1), (1, 2), (2, 1), (2, 2)} से {1, 2} तक एक फलन। क्योंकि अभीष्ट द्विआधारी संक्रिया ∗ के लिए तत्समक अवयव 1 है, इसलिए, ∗ (1, 1) = 1, ∗ (1, 2) = 2, ∗ (2, 1) = 2 और युग्म (2, 2) के लिए ही केवल विकल्प शेष रह जाता है। क्योंकि 2 का प्रतिलोम 2 है, इसलिए ∗ (2, 2) आवश्यक रूप से 1 के बराबर है। अतः अभीष्ट द्विआधारी संक्रियाओं की संख्या केवल एक है।
उदाहरण 50 तत्समक फलन IN : N → N पर विचार कीजिए, जो IN (x) = x,  x ∈ N द्वारा परिभाषित है। सिद्ध कीजिए कि, यद्यपि IN आच्छादक है किंतु निम्नलिखित प्रकार से परिभाषित फलन IN + IN : N → N आच्छादक नहीं है
x ∈ N द्वारा परिभाषित है। सिद्ध कीजिए कि, यद्यपि IN आच्छादक है किंतु निम्नलिखित प्रकार से परिभाषित फलन IN + IN : N → N आच्छादक नहीं है
(IN + IN) (x) = IN (x) + IN (x) = x + x = 2x
हल स्पष्टतया IN आच्छादक है किंतु IN + IN आच्छादक नहीं है। क्योंकि हम सहप्रांत N में एक अवयव 3 ले सकते हैं जिसके लिए प्रांत N में किसी एेसे x का अस्तित्व नहीं है कि (IN + IN) (x) = 2x = 3 हो।
उदाहरण 51 f(x) = sin x द्वारा प्रदत्त फलन f : 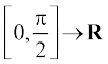 तथा g(x) = cos x द्वारा प्रदत्त फलन g :
तथा g(x) = cos x द्वारा प्रदत्त फलन g : 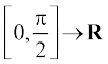 पर विचार कीजिए। सिद्ध कीजिए कि f तथा g एकैकी है, परंतु f + g एकैकी नहीं है।
पर विचार कीजिए। सिद्ध कीजिए कि f तथा g एकैकी है, परंतु f + g एकैकी नहीं है।
हल क्योंकि 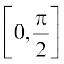 , के दो भिन्न-भिन्न अवयवों x1 तथा x2 के लिए sin x1 ≠ sin x2 तथा cos x1 ≠ cos x2 इसलिए f तथा g दोनों ही आवश्यक रूप से एकैकी हैं। परंतु (f+g) (0) =sin0 + cos0 = 1 तथा (f + g)
, के दो भिन्न-भिन्न अवयवों x1 तथा x2 के लिए sin x1 ≠ sin x2 तथा cos x1 ≠ cos x2 इसलिए f तथा g दोनों ही आवश्यक रूप से एकैकी हैं। परंतु (f+g) (0) =sin0 + cos0 = 1 तथा (f + g)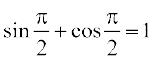 है। अतः f + g एकैकी नहीं है।
है। अतः f + g एकैकी नहीं है।
अध्याय 1 पर विविध प्रश्नावली
1. मान लीजिए कि f : R → R , f(x) = 10x + 7 द्वारा परिभाषित फलन है। एक एेसा फलन g : R → R ज्ञात कीजिए जिसके लिए gof = fog = 1R हो।
2. मान लीजिए कि f: W→W, f(n) =n – 1, यदि n विषम है तथा f(n) = n + 1, यदि n सम है, द्वारा परिभाषित है। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम ज्ञात कीजिए। यहाँ W समस्त पूर्णांकों का समुच्चय है।
3. यदि f : R → R जहाँ f(x) = x2 – 3x + 2 द्वारा परिभाषित है तो f (f(x)) ज्ञात कीजिए।
4. सिद्ध कीजिए कि f : R → {x ∈ R : – 1 < x < 1} जहाँ 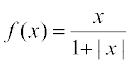 , x ∈ R द्वारा परिभाषित फलन एकैकी तथा आच्छादक है।
, x ∈ R द्वारा परिभाषित फलन एकैकी तथा आच्छादक है।
5. सिद्ध कीजिए कि f(x) = x3 द्वारा प्रदत्त फलन f : R → R एकैक (Injective) है।
6. दो फलनों f : N → Z तथा g : Z → Z के उदाहरण दीजिए जो इस प्रकार हों कि, gof एकैक है परंतु g एकैक नहीं है।
(संकेतन: f(x) = x तथा g(x) = |x| पर विचार कीजिए।)
7. दो फलनों f : N → N तथा g : N → N के उदाहरण दीजिए, जो इस प्रकार हों कि, gof आच्छादक है किंतु f आच्छादन नहीं है।
(संकेत: f(x) = x + 1 तथा  पर विचार कीजिए।
पर विचार कीजिए।
8. एक अरिक्त समुच्चय X दिया हुआ है। P(X) जो कि X के समस्त उपसमुच्चयों का समुच्चय है, पर विचार कीजिए। निम्नलिखित तरह से P(X) में एक संबंध R परिभाषित कीजिएः
P(X) में उपसमुच्चयों A, B के लिए, ARB, यदि और केवल यदि A ⊂ B है। क्या R, P(X) में एक तुल्यता संबंध है? अपने उत्तर का औचित्य भी लिखिए।
9. किसी प्रदत्त अरिक्त समुच्चय X के लिए एक द्विआधारी संक्रिया ∗ : P(X) × P(X) → P(X) पर विचार कीजिए, जो A ∗ B = A ∩ B,  A, B ∈ P(X) द्वारा परिभाषित है, जहाँ P(X) समुच्चय X का घात समुच्चय (Power set) है। सिद्ध कीजिए कि इस संक्रिया का तत्समक अवयव X है तथा संक्रिया ∗ के लिए P(X) में केवल X व्युत्क्रमणीय अवयव है।
A, B ∈ P(X) द्वारा परिभाषित है, जहाँ P(X) समुच्चय X का घात समुच्चय (Power set) है। सिद्ध कीजिए कि इस संक्रिया का तत्समक अवयव X है तथा संक्रिया ∗ के लिए P(X) में केवल X व्युत्क्रमणीय अवयव है।
10. समुच्चय {1, 2, 3, ... , n} से स्वयं तक के समस्त आच्छादक फलनों की संख्या ज्ञात कीजिए।
11. मान लीजिए कि S = {a, b, c} तथा T = {1, 2, 3} है। S से T तक के निम्नलिखित फलनों F के लिए F–1 ज्ञात कीजिए, यदि उसका अस्तित्व हैः
(i) F = {(a, 3), (b, 2), (c, 1)} (ii) F = {(a, 2), (b, 1), (c, 1)}
12. a ∗b = |a – b| तथा a o b = a,  a, b ∈ R द्वारा परिभाषित द्विआधारी संक्रियाओं ∗ : R × R → R तथा o : R × R → R पर विचार कीजिए। सिद्ध कीजिए कि ∗ क्रमविनिमेय है परंतु साहचर्य नहीं है, o साहचर्य है परंतु क्रमविनिमेय नहीं है। पुनः सिद्ध कीजिए कि सभी a, b, c ∈ R के लिए a ∗ (b o c) = (a ∗ b) o (a ∗ c) है। [यदि एेसा होता है, तो हम कहते हैं कि संक्रिया ∗ संक्रिया o पर वितरित (Distributes) होती है।] क्या o संक्रिया ∗ पर वितरित होती है? अपने उत्तर का औचित्य भी बतलाइए।
a, b ∈ R द्वारा परिभाषित द्विआधारी संक्रियाओं ∗ : R × R → R तथा o : R × R → R पर विचार कीजिए। सिद्ध कीजिए कि ∗ क्रमविनिमेय है परंतु साहचर्य नहीं है, o साहचर्य है परंतु क्रमविनिमेय नहीं है। पुनः सिद्ध कीजिए कि सभी a, b, c ∈ R के लिए a ∗ (b o c) = (a ∗ b) o (a ∗ c) है। [यदि एेसा होता है, तो हम कहते हैं कि संक्रिया ∗ संक्रिया o पर वितरित (Distributes) होती है।] क्या o संक्रिया ∗ पर वितरित होती है? अपने उत्तर का औचित्य भी बतलाइए।
13. किसी प्रदत्त अरिक्त समुच्चय X के लिए मान लीजिए कि ∗ : P(X) × P(X) → P(X), जहाँ A * B = (A – B) ∪ (B – A),  A, B ∈ P(X) द्वारा परिभाषित है। सिद्ध कीजिए कि रिक्त समुच्चय φ, संक्रिया ∗ का तत्समक है तथा P(X) के समस्त अवयव A व्युत्क्रमणीय है,ं इस प्रकार कि A–1 = A. (संकेत : (A – φ) ∪ (φ – A) = A. तथा (A – A) ∪ (A – A) = A ∗ A = φ).
A, B ∈ P(X) द्वारा परिभाषित है। सिद्ध कीजिए कि रिक्त समुच्चय φ, संक्रिया ∗ का तत्समक है तथा P(X) के समस्त अवयव A व्युत्क्रमणीय है,ं इस प्रकार कि A–1 = A. (संकेत : (A – φ) ∪ (φ – A) = A. तथा (A – A) ∪ (A – A) = A ∗ A = φ).
14. निम्नलिखित प्रकार से समुच्चय {0, 1, 2, 3, 4, 5} में एक द्विआधारी संक्रिया ∗ परिभाषित कीजिए

सिद्ध कीजिए कि शून्य (0) इस संक्रिया का तत्समक है तथा समुच्चय का प्रत्येक अवयव a≠0 व्युत्क्रमणीय है, इस प्रकार कि 6 – a, a का प्रतिलोम है।
15. मान लीजिए कि A = {– 1, 0, 1, 2}, B = {– 4, – 2, 0, 2} और f, g : A → B, क्रमशः f(x) = x2 – x, x ∈ A तथा 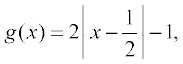
 x ∈ A द्वारा परिभाषित फलन हैं। क्या f तथा g समान हैं? अपने उत्तर का औचित्य भी बतलाइए। (संकेत: नोट कीजिए कि दो फलन f : A→ B तथा g : A → B समान कहलाते हैं यदि f(a) = g(a)
x ∈ A द्वारा परिभाषित फलन हैं। क्या f तथा g समान हैं? अपने उत्तर का औचित्य भी बतलाइए। (संकेत: नोट कीजिए कि दो फलन f : A→ B तथा g : A → B समान कहलाते हैं यदि f(a) = g(a)  a ∈ A हो।
a ∈ A हो।
16. यदि A = {1, 2, 3} हो तो एेसे संबंध जिनमें अवयव (1, 2) तथा (1, 3) हों और जो स्वतुल्य तथा सममित हैं किंतु संक्रामक नहीं है, की संख्या है
(A) 1 (B) 2 (C) 3 (D) 4
17. यदि A = {1, 2, 3} हो तो अवयव (1, 2) वाले तुल्यता संबंधों की संख्या है।
(A) 1 (B) 2 (C) 3 (D) 4
18. मान लीजिए कि f : R → R है तब निम्नलिखित प्रकार से परिभाषित चिह्न फलन (Signum Function) है।
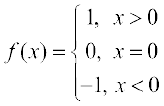
तथा g : R → R, g(x) = [x], द्वारा प्रदत्त महत्तम पूर्णांक फलन है, जहाँ [x], x से कम या x के बराबर पूर्णांक है, तो क्या fog तथा gof , अंतराल [0, 1] में संपाती (coincide) हैं?
19. समुच्चय {a, b} में द्विआधारी संक्रियाओं की संख्या है
(A) 10 (B) 16 (C) 20 (D) 8
सारांश
इस अध्याय में, हमने विविध प्रकार के संबंधों, फलनों तथा द्विआधारी संक्रियाओं का अध्ययन किया है। इस अध्याय की मुख्य विषय-वस्तु निम्नलिखित हैः
♦ X में, R = φ ⊂ X × X द्वारा प्रदत्त संबंध R, रिक्त संबंध होता है।
♦ X में, R = X × X द्वारा प्रदत्त संबंध R, सार्वत्रिक संबंध है।
♦ X में, एेसा संबंध कि  a ∈ X, (a, a) ∈ R, स्वतुल्य संबंध है।
a ∈ X, (a, a) ∈ R, स्वतुल्य संबंध है।
♦ X में, इस प्रकार का संबंध R, जो प्रतिबंध (a, b) ∈ R का तात्पर्य है कि (b, a) ∈ R को संतुष्ट करता है सममित संबंध है।
♦ X में, प्रतिबंध R, (a, b) ∈ R तथा (b, c) ∈ R ⇒ (a, c) ∈ R  a, b, c ∈ X को संतुष्ट करने वाला संबंध R संक्रामक संबंध है।
a, b, c ∈ X को संतुष्ट करने वाला संबंध R संक्रामक संबंध है।
♦ X में, संबंध R, जो स्वतुल्य, सममित तथा संक्रामक है, तुल्यता संबंध है।
♦ X में, किसी तुल्यता संबंध R के लिए a ∈ X के संगत तुल्यता वर्ग [a], X का वह उपसमुच्चय है जिसके सभी अवयव a से संबंधित हैं।
♦ एक फलन f : X → Y एकैकी (अथवा एकैक) फलन है, यदि f(x1) = f(x2) ⇒ x1 = x2,  x1, x2 ∈ X
x1, x2 ∈ X
♦ एक फलन f : X → Y आच्छादक (अथवा आच्छादी) फलन है, यदि किसी प्रदत्त y ∈ Y, ∃ x ∈ X, इस प्रकार कि f(x) = y
♦ एक फलन f : X → Y एकैकी तथा आच्छादक (अथवा एकैकी आच्छादी) फलन है, यदि f एकैकी तथा अच्छादक दोनों है।
♦ फलन f : A → B तथा g : B → C का संयोजन, फलन gof : A → C है, जो gof(x) = g(f(x)),  x ∈ A द्वारा प्रदत्त है।
x ∈ A द्वारा प्रदत्त है।
♦ एक फलन f : X → Y व्युत्क्रमणीय है, यदि ∃ g : Y → X, इस प्रकार कि gof = 1X तथा fog = 1Y.
♦ एक फलन f : X → Y व्युत्क्रमणीय है, यदि और केवल यदि f एकैकी तथा आच्छादक है।
♦ किसी प्रदत्त परिमित समुच्चय X के लिए फलन f : X → X एकैकी (तदानुसार आच्छादक) होता है, यदि और केवल यदि f आच्दछादक (तदानुसार एकैकी) है। यह किसी परिमित समुच्चय का अभिलाक्षणिक गुणधर्म (Characterstic Property) है। यह अपरिमित समुच्चय के लिए सत्य नहीं है।
♦ A में एक द्विआधारी संक्रिया ∗, A × A से A तक एक फलन ∗ है।
♦ एक अवयव e ∈ X, द्विआधारी संक्रिया ∗ : X × X → X, का तत्समक अवयव है, यदि a ∗ e = a = e ∗ a,  a ∈ X
a ∈ X
♦ कोई अवयव e ∈ X द्विआधारी संक्रिया ∗ : X × X → X, के लिए व्युत्क्रमणीय
होता है, यदि एक एेसे b ∈ X का अस्तित्व है कि a ∗ b = e = b ∗ a है जहाँ
e द्विआधारी संक्रिया ∗ का तत्समक है। अवयव b, a का प्रतिलोम कहलाता है, जिसे a–1 से निरूपित करते हैं।
♦ X का एक संक्रिया ∗, क्रमविनिमय है यदि a ∗ b = b ∗ a,  a, b ∈ X
a, b ∈ X
♦ X में, एक संक्रिया ∗, साहचर्य है यदि (a ∗ b) ∗ c = a ∗ (b ∗ c),a, b, c ∈ X
एेतिहासिक पृष्ठभूमि
फलन की संकल्पना, R. Descartes (सन् 1596-1650 ई.) से प्रारंभ हो कर एक लंबे अंतराल में विकसित हुई है। Descartes ने सन् 1637 ई. में अपनी पांडुलिपि “Geometrie” में शब्द ‘फलन’ का प्रयोग, ज्यामितीय वक्रों, जैसे अतिपरवलय (Hyperbola
