Table of Contents
अध्याय 2
प्रतिलोम त्रिकोणमितीय फलन
(Inverse Trigonometric Functions)
 Mathematics, in general, is fundamentally the science of self-evident things— FELIX KLEIN
Mathematics, in general, is fundamentally the science of self-evident things— FELIX KLEIN
2.1 भूमिका (प्दजतवकनबजपवद)

Arya Bhatta
अध्याय 1 में, हम पढ़ चुके हैं कि किसी फलन f का प्रतीक f–1 द्वारा निरूपित प्रतिलोम (Inverse) फलन का अस्तित्व केवल तभी है यदि f एकैकी तथा आच्छादक हो। बहुत से फलन एेसे हैं जो एकैकी, आच्छादक या दोनों ही नहीं हैं, इसलिए हम उनके प्रतिलोमों की बात नहीं कर सकते हैं। कक्षा XI में, हम पढ़ चुके हैं कि त्रिकोणमितीय फलन अपने स्वाभाविक (सामान्य) प्रांत और परिसर में एकैकी तथा आच्छादक नहीं होते हैं और इसलिए उनके प्रतिलोमों का अस्तित्व नहीं होता है। इस अध्याय में हम त्रिकोणमितीय फलनों के प्रांतों तथा परिसरों पर लगने वाले उन प्रतिबंधों (Restrictions) का अध्ययन करेंगे, जिनसे उनके प्रतिलोमों का अस्तित्व सुनिश्चित होता है और आलेखों द्वारा प्रतिलोमों का अवलोकन करेंगे। इसके अतिरिक्त इन प्रतिलोमों के कुछ प्रारंभिक गुणधर्म (Properties) पर भी विचार करेंगे।
प्रतिलोम त्रिकोणमितीय फलन, कलन (Calculus) में एक महत्वपूर्ण भूमिका निभाते हैं, क्योंकि उनकी सहायता से अनेक समाकल (Integrals) परिभाषित होते हैं। प्रतिलोम त्रिकोणमितीय फलनों की संकल्पना का प्रयोग विज्ञान तथा अभियांत्रिकी (Engineering) में भी होता है।
2.2 आधारभूत संकल्पनाएँ (ठेंपब ब्वदबमचजे)
कक्षा XI, में, हम त्रिकोणमितीय फलनों का अध्ययन कर चुके हैं, जो निम्नलिखित प्रकार से परिभाषित हैं
sine फलन, अर्थात्, sin : R → [–1,1]
cosine फलन, अर्थात्, cos : R → [–1,1]
tangent फलन, अर्थात्, tan रू R – { x : x = (2n + 1) 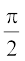 , n ∈ ρ} → R
, n ∈ ρ} → R
cotangent फलन, अर्थात्, cot : R – { x : x = nπ, n ∈ Z} → R
secant फलन, अर्थात् sec: R – { x : x = (2n+1) 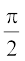 , n ∈ Z} → R – (– 1, 1)
, n ∈ Z} → R – (– 1, 1)
cosecant फलन, अर्थात्, cosec: R – { x : x = nπ, n ∈ Z} → R – (– 1, 1)
हम अध्याय 1 में यह भी सीख चुके हैं कि यदि f : X→ल् इस प्रकार है कि f(x) = y एक एकैकी तथा आच्छादक फलन हो तो हम एक अद्वितीय फलन g : Y→X इस प्रकार परिभाषित कर सकते हैं किg (y) = x, जहाँ x ∈ X तथा y=f(ग), y ∈ Y है। यहाँ g का प्रांत =f का परिसर और g का परिसर =f का प्रांत। फलन g को फलन f का प्रतिलोम कहते हैं और इसे f–1 द्वारा निरूपित करते हैं। साथ ही g भी एकैकी तथा आच्छादक होता है और g का प्रतिलोम फलन f होता हैं अतः g–1=(f –1)–1=f इसके साथ ही
(f–1of ) (x) = f–1(f (x))=f –1(y) = x
और (fof –1)(y) = f(f –1(y)) = f(x) = y
क्योंकि sine फलन का प्रांत वास्तविक संख्याओं का समुच्चय है तथा इसका परिसर संवृत अंतराल [–1, 1] है। यदि हम इसके प्रांत को 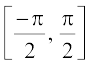 में सीमित (प्रतिबंधित) कर दें, तो यह परिसर [–1, 1] वाला, एक एकैकी तथा आच्छादक फलन हो जाता है। वास्तव में, sine फलन, अंतरालों
में सीमित (प्रतिबंधित) कर दें, तो यह परिसर [–1, 1] वाला, एक एकैकी तथा आच्छादक फलन हो जाता है। वास्तव में, sine फलन, अंतरालों 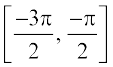 ]
]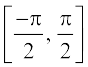
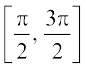 इत्यादि में, से किसी में भी सीमित होने से, परिसर [–1, 1] वाला, एक एकैकी तथा आच्छादक फलन हो जाता है। अतः हम इनमें से प्रत्येक अंतराल में, sine फलन के प्रतिलोम फलन को sin–1 (arc sine function) द्वारा निरूपित करते हैं। अतः sin–1 एक फलन है, जिसका प्रांत [– 1, 1] है, और जिसका परिसर
इत्यादि में, से किसी में भी सीमित होने से, परिसर [–1, 1] वाला, एक एकैकी तथा आच्छादक फलन हो जाता है। अतः हम इनमें से प्रत्येक अंतराल में, sine फलन के प्रतिलोम फलन को sin–1 (arc sine function) द्वारा निरूपित करते हैं। अतः sin–1 एक फलन है, जिसका प्रांत [– 1, 1] है, और जिसका परिसर 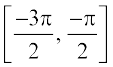 ]
]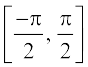 या
या 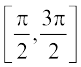 इत्यादि में से कोई भी अंतराल हो सकता है। इस प्रकार के प्रत्येक अंतराल के संगत हमें फलन sin–1 की एक शाखा (Branch) प्राप्त होती है। वह शाखा, जिसका परिसर
इत्यादि में से कोई भी अंतराल हो सकता है। इस प्रकार के प्रत्येक अंतराल के संगत हमें फलन sin–1 की एक शाखा (Branch) प्राप्त होती है। वह शाखा, जिसका परिसर 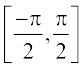 है, मुख्य शाखा (मुख्य मान शाखा) कहलाती है, जब कि परिसर के रूप में अन्य अंतरालों से sin–1 की भिन्न-भिन्न शाखाएँ मिलती हैं। जब हम फलन sin–1 का उल्लेख करते हैं, तब हम इसे प्रांत [–1, 1] तथा परिसर
है, मुख्य शाखा (मुख्य मान शाखा) कहलाती है, जब कि परिसर के रूप में अन्य अंतरालों से sin–1 की भिन्न-भिन्न शाखाएँ मिलती हैं। जब हम फलन sin–1 का उल्लेख करते हैं, तब हम इसे प्रांत [–1, 1] तथा परिसर 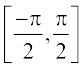 वाला फलन समझते हैं। इसे हम sin–1: [–1, 1] →
वाला फलन समझते हैं। इसे हम sin–1: [–1, 1] →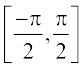 लिखते हैं।
लिखते हैं।
प्रतिलोम फलन की परिभाषा द्वारा, यह निष्कर्ष निकलता है कि sin (sin–1 x) = x , यदि – 1 ≤ x ≤1 तथा sin–1 (sin x) = x यदि 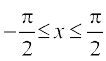 है। दूसरे शब्दों में, यदि y = sin–1 x हो तो sin y = x होता है।
है। दूसरे शब्दों में, यदि y = sin–1 x हो तो sin y = x होता है।

आकृति 2.1 (i)

आकृति 2.1 (ii)
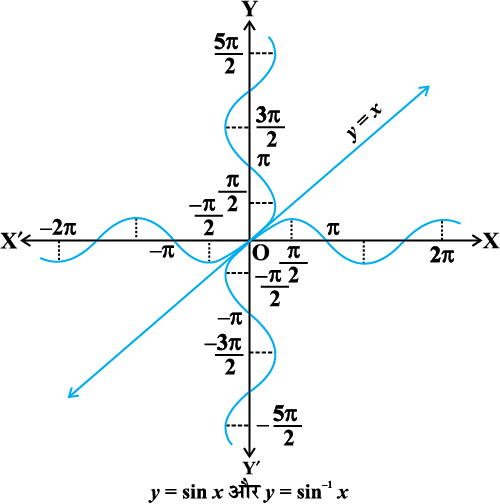
आकृति 2.1 (iii)
टिप्पणी
(ii) यह दिखलाया जा सकता है कि प्रतिलोम फलन का आलेख, रेखा y = x के परितः (Along), संगत मूल फलन के आलेख को दर्पण प्रतिबिंब (Mirror Image), अर्थात् परावर्तन (Reflection) के रूप में प्राप्त किया जा सकता है। इस बात की कल्पना, y = sin x तथा y = sin–1 x के उन्हीं अक्षों (Same axes) पर, प्रस्तुत आलेखों से की जा सकती है (आकृति 2.1 (iii) ) ।
sine फलन के समान cosine फलन भी एक एेसा फलन है जिसका प्रांत वास्तविक संख्याओं का समुच्चय है और जिसका परिसर समुच्चय [–1, 1] है। यदि हम cosine फलन के प्रांत को अंतराल [0, π] में सीमित कर दें तो यह परिसर [–1, 1] वाला एक एकैकी तथा आच्छादक फलन हो जाता है। वस्तुतः, cosine फलन, अंतरालों [–π, 0], [0,π], [πए2π] इत्यादि में से किसी में भी सीमित होने से, परिसर [–1, 1] वाला एक एकैकी आच्छादी (Bijective) फलन हो जाता है। अतः हम इन में से प्रत्येक अंतराल में cosine फलन के प्रतिलोम को परिभाषित कर सकते हैं। हम cosine फलन के प्रतिलोम फलन को cos–1 (arc cosine function) द्वारा निरूपित करते हैं। अतः cos–1 एक फलन है जिसका प्रांत [–1, 1] है और परिसर [–π, 0], [0,π], [π, 2π] इत्यादि में से कोई भी अंतराल हो सकता है। इस प्रकार के प्रत्येक अंतराल के संगत हमें फलन cos–1 की एक शाखा प्राप्त होती है। वह शाखा, जिसका परिसर [0, π] है, मुख्य शाखा (मुख्य मान शाखा) कहलाती है और हम लिखते हैं कि
cos–1 : [–1, 1] → [0, π]
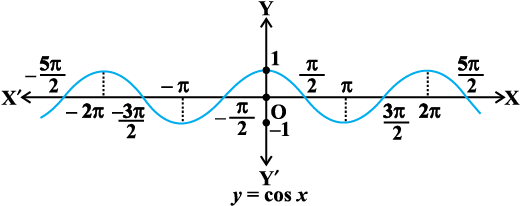
आकृति 2.2 (i)

आकृति 2.2 (ii)
आइए अब हम cosec–1x तथा sec–1x पर विचार करें।
क्योंकि cosec x = 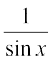 , इसलिए cosec फलन का प्रांत समुच्चय {x : x ∈ R और x ≠ nπ, n ∈ ρ} है तथा परिसर समुच्चय {y : y ∈ R, y ≥ 1 अथवा y ≤ –1}, अर्थात्, समुच्चय R – (–1, 1) है। इसका अर्थ है कि y = cosec x, –1 < y < 1 को छोड़ कर अन्य सभी वास्तविक मानों को ग्रहण करता है तथा यह π के पूर्णांक (Integral) गुणजों के लिए परिभाषित नहीं है। यदि हम cosec फलन के प्रांत को अंतराल
, इसलिए cosec फलन का प्रांत समुच्चय {x : x ∈ R और x ≠ nπ, n ∈ ρ} है तथा परिसर समुच्चय {y : y ∈ R, y ≥ 1 अथवा y ≤ –1}, अर्थात्, समुच्चय R – (–1, 1) है। इसका अर्थ है कि y = cosec x, –1 < y < 1 को छोड़ कर अन्य सभी वास्तविक मानों को ग्रहण करता है तथा यह π के पूर्णांक (Integral) गुणजों के लिए परिभाषित नहीं है। यदि हम cosec फलन के प्रांत को अंतराल 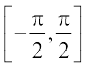 – {0}, में सीमित कर दें, तो यह एक एकैकी तथा आच्छादक फलन होता है, जिसका परिसर समुच्चय R – (– 1, 1). होता है। वस्तुतः cosec फलन, अंतरालों
– {0}, में सीमित कर दें, तो यह एक एकैकी तथा आच्छादक फलन होता है, जिसका परिसर समुच्चय R – (– 1, 1). होता है। वस्तुतः cosec फलन, अंतरालों 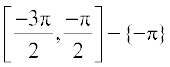 ,
, 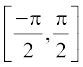 – {0},
– {0}, 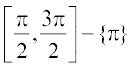 इत्यादि में से किसी में भी सीमित होने से एकैकी आच्छादी होता है और इसका परिसर समुच्चय R – (–1, 1) होता है। इस प्रकार cosec–1 एक एेसे फलन के रूप में परिभाषित हो सकता है जिसका प्रांत R – (–1, 1) है और परिसर अंतरालों
इत्यादि में से किसी में भी सीमित होने से एकैकी आच्छादी होता है और इसका परिसर समुच्चय R – (–1, 1) होता है। इस प्रकार cosec–1 एक एेसे फलन के रूप में परिभाषित हो सकता है जिसका प्रांत R – (–1, 1) है और परिसर अंतरालों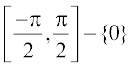 ए
ए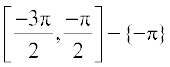 ए
ए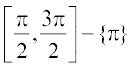 इत्यादि में से कोई भी एक हो सकता है। परिसर
इत्यादि में से कोई भी एक हो सकता है। परिसर 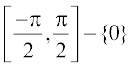 के संगत फलन को cosec–1 की मुख्य शाखा कहते हैं। इस प्रकार मुख्य शाखा निम्नलिखित तरह से व्यक्त होती हैः
के संगत फलन को cosec–1 की मुख्य शाखा कहते हैं। इस प्रकार मुख्य शाखा निम्नलिखित तरह से व्यक्त होती हैः
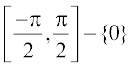
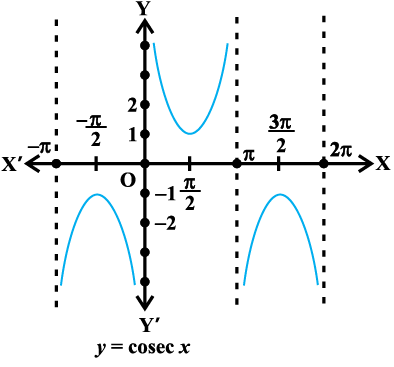
अाकृति 2.3 (i)

आकृति 2.3 (ii)
इसी तरह, sec x = 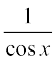 , ल = sec x का प्रांत समुच्चय R – {x : x = (2n+1)
, ल = sec x का प्रांत समुच्चय R – {x : x = (2n+1) 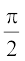 , n ∈ ρ} है तथा परिसर समुच्चय R – (–1, 1) है। इसका अर्थ है कि sec (secant) फलन –1 < y < 1 को छोड़कर अन्य सभी वास्तविक मानों को ग्रहण (Assumes) करता है और यह
, n ∈ ρ} है तथा परिसर समुच्चय R – (–1, 1) है। इसका अर्थ है कि sec (secant) फलन –1 < y < 1 को छोड़कर अन्य सभी वास्तविक मानों को ग्रहण (Assumes) करता है और यह 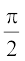 के विषम गुणजों के लिए परिभाषित नहीं है। यदि हम secant फलन के प्रांत को अंतराल [0, π] – {
के विषम गुणजों के लिए परिभाषित नहीं है। यदि हम secant फलन के प्रांत को अंतराल [0, π] – { 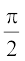 }, में सीमित कर दें तो यह एक एकैकी तथा आच्छादक फलन होता है जिसका परिसर समुच्चय R – (–1, 1) होता है। वास्तव में secant फलन अंतरालों [–πए0,–क्ष्
}, में सीमित कर दें तो यह एक एकैकी तथा आच्छादक फलन होता है जिसका परिसर समुच्चय R – (–1, 1) होता है। वास्तव में secant फलन अंतरालों [–πए0,–क्ष्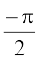 द्वए
द्वए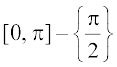 ए ख्πए2π] – {
ए ख्πए2π] – {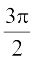 } इत्यादि में से किसी में भी सीमित होने से एकैकी आच्छादी होता है और इसका परिसर R– (–1, 1) होता है। अतः sec–1 एक एेसे फलन के रूप में परिभाषित हो सकता है जिसका प्रांत (–1, 1) हो और जिसका परिसर अंतरालों [– π, 0] – {
} इत्यादि में से किसी में भी सीमित होने से एकैकी आच्छादी होता है और इसका परिसर R– (–1, 1) होता है। अतः sec–1 एक एेसे फलन के रूप में परिभाषित हो सकता है जिसका प्रांत (–1, 1) हो और जिसका परिसर अंतरालों [– π, 0] – {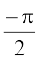 }, [0, π] – {
}, [0, π] – {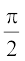 },[π, 2π] – {
},[π, 2π] – {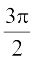 } इत्यादि में से कोई भी हो सकता है। इनमें से प्रत्येक अंतराल के संगत हमें फलन sec–1 की भिन्न-भिन्न शाखाएँ प्राप्त होती हैं। वह शाखा जिसका परिसर [0, π] – {
} इत्यादि में से कोई भी हो सकता है। इनमें से प्रत्येक अंतराल के संगत हमें फलन sec–1 की भिन्न-भिन्न शाखाएँ प्राप्त होती हैं। वह शाखा जिसका परिसर [0, π] – {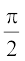 } होता है, फलन sec–1 की मुख्य शाखा कहलाती है। इसको हम निम्नलिखित प्रकार से व्यक्त करते हैंः
} होता है, फलन sec–1 की मुख्य शाखा कहलाती है। इसको हम निम्नलिखित प्रकार से व्यक्त करते हैंः
sec–1 : R – (–1,1) → [0, π] – {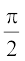 }
}
y = sec x तथा y = sec–1 x के आलेखों को आकृतियों 2.4 (i), (ii) में दिखलाया गया है।

आकृति 2.4 (i)
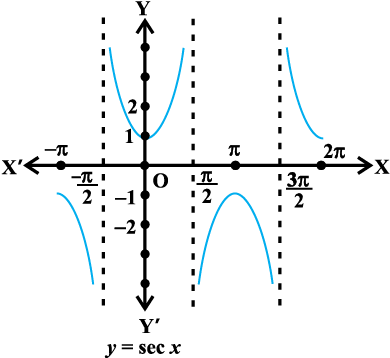
आकृति 2.4 (ii)
अंत में, अब हम tan–1 तथा cot–1 पर विचार करेंगे।
हमें ज्ञात है कि, tan फलन (tangent फलन) का प्रांत समुच्चय{x : x ∈ R तथा x ≠ (2n +1)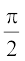 , n ∈ Z} है तथा परिसर R है। इसका अर्थ है कि tan फलन
, n ∈ Z} है तथा परिसर R है। इसका अर्थ है कि tan फलन 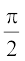 के विषम गुणजों के लिए परिभाषित नहीं है। यदि हम tangent फलन के प्रांत को अंतराल
के विषम गुणजों के लिए परिभाषित नहीं है। यदि हम tangent फलन के प्रांत को अंतराल 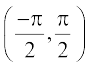 में सीमित कर दें, तो यह एक एकैकी तथा आच्छादक फलन हो जाता है जिसका परिसर समुच्चय R होता है। वास्तव में, tangent फलन, अंतरालों
में सीमित कर दें, तो यह एक एकैकी तथा आच्छादक फलन हो जाता है जिसका परिसर समुच्चय R होता है। वास्तव में, tangent फलन, अंतरालों 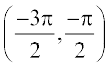 ,
, 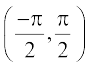 ,
, 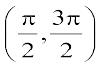 इत्यादि में से किसी में भी सीमित होने से एकैकी आच्छादी होता है और इसका परिसर समुच्चय R होता है। अतएव tan–1 एक एेसे फलन के रूप में परिभाषित हो सकता है, जिसका प्रांत R हो और परिसर अंतरालों
इत्यादि में से किसी में भी सीमित होने से एकैकी आच्छादी होता है और इसका परिसर समुच्चय R होता है। अतएव tan–1 एक एेसे फलन के रूप में परिभाषित हो सकता है, जिसका प्रांत R हो और परिसर अंतरालों 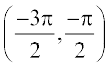 ,
, 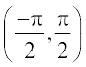 ,
, 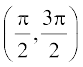 इत्यादि में से कोई भी हो सकता है। इन अंतरालों द्वारा फलन tan–1 की भिन्न-भिन्न शाखाएँ मिलती हैं। वह शाखा, जिसका परिसर
इत्यादि में से कोई भी हो सकता है। इन अंतरालों द्वारा फलन tan–1 की भिन्न-भिन्न शाखाएँ मिलती हैं। वह शाखा, जिसका परिसर 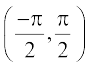 होता है, फलन tan–1 की मुख्य शाखा कहलाती है। इस प्रकार
होता है, फलन tan–1 की मुख्य शाखा कहलाती है। इस प्रकार
tan–1 : R → 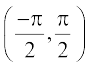
y = tan x तथा y = tan–1x के आलेखों को आकृतियों 2.5 (i), (ii) में दिखलाया गया है।

आकृति 2.5 (i)

आकृति 2.5 (ii)
हमें ज्ञात है कि cot फलन (cotangent फलन) का प्रांत समुच्चय {x : x ∈ R तथा x ≠ nπ, n ∈ ρ} है तथा परिसर समुच्चय R है। इसका अर्थ है कि cotangent फलन, π के पूर्णांकीय गुणजों के लिए परिभाषित नहीं है। यदि हम cotangent फलन के प्रांत को अंतराल (0, π) में सीमित कर दें तो यह परिसर R वाला एक एकैकी आच्छादी फलन होता है। वस्तुतः cotangent फलन अंतरालों (–π, 0), (0, π), (π, 2π) इत्यादि में से किसी में भी सीमित होने से एकैकी आच्छादी होता है और इसका परिसर समुच्चय R होता है। वास्तव में cot–1 एक एेसे फलन के रूप में परिभाषित हो सकता है, जिसका प्रांत R हो और परिसर, अंतरालों (–π, 0), (0, π), (π, 2π) इत्यादि में से कोई भी हो। इन अंतरालों से फलन cot–1 की भिन्न-भिन्न शाखाएँ प्राप्त होती हैं। वह शाखा, जिसका परिसर (0, π) होता है, फलन cot–1 की मुख्य शाखा कहलाती है। इस प्रकार
y = cot x तथा y = cot–1x के आलेखों को आकृतियों 2.6 (i), (ii) में प्रदर्शित किया गया है।

आकृति 2.6 (i)

आकृति 2.6 (ii)
निम्नलिखित सारणी में प्रतिलोम त्रिकोणमितीय फलनों (मुख्य मानीय शाखाओं) को उनके प्रांतों तथा परिसरों के साथ प्रस्तुत किया गया है।

टिप्पणी
1. sin–1x से (sin x)–1 की भ्रांति नहीं होनी चाहिए। वास्तव में (sin x)–1 = 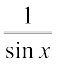 और यह तथ्य अन्य त्रिकोणमितीय फलनों के लिए भी सत्य होता है।
और यह तथ्य अन्य त्रिकोणमितीय फलनों के लिए भी सत्य होता है।
2. जब कभी प्रतिलोम त्रिकोणमितीय फलनों की किसी शाखा विशेष का उल्लेख न हो, तो हमारा तात्पर्य उस फलन की मुख्य शाखा से होता है।
3. किसी प्रतिलोम त्रिकोणमितीय फलन का वह मान, जो उसकी मुख्य शाखा में स्थित होता है, प्रतिलोम त्रिकोणमितीय फलन का मुख्य मान (Principal value) कहलाता है।
अब हम कुछ उदाहरणों पर विचार करेंगेः
उदाहरण 1 sin–1 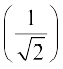 का मुख्य मान ज्ञात कीजिए।
का मुख्य मान ज्ञात कीजिए।
हल मान लीजिए कि sin–1 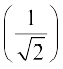 = y. अतः sin y =
= y. अतः sin y = 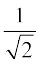 .
.
हमें ज्ञात है कि sin–1 की मुख्य शाखा का परिसर 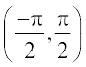 होता है और
होता है और 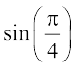 =
= 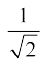 है। इसलिए sin–1
है। इसलिए sin–1 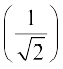 का मुख्य मान
का मुख्य मान 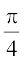 है।
है।
उदाहरण 2 cot–1  का मुख्य मान ज्ञात कीजिए।
का मुख्य मान ज्ञात कीजिए।
हल मान लीजिए कि cot–1  = y . अतएव
= y . अतएव
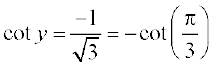 =
= 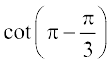 =
= 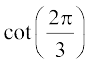 है।
है।
हमें ज्ञात है कि cot–1 की मुख्य शाखा का परिसर (0, π) होता है और cot 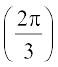 =
= 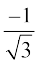 है। अतः cot–1
है। अतः cot–1  का मुख्य मान
का मुख्य मान 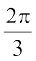 है।
है।
प्रश्नावली 2.1
निम्नलिखित के मुख्य मानों को ज्ञात कीजिएः
1. sin–1 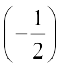 2. cos–1
2. cos–1 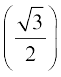 3. cosec–1 (2) 4. tan–1
3. cosec–1 (2) 4. tan–1 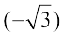 5. cos–1
5. cos–1 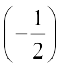 6. tan–1 (–1) 7. sec–1
6. tan–1 (–1) 7. sec–1 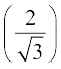 8. cot–1
8. cot–1 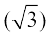 9. cos–1
9. cos–1 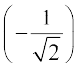 10. cosec–1 (
10. cosec–1 (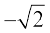 )
)
निम्नलिखित के मान ज्ञात कीजिएः
11. tan–1(1) + cos–1 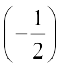 + sin–1
+ sin–1 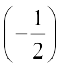 12. cos–1
12. cos–1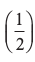 + 2 sin–1
+ 2 sin–1 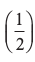
13. यदि sin–1 x = y, तो
(A) 0 ≤ y ≤ π (B) 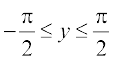
(C) 0 < y < π (D) 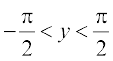
14. tan–1 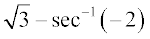 का मान बराबर है
का मान बराबर है
(A) π (B) 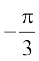 (C)
(C) 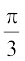 (D)
(D) 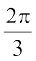
2.3 प्रतिलोम त्रिकोणमितीय फलनों के गुणधर्म (Properties of Inverse Trigonometric Functions)
इस अनुच्छेद में हम प्रतिलोम त्रिकोणमितीय फलनों के कुछ गुणधर्मों को सिद्ध करेंगे। यहाँ यह उल्लेख कर देना चाहिए कि ये परिणाम, संगत प्रतिलोम त्रिकोणमितीय फलनों की मुख्य शाखाओं के अंतर्गत ही वैध (Valid) है, जहाँ कहीं वे परिभाषित हैं। कुछ परिणाम, प्रतिलोम त्रिकोणमितीय फलनों के प्रांतों के सभी मानों के लिए वैध नहीं भी हो सकते हैं। वस्तुतः ये उन कुछ मानों के लिए ही वैध होंगे, जिनके लिए प्रतिलोम त्रिकोणमितीय फलन परिभाषित होते हैं। हम प्रांत के इन मानों के विस्तृत विवरण (Details) पर विचार नहीं करेंगे क्योंकि एेसी परिचर्चा (Discussion) इस पाठ्य पुस्तक के क्षेत्र से परे है।
स्मरण कीजिए कि, यदि y = sin–1x हो तो x = sin y तथा यदि x = sin y हो तो y = sin–1x होता है। यह इस बात के समतुल्य (Equivalent) है कि
sin (sin–1 x) = x, x ∈ [– 1, 1] तथा sin–1(sin x) = x, x ∈ 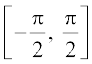
अन्य पाँच प्रतिलोम त्रिकोणमितीय फलनों के लिए भी यही सत्य होता है। अब हम प्रतिलोम त्रिकोणमितीय फलनों के कुछ गुणधर्मों को सिद्ध करेंगे।
1. (i) sin–1  = cosec–1 x, x ≥ 1 या x ≤ – 1
= cosec–1 x, x ≥ 1 या x ≤ – 1
(ii) cos–1  =sec–1x, x ≥ 1 या x ≤ – 1
=sec–1x, x ≥ 1 या x ≤ – 1
(iii) tan–1  = cot–1 x, x > 0
= cot–1 x, x > 0
पहले परिणाम को सिद्ध करने के लिए हम cosec–1 x = y मान लेते हैं, अर्थात्
अतएव  = sin y
= sin y
अतः sin–1  = y
= y
या sin–1  = cosec–1 x
= cosec–1 x
इसी प्रकार हम शेष दो भागों को सिद्ध कर सकते हैं।
2. (i) sin–1(–x) = – sin–1x, x ∈ [– 1, 1]
(ii) tan–1(–x) = – tan–1x, x ∈ R
(iii) cosec–1(–x) = – cosec–1 x, | x | ≥ 1
मान लीजिए कि sin–1(–x) = y, अर्थात् –x = sin y इसलिए x = – sin y, अर्थात्
x = sin (–y).
अतः sin–1x = – y = – sin–1(–x)
इस प्रकार sin–1(–x) = – sin–1x
इसी प्रकार हम शेष दो भागों को सिद्ध कर सकते हैं।
3. (i) cos–1 (–x) = π – cos–1 x, x ∈ [– 1, 1]
(ii) sec–1 (–x) = π –sec–1 x, | x | ≥ 1
(iii) cot–1 (–x) = π – cot–1 x, x ∈ R
मान लीजिए कि cos–1 (–x) = y अर्थात् – x = cos y इसलिए x = – cos y = cos (π – y)
अतएव cos–1 x = π – y = π – cos–1 (–x)
अतः cos–1 (–x) = π – cos–1 x
इसी प्रकार हम अन्य भागों को भी सिद्ध कर सकते हैं।
4. (i) sin–1 x + cos–1 x = 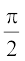 ए x ∈ [– 1, 1]
ए x ∈ [– 1, 1]
(ii) tan–1 x + cot–1 x = 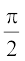 ए x ∈ R
ए x ∈ R
(iii) cosमब–1 x + sec–1 x =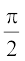 ए द्यxद्य ≥ 1
ए द्यxद्य ≥ 1
मान लीजिए कि sin–1 x = y, तो x = sin y = cos 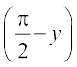
इसलिए cos–1 x = 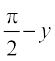 =
= 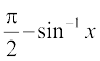
अतः sin–1 x + cos–1 x = 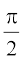
इसी प्रकार हम अन्य भागों को भी सिद्ध कर सकते हैं।
5. (i) tan–1x + tan–1 ल = tan–1 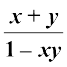 , गल ढ 1
, गल ढ 1
(ii) tan–1x – tan–1ल = tan–1 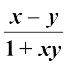 , गल झ – 1
, गल झ – 1
(iii) tan–1x + tan–1 ल = π + tan–1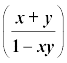 , x y > 1, x > 0, y > 0
, x y > 1, x > 0, y > 0
मान लीजिए कि tan–1x = θ तथा tan–1y = φ तो x = tan θ तथा y = tan φ
अब 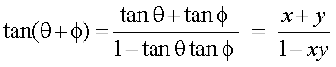
अतः θ + φ = tan–1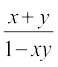
अतः tan–1 x + tan–1 y = tan–1 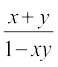
उपर्युक्त परिणाम में यदि y को – y द्वारा प्रतिस्थापित (Replace) करें तो हमें दूसरा परिणाम प्राप्त होता है और y को x द्वारा प्रतिस्थापित करने से तीसरा परिणाम प्राप्त होता है।
6. (i) 2tan–1 x = sin–1 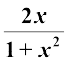 , | x | ≤ 1
, | x | ≤ 1
(ii) 2tan–1 x = cos–1 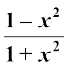 , x ≥ 0
, x ≥ 0
(iii) 2tan–1 x = tan–1 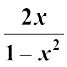 , – 1 ढ ग ढ 1
, – 1 ढ ग ढ 1
मान लीजिए कि tan–1 x = y, तो x = tan y
अब sin–1 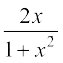 = sin–1
= sin–1 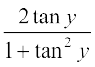
= sin–1 (sin 2 y) = 2 y = 2 tan–1 x
इसी प्रकार cos–1 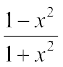 = cos–1
= cos–1 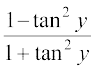 = cos–1 (cos 2y) = 2y = 2tan–1 x
= cos–1 (cos 2y) = 2y = 2tan–1 x
अब हम कुछ उदाहरणों पर विचार करेंगे।
उदाहरण 3 दर्शाइए कि
(i) sin–1 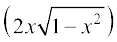 = 2 sin–1 x,
= 2 sin–1 x, 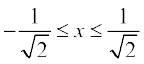
(ii) sin–1 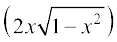 = 2 cos–1 x,
= 2 cos–1 x, 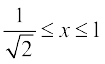
हल
(i) मान लीजिए कि x = sin θ तो sin–1 x = θ इस प्रकार
sin–1 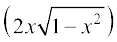 = sin–1
= sin–1 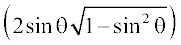
= sin–1 (2sinθ cosθ) = sin–1 (sin2θ) = 2θ
= 2 sin–1 ग
(ii) मान लीजिए कि x = cos θ तो उपर्युक्त विधि के प्रयोग द्वारा हमें
sin–1 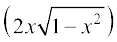 = 2 cos–1 x प्राप्त होता है।
= 2 cos–1 x प्राप्त होता है।
उदाहरण 4 सिद्ध कीजिए कि tan–1 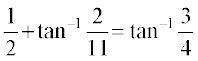
हल गुणधर्म 5 (i), द्वारा
बायाँ पक्ष = 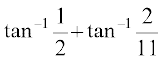
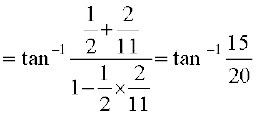 =
= 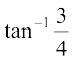 = दायाँ पक्ष
= दायाँ पक्ष
उदाहरण 5 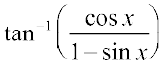 ,
, 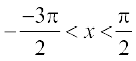 को सरलतम रूप में व्यक्त कीजिए।
को सरलतम रूप में व्यक्त कीजिए।
हल हम लिख सकते हैं कि
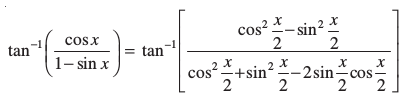
= 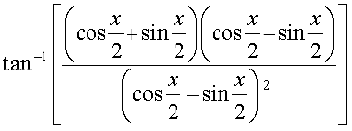
= 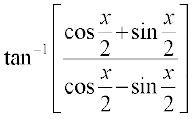
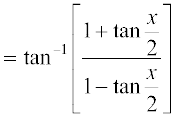
= 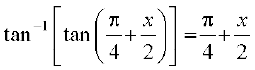
विकल्पतः
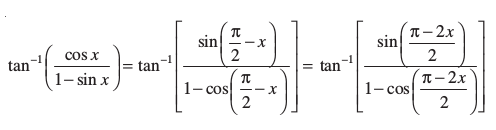
= 
= 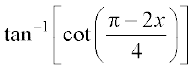
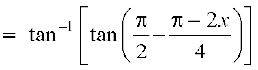
= 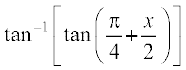
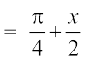
उदाहरण 6 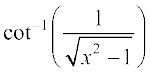 , x > 1 को सरलतम रूप में लिखिए।
, x > 1 को सरलतम रूप में लिखिए।
हल मान लीजिए कि x = sec θ, then 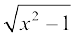 =
= 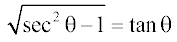
इसलिए 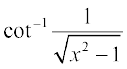 = cot–1 (cot θ) = θ = sec–1 x जो अभीष्ट सरलतम रूप है।
= cot–1 (cot θ) = θ = sec–1 x जो अभीष्ट सरलतम रूप है।
उदाहरण 7 सिद्ध कीजिए कि tan–1 x + 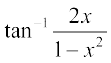 = tan–1
= tan–1 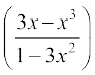 ,
, 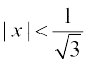
हल मान लीजिए कि x = tan θ. तो θ = tan–1 x है। अब
दायाँ पक्ष = 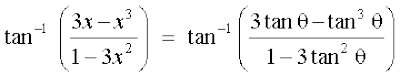
= tan–1 (tan3θ) = 3θ = 3tan–1 x = tan–1 x + 2 tan–1 x
= tan–1 x + tan–1 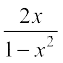 = बायाँ पक्ष (क्यों?)
= बायाँ पक्ष (क्यों?)
उदाहरण 8 cos (sec–1 x + cosec–1 ग), |गद्य ≥ 1 का मान ज्ञात कीजिए।
हल यहाँ पर cos (sec–1 x + cosec–1 x) = cos 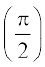 = 0
= 0
प्रश्नावली 2.2
निम्नलिखित को सिद्ध कीजिएः
1. 3sin–1 x = sin–1 (3x – 4x3), 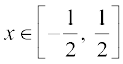
2. 3cos–1 x = cos–1 (4x3 – 3x), 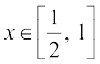
3. tan–1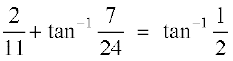
4. 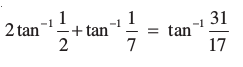
निम्नलिखित फलनों को सरलतम रूप में लिखिएः
5. 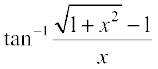 , x ≠ 0 6.
, x ≠ 0 6. 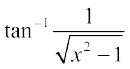 , |x| > 1
, |x| > 1
7. 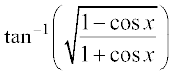 , 0 < x < π 8.
, 0 < x < π 8. 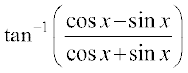 ,
, 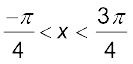
9. 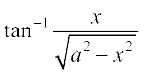 , |x| < a
, |x| < a
10. 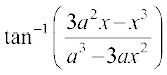 , a > 0;
, a > 0; 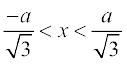
निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिएः
11. 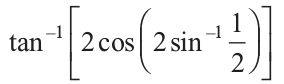 12. cot (tan–1a + cot–1a)
12. cot (tan–1a + cot–1a)
13.  , |x| < 1, y > 0 तथा गल < 1
, |x| < 1, y > 0 तथा गल < 1
14. यदि sin 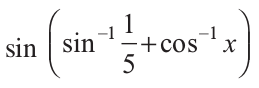 =1, तो x का मान ज्ञात कीजिए।
=1, तो x का मान ज्ञात कीजिए।
15. यदि 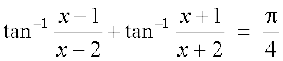 , तो x का मान ज्ञात कीजिए।
, तो x का मान ज्ञात कीजिए।
प्रश्न संख्या 16 से 18 में दिए प्रत्येक व्यंजक का मान ज्ञात कीजिएः
16. 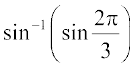 17.
17. 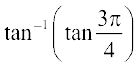
18. 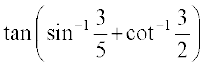
19. 
(A) 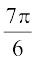 (B)
(B) 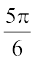 (C)
(C) 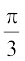 (D)
(D) 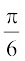
20. 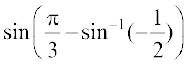 का मान है
का मान है
(A)  है (B)
है (B) 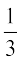 है (C)
है (C)  है (D) 1
है (D) 1
21. 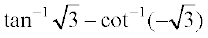 का मान
का मान
(A) π है (B) 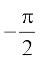 है (C) 0 है (D)
है (C) 0 है (D) 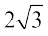
विविध उदाहरण
उदाहरण 9 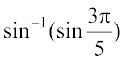 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
हल हमें ज्ञात है कि 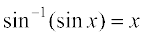 होता है। इसलिए
होता है। इसलिए 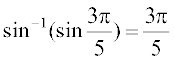
किंतु 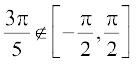 , जो sin–1 x की मुख्य शाखा है।
, जो sin–1 x की मुख्य शाखा है।
तथापि 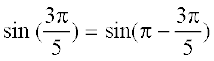 =
= 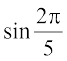 तथा
तथा 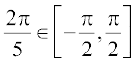
अतः 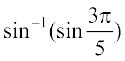 =
= 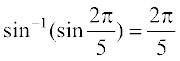
उदाहरण 10 दर्शाइए कि 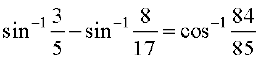
हल मान लीजिए कि 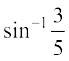 = x और
= x और 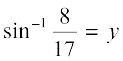
इसलिए sin x = 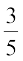 तथा
तथा 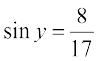
अब cos x = 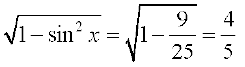 (क्यों?)
(क्यों?)
और cos y = 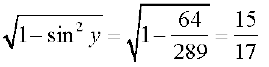
इस प्रकार cos (x – y) = cos x cos y + sin x sin y
= 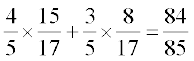
इसलिए x – y = 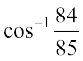
अतः 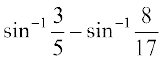 =
= 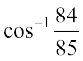
उदाहरण 11 दर्शाइए कि 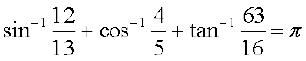
हल मान लीजिए कि 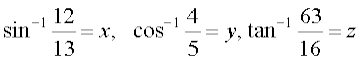
इस प्रकार 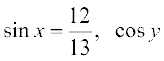 =
= 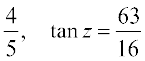
इसलिए 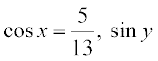 =
= 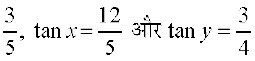
अब 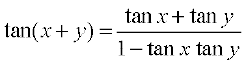
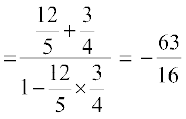
अतः 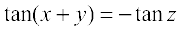
अर्थात् tan (x + y) = tan (–Ρ) या tan (x + y) = tan (π – Ρ)
इसलिए x + y = – Ρ or x + y = π – Ρ
क्योंकि x, y तथा Ρ धनात्मक हैं, इसलिए x + y ≠ – z (क्यों?)
अतः x + ल + Ρ = π या 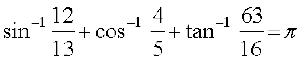
उदाहरण 12 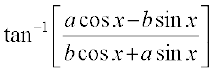 को सरल कीजिए, यदि
को सरल कीजिए, यदि 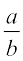 tan x > –1
tan x > –1
हल यहाँ
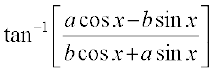 =
= 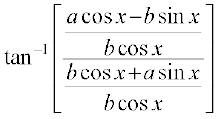 =
= 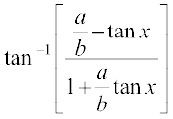
= 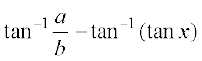 =
= 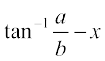
उदाहरण 13 tan–1 2x + tan–1 3x = 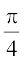 को सरल कीजिए।
को सरल कीजिए।
हल यहाँ दिया गया है कि tan–1 2x + tan–1 3x = 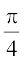
या 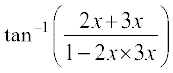 =
= 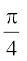
या 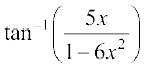 =
= 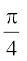
इसलिए 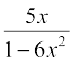 =
= 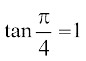
या 6x2 + 5x – 1 = 0 अर्थात् (6x – 1) (x + 1) = 0
जिससे प्राप्त होता है कि, x = 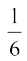 या x = – 1
या x = – 1
क्योंकि x = – 1, प्रदत्त समीकरण को संतुष्ट नहीं करता है, क्योंकि x = – 1 से समीकरण का बायाँ पक्ष ऋण हो जाता है। अतः प्रदत्त समीकरण का हल केवल 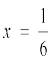 है।
है।
अध्याय 2 पर विविध प्रश्नावली
निम्नलिखित के मान ज्ञात कीजिएः
1. 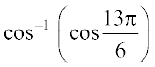
2. 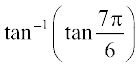
सिद्ध कीजिए
3. 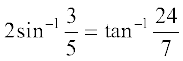
4. 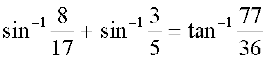
5. 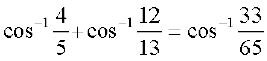
6. 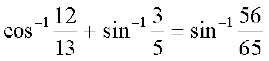
7. 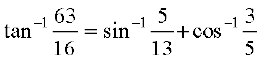
8. 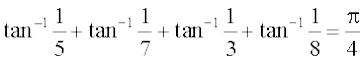
सिद्ध कीजिएः
9. 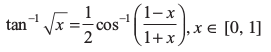
10. 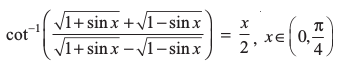
11. 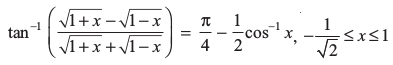 [संकेत: x = cos 2θ रखिए]
[संकेत: x = cos 2θ रखिए]
12. 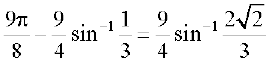
निम्नलिखित समीकरणों को सरल कीजिएः
13. 2tan–1 (cos x) = tan–1 (2 cosec x)
14. 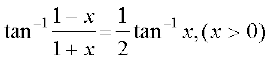
15. sin (tan–1 x, |x| < 1 बराबर होता हैः
(A) 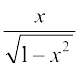
(B) 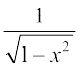
(C) 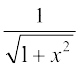
(D) 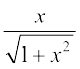
16. यदि sin–1 (1 – x) – 2 sin–1 x = 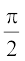 , तो x का मान बराबर हैः
, तो x का मान बराबर हैः
(A) 0, 
(B) 1, 
(C) 0
(D) 
17. 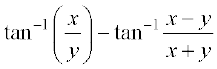 का मान हैः
का मान हैः
(A) 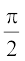 है।
है।
(B) 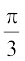 है।
है।
(C) 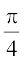 है।
है।
(D) 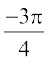
सारांश
♦ प्रतिलोम त्रिकोणमितीय फलनों (मुख्य शाखा) के प्रांत तथा परिसर निम्नलिखित सारणी में वर्णित हैंः
| फलन | प्रांत | परिसर(मुख्य शाखा) |
| y = sin–1x | [–1, 1] | 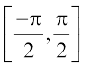 |
| y = cos–1x | [–1, 1] | [0, π] |
| y = cosec–1x | R – (–1,1 | 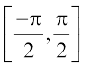 – {0} – {0} |
| y =sec–1x | R – (–1,1 | [0, π], – 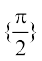 |
| y = tan–1x | R | (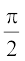 , , 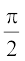 ) ) |
| y = cot–1x | R | 0, π) |
♦ sin–1x से (sin x)–1 की भ्रान्ति नहीं होनी चाहिए। वास्तव में (sin x)–1 = 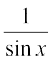 और इसी प्रकार यह तथ्य अन्य त्रिकोणमितीय फलनों के लिए सत्य होता है।
और इसी प्रकार यह तथ्य अन्य त्रिकोणमितीय फलनों के लिए सत्य होता है।
किसी प्रतिलोम त्रिकोणमितीय फलन का वह मान, जो उसकी मुख्य शाखा में स्थित होता है, प्रतिलोम त्रिकोणमितीय फलन का मुख्य मान (Principal Value) कहलाता है।
उपयुक्त प्रांतों के लिए
♦ y = sin–1 x ⇒ x = sin y
♦ ग = sin y ⇒ ल = sin–1 x
♦ sin (sin–1 x) = x
♦ sin–1 (sinx) = x
♦ sin–1 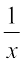 = cosec–1 x
= cosec–1 x
♦ cos–1 (–x) = π – cos–1 x
♦ cos–1 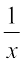 = sec–1x
= sec–1x
♦ cot–1 (–x) = π – cot–1 x
♦ tan–1 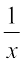 = cot–1 x
= cot–1 x
♦ sec–1 (–x) = π – sec–1 x
♦ sin–1 (–x) = – sin–1 x
♦ tan–1 (–x) = – tan–1 x
♦ tan–1 x + cot–1 x = 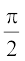
♦ cosec–1 (–x) = – cosec–1 x
♦ sin–1 x + cos–1 x = 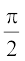
♦ cosec–1 x + sec–1 x = 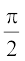
♦ tan–1x + tan–1y = tan–1 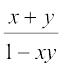 , गल < 1
, गल < 1
♦ 2tan–1x = tan–1 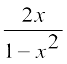 |x| <1
|x| <1
♦ tan–1x + tan–1y = π + tan–1 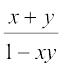 , गल > 1, x > 0, y > 0
, गल > 1, x > 0, y > 0
♦ tan–1x – tan–1y = tan–1 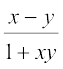 , गल > –1
, गल > –1
♦ 2tan–1 x = sin–1 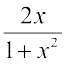 = cos–1
= cos–1 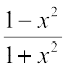 , 0 ≤ x ≤ 1
, 0 ≤ x ≤ 1
एेतिहासिक पृष्ठभूमि
एेसा विश्वास किया जाता है कि त्रिकोणमिती का अध्ययन सर्वप्रथम भारत में आरंभ हुआ था। आर्यभट्ट (476 ई.), ब्रह्मगुप्त (598 ई.) भास्कर प्रथम (600 ई.) तथा भास्कर द्वितीय (1114 ई.)ने प्रमुख परिणामों को प्राप्त किया था। यह संपूर्ण ज्ञान भारत से मध्यपूर्व और पुनः वहाँ से यूरोप गया। यूनानियों ने भी त्रिकोणमिति का अध्ययन आरंभ किया परंतु उनकी कार्य विधि इतनी अनुपयुक्त थी, कि भारतीय विधि के ज्ञात हो जाने पर यह संपूर्ण विश्व द्वारा अपनाई गई।
भारत में आधुनिक त्रिकोणमितीय फलन जैसे किसी कोण की ज्या (sine) और फलन के परिचय का पूर्व विवरण सिद्धांत (संस्कृत भाषा में लिखा गया ज्योतिषीय कार्य) में दिया गया है जिसका योगदान गणित के इतिहास में प्रमुख है।
भास्कर प्रथम (600 ई.) ने 90° से अधिक, कोणों के sinम के मान के लए सूत्र दिया था। सोलहवीं शताब्दी का मलयालम भाषा में sin (। + ठ) के प्रसार की एक उपपत्ति है। 18°ए 36°ए 54°ए 72°ए आदि के sinम तथा बवsinम के विशुद्ध मान भास्कर द्वितीय द्वारा दिए गए हैं।
sin–1 गए cos–1 गए आदि को चाप sin गए चाप cos गए आदि के स्थान पर प्रयोग करने का सुझाव ज्योतिषविदSir John F.W. Hersehel (1813 ई.) द्वारा दिए गए थे। ऊँचाई और दूरी संबंधित प्रश्नों के साथ Thales (600 ई. पूर्व) का नाम अपरिहार्य रूप से जुड़ा हुआ है। उन्हें मिश्र के महान पिरामिड की ऊँचाई के मापन का श्रेय प्राप्त है। इसके लिए उन्होंने एक ज्ञात ऊँचाई के सहायक दंड तथा पिरामिड की परछाइयों को नापकर उनके अनुपातों की तुलना का प्रयोग किया था। ये अनुपात हैं
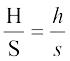 = tan (सूर्य का उन्नतांश)
= tan (सूर्य का उन्नतांश)
Thales को समुद्री जहाज की दूरी की गणना करने का भी श्रेय दिया जाता है। इसके लिए उन्होंने समरूप त्रिभुजों के अनुपात का प्रयोग किया था। ऊँचाई और दूरी संबधी प्रश्नों का हल समरूप त्रिभुजों की सहायता से प्राचीन भारतीय कार्यों में मिलते हैं।

