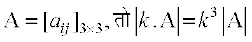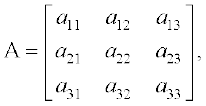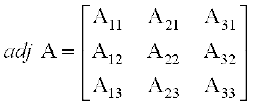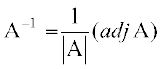Table of Contents
 All Mathematical truths are relative and conditional — C.P. Steinmetz
All Mathematical truths are relative and conditional — C.P. Steinmetz
4.1 भूमिका (Introduction)

a1 x + b1 y = c1
a2 x + b2 y = c2
को 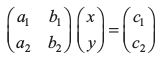 के रूप में व्यक्त कर सकते हैं। अब इन समीकरणों के निकाय का अद्वितीय हल है अथवा नहीं, इसको a1 b2 – a2 b1 संख्या द्वारा ज्ञात किया जाता है। (स्मरण कीजिए कि यदि
के रूप में व्यक्त कर सकते हैं। अब इन समीकरणों के निकाय का अद्वितीय हल है अथवा नहीं, इसको a1 b2 – a2 b1 संख्या द्वारा ज्ञात किया जाता है। (स्मरण कीजिए कि यदि 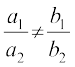 या a1 b2 – a2 b1 ≠ 0, हो तो समीकरणों के निकाय का हल अद्वितीय होता है) यह संख्या a1 b2 – a2 b1 जो समीकरणों के निकाय के अद्वितीय हल ज्ञात करती है, वह आव्यूह
या a1 b2 – a2 b1 ≠ 0, हो तो समीकरणों के निकाय का हल अद्वितीय होता है) यह संख्या a1 b2 – a2 b1 जो समीकरणों के निकाय के अद्वितीय हल ज्ञात करती है, वह आव्यूह 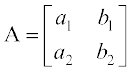 से संबंधित है और इसे A का सारणिक या det A कहते हैं। सारणिकों का इंजीनियरिंग, विज्ञान, अर्थशास्त्र, सामाजिक विज्ञान इत्यादि में विस्तृत अनुप्रयोग हैं।
से संबंधित है और इसे A का सारणिक या det A कहते हैं। सारणिकों का इंजीनियरिंग, विज्ञान, अर्थशास्त्र, सामाजिक विज्ञान इत्यादि में विस्तृत अनुप्रयोग हैं।
इस अध्याय में, हम केवल वास्तविक प्रविष्टियों के 3 कोटि तक के सारणिकों पर विचार करेंगे। इस अध्याय में सारणिकों के गुण धर्म, उपसारणिक, सह-ख.ड और त्रिभुज का क्षेत्रफल ज्ञात करने में सारणिकों का अनुप्रयोग, एक वर्ग आव्यूह के सहखंडज और व्युत्क्रम, रैखिक समीकरण के निकायों की संगतता और असंगतता और एक आव्यूह के व्युत्क्रम का प्रयोग कर दो अथवा तीन चरांकों के रैखिक समीकरणों के हल का अध्ययन करेंगे।
4.2 सारणिक (Determinant)
हम n कोटि के प्रत्येक वर्ग आव्यूह A = [aij] को एक संख्या (वास्तविक या सम्मिश्र) द्वारा संबंधित करा सकते हैं जिसे वर्ग आव्यूह का सारणिक कहते हैं। इसे एक फलन की तरह सोचा जा सकता है जो प्रत्येक आव्यूह को एक अद्वितीय संख्या (वास्तविक या सम्मिश्र) से संबंधित करता है।
यदि M वर्ग आव्यूहों का समुच्चय है, k सभी संख्याओं (वास्तविक या सम्मिश्र) का समुच्चय है और f : M → K, f(A) = k, के द्वारा परिभाषित है जहाँ A ∈ M और k ∈ K तब f (A) , A का सारणिक कहलाता है। इसे |A| या det (A) या ∆ के द्वारा भी निरूपित किया जाता है।
यदि A = 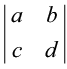 तो A के सारणिक को |A| =
तो A के सारणिक को |A| = 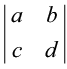 = det (A) द्वारा लिखा जाता है।
= det (A) द्वारा लिखा जाता है।
टिप्पणी
(i) आव्यूह A के लिए, |A| को A का सारणिक पढ़ते हैं।
(ii) केवल वर्ग आव्यूहों के सारणिक होते हैं।
4.2.1 एक कोटि के आव्यूह का सारणिक (Determinant of a matrix of order one)
माना एक कोटि का आव्यूह A = [a] हो तो A के सारणिक को a के बराबर परिभाषित किया जाता है।
4.2.2 द्वितीय कोटि के आव्यूह का सारणिक (Determinant of a matrix of order two)
माना 2 × 2 कोटि का आव्यूह A = 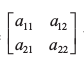 है।
है।
तो A के सारणिक को इस प्रकार से परिभाषित किया जा सकता हैः
det (A) = |A| = ∆ = 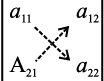 = a11a22 – a21a12
= a11a22 – a21a12
उदाहरण 1 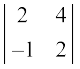 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
हल 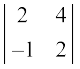 = 2(2) – 4(–1) = 4 + 4 = 8
= 2(2) – 4(–1) = 4 + 4 = 8
उदाहरण 2 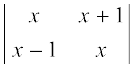 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
हल 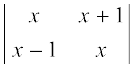 = x (x) – (x + 1) (x – 1) = x2 – (x2 – 1) = x2 – x2 + 1 = 1
= x (x) – (x + 1) (x – 1) = x2 – (x2 – 1) = x2 – x2 + 1 = 1
4.2.3 3 × 3 कोटि के आव्यूह का सारणिक (Determinant of a matrix of order 3 × 3)
तृतीय कोटि के आव्यूह के सारणिक को द्वितीय कोटि के सारणिकों में व्यक्त करके ज्ञात किया जाता है। यह एक सारणिक का एक पंक्ति (या एक स्तंभ) के अनुदिश प्रसरण कहलाता है। तृतीय कोटि के सारणिक को छः प्रकार से प्रसारित किया जाता है तीनों पंक्तियों (R1, R2 तथा R3) में से प्रत्येक के संगत और तीनों स्तंभ (C1, C2 तथा C3) में से प्रत्येक के संगत दर्शाए गए प्रसरण समान परिणाम देते हैें जैसा कि निम्नलिखित स्थितियों में स्पष्ट किया गया है।
वर्ग आव्यूह A = [aij]3 × 3 , के सारणिक पर विचार करते हैं।
जहाँ | A | = 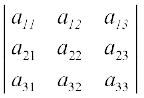
प्रथम पंक्ति (R1) के अनुदिश प्रसरण
| A | = 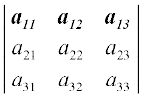
चरण 1 R1 के पहले अवयव a11 को (–1)(1 + 1) 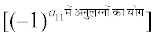 और सारणिक |A| की पहली पंक्ति (R1) तथा पहला स्तंभ (C1) के अवयवों को हटाने से प्राप्त द्वितीय कोटि के सारणिक से गुणा कीजिए क्योंकि a11, R1 और C1 में स्थित है
और सारणिक |A| की पहली पंक्ति (R1) तथा पहला स्तंभ (C1) के अवयवों को हटाने से प्राप्त द्वितीय कोटि के सारणिक से गुणा कीजिए क्योंकि a11, R1 और C1 में स्थित है
अर्थात् (–1)1 + 1 a11 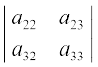
चरण 2 क्योंकि a12, R1 तथा C2 में स्थित है इसलिए R1 के दूसरे अवयव a12 को (–1)1 + 2 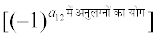 और सारणिक | A | की पहली पंक्ति (R1) व दूसरे स्तंभ (C2) को हटाने से प्राप्त द्वितीय क्रम के सारणिक से गुणा कीजिए
और सारणिक | A | की पहली पंक्ति (R1) व दूसरे स्तंभ (C2) को हटाने से प्राप्त द्वितीय क्रम के सारणिक से गुणा कीजिए
अर्थात् (–1)1 + 2 a12 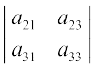
चरण 3 क्योंकि a13, R1 तथा C3 में स्थित है इसलिए R1 के तीसरे अवयव को (–1)1 + 3 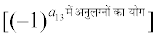 और सारणिक | A | की पहली पंक्ति (R1) व तीसरे स्तंभ (C3) को हटाने से प्राप्त तृतीय कोटि के सारणिक से गुणा कीजिए
और सारणिक | A | की पहली पंक्ति (R1) व तीसरे स्तंभ (C3) को हटाने से प्राप्त तृतीय कोटि के सारणिक से गुणा कीजिए
अर्थात् (–1)1 + 3 a13 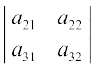
चरण 4 अब A का सारणिक अर्थात् | A | के व्यंजक को उपरोक्त चरण 1, 2 व 3 से प्राप्त तीनों पदों का योग करके लिखिए अर्थात्
det A = |A| = (–1)1 + 1 a11 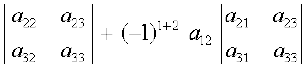
+ 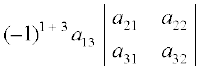
या |A| = a11 (a22 a33 – a32 a23) – a12 (a21 a33 – a31 a23)
+ a13 (a21 a32 – a31 a22)
= a11 a22 a33 – a11 a32 a23 – a12 a21 a33 + a12 a31 a23 + a13 a21 a32
– a13 a31 a22 ... (1)
टिप्पणी हम चारों चरणों का एक साथ प्रयोग करेंगे।
द्वितीय पंक्ति (R2) के अनुदिश प्रसरण
| A | = 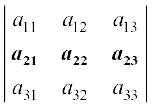
R2 के अनुदिश प्रसरण करने पर, हमें प्राप्त होता है
| A | = 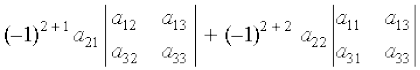
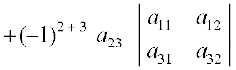
= – a21 (a12 a33 – a32 a13) + a22 (a11 a33 – a31 a13)
– a23 (a11 a32 – a31 a12)
| A | = – a21 a12 a33 + a21 a32 a13 + a22 a11 a33 – a22 a31 a13 – a23 a11 a32
+ a23 a31 a12
= a11 a22 a33 – a11 a23 a32 – a12 a21 a33 + a12 a23 a31 + a13 a21 a32
– a13 a31 a22 ... (2)
पहले स्तंभ (C1) के अनुदिश प्रसरण
| A | = 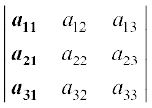
C1, के अनुदिश प्रसरण करने पर हमें प्राप्त होता है
| A | = 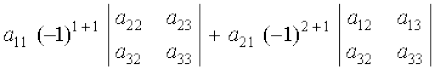
+ 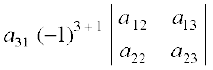
= a11 (a22 a33 – a23 a32) – a21 (a12 a33 – a13 a32) + a31 (a12 a23 – a13 a22)
| A | = a11 a22 a33 – a11 a23 a32 – a21 a12 a33 + a21 a13 a32 + a31 a12 a23
– a31 a13 a22
= a11 a22 a33 – a11 a23 a32 – a12 a21 a33 + a12 a23 a31 + a13 a21 a32
– a13 a31 a22 ... (3)
(1), (2) और (3) से स्पष्ट है कि |A| का मान समान है। यह पाठकों के अभ्यास के लिए छोड़ दिया गया है कि वे यह सत्यापित करें कि |A| का R3, C2 और C3 के अनुदिश प्रसरण (1), (2) और (3) से प्राप्त परिणामों के समान है।
अतः एक सारणिक को किसी भी पंक्ति या स्तंभ के अनुदिश प्रसरण करने पर समान मान प्राप्त होता है।
टिप्पणी
(i) गणना को सरल करने के लिए हम सारणिक का उस पंक्ति या स्तंभ के अनुदिश प्रसरण करेंगे जिसमें शून्यों की संख्या अधिकतम होती है।
(ii) सारणिकों का प्रसरण करते समय (–1)i + j से गुणा करने के स्थान पर, हम (i + j) के सम या विषम होने के अनुसार +1 या –1 से गुणा कर सकते हैं।
(iii) मान लीजिए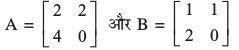 तो यह सिद्ध करना सरल है कि
तो यह सिद्ध करना सरल है कि
A = 2B. किंतु |A| = 0 – 8 = – 8 और |B| = 0 – 2 = – 2 है।
अवलोकन कीजिए कि |A| = 4(– 2) = 22|B| या |A| = 2n|B|, जहाँ n = 2, वर्ग आव्यूहों A व B की कोटि है।
व्यापक रूप में, यदि A = kB, जहाँ A व B वर्ग आव्यूहों की कोटि n है, तब | A| = kn | B |, जहाँ n = 1, 2, 3 है।
उदाहरण 3 सारणिक ∆ = 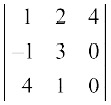 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
हल ध्यान दीजिए कि तीसरे स्तंभ में दो प्रविष्टियाँ शून्य हैं। इसलिए तीसरे स्तंभ (C3) के अनुदिश प्रसरण करने पर हमें प्राप्त होता है कि
∆ = 
= 4 (–1 – 12) – 0 + 0 = – 52
उदाहरण 4 ∆ = 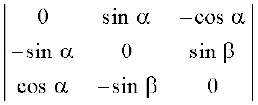 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
हल R1 के अनुदिश प्रसरण करने पर हमें प्राप्त होता है कि
∆ = 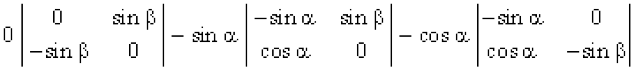
= 0 – sin α (0 – sin β cos α) – cos α (sin α sin β – 0)
= sin α sin β cos α – cos α sin α sin β = 0
उदाहरण 5 यदि 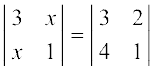 तो x के मान ज्ञात कीजिए।
तो x के मान ज्ञात कीजिए।
हल दिया है कि 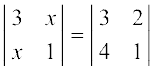
अर्थात् 3 – x2 = 3 – 8
अर्थात् x2 = 8
अतः x = 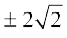
प्रश्नावली 4.1
प्रश्न 1 से 2 तक में सारणिकों का मान ज्ञात कीजिए
1. 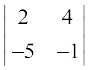
2. (i) 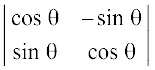 (ii)
(ii) 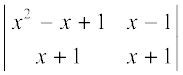

5. निम्नलिखित सारणिकों का मान ज्ञात कीजिए
(i) 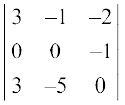 (ii)
(ii) 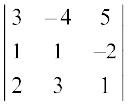 (iii)
(iii) 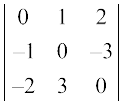
(iv) 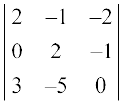
6. यदि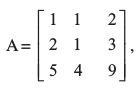 हो तो | A | ज्ञात कीजिए।
हो तो | A | ज्ञात कीजिए।
7. x के मान ज्ञात कीजिए यदि
(i) 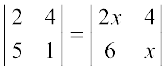 (ii)
(ii) 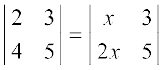
8. यदि 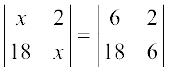 हो तो x बराबर हैः
हो तो x बराबर हैः
(A) 6 (B) ± 6 (C) – 6 (D) 0
4.3 सारणिकों के गुणधर्म (Properties of Determinants)
पिछले अनुच्छेद में हमने सारणिकों का प्रसरण करना सीखा है। इस अनुच्छेद में हम सारणिकों के कुछ गुणधर्मों को सूचीबद्ध करेंगे जिससे एक पंक्ति या स्तंभ में शून्य की संख्याओं को अधिकतम प्राप्त करने से इनका मान ज्ञात करना सरल हो जाता है। ये गुणधर्म किसी भी कोटि के सारणिक के लिए सत्य हैं किंतु हम स्वयं को इन्हें केवल तीसरी कोटि तक के सारणिकों तक सीमित रखेंगे।
गुणधर्म 1 किसी सारणिक का मान इसकी पंक्तियों और स्तंभों के परस्पर परिवर्तित करने पर अपरिवर्तित रहता है।
सत्यापन – मान लीजिए ∆ = 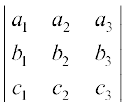
प्रथम पंक्ति के अनुदिश प्रसरण करने पर, हम प्राप्त करते हैं कि
∆ = 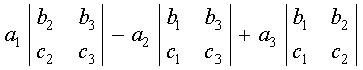
= a1 (b2 c3 – b3 c2) – a2 (b1 c3 – b3 c1) + a3 (b1 c2 – b2 c1)
∆ की पंक्तियों को स्तंभों में परिवर्तित करने पर हमें सारणिक
∆1 = 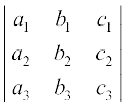 प्राप्त होता है।
प्राप्त होता है।
∆1 को प्रथम स्तंभ के अनुदिश प्रसरण करने पर हम पाते हैं कि
∆1 = a1 (b2 c3 – c2 b3) – a2 (b1 c3 – b3 c1) + a3 (b1 c2 – b2 c1)
अतः ∆ = ∆1
टिप्पणी उपर्युक्त व्याख्या से स्पष्ट है कि यदि A एक वर्ग आव्यूह है तो det (A) = det (A′), जहाँ A′ए Α का परिवर्त है।
टिप्पणी यदि Ri = i वीं पंक्ति और Ci = i वाँ स्तंभ है, तो पंक्तियों और स्तंभों के परस्पर परिवर्तन को हम संकेतन में Ci ↔ Ri लिखेंगे।
आइए हम उपरोक्त गुणधर्म को उदाहरण द्वारा सत्यापित करें।
उदाहरण 6 ∆ = 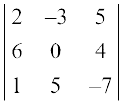 के लिए गुणधर्म 1 का सत्यापन कीजिए।
के लिए गुणधर्म 1 का सत्यापन कीजिए।
हल सारणिक का प्रथम पंक्ति के अनुदिश प्रसरण करने पर,
∆ = 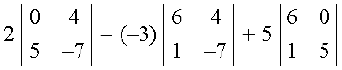
= 2 (0 – 20) + 3 (– 42 – 4) + 5 (30 – 0)
= – 40 – 138 + 150 = – 28
पंक्तियों और स्तंभों को परस्पर परिवर्तन करने पर हमें प्राप्त होता है।
∆1 = 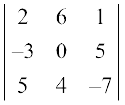 (पहले स्तंभ के अनुदिश प्रसरण करने पर)
(पहले स्तंभ के अनुदिश प्रसरण करने पर)
= 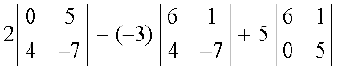
= 2 (0 – 20) + 3 (– 42 – 4) + 5 (30 – 0)
= – 40 – 138 + 150 = – 28
स्पष्टत: ∆ = ∆1
अत: गुणधर्म 1 सत्यापित हुआ।
गुणधर्म 2 यदि एक सारणिक की कोई दो पंक्तियों (या स्तंभों) को परस्पर परिवर्तित कर दिया जाता है, तब सारणिक का चिह्न परिवर्तित हो जाता है।
सत्यापन मान लीजिए ∆ = 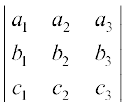
प्रथम पंक्ति के अनुदिश प्रसरण करने पर हम पाते हैं
∆ = a1 (b2 c3 – b3 c2) – a2 (b1 c3 – b3 c1) + a3 (b1 c2 – b2 c1)
पहली और तीसरी पंक्तियों को परस्पर परिवर्तित करने अर्थात् R2↔R3 से प्राप्त नया सारणिक
∆1 = 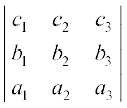
है। इसे तीसरी पंक्ति के अनुदिश प्रसरण करने पर,
∆1 = a1 (c2 b3 – b2 c3) – a2 (c1 b3 – c3 b1) + a3 (b2 c1 – b1 c2)
= – [a1 (b2 c3 – b3 c2) – a2 (b1 c3 – b3 c1) + a3 (b1 c2 – b2 c1)] प्राप्त होता है।
यह स्पष्ट है कि ∆1 = – ∆
इसी प्रकार, हम किन्हीं दो स्तंभों को परस्पर परिवर्तित करके उक्त परिणाम को सत्यापित कर सकते हैं।
टिप्पणी हम पंक्तियों के परस्पर परिवर्तन को Ri ↔ Rj और स्तंभों के परस्पर परिवर्तन को
Ci ↔ Cj के द्वारा निर्दिष्ट करते हैं।
उदाहरण 7 यदि ∆ = 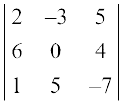 है तो गुणधर्म 2 का सत्यापन कीजिए।
है तो गुणधर्म 2 का सत्यापन कीजिए।
हल हम ज्ञात कर चुके हैं कि ∆ = 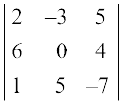 = – 28 (देखिए उदाहरण 6)
= – 28 (देखिए उदाहरण 6)
R2 और R3 को परस्पर परिवर्तित करने पर अर्थात् R2 ↔ R3 से
∆1 = 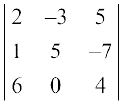 प्राप्त होता है।
प्राप्त होता है।
सारणिक ∆1 को पहली पंक्ति के अनुदिश प्रसरण करने पर हम प्राप्त करते हैं कि
∆1 = 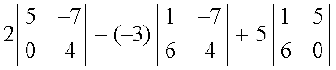
= 2 (20 – 0) + 3 (4 + 42) + 5 (0 – 30)
= 40 + 138 – 150 = 28
स्पष्टतया ∆1 = – ∆
अत: गुणधर्म 2 सत्यापित हुआ।
गुणधर्म 3 यदि एक सारणिक की कोई दो पंक्तियाँ (अथवा स्तंभ) समान हैं (सभी संगत अवयव समान हैं), तो सारणिक का मान शून्य होता है।
उपपत्ति यदि हम सारणिक ∆ की समान पंक्तियों (या स्तंभों) को परस्पर परिवर्तित कर देते हैं तो ∆ का मान परिवर्तित नहीं होता है।
तथापि, गुणधर्म 2 के अनुसार ∆ का चिह्न बदल गया है।
इसलिए ∆ = – ∆
या ∆ = 0
आइए हम उपरोक्त गुणधर्म का एक उदाहरण के द्वारा सत्यापन करते हैं।
उदाहरण 8 ∆ = 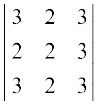 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
हल पहली पंक्ति के अनुदिश प्रसरण करने पर हम प्राप्त करते हैं कि
∆ = 3 (6 – 6) – 2 (6 – 9) + 3 (4 – 6)
= 0 – 2 (–3) + 3 (–2) = 6 – 6 = 0
यहाँ R2 और R3 समान हैं।
गुणधर्म 4 यदि एक सारणिक के किसी एक पंक्ति (अथवा स्तंभ) के प्रत्येक अव्यव को एक अचर k, से गुणा करते हैं तो उसका मान भी k से गुणित हो जाता है।
सत्यापन मान लीजिए ∆ = 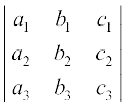
इसकी प्रथम पंक्ति के अवयवों को k से गुणा करने पर प्राप्त सारणिक ∆1 है तो
∆1 = 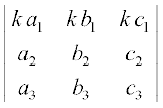
प्रथम पंक्ति के अनुदिश प्रसरण करने पर, हम प्राप्त करते हैं कि
∆1 = k a1 (b2 c3 – b3 c2) – k b1 (a2 c3 – c2 a3) + k c1 (a2 b3 – b2 a3)
= k [a1 (b2 c3 – b3 c2) – b1 (a2 c3 – c2 a3) + c1 (a2 b3 – b2 a3)] = k ∆
अतः 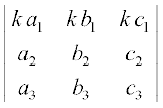 = k
= k 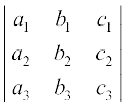
टिप्पणी
(i) इस गुणधर्म के अनुसार, हम एक सारणिक की किसी एक पंक्ति या स्तभों से सार्व उभयनिष्ठ गुणनखंड बाहर निकाल सकते हैं।
(ii) यदि एक सारणिक की किन्हीं दो पंक्तियों (या स्तंभों) के संगत अवयव समानुपाती (उसी अनुपात में) है, तब उसका मान शून्य होता है। उदाहरणतः
∆ = 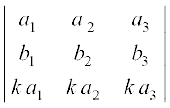 = 0 (पंक्तियाँ R2 व R3 समानुपाती है)
= 0 (पंक्तियाँ R2 व R3 समानुपाती है)
उदाहरण 9 सारणिक 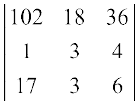 का मान ज्ञात कीजिए
का मान ज्ञात कीजिए
हल ध्यान दीजिए कि 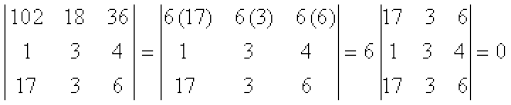
(गुणधर्म 3 और 4 )
गुणधर्म 5 यदि एक सारणिक की एक पंक्ति या स्तंभ के कुछ या सभी अवयव दो (या अधिक) पदों के योगफल के रूप में व्यक्त हों तो सारणिक को दो (या अधिक) सारणिकों के योगफल के रूप में व्यक्त किया जा सकता है।
उदाहरणतया 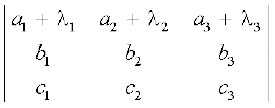 =
= 
सत्यापन बाँया पक्ष = 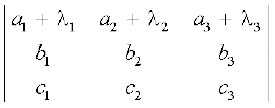
प्रथम पंक्ति के अनुदिश प्रसरण करने पर हम पाते हैं कि
∆ = (a1 + λ1) (b2 c3 – c2 b3) – (a2 + λ2) (b1 c3 – b3 c1)
+ (a3 + λ3) (b1 c2 – b2 c1)
= a1 (b2 c3 – c2 b3) – a2 (b1 c3 – b3 c1) + a3 (b1 c2 – b2 c1)
+ λ1 (b2 c3 – c2 b3) – λ2 (b1 c3 – b3 c1) + λ3 (b1 c2 – b2 c1)
(पदों को व्यवस्थित करने पर)
= 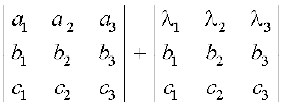 = दाँया पक्ष
= दाँया पक्ष
इसी प्रकार दूसरी पंक्तियों व स्तंभों के लिए हम गुणधर्म 5 का सत्यापन कर सकते हैं।
उदाहरण 10 दर्शाइए कि 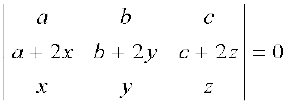
हल हम जानते हैं कि 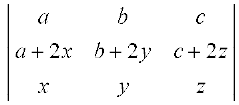 =
= 
(गुणधर्म 5 के द्वारा)
= 0 + 0 = 0 (गुणधर्म 3 और 4 का प्रयोग करने पर)
गुणधर्म 6 यदि एक सारणिक के किसी पंक्ति या स्तंभ के प्रत्येक अवयव में, दूसरी पंक्ति या स्तंभ के संगत अवयवों के समान गुणजों को जोड़ दिया जाता है तो सारणिक का मान वही रहता है। अर्थात्, यदि हम Ri → Ri + kRj या Ci → Ci + kCj का प्रयोग करें तो सारणिक का मान वही रहता है।
सत्यापन
मान लीजिए ∆ = 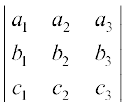 और ∆1 =
और ∆1 =  ,
,
जहाँ ∆1 संक्रिया R1 → R1 + kR3 के प्रयोग द्वारा प्राप्त होता है
यहाँ हम तीसरी पंक्ति (R3) के अवयवों को अचर k से गुणा करके और उन्हें पहली पंक्ति (R1) के संगत अवयवों में जोड़ते हैं।
संकेतन द्वारा इस संक्रिया को इस प्रकार लिखते हैं कि R1 → R1 + k R3
अब पुन:
∆1 = 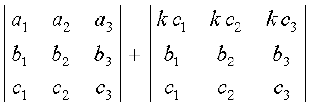 (गुणधर्म 5 के द्वारा)
(गुणधर्म 5 के द्वारा)
= ∆ + 0 (जब कि R1 और R3 समानुपाती हैं)
अतः ∆ = ∆1
टिप्पणी
(i) यदि सारणिक ∆ में Ri → kRi या Ci → kCi के प्रयोग से प्राप्त सारणिक ∆1 है, तो
∆1 = k∆.
(ii) यदि एक साथ Ri → Ri + kRj जैसी संक्रियाओं का एक से अधिक बार प्रयोग किया गया हो तो ध्यान देना चाहिए कि पहली संक्रिया से प्रभावित पंक्ति का अन्य संक्रिया में प्रयोग नहीं होना चाहिए। ठीक इसी प्रकार की टिप्पणी स्तंभों की संक्रियाओं में प्रयोग की जाती है।
उदाहरण 11 सिद्ध कीजिए कि ∆ = 
हल सारणिक ∆ में R2 → R2 – 2R1 और R3 → R3 – 3R1 का प्रयोग करने पर हम पाते हैं कि
∆ = 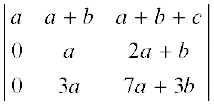
पुनः R3 → R3 – 3R2 , का प्रयोग करने से हम पाते हैं कि
∆ = 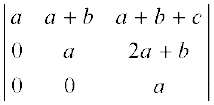
C1 के अनुदिश प्रसरण करने पर
∆ = 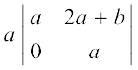 + 0 + 0
+ 0 + 0
= a (a2 – 0) = a (a2) = a3 प्राप्त होता है।
उदाहरण 12 प्रसरण किए बिना सिद्ध कीजिए कि
∆ = 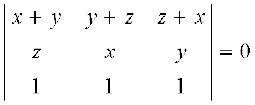
हल ∆ में R1 → R1 + R2 का प्रयोग करने पर हम पाते हैं
∆ = 
अब R1 और R3 के अवयव समानुपाती हैं।
इसलिए ∆ = 0
उदाहरण 13 निम्नलिखित का मान ज्ञात कीजिए
∆ = 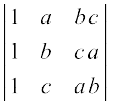
हल R2 → R2 – R1 और R3 → R3 – R1, का प्रयोग करने पर हम पाते हैं कि
∆ = 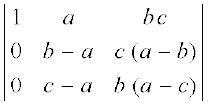
R2 और R3 से क्रमशः (b – a) और (c – a) उभयनिष्ठ लेने पर हम पाते हैं कि
∆ = 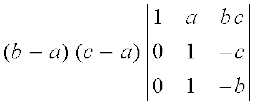
= (b – a) (c – a) [(– b + c)] (पहले स्तंभ के अनुदिश प्रसरण करने पर)
= (a – b) (b – c) (c – a)
उदाहरण 14 सिद्ध कीजिए कि 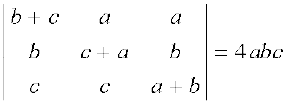
हल मान लीजिए
∆ = 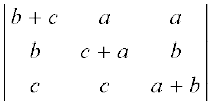
सारणिक पर R1 → R1 – R2 – R3 का प्रयोग करने पर हम पाते हैं कि
∆ = 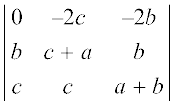
R1 के अनुदिश प्रसरण करने पर हम पाते हैं कि
∆ = 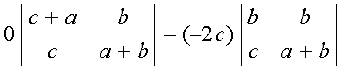
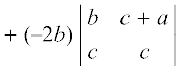
= 2 c (a b + b2 – bc) – 2 b (b c – c2 – ac)
= 2 a b c + 2 cb2 – 2 bc2 – 2 b2c + 2 bc2 + 2 abc
= 4 abc
उदाहरण 15 यदि x, y, z विभिन्न हों और 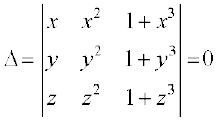 ,
,
तो दर्शाइए कि 1 + xyz = 0
हल हमें ज्ञात है ∆ = 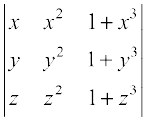
∆ =  (गुणधर्म 5 के प्रयोग द्वारा)
(गुणधर्म 5 के प्रयोग द्वारा)
=  (C3↔C2 और तब C1 ↔ C2 के प्रयोग द्वारा)
(C3↔C2 और तब C1 ↔ C2 के प्रयोग द्वारा)
= 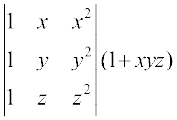
= 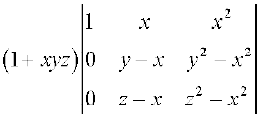 (R2→R2– R1 और R3 → R3–R1 का प्रयोग करने पर)
(R2→R2– R1 और R3 → R3–R1 का प्रयोग करने पर)
R2 से (y – x) और R3 से (z – x) उभयनिष्ठ लेने पर हम प्राप्त करते हैं कि
∆ = 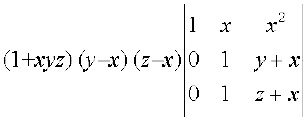
= (1 + xyz) (y – x) (z – x) (z – y) (C1 के अनुदिश प्रसरण करने पर)
चूँकि ∆ = 0 और x, y और z सभी भिन्न हैं,
अतः x – y ≠ 0, y – z ≠ 0, z – x ≠ 0, से हमें 1 + xyz = 0 प्राप्त होता है।
उदाहरण 16 दर्शाइए कि 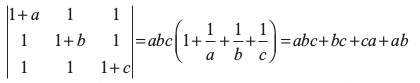
हल R1, R2 और R3 में से क्रमशः a, b और c उभयनिष्ठ लेने पर हम प्राप्त करते हैं कि
बाँया पक्ष = 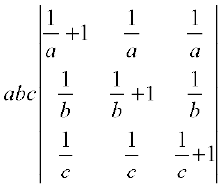
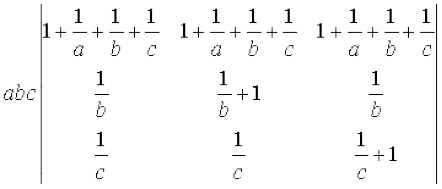
R1→ R1 + R2 + R3 का प्रयोग करने पर हम पाते हैं कि
∆ = 
या ∆ = 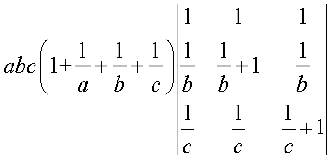
अब C2 → C2 – C1 और C3 → C3 – C1 का प्रयोग करने पर हम पाते हैं कि
∆ = 
= 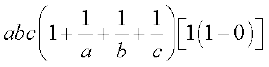
= 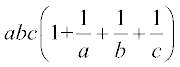 = abc + bc + ca + ab = दाँया पक्ष
= abc + bc + ca + ab = दाँया पक्ष
टिप्पणी अन्य विधि द्वारा C1 → C1 – C2 व C3 → C3 – C2, का अनुप्रयोग करके तथा
C1→ C1 – a C3 का प्रयोग करके उपरोक्त उदाहरण को हल करने का प्रयत्न करें।
प्रश्नावली 4.2
बिना प्रसरण किए और सारणिकों के गुणधर्मों का प्रयोग करके निम्नलिखित प्रश्न 1 से 5 को सिद्ध कीजिए।
1. 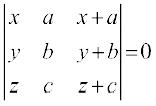 2.
2. 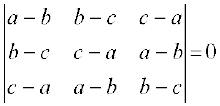 3.
3. 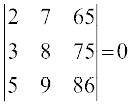
4. 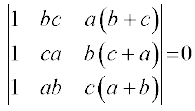 5.
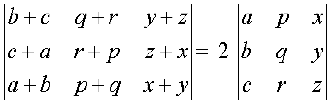
5. 
सारणिकों के गुणधर्मों का प्रयोग करके प्रश्न 6 से 14 तक को सिद्ध कीजिएः
6. 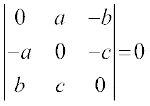 7.
7. 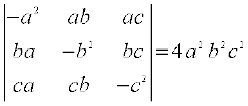
8. (i) 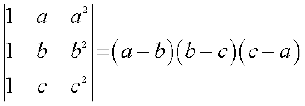
(ii) 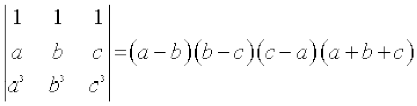
9. 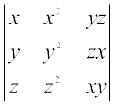 = (x – y) (y – z) (z – x) (xy + yz + zx)
= (x – y) (y – z) (z – x) (xy + yz + zx)
10. (i) 
(ii) 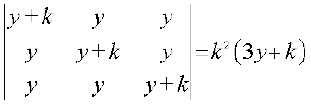
11. (i) 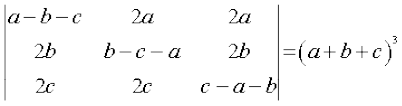
(ii) 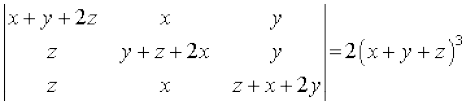
12. 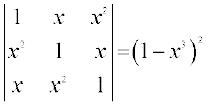
13. 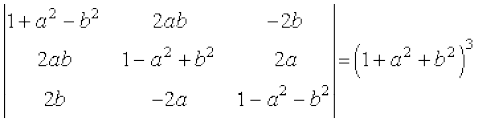
14. 
प्रश्न संख्या 15 तथा 16 में सही उत्तर चुनिए।
15. यदि A एक 3 × 3 कोटि का वर्ग आव्यूह है तो |kA| का मान होगाः
(A) k |A| (B) k2|A| (C) k3|A| (D) 3k|A|
16. निम्नलिखित में से कौन सा कथन सही है।
(A) सारणिक एक वर्ग आव्यूह है।
(B) सारणिक एक आव्यूह से संबद्ध एक संख्या है।
(C) सारणिक एक वर्ग आव्यूह से संबद्ध एक संख्या है।
(D) इनमें से कोई नहीं।
4.4 त्रिभुज का क्षेत्रफल (Area of a Triangle)
हमने पिछली कक्षाओं में सीखा है कि एक त्रिभुज जिसके शीर्षबिंदु (x1, y1), (x2, y2) तथा (x3, y3), हों तो उसका क्षेत्रफल व्यंजक  [x1(y2–y3) + x2 (y3–y1) + x3 (y1–y2)] द्वारा व्यक्त किया जाता है। अब इस व्यंजक को सारणिक के रूप में इस प्रकार लिखा जा सकता हैः
[x1(y2–y3) + x2 (y3–y1) + x3 (y1–y2)] द्वारा व्यक्त किया जाता है। अब इस व्यंजक को सारणिक के रूप में इस प्रकार लिखा जा सकता हैः
∆ = 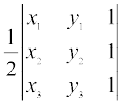 ... (1)
... (1)
टिप्पणी
(i) क्योंकि क्षेत्रफल एक धनात्मक राशि होती है इसलिए हम सदैव (1) में सारणिक का निरपेक्ष मान लेते हैं।
(ii) यदि क्षेत्रफल दिया हो तो गणना के लिए सारणिक का धनात्मक और ऋणात्मक दोनों मानों का प्रयोग कीजिए।
(iii) तीन संरेख बिंदुओं से बने त्रिभुज का क्षेत्रफल शून्य होगा।
उदाहरण 17 एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (3, 8), (– 4, 2) और (5, 1) हैं।
हल त्रिभुज का क्षेत्रफलः
∆ = 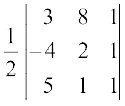 =
= 
= 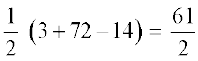
उदाहरण 18 सारणिकों का प्रयोग करके A(1, 3) और B (0, 0) को जोड़ने वाली रेखा का समीकरण ज्ञात कीजिए और k का मान ज्ञात कीजिए यदि एक बिंदु D(k, 0) इस प्रकार है कि ∆ ABD का क्षेत्रफल 3 वर्ग इकाई है।
हल मान लीजिए AB पर कोई बिंदु P (x, y) है तब ∆ ABP का क्षेत्रफल = 0 (क्यों?)
इसलिए 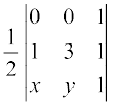 = 0
= 0
इससे प्राप्त है 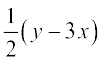 = 0 या y = 3x
= 0 या y = 3x
जो अभीष्ट रेखा AB का समीकरण है।
किंतु ∆ ABD का क्षेत्रफल 3 वर्ग इकाई दिया है अतः
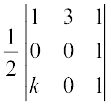 =±3हमेंप्राप्तहै
=±3हमेंप्राप्तहै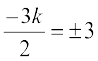 ,i.e.,k=
,i.e.,k=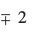
प्रश्नावली 4.3
1. निम्नलिखित प्रत्येक में दिए गए शीर्ष बिंदुओं वाले त्रिभुजों का क्षेत्रफल ज्ञात कीजिए।
(i) (1, 0), (6, 0), (4, 3) (ii) (2, 7), (1, 1), (10, 8)
(iii) (–2, –3), (3, 2), (–1, –8)
2. दर्शाइए कि बिंदु A (a, b + c), B (b, c + a) और C (c, a + b) संरेख हैं।
3. प्रत्येक में k का मान ज्ञात कीजिए यदि त्रिभुजों का क्षेत्रफल 4 वर्ग इकाई है जहाँ शीर्षबिंदु निम्नलिखित हैंः
(i) (k, 0), (4, 0), (0, 2) (ii) (–2, 0), (0, 4), (0, k)
4. (i) सारणिकों का प्रयोग करके (1, 2) और (3, 6) को मिलाने वाली रेखा का समीकरण ज्ञात कीजिए।
(ii) सारणिकों का प्रयोग करके (3, 1) और (9, 3) को मिलाने वाली रेखा का समीकरण ज्ञात कीजिए।
5. यदि शीर्ष (2, –6), (5, 4) और (k, 4) वाले त्रिभुज का क्षेत्रफल 35 वर्ग इकाई हो तो k का मान हैः
(A) 12 (B) –2 (C) –12, –2 (D) 12, –2
4.5 उपसारणिक और सहखंड (Minor and Co-factor)
इस अनुच्छेद में हम उपसारणिकों और सहखंडों का प्रयोग करके सारणिको के प्रसरण का विस्तृत रूप लिखना सीखेंगे।
परिभाषा 1 सारणिक के अवयव aij का उपसारणिक एक सारणिक है जो i वी पंक्ति और j वाँ स्तंभ जिसमें अवयव aij स्थित है, को हटाने से प्राप्त होता है। अवयव aij के उपसारणिक को Mij के द्वारा व्यक्त करते हैं।
टिप्पणी n(n ≥ 2) क्रम के सारणिक के अवयव का उपसारणिक n – 1 क्रम का सारणिक होता है।
उदाहरण 19 सारणिक 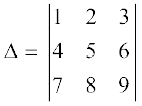 में अवयव 6 का उपसारणिक ज्ञात कीजिए।
में अवयव 6 का उपसारणिक ज्ञात कीजिए।
हल क्योंकि 6 दूसरी पंक्ति एवं तृतीय स्तंभ में स्थित है। इसलिए इसका उपसारिणक = M23 निम्नलिखित प्रकार से प्राप्त होता है।
M23 = 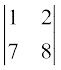 = 8 – 14 = – 6 (∆ से R2 और C3 हटाने पर)
= 8 – 14 = – 6 (∆ से R2 और C3 हटाने पर)
परिभाषा 2 एक अवयव aij का सहखंड जिसे Aij द्वारा व्यक्त करते हैं, जहाँ
Aij = (–1)i + j Mij,
के द्वारा परिभाषित करते हैं जहाँ aij का उपसारणिक Mij है।
उदाहरण 20 सारणिक 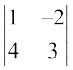 के सभी अवयवों के उपसारणिक व सहखंड ज्ञात कीजिए।
के सभी अवयवों के उपसारणिक व सहखंड ज्ञात कीजिए।
हल अवयव aij का उपसारणिक Mij है।
यहाँ a11 = 1, इसलिए M11 = a11का उपसारणिक = 3
M12 = अवयव a12 का उपसारणिक = 4
M21 = अवयव a21 का उपसारणिक = – 2
M22 = अवयव a22 का उपसारणिक = 1
अब aij का सहखंड Aij है। इसलिए
A11 = (–1)1 + 1 M11 = (–1)2 (3) = 3
A12 = (–1)1 + 2 M12 = (–1)3 (4) = – 4
A21 = (–1)2 + 1 M21 = (–1)3 (–2) = 2
A22 = (–1)2 + 2 M22 = (–1)4 (1) = 1
उदाहरण 21 ∆ = 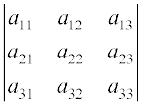 के अवयवों a11 तथा a21 के उपसारणिक और सहखंड
के अवयवों a11 तथा a21 के उपसारणिक और सहखंड
ज्ञात कीजिए।
हल उपसारणिक और सहखंड की परिभाषा द्वारा हम पाते हैंः
a11 का उपसारणिक = M11 = 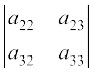 = a22 a33– a23 a32
= a22 a33– a23 a32
a11 का सहखंड = A11 = (–1)1+1 M11 = a22 a33 – a23 a32
a21 का उपसारणिक = M21 = 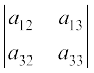 = a12 a33 – a13 a32
= a12 a33 – a13 a32
a21 का सहखंड = A21 = (–1)2+1 M21 = (–1) (a12 a33 – a13 a32) = – a12 a33 + a13 a32
टिप्पणी उदाहरण 21 में सारणिक ∆ का R1 के सापेक्ष प्रसरण करने पर हम पाते हैं कि
∆ = (–1)1+1 a11 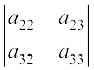 + (–1)1+2 a12
+ (–1)1+2 a12 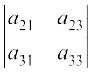 + (–1)1+3 a13
+ (–1)1+3 a13 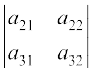
= a11 A11 + a12 A12 + a13 A13, जहाँ aij का सहखंड Aij हैं।
= R1 के अवयवों और उनके संगत सहखंडों के गुणनफल का योग।
इसी प्रकार ∆ का R2, R3, C1, C2 और C3 के अनुदिश 5 प्रसरण अन्य प्रकार से हैं।
अतः सारणिक ∆, किसी पंक्ति (या स्तंभ) के अवयवों और उनके संगत सहखंडों के गुणनफल का योग है।
टिप्पणी यदि एक पंक्ति (या स्तंभ) के अवयवों को अन्य पंक्ति (या स्तंभ) के सहखंडों से गुणा किया जाए तो उनका योग शून्य होता है। उदाहरणतया, माना ∆ = a11 A21 + a12 A22 + a13 A23 तबः
∆ = a11 (–1)1+1 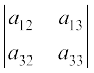 + a12 (–1)1+2
+ a12 (–1)1+2 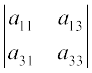 + a13 (–1)1+3
+ a13 (–1)1+3 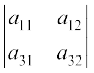
= 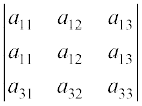 = 0 ( क्योंकि R1 और R2 समान हैं)
= 0 ( क्योंकि R1 और R2 समान हैं)
इसी प्रकार हम अन्य पंक्तियों और स्तंभों के लिए प्रयत्न कर सकते हैं।
उदाहरण 22 सारणिक 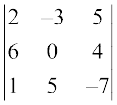 के अवयवों के उपसारणिक और सहखंड ज्ञात कीजिए और सत्यापित कीजिए कि a11 A31 + a12 A32 + a13 A33= 0 है।
के अवयवों के उपसारणिक और सहखंड ज्ञात कीजिए और सत्यापित कीजिए कि a11 A31 + a12 A32 + a13 A33= 0 है।
हल यहाँ M11 =  = 0 –20 = –20; इसलिए A11 = (–1)1+1 (–20) = –20
= 0 –20 = –20; इसलिए A11 = (–1)1+1 (–20) = –20
M12 = 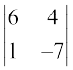 = – 42 – 4 = – 46; इसलिए A12 = (–1)1+2 (– 46) = 46
= – 42 – 4 = – 46; इसलिए A12 = (–1)1+2 (– 46) = 46
M13 = 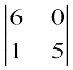 = 30 – 0 = 30; इसलिए A13 = (–1)1+3 (30) = 30
= 30 – 0 = 30; इसलिए A13 = (–1)1+3 (30) = 30
M21 = 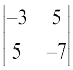 = 21 – 25 = – 4; इसलिए A21 = (–1)2+1 (– 4) = 4
= 21 – 25 = – 4; इसलिए A21 = (–1)2+1 (– 4) = 4
M22 = 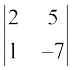 = –14 – 5 = –19; इसलिए A22 = (–1)2+2 (–19) = –19
= –14 – 5 = –19; इसलिए A22 = (–1)2+2 (–19) = –19
M23 = 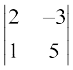 = 10 + 3 = 13; इसलिए A23 = (–1)2+3 (13) = –13
= 10 + 3 = 13; इसलिए A23 = (–1)2+3 (13) = –13
M31 = 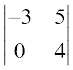 = –12 – 0 = –12; इसलिए A31 = (–1)3+1 (–12) = –12
= –12 – 0 = –12; इसलिए A31 = (–1)3+1 (–12) = –12
M32 = 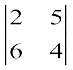 = 8 – 30 = –22; इसलिए A32 = (–1)3+2 (–22) = 22
= 8 – 30 = –22; इसलिए A32 = (–1)3+2 (–22) = 22
और M33 = 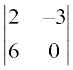 = 0 + 18 = 18; इसलिए A33 = (–1)3+3 (18) = 18
= 0 + 18 = 18; इसलिए A33 = (–1)3+3 (18) = 18
अब a11 = 2, a12 = –3, a13 = 5; तथा A31 = –12, A32 = 22, A33 = 18 है।
इसलिए a11 A31 + a12 A32 + a13 A33
= 2 (–12) + (–3) (22) + 5 (18) = –24 – 66 + 90 = 0
प्रश्नावली 4.4
निम्नलिखित सारणिकों के अवयवों के उपसारणिक एवं सहखंड लिखिए।
1. (i) 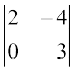 (ii)
(ii) 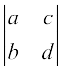
2. (i)  (ii)
(ii) 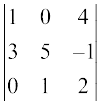
3. दूसरी पंक्ति के अवयवों के सहखंडों का प्रयोग करके ∆ = 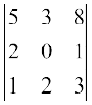 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
4. तीसरे स्तंभ के अवयवों के सहखंडों का प्रयोग करके ∆ = 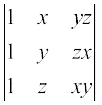 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
5. यदि ∆ = 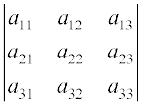 और aij का सहखंड Aij हो तो ∆ का मान निम्नलिखित रूप में व्यक्त किया जाता हैः
और aij का सहखंड Aij हो तो ∆ का मान निम्नलिखित रूप में व्यक्त किया जाता हैः
(A) a11 A31+ a12 A32 + a13 A33 (B) a11 A11+ a12 A21 + a13 A31
(C) a21 A11+ a22 A12 + a23 A13 (D) a11 A11+ a21 A21 + a31 A31
4.6 आव्यूह के सहखंडज और व्युत्क्रम (Adjoint and Inverse of a Matrix)
पिछले अध्याय में हमने एक आव्यूह के व्युत्क्रम का अध्ययन किया है। इस अनुच्छेद में हम एक आव्यूह के व्युत्क्रम के अस्तित्व के लिए शर्तों की भी व्याख्या करेंगे।
A–1 ज्ञात करने के लिए पहले हम एक आव्यूह का सहखंडज परिभाषित करेंगे।
4.6.1 आव्यूह का सहखंडज (Adjoint of a matrix)
परिभाषा 3 एक वर्ग आव्यूह A = [aij] का सहखंडज, आव्यूह [Aij] के परिवर्त के रूप में परिभाषित है, जहाँ Aij, अवयव aij का सहखंड है। आव्यूह A के सहखंडज को adj A के द्वारा व्यक्त करते हैं।
मान लीजिए A = है।
है।
तब adj A =
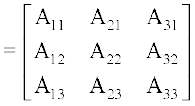 होता है।
होता है।
उदाहरण 23 आव्यूह 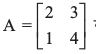 का सहखंडज ज्ञात कीजिए।
का सहखंडज ज्ञात कीजिए।
हल हम जानते हैं कि A11 = 4, A12 = –1, A21 = –3, A22 = 2
अतः adj A = 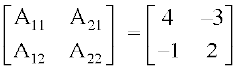
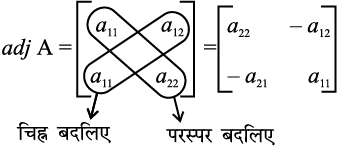
टिप्पणी 2 × 2 कोटि के वर्ग आव्यूह A = 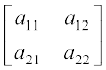 का सहखंडज adj A, a11 और a22 को परस्पर बदलने एवं a12 और a21 के चिह्न परिवर्तित कर देने से भी प्राप्त किया जा सकता है जैसा नीचे दर्शाया गया है।
का सहखंडज adj A, a11 और a22 को परस्पर बदलने एवं a12 और a21 के चिह्न परिवर्तित कर देने से भी प्राप्त किया जा सकता है जैसा नीचे दर्शाया गया है।
हम बिना उपपत्ति के निम्नलिखित प्रमेय निर्दिष्ट करते हैं।
प्रमेय 1 यदि A कोई n कोटि का आव्यूह है तो, A(adj A) = (adj A) A =  , जहाँ I, n कोटि का तत्समक आव्यूह है।
, जहाँ I, n कोटि का तत्समक आव्यूह है।
सत्यापनः मान लीजिए
A =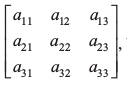 है तब
है तब 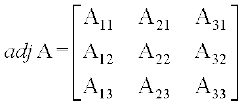
क्योंकि एक पंक्ति या स्तंभ के अवयवों का संगत सहखंडों की गुणा का योग |A| के समान होता है अन्यथा शून्य होता है।
इस प्रकार A (adj A) = 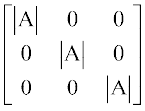 =
= 
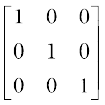 =
=  I
I
इसी प्रकार, हम दर्शा सकते हैं कि (adj A) A = |A| I
अतः A (adj A) = (adj A) A = |A| I सत्यापित है।
परिभाषा 4 एक वर्ग आव्यूह A अव्युत्क्रमणीय (singular) कहलाता है यदि  = 0 है।
= 0 है।
उदाहरण के लिए आव्यूह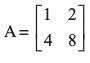 A = का सारणिक शून्य है। अतः A अव्युत्क्रमणीय है।
A = का सारणिक शून्य है। अतः A अव्युत्क्रमणीय है।
परिभाषा 5 एक वर्ग आव्यूह A व्युत्क्रमणीय (non-singular) कहलाता है यदि  ≠ 0
≠ 0
मान लीजिए A =  हो तो
हो तो  =
=  = 4 – 6 = – 2 ≠ 0 है।
= 4 – 6 = – 2 ≠ 0 है।
अतः A व्युत्क्रमणीय है।
हम निम्नलिखित प्रमेय बिना उपपत्ति के निर्दिष्ट कर रहे हैं।
प्रमेय 2 यदि A तथा B दोनों एक ही कोटि के व्युत्क्रमणीय आव्यूह हों तो AB तथा BA भी उसी कोटि के व्युत्क्रमणीय आव्यूह होते हैं।
प्रमेय 3 आव्यूहों के गुणनफल का सारणिक उनके क्रमशः सारणिकों के गुणनफल के समान होता है अर्थात्  =
= 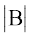
 , जहाँ A तथा B समान कोटि के वर्ग आव्यूह हैं।
, जहाँ A तथा B समान कोटि के वर्ग आव्यूह हैं।
टिप्पणी हम जानते हैं कि (adj A) A = प्
प्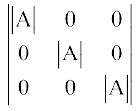
दोनों ओर आव्यूहों का सारणिक लेने पर,
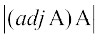 =
=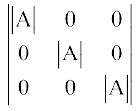
अर्थात् |(adj A)| |A| =  (क्यों?)
(क्यों?)
अर्थात् |(adj A)| |A| = 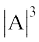 (1)
(1)
अर्थात् |(adj A)| = 
व्यापक रुप से, यदि n कोटि का एक वर्ग आव्यूह A हो तो |adjA| = |A|n – 1 होगा।
प्रमेय 4 एक वर्ग आव्यूह A के व्युत्क्रम का अस्तित्व है, यदि और केवल यदि A व्युत्क्रमणीय आव्यूह है।
उपपत्ति मान लीजिए n कोटि का व्युत्क्रमणीय आव्यूह A है और n कोटि का तत्समक आव्यूह I है।
तब n कोटि के एक वर्ग आव्यूह B का अस्तित्व इस प्रकार हो ताकि AB = BA = I
अब AB = I है तो |AB| = |I| या |A| |B| = 1 (क्योंकि |I| = 1, |AB| = |A| |B|)
इससे प्राप्त होता है |A| ≠ 0. अतः A व्युत्क्रमणीय है।
विलोमतः मान लीजिए A व्युत्क्रमणीय है। तब |A| ≠ 0
अब A (adj A) = (adj A) A =द्य।द्यI (प्रमेय 1)
या 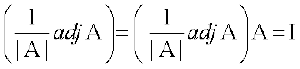
या AB = BA = I, जहाँ B = 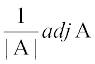
अतः A के व्युत्क्रम का अस्तित्व है और A–1 =। 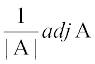
उदाहरण 24 यदि A =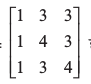 हो तो सत्यापित कीजिए कि A. adj A =
हो तो सत्यापित कीजिए कि A. adj A =  . I और A–1
. I और A–1
ज्ञात कीजिए।
हल हम पाते हैं कि = 1 (16 – 9) –3 (4 – 3) + 3 (3 – 4) = 1 ≠ 0
= 1 (16 – 9) –3 (4 – 3) + 3 (3 – 4) = 1 ≠ 0
अब A11 = 7, A12 = –1, A13 = –1, A21 = –3, A22 = 1, A23 = 0, A31 = –3, A32 = 0, A33 = 1
इसलिए adj A =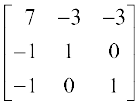
अब A.(adj A) =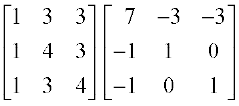
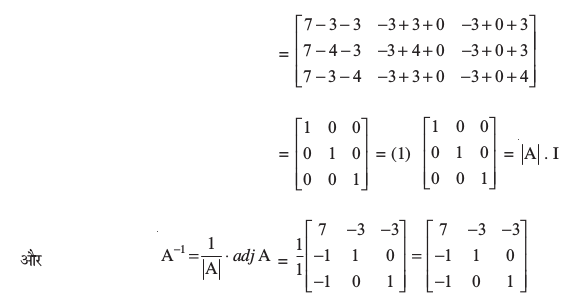
उदाहरण 25 यदि 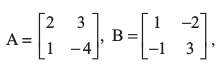 तो सत्यापित कीजिए कि (AB)–1 = B–1A–1 है।
तो सत्यापित कीजिए कि (AB)–1 = B–1A–1 है।
हल हम जानते हैं कि AB = 
क्योंकि  = –11 ≠ 0, (AB)–1 का अस्तित्व है और इसे निम्नलिखित प्रकार से व्यक्त किया जाता है।
= –11 ≠ 0, (AB)–1 का अस्तित्व है और इसे निम्नलिखित प्रकार से व्यक्त किया जाता है।
(AB)–1 =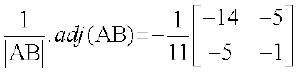
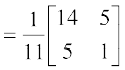
और  = –11 ≠ 0 व
= –11 ≠ 0 व 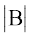 = 1 ≠ 0. इसलिए A–1 और B–1 दोनों का अस्तित्व है और जिसे निम्नलिखित रूप में व्यक्त किया जा सकता है।
= 1 ≠ 0. इसलिए A–1 और B–1 दोनों का अस्तित्व है और जिसे निम्नलिखित रूप में व्यक्त किया जा सकता है।
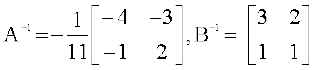
इसलिए 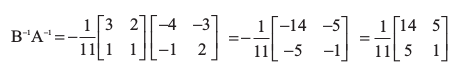
अतः (AB)–1 = B–1 A–1 है।
उदाहरण 26 प्रदर्शित कीजिए कि आव्यूह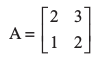 A = समीकरण A2 – 4A + I = O, जहाँ I
A = समीकरण A2 – 4A + I = O, जहाँ I
2 × 2 कोटि का एक तत्समक आव्यूह है और O, 2 × 2 कोटि का एक शून्य आव्यूह है। इसकी सहायता से A–1 ज्ञात कीजिए।
हल हम जानते हैं कि
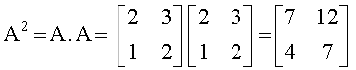
अतः A2 – 4A + I = 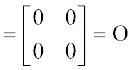
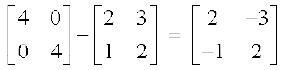
अब A2 – 4A + I = O
इसलिए A A – 4A = – I
या A A (A–1) – 4 A A–1 = – I A–1 (दोनों ओर A–1 से उत्तर गुणन द्वारा क्योंकि |A| ≠ 0)
या A (A A–1) – 4I = – A–1
या AI – 4I = – A–1
या A–1 = 4I – A = 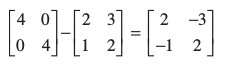
अतः 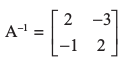
प्रश्नावली 4.5
प्रश्न 1 और 2 में प्रत्येक आव्यूह का सहखंडज (adjoint) ज्ञाात कीजिए



4.7 सारणिकों और आव्यूहों के अनुप्रयोग (Applications of Determinants and Matrices)
इस अनुच्छेद में हम दो या तीन अज्ञात राशियों के रैखिक समीकरण निकाय के हल और रैखिक समीकरणों के निकाय की संगतता की जाँच में सारणिकों और आव्यूहों के अनुप्रयोगों का वर्णन करेंगे।
संगत निकाय: निकाय संगत कहलाता है यदि इसके हलों (एक या अधिक) का अस्तित्व होता है।
असंगत निकायः निकाय असंगत कहलाता है यदि इसके किसी भी हल का अस्तित्व नहीं होता है।
टिप्पणी इस अध्याय में हम अद्वितीय हल के समीकरण निकाय तक सीमित रहेंगे।
4.7.1 आव्यूह के व्युत्क्रम द्वारा रैखिक समीकरणों के निकाय का हल (Solution of a system of linear equations using inverse of a matrix)
आइए हम रैखिक समीकरणों के निकाय को आव्यूह समीकरण के रूप में व्यक्त करते हैं और आव्यूह के व्युत्क्रम का प्रयोग करके उसे हल करते हैं।
निम्नलिखित समीकरण निकाय पर विचार कीजिए

स्थिति 1 यदि A एक व्युत्क्रमणीय आव्यूह है तब इसके व्युत्क्रम का अस्तित्व है। अतः AX = B से हम पाते हैं कि
A–1 (AX) = A–1 B (A–1 से पूर्व गुणन के द्वारा)
या (A–1A) X = A–1 B (साहचर्य गुणन द्वारा)
या I X = A–1 B
या X = A–1 B
यह आव्यूह समीकरण दिए गए समीकरण निकाय का अद्वितीय हल प्रदान करता है क्योंकि एक आव्यूह का व्युत्क्रम अद्वितीय होता है। समीकरणों के निकाय के हल करने की यह विधि आव्यूह विधिकहलाती है।
स्थिति 2 यदि A एक अव्युत्क्रमणीय आव्यूह है तब |A| = 0 होता है।
इस स्थिति में हम (adj A) B ज्ञात करते हैं।
यदि (adj A) B ≠ O, (O शून्य आव्यूह है), तब कोई हल नहीं होता है और समीकरण निकाय असंगत कहलाती है।
यदि (adj A) B = O, तब निकाय संगत या असंगत होगी क्योंकि निकाय के अनंत हल होंगे या कोई भी हल नहीं होगा।
उदाहरण 27 निम्नलिखित समीकरण निकाय को हल कीजिएः
2x + 5y = 1
3x + 2y = 7
हल समीकरण निकाय AX = B के रूप में लिखा जा सकता है, जहाँ
अब,  = –11 ≠ 0, अतः A व्युत्क्रमणीय आव्यूह है इसलिए इसके व्युत्क्रम का अस्तित्व है। और इसका एक अद्वितीय हल है।
= –11 ≠ 0, अतः A व्युत्क्रमणीय आव्यूह है इसलिए इसके व्युत्क्रम का अस्तित्व है। और इसका एक अद्वितीय हल है।
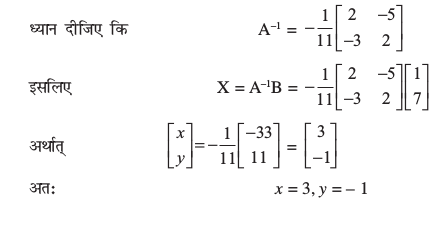
उदाहरण 28 निम्नलिखित समीकरण निकाय
3x – 2y + 3z = 8
2x + y – z = 1
4x – 3y + 2z = 4
को आव्यूह विधि से हल कीजिए।
हल समीकरण निकाय को AX = B के रूप में व्यक्त किया जा सकता है जहाँ

हम देखते हैं कि
 = 3 (2 – 3) + 2(4 + 4) + 3 (– 6 – 4) = – 17 ≠ 0 है।
= 3 (2 – 3) + 2(4 + 4) + 3 (– 6 – 4) = – 17 ≠ 0 है।
अतः A व्युत्क्रमणीय है, और इसके व्युत्क्रम का अस्तित्व है।
A11 = –1, A12 = – 8, A13 = –10
A21 = –5, A22 = – 6, A23 = 1
A31 = –1, A32 = 9, A33 = 7
इसलिए A–1 =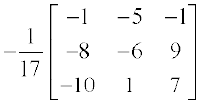
और ग् त्र्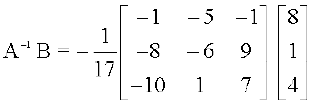
अतः 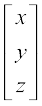 त्र्
त्र् 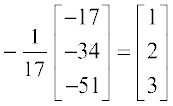
अतः x = 1, y = 2 व z = 3
उदाहरण 29 तीन संख्याओं का योग 6 है। यदि हम तीसरी संख्या को 3 से गुणा करके दूसरी संख्या में जोड़ दें तो हमें 11 प्राप्त होता है। पहली ओर तीसरी को जोड़ने से हमें दूसरी संख्या का दुगुना प्राप्त होता है। इसका बीजगणितीय निरूपण कीजिए और आव्यूह विधि से संख्याएँ ज्ञात कीजिए।
हल मान लीजिए पहली, दूसरी व तीसरी संख्या क्रमशः x, y और z, द्वारा निरूपित है। तब दी गई शर्तों के अनुसार हमें प्राप्त होता हैः
x + y + z = 6
y + 3z = 11
x + z = 2y
या x – 2y + z = 0
इस निकाय को A X = B के रूप में लिखा जा सकता है जहाँ
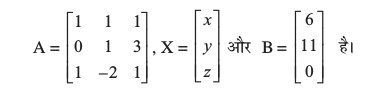
यहाँ 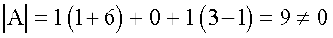 है। अब हम adj A ज्ञात करते हैं।
है। अब हम adj A ज्ञात करते हैं।
A11 = 1 (1 + 6) = 7, A12 = – (0 – 3) = 3, A13 = – 1
A21 = – (1 + 2) = – 3, A22 = 0, A23 = – (– 2 – 1) = 3
A31 = (3 – 1) = 2, A32 = – (3 – 0) = – 3, A33 = (1 – 0) = 1
अतः adj A =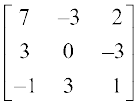
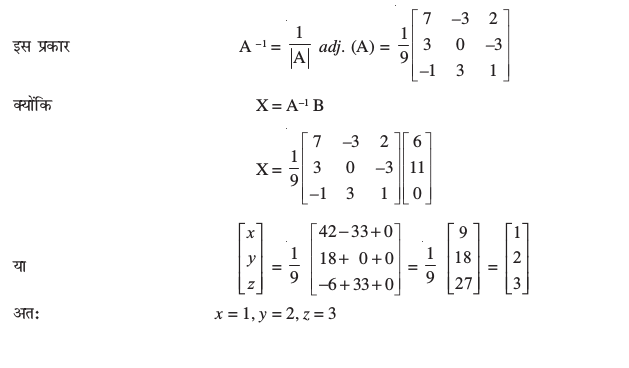
प्रश्नावली 4.6
निम्नलिखित प्रश्नों 1 से 6 तक दी गई समीकरण निकायों का संगत अथवा असंगत के रूप में वर्गीकरण कीजिए
1. x + 2y = 2 2. 2x – y = 5 3. x + 3y = 5
2x + 3y = 3 x + y = 4 2x + 6y = 8
4. x + y + z = 1 5. 3x–y – 2z = 2 6. 5x – y + 4z = 5
2x + 3y + 2z = 2 2y – z = –1 2x + 3y + 5z = 2
ax + ay + 2az = 4 3x – 5y = 3 5x – 2y + 6z = –1
निम्नलिखित प्रश्न 7 से 14 तक प्रत्येक समीकरण निकाय को आव्यूह विधि से हल कीजिए।
7. 5x + 2y = 4 8. 2x – y = –2 9. 4x – 3y = 3
7x + 3y = 5 3x + 4y = 3 3x – 5y = 7
10. 5x + 2y = 3 11. 2x + y + z = 1 12. x – y + z = 4
3x + 2y = 5 x – 2y – z = 3/2 2x + y – 3z = 0
3y – 5z = 9 x + y + z = 2
13. 2x + 3y +3 z = 5 14. x – y + 2z = 7
x – 2y + z = – 4 3x + 4y – 5z = – 5
3x – y – 2z = 3 2x – y + 3z = 12
15. यदि A =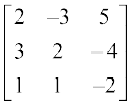 है तो A–1 ज्ञात कीजिए। A–1 का प्रयोग करके निम्नलिखित समीकरण निकाय को हल कीजिए।
है तो A–1 ज्ञात कीजिए। A–1 का प्रयोग करके निम्नलिखित समीकरण निकाय को हल कीजिए।
2x – 3y + 5z = 11
3x + 2y – 4z = – 5
x + y – 2z = – 3
16. 4 kg प्याज, 3 kg गेहूँ और 2 kg चावल का मूल्य Rs 60 है। 2 kg प्याज, 4 kg गेहूँ और 6 kg चावल का मूल्य Rs 90 है। 6 kg प्याज, 2 kg और 3 kg चावल का मूल्य Rs 70 है। आव्यूह विधि द्वारा प्रत्येक का मूल्य प्रति kg ज्ञात कीजिए।
विविध उदाहरण
उदहारण 30 यदि a, b, c धनात्मक और भिन्न हैं तो दिखाइए कि सारणिक
∆ =  का मान ऋणात्मक है।
का मान ऋणात्मक है।
हल C1 → C1 + C2 + C3 का प्रयोग करने पर
∆ =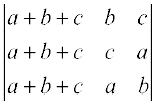 = (a + b + c)
= (a + b + c)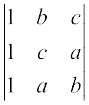
= (a + b + c)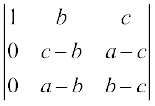 (R2→R2–R1,और R3→R3–R1 का प्रयोग करने पर)
(R2→R2–R1,और R3→R3–R1 का प्रयोग करने पर)
= (a + b + c) [(c – b) (b – c) – (a – c) (a – b)] (C1 के अनुदिश प्रसरण करने पर)
=( a + b + c)(– a2 – b2 – c2 + ab + bc + ca)
= 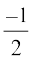 (a + b + c) (2a2 + 2b2 + 2c2 – 2ab – 2bc – 2ca)
(a + b + c) (2a2 + 2b2 + 2c2 – 2ab – 2bc – 2ca)
= 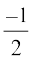 (a + b + c) [(a – b)2 + (b – c)2 + (c – a)2]
(a + b + c) [(a – b)2 + (b – c)2 + (c – a)2]
जो ऋणात्मक है ( क्योंकि a + b + c > 0 और (a – b)2 + (b – c)2 + (c – a)2 > 0)
उदाहरण 31 यदि a, b, c समांतर श्रेढ़ी में हाें तो निम्नलिखित सारणिक का मान ज्ञात कीजिए
∆ =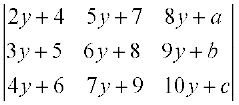
हल R1 → R1 + R3 – 2R2 का प्रयोग करने पर
∆ =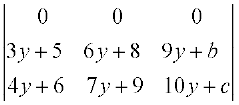 = 0 (क्योंकि 2b = a + c)
= 0 (क्योंकि 2b = a + c)
उदाहरण 32 दर्शाइए कि सारणिक
∆ =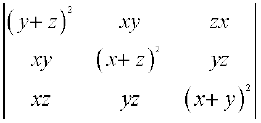 = 2xyz (x + y + z)3
= 2xyz (x + y + z)3
हल सारणिक में R1 → xR1, R2 → yR2 , R3 → zR3 का प्रयोग करने और xyz, से भाग करने पर हम प्राप्त करते हैं कि सारणिक
∆ = 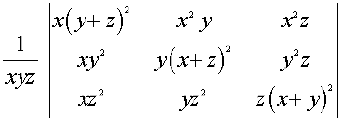
C1 , C2 और C3 से क्रमशः x, y, z उभयनिष्ठ लेने पर,
∆ = 
C2 → C2– C1, C3 → C3– C1, का प्रयोग करने पर हम प्राप्त करते हैं कि
∆ = 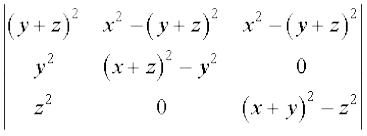
अब C2 और C3 से (x + y + z) उभयनिष्ठ लेने पर, प्राप्त सारणिक
∆ = (x + y + z)2 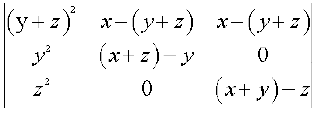
R1 → R1 – (R2 + R3) का प्रयोग करने पर हम निम्नलिखित सारणिक प्राप्त करते हैं
∆ = (x + y + z)2 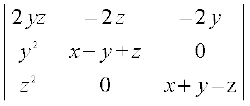
C2 → (C2 +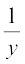 C1) और
C1) और 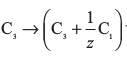 का प्रयोग करने पर प्राप्त सारणिक
का प्रयोग करने पर प्राप्त सारणिक
∆ = (x + y + z)2 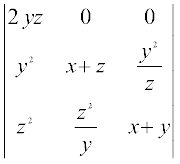
R1 के अनुदिश प्रसरण करने पर
∆ = (x + y + z)2 (2yz) [(x + z) (x + y) – yz] = (x + y + z)2 (2yz) (x2 + xy + xz)
= (x + y + z)3 (2xyz) प्राप्त होता है।
उदाहरण 33 आव्यूहों के गुणनफल 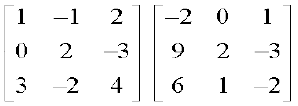 का प्रयोग करते हुए निम्नलिखित समीकरण निकाय को हल कीजिएः
का प्रयोग करते हुए निम्नलिखित समीकरण निकाय को हल कीजिएः
x – y + 2z = 1
2y – 3z = 1
3x – 2y + 4z = 2
हल दिया गया गुणनफल 
= 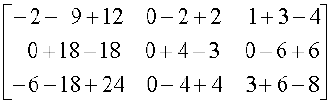
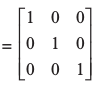
अतः 
अब दिए गए समीकरण निकाय को आव्यूह के रूप निम्नलिखित रूप में लिखा जा सकता है

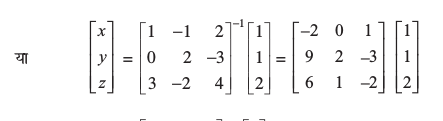
= 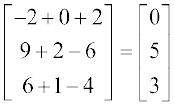
अतः x = 0, y = 5 और z = 3
उदाहरण 34 सिद्ध कीजिए कि सारणिक
∆ = 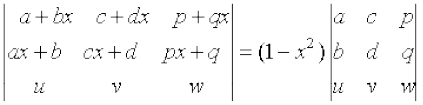
हल सारणिक ∆ पर R1 → R1 – x R2 का प्रयोग करने पर हमें
D = प्राप्त होता है
प्राप्त होता है
=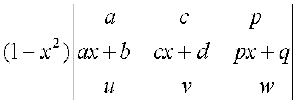
R2 → R2 – x R1, का प्रयोग करने पर हमें सारणिक
∆ =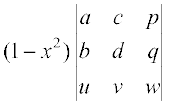 प्राप्त होता है।
प्राप्त होता है।
अध्याय 4 पर विविध प्रश्नावली
1. सिद्ध कीजिए कि सारणिक 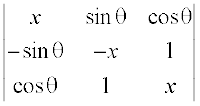 , θ से स्वतंत्र है।
, θ से स्वतंत्र है।
2. सारणिक का प्रसरण किए बिना सिद्ध कीजिए कि 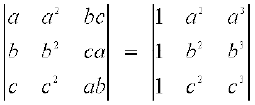
3.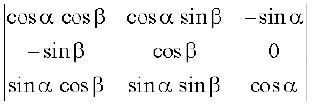 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
4. यदि a, b और c वास्तविक संख्याएँ हो और सारणिक
∆ = 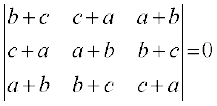
हो तो दर्शाइए कि या तो a + b + c = 0 या a = b = c है।
5. यदि a ≠ 0 हो तो समीकरण 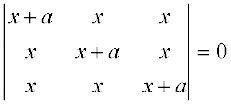 को हल कीजिए।
को हल कीजिए।
6. सिद्ध कीजिए कि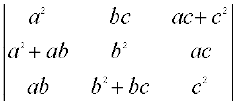 = 4a2b2c2
= 4a2b2c2
7.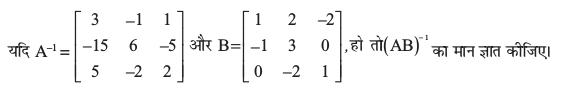
8.
मान लीजिए A = हो तो सत्यापित कीजिए कि
(i) [adj A]–1 = adj (A–1) (ii) (A–1)–1 = A
9.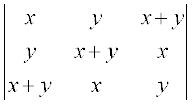 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
10. 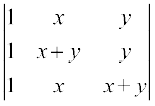 का मान ज्ञात कीजिए।
का मान ज्ञात कीजिए।
सारणिकों के गुणधर्मों का प्रयोग करके निम्नलिखित 11 से 15 तक प्रश्नों को सिद्ध कीजिएः
11.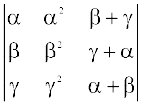 = (β – γ) (γ – α) (α – β) (α + β + γ)
= (β – γ) (γ – α) (α – β) (α + β + γ)
12.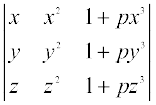 = (1 + pxyz) (x – y) (y – z) (z – x),
= (1 + pxyz) (x – y) (y – z) (z – x),
13.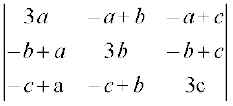 = 3(a + b + c) (ab + bc + ca)
= 3(a + b + c) (ab + bc + ca)
14.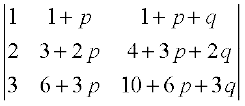 त्र् 1
त्र् 1
15.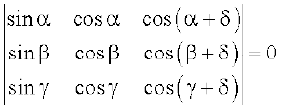
16. निम्नलिखित समीकरण निकाय को हल कीजिए
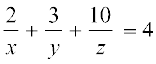
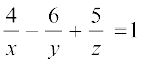
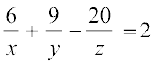
निम्नलिखित प्रश्नों 17 से 19 में सही उत्तर का चुनाव कीजिए।
17. यदि a, b, c समांतर श्रेढ़ी में हों तो सारणिक
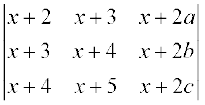
का मान होगाः
(A) 0 (B) 1 (C) x (D) 2x
18. यदि x, y, z शून्येतर वास्तविक संख्याएँ हों तो आव्यूह 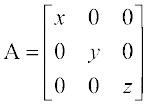 का व्युत्त्क्रम हैः
का व्युत्त्क्रम हैः
(A)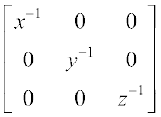 (ठ)
(ठ)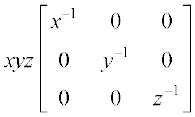
(C)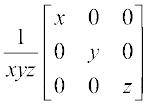 (क्)
(क्) 
19.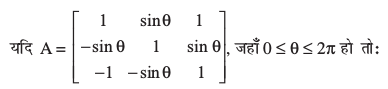
(A) det(A) = 0 (B) det(A) ∈ (2, ∞)
(C) det(A) ∈ (2, 4) (D) det(A) ∈ [2, 4].
सारांश
- आव्यूह
![]() का सारणिक
का सारणिक ![]() के द्वारा दिया जाता है।
के द्वारा दिया जाता है। - आव्यूह
![image239]() का सारणिक
का सारणिक
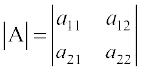 = a11 a22 – a12 a21 के द्वारा दिया जाता है।
= a11 a22 – a12 a21 के द्वारा दिया जाता है।
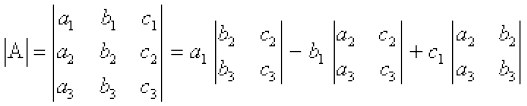
किसी वर्ग आव्यूह । के लिए, द्य।द्य निम्नलिखित गुणधर्मों को संतुष्ट करता है।
-
![]() =
= ![]() , जहाँ = A का परिवर्त है।
, जहाँ = A का परिवर्त है। - यदि हम दो पंक्तियों या स्तंभों को परस्पर बदल दें तो सारणिक का चिह्न बदल जाता है।
- यदि सारणिक की कोई दो पंक्ति या स्तंभ समान या समानुपाती हों तो सारणिक का मान शून्य होता है।
- यदि हम एक सारणिक की एक पंक्ति या स्तंभ को अचर k, से गुणा कर दें तो सारणिक का मान k गुना हो जाता है।
- एक सारणिक को k से गुणा करने का अर्थ है कि उसके अंदर केवल किसी एक पंक्ति या स्तंभ के अवयवों को k से गुणा करना।
- यदि
![]()
![]()
- यदि एक सारणिक के एक पंक्ति या स्तंभ के अवयव दो या अधिक अवयवों के योग के रूप में व्यक्त किए जा सकते हों तो उस दिए गए सारणिक को दो या अधिक सारणिकों के योग के रूप में व्यक्त किया जा सकता है।
- यदि एक सारणिक के किसी एक पंक्ति या स्तंभ के प्रत्येक अवयव के समगुणज अन्य पंक्ति या स्तंभ के संगत अवयवों में जोड़ दिए जाते हैं तो सारणिक का मान अपरिवर्तित रहता है।
- (x1, y1), (x2, y2) और (x3, y3) शीर्षों वाली त्रिभुज का क्षेत्रफल निम्नलिखित रूप द्वारा दिया जाता हैः
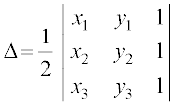
- दिए गए आव्यूह A के सारणिक के एक अवयव aij का उपसारणिक, i वीं पंक्ति और
- aij का सहखंड Aij = (– 1)i+j Mij द्वारा दिया जाता है।
- A के सारणिक का मान
![]() = a11 A11 + a12 A12 + a13 A13 है और इसे एक पंक्ति या स्तंभ के अवयवों और उनके संगत सहखंडों के गुणनफल का योग करके प्राप्त किया जाता है।
= a11 A11 + a12 A12 + a13 A13 है और इसे एक पंक्ति या स्तंभ के अवयवों और उनके संगत सहखंडों के गुणनफल का योग करके प्राप्त किया जाता है। - यदि एक पंक्ति (या स्तंभ) के अवयवों और अन्य दूसरी पंक्ति (या स्तंभ) के सहखंडों की गुणा कर दी जाए तो उनका योग शून्य होता है उदाहरणतया
a11 A21 + a12 A22 + a13 A23 = 0
- यदि आव्यूह
![]() तो सहखंडज
तो सहखंडज ![]() होता है, जहाँ aij का सहखंड Aij है।
होता है, जहाँ aij का सहखंड Aij है। - A (adj A) = (adj A) A =
![]() I, जहाँ A, n कोटि का वर्ग आव्यूह है।
I, जहाँ A, n कोटि का वर्ग आव्यूह है। - यदि कोई वर्ग आव्यूह क्रमशः अव्युत्क्रमणीय या व्युत्क्रमणीय कहलाता है यदि
![]() = 0 या
= 0 या - यदि AB = BA = I, जहाँ B एक वर्ग आव्यूह है तब A का व्युत्क्रम B होता है और
A–1 = B या B–1 = A और इसलिए (A–1)–1 = A
- किसी वर्ग आव्यूह A का व्युत्क्रम है यदि और केवल यदि A व्युत्क्रमणीय है।
![]()
- यदि a1 x + b1 y + c1 z = d1
a2 x + b2 y + c2 z = d2
a3 x + b3 y + c3 z = d3
तब इन समीकरणों को A X = B के रूप में लिखा जा सकता है।
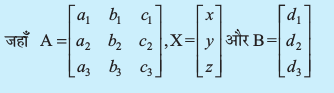
- समीकरण AX = B का अद्वितीय हल X = A–1 B द्वारा दिया जाता है जहाँ
![]()
- समीकरणों का एक निकाय संगत या असंगत होता है यदि इसके हल का अस्तित्व है अथवा नहीं है।
- आव्यूह समीकरण AX = B में एक वर्ग आव्यूह A के लिए
(i) यदि  ≠0, तो अद्वितीय हल का अस्तित्व है।
≠0, तो अद्वितीय हल का अस्तित्व है।
(ii) यदि  = 0 और (adj A) B ≠ O, तो किसी हल का अस्तित्व नहीं है।
= 0 और (adj A) B ≠ O, तो किसी हल का अस्तित्व नहीं है।
(iii) यदि  = 0 और (adj A) B = O, तो निकाय संगत या असंगत होती है।
= 0 और (adj A) B = O, तो निकाय संगत या असंगत होती है।
एेतिहासिक पृष्ठभूमि
गणना बोर्ड पर छड़ों का प्रयोग करके कुछ रैखिक समीकरणों की अज्ञात राशियों के गुणांकों को निरूपित करने की चीनी विधि ने वास्तव में विलोपन की साधारण विधि की खोज करने में सहायता की है। छड़ों की व्यवस्था क्रम एक सारणिक में संख्याओं की उचित व्यवस्था क्रम जैसी थी। इसलिए एक सारणिक की सरलीकरण में स्तंभों या पंक्तियों के घटाने का विचार उत्पन्न करने में चीनी प्रथम विचारकों में थे (‘Mikami, China, pp 30, 93).
सत्रहवीं शताब्दी के महान जापानी गणितज्ञ Seki Kowa द्वारा 1683 में लिखित पुस्तक 'Kai Fukudai no Ho' से ज्ञात होता है कि उन्हें सारणिकों और उनके प्रसार का ज्ञान था। परंतु उन्होंने इस विधि का प्रयोग केवल दो समीकरणों से एक राशि के विलोपन में किया परंतु युगपत रैखिक समीकरणों के हल ज्ञात करने में इसका सीधा प्रयोग नहीं किया था। ‘T. Hayashi, “The Fakudoi and Determinants in Japanese Mathematics,” in the proc. of the Tokyo Math. Soc., V.
Vendermonde पहले व्यक्ति थे जिन्होनें सारणिकों को स्वतंत्र फलन की तरह से पहचाना इन्हें विधिवत इसका अन्वेषक (संस्थापक) कहा जा सकता है। Laplace (1772) ने सारणिकों को इसके पूरक उपसारणिकों के रूप में व्यक्त करके प्रसरण की व्यापक विधि दी। 1773 में Lagrange ने दूसरे व तीसरे क्रम के सारणिकों को व्यवहृत किया और सारणिकों के हल के अतिरिक्त उनका अन्यत्र भी प्रयोग किया। 1801 में Gauss ने संख्या के सिद्धांतों में सारणिकों का प्रयोग किया।
अगले महान योगदान देने वाले Jacques - Philippe - Marie Binet, (1812) थे जिन्होंने m-स्तंभों और n-पंक्तियों के दो आव्यूहों के गुणनफल से संबंधित प्रमेय का उल्लेख किया जो विशेष स्थिति m = n में गुणनफल प्रमेय में बदल जाती है।
उसी दिन Cauchy (1812) ने भी उसी विषय-वस्तु पर शोध प्रस्तुत किए। उन्होंने आज केे व्यावहारिक सारणिक शब्द का प्रयोग किया। उन्होंने Binet से अधिक संतुष्ट करने वाली गुणनफल प्रमेय की उपपत्ति दी।
इन सिद्धांतों पर महानतम योगदान वाले Carl Gustav Jacob Jacobi थे। इसके पश्चात सारणिक शब्द को अंतिम स्वीकृति प्राप्त हुई।

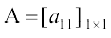
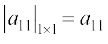
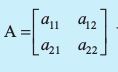

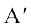 =
=