Table of Contents
ifjf'k"V 1
xf.kr esa miifÙk;k¡
(Proofs in Mathematics)
Proofs are to Mathematics what calligraphy is to poetry.
Mathematical works do consist of proofs just as
poems do consist of characters — Vladimir Arnold
A.1.1 Hkwfedk (Introduction)
d{kk IX] X rFkk XI esa ge dFku] la;qDr dFku] dFku osQ fu"ks/u] foykse rFkk izfr/ukRed Lo:i vkSj vfHkx`ghr] vuqekfur dFku] lkè; rFkk fuxeukRed foospu dh ladYiukvksa osQ ckjs esa i<+ pqosQ gSaA
;gk¡ ge xf.krh; lkè;ksa dks fl¼ (izekf.kr) djus dh fofHkUu fof/;ksa ij fopkj djsaxsA
A.1.2 miifÙk D;k gS? (What is a Proof?)
fdlh xf.krh; dFku dh miifÙk esa dFkuksa dk ,d vuqØe varfoZ"V gksrk gS] ftlosQ izR;sd dFku osQ vkSfpR; dks fdlh ifjHkkf"kr in ;k fdlh vfHkx`ghr ;k fdlh ,slh lkè; }kjk izekf.kr djrs gSa] ftls fuxefud fof/ rFkk oqQN vifjHkkf"kr inksa }kjk osQoy Lohdk;Z rkfoZQd fu;eksa dk iz;ksx djosQ iwoZ izfrikfnr fd;k tk pqdk gksA
bl izdkj izR;sd miifÙk fuxefud rdks± dh ,d Üka`[kyk gksrh gS] ftuesa ls izR;sd dh viuh ifjdYiuk,¡ rFkk fu"d"kZ gksrs gSaA vf/drj ge fdlh lkè; dks mlesa fn, gq, rF;ksa ls izR;{k jhfr }kjk fl¼ djrs gSaA ijarq dHkh&dHkh lkè; dks lh/s fl¼ djus dh vis{kk mlosQ lerqY; lkè; dks fl¼ djuk vklku gksrk gSA bl izdkj fdlh lkè; dks fl¼ djus dh nks fof/;k¡ iznf'kZr gksrh gSa] uker% izR;{k miifÙk vFkok vizR;{k miifÙk rFkk blosQ vfrfjDr izR;sd fof/ esa rhu fHkUu&fHkUu rjhosQ gksrs gSa] ftudh ppkZ uhps dh xbZ gSA
izR;{k miifÙk ;g lkè; dh og miifÙk gS] ftls ge lh/s #i esa iznÙk rF;ksa ls izkjaHk dj lkè; dh miifÙk LFkkfir djrs gSaA
(i) lh/k&lh/k mixeu (Approach) ;g rdks± dh ,d Üka`[kyk gS] tks iznÙk vFkok dfYir rF;ksa ls lh/s izkjaHk djosQ] vfHkx`ghrksa] ifjHkkf"kr inksa rFkk iwoZ izekf.kr lkè;ksa dh lgk;rk ls roZQ osQ fu;eksa osQ iz;ksx }kjk] fl¼ fd, tkus okys fu"d"kZ dks izekf.kr djrh gSA
fuEufyf[kr mnkgj.k ij fopkj dhft,%
mnkgj.k 1 ;fn x2 – 5x + 6 = 0 rks x = 3 ;k x = 2 gSA
gy x2 – 5x + 6 = 0 (fn;k gS)
⇒ (x – 3) (x – 2) = 0 (,d O;atd dks rqY; O;atd ls cnyus ij)
⇒ x – 3 = 0 ;k x – 2 = 0 (iwoZizekf.kr lkè; ab = 0 rc a = 0 ;k b = 0, a, b ∈ R }kjk)
⇒ x – 3 + 3 = 0 + 3 ;k x – 2 + 2 = 0 + 2 (lehdj.k osQ nksuksa i{kksa esa leku la[;k tksM+us ls mldh izo`Qfr ifjofrZr ugha gksrh gSA)
⇒ x + 0 = 3 ;k x + 0 = 2 (;ksx osQ varxZr iw.kk±d osQ rRled(Identity) xq.k osQ iz;ksx }kjk)
⇒ x = 3 ;k x = 2 (;ksx osQ varxZr iw.kk±d osQ rRled xq.k osQ iz;ksx }kjkA)
x2 – 5x + 6 = 0 ⇒ x = 3 ;k x = 2
;gk¡ p iznÙk dFku “x2 – 5x + 6 = 0” gS vkSj q fu"d"kZ dFku “x = 3 ;k x = 2” gSA
dFku p osQ O;atd x2 – 5x + 6 dks] blosQ rqY; ,d vU; O;atd (x – 3) (x – 2) ls izfrLFkkfir dj osQ ge ,d O;atd r:“(x – 3) (x – 2) = 0” izkIr djrs gSa
;gk¡ nks iz'u mBrs gSa%
(i) O;atd (x – 3) (x – 2) fdl izdkj O;atd x2 – 5x + 6 osQ leku (rqY;) gS ?
(ii) fdlh O;atd dks mlosQ leku ,d vU; O;atd ls ge dSls izfrLFkkfir dj ldrs gSa? buesa ls izFke dks ge fiNyh d{kkvksa esa xq.ku[kaM }kjk fl¼ dj pqosQ gSa vFkkZr~
x2 – 5x + 6 = x2 – 3x – 2x + 6 = x (x – 3) – 2 (x – 3) = (x – 3) (x – 2)
f}rh; iz'u roZQ osQ oS/ :i (roZQ osQ fu;eksa) }kjk laHko gksrk gSA
blosQ mijkar r iwoZdFku (Premise) ;k iznÙk dFku gks tkrk gS] ftlls dFku s: “ x – 3 = 0 ;k x – 2 = 0” izkIr gksrk gSA izR;sd pj.k (steps) dk vkSfpR; dks"Bd (brackets) esa fn;k gSA
;g izfØ;k fujarj rc rd pyrh jgrh gS tc rd ge vafre fu"d"kZ ij ugha igq¡p tkrs gSaA
roZQ dh izrhdkRed lerqY;rk fuxeu }kjk ;g izekf.kr djus esa gS fd p ⇒ q lR; gSA
p ls izkjaHk djosQ fuxeu }kjk p ⇒ r ⇒ s ⇒ … ⇒ q dks izekf.kr dhft,A vr%
“p ⇒ q” lR; gSA
mnkgj.k 2 fl¼ dhft, dh iQyu f : R → R tks f(x) = 2x + 5 }kjk ifjHkkf"kr gS] ,d ,oSQdh (one-one) iQyu gS
miifÙk è;ku nhft, fd iQyu f ,oSQdh gksxk ;fn f(x1) = f(x2) ⇒ x1 = x2
(,oSQdh iQyu dh ifjHkk"kk)
vc eku yhft, fd f(x1) = f(x2) vFkkZr~ 2x1+ 5 = 2x2 + 5
⇒ 2x1+ 5 – 5 = 2x2 + 5 – 5 (nksuksa i{kksa esa leku la[;k tksM+us ls)
⇒ 2x1+ 0 = 2x2 + 0
⇒ 2x1 = 2x2 (okLrfod la[;kvksa esa ;ksT; rRled dk xq.k)
⇒ 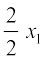 =
= 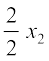 (nksuksa i{kksa dks leku 'kwU;srj la[;k ls foHkkftr djus ls)
(nksuksa i{kksa dks leku 'kwU;srj la[;k ls foHkkftr djus ls)
⇒ x1 = x2
vr% iQyu ,oSQdh gSA
(ii) xf.krh; vkxeu
xf.krh; vkxeu] lkè;ksa dks fl¼ djus dh ,d ,slh fof/ gS] ftldk Lo:i fuxefud gksrk gSA bl fof/ esa miifÙk iw.kZ:is.k fuEufyf[kr vfHkx`ghr ij vk/kfjr gksrh gSaA
N osQ ,d iznÙk mileqPp; S esa] ;fn
(i) izko`Qr la[;k 1 ∈ S rFkk
(ii) izko`Qr la[;k k + 1 ∈ S tc dHkh k ∈ S, rks S = N
xf.krh; vkxeu dk fl¼kar ;g gS fd ;fn ,d dFku “S(n), n = 1 osQ fy, lR; gS” (vFkok fdlh vU; izkjafHkd la[;k j osQ fy, lR; gS) vkSj ;fn dFku n = k osQ fy, lR; gksus esa ;g varfuZfgr gS fd og n = k + 1 osQ fy, vfuok;Zr% lR; gS (tc dHkh /u iw.kk±d k ≥ j), rks iznÙk dFku fdlh Hkh /u iw.kk±d n, tgk¡ n ≥ j osQ fy, lR; gksrk gSA
vc ge oqQN mnkgj.k ysrs gSaA
mnkgj.k 3 ;fn A = 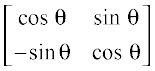 , rks fn[kkb, fd An =
, rks fn[kkb, fd An = 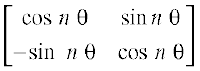
gy eku fy;k fd P(n) : An = 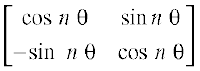
ge ns[krs gSa fd P(1) : A1 = 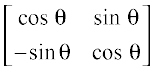
vr% P(1) lR; gSA
vc eku fy;k fd P(k) lR; gS] vFkkZr~
P(k) : Ak = 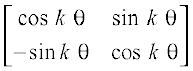
rks ge fl¼ djuk pkgrs gSa fd P(k + 1) lR; gS] tc dHkh P(k) lR; gS] vFkkZr~
P(k + 1) : Ak+1 = 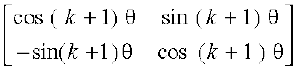 lR; gS
lR; gS
iqu% Ak+1 = Ak . A
pw¡fd P(k) lR; gS] blfy,
Ak+1 = 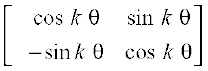
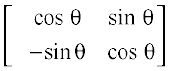
= 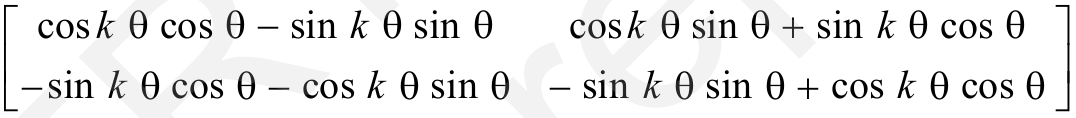
(vkO;wg xq.ku }kjk)
=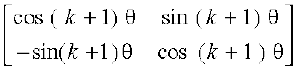
vr% P(k + 1) lR; gS] tc dHkh P(k) lR; gSA
vr,o P(n), n osQ lHkh ekuksa (/u iw.kk±d) osQ fy, lR; gSA
(iii) fofHkUu fLFkfr;ksa esa fo[kaMu }kjk vFkok fu%'ks"k.k }kjk miifÙk
dFku p ⇒ q dks fl¼ djus dh ;g fof/ osQoy rHkh laHko gS] tc p dks vusd dFkuksa r, s, t (eku fy;k) esa fo[kafMr fd;k tk ldrk gks tSlk fd p = r 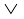 s
s 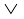 t (tgk¡ “
t (tgk¡ “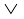 ” izrhd gS “;k” osQ fy,)
” izrhd gS “;k” osQ fy,)
;fn lizfrca/ dFkuksa r ⇒ q;
s ⇒ q;
rFkk t ⇒ q
dks izekf.kr fd;k tk,] rks (r 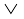 s
s 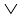 t) ⇒ q, fl¼ gks tkrk gS vkSj bl izdkj p ⇒ q izekf.kr gksrk gSA
t) ⇒ q, fl¼ gks tkrk gS vkSj bl izdkj p ⇒ q izekf.kr gksrk gSA
bl fof/ esa ifjdYiuk dh izR;sd laHko n'kk dks tk¡pk tkrk gSA ;g fof/ O;kogkfjd :i ls osQoy rHkh lqfo/ktud gS tc fo[k.Mu }kjk izkIr dFkuksa dh la[;k de gksA
mnkgj.k 4 fdlh f=kHkqt ABC, esa fl¼ dhft, fd
a = b cos C + c cos B
gy eku yhft, fd p dFku “ABC ,d f=kHkqt gS ” rFkk q dFku
“a = b cos C + c cos B” gS
eku yhft, fd ABC ,d f=kHkqt gSA 'kh"kZ A ls BC (vko';drkuqlkj c<+kbZ xbZ) ij yac AD [khafp,A
gesa Kkr gS fd ,d f=kHkqt ;k rks U;wudks.k f=kHkqt ;k vf/ddks.k f=kHkqt ;k ledks.k f=kHkqt gksrk gS] blfy, ge p dks r, s rFkk t esa fo[kf.Mr dj ldrs gSa] tgk¡
r : ABC ,d U;wudks.k f=kHkqt gS] ftlesa ∠C U;wudks.k gSaA
s : ABC ,d vf/ddks.k f=kHkqt gS] ftlesa ∠C vf/ddks.k gSA
t : ABC ,d ledks.k f=kHkqt gS] ftlesa ∠C ledks.k gSA
vr% ge lkè; dks mi;qZDr rhuksa laHkkoukvksa osQ fy, vyx&vyx fl¼ djrs gSaA
n'kk (i) tc ∠A, ∠B, rFkk ∠C rhuksa gh U;wudks.k gSa (vko`Qfr A1.1)
ledks.k f=kHkqt ADB, }kjk
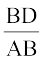 = cos B
= cos B
vFkkZr~ BD = AB cos B = c cos B
ledks.k f=kHkqt ADC }kjk
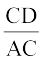 = cos C
= cos C
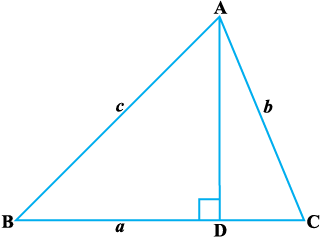
vko`Qfr A1-1
vFkkZr~ CD = AC cos C
= b cos C
vc a = BD + CD
= c cos B + b cos C ... (1)
n'kk (ii) tc ∠C vf/ddks.k gS (vko`Qfr A1.2)
ledks.k f=kHkqt ADB }kjk
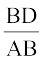 = cos B
= cos B
vFkkZr~ BD = AB cos B
= c cos B
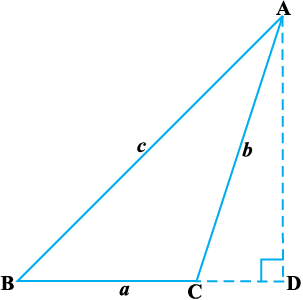
vko`Qfr A1-2
ledks.k f=kHkqt ADC }kjk
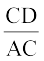 = cos ∠ ACD
= cos ∠ ACD
= cos (180 – C)
= – cos C
vFkkZr~ CD = – AC cos C
= – b cos C
vc a = BC = BD – CD
vFkkZr~ a = c cos B – ( – b cos C)
a = c cos B + b cos C ... (2)
n'kk (iii) tc ∠C ledks.k gS (vko`Qfr A1.3)
f=kHkqt ACB, }kjk
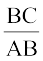 = cos B
= cos B

vko`Qfr A1-3
vFkkZr~ BC = AB cos B
rFkk a = c cos B,
b cos C = b cos 900 = 0
vr% ge fy[k ldrs gSa a = 0 + c cos B
= b cos C + c cos B ... (3)
lehdj.k (1), (2) rFkk (3) ls ge ikrs gSa] fd fdlh f=kHkqt ABC esa
a = b cos C + c cos B
n'kk (i) ls r ⇒ q izekf.kr gSA
n'kk (ii) ls s ⇒ q izekf.kr gSA
rFkk n'kk (iii) ls t ⇒ q izekf.kr gSA
vr% (r 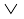 s
s 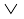 t) ⇒ q izekf.kr gS vFkkZr~ p ⇒ q izekf.kr gS]
t) ⇒ q izekf.kr gS vFkkZr~ p ⇒ q izekf.kr gS]
vizR;{k miifÙk% fn, x, lkè; dks lh/s izekf.kr djus osQ ,ot esa] ge mlosQ lerqY; fdlh lkè; dks fl¼ djosQ] iznÙk lkè; dks izekf.kr djrs gSa
(i) fojks/ksfDr }kjk miifÙk (Reductio Ad Absurdum):
;gk¡ ge bl ekU;rk ls izkjaHk djrs gSa fd ifjdYiuk lR; gS rFkk fu"d"kZ vlR; gSA roZQ osQ fu;eksa osQ iz;ksx }kjk ge bl fu"d"kZ ij igq¡prs gSa fd ,d Kkr lR; dFku] vlR; gS] tks ,d fojks/ksfDr gSA vr% iznÙk dFku lR; gS bl fof/ dks ,d mnkgj.k }kjk le>rs gSaA
mnkgj.k 5 lHkh vHkkT; la[;kvksa dk leqPp; vifjfer (Infinite) gksrk gSA
gy eku yhft, fd leLr vHkkT; la[;kvksa (Prime Numbers) dk leqPp; P gS tks vifjfer gSA ge bl dFku osQ fu"ks/ (Negation) dks] vFkkZr leLr vHkkT; la[;kvksa dk leqPp; vifjfer ugha gS] lR; eku ysrs gaS] vFkkZr~ leLr vHkkT; la[;kvksa dk leqPp; ifjfer gSA blfy, ge leLr vHkkT; la[;kvksa dks lwphc¼ dj ldrs gSaA eku yhft, fd P1, P2, P3,..., Pk leLr vHkkT; la[;kvksa dh lwph gSA vc eku yhft,
N = (P1 P2 P3…Pk) + 1 ... (1)
Li"V gS fd N vHkkT; la[;kvksa dh lwph esa ugha gS] D;ksafd ;g lwph dh fdlh Hkh la[;k ls vf/d gSA
N ;k rks vHkkT; la[;k gS ;k la;qDr la[;k gSA
;fn N vHkkT; la[;k gS rks (1) ls Li"V gksrk gS fd ,d ,slh vHkkT; la[;k dk vfLrRo gS] tks lwph esa ugha gSA
nwljh vksj] ;fn N ,d la;qDr la[;k gS] rks bldk de ls de ,d vHkkT; Hkktd (Divisor) gksuk pkfg,A ijarq lwph dh dksbZ Hkh la[;k N dks foHkkftr (iw.kZ:i ls) ugha dj ldrh gS] D;ksafd muesa ls fdlh osQ }kjk N dks foHkkftr djus ij 'ks"kiQy lnSo 1 cprk gSA vr% N dk vHkkT; Hkktd lwph osQ vfrfjDr dksbZ vU; la[;k gSA
fdarq ;g] bl dFku dk fd geus lHkh vHkkT; la[;kvksa dh lwph cuk yh gS] fojks/ksfDr gSA
bl izdkj gekjh iwoZ/kj.kk fd lHkh vHkkT; la[;kvksa dk leqPp; ifjfer gS] vlR; gSA
vr% lHkh vHkkT; la[;kvksa dk leqPp; vifjfer gksrk gSA
fVIi.kh (è;ku nhft, fd mi;qZDr miifÙk esa fofHkUu n'kkvksa esa fo[k.Mu }kjk miifÙk dh fof/ dk mi;ksx Hkh gS)
(ii) iznÙk dFku dk izfr/ukRed (contrapositive) dFku osQ iz;ksx }kjk miifÙk%
;gk¡ lizfrca/ dFku p ⇒ q dks fl¼ djus osQ LFkku ij ge mlosQ lerqY; dFku ~ q ⇒ ~ p dks fl¼ djrs gSaA (fo|kFkhZ lerqY;rk dks lR;kfir dj ldrs gSa)A
fdlh fn, gq, lizfrca/ dFku osQ fu"d"kZ rFkk ifjdYiuk dk fofue; djosQ muesa ls izR;sd dk fu"ks/u djus ls iznÙk dFku dk izfr/ukRed dFku curk gSA
mnkgj.k 6 fl¼ dhft, fd f(x) = 2x + 5 }kjk ifjHkkf"kr iQyu f : R → R ,oSQdh iQyu gSA
gy iQyu ,oSQdh gksrk gS] ;fn f(x1) = f(x2) ⇒ x1 = x2.
bldk iz;ksx djosQ gesa izekf.kr djuk gS fd “2x1+ 5 = 2x2 + 5” ⇒ “x1 = x2” ;g p ⇒ q, osQ :i dk gS] tgk¡ 2x1+ 5 = 2x2 + 5 dFku p gS rFkk x1 = x2 dFku q gSA bl ckr dks ge mnkgj.k 2 esa ¶izR;{k fof/¸ }kjk fl¼ dj pqosQ gSaA
ge bls iznÙk dFku osQ izfr/ukRed dFku osQ iz;ksx }kjk Hkh izekf.kr dj ldrs gSaA fn, x, dFku dk izfr/ukRed dFku ~ q ⇒ ~ p gS] vFkkZr~ “;fn f(x1) = f(x2) rks x1 = x2” dk
izfr/ukRed gS “;fn x1≠ x2 rks f(x1) ≠ f(x2)”
vc x1 ≠ x2
⇒ 2x1 ≠ 2x2
⇒ 2x1+ 5 ≠ 2x2 + 5
⇒ f(x1) ≠ f(x2).
D;ksafd “~ q ⇒ ~ p”, vkSj “p ⇒ q” lerqY; gS] bl izdkj miifÙk iw.kZ gSA
mnkgj.k 7 izekf.kr dhft, fd ¶;fn vkO;wg A, Invertible gS] rks A, Non-singular gS¸
gy mi;qZDr dFku dks izrhdkRed :i esa fy[kus ij p ⇒ q tgk¡ p dFku “vkO;wg A, invertible gS” rFkk q dFku “A, non-singular gSA”
iznÙk dFku dks izekf.kr djus osQ ,ot esa ge blosQ izfr/ukRed dFku dks izekf.kr djrs gSa] vFkkZr~ ;fn A ,d non-singular vkO;wg ugha gS] rks vkO;wg A invertible ugha gSA
;fn A ,d non-singular vkO;wg ugha gS rks bldk vFkZ gqvk |A| = 0 gSA
vc A–1 = 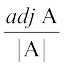 dk vfLrRo ugha gS] D;ksafd |A| = 0
dk vfLrRo ugha gS] D;ksafd |A| = 0
vr% A, Invertible ugha gSA
bl izdkj geus ;g izekf.kr dj fn;k fd ;fn A ,d non-singular vkO;wg ugha gS rks A, invertible ugha gSA vFkkZr~ ~ q ⇒ ~ p.
vr% ;fn ,d vkO;wg A invertible gS] rks A non-singular gSA
(iii) izR;qnkgj.k (counter example) }kjk miifÙk%
xf.kr osQ bfrgkl eas ,sls volj Hkh vkrs gSa] tc fdlh ifjdfYir O;kidhdj.k dh oS/ miifÙk Kkr djus osQ lHkh iz;kl vliQy gks tkrs gSa vkSj O;kidhdj.k osQ lR;eku dh vfuf'prrk vfu.khZr cuh jgrh gSA
,slh fLFkfr esa ;g ykHkizn gS fd] dFku dks vlR; fl¼ djus osQ fy,] ge ,d mnkgj.k <w¡<+ losaQA fdlh dFku dks vekU; djus okyk mnkgj.k izR;qnkgj.k dgykrk gSA
D;ksafd lkè; p ⇒ q dk [kaMu] lkè; ~ (p ⇒ q) dh osQoy ek=k ,d miifÙk gksrk gSA vr% ;g Hkh miifÙk dh ,d fof/ gSA
mnkgj.k 8 dFku% izR;sd n ∈ N osQ fy,] (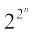 + 1) ,d vHkkT; la[;k gSA
+ 1) ,d vHkkT; la[;k gSA
;g dFku fuEufyf[kr izs{k.kksa osQ vk/kj ij ,d le; lR; le>k x;k Fkk%
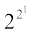 + 1 = 22 + 1 = 5 tks fd ,d vHkkT; la[;k gSA
+ 1 = 22 + 1 = 5 tks fd ,d vHkkT; la[;k gSA
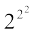 + 1 = 24 + 1 = 17 tks fd vHkkT; la[;k gSA
+ 1 = 24 + 1 = 17 tks fd vHkkT; la[;k gSA
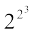 + 1 = 28 + 1 = 257 tks fd ,d vHkkT; gSA
+ 1 = 28 + 1 = 257 tks fd ,d vHkkT; gSA
;|fi] izFke n`f"V esa ;g O;kidhdj.k lgh izrhr gksrk gSA varrksxRok ;g izfrikfnr fd;k x;k fd 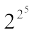 + 1 = 232 + 1 = 4294967297 ,d vHkkT; la[;k ugha gS D;ksafd 4294967297 = 641 × 6700417 gSA tks nks la[;kvksa dk xq.kuiQy gS (1 rFkk Loa; osQ vfrfjDr) bl izdkj ;g O;kidhdj.k fd ¶izR;sd n osQ fy,
+ 1 = 232 + 1 = 4294967297 ,d vHkkT; la[;k ugha gS D;ksafd 4294967297 = 641 × 6700417 gSA tks nks la[;kvksa dk xq.kuiQy gS (1 rFkk Loa; osQ vfrfjDr) bl izdkj ;g O;kidhdj.k fd ¶izR;sd n osQ fy,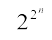 + 1 ,d vHkkT; la[;k gS ∀ n ∈ N+” vlR; gSA
+ 1 ,d vHkkT; la[;k gS ∀ n ∈ N+” vlR; gSA
ek=k osQoy ;g ,d mnkgj.k fd 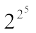 + 1 vHkkT; ugha gS] dk mnkgj.k O;kidhdj.k dks [kafMr djus osQ fy, i;kZIr gSA
+ 1 vHkkT; ugha gS] dk mnkgj.k O;kidhdj.k dks [kafMr djus osQ fy, i;kZIr gSA
vr% geus fl¼ dj fn;k fd dFku ¶izR;sd n ∈ N osQ fy,]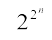 + 1 ,d vHkkT; la[;k gS” lR; ugha gSA
+ 1 ,d vHkkT; la[;k gS” lR; ugha gSA
mnkgj.k 9 dFku ¶izR;sd larr iQyu vodyuh; gksrk gSA¸ ij fopkj dhft,A
miifÙk% ge fuEufyf[kr iQyuksa ij fopkj djrs gSa%
(i) f (x) = x2
(ii) g (x) = ex
(iii) h (x) = sin x
;s lHkh iQyu x osQ lHkh ekuksa osQ fy, larr gSaA ;fn ge vodyuh;rk ij fopkj djsa rks ;s x osQ lHkh ekuksa osQ fy, vodyuh; gSaA ;g gesa bl fo'okl osQ fy, iszfjr djrk gS fd dFku ¶izR;sd larr iQyu vodyuh; gksrk gS¸ lR; gSA ¯drq ;fn ge iQyu “φ(x) = |x|” dh vodyuh;rk dh tk¡p djsa] tks fd larr gS] rks ge ns[krs gSa fd ;g x = 0 ij vodyuh; ugha gSA bldk rkRi;Z ;g gqvk fd dFku ¶izR;sd larr iQyu vodyuh; gksrk gS¸ vlR; gSA iQyu “φ(x) = |x|” dk osQoy ;g ,d mnkgj.k] O;kidhdj.k dk [kaMu djus osQ fy, i;kZIr gSA vr% iQyu “φ(x) = |x|” dks fn, x, dFku vFkkZr~] ¶izR;sd lrr iQyu vodyuh; gksrk gSAa¸ osQ [kaMu dk izR;qnkgj.k dgrs gSaA