Table of Contents
ifjf'k"V 2
xf.krh; fun'kZu
(Mathematical Modelling)
A.2.1 Hkwfedk (Introduction)
d{kk XI esa ge xf.krh; fun'kZu dks okLrfod thou dh leL;kvksa osQ oqQN va'k dk xf.krh; Hkk"kk esa vè;;u osQ ,d iz;kl osQ :i esa tku pqosQ gaS] vFkkZr~] mi;qDr izfrca/ksa dk iz;ksx djosQ fdlh HkkSfrd fLFkfr dk xf.krh; :ikarj.k gh xf.krh; fun'kZu gSA eksVs rkSj ij xf.krh; fun'kZu ,d izfØ;k gS] ftlesa ge viuh #fp osQ lk/uksa ;k oLrqvksa osQ O;ogkj dk o.kZu djus gsrq fun'kks± (Models) dh jpuk] fofo/ izdkj ls 'kCnksa] vkjs[kksa ;k js[kkfp=kksa] oaQI;wVj izksxzkeksa] xf.krh; lw=kksa vkfn osQ iz;ksx }kjk djrs gSaA
fiNyh d{kkvksa esa geus ns[kk gS fd] fofo/ xf.krh; ladYiukvksa osQ iz;ksx ls lacaf/r vf/dka'k iz'uksa osQ gy osQ fy, ,d izdkj ls xf.krh; fun'kZu dh vko';drk iM+rh gSA vr% ;g egRoiw.kZ gS fd xf.krh; fun'kZu dk vè;;u ,d i`Fko~Q fo"k; osQ :i esa fd;k tkuk pkfg,A
bl vè;k; (ifjf'k"V) esa ge iqu% xf.krh; fun'kZu dk vè;;u okLrfod thou dh oqQN ,slh leL;kvksa osQ fy, djsaxs] ftuesa vkO;wg] dyu rFkk jSf[kd izksxzkeu dh izkfof/vksa dk iz;ksx fd;k tkrk gSA
A.2.2 xf.krh; fun'kZu D;ksa\ (Why Mathematical Modelling?)
fo|kfFkZ;ksa dks vadxf.kr] chtxf.kr] f=kdks.kfefr rFkk jSf[kd izksxzkeu vkfn osQ 'kkfCnd iz'uksa dks gy djus dk Kku gSA dHkh&dHkh ge ifjfLFkfrtU; iz'uksa dks HkkSfrd :i ls mudh xgjkbZ esa x, fcuk gh ljy djrs gSaA ifjfLFkfrtU; iz'uksa dks gy djus osQ fy, HkkSfrd :i ls mudh xgjkbZ esa tkus dh vko';drk iM+rh gS] vFkkZr~ HkkSfrd fu;eksa rFkk oqQN izrhdksa osQ iz;ksx dh vko';drk ftlls izkIr xf.krh; ifj.kkeksa dk laxr izk;ksfxd ekuksa ls rqyuk dh tk losQA vusd izLrqr iz'uksa dks ljy djus osQ fy, gesa ,d dkS'ky dh vko';drk iM+rh gS ftls xf.krh; fun'kZu dgrs gSaA vkb, ge fuEufyf[kr leL;kvksa ij fopkj djsa%
(i) fdlh unh dh pkSM+kbZ Kkr djuk (fo'ks"k :i ls tc unh dks ikj djuk dfBu gks)A
(ii) fdlh xksys osQ isaQdus gsrq egÙke dks.k Kkr djuk (xksyk isaQdus okys dh Å¡pkbZ] ekè;e dk izfrjks/] xq:Rokd"kZ.k g vkfn izkpyksa ij fopkj djrs gq,)A
(iii) fdlh ehukj dh Å¡pkbZ Kkr djuk (fo'ks"k:i ls tc ehukj dk 'kh"kZ vxE; gks)A
(iv) lw;Z dh lrg dk rkieku Kkr djukA
(v) Kkr djuk fd ân; jksfx;ksa dks fyÝV osQ iz;ksx dk fu"ks/ D;ksa gS (fcuk ekuo 'kjhj fØ;k foKku tkus)A
(vi) i`Foh dk nzO;eku Kkr djukA
(vii) [kM+h iQly ls Hkkjr esa nkyksa dh iSnkokj dk vuqeku yxkuk (tc fdlh dks iQly osQ dkVus dh vuqefr ugha gS)A
(viii) fdlh O;fDr osQ 'kjhj esa jDr dk vk;ru Kkr djuk (O;fDr dk jDr fudkyus dh vuqefr ugha gS)A
(ix) lu~ 2009 bZ- esa Hkkjr dh tula[;k dk vuqeku yxkuk (tc fd lu~ 2009 bZ- rd izrh{kk djus dh vuqefr ugha gS)A
mi;qZDr lHkh leL;kvksa dks xf.krh; fun'kZu osQ iz;ksx }kjk ljy fd;k tk ldrk gS vkSj okLro esa ljy fd;k tk pqdk gSA oLrqr% buesa ls oqQN leL;kvksa dks ljy djus dh fof/;ksa dk vè;;u vki blh ikB~;iqLrd esa djsaxsA rFkkfi ;g f'k{kkizn gksxk ;fn vki budks Lo;a ljy djus dk iz;kl djsa og Hkh fcuk xf.kr osQ iz;ksx fd,A rc vki xf.kr dh {kerk rFkk xf.krh; fun'kZu dh vko';drk osQ egÙo dks le> losaQxsA
A.2.3 xf.krh; fun'kZu osQ fl¼kar (Principles of Mathematical Modelling)
xf.krh; fun'kZu ,d fl¼kar;qDr fØ;k gS vr% blls lacaf/r oqQN fl¼kar gSaA bu fl¼karksa dk Lo:i yxHkx nk'kZfud gSaA xf.krh; fun'kZu osQ oqQN ewy fl¼karksa dks vuqns'kkRed :i esa uhps lwphc¼ fd;k x;k gS%
(i) fun'kZ dh vko';drk dks igpkfu, (ge ekWMy D;ksa [kkst jgs gSa)A
(ii) ekWMy osQ fy, izkpyksa@pjksa dks lwphc¼ dhft, (ge D;k Kkr djuk pkgrs gSa)A
(iii) miyC/ izklafxd vk¡dM+ksa dks igpkfu, (D;k fn;k gqvk gS)A
(iv) iz;ksx ;ksX; ifjfLFkfr;ksa dks igpkfu, (iwoZ/kj.kk] dYiuk)A
(v) fu;a=kd HkkSfrd fu;eksa dks igpkfu,A
(vi) igpkfu,%
(a) iz;qDr gksus okys lehdj.kA
(b) dh tkus okyh x.kukA
(c) ifj.kkeLo:i izkIr gksus okyk gyA
(vii) mu ijh{k.kksa dks igpkfu, ftuls fuEufyf[kr tk¡p dh tk losQ%
(a) ekWMy rFkk mlls lacaf/r fu;eksa ,oa dYiukvksa dk laxr gksukA
(b) ekWMy dh mi;ksfxrkA
(viii) mu izkpyksa dks igpkfu, tks ekWMy dks lq/kj losaQA
fun'kZu osQ mi;qZDr fl¼karksa osQ vk/kj ij gesa xf.krh; fun'kZu osQ fuEufyf[kr pj.k izkIr gksrs gSa%
pj.k 1: HkkSfrd fLFkfr dks igpkfu,A
pj.k 2: izkpyksa @ pjksa osQ p;u vkSj Kkr HkkSfrd fu;eksa rFkk izrhdksa osQ iz;ksx }kjk HkkSfrd fLFkfr dks xf.krh; ekWMy esa ifjofrZr dhft,A
pj.k 3: xf.krh; iz'uksa osQ gy Kkr dhft,A
pj.k 4: izkIr ifj.kke dh ewy iz'u (leL;k) osQ lanHkZ esa O;k[;k dhft, vkSj mldh (ifj.kke) izs{k.kksa vFkok iz;ksxksa ls rqyuk dhft,A
pj.k 5: ;fn ifj.kke yxHkx esy [kkrs gSa] rks ekWMy dks Lohdkj dhft, vU;Fkk HkkSfrd fLFkfr dh ifjdYiuk @ dYiuk dks la'kksf/r dhft, vkSj pj.k 2 ij tkb,A
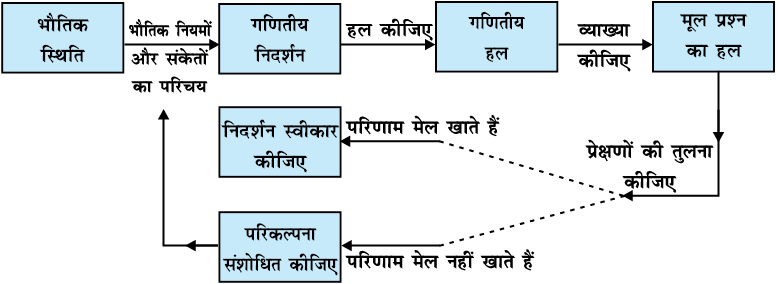
mi;qZDr pj.kksa dks uhps n'kkZ, vkjs[k esa ns[kk tk ldrk gS%
mnkgj.k 1 xf.krh; funZ'ku osQ iz;ksx }kjk ,d nh xbZ ehukj dh Å¡pkbZ Kkr dhft,A
gy pj.k 1 ¶,d nh xbZ ehukj dh Å¡pkbZ Kkr djuk¸ iznÙk HkkSfrd fLFkfr gSA
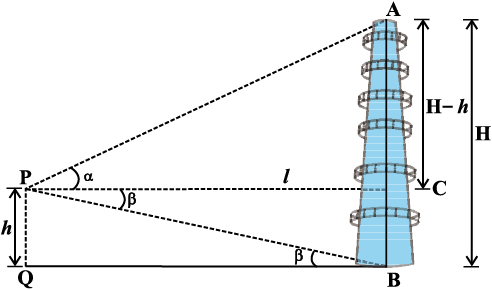
pj.k 2 eku yhft, fd AB nh xbZ ehukj gS (vko`Qfr A.2.2)A eku yhft, PQ ehukj dh Å¡pkbZ ukius okyk ,d izs{kd gS] ftldh vk¡[k ¯cnq P ij gSA eku yhft, fd PQ = h rFkk ehukj dh Å¡pkbZ H gSA iqu% eku yhft, fd izs{kd dh vk¡[k ls ehukj osQ f'k[kj ('kh"kZ) dk mUu;u&dks.k α gS rFkk l = QB = PC
vko`Qfr A.2.1
vc tan α = 
;k H = h + l tan α ... (1)
pj.k 3 è;ku nhft, fd izkpy h, l rFkk α osQ eku izs{kd dks Kkr gSa vr% ifj.kke (1) ls leL;k dk gy izkIr gksrk gSA
pj.k 4 ml n'kk esa tc ehukj dk vk/kj vxE; gks] vFkkZr~ tc izs{kd dks l dk eku Kkr ugha gks] rc eku yhft, fd ehukj osQ vk/kj B dk ¯cnq P ls voueu&dks.k β gSA vr% ∆ PQB ls gesa izkIr gksrk gS fd
vko`Qfr A.2.2
tan β = 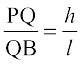 ;k l = h cot β
;k l = h cot β
pj.k 5 bl fLFkfr esa bl pj.k dh vko';drk ugha gS D;ksafd h, l, α rFkk β izkpyksa osQ lgh eku Kkr gSaA
mnkgj.k 2 eku yhft, fd ,d O;kolkf;d iQeZ rhu izdkj osQ mRikn P1, P2 vkSj P3 dk mRiknu djrh gS] ftuesa rhu izdkj ds dPps eky R1, R2 rFkk R3dk iz;ksx gksrk gSA eku yhft, fd iQeZ ls nks xzkgd F1 vkSj F2 [kjhn dh ek¡x djrs gSaA ;g ekurs gq, fd iQeZ osQ ikl R1, R2 rFkk R3 dh lhfer ek=kk gS] ,d ekWMy cukb,] tks ek¡x dks iwjk djus osQ fy, dPps eky R1, R2 vkSj R3 dh ek=kkvksa dks lqfuf'pr djsA
gy pj.k 1 bl leL;k esa HkkSfrd fLFkfr dh igpku HkyhHkk¡fr gSA
pj.k 2 eku yhft, fd A ,d vkO;wg gS] tks xzkgdksa F1 rFkk F2 dh vko';drk dks fu:fir djrk gSA rc A dk :i ,slk gksxk]
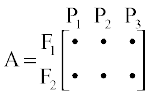
eku yhft, fd B ,d vkO;wg gS] tks mRikn P1, P2 rFkk P3 dh izR;sd bdkbZ osQ mRiknu gsrq dPps eky R1, R2 rFkk R3, dh vko';d ek=kkvksa dks fu:fir djrk gSA rc B uhps fn, x, izdkj dk gksxk]
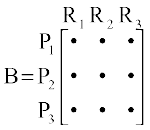
pj.k 3 è;ku nhft, fd A rFkk B vkO;wgksa dk xq.kuiQy (tks bl fLFkfr esa lqifjHkkf"kr gS) fuEufyf[kr vkO;wg }kjk izkIr gksrk gSA
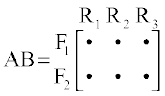
ftlls okLro esa xzkgdksa F1 rFkk F2 osQ iQjekb'kksa dks iwjk djus gsrq dPps eky R1, R2 rFkk R3 dh okafNr ek=kk,¡ Kkr gksrh gSaA
mnkgj.k 3 mnkgj.k 2 osQ ekWMy dh O;k[;k dhft,] tc fd
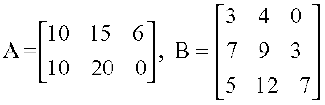
rFkk dPps eky dh miyC/ ek=kk,¡ R1 dh 330 bdkbZ;k¡, R2 dh 455 bdkbZ;k¡ vkSj R3 dh 140 bdkbZ;k¡ gSaA
gy uksV dhft, fd
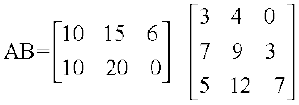 =
= 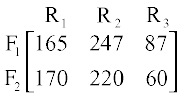
;g Li"Vr;k n'kkZrk gS fd F1 vkSj F2 dh ek¡x dks iwjk djus osQ fy, dPps eky R1 dh 335 bdkbZ] R2 dh 467 bdkbZ rFkk R3 dh 147 bdkbZ dh vko';drk gS tks fd dPps eky dh miyC/ ek=kkvksa ls vf/d gSA D;ksafd rhuksa mRiknksa dh izR;sd bdkbZ osQ fuekZ.k gsrq dPps eky osQ visf{kr ek=kk,¡ fuf'pr gSa] blfy, ge ;k rks dPps eky dh miyC/ ek=kkvksa osQ c<+kus dh ek¡x dj ldrs gSa vFkok ge xzkgdksa ls mudh ek¡xksa dks de djus dk fuosnu dj ldrs gSaA
fVIi.kh ;fn ge mnkgj.k 3 esa A dks A1 ls cny nsa] tgk¡
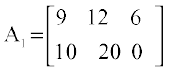
vFkkZr~] ;fn xzkgd yksx viuh ek¡xksa dks de djus osQ fy, eku tkrs gSa] rks

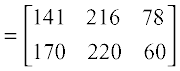
;gk¡ R1 dh 311, R2 dh 436 rFkk R3 dh 138 bdkb;k¡ vkisf{kr gSa tks fd dPps eky dh miyC/ ek=kkvksa vFkkZr~ R1 dh 330] R2 dh 455 rFkk R3 dh 140 bdkb;ksa ls de gSaA
fVIi.kh ge A dks iqu% bl izdkj la'kksf/r dj ldrs gSa ftlls miyC/ dPps eky dk iw.kZr;k mi;ksx gks tk,A
bl izdkj ;fn xzkgdksa dh ek¡x dks iwjk djus osQ fy, A1 osQ }kjk Ø;&vkns'k fn, tkrs gSa] rks iQeZ nksuksa xzkgdksa osQ Ø;&vkns'kksa dks ljyrk ls iwjk dj ldrk gSA
iwNrkN iznÙk B rFkk miyC/ dPps eky dh fu/kZfjr ek=kkvksa osQ fy, D;k ge] iQeZ osQ ekfyd dh lgk;rkFkZ] ,d ,slk xf.krh; ekWMy cuk ldrs gS] ftlls og xzkgdksa ls vuqjks/ dj losQ fd os viuh ek¡xksa dks bl izdkj la'kksf/r djsa fd miyC/ dPpk eky iw.kZr;k mi;ksx esa vk tk,A
bl iwNrkN dk mÙkj fuEufyf[kr mnkgj.k esa fn;k x;k gS%
mnkgj.k 4 eku fyft, fd P1, P2, P3 rFkk R1, R2, R3 mlh izdkj gS tSlk mnkgj.k 2 esa fn;k gSA eku yhft, fd iQeZ osQ ikl R1 dh 330] R2 dh 455 vkSj R3 dh 140 bdkb;k¡ miyC/ gSa vkSj eku yhft, fd rhuksa mRikn dh izR;sd bdkbZ osQ fuekZ.k osQ fy, dPps eky R1, R2 rFkk R3, dh ek=kk,¡ fuEufyf[kr vkO;wg ls izkIr gksrha gSa
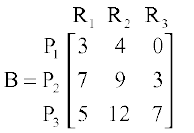
izR;sd mRikn dh fdruh bdkb;k¡ cukb tk,¡ fd miyC/ dPps eky dk mi;ksx iw.kZr;k gks tk,\
gy pj.k 1 fLFkfr ljyrk ls igpku ;ksX; gSA
pj.k 2 eku yhft, fd iQeZ P1 dh x bdkb;ksa , P2 dh y rFkk P3 dh z bdkb;ksa dk mRiknu djrh gSA D;ksafd mRikn P1 osQ fy, R1 dh 3, P2 osQ fy, R1 dh 7 rFkk P3 osQ fy, R1 dh 5 bdkb;ksa dh vko';drk iM+rh gS (vkO;wg B nsf[k,) vkSj R1 dh oqQy 330 bdkb;k¡ miyC/ gSa] vr%
3x + 7y + 5z = 330 (dPps eky R1 osQ fy,)
blh izdkj 4x + 9y + 12z = 455 (dPps eky R2 osQ fy,)
vkSj 3y + 7z = 140 (dPps eky R3 osQ fy,)
bl (mi;qZDr) lehdj.k fudk; dks vkO;wg :i esa fuEu izdkj O;Dr dj ldrs gSa]
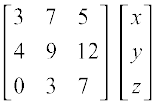 =
= 
pj.k 3 izkjfEHkd iafDr lafØ;k }kjk] gesa izkIr gksrk gS_
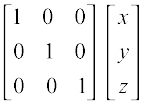 =
= 
blls x = 20, y = 35 rFkk z = 5 feyrk gSA vr,o iQeZ P1 dh 20, P2 dh 35 rFkk P3 dh 5 bdkb;k¡ mRiUu dj ldrh gSA
fVIi.kh dksbZ Hkh ns[k ldrk gS fd ;fn fuekZrk xzkgdksa F1 vkSj F2 dh ek¡xksa (tSlk mnkgj.k 3 esa gS) ij fopkj fd, fcuk gh osQoy miyC/ dPps eky osQ vuqlkj mRiknu djus dk fu.kZ; ysrk gS] rks og mudh ek¡xksa dks iwjk ugha dj ldrk gS] D;ksafd F1 us P3 dh 6 bdkb;k¡ ek¡xh gS tc fd fuekZrk mldh osQoy 5 bdkb;k¡ gh cuk ldrk gSA
mnkgj.k 5 ,d nok&fuekZrk M1 vkSj M2 nokb;ksa dh mRiknu&;kstuk cukrk gSA M1 dh 20]000 rFkk M2 dh 40]000 cksryksa osQ fy, nok cukus gsrq ;Fks"V dPpk&eky miyC/ gS] ¯drq mlosQ ikl osQoy 45]000 cksrysa gSa] ftuesa og nksuksa esa ls dksbZ Hkh nok Hkj ldrk gSA M1 dh 1]000 cksrysa Hkjus osQ fy, i;kZIr eky rS;kj djusa esa 3 ?kaVs vkSj M2 dh 1000 cksrysa Hkjus osQ fy, i;kZIr eky rS;kj djusa esa 1 ?kaVk yxrs gSa rFkk bl izfØ;k osQ fy, osQoy 66 ?kaVs miyC/ gSaA M1 dh izR;sd cksry ij Rs 8 rFkk M2 dh izR;sd cksry ij Rs 7 ykHk gksrk gSA nok&fuekZrk] egÙke ykHk vftZr djus gsrq] viuh mRiknu&;kstuk fdl izdkj cuk,\
gy pj.k 1 iznÙk ifjdYiuk osQ varxZr] egÙke ykHk vftZr djus gsrq] nokvksa M1 rFkk M2 dh cksryksa dh la[;k Kkr djukA
pj.k 2 eku yhft, fd nok M1 dh x vkSj nok M2 dh y cksrysa gSaA D;ksafd M1 dh izR;sd cksry ij ykHk Rs 8 rFkk M2 dh izR;sd cksry ij ykHk Rs 7 gksrk gS] vr% mn~ns';&iQyu (objective function)] ftls vf/dre djuk gS uhps fy[ks lehdj.k ls fn;k x;k gSA
Z ≡ Z (x, y) = 8x + 7y
bl mn~ns';&iQyu dk fuEufyf[kr izfrca/ksa (O;ojks/ksa) osQ varxZr vf/dre djuk gS (jSf[kd izksxzkeu osQ vè;k; 12 ij è;ku nhft,)A
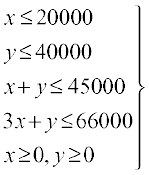 ... (1)
... (1)
pj.k 3 iznÙk O;ojks/ksa (constraints) (1) osQ varxZr Nk;kafdr {ks=k OPQRST lqlaxr&{ks=k gS (vkd`fr A.2.3) ¯cnqvksa O, P, Q, R, S rFkk T dksauh; osQ funsZ'kkad Øe'k% (0, 0), (20000, 0), (20000, 6000), (10500, 34500), (5000, 40000) rFkk (0, 40000) gSaA
uksV dhft, fd
P (0, 0) ij Z = 0
P (20000, 0) ij Z = 8 × 20000 = 160000
Q (20000, 6000) ij Z = 8 × 20000 + 7 × 6000 = 202000
R (10500, 34500) ij Z = 8 × 10500 + 7 × 34500 = 325500
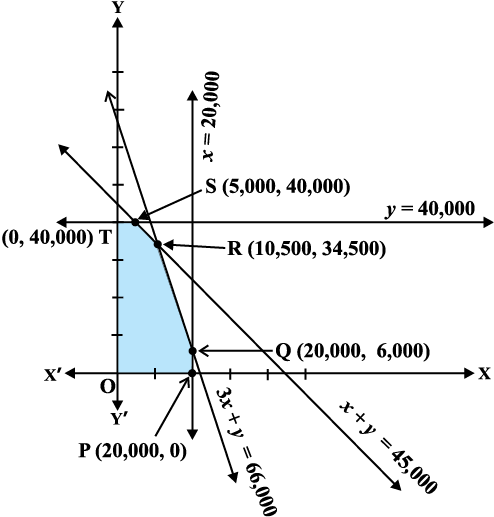
vkd`fr A.2.3
S = (5000, 40000) ij Z = 8 × 5000 + 7 × 40000 = 320000
T = (0, 40000) ij Z = 7 × 40000 = 280000
è;ku nhft, fd x = 10500 vkSj y = 34500 ij egÙke ykHk vftZr gksrk gS] tks fd Rs 325500 gSA vr% fuekZrk (mRiknd) dks Rs 325500 dk egÙke ykHk vftZr djus osQ fy, M1 dh 10500 rFkk M2 dh 34500 cksrysa mRiUu djuh pkfg,A
mnkgj.k 6 eku yhft, fd ,d oaQiuh dksbZ u;k mRikn cukuk pkgrh gS] ftl ij oqQN ykxr (fLFkj vkSj pj ykxr) vkrh gS vkSj eku yhft, fd oaQiuh ml mRikn dks ,d fLFkj ewY; ij foØ; djus dh ;kstuk cukrh gSA bl fLFkfr esa ykHk&gkfu osQ ijh{k.k gsrq ,d xf.krh; ekWMy cukb,A
gy pj.k 1 ;gk¡ fLFkfr Li"Vr;k igpku ;ksX; gSA
pj.k 2 lw=k.k ls gesa Kkr gS dh ykxr nks izdkj dh gksrh gS] fLFkj rFkk pjA fLFkj ykxr mRikn dh la[;k ls Lora=k gksrh gS (tSls fdjk;k] 'kqYd vkfn)] tc fd pj ykxr mRikn dh la[;k c<+us ls c<+rh gS (tSls lkexzh] iSfdax bR;kfn)A izkjaHk esa ge eku ysrs gSa fd pj ykxr mRikn dh la[;k dh vuqØekuqikrh gS & blls gekjk ekWMy ljy gks tkrk gSA daiuh dks oqQN /u jkf'k foØ; }kjk izkIr gksrh gS] vkSj og (daiuh) ;g lqfuf'pr djuk pkgrh gS fd ;g izkIr /u egÙke gSA
lqfo/k osQ fy,] ge ;g eku ysrs gSa fd izR;sd mRikfnr bdkbZ rRdky csp nh tkrh gSA
xf.krh; ekWMy
eku yhft, fd mRikfnr rFkk foØ; dh xbZ bdkb;ksa dh la[;k x gS]
C = mRiknu dh oqQy ykxr gS (#i;ksa esa)
I = foØ; ls gksus okyh oqQy vk; gS (#i;ksa esa)
P = oqQy ykHk gS (#i;ksa esa)
gekjh I mi;qZDr ekU;rk (assumption) osQ vuqlkj C nks Hkkxksa ls fey dj curk gS%
fLFkj ykxr = a (#i;ksa esa),
pj ykxr = b (#i, izfr bdkbZ).
vr,o C = a + bx ... (1)
lkFk gh vk; I foØ; ewY; s (#i, izfr bdkbZ) ij fuHkZj gS]
vr% I = sx ... (2)
ykHk P vk; vkSj ykxr osQ varj osQ cjkcj gksrk gS] bl izdkj
P = I – C
= sx – (a + bx)
= (s – b) x – a ... (3)
bl izdkj vc gesa pj jkf'kvksa x, C, I, P, a, b, rFkk s osQ chp (1)] (2) rFkk (3) esa n'kkZ, ikjLifjd laca/ksa dk ,d xf.krh; ekWMy izkIr gksrk gSA bu pj jkf'kvksa dk oxhZdj.k bl izdkj gS]
Lora=k x
vkfJr (ijra=k) C, I, P
izkpy a, b, s
mRiknd dks x, a, b, s, dh tkudkjh gS vkSj og P Kkr dj ldrk gSA
pj.k 3 laca/ (3) }kjk ge ns[krs gSa fd le foPNsnu ¯cnq (u dksbZ ykHk vkSj u dksbZ gkfu) osQ fy, P = 0, vFkkZr~, 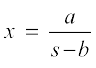 bdkb;k¡A
bdkb;k¡A
pj.k 4 rFkk 5 le foPNsnu ¯cnq osQ fopkj ls ge fu"d"kZ fudky ldrs gSa fd ;fn daiuh oqQN bdkb;k¡ gh mRikfnr djrh gS] vFkkZr~ 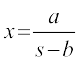 bdkb;ksa ls de gks rks mls gkfu gksxh vkSj ;fn og vf/d bdkb;k¡ mRikfnr djrh gS] vFkkZr~
bdkb;ksa ls de gks rks mls gkfu gksxh vkSj ;fn og vf/d bdkb;k¡ mRikfnr djrh gS] vFkkZr~ 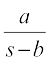 bdkb;ksa ls vf/d rks mls ykHk gksxkA blosQ vfrfjDr] ;fn le foPNsnu ¯cnq vokLrfod fl¼ gksrk gS] rc dksbZ vU; ekWMy iz;qDr fd;k tk ldrk gS vFkok /u izokg ls lacaf/r vfHk/kj.kkvksa esa la'kks/u fd;k tk ldrk gSA
bdkb;ksa ls vf/d rks mls ykHk gksxkA blosQ vfrfjDr] ;fn le foPNsnu ¯cnq vokLrfod fl¼ gksrk gS] rc dksbZ vU; ekWMy iz;qDr fd;k tk ldrk gS vFkok /u izokg ls lacaf/r vfHk/kj.kkvksa esa la'kks/u fd;k tk ldrk gSA
fVIi.kh laca/ (3) ls] gesa ;g Hkh feyrk gS fd]
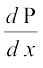 = s – b
= s – b
vFkkZr~] x osQ lkis{k P osQ ifjorZu dh nj] jkf'k s – b ij fuHkZj djrh gS tks fd mRikn osQ foØ; ewY; rFkk mlosQ pj ykxr osQ varj osQ cjkcj gSA vr% ykHk vftZr djus osQ fy, bl jkf'k dks /ukRed gksuk pkfg, vkSj izpqj ek=kk esa ykHk vftZr djus osQ fy, gesa cgqr vf/d ek=kk mRikfnr djuh pkfg, lkFk gh lkFk pj ykxr dks de djus dk iz;kl Hkh djuk pkfg,A
mnkgj.k 7 eku yhft, fd ,d VSad esa 1000 fyVj yo.k&ty gS ftlesa izfr fyVj 250 g yo.k gSA 200 g/L yo.k okyk yo.k&ty] 25 L/min dh nj ls VSad esa vk jgk gS rFkk bl izdkj izkIr feJ.k leku nj ls VSad ls ckgj fudy jgk gSA fdlh {k.k t ij VSad esa yo.k dh ek=kk D;k gS\
gy pj.k 1 ;gk¡ fLFkfr ljyrk ls igpku djus osQ ;ksX; gSA
pj.k 2 eku yhft, fd y = y (t) }kjk varokZg&cfgokZg izkjaHk gksus osQ ckn] fdlh le; t (feuV esa) ij] VSad esa mifLFkr yo.k dh ek=kk (fdyks xzke esa) lwfpr (izdV) gksrh gSA tc t = 0, vFkkZr~ varokZg&cfgokZg izkjaHk gksus ls iwoZ y = 250 g × 1000 = 250 kg
è;ku nhft, fd y esa ifjorZu] feJ.k esa varokZg&cfgokZg osQ dkj.k gksrk gS
vc VSad esa yo.k&ty dk varokZg] 5 kg/min (D;ksafd 25 × 200 g = 5 kg) dh nj ls yo.k ykrk gS rFkk yo.k&ty dk cfgokZg 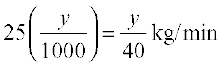 (D;ksafd t le; ij VSad esa yo.k dh ek=kk
(D;ksafd t le; ij VSad esa yo.k dh ek=kk 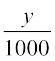 kg gS)
kg gS)
vr% t osQ lkis{k VSad esa yo.k dh ek=kk esa ifjorZu dh nj fuEufyf[kr lehdj.k ls izkIr gksrh gS]
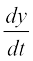 =
= 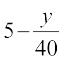 (D;ksa?)
(D;ksa?)
;k 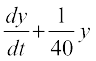 = 5 ... (1)
= 5 ... (1)
;g ifj.kke iznÙk leL;k dk ,d xf.krh; ekWMy nsrk gSA
pj.k 3 ifj.kke (1) ,d jSf[kd lehdj.k gS] ftls vklkuh ls ljy fd;k tk ldrk gSA lehdj.k (1) dk gy uhps fn;k gS
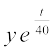 =
= 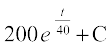 ;k y (t) = 200 + C
;k y (t) = 200 + C 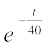 ... (2)
... (2)
tgk¡ C lekdyu dk vpj gSA
è;ku nhft, fd Kkr gS fd tc t = 0, y = 250. vr,o, 250 = 200 + C
vFkok C = 50
rc lehdj.k (2) uhps fyf[kr :i esa ifjofrZr gks tkrk gS]
y = 200 + 50 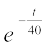 ... (3)
... (3)
;k 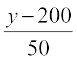 =
= 
;k 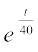 =
= 
vr% t = 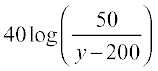 ... (4)
... (4)
bl izdkj lehdj.k (4) og le; t nsrk gS] tc VSad esa yo.k dh ek=kk y kg gSA
pj.k 4 lehdj.k (3) ls ge fu"d"kZ fudkyrs gSa fd lnSo y > 200 D;ksafd 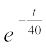 dk eku loZnk /ukRed jgrk gS
dk eku loZnk /ukRed jgrk gS
vr% VSad esa yo.k dh U;wure ek=kk yxHkx 200 kg (fdarq Bhd&Bhd 200 kg ugha) gks ldrh gSA blosQ vfrfjDr lehdj.k (4) ls ge fu"d"kZ fudkyrs gSa fd t > 0 ;fn vkSj osQoy ;fn 0 < y – 200 < 50 vFkkZr~ ;fn vkSj osQoy ;fn 200 < y < 250 varxZr VSad osQ yo.k&ty osQ varokZg vkSj cfgokZg osQ izkjaHk gksus osQ ckn yo.k dh ek=kk 200 kg vkSj 250 kg osQ eè; gSA
xf.krh; fun'kZu dh ifjlhek,¡ (Limitations)
vHkh rd vusd xf.krh; ekWMy fodflr fd, x, gSa vkSj mudk vuqiz;ksx (application) vusdkusd ifjfLFkfr;ksa dks xgurk ls le>us esa liQyrkiwoZd fd;k tk pqdk gSA oqQN fo"k; tSls xf.krh; HkkSfrdh] xf.krh; vFkZ'kkL=k] lafØ;k foKku (operations research)] tho&xf.kr (Bio-mathematics) vkfn] xf.krh; fun'kZu osQ (yxHkx) i;kZ;okph@lekukFkhZ gSaA
ijarq] vkt Hkh dbZ ifjfLFkfr;k¡ ,slh gS] ftuosQ ekWMy vHkh cuus gSaA ftlosQ ihNs dkj.k ;g gS fd ;k rks os ifjfLFkfr;k¡ cgqr tfVy gSa vFkok fodflr ekWMy xf.krkuqlkj vlkè; gSaA
'kfDr'kkyh daI;wVjksa rFkk vfr&daI;wVjksa (Super Computers) osQ fodkl us] ifjfLFkfr;ksa dh ,d cgqr cM+h la[;k osQ fy,] xf.krkuqlkj ekWMy cukus esa] gesa l{ke cuk fn;k gSA
Rofjr (fast) rFkk mUur daI;wVj osQ dkj.k ;g laHko gks ldk gS fd ge vf/d ;FkkFkZ ekWMyksa dh jpuk dj ldrs gSa ftuosQ }kjk izs{k.k osQ lkFk csgrj lgefr izkIr dh tk ldrh gSA
rFkkfi gekjs ikl] fdlh xf.krh; ekWMy esa iz;qDr fofHkUu pjksa osQ p;u rFkk bu pjksa osQ ewY;kdau gsrq vPNs ekxZn'kZd fl¼kar ugha gSA okLro esa ge ik¡p ;k N% pjksa dk p;u djosQ ¯dgh Hkh vk¡dM+ksa osQ fy, cgqr gn rd ;FkkFkZ (accurate) ekWMyksa dk fuekZ.k dj ldrs gSaA buosQ Bhd&Bhd ewY;kadu gsrq gesa pjksa dh la[;k de ls de j[kuh pkfg,A
c`gr~ vFkok tfVy ifjfLFkfr;ksa ds xf.krh; fun'kZu dh viuh fo'ks"k (fof'k"V) leL;k,¡ gksrh gSA bl izdkj dh ifjfLFkfr;k¡ izk;% i;kZoj.k (environment)] leqnz foKku (oceanography)] tula[;k fu;a=k.k (population control) vkfn osQ yksd fun'kks± (world models) osQ vè;;u esa vkrh gSaA f'k{kk dh lHkh 'kk[kkvksa&xf.kr] daI;wVj foKku] HkkSfrdh] vfHk;af=kdh] lekt'kkL=k vkfn osQ xf.krh; fun'kZd] bl pqukSrh dk lkeuk lkgliwoZd dj jgs gSaA