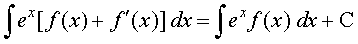Table of Contents
vè;k; 7
lekdyu Integrals
Just as a mountaineer climbs a mountain – because it is there, so a good mathematics student studies new material because it is there. – James B. Bristol
7.1 Hkwfedk (Introduction)
vody xf.kr vodyt dh ladYiuk ij osaQfnzr gSA iQyuksa osQ vkys[kksa osQ fy, Li'kZ js[kk,¡ ifjHkkf"kr djus dh leL;k ,oa bl izdkj dh js[kkvksa dh izo.krk dk ifjdyu djuk vodyt osQ fy, ewy vfHkizsj.k FkkA lekdyu xf.kr] iQyuksa osQ vkys[k ls f?kjs {ks=k osQ {ks=kiQy dks ifjHkkf"kr djus ,oa blosQ {ks=kiQy dk ifjdyu djus dh leL;k ls iszfjr gSA

(1646–1716)
;fn ,d iQyu f fdlh varjky I esa vodyuh; gS vFkkZr~ I osQ izR;sd ¯cnq ij iQyu osQ vodyt f′ dk vfLrRo gS] rc ,d LokHkkfod iz'u mBrk gS fd ;fn I osQ izR;sd ¯cnq ij f′ fn;k gqvk gS rks D;k ge iQyu f Kkr dj ldrs gSa\ os lHkh iQyu ftuls gesa ,d iQyu muosQ vodyt osQ :i esa izkIr gqvk gS] bl iQyu osQ izfrvodyt (iwoZx) dgykrs gSaA vxzr% og lw=k ftlls ;s lHkh izfrvodyt izkIr gksrs gSa] iQyu dk vfuf'pr lekdyu dgykrk gS vkSj izfrvodyt Kkr djus dk ;g izØe lekdyu djuk dgykrk gSA bl izdkj dh leL;k,¡ vusd O;kogkfjd ifjfLFkfr;ksa esa vkrh gSaA mnkgj.kr% ;fn gesa fdlh {k.k ij fdlh oLrq dk rkR{kf.kd osx Kkr gS] rks LokHkkfod iz'u ;g mBrk gS fd D;k ge fdlh {k.k ij ml oLrq dh fLFkfr Kkr dj ldrs gSa\ bl izdkj dh vusd O;kogkfjd ,oa lS¼kafrd ifjfLFkfr;k¡ vkrh gSa] tgk¡ lekdyu dh lafØ;k fufgr gksrh gSA lekdyu xf.kr dk fodkl fuEufyf[kr izdkj dh leL;kvksa osQ gy djus osQ iz;klksa dk izfriQy gSA
(a) ;fn ,d iQyu dk vodyt Kkr gks] rks ml iQyu dks Kkr djus dh leL;k]
(b) fuf'pr izfrca/ksa osQ varxZr iQyu osQ vkys[k ls f?kjs {ks=k dk {ks=kiQy Kkr djus dh leL;kA
mi;qZDr nksuks leL;k,¡ lekdyuksa osQ nks :iksa dh vksj izsfjr djrh gSa] vfuf'pr lekdyu ,oa fuf'pr lekdyuA bu nksuksa dk lfEefyr :i lekdyu xf.kr dgykrk gSA
vfuf'pr lekdyu ,oa fuf'pr lekdyu osQ eè; ,d laca/ gS ftls dyu dh vk/kjHkwr izes; osQ :i esa tkuk tkrk gSA ;g izes; fuf'pr lekdyu dks foKku ,oa vfHk;kaf=kdh osQ fy, ,d O;kogkfjd vkS”kkj osQ :i esa rS;kj djrh gSA vFkZ'kkL=k] foÙk ,oa izkf;drk tSls fofHkUu {ks=kksa ls vusd izdkj dh #fpdj leL;kvksa dks gy djus osQ fy, Hkh fuf'pr lekdyu dk mi;ksx fd;k tkrk gSA
bl vè;k; esa] ge vius vkidks vfuf'pr ,oa fuf'pr lekdyuksa ,oa lekdyu dh oqQN fof/;ksa lfgr muosQ izkjafHkd xq.k/eks± osQ vè;;u rd lhfer j[ksaxsA
7.2 lekdyu dks vodyu osQ O;qRØe izØe osQ :i esa (Integration as the Inverse Process of Differentiation)
vodyu osQ O;qRØe izØe dks lekdyu dgrs gSaA fdlh iQyu dk vodyu Kkr djus osQ LFkku ij gesa iQyu dk vodyt fn;k gqvk gS vkSj bldk iwoZx vFkkZr~ okLrfod iQyu Kkr djus osQ fy, dgk x;k gSA ;g izØe lekdyu vFkok izfr&vodyu dgykrk gSA
vkb, fuEufyf[kr mnkgj.kksa ij fopkj djsa]
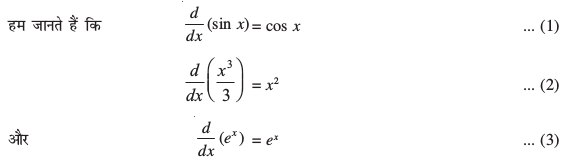
ge izsf{kr djrs gSa fd lehdj.k (1) esa iQyu cos x iQyu sin x dk vodyt gSA bls ge bl izdkj Hkh dgrs gSa fd cos x dk izfrvodyt (vFkok lekdyu) sin x gSA blh izdkj (2) ,oa (3) ls x2 vkSj ex osQ izfrvodyt (vFkok lekdyu) Øe'k%vkSj ex gSA iqu% ge uksV djrs gSa fd fdlh Hkh okLrfod la[;k C] ftls vpj iQyu ekuk tkrk gS] dk vodyt 'kwU; gS] vkSj blfy, ge (1)] (2) vkSj (3) dks fuEufyf[kr :i esa fy[k ldrs gSa%
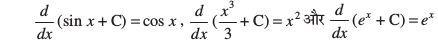
bl izdkj ge ns[krs gSa fd mi;qZDr iQyuksa osQ izfrvodyt vFkok lekdyu vf¼rh; ugha gSaA oLrqr% bu iQyuksa esa ls izR;sd iQyu osQ vifjfer izfrvodyt gSa] ftUgsa ge okLrfod la[;kvksa osQ leqPp; ls LosPN vpj C dks dksbZ eku iznku djosQ izkIr dj ldrs gSaA ;gh dkj.k gS fd C dks izFkkuqlkj LosPN vpj dgrs gSaA oLrqr% C ,d izkpy gS] ftlosQ eku dks ifjofrZr djosQ ge fn, gq, iQyu osQ

fVIi.kh leku vodyt okys iQyuksa esa ,d vpj dk varj gksrk gSA bldks n'kkZus osQ fy,] eku yhft, g vkSj h ,sls nks iQyu gSa ftuosQ vodyt varjky I esa leku gaS
f (x) = g (x) – h (x),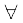 x ∈ I }kjk ifjHkkf"kr iQyu f = g – h ij fopkj dhft,
x ∈ I }kjk ifjHkkf"kr iQyu f = g – h ij fopkj dhft,
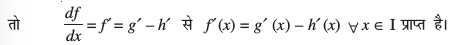
vFkok f′ (x) = 0,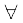 x ∈ I (ifjdYiuk ls)
x ∈ I (ifjdYiuk ls)
vFkkZr~ I esa x osQ lkis{k f osQ ifjorZu dh nj 'kwU; gS vkSj blfy, f ,d vpj gSA
mi;qZDr fVIi.kh osQ vuqlkj ;g fu"d"kZ fudkyuk U;k;laxr gS fd ifjokj {F + C, C ∈ R}, f osQ lHkh izfrvodytksa dks iznku djrk gSA
vc ge ,d u, izrhd ls ifjfpr gksrs gSa tks fd izfrvodytksa osQ iwjs ifjokj dks fu:fir djsxkA ;g izrhd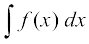 gS] bls x osQ lkis{k f dkvfuf'pr lekdyu osQ :i esa i<+k tkrk gSA
gS] bls x osQ lkis{k f dkvfuf'pr lekdyu osQ :i esa i<+k tkrk gSA
izrhdr% ge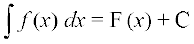 fy[krs gSaA
fy[krs gSaA
laosQru fn;k gqvk gS fd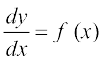 , rks ge y =
, rks ge y =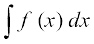 fy[krs gSaA
fy[krs gSaA
lqfo/k osQ fy, ge fuEufyf[kr izrhdksa@inksa@okD;ka'kksa dks muosQ vFkks± lfgr lkj.kh 7-1 esa mYysf[kr djrs gaS%
| izrhd@in@okD;ka'k | vFkZ |
|---|---|
| ∫ f ( x ) dx | f dk x osQ lkis{k lekdyu |
| ∫ f ( x ) dx esa x | lekdyu dk pj |
| lekdyu djuk | lekdyu Kkr djuk |
| f dk lekdyu | ,d iQyu F ftlosQ fy, F′(x) = f (x) |
| lekdyu lafØ;k | lekdyu Kkr djus dk izØe |
| lekdyu dk vpj | dksbZ Hkh okLrfod la[;k ftls vpj iQyu dgrs gaSA |
ge igys ls gh cgqr ls izeq[k iQyuksa osQ vodytksa osQ lw=k tkurs gSaA bu lw=kksa osQ laxr ge lekdyu osQ izkekf.kd lw=kksa dks rqjar fy[k ldrs gSaAkd lw=kksa dh lwph fuEufyf[kr gSa ftldk mi;ksx ge nwljs iQyuksa osQ lekdyuksa dks Kkr djus esa djsaxsA


fVIi.kh iz;ksx esa ge izk;% ml varjky dk ftØ ugha djrs ftlesa fofHkUu iQyu ifjHkkf"kr gSa rFkkfi fdlh Hkh fof'k"V iz'u osQ lanHkZ esa bldks Hkh è;ku esa j[kuk pkfg,A
7.2.1 vfuf'pr lekdyu dk T;kferh; fu:i.k (Geometrical interpretation of indefinite integral)
eku yhft, fd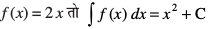 rFkk C osQ fofHkUu ekuksa osQ fy, ge fofHkUu lekdyu ikrs gSaA ijarq T;kferh; n`f"V ls ;s lHkh lekdyu leku gSaA bl izdkj
rFkk C osQ fofHkUu ekuksa osQ fy, ge fofHkUu lekdyu ikrs gSaA ijarq T;kferh; n`f"V ls ;s lHkh lekdyu leku gSaA bl izdkj
y = x2 + C, tgk¡ C ,d LosPN vpj gS] lekdyuksa osQ ,d ifjokj dks fu:fir djrk gSA C, dks fofHkUu eku iznku djosQ ge ifjokj osQ fofHkUu lnL; izkIr djrs gSaA bu lcdk lfEefyr :i vfuf'pr lekdyu gSA Li"Vr;k izR;sd lekdyu ,d ijoy; dks fu:fir djrk gS ftldk v{k y-v{k osQ vuqfn'k gSA
Li"Vr;k C = 0 osQ fy, ge y = x2 ikrs gSa tks ,d ,slk ijoy; gS ftldk 'kh"kZ ewy ¯cnq ij gSA C = 1 osQ fy, oØ y = x2 + 1 ijoy; y = x2 dks ,d bdkbZ y-v{k osQ vuq /ukRed fn'kk esa LFkkukarfjr djus ij izkIr gksrk gSA C = – 1, osQ fy,] oØ y = x2 – 1 ijoy; y = x2 dks ,d bdkbZ y-v{k osQ vuqfn'k ½.kkRed fn'kk esa LFkkukarfjr djus ij izkIr gksrk gSA bl izdkj C, osQ izR;sd /ukRed eku osQ fy,] ifjokj
osQ izR;sd ijoy; dk 'kh"kZ y-v{k dh /ukRed fn'kk esa gS vkSj C osQ ½.kkRed ekuksa osQ fy, izR;sd ijoy; dk 'kh"kZ y-v{k dh ½.kkRed fn'kk esa gSA bu ijoy;ksa esa ls oqQN dks vko`Qfr 7-1 esa n'kkZ;k x;k gSA
vc ge bu ijoy;ksa osQ js[kk x = a }kjk izfrPNsnu ij fopkj djrs gSaA vko`Qfr 7-1 esa geus a > 0 fy;k gSA ;g fu"d"kZ a < 0 osQ fy, Hkh lR; gSA ;fn js[kk x = a ijoy;ksa y = x2, y = x2 + 1, y = x2 + 2, y = x2 – 1, y = x2 – 2 dks Øe'k% ¯cnqvksa P0, P1, P2, P–1, P–2 bR;kfn ij dkVrh gS
rks bu lHkh ¯cnqvksa ij dk eku 2a gSA ;g fufnZ"V djrk gS fd bu lHkh ¯cnqvksa ij oØksa dh Li'kZ js[kk,¡ lekarj gSaA
bl izdkj 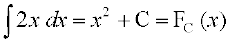 (eku yhft,) ls izkIr gksrk gS fd oØksa
(eku yhft,) ls izkIr gksrk gS fd oØksa
y = FC (x), C ∈ R, osQ js[kk x = a, }kjk izfrPNsnu ¯cnqvksa ij oØksa dh Li'kZ js[kk,¡ lekarj gSa tgk¡ a ∈ R vxzr% fuEufyf[kr dFku 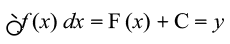 (eku yhft,) oØksa osQ ifjokj dks fu:fir djrk gSA C osQ fofHkUu ekuksa osQ laxr gesa bl ifjokj osQ fofHkUu lnL; izkIr gksrs gSa vkSj bu lnL;ksa esa ls ge fdlh ,d lnL; dks Lo;a osQ lekUrj LFkkukarfjr djosQ izkIr dj ldrs gSaA vfuf'pr lekdyu dk T;kferh; fu:i.k ;gh gSA
(eku yhft,) oØksa osQ ifjokj dks fu:fir djrk gSA C osQ fofHkUu ekuksa osQ laxr gesa bl ifjokj osQ fofHkUu lnL; izkIr gksrs gSa vkSj bu lnL;ksa esa ls ge fdlh ,d lnL; dks Lo;a osQ lekUrj LFkkukarfjr djosQ izkIr dj ldrs gSaA vfuf'pr lekdyu dk T;kferh; fu:i.k ;gh gSA

vko`Qfr 7.1
7.2.2 vfuf'pr lekdyuksa osQ oqQN xq.k/eZ (Some properties of indefinite integrals)
bl mi ifjPNsn esa ge vfuf'pr lekdyu osQ oqQN xq.k/eks± dks O;qRiUu djsaxsA
(i) fuEufyf[kr ifj.kkeksa osQ lanHkZ esa vodyu ,oa lekdyu osQ izØe ,d nwljs osQ O;qRØe gSa%
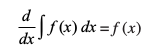
vkSj ∫f′( x ) dx= f(x) + C, tgk¡ C ,d LosPN vpj gSA
miifÙk eku yhft, fd F] f dk ,d izfrvodyt gSa vFkkZr~
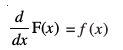
rks 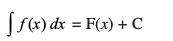
blfy, 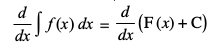
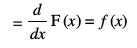
blh izdkj ge ns[krs gSa fd
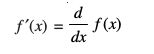
vkSj blfy, 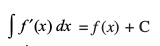
tgk¡ C ,d LosPN vpj gS ftls lekdyu vpj dgrs gSaA
(ii) ,sls nks vfuf'pr lekdyu ftuosQ vodyt leku gSa oØksa osQ ,d gh ifjokj dks izsfjr djrs gSa vkSj bl izdkj lerqY; gSaA
miifÙk eku yhft, f ,oa g ,sls nks iQyu gSa ftuesa
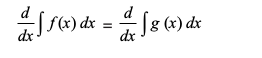
vFkok 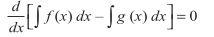
vr% 
vFkok 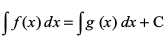
blfy, oØksa osQ ifjokj 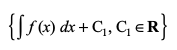
,oa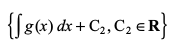 lerqY; gSaA
lerqY; gSaA
bl izdkj 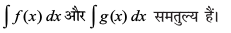
fVIi.kh nks ifjokjksa 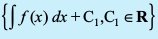 ,oa
,oa 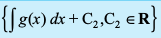 dh lerqY;rk dks izFkkuqlkj
dh lerqY;rk dks izFkkuqlkj
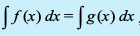 , fy[kdj O;Dr djrs gSa ftlesa izkpy dk o.kZu ugha gSA
, fy[kdj O;Dr djrs gSa ftlesa izkpy dk o.kZu ugha gSA
(iii) 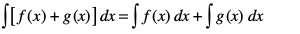
miifÙk xq.k/eZ (i) ls

vU;Fkk gesa Kkr gS fd
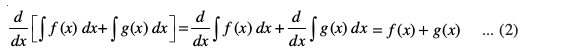
bl izdkj xq.k/eZ (ii) osQ lanHkZ esa (1) vkSj (2) ls izkIr gksrk gS fd
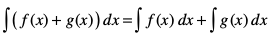
(iv) fdlh okLrfod la[;k k, osQ fy, 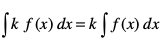
miifÙk xq.k/eZ (i) }kjk 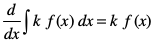
vkSj 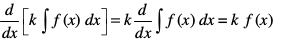
blfy, xq.k/eZ (ii) dk mi;ksx djrs gq, ge ikrs gSa fd 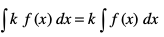
(v) izxq.kksa (iii) vkSj (iv) dk f1, f2, ..., fn iQyuksa dh fuf'pr la[;k vkSj okLrfod la[;kvksa k1, k2, ..., kn osQ fy, Hkh O;kidhdj.k fd;k tk ldrk gS tSlk fd uhps fn;k x;k gS
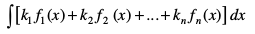
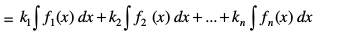
fn, gq, iQyu dk izfrvodyt Kkr djus osQ fy, ge varKkZu ls ,sls iQyu dh [kkst djrs gSa ftldk vodyt fn;k gqvk iQyu gSA vHkh"V iQyu dh bl izdkj dh [kkst] tks fn, gq, iQyu osQ izfr vodyt Kkr djus osQ fy, dh tkrh gS] dks fujh{k.k }kjk lekdyu dgrs gSaA bls ge oqQN mnkgj.kksa ls le>rs gSaA
mnkgkj.k 1 fujh{k.k fof/ dk mi;ksx djrs gq, fuEufyf[kr iQyuksa dk izfrvodyt Kkr dhft,A
(i) cos 2x (ii) 3x2 + 4x3 (iii)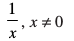
gy
(i) ge ,d ,sls iQyu dh [kkst djuk pkgrs gSa ftldk vodyt cos 2x gS
ge tkurs gSa fd 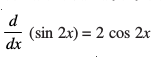
vFkok 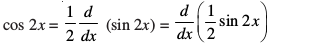
blfy, cos 2x dk ,d izfrvodyt 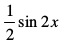 gSA
gSA
(ii) ge ,d ,sls iQyu dh [kkst djuk pkgrs gSa ftldk vodyt 3x2 + 4x3 gSA
vc 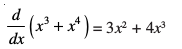
blfy, 3x2 + 4x3 dk izfrvodyt x3 + x4 gSA
(iii) ge tkurs gSa
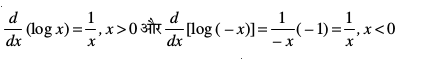
bu nksuksa dks la?kfVr djus ij ge ikrs gSa 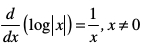
blfy, 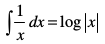 ] tks fd
] tks fd 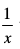 osQ izfrvodytksa esa ls ,d gSA
osQ izfrvodytksa esa ls ,d gSA
mnkgj.k 2 fuEufyf[kr lekdyuksa dks Kkr dhft,
(i)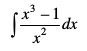 (ii)
(ii)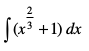 (iii)
(iii)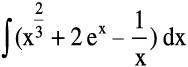
gy ge izkIr djrs gSa%
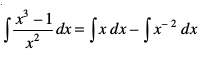 (xq.k/eZ v ls)
(xq.k/eZ v ls)
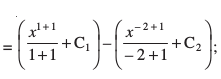 C1, C2 lekdyu vpj gSaA
C1, C2 lekdyu vpj gSaA
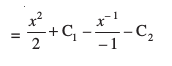
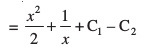
 ,d vU; lekdyu vpj gSA
,d vU; lekdyu vpj gSA
fVIi.kh blls vkxs ge osQoy vafre mÙkj esa gh] ,d lekdyu vpj fy[ksaxsA
(ii) ;gk¡
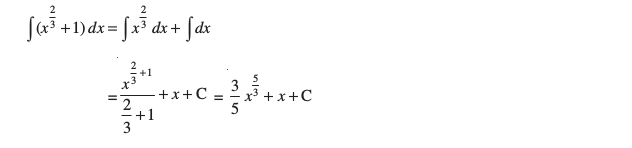
(iii) ;gk¡ 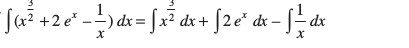
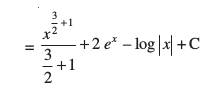
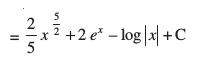
mnkgj.k 3 fuEufyf[kr lekdyuksa dks Kkr dhft,
(i)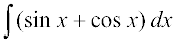 (ii)
(ii)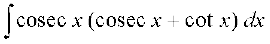
(iii)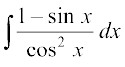
gy
(i) ;gk¡
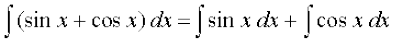
=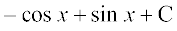
(ii) ;gk¡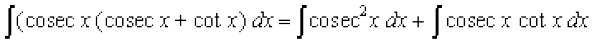
=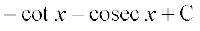
(iii) ;gk¡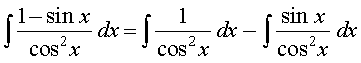
=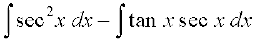
=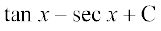
mnkgj.k 4 f(x) = 4x3 – 6 }kjk ifjHkkf"kr iQyu f dk izfrvodyt F Kkr dhft, tgk¡
F(0) = 3 gSA
gy f(x) dk ,d izfr vodyt x4 – 6x gS
pw¡fd 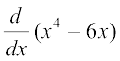 = 4x3 – 6, blfy, izfrvodyt F,
= 4x3 – 6, blfy, izfrvodyt F,
F(x) = x4 – 6x + C, }kjk ns; gS tgk¡ C vpj gSA
fn;k gqvk gS fd F(0) = 3
blls izkIr gksrk gS 3 = 0 – 6 × 0 + C
vFkok C = 3
vr% vHkh"V izfrvodyt] F (x) = x4 – 6x + 3 }kjk ifjHkkf"kr ,d vf}rh; iQyu gSA
fVIi.kh
(i) ge ns[krs gSa fd ;fn f dk izfrvodyt F gS rks F + C, tgk¡ C ,d vpj gS] Hkh f dk ,d izfrvodyt gSA bl izdkj ;fn gesa iQyu f dk ,d izfrvodyt F Kkr gS rks ge F esa dksbZ Hkh vpj tksM+dj f osQ vuar izfrvodyt fy[k ldrs gSa ftUgsa F (x) + C, C ∈ R osQ :i esa vfHkO;Dr fd;k tk ldrk gSA vuqiz;ksxksa esa lkekU;r% ,d vfrfjDr izfrca/ dks larq"V djuk vko';d gksrk gS ftlls C dk ,d fof'k"V eku izkIr gksrk gS vkSj ftlosQ ifj.kkeLo:i fn, gq, iQyu dk ,d vf}rh; izfrvodyt izkIr gksrk gSA
(ii) dHkh&dHkh F dks izkjafHkd iQyuksa tSls fd cgqin] y?kqx.kdh;] pj ?kkrkadh] f=kdks.kferh;] vkSj izfrykse f=kdks.kferh;] bR;kfn osQ :i esa vfHkO;Dr djuk vlaHko gksrk gSA blfy, 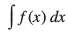 Kkr djuk vo#¼ gks tkrk gSA mnkgj.kr% fujh{k.k fof/ ls
Kkr djuk vo#¼ gks tkrk gSA mnkgj.kr% fujh{k.k fof/ ls 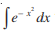 dks Kkr djuk vlaHko gS D;ksafd fujh{k.k ls ge ,slk iQyu Kkr ugha dj ldrs ftldk vodyt
dks Kkr djuk vlaHko gS D;ksafd fujh{k.k ls ge ,slk iQyu Kkr ugha dj ldrs ftldk vodyt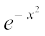 gSA
gSA
(iii) ;fn lekdy dk pj x, osQ vfrfjDr vU; dksbZ gS rks lekdyu osQ lw=k rnuqlkj :ikarfjr dj fy, tkrs gSaA mnkgj.kr%
7.2.3 vodyu ,oa lekdyu dh rqyuk (Comparision between differentiation and integration)
1. nksuksa iQyuksa ij lafØ;k,¡ gSaA
2. nksuksa jSf[kdrk osQ xq.k/eZ dks larq"V djrs gSa vFkkZr~
(i) 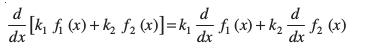
(ii) 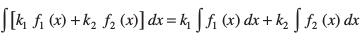
;gk¡ k1, k2 vpj gSA
3. ge igys ls gh tkurs gSa fd lHkh iQyu vodyuh; ugha gksrs gSaA Bhd blh izdkj lHkh iQyu lekdyuh; Hkh ugha gksrs gSaA ge vuodyuh; vkSj vlekdyuh; iQyuksa osQ fo"k; esa mPp d{kkvksa esa vè;;u djsaxsA
4. ;fn fdlh iQyu osQ vodyt dk vfLrRo gS rks og vf}rh; gksrk gS ijarq fdlh iQyu osQ lekdyu osQ lkFk ,slk ugha gS rFkkfi os fdlh ;ksT; vpj rd lhfer vf}rh; gksrs gSa vFkkZr fdlh iQyu osQ nks lekdyuksa esa ges'kk ,d vpj dk varj gksrk gSA
5. ;fn fdlh cgqin iQyu P dk vodyu fd;k tkrk gS rks ifj.kkeLo:i ,d ,slk cgqin feyrk gS ftldh ?kkr cgqin P dh ?kkr ls ,d de gksrh gSA tc fdlh cgqin iQyu P dk lekdyu fd;k tkrk gS rks ifj.kkeLo:i ,d ,slk cgqin izkIr gksrk gS ftldh ?kkr cgqin P dh ?kkr ls ,d vf/d gksrh gSA
6. ge vodyt dh ppkZ ,d ¯cnq ij djrs gaS ijarq lekdyu dh ppkZ ,d ¯cnq ij dHkh ugha gksrhA ge fn, gq, iQyu osQ lekdyu dh ppkZ ml varjky ij djrs gSa ftl ij lekdyu ifjHkkf"kr gksrk gS tSlkfd ge ifjPNsn 7-7 esa ppkZ djsaxsA
7. ,d iQyu osQ vodyt dk T;kferh; vFkZ Hkh gksrk gS tSls fd fn, gq, oØ osQ fn, gq, ¯cnq ij Li'kZ js[kk dh izo.krk] ml ¯cnq ij iQyu osQ vodyt osQ eku osQ cjkcj gksrh gSA blh izdkj fn, gq, iQyu dk vfuf'pr lekdyu ,d nwljs osQ lekarj fLFkr oØksa osQ ifjokj dks fu:fir djrk gS] ftlesa lekdyu osQ pj dks fu:fir djus okys v{k osQ vuqyac js[kk osQ lHkh oØksa osQ izfrPNsnu ¯cnqvksa ij Li'kZ js[kk,¡ lekarj gksrh gSA
8. oqQN HkkSfrd ek=kk,¡ Kkr djus esa vodyt dk mi;ksx gksrk gS mnkgj.kr% fdlh d.k }kjk fdlh le; t esa r; dh xbZ nwjh ;fn Kkr gS rks fn, x, le; ckn osx Kkr djus esa vodyt lgk;d gksrk gSA mlh izdkj fdlh le; t ij ;fn osx Kkr gS rks fn, x, le; esa r; nwjh Kkr djus osQ fy, lekdyu dk mi;ksx gksrk gSA
9. vodyt ,d ,slk izØe gS ftlesa lhek dk Hkko lekfgr gS Bhd mlh izdkj dk Hkko lekdyu esa Hkh lekfgr gS ftlosQ ckjs esa ge ifjPNsn 7-7 esa vè;;u djsaxsA
10. vodyu ,oa lekdyu osQ izØe ,d nwljs osQ O;qRØe gS tSlk fd ifjPNsn 7-2-2 (i) esa ppkZ dh tk pqdh gSA
iz'ukoyh 7-1
fuEufyf[kr iQyuksa osQ izfrvodyt (lekdyu) fujh{k.k fof/ }kjk Kkr dhft,A
1. sin 2x 2. cos 3x 3. e2x
4. (ax + b)2 5. sin 2x – 4 e3x
fuEufyf[kr lekdyuksa dks Kkr dhft,%
6.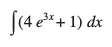 7.
7.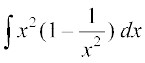 8.
8.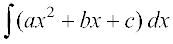
9. 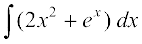 10.
10. 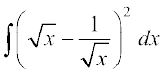 11.
11. 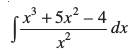
12.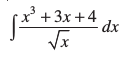 13.
13.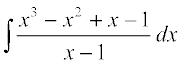 14.
14.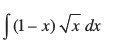
15. 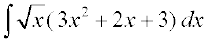 16.
16.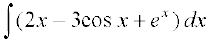
17.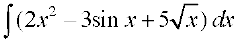 18.
18.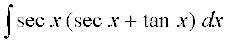
19. 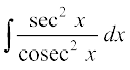 20.dx
20.dx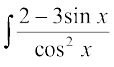
iz'u 21 ,oa 22 esa lgh mÙkj dk p;u dhft,%
21.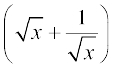 dk izfrvodyt gS%
dk izfrvodyt gS%
(A)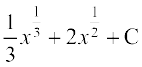 (B)
(B)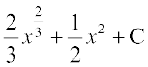
(C)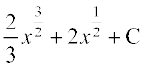 (D)
(D)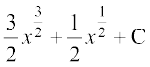
22. ;fn 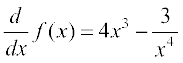 ftlesa f(2) = 0 rks f(x) gS%
ftlesa f(2) = 0 rks f(x) gS%
(A)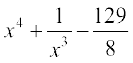 (B)
(B)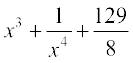
(C)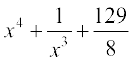 (D)
(D)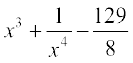
7.3 lekdyu dh fof/;k¡ (Methods of Integration)
fiNys ifjPNsn esa geus ,sls lekdyuksa dh ppkZ dh Fkh] tks oqQN iQyuksa osQ vodytksa ls ljyrkiwoZd izkIr fd, tk ldrs gSaA ;g fujh{k.k ij vk/kfjr fof/ Fkh] blesa ,sls iQyu F dh [kkst dh tkrh gS ftldk vodyt f gS blls f osQ lekdyu dh izkfIr gksrh gSA rFkkfi fujh{k.k ij vk/kfjr ;g fof/ vusd iQyuksa dh fLFkfr esa cgqr mfpr ugha gSA vr% lekdyuksa dks izkekf.kd :i esa ifjofrZr djrs gq, mUgsa Kkr djus osQ fy, gesa vfrfjDr fof/;k¡ fodflr djus dh vko';drk gSA buesa eq[; fof/;k¡ fuEufyf[kr ij vk/kfjr gSa%
1. izfrLFkkiu }kjk lekdyu
2. vkaf'kd fHkUuksa esa fo;kstu }kjk lekdyu
3. [kaM'k% lekdyu
7.3.1 izfrLFkkiu }kjk lekdyu (Integration by substitution)
bl mi ifjPNsn esa ge izfrLFkkiu fof/ }kjk lekdyu ij fopkj djsaxsA Lora=k pj x dks t esa ifjofrZr djus osQ fy, x = g (t) izfrLFkkfir djrs gq, fn, x, lekdyu 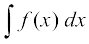 dks vU; :i esa ifjofrZr fd;k tk ldrk gSA
dks vU; :i esa ifjofrZr fd;k tk ldrk gSA
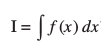 ij fopkj dhft,
ij fopkj dhft,
vc x = g(t) izfrLFkkfir dhft, rkfd 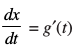
ge dx = g′(t) dt fy[krs gSaA
bl izdkj I = 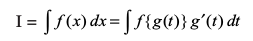
izfrLFkkiu }kjk lekdyu osQ fy, ;g pj ifjorZu dk lw=k gekjs ikl miyC/ ,d egRoiw.kZ
lk/u gSA mi;ksxh izfrLFkkiu D;k gksxk bldk vuqeku yxkuk ges'kk egRoiw.kZ gSA lkekU;r% ge ,d ,sls iQyu osQ fy, izfrLFkkiu djrs gSa ftldk vodyt Hkh lekdY; esa lfEefyr gksa] tSlk fd fuEufyf[kr mnkgj.kksa }kjk Li"V fd;k x;k gSA
mnkgj.k 5 fuEufyf[kr iQyuksa dk x osQ lkis{k lekdyu dhft,
(i) sin mx (ii) 2x sin (x2 + 1) (iii)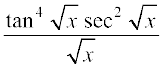
(iv)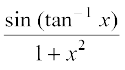
gy
(i) ge tkurs gSa fd mx dk vodyt m gSA vr% ge mx = t izfrLFkkiu djrs gSa] rkfd
mdx = dt
blfy, 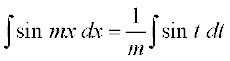
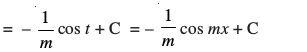
(ii) x2 + 1 dk vodyt 2x gSA vr% ge x2 + 1 = t osQ izfrLFkkiu dk mi;ksx djrs gSa rkfd
2x dx = dt
blfy, 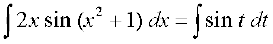
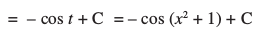
(iii)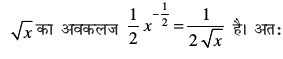 ge
ge
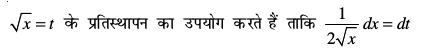 ftlls dx = 2t dt izkIr gksrk gSA
ftlls dx = 2t dt izkIr gksrk gSA
izkIr gksrk gS A
vr% 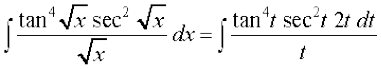 =
=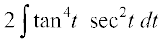
fiQj ls ge nwljk izfrLFkkiu tan t = u djrs gSa rkfd sec2 t dt = du
blfy, 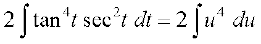 =
=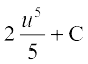
=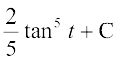 (D;ksafd u = tan t)
(D;ksafd u = tan t)
=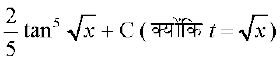
vr%
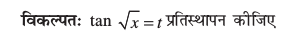
(iv)  gSA vr% ge tan–1 x = t izfrLFkkiu dk mi;ksx djrs gSa rkfd
gSA vr% ge tan–1 x = t izfrLFkkiu dk mi;ksx djrs gSa rkfd
blfy, 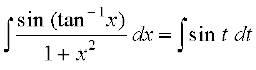
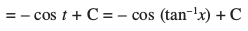
vc ge oqQN egRoiw.kZ lekdyuksa ftuesa f=kdks.kferh; iQyuksa vkSj muosQ izkekf.kd lekdyuksa dk mi;ksx izfrLFkkiu fof/ esa fd;k x;k gS] ij ppkZ djrs gSaA
(i)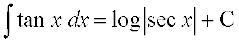
ge ikrs gSa fd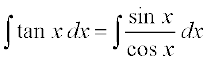
cos x = t, izfrLFkkfir dhft, rkfd sin x dx = – dt
rc 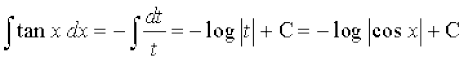
vFkok 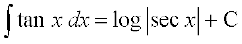
(ii)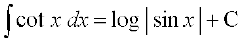
ge ikrs gSa fd 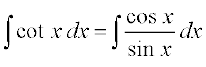
sin x = t izfrLFkkfir dhft, rkfd cos x dx = dt
rc 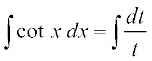
= 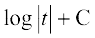
=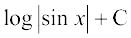
(iii)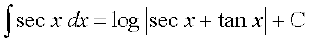
gesa Kkr gS fd,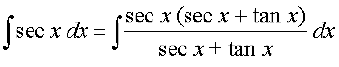
sec x + tan x = t izfrLFkkfir djus ij sec x (tan x + sec x) dx = dt
blfy, 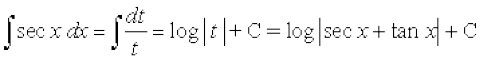
(iv)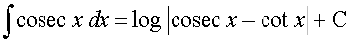
ge ikrs gSa fd, 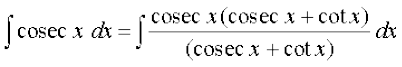
cosec x + cot x = t izfrLFkkfir dhft,
rkfd&& cosec x (cot x + cosec x) dx = dt
blfy,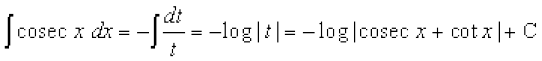
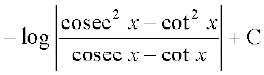
+ 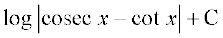
mnkgj.k 6 fuEufyf[kr lekdyuksa dks Kkr dhft,%
(i)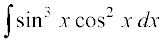
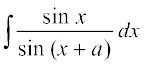 (ii)
(ii)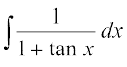 (iii)
(iii)
gy
(i) ;gk¡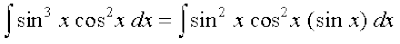
=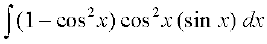
t = cos x izfrLFkkfir dhft, rkfd dt = – sin x dx
blfy,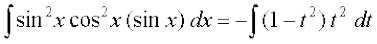
=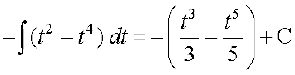
=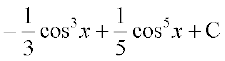
(ii) x + a = t izfrLFkkfir djus ij dx = dt
blfy,
=
=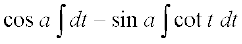
=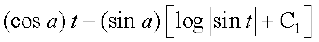
= 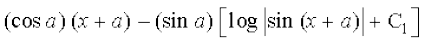
=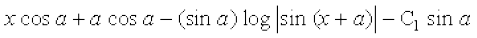
vr% 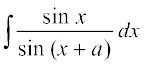 = x cos a – sin a log
= x cos a – sin a log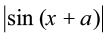 + C
+ C
tgk¡ C = – C1 sin a + a cos a, ,d vU; LosPN vpj gSA
(iii)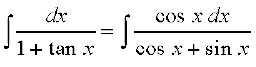
=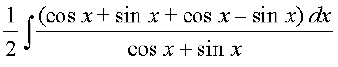
=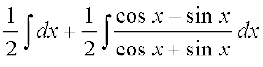
=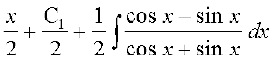
vc =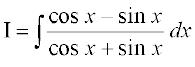 ij fopkj dhft,A
ij fopkj dhft,A
vc cos x + sin x = t izfrLFkkfir dhft, rkfd (–sin x + cos x) dx = dt
blfy, 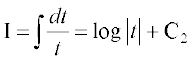
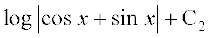
I dks (1) esa j[kus ij ge ikrs gSa
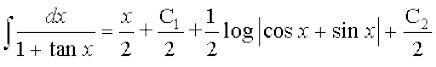
=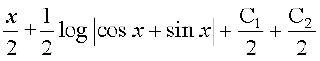
= 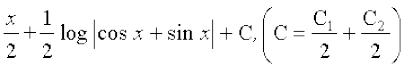
=
iz'ukoyh 7-2
1 ls 37 rd osQ iz'uksa esa izR;sd iQyu dk lekdyu Kkr dhft,A
1.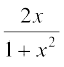 2.
2.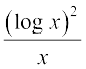 3.
3.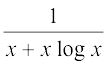
4.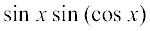 5.
5.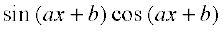
6.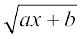 7.
7.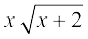 8.
8.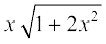
9.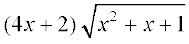 10.
10.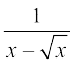 11.
11.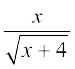 , x > 0
, x > 0
12.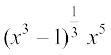 13.
13.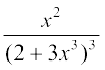 14.
14.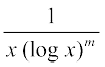 , x > 0, m ≠ 1
, x > 0, m ≠ 1
15.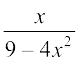 16.
16.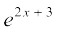 17.
17.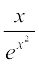
18.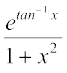 19.
19.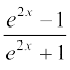 20.
20.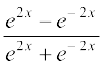
21.tan2 (2x – 3) 22. sec2 (7 – 4x) 23.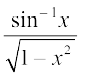
24.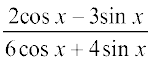 25.
25.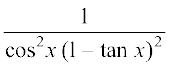 26.
26.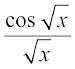
27.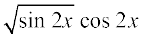 28.
28.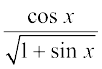 29.cot x log sin x
29.cot x log sin x
30.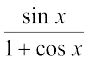 31.
31.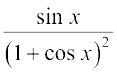 32.
32.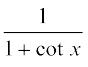
33.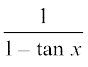 34.
34.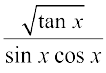 35.
35.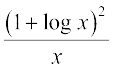
36.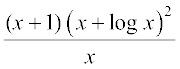 37.
37.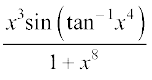
iz'u 38 ,oa 39 esa lgh mÙkj dk p;u dhft,%
38.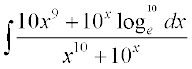
(A) 10x – x10 + C (B) 10x + x10 + C
(C) (10x – x10)–1 + C (D) log (10x + x10) + C
39.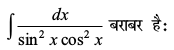
(A) tan x + cot x + C (B) tan x – cot x + C
(C) tan x cot x + C (D) tan x – cot 2x + C
7.3.2 f=kdks.kferh; loZ&lfedkvksa osQ mi;ksx }kjk lekdyu (Integration using trigonometric identities)
tc lekdY; esa oqQN f=kdks.kferh; iQyu fufgr gksrs gSa] rks ge lekdyu Kkr djus osQ fy, oqQN Kkr loZlfedkvksa dk mi;ksx djrs gSa tSlk fd fuEufyf[kr mnkgj.kksa osQ }kjk le>k;k x;k gSA
mnkgj.k 7 fuEufyf[kr dks Kkr dhft,
(i)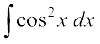 (ii)
(ii)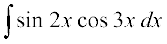 (iii)
(iii)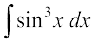
gy
(i) loZlfedk cos 2x = 2 cos2 x – 1 dks Lej.k dhft, ftlls
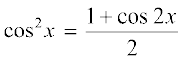 izkIr gksrk gSA
izkIr gksrk gSA
blfy,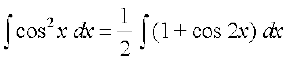
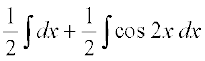 =
= 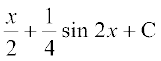
(ii) loZlfedk sin x cos y =  [sin (x + y) + sin (x – y)] , dks Lej.k dhft,
[sin (x + y) + sin (x – y)] , dks Lej.k dhft,
rc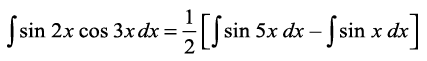
= 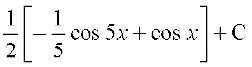
=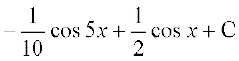
(iii) loZlfedk sin 3x = 3 sin x – 4 sin3 x ls ge ikrs gSa fd
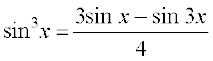
blfy,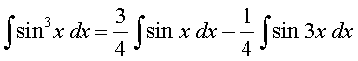
=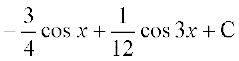
fodYir%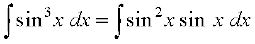 =
=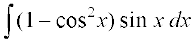
cos x = t j[kus ij – sin x dx = dt
blfy, 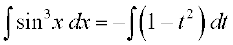 =
=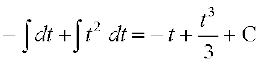
=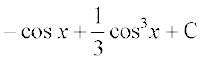
fVIi.kh f=kdks.kferh; loZ&lfedkvksa dk mi;ksx djrs gq, ;g n'kkZ;k tk ldrk gS fd nksuksa mÙkj lerqY; gSaA
iz'ukoyh 7-3
1 ls 22 rd osQ iz'uksa esa izR;sd iQyu dk lekdyu Kkr dhft,A
1. sin2 (2x + 5) 2. sin 3x cos 4x 3. cos 2x cos 4x cos 6x
4. sin3 (2x + 1) 5. sin3 x cos3 x 6. sin x sin 2x sin 3x
7. sin 4x sin 8x 8.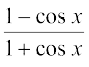
9.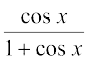
10. sin4 x 11. cos4 2x 12.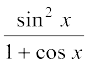
13.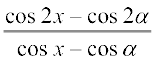
14.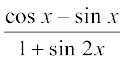 15. tan3 2x sec 2x
15. tan3 2x sec 2x
16. tan4x 17.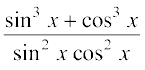
18.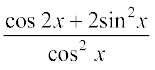
19.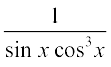
20.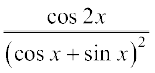
21. sin – 1 (cos x)
22.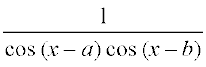
iz'u 23 ,oa 24 esa lgh mÙkj dk p;u dhft,A
23. 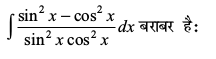
(A) tan x + cot x + C (B) tan x + cosec x + C
(C) – tan x + cot x + C (D) tan x + sec x + C
24.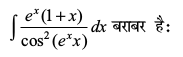
(A) – cot (exx) + C (B) tan (xex) + C
(C) tan (ex) + C (D) cot (ex) + C
7.4 oqQN fof'k"V iQyuksa osQ lekdyu (Integrals of Some Particular Functions)
bl ifjPNsn esa ge fuEufyf[kr egRoiw.kZ lekdyu lw=kksa dh O;k[;k djsaxs vkSj cgqr ls nwljs lacaf/r izkekf.kd lekdyuksa dks Kkr djus esa mudk iz;ksx djsaxsA
(1)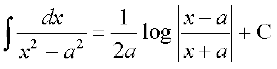 (2)
(2)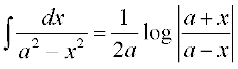 + C
+ C
(3)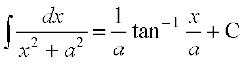 (4)
(4)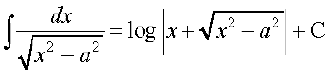
(5)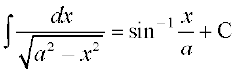 (6)
(6)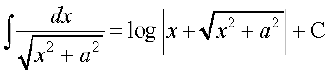
vc ge mi;qZDr ifj.kkeksa dks fl¼ djrs gSaA
(1) ge tkurs gSa fd 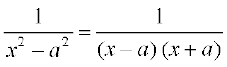
= 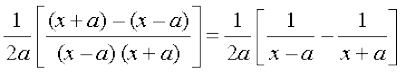
blfy, 
= 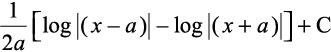
= 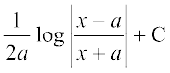
(2) mi;qZDr (1) osQ vuqlkj ge ikrs gSa fd
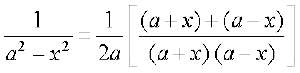 =
=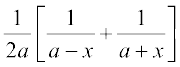
blfy,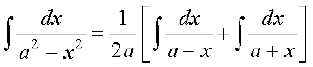
=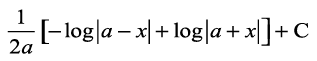
=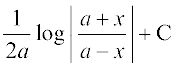
fVIi.kh (1) esa mi;ksx dh xbZ fof/ dh O;k[;k ifjPNsn 7-5 esa dh tk,xhA
(3) x = a tan θ j[kus ij dx = a sec2 θ dθ
blfy, 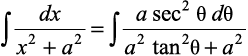
=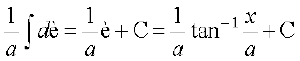
=
(4) eku yhft, x = a secθ rc dx = a sec θ tan θ dθ
blfy,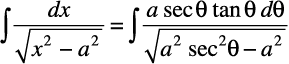
=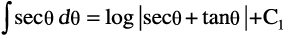
= 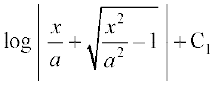
=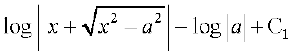
=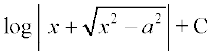 tgk¡ C = C1 – log=
tgk¡ C = C1 – log= 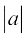
(5) eku yhft, fd x = a sin θ rc dx = a cos θ dθ
blfy,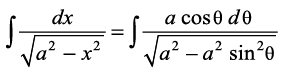 =
=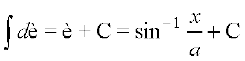
(6) eku yhft, fd x = a tan θ rc dx = a sec2θ dθ
blfy,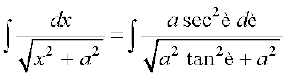
=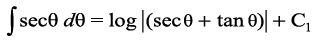
=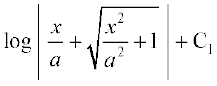
=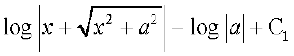
=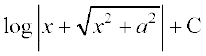 tgk¡ C = C1 – log=
tgk¡ C = C1 – log= 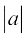
bu izkekf.kd lw=kksa osQ iz;ksx ls vc ge oqQN vkSj lw=k izkIr djrs gSa tks vuqiz;ksx dh n`f"V ls mi;ksxh gSa vkSj nwljs lekdyuksa dk eku Kkr djus osQ fy, budk lh/k iz;ksx fd;k tk ldrk gSA
(7) lekdyu 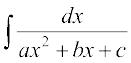 , Kkr djus osQ fy, ge
, Kkr djus osQ fy, ge
ax2 + bx + c =  fy[krs gSaA
fy[krs gSaA
vc 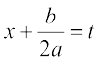 j[kus ij dx = dt ,o
j[kus ij dx = dt ,o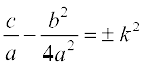 a fy[krs gq, ge ikrs gSa fd
a fy[krs gq, ge ikrs gSa fd 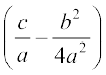 osQ fpÉ ij fuHkZj djrs gq, ;g lekdyu
osQ fpÉ ij fuHkZj djrs gq, ;g lekdyu 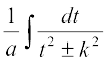 osQ :i esa ifjofrZr gks tkrk gS vkSj bl izdkj bldk eku Kkr fd;k tk ldrk gSA
osQ :i esa ifjofrZr gks tkrk gS vkSj bl izdkj bldk eku Kkr fd;k tk ldrk gSA
(8)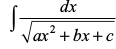 , osQ izdkj osQ lekdyu dks Kkr djus osQ fy, (7) dh Hkk¡fr vkxs c<+rs gq, izkekf.kd lw=kksa dk mi;ksx djosQ lekdyu Kkr fd;k tk ldrk gSA
, osQ izdkj osQ lekdyu dks Kkr djus osQ fy, (7) dh Hkk¡fr vkxs c<+rs gq, izkekf.kd lw=kksa dk mi;ksx djosQ lekdyu Kkr fd;k tk ldrk gSA
(9)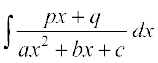
, tgk¡ p, q, a, b, c vpj gSa] osQ izdkj osQ lekdyu Kkr djus osQ fy, ge ,slh nks okLrfod la[;k,¡ A rFkk B Kkr djrs gSa rkfd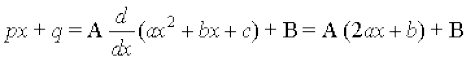
A rFkk B, Kkr djus osQ fy, ge nksuksa i{kksa ls x osQ xq.kkadksa ,oa vpjksa dks leku djrs gSaA A rFkk B osQ Kkr gks tkus ij lekdyu Kkr izkekf.kd :i esa ifjofrZr gks tkrk gSA
(10)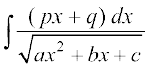 , osQ izdkj osQ lekdyu dk eku Kkr djus osQ fy, ge (9) dh Hkk¡fr vkxs c<+rs gSa vkSj lekdyu dks Kkr izkekf.kd :iksa esa ifjofrZr djrs gSaA
, osQ izdkj osQ lekdyu dk eku Kkr djus osQ fy, ge (9) dh Hkk¡fr vkxs c<+rs gSa vkSj lekdyu dks Kkr izkekf.kd :iksa esa ifjofrZr djrs gSaA
vkb, mi;qZDr fof/;ksa dks oqQN mnkgj.kksa dh lgk;rk ls le>rs gSaA
mnkgj.k 8 fuEufyf[kr lekdyuksa dks Kkr dhft,
(i)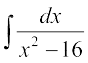 (ii)
(ii)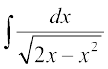
gy
(i) ;gk¡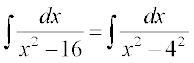 =
=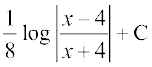 [7.4 (1) ls]
[7.4 (1) ls]
(ii)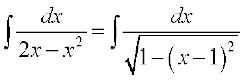
x – 1 = t j[kus ij dx = dt
blfy,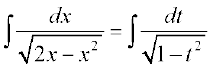 =
=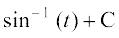
= 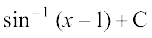 [7.4 (5) ls]
[7.4 (5) ls]
mnkgj.k 9 fuEufyf[kr lekdyuksa dks Kkr dhft,A
(i)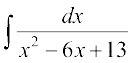 (ii)
(ii)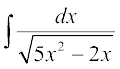 (iii)
(iii)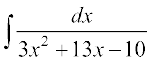
gy
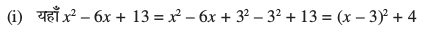
blfy, 
eku yhft, x – 3 = t rc dx = dt
blfy,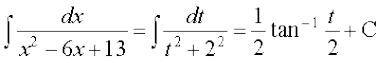 [7.4 (3) ls]
[7.4 (3) ls]
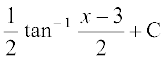
(ii) fn;k gqvk lekdyu 7-4(7) osQ :i dk gSA ge lekdY; osQ gj dks fuEufyf[kr izdkj ls fy[krs gSa
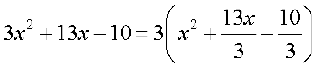
=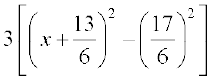 (iw.kZ oxZ cukus ij)
(iw.kZ oxZ cukus ij)
blfy,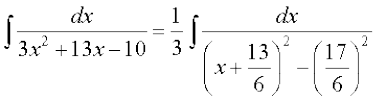
vc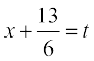 j[kus ij dx = dt
j[kus ij dx = dt
blfy, 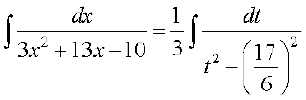
=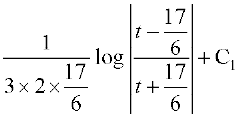 [7.4 (i) ls]
[7.4 (i) ls]
= =
= 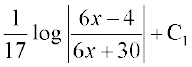
=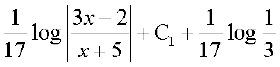
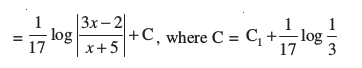
(iii) ;gk¡ 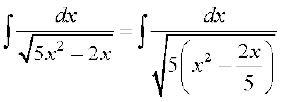
 (iw.kZ oxZ cukus ij)
(iw.kZ oxZ cukus ij)
vc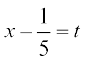 j[kus ij dx = dt
j[kus ij dx = dt
blfy, 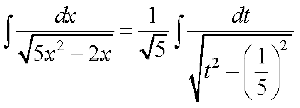
=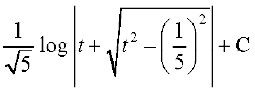 [7.4 (4) ls]
[7.4 (4) ls]
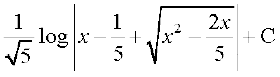
= 
mnkgj.k 10 fuEufyf[kr lekdyuksa dks Kkr dhft,
(i)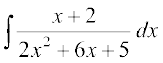 (ii)
(ii)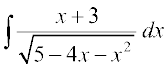
gy
(i) lw=k 7-4(9) dk mi;ksx djrs gq, ge vfHkO;Dr djrs gSa
x + 2 = 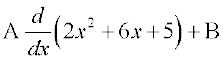
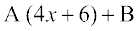
nksuksa i{kksa ls x osQ xq.kkadksa ,oa vpjksa dks leku djus ij ge ikrs gSa%

blfy,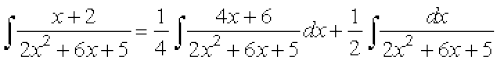
=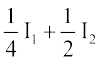 (eku yhft,) ... (1)
(eku yhft,) ... (1)
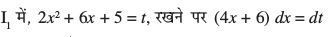
blfy, 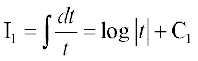
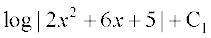
vkSj  =
=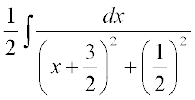
vc 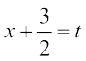 j[kus ij dx = dt, ge ikrs gSa
j[kus ij dx = dt, ge ikrs gSa
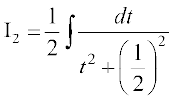 =
=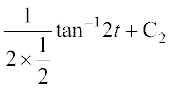 [7.4 (3) ls]
[7.4 (3) ls]
= 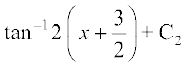 =
=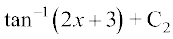
(2) vkSj (3) dk mi;ksx (1) esa djus ij ge ikrs gSa
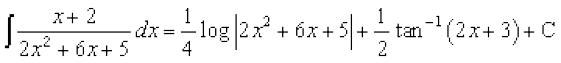 ... (3)
... (3)
tgk¡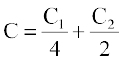
(ii) ;g lekdyu 7-4 (10) osQ :i esa gSA vkb, 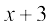 dks fuEufyf[kr :i esa vfHkO;Dr djrs gSa
dks fuEufyf[kr :i esa vfHkO;Dr djrs gSa
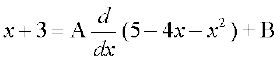 = A (– 4 – 2x) + B
= A (– 4 – 2x) + B
nksuksa i{kksa ls x osQ xq.kkadksa ,oa vpjksa dks leku djus ij ge ikrs gSa
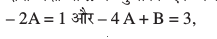
vFkkZr~ 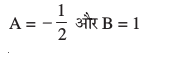
blfy,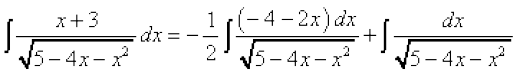
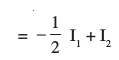
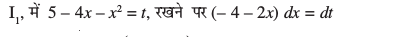
blfy,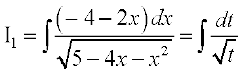 =
=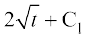
=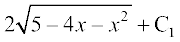
vc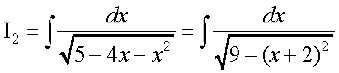 ij fopkj dhft,
ij fopkj dhft,
x + 2 = t j[kus ij dx = dt
blfy,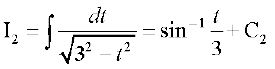
=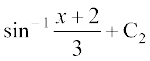
lehdj.kksa (2) ,oa (3) dks (1) esa izfrLFkkfir djus ij ge
=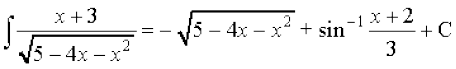 izkIr djrs gSa, tgk¡a
izkIr djrs gSa, tgk¡a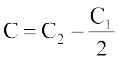
iz'ukoyh 7-4
iz'u 1 ls 23 rd osQ iQyuksa dk lekdyu dhft,A
1.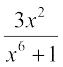 2.
2.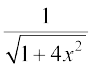 3.
3.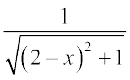
4.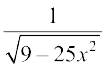 5.
5.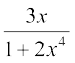 6.
6.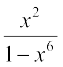
7.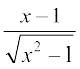 8.
8.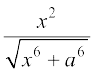 9.
9.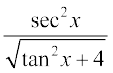
10.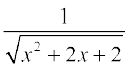 11.
11.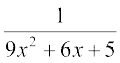 12.
12.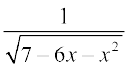
13.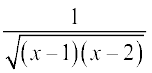 14.
14.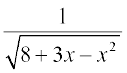 15.
15.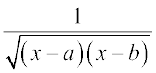
16.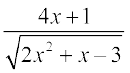 17.
17.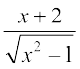 18.
18.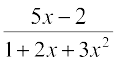
19.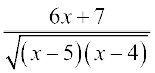 20.
20.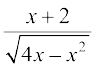 21.
21.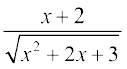
22.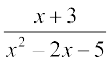 23.
23.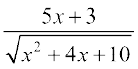
iz'u 24 ,oa 25 esa lgh mÙkj dk p;u dhft,%
24.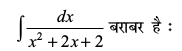
(A) x tan–1 (x + 1) + C (B) tan–1 (x + 1) + C
(C) (x + 1) tan–1x + C (D) tan–1x + C
25.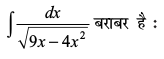
(A)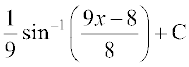 (B)
(B)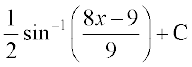
(C)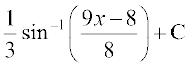 (D)
(D)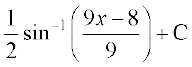
7.5 vkaf'kd fHkUuksa }kjk lekdyu (Integration by Partial Fractions)
Lej.k dhft, fd ,d ifjes; iQyu 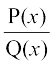 , nks cgqinksa osQ vuqikr osQ :i esa ifjHkkf"kr fd;k tkrk gS tgk¡ P(x) ,oa Q(x), x esa cgqin gSa rFkk Q(x) ≠ 0. ;fn P(x) dh ?kkr Q(x) dh ?kkr ls de gS] rks ifjes; iQyu mfpr ifjes; iQyu dgykrk gS vU;Fkk fo"ke ifjes; iQyu dgykrk gSA fo"ke ifjes; iQyuksa dks yEch Hkkx fof/ }kjk mfpr ifjes; iQyu osQ :i esa ifjofrZr fd;k tk ldrk gSA bl izdkj ;fn
, nks cgqinksa osQ vuqikr osQ :i esa ifjHkkf"kr fd;k tkrk gS tgk¡ P(x) ,oa Q(x), x esa cgqin gSa rFkk Q(x) ≠ 0. ;fn P(x) dh ?kkr Q(x) dh ?kkr ls de gS] rks ifjes; iQyu mfpr ifjes; iQyu dgykrk gS vU;Fkk fo"ke ifjes; iQyu dgykrk gSA fo"ke ifjes; iQyuksa dks yEch Hkkx fof/ }kjk mfpr ifjes; iQyu osQ :i esa ifjofrZr fd;k tk ldrk gSA bl izdkj ;fn 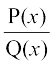 fo"ke ifjes; iQyu gS] rks
fo"ke ifjes; iQyu gS] rks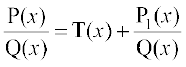 , tgk¡ T(x) x esa ,d cgqin gS vkSj
, tgk¡ T(x) x esa ,d cgqin gS vkSj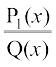 ,d mfpr ifjes; iQyu gSA ge tkurs gSa fd ,d cgqin dk lekdyu oSQls fd;k tkrk gS] vr% fdlh Hkh ifjes; iQyu dk lekdyu fdlh mfpr ifjes; iQyu osQ lekdyu dh leL;k osQ :i esa ifjofrZr gks tkrk gSA ;gk¡ ij ge ftu ifjes; iQyuksa osQ lekdyu ij fopkj djsaxs] muosQ gj jSf[kd vkSj f}?kkr xq.ku[kaMksa esa fo?kfVr gksus okys gksaxsA
,d mfpr ifjes; iQyu gSA ge tkurs gSa fd ,d cgqin dk lekdyu oSQls fd;k tkrk gS] vr% fdlh Hkh ifjes; iQyu dk lekdyu fdlh mfpr ifjes; iQyu osQ lekdyu dh leL;k osQ :i esa ifjofrZr gks tkrk gSA ;gk¡ ij ge ftu ifjes; iQyuksa osQ lekdyu ij fopkj djsaxs] muosQ gj jSf[kd vkSj f}?kkr xq.ku[kaMksa esa fo?kfVr gksus okys gksaxsA
eku yhft, fd ge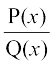 dk eku Kkr djuk pkgrs gSa tgk¡
dk eku Kkr djuk pkgrs gSa tgk¡ 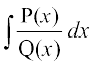 ,d mfpr ifjes; iQyu gSA ,d fof/] ftls vkaf'kd fHkUuksa esa fo;kstu osQ uke ls tkuk tkrk gS] dh lgk;rk ls fn, gq, lekdY; dks lk/kj.k ifjes; iQyuksa osQ ;ksx osQ :i es fy[kk tkuk laHko gSA blosQ i'pkr~ iwoZ Kkr fof/;ksa dh lgk;rk ls lekdyu ljyrkiwoZd fd;k tk ldrk gSA fuEufyf[kr
,d mfpr ifjes; iQyu gSA ,d fof/] ftls vkaf'kd fHkUuksa esa fo;kstu osQ uke ls tkuk tkrk gS] dh lgk;rk ls fn, gq, lekdY; dks lk/kj.k ifjes; iQyuksa osQ ;ksx osQ :i es fy[kk tkuk laHko gSA blosQ i'pkr~ iwoZ Kkr fof/;ksa dh lgk;rk ls lekdyu ljyrkiwoZd fd;k tk ldrk gSA fuEufyf[kr
lkj.kh 7-2 fufnZ"V djrh gS] fd fofHkUu izdkj osQ ifjes; iQyuksa osQ lkFk fdl izdkj osQ ljy vkaf'kd fHkUuksa dks lac¼ fd;k tk ldrk gSA
lkj.kh 7-2

mi;qZDr lkj.kh esa A, B ,oa C okLrfod la[;k,¡ gSa ftudks mfpr fof/ ls Kkr djrs gSaA
mnkgj.k 11 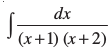 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy fn;k gqvk lekdY; ,d mfpr ifjes; iQyu gS blfy, vkaf'kd fHkUuksa osQ :i [lkj.kh 7.2 (i)], dk mi;ksx djrs gq,] ge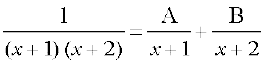 fy[krs gSa --- (1)
fy[krs gSa --- (1)
tgk¡ A vkSj B okLrfod la[;k,¡ gSa ftudks gesa mfpr fof/ ls Kkr djuk gSA ge ikrs gSa
1 = A (x + 2) + B (x + 1)
x osQ xq.kkadksa ,oa vpj inksa dks leku djus ij ge ikrs gSa
A + B = 0
,oa 2A + B = 1
bu lehdj.kksa dks gy djus ij gesa A = 1 vkSj B = – 1 izkIr gksrk gSA
bl izdkj lekdY; fuEufyf[kr :i esa izkIr gksrk gS 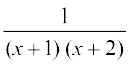 =
=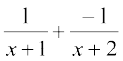
blfy, 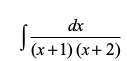 =
=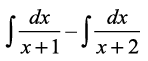
=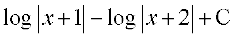
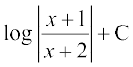
fVIi.kh mi;qZDr lehdj.k (1) ,d loZlfedk gS vFkkZr~ ,d ,slk dFku tks x osQ lHkh Lohdk;Z lHkh ekuksa osQ fy, lR; gSA oqQN ys[kd laosQr ≡ dk mi;ksx ;g n'kkZus osQ fy, djrs gSa fd fn;k gqvk dFku ,d loZlfedk gS vkSj laosQr = dk mi;ksx ;g n'kkZus osQ fy, djrs gSa fd fn;k gqvk dFku ,d lehdj.k gS vFkkZr~ ;g n'kkZus osQ fy, fd fn;k gqvk dFku x osQ fuf'pr ekuksa osQ fy, lR; gSA
mnkgj.k 12 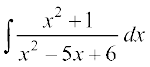 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy ;gk¡ lekdY; 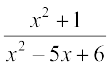 ,d mfpr ifjes; iQyu ugha gS blfy, ge x2 + 1 dks
,d mfpr ifjes; iQyu ugha gS blfy, ge x2 + 1 dks
x2 – 5x + 6 ls Hkkx djrs gSa vkSj ge ikrs gSa fd
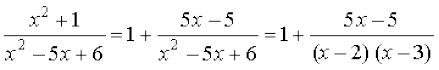
eku yhft, fd 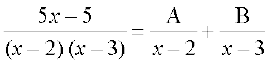
rkfd 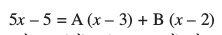
nksuksa i{kksa ls x osQ xq.kkadksa ,oa vpj inksa dks leku djus ij ge ikrs gSa A + B = 5 vkSj
3A + 2B = 5.
bu lehdj.kksa dks gy djus ij ge
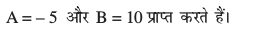
vr%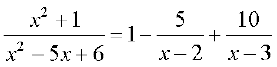
blfy,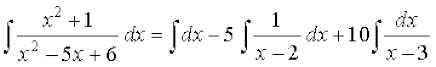
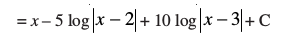
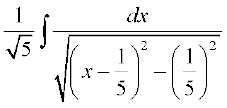
mnkgj.k 13 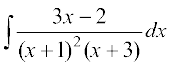 dk eku Kkr dhft,A
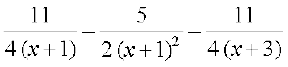
dk eku Kkr dhft,A
gy fn;k gqvk lekdY; lkj.kh 7-2(4) esa fn, gq, lekdY; osQ :i dk gSA vr% ge
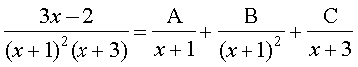 fy[krs gSa
fy[krs gSa
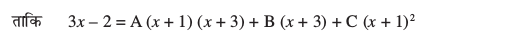
= A (x2 + 4x + 3) + B (x + 3) + C (x2 + 2x + 1 )
nksuksa i{kksa ls x2 osQ xq.kkadksa, x osQ xq.kkadksa ,o vpj inksa dh rqyuk djus ij ikrs gSa fd A + C = 0, 4A + B + 2C = 3 vkSj 3A + 3B + C = – 2 bu lehdj.kksa dks gy djus ij ge 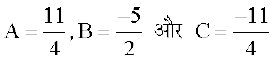 ikrs gSaA bl izdkj lekdY; fuEufyf[kr :i esa izkIr gksrk gSA
ikrs gSaA bl izdkj lekdY; fuEufyf[kr :i esa izkIr gksrk gSA
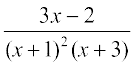
lfy,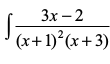 =
=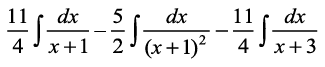
=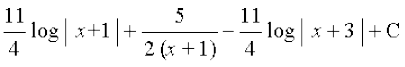
=
mnkgj.k 14 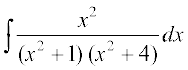 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy 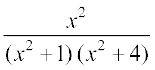 dks yhft, vkSj x2 = y jf[k,
dks yhft, vkSj x2 = y jf[k,
rc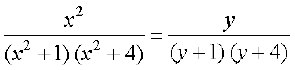
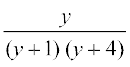 =
=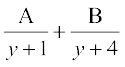 osQ :i esa fyf[k,
osQ :i esa fyf[k,
rkfd y = A (y + 4) + B (y + 1)
nksuksa i{kksa ls y osQ xq.kkadksa ,oa vpj inksa dh rqyuk djus ij ge ikrs gSa A + B = 1 vkSj 4A + B = 0, ftlls izkIr gksrk gS
A=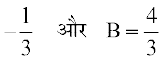
vr% 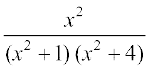 =
=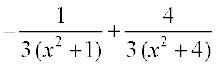
blfy,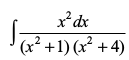 =
=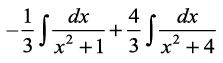
=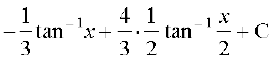
=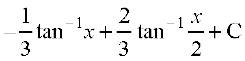
mi;qZDr mnkgj.k esa osQoy vkaf'kd fHkUu okys Hkkx osQ fy, izfrLFkkiu fd;k x;k Fkk u fd lekdyu okys Hkkx osQ fy,A vc ge ,d ,sls mnkgj.k dh ppkZ djrs gSa ftlesa lekdyu osQ fy, izfrLFkkiu fof/ ,oa vkaf'kd fHkUu fof/ nksuksa dks la;qDr :i ls iz;qDr fd;k x;k gSA
mnkgj.k 15 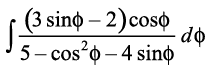 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy eku yhft, y = sinφ
rc dy = cosφ dφ
blfy, 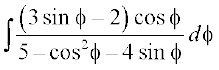 =
=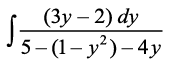
=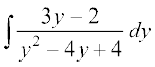 =
=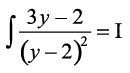 (eku yhft,)
(eku yhft,)
vc ge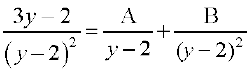 fy[krs gSa [lkj.kh 7.2 (2) ls]
fy[krs gSa [lkj.kh 7.2 (2) ls]
blfy, 3y – 2 = A (y – 2) + B
nksuksa i{kksa ls y osQ xq.kkad ,oa vpj inksa dh rqyuk djus ij ge ikrs gSa] A = 3 ,oa
B – 2A = – 2, ftlls gesa A = 3 ,oa B = 4 izkIr gksrk gSA
blfy, vHkh"V lekdyu fuEufyf[kr :i esa izkIr gksrk gSA
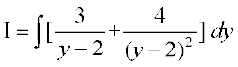 =
=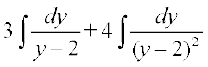
=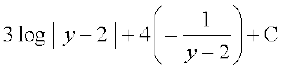
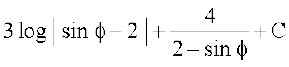
=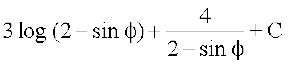 = (D;ksafd 2 – sin φ ges'kk /ukRed gS)
= (D;ksafd 2 – sin φ ges'kk /ukRed gS)
mnkgj.k 16 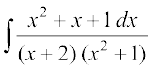 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy fn;k gqvk lekdY; ,d mfpr ifjes; iQyu gSA ifjes; iQyu dks vkaf'kd fHkUuksa esa
fo?kfVr djrs gSa [lkj.kh 2.2(5)]A
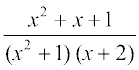 =
=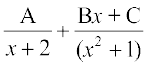
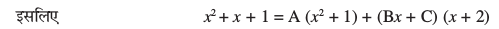
nksuksa i{kksa ls x2 osQ xq.kkadksa, x osQ xq.kkadksa ,oa vpj inksa dh rqyuk djus ij ge A + B =1,
2B + C = 1 vkSj A + 2C = 1 izkIr djrs gSaA
bu lehdj.kksa dks gy djus ij ge 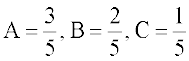 ikrs gSaA
ikrs gSaA
bl izdkj lekdY; fuEufyf[kr :i esa izkIr gksrk gS
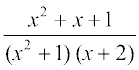 =
=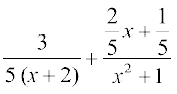
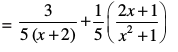
blfy,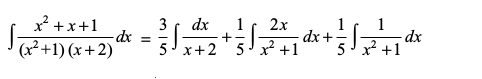
= 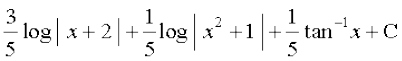
iz'ukoyh 7-5
1 ls 21 rd osQ iz'uksa esa ifjes; iQyuksa dk lekdyu dhft,A
1.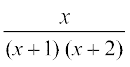 2.
2.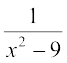 3.
3.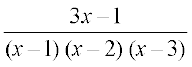
4.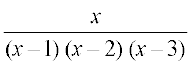 5.
5.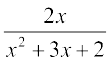
6.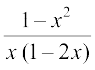 7.
7.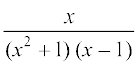 8.
8.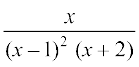
9.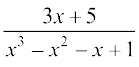 10.
10.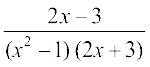 11.
11.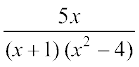
12.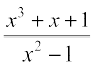 13.
13.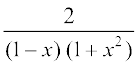 14.
14.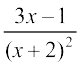
15.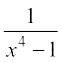 16.
16.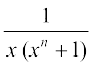 [laosQr% va'k ,oa gj dks x n – 1 ls xq.kk dhft, vkSj xn = t jf[k, ]
[laosQr% va'k ,oa gj dks x n – 1 ls xq.kk dhft, vkSj xn = t jf[k, ]
17.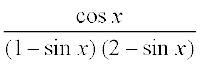 [laosQr% sin x = t jf[k,]
[laosQr% sin x = t jf[k,]
18.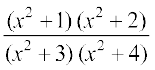 19.
19.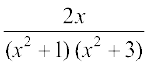 20.
20.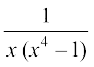
21. 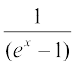 [laosQr% ex = t jf[k,] iz'u 22 ,oa 23 esa lgh mÙkj dk p;u dhft,A
[laosQr% ex = t jf[k,] iz'u 22 ,oa 23 esa lgh mÙkj dk p;u dhft,A
22.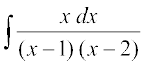 cjkcj gS%
cjkcj gS%
(A)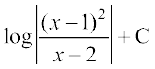 (B)
(B)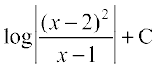
(C)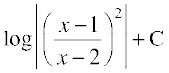 (D)
(D)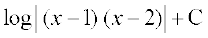
23.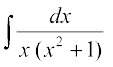 cjkcj gS%
cjkcj gS%
(A)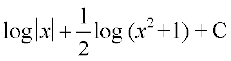 (B)
(B)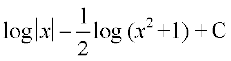
(C)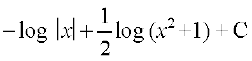 (D)
(D)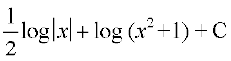
7.6 [kaM'k% lekdyu (Integration by Parts)
bl ifjPNsn esa ge lekdyu dh ,d vkSj fof/ dh ppkZ djsaxs tks fd nks iQyuksa osQ xq.kuiQy dk lekdyu djus esa cgqr mi;ksxh gSA
;fn ,dy pj x (eku yhft,) esa u vkSj v nks vodyuh; iQyu gS rks vodyu osQ xq.kuiQy fu;e osQ vuqlkj ge ikrs gSa fd
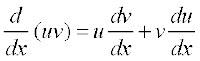
nksuksa i{kksa dk lekdyu djus ij ge ikrs gSa fd
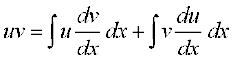
vFkok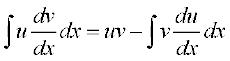
... (1)
eku yhft, fd u = f (x) vkSj 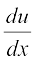 = g (x) rc
= g (x) rc
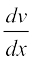 =f′ (x) vkSj v =
=f′ (x) vkSj v = 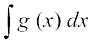
blfy, lehdj.k (1) dks fuEufyf[kr :i esa fy[kk tk ldrk gS
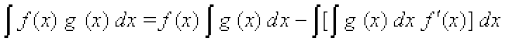
vFkkZr~ 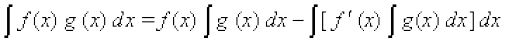
;fn ge f dks izFke iQyu vkSj g dks nwljk iQyu eku ysa rks bl lw=k dks fuEufyf[kr :i esa O;Dr fd;k tk ldrk gSA
“nks iQyuksa osQ xq.kuiQy dk lekdyu =(izFke iQyu) × (f}rh; iQyu dk lekdyu) — [(izFke iQyu dk vodyu xq.kkad) × (f}rh; iQyu dk lekdyu)] dk lekdyu”
mnkgj.k 17 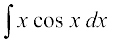 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy f (x) = x (izFke iQyu) vkSj g (x) = cos x (f}rh; iQyu) jf[k,A rc [kaM'k% lekdyu ls izkIr gksrk gS fd
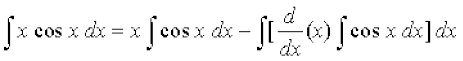
= 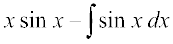 = x sin x + cos x + C
= x sin x + cos x + C
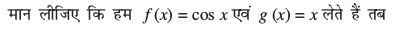
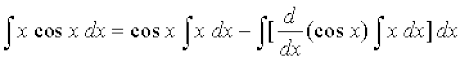
= 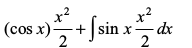
bl izdkj ge ns[krs gSa fd lekdyu 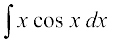 , rqyukRed n`f"V ls x dh vf/d ?kkr okys vf/d dfBu lekdyu eas ifjofrZr gks tkrk gSA blfy, izFke iQyu ,oa f}rh; iQyu dk mfpr p;u egRoiw.kZ gSA
, rqyukRed n`f"V ls x dh vf/d ?kkr okys vf/d dfBu lekdyu eas ifjofrZr gks tkrk gSA blfy, izFke iQyu ,oa f}rh; iQyu dk mfpr p;u egRoiw.kZ gSA
fVIi.kh
1. ;g o.kZuh; gSa] fd [kaM'k% lekdyu nks iQyuksa osQ xq.kuiQy dh lHkh fLFkfr;ksa esa iz;qDr ugha gS] mnkgj.kr;k 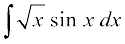 dh fLFkfr esa ;g fof/ dke ugha djrh gSA bldk dkj.k ;g gS fd ,slk dksbZ iQyu vfLrRo es gh ugha gS ftldk vodyt
dh fLFkfr esa ;g fof/ dke ugha djrh gSA bldk dkj.k ;g gS fd ,slk dksbZ iQyu vfLrRo es gh ugha gS ftldk vodyt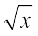 sin x gSA
sin x gSA
2. è;ku nhft, fd f}rh; iQyu dk lekdyu Kkr djrs le; geus dksbZ lekdyu vpj ugha tksM+k FkkA ;fn ge f}rh; iQyu cos x osQ lekdyu dks sin x + k, osQ :i esa fy[krs gSa] tgk¡ k dksbZ vpj gS] rc
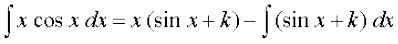
=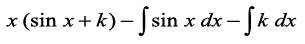
= 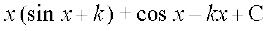
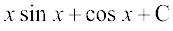 =
=
;g n'kkZrk gS fd [kaM'k% lekdyu fof/ osQ iz;ksx ls vafre ifj.kke Kkr djus osQ fy, f}rh; iQyu osQ lekdyu esa vpj dk tksM+uk O;FkZ gSA
3. lkekU;r% ;fn dksbZ iQyu x dh ?kkr osQ :i esa gS vFkok x dk cgqin gS rks ge bls izFke iQyu osQ :i es ysrs gSaA rFkkfi ,slh fLFkfr esa tgk¡ nwljk iQyu izfrykse f=kdks.kferh; iQyu vFkok y?kqx.kdh; iQyu gS] rks ge mudks izFke iQyu osQ :i es ysrs gSaA
mnkgj.k 18 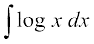 Kkr dhft,A
Kkr dhft,A
gy izkjEHk djus osQ fy, ge ,sls iQyu dk vuqeku yxkus esa vleFkZ gSa ftldk vodyt log x gSA ge log x dks izFke iQyu ,oa vpj iQyu 1 dks f}rh; iQyu ysrs gSaA nwljs iQyu dk lekdyu x gSA
vr% 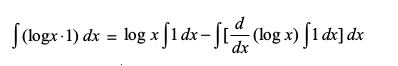
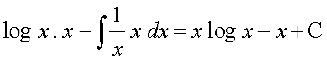
mnkgj.k 19 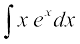 Kkr dhft,A
Kkr dhft,A
gy x izFke iQyu ,oa ex dks f}rh; iQyu osQ :i esa yhft,
nwljs iQyu dk lekdyu = ex
blfy, 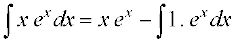 = xex – ex + C
= xex – ex + C
mnkgj.k 20 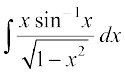 Kkr dhft,A
Kkr dhft,A
gy eku yhft, izFke iQyu = sin – 1x, vkSj f}rh; iQyu =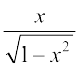
vc ge f}rh; iQyu dk lekdyu Kkr djrs gSa vFkkZr~ 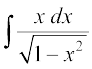 Kkr djrs gSaA
Kkr djrs gSaA
1.088 mm
t = 1 – x2 jf[k,
rc dt = – 2x dx
blfy,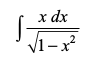 =
=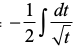 =
=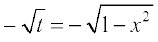
vr%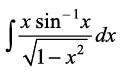 =
=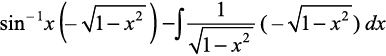
=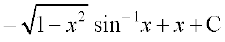 =
=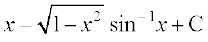
fodYir% sin–1 x = θ izfrLFkkfir djus ij vkSj rc [kaM'k% lekdyu dk mi;ksx djrs gq, Hkh bl lekdyu dks gy fd;k tk ldrk gSA
mnkgj.k 21 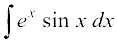 Kkr dhft,A
Kkr dhft,A
gy ex dks izFke iQyu ,oa sin x dks f}rh; iQyu osQ :i esa yhft,A rc [kaM'k% lekdyu ls ge ikrs gSa fd
I=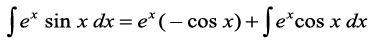
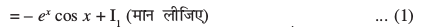
I1 esa ex ,oa cos x dks Øe'k% izFke ,oa f}rh; iQyu ekurs gq, ge ikrs gSa fd
I=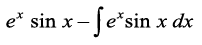
I1 dk eku (1) esa j[kus ij ge ikrs gSa fd
I= 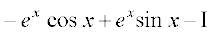 vFkok 2I= ex (sin x – cos x)
vFkok 2I= ex (sin x – cos x)
vr%I= 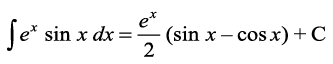
fodYir% sin x dks izFke iQyu ,oa ex dks f}rh; iQyu ysus ij Hkh mi;qZDr lekdyu dks Kkr fd;k tk ldrk gSA
7.6.1 ![]() osQ izdkj dk lekdyu
osQ izdkj dk lekdyu
gesa Kkr gS fd I= 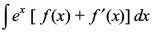 =
=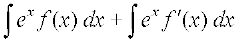
=
I1 esa f (x) ,oa ex dks Øe'k% izFke ,oa f}rh; iQyu ysrs gq, ,oa [kaM'k% lekdyu }kjk ge ikrs gSa
I1 = f (x) ex –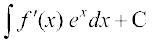
I1 dks (1) esa izfrLFkkfir djus ij ge ikrs gSa
I=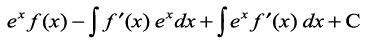 =
=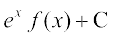
vr% 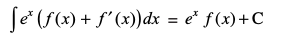
mnkgj.k 22 Kkr dhft,
(i)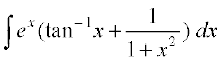 (ii)
(ii)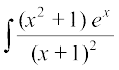 dx
dx
gy
(i) ;gk¡ I=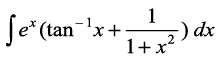
vc f (x) = tan– 1x, yhft,] rc f′(x) =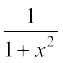
vr% fn;k gqvk lekdY; ex [f (x) + f ′(x)] osQ :i esa gSA
blfy, I=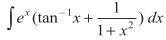 = ex tan– 1x + C
= ex tan– 1x + C
(ii) eku yhft, fd I=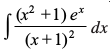
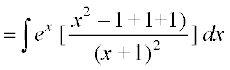 dx
dx
=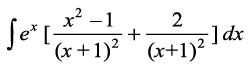
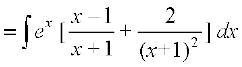
eku yhft, fd 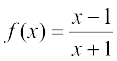 rc
rc 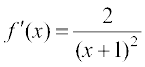
vr% fn;k gqvk lekdY; ex [f (x) + f ′(x)] osQ :i esa gSA
blfy, 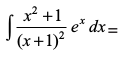
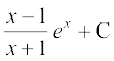
iz'ukoyh 7-6
1 ls 22 rd osQ iz'uksa osQ iQyuksa dk lekdyu dhft,A
1. x sin x 2. x sin 3x 3. x2 ex 4. x log x
5. x log2 x 6. x2 log x 7. x sin– 1x 8. x tan–1 x
9. x cos–1 x 10. (sin–1x)2 11.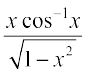 12. x sec2 x
12. x sec2 x
13. tan–1x 14. x (log x)2 15. (x2 + 1) log x
16. ex (sinx + cosx) 17.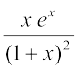 18.
18.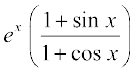
19.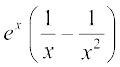 20.
20.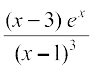 21. e2x sin x
21. e2x sin x
22.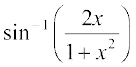
iz'u 23 ,oa 24 esa lgh mÙkj dk p;u dhft,A
23.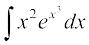 cjkcj gS%
cjkcj gS%
(A)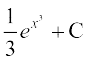 (B)
(B)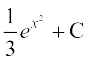
(C)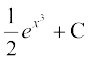 (D)
(D)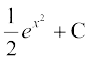
24.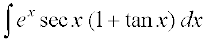 cjkcj gS%
cjkcj gS%
(A) ex cos x + C (B) ex sec x + C
(C) ex sin x + C (D) ex tan x + C
7.6.2 oqQN vU; izdkj osQ lekdyu (Integrals of some more types)
;gk¡ ge [kaM'k% lekdyu fof/ ij vk/kfjr oqQN fof'k"V izdkj osQ izkekf.kd lekdyuksa dh ppkZ djsaxsA tSls fd
(i)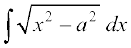 (ii)
(ii)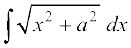 (iii)
(iii)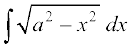
(i) eku yhft, fd 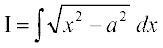
vpj iQyu 1 dks f}rh; iQyu ekurs gq, vkSj [kaM'k% lekdyu }kjk ge ikrs gSa
I=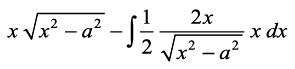
=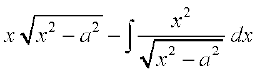 =
=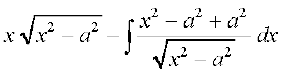
=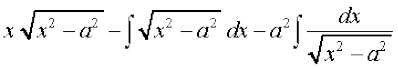
=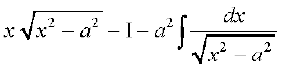
vFkok 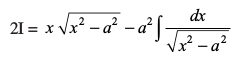
vFkok I=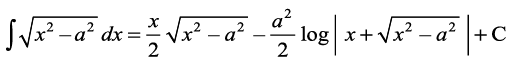
blh izdkj nwljs nks lekdyuksa esa vpj iQyu 1 dks f}rh; iQyu ysdj ,oa [kaM'k% lekdyu fof/ }kjk ge ikrs gSa
(ii)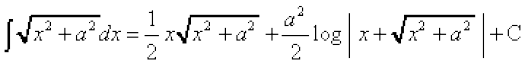
(iii)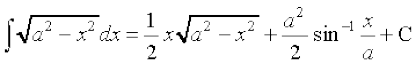
fodYir% lekdyuksa (i), (ii) ,oa (iii) esa Øe'k% x = a secθ, x = a tanθ vkSj
x = a sinθ, izfrLFkkiu djus ij Hkh bu lekdyuksa dks Kkr fd;k tk ldrk gSA
mnkgj.k 23 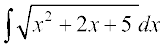 Kkr dhft,A
Kkr dhft,A
gy è;ku nhft, fd 
vc 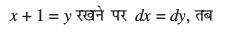
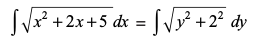
=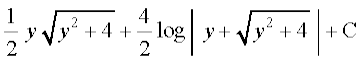 [7.6.2 (ii)osQ mi;ksx ls]
[7.6.2 (ii)osQ mi;ksx ls]
=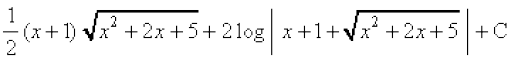
mnkgj.k 24 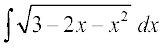 Kkr dhft,A
Kkr dhft,A
gy è;ku nhft, fd 
vc 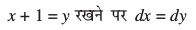
bl izdkj 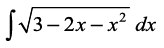 =
=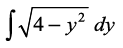
= 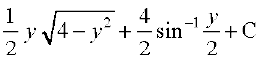 [7.6.2 (iii)osQ mi;ksx ls]
[7.6.2 (iii)osQ mi;ksx ls]
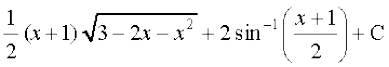
iz'ukoyh 7-7
1 ls 9 rd osQ iz'uksa osQ iQyuksa dk lekdyu dhft,A
1.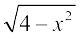 2.
2.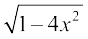 3.
3.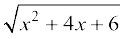
4.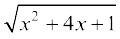 5.
5.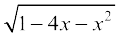 6.
6.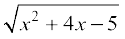
7.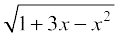 8.
8.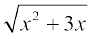 9.
9.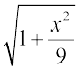
iz'u 10 ,oa 11 esa lgh mÙkj dk p;u dhft,A
10.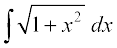 cjkcj gS%
cjkcj gS%
(A) (B)
(B)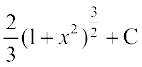
(C)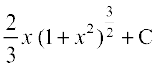 (D)
(D)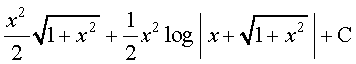
11.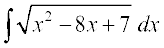 cjkcj gS
cjkcj gS
(A)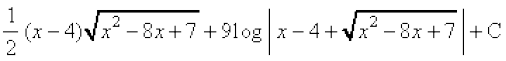
(B)
(C)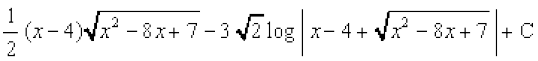
(D)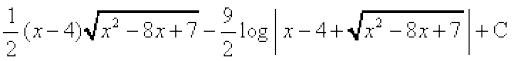
7.7 fuf'pr lekdyu (Definite Integral)
fiNys ifjPNsnksa esa geus vfuf'pr lekdyuksa osQ ckjs esa vè;;u fd;k gS vkSj oqQN fof'k"V iQyuksa osQ lekdyuksa lfgr vfuf'pr lekdyuksa dks Kkr djus dh oqQN fof/;ksa ij ppkZ dh gSA bl ifjPNsn esa ge fdlh iQyu osQ fuf'pr lekdyu dk vè;;u djsaxsA fuf'pr lekdyu dk ,d vf}rh; eku gksrk gSA ,d fuf'pr lekdyu dks 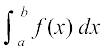 , ls fufnZ"V fd;k tkrk gS tgk¡
, ls fufnZ"V fd;k tkrk gS tgk¡
b] lekdyu dh mPp lhek rFkk a, lekdyu dh fuEu lhek dgykrh gSaA fuf'pr lekdyu dk ifjp;] ;k rks ;ksxksa dh lhek osQ :i esa djk;k tkrk gS vFkok ;fn varjky [a, b] esa bldk dksbZ izfrvodyt F gS rks fuf'pr lekdyu dk eku vafre ¯cnqvksa ij F osQ ekuksa osQ varj vFkkZr~ F(b) – F(a) osQ cjkcj gksrk gS] osQ :i esa djk;k tkrk gSA fuf'pr lekdyu osQ bu nksuksa :iksa dh ge vyx&vyx ppkZ djsaxsA
7.7.1 ;ksxiQy dh lhek osQ :i esa fuf'pr lekdyu (Definite integral as the limit of a sum)
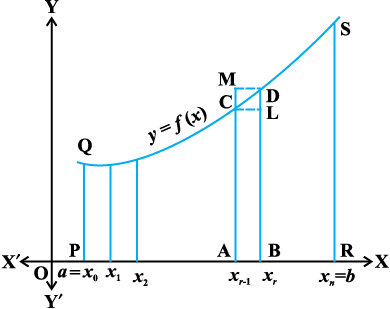
eku yhft, fd ,d can varjky [a, b] ij ,d larr iQyu f ifjHkkf"kr gSA eku yhft, fd iQyu osQ lHkh eku ½.ksÙkj gSa blfy, iQyu dk vkys[k x-v{k ls Åij ,d oØ gSA
oØ y = f(x), x = a, x = b ,oa x-v{k ls f?kjs {ks=k dk {ks=kiQy gh fuf'pr lekdyu 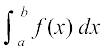 gSA bl {ks=kiQy dks Kkr djus osQ fy,] bl oØ] x-v{k ,oa dksfV;ksa x = a ,oa x = b osQ chp f?kjs {ks=k PRSQP dks yhft, (vko`Qfr 7-2 nsf[k,)A
gSA bl {ks=kiQy dks Kkr djus osQ fy,] bl oØ] x-v{k ,oa dksfV;ksa x = a ,oa x = b osQ chp f?kjs {ks=k PRSQP dks yhft, (vko`Qfr 7-2 nsf[k,)A
varjky [a, b] dks [x0, x1], [x1, x2] ,..., [xr – 1, xr] [xn – 1, xn] ls fufnZ"V n leku mivarjkyksa esa foHkkftr dhft, tgk¡ x0 = a, x1 = a + h, x2 = a + 2h,...., xr = a + rh rFkk
xn = b = a + nh vFkok 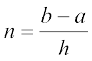 è;ku nhft, ;fn n → ∞ rks h → 0
è;ku nhft, ;fn n → ∞ rks h → 0
pfpZr {ks=k PRSQP, n mi{ks=kksa dk ;ksx gS tgk¡ izR;sd mi{ks=k mivarjkyksa [xr – 1, xr], r = 1, 2, 3, …, n ij ifjHkkf"kr gSA
vko`Qfr 7-2 ls ge ikrs gSa fd
vko`Qfr 7-2
Li"Vr% ;fn xr – xr–1 → 0 vFkkZr~ h → 0, rks lehdj.k (1) es n'kkZ, x, rhuksa {ks=kiQy ,d nwljs osQ yxHkx leku gks tkrs gSaA vc ge fuEufyf[kr ;ksxiQyksa dk fuekZ.k djrs gSa
sn = h [f(x0) + … + f(xn - 1)] = 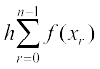 ... (2)
... (2)
vkSj Sn =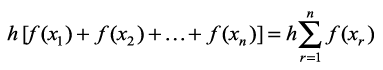 ...(3)
...(3)
=
;gk¡ sn ,oa Sn mivarjkyksa [xr–1, xr] r = 1, 2, 3, …, n, ij cus Øe'k% fuEu vk;rksa ,oa mPp vk;rksa osQ {ks=kiQyksa osQ ;ksx dks fufnZ"V djrk gSA vlfedk (1) osQ lanHkZ esa fdlh LosPN mi varjky [xr–1, xr] osQ fy, ge ikrs gSa fd
sn < {ks=k PRSQP dk {ks=kiQy < Sn
;fn 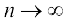 ] rks iV~fV;k¡ ladh.kZ ls ladh.kZ gksrh pyh tkrh gSa vkSj ;g eku fy;k tkrk gSa fd (2) vkSj (3) osQ lhfer eku ,d leku gSa rFkk mHk;fu"B lhfer eku gh oØ osQ vUrZxr vHkh"V {ks=kiQy gSA
] rks iV~fV;k¡ ladh.kZ ls ladh.kZ gksrh pyh tkrh gSa vkSj ;g eku fy;k tkrk gSa fd (2) vkSj (3) osQ lhfer eku ,d leku gSa rFkk mHk;fu"B lhfer eku gh oØ osQ vUrZxr vHkh"V {ks=kiQy gSA
lakosQfrd Hkk"kk esa ge bls fuEufyf[kr izdkj fy[krs gSa
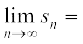
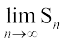 =
=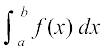 {ks=k PRSQP dk {ks=kiQy =
{ks=k PRSQP dk {ks=kiQy = 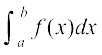 ... (5)
... (5)
blls ;g irk pyrk gS fd vHkh"V {ks=kiQy oØ osQ uhps osQ vk;rksa ,oa oØ osQ Åij osQ vk;rksa osQ chp osQ fdlh {ks=kiQy dk lhfer eku Hkh gSA lqfo/k osQ fy, ge izR;sd mivarjky osQ ck;sa fdukjs ij oØ dh m¡pkbZ osQ cjkcj m¡pkbZ okys vk;rksa dks ysaxsA vr% ge (5) dks nqckjk fuEufyf[kr :i esa fy[krs gSaA
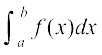 =
= 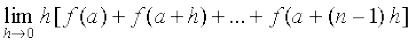
vFkok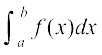 =
=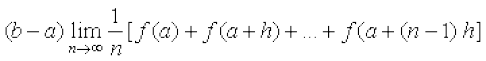 =... (6)
=... (6)
tgk¡ h =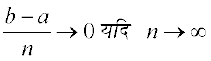
mi;qZDr O;atd (6) ;ksxiQy dh lhek osQ :i esa fuf'pr lekdyu dh ifjHkk"kk dgykrk gSA
fVIi.kh fdlh fof'k"V varjky ij ,d iQyu osQ fuf'pr lekdyu dk eku iQyu ,oa varjky ij fuHkZj djrk gS ijarq lekdyu osQ ml pj ij ugha ftldk p;u ge Lora=k pj dks fu:fir djus osQ fy, djrs gSaA ;fn x osQ LFkku ij Lora=k pj dks t vFkok u ls fufnZ"V fd;k tkrk gS rks ge lekdyu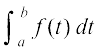 osQ LFkku ij osQoy lekdyu
osQ LFkku ij osQoy lekdyu 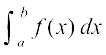 vFkok
vFkok 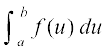 fy[krs gSaA vr% fuf'pr lekdyu osQ fy, lekdyu pj ,d ewd pj dgykrk gSA
fy[krs gSaA vr% fuf'pr lekdyu osQ fy, lekdyu pj ,d ewd pj dgykrk gSA
mnkgj.k 25 ;ksxiQy dh lhek osQ :i esa 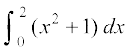 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy ifjHkk"kk osQ vuqlkj
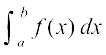
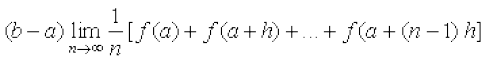 =
=
tgk¡ h =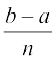
bl mnkgj.k esas 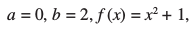
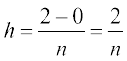
blfy,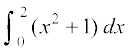
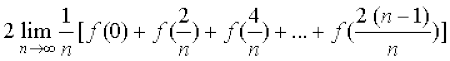
=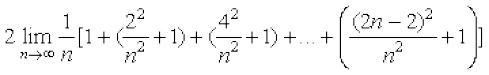
=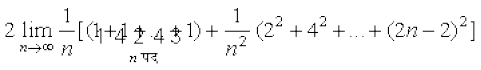
= 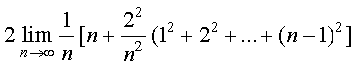
=
=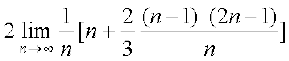
=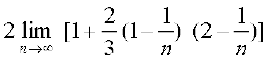 =
=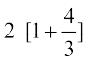 =
=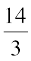
mnkgj.k 26 ;ksxiQy dh lhek osQ :i esa 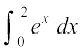 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy ifjHkk"kk osQ vuqlkj
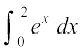 =
=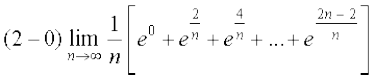 =
=
xq.kksÙkj Js.kh osQ n inksa osQ ;ksxiQy osQ lw=k dk mi;ksx djrs gq, tgk¡ a = 1,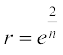 ,
,
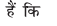
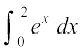
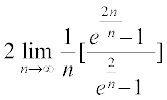 =
= 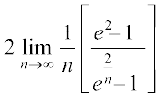
=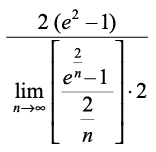 = e2 – 1 [
= e2 – 1 [

iz'ukoyh 7-8
;ksxksa dh lhek osQ :i esa fuEufyf[kr fuf'pr lekdyuksa dk eku Kkr dhft,A
1.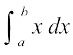 2.
2.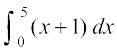 3.
3.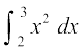
4.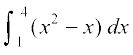 5.
5.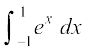 6.
6.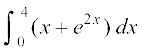
7.8 dyu dh vk/kjHkwr izes; (Fundamental Theorem of Calculus)
7.8.1 {ks=kiQy iQyu (Area function)
geus 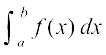 dks oØ y = f(x), x-v{k] ,oa dksfV;ksa x = a rFkk x = b ls f?kjs {ks=k osQ {ks=kiQy osQ :i esa ifjHkkf"kr fd;k gSA eku yhft, [a, b] esa x dksbZ ¯cnq gS rc
dks oØ y = f(x), x-v{k] ,oa dksfV;ksa x = a rFkk x = b ls f?kjs {ks=k osQ {ks=kiQy osQ :i esa ifjHkkf"kr fd;k gSA eku yhft, [a, b] esa x dksbZ ¯cnq gS rc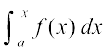 vko`Qfr 7-3 esa gYdk Nk;kafoQr {ks=k osQ {ks=kiQy dks fu:fir djrk gS [;gk¡ ;g eku fy;k x;k gS fd x ∈ [a, b] osQ fy, f(x) > 0 gSA fuEufyf[kr dFku lkekU;r% vU; iQyuksa osQ fy, Hkh lR; gSA bl Nk;kafoQr {ks=k dk {ks=kiQy x osQ eku ij fuHkZj gSA
vko`Qfr 7-3 esa gYdk Nk;kafoQr {ks=k osQ {ks=kiQy dks fu:fir djrk gS [;gk¡ ;g eku fy;k x;k gS fd x ∈ [a, b] osQ fy, f(x) > 0 gSA fuEufyf[kr dFku lkekU;r% vU; iQyuksa osQ fy, Hkh lR; gSA bl Nk;kafoQr {ks=k dk {ks=kiQy x osQ eku ij fuHkZj gSA
nwljs 'kCnksa esa bl Nk;kafoQr {ks=k dk {ks=kiQy x dk ,d iQyu gSA ge x osQ bl iQyu dks A(x) ls fufnZ"V djrs gSaA bl iQyu A(x) dks ge {ks=kiQy iQyu dgrs gSa vkSj ;g gesa fuEufyf[kr lw=k ls izkIr gksrk gSA
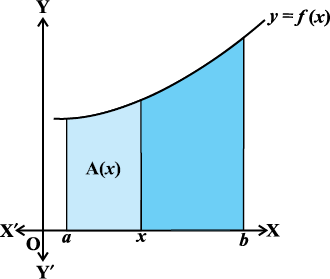
vko`Qfr 7-3
A(x) =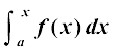
bl ifjHkk"kk ij vk/kfjr nks vk/kjHkwr izes; gSaA rFkkfi ge ;gk¡ ij osQoy budh O;k[;k djsaxs D;ksafd budh miifÙk bl ikB~;iqLrd dh lhek osQ ckgj gSA
7.8.2 izes; 1 lekdyu xf.kr dh izFke vk/kjHkwr izes; (First fundamental theorem of integral calculus)
eku yhft, fd can varjky [a, b] ij f ,d larr iQyu gS vkSj A (x) {ks=kiQy iQyu gSA rc lHkh x ∈ [a, b] osQ fy, A′(x) = f (x)
7.8.3 lekdyu xf.kr dh f}rh; vk/kjHkwr izes; (Second fundamental theorem of integral calculus)
ge uhps ,d ,sls egRoiw.kZ izes; dh O;k[;k djrs gSa ftldh lgk;rk ls ge izfrvodyt dk mi;ksx djrs gq, fuf'pr lekdyuksa dk eku Kkr djrs gSaA
izes; 2 eku yhft, fd can varjky [a, b] ij f ,d larr iQyu gS vkSj f dk izfrvodyt F gSA rc
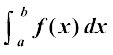 =
=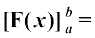 F (b) – F(a)
F (b) – F(a)
fVIi.kh
1. 'kCnksa esa ge izes; 2 dks bl izdkj O;Dr djrs gSa fd 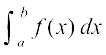 =(f osQ izfr vodyt F dk mPp lhek b ij eku) – (mlh izfr vodyt dk fuEu lhek a ij eku)A
=(f osQ izfr vodyt F dk mPp lhek b ij eku) – (mlh izfr vodyt dk fuEu lhek a ij eku)A
2. ;g izes; vR;ar mi;ksxh gS D;ksafd ;g gesa ;ksxiQy dh lhek Kkr fd, fcuk fuf'pr lekdyu dks Kkr djus dh vklku fof/ iznku djrh gSA
3. ,d fuf'pr lekdyu Kkr djus esa tfVy lafØ;k ,d ,sls iQyu dk izkIr djuk gS ftldk vodyt fn;k x;k lekdY; gSA ;g vodyu vkSj lekdyu osQ chp laca/ dks vkSj etcwr djrk gSA
4.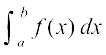 esa] [a, b] ij iQyu f dk lqifjHkkf"kr ,oa larr gksuk vko';d gSA mnkgj.kr% fuf'pr lekdyu
esa] [a, b] ij iQyu f dk lqifjHkkf"kr ,oa larr gksuk vko';d gSA mnkgj.kr% fuf'pr lekdyu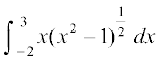 dh ppkZ djuk Hkzkafrewyd gSa D;ksafd can varjky [– 2, 3] osQ Hkkx – 1 < x < 1 osQ fy, f(x)=
dh ppkZ djuk Hkzkafrewyd gSa D;ksafd can varjky [– 2, 3] osQ Hkkx – 1 < x < 1 osQ fy, f(x)=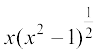 }kjk vfHkO;Dr iQyu f ifjHkkf"kr ugh gSA
}kjk vfHkO;Dr iQyu f ifjHkkf"kr ugh gSA 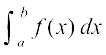 Kkr djus osQ pj.k (Steps for calculating
Kkr djus osQ pj.k (Steps for calculating 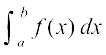 )
)
(i) vfuf'pr lekdyu Kkr dhft,A eku yhft, ;g F(x) gSA lekdyu vpj C dks ysus dh vko';drk ugha gS D;ksafd ;fn ge F(x) osQ LFkku ij F(x) + C ij fopkj djsa rks ikrs gSa fd
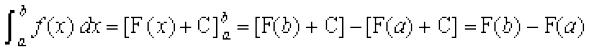
bl izdkj fuf'pr lekdyu dk eku Kkr djus esa LosPN vpj foyqIr gks tkrk gSA
(ii)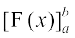 = F(b) – F(a) Kkr dhft,] tks fd
= F(b) – F(a) Kkr dhft,] tks fd 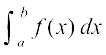 dk eku gSA
dk eku gSA
mnkgj.k 28 fuEufyf[kr lekdyuksa dk eku Kkr dhft,A
(i)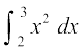 (ii)
(ii)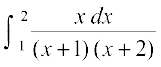 (iii)
(iii)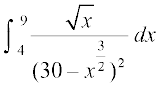
(iv)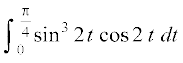
gy
(i) eku yhft, 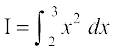 gSA D;ksafd
gSA D;ksafd 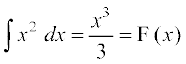
blfy, f}rh; vk/kjHkwr izes; ls ge ikrs gSa fd
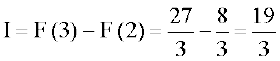
(ii) eku yhft, fd 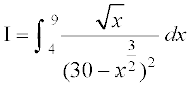 loZizFke ge lekdY; dk izfrvodyt Kkr djrs gSaA
loZizFke ge lekdY; dk izfrvodyt Kkr djrs gSaA
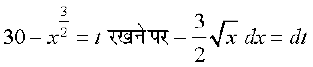 vFkok
vFkok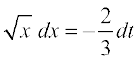
bl izdkj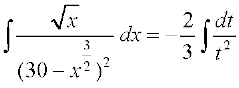 =
= 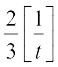 =
=
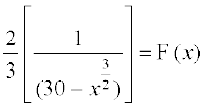
blfy, dyu dh f}rh; vk/kjHkwr izes; ls ge ikrs gSa%
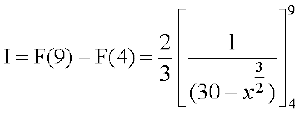 =
=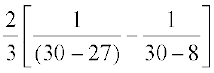 =
=
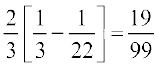
(iii) eku yhft, 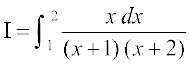
vkaf'kd fHkUu dk mi;ksx djrs gq, ge ikrs gSa fd
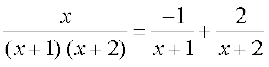
blfy,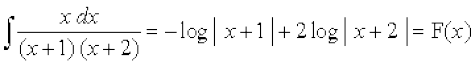
vr% dyu dh f}rh; vk/kjHkwr izes; ls ge ikrs gSa fd
I = F(2) – F(1) = [– log3 + 2 log4] – [– log2 + 2 log3]
= – 3 log3 + log2 + 2 log4 = 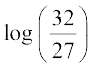
(iv) eku yhft,] 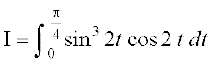 vc
vc 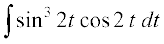
 ij fopkj dhft,
ij fopkj dhft,
sin 2t = u j[kus ij 2 cos 2t dt = du vFkok cos 2t dt = du
vr% 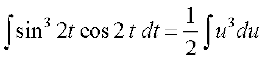
t =
blfy, dyu dh f}rh; vk/kjHkwr izes; ls
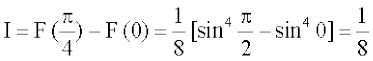
iz'ukoyh 7-9
1 ls 20 rd osQ iz'uksa esa fuf'pr lekdyuksa dk eku Kkr dhft,A
1.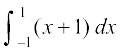 2.
2.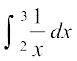 3.
3.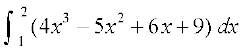
4.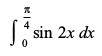 5.
5. 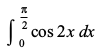 6.
6.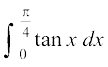 7.
7.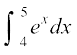
8.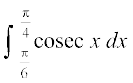 9.
9.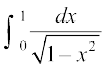 10.
10.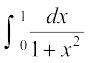 11.
11.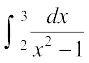
12.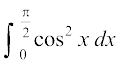 13.
13.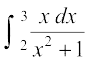 14.
14.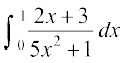 15.
15.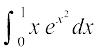
16.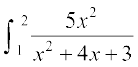 17.
17.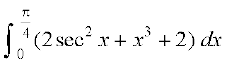
18.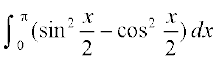 19.
19.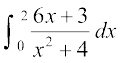
20.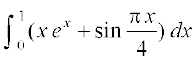
iz'u 21 ,oa 22 esa lgh mÙkj dk p;u dhft,A
21.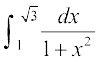 cjkcj gS%
cjkcj gS%
(A)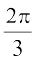 (B)
(B)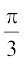 (C)
(C)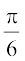 (D)
(D)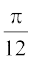
22.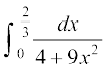 cjkcj gS%
cjkcj gS%
(A)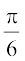 (B)
(B)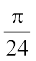 (C)
(C)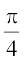 (D)
(D)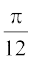
7.9 izfrLFkkiu }kjk fuf'pr lekdyuksa dk eku Kkr djuk (Evaluation of Definite Integrals by Substitution)
fiNys ifjPNsnksa esa geus vfuf'pr lekdyu Kkr djus dh vusd fof/;ksa dh ppkZ dh gSA vfuf'pr lekdyu Kkr djus dh egRoiw.kZ fof/;ksa esa ,d fof/ izfrLFkkiu fof/ gSA
izfrLFkkiu fof/ ls 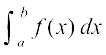 dk eku Kkr djus osQ fy, vko';d pj.k fuEufyf[kr gS%
dk eku Kkr djus osQ fy, vko';d pj.k fuEufyf[kr gS%
1. lekdyu osQ ckjs esa lhekvksa osQ fcuk fopkj dhft, vkSj y = f(x) vFkok x = g(y) izfrLFkkfir dhft, rkfd fn;k gqvk lekdyu ,d Kkr :i esa ifjofrZr gks tk,A
2. lekdyu vpj dh O;k[;k fd, fcuk u, lekdY; dk u, pj osQ lkis{k lekdyu dhft,A
3. u, pj osQ LFkku ij iqu% izfrLFkkiu dhft, vkSj mÙkj dks ewy pj osQ :i esa fyf[k,A
4. pj.k (3) ls izkIr mÙkj dk lekdyu dh nh gqbZ lhekvksa ij eku Kkr dhft, vkSj mPp lhek okys eku ls fuEu lhek okys eku dk varj Kkr dhft,A
fVIi.kh bl fof/ dks rhozrj cukus osQ fy, ge fuEufyf[kr izdkj vkxs c<+ ldrs gSaA pj.k (1) ,oa (2) dks djus osQ ckn pj.k (3) dks djus dh vko';drk ugha gSA ;gk¡ lekdyu dks u, pj osQ :i esa j[kk tkrk gS vkSj lekdyu dh lhekvksa dks u, pj osQ vuqlkj ifjofrZr dj ysrs gSa rkfd ge lh/s vafre pj.k dh fØ;k dj losaQA
vkb, bls ge mnkgj.kksa ls le>rs gSaA
mnkgj.k 29 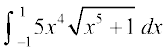 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy t = x5 + 1, j[kus ij dt = 5x4 dx
blfy,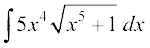 =
=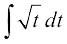 =
=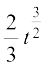 =
=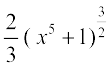
vr% 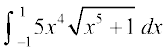 =
=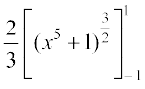
=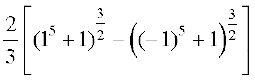
= 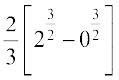 =
=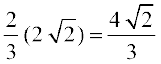 =
=
fodYir% loZizFke ge lekdyu dk :ikarj.k djrs gSa vkSj rc :ikarfjr lekdyu dk u;h lhekvksa osQ vuqlkj eku Kkr djrs gSaA
eku yhft, t = x5 + 1. rc dt = 5 x4 dx uksV dhft, fd
tc x = – 1 rks t = 0 vkSj tc x = 1 rks t = 2
vr% tSls&tSls x, – 1 ls 1 rd ifjofrZr gksrk gS oSls&oSls t] 0 ls 2 rd ifjofrZr gksrk gSA
blfy,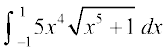 =
=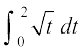
= 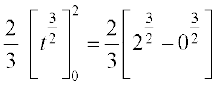 =
=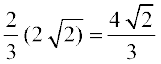
mnkgj.k 30 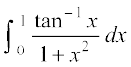
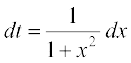 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy eku yhft, 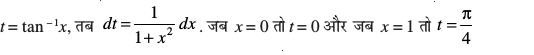
vr% tSls&tSls x, 0 ls 1 rd ifjofrZr gksrk gS oSls&osSls t, 0 ls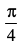 rd ifjofrZr gksrk gSA
rd ifjofrZr gksrk gSA
blfy,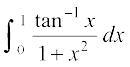 =
=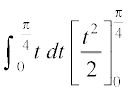 =
=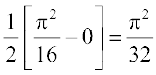
iz'ukoyh 7-10
1 ls 8 rd osQ iz'uksa lekdyuksa dk eku izfrLFkkiu dk mi;ksx djrs gq, Kkr dhft,A
1.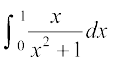
2.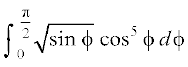
3.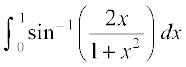
4.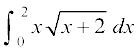 (x + 2 = t2 jf[k,)5.
(x + 2 = t2 jf[k,)5.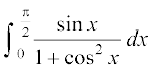
6.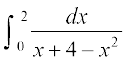 7.
7.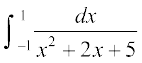 8.
8.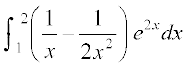
iz'u 9 ,oa 10 esa lgh mÙkj dk p;u dhft,A
9. lekdyu 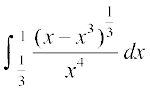 dk eku gS%
dk eku gS%
(A) 6 (B) 0 (C) 3 (D) 4
10. ;fn f(x) = 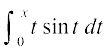 rc f′(x) gS%
rc f′(x) gS%
(A) cosx + x sinx (B) x sinx (C) x cosx (D) sinx + x cosx
7.10 fuf'pr lekdyuksa osQ oqQN xq.k/eZ (Some Properties of Definite Integrals)
fuf'pr lekdyuksa osQ oqQN egRoiw.kZ xq.k/eks± dks ge uhps lwphc¼ djrs gSaA ;s xq.k /eZ fuf'pr lekdyuksa dk eku vklkuh ls Kkr djus esa mi;ksxh gksaxsA
P0 :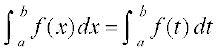
P1 :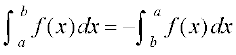 fof'k"Vr;k
fof'k"Vr;k 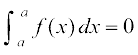
P2 :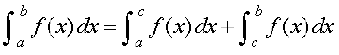
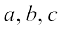 ]okLrfod la[;k,¡ gSaA
]okLrfod la[;k,¡ gSaA
P3 :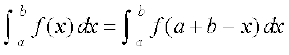
P4 :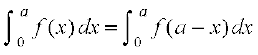 (è;ku nhft, fd P4, P3 dh ,d fof'k"V fLFkfr gS)
(è;ku nhft, fd P4, P3 dh ,d fof'k"V fLFkfr gS)
P5 :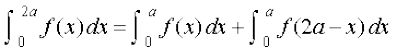
P6 :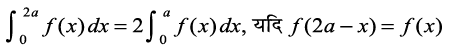
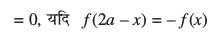
P7 : (i) 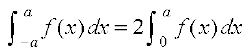 , ;fn f ,d le iQyu gS vFkkZr~ ;fn f(– x) = f(x)
, ;fn f ,d le iQyu gS vFkkZr~ ;fn f(– x) = f(x)
(ii)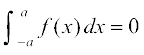 ;fn f ,d fo"ke iQyu gS vFkkZr~ ;fn f (–x) = –f (x)
;fn f ,d fo"ke iQyu gS vFkkZr~ ;fn f (–x) = –f (x)
,d&,d djosQ ge bu xq.k/eks± dh miifÙk djrs gSaA
P0 dh miifÙk x = t izfrLFkkiu djus ij lh/s izkIr gksrh gSA
P1 dh miifÙk eku yhft, fd f dk izfrvodyt F gSA rc dyu dh f}rh; vk/kjHkwr
izes; ls ge ikrs gSa fd 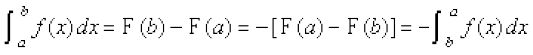
;gk¡ ge iszf{kr djrs gSa fd ;fn a = b, rc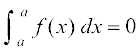
P2 dh miifÙk eku yhft, fd f dk izfrvodyt F gS] rc
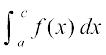 = F(b) – F(a) ... (1)
= F(b) – F(a) ... (1)
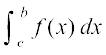 = F(c) – F(a) ... (2)
= F(c) – F(a) ... (2)
vkSj 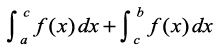 = F(b) – F(c) ... (3)
= F(b) – F(c) ... (3)
(2) vkSj (3) dks tksM+us ij ge ikrs gSa fd
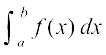
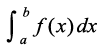 = F(b) – F(a) =
= F(b) – F(a) =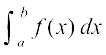
blls xq.k/eZ P2 fl¼ gksrk gSA
P3 dh miifÙk eku yhft, fd t = a + b – x. rc dt = – dx. tc x = a rc, t = b vkSj tc x = b rc t = a blfy,
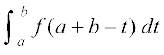 =
=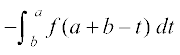
=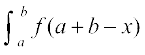 (P 1 ls)
(P 1 ls)
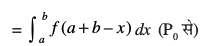
P4 dh miifÙk t = a – x jf[k, vkSj P3 dh rjg vkxs cf<+,A vc dt = – dx,
tc x = a, t = 0
P5 dh miifÙk P2, dk mi;ksx djrs gq, ge ikrs gSa fd
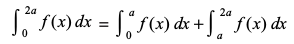
nk,¡ i{k osQ nwljs lekdyu esa t = 2a – x izfrLFkkfir dhft,] rc dt = – dx vkSj tc
x = a, rc t = a vkSj tc x = 2a, rc t = 0 vkSj x = 2a – t Hkh izkIr gksrk gSA
blfy, nwljk lekdyu
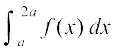 =
=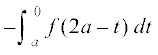
= 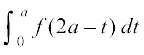 =
=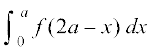 izkIr gksrk gSA
izkIr gksrk gSA
vr%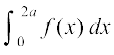 =
=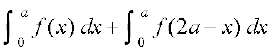
P6 dh miifÙk P5, dk mi;ksx djrs gq, ge ikrs gSa fd
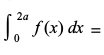
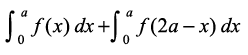
vc ;fn 
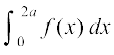
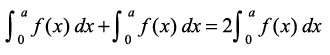
vkSj ;fn f(2a – x) = – f(x), rc (1) fuEufyf[kr :i esa ifjofrZr gks tkrk gSa
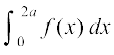 =
=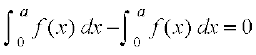
P7 dh miifÙk
P2 dk mi;ksx djrs gq, ge ikrs gSa fd 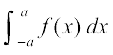 =
=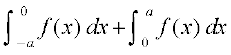
nk;sa i{k osQ izFke lekdyu esa t = – x j[kus ij
dt = – dx tc x = – a rc t = a vkSj tc x = 0, rc t = 0 vkSj x = – t Hkh izkIr gksrk gSA
blfy,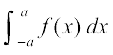 =
=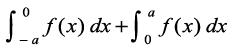
=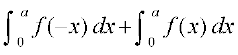 (P0 ls)
(P0 ls)
(i) vc ;fn f ,d le iQyu gS rc f (–x) = f (x) rks (1) ls izkIr gksrk gS fd
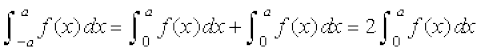
(ii) ;fn f fo"ke iQyu gS rc f (–x) = – f (x) rks (1) ls izkIr gksrk gS fd
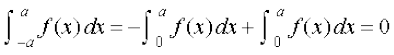
mnkgj.k 31 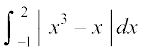 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy ge ns[krs gSa fd [ –1, 0] ij x3 – x ≥ 0 vkSj [0, 1] ij x3 – x ≤ 0 vkSj [1, 2] ij x3 – x ≥ 0 rc ge fy[k ldrs gSa fd
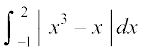 =
=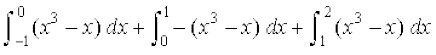
=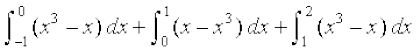 (P2 ls)
(P2 ls)
=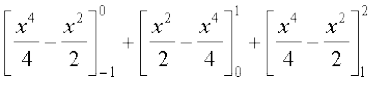
=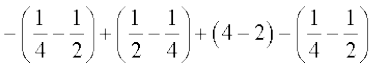
=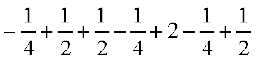 =
=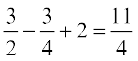
mnkgj.k 32 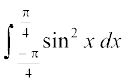 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy ge izsf{kr djrs gSa fd sin2 x ,d le iQyu gSA
blfy,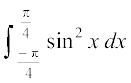 =
=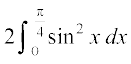 [P7 (1)ls]
[P7 (1)ls]
= 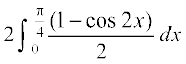 =
= 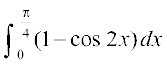
= 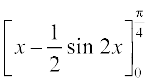 =
= 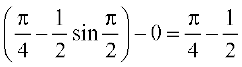
mnkgj.k 33 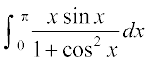 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy eku yhft, fd I =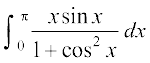 =
=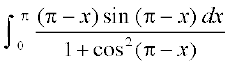 (P4 ls)
(P4 ls)
=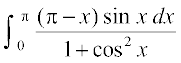 =
=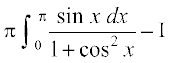
vFkok 2I= 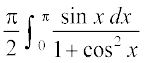
vFkok I =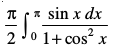
cos x =t j[kus ij – sin x dx = dt
tc x = 0 rc t = 1 vkSj tc x = π rc t = – 1 gSA blfy, ge ikrs gSa fd
I =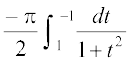 =
=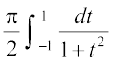 (P1 ls)
(P1 ls)
I = 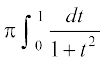 D;ksafd
D;ksafd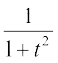 ,d leiQyu gS (P7 ls)
,d leiQyu gS (P7 ls)
= 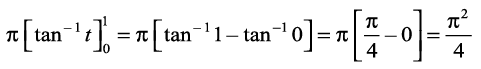
mnkgj.k 34  dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy eku yhft, fd I = 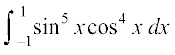 vkSj f(x) = sin5 x cos4 x
vkSj f(x) = sin5 x cos4 x
rc 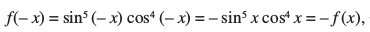 vFkkZr~ f ,d fo"ke iQyu gS blfy, I = 0 [P7 (ii) ls]
vFkkZr~ f ,d fo"ke iQyu gS blfy, I = 0 [P7 (ii) ls]
mnkgj.k 35 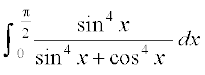 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy eku yhft, fd I = 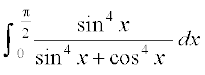
rc I =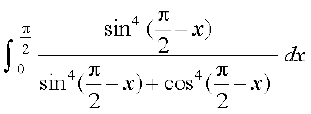 (P4 ls)
(P4 ls)
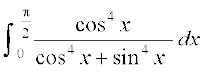
(1) vkSj (2) dks tksM+us ij ge ikrs gSa fd
2I =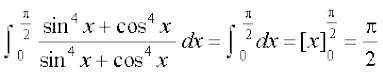
vr% I =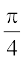
mnkgj.k 36 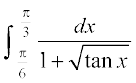 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy eku yhft, fd I =
rc I =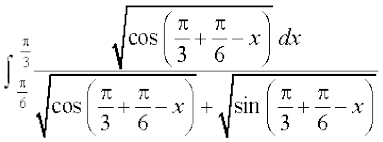 (1)
(1)
I = 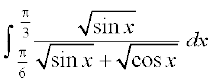 (P3 ls)
(P3 ls)
(1) vkSj (2) dks tksM+us ij ge ikrs gSa fd 2I =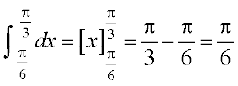
vr% I =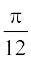
mnkgj.k 37 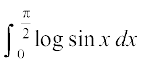 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy eku yhft, fd I =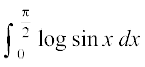
rc I =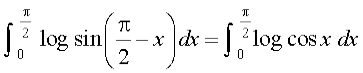 (P4 ls)
(P4 ls)
I osQ nksuksa ekuksa dks tksM+us ij ge ikrs gSa
2I =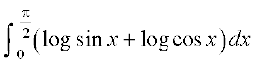
= ( log2 tksM+us ,oa ?kVkus ij)
( log2 tksM+us ,oa ?kVkus ij)
=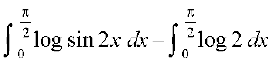 (D;ksa?)
(D;ksa?)
izFke lekdyu esa 2x = t j[kus ij 2 dx = dt tc x = 0 rks t = 0 vkSj tc x =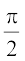 rks t = π
rks t = π
blfy, 2I =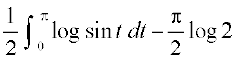
=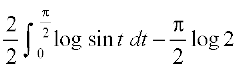 [P6 ls D;ksafd sin (π – t) = sin t)
[P6 ls D;ksafd sin (π – t) = sin t)
=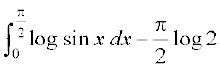 (pj t dks x esa ifjofrZr djus ij)
(pj t dks x esa ifjofrZr djus ij)
=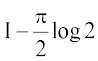
vr% 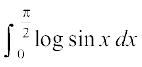 =
=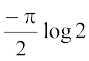
iz'ukoyh 7-11
fuf'pr lekdyuksa osQ xq.k/eks± dk mi;ksx djrs gq, 1 ls 19 rd osQ iz'uksa esa lekdyuksa dk eku Kkr dhft,A
1.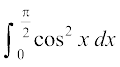 2.
2.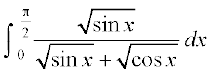 3.
3.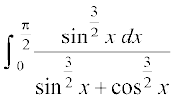
4.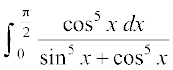 5.
5.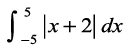 6.
6.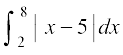
7.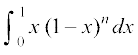 8.
8.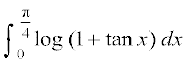 9.
9.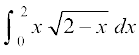
10.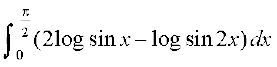 11.
11.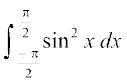
12.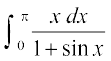 13.
13.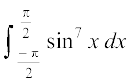 14.
14.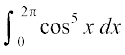
15.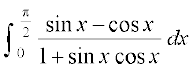 16.
16.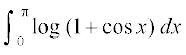 17.
17.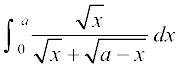
18.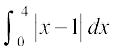
19.n'kkZb, fd 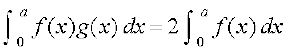 ;fn f vkSj g dks f(x) =f(a – x) ,oa
;fn f vkSj g dks f(x) =f(a – x) ,oa
g(x) + g(a – x) = 4 osQ :i esa ifjHkkf"kr fd;k x;k gSA
iz'u 20 ,oa 21 esa lgh mÙkj dk p;u dhft,A
20.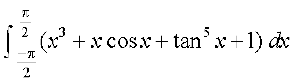 dk eku gS%
dk eku gS%
(A) 0 (B) 2 (C) π (D) 1
21.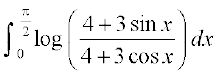 dk eku gS%
dk eku gS%
(A) 2 (B)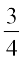 (C) 0 (D) –2
(C) 0 (D) –2
fofo/ mnkgj.k
mnkgj.k 38 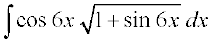 Kkr dhft,A
Kkr dhft,A
gy t = 1 + sin 6x, j[kus ij dt = 6 cos 6x dx
blfy,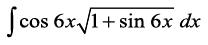 =
=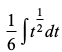
=
mnkgj.k 39 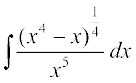 Kkr dhft,A
Kkr dhft,A
gy ge izkIr djrs gSa fd
vc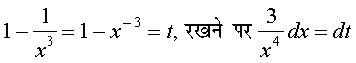
blfy,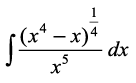 =
=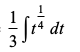
=
mnkgj.k 40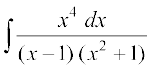 Kkr dhft,A
Kkr dhft,A
gy ge izkIr djrs gSa fd 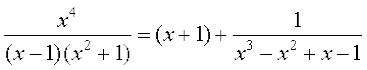
= 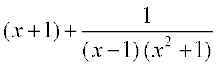
vc  osQ :i esa vfHkO;Dr djrs gSa
osQ :i esa vfHkO;Dr djrs gSa
blfy,
1 = A (x2 + 1) + (Bx + C) (x – 1)
= (A + B) x2 + (C – B) x + A – C
nksuksa i{kksa osQ xq.kkadksa dh rqyuk djus ij ge ikrs gSa fd A + B = 0, C – B = 0 vkSj
A – C = 1, ftlls izkIr gksrk gS fd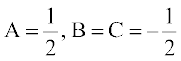
A, B ,oa C dk eku (2) esa izfrLFkkfir djus ij ge ikrs gSa fd
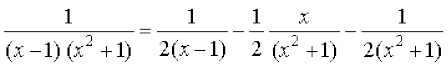
(3) dks (1) esa izfrLFkkfir djus ij ge ikrs gSa fd
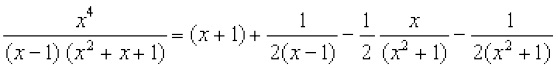
blfy, 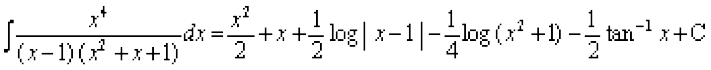
mnkgj.k 41 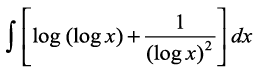 Kkr dhft,
Kkr dhft,
gy eku yhft, 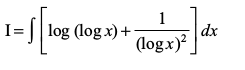
=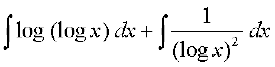
vkb,] izFke lekdyu esa 1 dks f}rh; iQyu osQ :i esa ysrs gSaA rc [kaM'k% lekdyu ls ge ikrs gSa fd
I =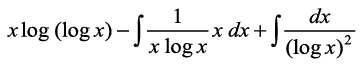
=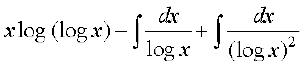
iqu% 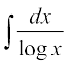 ij fopkj dhft,] 1 dks f}rh; iQyu osQ :i esa yhft, vkSj [kaM'k% fof/ }kjk lekdyu dhft,] bl izdkj ge ikrs gSa fd
ij fopkj dhft,] 1 dks f}rh; iQyu osQ :i esa yhft, vkSj [kaM'k% fof/ }kjk lekdyu dhft,] bl izdkj ge ikrs gSa fd
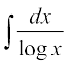 =
=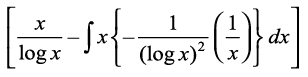
(2) dks (1), esa j[kus ij ge ikrs gSa
I =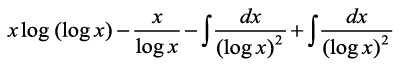
I = 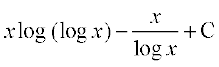
mnkgj.k 42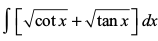 Kkr dhft,A
Kkr dhft,A
gy ge ikrs gSa fd 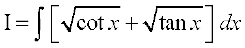
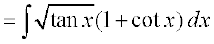
vc tan x = t2, j[kus ij sec2 x dx = 2t dt
vFkok dx =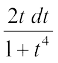
rc 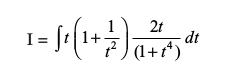
=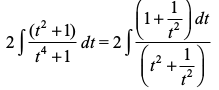 =
=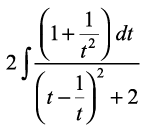
iqu% 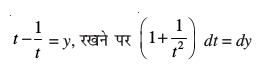
rc I=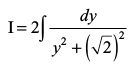
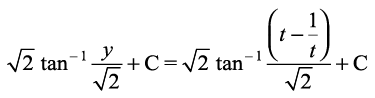
=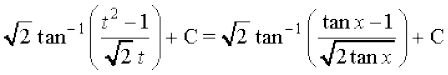
mnkgj.k 43 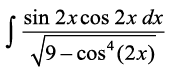 Kkr dhft,A
Kkr dhft,A
gy eku yhft, fd 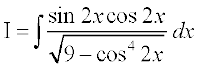
vc cos2 (2x) =t j[kus ij 4 sin 2x cos 2x dx = -dt
blfy,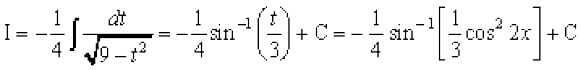
mnkgj.k 44 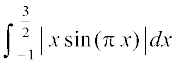 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy ;gk¡ f(x) =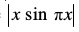 =
= 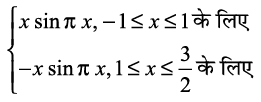
blfy,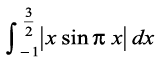 =
=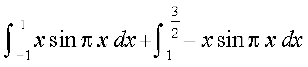
=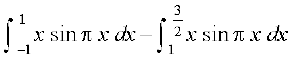
nk;sa i{k osQ nksuksa lekdyuksa dk lekdyu djus ij ge ikrs gSa fd
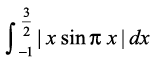 =
=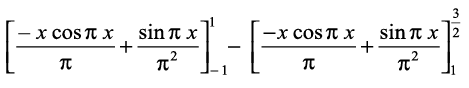
=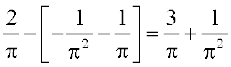
mnkgj.k 45 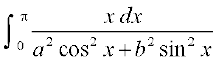 dk eku Kkr dhft,A
dk eku Kkr dhft,A
gy eku yhft, fd I=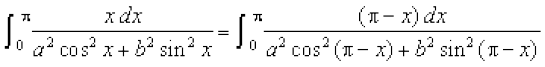
(P4osQ mi;ksx ls)
=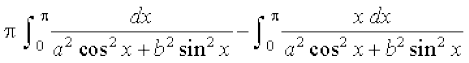
= 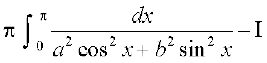
vr% 2I=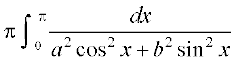
vFko I= 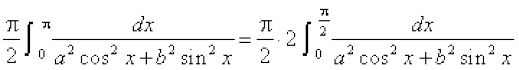
(P6 osQ mi;ksx ls)
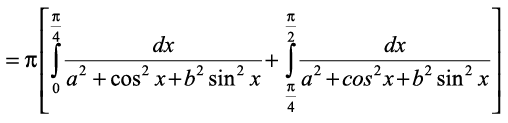
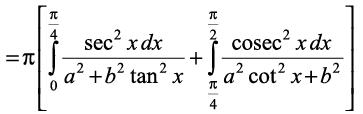
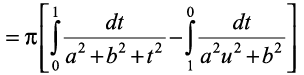 (jf[k, tanx = t vkSj cot x = u)
(jf[k, tanx = t vkSj cot x = u)
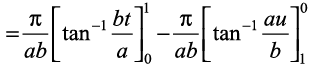
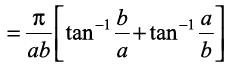
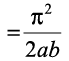
vè;k; 7 ij fofo/ iz'ukoyh
1 ls 24 rd osQ iz'uksa osQ iQyuksa dk lekdyu dhft,A
1.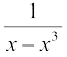 2.
2.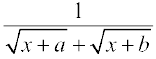
3.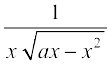 [laosQr : x =
[laosQr : x =  jf[k,] 4.
jf[k,] 4.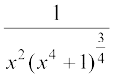
5.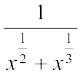 [laosQr
[laosQr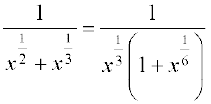 x = t6 jf[k,]
x = t6 jf[k,]
6.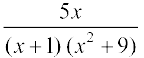 7.
7.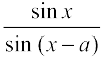 8.
8.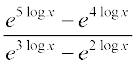
9.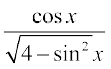 10.
10.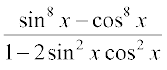 11.
11.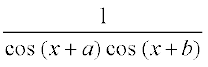
12.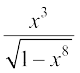 13.
13.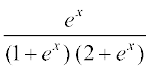 14.
14.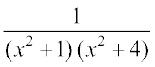
15.cos3x elog sinx 16. e3 logx (x4 + 1)– 1 17. f′(ax + b) [f(ax + b)]n
18.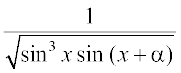 19.
19.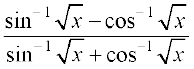 , (x ∈ [0, 1])
, (x ∈ [0, 1])
20.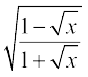 21.
21.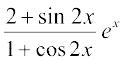 22.
22.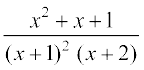
23.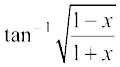 24.
24.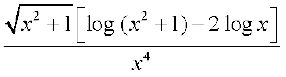
25 ls 33 rd osQ iz'uksa esa fuf'pr lekdyuksa dk eku Kkr dhft,A
25.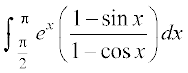 26.
26.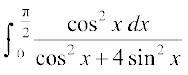 27.
27.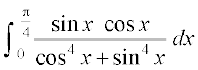
28.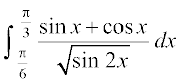 29.
29.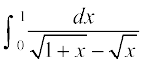 30.
30.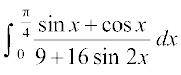
31.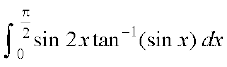 32.
32.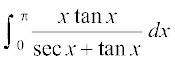
33.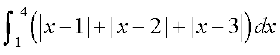
fuEufyf[kr dks fl¼ dhft, (iz'u 34 ls 39 rd)A
34.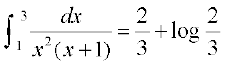
35.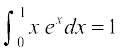
36.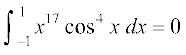 37.
37.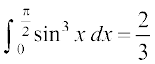
38.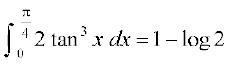
39.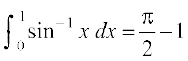
40. ;ksxiQy dh lhek osQ :i esa 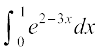 dk eku Kkr dhft,A
dk eku Kkr dhft,A
41 ls 44 rd osQ iz'uksa esa lgh mÙkj dk p;u dhft,A
41.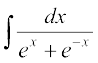
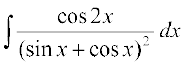 cjkcj gS%
cjkcj gS%
(A) tan–1 (ex) + C (B) tan–1 (e–x) + C
(C) log (ex – e–x) + C (D) log (ex + e–x) + C
42. 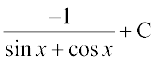 cjkcj gS%
cjkcj gS%
(A) 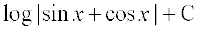 (B)
(B) 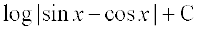
(C) 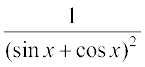 (D)
(D) 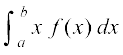
43. ;fn f (a + b – x) = f (x), rks 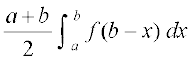 cjkcj gS%
cjkcj gS%
(A) 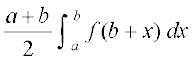 (B)
(B) 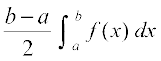
(C) 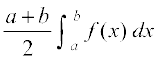 (D)
(D) 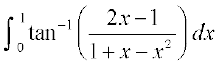
44. 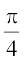 dk eku gS%
dk eku gS%
(A) 1 (B) 0 (C) –1 (D)
lkjka'k
- lekdyu] vodyu dk O;qRØe izØe gSA vodyu xf.kr esa gesa ,d iQyu fn;k gqvk gksrk gS vkSj gesa bl iQyu dk vodyt vFkok vody Kkr djuk gksrk gS ijarq lekdyu xf.kr esa gesa ,d ,slk iQyu Kkr djuk gksrk gS ftldk vody fn;k gqvk gksrk gSA vr% lekdyu ,d ,slk izØe gS tks fd vodyu dk O;qRØe gSA
eku yhft, fd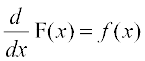 rc ge
rc ge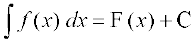 fy[krs gSaA ;s lekdyu vfuf'pr lekdyu vFkok O;kid lekdyu dgykrs gSaA C lekdyu vpj dgykrk gSA bu lHkh lekdyuksa esa ,d vpj dk varj gksrk gSA
fy[krs gSaA ;s lekdyu vfuf'pr lekdyu vFkok O;kid lekdyu dgykrs gSaA C lekdyu vpj dgykrk gSA bu lHkh lekdyuksa esa ,d vpj dk varj gksrk gSA
- T;kfefr n`f"V ls vfuf'pr lekdyu oØksa osQ ifjokj dk lewg gS ftlesa izR;sd lnL; y&v{k osQ vuqfn'k Åij dh rji+Q vFkok uhps dh rji+Q Lo;a osQ lekarj LFkkukarfjr djosQ izkIr fd;k tk ldrk gSA
- vfuf'pr lekdyu osQ oqQN xq.k/eZ fuEufyf[kr gSA
1. 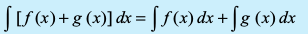
2. fdlh Hkh okLrfod la[;k k, osQ fy, 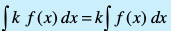
vf/d O;kidr%] ;fn f1, f2, f3,..., fn , iQyu gSa rFkk k1, k2,...,kn , okLrfod la[;k,¡ gSa rks
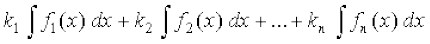
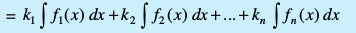
oqQN izkekf.kd lekdyu
(i)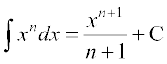 n ≠ – 1. fof'k"Vr%
n ≠ – 1. fof'k"Vr% 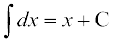
(ii)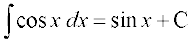 (iii)
(iii)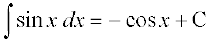
(iv)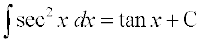 (v)
(v)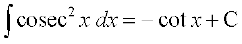
(vi)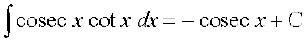
(vii)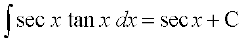 (viii)
(viii)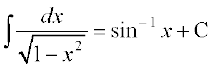
(ix)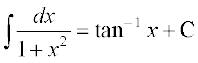 (x)
(x)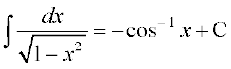
(xi)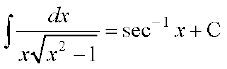 (xii)
(xii)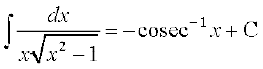
(xiii)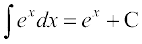 (xiv)
(xiv)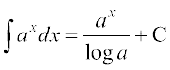
(xv)
- vkaf'kd fHkUuksa }kjk lekdyu
Lej.k dhft, fd ,d ifjes; iQyu 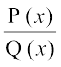 , nks cgqinksa dk vuqikr gS ftlesa P(x) vkSj Q(x), x osQ cgqin gSa vkSj Q(x) ≠ 0. ;fn cgqin P(x) dh ?kkr cgqin Q(x), dh ?kkr ls vf/d gS rks ge P(x) dks Q(x) ls foHkkftr djrs gSa rkfd
, nks cgqinksa dk vuqikr gS ftlesa P(x) vkSj Q(x), x osQ cgqin gSa vkSj Q(x) ≠ 0. ;fn cgqin P(x) dh ?kkr cgqin Q(x), dh ?kkr ls vf/d gS rks ge P(x) dks Q(x) ls foHkkftr djrs gSa rkfd 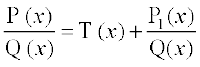 osQ :i esa fy[kk tk losQ tgk¡ T(x), ,d cgqin gS vkSj P1(x) dh ?kkr Q(x) dh ?kkr ls de gSA cgqin gksus osQ dkj.k T(x) dk lekdyu vklkuh ls Kkr fd;k tk ldrk gSA
osQ :i esa fy[kk tk losQ tgk¡ T(x), ,d cgqin gS vkSj P1(x) dh ?kkr Q(x) dh ?kkr ls de gSA cgqin gksus osQ dkj.k T(x) dk lekdyu vklkuh ls Kkr fd;k tk ldrk gSA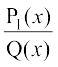 dks fuEufyf[kr izdkj dh vkaf'kd fHkUuksa osQ ;ksxiQy osQ :i esa O;Dr djrs gq, bldk lekdyu Kkr fd;k tk ldrk gSA
dks fuEufyf[kr izdkj dh vkaf'kd fHkUuksa osQ ;ksxiQy osQ :i esa O;Dr djrs gq, bldk lekdyu Kkr fd;k tk ldrk gSA
1.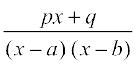
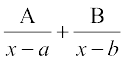 =, a ≠ b
=, a ≠ b
2.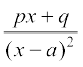 =
=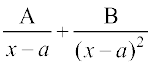
3.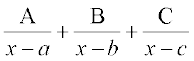 =
=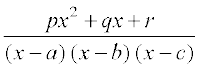
4.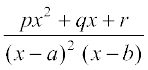 =
=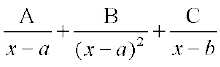
5.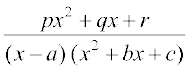 =
=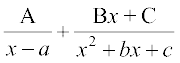 ,
,
tgk¡ x2 + bx + c osQ vkxs vkSj xq.ku[kaM ugha fd, tk ldrsA
- izfrLFkkiu }kjk lekdyu
lekdyu osQ pj esa ifjorZu fn, gq, lekdyu dks fdlh ,d vk/kjHkwr lekdyu esa ifjofrZr dj nsrk gSA ;g fof/ ftlesa ge ,d pj dks fdlh nwljs pj esa ifjofrZr djrs gSa izfrLFkkiu fof/ dgykrh gSA tc lekdY; esa oqQN f=kdks.kferh; iQyu lfEefyr gksa rks ge lekdyu Kkr djus osQ fy, oqQN lqifjfpr loZ lfedkvksa dk mi;ksx djrs gSaA izfrLFkkiu fof/ dk mi;ksx djrs gq, ge fuEufyf[kr izkekf.kd lekdyuksa dks izkIr djrs gSa%
(i)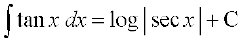 (ii)
(ii)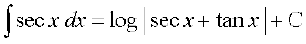
(iii)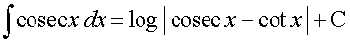
(iv)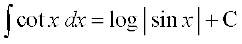
- oqQN fof'k"V iQyuksa osQ lekdyu
(i)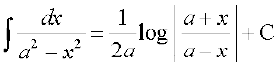
(ii)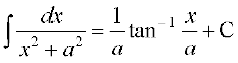 (iii)
(iii)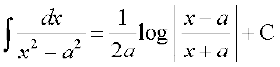
(iv)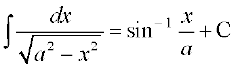 (v)
(v)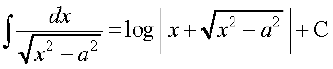
(vi)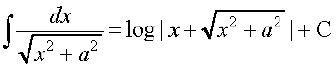
[kaM'k% lekdyu
fn, gq, iQyuksa f1 rFkk f2, osQ fy, ge izkIr djrs gSa fd
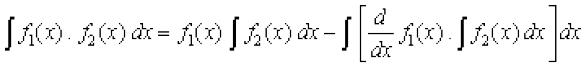 , vFkkZr~ nks iQyuksa osQ xq.kuiQy dk lekdyu = izFke iQyu × f}rh; iQyu dk lekdyu – {izFke iQyu dk vody xq.kkad × f}rh; iQyu dk lekdyu} dk lekdyu . izFke iQyu ,oa f}rh; iQyu osQ p;u esa lko/kuh j[kuh pkfg,A Li"Vr;k gesa ,sls iQyu dks f}rh; iQyu osQ :i esa ysuk pkfg, ftldk lekdyu gesa Hkfy&Hkk¡fr Kkr gSA
, vFkkZr~ nks iQyuksa osQ xq.kuiQy dk lekdyu = izFke iQyu × f}rh; iQyu dk lekdyu – {izFke iQyu dk vody xq.kkad × f}rh; iQyu dk lekdyu} dk lekdyu . izFke iQyu ,oa f}rh; iQyu osQ p;u esa lko/kuh j[kuh pkfg,A Li"Vr;k gesa ,sls iQyu dks f}rh; iQyu osQ :i esa ysuk pkfg, ftldk lekdyu gesa Hkfy&Hkk¡fr Kkr gSA
-
![]()
- oqQN fof'k"V izdkj osQ lekdyu
(i)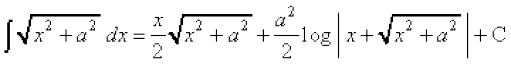
(ii)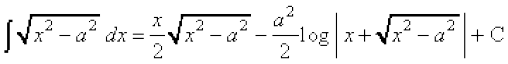
(iii)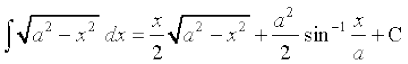
(iv) osQ izdkj osQ lekdyuksa dks izkekf.kd :i esa fuEufyf[kr fof/ }kjk ifjofrZr fd;k tk ldrk gS%
osQ izdkj osQ lekdyuksa dks izkekf.kd :i esa fuEufyf[kr fof/ }kjk ifjofrZr fd;k tk ldrk gS%
ax2 + bx + c = 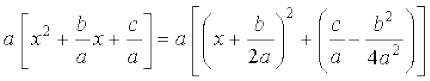
(v) osQ izdkj osQ lekdyuksa dks izkekf.kd :i esa ifjofrZr fd;k tk ldrk gSa%
osQ izdkj osQ lekdyuksa dks izkekf.kd :i esa ifjofrZr fd;k tk ldrk gSa%
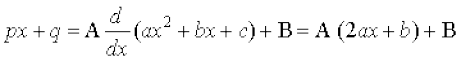 rFkk B dk eku Kkr djus osQ fy, nksuksa i{kksa ls xq.kkadksa dh rqyuk dh tkrh gSA
rFkk B dk eku Kkr djus osQ fy, nksuksa i{kksa ls xq.kkadksa dh rqyuk dh tkrh gSA
, A
- geus
![]() dks] oØ y = f(x), a ≤ x ≤ b, x-v{k ,oa dksfV;ksa x = a vkSj x = b ls f?kjs {ks=k osQ {ks=kiQy osQ :i esa ifjHkkf"kr fd;k gSA eku yhft, [a, b] esa x ,d ¯cnq gS rc
dks] oØ y = f(x), a ≤ x ≤ b, x-v{k ,oa dksfV;ksa x = a vkSj x = b ls f?kjs {ks=k osQ {ks=kiQy osQ :i esa ifjHkkf"kr fd;k gSA eku yhft, [a, b] esa x ,d ¯cnq gS rc![]() {ks=kiQy iQyu A(x) dks fu:fir djrk gSA
{ks=kiQy iQyu A(x) dks fu:fir djrk gSA ![]() {ks=kiQy iQyu dh ladYiuk gesa dyu dh vk/kjHkwr izes; dh vksj fuEufyf[kr :i esa izsfjr djrh gSA
{ks=kiQy iQyu dh ladYiuk gesa dyu dh vk/kjHkwr izes; dh vksj fuEufyf[kr :i esa izsfjr djrh gSA - lekdyu xf.kr dh izFke vk/kjHkwr izes; eku yhft, fd {ks=kiQy iQyu A(x)=
![]() ∀ x ≥ a, }kjk ifjHkkf"kr gS tgk¡ iQyu f varjky [a, b] ij larr iQyu ekuk x;k gSA rc A′(x) = f(x) ∀ x ∈ [a, b]
∀ x ≥ a, }kjk ifjHkkf"kr gS tgk¡ iQyu f varjky [a, b] ij larr iQyu ekuk x;k gSA rc A′(x) = f(x) ∀ x ∈ [a, b]
- lekdyu xf.kr dh f}rh; vk/kjHkwr izes;
eku yhft, fdlh can varjky [a, b] ij f, x dk larr iQyu gS vkSj F ,d nwljk iQyu gS tgk¡
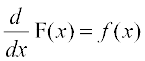 fosQ izkUr osQ lHkh x osQ fy, gS] rc
fosQ izkUr osQ lHkh x osQ fy, gS] rc
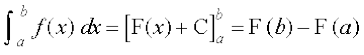
;g ifjlj [a, b] ij f dk fuf'pr lekdyu dgykrk gS tgk¡ a rFkk b lekdyu dh lhek,¡ dgykrh gSa a fuEu lhek dgykrh gS vkSj b dks mPp lhek dgrs gSaA