Table of Contents
vè;k; 8
lekdyuksa osQ vuqiz;ksx
(Application of Integrals)
One should study Mathematics because it is only through Mathematics that nature can be conceived in harmonious form. – Birkhoff
8.1 Hkwfedk (Introduction)
T;kfefr esa] geus f=kHkqtksa vk;rksa] leyac prqHkqZtksa ,oa o`Ùkksa lfgr fofHkUu T;kferh; vko`Qfr;ksa osQ {ks=kiQy osQ ifjdyu osQ fy, lw=kksa dk vè;;u fd;k gSA okLrfod thou dh vusd leL;kvksa osQ fy, xf.kr osQ vuqiz;ksx esa bl izdkj osQ lw=k ewy gksrs gSaA izkjafHkd T;kfefr osQ lw=kksa dh lgk;rk ls ge vusd lk/kj.k vko`Qfr;ksa osQ {ks=kiQy dk ifjdyu dj ldrs gSaA ;|fi ;s lw=k oØksa }kjk f?kjs {ks=kiQy osQ ifjdyu osQ fy, vi;kZIr gSa blosQ fy, gesa lekdyu xf.kr dh oqQN ladYiukvksa dh vko';drk gksxhA

A.L. Cauchy
(1789-1857)
fiNys vè;k; esa geus ;ksxiQy dh lhek osQ :i esa fuf'pr lekdyuksa dk ifjdyu djrs le; oØ y = f (x), dksfV;ksa
x = a, x = b ,oa x-v{k ls f?kjs {ks=kiQy dks Kkr djus dk vè;;u fd;k gSA bl vè;k; esa ge lk/kj.k oØksa osQ varxZr] ljy js[kkvksa ,oa o`Ùkksa] ijoy;ksa] rFkk nh?ko`Ùkksa (osQoy ekud :i) dh pkiksa osQ chp f?kjs {ks=kiQy dks Kkr djus osQ fy, lekdyuksa osQ ,d fof'k"V vuqiz;ksx dk vè;;u djsaxsA mijksDr oØksa ls f?kjs {ks=kiQy dks Hkh Kkr djsaxsA
8.2 lk/kj.k oØksa osQ varxZr {ks=kiQy (Area Under Simple Curves)
fiNys vè;k; esa geus] ;ksxiQy dh lhek osQ :i esa fuf'pr lekdyu ,oa dyu dh vk/kjHkwr izes; dk mi;ksx djrs gq, fuf'pr lekdyu dk ifjdyu oSQls fd;k tk,] dk vè;;u fd;k gSA vc ge oØ y = f(x), x-v{k ,oa dksfV;k¡ x = a rFkk x = b ls f?kjs {ks=kiQy dks Kkr djus dh vklku ,oa varKkZu ls izkIr fof/ dh ppkZ djrs gSaA vko`Qfr 8-1 ls ge oØ osQ varxZr {ks=kiQy dks cgqr lh iryh ,oa mèokZ/j cgqr lh ifV~V;ksa ls fufeZr eku ldrs gSaA y m¡pkbZ ,oa dx pkSM+kbZ okyh ,d LosPN iV~Vh ij fopkj dhft,] blesa dA (izkjafHkd iV~Vh dk {ks=kiQy) = ydx, tgk¡ y = f(x) gSA
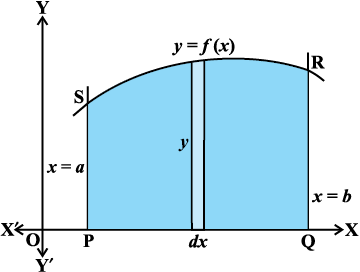
vko`Qfr 8-1
;g {ks=kiQy izkjafHkd {ks=kiQy dgykrk gS tks fd {ks=k osQ Hkhrj fdlh LosPN fLFkfr ij LFkkfir gS ,oa a rFkk b osQ eè; x osQ fdlh eku ls fofufnZ"V gSA oØ y = f (x), dksfV;ksa x = a, x = b ,oa x&v{k ls f?kjs {ks=k osQ oqQy {ks=kiQy A dks] {ks=k PQRSP esa lHkh iryh ifV~V;ksa osQ {ks=kiQyksa osQ ;ksxiQy osQ ifj.kke osQ :i esa ns[k ldrs gSaA lkaosQfrd Hkk"kk esa ge bls bl izdkj vfHkO;Dr djrs gSa%
A = 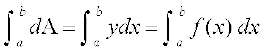
oØ x = g (y), y-v{k ,oa js[kk,¡ y = c, y = d ls f?kjs {ks=k dk {ks=kiQy fuEufyf[kr lw=k }kjk izkIr fd;k tkrk gSA
A = 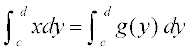
;gk¡ ge {kSfrt ifV~V;ksa ij fopkj djrs gSa tSlk fd vko`Qfr 8-2 esa n'kkZ;k x;k gSA
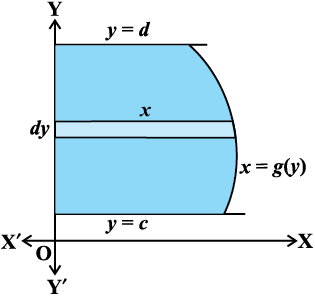
vko`Qfr 8-2
fVIi.kh ;fn pfpZr oØ dh fLFkfr x-v{k osQ uhps gS] rks tSlk fd vko`Qfr 8-3 esa n'kkZ;k x;k gS] tgk¡ x = a ls x = b rd f (x) < 0 blfy, fn, gq, oØ] x-v{k ,oa dksfV;ksa x = a, x = b ls f?kjs {ks=k dk {ks=kiQy ½.kkRed gks tkrk gS] ijarq ge {ks=kiQy osQ osQoy la[;kRed eku dh gh ppkZ djrs gSaA blfy, ;fn {ks=kiQy ½.kkRed gS rks ge blosQ fujis{k eku] vFkkZr~ 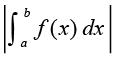 dks ysrs gSaA
dks ysrs gSaA
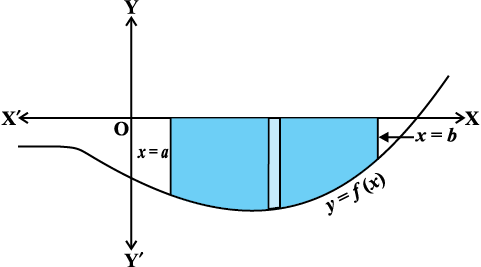
vko`Qfr 8-3
lkekU;r% ,slk gks ldrk gS fd oØ dk oqQN Hkkx x-v{k osQ Åij gS rFkk oqQN Hkkx x-v{k osQ uhps gS] tSlk fd vko`Qfr 8-4 esa n'kkZ;k x;k gSA ;gk¡ A1 < 0 rFkk A2 > 0 gS] blfy, oØ y = f (x), x-v{k ,oa dksfV;ksa x = a rFkk x = b ls f?kjs {ks=k dk {ks=kiQy A lw=k A =  + A2 }kjk izkIr fd;k tkrk gSA
+ A2 }kjk izkIr fd;k tkrk gSA
mnkgj.k 1 o`Ùk x2 + y2 = a2 dk {ks=kiQy Kkr dhft,A
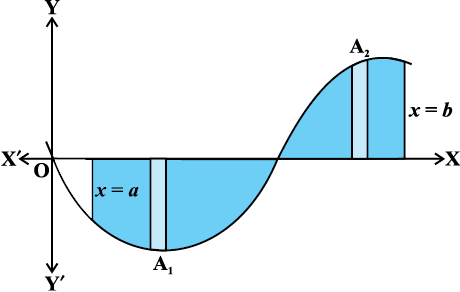
vko`Qfr 8-4
gy vko`Qfr 8-5 esa fn, gq, o`Ùk ls f?kjs gq, {ks=k dk oqQy {ks=kiQy
= 4 (fn, gq, oØ] x-v{k ,oa dksfV;ksa x = 0 rFkk x = a ls f?kjs {ks=k AOBA dk {ks=kiQy) [D;ksafd o`Ùk x-v{k ,oa y-v{k nksuksa osQ ifjr% lefer gS]
= 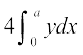 (mèokZ/j ifV~V;k¡ ysrs gq,)
(mèokZ/j ifV~V;k¡ ysrs gq,)
= 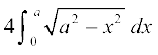 ,
,
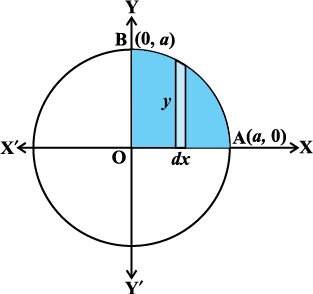
vko`Qfr 8-5
D;ksafd x2 + y2 = a2 ls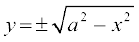 izkIr gksrk gSA
izkIr gksrk gSA
tSlk fd {ks=k AOBA izFke prqFkk±'k esa lfEefyr gS blfy, y dks /ukRed fy;k tkrk gSA lekdyu djus ij fn, gq, o`Ùk ls f?kjk {ks=kiQy fuEufyf[kr :i esa izkIr gksrk gS%
= 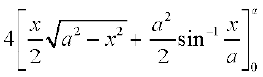 =
= 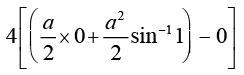
= 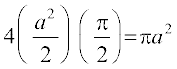
fodYir% tSlk fd vko`Qfr 8-6 esa n'kkZ;k x;k gS {kSfrt ifV~V;ksa dh ppkZ djrs gq, o`Ùk }kjk f?kjs {ks=k dk oqQy {ks=kiQy
= 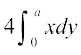 =
= 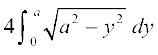
= 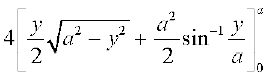
= 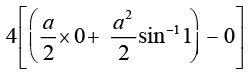
= 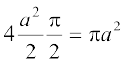
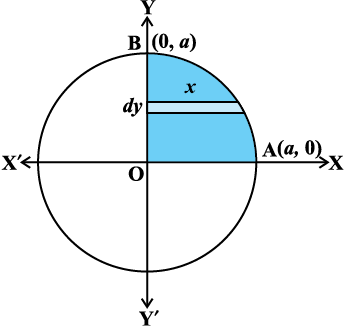
vko`Qfr 8-6
mnkgj.k 2 nh?kZo`Ùk 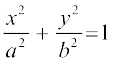 ls f?kjs {ks=k dk {ks=kiQy dk Kkr dhft,A
ls f?kjs {ks=k dk {ks=kiQy dk Kkr dhft,A
gy vko`Qfr 8.7 esa nh?kZo`Ùk ls f?kjs {ks=k ABA′B′A dk {ks=kiQy
= 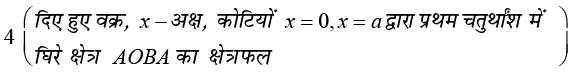
(D;ksafd nh?kZo`Ùk x-v{k ,oa y-v{k nksuksa osQ ifjr% lefer gS)
= 
vc 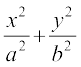 = 1 ls
= 1 ls 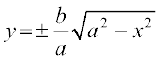 izkIr gksrk gS] ijarq {ks=k AOBA izFke prqFkk±'k esa gS blfy, y /ukRed fy;k tkrk gS] blfy, vHkh"V {ks=kiQy
izkIr gksrk gS] ijarq {ks=k AOBA izFke prqFkk±'k esa gS blfy, y /ukRed fy;k tkrk gS] blfy, vHkh"V {ks=kiQy
= 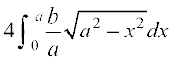
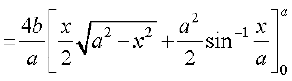 (D;ksa?)
(D;ksa?)
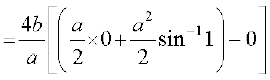
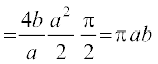 gSA
gSA
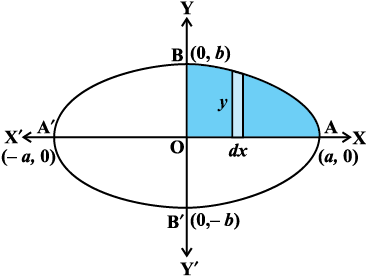
vko`Qfr 8-7
fodYir% tSlk fd vko`Qfr 8-8 esa n'kkZ;k x;k gS {kSfrt ifV~V;ksa dh ppkZ djrs gq, nh?kZo`Ùk dk {ks=kiQy
= 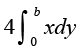 =
= 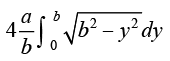 (D;ksa?)
(D;ksa?)
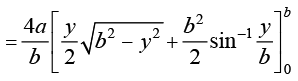
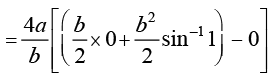
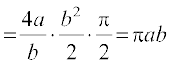 gSA
gSA
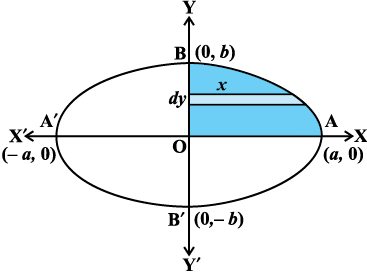
vko`Qfr 8-8
8.2.1 ,d oØ ,oa ,d js[kk ls f?kjs {ks=k dk {ks=kiQy (The area of the region bounded by a curve and a line)
bl miifjPNsn esa] ge ,d js[kk vkSj ,d o`Ùk] ,d js[kk vkSj ,d ijoy;] rFkk ,d js[kk vkSj ,d nh?kZo`Ùk ls f?kjs {ks=k dk {ks=kiQy Kkr djsaxs mijksDr pfrZr oØksa osQ lehdj.k osQoy izkekf.kd :i esa gh vè;;u fd, tk,¡xs D;ksafd vU; :iksa okys lehdj.k dk mi;ksx bl ikB~;iqLrd osQ vè;;u {ks=k ls ckgj gSaA
mnkgj.k 3 oØ y = x2 ,oa js[kk y = 4 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
gy D;ksafd fn, gq, lehdj.k y = x2 }kjk fu:fir oØ y-v{k osQ ifjr% lefer ,d ijoy; gSA blfy, vko`Qfr 8-9 ls {ks=k AOBA dk vHkh"V {ks=kiQy fuEufyf[kr :i esa izkIr gksrk gS%
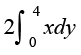 = 2 (fn, gq, oØ] y –v{k ,oa js[kkvksa y = 0 rFkk y = 4 ls f?kjs {ks=k BOND dk {ks=kiQy)
= 2 (fn, gq, oØ] y –v{k ,oa js[kkvksa y = 0 rFkk y = 4 ls f?kjs {ks=k BOND dk {ks=kiQy)
= 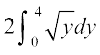 (D;ksa?)
(D;ksa?)
= 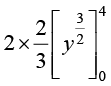
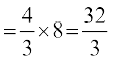
;gk¡ geus {kSfrt ifV~V;k¡ yh gSa tSlk fd vko`Qfr 8-9 esa n'kkZ;k x;k gSA

vko`Qfr 8-9
fodYir% {ks=k AOBA dk {ks=kiQy izkIr djus osQ fy, ge PQ tSlh mQèokZ/j ifV~V;k¡ ys ldrs gSa tSlk fd vko`Qfr 8-10 esa n'kkZ;k x;k gSA blosQ fy, ge lehdj.kksa x2 = y ,oa y = 4 dks gy djrs gSa ftlls x = –2 ,oa x = 2 izkIr gksrk gSA
bl izdkj {ks=k AOBA dks oØksa y = x2, y = 4 ,oa dksfV;ksa x = –2 rFkk x = 2 ls f?kjk {ks=k ifjHkkf"kr fd;k tk ldrk gSA

vko`Qfr 8-10
blfy, {ks=k AOBA dk {ks=kiQy
= 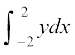 [y = (¯cnq Q dk y funs±'kkad – ¯cnq P dk y funsZ'kkad) = 4 – x2]
[y = (¯cnq Q dk y funs±'kkad – ¯cnq P dk y funsZ'kkad) = 4 – x2]
= 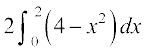 (D;ksa?)
(D;ksa?)
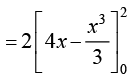
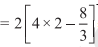
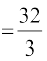
fVIi.kh mijksDr mnkgj.kksa ls ;g fu"d"kZ fudyrk gS fd fdlh {ks=k dk {ks=kiQy Kkr djus osQ fy, ge mQèokZ/j vFkok {kSfrt ifV~V;ksa esa ls fdlh dks Hkh ys ldrs gSaA blls vkxs ge bu nksuksa ifV~V;ksa esa ls fdlh ,d dh ppkZ djsaxs] mQèokZ/j ifV~V;ksa dks lkekU;r% vf/d izkFkfedrk nh tk,xhA
mnkgj.k 4 izFke prqFkk±'k esa o`Ùk x2 + y2 = 32, js[kk y = x, ,oa x-v{k ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A

vko`Qfr 8-11
gy fn, gq, lehdj.k gSa%
y = x ... (1)
vkSj x2 + y2 = 32 ... (2)
lehdj.k (1) rFkk (2) dks gy djus ij ge ikrs gSa fd fn;k gqvk o`Ùk ,oa nh gqbZ js[kk ,d nwljs dks izFke prqFkk±'k esa B(4, 4) ij feyrs gSa (vko`Qfr 8-11)A x-v{k osQ Åij BM yEc [khafp,A
blfy,] vHkh"V {ks=kiQy = {ks=k OBMO dk {ks=kiQy + {ks=k BMAB dk {ks=kiQy
vc] {ks=k OBMO dk {ks=kiQy
= 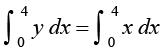 =
= 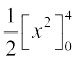 = 8 ... (3)
= 8 ... (3)
iqu% {ks=k BMAB dk {ks=kiQy
= 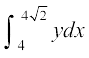 =
= 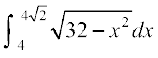
= 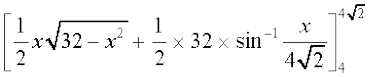
= 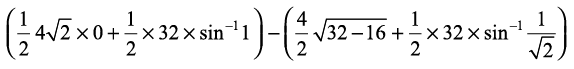
= 8 π – (8 + 4π) = 4π – 8 ... (4)
lehdj.k (3) ,oa (4) dk ;ksxiQy Kkr djus ij ge vHkh"V {ks=kiQy A = 4π ikrs gSaA
mnkgj.k 5 nh?kZo`Ùk 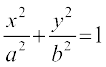 ,oa dksfV;ksa x = 0 vkSj x = ae, ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,] tgk¡ b2 = a2 (1 – e2) ,oa e < 1 gSA
,oa dksfV;ksa x = 0 vkSj x = ae, ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,] tgk¡ b2 = a2 (1 – e2) ,oa e < 1 gSA
gy {ks=k BOB′RFSB dk vHkh"V {ks=kiQy fn, gq, nh?kZo`Ùk ,oa js[kkvksa x = 0 rFkk x = ae ls f?kjk gqvk gS(vko`Qfr 8-12)A
è;ku nhft, fd {ks=k BOB′RFSB dk {ks=kiQy
= 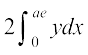 =
= 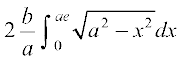
= 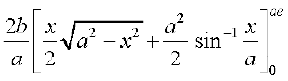
= 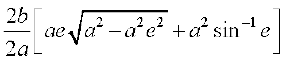
= 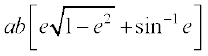
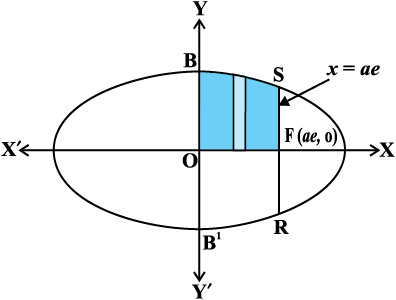
vko`Qfr 8-12
iz'ukoyh 8-1
1. oØ y2 = x, js[kkvksa x = 1, x = 4 ,oa x-v{k ls f?kjs {ks=k dk izFke ikn esa {ks=kiQy Kkr dhft,A
2. izFke prqFkk±'k esa oØ y2 = 9x, x = 2, x = 4 ,oa x-v{k ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
3. izFke prqFkk±'k esa x2 = 4y, y = 2, y = 4 ,oa y-v{k ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
4. nh?kZo`Ùk 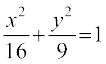 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
5. nh?kZo`Ùk 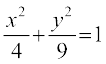 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
6. izFke prqFkk±'k esa o`Ùk x2 + y2 = 4, js[kk x =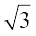 y ,oa x-v{k }kjk f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
y ,oa x-v{k }kjk f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
7. Nsnd js[kk 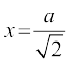 }kjk o`Ùk x2 + y2 = a2 osQ NksVs Hkkx dk {ks=kiQy Kkr dhft,A
}kjk o`Ùk x2 + y2 = a2 osQ NksVs Hkkx dk {ks=kiQy Kkr dhft,A
8. ;fn oØ x = y2 ,oa js[kk x = 4 ls f?kjk gqvk {ks=kiQy js[kk x = a }kjk nks cjkcj Hkkxksa esa foHkkftr gksrk gS rks a dk eku Kkr dhft,A
9. ijoy; y = x2 ,oa y = 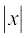 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
10. oØ x2 = 4y ,oa js[kk x = 4y – 2 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
11. oØ y2 = 4x ,oa js[kk x = 3 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
iz'u 12 ,oa 13 esa lgh mÙkj dk p;u dhft,%
12. izFke prqFkk±'k esa o`Ùk x2 + y2 = 4 ,oa js[kkvksa x = 0, x = 2 ls f?kjs {ks=k dk {ks=kiQy gS%
(A) π (B) 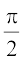 (C)
(C) 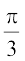 (D)
(D) 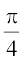
13. oØ y2 = 4x, y-v{k ,oa js[kk y = 3 ls f?kjs {ks=k dk {ks=kiQy gS%
(A) 2 (B)  (C)
(C)  (D)
(D) 
8.3 nks oØksa osQ eè;orhZ {ks=k dk {ks=kiQy (Area Between Two Curves)
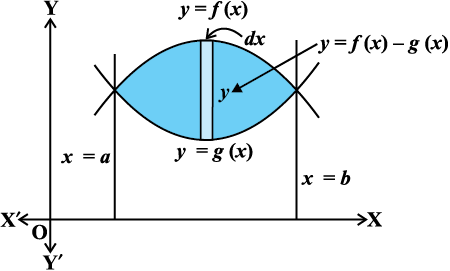
yScfu”k dh psruk ,oa varKkZu dh lPpkbZ osQ iQyLo:i fdlh {ks=k dks izkjafHkd {ks=kiQy dh c`gr~ la[;k esa ifV~V;k¡ dkVdj vkSj bu izkjafHkd {ks=kiQyksa dk ;ksxiQy Kkr dj] {ks=kiQy osQ ifjdyu dh fØ;k lekdyu dgykrh gSA dYiuk dhft,] gesa nks oØ y = f (x) vkSj y = g (x) fn, gq, gSa tgk¡ [a, b]esa f(x) ≥ g(x) tSlk fd vko`Qfr 8-13 esa n'kkZ;k x;k gSA fn, gq, oØksa osQ lehdj.k ls y dk mHk;fu"B eku ysrs gq, bu nksuksa oØksa osQ izfrPNsnd ¯cnq x = a rFkk x = b }kjk ns; gSaA
lekdyu osQ lw=k dk LFkkiu djus osQ fy, izkjafHkd {ks=kiQy dks mQèokZ/j ifV~V;ksa osQ :i esa ysuk lqfo/ktud gSA tSlk fd vko`Qfr 8-13 esa n'kkZ;k x;k gSA izkjafHkd iV~Vh dh m¡QpkbZ
f(x) – g(x) ,oa pkSM+kbZ dx gS] blfy, izkjafHkd {ks=kiQy
dA = [f(x) – g(x)] dx, rFkk oqQy {ks=kiQy A = 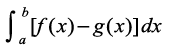
vko`Qfr 8-13
fodYir%
A = [oØ y = f (x), x-v{k rFkk js[kkvksa x = a, x = b ls f?kjs {ks=k dk {ks=kiQy]
– [oØ y = g (x), x-v{k ,oa js[kkvksa x = a, x = b ls f?kjs {ks=k dk {ks=kiQy]
= 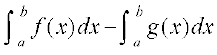 =
=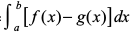 tgk¡ [a, b] esa f (x) ≥ g (x)
tgk¡ [a, b] esa f (x) ≥ g (x)
;fn [a, c] esa f (x) ≥ g (x) rFkk [c, b] esa f (x) ≤ g (x) tgk¡ a < c < b tSlk fd vko`Qfr 8-14 esa n'kkZ;k x;k gS] rks oØksa ls f?kjs {ks=kksa dk {ks=kiQy fuEufyf[kr izdkj fy[kk tk ldrk gS%
{ks=kiQy = {ks=k ACBDA dk {ks=kiQy + {ks=k BPRQB dk {ks=kiQy
= 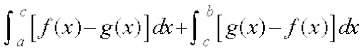

vko`Qfr 8-14
mnkgj.k 6 nks ijoy;ksa y = x2 ,oa y2 = x ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
gy tSlk fd vko`Qfr 8-15 esa n'kkZ;k x;k gS] bu nksuksa ijoy;ksa osQ izfrPNsnd ¯cnq O (0, 0) ,oa A (1, 1) gSA
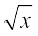 = f(x) vkSj y = x2 = g (x), tgk¡ [0, 1] esa f (x) ≥ g (x) gSA
= f(x) vkSj y = x2 = g (x), tgk¡ [0, 1] esa f (x) ≥ g (x) gSAblfy, Nk;kafoQr {ks=k dk vHkh"V {ks=kiQy
= 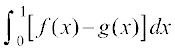
= 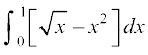
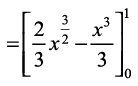 =
= 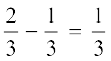

vko`Qfr 8-15
mnkgj.k 7 x-v{k osQ Åij rFkk o`Ùk x2 + y2 = 8x ,oa ijoy; y2 = 4x osQ eè;orhZ {ks=k dk {ks=kiQy Kkr dhft,A
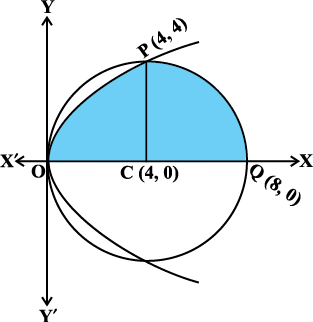
vko`Qfr 8-16
gy o`Ùk dk fn;k gqvk lehdj.k x2 + y2 = 8x, (x – 4)2 + y2 = 16 osQ :i esa vfHkO;Dr fd;k tk ldrk gSA bl o`Ùk dk osaQnz ¯cnq (4, 0) gS rFkk f=kT;k 4 bdkbZ gSA ijoy; y2 = 4x osQ lkFk blosQ izfrPNsn ls izkIr gksrk gS%
x2 + 4x = 8x
vFkok x2 – 4x = 0
vFkok x (x – 4) = 0
vFkok x = 0, x = 4
bl izdkj bu nks oØksa osQ izfrPNsn ¯cnq O(0, 0) ,oa x-v{k ls Åij P(4,4) gSaA
vko`Qfr 8-16 ls x-v{k ls mij bu nksuksa oØksa osQ eè; lfEefyr {ks=k OPQCO dk {ks=kiQy
= ({ks=k OCPO dk {ks=kiQy) + ({ks=k PCQP dk {ks=kiQy)
= 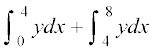
= 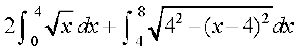 (D;ksa\)
(D;ksa\)
= 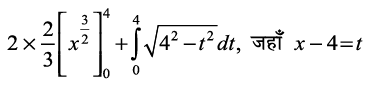
= 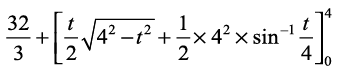
= 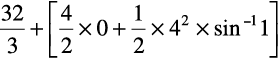
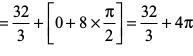 =
= 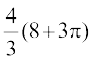
mnkgj.k 8 vko`Qfr 8-17 esa AOBA izFke prqFkk±'k esa nh?kZo`Ùk 9x2 + y2 = 36 dk ,d Hkkx gS ftlesa OA = 2 bdkbZ rFkk OB = 6 bdkbZ gSA y?kq pki AB ,oa thok AB osQ eè;orhZ {ks=k dk {ks=kiQy Kkr dhft,A
gy nh?kZo`Ùk dk fn;k gqvk lehdj.k 9x2 + y2 = 36, vFkkZr~ 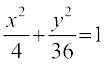 vFkok
vFkok 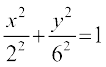 osQ :i esa vfHkO;Dr fd;k tk ldrk gS vkSj blfy, bldk vkdkj vko`Qfr 8-17 esa fn, gq, vkdkj tSlk gSA
osQ :i esa vfHkO;Dr fd;k tk ldrk gS vkSj blfy, bldk vkdkj vko`Qfr 8-17 esa fn, gq, vkdkj tSlk gSA

vko`Qfr 8-17
blosQ vuqlkj] thok AB dk lehdj.k gS%
y – 0 = 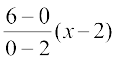
vFkok y = – 3 (x – 2)
vFkok y = – 3x + 6
vko`Qfr 8-17 esa n'kkZ;s Nk;kafoQr {ks=k dk {ks=kiQy
= 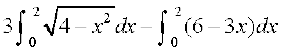 (D;ksa\)
(D;ksa\)
= 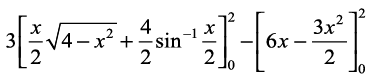
= 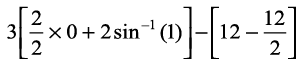
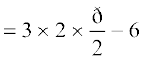 = 3π – 6
= 3π – 6
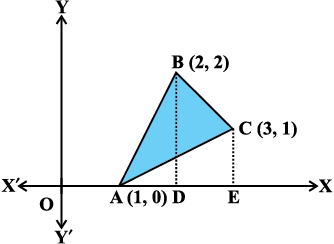
mnkgj.k 9 lekdyu dk mi;ksx djrs gq, ,d ,sls f=kHkqt dk {ks=kiQy Kkr dhft, ftlosQ 'kh"kZ (1, 0), (2, 2) ,oa (3, 1) gSaA
vko`Qfr 8-18
gy eku yhft, A(1, 0), B(2, 2) ,oa C(3, 1) f=kHkqt ABC osQ 'kh"kZ gSa (vko`Qfr 8-18)
∆ ABC dk {ks=kiQy = ∆ ABD dk {ks=kiQy + leyac prqHkqZt BDEC dk {ks=kiQy – ∆ AEC dk {ks=kiQy
vc Hkqtk,¡ AB, BC ,oa CA osQ lehdj.k Øe'k%
y = 2(x – 1), y = 4 – x, y =  (x – 1) gSaA
(x – 1) gSaA
vr% ∆ ABC dk {ks=kiQy
= 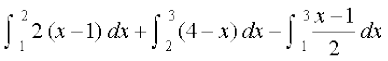
= 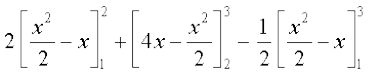
= 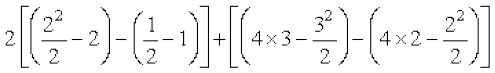
– 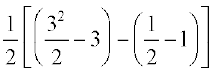 =
= 
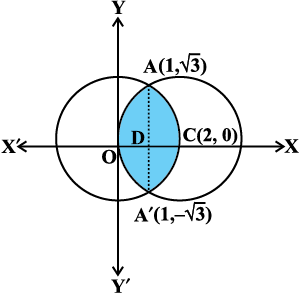
mnkgj.k 10 nks o`Ùkksa x2 + y2 = 4 ,oa (x – 2)2 + y2 = 4 osQ eè;orhZ {ks=k dk {ks=kiQy Kkr dhft,A
vko`Qfr 8-19
gy fn, gq, o`Ùkksa osQ lehdj.k gSa%
x2 + y2 = 4 ... (1)
vkSj (x – 2)2 + y2 = 4 ... (2)
lehdj.k (1) ,slk o`Ùk gS ftldk osaQnz ewy ¯cnq O ij gS vksj ftldh f=kT;k 2 bdkbZ gSA lehdj.k (2) ,d ,slk o`Ùk gS ftldk osaQnz C(2, O) gS vkSj ftldh f=kT;k 2 bdkbZ gSA lehdj.k (1) vkSj (2) dks gy djus ij ge ikrs gSa%
(x –2)2 + y2 = x2 + y2
vFkok x2 – 4x + 4 + y2 = x2 + y2
vFkok x = 1 ftlls y = 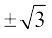 izkIr gksrk gSA
izkIr gksrk gSA
vr% fn, gq, o`Ùkksa osQ izfrPNsnu ¯cnq A(1, 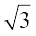 ) vkSj A′(1,
) vkSj A′(1, 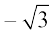 ) gS] tSlk vko`Qfr 8-19 esa n'kkZ;k x;k gSA
) gS] tSlk vko`Qfr 8-19 esa n'kkZ;k x;k gSA
o`Ùkksa osQ eè;orhZ {ks=k OACA′O dk vHkh"V
{ks=kiQy = 2 [{ks=k ODCAO dk {ks=kiQy] (D;ksa?)
= 2 [{ks=k ODAO dk {ks=kiQy + {ks=k DCAD dk {ks=kiQy]
= 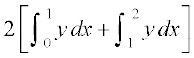
= 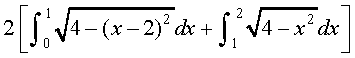 (D;ksa?)
(D;ksa?)
= 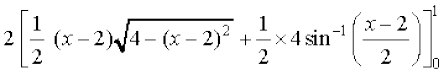 +
+

= 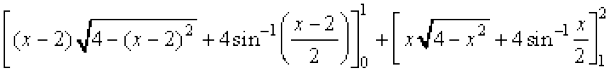
= 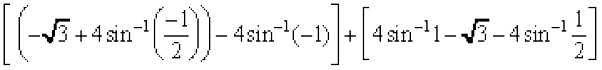
= 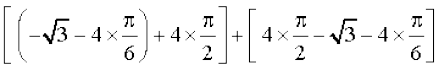
= 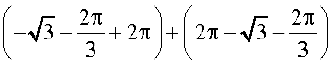
= 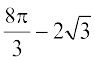
iz'ukoyh 8-2
1. ijoy; x2 = 4y vkSj o`Ùk 4x2 + 4y2 = 9 osQ eè;orhZ {ks=k dk {ks=kiQy Kkr dhft,A
2. oØksa (x – 1)2 + y2 = 1 ,oa x2 + y2 = 1 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
3. oØksa y = x2 + 2, y = x, x = 0 ,oa x = 3 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
4. lekdyu dk mi;ksx djrs gq, ,d ,sls f=kHkqt dk {ks=kiQy Kkr dhft, ftlosQ 'kh"kZ
(– 1, 0), (1, 3) ,oa (3, 2) gSaA
5. lekdyu dk mi;ksx djrs gq, ,d ,sls f=kdks.kh; {ks=k dk {ks=kiQy Kkr dhft, ftldh Hkqtkvksa osQ lehdj.k y = 2x + 1, y = 3x + 1 ,oa x = 4 gSaA
iz'u 6 ,oa 7 esa lgh mÙkj dk p;u dhft,%
6. o`Ùk x2 + y2 = 4 ,oa js[kk x + y = 2 ls f?kjs NksVs Hkkx dk {ks=kiQy gS%
(A) 2 (π – 2) (B) π – 2 (C) 2π – 1 (D) 2 (π + 2)
7. oØksa y2 = 4x ,oa y = 2x osQ eè;orhZ {ks=k dk {ks=kiQy gS%
(A)  (B)
(B) 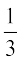 (C)
(C)  (D)
(D) 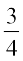
fofo/ mnkgj.k
mnkgj.k 11 ijoy; y2 = 4ax vkSj mlosQ ukfHkyac ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
gy vko`Qfr 8.20 ls] ijoy; y2 = 4ax dk 'kh"kZ ewy ¯cnq ij gSA ukfHkyac thok LSL′ dk lehdj.k x = a gSA fn;k gqvk ijoy; x-v{k osQ ifjr% lefer gSA
{ks=k OLL′O dk vHkh"V {ks=kiQy = 2 (+{ks=k OLSO dk {ks=kiQy)
= 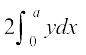 =
= 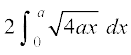
= 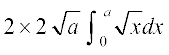
= 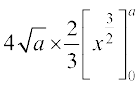 =
= 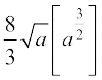 =
= 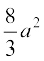

vko`Qfr 8-20
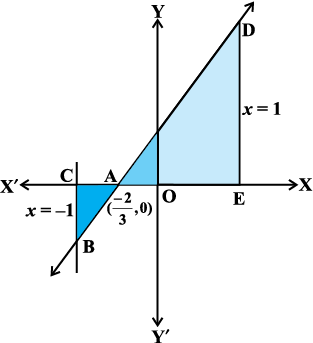
mnkgj.k 12 js[kk y = 3x + 2, x-v{k ,oa dksfV;ksa x = –1 ,oa x = 1 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
gy tSlk fd vko`Qfr 8-21 esa n'kkZ;k x;k gS] js[kk
y = 3x + 2, x-v{k dks x = 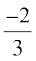 ij feyrh gS vkSj
ij feyrh gS vkSj 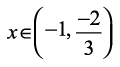 osQ fy, bldk vkys[k x-v{k osQ uhps gS rFkk
osQ fy, bldk vkys[k x-v{k osQ uhps gS rFkk 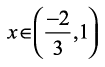 osQ fy, bldk vkys[k x-v{k ls Åij gSA
osQ fy, bldk vkys[k x-v{k ls Åij gSA
vHkh"V {ks=kiQy = {ks=k ACBA dk {ks=kiQy + {ks=k ADEA dk {ks=kiQy
= 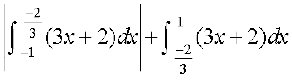
= 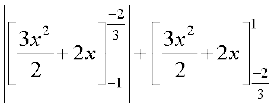 =
= 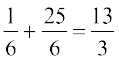
vko`Qfr 8-21
mnkgj.k 13 x = 0 ,oa x = 2π osQ eè; oØ
y = cosx ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
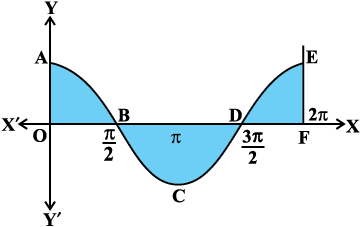
gy vko`Qfr 8-22 ls] vHkh"V {ks=kiQy
= {ks=k OABO dk {ks=kiQy + {ks=k BCDB dk {ks=kiQy + {ks=k DEFD dk {ks=kiQy
blfy, vHkh"V {ks=kiQy
= 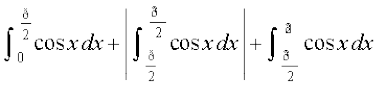
= 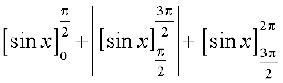 = 1 + 2 + 1 = 4
= 1 + 2 + 1 = 4
vko`Qfr 8-22
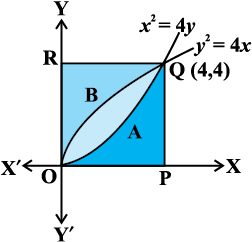
mnkgj.k 14 fl¼ dhft, fd oØ y2 = 4x ,oa x2 = 4y, js[kkvksa x = 0, x = 4, y = 4 ,oa y = 0 ls f?kjs oxZ osQ {ks=kiQy dks rhu cjkcj Hkkxksa esa foHkkftr djrs gSaA
gy è;ku nhft, fd ijoy;ksa y2 = 4x ,oa x2 = 4y osQ izfrPNsn ¯cnq (0,0) ,oa (4,4) gSa tSlk fd vko`Qfr 8-23 esa n'kkZ;k x;k gSA
vc oØksa y2 = 4x ,oa x2 = 4y ls f?kjs {ks=k OAQBO dk {ks=kiQy
= 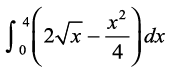 =
= 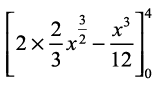
= 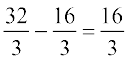 ... (1)
... (1)
iqu% oØksa x2 = 4y, x = 0, x = 4 ,oa x-v{k ls f?kjs {ks=k OPQAO dk {ks=kiQy =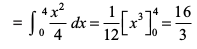 ... (2)
... (2)
blh izdkj oØ y2 = 4x, y-v{k, y = 0 ,oa y = 4 ls f?kjs {ks=k OBQRO dk {ks=kiQy=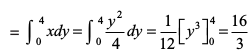 ... (3)
... (3)
vko`Qfr 8-23
lehdj.kksa (1)] (2) rFkk (3) ls ;g fu"d"kZ fudyrk gS fd
{ks=k OAQBO dk {ks=kiQy = {ks=k OPQAO dk {ks=kiQy = {ks=k OBQRO dk {ks=kiQy vFkkZr~] ijoy;ksa y2 = 4x ,oa x2 = 4y ls f?kjk {ks=kiQy fn, gq, oxZ osQ {ks=kiQy dks rhu cjkcj Hkkxksa esa foHkkftr djrk gSA
mnkgj.k 15 {ks=k {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2}dk {ks=kiQy Kkr dhft,A
gy vkb, loZizFke ge ml {ks=k dk js[kkfp=k rS;kj djsa ftldk gesa {ks=kiQy Kkr djuk gSA ;g {ks=k fuEufyf[kr {ks=kksa dk eè;orhZ {ks=k gS%
A1 = {(x ,y) : 0 ≤ y ≤ x2+ 1}
A2 = {(x, y) : 0 ≤ y ≤ x + 1}
vkSj A3 = {(x, y) : 0 ≤ x ≤ 2}
oØksa y = x2 + 1 ,oa y = x + 1 osQ izfrPNsn ¯cnq P(0, 1) ,oa Q(1, 2) gSaA vko`Qfr 8-24 ls] vHkh"V {ks=k] Nk;kafdr {ks=k OPQRSTO gS ftldk {ks=kiQy
= {ks=k OTQPO dk {ks=kiQy + {ks=k TSRQT dk {ks=kiQy
= 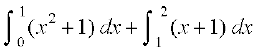 (D;ksa?)
(D;ksa?)
= 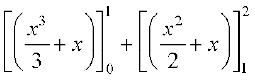
=  =
= 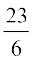
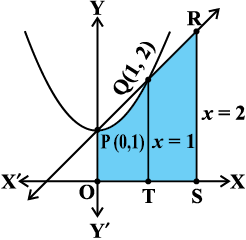
vko`Qfr 8-24
vè;k; 8 ij fofo/ iz'ukoyh
1. fn, gq, oØksa ,oa js[kkvksa ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,%
(i) y = x2; x = 1, x = 2 ,oa x-v{k
(ii) y = x4; x = 1, x = 5 ,o x-v{k
2. oØksa y = x ,oa y = x2 osQ eè;orhZ {ks=k dk {ks=kiQy Kkr dhft,A
3. izFke prqFkk±'k esa lfEefyr ,oa y = 4x2, x = 0, y = 1 rFkk y = 4 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
4. y = 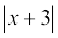 dk xzki+Q [khafp, ,oa
dk xzki+Q [khafp, ,oa 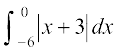 dk eku Kkr dhft,A
dk eku Kkr dhft,A
5. x = 0 ,oa x = 2π rFkk oØ y = sinx ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
6. ijoy; y2 = 4ax ,oa js[kk y = mx ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
7. ijoy; 4y = 3x2 ,oa js[kk 2y = 3x + 12 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
8. nh?kZo`Ùk 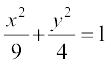 ,oa js[kk
,oa js[kk 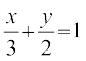 ls f?kjs y?kq {ks=k dk {ks=kiQy Kkr dhft,A
ls f?kjs y?kq {ks=k dk {ks=kiQy Kkr dhft,A
9. nh?kZo`Ùk 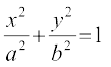 ,oa js[kk
,oa js[kk 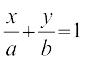 ls f?kjs y?kq {ks=k dk {ks=kiQy Kkr dhft,A
ls f?kjs y?kq {ks=k dk {ks=kiQy Kkr dhft,A
10. ijoy; x2 = y, js[kk y = x + 2 ,oa x-v{k ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
11. lekdyu fof/ dk mi;ksx djrs gq, oØ 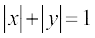 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
[laosQr : vko';d {ks=k] js[kkvksa x + y = 1, x– y = 1, – x + y = 1 ,oa – x – y = 1 ls f?kjk gS]
12. oØksa {(x, y) : y ≥ x2 rFkk y = 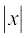 } ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
} ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
13. lekdyu fof/ dk mi;ksx djrs gq, ,d ,sls f=kHkqt ABC, dk {ks=kiQy Kkr dhft, ftlosQ 'kh"kks± osQ funsZ'kkad A(2, 0), B (4, 5) ,oa C (6, 3) gSaA
14. lekdyu fof/ dk mi;ksx djrs gq,] js[kkvksa 2x + y = 4, 3x – 2y = 6 ,oa x – 3y + 5 = 0 ls f?kjs {ks=k dk {ks=kiQy Kkr dhft,A
15. {ks=k {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}dk {ks=kiQy Kkr dhft,A
16 ls 20 rd iz'uksa esa lgh mÙkj dk p;u dhft,%
16. oØ y = x3, x-v{k ,oa dksfV;ksa x = – 2, x = 1 ls f?kjs {ks=k dk {ks=kiQy gS%
(A) – 9 (B) 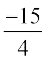 (C)
(C) 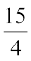 (D)
(D) 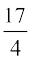
17. oØ y = x |x|, x-v{k ,oa dksfV;ksa x = – 1 rFkk x = 1 ls f?kjs {ks=k dk {ks=kiQy gS%
(A) 0 (B) 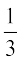 (C)
(C)  (D)
(D) 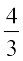
[laosQr : y = x2 ;fn x > 0 ,oa y = – x2 ;fn x < 0]
18. {ks=k y2 ≥ 6x vkSj o`Ùk x2 + y2 = 16 esa lfEefyr {ks=k dk {ks=kiQy gS%
(A) 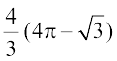 (B)
(B) 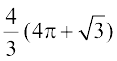 (C)
(C) 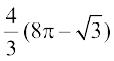 (D)
(D) 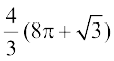
19. y-v{k, y = cos x ,oa y = sin x, 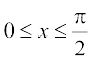 ls f?kjs {ks=k dk {ks=kiQy gS%
ls f?kjs {ks=k dk {ks=kiQy gS%
(A) 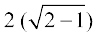 (B)
(B) 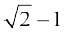 (C)
(C) 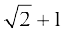 (D)
(D) 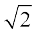
lkjka'k
- oØ y = f(x), x-v{k ,oa js[kkvksa x = a rFkk x = b (b > a) ls f?kjs {ks=k osQ {ks=kiQy dk lw=k :
![eq3]()
- oØ x = φ (y), y-v{k ,oa js[kkvksa y = c, y = d ls f?kjs {ks=k osQ dk lw=k:{ks=kiQy
![eq4]() gSA
gSA - nks oØksa y = f (x), y = g (x) ,oa js[kk,¡ x = a, x = b osQ eè; f?kjs {ks=k dk {ks=kiQy fuEufyf[kr lw=k }kjk ns; gS?
![]() , tgk¡ [a, b] esa f (x) ≥ g (x)
, tgk¡ [a, b] esa f (x) ≥ g (x) - ;fn [a, c] esa f (x) ≥ g (x) ,oa [c, b] esa f (x) ≤ g (x) , a < c < b, rks ge {ks=kiQy dks fuEufyf[kr izdkj ls fy[krs gSa% {ks=kiQy =
![]()
,sfrgkfld i`"BHkwfe
lekdyu xf.kr dk izkjaHk xf.kr osQ izkjafHkd fodkl dky ls gh gqvk gSA ;g izkphu ;wukuh xf.krKksa }kjk fodflr fu%'ks"krk fof/ ij vk/kfjr gSA bl fof/ dk izkjaHk leryh; vko`Qfr;ksa osQ {ks=kiQy vkSj Bksl oLrqvksa osQ vk;ru dh x.kuk ls gqvkA bl rjg ls fu%'ks"krk fof/] lekdyu fof/ dh izkjafHkd fLFkfr osQ :i esa le>h tk ldrh gSA fu%'ks"krk fof/ dk loksZRd`"V fodkl izkjafHkd dky esa ;wMksDl (Eudoxus (440 bZ- iw-) vkSj vk£dfeMht (Archimedes (300 bZ- iw-) osQ dk;ks± ls izkIr gqvk gSA
dyu osQ fl¼kar dk Øec¼ fodkl bZlk osQ i'pkr~ 17oha 'krkCnh esa gqvkA lu~ 1665 esa U;wVu us dyu ij viuk dk;Z izokgu fl¼kar (Theory of fluxion) osQ :i esa izkjaHk fd;kA mUgksaus bl fl¼kar dk iz;ksx oØ osQ fdlh ¯cnq ij Li'khZ vkSj oØrk&f=kT;k Kkr djus esa fd;kA U;wVu us O;qRØe iQyu dh /kj.kk ls ifjp; djk;k vkSj bldks izfrvodyt (vfuf'pr lekdyu) ;k Lif'kZ;ksa dh O;qRØe fof/ (Inverse Method of tangents) dk ukedj.k fd;kA
1684–86, osQ chp esa ySofu”k (Leibnitz) us ,d izi=k ,dVk bjksfMVksfj;e (Acta Eruditorum) esa izdkf'kr fd;k vkSj bls oSQyD;wyl lEeSVksfj;l (Calculous Summatorius) uke fn;k] D;ksafd ;g vuar NksVs {ks=kiQyksa osQ ;ksxiQy ls lacaf/r Fkk] ogha ij mUgksaus bls ;ksxiQy osQ izrhd ‘∫’ }kjk O;Dr fd;kA lu~ 1696 bZ- esa mUgksaus ts- cjukSyh (J.Bernoulli) osQ lq>ko dks ekudj vius izi=k dks dSyD;wyl baVsxzkyh (Calculus Integrali) uke esa ifjofrZr dj fn;kA ;g U;wVu }kjk Lif'kZ;ksa dh O;qRØe fof/ osQ laxr FkkA
U;wVu vkSj ySofu”k nksuksa us iw.kZr% Lora=k ekxZ viuk;k tks ewyr% fHkUu FksA rFkkfi mu nksuksa osQ fl¼karksa osQ laxr izfriQy rRle ik, x,A ySofu”k us fuf'pr lekdyu dh /kj.kk dk iz;ksx fd;kA
;g fuf'pr gS fd mUgksaus gh loZizFke izfrvodyt vkSj fuf'pr lekdyu osQ chp osQ laca/ dks Li"Vr;k ljkgkA
fu"d"kZ ;g gS fd lekdyu xf.kr osQ vk/kjHkwr /kj.kkvksa] fl¼karksa rFkk vodyu xf.kr ls blosQ izkjafHkd laca/ksa dk fodkl ih-Mh- iQekZ] U;wVu] vkSj ySofu”k osQ dk;ks± }kjk 17oha 'krkCnh osQ var esa gqvkA rFkkfi bldk vkSfpR;] lhek dh ladYiuk osQ vk/kj ij 19oha 'krkCnh osQ izkjaHk esa ,-,y-dks'kh (A.L.Cauchy) osQ }kjk fd;k x;kA var esa yh lksiQh (Lie Sophie) dk fuEufyf[kr m¼j.k o.kZuh; gSA "It may be said that the conceptions of differential quotient and integral which in their origin certainly go back to Archimedes were introduced in Science by the investigations of Kepler, Descartes, Cavalieri, Fermat and Wallis... The discovery that differentiation and integration are inverse operations belongs to Newton and Leibnitz".
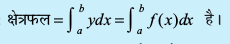
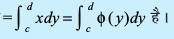
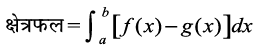 ,
,