Table of Contents
vè;k; 9
vody lehdj.k
(Differential Equations)
He who seeks for methods without having a definite problem in mind seeks for the most part in vain – D. Hilbert
9.1 Hkwfedk (Introduction)
d{kk XI ,oa bl iqLrd osQ vè;k; 5 esa geus ppkZ dh Fkh] fd ,d Lora=k pj osQ lkis{k fdlh iQyu f dk vodyt oSQls Kkr fd;k tkrk gS vFkkZr~ fdlh iQyu f dh ifjHkkf"kr izkar osQ izR;sd x osQ fy,] f′(x) oSQls Kkr fd;k tkrk gSA blosQ vfrfjDr lekdy xf.kr osQ vè;k; esa geus ppkZ dh Fkh] fd ;fn fdlh iQyu f dk vodyt iQyu g gS rks iQyu f oSQls Kkr fd;k tk,A bldks fuEu :i esa lw=kc¼ fd;k tk ldrk gS%

Henri Poincare (1854-1912 )
fdlh fn, gq, iQyu g osQ fy, iQyu f Kkr dhft, rkfd
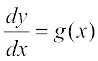 tgk¡ y = f (x) .... (1)
tgk¡ y = f (x) .... (1)
lehdj.k (1) osQ :i okys lehdj.k dks vody lehdj.k dgrs gSaA bldh vkSipkfjd ifjHkk"kk ckn esa nh tk,xhA
vody lehdj.kksa dk mi;ksx eq[; :i ls HkkSfrdh] jlk;u foKku] tho foKku] ekuo foKku] HkwfoKku] vFkZ'kkL=k vkfn fofHkUu {ks=kksa esa fd;k tkrk gSA vr% lHkh vR;k/qfud oSKkfud vUos"k.kksa osQ fy, vody lehdj.kksa osQ xgu vè;;u dh vR;ar vko';drk gSA bl vè;k; esa] ge vody lehdj.k dh oqQN vk/kjHkwr ladYiukvksa] vody lehdj.k osQ O;kid ,oa fof'k"V gy] vody lehdj.k dk fuekZ.k] izFke dksfV ,oa izFke ?kkr osQ vody lehdj.k dks gy djus dh oqQN fof/;k¡ vkSj fofHkUu {ks=kksa esa vody lehdj.kksa osQ oqQN mi;ksxksa osQ ckjs esa vè;;u djsaxsA
9.2 vk/kjHkwr ladYiuk,¡ (Basic Concepts)
ge igys ls gh fuEufyf[kr izdkj osQ lehdj.kksa ls ifjfpr gSa
x2 – 3x + 3 = 0 ... (1)
sin x + cos x = 0 ... (2)
x + y = 7 ... (3)
vkb, fuEufyf[kr lehdj.k ij fopkj djsa
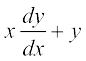 = 0 ... (4)
= 0 ... (4)
ge ikrs gSa fd lehdj.kksa (1)] (2) ,oa (3) esa osQoy Lora=k vkSj@vFkok vkfJr pj (,d ;k vf/d) 'kkfey gSa tc fd lehdj.k (4) esa pj osQ lkFk&lkFk Lora=k pj (x) osQ lkis{k vkfJr pj (y) dk vodyt Hkh 'kkfey gSA bl izdkj dk lehdj.k vody lehdj.k dgykrk gSA
lkekU;r% ,d ,slk lehdj.k] ftlesa Lora=k pj (pjksa) osQ lkis{k vkfJr pj osQ vodyt lfEefyr gksa] vody lehdj.k dgykrk gSA
,d ,slk vody lehdj.k] ftlesa osQoy ,d Lora=k pj osQ lkis{k] vkfJr pj osQ vodyt lfEefyr gksa] lkekU; vody lehdj.k dgykrk gSA mnkgj.kr;k
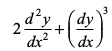 = 0 ... (5)
= 0 ... (5)
,d lkekU; vody lehdj.k gSA
fu%lUnsg ,sls Hkh vody lehdj.k gksrs gSa ftuesa ,d ls vf/d Lora=k pjksa osQ lkis{k vodyt 'kkfey gksrs gSa] bl izdkj osQ vody lehdj.k vkaf'kd vody lehdj.k dgykrs gSaA ysfdu bl Lrj ij ge vius vki dks osQoy lkekU; vody lehdj.kksa osQ vè;;u rd lhfer j[ksaxsA blls vkxs ge lkekU; vody lehdj.k osQ fy, vody lehdj.k 'kCn dk gh mi;ksx djsaxsA
fVIi.kh
1. ge vodytksa osQ fy, fuEufyf[kr laosQrksa osQ mi;ksx dks ojh;rk nsaxs
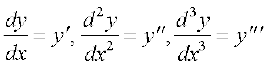
2. mPp dksfV okys vodytksa osQ fy,] brus vf/d MS'kksa (dashes) dks mPp izR;; osQ :i esa iz;qDr djuk vlqfo/ktud gksxk blfy, nosa dksfV okys vodyt 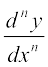 osQ fy, ge laosQr yn dk mi;ksx djsaxsA
osQ fy, ge laosQr yn dk mi;ksx djsaxsA
9.2.1 vody lehdj.k dh dksfV (Order of a differential equation)
fdlh vody lehdj.k dh dksfV ml vody lehdj.k eas lfEefyr Lora=k pj osQ lkis{k vkfJr pj osQ mPpre dksfV osQ vodyt dh dksfV }kjk ifjHkkf"kr gksrh gSA
fuEufyf[kr vody lehdj.kksa ij fopkj dhft,%
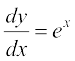 ... (6)
... (6)
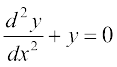 ... (7)
... (7)
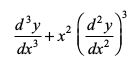 ...(8)
...(8)
lehdj.k (6)] (7) ,oa (8) esa Øe'k% izFke] f}rh; ,oa r`rh; dksfV osQ mPpre vodyt mifLFkr gSa blfy, bu lehdj.kksa dh dksfV Øe'k% 1] 2 ,oa 3 gSA
9.2.2 vody lehdj.k dh ?kkr (Degree of a differential equation)
fdlh vody lehdj.k dh ?kkr dk vè;;u djus osQ fy, eq[; ¯cnq ;g gS fd og vody lehdj.k] vodytksa y′, y″, y″′ bR;kfn esa cgqin lehdj.k gksuk pkfg,A fuEufyf[kr lehdj.kksa ij fopkj dhft,%
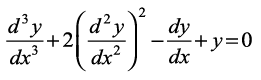 ... (9)
... (9)
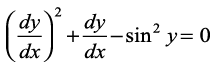 ... (10)
... (10)
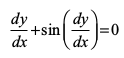 ... (11)
... (11)
ge izsf{kr djrs gSa fd lehdj.k (9) y″′, y″ ,oaa y′ esa cgqin lehdj.k gSA lehdj.k (10) y′ esa cgqin lehdj.k gS (;|fi ;g y esa cgqin ugha gS) bl izdkj osQ vody lehdj.kksa dh ?kkr dks ifjHkkf"kr fd;k tk ldrk gSA ijarq lehdj.k (11) y′ esa cgqin lehdj.k ugha gS vkSj bl izdkj osQ vody lehdj.k dh ?kkr dks ifjHkkf"kr ugha fd;k tk ldrk gSA
;fn ,d vody lehdj.k vodytksa dk cgqin lehdj.k gS rks ml vody lehdj.k dh ?kkr ls gekjk rkRi;Z gS ml vody lehdj.k esa mifLFkr mPpre dksfV osQ vodyt dh mPpre ?kkr (/ukRed iw.kk±d)
mijksDr ifjHkk"kk osQ lanHkZ esa ge izsf{kr dj ldrs gSa fd lehdj.kksa (6)] (7)] (8) ,oa (9) esa ls izR;sd dh ?kkr 1 gS] lehdj.k (10) dh ?kkr 2 gS tc fd vody lehdj.k (11) dh ?kkr ifjHkkf"kr ugha gSA
fVIi.kh fdlh vody lehdj.k dh dksfV ,oa ?kkr (;fn ifjHkkf"kr gks) ges'kk
/ukRed iw.kk±d gksrs gSaA
mnkgj.k 1 fuEufyf[kr vody lehdj.kksa esa ls izR;sd dh dksfV ,oa ?kkr (;fn ifjHkkf"kr gks) Kkr dhft,%
(i) 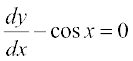 (ii)
(ii) 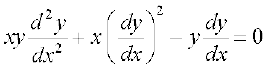
(iii) 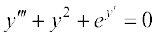
gy
(i) bl vody lehdj.k esa mifLFkr mPpre dksfV vodyt 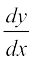 gSA blfy, bldh dksfV 1 gSA ;g y′ esa cgqin lehdj.k gS ,oa
gSA blfy, bldh dksfV 1 gSA ;g y′ esa cgqin lehdj.k gS ,oa 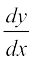 dh vf/dre ?kkrkad 1 gS] blfy, bl vody lehdj.k dh ?kkr 1 gSA
dh vf/dre ?kkrkad 1 gS] blfy, bl vody lehdj.k dh ?kkr 1 gSA
(ii) bl vody lehdj.k esa mifLFkr mPpre dksfV vodyt 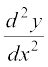 gS A blfy, bldh dksfV 2 gSA ;g vody lehdj.k
gS A blfy, bldh dksfV 2 gSA ;g vody lehdj.k 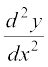 ,oa
,oa 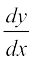 esa cgqin lehdj.k gS vkSj
esa cgqin lehdj.k gS vkSj 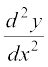 dh vf/dre ?kkrkad 1 gS] blfy, bl vody lehdj.k dh ?kkr 1 gSA
dh vf/dre ?kkrkad 1 gS] blfy, bl vody lehdj.k dh ?kkr 1 gSA
(iii) bl vody lehdj.k esa mifLFkr mPpre dksfV vodyt 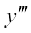 gSA blfy, bldh dksfV 3 gSA bl lehdj.k dk ck;k¡ i{k vodytksa esa cgqin ugha gS blfy, bldh ?kkr ifjHkkf"kr ugha gSA
gSA blfy, bldh dksfV 3 gSA bl lehdj.k dk ck;k¡ i{k vodytksa esa cgqin ugha gS blfy, bldh ?kkr ifjHkkf"kr ugha gSA
iz'ukoyh 9-1
1 ls 10 rd osQ iz'uksa esa izR;sd vody lehdj.k dh dksfV ,oa ?kkr (;fn ifjHkkf"kr gks) Kkr dhft,A
1. 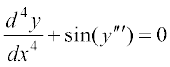 2. y′ + 5y = 0 3.
2. y′ + 5y = 0 3. 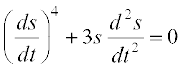
4. 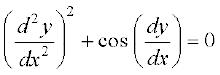 5.
5. 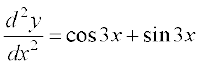
6. 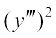 + (y″)3 + (y′)4 + y5 = 0 7.
+ (y″)3 + (y′)4 + y5 = 0 7. 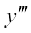 + 2y″ + y′ = 0
+ 2y″ + y′ = 0
8. y′ + y = ex 9. y″ + (y′)2 + 2y = 0 10. y″ + 2y′ + sin y = 0
11. vody lehdj.k
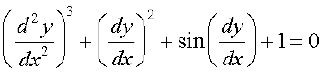 dh ?kkr gS%
dh ?kkr gS%
(A) 3 (B) 2 (C) 1 (D) ifjHkkf"kr ugha gS
12. vody lehdj.k 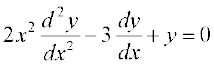 dh dksfV gS%
dh dksfV gS%
(A) 2 (B) 1 (C) 0 (D) ifjHkkf"kr ugha gS
9.3. vody lehdj.k dk O;kid ,oa fof'k"V gy (General and Particular Solutions of a Differential Equation)
fiNyh d{kkvksa esa geus fuEufyf[kr izdkj osQ lehdj.kksa dks gy fd;k gS%
x2 + 1 = 0 ... (1)
sin2 x – cos x = 0 ... (2)
lehdj.kksa (1) rFkk (2) dk gy ,d ,slh okLrfod vFkok lfEeJ la[;k gS tks fn, gq, lehdj.k dks larq"V djrh gS vFkkZr~ tc bl la[;k dks lehdj.k esa vKkr x osQ LFkku ij izfrLFkkfir dj fn;k tkrk gS rks nk;k¡ i{k vkSj ck;k¡ i{k vkil esa cjkcj gks tkrs gaSA
vc vody lehdj.k 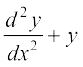 = 0 ... (3)
= 0 ... (3)
ij fopkj djrs gSaA
izFke nks lehdj.kksa osQ foijhr bl vody lehdj.k dk gy ,d ,slk iQyu φ gS tks bl lehdj.k dks larq"V djsxk vFkkZr~ tc bl iQyu φ dks vody lehdj.k esa vKkr y (vkfJr pj) osQ LFkku ij izfrLFkkfir dj fn;k tkrk gS rks ck;k¡ i{k vkSj nk;k¡ i{k cjkcj gks tkrs gSaA
oØ y = φ (x) vody lehdj.k dk gy oØ (lekdyu oØ) dgykrk gSA fuEufyf[kr iQyu ij fopkj dhft,
y = φ (x) = a sin (x + b) ... (4)
tgk¡ a, b ∈ R. ;fn bl iQyu vkSj blosQ vodytksa dks lehdj.k (3) esa izfrLFkkfir dj fn;k tk, rks ck;k¡ i{k vkSj nk;k¡ i{k cjkcj gks tkrs gSaA blfy, ;g iQyu vody lehdj.k (3) dk gy gSA
eku yhft, fd a vkSj b dks oqQN fof'k"V eku a = 2 ,oa 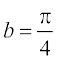 ns fn, tkrs gSa rks gesa fuEufyf[kr iQyu izkIr gksrk gS%
ns fn, tkrs gSa rks gesa fuEufyf[kr iQyu izkIr gksrk gS%
y = φ1(x) = 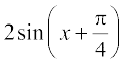 ... (5)
... (5)
;fn bl iQyu vkSj blosQ vodytksa dks lehdj.k (3) esa izfrLFkkfir dj fn;k tk, rks iqu% ck;k¡ i{k vkSj nk;k¡ i{k cjkcj gks tkrs gaSA blfy, φ1 Hkh lehdj.k (3) dk ,d gy gSA
iQyu φ esa nks LosPN vpj (izkpy) a, b lfEefyr gSa rFkk ;g iQyu fn, gq, vody lehdj.k dk O;kid gy dgykrk gSA tcfd iQyu φ1 esa dksbZ Hkh LosPN vpj lfEefyr ugha gS ysfdu izkpyksa a rFkk b osQ fof'k"V eku mifLFkr gSa vkSj blfy, bldks vody lehdj.k dk fof'k"V gy dgk tkrk gSA
,slk gy] ftlesa LosPN vpj mifLFkr gks vody lehdj.k dk O;kid gy dgykrk gSA
,slk gy] tks LosPN vpjkas ls eqDr gS vFkkZr~ O;kid gy esa LosPN vpjksa dks fof'k"V eku nsus ij izkIr gy] vody lehdj.k dk fof'k"V gy dgykrk gSA
mnkgj.k 2 lR;kfir dhft, fd iQyu y = e–3x, vody lehdj.k 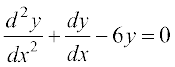 dk ,d gy gSA
dk ,d gy gSA
gy fn;k gqvk iQyu y = e–3x gSA blosQ nksuksa i{kksa dk x osQ lkis{k vodyu djus ij ge izkIr djrs gS%
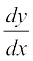 = 3e–3x ... (1)
= 3e–3x ... (1)
vc lehdj.k (1) dk x osQ lkis{k iqu% vodyu djus ij ge ns[krs gSa fd
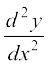 = 9e–3x
= 9e–3x
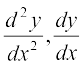 vkSj y dk eku] fn, x, vody lehdj.k esa izfrLFkkfir djus ij ij ge ikrs gSa fd ck;k¡ i{k = 9 e–3x + (–3e–3x) – 6.e–3x = 9 e–3x – 9 e–3x = 0 = nk;k¡ i{k
vkSj y dk eku] fn, x, vody lehdj.k esa izfrLFkkfir djus ij ij ge ikrs gSa fd ck;k¡ i{k = 9 e–3x + (–3e–3x) – 6.e–3x = 9 e–3x – 9 e–3x = 0 = nk;k¡ i{k
blfy, fn;k gqvk iQyu fn, gq, vody lehdj.k dk ,d gy gSA
mnkgkj.k 3 lR;kfir dhft, fd iQyu y = a cos x + b sin x, ftlesa a, b ∈ R, vody lehdj.k 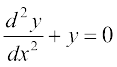 dk gy gSA
dk gy gSA
gy fn;k gqvk iQyu gS
y = a cos x + b sin x ... (1)
lehdj.k (1) osQ nksuksa i{kksa dk x, osQ lkis{k mÙkjksÙkj vodyu djus ij ge ns[krs gaS%
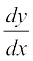 = –a sin x + b cos x
= –a sin x + b cos x
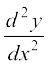 = – a cos x – b sin x
= – a cos x – b sin x
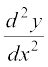 ,oa y dk eku fn, gq, vody lehdj.k esa izfrLFkkfir djus ij izkIr djrs gSa%
,oa y dk eku fn, gq, vody lehdj.k esa izfrLFkkfir djus ij izkIr djrs gSa%
ck;k¡ i{k = (– a cos x – b sin x) + (a cos x + b sin x) = 0 = nk;k¡ i{k
blfy, fn;k gqvk iQyu] fn, gq, vody lehdj.k dk gy gSA
iz'ukoyh 9-2
1 ls 10 rd izR;sd iz'u esa lR;kfir dhft, fd fn;k gqvk iQyu (Li"V vFkok vLi"V) laxr vody lehdj.k dk gy gS%
1. y = ex + 1 : y″ – y′ = 0
2. y = x2 + 2x + C : y′ – 2x – 2 = 0
3. y = cos x + C : y′ + sin x = 0
4. y = 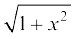 : y′ =
: y′ = 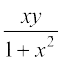
5. y = Ax : xy′ = y (x ≠ 0)
6. y = x sin x : xy′ = y + x 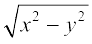 (x ≠ 0 vkSj x > y vFkok x < – y)
(x ≠ 0 vkSj x > y vFkok x < – y)
7. xy = log y + C : y′ = 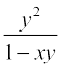 (xy ≠ 1)
(xy ≠ 1)
8. y – cos y = x : (y sin y + cos y + x) y′ = y
9. x + y = tan–1y : y2 y′ + y2 + 1 = 0
10. y = 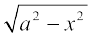 x ∈ (– a, a) : x + y
x ∈ (– a, a) : x + y 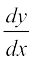 = 0 (y ≠ 0)
= 0 (y ≠ 0)
11. pkj dksfV okys fdlh vody lehdj.k osQ O;kid gy esa mifLFkr LosPN vpjksa dh la[;k gS%
(A) 0 (B) 2 (C) 3 (D) 4
12. rhu dksfV okys fdlh vody lehdj.k osQ fof'k"V gy esa mifLFkr LosPN vpjksa dh la[;k gS%
(A) 3 (B) 2 (C) 1 (D) 0
9.4. fn, gq, O;kid gy okys vody lehdj.k dk fuekZ.k (Formation of a Differential Equation whose Solution is Given)
ge tkurs gSa fd lehdj.k
x2 + y2 + 2x – 4y + 4 = 0 ... (1)
,d ,sls o`r dks fu:fir djrk gS ftldk osaQnz (&1] 2) gS vkSj f=kT;k 1 bdkbZ gSA
lehdj.k (1) dk x, osQ lkis{k vodyu djus ij izkIr djrs gSa
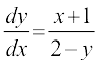 , (y ≠ 2) ... (2)
, (y ≠ 2) ... (2)
;g ,d vody lehdj.k gSA vki ckn esa ns[ksaxs fd (vuqHkkx 9-5-1 dk mnkgj.k 9 nsf[k,) fd ;g lehdj.k o`Ùkksa osQ ,d oqQy dks fu:fir djrk gS vkSj ml oqQy dk ,d lnL; lehdj.k (1) esa fn;k gqvk o`r gSA vkb, fuEufyf[kr lehdj.k ij fopkj djsa%
x2 + y2 = r2 ... (3)
r, dks fofHkUu eku nsus ij gesa oqQy osQ fHkUu lnL; izkIr gksrs gSa mnkgj.kr% x2 + y2 = 1, x2 + y2 = 4, x2 + y2 = 9 bR;kfn (vko`Qfr 9-1 nsf[k,)A bl izdkj lehdj.k (3) ,d ,sls laosaQnzh o`Ùkksa osQ oqQy dks fu:fir djrk gS ftudk osaQnz ewy ¯cnq gS vkSj ftudh f=kT;k,¡ fHkUu gSaA

vko`Qfr 9-1
gekjh #fp bl oqQy osQ izR;sd lnL; }kjk larq"V fd, tkus okyk vody lehdj.k Kkr djus esa gSaA ;g lehdj.k r ls eqDr gksuk pkfg, D;ksafd oqQy osQ fofHkUu lnL;ksa osQ fy, r dk eku fHkUu gSA lehdj.k (3) dk x osQ lkis{k vodyu djus ij ;g lehdj.k izkIr fd;k tkrk gSA vFkkZr~
2x + 2y 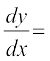 0 vFkok x + y
0 vFkok x + y 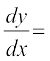 0 ... (4)
0 ... (4)
;g vody lehdj.k] lehdj.k (3) }kjk fu:fir losaQnzh o`Ùkksa osQ oqQy dks fu:fir djrk gSA
vkb, fiQj ls fuEufyf[kr lehdj.k ij fopkj djsa%
y = mx + c ... (5)
izkpyksa m rFkk c, osQ fofHkUu ekuksa ls gesa oqQy osQ fofHkUu lnL; izkIr gksrs gSa mnkgj.kr;k
y = x (m = 1, c = 0)
y = 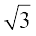 x (m =
x (m = 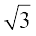 , c = 0)
, c = 0)
y = x + 1 (m = 1, c = 1)
y = – x (m = – 1, c = 0)
y = – x – 1 (m = – 1, c = – 1)
bR;kfn (vko`Qfr 9-2 nsf[k,)A
bl izdkj lehdj.k (5) ljy js[kkvksa osQ oqQy dks fu:fir djrk gS ftlesa m, c izkpy gSA
vc gekjh #fp bl oqQy osQ izR;sd lnL; }kjk larq"V fd, tkus okyk vody lehdj.k Kkr djus esa gSA blosQ vfrfjDr og lehdj.k m rFkk c ls eqDr gksuk pkfg, D;ksafd oqQy osQ fofHkUu lnL;ksa osQ fy, m rFkk c dk eku fHkUu gSA ;g vody lehdj.k] lehdj.k (5) dk x osQ lkis{k Øekuqlkj nks ckj vodyu djus ij izkIr gksrk gS vFkkZr~
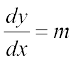 rFkk
rFkk 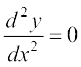 ... (6)
... (6)
lehdj.k (6)] lehdj.k (5) }kjk fn, gq, ljy js[kkvksa osQ oqQy dks fu:fir djrk gSA
fVIi.kh lehdj.k (3) rFkk (5) Øe'k% lehdj.k (4) ,oa (6) osQ O;kid gy gSaA
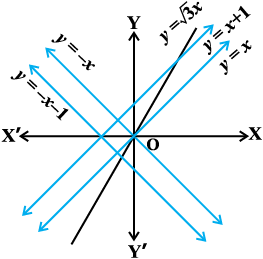
vko`Qfr 9-2
9.4.1 fn, gq, oØkas osQ oqQy dks fu:fir djus okys vody lehdj.k osQ fuekZ.k dh izfØ;k (Procedure to form a Differential Equation that will represent a given Family of curves)
(a) ;fn fn, gq, oØksa dk oqQy F1 osQoy ,d izkpy ij fuHkZj djrk gS rks bls fuEufyf[kr :i okys lehdj.k }kjk fu:fir fd;k tkrk gS%
F1 (x, y, a) = 0 ... (1)
mnkgj.kr%] ijoy;ksa y2 = ax dk oqQy f(x, y, a) : y2 = ax osQ :i okys lehdj.k }kjk fu:fir fd;k tk ldrk gSA
lehdj.k (1) dk x osQ lkis{k vodyu djus ij gesa y′, y, x, ,oa a dks lfEefyr djus okyk ,d lehdj.k fuEufyf[kr :i esa izkIr gksrk gS%
g (x, y, y′, a) = 0 ... (2)
lehdj.k (1) rFkk (2) ls a dks foyqIr djus ij gesa vko';d vody lehdj.k fuEufyf[kr :i esa izkIr gksrk gS%
F (x, y, y′) = 0 ... (3)
(b) ;fn fn, gq, oØksa dk oqQy F2 izkpyksa a, rFkk b ij fuHkZj djrk gS rks bls fuEufyf[kr :i okys lehdj.k }kjk fu:fir fd;k tkrk gS%
F2 (x, y, a, b) = 0 ... (4)
lehdj.k (4) dk x osQ lkis{k vodyu djus ij gesa y′, x, y, a, b dks lfEefyr djus okyk ,d lehdj.k fuEufyf[kr :i esa izkIr gksrk gS%
g (x, y, y′, a, b) = 0 ... (5)
ijarq nks lehdj.kksa dh lgk;rk ls nks izkpyksa dks foyqIr djuk lEHko ugha gS blfy, gesa ,d rhljs lehdj.k dh vko';drk gSA ;g lehdj.k] lehdj.k (5) dk x osQ lkis{k vodyu djus ij fuEufyf[kr :i esa izkIr fd;k tkrk gS%
h (x, y, y′, y″, a, b) = 0 ... (6)
lehdj.k (4)] (5) ,oa (6) ls a rFkk b dks foyqIr djus ij gesa vko';d vody lehdj.k fuEufyf[kr :i esa izkIr gksrk gS%
F (x, y, y′, y″) = 0 ... (7)
fVIi.kh fdlh oØ oqQy dks fu:fir djus okys vody lehdj.k dh dksfV mruh gh gksrh gS ftrus ml oØ oqQy osQ laxr lehdj.k esa LosPN vpj gksrs gSaA
mnkgj.k 4 oØksa osQ oqQy y = mx dks fu:fir djus okys vody lehdj.k dks Kkr dhft, tcfd m ,d LosPN vpj gSA
gy fn;k gqvk gS fd
y = mx ... (1)
lehdj.k (1) osQ nksuks i{kksa dk x osQ lkis{k vodyu djus ij ge izkIr djrs gSaA
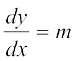
m dk eku lehdj.k (1) esa izfrLFkkfir djus ij gesa 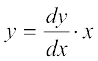 vFkok
vFkok 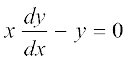 izkIr gksrk gSA ;g izkpy m ls eqDr gS vkSj blfy, ;g vHkh"V vody lehdj.k gSA
izkIr gksrk gSA ;g izkpy m ls eqDr gS vkSj blfy, ;g vHkh"V vody lehdj.k gSA
mnkgj.k 5 oØksa osQ oqQy y = a sin (x + b), ftlesa a, b LosPN vpj gSa] dks fu:fir djus okys vody lehdj.k dks Kkr dhft,A
gy fn;k gqvk gS fd y = a sin (x + b) ... (1)
lehdj.k (1) osQ nksuksa i{kksa dk x osQ lkis{k mÙkjksÙkj vodyu djus ij ge izkIr djrs gS%
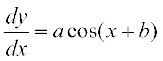 ... (2)
... (2)
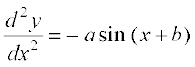 ... (3)
... (3)
lehdj.k (1)] (2) rFkk (3) ls a rFkk b dks foyqIr djus ij ge izkIr djrs gSaA
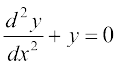 ... (4)
... (4)
lehdj.k (4) LosPN vpjksa a rFkk b ls eqDr gS vkSj blfy, ;g vHkh"V vody lehdj.k gSA
mnkgj.k 6 ,sls nh?kZo`Ùkksa osQ oqQy dks fu:fir djus okyk vody lehdj.k Kkr dhft, ftudh ukfHk;k¡ x-v{k ij gSa rFkk ftudk osaQnz ewy ¯cnq gSA

vko`Qfr 9-3
gy ge tkurs gSa fd dfFkr nh?kZo`Ùkksa osQ oqQy dk lehdj.k fuEufyf[kr izdkj dk gksrk gS (vko`Qfr 9-3 nsf[k,)
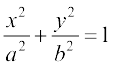 ... (1)
... (1)
lehdj.k (1) dk x osQ lkis{k vodyu djus ij gesa 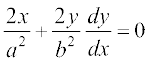 izkIr gksrk gSA
izkIr gksrk gSA
vFkok 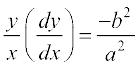 ... (2)
... (2)
lehdj.k (2) osQ nksuksa i{kksa dk x osQ lkis{k vodyu djus ij gesa izkIr gksrk gS% 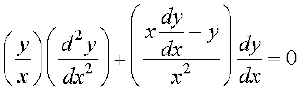
vFkok 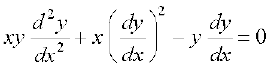 ... (3)
... (3)
lehdj.k (3) vHkh"V vody lehdj.k gSA
mnkgj.k 7 x&v{k dks ewy ¯cnq ij Li'kZ djus okys o`Ùkksa osQ oqQy dk vody lehdj.k Kkr dhft,A
gy eku yhft,] x&v{k dks ewy ¯cnq ij Li'kZ djus okys o`Ùkksa osQ oqQy dks C ls fufnZ"V fd;k tkrk gSA (0, a) ml oqQy osQ fdlh lnL; osQ osaQnz ¯cnq osQ funsZ'kkad gSa (vko`Qfr 9-4 nsf[k,)A blfy, oqQy C dk lehdj.k gS%


vko`Qfr 9-4
ftlesa a ,d LosPN vpj gSA lehdj.k (1) osQ nksuksa i{kksa dk x osQ lkis{k vodyu djus ij izkIr djrs gSa%
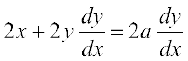
vFkok 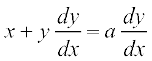
vFkok 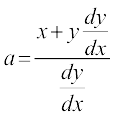 ... (2)
... (2)
lehdj.k (2) ls a dk eku lehdj.k (1) esa j[kus ij izkIr djrs gSa%
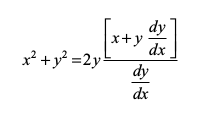
vFkok 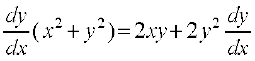
vFkok 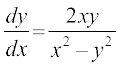
;g fn, gq, o`Ùkksa osQ oqQy dk vHkh"V vody lehdj.k gSA
mnkgj.k 8 ,sls ijoy;ksa osQ oqQy dks fu:fir djus okyk vody lehdj.k Kkr dhft, ftudk 'kh"kZ ewy ¯cnq ij gS rFkk ftudk v{k /ukRed x-v{k dh fn'kk esa gSA
gy eku yhft, fd mijksDr pfpZr ijoy;ksa osQ oqQy dks P ls fufnZ"V fd;k tkrk gS vkSj ml oqQy osQ fdlh lnL; dh ukfHk (a, 0) ij gS ftlesa a ,d /ukRed LosPN vpj gS (vko`Qfr 9-5 nsf[k,)A blfy, oqQy P dk lehdj.k gS%
y2 = 4ax ... (1)
lehdj.k (1) osQ nksuksa i{kksa dk x osQ lkis{k vodyu djus ij ge ikrs gSa%
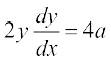 ... (2)
... (2)
lehdj.k (2) ls 4a dk eku lehdj.k (1) esa j[kus ij ge ikrs gSa%
s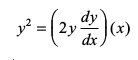
vFkok 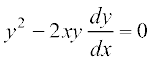 ... (3)
... (3)
lehdj.k (3) fn, gq, ijoy;ksa osQ oqQy dk vody lehdj.k gSA

vko`Qfr 9-5
iz'ukoyh 9-3
1 ls 5 rd izR;sd iz'u esa] LosPN vpjksa a rFkk b dks foyqIr djrs gq, fn, gq, oØksa osQ oqQy dks fu:fir djus okyk vody lehdj.k Kkr dhft,A
1. 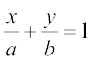 2. y2 = a (b2 – x2) 3. y = a e3x + b e– 2x
2. y2 = a (b2 – x2) 3. y = a e3x + b e– 2x
4. y = e2x (a + bx) 5. y = ex (a cos x + b sin x)
6. y-v{k dks ewy ¯cnq ij Li'kZ djus okys o`Ùkksa osQ oqQy dk vody lehdj.k Kkr dhft,A
7. ,sls ijoy;ksa osQ oqQy dk vody lehdj.k fufeZr dhft, ftudk 'kh"kZ ewy ¯cnq ij gS vkSj ftudk v{k /ukRed y-v{k dh fn'kk esa gSA
8. ,sls nh?kZo`Ùkksa osQ oqQy dk vody lehdj.k Kkr dhft, ftudh ukfHk;k¡ y-v{k ij gSa rFkk ftudk osaQnz ewy ¯cnq gSA
9. ,sls vfrijoy;ksa osQ oqQy dk vody lehdj.k Kkr dhft, ftudh ukfHk;k¡ x-v{k ij gSa rFkk ftudk osaQnz ewy ¯cnq gSA
10. ,sls o`Ùkksa osQ oqQy dk vody lehdj.k Kkr dhft, ftudk osaQnz y-v{k ij gS vkSj ftudh f=kT;k 3 bdkbZ gSA
11. fuEufyf[kr vody lehdj.kksa esa ls fdl lehdj.k dk O;kid gy y = c1 ex + c2 e–x gS\
(A) 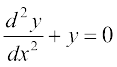 (B)
(B) 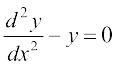 (C)
(C) 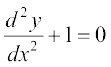 (D)
(D) 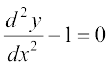
12. fuEufyf[kr lehdj.kksa esa ls fdl lehdj.k dk ,d fof'k"V gy y = x gS\
(A) 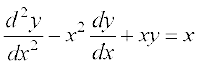 (B)
(B) 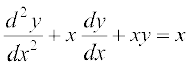
(C) 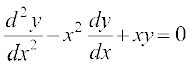 (D)
(D) 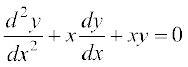
9.5. izFke dksfV ,oa izFke ?kkr osQ vody lehdj.kksa dks gy djus dh fof/;k¡ (Methods of Solving First order, First Degree Differential Equations)
bl ifjPNsn esa ge izFke dksfV ,oa izFke ?kkr osQ vody lehdj.kksa dks gy djus dh rhu
fof/;ksa dh ppkZ djsaxsA
9.5.1 i`FkDdj.kh; pj okys vody lehdj.k (Differential equations with variables separable)
izFke dksfV ,oa izFke ?kkr dk vody lehdj.k fuEufyf[kr :i dk gksrk gS%
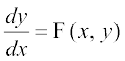 ... (1)
... (1)
;fn F (x, y) dks xq.kuiQy g (x), h(y) osQ :i esa vfHkO;Dr fd;k tk ldrk gS tgk¡ g(x), x dk iQyu gS vkSj h(y), y dk ,d iQyu gS rks lehdj.k (1) i`FkDdj.kh; pj okyk lehdj.k dgykrk gSA ,slk gksus ij lehdj.k (1) dks fuEufyf[kr :i esa fy[kk tk ldrk gS%
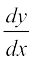 = h (y) . g (x) ... (2)
= h (y) . g (x) ... (2)
;fn h (y) ≠ 0, rks pjksa dks i`Fko~Q djrs gq, lehdj.k (2) dks
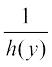 dy = g (x) dx ... (3)
dy = g (x) dx ... (3)
osQ :i esa fy[kk tk ldrk gSA lehdj.k (3) osQ nksuksa i{kksa dk lekdyu djus ij ge izkIr djrs gSa%
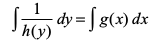 ... (4)
... (4)
bl izdkj lehdj.k (4)] fn, gq, vody lehdj.k dk gy fuEufyf[kr :i esa iznku djrk gS%
H(y) = G(x) + C ... (5)
;gk¡ H (y) ,oa G (x) Øe'k% 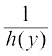 ,oa g (x) osQ izfrvodyt gSa vkSj C LosPN vpj gSA
,oa g (x) osQ izfrvodyt gSa vkSj C LosPN vpj gSA
mnkgj.k 9 vody lehdj.k 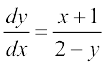 , (y ≠ 2) dk O;kid gy Kkr dhft,A
, (y ≠ 2) dk O;kid gy Kkr dhft,A
gy fn;k x;k gS fd
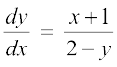 (y ≠ 2) ... (1)
(y ≠ 2) ... (1)
lehdj.k (1) esa pjksa dks i`Fko~Q djus ij ge izkIr djrs gSa%
(2 – y) dy = (x + 1) dx ... (2)
lehdj.k (2) osQ nksuksa i{kksa dk lekdyu djus ij ge izkIr djrs gSa%
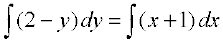
vFkok 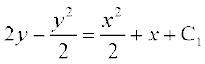
vFkok x2 + y2 + 2x – 4y + 2 C1 = 0
vFkok x2 + y2 + 2x – 4y + C = 0 ... (3)
tgk¡ C = 2C1
lehdj.k (3) vody lehdj.k (1) dk O;kid gy gSA
mnkgj.k 10 vody lehdj.k 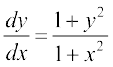 dk O;kid gy Kkr dhft,A
dk O;kid gy Kkr dhft,A
gy pw¡fd 1 + y2 ≠ 0, blfy, pjksa dks i`Fko~Q djrs gq, fn;k gqvk vody lehdj.k fuEufyf[kr :i esa fy[kk tk ldrk gS%
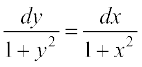 ... (1)
... (1)
lehdj.k (1) osQ nksuksa i{kksa dk lekdyu djrs gq, ge ikrs gSa%
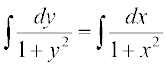
vFkok tan–1 y = tan–1x + C
;g lehdj.k (1) dk O;kid gy gSA
mnkgj.k 11 vody lehdj.k 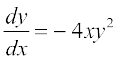 dk fof'k"V gy Kkr dhft,] ;fn y = 1 tc
dk fof'k"V gy Kkr dhft,] ;fn y = 1 tc
x = 0 gks
gy ;fn y ≠ 0, fn;k gqvk vody lehdj.k fuEufyf[kr :i esa fy[kk tk ldrk gS%
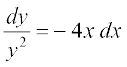 ... (1)
... (1)
lehdj.k (1) osQ nksuksa i{kksa dk lekdyu djus ij ge ikrs gSa%
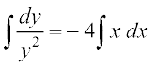
vFkok 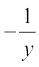 = – 2x2 + C
= – 2x2 + C
vFkok 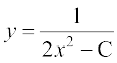 ... (2)
... (2)
lehdj.k (2) esa y = 1 vkSj x = 0 izfrLFkkfir djus ij gesa C = – 1 izkIr gksrk gSA
C dk eku lehdj.k (2) esa izfrLFkkfir djus ij fn, gq, vody lehdj.k dk fof'k"V gy 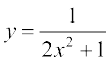 izkIr gksrk gSA
izkIr gksrk gSA
mnkgj.k 12 ¯cnq (1] 1) ls xqtjus okys ,d ,sls oØ dk lehdj.k dhft, ftldk vody lehdj.k x *dy = (2x2 + 1) *dx (x ≠ 0) gSA
gy fn, gq, vody lehdj.k dks fuEufyf[kr :i es vfHkO;Dr fd;k tk ldrk gS%
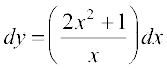
vFkok 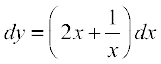 ... (1)
... (1)
lehdj.k (1) osQ nksuksa i{kksa dk lekdyu djus ij ge izkIr djrs gSa%
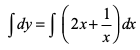
vFkok 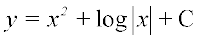 ... (2)
... (2)
lehdj.k (2) fn, gq, vody lehdj.k osQ gy oØksa osQ oqQy dks fu:fir djrk gS ijarq ge bl oqQy osQ ,d ,sls fof'k"V lnL; dk lehdj.k Kkr djuk pkgrs gSa tks ¯cnq (1] 1) ls xqtjrk gksA
* yScuht }kjk iznÙk laosQr 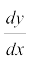 vR;ar yphyk gS] rFkk cgqr lh x.kuk ,oa vkSipkfjd :ikarj.kksa esa iz;qDr gksrk gS] tgk¡ ge dx vkSj dy dks lk/kj.k la[;kvksa dh rjg O;ogkj esa ykrs gSaA dx vkSj dy dks i`Fko~Q&i`Fko~Q lÙkk ekudj ge cgqr lh x.kukvksa dh lqLi"kV O;k[;k dj ldrs gSaA lanHkZ% Introduction to calculus and Analysis, volume-I page 172, By Richard Courant, Fritz John Spinger — Verlog New York.
vR;ar yphyk gS] rFkk cgqr lh x.kuk ,oa vkSipkfjd :ikarj.kksa esa iz;qDr gksrk gS] tgk¡ ge dx vkSj dy dks lk/kj.k la[;kvksa dh rjg O;ogkj esa ykrs gSaA dx vkSj dy dks i`Fko~Q&i`Fko~Q lÙkk ekudj ge cgqr lh x.kukvksa dh lqLi"kV O;k[;k dj ldrs gSaA lanHkZ% Introduction to calculus and Analysis, volume-I page 172, By Richard Courant, Fritz John Spinger — Verlog New York.
blfy, lehdj.k (2) esa x = 1, y = 1 izfrLFkkfir djus ij gesa C = 0 izkIr gksrk gSA C dk eku lehdj.k (2) esa izfrLFkkfir djus ij gesa vHkh"V oØ dk lehdj.k y = x2 + log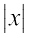 osQ :i esa izkIr gksrk gSA
osQ :i esa izkIr gksrk gSA
mnkgj.k 13 ¯cnq (–2, 3), ls xqtjus okys ,sls oØ dk lehdj.k Kkr dhft, ftlosQ fdlh ¯cnq (x, y) ij Li'kZ js[kk dh izo.krk 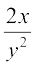 gSA
gSA
gy ge tkurs gSa fd fdlh oØ dh Li'kZ js[kk dh izo.krk 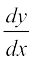 osQ cjkcj gksrh gSA blfy,
osQ cjkcj gksrh gSA blfy,
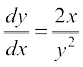 ... (1)
... (1)
pjksa dks i`Fko~Q djrs gq, lehdj.k (1) dks fuEufyf[kr :i esa fy[kk tk ldrk gS%
y2 dy = 2x dx ... (2)
lehdj.k (2) osQ nksuksa i{kksa dk lekdyu djus ij ge izkIr djrs gSa%
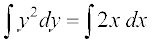
vFkok 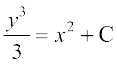 ... (3)
... (3)
lehdj.k (3) esa x = –2, y = 3 izfrLFkkfir djus ij gesa C = 5 izkIr gksrk gSA
C dk eku lehdj.k (3) esa izfrLFkkfir djus ij gesa vHkh"V oØ dk lehdj.k 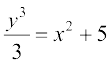 vFkok
vFkok 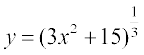
osQ :i esa izkIr gksrk gSA
mnkgj.k 14 fdlh cSad esa ewy/u dh o`f¼ 5% okf"kZd dh nj ls gksrh gSA fdrus o"kks± esa Rs 1000 dh jkf'k nqxquh gks tk,xh\
gy eku yhft, fdlh le; t ij ewy/u P gSA nh gqbZ leL;k osQ vuqlkj
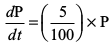
vFkok 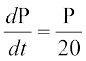 ... (1)
... (1)
lehdj.k (1) esa pjksa dks i`Fko~Q djus ij] ge izkIr djrs gSa%
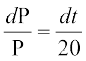 ... (2)
... (2)
lehdj.k (2) osQ nksuksa i{kksa dk lekdyu djus ij ge izkIr djrs gSa%
log P = 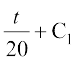
vFkok 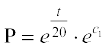
vFkok 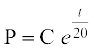 (tgk¡
(tgk¡ 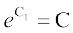 ) ... (3)
) ... (3)
vc P = 1000, tc t = 0
P vkSj t dk eku lehdj.k (3) esa j[kus ij ge C = 1000 izkIr djrs gSaA
blfy, lehdj.k (3) ls ge izkIr djrs gSa%
P = 1000 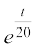
eku yhft, t o"kks± esa ewy/u nqxquk gks tkrk gS] rc
2000 = 1000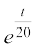 ⇒ t = 20 loge2
⇒ t = 20 loge2
iz'ukoyh 9-4
1 ls 10 rd osQ iz'uksa esa] izR;sd vody lehdj.k dk O;kid gy Kkr dhft,A
1. 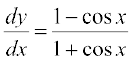 2.
2. 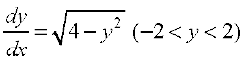
3. 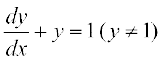 4. sec2 x tan y dx + sec2 y tan x dy = 0
4. sec2 x tan y dx + sec2 y tan x dy = 0
5. (ex + e–x) dy – (ex – e–x) dx = 0 6. 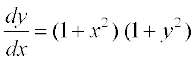
7. y log y dx – x dy = 0 8. 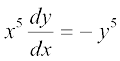 9.
9. 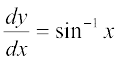 10. ex tan y dx + (1 – ex) sec2 y dy = 0
10. ex tan y dx + (1 – ex) sec2 y dy = 0
11 ls 14 rd osQ iz'uksa esa] izR;sd vody lehdj.k osQ fy, fn, gq, izfrca/ dks larq"V djus okyk fof'k"V gy Kkr dhft,A
11. 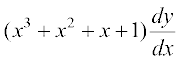 = 2x2 + x; y = 1 ;fn x = 0
= 2x2 + x; y = 1 ;fn x = 0
12. 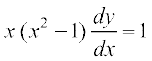 ; y = 0 ;fn x = 2
; y = 0 ;fn x = 2
13. 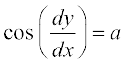 (a ∈ R); y = 1 ;fn x = 0
(a ∈ R); y = 1 ;fn x = 0
14. 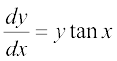 ; y = 2 ;fn x = 0
; y = 2 ;fn x = 0
15. ¯cnq (0] 0) ls xqtjus okys ,d ,sls oØ dk lehdj.k Kkr dhft, ftldk vody lehdj.k y′ = ex sin x gSA
16. vody lehdj.k 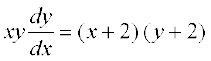 osQ fy, ¯cnq (1] &1) ls xqtjus okyk oØ Kkr dhft,A
osQ fy, ¯cnq (1] &1) ls xqtjus okyk oØ Kkr dhft,A
17. ¯cnq (0, –2) ls xqtjus okys ,d ,sls oØ dk lehdj.k Kkr dhft, ftlosQ fdlh ¯cnq
(x, y) ij Li'kZ js[kk dh izo.krk vkSj ml ¯cnq osQ y funsZ'kkad dk xq.kuiQy ml ¯cnq osQ x funsZ'kkad osQ cjkcj gSA
18. ,d oØ osQ fdlh ¯cnq (x, y) ij Li'kZ js[kk dh izo.krk] Li'kZ ¯cnq dks] ¯cnq (– 4, –3). ls feykus okys js[kk[kaM dh izo.krk dh nqxquh gSA ;fn ;g oØ ¯cnq (–2, 1) ls xq”kjrk gks rks bl oØ dk lehdj.k Kkr dhft,A
19. ,d xksykdkj xqCckjs dk vk;ru] ftls gok Hkjdj iqQyk;k tk jgk gS] fLFkj xfr ls cny jgk gS ;fn vkjaHk esa bl xqCckjs dh f=kT;k 3 bZdkbZ gS vkSj 3 lsosaQM ckn 6 bZdkbZ gS] rks t lsosaQM ckn ml xqCckjs dh f=kT;k Kkr dhft,A
20. fdlh cSad esa ewy/u dh o`f¼ r% okf"kZd dh nj ls gksrh gSA ;fn 100 #i;s 10 o"kks± esa nqxqus gks tkrs gSa] rks r dk eku Kkr dhft,A (loge2 = 0.6931).
21. fdlh cSad esa ewy/u dh o`f¼ 5% okf"kZd dh nj ls gksrh gSA bl cSad esa Rs 1000 tek djk, tkrs gSaA Kkr dhft, fd 10 o"kZ ckn ;g jkf'k fdruh gks tk,xh\ (e0.5 = 1.648)
22. fdlh thok.kq lewg esa thok.kqvksa dh la[;k 1] 00]000 gSA 2 ?kaVks esa budh la[;k esa 10% dh o`f¼ gksrh gSA fdrus ?kaVksa esa thok.kqvksa dh la[;k 2]00]000 gks tk,xh] ;fn thok.kqvksa osQ o`f¼ dh nj muosQ mifLFkr la[;k osQ lekuqikrh gSA
23. vody lehdj.k 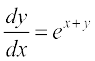 dk O;kid gy gS%
dk O;kid gy gS%
(A) ex + e–y = C (B) ex + ey = C
(C) e–x + ey = C (D) e–x + e–y = C
9.5.2 le?kkrh; vody lehdj.k (Homogenous differential equations)
x ,oa y osQ fuEufyf[kr iQyuksa ij fopkj dhft,
F1 (x, y) = y2 + 2xy, F2 (x, y) = 2x – 3y,
F3 (x, y) = 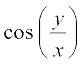 , F4 (x, y) = sin x + cos y
, F4 (x, y) = sin x + cos y
;fn mijksDr iQyuksa esa x vkSj y dks fdlh 'kwU;srj vpj λ osQ fy, Øe'k% λx ,oa λy ls izfrLFkkfir dj fn;k tk, rks ge izkIr djrs gSa%
F1 (λx, λy) = λ2 (y2 + 2xy) = λ2 F1 (x, y)
F2 (λx, λy) = λ (2x – 3y) = λ F2 (x, y)
F3 (λx, λy) = 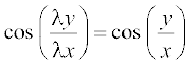 = λ0 F3 (x, y)
= λ0 F3 (x, y)
F4 (λx, λy) = sin λx + cos λy ≠ λn F4 (x, y), fdlh Hkh is osQ fy,
;gk¡ ge izsf{kr djrs gSa fd iQyuksa F1, F2, F3 dks F(λx, λy) = λn F (x, y) osQ :i esa fy[kk tk ldrk gS ijarq iQyu F4 dks bl :i esa ugha fy[kk tk ldrk gSA blls ge fuEufyf[kr ifjHkk"kk izkIr djrs gSaA
iQyu F(x, y), n ?kkr okyk le?kkrh; iQyu dgykrk gSA ;fn fdlh 'kwU;srj vpj λ osQ fy, F (λx, λy) = λn F(x, y)
ge uksV djrs gSa fd mijksDr mnkgj.kksa esa F1, F2, F3 Øe'k% 2, 1, 0 ?kkr okys le?kkrh; iQyu gSa tcfd F4 le?kkrh; iQyu ugha gSA
ge ;g Hkh izsf{kr djrs gSa fd

vFkok 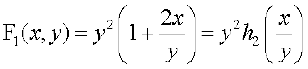 ,
,

vFkok  ,
,
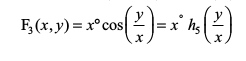
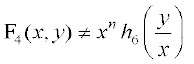 , n
, n 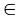 N osQ fdlh Hkh eku osQ fy,
N osQ fdlh Hkh eku osQ fy,
vFkok F4 (x, y) ≠ 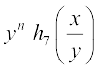 , n ∈ N
, n ∈ N
blfy, ,d iQyu F (x, y), n ?kkr okyk le?kkrh; iQyu dgykrk gS ;fn
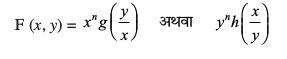
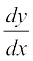 = F (x, y) osQ :i okyk vody lehdj.k le?kkrh; dgykrk gS ;fn F (x, y) 'kwU; ?kkr okyk le?kkrh; iQyu gSA
= F (x, y) osQ :i okyk vody lehdj.k le?kkrh; dgykrk gS ;fn F (x, y) 'kwU; ?kkr okyk le?kkrh; iQyu gSA
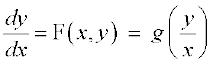 ... (1)
... (1)
osQ :i okys le?kkrh; vody lehdj.k dks gy djus osQ fy, ge 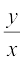 = v vFkkZr~
= v vFkkZr~
y = v x ... (2)
izfrLFkkfir djrs gSa
lehdj.k (2) dk x osQ lkis{k vodyu djus ij ge izkIr djrs gSa%
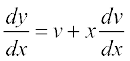 ... (3)
... (3)
lehdj.k (3) ls 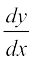 dk eku lehdj.k (1) esa izfrLFkkfir djus ij ge izkIr djrs gSa%
dk eku lehdj.k (1) esa izfrLFkkfir djus ij ge izkIr djrs gSa%
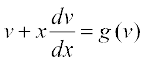
vFkkZr~ 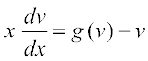 ... (4)
... (4)
lehdj.k (4) esa pjksa dks i`Fko~Q djus ij ge izkIr djrs gSa%
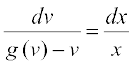 ... (5)
... (5)
lehdj.k (5) osQ nksuksa i{kksa dk lekdyu djus ij gesa izkIr gksrk gS%
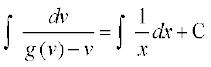 ... (6)
... (6)
;fn v dks 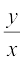 ls izfrLFkkfir dj fn;k tk, rks lehdj.k (6)] vody lehdj.k (1) dk O;kid gy iznku djrk gSA
ls izfrLFkkfir dj fn;k tk, rks lehdj.k (6)] vody lehdj.k (1) dk O;kid gy iznku djrk gSA
fVIi.kh ;fn le?kkrh; vody lehdj.k 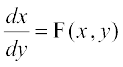 osQ :i esa gSA tgk¡
osQ :i esa gSA tgk¡
F (x, y) 'kwU; ?kkr okyk le?kkrh; iQyu gS rks ge 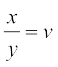 vFkkZr] x = vy izfrLFkkfir djrs gSa vkSj fiQj mijksDr ppkZ osQ vuqlkj
vFkkZr] x = vy izfrLFkkfir djrs gSa vkSj fiQj mijksDr ppkZ osQ vuqlkj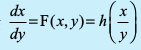 osQ :i esa fy[kdj O;kid gy Kkr djus osQ fy, vkxs c<+rs gSaA
osQ :i esa fy[kdj O;kid gy Kkr djus osQ fy, vkxs c<+rs gSaA
mnkgj.k 15 n'kkZb, fd vody lehdj.k (x – y) 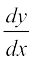 = x + 2y le?kkrh; gS vkSj bldk gy Kkr dhft,A
= x + 2y le?kkrh; gS vkSj bldk gy Kkr dhft,A
gy fn, x, vody lehdj.k dks fuEufyf[kr :i esa vfHkO;Dr fd;k tk ldrk gS%
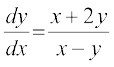 ... (1)
... (1)
eku yhft, F (x, y) = 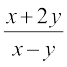
vc 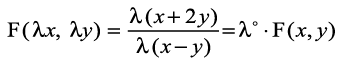
blfy, F(x, y) 'kwU; ?kkr okyk le?kkrh; iQyu gSA
vr% fn;k gqvk vody lehdj.k ,d le?kkrh; vody lehdj.k gSA
fodYir%
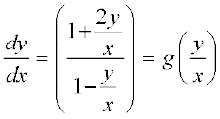 ... (2)
... (2)
lehdj.k (2) dk nk;k¡ i{k 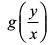 osQ :i esa gS blfy, ;g 'kwU; ?kkr okyk ,d le?kkrh; iQyu gSA blfy, lehdj.k (1) ,d le?kkrh; vody lehdj.k gSA
osQ :i esa gS blfy, ;g 'kwU; ?kkr okyk ,d le?kkrh; iQyu gSA blfy, lehdj.k (1) ,d le?kkrh; vody lehdj.k gSA
bldks gy djus osQ fy, ge izfrLFkkiu djrs gS%a
y = vx ... (3)
lehdj.k (3) dk x osQ lkis{k vodyu djus ij ge izkIr djrs gSa%
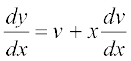 ... (4)
... (4)
lehdj.k (1) esa y ,oa 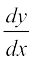 dk eku izfrLFkkfir djus ij ge izkIr djrs gSa%
dk eku izfrLFkkfir djus ij ge izkIr djrs gSa%
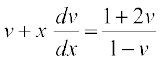
vFkkZr~ 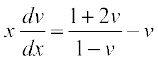
vFkkZr~ 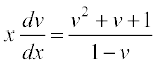
vFkkZr~ 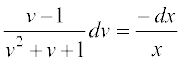 ... (5)
... (5)
lehdj.k (5) osQ nksuksa i{kksa dk lekdyu djus ij ge izkIr djrs gSa%
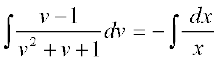
vFkok 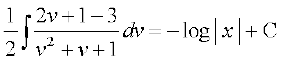
vFkok 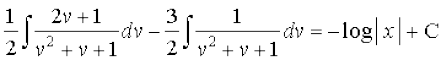
vFkok 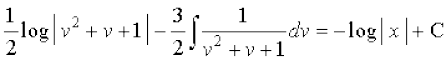
vFkok 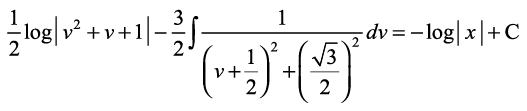
vFkok 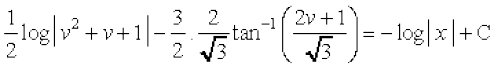
vFkok 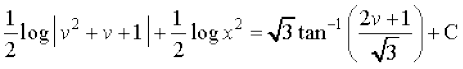
v dks 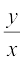 , ls izfrLFkkfir djus ij ge izkIr djrs gSa%
, ls izfrLFkkfir djus ij ge izkIr djrs gSa%
vFkok 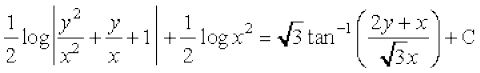
vFkok 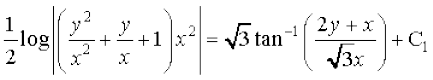
vFkok 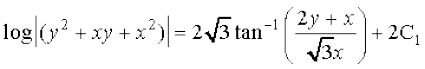
vFkok 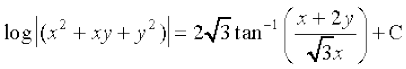
;g vody lehdj.k (1) dk O;kid gy gSA
mnkgj.k 16 n'kkZb, fd vody lehdj.k 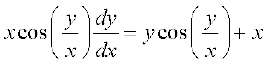 le?kkrh; gS vkSj bldk gy Kkr dhft,A
le?kkrh; gS vkSj bldk gy Kkr dhft,A
gy fn;k gqvk vody lehdj.k fuEufyf[kr :i esa fy[kk tk ldrk gS%
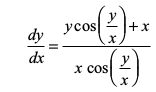 ... (1)
... (1)
;gk¡ 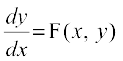 osQ :i dk vody lehdj.k gSA
osQ :i dk vody lehdj.k gSA
;gk¡ F (x, y) = 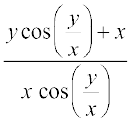 gSA
gSA
x dks λx ls ,oa y dks λy ls izfrLFkkfir djus ij ge izkIr djrs gSa%
F (λx, λy) = 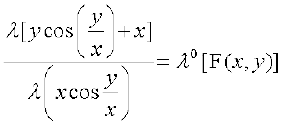
F (x, y) 'kwU; ?kkr okyk le?kkrh; iQyu gS] blfy, fn;k gqvk vody lehdj.k ,d le?kkrh; vody lehdj.k gSA bldks gy djus osQ fy, ge izfrLFkkiu djrs gSa%
y = vx ... (2)
lehdj.k (2) dk x osQ lkis{k vodyu djus ij ge izkIr djrs gSa%
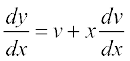 ... (3)
... (3)
lehdj.k (1) esa y ,oa 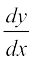 dk eku izfrLFkkfir djus ij ge izkIr djrs gSa%
dk eku izfrLFkkfir djus ij ge izkIr djrs gSa%
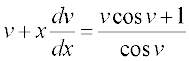
vFkok 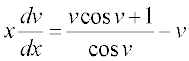
vFkok 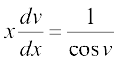
vFkok 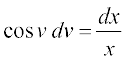
blfy, 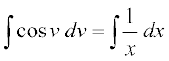
vFkok sin v = log 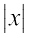 + log
+ log 
vFkok sin v = log 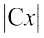
v dks 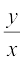 izfrLFkkfir djus ij ge izkIr djrs gSaA
izfrLFkkfir djus ij ge izkIr djrs gSaA
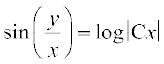
;g vody lehdj.k (1) dk O;kid gy gSA
mnkgj.k 17 n'kkZb, fd vody lehdj.k 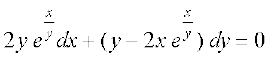 le?kkrh; gS vkSj ;fn] x = 0 tc y = 1 fn;k gqvk gks rks bl lehdj.k dk fof'k"V gy Kkr dhft,A
le?kkrh; gS vkSj ;fn] x = 0 tc y = 1 fn;k gqvk gks rks bl lehdj.k dk fof'k"V gy Kkr dhft,A
gy fn;k gqvk vody lehdj.k fuEufyf[kr :i esa fy[kk tk ldrk gS%
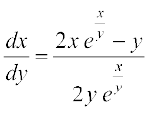 ... (1)
... (1)
eku yhft, F(x, y) 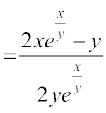 rc F(λx, λy)
rc F(λx, λy)
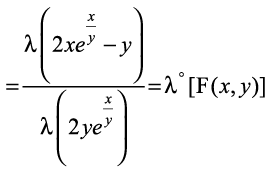
vr% F (x, y) 'kwU; ?kkr okyk le?kkrh; iQyu gSA
blfy,] fn;k gqvk vody lehdj.k ,d le?kkrh; vody lehdj.k gSA
bldk gy Kkr djus osQ fy,] ge x = vy izfrLFkkiu djrs gSaA
lehdj.k (2) dk y osQ lkis{k vodyu djus ij ge izkIr djrs gSa%
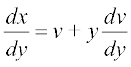
lehdj.k (1) esa 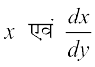 dk eku izfrLFkkfir djus ij ge izkIr djrs gSa%
dk eku izfrLFkkfir djus ij ge izkIr djrs gSa%
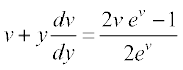
vFkok 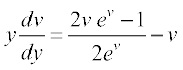
vFkok 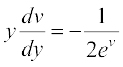
vFkok 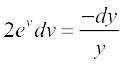
vFkok 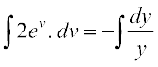
vFkok 2 ev = – log |y| + C
v dks  ls izfrLFkkfir djus ij ge izkIr djrs gSa%
ls izfrLFkkfir djus ij ge izkIr djrs gSa%
2 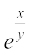 + log |y| = C ... (3)
+ log |y| = C ... (3)
lehdj.k (3) esa] x = 0 ,oa y = 1 izfrLFkkfir djus ij ge izkIr djrs gSa%
2 e0 + log |1| = C ⇒ C = 2
C dk eku lehdj.k (3) esa izfrLFkkfir djus ij ge izkIr djrs gSa%
2 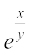 + log |y| = 2
+ log |y| = 2
;g fn, gq, vody lehdj.k dk ,d fof'k"V gy gSA
mnkgj.k 18 n'kkZb, fd oØksa dk oqQy] ftuosQ fdlh ¯cnq (x, y) ij Li'kZ js[kk dh izo.krk 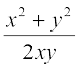 gS] x2 – y2 = cx }kjk iznÙk gSA
gS] x2 – y2 = cx }kjk iznÙk gSA
gy ge tkurs gSa fd ,d oØ osQ fdlh ¯cnq ij Li'kZ js[kk dh izo.krk 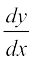 osQ cjkcj gksrh gSA
osQ cjkcj gksrh gSA
blfy, 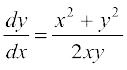 ;k
;k 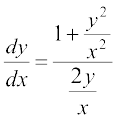 ... (1)
... (1)
Li"Vr% lehdj.k (1) le?kkrh; vody lehdj.k gSA
bldks gy djus osQ fy, ge y = vx izfrLFkkiu djrs gaSA
y = vx oQk x osQ lkis{k vodyu djus ij ge ikrs gSa%
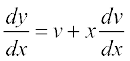 ;k
;k 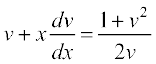
vr% 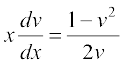 ;k
;k 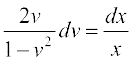 ;k
;k 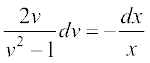
blfy, 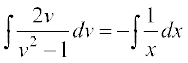
vFkok 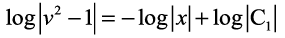
vFkok 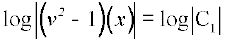
vFkok (v2 – 1) x = ± C1
v dks  ls izfrLFkkfir djus ij ge izkIr djrs gSa%
ls izfrLFkkfir djus ij ge izkIr djrs gSa%
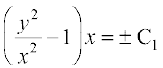
vFkok (y2 – x2) = ± C1 x ;k x2 – y2 = Cx
iz'ukoyh 9-5
1 ls 10 rd osQ izR;sd iz'u esa n'kkZb, fd fn;k gqvk vody lehdj.k le?kkrh; gS vkSj buesa ls izR;sd dks gy dhft,%
1. (x2 + xy) dy = (x2 + y2) dx 2. 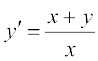
3. (x – y) dy – (x + y) dx = 0 4. (x2 – y2) dx + 2xy dy = 0
5. 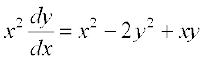 6. x dy – y dx =
6. x dy – y dx = 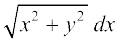
7. 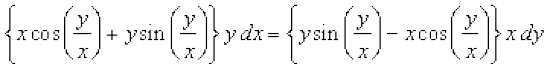
8. 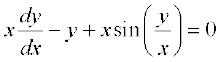 9.
9. 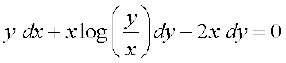
10. 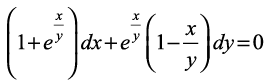
11 ls 15 rd osQ iz'uksa esa izR;sd vody lehdj.k osQ fy, fn, gq, izfrca/ dks larq"V djus okyk fof'k"V gy Kkr dhft,A
11. (x + y) dy + (x – y) dx = 0; y = 1 ;fn x = 1
12. x2 dy + (xy + y2) dx = 0; y = 1 ;fn x = 1
13. 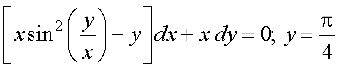 ;fn x = 1
;fn x = 1
14. 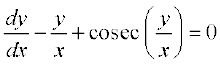 ; y = 0 ;fn x = 1
; y = 0 ;fn x = 1
15. 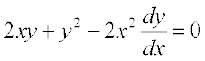 ; y = 2 ;fn x = 1
; y = 2 ;fn x = 1
16. 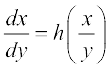 osQ :i okys le?kkrh; vody lehdj.k dks gy djus osQ fy, fuEufyf[kr esa ls dkSu lk izfrLFkkiu fd;k tkrk gS%
osQ :i okys le?kkrh; vody lehdj.k dks gy djus osQ fy, fuEufyf[kr esa ls dkSu lk izfrLFkkiu fd;k tkrk gS%
(A) y = vx (B) v = yx (C) x = vy (D) x = v
17. fuEufyf[kr esa ls dkSu lk le?kkrh; vody lehdj.k gS\
(A) (4x + 6y + 5) dy – (3y + 2x + 4) dx = 0
(B) (xy) dx – (x3 + y3) dy = 0
(C) (x3 + 2y2) dx + 2xy dy = 0
(D) y2 dx + (x2 – xy – y2) dy = 0
9.5.3 jSf[kd vody lehdj.k (Linear differential equations)
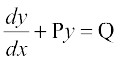 ,
,
osQ :i okyk vody lehdj.k] ftlesa P ,oa Q vpj vFkok osQoy x osQ iQyu gSa] izFke dksfV dk jSf[kd vody lehdj.k dgykrk gSA izFke dksfV osQ jSf[kd vody lehdj.k osQ oqQN mnkgj.k bl izdkj gSa%
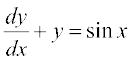
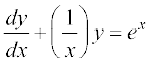
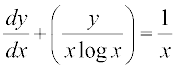
izFke dksfV osQ jSf[kd vody lehdj.k dk nwljk :i lsosaQM 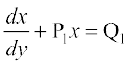 gS] ftlesa P1 vkSj Q1 vpj vFkok osQoy y osQ iQyu gSaA bl izdkj osQ vody lehdj.k osQ oqQN mnkgj.k fuEufyf[kr gSa%
gS] ftlesa P1 vkSj Q1 vpj vFkok osQoy y osQ iQyu gSaA bl izdkj osQ vody lehdj.k osQ oqQN mnkgj.k fuEufyf[kr gSa% 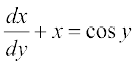
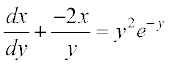
izFke dksfV osQ jSf[kd vody lehdj.k
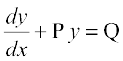 ... (1)
... (1)
dks gy djus osQ fy, lehdj.k osQ nksuksa i{kksa dks x osQ iQyu g (x) ls xq.kk djus ij ge izkIr djrs gSa%
g (x) 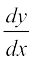 + P.g (x) y = Q.g (x) ... (2)
+ P.g (x) y = Q.g (x) ... (2)
g (x) dk p;u bl izdkj dhft, rkfd lehdj.k dk ck;k¡ i{k y . g (x) dk vodyt cu tk,%
vFkkZr~ g (x) 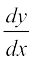 + P.g (x) y =
+ P.g (x) y = 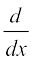 [y.g (x)]
[y.g (x)]
vFkok g (x) 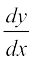 + P.g (x) y = g (x)
+ P.g (x) y = g (x) 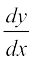 + y g′(x)
+ y g′(x)
⇒ P.g (x) = g′(x)
vFkok 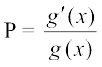
nksuksa i{kksa dk x osQ lkis{k lekdyu djus ij ge izkIr djrs gSa%
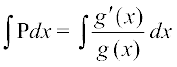
vFkok 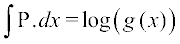
vFkok g (x) = 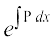
lehdj.k (1) dks g(x) = e∫pdx ls xq.kk djus ij ml lehdj.k dk ck;k¡ i{k x rFkk y osQ fdlh iQyu dk vodyt cu tkrk gSA ;g iQyu g(x) = e∫pdx fn, gq, vody lehdj.k dk lekdyu xq.kd (I.F.) dgykrk gSA
lehdj.k (2) esa g(x) dk eku izfrLFkkfir djus ij ge izkIr djrs gSa%
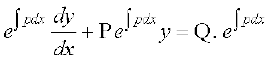
vFkok 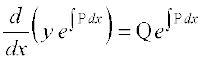
nksuksa i{kksa dk x, osQ lkis{k lekdyu djus ij ge izkIr djrs gSa%
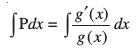
vFkok 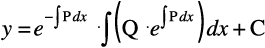
;g vody lehdj.k dk O;kid gy gSA
izFke dksfV osQ jSf[kd vody lehdj.k dks gy djus osQ fy, lfEefyr pj.k%
(i) fn, gq, vody lehdj.k dks 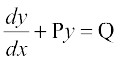 osQ :i esa fyf[k, ftlesa P, Q vpj vFkok osQoy x osQ iQyu gSaA
osQ :i esa fyf[k, ftlesa P, Q vpj vFkok osQoy x osQ iQyu gSaA
(ii) lekdyu xq.kd (I.F.) = 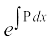 Kkr dhft,A
Kkr dhft,A
(iii) fn, gq, vody lehdj.k dk gy fuEufyf[kr :i esa fyf[k,%
y . (I.F.) = 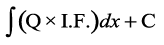
;fn izFke dksfV dk jSf[kd vody lehdj.k 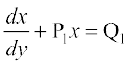 osQ :i esa gS ftlesa P1 vkSj Q1 vpj vFkok osQoy y osQ iQyu gSa] rc I.F. =
osQ :i esa gS ftlesa P1 vkSj Q1 vpj vFkok osQoy y osQ iQyu gSa] rc I.F. = 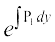 vkSj
vkSj
x . (I.F.) = 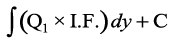 vody lehdj.k dk gy gSA
vody lehdj.k dk gy gSA
mnkgj.k 19 vody lehdj.k 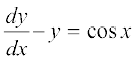 dk O;kid gy Kkr dhft,A
dk O;kid gy Kkr dhft,A
gy fn;k gqvk vody lehdj.k
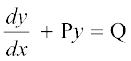 gS, tgk¡ P = –1 vkSj Q = cos x
gS, tgk¡ P = –1 vkSj Q = cos x
blfy, 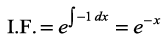
lehdj.k osQ nksuksa i{kksa dks I.F. ls xq.kk djus ij ge izkIr djrs gSa%
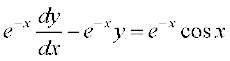
vFkok 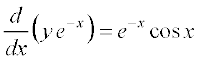
nksuksa i{kksa dk x osQ lkis{k lekdyu djus ij ge izkIr djrs gSa%
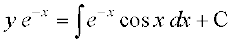 ... (1)
... (1)
eku yhft, fd I = 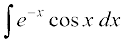
= 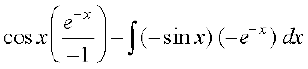
= 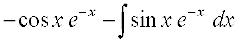
= 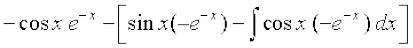
= 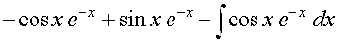
vFkok I = – e–x cos x + sin x e–x – I
vFkok 2I = (sin x – cos x) e–x
vFkok I = 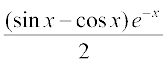
lehdj.k (1) esa I dk eku izfrLFkkfir djus ij ge izkIr djrs gSa%
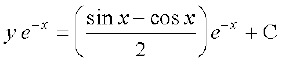
vFkok 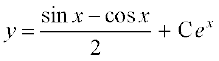
;g fn, gq, vody lehdj.k dk O;kid gy gSA
mnkgj.k 20 vody lehdj.k 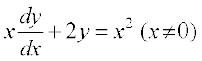 dk O;kid gy Kkr dhft,A
dk O;kid gy Kkr dhft,A
gy fn;k gqvk vody lehdj.k gS%
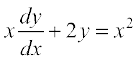 ... (1)
... (1)
lehdj.k (1) osQ nksuksa i{kksa dks x ls Hkkx nsus ij ge izkIr djrs gSa%
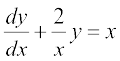
;g] 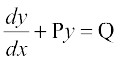 , osQ :i dk jSf[kd vody lehdj.k gSA ;gk¡
, osQ :i dk jSf[kd vody lehdj.k gSA ;gk¡ 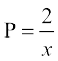 ,oa Q = x gSA
,oa Q = x gSA
blfy, I.F. = 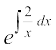 = e2 log x =
= e2 log x = 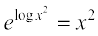
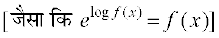
blfy, fn, gq, lehdj.k dk gy gS%
y . x2 = 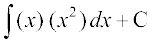 =
= 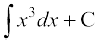
vFkok 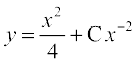
;g fn, gq, vody lehdj.k dk O;kid gy gSA
mnkgj.k 21 vody lehdj.k y dx – (x + 2y2) dy = 0 dk O;kid gy Kkr dhft,A
gy fn;k gqvk vody lehdj.k fuEufyf[kr :i esa fy[kk tk ldrk gS%
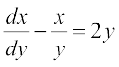
;g] 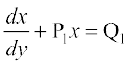 , osQ :i okyk jSf[kd vody lehdj.k gSA ;gk¡
, osQ :i okyk jSf[kd vody lehdj.k gSA ;gk¡ 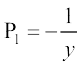 ,oa
,oa
Q1 = 2y gSA blfy, 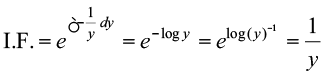
vr% fn, gq, vody lehdj.k dk gy gS%
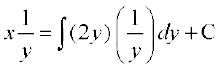
vFkok 
vFkok 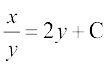
vFkok x = 2y2 + Cy
;g fn, gq, vody lehdj.k dk O;kid gy gSA
mnkgj.k 22 vody lehdj.k
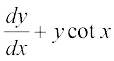 = 2x + x2 cot x (x ≠ 0)
= 2x + x2 cot x (x ≠ 0)
dk fof'k"V gy Kkr dhft,] fn;k gqvk gS fd y = 0 ;fn 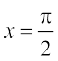
gy fn;k gqvk vody lehdj.k 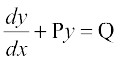 , osQ :i dk jSf[kd vody lehdj.k gSA ;gk¡ P = cot x vkSj Q = 2x + x2 cot x gSA blfy,
, osQ :i dk jSf[kd vody lehdj.k gSA ;gk¡ P = cot x vkSj Q = 2x + x2 cot x gSA blfy,
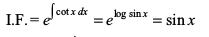
vr% vody lehdj.k dk gy gS%
y . sin x = ∫(2x + x2 cot x) sin x dx + C
vFkok y sin x = ∫2x sin x dx + ∫x2 cos x dx + C
vFkok y sin x = 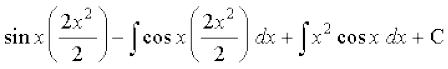
vFkok 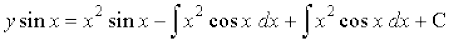
vFkok y sin x = x2 sin x + C ... (1)
lehdj.k (1) esa y = 0 ,oa 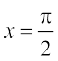 izfrLFkkfir djus ij ge izkIr djrs gSa%
izfrLFkkfir djus ij ge izkIr djrs gSa%
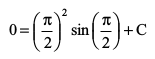
vFkok 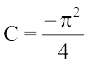
lehdj.k (1) esa C dk eku izfrLFkkfir djus ij ge izkIr djrs gSa%
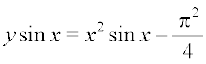
vFkok 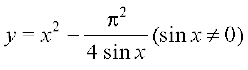
;g fn, gq, vody lehdj.k dk fof'k"V gy gSA
mnkgj.k 23 fcUnq (0] 1) ls xqtjus okys ,d oØ dk lehdj.k Kkr dhft,] ;fn bl oØ osQ fdlh ¯cnq (x, y) ij Li'kZ js[kk dh izo.krk] ml ¯cnq osQ x funsZ'kkad (Hkqt) rFkk x funsZ'kkad vkSj y funsZ'kkad (dksfV) osQ xq.kuiQy osQ ;ksx osQ cjkcj gSA
gy ge tkurs gSa fd oØ dh Li'kZ js[kk dh izo.krk 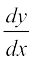 osQ cjkcj gksrh gSA blfy,
osQ cjkcj gksrh gSA blfy,
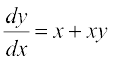
vFkok 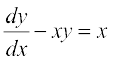 ... (1)
... (1)
lehdj.k (1)] 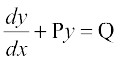 osQ :i dk jSf[kd vody lehdj.k gSA ;gk¡ P = – x ,oa
osQ :i dk jSf[kd vody lehdj.k gSA ;gk¡ P = – x ,oa
Q = x gSA blfy,
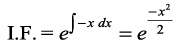
vr% fn, gq, lehdj.k dk gy gS%
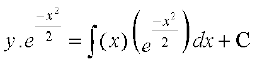 ... (2)
... (2)
eku yhft, 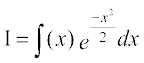
eku yhft, 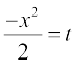 , rc – x dx = dt ;k x dx = – dt
, rc – x dx = dt ;k x dx = – dt
blfy, 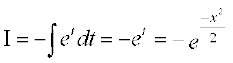
lehdj.k (2) esa I dk eku izfrLFkkfir djus ij] ge ikrs gSa%
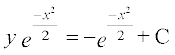
vFkok 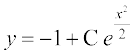 ... (3)
... (3)
lehdj.k (3) oØksa osQ oqQy dk lehdj.k gS ijarq ge bl oqQy osQ ,sls lnL; dk lehdj.k Kkr djuk pkgrs gSa tks ¯cnq (0]1) ls xqtjrk gksA lehdj.k (3) esa x = 0 ,oa y = 1 izfrLFkkfir djus ij ge ikrs gSa%
1 = – 1 + C . eo vFkok C = 2
lehdj.k (3) esa C dk eku izfrLFkkfir djus ij ge izkIr djrs gSa%
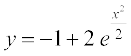
;g oØ dk vHkh"V lehdj.k gSA
iz'ukoyh 9-6
1 ls 12 rd osQ iz'uksa esa] izR;sd vody lehdj.k dk O;kid gy Kkr dhft,%
1. 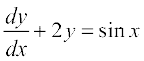 2.
2. 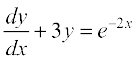 3.
3. 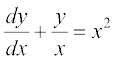
4. 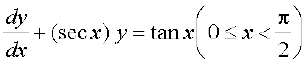 5.
5. 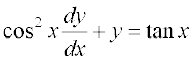
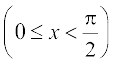
6. 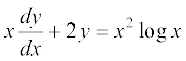 7.
7. 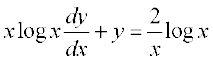
8. (1 + x2) dy + 2xy dx = cot x dx (x ≠ 0)
9. 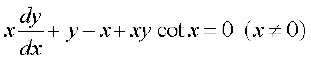 10.
10. 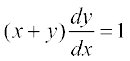
11. y dx + (x – y2) dy = 0 12. 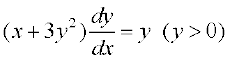 .
.
13 ls 15 rd osQ iz'uksa esa izR;sd vody lehdj.k osQ fy, fn, gq, izfrca/ dks larq"V djus okyk fof'k"V gy Kkr dhft,%
13. 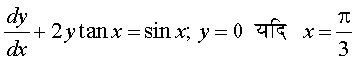
14. 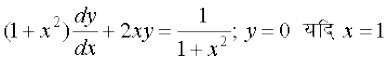
15. 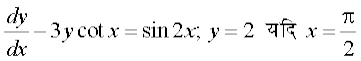
16. ewy ¯cnq ls xq”kjus okys ,d oØ dk lehdj.k Kkr dhft, ;fn bl oØ osQ fdlh ¯cnq (x, y) ij Li'kZ js[kk dh izo.krk ml ¯cnq osQ funsZ'kkadksa osQ ;ksx osQ cjkcj gSA
17. ¯cnq (0] 2) ls xqtjus okys oØ dk lehdj.k Kkr dhft, ;fn bl oØ osQ fdlh ¯cnq osQ funsZ'kkadksa dk ;ksx ml ¯cnq ij [khaph xbZ Li'kZ js[kk dh izo.krk osQ ifjek.k ls 5
vf/d gSA
18. vody lehdj.k 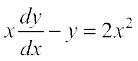 dk lekdyu xq.kd gS%
dk lekdyu xq.kd gS%
(A) e–x (B) e–y (C)  (D) x
(D) x
19. vody lehdj.k 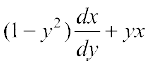 =
= 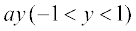 dk lekdyu xq.kd gS%
dk lekdyu xq.kd gS%
(A) 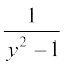 (B)
(B) 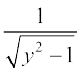 (C)
(C) 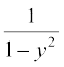 (D)
(D) 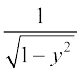
fofo/ mnkgj.k
mnkgj.k 24 lR;kfir dhft, fd iQyu y = c1 eax cos bx + c2 eax sin bx, tgk¡ c1, c2 LosPN vpj gS] vody lehdj.k
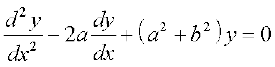 dk gy gSA
dk gy gSA
gy fn;k gqvk iQyu gS%
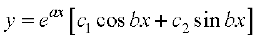 ... (1)
... (1)
lehdj.k (1) osQ nksuksa i{kksa dk x osQ lkis{k vodyu djus ij ge ikrs gSa fd
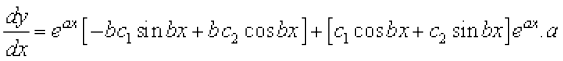
vFkok 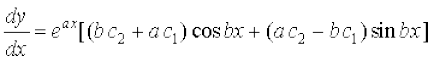 ... (2)
... (2)
lehdj.k (2) osQ nksuksa i{kksa dk x, osQ lkis{k vodyu djus ij ge ikrs gSa fd
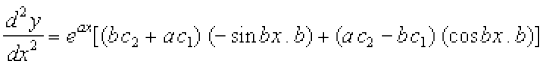
+ 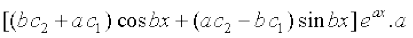
= 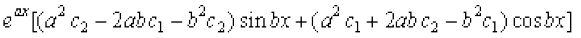
fn, x, vody lehdj.k esa 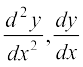 ,oa y dk eku izfrLFkkfir djus ij ge ikrs gSa%
,oa y dk eku izfrLFkkfir djus ij ge ikrs gSa%
ck;k¡ i{k 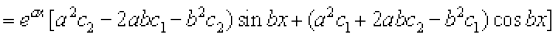
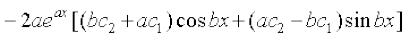
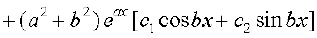
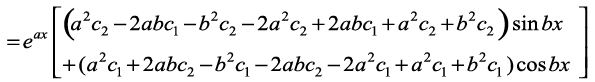
= 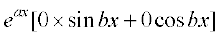 = eax × 0 = 0 = nk;k¡ i{k
= eax × 0 = 0 = nk;k¡ i{k
blfy, fn;k gqvk iQyu fn, gq, vody lehdj.k dk gy gSA
mnkgj.k 25 f}rh; prqFkk±'k esa ,sls o`Ùkksa osQ oqQy dk vody lehdj.k Kkr dhft, tks funsZ'kkad v{kksa dk Li'kZ djrs gSaA
gy eku yhft,] funsZ'kkad v{kksa dks Li'kZ djus okyk vkSj f}rh; prqFkk±'k esa cuk o`Ùkksa dk oqQy C }kjk fufnZ"V fd;k tkrk gSA bl oqQy osQ fdlh lnL; osQ osaQnz ¯cnq osQ funs±'kkad (–a, a) gSa (vko`Qfr 9-6 nsf[k,)A
oqQy C dks fu:fir djus okyk lehdj.k gS%
(x + a)2 + (y – a)2 = a2 ... (1)
vFkok x2 + y2 + 2ax – 2ay + a2 = 0 ... (2)
lehdj.k (2) dk x osQ lkis{k vodyu djus ij ge ikrs gaS%
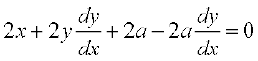
vFkok 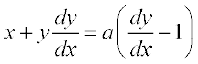
vFkok 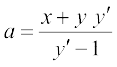
lehdj.k (1) esa a dk eku izfrLFkkfir djus ij ge ikrs gSa%
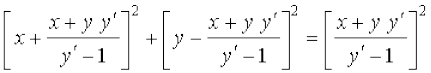
vFkok 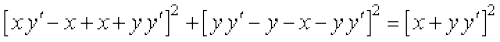
vFkok (x + y)2 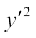 + [x + y]2 = [x + y y′]2
+ [x + y]2 = [x + y y′]2
vFkok (x + y)2 [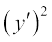 + 1] = [x + y y′]2
+ 1] = [x + y y′]2
tks fn, gq, o`Ùkksa osQ oqQy dks fu:fir djus okyk vody lehdj.k gSA
mnkgj.k 26 vody lehdj.k 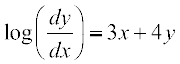 dk fof'k"V gy Kkr dhft,A fn;k gqvk gS fd y = 0 ;fn x = 0
dk fof'k"V gy Kkr dhft,A fn;k gqvk gS fd y = 0 ;fn x = 0
gy fn;k gqvk vody lehdj.k fuEufyf[kr :i esa fy[kk tk ldrk gS%
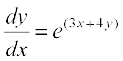
vFkok 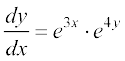 ... (1)
... (1)
pjksa dks i`Fko~Q djus ij ge ikrs gSa]
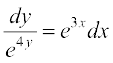
blfy, 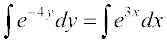
vFkok 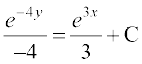
vFkok 4 e3x + 3 e– 4y + 12 C = 0 ... (2)
lehdj.k (2) esa x = 0 ,oa y = 0 izfrLFkkfir djus ij ge ikrs gSa%
4 + 3 + 12 C = 0 vFkok C = 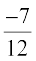
lehdj.k (2) esa C dk eku izfrLFkkfir djus ij ge]
4 e3x + 3 e– 4y – 7 = 0, izkIr djrs gSa
;g fn, gq, vody lehdj.k dk ,d fof'k"V gy gSA

vko`Qfr 9-6
mnkgj.k 27 vody lehdj.k
(x dy – y dx) y sin 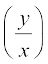 = (y dx + x dy) x cos
= (y dx + x dy) x cos 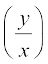 dks gy dhft,A
dks gy dhft,A
gy fn;k gqvk vody lehdj.k fuEufyf[kr :i esa fy[kk tk ldrk gSA
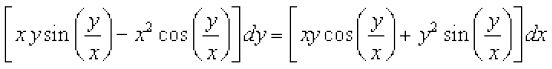
vFkok 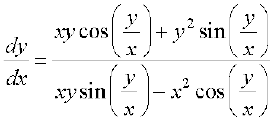
nk;sa i{k ij va'k ,oa gj nksuksa dks x2 ls Hkkx nsus ij ge ikrs gSa%
 ... (1)
... (1)
Li"Vr% lehdj.k (1)] 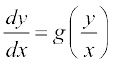 osQ :i dk le?kkrh; vody lehdj.k gS] blfy, bl lehdj.k dks gy djus osQ fy, ge
osQ :i dk le?kkrh; vody lehdj.k gS] blfy, bl lehdj.k dks gy djus osQ fy, ge
y = vx ... (2)
izfrLFkkfir djrs gSaA
vFkok 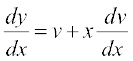
vFkok 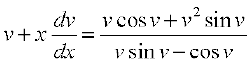 [lehdj.k (1) vkSj (2) dk iz;ksx djus ij]
[lehdj.k (1) vkSj (2) dk iz;ksx djus ij]
vFkok 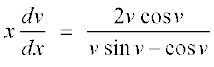
vFkok 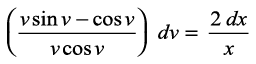
blfy, 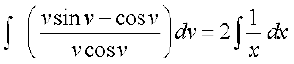
vFkok 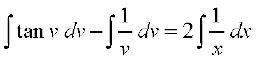
vFkok 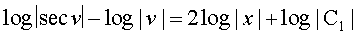
vFkok 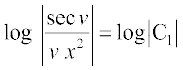
vFkok 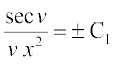 ... (3)
... (3)
lehdj.k (3) esa v dks 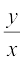 ls izfrLFkkfir djus ij ge ikrs gSa fd
ls izfrLFkkfir djus ij ge ikrs gSa fd
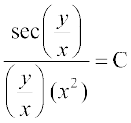 ] tgk¡ C = ± C1
] tgk¡ C = ± C1
vFkok 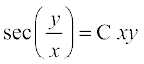
;g fn, gq, vody lehdj.k dk O;kid gy gSA
mnkgj.k 28 vody lehdj.k
(tan–1y – x) dy = (1 + y2) dx dk gy Kkr dhft,A
gy fn;k gqvk vody lehdj.k fuEufyf[kr :i esa fy[kk tk ldrk gS%
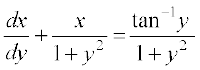 ... (1)
... (1)
lehdj.k (1)] 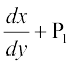 x = Q1, osQ :i dk jSf[kd vody lehdj.k gSA ;gk¡
x = Q1, osQ :i dk jSf[kd vody lehdj.k gSA ;gk¡
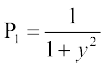 ,oa
,oa 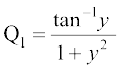 gSA blfy,
gSA blfy,
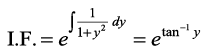
blfy, fn, gq, vody lehdj.k dk gy gS%
 ... (2)
... (2)
eku yhft, 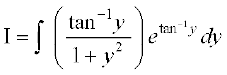
tan–1 y = t izfrLFkkfir djus ij ge ikrs gSa fd 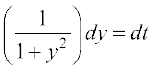
vr% I = 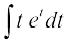 , I = t et – ∫1 . et et, I = t et – et = et (t – 1)
, I = t et – ∫1 . et et, I = t et – et = et (t – 1)
vFkok I = 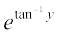 (tan–1y –1)
(tan–1y –1)
lehdj.k (2) esa I dk eku izfrLFkkfir djus ij ge
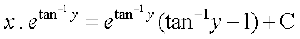 ikrs gSa
ikrs gSa
vFkok x = 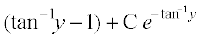
;g fn, gq, vody lehdj.k dk O;kid gy gSA
vè;k; 9 ij fofo/ iz'ukoyh
1. fuEufyf[kr vody lehdj.kksa esa ls izR;sd dh dksfV ,oa ?kkr (;fn ifjHkkf"kr gks) Kkr dhft,A
(i) 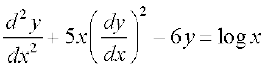 (ii)
(ii) 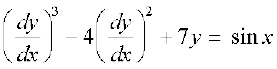
(iii) 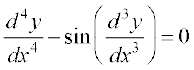
2. fuEufyf[kr iz'uksa esa izR;sd osQ fy, lR;kfir dhft, fd fn;k gqvk iQyu (vLi"V vFkok Li"V) laxr vody lehdj.k dk gy gSA
(i) xy = a ex + b e–x + x2 : 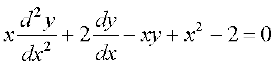
(ii) y = ex (a cos x + b sin x) : 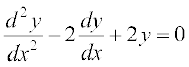
(iii) y = x sin 3x : 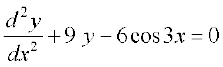
(iv) x2 = 2y2 log y : 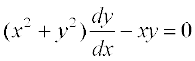
3. (x – a)2 + 2y2 = a2, }kjk fu:fir oØksa osQ oqQy dk vody lehdj.k fufeZr dhft, tgk¡ a ,d LosPN vpj gSA
4. fl¼ dhft, fd x2 – y2 = c (x2 + y2)2 tgk¡ c ,d izkpy gS] vody lehdj.k
(x3 – 3x y2) dx = (y3 – 3x2y) dy dk O;kid gy gSA
5. izFke prqFkk±'k esa ,sls o`Ùkksa osQ oqQy dk vody lehdj.k Kkr dhft, tks funsZa'kakd v{kksa dks Li'kZ djrs gSaA
6. vody lehdj.k 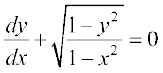 ] tcfd x ≠1 dk O;kid gy Kkr dhft,A
] tcfd x ≠1 dk O;kid gy Kkr dhft,A
7. n'kkZb, fd vody lehdj.k 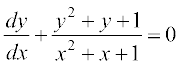 dk O;kid gy
dk O;kid gy
(x + y + 1) = A (1 – x – y – 2xy) gS] ftlesa A ,d izkpy gSA
8. ¯cnq 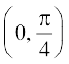 ls xqtjus okys ,d ,sls oØ dk lehdj.k Kkr dhft, ftldk vody lehdj.k sin x cos y dx + cos x sin y dy = 0 gSA
ls xqtjus okys ,d ,sls oØ dk lehdj.k Kkr dhft, ftldk vody lehdj.k sin x cos y dx + cos x sin y dy = 0 gSA
9. vody lehdj.k (1 + e2x) dy + (1 + y2) ex dx = 0 dk ,d fof'k"V gy Kkr dhft,] fn;k gqvk gS fd y = 1 ;fn x = 0.
10. vody lehdj.k 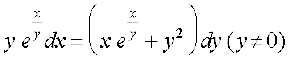 dk gy Kkr dhft,A
dk gy Kkr dhft,A
11. vody lehdj.k (x – y) (dx + dy) = dx – dy dk ,d fof'k"V gy Kkr dhft,] fn;k gqvk gS fd y = –1, ;fn x = 0 (laosQr: x – y = t j[ksa)A
12. vody lehdj.k 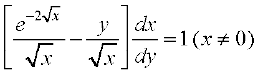 dk gy Kkr dhft,A
dk gy Kkr dhft,A
13. vody lehdj.k 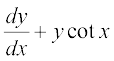 = 4x cosec x (x ≠ 0) dk ,d fof'k"V gy Kkr dhft,] fn;k gqvk gS fd y = 0 ;fn
= 4x cosec x (x ≠ 0) dk ,d fof'k"V gy Kkr dhft,] fn;k gqvk gS fd y = 0 ;fn 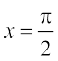 .
.
14. vody lehdj.k (x + 1) 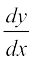 = 2 e–y – 1 dk ,d fof'k"V gy Kkr dhft,] fn;k gqvk gS fd y = 0 ;fn x = 0.
= 2 e–y – 1 dk ,d fof'k"V gy Kkr dhft,] fn;k gqvk gS fd y = 0 ;fn x = 0.
15. fdlh xk¡o dh tula[;k dh o`f¼ dh nj fdlh Hkh le; ml xk¡o osQ fuokfl;ksa dh la[;k osQ lekuqikrh gSA ;fn lu~ 1999 esa xk¡o dh tula[;k 20]000 Fkh vkSj lu~ 2004 esa 25]000 Fkh] rks Kkr dhft, fd lu~ 2009 esa xk¡o dh tula[;k D;k gksxh\
16. vody lehdj.k 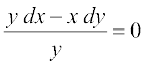 dk O;kid gy gS%
dk O;kid gy gS%
(A) xy = C (B) x = Cy2 (C) y = Cx (D) y = Cx2
17. 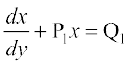 osQ :i okys vody lehdj.k dk O;kid gy gS%
osQ :i okys vody lehdj.k dk O;kid gy gS%
(A) 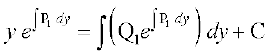
(B) 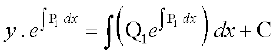
(C) 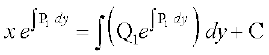
(D) 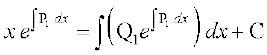
18. vody lehdj.k ex dy + (y ex + 2x) dx = 0 dk O;kid gy gS%
(A) x ey + x2 = C (B) x ey + y2 = C (C) y ex + x2 = C (D) y ey + x2 = C
lkjka'k
,d ,slk lehdj.k ftlesa Lora=k pj (pjksa) osQ lkis{k vkfJr pj osQ vodyt (vodytksa) lfEefyr gksa] vody lehdj.k dgykrk gSA
fdlh vody lehdj.k esa lfEefyr mPpre vodyt dh dksfV] ml vody lehdj.k dh dksfV dgykrh gSA
;fn dksbZ vody lehdj.k vodytksa esa cgqin lehdj.k gSa rks ml vody lehdj.k dh ?kkr ifjHkkf"kr gksrh gSA
fdlh vody lehdj.k dh ?kkr (;fn ifjHkkf"kr gks) ml vody lehdj.k esa lfEefyr mPpre dksfV vodyt dh mPpre ?kkr (osQoy /ukRed iw.kk±d) gksrh gSA
,d fn, gq, vody lehdj.k dks larq"V djus okyk iQyu ml vody lehdj.k dk gy dgykrk gSA ,d ,slk gy ftlesa mrus gh LosPN vpj gksa] ftruh ml vody lehdj.k dh dksfV gS] O;kid gy dgykrk gS vkSj LosPN vpjksa ls eqDr gy fof'k"V gy dgykrk gSA
fdlh fn, gq, iQyu ls vody lehdj.k cukus osQ fy, ge ml iQyu dk mÙkjksÙkj mruh gh ckj vodyu djrs gSa ftrus ml iQyu esa LosPN vpj gksrs gSa vkSj rc LosPN vpjksa dks foyqIr djrs gSaA
pj i`FkDdj.kh; fof/ ,sls lehdj.k dks gy djus osQ fy, mi;ksx dh tkrh gS ftlesa pjksa dks iwjh rjg ls i`Fko~Q~ fd;k tk ldrk gS vFkkZr~ y okys in dy osQ lkFk jgus pkfg, vkSj x okys in dx osQ lkFk jgus pkfg,A
,d ,slk vody lehdj.k] ftldks 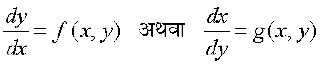 osQ :i esa vfHkO;Dr fd;k tk ldrk gS] tgk¡ f (x, y) ,oa g(x, y) 'kwU; ?kkr okys le?kkrh; iQyu gSa] le?kkrh; vody lehdj.k dgykrk gSA
osQ :i esa vfHkO;Dr fd;k tk ldrk gS] tgk¡ f (x, y) ,oa g(x, y) 'kwU; ?kkr okys le?kkrh; iQyu gSa] le?kkrh; vody lehdj.k dgykrk gSA
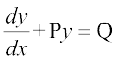 , osQ :i okyk vody lehdj.k] ftlesa P rFkk Q vpj vFkok osQoy x osQ iQyu gSa] izFke dksfV jSf[kd vody lehdj.k dgykrk gSA
, osQ :i okyk vody lehdj.k] ftlesa P rFkk Q vpj vFkok osQoy x osQ iQyu gSa] izFke dksfV jSf[kd vody lehdj.k dgykrk gSA
,sfrgkfld i`"BHkwfe
vody lehdj.k foKku dh izeq[k Hkk"kkvksa esa ls ,d gSA jkspd rF; ;g gS fd vody lehdj.kksa dk vfLrRo uoacj 11] 1675 Gottfried Wilthelm Freiherr Leibnitz (1646-1716) us loZizFke loZlfedk]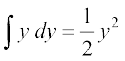 , dks fyf[kr :i esa izLrqr fd;k rFkk muls nksuksa izrhdksa ∫ vkSj dy ls ifjfpr djk;kA oLrqr% Leibnitz ,slh oØ dks Kkr djus dh leL;k esa eXu Fks ftldh Li'kZ js[kk fufnZ"V gksa] bl leL;k us lu~ 1691 esa mUgsa ^pjksa osQ i`FkDdj.kh; fof/* osQ vUos"k.k dk ekxZn'kZu djk;kA ,d o"kZ i'pkr~ mUgksaus ^izFke dksfV osQ le?kkrh; lehdj.kksa osQ gy djus dh fof/* dk lw=khdj.k fd;kA os vkxs c<+s vkSj vYi le; esa mUgksaus ^izFke dksfV osQ jSf[kd vody lehdj.kksa dks gy djus dh fof/* dk vUos"k.k fd;kA fdruk vk'p;Ztud gS fd mi;qZDr lHkh fof/;ksa dh [kkst vosQys ,d O;fDr }kjk vody lehdj.kksa osQ tUe osQ iPphl o"kks± osQ vYikof/ osQ varxZr laiUu gqbZA
, dks fyf[kr :i esa izLrqr fd;k rFkk muls nksuksa izrhdksa ∫ vkSj dy ls ifjfpr djk;kA oLrqr% Leibnitz ,slh oØ dks Kkr djus dh leL;k esa eXu Fks ftldh Li'kZ js[kk fufnZ"V gksa] bl leL;k us lu~ 1691 esa mUgsa ^pjksa osQ i`FkDdj.kh; fof/* osQ vUos"k.k dk ekxZn'kZu djk;kA ,d o"kZ i'pkr~ mUgksaus ^izFke dksfV osQ le?kkrh; lehdj.kksa osQ gy djus dh fof/* dk lw=khdj.k fd;kA os vkxs c<+s vkSj vYi le; esa mUgksaus ^izFke dksfV osQ jSf[kd vody lehdj.kksa dks gy djus dh fof/* dk vUos"k.k fd;kA fdruk vk'p;Ztud gS fd mi;qZDr lHkh fof/;ksa dh [kkst vosQys ,d O;fDr }kjk vody lehdj.kksa osQ tUe osQ iPphl o"kks± osQ vYikof/ osQ varxZr laiUu gqbZA
izkjaHk esa osQoy lehdj.kksa osQ ^gy* djus dh izfof/ dks vody lehdj.kksa osQ ^lekdyu* osQ :i esa fufnZ'V fd;k x;k FkkA ;g 'kCn lu~ 1690 esa izFker% James Bernoulli, (1654&1705) }kjk izpyu esa yk;k x;kA 'kCn ^gy* dk loZizFke iz;ksx Joseph Louis Lagrange (1736&1813)] }kjk lu~ 1774 esa fd;k x;kA ;g ?kVuk vody lehdj.kksa osQ tUe ls yxHkx 100 o"kks± ckn ?kfVr gqbZA ;s Jules Henri Poincare (1854&1912)] Fks] ftUgksaus 'kCn ^gy* osQ iz;ksx osQ fy, vdkV~; roZQ izLrqr fd;k] iQyr% vk/qfud 'kCnkoyh esa 'kCn gy dks viuk mfpr LFkku izkIr gqvkA ^pjksa osQ i`FDdj.kh; fof/ dk ukedj.k John Bernoulli (1667&1748)] James Bernoulli osQ vuqt }kjk fd;k x;kA ebZ 20] 1715 dks Leibnitz dks fy[ks vius i=k esa] mUgksus fuEufyf[kr vody lehdj.k osQ gy dh [kkst fd,
x2 y″ = 2y
osQ gy rhu izdkj dh oØksa uker% ijoy;] vfrijoy; vkSj ?kuh; oØksa osQ ,d lewg dk ekxZn'kZu djkrs gSaA ;g n'kkZrk gS fd ,sls ljy fn[kkbZ iM+us okys vody lehdj.kksa osQ gy oSQls ukuk :i /kj.k djrs gSaA 20oha 'krkCnh osQ mrjk/Z esa ^vody lehdj.kksa osQ xq.kkRed fo'ys"k.k* 'kh"kZd osQ varxZr vody lehdj.kksa osQ gyksa dh tfVy izo`Qfr osQ vkfo"dkj gsrq è;ku vkdf"kZr fd;k x;kA vktdy blus yxHkx lHkh vfo"dkjksa gsrq vR;ar izfof/ osQ :i esa izeq[k LFkku izkIr dj fy;k gSA