Table of Contents
vè;k; 10
lfn'k chtxf.kr (Vector Algebra)
In most sciences one generation tears down what another has built and what one has established another undoes. In Mathematics alone each generation builds a new story to the old structure. – Herman Hankel
10.1 Hkwfedk (Introduction)
vius nSfud thou esa gesa vusd iz'u feyrs gSa tSls fd vkidh Å¡pkbZ D;k gS\ ,d iqQVcky osQ f[kykM+h dks viuh gh Vhe osQ nwljs f[kykM+h osQ ikl xsan igq¡pkus osQ fy, xsan ij fdl izdkj izgkj djuk pkfg,\ voyksdu dhft, fd izFke iz'u dk laHkkfor mÙkj 1-6 ehVj gks ldrk gSA ;g ,d ,slh jkf'k gS ftlesa osQoy ,d eku ifjek.k tks ,d okLrfod la[;k gS] lfEefyr gSA ,slh jkf'k;k¡ vfn'k dgykrh gSA rFkkfi nwljs iz'u dk mÙkj ,d ,slh jkf'k gS (ftls cy dgrs gSa) ftlesa ekalisf'k;ksa dh 'kfDr ifjek.k osQ lkFk&lkFk fn'kk (ftlesa nwljk f[kykM+h fLFkr gS) Hkh lfEefyr gSA ,slh jkf'k;ka¡ lfn'k dgykrh gSA xf.kr] HkkSfrdh ,oa vfHk;kaf=kdh esa ;s nksuksa izdkj dh jkf'k;k¡ uker% vfn'k jkf'k;k¡] tSls fd yackbZ] nzO;eku] le;] nwjh] xfr] {ks=kiQy] vk;ru] rkieku] dk;Z] /u] oksYVrk] ?kuRo] izfrjks/d bR;kfn ,oa lfn'k jkf'k;k¡ tSls fd foLFkkiu] osx] Roj.k] cy] Hkkj] laosx] fo|qr {ks=k dh rhozrk bR;kfn cgq/k feyrh gaSA
bl vè;k; esa ge lfn'kksa dh oqQN vk/kjHkwr ladYiuk,¡] lfn'kksa dh fofHkUu lafØ;k,¡ vkSj buosQ chth; ,oa T;kferh; xq.k/eks± dk vè;;u djsaxsA bu nksuksa izdkj osQ xq.k/eks± dk lfEefyr :i lfn'kksa dh ladYiuk dk iw.kZ vuqHkwfr nsrk gS vkSj mi;qZDr p£pr {ks=kksa esa budh fo'kky mi;ksfxrk dh vksj izsfjr djrk gSA

W.R. Hamilton
(1805-1865)
10.2 oqQN vk/kjHkwr ladYiuk,¡ (Some Basic Concepts)
eku yhft, fd fdlh ry vFkok f=k&foeh; varfj{k esa l dksbZ ljy js[kk gSA rhj osQ fu'kkuksa dh lgk;rk ls bl js[kk dks nks fn'kk,¡ iznku dh tk ldrh gSaA bu nksuksa esa ls fuf'pr fn'kk okyh dksbZ Hkh ,d js[kk fn"V js[kk dgykrh gS [vko`Qfr 10.1 (i), (ii)]A
vc izsf{kr dhft, fd ;fn ge js[kk ‘l’ dks js[kk[kaM AB rd izfrcaf/r dj nsrs gSa rc nksuksa es ls fdlh ,d fn'kk okyh js[kk ‘l’ ij ifjek.k fu/kZfjr gks tkrk gSA bl izdkj gesa ,d fn"V js[kk[kaM izkIr gksrk gS (vko`Qfr 10.1(iii))A vr% ,d fn"V js[kk[kaM esa ifjek.k ,oa fn'kk nksuksa gksrs gSaA
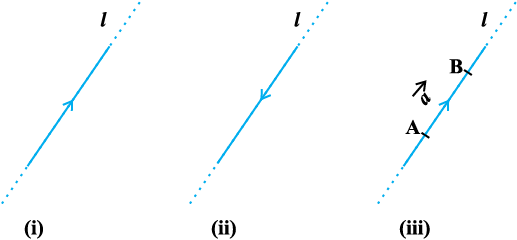
vko`Qfr 10-1
ifjHkk"kk 1 ,d ,slh jkf'k ftlesa ifjek.k ,oa fn'kk nksuksa gksrs gSa] lfn'k dgykrh gSA
è;ku nhft, fd ,d fn"V js[kk[kaM lfn'k gksrk gS (vko`Qfr 10.1(iii)), ftls 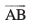 vFkok
vFkok
lk/kj.kr%  , osQ :i esa fufnZ"V djrs gSa vkSj bls lfn'k ^
, osQ :i esa fufnZ"V djrs gSa vkSj bls lfn'k ^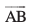 * vFkok lfn'k ^
* vFkok lfn'k ^ * osQ :i esa i<+rs gSaA
* osQ :i esa i<+rs gSaA
og ¯cnq A tgk¡ ls lfn'k 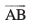 izkjaHk gksrk gS] izkjafHkd ¯cnq dgykrk gS vkSj og ¯cnq B tgk¡ ij lfn'k
izkjaHk gksrk gS] izkjafHkd ¯cnq dgykrk gS vkSj og ¯cnq B tgk¡ ij lfn'k 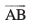 , lekIr gksrk gS vafre ¯cnq dgykrk gSA fdlh lfn'k osQ izkjafHkd ,oa vafre ¯cnqvksa osQ chp dh nwjh lfn'k dk ifjek.k (vFkok yackbZ) dgykrk gS vkSj bls |
, lekIr gksrk gS vafre ¯cnq dgykrk gSA fdlh lfn'k osQ izkjafHkd ,oa vafre ¯cnqvksa osQ chp dh nwjh lfn'k dk ifjek.k (vFkok yackbZ) dgykrk gS vkSj bls |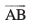 | vFkok |
| vFkok | | osQ :i esa fufnZ"V fd;k tkrk gSA rhj dk fu'kku lfn'k dh fn'kk dks fufnZ"V djrk gSA
| osQ :i esa fufnZ"V fd;k tkrk gSA rhj dk fu'kku lfn'k dh fn'kk dks fufnZ"V djrk gSA
fVIi.kh D;ksafd yackbZ dHkh Hkh ½.kkRed ugha gksrh gS blfy, laosQru | | < 0 dk dksbZ vFkZ ugha gSA
| < 0 dk dksbZ vFkZ ugha gSA
fLFkfr lfn'k (Position Vector)
d{kk XI ls] f=k&foeh; nf{k.kkorhZ ledksf.kd funsZ'kkad i¼fr dks Lej.k dhft,
(vko`Qfr 10-2(i))A varfj{k esa ewy ¯cnq O(0, 0, 0) osQ lkis{k ,d ,slk ¯cnq P yhft, ftlosQ funsZ'kkad (x, y, z) gSA rc lfn'k 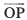 ftlesa O vkSj P Øe'k% izkjafHkd ,oa vafre ¯cnq gSa] O osQ
ftlesa O vkSj P Øe'k% izkjafHkd ,oa vafre ¯cnq gSa] O osQ
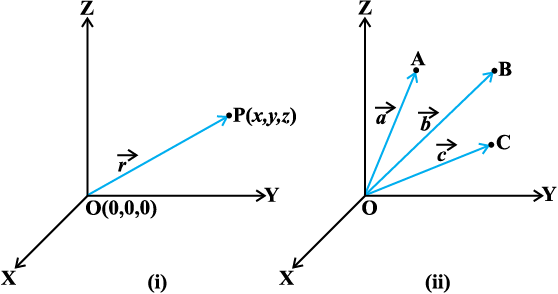
vko`Qfr 10-2
lkis{k ¯cnq P dk fLFkfr lfn'k dgykrk gSA nwjh lw=k (d{kk XI ls) dk mi;ksx djrs gq, 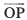 (vFkok
(vFkok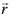 ) dk ifjek.k fuEufyf[kr :i esa izkIr gksrk gS%
) dk ifjek.k fuEufyf[kr :i esa izkIr gksrk gS%
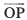 =
=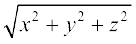
O;ogkj esa ewy ¯cnq O osQ lkis{k] ¯cnqvksa A, B, C bR;kfn osQ fLFkfr lfn'k Øe'k% 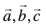 ls fufnZ"V fd, tkrs gaS [vko`Qfr 10.2(ii)]A
ls fufnZ"V fd, tkrs gaS [vko`Qfr 10.2(ii)]A
fno~Q&dkslkbu (Direction Cosines)
,d ¯cnq P(x, y, z) dk fLFkfr lfn'k  yhft, tSlk fd vko`Qfr 10-3 esa n'kkZ;k x;k gSA lfn'k
yhft, tSlk fd vko`Qfr 10-3 esa n'kkZ;k x;k gSA lfn'k 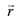 }kjk x, y ,oa z-v{k dh /ukRed fn'kkvksa osQ lkFk cuk, x, Øe'k% dks.k α, β, ,oa γ fn'kk dks.k dgykrs gSaA bu dks.kksa osQ dkslkbu eku vFkkZr~ cosα, cosβ ,oa cosγ lfn'k
}kjk x, y ,oa z-v{k dh /ukRed fn'kkvksa osQ lkFk cuk, x, Øe'k% dks.k α, β, ,oa γ fn'kk dks.k dgykrs gSaA bu dks.kksa osQ dkslkbu eku vFkkZr~ cosα, cosβ ,oa cosγ lfn'k 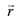 osQ fno~Q&dkslkbu dgykrs gSa vkSj lkekU;r% budks Øe'k% l, m ,oa n ls fufnZ"V fd;k tkrk gSA
osQ fno~Q&dkslkbu dgykrs gSa vkSj lkekU;r% budks Øe'k% l, m ,oa n ls fufnZ"V fd;k tkrk gSA
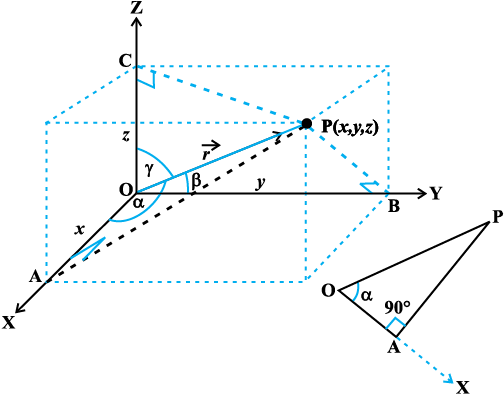
vko`Qfr 10-3
vko`Qfr 10.3, ls ge ns[krs gSa fd f=kHkqt OAP ,d ledks.k f=kHkqt gS vkSj bl f=kHkqt ls ge  izkIr djrs gSaA blh izdkj ledks.k f=kHkqtksa OBP ,oa OCP ls ge
izkIr djrs gSaA blh izdkj ledks.k f=kHkqtksa OBP ,oa OCP ls ge 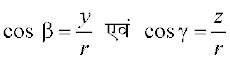 fy[k ldrs gSaA bl izdkj ¯cnq P osQ funsZ'kkadksa dks (lr, mr, nr) osQ :i esa vfHkO;Dr fd;k tk ldrk gSA fno~Q&dkslkbu osQ lekuqikrh la[;k,¡ lr, mr ,oa nr lfn'k
fy[k ldrs gSaA bl izdkj ¯cnq P osQ funsZ'kkadksa dks (lr, mr, nr) osQ :i esa vfHkO;Dr fd;k tk ldrk gSA fno~Q&dkslkbu osQ lekuqikrh la[;k,¡ lr, mr ,oa nr lfn'k 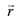 osQ fno~Q&vuqikr dgykrs gSa vkSj budks Øe'k% a, b rFkk c ls fufnZ"V fd;k tkrk gSA
osQ fno~Q&vuqikr dgykrs gSa vkSj budks Øe'k% a, b rFkk c ls fufnZ"V fd;k tkrk gSA
fVIi.kh ge uksV dj ldrs gSa fd l2 + m2 + n2 = 1 ijarq lkekU;r% a2 + b2 + c2 ≠ 1
10.3 lfn'kksa osQ izdkj (Types of Vectors)
'kwU; lfn'k [Zero (null) Vector] ,d lfn'k ftlosQ izkjafHkd ,oa vafre ¯cnq laikrh gksrs gSa] 'kwU; lfn'k dgykrk gS vkSj bls 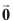 osQ :i esa fufnZ"V fd;k tkrk gSA 'kwU; lfn'k dks dksbZ fuf'pr fn'kk iznku ugha dh tk ldrh D;ksafd bldk ifjek.k 'kwU; gksrk gS vFkok fodYir% bldks dksbZ Hkh fn'kk /kj.k fd, gq, ekuk tk ldrk gSA lfn'k
osQ :i esa fufnZ"V fd;k tkrk gSA 'kwU; lfn'k dks dksbZ fuf'pr fn'kk iznku ugha dh tk ldrh D;ksafd bldk ifjek.k 'kwU; gksrk gS vFkok fodYir% bldks dksbZ Hkh fn'kk /kj.k fd, gq, ekuk tk ldrk gSA lfn'k 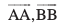 'kwU; lfn'k dks fu:fir djrs gSaA
'kwU; lfn'k dks fu:fir djrs gSaA
ek=kd lfn'k (Unit Vector) ,d lfn'k ftldk ifjek.k ,d (vFkok 1 bdkbZ) gS ek=kd lfn'k dgykrk gSA fdlh fn, gq, lfn'k  dh fn'kk esa ek=kd lfn'k dks
dh fn'kk esa ek=kd lfn'k dks 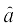 ls fufnZ"V fd;k tkrk gSA
ls fufnZ"V fd;k tkrk gSA
lg&vkfne lfn'k (Co-initial Vectors) nks vFkok vf/d lfn'k ftudk ,d gh izkjafHkd ¯cnq gS] lg vkfne lfn'k dgykrs gSaA
lajs[k lfn'k (Collinear Vectors) nks vFkok vf/d lfn'k ;fn ,d gh js[kk osQ lekarj gS rks os lajs[k lfn'k dgykrs gSaA
leku lfn'k (Equal Vectors) nks lfn'k  leku lfn'k dgykrs gSa ;fn muosQ ifjek.k ,oa fn'kk leku gSaA budks
leku lfn'k dgykrs gSa ;fn muosQ ifjek.k ,oa fn'kk leku gSaA budks 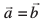 osQ :i esa fy[kk tkrk gSA
osQ :i esa fy[kk tkrk gSA
½.kkRed lfn'k (Negative of a Vector) ,d lfn'k ftldk ifjek.k fn, gq, lfn'k (eku yhft, 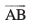 ) osQ leku gS ijarq ftldh fn'kk fn, gq, lfn'k dh fn'kk osQ foijhr gS] fn, gq, lfn'k dk ½.kkRed dgykrk gSA mnkgj.kr% lfn'k
) osQ leku gS ijarq ftldh fn'kk fn, gq, lfn'k dh fn'kk osQ foijhr gS] fn, gq, lfn'k dk ½.kkRed dgykrk gSA mnkgj.kr% lfn'k 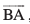 , lfn'k
, lfn'k 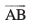 dk ½.kkRed gS vkSj bls
dk ½.kkRed gS vkSj bls 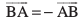 osQ :i esa fy[kk tkrk gSA
osQ :i esa fy[kk tkrk gSA
fVIi.kh mi;qZDr ifjHkkf"kr lfn'k bl izdkj gS fd muesa ls fdlh dks Hkh mlosQ ifjek.k ,oa fn'kk dks ifjofrZr fd, fcuk Lo;a osQ lekarj foLFkkfir fd;k tk ldrk gSA bl izdkj osQ lfn'k Lora=k lfn'k dgykrs gSaA bl iwjs vè;k; esa ge Lora=k lfn'kksa dh gh ppkZ djsaxsA
mnkgj.k 1 nf{k.k ls 30° if'pe esa] 40 km osQ foLFkkiu dk vkys[kh; fu:i.k dhft,A
gy lfn'k 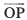 vHkh"V foLFkkiu dks fu:fir djrk gS (vko`Qfr 10-4 nsf[k,)A
vHkh"V foLFkkiu dks fu:fir djrk gS (vko`Qfr 10-4 nsf[k,)A
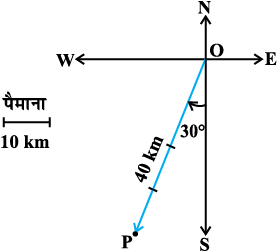
vko`Qfr 10-4
mnkgj.k 2 fuEufyf[kr ekiksa dks vfn'k ,oa lfn'k osQ :i esa Js.khc¼ dhft,A
(i) 5 s (ii) 1000 cm3 (iii) 10 N
(iv) 30 km/h (v) 10 g/cm3
(vi) 20 m/s mÙkj dh vksj
gy
(i) le;&vfn'k (ii) vk;ru&vfn'k (iii) cy&lfn'k
(iv) xfr&vfn'k (v) ?kuRo&vfn'k (vi) osx&lfn'k
mnkgj.k 3 vko`Qfr 10-5 esa dkSu ls lfn'k
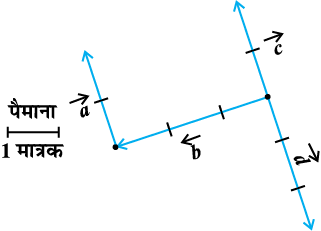
vko`Qfr 10-5
(i) lajs[k gSa
(ii) leku gSa
(iii) lg&vkfne gSa
gy

iz'ukoyh 10-1
1. mÙkj ls 30° iwoZ esa 40 km osQ foLFkkiu dk vkys[kh; fu:i.k dhft,A
2. fuEufyf[kr ekikas dks vfn'k ,oa lfn'k osQ :i esa Js.khc¼ dhft,A
(i) 10 kg (ii) 2 ehVj mÙkj&if'pe (iii) 40°
(iv) 40 okV (v) 10–19 owQyac (vi) 20 m/s2
3. fuEufyf[kr dks vfn'k ,oa lfn'k jkf'k;ksa osQ :i esa Js.khc¼ dhft,A
(i) le; dkyka'k (ii) nwjh (iii) cy
(iv) osx (v) dk;Z
4. vko`Qfr 10-6 (,d oxZ) esa fuEufyf[kr lfn'kksa dks igpkfu,A
(i) lg&vkfne (ii) leku
(iii) lajs[k ijarq vleku
5. fuEufyf[kr dk mÙkj lR; vFkok vlR; osQ :i esa nhft,A
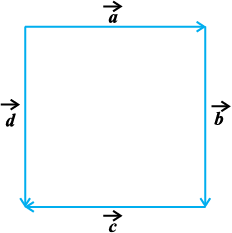
vko`Qfr 10-6
(i)  rFkk
rFkk 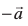 lajs[k gSaA
lajs[k gSaA
(ii) nks lajs[k lfn'kksa dk ifjek.k lnSo leku gksrk gSA
(iii) leku ifjek.k okys nks lfn'k lajs[k gksrs gSaA
(iv) leku ifjek.k okys nks lajs[k lfn'k leku gksrs gSaA
10.4 lfn'kksa dk ;ksxiQy (Addition of Vectors)
lfn'k 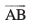 ls lk/kj.kr% gekjk rkRi;Z gS ¯cnq A ls ¯cnq B rd foLFkkiuA vc ,d ,slh fLFkfr dh ppkZ dhft, ftlesa ,d yM+dh ¯cnq A ls ¯cnq B rd pyrh gS vkSj mlosQ ckn ¯cnq B ls ¯cnq C rd pyrh gS (vko`Qfr 10.7)A ¯cnq A ls ¯cnq C rd yM+dh }kjk fd;k x;k oqQy foLFkkiu lfn'k,
ls lk/kj.kr% gekjk rkRi;Z gS ¯cnq A ls ¯cnq B rd foLFkkiuA vc ,d ,slh fLFkfr dh ppkZ dhft, ftlesa ,d yM+dh ¯cnq A ls ¯cnq B rd pyrh gS vkSj mlosQ ckn ¯cnq B ls ¯cnq C rd pyrh gS (vko`Qfr 10.7)A ¯cnq A ls ¯cnq C rd yM+dh }kjk fd;k x;k oqQy foLFkkiu lfn'k, 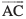 ls izkIr gksrk gS vkSj bls
ls izkIr gksrk gS vkSj bls 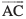 =
= 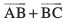 osQ :i esa vfHkO;Dr fd;k tkrk gSA
osQ :i esa vfHkO;Dr fd;k tkrk gSA
;g lfn'k ;ksx dk f=kHkqt fu;e dgykrk gSA
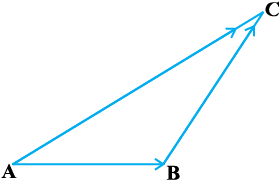
vko`Qfr 10-7
lkekU;r%] ;fn gekjs ikl nks lfn'k  rFkk
rFkk 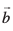 gSa [vko`Qfr 10.8 (i)], rks mudk ;ksx Kkr djus osQ fy, mUgsa bl fLFkfr esa yk;k tkrk gS] rkfd ,d dk izkjafHkd ¯cnq nwljs osQ vafre ¯cnq osQ laikrh gks tk, [vko`Qfr 10.8(ii)]A
gSa [vko`Qfr 10.8 (i)], rks mudk ;ksx Kkr djus osQ fy, mUgsa bl fLFkfr esa yk;k tkrk gS] rkfd ,d dk izkjafHkd ¯cnq nwljs osQ vafre ¯cnq osQ laikrh gks tk, [vko`Qfr 10.8(ii)]A
mnkgj.kr% vko`Qfr 10.8 (ii) esa] geus lfn'k 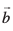 osQ ifjek.k ,oa fn'kk dks ifjofrZr fd, fcuk bl izdkj LFkkukarfjr fd;k gS rkfd bldk izkjafHkd ¯cnq]
osQ ifjek.k ,oa fn'kk dks ifjofrZr fd, fcuk bl izdkj LFkkukarfjr fd;k gS rkfd bldk izkjafHkd ¯cnq]  osQ vafre ¯cnq osQ laikrh gS rc f=kHkqt ABC dh rhljh Hkqtk AC }kjk fu:fir lfn'k
osQ vafre ¯cnq osQ laikrh gS rc f=kHkqt ABC dh rhljh Hkqtk AC }kjk fu:fir lfn'k 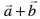 gesa lfn'kksa
gesa lfn'kksa  rFkk
rFkk 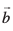 dk ;ksx (vFkok ifj.kkeh) iznku djrk gS] vFkkZr~~ f=kHkqt ABC esa ge ikrs gSa fd
dk ;ksx (vFkok ifj.kkeh) iznku djrk gS] vFkkZr~~ f=kHkqt ABC esa ge ikrs gSa fd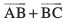 =
= 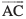 [vko`Qfr 10.8 (ii)]A
[vko`Qfr 10.8 (ii)]A
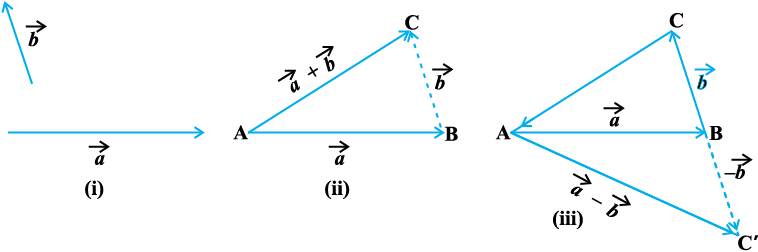
vko`Qfr 10-8
vc iqu% D;ksafd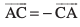 , blfy, mi;qZDr lehdj.k ls ge ikrs gSa fd
, blfy, mi;qZDr lehdj.k ls ge ikrs gSa fd
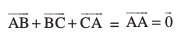
bldk rkRi;Z ;g gS fd fdlh f=kHkqt dh Hkqtkvksa dks ;fn ,d Øe esa fy;k tk, rks ;g 'kwU; ifj.kkeh dh vksj izsfjr djrk gS D;ksafd izkjafHkd ,oa vafre ¯cnq laikrh gks tkrs gSa [vko`Qfr 10.8(iii)]A
vc ,d lfn'k 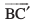 dh jpuk bl izdkj dhft, rkfd bldk ifjek.k lfn'k
dh jpuk bl izdkj dhft, rkfd bldk ifjek.k lfn'k 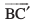 , osQ ifjek.k osQ leku gks] ijarq bldh fn'kk
, osQ ifjek.k osQ leku gks] ijarq bldh fn'kk 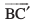 dh fn'kk osQ foijhr gks vko`Qfr 10-8(iii) vFkkZr~~
dh fn'kk osQ foijhr gks vko`Qfr 10-8(iii) vFkkZr~~
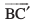 =
= 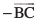 rc f=kHkqt fu;e dk vuqiz;ksx djrs gq, [vko`Qfr 10-8(iii)] ls ge ikrs gSa fd
rc f=kHkqt fu;e dk vuqiz;ksx djrs gq, [vko`Qfr 10-8(iii)] ls ge ikrs gSa fd 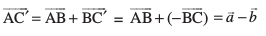
lfn'k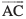 ,
,  osQ varj dks fu:fir djrk gSA
osQ varj dks fu:fir djrk gSA
vc fdlh unh osQ ,d fdukjs ls nwljs fdukjs rd ikuh osQ cgko dh fn'kk osQ yacor~~ tkus okyh ,d uko dh ppkZ djrs gSaA rc bl uko ij nks osx lfn'k dk;Z dj jgs gSa] ,d batu }kjk uko dks fn;k x;k osx vkSj nwljk unh osQ ikuh osQ cgko dk osxA bu nks osxksa osQ ;qxir izHkko ls uko okLro esa ,d fHkUu osx ls pyuk 'kq: djrh gSA bl uko dh izHkkoh xfr ,oa fn'kk (vFkkZr~~ ifj.kkeh osx) osQ ckjs esa ;FkkFkZ fopkj ykus osQ fy, gekjs ikl lfn'k ;ksxiQy dk fuEufyf[kr fu;e gSA
;fn gekjs ikl ,d lekarj prqHkqZt dh
nks layXu Hkqtkvksa ls fu:fir fd, tkus okys (ifjek.k ,oa fn'kk lfgr) nks lfn'k  gS (vko`Qfr 10-9) rc lekarj prqHkqZt dh bu nksuksa Hkqtkvksa osQ mHk;fu"B ¯cnq ls xqtjus okyk fod.kZ bu nksuksa lfn'kksa osQ ;ksx
gS (vko`Qfr 10-9) rc lekarj prqHkqZt dh bu nksuksa Hkqtkvksa osQ mHk;fu"B ¯cnq ls xqtjus okyk fod.kZ bu nksuksa lfn'kksa osQ ;ksx 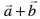 dks ifjek.k ,oa fn'kk lfgr fu:fir djrk gSA ;g lfn'k ;ksx dk lekarj prqHkqZt fu;e dgykrk gSA
dks ifjek.k ,oa fn'kk lfgr fu:fir djrk gSA ;g lfn'k ;ksx dk lekarj prqHkqZt fu;e dgykrk gSA
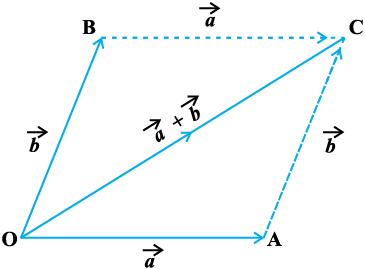
vko`Qfr 10-9
fVIi.kh f=kHkqt fu;e dk mi;ksx djrs gq, vko`Qfr 10-9 ls ge uksV dj ldrs gSa fd 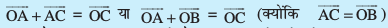 tks fd lekarj prqHkqZt fu;e gSA vr% ge dg ldrs gaS fd lfn'k ;ksx osQ nks fu;e ,d nwljs osQ lerqY; gSaA
tks fd lekarj prqHkqZt fu;e gSA vr% ge dg ldrs gaS fd lfn'k ;ksx osQ nks fu;e ,d nwljs osQ lerqY; gSaA
lfn'k ;ksxiQy osQ xq.k/eZ (Properties of vector addition)
xq.k/eZ 1 nks lfn'kksa  osQ fy,
osQ fy,
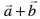 =
= 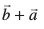 (Øefofue;rk)
(Øefofue;rk)
miifÙk lekarj prqHkqZt ABCD dks yhft, (vko`Qfr 10-10) eku yhft, 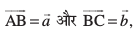 rc f=kHkqt ABC esa f=kHkqt fu;e dk mi;ksx djrs gq, ge ikrs gSa fd
rc f=kHkqt ABC esa f=kHkqt fu;e dk mi;ksx djrs gq, ge ikrs gSa fd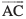 =
= 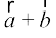
vc] D;ksafd lekarj prqHkqZt dh lEeq[k Hkqtk,¡ leku ,oa lekarj gS] blfy, vko`Qfr 10-10 esa 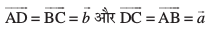 gSA iqu% f=kHkqt ADC esa f=kHkqt fu;e osQ iz;ksx ls
gSA iqu% f=kHkqt ADC esa f=kHkqt fu;e osQ iz;ksx ls 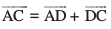 =
= 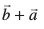
vr% 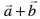 =
= 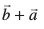
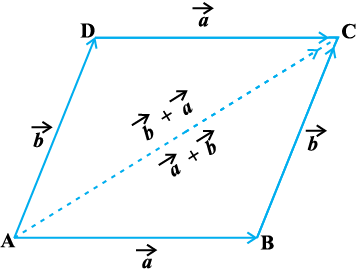
vko`Qfr 10-10
xq.k/eZ 2 rhu lfn'kksa 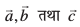 osQ fy,
osQ fy, 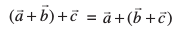 (lkgp;Z xq.k)
(lkgp;Z xq.k)
miifÙk eku yhft,] lfn'kksa 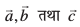 dks Øe'k%
dks Øe'k% 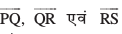 ls fu:fir fd;k x;k gS tSlk fd vko`Qfr 10.11(i) vkSj (ii) esa n'kkZ;k x;k gSA
ls fu:fir fd;k x;k gS tSlk fd vko`Qfr 10.11(i) vkSj (ii) esa n'kkZ;k x;k gSA

vko`Qfr 10-11
rc 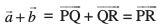
vkSj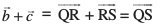
blfy,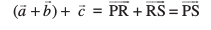
vkSj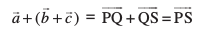
vr%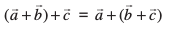
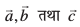 dk ;ksxiQy dks"Bdksa dk mi;ksx fd, fcuk
dk ;ksxiQy dks"Bdksa dk mi;ksx fd, fcuk 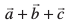 osQ :i esa fy[krs gSaA
osQ :i esa fy[krs gSaA uksV dhft, fd fdlh lfn'k  osQ fy, ge ikrs gSa%
osQ fy, ge ikrs gSa%
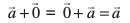
;gk¡ 'kwU; lfn'k 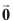 lfn'k ;ksxiQy osQ fy, ;ksT; loZlfedk dgykrk gSA
lfn'k ;ksxiQy osQ fy, ;ksT; loZlfedk dgykrk gSA
10.5 ,d vfn'k ls lfn'k dk xq.ku (Multiplication of a Vector by a Scalar)
eku yhft, fd  ,d fn;k gqvk lfn'k gS vkSj λ ,d vfn'k gSA rc lfn'k
,d fn;k gqvk lfn'k gS vkSj λ ,d vfn'k gSA rc lfn'k  dk vfn'k λ, ls xq.kuiQy ftls λ
dk vfn'k λ, ls xq.kuiQy ftls λ osQ :i esa fufnZ"V fd;k tkrk gS] lfn'k
osQ :i esa fufnZ"V fd;k tkrk gS] lfn'k  dk vfn'k λ ls xq.ku dgykrk gSA uksV dhft, fd λ
dk vfn'k λ ls xq.ku dgykrk gSA uksV dhft, fd λ Hkh lfn'k
Hkh lfn'k  osQ lajs[k ,d lfn'k gSA λ osQ eku /ukRed vFkok ½.kkRed gksus osQ vuqlkj λ
osQ lajs[k ,d lfn'k gSA λ osQ eku /ukRed vFkok ½.kkRed gksus osQ vuqlkj λ dh fn'kk]
dh fn'kk]  osQ leku vFkok foijhr gksrh gSA λ
osQ leku vFkok foijhr gksrh gSA λ dk ifjek.k
dk ifjek.k  osQ ifjek.k dk |λ| xq.kk gksrk gS] vFkkZr~~
osQ ifjek.k dk |λ| xq.kk gksrk gS] vFkkZr~~
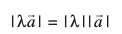
,d vfn'k ls lfn'k osQ xq.ku dk T;kferh; pk{kq"khdj.k [:i dh dYiuk (visualisation)] vko`Qfr 10-12 esa nh xbZ gSA
tc λ = – 1, rc 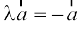 tks ,d ,slk lfn'k gS ftldk ifjek.k
tks ,d ,slk lfn'k gS ftldk ifjek.k  osQ leku gS vkSj fn'kk
osQ leku gS vkSj fn'kk  dh fn'kk osQ foijhr gSA lfn'k –
dh fn'kk osQ foijhr gSA lfn'k – lfn'k
lfn'k  dk ½.kkRed (vFkok ;ksT; izfrykse)dgykrk gS vkSj ge ges'kk
dk ½.kkRed (vFkok ;ksT; izfrykse)dgykrk gS vkSj ge ges'kk 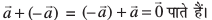
vkSj ;fn 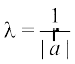 , fn;k gqvk gS fd
, fn;k gqvk gS fd 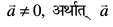 ,d 'kwU; lfn'k ugha gS rc
,d 'kwU; lfn'k ugha gS rc
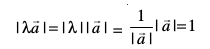

vko`Qfr 10-12
bl izdkj λ ,
, dh fn'kk esa ek=kd lfn'k dks fu:fir djrk gSA ge bls
dh fn'kk esa ek=kd lfn'k dks fu:fir djrk gSA ge bls
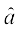 =
= 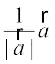 osQ :i esa fy[krs gSaA
osQ :i esa fy[krs gSaA
fVIi.kh fdlh Hkh vfn'k k osQ fy, 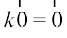
10.5.1 ,d lfn'k osQ ?kVd (Components of a vector)
vkbZ, ¯cnqvksa A(1, 0, 0), B(0, 1, 0) vkSj C(0, 0, 1) dks Øe'k% x-v{k, y-v{k ,oa z-v{k ij ysrs gSaA rc Li"Vr%
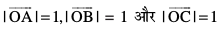
lfn'k 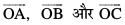 ftuesa ls izR;sd dk ifjek.k 1 gSa Øe'k% OX, OY vkSj OZ v{kksa osQ vuqfn'k ek=kd lfn'k dgykrs gSa vkSj budks Øe'k%
ftuesa ls izR;sd dk ifjek.k 1 gSa Øe'k% OX, OY vkSj OZ v{kksa osQ vuqfn'k ek=kd lfn'k dgykrs gSa vkSj budks Øe'k% 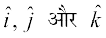 }kjk fufnZ"V fd;k tkrk gS (vko`Qfr 10-13)A
}kjk fufnZ"V fd;k tkrk gS (vko`Qfr 10-13)A
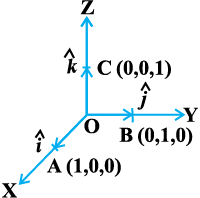
vko`Qfr 10-13
vc ,d ¯cnq P(x, y, z) dk fLFkfr lfn'k 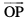 yhft, tSlk fd vko`Qfr 10-14 esa n'kkZ;k x;k gSA eku yhft, fd ¯cnq P1 ls ry XOY ij [khaps x, yac dk ikn ¯cnq P1 gSA bl izdkj ge ns[krs gSa fd P1 P, z-v{k osQ lekarj gSA D;ksafd
yhft, tSlk fd vko`Qfr 10-14 esa n'kkZ;k x;k gSA eku yhft, fd ¯cnq P1 ls ry XOY ij [khaps x, yac dk ikn ¯cnq P1 gSA bl izdkj ge ns[krs gSa fd P1 P, z-v{k osQ lekarj gSA D;ksafd 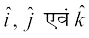 Øe'k% x, y ,oa z-v{kosQ vuqfn'k ek=kd lfn'k gS vkSj P osQ funsZ'kkadksa dh ifjHkk"kk osQ vuqlkj ge ikrs gSa fd
Øe'k% x, y ,oa z-v{kosQ vuqfn'k ek=kd lfn'k gS vkSj P osQ funsZ'kkadksa dh ifjHkk"kk osQ vuqlkj ge ikrs gSa fd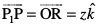 . blh izdkj
. blh izdkj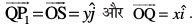 . bl izdkj ge ikrs gSa fd
. bl izdkj ge ikrs gSa fd
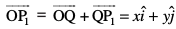
vkSj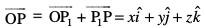
bl izdkj O osQ lkis{k P dk fLFkfr lfn'k 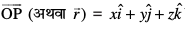 osQ :i esa izkIr gksrk gSA
osQ :i esa izkIr gksrk gSA
fdlh Hkh lfn'k dk ;g :i ?kVd :i dgykrk gSA ;gk¡ x, y ,oa z, 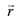 osQ vfn'k ?kVd dgykrs gSa vkSj
osQ vfn'k ?kVd dgykrs gSa vkSj 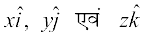 Øekxr v{kksa osQ vuqfn'k
Øekxr v{kksa osQ vuqfn'k 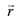 osQ lfn'k ?kVd dgykrs gSaA dHkh&dHkh x, y ,oa z dks ledksf.kd ?kVd Hkh dgk tkrk gSA
osQ lfn'k ?kVd dgykrs gSaA dHkh&dHkh x, y ,oa z dks ledksf.kd ?kVd Hkh dgk tkrk gSA
fdlh lfn'k 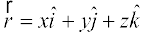 , dh yackbZ ikbFkkxksjl izes; dk nks ckj iz;ksx djosQ rqjar Kkr dh tk ldrh gSA ge uksV djrs gSa fd ledks.k f=kHkqt OQP1 esa (vko`Qfr 10.14)
, dh yackbZ ikbFkkxksjl izes; dk nks ckj iz;ksx djosQ rqjar Kkr dh tk ldrh gSA ge uksV djrs gSa fd ledks.k f=kHkqt OQP1 esa (vko`Qfr 10.14)
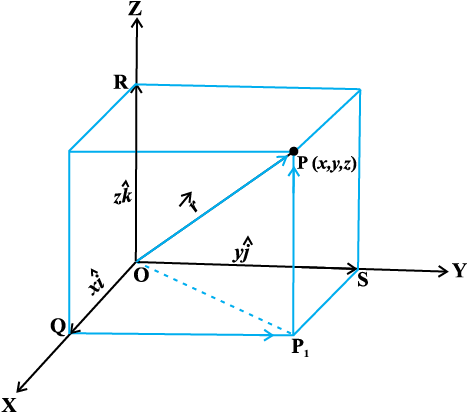
vko`Qfr 10-14
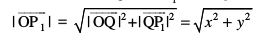
vkSj ledks.k f=kHkqt OP1P, esa ge ikrs gSa fd
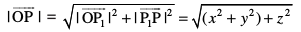
vr% fdlh lfn'k 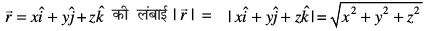 osQ :i esa izkIr gksrh gSA
osQ :i esa izkIr gksrh gSA
;fn nks lfn'k  ?kVd :i esa Øe'k%
?kVd :i esa Øe'k% 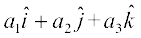 vkSj
vkSj 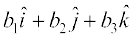 }kjk fn, x, gSa rks
}kjk fn, x, gSa rks
(i) lfn'kksa  dks ;ksx
dks ;ksx
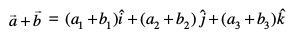 osQ :i esa izkIr gksrk gSA
osQ :i esa izkIr gksrk gSA
(ii) lfn'k  dk varj
dk varj
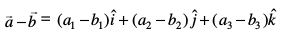 osQ :i esa izkIr gksrk gSA
osQ :i esa izkIr gksrk gSA
(iii) lfn'k  leku gksrs gSa ;fn vkSj osQoy ;fn
leku gksrs gSa ;fn vkSj osQoy ;fn
a1 = b1, a2 = b2 vkSj a3 = b3
(iv) fdlh vfn'k λ ls lfn'k  dk xq.ku
dk xq.ku
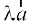 =
= 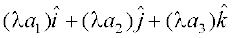 }kjk iznÙk gSA
}kjk iznÙk gSA
lfn'kksa dk ;ksxiQy vkSj fdlh vfn'k ls lfn'k dk xq.ku lfEefyr :i esa fuEufyf[kr forj.k&fu;e ls feyrk gS
eku yhft, fd  dksbZ nks lfn'k gSa vkSj k ,oa m nks vfn'k gSa rc
dksbZ nks lfn'k gSa vkSj k ,oa m nks vfn'k gSa rc
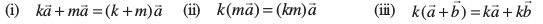
fVIi.kh
1. vki izsf{kr dj ldrs gSa fd λ osQ fdlh Hkh eku osQ fy, lfn'k 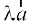 ges'kk lfn'k
ges'kk lfn'k  osQ lajs[k gSA okLro esa nks lfn'k
osQ lajs[k gSA okLro esa nks lfn'k  lajs[k rHkh gksrs gSa ;fn vkSj osQoy ;fn ,d ,sls 'kwU;srj vfn'k λ dk vfLrRo gSa rkfd
lajs[k rHkh gksrs gSa ;fn vkSj osQoy ;fn ,d ,sls 'kwU;srj vfn'k λ dk vfLrRo gSa rkfd 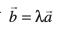 gksA ;fn lfn'k
gksA ;fn lfn'k  ?kVd :i esa fn, gq, gSa] vFkkZr~~
?kVd :i esa fn, gq, gSa] vFkkZr~~  rc nks lfn'k lajs[k gksrs gSa ;fn vkSj osQoy ;fn
rc nks lfn'k lajs[k gksrs gSa ;fn vkSj osQoy ;fn
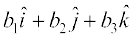 =
= 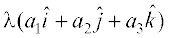
⇔ 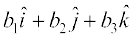 =
= 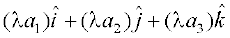
⇔ 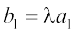 ,
, 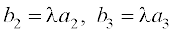
⇔ 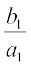 =
= 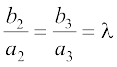
2. ;fn  =
= 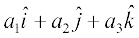 rc a1, a2, a3 lfn'k
rc a1, a2, a3 lfn'k  osQ fno~Q&vuqikr dgykrs gSaA
osQ fno~Q&vuqikr dgykrs gSaA
3. ;fn l, m, n fdlh lfn'k osQ fno~Q&dkslkbu gSa rc
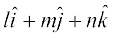 =
= 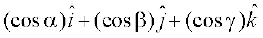
fn, gq, lfn'k dh fn'kk esa ek=kd lfn'k gS tgk¡ α, β ,oa γ fn, gq, lfn'k }kjk Øe'k% x, y ,oa z v{k osQ lkFk cuk, x, dks.k gSaA
mnkgj.k 4 x, y vkSj z osQ eku Kkr dhft, rkfd lfn'k 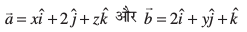 leku gSaA
leku gSaA
gy è;ku nhft, fd nks lfn'k leku gksrs gSa ;fn vkSj osQoy ;fn muosQ laxr ?kVd leku gSA vr% fn, gq, lfn'k  leku gksaxs ;fn vkSj osQoy ;fn x = 2, y = 2, z = 1
leku gksaxs ;fn vkSj osQoy ;fn x = 2, y = 2, z = 1
mnkgj.k 5 eku yhft, 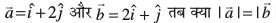 gS? D;k lfn'k
gS? D;k lfn'k  leku gSa\
leku gSa\
gy ;gk¡ 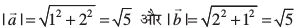
blfy, 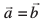 ijarq fn, gq, lfn'k leku ugha gSa D;ksafd buosQ laxr ?kVd fHkUu gSaA
ijarq fn, gq, lfn'k leku ugha gSa D;ksafd buosQ laxr ?kVd fHkUu gSaA
mnkgj.k 6 lfn'k 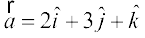 osQ vuqfn'k ek=kd lfn'k Kkr dhft,A
osQ vuqfn'k ek=kd lfn'k Kkr dhft,A
gy lfn'k  osQ vuqfn'k ek=kd lfn'k
osQ vuqfn'k ek=kd lfn'k 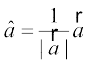 }kjk izkIr gksrk gSA
}kjk izkIr gksrk gSA
vc 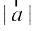 =
= 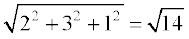
blfy, 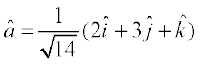 =
= 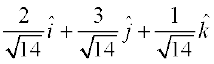
mnkgj.k 7 lfn'k 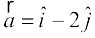 osQ vuqfn'k ,d ,slk lfn'k Kkr dhft, ftldk ifjek.k 7 bdkbZ gSA
osQ vuqfn'k ,d ,slk lfn'k Kkr dhft, ftldk ifjek.k 7 bdkbZ gSA
gy fn, gq, lfn'k  osQ vuqfn'k ek=kd lfn'k
osQ vuqfn'k ek=kd lfn'k 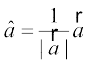 =
=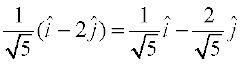 gSA
gSA
blfy,  osQ vuqfn'k vkSj 7 ifjek.k okyk lfn'k
osQ vuqfn'k vkSj 7 ifjek.k okyk lfn'k 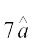 =
= 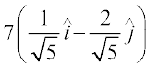 =
= 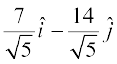 gSA
gSA
mnkgj.k 8 lfn'kksa 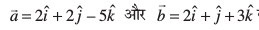 osQ ;ksxiQy osQ vuqfn'k ek=kd lfn'k Kkr dhft,A
osQ ;ksxiQy osQ vuqfn'k ek=kd lfn'k Kkr dhft,A
gy fn, gq, lfn'kksa dk ;ksxiQy
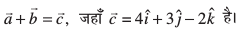
vkSj 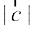 =
= 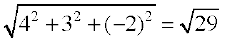
vr% vHkh"V ek=kd lfn'k
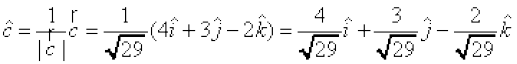 gSA
gSA
mnkgj.k 9 lfn'k 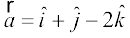 osQ fno~Q&vuqikr fyf[k, vkSj bldh lgk;rk ls fno~Q&dkslkbu Kkr dhft,A
osQ fno~Q&vuqikr fyf[k, vkSj bldh lgk;rk ls fno~Q&dkslkbu Kkr dhft,A
gy è;ku nhft, fd lfn'k 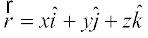 osQ fno~Q&vuqikr a, b, c lfn'k osQ] Øekxr ?kVd x, y, z gksrs gSaA blfy, fn, gq, lfn'k osQ fy, ge ikrs gSa fd a = 1, b = 1 vkSj c = –2 gSA iqu% ;fn l, m vkSj n fn, gq, lfn'k osQ fno~Q&dkslkbu gSa rks%
osQ fno~Q&vuqikr a, b, c lfn'k osQ] Øekxr ?kVd x, y, z gksrs gSaA blfy, fn, gq, lfn'k osQ fy, ge ikrs gSa fd a = 1, b = 1 vkSj c = –2 gSA iqu% ;fn l, m vkSj n fn, gq, lfn'k osQ fno~Q&dkslkbu gSa rks%
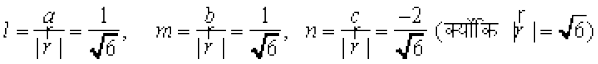
vr% fno~Q&dkslkbu 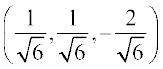 gSaA
gSaA
10.5.2 nks ¯cnqvksa dks feykus okyk lfn'k (Vector joining two points)
;fn P1(x1, y1, z1) vkSj P2(x2, y2, z2) nks ¯cnq gSa rc P1 dks P2 ls feykus okyk lfn'k 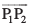 gS (vko`Qfr 10-15)A P1 vkSj P2 dks ewy ¯cnq O ls feykus ij vkSj f=kHkqt fu;e dk iz;ksx djus ij ge f=kHkqt OP1P2 ls ikrs gSa fd
gS (vko`Qfr 10-15)A P1 vkSj P2 dks ewy ¯cnq O ls feykus ij vkSj f=kHkqt fu;e dk iz;ksx djus ij ge f=kHkqt OP1P2 ls ikrs gSa fd 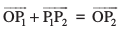
lfn'k ;ksxiQy osQ xq.k/eks± dk mi;ksx djrs gq, mi;qZDr lehdj.k fuEufyf[kr :i ls fy[kk tkrk gSA
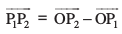
vFkkZr~~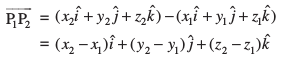
lfn'k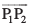 dk ifjek.k
dk ifjek.k 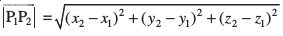 osQ :i esa izkIr gksrk gSA
osQ :i esa izkIr gksrk gSA
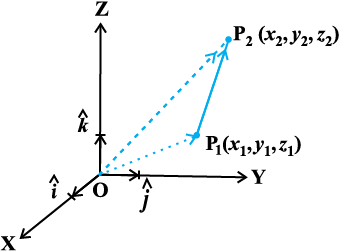
vko`Qfr 10-15
mnkgj.k10 ¯cnqvksa P(2, 3, 0) ,oa Q(– 1, – 2, – 4) dks feykus okyk ,oa P ls Q dh rjiQ fn"V lfn'k Kkr dhft,A
gy D;ksafd lfn'k P ls Q dh rjiQ fn"V gS] Li"Vr% P izkjafHkd ¯cnq gS vkSj Q vafre ¯cnq gS] blfy, P vkSj Q dks feykus okyk vHkh"V lfn'k ,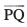 fuEufyf[kr :i esa izkIr gksrk gSA
fuEufyf[kr :i esa izkIr gksrk gSA
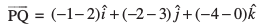
vFkkZr~~ 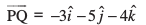
10.5.3 [kaM lw=k (Section Formula)
eku yhft, ewy ¯cnq O osQ lkis{k P vkSj Q nks ¯cnq gSa ftudks fLFkfr lfn'k  ls fu:fir fd;k x;k gSA ¯cnqvksa P ,oa Q dks feykus okyk js[kk [kaM fdlh rhljs ¯cnq R }kjk nks izdkj ls foHkkftr fd;k tk ldrk gSA var% (vko`Qfr 10-16) ,oa cká (vko`Qfr 10-17)A ;gk¡ gekjk mn~ns'; ewy ¯cnq O osQ lkis{k ¯cnq R dk fLFkfr lfn'k
ls fu:fir fd;k x;k gSA ¯cnqvksa P ,oa Q dks feykus okyk js[kk [kaM fdlh rhljs ¯cnq R }kjk nks izdkj ls foHkkftr fd;k tk ldrk gSA var% (vko`Qfr 10-16) ,oa cká (vko`Qfr 10-17)A ;gk¡ gekjk mn~ns'; ewy ¯cnq O osQ lkis{k ¯cnq R dk fLFkfr lfn'k 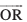 Kkr djuk gSA ge nksuksa fLFkfr;ksa dks ,d&,d djosQ ysrs gSaA
Kkr djuk gSA ge nksuksa fLFkfr;ksa dks ,d&,d djosQ ysrs gSaA
fLFkfr 1 tc R, PQ dks var% foHkkftr djrk gS (vko`Qfr 10-16)A ;fn R,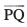 dks bl izdkj foHkkftr djrk gS fd
dks bl izdkj foHkkftr djrk gS fd 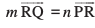 ,tgk¡ m vkSj n /ukRed vfn'k gSa rks ge dgrs gSa fd ¯cnq R,
,tgk¡ m vkSj n /ukRed vfn'k gSa rks ge dgrs gSa fd ¯cnq R, 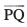 dks m : n osQ vuqikr esa var% foHkkftr djrk gSA vc f=kHkqtksa ORQ ,oa OPR ls
dks m : n osQ vuqikr esa var% foHkkftr djrk gSA vc f=kHkqtksa ORQ ,oa OPR ls
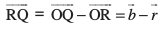
vkSj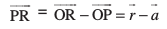
blfy, 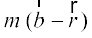 =
= 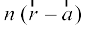 (D;ksa\)
(D;ksa\)
vFkok 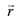 =
= 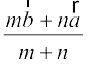 (ljy djus ij)
(ljy djus ij)
vr% ¯cnq R tks fd P vkSj Q dks m : n osQ vuqikr esa var% foHkkftr djrk gS dk fLFkfr lfn'k
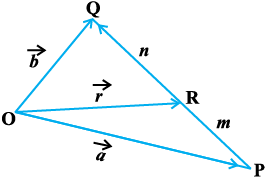
vko`Qfr 10-16

fLFkfr II tc R, PQ dks cká foHkkftr djrk gS (vko`Qfr 10-17)A ;g lR;kiu djuk ge ikBd osQ fy, ,d iz'u osQ :i esa NksM+rs gSa fd js[kk[kaM PQ dks m : n osQ vuqikr esa cká foHkkftr djus okys ¯cnq R 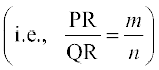 dk fLFkfr lfn'k
dk fLFkfr lfn'k 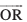 =
= 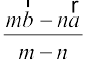 osQ :i esa izkIr gksrk gSA
osQ :i esa izkIr gksrk gSA
fVIi.kh ;fn R, PQ dk eè; ¯cnq gS rks m = n vkSj blfy, fLFkfr i ls 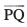 osQ eè; ¯cnq R dk fLFkfr lfn'k
osQ eè; ¯cnq R dk fLFkfr lfn'k 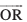 =
= 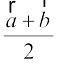 osQ :i esa gksxkA
osQ :i esa gksxkA
mnkgj.k 11 nks ¯cnq P vkSj Q yhft, ftuosQ fLFkfr lfn'k 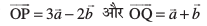 gSaA ,d ,sls ¯cnq R dk fLFkfr lfn'k Kkr dhft, tks P ,oa Q dks feykus okyh js[kk dks 2:1 osQ vuqikr esa (i) var% (ii) cká foHkkftr djrk gSA
gSaA ,d ,sls ¯cnq R dk fLFkfr lfn'k Kkr dhft, tks P ,oa Q dks feykus okyh js[kk dks 2:1 osQ vuqikr esa (i) var% (ii) cká foHkkftr djrk gSA
vko`Qfr 10-17
gy
(i) P vkSj Q dks feykus okyh js[kk dks 2:1 osQ vuqikr esa var% foHkkftr djus okys ¯cnq R dk fLFkfr lfn'k gS%
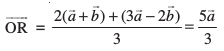
(ii) P vkSj Q dks feykus okyh js[kk dks 2:1 osQ vuqikr esa cká foHkkftr djus okys ¯cnq R dk fLFkfr lfn'k gS%
mnkgj.k 12 n'kkZb, fd ¯cnq 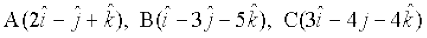 ,d ledks.k f=kHkqt osQ 'kh"kZ gSaA
,d ledks.k f=kHkqt osQ 'kh"kZ gSaA
gy ge ikrs gSa fd
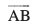 =
= 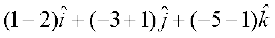
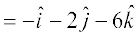
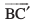 =
= 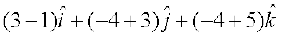
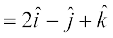
vkSj =
= 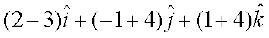
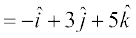
blosQ vfrfjDr è;ku nhft, fd
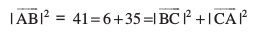
vr% fn;k gqvk f=kHkqt ,d ledks.k f=kHkqt gSA
iz'ukoyh 10-2
1. fuEufyf[kr lfn'kksa osQ ifjek.k dk ifjdyu dhft,%
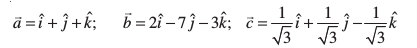
2. leku ifjek.k okys nks fofHkUu lfn'k fyf[k,A
3. leku fn'kk okys nks fofHkUu lfn'k fyf[k,A
4. x vkSj y osQ eku Kkr dhft, rkfd lfn'k 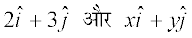 leku gksaA
leku gksaA
5. ,d lfn'k dk izkjafHkd ¯cnq (2] 1) gS vkSj vafre ¯cnq (&5] 7) gSA bl lfn'k osQ vfn'k ,oa lfn'k ?kVd Kkr dhft,A
6. lfn'k 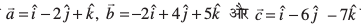 dk ;ksxiQy Kkr dhft,A
dk ;ksxiQy Kkr dhft,A
7. lfn'k 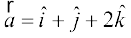 osQ vuqfn'k ,d ek=kd lfn'k Kkr dhft,A
osQ vuqfn'k ,d ek=kd lfn'k Kkr dhft,A
8. lfn'k 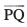 osQ vuqfn'k ek=kd lfn'k Kkr dhft, tgk¡ ¯cnq P vkSj Q Øe'k% (1] 2] 3) vkSj (4] 5] 6) gSaA
osQ vuqfn'k ek=kd lfn'k Kkr dhft, tgk¡ ¯cnq P vkSj Q Øe'k% (1] 2] 3) vkSj (4] 5] 6) gSaA
9. fn, gq, lfn'kksa 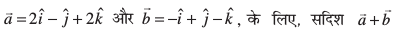 osQ vuqfn'k ek=kd lfn'k Kkr dhft,A
osQ vuqfn'k ek=kd lfn'k Kkr dhft,A
10. lfn'k 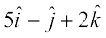 osQ vuqfn'k ,d ,slk lfn'k Kkr dhft, ftldk ifjek.k 8 bdkbZ gSA
osQ vuqfn'k ,d ,slk lfn'k Kkr dhft, ftldk ifjek.k 8 bdkbZ gSA
11. n'kkZb, fd lfn'k 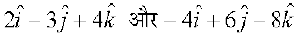 lajs[k gSaA
lajs[k gSaA
12. lfn'k 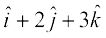 dh fno~Q cosine Kkr dhft,A
dh fno~Q cosine Kkr dhft,A
13. ¯cnqvksa A(1, 2, –3) ,oa B(–1, –2, 1) dks feykus okys ,oa A ls B dh rji+Q fn"V lfn'k dh fno~Q cosine Kkr dhft,A
14. n'kkZb, fd lfn'k 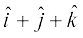 v{kksa OX, OY ,oa OZ osQ lkFk cjkcj >qdk gqvk gSA
v{kksa OX, OY ,oa OZ osQ lkFk cjkcj >qdk gqvk gSA
15. ¯cnqvksa P (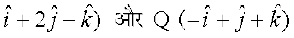 dks feykus okyh js[kk dks 2%1 osQ vuqikr esas (i) var% (ii) cká] foHkkftr djus okys ¯cnq R dk fLFkfr lfn'k Kkr dhft,A
dks feykus okyh js[kk dks 2%1 osQ vuqikr esas (i) var% (ii) cká] foHkkftr djus okys ¯cnq R dk fLFkfr lfn'k Kkr dhft,A
16. nks ¯cnqvksa P(2, 3, 4) vkSj Q(4, 1, –2) dks feykus okys lfn'k dk eè; ¯cnq Kkr dhft,A
17. n'kkZb, fd ¯cnq A, B vkSj C, ftuosQ fLFkfr lfn'k Øe'k% 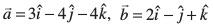 vkSj
vkSj 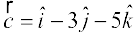 gSa] ,d ledks.k f=kHkqt osQ 'kh"kks± dk fuekZ.k djrs gSaA
gSa] ,d ledks.k f=kHkqt osQ 'kh"kks± dk fuekZ.k djrs gSaA
18. f=kHkqt ABC (vko`Qfr 10.18), osQ fy, fuEufyf[kr esa ls dkSu lk dFku lR; ugha gSA

vko`Qfr 10-18
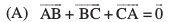
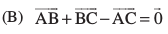
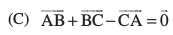
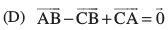
19. ;fn  nks lajs[k lfn'k gSa rks fuEufyf[kr esa ls dkSu lk dFku lgh ugha gS%
nks lajs[k lfn'k gSa rks fuEufyf[kr esa ls dkSu lk dFku lgh ugha gS%

10.6 nks lfn'kksa dk xq.kuiQy (Product of Two Vectors)
vHkh rd geus lfn'kksa osQ ;ksxiQy ,oa O;odyu osQ ckjs esa vè;;u fd;k gSA vc gekjk mn~ns'; lfn'kksa dk xq.kuiQy uked ,d nwljh chth; lafØ;k dh ppkZ djuk gSA ge Lej.k dj ldrs gSa fd nks la[;kvksa dk xq.kuiQy ,d la[;k gksrh gS] nks vkO;wgksa dk xq.kuiQy ,d vkO;wg gksrk gS ijarq iQyuksa dh fLFkfr esa ge mUgsa nks izdkj ls xq.kk dj ldrs gSa uker% nks iQyuksa dk ¯cnqokj xq.ku ,oa nks iQyuksa dk la;kstuA blh izdkj lfn'kksa dk xq.ku Hkh nks rjhosQ ls ifjHkkf"kr fd;k tkrk gSA uker% vfn'k xq.kuiQy tgk¡ ifj.kke ,d vfn'k gksrk gS vkSj lfn'k xq.kuiQy tgk¡ ifj.kke ,d lfn'k gksrk gSA lfn'kksa osQ bu nks izdkj osQ xq.kuiQyksa osQ vk/kj ij T;kferh] ;kaf=kdh ,oa vfHk;kaf=kdh esa buosQ fofHkUu vuqiz;ksx gSaA bl ifjPNsn esa ge bu nks izdkj osQ xq.kuiQyksa dh ppkZ djsaxsA
10.6.1 nks lfn'kksa dk vfn'k xq.kuiQy [Scalar (or dot) product of two vectors]
ifjHkk"kk 2 nks 'kwU;srj lfn'kksa  dk vfn'k xq.kuiQy
dk vfn'k xq.kuiQy 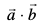 }kjk fufnZ"V fd;k tkrk gS vkSj bls
}kjk fufnZ"V fd;k tkrk gS vkSj bls 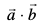 =
=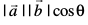 osQ :i es ifjHkkf"kr fd;k tkrk gSA
osQ :i es ifjHkkf"kr fd;k tkrk gSA
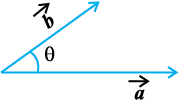
tgk¡ θ, 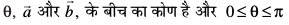 (vko`Qfr 10-19)A
(vko`Qfr 10-19)A
;fn  rks θ ifjHkkf"kr ugha gS vkSj bl fLFkfr eas ge
rks θ ifjHkkf"kr ugha gS vkSj bl fLFkfr eas ge 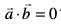 ifjHkkf"kr djrs gSaA
ifjHkkf"kr djrs gSaA
izs{k.k
1. 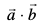 ,d okLrfod la[;k gSA
,d okLrfod la[;k gSA
2. eku yhft, fd  nks 'kwU;srj lfn'k gSa rc
nks 'kwU;srj lfn'k gSa rc 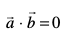 ;fn vkSj osQoy ;fn
;fn vkSj osQoy ;fn  ijLij yacor~~ gSa vFkkZr~~
ijLij yacor~~ gSa vFkkZr~~ 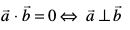
3.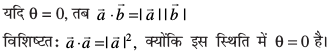
4. ;fn θ = π, rc 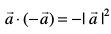
fof'k"Vr% 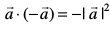 , tSlk fd bl fLFkfr esa θ, π osQ cjkcj gSA
, tSlk fd bl fLFkfr esa θ, π osQ cjkcj gSA
5. isz{k.k 2 ,oa 3 osQ lanHkZ esa ijLij yacor~ ek=kd lfn'kksa  osQ fy, ge ikrs gSa fd
osQ fy, ge ikrs gSa fd
vko`Qfr 10-19
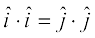 =
= 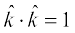
rFkk 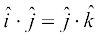 =
= 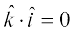
6. nks 'kwU;srj lfn'kksa  osQ chp dk dks.k θ,
osQ chp dk dks.k θ,
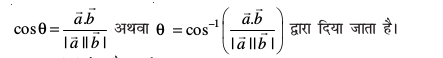
7. vfn'k xq.kuiQy Øe fofues; gS vFkkZr~~
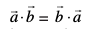 (D;ksa?)
(D;ksa?)
vfn'k xq.kuiQy osQ nks egRoiw.kZ xq.k/eZ (Two important properties of scalar product)
xq.k/eZ 1 (vfn'k xq.kuiQy dh ;ksxiQy ij forj.k fu;e) eku yhft, 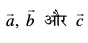 rhu lfn'k gSa rc
rhu lfn'k gSa rc 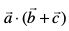 =
= 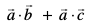
xq.k/eZ 2 eku yhft,  nks lfn'k gSa vkSj λ ,d vfn'k gS] rks
nks lfn'k gSa vkSj λ ,d vfn'k gS] rks
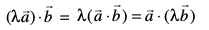
;fn nks lfn'k ?kVd :i esa 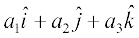 ,oa
,oa 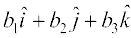 , fn, gq, gSa rc mudk vfn'k xq.kuiQy fuEufyf[kr :i esa izkIr gksrk gS
, fn, gq, gSa rc mudk vfn'k xq.kuiQy fuEufyf[kr :i esa izkIr gksrk gS
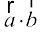 =
= 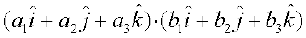
= 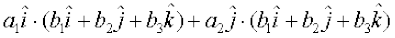 +
+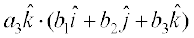
= 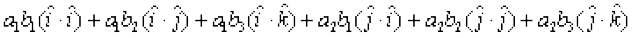
+ 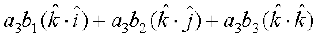
(mi;qZDr xq.k/eZ 1 vkSj 2 dk mi;ksx djus ij)
= a1b1 + a2b2 + a3b3 (iz{ks.k 5 dk mi;ksx djus ij)
bl izdkj 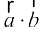 =
= 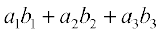
10.6.2 ,d lfn'k dk fdlh js[kk ij lkFk iz{ksi (Projection of a vector on a line)
eku yhft, fd ,d lfn'k 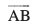 fdlh fn"V js[kk l (eku yhft,) osQ lkFk okekorZ fn'kk esa θ dks.k cukrk gSA (vko`Qfr 10-20 nsf[k,) rc
fdlh fn"V js[kk l (eku yhft,) osQ lkFk okekorZ fn'kk esa θ dks.k cukrk gSA (vko`Qfr 10-20 nsf[k,) rc 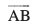 dk l ij iz{ksi ,d lfn'k
dk l ij iz{ksi ,d lfn'k 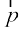 (eku yhft,) gS ftldk ifjek.k
(eku yhft,) gS ftldk ifjek.k 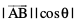 gS vkSj ftldh fn'kk dk l dh fn'kk osQ leku vFkok foijhr gksuk bl ckr ij fuHkZj gS fd
gS vkSj ftldh fn'kk dk l dh fn'kk osQ leku vFkok foijhr gksuk bl ckr ij fuHkZj gS fd 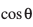 /ukRed gS vFkok ½.kkRedA lfn'k
/ukRed gS vFkok ½.kkRedA lfn'k 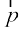 dks iz{ksi lfn'k dgrs gSa vkSj bldk ifjek.k |
dks iz{ksi lfn'k dgrs gSa vkSj bldk ifjek.k |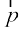 |, fu£n"V js[kk l ij lfn'k
|, fu£n"V js[kk l ij lfn'k 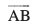 dk iz{ksi dgykrk gSA mnkgj.kr% fuEufyf[kr esa ls izR;sd vko`Qfr esa lfn'k
dk iz{ksi dgykrk gSA mnkgj.kr% fuEufyf[kr esa ls izR;sd vko`Qfr esa lfn'k 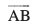 dk js[kk l ij iz{ksi lfn'k
dk js[kk l ij iz{ksi lfn'k 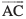 gSA [vko`Qfr 10.20 (i) ls (iv) rd]
gSA [vko`Qfr 10.20 (i) ls (iv) rd]
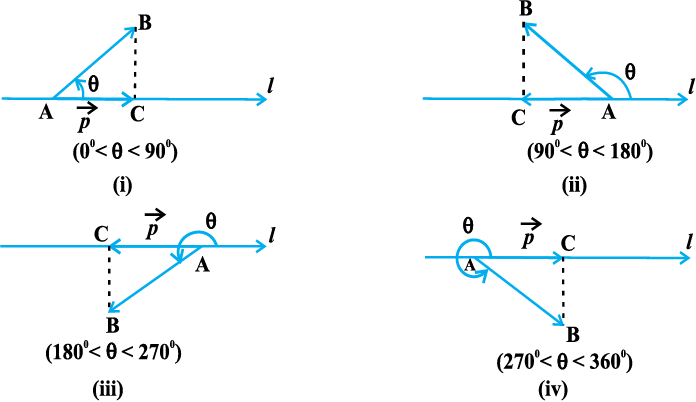
vko`Qfr 10-20
izs{k.k
1. js[kk l osQ vuqfn'k ;fn 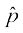 ek=kd lfn'k gS rks js[kk l ij lfn'k
ek=kd lfn'k gS rks js[kk l ij lfn'k  dk iz{ksi
dk iz{ksi 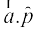 ls izkIr gksrk gSA
ls izkIr gksrk gSA
2. ,d lfn'k  dk nwljs lfn'k
dk nwljs lfn'k 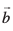 , ij iz{ksi
, ij iz{ksi 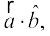 vFkok
vFkok  ls izkIr gksrk gSA
ls izkIr gksrk gSA
3- ;fn θ = 0, rks 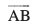 dk iz{ksi lfn'k Lo;a
dk iz{ksi lfn'k Lo;a 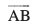 gksxk vkSj ;fn θ = π rks
gksxk vkSj ;fn θ = π rks 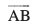 dk iz{ksi lfn'k
dk iz{ksi lfn'k 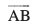 gksxkA
gksxkA
4- ;fn 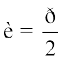 vFkok
vFkok 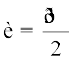 rks
rks 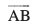 dk iz{ksi lfn'k 'kwU; lfn'k gksxkA
dk iz{ksi lfn'k 'kwU; lfn'k gksxkA
fVIi.kh ;fn α, β vkSj γ lfn'k 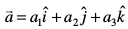 osQ fno~Q&dks.k gSa rks bldh fno~Q&dkslkbu fuEufyf[kr :i esa izkIr dh tk ldrh gSA
osQ fno~Q&dks.k gSa rks bldh fno~Q&dkslkbu fuEufyf[kr :i esa izkIr dh tk ldrh gSA
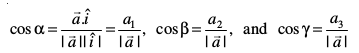
;g Hkh è;ku nhft, fd 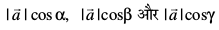 Øe'k% OX, OY rFkk OZ osQ vuqfn'k
Øe'k% OX, OY rFkk OZ osQ vuqfn'k  osQ iz{ksi gSa vFkkZr~~ lfn'k
osQ iz{ksi gSa vFkkZr~~ lfn'k  osQ vfn'k ?kVd a1, a2 vkSj a3 Øe'k% x, y, ,oa z v{k osQ vuqfn'k
osQ vfn'k ?kVd a1, a2 vkSj a3 Øe'k% x, y, ,oa z v{k osQ vuqfn'k  osQ iz{ksi gSA blosQ vfrfjDr ;fn
osQ iz{ksi gSA blosQ vfrfjDr ;fn  ,d ek=kd lfn'k gS rc bldks fno~Q&dkslkbu dh lgk;rk ls
,d ek=kd lfn'k gS rc bldks fno~Q&dkslkbu dh lgk;rk ls
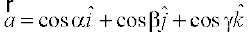
osQ :i esa vfHkO;Dr fd;k tk ldrk gSA
mnkgj.k 13 nks lfn'kksa  osQ ifjek.k Øe'k% 1 vkSj 2 gS rFkk
osQ ifjek.k Øe'k% 1 vkSj 2 gS rFkk 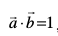 , bu lfn'kksa osQ chp dk dks.k Kkr dhft,A
, bu lfn'kksa osQ chp dk dks.k Kkr dhft,A
gy fn;k gqvk gS 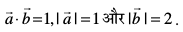 . vr%
. vr%
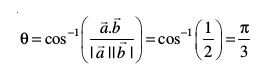
mnkgj.k 14 lfn'k 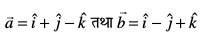 osQ chp dk dks.k Kkr dhft,A
osQ chp dk dks.k Kkr dhft,A
gy nks lfn'kksa  osQ chp dk dks.k θ fuEu }kjk iznÙk gS
osQ chp dk dks.k θ fuEu }kjk iznÙk gS
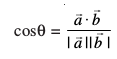 ls izkIr gksrk gSA
ls izkIr gksrk gSA
vc 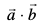 =
= 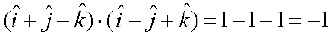
blfy,] ge ikrs gSa fd cosθ = 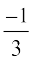
vr% vHkh"V dks.k θ = 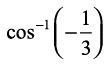 gSA
gSA
mnkgj.k 15 ;fn 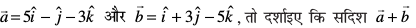 vkSj
vkSj 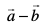 yacor~ gSA
yacor~ gSA
gy ge tkurs gSa fd nks 'kwU;srj lfn'k yacor~~ gksrs gSa ;fn mudk vfn'k xq.kuiQy 'kwU; gSA

mnkgj.k 16 lfn'k 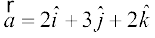 dk] lfn'k
dk] lfn'k 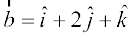 ij iz{ksi Kkr dhft,A
ij iz{ksi Kkr dhft,A
gy lfn'k  dk lfn'k
dk lfn'k 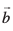 ij iz{ksi
ij iz{ksi
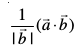 =
= 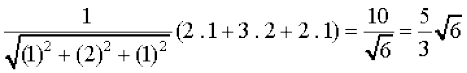 gSA
gSA
mnkgj.k 17 ;fn nks lfn'k bl izdkj gSa fd
bl izdkj gSa fd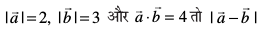 Kkr dhft,A
Kkr dhft,A
gy ge ikrs gSa fd
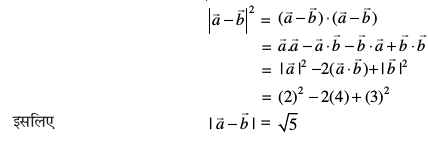
mnkgj.k 18 ;fn  ,d ek=kd lfn'k gS vkSj
,d ek=kd lfn'k gS vkSj 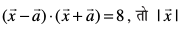 Kkr dhft,A
Kkr dhft,A
gy D;ksafd  ,d ek=kd lfn'k gS] blfy,
,d ek=kd lfn'k gS] blfy, 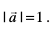 ;g Hkh fn;k gqvk gS fd
;g Hkh fn;k gqvk gS fd

mnkgj.k 19 nks lfn'kksa  , osQ fy, lnSo
, osQ fy, lnSo 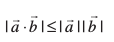 (Cauchy-Schwartz vlfedk)A
(Cauchy-Schwartz vlfedk)A
gy nh gqbZ vlfedk lgt :i esa Li"V gS ;fn  okLro esa bl fLFkfr esa ge ikrs gSa fd
okLro esa bl fLFkfr esa ge ikrs gSa fd 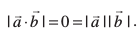 . blfy, ge dYiuk djrs gSa fd
. blfy, ge dYiuk djrs gSa fd 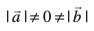 rc gesa
rc gesa
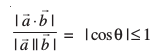 feyrk gSA
feyrk gSA
blfy,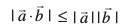
mnkgj.k 20 nks lfn'kksa  (f=kHkqt&vlfedk)
(f=kHkqt&vlfedk)
gy nh gqbZ vlfedk] nksuksa fLFkfr;ksa 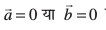 esa lgt :i ls Li"V gS (D;ksa ?)A blfy, eku yhft, fd
esa lgt :i ls Li"V gS (D;ksa ?)A blfy, eku yhft, fd 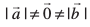 rc
rc
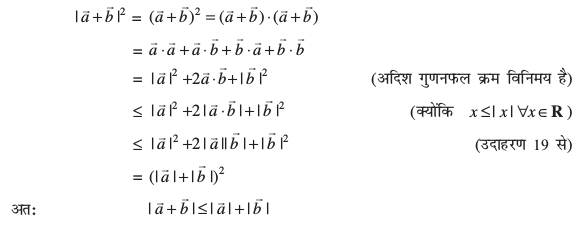
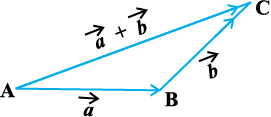
vko`Qfr 10-21
fVIi.kh ;fn f=kHkqt&vlfedk esa lfedk /kj.k gksrh gS (mi;qZDr mnkgj.k 20 esa) vFkkZr~~
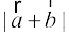 =
=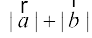 , rc
, rc
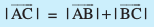
¯cnq A, B vkSj C lajs[k n'kkZrk gSA
mnkgj.k 21 n'kkZb, fd ¯cnq 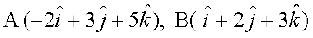 vkSj
vkSj 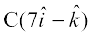 lajs[k gSA
lajs[k gSA
gy ge izkIr djrs gSa%
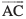 =
=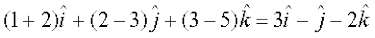
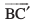 =
=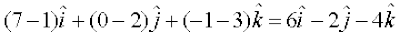
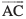 =
=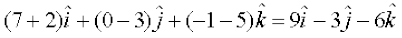
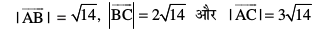
blfy,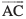 =
=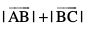
vr% ¯cnq A, B vkSj C lajs[k gSaA
fVIi.kh mnkgj.k 21 esa è;ku nhft, fd 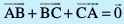 ijarq fiQj Hkh ¯cnq A, B vkSj C f=kHkqt osQ 'kh"kks± dk fuekZ.k ugha djrs gSaA
ijarq fiQj Hkh ¯cnq A, B vkSj C f=kHkqt osQ 'kh"kks± dk fuekZ.k ugha djrs gSaA
iz'ukoyh 10-3
1. nks lfn'kksa 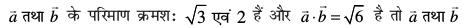 osQ chp dk dks.k Kkr dhft,A
osQ chp dk dks.k Kkr dhft,A
2. lfn'kksa 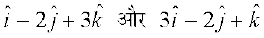 osQ chp dk dks.k Kkr dhft,A
osQ chp dk dks.k Kkr dhft,A
3. lfn'k 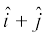 ij lfn'k
ij lfn'k 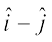 dk iz{ksi Kkr dhft,A
dk iz{ksi Kkr dhft,A
4. lfn'k 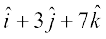 dk] lfn'k
dk] lfn'k 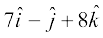 ij iz{ksi Kkr dhft,A
ij iz{ksi Kkr dhft,A
5. n'kkZb, fd fn, gq, fuEufyf[kr rhu lfn'kksa esa ls izR;sd ek=kd lfn'k gS]
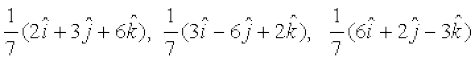
;g Hkh n'kkZb, fd ;s lfn'k ijLij ,d nwljs osQ yacor~ gSaA
6. ;fn 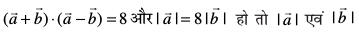 Kkr dhft,A
Kkr dhft,A
7. 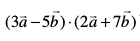 dk eku Kkr dhft,A
dk eku Kkr dhft,A
8. nks lfn'kksa  osQ ifjek.k Kkr dhft,] ;fn buosQ ifjek.k leku gS vkSj bu osQ chp dk dks.k 60° gS rFkk budk vfn'k xq.kuiQy
osQ ifjek.k Kkr dhft,] ;fn buosQ ifjek.k leku gS vkSj bu osQ chp dk dks.k 60° gS rFkk budk vfn'k xq.kuiQy  gSA
gSA
9. ;fn ,d ek=kd lfn'k 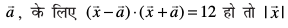 Kkr dhft,A
Kkr dhft,A
10. ;fn 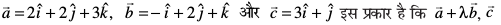 ij yac gS] rks λ dk eku Kkr dhft,A
ij yac gS] rks λ dk eku Kkr dhft,A
11. n'kkZb, fd nks 'kwU;srj lfn'kksa  osQ fy,
osQ fy, 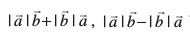 ij yac gSA
ij yac gSA
12. ;fn 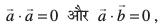 , rks lfn'k
, rks lfn'k 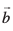 osQ ckjs esa D;k fu"d"kZ fudkyk tk ldrk gS?
osQ ckjs esa D;k fu"d"kZ fudkyk tk ldrk gS?
13. ;fn 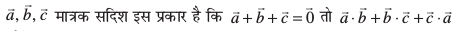 dk eku Kkr dhft,A
dk eku Kkr dhft,A
14. ;fn 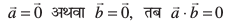 ijarq foykse dk lR; gksuk vko';d ugha gSA ,d mnkgj.k }kjk vius mÙkj dh iqf"V dhft,A
ijarq foykse dk lR; gksuk vko';d ugha gSA ,d mnkgj.k }kjk vius mÙkj dh iqf"V dhft,A
15. ;fn fdlh f=kHkqt ABC osQ 'kh"kZ A, B, C Øe'k% (1, 2, 3), (–1, 0, 0), (0, 1, 2) gSa rks ∠ABC Kkr dhft,A [∠ABC, lfn'kksa 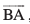 ,oa
,oa 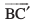 osQ chp dk dks.k gS]
osQ chp dk dks.k gS]
16. n'kkZb, fd ¯cnq A(1, 2, 7), B(2, 6, 3) vkSj C(3, 10, –1) lajs[k gSaA
17. n'kkZb, fd lfn'k 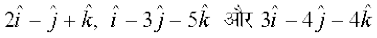 ,d ledks.k f=kHkqt osQ 'kh"kks± dh jpuk djrs gSaA
,d ledks.k f=kHkqt osQ 'kh"kks± dh jpuk djrs gSaA
18. ;fn 'kwU;srj lfn'k  dk ifjek.k ‘a’ gS vkSj λ ,d 'kwU;rsj vfn'k gS rks λ
dk ifjek.k ‘a’ gS vkSj λ ,d 'kwU;rsj vfn'k gS rks λ ,d ek=kd lfn'k gS ;fn
,d ek=kd lfn'k gS ;fn
(A) λ = 1 (B) λ = – 1 (C) a = |λ| (D) a = 1/|λ|
10.6.3 nks lfn'kksa dk lfn'k xq.kuiQy [Vector (or cross) product of two vectors]
ifjPNsn 10-2 esa geus f=k&foeh; nf{k.kkorhZ ledksf.kd funsZ'kkad i¼fr dh ppkZ dh FkhA bl i¼fr esa /ukRed x-v{k dks okekorZ ?kqekdj /ukRed y-v{k ij yk;k tkrk gS rks /ukRed z-v{k dh fn'kk esa ,d nf{k.kkorhZ (izkekf.kd) isap vxzxr gks tkrh gS [vko`Qfr 10.22(i)]A
,d nf{k.kkorhZ funsZ'kkad i¼fr esa tc nk,¡ gkFk dh m¡xfy;ksa dks /ukRed x-v{k dh fn'kk ls nwj /ukRed y-v{k dh rji+Q oqaQry fd;k tkrk gS rks v¡xwBk /ukRed z-v{k dh vksj laosQr djrk [vko`Qfr 10-22 (ii)] gSA

vko`Qfr 10-22
ifjHkk"kk 3 nks 'kwU;srj lfn'kksa  , dk lfn'k xq.kuiQy
, dk lfn'k xq.kuiQy 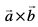 ls fufnZ"V fd;k tkrk gS vkSj
ls fufnZ"V fd;k tkrk gS vkSj 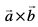 =
= 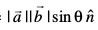 osQ :i esa ifjHkkf"kr fd;k tkrk gS tgk¡ θ,
osQ :i esa ifjHkkf"kr fd;k tkrk gS tgk¡ θ,  osQ chp dk dks.k gS vkSj
osQ chp dk dks.k gS vkSj 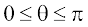 gSA ;gk¡
gSA ;gk¡ 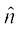 ,d ek=kd lfn'k gS tks fd lfn'k
,d ek=kd lfn'k gS tks fd lfn'k  , nksuksa ij yac gSA bl izdkj
, nksuksa ij yac gSA bl izdkj 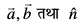 ,d nf{k.kkorhZ i¼fr dks fufeZr djrs gSa (vko`Qfr 10-23) vFkkZr~~ nf{k.kkorhZ i¼fr dks
,d nf{k.kkorhZ i¼fr dks fufeZr djrs gSa (vko`Qfr 10-23) vFkkZr~~ nf{k.kkorhZ i¼fr dks 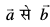 dh rji+Q ?kqekus ij ;g
dh rji+Q ?kqekus ij ;g 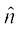 dh fn'kk esa pyrh gSA
dh fn'kk esa pyrh gSA
;fn  rc θ ifjHkkf"kr ugha gS vkSj bl fLFkfr eas ge
rc θ ifjHkkf"kr ugha gS vkSj bl fLFkfr eas ge 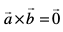 ifjHkkf"kr djrs gSaA
ifjHkkf"kr djrs gSaA
izs{k.k%
1. 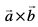 ,d lfn'k gSA
,d lfn'k gSA
2. eku yhft,  nks 'kwU;srj lfn'k gSa rc
nks 'kwU;srj lfn'k gSa rc 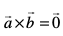 ;fn vkSj osQoy ;fn
;fn vkSj osQoy ;fn  ,d nwljs osQ lekarj (vFkok lajs[k) gSa vFkkZr~~
,d nwljs osQ lekarj (vFkok lajs[k) gSa vFkkZr~~
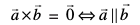
fof'k"Vr% 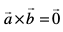 vkSj
vkSj 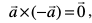 , D;ksafd izFke fLFkfr esa θ = 0 rFkk f}rh; fLFkfr esa θ = π, ftlls nksuksa gh fLFkfr;ksa esa sinθ dk eku 'kwU; gks tkrk gSA
, D;ksafd izFke fLFkfr esa θ = 0 rFkk f}rh; fLFkfr esa θ = π, ftlls nksuksa gh fLFkfr;ksa esa sinθ dk eku 'kwU; gks tkrk gSA
3. ;fn 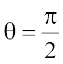 rks
rks 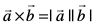
vko`Qfr 10-23
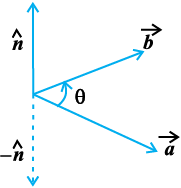
4. izs{k.k 2 vkSj 3 osQ lanHkZ esa ijLij yacor~ ek=kd lfn'kksa 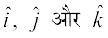 osQ fy, (vko`Qfr 10-24), ge ikrs gSa fd
osQ fy, (vko`Qfr 10-24), ge ikrs gSa fd
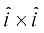 =
=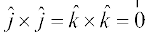
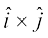 =
= 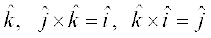
5. lfn'k xq.kuiQy dh lgk;rk ls nks lfn'kksa 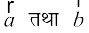 osQ chp dk dks.k θ fuEufyf[kr :i esa izkIr gksrk gS
osQ chp dk dks.k θ fuEufyf[kr :i esa izkIr gksrk gS
sinθ =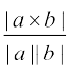
6. ;g loZnk lR; gS fd lfn'k xq.kuiQy Øe fofue; ugha gksrk gS D;ksafd 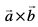 =
= 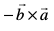 okLro esa
okLro esa 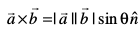 , tgk¡
, tgk¡ 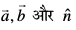 ,d nf{k.kkorhZ i¼fr dks fu£er djrs gSa vFkkZr~~ θ,
,d nf{k.kkorhZ i¼fr dks fu£er djrs gSa vFkkZr~~ θ, 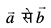 dh rjiQ pØh; Øe gksrk gSA vko`Qfr 10-25(i) tcfd
dh rjiQ pØh; Øe gksrk gSA vko`Qfr 10-25(i) tcfd 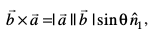 , tgk¡
, tgk¡ 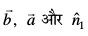 ,d nf{k.kkorhZ i¼fr dks fufeZr djrs gSa vFkkZr~~ θ,
,d nf{k.kkorhZ i¼fr dks fufeZr djrs gSa vFkkZr~~ θ,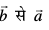 dh vksj pØh; Øe gksrk gS vko`Qfr 10-25(ii)A
dh vksj pØh; Øe gksrk gS vko`Qfr 10-25(ii)A
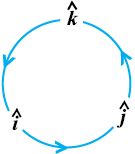
vko`Qfr 10-24
vr% ;fn ge ;g eku ysrs gSa fd  nksuksa ,d gh dkx”k osQ ry esa gSa rks
nksuksa ,d gh dkx”k osQ ry esa gSa rks 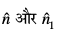 nksuksa dkx”k osQ ry ij yac gksaxs ijarq
nksuksa dkx”k osQ ry ij yac gksaxs ijarq 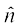 dkx”k ls Åij dh rji+Q fn"V gksxk vkSj
dkx”k ls Åij dh rji+Q fn"V gksxk vkSj 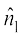 dkx”k ls uhps dh rji+Q fn"V gksxk vFkkZr~~
dkx”k ls uhps dh rji+Q fn"V gksxk vFkkZr~~ 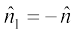
bl izdkj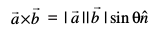
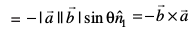
7. izs{k.k 4 vkSj 6 osQ lanHkZ esa
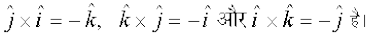
8. ;fn  f=kHkqt dh layXu Hkqtkvksa dks fu:fir djrs gSa rks f=kHkqt dk {ks=kiQy
f=kHkqt dh layXu Hkqtkvksa dks fu:fir djrs gSa rks f=kHkqt dk {ks=kiQy 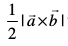 osQ :i esa izkIr gksrk gSA
osQ :i esa izkIr gksrk gSA
f=kHkqt osQ {ks=kiQy dh ifjHkk"kk osQ vuqlkj ge vko`Qfr 10-26 ls ikrs gSa fd f=kHkqt ABC dk {ks=kiQy = 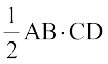 . ijarq
. ijarq 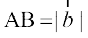 (fn;k gqvk gS) vkSj CD =
(fn;k gqvk gS) vkSj CD = 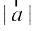 sinθ
sinθ
vr% f=kHkqt ABC dk {ks=kiQy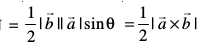

vko`Qfr 10-25
9. ;fn  lekarj prqHkZqt dh layXu Hkqtkvksa dks fu:fir djrs gSa rks lekarj prqHkqZt dk {ks=kiQy
lekarj prqHkZqt dh layXu Hkqtkvksa dks fu:fir djrs gSa rks lekarj prqHkqZt dk {ks=kiQy 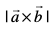 osQ :i esa izkIr gksrk gSA
osQ :i esa izkIr gksrk gSA
vko`Qfr 10-27 ls ge ikrs gSa fd lekarj prqHkaZt ABCD dk {ks=kiQy = AB. DE.
ijarq 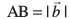 (fn;k gqvk gS), vkSj
(fn;k gqvk gS), vkSj 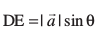 vr%
vr%
lekarj prqHkqZt ABCD dk {ks=kiQy = 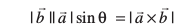
vc ge lfn'k xq.kuiQy osQ nks egRoiw.kZ xq.kksa dks vfHkO;Dr djsaxsA
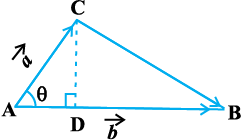
vko`Qfr 10-26
xq.k/eZ lfn'k xq.kuiQy dk ;ksxiQy ij forj.k fu;e (Distributivity of vector product over addition) ;fn 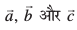 rhu lfn'k gSa vkSj λ ,d vfn'k gS rks
rhu lfn'k gSa vkSj λ ,d vfn'k gS rks
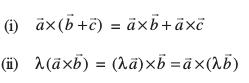
eku yhft, nks lfn'k  ?kVd :i esa Øe'k%
?kVd :i esa Øe'k% 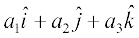 vkSj
vkSj 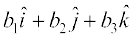 fn, gq, gSa rc mudk lfn'k xq.kuiQy
fn, gq, gSa rc mudk lfn'k xq.kuiQy
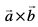 =
= 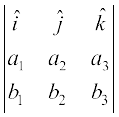 }kjk fn;k tk ldrk gSA
}kjk fn;k tk ldrk gSA
O;k[;k ge ikrs gSa
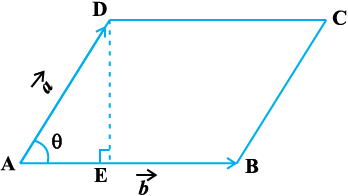
vko`Qfr 10-27
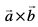 =
=
= 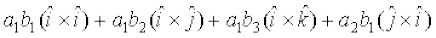
+ 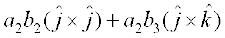
+ 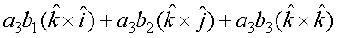 ( xq.k/eZ 1 ls)
( xq.k/eZ 1 ls)
= 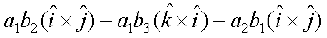
+ 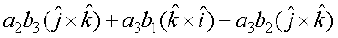
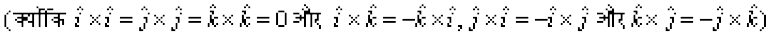
= 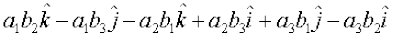
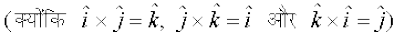
= 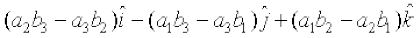
= 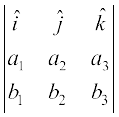
mnkgj.k 22 ;fn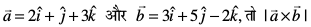 Kkr dhft,A
Kkr dhft,A
gy ;gk¡
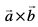 =
=
= 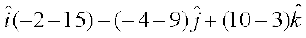
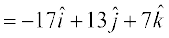
vr% 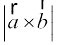 =
=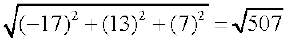
mnkgj.k 23 lfn'k 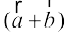 vkSj
vkSj 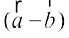 esa ls izR;sd osQ yacor~ ek=kd lfn'k Kkr dhft, tgk¡
esa ls izR;sd osQ yacor~ ek=kd lfn'k Kkr dhft, tgk¡
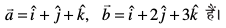
gy ge ikrs gSa fd 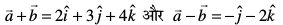
,d lfn'k] tks 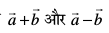 nksuks ij yac gS] fuEufyf[kr }kjk iznÙk gS
nksuks ij yac gS] fuEufyf[kr }kjk iznÙk gS
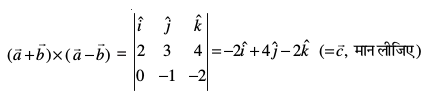
vc 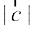 =
=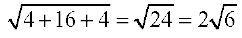
vr% vHkh"V ek=kd lfn'k
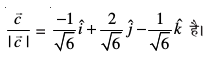
fVIi.kh fdlh ry ij nks yacor~ fn'kk,¡ gksrh gSaA vr%  ij nwljk yacor~ ek=kd lfn'k
ij nwljk yacor~ ek=kd lfn'k 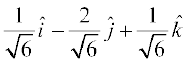 gksxkA ijarq ;g
gksxkA ijarq ;g 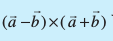 dk ,d ifj.kke gSA
dk ,d ifj.kke gSA
mnkgj.k 24 ,d f=kHkqt dk {ks=kiQy Kkr dhft, ftlosQ 'kh"kZ ¯cnq A(1, 1, 1), B(1, 2, 3) vkSj C(2, 3, 1) gSaA
gy ge ikrs gSa fd . fn, gq, f=kHkqt dk {ks=kiQy
. fn, gq, f=kHkqt dk {ks=kiQy 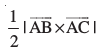 gSA
gSA
vc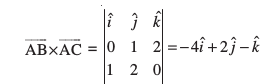
blfy,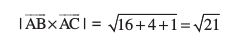
vr% vHkh"V {ks=kiQy 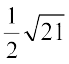 gSA
gSA
mnkgj.k 25 ml lekarj prqHkqZt dk {ks=kiQy Kkr dhft, ftldh layXu Hkqtk,¡ 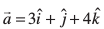 vkSj
vkSj 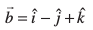 }kjk nh xbZ gSaA
}kjk nh xbZ gSaA
gy fdlh lekarj prqHkqZt dh layXu Hkqtk,¡  gSa rks mldk {ks=kiQy
gSa rks mldk {ks=kiQy 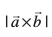 }kjk izkIr gksrk gSA
}kjk izkIr gksrk gSA
vc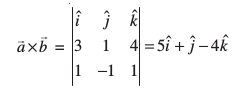
blfy, 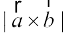 =
=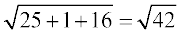
bl izdkj vko';d {ks=kiQy 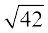 gSA
gSA
iz'ukoyh 10-4
1. 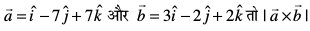 Kkr dhft,A
Kkr dhft,A
2. lfn'k 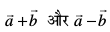 dh yac fn'kk esa ek=kd lfn'k Kkr dhft, tgk¡
dh yac fn'kk esa ek=kd lfn'k Kkr dhft, tgk¡ 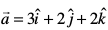 vkSj
vkSj 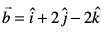 gSA
gSA
3. ;fn ,d ek=kd lfn'k  ,
, 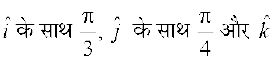 osQ lkFk ,d U;wu dks.k θ cukrk gS rks θ dk eku Kkr dhft, vkSj bldh lgk;rk ls
osQ lkFk ,d U;wu dks.k θ cukrk gS rks θ dk eku Kkr dhft, vkSj bldh lgk;rk ls osQ ?kVd Hkh Kkr dhft,A
osQ ?kVd Hkh Kkr dhft,A
4. n'kkZb, fd 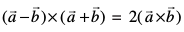
5. λ vkSj µ Kkr dhft,] ;fn 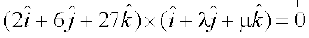
6. fn;k gqvk gS fd �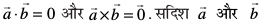 osQ ckjs esa vki D;k fu"d"kZ fudky ldrs gSa?
osQ ckjs esa vki D;k fu"d"kZ fudky ldrs gSa?
7. eku yhft, lfn'k 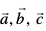 Øe'k%
Øe'k% 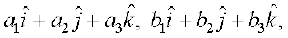
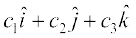 osQ :i esa fn, gq, gSa rc n'kkZb, fd
osQ :i esa fn, gq, gSa rc n'kkZb, fd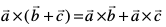
8. ;fn 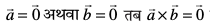 gksrk gSA D;k foykse lR; gS\ mnkgj.k lfgr vius mÙkj dh iqf"V dhft,A
gksrk gSA D;k foykse lR; gS\ mnkgj.k lfgr vius mÙkj dh iqf"V dhft,A
9. ,d f=kHkqt dk {ks=kiQy Kkr dhft, ftlosQ 'kh"kZ A(1, 1, 2), B(2, 3, 5) vkSj C(1, 5, 5) gSaA
10. ,d lekarj prqHkqZt dk {ks=kiQy Kkr dhft, ftldh layXu Hkqtk,¡ lfn'k 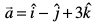 vkSj
vkSj 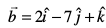 }kjk fu/kZfjr gSaA
}kjk fu/kZfjr gSaA
11. eku yhft, lfn'k  bl izdkj gSa fd
bl izdkj gSa fd 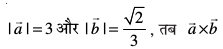 ,d ek=kd lfn'k gS ;fn
,d ek=kd lfn'k gS ;fn  osQ chp dk dks.k gS%
osQ chp dk dks.k gS%
(A) π/6 (B) π/4 (C) π/3 (D) π/2
12. ,d vk;r osQ 'kh"kks± A, B, C vkSj D ftuosQ fLFkfr lfn'k Øe'k%
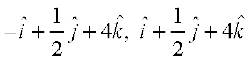 ,
, 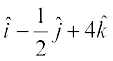 vkSj
vkSj 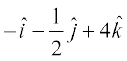 , gSa dk {ks=kiQy gS%
, gSa dk {ks=kiQy gS%
(A)  (B) 1
(B) 1
(C) 2 (D) 4
fofo/ mnkgj.k
mnkgj.k 26 XY-ry esa lHkh ek=kd lfn'k fyf[k,A
gy eku yhft, fd 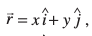 XY-ry esa ,d ek=kd lfn'k gS (vko`Qfr 10-28)A rc vko`Qfr osQ vuqlkj ge ikrs gSa fd x = cos θ vkSj y = sin θ (D;ksafd |
XY-ry esa ,d ek=kd lfn'k gS (vko`Qfr 10-28)A rc vko`Qfr osQ vuqlkj ge ikrs gSa fd x = cos θ vkSj y = sin θ (D;ksafd |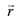 | 1). blfy, ge lfn'k
| 1). blfy, ge lfn'k 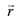 dks]
dks]
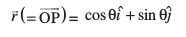
osQ :i esa fy[k ldrs gSaA
Li"Vr% 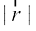 =
=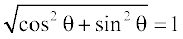

vko`Qfr 10-28
tSls&tSls θ, 0 ls 2π, rd ifjofrZr gksrk gS ¯cnq P (vko`Qfr 10-28) okekorZ fn'kk esa o`r
x2 + y2 = 1 dk vuqjs[k.k djrk gS vkSj bleas lHkh laHkkfor fn'kk,¡ lfEefyr gSaA vr% (1) ls XY-ry esa izR;sd ek=kd lfn'k izkIr gksrk gSA
mnkgj.k 27 ;fn ¯cnqvksa A, B, C vkSj D, osQ fLFkfr lfn'k Øe'k% 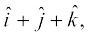
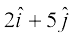 ,
, 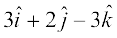
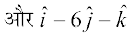 gS] rks ljy js[kkvksa AB rFkk CD osQ chp dk dks.k Kkr dhft,A fuxeu dhft, fd AB vkSj CD lajs[k gSaA
gS] rks ljy js[kkvksa AB rFkk CD osQ chp dk dks.k Kkr dhft,A fuxeu dhft, fd AB vkSj CD lajs[k gSaA
gy uksV dhft, fd ;fn θ, AB vkSj CD, osQ chp dk dks.k gS rks θ,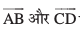 osQ chp dk Hkh dks.k gSA
osQ chp dk Hkh dks.k gSA
vc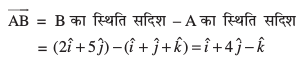
blfy,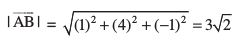
blh izdkj 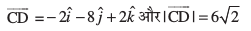

= 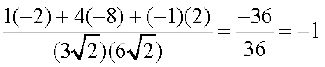
D;ksafd 0 ≤ θ ≤ π, blls izkIr gksrk gS fd θ = π. ;g n'kkZrk gS fd AB rFkk CD ,d nwljs osQ lajs[k gSaA
fodYir% 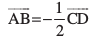 ] blls dg ldrs fd
] blls dg ldrs fd 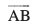 vkSj
vkSj  lajs[k lfn'k gSaA
lajs[k lfn'k gSaA
mnkgj.k 28 eku yhft, 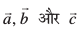 rhu lfn'k bl izdkj gSa fd
rhu lfn'k bl izdkj gSa fd 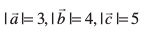 vkSj buesa ls izR;sd] vU; nks lfn'kksa osQ ;ksxiQy ij yacor~ gaS rks]
vkSj buesa ls izR;sd] vU; nks lfn'kksa osQ ;ksxiQy ij yacor~ gaS rks] 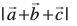 Kkr dhft,A
Kkr dhft,A
gy fn;k gqvk gS fd 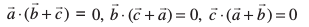
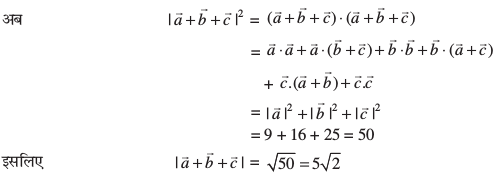
mnkgj.k 29 rhu lfn'k 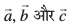 izfrca/
izfrca/ 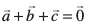 dks larq"V djrs gSaA ;fn
dks larq"V djrs gSaA ;fn
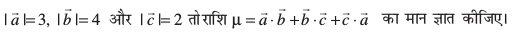
gy D;ksafd 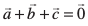 , blfy, ge ikrs gSa fd
, blfy, ge ikrs gSa fd
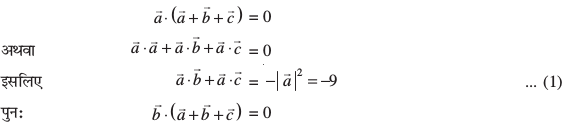

;k 2µ = – 29, i.e., µ=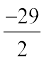
mnkgj.k 30 ;fn ijLij yacor~ ek=kd lfn'kksa 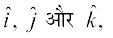 dh nf{k.kkorhZ i¼fr osQ lkis{k
dh nf{k.kkorhZ i¼fr osQ lkis{k
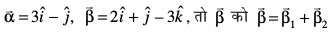 osQ :i esa vfHkO;Dr dhft, tgk¡
osQ :i esa vfHkO;Dr dhft, tgk¡ 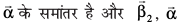 osQ yacor~ gSA
osQ yacor~ gSA
��gy eku yhft, fd 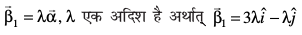

vè;k; 10 ij fofo/ iz'ukoyh
1. XY-ry esa] x-v{k dh /ukRed fn'kk osQ lkFk okekorZ fn'kk esa 30° dk dks.k cukus okyk ek=kd lfn'k fyf[k,A
2. ¯cnq P(x1, y1, z1) vkSj Q(x2, y2, z2) dks feykus okys lfn'k osQ vfn'k ?kVd vkSj ifjek.k Kkr dhft,A
3. ,d yM+dh if'pe fn'kk esa 4 km pyrh gSA mlosQ i'pkr~ og mÙkj ls 30° if'pe dh fn'kk esa 3 km pyrh gS vkSj :d tkrh gSA izLFkku osQ izkjafHkd ¯cnq ls yM+dh dk foLFkkiu Kkr dhft,A
4. ;fn  ? vius mÙkj dh iqf"V dhft,A
? vius mÙkj dh iqf"V dhft,A
5. x dk og eku Kkr dhft, ftlosQ fy, 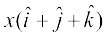 ,d ek=kd lfn'k gSA
,d ek=kd lfn'k gSA
6. lfn'kksa 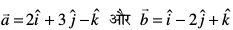 osQ ifj.kkeh osQ lekarj ,d ,slk lfn'k Kkr dhft, ftldk ifjek.k 5 bdkbZ gSA
osQ ifj.kkeh osQ lekarj ,d ,slk lfn'k Kkr dhft, ftldk ifjek.k 5 bdkbZ gSA
7. ;fn 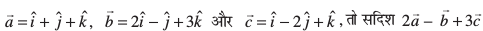 osQ lekarj ,d ek=kd lfn'k Kkr dhft,A
osQ lekarj ,d ek=kd lfn'k Kkr dhft,A
8. n'kkZb, fd ¯cnq A(1, – 2, – 8), B(5, 0, –2) vkSj C(11, 3, 7) lajs[k gS vkSj B }kjk AC dks foHkkftr djus okyk vuqikr Kkr dhft,A
9. nks ¯cnqvksa 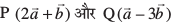 dks feykus okyh js[kk dks 1%2 osQ vuqikr es cká foHkkftr djus okys ¯cnq R dk fLFkfr lfn'k Kkr dhft,A ;g Hkh n'kkZb, fd ¯cnq P js[kk[kaM RQ dk eè; ¯cnq gSA
dks feykus okyh js[kk dks 1%2 osQ vuqikr es cká foHkkftr djus okys ¯cnq R dk fLFkfr lfn'k Kkr dhft,A ;g Hkh n'kkZb, fd ¯cnq P js[kk[kaM RQ dk eè; ¯cnq gSA
10. ,d lekarj prqHkqZt dh layXu Hkqtk,¡ 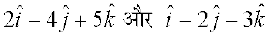 gaSA blosQ fod.kZ osQ lekarj ,d ek=kd lfn'k Kkr dhft,A bldk {ks=kiQy Hkh Kkr dhft,A
gaSA blosQ fod.kZ osQ lekarj ,d ek=kd lfn'k Kkr dhft,A bldk {ks=kiQy Hkh Kkr dhft,A
11. n'kkZb, fd OX, OY ,oa OZ v{kksa osQ lkFk cjkcj >qosQ gq, lfn'k dh fno~Q&dkslkbu dksT;k,¡ 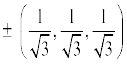 gSA
gSA
12. eku yhft, 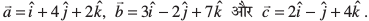 ,d ,slk lfn'k
,d ,slk lfn'k 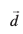 Kkr dhft, tks
Kkr dhft, tks  �� nksuksa ij yac gS vkSj
�� nksuksa ij yac gS vkSj 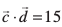
13. lfn'k 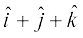 dk] lfn'kksa
dk] lfn'kksa 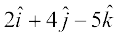 vkSj
vkSj 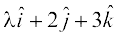 osQ ;ksxiQy dh fn'kk esa ek=kd lfn'k osQ lkFk vfn'k xq.kuiQy 1 osQ cjkcj gS rks
osQ ;ksxiQy dh fn'kk esa ek=kd lfn'k osQ lkFk vfn'k xq.kuiQy 1 osQ cjkcj gS rks 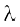 dk eku Kkr dhft,A
dk eku Kkr dhft,A
14. ;fn 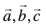 leku ifjek.kksa okys ijLij yacor~ lfn'k gSa rks n'kkZb, fd lfn'k
leku ifjek.kksa okys ijLij yacor~ lfn'k gSa rks n'kkZb, fd lfn'k 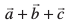 lfn'kksa
lfn'kksa 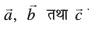 osQ lkFk cjkcj >qdk gqvk gSA
osQ lkFk cjkcj >qdk gqvk gSA
15. fl¼ dhft, fd 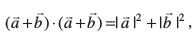 , ;fn vkSj osQoy ;fn
, ;fn vkSj osQoy ;fn 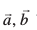 yacor~ gSaA ;g fn;k gqvk gS fd
yacor~ gSaA ;g fn;k gqvk gS fd 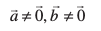
16 ls 19 rd osQ iz'uksa esa lgh mÙkj dk p;u dhft,A
16. ;fn nks lfn'kksa  osQ chp dk dks.k θ gS rks
osQ chp dk dks.k θ gS rks 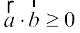 gksxk ;fn%
gksxk ;fn%
(A) 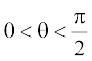 (B)
(B) 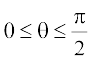
(C) 0 < θ < π (D) 0 ≤ θ ≤ π
17. eku yhft,  nks ek=kd lfn'k gSa vkSj muosQ chp dk dks.k θ gS rks
nks ek=kd lfn'k gSa vkSj muosQ chp dk dks.k θ gS rks 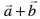 ,d ek=kd lfn'k gS ;fn%
,d ek=kd lfn'k gS ;fn%
(A) 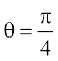 (B)
(B) 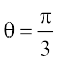 (C)
(C) 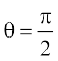 (D)
(D) 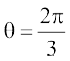
18. 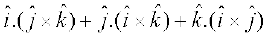 dk eku gS
dk eku gS
(A) 0 (B) –1 (C) 1 (D) 3
19. ;fn nks lfn'kksa  osQ chp dk dks.k θ gS rks
osQ chp dk dks.k θ gS rks 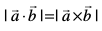 tc θ cjkcj gS%
tc θ cjkcj gS%
(A) 0 (B) 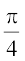 (C)
(C) 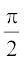 (D) π
(D) π
lkjak'k
- ,d ¯cnq P(x, y, z) dh fLFkfr lfn'k
![eq86]() gS vkSj ifjek.k
gS vkSj ifjek.k ![]() gSA
gSA - ,d lfn'k osQ vfn'k ?kVd blosQ fno~Q&vuqikr dgykrs gSa vkSj Øekxr v{kksa osQ lkFk blosQ iz{ksi dks fu:fir djrs gSaA
- ,d lfn'k dk ifjek.k (r), fno~Q&vuqikr a, b, c vkSj fno~Q&dkslkbu (l, m, n) fuEufyf[kr :i esa lacaf/r gSa%
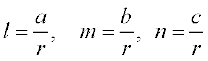
- f=kHkqt dh rhuksa Hkqtkvksa dks Øe esa ysus ij mudk lfn'k ;ksx
![0]() gSA
gSA - nks lg&vkfne lfn'kksa dk ;ksx ,d ,sls lekarj prqHkqZt osQ fod.kZ ls izkIr gksrk gS ftldh layXu Hkqtk,¡ fn, gq, lfn'k gSaA
- ,d lfn'k dk vfn'k λ ls xq.ku blosQ ifjek.k dks |λ| osQ xq.kt esa ifjofrZr dj nsrk gS vkSj λ dk eku /ukRed vFkok ½.kkRed gksus osQ vuqlkj bldh fn'kk dks leku vFkok foijhr j[krk gSA
- fn, gq, lfn'k
![ablue]() osQ fy, lfn'k
osQ fy, lfn'k ![eq752]() dh fn'kk esa ek=kd lfn'k gSA
dh fn'kk esa ek=kd lfn'k gSA - fcnqvksa P vkSj Q ftuosQ fLFkfr lfn'k Øe'k%
![arb blue]() gSa] dks feykus okyh js[kk dks m : n osQ vuqikr esa foHkkftr djus okys ¯cnq R dk fLFkfr lfn'k (i)
gSa] dks feykus okyh js[kk dks m : n osQ vuqikr esa foHkkftr djus okys ¯cnq R dk fLFkfr lfn'k (i) ![eq753]() var% foHkktu ij (ii)
var% foHkktu ij (ii) ![eq754]() cká foHkktu ij] osQ :i esa izkIr gksrk gSA
cká foHkktu ij] osQ :i esa izkIr gksrk gSA - nks lfn'kksa
![arb blue]() osQ chp dk dks.k θ gS rks mudk vfn'k xq.kuiQy
osQ chp dk dks.k θ gS rks mudk vfn'k xq.kuiQy ![eq755]() osQ :i esa izkIr gksrk gSA ;fn
osQ :i esa izkIr gksrk gSA ;fn ![eq757]() fn;k gqvk gS rks lfn'kksa
fn;k gqvk gS rks lfn'kksa ![arb blue]() � osQ chp dk dks.k ‘θ’,
� osQ chp dk dks.k ‘θ’, ![eq759]() ls izkIr gksrk gSA
ls izkIr gksrk gSA - ;fn nks lfn'kksa
![arb blue]() osQ chp dk dks.k θ gS rks mudk lfn'k xq.kuiQy
osQ chp dk dks.k θ gS rks mudk lfn'k xq.kuiQy
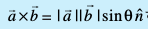 osQ :i esa izkIr gksrk gSA tgk¡
osQ :i esa izkIr gksrk gSA tgk¡ 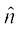 ,d ,slk ek=kd lfn'k gS tks
,d ,slk ek=kd lfn'k gS tks  dks lfEefyr djus okys ry osQ yacor~ gS rFkk
dks lfEefyr djus okys ry osQ yacor~ gS rFkk 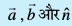 nf{k.kkorhZ ledksf.kd funsZ'kkad i¼fr dks fufeZr djrs gSaA
nf{k.kkorhZ ledksf.kd funsZ'kkad i¼fr dks fufeZr djrs gSaA- ;fn
![eq763]() ,d vfn'k gS rks
,d vfn'k gS rks
,sfrgkfld i`"BHkwfe
lfn'k 'kCn dk O;qRiUu ySfVu Hkk"kk osQ ,d 'kCn osDVl (vectus) ls gqvk gS ftldk vFkZ gS gLrxr djukA vk/qfud lfn'k fl¼kar osQ Hkzw.kh; fopkj dh frfFk lu~ 1800 osQ vklikl ekuh tkrh gS] tc Caspar Wessel (1745&1818 bZ-) vkSj Jean Robert Argand (1768-1822 bZ-) us bl ckr dk o.kZu fd;k fd ,d funsZ'kkad ry esa fdlh fn"V js[kk[kaM dh lgk;rk ls ,d lfEeJ la[;k a + ib dk T;kferh; vFkZ fuoZpu dSls fd;k tk ldrk gSA ,d vk;fj'k xf.krK] William Rowen Hamilton (1805-1865 bZ-) us viuh iqLrd] "Lectures on Quaternions" (1853 bZ-) esa fn"V js[kk[kaM osQ fy, lfn'k 'kCn dk iz;ksx lcls igys fd;k FkkA prq"V;h;ksa (quaternians) [oqQN fuf'pr chth; fu;eksa dk ikyu djrs gq, 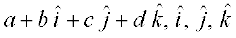 osQ :i okys pkj okLrfod la[;kvksa dk leqPp;] dh gSfeYVu fof/ lfn'kksa dks f=k&foeh; varfj{k esa xq.kk djus dh leL;k dk ,d gy FkkA rFkkfi ge ;gk¡ bl ckr dk ftØ vo'; djsaxs fd lfn'k dh ladYiuk vkSj muosQ ;ksxiQy dk fopkj cgqr& fnuksa igys ls Plato (384-322 bZlk iwoZ) osQ ,d f'k"; ,oa ;wukuh nk'kZkfud vkSj oSKkfud Aristotle (427-348 bZlk iwoZ) osQ dky ls gh FkkA ml le; bl tkudkjh dh dYiuk Fkh fd nks vFkok vf/d cyksa dh la;qDr fØ;k mudks lekarj prqHkqZt osQ fu;ekuqlkj ;ksx djus ij izkIr dh tk ldrh gSA cyksa osQ la;kstu dk lgh fu;e] fd cyksa dk ;ksx lfn'k :i esa fd;k tk ldrk gS] dh [kkst Sterin Simon(1548-1620 bZ-) }kjk yacor~ cyksa dh fLFkfr esa dh xbZA lu~ 1586 esa mUgksaus viuh 'kks/iqLrd] "DeBeghinselen der Weeghconst" (otu djus dh dyk osQ fl¼kar) esa cyksa osQ ;ksxiQy osQ T;kferh; fl¼kar dk fo'ys"k.k fd;k Fkk ftlosQ dkj.k ;kaf=kdh osQ fodkl esa ,d eq[; ifjorZu gqvkA ijarq blosQ ckn Hkh lfn'kksa dh O;kid ladYiuk osQ fuekZ.k esa 200 o"kZ yx x,A
osQ :i okys pkj okLrfod la[;kvksa dk leqPp;] dh gSfeYVu fof/ lfn'kksa dks f=k&foeh; varfj{k esa xq.kk djus dh leL;k dk ,d gy FkkA rFkkfi ge ;gk¡ bl ckr dk ftØ vo'; djsaxs fd lfn'k dh ladYiuk vkSj muosQ ;ksxiQy dk fopkj cgqr& fnuksa igys ls Plato (384-322 bZlk iwoZ) osQ ,d f'k"; ,oa ;wukuh nk'kZkfud vkSj oSKkfud Aristotle (427-348 bZlk iwoZ) osQ dky ls gh FkkA ml le; bl tkudkjh dh dYiuk Fkh fd nks vFkok vf/d cyksa dh la;qDr fØ;k mudks lekarj prqHkqZt osQ fu;ekuqlkj ;ksx djus ij izkIr dh tk ldrh gSA cyksa osQ la;kstu dk lgh fu;e] fd cyksa dk ;ksx lfn'k :i esa fd;k tk ldrk gS] dh [kkst Sterin Simon(1548-1620 bZ-) }kjk yacor~ cyksa dh fLFkfr esa dh xbZA lu~ 1586 esa mUgksaus viuh 'kks/iqLrd] "DeBeghinselen der Weeghconst" (otu djus dh dyk osQ fl¼kar) esa cyksa osQ ;ksxiQy osQ T;kferh; fl¼kar dk fo'ys"k.k fd;k Fkk ftlosQ dkj.k ;kaf=kdh osQ fodkl esa ,d eq[; ifjorZu gqvkA ijarq blosQ ckn Hkh lfn'kksa dh O;kid ladYiuk osQ fuekZ.k esa 200 o"kZ yx x,A
lu~ 1880 esa ,d vesfjdh HkkSfrd 'kkL=kh ,oa xf.krK Josaih Willard Gibbs (1839-1903 bZ-) vkSj ,d vaxzst vfHk;ark Oliver Heaviside (1850-1925 bZ-) us ,d prq"V;h osQ okLrfod (vfn'k) Hkkx dks dkYifud (lfn'k) Hkkx ls i`Fko~Q djrs gq, lfn'k fo'ys"k.k dk l`tu fd;k FkkA lu~ 1881 vkSj 1884 esa Gibbs us "Entitled Element of Vector Analysis" uked ,d 'kks/ iqfLrdk NiokbZA bl iqLrd esa lfn'kksa dk ,d Øec¼ ,oa laf{kIr fooj.k fn;k gqvk FkkA rFkkfi lfn'kksa osQ vuqiz;ksx dk fu:i.k djus dh dhfrZ
D. Heaviside vkSj P.G. Tait (1831-1901 bZ-) dks izkIr gS ftUgksaus bl fo"k; osQ fy, lkFkZd ;ksxnku fn;k gSA
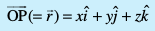
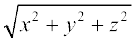
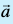
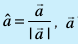 dh fn'kk esa ek=kd lfn'k gSA
dh fn'kk esa ek=kd lfn'k gSA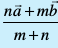 var% foHkktu ij
var% foHkktu ij 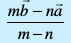 cká foHkktu ij] osQ :i esa izkIr gksrk gSA
cká foHkktu ij] osQ :i esa izkIr gksrk gSA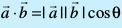 osQ :i esa izkIr gksrk gSA ;fn
osQ :i esa izkIr gksrk gSA ;fn 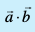
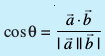
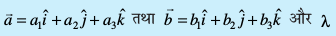 ,d vfn'k gS rks
,d vfn'k gS rks