Table of Contents
vè;k; 11
f=k&foeh; T;kfefr
(Three Dimensional Geometry)
The moving power of mathematical invention is not reasoning but imagination. – A.DEMORGAN
11.1 Hkwfedk (Introduction)
d{kk XI esa] oS'ysf"kd T;kfefr dk vè;;u djrs le; f}&foeh; vkSj f=k&foeh; fo"k;ksa osQ ifjp; esa geus Lo;a dks osQoy dkrhZ; fof/ rd lhfer j[kk gSA bl iqLrd osQ fiNys vè;k; esa geus lfn'kksa dh ewy ladYiukvksa dk vè;;u fd;k gSA vc ge lfn'kksa osQ chtxf.kr dk f=k&foeh; T;kfefr esa mi;ksx djsaxsA f=k&foeh; T;kfefr esa bl mikxe dk mn~ns'; gS fd ;g blosQ vè;;u dks vR;ar ljy ,oa lq#fpiw.kZ (lqxzkg;) cuk nsrk gSA*
bl vè;k; esa ge nks ¯cnqvksa dks feykus okyh js[kk osQ fnd~&dksT;k o fno~Q&vuqikr dk vè;;u djsaxs vkSj fofHkUu fLFkfr;ksa esa varfj{k esa js[kkvksa vkSj ryksa osQ lehdj.kksa] nks js[kkvksa] nks ryksa o ,d js[kk vkSj ,d ry osQ chp dk dks.k] nks fo"keryh; js[kkvksa osQ chp U;wure nwjh o ,d ry dh ,d ¯cnq ls nwjh osQ fo"k; esa Hkh fopkj foe'kZ djsaxsA mijksDr ifj.kkeksa esa ls vf/dka'k ifj.kkeksa dks lfn'kksa osQ :i esa izkIr djrs gSaA rFkkfi ge budk dkrhZ; :i esa Hkh vuqokn djsaxs tks dkykarj esa fLFkfr dk Li"V T;kferh; vkSj fo'ys"k.kkRed fp=k.k izLrqr dj losQxkA

Leonhard Euler
(1707-1783)
11.2 js[kk osQ fno~Q&dkslkbu vkSj fno~Q&vuqikr (Direction Cosines and Direction Ratios of a Line)
vè;k; 10 esa] Lej.k dhft,] fd ewy ¯cnq ls xqtjus okyh lfn'k js[kk L }kjk x, y vkSj z-v{kksa osQ lkFk Øe'k α] β vkSj γ cuk, x, dks.k fno~Q&dks.k dgykrs gSa rc bu dks.kksa dh dkslkbu uker% cosα, cosβ vkSj cosγ js[kk L osQ fno~Q&dkslkbu (direction cosines or dc's)dgykrh gSaA
;fn ge L dh fn'kk foijhr dj nsrs gSa rks fno~Q&dks.k] vius laiwjdksa esa vFkkZr~ π-α, π-β vkSj π-γ ls cny tkrs gSaA bl izdkj] fno~Q&dkslkbu osQ fpÉ cny tkrs gSaA
* For various activities in three dimensional geometry, one may refer to the Book
“A Hand Book for designing Mathematics Laboratory in Schools”, NCERT, 2005
è;ku nhft,] varfj{k esa nh xbZ js[kk dks nks foijhr fn'kkvksa esa c<+k ldrs gSa vkSj blfy, blosQ fno~Q&dkslkbu osQ nks lewg gSaA blfy, varfj{k esa Kkr js[kk osQ fy, fno~Q&dkslkbu osQ vf}rh; lewg osQ fy,] gesa Kkr js[kk dks ,d lfn'k js[kk ysuk pkfg,A bu vf}rh; fno~Q&dkslkbu dks
l, m vkSj n osQ }kjk fufnZ"V fd, tkrs gSaA
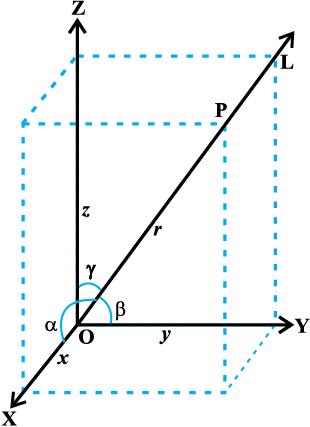
vko`Qfr 11-1
fVIi.kh varfj{k esa nh xbZ js[kk ;fn ewy ¯cnq ls ugha xqtjrh gS rks bldh fno~Q&dkslkbu dks Kkr djus osQ fy,] ge ewy ¯cnq ls nh xbZ js[kk osQ lekarj ,d js[kk [khaprs gSaA vc ewy ¯cnq ls buesa ls ,d lfn'k js[kk osQ fno~Q&vuqikr Kkr djrs gSa D;ksafd nks lekarj js[kkvksa osQ fno~Q&vuqikrksa osQ lewg leku (ogh) gksrs gSaA
,d js[kk osQ fno~Q&dkslkbu osQ lekuqikrh la[;kvksa dks js[kk osQ fno~Q&vuqikr (direction ratios or dr's) dgrs gSaA ;fn ,d js[kk osQ fno~Q&dkslkbu l, m, n o fno~Q&vuqikr a, b, c gksa rc fdlh 'kwU;srj λ ∈ R osQ fy, a = λl, b=λm vkSj c = λn
fVIi.kh oqQN ys[kd fno~Q&vuqikrksa dks fno~Q&la[;k,¡ Hkh dgrs gSaA
eku yhft, ,d js[kk osQ fno~Q&vuqikr a, b, c vkSj js[kk dh fno~Q&dkslkbu l, m, n gSA rc
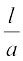 =
= 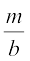 =
= 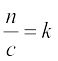 (eku yhft,), k ,d vpj gSA
(eku yhft,), k ,d vpj gSA
blfy, l = ak, m = bk, n = ck ... (1)
ijarq l2 + m2 + n2 = 1
blfy, k2 (a2 + b2 + c2) = 1
;k k = 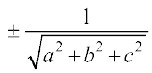
vr% (1) ls] js[kk dh fno~Q&dkslkbu (d.c.’s )
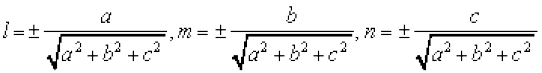
fdlh js[kk osQ fy, ;fn js[kk osQ fno~Q&vuqikr Øe'k% a, b, c gS] rks ka, kb, kc; k ≠ 0 Hkh fno~Q&vuqikrksa dk ,d lewg gSA blfy, ,d js[kk osQ fno~Q&vuqikrksa osQ nks lewg Hkh lekuqikrh gksaxsA vr% fdlh ,d js[kk osQ fno~Q&vuqikrksa osQ vla[; lewg gksrs gSaA
11.2.1 js[kk dh fno~Q&dkslkbu esa laca/ (Relation between the direction cosines of a line)
eku yhft, fd ,d js[kk RS dh fno~Q&dkslkbu l, m, n gSA ewy ¯cnq ls nh xbZ js[kk osQ lekarj ,d js[kk [khafp, vkSj bl ij ,d ¯cnq P(x, y, z) yhft,A P ls x-v{k ij yac PA [khafp,
(vko`Qfr 11-2)A
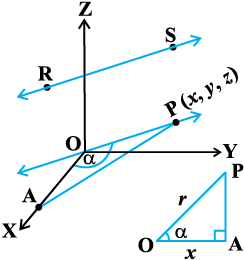
vko`Qfr 11-2
;fn OP = r. rks 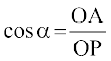
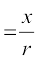 . ftlls x = lr izkIr gksrk gSA blh izdkj y = mr vkSj z = nr.
. ftlls x = lr izkIr gksrk gSA blh izdkj y = mr vkSj z = nr.
blfy, x2 + y2 + z2 = r2 (l2 + m2 + n2)
ijarq x2 + y2 + z2 = r2
vr% l2 + m2 + n2 = 1
11.2.2 nks ¯cnqvksa dks feykus okyh js[kk dh fno~Q&dkslkbu (Direction cosines of a line passing through two points)
D;ksafd nks fn, ¯cnqvksa ls gksdj tkus okyh js[kk vf}rh; gksrh gSA blfy, nks fn, x, ¯cnqvksa
P(x1, y1, z1) vkSj Q(x2, y2, z2) ls xqtjus okyh js[kk dh fno~Q&dkslkbu dks fuEu izdkj ls Kkr dj ldrs gSa (vko`Qfr 11-3(a)A
eku yhft, fd js[kk PQ dh fno~Q&dkslkbu l, m, n gSa vkSj ;g x, y vkSj z-v{k osQ lkFk dks.k Øe'k% α, β, γ cukrh gSaA
eku yhft, P vkSj Q ls yac [khafp, tks XY-ry dks R rFkk S ij feyrs gSaA P ls ,d vU; yac [khafp, tks QS dks N ij feyrk gSA vc ledks.k f=kHkqt PNQ esa, ∠PQN = γ (vko`Qfr 11.3 (b)) blfy,
cosγ = 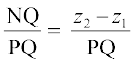

vko`Qfr 11-3
blh izdkj cosα = 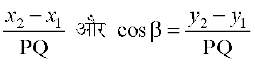
vr% ¯cnqvksa P(x1, y1, z1) rFkk Q(x2, y2, z2) dks tksM+us okys js[kk[kaM PQ fd fno~Q&dkslkbu
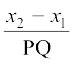 ,
, 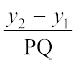 ,
, 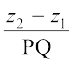 gSaA
gSaA
tgk¡ PQ = 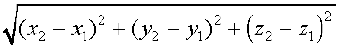
fVIi.kh ¯cnqvksa P(x1, y1, z1) rFkk Q(x2, y2, z2) dks tksM+us okys js[kk[kaM osQ fno~Q&vuqikr fuEu izdkj ls fy, tk ldrs gSaA
x2 – x1, y2 – y1, z2 – z1, ;k x1 – x2, y1 – y2, z1 – z2
mnkgj.k 1 ;fn ,d js[kk x, y rFkk z-v{kksa dh /ukRed fn'kk osQ lkFk Øe'k% 90°, 60° rFkk 30° dk dks.k cukrhs gS rks fno~Q&dkslkbu Kkr dhft,A
gy eku yhft, js[kk dh fno~Q&dkslkbu l, m, n gSA rc l = cos 90° = 0, m = cos 60° =  ,
,
n = cos 30° = 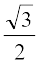
mnkgj.k 2 ;fn ,d js[kk osQ fno~Q&vuqikr 2] &1] &2 gSa rks bldh fno~Q&dkslkbu Kkr dhft,A
gy fno~Q&dkslkbu fuEuor~ gSa
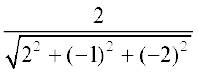 ,
, 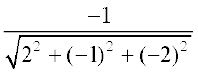 ,
, 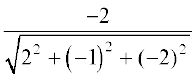
vFkkZr~ 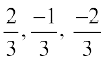
mnkgj.k 3 nks ¯cnqvksa (– 2, 4, – 5) vkSj (1, 2, 3) dks feykus okyh js[kk dh fno~Q&dkslkbu Kkr dhft,A
gy ge tkurs gSa fd nks ¯cnqvksa P (x1, y1, z1) vkSj Q(x2, y2, z2) dks feykus okyh js[kk dh fno~Q&dkslkbu
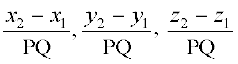
gSa] tgk¡ PQ = 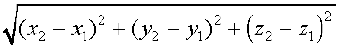
;gk¡ P vkSj Q Øe'k% (– 2, 4, – 5) vkSj (1, 2, 3) gSaA
blfy, PQ =  =
= 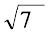
blfy, nks ¯cnqvksa dks feykus okyh js[kk dh fno~Q&dkslkbu gSa%
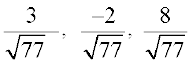
mnkgj.k 4 x, y vkSj z-v{kksa dh fno~Q&dkslkbu Kkr dhft,A
gy x-v{k Øe'k% x, y vkSj z-v{k osQ lkFk 0°, 90° vkSj 90° osQ dks.k cukrk gSA blfy, x-v{k dh fno~Q&dkslkbu cos 0°, cos 90°, cos 90° vFkkZr~ 1,0,0 gSaA
blh izdkj y-v{k vkSj z-v{k dh fno~Q&dkslkbu Øe'k% 0, 1, 0 vkSj 0, 0, 1 gSaA
mnkgj.k 5 n'kkZb, fd ¯cnq A (2, 3, – 4), B (1, – 2, 3) vkSj C (3, 8, – 11) lajs[k gSaA
gy A vkSj B (dks feykus okyh js[kk osQ fno~Q&vuqikr
1 –2, –2 –3, 3 + 4 vFkkZr~ – 1, – 5, 7 gSaA
B (vkSj C dks feykus okyh js[kk osQ fno~Q&vuqikr 3 –1, 8 + 2, – 11 – 3, vFkkZr~, 2, 10, – 14 gSaA
Li"V gS fdABvkSj BC osQ fno~Q&vuqikr lekuqikrh gSaA vr% AB vkSj BC lekarj gSaAq ijarq ABvkSj BC nksuksa esa B (mHk;fu"B gSA vr% A, B, vkSj C lajs[k ¯cnq gSaA
iz'ukoyh 11-1
1. ;fn ,d js[kk x, y vkSj z-v{k osQ lkFk Øe'k% 90°, 135°, 45° osQ dks.k cukrh gS rks bldh fno~Q&dkslkbu Kkr dhft,A
2. ,d js[kk dh fno~Q&dkslkbu Kkr dhft, tks funsZ'kka{kksa osQ lkFk leku dks.k cukrh gSA
3. ;fn ,d js[kk osQ fno~Q&vuqikr –18, 12, – 4, gSa rks bldh fno~Q&dkslkbu D;k gSa\
4. n'kkZb, fd ¯cnq (2, 3, 4), (– 1, – 2, 1), (5, 8, 7) lajs[k gSaA
5. ,d f=kHkqt dh Hkqtkvksa dh fno~Q&dkslkbu Kkr dhft, ;fn f=kHkqt osQ 'kh"kZ ¯cnq
(3, 5, – 4), (– 1, 1, 2) vkSj (– 5, – 5, – 2) gSaA
11.3 varfj{k esa js[kk dk lehdj.k (Equation of a Line in Space)
d{kk XI esa f}&foeh; ry esa js[kkvksa dk vè;;u djus osQ i'pkr~ vc ge varfj{k esa ,d js[kk osQ lfn'k rFkk dkrhZ; lehdj.kksa dks Kkr djsaxsA
,d js[kk vf}rh;r% fu/kZfjr gksrh gS] ;fn
(i);g fn, ¯cnq ls nh xbZ fn'kk ls gksdj tkrh gS] ;k
(ii);g nks fn, x, ¯cnqvksa ls gksdj tkrh gSA
11.3.1 fn, x, ¯cnq A ls tkus okyh rFkk fn, x, lfn'k ![]() osQ lekarj js[kk dk lehdj.k (Equation of a line through a given point A and parallel to a given vector
osQ lekarj js[kk dk lehdj.k (Equation of a line through a given point A and parallel to a given vector ![]() )
)
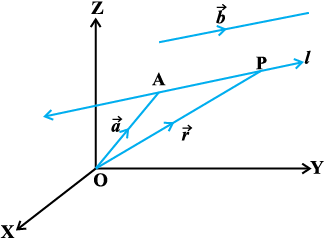
vko`Qfr 11-4
ledksf.kd funsZ'kka{k fudk; osQ ewy ¯cnq O osQ lkis{k eku yhft, fd ¯cnq A dk lfn'k  gSA eku yhft, fd ¯cnq A ls tkus okyh rFkk fn, x, lfn'k
gSA eku yhft, fd ¯cnq A ls tkus okyh rFkk fn, x, lfn'k  osQ lekarj js[kk l gSA eku yhft, fd l ij fLFkr fdlh LosPN ¯cnq P dk fLFkfr lfn'k
osQ lekarj js[kk l gSA eku yhft, fd l ij fLFkr fdlh LosPN ¯cnq P dk fLFkfr lfn'k  gS (vko`Qfr 11-4)A
gS (vko`Qfr 11-4)A
rc 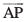 lfn'k
lfn'k 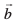 osQ lekarj gS vFkkZr~
osQ lekarj gS vFkkZr~ 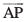 =λ
=λ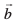 , tgk¡ λ ,d okLrfod la[;k gSA
, tgk¡ λ ,d okLrfod la[;k gSA
ijarq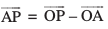
vFkkZr~ λ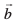 =
= 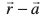
foykser% izkpy λ osQ izR;sd eku osQ fy, ;g lehdj.k js[kk osQ fdlh ¯cnq P dh fLFkfr iznku djrk gSA vr% js[kk dk lfn'k lehdj.k gS%
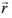 =
=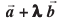 ... (1)
... (1)
fVIi.kh ;fn 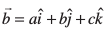 gS rks js[kk osQ fno~Q&vuqikr a, b, c gS vkSj foykser% ;fn ,d js[kk osQ fno~Q&vuqikr a, b, c gksa rks
gS rks js[kk osQ fno~Q&vuqikr a, b, c gS vkSj foykser% ;fn ,d js[kk osQ fno~Q&vuqikr a, b, c gksa rks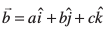 js[kk osQ lekarj gksxkA ;gk¡ b dks
js[kk osQ lekarj gksxkA ;gk¡ b dks 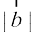 u le>k tk,A
u le>k tk,A
lfn'k :i ls dkrhZ; :i O;qRiUu djuk (Derivation of Cartesian Form from Vector Form)
eku yhft, fd fn, ¯cnq A osQ funsZ'kkad (x1, y1, z1) gSa vkSj js[kk dh fno~Q&dkslkbu
a, b, c gSa eku yhft, fdlh ¯cnq P osQ funsZ'kkad (x, y, z) gSaA rc
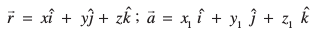
vkSj 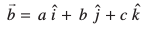
bu ekuksa dks (1) esa izfrLFkkfir djosQ 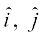 vkSj
vkSj 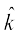 , osQ xq.kkadksa dh rqyuk djus ij ge ikrs gSa fd
, osQ xq.kkadksa dh rqyuk djus ij ge ikrs gSa fd
x = x1 + λa;y = y1 + λ b;z = z1+ λc ... (2)
;s js[kk osQ izkpy lehdj.k gSaA (2) ls izkpy λ dk foyksiu djus ij] ge ikrs gSa%
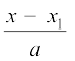 =
= 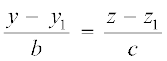 ... (3)
... (3)
;g js[kk dk dkrhZ; lehdj.k gSA
fVIi.kh ;fn js[kk dh fno~Q&dkslkbu l, m, n gSa] rks js[kk dk lehdj.k
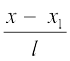 =
= 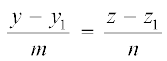 gSaA
gSaA
mnkgj.k 6 ¯cnq (5, 2, – 4) ls tkus okyh rFkk lfn'k 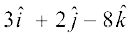 osQ lekarj js[kk dk lfn'k rFkk dkrhZ; lehdj.kksa dks Kkr dhft,A
osQ lekarj js[kk dk lfn'k rFkk dkrhZ; lehdj.kksa dks Kkr dhft,A
gy gesa Kkr gS] fd
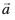 =
= 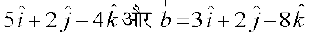
blfy,] js[kk dk lfn'k lehdj.k gS%
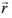 =
= 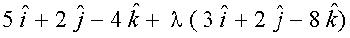 [(1) ls]
[(1) ls]
pw¡fd js[kk ij fLFkr fdlh ¯cnq P x, y, z) dh fLFkfr lfn'k 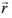 gS] blfy,
gS] blfy,
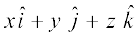 =
= 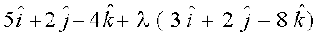
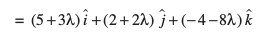
λ dk foyksiu djus ij ge ikrs gSa fd
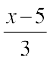 =
= 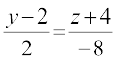
tks js[kk osQ lehdj.k dk dkrhZ; :i gSA
11.3.2 nks fn, x, ¯cnqvksa ls tkus okyh js[kk dk lehdj.k (Equation of a line passing through two given points)
eku yhft, ,d js[kk ij fLFkr nks ¯cnqvksa A(x1, y1, z1) vkSj B(x2, y2, z2), osQ fLFkfr lfn'k Øe'k% 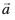 vkSj
vkSj 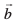 gSa (vko`Qfr 11.5)A
gSa (vko`Qfr 11.5)A
eku yhft, 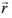 ,d LosPN ¯cnq P dk fLFkfr lfn'k gSA rc P js[kk ij gS ;fn vkSj osQoy ;fn
,d LosPN ¯cnq P dk fLFkfr lfn'k gSA rc P js[kk ij gS ;fn vkSj osQoy ;fn 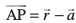 rFkk
rFkk 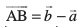 lajs[k lfn'k gSaA blfy, P js[kk ij fLFkr gS ;fn vkSj osQoy ;fn
lajs[k lfn'k gSaA blfy, P js[kk ij fLFkr gS ;fn vkSj osQoy ;fn
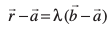
;k 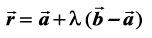 , λ ∈ R ... (1)
, λ ∈ R ... (1)
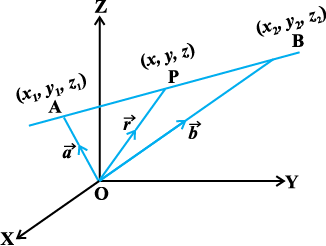
vko`Qfr 11-5
tks js[kk dk lfn'k lehdj.k gSA
lfn'k :i ls dkrhZ; :i O;qRiUu djuk
ge ikrs gSa fd
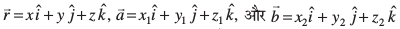
bu ekuksa dks (1) esa izfrLFkkfir djus ij ge ikrs gSa fd
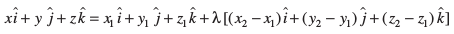
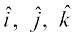 osQ xq.kkadksa dh rqyuk djus ij ge ikrs gSa fd
osQ xq.kkadksa dh rqyuk djus ij ge ikrs gSa fd
x = x1 + λ (x2 – x1); y = y1 + λ (y2 – y1); z = z1 + λ (z2 – z1)
λ dk foyksiu djus ij ge ikrs gSa fd
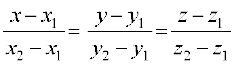
tks js[kk osQ lehdj.k dk dkrhZ; :i gSA
mnkgj.k 7 ¯cnqvksa (–1, 0, 2) vkSj (3, 4, 6) ls gksdj tkus okyh js[kk dk lfn'k lehdj.k Kkr dhft,A
gy eku yhft, 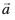 vkS
vkS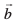 j¯cnqvksa A(– 1, 0, 2) vkSj B(3, 4, 6) osQ fLFkfr lfn'k gSaA
j¯cnqvksa A(– 1, 0, 2) vkSj B(3, 4, 6) osQ fLFkfr lfn'k gSaA
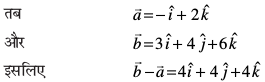
eku yhft, fd js[kk ij fLFkr fdlh LosPN ¯cnq P dk fLFkfr lfn'k 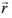 gSA vr% js[kk dk lfn'k lehdj.k
gSA vr% js[kk dk lfn'k lehdj.k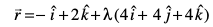
mnkgj.k 8 ,d js[kk dk dkrhZ; lehdj.k 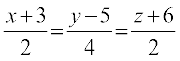 gSA bl js[kk dk lfn'k lehdj.k Kkr dhft,A
gSA bl js[kk dk lfn'k lehdj.k Kkr dhft,A
gy fn, x, lehdj.k dk ekud :i
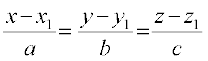
ls rqyuk djus ij ge ikrs gSa fd x1 = – 3, y1 = 5, z1 = – 6; a = 2, b = 4, c = 2
bl izdkj vHkh"V js[kk ¯cnq (– 3, 5, – 6) ls gksdj tkrh gS rFkk lfn'k 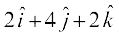 osQ lekarj gSA eku yhft, fd js[kk ij fLFkr fdlh ¯cnq dh fLFkfr lfn'k
osQ lekarj gSA eku yhft, fd js[kk ij fLFkr fdlh ¯cnq dh fLFkfr lfn'k  gS rks js[kk dk lfn'k lehdj.k
gS rks js[kk dk lfn'k lehdj.k
}kjk iznÙk gSA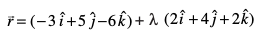
11.4 nks js[kkvksa osQ eè; dks.k (Angle between two lines)
eku yhft, fdL1 vkSjL2 ewy ¯cnq ls xqtjus okyh nks js[kk,¡ gSa ftuosQ fno~Q&vuqikr Øe'k% a1, b1, c1 vkSj a2, b2, c2, gSA iqu% eku yhft,fd L1 ij ,d ¯cnq P rFkk L2 ij ,d ¯cnq QgSA vko`Qfr 11-6 esa fn, x, lfn'k OP vkSj OQ ij fopkj dhft,A eku yhft, fd OP vkSj OQ osQ chp U;wu dks.k θ gSA vc Lej.k dhft, fd lfn'kksa OP vkSj OQ osQ ?kVd Øe'k% a1, b1, c1 vkSj a2, b2, c2 gSaA blfy, muosQ chp dk dks.k θ
cosθ =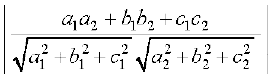 }kjk iznÙk gSA
}kjk iznÙk gSA
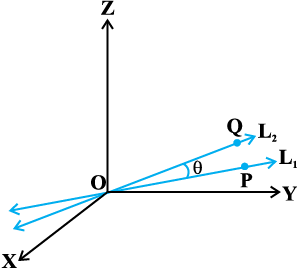
vko`Qfr 11-6
iqu% sin θosQ :i esa] js[kkvksa osQ chp dk dks.k
sin θ=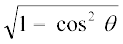
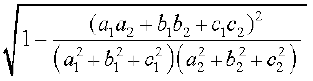
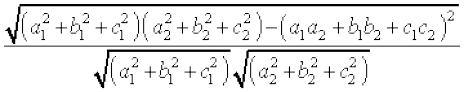
 .... (2)
.... (2)
fVIi.kh ml fLFkfr esa tc js[kk,¡ L1 vkSjL2 ewy ¯cnq ls ugha xqtjrh gS rks ge L1 vkSj L2 osQ lekarj] ewy ¯cnq ls xqtjus okyh js[kk,¡ Øe'k% ysrs gSaA ;fn js[kkvksa Øe'k% 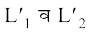 ysrs gSaA ;fn js[kkvksa L1 vkSj L2 osQ fno~Q&vuqikrksa osQ ctk; fno~Q&dkslkbu nh xbZ gks tSls L1 osQ fy, l1, m1, n1 vkSj L2 osQ fy, l2, m2, n2 rks (1) vkSj (2) fuEufyf[kr izk:i ysaxsA
ysrs gSaA ;fn js[kkvksa L1 vkSj L2 osQ fno~Q&vuqikrksa osQ ctk; fno~Q&dkslkbu nh xbZ gks tSls L1 osQ fy, l1, m1, n1 vkSj L2 osQ fy, l2, m2, n2 rks (1) vkSj (2) fuEufyf[kr izk:i ysaxsA
cosθ = |l1 l2 + m1m2 + n1n2| (D;ksafd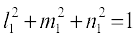
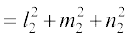 )... (3)
)... (3)
vkSj sin θ =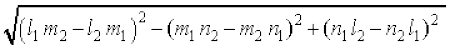 ... (4)
... (4)
fno~Q&vuqikr a1, b1, c1 vkSj a2, b2, c2 okyh js[kk,¡
(i)yacor~~ gS] ;fn θ = 90°, vFkkZr~ (1) ls a1a2 + b1b2 + c1c2 = 0
(ii)lekarj gS] ;fn θ = 0, vFkkZr~ (2) ls 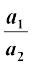
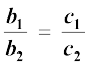
vc ge nks js[kkvksa osQ chp dk dks.k Kkr djsaxs ftuosQ lehdj.k fn, x, gSaA ;fn mu js[kkvksa 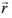 =
=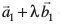 vkSj =
vkSj =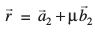 osQ chp U;wu dks.k θ g
osQ chp U;wu dks.k θ g
rc 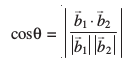
dkrhZ; :i esa ;fn js[kkvksa%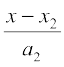 =
=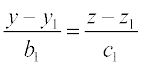 ... (1)
... (1)
vkSj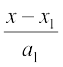 =
=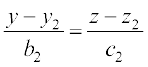 ... (2)
... (2)
cos θ ==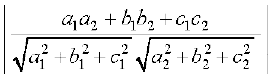
osQ chp dk dks.k θ gS tgk¡ js[kk,¡ (1) o (2) osQ fno~Q&vuqikr Øe'k% a1, b1, c1 rFkk a2, b2, c2 gS rc
mnkgj.k 9 fn, x, js[kk&;qXe
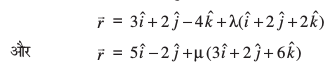
osQ eè; dks.k Kkr dhft,
gy eku yhft, 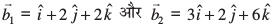
nksuksa js[kkvksa osQ eè; dks.k θ gS] blfy,
cosθ =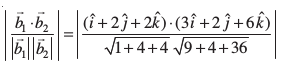
= 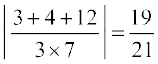
vr% θ = cos–1 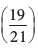
mnkgj.k 10 js[kk&;qXe%
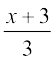 =
=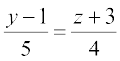
vkSj =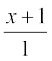 =
=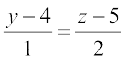
osQ eè; dks.k Kkr dhft,A
gy igyh js[kk osQ fno~Q&vuqikr 3] 5] 4 vkSj nwljh js[kk osQ fno~Q&vuqikr 1] 1] 2 gSaA ;fn muosQ chp dk dks.k θ gks rc
cosθ = 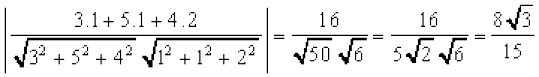 =
=
vr% vHkh"V dks.k cos–1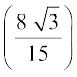 gSA
gSA
11.5 nks js[kkvksa osQ eè; U;wure nwjh (Shortest Distance between two lines)
varfj{k esa ;fn nks js[kk,¡ ijLij izfrPNsn djrh gS rks muosQ chp dh U;wure nwjh 'kwU; gSA vkSj varfj{k esa ;fn nks js[kk,¡ lekarj gS rks muosQ chp dh U;wure nwjh] muosQ chp yacor~~ nwjh gksxh vFkkZr~ ,d js[kk osQ ,d ¯cnq ls nwljh js[kk ij [khapk x;k yacA
blosQ vfrfjDr varfj{k esa] ,slh Hkh js[kk,¡ gksrh gS tks u rks izfrPNsnh vkSj u gh lekarj gksrh gSA okLro esa ,slh js[kkvksa osQ ;qXe vleryh; gksrs gSa vkSj bUgsa fo"keryh; js[kk,¡ (skew lines) dgrs gSaA mnkgj.kr;k ge vko`Qfr 11-7 esa x, y vkSj z-v{k osQ vuqfn'k Øe'k% 1] 3] 2 bdkbZ osQ vkdkj okys dejs ij fopkj djrs gSaA
js[kk GE Nr osQ fod.kZ osQ vuqfn'k gS vkSj js[kk DB, A osQ Bhd Åij Nr osQ dksus ls xqtjrh gqbZ nhokj osQ fod.kZ osQ vuqfn'k gSA ;s js[kk,¡ fo"keryh; gSa D;ksafd os lekarj ugha gS vkSj dHkh feyrh Hkh ugha gSaA
nks js[kkvksa osQ chp U;wure nwjh ls gekjk vfHkizk; ,d ,sls js[kk[kaM ls gS tks ,d js[kk ij fLFkr ,d ¯cnq dks nwljh js[kk ij fLFkr vU; ¯cnq dks feykus ls izkIr gksa rkfd bldh yackbZ U;wure gksA
U;wure nwjh js[kk[kaM nksuksa fo"keryh; js[kkvksa ij yac gksxkA
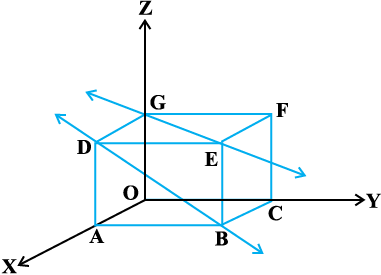
vko`Qfr 11-7
11.5.1 nks fo"keryh; js[kkvksa osQ chp dh nwjh (Distance between two skew lines)
vc ge js[kkvksa osQ chp dh U;wure nwjh fuEufyf[kr fof/ ls Kkr djrs gSaA eku yhft, l1 vkSj l2 nks fo"keryh; js[kk,¡ gS ftuosQ lehdj.k (vko`Qfr 11.8) fuEufyf[kr gSa%
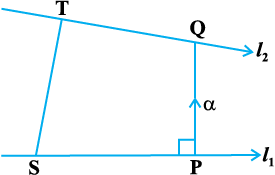
vko`Qfr 11-8

js[kk l1 ij dksbZ ¯cnq S ftldh fLFkfr lfn'k 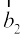 vkSj l2 ij dksbZ ¯cnq T ftldh fLFkfr lfn'k
vkSj l2 ij dksbZ ¯cnq T ftldh fLFkfr lfn'k 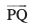 . gS] yhft,A rc U;wure nwjh lfn'k dk ifjek.k] ST dk U;wure nwjh dh fn'kk esa iz{ksi dh eki osQ leku gksxk (vuqPNsn 10.6.2)A
. gS] yhft,A rc U;wure nwjh lfn'k dk ifjek.k] ST dk U;wure nwjh dh fn'kk esa iz{ksi dh eki osQ leku gksxk (vuqPNsn 10.6.2)A
;fn l1 vkSj l2 osQ chp dh U;wure nwjh lfn'k 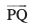 gS rks ;g nksuksa b1 vkSj b2 ij yac gksxhA
gS rks ;g nksuksa b1 vkSj b2 ij yac gksxhA 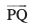 dh fn'kk esa bdkbZ lfn'k
dh fn'kk esa bdkbZ lfn'k 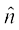 bl izdkj gksxh fd
bl izdkj gksxh fd
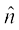 =
=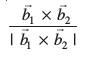
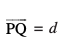


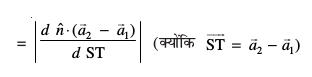
blfy, vHkh"V U;wure nwjh 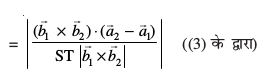
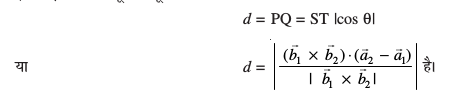
dkrhZ; :i (Cartesian Form)
js[kkvksa%
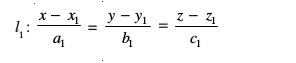
l2 :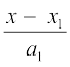 =
=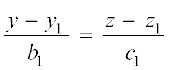
osQ chp dh U;wure nwjh gS%
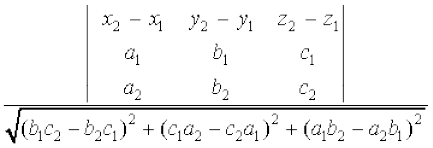
11.5.2 lekarj js[kkvksa osQ chp dh nwjh (Distance between parallel lines)
;fn nks js[kk,¡ l1 ;fn l2 lekarj gSa rks os leryh; gksrh gSaA ekuk nh xbZ js[kk,¡ Øe'k%
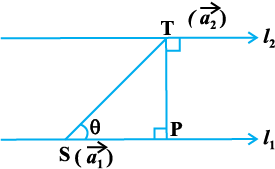
vko`Qfr 11-9
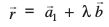 ... (1)
... (1)
vkSj
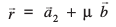
gSa] tgk¡ l1 ij ¯cnq S dk fLFkfr lfn'kvkSj l2 ij ¯cnq T dk fLFkfr lfn'k gS (vko`Qfr 11.9)
D;ksafd l1, vkSj l2 leryh; gSA ;fn ¯cnq T ls l1 ij Mkys x, yac dk ikn P gS rc js[kkvksa l1 vkSj l2 osQ chp dh nwjh = |TP|
eku yhft, fd lfn'kksa 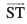 vkSj
vkSj 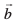 osQ chp dk dks.k θ gSA rc]
osQ chp dk dks.k θ gSA rc]
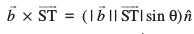
stgk¡ js[kkvksa l1 vkSj l2 osQ ry ij yac bdkbZ lfn'k 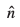 gSa
gSa
ijarq 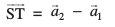
blfy, (3) ls ge ikrs gSa fd
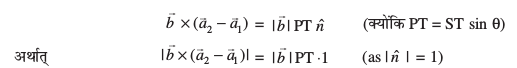
blfy, Kkr js[kkvksa osQ chp U;wure nwjh
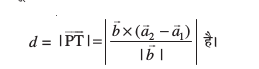
mnkgj.k 11 js[kkvksa l1 vkSj l2 osQ chp dh U;wure nwjh Kkr dhft, ftuosQ lfn'k lehdj.k gS%
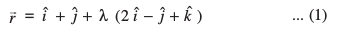
vkSj 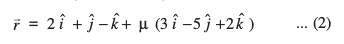
gy lehdj.k (1) o (2) dh 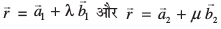 vkSj , ls rqyuk djus ij ge ikrs gSa fd
vkSj , ls rqyuk djus ij ge ikrs gSa fd
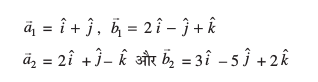
blfy,
vkSj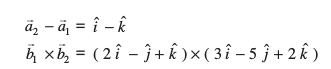
=
bl izdkj 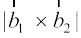 =
=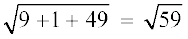
blfy, nh xbZ js[kkvksa osQ chp dh U;wure nwjh
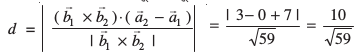
mnkgj.k 12 fuEufyf[kr nh xbZ js[kkvksa l1 vkSj l2 :
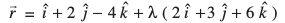
vkSj =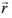 =
=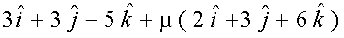 osQ chp U;wure nwjh Kkr dhft,A
osQ chp U;wure nwjh Kkr dhft,A
gy nksuksa js[kk,¡ lekraj gSaA (D;ksa\) gesa izkIr gS fd
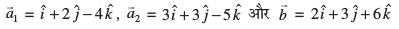
blfy, js[kkvksa osQ chp dh nwjh
d= 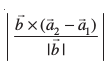 =
= 
= 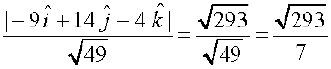 gSA
gSA
iz'ukoyh 11-2
1. n'kkZb, fd fno~Q&dkslkbu 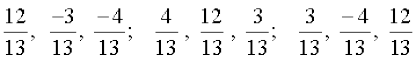 okyh rhu js[kk,¡ ijLij yacor~ gSaA
okyh rhu js[kk,¡ ijLij yacor~ gSaA
2. n'kkZb, fd ¯cnqvksa (1, – 1, 2), (3, 4, – 2) ls gksdj tkus okyh js[kk ¯cnqvksa (0, 3, 2) vkSj (3, 5, 6) ls tkus okyh js[kk ij yac gSA
3. n'kkZb, fd ¯cnqvksa (4, 7, 8), (2, 3, 4) ls gksdj tkus okyh js[kk] ¯cnqvksa (– 1, – 2, 1), (1, 2, 5) ls tkus okyh js[kk osQ lekarj gSA
4.
5. ¯cnq ftldh fLFkfr lfn'k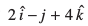 ls xq”kjus o lfn'k
ls xq”kjus o lfn'k 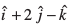 dh fn'kk esa tkus okyh js[kk dk lfn'k vkSj dkrhZ; :iksa esa lehdj.k Kkr dhft,A
dh fn'kk esa tkus okyh js[kk dk lfn'k vkSj dkrhZ; :iksa esa lehdj.k Kkr dhft,A
6. ml js[kk dk dkrhZ; lehdj.k Kkr dhft, tks ¯cnq (– 2, 4, – 5) ls tkrh gS vkSj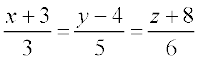 osQ lekarj gSA
osQ lekarj gSA
7. ,d js[kk dk dkrhZ; lehdj.k 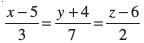 gSA bldk lfn'k lehdj.k Kkr dhft,A
gSA bldk lfn'k lehdj.k Kkr dhft,A
8. ewy ¯cnq vkSj (5, – 2, 3) ls tkus okyh js[kk dk lfn'k rFkk dkrhZ; :iksa esa lehdj.k Kkr dhft,A
9. ¯cnqvksa (3, – 2, – 5), vkSj (3, – 2, 6) ls xq”kjus okyh js[kk dk lfn'k rFkk dkrhZ; :iksa esa lehdj.k dks Kkr dhft,A
10.fuEufyf[kr js[kk&;qXeksa osQ chp dk dks.k Kkr dhft,%
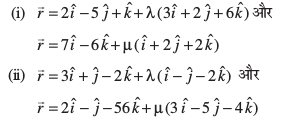
11. fuEufyf[kr js[kk&;qXeksa osQ chp dk dks.k Kkr dhft,%
(i)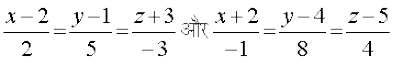
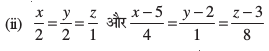
12. p dk eku Kkr dhft, rkfd js[kk,¡ 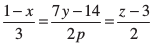
vkSj 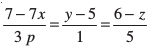 ijLij yac gksaA
ijLij yac gksaA
13. fn[kkb, fd js[kk,¡ 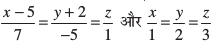 ijLij yac gSaA
ijLij yac gSaA
14. js[kkvksa 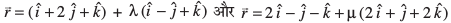 osQ chp dh U;wure nwjh Kkr dhft,%
osQ chp dh U;wure nwjh Kkr dhft,%
15. js[kkvksa 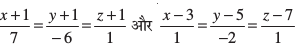 osQ chp dh U;wure nwjh Kkr dhft,A
osQ chp dh U;wure nwjh Kkr dhft,A
16. js[kk,¡] ftuosQ lfn'k lehdj.k fuEufyf[kr gS] osQ chp dh U;wure nwjh Kkr dhft,%
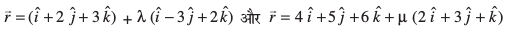
17. js[kk,¡] ftudh lfn'k lehdj.k fuEufyf[kr gSa] osQ chp dh U;wure Kkr dhft,%
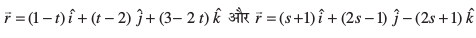
11.6 lery (Plane)
,d lery dks vf}rh; :i ls Kkr fd;k tk ldrk gS ;fn fuEufyf[kr esa ls dksbZ ,d 'krZ Kkr gks%
(i)lery dk vfHkyac vkSj ewy ¯cnq ls lery dh nwjh Kkr gS] vFkkZr~ vfHkyac :i esa lery dk lehdj.k
(ii);g ,d ¯cnq ls xq”kjrk gS vkSj nh xbZ fn'kk osQ yacor~ gSA
(iii);g fn, x, rhu vlajs[k ¯cnqvksa ls xq”kjrk gSA
vc ge leryksa osQ lfn'k vkSj dkrhZ; lehdj.kksa dks izkIr djsaxsA
�11.6.1 vfHkyac :i esa lery dk lehdj.k (Equation of a Plane in normal form)
,d lery ij fopkj dhft, ftldh ewy ¯cnq ls yacor~ nwjh d (d ≠ 0) gS (vko`Qfr 11-10)A
;fn 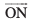 ewy ¯cnq ls ry ij yac gS rFkk
ewy ¯cnq ls ry ij yac gS rFkk 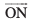 osQ vuqfn'k
osQ vuqfn'k 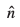 ek=kd vfHkyac lfn'k gS rc
ek=kd vfHkyac lfn'k gS rc 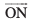 = d
= d 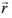 gSA eku yhft, fd lery ij dksbZ ¯cnq P gSA blfy,]
gSA eku yhft, fd lery ij dksbZ ¯cnq P gSA blfy,]  ,
,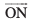 ij yac gSA
ij yac gSA
vr%

vko`Qfr 11-10
eku yhft, P dh fLFkfr lfn'k 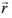 gS rks
gS rks 
bl izdkj (1) dk :i fuEufyf[kr gS%
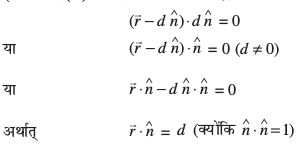
;g lery dk lfn'k lehdj.k gSA
dkrhZ; :i (Cartesian Form)
lery dk lfn'k lehdj.k gS tgkW 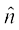 lery osQ vfHkyac bdkbZ lfn'k gSA eku yhft, lery ij dksbZ ¯cnq P (x, y, z) gSA rc
lery osQ vfHkyac bdkbZ lfn'k gSA eku yhft, lery ij dksbZ ¯cnq P (x, y, z) gSA rc
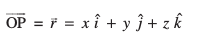
eku yhft, 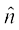 dh fno~Q&dkslkbu l, m, n gSaA rc
dh fno~Q&dkslkbu l, m, n gSaA rc
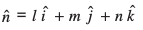
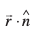 osQ ekuksa dks (2) esa izfrLFkkfir djus ij ge ikrs gSa]
osQ ekuksa dks (2) esa izfrLFkkfir djus ij ge ikrs gSa]
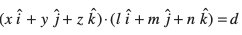
vFkkZr~ lx + my + nz = d ... (3)
;g lery dk dkrhZ; lehdj.k gSA
fVIi.kh lehdj.k (3) iznf'kZr djrk gS fd ;fn 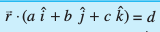 ,d lery dk lfn'k lehdj.k gS rks ax + by + cz = d lery dk dkrhZ; lehdj.k gS tgk¡ a, b vkSj c lery osQ vfHkyac osQ fno~Q&vuqikr gSaA
,d lery dk lfn'k lehdj.k gS rks ax + by + cz = d lery dk dkrhZ; lehdj.k gS tgk¡ a, b vkSj c lery osQ vfHkyac osQ fno~Q&vuqikr gSaA
mnkgj.k 13 ml lery dk lfn'k lehdj.k Kkr dhft, tks ewy ¯cnq ls 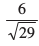 dh nwjh ij gS
dh nwjh ij gS
vkSj ewy ¯cnq ls bldk vfHkyac lfn'k 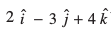 gSA
gSA
gy eku yhft, 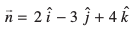 gSA rc
gSA rc
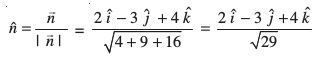
blfy, lery dk vHkh"V lehdj.k
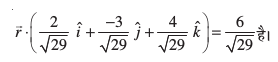
mnkgj.k 14 lery = 0 ij ewy ¯cnq ls Mkys x, yac bdkbZ lfn'k dh fno~Q&dkslkbu Kkr dhft,A
gy lery osQ Kkr lehdj.k dks bl izdkj O;Dr fd;k tk ldrk gS%
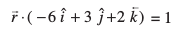
vc 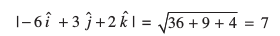 ... (1)
... (1)
blfy, (1) osQ nksuksa i{kksa dks 7 ls Hkkx djus ij ge ikrs gSa fd
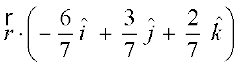 =
=
tks fd lery dk lehdj.k 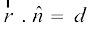 osQ :i dk gSA
osQ :i dk gSA
blls Li"V gS fd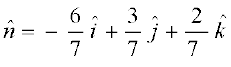 lery osQ yac bdkbZ lfn'k gS tks ewy ¯cnq ls xqtjrk gSA bl izdkj
lery osQ yac bdkbZ lfn'k gS tks ewy ¯cnq ls xqtjrk gSA bl izdkj 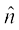 dh fno~Q&dkslkbu
dh fno~Q&dkslkbu 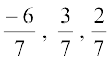 gS
gS
mnkgj.k 15 lery 2x – 3y + 4z – 6 = 0 dh ewy ¯cnq ls nwjh Kkr dhft,A
gy D;ksafd ry osQ vfHkyac osQ fno~Q&vuqikr 2, –3, 4 gSa blfy, bldh fno~Q&dkslkbu gSa%
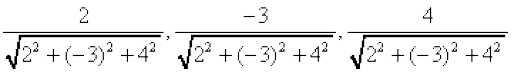 vFkkZr~
vFkkZr~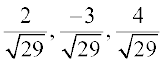
blfy, lehdj.k 2x – 3y + 4z – 6 = 0 vFkkZr~ 2x – 3y + 4z = 6 dks 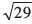 ls Hkkx djus ij ge izkIr djrs gSa%aA
ls Hkkx djus ij ge izkIr djrs gSa%aA
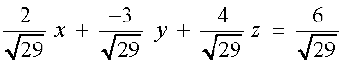
vkSj ;g lx + my + nz = d, osQ :i esa gS tgk¡ ewy ¯cnq ls lery dh nwjh d gSA blfy, lery dh ewy ¯cnq ls nwjh 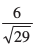 gSaAs
gSaAs
mnkgj.k 16 ewy ¯cnq ls lery 2x – 3y + 4z – 6 = 0 ij Mkys x, yac osQ ikn osQ funsZ'kkad Kkr dhft,A
gy eku yhft, ewy ¯cnq ls lery in Mkys x, yac osQ ikn P osQ funsZ'kkad (x1, y1, z1) gS (vko`Qfr 11.11)A
rc js[kk OP osQ fno~Q&vuqikr x1, y1, z1 gSaA
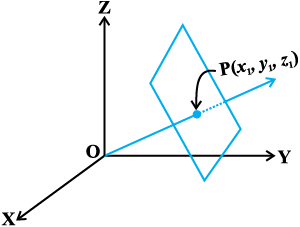
vko`Qfr 11-11
lery dh lehdj.k dks vfHkyac osQ :i esa fy[kus ij ge ikrs gSa fd
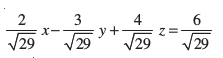
tgk¡ OP osQ fno~Q&vuqikr 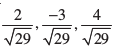 gSaA
gSaA
D;ksafd ,d js[kk osQ fno~Q&dkslkbu vkSj fno~Q&vuqikr lekuqikrh gksrs gSaA vr%
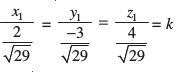
vFkkZr~ 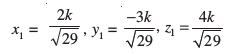
bu ekuksa dks lery osQ lehdj.k esa izfrLFkkfir djus ij ge ikrs gSa fd k = 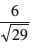
vr% yac osQ ikn osQ funsZ'kkad 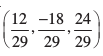 gSA
gSA
fVIi.kh ;fn ewy ¯cnq ls lery dh nwjh d gks vkSj lery osQ vfHkyac dh fno~Q&dkslkbu l, m, n gksa rc yac dk ikn (ld, md, nd) gksrk gSA
11.6.2 ,d fn, lfn'k osQ vuqyac rFkk fn, ¯cnq ls gksdj tkus okys lery dk lehdj.k (Equation of a plane perpendicular to a given vector and passing through a given point)
varfj{k esa] ,d fn, x, lfn'k osQ vuqyac vusoQ lery gks ldrs gSa ijarq ,d fn, x, ¯cnq P x1, y1, z1) ls bl izdkj dk osQoy ,d lery dk vfLrRo gksrk gS (nsf[k, vko`Qfr 11-12)A
eku yhft, fd lery ,d ¯cnq A, ftldh fLFkfr lfn'k 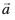 gS] ls tkrk gS vkSj lfn'k
gS] ls tkrk gS vkSj lfn'k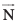 osQ vuqyac gSA eku yhft, fd lery ij fdlh ¯cnq P dk fLFkfr lfn'k gS (vko`Qfr 11-13)A
osQ vuqyac gSA eku yhft, fd lery ij fdlh ¯cnq P dk fLFkfr lfn'k gS (vko`Qfr 11-13)A
rc ¯cnq P lery esa fLFkr gksrk gS] ;fn vkSj osQoy ;fn 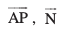 , ij yac gS] vFkkZr~
, ij yac gS] vFkkZr~ 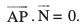 = 0. ijarq
= 0. ijarq 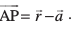 blfy,
blfy,
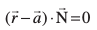 ......(1)
......(1)
;g lery dk lfn'k lehdj.k gSA

vko`Qfr 11-12
dkrhZ; :i (Cartesian Form)
eku yhft, fd fn;k ¯cnq A (x1, y1, z1) vkSj lery ij dksbZ ¯cnq P (x, y, z)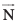 osQ
osQ
fno~Q&vuqikr A, B rFkk C gSa] rc
osQ fno~Q&vuqikr A, B rFkk C gSa] rc
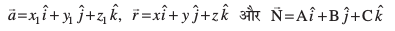
vc 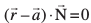
blfy, 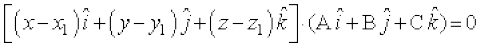
vFkkZr~ A(x – x1) + B(y – y1) + C(z – z1) = 0
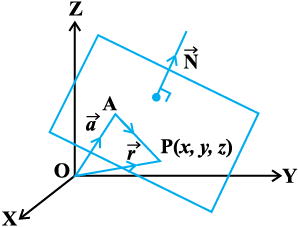
vko`Qfr 11-13
mnkgj.k 17 ml lery dk lfn'k vkSj dkrhZ; lehdj.k Kkr dhft,] tks ¯cnq (5, 2, – 4) ls tkrk gS vkSj 2, 3, – 1 fno~Q&vuqikr okyh js[kk ij yac gSA
gy ge tkurs gSa fd ¯cnq (5, 2, – 4) dk fLFkfr lfn'k 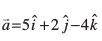 gS vkSj lery osQ yac dk vfHkyac lfn'k
gS vkSj lery osQ yac dk vfHkyac lfn'k 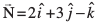 gSA
gSA
blfy, lery dk lfn'k lehdj.k 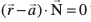 ls iznÙk gSA
ls iznÙk gSA
;k 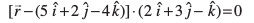
(1) dks dkrhZ; :i esa :ikarj.k djus ij ge ikrs gSa] fd
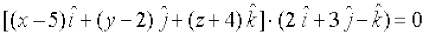
;k 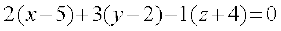
vFkkZr~ 2x + 3y – z = 20
tks lery dk dkrhZ; lehdj.k gSA
11.6.3 rhu vlajs[kh; ¯cnqvksa ls gksdj tkus okys lery dk lehdj.k (Equation of a plane passing through three non-collinear points)
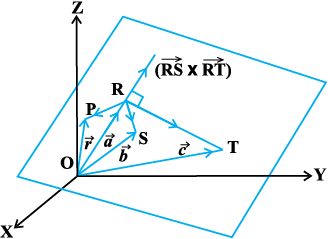
vko`Qfr 11-14
eku yhft, lery ij fLFkr rhu vlajs[k ¯cnqvksa R, S vkSj T osQ fLFkfr lfn'k Øe'k% 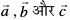 gSa (vko`Qfr 11.14)A
gSa (vko`Qfr 11.14)A
lfn'k 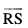 vkSj
vkSj 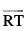 fn, lery esa gSaA blfy, lfn'k
fn, lery esa gSaA blfy, lfn'k 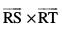 ¯cnqvksa R, S vkSj T dks vUrfoZ"V djus okys lery ij yac gksxkA eku yhft, lery esa dksbZ ¯cnq P dk fLFkfr lfn'k
¯cnqvksa R, S vkSj T dks vUrfoZ"V djus okys lery ij yac gksxkA eku yhft, lery esa dksbZ ¯cnq P dk fLFkfr lfn'k 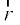 gSA blfy, R ls tkus okys rFkk lfn'k
gSA blfy, R ls tkus okys rFkk lfn'k 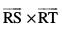 ij yac] lery dk lehdj.k
ij yac] lery dk lehdj.k 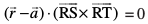 gSA
gSA
;k 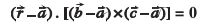
;g rhu vlajs[k ¯cnqvksa ls xqtjus okys lery osQ lehdj.k dk lfn'k izk:i gSA
fVIi.kh mijksDr izfØ;k esa rhu vlajs[k ¯cnq dguk D;ksa vko';d gS\ ;fn ¯cnq ,d gh js[kk ij fLFkr gSa rc mlls xqtjus okys dbZ lery gksaxs (vko`Qfr 11-15)A
;s lery ,d iqLrd osQ i`"Bksa dh Hkk¡fr gksaxs tgk¡ ¯cnqvksa R, S vkSj T dks varfoZ"V djus okyh js[kk iqLrd osQ i`"Bksa osQ ca/u okys LFkku dk lnL; gSA
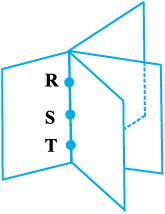
vko`Qfr 11-15
dkrhZ; :i (Cartesian Form)
eku yhft, ¯cnqvksa R, S vkSj T osQ funsZ'kkad Øe'k% (x1, y1, z1), (x2, y2, z2) vkSj (x3, y3, z3) gSaA eku yhft, fd lery ij fdlh ¯cnq P osQ funsZ'kkad (x, y, z) o bldk fLFkfr lfn'k 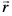 gSA rc
gSA rc
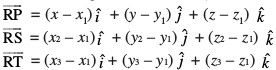
bu ekuksa dks lfn'k izk:i osQ lehdj.k (1) esa izfrLFkkiu djus ij ge ikrs gSa fd
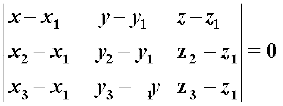
tks rhu ¯cnqvksa (x1, y1, z1), (x2, y2, z2) vkSj (x3, y3, z3) ls xq”kjus okys lery osQ lehdj.k dk dkrhZ; izk:i gSA
mngkj.k 18 ¯cnqvksa R(2, 5, – 3), S(– 2, – 3, 5) vkSj T(5, 3,– 3) ls tkus okys lery dk lfn'k lehdj.k Kkr dhft,A
gy eku yhft, 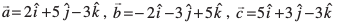
rc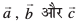 ls tkus okys lery dk lfn'k lehdj.k fuEufyf[kr gSa%
ls tkus okys lery dk lfn'k lehdj.k fuEufyf[kr gSa%
;k 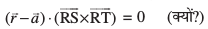
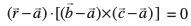
vFkkZr~ 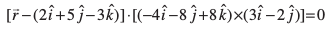
11.6.4 lery osQ lehdj.k dk var% [kaM&:i (Intercept form of the equation of a plane)
bl vuqPNsn esa] ge lery osQ lehdj.k dks] mlosQ }kjk funsZ'kka{kksa ij dVs var% [kaM osQ :i esa Kkr djsaxsA eku yhft, lery dk lehdj.k
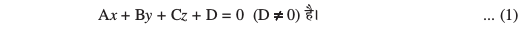
eku yhft, lery }kjk x, y, vkSj z-v{kksa ij dVs var% [kaM Øe'k% a, b vkSj c (vko`Qfr 11.16) gSaA
Li"Vr% lery x, y vkSj z-v{kksa ls Øe'k% ¯cnqvksa (a, 0, 0), (0, b, 0), vkSj (0, 0, c) ij feyrk gSA

vko`Qfr 11-16
blfy, 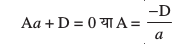
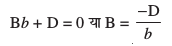
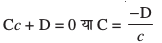
bu ekuksa dks lery osQ lehdj.k (1) esa izfrLFkkfir djus vkSj ljy djus ij ge ikrs gSa fd

tks var% [kaM :i esa lery dk vHkh"V lehdj.k gSA
mnkgj.k 19 ml lery dk lehdj.k Kkr dhft, tks x, y vkSj z-v{kksa ij Øe'k% 2] 3 vkSj 4 var% [kaM dkVrk gSA

;gk¡ a = 2, b = 3, c = 4 Kkr gSaA
a, b vkSj c osQ bu ekuksa dks (1) esa izfrLFkkfir djus ij ge lery dk vHkh"V lehdj.k 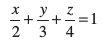 ;k 6x + 4y + 3z = 12 izkIr djrs gSaA
;k 6x + 4y + 3z = 12 izkIr djrs gSaA
11.6.5 nks fn, leryksa osQ izfrPNsnu ls gksdj tkus okyk lery (Plane passing through the intersection of two given planes)
eku yhft, π1 vkSj π2 nks lery] ftuosQ lehdj.k Øe'k%  gSa buosQ izfrPNsnu js[kk ij fLFkr fdlh ¯cnq dk fLFkfr lfn'k bu nksauksa lehdj.kksa dks larq"V djsxk (vko`Qfr 11.17)A
gSa buosQ izfrPNsnu js[kk ij fLFkr fdlh ¯cnq dk fLFkfr lfn'k bu nksauksa lehdj.kksa dks larq"V djsxk (vko`Qfr 11.17)A
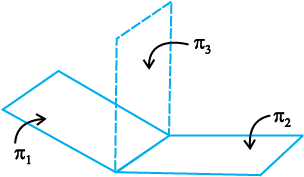
vko`Qfr 11-17
;fn bl js[kk ij fLFkr fdlh ¯cnq dh fLFkfr lfn'k gS] rks
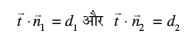
blhfy, λ osQ lHkh okLrfod ekuksa osQ fy, ge ikrs gSa fd
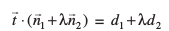
D;ksafd 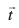 LosPN gS blfy, ;g js[kk osQ fdlh ¯cnq dks larq"V djrk gSA
LosPN gS blfy, ;g js[kk osQ fdlh ¯cnq dks larq"V djrk gSA
bl izdkj lehdj.k 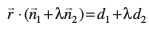 lery π3 dks fu:fir djrk gS tks ,slk gS fd ;fn dksbZ lfn'k,
lery π3 dks fu:fir djrk gS tks ,slk gS fd ;fn dksbZ lfn'k, 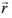 π1 vkSj π2, osQ lehdj.kksa dks larq"V djrk gS rks og π3 dks vo'; larq"V djsxkA vr% leryksa
π1 vkSj π2, osQ lehdj.kksa dks larq"V djrk gS rks og π3 dks vo'; larq"V djsxkA vr% leryksa 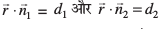 osQ izfrPNsnu js[kk ls tkus okys fdlh lery dk lehdj.k
osQ izfrPNsnu js[kk ls tkus okys fdlh lery dk lehdj.k 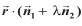 = d1 + λd2 gSA ... (1)
= d1 + λd2 gSA ... (1)
dkrhZ; :i (Cartesian Form)
dkrhZ; :i osQ fy, ekuk
vkSj 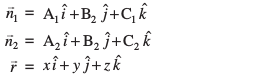
rks (1) dk ifjofrZr :i gS%
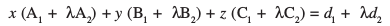
tks izR;sd λ osQ fy, fn, leryksa osQ izfrPNsnu js[kk ls gksdj tkus okys fdlh lery dk dkrhZ; lehdj.k gSA
mnkgj.k 20 leryksa 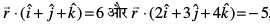 osQ izfrPNsnu rFkk ¯cnq (1,1,1) ls tkus okys lery dk lfn'k lehdj.k Kkr dhft,A
osQ izfrPNsnu rFkk ¯cnq (1,1,1) ls tkus okys lery dk lfn'k lehdj.k Kkr dhft,A
gy ;gk¡ 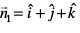 vkSj
vkSj 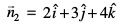 vkSj d1 = 6 vkSj d2 = –5 gSaA
vkSj d1 = 6 vkSj d2 = –5 gSaA
blfy, lw=k 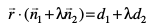 dk iz;ksx djus ij]
dk iz;ksx djus ij]
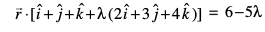
;k 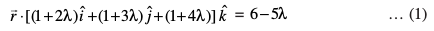
tgk¡ λ ,d okLrfod la[;k gSA
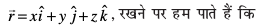
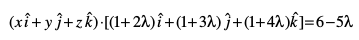
;k 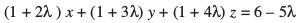
;k 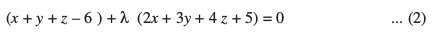
vc iz'ukuqlkj vHkh"V lery ¯cnq (1, 1, 1) ls tkrk gS] vr% ;g ¯cnq] (2) dks larq"V djsxk vFkkZr~
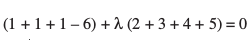
;k λ = 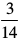
λ osQ bl eku dks (1) esa izfrLFkkfir djus ij ge ikrs gSa] fd
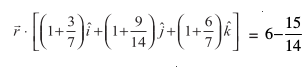
;k 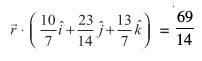
;k 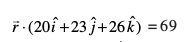
tks lery dk vHkh"V lfn'k lehdj.k gSA
11.7 nks js[kkvksa dk lg&ryh; gksuk (Coplanarity of two lines)
eku yhft, fd nks Kkr js[kk,¡%
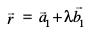
rFkk 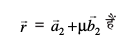
js[kk (1) ¯cnq A, ftldh fLFkfr lfn'k 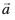 gS] ls gksdj tkrh gS rFkk
gS] ls gksdj tkrh gS rFkk 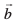 osQ lekarj gSA js[kk (2) ¯cnq B (ftldh fLFkfr lfn'k
osQ lekarj gSA js[kk (2) ¯cnq B (ftldh fLFkfr lfn'k 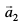 gS] ls gksdj tkrh gS rFkk
gS] ls gksdj tkrh gS rFkk 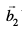 osQ lekarj gSA rc
osQ lekarj gSA rc
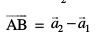
Kkr js[kk,¡ lg&ryh; gSa] ;fn 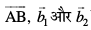 osQoy ;fn lg&ryh; gSaA vFkkZr~
osQoy ;fn lg&ryh; gSaA vFkkZr~
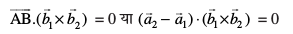
dkrhZ; :i (Cartesian Form)
eku yhft, fd ¯cnqvksa A vkSj B (osQ funsZ'kkad Øe'k% (x1, y1, z1) vkSj (x2, y2, z2) gSaA eku yhft, fd 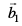 vkSj
vkSj 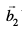 osQ fno~Q&vuqikr Øe'k% a1, b1, c1 rFkk a2, b2, c2 gSA rc
osQ fno~Q&vuqikr Øe'k% a1, b1, c1 rFkk a2, b2, c2 gSA rc
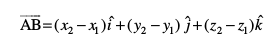
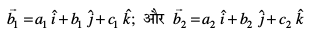
Kkr js[kk,¡ lg&ryh; gSa] ;fn vkSj osQoy ;fn 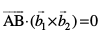 ftls fuEufyf[kr dkrhZ; :i esa O;Dr dj ldrs gSaA
ftls fuEufyf[kr dkrhZ; :i esa O;Dr dj ldrs gSaA
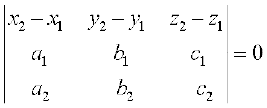 ... (4)
... (4)
mnkgj.k 21 n'kkZb, fd js[kk,¡
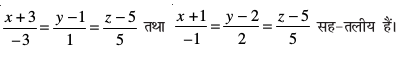
gy ;gk¡ gesa Kkr gS fd x1 = – 3, y1 = 1, z1 = 5, a1 = – 3, b1 = 1, c1 = 5
x2 = – 1, y2 = 2, z2 = 5, a2 = –1, b2 = 2, c2 = 5
vc fuEufyf[kr lkjf.kd ysus ij ge ikrs gSa fd
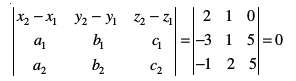
blfy, js[kk,¡ le&ryh; gSaA
11.8 nks leryksa osQ chp dk dks.k (Angle between two planes)
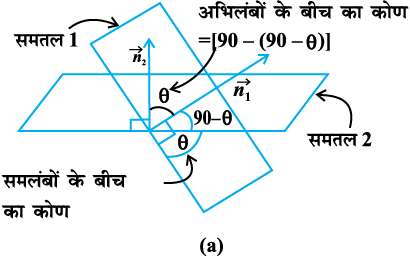
ifjHkk"kk 2 nks leryksa osQ chp dk dks.k muosQ vfHkyacksa osQ eè;LFk dks.k }kjk ifjHkkf"kr gS (vko`Qfr 11.18 (a))A è;ku nhft, fd ;fn nks leryksa osQ chp dk dks.k θ gS rks 180 – θ (vko`Qfr 11.18 (b)) Hkh muosQ chp dk dks.k gSA ge U;wu dks.k dks gh leryksa osQ chp dk dks.k ysaxsA
eku yhft, fd leryksa] 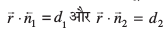 osQ chp dk dks.k θ gSA rc fdlh lkoZ ¯cnq ls leryksa ij [khaps x, vfHkyacksa osQ chp dk dks.k θ gSA
osQ chp dk dks.k θ gSA rc fdlh lkoZ ¯cnq ls leryksa ij [khaps x, vfHkyacksa osQ chp dk dks.k θ gSA
rc 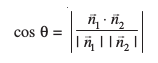

fVIi.kh nksuksa lery ijLij yacor~~ gS ;fn 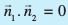 vkSj lekarj gS ;fn
vkSj lekarj gS ;fn 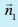 vkSj
vkSj 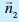 lekarj gSaA
lekarj gSaA
dkrhZ; :i (Cartesian Form)
eku yhft, leryksa%
A1 x + B1 y + C1z + D1 = 0 vkSj A2x + B2 y + C2 z + D2 = 0
osQ chp dk dks.k θ gSA
cosθ = 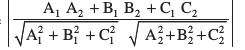
fVIi.kh
1. ;fn nksuksa lery ijLij yac gS rc θ = 90° vkSj bl rjg cosθ = 0. vr%
cos θ = A1A2 + B1B2 + C1C2 = 0
2. ;fn nksuksa lery lekarj gSa rks 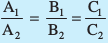
mnkgj.k 22 nks leryksa 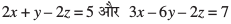 osQ chp dk dks.k lfn'k fof/ }kjk Kkr dhft,A
osQ chp dk dks.k lfn'k fof/ }kjk Kkr dhft,A
gy nks leryksa osQ chp dk dks.k ogh gS tks muosQ vfHkyacksa osQ chp dk dks.k gSA leryksa osQ fn, x, lehdj.kksa ls leryksa osQ lfn'k vfHkyac
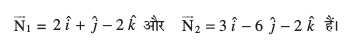
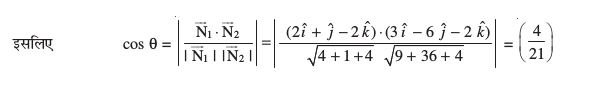
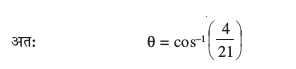
mnkgj.k 23 nks leryksa 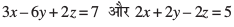 osQ chp dk dks.k Kkr dhft,A
osQ chp dk dks.k Kkr dhft,A
gy leryksa dh Kkr lehdj.kksa dh rqyuk lehdj.kksa

ls djus ij ge ikrs gSa fd% 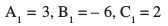
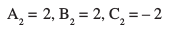
iqu% cos θ 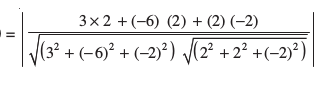
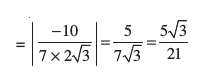
blfy, 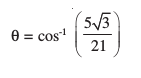
11.9 lery ls fn, x, ¯cnq dh nwjh (Distance of a point from a plane)
lfn'k :i (Vector Form)
,d ¯cnq P ftldk fLFkfr lfn'k 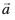 vkSj ,d lery π1 ftldk lehdj.k
vkSj ,d lery π1 ftldk lehdj.k 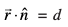 (vko`Qfr 11.19) ij fopkj dhft,A
(vko`Qfr 11.19) ij fopkj dhft,A
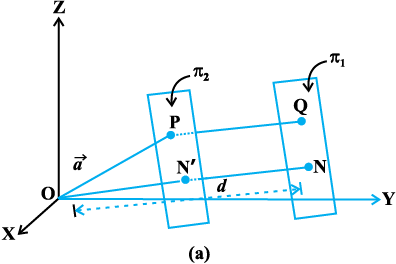
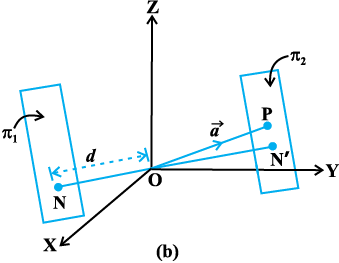
iqu% ¯cnq P ls lery π1 osQ lekarj lery π2 ij fopkj dhft,A lery π2 osQ vfHkyac bdkbZ lfn'k  gSA vr% bldk lehdj.k
gSA vr% bldk lehdj.k 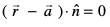 gSA
gSA
vFkkZr~ 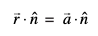
vr%] ewy ¯cnq ls bl lery dh nwjh ON′ 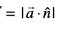 gSA blfy, P ls lery π1 ls nwjh (vko`Qfr 11.21 (a))
gSA blfy, P ls lery π1 ls nwjh (vko`Qfr 11.21 (a))
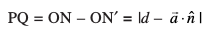
gS] tks ,d ¯cnq ls Kkr lery ij yac dh yackbZ gSA vko`Qfr 11.19 (b) osQ fy, ge blh izdkj dk ifj.kke LFkkfir dj ldrs gSaA
fVIi.kh
1. ;fn lery π2 dk lehdj.k 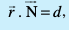 osQ :i dk gS] tgk¡
osQ :i dk gS] tgk¡ 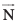 lery ij vfHkyac gS rks ykafcd nwjh
lery ij vfHkyac gS rks ykafcd nwjh 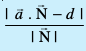 gSA
gSA
2. ewy ¯cnq O ls lery 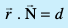 dh nwjh
dh nwjh 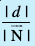 gS (D;ksafd
gS (D;ksafd 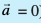 )A
)A
dkrhZ; :i (Cartesian Form)
eku yhft, fd P (x1, y1, z1) ,d fn;k ¯cnq gS ftldk fLFkfr lfn'k 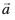 gS rFkk fn, lery dk dkrhZ; lehdj.k
gS rFkk fn, lery dk dkrhZ; lehdj.k
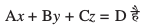
rc 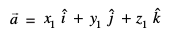
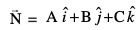
vr% (1) osQ }kjk P ls lery ij yac dh yackbZ
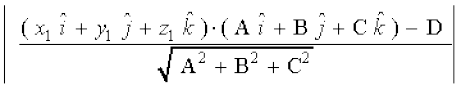
= 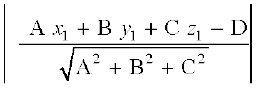
mnkgj.k 24 ¯cnq (2, 5, – 3) dh lery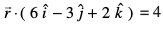 ls nwjh Kkr dhft,A
ls nwjh Kkr dhft,A
gy ;gk¡ 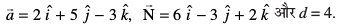
blfy, ¯cnq (2, 5, – 3) dh fn, lery ls nwjh gS%
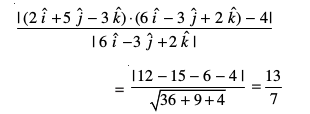
11.10 ,d js[kk vkSj ,d lery osQ chp dk dks.k (Angle between a line and a plane)
ifjHkk"kk 2 ,d js[kk vkSj ,d lery osQ chp dk dks.k] js[kk vkSj lery osQ vfHkyac osQ chp osQ dks.k dk dks.k (complementary angle) iwjd gksrk gS (vko`Qfr 11.20)A
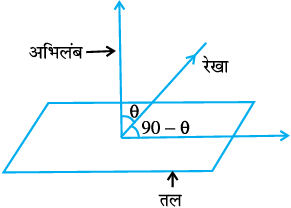
vko`Qfr 11-20
lfn'k :i (Vector Form)
eku yhft, fd js[kk dk lehdj.k 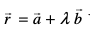 gS rFkk lery dk lehdj.k
gS rFkk lery dk lehdj.k 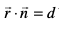 gSA rc js[kk vkSj lery osQ vfHkyac osQ chp dk dks.k θ, fuEufyf[kr lw=k }kjk O;Dr fd;k tk ldrk gSA
gSA rc js[kk vkSj lery osQ vfHkyac osQ chp dk dks.k θ, fuEufyf[kr lw=k }kjk O;Dr fd;k tk ldrk gSA
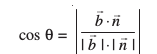
vkSj bl izdkj js[kk vkSj lery osQ chp dk dks.k φ, 90° – θ, }kjk iznÙk gS vFkkZr~
sin (90° – θ) = cos θ
vFkkZr~] s 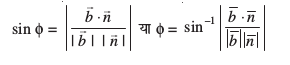
mnkgj.k 25 js[kk 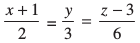 vkSj lery 10 x+2y – 11 z = 3 osQ chp dk dks.k Kkr dhft,A
vkSj lery 10 x+2y – 11 z = 3 osQ chp dk dks.k Kkr dhft,A
gy eku yhft, fd js[kk vksj lery osQ vfHkyac osQ chp dk dks.k θ gSA fn, x, js[kk rFkk lery osQ lehdj.kksa dks lfn'k :i esa O;Dr djus ij ge
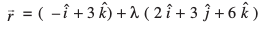
vkSj 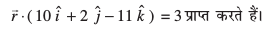
;gk¡ 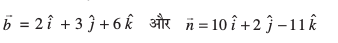
vr% 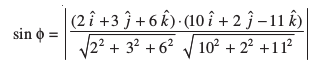
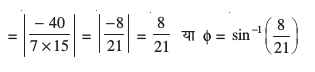
iz'ukoyh 11-3
1. fuEufyf[kr iz'uksa esa ls izR;sd esa lery osQ vfHkyac dh fno~Q&dkslkbu vkSj ewy ¯cnq ls nwjh Kkr dhft,%
(a) z = 2 (b) x + y + z = 1
(c) 2x + 3y-z = 5 (d) 5y + 8 = 0
2. ml lery dk lfn'k lehdj.k Kkr dhft,] tks ewy ¯cnq ls 7 ek=kd nwjh ij gS] vkSj lfn'k 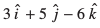 ij vfHkyac gSA
ij vfHkyac gSA
3. fuEufyf[kr leryksa dk dkrhZ; lehdj.k Kkr dhft,%
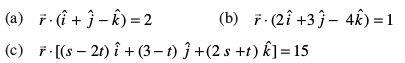
4. fuEufyf[kr fLFkfr;ksa esa] ewy ¯cnq ls [khaps x, yac osQ ikn osQ funsZ'kkad Kkr dhft,A
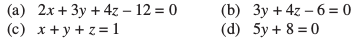
5. fuEufyf[kr izfrca/ksa osQ varxZr leryksa dk lfn'k ,oa dkrhZ; lehdj.k Kkr dhft, tks%
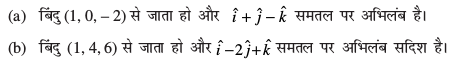
6. mu leryksa dk lehdj.k Kkr dhft, tks fuEufyf[kr rhu ¯cnqvksa ls xqtjrk gSA
(a) (1, 1, – 1), (6, 4, – 5), (– 4, – 2, 3)
(b) (1, 1, 0), (1, 2, 1), (– 2, 2, – 1)
7. lery 2x + y – z = 5 }kjk dkVs x, var% [kaMksa dks Kkr dhft,A
8. ml lery dk lehdj.k Kkr dhft, ftldk y&v{k ij var%[kaM 3 vkSj tks ry Z OX osQ lekarj gSA
9. ml lery dk lehdj.k Kkr dhft, tks leryksa 3x – y + 2z – 4 = 0 vkSj
x + y + z – 2 = 0 osQ izfrPNsnu rFkk ¯cnq (2, 2, 1) ls gksdj tkrk gSA
10. ml lery dk lfn'k lehdj.k Kkr dhft, tks leryksa 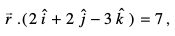
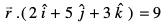 osQ izfrPNsnu js[kk vkSj (2, 1, 3) ls gksdj tkrk gSA
osQ izfrPNsnu js[kk vkSj (2, 1, 3) ls gksdj tkrk gSA
11. ryksa x + y + z = 1 vkSj 2x + 3y + 4z = 5 osQ izfrPNsnu js[kk ls gksdj tkus okys rFkk ry x – y + z = 0 ij yacor~ ry dk lehdj.k Kkr dhft,A
12. leryksa] ftuosQ lfn'k lehdj.k 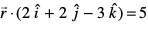 vkSj
vkSj 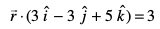
gSa] osQ chp dk dks.k Kkr dhft,A
13. fuEufyf[kr iz'uksa esa Kkr dhft, fd D;k fn, x, leryksa osQ ;qXe lekarj gS vFkok yacor~ gSa] vkSj ml fLFkfr esa] tc ;s u rks lekarj gS vkSj u gh yacor~~ rks muosQ chp dk dks.k Kkr dhft,A
(a) 7x + 5y + 6z + 30 = 0 vkSj 3x – y – 10z + 4 = 0
(b) 2x + y + 3z – 2 = 0 vkSj x – 2y + 5 = 0
(c) 2x – 2y + 4z + 5 = 0 vkSj 3x – 3y + 6z – 1 = 0
(d) 2x – y + 3z – 1 = 0 vkSj 2x – y + 3z + 3 = 0
(e) 4x + 8y + z – 8 = 0 vkSj y + z – 4 = 0
14. fuEufyf[kr iz'uksa esa izR;sd fn, x, ¯cnq ls fn, x, laxr leryksa dh nwjh Kkr dhft,A
¯cnq lery
(a) (0, 0, 0) 3x – 4y + 12 z = 3
(b) (3, – 2, 1) 2x – y + 2z + 3 = 0
(c) (2, 3, – 5) x + 2y – 2z = 9
(d) (– 6, 0, 0) 2x – 3y + 6z – 2 = 0
fofo/ mnkgj.k
mnkgj.k 26 ,d js[kk] ,d ?ku osQ fod.kks± osQ lkFk α, β, γ, δ, dks.k cukrh gS rks fl¼ dhft, fd
cos2 α + cos2 β + cos2 γ + cos2 δ = 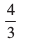
gy ,d ?ku] ,d ledksf.kd "kV~iQydh; gksrk gS ftldh yackbZ] pkSM+kbZ vkSj Å¡pkbZ leku gksrs gSaA
eku yhft, fd OADBEFCG ,d ?ku ftldh izR;sd Hkqtk a yackbZ dh gS (vko`Qfr 11.21)A
OE, AF, BG vkSj CD pkj fod.kZ gSaA
nks ¯cnqvksa O rFkk E dks feykus okyh js[kk OE vFkkZr~ fod.kZ OE osQ fno~Q&dkslkbu

vko`Qfr 11-21
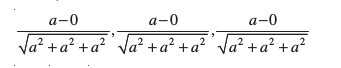
vFkkZr~ 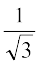 ,
, 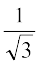 ,
, 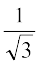
gSaA blh izdkj AF, BG vkSj CD dh fno~Q&dkslkbu Øe'k%
– 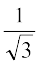 ,
, 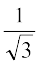 ,
, 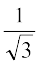 ;
; 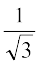 , –
, – 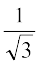 ,
, 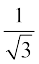 vkSj
vkSj 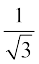 ,
, 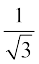 , –
, – 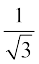 , gSaA
, gSaA
eku yhft, nh xbZ js[kk tks OE, AF, BG, vkSj CD, osQ lkFk Øe'k% α, β, γ, vkSj δ dks.k cukrh gS] dh fno~Q&dkslkbu l, m, n gSaA
rc cosα = 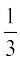 (l + m+ n); cos β =
(l + m+ n); cos β = 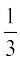 (– l + m + n)
(– l + m + n)
cosγ = 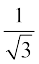 (l – m + n); cos δ =
(l – m + n); cos δ = 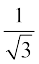 (l + m – n)
(l + m – n)
oxZ djosQ tksM+us ij ge ikrs gSa fd
cos2 α + cos2 β + cos2 γ + cos2 δ
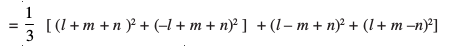
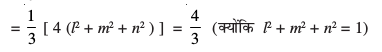
mnkgj.k 27 ml ry dk lehdj.k Kkr dhft, ftlesa ¯cnq (1, – 1, 2) varfoZ"V gS vkSj tks leryksa 2x + 3y-2z=5vkSj x+2y – 3z = 8 esa ls izR;sd ij yac gSA
gy fn, x, ¯cnq dks varfoZ"V djus okys lery dk lehdj.k
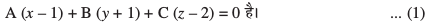
leryksa 2x + 3y-2z=5 vkSj x+2y – 3z = 8, osQ lkFk (1) }kjk iznÙk lery ij yac gksus osQ izfrca/ dk iz;ksx djus ij ge ikrs gSa fd
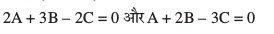
bu lehdj.kksa dks gy djus ij ge ikrs gSa fd A = – 5C vkSj B = 4C
vr% vHkh"V lehdj.k gS%
– 5C (x – 1) + 4 C (y + 1) + C(z – 2) = 0
vFkkZr~ 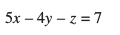
mnkgj.k 28 ¯cnq P(6, 5, 9) ls ¯cnqvksa A (3, – 1, 2), B (5, 2, 4) vkSj C(– 1, – 1, 6) }kjk
fu/kZfjr lery dh nwjh Kkr dhft,A
gy eku yhft, fd lery esa rhu ¯cnq A, B, rFkk C gSaA ¯cnq P ls lery ij yac dk ikn D gSA gesa vHkh"V nwjh PD Kkr djuh gS tgk¡ PD ,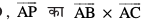 ij iz{ksi gSA
ij iz{ksi gSA
vr%
iqu% 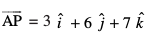
vkSj 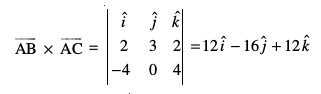

vr% 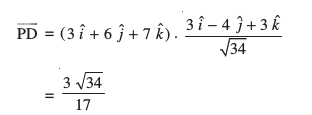
fodYir% ¯cnq A, B vkSj C ls xq”kjus okys lery dk lehdj.k Kkr dhft, vkSj rc ¯cnq P dh lery ls nwjh Kkr dhft,A
mnkgj.k 29 n'kkZb, fd js[kk,¡
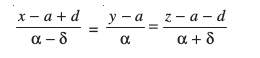
vkSj 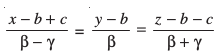 lg&ryh; gSaA
lg&ryh; gSaA
gy ;gk¡ Kkr gS fd
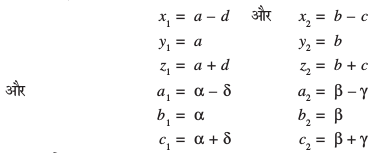
vc lkjf.kd
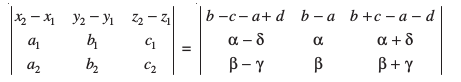
ij fopkj dhft,A
rhljs LraHk dks igys LraHk esa tksM+us ij ge ikrs gSaA
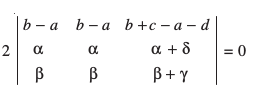
D;ksafd izFke vkSj f}rh; LraHk leku gSaA vr% nksuksa js[kk,¡ lg&ryh; gSaA
mnkgj.k 30 ml ¯cnq osQ funsZ'kkad Kkr dhft, tgk¡ ¯cnqvksa A(3, 4, 1) vkSj B(5, 1, 6) dks feykus okyh js[kk XY-ry dks dkVrh gSaA
gy ¯cnqvksa A vkSj B (ls tkus okyh js[kk dk lfn'k lehdj.k%
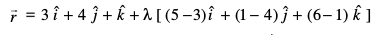
vFkkZr~ eq 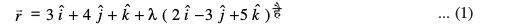
eku yhft, P og ¯cnq gS tgk¡ js[kk AB, XY-ry dks izfrPNsn djrh gSA rc ¯cnq P dk fLFkfr lfn'k 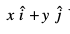 osQ :i esa gSA
osQ :i esa gSA
;g ¯cnq vo'; gh lehdj.k (1) dks larq"V djrk gSA (D;ksa?)
vFkkZr~ 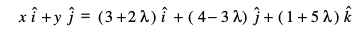
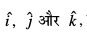 osQ xq.kkadksa dh rqyuk djus ij ge ikrs gSa
osQ xq.kkadksa dh rqyuk djus ij ge ikrs gSa
x = 3 + 2 λ
y = 4 – 3 λ
0 = 1 + 5 λ
mijksDr lehdj.kksa dks gy djus ij ge ikrs gSa fd
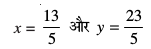
vr% vHkh"V ¯cnq osQ funsZ'kkad 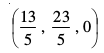 gSaA
gSaA
vè;k; 11 ij fofo/ iz'ukoyh
1. fn[kkb, fd ewy ¯cnq ls (2] 1] 1) feykus okyh js[kk] ¯cnqvksa (3] 5 &1) vkSj
(4] 3] &1) ls fu/kZfjr js[kk ij yac gSA
2. ;fn nks ijLij yac js[kkvksa dh fno~Q&dkslkbu l1, m1, n1 vkSj l2, m2, n2 gkas rks fn[kkb, fd bu nksuksa ij yac js[kk dh fno~Q&dkslkbu
m1 n2 – m2 n1, n1 l2 – n2 l1, l1 m2 – l2 – m1 gSaA
3. mu js[kkvksa osQ eè; dks.k Kkr dhft,] ftuosQ fno~Q&vuqikr a, b, c vkSj b – c, c – a, a-b gSaA
4. x-v{k osQ lekarj rFkk ewy&¯cnq ls tkus okyh js[kk dk lehdj.k Kkr dhft,A
5. ;fn ¯cnqvksa A, B, C, vkSj D osQ funsZ'kkad Øe'k% (1, 2, 3), (4, 5, 7), (– 4, 3, – 6) vkSj (2, 9, 2) gSa rks ABvkSj CD js[kkvksa osQ chp dk dks.k Kkr dhft,A
6. ;fn js[kk,¡ 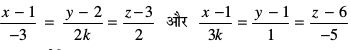 ijLij yac gksa rks k dk eku Kkr dhft,A
ijLij yac gksa rks k dk eku Kkr dhft,A
7. ¯cnq (1, 2, 3) ls tkus okyh rFkk ry 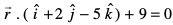 ij yacor~ js[kk dk
ij yacor~ js[kk dk
lfn'k lehdj.k Kkr dhft,A
8. ¯cnq (a, b, c) ls tkus okys rFkk ry 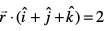 osQ lekarj ry dk lehdj.k Kkr dhft,A
osQ lekarj ry dk lehdj.k Kkr dhft,A
9.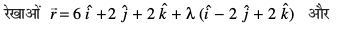
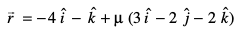 osQ chp dh U;wure nwjh Kkr dhft,A
osQ chp dh U;wure nwjh Kkr dhft,A
10. ml ¯cnq osQ funsZ'kkad Kkr dhft, tgk¡ ¯cnqvksa (5, 1, 6) vkSj (3, 4, 1) dks feykus okyh js[kk YZ-ry dks dkVrh gSA
11. ml ¯cnq osQ funsZ'kkad Kkr dhft, tgk¡ ¯cnqvksa (5, 1, 6) vkSj (3, 4, 1) dks feykus okyh js[kk ZX-ry dks dkVrh gSA
12. ml ¯cnq osQ funsZ'kkad Kkr dhft, tgk¡ ¯cnqvksa (3, – 4, – 5) vkSj (2, – 3, 1) ls xq”kjus okyh js[kk] lery 2x + y + z=7osQ ikj tkrh gSA
13. ¯cnq (– 1, 3, 2) ls tkus okys rFkk leryksa x+2y + 3z=5vkSj 3x + 3y + z = 0 esa ls izR;sd ij yac lery dk lehdj.k Kkr dhft,A
14. ;fn ¯cnq (1, 1, p) vkSj (– 3, 0, 1) lery 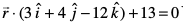 ls leku nwjh ij fLFkr gksa] rks p dk eku Kkr dhft,A
ls leku nwjh ij fLFkr gksa] rks p dk eku Kkr dhft,A
15. leryksa 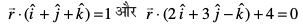 osQ izfrPNsnu js[kk ls tkus okys rFkk x-v{k osQ lekarj ry dk lehdj.k Kkr dhft,A
osQ izfrPNsnu js[kk ls tkus okys rFkk x-v{k osQ lekarj ry dk lehdj.k Kkr dhft,A
16. ;fn O ewy ¯cnq rFkk ¯cnq P osQ funsZ'kkad (1, 2, – 3), gSa rks ¯cnq P ls tkus okys rFkk OP osQ yacor~ ry dk lehdj.k Kkr dhft,A
17. leryksa 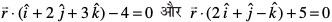 osQ izfrPNsnu js[kk dks varfoZ"V djus okys rFkk ry
osQ izfrPNsnu js[kk dks varfoZ"V djus okys rFkk ry 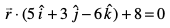 osQ yacor~ ry dk lehdj.k Kkr dhft,A
osQ yacor~ ry dk lehdj.k Kkr dhft,A
18. ¯cnq (– 1, – 5, – 10) ls js[kk 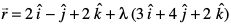 vkSj lery
vkSj lery 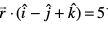 osQ izfrPNsnu ¯cnq osQ eè; dh nwjh Kkr dhft,A
osQ izfrPNsnu ¯cnq osQ eè; dh nwjh Kkr dhft,A
19. ¯cnq (1, 2, 3) ls tkus okyh rFkk leryksa 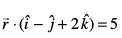 vkSj
vkSj 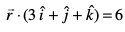 osQ lekarj js[kk dk lfn'k lehdj.k Kkr dhft,A
osQ lekarj js[kk dk lfn'k lehdj.k Kkr dhft,A
20. ¯cnq (1, 2, – 4) ls tkus okyh vkSj nksuksa js[kkvksa 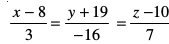 vkSj
vkSj
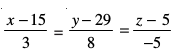 ij yac js[kk dk lfn'k lehdj.k Kkr dhft,A
ij yac js[kk dk lfn'k lehdj.k Kkr dhft,A
21. ;fn ,d lery osQ var%[kaM a, b, c gSa vkSj bldh ewy ¯cnq ls nwjh p bdkbZ gSa rks fl¼ dhft, fd 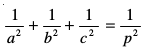
iz'uksa 22 vkSj 23 esa lgh mÙkj dk pquko dhft,A
22. 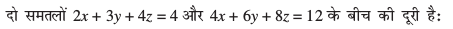
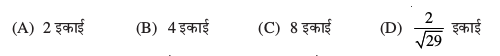
23. 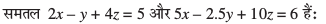
(A) ijLij yac (B) lekarj
lkjka'k
- ,d js[kk dh fno~Q&dkslkbu js[kk }kjk funsZ'kka{kksa dh /u fn'kk osQ lkFk cuk, dks.kksa dh dkslkbu gksrh gSA
- ;fn ,d js[kk dh fno~Q&dkslkbu l, m, n gSa rks l2 + m2 + n2 = 1
- nks ¯cnqvksa P (x1, y1, z1) vkSj Q (x2, y2, z2) dks feykus okyh js[kk dh fno~Q&dkslkbu
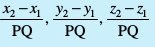 gSa
gSa
tgk¡ aPQ = 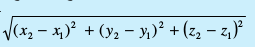
- ,d js[kk dk fno~Q&vuqikr os la[;k,¡ gSa tks js[kk dh fno~Q&dkslkbu osQ lekuqikrh gksrh gSaA
- ;fn ,d js[kk dh fno~Q&dkslkbu l, m, n vkSj fno~Q&vuqikr a, b, c gSa rks
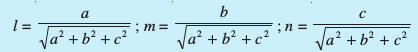
- fo"keryh; js[kk,¡ varfj{k dh os js[kk,¡ tks u rks lekarj gSa vkSj u gh izfrPNsnh gSaA ;g js[kk,¡ fofHkUu ryksa esa gksrh gSaA
- fo"keryh; js[kkvksa osQ chp dk dks.k og dks.k gS tks ,d fdlh ¯cnq (ojh;rk ewy ¯cnq dh) ls fo"keryh; js[kkvksa esa ls izR;sd osQ lekarj [khaph xbZ nks izfrPNsnh js[kkvksa osQ chp esa gSA
- ;fn l1, m1, n1 vkSj l2, m2, n2 fno~Q&dkslkbu okyh nks js[kkvksa osQ chp U;wudks.k θ gS rc
cos θ = |l1l2 + m1m2 + n1n2|
- ;fn a1, b1, c1 vkSj a2, b2, c2 fno~Q&vuqikrksa okyh nks js[kkvksa osQ chp dk U;wu dks.k θ gS rc
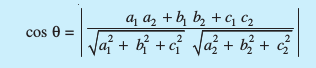
- ,d Kkr ¯cnq ftldh fLFkfr lfn'k
![ablu]() gS ls xq”kjus okyh vkSj lfn'k
gS ls xq”kjus okyh vkSj lfn'k ![b blu]() osQ lekarj js[kk dk lfn'k lehdj.k
osQ lekarj js[kk dk lfn'k lehdj.k ![eq239]() gSA
gSA - ¯cnq (x1, y1, z1) ls tkus okyh js[kk ftldh fno~Q&dkslkbu l, m, n gSa] dk lehdj.k
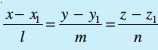 gSA
gSA
- nks ¯cnqvksa ftuosQ fLFkfr lfn'k
![ablu]() vkSj
vkSj ![b blu]() gS ls tkus okyh js[kk osQ lehdj.k dk lfn'k lehdj.k
gS ls tkus okyh js[kk osQ lehdj.k dk lfn'k lehdj.k ![eq240]() gSA
gSA - nks ¯cnqvksa (x1, y1, z1) vkSj (x2, y2, z2) ls tkus okyh js[kk dk dkrhZ; lehdj.k
![]() gSaA
gSaA - ;fn nks js[kkvksa
![eq241]() , osQ chp dk U;wudks.k θ gS rks
, osQ chp dk U;wudks.k θ gS rks ![eq242]()
- ;fn nks js[kkvksa
![eq243]() vkSj
vkSj
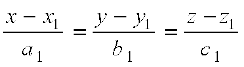 osQ chp dk dks.k θ gS rc
osQ chp dk dks.k θ gS rc
cos θ = |l1l2 + m1m2 + n1n2|.
- nks fo"keryh; js[kkvksa osQ chp dh U;wure nwjh og js[kk[kaM gS tks nksuksa js[kkvksa ij yac gSaA
- nks js[kkvksa
![eq244]() osQ chp U;wure nwjh
osQ chp U;wure nwjh ![eq245]() gSA
gSA - nks js[kkvksa
![eq246]() osQ chp U;wure nwjh
osQ chp U;wure nwjh
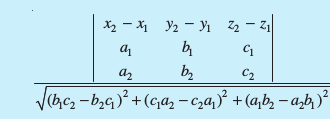 gSA
gSA- nks lekarj js[kkvksa
![eq248]()
![eq249]() gSA
gSA - ,d lery] ftldh ewy ¯cnq ls nwjh d rFkk lery ij ewy ¯cnq ls vfHkyac bdkbZ lfn'k
![nblu]() gS] dk lfn'k :i esa lehdj.k
gS] dk lfn'k :i esa lehdj.k ![eq250]() gSA
gSA - ,d lery] ftldh ewy ¯cnq ls nwjh d rFkk lery osQ vfHkyac dh fno~Q&dkslkbu
l, m, n gS] dk lehdj.k lx + my + nz = d gSA
- ,d ¯cnq ftldk fLFkfr lfn'k
![ablu]() ls tkus okyk vkSj lfn'k
ls tkus okyk vkSj lfn'k ![nb2]() ij yac lery dk lehdj.k
ij yac lery dk lehdj.k ![eq251]() gSA
gSA - ,d fn, x, ¯cnq (x1, y1, z1) tkus okys vkSj ,d nh xbZ js[kk ftlosQ fno~Q&vuqikr A, B, C gS] ij yac lery dk lehdj.k A (x – x1) + B (y – y1) + C (z – z1 ) = 0 gSA
- rhu vlajs[k ¯cnqvksa (x1, y1, z1), (x2, y2, z2) vkSj (x3, y3, z3) ls tkus okys lery dk lehdj.k gS%
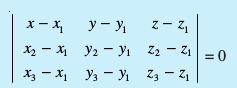
- rhu ¯cnqvksa ftuosQ fLFkfr lfn'k
![eq253]() dks varfoZ"V djus okys lery dk lfn'k lehdj.k
dks varfoZ"V djus okys lery dk lfn'k lehdj.k ![eq254]()
- ,d lery tks funsZ'kka{kksa dks (a, 0, 0), (0, b, 0) vkSj (0, 0, c) ij dkVrk gS] dk lehdj.k
![eq255]() gSA
gSA - leryksa
![eq256]() osQ izfrPNsnu ls xqtjus okys lery dk lfn'k lehdj.k
osQ izfrPNsnu ls xqtjus okys lery dk lfn'k lehdj.k ![eq257]() gS, tgk¡ λ ,d izkpy gSA
gS, tgk¡ λ ,d izkpy gSA - leryksa
A1 x + B1 y + C1 z + D1 = 0
vkSj A2 x + B2 y + C2 z + D2 = 0
osQ izfrPNsnu ls xqtjus okys lery dk lehdj.k
(A1 x + B1 y + C1 z + D1) + λ(A2 x + B2 y + C2 z + D2) = 0 gSA
- nks js[kk,a
![eq258]() lg&ryh; gSa ;fn
lg&ryh; gSa ;fn ![eq259]()
- ;fn mijksDr js[kk,a fcanqvksa A( x1, y1, z1) rFkk B(x2, y2, z2) ls xq”kjrh gS rc leryh; gSa ;fn
![eq260]()
- nks ry ftlosQ lfn'k :i
![eq261]() gSa rFkk buosQ chp dk U;wu dks.k
gSa rFkk buosQ chp dk U;wu dks.k ![eq262]()
-
![eq263]()
- ryksa A1x + B1y + C1z + D1 = 0 rFkk
θ = cos-1 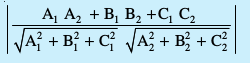
- lfn'k :i esa] ,d ¯cnq ftldk fLFkfr lfn'k gS] ls ry ls nwjh gSA
- ,d ¯cnq (x1, y1, z1) dh ry Ax + By + Cz + D = 0 ls nwjh
![eq265]() gSA
gSA
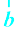
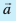
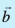
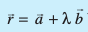 gSA
gSA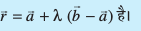 gSA
gSA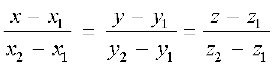
 ,
,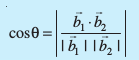
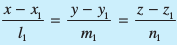
 osQ chp U;wure nwjh
osQ chp U;wure nwjh 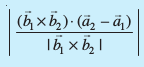
 osQ chp U;wure nwjh
osQ chp U;wure nwjh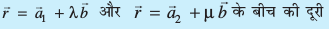
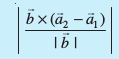
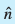
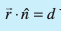 gSA
gSA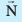
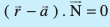 gSA
gSA
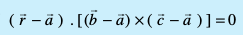
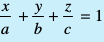 gSA
gSA osQ izfrPNsnu ls xqtjus okys lery dk lfn'k lehdj.k
osQ izfrPNsnu ls xqtjus okys lery dk lfn'k lehdj.k 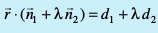 gS
gS
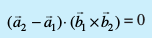
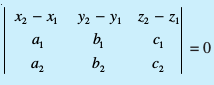
 gSa rFkk buosQ chp dk U;wu dks.k
gSa rFkk buosQ chp dk U;wu dks.k 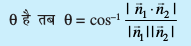
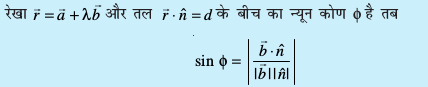
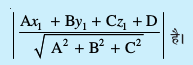 gSA
gSA