Table of Contents
vè;k;12
jSf[kd izksxzkeu Linear Programming
The mathematical experience of the student is incomplete if he never had the opportunity to solve a problem invented by himself. — G POLYA
12.1 Hkwfedk (Introduction)
fiNyh d{kkvksa esa ge jSf[kd lehdj.kksa vkSj fnu izfr fnu dh leL;kvksa esa muosQ vuqiz;ksx ij fopkj&foe'kZ dj pqosQ gSaA d{kk XI esa geus nks pj jkf'k;ksa okys jSf[kd vlfedkvksa vkSj jSf[kd vlfedkvksa osQ fudk;ksa osQ vkys[kh; fu:i.k ls gy fudkyus osQ fo"k; esa vè;;u dj pqosQ gSaA xf.kr esa dbZ vuqiz;ksxksa esa [email protected] osQ fudk; lfEefyr gSaA bl vè;k; esa ge jSf[kd [email protected] osQ fudk;ksa dk uhps nh xbZ oqQN okLrfod thou dh leL;kvksa dks gy djus esa mi;ksx djsaxsA
,d iQuhZpj O;kikjh nks oLrqvksa tSls es”k vkSj oqQ£l;ksa dk O;olk; djrk gSA fuos'k osQ fy, mlosQ ikl Rs 50]000 vkSj j[kus osQ fy, osQoy 60 oLrqvksasa osQ fy, LFkku gSA ,d es”k ij Rs 2500 vkSj ,d oqQlhZ ij Rs 500 dh ykxr vkrh gSA og vuqeku yxkrk gS fd ,d es”k dks cspdj og Rs 250 vkSj ,d oqQlhZ dks cspus ls Rs 75 dk ykHk dek ldrk gSA eku yhft, fd og lHkh oLrqvksasa dks csp ldrk gS ftudks fd og [kjhnrk gS rc og tkuuk pkgrk gS fd fdruh es”kksa ,oa oqQflZ;ksa dks [kjhnuk pkfg, rkfd miyC/ fuos'k jkf'k ij mldk ldy ykHk vf/dre gksA

L. Kantorovich
bl izdkj dh leL;kvksa ftuesa lkekU; izdkj dh leL;kvksa esa ykHk dk vf/drehdj.k vkSj ykxr dk U;wurehdj.k [kkstus dk iz;kl fd;k tkrk gS] b"Vredkjh leL;k,¡ dgykrh gSaA vr% b"Vredkjh leL;k esa vf/dre ykHk] U;wure ykxr ;k lalk/uksa dk U;wure mi;ksx lfEefyr gSA
jSf[kd izksxzkeu leL;k,¡ ,d fo'ks"k ysfdu ,d egÙoiw.kZ izdkj dh b"Vredkjh leL;k gS vkSj mijksDr mfYyf[kr b"Vredkjh leL;k Hkh ,d jSf[kd izksxzkeu leL;k gSA m|ksx] okf.kT;]
izca/u foKku vkfn esa foLr`r lqlaxrrk osQ dkj.k jSf[kd izksxzkeu leL;k,¡ vR;f/d egÙo dh gSaA
bl vè;k; esa] ge oqQN jSf[kd izksxzkeu leL;k,¡ vkSj mudk vkys[kh fof/ }kjk gy fudkyus dk vè;;u djsaxsA ;|fi bl izdkj leL;kvksa dk gy fudkyus osQ fy, vU; fof/;k¡ Hkh gSaA
12.2 jSf[kd izksxzkeu leL;k vkSj mldk xf.krh; lw=khdj.k (Linear Programming Problem and its Mathematical Formulation)
ge viuk fopkj foe'kZ mijksDr mnkgj.k osQ lkFk izkjaHk djrs gSa tks fd nks pj jkf'k;ksa okyh leL;k osQ xf.krh; lw=khdj.k vFkok xf.krh; izfr:i dk ekxZn'kZu djsxkA bl mnkgj.k esa geus è;kuiwoZd ns[kk fd
(i) O;kikjh viuh /u jkf'k dks es”kksa ;k oqQflZ;ksa ;k nksuksa osQ la;kstuksa esa fuos'k dj ldrk gSA blosQ vfrfjDr og fuos'k osQ fofHkUu ;kstukRed fof/;ksa ls fofHkUu ykHk dek losQxkA
(ii) oqQN vf/d egÙoiw.kZ fLFkfr;k¡ ;k O;ojks/ksa dk Hkh lekos'k gS tSls mldk fuos'k vf/dre Rs 50]000 rd lhfer gS rFkk mlosQ ikl vf/dre 60 oLrqvksasa dks j[kus osQ fy, LFkku miyC/ gSA
eku yhft, fd og dksbZ oqQlhZ ugha [kjhnrk osQoy es”kksa osQ [kjhnus dk fu'p; djrk gS] blfy, og 50,000 ÷ 2500, ;k 20 es”kksa dks [kjhn ldrk gSA bl fLFkfr esa mldk ldy ykHk
Rs (250 × 20) ;k Rs 5000 gksxkA
eku yhft, fd og dksbZ es”k u [kjhndj osQoy oqQ£l;k¡ gh [kjhnus dk p;u djrk gSA rc og viuh miyC/ Rs 50]000 dh jkf'k esa 50,000 ÷ 500, vFkkZr~ 100 oqQ£l;k¡ gh [kjhn ldrk gSA ijarq og osQoy 60 uxksa dks gh j[k ldrk gSA vr% og 60 oqQ£l;k¡ ek=k [kjhnus osQ fy, ckè; gksxkA ftlls mls ldy ykHk Rs 60 × 75 vFkkZr~ Rs 4500 gh gksxkA
,slh vkSj Hkh cgqr lkjh laHkkouk,¡ gSaA mnkgj.k osQ fy, og 10 es”kksa vkSj 50 oqQ£l;k¡ [kjhnus dk p;u dj ldrk gS] D;ksafd mlosQ ikl 60 oLrqvksasa dks j[kus dk LFkku miyC/ gSA bl fLFkfr esa mldk ldy ykHk Rs (10 × 250 + 50 × 75), vFkkZr~ Rs 6250 bR;kfnA
vr% ge Kkr djrs gSa fd iQuhZpj O;kikjh fofHkUu p;u fof/;ksa osQ }kjk viuh /u jkf'k dk fuos'k dj ldrk gS vkSj fofHkUu fuos'k ;kstukvksa dks viukdj fofHkUu ykHk dek losQxkA
vc leL;k ;g gS fd mls viuh /u jkf'k dks vf/dre ykHk izkIr djus osQ fy, fdl izdkj fuos'k djuk pkfg,\ bl iz'u dk mÙkj nsus osQ fy, gesa leL;k dk xf.krh; lw=khdj.k djus dk iz;kl djuk pkfg,A
12.2.1 leL;k dk xf.krh; lw=khdj.k (Mathematical Formulation of the Problem)
eku yhft, fd es”kksa dh la[;k x vkSj oqQflZ;ksa dh la[;k y gS ftUgsa iQuhZpj O;kikjh [kjhnrk gSA Li"Vr% x vkSj y ½.ksrj gSa] vFkkZr~

D;kasfd es”kksa vkSj oqQflZ;ksa dh la[;k ½.kkRed ugha gks ldrh gSA
O;kikjh (O;olk;h) ij vf/dre /u jkf'k (;gk¡ ;g Rs 50]000 gS) dk fuos'k djus dk O;ojks/ gS vkSj O;olk;h osQ ikl osQoy vf/dre oLrqvksasa (;gk¡ ;g 60 gS) dks j[kus osQ fy, LFkku dk Hkh O;ojks/ gSA
xf.krh; :i esa O;Dr djus ij
2500x + 500y ≤ 50,000 (fuos'k O;ojks/ )
;k 5x + y ≤ 100 ... (3)
vkSj x + y ≤ 60 (laxzg.k O;ojks/) ... (4)
O;olk;h bl izdkj ls fuos'k djuk pkgrk gS mldk ykHk Z (ekuk) vf/dre gks vkSj ftls x vkSj y osQ iQyu osQ :i esa fuEufyf[kr izdkj ls O;Dr fd;k tk ldrk gS%
Z = 250x + 75y (mís'kh; iQyu dgykrk gS)
iznÙk leL;k dk vc xf.krh; :i esa ifjofrZr gks tkrh gS%
Z = 250x + 75y dk vf/drehdj.k dhft,
tgk¡ O;ojks/ fuEufyf[kr gS
5x + y ≤ 100
x + y ≤ 60
x ≥ 0, y ≥ 0
blfy, gesa jSf[kd iQyu Z dk vf/drehdj.k djuk gS tcfd ½.ksrj pjksa okyh jSf[kd vlfedkvksa osQ :i oqQN fo'ks"k fLFkfr;ksa osQ O;ojks/ O;Dr fd, x, gSaA oqQN vU; leL;k,¡ Hkh gSa ftuesa jSf[kd iQyu dk U;wurehdj.k fd;k tkrk gS tcfd ½.ksrj pj okyh jSf[kd vlfedkvksa osQ :i esa oqQN fo'ks"k fLFkfr;ksa osQ O;ojks/ O;Dr fd, tkrs gSA ,slh leL;kvksa dks jSf[kd izksxzkeu leL;k dgrs gSaA
vr% ,d jSf[kd izksxzkeu leL;k og leL;k gS tks fd x vkSj y tSls oqQN vusd pjksa osQ ,d jSf[kd iQyu Z (tks fd mís'; iQyu dgykrk gS) dk b"Vre lqlaxr@vuqowQyre lqlaxr eku (vf/dre ;k U;wure eku) Kkr djus ls lacaf/r gSA izfrca/ ;g gS fd pj ½.ksrj iw.kk±d gSa vkSj ;s jSf[kd vlfedkvkas osQ leqPp; jSf[kd O;ojks/ksa dks larq"V djrs gSaA jSf[kd in ls rkRi;Z gS fd leL;k esa lHkh xf.krh; laca/ jSf[kd gSa tcfd izksxzkeu ls rkRi;Z gS fd fo'ks"k izksxzke ;k fo'ks"k fØ;k ;kstuk Kkr djukA
vkxs c<+us ls iwoZ ge vc oqQN inksa (ftudk iz;ksx Åij gks pqdk gS) dks vkSipkfjd :i ls ifjHkkf"kr djsaxs ftudk fd iz;ksx ge jSf[kd izksxzke leL;kvksa esa djsaxs%
mís'; iQyu jSf[kd iQyu Z = ax + by, tcfd a, b vpj gS ftudk vf/drehdj.k ;k U;wurehdj.k gksuk gS ,d jSf[kd mís'; iQyu dgykrk gSA
mijksDr mnkgj.k esa Z = 250x + 75y ,d jSf[kd mís'; iQyu gSA pj x vkSj y fu.kkZ;d pj dgykrs gSaA
O;ojks/ ,d jSf[kd izksxzkeu leL;k osQ pjksa ij jSf[kd vlfedkvksa ;k lehdj.k ;k izfrca/ O;ojks/ dgykrs gSaA izfrca/ x ≥ 0, y ≥ 0 ½.ksrj O;ojks/ dgykrs gSaA mijksDr mnkgj.k esa (1) ls (4) rd vlfedkvksa dk leqPp; O;ojks/ dgykrs gSaA
b"Vre lqlaxr leL;k,¡ fuf'pr O;ojks/ksa osQ v/hu vlfedkvksa osQ leqPp; }kjk fu/kZfjr leL;k tks pjksa (;Fkk nks pj x vkSj y ) esa jSf[kd iQyu dks vf/dre ;k U;wure djs] b"Vre lqlaxr leL;k dgykrh gSA jSf[kd izksxzkeu leL;k,¡ ,d fof'k"V izdkj dh b"Vre lqlaxr leL;k gSA lqlaxr leL;k O;kikjh }kjk es”kksa rFkk oqQflZ;ksa dh [kjhn esa iz;qDr ,d b"Vre lqlaxr leL;k rFkk jSf[kd izksxzkeu dh leL;k dk ,d mnkgj.k gSA
vc ge foospuk djsaxs fd ,d jSf[kd izksxzkeu leL;k dks fdl izdkj gy fd;k tkrk gSA bl vè;k; esa ge osQoy vkys[kh; fof/ ls gh lacaf/r jgsaxsA
12.2.2 jSf[kd izksxzkeu leL;kvksa dks gy djus dh vkys[kh; fof/ (Graphical Method of Solving Linear Programming Problems)
d{kk XI, esa ge lh[k pqosQ gS fd fdl izdkj nks pjksa x vkSj y ls lacaf/r jSf[kd vlehdj.k fudk;ksa dk vkjs[k [khaprs gSa rFkk vkjs[kh; fof/ }kjk gy Kkr djrs gSaA vc gesa vuqPNsn 12-2 esa foospu dh gqbZ es”kksa vkSj oqQflZ;ksa esa fuos'k dh leL;k dk mYys[k djsaxsA vc ge bl leL;k dks vkjs[k }kjk gy djsaxsA vc gesa jSf[kd vlehdj.kksa osQ :i iznÙk O;ojks/ksa dk vkjs[k [khapsa%

vko`Qfr 12.1
5x + y ≤ 100 ... (1)
x + y ≤ 60 ... (2)
x ≥ 0 ... (3)
y ≥ 0 ... (4)
bl fudk; dk vkjs[k (Nk;kafdr {ks=k) esa vlehdj.kksa (1) ls (4) rd osQ }kjk fu;r lHkh v/Zryksa osQ mHk;fu"B ¯cnqvksa ls fufeZr gSaA bl {ks=k esa izR;sd ¯cnq O;kikjh (O;olk;h) dks es”kksa vkSj oqQflZ;ksa esa fuos'k djus osQ fy, lqlaxr fodYi izLrqr djrk gSA blfy, ;g {ks=k leL;k dk lqlaxr {ks=k dgykrk gS (vko`Qfr 12-1)A bl {ks=k dk izR;sd ¯cnq leL;k dk lqlaxr gy dgykrk gSA
vr% ge fuEu dks ifjHkkf"kr djrs gSa%
lqlaxr {ks=k iznÙk leL;k osQ fy, ,d jSf[kd izksxzkeu leL;k osQ ½.ksrj O;ojks/ x, y ≥ 0 lfgr lHkh O;ojks/ksa }kjk fu;r mHk;fu"B {ks=k lqlaxr {ks=k (;k gy {ks=k) dgykrk gS vko`Qfr 12-1 esa {ks=k OABC (Nk;kafdr) leL;k osQ fy, lqlaxr {ks=k gSA lqlaxr {ks=k osQ vfrfjDr tks {ks=k gS mlss vlqlaxr {ks=k dgrs gSaA
lqlaxr gy lewg lqlaxr {ks=k osQ var% Hkkx rFkk lhek osQ lHkh ¯cnq O;ojks/ksa osQ lqlaxr gy dgykrs gSaA vko`Qfr 12-1 esa lqlaxr {ks=k OABC osQ var% Hkkx rFkk lhek osQ lHkh ¯cnq leL;k osQ lqlaxr gy iznf'kZr dgrs gSaA mnkgj.k osQ fy, ¯cnq (10] 50) leL;k dk ,d lqlaxr gy gS vkSj blh izdkj ¯cnq (0] 60)] (20] 0) bR;kfn Hkh gy gSaA
lqlaxr gy osQ ckgj dk dksbZ Hkh ¯cnq vlqlaxr gy dgykrk gSa mnkgj.k osQ fy, ¯cnq
(25] 40) leL;k dk vlqlaxr gy gSA
b"Vre@vuqowQyre (lqlaxr) gy% lqlaxr {ks=k esa dksbZ ¯cnq tks mís'; iQyu dk b"Vre eku (vf/dre ;k U;wure) ns] ,d b"Vre gy dgykrk gSA
vc ge ns[krs gSa fd lqlaxr {ks=k OABC esa izR;sd ¯cnq (1) ls (4) rd esa iznÙk lHkh O;ojks/ksa dks larq"V djrk gS vkSj ,sls vuar ¯cnq gSaA ;g Li"V ugha gS fd ge mís'; iQyu
Z = 250x + 75y osQ vf/dre eku okys ¯cnq dks fdl izdkj Kkr djus dk iz;kl djsaA bl fLFkfr dks gy djus osQ fy, ge fuEu izes;ksa dk mi;ksx djsaxs tks fd jSf[kd izksxzkeu leL;kvksa dks gy djus esa ewy fl¼kar (vk/kjHkwr) gSA bu izes;ksa dh miifr bl iqLrd osQ fo"k;&oLrq ls ckgj gSA
izes; 1 ekuk fd ,d jSf[kd izksxzkeu leL;k osQ fy, R lqlaxr {ks=k* (mÙky cgqHkqt) gS vkSj ekuk fd Z = ax + by mís'; iQyu gSA tc Z dk ,d b"Vre eku (vf/dre ;k U;wure) gks tgk¡ O;ojks/kas ls lacaf/r pj x vkSj y jSf[kd vlehdj.kksa }kjk O;Dr gks rc ;g b"Vre eku lqlaxr {ks=k osQ dksus ('kh"kZ) ij vofLFkr gksus pkfg,A
izes; 2 ekuk fd ,d jSf[kd izksxzkeu leL;k osQ fy, R lqlaxr {ks=k gS rFkk Z = ax + by mís'; iQyu gSA ;fn R ifjc¼ {ks=k gks rc mís'; iQyu Z, R esa nksuksa vf/dre vkSj U;wure eku j[krk gS vkSj buesa ls izR;sd R osQ dksuh; (corner) ¯cnq ('kh"kZ) ij fLFkr gksrk gSA
fVIi.kh ;fn R vifjc¼ gS rc mís'; iQyu dk vf/dre ;k U;wure eku dk vfLrRo ugha Hkh gks ldrk gSA fiQj Hkh ;fn ;g fo|eku gS rks R osQ dksuh; ¯cnq ij gksuk pkfg,] (izes; 1 osQ vuqlkj)
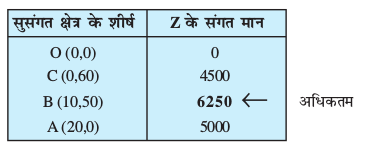
mijksDr mnkgj.k esa ifjc¼ (lqlaxr) {ks=k osQ dksuh; ¯cnq O, A, B vkSj C gSa vkSj ¯cnqvksa osQ funsZ'kkad Kkr djuk ljy gS ;Fkk (0, 0), (20, 0), (10, 50) vkSj (0, 60) Øe'k% dksuh; ¯cnq gSaA vc gesa bu ¯cnqvksa ij, Z dk eku Kkr djuk gSA
og bl izdkj gS%
ge fujh{k.k djrs gSa fd O;olk;h dks fuos'k ;kstuk (10] 50) vFkkZr~ 10 es”kksa vkSj 50 oqQflZ;ksa osQ [kjhnus esa vf/dre ykHk gksxkA

bl fof/ esa fuEu inksa dk lekfo"V gSa%
1. jSf[kd izksxzkeu leL;k dk lqlaxr {ks=k Kkr dhft, vkSj mlosQ dksuh; ¯cnqvksa ('kh"kZ) dks ;k rks fujh{k.k ls vFkok nks js[kkvksa osQ izfrPNsn ¯cnq dks nks js[kkvksa dh lehdj.kksa dks gy djosQ ml ¯cnq dks Kkr dhft,A
2. mís'; iQyu Z = ax + by dk eku izR;sd dksuh; ¯cnq ij Kkr dhft,A ekuk fd M vkSj m, Øe'k% bu ¯cnqvksa ij vf/dre rFkk U;wure eku iznf'kZr djrs gSaA
3. (i) tc lqlaxr {ks=k ifjc¼ gS] M vkSj m, Z osQ vf/dre vkSj U;wure eku gaSA
(ii) ,slh fLFkfr esa tc lqlaxr {ks=k vifjc¼ gks rks ge fuEufyf[kr fof/ dk mi;ksx djrs gSaA
4. (a) M dks Z dk vf/dre eku ysrs gSa ;fn ax + by > M }kjk izkIr v/Z&ry dk dksbZ ¯cnq lqlaxr {ks=k esa u iM+s vU;Fkk Z dksbZ vf/dre eku ugha gSA
(b) blh izdkj, m, dks Z dk U;wure eku ysrs gaS ;fn ax + by < m }kjk izkIr [kqys v/Zry vkSj lqlaxr {ks=k esa dksbZ ¯cnq mHk;fu"B ugha gSA vU;Fkk Z dk dksbZ U;wure eku ugha gSA
* lqlaxr {ks=k dk dksuh; ¯cnq {ks=k dk gh dksbZ ¯cnq gksrk gS tks nks js[kkvksa dk izfrPNsnu ¯cnq gSA
** ,d jSf[kd lehdj.k fudk; dk lqlaxr {ks=k ifjc¼ dgk tkrk gS ;fn ;g ,d o`r osQ varxZr ifjc¼ fd;k tk ldrk gS vU;Fkk bls vifjc¼ dgrs gSaA vifjc¼ ls rkRi;Z gS fd lqlaxr {ks=k fdlh Hkh fn'kk esa vlhfer :i ls c<+k;k tk ldrk gSA
ge vc oqQN mnkgj.kksa osQ }kjk dksuh; fof/ osQ inksa dks Li"V djsaxs%
mnkgj.k 1 vkys[k }kjk fuEu jSf[kd izksxzkeu leL;k dks gy dhft,%

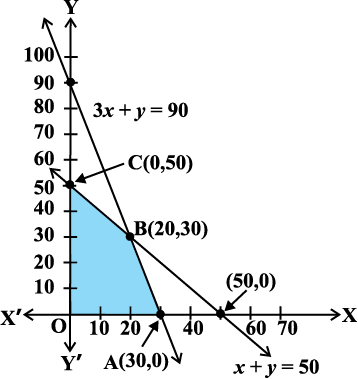

fuEu O;ojks/ksa osQ varxZr
x + y ≤ 50 ... (1)
3x + y ≤ 90 ... (2)
x ≥ 0, y ≥ 0 ... (3)
Z 4x + y dk vf/dre eku Kkr dhft,%
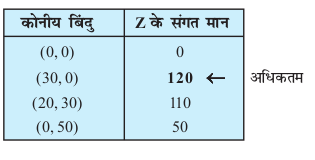
dksuh; ¯cnqvksa O, A, B vkSj C osQ funsZ'kkad Øe'k% (0, 0), (30, 0), (20, 30) vkSj (0, 50) gSaA
vc izR;sd dksuh; ¯cnq ij Z dk eku Kkr djrs gSaA
vr% ¯cnq (30] 0) ij Z dk vf/dre eku 120 gSA
mnkgj.k 2 vkys[kh; fof/ }kjk fuEu jSf[kd izksxzkeu leL;k dks gy dhft,A
fuEu O;ojks/ksa osQ varxZr
x + 2y ≥ 10 ... (1)
3x + 4y ≤ 24 ... (2)
x ≥ 0, y ≥ 0 ... (3)
Z = 200 x + 500 y dk U;wure eku Kkr dhft,

vko`Qfr 12.3
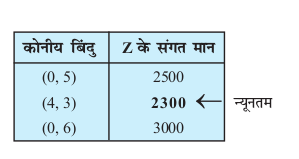
gy vko`Qfr 12-3 esa Nk;kafdr {ks=k] (1) ls (3) osQ O;ojks/ksa osQ fudk; }kjk fu/kZfjr lqlaxr {ks=k ABC gS tks ifjc¼ gSA dksuh; ¯cnqvksa A, B vkSj C osQ funsZ'kkad Øe'k% (0, 5), (4, 3) vkSj (0, 6) gSaA ge bu ¯cnqvksa ij Z = 200x + 500y dk eku Kkr djrs gSa
vr% ¯cnq (4] 3) ij Z dk U;wure eku Rs 2300 izkIr gksrk gSA
mnkgj.k 3 vkys[kh; fof/ ls fuEu leL;k dks gy dhft,%
fuEu O;ojks/ksa osQ varxZr
x + 3y ≤ 60 ... (1)
x + y ≥ 10 ... (2)
x ≤ y ... (3)
x ≥ 0, y ≥ 0 ... (4)

vko`Qfr 12.4

Z = 3x =+ 9y dk U;wure vkSj vf/dre eku Kkr dhft,A
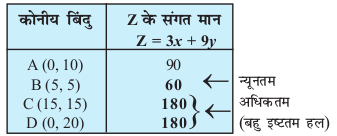
gy lcls igys ge (1) ls (4) rd dh jSf[kd vlfedkvksa osQ fudk; osQ lqlaxr {ks=k dk vkys[k [khaprs gSaA lqlaxr {ks=k ABCD dks vko`Qfr 12-4 esa fn[kk;k x;k gSA {ks=k ifjc¼ gSA dksuh; ¯cnqvksa A, B, C vkSj D osQ funsZ'kkad Øe'k% (0, 10), (5, 5), (15, 15) vkSj (0 20) gSaA vc ge Z osQ U;wure vkSj vf/dre eku Kkr djus osQ fy, dksuh; ¯cnq fof/ dk mi;ksx djrs gSaA
lkj.kh ls ge lqlaxr {ks=k ¯cnq B (5] 5) ij Z dk U;wure eku 60 izkIr djrs gSaA
Z dk vf/dre eku lqlaxr {ks=k osQ nks dksuh; ¯cnqvksa izR;sd C (15, 15) vkSj D (0, 20) ij 120 izkIr gksrk gSA
fVIi.kh fujh{k.k dhft, fd mijksDr mnkgj.k esa] leL;k dksuh; ¯cnqvksa C vkSj D, ij leku b"Vre gy j[krh gS] vFkkZr~ nksuksa ¯cnq ogh vf/dre eku 180 mRiUu djrs gSaA ,slh fLFkfr;ksa esa nks dksuh; ¯cnqvksa dks feykus okys js[kk[kaM CD ij izR;sd ¯cnq rFkk C vkSj D Hkh ,d gh vf/dre eku nsrs gSaA ogh ml fLFkfr esa Hkh lR; gS ;fn nks ¯cnq ogh U;wure eku mRiUu djrs gSaA
mnkgj.k 4 vkys[kh; fof/ }kjk mís'; iQyu Z = –50x + 20y dk U;wure eku fuEufyf[kr O;ojks/ksa osQ varxZr Kkr dhft,%
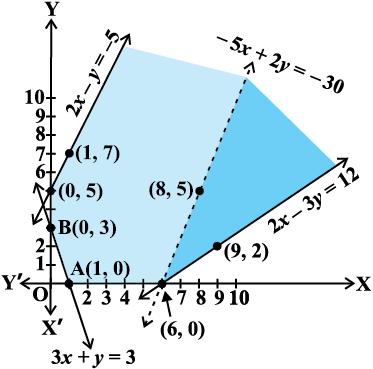
gy lcls igys ge (1) ls (4) rd osQ vlehdj.k fudk; }kjk lqlaxr {ks=k dk vkys[k [khaprs gSA vko`Qfr 12-5 esa lqlaxr {ks=k (Nk;kafdr) fn[kk;k x;k gSA fujh{k.k dhft, fd lqlaxr {ks=k vifjc¼ gSA
vc ge dksuh; ¯cnqvksa ij Z dk eku Hkh Kkr djsaxs%
vko`Qfr 12. 5

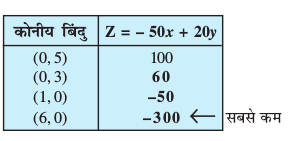
2x – y ≥ – 5 ... (1)
3x + y ≥ 3 ... (2)
2x – 3y ≤ 12 ... (3)
x ≥ 0, y ≥ 0 ... (4)
bl lkj.kh ls ge Kkr djrs gSa fd dksuh; ¯cnq (6] 0) ij Z dk lcls de eku &300 gSA D;k ge dg ldrs gSa fd Z dk U;wure eku &300 gS\ è;ku nhft, fd ;fn {ks=k ifjc¼ gksrk rks ;g Z dk lcls de eku (izes; 2 ls) gksrkA ysfdu ge ;gk¡ ns[krs gSa fd lqlaxr {ks=k vifjc¼ gSA blfy, &300] Z dk U;wure eku gks Hkh ldrk gS vkSj ugha HkhA bl leL;k dk fu"d"kZ Kkr djus osQ fy, ge fuEufyf[kr vlehdj.k dk vkys[k [khaprs gSa%
– 50x + 20y < – 300
vFkkZr~ – 5x + 2y < – 30
vkSj tk¡p dhft, fd vkys[k }kjk izkIr [kqys v/Zry o lqlaxr {ks=k esa mHk;fu"B ¯cnq gSa ;k ugha gSA ;fn blesa mHk;fu"B ¯cnq gSa] rc Z dk U;wure eku &300 ugha gksxkA vU;Fkk] Z dk U;wure eku&300 gksxkA
tSlk fd vko`Qfr 12-5 esa fn[kk;k x;k gSA blfy,] Z = –50 x + 20 y, dk iznÙk O;ojks/ksa osQ ifjizs{; eas U;wure eku ugha gSA
mijksDr mnkgj.k es D;k vki tk¡p dj ldrs gSa fd Z = – 50 x + 20 y, (0] 5) ij
vf/dre eku 100 j[krk gS\ blosQ fy,] tk¡p dhft, fd D;k – 50 x + 20 y > 100 dk vkjs[k lqlaxr {ks=k osQ lkFk mHk;fu"B ¯cnq j[krk gSA
mnkgj.k 5 fuEufyf[kr O;ojks/ksa osQ varxZr] Z = 3x + 2y dk U;wurehdj.k dhft,%
x + y ≥ 8 ... (1)
3x + 5y ≤ 15 ... (2)
x ≥ 0, y ≥ 0 ... (3)
gy vlfedkvksa (1) ls (3) dk vkys[k [khafp, (vko`Qfr 12-6)A D;k dksbZ lqlaxr {ks=k gS\ ;g ,slk D;ksa gS\
vko`Qfr 12-6 ls vki Kkr dj ldrs gS fd ,slk dksbZ ¯cnq ugha gS tks lHkh O;ojks/ksa dks ,d lkFk larq"V dj losQA vr%] leL;k dk lqlaxr gy ugha gSA
fVIi.kh mnkgj.kksa ls ftudk foospu ge vc rd dj pqosQ gSa ftlosQ vk/kj ij ge oqQN jSf[kd izksxzkeu leL;kvksa dh lkekU; fo'ks"krkvksa dk mYys[k djrs gSaA
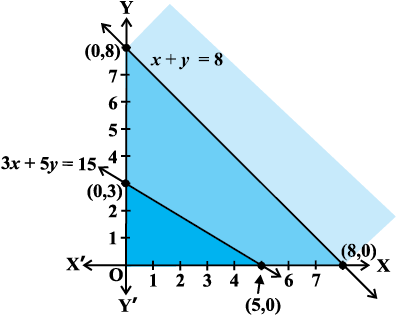
vko`Qfr 12.6
(1) lqlaxr {ks=k lnSo mÙky cgqHkqt gksrk gSA
(2) mís'; iQyu dk vf/dre (;k U;wure) gy lqlaxr {ks=k osQ 'kh"kZ ij (dksus ij) fLFkr gksrk gSA ;fn mís'; iQyu osQ nks dksuh; ¯cnq ('kh"kZ) ,d gh vf/dre (;k U;wure) eku iznku djrs gaS rks bu ¯cnqvksa osQ feykus okyh js[kk[kaM dk izR;sd ¯cnq Hkh leku vf/dre (;k U;wure) eku nsxkA
iz'ukoyh 12-1
xzki+Qh; fof/ ls fuEu jSf[kd izksxzkeu leL;kvksa dks gy dhft,%
1. fuEu vojks/ksa osQ varxZr Z = 3x + 4y dk vf/drehdj.k dhft,%
x + y ≤ 4, x ≥ 0, y ≥ 0
2. fuEu vojks/ksa osQ varxZr Z = – 3x + 4 y dk U;wurehdj.k dhft,%
x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0
3. fuEu vojks/ksa osQ varxZr Z = 5x + 3y dk vf/drehdj.k dhft,%
3 x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
4. fuEu vojks/ksa osQ varxZr Z = 3x + 5y dk U;wurehdj.k dhft,_
x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0
5. fuEu vojks/ksa osQ varxZr Z = 3x + 2y dk U;wurehdj.k dhft,%
x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0
6. fuEu vojks/ksa osQ varxZr Z = x + 2y dk U;wurehdj.k dhft,%
2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0
fn[kkb, fd Z dk U;wure eku nks ¯cnqvksa ls vf/d ¯cnqvksa ij ?kfVr gksrk gSA
7. fuEu vojks/ksa osQ varxZr Z = 5x + 10 y dk U;wurehdj.k rFkk vf/drehdj.k dhft,% x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0
8. fuEu vojks/ksa osQ varxZr Z = x + 2y dk U;wurehdj.k rFkk vf/drehdj.k dhft,%
x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0
9. fuEu vojks/ksa osQ varxZr Z = – x + 2y dk vf/drehdj.k dhft,%
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0
10. fuEu vojks/ksa osQ varxZr Z = x + y dk vf/drehdj.k dhft,%
x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0
12.3 jSf[kd izksxzkeu leL;kvksa osQ fHkUu izdkj (Different Types of Linear Programming Problems)
oqQN egÙoiw.kZ jSf[kd izksxzkeu leL;k,¡ uhps lwwphc¼ gaS%
1. mRiknu laca/h leL;k,¡ bl izdkj dh leL;kvksa esa ge Kkr djrs gSa fd fofHkUu mRiknuksa osQ fdrus ux cukus esa ,d fuf'pr tu'kfDr] e'khu osQ ?kaVs] izR;sd ux osQ fuekZ.k esa O;;] Je osQ ?kaVs] eky HkaMkj.k xksnke esa izR;sd mRiknu dks j[kus osQ fy, LFkku vkfn dks n`f"V esa j[krs gq, vf/dre ykHk dek;k tk losQA
2. vkgkj laca/h leL;k,¡ bl izdkj dh leL;kvksa esa ge Kkr djrs gSa fd fofHkUu izdkj osQ ?kVd@iks"kd rRo vkgkj esa fdruh ek=kk esa iz;ksx fd, tk,¡ ftlls mlesa lHkh iks"kd rRoksa dh U;wure vko';d ek=kk de ls de ykxr ij izkIr gksA
3. ifjogu laca/h leL;k,¡ bl izdkj dh leL;kvksa esa ge ifjogu iz.kkyh dks r; djrs gSa ftlls la;a=kksa @ dkj[kkus ls fofHkUu LFkkuksa ij fLFkr fofHkUu cktkjksa esa mRiknuksa dks Hkstus esa ifjogu O;; U;wure gksA
vc gesa bl izdkj dh oqQN jSf[kd izksxzkeu leL;kvksa dks gy djuk pkfg,
mnkgj.k 6 (vkgkj laca/h leL;k): ,d vkgkj foKkuh nks izdkj osQ HkksT;ksa dks bl izdkj feykuk pkgrk gS fd feJ.k esa foVkfeu A dk ?kVd de ls de 8 ek=kd vkSj foVkfeu C dk ?kVd de ls de 10 ek=kd gksA HkksT; I esa 2 ek=kd foVkfeu A izfr kg vkSj 1 ek=kd foVkfeu C izfr kg gSA tcfd HkksT; II esa 1 ek=kd foVkfeu A izfr kg vkSj 2 ek=kd foVkfeu C izfr kg gSA fn;k gS fd izfr kg HkksT; I dks [kjhnus esa Rs 50 vkSj izfr kg HkksT; II dks [kjhnus esa Rs 70 yxrs gSaA bl izdkj osQ HkksT; feJ.k dk U;wure ewY; Kkr dhft,A
gy ekuk fd feJ.k esa HkksT; I dk x kg vkSj HkksT; II dk y kg gSA Li"Vr% x ≥ 0 y ≥ 0. ge iznÙk vk¡dM+ksa ls fuEu lkj.kh cukrs gSaA
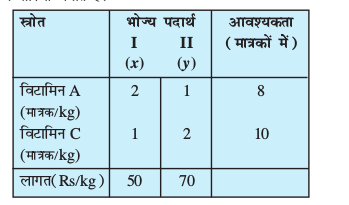
pw¡fd feJ.k esa foVkfeu A dh de ls de 8 ek=kd vkSj foVkfeu C osQ 10 ek=kd gksus pkfg,] vr% fuEufyf[kr O;ojks/ izkIr gksrs gSa
2x + y ≥ 8
x + 2y ≥ 10
HkksT; I osQ x kg vkSj HkksT; II osQ y kg [kjhnus dk oqQy ewY; Z gS tgk¡
Z = 50x + 70y
vr% leL;k dk xf.krh; lw=khdj.k fuEufyf[kr gS%
fuEu O;ojks/ksa osQ varxZr
2x + y ≥ 8 ... (1)
x + 2y ≥ 10 ... (2)
x, y ≥ 0 ... (3)
Z = 50x + 70y dk U;wurehdj.k dhft,
vlehdj.kksa (1) ls (3) rd osQ vkys[kksa }kjk fu/kZfjr lqlaxr {ks=k dks vko`Qfr 12-7 esa fn[kk;k x;k gSA
vko`Qfr 12.7
;gk¡ ge ns[krs gaS fd lqlaxr {ks=k vifjc¼ gSA
gesa dksuh; ¯cnqvksa A(0,8), B(2,4) vkSj C(10,0) ij Z dk eku Kkr djuk gSA
lkj.kh esa] ¯cnq (2] 4) ij Z dk lcls de eku 380 gS] D;k ge dg ldrs gSa fd Z dk U;wure eku 380 gS (D;ksa\) ;kn dhft, fd lqlaxr {ks=k vifjc¼ gSA blfy, gesa fuEufyf[kr vlehdj.k dk vkys[k [khapuk iM+sxkA
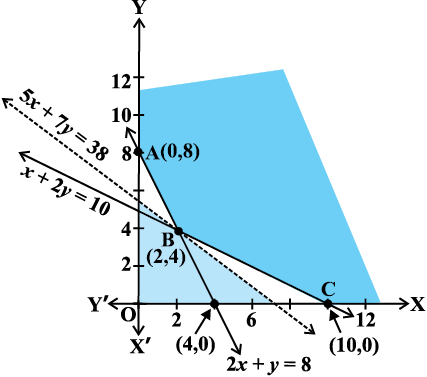
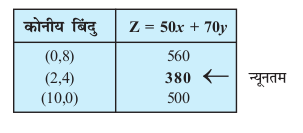
50x + 70y < 380
vFkkZr~ 5x + 7y < 38
tk¡p djus osQ fy, fd D;k vlehdj.k }kjk fu/kZfjr ifj.kkeh [kqyk v/Zry] lqlaxr {ks=k osQ lkFk dksbZ mHk;fu"B ¯cnq j[krk gSA vko`Qfr 12-7 esa ge ns[krs gSa fd ;gk¡ dksbZ mHk;fu"B ¯cnq ugha gSA
vr%] ¯cnq (2] 4) ij Z dk izkIr U;wure eku 380 gSA blfy, vkgkj foKkuh dh b"Vre feJ.k ;kstuk HkksT; ‘I’ dh 2 kg vkSj HkksT; ‘II’ osQ 4 kg osQ feJ.k cukus dh gks ldrh gS vkSj bl ;kstuk osQ varxZr feJ.k dk U;wure ewY; Rs 380 gksxkA
mnkgj.k 7 (vkcaVu leL;k) fdlkuksa dh ,d lgdkjh lfefr osQ ikl nks i+Qlyksa X vkSj Y dks mxkus osQ fy, 50 gsDVs;j Hkwfe gSA iQlyksa X vkSj Y ls izfr gsDVs;j ykHk dk Øe'k% Rs 10,500 vkSj Rs 9,000 dk vuqeku yxk;k x;k gSA iQlyksa X vkSj Y osQ fy, vir`.k fu;a=k.k osQ fy, 'kkd&uk'kh nzo dk Øe'k% 20 fyVj rFkk 10 fyVj izfr gsDVs;j iz;ksx fd;k tkrk gSA blosQ vfrfjDr iz;qDr Hkwfe ls tqM+h ukfy;ksa ls lac¼ rkykc ij fuHkZj tho/kfj;ksa ,oa eNfy;ksa dh thou&lqj{kk gsrq 'kkduk'kh dh ek=kk 800 fyVj ls vf/d u gksA izR;sd i+Qly osQ fy, fdruh Hkwfe dk vkcaVu gksuk pkfg, rkfd lfefr osQ ldy ykHk dk vf/drehdj.k fd;k tk losQ\
gy ekuk fd X iQly osQ fy, x gsDVs;j Hkwfe rFkk Y iQly osQ y gsDVs;j Hkwfe dk vkcaVu gksrk gSA Li"Vr% x ≥ 0, y ≥ 0
X iQly ij izfr gsDVs;j ykHk = Rs 10500
Y iQly ij izfr gsDVs;j ykHk = Rs 9000
blfy, oqQy ykHk = Rs (10500x + 9000y)
leL;k dk xf.krh; lw=khdj.k fuEu gS%
fuEu vojks/ksa osQ varxZr
x + y ≤ 50 (Hkwfe laca/h O;ojks/) ... (1)
20x + 10y ≤ 800 ('kkduk'kh dk mi;ksx laca/h O;ojks/)
vFkkZr~ 2x + y ≤ 80 ... (2)
x ≥ 0, y ≥ 0 ... (3)
Z = 10500 x + 9000 y dk vf/drehdj.k dhft,
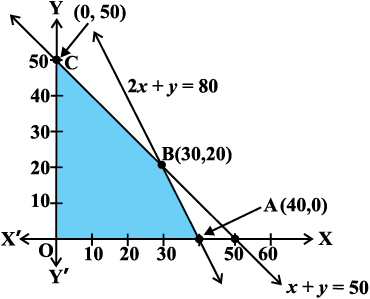
vc ge (1) ls (3) rd vlehdj.k fudk; dk vkys[k [khprs gSaA vko`Qfr 12-8 esa lqlaxr {ks=k OABC dks Nk;kafdr fn[kk;k x;k gSA fujh{k.k dhft, fd lqlaxr {ks=k ifjc¼ gSA
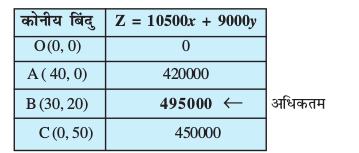
dksuh; ¯cnqvksa osQ funsZ'kkad Øe'k% (0, 0), (40, 0), (30, 20) vkSj (0, 50) gaSA mís'; iQyu
Z = 10500 x + 9000y dk eku bu 'kh"kks± ij fudkyuk pkfg, rkfd ml 'kh"kZ dks Kkr fd;k tk losQ ftl ij vf/dre ykHk gksrk gSA
vr% lfefr dks X iQly osQ fy, 30 gsDV;j vkSj Y iQly osQ 20 gsDV;j dk vkcaVu gksxk rkfd vf/dre ykHk Rs 4,95,000 dk gks losQA
mnkgj.k 8 mRiknu laca/h leL;k (Manufacturing Problem) ,d fuekZ.kdrkZ daiuh ,d mRikn osQ nks uewus (izfreku) A vkSj B cukrh gSA uewuk A osQ izR;sd ux cukus osQ fy, 9 Je ?kaVs vkSj 1 ?kaVk ikWfy'k djus osQ fy, yxrk gS tcfd uewuk B osQ izR;sd ux osQ cukus esa 12 Je ?kaVs rFkk ikWfy'k djus esa 3 Je ?kVksa dh vko';drk gksrh gSA cukus rFkk ikWfy'k djus osQ fy, miyC/ vf/dre Je ?kaVs Øe'k% 180 rFkk 30 gSaA oaQiuh uewuk A osQ izR;sd ux ij Rs 8000 rFkk uewuk B osQ izR;sd ux ij Rs12000 dk ykHk dekrh gSA uewuk A vkSj uewuk B osQ fdrus uxksa dk vf/dre ykHk dekus osQ fy, izfr lIrkg fuekZ.k djuk pkfg,\ izfr lIrkg vf/dre ykHk D;k gS\
gy eku yhft, fd uewuk A osQ uxksa dh la[;k x gS rFkk uewuk B osQ uxksa dh la[;k y gSA
blfy, oqQy ykHk = (Rs 8000 x + 12000 y)
vr% Z = 8000 x + 12000 y
vc gekjs ikl iznÙk leL;k dk xf.krh; lw=khdj.k fuEufyf[kr gS%
fuEu O;ojks/ksa osQ varxZr
9x + 12y ≤ 180
vFkkZr~ 3x + 4y ≤ 60 (x<+us dk O;ojks/) ... (1)
x + 3y ≤ 30 (ikWfy'k dk O;ojks/) ... (2)
x ≥ 0, y ≥ 0 (½.ksrj O;ojks/) ... (3)
Z = 8000 x + 12000 y dk vf/drehdj.k dhft,A
jSf[kd vlehdj.k (1) ls (3) }kjk fu/kZfjr lqlaxr {ks=k OABC (Nk;kafdr)
vko`Qfr 12-9 esa fn[kk;k x;k gSA è;ku nhft, fd lqlaxr {ks=k ifjc¼ gSA
izR;sd dksuh; ¯cnq ij mís'; iQyu Z dk eku dh x.kuk dh xbZ gS tSlk fd fuEu lkj.kh esa fn[kk;k x;k gS%
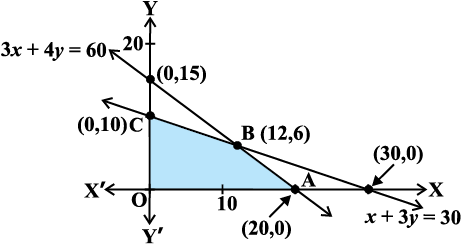
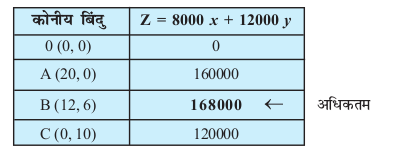
ge 'kh"kZ B (12, 6) ij Z dk vf/dre eku Rs 1,68,000 ikrs gSaA vr% oaQiuh dks uewuk A osQ 12 ux rFkk uewuk B osQ 6 uxksa osQ mRiknu ij vf/dre ykHk dekus osQ fy, djuk pkfg, vkSj vf/dre ykHk Rs 1,68,000 gksxkA
iz'ukoyh 12-2
1. js'kek nks izdkj osQ HkksT; P vkSj Q dks bl izdkj feykuk pkgrh gS fd feJ.k esa foVkfeu vo;oksa esa 8 ek=kd foVkfeu A rFkk 11 ek=kd foVkfeu B gksaA HkksT; P dh ykxr Rs 60@kg vkSj HkksT; Q dh ykxr Rs 80@kg gSA HkksT; P esa 3 ek=kd@kg foVkfeu A vkSj 5 ek=kd@kg foVkfeu B gS tcfd HkksT; Q esa 4 ek=kd@kg foVkfeu A vkSj 2 ek=kd@kg foVkfeu gSA feJ.k dh U;wure ykxr Kkr dhft,A
2. ,d izdkj osQ osQd dks 200 g vkVk rFkk 25 g olk (fat)dh vko';drk gksrh gS rFkk nwljh izdkj osQ osQd osQ fy, 100 g vkVk rFkk 50 g olk dh vko';drk gksrh gSA osQdksa dh vf/dre la[;k crkvks tks 5 fdyks vkVs rFkk 1 fdyks olk ls cu ldrs gSa] ;g eku fy;k x;k gS fd osQdksa dks cukus osQ fy, vU; inkFkks± dh deh ugha jgsxhA
3. ,d dkj[kkus esa Vsful osQ jSosQV rFkk fØosQV osQ cYys curs gSaA ,d Vsful jSosQV cukus osQ fy, 1-5 ?kaVk ;kaf=kd le; rFkk 3 ?kaVs f'kYidkj dk le; yxrk gSA ,d fØosQV cYys dks rS;kj djus esa 3 ?kaVs ;kaf=kd le; rFkk 1 ?kaVk f'kYidkj dk le; yxrk gSA ,d fnu esa dkj[kkus esa fofHkUu ;a=kksa ij miyC/ ;kaf=kd le; osQ 42 ?kaVs vkSj f'kYidkj le; osQ 24 ?kaVs ls vf/d ugha gSaA
(i) jSosQVksa vkSj cYyksa dks fdruh la[;k esa cuk;k tk, rkfd dkj[kkuk iwjh {kerk ls dk;Z djs\
(ii) ;fn jSosQV vkSj cYys ij ykHk Øe'k% Rs 20 rFkk Rs 10 gksa rks dkj[kkus dk
vf/dre ykHk Kkr dhft, ;fn dkj[kkuk iwjh {kerk ls dk;Z djsA
4. ,d fuekZ.kdrkZ uV vkSj cksYV dk fuekZ.k djrk gSA ,d iSosQV uVksa osQ fuekZ.k esa e'khu A ij ,d ?kaVk vkSj e'khu B ij 3 ?kaVs dke djuk iM+rk gS] tcfd ,d iSosQV cksYV osQ fuekZ.k esa 3 ?kaVs e'khu A ij vkSj 1 ?kaVk e'khu B ij dke djuk iM+rk gSA og uVksa ls
Rs 17-50 izfr iSosQV vkSj cksYVksa ij Rs 7-00 izfr iSosQV ykHk dekrk gSA ;fn izfrfnu e'khuksa dk vf/dre mi;ksx 12 ?kaVs fd;k tk, rks izR;sd (uV vkSj cksYV) osQ fdrus iSosQV mRikfnr fd, tk,¡ rkfd vf/dre ykHk dek;k tk losQA
5. ,d dkj[kkus esa nks izdkj osQ isap A vkSj B curs gSaA izR;sd osQ fuekZ.k esa nks e'khuksa osQ iz;ksx dh vko';drk gksrh gS] ftlesa ,d Lopkfyr vkSj nwljh gLrpkfyr gSA ,d iSosQV isap A osQ fuekZ.k esa 4 feuV Lopkfyr vkSj 6 feuV gLrpkfyr e'khu] rFkk ,d iSosQV isap B osQ fuekZ.k esa 6 feuV Lopkfyr vkSj 3 feuV gLrpkfyr e'khu dk dk;Z gksrk gSA izR;sd e'khu fdlh Hkh fnu osQ fy, vf/dre 4 ?kaVs dke osQ fy, miyC/ gSA fuekZrk isap A osQ izR;sd iSosQV ij Rs 7 vkSj isap B osQ izR;sd iSosQV ij Rs 10 dk ykHk dekrk gSA ;g ekurs gq, fd dkj[kkus esa fufeZr lHkh isapksa osQ iSosQV fcd tkrs gSa] Kkr dhft, fd izfrfnu fdrus iSosQV fofHkUu isapksa osQ cuk, tk,¡ ftlls ykHk vf/dre gks rFkk vf/dre ykHk Kkr dhft,A
6. ,d oqQVhj m|ksx fuekZrk iSMsLVy ySai vkSj ydM+h osQ 'ksM cukrk gSA izR;sd osQ fuekZ.k esa ,d jxM+us @ dkVus vkSj ,d Lizs;j dh vko';drk iM+rh gSA ,d ySai osQ fuekZ.k esa 2 ?kaVs jxM+us@dkVus vkSj 3 ?kaVs Lizs;j dh vko';drk gksrh gS] tcfd ,d 'ksM osQ fuekZ.k esa 1 ?kaVk jxM+us@dkVus vkSj 2 ?kaVs Lizs;j dh vko';drk gksrh gSA Lizs;j dh e'khu izfrfnu
vf/dre 20 ?kaVs vkSj jxM+us@dkVus dh e'khu izfrfnu vf/dre 12 ?kaVs osQ fy, miyC/ gSA ,d ySai dh fcØh ij Rs 5 vkSj ,d 'ksM dh fcØh ij Rs 3 dk ykHk gksrk gSA ;g ekurs gq, fd lHkh fufeZr ySai vkSj 'ksM fcd tkrs gS] rks crkb, og fuekZ.k dh izfrfnu oSQlh ;kstuk cuk, fd ykHk vf/dre gks\
7. ,d oaQiuh IykbZoqM osQ vuwBs Le`fr fpÉ dk fuekZ.k djrh gSA A izdkj osQ izfr Le`fr fpÉ osQ fuekZ.k esa 5 feuV dkVus vkSj 10 feuV tksM+us esa yxrs gSaA B izdkj osQ izfr Le`fr fpÉ osQ fy, 8 feuV dkVus vkSj 8 feuV tksM+us esa yxrs gSaA fn;k x;k gS fd dkVus osQ fy, oqQy le; 3 ?kaVs 20 feuV rFkk tksM+us osQ fy, 4 ?kaVs miyC/ gSaA izR;sd A izdkj osQ Le`fr fpÉ ij Rs 5 vkSj izR;sd B izdkj osQ Le`fr fpÉ ij Rs 6 dk ykHk gksuk gSA Kkr dhft, fd ykHk osQ vf/drehdj.k osQ fy, izR;sd izdkj osQ fdrus&fdrus Le`fr fpÉksa dk daiuh }kjk fuekZ.k gksuk pkfg,\
8. ,d lkSnkxj nks izdkj osQ futh daI;wVj&,d MsLdVkWi uewuk vkSj nwljk iksVZscy uewuk] ftudh dhersa Øe'k% Rs 25]000 vkSj Rs 40]000 gksxh] cspus dh ;kstuk cukrk gSA og vuqeku yxkrk gS fd daI;wVjksa dh oqQy ekfld ek¡x 250 uxksa ls vf/d ugha gksxhA izR;sd izdkj osQ daI;wVjksa osQ uxksa dh la[;k Kkr dhft, ftls lkSnkxkj vf/dre ykHk izkIr djus osQ fy, laxzg djsa ;fn mlosQ ikl fuos'k osQ fy, Rs 70 yk[k ls vf/d ugha gS vkSj ;fn MsLdVkWi uewus ij mldk ykHk Rs 4500 vkSj iksVsZcy uewus ij Rs 5000 ykHk gksA
9. ,d HkksT; inkFkZ esa de ls de 80 ek=kd foVkfeu A vkSj 100 ek=kd [kfut gksuk pkfg,A nks izdkj osQ HkksT; F1 vkSj F2 miyC/ gSaA HkksT; F1 dh ykxr Rs 4 izfr ek=kd vkSj F2 dh ykxr Rs 5 izfr ek=kd gSA HkksT; F1 dh ,d bdkbZ esa de ls de 3 ek=kd foVkfeu A vkSj 4 ek=kd [kfut gSA F2 dh izfr bdkbZ esa de ls de 6 ek=kd foVkfeu A vkSj 3 ek=kd [kfut gSaA bldks ,d jSf[kd izksxzkeu leL;k osQ :i esa lw=kc¼ dhft,A ml vkgkj dk U;wure ewY; Kkr dhft,] ftlesa bu nks HkksT;ksa dk feJ.k gS vkSj mlesa U;wure iks"kd rRo gSaA
10. nks izdkj osQ moZjd F1 vkSj F2 gSA F1 esa 10% ukbVªkstu vkSj 6% iQkLiQksfjd vEy gSA rFkk F2 esa 5% ukbVªkstu rFkk 10% iQkLiQksfjd vEy gSA feVðh dh fLFkfrvksa dk ijh{k.k djus osQ i'pkr~ ,d fdlku ikrk gS fd mls viuh iQly osQ fy, 14 kg ukbVªkstu vkSj 14 kg iQkLiQksfjd vEy dh vko';drk gSA ;fn F1 dh dher Rs 6/kg vkSj F2 dh dher Rs 5/kg gS] izR;sd izdkj dk fdruk moZjd mi;ksx osQ fy, pkfg, rkfd U;wure ewY; ij okafNr iks"kd rRo fey losQA U;wure ykxr D;k gSA
11. fuEufyf[kr vlehdj.k fudk;% 2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 ls fu/kZfjr lqlaxr {ks=k osQ dksuh; ¯cnq% (0, 0), (5, 0), (3, 4) vkSj (0, 5) gSA ekukfd Z = px + qy, tgk¡
p, q > 0, p rFkk q osQ fy, fuEufyf[kr esa dkSu izfrca/ mfpr gS rkfd Z dk vf/dre (3] 4) vkSj (0] 5) nksuksa ij ?kfVr gksrk gS
(A) p = q (B) p = 2q (C) p = 3q (D) q = 3p
fofo/ mnkgj.k
mnkgj.k 9 (vkgkj leL;k) ,d vkgkjfon~ nks HkksT;ksa P vkSj Q dk mi;ksx djrs gq, ,d fo'ks"k vkgkj rS;kj djrk gSA HkksT; P dk izR;sd iSosQV (ftlesa 30 xzke var£o"V gS) esa dSfY'k;e osQ 12 ek=kd ykSg rRo osQ 4 ek=kd] dksysLVªksy osQ 6 ek=kd vkSj foVkfeu A osQ 6 ek=kd var£o"V gSa tcfd mlh ek=k osQ HkksT; Q osQ iSosQV esa oSQfY'k;e rRo osQ 3 ek=kd] ykSg rRo osQ 20 ek=kd] dksysLVªksy osQ 4 ek=kd vkSj foVkfeu A osQ 3 ek=kd varfoZ"V gSA vkgkj esa de ls de 240 ek=kd oSQfY'k;e] ykSg rRo osQ de ls de 460 ek=kd] vkSj dksysLVªksy osQ vf/d ls vf/d 300 ek=kd visf{kr gSaA izR;sd HkksT; osQ fdrus iSosQVksa dk mi;ksx fd;k tk, rkfd vkgkj esa foVkfeu A dh ek=kk dk U;wure fd;k tk losQA
gy ekuk fd HkksT;ksa P vkSj Q osQ iSosQVksa dh la[;k Øe'k% x vkSj y gSA Li"Vr% x ≥ 0, y ≥ 0. iznÙk leL;k dk xf.krh; lw=khdj.k fuEu gS
fuEu O;ojks/ksa osQ varxZr
12x + 3y ≥ 240 (oSQfY'k;e dk O;ojks/) vFkkZr~ 4x + y ≥ 80 ... (1)
4x + 20y ≥ 460 (ykSg rRo dk O;ojks/) vFkkZr~ x + 5y ≥ 115 ... (2)
6x + 4y ≤ 300 (dksysLVªksy dk O;ojks/) vFkkZr~ 3x + 2y ≤ 150 ... (3)
x ≥ 0, y ≥ 0 x ≥ 0, y ≥ 0 ... (4)
Z = 6x + 3y (foVkfeu A) dk U;wurehdj.k dhft,A
vlehdj.kksa (1) ls (4) rd dk vkys[ku O;ojks/ksa (1) ls (4) rd osQ varxZr vko`Qfr 12-10 esa n'kkZ;k x;k gSA mlesa lqfuf'pr lqalxr {ks=k (Nk;kafdr) ij è;ku nhft, tks ifjc¼ gSA

vko`Qfr 12. 10
dksuh; ¯cnqvksa L, M vkSj N osQ funsZ'kkad Øe'k% (2, 72), (15, 20) vkSj (40, 15) gSaA bu ¯cnqvksa ij Z dk eku fuEufyf[kr lkj.kh esa fn;k x;k gSA
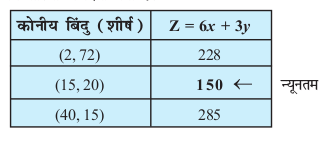
lkj.kh ls] ge Z dk eku ¯cnq (15, 20) ij U;wure ikrs gSaA vr% leL;k esa iznÙk O;ojks/ksa osQ vk/hu foVkfeu A dk eku U;wure rc gksxk tcfd HkksT; P osQ 15 iSosQV vkSj HkksT; Q osQ 20 iSosQV dk mi;ksx fo'ks"k vkgkj osQ izca/ esa fd;k tk;A foVkfeu A dk U;wure eku 150 ek=k dk gksxkA
mnkgj.k 10 mRiknu laca/h leL;k (Manufacturing problem) ,d mRiknu osQ dkj[kkus esa rhu e'khusa I, II vkSj III yxh gSaA e'khusa I vkSj II vf/dre 12 ?kaVs rd pyk, tkus dh {kerk j[krh gSA tcfd e'khu III izfrfnu de ls de 5 ?kaVs pyuk pkfg,A fuekZ.kdrkZ osQoy nks izdkj osQ lkeku M vkSj N dk mRiknu djrk gS] ftuesa izR;sd osQ mRiknu esa rhuksa e'khuksa dh vko';drk gksrh gSA M vkSj N osQ izR;sd mRikn osQ ,d ux mRiknu esa rhuksa e'khuksa osQ laxr yxs le; (?kaVkas esa) fuEu fyf[kr lkj.kh esa fn, gSaA
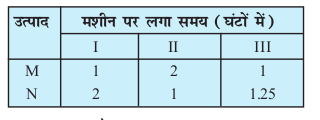
og mRikn M ij Rs 600 izfr ux vkSj mRikn N ij Rs 400 izfr ux dh nj ls ykHk dekrh gSA ekurs gq, fd mlosQ lHkh mRikn fcd tkrs gSa] ftudk mRiknu fd;k x;k gS] rc Kkr dhft, fd izR;sd mRikn osQ fdrus uxksa dk mRiknu fd;k tk,] ftlls ykHk dk vf/drehdj.k gks\
vf/dre ykHk D;k gksxk\
gy ekuk fd mRikn M vkSj N osQ uxksa dh la[;k Øe'k% x vkSj y gSA
mRiknu ij oqQy ykHk = Rs (600 x + 400 y)
iznÙk leL;k dk xf.krh; lw=kc¼ :i fuEufyf[kr gS%
Z = 600 x + 400 y dk vf/drehdj.k dhft,
tgk¡ O;ojks/ fuEufyf[kr gSaA
x + 2y ≤ 12 (e'khu I ij O;ojks/) ... (1)
2x + y ≤ 12 (e'khu II ij O;ojks/) ... (2)
x +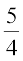 y ≥ 5 (e'khu III ij O;ojks/) ... (3)
y ≥ 5 (e'khu III ij O;ojks/) ... (3)
x ≥ 0, y ≥ 0 ... (4)
ge O;ojks/ksa (1) ls (4) dk vkys[ku djrs gSaA vko`Qfr 12-11 esa fn[kk;k x;k lqlaxr {ks=k ABCDE (Nk;kafdr) gS ftldks O;ojks/ksa (1) ls (4) rd }kjk fu/kZfjr fd;k x;k gSA voyksdu dhft, fd lqlaxr {ks=k ifjc¼ gS] dksuh; ¯cnqvksa A, B, C, D vkSj E osQ funsZ'kkad Øe'k% (5, 0) (6, 0), (4, 4), (0, 6) vkSj (0, 4) gSaA

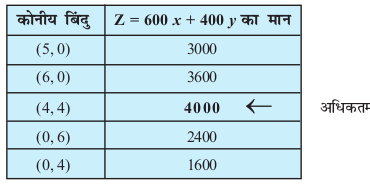
ge ns[krs gSa fd ¯cnq (4] 4) Z dk vf/dre eku gSA vr% mRiknd dks vf/dre
Rs 4000 ykHk dekus osQ fy, izR;sd mRikn osQ 4 uxksa dk mRiknu djuk pkfg,A
mnkgj.k 11 ifjogu laca/h leL;k (Transportation Problem) P vkSj Q nks LFkkuksa ij nks dkj[kkus LFkkfir gSaA bu LFkkuksa ls lkeku A, B vkSj C ij fLFkr rhu fMiks esa Hksts tkrs gSaA bu fMiks dh lkIrkfgd vko';drk Øe'k% 5] 5 vkSj 4 lkeku dh ux gSa] tc fd P vkSj Q dh LFkkfir dkj[kkuksa dh mRiknu {kerk 8 vkSj 6 ux gSaA
izfr ux ifjogu O;; fuEu lkj.khc¼ gS%
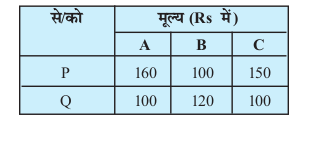
izR;sd dkj[kkus ls fdrus ux lkeku izR;sd fMiks dks Hkstk tk, ftlls ifjogu O;; U;wure gks\ U;wure ifjogu O;; D;k gksxkA
gy vko`Qfr 12-12 }kjk bl leL;k dks fuEufyf[kr :i esa O;Dr fd;k tk ldrk gSA
ekuk fd eky osQ x uxksa vkSj y uxksa dks dkj[kkuk P ls Øe'k% A vkSj B fMiks dks Hkstk x;kA rc (8 – x – y) uxksa dks C fMiks rd Hkstk tk,xk (D;ksa\)
vr% x ≥ 0, y ≥ 0 vkSj 8 – x – y ≥ 0
vFkkZr~ x ≥ 0, y ≥ 0 vkSj x + y ≤ 8
vc fMiks A ij lkeku dh lkIrkfgd vko';drk 5 ux gSA D;ksafd P dkj[kkus ls x ux
fMiks A dks Hksts tk pqosQ gSa blfy, dkj[kkus Q ls (5 – x) ux] fMiks A dks Hksts tk,¡xsA Li"Vr% 5 – x ≥ 0, vFkkZr~ x ≤ 5 gSA

vko`Qfr 12.12
blh izdkj (5 – y) vkSj 6 – (5 – x + 5 – y) = x + y – 4 ux dkj[kkus Q ls Øe'k% fMiks B vkSj C dks Hksts tk,¡xsA vr%
5 – y ≥ 0, x + y – 4 ≥ 0
vFkkZr~ y ≤ 5, x + y ≥ 4
laiw.kZ ifjogu O;;] tks Z }kjk fn;k x;k gS fuEu gS%
Z = 160 x + 100 y + 100 ( 5 – x) + 120 (5 – y) + 100 (x + y – 4) + 150 (8 – x – y)
= 10 (x – 7 y + 190)
blfy, leL;k xf.krh; :i esa fuEufyf[kr :i ls O;Dr dh tk ldrh gS%
fuEu O;ojks/ksa osQ varxZr
x ≥ 0, y ≥ 0 ... (1)
x + y ≤ 8 ... (2)
x ≤ 5 ... (3)
y ≤ 5 ... (4)
x + y ≥ 4 ... (5)
Z = 10 (x – 7y + 190) dk U;wurehdj.k dhft,
O;ojks/ksa (1) ls (5) }kjk fu/kZfjr Nk;kafdr {ks=k ABCDEF lqlaxr {ks=k gS (vko`Qfr 12-13)
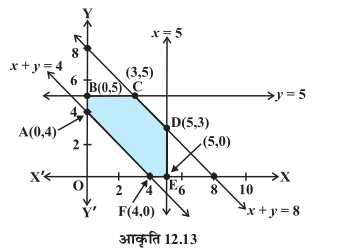
voyksdu dhft, fd lqlaxr {ks=k ifjc¼ gSA lqlaxr {ks=k osQ dksuh; ¯cnqvksa osQ funsZ'kkad (0, 4), (0, 5), (3, 5), (5, 3), (5, 0) vkSj(4, 0) gSaA ge bu ¯cnqvksa ij Z dk eku Kkr djrs gSa%
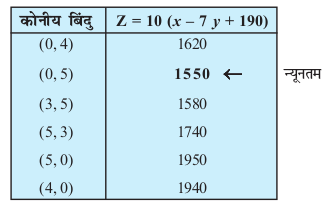
lkj.kh ls Kkr gksrk gS fd ¯cnq (0] 5) ij Z dk U;wure eku 1550 gSA
vr% b"Vre ifjogu fLFkfr osQ vuqlkj dkj[kkuk P ls 5, 0 vkSj 3 ux vkSj dkj[kkus Q ls Øe'k% fMiks A, B vkSj C rd 5] 0 vkSj 1 ux Hkstk tk,xkA blh fLFkfr osQ laxr U;wure ifjogu O;; Rs 1550 gksxkA
vè;k; 12 ij fofo/ iz'ukoyh
1. mnkgj.k 9 ij è;ku dhft,A vkgkj esa foVkfeu A dh ek=kk dk vf/drehdj.k djus osQ fy, izR;sd HkksT; osQ fdrus iSosQVksa dk mi;ksx gksuk pkfg,\ vkgkj esa foVkfeu A dh
vf/dre ek=kk D;k gS\
2. ,d fdlku nks izdkj osQ pkjs P vkSj Q dks feykrk (feJ.k) gSA P izdkj osQ pkjs] ftldk ewY; Rs 250 izfr FkSyk tksfd iks"kd rRo A osQ 3 ek=kd] rRo B osQ 2-5 ek=kd vkSj rRo C osQ 2 ek=kd j[krk gS tcfd Q izdkj dk pkjk ftldk ewY; Rs 200 izfr FkSyk gS] iks"kd rRo A dk 1-5 ek=kd] rRo B dk 11-25 ek=kd vkSj rRo C osQ rhu ek=kd j[krk gSA iks"kd rRoksa A, B, vkSj C dh U;wure vko';drk,¡ Øe'k% 18 ek=kd] 45 ek=kd vkSj 24 ek=kd gSaA izR;sd izdkj osQ FkSyksa dh la[;k Kkr dhft, rkfd feJ.k osQ izR;sd FkSys dk ewY; U;wure gks\ feJ.k osQ izR;sd FkSys dk U;wure ewY; D;k gS\
3. ,d vkgkjfon~ nks izdkj osQ HkksT;ksa X vkSj Y dks bl izdkj feykuk pkgrk gS fd feJ.k esa foVkfeu A, dh de ls de 10 ek=kd] foVkfeu B dh de ls de 12 ek=kd vkSj foVkfeu C dh 8 ek=kd gksa 1 kg HkksT;ksa esa foVkfeuksa dh ek=kk fuEufyf[kr lkj.kh esa nh xbZ gSA
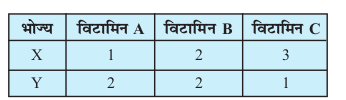
HkksT; X osQ 1 kg dk ewY; Rs 16 vkSj HkksT; y osQ 1 kg dk ewY; Rs 20 gSA okafNr vkgkj osQ fy, feJ.k dk U;wure ewY; Kkr dhft,A
4. ,d fuekZrk nks izdkj osQ f[kykSus A vkSj B cukrk gSA bl mís'; osQ fy, fuekZ.k esa rhu e'khuksa dh vko';drk iM+rh gS vkSj izR;sd izdkj osQ f[kykSus osQ fuekZ.k osQ fy, yxk le; (feuVksa esa) fuEufyf[kr gSA
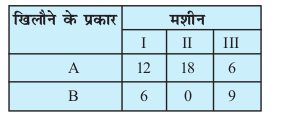
izR;sd e'khu vf/dre 6 ?kaVs izfrfnu osQ fy, miyC/ gSA ;fn A izdkj osQ f[kykSus dh fcØh ij Rs 7-50 ykHk vkSj B izdkj osQ f[kykSus ij Rs 5 dk ykHk gks rks n'kkZb, fd vf/dre ykHk dekus osQ fy, izfrfnu A izdkj osQ 15 f[kykSus vkSj B izdkj 30 f[kykSus fu£er gksus pkfg,A
5. ,d gokbZ tgkt vf/dre 200 ;kf=k;ksa dks ;k=kk djk ldrk gSA izR;sd izFke Js.kh osQ fVdV ij Rs 1000 vkSj lLrs Js.kh osQ fVdV ij Rs 600 dk ykHk dek;k tk ldrk gSA ,;jykbu de ls de 20 lhVsa izFke Js.kh osQ fy, vkjf{kr djrh gSA rFkkfi izFke Js.kh dh vis{kk de ls de 4 xqus ;k=kh lLrh Js.kh osQ fVdV ls ;k=kk djus dks ojh;rk nsrs gSaA Kkr dhft, fd izR;sd izdkj osQ fdrus&fdrus fVdV csps tk,¡ rkfd ykHk dk
vf/drehdj.k gks\ vf/dre ykHk fdruk gS\
6. nks vUu HkaMkjksa A vkSj B dh HkaMkj.k {kerk Øe'k% 100 fDoaVy vkSj 50 fDoaVy gSA mUgsa rhu jk'ku dh nqdkuksa D, E vkSj F ij vUu miyC/ djkuk iM+rk gS] ftudh vko';drk,¡ Øe'k% 60] 50] vkSj 40 fDoaVy gSaA
HkaMkjksa ls nqdkuksa dks izfr fDoaVy ifjogu O;; fuEu lkj.kh osQ vuqlkj gS%
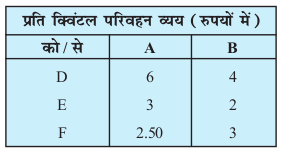
ifjogu O;; osQ U;wurehdj.k osQ fy, vkiwfrZ dk ifjogu oSQls fd;k tk,\ U;wure ifjogu ewY; D;k gS\
7. ,d rsy dkj[kkus esa nks fMiks A rFkk B gSa] ftudh {kerk,¡ Øe'k% 7000 fyVj vkSj 4000 fyVj dh gSaA dkj[kkus }kjk rhu isVªksy iaiksa D, E vkSj F osQ fy, vkiwfrZ djuh gS] ftudh vko';drk,¡ Øe'k% 4500 fyVj] 3000 fyVj vkSj 3500 fyVj dh gSA fMiks ls isVªksy iaiksa dh nwfj;k¡ (km esa) fuEukafdr lkj.kh osQ vuqlkj gS%
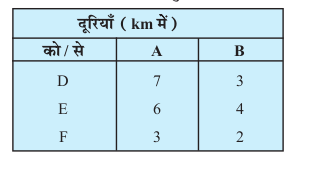
;g ekurs gq, fd ifjogu O;; izfr 10 fyVj ij izfr fdyksehVj 1 #i;k gS] Kkr dhft, fd oSQlh vkiwfrZ ;kstuk viukbZ tk,] ftlls ifjogu O;; dk U;wurehdj.k gks tk,\ U;wure O;; D;k gS\
8. ,d iQy mRiknd vius ckx esa nks izdkj osQ [kknksa P czkaM vkSj Q czkaM dk mi;ksx dj ldrk gSA feJ.k osQ izR;sd FkSys esa ukbVªkstu] iQkLiQksfjd vEy] iksVk'k vkSj Dyksjhu dh ek=kk (kg esa) lkj.kh esa fn;k x;k gSA ijh{k.k laosQr nsrs gS fd ckx dks de ls de 250 kg iQkLiQksfjd vEy] de ls de 270 kg iksVk'k vkSj Dyksjhu dh vf/d ls vf/d 310 kg dh vko';drk gSA
;fn mRiknd ckx osQ fy, feykbZ tkus okyh ukbVªkstu dh ek=kk dk U;wurehdj.k djuk pkgrk gS rFkk] izR;sd feJ.k osQ fdrus FkSyksa dk mi;ksx gksuk pkfg,\ feykbZ tkus okyh ukbVªkstu dh fuEure ek=kk D;k gS\
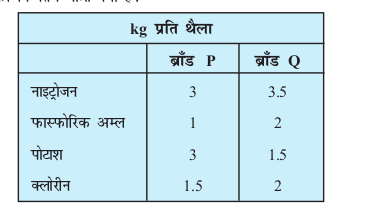
9. mijksDr iz'u 8 ij è;ku nhft,A ;fn mRiknd ckx esa feykbZ tkus okyh ukbVªkstu dh ek=kk dk vf/drehdj.k pkgrk gS rks feJ.k osQ fdrus FkSyksa dks feyk;k tkuk pkfg,\ feykbZ tkus okyh ukbVªkstu dh vf/dre ek=kk D;k gS\
10. ,d f[kykSuk oaQiuh] A vkSj B nks izdkj dh xqfM+;ksa dk fuekZ.k djrh gSA ek£dV ijh{k.kksa rFkk miyC/ lalk/uksa ls laosQr feyrk gS fd lfEefyr mRiknu Lrj izfr lIrkg 1200 xqfM+;ksa ls vf/d ugha gksuk pkfg, vkSj B izdkj dh xqfM+;ksa dh vf/d ls vf/d ek¡x A izdkj dh xqfM+;ksa dh vk/h gSA blosQ vfrfjDr A izdkj dh xqfM+;ksa dk mRiknu Lrj nwljs izdkj dh xqfM+;ksa osQ mRiknu Lrj osQ rhu xqus ls 600 ux vf/d gSA ;fn daiuh A vkSj B izR;sd xqfM+;k ij Øe'k% Rs 12 vkSj Rs 16 dk ykHk dekrh gS] ykHk dk vf/drehdj.k djus osQ fy, izR;sd osQ fdrus uxksa dk lkIrkfgd mRiknu djuk pkfg,A
lkjka'k
- ,d jSf[kd izksxzkeu leL;k og leL;k gS tks dbZ pjksa osQ jSf[kd iQyu osQ b"Vre eku (vf/dre ;k U;wure) dks Kkr djus ls lacaf/r iQyu dks mís'; iQyu dgrs gSaA tc izfrca/ ;g gks fd pj ½.ksrj gksa vkSj jSf[kd vlehdj.kksa (ftudks jSf[kd O;ojks/ dgrs gSa) dks larq"V djrs gksaA pjksa dks dHkh&dHkh fu.kkZ;d pj dgrs gSa vkSj ½.ksrj gSaA
- oqQN egÙoiw.kZ jSf[kd izksxzkeu leL;k,¡ fuEufyf[kr gSa%
(i) vkgkj laca/h leL;k
(ii) mRiknu laca/h leL;k
(iii) ifjogu laca/h leL;k
- lHkh O;ojks/ksa vkSj ½.ksrj O;ojks/ksa x ≥ 0, y ≥ 0 }kjk fu/kZfjr mHk;fu"B {ks=k] ,d js[kh; izksxzkeu leL;k dk lqlaxr {ks=k (;k gy leqPp;) dgykrk gSA
- lqlaxr {ks=k osQ var% Hkkx osQ rFkk lhekar ¯cnq O;ojks/ksa osQ lqlaxr gyksa dks iznf'kZr djrs gSaA
- lqlaxr {ks=k osQ cká Hkkx osQ fdlh Hkh ¯cnq dks vlaxr gy dgrs gSaA
- lqlaxr {ks=k esa dksbZ ¯cnq tks mís'; iQyu dk b"Vre eku (vf/dre ;k U;wure) ,d nsrk gS rks bls b"Vre gy dgrs gSaA
- fuEufyf[kr izes; jSf[kd izksxzkeu leL;kvksa dks gy djus osQ fy, vk/kjHkwr egÙo osQ gSa%
izes; 1% ekuk fd R ,d jSf[kd izksxzkeu leL;k osQ fy, lqlaxr {ks=k (mÙky cgqHkqt) gS vkSj ekuk fd Z = ax + by mís'; iQyu gSA tc Z ,d b"Vre eku (vf/dre ;k U;wure) nsrk gS tgk¡ jSf[kd vlehdj.k pjksa x vkSj y }kjk O;ojks/ksa osQ :i esa of.kZr gS rks ;g b"Vre eku lqlaxr {ks=k osQ ,d dksuh; ¯cnq ('kh"kZ) ij gksuk gh pkfg,A
izes; 2% ekuk fd R ,d jSf[kd izksxzkeu leL;k osQ fy, lqlaxr {ks=k (mÙky cgqHkqt) gS vkSj ekuk fd Z = ax + by mís'; iQyu gSA tc ;fn R ifjc¼ gS rc mís'; iQyu] R esa ,d vf/dre vkSj ,d U;wure nksuksa gh nsrk gS vkSj buesa ls izR;sd ¯cnq R osQ dksuh; ¯cnq ('kh"kZ) ij fLFkr gksrk gSA
- ;fn lqlaxr {ks=k vifjc¼ gS rc vf/dre ;k U;wure vfLrRo esa ugha Hkh gks ldrk gSA rFkkfi ;fn ;g vfLrRo esa gksrk gS rks R osQ dksuh; ¯cnq ij fLFkr gksuk pkfg,A
dksuh; ¯cnq fof/% ,d jSf[kd leL;k dks gy djus osQ fy, ;g fof/ fuEu inksa esa fØ;kfUor gksrh gS%
(1) jSf[kd izksxzkeu leL;k osQ lqlaxr {ks=k dks Kkr dhft, rFkk blosQ dksuh; ¯cnq ('kh"kks±) dks Kkr dhft,A
(2) izR;sd dksuh; ¯cnq ij mís'; iQyu Z = ax + by dk eku Kkr dhft,A eku yhft, bu ¯cnqvksa ij vf/dre vkSj U;wure eku Øe'k% M rFkk m gSaA
(3) ;fn lqlaxr {ks=k ifjc¼ gS] rks M vkSj m Øe'k% mís'; iQyu osQ vf/dre rFkk U;wure eku gaSA
;fn lqlaxr {ks=k vifjc¼ gS rc
(i) mís'; iQyu dk M vf/dre eku gS ;fn ax + by > M osQ }kjk fu/kZfjr [kqyk v/Zry lqlaxr {ks=k osQ lkFk dksbZ mHk;fu"B ¯cnq ugha j[krk gSA vU;Fkk mís'; iQyu dk vf/dre eku ugha gSA
(ii) mís'; iQyu dk U;wure eku m gS ;fn ax + by < m }kjk fu/kZfjr [kqyk
v/Zry vkSj lqlaxr {ks=k esa dksbZ ¯cnq mHk;fu"B ugha gSA vU;Fkk mís'; iQyu dk dksbZ U;wure eku ugha gSA
;fn lqlaxr {ks=k osQ nks dksuh; ¯cnqvksa dk b"Vre eku ,d gh izdkj dk gS vFkkZr~ nksuksa ogh vf/dre ;k U;wure eku iznku djrs gS rc bu nksuksa ¯cnqvksa dks feykus okys js[kk[kaM osQ fdlh Hkh ¯cnq ij Hkh mlh izdkj dk b"Vre gy gSA
,sfrgkfld fVIi.kh
f}rh; fo'o ;q¼ esa] tc ;q¼ lapkyu dh ;kstuk cuh] ftlls fd 'k=kqvksa dks
U;wure O;; ij vf/dre gkfu igq¡ps] jSf[kd izksxzkeu fof/ vfLrRo esa vkbZA
jSf[kd izksxzkeu osQ {ks=k esa izFke izksxzkeu dk lw=kikr :lh xf.krK L.Kantoro Vich rFkk vesfjdh vFkZ'kkL=kh F.L.Hitch Cock us 1941 esa fd,A nksuksa us Lora=k :i ls dk;Z fd;kA bl izksxzkeu dks ifjogu&leL;k osQ uke ls tkuk x;kA lu~ 1945 esa vaxzst vFkZ'kkL=kh G.Stigler us jSf[kd izksxzkeu leL;k] osQ varxZr b"Vre vkgkj laca/h leL;k dk o.kZu fd;kA
lu~ 1947 esa G.B. Dantzig us ,d n{krk iw.kZ fof/ tks flaiysDl fof/ osQ uke ls izfl¼ gS] dk lq>ko fn;k tks jSf[kd izksxzkeu leL;kvksa dks lhfer izØeksa esa gy djus dh l'kDr fof/ gSA
jSf[kd izksxzkeu fof/ ij izkjfHkd dk;Z djus osQ dkj.k lu~ 1975 esa L.Katorovich vkSj vesfjdh xf.kr; vFkZ'kkL=kh T.C.Koopmans dks vFkZ 'kkL=k esa ukscsy iqjLdkj iznku fd;k x;kA ifjdyu rFkk vko';d lkWÝVos;j osQ vkxeu osQ lkFk dbZ {ks=kksa dh tfVy leL;kvksa esa jSf[kd izksxzkeu izfof/ osQ vuqiz;ksx esa mÙkjksrj o`f¼ gks jgh gSA
——