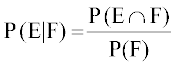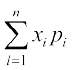Table of Contents
vè;k;13
izkf;drk Probability
The Theory of probabilities is simply the science of logic quantitatively treated – C.S. PEIRCE
13.1 Hkwfedk (Introduction)

Pierre de Fermat
(1601-1665)
igys dh d{kkvksa esa geus izkf;drk dks fdlh ;kn`fPNd ijh{k.k dh ?kVukvksa osQ ?kfVr gksus dh vfuf'prrk dh eki osQ :i esa i<+k FkkA geus :lh xf.krK ,-,u- dkSYeksxzksc (1903&1987) }kjk izfrikfnr vfHkx`fgrh; n`f"Vdks.k dk mi;ksx fd;k Fkk vkSj izkf;drk dks ijh{k.k osQ ifj.kkeksa ij ifjHkkf"kr iQyu osQ :i esa fu:fir fd;k FkkA geus lelaHkkO; ifj.kkeksa dh n'kk esa izkf;drk osQ vfHkx`fgrh; n`f"Vdks.k vkSj Dykfldy fl¼kar (classical theory) esa led{krk Hkh LFkkfir dh FkhA bl led{krk osQ vk/kj ij geus vlarr izfrn'kZ lef"V dh ?kVukvksa dh izkf;drk Kkr dh FkhA geus izkf;drk osQ ;ksx fu;e dk Hkh vè;;u fd;k gSA bl vè;k; esa ge fdlh ?kVuk dh lizfrca/ izkf;drk (conditional probability) osQ ckjs esa fopkj djsaxs] tcfd fdlh vU; ?kVuk osQ ?kfVr gksus dh lwpuk gekjs ikl gks] rFkk bl egÙoiw.kZ vo/kj.kk dh lgk;rk ls cst&izes; (Bayes' theorem), izkf;drk dk xq.ku fu;e rFkk Lora=k ?kVukvksa osQ ckjs esa le>asxsA ge ;kn`fPNd pj (random variable) vkSj blosQ izkf;drk caVu dh egÙoiw.kZ vo/kj.kk dks Hkh le>asxs rFkk fdlh izkf;drk caVu osQ ekè; (mean) o izlj.k osQ ckjs esa Hkh i<+saxsA vè;k; osQ vafre vuqHkkx esa ge ,d egÙoiw.kZ vlarr izkf;drk caVu (discrete probability distribution) osQ ckjs esa i<+saxs ftls f}in caVu dgk tkrk gSA bl vè;k; esa ge ,sls ijh{k.k ysaxs ftuosQ ifj.kke lelaHkkO; gksrs gSa] tc rd fd vU;Fkk u dgk x;k gksA
13.2 lizfrca/ izkf;drk (Conditional Probability)
vHkh rd geus fdlh ?kVuk dh izkf;drk Kkr djus ij ppkZ dh gSA ;fn gesa fdlh izfrn'kZ lef"V dh nks ?kVuk,¡ nh xbZ gksa] rks D;k fdlh ,d ?kVuk osQ ?kfVr gksus dh lwpuk dk izHkko nwljh ?kVuk dh izkf;drk ij iM+rk gS\ vkb, bl iz'u osQ mÙkj osQ fy, ,d ;kn`fPNd ijh{k.k ij fopkj djsa ftlosQ ifj.kke lelaHkkO; gSaA
vkb, vc rhu U;kÕ; (fair) flDdksa dks mNkyus osQ ijh{k.k ij fopkj dhft,A bl ijh{k.k dk izfrn'kZ lef"V gS%
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
D;ksafd flDosQ U;kÕ; gSa] blfy, ge izfrn'kZ lef"V osQ izR;sd izfrn'kZ ¯cnq dh izkf;drk 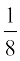 fufnZ"V dj ldrs gSaA eku yhft, E ?kVuk ¶U;wure nks fpr izdV gksuk¸ vkSj F ?kVuk ¶igys flDosQ ij iV iznf'kZr gksuk¸ dks fu:fir djrs gSaA
fufnZ"V dj ldrs gSaA eku yhft, E ?kVuk ¶U;wure nks fpr izdV gksuk¸ vkSj F ?kVuk ¶igys flDosQ ij iV iznf'kZr gksuk¸ dks fu:fir djrs gSaA
rc E = {HHH, HHT, HTH, THH}
vkSj F = {THH, THT, TTH, TTT}
blfy, P(E) = P ({HHH}) + P ({HHT}) + P ({HTH}) + P ({THH})
= 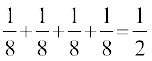 (D;ksa ?)
(D;ksa ?)
vkSj P(F) = P ({THH}) + P ({THT}) + P ({TTH}) + P ({TTT})
= 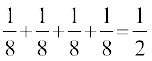
lkFk gh E ∩ F = {THH}
blfy, P(E ∩ F) = P({THH}) = 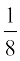
vc eku yhft, gesa fn;k x;k gS fd igys flDosQ ij iV izdV gksrk gS vFkkZr~~ ?kVuk F ?kfVr gqbZ gS] rc ?kVuk E dh izkf;drk D;k gS\ F osQ ?kfVr gksus dh lwpuk ij ;g fuf'pr gS fd E dh izkf;drk Kkr djus osQ fy, mu izfrn'kZ ¯cnqvksa ij fopkj ugha fd;k tk,xk ftueas igys flDosQ ij iV ugha gSA ?kVuk E osQ fy, bl lwpuk ls izfrn'kZ lef"V S ls ?kVdj bldk mileqPp; F cu x;k gSA vU; 'kCnksa esa] bl vfrfjDr lwpuk us gesa okLro esa ;g crk;k gS fd gkykr dks ,d ,sls u, ;kn`fPNd ijh{k.k osQ :i esa le>uk pkfg, ftldk izfrn'kZ lef"V osQoy mu ifj.kkeksa dk leqPp; gS tks fd ?kVuk F osQ vuqowQy gSA
vc F dk og izfrn'kZ ¯cnq tks E osQ Hkh vuqowQy gS_ THH gSA vr%
F dks izfrn'kZ lef"V ekurs gq, ?kVuk E dh izkf;drk = 
;k F dk ?kfVr gksuk fn;k x;k gksus ij E dh izkf;drk = 
?kVuk E dh bl izkf;drk dks lizfrca/ izkf;drk dgrs gSa] tcfd Kkr gS fd ?kVuk F ?kfVr gks pqdh gS] vkSj bls P (E|F) }kjk n'kkZrs gSaA
vFkkZr~~ P(E|F) = 
uksV dhft, fd F osQ oks vo;o tks ?kVuk E osQ Hkh vuqowQy gSa] E rFkk F osQ lk>s vo;o gksrs gSa] vFkkZr~~ E ∩ F osQ izfrn'kZ ¯cnq gSaA
vr% ge ?kVuk E dh lizfrca/ izkf;drk] tcfd Kkr gS fd ?kVuk F ?kfVr gks pqdh gS dks fuEu izdkj ls Kkr dj ldrs gSaA
P(E|F) = 
= 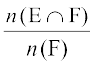
vc va'k o gj dks izfrn'kZ lef"V osQ vo;oksa dh oqQy la[;k ls foHkkftr djus ij ge ns[krs gSa fd P (E|F) dks fuEu izdkj ls fy[kk tk ldrk gS%
P(E|F) = 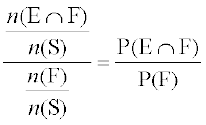 ... (1)
... (1)
uksV dhft, fd (1) rHkh ekU; gS tc P(F) ≠ 0 vFkkZr~~ F ≠ φ (D;ksa?)
vr% ge lizfrca/ izkf;drk dks fuEu izdkj ls ifjHkkf"kr dj ldrs gSa%
ifjHkk"kk 1 ;fn E rFkk F fdlh ;kn`fPNd ijh{k.k osQ izfrn'kZ lef"V ls lcaf/r nks ?kVuk,¡ gSa] rks F osQ ?kfVr gksus dh lwpuk ij] E dh izkf;drk fuEufyf[kr lw=k ls izkIr gksrh gS%
P(E|F) = 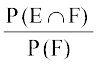 , tcfd P(F) ≠ 0
, tcfd P(F) ≠ 0
13.2.1 lizfrca/ izkf;drk osQ xq.k (Properties of conditional probability)
eku ysa fd E rFkk F fdlh izfrn'kZ lef"V S dh nks ?kVuk,¡ gSa
xq.k 1 P (S|F) = P (F|F) = 1
gesa Kkr gS fd P(S|F) = 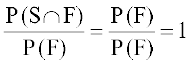
lkFk gh P(F|F) = 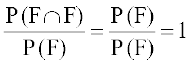
vr% P(S|F) = P(F|F) = 1
xq.k 2 ;fn A vkSj B izfrn'kZ lef"V S dh dksbZ nks ?kVuk,¡ gSa vkSj F ,d vU; ?kVuk bl izdkj gS fd P(F) ≠0, rc
P[(A ∪ B)|F)] = P(A|F) + P(B|F) – P[(A ∩ B)|F]
fo'ks"k :i ls] ;fn A vkSj B ijLij viothZ ?kVuk,¡ gksa] rks
P[(A∪B)|F)] = P(A|F) + P(B|F)
ge tkurs gSa fd
P[(A∪B)|F)] = 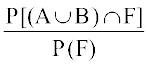
= 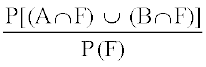
(leqPp;ksa osQ loZfu"B ij lfEeyu osQ caVu fu;e }kjk)
= 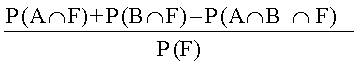
= 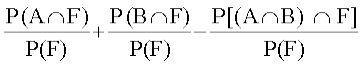
= P(A|F) + P(B|F) – P(A∩B|F)
tc A rFkk B ijLij viothZ gksa rks
P[(A ∩ B)|F)] = 0
⇒ P[(A ∪ B)|F)] = P(A|F) + P(B|F)
vr% tc A rFkk B ijLij viothZ ?kVuk,¡ gksa rks P(A ∪ B) = P(A|F) + P(B|F)
xq.k 3 P (E′|F) = 1 – P(E|F)
xq.k 1 ls gesa Kkr gS fd P (S|F) = 1
⇒ P [(E ∪ E′)|F)] = 1 D;ksafd S = E ∪ E′
⇒ P (E|F) + P (E′|F) = 1 D;ksafd E rFkk E′ ijLij viothZ ?kVuk,¡ gSa
vr% P (E′|F) = 1 − P (E|F)
vkb, vc dqN mnkgj.k ysaA
mnkgj.k 1 ;fn P (A) = 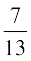 , P (B) =
, P (B) = 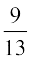 vkSj P (A ∩ B) =
vkSj P (A ∩ B) = 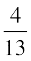 , rks P (A|B) Kkr dhft,A
, rks P (A|B) Kkr dhft,A
gy ge tkurs gSa fd 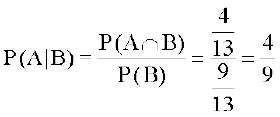
mnkgj.k 2 ,d ifjokj esa nks cPps gSaA ;fn ;g Kkr gks fd cPpksa esa ls de ls de ,d cPpk yM+dk gS] rks nksuksa cPpksa osQ yM+dk gksus dh D;k izkf;drk gS\
gy eku yhft, b yM+osQ dks o g yM+dh dks fu:fir djrs gSaA ijh{k.k dk izfrn'kZ lef"V gS%
S = {(b,b), (g,b), (b,g), (g,g)}
eku yhft, E rFkk F Øe'k% fuEufyf[kr ?kVukvksa dks n'kkZrs gSa%
E : ^nksuksa cPps yM+osQ gSa*
F : ^cPpksa esa ls de ls de ,d yM+dk gS*
rc E = {(b,b)} vkSj F = {(b,b), (g,b), (b,g)}
vc E ∩ F = {(b,b)}
vr% P(F) = 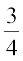 vkSj P (E ∩ F ) =
vkSj P (E ∩ F ) = 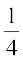
blfy, P(E|F) = 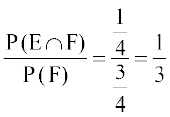
mnkgj.k 3 ,d cDls esa nl dkMZ 1 ls 10 rd iw.kk±d fy[k dj j[ks x, vkSj mUgas vPNh rjg feyk;k x;kA bl cDls ls ,d dkMZ ;kn`PN;k fudkyk x;kA ;fn ;g Kkr gks fd fudkys x, dkMZ ij la[;k 3 ls vf/d gS] rks bl la[;k osQ le gksus dh D;k izkf;drk gS\
gy eku yhft, fd A ?kVuk ^fudkys x, dkMZ ij le la[;k gS* vkSj B ?kVuk ^fudkys x, dkMZ ij la[;k 3 ls cM+h gS* dks fu:fir djrs gSaA gesa P(A|B) Kkr djuk gSA
bl ijh{k.k dk izfrn'kZ lef"V gS% S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
rc A = {2, 4, 6, 8, 10}, B = {4, 5, 6, 7, 8, 9, 10}
vkSj A ∩ B = {4, 6, 8, 10}
vc P(A) = 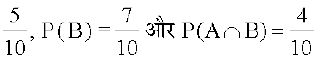
rc P(A|B) = 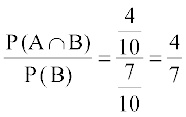
mnkgj.k 4 ,d ikB'kkyk esa 1000 fo|kFkhZ gSa] ftuesa ls 430 yM+fd;k¡ gSaA ;g Kkr gS fd 430 esa ls 10% yM+fd;k¡ d{kk XII esa i<+rh gSaA D;k izkf;drk gS fd ,d ;kn`PN;k pquk x;k fo|kFkhZ d{kk XII esa i<+rk gS ;fn ;g Kkr gS fd pquk x;k fo|kFkhZ yM+dh gS\
gy eku yhft, E ?kVuk ^;kn`PN;k pquk x;k fo|kFkhZ d{kk XII esa i<+rk gS* vkSj F ?kVuk ^;kn`PN;k pquk x;k fo|kFkhZ yM+dh gS*] dks O;Dr djrs gSaA gesa P (E|F) Kkr djuk gSA
vc P(F) = 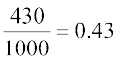 vkSj
vkSj 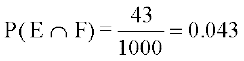 (D;ksa?)
(D;ksa?)
rc P(E|F) = 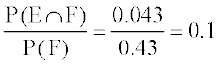
mnkgj.k 5 ,d ikls dks rhu ckj mNkyus ds ijh{k.k esa ?kVuk A rFkk B dks fuEu izdkj ls ifjHkkf"kr fd;k x;k gS%
A : ^rhljh mNky ij la[;k 4 izdV gksuk*
B : ^igyh mNky ij la[;k 6 vkSj nwljh mNky ij la[;k 5 izdV gksuk*
;fn B dk ?kfVr gksuk fn;k x;k gS] rks ?kVuk A dh izkf;drk Kkr dhft,A
gy izfrn'kZ lef"V esa 216 ifj.kke gSaA
vc] B = {(6,5,1), (6,5,2), (6,5,3), (6,5,4), (6,5,5), (6,5,6)}
A = 
vkSj A ∩ B = {(6,5,4)}
vc P(B) = 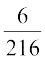 vkSj P(A ∩ B) =
vkSj P(A ∩ B) = 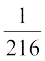
rc P(A|B) = 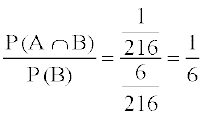
mnkgj.k 6 ,d ikls dks nks ckj mNkyk x;k vkSj izdV gqbZ la[;kvksa dk ;ksx 6 ik;k x;kA la[;k 4 osQ U;wure ,d ckj izdV gksus dh lizfrca/ izkf;drk Kkr dhft,A
gy eku yhft, E ?kVuk ^la[;k 4 dk U;wure ,d ckj izdV gksuk* vkSj F ?kVuk ^nksuksa iklksa ij izdV la[;kvksa dk ;ksx 6 gksus* dks n'kkZrs gSaA
rc E = {(4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (1,4), (2,4), (3,4), (5,4), (6,4)}
vkSj F = {(1,5), (2,4), (3,3), (4,2), (5,1)}
ge tkurs gSa fd P(E) = 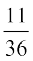 ] P(F) =
] P(F) = 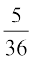
rFkk E ∩ F = {(2,4), (4,2)}
vc P(E ∩ F) = 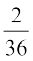
vr% okafNr izkf;drk
P(E|F) = 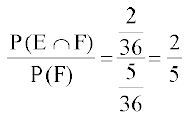
vHkh rd geus mu ijh{k.kksa ij fopkj fd;k gS ftuosQ lHkh ifj.kke lelaHkkO; FksA bu ijh{k.kksa osQ fy, geusa lizfrca/ izkf;drk dks ifjHkkf"kr fd;k gSA rFkkfi lizfrca/ izkf;drk dh ;gh ifjHkk"kk] O;kid :i ls] ml fLFkfr es Hkh iz;ksx dh tk ldrh gS] tc ekSfyd ?kVuk,¡ lelaHkkO; u gksaA izkf;drkvksa P(E∩F) rFkk P (F) dk ifjdyu rnuqlkj fd;k tkrk gSA
vkb, fuEufyf[kr mnkgj.k ls bls le>saA
mnkgj.k 7 ,d flDosQ dks mNkyus osQ ijh{k.k ij fopkj dhft,A ;fn flDosQ ij fpr izdV gks rks flDosQ dks iqu% mNkysa ijarq ;fn flDosQ ij iV izdV gks rks ,d ikls dks isaQosaQA ;fn ?kVuk ^de ls de ,d iV izdV gksuk* dk ?kfVr gksuk fn;k x;k gS rks ?kVuk ^ikls ij 4 ls cM+h la[;k izdV gksuk* dh lizfrca/ izkf;drk Kkr dhft,A
gy ijh{k.k osQ ifj.kkeksa dks fp=k 13-1 ls O;Dr fd;k tk ldrk gSA bl izdkj osQ fp=k dks o`{kkjs[k dgrs gSaA
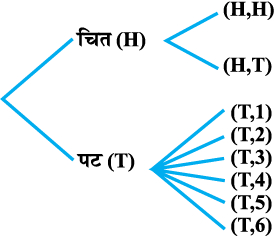
vko`Qfr 13.1
ijh{k.k dk izfrn'kZ lef"V gS%
S = {(H,H), (H,T), (T,1), (T,2), (T,3), (T,4), (T,5), (T,6)}
tgk¡ (H,H) n'kkZrk gS fd nksuksa mNkykas ij fpr izdV gqvk gS] rFkk (T, i) n'kkZrk gS fd igyh mNky ij iV izdV gqvk vkSj ikls dks isaQdus ij la[;k i izdV gqbZA
vr% 8 ekSfyd ?kVukvksa (H,H), (H,T), (T,1), (T,2), (T,3) (T,4), (T,5), (T,6) dh Øe'k% 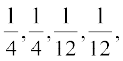
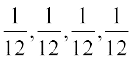 izkf;drk fu/kZfjr dh tk ldrh gS] tSlk fd fp=k 13-2 ls Li"V gSA
izkf;drk fu/kZfjr dh tk ldrh gS] tSlk fd fp=k 13-2 ls Li"V gSA
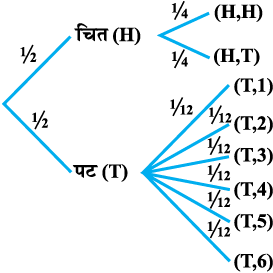
vko`Qfr 13.2
eku ysa F ?kVuk ^U;wure ,d iV izdV gksuk* vkSj E ?kVuk ^ikls ij 4 ls cM+h la[;k izdV gksuk* dks n'kkZrs gSaA
rc F = {(H,T), (T,1), (T,2), (T,3), (T,4), (T,5), (T,6)}
E = {(T,5), T,6)} vkSj E ∩ F = {(T,5), (T,6)}
vc P(F) = P({(H,T)}) + P ({(T,1)}) + P ({(T,2)}) + P ({(T,3)}) +
P ({(T,4)}) + P({(T,5)}) + P({(T,6)})
= 
vkSj P (E ∩ F) = P ({(T,5)}) + P ({(T,6)}) = 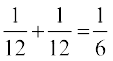
vr% P(E|F) = 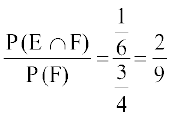
iz'ukoyh 13.1
1. ;fn E vkSj F bl izdkj dh ?kVuk,¡ gSa fd P (E) = 0.6, P (F) = 0.3 vkSj
P (E ∩ F) = 0.2] rks P (E|F) vkSj P (F|E) Kkr dhft,A
2. P(A|B) Kkr dhft,] ;fn P(B) = 0.5 vkSj P (A ∩ B) = 0.32
3. ;fn P(A) = 0.8, P(B) = 0.5 vkSj P (B|A) = 0.4 Kkr dhft,
(i) P(A ∩ B) (ii) P(A|B) (iii) P(A ∪ B)
4. P(A ∪ B) Kkr dhft, ;fn 2 P(A) = P(B) = 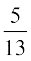 vkSj
vkSj 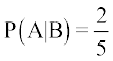
5. ;fn P(A) = 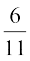 , P(B) =
, P(B) = 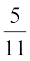 vkSj P(A ∪ B)
vkSj P(A ∪ B) 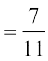 rks Kkr dhft,
rks Kkr dhft,
(i) P(A∩B) (ii) P(A|B) (iii) P(B|A)
fuEufyf[kr iz'u 6 ls 9 rd P(E|F) Kkr dhft,A
6. ,d flDosQ dks rhu ckj mNkyk x;k gS%
(i) E : rhljh mNky ij fpr F : igyh nksuksa mNkyksa ij fpr
(ii) E : U;wure nks fpr F : vf/dre ,d fpr
(iii) E : vf/dre nks iV F : U;wure nks iV
7. nks flDdksa dks ,d ckj mNkyk x;k gS%
(i) E : ,d flDosQ ij iV izdV gksrk gS F : ,d flDosQ ij fpr izdV gksrk gS
(ii) E : dksbZ iV izdV ugha gksrk gS F dksbZ fpr izdV ugha gksrk gS
8. ,d ikls dks rhu ckj mNkyk x;k gS%
E : rhljh mNky ij la[;k 4 izdV gksuk
F : igyh nks mNkyksa ij Øe'k% 6 rFkk 5 izdV gksuk
9. ,d ikfjokfjd fp=k esa ekrk] firk o iq=k ;kn`PN;k [kM+s gSa%
E : iq=k ,d fljs ij [kM+k gS F : firk eè; esa [kM+s gSa
10. ,d dkys vkSj ,d yky ikls dks mNkyk x;k gS%
(a) iklksa ij izkIr la[;kvksa dk ;ksx 9 gksus dh lizfrca/ izkf;drk Kkr dhft, ;fn ;g Kkr gks fd dkys ikls ij 5 izdV gqvk gSA
(b) iklksa ij izkIr laa[;kvksa dk ;ksx 8 gksus dh lizfrca/ izkf;drk Kkr dhft, ;fn ;g Kkr gks fd yky ikls ij izdV la[;k 4 ls de gSA
11. ,d U;kÕ; ikls dks mNkyk x;k gSA ?kVukvksa E = {1,3,5}, F = {2,3}, vkSj G = {2,3,4,5} osQ fy, fuEufyf[kr Kkr dhft,%
(i) P (E|F) vkSj P (F|E) (ii) P (E|G) vkSj P (G|E)
(iii) P (E ∪ F|G) vkSj P (E ∩ F|G)
12. eku ysa fd tUe ysus okys cPps dk yM+dk ;k yM+dh gksuk lelaHkkO; gSA ;fn fdlh ifjokj esa nks cPps gSa] rks nksuksa cPpksa osQ yM+dh gksus dh lizfrca/ izkf;drk D;k gS] ;fn ;g fn;k x;k gS fd (i) lcls NksVk cPpk yM+dh gS (ii) U;wure ,d cPpk yM+dh gSA
13. ,d izf'k{kd osQ ikl 300 lR;@vlR; izdkj osQ vklku iz'u 200 lR;@vlR; izdkj osQ dfBu iz'u] 500 cgq&fodYih; izdkj osQ vklku iz'u vkSj 400 cgq&fodYih; izdkj osQ dfBu iz'uksa dk laxzg gSA ;fn iz'uksa osQ laxzg ls ,d iz'u ;kn`PN;k pquk tkrk gS] rks ,d vklku iz'u dh cgq&fodYih; gksus dh izkf;drk D;k gksxh\
14. ;g fn;k x;k gS fd nks iklksa dks isaQdus ij izkIr la[;k,¡ fHkUu&fHkUu gSaA nksuksa la[;kvksa dk ;ksx 4 gksus dh izkf;drk Kkr dhft,A
15. ,d ikls dks isaQdus osQ ijh{k.k ij fopkj dhft,A ;fn ikls ij izdV la[;k 3 dk xq.kt gS rks ikls dks iqu% isaQosaQ vkSj ;fn dksbZ vU; la[;k izdV gks rks ,d flDosQ dks mNkysaA ?kVuk ^U;wure ,d ikls ij la[;k 3 izdV gksuk* fn;k x;k gS rks ?kVuk ^flDosQ ij iV izdV gksus* dh lizfrca/ izkf;drk Kkr dhft,A
fuEufyf[kr iz'uksa esa ls izR;sd esa lgh mÙkj pqusaA
16. ;fn P (A) = 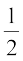 , P(B) = 0 rc P (A|B) gS%
, P(B) = 0 rc P (A|B) gS%
(A) 0 (B) 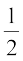 (C) ifjHkkf"kr ugha (D) 1
(C) ifjHkkf"kr ugha (D) 1
17. ;fn A vkSj B nks ?kVuk,¡ bl izdkj gSa fd P (A|B) = P (B|A) ≠ 0 rc
(A) A ⊂ B (B) A = B (C) A ∩ B = φ
(D) P (A) = P(B)
13.3 izkf;drk dk xq.ku fu;e (Multiplication Theorem on Probability)
eku yhft, fd E rFkk F ,d izfrn'kZ lef"V S dh nks ?kVuk,¡ gSaA Li"Vr;k leqPp;
E ∩ F nksuksa ?kVukvksa E rFkk F osQ ?kfVr gksus dks n'kkZrk gSA vU; 'kCnksa esa E ∩ F ?kVukvksa E rFkk F osQ ;qxir~ ?kfVr gksus dks n'kkZrk gSA ?kVuk E ∩ F dks EF Hkh fy[kk tkrk gSA
izk;% gesa l;qaDr ?kVuk EF dh izkf;drk Kkr djus dh vko';drk gksrh gSA mnkgj.k osQ fy,] ,d osQ ckn nwljk iÙkk fudkyus osQ ijh{k.k esa ge feJ ?kVuk ^,d ckn'kkg vkSj ,d jkuh* dh izkf;drk Kkr djus esa bPNqd gks ldrs gSaA ?kVuk EF dh izkf;drk Kkr djus osQ fy, ge lizfrca/ izkf;drk dk mi;ksx djrs gSa tSlk fd uhps fn[kk;k x;k gSA
ge tkurs gSa fd ?kVuk F osQ fn, tkus ij ?kVuk E dh lizfrca/ izkf;drk dks
P(E|F) }kjk n'kkZrs gSa vkSj bls fuEufyf[kr izdkj ls Kkr djrs gSaA
P(E|F) = 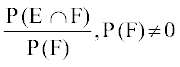
mijksDr ifj.kke ls ge fy[k ldrs gSa fd
P(E ∩ F) = P (F) . P (E|F) ... (1)
ge ;g Hkh tkurs gSa fd
P(F|E) = 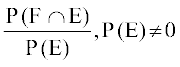
;k P(F|E) = 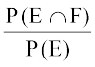 (D;ksafd E ∩ F = F ∪ E)
(D;ksafd E ∩ F = F ∪ E)
vr% P(E ∩ F) = P(E) . P(F|E) ... (2)
(1) vkSj (2) dks feykus ls gesa izkIr gksrk gS fd
P(E ∩ F) = P(E) P(F|E) = P(F). P(E|F) tc fd P(E) ≠ 0 vkSj P(F) ≠ 0
mijksDr ifj.kke dks ^izkf;drk dk xq.ku fu;e* dgrs gSaA vkb, ,d mnkgj.k ysaA
mnkgj.k 8 ,d dy'k esa 10 dkyh vkSj 5 li+sQn xsansaa gSaA nks xsan ,d osQ ckn ,d fudkyh tkrh gSa vkSj igyh xsan nwljs osQ fudkyus ls igys okil ugha j[kh tkrh gSaA eku yhft, fd dy'k esa ls izR;sd xsan dk fudkyuk lelaHkkO; gS] rks nksuksa dkys xsan fudyus dh D;k izkf;drk gS\
gy ekuk fd E ^igyh dkyh xsan osQ fudyus* dh ?kVuk gS vkSj F ^nwljh dkyh xsan osQ fudyus* dh ?kVuk gSA gesa P(E∩F) ;k P (EF) Kkr djuk gSA
vc P(E) = P (igyh fudky esa dkyh xsan fudkyuk) = 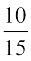
lkFk gh fn;k x;k gS fd igyh fudky esa dkyh xsan fudyh gS vFkkZr~~ ?kVuk E ?kfVr gqbZ gS] vc dy'k esa 9 dkyh xsan vkSj 5 li+sQn xsan jg xbZ gSaA blfy,] nwljh xsan dkyh gksus dh izkf;drk tc fd igyh xsan dk dkyk gksuk gesa Kkr gS] oqQN vkSj ugha osQoy F dk lizfrca/ izkf;drk gS tc E dk ?kfVr gksuk Kkr gSA
vFkkZr~~ P(F|E) = 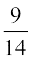
vc izkf;drk osQ xq.ku fu;e }kjk gesa izkIr gksrk gS
P(E∩F) = P(E) P(F|E) = P(E) . P(F|E) . P(G|EF)
= 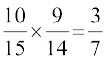
nks ls vf/d ?kVukvksa osQ fy, izkf;drk dk xq.ku fu;e ;fn E, F vkSj G ,d izfrn'kZ lef"V dh ?kVuk,¡ gSa rks
P(E∩F∩G) = P(E) P(F|E) P(G|E∩F) = P(E) P(F|E) P(G|EF)
blh izdkj izkf;drk osQ xq.ku fu;e dk foLrkj pkj ;k vf/d ?kVukvksa osQ fy, Hkh fd;k tk ldrk gSA fuEufyf[kr mnkgj.k rhu ?kVukvksa osQ fy, izkf;drk osQ xq.ku fu;e dk n`"Vkar izLrqr djrk gSA
mnkgj.k 9 52 iÙkksa dh vPNh rjg isaQVh xbZ xM~Mh esa ls ,d osQ ckn ,d rhu iÙks fcuk izfrLFkkfir fd, fudkys x,A igys nkss iÙkksa dk ckn'kkg vkSj rhljs dk bDdk gksus dh D;k izkf;drk gS\
gy eku ysa fd K ?kVuk ^fudkyk x;k iÙkk ckn'kkg gS* dks vkSj A ?kVuk ^fudkyk x;k iÙkk bDdk gS* dks O;Dr djrs gSaA Li"Vr;k gesa P (KKA) Kkr djuk gSA
vc P(K) = 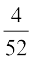
lkFk gh P(K|K) ;g Kkr gksus ij fd ^igys fudkyk x;k iÙkk ckn'kkg gS* ij nwljs iÙks dk ckn'kkg gksus dh izkf;drk dks n'kkZrk gSA vc xM~Mh esa (52 − 1) = 51 iÙks gSa ftuesa rhu ckn'kkg gS
blfy, P(K|K) = 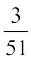
varr% P(A|KK) rhljs fudkys x, iÙks dk bDdk gksus dh lizfrca/ izkf;drk gS tc fd gesa Kkr gS fd nks ckn'kkg igys gh fudkys tk pqds gSaA vc xM~Mh esa 50 iÙks jg x, gSa
blfy, P(A|KK) = 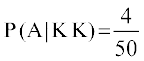
izkf;drk osQ xq.ku fu;e }kjk gesa izkIr gksrk gS fd
P(KKA) = P(K) P(K|K) P(A|KK)
= 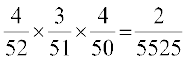
13.4 Lora=k ?kVuk,¡ (Independent Events)
52 iÙkksa dh xM~Mh esa ls ,d iÙkk fudkyus osQ ijh{k.k ij fopkj dhft, ftlesa izR;sd ekSfyd ?kVuk dks lelaHkkO; ekuk x;k gSA ;fn E rFkk F Øe'k% ?kVukvksa ^fudkyk x;k iÙkk fpM+h dk gS* vkSj ^fudkyk x;k iÙkk ,d bDdk gS* dks O;Dr djrs gSa] rks
P(E) = 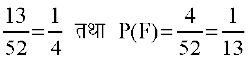
lkFk gh ^E vkSj F* ?kVuk ^fudkyk x;k iÙkk fpM+h dk bDdk gS* dks O;Dr djrh gS] blfy,
P(E ∩ F) = 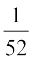
vr% P(E|F) = 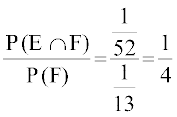
D;ksafd P(E) = 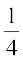 = P (E|F), ge dg ldrs gSa fd ?kVuk F osQ ?kfVr gksus dh lwpuk us ?kVuk E dh izkf;drk ij dksbZ izHkko ugha Mkyk gSA
= P (E|F), ge dg ldrs gSa fd ?kVuk F osQ ?kfVr gksus dh lwpuk us ?kVuk E dh izkf;drk ij dksbZ izHkko ugha Mkyk gSA
gesa ;g Hkh izkIr gS fd
P(F|E) = 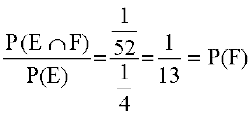
iqu% P(F) = 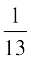 = P(F|E) n'kkZrk gS fd ?kVuk E osQ ?kfVr gksus dh lwpuk us ?kVuk F dh izkf;drk ij dksbZ izHkko ugha Mkyk gSA
= P(F|E) n'kkZrk gS fd ?kVuk E osQ ?kfVr gksus dh lwpuk us ?kVuk F dh izkf;drk ij dksbZ izHkko ugha Mkyk gSA
vr% E rFkk F bl izdkj dh ?kVuk,¡ gS fd fdlh ,d ?kVuk osQ ?kfVr gksus dh lwpuk nwljh ?kVuk dh izkf;drk ij dksbZ izHkko ugha Mkyrh gSA
bl izdkj dh ?kVukvksa dks ^Lora=k ?kVuk,¡* dgrs gSaA
ifjHkk"kk 2 nks ?kVukvksa E rFkk F dks Lora=k ?kVuk,¡ dgrs gSa ;fn
P(F| E) = P(F) tcdh P(E) ≠ 0
P(E| F) = P(E) tcdh P(F) ≠ 0
vr% bl ifjHkk"kk esa P(E) vkSj P(F) dk 'kwU;sÙkj gksuk vko';d gSA
vc izkf;drk osQ xq.ku fu;e ls
P(E ∩ F) = P(E) . P(F|E) ... (1)
;fn E vkSj F Lora=k ?kVuk,¡ gksa rks (1) ls gesa izkIr gksrk gS fd
P(E ∩ F) = P(E). P(F) ... (2)
vr% (2) osQ mi;ksx ls ge nks ?kVukvksa dh Lora=krk dks fuEufyf[kr rjg ls Hkh ifjHkkf"kr dj ldrs gSaA
ifjHkk"kk 3 eku ysa E vkSj F fdlh ;kn`fPNd ijh{k.k osQ izfrn'kZ lef"V dh nks ?kVuk,¡ gSa] rks E vkSj F Lora=k ?kVuk,¡ gksrh gSa ;fn
P(E ∩ F) = P(E) P(F)
fVIi.kh
1. nks ?kVukvksa E rFkk F dks ijkfJr (dependent) dgrs gSa] ;fn os Lora=k u gksa vFkkZr~~ ;fn P(E ∩ F ) ≠ P(E) . P(F)
2. dHkh&dHkh Lora=k ?kVukvksa vkSj ijLij viothZ ?kVukvksa osQ chp Hkze iSnk gks tkrk gSA ^Lora=k ?kVukvksa* dh ifjHkk"kk ^?kVukvksa dh izkf;drk* osQ :i esa dh xbZ gS tc fd ^ijLij viothZ ?kVukvksa* dh ifjHkk"kk ^?kVukvksa* osQ :i esa dh xbZ gSA blosQ vfrfjDr] ijLij viothZ ?kVukvksa esa dksbZ Hkh ifj.kke lkoZ dnkfi ugha gks ldrk gS ¯drq Lora=k ?kVukvksa esa ifj.kke lkoZ Hkh gks ldrs gSa] ;fn izR;sd ?kVuk vfjDr gSA Li"Vr;k ^Lora=k ?kVuk,¡* vkSj ^ijLij viothZ ?kVuk,¡* lekukFkhZ ugha gSaA
nwljs 'kCnksa esa] ;fn nks ,slh Lora=k ?kVuk,¡ ?kVrh gSa ftudh izf;drk 'kwU;srj gS] rks og ijLij viothZ ugha gks ldrh gSaA foykser% ;fn nks 'kwU;srj izkf;drk okyh ijLij viothZ ?kVuk,¡ ?kVrh gSa] rks og Lora=k ugha gks ldrh gSaA
3. nks ;kn`fPNd ijh{k.k Lora=k dgykrs gSa] ;fn izR;sd ?kVuk ;qXe E vkSj F osQ fy,] tgk¡ E igys ijh{k.k ls rFkk F nwljs ijh{k.k ls lacaf/r gSa] ?kVukvksa E rFkk F osQ ,d lkFk ?kfVr gksus dh izkf;drk] tc nksuksa ijh{k.k laiUu fd, tk,¡] izkf;drk P(E) vkSj P(F) osQ xq.kuiQy osQ cjkcj gksrh gSa] ftudk ifjdyu nksuksa ijh{k.kksa osQ vk/kj ij vyx&vyx fd;k tkrk gSA vFkkZr~~ P(E∩F) = P(E) . P(F)
4. rhu ?kVukvksa A, B vkSj C dks Lora=k dgk tkrk gS ;fn vkSj osQoy ;fn
P(A∩B) = P(A) P(B)
P(A∩C) = P(A) P(C)
P(B∩C) = P(B) P(C)
vkSj P(A∩B∩C) = P(A) P(B) P(C)
;fn mijksDr esa ls de ls de ,d Hkh 'krZ lR; ugha gksrh gS rks nh xbZ ?kVukvksa dks Lora=k ugha dgk tkrk gSA
mnkgj.k 10 ,d ikls dks ,d ckj mNkyk tkrk gSA ?kVuk ^ikls ij izkIr la[;k 3 dk vioR;Z gS*] dks E ls vkSj ^ikls ij izkIr la[;k le gS*] dks F ls fu:fir fd;k tk, rks crk,¡ D;k ?kVuk,¡ E vkSj F Lora=k gSa\
gy ge tkurs gSa fd bl ijh{k.k dk izfrn'kZ lef"V gS% S = {1, 2, 3, 4, 5, 6}
vc E = {3, 6}, F = {2, 4, 6} vkSj E ∩ F = {6}
rc P(E) = 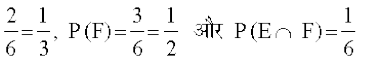
Li"Vr;k P(E ∩ F) = P(E). P(F)
vr% E vkSj F Lora=k ?kVuk,¡ gSaA
mnkgj.k 11 ,d vufHkur (unbiased) ikls dks nks ckj mNkyk x;kA eku ysa A ?kVuk ^igyh mNky ij fo"ke la[;k izkIr gksuk* vkSj B ?kVuk ^f}rh; mNky ij fo"ke la[;k izkIr gksuk* n'kkZrs gSaA ?kVukvksa A vkSj B osQ Lokra=; dk ijh{k.k dhft,A
gy ;fn lHkh 36 ekSfyd ?kVukvksa dks lelaHkkO; eku ysa rks
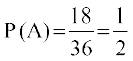 vkSj
vkSj 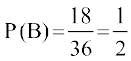
lkFk gh P(A ∩ B) = P (nksuksa mNkyksa esa fo"ke la[;k izkIr gksuk)
= 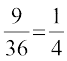
vc P(A) . P(B) = 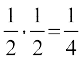
Li"Vr;k P(A ∩ B) = P(A) . P(B)
vr% A vkSj B Lora=k ?kVuk,¡ gSaA
mnkgj.k 12 rhu flDdksa dks mNkyk x;k gSA eku ysa E ?kVuk ^rhu fpr ;k rhu iV izkIr gksuk* vkSj F ?kVuk ^U;wure nks fpr izkIr gksuk* vkSj G ?kVuk ^vf/dre nks iV izkIr gksuk* dks fu:fir djrs gSaA ;qXe (E,F), (E,G) vkSj (F,G) esa dkSu&dkSu ls Lora=k gSa\ dkSu&dkSu ls ijkfJr gSa\
gy ijh{k.k dk izfrn'kZ lef"V gS %
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Li"Vr;k E = {HHH, TTT}, F= {HHH, HHT, HTH, THH}
vkSj G = {HHT, HTH, THH, HTT, THT, TTH, TTT}
lkFk gh E ∩ F = {HHH}, E ∩ G = {TTT}, F ∩ G = { HHT, HTH, THH}
blfy, P(E) = 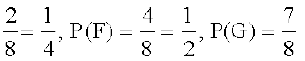
P(E ∩ F) = 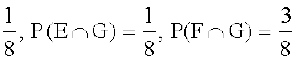
lkFk gh P(E) . P(F) = 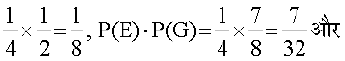
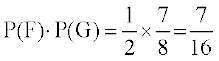
vr% P(E ∩ F) = P(E) . P(F)
P(E ∩ G) ≠ P(E) . P(G)
vkSj P(F ∩ G) ≠ P(F) . P(G)
blfy, ?kVuk,¡ (E vkSj F) Lora=k gSa tcdh ?kVuk,¡ (F vkSj G) vkSj (E vkSj G) ijkfJr gSaA
mnkgj.k 13 fl¼ dhft, fd ;fn E vkSj F nks Lora=k ?kVuk,¡ gSa rks E vkSj F′ Hkh Lora=k gksaxhA
gy D;ksafd E rFkk F Lora=k gS] blfy,
P(E ∩ F) = P(E) . P(F) ... (1)
fp=k 13.3, osQ osu&vkjs[k ls ;g Li"V gS fd E ∩ F vkSj E ∩ F′ ijLij viothZ gSa vkSj lkFk gh
E = (E ∩ F) ∪ (E ∩ F′)
D;ksafd E ∩ F vkSj E ∩ F′ ijLij viothZ gSa]
blfy, P(E) = P(E ∩ F) + P(E ∩ F′)
;k P(E ∩ F′) = P(E) − P(E ∩ F)
= P(E) − P(E) . P(F) (1) ls
= P(E) [1 − P(F]
= P(E) . P(F′)
vr% E vkSj F′ Lora=k ?kVuk,¡ gSaA
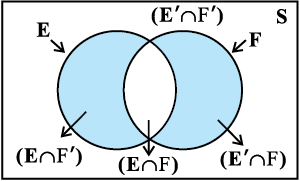
vko`Qfr 13.3
fVIi.kh blh izdkj ;g n'kkZ;k tk ldrk gS fd ;fn
(a) E′ rFkk F Lora=k gSa
(b) E′ rFkk F′ Lora=k gSaA
mnkgj.k 14 ;fn A vkSj B Lora=k ?kVuk,¡ gSa rks A ;k B esa ls U;wure ,d osQ gksus dh izkf;drk = 1− P(A′) P(B′)
= P(A) + P(B) − P(A ∩ B)
= P(A) + P(B) − P(A) P(B)
= P(A) + P(B) [1−P(A)]
= P(A) + P(B) . P(A′)
= 1− P(A′) + P(B) P(A′)
= 1− P(A′) [1− P(B)]
= 1− P(A′) P (B′)
iz'ukoyh 13.2
1. ;fn P(A) 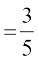 ] P (B)
] P (B) 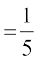 vkSj A rFkk B Lora=k ?kVuk,¡ gSa rks P (A ∩ B) Kkr dhft,A
vkSj A rFkk B Lora=k ?kVuk,¡ gSa rks P (A ∩ B) Kkr dhft,A
2. 52 iÙkksa dh ,d xM~Mh esa ls ;kn`PN;k fcuk izfrLFkkfir fd, x, nks iÙks fudkys x,A nksuksa iÙkksa osQ dkys jax dk gksus dh izkf;drk Kkr dhft,A
3. larjksa osQ ,d fMCcs dk fujh{k.k mlesa ls rhu larjksa dks ;kn`PN;k fcuk izfrLFkkfir fd, gq, fudky dj fd;k tkrk gSA ;fn rhuksa fudkys x, larjs vPNs gksa rks fMCcs dks fcØh osQ fy, Loho`Qr fd;k tkrk gS vU;Fkk vLoho`Qr dj nsrs gSaA ,d fMCck ftlesa 15 larjs gSa ftuesa ls 12 vPNs o 3 [kjkc larjs gSa] osQ fcØh osQ fy, Loho`Qr gksus dh izkf;drk Kkr dhft,A
4. ,d U;kÕ; flDdk vkSj ,d vfHkur ikls dks mNkyk x;kA eku ysa A ?kVuk ^flDosQ ij fpr izdV gksrk gS* vkSj B ?kVuk ^ikls ij la[;k 3 izdV gksrh gS* dks fu:fir djrs gSaA fujh{k.k dhft, fd ?kVuk,¡ A vkSj B Lora=k gSa ;k ugha\
5. ,d ikls ij 1, 2, 3 yky jax ls vkSj 4, 5, 6 gjs jax ls fy[ks x, gSaA bl ikls dks mNkyk x;kA eku ysa A ?kVuk ^la[;k le gS* vkSj B ?kVuk ^la[;k yky jax ls fy[kh xbZ gS*] dks fu:fir djrs gSaA D;k A vkSj B Lora=k gSa\
6. eku ysa E rFkk F nks ?kVuk,¡ bl izdkj gSa fd P(E) 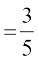 , P (F)
, P (F) 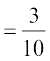 vkSj P (E ∩ F) =
vkSj P (E ∩ F) = 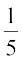 rc D;k E rFkk F Lora=k gSa?
rc D;k E rFkk F Lora=k gSa?
7. A vkSj B ,slh ?kVuk,¡ nh xbZ gSa tgk¡ 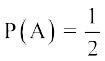 , P (A ∪ B)
, P (A ∪ B) 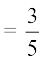 rFkk P(B) = p.
rFkk P(B) = p.
p dk eku Kkr dhft, ;fn (i) ?kVuk,¡ ijLij viothZ gSaA (ii) ?kVuk,¡ Lora=k gSaA
8. eku ysa A vkSj B Lora=k ?kVuk,¡ gSa rFkk P(A) = 0.3 vkSj P(B) = 0.4. rc
(i) P (A ∩ B) (ii) P (A ∪ B)
(iii) P(A|B) (iv) 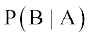 Kkr dhft,A
Kkr dhft,A
9. nh xbZ ?kVuk,¡ A vkSj B ,slh gSa] tgk¡ P(A)  , P (B) =
, P (B) = 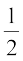 vkSj P(A ∩ B) =
vkSj P(A ∩ B) = 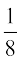 rc P(A&ugha vkSj B&ugha) Kkr dhft,A
rc P(A&ugha vkSj B&ugha) Kkr dhft,A
10. eku ysa A rFkk B Lora=k ?kVuk,¡ gSa vkSj P(A) = 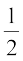 rFkk P(B) =
rFkk P(B) = 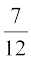 vkSj P (A&ugha vkSj B&ugha)
vkSj P (A&ugha vkSj B&ugha)  . D;k A vkSj B Lora=k
. D;k A vkSj B Lora=k
?kVuk,¡ gSa\
11. A vkSj B Lora=k ?kVuk,¡ nh xbZ gSa tgk¡ P(A) = 0.3, P(B) = 0.6 rks
(i) P(A vkSj B) (ii) P(A vkSj B&ugha)
(iii) P(A ;k B) (iv) P(A vkSj B esa dksbZ Hkh ugha) dk eku Kkr dhft,A
12. ,d ikls dks rhu ckj mNkyk tkrk gS rks de ls de ,d ckj fo"ke la[;k izkIr gksus dh izkf;drk Kkr dhft,A
13. nks xsan ,d ckWDl ls fcuk izfrLFkkfir fd, fudkyh tkrh gSA ckWDl esa 10 dkyh vkSj 8 yky xsnsa gSa rks izkf;drk Kkr dhft, (i) nksuksa xsansaa yky gksa (ii) izFke dkyh ,oa nwljh yky gks (iii) ,d dkyh rFkk nwljh yky gksA
14. ,d fo'ks"k leL;k dks A vkSj B }kjk Lora=k :i ls gy djus dh izkf;drk,¡ Øe'k% 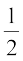 vkSj
vkSj 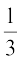 gSaA ;fn nksuksa] Lora=k :i ls] leL;k gy djus dk iz;kl djrs gSa] rks izkf;drk Kkr dhft, fd
gSaA ;fn nksuksa] Lora=k :i ls] leL;k gy djus dk iz;kl djrs gSa] rks izkf;drk Kkr dhft, fd
(i) leL;k gy gks tkrh gS
(ii) muesa ls rF;r% dksbZ ,d leL;k gy dj ysrk gSA
15. rk'k osQ 52 iÙkksa dh ,d lqfefJr xM~Mh ls ,d iÙkk ;kn`PN;k fudkyk tkrk gSA fuEufyf[kr esa ls fdu n'kkvksa esa ?kVuk,¡ E vkSj F Lora=k gSa?
(i) E : ‘fudkyk x;k iÙkk gqoqQe dk gS’
F : ‘fudkyk x;k iÙkk bDdk gS’
(ii) E : ‘fudkyk x;k iÙkk dkys jax dk gS’
F : ‘fudkyk x;k iÙkk ,d ckn'kkg gS’
(iii) E : ‘fudkyk x;k iÙkk ,d ckn'kkg ;k ,d csxe gS’
F : ‘fudkyk x;k iÙkk ,d csxe ;k ,d xqyke gS’
16. ,d Nk=kkokl esa 60% fo|kFkhZ ¯gnh dk] 40% vaxzs”kh dk vkSj 20% nksuksa v[kckj i<+rs gSaA ,d Nk=kk dks ;kn`PN;k pquk tkrk gSA
(a) izkf;drk Kkr dhft, fd og u rks ¯gnh vkSj u gh vaxzs”kh dk v[kckj i<+rh gSA
(b) ;fn og ¯gnh dk v[kckj i<+rh gS rks mlosQ vaxzs”kh dk v[kckj Hkh i<+us okyh gksus dh izkf;drk Kkr dhft,A
(c) ;fn og vaxzs”kh dk v[kckj i<+rh gS rks mlosQ ¯gnh dk v[kckj Hkh i<+us okyh gksus dh izkf;drk Kkr dhft,A
17. ;fn iklksa dk ,d tksM+k mNkyk tkrk gS rks izR;sd ikls ij le vHkkT; la[;k izkIr djus dh izkf;drk fuEufyf[kr esa ls D;k gS\
(A) 0 (B) 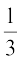 (C)
(C) 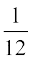 (D)
(D) 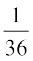
18. nks ?kVukvksa A vkSj B dks ijLij Lora=k dgrs gSa] ;fn
(A) A vkSj B ijLij viothZ gSa (B) P(A′B′) = [1–P(A)][1–P(B)]
(C) P(A) = P(B) (D) P(A) + P(B) = 1
13.5 cs”k&izes; (Bayes' Theorem)
eku yhft, fd nks FkSys I vkSj II fn, x, gSaA Fksyk I esa 2 li+sQn vkSj 3 yky xsansaa gSaA vkSj FkSyk II esa 4 li+sQn vkSj 5 yky xsansaa gSaA fdlh ,d FkSys esa ls ,d xsan ;kn`PN;k fudkyh tkrh gSA ge fdlh ,d FkSys dks pquus dh izkf;drk 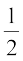 Kkr dj ldrs gSa ;k fdlh fo'ks"k FkSys (eku ysa FkSyk I) esa ls ,d fo'ks"k jax (eku ysa li+sQn) xsan dks fudkyus dh izkf;drk Hkh Kkr dj ldrs gSaA vU; 'kCnksa esa ge fdlh fo'ks"k jax dh xsan fudkyus dh izkf;drk Kkr dj ldrs gSa] ;fn gesa ;g fn;k x;k gks fd xsan dkSu&ls FkSys ls fudkyh xbZ gSA ysfdu D;k ge bl ckr dh izkf;drk Kkr dj ldrs gSa fd xsan fdlh fo'ks"k FkSys (eku ysa FkSyk&II) ls fudkyh xbZ gS ;fn gesa fudkyh xbZ xsan dk jax irk gS\ ;gk¡ gesa FkSyk&II osQ pquus dh izfrykse (reverse)izkf;drk Kkr djuh gS tcfd blosQ ckn gksus okyh ?kVuk dk gesa Kku gSA izfl¼ xf.krK tkWu cs”k us izfrykse izkf;drk Kkr djus dh leL;k dk lek/ku lizfrca/ izkf;drk osQ mi;ksx }kjk fd;k gSA muosQ }kjk cuk;k x;k lw=k ^cs”k&izes;* osQ uke ls tkuk tkrk gS tks mudh e`R;ksijkar 1763 esa izdkf'kr gqvk FkkA cs”k&izes; osQ dFku o izek.k ls iwoZ vkb, ,d ifjHkk"kk vkSj oqQN izkjafHkd ifj.kkeksa ij fopkj dhft,A
Kkr dj ldrs gSa ;k fdlh fo'ks"k FkSys (eku ysa FkSyk I) esa ls ,d fo'ks"k jax (eku ysa li+sQn) xsan dks fudkyus dh izkf;drk Hkh Kkr dj ldrs gSaA vU; 'kCnksa esa ge fdlh fo'ks"k jax dh xsan fudkyus dh izkf;drk Kkr dj ldrs gSa] ;fn gesa ;g fn;k x;k gks fd xsan dkSu&ls FkSys ls fudkyh xbZ gSA ysfdu D;k ge bl ckr dh izkf;drk Kkr dj ldrs gSa fd xsan fdlh fo'ks"k FkSys (eku ysa FkSyk&II) ls fudkyh xbZ gS ;fn gesa fudkyh xbZ xsan dk jax irk gS\ ;gk¡ gesa FkSyk&II osQ pquus dh izfrykse (reverse)izkf;drk Kkr djuh gS tcfd blosQ ckn gksus okyh ?kVuk dk gesa Kku gSA izfl¼ xf.krK tkWu cs”k us izfrykse izkf;drk Kkr djus dh leL;k dk lek/ku lizfrca/ izkf;drk osQ mi;ksx }kjk fd;k gSA muosQ }kjk cuk;k x;k lw=k ^cs”k&izes;* osQ uke ls tkuk tkrk gS tks mudh e`R;ksijkar 1763 esa izdkf'kr gqvk FkkA cs”k&izes; osQ dFku o izek.k ls iwoZ vkb, ,d ifjHkk"kk vkSj oqQN izkjafHkd ifj.kkeksa ij fopkj dhft,A
13.5.1 ,d izfrn'kZ lef"V dk foHkktu (Partition of a sample space)
?kVukvksa E1, E2 ... En osQ leqPp; dks izfrn'kZ lef"V S osQ foHkktu dks fu:fir djrk gS ;fn
(a) Ei ∩ Ej = φ, i ≠ j, i, j = 1, 2, 3, ...n
(b) E1 ∪ Ε2 ∪...∪ En= S rFkk
(c) P(Ei) > 0, izR;sd i = 1, 2, ..., n osQ fy,
nwljs 'kCnksa esa] ?kVuk,¡ E1, Ε2, ... En izfrn'kZ lef"V S osQ foHkktu dks fu:fir djrh gSa ;fn os ;qXer% vla;qDr gSa] lexz gS rFkk mudh izkf;drk 'kwU;srj gSA
mnkgj.kr% ge ns[krs gSa fd dksbZ ?kVuk E vkSj mldh iwjd ?kVuk E′ izfrn'kZ lef"V S dk foHkktu gS D;ksafd E ∩ E′ = φ vkSj E ∪ E′ = S.
osu&vkjs[k fp=k 13.3, ls ge vklkuh ls izs{k.k dj ldrs gSa fd ;fn E vkSj F fdlh izfrn'kZ lef"V S, osQ laxr dksbZ nks ?kVuk,¡ gSa] rks {E ∩ F, E ∩ F′} leqPp; E dk ,d foHkktu gSA
leqPp; {E′ ∩ F, E ∩ F, E ∩ F′} leqPp; E ∪ F dk ,d foHkktu gS vkSj leqPp;
{E ∩ F′, E ∩ F, E′ ∩ F, E′ ∩ F′} laiw.kZ izfrn'kZ S dk ,d foHkktu gSA
vc ge laiw.kZ izkf;drk dh izes; dks fl¼ djsaxsA
13.5.2 laiw.kZ izkf;drk dh izes; (Theorem of Total Probability)
eku ysa {E1, E2,...,En} izfrn'kZ lef"V S, dk ,d foHkktu gS vkSj eku ysa fd izR;sd ?kVuk E1, E2 ,...,En dh izkf;drk 'kwU;sÙkj gSA eku yhft, A izfrn'kZ lef"V osQ laxr ,d ?kVuk gS] rc,
P(A) = P(E1) P(A|E1) + P(E2) P(A|E2) + ... + P(En) P(A|En)
= 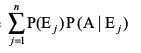
miifÙk fn;k x;k gS fd E1, E2, ..., En izfrn'kZ lef"V S dk ,d foHkktu gS (fp=k 13-4) blfy,]
vko`Qfr 13.4
S = E1 ∪ E2 ∪ ... ∪ En ... (1)
vkSj Ei ∩ Ej = φ ∀ i ≠ j, i, j = 1, 2, ...., n
gesa Kkr gS fd fdlh ?kVuk A, osQ fy,
A = A ∩ S
= A ∩ (E1 ∪ E2 ... En)
= (A ∩ E1) ∪ (A ∩ E2) ∪ ...∪ (A ∩ En)
lkFk gh A ∩ Ei, vkSj A ∩ Ej, Øe'k% leqPp;ks Ei vkSj Ej osQ mileqPp; gSa tks i ≠ j, osQ fy, vla;qDr gS blfy, i ≠ j, i, j = 1, 2 ..., n osQ fy, A ∩ Ei vkSj A ∩Ej Hkh vla;qDr gSaA
blfy, P(A) = P[(A ∩ E1) ∪ (A ∩ E2) ∪ .....∪ (A ∩ En)]
= P(A ∩ E1) + P(A ∩ E2) + ... + P(A ∩ En)
vc P(A ∩ Ei) = P(Ei) P(A|Ei) D;ksafd P (Ei) ≠ 0∀i = 1,2,..., n
izkf;drk osQ xq.ku fu;e }kjk ge tkurs gSa fd
blfy, P(A) = P(E1) P(A|E1) + P(E2) P(A|E2) + ... + P(En) P(A|En)
;k P(A) =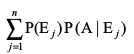
mnkgj.k 15 fdlh O;fDr us ,d fuekZ.k dk;Z dk Bsdk fy;k gSA gM+rky gksus dh izkf;drk 0-65 gSA gM+rky u gksus dh rFkk gM+rky gksus dh fLFkfr;ksa esa fuekZ.k dk;Z osQ le;kuqlkj iw.kZ gksus dh izkf;drk,¡ Øe'k% 0-80 rFkk 0-32 gSaA fuekZ.k dk;Z osQ le;kuqlkj iw.kZ gksus dh izkf;drk Kkr dhft,A
P(B) = 0.65, P (gM+rky ugha) = P(B′) = 1 − P(B) = 1 − 0.65 = 0.35
P(A | B) = 0.32, P(A | B′) = 0.80
D;ksafd ?kVuk,¡ B vkSj B′ lef"V leqPp; osQ foHkktu gSa blfy, laiw.kZ izkf;drk izes; }kjk
= P(B) . P(A | B) + P(B′) P(A | B′)
= 0.65 × 0.32 + 0.35 × 0.8
= 0.208 + 0.28 = 0.488
vr% fuekZ.k dk;Z le;kuqlkj iw.kZ gksus dh izkf;drk 0-488 gSA
vc ge cs”k&izes; dk izdFku djsaxs rFkk bls fl¼ djsaxsA
cs”k&izes; (Bayes' Theorem) ;fn E1, E2 ,..., En vfjDr ?kVuk,¡ gSa tks fd izfrn'kZ lef"V S osQ foHkktu dk fuekZ.k djrh gSa vFkkZr~~ E1, E2 ,...., En ;qXer% vla;qDr gSa vkSj E1∪ E2∪ ,..., ∪ En = S vkSj A dksbZ ,slh ?kVuk gS ftldh izkf;drk 'kwU;srj gS] rks
P(Ei|A) = 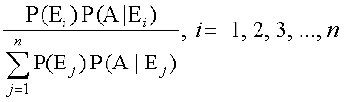
miifÙk gesa Kkr gS fd
P(Ei|A) = 
= 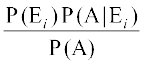 (izkf;drk osQ xq.ku fu;e ls)
(izkf;drk osQ xq.ku fu;e ls)
= 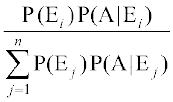 (laiw.kZ izkf;drk osQ fu;e ls)
(laiw.kZ izkf;drk osQ fu;e ls)
fVIi.kh cs”k&izes; osQ vuqiz;ksx esa fuEufyf[kr 'kCnkoyh dk mi;ksx djrs gSa
?kVukvksa E1, E2, ... En dks ifjdYiuk,¡ (hypotheses)dgrs gSaA
P(Ei) dks ifjdYiuk Ei dh iwoZdkyhu (a priori) izkf;drk dgrs gSaA lizfrca/ izkf;drk
P(EiA) dks ifjdYiuk Ei dh mÙkjdkyhu (a posteriori) izkf;drk dgrs gSaA
cs”k izes; dks ^dkj.kksa* dh izkf;drk dk lw=k Hkh dgk tkrk gSA D;ksafd Ei izfrn'kZ lef"V S osQ ,d foHkktu dk fuekZ.k djrs gSa blfy, ?kVukvksa Ei esa ls ,d le; esa ,d vkSj osQoy
,d gh ?kfVr gksrh gS (vFkkZr~~ Ei esa ls osQoy ,d gh ?kVuk ?kVrh gS vkSj ,d ls vf/d ugha ?kV ldrh gS) vr% mijksDr lw=k gesa fdlh fo'ks"k Ei (vFkkZr~~ ,d dkj.k)dh izkf;drk nsrk gS tcfd ?kVuk A dk ?kfVr gksuk fn;k x;k gSA
cs”k&izes; dh fofo/ ifjfLFkfr;ksa esa mi;ksfxrk gSA buesa ls oqQN dks fuEufyf[kr mnkgj.kksa esa Li"V fd;k x;k gSA
mnkgj.k 16 nks FkSys I vkSj II fn, gSaA FkSys I esa 3 yky vkSj 4 dkyh xsansaa gSa tc fd FkSys II esa 5 yky vkSj 6 dkyh xsansaa gSaA fdlh ,d FkSys esa ls ;kn`PN;k ,d xsan fudkyh xbZ gS tks fd yky jax dh gSA bl ckr dh D;k izkf;drk gS fd ;g xsan FkSys II ls fudkyh xbZ gS\
gy FkSys I dk p;u gksuk dks E1 ls vkSj FkSys II osQ p;u dks E2 eku yhft,A eku yhft, fd yky jax dh xsan fudyus dh ?kVuk dks A ls fu:fir djrs gSaA
rc P(E1) = P(E2) = 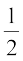
lkFk gh P(A|E1) = P(FkSys I esa ls yky jax dh xsan fudkyuk) = 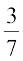
vkSj P(A|E2) = P(FkSys II esa ls yky jax dh xsan fudkyuk) = 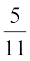
vc FkSys II esa ls xsan fudkyus dh izkf;drk] tc fd ;g Kkr gS fd og yky jax dh gS = P(E2|A), cs”k&izes; }kjk
P(E2|A) = 
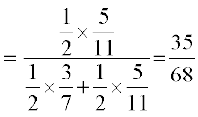
mnkgj.k 17 rhu vfHkUu fMCcs I, II vkSj III fn, x, gSa tgk¡ izR;sd esa nks flDosQ gSaA fMCcs I esa nksuksa flDosQ lksus osQ gS] fMCcs II esa nksuksa flDosQ pk¡nh osQ gSa vkSj fMCcs III esa ,d lksus vkSj ,d pk¡nh dk flDdk gSA ,d O;fDr ;kn`PN;k ,d fMCck pqurk gS vkSj mlesa ls ;kn`PN;k ,d flDdk fudkyrk gSA ;fn flDdk lksus dk gS] rks bl ckr dh D;k izkf;drk gS fd fMCcs esa nwljk flDdk Hkh lksus dk gh gS\
gy eku ysa E1, E2 vkSj E3 Øe'k% fMCcs I, II vkSj III osQ p;u dks fu:fir djrs gSa
rc P(E1) = P(E2) = P(E3) = 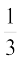
lkFk gh eku ysa A ?kVuk ^fudkyk x;k flDdk lksus dk gS* dks n'kkZrk gSA
rc P(A|E1) = P(fMCcs I ls lksus dk flDdk fudyuk) =  = 1
= 1
P(A|E2) = P(fMCcs II ls lksus dk ,d flDdk fudyuk) = 0
P(A|E3) = P(fMCcs III ls lksus dk flDdk fudyuk) = 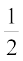
vc fMCcs esa nwljk flDdk Hkh lksus dk gksus dh izkf;drk
= fudkyk x;k lksus dk flDdk fMCcs I ls gksus dh izkf;drk
= P(E1|A)
vc cs”k&izes; }kjk
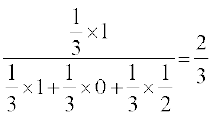
P(E1|A) = 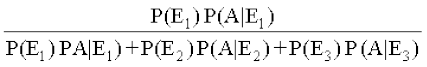
= 
mnkgj.k 18 eku ysa fd ,d ,p-vkbZ-oh- ijh{k.k dh fo'oluh;rk fuEufyf[kr izdkj ls fufnZ"V dh xbZ gSA
,p-vkbZ-oh- iksthfVo O;fDr;ksa osQ fy, ijh{k.k 90% irk yxkus esa vkSj 10% irk u yxkus esa l{ke gSA ,p-vkbZ-oh- ls Lora=k O;fDr;ksa osQ fy, ijh{k.k] 99% lgh irk yxkrk gS ;kuh ,p-vkbZ-oh usxsfVo crkrk gS tcfd 1% ijhf{kr O;fDr;ksa osQ fy, ,p-vkbZ-oh- iksthfVo crkrk gSA ,d cM+h tula[;k] ftlesa 0.1% O;fDr ,p-vkbZ-oh- xzLr gS] esa ls ,d O;fDr ;kn`PN;k pquk tkrk gS vkSj ml dk ijh{k.k fd;k tkus ij jksxfoKkuh ,p-vkbZ-oh- dh mifLFkfr crkrk gSA D;k izkf;drk gS fd og O;fDr okLro esa ,p-vkbZ-oh- (iksthfVo) gS\
gy eku ysa E pqus x, O;fDr osQ okLro esa ,p-vkbZ-oh- iksthfVo gksus dh ?kVuk vkSj A O;fDr osQ ,p-vkbZ-oh- ijh{k.k esa iksthfVo gksus dh ?kVuk dks n'kkZrs gSaA gesa P(E|A) Kkr djuk gSA
lkFk gh E′ pqus x, O;fDr osQ ,p-vkbZ-oh- iksthfVo u gksus dh ?kVuk dks n'kkZrk gSA
Li"Vr;k {E, E′} tula[;k esa lHkh O;fDr;ksa osQ izfrn'kZ lef"V dk ,d foHkktu gSA gesa Kkr gS
P(E) = 0.1% 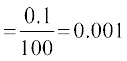
P(E′) = 1 – P (E) = 0.999
P(A| E) = P (O;fDr dk ijh{k.k esa ,p-vkbZ-oh- iksthfVo n'kkZuk tcfd fn;k x;k gS fd og okLro esa ,p-vkbZ-oh- iksthfVo gS) = 90% = 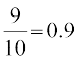
vkSj P(A|E′) = P (O;fDr dk ijh{k.k esa ,p-vkbZ-oh- iksthfVo n'kkZuk tc fd fn;k x;k gS fd og okLro esa ,p-vkbZ-oh- iksthfVo ugha gS) = 1% = 0.01
vc cs”k&izes; }kjk
P(E|A) = 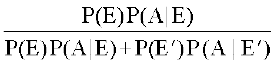
= 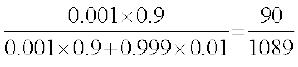 = 0.083 (yxHkx)
= 0.083 (yxHkx)
vr% ,d ;kn`PN;k pqus x, O;fDr osQ okLro esa ,p-vkbZ-oh- iksthfVo gksus dh izkf;drk tc fd Kkr gS fd mldk ,p-vkbZ-oh- ijh{k.k iksthfVo gS] 0.083 gSA
mnkgj.k 19 ,d cksYV cukus osQ dkj[+kkus esa e'khusa (;a=k) A, B vkSj C oqQy mRiknu dk Øe'k% 25%, 35% vkSj 40% cksYV cukrh gSaA bu e'khuksa osQ mRiknu dk Øe'k% 5] 4] vkSj 2 izfr'kr Hkkx [kjkc (=kqfViw.kZ) gSaA cksYVksa osQ oqQy mRiknu esa ls ,d cksYV ;kn`PN;k fudkyk tkrk gS vkSj og [kjkc ik;k tkrk gSA bldh D;k izkf;drk gS fd ;g cksYV e'khu B }kjk cuk;k x;k gS\
gy eku fy;k fd ?kVuk,¡ B1, B2, B3 fuEu izdkj gS%
B1 : cksYV e'khu A }kjk cuk;k x;k gS
B2 : cksYV e'khu B }kjk cuk;k x;k gS
B3 : cksYV e'khu C }kjk cuk;k x;k gS
Li"V gS fd ?kVuk,¡ B1, B2, B3 ijLij viothZ vkSj ifjiw.kZ gSA eku fy;k fd ?kVuk E fuEu izdkj gS% E cksYV [kjkc gSA
?kVuk E, ?kVukvksa B1 ;k B2 ;k B3 osQ lkFk ?kfVr gksrh gSA fn;k gS%
P(B1) = 25% = 0.25, P (B2) = 0.35 vkSj P(B3) = 0.40
iqu% P(E|B1) = cksYV osQ [kjkc gksus dh izkf;drk tc fd fn;k gks fd og e'khu B }kjk fufeZr gS
= 5% = 0.05
blh izdkj P(E|B2) = 0.04, P(E|B3) = 0.02
cs”k&izes; }kjk gesa Kkr gS fd
P(B2|E) = 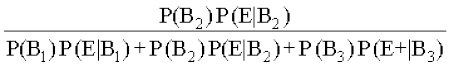
= 
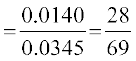
mnkgj.k 20 ,d MkWDVj dks ,d jksxh dks ns[kus vkuk gSA igys osQ vuqHkoksa ls ;g Kkr gS fd mlosQ Vªsu] cl] LowQVj ;k fdlh vU; okgu ls vkus dh izkf;drk,¡ Øe'k% 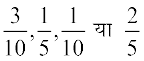 gS ;fn og Vsªu] cl ;k LowQVj ls vkrk gS rks mlosQ nsj ls vkus dh izkf;drk,¡ Øe'k%
gS ;fn og Vsªu] cl ;k LowQVj ls vkrk gS rks mlosQ nsj ls vkus dh izkf;drk,¡ Øe'k% 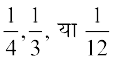 gS] ijarq fdlh vU; okgu ls vkus ij mls nsj ugha gksrh gSA ;fn og nsj ls vk;k] rks mlosQ Vsªu ls vkus dh izkf;drk Kkr dhft,A
gS] ijarq fdlh vU; okgu ls vkus ij mls nsj ugha gksrh gSA ;fn og nsj ls vk;k] rks mlosQ Vsªu ls vkus dh izkf;drk Kkr dhft,A
gy eku yhft, fd ^MkWDVj osQ jksxh osQ ;gk¡ nsj ls vkus* dh ?kVuk E gSA ;fn MkWDVj osQ Vsªu] cl] LowQVj ;k fdlh vU; okgu }kjk vkus dh ?kVuk,¡ Øe'k% T1, T2, T3, vkSj T4 gks] rks
P(T1) = 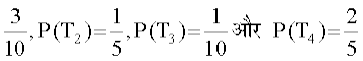 (fn;k gS)
(fn;k gS)
P(E|T1) = MkWDVj osQ Vsªu }kjk vkus ij nsj ls igq¡pus dh izkf;drk = 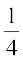
blh izdkj, P(E|T2) = 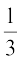 , P (E|T3) =
, P (E|T3) = 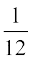 , P(E|T4) = 0, D;ksafd vU; okgu }kjk vkus ij mls nsjh ugha gksrhA
, P(E|T4) = 0, D;ksafd vU; okgu }kjk vkus ij mls nsjh ugha gksrhA
vc cs”k&izes; }kjk
P(T1|E) = MkWDVj }kjk nsj ls vkus ij Vsªu }kjk vkus dh izkf;drk
= 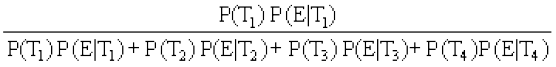
= 
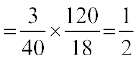
vr% vHkh"V izkf;drk 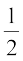 gSA
gSA
mnkgj.k 21 ,d O;fDr osQ ckjs esa Kkr gS fd og 4 esa ls 3 ckj lR; cksyrk gSA og ,d ikls dks mNkyrk gS vkSj crykrk gS fd ml ij vkus okyh la[;k 6 gSA bl dh izkf;drk Kkr dhft, fd ikls ij vkus okyh la[;k okLro esa 6 gSA
gy eku yhft, fd E] ^O;fDr }kjk ikls dks mNky dj ;g crkus dh fd ml ij vkus okyh la[;k 6 gS* dh ?kVuk gSA eku yhft, fd S1] ikls ij la[;k 6 vkus dh ?kVuk vkSj S2 ikls ij la[;k 6 ugha vkus dh ?kVuk gSaA rc
P(S1) = la[;k 6 vkus dh ?kVuk dh izkf;drk = 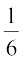
P(S2) = la[;k 6 ugha vkus dh ?kVuk dh izkf;drk = 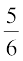
P(E|S1) = O;fDr }kjk ;g crkus ij fd ikls fd la[;k 6 vkbZ gS tcfd ikls ij vkus okyh la[;k okLro esa 6 gS] dh izkf;drk
= O;fDr }kjk lR; cksyus dh izkf;drk = 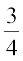
P(E|S2) = O;fDr }kjk ;g crkus ij fd ikls ij la[;k 6 vkbZ gS tcfd ikls ij vkus okyh la[;k okLro esa 6 ugha gS] dh izkf;drk
= O;fDr }kjk lR; ugha cksyus dh izkf;drk 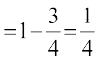
vc cs”k&izes; }kjk
P(S1|E) = O;fDr }kjk ;g crkus dh izkf;drk fd la[;k 6 izdV gqbZ gS] tc okLro esa la[;k 6 gS
= 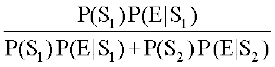 =
= 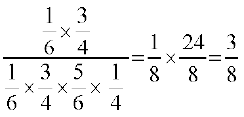
vr% vHkh"V izkf;drk 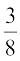 gSA
gSA
iz'ukoyh 13.3
1. ,d dy'k esa 5 yky vkSj 5 dkyh xsnsa gSaA ;kn`PN;k ,d xsan fudkyh tkrh gS] bldk jax uksV djus osQ ckn iqu% dy'k esa j[k nh tkrh gSA iqu% fudkys x, jax dh 2 vfrfjDr xsansaa dy'k esa j[k nh tkrh gS rFkk dy'k esa ls ,d xsan fudkyh tkrh gSA nwljh xsansaa dh yky gksus dh izkf;drk D;k gS\
2. ,d FkSys esa 4 yky vkSj 4 dkyh xsansaa gSa vkSj ,d vU; FkSys esa 2 yky vkSj 6 dkyh xsansa gSaA nksuksa FkSyksa esa ls ,d dks ;kn`PN;k pquk tkrk gS vkSj mlesa ,d xsan fudkyh tkrh gS tks fd yky gSA bl ckr dh D;k izkf;drk gS fd xsan igys FkSys ls fudkyh xbZ gS\
3. ;g Kkr gS fd ,d egkfo|ky; osQ Nk=kksa esa ls 60% Nk=kkokl esa jgrs gSa vkSj 40% Nk=kkokl esa ugha jgrs gSaA iwoZorhZ o"kZ osQ ifj.kke lwfpr djrs gSa fd Nk=kkokl esa jgus okys Nk=kksa esa ls 30% vkSj Nk=kkokl esa u jgus okys Nk=kksa esa ls 20% Nk=kksa us A&xzsM fy;kA o"kZ osQ var esa egkfo|ky; osQ ,d Nk=k dks ;kn`PN;k pquk x;k vkSj ;g ik;k x;k fd mls A-xzsM feyk gSA bl ckr dh D;k izkf;drk gS fd og Nk=k Nk=kkokl es jgus okyk gS\
4. ,d cgqfodYih iz'u dk mÙkj nsus esa ,d fo|kFkhZ ;k rks iz'u dk mÙkj tkurk gS ;k og vuqeku yxkrk gSA eku ysa fd mlosQ mÙkj tkuus dh izkf;drk 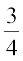 gS vkSj vuqeku yxkus dh izkf;drk
gS vkSj vuqeku yxkus dh izkf;drk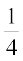 gSA eku ysa fd Nk=k osQ iz'u osQ mÙkj dk vuqeku yxkus ij lgh mÙkj nsus dh izkf;drk
gSA eku ysa fd Nk=k osQ iz'u osQ mÙkj dk vuqeku yxkus ij lgh mÙkj nsus dh izkf;drk 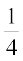 gS rks bl ckr dh D;k izkf;drk gS fd dksbZ Nk=k iz'u dk mÙkj tkurk gS ;fn ;g Kkr gS fd mlus lgh mÙkj fn;k gS\
gS rks bl ckr dh D;k izkf;drk gS fd dksbZ Nk=k iz'u dk mÙkj tkurk gS ;fn ;g Kkr gS fd mlus lgh mÙkj fn;k gS\
5. fdlh fo'ks"k jksx osQ lgh funku osQ fy, jDr dh tk¡p 99% vljnkj gS] tc okLro esa jksxh ml jksx ls xzLr gksrk gSA ¯drq 0.5% ckj fdlh LoLFk O;fDr dh jDr tk¡p djus ij funku xyr fjiksVZ nsrk gS ;kuh O;fDr dks jksx ls xzLr crykrk gSA ;fn fdlh tuleqnk; esa 0-1% yksx ml jksx ls xzLr gS rks D;k izkf;drk gS fd dksbZ ;kn`PN;k pquk x;k O;fDr ml jksx ls xzLr gksxk ;fn mlosQ jDr dh tk¡p esa ;g crk;k tkrk gS fd mls ;g jksx gS\
6. rhu flDosQ fn, x, gSaA ,d flDosQ osQ nksuksa vksj fpr gh gSA nwljk flDdk vfHkur gS ftlesa fpr 75% ckj izdV gksrk gS vkSj rhljk vufHkru flDdk gSA rhuksa esa ls ,d flDosQ dks ;kn`PN;k pquk x;k vkSj mls mNkyk x;k gSA ;fn flDosQ ij fpr izdV gks] rks D;k izkf;drk gS fd og nksuksa fpr okyk flDdk gS\
7. ,d chek oaQiuh 2000 LowQVj pkydksa] 4000 dkj pkydksa vkSj 6000 Vªd pkydksa dk chek djrh gSA nq?kZVukvksa dh izkf;drk,¡ Øe'k% 0-01] 0-03 vkSj 0-15 gSA cheko`Qr O;fDr;ksa (pkydksa) esa ls ,d nq?kZVukxzLr gks tkrk gSA ml O;fDr osQ LowQVj pkyd gksus dh izkf;drk D;k gS\
8. ,d dkj[kkus esa A vkSj B nks e'khus yxh gSaA iwoZ fooj.k ls irk pyrk gS fd oqQy mRiknu dk 60% e'khu A vkSj 40% e'khu B }kjk fd;k tkrk gSA blosQ vfrfjDr e'khu A dk 2% vkSj e'khu B dk 1% mRiknu [kjkc gSA ;fn oqQy mRiknu dk ,d <sj cuk fy;k tkrk gS vkSj ml <sj ls ;kn`PN;k fudkyh xbZ oLrq [kjkc gks] rks bl oLrq osQ ^e'khu A* }kjk cus gksus dh izkf;drk D;k gksxh\
9. nks ny ,d fuxe osQ funs'kd eaMy esa LFkku ikus dh izfrLi/kZ esa gSaA igys rFkk nwljs ny osQ thrus dh izkf;drk,¡ Øe'k% 0-6 rFkk 0-4 gSaA blosQ vfrfjDr ;fn igyk ny thrrk gS rks ,d u, mRikn osQ izkjEHk gksus dh izkf;drk 0-7 gS vkSj ;fn nwljk ny thrrk gS rks bl ckr dh laxr izkf;drk 0-3 gSA bldh izkf;drk Kkr dhft, fd u;k mRiknu nwljs ny }kjk izkjEHk fd;k x;k FkkA
10. eku yhft, fd dksbZ yM+dh ,d iklk mNkyrh gSA ;fn mls 5 ;k 6 dh la[;k izkIr gksrh gS rks og ,d flDosQ dks rhu ckj mNkyrh gS vkSj ^fprksa* dh la[;k uksV djrh gSA ;fn mls 1] 2] 3 ;k 4 dh la[;k izkIr gksrh gS rks og ,d flDosQ dks ,d ckj mNkyrh gS vkSj ;g uksV djrh gS fd ml ij ^fpr* ;k ^iV* izkIr gqvkA ;fn mls Bhd ,d fpr izkIr gksrk gS] rks mlosQ }kjk mNkys x, ikls ij 1] 2] 3 ;k 4 izkIr gksus dh izkf;drk D;k gS\
11. ,d O;kolkf;d fuekZrk osQ ikl A, B rFkk C e'khu vkWijsVj gSaA izFke vkWijsVj A 1% [kjkc lkexzh mRikfnr djrk gaS rFkk vkWijsVj B vkSj C Øe'k% 5% vkSj 7% [kjkc lkexzh mRikfnr djrk gSA dk;Z ij A oqQy le; dk 50% yxkrk gS] B oqQy le; dk 30% rFkk C oqQy le; dk 20% yxkrk gSA ;fn ,d [kjkc lkexzh mRikfnr gS rks bls A }kjk mRikfnr fd, tkus dh izkf;drk D;k gS?
12. 52 rk'kksa dh xM~Mh ls ,d iÙkk [kks tkrk gSA 'ks"k iÙkksa ls nks iÙks fudkys tkrs gSa tks b±V osQ iÙks gSaA [kks x, iÙks dh b±V gksus dh izkf;drk D;k gS\
13. A }kjk lR; cksyus dh izkf;drk 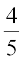 gSA ,d flDdk mNkyk tkrk gS rFkk A crkrk gS fd fpr iznf'kZr gqvkA okLrfod :i esa fpr izdV gksus dh izkf;drk gS%
gSA ,d flDdk mNkyk tkrk gS rFkk A crkrk gS fd fpr iznf'kZr gqvkA okLrfod :i esa fpr izdV gksus dh izkf;drk gS%
(A) 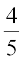 (B)
(B) 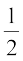 (C)
(C) 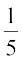 (D)
(D) 
14. ;fn A vkSj B ,slh ?kVuk,¡ gSa fd A ⊂ B rFkk P(B) ≠ 0 rks fuEu esa ls dkSu Bhd gS%
(A) 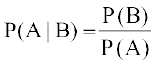 (B) P(A|B) < P(A)
(B) P(A|B) < P(A)
(C) P(A|B) ≥ P(A) (D) buesa ls dksbZ ugha
13.6 ;kn`fPNd pj vkSj blosQ izkf;drk caVu (Random Variables and its Probability Distribution)
ge] ;kn`fPNd ijh{k.kksa vkSj muosQ izfrn'kZ fuekZ.k osQ ckjs esa igys gh lh[k pqosQ gSa bu ijh{k.kksa esa ls vf/drj esa ge fo'ks"k ifj.kke osQ bPNqd ugha Fks ¯drq bu ifj.kkeksa ls
lacaf/r fdlh la[;k esa bPNqd FksA
vkb, oqQN ijh{k.kksa vkSj muosQ ifj.kkeksa ij fopkj djsaA
(i) nks iklksa dks isaQdus osQ ijh{k.k esa ge nksuksa iklksa ij izdV la[;kvksa osQ ;ksx esa bPNqd gks ldrs gSaA
(ii) ,d flDosQ dks 50 ckj mNkyus esa gekjh #fp fprksa dh la[;k esa gks ldrh gSA
(iii) 20 oLrqvksa osQ ,d <sj ls] ftlesa 6 [kjkc gS] 4 oLrqvksa dks (,d ds ckn ,d) fudkyus osQ ijh{k.k esa gekjh #fp 4 oLrqvksa osQ izfrn'kZ esa [kjkc oLrqvksa dh la[;k esa gks ldrh gS u dh [kjkc vkSj Bhd oLrqvksa osQ fdlh fo'ks"k vuqØe esaA
mi;qZDr esa ls izR;sd ijh{k.k esa gekjs ikl ,d fu;e gS tks izR;sd ifj.kke osQ laxr ,d okLrfod la[;k fufnZ"V djrk gSA ijh{k.k osQ izR;sd ifj.kke osQ fy, ;g okLrfod la[;k vyx&vyx Hkh gks ldrh gSA blfy, ;g ,d pj gSA lkFk gh bldk eku fdlh ;kn`fPNd ijh{k.k osQ ifj.kkeksa ij fuHkZj djrk gS blfy, bls ;kn`fPNd pj dgrs gSaA ,d ;kn`fPNd pj dks lkekU;r% X ls O;Dr djrs gSaA
;fn vki ,d iQyu dh ifjHkk"kk dk Lej.k dhft, rks ik,¡xs fd okLro esa ,d ;kn`fPNd pj X, iQyu gksrk gS ftldk izkar (domain) ;kn`fPNd ijh{k.k osQ ifj.kkeksa dk leqPp; (;k izfrn'kZ lef"V) gksrk gSA ,d ;kn`fPNd pj dksbZ Hkh okLrfod eku ys ldrk gS] blfy, bldk lgizkar (codomain) okLrfod la[;kvksa dk leqPp; gksrk gSA vr% ,d ;kn`fPNd pj dks fuEu izdkj ls ifjHkkf"kr dj ldrs gSaA
ifjHkk"kk 4 ,d ;kn`fPNd pj og iQyu gksrk gS ftldk izkar fdlh ;kn`fPNd ijh{k.k dk izfrn'kZ lef"V gksrk gSA
mnkgj.k osQ fy,] vkb, ,d flDosQ dks nks ckj vuqØe esa mNkys tkus osQ ijh{k.k ij fopkj dhft,A bl ijh{k.k dk izfrn'kZ lef"V gS%
S = {HH, HT, TH, TT}
;fn X, izkIr fprksa dh la[;k dks O;Dr djrk gS rks X ,d ;kn`fPNd pj gS vkSj izR;sd ifj.kke osQ fy, bldk eku fuEu izdkj ls fn;k x;k gS%
X (HH) = 2, X (HT) = 1, X (TH) = 1, X (TT) = 0.
,d gh izfrn'kZ lef"V ij ,d ls vf/d ;kn`fPNd pj ifjHkkf"kr fd, tk ldrs gSaA mnkgj.k osQ fy, eku ysa fd Y] izfrn'kZ lef"V S osQ izR;sd ifj.kke osQ fy, fprksa dh la[;k ls iVksa dh la[;k osQ ?kVko dks O;Dr djrk gSA rc
Y (HH) = 2, Y (HT) = 0, Y (TH) = 0, Y (TT) = − 2.
vr% ,d izfrn'kZ lef"V S esa X vkSj Y nks fHkUu ;kn`fPNd pj ifjHkkf"kr fd, x, gaSA
mnkgj.k 22 ,d O;fDr ,d flDosQ dks rhu ckj mNkyus dk [ksy [ksyrk gSA [ksy osQ vk;kstd }kjk ml O;fDr dks izR;sd fpr osQ fy, Rs 2 nsrk gS vkSj izR;sd iV osQ fy, og O;fDr vk;kstd dks Rs 1.50 nsrk gSA eku ysa X O;fDr }kjk thrh xbZ ;k gkjh xbZ jkf'k dks O;Dr djrk gSA n'kkZ,¡ fd X ,d ;kn`fPNd pj gS vkSj bls ijh{k.k osQ izfrn'kZ lef"V osQ iQyu osQ :i esa iznf'kZr dhft,A
gy X ,slh la[;k gS ftldk eku fdlh ;kn`fPNd ijh{k.k osQ ifj.kkeksa ij ifjHkkf"kr gSA blfy, X ,d ;kn`fPNd pj gSA
vc ijh{k.k dk izfrn'kZ lef"V gS%
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
rc
X (HHH) = Rs (2 3) = Rs 6
3) = Rs 6
X (HHT) = X (HTH) = X (THH) = Rs (2 2 − 1
2 − 1 1.50) = Rs 2.50
1.50) = Rs 2.50
X (HTT) = X (THT) = X (TTH) = Rs (1 2 − 2
2 − 2 1.50) = − Re 1
1.50) = − Re 1
vkSj X (TTT) = − Rs (3 1.50) = − Rs 4.50
1.50) = − Rs 4.50
;gk¡ ½.k fpÉ] f[kykM+h dh gkfu dks n'kkZ jgk gSA vr% izfrn'kZ lef"V osQ izR;sd vo;o osQ fy, X dk ,d vf}rh; eku gS] blfy, X izfrn'kZ lef"V ij ,d iQyu gS ftldk ifjlj gS%
{−1, 2.50, − 4.50, 6}
mnkgj.k 23 ,d FkSys esa 2 li+sQn vkSj 1 yky xsan gSaA ;kn`PN;k ,d xsan fudkyh xbZ vkSj mldk jax uksV djus osQ ckn mls iqu% FkSys esa Mkyk x;kA bl izfØ;k dks iqu% fd;k x;kA ;fn X nks fudkyksa esa liQyrk dh la[;k dks n'kkZrk gS rks] X dk fooj.k nsa] tgk¡ ,d yky xsan dk fudyuk liQyrk ekuk x;k gSA
gy eku yas fd FkSys esa j[kh xsanksa dks w1, w2, r ls O;Dr djrs gSaA
rc izfrn'kZ lef"V gS%
S = {w1 w1, w1 w2, w2 w2, w2 w1, w1 r, w2 r, r w1, r w2, r r}
vc X = yky xsanksa dh la[;k = liQyrk dh la[;k
blfy, X ({w1, w1}) = X ({w1 w2}) = X ({ w2 w2}) = X ({w2 w1}) = 0
X ({w1, r}) = X ({w2 r}) = X ({ rw1}) = X ({rw2}) = 1 vkSj X ({rr}) = 2
vr% X ,d ;kn`fPNd pj gS tks 0, 1 ;k 2 eku ys ldrk gSA
13.6.1 ,d ;kn`fPNd pj dh izkf;drk caVu (Probability distribution of a random variable)
vkb, nl ifjokjksa f1, f2 ... f10 ls ,d ifjokj dks bl izdkj pquus osQ ijh{k.k ij fopkj djsa fd izR;sd ifjokj dk pquko lelaHkkO; gksA eku ysa fd ifjokjksa f1, f2 ...f10 esa Øe'k% 3, 4, 3, 2, 5, 4, 3, 6, 4, 5 lnL; gSaA
vkb, ,d ifjokj dks pqus o mlosQ lnL;ksa dh la[;k dks uksV dj] X ls O;Dr dhft,A Li"Vr;k X ,d ;kn`fPNd pj gS ftls fuEu izdkj ls ifjHkkf"kr fd;k x;k gS%
X(f1) = 3, X(f2) = 4, X(f3) = 3, X(f4) = 2, X(f5) = 5,
X(f6) = 4, X(f7) = 3, X(f8) = 6, X(f9) = 4, X(f10) = 5
vr% 2] 3] 4] 5] 6 esa ls X dksbZ Hkh eku ys ldrk gS
vc X dk eku 2 gksxk tcfd ifjokj f4 dks pquk x;k gksA X dk eku 3 gks ldrk gS tc f1, f3, f7 esa ls fdlh ifjokj dks pquk tk,A blh izdkj
X = 4, tc ifjokj f2, f6 ;k f9 dks pquk tk,xk
X = 5, tc ifjokj f5 ;k f10 dks pquk tk,xk
vkSj X = 6, tc ifjokj f8 dks pquk tk,xk
pw¡fd geus ekuk gS fd izR;sd ifjokj dk pquk tkuk lelaHkkO; gS] blfy, ifjokj f4 osQ pqus tkus dh izkf;drk 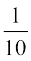 gSA
gSA
vr% X dk eku 2 gksus dh izkf;drk 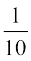 gSA
gSA
ge fy[krs gSa P(X = 2) =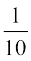
lkFk gh f1, f2, ;k f7 ls fdlh Hkh ,d ifjokj dks pquus dh izkf;drk
P ({f1, f2, f3}) = 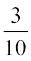 gSA
gSA
vr% X dk eku 3 gksus dh izkf;drk = 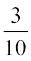
ge fy[krs gSa P (X = 3) = 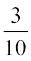
blh izdkj ge ikrs gSa fd
P(X = 4) = P({f2, f6, f9}) =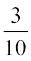 , P(X = 5) = P({f5, f10}) =
, P(X = 5) = P({f5, f10}) =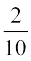
vkSj P(X = 6) = P({f8}) =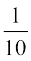
bl izdkj dk fooj.k ftlesa ;kn`fPNd pj osQ lkFk mldh laxr izkf;drkvksa dks fy[kk tkrk gS] dks ;kn`fPNd pj X dh izkf;drk caVu dgrs gSaA
O;kidr% ,d ;kn`fPNd pj X dh izkf;drk caVu dks fuEu izdkj ls ifjHkkf"kr fd;k tkrk gSA
ifjHkk"kk 5 fdlh ;kn`fPNd pj X dh izkf;drk caVu la[;kvksa dh fuEufyf[kr iz.kkyh (fudk;) gksrk gS
X : x1 x2 ... xn
P(X) : p1 p2 ... pn
tgk¡ 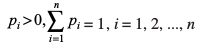
okLrfod la[;k,¡ x1, x2, ... xn ;kn`fPNd pj X osQ laHko eku (ewY;) gS vkSj pi (i = 1, 2, ... n) ;kn`fPNd pj X dk eku xi gksus dh izkf;drk gS vFkkZr~~ P (X=xi) = pi
fVIi.kh ;fn xi ;kn`fPNd pj X, dk dksbZ laHko ewY; gS rks dFku X = xi izfrn'kZ lef"V osQ oqQN ¯cnq (vksa) osQ fy, gh lR; gksrk gSA vr% X dk xi ewY; ysus dh izkf;drk lnSo 'kwU;sÙkj gksrh gS vFkkZr~~ P(X = xi) ≠ 0A
lkFk gh X osQ lHkh laHkkfor ekuksa osQ fy, izfrn'kZ lef"V osQ lHkh ¯cnqvksa dk lekos'k gks tkrk gSA blfy, fdlh izkf;drk caVu osQ fy, lHkh izkf;drkvksa dk ;ksx ,d gksuk pkfg,A
mnkgj.k 24 rk'k osQ 52 iÙkksa dh ,d lqfefJr xM~Mh ls nks iÙks mÙkjksÙkj izfrLFkkiuk osQ lkFk fudkys tkrs gSaA bDdksa dh la[;k dk izkf;drk caVu Kkr dhft,A
gy bDdksa dh la[;k ,d ;kn`fPNd pj gSA bldks ge X ls fu:fir djrs gSaA Li"Vr;k X dk eku 0, 1, ;k 2 gSA D;ksafd iÙkksa dks izfrLFkkiuk osQ lkFk fudkyk x;k gS blfy, nksuksa iÙkksa dk fudkyuk Lora=k ijh{k.k gSaA
blfy, P(X = 0) = P(bDdk ugha vkSj bDdk ugha)
= P(bDdk ugha) × P (bDdk ugha)
= 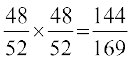
vkSj P(X = 1) = P(bDdk vkSj bDdk ugha vFkok bDdk ugha vkSj bDdk)
= P(bDdk) . P(bDdk ugha) + P (bDdk ugha) . P (bDdk)
= 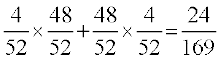
vkSj P(X = 2) = P(bDdk vkSj bDdk) = P(bDdk) % P(bDdk)
= 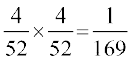
vr% vHkh"V izkf;drk caVu gS%
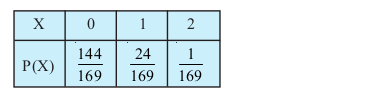
mnkgj.k 25 iklksa osQ ,d tksM+s dks rhu ckj mNkyus ij f}dksa (doublets) dh la[;k dk izkf;drk caVu Kkr dhft,A
gy eku yhft, fd X f}dksa dh la[;k fu:fir djrk gSA
(1,1) , (2,2), (3,3), (4,4), (5,5), vkSj (6,6) laHko f}d gSaA
Li"V gS fd X dk eku 0, 1, 2, ;k 3 gSA
,d f}d izkIr gksus dh izkf;drk 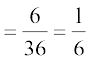
,d f}d izkIr u gksus dh izkf;drk 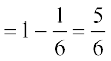
vc
P(X = 0) = P(,d Hkh f}d ugha) = 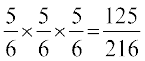
P(X = 1) = P(,d f}d vkSj nks f}d ugha)
= 
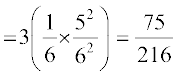
P(X = 2) = P (nks f}d vkSj ,d f}d ugha)
= 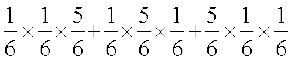
= 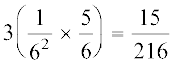
P(X = 3) = P (rhu f}d) 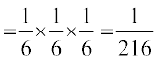
vr% X dk vHkh"V izkf;drk caVu fuEufyf[kr gSa%
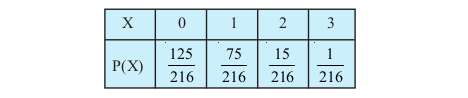
lR;kiu izkf;drkvksa dk ;ksx
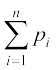 =
= 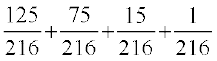
= 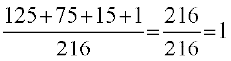
vr% mijksDr izkf;drk caVu lgh gSA
mnkgj.k 26 eku ysa fdlh ;kn`fPNd pqus x, fo|ky;h fnol esa i<+kbZ ds ?kaVksa dks X ls n'kkZ;k tkrk gSA X osQ eku x ysus dh izkf;drk fuEufyf[kr rjg ls gS] tgk¡ k ,d okLrfod la[;k gS%
P(X = x) = 
(a) k dk eku Kkr dhft,
(b) bl ckr dh D;k izkf;drk gS fd vki
U;wure nks ?kaVs i<+rs gSa\ rF;r% nks ?kaVs i<+rs gSa\ vf/dre nks ?kaVs i<+rs gSa\
gy X dk izkf;drk caVu uhps fn;k x;k gS%

(a) gesa Kkr gS fd 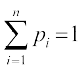
blfy, 0.1 + k + 2k + 2k + k = 1
⇒ k = 0.15
(b) P(vki U;wure nks ?kaVs i<+rs gSaa) = P (X ≥ 2)
= P (X = 2) + P (X = 3) + P (X = 4)
= 2k + 2k + k = 5k = 5 × 0.15 = 0.75
P(vki rF;r% nks ?kaVs i<+rs gSa) = P (X = 2)
= 2k = 2 × 0.15 = 0.3
P(vki vf/dre nks ?kaVs i<+rs gSa) = P (X ≤ 2)
= P (X = 0) + P(X = 1) + P(X = 2)
= 0.1 + k + 2k = 0.1 + 3k = 0.1 + 3 × 0.15 = 0.55
13.6.2 ;kn`fPNd pj dk ekè; (Mean of a random variable)
cgqr lh leL;kvksa esa fdlh ;kn`fPNd pj ds fdlh y{k.k dks ,dy la[;k ls n'kkZuk okaNuh; gksrk gS] ftls pj dh izkf;drk caVu ls Kkr dj ldrs gSa ,slh gh oqQN la[;k,¡ ekè;] ekè;d o cgqyd gksrs gSaA bl d{kk esa ge ekè; ij ppkZ djsaxsA ekè; vofLFkfr ;k osaQnzh; izo`fr dh eki bu vFkks± esa gS fd ;g fdlh ;kn`fPNd pj osQ eè;eku ;k vkSlr eku dks bafxr djrk gSA
ifjHkk"kk 6 eku ysa X ,d ;kn`fPNd pj gS ftlosQ laHkkfor eku x1, x2, x3, ..., xn dh Øe'k% izkf;drk p1, p2, p3, ..., pn gSA X dk ekè;] ftls  , ls O;Dr djrs gSa] la[;k
, ls O;Dr djrs gSa] la[;k 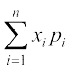 gksrh gSA vFkkZr~~ x dk ekè;] pj X, osQ laHkkfor ekuksa dk Hkkfjr vkSlr gksrk gS] tc izR;sd eku dks mldh laxr izkf;drk ls Hkkfjr fd;k x;k gksA
gksrh gSA vFkkZr~~ x dk ekè;] pj X, osQ laHkkfor ekuksa dk Hkkfjr vkSlr gksrk gS] tc izR;sd eku dks mldh laxr izkf;drk ls Hkkfjr fd;k x;k gksA
;kn`fPNd pj X osQ ekè; dks X dh izR;k'kk (Expectation) Hkh dgrs gSa] ftls
E (X) ls O;Dr djrs gSaA vr%
E(X) = µ =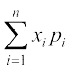 = x1p1+ x2p2 + ... + xnpn
= x1p1+ x2p2 + ... + xnpn
vU; 'kCnksa esa
;kn`fPNd pj X dk ekè; ;k izR;k'kk X osQ lHkh laHkkfor ekuksa dk mudh laxr izkf;drkvksa osQ xq.ku dk ;ksx gksrk gSA
mnkgj.k 27 eku ysa fd iklksa osQ ,d tksM+s dks mNkyk tkrk gS vkSj ;kn`fPNd pj X] iklksa ij izkIr la[;kvksa dk ;ksx fy;k tkrk gSA X dk ekè; ;k izR;k'kk Kkr dhft,A
gy bl ijh{k.k dk izfrn'kZ lef"V 36 ekSfyd ?kVukvksa ls fufeZr gqvk gS] ftUgsa Øfer ;qXe (xi, yi) osQ :i esa fy[kk tk ldrk gS tgk¡ xi = 1, 2, 3, 4, 5, 6 vkSj yi = 1, 2, 3, 4, 5, 6.
;kn`fPNd pj X osQ eku vFkkZr~~ iklksa ij izkIr la[;kvksa dk ;ksx 2] 3] 4] 5] 6] 7] 8] 9] 10] 11 ;k 12 gks ldrk gS
vc P(X = 2) = P({(1, 1)}) 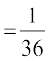
P(X = 3) = P({(1, 2), (2, 1)}) 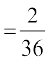
P(X = 4) = P({(1, 3), (2, 2), (3, 1)}) 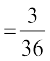
P(X = 5) = P({(1, 4), (2, 3), (3, 2), (4, 1)})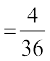
P(X = 6) = P({(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)})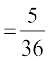
P(X = 7) = P({(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)})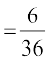
P(X = 8) = P({(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)})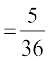
P(X = 9) = P({(3, 6), (4, 5), (5, 4), (6, 3)})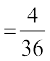
P(X = 10) = P({(4, 6), (5, 5), (6, 4)})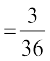
P(X = 11) = P({(5, 6), (6, 5)})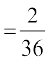
P(X = 12) = P({(6, 6) 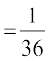
X dk izkf;drk caVu gS%

blfy, µ = E(X) = 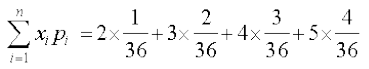
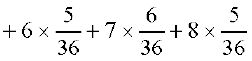
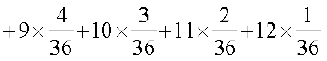
= 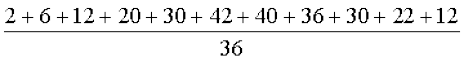 = 7
= 7
vr% nks iklksa osQ isaQdus ij izdV la[;kvksa osQ ;ksx dk ekè; 7 gSA
13.6.3 ;kn`fPNd pj dk izlj.k (Variance of a random variable)
;kn`fPNd pj dk ekè; ml pj osQ ekuksa esa fopj.k osQ ckjs esa dksbZ lwpuk ugha nsrk gSA lkFk gh fofHkUu izkf;drk caVu okys ;kn`fPNd pjksa osQ ekè; leku gks ldrs gSa] tSlk fd X vkSj Y osQ fuEufyf[kr caVuksa esa fn[kk;k x;k gSA
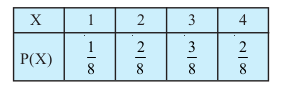
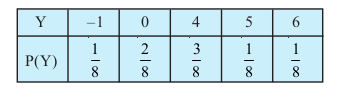
Li"Vr;k 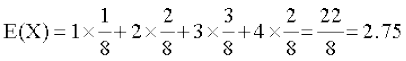
vkSj 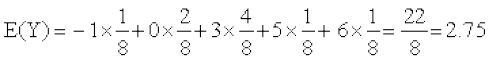
pj X vkSj Y vyx&vyx gSa ;|fi muosQ ekè; leku gSa ;g bu pjksa osQ fp=kkRed fu:i.k ls Hkh vklkuh ls izsf{kr fd;k tk ldrk gS (vko`Qfr 13-5)A
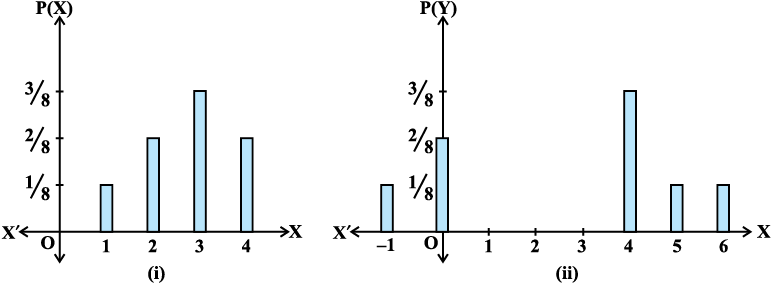
vko`Qfr 13.5
X dks Y ls vyx djus osQ fy, gesa ;kn`fPNd pj osQ eku esa fc[kjko dh lhek rd osQ eki dh vko';drk gSA geus lkaf[;dh esa i<+k gS fd vk¡dM+ksa esa fopj.k ;k fc[kjko dh eki gh izlj.k gSA blh izdkj ;kn`fPNd pj osQ ewY;ksa esa fc[kjko dks izlj.k ls ekik tk ldrk gSA
ifjHkk"kk 7 eku yhft, X ,d ;kn`fPNd pj gS ftlosQ laHkkfor ewY; x1, x2 ...xn laxr izkf;drkvksa p(x1), p(x2), ..., p(xn) osQ lkFk fo|eku gSaA
eku ysa µ = E (X), X dk ekè; gSA X dk izlj.k var (X) ;k 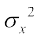 }kjk fu:fir] dks fuEu izdkj ls ifjHkkf"kr fd;k tkrk gS_
}kjk fu:fir] dks fuEu izdkj ls ifjHkkf"kr fd;k tkrk gS_
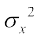 =
= 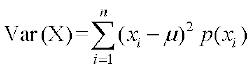
;k lerqY;r% 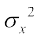 =
= 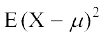
½.ksÙkj la[;k 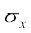 =
= 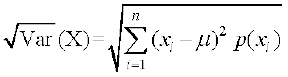
dks ;kn`fPNd pj X dk ekud fopyu (standard deviation) dgrs gSaA
;kn`fPNd pj dk izlj.k Kkr djus dk vU; lw=k
ge tkurs gSa fd
Var(X) = 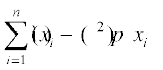
= 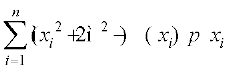
= 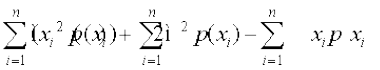
= 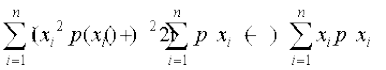
= 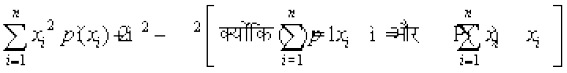
= 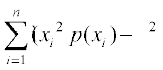
;k Var(X) = 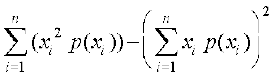
;k Var(X) = 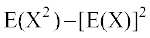 ] tgk¡ E(X2) =
] tgk¡ E(X2) =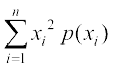
mngkj.k 28 ,d vufHkur ikls dks isaQdus ij izkIr la[;kvksa dk izlj.k Kkr dhft,A
gy ijh{k.k dk izfrn'kZ lef"V gS S = {1, 2, 3, 4, 5, 6}
eku ysa X, ikls ij izdV la[;k dks O;Dr djrk gSA rc X ,d ;kn`fPNd pj gS tks 1, 2, 3, 4, 5, ;k 6 eku ys ldrk gSA
lkFk gh P(1) = P (2) = P (3) = P (4) = P (5) = P (6) = 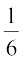
blfy, X dk izkf;drk caVu gS%
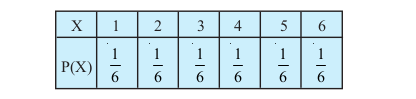
vc E(X) = 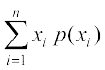
= 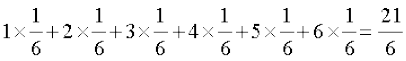
lkFk gh E(X2) = 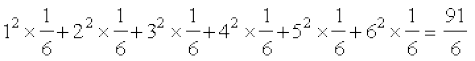
vr% Var(X) = E (X2) – (E(X))2
= 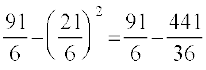
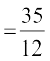
mnkgj.k 29 rk'k osQ 52 iÙkksa dh ,d Hkyh&Hkk¡fr isaQVh xbZ xM~Mh esa ls nks iÙks mÙkjksÙkj fcuk izfrLFkkiuk osQ (;k ,d lkFk) fudkys tkrs gSaA ckn'kkgksa dh la[;k dk ekè;] izlj.k o ekud&fopyu Kkr dhft,A
gy eku yhft, fd nks iÙks fudkyus esa ckn'kkgksa dh la[;k dks X ls O;Dr djrs gSaA X ,d ;kn`fPNd pj gS tks 0 , 1 ;k 2 eku ys ldrk gSA
vc P(X = 0) = P(dksbZ ckn'kkg ugha) 
P(X = 1) = P(,d ckn'kkg vkSj ,d ckn'kkg ugha) 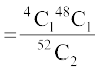
= 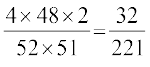
vkSj P(X = 2) = P (nksuksa ckn'kkg) 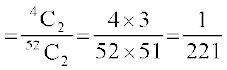
vr% X dk izkf;drk caVu gS%
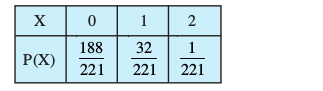
vc ekè; X = E(X) = 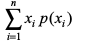
= 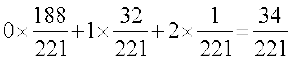
lkFk gh E(X2) = 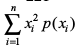 =
= 
vc Var(X) = E(X2) – [E(X)]2
= 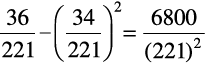
blfy, 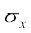 =
= 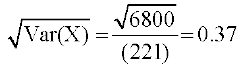 (yxHkx)
(yxHkx)
iz'ukoyh 13.4
1. crkb, fd fuEufyf[kr izkf;drk caVuksa esa dkSu ls ,d ;kn`fPNd pj osQ fy, laHko ugha gSA viuk mÙkj dkj.k lfgr fyf[k,A
(i)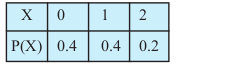
(ii)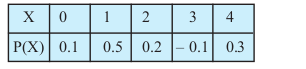
(iii)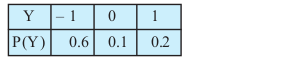
(iv)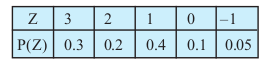
2. ,d dy'k esa 5 yky vkSj 2 dkyh xsan gSaA nks xsan ;kn`PN;k fudkyh xbZA eku yhft, X dkyh xsanksa dh la[;k dks O;Dr djrk gSA X osQ laHkkfor eku D;k gS\ D;k X ;kn`fPNd pj gS\
3. eku yhft, X fprksa dh la[;k vkSj iVksa dh la[;k esa varj dks O;Dr djrk gS] tc ,d flDosQ dks 6 ckj mNkyk tkrk gSA X osQ laHkkfor ewY; D;k gS?
4. fuEufyf[kr osQ izkf;drk caVu Kkr dhft,%
(i) ,d flDosQ dh nks mNkyksa esa fprksa dh la[;k dk
(ii) rhu flDdksa dks ,d lkFk ,d ckj mNkyus ij iVksa dh la[;k dk
(iii) ,d flDosQ dh pkj mNkyksa esa fprksa dh la[;k dk
5. ,d iklk nks ckj mNkyus ij liQyrk dh la[;k dk izkf;drk caVu Kkr dhft, tgk¡
(i) ^4 ls cM+h la[;k* dks ,d liQyrk ekuk x;k gSA
(ii) ^ikls ij la[;k 6 izdV gksuk* dks ,d liQyrk ekuk x;k gSA
6. 30 cYcksa osQ ,d <sj ls] ftles 6 cYc [kjkc gSa 4 cYcksa dk ,d uewuk (izfrn'kZ) ;kn`PN;k fcuk izfrLFkkiuk osQ fudkyk tkrk gSA [kjkc cYcksa dh la[;k dk izkf;drk caVu Kkr dhft,A
7. ,d flDdk leloZ; larqfyr ugha gS ftlesa fpr izdV gksus dh laHkkouk iV izdV gksus dh laHkkouk dh rhu xquh gSA ;fn flDdk nks ckj mNkyk tkrk gS rks iVksa dh la[;k dk izkf;drk caVu Kkr dhft,A
8. ,d ;kn`fPNd pj X dk izkf;drk caVu uhps fn;k x;k gSA

Kkr dhft,
(i) k (ii) P(X < 3) (iii) P(X > 6) (iv) P(0 < X < 3)
9. ,d ;kn`fPNd pj X dk izkf;drk iQyu P(x) fuEu izdkj ls gS] tgk¡ k dksbZ la[;k gS
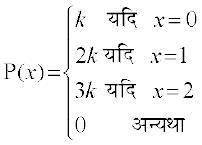
(a) k dk eku Kkr dhft,
(b) P (X < 2), P (X ≤ 2), P(X ≥ 2) Kkr dhft,A
10. ,d U;kÕ; flDosQ dh rhu mNkyksa ij izkIr fprksa dh la[;k dk ekè; Kkr dhft,A
11. nks iklksa dks ;qXer~ mNkyk x;kA ;fn X, NDdksa dh la[;k dks O;Dr djrk gS] rks X dh izR;k'kk Kkr dhft,A
12. izFke N% /u iw.kk±dksa esa ls nks la[;k,¡ ;kn`PN;k (fcuk izfrLFkkiu) pquh xbZA eku ysa X nksuksa la[;kvksa esa ls cM+h la[;k dks O;Dr djrk gSA E(X) Kkr dhft,A
13. eku yhft, nks iklksa dks iasQdus ij izkIr la[;kvksa osQ ;ksx dks X ls O;Dr fd;k x;k gSA X dk izlkj.k vkSj ekud fopyu Kkr dhft,A
14. ,d d{kk esa 15 Nk=k gSa ftudh vk;q 14] 17] 15] 14] 21] 17] 19] 20] 16] 18] 20] 17] 16] 19 vkSj 20 o"kZ gSaA ,d Nk=k dks bl izdkj pquk x;k fd izR;sd Nk=k osQ pqus tkus dh laHkkouk leku gS vkSj pqus x, Nk=k dh vk;q (X) dks fy[kk x;kA ;kn`fPNd pj X dk izkf;drk caVu Kkr dhft,A X dk ekè;] izlj.k o ekud fopyu Hkh Kkr dhft,A
15. ,d cSBd esa 70% lnL;ksa us fdlh izLrko dk vuqeksnu fd;k vkSj 30% lnL;ksa us fojks/ fd;kA ,d lnL; dks ;kn`PN;k pquk x;k vkSj] ;fn ml lnL; us izLrko dk fojks/ fd;k gks rks X = 0 fy;k x;k] tc fd ;fn mlus izLrko dk vuqeksnu fd;k gks rks X = 1 fy;k x;kA E(X) vkSj var (X) Kkr dhft,A
fuEufyf[kr esa ls izR;sd esa lgh mÙkj pqusaA
16. ,sls ikls] ftlosQ rhu iQydksa ij 1 vU; rhu ij 2 vkSj ,d iQyd ij 5 fy[kk x;k gS] dks mNkyus ij izkIr la[;kvksa dk ekè; gS%
(A) 1 (B) 2 (C) 5 (D) 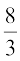
17.eku yhft, rk'k dh ,d xM~Mh ls ;kn`PN;k nks iÙks fudkys tkrs gSaA eku yhft, X bDdksa
dh la[;k izdV djrk gSA rc E(X) dk eku gS%
(A) 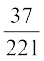 (B)
(B) 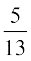 (C)
(C) 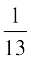 (D)
(D) 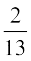
13.7 cjukSyh ijh{k.k vkSj f}in caVu (Bernoulli Trails and Binomial Distribution)
13.7.1 cjukSyh ijh{k.k
vusd iz;ksxksa dh izo`Qfr f}ifj.kkeh gksrh gSA mnkgj.kkFkZ mNkyk x;k flDdk ,d ^fpr* ;k ,d ^iV* n'kkZrk gS] fdlh iz'u dk mÙkj ^gk¡* ;k ^ugha* gks ldrk gS] ,d vaMs ls cPpk ^fudy pqdk gS* ;k ^ugha fudyk gS] ,d fu.kZ; ^gk¡* ;k ^ugha* gS vkfnA bl izdkj dh fLFkfr;ksa esa ,slk izpyu gS fd izkIr ifj.kkeksa esa ls ,d dks ^liQyrk* vkSj nwljs dks ^vliQyrk* dgk tkrk gSA mnkgj.k osQ fy,] ,d flDosQ dks mNkyus ij ^fpr* vkus dks liQyrk ekuk tk, rks ^iV* vkus dks vliQyrk dgk tk,xkA
izR;sd ckj] tc ge ,d flDdk mNkyrs gSa ;k ,d iklk mNkyrs gSa ;k dksbZ vU; iz;ksx djrs gSa] rc ge bls ,d ijh{k.k (trial) dgrs gSaA ;fn ,d flDdk eku yhft,] pkj ckj mNkyk tk, rks ijh{k.kksa dh la[;k 4 gksxh vkSj buesa ls izR;sd osQ ifj.kke rF;r% nks gksaxs vFkkZr~~ liQyrk ;k vliQyrkA fdlh ,d ijh{k.k dk ifj.kke fdlh nwljs ijh{k.k osQ ifj.kke ls Lora=k gksrk gSA bl izdkj osQ izR;sd ijh{k.k esa liQyrk (;k vliQyrk) dh izkf;drk,¡ vpj gksrh gSA bl izdkj osQ Lora=k ijh{k.k] ftuosQ osQoy nks ifj.kke gksrs gSa tks izk;% ^liQyrk* ;k ^vliQyrk* dgykrs gSa] cjukSyh ijh{k.k dgykrs gSaA
ifjHkk"kk 8 ,d ;kn`fPNd iz;ksx osQ ijh{k.kksa dks cjukSyh ijh{k.k dgrs gSa ;fn os fuEufyf[kr 'krks± dks larq"V djrs gSa%
(i) ijh{k.kksa dh la[;k fuf'pr (ifjfer) gksuh pkfg,
(ii) ijh{k.k Lora=k gksus pkfg,
(iii) izR;sd ijh{k.k osQ rF;r% nks gh ifj.kke gksus pkfg,] liQyrk ;k vliQyrk
(iv) fdlh ifj.kke dh izkf;drk izR;sd ijh{k.k esa leku jguh pkfg,
mnkgj.k osQ fy, ,d ikls dks 50 ckj mNkyuk] 50 cjukSyh ijh{k.kksa dh fLFkfr gS] ftlesa izR;sd ijh{k.k dk ifj.kke liQyrk (eku ysa le la[;k izdV gksuk) ;k vliQyrk (fo"ke la[;k izdV gksuk) gS vkSj lHkh 50 mNkyks esa liQyrk dh izkf;drk (p) ,d leku gSA fu%lUnsg ikls dh mÙkjksÙkj mNkysa Lora=k iz;ksx gksrs gSaA ;fn iklk U;kÕ; gS vkSj blosQ N% iQydksa ij N% la[;k,¡ 1 ls 6 rd fy[kh xbZ gS rks p = 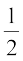 liQyrk dh vkSj q = 1 – p =
liQyrk dh vkSj q = 1 – p = 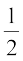 vliQyrk dh izkf;drk gSA
vliQyrk dh izkf;drk gSA
mnkgj.k 30 7 yky vkSj 9 dkyh xsanksa okys ,d dy'k esa ls mÙkjksÙkj N% xsan fudkyh xbZA crkb, fd xsan fudkyus osQ ijh{k.k cjukSyh ijh{k.k gSa ;k ugha ;fn izR;sd fudky osQ ckn xsan dks
(i) izfrLFkkfir fd;k x;k gksA
(ii) izfrLFkkfir u fd;k x;k gksA
gy
(i) ijh{k.kksa dh la[;k ifjfer (fuf'pr) gSA tc xsan dks fudkyus osQ ckn dy'k esa iqu% izfrLFkkfir fd;k x;k gks rks liQyrk (eku ysa yky xsan fudyuk) dh izkf;drk p = 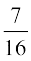 gS tks fd lHkh N% ijh{k.kksa esa leku gS vr% xasnksa dks izfrLFkkiuk osQ lkFk fudkyuk cjukSyh ijh{k.k gSaA
gS tks fd lHkh N% ijh{k.kksa esa leku gS vr% xasnksa dks izfrLFkkiuk osQ lkFk fudkyuk cjukSyh ijh{k.k gSaA
(ii) tc xsanksa dks fcuk izfrLFkkiuk osQ fudkyk x;k rks igys ijh{k.k esa liQyrk (vFkkZr~ yky xsan dk fudyuk) dh izkf;drk 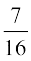 gS] nwljs ijh{k.k esa
gS] nwljs ijh{k.k esa 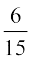 gS vkSj bl rjg Li"Vr;k lHkh ijh{k.kksa esa liQyrk dh izkf;drk leku ugha gS] vr% ;g ijh{k.k cjukSyh ijh{k.k ugha gSaA
gS vkSj bl rjg Li"Vr;k lHkh ijh{k.kksa esa liQyrk dh izkf;drk leku ugha gS] vr% ;g ijh{k.k cjukSyh ijh{k.k ugha gSaA
13.7.2 f}in caVu (Binomial Distribution)
,d flDosQ osQ mNkyus osQ iz;ksx ij fopkj dhft, ftlesa izR;sd ijh{k.k dk ifj.kke liQyrk (eku ysa fpr) ;k vliQyrk (iV) gksrs gSaA izR;sd ijh{k.k esa liQyrk vkSj vliQyrk dks Øe'k% S vkSj F eku yhft,A
dYiuk dhft, fd ge N% ijh{k.kksa esa ,d liQyrk osQ fofHkUu rjhdksa dks Kkr djus esa bPNqd gSaA Li"Vr;k N% fofHkUu rjhosQ gSa tSlk fd uhps lwphc¼ fd;k x;k gS%
SFFFFF, FSFFFF, FFSFFF, FFFSFF, FFFFSF, FFFFFS
blh izdkj] nks liQyrk,¡ vkSj pkj vliQyrk,¡ 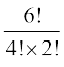 Øep; esa gks ldrh gaSA bu lHkh Øep;ksa dh lwph cukuk dki+Qh yack dk;Z gksxkA blfy,] 0] 1] 2] ---] n liQyrkvksa dh izkf;drk Kkr djuk yack vkSj le; ysus okyk dk;Z gks ldrk gSA n cjukSyh ijh{k.kksa esa ls liQyrkvksa dh la[;k dh izkf;drk Kkr djus osQ fy, ,d lw=k dk fuekZ.k fd;k x;k gS] ftlls x.kuk esa yxus okys le; vkSj laHko ifj.kkeksa dh lwph cukus ls cpk tk ldrk gSA bl mn~ns'; osQ fy, rhu cjukSyh ijh{k.kksa ls cus ;kn`fPNd iz;ksx dks ysrs gSa ftlesa izR;sd ijh{k.k esa liQyrk vkSj vliQyrk dh izkf;drk,¡ Øe'k% p rFkk q gSaA bl iz;ksx (ijh{k.k) dk izfrn'kZ lef"V dkrhZ; xq.ku
Øep; esa gks ldrh gaSA bu lHkh Øep;ksa dh lwph cukuk dki+Qh yack dk;Z gksxkA blfy,] 0] 1] 2] ---] n liQyrkvksa dh izkf;drk Kkr djuk yack vkSj le; ysus okyk dk;Z gks ldrk gSA n cjukSyh ijh{k.kksa esa ls liQyrkvksa dh la[;k dh izkf;drk Kkr djus osQ fy, ,d lw=k dk fuekZ.k fd;k x;k gS] ftlls x.kuk esa yxus okys le; vkSj laHko ifj.kkeksa dh lwph cukus ls cpk tk ldrk gSA bl mn~ns'; osQ fy, rhu cjukSyh ijh{k.kksa ls cus ;kn`fPNd iz;ksx dks ysrs gSa ftlesa izR;sd ijh{k.k esa liQyrk vkSj vliQyrk dh izkf;drk,¡ Øe'k% p rFkk q gSaA bl iz;ksx (ijh{k.k) dk izfrn'kZ lef"V dkrhZ; xq.ku
S = {SSS, SSF, SFS, FSS, SFF, FSF, FFS, FFF} gS
liQyrkvksa dh la[;k ,d ;kn`fPNd pj X gS vkSj 0, 1, 2, ;k 3 eku ys ldrk gSA liQyrkvksa dh la[;k dk izkf;drk caVu fuEufyf[kr izdkj ls izkIr fd;k x;k gSA
P(X = 0) = P(dksbZ liQyrk ugha)
= P({FFF}) = P(F) P(F) P(F)
= q . q . q = q3 (D;ksafd ijh{k.k Lora=k gSa)
P(X = 1) = P(,d liQyrk)
= P({SFF, FSF, FFS})
= P({SFF}) + P({FSF}) + P({FFS})
= P(S) P(F) P(F) + P(F) P(S) P(F) + P(F) P(F) P(S)
= p.q.q + q.p.q + q.q.p = 3qp2
P(X = 2) = P (nks liQyrk,¡)
= P({SSF, SFS, FSS})
= P({SSF}) + P({SFS}) + P({FSS})
= P(S) P(S) P(F) + P(S) P(F) P(S) + P(F) P(S) P(S)
= p.p.q. + p.q.p + q.p.p = 3qp2
vkSj P(X = 3) = P(rhu liQyrk,¡) = P ({SSS})
= P(S) . P(S) . P(S) = p3
vr% X dk izkf;drk caVu gS

lkFk gh (q + p)3 dk f}in foLrkj fuEufyf[kr gS
q3 + 3q2p + 3qp2 + p3
uksV dhft, fd 0] 1] 2] ;k 3 liQyrkvksa dh izkf;drk,¡ Øe'k% (q + p)3 osQ foLrkj dh igyh] nwljh] rhljh vkSj prqFkZ in gSaA
lkFk gh D;ksafd q + p = 1 gS ftlls ;g vFkZ fudyrk gS fd lHkh izkf;drkvksa dk ;ksx 1 gS tSlk fd vkisf{kr FkkA
vr% ge ;g fu"d"kZ fudky ldrs gSa fd n-cjukSyh ijh{k.kksa okys iz;ksx esa 0, 1, 2 ...., n liQyrkvksa dh izkf;drk,¡ (q + p)n osQ foLrkj dh izFke] f}rh;] r`rh;] ...noha in ls izkIr dh tk ldrh gSaA bl ifj.kke dks fl¼ djus osQ fy, ge n &cjukSyh ijh{k.kksa okys iz;ksx esa x&liQyrkvksa dh izkf;drk Kkr djrs gSaA
Li"Vr;k x liQyrkvksa (S) dh n'kk esa (n–x) vliQyrk,¡ (F) gksaxhA
vc x liQyrk,¡ (S) vkSj (n–x) vliQyrk,¡ (F), 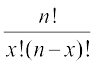 rjhdksa ls Øep; gksrh gSaA
rjhdksa ls Øep; gksrh gSaA
buesa ls izR;sd rjhosQ esa x liQyrkvksa vkSj (n − x) vliQyrkvksa dh izkf;drk
= P(x liQyrk,¡). 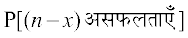
=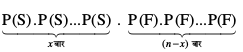 = px qn–x
= px qn–x
vr% n-cjukSyh ijh{k.kksa esa x liQyrkvksa dh izkf;drk 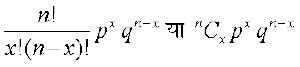 gSA
gSA
vr% P(x liQyrk,¡) = 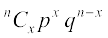 , x = 0, 1, 2, ..., n, (q = 1 – p)
, x = 0, 1, 2, ..., n, (q = 1 – p)
Li"Vr;k P (x liQyrk,¡) vFkkZr~~ 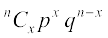 , (q + p)n osQ foLrkj dh (x + 1)oha in gSA
, (q + p)n osQ foLrkj dh (x + 1)oha in gSA
bl izdkj] n&cjukSyh ijh{k.kksa okys ,d iz;ksx esa liQyrkvksa dh la[;k dh izkf;drk caVu
(q + p)n osQ f}in&foLrkj }kjk izkIr dh tk ldrh gSA vr%] liQyrkvksa dh la[;k X dk caVu fuEufyf[kr izdkj ls fy[kk tk ldrk gSA

mi;qZDr izkf;drk caVu dks f}in caVu dgrs gSa ftlesa n rFkk p, izkpy gSa] D;ksafd n rFkk p osQ eku fn, gksus ij ge laiw.kZ izkf;drk caVu Kkr dj ldrs gSaA
x liQyrkvksa dh izkf;drk P (X = x) dks P(x) ls Hkh O;Dr djrs gSa vkSj bls
P(x) = nCxqn–xpx, x = 0, 1, ..., n (q = 1 – p) ls izkIr djrs gSaA
bl P(x) dks f}in caVu dk izkf;drk iQyu dgrs gSaA
,d n-cjukSyh ijh{k.kksa vkSj izR;sd ijh{k.k esa liQyrk dh izkf;drk p, okys f}in caVu dks B(n, p) ls O;Dr djrs gSaA
vkb, vc oqQN mnkgj.k ysaA
mnkgj.k 31 ;fn ,d U;kÕ; flDosQ dks 10 ckj mNkyk x;k rks fuEu dh izkf;drk,¡ Kkr dhft,%
(i) Bhd N% fpr
(ii) U;wure N% fpr
(iii) vf/dre N% fpr
gy ,d flDosQ dks ckjckj mNkyuk cjukSyh ijh{k.k gksrs gSaA 10 ijh{k.kksa esa fprkas dh la[;k dks X eku yhft,A
Li"Vr;k X caVu n = 10 vkSj p = 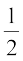 okyk f}in caVu gSA
okyk f}in caVu gSA
blfy, P(X = x) = nCxqn–xpx
;gk¡ n = 10, 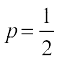 , q = 1 – p =
, q = 1 – p = 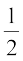
blfy, P(X = x) = 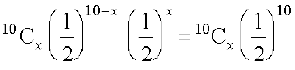
vc
(i) P(Bhd N% fpr) 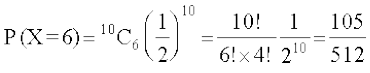
(ii) P(U;wure N% fpr) = P(X ≥ 6)
= P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10)
= 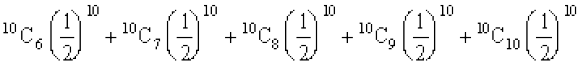
= 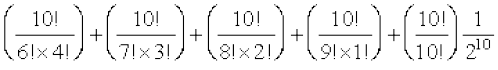
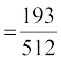
(iii) P (vf/dre N% fpr) = P (X ≤ 6)
= P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3)
+ P (X = 4) + P (X = 5) + P (X = 6)
= 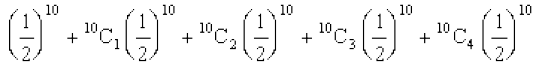
+ 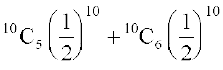
= 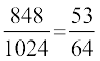
mnkgj.k 32 10% [kjkc vaMksa okys ,d <sj ls 10 vaMs mÙkjksÙkj izfrLFkkiuk osQ lkFk fudkys x,A bl ckr dh izkf;drk Kkr dhft, fd 10 vaMksa osQ izfrn'kZ esa de ls de ,d [kjkc vaMk gSA
gy eku yhft, X [kjkc vaMksa dh la[;k dks O;Dr djrk gSA D;ksafd vaMksa dks izfrLFkkiuk osQ lkFk fudkyk x;k gS blfy, ;g cjukSyh ijh{k.k gSaA Li"Vr;k X dk caVu n = 10 vkSj 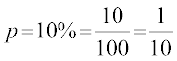 okyk f}in caVu gSA
okyk f}in caVu gSA
blfy, q = 1 – p = 1 – 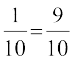
vc P(U;wure ,d [kjkc vaMk) = P(X ≥ 1) = 1 – P(X = 0)
= 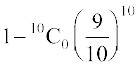
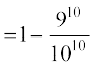
iz'ukoyh 13.5
1. ,d ikls dks 6 ckj mNkyk tkrk gSA ;fn ^ikls ij le la[;k izkIr gksuk* ,d liQyrk gS rks fuEufyf[kr dh izkf;drk,¡ D;k gksaxh\
(i) rF;r% 5 liQyrk,¡ ? (ii) U;wure 5 liQyrk,¡ ? (iii) vf/dre 5 liQyrk,¡\
2. iklksa osQ ,d tksM+s dks 4 ckj mNkyk tkrk gSA ;fn ^iklksa ij izkIr vadksa dk f}d gksuk* ,d liQyrk ekuh tkrh gS] rks 2 liQyrkvksa dh izkf;drk Kkr dhft,A
3. oLrqvksa osQ ,d <sj esa 5% =kqfV;qDr oLrq,¡ gSA bldh D;k izkf;drk gS fd 10 oLrqvksa osQ ,d izfrn'kZ esa ,d ls vf/d =kqfV;qDr oLrq,¡ ugha gkasxh\
4. 52 rk'k osQ iÙkksa dh ,d Hkyh&Hkk¡fr isaQVh xbZ xM~Mh esa ls 5 iÙks mÙkjksrj izfrLFkkiuk lfgr fudkys tkrs gSaA bldh D;k izkf;drk gS fd
(i) lHkh 5 iÙks gqoqQe osQ gksa ?
(ii) osQoy 3 iÙks gqoqQe osQ gksa ?
(iii) ,d Hkh iÙkk gqoqQe dk ugha gks ?
5. fdlh i+SQDVªh esa cus ,d cYc dh 150 fnuksa osQ mi;ksx osQ ckn Ý;w”k gksus dh izkf;drk 0-05 gSA bldh izkf;drk Kkr dhft, fd bl izdkj osQ 5 cYcksa esa ls
(i) ,d Hkh ugha (ii) ,d ls vf/d ugha
(iii) ,d ls vf/d (iv) de ls de ,d] 150 fnuksa ds mi;ksx osQ ckn Ý;w”k gks tk,¡xsA
6. ,d FkSys esa 10 xsanas gS ftuesa ls izR;sd ij 0 ls 9 rd osQ vadksa esa ls ,d vad fy[kk gSA ;fn FkSys ls 4 xsansaa mÙkjksrj iqu% okil j[krs gq, fudkyh tkrh gS] rks bldh D;k izkf;drk gS fd muesa ls fdlh Hkh xsan ij vad 0 u fy[kk gks\
7. ,d lR;&vlR; izdkj osQ 20&iz'uksa okyh ijh{kk esa eku ysa fd ,d fo|kFkhZ ,d U;kÕ; flDosQ dks mNky dj izR;sd iz'u dk mÙkj fu/kZfjr djrk gSA ;fn ikls ij fpr izdV gks rks og iz'u dk mÙkj ^lR;* nsrk gS vkSj ;fn iV izdV gks rks ^vlR;* fy[krk gSA bl dh izkf;drk Kkr dhft, fd og de ls de nks iz'uksa dk lgh mÙkj nsrk gSA
8. eku yhft, fd X dk caVu 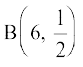 f}in caVu gSA n'kkZ,¡ fd X=3 vf/dre izkf;drk okyk ifj.kke gSA
f}in caVu gSA n'kkZ,¡ fd X=3 vf/dre izkf;drk okyk ifj.kke gSA
(laosQr : P(X = 3) lHkh P(xi), xi = 0,1,2,3,4,5,6 esa ls vf/dre gS)
9. ,d cgq&fodYih; ijh{kk esa 5 iz'u gS ftuesa izR;sd osQ rhu laHkkfor mÙkj gSaA bldh D;k izkf;drk gS fd ,d fo|kFkhZ osQoy vuqeku yxk dj pkj ;k vf/d iz'uksa osQ lgh mÙkj ns nsxk ?
10. ,d O;fDr ,d ykWVjh osQ 50 fVdV [kjhnrk gS] ftlesa mlosQ izR;sd esa thrus dh izkf;drk 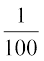 gSA bldh D;k izkf;drk gS fd og (a) U;wure ,d ckj (b) rF;r% ,d ckj (c) U;wure nks ckj] buke thr ysxkA
gSA bldh D;k izkf;drk gS fd og (a) U;wure ,d ckj (b) rF;r% ,d ckj (c) U;wure nks ckj] buke thr ysxkA
11. ,d ikls dks 7 ckj mNkyus ij rF;r% nks ckj 5 vkus dh izkf;drk Kkr dhft,A
12. ,d ikls dks N% ckj mNkyus ij vf/dre 2 ckj N% vkus dh izkf;drk Kkr dhft,A
13. ;g Kkr gS fd fdlh fo'ks"k izdkj dh fufeZr oLrqvksa dh la[;k esa 10% [kjkc gSA bldh D;k izkf;drk gS fd bl izdkj dh 12 oLrqvksa osQ ;kn`fPNd izfrn'kZ esa ls 9 [kjkc gksa\
14. ,d ckWDl esa 100 cYc gSaA ftlesa 10 =kqfV;qDr gSaA 5 cYc osQ uewus esa ls] fdlh Hkh cYc osQ =kqfV;qDr u gksus dh izkf;drk gS%
(A) 10–1 (B) 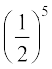 (C)
(C) 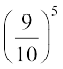 (D)
(D) 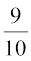
15. ,d Nk=k dh rSjkd u gksus dh izkf;drk 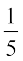 gSA rc 5 Nk=kksa esa ls 4 Nk=kksa dh rSjkd gksus dh izkf;drk gS%
gSA rc 5 Nk=kksa esa ls 4 Nk=kksa dh rSjkd gksus dh izkf;drk gS%
(A) 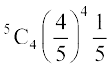 (B)
(B) 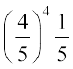
(C) 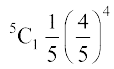 (D) buesa ls dksbZ ugha
(D) buesa ls dksbZ ugha
fofo/ mnkgj.k
mnkgj.k 33 pkj fMCcksa esa jxhau xsansaa fuEu lkj.kh esa n'kkZ, x, rjg ls vkacfVr dh xbZ gS%
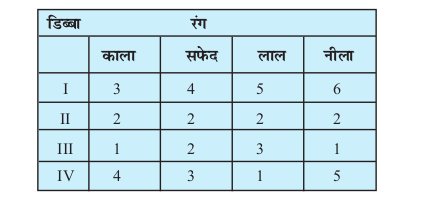
,d fMCcs dks ;kn`PN;k pquk x;k vkSj fiQj mlesa ls ,d xsan fudkyh xbZA ;fn xsan dk jax dkyk gS rks bldh D;k izkf;drk gS fd xsan dks fMCck& III ls fudkyk x;k gS?
gy eku yhft, A, E1, E2, E3 vkSj E4 fuEu izdkj ls ifjHkkf"kr ?kVuk,¡ gSa%
A : ,d dkyh xsan dk fudyuk E1 : fMCck&I dk pquko
E2 : fMCck&II dk pquko E3 : fMCck&III dk pquko
E4 : fMCck&IV dk pquko
D;ksafd fMCcksa dks ;kn`PN;k pquk x;k gS]
blfy, P(E1) = P(E2) = P(E3) = P(E4) 
lkFk gh P(A|E1) = 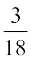 , P (A|E2) =
, P (A|E2) =  , P (A|E3) =
, P (A|E3) = 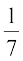 vkSj P (A|E4) =
vkSj P (A|E4) = 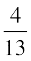
P(fMCck & III dk pquko] tc ;g Kkr gS fd dkyh xsan fudkyh xbZ gS)
= P(E3|A) cs”k&izes; ls
P(E3|A) = 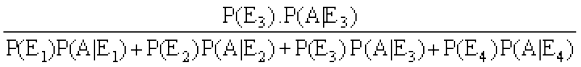
= 
mnkgj.k 34 f}in caVu 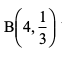 dk ekè; Kkr dhft,A
dk ekè; Kkr dhft,A
gy eku yas X og ;kn`fPNd pj gS ftldk izkf;drk caVu 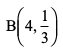 gSA
gSA
;gk¡ n = 4, p = 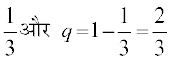
ge tkurs gSa fd P(X = x) = 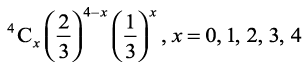
vFkkZr~ X dk caVu fuEufyf[kr gS is
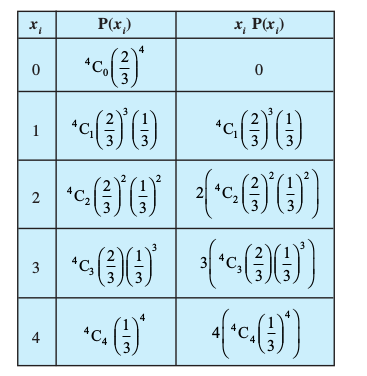
vc ekè; (µ) = 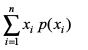
= 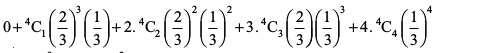
= 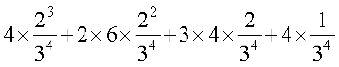
= 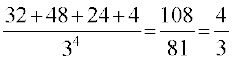
mnkgj.k 35 ,d fu'kkusckt osQ y{;&Hksnu dh izkf;drk 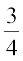 gSA og de ls de fdruh ckj xksyh pyk, fd y{; dks de ls de ,d ckj Hksnus dh izkf;drk 0-99 ls vf/d gks\
gSA og de ls de fdruh ckj xksyh pyk, fd y{; dks de ls de ,d ckj Hksnus dh izkf;drk 0-99 ls vf/d gks\
gy eku yhft, fd fu'kkusckt n ckj xksyh pykrk gSA fuLlansg n ckj xksyh pykuk n cjukSyh ijh{k.k gSaA
p = izR;sd ijh{k.k esa y{; Hksnu dh izkf;drk = 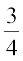 vkSj q = y{; dks u Hksnus dh izkf;drk =
vkSj q = y{; dks u Hksnus dh izkf;drk = 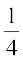
rc 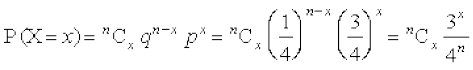
vc fn;k gS
P(U;wure ,d ckj y{; Hksnu) > 0.99
vFkkZr~~ P (x ≥ 1) > 0.99
blfy, 1 – P (x = 0) > 0.99
;k 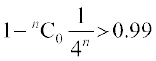
;k 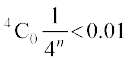 vFkkZr~
vFkkZr~ 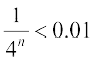
;k 4n > 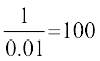 ... (1)
... (1)
vlfedk (1) dks larq"V djus okyh n dh U;wure eku 4 gSA
vr% fu'kkusckt dks de ls de 4 xksyh pykuh gksxhA
mnkgj.k 36 A vkSj B ckjh&ckjh ls ,d ikls dks mNkyrs gSa tc rd fd muesa ls dksbZ ,d ikls ij N% izkIr dj [ksy dks thr ugha ysrkA ;fn A [ksy dks 'kq: djsa rks muosQ thrus dh Øe'k% izkf;drk Kkr dhft,A
gy eku yhft, S liQyrk (ikls ij 6 izdV gksuk) dks vkSj F vliQyrk (ikls ij 6 izdV u gksuk) dks O;Dr djrs gSaA
vr% 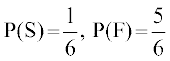
P(A osQ igyh mNky esa thruk) = P(S) = 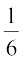
A dks rhljh mNky dk volj rc feyrk gS tc A igyh mNky esa vkSj B nwljh mNky esa vliQy gksrs gSaA blfy,
P(A dk rhljh mNky esa thruk) = P(FFS) = 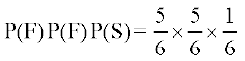
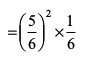
blh izdkj P(A dk ik¡poha mNky esa thruk) = P (FFFFS)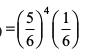
vkSj blh izdkj vU; vr% P(A thruk) =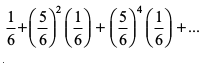
= 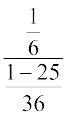 =
= 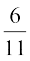
P(B thruk) = 1 – P(A thruk) = 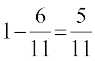
fVIi.kh ;fn a + ar + ar2 + ... + arn–1 + ..., tgk¡ r | < 1, rc bl vuar Js.kh dk ;ksx 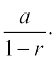 (nsf[k, d{kk XI dh ikB~;iqLrd dk A.1.3)
(nsf[k, d{kk XI dh ikB~;iqLrd dk A.1.3)
mnkgj.k 37 ;fn ,d e'khu leqfpr <ax ls LFkkfir dh tkrh gS rks ;g 90% Lohdk;Z oLrq mRikfnr djrh gSA ;fn ;g leqfpr <ax ls LFkkfir ugha dh tkrh gS rks ;g ek=k 40% Lohdk;Z oLrq cukrh gSA iwoZ vuqHko ;g n'kkZrk gS fd e'khu LFkkiu 80% leqfpr gSA ;fn ,d fuf'pr LFkkiu osQ ckn e'khu 2 Lohdk;Z oLrq mRikfnr djrh gS rks e'khu dh leqfpr <ax ls LFkkfir gksus dh izkf;drk Kkr dhft,A
gy eku yhft, A ,d ?kVuk gS ftlesa ,d e'khu nks Lohdk;Z oLrqvksa dk mRiknu djrh gSA
lkFk gh eku yhft, B1 lgh dk;Z iz.kkyh dh ?kVuk dks iznf'Zkr djrk gS vkSj B2 xyr dk;Z iz.kkyh dh ?kVuk dks iznf'kZr djrk gSA
vc P(B1) = 0.8, P(B2) = 0.2
P(A|B1) = 0.9 × 0.9 vkSj P(A|B2) = 0.4 × 0.4
blfy, P(B1|A) = 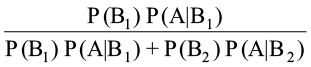
= 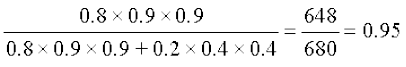
vè;k; 13 ij vk/kfjr fofo/ iz'ukoyh
1. A vkSj B bl izdkj ?kVuk,¡ gSa fd P (A) ≠ 0. P(B|A) Kkr dhft, ;fn
(i) A, leqPp; B dk mileqPp; gS (ii) A ∩ B = φ
2. ,d naifr osQ nks cPps gSa
(i) nksuksa cPpksa osQ yM+dk gksus dh izkf;drk Kkr dhft, ;fn ;g Kkr gSa fd nksuksa cPpksa esa ls de ls de ,d cPpk yM+dk gSA
(ii) nksuksa cPpksa osQ yM+dh gksus dh izkf;drk Kkr dhft, ;fn ;g Kkr gS fd cM+k cPpk yM+dh gSA
3. dYiuk dhft, fd 5% iq#"kksa vkSj 0.25% efgykvksa osQ cky li+sQn gSaA ,d li+sQn ckyksa okys O;fDr dks ;kn`fPNd pquk x;k gSA bl O;fDr osQ iq#"k gksus dh izkf;drk D;k gS\ ;g eku ysa fd iq#"kksa vkSj efgykvksa dh la[;k leku gSA
4. eku yhft, fd 90% yksx nkfgus gkFk ls dke djus okys gSaA bldh izkf;drk D;k gS fd 10 yksxksa esa ls ;kn`PN;k pqus x, vf/d ls vf/d 6 yksx nkfgus gkFk ls dke djus okys gksa\
5. ,d dy'k (ik=k) esa 25 xsansaa gSa] ftuesa ls 10 xsanksa ij fpÉ 'X' vafdr gS vkSj 'ks"k 15 ij fpÉ 'Y'. vafdr gSA dy'k esa ls ,d xsan ;kn`PN;k fudkyh tkrh gS vkSj ml ij vafdr fpÉ dks uksV (fy[k) djosQ mls dy'k esa izfrLFkkfir dj fn;k tkrk gsA ;fn bl izdkj ls 6 xsansaa fudkyh tkrh gksa] rks vxzfyf[kr izkf;drk,¡ Kkr dhft,A
(i) lHkh ij fpÉ 'X' vafdr gksA
(ii) 2 ls vf/d ij fpÉ 'Y' ugha vafdr gksA
(iii) de ls de 1 xsan ij fpÉ 'Y' vafdr gksA
(iv) 'X' rFkk 'Y' fpÉksa ls vafdr xsanksa dh la[;k,¡ leku gksaA
'X' fpÉ ls vafdr xsanksa dh la[;k dk ekè; Hkh Kkr dhft,A
6. ,d ck/k nkSM+ esa ,d izfr;ksxh dks 10 ck/k,¡ ikj djuh gS bldh izkf;drk fd og izR;sd ck/k dks ikj dj ysxk 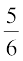 gSA bldh D;k izkf;drk gS fd og 2 ls de ck/kvksa dks fxjk nsxk (ugha ikj dj ik,xk)\
gSA bldh D;k izkf;drk gS fd og 2 ls de ck/kvksa dks fxjk nsxk (ugha ikj dj ik,xk)\
7. ,d ikls dks ckj&ckj rc rd mNkyk tkrk gS tc rd fd ml ij 6 dk vad rhu ckj izkIr ugha gks tkrkA bldh izkf;drk Kkr dhft, fd ikls ij rhljk 6 dk vad mls NBh ckj mNkyus ij izkIr gksrk gSA
8. ;fn ,d yhi o"kZ dks ;kn`PN;k pquk x;k gks rks bldh D;k izkf;drk gS fd ml o"kZ esa 53 eaxyokj gksaxs\
9. ,d iz;ksx osQ liQy gksus dk la;ksx mlosQ vliQy gksus ls nks xquk gSA izkf;drk Kkr dhft, fd vxys N% ijh{k.kksa esa de ls de 4 liQy gksaxsA
10. ,d O;fDr ,d U;kÕ; flDosQ dks fdruh ckj mNkys fd de ls de ,d fpr dh izkf;drk 90% ls vf/d gks?
11. ,d [ksy esa fdlh O;fDr dks ,d U;kÕ; ikls dks mNkyus osQ ckn N% izdV gksus ij ,d #i;k feyrk gS vkSj vU; dksbZ la[;k izdV gksus ij og ,d #i;k gkj tkrk gSA ,d O;fDr ;g fu.kZ; ysrk gS] fd og ikls dks rhu ckj isaQosQxk ysfdu tc Hkh N% izkIr gksxk og [ksyuk NksM+ nsxkA mlosQ }kjk thrh@gkjh xbZ jkf'k dh izR;k'kk Kkr dhft,A
12. eku yhft, gekjs ikl A, B, C vkSj D cDls gSa ftlesa j[kh laxejej dh yky] lisQn vkSj dkyh VqdfM+;ksa dk fooj.k fuEu rjhosQ ls gS ;kn`PN;k ,d ckWDl pquk tkrk gS rFkk blls ,d VqdM+k fudkyk tkrk gSA ;fn VqdM+k yky gks rks bls ckWDl A_ ckWDl B] ckWDl C ls fudkys tkus dh D;k izkf;drk gS\
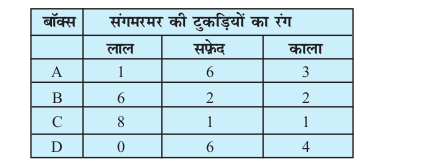
13. eku yhft, fdlh jksxh dks fny dk nkSjk iM+us dk la;ksx 40% gSA ;g eku fy;k tkrk gS fd è;ku vksj ;ksx fof/ fny dk nkSjk iM+us osQ [krjs dks 30% de dj nsrk gS vkSj nok }kjk [krjs dks 25% de fd;k tk ldrk gSA fdlh Hkh le; jksxh bu nksuksa esa ls fdlh ,d fodYi dk p;u djrk gSA ;g fn;k x;k gS fd mijksDr fodYiksa ls fdlh ,d dk pquko djus okys jksfx;ksa ls ;kn`PN;k pquk x;k jksxh fny osQ nkSjs ls xzflr gks tkrk gSA jksxh }kjk è;ku vkSj ;ksx fof/ dk mi;ksx fd, tkus dh izkf;drk Kkr dhft,A
14. ;fn 2 dksfV osQ ,d lkjf.kd osQ lHkh vo;o 'kwU; ;k ,d gks rks lkjf.kd dk /ukRed eku gksus dh D;k izkf;drk gSaA (eku yhft, dh lkjf.kd osQ izR;sd vo;o Lora=k :i ls pqus tk ldrs gSa rFkk izR;sd dh pqus tkus dh izkf;drk  gSA)
gSA)
15. ,d bysDVªkWfud ,lsacyh osQ nks lgk;d fudk; A vkSj B gSaA iwoZorhZ fujh{k.k }kjk fuEu izkf;drk,¡ Kkr gS%
P(A osQ vliQy gksus dh ) = 0.2
P(B osQ vosQys vliQy gksus dh ) = 0.15
P(A vkSj B osQ vliQy gksus dh ) = 0.15
rks] fuEu izkf;drk,¡ Kkr dhft,%
(i) P(A vliQy/B vliQy gks pqdh gks)
(ii) P(A osQ vosQys vliQy gksus dh )
16. FkSyk 1 esa 3 yky rFkk 4 dkyh xsansa gS rFkk FkSyk II esa 4 yky vkSj 5 dkyh xasnsa gSaA ,d xsan dks FkSyk 1 ls FkSyk 2 esa LFkkukarfjr fd;k tkrk gS vkSj rc ,d xsan FkSyk 2 ls fudkyh tkrh gSA fudkyh xbZ xsan yky jax dh gSA LFkkukarfjr xsan dh dkyh gksus dh izkf;drk Kkr dhft,A
fuEufyf[kr iz'uksa esa lgh mÙkj dk pquko dhft,%
17. ;fn A vkSj B nks ,slh ?kVuk,¡ gS fd P(A) ≠ 0 vkSj P(B/ A) = 1, rc
(A) A ⊂ B (B) B ⊂ A (C) B = φ (D) A = φ
18. ;fn P(A/B) > P(A), rc fuEu esa ls dkSu lgh gSA
(A) P(B|A) < P(B) (B) P(A ∩ B) < P(A) . P(B)
(C) P(B|A) > P(B) (D) P(B|A) = P(B)
19. ;fn A vkSj B ,slh nks ?kVuk,¡ gaS fd
P(A) + P(B) – P(A vkSj B) = P(A), rc
(A) P(B|A) = 1 (B) P(A|B) = 1
(C) P(B|A) = 0 (D) P(A|B) = 0
lkjka'k
bl vè;k; osQ eq[; ¯cnq fuEu izdkj ls gSa
- ?kVuk E dh lizfrca/ izkf;drk tc fd ?kVuk F nh xbZ gS] fuEu izdkj ls Kkr dh tkrh gS
![]() , P (F) ≠ 0
, P (F) ≠ 0 - 0 ≤ P (E|F) ≤ 1, P (E′| F) = 1 – P (E|F)
P (E ∪ F|G) = P (E|G) + P (F|G) – P (E ∩ F|G)
- P (E ∩ F) = P (E) P (F|E), P (E) ≠ 0
;k P (E ∩ F) = P (F) (E|F), P (F) ≠ 0
- ;fn E vkSj F Lora=k ?kVuk,¡ gSa rks
P (E ∩ F) = P (E) P (F)
vkSj P (E|F) = P (E), P (F) ≠ 0
P (F|E) = P (F), P(E) ≠ 0
- laiw.kZ izkf;drk dh izes;%
eku ysa {E1, E2, ...En) izfrn'kZ lef"V S dk ,d foHkktu gS vkSj E1, E2, ...En, esa izR;sd dh izkf;drk 'kwU;sÙkj gSA lkFk gh A izfrn'kZ lef"V ls lacf/r ,d ?kVuk gS] rc
P(A) = P(E1) P (A|E1) + P (E2) P (A|E2) + ... + P (En) P(A|En)
- cs”k&izes;% ;fn E1, E2, ....En izfrn'kZ lef"V S osQ foHkktu dk fuekZ.k djrh gaS vFkkZr~~ E1, E2, ..., En ;qXer% vla;qDr gSa vkSj E1 4 E2 4 ...4 En = S vkSj A ,d 'kwU;srj izkf;drk dh ?kVuk gS rc
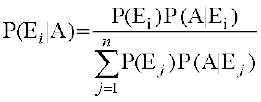
- ,d ;kn`fPNd pj fdlh ;kn`fPNd ijh{k.k osQ izfrn'kZ lef"V ij ifjHkkf"kr okLrfod eku iQyu gksrk gSA
- ;kn`fPNd pj X dh izkf;drk caVu la[;kvksa dh fuEufyf[kr iz.kkyh gS
X : x1 x2 ... xn
P(X) : p1 p2 ... pn
tgk¡ 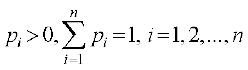
- eku ysa X ,d ;kn`fPNd pj gS ftlosQ laHkkfor ewY; x1, x2, x3, ... ,xn gSa ftudh Øe'k% izkf;drk,¡ p1, p2, p3, ..., pn gSaA X dk ekè;] µ ls O;Dr] la[;k
![]() gSA
gSA
;kn`fPNd pj X osQ ekè; dks X, dh izR;k'kk Hkh dgrs gSa ftls E (X) ls O;Dr djrs gSaA
- eku ysa X ,d ;kn`fPNd pj gS ftlosQ laHkkfor ewY; x1, x2,...,xn gSa ftudh Øe'k% izkf;drk,¡ p1, p2, ..., pn gSaA eku yhft, µ = E (X), X dk ekè; gSA
X, dk izlj.k] var (X) ;k σx2 ls O;Dr] dks fuEu izdkj ls ifjHkkf"kr fd;k tkrk gS 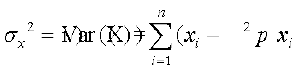
;k lerqY;r% σx2 = E (X – µ)2
½.ksrj la[;k 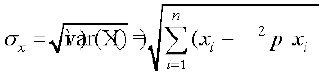
dks ;kn`fPNd pj X dh ekud fopyu dgrs gSaA
- var (X) = E (X2) – [E(X)]2
- fdlh ;kn`fPNd iz;ksx osQ ijh{k.kksa dks cjukSyh ijh{k.k dgrs gSa ;fn os fuEufyf[kr 'krks± dks larq"V djrs gSa%
(i) ijh{k.kksa dh la[;k fuf'pr (ifjfer) gksuh pkfg,
(ii) ijh{k.k Lora=k gksus pkfg,
(iii) izR;sd ijh{k.k osQ rF;r% nks gh ifj.kke gksus pkfg,% liQyrk ;k vliQyrk
(iv) fdlh ifj.kke dh izkf;drk izR;sd ijh{k.k esa ,d gh (leku) jguh pkfg,A
- f}in caVu B (n, p), osQ fy, P (X = x) = nCx q n–x px
,sfrgkfld uksV
,d ikls ij vk/kfjr [ksy esa izkf;drk (volj) osQ eki dk igyk lanHkZ nk¡rs osQ nSoh izglu ij ,d O;k[;k esa feyrk gSA tsjuheksadkWjMu (1501&1576) us tq, osQ [ksy ij ,d foLr`r fuca/ ftldk uke ^fycj Ms ywMks vydk,* fy[kk Fkk tks muosQ e`R;ksijkar 1663 esa izdkf'kr gqvk FkkA bl fuca/ esa mUgksaus nks iklksa dks mNkyus ij izR;sd ?kVuk osQ vuqowQy ifj.kkeksa dh la[;k osQ ckjs esa crk;k gSA xSfyfy;ks (1564&1642) us rhu iklksa osQ ,d [ksy esa la;ksx osQ eki osQ laca/ esa vkdfLed fVIi.kh dh gSA xSfyfy;ks us fo'ys"k.k fd;k Fkk fd tc rhu iklksa dks mNkyk tkrk gS rks izdV la[;kvksa osQ ;ksx dk 10 gksuk ;ksx 9 ls vf/d laHkkO; gS D;ksafd ;ksx dks nl gksus osQ vuqowQy ifj.kkeksa dh la[;k ;ksx 9 osQ vuqowQy ifj.kkeksa dh la[;k ls vf/d gSA
bl izkjafHkd ;ksxnku osQ vfrfjDr ;g lkekU;r% ekuk tkrk gS fd izkf;drk osQ foKku dk izekf.kd mn~xe l=kgoha 'krkCnh osQ nks egku xf.krKksa ikWLdy (1623&1662) vkSj ihvjs n~ i+QekZ (1601&1665) osQ eè; gq, i=k O;ogkj ls gqvk gSA ,d i+zQakfllh tqvkjh 'ksosfy;j Ms esjs us lSa¼kfrd roZQ vkSj tq, esa ,df=kr izs{k.kksa esa var£ojks/ dh O;k[;k osQ fy, ikWLdy ls iwNkA bl iz'u osQ gy osQ fy, 1654 osQ bnZ&fxnZ ikWLdy vkSj i+QekZ osQ chp gq, i=k O;ogkj dh Üka`[kyk esa izkf;drk osQ foKku dh izFke uhao j[kh xbZA ikWLdy us leL;k dks chtxf.krh; :i esa gy fd;k tcfd i+QekZ us lap; dh fof/;ksa dk mi;ksx fd;kA
egku gkySaM fuoklh oSKkfud átsu (1629&1695) dks ikWLdy vkSj i+QekZ osQ eè; gq, i=k O;ogkj osQ ckjs esa tkudkjh feyh rks mUgksaus izkf;drk dh izFke iqLrd ^Ms jsf'k;ksflful bu ywMks vyk;* dks izdkf'kr fd;k ftlesa la;ksx osQ [ksy esa izkf;drk ij cgqr lkjh jkspd ysfdu dfBu leL;kvksa osQ gy izLrqr fd,A izkf;drk fl¼kar ij vxyk egku dk;Z tSdc cjukSyh (1654&1705) us ,d iqLrd ^vklZ oaQtsdVsaMh* osQ :i esa fd;k tks muds e`R;ksijkar muosQ Hkrhts fudkWyl cjukSyh us 1713 esa izdkf'kr dh FkhA mUgsa ,d egÙoiw.kZ izkf;drk caVu ^f}in caVu* dh [kkst dk Js; Hkh tkrk gSA izkf;drk ij vxyk vkd"kZd dk;Z ^vczkge Ms eksfo;j (1667&1754) dh iqLrd ^n MkWfDVªu vkWiQ pkal* esa fo|eku gS ftls 1718 esa izdkf'kr fd;k x;k FkkA FkkWel cs”k (1702&1761) us muosQ uke ij izfl¼ izes; ^cs”k&izes;* dks O;qRiUu djus osQ fy, lizfrca/ izkf;drk dk mi;ksx fd;kA izfl¼ [kxksy'kkL=kh ^fi;js lkbeu Ms ykWiykl (1749&1827) us Hkh izkf;drk fl¼kar ij dk;Z fd;k vkSj 1812 esa ,d iqLrd ^fFk;ksjh ,ukWfyfVd Msl izkscsfcfyfV”k* izdkf'kr dhA blosQ ckn :lh xf.krKksa 'ksch'kso (1821&1894)] ekWjdkso (1856&1922)] ,- fy;kiksukso (1821&1918) vkSj ,-,u- dkWYeksxzkso (1903&1987) us izkf;drk fl¼kar ij lkFkZd ;ksxnku fn;kA dkWYeksxzkso us izkf;drk dk leqPp; iQyu osQ :i esa lw=kikr fd;kA ftls 1933 esa izdkf'kr iqLrd ^izkf;drk dk vk/kjHkwr fl¼kar* esa izkf;drk osQ vfHkx`fgrh; n`f"Vdks.k osQ uke ls tkuk tkrk gSA
——