Table of Contents

QR12091C1.tif


अध्याय 1


वैद्युत आवेश तथा क्षेत्र


 1.1 भूमिका

हम सभी को, विशेषकर शुष्क मौसम में, स्वेटर अथवा संश्लिष्ट वस्त्रों को शरीर से उतारते समय चट-चट की ध्वनिसुनने अथवा चिनगारियाँ देखने का अनुभव होगा। महिलाओें के वस्त्रों जैसे पॉलिएस्टर साड़ी के साथ तो एेसी घटना होना प्रायः अनिवार्य होता है। क्या आपने कभी इस परिघटना का स्पष्टीकरण खोजने का प्रयास किया है? विद्युत विसर्जन का एक अन्य सामान्य उदाहरण आकाश में गर्जन के समय तड़ित दिखाई देना है। विद्युत झटके के संवेदन का अनुभव हमें उस समय भी होता है जब हम किसी कार का दरवाज़ा खोलते हैं अथवा जब हम अपनी बस की सीट पर खिसकने के पश्चात उसमें लगी लोहे की छड़ को पकड़ते हैं। इन अनुभवों के होने के कारण हमारे शरीर में से होकर उन वैद्युत आवेशों का विसर्जित होना है जो विद्युतरोधी पृष्ठों पर रगड़ के कारण एकत्र हो जाते हैं। आपने यह भी सुना होगा कि यह वैद्युत आवेश (स्थिरवैद्युत) के उत्पन्न होने के कारण है। इस अध्याय तथा अगले अध्याय में भी हम इसी विषय पर चर्चा करेंगे। स्थिर से तात्पर्य है वह सब कुछ जो समय के साथ परिवर्तित अथवा गतिमय नहीं होता। स्थिरवैद्युतिकी के अंतर्गत हम स्थिर आवेशों द्वारा उत्पन्न बलों, क्षेत्रों तथा विभवों के विषय में अध्ययन करते हैं।


1.2 वैद्युत आवेश

इतिहास के अनुसार लगभग 600 ई. पूर्व हुई इस तथ्य की खोज का श्रेय, कि ऊन अथवा रेशमी-वस्त्र से रगड़ा गया एेम्बर हलकी वस्तुओं को आकर्षित करता है, ग्रीस देश के मिलेटस के निवासी थेल्स को जाता है। ‘इलेक्ट्रिसिटी’ शब्द भी ग्रीस की भाषा के शब्द इलेक्ट्रॉन से व्युत्पन्न हुआ है जिसका अर्थ एेम्बर है। उस समय पदार्थों के एेसे बहुत से युगल ज्ञात थे जो परस्पर रगड़े जाने पर भूसे के तिनकों, सरकंडे की गोलियों, कागज़ के छोटे टुकड़ों आदि हलकी वस्तुओं को आकर्षित कर लेते थे। आप इस प्रकार के प्रभाव का अनुभव अपने घर पर निम्नलिखित क्रियाकलाप द्वारा कर सकते हैं। सफ़ेद कागज़ की लंबी पतली पट्टियाँ काटकर उन पर धीरे से इस्तरी कीजिए। इन पट्टियों को टेलीविज़न के पर्दे अथवा कंप्यूटर के मॉनिटर के निकट लाइए। आप देखेंगे कि पट्टियाँ पर्दे की ओर आकर्षित हो जाती हैं। वास्तव में वे कुछ क्षण तक पर्दे से चिपकी रहती हैं।

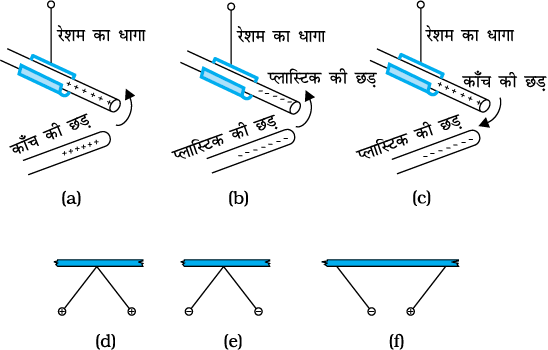
1916.png
चित्र 1.1 छड़ें तथा सरकंडे की गोलियाँः सजातीय आवेश एक-दूसरे को प्रतिकर्षित तथा विजातीय आवेश एक-दूसरे को आकर्षित करते हैं।

1935.png
सरल स्थिर वैद्युतकीय प्रयोगों से संबंधित प्रभावी सजीव चित्रण

http://demoweb.physics.ucla.edu/content/100-simple

electrostatic-experiments

यह भी प्रेक्षित किया गया कि यदि ऊन अथवा रेशम के कपड़े से रगड़ी हुई दो काँच की छड़ों को एक-दूसरे के निकट लाएँ तो वे एक-दूसरे को प्रतिकर्षित करती हैं [चित्र 1.1(a)]। ऊन की वे लड़ियाँ अथवा रेशम के कपड़े के वे टुकड़े जिनसे इन छड़ों को रगड़ा गया था, वे भी परस्पर एक-दूसरे को प्रतिकर्षित करते हैं परंतु काँच की छड़ तथा ऊन एक-दूसरे को आकर्षित करते हैं। इसी प्रकार, बिल्ली की समूर से रगड़ी हुई दो प्लास्टिक की छड़ें एक-दूसरे को प्रतिकर्षित करती हैं [चित्र 1.1(b)] परंतु समूर को आकर्षित करती हैं। इसके विपरीत, प्लास्टिक की छड़ें काँच की छड़ों को आकर्षित करती हैं [चित्र 1.1(c)] तथा सिल्क अथवा ऊन जिससे काँच की छड़ों को रगड़ा गया था, को प्रतिकर्षित करती हैं। काँच की छड़ समूर को प्रतिकर्षित करती है।

यदि समूर से रगड़ी हुई किसी प्लास्टिक की छड़ को रेशम अथवा नायलॉन के धागों से लटकी हुई दो छोटी सरकंडे की गोलियों (आजकल हम पॉलिएस्टरीन की गोलियाँ भी उपयोग कर सकते हैं) से स्पर्श करा दें, तो ये गोलियाँ एक-दूसरे को प्रतिकर्षित करती हैं [चित्र 1.1(d)] तथा स्वयं छड़ से भी प्रतिकर्षित होती हैं। यही प्रभाव उस समय भी दिखाई देता है जब सरकंडे की गोलियों को रेशम से रगड़ी काँच की छड़ से स्पर्श कराते हैं [चित्र 1.1(e)]। यह एक नाटकीय प्रेक्षण है कि काँच की छड़ से स्पर्श की हुई सरकंडे की गोली दूसरी प्लास्टिक छड़ से स्पर्श की गई सरकंडे की गोली को आकर्षित करती है [चित्र 1.1(f)]।

वर्षों के प्रयास तथा सावधानीपूर्वक किए गए प्रयोगों एवं उनके विश्लेषणों द्वारा सरल प्रतीत होने वाले ये तथ्य स्थापित हो पाए हैं। विभिन्न वैज्ञानिकों द्वारा किए गए बहुत से सावधानीपूर्ण अध्ययनों के पश्चात यह निष्कर्ष निकाला गया है कि एक राशि होती है, जिसे वैद्युत आवेश कहते हैं और यह केवल दो प्रकार के ही हो सकते हैं। वैद्युत आवेश कहलाने वाली राशि के केवल दो प्रकार ही होते हैं। हम कहते हैं कि प्लास्टिक एवं काँच की छड़, रेशम, समूर, सरकंडे की गोलियाँ आदि पिंड विद्युन्मय हो गए हैं। रगड़ने पर ये वैद्युत आवेश अर्जित कर लेते हैं। सरकंडे की गोलियों पर किए गए ये प्रयोग यह सुझाते हैं कि आवेश दो प्रकार के होते हैं तथा हम यह पाते हैं कि (i) सजातीय आवेश एक-दूसरे को प्रतिकर्षित तथा (ii) विजातीय आवेश एक-दूसरे को आकर्षित करते हैं। ये प्रयोग यह भी प्रदर्शित करते हैं कि स्पर्श करने पर, आवेश छड़ से सरकंडे की गोली में स्थानांतरित हो जाते हैं। यह कहा जाता है कि सरकंडे की गोलियाँ स्पर्श द्वारा विद्युन्मय अथवा आवेशित (आविष्ट) होती हैं। वह गुण जो दो प्रकार के आवेशों में भेद करता है, आवेश की ध्रुवता कहलाता है।

जब काँच की छड़ को रेशम से रगड़ते हैं तो छड़ एक प्रकार का आवेश अर्जित करती है तथा रेशम दूसरे प्रकार का आवेश अर्जित करता है। यह उन सभी वस्तुओं के युगल के लिए सत्य है जो विद्युन्मय होने के लिए परस्पर रगड़े जाते हैं। अब यदि विद्युन्मय काँच की छड़ को उस रेशम के संपर्क में लाते हैं जिससे उसे रगड़ा गया था, तो वे अब एक-दूसरे को आकर्षित नहीं करते। ये अब अन्य हलकी वस्तुओं को भी आकर्षित अथवा प्रतिकर्षित नहीं करते जैसा कि ये विद्युन्मय होने पर कर रहे थे।

इस प्रकार, रगड़ने के पश्चात वस्तुओं द्वारा अर्जित आवेश आवेशित वस्तुओं को एक-दूसरे के संपर्क में लाने पर लुप्त हो जाता है। इन प्रेक्षणों से आप क्या निष्कर्ष निकाल सकते हैं? यह तो केवल इतना बताता है कि वस्तुओं द्वारा अर्जित विजातीय आवेश एक-दूसरे के प्रभाव को निष्फल कर देते हैं। इसीलिए अमेरिकी वैज्ञानिक बेंजामिन फ्रेंकलिन ने आवेशों को धनात्मक तथा ऋणात्मक कहा। हम जानते हैं कि जब हम किसी धनात्मक संख्या को उसी परिमाण की ऋणात्मक संख्या से जोड़ते हैं तो योगफल शून्य होता है। आवेशों को धनात्मक तथा ऋणात्मक नाम देने के पीछे भी यही तर्क रहा होगा। परिपाटी के अनुसार काँच की छड़ अथवा बिल्ली के समूर पर आवेश धनात्मक कहलाता है तथा प्लास्टिक-छड़ अथवा रेशम पर आवेश ऋणात्मक कहलाता है। जब किसी वस्तु पर कोई आवेश होता है तो वह वस्तु विद्युन्मय अथवा आवेशित (आविष्ट) कही जाती है। जब उस पर कोई आवेश नहीं होता तब उसे अनावेशित कहते हैं।


विद्युत तथा चुंबकत्व का एकीकरण

प्राचीन काल में विद्युत तथा चुंबकत्व पृथक विषय समझे जाते थे। विद्युत के अंतर्गत काँच की छड़ों, बिल्ली के समूर, बैटरी, तड़ित आदि के आवेशों पर चर्चा होती थी जबकि चुंबकत्व के अंतर्गत चुंबकों, लौह-छीलन, चुंबकीय सुई आदि में अन्योन्य क्रिया का वर्णन किया जाता था। सन 1820 ई. में डेनमार्क के वैज्ञानिक अॉर्स्टेड ने यह पाया कि चुंबकीय सुई के निकट रखे तार से विद्युत धारा प्रवाहित करने पर सुई विक्षेपित हो जाती है। एेम्पियर तथा फैराडे ने इस प्रेक्षण का यह कहकर पोषण किया कि गतिशील आवेश चुंबकीय क्षेत्र उत्पन्न करते हैं तथा गतिशील चुंबक विद्युत धारा उत्पन्न करते हैं। विद्युत तथा चुंबकत्व में एकीकरण तब स्थापित हुआ जब स्कॉटलैंड के भौतिकविद मैक्सवेल तथा हॉलैंड के भौतिकविद लोरेंज ने एक सिद्धांत प्रतिपादित किया जिसमें उन्होंने यह दर्शाया कि ये दोनों विषय एक-दूसरे पर निर्भर हैं। इस क्षेत्र को वैद्युतचुंबकत्व कहते हैं। हमारे चारों ओर की अधिकांश परिघटनाओं की व्याख्या वैद्युतचुंबकत्व के अंतर्गत की जा सकती है। वस्तुतः वे सभी बल जिनके विषय में हम विचार करते हैं, जैसे घर्षण पदार्थ को संयोजित रखने के लिए उनके परमाणुओं के बीच लगने वाला रासायनिक बल यहाँ तक कि सजीवों की कोशिकाओं में होने वाली प्रक्रियाओं की व्याख्या करने वाले बलों का उद्भव भी वैद्युतचुंबकीय बलों से हुआ है। वैद्युतचुंबकीय बल प्रकृति के मूल बलों में से एक है।

मैक्सवेल ने चार समीकरण प्रस्तुत किए जिनकी क्लासिकल वैद्युतचुंबकत्व में वही भूमिका है, जो यांत्रिकी में न्यूटन की गति की समीकरणों तथा गुरुत्वाकर्षण नियम की है। उन्होंने यह भी प्रमाणित किया कि प्रकाश की प्रकृति वैद्युतचुंबकीय है तथा इसकी चाल केवल विद्युत तथा चुंबकीय मापों द्वारा प्राप्त की जा सकती है। उन्होंने यह भी दावा किया कि प्रकाशिकी के विज्ञान तथा विद्युत एवं चुंबकत्व में प्रगाढ़ संबंध है।

विद्युत एवं चुंबकत्व का विज्ञान आधुनिक प्रौद्योगिक सभ्यता की नींव है। विद्युत शक्ति, दूरसंचार, रेडियो और टेलीविज़न तथा दैनिक जीवन में उपयोग होने वाली विस्तृत प्रकार की प्रायोगिक युक्तियाँ इसी विज्ञान के सिद्धांतों पर आधारित हैं। यद्यपि गतिशील आवेशित कण विद्युत तथा चुंबकीय दोनों बल आरोपित करते हैं, परंतु एेसे निर्देश फ्रेम जिसमें सभी आवेश विराम में हों, आरोपित बल केवल विद्युत बल होते हैं। आप जानते हैं कि गुरुत्वाकर्षण बल दीर्घ-परासी बल है। इसका प्रभाव वहाँ भी अनुभव किया जाता है, जहाँ अन्योन्य क्रिया करने वाले कणों के बीच की दूरी अत्यधिक होती है क्योंकि यह बल अन्योन्य क्रिया करने वाले पिंडों के बीच की दूरी के वर्ग के व्युत्क्रमानुसार घटता है। इस अध्याय के अंतर्गत हम यह सीखेंगे कि विद्युत बल भी उतना ही व्यापक है तथा वास्तव में गुरुत्वाकर्षण बल की तुलना में परिमाण की कोटि कई गुना प्रबल है (भौतिकी पाठ्यपुस्तक कक्षा 11 का अध्याय 1 देखिए)।


आवेशों की उपस्थिति के संसूचन के लिए एक सरल उपकरण स्वर्ण पत्र विद्युतदर्शी है 

[चित्र 1.2 (a)]। इसमें एक बॉक्स में धातु की एक छड़ ऊर्ध्वाधरतः लगी होती है जिसके निचले सिरे पर सोने के वर्क की दो पट्टियाँ बँधी होती हैं। जब कोई आवेशित वस्तु छड़ के ऊपरी सिरे को छूती है तो छड़ में होता हुआ आवेश सोने के वर्कों पर आ जाता है और वे एक-दूसरे से दूर हट जाते हैं। आवेश जितना अधिक होता है, वर्कों के निचले सिरों के बीच उतनी ही अधिक दूरी हो जाती है।

विद्यार्थी नीचे बताए अनुसार सरल विद्युतदर्शी बना सकते हैं [चित्र 1.2(b)]। परदे लटकाने वाली एेलुमिनियम की एेसी बारीक छड़ लीजिए जिसके दोनों सिरों पर गोले जुड़े हों। इसका लगभग 20 cm लंबा एक टुकड़ा इस प्रकार काटिए जिससे छड़ का एक सिरा चपटा तथा दूसरा सिरा गोले वाला बन जाए। एक इतनी बड़ी बोतल लीजिए जिसके मुंँह पर कॉर्क लगाकर उस कॉर्क में छेद करके चित्र में दर्शाए अनुसार इस छड़ को फिट किया जा सके। छड़ का गोले वाला सिरा बोतल के बाहर तथा कटा सिरा बोतल के भीतर रखना चाहिए। लंबा पतला एेलुमिनियम पत्र (लगभग 6 cm) लेकर इसे बीच में मोड़िए और इसे छड़ के चपटे सिरे पर सेल्युलोस-टेप के साथ जोड़ दीजिए। इस प्रकार आपके विद्युतदर्शी के पत्र बन जाते हैं। अब कॉर्क को बोतल में इस प्रकार फिट करिए कि छड़ का गोले वाला सिरा कॉर्क से लगभग 5 cm बाहर निकला रहे। बोतल के भीतर एक कागज़ का पैमाना पहले से ही पत्रों की पृथकता को मापने के लिए लगाया जा सकता है। पत्रों की पृथकता विद्युतदर्शी पर आवेश की मात्रा की एक माप होती है।

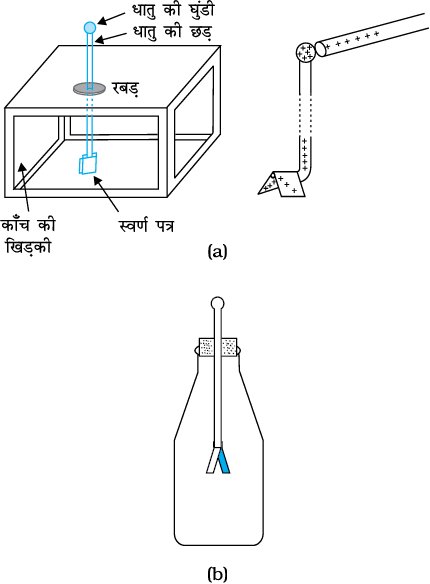
1973.png

चित्र 1.2 विद्युतदर्शी (a) स्वर्ण पत्र विद्युतदर्शी 
(b) सरल विद्युतदर्शी की रूपरेखा।


1987.png
चित्र 1.3 कागज़-पट्टी प्रयोग।

यह समझने के लिए कि विद्युतदर्शी किस प्रकार कार्य करता है सफ़ेद कागज़ की वह पट्टियाँ लीजिए जिनका उपयोग हमने आवेशित वस्तुओं द्वारा आकर्षण देखने के लिए किया था। पट्टी को आधा मोड़िए ताकि पट्टी पर मोड़ का निशान बन जाए। पट्टी को खोलिए तथा इस पर चित्र 1.3 में दर्शाए अनुसार, पर्वतीय मोड़ बनाकर हलकी इस्तरी कीजिए। इसे मोड़ पर चुटकी भरकर पकड़िए। आप यह पाएँगे कि दोनों अर्धभाग एक-दूसरे से दूर जाते हैं। यह दर्शाता है कि इस्तरी करने पर पट्टी आवेश अर्जित कर लेती है। जब आप पट्टी को आधा मोड़ते हैं तो दोनों अर्धभागों पर सजातीय आवेश होता है, अतः वे एक-दूसरे को प्रतिकर्षित करते हैं। पत्र विद्युतदर्शी में भी यही प्रभाव दिखाई देता है। परदे की छड़ के गोले को विद्युन्मय वस्तु से स्पर्श कराने पर परदे की छड़ पर आवेश स्थानांतरित होकर उसके दूसरे सिरे पर जुड़े एेलुमिनियम पत्रों पर पहुँच जाता है। पत्र के दोनों अर्धभाग सजातीय आवेश अर्जित करने के कारण एक-दूसरे को प्रतिकर्षित करते हैं। पत्रों की अपसारिता द्वारा उन पर आवेश की मात्रा सुनिश्चित की जाती है। आइए, अब पहले यह समझें कि द्रव्य से बनी वस्तुएँ क्यों आवेश को अर्जित करती हैं।

सभी पदार्थ परमाणुओं और/अथवा अणुओं से बने हैं। यद्यपि वस्तुएँ सामान्यतः वैद्युत उदासीन होती हैं, उनमें आवेश तो होते हैं परंतु उनके ये आवेश ठीक-ठीक संतुलित होते हैं। अणुओं को सँभालने वाला रासायनिक बल, ठोसों में परमाणुओं को एकसाथ थामे रखने वाले बल, गोंद का आसंजक बल, पृष्ठ तनाव से संबद्ध बल–इन सभी बलों की मूल प्रकृति वैद्युतीय है, और ये आवेशित कणों के बीच लगने वाले विद्युत बलों से उत्पन्न होते हैं। इस प्रकार, वैद्युतचुंबकीय बल सर्वव्यापी है और यह हमारे जीवन से संबद्ध प्रत्येक क्षेत्र में सम्मिलित है। अतः यह आवश्यक है कि हम इस प्रकार के बल के विषय में अधिक जानकारी प्राप्त करें।

किसी उदासीन वस्तु को आवेशित करने के लिए हमें उससे एक प्रकार के आवेश को जोड़ने अथवा हटाने की आवश्यकता होती है। जब हम यह कहते हैं कि कोई वस्तु आवेशित है तो हम सदैव ही इस आवेश के आधिक्य अथवा अभाव का उल्लेख करते हैं। ठोसों में कुछ इलेक्ट्रॉन परमाणु में कम कसकर आबद्ध होने के कारण, वे आवेश होते हैं जो एक वस्तु से दूसरी वस्तु में स्थानांतरित हो जाते हैं। इस प्रकार कोई वस्तु अपने कुछ इलेक्ट्रॉन खोकर धनावेशित हो सकती है। इसी प्रकार किसी वस्तु को इलेक्ट्रॉन देकर ऋणावेशित भी बनाया जा सकता है। जब हम काँच की छड़ को रेशम से रगड़ते हैं तो छड़ के कुछ इलेक्ट्रॉन रेशम के कपड़े में स्थानांतरित हो जाते हैं। इस प्रकार छड़ धनावेशित तथा रेशम ऋणावेशित हो जाता है। रगड़ने की प्रक्रिया में कोई नया आवेश उत्पन्न नहीं होता। साथ ही स्थानांतरित होने वाले इलेक्ट्रॉनों की संख्या वस्तु में उपस्थित इलेक्ट्रॉनों की संख्या की तुलना में एक बहुत छोटा अंश होती है। और केवल वस्तु के कम कसकर आबद्ध इलेक्ट्रॉन ही रगड़कर एक वस्तु से दूसरी वस्तु में स्थानांतरित किए जा सकते हैं। इसीलिए, जब किसी वस्तु को किसी अन्य वस्तु से रगड़ा जाता है, तो वस्तुएँ आवेशित हो जाती हैं और यही कारण है कि रगड़ द्वारा वस्तुओं पर आए आवेश को दर्शाने के लिए हमें पदार्थों के कुछ निश्चित युगलों तक ही अटके रहना पड़ता है।


1.3 चालक तथा विद्युतरोधी

हाथ में पकड़ी धातु की छड़ ऊन से रगड़े जाने पर आवेशित होने का कोई संकेत नहीं दर्शाती। परंतु, यदि धातु की छड़ पर लकड़ी अथवा प्लास्टिक का हैंडिल लगा है और उसके धातु के भाग को स्पर्श नहीं किया गया है, तो वह आवेशित होने का संकेत दे देती है। मान लीजिए हम किसी ताँबे के तार के एक सिरे को उदासीन सरकंडे की गोली से जोड़ देते हैं तथा दूसरे सिरे को ऋणावेशित प्लास्टिक-छड़ से जोड़ देते हैं तो हम यह पाते हैं कि सरकंडे की गोली ऋणावेशित हो जाती है। यदि इसी प्रयोग को नॉयलोन के धागे अथवा रबर के छल्ले के साथ दोहराएँ तो प्लास्टिक-छड़ से सरकंडे की गोली में कोई आवेश स्थानांतरित नहीं होता। छड़ से गोली में आवेश के स्थानांतरित न होने का क्या कारण है?

कुछ पदार्थ तुरंत ही अपने में से होकर विद्युत को प्रवाहित होने देते हैं जबकि कुछ अन्य एेसा नहीं करते। जो पदार्थ आसानी से अपने में से होकर विद्युत को प्रवाहित होने देते हैं उन्हें चालक कहते हैं। उनमें एेसे वैद्युत आवेश (इलेक्ट्रॉन) होते हैं जो पदार्थ के भीतर गति के लिए अपेक्षाकृत स्वतंत्र होते हैं। धातुएँ, मानव तथा जंतु शरीर और पृथ्वी चालक हैं। काँच, पॉर्सेलेन, प्लास्टिक, नॉयलोन, लकड़ी जैसी अधिकांश अधातुएँ अपने से होकर प्रवाहित होने वाली विद्युत पर उच्च प्रतिरोध लगाती हैं। इन्हें विद्युतरोधी कहते हैं। अधिकांश पदार्थ ऊपर वर्णित इन दो वर्गों में से किसी एक में आते हैं।*

जब कुछ आवेश किसी चालक पर स्थानांतरित होता है तो वह तुरंत ही उस चालक के समस्त पृष्ठ पर फैल जाता है। इसके विपरीत यदि कुछ आवेश किसी विद्युतरोधी को दें तो वह वहीं पर रहता है। एेसा क्यों होता है, यह आप अगले अध्याय में सीखेंगे।

पदार्थों का यह गुण हमें बताता है कि सूखे बालों में कंघी करने अथवा रगड़ने पर नॉयलोन या प्लास्टिक की कंघी क्यों आवेशित हो जाती है, परंतु धातु की वस्तुएँ जैसे चम्मच आवेशित क्यों नहीं होती? धातुओं से आवेश का क्षरण हमारे शरीर से होकर धरती में हो जाता है, एेसा होने का कारण यह है कि धातु तथा हमारा शरीर दोनों ही विद्युत के अच्छे चालक हैं।

जब हम किसी आवेशित वस्तु को पृथ्वी के संपर्क में लाते हैं तो उसका अतिरिक्त आवेश जोड़ने वाले चालक (जैसे हमारा शरीर) में से होते हुए क्षणिक विद्युत धारा उत्पन्न करके भूमि में चला जाता है। आवेशों के भूमि के साथ बंटन की इस प्रक्रिया को भूसंपर्कण (भूसंपर्कित करना) कहते हैं। भूसंपर्कण विद्युत परिपथों एवं अनुप्रयुक्तियों की सुरक्षा के लिए की गई एक व्यवस्था है। धातु की एक मोटी प्लेट को भूमि में गहराई तक गाड़ा जाता है तथा इस प्लेट से मोटे तारों को निकालकर भवनों में इन तारों का उपयोग मुख्य आपूर्ति के निकट भूसंपर्कण के लिए किया जाता है। हमारे घरों में विद्युत की आपूर्ति के लिए तीन तार उपयोग किए जाते है विद्युन्मय तार, उदासीन तार तथा भूसंपर्क तार। इनमें से पहले दो तार विद्युत धारा को शक्ति स्टेशन से युक्तियों तक ले जाते हैं तथा तीसरा तार भूमि में गड़ी धातु की प्लेट से जोड़ा जाता है। विद्युत अनुप्रयुक्तियों; जैसे – विद्युत इस्तरी, रेफ्रिजरेटर, टेलीविज़न के धातु के आवरण भूसंपर्क तार से जुड़े होते हैं। परिपथ में कोई त्रुटि होने पर अथवा विद्युन्मय तार का धातु के आवरण से स्पर्श होने पर आवेश भूमि में प्रवाहित हो जाता है। इन अनुप्रयुक्तियों को कोई हानि नहीं होती तथा मनुष्यों को कोई क्षति भी नहीं होती; यदि भूसंपर्क तार न हो तो क्षति पहुँचना/दुर्घटना होना अपरिहार्य हो जाएगा, क्योंकि मानव शरीर विद्युत का अच्छा चालक है।

* एक तीसरी श्रेणी जिसे अर्धचालक कहते हैं, आवेशों की गति में अवरोध उत्पन्न करती है। इस अवरोध का परिमााण चालकों तथा विद्युतरोधियों के मध्यवर्ती होता है।


1.4 प्रेरण द्वारा आवेशन

जब हम किसी सरकंडे की गोली से किसी आवेशित प्लास्टिक-छड़ को स्पर्श कराते हैं तो छड़ का कुछ आवेश सरकंडे की गोली पर स्थानांतरित हो जाता है और वह आवेशित हो जाती है। इस प्रकार सरकंडे की गोली संपर्क द्वारा आवेशित होती है। तब यह प्लास्टिक-छड़ से प्रतिकर्षित होती है तथा काँच की छड़ जो विजातीय आवेशित है, की ओर आकर्षित होती है। परंतु, कोई विद्युन्मय छड़ हलकी वस्तुओं को क्यों आकर्षित करती है, इस प्रश्न का उत्तर अभी भी नहीं मिल पाया है। आइए, हम यह समझने का प्रयास करें कि निम्नलिखित प्रयोग को करने पर क्या हो सकता है।

(i) विद्युतरोधी स्टैंडों पर रखे दो धातु के गोलों A एवं B को चित्र 1.4 (a) में दर्शाए अनुसार एक दूसरे के संपर्क में लाइए।

(ii) एक धनावेशित छड़ इन गोलों में किसी एक (माना A) के निकट लाइए तथा यह सावधानी बरतिए कि छड़ गोले से स्पर्श न करे। गोले के मुक्त इलेक्ट्रॉन छड़ की ओर आकर्षित होते हैं। गोले B के पिछले पृष्ठ पर धनावेश का आधिक्य हो जाता है। दोनों प्रकार के आवेश धातु के गोलों में आबद्ध रहते हैं, पलायन नहीं कर पाते। अतः वे पृष्ठों पर ही चित्र 1.4(b) में दर्शाए अनुसार रहते हैं। गोले A के बाएँ पृष्ठ पर ऋणावेश का आधिक्य तथा गोले के दाएँ पृष्ठ पर धनात्मक आवेश का आधिक्य होता है। तथापि गोले के सारे इलेक्ट्रॉन गोले A के बाएँ पृष्ठ पर संचित नहीं होते। जैसे ही गोले A के बाएँ पृष्ठ पर इलेक्ट्रॉन एकत्र होने शुरू होते हैं अन्य इलेक्ट्रॉन इनके द्वारा प्रतिकर्षित हो जाते हैं। कुछ ही क्षण में छड़ के आकर्षण के कारण क्रिया तथा संचित आवेशों के कारण प्रतिकर्षण के बीच साम्य स्थापित हो जाता है। चित्र 1.4(b) साम्यावस्था को दर्शाता है। इस प्रक्रिया को आवेश का प्रेरण कहते हैं तथा यह लगभग तात्कालिक है। जब तक काँच की छड़ गोले के निकट रहती है तब तक चित्र में दर्शाए अनुसार संचित आवेश पृष्ठ पर रहता है। यदि छड़ को हटा लेते हैं तो आवेशों पर कोई बाह्य बल कार्य नहीं करता तथा वे अपनी उदासीन अवस्था में वापस लौट जाते हैं।

2054.png
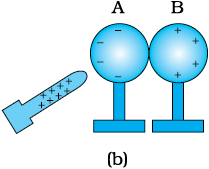
2063.png
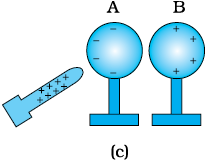
2073.png



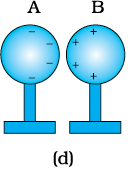
2083.png
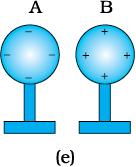
2093.png
चित्र 1.4 दो गोलों के साथ प्रेरण द्वारा आवेशन।

(iii) चित्र 1.4(c) में दर्शाए अनुसार काँच की छड़ को बाएँ गोले के निकट रखते हुए दोनों गोलों को एक-दूसरे से कुछ पृथक कीजिए। एेसा करने पर दोनों गोले विजातीय आवेशों द्वारा आवेशित होकर एक-दूसरे को आकर्षित करते हैं।

(iv) छड़ को हटा लीजिए। गोलों पर आवेश चित्र 1.4(d) में दर्शाए अनुसार स्वयं को पुनर्व्यवस्थित कर लेते हैं। अब दोनों गोलों के बीच पृथकन अधिक कीजिए। एेसा करने पर चित्र 1.4(e) में दर्शाए अनुसार आवेश गोलों पर एकसमान रूप से वितरित हो जाता है।

इस प्रक्रिया में धातु के गोले आवेशित हो जाते हैं। धनावेशित काँच की छड़ के आवेश की कोई क्षति नहीं होती, जो संपर्क द्वारा आवेशित करने की प्रक्रिया के विपरीत है।

जब किसी विद्युन्मय छड़ को हलकी वस्तुओं के निकट लाते हैं तो यही प्रभाव होता है। छड़ वस्तुओं के पास वाले पृष्ठ पर विजातीय आवेश प्रेरित करती है तथा सजातीय आवेश वस्तुओं के दूर वाले भाग पर पहुँच जाता है [एेसा तब भी होता है जब हलकी वस्तु चालक नहीं होती। यह प्रक्रिया किस प्रकार होती है इसका स्पष्टीकरण बाद में अनुच्छेद 1.10 तथा 2.10 में किया गया है ]। दोनों प्रकार के आवेशों के केंद्रों में कुछ पृथकन होता है। हम जानते हैं कि सजातीय आवेशों में प्रतिकर्षण तथा विजातीय आवेशों में आकर्षण होता है। तथापि, बल का परिमाण आवेशों के बीच दूरी पर निर्भर करने के कारण आकर्षण बल प्रतिकर्षण बल की तुलना में अधिक होता है। फलस्वरूप कागज़ के टुकड़े, सरकंडे की गोली आदि हलके होने के कारण छड़ की ओर खिंच आते हैं।

 

उदाहरण 1.1 

आप किसी धातु के गोले को स्पर्श किए बिना कैसे धनावेशित कर सकते हैं?

हल 

चित्र 1.5(a) में किसी विद्युतरोधी धातु के स्टैंड पर कोई अनावेशित धातु का गोला रखा दर्शाया गया है। चित्र 1.5(b) में दर्शाए अनुसार इस गोले के निकट कोई ऋणावेशित छड़ लाइए। गोले के मुक्त इलेक्ट्रॉन प्रतिकर्षण के कारण दूर जाकर दूरस्थ सिरे पर एकत्र हो जाते हैं। पास का सिरा इलेक्ट्रॉनों की कमी के कारण धनावेशित हो जाता है। जब गोले की धातु के मुक्त इलेक्ट्रॉनों पर लगने वाला नेट बल शून्य हो जाता है तो आवेशों के वितरण की यह प्रक्रिया बंद हो जाती है। किसी चालक तार द्वारा गोले को भूसंपर्कित कीजिए। इलेक्ट्रॉन भूमि में प्रवाहित हो जाएँगे जबकि पास के सिरे का धनावेश, छड़ के ऋणावेश के आकर्षण बल के कारण चित्र 1.5(c) में दर्शाए अनुसार बद्ध रहेगा। गोले का भूसंपर्क तोड़ दीजिए। पास के सिरे पर धनावेश की बद्धता बनी रहती है [चित्र 1.5(d)]। विद्युन्मय छड़ को हटा लीजिए। चित्र 1.5(e) में दर्शाए अनुसार धनावेश गोले के पृष्ठ पर एकसमान रूप से फैल जाता है।

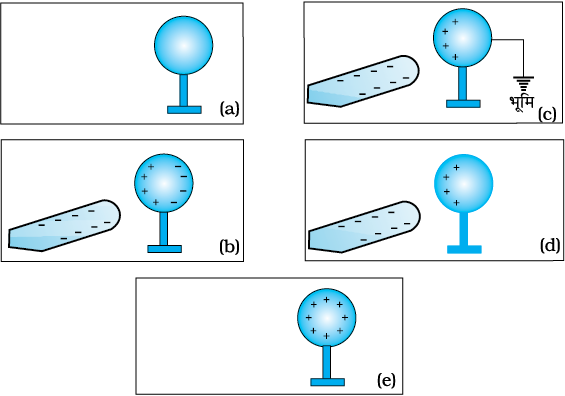
2031.png
चित्र 1.5

इस प्रयोग में धातु का गोला प्रेरण की प्रक्रिया द्वारा आवेशित हो जाता है तथा छड़ अपना कोई आवेश नहीं खोती।

प्रेरण द्वारा धातु के गोले को ऋणावेशित करने की प्रक्रिया के भी ये ही चरण होते हैं, इसमें धनावेशित छड़ गोले के समीप लाई जाती है। इस प्रकरण में इलेक्ट्रॉन भूमि से गोले में उस समय स्थानांतरित (प्रवाहित) होते हैं जब तार द्वारा गोले को भूसंपर्कित किया जाता है। क्या आप इसका कारण स्पष्ट कर सकते हैं?


1.5 वैद्युत आवेश के मूल गुण

हमने यह देखा है कि दो प्रकार के आवेश होते हैं– धनावेश तथा ऋणावेश तथा इनमें एक-दूसरे के प्रभाव को निरस्त करने की प्रवृत्ति होती है। अब, हम यहाँ वैद्युत आवेश के अन्य गुणों का वर्णन करेंगे।

यदि आवेशित वस्तुओं का साइज़ उनके बीच की दूरी की तुलना में बहुत कम होता है तो हम उन्हें बिंदु आवेश मानते हैं। यह मान लिया जाता है कि वस्तु का संपूर्ण आवेश आकाश में एक बिंदु पर संकेंद्रित है।


1.5.1 आवेशों की योज्यता

अब तक हमने आवेश की परिमाणात्मक परिभाषा नहीं दी है; इसे हम अगले अनुभाग में समझेंगे। अंतरिम रूप में हम यह मानेंगे कि एेसा किया जा सकता है और फिर आगे बढ़ेंगे। यदि किसी निकाय में दो बिंदु आवेश q1 तथा q2 हैं तो निकाय का कुल आवेश q1 तथा q2 को बीजगणितीय रीति से जोड़ने पर प्राप्त होता है, अर्थात आवेशों को वास्तविक संख्याओं की भाँति जोड़ा जा सकता है अथवा आवेश द्रव्यमान की भाँति अदिश राशि है। यदि किसी निकाय में n आवेश q1, q2 , q3... qn, हैं तो निकाय का कुल आवेश q1 + q2 + q3 + …+ qn है। आवेश का द्रव्यमान की भाँति ही परिमाण होता है दिशा नहीं होती। तथापि आवेश तथा द्रव्यमान में एक अंतर है। किसी वस्तु का द्रव्यमान सदैव धनात्मक होता है जबकि कोई आवेश या तो धनात्मक हो सकता है अथवा ऋणात्मक। किसी निकाय के आवेश का योग करते समय उसके उपयुक्त चिह्न का उपयोग करना होता है। उदाहरणार्थ, किसी निकाय में किसी यादृच्छिक मात्रक में मापे गए पाँच आवेश +1, +2, –3, +4 तथा –5 हैं, तब उसी मात्रक में निकाय का कुल आवेश = (+1) + (+2) + (–3) + (+4) + (–5) = –1 है।


1.5.2 वैद्युत आवेश संरक्षित है

हम इस तथ्य की ओर पहले ही संकेत दे चुके हैं कि जब वस्तुएँ रगड़ने पर आवेशित होती हैं तो एक वस्तु से दूसरी वस्तु में इलेक्ट्रॉनों का स्थानांतरण होता है, कोई नया आवेश उत्पन्न नहीं होता है, और न ही आवेश नष्ट होता है। वैद्युत आवेशयुक्त कणों को दृष्टि में लाएँ तो हमें आवेश के संरक्षण की धारणा समझ में आएगी। जब हम दो वस्तुओं को परस्पर रगड़ते हैं तो एक वस्तु जितना आवेश प्राप्त करती है, दूसरी वस्तु उतना आवेश खोती है। बहुत सी आवेशित वस्तुओं के किसी वियुक्त निकाय के भीतर, वस्तुओं में अन्योन्य क्रिया के कारण, आवेश पुनः वितरित हो सकते हैं, परंतु यह पाया गया है कि वियुक्त निकाय का कुल आवेश सदैव संरक्षित रहता है। आवेश-संरक्षण को प्रायोगिक रूप से स्थापित किया जा चुका है।

यद्यपि किसी प्रक्रिया में आवेशवाही कण उत्पन्न अथवा नष्ट किए जा सकते हैं, परंतु किसी वियुक्त निकाय के नेट आवेश को उत्पन्न करना अथवा नष्ट करना संभव नहीं है। कभी-कभी प्रकृति आवेशित कण उत्पन्न करती है कोई न्यूट्रॉन एक प्रोटॉन तथा एक इलेक्ट्रॉन में रूपांतरित हो जाता है। इस प्रकार उत्पन्न प्रोटॉन तथा इलेक्ट्रॉन पर, परिमाण में समान एवं विजातीय (विपरीत) आवेश उत्पन्न होते हैं तथा इस रचना से पूर्व और रचना के पश्चात का कुल आवेश शून्य रहता है।


1.5.3 वैद्युत आवेश का क्वांटमीकरण

प्रायोगिक रूप से यह स्थापित किया गया है कि सभी मुक्त आवेश परिमाण में आवेश की मूल इकाई, जिसे e द्वारा दर्शाया जाता है, के पूर्णांकी गुणज हैं। इस प्रकार, किसी वस्तु के आवेश q को सदैव इस प्रकार दर्शाया जाता है –

q = ne

यहाँ n कोई धनात्मक अथवा ऋणात्मक पूर्णांक है। आवेश की यह मूल इकाई इलेक्ट्रॉन अथवा प्रोटॉन के आवेश का परिमाण है। परिपाटी के अनुसार, इलेक्ट्रॉन के आवेश को ऋणात्मक मानते हैं; इसीलिए किसी इलेक्ट्रॉन पर आवेश –e तथा प्रोटॉन पर आवेश +e द्वारा व्यक्त करते हैं।

वैद्युत आवेश सदैव e का पूर्णांक गुणज होता है। इस तथ्य को आवेश का क्वांटमीकरण कहते हैं। भौतिकी में एेसी बहुत सी अवस्थितियाँ हैं जहाँ कुछ भौतिक राशियाँ क्वांटीकृत हैं। आवेश के क्वांटमीकरण का सुझाव सर्वप्रथम अंग्रेज़ प्रयोगकर्ता फैराडे द्वारा खोजे गए विद्युत अपघटन के प्रायोगिक नियमों से प्राप्त हुआ था। सन् 1912 में मिलिकन ने इसे वास्तव में प्रायोगिक रूप से निदर्शित किया था।

मात्रकों की अंतर्राष्ट्रीय प्रणाली (SI) में आवेश का मात्रक कूलॉम है, जिसका प्रतीक C है। एक कूलॉम को विद्युत धारा के मात्रक के पदों में परिभाषित किया जाता है जिसके विषय में आप अगले अध्याय में सीखेंगे। इस परिभाषा के अनुसार, एक कूलॉम वह आवेश है जो किसी तार में 1 A (एेेम्पियर) धारा 1 सेकंड तक प्रवाहित करता है [भौतिकी की पाठ्यपुस्तक कक्षा 11, भाग 1 का अध्याय 2 देखिए]। इस प्रणाली में, आवेश की मूल इकाई

e = 1.602192 × 10–19 C

इस प्रकार, –1C आवेश में लगभग 6 × 1018 इलेक्ट्रॉन होते हैं। स्थिरवैद्युतिकी में इतने विशाल परिमाण के आवेशों से यदा-कदा ही सामना होता है और इसीलिए हम इसके छोटे मात्रकों 1 µC (माइक्रोकूलॉम) = 10–6 C अथवा 1 mC (मिलीकूलॉम) = 10–3 C का उपयोग करते हैं।

यदि केवल इलेक्ट्रॉन तथा प्रोटॉन ही विश्व में आवेश के मूल मात्रक हैं तो सभी प्रेक्षित आवेशों को e का पूर्णांक गुणज होना चाहिए। इस प्रकार यदि किसी वस्तु में n1 इलेक्ट्रॉन तथा n2 प्रोटॉन हैं तो उस वस्तु पर कुल आवेश n2 × e + n1 × (–e) = (n2 – n1) e है। चूँकि n1 तथा n2 पूर्णांक हैं, इनका अंतर भी एक पूर्णांक है। अतः किसी वस्तु पर आवेश सदैव e का पूर्णांक गुणज होता है जिसे e के चरणों में ही घटाया अथवा बढ़ाया जा सकता है।

किंतु, मूल मात्रक e का साइज़ बहुत छोटा होता है और स्थूल स्तर पर हम कुछ µC के आवेशों को व्यवहार में लाते हैं, इस पैमाने पर यह तथ्य दृष्टिगोचर नहीं होता कि किसी वस्तु का आवेश e के मात्रकों में घट अथवा बढ़ सकता है। आवेश की कणिकीय प्रकृति लुप्त हो जाती है और यह सतत प्रतीत होता है।

इस स्थिति की तुलना बिंदु तथा रेखा की ज्यामितीय परिकल्पनाओं से की जा सकती है। दूर से देखने पर कोई बिंदुकित रेखा हमें सतत प्रतीत होती है परंतु वह वास्तव में सतत नहीं होती। जिस प्रकार एक-दूसरे के अत्यधिक निकट के बहुत से बिंदु हमें सतत रेखा का आभास देते हैं, उसी प्रकार एक साथ लेने पर बहुत से छोटे आवेशों का संकलन भी सतत आवेश वितरण जैसा दिखाई देता है।

स्थूल स्तर पर हम एेसे आवेशों से व्यवहार करते हैं जो इलेक्ट्रॉन e के आवेश की तुलना में परिमाण में अत्यधिक विशाल होते हैं। चूँकि e = 1.6 × 10–19 C, परिमाण में 1µC आवेश में एक इलेक्ट्रॉन के आवेश का लगभग 1013 गुना आवेश होता है। इस पैमाने पर, यह तथ्य कि किसी वस्तु में आवेश की कमी अथवा वृद्धि केवल e के मात्रकों में हीे हो सकती है, इस कथन से सर्वथा भिन्न नहीं है कि आवेश सतत मान ग्रहण कर सकता है। इस प्रकार, स्थूल स्तर पर आवेश के क्वांटीकरण का कोई व्यावहारिक महत्त्व नहीं है तथा इसकी उपेक्षा की जा सकती है। सूक्ष्म स्तर पर जहाँ आवेश के परिमाण e के कुछ दशक अथवा कुछ शतक कोटि के होते हैं अर्थात जिनकी गणना की जा सकती है, वहाँ पर आवेश विविक्त प्रतीत होते हैं तथा आवेश के क्वांटमीकरण की उपेक्षा नहीं की जा सकती। अतः यह जानना बहुत महत्वपूर्ण है कि किस परिमाण के आवेश की बात हो रही है।


उदाहरण 1.2 

यदि किसी पिंड से एक सेकंड में 109 इलेक्ट्रॉन किसी अन्य पिंड में स्थानांतरित होते हैं तो 1C आवेश के स्थानांतरण में कितना समय लगेगा?

हल 

1सेकंड में पिंड से 109 इलेक्ट्रॉन निकलते हैं, अतः पिंड द्वारा 1s में दिया जाने वाला आवेश 1.6 × 10–19 × 109 C = 1.6 × 10–10 C

तब 1 C आवेश के संचित होने के समय का आकलन 1 C ÷ (1.6 × 10–10 C/s) = 6.25 × 109 s = 6.25 × 109 ÷ (365 × 24 × 3600) वर्ष = 198 वर्ष। इस प्रकार जिस पिंड से 109 इलेक्ट्रॉन प्रति सेकंड की दर से उत्सर्जन हो रहा है, उससे 1 C आवेश संचित करने में लगभग 200 वर्ष लगेंगे। अतः बहुत से व्यावहारिक कार्यों की दृष्टि से एक कूलॉम आवेश का एक अति विशाल मात्रक है।

तथापि यह जानना भी अति महत्वपूर्ण है कि किसी पदार्थ के 1 घन सेंटीमीटर टुकड़े में लगभग कितने इलेक्ट्रॉन होते हैं। 1 cm भुजा के ताँबे के घन में लगभग 2.5 × 1024 इलेक्ट्रॉन होते हैं।


उदाहरण 1.3

एक कप जल में कितने धन तथा ऋण आवेश होते हैं?

हल 

मान लीजिए कि एक कप जल का द्रव्यमान 250 g है। जल का अणु द्रव्यमान 18 g है। इस प्रकार एक मोल (= 6.02 × 1023 अणु) जल का द्रव्यमान 18 g है। अतः एक कप जल में अणुओं की संख्या = (250/18) × 6.02 × 1023 ।

जल के प्रत्येक अणु में दो हाइड्रोजन परमाणु तथा एक अॉक्सीजन परमाणु होता है, अर्थात, 10 इलेक्ट्रॉन तथा 10 प्रोटॉन होते हैं। अतः कुल धन तथा कुल ऋण आवेश परिमाण में समान होते हैं। आवेश का यह परिमाण = (250/18) × 6.02 × 1023 × 10 × 1.6 × 10–19 C = 1.34 × 107 C



1.6 कूलॉम नियम

कूलॉम नियम दो बिंदु आवेशों के बीच लगे बल के विषय में एक मात्रात्मक प्रकथन है। जब आवेशित वस्तुओं के साइज़ उनको पृथक करने वाली दूरी की तुलना में बहुत कम होते हैं तो एेसी आवेशित वस्तुओं के साइज़ों की उपेक्षा की जा सकती है और उन्हें बिंदु आवेश माना जा सकता है। कूलॉम ने दो बिंदु आवेशों के बीच लगे बल की माप की और यह पाया कि यह बल दोनों आवेशों के परिमाणों के गुणनफल के अनुक्रमानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती है तथा यह दोनों आवेशों को मिलाने वाली रेखा के अनुदिश कार्य करता है। इस प्रकार यदि दो बिंदु आवेशों q1 तथा q2 के बीच निर्वात में पृथकन r है, तो इनके बीच लगे बल (F) का परिमाण है

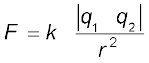3395.png (1.1)

अपने प्रयोगों से किस प्रकार कूलॉम इस नियम तक पहुँचे? कूलॉम ने धातु के दो आवेशित गोलों के बीच लगे बल की माप के लिए एेंठन तुला* का उपयोग किया। जब दो गोलों के बीच पृथकन प्रत्येक गोले की त्रिज्या की तुलना में बहुत अधिक होता है तो प्रत्येक आवेशित गोले को बिंदु आवेश मान सकते हैं। तथापि आरंभ करते समय गोलों पर आवेश अज्ञात थे। तब वह किस प्रकार समीकरण (1.1) जैसे संबंध को खोज पाए? कूलॉम ने निम्नलिखित सरल उपाय सोचा–मान लीजिए धातु के गोले पर आवेश q है। यदि इस गोले को इसके सर्वसम किसी अन्य अनावेशित गोले के संपर्क में रख दें तो आवेश q दोनों गोलों पर फैल जाएगा। सममिति के अनुसार, प्रत्येक गोले पर q/2* आवेश होगा। इस प्रक्रिया को दोहराकर हम q/2, q/4 आदि आवेश प्राप्त कर सकते हैं। कूलॉम ने आवेशों के नियत युगल के लिए दूरियों में परिवर्तन करके विभिन्न दूरियों के लिए बल की माप की। तत्पश्चात उन्होंने प्रत्येक युगल के लिए दूरी नियत रखकर युगलों में आवेशों में परिवर्तन किया। विभिन्न दूरियों पर आवेशों के विभिन्न युगलों के लिए बलों की तुलना करके कूलॉम समीकरण (1.1) के संबंध पर पहुँच गए।

* एेंठन तुला बल मापने की एक सुग्राही युक्ति है। इस तुला का उपयोग बाद में कैवेंडिश ने दो पिंडों के बीच लगे गुरुत्वाकर्षण बल की माप के लिए भी करके न्यूटन के गुरुत्वाकर्षण नियम को सत्यापित किया।

कूलॉम नियम जो कि एक सरल गणितीय कथन है, उस तक आरंभ में, ऊपर वर्णित प्रयोगों के आधार पर पहुँचा गया। यद्यपि इन मूल प्रयोगों ने इसे स्थूल स्तर पर स्थापित किया, अवपरमाणुक स्तर (r ~ 10–10 m) तक भी इसे स्थापित किया जा चुका है।

कूलॉम ने अपने नियम की खोज बिना आवेशों के परिमाणों के सही संज्ञान के, की थी। वास्तव में, इसे विपरीत अनुप्रयोग के लिए उपयोग में लाया जा सकता है–कूलॉम के नियम का उपयोग अब हम आवेश के मात्रक को परिभाषित करने के लिए कर सकते हैं। समीकरण (1.1) के संबंध में अब तक k का मान यादृच्छिक है। हम k के लिए किसी भी धनात्मक मान का चयन कर सकते हैं। k का चयन आवेश के मात्रक का साइज़ निर्धारित करता है। SI मात्रकों में k का मान लगभग 9 × 109 Nm2/C2

है। इस चयन के फलस्वरूप आवेश का जो मात्रक प्राप्त होता है उसे कूलॉम कहते हैं जिसकी परिभाषा हमने पहले अनुच्छेद 1.4 में दे दी है। समीकरण (1.1) में k का यह मान रखने पर हम यह पाते हैं कि q1 = q2 = 1 C तथा r = 1 m के लिए

F = 9 × 109 N

अर्थात 1 C वह आवेश है जो निर्वात में 1 m दूरी पर रखे इसी परिमाण के किसी अन्य सजातीय आवेश को 9 × 109 न्यूटन बल से प्रतिकर्षित करे। स्पष्ट रूप से, 1 C व्यावहारिक कार्यों के लिए आवेश का बहुत बड़ा मात्रक है। स्थिरवैद्युतिकी में, व्यवहार में इसके छोटे मात्रकों जैसे 1mC तथा 1 µC का उपयोग किया जाता है।

बाद की सुविधा के लिए समीकरण (1.1) के नियतांक k को प्रायः 

k = 1/4πε0 लिखते हैं, जिससे कूलॉम नियम को इस प्रकार व्यक्त किया जाता है

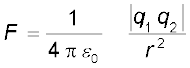3405.png (1.2)

ε0 को मुक्त आकाश या निर्वात की विद्युतशीलता अथवा परावैद्युतांक कहते हैं। SI मात्रकों में ε0 का मान

ε0= 8.854 × 10–12 C2 N–1m–2

बल एक सदिश है, अतः कूलॉम नियम को सदिश संकेतन में लिखना उत्तम होता है। मान लीजिए q1 तथा q2 आवेशों के स्थिति सदिश क्रमशः r1 तथा r2 हैं [चित्र 1.6(a) देखिए]। हम q2 के द्वारा q1 पर आरोपित बल को F12 तथा q1 के द्वारा q2 पर आरोपित बल को F21 द्वारा व्यक्त करते हैं। दो बिंदु आवेशों q1 तथा q2 को सुविधा के लिए 1 तथा 2 अंक द्वारा व्यक्त किया गया है। साथ ही 1 से 2 की ओर जाते सदिश को r21 द्वारा व्यक्त किया गया है–

r21 = r2 – r1

* इसमें आवेशों की योज्यशीलता तथा आवेशों के संरक्षण की अवधारणाएँ अंतर्निहित हैं। दो आवेशों (प्रत्येक q/2) के संयोजन से कुल आवेश q बनता है।

इसी प्रकार 2 से 1 की ओर जाते सदिश को r12 द्वारा व्यक्त किया जाता है–

r12 = r1 – r2 = – r21

सदिशों r21 तथा r12 के परिमाणों का संकेतन क्रमशः r21 एवं r12 द्वारा होता है (rn21 = rn12)। किसी सदिश की दिशा का विशेष उल्लेख उस सदिश के अनुदिश एकांक सदिश द्वारा किया जाता है। बिंदु 1 से 2 की ओर (अथवा 2 से 1 की ओर) इंगित करने वाले एकांक सदिश की परिभाषा हम इस प्रकार करते है

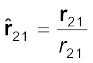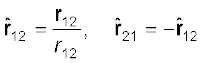
3419.png, 3424.png

क्रमशः r1 तथा r2 पर अवस्थित बिंदु आवेशों q1 v q2 के बीच लगे कूलॉम बल नियम को तब इस प्रकार व्यक्त किया जाता है

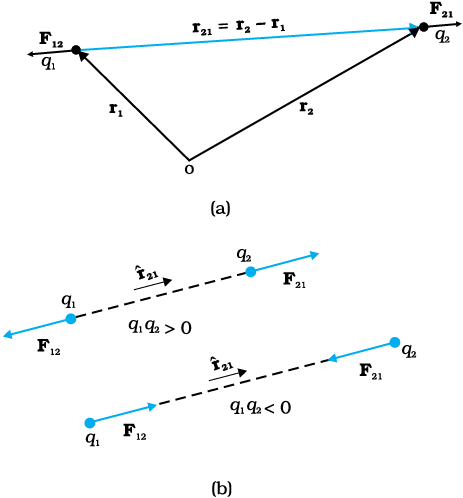
2250.png

चित्र 1.6 (a) ज्यामिति तथा 
(b) आवेशों के बीच आरोपित बल।

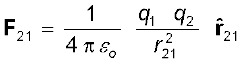
3429.png

(1.3)

Coulomb.tif

चार्ल्स अॉगस्टिन डे कूलॉम (1736 –1806)

चार्ल्स अॉगस्टिन डे कूलॉम (1736 – 1806) फ्रांसीसी भौतिकविद कूलॉम ने वेस्टइंडीज में एक फौजी इंजीनियर के रूप में अपना कैरियर आरंभ किया। सन् 1776 में वे पेरिस लौट आए तथा एक छोटी सी संपत्ति बनाकर एकांत में अपना शोध कार्य करने लगे। बल के परिमाण को मापने के लिए इन्होंने एक एेंठन तुला का आविष्कार किया और इसका उपयोग इन्होंने छोटे आवेशित गोलों के बीच लगने वाले आकर्षण अथवा प्रतिकर्षण बलों को ज्ञात करने में किया। इस प्रकार, सन् 1785 में ये व्युत्क्रम वर्ग नियम को खोज पाए जिसे आज कूलॉम का नियम कहते हैं। इस नियम का पूर्व अनुमान प्रिस्टले तथा कैवेंडिश ने लगा लिया था परंतु कैवेेंडिश ने अपने परिणाम कभी प्रकाशित नहीं किए। कूलॉम ने सजातीय तथा विजातीय चुंबकीय ध्रुवों के बीच लगने वाले व्युत्क्रम वर्ग नियम का भी पता लगाया।


समीकरण (1.3) के संबंध में कुछ टिप्पणियाँ प्रासंगिक हैं :

• समीकरण (1.3) q1 तथा q2 के किसी भी चिह्न, धनात्मक अथवा ऋणात्मक के लिए मान्य है। यदि q1 तथा q2 समान चिह्न के हैं (या तो दोनों ही धनात्मक अथवा दोनों ही ऋणात्मक हैं) तब F21,

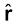3434.png21 के अनुदिश है, जो प्रतिकर्षण को प्रदर्शित करता है जैसा सजातीय आवेशों के लिए होना ही चाहिए। यदि q1 तथा q2 के विपरीत चिह्न हैं तब F21, –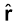3439.png21 के अनुदिश है, जो आकर्षण को प्रदर्शित करता है तथा विजातीय आवेशों के लिए हम इसी की आशा करते हैं। इस प्रकार हमें सजातीय तथा विजातीय आवेशों के प्रकरणों के लिए पृथक-पृथक समीकरण लिखने की आवश्यकता नहीं है। समीकरण (1.3) दोनों ही प्रकरणों को सही-सही प्रकट कर देती है [चित्र 1.6(b) देखिए]।

• q2 के कारण q1 पर आरोपित बल F12 को समीकरण (1.3) में 1 तथा 2 में सरल अंतर्परिवर्तन करके प्राप्त किया जा सकता है, अर्थात

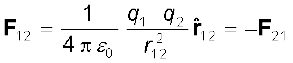
3444.png

इस प्रकार, कूलॉम नियम न्यूटन के गति के तृतीय नियम के अनुरूप ही है।

• कूलॉम नियम (समीकरण 1.3) से निर्वात में स्थित दो आवेशों q1 तथा q2 के बीच आरोपित बल प्राप्त होता है। यदि आवेश किसी द्रव्य में स्थित हैं अथवा दोनों आवेशों के बीच के रिक्त स्थान में कोई द्रव्य भरा है, तब इस द्रव्य के आवेशित अवयवों के कारण स्थिति जटिल बन जाती है। अगले अध्याय में हम द्रव्य में स्थिरवैद्युतिकी पर विचार करेंगे।


उदाहरण 1.4 

दो वैद्युत आवेशों के बीच स्थिर वैद्युत बल के लिए कूलॉम नियम तथा दो स्थिर बिंदु द्रव्यमानों के बीच गुरुत्वाकर्षण बल के लिए न्यूटन का नियम दोनों में ही बल आवेशों/द्रव्यमानों के बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। (a) इन दोनों बलों के परिमाण ज्ञात करके इनकी प्रबलताओं की तुलना की जाए (i) एक इलेक्ट्रॉन तथा एक प्रोटॉन के लिए, (ii) दो प्रोटॉनों के लिए। (b) इलेक्ट्रॉन तथा प्रोटॉन में पारस्परिक आकर्षण के वैद्युत बल के कारण इलेक्ट्रॉन तथा प्रोटॉन के त्वरण आकलित कीजिए जबकि इनके बीच की दूरी 1 Å (= 10-10 m) है। 

(mp = 1.67 × 10–27 K, me = 9.11 × 10–31 kg)

हल

(a) (i) एक इलेक्ट्रॉन तथा एक प्रोटॉन के बीच वैद्युत बल जबकि इनके बीच की दूरी r है

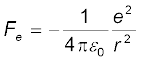
3449.png

यहाँ पर ऋणात्मक चिह्न आकर्षण बल को इंगित करता है। इसके तदनुरूपी गुरुत्वाकर्षण बल (जो सदैव धनात्मक है) :

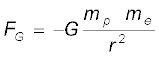
3454.png

यहाँ mp तथा me क्रमशः प्रोटॉन तथा इलेक्ट्रॉन के द्रव्यमान हैं।

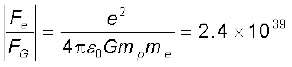
3459.png

(ii) इसी प्रकार r दूरी पर स्थित दो प्रोटॉनों के बीच वैद्युत बल तथा गुरुत्वाकर्षण बल के परिमाणों का अनुपात–

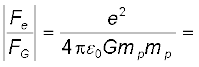3464.png 1.3 × 1036

तथापि यहाँ यह उल्लेख करना महत्वपूर्ण है कि यहाँ पर दो बलों के चिह्नों में अंतर है। दो प्रोटॉनों के लिए गुरुत्वाकर्षण बल आकर्षी है तथा कूलॉम बल प्रतिकर्षी है। नाभिक के भीतर इन बलों के वास्तविक मान (नाभिक के भीतर दो प्रोटॉनों के बीच की दूरी ~ 10-15 m है) : Fe ~ 230 N है जबकि FG ~ 1.9 × 10–34 N हैं।

इन दोनों बलों का (विमाहीन) अनुपात यह दर्शाता है कि गुरुत्वाकर्षण बल की तुलना में वैद्युत बल अत्यंत प्रबल होते हैं।

(b) एक प्रोटॉन द्वारा एक इलेक्ट्रॉन पर आरोपित वैद्युत बल F परिमाण में एक इलेक्ट्रॉन द्वारा एक प्रोटॉन पर आरोपित बल समान है; तथापि इलेक्ट्रॉन तथा प्रोटॉन के द्रव्यमान भिन्न होते हैं। इस प्रकार बल का परिमाण है

|F| = 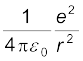3469.png = 8.987 × 109 Nm2/C2 × (1.6 ×10–19C)2 / (10–10m)2
= 2.3 × 10–8 N

न्यूटन के गति के दूसरे नियम F = ma के अनुसार इलेक्ट्रॉन में उत्पन्न त्वरण

a = 2.3×10–8 N / 9.11 ×10–31 kg = 2.5 × 1022 m/s2

इसकी गुरुत्वीय त्वरण से तुलना करने पर हम यह निष्कर्ष निकाल सकते हैं कि इलेक्ट्रॉन की गति पर गुरुत्वीय क्षेत्र का प्रभाव नगण्य है तथा किसी प्रोटॉन द्वारा इलेक्ट्रॉन पर आरोपित कूलॉम बल की क्रिया के अधीन इलेक्ट्रॉन में उत्पन्न त्वरण अत्यधिक है।

प्रोटॉन के लिए त्वरण का मान

2.3 × 10–8 N / 1.67 × 10–27 kg = 1.4 × 1019 m/s2 है।


उदाहरण 1.5 

धातु का आवेशित गोला A नाइलॉन के धागे से निलंबित है। विद्युतरोधी हत्थी द्वारा किसी अन्य धातु के आवेशित गोले B को A के इतने निकट लाया जाता है कि चित्र 1.7(a) में दर्शाए अनुसार इनके केंद्रों के बीच की दूरी 10 cm है। गोले A के परिणामी प्रतिकर्षण को नोट किया जाता है (उदाहरणार्थ– गोले पर चमकीला प्रकाश पुंज डालकर तथा अंशांकित पर्दे पर बनी इसकी छाया का विक्षेपण मापकर)। A तथा B गोलों को चित्र 1.7(b) में दर्शाए अनुसार, क्रमशः अनावेशित गोलों C तथा D से स्पर्श कराया जाता है। तत्पश्चात चित्र 1.7(c) में दर्शाए अनुसार C तथा D को हटाकर B को A के इतना निकट लाया जाता है कि इनके केंद्रों के बीच की दूरी 

5.0 cm हो जाती है। कूलॉम नियम के अनुसार A का कितना अपेक्षित प्रतिकर्षण है? गोले A तथा C एवं गोले B तथा D के साइज़ सर्वसम हैं। A तथा B के केंद्रों के पृथकन की तुलना में इनके साइज़ों की उपेक्षा कीजिए।

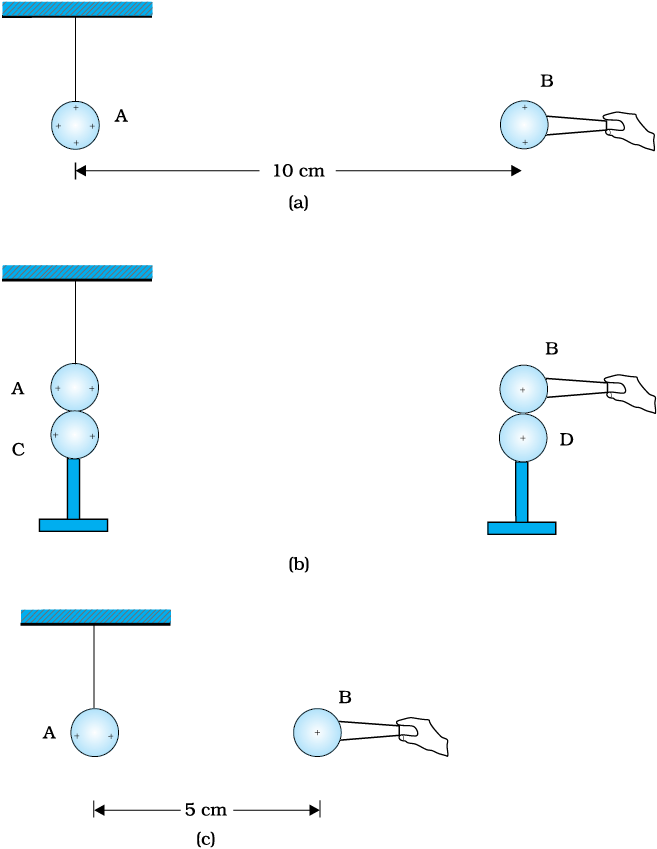
2327.png

चित्र 1.7
हल 

मान लीजिए गोले A पर मूल आवेश q तथा गोले B पर मूल आवेश q′ है। दोनों गोलों के केंद्रों के बीच दूरी r पर, प्रत्येक पर लगे स्थिर वैद्युत बल का परिमाण

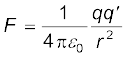
3474.png

यहाँ r की तुलना में गोलों A तथा B के साइज़ नगण्य हैं। जब कोई सर्वसम परंतु अनावेशित गोला C गोले A को स्पर्श करता है तो A तथा C पर आवेश का पुनर्वितरण होता है और सममिति द्वारा प्रत्येक गोले पर आवेश (q/2) होता है। इसी प्रकार, B तथा D के स्पर्श के पश्चात इनमें प्रत्येक पर पुनर्वितरित आवेश (q′/2) होता है। अब यदि A तथा B का पृथकन आधा रह जाए तो प्रत्येक पर स्थिरवैद्युत बल

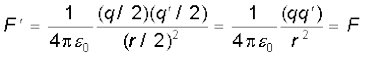
3479.png

इस प्रकार B के कारण A पर स्थिरवैद्युत बल अपरिवर्तित रहता है।


1.7 बहुल आवेशों के बीच बल

दो आवेशों के बीच पारस्परिक वैद्युत बल कूलॉम नियम द्वारा प्राप्त होता है। उस स्थिति में किसी आवेश पर आरोपित बल का परिकलन कैसे करें, जहाँ उसके निकट एक आवेश न होकर उसे बहुत से आवेश चारों ओर से घेरे हों? निर्वात में स्थित n स्थिर आवेशों q1, q2, q3, ..., qn के निकाय पर विचार कीजिए। q1 पर q2, q3, ..., qn के कारण कितना बल लगता है? इसका उत्तर देने के लिए कूलॉम नियम पर्याप्त नहीं है। याद कीजिए, यांत्रिक मूल के बलों का संयोजन सदिशों के संयोजन के समांतर चतुर्भुज नियम द्वारा किया जाता है। क्या यही स्थिरवैद्युत मूल के बलों पर भी लागू होता है?

प्रयोगों द्वारा यह सत्यापित हो चुका है कि किसी आवेश पर कई अन्य आवेशों के कारण बल उस आवेश पर लगे उन सभी बलों के सदिश योग के बराबर होता है जो इन आवेशों द्वारा इस आवेश पर एक-एक कर लगाया जाता है। किसी एक आवेश द्वारा लगाया गया विशिष्ट बल अन्य आवेशों की उपस्थिति के कारण प्रभावित नहीं होता। इसे अध्यारोपण का सिद्धांत कहते हैं।

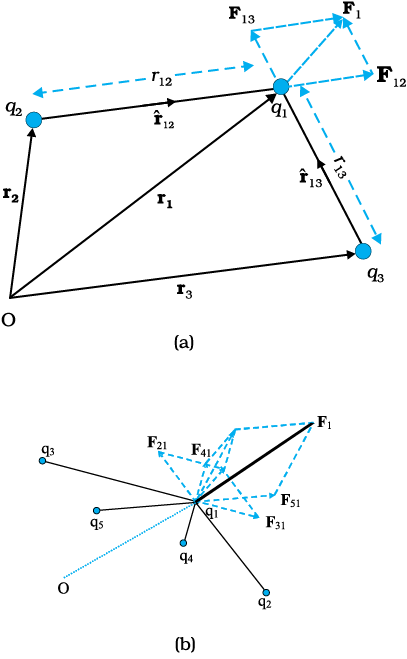
2299.png

चित्र 1.8 (a) तीन आवेशों (b) बहुल आवेशों के निकाय।

इस अवधारणा को भलीभाँति समझने के लिए तीन आवेशों q1, q2 तथा q3 के निकाय, जिसे चित्र 1.8(a) में दर्शाया गया है, पर विचार कीजिए। किसी एक आवेश, जैसे q1 पर अन्य दो आवेशों q2 तथा q3 के कारण बल को इनमें से प्रत्येक आवेश के कारण लगे बलों का सदिश संयोजन करके प्राप्त किया जा सकता है। इस प्रकार यदि q2 के कारण q1 पर बल को F12 द्वारा निर्दिष्ट किया जाता है, तो F12 को समीकरण (1.3) द्वारा अन्य आवेशों की उपस्थिति होते हुए भी इस प्रकार व्यक्त किया जाता है :

F12 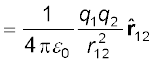3484.png


इसी प्रकार q3 के कारण q1 पर लगा कूलॉम बल जिसे F13 द्वारा निर्दिष्ट करते हैं तथा जिसे लिख सकते हैं

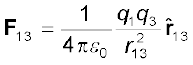
3489.png

यह भी q3 के कारण q1 पर लगा कूलॉम बल ही है, जबकि अन्य आवेश q2 उपस्थित हैं।

इस प्रकार q1 पर दो आवेशों q2 तथा q3 के कारण कुल बल F1 है

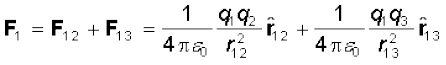3494.png (1.4)

चित्र 1.8(b) में दर्शाए अनुसार तीन से अधिक आवेशों के निकाय के लिए उपरोक्त परिकलन का व्यापकीकरण किया जा सकता है।

अध्यारोपण के सिद्धांत के अनुसार आवेशाें q1, q2, ..., qn के किसी निकाय में आवेश q1 पर q2 द्वारा लगा बल कूलॉम नियम द्वारा लगे बल के समान होता है, अर्थात यह अन्य आवेशों q3, q4, ..., qn की उपस्थिति से प्रभावित नहीं होता। आवेश q1 पर सभी आवेशों द्वारा लगा कुल बल F1 तब F12, F13, ..., F1n का सदिश योग होगा। अतः

1.b

1.a

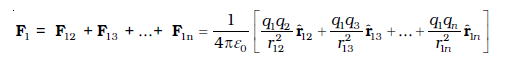
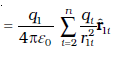
(1.5)

सदिशों के संयोजन की सामान्य विधि, समांतर चतुर्भुज के नियम द्वारा सदिश योग प्राप्त किया जाता है। वास्तव में मूल रूप से समस्त स्थिरवैद्युतिकी कूलॉम नियम तथा अध्यारोपण के सिद्धांत का एक परिणाम है।

 

उदाहरण 1.6 

तीन आवेशों q1, q2, q3 पर विचार कीजिए जिनमें प्रत्येक q के बराबर है तथा l भुजा वाले समबाहु त्रिभुज के शीर्षों पर स्थित है। त्रिभुज के केंद्रक पर चित्र 1.9 में दर्शाए अनुसार स्थित आवेश Q (जो q का सजातीय) पर कितना परिणामी बल लग रहा है?

 

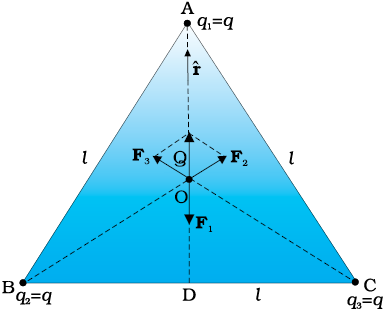
2393.png
चित्र 1.9

 

हल 

दिए गए l भुजा के समबाहु त्रिभुज ABC में यदि हम भुजा BC पर AD लंब खींचें तो AD = AC cos 30º = (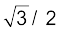3531.png) l तथा A से केंद्रक की दूरी AD = (2/3) AD = (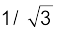3536.png)l सममिति से AO = BO = CO

इस प्रकार

A पर स्थित आवेश q के कारण Q पर बल, F1 = 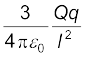3541.png AO के अनुदिश

B पर स्थित आवेश q के कारण Q पर बल, F2 = 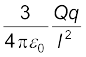3546.png BO के अनुदिश

C पर स्थित आवेश q के कारण Q पर बल, F3 = 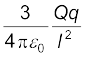3551.png CO के अनुदिश

बलों F2 तथा F3 का परिणामी समांतर चतुर्भुज नियम द्वारा 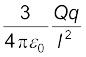3556.png OA के अनुदिश है। इसीलिए, Q पर कुल बल = 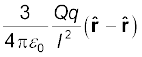3561.png = 0 यहाँ 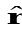3567.png, OA के अनुदिश एकांक सदिश है। सममिति द्वारा भी यह स्पष्ट है कि उन तीनों बलों का योग शून्य होगा।

मान लीजिए परिणामी बल शून्येतर था परंतु किसी दिशा में था। विचार कीजिए कि क्या हुआ होता यदि इस निकाय को O के गिर्द (परितः) 60º पर घूर्णन कराया जाता।

 

उदाहरण 1.7 

चित्र 1.10 में दर्शाए अनुसार किसी समबाहु त्रिभुज के शीर्षों पर स्थित आवेशों q, q, तथा –q पर विचार कीजिए। प्रत्येक आवेश पर कितना बल लग रहा है?

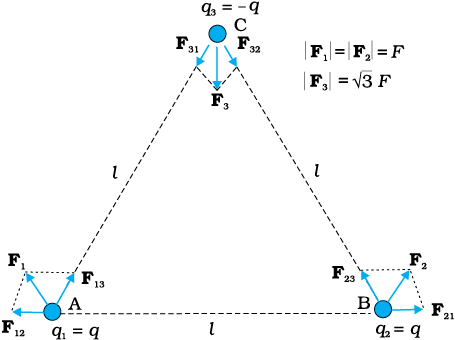
2368.png
चित्र 1.10

हल चित्र 1.10 में दर्शाए अनुसार, A पर स्थित आवेश q पर अन्य आवेशों जैसे B पर स्थित q के कारण बल F12 BA के अनुदिश तथा C पर स्थित –q के कारण बल F13 AC के अनुदिश है। समांतर चतुर्भुज नियम द्वारा A पर स्थित q पर कुल बल F1 है

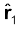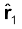F1 = F 3577.png यहाँ 3582.png BC के अनुदिश एकांक सदिश है।

आवेशों के प्रत्येक युगल के लिए आकर्षण अथवा प्रतिकर्षण बलों के परिमाण F समान हैं तथा 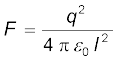3587.png

इस प्रकार B पर स्थित आवेश q पर कुल बल F2 = F 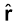3592.png2 यहाँ 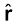3597.png2 AC के अनुदिश एकांक सदिश है।

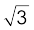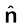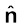इसी प्रकार, C पर स्थित आवेश –q पर कुल बल F3 = 3602.png F3607.png है। यहाँ 3612.pngएकांक सदिश है जिसकी दिशा ∠BCA को समद्विभाजित करने वाली रेखा के अनुदिश है।

यहाँ रोचक बात यह है कि तीनों आवेशों पर लगे बलों का योग शून्य है, अर्थात

F1 + F2 + F3 = 0

यह परिणाम चौंकाने वाला नहीं है। यह इस तथ्य का अनुसरण करता है कि कूलॉम नियम तथा न्यूटन के तृतीय नियम के बीच सामंजस्य है। इस कथन की निष्पत्ति आपके अभ्यास के लिए छोड़ी जा रही है।

 

1.8 विद्युत क्षेत्र

माना निर्वात में एक बिंदु आवेश Q मूल बिंदु O पर रखा है। यदि एक अन्य बिंदु आवेश q, बिंदु P पर रखा जाए, जहाँ OP = r, तो आवेश Q, q पर कूलॉम के नियमानुसार बल लगाएगा। हम यह प्रश्न पूछ सकते है यदि आवेश q को हटा लें तो Q के परिवेश में क्या बचेगा? क्या कुछ भी नहीं बचेगा? यदि एेसा है तो P पर आवेश q रखने पर इस पर बल कैसे लगता है? इस प्रकार के प्रश्नों का उत्तर देने के लिए प्रारंभिक वैज्ञानिकों ने क्षेत्र की अवधारणा प्रस्तुत की। इसके अनुसार हम कहते हैं कि आवेश Q अपने चारों ओर विद्युत क्षेत्र उत्पन्न करता है जब इसमें कोई अन्य आवेश q बिंदु P पर लाया जाता है तो क्षेत्र इस पर बल आरोपित करता है।

किसी बिंदु r पर आवेश Q द्वारा उत्पन्न विद्युत क्षेत्र

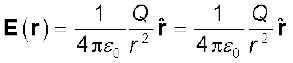
3617.png


(1.6)

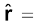यहाँ 3623.png r/r , मूल बिंदु से बिंदु r तक मात्रक सदिश है। इस प्रकार, समीकरण (1.6) स्थिति सदिश r के प्रत्येक मान के लिए विद्युत क्षेत्र का संगत मान बताती है। शब्द ‘क्षेत्र’ यह बताता है कि किस प्रकार कोई वितरित राशि (जो सदिश अथवा अदिश हो सकती है) स्थिति के साथ परिवर्तित होती है। आवेश के प्रभाव को विद्युत क्षेत्र के अस्तित्व में समाविष्ट किया गया है। आवेश Q द्वारा आवेश q पर आरोपित बल F को हम इस प्रकार प्राप्त करते है

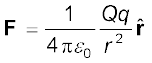3628.png (1.7)

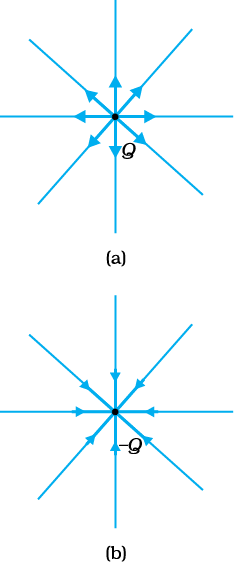
2442.png

चित्र 1.11 (a) आवेश Q के कारण विद्युत क्षेत्र, (b) आवेश –Q के कारण विद्युत क्षेत्र।

ध्यान दीजिए आवेश q भी आवेश Q पर परिमाण में समान परंतु दिशा में विपरीत बल आरोपित करता है। Q तथा q आवेशों के बीच स्थिरवैद्युत बल को हम आवेश q तथा Q के विद्युत क्षेत्र के बीच अन्योन्य क्रिया अथवा विलोमतः के रूप में समझ सकते हैं। यदि हम आवेश q की स्थिति को सदिश r द्वारा निर्दिष्ट करें, तो यह q की अवस्थिति पर एक बल F का अनुभव करता है जो आवेश q तथा विद्युत क्षेत्र E के गुणनफल के बराबर है। इस प्रकार

F(r) = q E(r) (1.8)

समीकरण (1.8) विद्युत क्षेत्र के SI मात्रक को N/C* के रूप में परिभाषित करती है।

यहाँ कुछ महत्वपूर्ण टिप्पणियाँ की जा सकती हैंः

(i) समीकरण (1.8) से यह निष्कर्ष निकाला जा सकता है कि यदि q एकांक है तो आवेश Q के कारण विद्युत क्षेत्र का आंकिक मान इसके द्वारा आरोपित बल के बराबर होता है। इस प्रकार दिक्स्थान में किसी बिंदु पर आवेश Q के कारण विद्युत क्षेत्र को उस बल के रूप में पारिभाषित किया जा सकता है जिसे कोई एकांक धनावेश उस बिंदु पर रखे जाने पर अनुभव करता है। वह आवेश Q जो विद्युत क्षेत्र उत्पन्न कर रहा है स्रोत आवेश कहलाता है तथा आवेश q जो स्रोत आवेश के प्रभाव का परीक्षण करता है, को परीक्षण आवेश कहते हैं। ध्यान दीजिए स्रोत आवेश को अपनी मूल अवस्थिति पर ही रहना चाहिए। तथापि, यदि किसी आवेश q को Q के चारों ओर कहीं लाया जाता है, तो Q स्वयं भी आवेश q के कारण वैद्युत बल का अनुभव करने के लिए बाध्य है और उसमें गति करने की प्रवृत्ति होगी। इससे मुक्ति का केवल एक ही उपाय है कि हम q को उपेक्षणीय छोटा बनाएँ, तब बल F उपेक्षणीय छोटा होता है परंतु अनुपात 

F/q एक परिमित राशि होती है तथा विद्युत क्षेत्र को पारिभाषित करती है

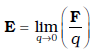1.d (1.9)

* अगले अध्याय में विद्युत क्षेत्र के लिए एक अन्य वैकल्पिक मात्रक V/m पर विचार किया जाएगा।

इस समस्या (आवेश Q को आवेश q की उपस्थिति के कारण विक्षुब्ध न होने देना) से मुक्ति का एक व्यावहारिक उपाय यह है कि आवेश Q की किन्हीं अनिर्दिष्ट बलों द्वारा अपनी अवस्थिति पर बाँधे रखा जाए। यह विलक्षण प्रतीत हो सकता है, परंतु व्यवहार में एेसा ही होता है। जब हम आवेशित की समतल चादर के कारण परीक्षण आवेश q पर लगे वैद्युत बल पर विचार करते हैं (अनुच्छेद 1.15), तब चादर पर आवेश, चादर के भीतर अनिर्दिष्ट आवेशित अवयवों द्वारा लगे बलों के कारण अपनी अवस्थितियों पर ही बँधे रहते हैं।

(ii) ध्यान दीजिए, आवेश Q के कारण विद्युत क्षेत्र E की परिभाषा यद्यपि प्रभावी रूप से परीक्षण आवेश q के पदों में की जाती है, तथापि यह q पर निर्भर नहीं करती है। इसका कारण यह है कि बल F आवेश q के अनुक्रमानुपाती है, इसलिए अनुपात F/q आवेश q पर निर्भर नहीं करता है। Q के कारण q पर बल आवेश q की किसी विशेष अवस्थिति से आवेश Q के चारों ओर के दिक्स्थान में कहीं भी हो सकती है। इस प्रकार Q के कारण विद्युत क्षेत्र E दिक्स्थान निर्देशांक r पर भी निर्भर करता है। सारे दिक्स्थान में आवेश की विभिन्न स्थितियों के लिए हमें विद्युत क्षेत्र E के भिन्न मान प्राप्त होते हैं। विद्युत क्षेत्र का अस्तित्व त्रिविमीय दिक्स्थान के प्रत्येक बिंदु पर होता है।

(iii) धनावेश के कारण विद्युत क्षेत्र आवेश से बाहर की ओर उन्मुख त्रिज्यीय होता है। इसके विपरीत, यदि स्रोत आवेश ऋणात्मक है तो विद्युत क्षेत्र सदिश, हर बिंदु पर त्रिज्यीय, किंतु अंदर की ओर उन्मुख होता है।

(iv) चूँकि आवेश Q के कारण आवेश q पर लगे बल F का परिमाण केवल आवेश Q से आवेश q के बीच की दूरी r पर निर्भर करता है, विद्युत क्षेत्र E का परिमाण भी केवल दूरी r पर निर्भर करता है। इस प्रकार, आवेश Q से समान दूरियों पर इसके कारण उत्पन्न विद्युत क्षेत्र E का परिमाण समान होता है। इस प्रकार किसी गोले के केंद्र पर स्थित बिंदु आवेश के कारण विद्युत क्षेत्र E का परिमाण उसके पृष्ठ के हर बिंदु पर समान होता है; दूसरे शब्दों में, वह क्षेत्र गोलीय रूप से सममित होता है।


1.8.1 आवेशों के निकाय के कारण विद्युत क्षेत्र

आइए, q1, q2, ..., qn आवेशों के एक निकाय पर विचार करते हैं जिनके किसी मूल बिंदु O के सापेक्ष स्थिति सदिश क्रमशः r1, r2, ..., rn हैं। किसी एकल आवेश के कारण दिक्स्थान के किसी बिंदु पर विद्युत क्षेत्र की ही भाँति आवेशों के निकाय के कारण दिक्स्थान के किसी बिंदु पर विद्युत क्षेत्र को उस बिंदु पर रखे किसी एकांक धनावेश द्वारा अनुभव किए जाने वाले बल द्वारा परिभाषित किया जाता है। यहाँ यह माना जाता है कि एकाक आवेश के कारण q1, q2, ..., qn आवेशों की मूल स्थितियाँ विक्षुब्ध नहीं होतीं। बिंदु P, जिसे स्थिति सदिश r द्वारा निर्दिष्ट किया जाता है, पर विद्युत क्षेत्र को निर्धारित करने के लिए हम कूलॉम नियम तथा अध्यारोपण के सिद्धांत का उपयोग करते हैं।

r1 पर स्थित आवेश q1 के कारण अवस्थिति r पर विद्युत क्षेत्र E1 इस प्रकार व्यक्त किया जाता है।

2502.png
चित्र 1.12 आवेशों के निकाय के कारण किसी बिंदु पर वैद्युत क्षेत्र पृथक-पृथक आवेशों के कारण उस बिंदु पर वैद्युत क्षेत्रों के सदिश योग के बराबर होता है।

E1 = 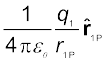3645.png

यहाँ 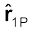3650.png आवेश q1 से P की दिशा में एकांक सदिश है तथा r1P आवेश q1 तथा P के बीच की दूरी है। इसी प्रकार r2 पर स्थित आवेश q2 के कारण अवस्थिति r पर विद्युत क्षेत्र E2 को इस प्रकार व्यक्त करते हैं

E2 = 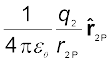3655.png

यहाँ 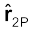3660.png आवेश q2 से P की दिशा में एकांक सदिश है तथा r2P आवेश q2 तथा P के बीच की दूरी है। इसी प्रकार के व्यंजक q3, q4, ..., qn आवेशों के विद्युत क्षेत्रों E3, E4, ..., En लिखे जा सकते हैं। अध्यारोपण सिद्धांत द्वारा आवेशों के निकाय के कारण r पर विद्युत क्षेत्र (चित्र 1.12 में दर्शाए अनुसार) इस प्रकार व्यक्त किया जा सकता है-

E(r) = E1 (r) + E2 (r) + … + En(r)

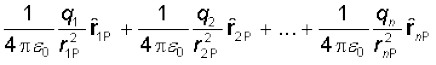
=3665.png

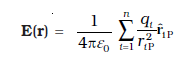1.e (1.10)

E एक सदिश राशि है जिसका मान दिक्स्थान में एक बिंदु से दूसरे बिंदु पर जाने पर परिवर्तित हो जाता है तथा यह स्रोत आवेशों की स्थितियों से निर्धारित होता है।


1.8.2 विद्युत क्षेत्र का भौतिक अभिप्राय

आपको आश्चर्य हो सकता है कि हमें यहाँ विद्युत क्षेत्र की धारणा से परिचित क्यों कराया जा रहा है। वैसे भी, आवेशों के किसी भी निकाय के लिए मापने योग्य राशि किसी आवेश पर लगा बल है जिसे सीधे ही कूलॉम नियम तथा अध्यारोपण सिद्धांत द्वारा (समीकरण 1.5) निर्धारित किया जा सकता है। फिर विद्युत क्षेत्र नामक इस मध्यवर्ती राशि को प्रस्तावित क्यों किया जा रहा है?

स्थिरवैद्युतिकी के लिए विद्युत क्षेत्र की अभिधारणा सुगम तो है पर वास्तव में आवश्यक नहीं है। विद्युत क्षेत्र आवेशों के किसी निकाय के वैद्युत पर्यावरण को अभिलक्षित करने का सुरुचि संपन्न उपाय है। आवेशों के निकाय के चारों ओर के दिक्स्थान में किसी बिंदु पर विद्युत क्षेत्र आपको यह बताता है कि निकाय को विक्षुब्ध किए बिना यदि इस बिंदु पर कोई एकांक धनात्मक परीक्षण आवेश रखे तो वह कितना बल अनुभव करेगा। विद्युत क्षेत्र आवेशों के निकाय का एक अभिलक्षण है तथा विद्युत क्षेत्र के निर्धारण के लिए आपके द्वारा उस बिंदु पर रखे जाने वाले परीक्षण आवेश पर निर्भर नहीं करता। भौतिकी में क्षेत्र शब्द का उपयोग व्यापक रूप से उस राशि को निर्दिष्ट करने के लिए किया जाता है, जो दिक्स्थान के प्रत्येक बिंदु पर पारिभाषित की जा सके तथा एक बिंदु से दूसरे बिंदु पर परिवर्तित होती हो। चूँकि बल सदिश राशि है, अतः विद्युत क्षेत्र एक सदिश राशि है।

तथापि विद्युत क्षेत्र की अभिधारणा की वास्तविक भौतिक सार्थकता तभी प्रकट होती है जब हम स्थिरवैद्युतिकी से बाहर निकलकर कालाश्रित वैद्युतचुंबकीय परिघटनाओं से व्यवहार करते हैं। मान लीजिए हम त्वरित गति से गतिमान दो दूरस्थ आवेशों q1 तथा q2 के बीच लगे बल पर विचार करते हैं। अब, वह अधिकतम चाल जिससे कोई संकेत अथवा सूचना एक स्थान से दूसरे स्थान तक जा सकती है, वह प्रकाश की चाल c है। इस प्रकार, q2 पर q1 की किसी गति का प्रभाव तात्क्षणिक उत्पन्न नहीं हो सकता। कारण (q1 की गति) तथा प्रभाव (q2 पर बल) के बीच कुछ न कुछ काल विलंब अवश्य होता है। यहीं पर सार्थक रूप में विद्युत क्षेत्र (सही अर्थों में वैद्युतचुंबकीय क्षेत्र) की अवधारणा स्वाभाविक एवं अति उपयोगी है। क्षेत्र का चित्रण इस प्रकार हैः आवेश q1 की त्वरित गति वैद्युतचुंबकीय तरंगें उत्पन्न करती है जो फिर प्रकाश की चाल से फैलकर q2 तक पहुँचती है तथा q2 पर बल लगाती है। क्षेत्र की अवधारणा काल विलंब का सुचारु रूप से स्पष्टीकरण करती है। इस प्रकार, यद्यपि वैद्युत तथा चुंबकीय बलों की संसूचना केवल आवेशों पर इनके प्रभावों (बलों) द्वारा ही की जा सकती है, उन्हें भौतिक सत्व माना जाता है, ये मात्र गणितीय रचनाएँ ही नहीं हैं। इनकी अपनी स्वतंत्र गतिकी है, अर्थात ये अपने नियमों के अनुसार विकसित होते हैं। ये ऊर्जा का परिवहन भी कर सकते हैं। इस प्रकार, कालाश्रित वैद्युतचुंबकीय क्षेत्रों का कोई स्रोत जिसे अल्प समय अंतराल के लिए खोलकर फिर बंद किया जा सकता है, ऊर्जा परिवहन करने वाले वैद्युतचुंबकीय क्षेत्रों को पीछे छोड़ देता है। क्षेत्र की अवधारणा सर्वप्रथम फैराडे ने प्रस्तावित की थी जो भौतिकी की प्रमुख अवधारणाओं में स्थान रखती है।


उदाहरण 1.8 

कोई इलेक्ट्रॉन 2.0 × 104 N C–1 परिमाण के एकसमान विद्युत क्षेत्र में
1.5 cm दूरी तक गिरता है [चित्र 1.13(a)]। क्षेत्र का परिमाण समान रखते हुए इसकी दिशा उत्क्रमित कर दी जाती है तथा अब कोई प्रोटॉन इस क्षेत्र में उतनी ही दूरी तक गिरता है [चित्र 1.13(b)]। दोनों प्रकरणों में गिरने में लगे समय की गणना कीजिए। इस परिस्थिति की ‘गुरुत्व के अधीन मुक्त पतन’ से तुलना कीजिए।

 

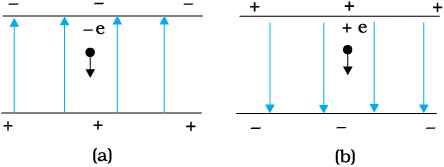
2483.png
चित्र 1.13
हल 

चित्र 1.13(a) में क्षेत्र उपरिमुखी है, अतः ऋणावेशित इलेक्ट्रॉन eE परिमाण का अधोमुखी बल अनुभव करता है, यहाँ E विद्युत क्षेत्र का परिमाण है। अतः इलेक्ट्रॉन का त्वरण

ae = eE/me

यहाँ me इलेक्ट्रॉन का द्रव्यमान है।

विरामावस्था से आरंभ करके, इलेक्ट्रॉन के मुक्त रूप से h दूरी तक गिरने में लगा समय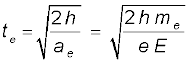3687.png

e = 1.6 × 10–19C, me = 9.11 × 10–31 kg,

E = 2.0 × 104 N C–1, h = 1.5 × 10–2 m,

te = 2.9 × 10–9s

चित्र 1.13 (b) में क्षेत्र अधोमुखी है, अतः धनावेशित प्रोटॉन eE परिमाण का अधोमुखी बल अनुभव करता है। अतः प्रोटॉन का त्वरण

ap = eE/mp

यहाँ mp प्रोटॉन का द्रव्यमान है; mp = 1.67 × 10–27 kg । अतः प्रोटॉन द्वारा गिरने में लिया गया समय 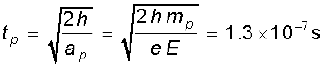3692.png

इस प्रकार, समान दूरी गिरने में भारी कण (प्रोटॉन) अधिक समय लेता है। ‘गुरुत्व के अधीन मुक्त पतन’ और इस पतन में यही मूल विषमता है क्योंकि गुरुत्व के अधीन पतन में समय वस्तु के द्रव्यमान पर निर्भर नहीं करता। ध्यान दीजिए यहाँ हमने पतन का समय परिकलित करते समय गुरुत्वीय त्वरण की उपेक्षा की है। यह देखने के लिए कि क्या यह न्यायसंगत है, आइए दिए गए विद्युत क्षेत्र में प्रोटॉन का त्वरण परिकलित करते है

3697.png 

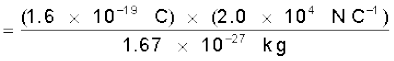
3702.png

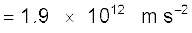
3707.png

यह त्वरण गुरुत्वीय त्वरण (9.8 m s–2) की तुलना में अत्यंत विशाल है। इलेक्ट्रॉन का त्वरण तो इस त्वरण से भी अधिक है। इस प्रकार, इस उदाहरण में गुरुत्वीय त्वरण के प्रभाव की उपेक्षा की जा सकती है।


उदाहरण 1.9 

दो बिंदु आवेश q1  तथा q2 जिनके परिमाण क्रमशः +10–8 C तथा –10–8 C हैं एक दूसरे से 0.1 m दूरी पर रखे हैं। चित्र 1.14 में दर्शाए बिंदुओं A, B तथा C पर विद्युत क्षेत्र परिकलित कीजिए।

 

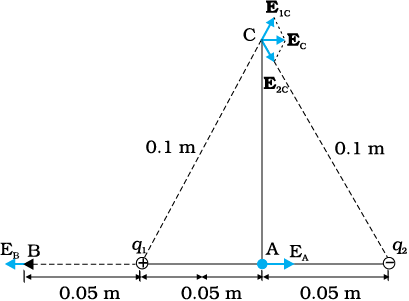
2582.png
चित्र 1.14

हल धनावेश q1 के कारण A पर विद्युत क्षेत्र सदिश E1A दाईं ओर निर्दिष्ट है तथा इसका परिमाण 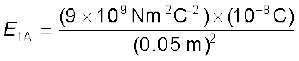3712.png = 3.6 × 104 N C–1

ऋणावेश q2 के कारण A पर विद्युत क्षेत्र सदिश E2A भी दाईं ओर निर्दिष्ट है तथा इसका परिमाण EA के समान है। अतः A पर कुल विद्युत क्षेत्र EA का परिमाण

EA = E1A + E2A = 7.2 × 104 N C–1 (यह दाईं ओर निर्दिष्ट है)

धनावेश q1 के कारण B पर विद्युत क्षेत्र सदिश E1B बाईं ओर निर्दिष्ट है तथा इसका परिमाण

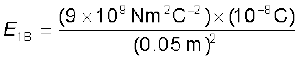3717.png= 3.6 × 104 N C–1

ऋणावेश q2 के कारण B पर विद्युत क्षेत्र सदिश E2B दाईं ओर निर्दिष्ट है तथा इसका परिमाण

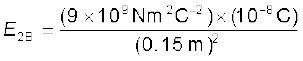3722.png= 4 × 103 N C–1

B पर कुल विद्युत क्षेत्र का परिमाण

EB = E1B – E2B = 3.2 × 104 N C–1 (यह बाईं ओर निर्दिष्ट है)

q1 तथा q2 में प्रत्येक के कारण बिंदु C पर विद्युत क्षेत्र सदिश का परिमाण समान है, अतः

3727.png = 9 × 103 N C–1

इन दोनों सदिशों की दिशाएँ चित्र 1.14 में दर्शायी गई हैं। इन दो सदिशों के परिणामी सदिश का परिमाण

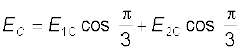3732.png= 9 × 103 N C–1 Ec दाईं ओर निर्दिष्ट है।


1.9 विद्युत क्षेत्र रेखाएँ

पिछले अनुभाग में हमने विद्युत क्षेत्र का अध्ययन किया। यह एक सदिश राशि है तथा इसे हम सदिशों की भाँति ही निरूपित कर सकते हैं। आइए किसी बिंदु आवेश के कारण E को चित्रात्मक निरूपित करने का प्रयास करते हैं। मान लीजिए बिंदु आवेश मूल बिंदु पर स्थित है। प्रत्येक बिंदु पर विद्युत क्षेत्र की दिशा के अनुदिश संकेत करते हुए क्षेत्र की तीव्रता की आनुपातिक लंबाई के सदिश खींचिए। चूँकि किसी बिंदु पर विद्युत क्षेत्र का परिमाण आवेश से उस बिंदु की दूरी के वर्ग के व्युत्क्रमानुसार घटता है, मूल बिंदु से दूर जाने पर सदिश की लंबाई निरंतर घटती जाती है तथा इसकी दिशा सदैव बहिर्मुखी अरीय संकेत करती है। चित्र 1.15 इसी चित्रण को दर्शाता है। इस चित्रण में प्रत्येक तीर विद्युत क्षेत्र अर्थात उस तीर के पुच्छ पर स्थित इकाई धन आवेश पर लगने वाला बल दर्शाता है। एक दिशा में संकेत करने वाले तीरों को मिलाने पर प्राप्त परिणामी चित्र क्षेत्र रेखा को निरूपित करता है। इस प्रकार हमें बहुत सी क्षेत्र रेखाएँ प्राप्त होती हैं जिनमें सभी बिंदु आवेश से बाहर की ओर संकेत करती हैं। क्या अब हमने विद्युत क्षेत्र की तीव्रता अथवा परिमाण के विषय में जानकारी नष्ट कर दी है, क्योंकि वह तो तीर की लंबाई में समाई हुई थी? नहीं। अब, क्षेत्र के परिमाण को क्षेत्र रेखाओं के घनत्व द्वारा निरूपित किया जाता है। आवेश के निकट E प्रबल होता है। अतः आवेश के निकट क्षेत्र रेखाओं का घनत्व अधिक होता है तथा क्षेत्र रेखाएँ सघन होती हैं। आवेश से दूर जाने पर क्षेत्र दुर्बल होता जाता है तथा क्षेत्र रेखाओं का घनत्व कम होता है परिणामस्वरूप रेखाएँ भी दूर-दूर होती हैं।

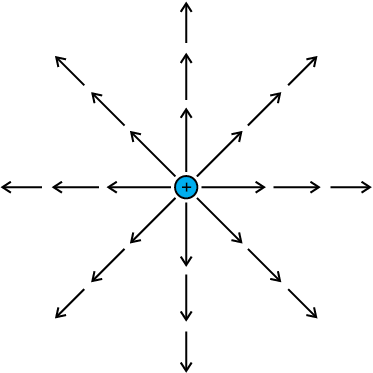
2542.png
चित्र 1.15 बिंदु आवेश का क्षेत्र।

कोई व्यक्ति अधिक रेखाएँ खींच सकता है। परंतु रेखाओं की संख्या महत्वपूर्ण नहीं है। वास्तव में किसी क्षेत्र में असंख्य रेखाएँ खींची जा सकती हैं। अतः महत्वपूर्ण यह है कि विभिन्न क्षेत्रों में रेखाओं का आपेक्षिक घनत्व क्या है?

हम कागज़ के पृष्ठ पर चित्र खींचते हैं अर्थात हम द्विविमीय चित्र खींचते हैं, परंतु हम तीन विमाओं में रहते हैं। अतः यदि हमें क्षेत्र रेखाओं के घनत्व का आकलन करना है तो हमें इन रेखाओं के लंबवत अनुप्रस्थ काट के प्रति एकांक क्षेत्रफल में क्षेत्र रेखाओं की संख्या पर विचार करना होता है। चूँकि किसी बिंदु आवेश से दूरी के वर्ग के अनुसार विद्युत क्षेत्र कम होता जाता है तथा आवेश को परिबद्ध करने वाला क्षेत्र दूरी के वर्ग के अनुसार बढ़ता जाता है, परिबद्ध क्षेत्र से गुजरने वाली क्षेत्र रेखाओं की संख्या सदैव नियत रहती है, चाहे आवेश से उस क्षेत्र की दूरी कुछ भी हो।

2641.png
चित्र 1.16 विद्युत क्षेत्र प्रबलता की दूरी पर निर्भरता तथा इसका क्षेत्र रेखाओं की संख्या से संबंध।

हमने आरंभ में यह कहा था कि क्षेत्र रेखाएँ दिक्स्थान के विभिन्न बिंदुओं पर विद्युत क्षेत्र की दिशा के विषय में सूचनाएँ पहुँचाती हैं। कुछ क्षेत्र रेखाओं का समुच्चय खींचने पर विभिन्न बिंदुओं पर क्षेत्र रेखाओं का आपेक्षिक संख्या घनत्व (अर्थात अत्यधिक निकटता) उन बिंदुओं पर विद्युत क्षेत्र की आपेक्षिक प्रबलता इंगित करता है। जहाँ क्षेत्र रेखाएँ सघन होती हैं वहाँ क्षेत्र प्रबल होता है तथा जहाँ दूर-दूर होती हैं वहाँ दुर्बल होता है। चित्र 1.16 में क्षेत्र रेखाओं का समुच्चय दर्शाया गया है। हम बिंदुओं R तथा S पर वहाँ की क्षेत्र रेखाओं के अभिलंबवत दो समान तथा छोटे क्षेत्र अवयवों की कल्पना कर सकते हैं। हमारे चित्रण में इन क्षेत्र अवयवों को काटने वाली क्षेत्र रेखाओं की संख्या इन बिंदुओं पर विद्युत क्षेत्रों के परिमाणों के अनुक्रमानुपाती है। चित्रण यह दर्शाता है कि बिंदु R पर क्षेत्र, बिंदु S पर क्षेत्र की तुलना में अधिक प्रबल है।

क्षेत्रफल पर अथवा क्षेत्र अवयव द्वारा अंतरित घन कोण* पर, क्षेत्र रेखाओं की निर्भरता को समझने के लिए आइए हम क्षेत्रफल और घन कोण (जो कोण का तीन विमाओं में व्यापकीकरण है) के बीच संबंध स्थापित करने का प्रयास करते हैं। याद कीजिए दो विमाओं में किसी (समतल) कोण की परिभाषा किस प्रकार की जाती है। मान लीजिए कोई छोटा अनुप्रस्थ रेखा अवयव ∆l बिंदु O से r दूरी पर रखा जाता है। तब O पर ∆l द्वारा अंतरित कोण का सन्निकटन ∆θ = ∆l/r के रूप में किया जा सकता है। इसी प्रकार, तीन विमाओं में किसी छोटे लंबवत क्षेत्र ∆S द्वारा दूरी r पर अंतरित घन कोण* को ∆Ω = ∆S/r2 व्यक्त किया जा सकता है। हम जानते हैं कि किसी दिए गए घन कोण में अरीय क्षेत्र रेखाओं की संख्या समान होती है। चित्र 1.16 में आवेश से r1 तथा r2 दूरियों पर स्थित दो बिंदुओं P1 तथा P2 के लिए घन कोण ∆Ω द्वारा P1 पर अंतरित क्षेत्र अवयव r12 ∆Ω तथा P2 पर अंतरित क्षेत्र अवयव r22 ∆Ω है। इन क्षेत्र अवयवों को काटने वाली रेखाओं की संख्या (मान लीजिए n) समान है। अतः एकांक क्षेत्र अवयव को काटने वाली क्षेत्र रेखाओं की संख्या P1 पर n/(r12 ∆Ω) तथा P2 पर n/(r22 ∆Ω) है। इस प्रकार स्पष्ट है कि क्षेत्र रेखाओं की संख्या और इसीलिए क्षेत्र-प्रबलता स्पष्ट रूप से 1/r2 पर निर्भर है।

क्षेत्र रेखाओं के चित्रण की खोज फैराडे ने आवेशित विन्यासों के चारों ओर विद्युत क्षेत्र का मानस प्रत्यक्षीकरण करने के एक अंतर्दर्शी अगणितीय उपाय को विकसित करने के लिए की थी। फैराडे ने इन्हें बल रेखाएँ कहा था। यह पद विशेषकर चुंबकीय क्षेत्रों के प्रकरण के लिए कुछ भ्रामक है। इनके लिए अधिक उचित पद क्षेत्र रेखाएँ (वैद्युत अथवा चुंबकीय) है जिसे हमने इस पुस्तक में अपनाया है।

* घन कोण शंकु की एक माप है। R त्रिज्या के गोले वाले दिए गए शंकु के परिच्छेद पर विचार कीजिए। शंकु के घन कोण ∆Ω की परिभाषा इसे ∆S/R2 के बराबर मानकर करते हैं, यहाँ ∆S शंकु द्वारा गोले पर काटा गया क्षेत्रफल है।

इस प्रकार विद्युत क्षेत्र रेखाएँ आवेशों के अभिविन्यास के चारों ओर विद्युत क्षेत्र के चित्रात्मक निरूपण का एक उपाय है। व्यापक रूप में, विद्युत क्षेत्र रेखा एक एेसा वक्र होती है जिसके किसी भी बिंदु पर खींचा गया स्पर्शी उस बिंदु पर लगे नेट बल की दिशा को निरूपित करता है। इस वक्र के किसी बिंदु पर, स्पष्ट रूप से, स्पर्शी द्वारा विद्युत क्षेत्र की दो संभावित दिशाओं में से कोई एक दिशा दर्शाने के लिए वक्र पर तीर का चिह्न अंकित करना आवश्यक है। क्षेत्र रेखा एक दिक्स्थान वक्र अर्थात तीन दिशाओं में वक्र होती है।

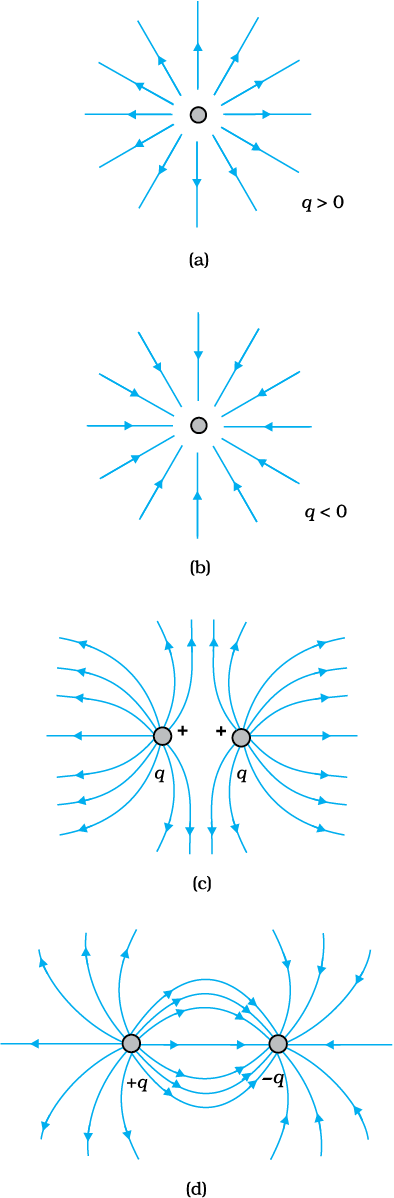
2614.png

चित्र 1.17 विभिन्न आवेश वितरणों के कारण क्षेत्र रेखाएँ।

न्यासों के चारों ओर क्षेत्र रेखाएँ दर्शायी गई हैं। जैसा कि पहले वर्णन किया जा चुका है, ये क्षेत्र रेखाएँ तीन विमीय दिक्स्थान में हैं यद्यपि चित्र में इन्हें केवल एक तल में दर्शाया गया है। एकल धनावेश के कारण क्षेत्र रेखाएँ त्रिज्यतः (अरीय) बहिर्मुखी होती हैं जबकि एकल ऋणावेश के कारण क्षेत्र रेखाएँ त्रिज्यतः अंतर्मुखी होती हैं। दो धनावेशों (q, q) के निकाय के चारों ओर की क्षेत्र रेखाएँ पारस्परिक प्रतिकर्षण का एक सजीव चित्रण प्रस्तुत करती हैं जबकि परिमाण में समान दो विजातीय आवेशों 

(q, –q) के निकाय, अर्थात किसी द्विध्रुव के चारों ओर क्षेत्र रेखाएँ आवेशों के बीच स्पष्ट पारस्परिक आकर्षण दर्शाती हैं। क्षेत्र रेखाएँ कुछ महत्वपूर्ण सामान्य गुणों का पालन करती हैं–

(i) क्षेत्र रेखाएँ धनावेश से आरंभ होकर ऋणावेश पर समाप्त होती हैं। यदि आवेश एकल है तो ये अनंत से आरंभ अथवा अनंत पर समाप्त हो सकती हैं।

(ii) किसी आवेश मुक्त क्षेत्र में, क्षेत्र रेखाओं को एेसे संतत वक्र माना जा सकता है जो कहीं नहीं टूटते।

(iii) दो क्षेत्र रेखाएँ एक-दूसरे को कदापि नहीं काटतीं। (यदि वे एेसा करें तो प्रतिच्छेदन बिंदु पर क्षेत्र की केवल एक दिशा नहीं होगी, जो निरर्थक है।

(iv) स्थिरवैद्युत क्षेत्र रेखाएँ बंद लूप नहीं बनातीं। यह विद्युत क्षेत्र की संरक्षणात्मक प्रकृति से अनुशासित है (अध्याय 2 देखिए)।


1.10 वैद्युत फ्लक्स

किसी dS क्षेत्रफल के छोटे पृष्ठ से उसके अभिलंबवत v वेग से प्रवाहित होने वाले किसी द्रव के प्रवाह पर विचार कीजिए। द्रव के प्रवाह की दर इस क्षेत्र से प्रति एकांक समय में गुजरने वाले आयतन v dS द्वारा प्राप्त होती है तथा यह उस तल से गुजरने वाले द्रव के फ्लक्स को निरूपित करती है। यदि इस तल (पृष्ठ) पर अभिलंब द्रव के प्रवाह की दिशा अर्थात v के समांतर नहीं है, और इनके बीच θ कोण बनता है तो v के लंबवत तल में प्रक्षेपित क्षेत्रफल dS cos θ होगा। अतः पृष्ठ dS से बाहर जाने वाला फ्लक्स v.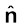3758.pngdS होता है। विद्युत क्षेत्र के प्रकरण के लिए, हम एक समतुल्य राशि को परिभाषित करते हैं और इसे वैद्युत फ्लक्स कहते हैं। तथापि हमें यह ध्यान में रखना चाहिए कि द्रव-प्रवाह के प्रकरण के विपरीत यहाँ प्राकृतिक नियमों के अनुसार प्रेक्षण योग्य राशि का कोई प्रवाह नहीं है।

उपरोक्त वर्णित विद्युत क्षेत्र रेखाओं के चित्रण में हमने देखा कि किसी बिंदु पर क्षेत्र के अभिलंबवत रखे एकांक क्षेत्रफल से गुजरने वाली क्षेत्र रेखाओं की संख्या उस बिंदु पर विद्युत क्षेत्र प्रबलता की माप होती है। इसका तात्पर्य यह है कि यदि हम किसी बिंदु पर E के अभिलंबवत कोई ∆S क्षेत्रफल का छोटा समतलीय अवयव रखें तो इससे गुजरने वाली क्षेत्र रेखाओं की संख्या E ∆S के अनुक्रमानुपाती* है। अब मान लीजिए हम क्षेत्रफल अवयव को किसी कोण θ पर झुका देते हैं। स्पष्ट है अब इस क्षेत्रफल अवयव से गुजरने वाली क्षेत्र रेखाओं की संख्या घट जाएगी। चूँकि E के अभिलंबवत क्षेत्रफल अवयव ∆S का प्रक्षेप ∆S cosθ है, अतः ∆S से गुजरने वाली क्षेत्र रेखाओं की संख्या E ∆S cosθ के अनुक्रमानुपाती है। जब θ = 90° होता है तो क्षेत्र रेखाएँ ∆S के समांतर हो जाती हैं और इससे कोई भी क्षेत्र रेखा नहीं गुजरती (चित्र 1.18 देखिए)।

* यह कहना उचित नहीं है कि क्षेत्र रेखाओं की संख्या E∆S के बराबर है। वास्तव में क्षेत्र रेखाओं की संख्या एेसा विषय है जो हम कितनी क्षेत्र रेखाएँ खींचने का चयन करते हैं, पर निर्भर है। अतः विभिन्न बिंदुओं पर दिए गए क्षेत्रफल से गुजरने वाली क्षेत्र रेखाओं की आपेक्षिक संख्या के ज्ञात होने में ही इनकी भौतिक सार्थकता है।

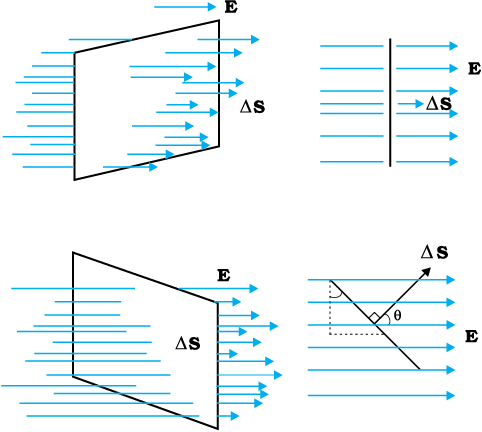
2687.png

चित्र 1.18 E तथा के बीच झुकाव θ पर फ्लक्स की निर्भरता।

बहुत से संदर्भों में क्षेत्रफल अवयव के परिमाण के साथ-साथ उसका दिक्विन्यास भी महत्वपूर्ण होता है। उदाहरण के लिए, किसी जल-प्रवाह में किसी रिंग से गुजरने वाले जल का परिमाण स्वाभाविक रूप से इस बात पर निर्भर करता है कि आप जल धारा में इसे किस प्रकार पकड़े हुए हैं। यदि आप इसे जल-प्रवाह के अभिलंबवत रखते हैं तो अन्य सभी दिक्विन्यासों की तुलना में इस विन्यास में रिंग से अधिकतम जल गुजरेगा। इससे यह निष्कर्ष निकलता है कि क्षेत्रफल-अवयव को सदिश के समान मानना चाहिए। इसमें परिमाण के साथ दिशा भी होती है। समतलीय क्षेत्र की दिशा कैसे निर्दिष्ट की जाए? स्पष्ट रूप से तल पर अभिलंब तल का दिक्विन्यास निर्दिष्ट करता है। इस प्रकार समतलीय क्षेत्र सदिश की दिशा इसके अभिलंब के अनुदिश होती है।

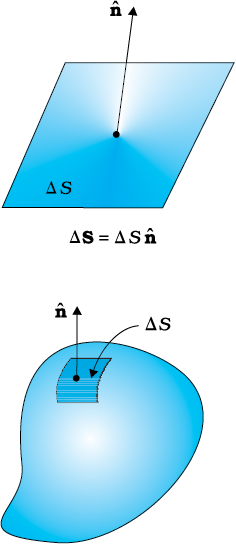
2699.png

चित्र 1.19 अभिलंब तथा ∆S को परिभाषित करने की परिपाटी।

किसी वक्रित पृष्ठ के क्षेत्रफल को किसी सदिश से कैसे संबद्ध किया जाता है? हम यह कल्पना करते हैं कि वक्रित पृष्ठ बहुत से छोटे-छोटे क्षेत्रफल अवयवों में विभाजित है। इनमें से प्रत्येक छोटा क्षेत्रफल अवयव समतलीय माना जा सकता है और पहले स्पष्टीकरण के अनुसार इससे सदिश संबद्ध किया जा सकता है।

यहाँ एक संदिग्धता पर ध्यान दीजिए। किसी क्षेत्रफल अवयव की दिशा उसके अभिलंब के अनुदिश होती है। परंतु अभिलंब दो दिशाएँ संकेत कर सकता है। किसी क्षेत्रफल अवयव से संबद्ध सदिश की दिशा का चयन किस प्रकार किया जाता है? इस समस्या का समाधान इस संदर्भ में उचित कुछ परिपाटियों के निर्धारण द्वारा किया गया है। बंद पृष्ठों के प्रकरणों के लिए यह परिपाटी अति सरल है। किसी बंद पृष्ठ के प्रत्येक क्षेत्रफल अवयव से संबद्ध सदिश की दिशा बहिर्मुखी अभिलंब की दिशा मानी जाती है। इसी परिपाटी का उपयोग चित्र 1.19 में किया गया है। इस प्रकार, किसी बंद पृष्ठ के किसी बिंदु पर क्षेत्रफल अवयव सदिश ∆S का मान ∆S

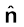3763.png होता है, यहाँ ∆S क्षेत्रफल सदिश का परिमाण तथा 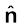3768.png इस बिंदु पर बहिर्मुखी अभिलंब की दिशा में एकांक सदिश है।

अब हम वैद्युत फ्लक्स की परिभाषा पर आते हैं। किसी क्षेत्रफल अवयव ∆S से गुजरने वाले वैद्युत फ्लक्स ∆φ की परिभाषा इस प्रकार करते हैं 

∆φ = E.∆S = E ∆S cosθ (1.11)

जो पहले की भाँति इस क्षेत्रफल अवयव को काटने वाली क्षेत्र रेखाओं की संख्या के अनुक्रमानुपाती है। यहाँ θ क्षेत्र अवयव ∆S तथा E के बीच का कोण है। पूर्वोक्त परिपाटी के अनुसार बंद पृष्ठ के लिए θ क्षेत्र-अवयव पर बहिर्मुखी अभिलंब तथा E के बीच का कोण है। ध्यान दीजिए, हम व्यंजक E ∆S cosθ पर दो ढंग से विचार कर सकते हैंः E (∆S cosθ ) अर्थात E पर क्षेत्र-अभिलंब के प्रक्षेप का E गुना, अथवा E⊥ ∆S अर्थात क्षेत्र-अवयव पर अभिलंब के अनुदिश E का अवयव गुना क्षेत्र-अवयव का परिमाण। वैद्युत फ्लक्स का मात्रक N C–1 m2 है।

समीकरण (1.11) से प्राप्त वैद्युत फ्लक्स की मूल परिभाषा को सैद्धांतिक रूप में, किसी दिए गए पृष्ठ से गुजरने वाले कुल फ्लक्स को परिकलित करने में उपयोग कर सकते हैं। इसके लिए हमें यह करना होता है कि हम पहले पृष्ठ को छोटे-छोटे क्षेत्रफल अवयवों में विभाजित करते हैं और फिर प्रत्येक अवयव के लिए फ्लक्स परिकलित करके उन्हें जोड़कर कुल फ्लक्स प्राप्त कर लेते हैं। अतः पृष्ठ S से गुजरने वाला कुल फ्लक्स φ है

φ ~ Σ E.∆S (1.12)

यहाँ सन्निकटन चिह्न लगाने का कारण यह है कि हमने छोटे क्षेत्रफल अवयव पर विद्युत क्षेत्र E को नियत माना है। गणितीय रूप से यह केवल तभी यथार्थ है जब आप सीमा ∆S → 0 लें तथा समीकरण (1.12) में योग को समाकलन के रूप में व्यक्त करें।


1.11 वैद्युत द्विध्रुव

परिमाण में समान एवं विजातीय बिंदु आवेशों q तथा –q का कोई युगल जिनके बीच पृथकन 2a है, वैद्युत द्विध्रुव कहलाता है। दोनों आवेशों को संयोजित करने वाली रेखा दिक्स्थान में किसी दिशा को परिभाषित करती है। परिपाटी के अनुसार –q से q की दिशा द्विध्रुव की दिशा कहलाती है। –q तथा q की अवस्थितियों का मध्य बिंदु द्विध्रुव का केंद्र कहलाता है।

प्रत्यक्ष रूप से वैद्युत द्विध्रुव का कुल आवेश शून्य होता है। परंतु इसका यह अर्थ नहीं है कि द्विध्रुव का विद्युत क्षेत्र शून्य है। चूँकि आवेश q तथा –q में कुछ पृथकन है, इनके कारण विद्युत क्षेत्र जब जोड़े जाते हैं तब ये एक-दूसरे को यथार्थ रूप से निरस्त नहीं करते। परंतु यदि द्विध्रुव बनाने वाले आवेशों के पृथकन की तुलना में दूरी अधिक (r >> 2a) है, तो q एवं –q के कारण क्षेत्र लगभग निरस्त हो जाते हैं। अतः अधिक दूरियों पर किसी वैद्युत द्विध्रुव के कारण विद्युत क्षेत्र 1/r2 (एकल आवेश q के कारण विद्युत क्षेत्र की r पर निर्भरता) से भी अधिक गति से मंद होता जाता है। यह गुणात्मक धारणा नीचे दिए गए सुस्पष्ट परिकलन से उत्पन्न हुई हैः


1.11.1 वैद्युत द्विध्रुव के कारण क्षेत्र

आवेशों के युगल (–q तथा q) के कारण दिक्स्थान में किसी बिंदु पर विद्युत क्षेत्र कूलॉम नियम तथा अध्यारोपण सिद्धांत से ज्ञात किया जा सकता है। निम्नलिखित दो प्रकरणों के परिणाम सरल हैंः
(i) जब बिंदु द्विध्रुव के अक्ष पर है, (ii) जब बिंदु द्विध्रुव के विषुवतीय तल, अर्थात द्विध्रुव अक्ष के केंद्र से गुजरने वाले द्विध्रुव अक्ष के लंबवत तल में है। किसी व्यापक बिंदु P पर विद्युत क्षेत्र, आवेश –q के कारण P पर विद्युत क्षेत्र E –q तथा आवेश +q के कारण P पर विद्युत क्षेत्र E+q को सदिशों के समांतर चतुर्भुज नियम द्वारा संयोजित करके प्राप्त किया जाता हैै।

(i) अक्ष पर स्थित बिंदुओं के लिए

मान लीजिए बिंदु P द्विध्रुव के केंद्र से q की ओर चित्र (1.20a) में दर्शाए अनुसार r दूरी पर है, तब

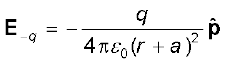3773.png [1.13(a)]

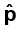यहाँ 3778.png द्विध्रुव अक्ष (–q से q की ओर) के अनुदिश एकांक सदिश है। साथ ही

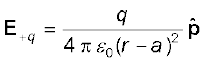3788.png [1.13(b)] P पर कुल विद्युत क्षेत्र है

1.f

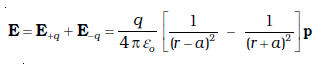
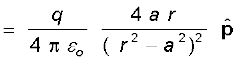3810.png (1.14) r >> a के लिए

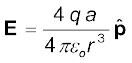3815.png (r >> a) (1.15)

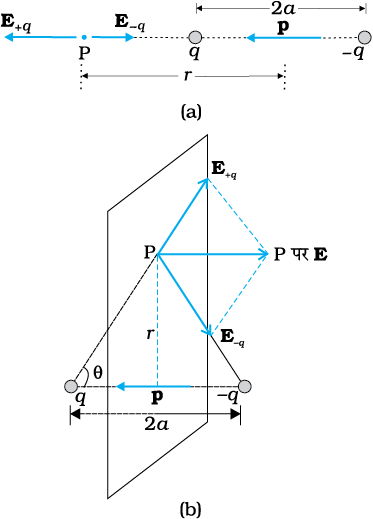
2760.png

चित्र 1.20 (a) अक्ष पर स्थित किसी बिंदु, (b) द्विध्रुव के विषुवतीय तल पर स्थित किसी बिंदु पर द्विध्रुव का विद्युत क्षेत्र।द्विध्रुव आघूर्ण p सदिश है जिसका परिमाण p = q × 2a  है तथा दिशा –q से q की ओर है।


(ii) विषुवतीय तल पर स्थित बिंदुओं के लिए

दो आवेशों +q तथा –q के कारण विद्युत क्षेत्रों के परिमाण

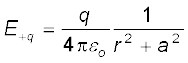3820.png [1.16(a)]

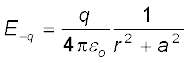3825.png [1.16(b)]

समान हैं।

E+q तथा E–q की दिशाएँ चित्र 1.20(b) में दर्शायी गई हैं। स्पष्ट है कि द्विध्रुव अक्ष के अभिलंबवत अवयव एक-दूसरे को निरस्त कर देते हैं। द्विध्रुव अक्ष के अनुदिश अवयव संयोजित हो जाते हैं। कुल विद्युत क्षेत्र 3830.png के विपरीत होता है। अतः

E = – (E +q + E –q) cosθ 3835.png


4244.png

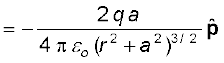3840.png (1.17)

अधिक दूरियों (r >> a) पर

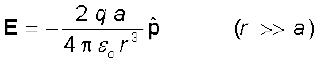3845.png (1.18)

समीकरणों (1.15) तथा (1.18) से स्पष्ट है कि अधिक दूरियों पर द्विध्रुव क्षेत्र में q तथा a पृथक रूप से सम्मिलित नहीं होते; यह इनके संयुक्त गुणनफल qa पर निर्भर करता है। इससे द्विध्रुव आघूर्ण की परिभाषा का संकेत मिलता है। किसी वैद्युत द्विध्रुव के द्विध्रुव आघूर्ण सदिश p की परिभाषा इस प्रकार की जा सकती हैः

p = q × 2a 3850.png (1.19)

अर्थात यह एक सदिश है जिसका परिमाण आवेश q तथा पृथकन 2a (आवेशों q, –q के युगल के बीच की दूरी) तथा दिशा –q से q की ओर होती है। p के पदों में, किसी द्विध्रुव का विद्युत क्षेत्र अधिक दूरियों पर एक सरल रूप ले लेता है।

द्विध्रुव अक्ष के किसी बिंदु पर

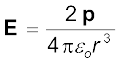3856.png (r >> a) (1.20)

विषुवतीय तल के किसी बिंदु पर

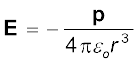3861.png (r >> a) (1.21)

इस महत्वपूर्ण तथ्य पर ध्यान दीजिए कि द्विध्रुव क्षेत्र अधिक दूरियों पर 1/r2 के रूप में नहीं वरन्1/r3 के रूप में मंद होता है। इसके अतिरिक्त द्विध्रुव क्षेत्र का परिमाण तथा दिशा केवल दूरी r पर ही निर्भर नही ंहै वरन् ये सदिश r तथा द्विध्रुव आघूर्ण p के बीच के कोण पर भी निर्भर करते है।

हम उसके बारे में सोच सकते हैं- जब द्विध्रुव आमाप 2a शून्य की ओर अग्रसर होता जाता है, तब आवेश q अनंत की ओर अग्रसर इस प्रकार होता जाता है कि गुणनफल p = q × 2a एक नियत परिमित संख्या होती है। इस प्रकार के द्विध्रुव को बिंदु द्विध्रुव कहते हैं। किसी बिंदु द्विध्रुव के लिए समीकरण (1.20) तथा (1.21) r के सभी मानों के लिए सत्य तथा यथार्थ हैं।


1.11.2 द्विध्रुवों की भौतिक सार्थकता

अधिकांश अणुओं में धनावेशों तथा ऋणावेशों* के केंद्र एक ही स्थान पर होते हैं। इसीलिए इनके द्विध्रुव आघूर्ण शून्य होते हैं। CO2 तथा CH4 अणु इसी प्रकार के हैं। विद्युत क्षेत्र आरोपित किए जाने पर ये द्विध्रुव आघूर्ण विकसित कर लेते हैं परंतु कुछ अणुओं मंें धनावेशों तथा ऋणावेशों के केंद्र संपाती नहीं होते। अतः विद्युत क्षेत्र की अनुपस्थिति में भी इनका अपना स्थायी द्विध्रुव आघूर्ण होता है। इस प्रकार के अणुओं को ध्रुवित अणु कहते हैं। जल का अणु, H2O, इस प्रकार के अणुओं का एक उदाहरण है। विविध पदार्थ विद्युत क्षेत्र की उपस्थिति अथवा अनुपस्थिति में रोचक गुण तथा महत्वपूर्ण अनुप्रयोग प्रस्तुत करते हैं।

 

उदाहरण 1.10 

±10 µC के दो आवेश एक-दूसरे से 5.0 mm दूरी पर स्थित हैं। (a) इस द्विध्रुव के अक्ष पर द्विध्रुव के केंद्र O से चित्र 1.21(a) में दर्शाए अनुसार, धनावेश की ओर 15 cm दूरी पर स्थित किसी बिंदु P पर तथा (b) द्विध्रुव के अक्ष के अभिलंबवत O से, चित्र 1.21(b) में दर्शाए अनुसार गुजरने वाली रेखा से 15 cm दूरी पर स्थित किसी बिंदु Q पर विद्युत क्षेत्र ज्ञात कीजिए।

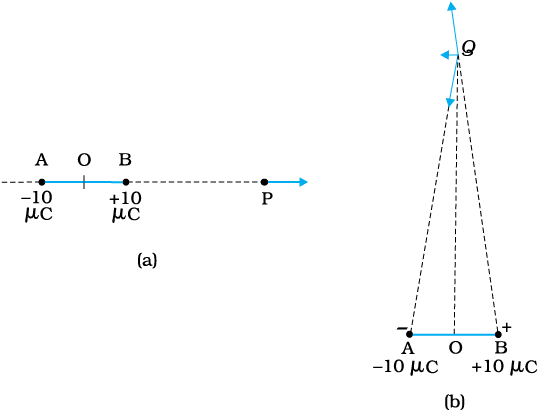
2750.png
चित्र 1.21
हल 

 (a) बिंदु P पर आवेश +10 µC के कारण क्षेत्र

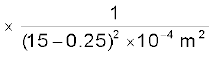
= 3866.png3871.png

= 4.13 × 106 N C–1 BP के अनुदिश

बिंदु P पर आवेश –10 µC के कारण क्षेत्र

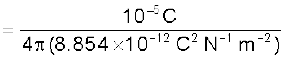
3876.png 3881.png

= 3.86 × 106 N C–1 PA के अनुदिश

A तथा B पर स्थित दो आवेशों के कारण P पर परिणामी विद्युत क्षेत्र = 2.7 × 105 N C–1 BP के अनुदिश है।

इस उदाहरण में अनुपात OP/OB काफी अधिक (=60) है। अतः, किसी द्विध्रुव के अक्ष पर अत्यधिक दूरी पर स्थित किसी बिंदु पर विद्युत क्षेत्र ज्ञात करने के लिए सीधे ही सूत्र के उपयोग द्वारा हम इसी के सन्निकट परिणाम की आशा कर सकते हैं। 2a पृथकन के ± q आवेशों से बने द्विध्रुव के लिए द्विध्रुव के अक्ष के केंद्र से r दूरी पर विद्युत क्षेत्र का परिमाण

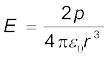3886.png (r/a >> 1)

यहाँ p = 2a q द्विध्रुव आघूर्ण का परिमाण है।

द्विध्रुΡव अक्ष पर विद्युत क्षेत्र की दिशा सदैव द्विध्रुव आघूर्ण सदिश के अनुदिश (अर्थात –q से q की ओर) होती है। यहाँ, p =10–5 C × 5 × 10–3 m = 5 × 10–8 C m

अतः

E =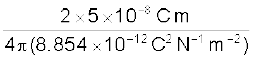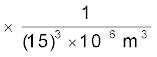3891.png3896.png = 2.6 × 105 N C–1

द्विध्रुव आघूर्ण की दिशा AB के अनुदिश है, तथा यह परिणाम पूर्व परिणाम के काफी निकट है।

(b) बिंदु B पर स्थित + 10 µC आवेश के कारण बिंदु Q पर विद्युत क्षेत्र

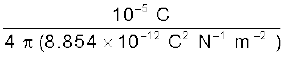
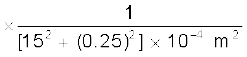
=3901.png 3906.png

= 3.99 × 106 N C–1 BQ के अनुदिश

बिंदु A पर स्थित –10 µC आवेश के कारण Q पर विद्युत क्षेत्र

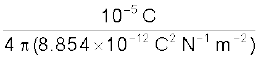
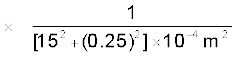
=3912.png3917.png

= 3.99 × 106 N C–1 QA के अनुदिश

स्पष्ट है कि इन दो समान परिमाण के बलों के OQ दिशा के अनुदिश घटक एक-दूसरे को निरस्त करते हैं परंतु BA के समांतर दिशा के अनुदिश घटक संयोजित हो जाते हैं। अतः A तथा B पर स्थित दो आवेशों के कारण Q पर परिणामी विद्युत क्षेत्र

= 2 × 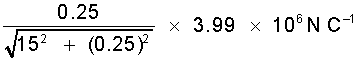3922.pngBA के अनुदिश

= 1.33 × 105 N C–1 BA के अनुदिश

(a) की ही भाँति द्विध्रुव के अक्ष के अभिलंबवत किसी बिंदु पर द्विध्रुव विद्युत क्षेत्र के लिए सीधे ही सूत्र के उपयोग द्वारा हम इसी परिणाम की अपेक्षा कर सकते हैं–

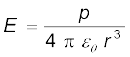3927.png (r/a >> 1)

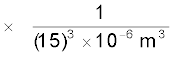
3932.png3937.png 

= 1.33 × 105 N C–1.

इस प्रकरण में विद्युत क्षेत्र की दिशा आघूर्ण सदिश की दिशा के विपरीत है। तथापि प्राप्त परिणाम पहले प्राप्त हुए परिणाम के अनुरूप हैं।

 

1.12 एकसमान बाह्य क्षेत्र में द्विध्रुव

चित्र 1.22 में दर्शाए अनुसार एकसमान विद्युत क्षेत्र E में रखे द्विध्रुव आघूर्ण p के स्थायी द्विध्रुव (स्थायी द्विध्रुव से हमारा तात्पर्य यह है कि p का E से स्वतंत्र अस्तित्व है; यह E द्वारा प्रेरित नहीं हुआ है।) पर विचार कीजिए।

यहाँ आवेश q पर qE तथा –q पर –qE बल लग रहे हैं। चूँकि E एकसमान है अतः द्विध्रुव पर नेट बल शून्य है। परंतु आवेशों में पृथकन है, अतः बल भिन्न बिंदु पर लगे हैं, जिसके परिणामस्वरूप द्विध्रुव पर बल आघूर्ण कार्य करता है। जब नेट बल शून्य है तो बल आघूर्ण (बल युग्म) मूल बिंदु पर निर्भर नहीं होता। इसका परिमाण प्रत्येक बल के परिमाण तथा बलयुग्म की भुजा (दो प्रतिसमांतर बलों के बीच लंबवत दूरी) के गुणनफल के बराबर होता है।

2810.png

चित्र 1.22 एकसमान विद्युत क्षेत्र में द्विध्रुव।

बल आघूर्ण का परिमाण = q E × 2 a sinθ

= 2 q a E sinθ

इसकी दिशा कागज़ के तल के अभिलंबवत इससे बाहर की ओर है।

p × E का परिमाण भी p E sinθ है तथा इसकी दिशा कागज़ के पृष्ठ के अभिलंबवत बाहर की ओर है। अतः

τ = p × E (1.22)


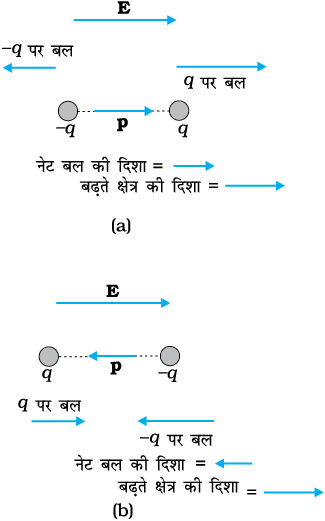
2826.png

चित्र 1.23 द्विध्रुव पर वैद्युत बल (a) p क्षेत्र E के समांतर (b) p क्षेत्र E के प्रतिसमांतर।

यह बल आघूर्ण द्विध्रुव को क्षेत्र E के साथ संरेखित करने की प्रवृत्ति रखेगा। जब p क्षेत्र E के साथ संरेखित हो जाता है तो बल आघूर्ण शून्य होता है।

जब क्षेत्र एकसमान नहीं होता तब क्या होता है? स्पष्ट है, उस प्रकरण में नेट बल शून्येतर हो सकता है। इसके अतिरिक्त, व्यापक रूप से निकाय पर पहले की ही भाँति एक बल आघूर्ण कार्य करेगा। यहाँ व्यापक प्रकरण अंतर्ग्रस्त है, अतः आइए एेसी सरल स्थिति पर विचार करते हैं जिसमें p क्षेत्र E के समांतर अथवा प्रतिसमांतर है। दोनों ही प्रकरणों में नेट बल आघूर्ण तो शून्य होता है परंतु यदि E एकसमान नहीं है तो द्विध्रुव पर एक नेट बल लगता है।

चित्र 1.23 स्वतः स्पष्टीकरण करता है। इसे आसानी से देखा जा सकता है कि जब p क्षेत्र E के समांतर है तो द्विध्रुव पर बढ़ते क्षेत्र की दिशा में एक नेट बल कार्य करता है। जब p क्षेत्र के E प्रतिसमांतर होता है तो द्विध्रुव पर घटते क्षेत्र की दिशा में एक नेट बल कार्य करता है। व्यापक रूप में, बल E के सापेक्ष p के दिक्विन्यास पर निर्भर करता है।

* धनात्मक बिंदु आवेशों के संग्रह को केंद्र की परिभाषा संहति केंद्र की ही भाँति की जाती है जिसके अनुसार 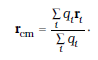1.g


इससे हमारा ध्यान घर्षण विद्युत के सामान्य प्रेक्षणों पर जाता है। शुष्क बालों में फेरी गई कंघी कागज़ के छोटे टुकड़ों को आकर्षित करती है। जैसाकि हम जानते हैं कि कंघी घर्षण द्वारा आवेश अर्जित करती है। परंतु कागज़ आवेशित नहीं है तो फिर इस आकर्षक बल का स्पष्टीकरण कैसे करें? पिछली चर्चा से संकेत पाकर हम कह सकते हैं कि आवेशित कंघी कागज़ के टुकड़ों को ध्रुवित कर देती है, अर्थात कागज़ के टुकड़ों में क्षेत्र की दिशा में नेट द्विध्रुव आघूर्ण प्रेरित कर देती है। इसके अतिरिक्त कंघी के कारण विद्युत क्षेत्र एकसमान नहीं है। इस असमान क्षेत्र के कारण द्विध्रुव पर एक नेट बल कार्यरत हो जाता है। इस स्थिति में यह आसानी से देखा जा सकता है कि कागज़ के टुकड़े कंघी की दिशा में गति करते हैं।


1.13 संतत आवेश वितरण

अब तक हमने विविक्त आवेशों q1, q2, ..., qn के आवेश विन्यास के विषय में चर्चा की है। इसका कारण यह है कि एेसे विन्यासों के लिए गणितीय परिकलन सरल होते हैं जिनमें कलन (कैलकुलस) की आवश्यकता नहीं होती। साथ ही, बहुत से कार्यों के लिए विविक्त आवेशों के पदों में कार्य करना व्यावहारिक नहीं होता और हमें संतत आवेश वितरण की आवश्यकता होती है। उदाहरणार्थ, किसी आवेशित चालक के पृष्ठ पर सूक्ष्म आवेशित अवयवों की अवस्थितियों के पदों में आवेश वितरण का विशेष रूप से उल्लेख करना व्यावहारिक नहीं है। चालक के पृष्ठ पर किसी क्षेत्रफल अवयव ∆S (जो स्थूल स्तर पर बहुत छोटा परंतु इलेक्ट्रॉनों की विशाल संख्या को सम्मिलित करने के लिए पर्याप्त है, देखिए चित्र 1.24) के विषय में विचार करके उस अवयव पर आवेश ∆Q का पृथक-पृथक उल्लेख करना अधिक उपयुक्त है। इसके बाद हम क्षेत्रफल अवयव पर पृष्ठीय आवेश घनत्व σ की परिभाषा इस प्रकार करते हैं–

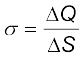3942.png (1.23)

2893.png

चित्र 1.24 रैखिक, पृष्ठीय, आयतनी घनत्वों की परिभाषा। प्रत्येक प्रकरण में चुने गए अवयव (∆l, ∆S, ∆V) स्थूलदर्शीय स्तर पर छोटे हैं परंतु इनमें सूक्ष्मदर्शीय स्तर के अवयवों की एक विशाल संख्या समाहित होती है।

एेसा हम चालक के पृष्ठ के विभिन्न बिंदुओं पर कर सकते हैं और इस प्रकार एक संतत

फलन σ (जिसे पृष्ठीय आवेश घनत्व कहते हैं) पर पहुँचते हैं। इस रूप में वर्णित पृष्ठीय आवेश घनत्व σ आवेश की क्वांटमता तथा सूक्ष्मदर्शीय स्तर* पर आवेश की असंतता वितरण की उपेक्षा करता है। σ स्थूलदर्शीय रूप में पृष्ठीय आवेश घनत्व है जो एक प्रकार से, सूक्ष्मदर्शीय रूप में बड़े परंतु स्थूलदर्शीय रूप में छोटे क्षेत्र अवयव ∆S पर सूक्ष्मदर्शीय आवेश घनत्व है। σ का मात्रक C/m2 है।

इसी प्रकार के दृष्टिकोण रैखिक आवेश वितरणों तथा आयतनी आवेश वितरणों पर भी लागू होते हैं। किसी तार का रैखिक आवेश घनत्व λ की परिभाषा

1.0

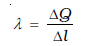
(1.24)

द्वारा की जाती है। यहाँ ∆l सूक्ष्म स्तर पर तार का रैखिक अवयव है। तथापि सूक्ष्म आवेशित अवयवों की एक विशाल संख्या इसमें सम्मिलित है तथा ∆Q इस रैखिक अवयव में समाए आवेश हैं। λ का मात्रक C/m है। इसी प्रकार से आयतनी आवेश घनत्व (सरल शब्दों में जिसे आवेश घनत्व भी कहा जाता है) की परिभाषा भी

1.25

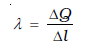
(1.25)

द्वारा की जाती है। यहाँ ∆Q स्थूल रूप में छोटे आयतन अवयव ∆V में समाए वे आवेश हैं जो सूक्ष्म आवेशित अवयवों की विशाल संख्या को सम्मिलित करते हैं। ρ का मात्रक C/m3 है।

यहाँ संतत आवेश वितरण की हमारी धारणा यांत्रिकी में हमारे द्वारा अपनाई गई संतत संहति वितरण की धारणा के ही समान है। जब हम किसी द्रव के घनत्व का उल्लेख करते हैं तो उस समय वास्तव में हम उसके स्थूल घनत्व का ही उल्लेख कर रहे होते हैं। हम द्रव को एक संतत तरल मान लेते हैं तथा उसकी विविक्त आणविक रचना की उपेक्षा कर देते हैं।

* सूक्ष्मदर्शीय स्तर पर, आवेश वितरण असंतत होता है। पृथक आवेश एक आवेशरहित मध्यवर्ती स्थान से पृथकृत होते हैं।

विविक्त आवेशों के निकाय के कारण विद्युत क्षेत्र प्राप्त करने [समीकरण (1.10)] की ही भाँति लगभग इसी ढंग से संतत आवेश वितरण के कारण विद्युत क्षेत्र प्राप्त किया जा सकता है। मान लीजिए किसी दिक्स्थान में संतत आवेश वितरण का आवेश घनत्व ρ है। कोई सुविधाजनक मूल बिंदु O चुनिए तथा मान लीजिए आवेश वितरण में किसी बिंदु का स्थिति सदिश r है। आवेश घनत्व ρ एक बिंदु से दूसरे बिंदु पर भिन्न हो सकता है, अर्थात यह r का फलन है। आवेश वितरण को ∆V आमाप के छोटे आयतन अवयवों में विभाजित कीजिए। आयतन अवयव ∆V में आवेश का परिमाण ρ∆V है।

अब स्थिति सदिश R के साथ किसी भी व्यापक बिंदु P (आवेश वितरण के भीतर अथवा बाहर) पर विचार कीजिए (चित्र 1.24)। कूलॉम नियम द्वारा आवेश ρ∆V के कारण विद्युत क्षेत्र

1.26

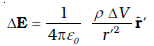
(1.26)

यहाँ r′ आवेश अवयव तथा P के बीच की दूरी है, तथा 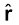3962.png′ आवेश अवयव से P की दिशा में एकांक सदिश है। अध्यारोपण सिद्धांत द्वारा आवेश वितरण के कारण कुल विद्युत क्षेत्र विभिन्न आयतन-अवयवों के कारण विद्युत क्षेत्रों का योग करने पर प्राप्त होता है।

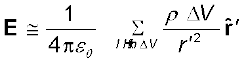3968.png (1.27)

ध्यान दीजिए ρ, r′, 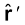3973.png सभी के मान एक बिंदु से दूसरे पर परिवर्तित हो सकते हैं। यथार्थ गणितीय विधि में हमें ∆V→0 लेना चाहिए और फिर यह योग एक समाकल बन जाता है। परंतु सरलता की दृष्टि से इस चर्चा को हम यही छोड़ रहे हैं। संक्षेप में कूलॉम नियम तथा अध्यारोपण सिद्धांत के उपयोग द्वारा किसी भी आवेश वितरण के लिए चाहे वह विविक्त हो अथवा संतत, अथवा अंशतः विविक्त और अंशतः संतत हो, विद्युत क्षेत्र ज्ञात किया जा सकता है।


1.14 गाउस नियम

वैद्युत फ्लक्स की अवधारणा के सरल अनुप्रयोग के रूप में आइए किसी r त्रिज्या के एेसे गोले जिसके केंद्र पर कोई बिंदु आवेश q परिबद्ध है, से गुजरने वाले कुल फ्लक्स पर विचार करें। चित्र 1.25 में दर्शाए अनुसार इस गोले को छोटे क्षेत्रफल अवयवों में विभाजित करते हैं।

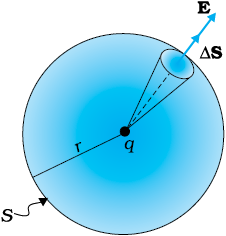
2875.png

चित्र 1.25 उस गोले से गुजरने वाला फ्लक्स जिसके केंद्र पर बिंदु आवेश q परिबद्ध है।

क्षेत्रफल अवयव ∆S से गुजरने वाला फ्लक्स

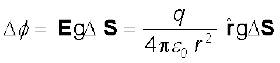3978.png (1.28)

2953.png
चित्र 1.26 सिलिंडर के पृष्ठ से गुजरने वाले एकसमान विद्युत क्षेत्र के फ्लक्स का परिकलन।

यहाँ हमने एकल आवेश q के कारण विद्युत क्षेत्र के लिए कूलॉम नियम का उपयोग किया है। एकांक सदिश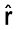3983.png केंद्र से क्षेत्र अवयव की ओर ध्रुवांतर रेखा के अनुदिश है। अब, चूँकि गोले के पृष्ठ के किसी भी बिंदु पर अभिलंब उस बिंदु पर ध्रुवांतर रेखा के अनुदिश होता है, क्षेत्र अवयव ∆S तथा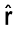3988.png दोनों एक ही दिशा में होते हैं। इसीलिए,

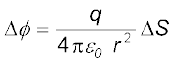3993.png (1.29)

चूँकि एकांक सदिश r का परिमाण 1 है।

गोले से गुजरने वाला कुल फ्लस्क सभी क्षेत्र-अवयवों से गुजरने वाले फ्लक्सों का योग करने पर प्राप्त होता है

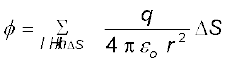
3998.png

चूँकि गोले का प्रत्येक क्षेत्र अवयव आवेश से समान दूरी r पर है, अतः

4003.png 

अब, चूँकि गोले का कुल पृष्ठीय क्षेत्र S = 4πr2 है, अतः

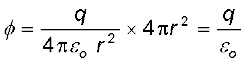4008.png (1.30)

समीकरण (1.30) स्थिरवैद्युतिकी के व्यापक परिणाम, जिसे गाउस नियम कहते हैं, का एक सरल दृष्टांत है। हम बिना उपपत्ति के गाउस नियम का इस प्रकार उल्लेख करते हैं-

किसी बंद पृष्ठ S से गुजरने वाला वैद्युत फ्लक्स

= q/ε0 (1.31)

यहाँ q पृष्ठ S द्वारा परिबद्ध कुल आवेश है।

इस नियम से यह उपलक्षित होता है कि यदि किसी बंद पृष्ठ द्वारा कोई आवेश परिबद्ध नहीं किया गया है तो उस पृष्ठ से गुजरने वाला कुल फ्लक्स शून्य होता है। इसे हम चित्र 1.26 की सरल अवस्थिति में सुस्पष्ट देख सकते हैं।

यहाँ विद्युत क्षेत्र एकसमान है तथा हम एक एेसे बंद बेलनाकार पृष्ठ के विषय में विचार कर रहे हैं जिसमें बेलन का अक्ष एकसमान क्षेत्र E के समांतर है। इसके पृष्ठ से गुजरने वाला कुल फ्लक्स φ हैै। φ = φ1 + φ2 + φ3 यहाँ φ1 तथा φ2 सिलिंडर के पृष्ठ 1 तथा 2 (वृत्ताकार अनुप्रस्थ परिच्छेद के) से गुजरने वाले फ्लक्स को निरूपित करते हैं तथा φ3 बंद पृष्ठ के वक्रित सिलिंडरी भाग से गुजरने वाले फ्लक्स को निरूपित करता है। चूँकि पृष्ठ 3 के प्रत्येक बिंदु पर अभिलंब E के लंबवत है, अतः फ्लक्स की परिभाषा के अनुसार φ3 = 0 । इसके अतिरिक्त पृष्ठ 2 पर बहिर्मुखी अभिलंब E के अनुदिश है तथा पृष्ठ 1 पर बहिर्मुखी अभिलंब E की दिशा के विपरीत है। अतः

φ1 = –E S1, φ2 = +E S2

S1 = S2 = S

यहाँ S वृत्ताकार अनुप्रस्थ काट का क्षेत्रफल है। इस प्रकार कुल फ्लक्स शून्य है, जैसा कि गाउस नियम से संभावित था। इस प्रकार जब आप पाएँ कि एक बंद पृष्ठ के अंदर नेट वैद्युत फ्लक्स शून्य है तो हम इस परिणाम पर पहुँचते हैं कि बंद पृष्ठ के अंतर्विष्ट कुल आवेश शून्य है।

गाउस नियम समीकरण (1.31) का अत्यधिक महत्व इस कारण से भी है कि यह व्यापक रूप से सत्य है, तथा केवल उन्हीं सरल प्रकरणों जिन पर हमने ऊपर विचार किया था, लागू नहीं होता है, वरन् सभी प्रकरणों में इसका प्रयोग किया जा सकता है। इस नियम के बारे में, आइए कुछ महत्वपूर्ण तथ्यों पर ध्यान दें-

(i) गाउस नियम प्रत्येक बंद पृष्ठ, चाहे उसकी आकृति तथा आमाप कुछ भी हो, के लिए सत्य है।

(ii) गाउस नियम समीकरण (1.31) के दक्षिण पक्ष के पद q में पृष्ठ द्वारा परिबद्ध सभी आवेशों का योग सम्मिलित है। ये आवेश पृष्ठ के भीतर कहीं भी अवस्थित हो सकते हैं।

(iii) उन परिस्थितियों जिनमें एेसे पृष्ठ का चयन किया जाता है कि कुछ आवेश पृष्ठ के भीतर तथा कुछ पृष्ठ के बाहर होते हैं, विद्युत क्षेत्र [जिसका फ्लक्स समीकरण (1.31) के वाम पक्ष में दृष्टिगोचर होता है] S के भीतर तथा बाहर स्थित सभी आवेशों के कारण है। तथापि, गाउस नियम के समीकरण के दक्षिण पक्ष में पद q केवल S के भीतर के कुल आवेशों को निरूपित करता है।

(iv) गाउस नियम के अनुप्रयोग के लिए चयन किए जाने वाले पृष्ठ को गाउसीय पृष्ठ कहते हैं। आप किसी भी गाउसीय पृष्ठ का चयन करके गाउस नियम लागू कर सकते हैं। तथापि, सावधान रहिए गाउसीय पृष्ठ को किसी भी विविक्त आवेश से नहीं गुजरना चाहिए। इसका कारण यह है कि विविक्त आवेशों के निकाय के कारण विद्युत क्षेत्र को किसी भी आवेश की अवस्थिति पर भलीभाँति परिभाषित नहीं किया गया है। (जैसे ही आप किसी आवेश के निकट जाते हैं, विद्युत क्षेत्र सभी मर्यादाओं से बाहर विकसित होता जाता है) परंतु गाउसीय पृष्ठ संतत आवेश वितरण से गुजर सकता है।

(v) जब निकाय में कुछ सममिति होती है तो विद्युत क्षेत्र के परिकलन को अधिक आसान बनाने के लिए गाउस नियम प्रायः उपयोगी होता है। उचित गाउसीय पृष्ठ का चयन इसे सुविधाजनक बना देता है।

(vi) अंत में, गाउस नियम कूलॉम नियम में अंतर्निहित दूरी पर व्युत्क्रम वर्ग निर्भरता पर आधारित है। गाउस नियम का कोई उल्लंघन व्युत्क्रम वर्ग नियम से विचलन को संकेत करेगा।


उदाहरण 1.11 

चित्र 1.27 में विद्युत क्षेत्र अवयव Ex = αx1/2, Ey = Ez = 0 है, जिसमें
α = 800 N/C m1/2 है। (a) घन से गुजरने वाला फ्लक्स, तथा (b) घन के भीतर आवेश परिकलित कीजिए। a = 0.1 m मानिए।

 

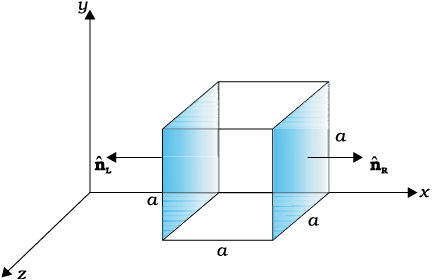
2940.png
चित्र 1.27
हल

(a) चूँकि विद्युत क्षेत्र का केवल x अवयव ही है, x दिशा के लंबवत फलकों के लिए, E तथा ∆S के बीच के कोण ± π/2 हैं। अतः फ्लक्स φ = E.∆S घन के केवल दो छायांकित फलकों को छोड़कर शेष सभी फलकों के लिए पृथक-पृथक रूप से शून्य है। अब, बाएँ फलक पर विद्युत क्षेत्र का परिमाण

EL = αx1/2 = αa1/2

(चूँकि बाएँ फलक पर x = a)

दाएँ फलक पर विद्युत क्षेत्र का परिमाण

ER = α x1/2 = α (2a)1/2

(चूँकि दाएँ फलक पर x = 2a )

इनके तद्नुरूपी फ्लक्स हैं

φL= EL.∆S = 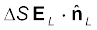4013.png=EL ∆S cosθ = –EL ∆S, चूँकि θ = 180°

= –ELa2

φR= ER.∆S = ER ∆S cosθ = ER ∆S, चूँकि θ = 0°

= ERa2

घन से गुजरने वाला नेट फ्लक्स

= φR + φL = ERa2 – ELa2 = a2 (ER – EL) = αa2 [(2a)1/2 – a1/2]

= αa5/2 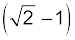4019.png

= 800 (0.1)5/2 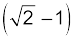4024.png

= 1.05 N m2 C–1

(b) हम घन के भीतर कुल आवेश q को ज्ञात करने के लिए गाउस नियम का उपयोग कर सकते हैं। हम जानते हैं कि φ = q/ε0 अथवा q = φε0 इसलिए

q = 1.05 × 8.854 × 10–12 C = 9.27 × 10–12 C

 


उदाहरण 1.12 

कोई विद्युत क्षेत्र धनात्मक x के लिए, धनात्मक x दिशा में एकसमान है तथा उसी परिमाण के साथ परंतु ऋणात्मक x के लिए, ऋणात्मक x दिशा में एकसमान है। यह दिया गया है कि E = 200 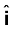4029.png N/C जबकि x > 0 तथा E = –200 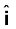4034.png N/C, जबकि x < 0 है। 20 cm लंबे 5 cm त्रिज्या के किसी लंबवृत्तीय सिलिंडर का केंद्र मूल बिंदु पर तथा इस अक्ष x के इस प्रकार अनुदिश है कि इसका एक फलक चित्र 1.28 में दर्शाए अनुसार x = +10 cm तथा दूसरा फलक x = –10 cm पर है। (a) प्रत्येक चपटे फलक से गुजरने वाला नेट बहिर्मुखी फ्लक्स कितना है? (b) सिलिंडर के पार्श्व से गुजरने वाला फ्लक्स कितना है? (c) सिलिंडर से गुजरने वाला नेट बहिर्मुखी फ्लक्स कितना है? (d) सिलिंडर के भीतर नेट आवेश कितना है?

हल

(a) चित्र में हम यह देखते हैं कि बाएँ फलक पर E तथा ∆S समांतर हैं। इसलिए बहिर्मुखी फ्लक्स है

φL= E.∆S = – 200 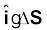4039.png

= + 200 ∆S, चूँकि 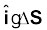4044.png= – ∆S

= + 200 × π (0.05)2 = + 1.57 N m2 C–1

दाएँ फलक पर E तथा ∆S समांतर हैं, इसलिए

φR = E.∆S = + 1.57 N m2 C–1

(b) सिलिंडर के पार्श्व के किसी भी बिंदु पर E क्षेत्र अवयव ∆S के लंबवत है, इसलिए
E.∆S = 0 इसलिए सिलिंडर के पार्श्व के बाहर फ्लक्स शून्य है।

(c) सिलिंडर से होकर नेट बहिर्मुखी फ्लक्स

φ = (1.57 + 1.57 + 0) = 3.14 N m2 C–1

 

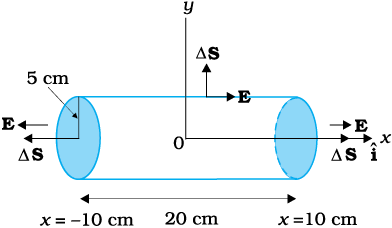
3026.png
चित्र 1.28

(d) सिलिंडर के भीतर नेट आवेश का मान गाउस नियम द्वारा ज्ञात किया जा सकता है जिससे हमें प्राप्त होता है

q = ε0φ

= 3.14 × 8.854 × 10–12 C

= 2.78 × 10–11 C


1.15 गाउस नियम के अनुप्रयोग

जैसी कि हम ऊपर चर्चा कर चुके हैं कि किसी व्यापक आवेश वितरण के कारण विद्युत क्षेत्र समीकरण (1.27) द्वारा व्यक्त किया जाता है। कुछ विशिष्ट प्रकरणों को छोड़कर, व्यवहार में, इस समीकरण में सम्मिलित संकलन (अथवा समाकलन) की प्रक्रिया दिक्स्थान के सभी बिंदुओं पर विद्युत क्षेत्र प्राप्त करने के लिए कार्यान्वित नहीं की जा सकती। तथापि, कुछ सममित आवेश विन्यासों के लिए गाउस नियम का उपयोग करके विद्युत क्षेत्र को सरल ढंग से प्राप्त करना संभव है। कुछ उदाहरणों से इसे आसानी से समझा जा सकता है।


1.15.1 अनंत लंबाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र

किसी अनंत लंबाई के एकसमान रैखिक आवेश घनत्व λ के सीधे पतले तार पर विचार कीजिए। स्पष्ट रूप से यह तार एक सममित अक्ष है। मान लीजिए हम O से P की दिशा में ध्रुवांतर (त्रिज्य सदिश) लेकर इसे तार के चारों ओर घूर्णन कराते हैं। इस प्रकार प्राप्त बिंदु P, P′, P′′ आवेशित तार के संदर्भ में संपूर्ण रूप से तुल्य हैं। इससे यह उपलक्षित होता है कि इन बिंदुओं पर विद्युत क्षेत्र का परिमाण समान होना चाहिए। प्रत्येक बिंदु पर विद्युत क्षेत्र की दिशा अरीय (त्रिज्यीय) होनी चाहिए (यदि λ > 0, तो बहिर्मुखी तथा यदि λ < 0, तो अंतर्मुखी)। यह चित्र 1.29 से स्पष्ट है।

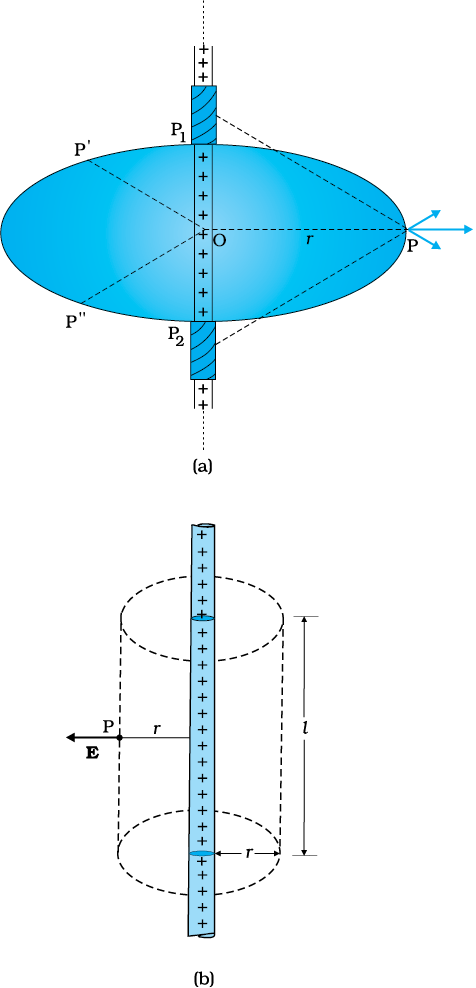
2996.png
चित्र 1.29 (a) अनंत लंबाई के एकसमान आवेशित पतले सीधे तार के कारण विद्युत क्षेत्र अरीय (त्रिज्यीय) होता है।
(b) एकसमान रैखिक आवेश घनत्व के लंबे पतले तार के लिए गाउसीय पृष्ठ।

दर्शाए अनुसार तार के रैखिक अवयवों P1 तथा P2 के युगल पर विचार करें। इस युगल के दो अवयवों द्वारा उत्पन्न विद्युत क्षेत्रों को संकलित करने पर प्राप्त परिणामी विद्युत क्षेत्र अरीय होता है [ध्रुवांतर के अभिलंबवत अवयव एक-दूसरे को निरस्त कर देते हैं]। यह इस प्रकार के सभी युगलों के लिए सत्य है। अतः किसी भी बिंदु P पर कुल विद्युत क्षेत्र अरीय है। अंत में, चूँकि तार अनंत है, तार की लंबाई के अनुदिश विद्युत क्षेत्र बिंदु P की स्थिति पर निर्भर नहीं करता। संक्षेप में, तार को अभिलंबवत काटने वाले तल में विद्युत क्षेत्र हर स्थान पर अरीय है तथा इसका परिमाण केवल त्रिज्य दूरी r पर निर्भर करता है।

विद्युत क्षेत्र परिकलित करने के लिए चित्र 1.29(b) में दर्शाए अनुसार किसी बेलनाकार गाउसीय पृष्ठ की कल्पना कीजिए। चूँकि विद्युत क्षेत्र हर स्थान पर अरीय है, बेलनाकार गाउसीय पृष्ठ के दो सिरों से गुजरने वाला फ्लक्स शून्य है। पृष्ठ के बेलनाकार भाग पर विद्युत क्षेत्र E पृष्ठ के हर बिंदु पर अभिलंबवत है तथा केवल r पर निर्भर होने के कारण इसका परिमाण नियत है। वक्रित भाग का पृष्ठीय क्षेत्रफल 2πrl है, यहाँ l सिलिंडर की लंबाई है।

गाउसीय पृष्ठ से गुज़रने वाला फ्लक्स

= पृष्ठ के वक्रित बेलनाकार भाग से गुज़रने वाला फ्लक्स

= E × 2πrl

पृष्ठ में λ l के बराबर आवेश सम्मिलित है। तब गाउस नियम से प्राप्त होता है

E × 2πrl = λl/ε0

अर्थात E =

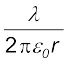
4049.png

सदिश रूप में किसी भी बिंदु पर विद्युत क्षेत्र E इस प्रकार व्यक्त किया जाता है

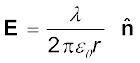4054.png (1.32)

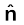यहाँ 4059.png तार के किसी बिंदु के अभिलंबवत गुजरने वाले तल में त्रिज्य एकांक सदिश है। जब λ धनात्मक होता है तो E बहिर्मुखी होता है और जब λ ऋणात्मक होता है, यह अंतर्मुखी होता है।

ध्यान दीजिए, जब हम सदिश A को एकांक सदिश से गुणित अदिश के रूप में, अर्थात
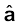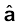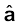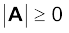A = A 4064.png के रूप में लिखते हैं तो अदिश A एक बीजगणितीय संख्या होती है। यह धनात्मक भी हो सकती है और ऋणात्मक भी। यदि A > 0 है तो A की दिशा एकांक सदिश 4070.png के समान होगी तथा यदि A < 0 है तो A की दिशा 4075.png की दिशा के विपरीत होगी। जब हम ऋणेतर मानों तक सीमित रखना चाहते हैं तो हम प्रतीक 4080.pngका उपयोग करते हैं तथा इसे A का माड्यूल्स (मापांक) कहते हैं। इस प्रकार 4085.png होता है।

यह भी ध्यान दीजिए कि उपरोक्त चर्चा में यद्यपि पृष्ठ (λl) द्वारा परिबद्ध आवेश को ही केवल सम्मिलित किया गया था, परंतु विद्युत क्षेत्र E समस्त तार पर आवेश के कारण है। साथ ही यह कल्पना कर लेना कि तार की लंबाई अनंत है इस कल्पना के बिना हम विद्युत क्षेत्र E को बेलनाकार गाउसीय पृष्ठ के अभिलंबवत नहीं ले सकते। तथापि, लंबे तार के बेलनाकार भागों के चारों ओर जहाँ अंत्य प्रभाव (end effects) की उपेक्षा की जा सकती है, विद्युत क्षेत्र के लिए समीकरण (1.32) सन्निकटतः सही है।


1.15.2 एकसमान आवेशित अनंत समतल चादर के कारण विद्युत क्षेत्र

मान लीजिए किसी अनंत समतल चादर (चित्र 1.30) का एकसमान पृष्ठीय आवेश घनत्व σ है। हम x-अक्ष को दिए गए तल के अभिलंबवत मानते हैं। सममिति के अनुसार विद्युत क्षेत्र y तथा z निर्देशांकों पर निर्भर नहीं करेगा तथा इसकी प्रत्येक बिंदु पर दिशा x-दिशा के समांतर होनी चाहिए।

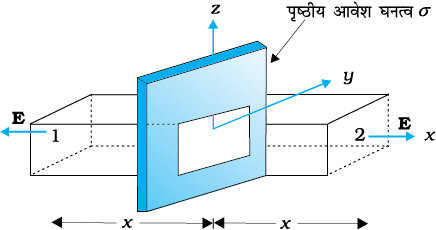
3081.png
चित्र 1.30 एकसमान आवेशित अनंत आवेश चादर के लिए गाउसीय पृष्ठ।

हम गाउसीय पृष्ठ को चित्र में दर्शाए अनुसार A अनुप्रस्थकाट क्षेत्रफल के आयताकार समांतर षट्फलक जैसा ले सकते हैं (वैसे तो बेलनाकार पृष्ठ से भी यह कार्य हो सकता है)। जैसा चित्र से दृष्टिगोचर होता है, केवल दो फलक 1 तथा 2 ही फ्लक्स में योगदान देंगे; विद्युत क्षेत्र रेखाएँ अन्य फलकों के समांतर हैं और वे इसीलिए कुल फ्लक्स में योगदान नहीं देतीं।

पृष्ठ 1 के अभिलंबवत एकांक सदिश –x दिशा में है जबकि पृष्ठ 2 के अभिलंबवत एकांक सदिश +x दिशा में है। अतः, दोनों पृष्ठों से गुजरने वाले फ्लक्स E.∆S बराबर हैं और संयोजित हो जाते हैं। इसीलिए गाउसीय पृष्ठ से गुजरने वाला नेट फ्लक्स 2 EA है। पृष्ठ द्वारा परिबद्ध आवेश σA है। इसीलिए गाउस नियम द्वारा हमें यह संबंध प्राप्त होता है

2 EA = σA/ε0

अथवा E = σ/2ε0

सदिश रूप में

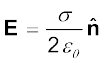4090.png (1.33)

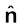यहाँ 4095.png तल के अभिलंबवत इससे दूर जाता हुआ एकांक सदिश है।

यदि σ धनात्मक है तो E तल से बहिर्मुखी तथा यदि σ ऋणात्मक है तो E तल से अंतर्मुखी होता है। ध्यान दीजिए गाउस नियम के अनुप्रयोग से हमें एक अतिरिक्त तथ्य यह प्राप्त होता है कि E, x पर भी निर्भर नहीं है।

किसी परिमित बड़ी समतलीय चादर के लिए समीकरण (1.33), सिरों से दूर समतलीय चादर के मध्यवर्ती क्षेत्रों में सन्निकटतः सत्य है।


1.15.3 एकसमान आवेशित पतले गोलीय खोल के कारण विद्युत क्षेत्र

मान लीजिए R त्रिज्या के पतले गोलीय खोल का एकसमान पृष्ठीय आवेश घनत्व σ है
(चित्र 1.31)। स्पष्ट रूप से इस स्थिति में गोलीय सममिति है। किसी बिंदु P पर चाहे वह भीतर है अथवा बाहर, विद्युत क्षेत्र केवल r पर निर्भर कर सकता है (यहाँ r खोल के केंद्र से उस बिंदु तक की त्रिज्य दूरी है।)तथा इस क्षेत्र को अरीय (अर्थात ध्रुवांतर के अनुदिश) होना चाहिए।

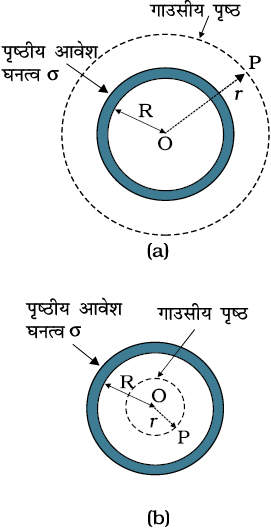
3054.png
चित्र 1.31 किसी बिंदु के लिए जो 
(a) r > R, (b) r < R पर है, गाउसीय पृष्ठ।

(i) खोल के बाहर विद्युत क्षेत्र–खोल के बाहर ध्रुवांतर r के किसी बिंदु P पर विचार कीजिए। बिंदु P पर E का परिकलन करने के लिए हम केंद्र O तथा त्रिज्या r के बिंदु P से गुजरने वाले गोले को गाउसीय पृष्ठ मानते हैं। दिए गए आवेश विन्यास के सापेक्ष इस गोले पर स्थित प्रत्येक बिंदु समतुल्य है। (गोलीय सममिति से हमारा यही अभिप्राय है।) इसीलिए गाउसीय पृष्ठ के प्रत्येक बिंदु पर विद्युत क्षेत्र का समान परिमाण E है तथा प्रत्येक बिंदु पर ध्रुवांतर के अनुदिश है। इस प्रकार प्रत्येक बिंदु पर E तथा ∆S समांतर हैं तथा प्रत्येक अवयव से गुज़रने वाला फ्लक्स E ∆S है। सभी ∆S का संकलन करने पर गाउसीय पृष्ठ से गुज़रने वाला फ्लक्स E × 4 π r2 है। परिबद्ध आवेश σ × 4 π R2 है। गाउस नियम से

E × 4 π r2 = 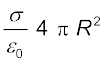4100.png

अथवा 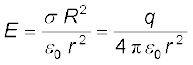4105.png

यहाँ q = 4 π R2 σ गोलीय खोल पर कुल आवेश है।

सदिश रूप में, 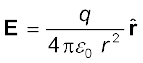4110.png (1.34)

यदि q > 0 है तो विद्युत क्षेत्र बहिर्मुखी होता है तथा यदि q < 0 है तो विद्युत क्षेत्र अंतर्मुखी होता है। तथापि, यह खोल के केंद्र O पर स्थित आवेश q द्वारा उत्पन्न विद्युत क्षेत्र है। अतः खोल के बाहर स्थित बिंदुओं पर एकसमान आवेशित गोलीय खोल के कारण विद्युत क्षेत्र इस प्रकार का होता है, जैसे कि खोल का समस्त आवेश उसके केंद्र पर स्थित है।

(ii) खोल के भीतर विद्युत क्षेत्र–चित्र 1.31(b) में बिंदु P खोल के भीतर है। इस प्रकरण

में भी गाउसीय पृष्ठ P से गुज़रने वाला वह गोला है जिसका केंद्र O है। पहले किए गए परिकलनों की ही भाँति गाउसीय पृष्ठ से गुजरने वाला फ्लक्स E × 4 π r2 है। तथापि इस प्रकरण में, गाउसीय पृष्ठ में कोई आवेश परिबद्ध नहीं है। तब गाउस नियम के अनुसार

E × 4 π r2 = 0

अर्थात E = 0 (r < R ) (1.35)

अर्थात एकसमान आवेशित पतले गोलीय खोल* के कारण उसके भीतर स्थित सभी बिंदुओं पर विद्युत क्षेत्र शून्य है। यह महत्वपूर्ण परिणाम गाउस नियम का प्रत्यक्ष निष्कर्ष है जो कूलॉम नियम से प्राप्त हुआ है। इस नियम का प्रायोगिक सत्यापन कूलॉम नियम में 1/r2 की निर्भरता की पुष्टि करता है।


उदाहरण 1.13 

परमाणु के प्रारंभिक प्रतिरूप में यह माना गया था कि आवेश Ze का बिंदु आमाप का धनात्मक नाभिक होता है जो त्रिज्या R तक एकसमान घनत्व के ऋणावेश से घिरा हुआ है। परमाणु पूर्ण रूप में विद्युत उदासीन है। इस प्रतिरूप के लिए नाभिक से r दूरी पर विद्युत क्षेत्र कितना है?

 

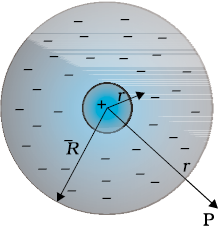
3141.png
चित्र 1.32 परमाणु का प्रारंभिक प्रतिरूप।
हलः 

चित्र 1.32 में इस प्रतिरूप का आवेश वितरण दर्शाया गया है। चूँकि परमाणु उदासीन (नाभिक में आवेश Z e + ऋणावेश) है, अतः R त्रिज्या के एकसमान गोलीय आवेश वितरण में कुल ऋणात्मक आवेश –Ze होना चाहिए। इससे हमें तुरंत ही ऋणात्मक आवेश घनत्व ρ प्राप्त हो जाता है। चूँकि हमारे पास कुल शून्य आवेश होना चाहिए, अतः

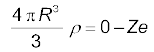
4115.png 

अथवा 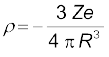4121.png

नाभिक से r दूरी पर स्थित बिंदु P पर विद्युत क्षेत्र E(r) ज्ञात करने के लिए हम गाउस नियम का उपयोग करते हैं। आवेश वितरण की गोलीय सममिति के कारण विद्युत क्षेत्र E(r) का परिणाम केवल त्रिज्य दूरी पर निर्भर करता है, यहाँ r की दिशा का कोई अर्थ नहीं हेाता। इसकी दिशा मूल बिंदु से P की ओर ध्रुवांतर r के अनुदिश (अथवा विपरीत) है। स्पष्ट रूप से इस प्रकरण में गाउसीय पृष्ठ एक गोलीय पृष्ठ है जिसका केंद्र नाभिक है। यहाँ हम दो स्थितियों r < R तथा r > R पर विचार करते हैं।

(i) r < R : गोलीय पृष्ठ द्वारा परिबद्ध वैद्युत फ्लक्स

φ = E (r) × 4 π r2

यहाँ E (r), r पर विद्युत क्षेत्र का परिमाण है। इसका कारण यह है गोलीय गाउसीय पृष्ठ के किसी भी बिंदु पर विद्युत क्षेत्र की दिशा पृष्ठ के उस बिंदु पर अभिलंबवत होती है तथा इसका परिमाण पृष्ठ के सभी बिंदुओं पर समान होता है।

यहाँ गाउसीय पृष्ठ द्वारा परिबद्ध आवेश q धनात्मक नाभिकीय आवेश तथा r त्रिज्या के गोले में विद्यमान ऋणात्मक आवेश है 

अर्थात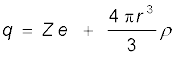4126.png

पहले प्राप्त आवेश घनत्व ρ का मान प्रतिस्थापित करने पर हमें प्राप्त होता है।

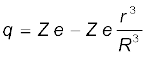
4131.png 

तब गाउस नियम से हमें प्राप्त होता है।

111

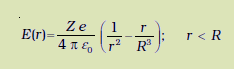
यहाँ विद्युत क्षेत्र त्रिज्यतः बहिर्मुखी निदर्शित है।

(ii) r > R : इस प्रकरण में, चूँकि परमाणु उदासीन है, गोलीय गाउसीय पृष्ठ द्वारा परिबद्ध आवेश शून्य है। इस प्रकार, गाउस नियम से

E (r) × 4 π r2 = 0  अथवा (r) = 0;  r > R

r = R, पर दोनों प्रकरणों से समान परिणाम, E = 0 प्राप्त होता है।

* इसकी तुलना भौतिकी पाठ्यपुस्तक कक्षा 11 के अनुभाग 8.5 में वर्णित एकसमान द्रव्यमान खोल से कीजिए।


सारांश

1. विद्युत तथा चुंबकीय बल परमाणुओं, अणुओं तथा स्थूल द्रव्य के गुणधर्मों का निर्धारण करते हैं।

2. घर्षण विद्युत के सरल प्रयोगों के आधार पर यह निष्कर्ष निकाला जा सकता है कि प्रकृति में दो प्रकार के आवेश होते हैं। सजातीय आवेशों में प्रतिकर्षण तथा विजातीय आवेशों में आकर्षण होता है। परिपाटी के अनुसार, रेशम से रगड़ने पर काँच की छड़ पर धनावेश होता है; तथा फर से रगड़ने पर प्लास्टिक की छड़ पर ऋणावेश होता है।

3. चालक अपने में से होकर सरलता से वैद्युत आवेश की गति होने देते हैं जबकि विद्युतरोधी एेसा नहीं करते। धातुओं में गतिशील आवेश इलेक्ट्रॉन होते हैं; वैद्युत अपघट्यों में धनायन तथा ऋणायन दोनों ही गति करते हैं।

4. वैद्युत आवेशों के तीन गुणधर्म होते हैं : क्वांटमीकरण, योज्यता तथा संरक्षण।

वैद्युत आवेश के क्वांटमीकरण से तात्पर्य है कि किसी वस्तु का कुल आवेश (q) सदैव ही आवेश के एक मूल क्वांटम (e) के पूर्णांकी गुणज अर्थात q = n e होता है, जहाँ

n = 0, ±1, ±2, ±3, .... है। प्रोटॉन तथा इलेक्ट्रॉन पर क्रमशः +e तथा –e आवेश होते हैं। स्थूल आवेशों जिनके लिए n एक अत्यधिक बड़ी संख्या होती है, में आवेश के क्वांटमीकरण की उपेक्षा की जा सकती है।

वैद्युत आवेशों की योज्यता से हमारा तात्पर्य यह है कि किसी निकाय का कुल आवेश उस निकाय के सभी एकाकी आवेशों का बीजगणितीय योग (अर्थात योग करते समय उनके चिह्नों को ध्यान में रखकर) होता है।

वैद्युत आवेशों के संरक्षण से हमारा तात्पर्य यह है कि किसी वियुक्त निकाय (isolated system) का कुल आवेश समय के साथ अपरिवर्तित रहता है। इसका अर्थ यह है कि जब घर्षण द्वारा वस्तुएँ आवेशित की जाती हैं तो आवेशों का एक वस्तु से दूसरी वस्तु में स्थानांतरण होता है, परंतु इस प्रक्रिया में न तो कोई आवेश उत्पन्न होता है और न ही नष्ट होता है।

5. कूलॉम नियम ः दो बिंदु आवेशों q1 तथा q2 के बीच पारस्परिक स्थिर वैद्युत बल, आवेशों के गुणनफल q1q2 के अनुक्रमानुपाती तथा उनके बीच की दूरी r21 के वर्ग के व्युत्क्रमानुपाती होता है। गणितीय रूप में

F21 = q2 पर q1 के कारण लगने वाला बल

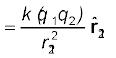
4152.png

यहाँ 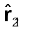4157.png आवेश q1 से q2 की दिशा में एकांक सदिश है तथा k = 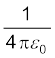4162.pngआनुपातिकता स्थिरांक है। SI मात्रकों में, आवेश का मात्रक कूलॉम है। नियतांक ε0 का प्रायोगिक मान है

ε0 = 8.854 × 10–12 C2 N–1 m–2

k का सन्निकट मान k = 9 × 109 N m2 C–2 होता है।

6. किसी प्रोटॉन तथा किसी इलेक्ट्रॉन के बीच वैद्युत बल तथा गुरुत्वाकर्षण बल का अनुपात है,

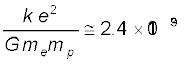
4167.png

7. अध्यारोपण सिद्धांत : यह सिद्धांत इस गुणधर्म पर आधारित है कि दो आवेशों के बीच लगने वाले आकर्षी अथवा प्रतिकर्षी बल किसी तीसरे (अथवा अधिक) अतिरिक्त आवेश की उपस्थिति से प्रभावित नहीं होते। आवेशों q1, q2, q3... के किसी समूह के लिए किसी आवेश (जैसे q1) पर बल, q1 पर q2 के कारण बल, q1 पर q3 के कारण बल आदि-आदि के सदिश योग के बराबर होता है। प्रत्येक युगल के लिए यह बल पहले वर्णित दो आवेशों के लिए कूलॉम के नियम द्वारा ही व्यक्त किया जाता है।

8. किसी आवेश विन्यास के कारण किसी बिंदु पर विद्युत क्षेत्र E किसी छोटे धनात्मक परीक्षण आवेश (test charge) q को उस बिंदु पर रखने पर उसके द्वारा अनुभव किए जाने वाले बल को उस आवेश के परिमाण द्वारा विभाजित करने पर प्राप्त होता है। किसी बिंदु आवेश q के कारण विद्युत क्षेत्र का कोई परिमाण 

4121

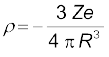
 होता है; यदि q धनात्मक है तो यह क्षेत्र अरीय (त्रिज्यीय) बहिर्मुखी होता है तथा यदि q ऋणात्मक है तो अरीय (त्रिज्यीय) अंतर्मुखी होता है। कूलॉम बल की भाँति विद्युत क्षेत्र भी अध्यारोपण सिद्धांत को संतुष्ट करता है।

9. विद्युत क्षेत्र रेखा एेसा वक्र है जिसके किसी भी बिंदु पर खींचा गया स्पर्शी, वक्र के उस बिंदु पर विद्युत क्षेत्र की दिशा बताता है। क्षेत्र रेखाओं की सापेक्षिक संकुलता विभिन्न बिंदुओं पर विद्युत क्षेत्र की सापेक्षिक तीव्रता को इंगित करती है। प्रबल विद्युत क्षेत्र में रेखाएँ पास-पास तथा दुर्बल क्षेत्र में ये एक-दूसरे से काफी दूर होती हैं। एकसमान (अथवा नियत) विद्युत क्षेत्र में क्षेत्र रेखाएँ एक-दूसरे से एकसमान दूरी पर समांतर सरल रेखाएँ होती हैं।

10. क्षेत्र रेखाओं की कुछ महत्वपूर्ण विशेषताएँ इस प्रकार हैं– (a) आवेशमुक्त दिक्स्थान में क्षेत्र रेखाएँ संतत वक्र होती हैं जो कहीं नहीं टूटतीं। (b) दो क्षेत्र रेखाएँ एक-दूसरे को कदापि नहीं काट सकतीं। (c) स्थिरवैद्युत क्षेत्र रेखाएँ धनावेश से आरंभ होकर ऋणावेश पर समाप्त हो जाती हैं– ये संवृत पाश (बंद लूप) नहीं बना सकतीं।

11. वैद्युत द्विध्रुव परिमाण में समान विजातीय दो आवेशों q तथा –q, जिनके बीच पृथकन 2a हो, का युग्म होता है। इसके द्विध्रुव आघूर्ण सदिश p का परिमाण 2qa होता है तथा यह द्विध्रुव अक्ष –q से q की दिशा में होता है।

12. किसी वैद्युत द्विध्रुव का इसके निरक्षीय/विषुवतीय समतल (अर्थात इसके अक्ष के लंबवत तथा इसके केंद्र से गुजरने वाले समतल) पर इसके केंद्र से r दूरी पर विद्युत क्षेत्र–

4178


4183

(r >> a के लिए)

4188

4193

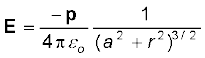
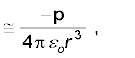
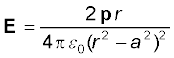
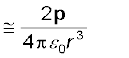
(r >> a के लिए)

इस तथ्य पर ध्यान देना चाहिए कि किसी द्विध्रुव का विद्युत क्षेत्र 1/r3 पर निर्भर होता है, जबकि किसी बिंदु आवेश के कारण विद्युत क्षेत्र 1/r2 पर निर्भर होता है।

13. किसी एकसमान विद्युत क्षेत्र E में कोई वैद्युत द्विध्रुव एक बल आघूर्ण τ का अनुभव करता है।

τ = p × E परंतु किसी नेट बल का अनुभव नहीं करता।

14. विद्युत क्षेत्र E का किसी लघु क्षेत्रफल-अवयव ∆S से गुजरने वाला फ्लक्स ∆φ = E.∆S

सदिश क्षेत्रफल-अवयव ∆S = ∆S 

4198

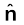
यहाँ ∆S क्षेत्रफल-अवयव का परिमाण तथा 

4203

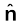
क्षेत्रफल-अवयव के लंबवत त्रिज्य एकांक सदिश है जिसे काफी छोटे क्षेत्र के लिए समतलीय माना जा सकता है। किसी बंद पृष्ठ के क्षेत्रफल-अवयव के लिए, 

4208

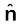
को परिपाटी के अनुसार बहिर्मुखी अभिलंब की दिशा माना जा सकता है।

15. गाउस नियम ः किसी बंद पृष्ठ S से होकर गुज़रने वाले किसी विद्युत क्षेत्र का फ्लक्स उस पृष्ठ S द्वारा परिबद्ध कुल आवेश का 1/ε0 गुना होता है। यह नियम विद्युत क्षेत्र के निर्धारण में विशेष रूप से तब उपयोगी होता है जबकि आवेश वितरण में सरल सममिति हो।

(i) एकसमान रैखिक आवेश घनत्व λ का पतला अनंत लंबाई का सीधा तार

4213

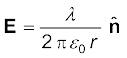
यहाँ r बिंदु की तार से लंबवत दूरी है तथा 

4229

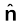
उस बिंदु से गुज़रने वाले तार के अभिलंबवत तल में त्रिज्य एकांक सदिश है।

(ii) एकसमान पृष्ठीय आवेश घनत्व σ की पतली अनंत समतल चादर

 

4223

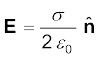
यहाँ 

4229

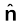
समतल के अभिलंबवत पार्श्व के दोनों ओर बहिर्मुखी एकांक सदिश है।

(iii) एकसमान पृष्ठीय आवेश घनत्व σ के पतले गोलीय खोल (या कोश)

4234

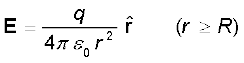
E = 0 (r < R)

यहाँ r गोलीय खोल के केंद्र से बिंदु की दूरी तथा R खोल की त्रिज्या है। खोल का कुल आवेश q है। जहाँ q = 4πR2σ है।


1.2


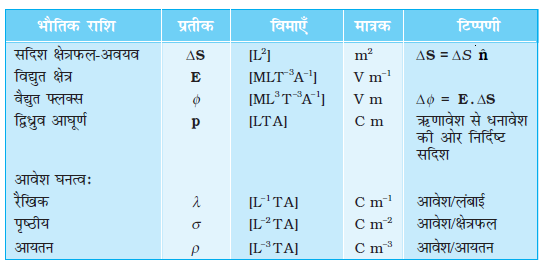
सममिति संक्रियाओं के विषय में

भौतिकी में हमारा प्रायः विभिन्न सममिति के निकायों से सामना होता है। इन सममितियों पर विचार करना सीधे-सीधेे परिकलनों की तुलना में कहीं अधिक शीघ्रता से परिणाम तक पहुँचने में सहायक होता है। उदाहरण के लिए, y-z तल के अनुदिश अनंत लंबाई की आवेश की एकसमान चादर (पृष्ठीय आवेश घनत्व σ) पर विचार कीजिए। यह निकाय अपरिवर्तित रहता है यदि (a) y-z तल के समांतर किसी भी दिशा में स्थानांतरित किया जाता है, (b) x-अक्ष के परितः किसी भी कोण पर घूर्णन कराया जाता है। जिस प्रकार यह निकाय इस प्रकार की सममिति संक्रियाओं के अधीन अपरिवर्तित रहता है, इसी प्रकार इसके गुणधर्म भी अपरिवर्तित रहने चाहिए। विशेष रूप से, इस उदाहरण में, विद्युत क्षेत्र E अपरिवर्तितत होना चाहिए।

y-अक्ष के अनुदिश स्थानांतरीय सममिति यह दर्शाती है कि किसी बिंदु (0, y1, 0) पर विद्युत क्षेत्र (0, y2, 0) पर विद्युत क्षेत्र के समान होना चाहिए। इसी प्रकार z-अक्ष के अनुदिश स्थानांतरीय सममिति यह दर्शाती है कि दो बिंदुओं (0, 0, z1) तथा (0, 0, z2) पर विद्युत क्षेत्र समान होना चाहिए। x- अक्ष के चारों ओर घूर्णन सममिति का उपयोग करके हम यह निष्कर्ष निकाल सकते हैं कि E y-z तल के लंबवत होना चाहिए, अर्थात यह x- दिशा के समांतर होना चाहिए।

अब किसी एेसी सममिति को सोचने का प्रयास कीजिए जो आपको यह बताए कि विद्युत क्षेत्र का परिमाण एक नियतांक है, जो x- निर्देशांक पर निर्भर नहीं करता। इस प्रकार यह कहा जा सकता है कि किसी अनंत लंबाई की एकसमान चालक चादर के कारण उत्पन्न विद्युत क्षेत्र का परिमाण दिक्स्थान में हर बिंदु पर समान होता है। तथापि चादर के दोनों ओर विद्युत क्षेत्र की दिशा एक-दूसरे के विपरीत होती है।

इसकी तुलना उन परिणामों से कीजिए जो कूलॉम नियम के उपयोग द्वारा सीधे परिकलन कर परिणाम पर पहुँचने के लिए आवश्यक हों।


विचारणीय विषय

1. आपको यह आश्चर्य हो सकता है कि नाभिक में प्रोटॉन जिन पर धनावेश है, सभी एक साथ कसे रहकर कैसे समाए हुए हैं। वे एक-दूसरे से दूर क्यों नहीं उड़ जाते? आप यह सीखेंगे कि एक तीसरे प्रकार का मूल बल भी है जिसे प्रबल बल कहते हैं और यही बल प्रोटॉनों को एक साथ बाँधे रखता है। परंतु दूरी का वह परिसर जिसमें यह बल प्रभावी होता है, बहुत छोटा ~ 10-14 m है। यथार्य रूप में यही नाभिक का साइज़ है। साथ ही क्वांटम यांत्रिकी के नियमों के अनुसार इलेक्ट्रॉनों को प्रोटॉनों के शीर्ष पर अर्थात नाभिक के भीतर बैठने की अनुमति भी नहीं है। इसी से परमाणुओं को उनकी रचना प्राप्त है और उनका प्रकृति में अस्तित्व है।

2. कूलॉम बल तथा गुरुत्वाकर्षण बल समान व्युत्क्रम वर्ग नियम का а¤Єа¤ѕа¤Іа¤Ё करते हैं। परंतु गुरुत्वाकर्षण बल का केवल एक ही चिह्न (सदैव आकर्षी) होता है, जबकि कूलॉम बल के दोनों चिह्न (आकर्षी तथा प्रतिकर्षी) हो सकते हैं, जिससे विद्युत बलों का а¤Ёа¤їа¤°а¤ёа¤Ё हो सकता है। यही कारण है कि अत्यंत दुर्बल बल होने а¤Єа¤° भी गुरुत्व बल प्रकृति में एक प्रबल तथा अधिक व्а¤