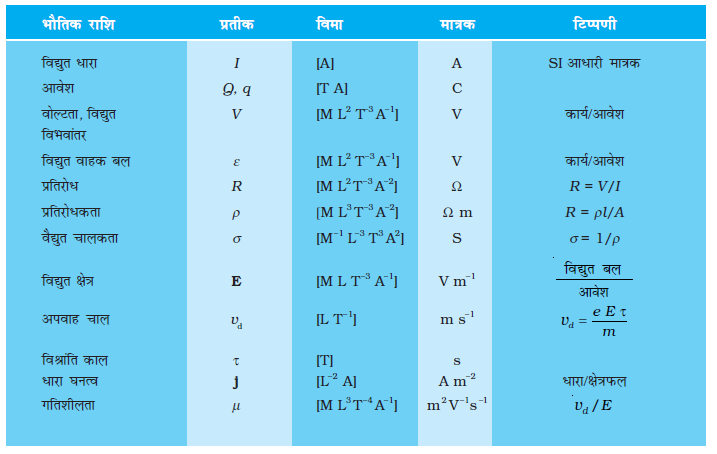
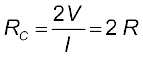Table of Contents

अध्याय 3
विद्युत धारा
3.1 भूमिका
अध्याय 1 में सभी आवेशों को चाहे वे स्वतंत्र हों अथवा परिबद्ध, विरामावस्था में माना गया था। गतिमान आवेश विद्युत धारा का निर्माण करते हैं। एेसी ही धारा प्रकृति में बहुत-सी स्थितियों में पाई जाती है। तड़ित एक एेसी परिघटना है जिसमें आवेश बादलों से पृथ्वी तक वायुमंडल से होकर पहुँचते हैं, जिनका परिणाम कभी-कभी भयंकर होता है। तड़ित में आवेश का प्रवाह स्थायी नहीं होता, परंतु हम अपने दैनिक जीवन में बहुत-सी युक्तियों में आवेशों को उसी प्रकार प्रवाहित होते हुए देखते हैं जिस प्रकार नदियों में जल प्रवाहित होता रहता है। टॉर्च तथा सेल से चलने वाली घड़ी इस प्रकार की युक्तियों के कुछ उदाहरण हैं। इस अध्ययन में हम अपरिवर्ती अथवा स्थायी विद्युत धारा से संबंधित कुछ मूल नियमों का अध्ययन करेंगे।
3.2 विद्युत धारा
आवेश प्रवाह के लंबवत एक लघु क्षेत्रफल की कल्पना कीजिए। इस क्षेत्र से होकर धनात्मक और ऋणात्मक दोनों ही प्रकार के आवेश अग्र अथवा पश्च दिशा में प्रवाहित हो सकते हैं। मान लीजिए, किसी काल-अंतराल t में इस क्षेत्र से प्रवाहित होने वाला नेट अग्रगामी धनावेश q+ (अर्थात अग्रगामी तथा पश्चगामी का अंतर) है। इसी प्रकार, मान लीजिए इसी क्षेत्र से प्रवाहित होने वाला नेट अग्रगामी ऋणावेश q– है। तब इस काल अंतराल t में इस क्षेत्र से प्रवाहित होने वाला नेट आवेश
q = q+– q– है। स्थायी धारा के लिए यह t के अनुक्रमानुपाती है और भागफल
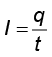 (3.1)
(3.1)
क्षेत्र से होकर अग्रगामी दिशा में प्रवाहित विद्युत धारा को परिभाषित करता है। (यदि यह संख्या ऋणात्मक है तो इससे यह संकेत प्राप्त होता है कि विद्युत धारा पश्चदिशा में है।)
विद्युत धाराएँ सदैव अपरिवर्ती नहीं होतीं, इसलिए अधिक व्यापक रूप में हम विद्युत धारा को निम्न प्रकार से परिभाषित करते हैं। मान लीजिए काल-अंतराल ∆t [अर्थात काल t तथा (t + ∆t) के बीच] में किसी चालक की अनुप्रस्थ काट से प्रवाहित होने वाला नेट आवेश ∆Q है। तब काल t पर चालक के इस अनुप्रस्थ काट से प्रवाहित विद्युत धारा को ∆Q या ∆t के अनुपात के मान के रूप में इस प्रकार परिभाषित किया जाता है जिसमें ∆t की सीमा शून्य की ओर प्रवृत्त है,
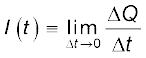
(3.2)
S I मात्रकों में विद्युत धारा का मात्रक एेम्पियर है। एक एेम्पियर को विद्युत धारा के चुंबकीय प्रभाव द्वारा परिभाषित किया जाता है जिसका हम अगले अनुच्छेद में अध्ययन करेंगे। घरेलू वैद्युत-साधित्रों में प्रवाहित होने वाली प्रतिरूपी विद्युत धारा के परिमाण की कोटि एक एेम्पियर होती है। जहाँ एक ओर किसी औसत तड़ित में हज़ारों एेम्पियर कोटि की धारा प्रवाहित हो जाती है, वहीं दूसरी ओर हमारी तंत्रिकाओं से प्रवाहित होने वाली धाराएँ कुछ माइक्रोएेम्पियर कोटि की होती हैं।
3.3 चालक में विद्युत धारा
यदि किसी वैद्युत आवेश पर कोई विद्युत क्षेत्र को अनुप्रयुक्त किया जाए तो वह एक बल का अनुभव करेगा। यदि यह गति करने के लिए स्वतंत्र है तो यह भी गतिमान होकर विद्युत धारा उत्पन्न करेगा। वायुमंडल के ऊपरी स्तर जिसे आयनमंडल कहते हैं, की भाँति प्रकृति में मुक्त आवेशित कण पाए जाते हैं। तथापि, अणुओं तथा परमाणुओं में ऋणावेशित इलेक्ट्रॉन तथा धनावेशित इलेक्ट्रॉन एक-दूसरे से परिबद्ध होने के कारण गति करने के लिए स्वतंत्र नहीं होते हैं। स्थूल पदार्थ अनेक अणुओं से निर्मित होते हैं, उदाहरण के लिए, एक ग्राम जल में लगभग 1022 अणु होते हैं। ये अणु इतने संकुलित होते हैं कि इलेक्ट्रॉन अब एक व्यष्टिगत नाभिक से ही जुड़ा नहीं रहता। कुछ पदार्थों में इलेक्ट्रॉन अभी भी परिबद्ध होते हैं, अर्थात विद्युत-क्षेत्र अनुप्रयुक्त करने पर भी त्वरित नहीं होते। कुछ दूसरे पदार्थों में विशेषकर धातुओं में कुछ इलेक्ट्रॉन स्थूल पदार्थ के भीतर वास्तविक रूप से, गति करने के लिए स्वतंत्र होते हैं। इन पदार्थों जिन्हें सामान्यतः चालक कहते हैं, में विद्युत क्षेत्र अनुप्रयुक्त करने पर विद्युत धारा उत्पन्न हो जाती है।
यदि हम ठोस चालक पर विचार करें तो वास्तव में इनमें परमाणु आपस में निकट रूप से, कस कर आबद्ध होते हैं जिसके कारण ऋण आवेशित इलेक्ट्रॉन विद्युत धारा का वहन करते हैं। तथापि, अन्य प्रकार के चालक भी होते हैं जैसे विद्युत अपघटनी विलयन, जिनमें धनावेश तथा ऋणावेश दोनों गति कर सकते हैं। हम अपनी चर्चा को ठोस चालकों पर ही केंद्रित रखेंगे जिसमें स्थिर धनायनों की पृष्ठभूमि में ऋण आवेशित इलेक्ट्रॉन विद्युत धारा का वहन करते हैं।
पहले हम एेसी स्थिति पर विचार करते हैं जहाँ कोई विद्युत क्षेत्र उपस्थित नहीं है। इलेक्ट्रॉन तापीय गति करते समय आबद्ध आयनों से संघट्ट करते हैं। संघट्ट के पश्चात इलेक्ट्रॉन की चाल अपरिवर्तित रहती है। अतः टकराने के बाद चाल की दिशा पूर्णतया यादृच्छिक होती है। किसी दिए हुए समय पर इलेक्ट्रॉनों की चाल की कोई अधिमानिक दिशा नहीं होती है। अतः औसत रूप से किसी एक विशेष दिशा में गमन करने वाले इलेक्ट्रॉनों की संख्या, उस दिशा के ठीक विपरीत दिशा में गमन करने वाले इलेक्ट्रॉनों की संख्या के ठीक बराबर होती है। अतः कोई नेट विद्युत धारा नहीं होगी।

चित्र 3.1 धात्विक बेलन के सिरों पर रखे +Q और –Q आवेश। आवेशों को उदासीन करने के लिए उत्पन्न विद्युत क्षेत्र के कारण इलेक्ट्रॉनों का अपवाह होगा। यदि आवेश +Q और –Q की पुनः पूर्ति सतत न की गई तो कुछ देर में विद्युत धारा प्रवाह समाप्त हो जाएगा।
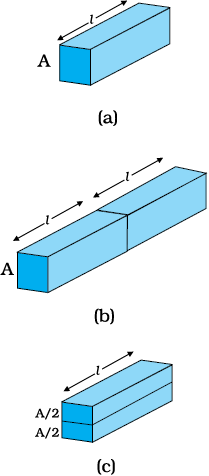
चित्र 3.2 लंबाई l तथा अनुप्रस्थ काट क्षेत्रफल A की आयताकार सिल्ली के संबंध R = ρl/A का निदर्श चित्र।
आइए अब हम यह देखें कि इस प्रकार के चालक के किसी टुकड़े पर कोई विद्युत क्षेत्र अनुप्रयुक्त करने पर क्या होता है। अपने विचारों को केंद्रित करने के लिए R त्रिज्या के बेलनाकार चालक की कल्पना कीजिए (चित्र 3.1)। मान लीजिए परावैद्युत पदार्थ की बनी दो पतली वृत्ताकार डिस्क लेते हैं जिनकी त्रिज्याएँ चालक के समान हैं और जिनमें एक पर धनावेश +Q तथा दूसरे पर ऋणावेश –Q एकसमान रूप से वितरित हैं। इन दोनों डिस्कों को बेलन की दो चपटी पृष्ठों से जोड़ देते हैं। एेसा करने पर एक विद्युत क्षेत्र उत्पन्न हो जाएगा जिसकी दिशा धनावेश से ऋणावेश की ओर होगी। इस क्षेत्र के कारण इलेक्ट्रॉन +Q की तरफ त्वरित होंगे। इस प्रकार वे आवेशों को उदासीन करने के लिए गति करेंगे। जब तक इलेक्ट्रॉन का प्रवाह बना रहेगा, विद्युत धारा बनी रहेगी। इस प्रकार विचाराधीन परिस्थिति में बहुत अल्प समय के लिए विद्युत धारा बहेगी और उसके पश्चात कोई धारा नहीं होगी।
हम एेसी युक्तियों की भी कल्पना कर सकते हैं जो बेलन के सिरों पर, चालक के अंदर गतिमान इलेक्ट्रॉनों द्वारा उदासीन सभी आवेशों की नए आवेशों से पुनः पूर्ति कराएँ। उस प्रकाश में चालक में एक स्थायी विद्युत क्षेत्र स्थापित होगा, जिसके परिणामस्वरूप जो धारा उत्पन्न होगी वह अल्पावधि की न होकर, सतत विद्युत धारा होगी। इस प्रकार स्थायी विद्युत क्षेत्र उत्पन्न करने वाली युक्तियाँ विद्युत सेल अथवा बैटरियाँ होती हैं जिनके विषय में हम इस अध्याय में आगे अध्ययन करेंगे। अगले अनुभागों में हम चालकों में स्थायी विद्युत-क्षेत्रों से प्राप्त स्थायी विद्युत धारा का अध्ययन करेंगे।
3.4 ओम का नियम
विद्युत धारा के प्रवाह के लिए उत्तरदायी भौतिक युक्तियों की खोज से काफी पहले जी. एस. ओम ने सन् 1828 में धारा प्रवाह से संबद्ध एक मूल नियम की खोज कर ली थी। एक चालक की परिकल्पना कीजिए जिससे धारा I प्रवाहित हो रही है और मान लीजिए V, चालक के सिरों के मध्य विभवान्तर है। तब ओम के नियम का कथन है कि
V ∝ I
अथवा V = R I (3.3)
यहाँ आनुपातिकता स्थिरांक R, चालक का प्रतिरोध कहलाता है। प्रतिरोध का SI मात्रक ओम है और यह प्रतीक Ω द्वारा निर्दिष्ट किया जाता है। प्रतिरोध R चालक के केवल पदार्थ पर ही नहीं बल्कि चालक के विस्तार पर भी निर्भर करता है। प्रतिरोध की चालक के विस्तार पर निर्भरता नीचे दिए अनुसार आसानी से ज्ञात की जा सकती है।

जॉर्ज साइमन ओम (1787–1854)
जर्मन भौतिकविज्ञानी, म्यूनिख में प्रोफ़ेसर थे। ओम ने अपने नियम की खोज ऊष्मा-चालन से सदृश्य के आधार पर की– विद्युत क्षेत्र ताप-प्रवणता के तुल्य है और विद्युत धारा ऊष्मा-प्रवाह के।
लंबाई l तथा अनुप्रस्थ काट क्षेत्रफल A की किसी आयताकार सिल्ली पर विचार कीजिए जो समीकरण (3.3) को संतुष्ट करता है [चित्र 3.2 ]। कल्पना कीजिए एेसी दो सर्वसम सिल्लियाँ सिरे से सिरे को मिलाते हुए इस प्रकार रखी हुई हैं कि संयोजन की लंबाई 2l है। इस संयोजन से उतनी ही धारा प्रवाहित होगी जितनी कि दोनों में से किसी एक सिल्ली से होगी। यदि पहली सिल्ली के सिरों के मध्य विभवांतर V है, तब दूसरी सिल्ली के सिरों के मध्य भी विभवांतर V होगा, क्योंकि दूसरी सिल्ली पहली के समान है और दोनों से समान धारा प्रवाहित हो रही है। स्पष्टतया संयोजन के सिरों के मध्य विभवांतर, दो पृथक सिल्लियों के मध्य विभवांतरों का योग है, अतः 2V के बराबर है। संयोजन से होकर प्रवाहित धारा I है तब समीकरण (3.3) से संयोजन का प्रतिरोध RC
![2814.png]() (3.4)
(3.4)
चूँकि V/I = R, दोनों में से किसी एक सिल्ली का प्रतिरोध है। इस प्रकार चालक की लंबाई दोगुनी करने पर इसका प्रतिरोध दोगुना हो जाता है। तब व्यापक रूप से प्रतिरोध लंबाई के अनुक्रमानुपाती होता है
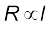 (3.5)
(3.5)
इसके बाद इस सिल्ली को लंबाई में दो समान भागों में विभाजित करने की कल्पना कीजिए जिससे कि सिल्ली को लंबाई l की दो सर्वसम सिल्लियों जिनमें प्रत्येक का अनुप्रस्थ काट क्षेत्रफल A/2 है, के संयोजन जैसा समझा जा सके [चित्र 3.2 (c)]।
सिल्ली के सिरों के मध्य दिए गए विभवांतर V के लिए यदि पूरी सिल्ली से प्रवाहित होने वाली धारा I है तो स्पष्टता प्रत्येक आधी सिल्ली से प्रवाहित होने वाली धारा I/2 होगी। चूँकि आधी सिल्ली के सिरों के मध्य विभवांतर V है, अर्थात उतना ही है जितना कि पूरी सिल्ली के सिरों के मध्य विभवांतर है, इसलिए प्रत्येक आधी सिल्ली का प्रतिरोध R1 इस प्रकार व्यक्त किया जा सकता है
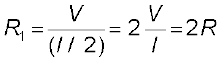 (3.6)
(3.6)
इस प्रकार चालक की अनुप्रस्थ काट के क्षेत्रफल को आधा करने पर प्रतिरोध दोगुना हो जाता है। व्यापक रूप से तब प्रतिरोध R, अनुप्रस्थ काट क्षेत्रफल (A) के व्युत्क्रमानुपाती होता है, अर्थात
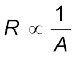 (3.7)
(3.7)
समीकरण (3.5) और (3.7) के संयोजन से
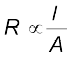 (3.8)
(3.8)
अतः, किसी दिए गए चालक के लिए
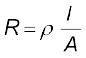 (3.9)
(3.9)
यहाँ ρ एक आनुपातिकता स्थिरांक है जो चालक के पदार्थ की प्रकृति पर निर्भर करता है, इसके विस्तार पर नहीं। ρ को प्रतिरोधकता कहते हैं।
समीकरण (3.9) का प्रयोग करने पर, ओम के नियम को इस प्रकार व्यक्त कर सकते हैं
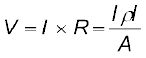 (3.10)
(3.10)
विद्युत धारा प्रति एकांक क्षेत्र (धारा के अभिलंबवत ली गई) I/A धारा घनत्व कहलाता है और j द्वारा निर्दिष्ट किया जाता है। धारा घनत्व का SI मात्रक A/m2 है। इसके अतिरिक्त यदि एकसमान विद्युत क्षेत्र E के किसी चालक की लंबाई l है तो इस चालक के सिरों के बीच विभवांतर का परिणाम El होता है। इसका उपयोग करने पर समीकरण (3.10) को इस प्रकार व्यक्त करते हैं
E l = j ρ l
अथवा E = j ρ (3.11)
E तथा j के परिमाण के लिए उपरोक्त समीकरण को अवश्य ही सदिश रूप में व्यक्त किया जा सकता है। धारा घनत्व (जिसे हमने धारा के अभिलंबवत प्रति एकांक क्षेत्रफल के रूप में परिभाषित किया है) भी E की ओर निर्दिष्ट है और j (≡ jE/E) एक सदिश भी है। इस प्रकार समीकरण (3.11) को इस प्रकार से व्यक्त करते हैं
E = jρ (3.12)
अथवा j = σ E (3.13)
जहाँ σ =1/ρ को चालकता कहते हैं। ओम के नियम को प्रायः समीकरण (3.3) के अलावा समीकरण (3.13) द्वारा भी समतुल्य रूप में व्यक्त किया जाता है। अगले अनुच्छेद में हम ओम के नियम के उद्गम को इस रूप में समझने का प्रयास करेंगे जैसे कि यह इलेक्ट्रॉनों के अपवाह के अभिलक्षणों से उत्पन्न हुआ है।
3.5 इलेक्ट्रॉन का अपवाह एवं प्रतिरोधकता का उद्गम
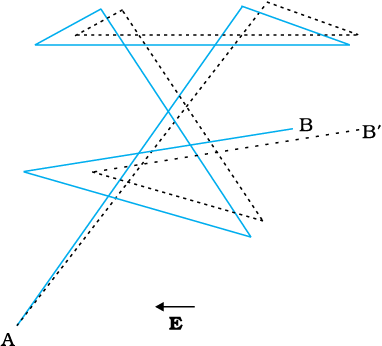
चित्र 3.3 किसी बिंदु A से दूसरे बिंदु B तक बारम्बार संघट्टों के द्वारा इलेक्ट्रॉन की गति तथा संघट्टों के बीच रैखिक गति का आरेखीय चित्रण (सतत रेखाएँ)। यदि दर्शाए अनुसार कोई विद्युत क्षेत्र लगाया जाता है तो इलेक्ट्रॉन B' पर रुक जाता है (बिंदुकृत रेखाएँ)। विद्युत क्षेत्र के विपरीत दिशा में मामूली अपवाह दिखलाई दे रहा है।
हमने पहले देखा है कि जब कोई इलेक्ट्रॉन किसी भारी आयन से संघट्ट करता है तो संघट्ट के बाद उसी चाल से चलता है लेकिन इसकी दिशा यादृच्छिक हो जाती है। यदि हम सभी इलेक्ट्रॉनों पर विचार करें तो उनका औसत वेग शून्य होगा, क्योंकि उनकी दिशाएँ यादृच्छिक हैं। इस प्रकार यदि ith इलेक्टॉन (i = 1, 2, 3, ... N) का वेग किसी दिए समय में vi हो तो
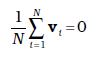 (3.14)
(3.14)
अब एेसी स्थिति पर विचार करें जब यह चालक किसी विद्युत क्षेत्र में उपस्थित है। इस क्षेत्र के कारण इलेक्ट्रॉन में त्वरण उत्पन्न होगा
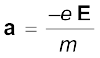 (3.15)
(3.15)
जहाँ –e इलेक्ट्रॉन का आवेश तथा m इसका द्रव्यमान है। दिए गए समय t में ith इलेक्ट्रॉन पर पुनः विचार करें। यह इलेक्ट्रॉन t के कुछ समय पहले अंतिम बार संघट्ट करेगा और मान लीजिए, ti इसके अंतिम संघट्ट के बाद व्यतीत समय है। यदि vi अंतिम संघट्ट के तुरंत पश्चात का वेग था तब समय t पर इसका वेग
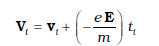 (3.16)
(3.16)
चूँकि अपने अंतिम संघट्ट से आरंभ करने के पश्चात यह इलेक्ट्रॉन किसी समय अंतराल ti के लिए समीकरण (3.15) द्वारा दिए गए त्वरण के साथ त्वरित हुआ था। सभी इलेक्ट्रॉनों का समय t पर औसत वेग सभी Vi का औसत है। vi का औसत शून्य है [समीकरण (3.14)] क्योंकि संघट्ट के तुरंत बाद एक इलेक्ट्रॉन के वेग की दिशा पूर्णतया यादृच्छिक होती है। इलेक्ट्रॉनों के संघट्ट नियमित काल-अंतरालों पर न होकर यादृच्छिक समय में होते हैं। यदि लगातार (क्रमिक) संघट्टों के बीच औसत समय को हम लोग τ से निर्दिष्ट करें तो किसी दिए गए समय में कुछ इलेक्ट्रॉन τ से ज्यादा और कुछ τ से कम समय व्यतीत किए होंगे। दूसरे शब्दों में, जैसे-जैसे हम i = 1, 2 ..... N विभिन्न मान देते हैं तो हमें समीकरण (3.16) के अनुसार समय ti के मान कुछ के लिए τ से ज्यादा होंगे तथा कुछ के लिए τ से कम होंगे। तब ti का औसत मान τ होगा (जिसे विश्रांति काल कहते हैं)। इस प्रकार किसी दिए समय t पर N इलेक्ट्रॉनों के लिए समीकरण (3.16) का औसत लेने पर हमें औसत वेग vd प्राप्त होता है
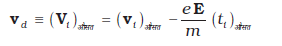
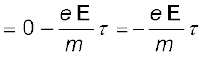 (3.17)
(3.17)
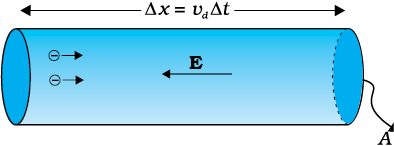
चित्र 3.4 धात्विक चालक में विद्युत धारा। धातु में धारा घनत्व का परिमाण एकांक क्षेत्रफल तथा vd ऊँचाई के बेलन में अंतर्विष्ट आवेश के परिमाण के बराबर है।
यह अंतिम परिणाम आश्चर्यजनक है। यह हमें बताता है कि इलेक्ट्रॉन, यद्यपि त्वरित है, एक औसत वेग से गतिमान है जो समय पर निर्भर नहीं करता है। यह परिघटना अपवाह की है और समीकरण (3.17) का वेग vd अपवाह वेग कहलाता है।
अपवाह के कारण, विद्युत क्षेत्र E के लंबवत किसी क्षेत्र से होकर आवेशों का नेट परिवहन होगा। चालक के अंदर एक समतलीय क्षेत्र पर विचार करें जो कि E के समांतर क्षेत्र पर अभिलंब है (चित्र 3.4)। तब अपवाह के कारण, अत्यणु समय ∆t में, क्षेत्र की बायीं ओर के सभी इलेक्ट्रॉन |vd|∆t दूरी पार कर लिए होंगे। यदि चालक में प्रति एकांक आयतन मुक्त इलेक्ट्रॉनों की संख्या n है तो n ∆t|vd|A एेसे इलेक्ट्रॉन होंगे। चूँकि प्रत्येक इलेक्ट्रॉन आवेश –e वहन करता है, ∆t समय में क्षेत्र A की दायीं ओर परिवहित कुल आवेश –ne A|vd|∆t है। E बायीं ओर निर्दिष्ट है, अतः इस क्षेत्र से होकर E के अनुदिश परिवहित कुल आवेश इसके ऋणात्मक होगा। परिभाषानुसार [समीकरण (3.2)] क्षेत्र A को समय ∆t में पार करने वाले आवेश I ∆t होंगे, यहाँ I धारा का परिमाण है। अतः
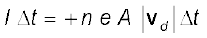 (3.18)
(3.18)
|vd| के मान को समीकरण (3.17) से प्रतिस्थापित करने पर
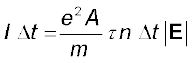 (3.19)
(3.19)
परिभाषानुसार, धारा घनत्व के परिमाण |j| से I संबंधित है
I = |j|A (3.20)
अतः समीकरण (3.19) तथा (3.20) से,
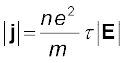 (3.21)
(3.21)
सदिश j, E के समांतर है, इसलिए हम समीकरण (3.21) को सदिश रूप में लिख सकते हैं
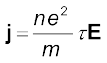 (3.22)
(3.22)
अगर हम चालकता σ का तादात्म्य स्थापित करें
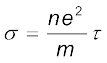
तो समीकरण (3.13) से तुलना करने पर यह व्यक्त होता है कि समीकरण (3.22) तथ्यतः ओम का नियम है। यदि हम चालकता को σ द्वारा निर्दिष्ट करें तो 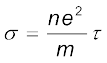 (3.23)
(3.23)
इस प्रकार हम देखते हैं कि विद्युत चालकता का एक बहुत सरल चित्रण ओम के नियम की प्रतिकृति तैयार करता है। अवश्य ही हमने यह पूर्वधारणा बनाई है कि τ और n, E से स्वतंत्र स्थिरांक हैं। अगले अनुच्छेद में हम ओम के नियम की सीमाओं का विवेचन करेंगे।
उदाहरण 3.1
(a) 1.0 × 10−7 m2 अनुप्रस्थ काट क्षेत्रफल वाले ताँबे के तार में 1.5 A धारा प्रवाहित हो रही है। इसमें चालक इलेक्ट्रॉनों की औसत अपवाह चाल का आकलन कीजिए। मान लीजिए कि ताँबे का प्रत्येक परमाणु धारा के प्रवाह में एक चालक इलेक्ट्रॉन का योगदान करता है। ताँबे का घनत्व 9.0 × 103 kg/m3 तथा इसका परमाणु द्रव्यमान 63.5 u है। (b) ऊपर निकाली गई अपवाह चाल की निम्नलिखित उदाहरणों से तुलना कीजिए। (i) सामान्य तापों पर ताँबे के परमाणुओं की तापीय चाल (ii) चालक के अनुदिश विद्युत क्षेत्र की संचरण चाल जो अपवाह गति उत्पन्न करती है।
हल
(a) चालक इलेक्ट्रॉन के अपवाह वेग की दिशा विद्युत क्षेत्र की दिशा के विपरीत है अर्थात इलेक्ट्रॉन बढ़ते हुए विभव की दिशा में अपवाह करते हैं। अपवाह चाल vd समीकरण (3.18) से व्यक्त होगी,
vd = (I/neA)
अब e = 1.6 × 10–19 C, A = 1.0 × 10–7m2, I = 1.5 A है। चालक इलेक्ट्रॉनों का घनत्व, n प्रति घन मीटर में परमाणुओं की संख्या के बराबर है (मान लीजिए कि प्रति ताँबे के परमाणु में एक चालक इलेक्ट्रॉन है जो संयोजकता इलेक्ट्रॉन की संख्या 1 के अनुसार यथोचित है)। एक घन मीटर ताँबे का द्रव्यमान 9.0 × 103 kg है। चूँकि 6.0 × 1023 ताँबे के परमाणुओं का द्रव्यमान 63.5 g है, अतः
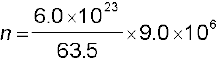
= 8.5 × 1028 m–3
जिससे हमें अपवाह चाल का निम्न मान प्राप्त होता हैः
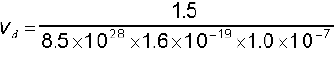
= 1.1 × 10–3 m s–1
= 1.1 mm s–1
(b) (i) ताप T पर M द्रव्यमान के ताँबे के एक परमाणु की तापीय चाल* विशिष्ट रूप से
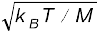
की कोटि की है। जिसे [<(1/2) Mv2 > = (3/2) kBT ] से प्राप्त
किया गया है। यहाँ kB बोल्ट्ज़मैन नियतांक है। 300 K पर ताँबे के लिए यह लगभग
2 × 102 m/s है। यह किसी चालक में ताँबे के परमाणुओं की यादृच्छिक कंपन चालों को इंगित करता है। ध्यान दीजिए कि इलेक्ट्रॉनों की अपवाह चाल बहुत कम है। साधारण ताप पर यह इलेक्ट्रॉनों की प्रतिरूपी तापीय चाल की लगभग 10−5 गुनी होती है।
(ii) चालक के अनुदिश गतिशील विद्युत क्षेत्र की चाल किसी विद्युत चुंबकीय तरंग की चाल अर्थात 3.0 × 108 m s–1 के बराबर है। (इसके नियम में आप अध्याय 8 में पढ़ेंगे)। इसकी तुलना में अपवाह चाल बहुत ही कम है, 10–11 गुणक द्वारा कम।
* भौतिकी पाठ्यपुस्तक, कक्षा 11, अध्याय 13 का समीकरण (13.23) देखिए।
उदाहरण 3.2
(a) उदाहरण 3.1 में कुछ एेम्पियर धारा के परिसर में किसी इलेक्ट्रॉन की अपवाह गति केवल कुछ mm s−1 ही आकलित की गई है। तब परिपथ बंद करते ही लगभग उसी क्षण धारा कैसे स्थापित हो जाती है?
(b) किसी चालक के अंदर इलेक्ट्रॉन अपवाह विद्युत क्षेत्र में इलेक्ट्रॉनों द्वारा अनुभव किए गए बल के कारण उत्पन्न होता है। लेकिन बल द्वारा त्वरण उत्पन्न होना चाहिए। तब इलेक्ट्रॉन अपरिवर्ती औसत अपवाह वेग क्यों प्राप्त कर लेते हैं?
(c) यदि इलेक्ट्रॉन का अपवाह वेग इतना कम है और इलेक्ट्रॉन का आवेश भी कम है तो फिर किसी चालक में हम अधिक मात्रा में धारा कैसे प्राप्त कर सकते हैं?
(d) जब किसी धातु में इलेक्ट्रॉन कम विभव से अधिक विभव की ओर अपवाह करते हैं तो क्या इसका तात्पर्य यह है कि धातु में सभी मुक्त इलेक्ट्रॉन एक ही दिशा में गतिमान हैं?
(e) क्या उत्तरोत्तर संघट्टों (धातु के धनायनों के साथ) के बीच इलेक्ट्रॉनों के पथ (i) विद्युत क्षेत्र की अनुपस्थिति में, (ii) विद्युत क्षेत्र की उपस्थिति में, सरल रेखीय हैं?
हल
(a) पूर्ण परिपथ में विद्युत क्षेत्र लगभग तत्काल स्थापित हो जाता है (प्रकाश के वेग से) जो प्रत्येक बिंदु पर स्थानीय इलेक्ट्रॉन अपवाह उत्पन्न करता है। परिपथ में विद्युत धारा स्थापित होने के लिए यह प्रतीक्षा नहीं करनी पड़ती कि इलेक्ट्रॉन चालक में एक सिरे से दूसरे सिरे तक जाएंगे। फिर भी, धारा स्थायी मान प्राप्त करने में अल्प समय अवश्य लेती है।
(b) प्रत्येक मुक्त इलेक्ट्रॉन त्वरित होता है जिससे उसकी अपवाह चाल तब तक बढ़ती है जब तक वह धातु के धनायनों से संघट्ट नहीं करता। संघट्ट के पश्चात यह अपनी अपवाह चाल खो देता है। पर यह पुनः त्वरित होता है तथा पुनः इसके अपवाह वेग में तब तक वृद्धि होती है जब यह पुनः संघट्ट नहीं करता और यह क्रम चलता रहता है। अतः औसतन इलेक्ट्रॉन केवल अपवाह चाल प्राप्त कर पाता है।
(c) सरल है, क्योंकि चालक में इलेक्ट्रॉन संख्या घनत्व अत्यधिक (~ 1029 m–3) है।
(d) किसी प्रकार नहीं। इलेक्ट्रॉनों की अपवाह चाल उनके अत्यधिक यादृच्छिक वेग पर अध्यारोपित होती है।
(e) विद्युत क्षेत्र की अनुपस्थिति में पथ ऋजु-रेखीय हैं जबकि विद्युत क्षेत्र की उपस्थिति में पथ व्यापक रूप से वक्रित होते हैं।
3.5.1 गतिशीलता
जैसा कि हम देख चुके हैं, चालकता गतिमान आवेश वाहकों से उत्पन्न होती है। धातुओं में यह गतिमान आवेश वाहक इलेक्ट्रॉन हैं, आयनित गैस में ये इलेक्ट्रॉन तथा धन आवेशित आयन हैं, विद्युत अपघट्य में ये धनायन तथा ऋणायन दोनों हो सकते हैं।
एक महत्वपूर्ण राशि गतिशीलता µ है जिसे प्रति एकांक विद्युत क्षेत्र के अपवाह वेग के परिमाण के रूप में परिभाषित करते हैं
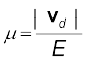 (3.24)
(3.24)
गतिशीलता का SI मात्रक m2/Vs है और इसके प्रायोगिक मात्रक (cm2/Vs) का 104 गुना है। गतिशीलता धनात्मक होती है। समीकरण (3.17) में,
vd = 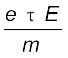
अतः
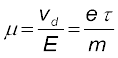 (3.25)
(3.25)
जहाँ τ इलेक्ट्रॉन के लिए संघट्टन का औसत समय है।
3.6 ओम के नियम की सीमाएँ
यद्यपि ओम का नियम पदार्थों के विस्तृत वर्ग के लिए मान्य है, विद्युत परिपथों में उपयोग होने वाले कुछ एेसे पदार्थ एवं युक्तियाँ विद्यमान हैं जहाँ V तथा I की आनुपातिकता लागू नहीं होती है। मोटे तौर पर, यह विचलन निम्नलिखित एक या अधिक प्रकार का हो सकता है

चित्र 3.5 बिंदुकित रेखा रैखिक ओम-नियम को निरूपित करती है। सतत रेखा अच्छे चालक के लिए V तथा I के संबंध को दर्शाती है।
(a) V की I से आनुपातिकता समाप्त हो जाती है (चित्र 3.5)
(b) V तथा I के मध्य संबंध V के चिह्न पर निर्भर करता है। दूसरे शब्दों में, यदि कुछ V के लिए धारा I है, तो V का परिमाण स्थिर रख कर इसकी दिशा बदलने पर, विपरीत दिशा में I के समान परिमाण की धारा उत्पन्न नहीं होती है (चित्र 3.6)। उदाहरण के लिए, डायोड में एेसा होता है जिसका अध्ययन हम अध्याय 14 में करेंगे।
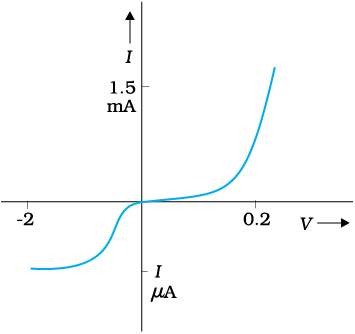
चित्र 3.6 डायोड के अभिलाक्षणिक वक्र। वोल्टता तथा धारा के ऋण व धन मानों के लिए विभिन्न पैमानों को नोट कीजिए।
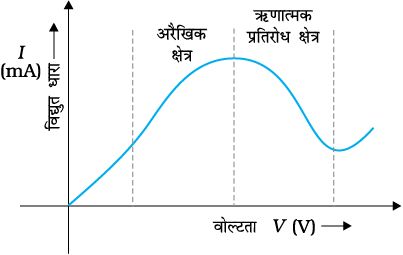
चित्र 3.7 GaAs में वोल्टता के सापेक्ष धारा में परिवर्तन।
(c) V तथा I के मध्य संबंध एकमात्र संबंध नहीं है अर्थात उसी धारा I के लिए V के एक से अधिक मान हो सकते हैं (चित्र 3.7)।
पदार्थ तथा युक्तियाँ जो समीकरण (3.3) के रूप में ओम के नियम का पालन नहीं करती हैं, यथार्थ में, इलेक्ट्रॉनिक परिपथ में व्यापक रूप से उपयोग की जाती हैं। तथापि इस अध्याय तथा परवर्ती अध्याय में, हम उस पदार्थ में विद्युत धारा का अध्ययन करेंगे जो ओम के नियम का पालन करते हैं।
3.7 विभिन्न पदार्थों की प्रतिरोधकता
विविध सामान्य पदार्थों की प्रतिरोधकता सारणी 3.1 में सूचीबद्ध हैं। प्रतिरोधकता पर निर्भरता तथा उनके बढ़ते हुए मान के अनुसार पदार्थों का वर्गीकरण चालक, अर्धचालक तथा विद्युतरोधी में किया जाता है। धातुओं की प्रतिरोधकता 10–8 Ωm से 10–6 Ωm के परिसर में होती है। इसके विपरीत मृत्तिका (सिरेमिक), रबर तथा प्लास्टिक जैसे विद्युतरोधी पदार्थ भी हैं जिनकी प्रतिरोधकता, धातुओं की तुलना में 1018 गुनी या अधिक है। इन दोनों के मध्य अर्धचालक हैं। इनकी प्रतिरोधकता, तथापि ताप बढ़ाने पर अभिलाक्षणिक रूप से घटती है। अर्धचालक की प्रतिरोधकता उपयुक्त अशुद्धियों को अल्प मात्रा में मिलाने पर कम की जा सकती है। इस अंतिम विशिष्टता का लाभ, इलेक्ट्रॉनिक युक्तियों में उपयोग होने वाले अर्धचालकों के निर्माण में किया जाता है।
घरेलू या प्रयोगशालाओं में प्रयोग हेतु व्यापारिक दृष्टिकोण से बनाए जाने वाले प्रतिरोधक मुख्यतः दो प्रकार के होते हैं–तार आबद्ध प्रतिरोधक तथा कार्बन प्रतिरोधक। तार आबद्ध प्रतिरोधक किसी मिश्रातु, जैसे मैंगनिन, कान्सटेन्टन, निक्रोम या उनके जैसे तारों को लपेट कर बनाए जाते हैं। बहुधा इन पदार्थों का चयन इस तथ्य से निर्धारित होता है कि इनकी प्रतिरोधकता पर ताप का प्रभाव अपेक्षाकृत नगण्य है।
इन प्रतिरोधों का परिसर एक ओम के किसी अंश से लेकर कुछ सौ ओम तक होता है। उच्चतर परिसर के प्रतिरोधक मुख्यतः कार्बन से बनाए जाते हैं। कार्बन के प्रतिरोधक सुसंहत और सस्ते होते हैं, इसलिए इलेक्ट्रॉनिक परिपथों में व्यापक रूप से उपयोग किए जाते हैं। कार्बन प्रतिरोधक आमाप में छोटे होते हैं, अतः उनके मान वर्ण कोड के द्वारा व्यक्त किए जाते हैं।
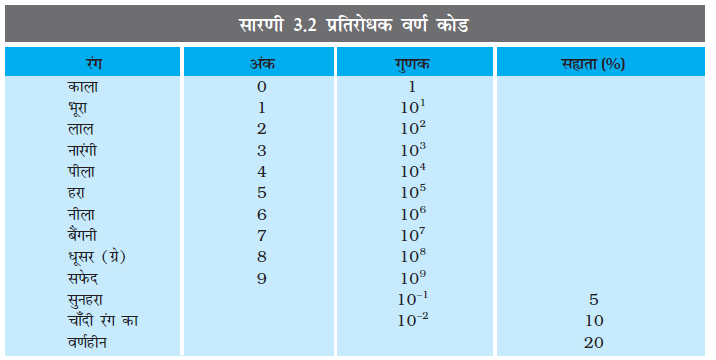
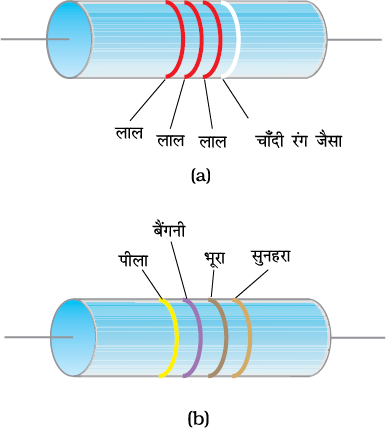
(b) (47 × 10Ω) ± 5%
प्रतिरोधक पर समाक्ष रंगीन वलयों का समूह होता है जिनकी सार्थकता सारणी 3.2 में सूचीबद्ध की गई है। सिरे से पहली दो धारियाँ ओम में प्रतिरोध के पहले दो सार्थक अंकों को निर्देशित करती हैं। तीसरी धारी दशमलव गुणक को निर्देशित करती है (जैसा कि सारणी 3.2 में सूचीबद्ध है) तथा अंतिम धारी सह्यता अथवा निर्देशित मान के प्रतिशत में संभावित विचरण को व्यक्त करती है। कभी-कभी यह अंतिम धारी नहीं होती है जिसका आशय यह है कि सह्यता 20% है (चित्र 3.8)। उदाहरण के लिए, यदि चार रंग नारंगी, नीला, पीला और सुनहरा हैं, तो प्रतिरोध का मान 5% सह्यता मान के साथ 36 × 104 Ω होगा।
3.8 प्रतिरोधकता की ताप पर निर्भरता
पदार्थ की प्रतिरोधकता ताप पर निर्भर पाई जाती है। विभिन्न पदार्थ एक जैसी निर्भरता प्रदर्शित नहीं करते। एक सीमित ताप परिसर में, जो बहुत अधिक नहीं होता, किसी धात्विक चालक की लगभग प्रतिरोधकता को इस प्रकार व्यक्त करते हैं
ρT = ρ0 [1 + α (T–T0)] (3.26)जहाँ ρT ताप T पर प्रतिरोधकता है तथा ρ0 संदर्भ ताप T0 पर इसका माप है। α को प्रतिरोधकता ताप-गुणांक कहते हैं और समीकरण (3.26) से α की विमा (ताप)–1 है। धातुओं के लिए α का मान धनात्मक होता है तथा T0 = 0°C पर कुछ धातुओं के लिए α का मान सारणी 3.1 में सूचीबद्ध है।
समीकरण (3.26) के संबंध से यह ध्वनित होता है कि T और ρT के बीच ग्राफ एक सरल रेखा होती है। तथापि, 0°C से बहुत कम तापों पर, ग्राफ एक सरल रेखा से काफी विचलित हो जाता है।
अतः समीकरण (3.26) को किसी संदर्भ ताप T0 के लगभग किसी सीमित परिसर में उपयोग कर सकते हैें, जहाँ ग्राफ करीब-करीब एक सरल रेखा होगी।
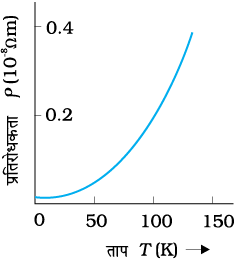
चित्र 3.9 ताप T के फलन के रूप में ताँबे की प्रतिरोधकता

चित्र 3.10 परम ताप T के फलन के रूप में निक्रोम की प्रतिरोधकता।
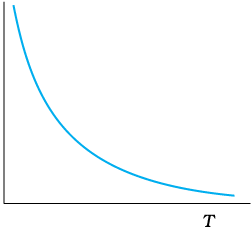
चित्र 3.11 विशिष्ट अर्द्धचालक के लिए प्रतिरोधकता की
ताप-निर्भरता।
कुछ पदार्थ जैसे कि निक्रोम (जो कि निकैल, लोहा तथा क्रोमियम की मिश्रातु है) बहुत दुर्बल ताप-निर्भरता प्रदर्शित करता है (चित्र 3.10)। मैंगनीन तथा कांसटेंटन में भी इसी प्रकार के गुण हैं। चूँकि इनके प्रतिरोध की ताप-निर्भरता बहुत कम है, इसलिए ये पदार्थ तार आबद्ध मानक प्रतिरोधकों के निर्माण में व्यापक रूप से उपयोग किए जाते हैं।
धातुओं के विपरीत, अर्धचालकों की प्रतिरोधकता ताप में वृद्धि होने पर कम हो जाती है। इस प्रारूपिक निर्भरता को चित्र 3.11 में दर्शाया गया है।
हम समीकरण (3.23) में व्युत्पन्न परिणामों के आधार पर प्रतिरोधकता की ताप-निर्भरता को गुणात्मक रूप में समझ सकते हैं। इस समीकरण से किसी पदार्थ की प्रतिरोधकता व्यक्त की जाती है
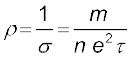 (3.27)
(3.27)
किसी पदार्थ की प्रतिरोधकता प्रति एकांक आयतन में इलेक्ट्रॉनों की संख्या तथा उसमें होने वाले संघट्टों पर प्रतिलोमी रूप से निर्भर करती है। जैसे-जैसे हम ताप बढ़ाते हैं, विद्युत धारा वहने करने वाले इलेक्ट्रॉनों की औसत चाल बढ़ती जाती है जिसके परिणामस्वरूप संघट्ट की आवृत्ति भी बढ़ती जाती है। इसलिए संघट्टों का औसत समय τ, ताप के साथ घटता है।
धातुओं में n की ताप निर्भरता उपेक्षणीय है, इसलिए ताप बढ़ने से τ के मान के घटने के कारण ρ बढ़ता है, जैसा कि हमने प्रेक्षण किया है।
तथापि, विद्युतरोधियों एवं अर्धचालकों में ताप में वृद्धि के साथ n में भी वृद्धि होती है। यह वृद्धि समीकरण (3.23) में τ में होने वाली किसी भी कमी से भी अधिक की क्षतिपूर्ति करती है जिसके फलस्वरूप एेसे पदार्थों के लिए प्रतिरोधकता ρ का मान ताप के साथ घट जाता है।
उदाहरण 3.3
किसी विद्युत टोस्टर में निक्रोम के तापन अवयव का उपयोग होता है। जब इससे एक नगण्य लघु विद्युत धारा प्रवाहित होती है तो कक्ष ताप पर (27.0 °C) इसका प्रतिरोध 75.3 Ω पाया जाता है। जब इस टोस्टर को 230 V आपूर्ति से संयोजित करते हैं तो कुछ सेकंड में परिपथ में 2.68 A की स्थायी धारा स्थापित हो जाती है। निक्रोम-अवयव
का स्थायी ताप क्या है? निक्रोम को सम्मिलित ताप परिसर में प्रतिरोध ताप गुणांक
1.70 × 10–4 °C–1 है।
हल
जब अवयव में धारा बहुत कम है तो तापीय प्रभावों की उपेक्षा की जा सकती है और तब अवयव का ताप T1 कमरे के ताप के बराबर हो जाता है। जब टोस्टर को आपूर्ति से संयोजित किया जाएगा, तो प्रारंभिक धारा स्थायी मान 2.68 A से कुछ अधिक हो जाएगी। परंतु विद्युत धारा के तापीय प्रभाव के कारण ताप बढ़ेगा। यह प्रतिरोध को बढ़ाएगा फलस्वरूप परिपथ की विद्युत धारा में कुछ कमी उत्पन्न होगी। कुछ सेकंड में स्थायी अवस्था प्राप्त हो जाएगी तथा ताप और नहीं बढ़ेगा। अवयव का प्रतिरोध तथा आपूर्ति से ली गई विद्युत धारा दोनों स्थायी मान प्राप्त कर लेंगे। तब स्थायी ताप T2 पर प्रतिरोध R2 का मान
R2 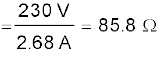
संबंध R2 = R1 [1 + α (T2 – T1)] का उपयोग संबंध
α = 1.70 × 10–4 °C–1 के साथ करने पर हमें प्राप्त होता है
T2 – T1 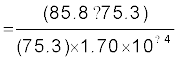 = 820 °C
= 820 °C
अर्थात, T2= (820 + 27.0) °C = 847 °C
इस प्रकार, तापन अवयव का ताप (जब धारा के कारण तापीय प्रभाव प्रतिवेश में हुए ऊष्मा क्षय के बराबर है) 847 °C है।
उदाहरण 3.4
प्लैटिनम प्रतिरोध तापमापी के प्लैटिनम के तार का प्रतिरोध हिमांक पर
5 Ω तथा भाप बिंदु पर 5.23 Ω है। जब तापमापी को किसी तप्त-ऊष्मक में प्रविष्ट कराया जाता है तो प्लैटिनम के तार का प्रतिरोध 5.795 Ω हो जाता है। ऊष्मक का ताप परिकलित कीजिए।
हल R0 = 5 Ω, R100 = 5.23 Ω तथा Rt = 5.795 Ω
अब, t = 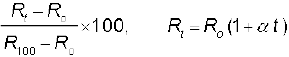
= 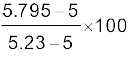
= 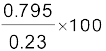 = 345.65 oC
= 345.65 oC
3.9 विद्युत ऊर्जा, शक्ति
किसी चालक AB पर विचार कीजिए जिसमें A से B की ओर I धारा प्रवाहित हो रही है। A तथा B पर विद्युत विभव क्रमशः V(A) एवं V(B) से निरूपित किए गए हैं। चूँकि धारा A से B की ओर प्रवाहित हो रही है, V(A) > V(B) और चालक AB के सिरों के बीच विभवांतर V = V(A) – V(B) > 0 है।
∆t काल अंतराल में, आवेश की एक मात्रा ∆Q = I ∆t A से B की ओर चलती है। परिभाषानुसार बिंदु A पर आवेश की स्थितिज ऊर्जा Q V(A) थी तथा इसी प्रकार बिंदु B पर आवेश की स्थितिज ऊर्जा Q V(B) है। इसलिए स्थितिज ऊर्जा में यह परिवर्तन ∆Upot है
∆Upot = अंतिम स्थितिज ऊर्जा – प्रारंभिक स्थितिज ऊर्जा
= ∆Q[(V (B) – V (A)] = –∆Q V
= –I V∆t < 0 (3.28)
यदि आवेश चालक के अंदर बिना संघट्ट किए गतिमान हैं तो उनकी गतिज ऊर्जा भी परिवर्तित होती है जिससे कि समस्त ऊर्जा अपरिवर्तित रहे। समस्त ऊर्जा के संरक्षण से यह परिणाम निकलता है कि
∆K = –∆Upot (3.29)
अथवा
∆K = I V∆t > 0 (3.30)
अतः चालक के अंदर विद्युत क्षेत्र के प्रभाव से अगर आवेश मुक्त रूप से गतिमान रहते तो उनकी गतिज ऊर्जा बढ़ जाती। तथापि, हमने पहले समझा है कि सामान्य तौर पर, आवेश त्वरित गति से गमन नहीं करते हैं बल्कि अपरिवर्ती अपवाह वेग से चलते हैं। यह पारगमन की अवधि में आयनों तथा परमाणुओं से संघट्ट के कारण होता है। संघट्टों के समय आवेशों द्वारा प्राप्त की गई ऊर्जा, परमाणुओं के साथ आपस में बाँट ली जाती है। परमाणु ज्यादा प्रबल रूप से कंपन करते हैं अर्थात चालक गर्म हो जाते हैं। इस प्रकार एक वास्तविक चालक में काल अंतराल ∆t में ऊष्मा के रूप में क्षयित ऊर्जा का परिमाण
∆W = I V∆t (3.31)
प्रति एकांक समय में क्षय हुई ऊर्जा क्षयित शक्ति के बराबर है P = ∆W/∆t और हम प्राप्त कर सकते हैं
P = I V (3.32)
ओम के नियम V = IR का उपयोग करने पर हम पाते हैं
P = I 2 R = V 2/R (3.33)
जो कि R प्रतिरोध के चालक जिससे I विद्युत धारा प्रवाहित हो रही है, में होने वाला शक्ति क्षय (ओमी क्षय) है। यह वही शक्ति है जो, उदाहरण के लिए किसी तापदीप्त विद्युत लैंप की कुंडली को प्रदीप्त करती है, जिसके कारण वह ऊष्मा तथा प्रकाश को विकिरण करता है।
यह शक्ति कहाँ से आती है? जैसा कि हम पहले स्पष्ट कर चुके हैं कि किसी चालक में स्थायी धारा का प्रवाह बनाए रखने के लिए हमें एक बाह्य स्रोत की आवश्यकता होती है। स्पष्टतया यही स्रोत है जिसे इस शक्ति की आपूर्ति करनी चाहिए। चित्र (3.12) में विद्युत सेल के साथ दर्शाए गए एक सरल परिपथ में यह सेल की ही रासायनिक ऊर्जा है जो इस शक्ति की आपूर्ति जब तक कर सके, करती है।
समीकरणों (3.32) तथा (3.33) में शक्ति के लिए दिए गए व्यंजक से यह स्पष्ट होता है कि किसी प्रतिरोधक R में क्षयित शक्ति उस चालक में प्रवाहित धारा तथा उसके सिरों पर वोल्टता पर किस प्रकार निर्भर करती है।
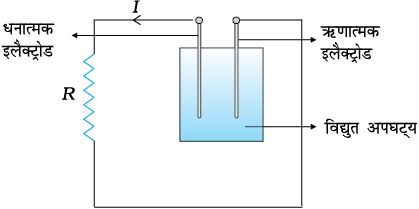
चित्र 3.12 सेल के टर्मिनलों से संयोजित प्रतिरोधक में R ऊष्मा उत्पन्न होती है। प्रतिरोधक R में क्षयित ऊर्जा विद्युत अपघट्य की रासायनिक ऊर्जा से आती है।
समीकरण (3.33) का विद्युत शक्ति संचरण में महत्वपूर्ण अनुप्रयोग है। विद्युत शक्ति का संचरण पावर स्टेशन से घरों तथा कारखानों में संचरण केबल द्वारा किया जाता है जो कि सैकड़ों मील दूर हो सकते हैं। स्पष्ट है कि हम पावर स्टेशनों से घरों तथा कारखानों से जोड़ने वाले संचरण केबिल में होने वाले शक्ति क्षय को न्यूनतम करना चाहेंगे। अब समझेंगे कि इसमें हम कैसे सफल हो सकते हैं। एक युक्ति R पर विचार करें जिसमें Rc प्रतिरोध वाले संचरण केबिल से होकर शक्ति P को पहुँचाना है, जिसे अंतिमतः क्षयित होना है यदि R के सिरों के बीच वोल्टता V है और उससे I विद्युत धारा प्रवाहित हो रही है तो
P = V I (3.34)
पावर स्टेशन से युक्ति को संयोजित करने वाले संयोजी तारों का प्रतिरोध परिमित है और यह Rc है। संयोजक तारों में ऊर्जा क्षय Pc जो कि व्यर्थ व्यय होता है
Pc = I2 Rc
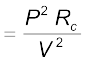
(3.35)
समीकरण (3.32) से। अतः शक्ति P की किसी युक्ति को संचालित करने के लिए, संयोजक तार में शक्ति अपव्यय V 2 के व्युत्क्रमानुपाती है। पावर स्टेशन से आने वाले संचरण केबल सैकड़ों मील लंबे होते हैं तथा उनका प्रतिरोध Rc काफी अधिक होता है। संचरण में होने वाले शक्ति-क्षय Pc को कम करने के लिए इन विद्युतवाही तारों में बृहत वोल्टता V पर विद्युत धारा प्रवाहित की जाती है। यही कारण है कि इन शक्ति संचरण लाइनों पर उच्च वोल्टता के खतरे का चिह्न बना होता है, जो कि आबादी वाले क्षेत्र से दूर जाने पर एक सामान्य दृश्य होता है। इतनी उच्च वोल्टता पर विद्युत का प्रयोग सुरक्षित नहीं है। अतः इस धारा की वोल्टता को उपयोग के लिए उपयुक्त मान तक एक युक्ति द्वारा जिसे ट्रांसफार्मर कहते हैं, कम किया जाता है।
3.10 प्रतिरोधकों का संयोजन-श्रेणी संयोजन तथा पार्श्व संयोजन
ओम के नियम से, एक एकल प्रतिरोधक R जिसके सिरों के मध्य विभवांतर V है, से प्रवाहित धारा I = V/R व्यक्त की जाती है। कभी-कभी प्रतिरोधक एक दूसरे से संयोजित रहते हैं तथा इस प्रकार संयोजनों के तुल्य प्रतिरोध के परिकलन के लिए कुछ सरल नियम हैं।

चित्र 3.13 दो प्रतिरोधकों R1 एवं R2 का श्रेणी संयोजन।
दो प्रतिरोधक श्रेणीक्रम में कहे जाते हैं यदि उनमें से केवल एक अंत्य बिंदु संयोजित होता है (चित्र 3.13)। यदि एक तीसरा प्रतिरोधक, दोनों के श्रेणी संयोजन से जोड़ा जाता है (चित्र 3.14), तो तीनों को श्रेणीक्रम में संयोजित कहते हैं। स्पष्टतः हम इस परिभाषा का विस्तार अनेक प्रतिरोधकों के श्रेणी संयोजन के लिए कर सकते हैं।
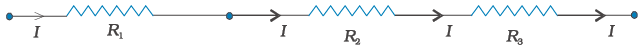
चित्र 3.14 तीन प्रतिरोधकों R1, R2 एवं R3 का श्रेणी संयोजन।
दो या अधिक प्रतिरोधक पार्श्व में संयोजित कहे जाते हैं यदि सभी प्रतिरोधकों के एक सिरे आपस में जुड़े हों और उसी तरह दूसरे सिरे भी आपस में संबंधित हों (चित्र 3.15)।
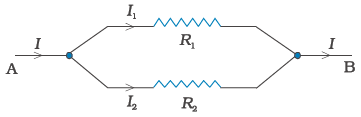
चित्र 3.15 दो प्रतिरोधकों R1 तथा R2 का पार्श्व संयोजन।
दो प्रतिरोधकों R1 तथा R2 के श्रेणी संयोजन पर विचार करते हैं। जो आवेश R1 से प्रस्थान कर रहा है उसे R2 में प्रवेश करना चाहिए। चूँकि विद्युत धारा, आवेश के प्रवाह दर की माप है, इसका अर्थ यह है कि यही धारा R1 तथा R2 से होकर प्रवाहित हो रही है। ओम के नियम से–
R1 के मध्य विभवांतर = V1 = I R1, तथा
R2 के मध्य विभवांतर = V2 = I R2
संयोजन के मध्य विभवांतर V, V1+V2 के बराबर है। अतः
V = V1+ V2 = I (R1 + R2) (3.36)
यह एेसा है जैसे कि संयोजन का तुल्य प्रतिरोध Req था, जो कि ओम के नियम से
Req
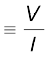 = (R1 + R2) (3.37)
= (R1 + R2) (3.37)
यदि हमारे पास तीन प्रतिरोधक श्रेणीक्रम में संयोजित होते तो इसी प्रकार
V = I R1 + I R2 + I R3 = I (R1+ R2+ R3) (3.38)
स्पष्ट रूप से इसे प्रतिरोधकों की किसी भी संख्या n, R1, R2 ....., Rn के श्रेणीक्रम में संयोजन के लिए विस्तार कर सकते हैं। तुल्य प्रतिरोध Req होगा
Req = R1 + R2 + . . . + Rn (3.39)
अब दो प्रतिरोधकों के पार्श्व संयोजन पर विचार करते हैं (चित्र 3.15)। जो आवेश A की बायीं ओर से अंदर प्रवाहित होता है, आंशिक रूप से R1 से होकर तथा आंशिक रूप से R2 से होकर बाहर प्रवाहित होता है। चित्र में दर्शायी विद्युत धाराएँ I, I1, I2 निर्दिष्ट बिंदुओं पर आवेश प्रवाह की दर हैं। अतः
I = I1 + I2 (3.40)
R1 पर ओम का नियम लागू करने पर, A तथा B के मध्य विभवांतर
V = I1 R1 (3.41)
इसी तरह, R2 पर ओम का नियम लागू करने पर
V = I2 R2 (3.42)
(3.43)
यदि संयोजन को एक तुल्य प्रतिरोध Req से प्रतिस्थापित करें तो ओम के नियम से हमें प्राप्त होगा
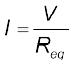 (3.44)
(3.44)
अतः
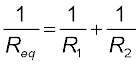 (3.45)
(3.45)
हम आसानी से यह समझ सकते हैं कि तीन प्रतिरोधकों के पार्श्वक्रम में इसे कैसे विस्तृत कर सकते हैं चित्र ( 3.16)।

चित्र 3.16 तीन प्रतिरोधकों R1, R2 तथा R3 का पार्श्व संयोजन।
ठीक पहले की तरह
I = I1 + I2 + I3 (3.46)
और R1, R2 तथा R3 पर ओम का नियम लागू करने पर हम पाते हैं
V = I1 R1, V = I2 R2, V = I3 R3 (3.47)
जिससे कि,
I = I1 + I2 + I3 =
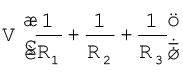 (3.48)
(3.48)
एक समतुल्य प्रतिरोध Req जो कि संयोजन को प्रतिस्थापित करता है, इस प्रकार होगा कि
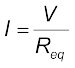 (3.49)
(3.49)
अतः
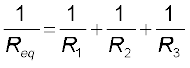 (3.50)
(3.50)
पार्श्व में संयोजित प्रतिरोधकों की किसी भी संख्या के लिए इसी आधार पर हम व्यंजक लिख सकते हैं। पार्श्व में जुड़े n प्रतिरोधकों R1, R2 . . . ,Rn का तुल्य प्रतिरोध है
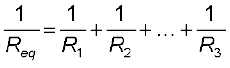 (3.51)
(3.51)
तुल्य प्रतिरोधकों के इन सूत्रों [समीकरण (3.39) तथा समीकरण (3.51)] को अधिक जटिल परिपथों की धारा एवं वोल्टता ज्ञात करने के लिए उपयोग कर सकते हैं। उदाहरण के लिए चित्र (3.17) के परिपथ पर विचार कीजिए, जहाँ तीन प्रतिरोधक R1, R2 तथा R3 हैं। R2 तथा R3 पार्श्वक्रम में हैं, अतः हम उन्हें बिंदु B एवं C के मध्य एक तुल्य प्रतिरोध
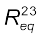 से प्रतिस्थापित कर सकते हैं
से प्रतिस्थापित कर सकते हैं
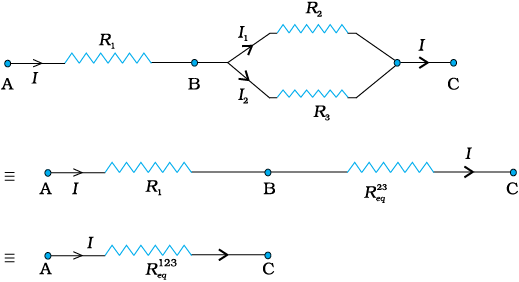
चित्र 3.17 तीन प्रतिरोधकों R1, R2 तथा R3 का संयोजन। ≡ प्रतिरोधक R1 के साथ श्रेणीक्रम में संयोजित R2 तथा R3के पार्श्वक्रम का तुल्य प्रतिरोधक
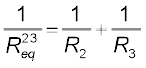
अथवा, 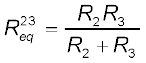 (3.52)
(3.52)
परिपथ में अब R1 तथा 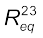 श्रेणी संयोजन में हैं, अतः उनके संयोजन को एक तुल्य प्रतिरोध
श्रेणी संयोजन में हैं, अतः उनके संयोजन को एक तुल्य प्रतिरोध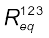 से प्रतिस्थापित कर सकते हैं
से प्रतिस्थापित कर सकते हैं
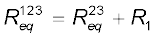 (3.53)
(3.53)
यदि A तथा C के मध्य वोल्टता V है, तो प्राप्त विद्युत धारा का मान
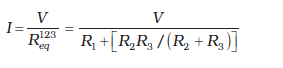
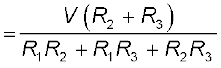 (3.54)
(3.54)
3.11 सेल, विद्युत वाहक बल (emf), आंतरिक प्रतिरोध
हमने पहले ही उल्लेख किया है कि विद्युत अपघटनी सेल विद्युत परिपथ में स्थायी धारा को बनाए रखने के लिए एक सरल युक्ति है। जैसा कि चित्र 3.18 में दिखाया गया है, मूल रूप से एक सेल के दो इलैक्ट्रोड होते हैं, जो कि धनात्मक (P) तथा ऋणात्मक (N) कहलाते हैं। ये एक विद्युत अपघटनी विलयन में डूबे रहते हैं। विलयन में डूबे इलैक्ट्रोड विद्युत अपघट्य के साथ आवेशों का आदान-प्रदान करते हैं। इसके फलस्वरूप धनात्मक इलैक्ट्रोड के ठीक पास विद्युत अपघटनी विलयन के किसी बिंदु A पर [चित्र (3.18(a)] तथा स्वयं इस इलैक्ट्रोड के बीच एक विभवांतर V+ (V+ > 0) होता है। इसी प्रकार ऋणात्मक इलैक्ट्रोड अपने ठीक पास के विद्युत अपघटनी विलयन के किसी बिंदु B के सापेक्ष एक ऋणात्मक विभव – (V– ) (V– 0) पर हो जाता है। जब कोई विद्युत धारा नहीं प्रवाहित होती है तो समस्त विद्युत अपघटनी विलयन का समान विभव होता है, जिससे कि P तथा N के मध्य विभवांतर V+ – (–V–) = V+ + V– रहता है। इस अंतर को सेल का विद्युत वाहक बल (emf) कहते हैं और इसे ε से निर्दिष्ट करते हैं। इस प्रकार
0) पर हो जाता है। जब कोई विद्युत धारा नहीं प्रवाहित होती है तो समस्त विद्युत अपघटनी विलयन का समान विभव होता है, जिससे कि P तथा N के मध्य विभवांतर V+ – (–V–) = V+ + V– रहता है। इस अंतर को सेल का विद्युत वाहक बल (emf) कहते हैं और इसे ε से निर्दिष्ट करते हैं। इस प्रकार
ε = V++V– > 0 (3.55)
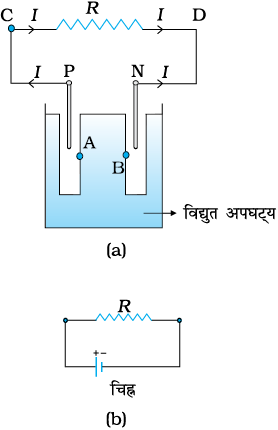
चित्र 3.18 (a) धनात्मक टर्मिनल P तथा ऋणात्मक टर्मिनल N के साथ एक विद्युत अपघटनीय सेल का रेखा चित्र। स्पष्टता के लिए इलैक्ट्रोडों के मध्य अंतराल बढ़ाए गए हैं। विद्युत अपघट्य में A तथा B बिंदु प्रारूपिक तौर पर Pएवं N के निकट हैं।
(b) एक सेल का संकेत। + चिह्न P को तथा – का चिह्न N इलैक्ट्रोड को इंगित करता है। सेल के साथ विद्युतीय संयोजन P तथा N पर बनाए जाते हैं।
ध्यान दीजिए कि ε वास्तव में एक विभवांतर है, बल नहीं। तथापि, इसके नाम के लिए विद्युत वाहक बल का उपयोग एेतिहासिक कारणों से करते हैं और यह नाम उस समय दिया गया था जब यह परिघटना उचित रूप से समझी नहीं गई थी।
ε का महत्त्व समझने के लिए, सेल से संयोजित एक प्रतिरोधक R पर विचार कीजिए (चित्र 3.18)। R से होकर एक विद्युत धारा C से D की ओर प्रवाहित होती है। जैसी कि पहले व्याख्या की जा चुकी है, एक स्थायी धारा बनाए रखी जाती है, क्योंकि विद्युत धारा, विद्युत अपघट्य से होकर N से P की ओर प्रवाहित होती है। स्पष्टतः विद्युत अपघट्य से होकर यही धारा N से P की ओर प्रवाहित होती है जबकि R से होकर यही धारा P से N की ओर प्रवाहित होती है।
जिस विद्युत अपघट्य से होकर यह धारा प्रवाहित होती है उसका एक परिमित प्रतिरोध r होता है, जिसे सेल का आंतरिक प्रतिरोध कहते हैं। पहले हम एेसी स्थिति पर विचार करें जब R अनंत है जिससे कि I = V/R = 0, जहाँ V, P तथा N के मध्य विभवांतर है।
अब,
V = P तथा A के मध्य विभवांतर
+ A तथा B के मध्य विभवांतर
+ B तथा N के मध्य विभवांतर
= ε (3.56)
अतः विद्युत वाहक बल ε एक खुले परिपथ में (अर्थात जब सेल से होकर कोई धारा नहीं प्रवाहित हो रही है) धनात्मक तथा ऋणात्मक इलैक्ट्रोड के मध्य विभवांतर है।
तथापि, यदि R परिमित है तो I शून्य नहीं होगा। उस स्थिति में P तथा N के मध्य विभवांतर
V = V++ V– – I r
= ε – I r (3.57)
A तथा B के मध्य विभवांतर के लिए व्यजंक (I r) में ऋणात्मक चिह्न पर ध्यान दीजिए। यह इसलिए है कि विद्युत अपघट्य में धारा I, B से A की ओर प्रवाहित होती है।
प्रायोगिक परिकलनों में, जब धारा I एेसी है कि ε >> I r, तब परिपथ में सेल के आंतरिक प्रतिरोध को नगण्य माना जा सकता है। सेल के आंतरिक प्रतिरोध के वास्तविक मान, विभिन्न सेलों के लिए भिन्न-भिन्न होते हैं। तथापि, शुष्क सेल के लिए आंतरिक प्रतिरोध, सामान्य विद्युत अपघटनी सेल से बहुत अधिक होता है।
हमने यह भी अवलोकन किया है कि जब R से होकर विभवांतर V है तो ओम के नियम से
V = I R (3.58)
समीकरण (3.57) तथा (3.58) को संयोजित करने पर,
I R = ε – I r
अथवा
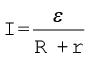 (3.59)
(3.59)
R = 0 के लिए सेल से अधिकतम धारा प्राप्त की जा सकती है Iअधिकतम = ε/r तथापि अधिकांश सेलों में अधिकतम अनुमत धारा इससे बहुत कम होती है जिससे सेल को स्थायी क्षति से बचाया जा सके।
बादलों में आवेश
पुरातन काल में तड़ित को अलौलिक उद्गम की वायुमंडलीय स्फुर क्षणदीप्ति समझा गया। इसे ईश्वर का महान हथियार माना गया। किन्तु आज तड़ित की परिघटना की, भौतिकी के प्राथमिक सिद्धांतों द्वारा, वैज्ञानिक रूप से व्याख्या की जा सकती है।
वायुमंडलीय विद्युत, विद्युत आवेशोें के पृथक्करण के कारण उत्पन्न होती है। आयनमंडल तथा चुंबकमंडल में सौर पार्थिव पारस्परिक क्रिया से प्रबल विद्युत धारा पैदा होती है। निचले वायुमंडल में धारा दुर्बल होती है तथा तड़ित झंझावत द्वारा पोषित की जाती है।
बादलों में बर्फ के कण होते हैं जो विकसित होते हैं, टकराते हैं, टूटते हैं तथा टुकड़े-टुकड़े होकर पृथक हो जाते हैं। छोटे वाले कण धनात्मक आवेश तथा बड़े वाले ऋणात्मक आवेश प्राप्त करते हैं। ये आवेशित कण बादलों के ऊर्ध्ववाह एवं गुरुत्व के कारण पृथक हो जाते हैं। बादल के ऊपरी भाग धनात्मक तथा मध्य भाग ऋणात्मक आवेशित हो जाते हैं जिसके कारण द्विध्रुव की संरचना होती है। कभी-कभी बादलों के तल पर एक अत्यंत दुर्बल धनावेश पाए जाते हैं। तड़ित झंझावात की परिवृद्धि के समय धरती धनावेशित हो जाती है। साथ ही, अंतरिक्ष तथा रेडियोधर्मी विकिरणेें वायु को धन तथा ऋण आयनों में आयनित करती हैं और हवा वैद्युत चालक (दुर्बल रूप से) हो जाती है। धरती तथा बादल के मध्य के अतिरिक्त आवेशों का पृथक्करण बादल के अंदर भी विशाल मात्रा में विद्युत विभव उत्पन्न करता है। यह दसों लाख वोल्ट के बराबर हो सकता है और अंततः वायु में विद्युत प्रतिरोध, भंग हो जाता है तथा तड़ित स्फुर क्षणदीप्ति प्रारंभ हो जाती है एवं हज़ारों एेम्पियर की धारा प्रवाहित होती है। विद्युत क्षेत्र 105 V/m की कोटि का होता है। एक तड़ित स्फुर क्षणदीप्ति औसत रूप से चार वज्रपातों की शृंखलाओं से संगठित होता है तथा प्रत्येक स्फुर क्षणदीप्ति की अवधि लगभग 30 s होती है। प्रति वज्रपात का औसत शीर्ष सामर्थ्य लगभग 1012 W होता है।
शुष्क मौसम में भी वायुमंडल में आवेश होते हैं। शुष्क मौसम का विद्युत क्षेत्र, आयनमंडल से धरती के पृष्ठ पर धारा प्रवाह (जो कि पीकोएेम्पियर प्रति वर्गमीटर की कोटि का होता है) के अतिरिक्त धरती पर पृष्ठीय आवेश घनत्व के अस्तित्व तथा वायुमंडलीय चालकता के कारण उत्पन्न होता है। धरती पर पृष्ठीय आवेश ऋणात्मक होता है; विद्युत क्षेत्र अधोमुखी निर्दिष्ट होता है। धरती पर औसत विद्युत क्षेत्र लगभग 120 V/m होता है जो –1.2 × 10–9 C/m2 पृष्ठीय आवेश घनत्व के संगत है। धरती के समस्त पृष्ठ सतह पर, कुल ऋणात्मक आवेश की मात्रा लगभग 600 kC है। वायुमंडल में बराबर मात्रा में धनात्मक आवेश होते हैं। इस विद्युत क्षेत्र को हम अपने दैनिक जीवन में अनुभव नहीं कर पाते। इसका कारण यह है कि वास्तव में हमारे शरीर सहित, सभी वस्तुएँ वायु की तुलना में चालक हैं।
उदाहरण 3.5
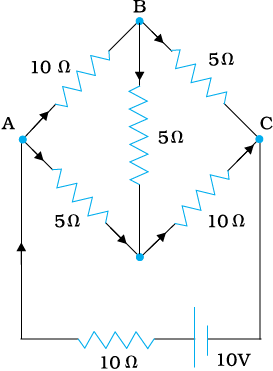
चित्र 3.17 में दिखाए गए अनुसार 1 Ω आंतरिक प्रतिरोध के 16 V की एक बैटरी से प्रतिरोधों के एक नेटवर्क को जोड़ा गया है। (a) नेटवर्क के तुल्य प्रतिरोध परिकलित कीजिए।
(b) प्रत्येक प्रतिरोधक में धारा का मान ज्ञात कीजिए तथा (c) वोल्टता पात VAB, VBC तथा VCD ज्ञात कीजिए।
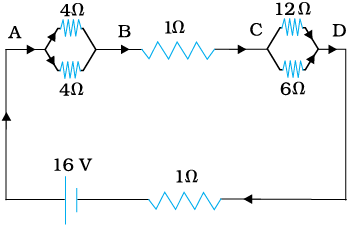
चित्र 3.19
हल
(a) नेटवर्क श्रेणी तथा पार्श्वक्रम में संबद्ध प्रतिरोधकों का एक सरल संयोजन है। पहले 4Ω के पार्श्वक्रम में दो प्रतिरोधों का समतुल्य प्रतिरोध = [(4 × 4)/(4 + 4)] Ω = 2 Ω है।
इसी प्रकार, 12 Ω तथा 6 Ω के पार्श्वक्रम में संबद्ध प्रतिरोधकों का समतुल्य प्रतिरोध है
[(12 × 6)/(12 + 6)] Ω = 4 Ω
इन दोनों तुल्य प्रतिरोधों (2 Ω तथा 4 Ω) को 1 Ω प्रतिरोधक के साथ श्रेणीक्रम में संयोजित करके नेटवर्क का समतुल्य प्रतिरोध R ज्ञात कर लेते हैं, अर्थात
R = 2 Ω + 4 Ω + 1 Ω = 7 Ω
(b) परिपथ में कुल धारा
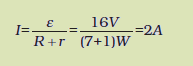
A व B के मध्य प्रतिरोधकों पर विचार कीजिए। यदि 4 Ω के प्रतिरोधकों में से किसी एक में धारा I1 है तथा दूसरे में I2 है तो
I1 × 4 = I2 × 4
अर्थात I1 = I2 जो भुजाओं की सममिति से भी स्पष्ट है। किंतु I1 + I2 = I = 2 A। इसलिए I1 = I2 = 1 A अर्थात प्रत्येक 4 Ω प्रतिरोधक में धारा 1 A है। बिंदुओं B तथा C के बीच संयोजित 1 Ω के प्रतिरोधक से प्रवाहित होने वाली धारा का मान 2A है।
पुनः C व D के मध्य प्रतिरोधकों पर विचार कीजिए। यदि 12 Ω प्रतिरोधक में धारा I3 तथा 6 Ω प्रतिरोधक में धारा I4 हो, तो
I3 × 12 = I4 × 6, अर्थात I4 = 2I3
किंतु I3 + I4 = I = 2 A
इस प्रकार
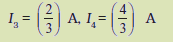
अर्थात 12 Ω प्रतिरोधक में धारा (2/3) A जबकि 6 Ω प्रतिरोधक में धारा (4/3) A है।
(c) AB के मध्य वोल्टता पात
VAB = I1 × 4 Ω = 1 A × 4 Ω = 4 V
जिसे A व B के मध्य संपूर्ण धारा को A व B के मध्य समतुल्य प्रतिरोध के गुणनफल से भी प्राप्त कर सकते हैं। अर्थात
VAB = 2 A × 2 Ω = 4 V
BC के मध्य वोल्टता पात
VBC = 2 A × 1 Ω = 2 V
अंत में, CD के मध्य वोल्टता पात
VCD = 12 Ω × I3 = 12 Ω × (2/3)A = 8 V
जिसे C व D के मध्य संपूर्ण धारा को C व D के मध्य समतुल्य प्रतिरोध के गुणनफल से भी प्राप्त कर सकते हैं। अर्थात
VCD = 2 A × 4 Ω = 8 V
ध्यान दीजिए कि A D के मध्य कुल वोल्टता पात 4 V + 2 V + 8 V = 14 V है। इस प्रकार से बैटरी के सिरों के मध्य वोल्टता 14 V है जबकि विद्युत वाहक बल 16 V है। वोल्टता में क्षति
(= 2 V) बैटरी के आंतरिक प्रतिरोध =1 Ω के द्वारा होती है, 2 A × 1 Ω = 2 V।
3.12 श्रेणी तथा पार्श्वक्रम में सेल
प्रतिरोधकों की भाँति, विद्युत परिपथ में सेलों को भी संयोजित किया जा सकता है। प्रतिरोधकों की ही भाँति परिपथ में धारा तथा विभवांतर के परिकलन के लिए सेलों के संयोजन को एक तुल्य सेल से प्रतिस्थापित किया जा सकता है।
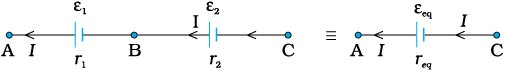
चित्र 3.20 विद्युत वाहक बल ε1 तथा ε2 के दो सेल श्रेणीक्रम में संयोजित हैं। r1 तथा r2 उनके आंतरिक प्रतिरोध हैं। A तथा C के मध्य संबंधन के लिए संयोजन को विद्युत वाहक बल εeq तथा आंतरिक प्रतिरोध req के एक सेल के जैसा समझा जा सकता है।
पहले, श्रेणीक्रम में दो सेलों पर विचार करें (चित्र 3.20), जहाँ प्रत्येक के एक टर्मिनल को मुक्त छोड़कर, दोनों सेलों के एक टर्मिनल एक दूसरे से संयोजित हैं। ε1, ε2 दोनों सेलों के विद्युत वाहक बल हैं, तथा r1, r2 क्रमशः उनके आंतरिक प्रतिरोध हैं।
चित्र 3.20 में दर्शाए अनुसार मानिए बिंदु A, B तथा C पर, विभव क्रमशः V (A), V (B) तथा V (C) हैं। तब V (A) – V (B) पहले सेल के धनात्मक तथा ऋणात्मक टर्मिनल के मध्य विभवांतर है। समीकरण (3.57) में इसे हमने पहले ही परिकलित किया है, अतः
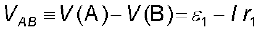 (3.60)
(3.60)
इसी प्रकार
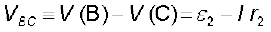 (3.61)
(3.61)
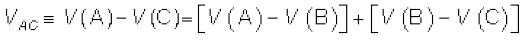
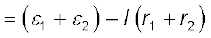 (3.62)
(3.62)
यदि हम संयोजन को A तथा C के मध्य किसी एकल सेल से प्रतिस्थापित करना चाहें जिसका विद्युत वाहक बल εeq तथा आंतरिक प्रतिरोध req हो, तब हमें प्राप्त होता है
VAC = εeq– Ireq (3.63)
समीकरणों (3.62) तथा (3.63) को संयोजित करने पर
εeq = ε1 + ε2 (3.64)
तथा req = r1 + r2 (3.65)
चित्र 3.20 में हमने पहले सेल के ऋणात्मक इलैक्ट्रोड को दूसरे सेल के धनात्मक इलैक्ट्रोड से संबद्ध किया है। इसके स्थान पर यदि हम दोनों सेलों के ऋणात्मक टर्मिनलों को संबद्ध करें, तो समीकरण (3.61) से VBC = –ε2–Ir2
और हमें प्राप्त होता हैः
εeq = ε1 – ε2 (ε1 > ε2) (3.66)
स्पष्टतः श्रेणी संयोजन के नियम को सेलों की किसी भी संख्या के लिए विस्तारित किया जा सकता हैः
(i) n सेलों के श्रेणी संयोजन का तुल्य विद्युत वाहक बल उनके व्यष्टिगत विद्युत वाहक बलों का योग मात्र है, तथा
(ii) n सेल के श्रेणी संयोजन का तुल्य आंतरिक प्रतिरोध उनके आंतरिक प्रतिरोधों का योग मात्र है।
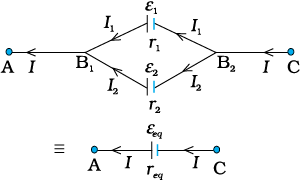
चित्र 3.21 दो सेलों का पार्श्व संयोजन A तथा C के बीच इस संयोजन को आंतरिक प्रतिरोध req तथा विद्युत वाहकबल εeq (जिनके मान समीकरण
(3.73 तथा (3.74) में दिए गए हैं) के किसी एकल सेल से प्रतिस्थापित कर सकते हैं।
एेसा तब है, जब धारा प्रत्येक सेल के धनात्मक इलैक्ट्रोड से निकलती है। यदि इस संयोजन में धारा किसी सेल के ऋणात्मक इलैक्ट्रोड से निकले तो εeq के व्यंजक में, सेल का विद्युत वाहक बल ऋणात्मक चिह्न के साथ सम्मिलित होता है, जैसा कि समीकरण (3.66) में हुआ है।
अब हम सेलों के पार्श्व संयोजन पर विचार करते हैं। I1 तथा I2 सेल के धनात्मक इलैक्ट्रोड से निकलने वाली धाराएँ हैं। दो विद्युत धाराएँ I1 तथा I2 बिंदु B1 पर प्रवेश करती हैं जबकि इस बिंदु से I धारा बाहर निकलती है।
चूँकि उतने ही आवेश अन्दर प्रवाहित होते हैं जितने कि बाहर, हमें प्राप्त होता है
I = I1 + I2 (3.67)
मान लीजिए बिंदुओं B1 तथा B2 पर विभव क्रमशः V (B1) तथा V (B2) हैं। तब पहले सेल पर विचार करने पर इसके टर्मिनलों के मध्य विभवांतर 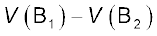 होगा। अतः समीकरण (3.57) से
होगा। अतः समीकरण (3.57) से
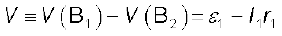 (3.68)
(3.68)
बिंदु B1 तथा B2 इसी प्रकार ठीक-ठीक दूसरे सेल से भी संबद्ध हैं। अतः यहाँ दूसरे सेल पर विचार करने से हमें प्राप्त होता है
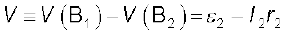 (3.69)
(3.69)
पिछले तीनों समीकरणों को संयोजित करने पर
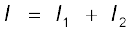
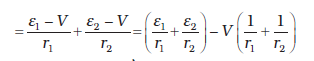 (3.70)
(3.70)
इस प्रकार V का मान है
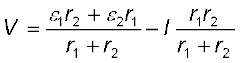 (3.71)
(3.71)
यदि सेलों के इस संयोजन को हम बिंदु B1 और B2 के बीच किसी एेसे एकल सेल से प्रतिस्थापित करें जिसका विद्युत वाहक बल εeq तथा आंतरिक प्रतिरोध req हो तो हमें प्राप्त होता है
V = εeq – I req (3.72)
समीकरण (3.71) तथा (3.72) समान होने चाहिए, अतः
εeq =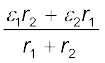 (3.73)
(3.73)
req =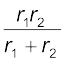 (3.74)
(3.74)
इन समीकरणों को हम और सरल रूप में तरीके से प्रस्तुत कर सकते हैं
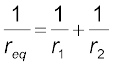 (3.75)
(3.75)
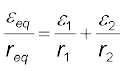 (3.76)
(3.76)

गुस्ताव रॉबर्ट किरखोफ (1824 – 1887)
जर्मनी के भौतिकविज्ञानी हीडलबर्ग एवं बर्लिन में प्रोप़ेηसर रहे। मुख्यतः स्पेक्ट्रमिकी के विकास के लिए जाने जाते हैं। उन्होंने गणितीय भौतिकी में भी काफी महत्वपूर्ण योगदान किया जिसमें परिपथों के लिए प्रथम एवं द्वितीय नियम शामिल हैं।
चित्र (3.21) में हमने दोनों टर्मिनलों को एक साथ तथा इसी प्रकार दोनों ऋण टर्मिनलों को भी एक साथ संबद्ध किया है जिससे विद्युत धाराएँ I1 तथा I2 धन टर्मिनलों से बाहर निकलती हैं। यदि दूसरे का ऋणात्मक टर्मिनल पहले के धनात्मक टर्मिनल से संबद्ध कर दिया जाए, तब भी समीकरण (3.75) तथा (3.76) ε 2 → –ε2 के साथ मान्य होंगे।
समीकरण (3.75) तथा (3.76) को आसानी से विस्तारित किया जा सकता है। यदि हमारे पास n सेल हैं जिनके विद्युत वाहक बल ε1, ... εn तथा आंतरिक प्रतिरोध r1, . . . rn हैं और वे पार्श्व संबंधन में हैं तो यह संयोजन उस एकल सेल के तुल्य होगा जिसका विद्युत वाहक बल εeq तथा आंतरिक प्रतिरोध req है जिससे कि
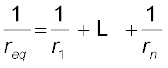 (3.77)
(3.77)
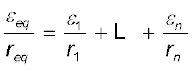 (3.78)
(3.78)
3.13 किरखोफ के नियम
विद्युत परिपथों में कभी-कभी कई प्रतिरोधक एवं सेल जटिल ढंग से संबद्ध होते हैं। श्रेणी एवं पार्श्व संयोजन के लिए जो सूत्र हमने पहले व्युत्पन्न किए हैं, वे परिपथ के सभी विद्युत धाराओं तथा विभवांतरों के लिए हमेशा पर्याप्त नहीं होते। दो नियम, जिन्हें किरखोफ के नियम कहते हैं, विद्युत परिपथों के विश्लेषण में बहुत उपयोगी होते हैं।
दिए गए परिपथ में हम प्रत्येक प्रतिरोधक में प्रवाहित धारा को किसी प्रतीक जैसे I से नामांकित करते हुए और तीर के चिह्न द्वारा प्रतिरोध के अनुदिश धारा के प्रवाह को निर्दिष्ट करते हुए आगे बढ़ते हैं। यदि अंततः I धनात्मक निर्धारित होता है तो प्रतिरोधक में विद्युत धारा की वास्तविक दिशा, तीर की दिशा में है। यदि यह ऋणात्मक निकलता है, तो वास्तव में विद्युत धारा तीर की दिशा के विपरीत प्रवाहित हो रही है। इसी प्रकार, प्रत्येक स्रोत (अर्थात सेल या विद्युत शक्ति का कोई दूसरा स्रोत) के लिए धनात्मक तथा ऋणात्मक इलैक्ट्रोड को, सेल में प्रवाह हो रही धारा के संकेत के अलावा एक निर्देशित तीर से चिह्नित करते हैं। यह हमें धनात्मक टर्मिनल P तथा ऋणात्मक टर्मिनल N के बीच विभवांतर बताएगा, V = V (P) – V (N) = ε – I r [समीकरण (3.57), I यहाँ सेल के अंदर N से होकर P की ओर प्रवाहित होने वाली विद्युत धारा है]। यदि सेल से होकर बहने वाली धारा को चिह्नित करते हुए हम P से N की ओर बढ़ते हैं तो स्पष्टतः
V = ε + I r (3.79)

चित्र 3.22 संधि a पर निकलने वाली विद्युत धारा I1 + I2 तथा प्रवेश करने वाली विद्युत धारा I3 है। संधि के नियमानुसार I3 = I1 + I2. बिंदु h पर प्रवेश करने वाली धारा I1 है। h से निकलने वाली भी एक ही धारा है और संधि नियम से, ये भी I1 होगा। दो पाशों ‘ahdcba’ तथा ‘ahdefga’ के लिए पाश नियम प्रदत्त करते हैं –30I1 – 41I3 + 45 = 0 तथा –30I1 + 21I2 – 80 = 0ा
चिह्नों को बनाने कि प्रक्रिया को स्पष्ट करने के बाद अब हम नियमों तथा उपपत्तियों को अभिव्यक्त करेंगे ः
(a) संधि नियम–किसी संधि पर संधि से प्रवेश करने वाली विद्युत धाराओं क योग इस संधि से निकलने वाली विद्युत धाराओं के योग के बराबर होता है (चित्र 3.22)।
इस नियम का प्रमाण इस तथ्य से समझते हैं कि जब विद्युत धारा स्थायी होती है, किसी संधि या चालक के किसी बिंदु पर आवेश संचित नहीं होता है। अतः प्रवेश करने वाली कुल विद्युत धाराएँ (जो कि संधि में आवेश के प्रवाह की दर है) बाहर निकलने वाली कुल विद्युत धाराओं के बराबर होती हैं।
(b) पाश (लूप) नियम–प्रतिरोधकों तथा सेलों से सम्मिलित किसी बंद पाश के चारों ओर विभव में परिवर्तनों का बीजगणितीय योग शून्य होता है (चित्र 3.22)।
यह नियम भी सुस्पष्ट है, क्योंकि विद्युत विभव बिंदु की अवस्थिति पर निर्भर करता है। अतः किसी बिंदु से प्रस्थान कर यदि हम वापस उसी बिंदु पर आते हैं, तो कुल परिवर्तन शून्य होने चाहिए। एक बंद पाश में हम प्रस्थान बिंदु पर वापस आ जाते हैं, यह नियम इसीलिए है।
उदाहरण 3.6
10 V तथा नगण्य आंतरिक प्रतिरोध की बैटरी एक घनीय परिपथ जाल (नेटवर्क) के विकर्णतः सम्मुख कोनों से जुड़ी है। परिपथ जाल में 1 Ω प्रतिरोध के 12 प्रतिरोधक हैं (चित्र 3.23)। परिपथ जाल का समतुल्य प्रतिरोध तथा घन के प्रत्येक किनारे के अनुदिश विद्युत धारा ज्ञात कीजिए।

चित्र 3.23
हल
परिपथ जाल को प्रतिरोधकों के सरल श्रेणी एवं पार्श्व संयोजन में परिवर्त्य नहीं किया जा सकता तथापि प्रश्न में स्पष्ट सममिति है जिसके उपयोग द्वारा परिपथ जाल के समतुल्य प्रतिरोध को ज्ञात किया जा सकता है।
AA', AD तथा AB पथों को परिपथ जाल में सममितीय विधि से रखा गया है। इसलिए प्रत्येक में समान विद्युत धारा, मान लीजिए I प्रवाहित होनी चाहिए। इसके अतिरिक्त A', B व D सिरों पर आगत धारा I को दो समान निर्गत शाखाओं में टूटना चाहिए। इस प्रकार, घन के सभी 12 किनारों में धारा को सरलतापूर्वक I के पद में लिख सकते हैं। इसमें किरखोफ के प्रथम नियम तथा प्रश्न की सममिति का उपयोग करते हैं।
आगे एक बंद पाश जैसे ABCC' EA लीजिए और उस पर किरखोफ का द्वितीय नियम लागू कीजिए ः
–IR – (1/2)IR – IR + ε = 0
यहाँ प्रत्येक किनारे का प्रतिरोध R है तथा बैटरी का विद्युत वाहक बल ε है।
इस प्रकार,
ε =5/2IR
परिपथ जाल (नेटवर्क) का समतुल्य प्रतिरोध Req निम्नवत् हैः
Req =ε/3I
= 5/6R
R = 1 Ω के लिए Req = (5/6) Ω तथा ε = 10 V के लिए, परिपथ जाल (नेटवर्क) में कुल धारा है
3I = 10 V/(5/6) Ω = 12 A अर्थात I = 4 A
प्रत्येक किनारे में प्रवाहित होने वाली धारा को अब चित्र 3.23 से जाना जा सकता है।
इस बात पर ध्यान दिया जाना चाहिए कि परिपथ नेटवर्क की सममिति के कारण उदाहरण 3.6 में किरखोफ के नियमों की विशाल शक्ति का उपयोग नहीं किया गया है। एक सामान्य परिपथ नेटवर्क में सममिति के कारण इस प्रकार का सरलीकरण नहीं होता। इसलिए संधियों एवं बंद पाशों में (इनकी संख्या उतनी होनी चाहिए जितनी कि नेटवर्क में अज्ञात राशियाँ हैं) किरखोफ के नियमों के उपयोग द्वारा समस्या को हल कर सकते हैं। यह उदाहरण 3.7 में स्पष्ट किया गया है।
उदाहरण 3.7
चित्र 3.24 में दिखलाए गए नेटवर्क की प्रत्येक शाखा में धारा ज्ञात कीजिए।
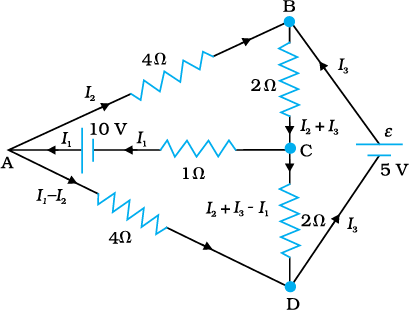
चित्र 3.24
हल
नेटवर्क की प्रत्येक शाखा के लिए एक अज्ञात धारा निर्धारित की गयी है जिसे किरखोफ के नियम को लागू कर ज्ञात करना है। प्रारंभ में ही अज्ञातों की संख्या कम करने के लिए प्रत्येक शाखा में अज्ञात विद्युत धारा को निर्दिष्ट करने हेतु किरखोफ के प्रथम नियम का उपयोग करते हैं। इस प्रकार, हमारे पास तीन अज्ञात धाराएँ I1, I2 तथा I3 हैं जिन्हें तीन विभिन्न बंद पाशों में किरखोफ के द्वितीय नियम के उपयोग से ज्ञात कर सकते हैं।
बंद पाश ADCA में किरखोफ के द्वितीय नियम के उपयोग से हमें निम्नलिखित व्यंजक प्राप्त होता है–
10 – 4(I1– I2) + 2(I2 + I3 – I1) – I1 = 0 [3.80 (a)]
अर्थात 7I1– 6I2 – 2I3 = 10
बंद पाश ABCA के लिए हमें प्राप्त होता है
10 – 4I2– 2 (I2 + I3) – I1 = 0
अर्थात I1 + 6I2 + 2I3 =10 [3.80 (b)]
बंद पाश BCDEB के लिए हमें प्राप्त है
5 – 2 (I2 + I3) – 2 (I2 + I3 – I1) = 0
अर्थात 2I1 – 4I2 – 4I3 = –5 [3.80 (c)]
समीकरण (a), (b) व (c) तीन युगपत समीकरण हैं जिनमें तीन राशियाँ अज्ञात हैं, इन्हें सामान्य विधि से हल किया जा सकता है। इस प्रकार,
I1 = 2.5A, I2 =5/8
A, I3 = 15/8
A
परिपथ जाल की विभिन्न शाखाओं में धाराएँ इस प्रकार हैंः
AB :5/8
A, CA :2(1/2)
A, DEB :1(7/8)
A
AD :1(7/8)
A, CD : 0 A, BC : 2(1/2)
A
यह आसानी से सत्यापित किया जा सकता है कि यदि किरखोफ के नियम को शेष बंद पाशों में उपयोग किया जाए तो हमें कोई अन्य स्वतंत्र समीकरण नहीं प्राप्त होगा अर्थात धाराओं के उपरोक्त मान नेटवर्क के हर बंद पाश के लिए द्वितीय नियम को संतुष्ट करेंगे। उदाहरण के तौर पर बंद परिपथ BADEB के लिए कुल वोल्टता पात
5V+(5/8X4)V-(15/8X4)V
शून्य होगा, जैसा कि किरखोफ के द्वितीय नियम द्वारा अपेक्षित है।
3.14 व्हीटस्टोन सेतु
किरखोफ के एक अनुप्रयोग के रूप में चित्र 3.25 में दिखाए परिपथ पर विचार कीजिए, जो कि व्हीटस्टोन सेतु कहलाता है। सेतु में चार प्रतिरोधक R1, R2, R3 तथा R4 होते हैं। विकर्णतः विपरीत बिंदुओं (चित्र में A तथा C) के एक युग्म से कोई विद्युत स्रोत संबद्ध है। यह (अर्थात AC) बैटरी भुजा कहलाती है। दूसरे दो शीर्ष बिंदुओं, B तथा D के मध्य एक गैल्वेनोमीटर (जो विद्युत धारा के संसूचन की एक युक्ति है) संबद्ध है। यह लाइन, जिसे चित्र में BD से दिखाया गया है, गैल्वेनोमीटर भुजा कहलाती है।
सरलता के लिए हम कल्पना करते हैं कि सेल में कोई आंतरिक प्रतिरोध नहीं है। सामान्यतः G से होकर विद्युत धारा Ig तथा सभी प्रतिरोधकों से होकर भी धारा प्रवाहित होगी। उस संतुलित सेतु का उदाहरण एक विशेष महत्व रखता है जिसमें प्रतिरोधक एेसे हों कि Ig = 0। हम आसानी से एेसी संतुलन अवस्था प्राप्त कर सकते हैं जिससे G से होकर कोई धारा प्रवाहित नहीं होती। एेसे प्रकरण में, संधि D तथा B के लिए (चित्र देखिए) किरखोफ के संधि नियम को अनुप्रयुक्त करने पर हमें संबंध I1 = I3 तथा I2 = I4 तुरंत प्राप्त हो जाते हैं। उसके बाद, हम बंद पाशों ADBA तथा CBDC पर किरखोफ के पाश नियम को अनुप्रयुक्त करते हैं। पहले पाश से प्राप्त होता है
–I1 R1 + 0 + I2 R2 = 0 (Ig = 0) (3.81)
तथा I3 = I1, I4 = I2 को उपयोग करने पर द्वितीय पाश से प्राप्त होता है
I2 R4 + 0 – I1 R3 = 0 (3.82)
समीकरण (3.81) से हम प्राप्त करते हैं
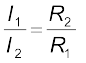

चित्र 3.25 व्हीटस्टोन सेतु
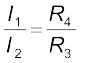
अतः हम प्रतिबंध प्राप्त करते हैं।
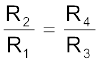 [3.83(a)]
[3.83(a)]
चार प्रतिरोधकों में संबंध दिखलाने वाले समीकरण [3.83(a)] को गैल्वेनोमीटर में शून्य अथवा नगण्य विक्षेप के लिए संतुलन प्रतिबंध कहते हैं।
व्हीटस्टोन सेतु तथा इसका संतुलन प्रतिबंध अज्ञात प्रतिरोध के निर्धारण के लिए एक प्रायोगिक विधि देता है। कल्पना कीजिए कि हमारे पास कोई अज्ञात प्रतिरोध है जिसे हम चौथी भुजा में लगाते हैं; इस प्रकार R4 ज्ञात नहीं है। ज्ञात प्रतिरोधकों R1 तथा R2 को सेतु की पहली तथा दूसरी भुजा में रखते हुए, हम R3 को तब तक परिवर्तित करते जाते हैं जब तक गैल्वेनोमीटर नगण्य विक्षेप नहीं दिखलाता है। सेतु तब संतुलित है तथा संतुलन प्रतिबंध से अज्ञात प्रतिरोध R4 का मान प्राप्त होता है,
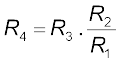 [3.83(b)]
[3.83(b)]
इस सिद्धांत को उपयोग करने वाली प्रायोगिक युक्ति मीटर सेतु कहलाती है। इसकी विवेचना अगले अनुच्छेद में की जाएगी।
उदाहरण 3.8
व्हीटस्टोन सेतु की चार भुजाओं (चित्र 3.26) के प्रतिरोध निम्नवत हैंः
AB = 100 Ω, BC = 10 Ω, CD = 5 Ω तथा DA = 60 Ω।
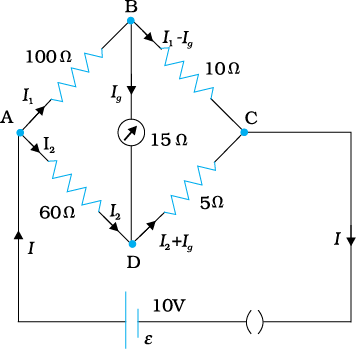
चित्र 3.26
15 Ω प्रतिरोध के एक गैल्वेनोमीटर को BD के बीच जोड़ा गया है। गैल्वेनोमीटर से प्रवाहित होने वाली धारा को परिकलित कीजिए। AC के मध्य 10 V विभवांतर है।
हल
पाश BADB पर विचार करने पर
100I1 + 15Ig – 60I2 = 0
अथवा 20I1 + 3Ig – 12I2= 0 [3.84(a)]
पाश BCDB पर विचार करने पर
10 (I – Ig) – 15Ig – 5 (I2 + Ig) = 0
10I1 – 30Ig – 5I2 = 0
2I1 – 6Ig – I2 = 0 [3.84(b)]
पाश ADCEA पर विचार करने पर
60I2 + 5 (I2 + Ig) = 10
65I2 + 5Ig = 10
13I2 + Ig = 2 [3.84(c)]
समीकरण [3.84(b)] को 10 से गुणा करने पर
20I1 – 60Ig – 10I2 = 0 [3.84(d)]
समीकरणों [3.84(d)] व [3.84 (a)] से हमें निम्नलिखित व्यंजक प्राप्त होता है
63Ig – 2I2 = 0
I2 =
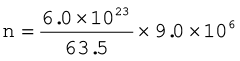
Ig = 31.5Ig [3.84(e)]
I2 के मान को समीकरण [3.84(c)] में स्थानापन्न करने पर
13 (31.5Ig ) + Ig = 2
410.5 Ig = 2
Ig = 4.87 mA
3.15 मीटर सेतु
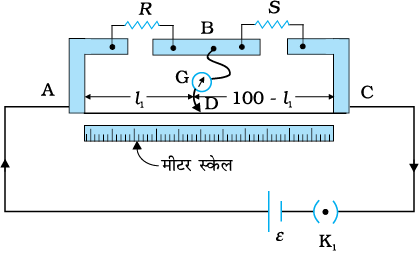
चित्र 3.27 एक मीटर सेतु तार AC एक मीटर लंबा है। R एक प्रतिरोध है जिसका मापन करना है तथा S एक मापक प्रतिरोध है।
मीटर सेतु को चित्र 3.27 में दिखाया गया है। यह एक मीटर लंबे एकसमान अनुप्रस्थ काट क्षेत्रफल वाले तार से निर्मित होता है जिसे लंबवत धातु की दो मोटी पट्टिकाओं के मध्य कस दिया जाता है, जैसा कि दिखाया गया है। धात्विक पट्टिका में दो रिक्तियाँ होती हैं जिनके मध्य प्रतिरोधकों को संयोजित किया जा सकता है। अंत्य बिंदु जहाँ तार कसे रहते हैं, एक कुंजी द्वारा सेल से जुड़े रहते हैं। गैल्वेनोमीटर का एक सिरा रिक्तियों के मध्य बीचोबीच धात्विक पट्टिका से जुड़ा रहता है। गैल्वेनोमीटर का दूसरा सिरा जॉकी से जुड़ा रहता है। जॉकी, तत्वतः एक धात्विक छड़ होती है जिसका एक सिरा क्षुर-धार होता है तथा जिसे विद्युत संयोजन बनाने के लिए तार के ऊपर सरका सकते हैं।
R एक अज्ञात प्रतिरोध है जिसका मान हम ज्ञात करना चाहते हैं। इसे दोनों में से किसी एक रिक्ति में संयोजित कर देते हैं। दूसरी रिक्ति के मध्य एक मानक ज्ञात प्रतिरोध S संयोजित करते हैं। जॉकी के तार पर किसी बिंदु D जो कि सिरे A से l cm की दूरी पर है, स्पर्श करते हैं। जॉकी को तार के अनुदिश सरका सकते हैं। तार के AD भाग का प्रतिरोध Rcml है जहाँ Rcm तार का प्रति एकांक cm प्रतिरोध है। इस प्रकार DC भाग का प्रतिरोध Rcm (100–l) है।
चार भुजाएँ AB, BC, DA तथा CD [जिनके प्रतिरोध क्रमशः R, S, Rcm l तथा Rcm (100–l) हैं] स्पष्टतः, AC बैटरी भुजा तथा BD गैल्वेनोमीटर भुजा के साथ एक व्हीटस्टोन सेतु का निर्माण करते हैं। यदि जॉकी को तार के अनुदिश सरकाया जाता है तो एक स्थान (संतुलन बिंदु) एेसा आएगा जहाँ गैल्वेनोमीटर कोई धारा नहीं दर्शाएगा। मान लीजिए कि संतुलन बिंदु पर सिरे से जॉकी की दूरी l= l1 है, तब संतुलन बिंदु पर सेतु के चार प्रतिरोधों के मान R, S, Rcm l1 तथा Rcm(100–l1) हैं। संतुलन प्रतिबंध के लिए समीकरण [3.83(a)] के अनुसार
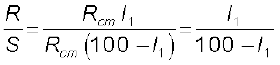 (3.85)
(3.85)
अतः जैसे ही हम l1 का मान ज्ञात करते हैं, मानक ज्ञात प्रतिरोध S के पदों में अज्ञात प्रतिरोध R का मान प्राप्त हो जाता है।
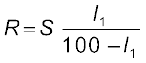 (3.86)
(3.86)
S के विभिन्न मानों को चुनने पर हमें l1 के विभिन्न मान प्राप्त होते हैं और हर बार R का परिकलन करते हैं। निस्संदेह l1 के मापन में त्रुटि के परिणामस्वरूप R में त्रुटि आ जाएगी। यह दिखाया जा सकता है कि संतलुन बिंदु को सेतु के तार के मध्य के समीप अर्थात l1 को 50 cm के निकट रखकर समायोजित करने से (इसके लिए S का उचित चुनाव करना आवश्यक है) R में प्रतिशत त्रुटि को न्यूनतम किया जा सकता है।
उदाहरण 3.9
चित्र 3.27 में दर्शाए गए मीटर सेतु में बिंदु A से 33.7 cm की दूरी पर शून्य विक्षेप बिंदु प्राप्त होता है। S प्रतिरोध के पार्श्व में 12 Ω के एक अन्य प्रतिरोध संयोजित करने पर शून्य विक्षेप बिंदु 51.9 cm की दूरी पर प्राप्त होता है। R तथा S के मान परिकलित कीजिए।
हल
प्रथम शून्य विक्षेप बिंदु से;
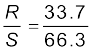
(3.87)
प्रतिरोध S के पार्श्व में 12Ω का प्रतिरोध संयोजित करने पर कुल प्रतिरोध S से Seq हो जाता है, जहाँ
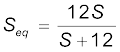
तथा नए संतुलन प्रतिबंध से हमें प्राप्त होता है
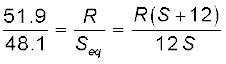 (3.88)
(3.88)
समीकरण (3.87) से R/S का मान रखने पर
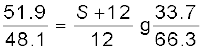
S = 13.5Ω समीकरण (3.87) में S का मान रखने पर, R = 6.86 Ω
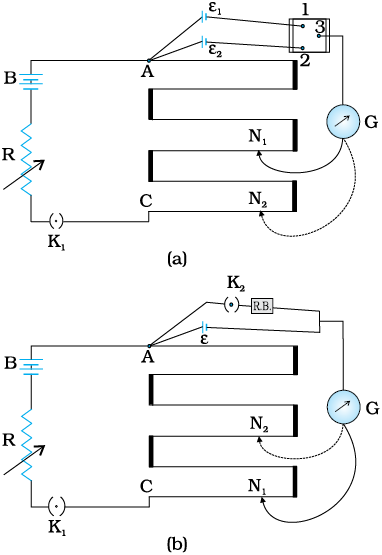
3.16 पोटेंशियोमीटर (विभवमापी)
यह एक सर्वतोमुखी उपकरण है। मौलिक रूप से यह एकसमान तार का एक लंबा टुकड़ा है, बहुधा तार की लंबाई कुछ मीटर होती है जिसे किसी मानक सेल (B) के सिरों से संबद्ध करते हैं। वास्तविक बनावट में तार को कभी-कभी एक साथ अगल-बगल रख कर कई टुकड़ों में काट दिया जाता है तथा सिरों पर एक मोटी धात्विक पट्टी जोड़ दी जाती है (चित्र 3.28) । चित्र में तार A से C तक फैली हुई है। छोटा ऊर्ध्वाकार हिस्सा धातु की मोटी पट्टी है जो तार के विभिन्न खंडों को जोड़ती है।
तार से होकर कोई धारा I प्रवाहित होती है जो परिपथ में एक धारा नियंत्रक द्वारा परिवर्तित की जा सकती है। चूँकि तार एकसमान है अतः अंत्य A तथा A से l की दूरी पर स्थित किसी बिंदु के बीच विभवांतर
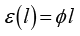 (3.89)
(3.89)
जहाँ φ, प्रति एकांक लंबाई वोल्टता पात है।
चित्र 3.28 (a) दो सेलों के विद्युत वाहक बल ε1 तथा ε2 की तुलना के लिए पोटेंशियोमीटर का अनुप्रयोग दिखाता है। बिंदु 1, 2, 3 द्विगामी कुंजी की रचना करते हैं। पहले कुंजी की उस स्थिति पर विचार करें जहाँ 1 और 3 संयोजित हैं जिससे कि गैल्वेनोमीटर ε1 से संबद्ध है। जॉकी को तार के अनुदिश तब तक सरकाया जाता है जब तक A से l1 की दूरी पर, किसी बिंदु N1 पर, गैल्वेनोमीटर में कोई विक्षेप नहीं होता है। बंद पाश
AN1 G 31A पर किरखोफ का नियम लागू करने पर हम प्राप्त करते हैं
φ l1 + 0 – ε1 = 0 (3.90)
इसी प्रकार यदि दूसरे विद्युत वाहक बल ε2 के लिए तार की लंबाई AN2 = l2 पर संतुलित होता है तो
φ l2 + 0 – ε2 = 0 (3.91)
पिछले दो समीकरणों से
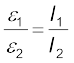 (3.92)
(3.92)
चित्र 3.28 एक पोटेंशियोमीटर, G एक गैल्वनोमीटर तथा R एक धारा नियंत्रक है।
1, 2, 3 द्विमार्गी कुंजी के सिरे हैं
(a) दो सेल के विद्युत वाहक बलों की तुलना के लिए परिपथ (b) सेल का आंतरिक प्रतिरोध ज्ञात करने के लिए परिपथ।
इस प्रकार की सरल प्रायोगिक व्यवस्था से दो स्रोतों (ε1,ε2) के विद्युत वाहक बल की तुलना कर सकते हैं। व्यवहार में, दोनों में से एक सेल का चुनाव मानक सेल के रूप में किया जाता है। इस मानक सेल का जिसका विद्युत वाहक बल उच्च कोटि की परिशुद्धता से ज्ञात करते हैं। तब समीकरण (3.92) से दूसरे सेल के विद्युत वाहक बल को आसानी से परिकलित किया जा सकता है।
विभवमापी को हम किसी सेल के आंतरिक प्रतिरोध के मापन के लिए भी उपयोग कर सकते हैं [चित्र 3.28 (b)] । इसके लिए सेल (emf ε ), जिसका आंतरिक प्रतिरोध (r) ज्ञात करना है, को एक कुंजी K2 को खुला रख कर, लंबाई AN1 = l1 पर संतुलन प्राप्त करते हैं। तब,
ε = φ l1 [3.93(a)]
जब K2 को बंद करते हैं तो सेल प्रतिरोध बॉक्स (R) से होकर एक धारा I प्रेषित करता है। यदि V सेल का टर्मिनल विभवांतर है तथा संतुलन बिंदु लंबाई AN2 = l2 पर प्राप्त होता है,
V = φ l2 [3.93(b)]
अतः हम पाते हैं, ε/V = l1/l2 [3.94(a)]
किंतु, ε = I (r + R) तथा V = IR. हमें प्राप्त होता है
ε/V = (r+R)/R [3.94(b)]
समीकरण [3.94(a)] तथा [3.94(b)] से हम प्राप्त करते हैं
(R+r)/R = l1/l2
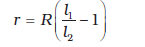 (3.95)
(3.95)
समीकरण (3.95) का उपयोग करके हम दिए गए सेल के आंतरिक प्रतिरोध ज्ञात कर सकते हैं।
पोटेंशियोमीटर को उपयोग करने का एक लाभ यह है कि यह मापन किए जा रहे विभव स्रोत से कोई धारा प्राप्त नहीं करता है। इसलिए इसके द्वारा किए गए मापन स्रोत के आंतरिक प्रतिरोध द्वारा प्रभावी नहीं होते।
उदाहरण 3.10
R Ω का कोई प्रतिरोध एक पोटेंशियोमीटर से विद्युत धारा प्राप्त कर रहा है पोटेंशियोमीटर का कुल प्रतिरोध R0 Ω है (चित्र 3.29)। पोटेंशियोमीटर को वोल्टता V की आपूर्ति की गयी है। जब सर्पी संपर्क (सरकने वाला भाग या स्लाइड) पोटेंशियोमीटर के तार के मध्य में हो तो R के सिरों पर वोल्टता के लिए व्यंजक प्राप्त कीजिए।
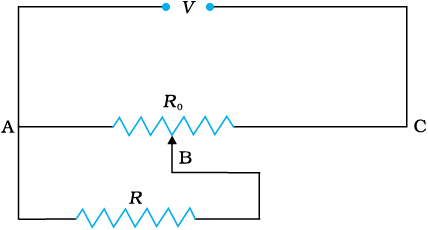
चित्र 3.29
हल
जब जॉकी पोटेंशियोमीटर के तार के मध्य में है तो इस तार की आधी लंबाई का कुल प्रतिरोध (R0/2) होगा। अब चूँकि A व B के बीच R0 तथा R पार्श्वक्रम में हैं, अतः उनके बीच का तुल्य प्रतिरोध R1 बिंदुओं A व B के मध्य केवल उसके आधे बीच का कुल प्रतिरोध (R0/2) होगा। R1 निम्नलिखित व्यंजक द्वारा दिया जाएगा,
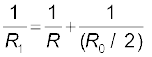
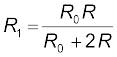
इस प्रकार A व C के मध्य कुल प्रतिरोध A व B के मध्य तथा B व C के मध्य के प्रतिरोधों के योग के बराबर होगा अर्थात यह R1 + R0/2 होगा।
पोटेंशियोमीटर से प्रवाहित होने वाली धारा निम्नलिखित होगी
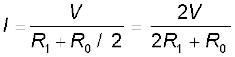
पोटेंशियोमीटर से ली गयी वोल्टता V1 धारा I तथा प्रतिरोध R1 के गुणनफल के बराबर होती है
V1 = I R1 =
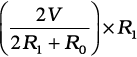
R1 का मान रखने पर हमें निम्नलिखित मान मिलता है

सारांश
1. किसी चालक के दिए गए क्षेत्रफल से प्रवाहित धारा उस क्षेत्रफल से प्रति एकांक समय में गुज़रने वाला नेट आवेश होता है।
2. एक स्थायी धारा बनाए रखने के लिए हमें एक बंद परिपथ चाहिए जिसमें एक बाह्य स्रोत विद्युत आवेश को निम्न से उच्च स्थितिज ऊर्जा की ओर प्रवाहित कराता है। आवेश को निम्न से उच्च स्थितिज ऊर्जा (अर्थात स्रोत के एक टर्मिनल से दूसरे तक) की ओर ले जाने में स्रोत द्वारा प्रति एकांक आवेश पर किया गया कार्य स्रोत का विद्युत वाहक बल (electromotive force) या emf कहलाता है। ध्यान दीजिए कि emf एक बल नहीं है, बल्कि यह खुले परिपथ में स्रोत के दोनों टर्मिनलों के बीच वोल्टता का अंतर है।
3. ओम का नियम– किसी चालक में प्रवाहित धारा I उसके सिरों के बीच विभवांतर V के अनुक्रमानुपातिक है अर्थात V ∝ I अथवा V = RI, जहाँ R को चालक का प्रतिरोध कहते हैं। प्रतिरोध का मात्रक ओम है– 1 Ω = 1 V A−1
4. चालक के प्रतिरोध R, संबंध
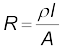
के द्वारा चालक की लंबाई और अनुप्रस्थ काट पर निर्भर है, जहाँ ρ, जिसे प्रतिरोधकता कहते हैं, पदार्थ का गुण है जो ताप और दाब पर निर्भर करता है।
5. पदार्थों की विद्युत प्रतिरोधकता विस्तृत परिसर में परिवर्तित होती है। धातुओं की प्रतिरोधकता कम (10−8 Ω m से 10−6 Ω m परिसर में) होती है। विद्युतरोधी जैसे काँच या रबर की प्रतिरोधकता 1022 से 1024 गुना होती है, लघुगणकीय पैमाने पर, अर्द्धचालकों जैसे Si और Ge की प्रतिरोधकता उसके मध्य परिसर में होती है।
6. अधिकतर पदार्थों में धारा के वाहक इलेक्ट्रॉन होते हैं, कुछ स्थितियों उदाहरणार्थ, आयनी क्रिस्टलों और विद्युत अपघट्य, में धारा वहन धनायनों तथा ऋणायनों द्वारा होता है।
7. धारा घनत्व j प्रति सेकंड प्रति एकांक प्रवाह के अभिलंब, क्षेत्रफल से प्रवाहित आवेश की मात्रा देता है
j = nqvd
जहाँ n आवेश वाहकों, जिनमें प्रत्येक का आवेश q है, की संख्या घनत्व (प्रति एकांक आयतन में संख्या) तथा आवेश वाहकों का अपवाह वेग vd है। इलेक्ट्रॉन के लिए
q = −e है। यदि j एक अनुप्रस्थ काट A के अभिलंब है और क्षेत्रफल पर एकसमान है तो क्षेत्रफल में धारा का परिमाण I (= nevd A) है।
8. E = V/l, I = nevd A और ओम के नियम का उपयोग करते हुए निम्न व्यंजक प्राप्त होता है
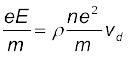
यदि हम मान लें कि इलेक्ट्रॉन धातु के आयनों से संघट्ट करते (टकराते) हैं जो उन्हें यादृच्छिकतः विक्षेपित कर देते हैं तो बाह्य बल E के कारण धातु में इलेक्ट्रॉनों पर लगने वाले बल eE और अपवाह वेग vd (त्वरण नहीं) में आनुपातिकता को समझा जा सकता है। यदि एेसे संघट्ट औसत काल अंतराल τ में होते हैं तो
vd = aτ = eEτ/m
जहाँ a इलेक्ट्रॉन का त्वरण है। अतः
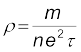
9. उस ताप परिसर में जिसमें प्रतिरोधकता ताप के साथ रैखिक रूप से बढ़ती है, प्रतिरोधकता के ताप गुणांक α को प्रति एकांक ताप वृद्धि से प्रतिरोधकता में भिन्नात्मक वृद्धि के रूप में परिभाषित किया जाता है।
10. ओम के नियम का पालन बहुत से पदार्थ करते हैं परंतु यह प्रकृति का मूलभूत नियम नहीं है। यह असफल है यदि
(a) V अरैखिक रूप से I पर निर्भर है।
(b) V के उसी परम मान के लिए V और I में संबंध V के चिह्न पर निर्भर है।
(c) V और I में संबंध अद्वितीय नहीं है।
(a) का एक उदाहरण यह है कि जब ρ, I के साथ बढ़ता है (यद्यपि ताप को स्थिर रखते हैं)। एक दिष्टकारी (rectifier) (a) तथा (b) लक्षणों को संयोजित करता है।
Ga As (c) लक्षण को दर्शाता है।
11. जब ε विद्युत वाहक बल के एक स्रोत को बाह्य प्रतिरोध R से संयोजित किया जाता है तो R पर वोल्टता Vबाह्य निम्न द्वारा दी जाती है
Vबाह्य = IR =
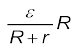
जहाँ r, स्रोत का आंतरिक प्रतिरोध है।
12. (a) श्रेणी में संयोजित n प्रतिरोधों का कुल प्रतिरोध R
R = R1 + R2 +..... + Rn
(b) पार्श्व में संयोजित n प्रतिरोधाें का कुल प्रतिरोध R
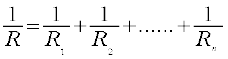
द्वारा दिया जाता है।
13. किरखोफ के नियम–
(a) प्रथम नियम (संधि नियम)– परिपथ के अवयवों की किसी संधि पर आगत धाराओं का योग निर्गत धाराओं के योग के तुल्य होना चाहिए।
(b) द्वितीय नियम [पाश नियम]– किसी बंद पाश (लूप) के चारों ओर विभव में परिवर्तन का बीजगणितीय योग शून्य होना चाहिए।
14. व्हीटस्टोन सेतु जैसा कि पाठ्यपुस्तक में दिखाया गया है, चार प्रतिरोधों – R1, R2, R3, R4 का विन्यास है तथा शून्य विक्षेप अवस्था में
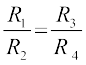
द्वारा यदि तीन प्रतिरोध ज्ञात हों तो चौथे प्रतिरोध के अज्ञात मान को निर्धारित किया जा सकता है।
15. पोटेंशियोमीटर विभवों की तुलना करने वाली एक युक्ति है। चूँकि इस विधि में कोई धारा प्रवाहित न होने वाली स्थिति होती है, यह युक्ति विभवांतर मापने; किसी सेल का आंतरिक प्रतिरोध मापने तथा दो स्रोतों के विद्युत वाहक बल emf की तुलना करने में प्रयुक्त होता है।
विचारणीय विषय
1. यद्यपि हम धारा की दिशा को परिपथ में एक तीर से दर्शाते हैं परंतु यह एक अदिश राशि है। धाराएँ सदिश योग के नियम का पालन नहीं करतीं। धारा एक अदिश है, इसे इसकी परिभाषा से भी समझ सकते हैं ः किसी अनुप्रस्थ काट से प्रवाहित विद्युत धारा I दो सदिशों के अदिश गुणनफल द्वारा व्यक्त की जाती है
I = j . ∆S
जहाँ j तथा ∆S सदिश हैं।
2. पाठ्य में प्रदर्शित किसी प्रतिरोधक और किसी डायोड के V-I वक्र पर ध्यान दीजिए। प्रतिरोधक ओम के नियम का पालन करता है जबकि डायोड नहीं करता है। यह दृढ़कथन कि V = IR ओम के नियम का प्रकथन है, सत्य नहीं है। यह समीकरण प्रतिरोध को परिभाषित करता है और इसे सभी चालक युक्तियों में प्रयुक्त कर सकते हैं चाहे वह ओम के नियम का पालन करती हैं या नहीं। ओम का नियम दावा करता है कि V तथा I के बीच ग्राफ रैखिक है अर्थात R, V पर निर्भर नहीं करता है। ओम के नियम का समीकरण
E = ρ j
ओम के नियम के दूसरे प्रकथन की ओर ले जाता है, अर्थात कोई चालक पदार्थ तभी ओम के नियम का पालन करता है जब उस पदार्थ की प्रतिरोधकता लगाए गए विद्युत क्षेत्र के परिमाण और दिशा पर निर्भर नहीं करती।
3. समांगी चालक जैसे सिल्वर या अर्द्धचालक जैसे शुद्ध जर्मेनियम या अशुद्धियुक्त जर्मेनियम विद्युत क्षेत्र के मान के कुछ परिसर में ओम के नियम का पालन करते हैं। यदि क्षेत्र अति प्रबल है तो इन सभी उदाहरणों में ओम के नियम का पालन नहीं होगा।
4. विद्युत क्षेत्र E में इलेक्ट्रॉन की गति (i) यादृच्छिक संघट्टों के कारण (ii) E के कारण उत्पन्न गतियों के योग के बराबर है। यादृच्छिक संघट्टों के कारण गति का औसत शून्य हो जाता है और vd (अपवाह चाल) में योगदान नहीं करता (देखिए अध्याय 11, कक्षा XI की पाठ्यपुस्तक)। इस प्रकार इलेक्ट्रॉन की अपवाह चाल vd केवल इलेक्ट्रॉन पर लगाए गए विद्युत क्षेत्र के कारण ही है।
5. संबंध j = ρ v प्रत्येक प्रकार के आवेश वाहक पर अलग-अलग प्रयुक्त होना चाहिए। किसी चालक तार में कुल धारा तथा धारा घनत्व धन और ऋण दोनों प्रकार के आवेशों से उत्पन्न होती है।
j = ρ+v+ + ρ− v−
ρ = ρ+ + ρ−
एक उदासीन तार जिसमें धारा प्रवाहित हो रही है, में
ρ+ = – ρ−
इसके अतिरिक्त, v+ ~ 0 है जिसके कारण हमें प्राप्त होता है
ρ = 0
j = ρ– v
इस प्रकार संबंध j = ρ v कुल धारा आवेश घनत्व पर लागू नहीं होता।
6. किरखोफ का संधि नियम आवेश संरक्षण नियम पर आधारित है ः किसी संधि पर निर्गत धाराओं का योग संधि पर आगत धाराओं के योग के तुल्य होता है। तारों को मोड़ने या पुनः अभिविन्यसित करने के कारण किरखोफ के संधि नियम की वैधता नहीं बदलती।
अभ्यास
3.1 किसी कार की संचायक बैटरी का विद्युत वाहक बल 12 V है। यदि बैटरी का आंतरिक प्रतिरोध 0.4 Ω हो, तो बैटरी से ली जाने वाली अधिकतम धारा का मान क्या है?
3.2 10 V विद्युत वाहक बल वाली बैटरी जिसका आंतरिक प्रतिरोध 3 Ω है, किसी प्रतिरोधक से संयोजित है। यदि परिपथ में धारा का मान 0.5 A हो, तो प्रतिरोधक का प्रतिरोध क्या है? जब परिपथ बंद है तो सेल की टर्मिनल वोल्टता क्या होगी?
3.3 (a) 1 Ω, 2 Ω और 3 Ω के तीन प्रतिरोधक श्रेणी में संयोजित हैं। प्रतिरोधकों के संयोजन का कुल प्रतिरोध क्या है?
(b) यदि प्रतिरोधकों का संयोजन किसी 12 V की बैटरी जिसका आंतरिक प्रतिरोध नगण्य है, से संबद्ध है, तो प्रत्येक प्रतिरोधक के सिरों पर वोल्टता पात ज्ञात कीजिए।
3.4 (a) 2 Ω, 4 Ω और 5 Ω के तीन प्रतिरोधक पार्श्व में संयोजित हैं। संयोजन का कुल प्रतिरोध क्या होगा?
(b) यदि संयोजन को 20 V के विद्युत वाहक बल की बैटरी जिसका आंतरिक प्रतिरोध नगण्य है, से संबद्ध किया जाता है, तो प्रत्येक प्रतिरोधक से प्रवाहित होने वाली धारा तथा बैटरी से ली गई कुल धारा का मान ज्ञात कीजिए।
3.5 कमरे के ताप (27.0 °C) पर किसी तापन-अवयव का प्रतिरोध 100 Ω है। यदि तापन-अवयव का प्रतिरोध 117 Ω हो तो अवयव का ताप क्या होगा? प्रतिरोधक के पदार्थ का ताप-गुणांक 1.70 × 10−4 °C−1 है।
3.6 15 मीटर लंबे एवं 6.0 × 10−7 m2 अनुप्रस्थ काट वाले तार से उपेक्षणीय धारा प्रवाहित की गई और इसका प्रतिरोध 5.0 Ω मापा गया। प्रायोगिक ताप पर तार के पदार्थ की प्रतिरोधकता क्या होगी?
3.7 सिल्वर के किसी तार का 27.5 °C पर प्रतिरोध 2.1 Ω और 100 °C पर प्रतिरोध 2.7 Ω है। सिल्वर की प्रतिरोधकता ताप-गुणांक ज्ञात कीजिए।
3.8 निक्रोम का एक तापन-अवयव 230 V की सप्लाई से संयोजित है और 3.2 A की प्रारंभिक धारा लेता है जो कुछ सेकंड में 2.8 A पर स्थायी हो जाती है। यदि कमरे का ताप 27.0 °C है तो तापन-अवयव का स्थायी ताप क्या होगा? दिए गए ताप-परिसर में निक्रोम का औसत प्रतिरोध का ताप-गुणांक 1.70 × 10-4 °C−1 है।
3.9 चित्र 3.30 में दर्शाए नेटवर्क की प्रत्येक शाखा में प्रवाहित धारा ज्ञात कीजिए।
चित्र 3.30
3.10 (a) किसी मीटर-सेतु में [चित्र 3.27] जब प्रतिरोधक S = 12.5Ω हो तो संतुलन बिंदु, सिरे A से 39.5 cm की लंबाई पर प्राप्त होता है। R का प्रतिरोध ज्ञात कीजिए। व्हीटस्टोन सेतु या मीटर सेतु में प्रतिरोधकों के संयोजन के लिए मोटी कॉपर की पत्तियाँ क्यों प्रयोग में लाते हैं?
(b) R तथा S को अंतर्बदल करने पर उपरोक्त सेतु का संतुलन बिंदु ज्ञात कीजिए।
(c) यदि सेतु के संतुलन की अवस्था में गैल्वेनोमीटर और सेल को अंतर्बदल कर दिया जाए तब क्या गैल्वेनोमीटर कोई धारा दर्शाएगा?
3.11 8 V विद्युत वाहक बल की एक संचायक बैटरी जिसका आंतरिक प्रतिरोध 0.5 Ω है, को श्रेणीक्रम में 15.5 Ω के प्रतिरोधक का उपयोग करके 120 V के dc स्रोत द्वारा चार्ज किया जाता है। चार्ज होते समय बैटरी की टर्मिनल वोल्टता क्या है? चार्जकारी परिपथ में प्रतिरोधक को श्रेणीक्रम में संबद्ध करने का क्या उद्देश्य है?
3.12 किसी पोटेंशियोमीटर व्यवस्था में, 1.25 V विद्युत वाहक बल के एक सेल का संतुलन बिंदु तार के 35.0 cm लंबाई पर प्राप्त होता है। यदि इस सेल को किसी अन्य सेल द्वारा प्रतिस्थापित कर दिया जाए तो संतुलन बिंदु 63.0 cm पर स्थानांतरित हो जाता है। दूसरे सेल का विद्युत वाहक बल क्या है?
3.13 किसी ताँबे के चालक में मुक्त इलेक्ट्रॉनों का संख्या घनत्व उदाहरण 3.1 में 8.5 × 1028 m3 आकलित किया गया है। 3 m लंबे तार के एक सिरे से दूसरे सिरे तक अपवाह करने में इलेक्ट्रॉन कितना समय लेता है? तार की अनुप्रस्थ-काट 2.0 × 10−6 m2 है और इसमें 3.0 A धारा प्रवाहित हो रही है।
अतिरिक्त अभ्यास
3.14 पृथ्वी के पृष्ठ पर ऋणात्मक पृष्ठ-आवेश घनत्व 10−9 C cm−2 है। वायुमंडल के ऊपरी भाग और पृथ्वी के पृष्ठ के बीच 400 kV विभवांतर (नीचे के वायुमंडल की कम चालकता के कारण) के परिणामतः समूची पृथ्वी पर केवल 1800 A की धारा है। यदि वायुमंडलीय विद्युत क्षेत्र बनाए रखने हेतु कोई प्रक्रिया न हो तो पृथ्वी के पृष्ठ को उदासीन करने हेतु (लगभग) कितना समय लगेगा? (व्यावहारिक रूप में यह कभी नहीं होता है क्योंकि विद्युत आवेशों की पुनः पूर्ति की एक प्रक्रिया है यथा पृथ्वी के विभिन्न भागों में लगातार तड़ित झंझा एवं तड़ित का होना)।
(पृथ्वी की त्रिज्या = 6.37 × 106 m)।
3.15 (a) छः लेड एसिड संचायक सेलों को जिनमें प्रत्येक का विद्युत वाहक बल 2 V तथा आंतरिक प्रतिरोध 0.015 Ω है, के संयोजन से एक बैटरी बनाई जाती है। इस बैटरी का उपयोग
8.5 Ω प्रतिरोधक जो इसके साथ श्रेणी संबद्ध है, मेें धारा की आपूर्ति के लिए किया जाता है। बैटरी से कितनी धारा ली गई है एवं इसकी टर्मिनल वोल्टता क्या है?
(b) एक लंबे समय तक उपयोग में लाए गए संचायक सेल का विद्युत वाहक बल 1.9 V और विशाल आंतरिक प्रतिरोध 380 Ω है। सेल से कितनी अधिकतम धारा ली जा सकती है? क्या सेल से प्राप्त यह धारा किसी कार की प्रवर्तक-मोटर को स्टार्ट करने में सक्षम होगी?
3.16 दो समान लंबाई की तारों में एक एेलुमिनियम का और दूसरा कॉपर का बना है। इनके प्रतिरोध समान हैं। दोनों तारों में से कौन-सा हलका है? अतः समझाइए कि ऊपर से जाने वाली बिजली केबिलों में एेलुमिनियम के तारों को क्यों पसंद किया जाता है? (ρAl = 2.63 × 10−8 Ωm, ρCu= 1.72 × 10−8 Ωm, Al का आपेक्षिक घनत्व = 2.7, कॉपर का आपेक्षिक घनत्व = 8.9)
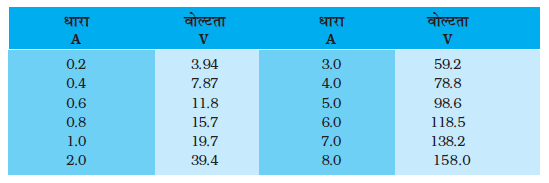
3.17 मिश्रातु मैंगनिन के बने प्रतिरोधक पर लिए गए निम्नलिखित प्रेक्षणों से आप क्या निष्कर्ष निकाल सकते हैं?
3.18 निम्नलिखित प्रश्नों के उत्तर दीजिए–
(a) किसी असमान अनुप्रस्थ काट वाले धात्विक चालक से एकसमान धारा प्रवाहित होती है। निम्नलिखित में से चालक में कौन-सी अचर रहती है–धारा, धारा घनत्व, विद्युत क्षेत्र, अपवाह चाल।
(b) क्या सभी परिपथीय अवयवों के लिए ओम का नियम सार्वत्रिक रूप से लागू होता है? यदि नहीं, तो उन अवयवों के उदाहरण दीजिए जो ओम के नियम का पालन नहीं करते।
(c) किसी निम्न वोल्टता संभरण जिससे उच्च धारा देनी होती है, का आंतरिक प्रतिरोध बहुत कम होना चाहिए, क्यों?
(d) किसी उच्च विभव (H.T) संभरण, मान लीजिए 6 kV, का आंतरिक प्रतिरोध अत्यधिक होना चाहिए, क्यों?
3.19 सही विकल्प छाँटिए–
(a) धातुओं की मिश्रातुओं की प्रतिरोधकता प्रायः उनकी अवयव धातुओं की अपेक्षा (अधिक/कम) होती है।
(b) आमतौर पर मिश्रातुओं के प्रतिरोध का ताप-गुणांक, शुद्ध धातुओं के प्रतिरोध के ताप-गुणांक से बहुत कम/अधिक होती है।
(c) मिश्रातु मैंगनिन की प्रतिरोधकता ताप में वृद्धि के साथ लगभग (स्वतंत्र है/तेजी से
बढ़ती है)।
(d) किसी प्रारूपी विद्युतरोधी (उदाहरणार्थ, अंबर) की प्रतिरोधकता किसी धातु की प्रतिरोधकता की तुलना में (1022/1023) कोटि के गुणक से बड़ी होती है।
3.20 (a) आपको R प्रतिरोध वाले n प्रतिरोधक दिए गए हैं। (i) अधिकतम (ii) न्यूनतम प्रभावी प्रतिरोध प्राप्त करने के लिए आप इन्हें किस प्रकार संयोजित करेंगे? अधिकतम और न्यूनतम प्रतिरोधों का अनुपात क्या होगा?
(b) यदि 1 Ω, 2 Ω, 3 Ω के तीन प्रतिरोध दिए गए हों तो उनको आप किस प्रकार संयोजित करेंगे कि प्राप्त तुल्य प्रतिरोध हों : (i) (11/3) Ω (ii) (11/5) Ω, (iii) 6 Ω, (iv) (6/11) Ω ?
(c) चित्र 3.31 में दिखाए गए नेटवर्कों का तुल्य प्रतिरोध प्राप्त कीजिए।
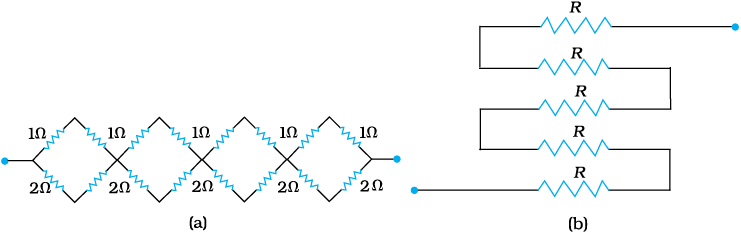
चित्र 3.31
3.21 किसी 0.5 Ω आंतरिक प्रतिरोध वाले 12 V के एक संभरण (supply) से चित्र 3.32 में दर्शाए गए अनंत नेटवर्क द्वारा ली गई धारा का मान ज्ञात कीजिए। प्रत्येक प्रतिरोध का मान 1 Ω है।
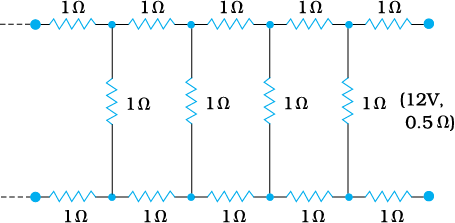
चित्र 3.32
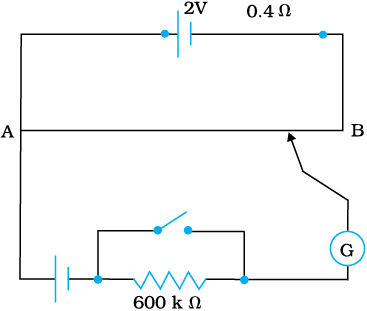
3.22 चित्र 3.33 में एक पोटेंशियोमीटर दर्शाया गया है जिसमें एक 2.0 V और आंतरिक प्रतिरोध 0.40 Ω का कोई सेल, पोटेंशियोमीटर के प्रतिरोधक तार AB पर वोल्टता पात बनाए रखता है। कोई मानक सेल जो 1.02 V का अचर विद्युत वाहक बल बनाए रखता है (कुछ mA की बहुत सामान्य धाराओं के लिए) तार की 67.3 cm लंबाई पर संतुलन बिंदु देता है। मानक सेल से अति न्यून धारा लेना सुनिश्चित करने के लिए इसके साथ परिपथ में श्रेणी 600 kΩ का एक अति उच्च प्रतिरोध इसके साथ संबद्ध किया जाता है, जिसके संतुलन बिंदु प्राप्त होने के निकट लघुपथित (shorted) कर दिया जाता है। इसके बाद मानक सेल को किसी अज्ञात विद्युत वाहक बल ε के सेल से प्रतिस्थापित कर दिया जाता है जिससे संतुलन बिंदु तार की 82.3 cm लंबाई पर प्राप्त होता है।
(a) ε का मान क्या है?
(b) 600 kΩ के उच्च प्रतिरोध का क्या प्रयोजन है?
(c) क्या इस उच्च प्रतिरोध से संतुलन बिंदु प्रभावित होता है?
(d) उपरोक्त स्थिति में यदि पोटेंशियोमीटर के परिचालक सेल का विद्युत वाहक बल 2.0 V के स्थान पर 1.0 V हो तो क्या यह विधि फिर भी सफल रहेगी?
(e) क्या यह परिपथ कुछ mV की कोटि के अत्यल्प विद्युत वाहक बलों (जैसे कि किसी प्रारूपी तापवैद्युत युग्म का विद्युत वाहक बल) के निर्धारण में सफल होगी? यदि नहीं तो आप इसमें किस प्रकार संशोधन करेंगे?
चित्र 3.33
3.23 चित्र 3.34 में किसी 1.5 V के सेल का आंतरिक प्रतिरोध मापने के लिए एक 2.0 V का पोटेंशियोमीटर दर्शाया गया है। खुले परिपथ में सेल का संतुलन बिंदु 76.3 cm पर मिलता है। सेल के बाह्य परिपथ में 9.5 Ω प्रतिरोध का एक प्रतिरोधक संयोजित करने पर संतुलन बिंदु पोटेंशियोमीटर के तार की 64.8 cm लंबाई पर पहुँच जाता है। सेल के आंतरिक प्रतिरोध का मान ज्ञात कीजिए।