Table of Contents
अध्याय 4
गतिमान आवेश और चुंबकत्व
4.1 भूमिका
2000 वर्ष से भी पहले विद्युत तथा चुंबकत्व दोनों ही के बारे में लोगों को ज्ञान था। फिर भी लगभग 200 वर्ष पूर्व, 1820 में* यह स्पष्ट अनुभव किया गया कि इन दोनों में अटूट संबंध है। 1820 की ग्रीष्म ऋतु में, डच भौतिकविज्ञानी हैंस क्रिश्चियन अॉर्स्टेड ने, अपने एक भाषण के दौरान प्रयोग प्रदर्शित करते हुए देखा कि एक सीधे तार में विद्युत धारा प्रवाहित करने पर पास रखी हुई चुंबकीय सुई में सुस्पष्ट विक्षेप प्राप्त होता है। उन्होंने इस परिघटना पर शोध आरंभ किया। उन्होंने पाया कि चुंबकीय सुई तार के अभिलंबवत तल में तार की स्थिति के केंद्रतः वृत्त की स्पर्श रेखा के समांतर संरेखित होती है। इस स्थिति को चित्र 4.1(a) में दर्शाया गया है। पर यह देखने के लिए तार में पर्याप्त धारा प्रवाहित होनी चाहिए और चुंबकीय सुई तार के काफी निकट रखी होनी चाहिए ताकि पृथ्वी के चुंबकीय क्षेत्र की उपेक्षा की जा सके। यदि तार में धारा की दिशा विपरीत कर दी जाए तो चुंबकीय सुई भी घूम कर विपरीत दिशा में संरेखित हो जाती है [चित्र 4.1(b) देखिए]। तार में धारा का परिमाण बढ़ाने या सुई को तार के निकट लाने से चुंबकीय सुई का विक्षेप बढ़ जाता है। तार के चारों ओर यदि लौह चूर्ण छिड़कें तो इसके कण तार के चारों ओर संकेंद्री वृत्तों में व्यवस्थित हो जाते हैं [चित्र 4.1(c) देखिए]। इस परिघटना से अॉर्स्टेड ने निष्कर्ष निकाला कि गतिमान आवेश (धारा) अपने चारों ओर एक चुंबकीय क्षेत्र उत्पन्न करते हैं।
इसके पश्चात प्रयोगों की गति तीव्र हो गई। सन 1864 में विद्युत तथा चुंबकत्व के सर्वमान्य नियमों को जेम्स मैक्सवेल ने एकीकृत करके नए नियम बनाए और यह स्पष्ट अनुभव किया कि प्रकाश वास्तव में विद्युत चुंबकीय तरंगें हैं। हर्ट्ज़ ने रेडियो तरंगों की खोज की तथा 19वीं शताब्दी के अंत तक सर जे.सी. बोस तथा मार्कोनी ने इन तरंगों को उत्पन्न किया। 20वीं शताब्दी में विज्ञान तथा प्रौद्योगिकी में आश्चर्यजनक प्रगति हुई है। यह प्रगति विद्युत चुंबकत्व के हमारे बढ़ते ज्ञान तथा विद्युत चुंबकीय तरंगों को उत्पन्न, प्रबर्धित, प्रेषित तथा संसूचित करने वाली युक्तियों की खोज के कारण हुई है।
चित्र 4.1 एक सीधे लंबे धारावाही तार के कारण उत्पन्न चुंबकीय क्षेत्र। तार, कागज़ के तल पर अभिलंबवत है। तार के चारों ओर चुंबकीय सुइयों की एक मुद्रिका बनाई गई है। चुंबकीय सुइयों का अभिविन्यास– (a) जब धारा कागज़ के तल से बाहर की ओर प्रवाहित होती है।
(b) जब धारा कागज़ के तल से अंदर की ओर प्रवाहित होती है। (c) लौह चूर्ण कणों का तार के चारों ओर अभिविन्यास। सुइयों के काले सिरे उत्तरी ध्रुव प्रदर्शित करते हैं। यहाँ भू-चुंबकत्व के प्रभाव की उपेक्षा की गई है।
इस अध्याय में हम यह देखेंगे कि चुंबकीय क्षेत्र किस प्रकार आवेशित कणों; जैसे–इलेक्ट्रॉन, प्रोटॉन तथा विद्युत धारावाही तारों पर बल आरोपित करते हैं। हम यह भी सीखेंगे कि विद्युत धाराएँ किस प्रकार चुंबकीय क्षेत्र उत्पन्न करती हैं। हम यह देखेंगे कि साइक्लोट्रॉन में किस प्रकार कणों को अति उच्च ऊर्जाओं तक त्वरित किया जा सकता है। हम गैल्वेनोमीटर द्वारा विद्युतधाराओं एवं वोल्टताओं के संसूचन के विषय में भी अध्ययन करेंगे।
इस अध्याय तथा आगे आने वाले चुंबकत्व के अध्यायों में हम निम्नलिखित परिपाटी को अपनाएँगे। कागज़ के तल से बाहर की ओर निर्गत विद्युत धारा अथवा क्षेत्र (विद्युत अथवा चुंबकीय) को एक बिंदु () द्वारा व्यक्त किया जाता है। कागज़ के तल में भीतर की ओर जाती विद्युत धारा अथवा विद्युत क्षेत्र को एक क्रॉस (
)* द्वारा व्यक्त किया जाता है। चित्र 4.1(a) तथा 4.1(b) क्रमशः इन दो स्थितियों के तदनुरूपी हैं।
हैंस क्रिश्चियन अॉर्स्टेड (1777–1851)
डेनमार्क के भौतिकविज्ञानी एवं रसायनज्ञ, कॉपेनहेगन में प्रोफ़ेसर थे। उन्होंने यह देखा कि किसी चुंबकीय सुई को जब एक एेसे तार के पास रखा जाता है जिसमें विद्युत धारा प्रवाहित हो रही हो तो उसमें विक्षेप होता है। इस खोज ने वैद्युत एवं चुंबकीय प्रक्रमों के बीच संबंध का पहला आनुभविक प्रमाण प्रस्तुत किया।
4.2 चुंबकीय बल
4.2.1 स्रोत और क्षेत्र
किसी चुंबकीय क्षेत्र B की अभिधारणा को प्रस्तावित करने से पहले हम संक्षेप में यह दोहराएँगे कि हमने अध्याय 1 के अंतर्गत विद्युत क्षेत्र E के विषय में क्या सीखा है। हमने यह देखा है कि दो आवेशों के बीच अन्योन्य क्रिया पर दो चरणों में विचार किया जा सकता है। आवेश Q जोकि विद्युत क्षेत्र का स्रोत है, एक विद्युत क्षेत्र E उत्पन्न करता है–
E = Q
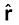/ (4πε0)r2 (4.1)
यहाँ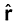 
, r के अनुदिश एकांक सदिश है तथा क्षेत्र E एक सदिश क्षेत्र है। कोई आवेश q इस क्षेत्र से अन्योन्य क्रिया करके एक बल F का अनुभव करता है
F = q E = q Q
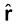
/ (4πε0 ) r2 (4.2)
हेंड्रिक एेंटून लोरेंज़ (1853 – 1928)
लोरेंज़ डेनमार्क के सैद्धांतिक भौतिकविज्ञानी, लिडेन में प्रोफ़ेसर थे। उन्होंने विद्युत, चुंबकत्व तथा यांत्रिकी में संबंध की खोज की। प्रकाश उत्सर्जकों पर चुंबकीय क्षेत्र के प्रेक्षित प्रभावों (जीमान प्रभाव) की व्याख्या करने के लिए इन्होंने परमाणु में वैद्युत आवेशों के अस्तित्व होने को अभिगृहीत किया। इसके लिए इन्हें 1902 में नोबेल पुरस्कार प्रदान किया गया। इन्होंने कुछ जटिल उलझन भरे गणितीय तर्कों के आधार पर कुछ रूपांतरण समीकरणों का एक समुच्चय व्युत्पन्न किया जिसे उनके सम्मान में लोरेंज़ रूपांतरण समीकरण कहते हैं। समीकरणों को व्युत्पन्न करते समय इन्हें इस तथ्य के बारे में यह ज्ञात नहीं था कि ये समीकरण काल तथा दिक्स्थान की नयी अभिधारणा पर अवलंबित हैं।
जैसा कि अध्याय 1 में निर्दिष्ट किया जा चुका है कि विद्युत क्षेत्र E मात्र शिल्प तथ्य ही नहीं है, परंतु इसकी भौतिक भूमिका भी है। यह ऊर्जा तथा संवेग संप्रेषित कर सकता है तथा यह तत्क्षण ही स्थापित नहीं हो जाता वरन इसके फैलने में परिमित समय लगता है। क्षेत्र की अभिधारणा को फैराडे द्वारा विशेष महत्त्व दिया गया तथा मैक्सवेल ने विद्युत तथा चुंबकत्व को एकीकृत करने में इस अभिधारणा को समावेशित किया। दिक्स्थान में प्रत्येक बिंदु पर निर्भर होने के साथ-साथ यह समय के साथ भी परिवर्तित हो सकता है, अर्थात यह समय का फलन है। इस अध्याय में हम अपनी चर्चा में, यह मानेंगे कि समय के साथ क्षेत्र में परिवर्तन नहीं होता।
किसी विशेष बिंदु पर विद्युत क्षेत्र एक अथवा अधिक आवेशों के कारण हो सकता है। यदि एक से अधिक आवेश हैं तो उनके कारण उत्पन्न क्षेत्र सदिश रूप से संयोजित हो जाते हैं। आप पहले अध्याय में यह सीख ही चुके हैं कि इसे अध्यारोपण का सिद्धांत कहते हैं। एक बार यदि क्षेत्र ज्ञात है तो परीक्षण आवेश पर बल को समीकरण (4.2) द्वारा ज्ञात किया जा सकता है।
जिस प्रकार स्थिर आवेश विद्युत क्षेत्र उत्पन्न करते हैं, विद्युत धाराएँ अथवा गतिमान आवेश (विद्युत क्षेत्र के साथ-साथ) चुंबकीय क्षेत्र उत्पन्न करते हैं जिसे B (r) द्वारा निर्दिष्ट किया जाता है तथा यह भी एक सदिश क्षेत्र है। इसके विद्युत क्षेत्र के समरूप बहुत से मूल गुण हैं। इसे दिक्स्थान के हर बिंदु पर परिभाषित किया जाता है (और साथ ही समय पर निर्भर कर सकता है)। प्रयोगों द्वारा यह पाया गया है कि यह अध्यारोपण के सिद्धांत का पालन करता है। अध्यारोपण का सिद्धांत इस प्रकार है–बहुत से स्रोतों का चुंबकीय क्षेत्र प्रत्येक व्यष्टिगत स्रोत के चुंबकीय क्षेत्रों का सदिश योग होता है।
4.2.2 चुंबकीय क्षेत्र, लोरेंज बल
मान लीजिए विद्युत क्षेत्र E (r) तथा चुंबकीय क्षेत्र B (r) दोनों की उपस्थिति में कोई बिंदु आवेश q (वेग v से गतिमान तथा किसी दिए गए समय t पर r पर स्थित) विद्यमान है। किसी आवेश q पर इन दोनों क्षेत्रों द्वारा आरोपित बल को इस प्रकार व्यक्त किया जा सकता है–
F = q [ E (r) + v × B (r)] = Fविद्युत +Fचुंबकीय (4.3)
इस बल को सर्वप्रथम एच.ए. लोरेंज ने एेम्पियर तथा अन्य वैज्ञानिकों द्वारा विस्तृत पैमाने पर किए गए प्रयोगों के आधार पर व्यक्त किया था। इस बल को अब लोरेंज बल कहते हैं। विद्युत क्षेत्र के कारण लगने वाले बल के बारे में तो आप विस्तार से अध्ययन कर ही चुके हैं। यदि हम चुंबकीय क्षेत्र के साथ अन्योन्य क्रिया पर ध्यान दें तो हमें निम्नलिखित विशेषताएँ मिलती हैं–
(i) यह q, v तथा B (कण के आवेश, वेग तथा चुंबकीय क्षेत्र) पर निर्भर करता है। ऋणावेश पर लगने वाला बल धनावेश पर लगने वाले बल के विपरीत होता है।
(ii) चुंबकीय बल q [ v × B ] वेग तथा चुंबकीय क्षेत्र का एक सदिश गुणनफल होता है। सदिश गुणनफल चुंबकीय क्षेत्र के कारण बल को समाप्त (शून्य) कर देता है। यह तब होता है जब बल, वेग तथा चुंबकीय क्षेत्र दोनों के लंबवत होता है (किसी दिशा में)। जब वेग तथा चुंबकीय क्षेत्र की दिशा एक दूसरे के समांतर या प्रतिसमांतर होती है। इसकी दिशा सदिश गुणनफल (क्रास गुणनफल) के लिए चित्र 4.2 में दर्शाए अनुसार पेंच नियम अथवा दक्षिण हस्त नियम द्वारा प्राप्त होती है।
(iii) यदि आवेश गतिमान नहीं है (तब |v|= 0) तो चुंबकीय बल शून्य होता है। केवल गतिमान आवेश ही बल का अनुभव करता है।
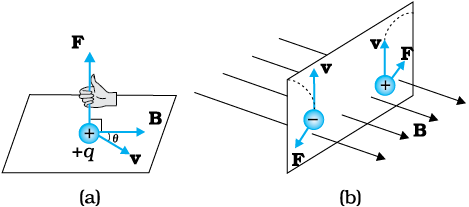
चित्र 4.2 आवेशित कण पर लगे बल की दिशा (a) चुंबकीय क्षेत्र B से θ कोण बनाते हुए v वेग से गतिमान कोई धनावेशित कण बल का अनुभव करता है जिसकी दिशा दक्षिण हस्त नियम द्वारा प्राप्त होती है। (b) चुंबकीय क्षेत्र की उपस्थिति में गतिशील आवेशित कण के विक्षेप q की दिशा –q के विक्षेप की दिशा के विपरीत होती है।
चुंबकीय क्षेत्र के लिए व्यंजक चुंबकीय क्षेत्र के मात्रक की परिभाषा देने में हमारी सहायता करता है। यदि बल के समीकरण में हल q, F तथा v सभी का मान एकांक मानें तो F = q
[v × B] =q v B sin θ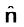 
, यहाँ θ वेग v तथा चुंबकीय क्षेत्र B के बीच का कोण है [चित्र 4.2 (a) देखिए]। चुंबकीय क्षेत्र B का परिमाण 1 SI मात्रक होता है, जबकि किसी एकांक आवेश (1 C), जो कि B के लंबवत 1m/s वेग v से गतिमान है, पर लगा बल 1 न्यूटन हो।
विमीय रीति से हम जानते हैं कि [B] = [F/qv] तथा B का मात्रक न्यूटन सेकंड/कूलॉम मीटर है। इस मात्रक को टेस्ला (T) कहते हैं जिसे निकोला टेस्ला (1856-1943) के नाम पर रखा गया है। टेस्ला एक बड़ा मात्रक है। अतः एक अपेक्षाकृत छोटे मात्रक गाउस (=10–4 टेस्ला) का प्रायः उपयोग किया जाता है। विश्व के चुंबकीय क्षेत्र के विस्तृत परिसर को सारणी 4.1 में दर्शाया गया है
4.2.3 विद्युत धारावाही चालक पर चुंबकीय बल
हम किसी एकल गतिमान आवेश पर चुंबकीय क्षेत्र द्वारा आरोपित बल के विश्लेषण का विस्तार विद्युत धारावाही सीधी छड़ के लिए कर सकते हैं। लंबाई l तथा एकसमान अनुप्रस्थ काट A की किसी छड़ पर विचार करते हैं। हम किसी चालक (जिसमें इलेक्ट्रॉन गतिशील वाहक हैं) की भाँति एक ही प्रकार के गतिशील वाहक मानेंगे। मान लीजिए इन गतिशील आवेश वाहकों का संख्या घनत्व n है तब चालक में कुल गतिशील आवेश वाहकों की संख्या nlA हुई। इस चालक छड़ में अपरिवर्ती विद्युत धारा I के लिए हम यह मान सकते हैं कि प्रत्येक गतिशील वाहक का अपवाह वेग vd है (अध्याय 3 देखिए)। किसी बाह्य चुंबकीय क्षेत्र B की उपस्थिति में इन वाहकों पर बल
F = (nlA)q vd × B
|(nq vd)|A विद्युत धारा I है (विद्युत धारा तथा विद्युत धारा घनत्व पर चर्चा के लिए अध्याय 3 देखिए।) इस प्रकार
F = [(nq vd )lA] × B = [ jlA ] × B
= Il × B (4.4)
यहाँ l एक सदिश है जिसका परिमाण l है जो कि छड़ की लंबाई है, तथा इसकी दिशा विद्युत धारा I के सर्वसम है। ध्यान दीजिए विद्युत धारा सदिश नहीं है। समीकरण (4.4) के अंतिम चरण में हमने सदिश चिह्न को j से l पर स्थानांतरित कर दिया है।
समीकरण (4.4) सीधी छड़ पर लागू होती है। इस समीकरण में B बाह्य चुंबकीय क्षेत्र है। यह विद्युत धारावाही छड़ द्वारा उत्पन्न क्षेत्र नहीं है। यदि तार की यादृच्छिक आकृति है, तो हम इस पर लॉरेंज बल का परिकलन, इसे रेखिक पट्टियों dlj का समूह मानकर तथा संकलन द्वारा कर सकते हैं
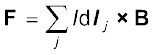
अधिकांश प्रकरणों में संकलन को समाकलन में परिवर्तित कर लेते हैं।
विद्युतशीलता (परावैद्युतांक) तथा चुंबकशीलता (पारगम्यता)
गुरुत्वाकर्षण के सार्वत्रिक नियम में हम यह कहते हैं कि दो बिंदु द्रव्यमान एक दूसरे पर बल आरोपित करते हैं जो उन द्रव्यमानों, m1, m2 के गुणनफल के अनुक्रमानुपाती तथा उनके बीच के दूरी r के वर्ग के व्युत्क्रमानुपाती होता है। इसे हम इस प्रकार F = Gm1m2/r2 व्यक्त करते हैं, यहाँ G गुरुत्वाकर्षण का सार्वत्रिक नियतांक है। इसी प्रकार स्थिरवैद्युतिकी में कूलॉम के नियम में, हम दो विद्युत आवेशों q1, q2 जिनके बीच r पृथकन है, लगने वाले बल को F = kq1q2/r2 द्वारा व्यक्त करते हैं, यहाँ k एक अनुक्रमानुपाती स्थिरांक है। SI मात्रकों में, k 1/4πε है, यहाँ ε माध्यम की विद्युतशीलता है। इसी प्रकार चुंबकत्व में भी हमें एक अन्य नियतांक प्राप्त होता है। SI मात्रकों में यह नियतांक
µ/4π है, यहाँ µ माध्यम की चुंबकशीलता है।
यद्यपि G, ε तथा µ अनुक्रमानुपाती नियतांक के रूप में प्रकट होते हैं, परंतु गुरुत्वाकर्षण बल तथा विद्युत चुंबकीय बल में एक अंतर है। जबकि गुरुत्वाकर्षण बल दो वस्तुओं के बीच के माध्यम की प्रकृति पर निर्भर नहीं करता, विद्युत चुंबकीय बल, दो आवेशों अथवा चुंबकों के बीच के माध्यम पर निर्भर करता है। अतः G एक सार्वत्रिक स्थिरांक है, ε तथा µ माध्यम पर निर्भर करते हैं। इनके विभिन्न माध्यमों के लिए भिन्न-भिन्न मान हैं। गुणनफल εµ का विद्युत चुंबकीय विकिरणों की चाल v से एक संबंध εµ =1/ v 2 है।
विद्युत परावैद्युतांक ε एक भौतिक राशि है जो यह स्पष्ट करती है कि कोई विद्युत क्षेत्र माध्यम को तथा माध्यम द्वारा किस प्रकार प्रभावित होता है। इसका निर्धारण अनुप्रयुक्त क्षेत्र के प्रत्युत्तर में माध्य के ध्रुवित होने के गुण, जिसके द्वारा यह किसी पदार्थ के भीतर के क्षेत्र को आंशिक रूप से निरसित करता है, से किया जाता है। इसी प्रकार चुंबकीय पारगम्यता µ किसी पदार्थ की चुंबकीय क्षेत्रों में चुंबकन अर्जित करने की सामर्थ्य होती है। इसकी माप चुंबकीय क्षेत्रों द्वारा पदार्थ को वेधन करने की सीमा से की जाती है।
उदाहरण 4.1
200 g द्रव्यमान तथा 1.5 m लंबाई के किसी सीधे तार से 2 A विद्युत धारा प्रवाहित हो रही है। यह किसी एकसमान क्षैतिज B चुंबकीय क्षेत्र द्वारा वायु के बीच में निलंबित है (चित्र 4.3)। चुंबकीय क्षेत्र का परिमाण ज्ञात कीजिए।
चित्र 4.3
हल
समीकरण (4.4) के अनुसार, तार बीच-वायु में निलंबित है इसके निलंबित रहने के लिए इस पर एक उपरिमुखी बल F जिसका परिमाण IlB लगना चाहिए जो इसके भार mg को संतुलित कर सके। अतः
m g = I lB
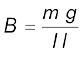
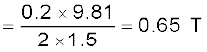
ध्यान दीजिए, यहाँ पर m/l अर्थात तार का प्रति एकांक लंबाई द्रव्यमान बताना पर्याप्त है। पृथ्वी के चुंबकीय क्षेत्र का मान लगभग 4 × 10–5 T है जिसकी हमने यहाँ उपेक्षा की है।
उदाहरण 4.2
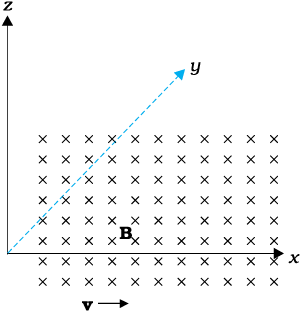
यदि चुंबकीय क्षेत्र धनात्मक y-अक्ष के समान्तर है तथा आवेशित कण धनात्मक x-अक्ष के अनुदिश गतिमान है (चित्र 4.4 देखिए), तो लोरेंज बल किस ओर लगेगा जबकि गतिमान कण (a) इलेक्ट्रॉन (ऋण आवेश) (b) प्रोटॉन (धन आवेश) है।
चित्र 4.4
हल कण के वेग v की दिशा x-अक्ष के अनुदिश है जबकि चुंबकीय क्षेत्र B की दिशा y-अक्ष के अनुदिश है, अतः लोरेंज बल v × B की दिशा z-अक्ष के अनुदिश (पेंच नियम अथवा दक्षिण हस्त अंगुष्ठ नियम) है। अतः (a) इलेक्ट्रॉन के लिए यह बल –z अक्ष के अनुदिश तथा (b) धनावेश (प्रोटॉन) के लिए यह +z अक्ष के अनुदिश है।
4.3 चुंबकीय क्षेत्र में गति
अब हम और अधिक विस्तार से चुंबकीय क्षेत्र में गतिशील आवेश के विषय में अध्ययन करेंगे। हमने यांत्रिकी (कक्षा 11 की पाठ्यपुस्तक का अध्याय 6 देखिए) में यह सीखा है कि यदि किसी बल का कण की गति की दिशा में (अथवा उसके विपरीत) कोई अवयव है तो वह बल उस कण पर कार्य करता है। चुंबकीय क्षेत्र में आवेश की गति के प्रकरण में, चुंबकीय बल कण के वेग की दिशा के लंबवत होता है। अतः कोई कार्य नहीं होता तथा वेग के परिमाण में भी कोई परिवर्तन नहीं होता (यद्यपि संवेग की दिशा में परिवर्तन हो सकता है। [ध्यान दीजिए, यह विद्युत क्षेत्र के कारण बल, qE, से भिन्न है, जिसका गति के समांतर (अथवा प्रतिसमांतर) अवयव हो सकता है और इस प्रकार संवेग के साथ-साथ ऊर्जा को भी स्थानांतरित कर सकता है।]
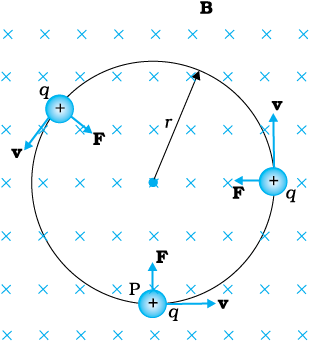
चित्र 4.5 वर्तुल गति
हम किसी एकसमान चुंबकीय क्षेत्र में आवेशित कण की गति पर विचार करेंगे। पहले उस स्थिति पर विचार कीजिए जिसमें वेग v चुंबकीय क्षेत्र B के लंबवत है। लंबवत बल q v × B अभिकेंद्र बल की भाँति कार्य करता है तथा चुंबकीय क्षेत्र के लंबवत वर्तुल गति उत्पन्न करता है। यदि v तथा B एक दूसरे के लंबवत हैं, तो कण (अर्थात किसी वृत्त के अनुदिश) वर्तुल गति करेगा (चित्र 4.5)।
यदि वेग v का कोई अवयव है, B के अनुदिश तो यह अवयव अपरिवर्तित रहता है, क्योंकि चुंबकीय क्षेत्र के अनुदिश गति को चुंबकीय क्षेत्र प्रभावित नहीं करेगा। B के लंबवत किसी तल में गति, पहले की भाँति, वर्तुल गति ही है जिससे यह अवयव कुंडलिनी गति उत्पन्न करता है (चित्र 4.6)।
चित्र 4.6 कुंडलिनी गति
आपने पिछली कक्षाओं में यह सीख लिया है (देखिए अध्याय 4 कक्षा 11) कि यदि किसी कण के वृत्ताकार पथ की त्रिज्या r है तो उस कण पर एक बल m v2 / r वृत्त के केंद्र की ओर तथा पथ के लंबवत कार्य करता है जिसे अभिकेंद्र बल कहते हैं। यदि वेग v चुंबकीय क्षेत्र B के लंबवत है, तो चुंबकीय बल वेग v तथा चुंबकीय क्षेत्र B के लंबवत होता है तथा अभिकेंद्र बल की भाँति इसका परिमाण q v B होता है। दोनों अभिकेंद्र बल के व्यंजकों को समीकरण के रूप में लिखने पर
m v 2/r = q v B,
r = m v / qB (4.5)
जितना अधिक संवेग होगा उतनी ही अधिक निर्मित वृत्त की त्रिज्या होगी तथा निर्मित वृत्त भी बड़ा होगा। यदि कोणीय आवृत्ति ω है तो v = ωr अतः
ω = 2π ν = q B/ m [4.6(a)]
कोणीय आवृत्ति ω वेग अथवा ऊर्जा पर निर्भर नहीं करती। यहाँ ν घूर्णन की आवृत्ति है। ν के ऊर्जा पर निर्भर न करने का साइक्लोट्रॉन के डिज़ाइन में एक महत्वपूर्ण अनुप्रयोग है (अनुभाग 4.4.2 देखिए)।
एक परिक्रमा पूरी करने में लगा समय T= 2π/ω ≡ 1/ν, यदि चुंबकीय क्षेत्र के समांतर वेग का कोई अवयव (v|| द्वारा निर्दिष्ट) है, कण का पथ कुंडलिनी (सर्पिलाकार) जैसा होगा। एक घूर्णन में कण द्वारा चुंबकीय क्षेत्र के अनुदिश चली गई दूरी को पिच या चूड़ी अंतराल कहते हैं। समीकरण [4.6 (a)] का उपयोग करने पर हमें प्राप्त होता है।
p = v ||T = 2πm v || / q B [4.6(b)]
गति के वृत्तीय अवयव की त्रिज्या को कुंडलिनी की त्रिज्या कहते हैं।
उदाहरण 4.3
6 × 10–4 T के चुंबकीय क्षेत्र के लंबवत 3 ×107 m/s की चाल से गतिमान किसी इलेक्ट्रॉन (द्रव्यमान 9 × 10-31 kg तथा आवेश 1.6 × 10–19 C) के पथ की त्रिज्या क्या है? इसकी क्या आवृत्ति होगी? इसकी ऊर्जा KeV में परिकलित कीजिए। ( 1 eV = 1.6 × 10–19 J)
हल
समीकरण (4.5) का उपयोग करने पर हम पाते हैं
r = m v / (qB) = 9 ×10–31 kg × 3 × 107 m s–1 / ( 1.6 × 10–19 C × 6 × 10–4 T)
= 28 × 10–2 m = 28 cm
ν = v / (2 πr) = 17×106 s–1 = 17×106 Hz =17 MHz.
E = (½ )mv 2 = (½ ) 9 × 10–31 kg × 9 × 1014 m2/s2 = 40.5 ×10–17 J
=4×10–16 J = 2.5 KeV
आवेशित कणों की कुंडलिनी गति तथा उत्तर ध्रुवीय ज्योति
ध्रुवीय क्षेत्रों जैसे अलास्का तथा उत्तरी कनाडा में आकाश में वर्णों का अत्यंत वैभवशाली दृश्य दिखाई देता है। नृत्य करते हरे गुलाबी प्रकरणों का दृष्टिगोचर होना जितना मनोहारी व चित्ताकर्षक है उतना ही उलझन पूर्ण भी है। भौतिकी में अब इस प्राकृतिक परिघटना का स्पष्टीकरण प्राप्त हो गया है जिसका इस अध्याय के अंतर्गत हम अध्ययन कर रहे हैं उससे संबंध रखता है।
मान लीजिए द्रव्यमान m तथा आवेश q का कोई कण आरंभिक वेग v से किसी चुंबकीय क्षेत्र B में प्रवेश करता है। मान लीजिए इस वेग का चुंबकीय क्षेत्र के समांतर अवयव vp तथा इस क्षेत्र के अभिलंबवत अवयव vn है। आवेशित कण पर चुंबकीय क्षेत्र के अनुदिश कोई बल नहीं है। वेग vp से निरंतर चुंबकीय क्षेत्र के समांतर गतिमान रहता है। कण पर कार्यरत वेग के अभिलंबवत अवयव के कारण इस पर लोरेंज बल (vn × B) कार्य करता है जिसकी दिशा vn तथा B दोनों के लंबवत होती है। जैसा कि अनुभाग 4.3.1 में देख चुके हैं, इस प्रकार कण में वर्तुल गति करने की प्रवृत्ति उत्पन्न हो जाती है तथा वह वर्तुल गति चुंबकीय क्षेत्र के लंबवत तल में होती है। जब यह गति चुंबकीय क्षेत्र के समांतर कण की गति से युग्मित हो जाती है तो परिणामी प्रक्षेप पथ रेखाओं के चुंबकीय क्षेत्र के अनुदिश कुंडलिनी होता है जैसा कि यहाँ चित्र (a) में दर्शाया गया है। यदि क्षेत्र रेखाएँ मुड़ भी जाती हैं तो भी कुंडलिनी पथ पर गतिशील कण पाश में फँसकर चुंबकीय क्षेत्र के चारों ओर गति करने के लिए निर्देशित होता है। चूँकि लोरेंज बल प्रत्येक बिंदु पर वेग के लंबवत है, क्षेत्र कण पर कोई कार्य नहीं करता तथा वेग का परिमाण समान रहता है।
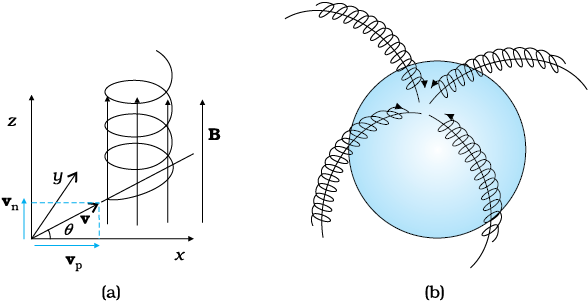
सौर प्रज्वाल के समय सूर्य से विशाल संख्या में इलेक्ट्रॉन तथा प्रोटॉन बाहर उत्सर्जित होते हैं। उनमें से कुछ पृथ्वी के चुंबकीय क्षेत्र के पाश में फँस जाते हैं तथा क्षेत्र रेखाओं के अनुदिश कुंडलिनी पथ पर गति करते हैं। पृथ्वी के चुंबकीय क्षेत्र की क्षेत्र रेखाएँ चुंबकीय ध्रुवों पर बहुत पास-पास आ जाती हैं [देखिए चित्र (b)] अतः ध्रुवों के निकट आवेशों का घनत्व बढ़ जाता है। ये आवेशित कण वायुमंडल के अणुओं से तथा परमाणुओं से टकराते हैं। उत्तेजित अॉक्सीजन परमाणु हरा प्रकाश उत्सर्जित करते हैं तथा उत्तेजित नाइट्रोजन परमाणु गुलाबी प्रकाश उत्सर्जित करते हैं। भौतिकी में इस परिघटना को उत्तर ध्रुवीय ज्योति कहते हैं।
4.4 संयुक्त विद्युत तथा चुंबकीय क्षेत्रों में गति
4.4.1 वेग वरणकर्ता
आप जानते हैं कि विद्युत तथा चुंबकीय दोनों क्षेत्रों की उपस्थिति में v वेग से गतिमान q आवेश के कण पर समीकरण (4.3) के अनुसार एक बल कार्य करता है जिसे इस प्रकार व्यक्त करते हैंः
F = q (E + v × B) = FE + FB
हम यहाँ चित्र 4.7 में दर्शाए अनुसार एक सरल स्थिति पर विचार करेंगे जिसमें विद्युत क्षेत्र तथा चुंबकीय क्षेत्र एक दूसरे के लंबवत हैं तथा कण का वेग इन दोनों क्षेत्रों के लंबवत है। तब
चित्र 4.7
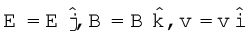
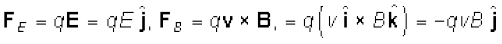
अतः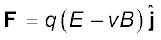 
इस प्रकार चित्र में दर्शाए अनुसार विद्युत बल तथा चुंबकीय बल एक दूसरे के विपरीत दिशा में हैं। मान लीजिए हम E तथा B के मानों को इस प्रकार समायोजित करते हैं कि इन बलों के परिमाण समान हो जाएँ तो आवेश पर कुल बल शून्य हो जाएगा तथा आवेश इन क्षेत्रों में बिना विक्षेपित हुए गमन करेगा। यह तब होगा जब
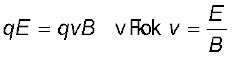(4.7)
इस शर्त का उपयोग विभिन्न गति से गतिमान आवेशों (चाहे उनके आवेश तथा द्रव्यमान कुछ भी हों) के पुंज से किसी विशेष वेग के आवेशित कणों को चुनने में किया जाता है। अतः क्रॉसित चुंबकीय व विद्युत क्षेत्र वेग वरणकर्ता के समान कार्य करते हैं। केवल E/B की चाल वाले कण ही इस क्रॉसित क्षेत्रों वाले स्थान से बिना विक्षेपित हुए गुज़रते हैं। इस विधि का उपयोग सन 1897 में जे. जे. थामसन ने इलेक्ट्रॉन का आवेश-द्रव्यमान अनुपात (e/m) मापने में किया था। इस सिद्धांत का उपयोग द्रव्यमान स्पेक्ट्रोमीटर में भी किया जाता है। यह एेसी युक्ति है जो आवेशित कणों को, प्रायः आयनों, उनके आवेश-द्रव्यमान अनुपात के अनुसार पृथक करती है।
4.4.2 साइक्लोट्रॉन
साइक्लोट्रॉन आवेशित कणों अथवा आयनों का उच्च ऊर्जाओं तक त्वरित करने वाला यंत्र है। इसका आविष्कर नाभिकीय संरचना के अन्वेषण के लिए सन् 1934 में ई.ओ. लोरेंज़ तथा एम. एस. लिविंग्स्टॉन ने किया था। आवेशित कणों की ऊर्जा में वृद्धि करने के लिए साइक्लोट्रॉन में संयुक्त रूप में विद्युत क्षेत्र तथा चुंबकीय क्षेत्र दोनों का उपयोग किया जाता है। चूँकि ये दोनों क्षेत्र एक दूसरे के लंबवत लगाए जाते हैं, इन्हें क्रॉसित क्षेत्र कहते हैं। साइक्लोट्रॉन में इस तथ्य का उपयोग किया जाता है कि "चुंबकीय क्षेत्र में परिक्रमण करने वाले आवेशित कणों की परिक्रमण की आवृत्ति कण की ऊर्जा पर निर्भर नहीं करती।" कण अधिकांश समय तक दो अर्धवृत्ताकार चक्रिका जैसे धातु के पात्रों, D1 तथा D2 के बीच गति करते हैं। इन धातु के पात्रों को ‘डीज’ (Dees) कहते हैं क्योंकि ये अंग्रेज़ी के वर्णमाला के अक्षर 'D' जैसे दिखाई देते हैं। चित्र 4.8 में साइक्लोट्रॉन का व्यवस्था आरेख दर्शाया गया है। धातु के बॉक्सों के भीतर कण परिरक्षित रहते हैं तथा इन पर विद्युत क्षेत्र कार्य नहीं करता। तथापि कण पर चुंबकीय क्षेत्र कार्य करता है जिसके कारण वह एक ‘डी’ के अंदर वर्तुल गति करता है। प्रत्येक बार जब कण एक ‘डी’ से दूसरी ‘डी’ में जाता है तो हर बार उस पर विद्युत क्षेत्र कार्य करता है। प्रत्यावर्ती रूप से विद्युत क्षेत्र का चिह्न परिवर्तित होता रहता है तथा इसका कण की वर्तुल गति के साथ सामंजस्य होता है। इससे यह सुनिश्चित होता है कि कण सदैव विद्युत क्षेत्र द्वारा त्वारित होता है। हर बार त्वरण से कण की ऊर्जा में वृद्धि होती है। जैसे-जैसे ऊर्जा में वृद्धि होती जाती है उसके वृत्ताकार पथ की त्रिज्या में भी वृद्धि होती है। अतः कण का पथ सर्पिलाकार होता है।
इस सारे संयोजन को निर्वातित किया जाता है ताकि आयनों तथा वायु के अणुओं के बीच संघट्ट न्यूनतम हो जाए। डीज़ पर एक उच्च प्रत्यावर्ती वोल्टता अनुप्रयुक्त की जाती है। चित्र 4.8 में दर्शाए गए आरेख में धनायन अथवा धनावेशित कण (कण प्रोटॉन) केंद्र P पर मुक्त किए जाते हैं। ये किसी एक ‘डी’ में अर्धवृत्ताकर पथ पर गमन करते हुए T/2 समय अंतराल में डीज़ के बीच के रिक्त स्थान में आते हैं। यहाँ T परिक्रमण काल है जिसका मान समीकरण (4.6) के अनुसार
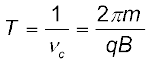
अथवा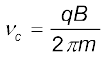 
(4.8)
प्रत्यक्ष तर्कों के आधार पर इस आवृत्ति को साइक्लोट्रॉन आवृत्ति कहते हैं तथा इसे νc द्वारा निर्दिष्ट किया जाता है।
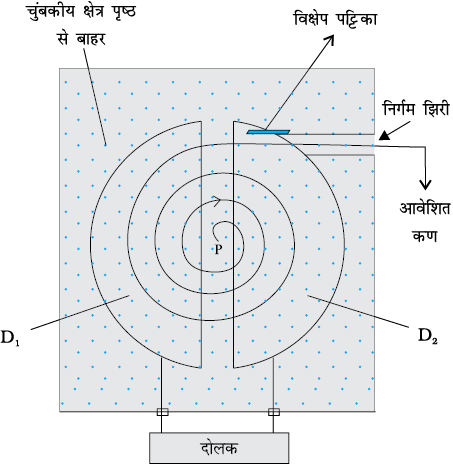
चित्र 4.8 साइक्लोट्रॉन का व्यवस्था आरेख। बिंदु P पर आवेशित कणों अथवा आयनों का स्रोत है। ये आवेशित कण या आयन एकसमान लंबवत चुंबकीय क्षेत्र B के कारण D1 तथा D2 डीज़ के भीतर-वृत्ताकार पथ पर गमन करते हैं। एक प्रत्यावर्ती वोल्टता स्रोत इन आवेशित कणों को उच्च चालों तक त्वरित करता है। अंततः आवेशित कण बाहरी द्वार से निकाल दिए जाते हैं।
साइक्लोट्रॉन में अनुप्रयुक्त वोल्टता की आवृत्ति νa को इस प्रकार समायोजित किया जाता है कि जितने समय में आयन अपना आधा परिक्रमण पूरा करता है उतने ही समय में डीज़ की ध्रुवता परिवर्तित हो जाती है। इसके लिए आवश्यक शर्त νa = νc को अनुनाद की शर्त कहते हैं। स्रोत का कला का समायोजन इस प्रकार किया जाता है कि जब धनायन D1 के छोर पर पहुँचता है तो उस समय D2 निम्न विभव पर होता है तथा आयन इस रिक्त स्थान में त्वरित होते हैं। डीज़ के भीतर कण एेसे क्षेत्र में गमन करते हैं जहाँ विद्युत क्षेत्र नहीं होता। हर बार कण एक डी से दूसरी डी पर जाने में कण की ऊर्जा में qV की वृद्धि होती है (यहाँ V डीज़ के बीच उस समय की वोल्टता है।) समीकरण (4.5) से यह स्पष्ट है कि कणों के पथों की त्रिज्या में हर बार, गतिज ऊर्जाओं में वृद्धि होने के कारण वृद्धि होती जाती है। आयन डीज़ के बीच बारंबार उस समय तक त्वरित होते रहते हैं जब तक कि वे लगभग डीज़ के बराबर त्रिज्या पाने के लिए आवश्यक ऊर्जा प्राप्त नहीं कर लेते। उस समय फिर से चुंबकीय क्षेत्र द्वारा विक्षेपित होकर निर्गम झिरी द्वारा निकाय से बाहर निकल जाते हैं। समीकरण (4.5) से, हमें प्राप्त होता है–
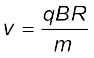(4.9)
यहाँ R निर्गम पर प्रक्षेप की त्रिज्या है तथा यह डीज़ की त्रिज्या के बराबर है।
अतः आयनों की गतिज ऊर्जा
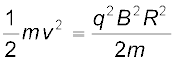(4.10)
साइक्लोट्रॉन का प्रचालन इस तथ्य पर आधारित है कि किसी आयन के एक परिक्रमण का समय आयन की चाल अथवा कक्षा की त्रिज्या पर निर्भर नहीं है। साइक्लोट्रॉन का उपयोग इसमें त्वरित ऊर्जायुक्त कणों द्वारा नाभिक पर बमबारी करके परिणामी नाभिकीय अभिक्रियाओं का अध्ययन करने के लिए किया जाता है। इसका उपयोग ठोसों में आयनों को रोपित करके उनके गुणों में सुधार करने और यहाँ तक कि नए पदार्थों को संश्लेषित करने में भी किया जाता है। इसका उपयोग रेडियोएक्टिव पदार्थों को उत्पन्न करने में किया जाता है। इन रेडियोएक्टिव पदार्थों को अस्पतालों में रोगी के निदान तथा उपचार में किया जाता है।
उदाहरण 4.4
साइक्लोट्रॉन की दोलित्र आवृत्ति 10 MHz है। प्रोटॉनों को त्वरित करने के लिए प्रचालन चुंबकीय क्षेत्र का मान कितना होना चाहिए। यदि डीज़ की त्रिज्या 60 cm है तो त्वरक द्वारा उत्पन्न प्रोटॉन पुंज की गतिज ऊर्जा MeV में परिकलित कीजिए।
(e =1.60 × 10–19 C, mp = 1.67 × 10–27 kg, 1 MeV = 1.6 × 10–13 J).
हल
दोलित्र आवृत्ति प्रोटॉन के साइक्लोट्रॉन के बराबर होनी चाहिए।
समीकरणों (4.5) तथा [4.6 (a)] का उपयोग करने पर हमें प्राप्त होता है
B = 2π m ν/q = 6.3 ×1.67 × 10–27 × 107 / (1.6 × 10–19) = 0.66 T
प्रोटॉन का अंतिम वेग
v = r × 2π ν = 0.6 m × 6.3 ×107 = 3.78 × 107 m/s.
E = ½ mv 2 = 1.67 ×10–27 × 14.3 × 1014 / (2 × 1.6 × 10–13) = 7 MeV
भारत में त्वरक
भारत त्वरक-आधारित अनुसंधान के क्षेत्र में प्रवेश करने वाला अग्रणी देश है। डॉ. मेघनाद साहा की दूरदर्शिता के कारण सन् 1953 में कोलकाता के साहा नाभिकीय भौतिकी संस्थान ने 37" साइक्लोट्रॉन स्थापित कर लिया था। इसके पश्चात तो शीघ्र ही भारत के विभिन्न संस्थानों; जैसे–टाटा भौमिक अनुसंधान संस्थान (TIFR), मुंबई; अलीगढ़ मुस्लिम विश्वविद्यालय, अलीगढ़; बोस इंस्टीट्यूट, कोलकाता तथा आंध्रा विश्वविद्यालय, वाल्टेयर में कोकरोफ्ट-वाल्टन प्रकार के कई त्वरक स्थापित हो गए।
साठ के दशक में तो कई वान डे ग्राफ त्वरक स्थापित हुए– 5.5 MV टर्मिनल मशीन भाभा परमाणु अनुसंधान केंद्र (BARC), मुंबई (1963); 2 MV टर्मिनल मशीन भारतीय प्रौद्योगिकी संस्थान, कानपुर; 400 kV टर्मिनल मशीन बनारस हिंदू विश्वविद्यालय, वाराणसी तथा पंजाबी विश्वविद्यालय, पटियाला। अमेरिका के रोशेस्टर विश्वविद्यालय द्वारा प्रदान किए गए 66 cm साइक्लोट्रॉन को पंजाब विश्वविद्यालय, चंडीगढ़ में स्थापित किया गया। एक लघु इलेक्ट्रॉन त्वरक पूना विश्वविद्यालय, पुणे में भी स्थापित किया गया।
सत्तर तथा अस्सी के दशकों में एक प्रमुख सूत्रपात परिवर्ती ऊर्जा साइक्लोट्रॉन केंद्र (VECC), कोलकाता द्वारा पूर्णतः भारतीय संसाधनों का उपयोग करके परिवर्ती ऊर्जा साइक्लोट्रॉन निर्मित करके किया गया; भाभा परमाणु अनुसंधान केंद्र (BARC) मुंबई ने 2 MV टैंडेम वान डे ग्राफ त्वरक विकसित एवं निर्मित किया तथा टाटा भौमिक अनुसंधान संस्थान में14 MV टैंडेम पेल्लेट्रॉन त्वरक स्थापित किया गया।
इसके पश्चात शीघ्र ही विश्वविद्यालय अनुदान आयोग (UGC), नयी दिल्ली ने अंतर विश्वविद्यालय सुविधा के रूप में अंतरविश्वविद्यालय त्वरक केंद्र (IUAC), नयी दिल्ली में एक 15 MV टैंडेम पेल्लेट्रॉन; भौतिकी संस्थान, भुवनेश्वर में एक 3 MV टैंडेम पेल्लेट्रॉन; अन्वेषण, भन्वेषण व अनुसंधान का परमाणु खनिज निदेशालय, हैदराबाद तथा इंदिरा गांधी परमाणु अनुसंधान केंद्र, कलपक्कम में दो 1.7 MV टैण्डेट्रॉन स्थापित कराए। TIFR तथा IUAC दोनों ही अपनी सुविधाएँ, अतिचालक LINAC मॉड्यूल जिनका उपयोग आयनों को उच्च ऊर्जाओं तक त्वरित करने में किया जाता है, के साथ आगे बढ़ा रहे हैं।
इन त्वरकों के अतिरिक्त परमाणु ऊर्जा विभाग ने भी बहुत से इलेक्ट्रॉन त्वरक विकसित किए हैं। राजा रामन्ना अग्रवर्ती प्रौद्योगिकी केंद्र, इंदौर में एक 2 GeV सिंक्रोट्रॉन विकिरण स्रोत निर्मित किया जा रहा है।
परमाणु ऊर्जा विभाग भविष्य में विकल्प के रूप में शक्ति उत्पादन तथा विखंडनीय पदार्थ के प्रजनन के लिए त्वरक प्रचालित संयंत्रों पर विचार कर रहा है।
4.5 विद्युत धारा अवयव के कारण चुंबकीय क्षेत्र, बायो-सावर्ट नियम
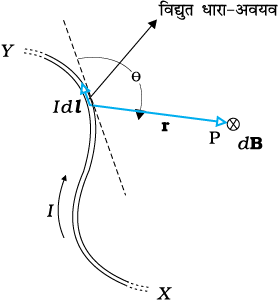
चित्र 4.9 बायो-सावर्ट नियम का निदर्श चित्र। विद्युतधारा-अवयव I dl, r दूरी पर स्थित बिंदु पर क्षेत्र dB उत्पन्नकरता है। ⊗ चिह्न यह इंगित करता है कि क्षेत्र कागज़ के तल के अभिलंबवत नीचे की ओर प्रभावी है।
जितने चुंबकीय क्षेत्र हमें ज्ञात हैं वे सभी विद्युत धाराओं (अथवा गतिशील आवेशों) तथा कणों के नैज चुंबकीय आघूर्णों के कारण उत्पन्न हुए हैं। यहाँ अब हम विद्युत धारा तथा उसके द्वारा उत्पन्न चुंबकीय क्षेत्र के बीच संबंध के बारे में अध्ययन करेंगे। यह संबंध बायो सावर्ट नियम द्वारा प्राप्त होता है। चित्र 4.9 में एक परिमित विद्युत धारा चालक XY दर्शाया गया है, जिसमें विद्युत धारा I प्रवाहित हो रही है। चालक के अतिअल्प अवयव dl पर विचार कीजिए। मान लीजिए हमें इस अवयव द्वारा इससे r दूरी पर स्थित किसी बिंदु P पर चुंबकीय क्षेत्र dB का मान निर्धारित करना है। मान लीजिए विस्थापन सदिश r तथा dl के बीच θ कोण बनता है। तब बायो-सावर्ट नियम के अनुसार चुंबकीय क्षेत्र dB का परिमाण विद्युत धारा I, लंबाई अवयव |dl|के अनुक्रमानुपाती तथा दूरी r के वर्ग के व्युत्क्रमानुपाती है। इस क्षेत्र की दिशा* dl तथा r के तलों के लंबवत होगी। अतः सदिश संकेत पद्धति में
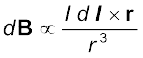
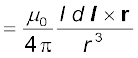[4.11(a)]
यहाँ µ0/4π अनुक्रमानुपातिक नियतांक है। उपरोक्त समीकरण तब लागू होता है जबकि माध्यम निर्वात होता है।
इस क्षेत्र का परिमाण
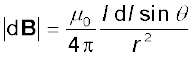[4.11(b)]
यहाँ हमने सदिश-गुणनफल के गुणधर्म |dl × r|= dl r sinθ का उपयोग किया है। चुंबकीय क्षेत्र के लिए समीकरण [4.11(a)] मूल समीकरण है। अनुक्रमानुपाती नियतांक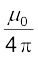 
का यथार्थ मान है–
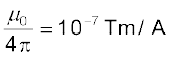[4.11(c)]
राशि µ0 को मुक्त आकाश (या निर्वात) की चुंबकशीलता नियतांक कहते हैं।
चुंबकीय क्षेत्र के बायो-सावर्ट नियम और स्थिरवैद्युतिकी के कूलॉम नियम में कुछ समानताएँ हैं तथा कुछ असमानताएँ। इसमें से कुछ निम्न प्रकार हैं-
(i) दोनों दीर्घ-परासी हैं, क्योंकि दोनों ही स्रोत से परीक्षण बिंदु तक की दूरी के वर्ग के व्युत्क्रमानुपाती होते हैं। दोनों ही क्षेत्रों पर अध्यारोपण सिद्धांत लागू होता है [इस संबंध में यह ध्यान दीजिए कि स्रोत I dl में चुंबकीय क्षेत्र रैखिक है जैसे कि अपने स्रोत, विद्युत आवेश में स्थिर वैद्युत क्षेत्र रैखिक है।]
* dl × r की दिशा दक्षिण हस्त पेंच नियम द्वारा भी प्राप्त होती है। dl तथा r के तलों को देखिए। कल्पना कीजिए कि आप पहले सदिश से दूसरे सदिश की ओर गमन कर रहे हैं। यदि गति वामावर्त है तो परिणामी आपकी ओर संकेत करेगा। यदि यह दक्षिणावर्त है तो परिणामी आपसे दूर की ओर होगा।
(ii) स्थिरवैद्युत क्षेत्र आदिश स्रोत, जैसे वैद्युत आवेश, द्वारा उत्पन्न होता है जबकि चुंबकीय क्षेत्र एक सदिश स्रोत जैसे, I dl द्वारा उत्पन्न होता है।
(iii) स्थिरवैद्युत क्षेत्र स्रोत को क्षेत्र के बिंदु से मिलाने वाले विस्थापन सदिश के अनुदिश होता है जबकि चुंबकीय क्षेत्र विस्थापन सदिश r तथा विद्युत धारा अवयव I dl दोनों के तलों के लंबवत होता है।
(iv) बायो-सावर्ट नियम में कोण पर निर्भरता है जो स्थिर वैद्युत क्षेत्र में नहीं होती। चित्र 4.9 में, दिशा dl (डैश युक्त रेखा में किसी भी बिंदु पर चुंबकीय क्षेत्र शून्य है। इस दिशा के अनुदिश
θ = 0, sin θ = 0 तथा समीकरण [4.11(a)], |dB| = 0
मुक्त दिक्स्थान की विद्युतशीलता, मुक्त दिक्स्थान की चुंबकशीलता तथा निर्वात में प्रकाश के वेग में एक रोचक संबंध है।
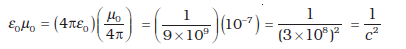
इस संबंध के विषय में हम विद्युत चुंबकीय तरंगों के अध्याय 8 में चर्चा करेंगे। चूँकि निर्वात में प्रकाश का वेग नियत है, गुणनफल µ0ε0 परिमाण में निश्चित है। ε0 तथा µ0 में से किसी भी एक मान का चयन करने पर अन्य का मान स्वतः निश्चित हो जाता है। SI मात्रकों में µ0 का एक निश्चित परिमाण 4π × 10–7 है।
उदाहरण 4.5
कोई विद्युत धारा अवयव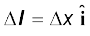 
जिससे एक उच्च धारा I = 10A प्रवाहित हो रही है, मूल बिंदु पर स्थित है (चित्र 4.10), y-अक्ष पर 0.5 m दूरी पर स्थित किसी बिंदु पर इसके कारण चुंबकीय क्षेत्र का क्या मान है। ∆x = 1 cm
चित्र 4.10
हल
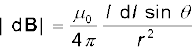[समीकरण (4.11द्वारा)]
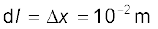, I = 10 A, r = 0.5 m = y,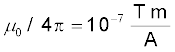 
θ = 90° ; sin θ = 1
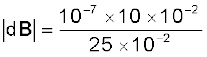= 4 × 10–8 T
इस चुंबकीय क्षेत्र की दिशा +z दिशा में है। इसका कारण यह है कि
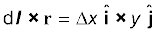
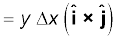
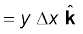
यहाँ हम आपको सदिश गुणनफलों के निम्नलिखित चक्रीय गुणों को याद कराते हैं
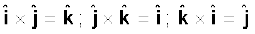
ध्यान दीजिए इस क्षेत्र का परिमाण लघु है।
अगले अनुभाग में हम वृत्ताकार पाश के कारण चुंबकीय क्षेत्र परिकलित करने के लिए बायो-सावर्ट नियम का उपयोग करेंगे।
4.6 विद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
इस अनुभाग में हम विद्युत धारावाही वृत्ताकार पाश के कारण उसके अक्ष के अनुदिश चुंबकीय क्षेत्र का मूल्यांकन करेंगे। इस मूल्यांकन में पिछले अनुभाग में वर्णित अत्यल्प विद्युत धारा अवयवाें (I dl) के प्रभाव को संयोजित किया जाएगा। हम यह मानते हैं कि प्रवाहित विद्युत धारा अपरिवर्ती है तथा मूल्यांकन मुक्त दिक्स्थान (निर्वात) में किया गया है।
चित्र 4.11 में वृत्ताकार पाश में स्थायी विद्युत धारा I प्रवाहित होते हुए दर्शाई गई है। पाश को मूल बिंदु पर x y तल में स्थित दर्शाया गया है तथा पाश का त्रिज्या R है। x-अक्ष ही लूप का अक्ष है। हमें इसी अक्ष के बिंदु P पर चुंबकीय क्षेत्र परिकलित करना है, मान लीजिए बिंदु P पाश के केंद्र से x दूरी पर स्थित है।
पाश के चालक अवयव dl पर विचार कीजिए, इसे चित्र 4.11 में दर्शायी गई है। dl के कारण चुंबकीय क्षेत्र का परिमाण बायो-सावर्ट नियम [समीकरण 4.11(a)] के अनुसार
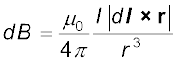(4.12)
अब r2 = x2 + R2। साथ ही, पाश का कोई भी अवयव, इस अवयव से अक्षीय बिंदु के विस्थापन सदिश के लंबवत होगा। उदाहरण के लिए, चित्र 4.11 में अवयव dl y-z दिशा में है जबकि विस्थापन सदिश r अवयव dl से अक्षीय बिंदु P तक x-y तल में है। अतः |dl × r|=r dl, इस प्रकार
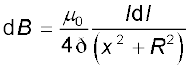(4.13)
dB की दिशा चित्र 4.11 में दर्शायी गई है। यह dl तथा r द्वारा बने तल के लंबवत है। इसका एक x- अवयव dBx तथा x- अक्ष के लंबवत अवयव dB⊥ है। जब x- अक्ष के लंबवत अवयवों को संयोजित करते हैं तो वे निरस्त हो जाते हैं तथा हमें शून्य परिणाम प्राप्त होता है। उदाहरण के लिए, चित्र 4.11 में दर्शाए अनुसार dl के कारण अवयव dB⊥ इसके त्रिज्यतः विपरीत dl अवयव के कारण योगदान द्वारा निरसित हो जाता है। इस प्रकार केवल x-अवयव ही बच पाता है। x-दिशा के अनुदिश नेट योगदान पाश के ऊपर dBx = dB cos θ को समाकलित करके प्राप्त किया जा सकता है।
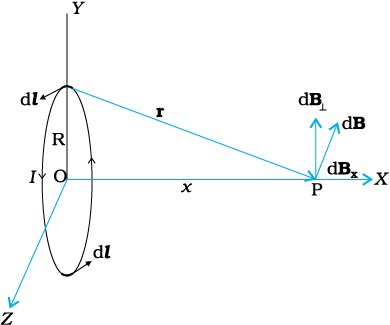
चित्र 4.11 त्रिज्या R विद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र। इस चित्र में रेखा अवयव dl के कारण चुंबकीय क्षेत्र dB तथा अक्ष के लंबवत कार्यरत इसके अवयवों को दर्शाया गया है।
चित्र 4.11 के लिए
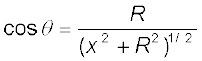(4.14)
समीकरणों (4.13) और (4.14),
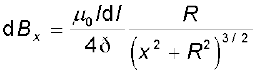
समस्त पाश पर dl अवयवों का संकलन, 2πR, प्राप्त होता है जो पाश की परिधि है। इस प्रकार
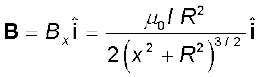(4.15)
उपरोक्त परिणाम की एक विशेष स्थिति के रूप में हम पाश के केंद्र पर चुंबकीय क्षेत्र प्राप्त कर सकते हैं। इस प्रकार यहाँ x = 0, तथा हमें प्राप्त होता है,
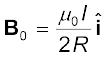(4.16)
वृत्ताकार तार के कारण चुंबकीय क्षेत्र रेखाएँ बंद वृत्ताकार पाश बनाती हैं जिन्हें चित्र 4.12 में दर्शाया गया है। चुंबकीय क्षेत्र की दिशा (एक अन्य) दक्षिण हस्त अंगुष्ठ नियम द्वारा होती है। यह नियम नीचे दिया गया है,
वृत्ताकार तार के चारों ओर अपने दाएँ हाथ की हथेली को इस प्रकार मोड़िए कि उँगलियाँ विद्युत धारा की दिशा की ओर संकेत करें, तब इस हाथ का फैला हुआ अँगूठा चुंबकीय क्षेत्र की दिशा बताता है।
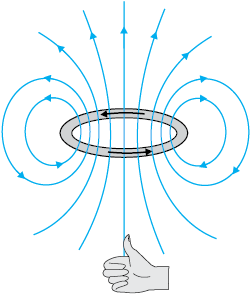
चित्र 4.12 किसी विद्युतवाही पाश का चुंबकीय क्षेत्र। पाठ की विषय वस्तु में वर्णित दक्षिण हस्त अंगुष्ठ नियम द्वारा उत्पन्न चुंबकीय क्षेत्र की दिशा निर्धारित होती है। पाश के ऊपरी पार्श्व को उत्तर ध्रुव तथा निचले पार्श्व को दक्षिण ध्रुव माना जा सकता है।
उदाहरण 4.6
चित्र 4.13 में दर्शाए अनुसार किसी सीधे तार जिसमें 12 A विद्युत धारा प्रवाहित हो रही है, को 2.0 cm त्रिज्या के अर्धवृत्ताकार चाप में मोड़ा गया है। इस चाप के केंद्र पर चुंबकीय क्षेत्र B को मानें।
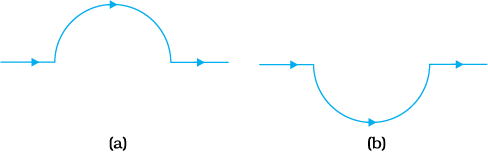
चित्र 4.13
(a) सीधे खंडों के कारण चुंबकीय क्षेत्र कितना है?
(b) किस रूप में अर्धवृत्त द्वारा B को दिया गया योगदान वृत्ताकार पाश के योगदान से भिन्न है और किस रूप में ये एक दूसरे के समान हैं।
(c) क्या आपके उत्तर में कोई परिवर्तन होगा यदि तार को उसी त्रिज्या के अर्धवृत्त में पहले की तुलना में चित्र 4.13 (b) में दर्शाए अनुसार उलटी दिशा में मोड़ दें।
हल
(a) सीधे खंडों के प्रत्येक अवयव के लिए dl तथा r समांतर हैं। अतः dl × r = 0। इस प्रकार सीधे खंड |B| को कोई योगदान नहीं देते।
(b) अर्धवृत्ताकार चाप के सभी खंडों के लिए, dl × r सभी एक दूसरे के समांतर हैं (कागज़ के तल में भीतर को जाते हुए)। इस प्रकार के सभी योगदान परिमाण में संयोजित हो जाते हैं। अतः अर्धवृत्ताकार चाप के लिए B की दिशा दक्षिण हस्त नियम द्वारा प्राप्त होती है। इसका परिमाण वृत्ताकार पाश के लिए B का आधा होता है। इस प्रकार B का मान 1.9 × 10–4 T है तथा दिशा कागज़ के तल के अभिलंबवत उसके भीतर जाते हुए है।
(c) B का परिमाण तो वही है जो (b) में है पर दिशा विपरीत है।
उदाहरण 4.7
10 cm त्रिज्या की 100 कसकर लपेटे गए फेरों की किसी एेसी कुंडली पर विचार कीजिए जिससे 1 A विद्युत धारा प्रवाहित हो रही है। कुंडली के केंद्र पर चुंबकीय क्षेत्र का परिमाण क्या है?
हल
चूँकि कुंडली कसकर लपेटी गई है अतः हम प्रत्येक वृत्ताकार अवयव की त्रिज्या R = 10 cm = 0.1 m मान सकते हैं। फेरों की संख्या N = 100 है, अतः चुंबकीय क्षेत्र का परिमाण
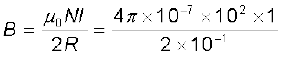
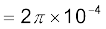T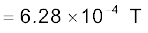
.
4.7 एेम्पियर का परिपथीय नियम
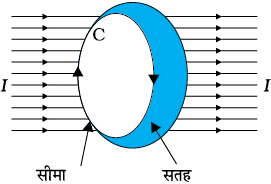
चित्र 4.14
बायो-सावर्ट नियम को अभिव्यक्त करने का एक अन्य वैकल्पिक तथा रुचिकर उपाय भी है। एेम्पियर के परिपथीय नियम में किसी खुले पृष्ठ जिसकी कोई सीमा हो, पर विचार किया जाता है। इस पृष्ठ से विद्युत धारा प्रवाहित होती है। हम यह विचार करते हैं कि सीमा रेखा बहुत से अल्प रेखा अवयवों से मिलकर बनी है। एेसे ही एक रेखा अवयव dl पर विचार कीजिए। हम इस अवयव पर चुंबकीय क्षेत्र के स्पर्शरेखीय घटक Bt का मान लेंगे तथा इसे अवयव dl की लंबाई से गुणा करेंगे। [ध्यान दीजिए Btdl=B.dl]। इस प्रकार के सभी गुणनफल एक दूसरे के साथ संयोजित किए जाते हैं। हम सीमा पर विचार करते हैं क्योंकि जैसे-जैसे अवयवों की लंबाई घटती है इनकी संख्या बढ़ती है। तब इनका योग एक समाकलन बन जाता है। एेम्पियर का नियम यह कहता है कि यह समाकलन पृष्ठ से प्रवाहित होने वाली कुल विद्युत धारा का µ0 गुना होता है, अर्थात
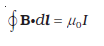[4.17(a)]
यहाँ I पृष्ठ से गुज़रने वाली कुल विद्युत धारा है। इस समाकलन को पृष्ठ की सीमारेखा C के संपाती बंद के ऊपर लिया गया है। उपरोक्त संबंध में दिशा सम्मिलित है जो दक्षिण हस्त नियम से प्राप्त होती है। अपने दाएँ हाथ की उँगलियों को उस दिशा में मोड़िए जिस दिशा में पाश समाकल ÜB.dl में सीमा रेखा मुड़ी है। तब अँगूठे की दिशा उस दिशा को बताती है जिसमें विद्युत धारा को धनात्मक माना गया है।
बहुत से अनुप्रयोगों के लिए समीकरण [4.17 (a)] का कहीं अधिक सरलीकृत रूप पर्याप्त सिद्ध होता है। हम यह मानेंगे कि, इस प्रकार के प्रकरणों में एेसे पाश (जिसे एेम्पियरीय पाश कहते हैं।) का चयन संभव है जो इस प्रकार का है कि पाश के प्रत्येक बिंदु पर या तो
(i) B पाश के स्पर्शरेखीय है तथा शून्येतर नियतांक B है, अथवा
(ii) B पाश के अभिलंबवत है, अथवा
(iii) B नष्ट हो जाता है।
अब मान लीजिए L पाश की वह लंबाई (भाग) है जिसके लिए B स्पर्शरेखीय है। मान लीजिए पाश में परिवद्ध विद्युत धारा Ie है। तब समीकरण (4.17) को इस प्रकार व्यक्त कर सकते हैं
BL =µ0Ie [4.17(b)]
आंद्रे एेम्पियर (1775 –1836)
आंद्रे मैरी एेम्पियर एक फ्रांसीसी भौतिक विज्ञानी, गणितज्ञ एवं रसायनज्ञ थे जिन्होंने विद्युतगतिकी विज्ञान की आधारशिला रखी। एेम्पियर एक बाल प्रतिभा थे जिसने 12 वर्ष की आयु में उच्च गणित में महारत हासिल कर ली थी। एेम्पियर ने अॉर्स्टेड की खोज का महत्त्व समझा और धारा विद्युत एवं चुंबकत्व में संबंध खोजने के लिए प्रयोगों की एक लंबी शृंखला पार की। इन खोजों की परिणति 1827 में, Mathematical theory of Electrodynamic Phenomena Deduced Solely from Experiments नामक पुस्तक के प्रकाशन के रूप में हुई। उन्होंने परिकल्पना की कि सभी चुंबकीय प्रक्रम, वृत्तवाही विद्युत धाराओं के कारण होते हैं। एेम्पियर स्वभाव से बहुत विनम्र और भुलक्कड़ थे। एक बार वह सम्राट नेपोलियन का रात्रिभोज का निमंत्रण भी भूल गए थे। 61 वर्ष की उम्र में न्यूमोनिया से उनकी मृत्यु हो गई। उनकी कब्र के पत्थर पर यह समाधि लेख उत्कीर्णित है – Tandem felix (अंत में प्रसन्न)।
जब किसी निकाय में इस प्रकार की सममिति हो जैसे कि चित्र 4.15 में सीधे विद्युत धारावाही अनंत तार के लिए है, तब एेम्पियर का नियम हमें चुंबकीय क्षेत्र का एक सरल मूल्यांकन करने योग्य बनाता है जो ठीक उसी प्रकार है जैसे कि गाउस नियम विद्युत क्षेत्र को निर्धारित करने में हमारी सहायता करता है। इसे नीचे दिए गए उदाहरण 4.9 में दर्शाया गया है। पाश की सीमा रेखा का चयन एक वृत्त है तथा चुंबकीय क्षेत्र वृत्त की परिधि के स्पर्शरेखीय है। समीकरण [4.17 (b)] के वाम पक्ष के लिए इस नियम से प्राप्त मान B. 2πr है। हम यह पाते हैं कि तार के बाहर r दूरी पर चुंबकीय क्षेत्र स्पर्शरेखीय है तथा इसे इस प्रकार व्यक्त किया जा सकता है।
B × 2πr = µ0 I,
B = µ0 I/ (2πr)
(4.18)
उपरोक्त परिणाम अनंत लंबाई के तार के लिए है जो कई दृष्टिकोणों से रोचक है–
(i) इसमें यह अंतर्निहित है कि r त्रिज्या के वृत्त के प्रत्येक बिंदु पर (तार को अक्ष के अनुदिश रखते हुए) क्षेत्र का परिमाण समान है। दूसरे शब्दों में चुंबकीय क्षेत्र में बेलनाकार सममिति है जो क्षेत्र सामान्यतः तीन निर्देशांकों पर निर्भर कर सकता है केवल एक ही निर्देशांक r पर निर्भर है। जहाँ कहीं भी सममिति होती है समस्याओं के हल सरल हो जाते हैं।
(ii) इस वृत्त के किसी भी बिंदु पर क्षेत्र की दिशा इसके स्पर्शरेखीय है। इस प्रकार चुंबकीय क्षेत्र की नियत परिमाण की रेखाएँ संकेंद्री वृत्त बनाती हैं। अब चित्र 4.1(c) पर ध्यान दीजिए, लौह चूर्ण वृत्त संकेंद्री में व्यवस्थित हुआ है। ये रेखाएँ जिन्हें हम चुंबकीय क्षेत्र रेखाएँ कहते है, बंद पाश बनाती हैं। यह स्थिरवैद्युत क्षेत्र रेखाओं से भिन्न हैं। स्थिरवैद्युत क्षेत्र रेखाएँ धन आवेशों से आरंभ तथा ऋण आवेशों पर समाप्त होती हैं। सीधे विद्युत धारावाही चालक के चुंबकीय क्षेत्र के लिए व्यंजक ओर्स्टेड प्रयोग का सैद्धांतिक स्पष्टीकरण करता है।
(iii) एक अन्य ध्यान देने योग्य रोचक बात यह है कि यद्यपि तार अनंत लंबाई का है, तथापि शून्येतर दूरी पर इसके कारण चुंबकीय क्षेत्र अनंत नहीं है। यह केवल तार के अत्यधिक पास आने पर विस्फुटित होता है। यह क्षेत्र विद्युत धारा के अनुक्रमानुपाती है तथा विद्युत धारा स्रोत (अनंत लंबाई के) से दूरी के व्युत्क्रमानुपाती है।
(iv) लंबे तार के कारण उत्पन्न चुंबकीय क्षेत्र की दिशा को निर्धारित करने का एक सरल नियम है। इस नियम को दक्षिण हस्त नियम* कहते हैं। यह इस प्रकार है
तार को अपने दाएँ हाथ में इस प्रकार पकड़िए कि आपका तना हुआ अँगूठा विद्युत धारा की दिशा की ओर संकेत करे। तब आपकी अँगुलियों के मुड़ने की दिशा चुंबकीय क्षेत्र की दिशा में होगी।
एेम्पियर का परिपथीय नियम बायो-सावर्ट नियम से भिन्न नहीं है। दोनों ही नियम विद्युत धारा तथा चुंबकीय क्षेत्र में संबंध व्यक्त करते हैं तथा दोनों ही स्थायी विद्युत धारा के समान भौतिक परिणामों को व्यक्त करते हैं। जो संबंध एेम्पियर के नियम तथा बायो-सावर्ट नियम के बीच है ठीक वही संबंध गाउस नियम तथा कूलॉम नियम के बीच में है। एेम्पियर का नियम तथा गाउस का नियम दोनों ही परिरेखा अथवा परिपृष्ठ पर किसी भौतिक राशि (चुंबकीय अथवा विद्युत क्षेत्र) का संबंध किसी अन्य भौतिक राशि जैसे अन्तः क्षेत्र में उपस्थित स्रोत (विद्युत धारा अथवा आवेश) के बीच संबंध व्यक्त करते हैं। यहाँ ध्यान देने योग्य बात यह भी है कि एेम्पियर का परिपथीय नियम केवल उन स्थायी विद्युत धाराओं पर लागू होता है जो समय के साथ परिवर्तित नहीं होतीं। निम्नलिखित उदाहरण हमें परिबद्ध विद्युत धारा का अर्थ समझने में सहायता करेगा।
उदाहरण 4.8
चित्र 4.15 में एक लंबा सीधा वृत्ताकार अनुप्रस्थ काट का (जिसकी त्रिज्या a है) विद्युत धारावाही तार जिससे स्थायी विद्युत धारा I प्रवाहित हो रही हो, दर्शाया गया है। स्थायी विद्युत धारा इस अनुप्रस्थ काट पर एकसमान रूप से वितरित है। क्षेत्रों r < a तथा r > a में चुंबकीय क्षेत्र परिकलित कीजिए
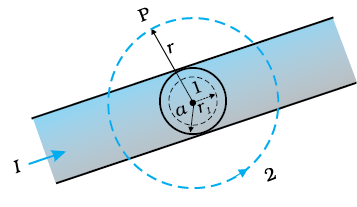
चित्र 4.15
हल
(a) प्रकरण r > a पर विचार कीजिए। जिस पाश पर 2 अंकित है वह अनुप्रस्थ काट के साथ संकेंद्री वृत्त के रूप में एेम्पियर पाश है। इस पाश के लिए
L = 2 π r
Ie = पाश द्वारा परिबद्ध विद्युत धारा = I
यह परिणाम किसी सीधे लंबे तार के लिए सुपरिचित व्यंजक है।
B (2π r) = µ0I
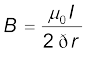[4.19(a)]
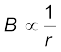(r > a)
(b) प्रकरण r < a पर विचार कीजिए। इसके लिए एेम्पियर पाश वह वृत्त है जिस पर 1 अंकित है। इस पाश के लिए वृत्त की त्रिज्या r लेने पर,
L = 2 π r
अब यहाँ परिबद्ध विद्युत धारा Ie का मान I नहीं है परंतु यह इस मान से कम है। चूँकि विद्युत धारा का विवरण एकसमान है, परिबद्ध विद्युत धारा के अंश का मान
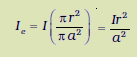
एेम्पियर के नियम का उपयोग करने पर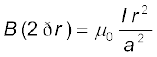 
[4.19(b)]
B ∝ r (r < a)
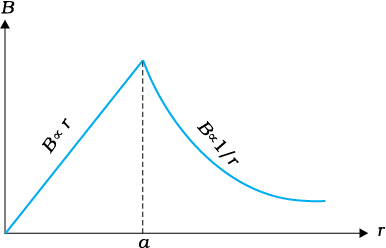
चित्र 4.16
चित्र (4.16) में B के परिमाण तथा तार के केंद्र से दूरी r के बीच ग्राफ दर्शाया गया है। चुंबकीय क्षेत्र की दिशा अपने-अपने वृत्ताकार पाशों (1 अथवा 2) के स्पर्शरेखीय है तथा यह इसी अनुभाग में पहले वर्णन किए जा चुके दक्षिण हस्त नियम से निर्धारित की गई है। इस उदाहरण में आवश्यक सममिति विद्यमान है इसलिए इसी पर एेम्पियर का नियम आसानी से लागू किया जा सकता है।
* कृपया ध्यान दीजिए–दो सुस्पष्ट (पृथक) नियम हैं जिन्हें दक्षिण हस्त नियम कहते हैं। इनमें से एक नियम विद्युत धारा पाश के अक्ष पर चुंबकीय क्षेत्र B की दिशा देता है तथा दूसरा सीधे विद्युत धारावाही चालक तार के लिए B की दिशा है। इन नियमों में अँगूठे तथा अँगुलियों की भिन्न भूमिका है।
यहाँ ध्यान देने योग्य बात यह है कि जबकि एेम्पियर के परिपथीय नियम को किसी भी पाश पर लागू किया जा सकता है परंतु यह हर प्रकरण में चुंबकीय क्षेत्र का मूल्यांकन सदैव ही आसान नहीं बनाता। उदाहरण के लिए, अनुभाग 4.6 में वर्णन किए गए वृत्ताकार पाश के प्रकरण में, इसे सरल व्यंजक B = µ0I/2R [समीकरण (4.16)] को, जोकि पाश के केंद्र पर चुंबकीय क्षेत्र के लिए है, प्राप्त करने के लिए लागू नहीं किया जा सकता। तथापि एेसी बहुत सी परिस्थितियाँ हैं जिनमें उच्च सममिति होती है तथा इस नियम को सुविधापूर्वक लागू किया जा सकता है। अगले अनुभाग में हम इसका उपयोग दो सामान्यतः उपयोग होने वाले अत्यंत उपयोगी चुंबकीय निकायों–परिनालिका एवं टोरॉइड द्वारा उत्पन्न चुंबकीय क्षेत्रों को परिकलित करने में करेंगे।
4.8 परिनालिका तथा टोरॉइड
परिनालिका तथा टोरॉइड एेसे दो उपकरण हैं जो चुंबकीय क्षेत्र उत्पन्न करते हैं। सिंक्रोट्रॉन में आवश्यक चुंबकीय क्षेत्र उत्पन्न करने के लिए इन दोनों का संयुक्त रूप से उपयोग किया जाता है। परिनालिका तथा टोरॉइड दोनों मेें ही हमें उच्च सममिति की एेसी स्थिति देखने को मिलती है जिनमें एेम्पियर-नियम आसानी से लागू किया जा सकता है।
4.8.1 परिनालिका
हम यहाँ एक लंबी परिनालिका के विषय में चर्चा करेंगे। लंबी परिनालिका से हमारा तात्पर्य यह है कि परिनालिका की लंबाई उसकी त्रिज्या की तुलना में अधिक है। परिनालिका में एक लंबा तार सर्पिल के आकार में लिपटा होता है जिसमें प्रत्येक फेरा अपने निकट के फेरे के साथ काफ़ी सटा होता है। इस प्रकार फेरे को एक वृत्ताकार पाश माना जा सकता है। किसी परिनालिका के सभी फेरों के कारण उत्पन्न कुल चुंबकीय क्षेत्र प्रत्येक फेरे के चुंबकीय क्षेत्रों का सदिश योग होता है। परिनालिका पर लपेटने के लिए इनैमलित तारों का उपयोग किया जाता है ताकि फेरे एक दूसरे से विद्युतरोधी रहें।
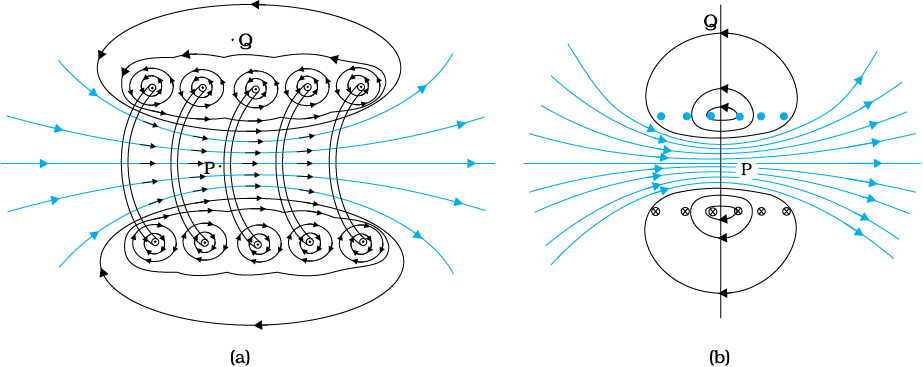
चित्र 4.17 (a) परिनालिका के किसी भाग जिसे स्पष्टता की दृष्टि से बाहर खींचा दर्शाया गया है, के कारण चुंबकीय क्षेत्र। केवल बाह्य अर्धवृत्ताकार भाग दर्शाया गया है। ध्यान से देखिए, किस प्रकार पास-पास स्थित फेरों के बीच चुंबकीय क्षेत्र एक दूसरे को निरसित कर देते हैं। (b) किसी परिमित परिनालिका का चुंबकीय क्षेत्र।
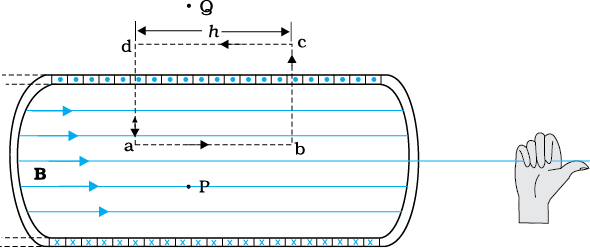
चित्र 4.18 अत्यधिक लंबी परिनालिका का चुंबकीय क्षेत्र। चुंबकीय क्षेत्र को निर्धारित करने के लिए हम एक आयताकार एेम्पियर-पाश a, b, c, d पर विचार करते हैं।
चित्र 4.17 में किसी परिमित परिनालिका का चुंबकीय क्षेत्र दर्शाया गया है। चित्र 4.17 (a) में हमने इस परिनालिका के एक खंड को विस्तारित करके दिखाया है। चित्र 4.17 (b) में वृत्ताकार पाश से यह स्पष्ट है कि दो पास-पास के फेरों के बीच चुंबकीय क्षेत्र नष्ट हो जाता है। चित्र 4.17 (b) में हम यह देखते हैं कि अन्तःभाग के मध्य बिंदु P पर चुंबकीय क्षेत्र एकसमान, प्रबल तथा परिनालिका के अक्ष के अनुदिश है। बाह्य भाग के मध्य बिंदु Q पर चुंबकीय क्षेत्र दुर्बल है और साथ ही यह परिनालिका के अक्ष के अनुदिश है तथा इसका लंबवत अथवा अभिलंबवत कोई घटक भी नहीं है। जैसे-जैसे परिनालिका की लंबाई में वृद्धि होती है वह लंबी बेलनाकार धातु के पटल जैसी दिखाई देने लगती है। चित्र 4.18 में यह आदर्शीकृत चित्रण निरूपित किया गया है। परिनालिका के बाहर चुंबकीय क्षेत्र शून्य होने लगता है। परिनालिका के भीतर हर बिंदु पर चुंबकीय क्षेत्र अक्ष के समांतर होता है।
किसी आयताकार एेम्पियर-पाश abcd पर विचार करिए। जैसा कि ऊपर तर्क दिया जा चुका है cd के अनुदिश क्षेत्र शून्य है। अनुप्रस्थ खंडों bc तथा ad के अनुदिश चुंबकीय क्षेत्र का घटक शून्य है। इस प्रकार ये दोनों खंड चुंबकीय क्षेत्र में कोई योगदान नहीं देते। मान लीजिए ab के अनुदिश चुंबकीय क्षेत्र B है, इस प्रकार, एेम्पियर-पाश की प्रासंगिक लंबाई L = h ।
मान लीजिए प्रति एकांक लंबाई फेरों की संख्या n है, तब फेरों की कुल संख्या nh है। इस प्रकार परिबद्ध विद्युत धारा है Ie = I (n h), यहाँ I परिनालिका में प्रवाहित विद्युत धारा है। एेम्पियर के परिपथीय नियम के अनुसार [समीकरण 4.17 (b) से]
BL = µ0Ie, B h = µ0I (n h)
B = µ0 n I (4.20)
क्षेत्र की दिशा दक्षिण हस्त नियम से प्राप्त होती है। परिनालिका का सामान्यतः उपयोग एकसमान चुंबकीय क्षेत्र प्राप्त करने के लिए किया जाता है। अगले अध्याय में हम यह देखेंगे कि परिनालिका में भीतर नर्म लौह क्रोड रखकर विशाल चुंबकीय क्षेत्र उत्पन्न करना संभव है।
4.8.2 टोरॉइड
यह एक वृत्ताकार खोखला छल्ला होता है जिस पर किसी तार के अत्यधिक फेरे पास-पास सटाकर लपेटे जाते हैं। इसे एक एेसी परिनालिका के रूप में भी देखा जा सकता है जिसे बंद करने के लिए वृत्ताकार मोड़ दिया गया है। इसे चित्र 4.19 (a) में दर्शाया गया है। इससे I विद्युत धारा प्रवाहित हो रही है। हम यह देखेंगे कि टोरॉइड के भीतर खुले दिक्स्थान में (बिंदु P) तथा टोरॉइड के बाहर (बिंदु Q) पर चुंबकीय क्षेत्र शून्य है। किसी आदर्श टोरॉइड जिसके फेरे सटाकर लिपटे होते हैं, के लिए टोरॉइड के भीतर चुंबकीय क्षेत्र B नियत रहता है।
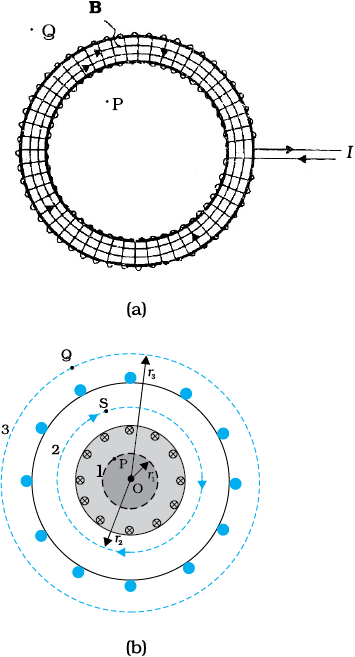
चित्र 4.19 (a) टोरॉइड से विद्युत धारा I प्रवाहित होते हुए (b) टोरॉइड की अनुप्रस्थ काट का दृश्य। एेम्पियर-परिपथीय नियम द्वारा टोरॉइड के केंद्र O से किसी यादृच्छिक दूरी r पर चुंबकीय क्षेत्र प्राप्त किया जा सकता है। 1,2, 3 द्वारा अंकित खंडित रेखाएँ इनके वृत्ताकार एेम्पियर-पाश हैं।
चित्र 4.19 (b) में टोरॉइड की अनुप्रस्थ काट दर्शायी गई है। वृत्ताकार-पाशों के लिए दक्षिण हस्त नियम के अनुसार टोरॉइड के भीतर चुंबकीय क्षेत्र की दिशा दक्षिणावर्त है। खंडित रेखाएँ जिन पर 1, 2, 3 अंकित हैं, इसके तीन एेम्पियर-पाश हैं। सममिति के अनुसार चुंबकीय क्षेत्र इन पाशों में प्रत्येक के स्पर्शरेखीय होना चाहिए तथा प्रत्येक पाश के लिए इसका परिमाण नियत होना चाहिए। पाश 2 तथा 3 इन दोनों द्वारा घेरे गए वृत्ताकार क्षेत्र टोरॉइड को काटते हैं; इस प्रकार विद्युत धारावाही तार को प्रत्येक फेरा पाश 2 को एक तथा पाश 3 को दो बार काटता है।
मान लीजिए पाश 1 के अनुदिश चुंबकीय क्षेत्र का परिमाण B1 है। तब एेम्पियर के परिपथीय नियम में [समीकरण 4.17 (a)] L = 2π r1
तथापि, यह पाश कोई विद्युत धारा परिबद्ध नहीं करता, अतः Ie = 0। इस प्रकार
B1 (2 π r1) = µ0(0), B1 = 0
इस प्रकार टोरॉइड के भीतर खुले क्षेत्र में किसी भी बिंदु P पर चुंबकीय क्षेत्र शून्य होता है।
अब हम यह दर्शाएँगे कि इसी प्रकार Q पर भी चुंबकीय क्षेत्र शून्य है। मान लीजिए पाश 3 के अनुदिश चुंबकीय क्षेत्र B3 है। एक बार फिर एेम्पियर के नियम के अनुसार L = 2 π r3, तथापि अनुप्रस्थ काट से हम यह देखते हैं कि कागज़ के तल से बाहर निकलती विद्युत धारा कागज़ के तल के भीतर जाती विद्युत धारा से ठीक-ठीक निरसित हो जाती है। अतः Ie= 0, तथा B3 = 0 । मान लीजिए टोरॉइड के भीतर चुंबकीय क्षेत्र B है। अब हम S पर चुंबकीय क्षेत्र के बारे में विचार करेंगे। एक बार फिर हम एेम्पियर के नियम का उपयोग [समीकरण
[4.17 (a)] के रूप में करते हैं। हम पाते हैं कि L = 2π r
परिबद्ध विद्युत धारा Ie का मान (टोरॉइडी कुंडली के N फेरोें के लिए)
N I है।
B (2πr) = µ0NI
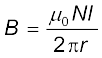
(4.21)
हम अब टोरॉइड तथा परिनालिका के लिए प्राप्त इन दो परिणामों की तुलना करेंगे। हम समीकरण (4.21) के व्यंजक की परिनालिका के लिए समीकरण (4.20) में दिए गए व्यंजक से तुलना करने के लिए समीकरण (4.21) को दुबारा नए रूप में व्यक्त करेंगे। मान लीजिए टोरॉइड की औसत त्रिज्या r है तथा इसमें प्रति एकांक लंबाई फेरों की संख्या n है, तब
N = 2πrn = टोरॉइड की (औसत) परिधि
× प्रति एकांक लंबाई फेरों की संख्या
तथा, इस प्रकार
B = µ0 n I, (4.22)
अर्थात, यही परिणाम हमें परिनालिका के लिए प्राप्त हुआ था।
आदर्श टोरॉइड मेें कुंडलियाँ पूर्णतः वृत्ताकार होती हैं। वास्तव में टोरॉइड के फेरे सर्पिलाकार कुंडली बनाते हैं तथा इसके बाहर सदैव ही एक क्षीण चुंबकीय क्षेत्र पाया जाता है।
चुंबकीय परिरोधन
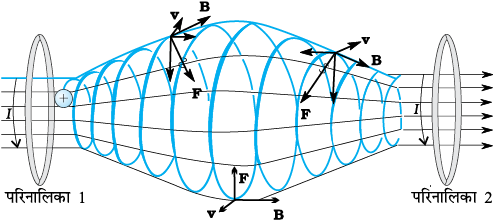
हमने अनुभाग 4.3 में यह देखा है (इस अध्याय के आरंभ में बॉक्स आवेशित कणों की सर्पिलाकार गति देखें) कि आवेशित कणों की कक्षाएँ सर्पिलाकार होती हैं। यदि चुंबकीय क्षेत्र असमान है, परंतु एक वर्तुल कक्षा में जिसका अधिक परिवर्तन नहीं होता है तब सर्पिल की त्रिज्या प्रबल चुंबकीय क्षेत्र में प्रवेश करने पर घटेगी तथा दुर्बल क्षेत्र में प्रवेश करने पर बढ़ेगी। हम दो परिनालिकाओं पर विचार करते हैं जो एक दूसरे से कुछ दूरी पर हैं तथा निर्वातित पात्र में परिबद्ध हैं। (नीचे दिए गए चित्र को देखें जिसमें हमने पात्र को नहीं दर्शाया है)। परिनालिकाओं के मध्य क्षेत्र में गति करने वाले आवेशित कण अपनी अपनी गति छोटी त्रिज्या से आरंभ करेंगे। जैसे क्षेत्र कम होगा, त्रिज्या में वृद्धि होगी तथा त्रिज्या में फिर कमी होगी जब परिनालिका 2 के कारण चुंबकीय क्षेत्र में वृद्धि होगी। परिनालिकाएँ दर्पण अथवा परावर्तक की भाँति कार्य करती हैं [जैसे ही कण परिनालिका 2 की तरफ़ पहुँचता है चित्र में बल F की दिशा देखें। इसका क्षैतिज घटक अग्रदिश गति के विरुद्ध है।] जिसके कारण कण दूसरी परिनालिका 2 के पास पहुँचते ही वापस भेज दिया जाता है। इस प्रकार की व्यवस्था एक चुंबकीय बोतल अथवा चुंबकीय पात्र की भाँति कार्य करेगी। कण पात्र के दोनों तरफ़ की सीमाओं को कभी स्पर्श नहीं करेगा। एेसी चुंबकीय बोतल संलयन प्रयोगों में उच्च ऊर्जा ‘प्लाज्मा’ को परिरोधित करने में बहुत उपयोगी है। अपने उच्च ताप के कारण ‘प्लाज्मा’ किसी भी पदार्थ की अन्य अवस्था को नष्ट कर देगा। एक अन्य उपयोगी संयोजन टोरॉइड है। टोकामैक में टोरॉइड की प्रमुख भूमिका निभाने की आशा की जाती है। टोकामैक संलयन शक्ति रिएक्टरों में प्लाज़्मा परिरोधन के लिए उपयोगी उपकरण है। यहाँ एक अंतर्राष्ट्रीय सहयोग अंतर्राष्ट्रीय ताप-नाभिकीय प्रयोगात्मक रिएक्टर (ITER) नियंत्रित संलयन प्राप्त करने के लिए फ्रांस में स्थापित हो रहा है जिसका भारत एक सहयोगी राष्ट्र है। ITER से सहयोग एवं परियोजना संबंधी विस्तृत जानकारी के लिए देखें http://www.iter.org.
उदाहरण 4.9
कोई परिनालिका जिसकी लंबाई 0.5 m तथा त्रिज्या 1 cm है, में 500 फेरे हैं। इसमें 5 A विद्युत धारा प्रवाहित हो रही है। परिनालिका के भीतर चुंबकीय क्षेत्र का परिमाण क्या है?
हल
प्रति एकांक लंबाई फेरों की संख्या
n = 500/0.5 = 1000 फेरे प्रति मीटर
लबाई l = 0.5 m तथा त्रिज्या r = 0.01 m। इस प्रकार, l/a = 50 अर्थात l >> a
अतः हम लंबी परिनालिका का सूत्र [समीकरण (4.20)] का उपयोग कर सकते हैं
B = µ0n I
= 4π × 10–7 × 103 × 5
= 6.28 × 10–3 T
4.9 दो समांतर विद्युत धाराओं के बीच बल–एेम्पियर
हम यह सीख चुके हैं कि किसी विद्युत धारावाही चालक के कारण चुंबकीय क्षेत्र उत्पन्न होता है तो बायो-सावर्ट नियम का पालन करता है। साथ ही हमने यह भी सीखा है कि विद्युत धारावाही चालक पर बाह्य चुंबकीय क्षेत्र बल आरोपित करता है। यह लोरेंज बल सूत्र का अनुगमन करता है। अतः यह आशा करना तर्कसंगत है कि एक-दूसरे के पास स्थित दो विद्युत धारावाही चालक एक दूसरे पर (चुंबकीय) बल आरोपित करेंगे। सन् 1820-25 की अवधि में एेम्पियर ने इस चुंबकीय बल की प्रकृति, इसकी विद्युत धारा के परिमाण, चालक की आकृति तथा आमाप पर निर्भरता के साथ इन चालकों के बीच की दूरी पर निर्भरता का अध्ययन किया। इस अनुभाग में हम दो समांतर विद्युत धारावाही चालकों के सरल उदाहरण पर ही चर्चा करेंगे जो कदाचित एेम्पियर के श्रम साध्य कार्यों के प्रति आभार प्रकट करने में हमारी सहायता करेंगे।
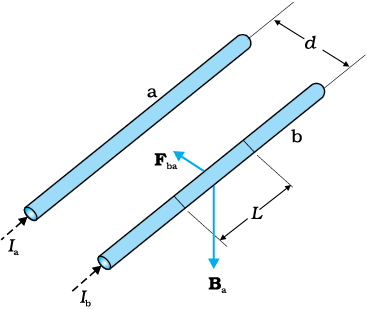
चित्र 4.20 दो लंबे सीधे, समांतर चालक जिनमें अपरिवर्ती धारा ia एवं ib प्रवाहित हो रही है और जो एक-दूसरे से dदूरी पर रखे हैं। चालक ‘a’ के कारण चालक ‘b’ पर उत्पन्न चुंबकीय क्षेत्र Ba है।
चित्र 4.20 में दो लंबे समांतर चालक a तथा b दर्शाए गए हैं जिनके बीच पृथकन d है तथा जिनसे (समांतर) क्रमशः Ia तथा Ib विद्युत धाराएँ प्रवाहित हो रही हैं। चालक ‘a’ चालक ‘b’ के अनुदिश प्रत्येक बिंदु पर समान चुंबकीय क्षेत्र Ba लगा रहा है। तब दक्षिण हस्त नियम के अनुसार इस चुंबकीय क्षेत्र की दिशा अधोमुखी (जब चालक क्षैतिजतः रखे होते हैं) है। एेम्पियर के परिपथीय नियम अथवा [समीकरण [4.19 (a)] के अनुसार इस चुंबकीय क्षेत्र का परिमाण
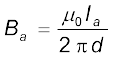
चालक ‘b’ जिससे विद्युत धारा Ib प्रवाहित हो रही है Ba के कारण पार्श्वतः एक बल का अनुमान करता है। इस बल की दिशा चालक ‘a’ की ओर होती है। (आप इसकी पुष्टि स्वयं कर सकते हैं) हम इस बल को Fba द्वारा नामांकित करते हैं, जोकि ‘a’ के कारण ‘b’ के खंड L पर लगा बल है। समीकरण (4.4) से इस बल का परिमाण
Fba = Ib L Ba
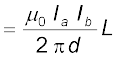(4.23)
वास्तव में ‘b’ के कारण ‘a’ पर बल को परिकलित करना संभव है। जिस प्रकार हमने ऊपर विचार किया था उसी प्रकार के विचारों के द्वारा हम ‘b’ में प्रवाहित विद्युत धारा के कारण ‘a’ के खंड L पर बल Fab के बराबर तथा ‘b’ की ओर निर्दिष्ट ज्ञात कर सकते हैं। यह परिमाण में Fba के बराबर तथा ‘b’ की ओर निर्दिष्ट होता है। इस प्रकार
Fba = –Fab (4.24)
ध्यान दीजिए, यह न्यूटन के तीसरे गति के नियम के अनुरूप है। इस प्रकार हमने समांतर चालकों तथा अपरिवर्ती विद्युत धाराओं के लिए यह तो दर्शा ही दिया है कि बायो-सावर्ट नियम तथा लोरेंज बल द्वारा प्राप्त परिणाम न्यूटन के गति के तीसरे नियम के अनुरूप है।*
हमने ऊपर प्राप्त परिणामों से यह पाया कि समान दिशा में प्रवाहित होने वाली विद्युत धाराएँ एक दूसरे को आकर्षित करती हैं। हम यह भी दर्शा सकते हैं कि विपरीत दिशाओं में प्रवाहित होने वाली विद्युत धाराएँ एक दूसरे को प्रतिकर्षित करती हैं। इस प्रकार
समांतर धाराएँ आकर्षित तथा प्रतिसमांतर धाराएँ प्रतिकर्षित करती हैं।
यह नियम उस नियम के विपरीत है जिसका हमने स्थिरवैद्युतिकी में अध्ययन किया था– "सजातीय आवेशों में प्रतिकर्षण तथा विजातीय आवेशों में आकर्षण होता है।" परंतु सजातीय (समांतर) धाराएँ एक दूसरे को आकर्षित करती हैं।
मान लीजिए fba बल Fba के प्रति एकांक लंबाई पर आरोपित बल के परिमाण को निरूपित करता है। तब समीकरण (4.23) से,
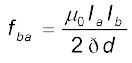(4.25)
उपरोक्त व्यंजक का उपयोग विद्युत धारा के मात्रक एेम्पियर (A) की परिभाषा को प्राप्त करने में किया जा सकता है। यह सात SI मूल मात्रकों में से एक है।
एक एेम्पियर वह अपरिवर्ती विद्युत धारा है जो दो लंबे, सीधे उपेक्षणीय अनुप्रस्थ काट के निर्वात में एक दूसरे से 1m दूरी पर स्थित समांतर चालकों में प्रवाहित हो, तो इनमें से प्रत्येक चालक की प्रति मीटर लंबाई पर 2 × 10–7N का बल उत्पन्न होता है।
‘एेम्पियर’ की यह परिभाषा सन् 1946 में अपनायी गई थी। यह एक सैद्धांतिक परिभाषा है। व्यवहार में हमें पृथ्वी के चुंबकीय क्षेत्र के प्रभाव को विलुप्त करना चाहिए तथा बहुत लंबे तारों के स्थान पर उचित ज्यामिति की बहुफेरों की कुंडलियाँ लेनी चाहिए। एक उपकरण, जिसे ‘धारा तुला’ कहते हैं, का उपयोग इस यांत्रिक बल की माप के लिए किया जाता है।
आवेश के SI मात्रक, अर्थात कूलॉम को अब हम एेम्पियर के पदों में परिभाषित कर सकते हैं।
जब किसी चालक में 1A की अपरिवर्ती विद्युत धारा प्रवाहित होती है तो उसकी अनुप्रस्थ काट से एक सेकंड में प्रवाहित आवेश की मात्रा एक कूलॉम (1C) होती है।
* इससे यह अर्थ निकलता है कि जब हमारे पास समय निर्भर विद्युत धाराएँ/अथवा गतिशील आवेश होती हैं तब आवेशों/चालकों के बीच बलों के लिए न्यूटन का तीसरा नियम लागू नहीं होता। न्यूटन के तीसरे नियम का आवश्यक परिणाम यांत्रिकी में किसी वियुक्त निकाय के संवेग का संरक्षण है। तथापि यह विद्युत चुंबकीय क्षेत्रों के साथ समय निर्भर स्थितियों के प्रकरण पर लागू होती है, परंतु इस शर्त के साथ कि क्षेत्रों द्वारा वहन संवेग को भी सम्मिलित किया जाए।
समांतर विद्युत धाराओं के बीच आकर्षण के लिए रागेट का सर्पिल
चुंबकीय प्रभाव सामान्यतः विद्युत प्रभावों से कम प्रभावी होते हैं। इसके परिणामस्वरूप विद्युत धाराओं के बीच बल, कारक µ के अल्पमान के कारण, अल्प परिमाण के होते हैं। इसीलिए विद्युत धाराओं के बीच आकर्षण अथवा प्रतिकर्षण के बलों को निदर्शित करना कठिन है। इस प्रकार प्रत्येक तार से 5 A विद्युत धारा तथा 1 cm पृथकन के लिए प्रति मीटर बल 5 × 10–4 N होता है जो कि लगभग 50 mg भार होता है। यह इस प्रकार होगा जैसे कि किसी घिरनी से डोरी द्वारा लटका 50 mg भार उस डोरी से बँधे तार को खींच रहा हो। इस भार के कारण तार में हुआ विस्थापन लगभग अदृश्य होगा।
कोमल कमानी का उपयोग करके हम समांतर विद्युत धाराओं की प्रभावी लंबाई में वृद्धि कर सकते हैं तथा पारे (मरकरी) का उपयोग करके हम कुछ मिलीमीटर के विस्थापनों को भी प्रभावशाली ढंग से प्रेक्षणीय बना सकते हैं। आपको एेसी विद्युत धारा आपूर्ति की आवश्यकता भी होगी जो लगभग 5 A की अचर विद्युत धारा प्रदान करे।
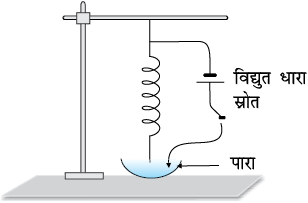
एक एेसी कोमल कमानी लीजिए जिसका प्राकृतिक दोलन काल लगभग 0.5 – 1 s हो। इसे ऊर्ध्वाधर लटकाकर इसके निचले सिरे पर चित्र में दर्शाए अनुसार एक नोंक जोड़िए। प्याली में थोड़ी मरकरी लीजिए तथा कमानी को इस प्रकार समायोजित कीजिए कि इसकी नोक मरकरी के पृष्ठ के ठीक ऊपर हो। दिष्ट विद्युत धारा (DC स्रोत) स्रोत लेकर इसके एक टर्मिनल को कमानी के ऊपरी सिरे से संयोजित कीजिए तथा दूसरे टर्मिनल को मरकरी में डुबोइए। यदि कमानी की नोंक मरकरी को स्पर्श करती है तो मरकरी से होते हुए विद्युत परिपथ पूरा हो जाता है।
मान लीजिए प्रारंभ में DC स्रोत ‘अॉफ’ है। मान लीजिए कमानी की नोंक इस प्रकार समायोजित है कि वह मरकरी के पृष्ठ को स्पर्श कर रही है। अब अचर विद्युत धारा स्रोत को ‘अॉन’ कीजिए तथा मंत्र-मुग्ध करने वाला परिणाम देखिए। कमानी एक झटके के साथ सिकुड़ती है, नोंक मरकरी से बाहर आ जाती है (लगभग 1mm), परिपथ टूट जाता है, विद्युत धारा प्रवाहित होना रुक जाता है, कमानी शिथिल हो जाती है तथा अपनी मूल स्थिति में आने का प्रयास करती है, कमानी की नोंक पुनः मरकरी के पृष्ठ को छूती है तथा परिपथ में विद्युत धारा प्रवाहित होने लगती है और यह चक्र टिक, टिक, टिक के साथ चलता रहता है। आरंभ में आपको अच्छा प्रभाव पाने के लिए कुछ समायोजन की आवश्यकता होती है।
क्योंकि मरकरी की वाष्प ज़हरीली होती है, अतः प्रयोग करते समय अपना चेहरा मरकरी से दूर रखिए। काफ़ी समय तक मरकरी की वाष्प के पास साँस मत खींचिए।
उदाहरण 4.10
किसी निर्धारित स्थान पर पृथ्वी के चुंबकीय क्षेत्र का क्षैतिज घटक 3.0 ×10–5 T है, तथा इस क्षेत्र की दिशा भौगोलिक दक्षिण से भौगोलिक उत्तर की ओर है। किसी अत्यधिक लंबे सीधे चालक से 1A की अपरिवर्ती धारा प्रवाहित हो रही है। जब यह तार किसी क्षैतिज मेज़ पर रखा है तथा विद्युत धारा के प्रवाह की दिशाएँ (a) पूर्व से पश्चिम की ओर; (b) दक्षिण से उत्तर की ओर हैं तो तार की प्रत्येक एकांक लंबाई पर बल कितना है?
हल
F = Il × B
F = IlB sinθ
प्रति एकांक लंबाई पर बल
f = F/l = I B sinθ
(a) जब विद्युत धारा पूर्व से पश्चिम की ओर प्रवाहित होती है, तब
θ = 90°
अतः
f = I B
= 1 × 3 × 10–5 = 3 × 10–5 N m–1
यह एेम्पियर की परिभाषा में वर्णित बल के मान 2×10–7 Nm–1 से बड़ा है। अतः एेम्पियर का मानकीकरण करने के लिए पृथ्वी के चुंबकीय क्षेत्र तथा अन्य भूले-भटके क्षेत्रों के प्रभावों को समाप्त करना महत्वपूर्ण है। बल की दिशा अधोमुखी है।
इस दिशा को ‘सदिशों के सदिश गुणनफल’ के दैशिक गुण के द्वारा प्राप्त किया जा
सकता है।
(b) जब विद्युत धारा के प्रवाह की दिशा दक्षिण से उत्तर की ओर है, तो
θ = 0o
f = 0
अतः चालक पर कोई बल कार्य नहीं करता।
4.10 विद्युत धारा पाश पर बल आघूर्ण, चुंबकीय द्विध्रुव
4.10.1 एकसमान चुंबकीय क्षेत्र में आयताकार विद्युत धारा पाश पर बल आघूर्ण
अब हम आपको यह दिखाएँगे कि एकसमान चुंबकीय क्षेत्र में स्थित कोई आयताकार पाश जिससे अपरिवर्ती विद्युत धारा I प्रवाहित हो रही है, एक बल आघूर्ण का अनुभव करता है। इस पर कोई नेट बल आरोपित नहीं होता। यह व्यवहार उस द्विध्रुव के व्यवहार के समरूपी है जो यह एकसमान विद्युत क्षेत्र में दर्शाता है (अनुभाग 1.12 देखिए)।
पहले हम उस सरल प्रकरण पर विचार करते हैं जिसमें आयताकार पाश इस प्रकार स्थित है कि एकसमान चुंबकीय क्षेत्र B पाश के तल में है। इसे चित्र 4.21 (a) में दर्शाया गया है।
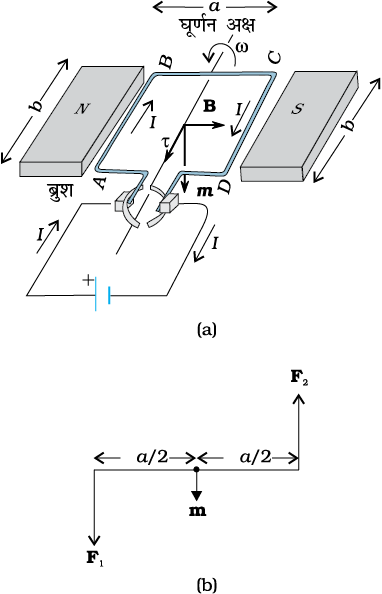
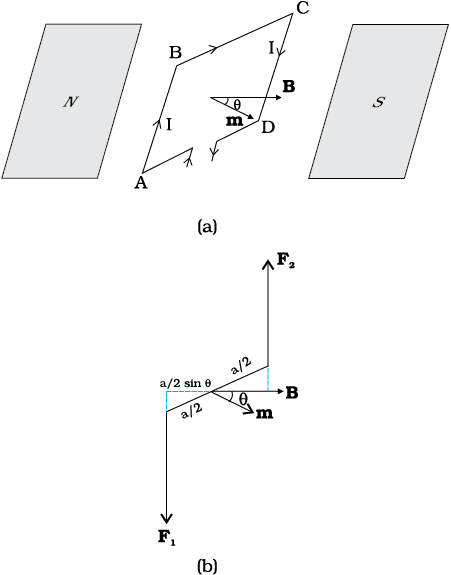
चित्र 4.21 (a) एकसमान चुंबकीय क्षेत्र में स्थित कोई विद्युत धारावाही आयताकार कुंडली। चुंबकीय आघूर्ण m अधोमुखी संकेत करता है। बल आघूर्ण τ अक्ष के अनुदिश है तथा इसकी प्रवृत्ति कुंडली को वामावर्त घूर्णन कराने की है। (b) कुंडली पर बल युग्म कार्य करते हुए।
चुंबकीय क्षेत्र पाश की दो भुजाओं AD तथा BC पर कोई बल आरोपित नहीं करता। यह पाश की भुजा AB के लंबवत है तथा इस पर बल F1 आरोपित करता है जिसकी दिशा पाश के तल में भीतर की ओर है। इस बल का परिमाण है ः
F1 = I b B
इसी प्रकार, चुंबकीय क्षेत्र भुजा CD पर एक बल F2 आरोपित करता है जो पाश के तल के बाहर की ओर है। इस बल का परिमाण है ः
F2 = I b B = F1
इसी प्रकार पाश पर आरोपित नेट बल शून्य है। बलों F1 तथा F2 के युगल के कारण पाश पर एक बल आघूर्ण कार्य करता है। चित्र 4.21 (b) में AD सिरे से पाश का एक दृश्य दिखाया गया है। यह स्पष्ट करता है कि यह बल आघूर्ण पाश में वामावर्त घूर्णन की प्रवृत्ति उत्पन्न करता है। इस बल आघूर्ण का परिमाण है ः
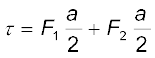
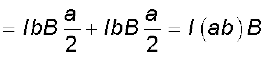
= I A B (4.26)
यहाँ A = ab आयत का क्षेत्रफल है।
अब हम आगे उस प्रकरण पर विचार करेंगे जिसमें पाश का तल चुंबकीय क्षेत्र के अनुदिश नहीं है, परंतु इनके बीच कोई कोण बनता है। हम चुंबकीय क्षेत्र B तथा कुंडली पर अभिलंब के बीच का कोण θ लेते हैं (पहला प्रकरण θ = π/2 के तदनुरूपी है)। चित्र 4.22 में यह व्यापक प्रकरण दर्शाया गया है।
भुजाओं BC तथा DA पर कार्यरत बल परिमाण में समान दिशा में विपरीत तथा कुंडली के अक्ष के अनुदिश कार्य करते हैं। ये बल BC तथा DA के संहति केंद्रों को संयोजित करते हैं। अक्ष के अनुदिश संरेखित होने के कारण ये एक दूसरे को निरस्त करते हैं, परिणामस्वरूप कोई नेट बल अथवा बल आघूर्ण नहीं है। भुजाओं AB तथा CD पर कार्यरत बल F1 तथा F2 हैं। ये भी परिमाण सहित समान एवं विपरीत हैं।
F1 = F2 = I b B
चित्र 4.22 (a) पाश ABCD का क्षेत्र सदिश चुंबकीय क्षेत्र से कोई यादृच्छिक कोण θ बनाता है। (b) पाश का ऊपरी दृश्य। भुजाओं AB तथा CD पर कार्यरत बल F1 तथा F2 दर्शाए गए हैं।
परंतु ये संरेख नहीं हैं। इसके परिणामस्वरूप पहले की तरह एक बल युग्म उत्पन्न होता है। तथापि, पिछले प्रकरण जिसमें पाश का तल चुंबकीय क्षेत्र के अनुदिश था, की तुलना में बल आघूर्ण का परिमाण अब कम है। इसका कारण यह है कि बलयुग्म बनाने वाले बलों के बीच की लंबवत दूरी कम हो गई है। चित्र 4.22(b) में सिरे AD से इस व्यवस्था का दृश्य दिखाया गया है। इसमें यह दर्शाया गया है कि ये दो बल एक बलयुग्म बनाते हैं। पाश पर बल आघूर्ण का परिमाण है ः
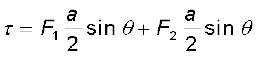
= I ab B sin θ
= I A B sin θ (4.27)
जैसे-जैसे θ 0, बलयुग्म के बलों के बीच लंबवत दूरी भी शून्य की ओर बढ़ती है। इससे बल संरेख बन जाते हैं तथा नेट बल तथा बल आघूर्ण शून्य हो जाते हैं। समीकरणों (4.26) तथा (4.27) के बल आघूर्णों को कुंडली के चुंबकीय आघूर्ण तथा चुंबकीय क्षेत्र के सदिश गुणनफल के रूप में व्यक्त कर सकते हैं। विद्युत धारा पाश के चुंबकीय आघूर्ण को हम इस प्रकार परिभाषित करते हैं
m = I A (4.28)
यहाँ क्षेत्र सदिश A की दिशा दक्षिण हस्त अंगुष्ठ नियम के अनुसार कागज़ के तल के भीतर की ओर निर्दिष्ट है (चित्र 4.21 देखिए) चूँकि m तथा B के बीच का कोण θ है, समीकरणों (4.26) तथा (4.27) को केवल एक व्यंजक द्वारा व्यक्त किया जा सकता है
(4.29)
यह स्थिरवैद्युतिकी के प्रकरण के सदृश है। [विद्युत क्षेत्र E में द्विध्रुव आघूर्ण pe का वैद्युत द्विध्रुव]
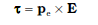
जैसा कि समीकरण (4.28) से स्पष्ट है, चुंबकीय क्षेत्र की विमाएँ [AL2] हैं तथा इसका मात्रक Am2 है।
समीकरण (4.29) से स्पष्ट है कि जब m चुंबकीय क्षेत्र B के समांतर अथवा प्रतिसमांतर होता है तो बल आघूर्ण τ विलुप्त हो जाता है। जब कुंडली पर बल आघूर्ण नहीं होता तो यह साम्यावस्था की ओर इंगित करता है (यह चुंबकीय आघूर्ण m की किसी वस्तु पर भी लागू होता है)। जब m तथा B समांतर होते हैं तो साम्यावस्था स्थायी होती है। कुंडली में कोई भी घूर्णन होने पर बल आघूर्ण उत्पन्न होता है जो कुंडली को वापस उसकी मूल स्थिति में ला देता है। जब ये प्रतिसमांतर होते हैं तो साम्यावस्था अस्थायी होती है क्योंकि कुंडली में कोई घूर्णन होने पर एक बल आघूर्ण उत्पन्न होता है जो इस घूर्णन में वृद्धि कर देता है। इस बल आघूर्ण की उपस्थिति के कारण ही लघु चुंबक अथवा कोई चुंबकीय द्विध्रुव बाह्य चुंबकीय क्षेत्र के साथ स्वयं को संरेखित कर लेता है।
यदि पाश में पास-पास सटे हुए N फेरे हैं तो बल आघूर्ण के लिए व्यंजक, समीकरण (4.29) अब भी लागू होता है। तब यह व्यंजक इस प्रकार व्यक्त किया जाता है
m = N I A (4.30)
उदाहरण 4.11
10 cm त्रिज्या की किसी कुंडली जिसमें पास-पास सटे 100 फेरे हैं, में 3.2 A विद्युत धारा प्रवाहित हो रही है। (a) कुंडली के केंद्र पर चुंबकीय क्षेत्र कितना है?
(b) इस कुंडली का चुंबकीय आघूर्ण क्या है?
यह कुंडली ऊर्ध्वाधर तल में रखी है तथा किसी क्षैतिज अक्ष जो उसके व्यास से संरेखित है, के परितः घूर्णन करने के लिए स्वतंत्र है। एक 2T का एकसमान चुंबकीय क्षेत्र क्षैतिज दिशा में है जो इस प्रकार है कि आरंभ में कुंडली का अक्ष चुंबकीय क्षेत्र की दिशा में है। चुंबकीय क्षेत्र के प्रभाव में कुंडली 90º के कोण पर घूर्णन कर जाती है। (c) आरंभिक तथा अंतिम स्थिति में कुंडली पर बल आघूर्ण के परिमाण क्या हैं? (d) 90º पर घूर्णन करने के पश्चात कुंडली द्वारा अर्जित कोणीय चाल कितनी है? कुंडली का जड़त्व आघूर्ण 0.1 kg m2 है।
हल
(a) समीकरण (4.16) से
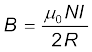
यहाँ, N = 100; I = 3.2 A, तथा R = 0.1 m इसलिए
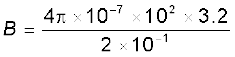
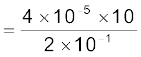(π × 3.2 = 10 का उपयोग करने पर)
= 2 × 10–3 T
B की दिशा दक्षिण हस्त अंगुष्ठ नियम द्वारा प्राप्त होती है।
(b) समीकरण (4.30) से चुंबकीय आघूर्ण
m = N I A = N I π r2 = 100 × 3.2 × 3.14 × 10–2 = 10 A m2
इस बार फिर दिशा दक्षिण हस्त अंगुष्ठ नियम द्वारा प्राप्त होती है।
(c)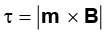 
[समीकरण (4.29) से]
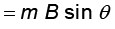
आरंभ मेें θ = 0, इस प्रकार आरंभिक बल आघूर्ण τi = 0, अंत में θ = π/2 (अथवा 90º) इस प्रकार अंतिम बल आघूर्ण τf = m B = 10 × 2 = 20 N m
(d) न्यूटन के द्वितीय नियम से
I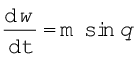 
यहाँ I कुंडली का जड़त्व आघूर्ण है। शृंखला नियम के अनुसार
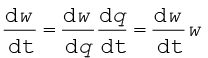
इसका उपयोग करने पर,
I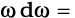 
θ = 0 से θ = π/2 तक समाकलन करने पर,
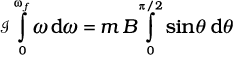
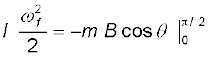= m B
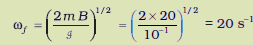
उदाहरण 4.12
(a) किसी चिकने क्षैतिज तल पर कोई विद्युत धारावाही वृत्ताकार पाश रखा है। क्या इस पाश के चारों ओर एेसा चुंबकीय क्षेत्र स्थापित किया जा सकता है कि यह पाश अपने अक्ष के चारों ओर स्वयं चक्कर लगाए (अर्थात ऊर्ध्वाधर अक्ष के चारों ओर)।
(b) कोई विद्युत वाही वृत्ताकार पाश किसी एकसमान बाह्य चुंबकीय क्षेत्र में स्थित है। यदि यह पाश घूमने के लिए स्वतंत्र है, तो इसके स्थायी संतुलन का दिक्विन्यास क्या होगा। यह दर्शाइए कि इसमें कुल क्षेत्र (बाह्य क्षेत्र + पाश द्वारा उत्पन्न क्षेत्र) का फ्लक्स अधिकतम होगा।
(c) अनियमित आकृति का कोई विद्युत धारावाही पाश किसी बाह्य चुंबकीय क्षेत्र में स्थित है। यदि तार लचीला है तो यह वृत्ताकार आकृति क्यों ग्रहण कर लेता है?
हल
(a) नहीं, क्योंकि इसके लिए ऊर्ध्वाधर दिशा में बल आघूर्ण τ की आवश्यकता होगी। परंतु
τ = I A × B, और चूँकि क्षैतिज पाश का क्षेत्रफल सदिश A ऊर्ध्वाधर दिशा में है, τ को B के किसी मान के लिए पाश के तल में होना चाहिए।
(b) स्थायी संतुलन वाला दिक्विन्यास वह है जिसमें पाश का क्षेत्रफल सदिश A बाह्य चुंबकीय क्षेत्र की दिशा में होता है। इस दिक्विन्यास में पाश द्वारा उत्पन्न चुंबकीय क्षेत्र बाह्य क्षेत्र की दिशा में ही है। इस प्रकार, दोनों क्षेत्र पाश के तल के लंबवत होने के कारण कुल क्षेत्र का अधिकतम फ्लक्स प्रदान करते हैं।
(c) यह क्षेत्र के लंबवत तल में वृत्ताकार पाश का रूप इसलिए ग्रहण कर लेता है ताकि इससे होकर अधिकतम फ्लक्स प्रवाहित हो सके। क्योंकि किसी दी गई परिमिति के लिए वृत्त का क्षेत्रफल किसी भी अन्य आकृति की तुलना में अधिकतम होता है।
4.10.2 वृत्ताकार विद्युत धारा पाश चुंबकीय द्विध्रुव
इस अनुभाग में हम मौलिक चुंबकीय तत्व के रूप में किसी विद्युत धारा पाश के विषय में विचार करेंगे। हम यह दर्शाएँगे कि वृत्ताकार विद्युत धारा पाश के कारण चुंबकीय क्षेत्र (अधिक दूरियों पर) व्यवहार में वैद्युत द्विध्रुव के विद्युत क्षेत्र से बहुत कुछ समान होता है। अनुभाग 4.6 में हमने R त्रिज्या के वृत्ताकार पाश जिससे अपरिवर्ती विद्युत धारा I प्रवाहित हो रही है, के कारण पाश के अक्ष चुंबकीय क्षेत्र का मूल्यांकन किया था। इस चुंबकीय क्षेत्र का परिमाण [समीकरण (4.15)],
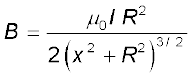
तथा इसकी दिशा अक्ष के अनुदिश थी जिसे दक्षिण हस्त अंगुष्ठ नियम द्वारा प्राप्त किया गया था (चित्र 4.12)। यहाँ पर x पाश के केंद्र से उसके अक्ष के अनुदिश दूरी है। यदि x >> R है, तो हम उपरोक्त व्यंजक के हर से R2 की उपेक्षा कर सकते हैं। इस प्रकार
ध्यान दीजिए, पाश का क्षेत्रफल A = πR2 , इस प्रकार
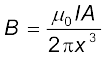
जैसा कि पहले हमने चुंबकीय आघूर्ण m के परिमाण की परिभाषा
m = I A के रूप में की थी
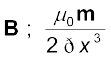
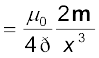[4.31(a)]
समीकरण [4.31(a)] का यह व्यंजक किसी स्थिरवैद्युत द्विध्रुव के विद्युत क्षेत्र के लिए पहले प्राप्त किए जा चुके व्यंजक से काफ़ी मेल खाता है। इस समानता को देखने के लिए हम प्रतिस्थापित करते हैं
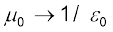
(स्थिरवैद्युत द्विध्रुव)
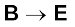(स्थिरवैद्युतीय क्षेत्र)
तब हमें प्राप्त होता है,
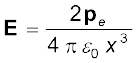
जो कि यथार्थ रूप से किसी वैद्युत द्विध्रुव का उसके अक्ष पर विद्युत क्षेत्र है। इसके विषय में हमने अध्याय 1 अनुभाग 1.10 [समीकरण (1.20)] में अध्ययन किया था।
यह दर्शाया जा सकता है कि उपरोक्त सदृशता को आगे भी ले जाया जा सकता है। हमने यह पाया था कि द्विध्रुव के लंबवत द्विविभाजक पर विद्युत क्षेत्र [समीकरण (1.21) देखिए]
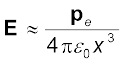
यहाँ x द्विध्रुव से दूरी है। यदि हम उपरोक्त संबंध में p m तथा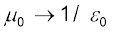 
से प्रतिस्थापित करें, तो हमें पाश के तल में किसी बिंदु जिसकी केंद्र से दूरी x है, के लिए B के परिणाम प्राप्त हो सकते हैं। x >>R के लिए
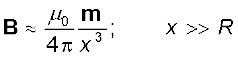[4.31(b)]
किसी बिंदु चुंबकीय द्विध्रुव के लिए समीकरणों [4.31(a)] तथा [4.31(b)] द्वारा दिए गए परिणाम यथार्थ बन जाते हैं।
उपरोक्त परिणाम किसी भी समतल पाश पर लागू होते दर्शाए जा सकते हैं। समतल विद्युत धारा पाश किसी अक्ष चुंबकीय द्विध्रुव के तुल्य होता है जिसका चुंबकीय आघूर्ण m = I A है जो कि वैद्युत द्विध्रुव आघूर्ण p के सदृश है। ध्यान दीजिए, इतना होते हुए भी एक मूल अंतर यह है कि कोई वैद्युत द्विध्रुव दो मूल इकाइयों – आवेशों (अथवा विद्युत एकध्रुवों) से मिलकर बनता है। जबकि चुंबकत्व में कोई चुंबकीय द्विध्रुव (अथवा विद्युत धारा पाश) एक अत्यंत मूल तत्व है। चुंबकत्व में विद्युत आवेशों के समतुल्य अर्थात चुंबकीय एकध्रुवों, का अस्तित्व अब तक अज्ञात है।
हमने यह दर्शाया कि कोई विद्युत धारा पाश (i) चुंबकीय क्षेत्र उत्पन्न करता है (चित्र 4.12 देखिए) तथा अधिक दूरियों पर एक चुंबकीय द्विध्रुव की तरह व्यवहार करता है तथा (ii) पर एक बल आघूर्ण कार्य करता है जैसे चुंबकीय सुई। इसके आधार पर एेम्पियर ने यह सुझाव दिया था कि समस्त चुंबकत्व प्रवाहित विद्युत धाराओं के कारण है। यह आंशिक रूप से सत्य प्रतीत होता है तथा अब तक कोई भी चुंबकीय एकध्रुव नहीं देखा जा सका है। तथापि मूल कण जैसे इलेक्ट्रॉन अथवा प्रोटॉन के भी नैज चुंबकीय आघूर्ण हैं जो प्रवाहित विद्युत धाराओं के कारण नहीं हैं।
4.10.3 परिक्रमी इलेक्ट्रॉन का चुंबकीय द्विध्रुव आघूर्ण
अध्याय 12 में हम हाइड्रोजन परमाणु के बोर मॉडल के विषय में अध्ययन करेंगे। कदाचित आपने इस मॉडल के बारे में सुना होगा। जिसे डेनमार्क के भौतिक विज्ञानी नील बोर ने सन् 1911 में प्रस्तावित किया था और जो नए प्रकार की यांत्रिकी जिसे क्वांटम यांत्रिकी कहते हैं, के लिए मील का एक पत्थर था। बोर मॉडल में, इलेक्ट्रॉन (एक ऋणावेशित कण) किसी धनावेशित नाभिक के चारों ओर ठीक उसी प्रकार परिक्रमा करता है जिस प्रकार कोई ग्रह सूर्य की परिक्रमा करता है। इलेक्ट्रॉन के प्रकरण में बल स्थिरवैद्युत (कूलॉम बल) होता है जबकि सूर्य ग्रह प्रकरण में यह गुरुत्वाकर्षण बल होता है। चित्र 4.23 में बोर मॉडल दर्शाया गया है।
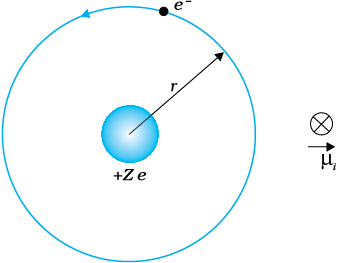
चित्र 4.23 हाइड्रोजन जैसे परमाणुओं के बोर मॉडल में, ऋणावेश युक्त इलेक्ट्रॉन केंद्रस्थ धनावेश युक्त (+Z e)नाभिक के चारों ओर एकसमान चाल से घूम रहा है। इलेक्ट्रॉन की एकसमान वर्तुल गति एक धारा लूप बनाती है। चुंबकीय आघूर्णों की दिशा कागज़ के तल के लंबवत भीतर की ओर है तथा इसे पृथक रूप चिह्न ⊗ द्वारा निर्दिष्ट किया गया है।
किसी स्थिर भारी नाभिक जिसका आवेश +Ze है, के चारों ओर (–e) आवेश का इलेक्ट्रॉन (e = + 1.6 × 10–19 C) एकसमान वर्तुल गति करता रहता है। इससे विद्युत धारा I बनती है। यहाँ
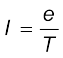(4.32)
यहाँ T परिक्रमण का आवर्तकाल है। यदि इलेक्ट्रॉन की कक्षा की त्रिज्या r तथा कक्षीय चाल v है, तो
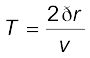(4.33)
समीकरण में T का मान प्रतिस्थापित करने पर I = ev/2πr
इस परिसंचारी विद्युत धारा के साथ एक चुंबकीय आघूर्ण संबद्ध होगा जिसे प्रायः µl द्वारा निर्दिष्ट करते हैं। समीकरण (4.28) से इसका परिमाण है µl = Iπr2 = evr/2
चित्र 4.23 में इस चुंबकीय आघूर्ण की दिशा कागज़ के तल में भीतर की ओर है। [इस परिणाम पर हमेें पहले वर्णन किए जा चुके दक्षिण हस्त नियम तथा इस तथ्य के आधार पर पहुंचे हैं कि ऋणावेशित इलेक्ट्रॉन वामावर्त गति कर रहा है जिसके फलस्वरूप विद्युत धारा दक्षिणावर्त है।] उपरोक्त व्यंजक के दक्षिण पक्ष को इलेक्ट्रॉन के द्रव्यमान me से गुणा एवं भाग करने पर हमें प्राप्त होता है
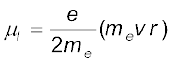
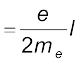[4.34(a)]
यहाँ, l केंद्रीय नाभिक के परितः इलेक्ट्रॉन के कोणीय संवेग का परिमाण है। सदिश रूप में
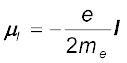[4.34(b)]
यहाँ ऋणात्मक चिह्न यहाँ यह संकेत देता है कि इलेक्ट्रॉन के कोणीय संवेग की दिशा चुंबकीय आघूर्ण की दिशा के विपरीत है। यदि हमने इलेक्ट्रॉन (जिस पर आवेश –e है) के स्थान पर (+q) आवेश का कोई कण लिया होता तो कोणीय संवेग तथा चुंबकीय आघूर्ण दोनों की एक ही दिशा होती। अनुपात
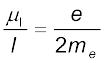(4.35)
इसे घूर्ण चुंबकीय अनुपात कहते हैं तथा यह एक नियतांक है। इलेक्ट्रॉन के लिए इस अनुपात का मान 8.8 × 1010 C /kg है जिसे प्रयोगों द्वारा सत्यापित किया जा चुका है।
यह तथ्य कि परमाण्विक स्तर तक भी चुंबकीय आघूर्ण विद्यमान है परमाण्विक आघूर्ण संबंधी एेम्पियर की साहसपूर्ण परिकल्पना की पुष्टि करता है। एेम्पियर के अनुसार, यह पदार्थों के चुंबकीय गुणों को भली-भाँति स्पष्ट करने में सहायक है। क्या हम उस परमाणवीय द्विध्रुव आघूर्ण को कोई निश्चित मान दे सकते हैं? इसका उत्तर है – हाँ। बोर मॉडल की परिधि में एेसा किया जाना संभव है। बोर ने यह परिकल्पना की थी कि कोणीय संवेग एक विविक्त मानाें का समुच्चय ही हो सकता है। अर्थात
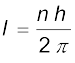(4.36)
यहाँ n एक प्राकृत संख्या, n = 1, 2, 3, ... है तथा h एक नियतांक है जिसे वैज्ञानिक मैक्स प्लांक के नाम पर (प्लांक नियतांक) कहते हैं तथा इसका मान h = 6.626 × 10–34 J s है। कोणीय वेग की विविक्तता संबंधी इस शर्त को बोर क्वांटीकरण-शर्त कहते हैं। इसके विषय में हम अध्याय 12 में विस्तार से चर्चा करेंगे। यहाँ हमारा उद्देश्य मात्र प्राथमिक द्विध्रुव आघूर्ण को परिकलित करने में इसका उपयोग करना है। n = 1 लेने पर समीकरण (4.34) से हमें प्राप्त होता है,
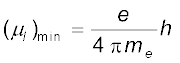
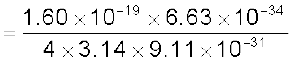
= 9.27 × 10–24 Am2 (4.37)
यहाँ अधोलिखित min का उपयोग न्यूनतम के लिए किया गया है। इस न्यूनतम मान को बोर मैग्नेटॉन कहते हैं।
एकसमान वर्तुल गति करने वाले प्रत्येक आवेश के पास कोई चुंबकीय आघूर्ण अवश्य ही संबद्ध होता है जिसे समीकरण (4.34) के समान किसी व्यंजक से व्यक्त किया जाता है। इस द्विध्रुव आघूर्ण को कक्षीय चुंबकीय आघूर्ण कहते हैं। इसीलिए µl में अधोलिखित ‘l’ लगा है। कक्षीय चुंबकीय आघूर्ण के अतिरिक्त इलेक्ट्रॉन का एक नैज चुंबकीय आघूर्ण भी होता है जिसका आंकिक मान वही है जैसा समीकरण (4.37) में दर्शाया गया है। इस आघूर्ण को चक्रण चुंबकीय आघूर्ण कहते हैं। परंतु हम तुरंत ही यह स्पष्ट कर देना चाहते हैं कि इसका यह अर्थ नहीं है कि इलेक्ट्रॉन घूर्णन गति करता है। इलेक्ट्रॉन एक मूल कण है तथा प्रचक्रमान लट्टू अथवा पृथ्वी की भाँति इसका अपना कोई घूर्णन अक्ष नहीं है जिस पर यह घूर्णन कर सके। इतना होने पर भी इसका एक नैज चुंबकीय आघूर्ण होता है। लोहे तथा अन्य चुंबकीय पदार्थों में चुंबकन की सूक्ष्म जड़ें इसी नैज चक्रण चुंबकीय आघूर्ण से निकलती प्रतीत होती हैं।
4.11 चल कुंडली गैल्वेनोमीटर
अध्याय 3 के अंतर्गत विद्युत परिपथों में प्रवाहित धाराओं तथा वोल्टताओं के विषय में विस्तार से चर्चा की जा चुकी है। परंतु हम इन्हें किस प्रकार मापते हैं। हम यह कैसे कहते हैं कि किसी परिपथ में 1.5 A विद्युत धारा प्रवाहित हो रही है अथवा किसी प्रतिरोधक के सिरों के बीच 1.2 V विभवांतर है। चित्र 4.24 में इसी उद्देश्य के उपयोग से किया जाने वाला उपयोगी उपकरण दर्शाया गया है जिसे चल कुंडली गैल्वेनोमीटर (moving coil galvanometer — MCG) कहते हैं। यह एक एेसी युक्ति है जिसके सिद्धांत को हमारे द्वारा अनुभाग में 4.10 में की गई चर्चा के आधार पर समझा जा सकता है।
चल कुंडली गैल्वेनोमीटर में किसी एकसमान त्रिज्य (अरीय) चुंबकीय क्षेत्र में किसी अक्ष पर घूर्णन करने के लिए अनेक फेरों वाली एक कुंडली होती है (चित्र 4.24)। इस कुंडली के भीतर एक बेलनाकार नर्म लोह क्रोड जो केवल चुंबकीय क्षेत्र को त्रिज्य ही नहीं बनाता वरन चुंबकीय क्षेत्र की प्रबलता में भी वृद्धि कर देता है। जब इस कुंडली से कोई विद्युत धारा प्रवाहित की जाती है तो इस पर एक बल आघूर्ण कार्य करता है। समीकरण (4.26) के अनुसार इस बल आघूर्ण τ का मान होता है
τ = NI AB
यहाँ, भौतिक राशियों के प्रतीकों के अपने सामान्य अर्थ हैं। चूँकि डिज़ाइन के अनुसार चुंबकीय क्षेत्र त्रिज्य है, हमने बल आघूर्ण के लिए दिए गए उपरोक्त व्यंजक में sin θ = 1 लिया है। यह चुंबकीय बल आघूर्ण NIAB कुंडली में घूर्णन की प्रवृत्ति उत्पन्न करता है जिसके फलस्वरूप कुंडली अपने अक्ष पर घूर्णन करती है। कुंडली से जुड़ी कमानी Sp में कुंडली के घूर्णन के विरोध में बल आघूर्ण kφ उत्पन्न हो जाता है जो कुंडली के बल आघूर्ण NIAB को संतुलित करता है; फलस्वरूप कुंडली में φ कोण का स्थायी कोणीय विक्षेप आ जाता है। साम्यावस्था में
kφ = NI AB
यहाँ k कमानी का एेंठन नियतांक है, अर्थात प्रति एकांक एेंठन प्रत्यानयन बल आघूर्ण है। विक्षेप φ का पाठ्यांक कमानी के साथ जुड़े संकेतक द्वारा पैमाने पर लिया जा सकता है। उपरोक्त व्यंजक के अनुसार φ का मान है
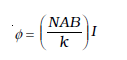(4.38)
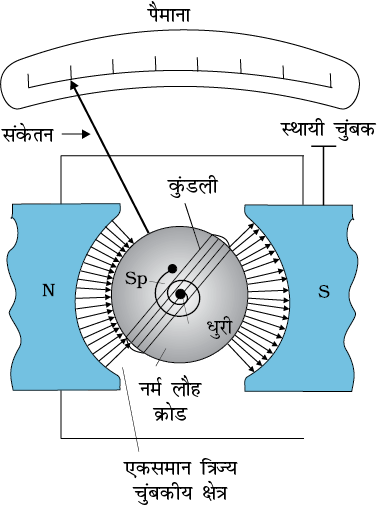
चित्र 4.24 चल कुंडली गैल्वेनोमीटर। इसके अवयवों का वर्णन पाठ में किया गया है। आवश्यकतानुसार इस उपकरण का उपयोग हम धारा का पता लगाने या धारा (एेमीटर), या फिर वोल्टता (वोल्टमीटर) का मान ज्ञात करने के लिए करते हैं।
कोष्ठक की राशि का मान किसी दिए गए गैल्वेनोमीटर के लिए एक नियतांक है। गैल्वेनोमीटर का उपयोग कई प्रकार से किया जा सकता है। इसका उपयोग एक संसूचक के रूप में यह ज्ञात करने के लिए किया जा सकता है कि परिपथ में कोई विद्युत धारा प्रवाहित हो रही है अथवा नहीं। इस प्रकार का उपयोग हमने व्हीटस्टोन सेतु व्यवस्था में किया था। जब गैल्वेनोमीटर का उपयोग संसूचक के रूप में करते हैं तो इसका संकेतक साम्यावस्था (शून्य विक्षेप स्थिति अर्थात जब कुुंडली में कोई विद्युत धारा प्रवाहित नहीं होती) पैमाने के मध्य में होता है न कि बाईं ओर जैसा कि चित्र 4.24 में दर्शाया गया है। प्रवाहित विद्युत धारा के अनुसार गैल्वेनोमीटर का संकेतक विद्युत धारा की दिशा के अनुरूप बाएँ अथवा दाएँ विक्षेपित हो जाता है।
गैल्वेनोमीटर का उपयोग इसी रूप में किसी परिपथ में प्रवाहित विद्युत धारा को मापने के लिए एेमीटर की भाँति नहीं किया जा सकता। इसके दो कारण हैं (i) गैल्वेनोमीटर एक अत्यंत सुग्राही युक्ति है, यह µA कोटि की विद्युत धारा के लिए पूर्ण पैमाना विक्षेप देती है। (ii) विद्युत धारा को मापने के लिए गैल्वेनोमीटर को परिपथ में श्रेणीक्रम में जोड़ना होता है। क्योंकि इसका प्रतिरोध अधिक होता है जो परिपथ में प्रवाहित होने वाली विद्युत धारा के मान को परिवर्तित कर देता है। इस परेशानी को दूर करने के लिए एक अल्प-मान वाला प्रतिरोध rs जिसे शंट कहते हैं, गैल्वेनोमीटर की कुंडली के पार्श्वक्रम में संयोजित किया जाता है जिससे अधिकांश विद्युत धारा इस शंट से प्रवाहित हो जाती है। इस प्रकार इस व्यवस्था का प्रतिरोध हो जाता है–
RG rs / (RG + rs) ~ rs यदि RG >> rs
यदि परिपथ के प्रतिरोध Re की तुलना में rs का मान कम है तो मापक यंत्र को परिपथ में जोड़ने का प्रभाव भी कम होगा जिसकी उपेक्षा की जा सकती है। इस व्यवस्था का एक योजना आरेख चित्र 4.25 में दिखाया गया है। इस प्रकार बने एेमीटर के पैमाने का अंशांकन कर दिया जाता है ताकि आसानी से धारा का मान पढ़ा जा सके। एेमीटर की सुग्राहिता की परिभाषा हम विक्षेप प्रति इकाई धारा के रूप में करते हैं। समीकरण (4.38) के अनुसार धारा सुग्राहिता है,
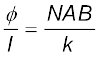(4.39)
किसी भी उत्पादक के लिए गैल्वेनोमीटर की सुग्राहिता में वृद्धि करने का सरल उपाय यह है कि वह कुंडली में फेरों की संख्या N में वृद्धि कर दे। हम अपने प्रयोग की आवश्यकता के अनुसार गैल्वेनोमीटर का चयन करते हैं।
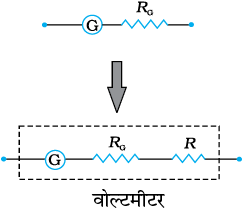
चित्र 4.25 एक अत्यल्प मान का शंट प्रतिरोध rs पार्श्वक्रम में लगाकर किसी गैल्वेनोमीटर (G) को एेमीटर (A) में रूपांतरित करना।
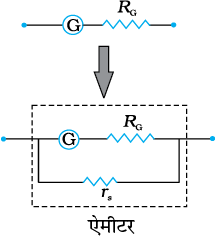
चित्र 4.26 श्रेणीक्रम में एक बड़ा प्रतिरोध R लगाकर गैल्वेनोमीटर (G) को वोल्टमीटर (V) में परिवर्तित करना।
धारामापी का उपयोग परिपथ के किसी अंश के सिरों के बीच विभवांतर ज्ञात करने के लिए वोल्टतामापी के रूप में भी हो सकता है। इस उद्देश्य के लिए इसको परिपथ के उस अंश के पार्श्वक्रम में लगाना होगा। और फिर, इसमें से अत्यल्प धारा प्रवाहित होनी चाहिए, अन्यथा, वोल्टता की माप मूल व्यवस्था को अत्यधिक विक्षुब्ध कर देगी। प्रायः हम मापक यंत्रों द्वारा उत्पन्न विक्षोभ को एक प्रतिशत से कम रखते हैं। माप की परिशुद्धता बनाए रखने के लिए, गैल्वेनोमीटर के श्रेणीक्रम में एक बड़ा प्रतिरोध R जोड़ा जाता है। इस व्यवस्था का योजना आरेख चित्र 4.26 में दर्शाया गया है। ध्यान दीजिए कि अब वोल्टमीटर का कुल प्रतिरोध,
RG + R =
R : अर्थात प्रतिरोध बहुत अधिक है।
वोल्टमीटर के पैमाने को अंशांकित कर दिया जाता है ताकि आसानी से वोल्टता का मान पढ़ा जा सके। किसी वोल्टमापी की वोल्टता सुग्राहिता की परिभाषा हम विक्षेप प्रति एकांक वोल्टता से करते हैं। समीकरण (4.38) से
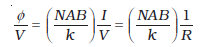(4.40)
यहाँ एक रोचक तथ्य ध्यान देने योग्य यह है कि धारा सुग्राहिता में वृद्धि करने पर यह आवश्यक नहीं है कि वोल्टता सुग्राहिता में भी वृद्धि हो जाएगी। आइए समीकरण (4.39) पर विचार करें जो धारा सुग्राहिता का माप बताती है। यदि N → 2N अर्थात यदि फेरों की संख्या दोगुनी कर दी जाए, तो
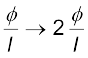
अर्थात धारा सुग्राहिता भी दोगुनी हो जाती है। किंतु, गैल्वेनोमीटर का प्रतिरोध भी दो गुना हो जाने की संभावना है क्योंकि यह तार की लंबाई के अनुक्रमानुपाती है। समीकरण (4.40) में N→2N एवं R→2R, अतः वोल्टता सुग्राहिता,
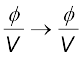
अपरिवर्तित रहती है। अतः व्यापक रूप से गैल्वेनोमीटर से एेमीटर में रूपांतरित करने के लिए जो संशोधन किए जाते हैं गैल्वेनोमीटर को वोल्टमीटर में परिवर्तित करने के लिए इनसे भिन्न संशोधन किए जाने चाहिए।
उदाहरण 4.13
नीचे दिखाए गए परिपथ में धारा का मान क्या है यदि दिखाया गया एेमीटर, (a) RG = 60.00 Ω प्रतिरोध का गैल्वेनोमीटर है। (b) भाग (a) में बताया गया गैल्वेनोमीटर ही है परंतु इसको rs = 0.02 Ω का शंट प्रतिरोध लगाकर एेमीटर में परिवर्तित किया गया है। (c) शून्य प्रतिरोध का एक आदर्श एेमीटर है।
चित्र 4.27
हल
(a) परिपथ में कुल प्रतिरोध है
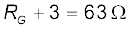इसलिए I = 3/63 = 0.048 A
(b) एेमीटर में रूपांतरित गैल्वेनोमीटर का प्रतिरोध
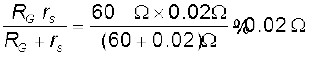
परिपथ में कुल प्रतिरोध
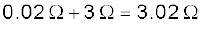अतः I = 3/3.02 = 0.99 A
(c) शून्य प्रतिरोध के आदर्श एेमीटर के लिए
I = 3/3 = 1.00 A
सारांश
1. चुंबकीय क्षेत्र B पर विद्युत क्षेत्र E की उपस्थिति में v वेग से गतिमान किसी आवेश q पर लगने वाले कुल बल को लोरेंज बल कहते हैं। इसे नीचे दिए गए व्यंजक द्वारा व्यक्त किया जाता है।
F = q (v × B + E)
चुंबकीय क्षेत्र q (v × B), v के अभिलंबवत है तथा किया गया कार्य शून्य है।
2. l लंबाई के किसी सीधे चालक जिससे स्थायी विद्युत धारा I प्रवाहित हो रही है, किसी एकसमान बाह्य चुंबकीय क्षेत्र में बल F का अनुभव करता है,
F = I l × B
यहाँ |l| = l तथा l की दिशा विद्युत धारा की दिशा द्वारा प्रदान की जाती है।
3. किसी एकसमान चुंबकीय क्षेत्र में, कोई आवेश q, B के अभिलंबवत तल में वृत्ताकार कक्षा में गतिमान है। इसकी एकसमान वर्तुल गति की आवृत्ति को साइक्लोट्रॉन आवृत्ति कहते हैं जिसे इस प्रकार व्यक्त किया जाता है–
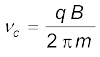
यह आवृत्ति कण की चाल तथा त्रिज्या पर निर्भर नहीं करती। इस तथ्य का उपयोग साइक्लोट्रॉन नामक मशीन में किया जाता है जो आवेशित कणों को त्वरित करने में उपयोगी होता है।
4. बायो-सावर्ट नियम के अनुसार dl लंबाई के किसी अवयव जिससे अपरिवर्ती विद्युत धारा I प्रवाहित हो रही है, के कारण r सदिश दूरी पर स्थित किसी बिंदु P पर चुंबकीय क्षेत्र dB इस प्रकार व्यक्त किया जाता है–
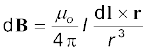
P पर कुल क्षेत्र प्राप्त करने के लिए हमें इस सदिश व्यंजक को चालक की समस्त लंबाई के लिए समाकलित करना चाहिए।
5. त्रिज्या R की वृत्ताकार कुंडली जिससे I धारा प्रवाहित हो रही है, के कारण केंद्र से अक्षीय दूरी x पर चुंबकीय क्षेत्र का परिमाण
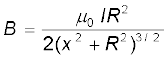
कुंडली के केंद्र पर इस क्षेत्र का परिमाण
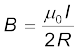
6. एेम्पियर का परिपथीय नियम ः मान लीजिए कोई खुला पृष्ठ S किसी पाश C द्वारा परिबद्ध है। तब एेम्पियर के नियम के अनुसार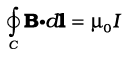 
यहाँ I पृष्ठ S से प्रवाहित विद्युत
धारा है। I का चिह्न दक्षिण हस्त नियम द्वारा निर्धारित किया जाता है। हमने यहाँ इस नियम के सरलीकृत रूप पर चर्चा की है। यदि B बंद वक्र की परिधि L के हर बिंदु पर स्पर्शी के अनुदिश निर्दिष्ट है तथा परिधि के अनुदिश इसका परिमाण नियत है तो
BL = µ0 Ie
यहाँ Ie बंद परिपथ द्वारा परिबद्ध नेट विद्युत धारा है।
7. किसी लंबे सीधे तार जिससे I विद्युत धारा प्रवाहित हो रही है, से R दूरी पर स्थित किसी बिंदु पर चुंबकीय क्षेत्र का परिमाण
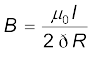
क्षेत्र रेखाएँ तार के साथ संकेंद्री वृत्त होती हैं।
8. किसी लंबी परिनालिका जिससे I विद्युत धारा प्रवाहित हो रही है, के भीतर चुंबकीय क्षेत्र B का परिमाण
B = µ0nI
यहाँ n परिनालिका की प्रति एकांक लंबाई में फेरों की संख्या है। किसी टोरॉइड के लिए चुंबकीय क्षेत्र B का परिमाण
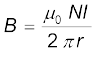
यहाँ n फेरों की कुल संख्या तथा r औसत त्रिज्या है।
9. समांतर विद्युत धाराएँ आकर्षित तथा प्रतिसमांतर विद्युत धाराएँ प्रतिकर्षित करती हैं।
10. बहुत पास लिपटे N फेरों तथा A क्षेत्रफल के समतलीय पाश जिससे विद्युत धारा I में प्रवाहित हो रही है, का एक चुंबकीय आघूर्ण m होता है
m = N I A
तथा m की दिशा दक्षिण हस्त अंगुष्ठ नियम से निर्धारित होती है। इस नियम के अनुसार, "अपने दाएँ हाथ की हथेली को इस प्रकार पाश के अनुदिश मोड़िए कि उँगलियाँ विद्युत धारा की दिशा में संकेत करें तो, बाहर की ओर खिंचा अँगूठा m (और A) की दिशा बताता है।
जब यह पाश किसी एकसमान चुंबकीय क्षेत्र B में रखा जाता है तो इस पर आरोपित बल F = 0
तथा इस पर बल आघूर्ण
τ = m × B
किसी चल कुंडली गैल्वेनोमीटर में इस बल आघूर्ण को कमानी द्वारा लगाया प्रति बल आघूर्ण संतुलित कर लेता है और तब हमें प्राप्त होता है
kφ = NI AB
यहाँ φ संतुलन विक्षेप है तथा k कमानी का एेंठन नियतांक है।
11. केंद्रीय नाभिक के चारों ओर गतिमान किसी इलेक्ट्रॉन का एक चुंबकीय आघूर्ण µl होता है जिसे इस प्रकार व्यक्त करते हैं ः
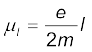
यहाँ l केंद्रीय नाभिक के परितः परिसंचारी इलेक्ट्रॉन का कोणीय संवेग का परिमाण है। µl के लघुतम मान को बोहर मेग्नेटॉन µB कहते हैं (µB = 9.27×10–24 J/T)।
12. किसी चल कुंडली गैल्वेनोमीटर को उसकी कुंडली के पार्श्वक्रम में कोई अल्प परिमाण का शंट प्रतिरोध rs संबद्ध करके एेमीटर में रूपांतरित किया जा सकता है। गैल्वेनोमीटर की कुंडली के साथ श्रेणीक्रम में अधिक परिमाण का प्रतिरोध संबद्ध करके उसे वोल्टमीटर में रूपांतरित किया जा सकता है।
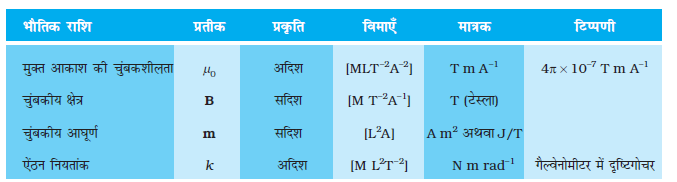
विचारणीय विषय
1. स्थिरवैद्युत क्षेत्र रेखाएँ धनावेश से आरंभ होकर ऋणावेश पर समाप्त हो जाती हैं अथवा अनंत पर लुप्त या विलीन हो जाती हैं। चुंबकीय क्षेत्र रेखाएँ सदैव बंद पाश बनाती हैं।
2. इस अध्याय में वर्णित विचार केवल अपरिवर्ती विद्युत धाराओं (जो समय के साथ परिवर्तित नहीं होती)के लिए ही लागू है।
समय के साथ परिवर्तित होने वाली विद्युत धाराओं के लिए न्यूटन का तीसरा नियम वैद्युतचुंबकीय क्षेत्र के संवेग का संज्ञान करने पर ही वैध होता है।
3. लोरेंज बल के समीकरण का स्मरण कीजिए,
F = q (v × B + E)
वेग निर्भर इस बल ने कुछ महानतम वैज्ञानिक विचारकों का ध्यान आकर्षित किया। यदि कोई प्रेेक्षक एक एेसे फ्रेम में पहुँच जाए जहाँ उसका क्षणिक वेेग v हो तो बल का चुंबकीय भाग शून्य हो जाता है। तब आवेशित कण की गति यह मानकर समझाई जा सकती है कि इस नए फ्रेम में एक उचित विद्युत क्षेत्र विद्यमान है। इस यांत्रिकी के विस्तार में हम नहीं जाएँगे। इसके विषय में आप आगे की कक्षाओं में पढ़ेंगे। लेकिन इस बात पर हम ज़ोर देना चाहेंगे कि इस विरोधाभास का समाधान इस तथ्य में निहित है कि विद्युत और चुंबकत्व एक-दूसरे से जुड़े हुए प्रक्रम हैं (विद्युतचुंबकत्व) और लोरेंज बल का व्यंजक, प्रकृति में किसी सार्वभौम वरीय संदर्भ फ्रेम में अंतर्निहित नहीं है।
4. एेम्पियर का परिपथीय नियम, बायो-सावर्ट नियम से अलग नहीं है। यह बायो-सावर्ट नियम से व्युत्पन्न किया जा सकता है। इसका बायो-सावर्ट नियम से वैसा ही संबंध है जैसा कि गाउस नियम का वूॅηलाम नियम से।
अभ्यास
4.1 तार की एक वृत्ताकार कुंडली में 100 फेरे हैं, प्रत्येक की त्रिज्या 8.0 cm है और इनमें 0.40 A विद्युत धारा प्रवाहित हो रही है। कुंडली के केंद्र पर चुंबकीय क्षेत्र का परिमाण क्या है?
4.2 एक लंबे, सीधे तार में 35 A विद्युत धारा प्रवाहित हो रही है। तार से 20 cm दूरी पर स्थित किसी बिंदु पर चुंबकीय क्षेत्र का परिमाण क्या है?
4.3 क्षैतिज तल में रखे एक लंबे सीधे तार में 50 A विद्युत धारा उत्तर से दक्षिण की ओर प्रवाहित हो रही है। तार के पूर्व में 2.5 m दूरी पर स्थित किसी बिंदु पर चुंबकीय क्षेत्र B का परिमाण और उसकी दिशा ज्ञात कीजिए।
4.4 व्योमस्थ खिंचे क्षैतिज बिजली के तार में 90 A विद्युत धारा पूर्व से पश्चिम की ओर प्रवाहित हो रही है। तार के 1.5 m नीचे विद्युत धारा के कारण उत्पन्न चुंबकीय क्षेत्र का परिमाण और दिशा क्या है?
4.5 एक तार जिसमें 8 A विद्युत धारा प्रवाहित हो रही है, 0.15 T के एकसमान चुंबकीय क्षेत्र में, क्षेत्र से 30° का कोण बनाते हुए रखा है। इसकी एकांक लंबाई पर लगने वाले बल का परिमाण और इसकी दिशा क्या है?
4.6 एक 3.0 cm लंबा तार जिसमें 10 A विद्युत धारा प्रवाहित हो रही है, एक परिनालिका के भीतर उसके अक्ष के लंबवत रखा है। परिनालिका के भीतर चुंबकीय क्षेत्र का मान 0.27 T है। तार पर लगने वाला चुंबकीय बल क्या है।
4.7 एक-दूसरे से 4.0 cm की दूरी पर रखे दो लंबे, सीधे, समांतर तारों A एवं B से क्रमशः 8.0 A एवं 5.0 A की विद्युत धाराएँ एक ही दिशा में प्रवाहित हो रही हैं। तार A के 10 cm खंड पर बल का आकलन कीजिए।
4.8 पास-पास फेरों वाली एक परिनालिका 80 cm लंबी है और इसमें 5 परतें हैं जिनमें से प्रत्येक में 400 फेरे हैं। परिनालिका का व्यास 1.8 cm है। यदि इसमें 8.0 A विद्युत धारा प्रवाहित हो रही है तो परिनालिका के भीतर केंद्र के पास चुंबकीय क्षेत्र B के परिमाण परिकलित कीजिए।
4.9 एक वर्गाकार कुंडली जिसकी प्रत्येक भुजा 10 cm है, में 20 फेरे हैं और उसमें 12 A विद्युत धारा प्रवाहित हो रही है। कुंडली ऊर्ध्वाधरतः लटकी हुई है और इसके तल पर खींचा गया अभिलंब 0.80 T के एकसमान चुंबकीय क्षेत्र की दिशा से 30° का एक कोण बनाता है। कुंडली पर लगने वाले बलयुग्म आघूर्ण का परिमाण क्या है?
4.10 दो चल कुंडली गैल्वेनोमीटर मीटरों M1 एवं M2 के विवरण नीचे दिए गए हैं ः
R1 = 10 Ω, N1 = 30,
A1 = 3.6 × 10–3 m2, B1 = 0.25 T
R2 = 14 Ω, N2 = 42,
A2 = 1.8 × 10–3 m2, B2 = 0.50 T (दोनों मीटरों के लिए स्प्रिंग नियतांक समान हैं)।
(a) M2 एवं M1 की धारा-सुग्राहिताओं, (b) M2 एवं M1 की वोल्टता-सुग्राहिताओं का अनुपात ज्ञात कीजिए।
4.11 एक प्रकोष्ठ में 6.5 G (1 G = 10–4 T) का एकसमान चुंबकीय क्षेत्र बनाए रखा गया है। इस चुंबकीय क्षेत्र में एक इलेक्ट्रॉन 4.8×106 m s–1 के वेग से क्षेत्र के लंबवत भेजा गया है। व्याख्या कीजिए कि इस इलेक्ट्रॉन का पथ वृत्ताकार क्यों होगा? वृत्ताकार कक्षा की त्रिज्या ज्ञात कीजिए।
(e = 1.6 ×10–19 C, me = 9.1×10–31 kg)
4.12 प्रश्न 4.11 में, वृत्ताकार कक्षा में इलेक्ट्रॉन की परिक्रमण आवृत्ति प्राप्त कीजिए। क्या यह उत्तर इलेक्ट्रॉन के वेग पर निर्भर करता है? व्याख्या कीजिए।
4.13 (a) 30 फेरों वाली एक वृत्ताकार कुंडली जिसकी त्रिज्या 8.0 cm है और जिसमें 6.0 A विद्युत धारा प्रवाहित हो रही है, 1.0 T के एकसमान क्षैतिज चुंबकीय क्षेत्र में ऊर्ध्वाधरतः लटकी है। क्षेत्र रेखाएँ कुंडली के अभिलंब से 60° का कोण बनाती हैं। कुंडली को घूमने से रोकने के लिए जो प्रतिआघूर्ण लगाया जाना चाहिए उसके परिमाण परिकलित कीजिए।
(b) यदि (a) में बतायी गई वृत्ताकार कुंडली को उसी क्षेत्रफल की अनियमित आकृति की समतलीय कुंडली से प्रतिस्थापित कर दिया जाए (शेष सभी विवरण अपरिवर्तित रहें) तो क्या आपका उत्तर परिवर्तित हो जाएगा?
अतिरिक्त अभ्यास
4.14 दो समकेंद्रिक वृत्ताकार कुंडलियाँ X और Y जिनकी त्रिज्याएँ क्रमशः 16 cm एवं 10 cm हैं, उत्तर-दक्षिण दिशा में समान ऊर्ध्वाधर तल में अवस्थित हैं। कुंडली X में 20 फेरे हैं और इसमें 16 A विद्युत धारा प्रवाहित हो रही है, कुंडली Y में 25 फेरे हैं और इसमें 18 A विद्युत धारा प्रवाहित हो रही है। पश्चिम की ओर मुख करके खड़ा एक प्रेक्षक देखता है कि X में धारा प्रवाह वामावर्त है जबकि Y में दक्षिणावर्त है। कुंडलियों के केंद्र पर, उनमें प्रवाहित विद्युत धाराओं के कारण उत्पन्न कुल चुंबकीय क्षेत्र का परिमाण एवं दिशा ज्ञात कीजिए।
4.15 10 cm लंबाई और 10–3 m2 अनुप्रस्थ काट के एक क्षेत्र में 100 G (1 G = 10–4 T) का एकसमान चुंबकीय क्षेत्र चाहिए। जिस तार से परिनालिका का निर्माण करना है उसमें अधिकतम 15 A विद्युत धारा प्रवाहित हो सकती है और क्रोड पर अधिकतम 1000 फेरे प्रति मीटर लपेटे जा सकते हैं। इस उद्देश्य के लिए परिनालिका के निर्माण का विवरण सुझाइए। यह मान लीजिए कि क्रोड लोह-चुंबकीय नहीं है।
4.16 I धारावाही, N फेरों और R त्रिज्या वाली वृत्ताकार कुंडली के लिए, इसके अक्ष पर, केंद्र से x दूरी पर स्थित किसी बिंदु पर चुंबकीय क्षेत्र के लिए निम्न व्यंजक है ः
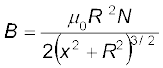
(a) स्पष्ट कीजिए, इससे कुंडली के केंद्र पर चुंबकीय क्षेत्र के लिए सुपरिचित परिणाम कैसे प्राप्त किया जा सकता है।
(b) बराबर त्रिज्या R, एवं फेरों की संख्या N, वाली दो वृत्ताकार कुंडलियाँ एक-दूसरे से R दूरी पर एक-दूसरे के समांतर, अक्ष मिला कर रखी गई हैं। दोनों में समान विद्युत धारा एक ही दिशा में प्रवाहित हो रही है। दर्शाइए कि कुंडलियों के अक्ष के लगभग मध्यबिंदु पर क्षेत्र, एक बहुत छोटी दूरी के लिए जो कि R से कम है, एकसमान है और इस क्षेत्र का लगभग मान निम्न है :
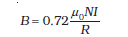
[बहुत छोटे से क्षेत्र पर एकसमान चुंबकीय क्षेत्र उत्पन्न करने के लिए बनायी गई ऊपर वर्णित व्यवस्था हेल्महोल्ट्ज कुंडलियों के नाम से जानी जाती है।]
4.17 एक टोरॉइड के (अलौह चुंबकीय) क्रोड की आंतरिक त्रिज्या 25 cm और बाह्य त्रिज्या 26 cm है। इसके ऊपर किसी तार के 3500 फेरे लपेटे गए हैं। यदि तार में प्रवाहित विद्युत धारा 11 A हो तो चुंबकीय क्षेत्र का मान क्या होगा। (i) टोरॉइड के बाहर (ii) टोरॉइड के क्रोड में (iii) टोरॉइड द्वारा घिरी हुई खाली जगह में।
4.18 निम्नलिखित प्रश्नों के उत्तर दीजिए :
(a) किसी प्रकोष्ठ में एक एेसा चुंबकीय क्षेत्र स्थापित किया गया है जिसका परिमाण तो एक बिंदु पर बदलता है, पर दिशा निश्चित है (पूर्व से पश्चिम)। इस प्रकोष्ठ में एक आवेशित कण प्रवेश करता है और अविचलित एक सरल रेखा में अचर वेग से चलता रहता है। आप कण के प्रारंभिक वेग के बारे में क्या कह सकते हैं।
(b) एक आवेशित कण, एक एेसे शक्तिशाली असमान चुंबकीय क्षेत्र में प्रवेश करता है जिसका परिमाण एवं दिशा दोनों एक बिंदु से दूसरे बिंदु पर बदलते जाते हैं, एक जटिल पथ पर चलते हुए इसके बाहर आ जाता है। यदि यह मान लें कि चुंबकीय क्षेत्र में इसका किसी भी दूसरे कण से कोई संघट्ट नहीं होता तो क्या इसकी अंतिम चाल, प्रारंभिक चाल के बराबर होगी?
(c) पश्चिम से पूर्व की ओर चलता हुआ एक इलेक्ट्रॉन एक एेसे प्रकोष्ठ में प्रवेश करता है जिसमें उत्तर से दक्षिण दिशा की ओर एकसमान एक वैद्युत क्षेत्र है। वह दिशा बताइए जिसमें एकसमान चुंबकीय क्षेत्र स्थापित किया जाए ताकि इलेक्ट्रॉन को अपने सरल रेखीय पथ से विचलित होने से रोका जा सके।
4.19 ऊष्मित कैथोड से उत्सर्जित और 2.0 kV के विभवांतर पर त्वरित एक इलेक्ट्रॉन, 0.15 T के एकसमान चुंबकीय क्षेत्र में प्रवेश करता है। इलेक्ट्रॉन का गमन पथ ज्ञात कीजिए यदि चुंबकीय क्षेत्र (a) प्रारंभिक वेग के लंबवत है (b) प्रारंभिक वेग की दिशा से 30° का कोण बनाता है।
4.20 प्रश्न 4.16 में वर्णित हेल्महोल्टज कुंडलियों का उपयोग करके किसी लघुक्षेत्र में 0.75 T का एकसमान चुंबकीय क्षेत्र स्थापित किया है। इसी क्षेत्र में कोई एकसमान स्थिरवैद्युत क्षेत्र कुंडलियों के उभयनिष्ठ अक्ष के लंबवत लगाया जाता है। (एक ही प्रकार के) आवेशित कणों का 15 kV विभवांतर पर त्वरित एक संकीर्ण किरण पुंज इस क्षेत्र में दोनों कुंडलियों के अक्ष तथा स्थिरवैद्युत क्षेत्र की लंबवत दिशा के अनुदिश प्रवेश करता है। यदि यह किरण पुंज 9.0 × 10–5 V m–1, स्थिरवैद्युत क्षेत्र में अविक्षेपित रहता है तो यह अनुमान लगाइए कि किरण पुंज में कौन से कण हैं। यह स्पष्ट कीजिए कि यह उत्तर एकमात्र उत्तर क्यों नहीं है।
4.21 एक सीधी, क्षैतिज चालक छड़ जिसकी लंबाई 0.45 m एवं द्रव्यमान 60 g है इसके सिरों पर जुड़े दो ऊर्ध्वाधर तारों पर लटकी हुई है। तारों से होकर छड़ में 5.0 A विद्युत धारा प्रवाहित हो
रही है।(a) चालक के लंबवत कितना चुंबकीय क्षेत्र लगाया जाए कि तारों में तनाव शून्य हो जाए।
(b) चुंबकीय क्षेत्र की दिशा यथावत रखते हुए यदि विद्युत धारा की दिशा उत्क्रमित कर दी
जाए तो तारों में कुल तनाव कितना होगा? (तारों के द्रव्यमान की उपेक्षा कीजिए)
g = 9.8 m s–2।
4.22 एक स्वचालित वाहन की बैटरी से इसकी चालन मोटर को जोड़ने वाले तारों में 300 A विद्युत धारा (अल्प काल के लिए) प्रवाहित होती है। तारों के बीच प्रति एकांक लंबाई पर कितना बल लगता है यदि इनकी लंबाई 70 cm एवं बीच की दूरी 1.5 cm हो। यह बल आकर्षण बल है या प्रतिकर्षण बल?
4.23 1.5 T का एक एकसमान चुंबकीय क्षेत्र, 10.0 cm त्रिज्या के बेलनाकार क्षेत्र में विद्यमान है। इसकी दिशा अक्ष के समांतर पूर्व से पश्चिम की ओर है। एक तार जिसमें 7.0 A विद्युत धारा प्रवाहित हो रही है इस क्षेत्र में होकर उत्तर से दक्षिण की ओर गुज़रती है। तार पर लगने वाले बल का परिमाण और दिशा क्या है, यदि
(a) तार अक्ष को काटता हो,
(b) तार N-S दिशा से घुमाकर उत्तर पूर्व-उत्तर पश्चिम दिशा में कर दिया जाए,
(c) N-S दिशा में रखते हुए ही तार को अक्ष से 6.0 cm नीचे उतार दिया जाए।
4.24 धनात्मक z-दिशा में 3000 G का एक एकसमान चुंबकीय क्षेत्र लगाया गया है। एक आयताकार लूप जिसकी भुजाएँ 10 cm एवं 5 cm और जिसमें 12 A धारा प्रवाहित हो रही है इस क्षेत्र में रखा है। चित्र 4.28 में दिखायी गई लूप की विभिन्न स्थितियों में इस पर लगने वाला बलयुग्म आघूर्ण क्या है? हर स्थिति में बल क्या है? स्थायी संतुलन वाली स्थिति कौन-सी है?
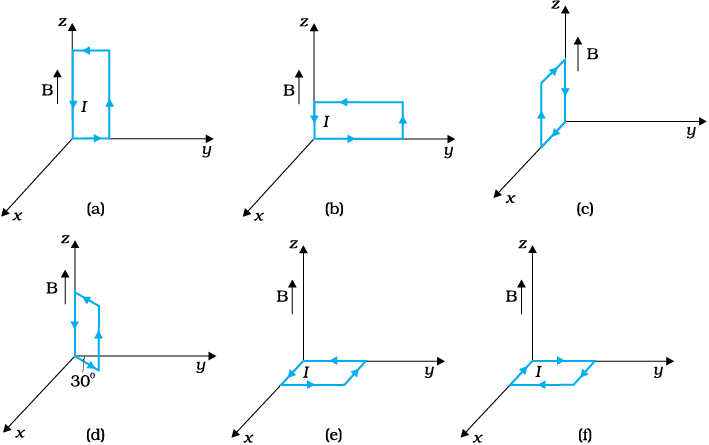
चित्र 4.28
4.25 एक वृत्ताकार कुंडली जिसमें 20 फेरे हैं और जिसकी त्रिज्या 10 cm है, एकसमान चुंबकीय क्षेत्र में रखी है जिसका परिमाण 0.10 T है और जो कुंडली के तल के लंबवत है। यदि कुंडली में 5.0 A विद्युत धारा प्रवाहित हो रही हो तो,
(a) कुंडली पर लगने वाला कुल बलयुग्म आघूर्ण क्या है?
(b) कुंडली पर लगने वाला कुल परिणामी बल क्या है?
(c) चुंबकीय क्षेत्र के कारण कुंडली के प्रत्येक इलेक्ट्रॉन पर लगने वाला कुल औसत बल
क्या है?
(कुंडली 10–5 m2 अनुप्रस्थ क्षेत्र वाले ताँबे के तार से बनी है, और ताँबे में मुक्त इलेक्ट्रॉन घनत्व 1029 m–3 दिया गया है)
4.26 एक परिनालिका जो 60 cm लंबी है, जिसकी त्रिज्या 4.0 cm है और जिसमें 300 फेरों वाली 3 परतें लपेटी गई हैं। इसके भीतर एक 2.0 cm लंबा, 2.5 g द्रव्यमान का तार इसके (केंद्र के निकट) अक्ष के लंबवत रखा है। तार एवं परिनालिका का अक्ष दोनों क्षैतिज तल में हैं। तार को परिनालिका के समांतर दो वाही संयोजकों द्वारा एक बाह्य बैटरी से जोड़ा गया है जो इसमें 6.0 A विद्युत धारा प्रदान करती है। किस मान की विद्युत धारा (परिवहन की उचित दिशा के साथ) इस परिनालिका के फेरों में प्रवाहित होने पर तार का भार सँभाल सकेगी?
g = 9.8 m s–2
4.27 किसी गैल्वेनोमीटर की कुंडली का प्रतिरोध 12 Ω है। 4 mA की विद्युत धारा प्रवाहित होने पर यह पूर्णस्केल विक्षेप दर्शाता है। आप इस गैल्वेनोमीटर को 0 से 18 V परास वाले वोल्टमीटर में कैसे रूपांतरित करेंगे?
4.28 किसी गैल्वेनोमीटर की कुंडली का प्रतिरोध 15 Ω है। 4 mA की विद्युत धारा प्रवाहित होने पर यह पूर्णस्केल विक्षेप दर्शाता है। आप इस गैल्वेनोमीटर को 0 से 6 A परास वाले एेमीटर में कैसे रूपांतरित करेंगे?