Table of Contents
अध्याय 5
चुंबकत्व एवं द्रव्य
5.1 भूमिका
चुंबकीय परिघटना प्रकृति में सार्वभौमिक है। विशाल दूरस्थ गैलेक्सियाँ, अतिसूक्ष्म अदृश्य परमाणु, मनुष्य और जानवर, सबमें भाँति-भाँति के स्रोतों से उत्पन्न भाँति-भाँति के चुंबकीय क्षेत्र व्याप्त हैं। भू-चुंबकत्व, मानवीय विकास से भी पूर्व से अस्तित्व में है। ‘चुंबक’ शब्द यूनान के एक द्वीप मैग्नेशिया के नाम से व्युत्पन्न है, जहाँ बहुत पहले 600 ईसा पूर्व चुंबकीय अयस्कों के भंडार मिले थे। इस द्वीप के गड़रियों ने शिकायत की कि उनके लकड़ी के जूते (जिनमें कीलें लगी हुई थीं), कई बार जमीन से चिपक जाते थे। लोहे की टोपी चढ़ी उनकी लाठी भी इसी प्रकार प्रभावित होती थी। चुंबकों के इस आकर्षित करने वाले गुण ने उनका घूमना-फिरना दूभर बना दिया था।
चुंबकों का दैशिक गुण भी प्राचीन काल से ज्ञात था। चुंबक का एक पतला लंबा टुकड़ा, स्वतंत्रतापूर्वक लटकाए जाने पर, हमेशा उत्तर-दक्षिण दिशा के अनुदिश ठहरता था। एेसा ही व्यवहार तब भी देखने में आता था जब इसको एक कॉर्क के ऊपर रख कर, उसको ठहरे हुए पानी में तैराया जाता था। प्राकृतिक रूप से पाए जाने वाले लोहे के एक अयस्क मैग्नेटाइट का एक नाम लोडस्टोन है, जिसका अर्थ है लीडिंग स्टोन अर्थात मार्गदर्शक पत्थर। इस गुण के तकनीकी उपयोग का श्रेय आमतौर पर चीनियों को दिया जाता है। 400 ईसा पूर्व की चीनी पाठ्यपुस्तकों में नौकायन में दिशा ज्ञान के लिए चुंबकीय सुइयों के उपयोग का ज़िक्र है। गोबी रेगिस्तान को पार करने वाले काफ़िले भी चुंबकीय सुइयों का उपयोग करते थे।
एक चीनी आख्यान में, लगभग 4000 वर्ष पुरानी, सम्राट ह्वेंग-ती की विजय गाथा है, जिसमें उसको अपने शिल्पकारों (जिन्हें आज की भाषा में आप इंजीनियर कहते हैं) के कारण विजय प्राप्त हुई थी। इन ‘इंजीनियरों’ ने एक रथ बनाया जिस पर उन्होंने चुंबक की बनी हुई एक प्रतिमा लगाई, जिसका एक हाथ बाहर फैला हुआ था। चित्र 5.1 में इस रथ का एक चित्रकार द्वारा दिया गया विवरण है। रथ पर लगी हुई प्रतिमा इस तरह घूम जाती थी कि उसकी अँगुली हमेशा दक्षिण की ओर संकेत करे। इस रथ के सहारे, घने कोहरे में ह्वेंग-ती की फ़ौजें दुश्मन के पीछे पहुँच गईं और आक्रमण कर उन्हें हरा दिया।
चित्र 5.1 रथ पर स्थापित प्रतिमा का हाथ हमेशा दक्षिण की ओर संकेत करता है। यह एक कलाकार द्वारा बनाया गया आरेख है, जिसमें एक प्राचीनतम ज्ञात कंपास दिखाया गया है, जो हजारों साल पुराना है।
पिछले अध्याय में हमने सीखा कि गतिशील आवेश या विद्युत धारा चुंबकीय क्षेत्र उत्पन्न करती है। यह खोज जो उन्नीसवीं शताब्दी के
पूर्वार्द्ध में की गई थी, इसका श्रेय अॉर्स्टेड, एेम्पियर, बायो एवं सावर्ट तथा अन्य कुछ लोगों को दिया जाता है।
प्रस्तुत अध्याय में हम चुंबकत्व पर एक स्वतंत्र विषय के रूप में दृष्टि डालेंगे।
चुंबकत्व संबंधी कुछ आम विचार इस प्रकार हैं–
(i) पृथ्वी एक चुंबक की भाँति व्यवहार करती है जिसका चुंबकीय क्षेत्र लगभग भौगोलिक दक्षिण से उत्तर की ओर संकेत करता है।
(ii) जब एक छड़ चुंबक को स्वतंत्रतापूर्वक लटकाया या शांत पानी पर तैराया जाता है तो यह उत्तर-दक्षिण दिशा में ठहरता है। इसका वह सिरा जो भौगोलिक उत्तर की ओर संकेत करता है, उत्तरी ध्रुव और जो भौगोलिक दक्षिण की ओर संकेत करता है, चुंबक का दक्षिणी ध्रुव कहलाता है।
(iii) दो पृथक-पृथक चुंबकों के दो उत्तरी ध्रुव (या दो दक्षिणी ध्रुव) जब पास-पास लाए जाते हैं तो वे एक-दूसरे को विकर्षित करते हैं। इसके विपरीत, एक चुंबक के उत्तर और दूसरे के दक्षिण ध्रुव एक-दूसरे को आकर्षित करते हैं।
(iv) किसी चुंबक के उत्तर और दक्षिण ध्रुवों को अलग-अलग नहीं किया जा सकता। यदि किसी छड़ चुंबक को दो भागों में विभाजित किया जाए तो हमें दो छोटे अलग-अलग छड़ चुंबक मिल जाएँगे, जिनका चुंबकत्व क्षीण होगा। वैद्युत आवेशों की तरह, विलगित चुंबकीय उत्तरी तथा दक्षिणी ध्रुवों जिन्हें चुंबकीय एकध्रुव कहते हैं, का अस्तित्व नहीं है।
(v) लौह और इसकी मिश्र-धातुओं से चुंबक बनाने संभव हैं।
इस अध्याय में हम एक छड़ चुंबक और एक बाह्य चुंबकीय क्षेत्र में इसके व्यवहार के वर्णन से प्रारंभ करेंगे। हम चुंबकत्व संबंधी गाउस का नियम बताएँगे। इसके बाद पृथ्वी के चुंबकीय क्षेत्र का विवरण देंगे। उसके बाद यह बताएँगे कि चुंबकीय गुणों के आधार पर पदार्थों का वर्गीकरण कैसे किया जाता है और फिर अनुचुंबकत्व, प्रतिचुंबकत्व तथा लौह-चुंबकत्व का वर्णन करेंगे और अंत में वैद्युत-चुंबक एवं स्थायी चुंबकों पर एक अनुभाग के साथ इसका समापन करेंगे।
5.2 छड़ चुंबक
प्रसिद्ध भौतिक विज्ञानी अल्बर्ट आइंसटीन के अति प्रारंभिक बचपन की स्मृतियों में से एक उस चुंबक से जुड़ी थी, जो उन्हें उनके एक संबंधी ने भेंट किया था। आइंसटीन उससे चमत्कृत हो गए थे और उससे खेलते हुए कभी थकते नहीं थे। उनको आश्चर्य होता था कि कैसे एक चुंबक उन कीलों और पिनों को अपनी ओर खींच लेती थी, जो उससे दूर रखे थे और किसी स्प्रिंग या धागे द्वारा उससे जुड़े भी नहीं थे।
हम अपने अध्ययन की शुरुआत लौह रेतन से करते हैं जो एक छोटे छड़ चुंबक के ऊपर रखी गई काँच की शीट पर छिड़का गया है। लौह रेतन की यह व्यवस्था चित्र 5.2 में दर्शायी गई है।
लौह रेतन के पैटर्न यह इंगित करते हैं कि चुंबक के दो ध्रुव होते हैं, वैसे ही जैसे वैद्युत द्विध्रुव के धनात्मक एवं ऋणात्मक आवेश। जैसा कि पहले भूमिका में बताया जा चुका है, एक ध्रुव को उत्तर और दूसरे को दक्षिण ध्रुव कहते हैं। जब छड़ चुंबक को स्वतंत्रतापूर्वक लटकाया जाता है तो ये ध्रुव क्रमशः लगभग भौगोलिक उत्तरी एवं दक्षिणी ध्रुवों की ओर संकेत करते हैं। लौह रेतन का इसी से मिलता-जुलता पैटर्न एक धारावाही परिनालिका के इर्द-गिर्द भी बनता है।
चित्र 5.2 एक छड़ चुंबक के इर्द-गिर्द लौह रेतन की व्यवस्था। यह पैटर्न चुंबकीय क्षेत्र रेखाओं की अनुकृति है। ये इंगित करते हैं कि छड़ चुंबक एक चुंबकीय द्विध्रुव है।
5.2.1 चुंबकीय क्षेत्र रेखाएँ
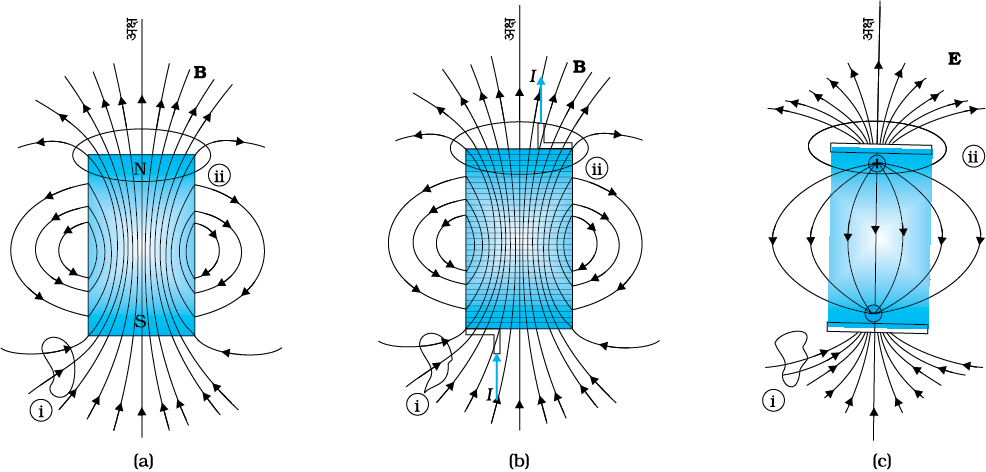
चित्र 5.3 क्षेत्र रेखाएँ (a) एक छड़ चुंबक की (b) एक सीमित आकार वाली धारावाही परिनालिका की, और (c) एक वैद्युत द्विध्रुव की। बहुत अधिक दूरी पर तीनों रेखा समुच्चय एक से हैं। i एवं ii अंकित वक्र, बंद गाउसीय पृष्ठ हैं।
लौह रेतन के बने पैटर्नों के आधार पर हम चुंबकीय क्षेत्र रेखाएँ* खींच सकते हैं। चित्र 5.3 में यह छड़ चुंबक और धारावाही परिनालिका, दोनों के लिए दर्शाया गया है। तुलना के लिए अध्याय एक चित्र 1.17(d) देखिए। विद्युत द्विध्रुव की वैद्युत बल रेखाएँ चित्र 5.3(c) में भी दर्शायी गई हैं। चुंबकीय क्षेत्र रेखाएँ, चुंबकीय क्षेत्र का दृश्य और अंतर्दृष्टिपरक प्रस्तुतीकरण हैं। इनके गुण हैंः
(i) किसी चुंबक (या धारावाही परिनालिका) की चुंबकीय क्षेत्र रेखाएँ संतत बंद लूप बनाती हैं। यह वैद्युत-द्विध्रुव के जैसी नहीं है, जहाँ ये रेखाएँ धनावेश से शुरू होकर ऋणावेश पर खत्म हो जाती हैं [चित्र 5.3(c) देखिए] या फिर अनंत की ओर चली जाती हैं।
* कुछ पाठ्यपुस्तकों में चुंबकीय क्षेत्र रेखाओं को चुंबकीय बल रेखाएँ कहा गया है। इस नामावली से बचना उचित होगा क्योंकि यह भ्रामक है। स्थिरवैद्युत के विपरीत चुंबकत्व में क्षेत्र रेखाएँ (गतिमान) आवेश पर बल की दिशा की सूचक नहीं हैं।
(ii) क्षेत्र रेखा के किसी बिंदु पर खींची गई स्पर्श रेखा उस बिंदु पर परिणामी चुंबकीय क्षेत्र B की दिशा बताती है।
(iii) क्षेत्र के लंबवत रखे गए तल के प्रति इकाई क्षेत्रफल से जितनी अधिक क्षेत्र रेखाएँ गुजरती हैं, उतना ही अधिक उस स्थान पर चुंबकीय क्षेत्र B का परिमाण होता है। चित्र 5.3 (a) में, क्षेत्र ii के आसपास B का परिमाण क्षेत्र i की तुलना में अधिक है।
(iv) चुंबकीय क्षेत्र रेखाएँ एक-दूसरे को काटती नहीं हैं। एेसा इसलिए है क्योंकि इस स्थिति में कटान बिंदु पर चुंबकीय क्षेत्र की दिशा एक ही नहीं रह जाती।
आप चाहें तो कई तरह से चुंबकीय क्षेत्र रेखाएँ आलेखित कर सकते हैं। एक तरीका यह है कि भिन्न-भिन्न जगहों पर एक छोटी चुंबकीय कंपास सुई रखिए और इसके दिक्विन्यास को अंकित कीजिए। इस तरह आप चुंबक के आस-पास विभिन्न बिंदुओं पर चुंबकीय क्षेत्र की दिशा जान सकेंगे।
5.2.2 छड़ चुंबक का एक धारावाही परिनालिका की तरह व्यवहार
पिछले अध्याय में हमने यह समझाया है कि किस प्रकार एक धारा लूप एक चुंबकीय द्विध्रुव की तरह व्यवहार करता है (अनुभाग 4.10 देखिए)। हमने एेम्पियर की इस परिकल्पना का जिक्र भी किया था कि सभी चुंबकीय परिघटनाओं को परिवाही धाराओं के प्रभावों के रूप में समझाया जा सकता है। याद कीजिए कि किसी धारावाही लूप से जुड़े चुंबकीय द्विध्रुव आघूर्ण m की परिभाषा m = NIA से दी जाती है, जहाँ N लूप में फेरों की संख्या, I धारा एवं A क्षेत्रफल-सदिश है [समीकरण (4.30) देखिए]।
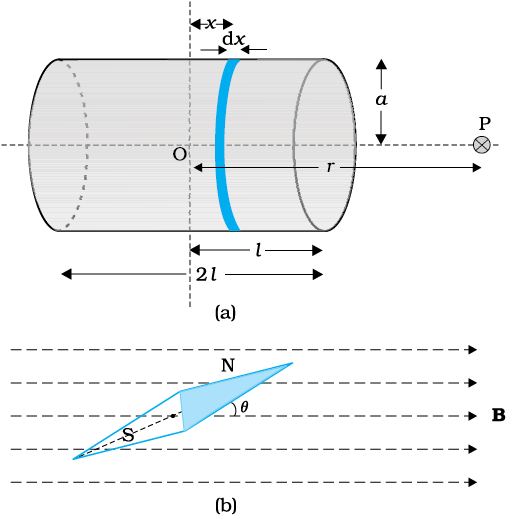
चित्र 5.4 (a) एक सीमित परिनालिका के अक्षीय क्षेत्र का परिकलन, ताकि इसकी छड़ चुंबक से साम्यता प्रदर्शित की जा सके। (b) एक समान चुंबकीय क्षेत्र B में रखी हुई चुंबकीय सूई। यह प्रबंध चुंबकीय क्षेत्र B अथवा चुंबकीय आघूर्ण m का आकलन करने में सहायक है।
एक छड़ चुंबक की चुंबकीय क्षेत्र रेखाओं की, एक धारावाही परिनालिका की चुंबकीय क्षेत्र रेखाओं से साम्यता यह सुझाती है कि जैसे परिनालिका बहुत-सी परिवाही धाराओं का योग है वैसे ही छड़ चुंबक भी बहुत-सी परिसंचारी धाराओं का योग हो सकता है। एक छड़ चुंबक के दो बराबर टुकड़े करना वैसा ही है जैसे एक परिनालिका को काटना। जिससे हमें दो छोटी परिनालिकाएँ मिल जाती हैं जिनके चुंबकीय क्षेत्र अपेक्षाकृत क्षीण होते हैं। क्षेत्र रेखाएँ संतत बनी रहती हैं, एक सिरे से बाहर निकलती हैं और दूसरे सिरे से अंदर प्रवेश करती हैं। एक छोटी चुंबकीय कंपास सुई को एक छड़ चुंबक एवं एक धारावाही सीमित परिनालिका के पास एक जगह से दूसरी जगह ले जाकर यह देखा जा सकता है कि दोनों के लिए चुंबकीय सुई में विक्षेपण एक जैसा है और इस तरह इस साम्यता का परीक्षण आसानी से किया जा सकता है।
इस साम्यता को और अधिक सुदृढ़ करने के लिए हम चित्र 5.4 (a) में दर्शायी गई सीमित परिनालिका के अक्षीय क्षेत्र की गणना करते हैं। हम यह प्रदर्शित करेंगे कि बहुत अधिक दूरी पर यह अक्षीय क्षेत्र छड़ चुंबक के अक्षीय क्षेत्र जैसा ही है।
माना कि चित्र 5.4 (a) में दर्शायी गई धारावाही परिनालिका की प्रति इकाई लंबाई में n फेरे हैं और इसकी त्रिज्या ‘a’ है। माना इसकी लंबाई 2l है। परिनालिका के केंद्र से r दूरी पर (बिंदु P) हम अक्षीय क्षेत्र ज्ञात कर सकते हैं। यह करने के लिए, परिनालिका का एक छोटा वृत्ताकार अंश dx मोटाई का लेते हैं जो इसके केंद्र से x दूरी पर है। इसमें n dx फेरे हैं। माना कि परिनालिका में I धारा प्रवाहित हो रही है। पिछले अध्याय के अनुभाग 4.6 में हमने एक वृत्ताकार लूप के अक्ष पर चुंबकीय क्षेत्र की गणना की थी। समीकरण (4.17) के अनुसार, वृत्ताकार अंश के कारण बिंदु P पर चुंबकीय क्षेत्र का परिमाण
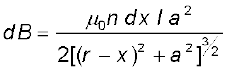
कुल क्षेत्र का परिमाण प्राप्त करने के लिए एेसे सभी अंशों के योगदान जोड़ने होंगे। दूसरे शब्दों में x = – l से x = + l तक समाकलन करना होगा।
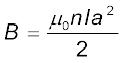
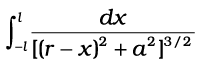
और
यह समाकलन त्रिकोणमितीय प्रतिस्थापन द्वारा किया जा सकता है। किंतु, हमारा उद्देश्य पूरा करने के लिए एेसा करना आवश्यक नहीं है। ध्यान दें कि x का परास −l से +l तक है। धारावाही परिनालिका के बहुत दूर स्थित अक्षीय बिंदु के लिए r >> a एवं r >> l । तब भिन्न में हर का लगभग मान हो जाएगा ः
= 
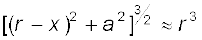
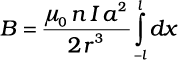
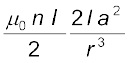(5.1)
ध्यान दीजिए कि धारावाही परिनालिका के चुंबकीय आघूर्ण का परिमाण m = n (2l) I (πa2) [अर्थात कुल फेरों की संख्या × धारा × अनुप्रस्थ काट का क्षेत्रफल]। अतः
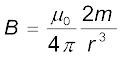(5.2)
यही समीकरण छड़ चुंबक की अक्ष पर दूर स्थित बिंदु के लिए भी है जिसे कोई भी प्रयोगात्मक विधि से प्राप्त कर सकता है। इस प्रकार, छड़ चुंबक और धारावाही परिनालिका एक जैसे चुंबकीय क्षेत्र उत्पन्न करते हैं। अतः एक छड़ चुंबक का चुंबकीय आघूर्ण, उतना ही चुंबकीय क्षेत्र उत्पन्न करने वाली समतुल्य धारावाही परिनालिका के चुंबकीय आघूर्ण के बराबर है।
कुछ पाठ्यपुस्तकें 2l लंबाई के एक छड़ चुंबक के उत्तर ध्रुव के लिए एक चुंबकीय आवेश +qm एवं दक्षिण (इसे ध्रुव शक्ति कहते हैं) ध्रुव के लिए –qm नियत करके इसका चुंबकीय आघूर्ण +qm(2l) नियत करती हैं। r दूरी पर qm के कारण क्षेत्र की तीव्रता µ0qm/4πr2 होगी और तब अक्षीय एवं अनुप्रस्थ दोनों स्थितियों में इस छड़ चुंबक के कारण चुंबकीय क्षेत्र उसी प्रकार ज्ञात किया जा सकता है जैसा कि वैद्युत द्विध्रुव के लिए किया गया था (देखिए अध्याय 1)। यह तरीका सरल भी है और आकर्षक भी। परंतु, चुंबकीय एकध्रुवों का अस्तित्व तो होता नहीं, इसलिए, हमने इस प्रस्तुति-विधि का उपयोग नहीं किया है।
5.2.3 एकसमान चुंबकीय क्षेत्र में द्विध्रुव
लौह रेतन (iron filling) से बने पैटर्न अर्थात चुंबकीय क्षेत्र रेखाएँ हमें चुंबकीय क्षेत्र B का एक सन्निकट मान बताते हैं। प्रायः हमें B का सही-सही मान जानने की आवश्यकता होती है। इसके लिए हम एक पतली चुंबकीय सुई का, जिसका चुंबकीय आघूर्ण m एवं जड़त्वाघूर्ण I ज्ञात हों, इस चुंबकीय क्षेत्र में दोलन कराते हैं। यह व्यवस्था चित्र 5.4 (b) में दर्शायी गई है।
चुंबकीय सुई पर बलआघूर्ण [समीकरण (4.29) देखिए]
τ = m × B (5.3)
जिसका परिमाण τ = mB sinθ
यहाँ τ प्रत्यानयन आघूर्ण है तथा कोण θ, m और B के बीच का कोण है।
अतः, संतुलनावस्था में
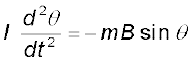
mB sinθ के साथ ऋणात्मक चिह्न यह निर्दिष्ट करता है कि प्रत्यानयन आघूर्ण विस्थापनकारी आघूर्ण के विपरीत दिशा में है। रेडियन में बहुत छोटे कोण के लिए हम sin θ ≈ θ लेते हैं। अतः,
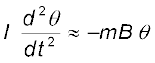
अथवा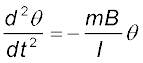 
यह सरल आवर्त गति दर्शाता है, जिसके लिए, कोणीय आवृत्ति का वर्ग ω2 = mB/I तथा दोलन काल है,
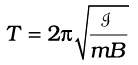(5.4)
अथवा 
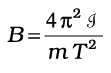(5.5)
चुंबकीय स्थितिज ऊर्जा के लिए व्यंजक प्राप्त करने के लिए हम उसी विधि का अनुसरण कर सकते हैं जो हमने वैद्युत स्थितिज ऊर्जा का व्यंजक प्राप्त करने के लिए अपनायी थी।
किसी चुंबकीय द्विध्रुव की चुंबकीय स्थितिज ऊर्जा Um इस प्रकार है
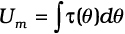
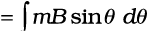
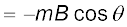
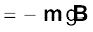(5.6)
इस बात को हमने पहले भी काफी जोर देकर कहा था कि स्थितिज ऊर्जा का शून्य हम अपनी सुविधानुसार निर्धारित कर सकते हैं। समाकलन नियंताक को शून्य लेने का अर्थ है कि हमने स्थितिज ऊर्जा का शून्य θ = 90o पर, अर्थात उस स्थिति को ले लिया है जिस पर सुई क्षेत्र के लंबवत है। समीकरण (5.6) यह दर्शाती है कि न्यूनतम स्थितिज ऊर्जा (= –mB) (अर्थात सर्वाधिक स्थायी अवस्था) θ = 0o पर होती है एवं अधिकतम स्थितिज ऊर्जा (= +mB) (अर्थात अधिकतम अस्थायी अवस्था) θ = 180o पर होती है।
उदाहरण 5.1
चित्र 5.4 (b) में, चुंबकीय सुई का चुंबकीय आघूर्ण 6.7 × 10–2 A m2 और जड़त्वाघूर्ण I = 7.5 × 10–6 kg m2 है। यह 6.70 s में 10 पूरे दोलन करती है। चुंबकीय क्षेत्र का परिमाण क्या है?
हल
दोलनकाल
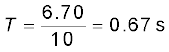
समीकरण (5.5) से प्राप्त होता है
= 
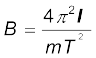
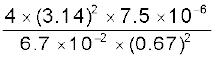
= 0.01 T
उदाहरण 5.2
एक छोटे छड़ चुंबक को जब 800 G के बाह्य चुंबकीय क्षेत्र में इस तरह रखा जाता है कि इसकी अक्ष क्षेत्र से 30o का कोण बनाए, तो यह 0.016 N m का बलआघूर्ण अनुभव करता है। (a) चुंबक का चुंबकीय आघूर्ण कितना है? (b) सर्वाधिक स्थायी स्थिति से सर्वाधिक अस्थायी स्थिति तक इसको घुमाने में कितना कार्य करना पड़ेगा? (c) छड़ चुंबक को यदि एक परिनालिका से प्रतिस्थापित कर दें जिसमें 1000 फेरे हों, जिसके अनुप्रस्थ काट का क्षेत्रफल
2 × 10–4 m2 हो और जिसका चुंबकीय आघूर्ण उतना ही हो जितना छड़ चुंबक का है, तो परिनालिका में प्रवाहित होने वाली धारा ज्ञात कीजिए।
हल
(a) समीकरण (5.3) के अनुसार τ = m B sin θ, θ = 30o, इसलिए sinθ =1/2
अतः, 0.016 = m × (800 × 10–4 T) × (1/2)
m = 160 × 2/800 = 0.40 A m2
(b) समीकरण (5.6) के अनुसार सर्वाधिक स्थायी स्थिति तब है जब θ = 0o एवं सर्वाधिक अस्थायी स्थिति तब है जब θ =180o
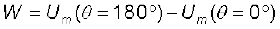
= 2 m B = 2 × 0.40 × 800 × 10–4 = 0.064 J
(c) समीकरण (4.30) के अनुसार ms = NIA भाग (a) में हमने ज्ञात किया है कि ms = 0.40 A m2
0.40 = 1000 × I × 2 × 10–4
I = 0.40 × 104/(1000 × 2) = 2A
उदाहरण 5.3
(a) क्या होता है जबकि एक चुंबक को दो खंडों में विभाजित करते हैं (i) इसकी लंबाई के लंबवत (ii) लंबाई के अनुदिश?
(b) एकसमान चुंबकीय क्षेत्र में रखी गई किसी चुंबकीय सुई पर बल आघूर्ण तो प्रभावी होता है पर इस पर कोई परिणामी बल नहीं लगता। तथापि, एक छड़ चुंबक के पास रखी लोहे की कील पर बल आघूर्ण के साथ-साथ परिणामी बल भी लगता है। क्यों?
(c) क्या प्रत्येक चुंबकीय विन्यास का एक उत्तरी और एक दक्षिणी ध्रुव होना आवश्यक है? एक टोरॉयड के चुंबकीय क्षेत्र के संबंध में इस विषय में अपनी टिप्पणी दीजिए।
(d) दो एक जैसी दिखाई पड़ने वाली छड़ें A एवं B दी गई हैं जिनमें कोई एक निश्चित रूप से चुंबकीय है, यह ज्ञात है (पर, कौन सी यह ज्ञात नहीं है)। आप यह कैसे सुनिश्चित करेंगे कि दोनों छड़ें चुंबकित हैं या केवल एक? और यदि केवल एक छड़ चुंबकित है तो यह कैसे पता लगाएँगे कि वह कौन सी है। [आपको छड़ों A एवं B के अतिरिक्त अन्य कोई चीज प्रयोग नहीं करनी है।]
हल
(a) दोनों ही प्रकरणों में आपको दो चुंबक प्राप्त होते हैं जिनमें से प्रत्येक में एक उत्तरी और एक दक्षिणी ध्रुव होता है।
(b) यदि क्षेत्र एकसमान हों केवल तभी चुंबक पर कोई बल नहीं लगता। परंतु छड़ चुंबक के कारण कील पर असमान क्षेत्र आरोपित होता है जिसके कारण कील में चुंबकीय आघूर्ण प्रेरित होता है। अतः इस पर परिणामी बल भी लगता है और बल आघूर्ण भी। परिणामी बल आकर्षण बल होता है, क्योंकि कील में प्रेरित दक्षिण ध्रुव (माना) इसमें प्रेरित उत्तरी ध्रुव की अपेक्षा चुंबक के अधिक निकट होता है।
(c) आवश्यक नहीं है। यह तभी सत्य होगा जब चुंबकीय क्षेत्र के स्रोत का परिणामी चुंबकीय आघूर्ण शून्य नहीं होगा। टोरॉयड या अनंत लंबाई की परिनालिका के लिए एेसा नहीं होता।
(d) चुंबकों के अलग-अलग सिरों को एक-दूसरे के पास लाने की कोशिश कीजिए। यदि किसी स्थिति में प्रतिकर्षण बल का अनुभव हो तो दोनों छड़ें चुंबकित हैं। यदि हमेशा आकर्षण बल ही लगे तो उनमें से एक छड़ चुंबकित नहीं है। यह देखने के लिए कि कौन-सी छड़ चुंबकित है, एक छड़ A मान लीजिए और इसका एक सिरा नीचे कीजिए; पहले दूसरी छड़ B के सिरे के पास लाइए और फिर बीच में। अगर आप पाएँ कि B के बीच में छड़ A आकर्षण बल अनुभव नहीं करती तो B चुंबकित है। और यदि आप पाएँ कि सिरे पर और बीच में आकर्षण बल बराबर है, तो छड़ A चुंबकित है।
5.2.4 स्थिरवैद्युत अनुरूप
समीकरणों (5.2), (5.3) एवं (5.4) के संगत विद्युत द्विध्रुव के समीकरणों (अध्याय 1 देखिए) से तुलना करने पर हम इस परिणाम पर पहुँचते हैं कि m चुंबकीय आघूर्ण वाले छड़ चुंबक का चुंबकीय क्षेत्र, इससे बहुत दूरी पर स्थित किसी बिंदु पर ज्ञात करने के लिए, हमें द्विध्रुव आघूर्णों वाले विद्युत द्विध्रुव के कारण उत्पन्न विद्युत क्षेत्र के समीकरण में, केवल निम्नलिखित प्रतिस्थापन करने होंगे–
, 
, 
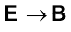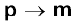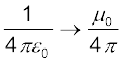
विशेषतः, r दूरी (r >> l के लिए, जहाँ l चुंबक की लंबाई है)पर एक छड़ चुंबक का विषुवतीय चुंबकीय क्षेत्र
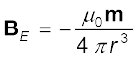(5.7)
इसी प्रकार, r दूरी (r >> l के लिए) पर एक छड़ चुंबक का अक्षीय चुंबकीय क्षेत्र
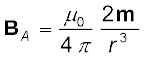(5.8)
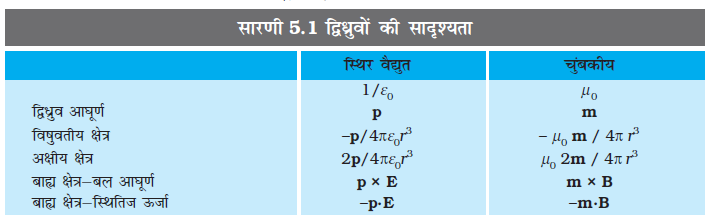
समीकरण (5.8), समीकरण (5.2) का सदिश रूप है। सारणी 5.1 विद्युत एवं चुंबकीय द्विध्रुवों के मध्य समानता दर्शाती है।
उदाहरण 5.4
5 cm लंबाई के छड़ चुंबक के केंद्र से 50 cm की दूरी पर स्थित बिंदु पर, विषुुवतीय एवं अक्षीय स्थितियों के लिए चुंबकीय क्षेत्र का परिकलन कीजिए। छड़ चुंबक का चुंबकीय आघूर्ण 0.40 A m2, जैसा कि उदाहरण 5.2 में है।
हल
समीकरण (5.7) के अनुसार,
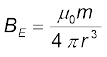
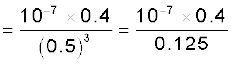
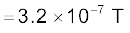
समीकरण (5.8) के अनुसार,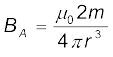 
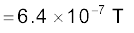
उदाहरण 5.5
चित्र 5.5 में O बिंदु पर रखी गई एक छोटी चुंबकीय सुई P दिखाई गई है। तीर इसके चुंबकीय आघूर्ण की दिशा दर्शाता है। अन्य तीर, दूसरी समरूप चुंबकीय सुई Q की विभिन्न स्थितियों (एवं चुंबकीय आघूर्ण के दिक्विन्यासों) को प्रदर्शित करते हैं।
(a) किस विन्यास में यह निकाय संतुलन में नहीं होगा?
(b) किस विन्यास में निकाय (i) स्थायी (ii) अस्थायी संतुलन में होंगे?
(c) दिखाए गए सभी विन्यासों में किसमें न्यूनतम स्थितिज ऊर्जा है?
चित्र 5.5
हल
किसी विन्यास की स्थितिज ऊर्जा, एक चुंबकीय द्विध्रुव (माना Q) की, दूसरे चुंबकीय द्विध्रुव (माना P) के चुंबकीय क्षेत्र के कारण उत्पन्न स्थितिज ऊर्जा है। आप समीकरण (5.7) एवं (5.8) द्वारा व्यक्त निम्नलिखित परिणाम प्रयोग में ला सकते हैं–
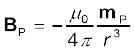(लंब समद्विभाजक पर)
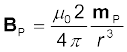(अक्ष पर)
जहाँ mP द्विध्रुव P का चुंबकीय आघूर्ण है।
संतुलन तब स्थायी होगा जब mQ एवं BP एक-दूसरे के समांतर होंगी और संतुलन अस्थायी तब होगा जब वे प्रतिसमांतर होंगी।
उदाहरणार्थ, विन्यास Q3 में, जिसके लिए Q द्विध्रुव P के लंब समद्विभाजक के अनुदिश है, Q का चुंबकीय आघूर्ण, स्थिति 3 में, चुंबकीय क्षेत्र के समांतर है, अतः Q3 स्थायी है
इस प्रकार,
(a) PQ1 एवं PQ2
(b) (i) PQ3, PQ6 (स्थायी); (ii) PQ5, PQ4 (अस्थायी)
(c) PQ6
5.3 चुंबकत्व एवं गाउस नियम
अध्याय 1 में हमने स्थिरवैद्युत के लिए गाउस के नियम का अध्ययन किया था। चित्र 5.3 (c) में हम देखते हैं कि i द्वारा अंकित बंद गाउसीय सतह से क्षेत्र रेखाओं की जितनी संख्या बाहर आती है, उतनी ही इसके अंदर प्रवेश करती है। इस बात की इस तथ्य से संगति बैठती है कि सतह द्वारा परिवेष्ठित कुल आवेश का परिमाण शून्य है। किंतु, उसी चित्र में, बंद सतह ii जो किसी धनावेश को घेरती है, के लिए परिणामी निर्गत फ्लक्स होता है।
यह स्थिति उन चुंबकीय क्षेत्रों के लिए पूर्णतः भिन्न है, जो संतत हैं और बंद लूप बनाते हैं। चित्र 5.3 (a) या 5.3 (b) में i या ii द्वारा अंकित गाउसीय सतहों का निरीक्षण कीजिए। आप पाएँगे कि सतह से बाहर आने वाली बल रेखाओं की संख्या इसके अंदर प्रवेश करने वाली संख्या के बराबर है। दोनों ही सतहों के लिए कुल चुंबकीय फ्लक्स शून्य है और यह बात किसी भी बंद सतह के लिए सत्य है।
कार्ल फ्रेड्रिक गाउस (1777 – 1855)
कार्ल फ्रेड्रिक गाउस (1777 – 1855) वे एक विलक्षण बाल-प्रतिभा थे। गणित, भौतिकी, अभियांत्रिकी, खगोलशास्त्र और यहाँ तक कि भू-सर्वेक्षण में भी उनको प्रकृति की अनुपम देन थी। संख्याओं के गुण उनको लुभाते थे और उनके कार्य में उनके बाद आने वाले जमाने के प्रमुख गणितीय विकास का पूर्वाभास होता है। 1833 में विल्हेम वेलसर के साथ मिलकर उन्होंने पहला विद्युतीय टेलिग्राफ बनाया। वक्र-पृष्ठों से संबंधित उनके गणितीय सिद्धांत ने बाद में रीमन द्वारा किए गए कार्य की आधारशिला रखी|
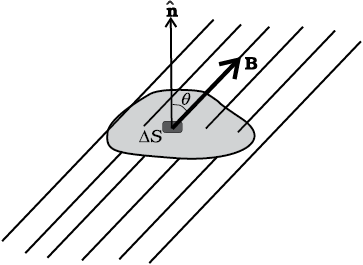
चित्र 5.6
किसी बंद सतह S का एक छोटा सदिश क्षेत्रफल अवयव ∆S लीजिए। जैसा कि चित्र 5.6 में दर्शाया गया है। ∆S से गुजरने वाला चुंबकीय फ्लक्स ∆φB = B.∆S है, जहाँ B, ∆S पर चुंबकीय क्षेत्र है। हम S को कई छोटे-छोटे अवयवों में बाँट लेते हैं और उनमें से प्रत्येक से गुजरने वाले फ्लक्सों के मान अलग-अलग निकालते हैं। तब, कुल फ्लक्स φB का मान है,
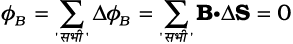(5.9)
जहाँ ‘सभी’ का अर्थ है सभी क्षेत्रफल अवयव ∆S । इसकी तुलना वैद्युतस्थितिकी के गाउस के नियम से कीजिए। जहाँ एक बंद सतह से गुजरने वाला वैद्युत फ्लक्स
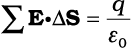
जहाँ q बंद सतह द्वारा परिबद्ध आवेश है।
चुंबकत्व एवं स्थिरवैद्युतिकी के गाउस नियमों के बीच का अंतर इसी तथ्य की अभिव्यक्ति है कि पृथक्कृत चुंबकीय ध्रुवों (जिन्हें एकध्रुव भी कहते हैं) का अस्तित्व नहीं होता। B का कोई उद्गम या अभिगम नहीं होता है। सरलतम चुंबकीय अवयव एक द्विध्रुव या धारा लूप है। सभी चुंबकीय परिघटनाएँ एक धारा लूप एवं/या द्विध्रुव व्यवस्था के रूप में समझायी जा सकती हैं।
चुंबकत्व के लिए गाउस का नियम है–
किसी भी बंद सतह से गुज़रने वाला कुल चुंबकीय फ्लक्स हमेशा शून्य होता है।
उदाहरण 5.6
नीचे दिए गए चित्रों में से कई में चुंबकीय क्षेत्र रेखाएँ गलत दर्शायी गई हैं [चित्रों में मोटी रेखाएँ]। पहचानिए कि उनमें गलती क्या है? इनमें से कुछ में वैद्युत क्षेत्र रेखाएँ ठीक-ठीक दर्शायी गई हैं। बताइए, वे कौन से चित्र हैं?
चित्र 5.7
हल
(a) गलत है। चुंबकीय बल रेखाएँ एक बिंदु से इस प्रकार नहीं निकल सकतीं जैसा कि चित्र में दिखाया गया है। किसी बंद सतह पर B का कुल फ्लक्स हमेशा शून्य ही होना चाहिए अर्थात, चित्र में जितनी क्षेत्र रेखाएँ सतह में प्रवेश करें उतनी ही इससे बाहर निकलनी चाहिए। दिखायी गई क्षेत्र रेखाएँ, वास्तव में, एक लंबे धनावेशित तार का विद्युत क्षेत्र प्रदर्शित करती हैं। सही चुंबकीय क्षेत्र रेखाएँ जैसा अध्याय 4 में बताया गया है, सीधे तार को चारों ओर से घेरने वाले वृत्तों के रूप में हैं।
(b) गलत है। चुंबकीय क्षेत्र रेखाएँ (विद्युत क्षेत्र रेखाओं की तरह ही) कभी भी एक-दूसरे को काट नहीं सकतीं। क्योंकि, अन्यथा कटान बिंदु पर क्षेत्र की दिशा संदिग्ध हो जाएगी। चित्र में एक गलती और भी है। स्थिर-चुंबकीय क्षेत्र रेखाएँ मुक्त आकाश में कभी भी बंद वक्र नहीं बना सकतीं। स्थिर-चुंबकीय क्षेत्र रेखा के बंद लूप को निश्चित रूप से एक एेसे प्रदेश को घेरना चाहिए जिसमें से होकर धारा प्रवाहित हो रही हो [इसके विपरीत वैद्युत क्षेत्र रेखाएँ कभी भी बंद लूप नहीं बना सकतीं, न तो मुक्त आकाश में और न ही तब जब लूप आवेश को घेरते हैं।]
(c) ठीक है। चुंबकीय रेखाएँ पूर्णतः एक टोरॉइड में समाहित हैं। यहाँ चुंबकीय क्षेत्र रेखाओं द्वारा बंद लूप बनाने में कोई त्रुटि नहीं है, क्योंकि प्रत्येक लूप एक एेसे क्षेत्र को घेरता है जिसमें से होकर धारा गुजरती है। ध्यान दीजिए कि चित्र में स्पष्टता लाने के लिए ही टोरॉइड के अंदर मात्र कुछ क्षेत्र रेखाएँ दिखायी गई हैं। तथ्य यह है कि टोरॉइड के फेरों के अंदर के संपूर्ण भाग में चुंबकीय क्षेत्र मौजूद रहता है।
(d) गलत है। परिनालिका की क्षेत्र रेखाएँ, इसके सिरों पर और इसके बाहर पूर्णतः सीधी और सिमटी हुई नहीं हो सकती हैं। एेसा होने से एेम्पियर का नियम भंग होता है। ये रेखाएँ सिरों पर वक्रित हो जानी चाहिए और इनको अंत में मिल कर बंद पाश बनाने चाहिए।
(e) सही है। एक छड़ चुंबक के अंदर एवं बाहर दोनों ओर चुंबकीय क्षेत्र होता है। अंदर क्षेत्र की दिशा पर अच्छी तरह ध्यान दीजिए। सभी क्षेत्र रेखाएँ उत्तर ध्रुव से नहीं निकलतीं (और न ही दक्षिण ध्रुव पर समाप्त होती हैं)। N-ध्रुव एवं S-ध्रुव के चारों तरफ क्षेत्र के कारण कुल फ्लक्स शून्य होता है।
(f) गलत है। संभावना यही है कि ये क्षेत्र रेखाएँ चुंबकीय क्षेत्र प्रदर्शित नहीं करतीं। ऊपरी भाग को देखिए। सभी क्षेत्र रेखाएँ छायित प्लेट से निकलती जान पड़ती हैं। इस प्लेट को घेरने वाली सतह से गुजरने वाले क्षेत्र का कुल फ्लक्स शून्य नहीं है। चुंबकीय क्षेत्र के संदर्भ में एेसा होना संभव नहीं है। दिखायी गई क्षेत्र रेखाएँ, वास्तव में, धनावेशित ऊपरी प्लेट एवं ऋणावेशित निचली प्लेट के बीच स्थिरवैद्युत क्षेत्र रेखाएँ हैं। [चित्र 5.7(e) एवं (f)] के बीच के अंतर को ध्यानपूर्वक ग्रहण करना चाहिए।
(g) गलत है। दो ध्रुवों के बीच चुंबकीय क्षेत्र रेखाएँ, सिरों पर, ठीक सरल रेखाएँ नहीं हो सकतीं। रेखाओं में कुछ फैलाव अवश्यम्भावी है अन्यथा, एेम्पियर का नियम भंग होता है। यह बात वैद्युत क्षेत्र रेखाओं के लिए भी लागू होती है।
उदाहरण 5.7
(a) चुंबकीय क्षेत्र रेखाएँ (हर बिंदु पर) वह दिशा बताती हैं जिसमें (उस बिंदु पर रखी) चुंबकीय सुई संकेत करती है। क्या चुंबकीय क्षेत्र रेखाएँ प्रत्येक बिंदु पर गतिमान आवेशित कण पर आरोपित बल रेखाएँ भी हैं?
(b) एक टोरॉइड में तो चुंबकीय क्षेत्र पूर्णतः क्रोड के अंदर सीमित रहता है, पर परिनालिका में एेसा नहीं होता। क्यों?
(c) यदि चुंबकीय एकल ध्रुवों का अस्तित्व होता तो चुंबकत्व संबंधी गाउस का नियम क्या रूप ग्रहण करता?
(d) क्या कोई छड़ चुंबक अपने क्षेत्र की वजह से अपने ऊपर बल आघूर्ण आरोपित करती है? क्या किसी धारावाही तार का एक अवयव उसी तार के दूसरे अवयव पर बल आरोपित करता है।
(e) गतिमान आवेशों के कारण चुंबकीय क्षेत्र उत्पन्न होते हैं। क्या कोई एेसी प्रणाली है जिसका चुंबकीय आघूर्ण होगा, यद्यपि उसका नेट आवेश शून्य है?
हल
(a) नहीं। चुंबकीय बल सदैव B के लंबवत होता है (क्योंकि चुंबकीय बल = q (v × B) अतः B की क्षेत्र रेखाओं को बल रेखाएँ कहना भ्रामक वक्तव्य है।
(b) यदि क्षेत्र रेखाएँ सिर्फ सीधी परिनालिका के दो सिरों के बीच सीमित होतीं तो प्रत्येक सिरे के अनुप्रस्थ काट से गुज़रने वाला फ्लक्स शून्य न होता। लेकिन, क्षेत्र B का किसी बंद सतह से गुज़रने वाला फ्लक्स तो सदैव शून्य ही होता है। टोरॉइड के विषय में यह समस्या ही खड़ी नहीं होती क्योंकि इसके कोई सिरे नहीं होते।
(c) चुंबकत्व संबंधी गाउस का नियम यह कहता है कि क्षेत्र B के कारण, किसी बंद सतह से गुज़रने वाला कुल फ्लक्स सदैव शून्य होता है। किसी बंद सतह S के लिए
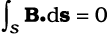
यदि एकल ध्रुवों का अस्तित्व होता तो (स्थिरवैद्युतिकी के गाउस नियम के अनुरूप) समीकरण के दायीं ओर सतह S से घिरे एकल ध्रुवों (चुंबकीय आवेशों) qm का योग आता। अर्थात समीकरण का रूप होता
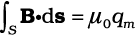जहाँ qm , S से घिरा चुंबकीय आवेश (एकल ध्रुव) है।
(d) नहीं। तार के अल्पांश द्वारा उत्पन्न चुंबकीय क्षेत्र के कारण इसके स्वयं के ऊपर कोई बल या बल आघूर्ण नहीं लगता। लेकिन इसके कारण उसी तार के दूसरे अल्पांश पर बल (या बल आघूर्ण) लगता है। (सीधे तार के विशेष मामले में, यह बल शून्य ही होता है)।
(e) हाँ। संपूर्ण व्यवस्था को देखें तो सभी आवेशों का औसत शून्य हो सकता है। फिर भी, यह हो सकता है कि विभिन्न धारा लूपों के कारण उत्पन्न चुंबकीय आघूर्णों का औसत शून्य न हो। हमारे समक्ष अनुचुंबकीय पदार्थों के संदर्भ में एेसे कई उदाहरण आएँगे जहाँ परमाणुओं का आवेश शून्य है लेकिन उनका द्विध्रुव-आघूर्ण शून्य नहीं है।
5.4 भू-चुंबकत्व
हमने पृथ्वी के चुंबकीय क्षेत्र का जिक्र पहले भी किया है। पृथ्वी के चुंबकीय क्षेत्र की तीव्रता, इसकी सतह पर, भिन्न स्थानों पर भिन्न होती है, पर इसका मान 10–5 T की कोटि का होता है।
पृथ्वी के चुंबकीय क्षेत्र का कारण क्या है, यह बहुत स्पष्ट नहीं है। प्रारंभ में यह सोचा गया कि पृथ्वी का चुंबकीय क्षेत्र इसके अंदर बहुत गहराई में रखे एक विशाल चुंबक के कारण है जो लगभग पृथ्वी के घूर्णन अक्ष के अनुदिश रखा है। परंतु, यह सरलीकृत चित्र निश्चित रूप से सही नहीं है। अब यह माना जाता है कि पृथ्वी का चुंबकीय क्षेत्र इसके बाह्य क्रोड के धात्विक तरलों (जो अधिकांशतः पिघला लोहा एवं निकिल है) की संवाहक गति के कारण उत्पन्न विद्युत धाराओं के परिणामस्वरूप अस्तित्व में आता है। इसको डायनेमो प्रभाव कहा जाता है।
पृथ्वी की चुंबकीय क्षेत्र रेखाएँ, पृथ्वी के केंद्र पर रखे (काल्पनिक) चुंबकीय द्विध्रुव के जैसी ही होती हैं। इस द्विध्रुव की अक्ष पृथ्वी के घूर्णन अक्ष के संपाती नहीं होती है, बल्कि वर्तमान में यह इससे लगभग 11.3° पर झुकी हुई है। इस दृष्टि से देखें तो चुुंबकीय ध्रुव वहाँ अवस्थित है जहाँ चुंबकीय बल रेखाएँ पृथ्वी में प्रवेश करती हैं अथवा इससे बाहर निकलती हैं। पृथ्वी के उत्तरी चुंबकीय ध्रुव की स्थिति 79.74° N अक्षांश एवं 71.8° W देशांतर पर है। यह स्थान उत्तरी कनाडा में है। चुंबकीय दक्षिणी ध्रुव अंटार्कटिका में, 79.74° S अक्षांश एवं 108.22° E देशांतर पर है।
वह ध्रुव जो पृथ्वी के भौगोलिक उत्तरी ध्रुव के निकट है उत्तरी चुंबकीय ध्रुव कहलाता है। इसी प्रकार पृथ्वी के भौगोलिक दक्षिण ध्रुव के निकट स्थित ध्रुव दक्षिणी चुंबकीय ध्रुव कहलाता है। ध्रुवों के नामकरण के संबंध में कुछ संभ्रम हैं। यदि आप पृथ्वी की चुंबकीय क्षेत्र रेखाओं को देखें (चित्र 5.8), तो छड़ चुंबक के विपरीत क्षेत्र रेखाएँ उत्तरी चुंबकीय ध्रुव (Nm) से पृथ्वी के अंदर प्रवेश करती हैं और दक्षिणी चुंबकीय ध्रुव (Sm) से बाहर आती हैं। यह परिपाटी इसलिए शुरू हुई क्योंकि चुंबकीय उत्तर वह दिशा थी जिसमें चुंबकीय सुई का उत्तरी सिरा संकेत करता था; चुंबक के ध्रुव को उत्तरी ध्रुव इसलिए कहा गया क्योंकि यह उत्तर दिशा का ज्ञान कराने में सहायक था। इस प्रकार, वास्तव में, उत्तरी चुंबकीय ध्रुव पृथ्वी के अंदर के छड़ चुंबक के दक्षिणी ध्रुव की तरह व्यवहार करता है एवं दक्षिणी चुंबकीय ध्रुव इस छड़ चुंबक के उत्तरी ध्रुव की तरह।
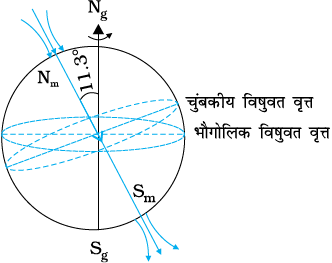
चित्र 5.8 पृथ्वी, एक विशाल चुंबकीय द्विध्रुव की भाँति।
उदाहरण 5.8
विषुवत रेखा पर पृथ्वी के चुंबकीय क्षेत्र का परिमाण लगभग 0.4 G है। पृथ्वी के चुंबक के द्विध्रुव आघूर्ण की गणना कीजिए।
हल
समीकरण (5.7) के अनुसार विषुवतीय चुंबकीय क्षेत्र का परिमाण,
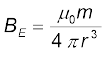
दिया हैः BE ~ 0.4 G = 4 × 10–5 T, r यहाँ पृथ्वी की त्रिज्या है, 6.4 × 106 m अतः
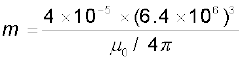=4 × 102 × (6.4 × 106)3 (µ0/4π = 10–7)
= 1.05 × 1023 A m2
यह मान भू-चुंबकत्व संबंधी पुस्तकों में दिए गए मान 8 × 1022 A m2 के बहुत निकट है।
5.4.1 चुंबकीय दिक्पात एवं नति
चित्र 5.9 क्षैतिज तल में घूमने के लिए स्वतंत्र चुंबकीय सुई, चुंबकीय उत्तर-दक्षिण दिशा में इंगित करती है।
पृथ्वी की सतह पर कोई बिंदु लीजिए। इस बिंदु से गुज़रने वाला देशांतर वृत्त भौगोलिक उत्तर-दक्षिण दिशा निर्दिष्ट करता है जिसकी उत्तरी ध्रुव की ओर जाने वाली रेखा यथार्थ उत्तर की ओर इंगित करती है। देशांतर वृत्त एवं पृथ्वी के घूर्णन अक्ष में से गुजरने वाला ऊर्ध्वाधर तल भौगोलिक याम्योत्तर कहलाता है। इसी प्रकार आप किसी स्थान विशेष पर चुंबकीय याम्योत्तर भी उस स्थान और चुंबकीय उत्तरी एवं दक्षिणी ध्रुवों को मिल जाने वाली काल्पनिक रेखा से गुज़रने वाले ऊर्ध्वाधर तल के रूप में परिभाषित कर सकते हैं। यह तल भी पृथ्वी की सतह को देशांतर जैसे ही एक वृत्त में काटेगा। एक चुंबकीय सुई जो क्षैतिज तल में घूमने के लिए स्वतंत्र है, तब चुंबकीय याम्योत्तर में रहेगी और इसका उत्तरी ध्रुव पृथ्वी के चुंबकीय उत्तरी ध्रुव की ओर संकेत करेगा। चूँकि चुंबकीय ध्रुवों को मिलाने वाली रेखा, पृथ्वी के भौगोलिक अक्ष की तुलना में किसी कोण पर झुकी रहती है, किसी स्थान पर चुंबकीय याम्योत्तर, भौगोलिक याम्योत्तर से एक कोण बनाती है। यही वह कोण है जो यथार्थ भौगोलिक उत्तर एवं चुंबकीय सुई द्वारा इंगित उत्तर के बीच बनता है। इस कोण को चुंबकीय दिक्पात अथवा केवल दिक्पात कहते हैं (चित्र 5.9)।
दिक्पात उच्चतर अक्षांशों पर अधिक एवं विषुवत रेखा के पास कम होता है, भारत में दिक्पात का मान कम है, यह दिल्ली में 0o 41′ E एवं मुंबई में 0°58′ W है। अतः दोनों ही स्थानों पर चुंबकीय सुई काफ़ी हद तक सही उत्तर दिशा दर्शाती है।
एक अन्य महत्वपूर्ण राशि भी है जिसमें आपकी रुचि हो सकती है। यदि कोई चुंबकीय सुई, एक क्षैतिज अक्ष पर इस प्रकार पूर्ण संतुलन में हो कि चुंबकीय याम्योत्तर के तल में घूम सके तो यह सुई क्षैतिज से एक कोण बनाएगी (चित्र 5.10)। यह नमन कोण (या आनति) कहलाता है। अतः आनति वह कोण है जो पृथ्वी का कुल चुंबकीय क्षेत्र BE पृथ्वी की सतह से बनाता है।
चित्र (5.11) पृथ्वी की सतह के किसी बिंदु P पर चुंबकीय याम्योत्तर तल दर्शाता है। यह तल पृथ्वी से गुजरने वाला एक खंड है। बिंदु P पर कुल चुंबकीय क्षेत्र को हम एक क्षैतिज अवयव HE एवं एक ऊर्ध्वाधर अवयव ZE में वियोजित कर सकते हैं। BE, HE से जो कोण बनाता है वही नमन कोण I है।
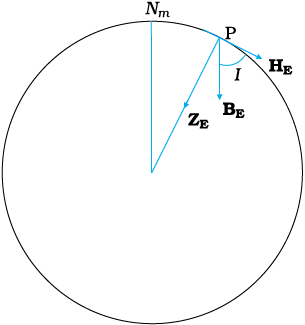
चित्र 5.10 दर्शाया गया वृत्त, पृथ्वी से गुज़रने वाला चुंबकीय याम्योत्तर का खंड है। BE एवं क्षैतिज अवयव HE के बीच बना कोण आनति है।
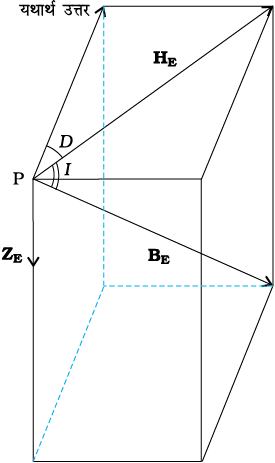
चित्र 5.11 पृथ्वी का चुंबकीय क्षेत्र BE, एवं इसके क्षैतिज एवं ऊर्ध्वाधर अवयव HE एवं ZE। दिक्पात कोण D एवं नमन कोण I भी दर्शाए गए हैं।
अधिकतर उत्तरी गोलार्ध में नमन वृत्त की सुई का उत्तरी ध्रुव नीचे की ओर झुकता है। इसी प्रकार अधिकांश दक्षिणी गोलार्ध में नमन सुई का दक्षिणी ध्रुव नीचे झुकता है।
पृथ्वी की सतह पर स्थित किसी बिंदु पर चुंबकीय क्षेत्र को पूरी तरह निर्दिष्ट करने के लिए हमें तीन राशियों का विवरण देना होता है, ये हैं- दिक्पात कोण D, आनति या नमन कोण I एवं पृथ्वी के चुंबकीय क्षेत्र का क्षैतिज अवयव HE । ये पृथ्वी के चुंबकीय क्षेत्र के घटक कहलाते हैं।
यहाँ ऊर्ध्वाधर घटक,
ZE = BE sinI
क्षैतिज घटक, [5.10(a)]
HE = BE cosI [5.10(b)]
जिससे हमें प्राप्त होता है
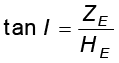[5.10(c)]
ध्रुवों पर हमारी चुंबकीय सुई को क्या हो जाता है?
चुंबकीय दिक्सूचक में एक चुंबकीय सुई एक धुरी पर स्वतंत्रतापूर्वक घूम सकती है। जब दिकसूचक को समतल में रखा जाता है तो इसकी चुंबकीय सुई उस स्थान पर पृथ्वी के चुंबकीय क्षेत्र के क्षैतिज अवयव की दिशा में ठहरती है। पृथ्वी पर कुछ स्थानों पर चुंबकीय खनिजों के भंडार पाए जाते हैं जिनके कारण दिक्सूचक सुई चुंबकीय याम्योत्तर सेहट जाती है। किसी स्थान पर दिक्पात का ज्ञान, हमें उस स्थान पर दिक्सूचक सुई के मान में संशोधन कर यथार्थ उत्तर दिशा जानने में सहायता करता है
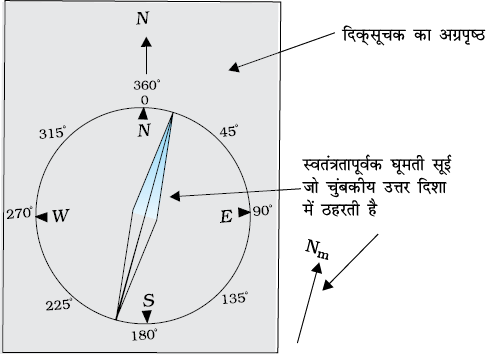
अतः चुंबकीय सुई को ध्रुव पर ले जाने का परिणाम क्या होगा? ध्रुव पर, या तो चुंबकीय क्षेत्र रेखाएँ ऊर्ध्वाधरतः अभिसरित होंगी या अपसरित होंगी इससे क्षैतिज घटक का मान उपेक्षणीय होगा। यदि सुई केवल क्षैतिज तल में ही घूमने के लिए स्वतंत्र होगी तो यह किसी भी दिशा में संकेत कर सकती है और इस कारण दिक्सूचक के रूप में इसकीकोई उपयोगिता नहीं रह जाएगी। इस स्थिति में जिस वस्तु की हमें आवश्यकता है वह है नमनदर्शी सुई जो एक एेसी दिक्सूचक सुई है जिसको पृथ्वी के चुंबकीय क्षेत्र से युक्त ऊर्ध्वाधर तल में घूमने के लिए धुरी पर रखा गया है। तब इस दिक्सूचक की सुई वह कोण दर्शाती है जो चुंबकीय क्षेत्र ऊर्ध्वाधर से बनाता है। चुंबकीय ध्रुवों पर यह सुई सीधे नीचे की ओर इंगित करती है।
उदाहरण 5.9
किसी स्थान के चुंबकीय याम्योत्तर में पृथ्वी के चुंबकीय क्षेत्र का क्षैतिज अवयव 0.26 G है एवं नमन कोण 60o है। इस स्थान पर पृथ्वी का चुंबकीय क्षेत्र क्या है?
हल
यह दिया गया है कि HE = 0.26 G, चित्र 5.11 से हम पाते हैं कि–
=
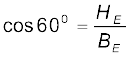
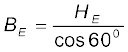
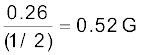
पृथ्वी का चुंबकीय क्षेत्र
यह नहीं मानना चाहिए कि पृथ्वी के अंदर गहराई में कोई विशाल छड़ चुंबक रखा है जो पृथ्वी के चुंबकीय क्षेत्र के लिए उत्तरदायी है। यद्यपि पृथ्वी के अंदर लोहे के प्रचुर भंडार हैं तथापि इसकी संभावना बहुत ही कम है कि लोहे का कोई विशाल ठोस खंड चुंबकीय उत्तरी ध्रुव से चुंबकीय दक्षिणी ध्रुव तक फैला हो। पृथ्वी का क्रोड बहुत गर्म तथा पिघली हुई अवस्था में है तथा लोहे एवं निकिल के आयन पृथ्वी के चुंबकीय क्षेत्र के लिए उत्तरदायी हैं। यह परिकल्पना संभावित जान पड़ती है। चंद्रमा जिसमें कोई द्रवीभूत क्रोड नहीं है, इसका कोई चुंबकीय क्षेत्र भी नहीं है। शुक्र ग्रह जिसकी घूर्णन गति अत्यंत मंद है इसका चुंबकीय क्षेत्र भी बहुत क्षीण है, जबकि बृहस्पति, जिसकी घूर्णन गति ग्रहों में सर्वाधिक है, इसका चुंबकीय क्षेत्र भी पर्याप्त शक्तिशाली है। किंतु, इन परिवाही धाराओं की उत्पत्ति के सही कारण और उनको बनाए रखने के लिए आवश्यक ऊर्जा आदि को बहुत अच्छी तरह से समझा नहीं जा सका है। ये एेसे प्रश्न हैं जो सतत शोध के लिए एक महत्वपूर्ण क्षेत्र प्रदान करते हैं।
स्थान परिवर्तन के साथ पृथ्वी के चुंबकीय क्षेत्र में होने वाले परिवर्तन भी अध्ययन का रोचक विषय है। सूर्य से उत्सर्जित होने वाले आवेशित कण एक प्रवाह के रूप में पृथ्वी की ओर आते हैं जिसे सौर पवन कहा जाता है। इन कणों की गति पृथ्वी के चुंबकीय क्षेत्र से प्रभावित होती है और ये स्वयं पृथ्वी की चुुंबकीय क्षेत्र व्यवस्था में बदलाव ला देते हैं। ध्रुवों के निकट पृथ्वी के चुंबकीय क्षेत्र की संरचना अन्य भागों से बिलकुल अलग होती है।
समय के साथ पृथ्वी के चुंबकीय क्षेत्र में होने वाले परिवर्तन भी कोई कम लुभावने नहीं हैं। इनमें अल्पकालिक परिवर्तन भी शामिल हैं जो शताब्दियों में नजर आने लगते हैं और दीर्घकालीन परिवर्तन भी जो लाखों वर्षों के दीर्घकाल में दृष्टिगत होते हैं। ज्ञात स्रोतों के अनुसार, 1580 ई. से 1820 ई. के बीच के 240 वर्षों के समय काल में लंदन में चुंबकीय दिक्पात के मान में 3.5o का अंतर रिकार्ड किया गया, जिससे यह संकेत मिलता है कि पृथ्वी का चुंबकीय क्षेत्र समय के साथ परिवर्तित होता है। यह पाया गया है कि 10 लाख वर्षों में पृथ्वी के चुंबकीय क्षेत्र की दिशा उलट जाती है। असिताश्म (Basalt) में लोहा होता है और असिताश्म ज्वालामुखी विस्फोट में बाहर निकलता है। जब यह ठंडा होकर ठोस में बदलता है तो इसके अंदर के छोटे-छोटे लौह-चुंबक चुंबकीय क्षेत्र की दिशा के समांतर समरेखित हो जाते हैं। एेसे चुंबकीय क्षेत्रों से युक्त असिताश्म भंडारों के भूवैज्ञानिक अध्ययनों से इस बात के प्रमाण मिले हैं कि पृथ्वी के चुंबकीय क्षेत्र की दिशा अतीत में कई बार उलट चुकी है।
5.5 चुंबकीकरण एवं चुंबकीय तीव्रता
पृथ्वी तत्वों एवं यौगिकों की विस्मयकारी विभिन्नताओं से भरपूर है। इसके अतिरिक्त, हम नए-नए मिश्रधातु, यौगिक, यहाँ तक कि तत्व भी संश्लेषित करते जा रहे हैं। आप इन सब पदार्थों को चुंबकीय गुणों के आधार पर वर्गीकृत करना चाहेंगे। प्रस्तुत अनुभाग में हम एेसे कुछ पदों की परिभाषा देंगे और उनके बारे में समझाएँगे जो इस वर्गीकरण में हमारी सहायता करेंगे।
हम यह देख चुके हैं कि परमाणु में परिक्रमण करते इलेक्ट्रॉन का एक चुंबकीय आघूर्ण होता है। पदार्थ के किसी बड़े टुकड़े में ये चुंबकीय आघूर्ण सदिश रूप से समाकलित होकर शून्येतर परिणामी चुंबकीय आघूर्ण प्रदान कर सकते हैं। किसी दिए गए नमूने का चुंबकन M हम इस प्रकार उत्पन्न हुए प्रति इकाई आयतन परिणामी चुंबकीय आघूर्ण के रूप में परिभाषित कर सकते हैं,
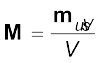(5.11)
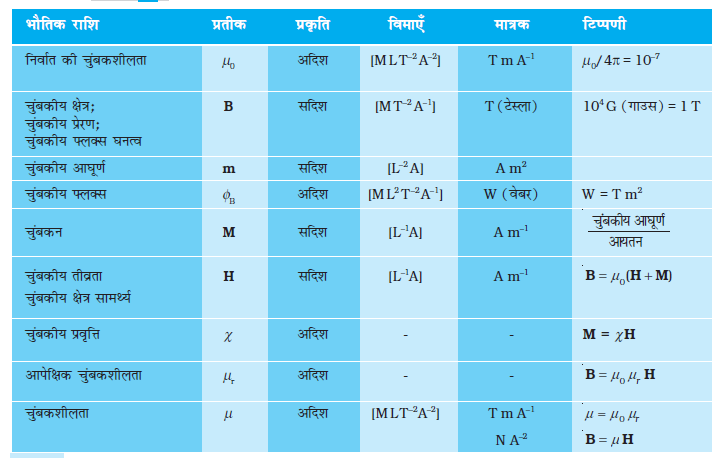
M एक सदिश राशि है जिसका विमीय सूत्र L–1 A एवं मात्रक A m–1 है।
एक लंबी परिनालिका लीजिए जिसकी प्रति इकाई लंबाई में n फेरे हों, और जिसमें I धारा प्रवाहित हो रही हो। इस परिनालिका के अंदर चुंबकीय क्षेत्र का परिमाण है,
B0 = µ0 nI (5.12)
यदि परिनालिका के अंदर शून्येतर चुंबकन का कोई पदार्थ भरा हो तो यहाँ क्षेत्र B0 से अधिक होगा। परिनालिका के अंदर परिणामी क्षेत्र B को लिख सकते हैं
B = B0 + Bm (5.13)
जहाँ Bm क्रोड के पदार्थ द्वारा प्रदत्त क्षेत्र है। यह पाया गया है कि यह अतिरिक्त क्षेत्र Bm पदार्थ के चुंबकन M के अनुक्रमानुपाती होता है और इसको हम निम्नवत व्यक्त कर सकते हैं
Bm = µ0M (5.14)
जहाँ µ0 वही नियंताक है (निर्वात की पारगम्यता) जो बायो-सावर्ट के नियम में उपयोग किया गया था।
सुविधा के लिए हम एक अन्य सदिश क्षेत्र H की बात करते हैं जिसे चुंबकीय तीव्रता कहा जाता है और जिसको निम्नलिखित समीकरण द्वारा परिभाषित किया जाता है
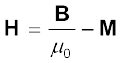(5.15)
जहाँ H की विमाएँ वहीं हैं जो M की और इसका मात्रक भी A m–1 ही है।
इस प्रकार कुल चुंबकीय क्षेत्र B को लिख सकते हैं
B = µ0 (H + M) (5.16)
उपरोक्त विवरण में आए पदों को व्युत्पन्न करने में हमने जिस पद्धति का प्रयोग किया है उसको दोहराते हैं। परिनालिका के अंदर के कुल चुंबकीय क्षेत्र को हमने दो अलग-अलग योगदानों के रूप में प्रस्तुत किया– पहला बाह्य कारक, जैसे कि परिनालिका में प्रवाहित होने वाली धारा का योगदान। यह H द्वारा व्यक्त किया गया है; और दूसरा चुंबकीय पदार्थ की विशेष प्रकृति के कारण अर्थात M। बाद वाली राशि (M) बाह्य कारकों द्वारा प्रभावित की जा सकती है। यह प्रभाव गणितीय रूप में इस प्रकार व्यक्त कर सकते हैंः
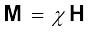(5.17)
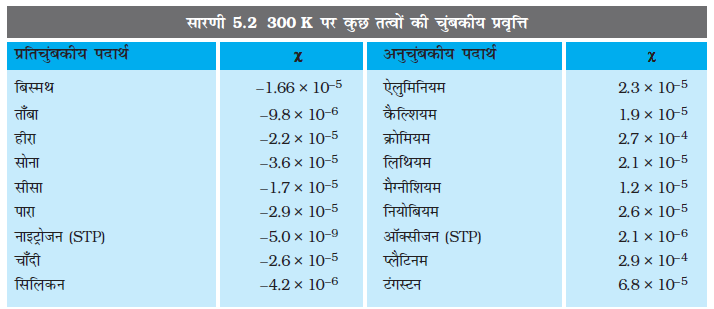
जहाँ χ एक विमाविहीन राशि है और इसे चुंबकीय प्रवृत्ति कहते हैं। यह किसी चुंबकीय पदार्थ पर बाह्य चुंबकीय क्षेत्र के प्रभाव का माप है। सारणी 5.2 में कुछ तत्वों की चुंबकीय प्रवृत्ति को सूचीबद्ध किया गया है। हम देखते हैं कि χ बहुत छोटे परिमाण वाली राशि है। कुछ पदार्थों के लिए इसका मान छोटा और धनात्मक है जिन्हें अनुचुंबकीय पदार्थ कहते हैं। कुछ पदार्थों के लिए इसका मान छोटा एवं ऋणात्मक है जिन्हें प्रतिचुंबकीय पदार्थ कहते हैं। प्रतिचुंबकीय पदार्थों में M एवं H विपरीत दिशाओं में होते हैं। समीकरण (5.16) एवं (5.17) से हम पाते हैं,
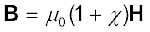(5.18)
= µ0 µr H
= µ H (5.19)
जहाँ, µr = (1 + χ) एक विमाविहीन राशि है जिसे हम पदार्थ की आपेक्षिक चुंबकशीलता या ‘आपेक्ष चुंबकीय पारगम्यता’ कहते हैं। यह स्थिरवैद्युतिकी के परावैद्युतांक के समतुल्य राशि है। पदार्थ की चुंबकशीलता µ है और इसकी विमाएँ तथा मात्रक वही हैं जो µ0 के हैं।
µ = µ0µr = µ0 (1+χ)
χ, µr एवं µ में तीन राशियाँ परस्पर संबंधित हैं। यदि इनमें से किसी एक का मान ज्ञात हो तो बाकी दोनों के मान ज्ञात किए जा सकते हैं।
उदाहरण 5.10
एक परिनालिका के क्रोड में भरे पदार्थ की आपेक्षिक चुंबकशीलता 400 है। परिनालिका के विद्युतीय रूप से पृथक्कृत फेरों में 2A की धारा प्रवाहित हो रही है। यदि इसकी प्रति 1m लंबाई में फेरों की संख्या 1000 है तो (a) H, (b) M, (c) B एवं (d) चुंबककारी धारा Im की गणना कीजिए।
हल
(a) क्षेत्र H क्रोड के पदार्थ पर निर्भर करता है और इसके लिए सूत्र है
H = nI = 1000 × 2.0 = 2 ×103 A/m
(b) चुंबकीय क्षेत्र B के लिए सूत्र है
B = µr µ0 H
= 400 × 4π ×10–7 (N/A2) × 2 × 103 (A/m)
= 1.0 T
(c) चुंबकन
M = (B– µ0 H)/ µ0
= (µr µ0 H–µ0 H)/µ0 = (µr – 1)H = 399 × H
≅ 8 × 105 A/m
(d) चुंबकन धारा IM वह अतिरिक्त धारा है जो क्रोड की अनुपस्थिति में परिनालिका के फेरों में प्रवाहित किए जाने पर इसके अंदर उतना ही क्षेत्र B उत्पन्न करेगी जितना क्रोड की उपस्थिति में होता। अतः B = µr n (I + IM) लेने पर I = 2 A, B = 1 T हमें प्राप्त होता है
IM = 794 A
5.6 पदार्थों के चुंबकीय गुण
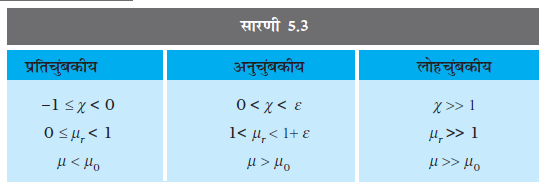
पिछले अनुभाग में वर्णित विचार हमें पदार्थों को प्रतिचुंबकीय, अनुचुंबकीय एवं लोहचुंबकीय श्रेणियों में वर्गीकृत करने में सहायता प्रदान करते हैं। चुंबकीय प्रवृत्ति χ की दृष्टि से देखें तो कोई पदार्थ प्रतिचुंबकीय है यदि इसके लिए χ ऋणात्मक है, अनुचुंबकीय होगा यदि χ धनात्मक एवं अल्प मान वाला है, और लोहचुंबकीय होगा यदि χ धनात्मक एवं अधिक मान वाला है।
अधिक मूर्त रूप में सारणी 5.3 पर एक दृष्टि हमें इन पदार्थों का एक अच्छा अनुभव प्रदान करती है। यहाँ ε एक छोटी धन संख्या है जो अनुचुंबकत्व का परिमाण निर्धारित करने के लिए लाई गई है। अब हम इन पदार्थों के बारे में कुछ विस्तार से चर्चा करेंगे।
5.6.1 प्रतिचुंबकत्व
प्रतिचुंबकीय पदार्थ वह होते हैं जिनमें बाह्य चुंबकीय क्षेत्र में अधिक तीव्रता वाले भाग से कम तीव्रता वाले भाग की ओर जाने की प्रवृत्ति होती है। दूसरे शब्दों में कहें तो चुंबक लोहे जैसी धातुओं को तो अपनी ओर आकर्षित करता है, परंतु यह प्रतिचुंबकीय पदार्थों को विकर्षित करेगा।
चित्र 5.12 (a), बाह्य चुंबकीय क्षेत्र में रखी प्रतिचुंबकीय पदार्थ की एक छड़ दर्शाता है। क्षेत्र रेखाएँ विकर्षित होती हैं या दूर हटती हैं इसलिए पदार्थ के अन्दर क्षेत्र कम हो जाता है सारणी 5.2 से यह स्पष्ट है कि अधिकांश मामलों में क्षेत्र की तीव्रता में यह कमी अत्यल्प होती है (105 भागों में एक भाग)। छड़ को किसी असमान चुंबकीय क्षेत्र में रखने पर इसकी प्रवृत्ति अधिक क्षेत्र से कम क्षेत्र की ओर जाने की होती है।
प्रतिचुंबकत्व की सरलतम व्याख्या इस प्रकार है–नाभिक के चारों ओर घूमते इलेक्ट्रॉनों के कारण कक्षीय कोणीय संवेग होता है। ये प्ररिक्रमण करते इलेक्ट्रॉन एक धारावाही लूप के समतुल्य होते हैं और इस कारण इनका कक्षीय चुंबकीय आघूर्ण होता है, प्रतिचुंबकीय पदार्थ वे होते हैं जिनके परमाणु में परिणामी चुंबकीय आघूर्ण शून्य होता है। जब कोई बाह्य चुंबकीय क्षेत्र आरोपित किया जाता है तो जिन इलेक्ट्रॉनों के कक्षीय चुंबकीय आघूर्ण क्षेत्र की दिशा में होते हैं उनकी गति मंद हो जाती है और जिनके चुुंबकीय आघूर्ण क्षेत्र के विपरीत दिशा में होते हैं उनकी गति बढ़ जाती है। एेसा लेंज के नियम के अनुसार प्रेरित धारा के कारण होता है जिसके विषय में आप अध्याय 6 में अध्ययन करेंगे। इस प्रकार पदार्थ में परिणामी चुंबकीय आघूर्ण आरोपित क्षेत्र के विपरीत दिशा में विकसित होता है और इस कारण यह प्रतिकर्षित होता है।
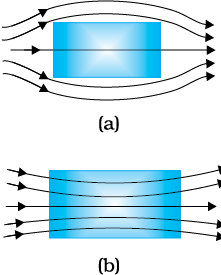
चित्र 5.12
एक (a) प्रतिचुंबकीय
(b) अनुचुंबकीय पदार्थ के निकट किसी बाह्य चुंबकीय क्षेत्र के कारण चुंबकीय क्षेत्र रेखाओं का व्यवहार।
कुछ प्रतिचुंबकीय पदार्थ हैं– बिस्मथ, ताँबा, सीसा, सिलिकन, नाइट्रोजन (STP पर), पानी एवं सोडियम क्लोराइड। प्रति चुंबकत्व सभी पदार्थों में विद्यमान होता है। परंतु, अधिकांश पदार्थों के लिए यह इतना क्षीण होता है कि अनुचुंबकत्व एवं लौह चुंबकत्व जैसे प्रभाव इस पर हावी हो जाते हैं।
सबसे अधिक असामान्य प्रतिचुंबकीय पदार्थ हैं अति चालक। ये एेसी धातुएँ हैं, जिनको यदि बहुत निम्न ताप तक ठंडा कर दिया जाता है तो ये पूर्ण चालकता एवं पूर्ण प्रतिचुंबकत्व दोनों प्रदर्शित करती हैं। चुंबकीय क्षेत्र रेखाएँ पूर्णतः इनके बाहर रहती हैं, χ = –1 एवं µr = 0। एक अतिचालक, एक चुंबक को प्रतिकर्षित करेगा और (न्यूटन के तृतीय नियमानुसार) स्वयं इसके द्वारा प्रतिकर्षित होगा। अतिचालकों में पूर्ण प्रतिचुंबकत्व की यह परिघटना इसके आविष्कारक के नाम पर माइस्नर प्रभाव कहलाती है। अनेक भिन्न परिस्थितियों में जैसे कि, चुंबकीकृत अधरगामी अति तीव्र रेलगाड़ियों को चलाने में अतिचालक चुंबकों का लाभ उठाया जा सकता है।
5.6.2 अनुचुंबकत्व
अनुचुंबकीय पदार्थ एेसे पदार्थ होते हैं जो बाह्य चुंबकीय क्षेत्र में रखे जाने पर क्षीण चुंबकत्व प्राप्त कर लेते हैं। उनमें क्षीण चुंबकीय क्षेत्र से सशक्त चुंबकीय क्षेत्र की ओर जाने की प्रवृत्ति होती है अर्थात ये चुंबक की ओर क्षीण बल द्वारा आकर्षित होते हैं।
किसी अनुचुंबकीय पदार्थ के परमाणुओं (या आयनों या अणुओं) का अपना स्वयं का स्थायी चुंबकीय द्विध्रुव आघूर्ण होता है। परमाणुओं की सतत यादृच्छिक तापीय गति के कारण कोई परिणामी चुंबकीकरण दृष्टिगत नहीं होता। पर्याप्त शक्तिशाली बाह्य चुंबकीय क्षेत्र B0 की उपस्थिति में एवं निम्न तापों पर अलग-अलग परमाणुओं के द्विध्रुव आघूर्ण सरल रेखाओं में और B0 की दिशा के अनुदिश संरेखित किए जा सकते हैं। चित्र 5.12 (b) बाह्य चुंबकीय क्षेत्र में रखी हुई अनुचुंबकीय पदार्थ की एक छड़ प्रदर्शित करता है। चुंबकीय क्षेत्र रेखाएँ पदार्थ के अंदर संकेंद्रित हो जाती हैं और अंदर चुंबकीय क्षेत्र बढ़ जाता है। अधिकतर मामलाें में, जैसा सारणी 5.2 से प्रकट है कि यह वृद्धि अति न्यून है, 105 भागों में एक भाग। असमान चुंबकीय क्षेत्र में रखने पर यह छड़ निम्न क्षेत्र से उच्च क्षेत्र की ओर चलने की चेष्टा करेगी।
कुछ अनुचुंबकीय पदार्थ हैं–एेलुमिनियम, सोडियम, कैल्शियम, अॉक्सीजन (STP पर) एवं कॉपर क्लोराइड। प्रयोगात्मक रूप से किसी अनुचुंबकीय पदार्थ का चुंबकन लगाए गए चुंबकीय क्षेत्र के अनुक्रमानुपाती एवं परम ताप T के व्युत्क्रमानुपाती होता है।
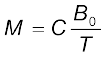[5.20(a)]
या दूसरे समतुल्य रूप में, समीकरण (5.12) एवं (5.17) के प्रयोग से
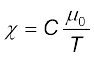[5.20(b)]
यह इसके शोधकर्ता पियरे क्यूरी (1859-1906) के सम्मान में क्यूरी का नियम कहलाता है। नियतांक C को क्यूरी नियतांक कहते हैं। अतः किसी अनुचुंबकीय पदार्थ के लिए χ एवं µr दोनों का मान न केवल पदार्थ पर निर्भर करता है, वरन् (एक सरल रूप में) इसके ताप पर भी निर्भर करता है। बहुत उच्च चुंबकीय क्षेत्रों में या बहुत निम्न ताप पर, चुंबकन अपना अधिकतम मान ग्रहण करने लगता है, जबकि सभी परमाण्वीय द्विध्रुव आघूर्ण चुंबकीय क्षेत्र में रेखाओं के अनुदिश संरेखित हो जाते हैं। यह संतृप्त चुंबकन मान Ms कहलाता है। इसके परे, क्यूरी का नियम [समीकरण (5.20)] मान्य नहीं रह जाता है।
5.6.3 लौह चुंबकत्व
लौह चुंबकीय पदार्थ एेसे पदार्थ होते हैं जो बाह्य चुंबकीय क्षेत्र में रखे जाने पर शक्तिशाली चुंबक बन जाते हैं। उनमें चुंबकीय क्षेत्र के क्षीण भाग शक्तिशाली भाग की ओर चलने की तीव्र प्रवृत्ति होती है अर्थात वे चुंबक की ओर भारी आकर्षण बल का अनुभव करते हैं। किसी लौह चुंबकीय पदार्थ के एकल परमाणुओं (या आयनों या अणुओं) का भी अनुचुंबकीय पदार्थों की तरह ही चुंबकीय द्विध्रुव आघूर्ण होता है। परंतु, वे एक-दूसरे के साथ इस प्रकार अन्योन्य क्रिया करते हैं कि एक स्थूल आयतन में (जिसे डोमेन कहते हैं) सब एक साथ एक दिशा में संरेखित हो जाते हैं। इस सहकारी प्रभाव की व्याख्या के लिए क्वांटम यांत्रिकी की आवश्यकता होती है, जो इस पाठ्यपुस्तक के क्षेत्र से बाहर है। प्रत्येक डोमेन का अपना परिणामी चुंबकन होता है। प्रारूपी डोमेन का आकार 1 mm है, और एक डोमेन में लगभग 1011 परमाणु होते हैं। प्रथमदृष्टया चुंबकन एक डोमेन से दूसरे डोमेन तक जाने पर यादृच्छिक रूप से बदलता है तथा कुल पदार्थ में कोई चुंबकन नहीं होता। यह चित्र 5.13 (a) में दिखाया गया है। जब हम बाह्य चुंबकीय क्षेत्र B0 लगाते हैं, तो डोमेन B0 के अनुदिश उन्मुख होने लगते हैं और साथ ही वे डोमेन जो B0 की दिशा में हैं, साइज़ में बढ़ने लगते हैं। डोमेनों का अस्तित्व और B0 के अनुदिश उनके होने वाली गति केवल अनुमान नहीं है। लौह चुंबकीय पदार्थ के पाउडर को किसी द्रव में छिड़क कर उसके निलंबन को सूक्ष्मदर्शी के द्वारा उसकी यादृच्छिक गति को देखा जा सकता है। चित्र 5.12 (b) वह स्थिति दर्शाता है जब सभी डोमेन पंक्तिबद्ध हो गए हैं और उन्होंने घुल-मिलकर एक अकेला विशाल डोमेन बना लिया है।
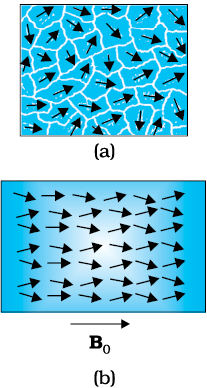
चित्र 5.13
(a) यादृच्छिक अभिविन्यासित डोमेन, (b) संरेखित डोमेन।
इस प्रकार एक लौह चुंबकीय पदार्थ में चुंबकीय क्षेत्र रेखाएँ बहुत अधिक संकेंद्रित हो जाती हैं। एक असमान चुंबकीय क्षेत्र में इस पदार्थ का नमूना अधिक शक्तिशाली चुंबकीय क्षेत्र वाले भाग की ओर चलने को प्रवृत्त होता है। हम यह सोच सकते हैं कि बाह्य क्षेत्र हटा लेने पर क्या होगा? कुछ चुंबकीय पदार्थों में चुंबकन बना रह जाता है। एेसे पदार्थों को कठोर चुंबकीय पदार्थ या कठोर लौह चुंबक कहा जाता है। एलनिको (लोहे, एेलुमिनियम, निकल, कोबाल्ट एवं ताँबे का एक मिश्रातु) एेसा ही एक पदार्थ है और प्राकृतिक रूप में उपलब्ध लोडस्टोन दूसरा। इन पदार्थों से स्थायी चुंबक बनते हैं और इनका उपयोग चुंबकीय सुई बनाने के अलावा अन्य कार्यों में भी होता है। दूसरी ओर लौह चुंबकीय पदार्थों की एक श्रेणी एेसी है जिनका चुंबकन बाह्य क्षेत्र को हटाते ही खत्म हो जाता है। नर्म लोहा एेसा ही एक पदार्थ है। उचित रूप से ही, एेसे पदार्थों को नर्म लौह चुंबकीय पदार्थ कहा जाता है। बहुत से तत्व लौह चुंबकीय हैं; जैसे–लोहा, कोबाल्ट, निकल, गैडोलिनियम आदि। इनकी आपेक्षिक चुंबकशीलता 1000 से अधिक है।
लौह चुंबकीय गुण भी ताप पर निर्भर करता है। पर्याप्त उच्च ताप पर एक लौह चुंबक, अनुचुंबक बन जाता है। ताप बढ़ने पर डोमेन संरचनाएँ विघटित होने लगती हैं। ताप बढ़ने पर चुंबकन का विलोपन धीरे-धीरे होता है। यह एक तरह का प्रावस्था (Phase) परिवर्तन है वैसे ही जैसे किसी ठोस मणिभ (क्रिस्टल) का पिघलना। वह ताप जिस पर कोई लौह चुंबक, अनुचुंबक में परिवर्तित हो जाता है क्यूरी ताप (Tc ) कहलाता है। सारणी 5.4 कुछ लौह चुंबकों के क्यूरी ताप दर्शाती है।
क्यूरी ताप से उच्चतर ताप पर अर्थात अनुचुंबकीय प्रावस्था में चुंबकीय प्रवृत्ति,
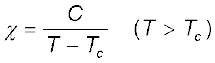
(5.21)
उदाहरण 5.11
लौह चुंबकीय पदार्थ लोहे में कोई डोमेन 10–4m भुजा वाले घन के रूप में है। डोमेन में लौह परमाणुओं की संख्या, अधिकतम संभावित चुंबकीय द्विध्रुव आघूर्ण और इसके चुंबकन का मान ज्ञात कीजिए। लोहे का परमाण्विक द्रव्यमान 55 g/mole और इसका घनत्व 7.9 g/cm3 है। यह मान लीजिए कि प्रत्येक लौह परमाणु का चुंबकीय द्विध्रुव आघूर्ण 9.27 × 10−24 A m2 है।
हल
घनीय डोमेन का आयतन होगा
V = (10–6 m)3 = 10–18 m3 = 10–12 cm3
इसका द्रव्यमान = आयतन × घनत्व = 7.9 g cm–3 × 10–12 cm3= 7.9 × 10–12 g
यह दिया गया है कि एक एवोगाद्रो संख्या (6.023 × 1023) के बराबर लौह परमाणुओं का द्रव्यमान 55 g है। अतः डोमेन में परमाणुओं की संख्या,
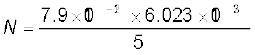
= 8.65 × 1010 परमाणु
अधिकतम संभावित चुंबकीय द्विध्रुव आघूर्ण mअधिकतम तब प्राप्त होता है (यद्यपि यह एक अवास्तविक स्थिति है), जब सभी परमाण्विक आघूर्ण पूर्णतः पंक्तिबद्ध हो जाते हैं। अतः
mअधिकतम = (8.65 × 1010) × (9.27 × 10–24)
= 8.0 × 10–13 A m2
परिणामी चुंबकन का मान
Mअधिकतम = mअधिकतम/डोमेन आयतन
= 8.0 × 10–13 A m2/10–18 m3
= 8.0 × 105 A m–1
लौह-चुंबकीय पदार्थों में B एवं H का संबंध बहुत जटिल है। प्रायः यह रैखिक संबंध नहीं होता एवं नमूने के चुंबकीय अतीत पर निर्भर करता है। चित्र 5.14 चुंबकन के एक चक्र में पदार्थ का व्यवहार चित्रित करता है। माना कि पदार्थ शुरू में बिलकुल विचुंबकित है। हम इसको परिनालिका में रखते हैं और परिनालिका में धारा का मान बढ़ाते हैं। पदार्थ में चुंबकीय क्षेत्र B का मान बढ़ता है और अंत में संतृप्त हो जाता है जैसा कि वक्र Oa में चित्रित है। यह व्यवहार दर्शाता है कि डोमेन तब तक पंक्तिबद्ध और एक-दूसरे में विलीन होते रहते हैं जब तक कि आगे वृद्धि असंभव न हो जाए। इससे आगे धारा (और इस कारण चुंबकीय तीव्रता H) को बढ़ाने का कोई उपयोग नहीं है। फिर, हम H को घटाते हुए शून्य पर ले आते हैं। H = 0 पर B ≠ 0 है। यह वक्र ab द्वारा प्रदर्शित है। H = 0 पर B का मान पदार्थ की चुंबकीय धारणशीलता या चुंबकत्वावशेष कहलाता है। चित्र 5.14 में BR ~ 1.2 T है, यहाँ निम्नष्ठ R धारणशीलता को इंगित करता है। बाह्य चुंबकनकारी क्षेत्र हटा लेने पर भी डोमेन पूर्णतः बेतरतीब विन्यास ग्रहण नहीं कर पाते। अब, परिनालिका में धारा की दिशा उलट देते हैं और धीरे-धीरे इसका मान बढ़ाते हैं। फलस्वरूप कुछ डोमेन पलटकर अपना विन्यास बदल लेते हैं, जब तक कि अंदर परिणामी क्षेत्र शून्य न हो जाए। यह वक्र bc द्वारा दर्शाया गया है। c बिंदु पर H का मान, पदार्थ की निग्राहिता कहलाती है। चित्र 5.14 में, Hc ∼ −90 A m−1। प्रतिलोम धारा का परिमाण बढ़ाते जाने पर हम एक बार फिर संतृप्तता की स्थिति प्राप्त कर लेते हैं। वक्र cd यही दर्शाता है। संतृप्त चुंबकीय क्षेत्र Bs ~ 1.5 T है। एक बार फिर, धारा को कम किया जाता है (वक्र de) और फिर उलट दिया जाता है (वक्र ea)। यह चक्र दोहराया जाता रहता है। इस विषय में हम निम्नलिखित प्रेक्षण लेते हैंः (i) जब H को कम किया जाता है, तो वक्र Oa पुनः अनुरेखित नहीं होता। H के दिए गए मान के लिए, B का कोई अद्वितीय मान लब्ध नहीं होता, बल्कि यह नमूने के पूर्व इतिहास पर निर्भर करता है। यह परिघटना चुंबकीय शैथिल्य (Hysterisis) कहलाती है। शब्द हिस्टेरिसिस का अर्थ चुंबकीय पश्चता है (‘इतिहास’ नहीं)।
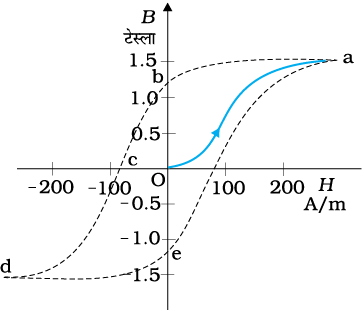
चित्र 5.14 चुंबकीय शैथिल्य पाश लौह-चुंबकीय पदार्थों के लिए B-H वक्र है।
5.7 स्थायी चुंबक एवं विद्युत चुंबक
वह पदार्थ जो कमरे के ताप पर अपने लौह-चुंबकीय गुण दीर्घ काल के लिए बनाए रख सकते हैं, स्थायी चुंबक कहलाते हैं। स्थायी चुंबक विभिन्न तरीकों से बनाए जा सकते हैं। लोहे की एक छड़ को उत्तर-दक्षिण दिशा में रख कर बार-बार इस पर हथौड़े से प्रहार करते हैं तो वह चुंबक बन जाती है। यह विधि चित्र 5.15 में दर्शायी गई है। यह चित्र एक 400 साल पुरानी पुस्तक से यह दर्शाने के लिए लिया गया है कि स्थायी चुंबक बनाने की कला काफी पुरानी है। स्थायी चुंबक बनाने के लिए एक स्टील की छड़ को पकड़ कर उसके ऊपर किसी छड़ चुंबक का एक सिरा एक ओर से दूसरी ओर स्पर्श कराते हुए बार-बार ले जाते हैं।
चित्र 5.15 एक लोहार, उत्तर-दक्षिण दिशा में रखी एक लाल गर्म लोहे की छड़ को हथौड़े से पीट कर चुंबक में बदलते हुए। यह आरेख सन 1600 में प्रकाशित, डॉ. विलियम गिल्बर्ट (जो इंग्लैंड की महारानी एलिजाबेथ के शाहीचिकित्सक थे) की पुस्तक, डे मैग्नेटे (De Magnete) से है।
स्थायी चुंबक बनाने का एक प्रभावी तरीका यह है कि किसी परिनालिका के अंदर एक लौह चुंबकीय पदार्थ की छड़ रखी जाए और उस परिनालिका में नियत दिष्ट धारा प्रवाहित की जाए। परिनालिका का चुंबकीय क्षेत्र छड़ को चुंबकित कर देता है।
चुंबकीय शैथिल्य वक्र (चित्र 5.14) हमें स्थायी चुंबकों के लिए उचित पदार्थ चुनने में सहायता करते हैं। शक्तिशाली चुंबक बनाने के लिए पदार्थ की उच्च चुंबकीय धारणशीलता और उच्च निग्राहिता होनी चाहिए ताकि इधर-उधर के चुंबकीय क्षेत्रों या तापीय उतार-चढ़ावों या क्षुद्र यांत्रिक हानियों के कारण इसका चुंबकत्व आसानी से खत्म न हो जाए।
इसके अलावा पदार्थ की उच्च चुंबकशीलता होनी चाहिए। स्टील एेसा ही एक पदार्थ है। इसकी धारणशीलता नर्म लोहे से कुछ कम है पर नर्म लोहे की निग्राहिता इतनी कम है कि सब गुणों को सोचें तो स्थायी चुंबक बनाने के लिए स्टील नर्म लोहे से बेहतर है। स्थायी चुंबकों के लिए उपयुक्त अन्य पदार्थों के नाम हैं–एेलनिको (लोहे, एलुमिनियम, निकल, कोबाल्ट एवं ताँबे का एक मिश्रातु), कोबाल्ट-स्टील एवं टिकोनल।
विद्युत चुंबक एेसे लौह चुंबकीय पदार्थों के बने होते हैं जिनकी चुंबकशीलता बहुत अधिक एवं धारणशीलता बहुत कम होती है। नर्म लोहा विद्युत चुंबकों के लिए एक उपयुक्त पदार्थ है। किसी परिनालिका के अंदर नर्म लोहे की छड़ रख कर हम उसमें नियत दिष्ट धारा प्रवाहित करते हैं, तो परिनालिका का चुंबकीय क्षेत्र हज़ार गुना बढ़ जाता है। जब हम परिनालिका में धारा प्रवाहित करना बंद कर देते हैं तो चुंबकीय क्षेत्र भी वस्तुतः समाप्त हो जाता है क्योंकि नर्म लोहे वाले क्रोड की चुंबकीय धारणशीलता बहुत कम है। यह व्यवस्था चित्र 5,16 में दर्शायी गई है।
चित्र 5.16 एक नर्म लौह-क्रोड युक्त परिनालिका विद्युत चुंबक की तरह व्यवहार करती है।
कुछ अनुप्रयोगों में पदार्थ एक लंबे समय तक चुंबकन के प्रत्यावर्ती चक्र से गुजरता है। ट्रांसफॉर्मर के क्रोड एवं टेलीफोन के डायफ्राम में एेसा ही होता है। इनमें प्रयुक्त पदार्थों के चुंबकीय शैथिल्य वक्र संकीर्ण होने चाहिए। परिणामस्वरूप इनमें ऊष्मा क्षय एवं ताप वृद्धि कम होगी। इन पदार्थों की प्रतिरोधकता भी कम होनी चाहिए ताकि भँवर धाराओं के कारण ऊर्जा क्षय में कमी रहे। भँवर धाराओं के विषय में हम अध्याय 6 में अध्ययन करेंगे।
विद्युत चुंबकों का अनुप्रयोग विद्युत घंटियों, ध्वनि विस्तारक एवं दूरभाष यंत्रों में होता है। विशालकाय विद्युत चुंबकों का क्रेनाें में मशीनों या लोहे एवं स्टील की भारी वस्तुओं को उठाने के लिए इस्तेमाल किया जाता है।
भारत के चुंबकीय क्षेत्र का मानचित्रण
अन्वेषण, संचार एवं नाविकी में व्यावहारिक अनुप्रयोगों के कारण दुनिया के अधिकतर देशों ने पृथ्वी के चुंबकीय क्षेत्र के एेसे नक्शे बनाए हैं जिनकी परिशुद्धता भौगोलिक नक्शों के साथ तुलनीय है। भारत में, दक्षिण में त्रिवेंद्रम से उत्तर में गुलमर्ग तक एक दर्जन से अधिक वेधशालाएँ हैं। ये वेधशालाएँ मुंबई के कोलाबा में स्थित, भारतीय भू-चुंबकत्व संस्थान (IIG) के अधीन कार्य करती हैं। भारतीय भू-चुंबकत्व संस्थान, कोलाबा एवं अलीबाग वेधशालाओं के विस्तार स्वरूप, औपचारिक रूप से 1971 में स्थापित किया गया। भारतीय भू-चुंबकत्व संस्थान अपनी देशव्यापी वेधशालाओं के माध्यम से भू, समुद्र तल एवं अंतरिक्ष के चुंबकीय क्षेत्र एवं उनमें होने वाले उतार-चढ़ावों पर निगाह रखता है। इसकी सेवाएँ तेल एवं प्राकृतिक गैस आयोग (ONGC), राष्ट्रीय समुद्र-विज्ञान संस्थान (NIO) एवं भारतीय अंतरिक्ष अनुसंधान संगठन (ISRO) द्वारा प्रयोग की जाती हैं। यह उस विश्वव्यापी व्यवस्था का अंग है जो लगातार प्रयत्नपूर्वक भू-चुंबकीय आंकड़ों को सुधारती रहती है। अब भारत का ‘गंगोत्री’ नामक एक स्थायी केंद्र है।
सारांश
1. चुंबकत्व विज्ञान एक प्राचीन विज्ञान है। यह अत्यंत प्राचीन काल से ज्ञात रहा है कि चुंबकीय पदार्थों में उत्तर-दक्षिण दिशा में संकेत करने की प्रवृत्ति होती है। समान ध्रुव एक-दूसरे को प्रतिकर्षित करते हैं और विपरीत ध्रुव आकर्षित। किसी छड़ चुंबक को काटकर दो भागों में विभाजित करें तो दो छोटे चुंबक बन जाते हैं। चुंबक के ध्रुव अलग नहीं किए जा सकते।
2. जब m चुंबकीय द्विध्रुव आघूर्ण वाले छड़ चुंबक को समांग चुंबकीय क्षेत्र B में रखते हैं, तो
(a) इस पर लगने वाला कुल बल शून्य होता है।
(b) बल आघूर्ण m × B होता है।
(c) इसकी स्थितिज ऊर्जा –m.B होती है, जहाँ हमने शून्य ऊर्जा को उस विन्यास में लिया है जब m चुंबकीय क्षेत्र B के लंबवत है।
3. लंबाई l एवं चुंबकीय आघूर्ण m का एक छड़ चुंबक लीजिए। इसके मध्य बिंदु से r दूरी पर, जहाँ r >> l, इस छड़ के कारण चुंबकीय क्षेत्र B का मान होगा,
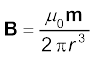(अक्ष के अनुदिश)
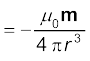
(विषुवत वृत्त के अनुदिश)
4. चुंबकत्व संबंधी गाउस के नियमानुसार, किसी बंद पृष्ठ में से गुजरने वाला कुल चुंबकीय फ्लक्स हमेशा शून्य होता है।
= 0
5. पृथ्वी का चुंबकीय क्षेत्र, पृथ्वी के केंद्र पर रखे एक चुंबकीय द्विध्रुव (परिकल्पित) के समतुल्य है। पृथ्वी के भौगोलिक उत्तरी ध्रुव के समीप के ध्रुव को उत्तरी चुंबकीय ध्रुव कहते हैं। इसी प्रकार से, पृथ्वी के भौगोलिक दक्षिणी ध्रुव के समीप के ध्रुव को दक्षिण चुंबकीय ध्रुव कहते हैं। यह द्विध्रुव पृथ्वी के घूर्णन अक्ष से एक छोटा कोण बनाता है। पृथ्वी की सतह पर चुंबकीय क्षेत्र का परिमाण ≈ 4 × 10–5 T है।
6. पृथ्वी की सतह पर इसके चुंबकीय क्षेत्र का विवरण देने के लिए तीन राशियाँ आवश्यक हैं– चुंबकीय क्षेत्र का क्षैतिज अवयव, चुंबकीय दिक्पात एवं चुंबकीय नति। ये पृथ्वी के चुंबकीय क्षेत्र के अवयव हैं।
7. माना कि कोई पदार्थ एक बाह्य चुंबकीय क्षेत्र B0 में रखा है। चुंबकीय तीव्रता की परिभाषा है,
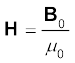
पदार्थ का चुंबकन M इसका द्विध्रुव आघूर्ण प्रति इकाई आयतन है। पदार्थ के अंदर चुंबकीय क्षेत्र
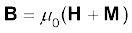
8. रैखिक पदार्थ के लिए,
M = χ H जिससे कि B = µ H
एवं χ पदार्थ की चुंबकीय प्रवृत्ति कहलाती है। राशियों χ, आपेक्षिक चुंबकशीलता µr एवं चुंबकशीलता µ में निम्नलिखित संबंध हैं–
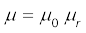
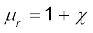
9. चुंबकीय पदार्थों को मोटे तौर पर तीन श्रेणियों में विभाजित करते हैं ः प्रतिचुंबकीय, अनुचुंबकीय एवं लौह चुंबकीय। प्रतिचुंबकीय पदार्थों के लिए χ का मान ऋणात्मक और प्रायः बहुत कम होता है, अनुचुंबकीय पदार्थों के लिए χ धनात्मक एवं बहुत कम है। लौह चुंबकों के लिए χ धनात्मक एवं बहुत अधिक मान वाला है और ये B एवं H के रैखिक संबंधों से भी पहचाने जाते हैं। वे शैथिल्यता का गुण प्रदर्शित करते हैं।
10. वे पदार्थ जो सामान्य ताप पर लंबे समय के लिए लौह चुंबकीय गुण दर्शाते हैं, स्थायी चुंबक कहलाते हैं।
विचारणीय विषय
1. गतिमान आवेशों/धाराओं के माध्यम से चुंबकीय प्रक्रमों की संतोषजनक समझ सन 1800 ई. के बाद पैदा हुई। लेकिन, चुंबकों के दैशिक गुणों का प्रौद्योगिकीय उपयोग इस वैज्ञानिक समझ से दो हजार वर्ष पूर्व होने लगा था। अतः अभियांत्रिक अनुप्रयोगों के लिए, वैज्ञानिक समझ का होना कोई आवश्यक शर्त नहीं है। आदर्श स्थिति यह है कि विज्ञान और अभियांत्रिकी एक-दूसरे से सहयोग करते हुए चलते हैं। कभी विज्ञान अभियांत्रिकी को आगे बढ़ाता है तो कभी अभियांत्रिकी विज्ञान को।
2. एकल चुंबकीय ध्रुवों का अस्तित्व नहीं होता। यदि आप एक चुंबक को काट कर दो टुकड़े करते हैं तो आपको दो छोटे चुंबक प्राप्त होते हैं। इसके विपरीत पृथक्कृत धनात्मक एवं ऋणात्मक विद्युत आवेशों का अस्तित्व है। एक इलेक्ट्रॉन पर आवेश का परिमाण e = 1.6 × 10–19 C होता है जो आवेश का सूक्ष्मतम मान है। अन्य सभी आवेश इस न्यूनतम इकाई आवेश के पूर्ण गुणांक होते हैं। दूसरे शब्दों में, आवेश क्वांटीकृत होते हैं। हमें ज्ञात नहीं है कि एकल चुंबकीय ध्रुवों का अस्तित्व क्यों नहीं है अथवा विद्युत आवेश क्वांटीकृत क्यों होता है?
3. इस तथ्य का कि चुंबकीय एकल ध्रुवों का अस्तित्व नहीं होता, एक परिणाम यह है कि चुंबकीय क्षेत्र रेखाएँ संतत हैं और बंद लूप बनाती हैं। इसके विपरीत, वैद्युत बल रेखाएँ धनावेश से शुरू होकर ऋणावेश पर समाप्त हो जाती हैं (या अनंत में लीन हो जाती हैं)।
4. पृथ्वी का चुंबकीय क्षेत्र इसके अंदर रखे एक विशाल छड़ चुंबक के कारण नहीं है। पृथ्वी का क्रोड गर्म एवं पिघली हुई अवस्था में है। शायद इस क्रोड में प्रवाहित होने वाली संवहन धाराएँ ही पृथ्वी के चुंबकीय क्षेत्र के लिए जिम्मेदार हैं। हम नहीं जानते कि वह कौन-सा ‘जनित्र’ प्रभाव है जो इन धाराओं को बनाये रखता है और पृथ्वी का चुंबकीय क्षेत्र लगभग हर दस लाख सालों में अपनी ध्रुवता क्यों उलट लेता है।
5. चुंबकीय प्रवृत्ति χ के मान में अत्यल्प अंतर से पदार्थ के व्यवहार में मूलभूत अंतर पाया जाता है, जैसे प्रतिचुंबक और अनुचुंबक के व्यवहारों में अंतर। प्रतिचुंबकीय पदार्थों के लिए χ = –10–5 जबकि अनुचुंबकीय पदार्थों के लिए χ = +10–5।
6. अतिचालक, परिपूर्ण प्रतिचुंबक (perfect diamagnetic) भी होते हैं। इसके लिए χ = –1, µr = 0, µ = 0। बाह्य चुंबकीय क्षेत्र पूर्णतः इसके बाहर ही रहता है। एक मनोरंजक तथ्य यह है कि यह पदार्थ एक परिपूर्ण चालक भी है। परंतु, एेसा कोई चिरसम्मत सिद्धांत नहीं है जो इन दोनों गुणों में एक सूत्रता ला सके। बार्डीन, कूपर एवं श्रीफर ने एक क्वांटम यांत्रिकीय सिद्धांत (BCS सिद्धांत) दिया है, जो इन प्रभावों की व्याख्या कर सकता है। BCS सिद्धांत 1957 में प्रस्तावित किया गया था और बाद में, 1970 में, भौतिकी के नोबेल पुरस्कार के रूप में इसको मान्यता प्राप्त हुई।
7. चुंबकीय शैथिल्यता की परिघटना, पदार्थों के प्रत्यास्थता संबंधी मिलते-जुलते व्यवहार की याद दिलाता है। जैसे–प्रतिबल, विकृति के अनुक्रमानुपाती होना आवश्यक नहीं है वैसे ही यहाँ H एवं B (या M) में रैखिक संबंध नहीं है। प्रतिबल-विकृति वक्र शैथिल्यता का प्रदर्शन करता है और इससे घिरा हुआ क्षेत्रफल प्रति इकाई आयतन में होने वाला ऊर्जा क्षय व्यक्त करता है। B-H चुंबकीय शैथिल्य वक्र की भी इसी तरह की व्याख्या की जा सकती है।
8. प्रतिचुंबकत्व सार्वत्रिक है। यह सभी पदार्थों में विद्यमान है। परंतु अनुचुंबकीय एवं लौह चुंबकीय पदार्थों में यह बहुत क्षीण होता है और इसका पता लगाना बहुत कठिन है।
9. हमने पदार्थों का प्रतिचुंबकीय, अनुचुंबकीय एवं लौह चुंबकीय रूपों में वर्गीकरण किया है। लेकिन चुंबकीय पदार्थों के इनके अलावा भी कुछ प्रकार हैं; जैसे–लघु लौह चुंबकीय (फेरी चुंबकीय), प्रतिलौह चुंबकीय, स्पिन-काँच आदि जिनके गुण बहुत ही असामान्य एवं रहस्यमय हैं।
अभ्यास
5.1 भू-चुंबकत्व संबंधी निम्नलिखित प्रश्नों के उत्तर दीजिए–
(a) एक सदिश को पूर्ण रूप से व्यक्त करने के लिए तीन राशियों की आवश्यकता होती है। उन तीन स्वतंत्र राशियों के नाम लिखिए जो परंपरागत रूप से पृथ्वी के चुंबकीय क्षेत्र को व्यक्त करने के लिए प्रयुक्त होती हैं।
(b) दक्षिण भारत में किसी स्थान पर नति कोण का मान लगभग 18o है। ब्रिटेन में आप इससे अधिक नति कोण की अपेक्षा करेंगे या कम की?
(c) यदि आप अॉस्ट्रेलिया के मेल्बोर्न शहर में भू-चुंबकीय क्षेत्र रेखाओं का नक्शा बनाएँ तो ये रेखाएँ पृथ्वी के अंदर जाएँगी या इससे बाहर आएँगी?
(d) एक चुंबकीय सुई जो ऊर्ध्वाधर तल में घूमने के लिए स्वतंत्र है, यदि भू-चुंबकीय उत्तर या दक्षिण ध्रुव पर रखी हो तो यह किस दिशा में संकेत करेगी?
(e) यह माना जाता है कि पृथ्वी का चुंबकीय क्षेत्र लगभग एक चुंबकीय द्विध्रुव के क्षेत्र जैसा है जो पृथ्वी के केंद्र पर रखा है और जिसका द्विध्रुव आघूर्ण 8 × 1022 JT–1 है। कोई ढंग सुझाइए जिससे इस संख्या के परिमाण की कोटि जाँची जा सके।
(f) भू-गर्भशास्त्रियों का मानना है कि मुख्य N-S चुंबकीय ध्रुवों के अतिरिक्त, पृथ्वी की सतह पर कई अन्य स्थानीय ध्रुव भी हैं, जो विभिन्न दिशाओं में विन्यस्त हैं। एेसा होना कैसे संभव है?
5.2 निम्नलिखित प्रश्नों के उत्तर दीजिए–
(a) एक जगह से दूसरी जगह जाने पर पृथ्वी का चुंबकीय क्षेत्र बदलता है। क्या यह समय के साथ भी बदलता है? यदि हाँ, तो कितने समय अंतराल पर इसमें पर्याप्त परिवर्तन होते हैं?
(b) पृथ्वी के क्रोड में लोहा है, यह ज्ञात है। फिर भी भूगर्भशास्त्री इसको पृथ्वी के चुंबकीय क्षेत्र का स्रोत नहीं मानते। क्यों?
(c) पृथ्वी के क्रोड के बाहरी चालक भाग में प्रवाहित होने वाली आवेश धाराएँ भू-चुंबकीय क्षेत्र के लिए उत्तरदायी समझी जाती हैं। इन धाराओं को बनाए रखने वाली बैटरी (ऊर्जा स्रोत) क्या हो सकती है?
(d) अपने 4-5 अरब वर्षों के इतिहास में पृथ्वी अपने चुंबकीय क्षेत्र की दिशा कई बार उलट चुकी होगी। भूगर्भशास्त्री, इतने सुदूर अतीत के पृथ्वी के चुंबकीय क्षेत्र के बारे में कैसे जान पाते हैं?
(e) बहुत अधिक दूरियों पर (30,000 km से अधिक) पृथ्वी का चुंबकीय क्षेत्र अपनी द्विध्रुवीय आकृति से काफी भिन्न हो जाता है। कौन से कारक इस विकृति के लिए उत्तरदायी हो
सकते हैं?
(f) अंतरातारकीय अंतरिक्ष में 10-12 T की कोटि का बहुत ही क्षीण चुंबकीय क्षेत्र होता है। क्या इस क्षीण चुंबकीय क्षेत्र के भी कुछ प्रभावी परिणाम हो सकते हैं? समझाइए।
[टिप्पणी ः प्रश्न 5.2 का उद्देश्य मुख्यतः आपकी जिज्ञासा जगाना है। उपरोक्त कई प्रश्नों के उत्तर या तो काम चलाऊ हैं या अज्ञात हैं। जितना संभव हो सका, प्रश्नों के संक्षिप्त उत्तर पुस्तक के अंत में दिए गए हैं। विस्तृत उत्तरों के लिए आपको भू-चुंबकत्व पर कोई अच्छी पाठ्यपुस्तक देखनी होगी।]
5.3 एक छोटा छड़ चुंबक जो एकसमान बाह्य चुंबकीय क्षेत्र 0.25 T के साथ 30o का कोण बनाता है, पर 4.5 × 10-2 J का बल आघूर्ण लगता है। चुंबक के चुंबकीय आघूर्ण का परिमाण क्या है?
5.4 चुंबकीय आघूर्ण m = 0.32 JT-1 वाला एक छोटा छड़ चुंबक, 0.15 T के एकसमान बाह्य चुंबकीय क्षेत्र में रखा है। यदि यह छड़ क्षेत्र के तल में घूमने के लिए स्वतंत्र हो, तो क्षेत्र के किस विन्यास में यह (i) स्थायी संतुलन और (ii) अस्थायी संतुलन में होगा? प्रत्येक स्थिति में चुंबक की स्थितिज ऊर्जा का मान बताइए।
5.5 एक परिनालिका में पास-पास लपेटे गए 800 फेरे हैं, तथा इसका अनुप्रस्थ काट का क्षेत्रफल
2.5 × 10-4 m2 है और इसमें 3.0 A धारा प्रवाहित हो रही है। समझाइए कि किस अर्थ में यह परिनालिका एक छड़ चुंबक की तरह व्यवहार करती है? इसके साथ जुड़ा हुआ चुंबकीय आघूर्ण कितना है?
5.6 यदि प्रश्न 5.5 में बताई गई परिनालिका ऊर्ध्वाधर दिशा के परितः घूमने के लिए स्वतंत्र हो और इस पर क्षैतिज दिशा में एक 0.25 T का एकसमान चुंबकीय क्षेत्र लगाया जाए, तो इस परिनालिका पर लगने वाले बल आघूर्ण का परिमाण उस समय क्या होगा, जब इसकी अक्ष आरोपित क्षेत्र की दिशा से 30o का कोण बना रही हो?
5.7 एक छड़ चुंबक जिसका चुंबकीय आघूर्ण 1.5 JT-1 है, 0.22 T के एक एकसमान चुंबकीय क्षेत्र के अनुदिश रखा है।
(a) एक बाह्य बल आघूर्ण कितना कार्य करेगा यदि यह चुंबक को चुंबकीय क्षेत्र के (i) लंबवत (ii) विपरीत दिशा में संरेखित करने के लिए घुमा दे।
(b) स्थिति (i) एवं (ii) में चुंबक पर कितना बल आघूर्ण होता है?
5.8 एक परिनालिका जिसमें पास-पास 2000 फेरे लपेटे गए हैं तथा जिसके अनुप्रस्थ काट का क्षेत्रफल 1.6 × 10-4 m2 है और जिसमें 4.0 A की धारा प्रवाहित हो रही है, इसके केंद्र से इस प्रकार लटकायी गई है कि यह एक क्षैतिज तल में घूम सके।
(a) परिनालिका के चुंबकीय आघूर्ण का मान क्या है?
(b) परिनालिका पर लगने वाला बल एवं बल आघूर्ण क्या है, यदि इस पर, इसकी अक्ष से 30o का कोण बनाता हुआ 7.5 × 10-2 T का एकसमान क्षैतिज चुंबकीय क्षेत्र लगाया जाए?
5.9 एक वृत्ताकार कुंडली जिसमें 16 फेरे हैं, जिसकी त्रिज्या 10 cm है और जिसमें 0.75 A धारा प्रवाहित हो रही है, इस प्रकार रखी है कि इसका तल, 5.0 × 10-2 T परिमाण वाले बाह्य क्षेत्र के लंबवत है। कुंडली, चुंबकीय क्षेत्र के लंबवत और इसके अपने तल में स्थित एक अक्ष के चारों तरफ घूमने के लिए स्वतंत्र है। यदि कुंडली को जरा-सा घुमा कर छोड़ दिया जाए तो यह अपनी स्थायी संतुलनावस्था के इधर-उधर 2.0 s-1 की आवृत्ति से दोलन करती है। कुंडली का अपने घूर्णन अक्ष के परितः जड़त्व-आघूर्ण क्या है?
5.10 एक चुंबकीय सुई चुंबकीय याम्योत्तर के समांतर एक ऊर्ध्वाधर तल में घूमने के लिए स्वतंत्र है। इसका उत्तरी ध्रुव क्षैतिज से 22o के कोण पर नीचे की ओर झुका है। इस स्थान पर चुंबकीय क्षेत्र के क्षैतिज अवयव का मान 0.35 G है। इस स्थान पर पृथ्वी के चुंबकीय क्षेत्र का परिमाण ज्ञात कीजिए।
5.11 दक्षिण अफ्रीका में किसी स्थान पर एक चुंबकीय सुई भौगोलिक उत्तर से 12o पश्चिम की ओर संकेत करती है। चुंबकीय याम्योत्तर में संरेखित नति-वृत्त की चुंबकीय सुई का उत्तरी ध्रुव क्षैतिज से 60o उत्तर की ओर संकेत करता है। पृथ्वी के चुंबकीय क्षेत्र का क्षैतिज अवयव मापने पर
0.16 G पाया जाता है। इस स्थान पर पृथ्वी के क्षेत्र का परिमाण और दिशा बताइए।
5.12 किसी छोटे छड़ चुंबक का चुंबकीय आघूर्ण 0.48 JT-1 है। चुंबक के केंद्र से 10 cm की दूरी पर स्थित किसी बिंदु पर इसके चुंबकीय क्षेत्र का परिमाण एवं दिशा बताइए यदि यह बिंदु (i) चुंबक के अक्ष पर स्थित हो (ii) चुंबक के अभिलंब समद्विभाजक पर स्थित हो।
5.13 क्षैतिज तल में रखे एक छोटे छड़ चुंबक का अक्ष, चुंबकीय उत्तर-दक्षिण दिशा के अनुदिश है। संतुलन बिंदु चुंबक के अक्ष पर, इसके केंद्र से 14 cm दूर स्थित है। इस स्थान पर पृथ्वी का चुंबकीय क्षेत्र 0.36 G एवं नति कोण शून्य है। चुंबक के अभिलंब समद्विभाजक पर इसके केंद्र से उतनी ही दूर (14 cm) स्थित किसी बिंदु पर परिणामी चुंबकीय क्षेत्र क्या होगा?
5.14 यदि प्रश्न 5.13 में वर्णित चुंबक को 180o से घुमा दिया जाए तो संतुलन बिंदुओं की नयी स्थिति क्या होगी?
5.15 एक छोटा छड़ चुंबक जिसका चुंबकीय आघूर्ण 5.25 × 10-2 JT-1 है, इस प्रकार रखा है कि इसका अक्ष पृथ्वी के क्षेत्र की दिशा के लंबवत है। चुंबक के केंद्र से कितनी दूरी पर, परिणामी क्षेत्र पृथ्वी के क्षेत्र की दिशा से 45o का कोण बनाएगा, यदि हम (a) अभिलंब समद्विभाजक पर देखें, (b) अक्ष पर देखें। इस स्थान पर पृथ्वी के चुंबकीय क्षेत्र का परिमाण 0.42 G है। प्रयुक्त दूरियों की तुलना में चुंबक की लंबाई की उपेक्षा कर सकते हैं।
अतिरिक्त अभ्यास
5.16 निम्नलिखित प्रश्नों के उत्तर दीजिए–
(a) ठंडा करने पर किसी अनुचुंबकीय पदार्थ का नमूना अधिक चुंबकन क्यों प्रदर्शित करता है? (एक ही चुंबककारी क्षेत्र के लिए)
(b) अनुचुंबकत्व के विपरीत, प्रतिचुंबकत्व पर ताप का प्रभाव लगभग नहीं होता। क्यों?
(c) यदि एक टोरॉइड में बिस्मथ का क्रोड लगाया जाए तो इसके अंदर चुंबकीय क्षेत्र उस स्थिति की तुलना में (किंचित) कम होगा या (किंचित) ज्यादा होगा, जबकि क्रोड खाली हो?
(d) क्या किसी लौह चुंबकीय पदार्थ की चुंबकशीलता चुंबकीय क्षेत्र पर निर्भर करती है? यदि हाँ, तो उच्च चुंबकीय क्षेत्रों के लिए इसका मान कम होगा या अधिक?
(e) किसी लौह चुंबक की सतह के प्रत्येक बिंदु पर चुंबकीय क्षेत्र रेखाएँ सदैव लंबवत होती हैं [यह तथ्य उन स्थिरवैद्युत क्षेत्र रेखाओं के सदृश है जो कि चालक की सतह के प्रत्येक बिंदु पर लंबवत होती हैं]। क्यों?
(f) क्या किसी अनुचुंबकीय नमूने का अधिकतम संभव चुंबकन, लौह चुंबक के चुंबकन के परिमाण की कोटि का होगा?
5.17 निम्नलिखित प्रश्नों के उत्तर दीजिए–
(a) लौह चुंबकीय पदार्थ के चुंबकन वक्र की अनुत्क्रमणीयता, डोमेनो के आधार पर गुणात्मक दृष्टिकोण से समझाइए।
(b) नर्म लोहे के एक टुकड़े के शैथिल्य लूप का क्षेत्रफल, कार्बन-स्टील के टुकड़े के शैथिल्य लूप के क्षेत्रफल से कम होता है। यदि पदार्थ को बार-बार चुंबकन चक्र से गुजारा जाए तो कौन सा टुकड़ा अधिक ऊष्मा ऊर्जा का क्षय करेगा?
(c) लौह चुंबक जैसा शैथिल्य लूप प्रदर्शित करने वाली कोई प्रणाली स्मृति संग्रहण की युक्ति है। इस कथन की व्याख्या कीजिए।
(d) कैसेट के चुंबकीय फीतों पर पर्त चढ़ाने के लिए या आधुनिक कंप्यूटर में स्मृति संग्रहण के लिए, किस तरह के लौह चुंबकीय पदार्थों का इस्तेमाल होता है?
(e) किसी स्थान को चुंबकीय क्षेत्र से परिरक्षित करना है। कोई विधि सुझाइए।
5.18 एक लंबे, सीधे, क्षैतिज केबल में, 2.5 A धारा, 10o दक्षिण-पश्चिम से 10o उत्तर-पूर्व की ओर प्रवाहित हो रही है। इस स्थान पर चुंबकीय याम्योत्तर भौगोलिक याम्योत्तर के 10o पश्चिम में है। यहाँ पृथ्वी का चुंबकीय क्षेत्र 0.33 G एवं नति कोण शून्य है। उदासीन बिंदुओं की रेखा निर्धारित कीजिए। (केबल की मोटाई की उपेक्षा कर सकते हैं)।
(उदासीन बिंदुओं पर, धारावाही केबल द्वारा चुंबकीय क्षेत्र, पृथ्वी के क्षैतिज घटक के चुंबकीय क्षेत्र के समान एवं विपरीत दिशा में होता है।)
5.19 किसी स्थान पर एक टेलिफोन केबल में चार लंबे, सीधे, क्षैतिज तार हैं जिनमें से प्रत्येक में
1.0 A की धारा पूर्व से पश्चिम की ओर प्रवाहित हो रही है। इस स्थान पर पृथ्वी का चुंबकीय क्षेत्र 0.39 G एवं नति कोण 35o है। दिक्पात कोण लगभग शून्य है। केबल के 4.0 cm नीचे और 4.0 cm ऊपर परिणामी चुंबकीय क्षेत्रों के मान क्या होंगे?
5.20 एक चुंबकीय सुई जो क्षैतिज तल में घूमने के लिए स्वतंत्र है, 30 फेरों एवं 12 cm त्रिज्या वाली एक कुंडली के केंद्र पर रखी है। कुंडली एक ऊर्ध्वाधर तल में है और चुंबकीय याम्योत्तर से 45o का कोण बनाती है। जब कुंडली में 0.35 A धारा प्रवाहित होती है, चुंबकीय सुई पश्चिम से पूर्व की ओर संकेत करती है।
(a) इस स्थान पर पृथ्वी के चुंबकीय क्षेत्र के क्षैतिज अवयव का मान ज्ञात कीजिए।
(b) कुंडली में धारा की दिशा उलट दी जाती है और इसको अपनी ऊर्ध्वाधर अक्ष पर वामावर्त दिशा में (ऊपर से देखने पर) 90o के कोण पर घुमा दिया जाता है। चुंबकीय सुई किस दिशा में ठहरेगी? इस स्थान पर चुंबकीय दिक्पात शून्य लीजिए।
5.21 एक चुंबकीय द्विध्रुव दो चुंबकीय क्षेत्रों के प्रभाव में है। ये क्षेत्र एक-दूसरे से 60o का कोण बनाते हैं और उनमें से एक क्षेत्र का परिमाण 1.2 × 10-2 T है। यदि द्विध्रुव स्थायी संतुलन में इस क्षेत्र से 15o का कोण बनाए, तो दूसरे क्षेत्र का परिमाण क्या होगा?
5.22 एक समोर्जी 18 keV वाले इलेक्ट्रॉनों के किरण पुंज पर जो शुरू में क्षैतिज दिशा में गतिमान है, 0.04 G का एक क्षैतिज चुंबकीय क्षेत्र, जो किरण पुंज की प्रारंभिक दिशा के लंबवत है, लगाया गया है। आकलन कीजिए 30 cm की क्षैतिज दूरी चलने में किरण पुंज कितनी दूरी ऊपर या नीचे विस्थापित होगा? (me = 9.11 × 10–31 kg, e = 1.60 × 10–19 C)।
[नोटः इस प्रश्न में आँकड़े इस प्रकार चुने गए हैं कि उत्तर से आपको यह अनुमान हो, कि TV सेट में इलेक्ट्रॉन गन से पर्दे तक इलेक्ट्रॉन किरण पुंज की गति भू-चुंबकीय क्षेत्र से किस प्रकार प्रभावित होती है]।
5.23 अनुचुंबकीय लवण के एक नमूने में 2.0 × 1024 परमाणु द्विध्रुव हैं जिनमें से प्रत्येक का द्विध्रुव आघूर्ण 1.5 × 10–23 J T–1 है। इस नमूने को 0.64 T के एक एकसमान चुंबकीय क्षेत्र में रखा गया और 4.2 K ताप तक ठंडा किया गया। इसमें 15% चुंबकीय संतृप्तता आ गई। यदि इस नमूने को 0.98 T के चुंबकीय क्षेत्र में 2.8 K ताप पर रखा हो तो इसका कुल द्विध्रुव आघूर्ण कितना होगा? (यह मान सकते हैं कि क्यूरी नियम लागू होता है।)
5.24 एक रोलैंड रिंग की औसत त्रिज्या 15 cm है और इसमें 800 आपेक्षिक चुंबकशीलता के लौह चुंबकीय क्रोड पर 3500 फेरे लिपटे हुए हैं। 1.2 A की चुंबककारी धारा के कारण इसके क्रोड में कितना चुंबकीय क्षेत्र (B) होगा?
5.25 किसी इलेक्ट्रॉन के नैज चक्रणी कोणीय संवेग S एवं कक्षीय कोणीय संवेग l के साथ जुड़े चुंबकीय आघूर्ण क्रमशः µs और µl है। क्वांटम सिद्धांत के आधार पर (और प्रयोगात्मक रूप से अत्यंत परिशुद्धतापूर्वक पुष्ट) इनके मान क्रमशः निम्न प्रकार दिए जाते हैं–
µS = –(e/m)S, एवं µl = –(e/2m)l
इनमें से कौन-सा व्यंजक चिरसम्मत सिद्धांतों के आधार पर प्राप्त करने की आशा की जा सकती है? उस चिरसम्मत आधार पर प्राप्त होने वाले व्यंजक को व्युत्पन्न कीजिए।