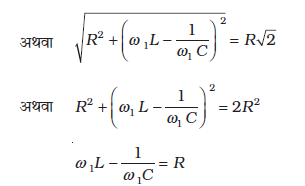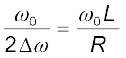Table of Contents

QR12091C7.tif

 

अध्याय 7


प्रत्यावर्ती धारा


7.1 भूमिका

अब तक हमने दिष्टधारा (dc) स्रोतों एवं दिष्टधारा स्रोतों से युक्त परिपथों पर विचार किया है। समय के साथ इन धाराओं की दिशा में परिवर्तन नहीं होता। तथापि, समय के साथ परिवर्तित होने वाली धाराओं और वोल्टताओं का मिलना एक आम बात है। हमारे घरोें एवं दफ्तरों में पाया जाने वाला मुख्य विद्युत प्रदाय (electric mains supply) एक एेसी ही वोल्टता का स्रोत है जो समय के साथ ज्या फलन (sine function) की भाँति परिवर्तित होता है। एेसी वोल्टता को प्रत्यावर्ती (ac) वोल्टता तथा किसी परिपथ में इसके द्वारा अचालित धारा को प्रत्यावर्ती धारा (ac धारा)* कहते हैं। आजकल जिन वैद्युत युक्तियों का हम उपयोग करते हैं उनमें से अधिकांश के लिए ac वोल्टता की ही आवश्यकता होती है। इसका मुख्य कारण यह है कि अधिकांश विद्युत कंपनियों द्वारा बेची जा रही विद्युत ऊर्जा प्रत्यावर्ती धारा के रूप में ही संप्रेषित एवं वितरित होती है। dc पर ac के उपयोग को वरीयता दिए जाने का मुख्य कारण यह है कि ac वोल्टताओं को ट्रांसफॉर्मरों द्वारा आसानी से एवं दक्षता के साथ एक वोल्टता से दूसरी वोल्टता में बदला जा सकता है। इसके अतिरिक्त ac के रूप में लंबी दूरियों तक वैद्युत ऊर्जा का संप्रेषण भी अपेक्षाकृत कम खर्चीला होता है। प्रत्यावर्ती धारा परिपथ एेसे अभिलक्षण प्रदर्शित करता है जिनका उपयोग दैनिक जीवन में काम आने वाली अनेक युक्तियों में किया जाता है। उदाहरणार्थ, जब हम अपने रेडियो को अपने मनपसंद स्टेशन से समस्वरित करते हैं तो ac परिपथों के एक विशिष्ट गुण का लाभ उठाते हैं जो उन अनेक गुणों में से एक है जिनका अध्ययन आप इस अध्याय में करेंगे

* ac वोल्टता एवं ac धारा, ये वाक्यांश असंगत एवं अनुप्रयुक्त हैं, क्योंकि इनका शाब्दिक अर्थ है क्रमशः ‘प्रत्यावर्ती धारा वोल्टता’ एवं ‘प्रत्यावर्ती धारा धारा’। तब भी संकेताक्षर ac समय के अनुसार सरल आवर्ती क्रम में परिवर्तित होने वाली वैद्युत राशि को व्यक्त करने के लिए इतनी सार्वभौमिक स्वीकृति पा चुका है कि इसके प्रयोग में हम प्रचलित परिपाटी का ही अनुसरण करेंगे। इसके अतिरिक्त, सामान्यतः प्रयुक्त होने वाले शब्द वोल्टता का अर्थ दो बिंदुओं के बीच विभवांतर होता है।


7.2 प्रतिरोधक पर प्रयुक्त ac वोल्टता

चित्र 7.1 में ac वोल्टता स्रोत ε से जुड़ा प्रतिरोधक R दर्शाया गया है। परिपथ आरेख में ac स्रोत का संकेत चिह्न

2768.png

है। यहाँ हम एक एेसे स्रोत की बात कर रहे हैं जो अपने सिरों के बीच ज्यावक्रीय रूप में परिवर्तनशील विभवांतर उत्पन्न करता है, माना कि यह विभवांतर जिसे ac वोल्टता भी कहा जाता है, निम्नलिखित प्रकार से व्यक्त किया जाए

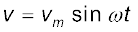
2773.png

(7.1)

यहाँ vm दोलायमान विभवांतर का आयाम एवं ω इसकी कोणीय आवृत्ति है।

1750.png
चित्र 7.1 प्रतिरोधक पर प्रयुक्त ac वोल्टता।

प्रतिरोधक में प्रवाहित होने वाली धारा का मान प्राप्त करने के लिए हम चित्र 7.1 में दर्शाए गए परिपथ पर किरखोफ का लूप नियम 

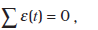77.1, (खण्ड 3.13 देखें) लागू करते हैं जिससे हमें प्राप्त होता है :

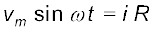
2791.png

अथवा

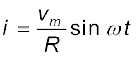
2796.png

चूँकि R एक नियतांक है, हम इस समीकरण को इस प्रकार व्यक्त कर सकते हैं :


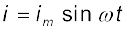2801.png (7.2)

यहाँ धारा आयाम im के लिए सूत्र है :

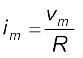2806.png (7.3)

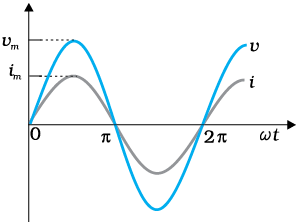
1767.png

चित्र 7.2 शुद्ध प्रतिरोधक में वोल्टता एवं धारा एक ही कला में हैं। निम्निष्ठ, शून्य तथा उच्चिष्ठ क्रमशः एक ही समय में बनते हैं।

समीकरण (7.3) ओम का नियम है जो प्रतिरोधकों के प्रकरण में ac एवं dc दोनों प्रकार की वोल्टताओं के लिए समान रूप से लागू होता है। समीकरण (7.1) एवं समीकरण (7.2) द्वारा व्यक्त किसी शुद्ध प्रतिरोधक के सिरों के बीच लगाई गई वोल्टता एवं इसमें प्रवाहित होने वाली धारा को चित्र 7.2 में समय के फलन के रूप में आलेखित किया गया है। इस तथ्य पर विशेष ध्यान दीजिए कि v एवं i दोनों ही शून्य, न्यूनतम एवं अधिकतम मानों की स्थितियाँ साथ-साथ ही प्राप्त करती हैं। अतः स्पष्ट है कि वोल्टता एवं धारा एक दूसरे के साथ समान कला में हैं।

Tesla.tif

निकोला टेस्ला (1836 – 1943)

निकोला टेस्ला (1856 – 1943) सर्बिया-अमेरिका के वैज्ञानिक, आविष्कर्ता एवं प्रतिभावान व्यक्ति। चुंबकीय क्षेत्र को घुमाने का उनका विचार ही व्यावहारिक रूप में सब प्रत्यावर्ती धारा मशीनों का आधार बना जिसके कारण विद्युत शक्ति के युग में प्रवेश किया जा सका। अन्य वस्तुओं के अतिरिक्त, प्रेरण मोटर, ac शक्ति की बहुफेज़ प्रणाली; रेडियो, टेलीविजन तथा अन्य वैद्युत उपकरणों पर लगने वाली उच्च आवृत्ति प्रेरण कुंडली (टेस्ला कुंडली) का आविष्कार भी उन्होंने किया। चुंबकीय क्षेत्र के SI मात्रक का नाम उनके सम्मान में रखा गया है।

हम देखते हैं कि प्रयुक्त वोल्टता की भाँति ही धारा भी ज्या-वक्रीय रूप में परिवर्तित होती है और तदनुसार ही प्रत्येक चक्र में इसके धनात्मक एवं ऋणात्मक मान प्राप्त होते हैं। अतः एक संपूर्ण चक्र में तात्क्षणिक धारा मानों का योग शून्य होता है तथा माध्य धारा शून्य होती है। तथापि माध्य धारा शून्य है इस तथ्य का यह अर्थ नहीं है कि व्यय होने वाली माध्य शक्ति भी शून्य है, और विद्युत ऊर्जा का क्षय नहीं हो रहा है। जैसा कि आप जानते हैं जूल i2R द्वारा व्यक्त होता है और i2 (जो सदैव धनात्मक ही होता है चाहे i धनात्मक हो या ऋणात्मक) पर निर्भर करता है, न कि i पर। अतः जब किसी प्रतिरोधक से ac धारा प्रवाहित होती है तो जूल तापन एवं वैद्युत ऊर्जा का क्षय होता है।


w.house.tif

जॉर्ज वेस्टिंगहाउस (1846 – 1914)

दिष्टधारा की तुलना में प्रत्यावर्ती धारा के प्रमुख पक्षधर। अतः दिष्टधारा के समर्थक थॉमस अल्वा एडीसन से उनका सीधा संघर्ष हुआ। वेस्टिंगहाउस का पूर्ण विश्वास था कि प्रत्यावर्ती धारा प्रौद्योगिकी के हाथ में ही वैद्युतीय भविष्य की कुंजी है। उन्होंने अपने नाम वाली प्रसिद्ध कम्पनी की स्थापना की और निकोला टेस्ला एवं अन्य आविष्कारकों को प्रत्यावर्ती धारा मोटरों एवं उच्च वोल्टता पर विद्युत धारा के संप्रेषण संबंधी उपकरणों के विकास के लिए नियुक्त किया, जिससे बड़े पैमाने पर प्रकाश प्राप्त करने का मार्ग खुला।


प्रतिरोधकता के क्षयित होने वाली तात्क्षणिक शक्ति होती है

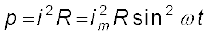2811.png (7 .4)

एक समय चक्र में p का माध्य मान है*

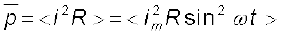2816.png [7.5(a)]

जहाँ किसी अक्षर के ऊपर लगी रेखा (यहाँ p) उसका माध्य मान निर्दिष्ट करती है एवं <......> यह सूचित करता है कि कोष्ठक के अंदर की राशि का माध्य लिया गया है। चूँकि i2m एवं R नियत राशियाँ हैं

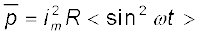2821.png [7.5(b)]

त्रिकोणमितीय सर्वसमिका sin2 ωt = (1/2) (1– cos 2ωt), का उपयोग करने पर < sin2 ωt > = (1/2) (1– < cos 2ωt >) और चूँकि < cos2ωt > = 0**, इसीलिए

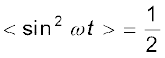
2826.png 

अतः,

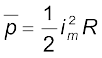2831.png [7.5(c)]

ac शक्ति को उसी रूप में व्यक्त करने के लिए जिसमें dc शक्ति (P = i2R) को व्यक्त किया जाता है धारा के एक विशिष्ट मान का उपयोग किया जाता है जिसे वर्ग माध्य मूल (rms) अथवा प्रभावी (effective) धारा (चित्र 7.3) कहते हैं और इसे Irms अथवा I द्वारा निर्दिष्ट किया जाता है।

 

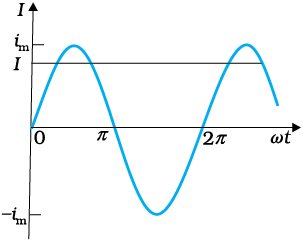
1789.png

 चित्र 7.3 rms धारा I, शिखरधारा im से सूत्र I =

3874.png
= 0.707 im 
द्वारा संबंधित है।


* किसी फलन F (t) का समयावधि T में माध्यमान ज्ञात करने के लिए सूत्र है

77.2

**

77.3


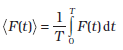
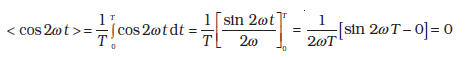
इसे इस प्रकार व्यक्त किया जाता है

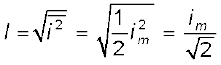
2836.png 

= 0.707 Im

(7.6)

I के पदों में व्यक्त करें तो P द्वारा निर्दिष्ट माध्य शक्ति

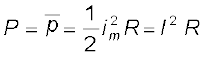2841.png (7.7)

इसी प्रकार, rms वोल्टता अथवा प्रभावी वोल्टता को हम व्यक्त करते हैं ः

V = 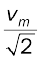2846.png = 0.707 vm (7.8)

समीकरण (7.3) के आधार पर

vm = imR

अथवा

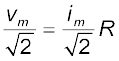
2851.png

अथवा V = IR (7.9)

समीकरण (7.9) ac धारा एवं ac वोल्टता के बीच संबंध बताती है जो dc में इन राशियों के संबंध के समान ही है। यह rms मानों की अवधारणा के लाभ दर्शाती है। rms मानों के पदों में, ac परिपथों के लिए शक्ति का समीकरण (7.7) एवं धारा तथा वोल्टता का संबंध वही है जो dc के लिए होता है।

परंपरा यह कि ac राशियों को उनके rms मानों के पदों में मापा और व्यक्त किया जाए। उदाहरणार्थ, घरेलू आपूर्ति मेें 220 V वोल्टता का rms मान है जिसका शिखर मान है

vm = 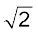2856.png V = (1.414)(220 V) = 311 V

वास्तव में, I अथवा rms धारा उस dc धारा के समतुल्य है जो वही माध्य शक्ति ह्रास करेगी जो प्रत्यावर्ती धारा करती है। समीकरण (7.7) को निम्नलिखित रूप में भी प्रस्तुत कर सकते हैं–

P = V2 / R = I V (चूँकि V = I R)


उदाहरण 7.1 

एक विद्युत बल्ब 220V आपूर्ति पर 100W शक्ति देने के लिए बनाया गया है।
(a) बल्ब का प्रतिरोध; (b) स्रोत की शिखर वोल्टता एवं (c) बल्ब में प्रवाहित होने वाली rms धारा ज्ञात कीजिए।

हल

(a) दिया है P = 100 W एवं V = 220 V। बल्ब का प्रतिरोध है :

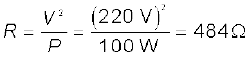
2861.png

(b) स्रोत की शिखर वोल्टता

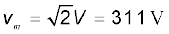
2866.png

(c) चूँकि, P = I V

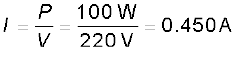
2871.png


7.3 ac धारा एवं वोल्टता का घूर्णी सदिश द्वारा निरूपण– कलासमंजक (फेजर्स)

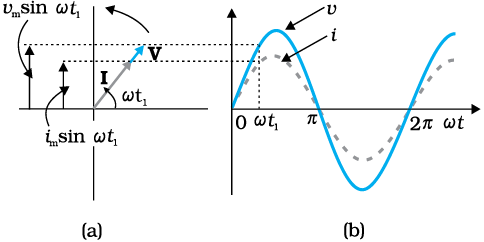
1853.png

चित्र 7.4 (a) चित्र 7.1 में दर्शाए गए परिपथ के लिए फेजर आरेख (b) v एवं i तथा ωt के बीच ग्राफ।

पिछले अनुभाग में हमने सीखा कि किसी प्रतिरोधक में प्रवाहित होने वाली धारा तथा ac वोल्टता समान कला में रहते हैं। परन्तु प्रेरक, संधारित्र अथवा इनके संयोजन युक्त परिपथों मेें एेसा नहीं होता है। ac परिपथ में धारा एवं वोल्टता के बीच कला संबंध दर्शाने के लिए हम फेजर्स की धारणा का उपयोग करते हैं। फेजर चित्र के उपयोग से ac परिपथ का विश्लेषण सरलतापूर्वक हो जाता है। फेजर* जैसा कि चित्र 7.4 में दर्शाया गया है, एक सदिश है जो मूल बिंदु के परितः कोणीय वेग ω से घूर्णन करता है। फेजर्स V एवं I के ऊर्ध्वाधर घटक ज्यावक्रीय रूप से परिवर्तनशील राशियाँ v एवं i निरूपित करते हैं। फेजर्स V एवं I के परिमाण इन दोलायमान राशियों के आयाम अथवा शिखरमान vm एवं im निरूपित करते हैं। चित्र 7.4(a) चित्र 7.1 के संगत किसी प्रतिरोधक के सिरों से जुड़ी ac वोल्टता की, किसी क्षण t1 पर, वोल्टता एवं धारा के फेजर्स और उनका पारस्परिक संबंध दर्शाता है। वोल्टता एवं धारा के ऊर्ध्वाधर अक्ष पर प्रक्षेप अर्थात vm sinω t एवं im sin ω t, क्रमशः, उस क्षण विशेष पर वोल्टता एवं धारा के मान निरूपित करते हैं। ज्यों-ज्यों वे आवृत्ति ω से घूर्णन करते हैं चित्र 7.4(b) में दर्शाए गए वक्र जैसे होते हैं।

चित्र 7.4(a) से हम यह समझ सकते हैं कि प्रतिरोधक के लिए फेजर्स V एवं I एक ही दिशा में होते हैं। एेसा हर समय होता है। इसका अर्थ है कि वोल्टता एवं धारा के बीच कला कोण शून्य होता है।


7.4 प्रेरक पर प्रयुक्त ac वोल्टता

1868.png
चित्र 7.5 प्रेरक से जुड़ा एक ac स्रोत।

चित्र 7.5 एक प्रेरक के सिरों पर लगा ac स्रोत दर्शाता है। प्रायः प्रेरक के लपेटों में लगे तार का अच्छा खासा प्रतिरोध होता है, लेकिन यहाँ हम यह मानेंगे कि इस प्रेरक का प्रतिरोध नगण्य है। अतः यह परिपथ विशुद्ध प्रेरणिक ac परिपथ है। माना कि स्रोत के सिरों के बीच वोल्टता v = vm sinω t है क्योंकि परिपथ में कोई प्रतिरोधक नहीं है। किरखोफ लूप नियम

77.1

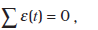
, का उपयोग करने से

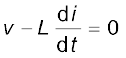2888.png (7.10)

यहाँ समीकरण का दूसरा पद प्रेरक में स्वप्रेरित फैराडे emf है, एवं L प्रेरक का स्व-प्रेरकत्व है। ऋणात्मक चिह्न लेंज के नियम का अनुसरण करने से समाविष्ट होता है (अध्याय 6)। समीकरण (7.1) एवं समीकरण (7.10) को संयोजित करने पर


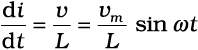2893.png (7.11)

समीकरण (7.11) में यह सन्निहित है कि धारा i(t) के लिए समीकरण समय का एेसा फलन होना चाहिए कि इसकी प्रवणता, di/dt एक ज्यावक्रीय रूप में परिवर्तनशील राशि हो जो स्रोत वोल्टता के साथ समान कला में रहती हो और जिसका आयाम vm/L द्वारा प्राप्त होता हो। धारा का मान प्राप्त करने के लिए, हम di/dt को समय के सापेक्ष समाकलित करते हैं,

77.5

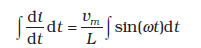
इससे हमें प्राप्त होता है :

77.6

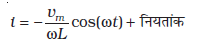
* यद्यपि ac परिपथ में वोल्टता एवं धारा को घूर्णन करते सदिशों-फेजर्स द्वारा निरूपित किया जाता है, अपने आप में वे सदिश नहीं हैं। वे अदिश राशियाँ हैं। होता यह है, कि आवर्ती रूप से परिवर्तित होते अदिशों की कलाएँ एवं आयाम गणितीय रूप से उसी प्रकार संयोजित होते हैं जैसे कि उन्हीं परिमाण एवं दिशाओं वाले घूर्णन सदिशों के प्रक्षेप। आवर्ती रूप से परिवर्तित होने वाली अदिश राशियों को, घूर्णन सदिशों द्वारा निरूपित करने से हम इन राशियों का संयोजन एक सरल विधि द्वारा, एक पहले से ही ज्ञात नियम का प्रयोग करके, कर सकते हैं।

 

यहाँ समाकलन नियतांक की विमा, धारा की विमा होती है और यह समय पर निर्भर नहीं करती। चूँकि, स्रोत का emf शून्य के परितः सममितीय रूप से दोलन करता है; वह धारा, जो इसके कारण बहती है, भी सममितीय रूप से दोलन करती है। अतः न तो धारा का कोई नियत, न ही समय पर निर्भर करने वाला अवयव, अस्तित्व में आता है। इसलिए, समाकलन नियतांक का मान शून्य होता है।

77.7

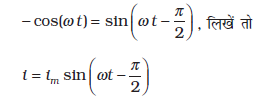
(7.12)

यहाँ

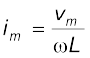
2938.png

धारा का आयाम है। राशि ω L प्रतिरोध के सदृश है, इसे प्रेरकीय प्रतिघात कहा जाता है एवं इसे XL द्वारा व्यक्त करते हैं।

XL = ω L (7.13)

तब, धारा का आयाम है :

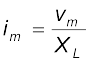2943.png (7. 14)

प्रेरकीय प्रतिघात की विमाएँ वही हैं तो प्रतिरोध की और इसका SI मात्रक ओम (Ω) है। प्रेरकीय प्रतिघात एक शुद्ध प्रेरणिक परिपथ में धारा को वैसे ही नियंत्रित करता है जैसे प्रतिरोध एक शुद्ध प्रतिरोधक परिपथ में। प्रेरकीय प्रतिघात, प्रेरकत्व एवं धारा की आवृत्ति के अनुक्रमानुपाती होता है।

स्रोत वोल्टता एवं प्रेरक में प्रवाहित होने वाली धारा के समीकरण (7.1) एवं (7.12) की तुलना से यह ज्ञात होता है कि धारा वोल्टता से π/2 अथवा (1/4) चक्र पीछे रहती है। चित्र 7.6 (a) प्रस्तुत प्रकरण के t1 क्षण पर, वोल्टता एवं धारा फेजर्स दर्शाता है। धारा फेजर I वोल्टता फेजर V से π/2 पीछे है। जब उन्हें ω आवृत्ति से वामावर्त दिशा में घूर्णन कराते हैं तो ये वोल्टता एवं धारा जनित करते हैं जो क्रमशः समीकरण (7.1) एवं (7.12) द्वारा व्यक्त की जाती है और जिसे चित्र 7.6 (b) में दर्शाया गया है।

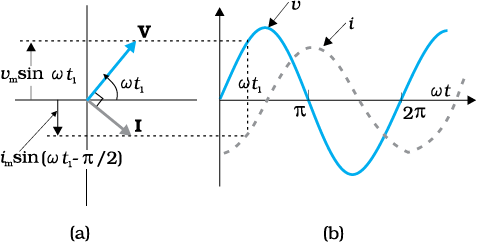
1917.png
चित्र 7.6 (a) चित्र 7.5 में दर्शाए गए परिपथ का फेजर आरेख 
(b) v एवं i तथा ωt के बीच ग्राफ़।

हम देखते हैं कि धारा, वोल्टता की अपेक्षा चौथाई आवर्त काल 

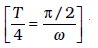77.8 के पश्चात अपने अधिकतम मान को प्राप्त करती है। आपने देखा कि एक प्रेरक में प्रतिघात होता है जो धारा को उसी प्रकार नियंत्रित करता है जैसे dc परिपथ में प्रतिरोध करता है। पर, क्या प्रतिरोध की तरह ही इसमें भी शक्ति व्यय होती है? आइए, इसका पता लगाने का प्रयास करें।

प्रेरक को आपूर्त तात्क्षणिक शक्ति

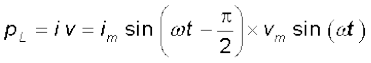
2960.png 

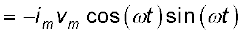
2965.png

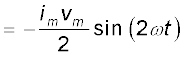
2970.png

अतः एक पूरे चक्र में माध्य शक्ति


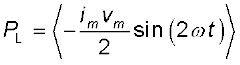
2975.png 

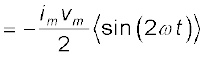2980.png= 0

क्योंकि, एक पूरे चक्र में sin(2ωt) का माध्य शून्य होता है

इसलिए एक पूरे चक्र में किसी प्रेरक को आपूर्त माध्य शक्ति भी शून्य होती है।

चित्र 7.7 में इस तथ्य को विस्तार में समझाया गया है।

 

उदाहरण 7.2 

25.0 mH का एक शुद्ध प्रेरक 220 V के एक स्रोत से जुड़ा है। यदि स्रोत की आवृत्ति 50 Hz हो तो परिपथ का प्रेरकीय प्रतिघात एवं rms धारा ज्ञात कीजिए।

हल 

प्रेरकीय प्रतिघात

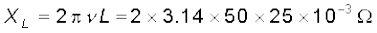
2985.png

= 7.85Ω

परिपथ में rms धारा

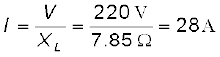
2990.png


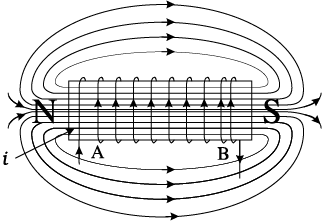
2000.png

0-1 कुंडली में प्रवाहित होने वाली धारा i, जो कुंडली में बिंदु A पर प्रवेश करती है, शून्य से अधिकतम मान तक बढ़ती है। फ्लक्स रेखाएँ स्थापित होती हैं अर्थात क्रोड चुंबकित होता है। दर्शायी गई ध्रुव स्थिति के लिए, वोल्टता एवं धारा दोनों धनात्मक होते हैं, अतः इनका गुणनफल p धनात्मक होता है। स्रोत से ऊर्जा अवशोषित होती है।

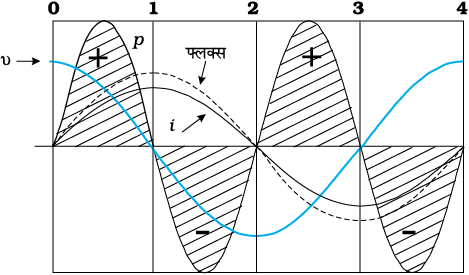
2030.png

वोल्टता/धारा का एक पूर्ण चक्र। ध्यान दीजिए कि धारा वोल्टता से पीछे है।

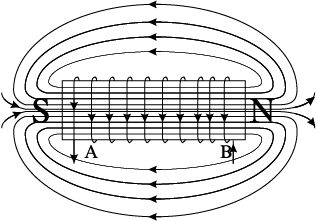
2011.png

1-2 कुंडली में प्रवाहित होने वाली धारा अभी भी धनात्मक है परन्तु कम हो रही है। आधे चक्र के अंत में क्रोड विचुंबकित हो जाता है और कुल फ्लक्स शून्य हो जाता है। वोल्टता v ऋणात्मक है (क्योंकि di/dt का मान ऋणात्मक होता है) वोल्टता एवं धारा का गुणनफल ऋणात्मक होता है और ऊर्जा स्रोत को लौटाई जाने लगती है।

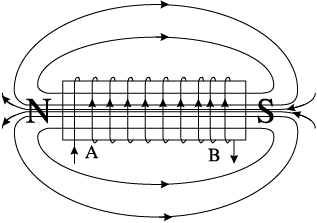
1990.png

2-3 धारा i ऋणात्मक हो जाती है अर्थात यह बिंदु B से प्रवेश कर बिंदु A से बाहर आती है। क्योंकि धारा की दिशा बदल गई है, चुंबक के ध्रुव भी बदल जाते हैं। धारा और वोल्टता दोनों ऋणात्मक हो जाते हैं अतः उनका गुणनफल p धनात्मक है। ऊर्जा अवशोषित होती है।

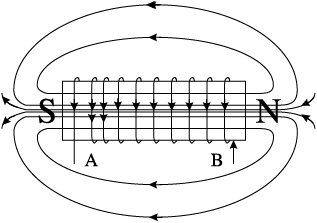
2021.png

3-4 धारा i कम होती है और 4 पर धारा शून्य हो जाती है। 4 पर क्रोड विचुंबकित हो जाता है तथा फ्लक्स शून्य है। वोल्टता धनात्मक एवं धारा ऋणात्मक हैं। अतः शक्ति ऋणात्मक है। जो ऊर्जा 2-3 चक्र के दौरान अवशोषित हुई थी ऊर्जा स्रोत को वापस लौटा दी जाती है।

चित्र 7.7 किसी प्रेरक का चुंबकन एवं विचुंबकन।


7.5 संधारित्र पर प्रयुक्त ac वोल्टता

चित्र 7.8 में एक संधारित्रीय ac परिपथ दर्शाया गया है जिसमें केवल एक संधारित्र एक एेसे ac स्रोत ε से जुड़ा है जो वोल्टता v = vm sin ωt प्रदान करता है।

जब dc परिपथ में वोल्टता स्रोत से किसी संधारित्र को जोड़ा जाता है तो इसमें धारा, उस अल्पकाल के लिए ही प्रवाहित होती है जो संधारित्र की प्लेटों पर एकत्रित होता है, उनके बीच विभवांतर बढ़ता है, जो धारा का विरोध करता है। अर्थात dc परिपथ में ज्यों-ज्यों संधारित्र आवेशित होता है यह परिपथ धारा को सीमित करता है अथवा उसके प्रवाह का विरोध करता है। जब संधारित्र पूरी तरह आवेशित हो जाता है तो परिपथ में धारा गिर कर शून्य हो जाती है।

2040.png

चित्र 7.8  एक संधारित्र से जुड़ी ac वोल्टता।

जब संधारित्र को ac स्रोत से जोड़ा जाता है, जैसा कि चित्र 7.8 में दर्शाया गया है तो यह धारा को नियंत्रित तो करता है, पर आवेश के प्रवाह को पूरी तरह रोकता नहीं है। क्योंकि धारा प्रत्येक अर्द्ध चक्र में प्रत्यावर्तित होती है संधारित्र भी एकांतर क्रम में आवेशित एवं अनावेशित होता है। माना कि किसी क्षण t पर संधारित्र पर आवेश q है। तो संधारित्र के सिरों के बीच तात्क्षणिक वोल्टता है,

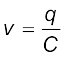2995.png (7.15)

किरखोफ के लूप नियम के अनुसार, स्रोत एवं संधारित्र के सिरों के बीच वोल्टताएँ समान हैं, अतः

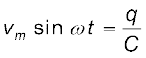
3000.png

धारा का मान ज्ञात करने के लिए हम संबंध

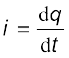
3005.png

का उपयोग करते हैं

3011.png

संबंध,

77.9

77.10

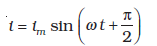
(7.16)

यहाँ, दोलायमान धारा का आयाम im = ωCvm है। इसको हम

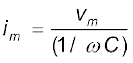
3047.png

के रूप में लिखें और विशुद्ध प्रतिरोधकीय परिपथ के तदनुरूपी सूत्र im= vm/R से तुलना करें तो हम पाते हें कि (1/ωC) की भूमिका प्रतिरोध जैसी ही है। इसको संधारित्र प्रतिघात कहते हैं और Xc से निरूपित करते हैं।

Xc= 1/ωC (7.17)

अतः धारा का आयाम है,

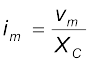3052.png (7.18)

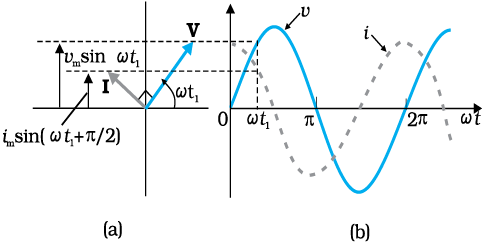
2084.png

चित्र 7.9 (a) चित्र 7.7 में दर्शाए गए परिपथ का फेजर आरेख 
(b) v एवं i का समय के सापेक्ष ग्राफ़।

संधारित्रीय प्रतिघात की विमाएँ वही हैं जो प्रतिरोध की और इसका SI मात्रक ओम (Ω) है। संधारित्रीय प्रतिघात उसी प्रकार विशुद्ध संधारित्रीय परिपथ में धारा को नियंत्रित करता है जैसे विशुद्ध प्रतिरोधकीय परिपथ में प्रतिरोध, परंतु इसका मान आवृत्ति एवं धारिता के व्युत्क्रमानुपाती होता है।

समीकरण (7.16) की स्रोत वोल्टता की समीकरण (7.1) से तुलना करने पर हम पाते हैं कि धारा, वोल्टता से π/2अग्रगामी होती है। चित्र 7.9 (a) किसी क्षण t1 पर फेजर आरेख दर्शाता है। यहाँ धारा फेजर I , वोल्टता फेजर V सेπ/2 कोण अग्रगामी है जब वे वामावर्त घूर्णन करते हैं। चित्र 7.9 (b), वोल्टता एवं धारा में समय के साथ होने वाला परिवर्तन दर्शाता है। हम देखते हैं कि धारा, वोल्टता की तुलना में चौथाई समयकाल पहले अधिकतम मान ग्रहण करती है।

संधारित्र को आपूर्त तात्क्षणिक शक्ति,

pc = i v = im cos(ωt)vm sin(ωt)

= imvm cos(ωt) sin(ωt)

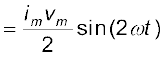
4124.png

(7.19)

अतः संधारित्र के प्रकरण में, माध्य शक्ति

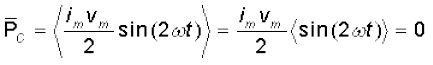
4129.png

क्योंकि एक पूर्ण चक्र पर <sin (2ωt)> = 0, चित्र 7.10 इसकी विस्तार से व्याख्या करता है।

इस प्रकार हम देखते हैं कि प्रेरक के प्रकरण में धारा, वोल्टता से π/2 कोण पश्चगामी एवं संधारित्र के प्रकरण में धारा, वोल्टता से π/2 कोण अग्रगामी होती है।


उदाहरण 7.3 

एक लैंप किसी संधारित्र के साथ श्रेणीक्रम में जुड़ा है। dc एवं ac संयोजनों के लिए अपने प्रेक्षणों की प्रागुक्ति कीजिए। प्रत्येक प्रकरण में बताइए कि संधारित्र की धारिता कम करने का क्या प्रभाव होगा?

हल 

जब संधारित्र के साथ किसी dc स्रोत को जोड़ते हैं तो संधारित्र आवेशित होता है और उसके पूर्ण आवेशन के बाद परिपथ में कोई धारा प्रवाहित नहीं होती और लैंप प्रकाशित नहीं होता है। इस मामले में C को कम करने से कोई परिवर्तन नहीं आएगा। ac स्रोत के साथ, संधारित्र 

(1/ωC) संधारित्रीय प्रतिघात लगाता है और परिपथ में धारा प्रवाहित होती है। परिणामतः लैंप प्रकाश देगा। C को कम करने से प्रतिघात बढ़ेगा और लैंप पहले की तुलना में दीप्ति से प्रकाशित होगा।

उदाहरण 7.4 

15.0 µF का एक संधारित्र,  220 V, 50 Hz स्रोत से जोड़ा गया है। परिपथ का संधारित्रीय प्रतिघात और इसमें प्रवाहित होने वाली (rms एवं शिखर) धारा का मान बताइए। 

यदि आवृत्ति को दोगुना कर दिया जाए तो संधारित्रीय प्रतिघात और धारा के मान पर क्या प्रभाव होगा?

हल  संधारित्रीय प्रतिघात है,

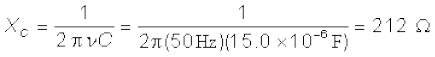
4134.png

rms धारा है

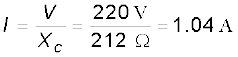
3057.png

शिखर धारा है

3062.png

यह धारा +1.47A एवं –1.47 A के बीच दोलन करती है और वोल्टता से π/2 कोण अग्रगामी होती है।

यदि आवृत्ति दोगुनी हो जाए तो संधारित्रीय प्रतिघात आधा रह जाता है, परिणामतः धारा दोगुनी हो जाती है।


उदाहरण 7.5 

एक प्रकाश बल्ब और एक सरल कुंडली प्रेरक, एक कुंजी सहित, चित्र में दर्शाए अनुसार, एक ac स्रोत से जोड़े गए हैं। स्विच को बंद कर दिया गया है और कुछ समय पश्चात एक लोहे की छड़ प्रेरक कुंडली के अंदर प्रविष्ट कराई जाती है।

 

2256.png
चित्र 7.11

छड़ को प्रविष्ट कराते समय प्रकाश बल्ब की चमक (a) बढ़ती है (b) घटती है (c) अपरिवर्तित रहती है। कारण सहित उत्तर दीजिए।

हल 

 जैसे-जैसे लोहे की छड़ कुंडली में प्रवेश करती है कुंडली के अंदर का चुंबकीय क्षेत्र इसे चुंबकित कर देता है जिससे कुंडली के अंदर चुंबकीय क्षेत्र बढ़ जाता है। अतः कुंडली का प्रेरकत्व बढ़ जाता है। परिणामतः कुंडली का प्रेरकीय प्रतिघात बढ़ जाता है। इस प्रकार प्रयुक्त ac वोल्टता का अधिकांश भाग प्रेरक के सिरों के बीच प्रभावी हो जाता है और बल्ब के सिरों के बीच वोल्टता कम रह जाती है। अतः बल्ब की दीप्ति कम हो जाती है।

 

2134.png

0-1 धारा i दर्शाए अनुसार प्रवाहित होती है एवं 0 पर अधिकतम मान से 1 पर शून्य हो जाती है। प्लेट A धनावेशित होती है जबकि प्लेट B पर ऋणात्मक आवेश q बढ़ता है जो 1 पर अधिकतम हो जाता है जहाँ धारा शून्य हो जाती है। वोल्टता vc = q/C आवेश q के साथ समान कला में रहती है और 1 पर शून्य हो जाती है। धारा और वोल्टता दोनों धनात्मक होती हैं। अतः p = vci धनात्मक है। इस चौथाई चक्र में जैसे-जैसे संधारित्र आवेशित होता है, यह स्रोत से ऊर्जा अवशोषित करता है।


2144.png

 1-2 धारा i की दिशा उलट जाती है। संगृहित आवेश समाप्त हो जाता है अर्थात संधारित्र इस चौथाई चक्र में विसर्जित हो जाता है। वोल्टता कम होती जाती है पर धनात्मक बनी रहती है। धारा ऋणात्मक है। अतः शक्ति जो इनका गुणनफल है, ऋणात्मक होती है। 0-1 चौथाई चक्र में अवशोषित ऊर्जा इस चौथाई चक्र में वापस मिल जाती है।

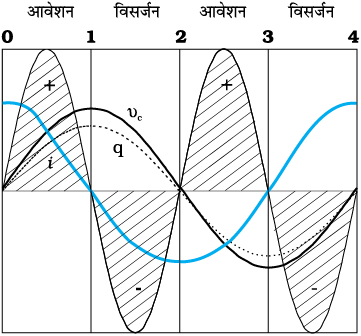
2174.png

वोल्टता/धारा/आवेश/शक्ति का एक पूर्ण चक्र। ध्यान दीजिए कि धारा वोल्टता की तुलना में अग्रगामी है।

2153.png

2-3 क्योंकि धारा i A से B की ओर बहती है, संधारित्र विपरीत ध्रुवता के साथ आवेशित होता है, अर्थात प्लेट B पर धनात्मक एवं प्लेट A पर ऋणात्मक आवेश आने लगता है। धारा एवं वोल्टता दोनों ही ऋणात्मक होते हैं। उनका गुणनफल p धनात्मक है। इस चौथाई चक्र में संधारित्र ऊर्जा अवशोषित करता है।

2163.png

3-4 क्षण 3 पर धारा i की दिशा में उत्क्रमण हो जाता है और यह B से A की ओर प्रवाहित होने लगती है। संग्रहित आवेश समाप्त हो जाता है और वोल्टता vc का परिमाण कम हो जाता है। जब 4 पर संधारित्र पूर्णतः आवेशित हो जाता है तो vc का मान शून्य हो जाता है। शक्ति ऋणात्मक होती है और 2-3 में अवशोषित ऊर्जा स्रोत को वापस लौटा दी जाती है। कुल अवशोषित ऊर्जा शून्य है।

चित्र 7.10 एक संधारित्र का आवेशन एवं निरावेशन।

7.6 श्रेणीबद्ध LCR परिपथ पर प्रयुक्त ac वोल्टता

चित्र 7.12, ac स्रोत ε से जुड़ा श्रेणीबद्ध LCR परिपथ दर्शाता है। पहले की ही भाँति हम ac स्रोत की वोल्टता v = vm sin ωt लेते हैं।

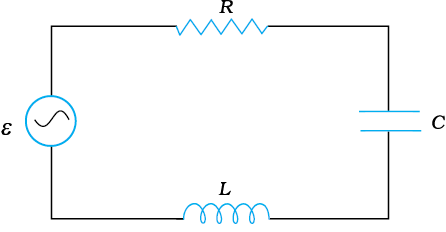
2222.png
चित्र 7.12 किसी ac स्रोत से संयोजित श्रेणीबद्ध LCR परिपथ।

यदि संधारित्र पर आवेश q एवं किसी क्षण t पर परिपथ में प्रवाहित धारा i है तो किरखोफ़ पाश नियम से

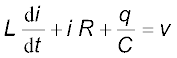3067.png (7.20)

हम तात्क्षणिक धारा i और प्रयुक्त प्रत्यावर्ती वोल्टता v के साथ इसका कला संबंध ज्ञात करना चाहते हैं। हम इस समस्या को हल करने के लिए दो विधियों का उपयोग करेंगे। पहली विधि में हम फेजर्स तकनीक का उपयोग करेंगे और दूसरी विधि में हम समीकरण (7.20) को विश्लेषणात्मक रूप से हल करके i की कालाश्रितता प्राप्त करेंगे।


7.6.1 फेजर आरेख द्वारा हल

चित्र 7.12 में दर्शाए गए परिपथ में प्रतिरोधक, प्रेरक एवं संधारित्र श्रेणीक्रम में जुड़े हैं। अतः किसी क्षण विशेष पर परिपथ के हर घटक में ac धारा, उसके आयाम एवं कला समान हैं। माना कि

i = im sin(ωt+φ) (7.21)

यहाँ φ स्रोत की वोल्टता और परिपथ में प्रवाहित होने वाली धारा में कला-अंतर है। पिछले अनुभागों में हमने जो सीखा है उसके आधार पर हम वर्तमान प्रकरण का एक फेजर आरेख बनाएँगे।

मान लीजिए कि समीकरण (7.21) द्वारा प्रदत्त परिपथ की धारा को फेजर I द्वारा व्यक्त करें। और प्रेरक, प्रतिरोधक, संधारित्र एवं स्रोत के सिरों के बीच वोल्टताओं को क्रमशः VL, VR, VC, एवं V से निरूपित करें तो पिछले अनुभाग से हम जानते हैं कि VR, I के समातंर है, VC धारा I से π/2 रेडियन पीछे है तथा VL , I से π/2 रेडियन आगे है। चित्र 7.13(a) में VL, VR, VC एवं I को समुचित कला संबंधों के साथ दर्शाया गया है।

 

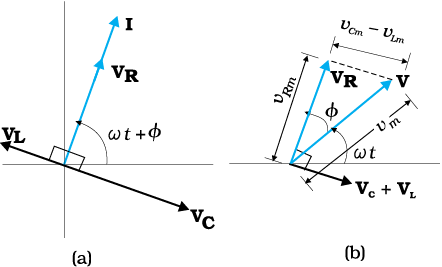
2241.png
चित्र 7.13 (a) फेजर्स VL, VR, VC, एवं I के बीच पारस्परिक संबंध (b) फेजर्स VL, VR, एवं (VL + VC) 
के बीच 7.12 में दर्शाए गए परिपथ के लिए संबंध।

इन फेजर्स की लंबाई अर्थात VR, VC एवं VL के आयाम हैं :

vRm = im R, vCm = im XC, vLm = im XL (7.22)

परिपथ के लिए वोल्टता समीकरण (7.20) को इस प्रकार लिखा जा सकता है

vL + vR + vC = v (7.23)

वह फेजर संबंध जिसके ऊर्ध्वाधर घटकों द्वारा उपरोक्त समीकरण बनती है, वह है

VL + VR + VC = V (7.24)

इस संबंध को चित्र 7.13 (b) में प्रस्तुत किया गया है। चूँकि, VC एवं VL सदैव एक ही सरल रेखा में और एक दूसरे की विपरीत दिशाओं में होते हैं, उनको एक एकल फेजर (VC + VL) के रूप में संयोजित किया जा सकता है जिसका परिमाण vCm – vLm होता है। चूँकि V उस समकोण त्रिभुज के कर्ण से निरूपित किया गया है जिसकी भुजाएँ VR एवं (VC + VL) हैं, पाइथागोरस प्रमेय द्वारा,

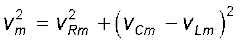
3072.png

समीकरण (7.22) से vRm, vCm, एवं vLm के मान प्रत्येक समीकरण में रखने पर

77.11

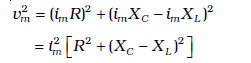
अथवा

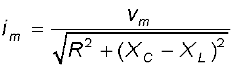3095.png[7.25(a)]

किसी परिपथ मेें प्रतिरोध से समतुल्यता के आधार पर हम ac परिपथ के लिए प्रतिबाधा, Z पद को उपयोग में लाएँ तो

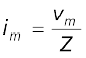3100.png [7.25(b)]

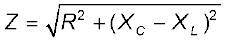
यहाँ 3105.png

(7.26)

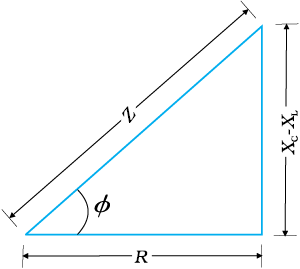
2285.png

चित्र 7.14 प्रतिबाधा आरेख।

चूँकि फेजर I सदैव फेजर VR के समांतर होता है, कला कोण φ VR एवं V के बीच बना कोण है और चित्र 7.14 के आधार पर इसका मान ज्ञात किया जा सकता है


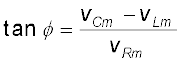
3110.png

समीकरण (7.22) का उपयोग करने पर,

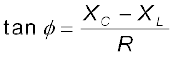
3115.png

(7.27)

समीकरणों (7.26) एवं (7.27) का ग्राफीय निरूपण चित्र (7.14) में प्रस्तुत किया गया है। यह प्रतिबाधा आरेख कहलाता है। यह एक समकोण त्रिभुज है जिसका कर्ण Z है।

समीकरण 7.25(a) धारा का आयाम बताती है एवं समीकरण (7.27) से कलाकोण का मान प्राप्त होता है। इनके साथ मिलकर समीकरण (7.21) पूर्णतः निर्दिष्ट हो जाती है।

यदि XC > XL, φ धनात्मक होता है तथा परिपथ का धारितात्मक व्यवहार प्रधान हो जाता है। परिणामतः परिपथ में धारा स्रोत वोल्टता से अग्र हो जाती है। यदि XC < XL, φ ऋणात्मक होता है तथा परिपथ का प्रेरकीय व्यवहार प्रमुख हो जाता है। परिणामतः परिपथ में धारा स्रोत वोल्टता से पश्च हो जाती है।

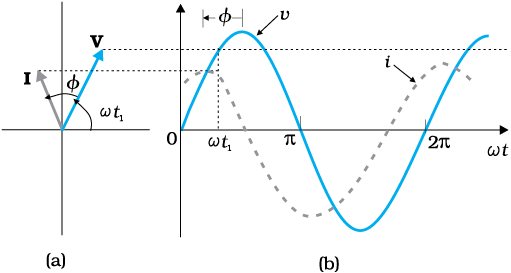
2299.png



चित्र 7.15, XC > XL के प्रकरण के लिए फेजर आरेख है और यह ω t के साथ v एवं i में होने वाले परिवर्तन को दर्शाता है।

इस प्रकार, फेजर्स तकनीक का उपयोग करके, हमने श्रेणीबद्ध LCR परिपथ में धारा का आयाम एवं कला ज्ञात कर ली है। लेकिन ac परिपथों के विश्लेषण की इस विधि में कुछ कमियाँ हैं। प्रथम तो यह कि फेज़र आरेख प्रारंभिक स्थितियों के विषय में कोई सूचना नहीं देते। आप t का कोई भी यादृच्छिक मान (जैसा कि इस अध्याय में सब जगह t1 लिया गया है) ले सकते हैं और विभिन्न फेजर्स के बीच सापेक्षिक कोण दर्शाते हुए अलग-अलग फेजर्स आरेख बना सकते हैं। इस प्रकार प्राप्त हल को स्थायी अवस्था हल कहते हैं। यह कोई व्यापक हल नहीं है। इसके अतिरिक्त एक क्षणिक हल भी होता है जो v = 0 के लिए भी लागू होता है। व्यापक हल, क्षणिक हल एवं स्थायी अवस्था हल के योग से प्राप्त होता है। पर्याप्त दीर्घकाल के पश्चात क्षणिक हल के प्रभाव निष्प्रभावी हो जाते हैं और परिपथ के आचरण का वर्णन स्थायी अवस्था द्वारा ही हल किया जाता है।


7.6.2 विश्लेषणात्मक हल

परिपथ के लिए वोल्टता समीकरण है,


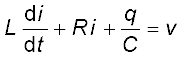
3120.png

= vm sin ωt

हम जानते हैं कि i = dq/dt इसलिए, di/dt = d2q/dt2 अतः, q के पदों में, वोल्टता समीकरण को लिख सकते हैं,


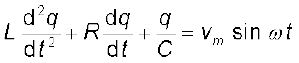3125.png (7.28)

यह किसी प्रणोदित अवमंदित दोलक के समीकरण जैसी ही है। [देखिए समीकरण (14.37(b) कक्षा 11 भौतिकी पाठ्यपुस्तक]। मान लिया कि इसका एक हल है,

q = qm sin (ω t + θ)


[7.29(a)]

ताकि, 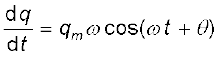3130.png [7.29(b)]

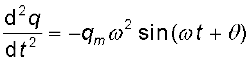एवं 3136.png [7.29(c)]

इन मानों को समीकरण (7.28) में रखने पर, हम पाते हैं


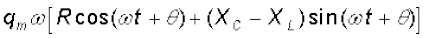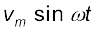3141.png= 3146.png (7.30)

यहाँ हमने Xc= 1/ωC एवं XL = ω L संबंधों का उपयोग किया है। समीकरण (7.30) के वाम पक्ष को

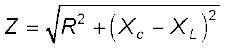
3151.png

से गुणा एवं विभाजित करने पर,

77.12


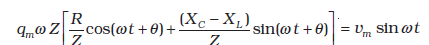
 (7.31)

अब, माना कि

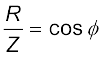
3175.png

तथा

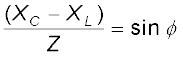
3180.png

ताकि 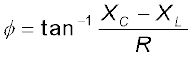3185.png

(7.32)

समीकरण (7.31) में यह मान प्रतिस्थापित करके सरलीकरण करने पर,


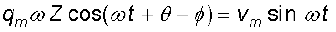
3190.png

(7.33)

इ स समीकरण के दोनों पक्षों की तुलना करने पर हम पाते हैं कि



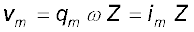
3196.png

यहाँ

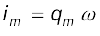3201.png [7.33 (a)]

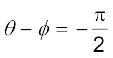एवं 3206.png अथवा

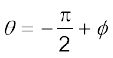
3211.png

[7.33 (b)]

इसलिए परिपथ में धारा का संबंध है

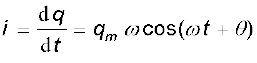
3216.png 

= im cos(ωt + θ)

अथवा i = imsin(ωt + φ) (7.34)

यहाँ


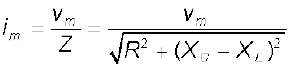3221.png [7.34 (a)]

एवं


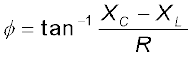
3226.png

अतः परिपथ में धारा के आयाम एवं कला के लिए विश्लेषणात्मक हल फेजर्स तकनीक से प्राप्त हल से मेल खाता है।


7.6.3 अनुनाद

श्रेणीबद्ध RLC परिपथ का एक रोचक अभिलक्षण अनुनाद की परिघटना है। अनुनाद एेसे सभी निकायों की एक सामान्य परिघटना है जिनमें एक विशिष्ट आवृत्ति से दोलन की प्रवृत्ति होती है। यह आवृत्ति उस निकाय की प्राकृतिक आवृत्ति कहलाती है। यदि इस प्रकार का कोई निकाय किसी एेसे ऊर्जा स्रोत द्वारा संचालित हो जिसकी आवृत्ति निकाय की प्राकृतिक आवृत्ति के सन्निकट हो तो निकाय बहुत अधिक आयाम के साथ दोलन करता हुआ पाया जाता है। इसका एक सुपरिचित उदाहरण झूले पर बैठा हुआ बच्चा है। झूले की, लोलक की ही तरह मूल बिन्दु के इधर-उधर दोलन की एक प्राकृतिक आवृत्ति होती है। यदि बच्चा रस्सी को नियमित समय-अंतरालों पर खींचता है और खींचने की आवृत्ति लगभग झूले के दोलनों की प्राकृतिक आवृत्ति के बराबर हो तो झूलने का आयाम अधिक होगा (देखिए कक्षा 11 का अध्याय 14)।

vm आयाम एवं ω आवृत्ति की वोल्टता द्वारा संचालित RLC परिपथ के लिए हम पाते हैं कि धारा आयाम,

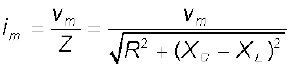
3231.png

यहाँ Xc = 1/ωC एवं XL = ω L अतः यदि ω को परिवर्तित किया जाए तो एक विशिष्ट आवृत्ति ω0 पर Xc = XL एवं प्रतिबाधा Z का मान न्यूनतम

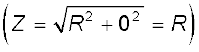
3236.png

हो जाता है। यह आवृत्ति अनुनादी आवृत्ति कहलाती है 

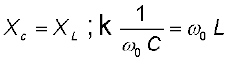
3241.png 

या 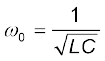3247.png

(7.35)

अनुनादी आवृत्ति पर धारा का आयाम अधिकतम होता है और इसका मान है, im = vm/R

चित्र 7.16 किसी RLC श्रेणीक्रम परिपथ के लिए ω के साथ Im का परिवर्तन दर्शाता है। यहाँ L = 1.00 mH, C = 1.00 nF है तथा R के दो अलग-अलग मान (i) R = 100 Ω एवं (ii) R = 200 Ω लिए गए हैं। प्रयुक्त स्रोत के लिए Vm = 100 V, इस प्रकरण में ω0 = (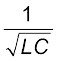3252.png) = 1.00×106 rad/s ।

हम देखते हैं कि अनुनादी आवृत्ति पर धारा का आयाम अधिकतम होता है। चूँकि im = vm / R अनुनाद की स्थिति में, प्रकरण (i) में धारा का परिमाण प्रकरण (ii) की स्थिति में धारा के परिमाण से दोगुना है।

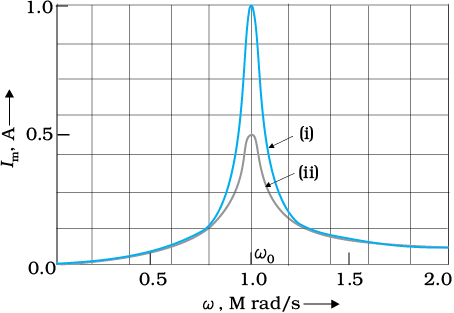
2333.png

चित्र 7.16 दो प्रकरणों (i) R = 100 Ω एवं (ii) R = 200 Ω के लिए. ω के साथ lm का परिवर्तन। दोनों प्रकरणों में L = 1.00 mH

अनुनादी परिपथों के तरह-तरह के अनुप्रयोग होते हैं उदाहरणार्थ, रेडियो एवं टीवी सेटों के समस्वरण की क्रियाविधि। किसी रेडियो का एेंटिना अनेक प्रसारक स्टेशनों से संकेतों का अभिग्रहण करता है। एेंटिना द्वारा अभिग्रहित संकेत, रेडियो के समस्वरण परिपथ में स्रोत का कार्य करते हैं, इसलिए परिपथ अनेक आवृत्तियों पर संचालित किया जा सकता है। परंतु किसी विशिष्ट रेडियो स्टेशन को सुनने के लिए हम रेडियो को समस्वरित करते हैं। समस्वरण के लिए हम समस्वरण परिपथ में लगे संधारित्र की धारिता को परिवर्तित कर परिपथ की आवृत्ति को परिवर्तित कर इस स्थिति में लाते हैं कि उसकी अनुनादी आवृत्ति अभिगृहित रेडियो संकेतों की आवृत्ति के लगभग बराबर हो जाए। जब एेसा होता है तो परिपथ में उस विशिष्ट रेडियो स्टेशन से आने वाले संकेतों की आवृत्ति के धारा आयाम का मान अधिकतम हो जाता है।

एक महत्वपूर्ण एवं ध्यान देने योग्य तथ्य यह है कि अनुनाद की परिघटना केवल उन्हीं परिपथों द्वारा प्रदर्शित की जाती है जिनमें L एवं C दोनों विद्यमान होते हैं। क्योंकि केवल तभी L एवं C के सिरों के बीच की वोल्टता (विपरीत कला में होने के कारण) एक दूसरे को निरस्त करती हैं और धारा आयाम vm/R होता है तथा कुल स्रोत वोल्टता R के सिरों के बीच ही प्रभावी पायी जाती है। इसका अर्थ यह हुआ कि RL या RC परिपथ में अनुनाद नहीं।

अनुनाद की तीक्ष्णता

श्रेणीबद्ध LCR परिपथ में धारा का आयाम,

77.13

 

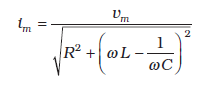
और इसका मान अधिकतम होता है, जब 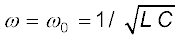3271.png तथा यह अधिकतम मान होता है

77.14

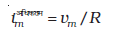
ω के ω0 के अतिरिक्त सभी मानों के लिए धारा का आयाम, इसके अधिकतम मान से कम होता है। मान लीजिए कि हम ω का एक एेसा मान चुनते हैं जिसके लिए धारा आयाम, अधिकतम मान का 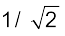3281.png गुना है। इस मान के लिए परिपथ में होने वाला शक्ति क्षय आधा हो जाता है। चित्र (7.16) के वक्र में हम देखते हैं कि ω के एेसे दो मान हैं, ω1 एवं ω2, जिनमें एक ω0 से कम है और दूसरा ω0 से अधिक। ये दोनों मान ω0 के इधर-उधर सममित रूप में स्थित होते हैं। हम लिख सकते हैं :

ω1 = ω0 + ∆ω

ω2 = ω0 – ∆ω

इन दोनों आवृत्तियों के बीच का अंतर ω1 – ω2 = 2∆ω प्रायः परिपथ का बैंड-विस्तार कहलाता है। राशि (ω0 / 2∆ω) को अनुनाद की तीव्रता का माप माना जाता है। ∆ω जितना छोटा होगा, अनुनाद उतना ही तीक्ष्ण या संकीर्ण होगा।

∆ω के लिए व्यंजक प्राप्त करने के लिए, ध्यान दें कि धारा-आयाम im =

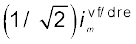
3286.png

तब होता है जब ω1 = ω0 + ∆ω, इसलिए

77.15

77.16

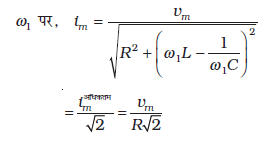
जिसको लिख सकते हैं

77.17

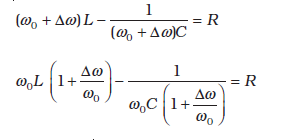
वामपक्ष के दूसरे पद में

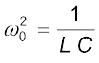
3348.png

का उपयोग करने पर

77.18

77.20


77.19

[7.36 (a)]
अतः, अनुनाद की तीक्ष्णता

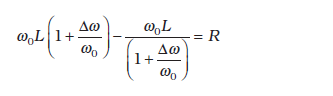
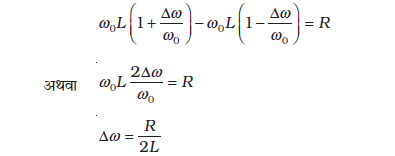
3413.png [7.36 (b)]

अनुपात 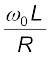3418.png को परिपथ का गुणवत्ता गुणांक Q भी कहते हैं

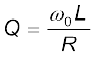
3423.png

[7.36 (c)]

समीकरण [7.36 (b)] एवं [7.36 (c)] से हम देखते हैं कि

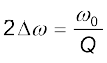
3428.png

अतः, Q का मान जितना अधिक होगा, 2∆ω अर्थात बैंड विस्तार का मान उतना ही कम होगा और अनुनाद उतना ही तीक्ष्ण होगा।

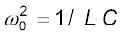
3433.png

का उपयोग करके समीकरण [7.36(c)] को समतुल्यतापूर्वक निम्न प्रकार से व्यक्त कर सकते हैं Q = 1/ω0CR

चित्र 7.15 से हम देखते हैं कि यदि अनुनाद की तीक्ष्णता कम हो तो न केवल शिखर धारा कम होती है, परिपथ अधिक बड़े आवृत्ति परिसर ∆ω के लिए अनुनाद के निकट रहता है और इसलिए परिपथ का समस्वरण अच्छा नहीं हो पाएगा। अतः अनुनाद जितना कम तीक्ष्ण होगा परिपथ की चयन क्षमता भी उतनी ही कम होगी। इसके विपरीत यदि अनुनाद तीक्ष्ण है तो परिपथ की चयन क्षमता भी अधिक होगी। समीकरण (7.36) से हम देखते हैं कि यदि गुणवत्ता गुणांक अधिक है, अर्थात R कम या L अधिक है तो परिपथ की चयन क्षमता अधिक होती है।


उदाहरण 7.6 

एक 200 Ω प्रतिरोधक एवं एक 15.0 µF संधारित्र, किसी 220 V, 50 Hz ac स्रोत से श्रेणीक्रम में जुड़े हैं। (a) परिपथ में धारा की गणना कीजिए; (b) प्रतिरोधक एवं संधारित्र के सिरों के बीच (rms) वोल्टता की गणना कीजिए। क्या इन वोल्टताओं का बीजगणितीय योग स्रोत वोल्टता से अधिक है? यदि हाँ, तो इस विरोधाभास का निराकरण कीजिए।

हल

दिया है

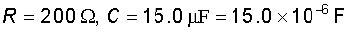
3438.png

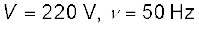
3443.png

(a) धारा की गणना करने के लिए, हमें परिपथ की प्रतिबाधा की आवश्यकता होती है। यह होता है–

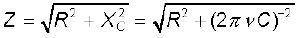
3448.png

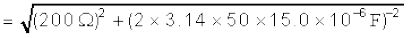
3454.png

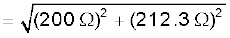
3459.png

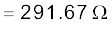
3464.png

इसलिए, परिपथ में धारा है,

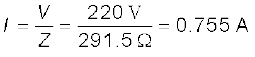
3469.png

(b) चूँकि पूरे परिपथ में समान धारा प्रवाहित हो रही है, इसलिए

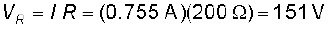
3474.png

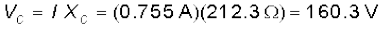
3479.png

दोनों वोल्टताओं VR एवं VC का बीजगणितीय योग 311.3 V है जो स्रोत वोल्टता 220 V से अधिक है। इस विरोधाभास का निराकरण किस प्रकार किया जाए? जैसा कि आपने पाठ में पढ़ा है, दोनों वोल्टताएँ समान कला में नहीं होती हैं। इसलिए उनको साधारण संख्याओं की तरह नहीं जोड़ा जा सकता है। इन वोल्टताओं में 90º का कला-अंतर होता है। इसलिए इनके योग का परिमाण पाइथागोरस के प्रमेय का उपयोग करके ज्ञात किया जा सकता है। अतः,

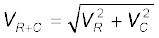
3484.png

= 220 V

इस प्रकार, यदि दो वोल्टताओं के बीच के कला-अंतर को गणना में लाते हुए प्रतिरोधक एवं संधारित्र के सिरों के बीच कुल वोल्टता ज्ञात की जाए तो यह स्रोत वोल्टता के बराबर ही पायी जाएगी।


7.7 ac परिपथों में शक्ति : शक्ति गुणांक

हम देख चुके हैं कि श्रेणीबद्ध RLC परिपथ में प्रयुक्त कोई वोल्टता v = vm sinωt इस परिपथ में धारा i = im sin(ωt + φ) प्रवाहित करती है। यहाँ,

77.21

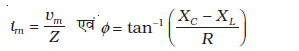
इसलिए स्रोत द्वारा आपूर्त तात्क्षणिक शक्ति p है,


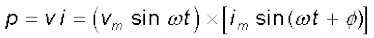
3511.png 

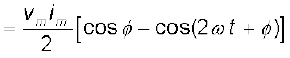3517.png (7.37)

एक पूर्ण चक्र में माध्य शक्ति समीकरण (7.37) के दाएँ पक्ष के दोनों पदों का माध्य लेने से प्राप्त हो सकती है। इनमें केवल दूसरा पद ही समय पर निर्भर करता है, और इसका माध्य शून्य है (कोज्या (cosine) का धनात्मक अर्द्ध इसके ऋणात्मक अर्द्ध को निरस्त कर देता है।) इसलिए,

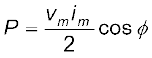
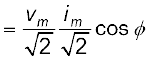
3522.png3527.png 

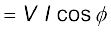3532.png [7.38(a)]

इसको इस प्रकार भी लिखा जा सकता है

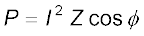3537.png [7.38(b)]

अतः क्षयित माध्य शक्ति, न केवल वोल्टता एवं धारा पर निर्भर करती है बल्कि उनके बीच के कला-कोण की कोज्या (cosine) पर भी निर्भर करती है। राशि cos φ को शक्ति गुणांक कहा जाता है। आइए निम्नलिखित प्रकरणों पर चर्चा करें :

प्रकरण (i) प्रतिरोधकीय परिपथ : यदि परिपथ में केवल शुद्ध R है तो यह परिपथ प्रतिरोधकीय परिपथ कहलाता है। इस परिपथ के लिए φ = 0, cos φ = 1 इसमें अधिकतम शक्ति क्षय होती है।

प्रकरण (ii) शुद्ध प्रेरकीय अथवा धारितीय परिपथ : यदि परिपथ में केवल एक प्रेरक अथवा संधारित्र हो तो हम जानते हैं कि धारा एवं वोल्टता के बीच कला अंतर π/2 होता है। इसलिए 

cos φ = 0 और इसलिए यद्यपि परिपथ में धारा प्रवाहित होती है तो भी कोई शक्ति क्षय नहीं होती। इस धारा को कभी-कभी वाटहीन धारा भी कहा जाता है।

प्रकरण (iii) श्रेणीबद्ध LCR परिपथ : किसी LCR परिपथ में शक्ति क्षय समीकरण (7.38) के अनुसार होता है। यहाँ φ = tan–1 (Xc – XL )/ R अतः किसी RL या RC या RCL परिपथ में φ शून्येतर हो सकता है। इन परिपथों में भी शक्ति केवल प्रतिरोधक में ही क्षयित होती है।

प्रकरण (iv) LCR परिपथ में अनुनाद स्थिति में शक्ति क्षयः अनुनाद की स्थिति में Xc – XL= 0 एवं φ = 0 इसलिए cosφ = 1 एवं P = I2Z = I2 R अर्थात परिपथ में अधिकतम शक्ति (R के माध्यम से) अनुनाद की स्थिति में क्षयित होती है।

 

उदाहरण 7.7 

(a) विद्युत शक्ति के परिवहन के लिए प्रयुक्त होने वाले परिपथों में निम्न शक्ति गुणांक, संप्रेषण में अधिक ऊर्जा का क्षय होगा, निर्दिष्ट करता है। इसका कारण समझाइए।

(b) परिपथ का शक्ति गुणांक, प्रायः परिपथ में उपयुक्त मान के संधारित्र का उपयोग करके सुधारा जा सकता है। यह तथ्य समझाइए।

हल 

(a) हम जानते हैं कि P = I V cos φ यहाँ cos φ शक्ति गुणांक है। दी गई वोल्टता पर वांछित शक्ति की आपूर्ति के लिए यदि cos φ का मान कम होगा तो हमें उसी अनुपात में धारा का मान बढ़ाना पड़ेगा। परन्तु इससे संप्रेषण में अधिक शक्ति क्षय (I2R) होगा।

(b) माना कि किसी परिपथ में धारा I वोल्टता से φ कोण पीछे रहती है तो इस परिपथ के लिए
cos φ =R/Z

हम शक्ति गुणांक का सुधार कर इसका मान 1 की ओर प्रवृत्त कर सकते हैं जिसके लिए Z का मान R हो यह प्रयास करना पड़ेगा। यह उपलब्धि कैसे होती है, आइए चित्र द्वारा इसे समझने का प्रयास करें। धारा I को हम दो घटकों में वियोजित करते हैं– Ip प्रयुक्त वोल्टता V की दिशा में एवं Iq वोल्टता की लंबवत दिशा में। Iq जैसा आप अनुभाग 7.7 में पढ़ चुके हैं, वाटहीन घटक कहलाता है क्योंकि धारा के इस घटक के संगत कोई शक्ति क्षय नहीं होता। IP को शक्ति घटक कहा जाता है, क्योंकि यह वोल्टता के साथ समान कला में है और इसी के साथ परिपथ में शक्ति क्षय होती है।

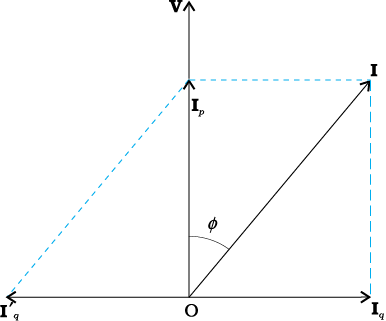
2414.png
चित्र 7.17

इस विश्लेषण से यह स्पष्ट है कि यदि हम शक्ति गुणांक में सुधार लाना चाहें तो पश्चगामी वाटहीन धारा Iq को उसी के बराबर अग्रगामी वाटहीन धारा I′q द्वारा उदासीन करना पड़ेगा। इसके लिए उपयुक्त मान का संधारित्र समांतर क्रम में संयोजित करना होगा ताकि Iq एवं I′q एक-दूसरे को निरस्त कर सकें और P प्रभावी रूप से Ip V हो सके।

 

उदाहरण 7.8 

283 V शिखर वोल्टता एवं 50 Hz आवृत्ति की एक ज्यावक्रीय वोल्टता एक श्रेणीबद्ध LCR परिपथ से जुड़ी है जिसमें R = 3 Ω, L = 25.48 mH, एवं C = 796 µF है। ज्ञात कीजिए (a) परिपथ की प्रतिबाधा; (b) स्रोत के सिरों के बीच लगी वोल्टता एवं परिपथ में प्रवाहित होने वाली धारा के बीच कला-अंतर; (c) परिपथ में होने वाला शक्ति-क्षय; एवं (d) शक्ति गुणांक।

हल

(a) परिपथ की प्रतिबाधा ज्ञात करने के लिए पहले हम XL एवं XC की गणना करेंगे।

XL = 2 πνL

= 2 × 3.14 × 50 × 25.48 × 10–3 Ω = 8 Ω

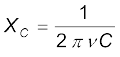
3542.png

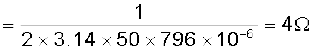
3547.png

इसलिए,

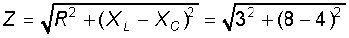
3552.png

= 5 Ω

(b) कला-अंतर, φ = tan–1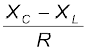3557.png

77.22

चूँकि φ का मान ऋणात्मक है, परिपथ में धारा स्रोत के सिरों के बीच वोल्टता से पीछे रहती है,

(c) परिपथ में शक्ति क्षय,

77.23

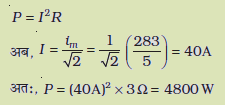
(d) शक्ति गुणांक =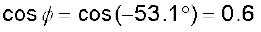3604.png 


उदाहरण 7.9 

माना कि पूर्व उदाहरण में वर्णित स्रोत की आवृत्ति परिवर्तनशील है। (a) स्रोत की किस आवृत्ति पर अनुनाद होगा। (b) अनुनाद की अवस्था में प्रतिबाधा, धारा एवं क्षयित शक्ति की गणना कीजिए।

हल

(a) वह आवृत्ति जिस पर अनुनाद होगा,

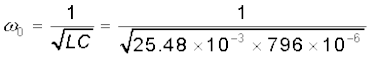
3609.png

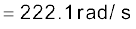
3614.png

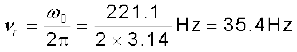
3619.png

(b) अनुनाद की स्थिति में प्रतिबाधा, Z प्रतिरोध, R के बराबर होती है अतः

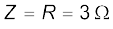
3624.png

अनुनाद स्थिति में rms धारा

77.24

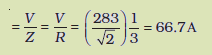
अनुनाद स्थिति में शक्ति क्षय

3646.png

प्रस्तुत प्रकरण में आप देख सकते हैं कि अनुनाद स्थिति में शक्ति क्षय उदाहरण 7.8 में हुए शक्ति क्षय से अधिक है।


उदाहरण 7.10 

किसी हवाई अड्डे पर सुरक्षा कारणों से, किसी व्यक्ति को धातु-संसूचक के द्वार पथ से गुजारा जाता है। यदि उसके पास कोई धातु से बनी वस्तु है, तो धातु संसूचक से एक ध्वनि निकलने लगती है। यह संसूचक किस सिद्धांत पर कार्य करता है?

हल 

धातु संसूचक ac परिपथों में अनुनाद के सिद्धांत पर कार्य करता है। जब आप किसी धातु संसूचक से गुजरते है तो वास्तव में आप अनेक फेरों वाली एक कुंडली से होकर गुजरते हैं। यह कुंडली एक एेसी समस्वरित संधारित्र से जुड़ी होती है जिसके कारण परिपथ अनुनाद की स्थिति में होता है। जब आप जेब में धातु लेकर कुंडली से गुजरते हैं तो परिपथ की प्रतिबाधा परिवर्तित हो जाती है, परिणामस्वरूप परिपथ में प्रवाहित होने वाली धारा में सार्थक परिवर्तन होता है। धारा का यह परिवर्तन संसूचित होता है एवं इलेक्ट्रॉनिक परिपथिकी के कारण चेतावनी की ध्वनि उत्पन्न होती है।

 

7.8 LC दोलन  

हम जानते हैं कि एक संधारित्र एवं एक प्रेरक क्रमशः वैद्युत एवं चुंबकीय ऊर्जा संचित कर सकते हैं। जब एक (पहले से आवेशित) संधारित्र एक प्रेरक के साथ जोड़ा जाता है तो संधारित्र पर आवेश एवं परिपथ में धारा, वैद्युत दोलनों की वैसी ही परिघटना प्रदर्शित करते हैं जैसी यांत्रिक प्रणालियों के दोलनों में देखी जाती है (अध्याय 14, कक्षा 11)।

माना कि किसी संधारित्र पर (t = 0) पर qm आवेश है और इसे एक प्रेरक से जोड़ा गया है जैसा चित्र 7.18 में दर्शाया गया है।

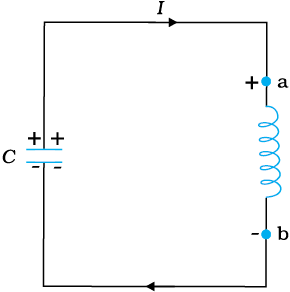
2484.png
चित्र 7.18 दर्शाए गए क्षण पर धारा बढ़ रही है अतः प्रेरक में प्रेरण द्वारा उत्पन्न की गई ध्रुवता वैसी ही होती है जैसी चित्र में दर्शायी गई है।

जैसे ही परिपथ पूर्ण होता है, संधारित्र पर आवेश कम होना प्रारंभ हो जाता है जिससे परिपथ में धारा प्रवाहित होने लगती है। माना कि किसी क्षण t पर आवेश q एवं परिपथ में धारा i है। चूँकि di/dt धनात्मक है, L में प्रेरित emf की ध्रुवता वही होगी जो चित्र में दर्शायी गई है, अर्थात vb < va । किरखोफ के लूप नियम के अनुसार,

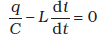77.25 (7.39)

i = – (dq/dt), क्योंकि प्रस्तुत प्रकरण में q कम हो रहा है, i बढ़ रहा है 

अतः समीकरण (7.39) को लिख सकते हैं :

77.26

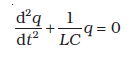
(7.40)

इस समीकरण का स्वरूप सरल आवर्त गति की समीकरण

77.27

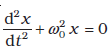
जैसा है। अतः, 

संधारित्र का आवेश सरल आवर्त दोलन करता है जिनकी प्राकृतिक आवृत्ति है,

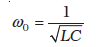77.28 (7.41)


और इसके परिमाण में समय के साथ ज्यावक्रीय रूप से परिवर्तन होता है जिसको हम निम्नलिखित सूत्र द्वारा व्यक्त कर सकते हैं :

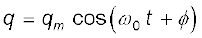3671.png (7.42)

यहाँ qm आवेश q का अधिकतम मान है एवं φ एक कला नियतांक है। चूंँकि, t = 0 पर q = qm, cos φ =1 या φ = 0 । इसलिए, प्रस्तुत प्रकरण में

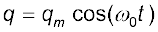3676.png (7.43)

77.29

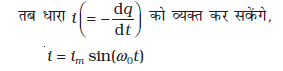
(7.44)

यहाँ

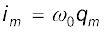
3696.png

आइए अब यह देखने की चेष्टा करें कि परिपथ में यह दोलन होते कैसे हैं?

चित्र 7.19(a) में प्रारंभिक आवेश qm युक्त एक संधारित्र एक आदर्श प्रेरक से जुड़ा दिखाया गया है। आवेशित संधारित्र में संचित वैद्युत ऊर्जा है

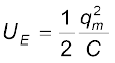
3702.png


। क्योंकि, परिपथ में कोई धारा प्रवाहित नहीं हो रही है, प्रेरक में ऊर्जा शून्य है। अतः LC परिपथ की कुल ऊर्जा है,

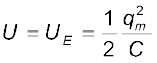
3707.png


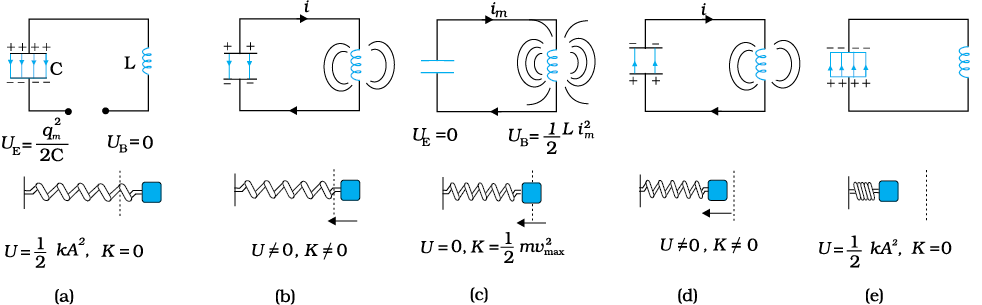
2520.png

चित्र 7.19 LC परिपथ के दोलन स्प्रिंग के सिरे पर लगे गुटके के दोलनों के समतुल्य हैं। 
चित्र में दोलनों के आधे चक्र को दर्शाया गया है।

t = 0 पर स्विच बंद कर दिया जाता है और संधारित्र विसर्जित होने लगता है [चित्र 7.19 (b)]। जैसे-जैसे धारा बढ़ती है प्रेरक में चुंबकीय क्षेत्र स्थापित होने लगता है और प्रेरक में चुंबकीय ऊर्जा के रूप मेें ऊर्जा संचित होने लगती है जिसका मान है UB = (1/2) Li2। जब im, (t = T/4 पर) धारा का मान अधिकतम im होता है, जैसा चित्र 7.19 (c) में दर्शाया गया है तो कुल ऊर्जा चुंबकीय क्षेत्र के रूप में संचित होती है जिसका मान है– UB = (1/2) Li2m । आप यह आसानी से जाँच सकते हैं कि अधिकतम वैद्युत ऊर्जा, अधिकतम चुंबकीय ऊर्जा के बराबर होती है। इस स्थिति में संधारित्र पर कोई आवेश और इसलिए कोई ऊर्जा नहीं होती। अब, जैसा चित्र 7.19 (d) में दर्शाया गया है, धारा संधारित्र को आवेशित करने लगती है। यह प्रक्रिया तब तक चलती रहती है जब तक कि (t = T/2 पर) संधारित्र पूरी तरह आवेशित नहीं हो जाता है [चित्र 7.19 (e)]। लेकिन, अब इसका आवेशन, चित्र 7.19 (a) में दर्शायी गई प्रारंभिक स्थिति की ध्रुवता को विपरीत ध्रुवता के साथ होता है। ऊपर बताई गई प्रक्रिया अब फिर से दोहराई जाएगी जिससे प्रणाली अपनी मूल अवस्था में लौट आएगी। अतः इस प्रणाली में ऊर्जा संधारित्र एवं प्रेरक के बीच दोलन करती है।

LC दोलन स्प्रिंग से जुड़े पिंड के यांत्रिक दोलनों की ही तरह है। चित्र 7.19 में प्रत्येक आकृति का नीचे का भाग यांत्रिक प्रणाली (स्प्रिंग से जुड़े पिंड) की संगत अवस्था प्रदर्शित करता है। जैसा पहले देखा गया है, m द्रव्यमान के ω0 आवृत्ति से दोलन करते पिंड के लिए, समीकरण है

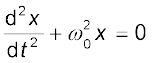
3712.png

यहाँ,

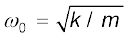
3727.png

, एवं k स्प्रिंग नियतांक है। इसलिए, x के संगत राशि q है। यांत्रिक प्रणाली के लिए, F = ma = m(dv/dt) = m(d2x/dt2)। विद्युतीय प्रणाली के लिए ε = –L(di/dt) = –L(d2q/dt2)। इन दो समीकरणों की तुलना करने पर, हम देखते हैं कि L द्रव्यमान m के समतुल्य है ः L धारा में परिवर्तन के प्रतिरोध का माप है। LC परिपथ के प्रकरण में,

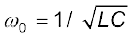
3722.png

एवं स्प्रिंग पर दोलन करते द्रव्यमान के लिए,


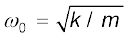
3727.png

। इसलिए 1/C स्प्रिंग नियतांक k के समतुल्य है। नियतांक, k (=F/x) व्यक्त करता है इकाई विस्थापन के लिए आवश्यक (बाह्य) बल, जबकि 1/C (=V/q) व्यक्त करता है इकाई आवेश संचित करने के लिए आवश्यक विभवांतर।

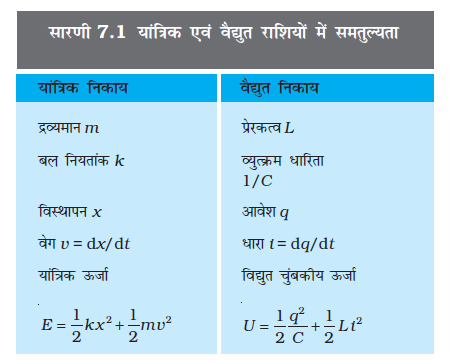
सारणी 7.1 में यांत्रिक एवं वैद्युत राशियों की सादृश्यता प्रस्तुत की गई है।

ध्यान दें कि LC दोलनों के संबंध में उपरोक्त चर्चा दो कारणों से यथार्थ नहीं है–

77.30

(i) प्रत्येक प्रेरक में कुछ न कुछ प्रतिरोध अवश्य होता है। यह प्रतिरोध आवेश एवं परिपथ में प्रवाहित धारा पर अवमंदक प्रभाव डालता है जिससे अंततः दोलन समाप्त हो जाते हैं।

(ii) यदि प्रतिरोध शून्य हो तो भी निकाय की कुल ऊर्जा नियत नहीं रहेगी। यह निकाय से विद्युत चुंबकीय तरंगों के रूप में विकिरित हो जाएगी (अगले अध्याय में इस विषय में विस्तार से चर्चा की गई है)। वास्तव में रेडियो एवं टीवी संप्रेषकों की कार्य प्रणाली इन्हीं विकिरणों के ऊपर निर्भर करती है।


दो अलग-अलग परिघटनाएँ, समान गणितीय व्यवहार

संभवतः आप कक्षा 11 की भौतिकी की पाठ्यपुस्तक के अनुभाग 14.10 में वर्णित प्रणोदित अवमंदित दोलक की तुलनाac से जुड़े LCR परिपथ से करना चाहें। हम यह टिप्पणी पहले ही कर चुके हैं कि कक्षा 11 की पाठ्यपुस्तक में दी गई समीकरण [14.37 (b)] और इस अध्याय में दी गई समीकरण (7.28) में यद्यपि अलग-अलग संकेत चिह्न एवं प्राचल प्रयुक्त किए गए हैं, फिर भी वे एक दूसरे से बिलकुल मिलती-जुलती हैं। आइए, इन दो स्थितियों में विभिन्न राशियों की समतुल्यता सूचीबद्ध करें–

 

77.31

ध्यान दें कि चूँकि विस्थापन (x), आवेश (q) के संगत होता है, आयाम (अधिकतम विस्थापन) A के संगत अधिकतम संचित आवेश, qm होगा। कक्षा 11 की समीकरण [14.39 (a)] अन्य प्राचलों के पदों में दोलनों का आयाम निर्दिष्ट करती है जो सुविधा के लिए यहाँ हम प्रस्तुत करते हैं ः

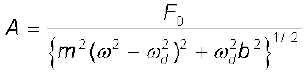
3899.png

उपरोक्त समीकरण में प्रत्येक प्राचल को उसके संगत वैद्युत राशि से प्रतिस्थापित करें और देखें कि क्या होता है। इससे, L,C, ω एवं ω0, को, संबंधों XL= ωL, XC = 1/ωC, एवं ω02 = 1/LC का उपयोग करके हटाएँ। जब आप समीकरण(7.33) एवं (7.34) का उपयोग करेंगे तो आप पाएँगे कि उनमें पूरा तालमेल है।

भौतिकी में एेसी अनेक स्थितियों से आपका सामना होगा जहाँ बिलकुल अलग भौतिक परिघटनाओं को एक जैसी गणितीय समीकरणों द्वारा व्यक्त किया जाता है। यदि आप उनमें से एक को सुलझा चुके हैं तो दूसरी को सुलझाने के लिए आप केवल संगत राशियों को प्रतिस्थापित करके नए संदर्भ में परिणाम की व्याख्या करें। हमारा सुझाव है कि आप भौतिकी के विभिन्न क्षेत्रों से इस प्रकार की समान परिस्थितियों को खोजें। हमें इन स्थितियों के अंतरों से भी अवगत होना चाहिए।


उदाहरण 7.11 

दर्शाइए कि LC परिपथ के मुक्त दोलनों में, संधारित्र एवं प्रेरक में संचित ऊर्जाओं का योग, समय के बदलने पर भी नहीं बदलता।

हल 

मान लीजिए कि किसी संधारित्र पर प्रारंभिक आवेश q0 है तथा यह संधारित्र L प्रेरकत्व के किसी प्रेरक के साथ जोड़ा गया है। जैसा आपने अनुभाग 7.8 में पढ़ा है, इस LC परिपथ में आवृत्ति (ω) यहाँ ω

77.32

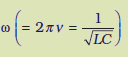
के दोलन बने रहेंगे।

किसी क्षण t पर, संधारित्र पर आवेश q एवं परिपथ में धारा i हैं,

q (t) = q0 cos ωt

i (t) = – q0 ω sin ωt

समय t पर, प्रेरक में संचित ऊर्जा

3742.png

समय t पर प्रेरक में संचित ऊर्जा

77.33

क्योंकि qo एवं C दोनों ही समय पर निर्भर नहीं करते इसलिए यह योग समय के साथ नहीं बदलता। ध्यान देने योग्य बात यह है कि ऊर्जाओं का यह योग संधारित्र की प्रारंभिक ऊर्जा के बराबर है। एेसा क्यों है? विचार कीजिए!


7.9 ट्रांसफॉर्मर

अनेक उद्देश्यों के लिए ac वोल्टता को एक मान से दूसरे अधिक या कम मान में परिवर्तित करना (या रूपांतरित करना) आवश्यक हो जाता है। एेसा अन्योन्य प्रेरण के सिद्धांत पर आधारित एक युक्ति के द्वारा किया जाता है जिसे ट्रांसफॉर्मर कहते हैं।

ट्रांसफार्मर में दो कुंडलियाँ होती हैं जो एक दूसरे से विद्युतरुद्ध होती हैं। वे एक कोमल-लौह-क्रोड पर लिपटी होती हैं। लपेटने की विधि या तो चित्र 7.20 (a) की भाँति होती है, जिसमें एक कुंडली दूसरी के ऊपर लिपटी होती है, या फिर चित्र 7.20 (b) की भाँति जिसमें दोनों कुंडलियाँ क्रोड की अलग-अलग भुजाओं पर लिपटी होती हैं। एक कुंडली को प्राथमिक कुंडली (primary coil) कहते हैं इसमें Np लपेटे होते हैं। दूसरी कुंडली को द्वितीयक कुंडली (secondary coil) कहते हैं, इसमें Ns लपेटे होते हैं। प्रायः प्राथमिक कुंडली निवेशी कुंडली होती है एवं द्वितीयक कुंडली ट्रांसफार्मर की निर्गत कुंडली होती है। 

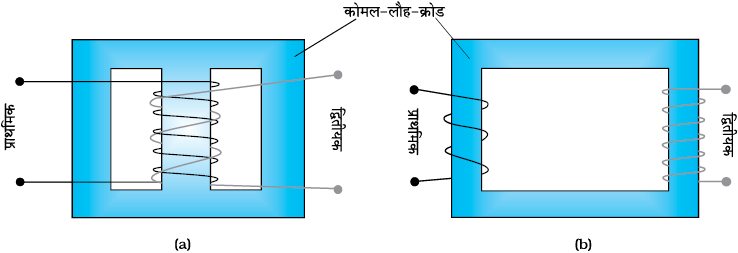
2613.png
चित्र 7.20 किसी ट्रांसफॉर्मर में प्राथमिक एवं द्वितीयक कुंडलियों को लपेटने की दो व्यवस्थाएँ ः 
(a) एक दूसरे के ऊपर लपेटी गई दो कुंडलियाँ (b) क्रोड की अलग-अलग भुजाओं पर लिपटी कुंडलियाँ

जब प्राथमिक कुंडली के सिरों के बीच प्रत्यावर्ती वोल्टता लगाई जाती है तो परिणामी धारा एक प्रत्यावर्ती चुंबकीय फ्लक्स उत्पन्न करती है जो द्वितीयक कुंडली से संयोजित होकर इसके सिरों के बीच एक emf प्रेरित करता है। इस emf का मान द्वितीयक कुंडली में फेरों की संख्या पर निर्भर करता है। हम मान लेते हैं कि हमारा ट्रांसफॉर्मर एक आदर्श ट्रांसफॉर्मर है जिसकी प्राथमिक कुंडली का प्रतिरोध नगण्य है, और क्रोड का संपूर्ण फ्लक्स प्राथमिक एवं द्वितीयक दोनों कुुंडलियों से गुजरता है। प्राथमिक कुुंडली के सिरों के बीच वोल्टता vp लगाने से, माना किसी क्षण t पर, इस कुंडली का प्रत्येक फेरा क्रोड में φ फ्लक्स उत्पन्न करता है।

तब Ns लपेटों वाली द्वितीयक कुंडली के सिरों के बीच प्रेरित emf या वोल्टता εs है

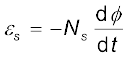3783.png (7.45)

प्रत्यावर्ती फ्लक्स, φ प्राथमिक कुंडली में भी एक emf प्रेरित करता है जिसे पश्च विद्युत वाहक बल कहते हैं। यह है,

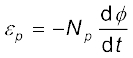3788.png (7.46)

लेकिन, εp = vp यदि एेसा नहीं होता तो प्रारंभिक कुंडली (जिसका प्रतिरोध हमने शून्य माना है) में अनंत परिमाण की धारा प्रवाहित होती। यदि द्वितीयक कुुंडली के सिरे मुक्त हों अथवा इससे बहुत कम धारा ली जा रही हो तो पर्याप्त सन्निकट मान तक

εs = vs

यहाँ vs द्वितीयक कुंडली के सिरों के बीच वोल्टता है। अतः समीकरणों (7.45) एवं (7.46) को हम इस प्रकार लिख सकते हैं 

77.34

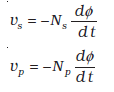
[7.46(a)]

समीकरण [7.45 (a)] एवं [7.46 (a)] से,

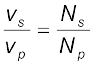3803.png (7.47)

ध्यान दीजिए कि उपरोक्त संबंध की व्युत्पत्ति में हमने तीन परिकल्पनाओं का उपयोग किया है जो इस प्रकार हैं– (i) प्राथमिक कुंडली का प्रतिरोध एवं इसमें प्रवाहित होने वाली धारा कम है; (ii) प्राथमिक एवं द्वितीयक कुंडली से समान फ्लक्स बाहर निकल पाता है; एवं (iii) द्वितीयक कुंडली में बहुत कम धारा प्रवाहित होती है।

यदि यह मान लिया जाए कि ट्रांसफॉर्मर की दक्षता 100% है (कोई ऊर्जा क्षय नहीं होता); तो निवेशी शक्ति, निर्गत शक्ति के बराबर होगी और चूँकि p = i v,

ipvp = isvs (7.48)

यद्यपि कुछ न कुछ ऊर्जा क्षय तो सदैव होता ही है, फिर भी यह एक अच्छा सन्निकटन है, क्योंकि एक भली प्रकार अभिकल्पित ट्रांसफॉर्मर की दक्षता 95% से अधिक होती है। समीकरण (7.47) एवं (7.48) को संयोजित करने पर,ip

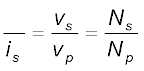3808.png (7.49)

क्योंकि i एवं v दोनों की दोलन आवृत्ति वही है जो ac स्रोत की, समीकरण (7.49) से संगत राशियों के आयामों अथवा rms मानों का अनुपात भी प्राप्त होता है।

अब, हम देख सकते हैं कि ट्रांसफॉर्मर किस प्रकार वोल्टता एवं धारा के मानों को प्रभावित करता है। हम जानते हैं कि:

77.40 (7.50)

अर्थात यदि द्वितीयक कुंडली में प्राथमिक कुंडली से अधिक फेरे हैं (Ns > Np) तो वोल्टता बढ़ जाती है (Vs > Vp) । इस प्रकार की व्यवस्था को उच्चायी ट्रांसफॉर्मर (step-up transformer) कहते हैं। तथापि, इस व्यवस्था में, द्वितीयक कुंडली में धारा प्राथमिक कुंडली से कम होती है (Np/Ns < 1 एवं Is < Ip)। उदाहरणार्थ, यदि किसी ट्रांसफॉर्मर की प्राथमिक कुंडली में 100 एवं द्वितीयक कुंडली में 200 फेरे हों तो Ns/Np = 2 एवं Np/Ns=1/2 । अतः 220V, 10A का निवेश, बढ़कर 440 V का निर्गम 5.0 A पर देगा।

यदि द्वितीयक कुंडली में प्राथमिक कुंडली से कम फेरे हैं (Ns < Np) तो यह ट्रांसफॉर्मर अपचयी (step-down transformer) है। इस ट्रांसफार्मर में Vs < Vp एवं Is > Ip अर्थात वोल्टता कम हो जाती है तथा धारा बढ़ जाती है।

ऊपर प्राप्त की गई समीकरण आदर्श ट्रांसफॉर्मरों के लिए ही लागू होती है (जिनमें कोई ऊर्जा क्षय नहीं होता)। परंतु वास्तविक ट्रॉसफॉर्मरों में निम्नलिखित कारणों से अल्प मात्रा में ऊर्जा क्षय होता है–

(i) फ्लक्स क्षरण–सदैव कुछ न कुछ फ्लक्स तो क्षरित होता ही है, अर्थात क्रोड के खराब अभिकल्पन या इसमें रही वायु रिक्ति के कारण, प्राथमिक कुंडली का समस्त फ्लक्स द्वितीयक कुंडली से नहीं गुजरता। प्राथमिक एवं द्वितीयक कुंडलियों को एक दूसरे के ऊपर लपेट कर फ्लक्स क्षरण को कम किया जाता है।

(ii) कुंडलनों का प्रतिरोध– कुंडलियाँ बनाने में लगे तारों का कुछ न कुछ प्रतिरोध तो होता ही है और इसलिए इन तारों में उत्पन्न ऊष्मा (I 2R) के कारण ऊर्जा क्षय होता है। उच्च धारा, निम्न वोल्टता कुंडलनों में मोटे तार का उपयोग करके, इनमें होने वाले ऊर्जा क्षय को कम किया जाता है।

(iii) भँवर धाराएँ–प्रत्यावर्ती चुंबकीय फ्लक्स, लौह-क्रोड में भँवर धाराएँ प्रेरित करके, इसे गर्म कर देता है। स्तरित क्रोड का उपयोग करके इस प्रभाव को कम किया जाता है।

(iv) शैथिल्य (Hysteresis)–प्रत्यावर्ती चुंबकीय क्षेत्र द्वारा क्रोड का चुंबकन बार-बार उत्क्रमित होता है। इस प्रक्रिया में व्यय होने वाली ऊर्जा क्रोड में ऊष्मा के रूप में प्रकट होती है। कम शैथिल्य वाले पदार्थ का क्रोड में उपयोग करके इस प्रभाव को कम रखा जाता है।

विद्युत ऊर्जा का लंबी दूरियों तक, बड़े पैमाने पर संप्रेषण एवं वितरण करने के लिए ट्रांसफॉर्मरों का उपयोग किया जाता है। जनित्र की निर्गत वोल्टता को उच्चायित किया जाता है (ताकि धारा कम हो जाती है और परिणामस्वरूप I2R हानि घट जाती है। इसकी लंबी दूरी के उपभोक्ता के समीप स्थित क्षेत्रीय उप-स्टेशन तक संप्रेषित किया जाता है। वहाँ वोल्टता को अपचयित किया जाता है। वितरण उप-स्टेशनों एवं खंभों पर फिर से अपचयित करके 240 V की शक्ति आपूर्ति हमारे घरों को पहुँचायी जाती है।


सारांश

1. जब किसी प्रतिरोधक R के सिरों पर कोई प्रत्यावर्ती वोल्टता


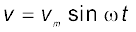
3904.png

लगाई जाती है तो उसमें धारा i = im sinωt संचालित होती है जहाँ,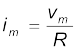

3909.png

. यह धारा प्रयुक्त वोल्टता की कला में होती है।

2. किसी प्रतिरोधक R से प्रवाहित प्रत्यावर्ती धारा i = im sinωt के लिए जूल तापन के कारण माध्य शक्ति क्षय (1/2)i2mR होता है। इसे उसी रूप में व्यक्त करने के लिए जिसमें dc शक्ति (P = I2R), को व्यक्त करते हैं, धारा के एक विशिष्ट मान का उपयोग किया जाता है। इसे वर्ग माध्य मूल (rms) धारा कहते हैं तथा I से व्यक्त करते हैं :


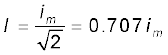
3914.png

इसी प्रकार, rms वोल्टता


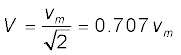
3919.png

माध्य शक्ति के लिए व्यंजक P = IV = I2R

3. किसी शुद्ध प्रेरक L के किसी पर प्रयुक्त ac वोल्टता v = vm sinωt इसमें i = im sin (ωt – π/2), धारा संचालित करता है, यहाँ


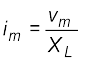
3924.png

जहाँ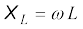

3929.png

XL को प्रेरणिक प्रतिघात कहते हैं। प्रेरक में धारा वोल्टता से π/2 रेडियन से पीछे होती है। एक पूरे चक्र में किसी प्रेरिक को आपूर्ति माध्य शक्ति शून्य होती है।

4. किसी संधारित्र के सिरों पर प्रयुक्त ac वोल्टता v = vm sinωt उसमें i = im sin (ωt + π/2) धारा संचालित करता है। यहाँ


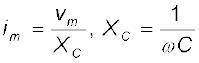
3934.png

XC को धारिता प्रतिघात कहते हैं। संधारित्र में प्रवाहित धारा प्रयुक्त वोल्टता से π/2 रेडियन आगे होती है। प्रेरक के समान ही एक पूरे चक्र में संधारित्र को आपूर्त माध्य शक्ति शून्य होती है।

5. वोल्टता v = vm sinωt, द्वारा संचालित किसी श्रेणीबद्ध LCR परिपथ में धारा का मान निम्नलिखित व्यंजक से दिया जाता है,

यहाँ


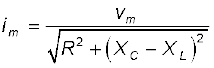
3939.png

तथा


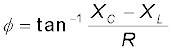
3944.png

होता है।


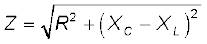
3949.png

को परिपथ की प्रतिबाधा कहते हैं।

एक पूरे चक्र में माध्य शक्ति क्षय को निम्न सूत्र से व्यक्त करते हैं,

P = V I cosφ

पद cosφ को शक्ति गुणांक कहते हैं।

6. किसी विशुद्ध प्रेरणिक अथवा धारिता परिपथ के लिए


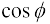
3954.png

= 0। एेसे परिपथ में यद्यपि धारा तो प्रवाहित होती है तथापि शक्ति क्षय नहीं होता है। एेसे उदाहरणों में धारा को वाटहीन (Wattless) धारा कहते हैं।

7. किसी ac परिपथ में धारा व वोल्टता के मध्य कला के संबंध को सुगमता से व्यक्त किया जा सकता है। इसमें वोल्टता तथा धारा को घूर्णी सदिशों से निरूपित करते हैं। घूर्णी सदिश को फेजर कहते हैं। फेजर एक सदिश के समान है जो


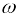
3959.png

चाल से मूल बिंदु के चतुर्दिश घूर्णन करता है। फेजर का परिमाण फेजर द्वारा निरूपित राशि (वोल्टता या धारा) के आयाम या शिखर मान को व्यक्त करता है।

फेजर-आरेख के उपयोग से किसी ac परिपथ का विश्लेषण आसान हो जाता है।

8. अनुनाद की घटना किसी श्रेणीबद्ध LCR परिपथ की एक रोचक विशिष्टता है। परिपथ अनुनाद को प्रदर्शित करता है अर्थात अनुनादी आवृत्ति


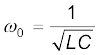
3964.png

पर धारा का आयाम अधिकतम होता है।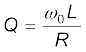

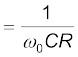
3969.png3974.png

द्वारा परिभाषित गुणता कारक (Quality Factor) Q अनुनाद की तीक्ष्णता का संकेतक है। Q का अधिक मान यह संकेत करता है कि धारा का शिखर अपेक्षाकृत अधिक तीक्ष्ण है।

9. ac स्रोत तथा प्रतिरोधक विहीन कोई एेसा परिपथ जिसमें कोई प्रेरक L तथा संधारित्र C (प्रारंभ में आवेशित) हैं, मुक्त दोलन प्रदर्शित करता है। संधारित्र का आवेश q एक सरल आवर्त गति करता हैः


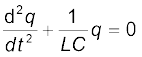
3979.png

इस प्रकार मुक्त दोलनों की आवृत्ति


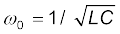
3984.png

होती है। निकाय की ऊर्जा संधारित्र तथा प्रेरक के मध्य दोलन करती है, किंतु उनका योग अथवा कुल ऊर्जा समय के साथ नियत रहती है।

10. ट्रांसफार्मर में एक लोहे का क्रोड होता है जिसमें फेरों की संख्या Np की एक प्राथमिक कुंडली तथा फेरों की संख्या Ns की एक द्वितीयक कुंडली लिपटी रहती है। यदि प्राथमिक कुंडली को किसी ac स्रोत से जोड़ दें, तो प्राथमिक एवं द्वितीयक वोल्टता निम्नलिखित व्यंजक द्वारा संबंधित होती हैं,

77.35

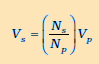
तथा दोनों धाराओं के मध्य के संबंध को निम्नलिखित सूत्र से व्यक्त करते हैं

77.36

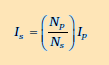
यदि प्राथमिक की तुलना में द्वितीयक कुंडली में फेरों की संख्या अधिक है तो वोल्टता उच्च हो जाती है (


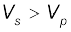
4015.png

)। इस प्रकार की युक्ति को उच्चायी ट्रांसफार्मर कहते हैं। किंतु यदि प्राथमिक की तुलना में द्वितीयक में फेरों की संख्या कम है तो ट्रांसफार्मर अपचयी होता है।


Untitled

विचारणीय विषय

1. जब ac वोल्टता या धारा को कोई मान दिया जाता है तो यह प्रायः धारा अथवा वोल्टता का rms मान होता है। आपके कमरे में लगे विद्युत स्विच के टर्मिनलों के बीच वोल्टता सामान्यतया 240 V होती है। यह वोल्टता के rms मान को निर्दिष्ट करती है। इस वोल्टता का आयाम


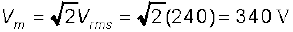
4064.png

है।

2. किसी ac परिपथ में प्रयुक्त अवयव की शक्ति संनिर्धारण माध्य शक्ति से निर्धारण को इंगित 

करती है।

3. किसी ac परिपथ में उपयुक्त शक्ति कभी भी ऋणात्मक नहीं होती।

4. प्रत्यावर्ती एवं दिष्ट धाराएँ दोनों एेम्पियर में मापी जाती हैं। किंतु प्रत्यावर्ती धारा के लिए एेम्पियर को किस प्रकार भौतिक रूप से परिभाषित किया जाए? जिस प्रकार dc एेम्पियर को परिभाषित करते हैं उसी प्रकार इसे (ac एेम्पियर को) ac धाराओं को वहन करने वाले दो समांतर तारों के अन्योन्य आकर्षण के रूप में परिभाषित नहीं कर सकते। ac धारा स्रोत की आवृत्ति के साथ दिशा परिवर्तित करती है जिससे माध्य आकर्षण बल शून्य हो जाता है। अतः ac एेम्पियर को किसी एेसे गुण के संबंध में परिभाषित करना चाहिए जो धारा की दिशा पर निर्भर न करता हो।

जूल तापन एक एेसा ही गुण है, तथा किसी परिपथ में प्रत्यावर्ती धारा के rms मान को एक एेम्पियर के रूप में परिभाषित करते हैं यदि यह धारा वही औसत ऊष्मीय प्रभाव उत्पन्न करती है, जैसा कि dc धारा की एक एेम्पियर उन्हीं परिस्थितियों में करती है।

5. किसी ac परिपथ में विभिन्न अवयवों के सिरों के बीच वोल्टताओं का योग करते समय उनकी कलाओं का उचित ध्यान रखना चाहिए। उदाहरणार्थ, यदि किसी RC परिपथ में VR और VC क्रमशः R व C के सिराें के बीच वोल्टता है तो RC संयोजन के सिरों के बीच वोल्टता

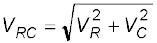
4069.png

होगी न कि VR + VC क्योंकि VC तथा VR के बीच कला-अंतर

4074.png

है।

6. यद्यपि किसी फेजर-आरेख में वोल्टता तथा धारा को सदिशों से निरूपित करते हैं तथापि ये राशियाँ वास्तव में सदिश नहीं हैं। ये अदिश राशियाँ हैं। एेसा होता है कि सरल आवर्त रूप से परिवर्तित होने वाले अदिशों की कलाएँ गणितीय रूप से उसी प्रकार संयोग करती हैं, जैसे कि तदनुसार परिमाणों व दिशाओं के घूर्णी सदिशों के प्रक्षेप करते हैं। ‘घूर्णी सदिश’, जो सरल आवर्त रूप से परिवर्तनशील अदिश राशियों का निरूपण करते हैं, हमें इन राशियों के जोड़ने की सरल विधि प्रदान करने के लिए सन्निविष्ट किए जाते हैं। इसके लिए हम उस नियम का उपयोग करते हैं जिसे हम सदिशों के संयोजन के नियम के रूप में पहले ही से जानते हैं।

7. किसी ac परिपथ में शुद्ध संधारित्रों तथा प्रेरकों से कोई शक्ति-क्षय संबद्ध नहीं होता। यदि ac परिपथ में किसी अवयव द्वारा शक्ति-क्षय होता है तो वह प्रतिरोधक अवयव है।

8. किसी LCR परिपथ में अनुनाद की परिघटना तब होती है जब XL = XC या


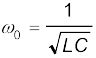
4079.png

। अनुनाद होने के लिए परिपथ में L व C दोनों अवयवों का होना आवश्यक है। इनमें से मात्र एक (L अथवा C) के होने से वोल्टता के निरस्त होने की संभावना नहीं होती और इस प्रकार अनुनाद संभव नहीं है।

9. किसी LCR परिपथ में शक्ति गुणांक (Power Factor) इस बात को मापता है कि परिपथ अधिकतम शक्ति व्यय करने के कितने समीप है।

10. जनित्रों एवं मोटरों में निवेश तथा निर्गत की भूमिकाएँ एक-दूसरे के विपरीत होती हैं। एक मोटर में वैद्युत ऊर्जा निवेश है तथा यांत्रिक ऊर्जा निर्गत है; जनित्र में यांत्रिक ऊर्जा निवेश है तथा वैद्युत ऊर्जा निर्गत है। दोनों युक्तियाँ ऊर्जा को एक प्रकार से दूसरे में रूपांतरित करती हैं।

11. एक ट्रांसफॉर्मर (उच्चायी) निम्न वोल्टता को उच्च वोल्टता में परिवर्तित करता है। यह ऊर्जा के संरक्षण के नियम का उल्लंघन नहीं करता है। धारा उसी अनुपात में घट जाती है।

12. यह चयन करना कि दोलन गति का विवरण ज्या (sine) या कोज्या (cosine) के द्वारा दिया जाता है अथवा इनके रैखिक संयोग द्वारा, महत्वहीन है क्योंकि शून्य-समय स्थिति में परिवर्तन एक को दूसरे में रूपांतरित कर देता है।




अभ्यास

7.1 एक 100 ω का प्रतिरोधक 200 V, 50 Hz आपूर्ति से संयोजित है।

(a) परिपथ में धारा का rms मान कितना है?

(b) एक पूरे चक्र में कितनी नेट शक्ति व्यय होती है।

7.2 (a) ac आपूर्ति का शिखर मान 300 V है। rms वोल्टता कितनी है?

(b) ac परिपथ में धारा का rms मान 10 A है। शिखर धारा कितनी है?

7.3 एक 44 mH का प्रेरित्र 220 V, 50 Hz आपूर्ति से जोड़ा गया है। परिपथ में धारा के rms मान को ज्ञात कीजिए।

7.4 एक 60 µF का संधारित्र 110 V, 60 Hz ac आपूर्ति से जोड़ा गया है। परिपथ में धारा के rms मान को ज्ञात कीजिए।

7.5 अभ्यास 7.3 व 7.4 में एक पूरे चक्र की अवधि में प्रत्येक परिपथ में कितनी नेट शक्ति अवशोषित होती है? अपने उत्तर का विवरण दीजिए।

7.6 एक LCR परिपथ की, जिसमें L = 2.0 H, C = 32 µF तथा R = 10 Ω अनुनाद आवृत्ति

परिकलित कीजिए। इस परिपथ के लिए Q का क्या मान है?

7.7 30 µF का एक आवेशित संधारित्र 27 mH के प्रेरित्र से जोड़ा गया है। परिपथ के मुक्त दोलनों की कोणीय आवृत्ति कितनी है?

7.8 कल्पना कीजिए कि अभ्यास 7.7 में संधारित्र पर प्रारंभिक आवेश 6 mC है। प्रारंभ में परिपथ में कुल कितनी ऊर्जा संचित होती है। बाद में कुल ऊर्जा कितनी होगी?

7.9 एक श्रेणीबद्ध LCR परिपथ को, जिसमें R = 20 Ω, L = 1.5 H तथा C = 35 µF, एक परिवर्ती आवृत्ति की 200 V ac आपूर्ति से जोड़ा गया है। जब आपूर्ति की आवृत्ति परिपथ की मूल आवृत्ति के बराबर होती है तो एक पूरे चक्र में परिपथ को स्थानांतरित की गई माध्य शक्ति कितनी होगी?

7.10 एक रेडियो को MW प्रसारण बैंड के एक खंड के आवृत्ति परास के एक ओर से दूसरी ओर (800 kHz से 1200 kHz) तक समस्वरित किया जा सकता है। यदि इसके LC परिपथ का प्रभावकारी प्रेरकत्व 200 µH हो, तो उसके परिवर्ती संधारित्र की परास कितनी होनी चाहिए?

[संकेत : समस्वरित करने के लिए मूल आवृत्ति अर्थात LC परिपथ के मुक्त दोलनों की आवृत्ति रेडियो तरंग की आवृत्ति के समान होनी चाहिए।]

7.11 चित्र 7.21 में एक श्रेणीबद्ध LCR परिपथ दिखलाया गया है जिसे परिवर्ती आवृत्ति के 230 V के स्रोत से जोड़ा गया है। L = 5.0 H, C = 80

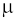4089.pngF, R = 40 Ω


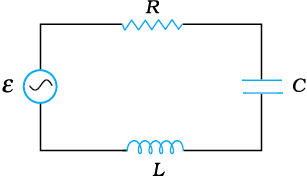
2727.png
चित्र 7.21

(a) स्रोत की आवृत्ति निकालिए जो परिपथ में अनुनाद उत्पन्न करे।

(b) परिपथ की प्रतिबाधा तथा अनुनादी आवृत्ति पर धारा का आयाम निकालिए।

(c) परिपथ के तीनों अवयवों के सिरों पर विभवपात के rms मानों को निकालिए। दिखलाइए कि अनुनादी आवृत्ति पर LC संयोग के सिरों पर विभवपात शून्य है।

अतिरिक्त अभ्यास

7.12 किसी LC परिपथ में 20 mH का एक प्रेरक तथा 50 µF का एक संधारित्र है जिस पर प्रारंभिक आवेश 10 mC है। परिपथ का प्रतिरोध नगण्य है। मान लीजिए कि वह क्षण जिस पर परिपथ बंद किया जाता है t = 0 है।

(a) प्रारंभ में कुल कितनी ऊर्जा संचित है? क्या यह LC दोलनों की अवधि में संरक्षित है?

(b) परिपथ की मूल आवृत्ति क्या है?

(c) किस समय पर संचित ऊर्जा

(i) पूरी तरह से वैद्युत है (अर्थात वह संधारित्र में संचित है)?

(ii) पूरी तरह से चुंबकीय है (अर्थात प्रेरक में संचित है)?

(d) किन समयों पर संपूर्ण ऊर्जा प्रेरक एवं संधारित्र के मध्य समान रूप से विभाजित है?

(e) यदि एक प्रतिरोधक को परिपथ में लगाया जाए तो कितनी ऊर्जा अंततः ऊष्मा के रूप में क्षयित होगी?

7.13 एक कुंडली को जिसका प्रेरण 0.50 H तथा प्रतिरोध 100 है, 240 V व 50 Hz की एक आपूर्ति से जोड़ा गया है।

(a) कुंडली में अधिकतम धारा कितनी है?

(b) वोल्टेज शीर्ष व धारा शीर्ष के बीच समय-पश्चता (time lag) कितनी है?

7.14 यदि परिपथ को उच्च आवृत्ति की आपूर्ति (240 V, 10 kHz) से जोड़ा जाता है तो अभ्यास 7.13 (a) तथा (b) के उत्तर निकालिए। इससे इस कथन की व्याख्या कीजिए कि अति उच्च आवृत्ति पर किसी परिपथ में प्रेरक लगभग खुले परिपथ के तुल्य होता है। स्थिर अवस्था के पश्चात किसी dc परिपथ में प्रेरक किस प्रकार का व्यवहार करता है।

7.15 40


4099.png

प्रतिरोध के श्रेणीक्रम में एक 100 µF के संधारित्र को 110 V, 60 Hz की आपूर्ति से जोड़ा गया है।

(a) परिपथ में अधिकतम धारा कितनी है?

(b) धारा शीर्ष व वोल्टेज़ शीर्ष के बीच समय-पश्चता कितनी है?

7.16 यदि परिपथ को 110 V, 12 kHz आपूर्ति से जोड़ा जाए तो अभ्यास (a) व (b) का उत्तर निकालिए। इससे इस कथन की व्याख्या कीजिए कि अति उच्च आवृत्तियों पर एक संधारित्र चालक होता है। इसकी तुलना उस व्यवहार से कीजिए जो किसी dc परिपथ में एक संधारित्र प्रदर्शित करता है।

7.17 स्रोत की आवृत्ति को एक श्रेणीबद्ध LCR परिपथ की अनुनादी आवृत्ति के बराबर रखते हुए तीन अवयवों L, C तथा R को समांतरक्रम में लगाते हैं। यह दर्शाइए कि समांतर LCR परिपथ में इस आवृत्ति पर कुल धारा न्यूनतम है। इस आवृत्ति के लिए अभ्यास 7.11 में निर्दिष्ट स्रोत तथा अवयवों के लिए परिपथ की हर शाखा में धारा के rms मान को परिकलित कीजिए।

7.18 एक परिपथ को जिसमें 80 mH का एक प्रेरक तथा 60 µF का संधारित्र श्रेणीक्रम में है, 230 V, 50 Hz की आपूर्ति से जोड़ा गया है। परिपथ का प्रतिरोध नगण्य है।

(a) धारा का आयाम तथा rms मानों को निकालिए।

(b) हर अवयव के सिरों पर विभवपात के rms मानों को निकालिए।

(c) प्रेरक में स्थानांतरित माध्य शक्ति कितनी है?

(d) संधारित्र में स्थानांतरित माध्य शक्ति कितनी है?

(e) परिपथ द्वारा अवशोषित कुल माध्य शक्ति कितनी है?

[‘माध्य में यह समाविष्ट है’ कि इसे ‘पूरे चक्र’ के लिए लिया गया है]।

7.19 कल्पना कीजिए कि अभ्यास 7.18 में प्रतिरोध 15

4104.png

है। परिपथ के हर अवयव को स्थानांतरित माध्य शक्ति तथा संपूर्ण अवशोषित शक्ति को परिकलित कीजिए।

7.20 एक श्रेणीबद्ध LCR परिपथ को जिसमें L = 0.12 H, C = 480 nF, R = 23


4109.png

, 230 V परिवर्ती आवृत्ति वाले स्रोत से जोड़ा गया है।

(a) स्रोत की वह आवृत्ति कितनी है जिस पर धारा आयाम अधिकतम है। इस अधिकतम मान को निकालिए।

(b) स्रोत की वह आवृत्ति कितनी है जिसके लिए परिपथ द्वारा अवशोषित माध्य शक्ति अधिकतम है।

(c) स्रोत की किस आवृत्ति के लिए परिपथ को स्थानांतरित शक्ति अनुनादी आवृत्ति की शक्ति की आधी है।

(d) दिए गए परिपथ के लिए Q कारक कितना है?

7.21 एक श्रेणीबद्ध LCR परिपथ के लिए जिसमें L = 3.0 H, C = 27 µF तथा R = 7.4

4114.png

अनुनादी आवृत्ति तथा Q कारक निकालिए। परिपथ के अनुनाद की तीक्ष्णता को सुधारने की इच्छा से "अर्ध उच्चिष्ठ पर पूर्ण चौड़ाई" को 2 गुणक द्वारा घटा दिया जाता है। इसके लिए उचित उपाय सुझाइए।

7.22 निम्नलिखित प्रश्नों के उत्तर दीजिए–

(a) क्या किसी ac परिपथ में प्रयुक्त तात्क्षणिक वोल्टता परिपथ में श्रेणीक्रम में जोड़े गए अवयवों के सिरों पर तात्क्षणिक वोल्टताओं के बीजगणितीय योग के बराबर होता है? क्या यही बात rms वोल्टताओं में भी लागू होती है?

(b) प्रेरण कुंडली के प्राथमिक परिपथ में एक संधारित्र का उपयोग करते हैं।

(c) एक प्रयुक्त वोल्टता संकेत एक dc वोल्टता तथा उच्च आवृत्ति के एक ac वोल्टता के अध्यारोपण से निर्मित है। परिपथ एक श्रेणीबद्ध प्रेरक तथा संधारित्र से निर्मित है। दर्शाइए कि dc संकेत C तथा ac संकेत L के सिरे पर प्रकट होगा।

(d) एक लैंप से श्रेणीक्रम में जुड़ी चोक को एक dc लाइन से जोड़ा गया है। लैंप तेजी से चमकता है। चोक में लोहे के क्रोड को प्रवेश कराने पर लैंप की दीप्ति में कोई अंतर नहीं पड़ता है। यदि एक ac लाइन से लैंप का संयोजन किया जाए तो तदनुसार प्रेक्षणों की प्रागुक्ति कीजिए।

(e) ac मेंस के साथ कार्य करने वाली फ्लोरोसेंट ट्यूब में प्रयुक्त चोक कुंडली की आवश्यकता क्यों होती है? चोक कुंडली के स्थान पर सामान्य प्रतिरोधक का उपयोग क्यों नहीं होता?

7.23 एक शक्ति संप्रेषण लाइन अपचयी ट्रांसफार्मर में जिसकी प्राथमिक कुंडली में 4000 फेरे हैं, 2300 वोल्ट पर शक्ति निवेशित करती है। 230 V की निर्गत शक्ति प्राप्त करने के लिए द्वितीयक में कितने फेरे होने चाहिए?

7.24 एक जल विद्युत शक्ति संयंत्र में जल दाब शीर्ष 300 m की ऊँचाई पर है तथा उपलब्ध जल प्रवाह 100 m3s–1 है। यदि टर्बाइन जनित्र की दक्षता 60% हो तो संयंत्र से उपलब्ध विद्युत शक्ति का आकलन कीजिए, g = 9.8 m s–2।

7.25 440 V पर शक्ति उत्पादन करने वाले किसी विद्युत संयंत्र से 15 km दूर स्थित एक छोटे से कस्बे में 220 V पर 800 kW शक्ति की आवश्यकता है। विद्युत शक्ति ले जाने वाली दोनों तार की लाइनों का प्रतिरोध 0.5


4119.png

प्रति किलोमीटर है। कस्बे को उप-स्टेशन में लगे

4000 – 220 V अपचयी ट्रांसफार्मर से लाइन द्वारा शक्ति पहुँचती है।

(a) ऊष्मा के रूप में लाइन से होने वाली शक्ति के क्षय का आकलन कीजिए।

(b) संयंत्र से कितनी शक्ति की आपूर्ति की जानी चाहिए, यदि क्षरण द्वारा शक्ति का क्षय नगण्य है।

(c) संयंत्र के उच्चायी ट्रांसफार्मर की विशेषता बतलाइए।

7.26 ऊपर किए गए अभ्यास को पुनः कीजिए। इसमें पहले के ट्रांसफार्मर के स्थान पर 40,000 – 220 V का अपचयी ट्रांसफार्मर है। [पूर्व की भाँति क्षरण के कारण हानियों को नगण्य मानिए, यद्यपि अब यह सन्निकटन उचित नहीं है क्योंकि इसमें उच्च वोल्टता पर संप्रेषण होता है]। अतः समझाइए कि क्यों उच्च वोल्टता संप्रेषण अधिक वरीय है?